ГОУ ВПО «Алтайский государственный университет
им. И.И. Ползунова»
В.М. Щербаков
Учебное пособие для студентов
дистанционной формы обучения
Барнаул 2009
Статика твердого тела
1 Основные понятия и аксиомы статики
§ 1 Основные понятия статики
Статика - раздел теоретической механики, в котором рассматривается учение о силах и условия равновесия тел под действием этих сил.
В теоретической механике в качестве материальных объектов рассматриваются:
-- материальная точка - материальное тело, обладающее массой и способностью взаимодействовать с другими телами, но размерами которого в данной конкретной задаче можно пренебречь.
-- механическая система - система взаимосвязанных материальных точек.
Под механической системой в абстрактном смысле можно понимать любое механическое устройство.
Абсолютно твёрдое тело - неизменяемая система материальных точек.
Сила - мера механического взаимодействия материальных объектов.
По своей природе сила - векторная величина и в общем случае характеризуется:
-численной величиной (модулем)
-линией действия и направлением
-точкой приложения.
вектор силы
точка приложения
линия действия
де
Рисунок 1
Линия действия силы - прямая, с которой совпадает вектор силы.
Совокупность нескольких сил, действующих на данное тело или механическую систему, называется системой сил.
Системы сил, оказывающие одинаковое механическое воздействие на материальный объект называются эквивалентными системами сил.
Одна сила, эквивалентная некоторой системе сил, называется равнодействующей силой.
Система сил, приложенная к материальному объекту, не нарушающая характер его механического движения, называется системой взаимно уравновешивающихся сил.
Силы, действующие на механическую систему, делят на внешние и внутренние.
Внешними называют силы, действующие на материальные точки данной механической системы со стороны материальных объектов, не входящих в эту систему.
Внутренними силами называют силы взаимодействия между материальными объектами данной механической системы.
В основе любых естественных наук, какой является и механика, лежат объективные законы природы, установленные опытным путем.
Эти законы называются аксиомами. Аксиомы не доказываются, их справедливость подтверждается многовековой практикой.
В статике используются аксиомы:
1. Аксиома покоя: Система взаимно уравновешивающихся сил не может нарушить исходного покоя механического объекта.
2. Аксиома равновесия двух сил: Две силы взаимно уравновешиваются только в том случае, если они имеют общую линию действия, равны по величине и направлены в разные стороны.
3. Аксиома присоединения или исключения взаимно уравновешивающихся сил: Если к механическому объекту, находящемуся под действием некоторой системы сил присоединить(или исключить) систему взаимно уравновешивающихся сил, то получится система сил, эквивалентная заданной.
Из аксиомы (3) вытекает важное следствие:
-механическое состояние твердого тела не изменится вследствие переноса силы вдоль её линии действия.
Рисунок 2
Вывод: Вектор силы - скользящий вектор.
4. Аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и представляется диагональю параллелограмма, построенного на этих силах.
Рисунок 3.
Из аксиомы(4) вытекает следствие, получившее название
Теорема о трёх силах: Если три непараллельные силы взаимно уравновешены, то они лежат в одной плоскости и линии их действия пересекаются в одной точке.
F3
Рисунок 4.
Доказательство: Пусть силы F1,F2,F3 взаимно уравновешены. Заменим силы F2 и F3 их равнодействующей R, приложенной в точке их пересечения В. Силы R и F1 эквивалентны исходной системе сил. Две же силы взаимно уравновешены, если они имеют общую линию действия. Следовательно линия действия силы F1 также пройдёт через точку В.
studfiles.net
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил.
Рассматриваемые в статике материальные тела принимаются как абсолютно твердые тела.
Абсолютно твердым телом (а.т.т.) называется такое тело, расстояние между двумя точками которого всегда остается постоянным.
Таким образом, в статике считается, что деформация тел под действием сил отсутствует.
Чтобы твердое тело под действием некоторой системы сил находилось в равновесии (в покое), необходимо, чтобы эта система сил удовлетворяла определенным условиям равновесия.
В статике твердого тела решаются следующие основные задачи:
Сложение сил и приведение системы сил, действующих на твердое тело, к простейшему виду.
Определение условий равновесия действующих на твердое тело систем сил.
Основной характеристикой в статике является сила.
Сила – это величина, являющаяся количественной мерой механического взаимодействия материальных тел.
Сила является векторной величиной, поэтому ее действие характеризуется:
Численной величиной, или модулем силы;
Направлением действия;
Точкой приложения силы.
Тело, не скрепленное с другими телами, называется свободным.
Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния равновесия или движения, то такие две системы сил называются эквивалентными.
Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной и эквивалентной нулю.
Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системе сил. Сила, равная равнодействующей по модулю, прямо противоположна по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
Силы, действующие на твердое тело, подразделяются на внешние и внутренние.
Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.
Сила, приложенная в какой-либо одной точке, называется сосредоточенной. Силы, действующие на ряд точек, называются распределенными.
А
Рис. 1.1
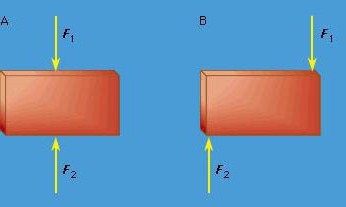
ксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в состоянии равновесия тогда и только тогда, когда эти силы равны по модулю (F1=F2) и направлены вдоль одной прямой в противоположные стороны (рис. 1.1). А
а)
б)
ксиома 2. Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил (рис. 1.2а, 1.2б).С
Рис. 1.2
в)
ледствие из аксиом: действие сил на абсолютно твердое тело не изменяется, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела (рис. 1.2в). 
Аксиома 3. Две силы, приложенные в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах (рис. 1.3).
В
Рис. 1.3
екторR равный диагонали параллелограмма, построенного на векторах F1 и F2, называется геометрической суммой векторов F1 и F2: 
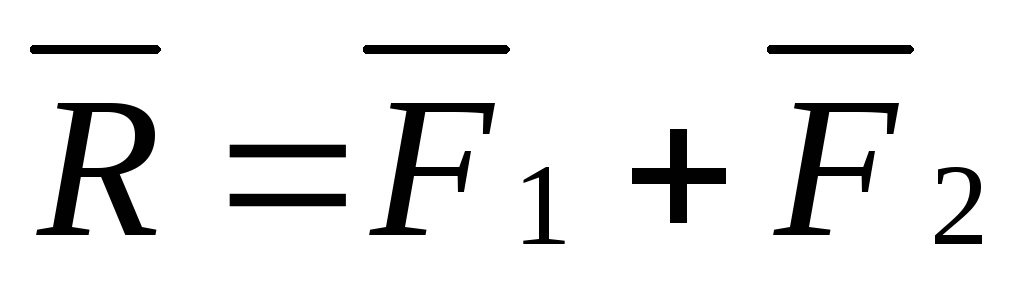
А
Рис. 1.4
ксиома 4.При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие (III з-н Ньютона) (рис. 1.4). С
илыF1=F2 и приложены к разным телам.
Свойство внутренних сил. При изучении равновесия твердого тела его внутренние силы образуют уравновешенную систему сил, поэтому их можно не учитывать в общем балансе сил.
Аксиома 5. (Принцип отвердевания). Равновесие изменяемого тела, находящегося под действием данной системы сил, не нарушается, если тело считать отвердевшим (абсолютно твердым).
studfiles.net
Аксиомы статики. - раздел Механика, Раздел Теоретическая механика
Данные аксиомы сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея – Ньютона являются одновременно и аксиомами статики.
1. Аксиома инерции.
Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. Равномерное и прямолинейное движение материальной точки является движением по инерции.
2. Аксиома равновесия двух сил
Две силы, приложенных к телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны.
Рис. 1.4
3. Аксиома присоединения и исключения уравновешивающихся сил.
Действие системы сил на твёрдое тело не изменяется, если к ней присоединить или из неё исключить систему взаимно уравновешивающихся сил.
Рис. 1.5
Пусть к твёрдому телу приложены силы 
, под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы 
и 
, которые взаимно уравновешиваются.
Если тело находится в движении, то оно будет двигаться под действием новой системы сил 
так же и под действием сил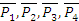 
, то есть основная система сил эквивалентна прежней.
Следствие. Не нарушая состояния абсолютно твёрдого тела, силу можно переносить вдоль линии её действия, сохраняя неизменными её модуль и направление.
Рис. 1.6
Предположим в т. А приложена 
. Приложим в точке В две силы 
и 
равные по модулю силе и направленные по линии действия в противоположные стороны. Затем отбросим силы и как взаимно- уравновешивающееся. Тогда к телу в точке В будет приложена сила =.
Таким образом, силу можно переносить в любую точку по линии действия, не изменяя её модуля и направления. Поэтому в статике сила рассматривается как скользящий вектор.
4. Аксиома параллелограмма сил
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
Рис. 1.7
5. Аксиома равенства действия и противодействия
Всякому действию соответствует равное и противоположно направленное противодействие. Эта аксиома утверждает, что силы действия друг на друга двух сил равны по модулю и направлены в противоположные стороны. Аксиома установлена Ньютоном.
Рис. 1.8 Рис. 1.9
В природе не существует одностороннего действия сил. Силы, действующие и противодействующие, приложены к разным телам, потому они не уравновешиваются.
6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердевании
Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении. Из этой, аксиомы следует, что условие равновесия сил приложенных к абсолютно твёрдому телу, должны и сохраняться для сил, приложенных к деформирующемуся телу. Однако в случае деформированного тела эти условия необходимы, но не достаточны.
Рис. 1.10
1.3. Несвободное твёрдое тело
Твёрдое тело, на перемещение которого не наложено никаких ограничений, называется свободным. Тело, ограничивающее свободу движения данного твёрдого тела, является по отношению к нему связью.
Твёрдое тело, свобода движения которого ограничена связями, называется несвободным. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождаемости твёрдых тел от связей).
Все связи можно разделить на несколько типов.
1. Идеально гладкая поверхность.
Рис. 1.11
Реакции опоры, приложены в точке опоры, всегда направлены перпендикулярно опоре.
2. Гибкая связь (трос, нить, цепь, канат)
Рис. 1.12
Реакция гибкой нити, направлена на нити к точке подвеса.
3. Жёсткий стержень
На схемах показывается толстой линией. Реакция стержня направлена вдоль стержня. Стержень может быть сжат или растянут. Точное направление реакции определяют, мысленно убрав стержень и анализируя направление перемещение узла.
 |
Рис. 1.13
4. Брус.
Рис. 1.14
5. Цилиндрическая шарнирно – неподвижная опора
Рис. 1.15
6. Цилиндрическая шарнирно – подвижная опора
Рис. 1.16
7. Защемление (заделка)
Рис. 1.17
8. Невесомый стержень, на концах которого шарниры
Рис. 1.18
9. Сферический шарнир
Рис. 1.19
10. Подпятник
(Совокупность цилиндрического шарнира и упорной поверхности)
Рис. 1.20
– Конец работы –
Эта тема принадлежит разделу:
ТЕХНИЧЕСКАЯ МЕХАНИКА... Раздел Теоретическая механика... Тверь г...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Аксиомы статики.
Система сходящихся сил 2.1.1 Равновесие твёрдого тела, к которому приложена система сходящихся сил. Сходящимися называются сил
Произвольная плоская система сил 2.2.1 Равновесие твёрдого тела при наличии плоской системы сил. Случай параллельных сил. Равнодейст
Системы сходящихся сил. Равнодействующую пространственной системы сил можн
Произвольная пространственная система сил. 3.2.1. Момент силы относительно точки. Момент силы относительно оси. Теория пар в пространстве. В случае п
ЦЕНТР ТЯЖЕСТИ. Сила тяжести – равнодействующая сил притяжения к Земле, она распределена по всему объёму тела. Сил
КИНЕМАТИКА. 1. ВВЕДЕНИЕ Кинематикой называется раздел механики, в котором изучается движ
Поступательное движение тела. Поступательным движением твердого тела называется
Вращательное движение твердого тела. Вращательным называется такое движение твердого тела, при котором точки тела движутся в плоскостях, перпен
Уравнения равномерного вращения тела Вращение тела с постоянной угловой скоростью называется равномерным
Уравнения равнопеременного вращения тела Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением. Если ве
Сложение скоростей. Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной трае
Сложение ускорений. Теорема Кориолиса. Найдем зависимость между абсолютным , относительным
Мгновенный центр скоростей (МЦС) МЦС называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. Теорема.
Определение скорости точки плоской фигуры с помощью МЦС Выберем за полюс точку Р. Тогда скорость произвольной точки А
Ускорения точек при плоском движении. Покажем, что ускорение любой точки М тела при плоском или параллельном движении (так же как и скорость) с
Мгновенный центр ускорений (МЦУ) МЦУ называется точка плоской фигуры, ускорение которой равно нулю. Если в данный момент времени за
Частные случаи определения МЦУ. 1. Известна точка, ускорение которой равно нулю. Эта
Основные способы вычисления углового ускорения при плоском движении. 1. Если известен закон изменения угла поворота или угловой скорости от времени, то углово
Сложение поступательных движений. Пусть твердое тело движется поступательно со
Сложение вращений вокруг двух параллельных осей. Рассмотрим случай, когда относи
Пара вращений. Рассмотрим частный случай, когда вращения вокруг параллельных осей направлены в разные стороны, но по моду
Сложение вращений вокруг пересекающихся осей. Рассмотрим случай сложения вращения вокр
Сложение поступательного и вращательного движений. 6.5.1. Скорость поступательного движения перпендикулярно к оси вращения (
Законы динамики. В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений.
Задачи динамики для свободной и несвободной материальной точки. Для свободной материальной точки задачами динамики являются: 1. Зная закон движения, определить действ
Прямолинейное движение точки. Из кинематики известно, что при прямолинейном движении скорость и ускорение точки все время направлены вдо
Криволинейное движение точки. Рассмотрим свободную материальную точку,
Количество движения и кинетическая энергия точки. Это основные динамические характеристики движения. Количеством движения точки называется векторная велич
Импульс силы. Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводим понятия об
Теорема об изменении количества движения точки. Так как масса точки постоянна, а ее ускорение , то ур
Работа силы. Мощность. Для характеристики действия, оказываемое силой на
Теорема об изменении кинетической энергии точки. Рассмотрим точку массой m, перемещающуюся под действием приложенных к ней сил из положения М0,
Теорема об изменении момента количества движения (теорема моментов). Иногда при изучении движения точки вместо изменения самого вектора (m
Прямолинейные колебания точки 4.1. Свободные колебания без учёта сил сопротивления. Рассмотрим точку М, движущуюся под де
Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания) Рассмотрим, как влияет на свободные колебания сопротивления среды, считая, что сила сопротивления пропорци
Вынужденные колебания. Резонанс. Рассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически
Механическая система. Механической системой материальных точек или тел называется такая их совокупность, в которой поло
Масса системы. Центр масс. Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения м
Дифференциальные уравнения движения системы. Рассмотрим систему, состоящую из «n» материальных точек. Выделим какую-нибудь точку системы с м
Теорема о движении центра масс. Сложим почленно левые и правые части уравнения (3).
Закон сохранения движения центра масс. Из теоремы о движении центра масс можно получить важные следствия. 1). Пусть сумма внешних сил, действую
Количество движения системы. Количеством движения системы будем называть векторную величину
Теорема об изменении количества движения. Рассмотрим систему, состоящую из «n» материальных точек, составим для этой системы дифференциальные уравне
Закон сохранения количества движения. Из теоремы об изменении количества движения системы можно получить важные следствия. 1). Пусть сумма вс
Момент инерции тела относительно оси. Положение центра масс характеризует распределение масс системы не полностью.
Главный момент количества движения системы. Главным моментом количества движения (или кинематическим моментом) системы относительно данного центра
Теорема об изменении главного момента количества движения системы (теорема моментов). Теорема моментов, доказанная для одной материальной точки, будет справедлива для каждой из точек системы. С
Закон сохранения главного момента количества движения. Из теоремы моментов можно получить следующие важные следствия. 1). Пусть сумма моментов относительно ц
Кинетическая энергия системы. Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических
Некоторые случаи вычисления работы. Рассмотрим следующие случаи. 1). Работа сил тяжести, действующих на систему. Работа силы тяжести, д
Теорема об изменении кинетической энергии системы. Показанная в п. 3.5. теорема справедлива для любой точки системы. Следовательно, если рассмотреть какую-нибуд
Потенциальное силовое поле и силовая функция. Работа на перемещениесилы F приложенной в точке
Потенциальная энергия Для потенциальных сил можно вывести понятие о потенциальной энергии, как о величине, «характеризу
Закон сохранения механической энергии Допустим, что все действующие на систему внешние и внутренние силы потенциальны. Тогда для каждой из т
allrefers.ru
Предмет статики. Основные понятия и определения
Статика – раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов.
Равновесие – такое механическое состояние тела, при котором оно находится в состоянии покоя или движется прямолинейно и равномерно относительно выбранной инерциальной системы отсчёта.
Все тела в природе взаимодействуют между собой и с окружающей средой.
Сила – векторная величина, характеризующаяся величиной (модулем силы), направлением и точкой приложения.
Система тел – совокупность тел, каким-либо образом связанных между собой.
Внутренние силы – силы, с которыми тела данной системы взаимодействуют друг с другом.
Внешние силы – силы, с которыми тела, не входящие в систему, взаимодействуют с телами данной системы.
Равнодействующая сила – это сила, равная эквивалентной системе сил по своему действию.
Система сходящихся сил – это такая система сил, линии действия которой пересекаются в одной точке.
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
В механике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел.
Равновесие механической системы – состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта.
Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называется эквивалентными.
Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
1) Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.
2) О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению.
3) О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.
4) О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.
5) Аксиома затвердевания. Если деформируемое телонаходилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.
6) Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
Классификация силовых систем: свободная, несвободная
Классификация сил: активные и реакции связей либо внешние и внутренние
Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены.
В любом другом случае тело является несвободным.
Связи – ограничения, налагаемые на свободу любого несвободного тела.
Силы, с которыми связи действуют на данное тело, называются реакциями связей.
Аксиома связей:
Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. Виды связей:
Гладкая поверхность (опора без трения)
Шероховатая поверхность
Цилиндрический шарнир (подшипник)
Сферический шарнир
Гибкая нить
Невесомый стержень
Жесткая заделка (защемление)
Опорные реакции балок
Шарнирно-подвижная опора
Шарнирно-неподвижная опора
Ж
есткая заделка
Сходящимися называются силы, линии действия(л.д.) которых пересекаются в одной точке.
Если у такой системы сил л.д. расположены в одной плоскости, то она называется плоской системой сходящихся сил. В любом другом случае система сходящихся сил пространственная.
Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения 
. Равнодействующая может быть найдена геометрическим способом – построением силового (векторного) многоугольника или аналитическим способом, проектируя силы на оси координат.
Геометрический способ:
Теорема: любая система сходящихся сил приводится к равнодействующей, равной геометрической сумме составляющих сил и приложенных в точках пересечения линий их действия.
Сложность данного подхода в сложности геометрических построений.
Для упрощения построений сложим геометрически силы следующим образом: конец предыдущей силы должен совпадать с началом следующего, а линии действия сил должны быть параллельны заданным.
Замыкающая, полученная таким образом, и будет являться вектором равнодействующей, причем он должен быть направлен то начала к концу.
Аналитический способ:
Проекцией силы на ось называется направленный отрезок, заключенный между перпендикулярами, проведенными к соответствующей оси из начала к концу вектора силы.
В случае пространственной системы сил используется метод двойного проецирования: сначала сила проецируется на плоскость, а затем определяются проекции полученной проекции на осях координат.
6. Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Геометрическое условие равновесия:
Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого.
Аналитическое условие равновесия:
Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0).
Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0).
Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат.
studfiles.net
Количество просмотров публикации Аксиомы статики - 411
Вычисление проекций силы.
Сложение и разложение сил.
Аксиомы статики.
Основные задачи статики.
Вопросы
1. Основными задачами статики являются:
а) преобразование различных систем сил в более простые, им эквивалентные;
б) определение условий равновесия твердых тел, находящихся под действием различных систем сил.
Аксиома 1. Твердое тело под действием двух сил будет находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис. 1.1).
Рис. 1.1. Равновесие тела под действием двух сил
Аксиома 2. Действие любой системы сил на твердое тело не изменится, в случае если к ней добавить или от нее отнять уравновешенную систему сил.
Следствие: Силу, не изменяя ее действия на твердое тело, можно переносить вдоль линии ее действия (рис.1.2) Данное обстоятельство позволяет считать силы в теоретической механике скользящими векторами.
Рис. 1.2. Перенос силы вдоль ее линии действия
Аксиома 3. (Правило параллелограмма). Две силы, приложенные в одной точке, имеют равнодействующую, определяемую диагональю параллелограмма, построенного на этих силах и приложенную в этой же точке (рис. 1.3).
Говорят также, что в данном случае равнодействующая К равна геометрической или векторной сумме сил А! и А@ . .
Рис. 1.3. Геометрическое сложение двух сил
Аксиома 4. Силы взаимодействия двух тел равны по величине и направлены вдоль одной прямой в противоположные стороны (третий закон Ньютона). Отметим, что в данном случае эти силы не уравновешивают друг друга так как приложены к разным телам (рис. 1.4).
Рис. 1.4. Иллюстрация третьего закона Ньютона
Аксиома 5. (Принцип освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, в случае если заменить все связи эквивалент-ными им по воздействию на тело силами, называемыми реакциями связей.
Аксиома 6. Равновесие деформируемого тела не нарушится, в случае если тело считать абсолютно твердым (другими словами: равновесие тела не нарушается при наложении на него дополнительных связей).
3. Сложение и разложение сил.
Различают геометрические и аналитический способы сложения сил. Рассмотрим первые из них.
Известно (аксиома 3), что два вектора можно сложить по правилу параллелограмма. Очевидно, что правилу параллелограмма эквивалентно правило треугольника (рис. 1.5). Последовательное применение правила треугольника позволяет определить геометрическую сумму нескольких сил (правило построения векторного многоугольника). Три вектора, не лежащие в одной плоскости, можно сложить используя правило параллелепипеда (рис.1.7).
Рис. 1.5. Правила сложения векторов: а) параллелограмма, б) треугольника, в) построение векторного многоугольника
Для разложения силы на две составляющие (ᴛ.ᴇ. замене одной силы системой двух сил, эквивалентных исходной силе) используют правило параллелограмма (рис 1.6). Заметим , что решение данной задачи не является однозначным.
Рис. 1.6. Разложения векторов на составляющие
В пространстве силу можно разложить на три составляющие используя правило параллелепипеда (рис.1.7).
Рис. 1.7. Разложения вектора К на составляющие А!, А@, А# по правилу параллелепипеда
Обычно при решении конкретных задач силы раскладывают на составляющие, параллельные осям прямоугольной декартовой системы координат. Алгебраические значения таких составляющих называются проекциями силы на координатные оси.
Проекция считается положительной, в случае если направление ее составляющей совпадает с положительным направлением соответствующей координатной оси. На рис. 1.8 приведены основные случаи, встречающиеся на практике при вычислении проекций векторов на оси прямоугольной системы координат.
Рис. 1.8. Вычисление проекций силы на координатные оси
Иногда для вычисления проекций на оси приходится предварительно находить проекцию этой силы на плоскость (рис. 1.9)
| |
Fxy=Fcosa,
Fx=Fxycosb= Fcosa cosb,
Fy=Fxy cosф=Fcosa cosф,
где Аxy - проекция силы А на плоскость (величина векторная).
Рис. 1.9. К определению проекции силы на плоскость
referatwork.ru
МБОУ Сухо-Сарматская СОШ
Реферат
по дисциплине «Прикладная механика»
на тему «Основные аксиомы статики. Условия равновесия тел под действием 3-х сил».
Выполнила учитель технологии:
Шаповалова Ирина Николаевна
Таганрог 2018
Содержание
Основные понятия статики
2. Аксиомы статики
3. Виды связей и их реакции
4. Система сходящихся сил
4.1. Геометрический способ сложения сходящихся сил
4.2. Разложение сил
4.3. Проекция силы на ось и на плоскость
4.4. Аналитический способ задания и сложения
4.5. Условия равновесия плоской системы сходящихся сил
4.6. Методические указания к решению задач по исследованию условий равновесия системы сходящихся сил
5. Литература
1. Основные понятия статики
Статикой называется раздел теоретической механики, в котором излагается общее учение о силах и изучаются условия равновесия тел, находящихся под действием сил. Силой называется физическая величина, являющаяся мерой механического взаимодействия тел. Сила – величина векторная. Она характеризуется величиной (модулем), направлением и точкой приложения. Основной единицей измерения силы является Ньютон [Н].В статике все тела считаются абсолютно твёрдыми, то есть под действием сил их форма и размеры остаются неизменными.Совокупность сил, приложенных к телу, называется системой сил. Если все силы лежат в одной плоскости, то такая система сил называется плоской. Если силы не лежат в одной плоскости, то они образуютпространственную систему сил.Тело, которое из данного положения может переместиться в любое положение в пространстве, называетсясвободным телом.Две системы сил называют эквивалентными одна другой, если каждая из них, действуя по отдельности, может сообщить покоящемуся телу одно и то же движение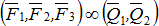 
.Система сил, под действием которой покоящееся тело не изменяет своего состояния покоя, называетсяуравновешенной или эквивалентной нулю – 
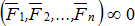.Сила, которая одна заменяет действие системы сил на твёрдое тело, называется равнодействующей – 
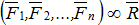.Силы могут быть сосредоточенные (рис. 1.1, а) и распределенные (рис. 1.1, б). Сила, приложенная к какой-нибудь одной точке тела, называется сосредоточенной.Система распределенных сил характеризуется интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в Ньютонах, деленных на метры (Н/м).
Рис. 1.1
Распределенную нагрузку в виде прямоугольника (равномерно распределенная нагрузка) или треугольника заменяют одной силой (равнодействующей), которую прикладывают в центре тяжести площади распределения (рис. 1.1, б). Величина равнодействующей численно равна площади фигуры, образованной распределенной нагрузкой: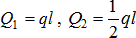 
.
2. Аксиомы статики
В основе статики лежат некоторые основные положения (аксиомы), которые являются обобщением многовекового производственного опыта человечества и теоретических исследований.
Аксиома 1. Если на свободное абсолютно твёрдое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис.1.2).
infourok.ru
В процессе изучения статики, которая является одним из составляющих разделов механики, основная роль отводится аксиомам и базовым понятиям. При этом основных аксиом всего пять. Некоторые из них известны со школьных уроков физики, поскольку являются законами Ньютона.
Для начала необходимо упомянуть, что статика является подразделом механики. Последнюю следует описать подробнее, поскольку она напрямую связана со статикой. При этом механика - более общий термин, объединяющий в себе динамику, кинематику и статику. Все эти предметы изучались в школьном курсе физике и известны каждому. Даже входящие в изучение статики аксиомы базируются на известных со школьных лет законах Ньютона. Однако их было три, в то время как базовых аксиом статики - пять. Большая часть из них касается правил сохранения равновесия и прямолинейного равномерного перемещения определённого тела или материальной точки.
Механикой является наука о наиболее простом способе движения материи - механическом. Наиболее простыми движениями принято считать действия, сводимые к перемещению в пространстве и времени физического объекта из одного положения в другое.
В теоретической механике изучаются общие законы движения без учета индивидуальных свойств тела, кроме свойства протяжённости и гравитации (из этого следуют свойства частиц материи взаимно притягиваться либо иметь определенный вес).
В число базовых определений входит механическая сила. Данным термином называется движение, в механической форме передающееся от одного тела второму во время взаимодействия. По многочисленным наблюдениям было определено, что сила считается величиной векторной, которая характеризуется направлением и точкой приложения.
По способу построения теоретическая механика схожа с геометрией: она так же базируется на определениях, аксиомах и теоремах. При этом на простых определениях связь не заканчивается. Большая часть рисунков, имеющих отношение к механике в целом и статике в частности, содержит геометрические правила и законы.
Теоретическая механика при этом включает три подраздела: статику, кинематику и динамику. В первой изучаются способы преобразования сил, приложенных к объекту и абсолютно твердому телу, а также условия возникновения равновесия. В кинематике рассматривается простое механическое движение, не учитывающее действующие силы. В динамике изучают движения точки, какой-либо системы или же твёрдого тела, учитывая действующие силы.
Для начала следует рассмотреть основные понятия, аксиомы статики, виды связей и их реакции. Статикой именуется состояние равновесия с силами, которые прилагаются к абсолютно твердому телу. В ее задачи входят два основных пункта: 1 - основные понятия и аксиомы статики включают замену дополнительной системы сил, что были приложены к телу другой системой, эквивалентной ей. 2 - вывод общих правил, при которых тело под влиянием приложенных сил остаётся в покоящимся состояние либо в процессе равномерного поступательного прямолинейного движения.
Объекты в таких системах принято называть материальной точкой - телом, размеры которого в поставленных условиях можно опустить. Совокупность точек или тел, каким-либо образом взаимосвязанных между собой, именуют системой. Силы взаимного воздействия между этими телами зовутся внутренними, а силы, влияющие на данную систему - внешними.
Равнодействующей силой в определённой системе называется сила, эквивалентная приведённой системе сил. Входящие в состав этой системы зовутся составляющими силами. Уравновешивающая сила по своей величине равняется равнодействующей, но направляется в противоположном направлении.
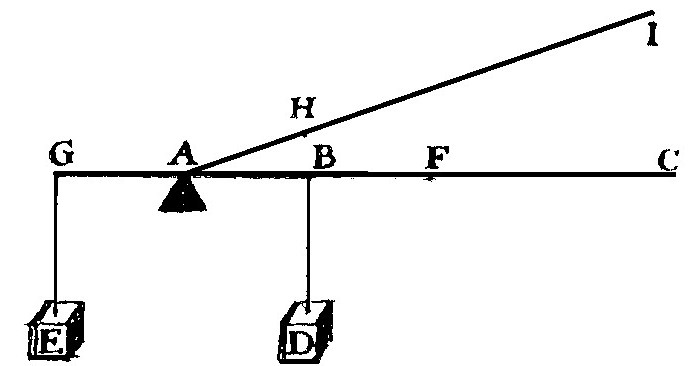
В статике при решении вопроса о смене системы сил, влияющих на твердое тело, или о равновесии сил используют геометрические свойства векторов сил. Из этого становится понятным определение геометрической статики. Аналитическая статика, базирующаяся на принципе допустимых перемещений, будет описана в динамике.
Условия нахождения тела в условиях равновесия выводятся из нескольких основных законов, используемых без дополнительных доказательств, но имеющих подтверждение в виде проведенных опытов, именуются аксиомами статики.
В теоретической механике материальной точке, системе и твердому телу может быть дано два определения: свободное и несвободное. Различия между этими словами состоят в том, что если на перемещение точки, тела или системы не налагаются заранее указанные ограничения, то данные объекты будут по определению свободными. В обратной ситуации объекты принято называть несвободными.
Физические обстоятельства, приводящие к ограничению свободы названных материальных объектов, именуются связями. В статике могут иметься простейшие связи, выполняемые разными твердыми или гибкими телами. Сила действия связи на точку, систему или тело именуется реакцией связи.
В обычной жизни связь может быть представлена нитями, шнурками, цепями или верёвками. В механике за данное определения принимают невесомые, гибкие и нерастяжимые связи. Реакции соответственно могут быть направлены по нити, веревке. При этом имеют место связи, линии действия которых нельзя определить сразу. В качестве примера основных понятий и аксиомы статики можно привести неподвижный цилиндрический шарнир.
В его состав входит неподвижный цилиндрический болт, на который надета втулка с цилиндрическим отверстием, диаметр которого не превышает величины болта. При скреплении тела с втулкой первое сможет вращаться лишь по оси шарнира. В идеальном шарнире (при условии пренебрежения трения поверхности втулки и болта) появляется преграда для смещения втулки по направлению, перпендикулярному поверхности болта и втулки. В связи с этим реакция в идеальном шарнире имеет направлении по нормали - радиусу болта. Под влиянием действующих сил втулка способна прижиматься к болту в произвольной точке. В связи с этим направление реакции у неподвижного цилиндрического шарнира заранее определить невозможно. По этой реакции может быть известно лишь ее расположение в плоскости, перпендикулярной к шарнирной оси.
Во время решения задач реакция шарнира будет устанавливаться аналитическим методом путём разложения вектора. Основные понятия и аксиомы статики включают данный способ. Значения проекций реакции вычисляется из уравнений равновесия. Так же поступают в иных ситуациях, включающих невозможность определения направления реакции связи.
В число основных определений можно включить систему сил, которые сходятся. Так называемой системой сходящихся сил будет называться система, линии действия в которой пересекаются в единственной точке. Данная система приводит к равнодействующей или пребывает в состоянии равновесия. Учитывается данная система и в ранее указанных аксиомах, поскольку связана с сохранением равновесия тела, о чем говорится сразу в нескольких положениях. Последние указывают как на причины, необходимые для создания равновесия, так и на факторы, которые не вызовут изменения данного состояния. Равнодействующая данной системы сходящийся силы равняется векторной сумме названных сил.
В основные понятия и аксиомы статики система сходящихся сил также включается при изучении. Для нахождения системы в равновесии механическим условием становится нулевое значение равнодействующей силы. Поскольку векторная сумма сил нулевая, то многоугольник считается замкнутым.
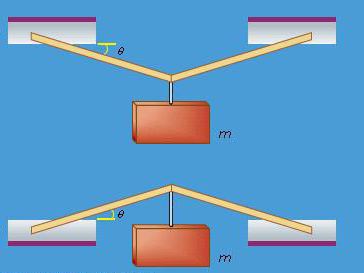
В аналитическом виде условие равновесия системы будет заключаться в следующем: пребывающая в равновесии пространственная система сходящихся сил будет иметь алгебраическую сумму проекций силы на каждую из осей координат, равной нулю. Поскольку в такой ситуации равновесия равнодействующая будет нулевой, то проекции на оси координат также будут нулевыми.
Под данным определением имеется в виду векторное произведение вектора точки приложения сил. Вектор момента силы направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
Этим определением именуется система, состоящая из пары параллельных сил, одинаковых по величине, направленных в противоположные направления и приложенных к телу.
Момент пары сил может считаться положительным, если силы пары направлены против часовой стрелки в правосторонней системе координат, и отрицательным - направлены по направлению часовой стрелки в левой системе координат. При переводе от правой системы координат к левой ориентация сил меняется на противоположную. Минимальное значение расстояния среди линий действия сил именуется плечом. Из этого следует, что момент пары сил является свободным вектором, по модулю равняющимся М=Fh и имеющим перпендикулярно плоскости действия направление, что с вершины данного вектора силы были ориентированы положительно.
Требуемым условием равновесия для произвольной пространственной системы сил, прилагаемой к твердому телу, считается обращение в нуль главного вектора и момента по отношению к любой точке пространства.
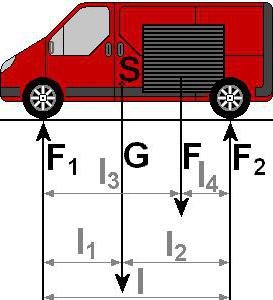
Из этого следует, что для достижения равновесия параллельных сил, располагаемых в одной плоскости, требуется и хватит того, что полученная сумма проекций сил на расположенную параллельно ось и алгебраическая сумма всех составляющих моментов, предоставленных сил относительно случайной точки, равняется нулю.
Согласно закону всемирного тяготения, на каждую частицу, находящуюся поблизости от поверхности Земли, влияют силы притяжения, именуемыми силами тяжести. При небольших размерах тела во всех технических приложениях можно считать силы тяжести отдельных частиц тела системой практически параллельных сил. Если все силы тяжести частиц мы будем считать параллельными, то их равнодействующая будет численно равна сумме весов всех частиц, т. е. весу тела.
Кинематикой именуется раздел из теоретической механики, который изучает механическое движение точки, системы точек и твердого тела в независимости от влияющих на них сил. Ньютон, исходя из материалистической позиции, считал объективным характер пространства и времени. Ньютон использовал определение абсолютного пространства и времени, но отделял их от перемещающейся материи, поэтому его можно назвать метафизиком. Диалектический материализм считает пространство и время объективными формами пребывания материи. Пространство и времени без материи не может существовать. В теоретической механике сказано, что пространство, включающее движущиеся тела, именуется трёхмерным эвклидовым пространством.
По сравнению с теоретической механикой, теория относительности основывается на иных представлениях о пространстве и времени. Помогло это возникновение новой геометрии, созданной Лобачевским. В отличие от Ньютона, Лобачевский не отделял пространство и время от видения, считая последнее изменением положения одних тел относительно других. В собственном произведении им было указано, что в природе человеком познается только движение, без коего чувственное представление становится невозможным. Из этого следует, что все прочие понятия, к примеру, геометрические, созданы разумом искусственно.
Из этого видно, что пространство рассматривается как проявление связи между перемещающими телами. Почти за век до возникновения теории относительности Лобачевский указал, что евклидова геометрия имеет отношение к абстрактным геометрически системам, тогда как в физическом мире пространственные взаимоотношения определяются физической геометрией, которая отличается от евклидовой, в которой свойства времени и пространства объединяются со свойствами материи, перемещающейся в пространстве и времени.
Не помешает заметить, что передовые ученые из России в области механики сознательно придерживались верных материалистических позиций в трактовке всех главных определений теоретической механики, в частности времени и пространства. При этом мнение о пространстве и времени в теории относительности сходны с представлениями о пространстве и времени сторонников марксизма, которые были созданы до возникновения работ о теории относительности.
При работе с теоретической механикой во время измерения пространства за главную единицу принимается метр, а за время - секунда. Время является одинаковым в каждой системе отсчета и находится вне зависимости от перемежения данных систем по отношению друг к другу. Время указывается символом и рассматривается в виде непрерывной изменчивой величины, используемой в роли аргумента. Во время измерения времени применяются определения промежутка времени, момента времени, начального времени, что входит в основные понятия и аксиомы статики.
В практическом применении основные понятия и аксиомы статики и техническая механика связаны между собой. В технической механике изучается как сам механический процесс движения, так и возможность его использования в практических целях. К примеру, при создании технических и строительных конструкций и проверки их на прочность, что требует знать кратко основные понятия и аксиомы статики. При этом такое краткое изучение подойдет только любителям. В профильных учебных заведениях эта тема имеет немалую важность, к примеру, в случае с системой сил, основными понятиями и аксиомами статики.
В технической механике так же применяются приведенные выше аксиомы. К примеру, аксиома 1, основные понятия и аксиомы статики связаны с данным разделом. При том что в самой первой аксиоме объясняется принцип сохранения равновесия. В технической механике немаловажная роль отводится не только созданию приборов, но и устойчивых конструкций, при строительстве которых устойчивость и прочность являются основными критериями. Однако создать нечто подобное без знания базовых аксиом будет невозможно.
К наиболее простым формам перемещения твердых тел относят поступательное и вращательное движение тела. В кинематике твердых тел при разных видах движений учитываются кинематические характеристики перемещения разных его точек. Вращательным движением тела вокруг неподвижной точки именуется такое движение, при котором прямая проходящая сквозь пару произвольных точек в процессе движения тела сохраняется в состоянии покоя. Данная прямая именуется осью вращения тел.
В тексте выше приводились кратко основные понятия и аксиомы статики. При этом существует большое количество сторонней информации, с помощью которой можно лучше узнать статику. Не стоит забывать базовые данные, в большинстве примеров основные понятия и аксиомы статики абсолютно твердое тело включают, поскольку это некий эталон для объекта, который может быть не достижим в нормальных условиях.
Затем следует вспомнить об аксиомах. К примеру, основные понятия и аксиомы статики, связи и их реакции входят в их число. Несмотря на то, что многие аксиомы лишь объясняют принцип сохранения равновесия или равномерного движения, это не отменяет их значимости. Начиная со школьного курса данные аксиомы и правила изучаются, поскольку являются всем известными законами Ньютона. Необходимость в их упоминании связана с практическим применением сведений статики и механики в целом. Примером послужила техническая механика, в которой, помимо создания механизмов, требуется понимать принцип конструирования устойчивых построек. Благодаря таким сведениям возможно правильное возведение обычных сооружений.
fb.ru
