 .
.1. Детерминированные и вероятностные математические модели в экономике. Преимущества и недостатки
Методы исследования экономических процессов базируются на использовании математических — детерминированных и вероятностных — моделей, представляющих изучаемый процесс, систему или вид деятельности. Такие модели дают количественную характеристику проблемы и служат основой для принятия управленческого решения при поисках оптимального варианта. Насколько обоснованы эти решения, являются ли они лучшими из возможных, учтены ли и взвешены все факторы, определяющие оптимальное решение, каков критерий, позволяющий определить, что данное решение действительно наилучшее, — таков круг вопросов, имеющих большое значение для руководителей производства, и ответ на которые можно найти с помощью методов исследования операций [Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, стр. 45].
Одним из принципов формирования системы управления является метод кибернетических (математических) моделей. Математическое моделирование занимает промежуточное положение между экспериментом и теорией: нет необходимости строить реальную физическую модель системы, ее заменит математическая модель. Особенность формирования системы управления заключается в вероятностном, статистическом подходе к процессам управления. В кибернетике принято, что любой процесс управления подвержен случайным, возмущающим воздействиям. Так, на производственный процесс оказывают влияния большое количество факторов, учесть которые детерминированным образом невозможно. Поэтому считается, что на производственный процесс воздействуют случайные сигналы. В силу этого планирование работы предприятия может быть только вероятностным.
По этим причинам часто, говоря о математическом моделировании экономических процессов, имеют в виду именно вероятностные модели.
Опишем каждый из типов математических моделей.
Детерминированные математические модели характеризуются тем, что описывают связь некоторых факторов с результативным показателем как функциональную зависимость, т. е. в детерминированных моделях результативный показатель модели представлен в виде произведения, частного, алгебраической суммы факторов, или в виде любой другой функции. Данный вид математических моделей наиболее распространен, поскольку, будучи достаточно простыми в применении (по сравнению вероятностными моделями), позволяет осознать логику действия основных факторов развития экономического процесса, количественно оценить их влияние, понять, какие факторы и в какой пропорции возможно и целесообразно изменить для повышения эффективности производства.
Вероятностные математические модели принципиально отличаются от детерминированных тем, что в вероятностных моделях взаимосвязь между факторами и результирующим признаком вероятностная (стохастическая): при функциональной зависимости (детерминированные модели) одному и тому же состоянию факторов соответствует единственное состояние результирующего признака, тогда как в вероятностных моделях одному и тому же состоянию факторов соответствует целое множество состояний результирующего признака [Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, с. 32-33].
Преимущество детерминированных моделей в простоте их применения. Основной недостаток — низкая адекватность реальной действительности, т. к., как было отмечено выше, большинство экономических процессов носит вероятностный характер.
Достоинством вероятностных моделей является то, что они, как правило, больше соответствуют реальной действительности (более адекватны), чем детерминированные. Однако, недостатком вероятностных моделей является сложность и трудоемкость их применения, так что во многих ситуациях достаточно бывает ограничиться детерминированными моделями.
2. Постановка задачи линейного программирования на примере задачи о пищевом рационе
Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.
Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам линейного программирования посвящено много работ зарубежных и, прежде всего, американских ученых.
Задача линейного программирования состоит в максимизации (минимизации) линейной функции.
, где
при ограничениях
(*)
причем все
Замечание. Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).
Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.
Итак, надо максимизировать функцию к удовлетворяющей системе ограничений.
Обратимся к одному из неравенств системы ограничений.
С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой , либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того чтобы выяснить это, надо проверить какая из них содержит точку ().
Замечание 2. Если , то проще взять точку (0;0).
Условия неотрицательности также определяют полуплоскости соответственно с пограничными прямыми . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы — это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую (где h — некоторая постоянная). Чаще всего берется прямая . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции.
Вектор в каждой точке перпендикулярен прямой , поэтому значение f будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой проводим прямые, смещаясь в направлении градиента (антиградиента).
Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.
Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:
Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
Находят полуплоскости, определяемые каждым из ограничений задачи.
Находят многоугольник решений.
Строят вектор .
Строят прямую .
Строят параллельные прямые в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.
Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
Задача о рациональном питании (задача о пищевом рационе)
Постановка задачи
Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно С1, С2, С3, С4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b1 единиц; углеводов — не менее b2 единиц; жиров — не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где aij (i=1,2,3,4; j=1,2,3) — какие-то определённые числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры).
| продукт | элементы | ||
| белки | углеводы | жиры | |
П1 П2 П3 П4 | A11 A21 A31 A41 | A12 A22 A32 A42 | A13 A23 A33 A43 |
Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.
Математическая модель
Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L): она линейно зависит от элементов решения x1, x2, x3, x4.
Целевая функция:
Система ограничений:
a11x1+a21x2+a31x3+a41x4 больше или равно b1
a12x1+a22x2+a32x3+a42x4 больше или равно b2
a13x1+a23x2+a32x3+a43x4 больше или равно b3
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4.
Таким образом, поставленная задача сводится к следующему: найти такие неотрицательные значения переменных x1, x2, x3, x4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
Список литературы
Гончаров В. В. Важнейшие понятия и концепции в современном управлении. — М.: МНИИПУ, 2002, 341 с.
История экономических учений. // Под ред. Н. А. Хохлова. — СПб: Питер, 2002, 324 с.
Казаков А. П., Минаев Н. В. Экономика. Курс лекций. Упражнения. Тесты и тренинги. — М.: Изд-во ЦИПКК АП, 1999, 359 с.
Макроэкономика. Учебное пособие. // Под ред. А. М. Бункина. — М.: Инфра-М, 1995, 337 с.
Нуриев, Розанова. Поведение потребителя в рыночной экономике. // Вопросы экономики, 2003, № 1, с. 4-9.
Социально-экономическая статистика. // Под ред. Г. Л. Громыко. — М.: Изд-во МГУ, 1999, 350 с.
Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, 160 с.
Ховард К., Эриашвили Н. Д., Никитин А. М. Экономическая теория. — М, 2000, 564 с.
Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, 259 с.
www.ronl.ru
1. Детерминированные и вероятностные математические модели в экономике. Преимущества и недостатки
Методы исследования экономических процессов базируются на использовании математических — детерминированных и вероятностных — моделей, представляющих изучаемый процесс, систему или вид деятельности. Такие модели дают количественную характеристику проблемы и служат основой для принятия управленческого решения при поисках оптимального варианта. Насколько обоснованы эти решения, являются ли они лучшими из возможных, учтены ли и взвешены все факторы, определяющие оптимальное решение, каков критерий, позволяющий определить, что данное решение действительно наилучшее, — таков круг вопросов, имеющих большое значение для руководителей производства, и ответ на которые можно найти с помощью методов исследования операций [Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, стр. 45].
Одним из принципов формирования системы управления является метод кибернетических (математических) моделей. Математическое моделирование занимает промежуточное положение между экспериментом и теорией: нет необходимости строить реальную физическую модель системы, ее заменит математическая модель. Особенность формирования системы управления заключается в вероятностном, статистическом подходе к процессам управления. В кибернетике принято, что любой процесс управления подвержен случайным, возмущающим воздействиям. Так, на производственный процесс оказывают влияния большое количество факторов, учесть которые детерминированным образом невозможно. Поэтому считается, что на производственный процесс воздействуют случайные сигналы. В силу этого планирование работы предприятия может быть только вероятностным.
По этим причинам часто, говоря о математическом моделировании экономических процессов, имеют в виду именно вероятностные модели.
Опишем каждый из типов математических моделей.
Детерминированные математические модели характеризуются тем, что описывают связь некоторых факторов с результативным показателем как функциональную зависимость, т. е. в детерминированных моделях результативный показатель модели представлен в виде произведения, частного, алгебраической суммы факторов, или в виде любой другой функции. Данный вид математических моделей наиболее распространен, поскольку, будучи достаточно простыми в применении (по сравнению вероятностными моделями), позволяет осознать логику действия основных факторов развития экономического процесса, количественно оценить их влияние, понять, какие факторы и в какой пропорции возможно и целесообразно изменить для повышения эффективности производства.
Вероятностные математические модели принципиально отличаются от детерминированных тем, что в вероятностных моделях взаимосвязь между факторами и результирующим признаком вероятностная (стохастическая): при функциональной зависимости (детерминированные модели) одному и тому же состоянию факторов соответствует единственное состояние результирующего признака, тогда как в вероятностных моделях одному и тому же состоянию факторов соответствует целое множество состояний результирующего признака [Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, с. 32-33].
Преимущество детерминированных моделей в простоте их применения. Основной недостаток — низкая адекватность реальной действительности, т. к., как было отмечено выше, большинство экономических процессов носит вероятностный характер.
Достоинством вероятностных моделей является то, что они, как правило, больше соответствуют реальной действительности (более адекватны), чем детерминированные. Однако, недостатком вероятностных моделей является сложность и трудоемкость их применения, так что во многих ситуациях достаточно бывает ограничиться детерминированными моделями.
2. Постановка задачи линейного программирования на примере задачи о пищевом рационе
Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок; позволяющего минимизировать суммарной километраж, была дана в работе советского экономиста А. Н. Толстого в 1930 году.
Систематические исследования задач линейного программирования и разработка общих методов их решения получили дальнейшее развитие в работах российских математиков Л. В. Канторовича, В. С. Немчинова и других математиков и экономистов. Также методам линейного программирования посвящено много работ зарубежных и, прежде всего, американских ученых.
Задача линейного программирования состоит в максимизации (минимизации) линейной функции.
, где
при ограничениях
(*)
причем все
Замечание. Неравенства могут быть и противоположного смысла. Умножением соответствующих неравенств на (-1) можно всегда получить систему вида (*).
Если число переменных системы ограничений и целевой функции в математической модели задачи равно 2, то её можно решить графически.
Итак, надо максимизировать функцию к удовлетворяющей системе ограничений.
Обратимся к одному из неравенств системы ограничений.
С геометрической точки зрения все точки, удовлетворяющие этому неравенству, должны либо лежать на прямой , либо принадлежать одной из полуплоскостей, на которые разбивается плоскость этой прямой. Для того чтобы выяснить это, надо проверить какая из них содержит точку ().
Замечание 2. Если , то проще взять точку (0;0).
Условия неотрицательности также определяют полуплоскости соответственно с пограничными прямыми . Будем считать, что система неравенств совместна, тогда полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты которых являются решением данной системы — это множество допустимых решений. Совокупность этих точек (решений) называется многоугольником решений. Он может быть точкой, лучом, многоугольником, неограниченной многоугольной областью. Таким образом, задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху (снизу). При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим прямую (где h — некоторая постоянная). Чаще всего берется прямая . Остается выяснить направление движения данной прямой. Это направление определяется градиентом (антиградиентом) целевой функции.
Вектор в каждой точке перпендикулярен прямой , поэтому значение f будет возрастать при перемещении прямой в направлении градиента (убывать в направлении антиградиента). Для этого параллельно прямой проводим прямые, смещаясь в направлении градиента (антиградиента).
Эти построения будем продолжать до тех пор, пока прямая не пройдет через последнюю вершину многоугольника решений. Эта точка определяет оптимальное значение.
Итак, нахождение решения задачи линейного программирования геометрическим методом включает следующие этапы:
Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
Находят полуплоскости, определяемые каждым из ограничений задачи.
Находят многоугольник решений.
Строят вектор .
Строят прямую .
Строят параллельные прямые в направлении градиента или антиградиента, в результате чего находят точку, в которой функция принимает максимальное или минимальное значение, либо устанавливают неограниченность сверху (снизу) функции на допустимом множестве.
Определяют координаты точки максимума (минимума) функции и вычисляют значение целевой функции в этой точке.
Задача о рациональном питании (задача о пищевом рационе)
Постановка задачи
Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно С1, С2, С3, С4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b1 единиц; углеводов — не менее b2 единиц; жиров — не менее b3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, где aij (i=1,2,3,4; j=1,2,3) — какие-то определённые числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры).
| продукт | элементы | ||
| белки | углеводы | жиры | |
П1 П2 П3 П4 | A11 A21 A31 A41 | A12 A22 A32 A42 | A13 A23 A33 A43 |
Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.
Математическая модель
Обозначим x1, x2, x3, x4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L): она линейно зависит от элементов решения x1, x2, x3, x4.
Целевая функция:
Система ограничений:
a11x1+a21x2+a31x3+a41x4 больше или равно b1
a12x1+a22x2+a32x3+a42x4 больше или равно b2
a13x1+a23x2+a32x3+a43x4 больше или равно b3
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения x1, x2, x3, x4.
Таким образом, поставленная задача сводится к следующему: найти такие неотрицательные значения переменных x1, x2, x3, x4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
Список литературы
Гончаров В. В. Важнейшие понятия и концепции в современном управлении. — М.: МНИИПУ, 2002, 341 с.
История экономических учений. // Под ред. Н. А. Хохлова. — СПб: Питер, 2002, 324 с.
Казаков А. П., Минаев Н. В. Экономика. Курс лекций. Упражнения. Тесты и тренинги. — М.: Изд-во ЦИПКК АП, 1999, 359 с.
Макроэкономика. Учебное пособие. // Под ред. А. М. Бункина. — М.: Инфра-М, 1995, 337 с.
Нуриев, Розанова. Поведение потребителя в рыночной экономике. // Вопросы экономики, 2003, № 1, с. 4-9.
Социально-экономическая статистика. // Под ред. Г. Л. Громыко. — М.: Изд-во МГУ, 1999, 350 с.
Толстова Ю. Н. Логика математического анализа экономических процессов. — М.: Наука, 2001, 160 с.
Ховард К., Эриашвили Н. Д., Никитин А. М. Экономическая теория. — М, 2000, 564 с.
Чесноков С. В. Детерминационный анализ социально-экономических данных. — М.: Наука, 1982, 259 с.
www.ronl.ru
Реферат на тему:
Математи́ческая моде́ль — это математическое представление реальности[1].
Математическое моделирование — процесс построения и изучения математических моделей.
Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю.
Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.
Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):
По учебнику Советова и Яковлева [3]: «модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.» (с. 6) «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием.» (с. 6) «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.»
По Самарскому и Михайлову [4], математическая модель — это «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д.» Существует в триадах «модель-алгоритм-программа». «Создав триаду „модель-алгоритм-программа“, исследователь получает в руки универсальный, гибкий и недорогой инструмент, который вначале отлаживается, тестируется в пробных вычислительных экспериментах. После того, как адекватность (достаточное соответствие) триады исходному объекту установлена, с моделью проводятся разнообразные и подробные „опыты“, дающие все требуемые качественные и количественные свойства и характеристики объекта.» (с.7-8)
По монографии Мышкиса [5]: «Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность S свойств реального объекта a с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т. д.). Для этого мы выбираем (как говорят, строим) „математический объект“ a' — систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т. д.,— исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах S. В этих условиях a' называется математической моделью объекта a относительно совокупности S его свойств.» (с.8)
По Севостьянову А. Г.[6] : «Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.»
Несколько менее общее определение математической модели, основанное на идеализации «вход — выход — состояние», заимствованной из теории автоматов, даёт Wiktionary: «Абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия.»[7]
Наконец, наиболее лаконичное определение математической модели: «Уравнение, выражающее идею.»[8]
Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий [9]:
и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.
Наряду с формальной классификацией, модели различаются по способу представления объекта:
Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями «чёрного ящика»[13] Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».
Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, содержательная модель[14]. Устоявшейся терминологии здесь нет, и другие авторы называют этот идеальный объект концептуальная модель[15], умозрительная модель[16] или предмодель[17]. При этом финальная математическая конструкция называется формальной моделью или просто математической моделью, полученной в результате формализации данной содержательной модели (предмодели). Построение содержательной модели может производиться с помощью набора готовых идеализаций, как в механике, где идеальные пружины, твёрдые тела, идеальные маятники, упругие среды и т. п. дают готовые структурные элементы для содержательного моделирования. Однако в областях знания, где не существует полностью завершенных формализованных теорий (передний край физики, биологии, экономики, социологии, психологии, и большинства других областей), создание содержательных моделей резко усложняется.
В работе Р. Пайерлса (англ. R. Реiеrls) [18] дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса[19] эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.
Эти модели «представляют собой пробное описание явления, причем автор либо верит в его возможность, либо считает даже его истинным». По Р. Пайерлсу это, например, модель Солнечной системы по Птолемею и модель Коперника (усовершенствованная Кеплером), модель атома Резерфорда и модель Большого Взрыва.
Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:
«У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что ваша теория правильна? Нет, просто-напросто это значит, что вам не удалось ее опровергнуть.»[20]
Если модель первого типа построена, то это означает что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.
Феноменологическая модель содержит механизм для описания явления. Однако этот механизм недостаточно убедителен, не может быть достаточно подтверждён имеющимися данными или плохо согласуется с имеющимися теориями и накопленным знанием об объекте. Поэтому феноменологические модели имеют статус вре́менных решений. Считается, что ответ всё ещё неизвестен и необходимо продолжить поиск «истинных механизмов». Ко второму типу Пайерлс относит, например, модели теплорода и кварковую модель элементарных частиц.
Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично, новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира, проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.
Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.
Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.
Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.
В модели типа 4 отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделью типа 3 (приближение) или 4 (опустим для ясности некоторые детали) — это зависит от явления, для изучения которого используется модель. Так, если модели линейного отклика применяются при отсутствии более сложных моделей (то есть не производится линеаризация нелинейных уравнений, а просто ищутся линейные уравнения, описываюшие объект), то это уже феноменологические линейные модели, и относятся они к следующему типу 4 (все нелинейные детали «для ясности» опускаем).
Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.
Эвристическая модель сохраняет лишь качественное подобие реальности и даёт предсказания только «по порядку величины». Типичный пример — приближение средней длины свободного пробега в кинетической теории. Оно даёт простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.
Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.
Р. Пайерлс приводит историю использования аналогий в первой статье В. Гейзенберга о природе ядерных сил. «Это произошло после открытия нейтрона, и хотя сам В. Гейзенберг понимал, что можно описывать ядра состоящими из нейтронов и протонов, он не мог все же избавиться от мысли, что нейтрон должен в конечном счете состоять из протона и электрона. При этом возникала аналогия между взаимодействием в системе нейтрон — протон и взаимодействием атома водорода и протоном. Эта-то аналогия и привела его к заключению, что должны существовать обменные силы взаимодействия между нейтроном и протоном, которые аналогичны обменным силам в системе H − H + , обусловленным переходом электрона между двумя протонами. … Позднее было все-таки доказано существование обменных сил взаимодействия между нейтроном и протоном, хотя ими не исчерпывалось полностью взаимодействие между двумя частицами… Но, следуя все той же аналогии, В. Гейзенберг пришёл к заключению об отсутствии ядерных сил взаимодействия между двумя протонами и к постулированию отталкивания между двумя нейтронами. Оба последних вывода находятся в противоречии с данными более поздних исследований».
А. Эйнштейн был одним из великих мастеров мысленного эксперимента. Вот один из его экспериментов. Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.
А вот и тип 8, широко распространенный в математических моделях биологических систем.
Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципам и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.
Один из самых знаменитых таких экспериментов — геометрия Лобачевского (Лобачевский называл её «воображаемой геометрией»). Другой пример — массовое производство формально — кинетических моделей химических и биологических колебаний, автоволн и др. Парадокс Эйнштейна — Подольского — Розена был задуман как модель 7 типа, для демонстрации противоречивости квантовой механики. Совершенно незапланированным образом он со временем превратился в модель 8 типа — демонстрацию возможности квантовой телепортации информации.
В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.
Рассмотрим механическую систему, состоящую из пружины, закрепленной с одного конца, и груза массой m, прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием x от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (F = − kx) после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:
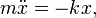
где означает вторую производную от x по времени:
 .
.
Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором».
По формальной классификации эта модель линейная, детерминисткая, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.
По отношению к реальности это, чаще всего, модель типа 4 упрощение («опустим для ясности некоторые детали»), поскольку опущены некоторые существенные универсальные особенности (например, диссипация). В некотором приближении (скажем, пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на её поведение. Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведет к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.
Впрочем, при уточнении модели сложность её математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).
Если применять модель гармонического осциллятора к объектам, далёким от физики, её содержательный статус может быть другим. Например, при приложении этой модели к биологическим популяциям, её следует отнести, скорее всего, к типу 6 аналогия («учтём только некоторые особенности»).
Гармонический осциллятор — пример так называемой «жёсткой» модели. Она получена в результате сильной идеализации реальной физической системы. Для решения вопроса о её применимости необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Иными словами, нужно исследовать «мягкую» модель, получающуюся малым возмущением «жёсткой». Она может задаваться, например, следующим уравнением:
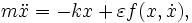
Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения,
— некоторый малый параметр. Явный вид функции f нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, решением уравнения гармонического осциллятора являются функции вида
, то есть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.
Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы.[21] Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.
Важнейшие математические модели обычно обладают важным свойством универсальности: принципиально разные реальные явления могут описываться одной и той же математической моделью. Скажем, гармонический осциллятор описывает не только поведение груза на пружине, но и другие колебательные процессы, зачастую имеющие совершенно иную природу: малые колебания маятника, колебания уровня жидкости в U-образном сосуде или изменение силы тока в колебательном контуре. Таким образом, изучая одну математическую модель, мы изучаем сразу целый класс описываемых ею явлений. Именно этот изоморфизм законов, выражаемых математическими моделями в различных сегментах научного знания, подвиг Людвига фон Берталанфи на создание «Общей теории систем».
Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются, как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.
Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.
Прямая задача: структура модели и все её параметры считаются известными, главная задача — провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолёт преодолеет звуковой барьер, не развалится ли он от флаттера, — вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический мост через реку Тей, конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул. [22]
В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.
Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего, структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение).
Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный И. Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.
В качестве другого примера можно привести математическую статистику. Задача этой науки — разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений[23]. Т.е. множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.
Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др.[24] Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.
Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением

где α — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция x(t) = x0eαt. Если рождаемость превосходит смертность (α > 0), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста
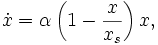
где xs — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению xs, причем такое поведение структурно устойчиво.
Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов x, число лис y. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерра:
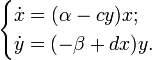
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.
wreferat.baza-referat.ru