Впервые кривые второго порядкаизучались одним из учеников Платона. Его работа заключалась в следующем: если взятьдве пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного,то получится конусная поверхность. Если же пересечь эту поверхность плоскостью,то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность,парабола, гипербола и несколько вырожденных фигур.

Однако эти научные знаниянашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическимтраекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно,что если придать телу первую космическую скорость, то оно будет двигаться по окружностивокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второйкосмической скорости тело по параболе покинет поле притяжения Земли.

1. Кривые второго порядка

Кривой 2-го порядка называетсялиния на плоскости, которая в некоторой декартовой системе координат определяетсяуравнением

ax2 + 2bxy + cy2+ 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты,причем a2 + b2 + c2 ≠ 0 .

Вид кривой зависит от четырёхинвариантов:

инварианты относительно поворотаи сдвига системы координат:

инвариант относительно поворотасистемы координат (полуинвариант):

Многие важные свойства кривыхвторого порядка могут быть изучены при помощи характеристической квадратичной формы,соответствующей уравнению кривой:

Или

λ2 − Iλ +D = 0.

Корни этого уравнения являютсясобственными значениями вещественной симметричной матрицы и, как следствие этого,всегда вещественны:

Кривые второго порядка классифицируютсяна невырожденные кривые и вырожденные.

Доказано, что кривая 2–гопорядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс,гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих),точка, пустое множество.

Иными словами, для каждойкривой 2-го порядка (для каждого уравнения) существует такая система координат,в которой уравнение кривой имеет вид:

1.1 Эллипс

Эллипсом называется геометрическоеместо точек плоскости, для которых сумма расстояний до двух фиксированных точекплоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющиеточку эллипса с фокусами, называются фокальными радиусами точки.

Если эллипс описывается каноническимуравнением

где a > 0, b > 0, a> b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметричнона оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где

Величина e = c/a называетсяэксцентриситетом эллипса.

По определению эллипса r1+ r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают,то эллипс является окружностью.

1.2 Гипербола

Гиперболой называется криваявторого порядка, которая в некоторой декартовой системе координат описывается уравнением

где a > 0, b > 0 — параметрыгиперболы.

Это уравнение называется каноническимуравнением гиперболы, а система координат, в которой гипербола описывается каноническимуравнением, называется канонической.

В канонической системе осикоординат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболыс осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосямигиперболы.

Рис.1

Прямые ay − bx = 0 иay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность,соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу,вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

Такая гипербола называетсясопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0.Говорят о паре сопряжённых гипербол.

1.3 Парабола

Параболой называется криваявторого порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2 px

где p > 0 — параметр параболы.

Такое уравнение называетсяканоническим уравнением параболы, а система координат, в которой парабола описываетсяканоническим уравнением, называется канонической.

В канонической системе осьабсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

Уравнения y2 = −2 px,x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координаттакже описывают параболы:

2. Теоремы, связанные скривыми второго порядка

Теоремма Паскамля — теоремапроективной геометрии, которая гласит, что:

Если шестиугольник вписанв окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу,даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат наодной прямой. Теорема Паскаля двойственна к теоремеБрианшона.

Теорема Брианшона являетсяклассической теоремой проективной геометрии. Она сформулируется следующим образом:

Если шестиугольник описаноколо конического сечения, то три диагонали, соединяющие противоположные вершиныэтого шестиугольника, проходят через одну точку.

В частности, в вырожденномслучае:

Если стороны шестиугольникапроходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположныевершины, проходят через одну точку.

Теорема Брианшона двойственнак теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература

1. Корн Г., Корн Т. Кривыевторого порядка (конические сечения) // Справочник по математике. — 4-е издание.— М: Наука, 1978. — С. 64-69.

2. Корн Г., Корн Т. 2.4-5.Характеристическая квадратичная форма и характеристическое уравнение // Справочникпо математике. — 4-е издание. — М: Наука, 1978. — С. 64.

3. В.А. Ильин, Э.Г. Позняк.Аналитическая геометрия, гл. 6. М.: «Наука», 1988.

www.ronl.ru

Реферат Кривые второго порядка

скачать

Реферат на тему:

План:

1 История
2 Инварианты
3 Характеристическая квадратичная форма и характеристическое уравнение
4 Классификация кривых второго порядка
- 4.1 Невырожденные кривые
- 4.2 Вырожденные кривые
5 Диаметры и центр кривой второго порядка
6 Главные оси и вершины кривой второго порядка
7 Уравнения
- 7.1 Общее уравнение в матричном виде
- 7.2 Канонический вид
- 7.3 Через эксцентриситет
- 7.4 Полярные координаты
- 7.5 Кривая, заданная своими пятью точками
- 7.6 Касательные и нормали
- 7.7 Полюсы и поляры
8 Теоремы, связанные с кривыми второго порядка

Введение

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

$~a_{11}x^2 + a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$

в котором по крайней мере один из коэффициентов $a_{11},~a_{12},~a_{22}$ отличен от нуля.

1. История

Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур (см. ниже).

Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

2. Инварианты

Вид кривой зависит от четырёх инвариантов:

инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
- $B=\begin{vmatrix} a_{11} & a_{13} \\ a_{13} & a_{33}\end{vmatrix}+\begin{vmatrix} a_{22} & a_{23} \\ a_{23} & a_{33}\end{vmatrix}$

3. Характеристическая квадратичная форма и характеристическое уравнение

Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой

$F_0(x,\,y) = a_{11}x^2 + 2a_{12}xy + a_{22}y^2.$

Так, например, невырожденная кривая $\left(\Delta\ne0\right)$ оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли $F_0(x,\,y)$ положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:

$\begin{vmatrix} a_{11} - \lambda & a_{12} \\ a_{12} & a_{22} - \lambda \end{vmatrix} = 0$

или

λ2 − Iλ + D = 0.

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы

$\begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix}$

и, как следствие этого, всегда вещественны.[1]

4. Классификация кривых второго порядка

4.1. Невырожденные кривые

Кривая второго порядка называется невырожденной, если $\Delta\ne0.$ Могут возникать следующие варианты:

Невырожденная кривая второго порядка называется центральной, если
- эллипс — при условии D > 0 и ΔI < 0;
  - частный случай эллипса — окружность — при условии I2 = 4D или a11 = a22,a12 = 0;
- мнимый эллипс (ни одной вещественной точки) — при условии ΔI > 0;
- гипербола — при условии D < 0;
Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0
- парабола — при условии D = 0.

4.2. Вырожденные кривые

Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:

вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;
пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
вырожденная парабола — при условии D = 0:
- пара вещественных параллельных прямых — при условии B < 0;
- одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;
- пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.

5. Диаметры и центр кривой второго порядка

Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:

$\left(a_{11}x + a_{12}y +a_{13}\right) \cos\theta + \left(a_{12}x + a_{22}y +a_{23}\right) \sin\theta = 0.$

Если выполняется условие $D\ne0,$ то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо параллельны, либо совпадают.

Координаты центра $\left(x_0,\;y_0\right)$ определяются системой уравнений:

$\begin{cases} a_{11}x_0 + a_{12}y_0 + a_{13} = 0 \\ a_{12}x_0 + a_{22}y_0 + a_{23} = 0 \end{cases}$

Решая эту систему относительно x0 и y0, получим:

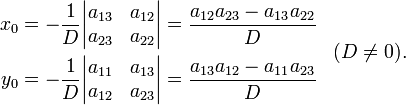
$\begin{align} x_0 = - \frac{1}{D} \begin{vmatrix} a_{13} & a_{12} \\ a_{23} & a_{22} \end{vmatrix} = \frac{a_{12}a_{23} - a_{13}a_{22}}{D} \\ y_0 = - \frac{1}{D} \begin{vmatrix} a_{11} & a_{13} \\ a_{12} & a_{23} \end{vmatrix} = \frac{a_{13}a_{12} - a_{11}a_{23}}{D} \end{align}\;\;\;(D\ne0).$

Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду

$a_{11} \bar x^2 + 2a_{12} \bar x \bar y + a_{22} \bar y^2 + \frac{\Delta}{D} = 0,\;\;\;\bar x = x - x_0,\;\;\;\bar y = y - y_0,$

где $\bar x,\;\bar y$ — координаты относительно новой системы.

6. Главные оси и вершины кривой второго порядка

Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая $\left(D\ne0\right)$ либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые $\left(D=0\right)$ имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.

Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям

$\begin{cases} \left(a_{11} - \lambda\right) \cos \theta + a_{12} \sin \theta = 0 \\ a_{12} \cos \theta + \left(a_{22} - \lambda\right) \sin \theta = 0 \end{cases},$

где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой

$\operatorname{tg}2\phi = \operatorname{tg}2\theta = \frac{2a_{12}}{a_{11}-a_{22}}.$

Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.

7. Уравнения

7.1. Общее уравнение в матричном виде

Общее уравнение кривой можно записать в матричном виде

$\begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = 0.$

7.2. Канонический вид

Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты $\Delta,\;D,\;I$ и корни характеристического уравнения $\lambda_1 \geqslant \lambda_2$ (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).

Для центральной кривой в каноническом виде её центр $\left(x_0,\;y_0\right)$ находится в начале координат.

7.3. Через эксцентриситет

Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду

$y^2=2px-(1-\varepsilon^2)x^2\ \ (p>0).$

В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых $\varepsilon \geqslant 0$ (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при $\varepsilon = 0$ кривая является окружностью, при $\varepsilon < 1$ — эллипсом, при $\varepsilon = 1$ — параболой, при $\varepsilon > 1$ — гиперболой.

Уравнение директрисы кривой выражается уравнением $x = - \frac{p}{\varepsilon \left( 1 + \varepsilon \right)},$ а координаты фокуса $x=\frac{p}{1+\varepsilon}, \;\; y = 0.$ Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно $\frac{p}{\varepsilon}.$

Если кривая второго порядка центральная (эллипс или гипербола), то прямая

$x = \frac{p}{1 - \varepsilon^2} = a$

является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы.

Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда).

7.4. Полярные координаты

Если взять в качестве полюса полярной системы координат $\left(\rho,\phi\right)$ фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симметрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид

$\rho=\frac{p}{1 + \varepsilon \cos \phi}.$

7.5. Кривая, заданная своими пятью точками

Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки $\left( x_1, y_1 \right),$ $\left( x_2, y_2 \right),$ $\left( x_3, y_3 \right),$ $\left( x_4, y_4 \right)$ и $\left( x_5, y_5 \right):$

$\begin{vmatrix} x^2 & xy & y^2 & x & y & 1 \\ x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ x_3^2 & x_3y_3 & y_3^2 & x_3 & y_3 & 1 \\ x_4^2 & x_4y_4 & y_4^2 & x_4 & y_4 & 1 \\ x_5^2 & x_5y_5 & y_5^2 & x_5 & y_5 & 1 \end{vmatrix} = 0.$

Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.

7.6. Касательные и нормали

Уравнение касательной к кривой второго порядка f(x,y) в её точке $\left(x_1, y_1\right)$ имеет вид:

$\left(a_{11}x_1+a_{12}y_1+a_{13}\right) x + \left(a_{12}x_1+a_{22}y_1+a_{23}\right) y + \left(a_{13}x_{1}+a_{23}y_{1}+a_{33}\right) = 0.$

Уравнение нормали к кривой второго порядка в точке $\left(x_1, y_1\right)$ имеет вид

$\frac{x-x_{1}}{a_{11}x_{1}+a_{12}y_{1}+a_{13}}=\frac{y-y_{1}}{a_{12}x_{1}+a_{22}y_{1}+a_{23}}.$

7.7. Полюсы и поляры

Уравнение

$\left(a_{11}x_1+a_{12}y_1+a_{13}\right) x + \left(a_{12}x_1+a_{22}y_1+a_{23}\right) y + \left(a_{13}x_{1}+a_{23}y_{1}+a_{33}\right) = 0$

помимо касательной опряделяет прямую, называемую полярой точки $\left(x_1, y_1\right)$ относительно кривой второго порядка, независимо от того, лежит ли эта точка на кривой или нет. При этом точка $\left(x_1, y_1\right)$ называется полюсом этой прямой. Поляра точки кривой есть её касательная в этой точке.

Теоремы о полюсах и полярах:

Если прямая, проведённая через полюс P, пересекает поляру в точке Q, а кривую второго порядка — в точках R1 и R2, то точки P и Q гармонически разделяют отрезок R1R2, т. е. выполняется условие $\frac{R_1P}{PR_2}=-\frac{R_1Q}{QR_2}.$
Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.
Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.
Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой пучка. Директрисса есть поляра фокуса.

Из этих утверждений, в частности, следует, что:

если через точку можно провести две касательные к кривой, то то поляра этой точки проходит через точки касания;
касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;
точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директриссе;
каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.

8. Теоремы, связанные с кривыми второго порядка

Теорема Паскаля: точки пересечения противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на одной прямой.
Теорема Брианшона: диагонали, проходящие через противоположные вершины шестиугольника, описанного около кривой второго порядка, пересекаются в одной точке.

wreferat.baza-referat.ru

Кривые второго порядка (работа 2)

Содержание

Введение

1.Кривые второго порядка

1.1 Эллипс

1.2 Гипербола

1.3 Парабола

2.Теоремы, связанные с кривыми второго порядка

Литература

Введение

Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.

Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

1. Кривые второго порядка

Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .

Вид кривой зависит от четырёх инвариантов:

инварианты относительно поворота и сдвига системы координат:

инвариант относительно поворота системы координат (полуинвариант):

Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:

Так, например, невырожденная кривая оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:

Или

λ2 − Iλ + D = 0.

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:

Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.

Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.

Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:

1.1 Эллипс

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.

Если эллипс описывается каноническим уравнением

где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где

Величина e = c/a называется эксцентриситетом эллипса.

По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают, то эллипс является окружностью.

1.2 Гипербола

Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

где a > 0, b > 0 — параметры гиперболы.

Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.

В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосями гиперболы.

Рис.1

Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.

1.3 Парабола

Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2 px

где p > 0 — параметр параболы.

Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.

В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:

2. Теоремы, связанные с кривыми второго порядка

Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:

Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.

Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:

Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.

В частности, в вырожденном случае:

Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.

Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература

Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: "Наука", 1988.

topref.ru

Кривые второго порядка - реферат

Содержание Введение 1.Кривые второго порядка 1.1 Эллипс 1.2 Гипербола 1.3 Парабола 2.Теоремы, связанные с кривыми второгопорядка Литература

Введение Впервые кривые второго порядкаизучались одним из учеников Платона. Его работа заключалась в следующем: если взятьдве пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного,то получится конусная поверхность. Если же пересечь эту поверхность плоскостью,то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность,парабола, гипербола и несколько вырожденных фигур.Однако эти научные знаниянашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическимтраекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно,что если придать телу первую космическую скорость, то оно будет двигаться по окружностивокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второйкосмической скорости тело по параболе покинет поле притяжения Земли.

1. Кривые второго порядка Кривой 2-го порядка называетсялиния на плоскости, которая в некоторой декартовой системе координат определяетсяуравнениемax2 + 2bxy + cy2+ 2dx + 2ey + f = 0где a, b, c, d, e, f — вещественные коэффициенты,причем a2 + b2 + c2 ≠ 0 .Вид кривой зависит от четырёхинвариантов:инварианты относительно поворотаи сдвига системы координат:/>/>/>инвариант относительно поворотасистемы координат (полуинвариант):/>Многие важные свойства кривыхвторого порядка могут быть изучены при помощи характеристической квадратичной формы,соответствующей уравнению кривой:/>

Так, например, невырожденнаякривая/>оказываетсявещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости оттого, будет ли/>положительно определённой, отрицательноопределённой, неопределённой или полуопределённой квадратичной формой, что устанавливаетсяпо корням характеристического уравнения:/>Илиλ2 − Iλ +D = 0.Корни этого уравнения являютсясобственными значениями вещественной симметричной матрицы и, как следствие этого,всегда вещественны:/>Кривые второго порядка классифицируютсяна невырожденные кривые и вырожденные.Доказано, что кривая 2–гопорядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс,гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих),точка, пустое множество.Иными словами, для каждойкривой 2-го порядка (для каждого уравнения) существует такая система координат,в которой уравнение кривой имеет вид:

/>1.1 Эллипс Эллипсом называется геометрическоеместо точек плоскости, для которых сумма расстояний до двух фиксированных точекплоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющиеточку эллипса с фокусами, называются фокальными радиусами точки.Если эллипс описывается каноническимуравнением/>где a > 0, b > 0, a> b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметричнона оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где/>Величина e = c/a называетсяэксцентриситетом эллипса.

/>По определению эллипса r1+ r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам/>Если фокусы эллипса совпадают,то эллипс является окружностью.1.2 ГиперболаГиперболой называется криваявторого порядка, которая в некоторой декартовой системе координат описывается уравнением/>где a > 0, b > 0 — параметрыгиперболы.Это уравнение называется каноническимуравнением гиперболы, а система координат, в которой гипербола описывается каноническимуравнением, называется канонической.В канонической системе осикоординат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.Точки пересечения гиперболыс осью OX ( ± a, 0) называются вершинами гиперболы.С осью OY гипербола не пересекается.Отрезки a и b называются полуосямигиперболы./>Рис.1Прямые ay − bx = 0 иay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность,соответствующая ветвь гиперболы приближается к одной из асимптот.Уравнение описывает гиперболу,вершины которой лежат на оси OY в точках (0, ± b)./>

/>Рис.2Такая гипербола называетсясопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0.Говорят о паре сопряжённых гипербол./>1.3 ПараболаПараболой называется криваявторого порядка, которая в некоторой декартовой системе координат описывается уравнениемy2 = 2 pxгде p > 0 — параметр параболы.Такое уравнение называетсяканоническим уравнением параболы, а система координат, в которой парабола описываетсяканоническим уравнением, называется канонической.В канонической системе осьабсцисс является осью симметрии параболы, а начало координат — её вершиной.

/>Рис.3Уравнения y2 = −2 px,x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координаттакже описывают параболы:/>

2. Теоремы, связанные скривыми второго порядка Теоремма Паскамля — теоремапроективной геометрии, которая гласит, что:Если шестиугольник вписанв окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу,даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат наодной прямой. Теорема Паскаля двойственна к теоремеБрианшона.Теорема Брианшона являетсяклассической теоремой проективной геометрии. Она сформулируется следующим образом:Если шестиугольник описаноколо конического сечения, то три диагонали, соединяющие противоположные вершиныэтого шестиугольника, проходят через одну точку.В частности, в вырожденномслучае:Если стороны шестиугольникапроходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположныевершины, проходят через одну точку.Теорема Брианшона двойственнак теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература 1. Корн Г., Корн Т. Кривыевторого порядка (конические сечения) // Справочник по математике. — 4-е издание.— М: Наука, 1978. — С. 64-69.2. Корн Г., Корн Т. 2.4-5.Характеристическая квадратичная форма и характеристическое уравнение // Справочникпо математике. — 4-е издание. — М: Наука, 1978. — С. 64.3. В.А. Ильин, Э.Г. Позняк.Аналитическая геометрия, гл. 6. М.: «Наука», 1988.

2dip.su

Кривые и поверхности второго порядка

Кафедра высшей математики

Курсовая работа

По линейной алгебре и аналитической геометрии

«Кривые и поверхности второго порядка»

Дубна 2002

Оглавление

Введение

Часть I. Исследование кривой второго порядка

1. Определение типа кривой с помощью инвариантов

2. Приведение к каноническому виду

3. Построение графиков

4. Вывод

Часть II. Исследование поверхности второго порядка

1. Определение типа поверхности.

2. Приведение к каноническому виду

3. Исследование формы поверхности методом сечений

4. Графики уравнения поверхности.

5. Вывод

Цель:

Целью данной курсовой работы является исследование кривой и поверхности второго порядка. Закрепление теоретических знаний и практических навыков по изучению и анализу свойств кривых и поверхностей второго порядка.

Постановка задачи:

I) Для данного уравнения кривой второго порядка:

1) Определить тип кривой с помощью инвариантов.

2) При a=0 записать каноническое уравнение прямой и определить расположение центра

3) Привести уравнение к каноническому виду, применяя параллельный перенос и поворот координатных осей.

II) Для данного уравнения плоскости второго порядка:

1) Исследовать форму поверхности методом сечений плоскостями, построить линии, полученные в сечениях.

2) Построить поверхность в канонической системе координат.

1. Определение типа кривой с помощью инвариантов

Для данного уравнения кривой второго порядка:

(5 - a)x2 + 4xy + 3y2 + 8x – 6y +5 = 0 (3.1)

определить зависимость типа кривой от параметра a с помощью инвариантов.

Для данного уравнения кривой второго порядка:

a11 = 5 - a, a12 = 2, a13 = 4, a22 = 2, a23 = -3, a33 = 5

Вычислим инварианты:

I1 = a11 + a22 = (5 - a) +2 = 7 - a

I2 == = (5 - a)2 – 4 = 6 -2a

I2 === (5 - a)10-24-24-32-9(5 - a)-20 = -a-95

Согласно классификации кривых второго порядка:

I. Если I2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:

I2 = 6 - 2a = 0, следовательно, при a = 3 уравнение определяет кривую параболического типа.

При a = 3 I3 = - a - 95 = -3 - 95 = 98 ¹ 0. Значит, при a = 3 уравнение (3.1) задаёт параболу.

II. Если I2 ¹ 0, то задаваемая кривая является центральной. Следовательно, при a ¹ 3 данное уравнение задаёт центральную кривую.

1. Если I2 > 0, то уравнение задаёт кривую эллиптического типа:

Значит, при a < 3 уравнение (3.1) задаёт кривую эллиптического типа.

a. Если I1 I3 < 0, то уравнение определяет эллипс:

I1 I3 = - (7 - a)(a+95) = a2+88a-665 < 0, при решении получаем a Î (-95 , 7). Следовательно, при a Î (-95 , 3) уравнение (3.1) задаёт эллипс.

b. Если I1 I3 > 0, то уравнение определяет эллипс:

I1 I3 = a2+88a-665 > 0, при решении получаем a Î (-¥, -95). Следовательно, при a Î (-¥ , -95) уравнение (3.1) задаёт мнимый эллипс.

c. Если I3 = 0, то уравнение определяет две мнимые пересекающиеся прямые:

I3 = -a - 95 = 0, при решении получаем a - 95. Следовательно, при a = - 95 уравнение (3.1) задаёт две мнимые пересекающиеся прямые.

2. Если I2 < 0, то уравнение задаёт кривую гиперболического типа:

Значит, при a > 3 уравнение (3.1) задаёт кривую гиперболического типа.

a. Если I3 ¹ 0, то уравнение определяет гиперболу:

I3 = -a - 95 ¹ 0, получаем a ¹ -95. Следовательно, при a Î (3 , +¥) уравнение (3.1) задаёт гиперболу.

Согласно полученным данным, построим таблицу:

a Î (-¥ , -95)	a = -95	a Î (-95 , 3)	a = 3	a Î (3 , +¥)
Мнимый эллипс	Две мнимые пересекающиеся прямые	Эллипс	Парабола	Гипербола

2. Приведение к каноническому виду

При a = 0 уравнение (3.1) принимает вид:

5x2 + 4xy + 2y2 + 8x - 6y + 5 = 0 (3.2)

Приведем уравнение кривой (3.2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.

a) Характеристическое уравнения для данной кривой будет иметь вид:

A(x, y) = 5x2 + 4xy + 2y2

Откуда следует, корни характеристического уравнения есть: l1 = 1, l2 = 6.

Расположение эллипса относительно начальной системы координат будет известно, если мы будем знать координаты центра и угловой коэффициент вещественной оси эллипса.

Уравнения для определения координат центра имеют вид:

Откуда мы находим x0 = - и y0 = . Следовательно, точка O¢ (-,) есть центр данной кривой.

Угловой коэффициент оси O¢X можем определить по формуле:

б) Совершим параллельный перенос начала координат в точку O¢ (x0, y0). При этом координаты x, y произвольной точки плоскости в системе координат xOy и координаты x', y' в новой системе координат x'O'y' связаны соотношениями:

Подставив данные выражения в уравнение (3.1), получим:

5(x0 + x¢)2 + 4(x0 + x¢)(y0 + y¢) + 2(y0 + y¢)2 + 8(x0 + x¢) - 6(y0 + y¢) + 5=0

Раскрыв скобки и приведя подобные члены, получим:

5x¢2+4x¢y¢+2y¢2+(10x0+4x0 + 8)x¢ + (4x0 + 4y0 - 6)y¢ + (5x02 + 4x0y0 + 2y02 + 8x0 - 6y0 + 5) = 0 (3.3)

В данном уравнении коэффициенты при x¢ и y¢ приравняем к нулю и получим систему уравнений:

Решив эту систему уравнений, мы получим, найденные уже раннее, координаты центра O¢ , x0 = - и y0 = . Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x'O'y' :

5x¢2 + 4x¢y¢ + 2y¢2 + () = 0

5x¢2 + 4x¢y¢ + 2y¢2 - = 0 (3.4)

в) Так как a12 = 2 ¹ 0, то для дальнейшего упрощения необходимо произвести поворота осей координат на угол a. При повороте осей координат на угол a координаты x', y' произвольной точки М плоскости в системе координат x'O'y' и координаты X, Y в новой системе координат XO'Y связаны соотношениями:

Подставим данные выражения в уравнение (3.4), получим:

5(Xcosa - Ysina)2 + 4(Xcosa - Ysina)(Xsina + Ycosa) + 2(Xsina + Ycosa)2 - = 0

(5cos2a + 4sinacosa + 2sin2a)X2 + (-6sinacosa + 4cos2a - 4sin2a)XY +

(5sin2a - 4sinacosa + 2cos2a)Y2 - = 0 (3.5)

В полученном выражении найдём такой угол a, чтобы коэффициент при XY стал равен нулю, для этого необходимо:

-6sinacosa + 4cos2a - 4sin2a = 0

2tg2a + 3tga - 2=0

Откуда, при решении, находим два значения tga = -2 и tga = .

В первом задании мы нашли, что угловой коэффициент вещественной оси O'X эллипса равен k = -2. Так как угловой коэффициент равен тангенсу, то из двух найдённых значений выберем tga = -2. Следовательно:

cosa = , sina =

Подставив данные значения для sina и cosa в уравнение (3.5), коэффициент при XY станет равным нулю, получим:

()X2 + ()Y2 - = 0

X2 + 6Y2 - = 0

(3.6)

- это каноническое уравнение данной кривой (3.1) при a = 0.

3. Построение графиков

Подтвердим результаты проведённого исследования данного уравнения кривой (3.1) второго порядка, построив соответствующие графики кривых при разных a.

При a = 3 уравнение (3.1) принимает вид:

2x2 + 4xy + 3y2 + 8x – 6y +5 = 0

Графиком данного уравнения является парабола:

При a = 6 уравнение (3.1) принимает вид:

x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0

Графиком данного уравнения является гипербола:

При a = 0 уравнение (3.1) принимает вид

5x2 + 4xy + 3y2 + 8y2 – 6y +5 = 0

Графиком данного уравнения является эллипс. Изобразим в данной системе также график канонического уравнения эллипса (3.6):

4. Вывод

Исследовав данное общее уравнение кривой второго порядка, мы установили, что при значении параметра a = 0 уравнение задаёт эллипс. Привели уравнение к каноническому виду, применяя преобразования параллельного переноса и поворота. При параллельном переносе коэффициенты при первых степенях стали равны нулю, при повороте координатных осей коэффициенты при смешанном произведении стали равны нулю. Построили графики для всех фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат.

1. Определение типа поверхности

Для данного уравнения поверхности второго порядка:

4x2 - z2 + 12xz + 6y - 8z + 5 = 0 (4.1)

Определить тип поверхности с помощью инвариантов.

4 + 0 -1 = 3

= - 4 – 36 = - 40

Определим характер расположения центра: Данная поверхность не имеет центра, так как выполняется условие I3 = 0, I4 ¹ 0. При этом инвариант I4 = 360 > 0, следовательно, графиком уравнения (4.1) является гиперболический параболоид.

2. Приведение к каноническому виду

Совершим параллельный перенос начала координат в некоторую точку O'(x0 ,y0, z0). При этом координаты x, y, z произвольной точки пространства в системе координат Oxyz и координаты x', y', z' этой же точки в новой системе координат в системе координат O'x'y'z' связаны соотношением:

(4.2)

Подставляя уравнения (4.2) в уравнение (4.1) получим уравнение поверхности S в новой системе координат O'x'y'z' :

4(x'+x0)2 - (z'+z0)2 + 12(x'+x0)(z'+z0) + 6y' - 8(z'+z0) + 5 = 0

4x'2 + 8x'x0 + 4x02 - z'2 - 2z'z0 - z02 + 12x'z' + 12z'z0 + 12x0z' + 12x0z0 + 6y' - 8z' - 8z0 + 5 = 0

4x'2 - z'2 + 12x'z' + 6y' + (12x0 - 2z0 - 8)z' + (8x0 + 12z0)x' + (4x02 - z02 + 12x0z0 - 8z0 +5)=0 (4.3)

Для того, чтобы новое начало координат O'(x0, y0, z0) было центром поверхности (4.1) необходимо и достаточно, чтобы в уравнении (4.3) отсутствовал член с x' и z' в первой степени:

Решая данную систему, находим x0 = и y0 = . Подставим полученные значения в уравнение (4.2):

4x'2 - z'2 + 12x'z' + 6y' + ()z' + ()x' + () = 0

4x'2 - z'2 + 12x'z' + 6y' + =0 (4.4)

Поскольку коэффициент при x'z' не равен нулю, то продолжим дальнейшее преобразование, совершив поворот осей координат на угол a. Координаты произвольной точки поверхности будут связаны следующими соотношениями:

(4.5)

Подставив выражения из (4.5) в уравнение (4.4), получим следующее:

4(Xcosa - Zsina)2 – (Xsina + Zcosa)2 + 12(Xcosa - Zsina)(Xsina + Zcosa) + 6Y + = 0

4X2cos2a - 8XZcosasina + 4Z2sin2a - X2sin2a - 2XZsin2a - 2XZcosasina -Z2cos2a + 12X2cosasina + 12XZcos2a - 12XZsin2a - 12Z2sinacosa + 6Y + = 0

(4cos2a-sin2a+12cosasina)X2+(4sin2a-cos2a-12sinacosa)+(-8cosasina-2cosasina+12cos2a-12sin2a)XZ+6Y+=0 (4.6)

Найдём угол a такой, что коэффициент при XZ будет равен нулю:

-8cosasina-2cosasina+12cos2a-12sin2a=0

6tg2a+5tga-6=0

D = 25+144 = 169 = 132

Откуда следует, что tga = или tga = . Возьмём tga = . Тогда найдём cosa==, sina=. Подставим найдённые значения в уравнение (4.6):

()X2+()Z2+()XZ+6Y+=0

(4.7)

- это каноническое уравнение поверхности (4.1). Оно имеет сдвиг по оси O'Y на (-).

3. Исследование формы поверхности методом сечений

Проведём исследование графика уравнения (4.7) методом сечения плоскостями.

Рассмотрим линии , полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:

Следовательно, уравнения проекций линий на плоскость ZO'X имеют вид:

Рассмотрим три случая:

Если h + >0, h >, запишем полученное уравнение в виде:

(4.8)

Уравнение (4.8) задаёт гиперболы с центрами в точках (0, h ,0).

Полуоси гипербол:

a = - действительная полуось, b = - мнимая полуось, увеличиваются с увеличением h. При различных значениях h получим семейство соответствующих гипербол:

h = 1 a=; b=;

h=2 a=; b=;

h=3 a=; b=;

Изобразим данные гиперболы на рисунке:

Если h + =0, h =, запишем полученное уравнение в виде:

или

Данное уравнение задаёт две пересекающиеся прямые. Изобразим их на рисунке:

Если h + < 0, h<, запишем полученное уравнение в виде:

Данное уравнение задаёт сопряжённые гиперболы с центрами в точке (0, h, 0).

Полуоси гипербол:

a=- действительная полуось, b=- мнимая полуось, увеличиваются с увеличением | h |.

При различных значениях h получаем семейство соответствующих гипербол:

h=-1 a=; b=;

h=-2 a=; b=;

h=-3 a=; b=;

Изобразим данные гиперболы на рисунке:

Рассмотрим линии , полученные в сечениях гиперболического параболоида плоскостями Z=h. Эти линии определяются системой уравнений:

Следовательно, уравнения проекций линий на плоскость XO'Y имеют вид:

: (4.9)

Уравнение (4.9) задаёт параболы, с вершинами в точках V(0, , h) и параметром

p=. При различных h получим семейство соответствующих парабол:

h = ±1 :

h = ±2 :

h = ±3 :

Изобразим данные параболы на рисунке:

Рассмотрим линии , полученные в сечениях гиперболического параболоида плоскостями X=h. Эти линии определяются системой уравнений:

Следовательно, уравнения проекций линий на плоскость YO'Z имеют вид:

(4.10)

Уравнение (4.10) задаёт параболы, с вершинами в V(h, ,0) и параметром p=. При различных h получаем семейство соответствующих парабол.

h = ±1 :

h = ±2 :

h = ±3 :

Изобразим данные параболы на рисунке:

4. Графики уравнения поверхности

Изобразим поверхность второго порядка в общеалгебраической и канонической системе координат.

График в общеалгебраической системе координат:

График в канонической системе координат:

5. Вывод

Исследовав каноническое уравнение (4.7) гиперболического параболоида, отметим следующее:

1. Оси O'Z и O'X являются осями симметрии поверхности. Центра симметрии у поверхности нет.

2. Рассекая поверхность горизонтальными плоскостями Y = h, в сечениях получаем:

h > - гиперболы с действительными осями, параллельными оси O'Z

h = - две пересекающиеся прямые

h < - сопряжённые гиперболы с действительными осями, параллельными оси O'Y

3. Рассекая поверхность плоскостями Z = h и X = h, в сечениях получаем параболы, с ветвями, направленными вниз (Z = h) или вверх (X = h).

4. Поверхность гиперболического параболоида бесконечна в направлении всех трёх координатных осей.

1. Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997.

2. Ильин В. А., Позняк Г. Д. Аналитическая геометрия. — М.: Наука, 1974.

www.referatmix.ru

Реферат: Кривые второго порядка

Содержание

Введение

1.Кривые второго порядка

1.1 Эллипс

1.2 Гипербола

1.3 Парабола

2.Теоремы, связанные с кривыми второго порядка

Литература

Введение

Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.

Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

1. Кривые второго порядка

Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .

Вид кривой зависит от четырёх инвариантов:

инварианты относительно поворота и сдвига системы координат:

инвариант относительно поворота системы координат (полуинвариант):

Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:

Или

λ2 − Iλ + в = 0.

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:

Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.

Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.

Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:

1.1 Эллипс

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.

Если эллипс описывается каноническим уравнением

где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где

Величина e = c/a называется эксцентриситетом эллипса.

По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают, то эллипс является окружностью.

1.2 Гипербола

Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

где a > 0, b > 0 — параметры гиперболы.

Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.

В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосями гиперболы.

Рис.1

Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.

1.3 Парабола

Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2 px

где p > 0 — параметр параболы.

Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.

В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

2. Теоремы, связанные с кривыми второго порядка

Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:

Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой.Теорема Паскаля двойственна к теореме Брианшона.

Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:

Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.

В частности, в вырожденном случае:

Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.

Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература

1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.

2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.

3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: "Наука", 1988.

www.yurii.ru

Курсовая работа - Кривые второго порядка

Содержание

Введение

1.Кривые второго порядка

1.1 Эллипс

1.2 Гипербола

1.3 Парабола

2.Теоремы, связанные с кривыми второгопорядка

Литература

Введение

1. Кривые второго порядка

ax2 + 2bxy + cy2+ 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты,причем a2 + b2 + c2 ≠ 0 .

Вид кривой зависит от четырёхинвариантов:

инварианты относительно поворотаи сдвига системы координат:

инвариант относительно поворотасистемы координат (полуинвариант):

Или

λ2 − Iλ +D = 0.

Кривые второго порядка классифицируютсяна невырожденные кривые и вырожденные.

1.1 Эллипс

Если эллипс описывается каноническимуравнением

Величина e = c/a называетсяэксцентриситетом эллипса.

По определению эллипса r1+ r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают,то эллипс является окружностью.

1.2 Гипербола

где a > 0, b > 0 — параметрыгиперболы.

Точки пересечения гиперболыс осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосямигиперболы.

Рис.1

Уравнение описывает гиперболу,вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

1.3 Парабола

y2 = 2 px

где p > 0 — параметр параболы.

В канонической системе осьабсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

Уравнения y2 = −2 px,x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координаттакже описывают параболы:

2. Теоремы, связанные скривыми второго порядка

Теоремма Паскамля — теоремапроективной геометрии, которая гласит, что:

В частности, в вырожденномслучае:

Теорема Брианшона двойственнак теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.

Литература

3. В.А. Ильин, Э.Г. Позняк.Аналитическая геометрия, гл. 6. М.: «Наука», 1988.

www.ronl.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..