|
|
|
|
 Far |
| WinNavigator |
| Frigate |
| Norton
Commander |
| WinNC |
| Dos
Navigator |
| Servant
Salamander |
| Turbo
Browser |
|
|
| Winamp,
Skins, Plugins |
| Необходимые
Утилиты |
| Текстовые
редакторы |
| Юмор |
|
|
|
File managers and best utilites |
Научно-исследовательская работа Дроби в жизни человека. Реферат дроби в жизни человека
Научно-исследовательская работа "Дроби в жизни человека"
Научно – исследовательская работа на конкурс исследовательских работ
и проектов школьников в области математики, прикладной математики «Математика вокруг нас»
Номинация- «Математика в моей жизни»
Тема: Дроби в жизни человека
Выполнил:
ученик 6 «А» класса МБОУ Школа №64
Железнодорожного района г .о. Самара
Новиков Иван
Научный руководитель:
Ларионова
Марина Михайловна
учитель математики
Самара, 2016 год
Оглавление
Введение. Актуальность исследования………………………………..……3
2. Основная часть
Дроби в жизни человека........................................................................................4
2.1 Что такое дробь, виды дроби............................................................................4
2.2 История возникновения дробей .....................................................................5
2.3 Дроби в повседневной жизни..........................................................................10
2.4 Мои наблюдения................................................................................................10
2.5 Достижения науки и техники...........................................................................11
3. Заключение...................................................................................................... ...11
4.Список литературы...............................................................................................12
5.Приложения……………………………….…………………………… ……....13-18
\
Введение
Еще в 5-м классе мы начали изучать дроби. Это очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними. С первого знакомства с ними было понятно, что без них не обойтись даже в обычной жизни, так как нам каждый день приходится сталкиваться с проблемой деления целого на части, и нам даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа. Мне стало интересно узнать: как и когда они появились. Нужны ли дроби? Важны ли они? Как часто в повседневной жизни мы сталкиваемся с ними? Какие профессии не могут обойтись без дробей?
Цель моего реферата: проследить историю развития понятия обыкновенной дроби, показать необходимость и важность использования дробей при решении практических задач в повседневной жизни.
Объект исследования: математика.
Предмет исследования: обыкновенные и десятичные дроби.
Методы исследования: анкетирование, сравнение, обобщение, анализ, изучение литературы и интернет ресурсов.
Цель: доказать необходимость использования дробей в повседневной жизни.
Задачи:
узнать, что такое дробь, какие виды дроби существуют
изучить историю возникновения дробей
рассмотреть применение дробей в повседневной жизни
провести анкетирование
оценить достижения науки в данной области.
Дроби в жизни человека
2.1 Что такое дробь, виды дроби
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дробь выражается отношением двух целых чисел m/n, где n - показывает на сколько долей разделена единица, а m – показывает сколько таких долей содержится в дроби.
В математике применяются следующие виды дробей:
Обыкновенная дробь имеет вид
или m/n где m и n - натуральные числа. Делимое (m) - называют числителем дроби, делитель (n) - называют знаменателем данной дроби. Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется-«солидус», а горизонтальная–«винкулум».Если числитель дроби меньше знаменателя, то дробь называется правильной (например 3/7), если больше или равен - неправильной (например 7/3).
Числа, в состав которых входит целое число и правильная дробь, называются смешанными. Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например, для смешанной дроби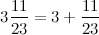 
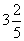число 3 - целая часть, 
а 2/5 - дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
.
2.2 История возникновения дробей
История возникновения дробей, как ни странно ведется еще с ранней стадии развития человечества. Так, например, первобытным людям приходилось делить добычу между участниками охоты, когда число животных оказывалось не кратным числу охотников. Им приходилось делить 2 животных на трёх охотников. Вот и получал каждый 2/3 добычи. В результате стали появляться дробные числа. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась в целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага. Поэтому второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, четверть шага. Можно сделать вывод, что дробные числа возникли как результат измерения величин.
Таким образом, во всех цивилизациях понятие дроби возникло из процесса дробления целого на равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от латинского «fractura», который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять, делить.
Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три – «треть», четыре – «четверть» и т. д.), для половины это не так – ее название во всех языках не имеет ничего общего со словом «два».
Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа. Важную роль играли также многочисленные заимствования идей при культурных контактах различных цивилизаций. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
У римлян основной единицей измерения массы, а также и денежной единицей служил «асс». Асс делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12. Со временем унции стали применяться для измерения любых величин. Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной. Данная система измерения до сих пор используется на мировом рынке драгоценных металлов.
У Египтян были основные, или единичные дроби. На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь, с которой они познакомились, была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными или основными дробями. У них числитель всегда единица.
Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф 
(ер, «[один] из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию (см. приложение № 1).
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (больше чем 1/2) (см. приложение № 2).
У жителей Вавилона использовались шестидесятеричные дроби, то есть те, у которых в знаменателе всегда была цифра 60. Кстати, именно от этой системы мы получили в наследство деление часа и геометрические углы.
В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах можно найти следующие названия дробей на Руст: полтина, четь, треть, полтреть и т. д. (см приложение № 3).
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
А вот история возникновения десятичных дробей, которыми мы пользуемся сегодня, ведется из древнего Китая. Они обозначали дробь словами, используя меры длины чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.
Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученного ал-Каши в 20-х годах XV века. Среднеазиатский город Самарканд был в XV веке большим научным центром. Там в знаменитой обсерватории, созданной видным астрономом Улугбеком, внуком Тамерлана, и работал в 20-х годах XV века крупный ученый того времени – Джемшид Гиясэддин ал-Каши. Это он впервые изложил учение о десятичных дробях в своей книге «Ключ арифметики», написанной в 1427 г. Он вводит специфическую для десятичных дробей запись: целая и дробная часть пишутся в одной строке. Для отделения первой части от дробной он не применяет запятую, а пишет целую часть черными чернилами, дробную же – красными или отделяет целую часть от дробной вертикальной чертой.
Но открытие десятичных дробей ал-Каши стало известно в Европе лишь спустя 300 лет после того, как эти дроби были в конце XVI века заново открыты фламандским инженером и ученом Симоном Стевиным (1548-1620). Его и считают создателем десятичных дробей. В своей книге «Десятая» он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании "изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов". Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их.
В XVII века происходит активное внедрение дробей в науку, вследствие чего, вместо разделительной полоски, в дробь была введена точка. А в 1617 году шотландский математик Джон Непер предложил ввести в качестве разделителя дроби – запятую. Именно благодаря этому мы и получили те дроби, которыми пользуемся сегодня.
Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби, хотя по сути они повторяют их.
2.3 Дроби в повседневной жизни
В настоящее время в науке и во всех отраслях народного хозяйства десятичные дроби и частный их вид, проценты, применяется намного чаще, чем обыкновенные дроби. Невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел. Мы привыкли пользоваться благами цивилизации – автомобилем, телефоном, телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. А сколько расчётов и вычислений делают конструкторы, инженеры, чтобы на свет всё время появлялись новинки, и везде в расчётах инженеров - конструкторов присутствуют дроби! Приведу такой пример. У нас в России стали выпускать новый современный пассажирский лайнер «Сухой Суперджет 100». Он имеет много положительных характеристик. Особенностью самолёта стал интерьер – 93 места с шагом кресел 86,36 см, что позволяет пассажирам чувствовать себя достаточно свободно: обычно у авиакомпаний этот шаг составляет 76,2 – 78,74 см. И это не является прихотью инженеров-конструкторов, а следствием точного расчета, основанного на полученных научных данных.
Еще в стародавние времена русские мастера-строители для того, чтобы получить качественный материал, например кирпич для строительства, использовали дроби, добавляя к определенным долям глины, определенные доли золы, извести и других компонентов. Именно поэтому храмы и церкви, возведённые в 9-11 веках, дошли до нас, что подтверждает высокое качества строительных материалов.
Десятичные дроби используются в различных отчётных документах в медицине, образовании, торговле, налоговой службе. А какая точность нужна в фармацевтике! При составлении лекарственных препаратов нужно предельное внимание при обращении с дробями.
А как близки дроби спортсменам! Возьмём для примера самый простой вид спорта – бег. В 1936 году легендарный Джесси Оуэнс в беге на 100 метров установил рекорд – 10,2 секунды. В течение двух десятков лет этот рекорд был пределом спортсменов-спринтеров. На Олимпиаде в Мехико в 1968 год этот рекорд был, наконец, побит – 9,9 секунды. В 2009 г. на данной дистанции установлен новый мировой рекорд – 9,58 секунды. Это время, показанное ямайским бегуном Усэйном Болтом, остается действующим мировым рекордом.
Интересна история золотой медали в конькобежном спорте на зимней Олимпиаде в Санкт-Мориц (Швейцария, 1948 г.). Оказывается, эту медаль не получил ни один конькобежец. На 2 месте пьедестала стояли 3 человека, на 3 месте – 2 человека, а 1 место осталось свободным. Вся причина опять же в десятичных дробях. В то время не учитывались сотые доли секунды, результаты у спортсменов оказались одинаковыми. Сейчас спортсмены борются даже не за десятые, а за сотые доли секунды! 0,01 доля секунды так мала, что за это время человек даже не успевает мигнуть. Судьбу призового места решает фотофиниш, который позволяет учитывать такие малые дробные числа. Сотые доли секунды позволили и мне завоевать золотую медаль в плавании вольным стилем на дистанции 50 метров.
Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дробные числа окружают нас и в быту, их можно отыскать и в комнате. Измеряя длину и ширину различных предметов, я ни разу не встретился с целым числом. В прошлом году перед ремонтом мы с папой решили две практические задачи с применением дробей, что помогло нам понять, сколько требуется обоев и краски для ремонта.
Моя мама бухгалтер, и она рассказала мне, что в бухгалтерии также используются дроби. Например, чтобы правильно рассчитать заработную плату и налоги, причитающиеся к уплате в бюджет, понадобятся десятичные дроби. Так ставка налога в Фонд медицинского страхования в 2015 году составляет 5,1%, а в Фонд социального страхования 2,9%.
И на кухне встречаются дроби. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда, расчета калорийности. Но сначала нужно купить определенное количество продуктов и рассчитать пропорции ингредиентов в составе блюда. Само блюдо нужно умело поделить на порции, в чем опять нам помогут дроби. В различных рецептах приготовления часто требуется взять 1/3 стакана сахара или 1/2 чайных ложки соды и т. д.
Дроби проникли даже в детскую художественную литературу! Например, в сказке Лии Гераскиной «В стране невыученных уроков» несчастный Витя Перестукин получил ответ своей задачи -1,5 землекопа. А в стихотворении Самуила Яковлевича Маршака «Про одного ученика и шесть единиц» одну из единиц ученик получил за неумение решать задачи на дроби.
Итак, делаем вывод, десятичные дроби и их частный вид «проценты» проникли во все сферы деятельности человека и успешно служат ему.
2.4 Мои наблюдения
Я провел анкетирование среди учащихся моего класса и их родителей. Результаты показали, что, к сожалению, не все одноклассники любят математику и не понимают, где в повседневной жизни можно встретить обыкновенные и десятичные дроби. Хорошо, что каждый из нас усвоил понятие математической дроби. Я рассказал, что выражение «попал в дроби» в переводе с немецкого языка означает попасть в трудное положение. Не так то и просты эти необыкновенные обыкновенные дроби! Результаты анкетирования см. в приложении № 4.
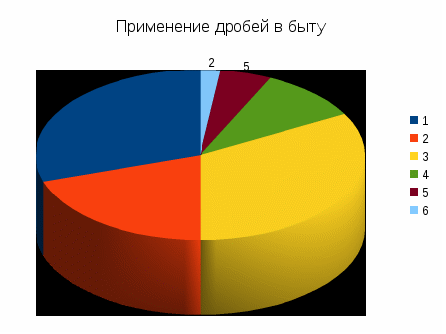
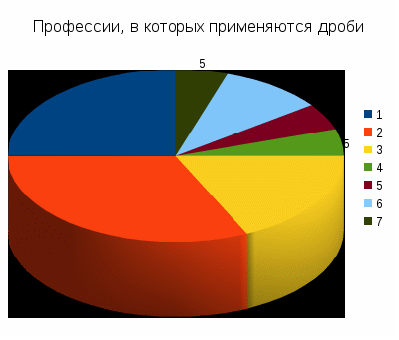
Отвечая на вопрос, где можно встретить по вашему мнению дроби в жизни, основная масса ребят и их родителей ответила - при оплате за коммунальные услуги, приготовление еды, строительство и ремонт (см. приложение № 5). Среди основных профессий, где применяются дроби были названы: бухгалтер, фармацевт, строитель, повар, продавец (см. приложение № 6)
2.5 Достижения науки и техники
Во второй половине 20 века возникла новая отрасль науки - промышленная электроника. Учёные исследуют строение вещества на клеточном, молекулярном и атомном уровнях. Трудно представить, насколько мала молекула. Все вещества на свете состоят из таких малых частиц – молекул. Если попросить всех жителей Земли дать по 1 000 000 000 молекул, то вы соберёте 0, 000 000 001 г вещества. Такую маленькую массу очень трудно ощутить на руке. Учёным приходится оперировать всё более мелкими единицами измерения. Эти сверхмалые величины: микро, нано («карлик»), пико и фемто обозначаются десятичными дробями со множеством нулей. Например, в 1 нанометре содержится 1 миллиардная часть метра: 1 нм =0,000000001 м. Эти величины можно увидеть только под электронным микроскопом. Применяя нанотехнологию, учёные выводят науку на совершенно новую ступень развития. Нет сомнения, что в новом веке, веке нанотехнологий, будут нужны ещё более точные дроби.
3. Заключение
В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось неразрешимыми, успешно решаются благодаря применению математики, тем самым расширяются возможности науки. Математика всегда была неотъемлемой и существенной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и развития личности. Сегодня можно с уверенностью сказать, что дроби – неотъемлемая часть нашей жизни.
В своей работе, я попытался показать, что практически во всех областях науки, техники, образования, медицины и т.д. применяются математические дроби. Знание понятия математическая дробь очень важно! Я считаю, что математика очень интересный и нужный предмет. Она позволяет развить умственные способности человека, тренирует память, усиливает быстроту мышления, умение прогнозировать, логически мыслить. Помните, математика жизненно необходима человечеству. Это ключ к прогрессу и процветанию.
4. Список используемой литературы
М.Я.Выгодский “Арифметика и алгебра в Древнем мире”(М. Наука,1967г)
Г.И.Глейзер “История математики в школе”(М. Просвещение,1964г)
И.Я.Депман “История арифметики” (М. Просвящение, 1959г)
Н.Я.Виленкин «За страницами учебника математики. Арифметика» (М. Просвещение, 2008)
5.Приложение № 1
Запись единичной дроби у древних египтян
Приложение 2
Специальные символы для дробей в Древнем Египте
Приложение № 3
Таблица № 1
Названия дробей на Руси
1/2 - половина, полтина1/3 – треть
1/4 – четь
1/6 – полтреть
1/8 - полчеть
1/12 –полполтреть
1/16 - полполчеть
1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь)
1/5 – пятина
1/7 - седьмина
1/10 - десятина
Приложение №4
Таблица № 2
Приложение № 5
Д
иаграмма № 1
Приложение № 6
Диаграмма № 2
Рецензия
на исследовательскую работу ученика 6 «А» класса МБОУ СОШ №64 города Самара Новикова Ивана .
Работа Новикова Ивана по теме «Дроби в жизни человека» посвящена исследованию истории развития обыкновенных и десятичных дробей , их необходимости и важности в повседневной жизни.
Тему «Дроби» начинают изучать с 5 класса. И , как показывает мне мой опыт ,это одна из наиболее сложных тем для усвоения детьми. При выполнении действий с дробями ученику требуется не только применить только что изученные правила ,но и вспомнить все, что было изучено ранее, в начальной школе. Степень сконцентрированности в этот момент максимальна и не удивительно, что появляется много вычислительных ошибок у детей. А если тема еще и не понятна или не интересна ,то вероятность не справиться с заданием возрастает многократно.
Как показывает практика работы в школе , когда ребенок более углубляется в изучение проходимого материала, то интерес к математике возрастает многократно. В своей работе Иван исследовал не только понятие дроби, но и проследил историю их возникновения, область применения дробей в повседневной жизни, их жизненную необходимость в некоторые моменты в нашей жизни.
Данная исследовательская работа содержит все необходимые структурные элементы для подобных работ – введение, основная часть, заключение, список источников информации, приложения. В работе чётко обозначены цель и задачи, которые были решены в процессе работы. Работа имеет большую практическую значимость и может быть использована и на уроках математики и во внеурочное время. Иваном проведена большая работа с литературой.
По мнению автора, эта тема является для него полезной, при выполнении работы Иван сделал для себя много важных открытий.
Работа Ивана показывает важность и актуальность математики в повседневной жизни.
Работа Новикова Ивана соответствует требованиям к исследовательским работам.
Учитель математики Ларионова М.М.
infourok.ru
Научно-исследовательская работа Дроби в жизни человека
Научно - исследовательская работа на конкурс исследовательских работ
и проектов школьников в области математики, прикладной математики «Математика вокруг нас»
Номинация- «Математика в моей жизни»
Тема: Дроби в жизни человека
Выполнил:
ученик 6 «А» класса МБОУ Школа №64
Железнодорожного района г .о. Самара
Новиков Иван
Научный руководитель:
Ларионова
Марина Михайловна
учитель математики
Самара, 2016 год
Оглавление
-
Введение. Актуальность исследования………………………………..……3
2. Основная часть
Дроби в жизни человека........................................................................................4
2.1 Что такое дробь, виды дроби............................................................................4
2.2 История возникновения дробей .....................................................................5
2.3 Дроби в повседневной жизни..........................................................................10
2.4 Мои наблюдения................................................................................................10
2.5 Достижения науки и техники...........................................................................11
3. Заключение...................................................................................................... ...11
4.Список литературы...............................................................................................12
5.Приложения……………………………….…………………………… ……....13-18
\
Введение
Еще в 5-м классе мы начали изучать дроби. Это очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними. С первого знакомства с ними было понятно, что без них не обойтись даже в обычной жизни, так как нам каждый день приходится сталкиваться с проблемой деления целого на части, и нам даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа. Мне стало интересно узнать: как и когда они появились. Нужны ли дроби? Важны ли они? Как часто в повседневной жизни мы сталкиваемся с ними? Какие профессии не могут обойтись без дробей?
Цель моего реферата: проследить историю развития понятия обыкновенной дроби, показать необходимость и важность использования дробей при решении практических задач в повседневной жизни.
Объект исследования: математика.
Предмет исследования: обыкновенные и десятичные дроби.
Методы исследования: анкетирование, сравнение, обобщение, анализ, изучение литературы и интернет ресурсов.
Цель: доказать необходимость использования дробей в повседневной жизни.
Задачи:
-
узнать, что такое дробь, какие виды дроби существуют
-
изучить историю возникновения дробей
-
рассмотреть применение дробей в повседневной жизни
-
провести анкетирование
-
оценить достижения науки в данной области.
Дроби в жизни человека
2.1 Что такое дробь, виды дроби
Дробь в математике - число, состоящее из одной или нескольких частей (долей) единицы. Дробь выражается отношением двух целых чисел m/n, где n - показывает на сколько долей разделена единица, а m - показывает сколько таких долей содержится в дроби.
В математике применяются следующие виды дробей:
Обыкновенная дробь имеет вид 
или m/n где m и n - натуральные числа. Делимое (m) - называют
числителем дроби, делитель (n) - называют знаменателем данной
дроби. Горизонтальная или косая линия в дроби обозначает деление.
Черта наклонная называется-«солидус», а
горизонтальная-«винкулум».
Если числитель дроби меньше знаменателя, то дробь называется правильной (например 3/7), если больше или равен - неправильной (например 7/3).
Числа, в состав которых входит целое
число</</font> и правильная дробь, называются смешанными.
Целое число называют целой частью смешанного
числа, а правильная дробь называется дробной
частью смешанного числа. Например, для
смешанной дроби 
число 3 - целая часть, 
а 2/5 -
дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.
Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
.
2.2 История возникновения дробей
История возникновения дробей, как ни странно ведется еще с ранней стадии развития человечества. Так, например, первобытным людям приходилось делить добычу между участниками охоты, когда число животных оказывалось не кратным числу охотников. Им приходилось делить 2 животных на трёх охотников. Вот и получал каждый 2/3 добычи. В результате стали появляться дробные числа. Кроме того, в жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась в целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага. Поэтому второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения. В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, четверть шага. Можно сделать вывод, что дробные числа возникли как результат измерения величин.
Таким образом, во всех цивилизациях понятие дроби возникло из процесса дробления целого на равные части. Русский термин «дробь», как и его аналоги в других языках, происходит от латинского «fractura», который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять, делить.
Первой дробью, с которой познакомились люди, была половина. Хотя названия всех следующих дробей связаны с названиями их знаменателей (три - «треть», четыре - «четверть» и т. д.), для половины это не так - ее название во всех языках не имеет ничего общего со словом «два».
Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа. Важную роль играли также многочисленные заимствования идей при культурных контактах различных цивилизаций. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
У римлян основной единицей измерения массы, а также и денежной единицей служил «асс». Асс делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12. Со временем унции стали применяться для измерения любых величин. Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 - «пять унций» и т.д. Три унции назывались четвертью, четыре унции - третью, шесть унций - половиной. Данная система измерения до сих пор используется на мировом рынке драгоценных металлов.
У Египтян были основные, или единичные дроби. На протяжении многих веков египтяне именовали дроби "ломаным числом", а первая дробь, с которой они познакомились, была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными или основными дробями. У них числитель всегда единица.
Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 2/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф 
(ер, «[один] из» или ре, рот) над числом для обозначения единичной
дроби в обычной записи, а в священных текстах использовали линию
(см. приложение № 1).
У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (больше чем 1/2) (см. приложение № 2).
У жителей Вавилона использовались шестидесятеричные дроби, то есть те, у которых в знаменателе всегда была цифра 60. Кстати, именно от этой системы мы получили в наследство деление часа и геометрические углы.
В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах можно найти следующие названия дробей на Руст: полтина, четь, треть, полтреть и т. д. (см приложение № 3).
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
А вот история возникновения десятичных дробей, которыми мы пользуемся сегодня, ведется из древнего Китая. Они обозначали дробь словами, используя меры длины чи, цуни, доли, порядковые, шерстинки, тончайшие, паутинки.
Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученного ал-Каши в 20-х годах XV века. Среднеазиатский город Самарканд был в XV веке большим научным центром. Там в знаменитой обсерватории, созданной видным астрономом Улугбеком, внуком Тамерлана, и работал в 20-х годах XV века крупный ученый того времени - Джемшид Гиясэддин ал-Каши. Это он впервые изложил учение о десятичных дробях в своей книге «Ключ арифметики», написанной в 1427 г. Он вводит специфическую для десятичных дробей запись: целая и дробная часть пишутся в одной строке. Для отделения первой части от дробной он не применяет запятую, а пишет целую часть черными чернилами, дробную же - красными или отделяет целую часть от дробной вертикальной чертой.
Но открытие десятичных дробей ал-Каши стало известно в Европе лишь спустя 300 лет после того, как эти дроби были в конце XVI века заново открыты фламандским инженером и ученом Симоном Стевиным (1548-1620). Его и считают создателем десятичных дробей. В своей книге «Десятая» он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании "изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов". Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их.
В XVII века происходит активное внедрение дробей в науку, вследствие чего, вместо разделительной полоски, в дробь была введена точка. А в 1617 году шотландский математик Джон Непер предложил ввести в качестве разделителя дроби - запятую. Именно благодаря этому мы и получили те дроби, которыми пользуемся сегодня.
Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид - проценты - применяются намного чаще, чем обыкновенные дроби, хотя по сути они повторяют их.
2.3 Дроби в повседневной жизни
В настоящее время в науке и во всех отраслях народного хозяйства десятичные дроби и частный их вид, проценты, применяется намного чаще, чем обыкновенные дроби. Невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел. Мы привыкли пользоваться благами цивилизации - автомобилем, телефоном, телевизором и прочей техникой, делающей нашу жизнь легче и интереснее. А сколько расчётов и вычислений делают конструкторы, инженеры, чтобы на свет всё время появлялись новинки, и везде в расчётах инженеров - конструкторов присутствуют дроби! Приведу такой пример. У нас в России стали выпускать новый современный пассажирский лайнер «Сухой Суперджет 100». Он имеет много положительных характеристик. Особенностью самолёта стал интерьер - 93 места с шагом кресел 86,36 см, что позволяет пассажирам чувствовать себя достаточно свободно: обычно у авиакомпаний этот шаг составляет 76,2 - 78,74 см. И это не является прихотью инженеров-конструкторов, а следствием точного расчета, основанного на полученных научных данных.
Еще в стародавние времена русские мастера-строители для того, чтобы получить качественный материал, например кирпич для строительства, использовали дроби, добавляя к определенным долям глины, определенные доли золы, извести и других компонентов. Именно поэтому храмы и церкви, возведённые в 9-11 веках, дошли до нас, что подтверждает высокое качества строительных материалов.
Десятичные дроби используются в различных отчётных документах в медицине, образовании, торговле, налоговой службе. А какая точность нужна в фармацевтике! При составлении лекарственных препаратов нужно предельное внимание при обращении с дробями.
А как близки дроби спортсменам! Возьмём для примера самый простой вид спорта - бег. В 1936 году легендарный Джесси Оуэнс в беге на 100 метров установил рекорд - 10,2 секунды. В течение двух десятков лет этот рекорд был пределом спортсменов-спринтеров. На Олимпиаде в Мехико в 1968 год этот рекорд был, наконец, побит - 9,9 секунды. В 2009 г. на данной дистанции установлен новый мировой рекорд - 9,58 секунды. Это время, показанное ямайским бегуном Усэйном Болтом, остается действующим мировым рекордом.
Интересна история золотой медали в конькобежном спорте на зимней Олимпиаде в Санкт-Мориц (Швейцария, 1948 г.). Оказывается, эту медаль не получил ни один конькобежец. На 2 месте пьедестала стояли 3 человека, на 3 месте - 2 человека, а 1 место осталось свободным. Вся причина опять же в десятичных дробях. В то время не учитывались сотые доли секунды, результаты у спортсменов оказались одинаковыми. Сейчас спортсмены борются даже не за десятые, а за сотые доли секунды! 0,01 доля секунды так мала, что за это время человек даже не успевает мигнуть. Судьбу призового места решает фотофиниш, который позволяет учитывать такие малые дробные числа. Сотые доли секунды позволили и мне завоевать золотую медаль в плавании вольным стилем на дистанции 50 метров.
Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дробные числа окружают нас и в быту, их можно отыскать и в комнате. Измеряя длину и ширину различных предметов, я ни разу не встретился с целым числом. В прошлом году перед ремонтом мы с папой решили две практические задачи с применением дробей, что помогло нам понять, сколько требуется обоев и краски для ремонта.
Моя мама бухгалтер, и она рассказала мне, что в бухгалтерии также используются дроби. Например, чтобы правильно рассчитать заработную плату и налоги, причитающиеся к уплате в бюджет, понадобятся десятичные дроби. Так ставка налога в Фонд медицинского страхования в 2015 году составляет 5,1%, а в Фонд социального страхования 2,9%.
И на кухне встречаются дроби. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда, расчета калорийности. Но сначала нужно купить определенное количество продуктов и рассчитать пропорции ингредиентов в составе блюда. Само блюдо нужно умело поделить на порции, в чем опять нам помогут дроби. В различных рецептах приготовления часто требуется взять 1/3 стакана сахара или 1/2 чайных ложки соды и т. д.
Дроби проникли даже в детскую художественную литературу! Например, в сказке Лии Гераскиной «В стране невыученных уроков» несчастный Витя Перестукин получил ответ своей задачи -1,5 землекопа. А в стихотворении Самуила Яковлевича Маршака «Про одного ученика и шесть единиц» одну из единиц ученик получил за неумение решать задачи на дроби.
Итак, делаем вывод, десятичные дроби и их частный вид «проценты» проникли во все сферы деятельности человека и успешно служат ему.
2.4 Мои наблюдения
Я провел анкетирование среди учащихся моего класса и их родителей. Результаты показали, что, к сожалению, не все одноклассники любят математику и не понимают, где в повседневной жизни можно встретить обыкновенные и десятичные дроби. Хорошо, что каждый из нас усвоил понятие математической дроби. Я рассказал, что выражение «попал в дроби» в переводе с немецкого языка означает попасть в трудное положение. Не так то и просты эти необыкновенные обыкновенные дроби! Результаты анкетирования см. в приложении № 4.
Отвечая на вопрос, где можно встретить по вашему мнению дроби в жизни, основная масса ребят и их родителей ответила - при оплате за коммунальные услуги, приготовление еды, строительство и ремонт (см. приложение № 5). Среди основных профессий, где применяются дроби были названы: бухгалтер, фармацевт, строитель, повар, продавец (см. приложение № 6)
2.5 Достижения науки и техники
Во второй половине 20 века возникла новая отрасль науки - промышленная электроника. Учёные исследуют строение вещества на клеточном, молекулярном и атомном уровнях. Трудно представить, насколько мала молекула. Все вещества на свете состоят из таких малых частиц - молекул. Если попросить всех жителей Земли дать по 1 000 000 000 молекул, то вы соберёте 0, 000 000 001 г вещества. Такую маленькую массу очень трудно ощутить на руке. Учёным приходится оперировать всё более мелкими единицами измерения. Эти сверхмалые величины: микро, нано («карлик»), пико и фемто обозначаются десятичными дробями со множеством нулей. Например, в 1 нанометре содержится 1 миллиардная часть метра: 1 нм =0,000000001 м. Эти величины можно увидеть только под электронным микроскопом. Применяя нанотехнологию, учёные выводят науку на совершенно новую ступень развития. Нет сомнения, что в новом веке, веке нанотехнологий, будут нужны ещё более точные дроби.
3. Заключение
В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось неразрешимыми, успешно решаются благодаря применению математики, тем самым расширяются возможности науки. Математика всегда была неотъемлемой и существенной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и развития личности. Сегодня можно с уверенностью сказать, что дроби - неотъемлемая часть нашей жизни.
В своей работе, я попытался показать, что практически во всех областях науки, техники, образования, медицины и т.д. применяются математические дроби. Знание понятия математическая дробь очень важно! Я считаю, что математика очень интересный и нужный предмет. Она позволяет развить умственные способности человека, тренирует память, усиливает быстроту мышления, умение прогнозировать, логически мыслить. Помните, математика жизненно необходима человечеству. Это ключ к прогрессу и процветанию.
4. Список используемой литературы
М.Я.Выгодский "Арифметика и алгебра в Древнем мире"(М. Наука,1967г)
Г.И.Глейзер "История математики в школе"(М. Просвещение,1964г)
И.Я.Депман "История арифметики" (М. Просвящение, 1959г)
Н.Я.Виленкин «За страницами учебника математики. Арифметика» (М. Просвещение, 2008)
5.Приложение № 1
Запись единичной дроби у древних египтян
Приложение 2
Специальные символы для дробей в Древнем Египте
Приложение № 3
Таблица № 1
Названия дробей на Руси
1/2 - половина, полтина
1/3 - треть
1/4 - четь
1/6 - полтреть
1/8 - полчеть
1/12 -полполтреть
1/16 - полполчеть
1/24 - полполполтреть (малая треть)
1/32 - полполполчеть (малая четь)
1/5 - пятина
1/7 - седьмина
1/10 - десятина
Приложение №4
Таблица № 2
Приложение № 5
Д
иаграмма № 1
Приложение № 6
Диаграмма № 2
Рецензия
на исследовательскую работу ученика 6 «А» класса МБОУ СОШ №64 города Самара Новикова Ивана .
Работа Новикова Ивана по теме «Дроби в жизни человека» посвящена исследованию истории развития обыкновенных и десятичных дробей , их необходимости и важности в повседневной жизни.
Тему «Дроби» начинают изучать с 5 класса. И , как показывает мне мой опыт ,это одна из наиболее сложных тем для усвоения детьми. При выполнении действий с дробями ученику требуется не только применить только что изученные правила ,но и вспомнить все, что было изучено ранее, в начальной школе. Степень сконцентрированности в этот момент максимальна и не удивительно, что появляется много вычислительных ошибок у детей. А если тема еще и не понятна или не интересна ,то вероятность не справиться с заданием возрастает многократно.
Как показывает практика работы в школе , когда ребенок более углубляется в изучение проходимого материала, то интерес к математике возрастает многократно. В своей работе Иван исследовал не только понятие дроби, но и проследил историю их возникновения, область применения дробей в повседневной жизни, их жизненную необходимость в некоторые моменты в нашей жизни.
Данная исследовательская работа содержит все необходимые структурные элементы для подобных работ - введение, основная часть, заключение, список источников информации, приложения. В работе чётко обозначены цель и задачи, которые были решены в процессе работы. Работа имеет большую практическую значимость и может быть использована и на уроках математики и во внеурочное время. Иваном проведена большая работа с литературой.
По мнению автора, эта тема является для него полезной, при выполнении работы Иван сделал для себя много важных открытий.
Работа Ивана показывает важность и актуальность математики в повседневной жизни.
Работа Новикова Ивана соответствует требованиям к исследовательским работам.
Учитель математики Ларионова М.М.
botana.cc
Проект «Дроби в нашей жизни»
Слайды и текст этой презентации
Слайд 1
Проект «Дроби в нашей жизни» Выполнил ученик 5 «А» класса: Чистяков Антон.
Слайд 2
Проблемные вопросы Зачем возникли дроби? Есть ли дроби в нашей жизни? Как знания дробей могут повлиять на нашу жизнь?
Слайд 3
Цели исследования: Узнать, где используются дроби в быту и в работе людей разных профессий. Составить примерный режим дня для ученика 5-го класса с использованием десятичных дробей. Составить примерное меню для ученика 5-го класса с использованием десятичных дробей.
Слайд 4
Из истории дробей
Слайд 5
Из истории обыкновенных дробей: С древних времен людям приходилось не только считать предметы, но и измерять длину, время, площадь, вести расчеты за купленные или проданные товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Приходилось учитывать и части, доли меры. Так появились дроби.
Слайд 6
Посмотрите, как изображали дроби в Древнем Египте:0 0 0 00 00В Древнем Китае вместо черты ставили точку:=Индийцы записывали так :Первой дробью, наверное, была дробь
Слайд 7
Дроби на Руси называли ДОЛЯМИ, Позже ЛОМАННЫМИ ЧИСЛАМИ. В старых руководствах находили следующие названия дробей…Дробинауси
Слайд 8
-Половина, полтина-Треть-Четь-Пятина-Полтреть-Седьмина-Полчеть- Десятина-Пол-полтретьПол-пол-треть (малая)-Пол-полчеть-Пол-полчеть (Малая)
Слайд 9
О десятичных дробяхК десятичным дробям математики пришли в разные времена в Азии и Европе. Целую часть от дробной отделяли в Китае особым знаком «дянь» (точка). Большое внимание дробям уделял средне-азиатский учёный аль-Коши. В Европе дроби были «открыты» нидерландским математиком и инженером С. Стевином. В России впервые изложил учение о десятичных дробях Леонтий Магницкий в своей «Арифметике».
Слайд 10
Посмотрите, как записывалась десятичная дробь 0,1
Слайд 11
● Тем, кто работает оператором теплосетей, нужны десятичные дроби для повышения и понижения температуры. ● Сварщикам десятичные дроби нужны для измерения длины сваренной трубы и ширины сварочного шва.
Слайд 12
Провизоры используют десятичные дроби при приготовлении лекарств
Слайд 13
● Повара применяют десятичные дроби для составления меню. ● Парикмахер применяет десятичные дроби для приготовления раствора для покраски волос и для завивки. ● В кулинарии при приготовлении блюд по рецептам.
Слайд 14
● В магазине при взвешивании товара. ● Экономисты и бухгалтеры используют десятичные дроби для составления отчетов, расчетов. ● Строители используют десятичные дроби для составления сметы.
Слайд 15
Исследование:Детям 11-15 лет на каждый килограмм своей массы необходимо употреблять в день: белков – 1,8 г, жиров -1,8 г, углеводов – 7,8 г. Посчитайте приближенно до граммов сколько должен употреблять ежедневно белков, жиров и углеводов мальчик 11 лет, масса которого равна 36,9 кг. Белков – 66,42г Жиров – 66,42г Углеводов – 287,82г
Слайд 16
Рацион питания (мальчик, 11 лет, вес 36,9 кг) Первый завтрак: каша (пшенная, овсяная, гречневая), горячий напиток (кофе, чай, какао), компот или молоко. Второй завтрак: омлет или сырники, горячий напиток (кофе, чай, какао), компот или молоко. Обед: овощной салат, первое - суп, второе – блюдо из мяса или рыбы и гарнир (каша или картофельное пюре), компот. Полдник: кефир или питьевой йогурт, печенье с добавлением цельных злаков, фрукты. Ужин: блюдо из овощей или творога, кефир или йогурт. 1-й завтрак дома (7-8 часов) – 20% калорийности суточного рациона; 2-й завтрак в школе (10-11 часов) – 20% калорийности суточного рациона; Обед дома или в школе (13-15 часов) – 35% калорийности суточного рациона; Ужин дома(19-20 часов) – 25% калорийности суточного рациона.
Слайд 17
Исследование:Учебные занятия в школе занимают 25% времени суток. Продолжительность ночного сна должно быть в 1,5 раза больше времени, проводимого в школе, не менее 1/16 части суток должен составлять активный отдых на свежем воздухе. Подготовка домашнего задания должна занимать 5/18 от времени, отведенного на учебные занятия. Досуг составляет около 1,8 времени от времени приготовления уроков дома. Время провождения около телевизора не должно превышать 1/6 части вашего досуга. Сон – 9ч Занятия в школе – 6ч Прогулка – 1час 30 минут Подготовка дом задания – 1 час 40мин Отдых – 3 ч Телевизор – 30 мин
Слайд 18
Примерный режим дня школьника: ● 7.00 – Подъём ● 7.00-7.30 – Утренняя гимнастика, водные процедуры, уборка постели, туалет ● 7.30-7-50 – Утренний завтрак ● 7.50-8.20 – Дорога в школу ● 8.30-14.40 – Занятия в школе ● 10.00 – Горячий завтрак в школе ● 13.00-14.00 – Горячий обед в школе ● 14.40-14.50 – Дорога из школы домой ● 15.00-15.30 – отдых ● 15.30-16.30 – Прогулка и игры на свежем воздухе ● 16.30-16.50 – Полдник ● 17.00-18.10 – Приготовление домашних заданий ● 18.10-19.00 – Прогулка на свежем воздухе ● 19.00-19.20 – Ужин ● 19.20-20.30 – Свободные занятия ● 20.30-21.00 – Приготовление ко сну ● 21.00-7.00 -- Сон
Слайд 19
1. Каждодневное меню должно состоять из нужных и полезных продуктов, доли которых определяются диетой. 2. Постоянное употребление продуктов быстрого приготовления приводит к тяжелым заболеваниям. 3. Режим питания должен быть постоянным, чтобы организм успевал перерабатывать пищу, не голодал и не перенасыщался. 4. Режим дня строится на основе биоритмов человека и нужен для того, чтобы не уставать и быть всегда в тонусе. 5. Продолжительность суток состоит из множества частей: сон, питание, учеба, различные занятия. 6. Десятичные дроби постоянно встречаются в жизни человека.Выводы:
Слайд 20
Вывод: Дроби возникли из практических нужд человека. 2. Задачи трехвековой давности актуальны и сейчас. Их решение требует немалой смекалки, сообразительности и умения рассуждать. 3. Старинные меры нужно знать не только для развития своего кругозора, но и потому что без прошлого невозможно будущее.
Слайд 21
Спасибо за внимание!!!!!!
lusana.ru
Реферат дроби нужны дроби важны
МБОУ НОШ №43 Реферат Дроби нужны, дроби важны.2013 г. Составили учащиеся 3 класса Б МБОУ НОШ №43 Большаков Никита, Киселев Егор, Фоменко Катя Руководитель Г.И.Саламатова , учитель начальных классов
Введение…………………………………………………………. 3 История развития обыкновенных дробей………………………6 Дроби в древнем Египте……………………………………….. 8 2.2 Дроби в древнем Риме………………………………………….. 9 Дроби в Вавилоне………………………………………………..10 Нумерация и дроби в древней Греции………………………. 11 Нумерация и дроби на Руси……………………….................. 12 2.6 Дроби в других государствах древности…………………….. 14 Возникновение современной записи дробей…………………..16 Сравнение обыкновенных дробей…………………………….. 17 3. Применение дробей в повседневной жизни …………………… 18 4. Заключение……………………………………………………… 26 Список используемой литературы……………………………….27 Приложения…………………………………………………………... 1. ВВЕДЕНИЕ Слыхали ли Вы о том, как ломают числа? А ведь ломаными числами пользуются и теперь, только называют их иначе. Попробуйте из торта получить четвертинку! Для этого надо разломить или разрезать весь торт на четыре равные части. Так и с числами: чтобы из одного получить половину, надо разделить или «разломить» единицу на два. Вот отсюда и пошло название ломаные числа. Теперь их называют дробями. Если единицу «разломим» на две части, получим дробь ½. Если разделим единицу на три, то получим дробь ⅓ и так далее. В 1 и 2 классе мы работали с числами, которые употребляются при счёте предметов (натуральными). Но в практике людям давно приходится делить целое на равное число частей, долей. Дробь – это или доля, или сумма нескольких одинаковых долей. Человек часто встречается с понятием «дробь» в жизни. Выбивать дробь зубами– стучать зубами (дрожа от холода, испуга ). (рис.1)
Рис.1
Русский народный танец невозможно представить без дробей и бега. (рис.2) рис.2 Барабанная дробь, представляющая собой поочередные удары. (рис 3)рис.3 На флоте, команда «дробь!» — прекращение огня.(рис 4) рис. 4 Номер через дробь ставят у домов, пронумерованных по двум пересекающимся улицам.(рис.5) рис.5 Дробь охотничья — снаряд патрона в виде мелких металлических шариков. Чаще всего стрельба дробью производится из охотничьего гладкоствольного оружия. (рис.6) рис.6 На уроках математики при изучении темы «Дроби» мы узнали, как сравнивать доли, решать простые задачи на нахождение доли от числа. Нам захотелось рассмотреть этот вопрос более основательно: рассмотреть более подробно этапы развития. Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни. Цель исследования - узнать о возникновении обыкновенных дробей, о значении дробей в других науках, кроме математики, а также показать наглядно применение дроби. Для достижения этой цели были сформулированы задачи: Изучить дроби во всех сферах. Научиться понимать дроби, решать задачи на них и активно применять в повседневной жизни. Объект исследования – математика. Предмет исследования – обыкновенные дроби. Гипотеза: повседневная жизнь человека не обходится без дробей. Актуальность и значимость нашей работы в том, что будет интересной для учащихся и полезной для учителей математики в качестве дополнительного материала при проведении уроков и мероприятий. ИСТОРИЯ РАЗВИТИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ Появление дробей связано у многих народов с делением добычи на охоте. В самых древних дошедших до нас письменных источниках – вавилонских глиняных табличках и египетских папирусах - встречаются не только целые числа, но и дроби. Дроби были нужны для измерения различных величин в случаях, когда единица измерения не укладывалась в измеряемой величине целое число раз. Тогда вводили новую, меньшую единицу измерения. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов, и оставался остаток меньше одного шага. Люди измеряли длины, площади земельных участков, объемы, массы тел, время, вели расчеты за купленные или проданные товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Названия единиц измерения стали первыми названиями дробей. Самая первая дробь, введенная раньше других, была половина. Даже ребёнку ясно, что такое половина яблока или булочки, и как сделать такое деление пополам на самом предмете. Похожие ситуации помогли и нашим далёким предкам понять, что такое половина. Долю называют половина. Слова с приставкой «пол» можно услышать часто: полчаса, полкилометра… Следующей дробью была треть. Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на три части – «треть». Долю называют «треть». Если целое разделили на 4 части, то получается «четверть». - А как называются другие доли? -А если разделить на пять частей, то что ли «пятерть», на шесть – «шестерть»? -Таких смешных слов в русском языке нет. Чтобы назвать доли пользуются словами «пятая», «шестая». В греческих сочинениях по математике дробей не встречалось. Греческие учёные считали, что математика должна заниматься только целыми числами. Современная форма записи обыкновенных дробей стала применяться лишь в 18 веке. Первым дробную черту стал применять арабский ученый ал-Халар. В Европе дробную черту для записи обыкновенных дробей использовал итальянский математик Леонардо Пизанский, названный также Фибоначчи. (рис.7) рис.7 ДРОБИ В ДРЕВНЕМ ЕГИПТЕ В древнем Египте архитектура достигла высокого развития. Об этом свидетельствуют сохранившиеся до наших дней египетские пирамиды. Разумеется, для того чтобы строить их, чтобы вычислить длины, площади и объёмы фигур, необходимо было знать арифметику. Египтяне писали на папирусах, то есть на свитках, изготовленных из стебля крупных тропических растений, носивших такое же название. Важнейшим по содержанию является «папирус Ахмеса», по имени одного из древнейших писцов, рукой которого он был написан. Его длина 544см, а ширина 33см; хранится он в Лондоне, в Британском музее. Этот старинный математический документ озаглавлен так: «Способы, при помощи которых можно дойти до понимания всех тёмных вещей, всех тайн, заключающихся в вещах». В этом папирусе имеются таблицы для представления некоторых дробей в виде суммы единичных дробей. Древние египтяне умели считать единичные дроби, а также дроби ⅔ и ¾. Египтяне пользовались единичными дробями даже тогда, когда имели дело с большим количеством долей. Такую дробь они представляли в виде суммы единичных дробей, т.е. дробей вида 1/n. Например, вместо 8/15 они писали 1/3+1/5, упуская знак «+»: 8/15 = 1/3 1/5. Египтяне умели умножать и делить дроби. А вот в старинном папирусе Ахмеса есть такая задача: "Разделить 7 хлебов между 8 людьми". Если разрезать каждый хлеб на 8 частей, придется провести 49 разрезов. А по-египетски эта задача решалась так. Дробь 7/8 записывали в виде долей: 1/2 + 1/4 + 1/8. Значит, каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезаем пополам, два хлеба - на 4 части и один хлеб - на 8 долей, после чего каждому даем его часть. 2.2 ДРОБИ В ДРЕВНЕМ РИМЕ Интересная система дробей была принята в Древнем Риме. Путь, время и другие величины сравнивали с весом. Единицу веса «асс» римляне делили на двенадцать долей. Одна двенадцатая называлась «унцией». Поэтому римлянин мог сказать, что он прошёл семь унций пути или прочёл пять унций книги. При этом имелось в виду, что пройдено 7/12 частей всего пути или прочтено 5/12 объёма всей книги. Двенадцатые доли дробились на двенадцать ещё и ещё… Даже сейчас иногда говорят: "Он скрупулезно изучил этот вопрос". Это значит, что вопрос изучен до конца, что ни одной самой малой неясности не осталось. А происходит странное слово "скрупулезно" от римского названия 1/288 асса - "скрупулус". (рис.8) рис.8 Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной. В ходу были и такие названия: «семис» - пол овина асса, «секстане» - шестая его доля, «семиунция» - полунции и т.д. Чтобы работать с дробями, надо было помнить для этих дробей и таблицу сложения, и таблицу умножения. Для облегчения работы составлялись специальные таблицы, некоторые из них дошли до нас. Сейчас «асс» - аптекарский фунт. 2.3 ДРОБИ В ВАВИЛОНЕ Около 4 тысяч лет назад в Месопотамию – долину между Тигром и Ефратом на территории нынешнего Ирака – пришли два кочевых народа: сумерийцы и аккадяне. Через два века они слились в одно мощное государство – Вавилон. Первые упоминания о дробях найдены на глиняных табличках Древнего Вавилона. Так как сама система исчисления в Вавилоне была шестидесятеричная, то вавилоняне предпочитали постоянный знаменатель «60». Но через шестидесятеричные дроби было довольно сложно точно выразить такие дроби, как 1/7, и их выражали приближенно. 1/7 ≈ 1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/120 Да-а-а, дело небыстрое, но, похоже, нашим предкам суета была неведома… Вавилонские мудрецы додумались разделить сутки на 24 часа. А затем час разделили на 60 минут и значительно позже минуту – на 60 секунд. Так же они разделили свою меру весов талант на 60 мин, а мину – на 60 шекелей. Соотношение часов, минут и секунд, принятое в Вавилоне, впоследствии перешло в Индию и в страны Европы и сохранилось в первоначальном виде до наших дней! (рис.9) рис.9
До наших дней сохранилось деление окружности на 360 градусов, градуса на 60 минут, а минуты на 60 секунд. 2.4 НУМЕРАЦИЯ И ДРОБИ В ДРЕВНЕЙ ГРЕЦИИ В греческих сочинениях по математике дробей не встречалось. Греческие учёные считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам и другому «чёрному люду». В Древней Греции арифметику – учение об общих свойствах чисел – отделяли от логистики – искусства исчисления. Греки считали, что дроби можно использовать только в логистике. Здесь мы впервые встречаемся с общим понятием дроби вида . Таким образом, можно считать, что впервые область натуральных чисел расширилась до области дополнительных рациональных чисел в Древней Греции не позднее V столетия до н. э. Греки свободно оперировали всеми арифметическими действиями с дробями, но числами их не признавали. 2.5 НУМЕРАЦИЯ ДРОБИ НА РУСИ Дроби на Руси называли долями, то есть маленькими числами. В старых рукописях встречаются следующие названия дробей: половина, полчеть, полополочеть, треть, полтреть. В русском языке слово дробь появилось в VIII веке, оно происходит от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в VII веке) дроби так и назывались — «ломаные числа». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять». И в «Арифметике» преподавателя навигацкой школы Леонтия Филипповича Магницкого были изложены сведения о дробях как о ломаных числах. Вот что там можно прочесть: «Число ломаное… есть токмо часть вещи, числом объявленная, сиречь полтина есть половина рубля, а пишется ещё ½ рубля…» Магницкий первым среди русских математиков рассказал, как производить действия с дробями и обыкновенными, и десятичными. (рис.10)рис.10 «Число ломаное не что же иное есть, токмо часть вещи, числом объявленная, сиречь полтина есть половина рубля, а пишется сие рубля, или, или пятая часть или две пятые части и всякии вещи яковые либо часть, объявлена числом, то есть ломаное число» (рис.11) рис.11 Существовало понятие «ломаное число» и в других странах. Оно ведёт своё начало от арабов. (рис.12) рис.12 Как свидетельствуют старинные памятники русской истории, наши предки-славяне, находившиеся в культурном общении с Византией, пользовались десятичной алфавитной славянской нумерацией, сходной с ионийской. Над буквами-числами ставился особый знак, названный титло. Для обозначения тысячи применялся другой знак, который приставлялся слева от букв. Старейшим арифметическим памятником Киевской Руси является сочинение о календаре, написанное на славянском языке в 1136году и названное «Учение им же ведати человеку числа всех лет», то есть «Наставление, как человеку познать счисление лет». автор сочинений – учёный монах Кирик Новгородец, о жизни которого известно немного. Кирик пользуется конкретными дробями: и т.д. В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси: 1/2 – половина, полтина 1/3 – треть 1/4 – четь 1/6 – полтреть 1/8 - полчеть 1/12 –полполтреть 1/16 - полполчеть 1/24 – полполполтреть (малая треть) 1/32 – полполполчеть (малая четь) 1/5 – пятина 1/7 - седьмина 1/10 - десятина Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I
2.6 ДРОБИ В ДРУГИХ ГОСУДАРСТВАХ ДРЕВНОСТИ Примерно во II в.н.э. в китайском трактате «Математика в девяти книгах» уже имеют место сокращения дробей и все действия с дробями. Эта книга была предназначена для землемеров, техников и счётных работников. Индия, одна из древнейших и величественных стран мира, является родиной позиционной десятичной нумерации(V-VII вв.н.э.). Индийцы широко употребляли «обыкновенные» дроби. Наше обозначение обыкновенных дробей при помощи числителя и знаменателя было принято в Индии ещё в VIIIв.н.э., однако запись была без дробной черты. Дробная черта стала применяться лишь в XIII веке. Широко известны математики древней Индии Ариабхатта(Vв.), Брахмагупта(VII в.), изложивший правила действий с дробями, мало отличавшиеся от наших, и Бхаскара(X в.). У них встречаются разные дроби: и основные, и произвольные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим. Около 1500 лет назад индусы первыми начали отделять чертой числитель от знаменателя. В VII в.н.э. жил известный армянский ученый Ананий Ширакаци, он писал книги по математике, географии и астрономии. Он составил обширные таблицы сложения, вычитания и умножения чисел. Среди книг Анания имеется также арифметика и сборник задач, названный «Вопросы и ответы». 1300 лет назад Ананий решал задачи на дроби, которые даже для многих учёных из Европы в то время казались трудными. Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. Иордан Неморарий (XIII ст.) выполняет деление дробей с помощью деления числителя на числитель и знаменателя на знаменатель, уподобляя деление умножению. Для этого приходится, члены первой дроби дополнять множителями: В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках. Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики. В ходе развития математики было замечено, что самыми удобными для вычисления являются десятичные дроби. С XVII – XVIII в. они получили всеобщее распространение, особенно после создания и введения в большинстве стран метрической системы мер. 2.7 ВОЗНИКНОВЕНИЕ СОВРЕМЕННОЙ ЗАПИСИ ДРОБИ В МАТЕМАТИКЕ Народы прошли через многие варианты записи дробей, пока не пришли к современной записи. Вначале в записи дробей не использовалась дробная черта. Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь. Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик. Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. А записывать дроби как сейчас стали арабы. Каждый может за версту Видеть дробную черту.Над чертой – числитель, знайте,Под чертою – знаменатель.Дробь такую, непременно,Надо звать обыкновенной. рис.13 Чтобы запомнить, что знаменатель - это нижняя часть дроби, мы выучили стихотворение: (рис.13) Знамёна упали, знаменатель - внизу, А числа сражались, числитель - вверху. 2.8 СРАВНЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ При сравнении дробей с одинаковыми знаменателями делили что-то целое на заданное количество частей и сравнивали нужное количество частей первой и второй дробей. Что больше 2/5 или 3/5? Делим пирог на 5 равных частей и видим, что две таких части меньше трёх таких же частей. При сравнении дробей с одинаковыми числителями рассуждали так: чем на большее количество частей делим одно и тоже число, тем меньше получается дробь. Но сравнивать приходилось и другие дроби не подходящие под эти правила. Сравнивать дроби, используя приём приведения дробей к общему знаменателю, люди научились гораздо позже, а до этого они пользовались многими другими способами, которые приводили их к верному результату. 1 способ: сравнение с половиной. Что больше 3/8 или 5/9 ? Если эти дроби сравнивать с 1/2 , то 3/8 меньше 1/2, а больше5/9 больше 1/2. Значит 5/9 больше 3/8 . 2 способ: сравнение путём добавления до единицы. Возьмём дроби 47/48 и 46/47 . Первую дробь дополняем до единицы дробью 1/8 , а вторую – 1/47. Но при сравнении дробей с одинаковыми числителями получаем, что 1/48 меньше 1/47 , значит 47/48 больше 46/47. 3 способ: сравнение правильной и неправильной дробей: любая правильная дробь меньше неправильной дроби. Действия с дробями и сейчас не всем легко даются. Пятьсот лет назад умение обращаться с дробями было вершиной арифметики, великие умы гордились этим знанием! Действия над дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». А сейчас мы изучаем дроби уже в младших классах…Чтобы облегчить действия с дробями, были придуманы десятичные дроби. Задачи на тему «Дроби» из нашего учебника: ПРИМЕНЕНИЕ ДРОБЕЙ В ПОВСЕДНЕВНОЙ ЖИЗНИ В жизни человек ежедневно сталкивается с дробями. Просыпаясь утром, мы смотрим на будильник и встречаемся с дробями. Садясь за школьную парту или приступая к работе, мы опять сталкиваемся с дробями. Дроби окружают нас. Мне стало интересно, а как часто и где мы с ними встречаемся? Живя в окружении дробей, мы не всегда их явно замечаем. Тем неимение, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее. Мы покажем лишь малую часть того, где можем увидеть присутствие дробей. Мы провели опрос на тему «Дроби в жизни моей семьи». Проанализировали 66 ответов. Сделали вывод, где используются дроби. Кулинария Лакомясь вкусным куском пирога, спросите у повара его состав. Ведь, во многих рецептах содержаться дроби. 1/3 часть опрошенных говорят об этом. В каждой семье делят угощения поровну. Время Для определения времени 1/3 часть опрошенных применяет дроби. Мы часто отвечаем на вопрос «который час?» дробям «Без четверти десять» - без пятнадцати минут десять; «Сейчас три часа без четверти» - 2 час 45 минут; «Четверть второго» - 1 час 15 минут. На каждую четверть часа приходится 15 минут. Каждые четверть часа бьют куранты. Медицина. В лечении используют дроби 122 опрошенных. Врач выписывает рецепт на лекарство, в котором указывает, что принимать следует по ½ или по ¼ части таблетки. Спорт. В спорте упоминают дроби 113 часть опрошенных. Команды играют в 1/8, ¼, ½ финала. Бюджет. При планировании бюджета используют дроби 113 часть опрошенных. В огороде при планировании посадок 16 часть респондентов используют дроби. Строительство. В строительстве применяет дроби 17 часть опрошенных. Для приготовления раствора для укладки стен нужно взять 2/3 песка и 1/3 цемента. Деньги Когда бы люди не использовали деньги, они обязательно встречаются с дробями: В настоящее время, российская копейка =1/100 рубля. Мерные системы 1сантиметр = 1/ 10 дециметра = 1/100 метра, Мода В любые времена в моде присутствовали дроби Всегда актуален фасон рукава три четверти.(рис.14) рис.14 А укороченные брюки 7/8 - это прекрасная деталь гардероба. Состав ткани Когда будете одеваться обратите внимание на ярлычок своей одежды: состав ткани (рис.15) в 100 % 58% шерсть 38% полиэстеррис.15 4% эластан Игры. • Достаньте целый круг и задайте Ребенку вопрос: "На что это похоже?" (например: круг - на яблоко, пирог, мяч и т.д.). Затем покажите второй круг, который состоит из двух половинок. Чем отличаются круги? Сколько частей во втором круге? Одинаковые ли круги? (целый и из двух частей, методом наложения половинок на целый круг). • Игра "Магазин": Ребенок в роли продавца, взрослый - покупатель, круги - это фрукты. Взрослый просит: "Дай мне, пожалуйста, целое яблоко, половинку яблока, одну вторую яблока". Затем меняются ролями. Игра станет более интересной, если добавить круги, разделенные на 3,4,5 частей и т.д.
Школа Оценки за четверть, т.е. оценки за ¼ учебного года.
И, конечно же, решая задачи и уравнения на уроках. География Во времена существования СССР, Россия занимала одну шестую часть суши и имела одну десятую населения. Во времена существования СССР, Россия занимала одну шестую часть суши и имела одну десятую населения. Пресса Мы сталкиваемся с дробями, читая газеты (рис.16) рис.16 Музыка Музыканты любят измерять такты четвертями Четверть в музыке - мера музыкального времени, равная 1/4 части целой ноты. Такты бывают 2/4, 3/8 могут быть и сложнее: 6/8, 1/9, 4/4, 5/4, 5/8 Бывают совсем редкостные, уникальные размеры такта. Так, в финале оперы «Снегурочка» Римский-Корсаков написал хор славления бога Ярилы-Солнца с размером такта в 11/4. Послушайте как звучит мелодия с размером такта 2/4
Творчество Учение о дробях всегда оставалось труднейшим разделом арифметики. Стихи и сказки помогают понять тему «Дроби». Мы делили апельсин Много нас, а он один. Эта долька для ежа, Эта долька для стрижа, Эта долька для утят, Эта долька для котят, Эта долька для бобра, А для волка кожура. Он сердит на нас - Беда, разбегайтесь кто – куда. - Однажды друзья решили измерить длину удава. Какую единицу измерения (мерку) они выбрали? - На каждой парте лежит модель удава и мерка, с помощью, которой нужно измерить длину удава. (Учащиеся выполняют задание парами, один ученик выполняет это задание на доске). - С какой трудностью столкнулись вы и герои мультфильма, при измерении длины удава? (Невозможно измерить длину удава только с помощью целых мерок, нужна ещё часть мерки). - Какой длины у вас получился удав? (Три целых мерки и ещё половина мерки) - Какой же длины получился удав у мартышки и слона? (38 попугаев и 1 попугайское крылышко) - Почему героям мультфильма пришлось для измерения длины удава добавить ещё и крылышко, а нам половину мерки? (Потому что целый попугай не уложился, как и целая мерка). - Чем по сравнению с попугаем является крылышко? Половина мерки? (Частью целого попугая, частью целой мерки) - Оказывается, не всегда можно выполнить измерения только с помощью целых мерок. И тут на помощь нам приходят дроби. Русский математик Л.Магницкий писал: Но несть той арифметик, Ижо в целых ответчик, А в долях сий ничтоже, Отвещати возможе. емже о ты радеяй, Буди в частях умеяй. Дроби всякие нужны, Дроби всякие важны. Дробь учи, тогда сверкнет тебе удача. Если будешь дроби знать, Точно смысл их понимать, Станет легкой даже трудная задача. О.Севостьянова Стихотворение про дробь. Дробь жила-была одна на свете. Ты узнаешь по примете: В верхнем домике живёт Замечательный народ- Звать его числитель -Могучий повелитель В нижнем домике живёт Знаменатель - злой народ: На него всегда все делят. Может злиться он хоть год На числитель всегда все отряды пустит в ход. А числитель без труда защищает всех всегда! Мухамедзянов Алексей, 6-а кл. МОУСОШ №3 4. ЗАКЛЮЧЕНИЕ В результате работы над проектом мы узнали историю развития обыкновенных дробей, сумели решить задачи связанные с дробями, и сами составили задачи по теме с практическим содержанием. В ходе их решения мы закрепили алгоритмы выполнения действий над дробями, нахождение числа по его части и части от числа. Особый интерес при работе над проектом мы испытали при решении задач с использованием дробей. Разнообразие предложенных задач и результаты анкетирования убедили нас в необходимости применения дробей в повседневной жизни и для многих профессий. Считаем, что материалы нашей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения внеклассных мероприятий по математике. Хотелось бы продолжить работу по нахождению применения дробей в различных профессиях и в жизненных ситуациях. Список литературы 1.Гельфанд М.Б., Павлович В.С. Внеклассная работа по математике. – М.: Издательство «Просвещение», 1965г. 2. Григорьева Г.И. Математика. Предметная неделя в школе. – М.: Глобус, 2008г. 3. Депман И.Я. Мир чисел. - М.: Детская литература, 1966 4. Занимательная математика в рассказах для детей / авт.-сост. А.П.Савин и др. – М.: АСТ: Астрель, 2011 5. Свечников А. А. Путешествие в историю математики, или Как люди научились считать - М., Педагогика-Пресс, 1995. 6. Нагибин Ф.Ф. Математическая шкатулка. – М.: Учпедгиз, 1958г 7. Перельман Я.И. Живая математика. – ОГИЗ, Гостехиздат, Москва, 1946г. 8. Совайленко В.К. Система обучения математике в 5-6 классах: Книга для учителя: Из опыта работы. – М.: Просвещение, 1991г. 9.Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949-1992. 10. Шейнина О.С., Соловьёва Г.М. Математика. Занятия школьного кружка. 5-6 кл. – М. Издательство НЦ ЭНАС, 2007г В газете “1 сентября” за январь 2012-го года были приведены интересные задачи с дробями. Уровень задач – 5-6 класс. Задачи демонстрируют жизненный подход к понятию дробь. 11. http://ru.wikipedia.org/wiki 12. http://mathege.ru/or/ege/Main Газета «Математика» (приложение к «Первое сентября»), 2005г. http://nova.rambler.ru. http://poverpoint-ppt.ru/
educontest.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|