

Министерство образования РФ
Санкт Петербургский государственный университет информационных технологий, механики и оптики
кафедра высшей математики
Реферат на тему
«Поверхности второго порядка»
Выполнил: студент 1 курса группы 1514 Блинов А.А.
Проверила: доцент Милованович Е.В.
Санкт-Петербург
2004 г.
Поверхности второго порядка
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоид.


Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:
 (1)
(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
 (2)
(2)
Исследуем уравнения (2) при различных значениях h.
Если  > c (c>0), то
> c (c>0), то и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.
Если  , то
, то и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости
и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости касаются эллипсоида).
касаются эллипсоида).
Если 
, то уравнения (2) можно представить в виде

откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями  и
и .
.
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.
2. Однополосный гиперболоид.


Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 , (a>0, b>0, c>0)
, (a>0, b>0, c>0)
(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения

и

из которых следует, что в сечениях получаются гиперболы.
Аналогично в плоскости x0zимеем гиперболу

В плоскости z=0 имеем эллипс (горловина)

Сечение z=±h, (h>0) даёт нам эллипс

Очевидно, что полуоси этого эллипса возрастают по мере удаления от начала координат.
В сечениях плоскостями, параллельными координатным плоскостям x0zиy0zполучим гиперболы.
3. Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Исследуем форму этой поверхности методом сечения.
1) Положим в уравнение x=0,получим

Это соотношение не имеет смысла, т.к. сумма квадратов не может быть отрицательным числом. Это означает, что данная поверхность не пересекается с координатной плоскостью y0z.
2) Положим в уравнениеy=0, получим
 ,
,
т.е. в координатной плоскости x0zмы имеем гиперболу.
3) В координатной плоскости x0yполучим также гиперболу

4) В координатной плоскости x=±h, (h>a) получим эллипсы

4. Эллиптический параболоид.


Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 ,
,
(7)
где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения

и

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
В сечении плоскостью z=h(h>0) имеем эллипс

Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.
Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
В случае p=q, то поверхность называется параболоидом вращения.
5. Гиперболический параболоид.
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
 , (p>0, q>0)
, (p>0, q>0)
(9)


рис.(5.1)
Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью xOz (y=0). Получаем уравнение

(10)

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h),получаются так же направленные вверх параболы.

рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
Получаем уравнение

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения

или

Проводя другие сечения, приходим к выводу, что поверхность имеет форму седла. (рис. 5.1)
6. Конус второго порядка.


(6.1)
Формула конуса: 
Определение: Канонической поверхностью называется поверхность, которая получается при движении прямой (образующей), проходящей через данную точку (вершину) и пересекающей данную линию (направляющую).
Если направляющей служит кривая второго порядка, то конус называется конусом второго порядка.
Если напраляющая есть замкнутая кривая, то конус представляет собой двуполостную поверхность, все образующие которой проходят через данную точку (вершину конуса). На рис. (6.1) изображён конус, имеющий уравнение  . Исследовать форму этого конуса нетрудно, проведя расзличные сечения этой поверхности.
. Исследовать форму этого конуса нетрудно, проведя расзличные сечения этой поверхности.
Отметим еще одну важную особенность уравнения конуса: как правило это однородное уравнение относительно разностей (x-a), (y-b), (z-c), где точкаM0(a,b,c) – вершина конуса. На рисунке 6.1 изображён конус с вершиной в начале координат, т.е. для данного конусаa=0,b=0,c=0.
7. Цилиндр

Формула эллиптического цилиндра: 
Определение: Цилиндрический поверхностьюили простоцилиндром называется всякая поверхность, которую можно получить движением прямой (образующей), перемещающейся параллельно некоторому данному векторуSи всё время пересекающей данную линию, которая называетсянаправляющей.
Если направляющей служит кривая второго порядка, то и цилиндр называется цилиндром второго порядка. Если образующие параллельны какой-либо координатной оси, то цилиндр называется прямым.
8. Поверхности вращения
Поверхность, образованная вращением плоской кривой вокруг оси, расположенной в её плоскости, называетсяповерхностью вращения. Эта ось называется осью вращения поверхности. Очевидно, если пересекать поверхность вращения плоскостями, перпендикулярными к оси вращения, то в сечениях будут окружности с центрами на оси вращения.
Рассмотрим правило получения уравнения поверхности, образованной вращением линии, лежащей в координатной плоскости вокруг оси координат.
Найдём уравнение поверхности, полученной от вращения этой линии вокруг оси Oz ( рис 8.1)

Введем на поверхности произвольную точку М(x,y,z) и проведем через нее плоскость, перпендикулярную к оси вращения. Обозначим через М1 иNточки пересечения построенной плоскости соответственно с данной линиейLи осью вращения (осьюOz). Координатыzвсех трёх точекM,M1иNравны между собой. Поэтому имею в виду, что координаты точкиNесть (0,0,z), найдем радиусNMокружности, получившейся в сечении поверхности плоскостью, как растояние между точкамиNиM, он равен . С другой стороны, так как точка М1лежит одновременно на окружности сечения и на линииL, то радиусNMравен абсолютной величине ординаты точкиM1. Следовательно, полагая в данном уравнении
. С другой стороны, так как точка М1лежит одновременно на окружности сечения и на линииL, то радиусNMравен абсолютной величине ординаты точкиM1. Следовательно, полагая в данном уравнении
Y=± ;Z=z
;Z=z
(координаты точки М1), получаем искомое уравнение поверхности вращения
F(± ,z) = 0.
,z) = 0.
Таким образом, мы приходим к следующему правилу: чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскостиy0z, вкруг оси 0z, нужно в уравнении этой линии заменитьyна ± .
.
При выборе знака перед радикалом следует придерживаться следующего правила: знак должен совпадать в соответствующих точках со знаком координаты yна исходной кривой.
Совершенно аналогичные правила будут для получения уравнений поверхностей вращения, получающихся вращением плоских линий вокруг других координатных осей.
Cписок использованной литературы:
1.Шипачёв В.С.:”Высшая математика”
2. Л.И.Брылевская, И.А.Лапин, Л.С.Ратафьева, О.Л.Суслина: «Элементы теории линейных пространств»
studfiles.net
Поверхности второго порядка
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
 Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:

(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h , где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
 (2)
(2)
Исследуем уравнения (2) при различных значениях h .
 >
c
(c>0), то
>
c
(c>0), то
 и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости
z=h
с данным эллипсоидом не существует.
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости
z=h
с данным эллипсоидом не существует.
 , то
, то
 и линия (2) вырождается в точки (0; 0; +
c
) и (0; 0; -
c
) (плоскости
и линия (2) вырождается в точки (0; 0; +
c
) и (0; 0; -
c
) (плоскости
 касаются эллипсоида).
касаются эллипсоида).


откуда следует, что плоскость
z=h
пересекает эллипсоид по эллипсу с полуосями
 и
и
 . При уменьшении
. При уменьшении
 значения
значения
 и
и
 увеличиваются и достигают своих наибольших значений при
увеличиваются и достигают своих наибольших значений при
 , т. е. в сечении эллипсоида координатной плоскостью
Oxy
получается самый большой эллипс с полуосями
, т. е. в сечении эллипсоида координатной плоскостью
Oxy
получается самый большой эллипс с полуосями
 и
и
 .
.
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz .
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.
2. Однополосный гиперболоид.
 Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (3)
(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
 и
и

из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
 или
или
 (4)
(4)

из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
 и
и
 ,
,
достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании
 величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно.
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (5)
(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
 и
и
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
или (6)
из которых следует, что при >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями и . При увеличении величины a* и b* тоже увеличиваются.
При уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости касаются данной поверхности).
При уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.
Величина a, b и c называются полуосями двуполостного гиперболоида.
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
(7)
где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
и
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
или (8)
из которых следует, что при плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями и . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.
Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
(9)
где p>0, q>0.
Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
(10)
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
Получаем уравнение
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
или
из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
и
точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
6. Конус второго порядка.
Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
(11)
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию
распадающуюся на две пересекающиеся прямые
и
Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
и
Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
или
из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями . При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.
При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).
Cписок использованной литературы:
1.Шипачёв В.С.:”Высшая математика”
referat.store
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоид.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:  (1)
(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
 (2)
(2)
Исследуем уравнения (2) при различных значениях h.
Если > c (c>0), то
> c (c>0), то  и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. Если
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. Если  , то
, то  и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости
и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости  касаются эллипсоида). Если
касаются эллипсоида). Если  , то уравнения (2) можно представить в виде
, то уравнения (2) можно представить в виде 
откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями  и
и  . При уменьшении
. При уменьшении  значения
значения  и
и  увеличиваются и достигают своих наибольших значений при
увеличиваются и достигают своих наибольших значений при  , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями
, т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями  и
и  .
.
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.
2. Однополосный гиперболоид.
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (3)
(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
 и
и
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
 или
или (4)
(4)

из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и  ,
,
достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании  величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно.
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида.
3. Двуполостный гиперболоид.Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (5)
(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
 и
и 
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
 или
или  (6)
(6)
из которых следует, что при  >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями
>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и  . При увеличении
. При увеличении  величины a* и b* тоже увеличиваются.
величины a* и b* тоже увеличиваются.
При  уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости
уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости  касаются данной поверхности).
касаются данной поверхности).
При  уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.
уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.
Величина a, b и c называются полуосями двуполостного гиперболоида.
4. Эллиптический параболоид.Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

 (7)
(7)
где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
 и
и 
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
 или
или  (8)
(8)
из которых следует, что при  плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями
плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями  и
и  . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.
. При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.
Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).
5. Гиперболический параболоид.Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
 (9)
(9)

где p>0, q>0.
Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
 (10)
(10)
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.

рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
Получаем уравнение

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
 или
или 
из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
 и
и 
точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
6. Конус второго порядка.Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

 (11)
(11)
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию

распадающуюся на две пересекающиеся прямые
 и
и 
Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
 и
и 
Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
 или
или 
из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями  . При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.
. При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.
При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).
Cписок использованной литературы:1.Шипачёв В.С.:”Высшая математика”
www.neuch.ru
Содержание.
· Понятие поверхности второго порядка.
1.Инварианты уравнения поверхности второго порядка.
· Классификация поверхностей второго порядка.
1. Классификация центральных поверхностей.
-1°. Эллипсоид.
-2°. Однополостный гиперболоид.
-3°. Двуполостный гиперболоид.-4°. Конус второго порядка.
2. Классификация нецентральных поверхностей.
-1°. Эллиптический цилиндр, гиперболический цилиндр, эллиптический параболоид, гиперболический параболоид.
-2°. Параболический цилиндр
•Исследование формы поверхностей второго порядка по их каноническим уравнениям.
1.Эллипсоид.2. Гиперболоиды.
- 1°. Однополостный гиперболоид.
-2°. Двуполостный гиперболоид.
3. Параболоиды.
-1°. Эллиптический параболоид.-2°. Гиперболический параболоид.
4.Конус и цилиндры второго порядка.
- 1°. Конус второго порядка.-2°. Эллиптический цилиндр.-3°. Гиперболический цилиндр.-4°. Параболический цилиндр.
Список использованной литературы.
§ 1. Понятие поверхности второго порядка.
Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11х2+ а22у2+a33z2+2a12xy+2a23уz +2a13xz +2а14x+2а24у+2а34z+а44=0(1)
в котором по крайней мере один из коэффициентовa11, а22, a33,a12,a23 ,a13отличен от нуля.
Уравнение (1) мы будем называтьобщим уравнением поверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение, полученное после преобразования координат, алгебраически эквивалентны.
 1.Инварианты уравнения поверхности второго порядка.
1.Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.
являются инвариантами уравнения(1)поверхности второго-порядка относительно преобразований декартовой системы координат.
Доказательство этого утверждения приведено в выпуске «Линейная алгебра» настоящего курса.
§ 2. Классификация поверхностей второго порядка
1. Классификация центральных поверхностей.Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид
a11х2+ а22у2+a33z2+ а44= 0 (2)
Так как инвариант I3для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равноa11•а22•a33, то коэффициентыa11,а22,a33удовлетворяют условию :
 |
Возможны следующие случаи:
-1°.Коэффициентыa11,а22,a33одного знака, а коэффициента44отличен от нуля.В этом случае поверхность S называетсяэллипсоидом.
Если коэффициентыa11,а22,a33,а44одного знака,то левая часть (2) ни при каких значенияхх, у, zне обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называетсямнимым эллипсоидом.
Если знак коэффициентовa11,а22,a33противоположен знаку коэффициентаа44, то поверхность S называетсявещественным эллипсоидом.В дальнейшем термином «эллипсоид» мы будем называть лишьвещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа

положительны. Обозначим эти числа соответственноа2,b2,с2. После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:

Уравнение (3) называетсяканоническим уравнением эллипсоида.
Если эллипсоид задан своим каноническим уравнением (3), то осиОх, ОуиОz.называются егоглавными осями.
-2°.Из четырех коэффициентовa11,а22,a33,а44два одногознака,а два других—противоположного.В этом случае поверхность S называетсяоднополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности,a11> 0,а22>0,a33<0,а44<0. Тогда числа

положительны. Обозначим эти числа соответственноа2, b2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:

Уравнение (4) называетсяканоническим уравнением однополостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (4), то осиОх, ОуиOzназываются егоглавными осями.
-3°.Знак одного из первых трех коэффициентовa11,а22,a33,а44противоположен знаку остальных коэффициентов.В этом случае поверхностьSназываетсядвуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности,a11< 0,а22<0,a33>0,а44<0. Тогда :

Обозначим эти числасоответственно через a2, b2, с2. Поcли несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:

Уравнение (5) называетсяканоническим уравнением двуполостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим
уравнением, то осиОх, ОуиОzназываются егоглавными осями.
-4°.Коэффициента44равен нулю.В этом случае поверхность S называетсяконусом второго порядка.
Если коэффициентыa11,а22,a33одного знака, то левая часть (2) обращается в нуль (а44=0) лишь длях=у=z=0,т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называетсямнимым конусом второго порядка.Если коэффициентыa11,а22,a33имеют разные знаки, то поверхность S являетсявещественнымконусом второго порядка.
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
a11> o,а22> 0,a33<0. Обозначим

соответственно череза2, b2,с2. Тогда уравнение (2) можно записать в виде

Уравнение (6) называетсяканоническим уравнением вещественного конуса второго порядка.
2. Классификация нецентральных поверхностей второго порядка.
Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариантI3равен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид
a´11х´2+ а´22у´2+a´33z´2+2а´14x´+2а´24у´+2а´34z´+а´44=0(7)
для системы координат Ox´y´z´
Так как инвариантI3=0 и его значение, вычисленное для уравнения (7), равно
a´11• а´22•a´33, то один или два из коэффициентовa´11, а´22,a´33равны нулю. В соответствии с этим рассмотрим следующие возможные случаи.
 -1°.Один из коэффициентовa´11, а´22,a´33равен нулю.Радиопределенности будем считать, чтоa´33=0(если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координатх', у', z'к новым координатамх, у,zпо формулам
-1°.Один из коэффициентовa´11, а´22,a´33равен нулю.Радиопределенности будем считать, чтоa´33=0(если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координатх', у', z'к новым координатамх, у,zпо формулам
Подставляях',у'и z', найденные из (8), в левую часть (7) и заменяя затем
a´11наa11,а´22наа22,а´34наpиа´44наq, получим следующее уравнение поверхности S в новой системе координатOxyz:
a11х2+ а22у2+ 2pz + q = 0(9)
 |
При этом, очевидно,эти плоскости будут мнимыми, если знакиa11иа22одинаковы, и вещественными, если знакиa11иа22различны.
2)Пустьр=0, q ≠ 0.Уравнение (9) принимает вид
a11х2+а22у2+ q = 0 (10)
Известно, чтоуравнение(10)являетсяуравнением цилиндра с образующими, параллельными осиОz.При этом еслиa11, а22,qимеют одинаковый знак, то левая часть (10) отлична от нуля для любыххи y, т. е.цилиндр будет мнимым.Если же среди коэффициентовa11, а22,qимеются коэффициенты разных знаков, тоцилиндр будет вещественным. Отметим, что в случае, когдаa11иа22имеютодинаковые знаки, aq—противоположный, то величины

положительны.
Обозначая их соответственно череза2и b2, мы приведем уравнение (10) к виду

Таким образом, в отмеченном случае мы имеемэллиптический цилиндр.В случае,a11и а22имеют различные знаки, мы получимгиперболический цилиндр.Легко убедиться, что уравнение гиперболического цилиндра может быть приведено к виду

3)Пустьр≠0.Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами

(0, 0, ).
При этом оставим старые обозначения координатх,у, z.Очевидно, для того чтобы получить уравнение поверхности S в новой системе координат, достаточно заменить в уравнении (9)

Получим следующее уравнение:
a11х2+а22у2+ 2pz = 0 (13)
Уравнение (13) определяет так называемыепараболоиды.Причем еслиa11и а22имеют одинаковый знак, то параболоид называетсяэллиптическим.Обычно уравнение эллиптического параболоида записывают в канонической форме:

Уравнение (14) легко получается из (13). Еслиa11и а22имеют разные знаки, то параболоид называетсягиперболическим.Каноническое уравнение гиперболического параболоида имеет вид

Это уравнение также легко может быть получено из (13).
-2°.Два из коэффициентовa´11, а´22,a´33равны нулю.Ради определенности будем считать, чтоa´11= 0иа´22= 0Перейдем отх,', у', z'к.новымкоординатамх, у,zпо формулам :

Подставляях', у'иz',найденные из (16) в левую часть (7) и заменяя затемa´33наa33 ,a´14нар,a´24наqиa´44наr, получим следующее уравнение поверхности S в новой системе координатОхуz:
a33z2+ 2px + 2qy + r = 0(17)
 1)Пустьр=0,q=0.Поверхность Sраспадается на пару параллельных плоскостей
1)Пустьр=0,q=0.Поверхность Sраспадается на пару параллельных плоскостей
При этом, очевидно, этиплоскости будутмнимыми, если знакиa33иr одинаковы, ивещественными, если знакиa33иr различны, причем приr = 0 эти плоскости сливаются в одну.
2)Хотя бы один из коэффициентовр илиq отличен от нуля.В этом случае повернем систему координат вокруг осиOzтак, чтобы новая ось абсцисс стала параллельной плоскости2рх+2qy+r=0.Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначениях, уи z для новых координат точек, уравнение (17) примет вид
a33z2+ 2q´y = 0(19)
которое являетсяуравнениемпараболического цилиндрас образующими, параллельными новой осиОх.
§ 3. Исследование формы поверхностей второго порядка по их каноническим уравнениям
 1. Эллипсоид.
1. Эллипсоид.
Из уравнения (3) вытекает, чтокоординатные плоскости являются плоскостями симметрии эллипсоида, а начало координат—центром симметрии.Числаа, b, сназываютсяполуосямиэллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтобы более наглядно представить себе формуэллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей.
Ради определенности рассмотрим линииLhпересечения эллипсоида с плоскостями
z = h(20)
параллельными плоскостиОху.Уравнение проекцииL*hлинииLhна плоскостьОхуполучается из уравнения (3), если положить в немz = h.Таким образом, уравнение этой проекции имеет вид

 Если положить
Если положить
то уравнение (21) можно записать в виде

 |
Представление об эллипсоиде можно получить следующим образом. Рассмотрим на плоскостиОхусемейство эллипсов (23) (рис. 1), полуосиа*иb*которых зависят отh(см. (22)), и каждый такой эллипс снабдим отметкой h, указывающей, на какую высоту по осиОzдолжен быть «поднят» этот эллипс. Мыполучим своего рода «карту» эллипсоида. Используя эту «карту», легко представить себе пространственный вид эллипсоида.
(Метод представления формы фигуры путем получения «карты» фигуры я привожу только для эллипсоида, представить форму других фигур этим методом можно аналогично)
Наглядное изображение эллипсоида находится на следующей странице.
Эллипсоид .
.
2. Гиперболоиды.
-1°.Однополостный гиперболоид.Обратимся к каноническому
 уравнению (4) однополостного гиперболоида
уравнению (4) однополостного гиперболоида
Из уравнения (4) вытекает, чтокоординатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.
 |
 -2°.Двуполостный гиперболоид.Из канонического уравнения (5)двуполостного гиперболоида вытекает, чтокоординатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.
-2°.Двуполостный гиперболоид.Из канонического уравнения (5)двуполостного гиперболоида вытекает, чтокоординатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.
 |
3. Параболоиды.
-1°.Эллиптический параболоид.Обращаясь к каноническому уравнению (14) эллиптического параболоида

мы видим, что для негоOxzиОуz являются плоскостями симметрии.Ось Oz, представляющая линию пересечения этих плоскостей, называетсяосью эллиптического параболоида.

 -2°.Гиперболический параболоид.Из канонического уравнения (15)
-2°.Гиперболический параболоид.Из канонического уравнения (15)
гиперболического параболоида вытекает, чтоплоскостиOxz иОуz являются плоскостями симметрии.ОсьOzназываетсяосью гиперболического пaраболоида.
Прим.: получение «карты высот» для гиперболического пaраболоида несколько отличается от аналогичной процедуры для вышеприведенных поверхностей 2-го порядка, поэтому я также включил его в свой реферат.
Линииz=hпересечения гиперболического параболоида плоскостямиz=h представляют собой при h>0 гиперболы

с полуосями
 |
 а приh < 0 —сопряженные гиперболы для гипербол (24)
а приh < 0 —сопряженные гиперболы для гипербол (24)
 |

 Используя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Используя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Из формул (25) и (27) вытекает, что прямые (28) являются асимптотами гипербол (24) и (26).Карта гиперболического параболоида дает представление о его пространственной форме. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостьюOxz(Оуz),когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостьюOyz (Oxz).
Прим.:Изображение гиперболического пaраболоида дано на следующей странице.
 Гиперболический параболоид.
Гиперболический параболоид.4. Конус и цилиндры второго порядка.
 -1°.Конус второго порядка
-1°.Конус второго порядка
 Убедимся, что вещественныйконус S образован прямыми линиями, проходящими через начало О координат.Естественно называть точку Овершиной конуса.
Убедимся, что вещественныйконус S образован прямыми линиями, проходящими через начало О координат.Естественно называть точку Овершиной конуса.
Для доказательства сформулированного утверждения, очевидно, достаточно установить, что прямая L, соединяющая произвольную, отличную от начала координат точкуМ0(х0, у0,z0)конуса (6) и начало координат О , целиком располагается на конусе, т. е. координаты(х, у, z)любой точкиМпрямойLудовлетворяют уравнению (6).
 Так как точкаМ0(х0, у0,z0)лежит на конусе (6), то :
Так как точкаМ0(х0, у0,z0)лежит на конусе (6), то :
 |
-2°.Эллиптическийцилиндр.
 |
 Состоит из прямых линий, параллельных оси Oz.
Состоит из прямых линий, параллельных оси Oz. -3°.Гиперболическийцилиндр.
-3°.Гиперболическийцилиндр.

Состоит из прямых линий, параллельных оси Oz.
-4°.Параболическийцилиндр.
a33z2+ 2q´y = 0(19)Путем переименования осей координат и простых арифметических операций из уравнения, (19) мы получим новое, компактное уравнениепараболическогоцилиндра.
 |

 |
superbotanik.net
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
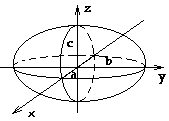
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением: 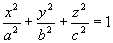 (1)
(1)
Уравнение (1) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
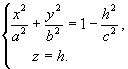 (2)
(2)
Исследуем уравнения (2) при различных значениях h.
 > c (c>0), то
> c (c>0), то 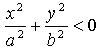 и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует.
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. 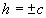 , то
, то 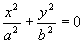 и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости
и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости 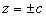 касаются эллипсоида).
касаются эллипсоида). 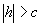
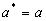
откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями 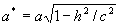 и
и 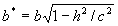 . При уменьшении
. При уменьшении  значения
значения 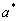 и
и 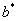 увеличиваются и достигают своих наибольших значений при
увеличиваются и достигают своих наибольших значений при 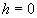 , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями
, т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями 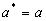 и
и 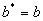 .
.
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой.

Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
 (3)
(3)
Уравнение (3) называется каноническим уравнением однополосного гиперболоида.
Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
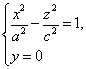 и
и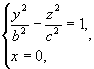
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
 или
или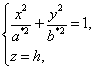 (4)
(4)
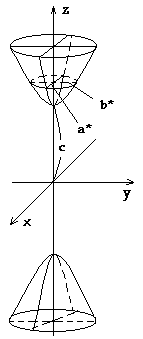
из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и 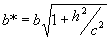 ,
,
достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании  величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно.
Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
Величины a, b, c называются полуосями однополосного гиперболоида.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
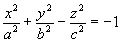 (5)
(5)
Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
 и
и 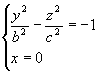
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
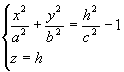 или
или  (6)
(6)
из которых следует, что при  >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями
>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями 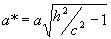 и
и 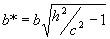 . При увеличении
. При увеличении 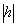 величины a* и b* тоже увеличиваются.
величины a* и b* тоже увеличиваются.
При 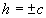 уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости
уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости 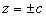 касаются данной поверхности).
касаются данной поверхности).
При 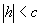 уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.
уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.
Величина a, b и c называются полуосями двуполостного гиперболоида.
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
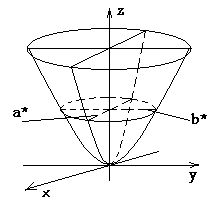
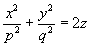 (7)
(7)
где p>0 и q>0.
Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
 и
и 
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
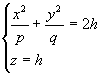 или
или  (8)
(8)
из которых следует, что при  плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями
плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями  и
и  . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.
. При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.
Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
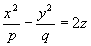 (9)
(9)

где p>0, q>0.
Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
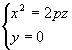 (10)
(10)
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
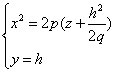
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
Получаем уравнение

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
 или
или 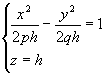
из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
 и
и 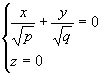
точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.
Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
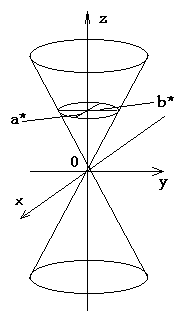
 (11)
(11)
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию
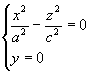
распадающуюся на две пересекающиеся прямые
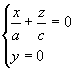 и
и 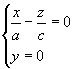
Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
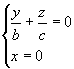 и
и 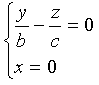
Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
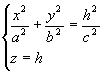 или
или 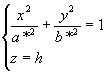
из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями 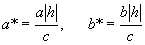 . При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.
. При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.
При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).
1.Шипачёв В.С.:”Высшая математика”
Дата добавления: 14.05.2001
www.km.ru
Содержание.
Понятие поверхности второго порядка. 1. Инварианты уравнения поверхности второго порядка.
Классификация поверхностей второго порядка. 1. Классификация центральных поверхностей.
1°. Эллипсоид.
2°. Однополостный гиперболоид.
3°. Двуполостный гиперболоид. 4°. Конус второго порядка.
2. Классификация нецентральных поверхностей.
1°. Эллиптический цилиндр, гиперболический цилиндр, эллиптический параболоид, гиперболический параболоид.
2°. Параболический цилиндр
• Исследование формы поверхностей второго порядка по их каноническим уравнениям.
Эллипсоид. 2. Гиперболоиды.
1°. Однополостный гиперболоид.
2°. Двуполостный гиперболоид.
3. Параболоиды.
1°. Эллиптический параболоид. 2°. Гиперболический параболоид.
4. Конус и цилиндры второго порядка.
1°. Конус второго порядка. 2°. Эллиптический цилиндр. 3°. Гиперболический цилиндр. 4°. Параболический цилиндр.
Список использованной литературы.
1. «Аналитическая геометрия» В.А. Ильин, Э.Г. Позняк
Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11х2 + а22у2 +a33z2+2a12xy + 2a23уz + 2a13xz + 2а14 x + 2а24у+2а34z +а44 = 0 (1)
в котором по крайней мере один из коэффициентов a11 , а22 , a33 , a12 , a23 , a13отличен от нуля.
Уравнение (1) мы будем называть общим уравнением поверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной декартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнение (1) и уравнение, полученное после преобразования координат, алгебраически эквивалентны.
1 . Инварианты уравнения поверхности второго порядка.
. Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.
являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы координат.
Доказательство этого утверждения приведено в выпуске «Линейная алгебра» настоящего курса.
1. Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид
a11х2 + а22у2 +a33z2 + а44 = 0 (2)
Так как инвариант I3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a11 • а22 • a33, то коэффициенты a11 ,а22 , a33 удовлетворяют условию :

Возможны следующие случаи:
1°. Коэффициенты a11 ,а22 , a33 одного знака, а коэффициент а44 отличен от нуля. В этом случае поверхность S называется эллипсоидом.
Если коэффициенты a11 ,а22 , a33 , а44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом.
Если знак коэффициентов a11 ,а22 , a33 противоположен знаку коэффициента а44, то поверхность S называется вещественным эллипсоидом. В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа

положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:

Уравнение (3) называется каноническим уравнением эллипсоида.
Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. называются его главными осями.
2°. Из четырех коэффициентов a11 ,а22 , a33 , а44 два одного знака, а два других—противоположного. В этом случае поверхность S называется однополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11 > 0,а22 >0, a33 <0, а44 <0. Тогда числа

положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:

Уравнение (4) называется каноническим уравнением однополостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу иOz называются его главными осями.
3°. Знак одного из первых трех коэффициентов a11 ,а22 , a33 , а44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a11 < 0,а22 <0, a33 >0, а44 <0. Тогда :

Обозначим эти числа соответственно через a2, b2, с2. Поcли несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:

Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим
уравнением, то оси Ох, Оу и Оz называются его главными осями.
4°. Коэффициент а44 равен нулю. В этом случае поверхность S называется конусом второго порядка.
Если коэффициенты a11 ,а22 , a33 одного знака, то левая часть (2) обращается в нуль (а44 =0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называется мнимым конусом второго порядка. Если коэффициенты a11 ,а22 , a33имеют разные знаки, то поверхность S является вещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
a11 > o, а22 > 0, a33 <0. Обозначим

соответственно через а2, b2, с2. Тогда уравнение (2) можно записать в виде

Уравнение (6) называется каноническим уравнением вещественного конуса второго порядка.
2. Классификация нецентральных поверхностей второго порядка.
Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариантI3 равен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид
a´11х´2 + а´22у´2 +a´33z´2 + 2а´14 x´ + 2а´24у´+2а´34z´ +а´44 = 0 (7)
для системы координат Ox´y´z´
Так как инвариант I3 =0 и его значение, вычисленное для уравнения (7), равно
a´11 • а´22 • a´33, то один или два из коэффициентов a´11 , а´22 , a´33равны нулю. В соответствии с этим рассмотрим следующие возможные случаи.
 1°. Один из коэффициентов a´11 , а´22 , a´33 равен нулю. Радиопределенности будем считать, что a´33 =0(если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координат х', у', z' к новым координатам х, у, z по формулам
1°. Один из коэффициентов a´11 , а´22 , a´33 равен нулю. Радиопределенности будем считать, что a´33 =0(если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координат х', у', z' к новым координатам х, у, z по формулам
Подставляя х', у' и z', найденные из (8), в левую часть (7) и заменяя затем
a´11 наa11, а´22 на а22 , а´34 на pи а´44 на q , получим следующее уравнение поверхности S в новой системе координатOxyz :
a11х2 + а22у2 + 2pz + q = 0 (9)
1 ) Пусть р=0, q =0. Поверхность S распадается на пару плоскостей
) Пусть р=0, q =0. Поверхность S распадается на пару плоскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a11 иа22 одинаковы, и вещественными, если знаки a11 иа22 различны.
2) Пусть р=0, q ≠ 0. Уравнение (9) принимает вид
a11х2 + а22у2 + q = 0 (10)
Известно, что уравнение (10) является уравнением цилиндра с образующими, параллельными оси Оz. При этом если a11 , а22 , q имеют одинаковый знак, то левая часть (10) отлична от нуля для любых х и y, т. е. цилиндр будет мнимым. Если же среди коэффициентов a11 , а22 , q имеются коэффициенты разных знаков, то цилиндр будет вещественным. Отметим, что в случае, когда a11 и а22 имеютодинаковые знаки, a q — противоположный, то величины

положительны.
Обозначая их соответственно через а2и b2, мы приведем уравнение (10) к виду

Таким образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, a11 и а22 имеют различные знаки, мы получим гиперболический цилиндр. Легко убедиться, что уравнение гиперболического цилиндра может быть приведено к виду

3) Пусть р≠0. Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами

(0, 0, ).
При этом оставим старые обозначения координатх, у, z. Очевидно, для того чтобы получить уравнение поверхности S в новой системе координат, достаточно заменить в уравнении (9)

Получим следующее уравнение:
a11х2 + а22у2 + 2pz = 0 (13)
Уравнение (13) определяет так называемые параболоиды. Причем если a11 и а22 имеют одинаковый знак, то параболоид называется эллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:

Уравнение (14) легко получается из (13). Если a11 и а22 имеют разные знаки, то параболоид называется гиперболическим. Каноническое уравнение гиперболического параболоида имеет вид

Это уравнение также легко может быть получено из (13).
2°. Два из коэффициентов a´11 , а´22 , a´33 равны нулю. Ради определенности будем считать, что a´11 = 0 и а´22 = 0 Перейдем от х,', у', z' к. новымкоординатам х, у, z по формулам :

Подставляя х', у' и z' , найденные из (16) в левую часть (7) и заменяя затем a´33 на a33 , a´14 на р , a´24 на q и a´44 на r, получим следующее уравнение поверхности S в новой системе координат Охуz :
a33 z2 + 2px + 2qy + r = 0 (17)
1 ) Пусть р=0, q=0. Поверхность S распадается на пару параллельных плоскостей
) Пусть р=0, q=0. Поверхность S распадается на пару параллельных плоскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a33 и r одинаковы, и вещественными, если знаки a33 и r различны, причем при r = 0 эти плоскости сливаются в одну.
2) Хотя бы один из коэффициентов р или q отличен от нуля. В этом случае повернем систему координат вокруг осиOz так, чтобы новая ось абсцисс стала параллельной плоскости 2рх+2qy+r=0. Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначения х, у и z для новых координат точек, уравнение (17) примет вид
a33 z2 + 2q´y = 0 (19)
которое является уравнением параболического цилиндра с образующими, параллельными новой оси Ох.
1 . Эллипсоид.
. Эллипсоид.
Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат—центром симметрии. Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтобы более наглядно представить себе формуэллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей.
Ради определенности рассмотрим линииLh пересечения эллипсоида с плоскостями
z = h (20)
параллельными плоскости Оху. Уравнение проекцииL*h линииLh на плоскость Оху получается из уравнения (3), если положить в немz = h. Таким образом, уравнение этой проекции имеет вид

Е сли положить
сли положить
то уравнение (21) можно записать в виде

т . е.L*h представляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (22). Так как Lh получается «подъемом»L*h на высоту h по оси Оz (см. (20)), то и Lh представляет собой эллипс.
. е.L*h представляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (22). Так как Lh получается «подъемом»L*h на высоту h по оси Оz (см. (20)), то и Lh представляет собой эллипс.
Представление об эллипсоиде можно получить следующим образом. Рассмотрим на плоскости Оху семейство эллипсов (23) (рис. 1), полуоси а* и b* которых зависят отh (см. (22)), и каждый такой эллипс снабдим отметкой h, указывающей, на какую высоту по оси Оz должен быть «поднят» этот эллипс. Мы получим своего рода «карту» эллипсоида. Используя эту «карту», легко представить себе пространственный вид эллипсоида.
(Метод представления формы фигуры путем получения «карты» фигуры я привожу только для эллипсоида, представить форму других фигур этим методом можно аналогично)
Наглядное изображение эллипсоида находится на следующей странице.
Эллипсоид .
2. Гиперболоиды.
1°. Однополостный гиперболоид. Обратимся к каноническому
у равнению (4) однополостного гиперболоида
равнению (4) однополостного гиперболоида
Из уравнения (4) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.

 2°. Двуполостный гиперболоид. Из канонического уравнения (5)двуполостного гиперболоида вытекает, что координатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.
2°. Двуполостный гиперболоид. Из канонического уравнения (5)двуполостного гиперболоида вытекает, что координатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.

3. Параболоиды.
1°. Эллиптический параболоид. Обращаясь к каноническому уравнению (14) эллиптического параболоида

мы видим, что для негоOxz и Оуz являются плоскостями симметрии. Ось Oz, представляющая линию пересечения этих плоскостей, называется осью эллиптического параболоида.

 2°. Гиперболический параболоид. Из канонического уравнения (15)гиперболического параболоида вытекает, что плоскости Oxz и Оуz являются плоскостями симметрии. ОсьOz называется осью гиперболического пaраболоида.
2°. Гиперболический параболоид. Из канонического уравнения (15)гиперболического параболоида вытекает, что плоскости Oxz и Оуz являются плоскостями симметрии. ОсьOz называется осью гиперболического пaраболоида.
Прим.: получение «карты высот» для гиперболического пaраболоида несколько отличается от аналогичной процедуры для вышеприведенных поверхностей 2-го порядка, поэтому я также включил его в свой реферат.
Линииz=h пересечения гиперболического параболоида плоскостямиz=h представляют собой при h>0 гиперболы

с полуосями

а приh < 0 —сопряженные гиперболы для гипербол (24)
приh < 0 —сопряженные гиперболы для гипербол (24)
 с полуосями
с полуосями
И
 спользуя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
спользуя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Из формул (25) и (27) вытекает, что прямые (28) являются асимптотами гипербол (24) и (26).Карта гиперболического параболоида дает представление о его пространственной форме. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостьюOxz (Оуz), когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостьюOyz (Oxz).
Прим.: Изображение гиперболического пaраболоида дано на следующей странице.
 иперболический параболоид.
иперболический параболоид.4. Конус и цилиндры второго порядка.
 1°. Конус второго порядка
1°. Конус второго порядка
 Убедимся, что вещественный конус S образован прямыми линиями, проходящими через начало О координат. Естественно называть точку О вершиной конуса.
Убедимся, что вещественный конус S образован прямыми линиями, проходящими через начало О координат. Естественно называть точку О вершиной конуса.
Для доказательства сформулированного утверждения, очевидно, достаточно установить, что прямая L, соединяющая произвольную, отличную от начала координат точку М0(х0, у0, z0) конуса (6) и начало координат О , целиком располагается на конусе, т. е. координаты (х, у, z) любой точки М прямойL удовлетворяют уравнению (6).
Т ак как точка М0(х0, у0, z0) лежит на конусе (6), то :
ак как точка М0(х0, у0, z0) лежит на конусе (6), то :
К оординаты (х, у, z) любой точки М прямой L равны соответственноtx0, ty0 , tz0, гдеt—некоторое число. Подставляя эти значения для х, у иz в левую часть (6), вынося затем t2 за скобку и учитывая (29), мы убедимся в том, что М лежит на конусе. Таким образом, утверждение доказано. Представление о форме конуса может быть получено методом сечений. Легко убедиться, что сечения конуса плоскостями z = h представляютсобой эллипсы с полуосями :
оординаты (х, у, z) любой точки М прямой L равны соответственноtx0, ty0 , tz0, гдеt—некоторое число. Подставляя эти значения для х, у иz в левую часть (6), вынося затем t2 за скобку и учитывая (29), мы убедимся в том, что М лежит на конусе. Таким образом, утверждение доказано. Представление о форме конуса может быть получено методом сечений. Легко убедиться, что сечения конуса плоскостями z = h представляютсобой эллипсы с полуосями :
2°. Эллиптический цилиндр.

 Состоит из прямых линий, параллельных оси Oz .
Состоит из прямых линий, параллельных оси Oz .
 3°. Гиперболический цилиндр.
3°. Гиперболический цилиндр.
 Состоит из прямых линий, параллельных оси Oz .
Состоит из прямых линий, параллельных оси Oz .
4°. Параболический цилиндр. a33 z2 + 2q´y = 0 (19) Путем переименования осей координат и простых арифметических операций из уравнения, (19) мы получим новое, компактное уравнение параболического цилиндра.



nreferat.ru
 Преподаватель: Лебедева Г.А. Иркутск 1999 Поверхности второго порядка Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени. 1. Эллипсоид.
Преподаватель: Лебедева Г.А. Иркутск 1999 Поверхности второго порядка Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени. 1. Эллипсоид.  Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:  (1) Уравнение (1) называется каноническим уравнением эллипсоида. Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями
(1) Уравнение (1) называется каноническим уравнением эллипсоида. Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями  (2) Исследуем уравнения (2) при различных значениях h. 1) Если
(2) Исследуем уравнения (2) при различных значениях h. 1) Если  > c (c>0), то
> c (c>0), то  и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. 2) Если
и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. 2) Если  , то
, то  и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости
и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости  касаются эллипсоида). 3) Если
касаются эллипсоида). 3) Если  , то уравнения (2) можно представить в виде
, то уравнения (2) можно представить в виде  откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями
откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями  и
и  . При уменьшении
. При уменьшении  значения
значения  и
и  увеличиваются и достигают своих наибольших значений при
увеличиваются и достигают своих наибольших значений при  , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями
, т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями  и
и  . Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz. Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой. 2. Однополосный гиперболоид.
. Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz. Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a=b=c эллипсоид является сферой. 2. Однополосный гиперболоид.  Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением  (3) Уравнение (3) называется каноническим уравнением однополосного гиперболоида. Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
(3) Уравнение (3) называется каноническим уравнением однополосного гиперболоида. Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения  и
и  из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями  или
или  (4) из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
(4) из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и  , достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании
, достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании  величины a* и b* возрастают бесконечно. Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.
величины a* и b* возрастают бесконечно. Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.  Величины a, b, c называются полуосями однополосного гиперболоида. 3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
Величины a, b, c называются полуосями однополосного гиперболоида. 3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением  (5) Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
(5) Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения  и
и  из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями
из которых следует, что в сечениях получаются гиперболы. Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями  или
или  (6) из которых следует, что при
(6) из которых следует, что при  >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями
>c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и  . При увеличении
. При увеличении  величины a* и b* тоже увеличиваются. При
величины a* и b* тоже увеличиваются. При  уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости
уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости  касаются данной поверхности). При
касаются данной поверхности). При  уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует. Величина a, b и c называются полуосями двуполостного гиперболоида. 4. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует. Величина a, b и c называются полуосями двуполостного гиперболоида. 4. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением 
 (7) где p>0 и q>0. Уравнение (7) называется каноническим уравнением эллиптического параболоида. Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения
(7) где p>0 и q>0. Уравнение (7) называется каноническим уравнением эллиптического параболоида. Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения  и
и  из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями  или
или  (8) из которых следует, что при
(8) из которых следует, что при  плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями
плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями  и
и  . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет. Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши. Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения). 5. Гиперболический параболоид. Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением
. При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет. Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши. Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения). 5. Гиперболический параболоид. Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением  (9)
(9)  где p>0, q>0. Уравнение (9) называется каноническим уравнением гиперболического параболоида. Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение
где p>0, q>0. Уравнение (9) называется каноническим уравнением гиперболического параболоида. Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение  (10) из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
(10) из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.  рассмотрим сечение данного параболоида плоскостью Oyz (x=0). Получаем уравнение
рассмотрим сечение данного параболоида плоскостью Oyz (x=0). Получаем уравнение  из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения  из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10). Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10). Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения  или
или  из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых
из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых  и
и  точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. 6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. 6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением 
 (11) Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию
(11) Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию  распадающуюся на две пересекающиеся прямые
распадающуюся на две пересекающиеся прямые  и
и  Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые
Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые  и
и  Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим
Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим  или
или  из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями
из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями  . При увеличении абсолютной величины h полуоси a* и b* также увеличиваются. При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0). Cписок использованной лит-ры: 1.Шипачёв В.С.:”Высшая мат-ка” Если сдал РЕФЕРАТ, то отправь свои данные в коллекцию!!!!!!!!!!!!!!!!!!!!!!!!
. При увеличении абсолютной величины h полуоси a* и b* также увеличиваются. При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0). Cписок использованной лит-ры: 1.Шипачёв В.С.:”Высшая мат-ка” Если сдал РЕФЕРАТ, то отправь свои данные в коллекцию!!!!!!!!!!!!!!!!!!!!!!!! works.tarefer.ru