Реферат "Плоскости в пространстве". Плоскость в пространстве реферат

Реферат "Плоскости в пространстве" | Социальная сеть работников образования

Муниципальное образовательное учреждение

Маклинская средняя полная общеобразовательная школа

с углубленным изучением отдельных предметов

РЕФЕРАТ

«Плоскости в пространстве»

Автор:  ученик 11А класса

Дворецкий Сергей

Руководитель-консультант:

Соколова Татьяна Владимировна

г. Малоярославец,  

2008 г.

Оглавление

1. Введение                                                                                                        3
2. Способы задания плоскости                                                                      4  
3. Взаимное расположение плоскостей в пространстве                           7
4. Параллельность плоскостей                                                                     8

1. Признаки параллельности плоскостей                                              8
2. Свойства параллельных плоскостей                                               10

5. Двугранные углы и угол между двумя плоскостями                         14

1. Двугранный угол и его измерение                                                    14
2. Угол между двумя плоскостями                                                        17

6. Перпендикулярность плоскостей                                                          19

6.1. Признаки перпендикулярности двух плоскостей                             19

6.2. Свойства  перпендикулярных плоскостей                                         20

7. Заключение                                                                                                  24

8. Список используемой литературы                                                         25

1. Введение.

 Из курса планиметрии мы знаем, что плоскость – это множество, элементами которого являются точки и в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямы.

Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.

Система аксиом стереометрии дает описание свойств пространства и основных его элементов. Понятия «точка», «прямая» и «плоскость» принимаются без определений: их описание и свойства содержатся в аксиомах. С  другой стороны, понятия «точка», «прямая», «плоскость» имеют наглядный смысл, отраженный на чертежах и рисунках.

Изучение пространства приводит к необходимости расширить систему аксиом планиметрии и рассмотреть новую группу аксиом, в которых выражены свойства взаимного расположения точек, прямых и плоскостей, что особенно важно для нас, в пространстве.

Цель реферата – получить наглядное представление о пространстве и способах расположения плоскостей в пространстве.

Для выполнения этой цели поставлены следующие задачи:

- рассмотреть способы задания плоскостей в пространстве,

- рассмотреть основные аксиомы стереометрии;

- изучить возможные варианты взаимного расположения плоскостей в пространстве,

- сформулировать основные признаки и свойства взаимного расположения плоскостей в пространстве;

- проиллюстрировать теоретический материал практическими примерами.

         2. Способы задания плоскости

Изучение пространства приводит к необходимости расширить систему аксиом.

Рассмотрим  аксиому R1. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Эта аксиома дает нам право рассматривать в любой плоскости пространства отрезки, прямые со всеми их свойствами, которые изучались в планиметрии. Например, если прямая а и не принадлежащая ей точка М лежат в некоторой плоскости α, то в этой плоскости можно провести через точку М прямую, параллельную прямой а, и притом только одну.

В аксиоме R3 говорится: какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Данной аксиомой утверждается, что для любой плоскости в пространстве можно выбрать любое количество точек в этой плоскости, равно как и сколько угодно точек вне её. В случае, если точка А лежит в (принадлежит) плоскости α, то записывают: А α и говорят, что плоскость α проходит через точку А. Если точка А не принадлежит плоскости α, то записывают:  А α и говорят, что плоскость α не проходит через точку А.

Плоскость в пространстве однозначно определяется:

- тремя точками, не лежащими на прямой. Аксиома R2 (аксиома плоскости) гласит:  Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну. Плоскость, которая проходит через точки А, В и С, не принадлежащие одной прямой  (С АВ), обозначается символически (АВС); если этой плоскостью является плоскость  α, то пишут α = (АВС) или (АВС)= α. Стол, имеющий три ножки, не может качаться на плоском полу. Его устойчивость объясняется тем, что концы трех его ножек (три точки) принадлежат одной плоскости – плоскости пола, но не принадлежат одной прямой. Плохо сделанный стол на четырех ножках качается на плоском полу, и под одну из его ножек что-нибудь стараются подложить.

- прямой и точкой, не лежащей на прямой.

По теореме 1 через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Доказательство. Пусть даны прямая а и не принадлежащая ей точка А. Выберем  на прямой а любые точки В и С. Через точки В и С проходит только одна прямая – прямая а. Так как точка А по условию теоремы не принадлежит прямой а, то точки А, В и С  не принадлежат одной прямой. По аксиоме R2 через точки А,В,С проходит только одна плоскость – плоскость АВС, которую обозначим α. Прямая а имеет с ней две общие точки – точки В и С, следовательно по аксиоме R4 (аксиоме прямой и плоскости -  Если прямая проходит через две точки плоскости, то она лежит в этой плоскости) эта прямая лежит в плоскости α. Таким образом, плоскость α проходит через прямую а и точку А и является искомой.

Докажем, что другой плоскости, проходящей через прямую а и точку А  а, не существует.

Предположим, что есть другая плоскость – α, проходящая через точку А и прямую а. Тогда плоскости α и α проходят через точки А, В и С, не принадлежащие одной прямой, а значит совпадают. Следовательно, плоскость α  единственная. Теорема доказана.

- двумя пересекающимися прямыми.

Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.

Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

Доказательство. Пусть данные прямые а и b пересекаются в точке С. Выберем на прямых а и b любые точки А и В, отличные от С: А а, В  b. Тогда точки А, В и  С не принадлежат одной прямой, и по аксиоме R2 через них можно провести только одну плоскость. Обозначим её α.

Точки А и С прямой а принадлежат плоскости α, значит, плоскость α проходит через прямую а (аксиома R4: Если прямая проходит через две точки плоскости, то она лежит в этой плоскости). Плоскость α проходит и через прямую b, так как точки В и С этой прямой принадлежат плоскости α.

Таким образом, плоскость α проходит через прямые а и b, следовательно является искомой.

Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые а и b, плоскость β.

Так как плоскость  β проходит через прямую а и не принадлежащую ей точку В, то по теореме 1 она совпадает с плоскостью α. Единственность плоскости α доказана.

- двумя параллельными прямыми.

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема 3. Через две параллельные прямые можно провести единственную плоскость.

Доказательство. Пусть а и b – данные параллельные прямые. Из определения параллельных прямых следует, что через прямые а и b можно провести плоскость. Обозначим её α и убедимся, что она единственна.

Допустим противное. Пусть  существует другая плоскость, отличная от α , которая содержит каждую из прямых а и b. Обозначим эту плоскость β.

Выберем на  прямой а точки В и С, на  прямой b – точку   А. В силу параллельности прямых а и b точки А, В и С не принадлежат одной прямой.

Каждая из плоскостей α и β содержит обе прямые а и b , значит, каждая из них проходит через точки А, В и С . Но по аксиоме R 2  через эти точки можно провести лишь одну плоскость. Следовательно, плоскости α и β  совпадают. Теорема доказана.

        3. Взаимное расположение плоскостей в пространстве

При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев.

1. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Аксиома R5 гласит: если две плоскости имеют общую точку, то пересечение этих плоскостей есть их общая прямая. Из этой аксиомы следует, что у плоскостей Такие плоскости называются пересекающимися.

2. Две плоскости не имеют общей точки.

3. Две плоскости совпадают

4. Параллельность плоскостей

1. Признаки параллельности плоскостей.

Две плоскости, не имеющие общей точки, называются параллельными.

Если плоскости α и β параллельны, то записывают: α || β или β || α. При этом также говорят, что плоскость α параллельна плоскости β или плоскость β параллельна плоскости α.

Ранее мы доказали, что в пространстве существуют параллельные плоскости. Но возникает вопрос: как определить, параллельны ли две данные плоскости? Ответить на этот вопрос помогают признаки параллельности двух плоскостей.

Теорема 4  (признак параллельности плоскостей). Если каждая из двух пересекающихся прямых одной плоскости параллельна другой плоскости, то данные плоскости параллельны.

Дано: а  α,  b  α,  а b=М,  ,  а || β, b|| β

Доказать: α || β.

Доказательство. Рассуждаем методом от противного. Предположим, что плоскости  α и β не параллельны. Тогда они пересекаются по некоторой прямой с.

В плоскости α  расположены прямая с и данные пересекающиеся прямые а и b. Так как из двух пересекающихся прямых не более, чем одна может быть параллельна данной прямой, то прямая с пересекает, по крайней мере, одну из прямых а и b. Пусть с пересекает прямую а в некоторой точке К: а  с = К.

Имеем: прямая с, следовательно, и точка К лежат в плоскости β. Значит, прямая а пересекает плоскость β. Это противоречит условию теоремы (α || β).

Также к противоречию с условием теоремы придем, если допустим, что пересекаются прямые с и b или прямая с пересекает обе прямые а и b.

         Таким образом, предположив, что плоскости α и β , мы пришли к противоречию. Это означает, что предположение не верно. Следовательно α || β. Теорема доказана.

Рассмотрим ещё один  признак параллельности плоскостей.

Теорема 5. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство. Пусть прямые а и b плоскости  α пересекаются в точке М, прямые а1 и b1 плоскости β параллельны соответственно прямым а и b. Тогда по признаку параллельности прямой и плоскости имеем:

а || а1, а1β       а || β;

b || b1, b1β       b || β

Таким образом, пересекающиеся прямые а и b в плоскости α параллельны плоскости β. По предидущей теореме плоскости α и β параллельны. Теорема доказана.

4.2. Свойства параллельных плоскостей.

Теорема 6. Прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.

Дано:  α || β,  γα=а,  γβ=b.

Доказать: а || b. 

Доказательство. Прямые  а и b лежат в одной плоскости  γ. Эти прямые не имеют общей точки, так как плоскости  α и β параллельны по определению. Теорема доказана.

Теорема 7. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Дано: α || β, а   α=А.

Доказать: α пересекает β.

Доказательство: Выберем в плоскости β любую точку С. Через эту точку и прямую а проведем плоскость γ.

Так как плоскость γ имеет с плоскостями α и β общие точки А и С соответственно, то она пересекает эти плоскости по некоторым прямым b и с, которые проходят соответственно через точки А и С. По предыдущей  теореме прямые b и с параллельны. Тогда в плоскости  γ прямая а пересекает (в точке А) прямую b , которая параллельна прямой с. Значит, прямая а пересекает и прямую с в некоторой точке В. Так как прямая с лежит в плоскости  β, то точка В является точкой пересечения прямой а и плоскости β. Теорема доказана.

Теорема 8. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

Дано: α || β, α  и γ  пересекаются.

Доказать: β и γ пересекаются.

Доказательство. Проведем в плоскости γ прямую а, пересекающую плоскость  α в некоторой точке В. Тогда по теореме 7 прямая а пересекает и плоскость β в некоторой точке А. Следовательно, плоскости  β и γ имеют общую точку А, т. е.  пересекаются. Теорема доказана. 

Вернемся к вопросу о существовании параллельных плоскостей.

Теорема 9. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

Дано: α, М; М α.

Доказать: существует единственная плоскость β такая, что М   β,  β  || α.

Доказательство. В данной плоскости α проведем две произвольные пересекающиеся прямые а и b. Через точку М проведем прямые а1 и b1, параллельные соответственно  а и b. Плоскость, проходящую через пересекающиеся прямые а и b , обозначим β. На основании теоремы 5 плоскость β параллельна плоскости  α.

Докажем  методом от противного, что β – единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку М проходит другая плоскость, например β, параллельная α.

Так как β   пересекает плоскость β (они имеют общую точку М), то по теореме 8  плоскость β пересекает и плоскость α (β  || α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку М можно провести плоскость, отличную от плоскости  β  и параллельную плоскости  α, неверно. Значит, плоскость β – единственна. Теорема доказана.

Данная теорема дает нам хороший способ построения в пространстве плоскости, параллельной данной плоскости.

Рассмотрим третий признак параллельности плоскостей.

Теорема 10. Две плоскости, параллельные третьей, параллельны.

Дано: α || β,  γ || β.

Доказать: α || γ.

Доказательство. Допустим, что плоскости α и γ пересекаются по некоторой прямой с. Выберем на прямой с произвольную точку М. Через эту точку проходят две различные плоскости α и γ, каждая из которых параллельна плоскости  β. Это противоречит теореме  9. Значит, предположение было неверно. Поэтому α || γ. Теорема доказана.

Рассмотрим задачу. Постройте сечение прямоугольной пирамиды РАВСDЕ плоскостью α, которая проходит через внутреннюю точку М основания АВСDЕ параллельно грани РАВ.

Решение. Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость  α параллельна грани РАВ, то: а) прямая пересечения плоскости  α с гранью АВС (плоскостью основания пирамиды) должна быть параллельна АВ; б) прямая пересечения плоскости α сгранью РАЕ – параллельна АР; в) прямая пересечения плоскости α с гранью РВС – параллельна РВ; г) прямая пересечения плоскости α с плоскостью РАD – параллельна РА, поэтому проводим: 1) через точку М прямую КF||АВ, КВС, FАЕ; 2)прямую FH||РА, НРЕ; 3)прямую КR||РВ, RРС; 4)прямую ML || АР, LРD. Пятиугольник HLRKF – искомое сечение. Доказательство проделайте самостоятельно

5.Двугранные углы и угол между двумя плоскостями.

5.1. Двугранный угол и его измерение.

Рассмотрим два полупространства, образованных непараллельными плоскостями. Пересечение этих пространств будем называть двугранным углом.

Прямую, по которой пересекаются плоскости – границы полупространств, называют ребром двугранного угла, а полуплоскости этих плоскостей, образующие двугранный угол,- гранями двугранного угла.

Двугранный угол с гранями α,  β и ребром а обозначают α а β. Можно использовать и такие обозначения двугранного угла К(АВ)Т;  α(АВ)β

Иногда говорят, что двугранный угол αаβ образован двумя полуплоскостями α и β, имеющими общую граничную прямую а.

Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, - модели двугранного угла.

Для  измерения двугранного угла введем понятие его линейного угла. На ребре а двугранного угла αаβ отметим произвольную точку О и в гранях α и β проведем из точки О соответственно лучи ОА и ОВ, перпендикулярные ребру а. Угол АОВ, образованный  этими лучами, называется линейным углом двугранного угла αаβ.

Так как ОАа и  ОВа, то плоскость АОВ перпендикулярна прямой  а. Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру.

Вследствие произвольного  выбора точки О на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны.

Действительно рассмотрим два линейных угла АОВ и АОВ двугранного угла αаβ. Лучи ОА и ОА лежат в одной грани α и перпендикулярны прямой а – ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправленны  лучи ОВ и ОВ. Тогда    АОВ =  АОВ (как углы с сонаправленными сторонами).

Таким образом нами доказана теорема 11. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. Иначе говоря, все линейные углы данного двугранного угла равны между собой.

Отсюда следует определение. Величиной двугранного угла называется величина его линейного угла.

Величина двугранного угла принадлежит промежутку (0  ;180  ). Двугранный угол является острым, прямым или тупым, если его линейный угол соответственно острый, прямой или тупой.

Аналогично тому, как и на плоскости, в пространстве определяются смежные и вертикальные двугранные углы.

5.2. Угол между двумя плоскостями.

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром. Если величина одного из них равна φ, то величины трех остальных равны соответственно 180  - φ, φ, 180   - φ. Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.

Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованный при их пересечении.

Угол между параллельными или совпадающими плоскостями полагается равным нулю.

Если величина угла между плоскостями α и β равна φ, то пишут (α;β) = φ. Так как двугранный угол измеряется своим линейным углом, то из выше приведенного определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это означает, что величина угла между плоскостями принадлежит промежутку  [0;90 ]

Проиллюстрируем теоретический материал примером решения задачи.

Задача. Отрезок DМ длинной 3,2 перпендикулярен плоскости ромба АВСД (АDС – тупой). Диагонали ромба равны 12 и 16. Найдите углы между плоскостями: а) АВС и МВС; б) АМD и СМD.

Решение. а)Пусть DE – высота ромба АВСD. Тогда по теореме о трех перпендикулярах МЕ ВС и DЕМ=φ – линейный угол двугранного угла, образованного плоскостями АВС и МВС. Найдём величину этого угла.

По условию задачи DМ(АВС), поэтому    МDЕ – прямоугольный, значит   tg φ=   . Так как DЕ – высота ромба АВСD, то DЕ= , где S  - площадь этого ромба. Сторона ВС ромба является гипотенузой прямоугольного треугольника ВОС, катеты ОВ и ОС которого равны 6 и 8. Значит ВС= =  =10

Учитывая, что S = хАСхВD=х12х16= 96,  находим: DЕ= Тогда tg φ=  = =, откуда φ = аrctg 

б)Так, как отрезок DМ-перпендикуляр к плоскости ромба АВСD, то АDDМ, CDDM значит  АDС =ψ – линейный угол двугранного угла, образованного пересекающимися плоскостями АDМ и СDМ. Найдем этот угол.

В треугольнике АСD по теореме косинусов находим

Cos ψ  ==-

откуда ψ = arcos (-)

Ответ: а) argtg ; б)arcos (-)

6. Перпендикулярность плоскостей

6.1. Признаки перпендикулярности двух плоскостей

Определение. Две плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90  .

Взаимную перпендикулярность плоскостей α и β обозначают  α  β. При этом также говорят, что плоскость α перпендикулярна плоскости β или плоскость β перпендикулярна плоскости α.

        Все четыре двугранных угла, образованные взаимно перпендикулярными плоскостями прямые. Примерами взаимно перпендикулярных плоскостей могут служить плоскости пола и стены комнаты в хорошо построенном доме, плоскости двух соседних граней куба или прямоугольного параллелепипеда. Для стены и потолка перпендикулярность проверяют при помощи «отвеса». А как проверить перпендикулярны ли две плоскости? Ответы на эти вопросы дают признаки перпендикулярности двух плоскостей, а также свойства, которыми обладают перпендикулярные плоскости.

        Рассмотрим признаки перпендикулярности двух плоскостей.

Теорема 12. (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Дано: α и β пересекаются; а  α;  аβ.

Доказать:  β  α.

Доказательство. Обозначим:  А=а  α, b= α   β. Так как по условию теоремы прямая а перпендикулярна плоскости α, то эта прямая перпендикулярна любой прямой, лежащей в плоскости α. Значит,  а b.

        Проведем в плоскости α через точку А прямую АС, перпендикулярную прямой b. Тогда     ВАС – линейный угол двугранного угла, образованного при пересечении плоскостей α и β. Так  как АВ  α,   то  ВАС = 90  . Это означает, что (α ; β) = 90  , т. е. α β (по определению перпендикулярности плоскостей). Теорема доказана.

Следствие 1. Если в плоскости есть хоть одна прямая, перпендикулярная другой плоскости, то эти плоскости взаимно перпендикулярны.

Следствие 2. Если плоскость перпендикулярна прямой, по которой пересекаются  две данные плоскости, то эта плоскость перпендикулярна каждой из данных плоскостей.

6.2. Свойства перпендикулярных плоскостей

Теорема 13. Если прямая лежит в одной из двух взаимно-перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна другой плоскости.

Дано: α    β ;    α     β=с;    а   α ,  а    с .

Доказать:    а  β.

Доказательство:  Обозначим О = а  с и в плоскости  β  проведем через точку О прямую b, перпендикулярную прямой с. Тогда (а;b) = 90 (как линейный угол прямого двугранного угла, образованного при пересечении плоскостей  α и β). Получаем (ас,  аb)  а  β    (по признаку перпендикулярности прямой и плоскости).  Теорема доказана.

Теорема 14. Если прямая, проведенная через точку одной из двух взаимно перпендикулярны плоскостей, перпендикулярна другой плоскости, то она лежит в первой из них.

Дано: α    β ,  А   а ,  А  α   а    β .

Доказать:   а   α.

Доказательство. Обозначим  с = α    β  и через точку А проведем в плоскости  α  прямую m, перпендикулярную прямой с. По теореме 28 прямая m перпендикулярна плоскости β. Так как в пространстве через точку можно провести лишь одну прямую, перпендикулярную данной плоскости, то прямая а совпадает с прямой m, лежащей в плоскости α. Значит,   а α. Теорема доказана.   

«Теорема отвеса». Если прямая, проведенная через точку одной из двух пересекающихся плоскостей, перпендикулярна другой плоскости и не лежит в первой, то данные плоскости не перпендикулярны.  

        В планиметрии две прямые, перпендикулярные третьей прямой, не могут пересекаться. Проводя аналогию, можно предположить, что не могут пересекаться и две плоскости, перпендикулярные третьей плоскости.   Однако это не так. Достаточно посмотреть на две соседние стены комнаты (надеемся, что они обе перпендикулярны к полу), чтобы убедиться, что эти стены не параллельны. Вообще, если две плоскости пересекаются по прямой, перпендикулярной третьей плоскости, то каждая из них перпендикулярна этой третьей плоскости. Верно и обратное утверждение.

Теорема 15. Если две плоскости, перпендикулярные третьей плоскости, пересекаются,  то прямая их пересечения перпендикулярна третьей плоскости.

Дано: α  γ,   β  γ,    α  β =а

Доказать: а   γ.

Доказательство. Отметим на прямой а произвольную точку А и проведем через неё прямую b, перпендикулярную плоскости γ. Так как точка А принадлежит плоскости   α (Аа = αβ), которая перпендикулярна плоскости γ, то прямая b лежит в плоскости α. Аналогично, точка А принадлежит плоскости β, поэтому прямая b лежит в плоскости β.

        Таким образом, прямая b проходит через точку А, перпендикулярна плоскости  γ и лежит в плоскостях α   и   β. Это означает, что прямая   b совпадает с прямой  а, т. е. а   γ.  Теорема доказана.

        В геометрии часто рассматриваются три попарно взаимно перпендикулярные плоскости, имеющие общую точку.

7. Заключение.

В основу написания реферата легли наглядные представления о пространстве, плоскости и пространственных фигурах полученные в процессе учебной деятельности в школе. Понятия  пространство и  плоскость, параллельность и перпендикулярность  послужили отправными точками для изучения признаков и свойств перпендикулярности и параллельности плоскостей. Так как активное и эффективное изучение стереометрии возможно лишь при решении задач различной сложности,  в реферате, приведено решение практических задач. Теоретический и практический материал в работе сопровождается построением стереометрических чертежей.

В реферате были рассмотрены способы задания плоскостей в пространстве, изучены возможные варианты взаимного расположения плоскостей в пространстве, приведены основные аксиомы стереометрии, доказаны теоремы стереометрии о взаимном расположении плоскостей в пространстве.

С помощью аксиом и теорем стереометрии  сформулированы основные признаки и свойства взаимного расположения плоскостей в пространстве, которые можно и необходимо использовать в практической деятельности. Поэтому вопросы, рассмотренные в реферате, имеют большое практическое значение. Свойства и признаки взаимного расположения плоскостей в пространстве широко используется во многих отраслях науки и техники, а особенно в машиностроении, геодезии и  особенно  в архитектуре.

Таким образом,  задачи,  поставленные в реферате, решены, цель достигнута.

8. Список используемой литературы

1. Костицин В. Н. Практические занятия по стереометрии / В. Н. Костицин. – М.: Издательство «Экзамен», 2004. – 160 с.

2. Потоскуев Е. В. Геометрия. 10 кл.: задачник для общеобразовательных учреждений с углубленным изучением математики/ Е. В. Потоскуев, Л. И. Звавич. – 3-е изд., стереотип. – М.: Дрофа, 2006. – 250 с.

3. Потоскуев Е. В. Геометрия. 10 кл.: учебник для общеобразовательных учреждений с углубленным изучением математики/ Е. В. Потоскуев, Л. И. Звавич. – 4-е изд., стереотип. – М.: Дрофа, 2005. – 223 с.

4. Потоскуев Е. В. Геометрия. 11 кл.: учебник для общеобразовательных учреждений с углубленным изучением математики/ Е. В. Потоскуев, Л. И. Звавич. – 3-е изд., стереотип. –с. М.: Дрофа, 2006. – 368 с.

5. Потоскуев Е. В. Геометрия. 11 кл.: задачник для общеобразовательных учреждений с углубленным изучением математики/ Е. В. Потоскуев, Л. И. Звавич. – 3-е изд., стереотип. – М.: Дрофа, 2005. – 235 с.

6. Поурочные разработки по геометрии: 10 класс/ Сост. В. А. Яровенко. – М.: ВАКО, 2007. – 304 с.

7. Роганин А. Н. Алгебра и геометрия в таблицах и схемах./ А. Н. Роганин, В. А. Дергачев. – Ростов на Дону: Феникс, 2006. – 222 с.

nsportal.ru

4 Прямая на плоскости

Если в системе координат 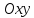на прямой, перпендикулярной нормальному вектору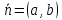, задана точка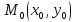, то выбрав на этой прямой произвольную точку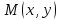, вектор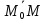можно записать через координаты в виде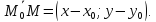

Используя условие перпендикулярности двух векторов 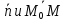, получаем уравнение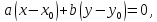(1)

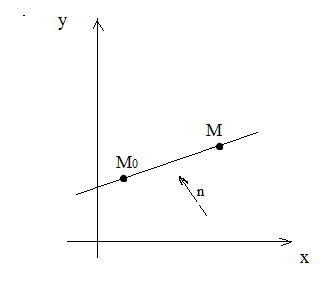
которое носит название уравнения прямой, проходящей через данную точку.

После раскрытия скобок уравнение (1) принимает вид:

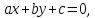(2)

где 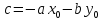. Уравнение (2) называетсяобщим уравнением прямой на плоскости.

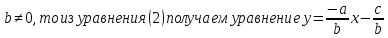Если , или

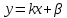, которое носит название уравнения прямой с угловым коэффициентом, а величина 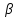определяет ординату точки пересечения прямой с осью .

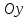Если на плоскости 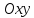заданы две точки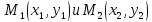, тоуравнение пучка прямых имеет вид: 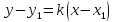(3)

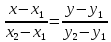(4)

Уравнение (4) называется уравнением прямой, проходящей через две заданные точки.

Возьмем точки 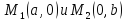и подставим в уравнение (4). Получим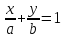–уравнение прямой в отрезках на осях. (5)

Если две прямые 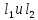заданы уравнениями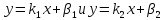, то тангенс угла между ними вычисляется по формуле

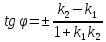(6)

В случае задания двух прямых общими уравнениями прямых 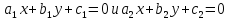можно выразить косинус одного из смежных углов между ними на основе формулы скалярного произведения двух нормальных векторов:

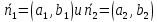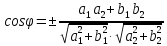(7)

Из формулы (7) следует условие перпендикулярности прямых:

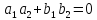, или ,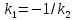

а из формулы (6) – условие параллельности прямых:

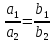или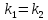

Для определения расстояния от точки 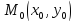до прямой, заданной в общем виде, можно использовать формулу.

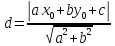Задания:

1. Дано общее уравнение прямой 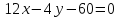. Написать:

а) уравнение с угловым коэффициентом; б) уравнение в отрезках на осях.

2. Написать уравнение прямой, проходящей через точку 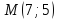и составляющей с осью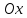угол в.

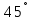3. Определить расстояние между прямыми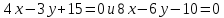

4. Написать уравнение перпендикуляра к прямой 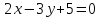, проходящего через точку.

5. Плоскость.

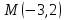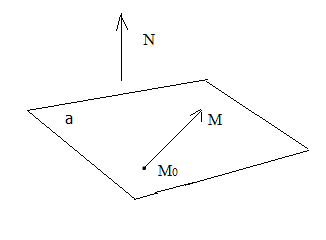
Уравнение плоскости, проходящей через точку 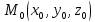и перпендикулярной вектору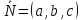, получается на основе использования скалярного произведения двух векторов. Пусть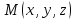- произвольная точка плоскости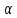. Тогда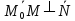и по условию перпендикулярности векторов

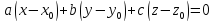(8)

Уравнение (8) называется уравнением плоскости, проходящей через заданную точку. После раскрытия скобок в данном уравнении получим общее уравнение плоскости в пространстве:

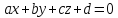(9)

Угол, образованный двумя плоскостями, находится по формуле:

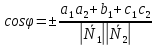, где 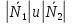- нормальные векторы плоскостей++.

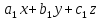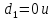
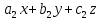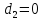Условие параллельности плоскостей имеет вид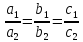

Условием перпендикулярности плоскостей является равенство:

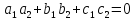(10)

Расстояние от точки 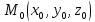до плоскости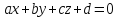определяется по формуле 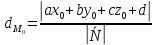(11)

Задания:

1. Составить уравнение плоскости, проходящей через точку 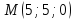и перпендикулярной вектору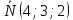

2. Написать уравнение плоскости, параллельной оси 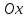и проходящей через точки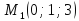и

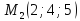
3. Составить уравнение плоскости, проходящей через точки 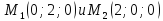и образующей угол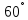с плоскостью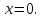

4. Найти расстояние от точки 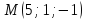до плоскости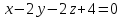

5. Прямая и плоскость в пространстве.

Прямая в пространстве может быть задана двумя пересекающимся плоскостями, уравнения которых 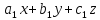+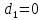и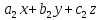+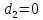. Тогда уравнения прямой будут

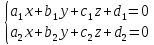(12)

Уравнения (12) называют общими уравнениями прямой.

Уравнения прямой 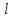, проходящей через точку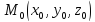и параллельной вектору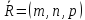, получаются на основе условия коллинеарности двух векторов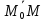и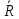: 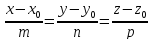- каноническое уравнение прямой

Вектор называетсянаправляющим вектором прямой.

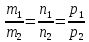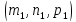Условие параллельности двух прямых имеет вид:, гдеи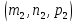координаты направляющих векторов.

Условие перпендикулярности двух прямых записывается в виде:

.

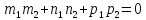Угол между прямой 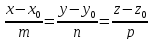и плоскостью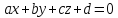определяется выражением 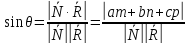(13)

Условие параллельности прямой и плоскости имеет вид:

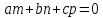(14)

Условием перпендикулярности прямой и плоскости являются равенства:

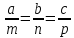(15)

Задания:

1. Написать уравнение прямой, проходящей через точк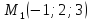и и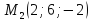и найти ее направляющие косинусы.

2. Показать, что прямая 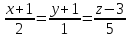параллельна плоскости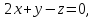а прямая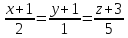лежит в этой плоскости.

Индивидуальные задания

studfiles.net

Читать курсовая по математике: "Плоскость и прямая в пространстве"

(Назад) (Cкачать работу)

Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!

СОДЕРЖАНИЕ ВВЕДЕНИЕ

Глава 1. Плоскость в пространстве

.1 Точка пересечения прямой с плоскостью

.2 Угол между прямой и плоскостью

Глава 2. Прямая в пространстве

.1 Различные случаи положения прямой в пространстве

.2 Угол между прямой и плоскостью

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ВВЕДЕНИЕ Всякое уравнение первой степени относительно координат x, y, z

+ By + Cz +D = 0 задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.

Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении коэффициенты A, B, C одновременно не равны 0. Особые случаи уравнения . D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

) как линия пересечения двух плоскостей,т.е. системой уравнений: A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; ) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями: =; ) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

Уравнения называются каноническими уравнениями прямой.

Вектор a называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений параметру t:

= x1 +mt, y = y1 + nt, z = z1 + рt. Решая систему как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:

= mz + a, y = nz + b От уравнений можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения: От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Системаравносильна системе x = x1, y = y1; прямая параллельна оси Oz.

Цель курсовой работы: изучить прямую и плоскость в пространстве.

Задачи курсовой работы: рассмотреть плоскость в пространстве, её уравнение, а также рассмотреть плоскость в пространстве.

Структура курсовой работы: введение, 2 главы, заключение, список использованных источников.

Глава 1. Плоскость в пространстве

Пусть плоскость Q задана уравнением общего типа: Ax+By+Cz+D=0, а прямая L в параметрическом виде: x=x1+mt, y=y1+nt, z=z1+pt, тогда чтобы найти точку пересечения прямой L и плоскости Q, нужно найти значение параметра t, при котором точка прямой будет лежать на плоскости. Подставив значение x, y, z, в уравнение плоскости и выразив t, получим Значение t будет единственным, если прямая и плоскость не параллельны.

Рассмотрим прямую L: и плоскость α:

+By+Cz+D=0. Прямая L и плоскость α:

а) перпендикулярны друг другу тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т. е.

б) параллельны друг другу тогда и только тогда, когда векторы и перпендикулярны, т. е. и Am + Bn + Ср = 0.

Угол α между нормальным вектором плоскости и направляющим вектором прямой вычисляется по формуле:

Совокупность всех плоскостей, проходящих через заданную прямую L, называется пучком плоскостей, а прямая L - осью пучка. Пусть ось пучка задана уравнениями

Почленно умножим второе уравнение системы на постоянную и сложим с первым уравнением: A1x+B1y+C1z+D1+ λ(A2x+B2y+C2z+D2)=0. Это уравнение имеет первую степень относительно х, у, z и, следовательно, при любом численном значении λ определяет плоскость. Так как данное уравнение есть следствие двух уравнений, то координаты точки, удовлетворяющие этим уравнениям будут удовлетворять и данному уравнению. Следовательно, при любом численном значении λ данное уравнение есть уравнение плоскости, проходящей через заданную прямую. Полученное уравнение есть уравнение пучка плоскостей.

Пример. Написать уравнение плоскости, проходящей через точку M1(2, -3, 4) параллельно прямым Решение. Запишем уравнение связки плоскостей, проходящих через данную точку M1: А (х - 2) + В (у + 3) + C(z - 4) = 0. Так как искомая плоскость должна быть параллельна данным прямым, то ее нормальный вектор должен быть перпендикулярен направляющим векторам этих прямых. Поэтому в качестве вектора N можно взять векторное произведение векторов :

Следовательно, А = 4, В = 30, С = - 8. Подставляя найденные значения А, В, С в уравнение связки плоскостей, получим

4(x-2)+30(y + 3) -8(z-4) =0 или 2x + 15у - 4z + 57 = 0. Пример. Найти точку пересечения прямой и плоскости 2х + 3y-2z + 2 = 0.

Решение. Запишем уравнения данной прямой в параметрическом виде: Подставим эти выражения для х, у, z в уравнение плоскости:

(2t+1)+3(3t-1)-2(2t+5)+2=0 Þ t=1.

Подставим t = 1 в параметрические уравнения прямой. Получим Итак, прямая и плоскость пересекаются в точке М(3, 2, 7).

Пример. Найти угол φ между прямой и плоскостью 4x-2y-2z+7=0.Решение. Применяем формулу (3.20). Так както

Следовательно,φ = 30°.

Глава 2. Прямая в пространстве Прямая линия в пространстве бесконечна, поэтому задавать ее удобнее отрезком. Из школьного курса Евклидовой геометрии известна аксиома, «через две точки в пространстве можно провести прямую и, притом, только одну». Следовательно, на эпюре прямая может быть задана двумя фронтальными и двумя горизонтальными проекциями точек. Но так как прямая - это прямая (а не кривая), то с полным основанием мы можем соединить эти точки отрезком прямой и получить фронтальную и горизонтальную проекции прямой (рис. 13). Доказательство от обратного: в плоскостях проекций V и Н заданы две проекции а' b' и ab (рис.14). Проведем через них плоскости, перпендикулярные к плоскостям проекций V и Н (рис.14), линией пересечения плоскостей будет прямая АВ.

В рассмотренных нами случаях прямые не были ни параллельными, ни перпендикулярными к плоскостям проекций V, Н, W. Большинство прямых занимает именно такое положение в пространстве и их называют прямыми общего положения. Они могут быть восходящими или нисходящими (разобраться самостоятельно).

На рис. 17 показана прямая общего положения, заданная тремя проекциями. Рассмотрим семейство прямых, обладающих важными свойствами - прямые, параллельные какой-либо плоскости проекци.

На рис. 17 показана прямая общего положения, заданная тремя проекциями.

Рассмотрим семейство прямых, обладающих важными свойствами - прямые, параллельные какой-либо плоскости проекций.

а) Горизонтальная прямая (иначе - горизонталь, прямая горизонтальною уровня). Так называется прямая, параллельная горизонтальной плоскости проекций. Ее изображение в пространстве и на эпюре показано на рис. 18. Горизонталь легко узнать на эпюре «в лицо»: ее фронтальная проекция всегда параллельна оси ОХ. Полностью важнейшее свойство горизонтали формулируются так:

У горизонтали - фронтальная проекция параллельна оси ОХ, а горизонтальная отражает натуральную величину. Попутно горизонтальная проекция горизонтали на эпюре позволяет определить угол ее наклона к плоскости V (угол b) и к плоскости W (у) - рис.18.

б) Фронтальная прямая (фронталь, прямая фронтального уровня) - это прямая, параллельная фронтальной плоскости проекций. Мы не иллюстрируем ее наглядным изображением, а показываем ее эпюр (рис. 19).

Эпюр фронтали характерен тем, что горизонтальная и профильная ее проекции параллельны соответственно осям X и Z, а фронтальная проекция располагается произвольно и показывает натуральную величину фронтали. Попутно на эпюре имеются углы наклона прямой к горизонтальной (а) и профильной (у) плоскостям проекций. Итак, еще раз: У фронтали - горизонтальная проекция параллельна оси ОХ, а фронтальная отражает

referat.co

Плоскости в пространстве | Бесплатные курсовые, рефераты и дипломные работы

Решение.

Используя формулу (1), получим

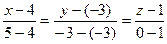или .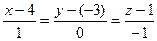

Равенство нулю второй дроби означает, что прямая принадлежит плоскости у = – 3.

Лекция 4

Контрольные вопросы:

1. Общее уравнение плоскости.

2. Уравнение плоскости, проходящей через три заданные точки.

3. Уравнение плоскости, проходящей через заданную точку перпендикулярно данному вектору.

4. Уравнение плоскости в отрезках.

5. Нормальное уравнение плоскости.

6. Угол между двумя плоскостями.

7. Условие параллельности плоскостей.

8. Условие перпендикулярности плоскостей.

9. Расстояние от точки до прямой.

1. … Общее уравнение плоскости Р имеет вид

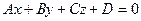, (1)

где 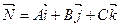– нормальный вектор плоскости (рис. 1).

Рис.1

Частные случаи общего уравнения плоскости:

1.Если 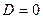, то оно принимает вид Ax+By+Cz=0. Этому уравнению удовлетворяет точка О(0;0;0). Следовательно, в этом случае плоскость проходит через начало координат.

2.Если C=0, то имеем уравнение Ax+By+D=0. Нормальный вектор 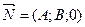перпендикулярен оси Oz. Следовательно, плоскость параллельна Oz; если В=0 – параллельна оси Oy, если A=0 – параллельна оси Ox.

3.Если C=D=0, то плоскость проходит через O(0;0;0) параллельно оси Oz, т.е. плоскость Ax+By=0 проходит через ось Oz. Аналогично, уравнениям By+Cz=0 и Ax+Cz=0 отвечают плоскости, проходящие соответственно через оси Ox и Oy.

4.Если A=B=0, то уравнение (14) принимает вид Cz +D=0, т.е. 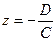. Плоскость параллельна плоскости Oxy. Аналогично, уравнениям Ax+D=0 и By+D=0 отвечают плоскости, соответственно параллельные плоскостям Oyz и Oxz.

5.Если A=B=D=0, то уравнение () примет вид Cz=0, т.е. z=0. Это уравнение плоскости Oxy. Аналогично: y=0 – уравнение плоскости Oxz; x=0 – уравнение плоскости Oyx.

2.Уравнение плоскости, проходящей через три заданные точк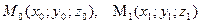и и 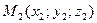имеет вид

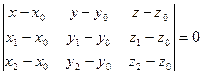. (2)

3.Уравнение плоскости, проходящей через заданную точку перпендикулярно данному вектору. Если в пространстве Oxyz плоскость Р задана точкой 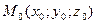и вектором 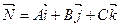, перпендикулярным этой плоскости (рис. 2), то уравнение плоскости имеет вид

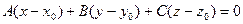. (3)

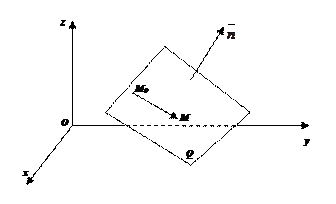
Рис. 2

4.Уравнение плоскости в отрезках. Если плоскость отсекает на осях Ох, Оу, Oz соответственно отрезки a, b, c (рис. 3), т.е. проходит через точки и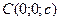, то уравнение плоскости имеет вид

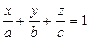. (4)

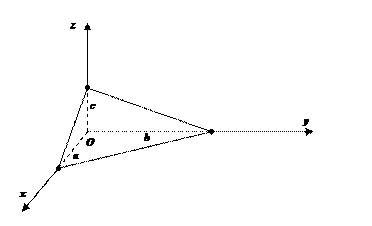
Рис. 3

Замечание. Уравнением (4) удобно пользоваться при построении плоскостей.

5.Нормальное уравнение плоскости. Положение плоскости Р определяется заданием единичного вектора , имеющего направление перпендикуляра ОК, проведенного на плоскость из начала координат, и длиной р этого перпендикуляра (рис. 4).

Рис. 4

Если α, β, γ – это углы, образованные единичным вектором с осями Ох, Оу, Oz соответственно, то уравнение плоскости имеет вид

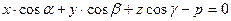. (5)

Замечание. Общее уравнение плоскости (1) можно привести к нормальному уравнению (15), умножив обе части уравнения (1) на нормирующий множитель 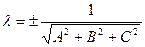, учитывая, что знак нормирующего множителя противоположен знаку свободного члена D общего уравнения плоскости.

6. Угол между двумя плоскостями, имеющими нормальные векторы 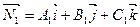и 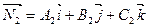(рис. 5), определяется как угол между 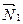и 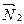; косинус этого угла находится по формуле

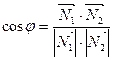
или

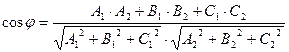. (6)

Рис. 5

Пример 3. Найти угол между плоскостью Р1, проходящей через точки А1(2; -4; 1), А2(-1; 2; 0), А3(0; -2; 3), и плоскостью Р2, заданной уравнением .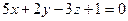

refac.ru

Смотрите также

• 
  Гимнастика для глаз реферат
• 
  Культура древнего китая реферат
• 
  Реферат по астрономии созвездия
• 
  Спорт и здоровье реферат
• 
  Реферат здоровье и спорт
• 
  Реферат экологические проблемы современности
• 
  Реферат по стоматологии ортопедической
• 
  М ю лермонтов реферат
• 
  Реферат пожары по обж
• 
  Реферат по гражданскому праву
• 
  Философское понятие истины реферат