(1)Результат измерений физической величины всегда отличается от истинного значения на некоторую величину, которая называется погрешностью
КЛАССИФИКАЦИЯ:
1. По способу выражения: абсолютные, приведенные и относительные
2. По источнику возникновения: методические и инструментальные.
3. По условиям и причинам возникновения: основные и дополнительные
4. По характеру изменения: систематические и случайные.
5. По зависимости от входной измеряемой величины: аддитивные и мультипликативные
6. По зависимости от инерционности: статические и динамические.
Абсолютная погрешность — это разность между измеренным и действительным значениями измеряемой величины:
(1)
где Аизм, А - измеряемое и действительное значения; ΔА - абсолютная погрешность.
Абсолютную погрешность выражают в единицах измеряемой величины. Абсолютную погрешность, взятую с обратным знаком, называют поправкой.
Относительная погрешность р равна отношению абсолютной погрешности ΔА к действительному значению измеряемой величины и выражается в процентах:
(2)
Приведенная погрешность измерительного прибора - это отношение абсолютной погрешности к номинальному значению. Номинальное значение для прибора с односторонней шкалой равно верхнему пределу измерения, для прибора с двусторонней шкалой (с нулем посередине) — арифметической сумме верхних пределов измерения:
пр. ном.
Погрешность метода обусловлена несовершенством применяемого метода измерения, неточностью формул и математических зависимостей, описывающий данный метод измерения, а также влиянием средства измерения на объект свойства которого изменяются.
Инструментальная погрешность (погрешность инструмента) обусловлена особенностью конструкции измерительного устройства, неточностью градуировки, шкалы, а также неправильностью установки измерительного устройства.
Инструментальная погрешность, как правило, указывается в паспорте на средство измерения и может быть оценена в числовом выражении.
Систематическая погрешность - постоянная или закономерно изменяющаяся погрешность при повторных измерениях одной и той же величины в одинаковых условиях измерения. Например, погрешность, возникающая при измерении сопротивления ампервольтметром, обусловленная разрядом батареи питания.
Случайная погрешность - погрешность измерения, характер изменения которой при повторных измерениях одной и той же величины в одинаковых условиях случайный. Например, погрешность отсчета при нескольких повторных измерениях.
Причиной случайной погрешности является одновременной действие многих случайных факторов, каждый из которых в отдельности мало влияет.
Случайная погрешность может быть оценена и частично снижена путём правильной обработки методами математической статистики, а также методами вероятности.
Основная погрешность - погрешность, возникающая в нормальных условиях применения средства измерения (температура, влажность, напряжение питания и др.), которые нормируются и указываются в стандартах или технических условиях.
Дополнительная погрешность обуславливается отклонением одной или нескольких влияющих величин от нормального значения. Например, изменение температуры окружающей среды, изменение влажности, колебания напряжения питающей сети. Значение дополнительной погрешности нормируется и указывается в технической документации на средства измерения.
Статическая погрешность - погрешность при измерении постоянной по времени величины. Например, погрешность измерения неизменного за время измерения напряжения постоянного тока.
Динамическая погрешность - погрешность измерения изменяющейся во времени величины. Например, погрешность измерения коммутируемого напряжения постоянного тока, обусловленная переходными процессами при коммутации, а также ограниченным быстродействием измерительного прибора.
studfiles.net
4
Точность косвенных измерений зависит как от надёжности используемых для расчёта данных, так и от структуры формул, связывающей эти данные с искомой величиной.
Точность измерений характеризуется их погрешностями. Абсолютная погрешность измерения по своему смыслу есть разность между результатом измерения и истинным значением измеряемой величины. Обозначая абсолютную погрешность измерения величины x символом x, получим
x = xизм − xист. | (2.1) |
Ясно, что измеряется абсолютная погрешность | x в тех же едини- |
цах, что и измеряемая величина x. |
|
Абсолютная погрешность ничего не говорит о качестве проводимых измерений. Одна и та же погрешность x = 1 мм при измерении длины комнаты не сыграет роли, при измерении длины стола может быть уже существенна, а при измерении диаметра болта совершенно недопустима. Качество измерения характеризует относительная погрешность отношение абсолютной погрешности к самой вели-
чине: |
|
|
|
|
|
ε(x) = | Δ(x) | = | xизм− xист | . | (2.2) |
xист |
| ||||
|
| xист |
| ||
Относительная погрешность безразмерная величина. Очень часто её выражают в процентах.
Согласно (2.1) и (2.2), чтобы найти абсолютную и относительную погрешности измерения, нужно знать не только измеренное, но и истинное значение интересующей нас величины. Цель измерений всегда состоит в том, чтобы узнать неизвестное заранее значение физической величины и оценить погрешность измерения. При оценках погрешностей учитываются условия проведения эксперимента, точность методики, качество приборов и ряд других факторов. Единого правила, шаблона, пригодного для всех случаев жизни, нет.
5
Говоря о погрешностях измерений, необходимо прежде всего упомянуть о грубых погрешностях (промахах), возникших вследствие недосмотра экспериментатора или неисправности аппаратуры. В эту группу входят погрешности, существенно превышающие ожидаемую при данных условиях. Например, при измерении длины линейкой промах может появиться в результате того, что один из концов измеряемого объекта оказался совмещённым не с “0” линейки, а, скажем, с делением “10” мм, причём отсчёт будет сделан без учёта этого обстоятельства.
Грубых ошибок следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбросить. Промахи выявляются при повторных измерениях, если они сделаны другим лицом, не знающим результатов предыдущего измерения.
Не связанные с грубыми ошибками, все погрешности делятся на систематические и случайные. Деление на систематчисекие и случайные погрешности обусловлено природой, т.е. причиной возникновения этих погрешностей.
Случайные погрешности меняют величину и знак от опыта к опыту. Причиной такого изменения могут быть, например, неодинаковая масса гирь одного номинала, изменяющаяся величина силы трения во вращающихся частях прибора и т.п. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто результаты не в точности равны друг другу, а “пляшут” вокруг некоторого среднего значения.
Случайные погрешности эксперимента исследуются путём сравнения результатов, полученных при нескольких измерениях, проведённых в одинаковых условиях. Если при двух-трёхизмерениях результаты совпали, то на этом следует остановиться. Если они расходятся, нужно попытаться понять причину расхождения и устранить её. Если устранить причину не удаётся, следует провести 10 12 измерений и, записав все результаты, обработать их в соответствии с полученной закономерностью разброса величин.
Систематические погрешности сохраняют свою величину и знак во время эксперимента. Они вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений.
Все факторы, обусловливающие систематические погрешности, можно разделить на четыре группы:
1. Погрешности, природа которых нам известна, и их значение может быть достаточно точно определено. Как правило, это погрешности методики измерения. Например, при взвешивании не учиты-
6
вается сила выталкивания воздуха. Такие погрешности устраняются путём введения соответствующих поправок. Величина поправок, которые ещё есть смысл вводить, устанавливается в зависимости от значения других погрешностей, сопровождающих данное измерение.
2.Погрешности, также обусловленные недостатками методики измерений, но о существовании которых не подозреваем, хотя они могут быть значительными. Например, если хотим измерить плотность какого-тометалла и для этого определим объём и массу образца, то совершим грубую ошибку, если образец содержал внутри пустоты. Здесь приведён простейший пример. При более сложных измерениях нужно всегда очень тщательно продумывать методику, чтобы избежать ошибок подобного рода. Один из наиболее надёжных способов провести измерение искомой величины совсем другим методом и в других условиях.
3.Погрешности, обусловленные объектом измерений. Эта группа ошибок, хотя и не связана непосредственно с измерительными операциями, может существенным образом исказить результат измерений.
Пример. Если для измерения электропроводности металла взят отрезок проволоки, имеющий утолщение или овальность, то, измерив диаметр проволоки в одном месте, можно допустить существенную ошибку. Для устранения погрешности такого сорта следует провести измерение диаметра проволоки в нескольких местах, а ещё лучше провести измерения на нескольких идентичных образцах. При этом такая погрешность из систематической переводится в случайную.
4.Погрешности известного происхождения, но неизвестной величины. К этой группе относится погрешность измерительных приборов: неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта. Именно эта группа ошибок и будет учитываться в лабораторном практикуме как систематическая погрешность. Способы определения систематической погрешности приборов будут рассмотрены в следующих разделах.
Различие между систематическими и случайными погрешностями не является абсолютным и связано с постановкой опыта. Например, производя измерение тока не одним, а несколькими одинаковыми амперметрами, мы превращаем систематическую ошибку, связанную с неточностью шкалы, в случайную, величина и знак которой зависят от того, какой поставлен амперметр в данном опыте. Однако во всяком опыте при заданной его постановке различие между систематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определённостью [3].
studfiles.net
Абсолютной погрешностью измерения называется величина, определяемая разницей между результатом измерения x и истинным значением измеряемой величины x0:
Δx = |x – x0|.
Величина δ, равная отношению абсолютной погрешности измерения к результату измерения, называется относительной погрешностью:
δ = 
Пример 2.1. Приближённым значением числа π является 3.14. Тогда погрешность его равна 0.00159… . Абсолютную погрешность можно считать равной 0.0016, а относительную погрешность равной 0.0016/3.14 = 0.00051 = 0.051 %.
Значащие цифры. Если абсолютная погрешность величины a не превышает одной единицы разряда последней цифры числа a, то говорят, что у числа все знаки верные. Приближённые числа следует записывать, сохраняя только верные знаки. Если, … например, абсолютная погрешность числа 52400 равна 100, то это число должно быть записано, например, в виде 524·10 2 или 0.524·10 5. Оценить погрешность приближённого числа можно, указав, сколько верных значащих цифр оно содержит. При подсчёте значащих цифр не считаются нули с левой стороны числа.
Например, число 0.0283 имеет три верных значащих цифры, а 2.5400 – пять верных значащих цифр.
Правила округления чисел. Если приближённое число содержит лишние (или неверные) знаки, то его следует округлить. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры (d) округлённого числа. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причём если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу.
Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются (как и лишние нули). Например, если погрешность измерения 0.001 мм, то результат 1.07005 округляется до 1.070. Если первая из изменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148935 с точностью измерения 50 имеет округление 148900. Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего чётного числа. Например, число 123.50 округляется до 124. Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. Например, число 6783.6 округляется до 6784.
Пример 2.2. При округлении числа 1284 до 1300 абсолютная погрешность составляет 1300 – 1284 = 16, а при округлении до 1280 абсолютная погрешность составляет 1280 – 1284 = 4.
Пример 2.3. При округлении числа 197 до 200 абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна 3/197 ≈ 0.01523 или приближённо 3/200 ≈ 1.5 %.
Пример 2.4. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая – 50 г. Взвешивание дало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превышает 50/3600 = 1.4 %.
Погрешности решения задачи на PC
В качестве основных источников погрешности обычно рассматривают три вида ошибок. Это так называемые ошибки усечения, ошибки округления и ошибки распространения. Например, при использовании итерационных методов поиска корней нелинейных уравнений результаты являются приближёнными в отличие от прямых методов, дающих точное решение.
Ошибки усечения
Этот вид ошибок связан с погрешностью, заложенной в самой задаче. Он может быть обусловлен неточностью определения исходных данных. Например, если в условии задачи заданы какие-либо размеры, то на практике для реальных объектов эти размеры известны всегда с некоторой точностью. То же самое касается любых других физических параметров. Сюда же можно отнести неточность расчётных формул и входящих в них числовых коэффициентов.
Ошибки распространения
Данный вид ошибок связан с применением того или иного способа решения задачи. В ходе вычислений неизбежно происходит накопление или, иначе говоря, распространение ошибки. Помимо того, что сами исходные данные не являются точными, новая погрешность возникает при их перемножении, сложении и т. п. Накопление ошибки зависит от характера и количества арифметических действий, используемых в расчёте.
Ошибки округления
Это тип ошибок связан с тем, что истинное значение числа не всегда точно сохраняется компьютером. При сохранении вещественного числа в памяти компьютера оно записывается в виде мантиссы и порядка примерно так же, как отображается число на калькуляторе.
refac.ru
Измерения многих величин, встречающихся в природе, не может быть точным. Измерение дает число, выражающее величину с той или иной степенью точности (измерение длины с точностью до 0,01 см, вычисление значения функции в точке с точностью до 
и т.д.), то есть приближенно, с некоторой погрешностью. Погрешность может быть задана наперед, или, наоборот, ее требуется найти.
Теория погрешностей имеет объектом своего изучения в основном приближенные числа. При вычислениях вместо 
обычно используют приближенные числа: 
(если точность не особо важна), 
(если точность важна). Как проводить вычисления с приближенными числами, определять их погрешности – этим занимается теория приближенных вычислений (теория погрешностей).
В дальнейшем точные … числа будем обозначать заглавными буквами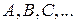 
, а соответствующие им приближенные – строчными 
Погрешности, возникающие на том или ином этапе решения задачи можно условно разделить на три типа:
1) Погрешность задачи. Этот тип погрешности возникает при построении математической модели явления. Далеко не всегда оказывается возможным учесть все факторы и степень их влияния на окончательный результат. То есть, математическая модель объекта не является его точным образом, не является точным его описание. Такая погрешность является неустранимой.
2) Погрешность метода. Эта погрешность возникает в результате подмены исходной математической модели более упрощенной, например, в некоторых задачах корреляционного анализа приемлемой является линейная модель. Такая погрешность является устранимой, так как на этапах вычисления она может свестись к сколь угодно малой величине.
3) Вычислительная («машинная») погрешность. Возникает при выполнении арифметических операций компьютером.
Определение 1.1. Пусть 
– точное значение величины (числа), 
– приближенное значение той же величины ( 
). Истинной абсолютной погрешностью 
приближенного числа называется модуль разности точного и приближенного значений:
. (1.1)
Пусть, например, =1/3. При вычислении на МК дали результат деления 1 на 3 как приближенное число =0,33. Тогда 
.
Однако в действительности в большинстве случаев точное значение величины не известно, а значит, нельзя применять (1.1), то есть нельзя найти истинную абсолютную погрешностью. Поэтому вводят другую величину, служащей некоторой оценкой (верхней границей для ).
Определение 1.2. Предельной абсолютной погрешностью 
приближенного числа , представляющее неизвестное точное число , называется такое возможно меньшее число, которого не превосходит истинная абсолютная погрешность , то есть 
. (1.2)
Для приближенного числа величин , удовлетворяющих неравенству (1.2), существует бесконечно много, но самым ценным из них будет наименьшее из всех найденных. Из (1.2) на основании определения модуля имеем 
, или сокращенно в виде равенства
. (1.3)
Равенство (1.3) определяет границы, в которых находится неизвестное точное число (говорят, что приближенное число выражает точное с предельной абсолютной погрешностью). Нетрудно видеть, что чем меньше , тем точнее определяются эти границы.
Например, если измерения некоторой величины дали результат 
см, при этом точность этих измерений не превосходила 1 см, то истинная (точная) длина 
см.
Пример 1.1. Дано число 
. Найти предельную абсолютную погрешность числа 
числом .
Решение: Из равенства (1.3) для числа ( =1,243; =0,0005) имеем двойное неравенство 
, то есть
(*)
Тогда задача ставится так: найти для числа предельную абсолютную погрешность 
, удовлетворяющую неравенству 
. Учитывая условие (*), получим (в (*) вычитаем 
из каждой части неравенства)
.
Так как в нашем случае 
, то 
, откуда =0,0035.
Ответ: =0,0035.
Предельная абсолютная погрешность часто плохо дает представление о точности измерений или вычислений. Например, =1 м при измерениях длины здания укажет, что они проводились не точно, а та же погрешность =1 м при измерениях расстояния между городами дает очень качественную оценку. Поэтому вводят другую величину.
Определение 1.3. Истинной относительной погрешностью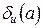 
числа , являющегося приближенным значением точного числа , называется отношение истинной абсолютной погрешности числа к модулю самого числа :
. (1.4)
Например, если 
соответственно точное и приближенное значения, то
.
Однако формула (1.4) неприменима, если не известно точное значение числа. Поэтому по аналогии с предельной абсолютной погрешностью вводят предельную относительную погрешность.
Определение 1.4. Предельной относительной погрешностью числа , являющегося приближенным значением неизвестного точного числа , называется возможно меньшее число 
, которого не превосходит истинная относительная погрешность 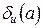, то есть
. (1.5)
Из неравенства (1.2) имеем 
; откуда, учитывая (1.5)
загрузка…
. (1.6)
Формула (1.6) имеет большую практическую применимость по сравнению с (1.5), так как в ней не участвует точное значение. Учитывая (1.6), (1.3), можно найти границы, в которых заключается точное значение неизвестной величины:
(приближенное число выражает неизвестное точное число с предельной относительной погрешностью ). Ясно, что чем меньше , тем точнее вычисляются границы точного числа .
Пример 1.2. Учитывая данные примера 1.1, найти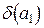 
.
Решение: Имеем =0,0035, . Тогда =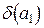 
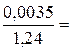0,0028.
Пример 1.3. Выяснить, какое из приближенных равенств точнее:
.
Решение:Для решения задачи необходимо найти предельные относительные погрешности чисел 
( 
), 
( 
) и сравнить их.
1) Находим сначала предельные абсолютные погрешности. При помощи калькулятора вычисляем числа , с большим числом знаков: =0,2727(27), =4,2426…. Тогда имеем (по определению)
,
.
2) Теперь вычисляем предельные относительные погрешности, пользуясь формулой (1.6):
,
.
Итак,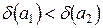 
. Значит, первое равенство точнее второго.
refac.ru
