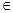 А, а если а не принадлежит А, то пишут: а
А, а если а не принадлежит А, то пишут: а А.
А.РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2 -5х+6=0;
6) множество действительных корней уравнения х2 +9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а А.
Например, пусть N–множество натуральных чисел. Тогда 5N, но N, N. Если А — множество корней уравнения х2 -5х+6=0, то 3 А, а 4А.
В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+, Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d, обозначают с помощью фигурных скобок: А={a; b; c; …;d}. Множество корней уравнения х2 -5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2 -5х+6=0}. Решив уравнение х2 -5х+6=0, мы можем записать множество А первым способом: А={2; 3}.
Другой пример: Х={х | -1 ≤ х < 4, х Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такой пример: F={f | │fґ(x)│≤ 1, 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А — пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А={х | хІ+9=0, хR} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и . Если, например, А — множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В А. Пустое множество считают подмножеством любого множества Х, т.е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.
Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.
Если Х У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если АВ, а В С, то АС.
Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому А С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств
Объединением АВ множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А В={х | хА или хВ}.
Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
На диаграмме объединение множеств А и В выделено штриховкой.
Если множество А определяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х), то А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k Z}, B={x | x=8n-4, n Z}. Тогда A B ={x | 4m, mZ}.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {Аα } называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются.
Таким образом, элемент хтогда и только тогда, когда найдется такой индекс α0 М, что х A α0.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись Если M=N, то имеем объединение последовательности множеств .
Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда = [0;2).
Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1A2 = A2 А1, и ассоциативна, т.е. (А1A2 ) А3 = А1(A2 А3 ).
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | хА и х В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7}.Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m Z}.
4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов.
Операцию пересечения можно определить и для произвольной системы множеств {Аα }, где α М. Пересечением системы множеств {Аα }, называется множество , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α М, т.е. = {x | xАα для каждого α М}.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись . Если M=N, то имеем пересечение последовательности множеств .
В рассмотренном выше примере системы множеств Аα =[0; α], αМ =(1; 2) получим:=[0;1].
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1 ∩A2 = A2 ∩А1 и (А1 ∩A2 )∩ А3 = А1 ∩(A2 ∩ А3 ).
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
А\В={х | х А и хВ},
что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность А\В выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А — множество всех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогда А\В — множество всех четных целых чисел, которые не делятся на 3, а В\А –множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество А и В таковы, что АВ. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СB А=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СU А=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x A}.
На диаграммах Эйлера-Венна можно так пояснить определения СВ А и СА:
www.ronl.ru
РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество — набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2-5х+6=0;
6) множество действительных корней уравнения х2+9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845−1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества? малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если, а не принадлежит А, то пишут: а А.
Например, пусть N-множество натуральных чисел. Тогда 5N, но N, N. Если, А — множество корней уравнения х2-5х+6=0, то 3 А, а 4А.
В математике часто исследуются так называемые числовые множества, т. е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+, Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество, А считается заданным, если относительно любого объекта, а можно установить, принадлежит этот объект множеству, А или не принадлежит; другими словами, если можно определить, является ли, а элементом множества, А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т. е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, …, d, обозначают с помощью фигурных скобок: А={a; b; c; …; d}. Множество корней уравнения х2-5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел -1, 0, 1, 2, поэтому В={-1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р (х), также записывают с помощью фигурных скобок: Х= Р (х), и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р (х). Например, А= х2-5х+6=0. Решив уравнение х2-5х+6=0, мы можем записать множество, А первым способом: А={2; 3}.
Другой пример: Х=х, т. е. Х есть множество целых чисел х, таких, что -1? х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такой пример: F= ¦fґ(x)¦? 1, 1 < x < 2, т. е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество, А — пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А= хІ+9=0, хR -множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
Включение и равенство множеств
Пусть Х и У — два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения или относятся только ко множествам и их не следует смешивать со знаками принадлежности и. Если, например, А — множество всех студентов вуза, а В — множество студентов-первокурсников этого вуза, то В есть подмножество А, т. е. В А. Пустое множество считают подмножеством любого множества Х, т. е. Ш Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х Х.
Если для двух множеств Х и У одновременно имеют место два включения Х У и У Х, т. е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В= хІ -5х+6=0, то А=В.
Если Х У, но Х? У, т. е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: NZ, ZQ, QR. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U.
Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т. п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество, А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если АВ, а В С, то АС.
Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х А; так как, А В, то х В, а так как В С, то из х В следует, что х С; значит, из того, что х А, следует хС, а поэтому, А С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств
Объединением АВ множеств, А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств, А или В.
Символическая запись этого определения: А В=х.
Здесь союз «или» понимается в смысле «неразделительного или», т. е. не исключается, что х может принадлежать и, А и В. Отметим, что в таком случае элемент х, входящий в оба множества, А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
На диаграмме объединение множеств, А и В выделено штриховкой.
Если множество, А определяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q (х), то, А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда, А В ={2; 3; 5; 6; 7}.
2) Пусть А=[-¼; 2], В=[ -2/3; 7/4]. Тогда, А В=[-2/3; 2].
3) Пусть А= х, B=x. Тогда A B = 4m, mZ.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже — на систему множеств. Система множеств определяется так: если каждому элементу б множества М отвечает множество Аб, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {Аб} называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аб. При этом общие элементы нескольких множеств не различаются.
Таким образом, элемент х тогда и только тогда, когда найдется такой индекс б 0 М, что х A б0.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись Если M=N, то имеем объединение последовательности множеств.
Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого б є М определим множество Аб =[0; б]; тогда = [0; 2).
Из определения операции объединения непосредственно следует, что она коммутативна, т. е. А1 A2 = A2 А1, и ассоциативна, т. е. (А1 A2) А3 = А1 (A2 А3).
Пересечение множеств
Пересечением, А? В множеств, А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств, А и В.
Символическая запись этого определения: А? В= х, А и х В.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
А? В
На диаграмме пересечение множеств, А и В выделено штриховкой.
Если множество, А задается характеристическим свойством Р (х), a множество В-свойством Q (х), то в, А? В входят элементы, одновременно обладающие и свойством Р (х), и свойством Q (х).
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7}. Тогда, А? В={5; 7}.
2) Пусть А=[-¼; 7/4], В=[-2/3; 3/2]. Тогда, А? В= [-¼; 3/2].
3) Пусть А= х=2k, k є Z, B=x. Тогда, А? В = x=6m, m Z.
4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда, А? В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т. е. множество всех квадратов.
Операцию пересечения можно определить и для произвольной системы множеств {Аб}, где б М. Пересечением системы множеств {Аб}, называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аб, б М, т. е. = x Аб для каждого б М.
В случае, когда М конечно и состоит из чисел 1, 2, …, n, применяется запись. Если M=N, то имеем пересечение последовательности множеств.
В рассмотренном выше примере системы множеств Аб =[0; б], бМ =(1; 2) получим: =[0;1].
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т. е. А1?A2 = A2 ?А1 и (А1?A2)? А3= А1?(A2? А3).
Разность множеств
Разностью АВ множеств, А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т. е.
АВ= х, А и хВ,
что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность АВ выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А В ={2; 7}, а ВА={3; 6}.
2. Пусть А=[-¼; 2], В=[-2/3; 7/4]. Тогда АВ=(7/4; 2], а ВА=[-2/3; -¼).
3. Пусть, А — множество всех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогда АВ — множество всех четных целых чисел, которые не делятся на 3, а ВА -множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество, А и В таковы, что АВ. Тогда дополнением множества, А до множества В называется разность ВА. В этом случае применяется обозначение СBА=ВА. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=UА и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА=x.
На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:
Показать Свернутьsinp.com.ua
РЕФЕРАТ
Множества. Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множество студентов в данной аудитории;
2) множество людей, живущих на нашей планете в данный момент времени;
3) множество точек данной геометрической фигуры;
4) множество чётных чисел;
5) множество корней уравнения х2-5х+6=0;
6) множество действительных корней уравнения х2+9=0;
Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект.
Объекты, составляющие данное множество, называют его элементами.
Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а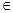 А, а если а не принадлежит А, то пишут: а
А, а если а не принадлежит А, то пишут: а А.
А.
Например, пусть N–множество натуральных чисел. Тогда 5 N , но
N , но
 N,
N,
 N. Если А - множество корней уравнения х2-5х+6=0, то 3
N. Если А - множество корней уравнения х2-5х+6=0, то 3 А, а 4
А, а 4 А.
А.
В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительных чисел.
Приняты также обозначения Z+, Q+, R+соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ-для множеств всех отрицательных целых, рациональных и действительных чисел.
Способы задания множества
Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества:
1) перечисление элементов множества;
2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d ,обозначают с помощью фигурных скобок: А={a; b; c; …;d} . Множество корней уравнения х2-5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2-5х+6=0}. Решив уравнение х2-5х+6=0, мы можем записать множество А первым способом: А={2; 3}.
Другой пример: Х={х | -1 ≤ х < 4, х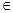 Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такой пример: F={f | │fґ(x)│≤ 1 , 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А - пустое (не содержит ни одного элемента) и пишут: А= Ш.
Например, А={х | хІ+9=0, х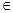 R} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
R} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет.
Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х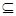 У или У
У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения
Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения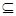 или
или относятся
относятся только ко множествам и их не следует смешивать со знаками принадлежности Î и
только ко множествам и их не следует смешивать со знаками принадлежности Î и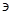 . Если, например, А - множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В
. Если, например, А - множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В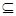 А. Пустое множество считают подмножеством любого множества Х, т.е. Ш
А. Пустое множество считают подмножеством любого множества Х, т.е. Ш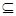 Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х
Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х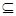 Х.
Х.
Если для двух множеств Х и У одновременно имеют место два включения Х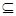 У и У
У и У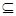 Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.
Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В.
Если Х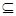 У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х
У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х У. Например: N
У. Например: N Z, Z
Z, Z Q, Q
Q, Q R. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
R. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:

С помощью такой диаграммы становиться наглядным, например, такое утверждение:
если А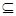 В, а В
В, а В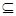 С, то А
С, то А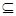 С.
С.

Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х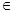 А; так как А
А; так как А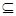 В, то х
В, то х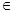 В, а так как В
В, а так как В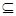 С, то из х
С, то из х В следует, что х
В следует, что х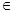 С; значит, из того, что х
С; значит, из того, что х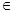 А, следует х
А, следует х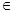 С, а поэтому А
С, а поэтому А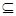 С.
С.
Операции над множествами
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
 Объединение множеств
Объединение множеств
Объединением А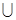 В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А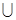 В={х | х
В={х | х А или х
А или х В}.
В}.
Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз).
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:

На диаграмме объединение множеств А и В выделено штриховкой.
Если множество А определяется характеристическим свойством Р (х), а множество В - характеристическим свойством Q(х), то А В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А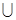 В ={2; 3; 5; 6; 7}.
В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А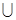 В=[-2/3; 2] .
В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k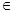 Z}, B={x | x=8n-4, n
Z}, B={x | x=8n-4, n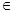 Z}. Тогда A
Z}. Тогда A B ={x | 4m, m
B ={x | 4m, m Z}.
Z}.
Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системы множеств {Аα} называется множество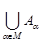 , состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются.
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются.
Таким образом, элемент х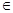
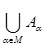 тогда и только тогда, когда найдется такой индекс α0
тогда и только тогда, когда найдется такой индекс α0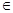 М, что х
М, что х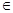 Aα0.
Aα0.
В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись Если M=N, то имеем объединение последовательности множеств
Если M=N, то имеем объединение последовательности множеств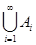 .
.
Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα=[0;α]; тогда = [0;2).
= [0;2).
Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1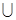 A2= A2
A2= A2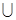 А1, и ассоциативна, т.е. (А1
А1, и ассоциативна, т.е. (А1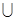 A2)
A2)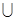 А3= А1
А3= А1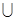 (A2
(A2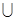 А3).
А3).
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | х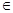 А и х
А и х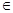 В}.
В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
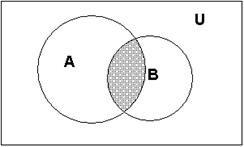
А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х).
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m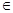 Z}.
Z}.
4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов.
Операцию пересечения можно определить и для произвольной системы множеств {Аα}, где α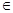 М. Пересечением системы множеств {Аα}, называется множество
М. Пересечением системы множеств {Аα}, называется множество , состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α
, состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α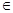 М, т.е.
М, т.е. = {x | x
= {x | x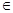 Аαдля каждого α
Аαдля каждого α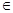 М}.
М}.
В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись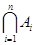 . Если M=N, то имеем пересечение последовательности множеств
. Если M=N, то имеем пересечение последовательности множеств .
.
В рассмотренном выше примере системы множеств Аα=[0; α], α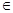 М =(1; 2) получим:
М =(1; 2) получим: =[0;1].
=[0;1].
Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1∩A2= A2∩А1и (А1∩A2)∩ А3= А1∩(A2∩ А3).
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
А\В={х | х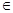 А и х
А и х В},
В},
что можно пояснить на диаграмме Эйлера-Венна следующим образом:

На диаграмме разность А\В выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А - множество всех четных целых чисел, В - множество всех целых чисел, делящихся на 3. тогда А\В - множество всех четных целых чисел, которые не делятся на 3, а В\А –множество всех нечетных целых чисел, кратных трем.
Дополнение множества
Пусть множество А и В таковы, что А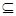 В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:
В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей: СА={x | x
СА={x | x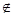 A}.
A}.
На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:


superbotanik.net
РЕФЕРАТ
Множества.Операции над множествами
СОДЕРЖАНИЕ
Способы задания множества
Включение и равенство множеств
Диаграммы Эйлера-Венна
Операции над множествами
а) Объединение множеств
б) Пересечение множеств
в) Разность множеств
Дополнение множества
Понятие множествапринадлежит к числу основных, неопределяемых понятий математики. Оно несводится к другим, более простым понятиям. Поэтому его нельзя определить, аможно лишь пояснить, указывая синонимы слова «множество» и приводя примерымножеств: множество – набор, совокупность, собрание каких-либо объектов(элементов), обладающих общим для всех их характеристическим свойством.
Примеры множеств:
1) множествостудентов в данной аудитории;
2) множество людей,живущих на нашей планете в данный момент времени;
3) множество точекданной геометрической фигуры;
4) множество чётныхчисел;
5) множество корнейуравнения х2-5х+6=0;
6) множестводействительных корней уравнения х2+9=0;
Основоположниктеории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множествоесть многое, мыслимое нами как единое». И хотя это высказывание учёного неявляется в полном смысле логическим определением понятия множества, но оноверно поясняет, что когда говорят о множестве, то имеют в виду некотороесобрание объектов, причём само это собрание рассматривается как единое целое,как один (новый) объект.
Объекты, составляющиеданное множество, называют его элементами.
Множество обычнообозначают большими латинскими буквами, а элементы множества − малымилатинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а />А, а если а непринадлежит А, то пишут: а />А.
Например, пусть N–множество натуральных чисел. Тогда 5/>N, но />/>N, />/>N. Если А — множество корней уравнения х2-5х+6=0,то 3 /> А, а4/>А.
В математикечасто исследуются так называемые числовые множества, т.е. множества, элементамикоторых являются числа. Для самых основных числовых множеств утвердилисьследующие обозначения:
N- множество всех натуральных чисел;
Z- множество всех целых чисел;
Q- множество всех рациональных чисел;
R- множество всех действительныхчисел.
Приняты также обозначенияZ+, Q+, R+ соответственно для множеств всех неотрицательных целых,рациональных и действительных чисел, и Z¯, Q¯, R¯ -для множеств всех отрицательных целых, рациональных идействительных чисел.
Способы заданиямножества
Множество Асчитается заданным, если относительно любого объекта а можно установить,принадлежит этот объект множеству А или не принадлежит; другими словами, еслиможно определить, является ли а элементом множества А или не является.Существуют два основных способа задания множества:
1) перечислениеэлементов множества;
2) указаниехарактеристического свойства элементов множества, т.е. такого свойства, которымобладают все элементы данного множества и только они.
Первым способом особенночасто задаются конечные множества. Например, множество студентов учебной группызадаётся их списком. Множество, состоящее из элементов a, b, c, … ,d, обозначают с помощью фигурных скобок: А={a; b; c; …;d}. Множество корней уравнения х2-5х+6=0состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2< х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}.
Второй способ заданиямножества является более универсальным. Множество элементов х, обладающихданным характеристическим свойством Р(х), также записывают с помощью фигурныхскобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, чтовыполняется свойство Р(х). Например, А={х | х2-5х+6=0}. Решивуравнение х2-5х+6=0, мы можем записать множество А первым способом:А={2; 3}.
Другой пример: Х={х | -1 ≤х < 4, х /> Z}, т.е. Х есть множество целых чиселх, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}.
Рассмотрим и такойпример: F={f | │f´(x)│≤ 1, 1 < x < 2}, т.е. F- множество функций f, производнаякоторых в интервале (1; 2) не превосходит по абсолютной величине числа 1.
Можетслучиться, что характеристическим свойством, определяющим множество А, необладает ни один объект. Тогда говорят, что множество А — пустое (не содержитни одного элемента) и пишут: А= Ø.
Например, А={х |х²+9=0, х/>R} –множество действительных чисел х, таких, что х²+9=0-пустое множество, т.к. таких действительных чисел нет.
Включение и равенствомножеств
Пусть Х и У – двамножества. Если каждый элемент х множества Х является элементом множества У, тоговорят, что множество Х содержится во множестве У и пишут: Х /> У или У />Х. Говорят также, что Хвключено в У или У включает Х, или что Х является подмножеством множества У.Знаки включения /> или /> относятся />только ко множествам иих не следует смешивать со знаками принадлежности Î и /> . Если, например, А — множествовсех студентов вуза, а В – множество студентов-первокурсников этого вуза, то Весть подмножество А, т.е. В /> А. Пустое множество считаютподмножеством любого множества Х, т.е. Ø /> Х, каким бы ни было множество Х.Ясно также, что каждое множество является подмножеством самого себя: Х />Х.
Если для двух множеств Хи У одновременно имеют место два включения Х />У и У /> Х, т.е. Х есть подмножествомножества У и У есть подмножество множества Х, то множества Х и У состоят изодних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У.Например, если А={2; 3}, а В={х | х² –5х+6=0}, то А=В.
Если Х />У, но Х≠ У, т.е.существует хотя бы один элемент множества У, не принадлежащий Х, то говорят,что Х есть собственное подмножество множества У, и пишут: Х /> У. Например: N/>Z, Z/>Q, Q/>R. Далее нам потребуется множество, которое содержит в качествесвоего подмножества любое другое множество. Такое «всеобъемлющее» множество будемназывать универсальным и обозначать буквой U .
Диаграммы Эйлера-Венна
Для наглядногопредставления множеств используют диаграммы Эйлера-Венна. В этом случаемножества обозначают областями на плоскости и внутри этих областей условнорасполагают элементы множества. Часто все множества на диаграмме размещаютвнутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чемодному множеству, то области, отвечающие таким множествам, должныперекрываться, чтобы общий элемент мог одновременно находиться всоответствующих областях. Выбор формы областей, изображающих множества надиаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольникии т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество Аявляется подмножеством множества В:
/>
С помощьютакой диаграммы становиться наглядным, например, такое утверждение:
если А/>В, а В />С, то А/>С.
/>
Строгое доказательство этогоутверждения, не опирающееся на диаграмму, можно провести так: пусть х />А; так как А /> В, то х /> В, а так как В/> С, то изх /> Вследует, что х /> С; значит, из того, что х /> А, следует х/>С, а поэтому А /> С.
Операции надмножествами
С помощьюнескольких множеств можно строить новые множества или, как говорят, производитьоперации над множествами. Мы рассмотрим следующие операции над множествами:объединение, пересечение, разность множеств, дополнение множества. Всерассматриваемые операции над множествами мы будем иллюстрировать на диаграммахЭйлера-Венна.
/>Объединение множеств
Объединением А/>В множеств А иВ называется множество, состоящее из всех элементов, принадлежащих хотя быодному из множеств А или В.
Символическая записьэтого определения: А />В={х | х/>А или х/>В}.
Здесь союз «или»понимается в смысле «неразделительного или», т.е. не исключается, что х можетпринадлежать и А и В. Отметим, что в таком случае элемент х, входящий в обамножества А и В, входит в их объединение только один раз (поскольку длямножества не имеет смысла говорить о том, что элемент входит в него несколькораз).
Пояснимопределение объединения множеств с помощью диаграммы Эйлера-Венна:
/>
На диаграмме объединениемножеств А и В выделено штриховкой.
Если множество Аопределяется характеристическим свойством Р (х), а множество В — характеристическим свойством Q(х),то А /> Всостоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двухмножеств:
1) Пусть А={2; 5; 7}, В={3;5; 6}. Тогда А /> В ={2; 3; 5; 6; 7}.
2) Пусть А=[-1/4; 2], В=[-2/3; 7/4]. Тогда А />В=[-2/3; 2] .
3) Пусть А= {х | х=8k, k /> Z}, B={x | x=8n-4, n /> Z}. Тогда A />B ={x | 4m, m/>Z}.
Операцияобъединения множеств может проводиться не только над двумя множествами.Определение объединения множеств можно распространить на случай любогоколичества множеств и даже – на систему множеств. Система множеств определяетсятак: если каждому элементу α множества М отвечает множество Аα,то совокупность всех таких множеств мы будем называть системой множеств.
Объединением системымножеств {Аα} называется множество />, состоящее из всех элементов,принадлежащих хотя бы одному из множеств Аα. При этом общиеэлементы нескольких множеств не различаются.
Таким образом, элемент х/>/>тогда и только тогда,когда найдется такой индекс α0 />М, что х />A α0.
В случае, когда М конечнои состоит из чисел 1, 2, …, n,применяется запись /> Если M=N, то имеемобъединение последовательности множеств />.
Рассмотрим ещё одинпример: пусть М=(1; 2) и для каждого α є М определим множество Аα=[0;α]; тогда />= [0;2).
Изопределения операции объединения непосредственно следует, что она коммутативна,т.е. А1/> A2 = A2/>А1, иассоциативна, т.е. (А1/> A2) /> А3 = А1/> (A2 /> А3).
Пересечение множеств
Пересечением А ∩ Вмножеств А и В называется множество, состоящее из всех элементов, принадлежащиходновременно каждому из множеств А и В.
Символическая записьэтого определения: А ∩ В={х | х/>А и х />В}.
Пояснимопределение пересечения множеств с помощью диаграммы Эйлера-Венна:
/>
А ∩ В
На диаграммепересечение множеств А и В выделено штриховкой.
Если множество А задаетсяхарактеристическим свойством Р(х), a множество В-свойством Q(х),то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), исвойством Q(х).
Примеры пересечений двухмножеств:
1) Пусть А={2; 5; 7;8}, В={3; 5; 6; 7}.Тогда А ∩ В={5; 7}.
2) Пусть А=[-1/4;7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2].
3) Пусть А= {х |х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m /> Z}.
4) Пусть А-множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В-множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е.множество всех квадратов.
Операциюпересечения можно определить и для произвольной системы множеств {Аα},где α /> М.Пересечением системы множеств {Аα}, называется множество />, состоящее извсех элементов, принадлежащих одновременно каждому из множеств Аα,α />М, т.е./>= {x | x/>Аα для каждогоα /> М}.
В случае,когда М конечно и состоит из чисел 1, 2, …, n, применяется запись />. Если M=N, то имеемпересечение последовательности множеств />.
Врассмотренном выше примере системы множеств Аα =[0; α],α/>М=(1; 2) получим:/>=[0;1].
Операцияпересечения множеств, как и операция объединения, очевидно, коммутативна иассоциативна, т.е. А1∩A2 = A2 ∩А1 и (А1∩A2)∩<sub/>А3= А1∩(A2 ∩ А3).
Разностьмножеств
Разностью А\Вмножеств А и В называется множество, состоящее из всех элементов множества А,которые не принадлежат множеству В, т.е.
А\В={х | х />А и х/>В},
что можнопояснить на диаграмме Эйлера-Венна следующим образом:
/>
На диаграммеразность А\В выделена штриховкой.
Примерыразностей множеств:
1. Пусть А={1; 2; 5;7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
2. Пусть А=[-1/4;2],В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4).
3. Пусть А — множествовсех четных целых чисел, В — множество всех целых чисел, делящихся на 3. тогдаА\В — множество всех четных целых чисел, которые не делятся на 3, а В\А–множество всех нечетных целых чисел, кратных трем.
Дополнениемножества
Пустьмножество А и В таковы, что А/>В. Тогда дополнением множества Адо множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества Вберётся универсальное множество U, топрименяется обозначение СА=СUА=U\А и такое множество просто называютдополнением множества А. Таким образом, символическая запись определениядополнения множества будет следующей: /> СА={x | x />A}.
На диаграммахЭйлера-Венна можно так пояснить определения СВА и СА:
/>
/>
www.ronl.ru
СОДЕРЖАНИЕ Способы задания множества Включение и равенство множеств Диаграммы Эйлера-Венна Операции над множествами а) Объединение множеств б) Пересечение множеств в) Разность множеств Дополнение множества
Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить, указывая синонимы слова «множество» и приводя примеры множеств: множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством. Примеры множеств: 1) множество студентов в данной аудитории; 2) множество людей, живущих на нашей планете в данный момент времени; 3) множество точек данной геометрической фигуры; 4) множество чётных чисел; 5) множество корней уравнения х2-5х+6=0; 6) множество действительных корней уравнения х2+9=0; Основоположник теории множеств немецкий математик Георг Кантор (1845-1918) писал: «Множество есть многое, мыслимое нами как единое». И хотя это высказывание учёного не является в полном смысле логическим определением понятия множества, но оно верно поясняет, что когда говорят о множестве, то имеют в виду некоторое собрание объектов, причём само это собрание рассматривается как единое целое, как один (новый) объект. Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А, а если а не принадлежит А, то пишут: а
А. Например, пусть N–множество натуральных чисел. Тогда 5
N , но
N,
N. Если А - множество корней уравнения х2-5х+6=0, то 3
А, а 4
А. В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых основных числовых множеств утвердились следующие обозначения: N- множество всех натуральных чисел; Z- множество всех целых чисел; Q- множество всех рациональных чисел; R- множество всех действительных чисел. Приняты также обозначения Z+ , Q+, R+ соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и ZЇ, QЇ, RЇ -для множеств всех отрицательных целых, рациональных и действительных чисел. Способы задания множества Множество А считается заданным, если относительно любого объекта а можно установить, принадлежит этот объект множеству А или не принадлежит; другими словами, если можно определить, является ли а элементом множества А или не является. Существуют два основных способа задания множества: 1) перечисление элементов множества; 2) указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они. Первым способом особенно часто задаются конечные множества. Например, множество студентов учебной группы задаётся их списком. Множество, состоящее из элементов a, b, c, … ,d ,обозначают с помощью фигурных скобок: А={a; b; c; …;d} . Множество корней уравнения х2-5х+6=0 состоит из двух чисел 2 и 3: А={2; 3}. Множество В целых решений неравенства -2 < х < 3 состоит из чисел –1, 0, 1, 2, поэтому В={–1; 0; 1; 2}. Второй способ задания множества является более универсальным. Множество элементов х, обладающих данным характеристическим свойством Р(х), также записывают с помощью фигурных скобок: Х={х | Р (х)}, и читают: множество Х состоит из элементов х, таких, что выполняется свойство Р(х). Например, А={х | х2-5х+6=0}. Решив уравнение х2-5х+6=0, мы можем записать множество А первым способом: А={2; 3}. Другой пример: Х={х | -1 ≤ х < 4, х
Z}, т.е. Х есть множество целых чисел х, таких, что –1 ≤ х < 4, значит, по-другому: Х={-1; 0; 1; 2; 3}. Рассмотрим и такой пример: F={f | │fґ(x)│≤ 1 , 1 < x < 2}, т.е. F- множество функций f, производная которых в интервале (1; 2) не превосходит по абсолютной величине числа 1. Может случиться, что характеристическим свойством, определяющим множество А, не обладает ни один объект. Тогда говорят, что множество А - пустое (не содержит ни одного элемента) и пишут: А= Ш. Например, А={х | хІ+9=0, х
R} –множество действительных чисел х, таких, что хІ+9=0- пустое множество, т.к. таких действительных чисел нет. Включение и равенство множеств Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х
У или У
Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У. Знаки включения
или
относятся
только ко множествам и их не следует смешивать со знаками принадлежности Î и
. Если, например, А - множество всех студентов вуза, а В – множество студентов-первокурсников этого вуза, то В есть подмножество А, т.е. В
А. Пустое множество считают подмножеством любого множества Х, т.е. Ш
Х, каким бы ни было множество Х. Ясно также, что каждое множество является подмножеством самого себя: Х
Х. Если для двух множеств Х и У одновременно имеют место два включения Х
У и У
Х, т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У. Например, если А={2; 3}, а В={х | хІ –5х+6=0}, то А=В. Если Х
У, но Х≠ У, т.е. существует хотя бы один элемент множества У, не принадлежащий Х, то говорят, что Х есть собственное подмножество множества У, и пишут: Х
У. Например: N
Z, Z
Q, Q
R. Далее нам потребуется множество, которое содержит в качестве своего подмножества любое другое множество. Такое «всеобъемлющее» множество будем называть универсальным и обозначать буквой U . Диаграммы Эйлера-Венна Для наглядного представления множеств используют диаграммы Эйлера-Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри прямоугольника, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях. Выбор формы областей, изображающих множества на диаграммах, может быть произвольным (круги, внутренности эллипсов, многоугольники и т.п.). Покажем, например, с помощью диаграммы Эйлера-Венна, что множество А является подмножеством множества В:
С помощью такой диаграммы становиться наглядным, например, такое утверждение: если А
В, а В
С, то А
С.
Строгое доказательство этого утверждения, не опирающееся на диаграмму, можно провести так: пусть х
А; так как А
В, то х
В, а так как В
С, то из х
В следует, что х
С; значит, из того, что х
А, следует х
С, а поэтому А
С. Операции над множествами С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Мы рассмотрим следующие операции над множествами: объединение, пересечение, разность множеств, дополнение множества. Все рассматриваемые операции над множествами мы будем иллюстрировать на диаграммах Эйлера-Венна.
Объединение множеств Объединением А
В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В. Символическая запись этого определения: А
В={х | х
А или х
В}. Здесь союз «или» понимается в смысле «неразделительного или», т.е. не исключается, что х может принадлежать и А и В. Отметим, что в таком случае элемент х, входящий в оба множества А и В, входит в их объединение только один раз (поскольку для множества не имеет смысла говорить о том, что элемент входит в него несколько раз). Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
На диаграмме объединение множеств А и В выделено штриховкой. Если множество А определяется характеристическим свойством Р (х), а множество В - характеристическим свойством Q(х), то А
В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств. Примеры объединений двух множеств: 1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А
В ={2; 3; 5; 6; 7}. 2) Пусть А=[-1/4; 2], В=[ -2/3; 7/4]. Тогда А
В=[-2/3; 2] . 3) Пусть А= {х | х=8k, k
Z}, B={x | x=8n-4, n
Z}. Тогда A
B ={x | 4m, m
Z}. Операция объединения множеств может проводиться не только над двумя множествами. Определение объединения множеств можно распространить на случай любого количества множеств и даже – на систему множеств. Система множеств определяется так: если каждому элементу α множества М отвечает множество Аα, то совокупность всех таких множеств мы будем называть системой множеств. Объединением системы множеств {Аα} называется множество
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств Аα. При этом общие элементы нескольких множеств не различаются. Таким образом, элемент х
тогда и только тогда, когда найдется такой индекс α 0
М, что х
A α0 . В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись
Если M=N, то имеем объединение последовательности множеств
. Рассмотрим ещё один пример: пусть М=(1; 2) и для каждого α є М определим множество Аα =[0;α]; тогда
= [0;2). Из определения операции объединения непосредственно следует, что она коммутативна, т.е. А1
A2 = A2
А1, и ассоциативна, т.е. (А1
A2)
А3 = А1
(A2
А3). Пересечение множеств Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В. Символическая запись этого определения: А ∩ В={х | х
А и х
В}. Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
А ∩ ВНа диаграмме пересечение множеств А и В выделено штриховкой. Если множество А задается характеристическим свойством Р(х), a множество В-свойством Q(х), то в А ∩ В входят элементы, одновременно обладающие и свойством Р(х), и свойством Q(х). Примеры пересечений двух множеств: 1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}. 2) Пусть А=[-1/4; 7/4], В=[-2/3; 3/2]. Тогда А ∩ В= [-1/4; 3/2]. 3) Пусть А= {х | х=2k, k є Z}, B={x | x=3n, n є Z}. Тогда А ∩ В ={x | x=6m, m
Z}. 4) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов. Операцию пересечения можно определить и для произвольной системы множеств {Аα}, где α
М. Пересечением системы множеств {Аα}, называется множество
, состоящее из всех элементов, принадлежащих одновременно каждому из множеств Аα, α
М, т.е.
= {x | x
Аα для каждого α
М}. В случае, когда М конечно и состоит из чисел 1, 2, … , n, применяется запись
. Если M=N, то имеем пересечение последовательности множеств
. В рассмотренном выше примере системы множеств Аα =[0; α], α
М =(1; 2) получим:
=[0;1]. Операция пересечения множеств, как и операция объединения, очевидно, коммутативна и ассоциативна, т.е. А1∩A2 = A2 ∩А1 и (А1∩A2)∩А3= А1∩(A2 ∩ А3). Разность множеств Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е. А\В={х | х
А и х
В}, что можно пояснить на диаграмме Эйлера-Венна следующим образом:
На диаграмме разность А\В выделена штриховкой. Примеры разностей множеств: 1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}. 2. Пусть А=[-1/4;2], В=[-2/3; 7/4]. Тогда А\В=(7/4;2], а В\А=[-2/3; -1/4). 3. Пусть А - множество всех четных целых чисел, В - множество всех целых чисел, делящихся на 3. тогда А\В - множество всех четных целых чисел, которые не делятся на 3, а В\А –множество всех нечетных целых чисел, кратных трем. Дополнение множества Пусть множество А и В таковы, что А
В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:
СА={x | x
A}. На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:
www.coolreferat.com