
 (9.2)
(9.2)Второй закон Ньютона (2.2), или, что то же самое, векторное уравнение движения, представляет собой три дифференциальных уравнения второго порядка по времени. Например, проектируя обе части (2.2) на оси декартовой системы координат, получим

 (9.2)
(9.2)
Различают две задачи динамики: 1) по заданному закону движения точки, т. е. по известному как функция  векторному соотношению
векторному соотношению  находят силу
находят силу  , действующую на точку; это прямая задача динамики
, действующую на точку; это прямая задача динамики
2) по заданной силе  находят закон движения точки
находят закон движения точки  ; это обратная (основная) задача динамики. Поговорим об основной задаче динамики более подробно. Для ее решения недостаточно знать только силу. Следует задать также механическое состояние в некоторый момент времени
; это обратная (основная) задача динамики. Поговорим об основной задаче динамики более подробно. Для ее решения недостаточно знать только силу. Следует задать также механическое состояние в некоторый момент времени  , т. е. начальные условия
, т. е. начальные условия  . Механическое состояние точки в момент
. Механическое состояние точки в момент  , т. е.
, т. е. однозначно определяется ее начальным механическим состоянием и условиями ее движения (уравнениями движения). Это следует из однозначности и единственности решения дифференциальных уравнений (2.2), удовлетворяющих данным начальным условиям. Сформулированное предложение о предсказуемости эволюции механической системы во времени при заданных начальном состоянии и условиях движения называется принципом механической причинности, или принципом механического детерминизма. Его суть наиболее точно и полно выразил Лаплас: «Разумное существо, которое в каждый момент знало бы все движущие силы природы и имело бы полную картину состояния, в котором природа находится, могло бы (если бы только его ум был в состоянии проанализировать эти данные) выразить одним уравнением как движение мельчайших атомов, так и движение самых больших тел мира. Ничто не осталось бы для него неизвестным, и оно могло бы обозреть одним взглядом как будущее, так и прошлое», т. е. по начальным состояниям и взаимодействиям состояние системы в любой момент времени в будущем определялось бы однозначно. Со времен Лапласа появились новые важные идеи. Вот одна из них.
однозначно определяется ее начальным механическим состоянием и условиями ее движения (уравнениями движения). Это следует из однозначности и единственности решения дифференциальных уравнений (2.2), удовлетворяющих данным начальным условиям. Сформулированное предложение о предсказуемости эволюции механической системы во времени при заданных начальном состоянии и условиях движения называется принципом механической причинности, или принципом механического детерминизма. Его суть наиболее точно и полно выразил Лаплас: «Разумное существо, которое в каждый момент знало бы все движущие силы природы и имело бы полную картину состояния, в котором природа находится, могло бы (если бы только его ум был в состоянии проанализировать эти данные) выразить одним уравнением как движение мельчайших атомов, так и движение самых больших тел мира. Ничто не осталось бы для него неизвестным, и оно могло бы обозреть одним взглядом как будущее, так и прошлое», т. е. по начальным состояниям и взаимодействиям состояние системы в любой момент времени в будущем определялось бы однозначно. Со времен Лапласа появились новые важные идеи. Вот одна из них.
Хотя уравнения, описывающие эволюцию механической системы во времени, вполне детерминированы, ее развитие во времени может различаться своими маршрутами. Это связано с чувствительностью некоторых систем к начальным условиям, а точнее, к даже малому изменению начального состояния. В классической динамике в качестве примера можно привести шарик, падающий на острие лезвия бритвы, траектория которого после соприкосновения существенно зависит от положения шарика относительно острия в момент времени  перед тем, как он касается лезвия.
перед тем, как он касается лезвия.
Решение уравнения (2.2), которое удовлетворяет какому-либо конкретному начальному условию, называют частным решением. Более важно найти решение, удовлетворяющее произвольным условиям, это так называемое общее решение.
В теории дифференциальных уравнений есть понятие первых интегралов. Первыми интегралами уравнений движения (9.2) будем называть такие функции  координат, скоростей и времени, которые обращаются в постоянные
координат, скоростей и времени, которые обращаются в постоянные  в силу этой системы дифференциальных уравнений
в силу этой системы дифференциальных уравнений
 . (10.2)
. (10.2)
Это означает, что система (9.2) может быть сведена к эквивалентной
 . (11.2)
. (11.2)
Условие функциональной независимости трех первых интегралов (рассматриваемых как функции скоростей) записывается виде неравенства нулю (функционального) определителя Якоби
 (12.2)
(12.2)
Если (12.2) выполнено, то три первых интеграла движения будут независимыми в смысле разрешимости системы конечных уравнений (10.2) относительно  . Условие (12.2) является необходимым и достаточным условием независимости первых интегралов движения. Далее, система (10.2) представляет собой систему дифференциальных уравнений 1-го порядка. Предположим, что мы свели ее к эквивалентной системе уравнений
. Условие (12.2) является необходимым и достаточным условием независимости первых интегралов движения. Далее, система (10.2) представляет собой систему дифференциальных уравнений 1-го порядка. Предположим, что мы свели ее к эквивалентной системе уравнений
 , (13.2)
, (13.2)
т. е. мы нашли  такие, что
такие, что
 . (14.2)
. (14.2)
 называют вторыми интегралами движения. Они являются независимыми, если уравнения (14.2) разрешимы относительно координат
называют вторыми интегралами движения. Они являются независимыми, если уравнения (14.2) разрешимы относительно координат . Условие независимости - неравенство нулю функционального определителя
. Условие независимости - неравенство нулю функционального определителя

 . (15.2)
. (15.2)
Решение системы (14.2) представляется в виде
 (16.2)
(16.2)
Найденные таким образом функции (16.2), являющиеся решением системы уравнений (9.2) и содержащие шесть произвольных постоянных интегрирования, называют общим решением, так как, придавая определенные значения постоянным  можно получить функции (10.2) при любых начальных условиях. Выражение постоянных
можно получить функции (10.2) при любых начальных условиях. Выражение постоянных  через начальные значения
через начальные значения  проводится элементарно в два приема.
проводится элементарно в два приема.
1. Из системы (10.2) при  имеем
имеем

 (17.2)
(17.2)
2. Подставляя в систему (14.2), взятую при  ,
,  из (17.2), находим
из (17.2), находим
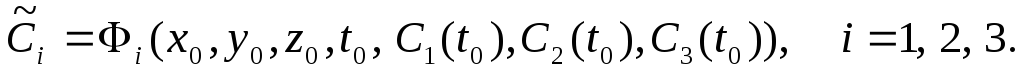 (18.2)
(18.2)
Найти общее решение уравнений движения - это значит полностью решить обратную задачу динамики.
Пример. Найти общее решение векторного уравнения движения (1.2), если сила зависит только от времени  .
.
Интегрируя (1.2) один раз, получаем три первых независимых интеграла движения
 ,
,
где постоянный вектор  - это начальная скорость
- это начальная скорость  . Интегрируя последнее уравнение, получаем три независимых вторых интеграла движения
. Интегрируя последнее уравнение, получаем три независимых вторых интеграла движения 
 .
.
Здесь  . Общее решение имеет вид
. Общее решение имеет вид
 .
.
Пример. Пусть проекции силы в уравнениях (9.2) зависят только от соответствующих координат. Найти все первые интегралы движения в этом случае и общее решение (в квадратурах).
Введем обозначения  . Тогда (9.2) можно переписать в виде
. Тогда (9.2) можно переписать в виде  . Последние уравнения, очевидно, имеют три первых интеграла
. Последние уравнения, очевидно, имеют три первых интеграла
 .
.
Откуда находим
 .
.
Знак перед корнем нужно выбирать в соответствии с начальным состоянием. Разделяя переменные и интегрируя, найдем
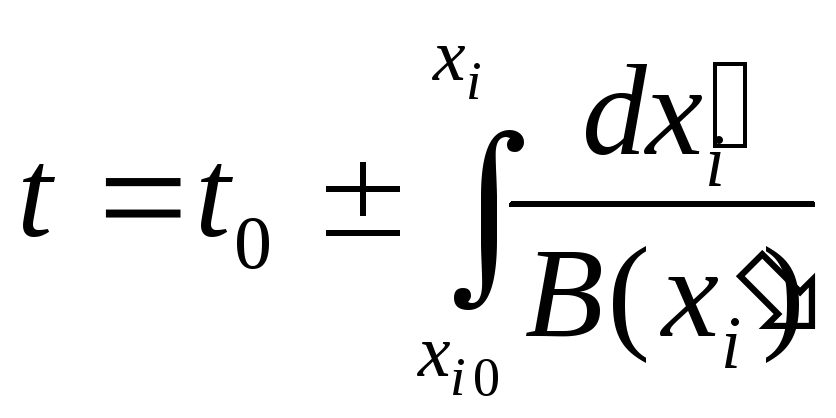 .
.
studfiles.net
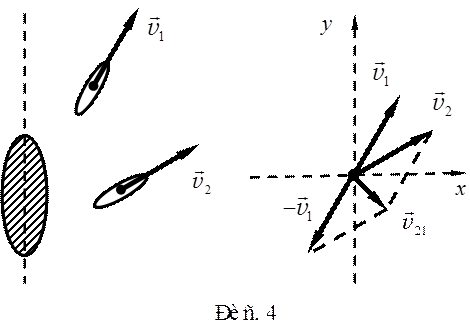
Задача 4. Два корабля движутся относительно острова со скоростью 4,8 и 6,4 м/с под углом 30 и 60° к востоку от меридиана соответственно. С какой скоростью второй корабль движется относительно первого?
| Дано:
| Решение. |
|
|

Для решения задачи воспользуемся формулой:
 ,
,
которая выражает принцип относительности движения и позволяет переходить от одной системы отсчета к другой. Тогда модуль относительной скорости
 ;
;

Этот путь поиска численного ответа в задаче основан на рис. 4 и не поз-воляет непосредственно указать в количественном виде направление результирующего вектора относительной скорости.
Эту же задачу можно решить другим способом. Выразим из формулы неизвестную относительную скорость:
 ,
,
возьмем проекции известных векторов и получим:
 ;
;
 ;
;
 ;
;
 .
.
Модуль относительной скорости, очевидно, равен квадратному корню из суммы квадратов проекций, и результат вычислений, безусловно, совпадет с результатом, полученным по формуле , в чем можно убедиться самостоятельно.
Преимущества второго способа заключаются в том, что, во-первых, его можно применять для любого количества складываемых (или вычитаемых) векторов (теорема косинусов позволяет работать только с парой векторов), а во-вторых, можно явно указать направление результирующего вектора, вычислив, например, угол между результирующим вектором и осью Ox:
 ;
;
 .
.
Отрицательное значение угла α означает, что угол нужно отложить вниз от оси Ox (по ходу часовой стрелки).
Ответ: скорость относительного движения кораблей равна 3,3  и направлена под углом 17° к оси Ox на юго-восток.
и направлена под углом 17° к оси Ox на юго-восток.
Обратная задача механики заключается в определении характеристик движения (скорости, ускорения и т. д.) по известной зависимости радиуса-вектора от времени. В общем случае задача решается на основе дифференциального исчисления и векторного анализа, другими словами, для решения обратной задачи механики необходимо уметь находить производные функций и знать правила работы с векторными величинами. Решение задачи 5 можно рассматривать как пример применения определений скорости, ускорения, траектории и других понятий кинематики.
Задача 5. Частица движется так, что зависимость ее координат от времени описывается выражениями:  и
и , где
, где ,
,  .Найти зависимость скорости и ускорения частицы от времени, ее тангенциальное и нормальное ускорение через 3,5 с после начала движения, а также радиус кривизны траектории в этот же момент времени и уравнение траектории.
.Найти зависимость скорости и ускорения частицы от времени, ее тангенциальное и нормальное ускорение через 3,5 с после начала движения, а также радиус кривизны траектории в этот же момент времени и уравнение траектории.
| Дано:
t = 3,5 c | СИ =0,053 м |
|
|
Знание зависимости координат движущегося тела от времени (эти функции часто называют законом движения) эквивалентно знанию радиуса-вектора:
 .
.
По определению скоростью тела является производная от радиуса-вектора по времени, тогда с учетом правил дифференцирования и таблицы производных получим:
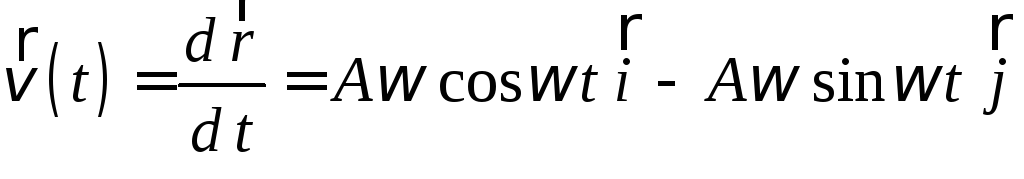 .
.
Очевидно, что в формуле сомножители перед ортами декартовых осей координат (с учетом знака) есть проекции вектора скорости на координатные оси.
По определению ускорением тела является производная от вектора скорости по времени, тогда с учетом правил дифференцирования и таблицы производных получим:
 .
.
По определению тангенциальным ускорением является производная от модуля скорости, а модуль скорости (как модуль любого вектора) есть квадратный корень из суммы квадратов проекций вектора на координатные оси:
 .
.
Оказалось, что модуль скорости не зависит от времени, и его производная по времени, очевидно, равна нулю в любой момент времени:
 .
.
Поскольку для полного, нормального и тангенциального ускорения справедлива формула
 ,
,
то в данной задаче полное ускорение частицы совпадает с ее нормальным ускорением и их в данный момент времени можно вычислить по формуле :

а модуль нормального и полного ускорения –
 ;
;

Такой же ответ для модуля нормального ускорения в данный момент времени можно было бы получить, если извлечь квадратный корень из суммы квадратов значений проекций вектора ускорения, вычисленных по формуле , но в данной задаче интересно было увидеть в формуле , что модуль ускорения не зависит от времени.
Радиус кривизны траектории движения частицы найдем из формулы, известной из школьного курса физики:
 .
.
Поскольку в данной задаче ни модуль ускорения, ни модуль скорости не зависят от времени, то и радиус кривизны траектории также будет постоянной величиной:
 ;
;
 .
.
Найдем уравнение траектории, по которой движется частица. По определению законы движения

п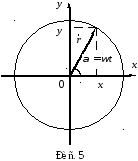 редставляют собой уравнения траектории, заданной впараметрической форме. Чтобы получить уравнение траектории в явном виде, нужно в выражениях системы избавиться от времени как от параметра. Часто для этого достаточно выразить время из одного выражения и подставить его во второе, но в этой задаче удобнее возвести оба выражения системы в квадрат и сложить левые и правые части получившихся формул. С учетом основного тригонометрического тождества и выражения получим:
редставляют собой уравнения траектории, заданной впараметрической форме. Чтобы получить уравнение траектории в явном виде, нужно в выражениях системы избавиться от времени как от параметра. Часто для этого достаточно выразить время из одного выражения и подставить его во второе, но в этой задаче удобнее возвести оба выражения системы в квадрат и сложить левые и правые части получившихся формул. С учетом основного тригонометрического тождества и выражения получим:
 .
.
Конечно, далее можно выразить зависимость y от x в явном виде, однако в этой задаче в этом нет необходимости, так как из математики хорошо известно, что формула

есть уравнение окружности радиуса R (рис. 5 иллюстрирует полученный результат).
Ответ: частица движется по окружности радиуса 5,3 см с постоянной по модулю скоростью и нормальным ускорением 3,6  .
.
studfiles.net
| Дано: R = 6,3 м l = v = const t = 1,2 с | Решение. |
|
|
При движении тела по окружности его ускорение можно разложить на две составляющие ускорения – тангенциальное и нормальное:
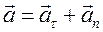 .
.
Если модуль скорости остается неизменным, то тангенциальное ускорение равно нулю. Следовательно, в этой задаче ускорение, с которым движется тело, является нормальным:
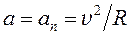 .
.
Скорость движения модели самолета найдем, учитывая, что при движении тела с постоянной по модулю скоростью путь (не перемещение), пройденный телом, можно вычислить по формуле:
 .
.
Подставляя в формулу путь, равный третьей части длины окружнос-ти, получим:
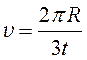 .
.
Тогда нормальное ускорение
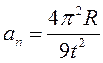 .
.
Модуль нормального ускорения, безусловно, не изменяется при движении тела, однако вектор нормального ускорения поворачивается и, следовательно, не остается постоянным. Тогда изменение ускорения равно модулю разности векторов ускорений, взятых в два разных момента времени:
 .
.
Из формулы следует, что для определения разности векторов надо ко второму вектору прибавить вектор, противоположный первому. Из рис. 3 видно, что длина такого вектора может быть найдена по теореме косинусов:
 ;
;

Направление вектора 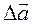 показано на рис. 3.
показано на рис. 3.
Ответ: модуль изменения ускорения равен 33  .
.
1.4. Относительность движения
Задача 4. Два корабля движутся относительно острова со скоростью 4,8 и 6,4 м/с под углом 30 и 60° к востоку от меридиана соответственно. С какой скоростью второй корабль движется относительно первого?
| Дано:
| Решение. |
|
|
Для решения задачи воспользуемся формулой:
 , которая выражает принцип относительности движения и позволяет переходить от одной системы отсчета к другой. Тогда модуль относительной скорости
, которая выражает принцип относительности движения и позволяет переходить от одной системы отсчета к другой. Тогда модуль относительной скорости
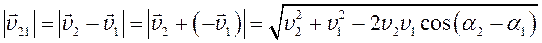 ;
;
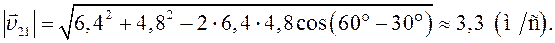
Этот путь поиска численного ответа в задаче основан на рис. 4 и не поз-воляет непосредственно указать в количественном виде направление результирующего вектора относительной скорости.
Эту же задачу можно решить другим способом. Выразим из формулы неизвестную относительную скорость:
 , возьмем проекции известных векторов и получим:
, возьмем проекции известных векторов и получим:
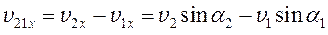 ;
;
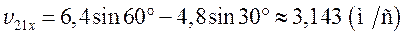 ;
;
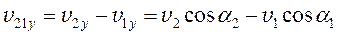 ;
;
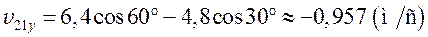 .
.
Модуль относительной скорости, очевидно, равен квадратному корню из суммы квадратов проекций, и результат вычислений, безусловно, совпадет с результатом, полученным по формуле , в чем можно убедиться самостоятельно.
Преимущества второго способа заключаются в том, что, во-первых, его можно применять для любого количества складываемых (или вычитаемых) векторов (теорема косинусов позволяет работать только с парой векторов), а во-вторых, можно явно указать направление результирующего вектора, вычислив, например, угол между результирующим вектором и осью Ox:
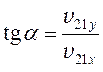 ;
;
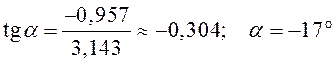 .
.
Отрицательное значение угла α означает, что угол нужно отложить вниз от оси Ox (по ходу часовой стрелки).
Ответ: скорость относительного движения кораблей равна 3,3 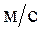 и направлена под углом 17° к оси Ox на юго-восток.
и направлена под углом 17° к оси Ox на юго-восток.
1.5. Обратная задача механики
Обратная задача механики заключается в определении характеристик движения (скорости, ускорения и т. д.) по известной зависимости радиуса-вектора от времени. В общем случае задача решается на основе дифференциального исчисления и векторного анализа, другими словами, для решения обратной задачи механики необходимо уметь находить производные функций и знать правила работы с векторными величинами. Решение задачи 5 можно рассматривать как пример применения определений скорости, ускорения, траектории и других понятий кинематики.
vunivere.ru
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
__________________
С. Н. Крохин
Краткий курс механики
Утверждено редакционно-издательским советом университета
в качестве программы и методических указаний по изучению курса «Физика»
для студентов заочной формы обучения
Омск 2006
УДК 530.1(075.8)
ББК 22.3
К83
Краткий курс механики: Программа и методические указания по изучению курса «Физика» / С. Н. Крохин; Омский гос. ун-т путей сообщения. Омск, 2006. 25 с.
Методические указания содержат рабочую программу раздела «Механика» дисциплины «Физика» и краткое теоретическое изложение основныхвопросов этого раздела.
Приведены определения физических величин, их единицы измерения в системе СИ, законы классической механики.
предназначены для самостоятельной работы студентов заочной формы обучения.
Библиогр.: 4 назв. Рис. 7.
Рецензенты: доктор техн. наук, профессор В. А. Нехаев;
канд. физ.-мат. наук, доцент В. И. Струнин.
________________________
© Омский гос. университет
путей сообщения, 2006

О Г Л А В Л Е Н И Е
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1. Рабочая программа дисциплины «Физика». Механика . . . . . . . . . . . . . . . . 6
2. Кинематика и динамика материальной точки. . . . . . . . . . . . . . . . . . . . . . . . 7
3. Кинематика и динамика вращения твердого тела вокруг
неподвижной оси . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14
4. Законы сохранения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18
Библиографический список. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24


Механика – раздел физики, изучающий закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение есть во всех высших и более сложных формах движения материи (химических, биологических и др.). Эти формы движения изучаются другими науками (химией, биологией и др.).
В основных учебных пособиях [1 – 4] вопросы по изучению механического движения излагаются подробно, зачастую с громоздкими математическими выкладками, что существенно затрудняет самостоятельную работу студентов.
В методических указаниях даны рабочая программа раздела «Механика», определения физических понятий, кратко излагаются основные физические законы и закономерности классической механики, приводится запись этих законов в математической форме.
В разделе «Механика» рассматриваются кинематика и динамика материальной точки, кинематика и динамика вращения твердого тела вокруг неподвижной оси и законы сохранения.
Для изучения раздела «Механика» необходимы знания из математики: элементов векторной алгебры (проекция вектора на ось, скалярное и векторное произведение и т. п.), дифференциального и интегрального исчисления (вычисление простейших производных и нахождение первообразных).
В методических указаниях из-за ограничений по объему издания не отражен экспериментальных материал.
Данные методические указания помогут студентам в самостоятельном изучении курса механики в период экзаменационной сессии.
МЕХАНИКА
1. Относительность механического движения. Система отсчета. Материальная точка (частица). Радиус-вектор. Траектория. Путь и перемещение. Скорость и ускорение.
2. Прямолинейное и криволинейное движение частицы. Касательное (тангенциальное) и нормальное ускорение.
3. Инерция. Инерциальные системы отсчета. Первый закон Ньютона. Сложение скоростей и принцип относительности в классической механике.
4. Взаимодействие тел. Сила. Инертность. Масса, плотность. Второй и третий законы Ньютона.
5. Силы в механике: гравитационная, тяжести, упругости, вес, выталкивающая, трения (покоя, скольжения, качения, вязкое).
6. Движение тела в поле силы тяжести. Свободное падение. Движение тела под действием нескольких сил. Равнодействующая.
7. Абсолютно твердое тело (АТТ). Центр инерции (центр масс) АТТ и закон его движения. Поступательное и вращательное движение АТТ. Система центра инерции.
8. Угловое перемещение, угловая скорость и угловое ускорение. Связь между кинематическими характеристиками поступательного и вращательного движения.
9. Момент силы. Момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения.
10. Изолированная система. Импульс (количество движения) тела. Закон сохранения импульса.
11. Момент импульса (момент количества движения). Собственный момент импульса. Закон сохранения момента импульса.
12. Механическая работа, мощность. Работа постоянной и переменной силы. Работа момента сил при вращательном движении.
13. Кинетическая энергия. Консервативные силы. Потенциальная энергия. Полная механическая энергия. Закон сохранения энергии в механике. Диссипация энергии. Общефизический закон сохранения энергии.
14. Абсолютно упругое и абсолютно неупругое столкновение частиц.
15. Простые механизмы: наклонная плоскость, блок, рычаг. «Золотое правило» механики. КПД механизма.

studfiles.net
КИНЕМАТИКА И ДИНАМИКА ЧАСТИЦ
В ПРИМЕРАХ РЕШЕНИЯ ЗАДАЧ
ОМСК 2009
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
–––––––––––––––––––––––––––––––––––––
Р. С. Курманов, Л. А. Литневский
КИНЕМАТИКА И ДИНАМИКА ЧАСТИЦ
В ПРИМЕРАХ РЕШЕНИЯ ЗАДАЧ
Утверждено редакционно-издательским советом университета
в качестве методических указаний к решению задач
для студентов первого курса дневного обучения
Омск 2009
УДК 530.1(075.8)
ББК 22.334я7
К93
Кинематика и динамика частиц в примерах решения задач: Методические указания к решению задач / Р. С. Курманов, Л. А. Литневский; Омский гос. ун-т путей сообщения. Омск, 2009. 33 с.
Приведены примеры решения типовых задач по всем темам раздела «Кинематика и динамика материальных точек» общего курса физики, краткие общие сведения по каждой теме этого раздела. В приложении даны основные правила работы с векторными величинами.
Предназначены для проведения практических занятий и организации самостоятельной работы студентов первого курса всех специальностей очной формы обучения.
Библиогр.: 3 назв. Табл. 1. Рис. 14. Прил. 1.
Рецензенты: канд. физ.-мат. наук, доцент Г. А. Вершинин;
канд. техн. наук, доцент А. Ю. Тэттэр.
________________________
© Омский гос. университет
путей сообщения, 2009
ОГЛАВЛЕНИЕ
Введение 5
Кинематика 6
Одномерное равноускоренное движение 6
Равноускоренное движение на плоскости 8
Движение по окружности с постоянной по модулю скоростью 10
Относительность движения 12
Обратная задача механики 14
Прямая задача механики 17
Динамика 19
Прямолинейное движение в вертикальном направлении 19
Прямолинейное движение в горизонтальном направлении 21
Движение по наклонной плоскости 23
Движение связанных тел 24
Движение под действием переменных сил 26
Движение тел с изменяющейся массой 28
Библиографический список 30
Приложение. Проекция вектора на ось 31
ВВЕДЕНИЕ
Классическая механика, разработанная Исааком Ньютоном более трехсот лет назад для описания движения планет Солнечной системы, оказалась применимой и для многих других тел, движение которых удовлетворяет нескольким условиям. Во-первых, тела должны двигаться со сравнительно небольшими скоростями (по сравнению со скоростью света в вакууме), в противном случае «работает»специальная теория относительности. Во-вторых, частицы не должны быть локализованы в слишком малой области пространства (механика Ньютона неприменима к электронам в атомах). Если это условие не выполняется, то необходимо использовать методыквантовой физики. В-третьих, размеры тел должны быть такими, чтобы ими можно было пренебречь по сравнению с масштабами движения (такие тела называются материальными точками или частицами).
Несмотря на «солидный возраст» механика Ньютонадо сих пор являетсянезаменимым инструментом при изучении движения окружающих нас предметов.
Механику Ньютона подразделяют на две взаимосвязанные и дополняющие друг друга части: кинематикуидинамикуи, кроме того, выделяют так называемыепрямуюи обратную задачи механики.
Как и любая наука, механика Ньютона оперирует набором понятий и терминов, без знания и понимания которых невозможно успешное освоение методов изучения явлений природы, которыми пользуются в этом разделе физики. Знание определений не является достаточным условием для понимания механики, еще необходимо уметь(знать как) применять определения и понятия, понимать, какими законами и формулами можно оперировать в конкретном случае.
Механика является важным разделом физики не только как самостоятельная область знаний. Физические величины, законы, методы описания природы, рассматриваемые в этом разделе, широко применяются во всех других разделах курса общей физики, а также и во многих других дисциплинах, изучаемых по программе высшей школы.
Решение задач является необходимым условием успешного изучения и понимания закономерностей физики.
КИНЕМАТИКА
Решение кинематических задач по механике опирается на знание нескольких формул кинематики и умение пользоваться векторной алгеброй и дифференциальным и интегральным исчислением. При рассмотрении приведенных ниже примеров решения задач необходимо обратить внимание на возможности, которые открываются при применении векторной алгебры.
Векторная алгебра, одним из создателей которой в ее современной форме был американский физик-теоретик Дж. У. Гиббс (1839 – 1903), является мощным универсальным инструментом решения задач по разделу «Кинематика».
studfiles.net
en.ppt-online.org
Государственный комитет Российской Федерации
по высшему образованию
Санкт-Петербургский государственный электротехнический университет
Кафедра теоретической механики
Курсовая работа по теоретической механики
Задание ¹1 Вариант ¹1
Студент: Виноградов К.Ю. ãð. 6361,ÔÀÂÒ
Преподаватель: Новиков Н.Б.
Дата: 24 февраля
Санкт-Петербург
1997 год.
Задача №1
По заданным кинематическим уравнениям движения точки определить:
1) траекторию точки
2) вектор скорости, вектор ускорения, а также радиус кривизны траектории точки в момент времени  , где
, где момент времени, когда впервые после начала движения точки выполняется условие
момент времени, когда впервые после начала движения точки выполняется условие , а
, а 0.1 с.
0.1 с.
 , см
, см
 , см
, см
Решение

 : x0=1, y0=5
: x0=1, y0=5







Задача №2
Точка движется в плоскости xoy по окружности радиуса R с центром в начале координат. Закон движения точки по траектории задан уравнением
 .
.
R=2 см, x0=0 см, y0=2 см,  , t1 - момент времени, когда впервые после начала движения выполняется условие: направление движения точки меняется на противоположное. t2=t1+1 с.
, t1 - момент времени, когда впервые после начала движения выполняется условие: направление движения точки меняется на противоположное. t2=t1+1 с.
Решение

t=0 с.  см.
см.

t2=2+1=3с.

| 2 | 0 | 0 | -1,123 | 0,899 | 0,063 | 0,8706 |
| 3 | -0,753 | -0,0376 | -0,452 | 0,482 | 0,0102 | 0,2424 |



studfiles.net