Реферат на тему:
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
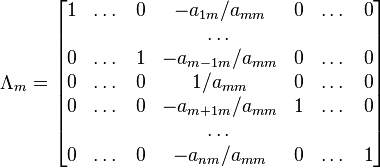 .
. Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n3).
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
Матричное уравнение AX = In для обратной матрицы X можно рассматривать как совокупность n систем вида Ax = b. Обозначим i-ый столбец матрицы X через Xi; тогда AXi = ei, ,поскольку i-м столбцом матрицы In является единичный вектор ei. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)[1].
Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA = LU. Пусть PA = B, B − 1 = D. Тогда из свойств обратной матрицы можно записать: D = U − 1L − 1. Если умножить это равенство на U и L то можно получить два равенства вида UD = L − 1 и DL = U − 1. Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для
из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)−1 = A−1P−1 = B−1 = D. получаем равенство A − 1 = DP.
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
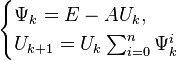
Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору
, обеспечивающие выполнение условия
(спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы
(а именно, если A — симметричная положительно определённая матрица и
, то можно взять
, где
; если же A — произвольная невырожденная матрица и
, то полагают
, где также
; можно конечно упростить ситуацию и, воспользовавшись тем, что
, положить
). Во-вторых, при таком задании начальной матрицы нет гарантии, что
будет малой (возможно, даже окажется
), и высокий порядок скорости сходимости обнаружится далеко не сразу.
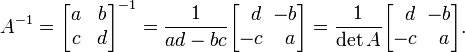
Обращение матрицы 2х2 возможно только при условии, что .
www.wreferat.baza-referat.ru
Пусть  – квадратная матрица
– квадратная матрица  -го порядка, а
-го порядка, а  – единичная матрица того же порядка.
– единичная матрица того же порядка.
Матрица  называется правой обратной по отношению к матрице
называется правой обратной по отношению к матрице  , если
, если  . Если же
. Если же  , то
, то  называется левой обратной к матрице
называется левой обратной к матрице  . Ясно, что
. Ясно, что  является квадратной матрицей порядка
является квадратной матрицей порядка  .
.
Теорема 4.1. Если у квадратной матрицы  существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
…
Доказательство. Пусть матрицы  и
и  такие, что
такие, что
 и
и 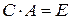 .
.
Тогда  . ■
. ■
В силу данной теоремы вводится следующее (основное)
Определение 4.1. Матрица  называется обратной по отношению к матрице
называется обратной по отношению к матрице  , если
, если
 . (4.1)
. (4.1)
В силу равенств (4.1) матрица  является обратной к матрице
является обратной к матрице  , то есть
, то есть  и
и  являются взаимно обратными матрицами.
являются взаимно обратными матрицами.
Обратная к  матрица обозначается символом
матрица обозначается символом  . Таким образом,
. Таким образом,  .
.
Если определитель матрицы равен нулю, то такую матрицу принято называть вырожденной, в противном случае – невырожденной.
Пусть матрица  является невырожденной, то есть
является невырожденной, то есть  . Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы
. Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы  :
:
 .
.
При транспонировании её получается матрица  , называемая присоединенной к матрице
, называемая присоединенной к матрице  :
:
 .
.
Теорема 4.2. Для того чтобы для матрицы  существовала обратная матрица
существовала обратная матрица  , необходимо и достаточно, чтобы матрица
, необходимо и достаточно, чтобы матрица  была невырожденной и при этом
была невырожденной и при этом
 , (4.2)
, (4.2)
где 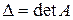 .
.
Доказательство необходимости. Если существует обратная матрица  , то
, то  . Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем:
. Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем:  . Но это означает, что
. Но это означает, что  .
.
Доказательство достаточности. Перемножая матрицы  и
и  , в силу теорем 3.1 и 3.2 получаем
, в силу теорем 3.1 и 3.2 получаем
 или
или  .
.
Отсюда следует, что матрица  является обратной по отношению к матрице
является обратной по отношению к матрице  , то есть имеет место формула (4.2). ■
, то есть имеет место формула (4.2). ■
Пример 1. Дана матрица
 .
.
Выяснить, существует ли обратная матрица  .
.
Решение. Вычислим определитель матрицы  . Прибавив к первой строке определителя матрицы
. Прибавив к первой строке определителя матрицы  его третью строку, получим определитель
его третью строку, получим определитель
 ,
,
у которого первая и четвертая строки совпадают. А это значит, что определитель равен нулю.
Итак, матрица  вырожденная, и, следовательно, обратная матрица
вырожденная, и, следовательно, обратная матрица  не существует.
не существует.
Пример 2. Для матрицы

найти обратную матрицу.
Решение. Вычислив определитель данной матрицы
 ,
,
можем утверждать, что обратная матрица для неё существует.
Найдём для каждого элемента  матрицы
матрицы  его алгебраическое дополнение
его алгебраическое дополнение  :
:
По формуле (4.2) найдём обратную матрицу
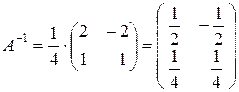 .
.
Проверка:
 .
.
Пример 3. Найти матрицу, обратную к матрице
 .
.
Решение. Вычислим определитель матрицы 
 .
.
Прибавив к элементам второго столбца соответствующие элементы первого столбца, получим
 .
.
Разложим определитель по элементам второй строки:
 .
.
Итак,  . То есть матрица
. То есть матрица  является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица
является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица  .
.
Найдем для каждого элемента матрицы  его алгебраическое дополнение:
его алгебраическое дополнение:
Составим присоединённую матрицу
 ,
,
и по формуле (4.2) найдём обратную матрицу
 .
.
Проверка:


 .
.
Пример 4. Дана матрица
 .
.
Определить, существует ли обратная матрица  , и если существует, то найти её.
, и если существует, то найти её.
Решение. Определитель матрицы 
 .
.
Следовательно, данная матрица невырожденная, и  существует. Согласно формуле (4.2),
существует. Согласно формуле (4.2),
 .
.
Найдём алгебраические дополнения элементов данной матрицы:
Тогда
 .
.
Проверка:

 .
.
Пример 5. Для матрицы

найти обратную матрицу.
Решение. Рассмотрим матричное уравнение
 , (4.3)
, (4.3)
где
 ,
,  ,
,  .
.
Умножив обе части уравнения (4.3) на матрицу  слева, получим
слева, получим
 . (4.4)
. (4.4)
Выражение (4.4) есть решение уравнения (4.3), которое в скалярной форме имеет вид:
 (4.5)
(4.5)
Решая систему (4.5), получаем

или, что то же самое,
 . (4.6)
. (4.6)
Выражение (4.6) есть (4.4). Следовательно,
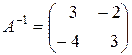 .
.
Проверка:
 .
.
Пример 6. Решить матричное уравнение
 . (4.7)
. (4.7)
Решение. Пусть
 ,
,  .
.
Тогда исходное уравнение запишется в виде
 . (4.8)
. (4.8)
Умножая обе части уравнения (4.8) слева на матрицу  , получаем
, получаем
 . (4.9)
. (4.9)
загрузка…
Вычислим обратную матрицу  , для чего найдем определитель
, для чего найдем определитель  и алгебраические дополнения элементов матрицы
и алгебраические дополнения элементов матрицы  :
:
 ,
,  ,
,  ,
,  ,
,  .
.
Итак,
 .
.
Проверим верность полученного результата:
 .
.
Таким образом, обратная матрица  вычислена верно.
вычислена верно.
Подставляя  в выражение (4.9), получаем
в выражение (4.9), получаем
 .
.
Проверка:







 .
.
Получили тождественное равенство. Следовательно, уравнение (4.7) решено верно:  .
.
ЗАДАЧИ
1.10. Найти обратные матрицы для следующих матриц:
1.11. Вычислить:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , если:
, если:
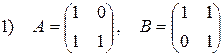 ;
;  .
.
refac.ru
Пусть  – квадратная матрица
– квадратная матрица  -го порядка, а
-го порядка, а  – единичная матрица того же порядка.
– единичная матрица того же порядка.
Матрица  называется правой обратной по отношению к матрице
называется правой обратной по отношению к матрице  , если
, если  . Если же
. Если же 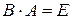 , то
, то  называется левой обратной к матрице
называется левой обратной к матрице  . Ясно, что
. Ясно, что  является квадратной матрицей порядка
является квадратной матрицей порядка  .
.
Теорема 4.1. Если у квадратной матрицы  существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
существуют как левая, так и правая обратные матрицы, то они совпадают между собой.
…
Доказательство. Пусть матрицы  и
и  такие, что
такие, что
 и
и 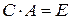 .
.
Тогда  . ■
. ■
В силу данной теоремы вводится следующее (основное)
Определение 4.1. Матрица  называется обратной по отношению к матрице
называется обратной по отношению к матрице  , если
, если
 . (4.1)
. (4.1)
В силу равенств (4.1) матрица  является обратной к матрице
является обратной к матрице  , то есть
, то есть  и
и  являются взаимно обратными матрицами.
являются взаимно обратными матрицами.
Обратная к  матрица обозначается символом
матрица обозначается символом  . Таким образом,
. Таким образом,  .
.
Если определитель матрицы равен нулю, то такую матрицу принято называть вырожденной, в противном случае – невырожденной.
Пусть матрица  является невырожденной, то есть
является невырожденной, то есть  . Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы
. Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы  :
:
 .
.
При транспонировании её получается матрица  , называемая присоединенной к матрице
, называемая присоединенной к матрице  :
:
 .
.
Теорема 4.2. Для того чтобы для матрицы  существовала обратная матрица
существовала обратная матрица  , необходимо и достаточно, чтобы матрица
, необходимо и достаточно, чтобы матрица  была невырожденной и при этом
была невырожденной и при этом
 , (4.2)
, (4.2)
где 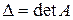 .
.
Доказательство необходимости. Если существует обратная матрица  , то
, то  . Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем:
. Отсюда, в силу того, что определитель произведения двух матриц равен произведению определителей сомножителей (см., например, [1], гл. 3, § 2, теорему 3), имеем:  . Но это означает, что
. Но это означает, что  .
.
Доказательство достаточности. Перемножая матрицы  и
и  , в силу теорем 3.1 и 3.2 получаем
, в силу теорем 3.1 и 3.2 получаем
 или
или  .
.
Отсюда следует, что матрица  является обратной по отношению к матрице
является обратной по отношению к матрице  , то есть имеет место формула (4.2). ■
, то есть имеет место формула (4.2). ■
Пример 1. Дана матрица
 .
.
Выяснить, существует ли обратная матрица  .
.
Решение. Вычислим определитель матрицы  . Прибавив к первой строке определителя матрицы
. Прибавив к первой строке определителя матрицы  его третью строку, получим определитель
его третью строку, получим определитель
 ,
,
у которого первая и четвертая строки совпадают. А это значит, что определитель равен нулю.
Итак, матрица  вырожденная, и, следовательно, обратная матрица
вырожденная, и, следовательно, обратная матрица  не существует.
не существует.
Пример 2. Для матрицы

найти обратную матрицу.
Решение. Вычислив определитель данной матрицы
 ,
,
можем утверждать, что обратная матрица для неё существует.
Найдём для каждого элемента  матрицы
матрицы  его алгебраическое дополнение
его алгебраическое дополнение  :
:
По формуле (4.2) найдём обратную матрицу
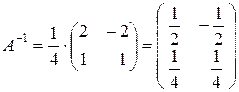 .
.
Проверка:
 .
.
Пример 3. Найти матрицу, обратную к матрице
 .
.
Решение. Вычислим определитель матрицы 
 .
.
Прибавив к элементам второго столбца соответствующие элементы первого столбца, получим
 .
.
Разложим определитель по элементам второй строки:
 .
.
Итак,  . То есть матрица
. То есть матрица  является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица
является невырожденной, а следовательно, по теореме 4.2 существует обратная к ней матрица  .
.
Найдем для каждого элемента матрицы  его алгебраическое дополнение:
его алгебраическое дополнение:
Составим присоединённую матрицу
 ,
,
и по формуле (4.2) найдём обратную матрицу
 .
.
Проверка:


 .
.
Пример 4. Дана матрица
 .
.
Определить, существует ли обратная матрица  , и если существует, то найти её.
, и если существует, то найти её.
Решение. Определитель матрицы 
 .
.
Следовательно, данная матрица невырожденная, и  существует. Согласно формуле (4.2),
существует. Согласно формуле (4.2),
 .
.
Найдём алгебраические дополнения элементов данной матрицы:
Тогда
 .
.
Проверка:

 .
.
Пример 5. Для матрицы

найти обратную матрицу.
Решение. Рассмотрим матричное уравнение
 , (4.3)
, (4.3)
где
 ,
,  ,
,  .
.
Умножив обе части уравнения (4.3) на матрицу  слева, получим
слева, получим
 . (4.4)
. (4.4)
Выражение (4.4) есть решение уравнения (4.3), которое в скалярной форме имеет вид:
 (4.5)
(4.5)
Решая систему (4.5), получаем

или, что то же самое,
 . (4.6)
. (4.6)
Выражение (4.6) есть (4.4). Следовательно,
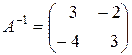 .
.
Проверка:
 .
.
Пример 6. Решить матричное уравнение
 . (4.7)
. (4.7)
Решение. Пусть
 ,
,  .
.
Тогда исходное уравнение запишется в виде
 . (4.8)
. (4.8)
Умножая обе части уравнения (4.8) слева на матрицу  , получаем
, получаем
 . (4.9)
. (4.9)
загрузка…
Вычислим обратную матрицу  , для чего найдем определитель
, для чего найдем определитель  и алгебраические дополнения элементов матрицы
и алгебраические дополнения элементов матрицы  :
:
 ,
,  ,
,  ,
,  ,
,  .
.
Итак,
 .
.
Проверим верность полученного результата:
 .
.
Таким образом, обратная матрица  вычислена верно.
вычислена верно.
Подставляя  в выражение (4.9), получаем
в выражение (4.9), получаем
 .
.
Проверка:







 .
.
Получили тождественное равенство. Следовательно, уравнение (4.7) решено верно:  .
.
ЗАДАЧИ
1.10. Найти обратные матрицы для следующих матриц:
1.11. Вычислить:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , если:
, если:
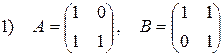 ;
;  .
.
refac.ru
Реферат на тему:
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
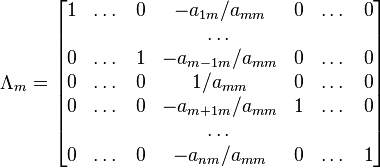 .
. Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n3).
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.
Матричное уравнение AX = In для обратной матрицы X можно рассматривать как совокупность n систем вида Ax = b. Обозначим i-ый столбец матрицы X через Xi; тогда AXi = ei, ,поскольку i-м столбцом матрицы In является единичный вектор ei. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)[1].
Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA = LU. Пусть PA = B, B − 1 = D. Тогда из свойств обратной матрицы можно записать: D = U − 1L − 1. Если умножить это равенство на U и L то можно получить два равенства вида UD = L − 1 и DL = U − 1. Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для
из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)−1 = A−1P−1 = B−1 = D. получаем равенство A − 1 = DP.
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
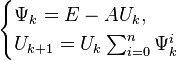
Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору
, обеспечивающие выполнение условия
(спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы
(а именно, если A — симметричная положительно определённая матрица и
, то можно взять
, где
; если же A — произвольная невырожденная матрица и
, то полагают
, где также
; можно конечно упростить ситуацию и, воспользовавшись тем, что
, положить
). Во-вторых, при таком задании начальной матрицы нет гарантии, что
будет малой (возможно, даже окажется
), и высокий порядок скорости сходимости обнаружится далеко не сразу.
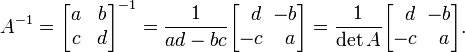
Обращение матрицы 2х2 возможно только при условии, что .
wreferat.baza-referat.ru