Доклад: Иррациональные уравнения и неравенства. Неравенства реферат по математике

Реферат Неравенство

скачать

Реферат на тему:

План:

1 Классификация неравенств
2 Решение неравенств второй степени
3 Решение неравенств методом интервалов
4 Равносильные переходы при решении иррациональных неравенств
5 Знаки неравенства
6 Примечание

Введение

О неравенствах в социально-экономическом смысле см. Социальное неравенство.

В математике неравенство есть утверждение об относительной величине или порядке двух объектов, или о том, что они просто не одинаковы).

запись $a < b \!\$ означает, что a меньше, чем b;
запись $a > b \!\$ означает, что a больше, чем b.
запись $a \neq b \!\$ означает, что a не равно b.

Эти математические отношения называются строгим неравенством. В противоположность им нестрогие неравенства означают следующее:

запись $a \leqslant b$ означает, что a меньше либо равно b;
запись $a \geqslant b$ означает, что a больше либо равно b.

Кроме того, иногда требуется показать, что одна из величин много больше другой, обычно на несколько порядков:

запись $a \gg b \!\$ означает, что a намного больше b.

Иногда не требуется знать результат и тогда можно определить формальное неравенство как два числа или алгебраических выражения, соединённые знаками >,<,≠.

1. Классификация неравенств

Неравенства, содержащие неизвестные величины, подразделяются на:[1]

алгебраические
трансцендентные

Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.

Пример: Неравнство $18x < 414 \!$ — алгебраическое, первой степени. Неравенство $2x^2-7x+6 > 0 \!$ — алгебраическое, второй степени. Неравенство $2^x > x+4 \!$ — трансцендентное.

2. Решение неравенств второй степени

Решение неравенства второй степени вида $ax^2+bx+c > 0\!$ или $ax^2+bx+c < 0\!$ можно рассматривать как нахождение промежутков, в которых квадратичная функция $f(x) = ax^2+bx+c\!$ принимает положительные или отрицательные значения (промежутки знакопостоянства).

3. Решение неравенств методом интервалов

Пусть у нас есть неравенство вида $f_1(x)\cdot f_2(x)\cdot f_3(x)\cdot f_4(x)\cdot\ldots\cdot f_N(x) > 0$ Для его решения нам необходимо:

разбить ось OX на интервалы знакопостоянства
поставить в каждом таком интервале знак неравенства на этом интервале ( $+\!$ , если больше нуля, $-\!$ если меньше)
выбрать те интервалы, где стоит знак начального неравенства

Крайними точками интервалов будут $-\infty$ , $+\infty$ и нули функций $f_1(x), f_2(x), f_3(x), f_4(x) \ldots f_N(x)\!$ .

4. Равносильные переходы при решении иррациональных неравенств

$\sqrt{f(x)} < g(x)$

$\left\{\begin{matrix} f(x) < g^2(x) \\ g(x) \geqslant 0 \\ f(x)\geqslant 0 \end{matrix}\right.$

$\sqrt{f(x)}>g(x)$

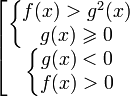
$\left[ \begin{matrix} \left\{\begin{matrix} f(x)>g^2(x) \\ g(x) \geqslant 0\end{matrix}\right. \\ \left\{\begin{matrix} g(x)<0 \\ f(x) > 0\end{matrix}\right. \end{matrix}\right.$

$\sqrt{f(x)} < \sqrt{g(x)}$

$\left\{\begin{matrix} f(x) < g(x) \\ f(x) \geqslant 0 \end{matrix}\right.$

5. Знаки неравенства

Русскоязычная традиция начертания знаков $\leqslant$ и $\geqslant$ отличается от принятой в англоязычной литературе.

Символ Код вЮникоде Названиев Юникоде Название HTMLшестн. HTMLдесят. HTMLобозн. LaTeX

$\leqslant$	U+2A7D	Less-than or slanted equal to	Меньше либо равно	⩽	⩽	отсутствует	\leqslant
$\geqslant$	U+2A7E	Greater-than or slanted equal to	Больше либо равно	⩾	⩾	отсутствует	\geqslant
$\le$	U+2264	Less-than or equal to	Меньше либо равно	≤	≤	≤	\le, \leq
$\ge$	U+2265	Greater-than or equal to	Больше либо равно	≥	≥	≥	\ge, \geq

6. Примечание

М. Я. Выгодский «Справочник по элементарной математике», М., 1974

wreferat.baza-referat.ru

Доклад - Иррациональные уравнения и неравенства

Колегаева Елена Михайловна, доцент кафедры математических методов и информационных технологий ДВАГС

I. Преобразование иррациональных выражений.

Иррациональным называется выражение, содержащее корни n-ой степени.

1) Одно из типичных преобразований иррациональных выражений – избавление от иррациональности в знаменателе.

а) Если в знаменателе стоит выражение вида , то необходимо числитель и знаменатель умножить на сопряженное к нему выражение . В этом случае применяется формула .

б) Если в знаменателе стоит выражение (или ), то числитель и знаменатель умножается, соответственно, на (или ). В этом случае применяются формулы

Пример 1. Избавиться от иррациональности в знаменателе:

а) ; б) ; в) ; г) ; д) ; е) .

Решение:

а) ;

б) ;

в) ;

г) ;

д) ;

е)

Отметим еще одно свойство:

которое часто применяется в преобразованиях.

Пример 2. Упростить выражение:

а) ; б) ; в) .

Решение:

а) , т.к. .

б) , т.к. .

в)

Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0.

1) Если n<-1, то

2) Если -1£n<0, то

3) Если 0<n<1, то

4) Если n³1, то

Ответ:

II. Иррациональные уравнения.

Рассмотрим уравнение вида .

Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть посторонние корни. Поэтому в уравнениях необходимо делать проверку.

Если уравнение содержит два и больше корней, то один из корней «уединяется», то есть уравнение приводится к виду .

Еще один способ решения – введение вспомогательной переменной.

Пример 3. Решить уравнения:

а) ;

б) ;

в) ;

г) .

Решение:

а) Û;

Проверка.

Þ х=-4 – посторонний корень,

– верно Þ х=2 – корень.

Ответ: х=2.

б)

Проверка.

– это выражение не существует, т.е.

– посторонний корень,

– верно Þ– корень.

Ответ: .

в)

Введем вспомогательную переменную Þ x2=t2–13

t2-13-2t=22; t2-2t-35=0,

t1=7; t2=-5.

Сделаем обратную замену:

Û х2+13=49 Û х2=36 Þ х=±6,

– не имеет решений.

Ответ: х=±6.

г)

Сделаем замену переменной. Положим . Тогда уравнение примет вид:

ÛÛ

ÞÛÛÛ.

Проверка показывает, что – корень.

Ответ: .

III. Решение иррациональных неравенств.

При решении этих неравенств следует помнить, что в четную степень можно возводить неравенства с неотрицательными членами.

Поэтому неравенство эквивалентно системам

или

Неравенство равносильно системе

Пример 4. Решить неравенства:

а) б)

в) г)

Решение.

а) ÛÛ

Решим третье неравенство системы методом интервалов:

x2-5x-14>0

x2-5x-14=0

(x-7)(x+2)>0

Найдем пересечение решений трех неравенств:

Ответ: -18£x<-2.

б)

если х-1£0, то неравенство верно, то есть х£1;

если x-1>0 и так как x2+1>0, возводим обе части в квадрат. Имеем:

ÛÛ x>1.

Объединяем два решения, получим х – любое.

Ответ: х – любое.

в)

ÛÛÛ

ÛÛ

Ответ: х³1.

г)

или

Û х³3

Ответ: .

Задачи для самостоятельного решения

Уважаемые ребята, ниже приводятся задания для самостоятельного решения, которые следует выполнить, оформить отдельно от заданий по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.

Наш адрес: 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ ( ХКЗФМШ).

М11.9.1. Упростить:

1) 2) 3)

4) , если , m>0, 0<n<1.

М11.9.2. Решить уравнения

;

М11.9.3. Решить неравенства:

;

www.ronl.ru

Читать реферат по математике: "Иррациональные уравнения и неравенства"

(Назад) скачать (Cкачать работу)

Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!

МОУ СОШ «УК №20»

Иррациональные

уравненияи неравенства

рефератпоалгебре

ученика 11 «В» класса

ТоросянаЛевона

Руководитель:

Олейникова Р. М.

Сочи 2002г.

Содержание.

Введение

Основные правила

Иррациональные уравнения:

Решение иррациональных уравнений стандартного вида.Решение иррациональных уравнений смешанного вида.Решение сложных иррациональных уравнений.

Иррациональные неравенства:

Решение иррациональных неравенств стандартного вида.Решение нестандартных иррациональных неравенств.Решение иррациональных неравенств смешанного вида.

Вывод

Список литературы

I. Введение

Я, Торосян Левон, ученик 11 «В» класса, выполнил реферат по теме: «Иррациональные уравнения и неравенства».

Особенностью моей работы является то, что в школьном курсе на решение иррациональных уравнений отводится очень мало времени, а ВУЗовские задания вообще не решаются. Решение иррациональных неравенств в школьном курсе не рассматри- вают, а на вступительных экзаменах эти задания часто дают. Я самостоятельно изучил правила решения иррациональных уравнений и неравенств. В реферате показаны решения как иррациональных уравнений и неравенств стандартного типа, так и повышенной сложности. Поэтому реферат можно использовать как учебное пособие для подготовки в ВУЗ, также рефератом можно пользоваться при изучении этой темы на факультативных занятиях.

II. Иррациональные уравнения

Иррациональным называется уравнение, в котором переменная содержится под знаком корня.

Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.

Иррациональные уравнения стандартного вида можно решить пользуясь следующим правилом:

Решение иррациональных уравнений стандартного вида:

а) Решить уравнение= x – 2,

Решение.

= x – 2,

2x – 1 = x2 – 4x + 4,Проверка:

x2 – 6x + 5 = 0,х = 5,= 5 – 2,

x1 = 5,3 = 3

x2 = 1 – постор. кореньх = 1,1 – 2 ,

Ответ: 5пост. к.1 -1.

б) Решить уравнение= х + 4,

Решение.

= х + 4,

Ответ: -1

в) Решить уравнение х – 1 =

Решение.

х – 1 =

х3 – 3х2 + 3х – 1 = х2 – х – 1,

х3 – 4х2 + 4х = 0,

х(х2 – 4х + 4) = 0,

х = 0илих2 – 4х + 4 = 0,

(х – 2)2 = 0,

х = 2

Ответ: 0; 2.

г) Решить уравнение х –+ 4 = 0,

Решение.

х –+ 4 = 0,

х + 4 = ,Проверка:

х2 + 8х + 16 = 25х – 50,х = 11,11 –+ 4 = 0,

х2 – 17х + 66 = 0,0 = 0

х1 = 11,х = 6,6 –+ 4 = 0,

х2 = 6.0 = 0.

Ответ: 6; 11.

Решение иррациональных уравнений смешанного вида:

Иррациональные уравнения, содержащие знак модуля:

а) Решить уравнение=

Решение.

= ,–+

Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:

илиОтвет:

б) Решить уравнение

Решение.

,–+

Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:

илиОтвет:.

а) Решить уравнение

Решение.

ОДЗ:

Пусть= t,t > 0

Сделаем обратную замену:

= 1/49,или= 7,

= ,

– (ур-ние не имеет решений)x = 3.

Ответ: 3

б) Решить уравнение

Решение.

Приведем все степени к одному основанию 2:

данное уравнение равносильно уравнению:

Ответ: 0,7

Иррациональное уравнение, содержащее иррациональность четной степени:

Решить уравнение

Решение.

возведем обе части уравнения в квадрат

3x – 5 – 2

2x – 2 = 2

x –1 =

xПроверка:

xx = 3,

4x1 = 1.

x = 1,75Ответ: 3.

Иррациональное уравнение, содержащее иррациональность нечетной степени:

Решить уравнение

Решение.

возведем обе части уравнения в куб

но, значит:

возведем обе части уравнения в куб

(25 + x)(3 – x) = 27,

Ответ: –24; 2.

Иррациональные уравнения, которые решаются заменой:

а) Решить уравнение

Решение.

Пусть= t,тогда= ,гдеt > 0

t –

Сделаем обратную замену:

= 2, возведем обе части в квадрат

Проверка: x = 2,5

Ответ: 2,5.

б) Решить уравнение

Решение.

Пусть= t,значит = ,где t > 0

t+ t – 6 = 0,

Сделаем обратную замену:

= 2, возведем обе части уравнения в четвертую степень

x + 8 = 16,Проверка:

x = 8,x = 2,

x = 2.6 = 6

Ответ: 2.

в) Решить уравнение

Решение.

Пусть= t,гдеt > 0

Сделаем обратную замену:

= 2, возведем обе части уравнения в квадрат

Проверка:

,Ответ: –5; 2.

Решение сложных иррациональных уравнений:

Иррациональное уравнение, содержащее двойную иррациональность:

Решить уравнение

Решение.

возведем обе части уравнения в куб

возведем обе части уравнения в квадрат

Пусть= t

t 2– 11t + 10 = 0,Сделаем обратную замену:Проверка:

= 10,или= 1,x = ,

x = -пост. корень0

Ответ:1.x = 1,

1 = 1

а) Решить уравнение lg3 + 0,5lg(x – 28) = lg

Решение.

lg3 + 0,5lg(x – 28) = lg,

lg(3 = lg,

Учитывая ОДЗ, данное уравнение равносильно системе:

Ответ: 32,75

б) Решить уравнение

Решение.

Ответ:; – 2; 3.

IV. Иррациональные неравенства

Неравенстваназываютсяиррациональными, если его неизвестное входит под знак корня (радикала).

Иррациональное неравенство видаравносильно системе неравенств:

Иррациональное неравенство видаравносильно совокуп-ности двух систем неравенств:

Решение иррациональных неравенств стандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

+–+Ответ:[1; 2).13x

б) Решить неравенство

Решение.

Данное неравенство равносильно двум системам неравенств:

Ответ:

в) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ: нет решений

Решение иррациональных неравенств нестандартного вида:

а) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

б) Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

Решение иррациональных неравенств с помощью правила знаков при умножении и делении:

а) Решить неравенство

Решение.

Учитывая то, чтои правило знаков при делении данное неравенство равносильно системе неравенств:

Ответ:

б) Решить неравенство (2x – 5)

Решение.

(2x – 5)

Учитывая то, чтои правило знаков при делении данное неравенство равносильно системе неравенств:

Ответ:

Решение иррациональных неравенств способом группировки:

Решить неравенство

Решение.

сгруппируем по два слагаемых

вынесем общий множитель за скобку

учитывая, что> 0 и правило знаков приумножении данное неравенство равносильно системе неравенств:

Ответ:( 0; 1 )

Иррациональное неравенство, содержащее двазнака иррациональности:

Решить неравенство

Решение.

Данное неравенство равносильно системе неравенств:

Ответ:

Решить неравенство

Решение.

Пусть= t, тогда= ,t > 0

Сделаем обратную замену:

возведем в квадрат обе части неравенства

Ответ:

Решение иррациональных неравенств смешанного вида:

а) Решить неравенство

Решение.

referat.co

Доклад: Иррациональные уравнения и неравенства. Неравенства реферат по математике

Реферат Неравенство

План:

Введение

1. Классификация неравенств

2. Решение неравенств второй степени

3. Решение неравенств методом интервалов

4. Равносильные переходы при решении иррациональных неравенств

5. Знаки неравенства

6. Примечание

Доклад - Иррациональные уравнения и неравенства

Читать реферат по математике: "Иррациональные уравнения и неравенства"

Смотрите также