.png)
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
.png)
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.
1. Прямоугольник — это параллелограмм.
Доказательство
Свойство объясняется действием признака 3 параллелограмма (то есть \angle A = \angle C, \angle B = \angle D)
2. Противоположные стороны равны.
AB = CD,\enspace BC = AD

3. Противоположные стороны параллельны.
AB \parallel CD,\enspace BC \parallel AD
4. Прилегающие стороны перпендикулярны друг другу.
AB \perp BC,\enspace BC \perp CD,\enspace CD \perp AD,\enspace AD \perp AB

5. Диагонали прямоугольника равны.
AC = BD

Доказательство
Согласно свойству 1 прямоугольник является параллелограммом, а значит AB = CD.

Следовательно, \triangle ABD = \triangle DCA по двум катетам (AB = CD и AD — совместный).
Если обе фигуры — ABC и DCA тождественны, то и их гипотенузы BD и AC тоже тождественны.
Значит, AC = BD.
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.

ABCD — параллелограмм \Rightarrow AB = CD, AC = BD по условию. \Rightarrow \triangle ABD = \triangle DCA уже по трем сторонам.
Получается, что \angle A = \angle D (как углы параллелограмма). И \angle A = \angle C, \angle B = \angle D.
Выводим, что \angle A = \angle B = \angle C = \angle D. Все они по 90^{\circ}. В сумме — 360^{\circ}.
Доказано!
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон.
Это свойство справедливо в силу теоремы Пифагора.
AC^2=AD^2+CD^2
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника.
\triangle ABC = \triangle ACD, \enspace \triangle ABD = \triangle BCD

8. Точка пересечения диагоналей делит их пополам.
AO = BO = CO = DO
.png)
9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности.

10. Сумма всех углов равна 360 градусов.
\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}
11. Все углы прямоугольника прямые.
\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника.

13. Вокруг прямоугольника всегда можно описать окружность.
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна 180^{\circ}
\angle ABC = \angle CDA = 180^{\circ},\enspace \angle BCD = \angle DAB = 180^{\circ}
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом).

academyege.ru
Нити параллелей и зелёных рек,
Протяните руку, руку протяните,
Надо, чтобы в дружбу верил каждый человек.
устанавливать связь между целью
учебной деятельности, её мотивом и её результатом
Что нарисовано на экране?
Назовите, одним словом.
На какие группы можно разделить данные линии?
Назовите прямые линии.
Назовите кривые линии.
Как отличить прямую линию от отрезка. Презентация
2.Игра “Я начну, а вы закончите”.
Часть прямой ограниченной с одной стороны – это ...
Часть прямой ограниченной с двух сторон – это ...
Прямая линия - ...
3.Работа в парах. Используя раздаточный материал построить: отрезок, прямую, луч, кривую.
2. Фронтальная работа.
учащиеся хором отвечают на вопросы учителя.
3.Работа в парах. Учащиеся выполняют работу и проводят взаимопроверку.
определять правила работы в парах;
Регулятивные:
умение работать по плану;
осуществлять контроль и самоконтроль;
совместно с учителем и одноклассниками давать оценку деятельности на уроке.
Познавательные:
находить ответы, на вопросы, используя свой жизненный опыт.
Коммуникативные:
слушать и понимать речь других;
умение с достаточной полнотой и точностью выражать свои мысли.
умение формулировать определение о геометрических линиях и строить эти линии;
умение участвовать в диалоге;
умение учащихся ориентироваться в окружающем мире и изученном материале.
– Как эти фигуры можно разделить на группы?
– Назовите, какого цвета треугольники.
– Какой из них имеет прямой угол? Докажите с помощью угольника.
– Если убрать треугольники и шестиугольники, то какие фигуры останутся?
– Какие углы имеют оставшиеся фигуры?
– Можно ли все оставшиеся четырёхугольники назвать прямоугольниками? А как вы думаете, какой четырёхугольник можно назвать прямоугольником?
Презентация.
2.Учащиеся выходят к доске и доказывают с помощью угольника, какие углы у геометрических фигур.
3.Тема урока
4.Постановка целей урока.
устанавливать связь между целью учебной деятельности, её мотивом и результатом.
Регулятивные:
определять и формулировать цель деятельности на уроке;
высказывать своё предположение на основе учебного материала.
Познавательные:
находить ответы, на вопросы, используя свой жизненный опыт;
ориентироваться в учебнике;
проводить анализ учебного материала.
Коммуникативные
слушать и понимать речь других;
умение с достаточной полнотой и точностью выражать свои мысли.
умение выполнять словесное рисование картин;
умение проводить анализ учебного материала;
умение ориентировать в учебнике.
– Как называется эта фигура? А как вы узнали?
Однажды квадрат встретил на своём пути такую фигуру. Презентация.
Стал квадрат к ней приглядываться. Что – то знакомое, родное увидел он в этой фигуре. Презентация.
– Давайте сравним эти две фигуры.
Используя линейку и угольник, измерьте стороны и углы фигуры. Сделайте выводы: 4 угла; все углы прямые; 4 стороны; противоположные стороны равны.
2.Прочитайте в учебнике, что такое прямоугольник.
3.Прослушать объяснение нового материала, которое дают авторы учебника. Электронное приложение
4.Практическая работа в парах.
Работа в тетрадях и с раздат. матер.
2.Практическая работа.
3.Работа в парах. Учащиеся выполняют работу и проводят взаимопроверку.
определять правила работы в парах;
устанавливать связь между целью учебной деятельности, её мотивом и результатом.
Регулятивные:
определять и формулировать цель деятельности на уроке;
высказывать своё предположение на основе учебного материала.
Познавательные:
ориентироваться в учебнике;
находить ответы, на вопросы, используя свой жизненный опыт;
проводить анализ учебного материала.
Коммуникативные:
слушать и понимать речь других;
умение с достаточной полнотой и точностью выражать свои мысли.
соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами;
формулировать правила о геометрических линиях;
называть части ломаной линии;
учащиеся научатся доказывать свою точку зрения и формулировать выводы.
2.Взаимопроверка выполненных заданий.
3.Работа по плакату “Геометрические фигуры”.
назвать фигуры, которые изображены на плакате. Презентация.
4.Работа в группах. Из предложенных геометрических фигур составить небольшую картинку. Презентация.
5.Самостоятельная работа. Решение задачи № 3, решение неравенств № 5.
Проверка выполненных заданий: доказать правильность используя математические правила.
3.Фронтальная работа по плакату.
4.Работа учащихся в группах. Защита полученных картинок.
определять правила работы в группах;
устанавливать связь между целью учебной деятельности, её мотивом и результатом.
Регулятивные:
высказывать своё предположение на основе учебного материала.
Познавательные:
ориентироваться в учебнике;
проводить анализ учебного материала; находить ответы, на вопросы, используя свой жизненный опыт.
Коммуникативные
слушать и понимать речь других;
умение с достаточной полнотой и точностью выражать свои мысли.
умение участвовать в диалоге;
умение учащихся ориентироваться в изученном материале;
соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами.
Оценить свою работу и работу товарищей на данном уроке. Приложение.
осуществлять контроль и самоконтроль.
– Приведите примеры прямоугольников, с которыми мы встречаемся в жизни.
Д/з: с. 14 № 4,6.
высказывать своё предположение на основе учебного материала.
Познавательные:
находить ответы, на вопросы, используя свой жизненный опыт и изученный материал.
Коммуникативные
слушать и понимать речь других;
умение с достаточной полнотой и точностью выражать свои мысли.
умение участвовать в диалоге;
умение учащихся ориентироваться в изученном материале и окружающем мире.
xn--i1abbnckbmcl9fb.xn--p1ai

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана.
Она считалась символом здоровья и служила опознавательным знаком. Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер. 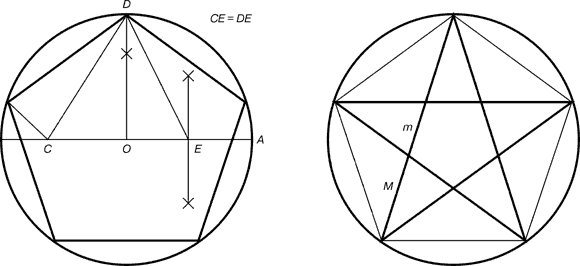
Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки, равные DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Интересно, что стороны пентаграммы, пересекаясь, образуют снова правильный пятиугольник, в котором пересечение диагоналей даёт нам новую пентаграмму и так далее до бесконечности.
Пентаграмма очень красива, недаром её помешают на свои флаги и гербы многие страны. На флагах многих государств изображена правильная пятиконечная звезда.
3. «Золотой» прямоугольник
В эпоху Возрождения «золотое» сечение было очень популярно среди художников, скульпторов, архитекторов. Так, выбирая размеры картины, художники старались, чтобы отношения её сторон равнялось числу Ф (приближенно равным 0,6). Такой прямоугольник стали называть «золотым», он обладает интересным свойством. Если от «золотого» прямоугольника со сторонами а и b (a > b) отрезать квадрат со стороной b, то получится опять «золотой» прямоугольник. Этот процесс можно продолжать до бесконечности. Каждый раз мы будем получать прямоугольник меньших размеров, но опять же «золотой».
4. «Золотое» сечение в живописи
«Пусть никто, не будучи математиком, не дерзнет читать мои труды».
Леонардо да Винчи
Леонардо да Винчи в своем творчестве не перестает восхищать зрителя пропорциями золотого сечения. Друг этого знаменитого художника, известный математик, Лука Пачоли называл «золотое» сечение божественной пропорцией. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Образцом того, как использовал «золотой» прямоугольник в своих творениях Леонардо да Винчи, может послужить его знаменитый портрет Моны Лизы, лицо которой прекрасно вписывается в такой прямоугольник.
Также портрет Джоконды долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.
Леонардо да Винчи «Мона Лиза» (Джоконда)


«Та́йная ве́черя» — фреска работы Леонардо да Винчи, изображающая сцену последнего ужина Христа со своими учениками. В этой картине присутствуют «золотые» прямоугольники.
infourok.ru