, (4.2)Множественная линейная регрессия. - раздел Экономика, ЭКОНОМЕТРИКА
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но, существует обычно несколько факторов, которые оказывают существенное влияние (например: на потребление того или иного товара влияют такие факторы, как цена товара, размер семьи, её состав, доход и т.д.). В этом случае следует попытаться выявить влияние этих факторов, введя их в модель, т.е. построить уравнение множественной регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
· Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, если анализируется спрос на мороженое летом и зимой, то фактор сезонности можно учесть бинарной переменной, принимающей значения 1 и 0. Аналогичным образом учитывается наличие балкона, этаж, тип здания (кирпичный или блочный дом) на рынке недвижимости и т. п.
· Факторы не должны быть коррелированы и тем более находиться в точной функциональной связи.
В случае учета влияния нескольких факторов линейная зависимость величины y от m переменных x1, x2,…, xmпримет вид:
y =q1x1+q2x2+…+qmxm . (4.1)
Конкретные значения независимых переменных будем отмечать двумя индексами: xi1, xi2,…, xim, (i = 1,2,…,n). Тогда можно записать уравнения
, (4.2)
где m – число рассматриваемых факторов.
Зависимость (4.2) будем называть множественной линейной регрессией.
Если зависимость величины y от переменных x1, x2,…, xmимеет вид
, i=1,2,…,n (4.3)
то, введя обозначение Fik=fk(xi), запишем формулу (4.3) в виде
. (4.4)
В качестве примеров зависимости типа (4.3) отметим квадратичную функцию y=a+bx+cx2 , полином третьей степени y=a+bx+cx2 +dx3 , тригонометрический полином y=q 1 sinx+q2sin2x+…+qm sin mx и др.
Сравнив формулы (4.2) и (4.4), нетрудно убедиться в том, что они отличаются только обозначениями заданных коэффициентов Fik и xik. В матричном виде имеем формулу
y=Fq+e , (4.5)
где
, 
, 
.
Для определения коэффициентов qk в формулах (4.2) или (4.4) воспользуемся методом наименьших квадратов:
min.
Необходимое условие экстремума функции F=F (q1,q2,…,qт)
, p=1,2,…,m
дает уравнение
(4.6)
В уравнении (4.6) переставим порядок суммирования :
(4.7)
В матричной форме система уравнений (4.7) относительно неизвестных значений переменной qk имеет вид
FTFq=FTy . (4.8)
Полагая, что матрица FTF неособенная, получим решение системы (4.8)
q=(FTF)-1FTy . (4.9)
В случае парной регрессии (3.1) вектор параметров q имеет вид
;
переменную x1 следует принять равной 1, а переменную x2=x; тогда матрица F принимает вид
.
Произведение матриц
представляет собой матрицу коэффициентов системы (3.6), а свободный член в формуле (4.8)
совпадает со свободными членами уравнений (3.6).
Точно также в случае множественной линейной регрессии для уравнения y=q0+q1x1+q2x2 первый столбец матрицы F состоит из 1, второй столбец - из заданных значений переменной x1, а третий – из значений x2:
;
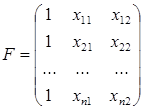Вектор параметров принимает вид
.
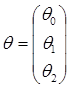– Конец работы –
Эта тема принадлежит разделу:
На сайте allrefs.net читайте: экономических специальностей...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Множественная линейная регрессия.
Состав исходной информации Основной базой исходной информации для эконометрических исследований служат данные статистики либо данны
Интерполяционный полином Лагранжа. Пусть имеется зависимость y = f(x) между величинами x и y, для которой нам известны отдельны
Случай 1. Через одну точку (x0, y0) можно провести пучок прямых y = y0+b(x-x0) (2
Случай 2. Через две различные точки (x0,y0), (x1,y1) проходит одна и только одна прям
Случай 3. Многочлен второй степени (квадратичная функция), график которой проходит через три точки (x0,y
Случай n. Теперь ясно, что интерполяционный полином Лагранжа n-ой степени, график которого проходит через n+1 точку
Парная линейная регрессия. Метод наименьших квадратов Пусть имеется n пар чисел (xi, yi), i=1,2,…,n, относительно которых предполагается, что
Нелинейные модели. Мы изучили применение метода наименьших квадратов для определения параметров, которые входят в фу
Системы одновременных эконометрических уравнений. Объектом статистического изучения в социально-экономических науках являются сложные системы. Изм
Составляющие временного ряда Временной ряд x(t) – это множество значений величины x, отвечающих последовательности момен
Определение составляющих временного ряда Одним из наиболее распространенных способов моделирования тенденции временного ряда является по
При этом коэффициенты ak, bk будут равны Если функция x (t) четная, т.е. выполняется равенство x (
Временной ряд как случайный процесс Пусть значение экономического показателя x( t ) в любой момент времени t представляет
Модели ARIMA В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральн
Учет сезонных составляющих Обобщение модели ARIMA, позволяющие учесть периодические (сезонные) составляющие временного ряд
Анализ погрешностей исходной информации Значения экономических показателей обычно известны неточно, с некоторой погрешностью. Рассмотрим
Доверительные интервалы Введем случайную величину . (13.1) Нетрудно проверить,
Расчет погрешностей. Эмпирические данные часто подвергаются математической обработке – над ними выполняются ари
Коэффициент детерминации. Коэффициент детерминации характеризует качество регрессион
Средняя ошибка аппроксимации. Фактические значения интересующей нас величины отличаются от рассчитанных по уравнению регресси
Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок Для нахождения неизвестных величин по результатам измерений, содержащих случайные погрешности, служит мет
Статистические гипотезы В предыдущих параграфах рассматривалась методика моделирования взаимосвязей экономических пока
F – статистика Значимость регрессионной модели определяется с помощью F-критерия Фишера. Для этого вычисляет
T – статистика Для оценки значимости отдельных параметров регрессионной модели y=a+bx+e их величина сравниваетс
allrefers.ru
Множественная линейная регрессия. - раздел Математика, ЭКОНОМЕТРИКА
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Но, существует обычно несколько факторов, которые оказывают существенное влияние (например: на потребление того или иного товара влияют такие факторы, как цена товара, размер семьи, её состав, доход и т.д.). В этом случае следует попытаться выявить влияние этих факторов, введя их в модель, т.е. построить уравнение множественной регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
· Факторы должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. Например, если анализируется спрос на мороженое летом и зимой, то фактор сезонности можно учесть бинарной переменной, принимающей значения 1 и 0. Аналогичным образом учитывается наличие балкона, этаж, тип здания (кирпичный или блочный дом) на рынке недвижимости и т. п.
· Факторы не должны быть коррелированы и тем более находиться в точной функциональной связи.
В случае учета влияния нескольких факторов линейная зависимость величины y от m переменных x1, x2,…, xmпримет вид:
y =q1x1+q2x2+…+qmxm . (4.1)
Конкретные значения независимых переменных будем отмечать двумя индексами: xi1, xi2,…, xim, (i = 1,2,…,n). Тогда можно записать уравнения
, (4.2)
где m – число рассматриваемых факторов.
Зависимость (4.2) будем называть множественной линейной регрессией.
Если зависимость величины y от переменных x1, x2,…, xmимеет вид
, i=1,2,…,n (4.3)
то, введя обозначение Fik=fk(xi), запишем формулу (4.3) в виде
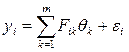. (4.4)
В качестве примеров зависимости типа (4.3) отметим квадратичную функцию y=a+bx+cx2 , полином третьей степени y=a+bx+cx2 +dx3 , тригонометрический полином y=q 1 sinx+q2sin2x+…+qm sin mx и др.
Сравнив формулы (4.2) и (4.4), нетрудно убедиться в том, что они отличаются только обозначениями заданных коэффициентов Fik и xik. В матричном виде имеем формулу
y=Fq+e , (4.5)
где
, 
, 
.
Для определения коэффициентов qk в формулах (4.2) или (4.4) воспользуемся методом наименьших квадратов:
min.
Необходимое условие экстремума функции F=F (q1,q2,…,qт)
, p=1,2,…,m
дает уравнение
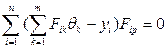(4.6)
В уравнении (4.6) переставим порядок суммирования :
(4.7)
В матричной форме система уравнений (4.7) относительно неизвестных значений переменной qk имеет вид
FTFq=FTy . (4.8)
Полагая, что матрица FTF неособенная, получим решение системы (4.8)
q=(FTF)-1FTy . (4.9)
В случае парной регрессии (3.1) вектор параметров q имеет вид
;
переменную x1 следует принять равной 1, а переменную x2=x; тогда матрица F принимает вид
.
Произведение матриц
представляет собой матрицу коэффициентов системы (3.6), а свободный член в формуле (4.8)
совпадает со свободными членами уравнений (3.6).
Точно также в случае множественной линейной регрессии для уравнения y=q0+q1x1+q2x2 первый столбец матрицы F состоит из 1, второй столбец - из заданных значений переменной x1, а третий – из значений x2:
;
Вектор параметров принимает вид
.
– Конец работы –
Эта тема принадлежит разделу:
На сайте allrefs.net читайте: "ЭКОНОМЕТРИКА"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Множественная линейная регрессия.
Состав исходной информации Основной базой исходной информации для эконометрических исследований служат данные статистики либо данны
Интерполяционный полином Лагранжа. Пусть имеется зависимость y = f(x) между величинами x и y, для которой нам известны отдельны
Случай 2. Через две различные точки (x0,y0), (x1,y1) проходит одна и только одна прям
Случай 3. Многочлен второй степени (квадратичная функция), график которой проходит через три точки (x0,y
Случай n. Теперь ясно, что интерполяционный полином Лагранжа n-ой степени, график которого проходит через n+1 точку
Парная линейная регрессия. Метод наименьших квадратов Пусть имеется n пар чисел (xi, yi), i=1,2,…,n, относительно которых предполагается, что
Нелинейные модели. Мы изучили применение метода наименьших квадратов для определения параметров, которые входят в фу
Системы одновременных эконометрических уравнений. Объектом статистического изучения в социально-экономических науках являются сложные системы. Изм
Составляющие временного ряда Временной ряд x(t) – это множество значений величины x, отвечающих последовательности момен
Определение составляющих временного ряда Одним из наиболее распространенных способов моделирования тенденции временного ряда является по
При этом коэффициенты ak, bk будут равны Если функция x (t) четная, т.е. выполняется равенство
Временной ряд как случайный процесс Пусть значение экономического показателя x( t ) в любой момент времени t представляет
Модели ARIMA В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральн
Учет сезонных составляющих Обобщение модели ARIMA, позволяющие учесть периодические (сезонные) составляющие временного ряд
Анализ погрешностей исходной информации Значения экономических показателей обычно известны неточно, с некоторой погрешностью. Рассмотрим
Доверительные интервалы Введем случайную величину . (13.1) Нетрудно прове
Расчет погрешностей. Эмпирические данные часто подвергаются математической обработке – над ними выполняются ари
Коэффициент детерминации. Коэффициент детерминации характеризует качество регре
Средняя ошибка аппроксимации. Фактические значения интересующей нас величины отличаются от рассчитанных по уравнению регресси
Принцип максимального правдоподобия. Построение регрессионных моделей при гетероскедастичности ошибок Для нахождения неизвестных величин по результатам измерений, содержащих случайные погрешности, служит мет
Статистические гипотезы В предыдущих параграфах рассматривалась методика моделирования взаимосвязей экономических пока
F – статистика Значимость регрессионной модели определяется с помощью F—критерия Фишера. Для этого вычисляе
T – статистика Для оценки значимости отдельных параметров регрессионной модели y=a+bx+e их величина сравнива
allrefers.ru
Министерство Образования Российской Федерации
Российский Государственный Гуманитарный Университет
Факультет информатики
Реферат по дисциплине:
«Прикладная статистика»
на тему: «Множественная регрессия в пакетах SPSS»
Выполнила: студентка 3 курса, ФИ, 1 группы
Проверил: Синицын В.Ю.
Москва 2005
Введение
SPSS - одна из старейших систем статистического анализа и управления данными, продукт фирмы SPSS Inc. (Statistical Products and Service Solution - Статистические продукты и сервисные решения), сегодня SPSS является одним из лидеров среди универсальных статистических пакетов.
Системные требования. Для работы базовой системы требуется процессор 386 (рекомендуется процессор 486/33Мгц), 4 Мб памяти (рекомендуется 8 Мб), Windows 3.1 или старше, 20 Мб пространства на диске.
Интерфейс. Пакет SPSS построен как традиционная база данных: накопление массива информации, его формализация и представление результатов статистической обработки массива в виде отчета. Но так как пакет предназначен для выполнения специализированной функции - обработки результатов опросов - он имеет структурное отличие от традиционных баз данных, выраженное в принципах формализации накопляемого массива исходной информации, принципах статистической обработки и представления результатов информации.
Но внешних отличий интерфейса от традиционных баз данных или электронных таблиц (MS Access, MS Excel и т.п.) нет, что значительно упрощает первое знакомство с пакетом и позволяет достаточно быстро начать процедуру ввода или импорта данных, кроме того, пакет включает справочник и глоссарий статистических терминов.
Множественный регрессионный анализ
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных
Эта задача решается с помощью множественного регрессионного анализа.
Обозначим
наблюдение переменной
, а объясняющих переменных —
Тогда модель множественной линейной регрессии можно представить в виде:
где
а
удовлетворяет приведенным выше предпосылкам.
Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.
Введем обозначения:
— матрица-столбец, или вектор, значений зависимой переменной размера
:
— матрица значений объясняющих переменных, или матрица плана размера
обращаем внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что в модели свободный член
умножается на фиктивную переменную хi0, принимающую значение 1 для всех
— матрица-столбец, или вектор, параметров размера
— матрица-столбец, или вектор случайных ошибок {возмущений) размера п.
Тогда в матричной форме модель примет вид:
применимметод наименьших квадратов. Так как произведение транспонированной матрицы
на саму матрицу
то условие минимизации остаточной суммы квадратов запишется в виде:
Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е.
, получим после раскрытия скобок:
есть матрица размера
, т.е. величина скалярная, следовательно, оно не меняется при транспонировании:
. Поэтому условие минимизации примет вид:
На основании необходимого условия экстремума функции нескольких переменных
, представляющей, необходимо приравнять нулю частные производные по этим переменным или в матричной форме — вектор частных производных
Для вектора частных производных доказаны следующие формулы:
где
и
— вектор-столбцы, а
— симметрическая матрица, вкоторой элементы, расположенные симметрично относительно главной диагонали, равны. Поэтому, полагая
, а матрицу
(она является симметрической), найдем
откуда получаем систему нормальных уравнений в матричной форме для определения вектора
:
Найдем матрицы, входящие в это уравнение. Матрица Х'Х представляет матрицу сумм первых степеней, квадратов и попарных произведений п наблюдений объясняющих переменных
Матрица 
есть вектор произведенийп наблюдений объясняющих и зависимой переменных:
В частном случае из рассматриваемого матричного уравнения с учетом 
и 
для одной объясняющей переменной
нетрудно получить уже рассматриваемую системунормальных уравнений для несгруппированных данных. Действительно, в этом случае матричное уравнение принимает вид:
откуда непосредственно следует система нормальных уравнений для несгруппированных данных.
Для решения матричного уравнения относительно вектора оценок параметров
необходимо ввести еще однупредпосылку б для множественного регрессионного анализа: матрица 
является неособенной, т.е. ее определитель не равен нулю. Следовательно, ранг матрицы 
равен ее порядку, т.е.
. Из матричной алгебры известно, что
, значит,
т.е. столбцы матрицы плана
должны быть линейно независимыми.
Решением уравнения является вектор
где
— матрица, обратная матрице коэффициентов системы), а
—матрица-столбец, или вектор, ее свободных членов.
Зная вектор
, выборочное уравнение множественной регрессии представим в виде
где
— групповая (условная) средняя переменной
при заданном векторе значений объясняющей переменной
На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии
и коэффициенты эластичности
:
Стандартизованный коэффициент регрессии 
показывает, на сколько величин
изменится в среднем зависимая переменная
приувеличении только
объясняющей переменной на
, а коэффициент эластичности
— на сколько процентов (от средней) изменится в среднем
при увеличении только
на 1%.
Пример использования Линейной регрессии в SPSS
Линейный регрессионный анализ позволяет получить предсказание значений зависимой переменной на основе значений независимых переменных.
Линейный регрессионный анализ является достаточно сложной статистической процедурой. Поэтому здесь ограничимся рассмотрением случая одной зависимой и одной независимой переменной и будем использовать процедуру простой линейной регрессии.
Для расчета линейной модели регрессии необходимо использовать пункты меню
Statistics – Regression - Linear –
выбрать переменную и поместить ее в окно Dependent (зависимая переменная) – выбрать переменную и поместить ее в окно Independet(s) (независимые переменные).
Нажав кнопку Statistics… можно задать расчет ряда коэффициентов регрессии, нажав кнопку Plots… - вид выводимых графиков в процедуре линейной регрессии (см. рис. 2.20), можно задать сохранение результатов процедуры "Линейная регрессия" (кнопка Save…) и параметры процедуры регрессии (кнопка Options…)
При интерпретации результатов, полученных в окне вывода программы SPSS, необходимо учитывать, что некоторые выходные данные требуются только при построении сложных регрессионных моделей. Поэтому рассмотрим только основные элементы выходных данных. В сноске к таблице Model Summary дается информация, которая показывает, насколько хорошо можно представить значение зависимой переменной на основе независимой:
R – коэффициент корреляции между переменными;
R-square - квадрат коэффициента корреляции (показывает, какая часть изменчивости зависимой переменной может быть объяснена независимой переменной).
При интерпретации выходных данных необходимо учитывать значимость коэффициентов (столбец Sig. таблицы ANOVA): линейная регрессионная модель зависимости является надежной, если уровень значимости не превышает 0.05 (5%).
В таблице Coefficients (коэффициенты) приводятся рассчитанные коэффициенты регрессионной модели: регрессионный коэффициент (тангенс угла наклона прямой), а также постоянная прямой. Значение в первой строке столбца В таблицы (Constant) – постоянная, во второй (где приведено имя переменной) – коэффициент (тангенс угла наклона прямой). С помощью этих чисел можно записать уравнение прямой:
Зависимая переменная = Коэффициент * Независимая
переменная + Постоянная
Теперь, используя это уравнение, можно по заданному значению независимой переменной вычислять значения (предсказанные) зависимой переменной.
В столбце Sig. таблицы Coefficients представлен уровень значимости для каждого регрессионного коэффициента. При 5%-ном уровне значимости можно считать неравными нулю только те коэффициенты, для которых значение Sig. не превышает 0.05.
Литература:
Сайт:
http://spss.ru
http://www.5ballov.ru/
Н.Ш. Кремер
«Теория вероятности и математическая статистика»
Руководство по использованию программы статистической обработки SPSS.
С.Ф. Борисова
«Компьютер и Интернет для социолога»
studfiles.net
