Исследовательская работа на тему "Многогранники в архитектуре". Многогранники в архитектуре реферат

Исследовательская работа на тему "Многогранники в архитектуре"

Глазковский филиал имени Героя Советского Союза Н.Н.Шерстова МБОУ Кочетовская СОШ Мичуринского района

Тамбовской области.

Открытая научно-практическая конференция обучающихся «Путь в науку»

Секция естественных наук

Исследовательская работа по математике

Многогранники

в архитектуре

Работу выполнила ученица 9Б класса

Занорина Юлия

научный руководитель: учитель математики

Щекочихина Лариса Александровна

Глазок – 2014

Содержание

Стр.

Вступление …………………………………….…………...…….……………....…3

1. История изучения многогранников…………………………..……….……...5

2. Правильные многогранники

2.1. Виды правильных многогранников…….………..……….….….…………….6

2.2. Некоторые свойства правильных многогранников …………….……………8

3. Пирамидальная форма в строительстве древнего мира……………………12

4. Стоечно-балочная и арочно-сводчатая системы в архитектуре.…….……......13

5. Особенности архитектурных строений XII -XVII веков……….……..........15

6. Применение принципов науки к решению проблем человечества…….…16

7. Особенности архитектурных строений в моем окружении…….……...….18

8. Дом моей мечты……………………………………………………….……..20

Выводы …………..…………………….……..…………………...……...............21

Заключение……..……………………………………..…………....…….................22

Библиографический список.……………………..………..……....……..………24

Приложение 1. Таблица ….........……………..….…………….....….….............25

Приложение 2. Рисунок 1 - 6...……...………….…………...…..…...................25

Рисунок 7-8……….…………..………….……...……..………26

Приложение 3. Фото 1 - 8 ...…….…………………………………...................27

Фото 9 - 14...…….……………………………….......................28

Математика предлагает архитектору ряд общих правил

организации частей в целое, которые помогают расположить

эти части в пространстве, так, что в них проявляется порядок.

Вступление.

Ни один из видов искусств так тесно не связан с геометрией как архитектура. Архитектурные произведения живут в пространстве, являются его частью, вписываясь в определенные геометрические формы. Кроме того, они состоят из отдельных деталей, каждая из которых также строится на базе определенного геометрического тела. Часто геометрические формы являются комбинациями различных геометрических тел.

Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности — от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книги Бранко Грюнбаума «Выпуклые многогранники».

Изучение многогранников на протяжении всей истории велось не только с позиций дальнейшего их применения, но и с целью осмысления философских вопросов об устройстве Вселенной и природе Пространства. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов. В данной работе я хочу рассмотреть, какова же цель применение многогранников в архитектуре. Так сформировалась тема моего исследования: роль многогранников в архитектуре.

Данная работа представляет собой теоретическое исследование, где в качестве объекта рассматривается связь между многогранниками и архитектурой сооружений. Предметом исследования являются многогранники. Целью исследования стал вопрос, каким образом форма многогранника нашла приложение в архитектуре.

В ходе исследования выстроились задачи:

• изучить историю возникновения многогранников;

• рассмотреть формы и свойства многогранников;

• проследить, как геометрическая фигура «многогранник» используется в архитектурных сооружениях.

Сложилась гипотеза, согласно которой, применение разных геометрических форм в архитектуре, в том числе многогранников, способствует созданию разнообразных архитектурных сооружений, непохожих друг на друга.

В ходе данного исследования, помимо описательного метода, я применяла частично – поисковый и аналитический. Все методы обеспечиваются обоснованностью исходных теоретических данных, с опорой на некоторые доказательства.

Теоретическая база исследовательской работы состоит из вэб-страниц (http://schools.techno.ru/sch758/2003/geomet/, http://architecturesss.blogspot.ru, http:www.nips.riss-telecom.ru/poly/ и др.), справочных материалов, соответствующей специализированной литературы (Семенов Е.Е. «Изучаем геометрию», Смирнова И.М. «В мире многогранников», Литвиненко В.Н. «Многогранники. Задачи и решения» и т.п.).

Теоретическая значимость результатов исследования обусловлена анализом принципов и способов применения многогранных форм в архитектуре.

Это исследование помогло бы привлечь внимание окружающих к математике, в частности, к многогранным формам, окружающим нас в повседневной жизни.

1. История изучения многогранников.

История многогранников уходит в глубокую древность и связана с именами таких ученых как Пифагор, Евклид, Архимед, Платон и Кеплер. Одной из первых и самых известных школ была Пифагорейская. Пифагорейцев поражала красота, совершенство и гармония правильных многоугольников. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ – идеалист Платон. С тех пор правильные многогранники (тетраэдр, куб, октаэдр, икосаэдр и додекаэдр) стали называться Платоновыми телами. Среди ученых, исследовавших многогранники, особое место принадлежит Иоганну Кеплеру (1571-1630). Вера в гармонию, красоту и математически закономерное устройство мироздания привела его к мысли о том, что пяти правильным многогранникам соответствуют только шесть (как казалось тогда) планет Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель имела единый центр – Солнце.

Идеи Пифагора, Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира вызывают сегодня лишь вежливую улыбку. Но эта теория нашла свое продолжение в интересной научной гипотезе московских инженеров начала 80-х годов ХХ века В.Макарова и В.Морозова, которые считают, что ядро Земли имеет форму и свойства растущего кристалла [1]. Лучи этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдровую структуру Земли. В земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения мирового океана. В этих узлах находится озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

2. Правильные многогранники.

2.1. Виды правильных многогранников.

Многогранник – это часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (гранями), соединенных таким образом, что каждая сторона (ребро) любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем, вокруг каждой вершины существует ровно один цикл многоугольников. Многогранник называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани, тогда грани его тоже выпуклы. Выпуклый многогранник разрезает пространство на две части — внешнюю и внутреннюю. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и к каждой вершине примыкает одно и то же число граней. Если все грани – правильные р-угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается {p, q}. Это обозначение в XIX веке было предложено швейцарским математиком Л.Шлефли.

Существует пять правильных многогранников. Простейший – правильный тетраэдр, гранями которого служат 4 равносторонних треугольника. Каждая его вершина является вершиной трех треугольников. Тетраэдру соответствует запись {3, 3}. Сумма плоских углов при каждой вершине равна 180˚. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Это частный случай треугольной пирамиды. Тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость α, проходящая через ребро АВ перпендикулярно к противоположному ребру СД, является плоскостью симметрии. (Приложение 2, Рисунок 1) У правильного тетраэдра – 3 оси симметрии и 6 плоскостей симметрии.

Наиболее известен из правильных многогранников куб. Это прямая квадратная призма, все шесть граней которой – квадраты. Так как к каждой вершине примыкают по 3 квадрата, куб обозначается {4, 3}. Сумма плоских углов при каждой вершине равна 270˚. У куба 6 граней, 8 вершин и 12 ребер. Куб имеет один центр симметрии - точку пересечения его диагоналей. Прямые a и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. (Приложение 2, Рисунок 2) Куб имеет 9 осей симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Таких плоскостей девять.

Если две конгруэнтные квадратные пирамиды с гранями, имеющими форму равносторонних треугольников, совместить основаниями, то получится правильный октаэдр. Он ограничен восемью равносторонними треугольниками, к каждой из вершин примыкают по 4 треугольника. Ему соответствует запись {3, 4}. Сумма плоских углов при каждой вершине равна 240˚. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер. Октаэдр имеет центр симметрии – свой центр, 9 осей симметрии и 9 плоскостей симметрии.

Рассмотрим прямую правильную пятиугольную антипризму, грани которой – равносторонние треугольники, и две правильные пятиугольные пирамиды, основания которых конгруэнтны основанию антипризмы, а грани имеют форму равносторонних треугольников. Если эти пирамиды присоединить к антипризме, совместив их основания, то получится правильный икосаэдр, который обозначается {3, 5}. К каждой вершине примыкают по 5 граней. Сумма плоских углов при каждой вершине равна 300˚. Таким образом, икосаэдр имеет 20 граней, 12 вершин и 30 ребер. Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

Еще один правильный многогранник – додекаэдр {5, 3}. Сумма плоских углов при каждой вершине равна 324˚. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Додекаэдр имеет один центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

2.2. Некоторые свойства правильных многогранников.

1. В выпуклом многограннике все грани – выпуклые многоугольники.

Докажем. Пусть F – грань многогранника М; А и В – точки, принадлежащие грани F. (Приложение 2, Рисунок 3) Из условия выпуклости многогранника М следует, отрезок АВ целиком содержится в многограннике М. Так как отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике. То есть F – выпуклый многоугольник.

2. Выпуклый многогранник может быть представлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Докажем. Пусть М – выпуклый многоугольник. S – произвольная точка многогранника М, не принадлежащая ни одной его грани. (Приложение 2, Рисунок 4) Соединим точку S с вершинами многогранника М отрезками. В силу выпуклости многогранника М все получившиеся отрезки и пирамиды целиком содержатся внутри многогранника М и все вместе составляют его.

3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.

Докажем. Предположим противное, то есть существуют точки А и В многогранника М, лежащие по разные стороны от плоскости некоторой его грани N. Рассмотрим пирамиды с вершинами в точках А и В, основаниями которых является грань N. (Приложение 2, Рисунок 5) В силу выпуклости многогранника, эти пирамиды целиком в нем содержатся.

4. В 1752 году Леонард Эйлер доказал свойство, связывающее число его вершин, ребер и граней, получившее название теоремы Эйлера, справедливой для любого выпуклого многогранника. (Приложение 1 Таблица).

Число вершин – число ребер + число граней = 2 (1)

5. Других видов правильных многогранников – нет.

Докажем. Так как каждое ребро в многограннике принадлежит ровно двум граням, а каждая грань имеет ровно p ребер, то, согласно теореме Эйлера: p · Г = 2Р

Поскольку каждое ребро имеет ровно два конца, а в каждой вершине сходится ровно q ребер, то q · В = 2Р. Итак, и (2)

Подставим отношение (2) в формулу Эйлера (1): (3)

Найдем Р из (3): P = 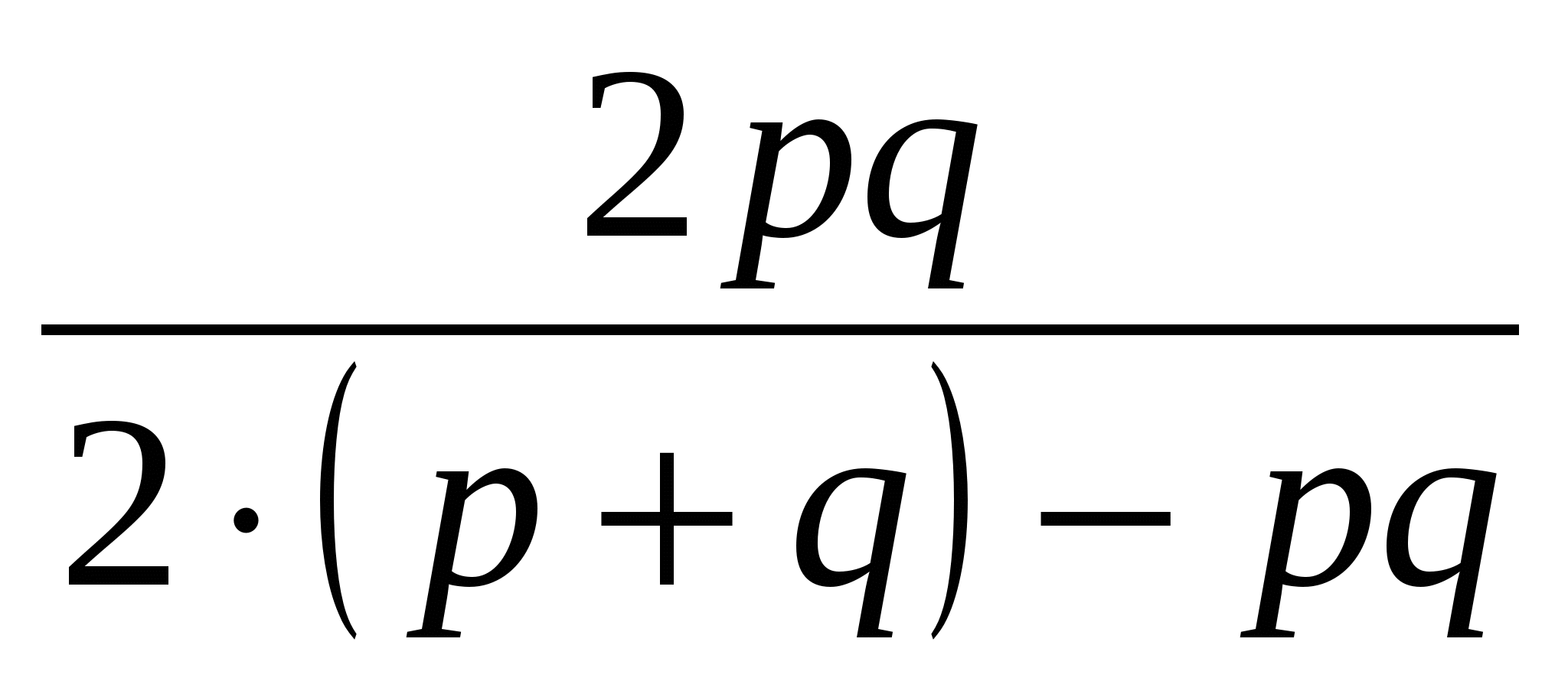(4)

Знаменатель дроби в (4) равен 4 - (p - 2)(q - 2). А так как знаменатель положителен, то (p - 2)(q - 2) < 4 (5)

С другой стороны, как число p сторон у грани, так и число q граней, сходящихся в вершине, не меньше 3. Поэтому уравнение (3) при условии p≥3 и q ≥3 имеет пять и только пять целочисленных решений (p , q): (3, 3), (3, 4), (4, 3), (3, 5), (5, 3).

К неравенству (5) можно также прийти, и рассматривая внутренние углы многогранников. Пусть {p, q} – произвольный правильный многогранник. Так как его гранями служат правильные р-угольники, градусная мера их внутренних углов будет равна 180 – или 180 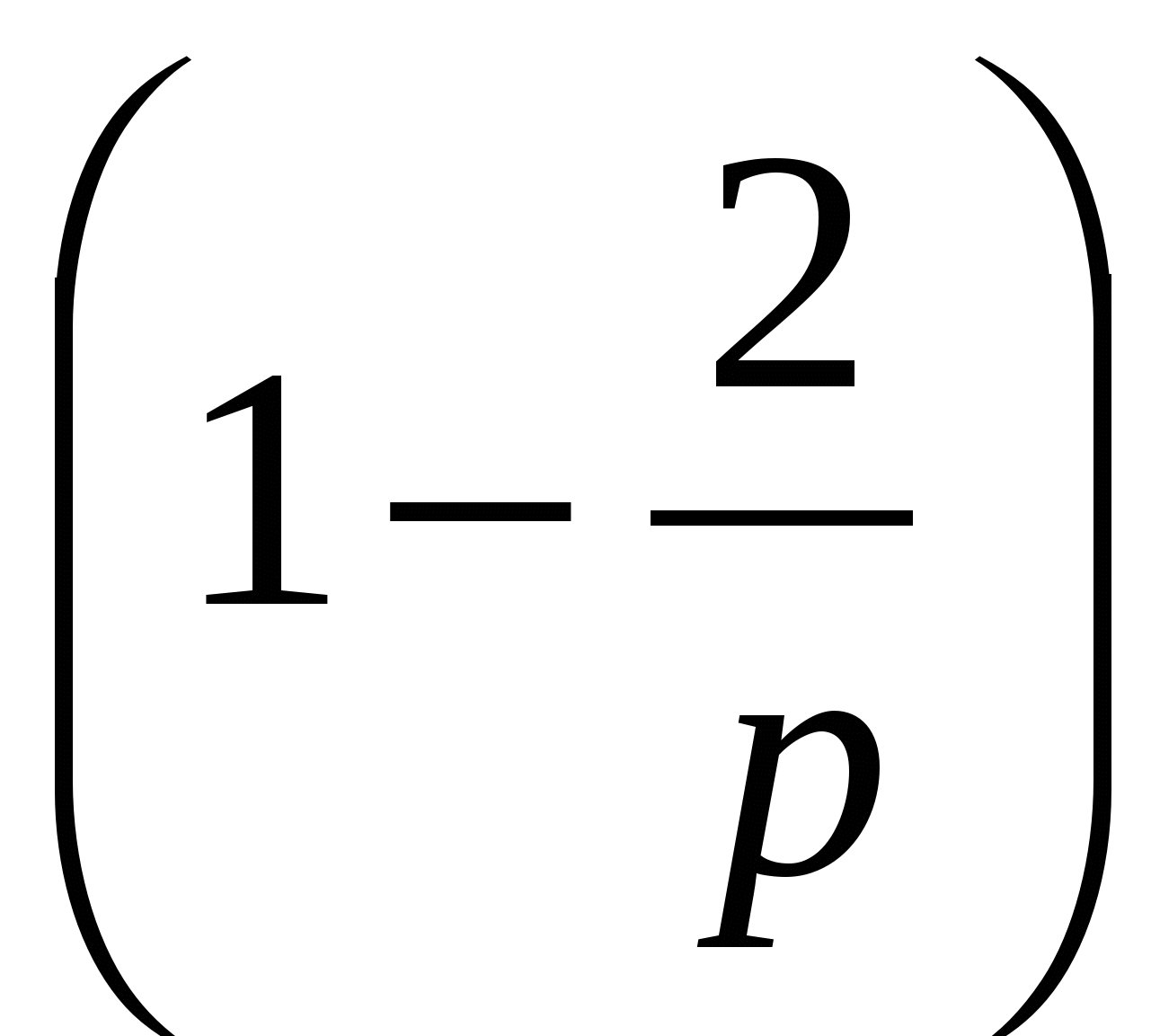(6)

Так как многогранник {p, q} выпуклый, сумма всех внутренних углов по граням, примыкающим к любой из его вершин, должна быть меньше 360˚. Но к каждой вершине примыкают q граней, значит, выполняется неравенство

180˚ 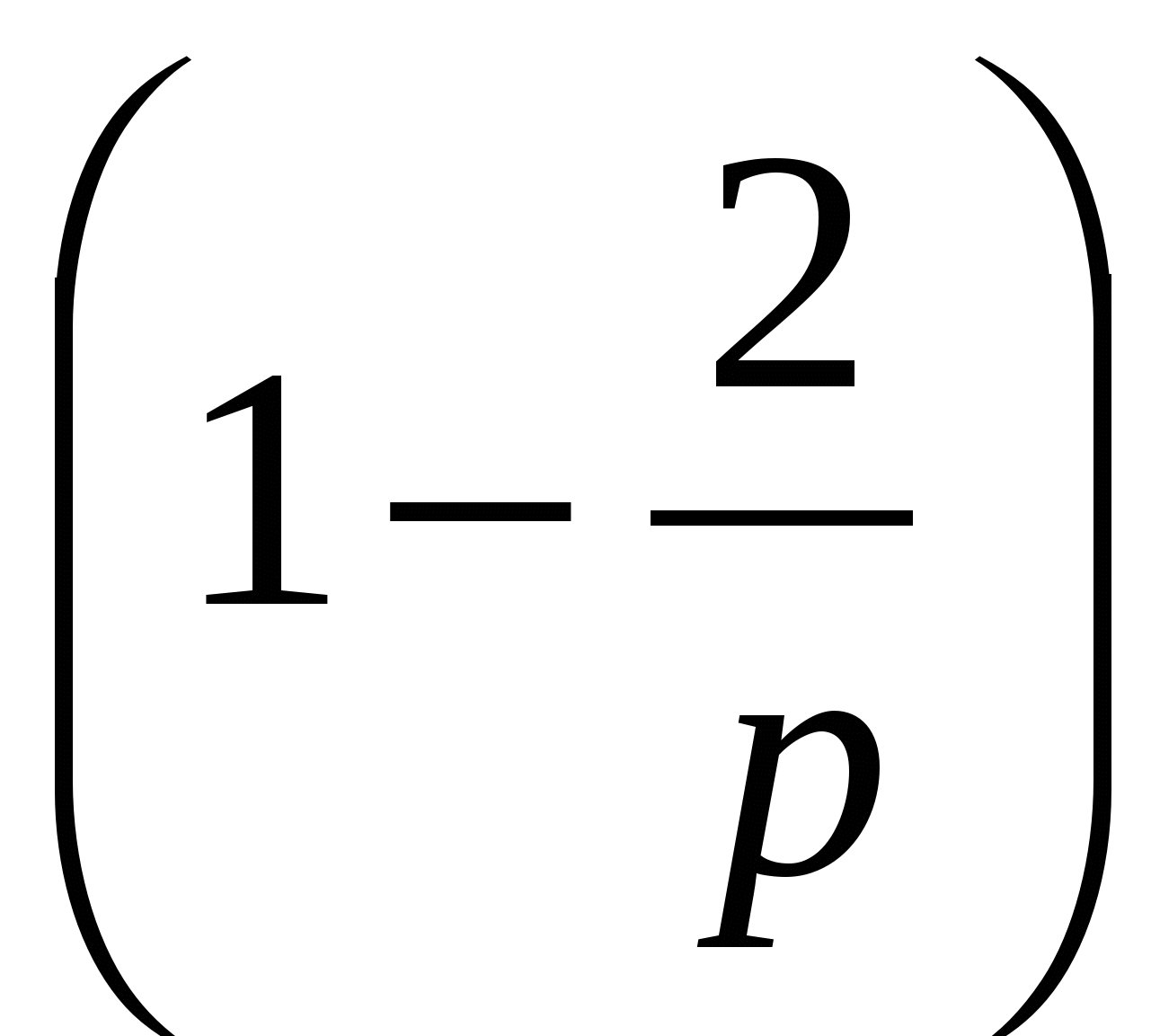q < 360˚ (7)

После несложных алгебраических преобразований полученное неравенство (7) приводится к виду (5). Нетрудно определить, что p и q должны быть больше 2. Подставляя в (5) р = 3, мы обнаруживаем, что единственными допустимыми значениями q в этом случае являются 3, 4 и 5, т.е. получаем многогранники {3, 3}, {3, 4} и {3, 5}. При р = 4 единственным допустимым значением q является 3, т.е. многогранник {4, 3}. При р = 5 неравенству (5) также удовлетворяет только q = 3, т.е. многогранник {5, 3}. При p > 5 допустимых значений q не существует. Следовательно, других правильных многогранников, кроме тел Платона, не существует.

5. Правильным многогранникам свойственна двойственность: если считать центры граней тетраэдра вершинами нового многогранника, то вновь получится тетраэдр; центры граней куба образуют октаэдр; центры граней октаэдра образуют куб; центры граней додекаэдра образуют икосаэдр; центры граней икосаэдра – додекаэдр. (Приложение 2, Рисунок 7)

Кроме того, ребра правильного многогранника равны между собой и равны также все двугранные углы, содержащие две грани с общим ребром. Следовательно, радиус вписанной и описанной сферы многогранника совпадают. Вершины любого правильного многогранника лежат на сфере. Помимо этой сферы, называемой «описанной сферой», имеются еще две. Одна из них, «срединная сфера», проходит через середины всех ребер, а другая, «вписанная сфера», касается всех граней в их центрах. Все три сферы имеют общий центр, который называется центром многогранника.

Симметрия многогранника – такое его движение в пространстве, которое оставляет неизменными множества вершин, ребер и граней. Существует одна симметрия, которая свойственна всем многогранникам. [3] Рассмотрим прямую правильную р-угольную призму. Пусть a – прямая, соединяющая центры оснований. (Приложение 2, Рисунок 6) Поворот вокруг a на любое целое кратное угла ˚ является симметрией. Пусть p – плоскость, проходящая посередине между основаниями, параллельна им. Отражение относительно плоскости p (движение, переводящее любую точку A в точку B, такую, что p пересекает отрезок AB под прямым углом и делит его пополам) – еще одна симметрия. Комбинируя отражение относительно плоскости p с поворотом вокруг прямой a, мы получим еще одну симметрию. Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника как твердого тела здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/р градусов вокруг прямой a есть произведение отражений относительно любых двух плоскостей, содержащих a и образующих относительно друг друга угол в 180/р градусов. Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.

Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра. Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии. Для наглядности полезно построить картонную модель правильного тетраэдра и убедиться, что тетраэдр действительно обладает 24 симметриями.

Еще в античной науке было установлено, что додекаэдр и икосаэдр основаны на «золотом сечении».

Рассмотрим еще вопрос: можно ли правильными многогранниками заполнить пространство так, чтобы между ними не было просветов. Оказывается, можно только с помощью одного правильного многогранника-куба. [2] Пространство можно заполнить и ромбическими додекаэдрами. Чтобы это понять, надо решить задачу.

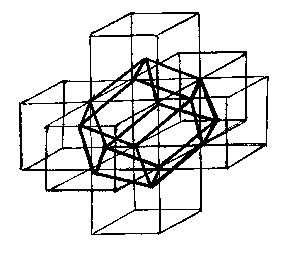
Задача. С помощью семи кубов, образующих пространственный "крест", постройте ромбододекаэдр и покажите, что ими можно заполнить пространство.

Решение. Рассмотрим часть кубической решетки. (Приложение 2, Рисунок 8) Средний куб оставим нетронутым, а в каждом из "окаймляющих" кубов проведем плоскости через все шесть пар противолежащих ребер. "Окаймляющие" кубы разобьются на шесть равных пирамид с квадратными основаниями и боковыми ребрами, равными половине диагонали куба. Пирамиды, примыкающие к нетронутому кубу, и образуют вместе с последним ромбический додекаэдр. Значит, ромбическими додекаэдрами можно заполнить все пространство. Как следствие получаем, что объем ромбического додекаэдра равен удвоенному объему куба, ребро которого совпадает с меньшей диагональю грани додекаэдра. Интересно, что пчелиные ячейки также являются геометрическими фигурами. Верхняя часть пчелиной ячейки представляет собой часть ромбододекаэдра.

Итак, правильные многогранники открыли нам попытки ученых приблизиться к тайне мировой гармонии и показали неотразимую привлекательность геометрии.

3. Пирамидальная форма в строительстве древнего мира.

Люди с древних времен, возводя свои жилища, думали, в первую очередь, об их прочности. Математик бы сказал, что здесь очень важна геометрическая форма (тело), в которое вписывается сооружение.

Самым прочным архитектурным сооружением считаются египетские пирамиды. Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет большой площади основания. С другой стороны, форма пирамиды обеспечивает уменьшение массы по мере увеличения высоты над землей, а, значит, делает ее более прочной в условиях земного тяготения. Великая египетская пирамида в Гизе – это единственное из Семи чудес света, сохранившееся до наших дней. (Приложение 3, Фото 1) Она стоит уже почти пять тысяч лет.

Вообще, первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Первые архитектурные сооружения (Пирамида Луны, конец первого тысячелетия до н.э. – начало н.э.; Пирамида Тенаюка, XII – XV века; Пирамида Кукулькана, VIII – XII века) строились из камней, кусков глины, дерева и влажного песка. Построить такое сооружение – трудная инженерная задача: края блоков должны быть выверены и выравненны с самого начала строительства, иначе они не сойдутся в одной точке на вершине пирамиды. Ошибка даже в два градуса могла бы привести к катастрофическим результатам [5]. Остается удивляться, как без современных научных приборов древние египтяне могли определить направление на нужную точку в воздухе и строить прямо по направлению на нее.

Если мы рассмотрим архитектурные сооружения, которые строились человеком, то можно отметить, что уже тогда человек выбирал самые выразительные по форме и величине камни. Все это говорит о том, что дизайн архитектурного сооружения начинал свое развитие уже с древних времен.

4. Стоечно-балочная и арочно-сводчатая системы в архитектуре.

На смену пирамидам пришла стоечно-балочная система. С точки зрения геометрии она представляет собой многогранник, который получится, если мысленно на два вертикально стоящих прямоугольных параллелепипеда поставить еще один прямоугольный параллелепипед.

Простейшая стоечно-балочная конструкция в процессе своего развития получала различную художественную разработку, в результате чего на каждом этапе истории Египта складывалась определённая система взаимосвязи конструкции и её художественного истолкования путём придания ей индивидуального характера, соответствующих пропорций, особых деталей, пластики и декоративных украшений. Эта система получила условное название ордера.

В развитии египетского ордера особенно заметные изменения наблюдаются в форме опор – столбов и колонн. Для раннего периода характерны опоры геометрически правильной формы, позднее (Новое царство) получают широкое распространение более сложные колонны, обычно подражающие формам растительного мира.

Египтяне умели строить и настоящие своды, но делали они это только исключительно при строительстве усыпальниц из кирпича, при возведении складских помещений и прокладке каналов. Лестницы стали использоваться гораздо позже, до этого в большинстве случаев для соединения различных уровней и этажей здания пользовались наклонной плоскостью – пандусом [9].

Чтобы стены зданий пересекались под прямым углом, использовалось известное древним египтянам соотношение сторон треугольника 3:4:5; угол между сторонами длиной 3 и 4 единицы – обязательно прямой, поэтому отношение короткой и длинной сторон плана помещения первоначально принимали равным 3:4. Позднее соотношение катетов египетского треугольника было заменено соотношением сторон прямоугольника, длину которых назначали по правилам золотой пропорции. Золотое сечение, золотую пропорцию размеров сторон помещения, высоты и ширины дверных и оконных проёмов находили делением отрезка длиной а в крайнем и среднем отношении. Делением его на две такие части x и (a – x) , большая из которых x будет средним геометрическим между длинами а и (а – x). Размер x находят из математической пропорции а:x = x:(а – x), откуда, положив а = 1, получают квадратное уравнение x2 + x – 1 = 0 и далее x ≈ 0,618. Следовательно, размеры сторон прямоугольника будут равны 0,618 и 1 – 0,618 ≈ 0,382, а их отношение 0,618:0,382 ≈ 1,62 [6].

Камень плохо работает на изгиб, но хорошо работает на сжатие. Это привело к использованию в архитектуре арок и сводов. Так возникла новая арочно-сводчатая конструкция. С появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей, вошли окружности, круги, сферы и круговые цилиндры. Первоначально в архитектуре использовались только полуциркульные арки или полусферические купола. Это означает, что граница арки представляла собой полуокружность, а купол – половину сферы [8]. Арочно-сводчатая конструкция позволяла древнеримским архитекторам возводить гигантские сооружения из камня. К ним относится знаменитый Колизей или амфитеатр Флавиев.

Нужно заметить, что до сих пор стоечно-балочная конструкция является наиболее распространенной в строительстве. Большинство современных зданий в своей основе имеют именно стоечно-балочную конструкцию (Приложение 3, Фото 2).

5. Особенности архитектурных строений XII -XVII веков.

В XII веке архитектура понимается уже как наука, как геометрия, имеющая практическое приложение. Усложнившаяся архитектурная практика готической эпохи, требовала от архитекторов специальных математических знаний. Готические сооружения были устремлены ввысь, поражали величественностью, главным образом за счет высоты. В их формах широко использовались пирамиды и конусы, гармонично сочетались множественные объёмы многогранников, объединённых в единую пирамидальную композицию. Были воздвигнуты величественные и обширные готические храмы и соборы, архитектура которых поражает многообразием форм многогранников, где единство и логика пропорционального строя пронизывали все многообразие архитектурных элементов. (Приложение 3, Фото 3). В процессе возведения готического храма перед архитектором вставали сложнейшие конструктивные задачи. Их конструкторская и техническая мысль носила чисто эмпирический характер. Геометрические методы позволяли архитектору готической эпохи определить пропорции здания, курватуру сводов и арок, толщину сводов и опор. С их помощью он выяснял взаимодействие сил распора и противостоящих ему сил и нагрузку, падающую на несущие части архитектурной конструкции. Они помогали ему при создании проекта будущего сооружения и при определении основных элементов архитектурной композиции, ее скульптурной и живописной декорации [9]. В XIII-XVII вв. многогранники были основой архитектурных строений, больше всего применялись кубы, но по мере развития, нашли применения и другие виды многогранников, такие как тетраэдр.

Геометрия сопровождала средневекового архитектора на всем его творческом пути, воспитывая его глаз на красоте геометрических форм, чистоте линий и точности пропорциональных соотношений. Она начиналась, когда готический архитектор приступал к созданию плана будущего сооружения, который он обычно не выражал в масштабе, лишь приблизительно намечая основные соотношения всех частей предполагаемого здания.

6. Применение принципов науки к решению проблем человечества.

Популяризатором геодезиков XX столетия был американский архитектор и инженер Фуллер Ричард Бакминстер, изучавший в конце 40-х годов свойства куполов. Фуллер надеялся, что геодезики помогут решить послевоенный жилищный кризис. Его заинтересовала конструкция геодезического купола прежде всего благодаря малой массе при большом внутреннем пространстве (геодезическая линия - это линия, соединяющая две точки на изогнутой поверхности) [7]. Размышляя о геометрических понятиях, Фуллер пришел к выводу, что можно создать восьмиугольную конструкцию, используя для этого прутья, изготовленные в виде переплетающихся треугольников.

Форма купола образуется благодаря особому соединению балок — в каждом узле сходятся ребра слегка различной длины, которые в целом образуют многогранник, близкий по форме к сегменту сферы (Приложение 3, Фото 4). Эта уникальная, куполообразная конструкция представляется в виде многогранника (икосаэдра), то есть двадцатигранника со сторонами в виде правильных треугольников. Эта фигура и разворачивается на плоскость, давая неискаженные соотношения по всей поверхности.

Чтобы понять, насколько новаторской и радикальной является идея создания геодезического купола, посмотрите на здания, которые вас окружают. Сколько из них имеют прямые углы? Скорее всего, вы ответите: «Все». В геодезическом куполе нет прямых углов. Ни одного!

Купола имеют ряд преимуществ, которые делают их уникальными архитектурными сооружениями. Это сетчатая оболочка, обладающая большой несущей способностью, причем, чем больше купол, тем она выше. Также эта конструкция обладает очень хорошими характеристиками прочности. Благодаря своей уникальной структуре, купол может принимать любые формы. Он представляет собой полусферу, а поскольку сферы охватывают наибольший объем при наименьшем пространстве, геодезический купол, согласно законам природы, позволяет, используя минимальное количество строительных материалов, охватить наибольшую площадь. Он является воплощением оригинальной идеи «сделай больше, затратив меньше». Простые сооружения создаются очень быстро из достаточно лёгких элементов силами небольшой строительной группы: структуры до 50 м собираются даже без строительного крана. На строительство купола требуется на 60% меньше строительных материалов, чем на сооружение обычной конструкции подобного размера.

Всего построено около трехсот тысяч «геодезических куполов», они широко используются как ангары, склады, оранжереи, планетарии, аудитории, эксплуатируются как жилища в местах со сложными погодными условиями (купол на Южном полюсе). Геодезические купола используются при создании туристических палаток, конференц-центров и кинотеатров. Эта конструкция рассматривается как подходящая для организации постоянно обитаемых станций на Луне и Марсе. [4]

Однако есть и недостатки. Обычно современные материалы для создания граней купола имеют прямоугольное сечение, их приходится дополнительно обрабатывать, придавая треугольное, из-за чего появляется много лишних отходов. Кроме того, из-за высокой стоимости жилые купола также не оправдали своих надежд. Хотя встречаются и куполообразные жилые дома (Приложение 3, Фото 5).

Благодаря своему футуристическому виду геодезики попали во множество фантастических произведений. В ряде из них купола накрывают целые колонии людей, осваивающих планеты звёздных систем. Также геодезические купола являются ключевым архитектурным элементом в произведениях из трилогии «Киберпространство» Уильяма Гибсона. Геодезический купол - одно из самых прочных сооружений на планете, а также одно из самых легких, дешевых, быстрых и простых в возведении.

7. Особенности архитектурных строений в моем окружении.

В ходе исследовательской работы меня заинтересовал такой вопрос: а какие формы архитектурных сооружений встречаются в моем окружении? Прежде всего, конечно же, это широко распространенные обычные здания, имеющие формы всевозможных прямых параллелепипедов. Их оказалось абсолютное большинство.

Есть и уникальные архитектурные сооружения! Кто был в Москве, знает, как красив Московский Кремль. Прекрасны его башни! Сколько интересных геометрических фигур положено в их основу! Вот, например, Набатная башня. На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а еще выше воздвигнута четырехугольная усеченная пирамида (Приложение 3, Фото 7). На ней расположены четыре арки, увенчанные восьмиугольной пирамидой. В Спасской башне Московского кремля в основании можно увидеть прямой параллелепипед, переходящий в средней части в фигуру, приближающуюся к цилиндру. Завершается же она пирамидой. (Приложение 3, Фото 6) Таким образом, можно говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей.

Заслуживают внимания здания православных храмов нашего города Мичуринска. Церковь Илии-пророка на площади имени Мичурина (Приложение 3, Фото 10) и гордость нашего города, памятник архитектуры федерального значения, храмовое сооружение второй половины XIX века, кафедральный собор Мичуринской епархии – Боголюбский (Приложение 3, Фото 9). Рассматривая эту церковь, я заметила, что основание Храма выполнено в виде равноконечного креста с одинаковыми фасадами с четырех сторон. Фасады подчинены точным законам осевой симметрии. Каждый фасад Храма делится четырьмя столбами-колоннами на три части, из которых средняя больше крайних. Все строение увенчано пятью шлемовидными главами. Круглая стена средней главы лежит на восьмигранном основании. Прочие главы находятся на выходящих между выступами углах и имеют форму восьмиугольных башен. Стиль куполов соответствует общему характеру здания: они вверху сужаются, подобно главам всех русских церквей.

Мое внимание привлекли также здания, в форме которых гармонично сочетаются множественные объёмы параллелепипедов, четырехгранных призм, объединённых в единую композицию, усложненных всевозможными барельефами, колоннами, полуцилиндрическими выступами или выемками. Это здания Мичуринского педагогического института, железнодорожного вокзала, Драматического театра (Приложение 3, Фото 11, 12, 13). Как писали «Тамбовские губернские ведомости» XIX века о здании Драматического театра: «здание не отличается вычурной архитектурой, но довольно обширно и симпатично». Конечно же, заслуживает внимания и архитектура здания моей школы, где геометрические формы являются комбинациями различных геометрических тел (Приложение 4, Фото 8). Это гармоничный комплекс, состоящий из двух прямых параллелепипедов различных по длине, но равных по высоте, примыкающих друг к другу. Кроме того, со стороны фасада к центральной части примыкает фигура, состоящая из двух полуцилиндров разного диаметра, расположенных один на другом. Стены заполнены вертикальными рядами окон. Крыша представляет собой сложное сочетание трехгранных призм, пирамид и фигур, приближающихся к конусу и усеченному конусу. В целом, архитектура здания школы определена единой закономерностью, симметричностью, что обеспечивает восприятие целостности и представление о порядке. Главное достоинство здания нашей школы – необычайной красоты фасад.

8. Дом моей мечты.

Анализируя некоторые архитектурные сооружения, и сравнивая геометрические формы, входящие в их конструкции, можно заметить, что, несмотря на похожесть зданий, в архитектуре каждого есть такие геометрические формы, которые делают их различными.

Работая над данным проектом, я задалась вопросом: «Каким бы я хотела видеть дом своей мечты?».

Ну, прежде всего, дом моей мечты должен быть необычным, выделяться своей архитектурой, как бы выпадая из контекста окружающей застройки, говоря "Посмотрите на меня!".

Я постаралась изобразить свои фантазии на бумаге, и в результате получилось ярко выраженное авангардное здание (Приложение 3 Фото 14). Все составляющие элементы архитектуры компонуются с помощью изгибов взятой за основу призматической формы. Некоторые их части существуют внутри этой формы, другие явно принадлежат улице, не покидая при этом зоны интерьера.

Я причисляю себя к числу людей, называемых экстравертами. Это люди, которые открыты внешнему миру и любят живое общение. А еще я очень люблю свет. Поэтому большая часть дома у меня будет выполнена в архитектурном стиле “Хай Тек”, где вся конструкция открыта для обозрения и можно видеть геометрию линий, которые идут параллельно или пересекаются, образуя ажурное пространство сооружения. Внешнее и внутреннее пространство дома объединено благодаря масштабным окнам и сложной геометрии элементов в конструкции. Кроме того, стеклянные фасады создают эффект зависания массивных балок в воздухе. Поэтому, находясь в гостиной, внутри здания, мы в то же время, как бы погружены в окружающий ландшафт. Все внутреннее пространство хорошо освещено, а удобные лестницы позволяют комфортно перемещаться.

Думаю, что в таком доме будет уютно и комфортно!

Выводы

Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. В результате проведенной исследовательской работы, проанализировав литературу и изучив многогранники, я сделала вывод, о том, что действительно многогранники нашли широкое применение в архитектуре. Современные здания и старинные церкви, построенные в форме многогранников, скрывают в себе некую тайну, встретившись с которой, человек считает необходимым разгадать её. Именно это завораживает и интригует взгляды людей.

Моя гипотеза о том, что применение разных геометрических форм в архитектуре, в том числе многогранников, способствует созданию разнообразных архитектурных сооружений, непохожих друг на друга, нашла свое подтверждение. Выполнив эту работу, я узнала много нового и интересного. Многогранники, как простейшие и красивые пространственные формы, применялись уже в древние и средние века. И сегодня определенные принципы науки применяют к решению некоторых проблем человечества. Математика предлагает архитектору ряд, если так можно назвать, общих правил организации частей в целое, которые помогают:

• расположить эти части в пространстве, так, что в них проявлялся порядок;

• установить определенное соотношение между размерами частей и задать для изменения размеров (уменьшения или увеличения) определенную единую закономерность, что обеспечивает восприятие целостности и представление о порядке;

• выделить определенное место в пространстве, где будет размещаться сооружение, описать его определенной математической формой, которая также позволит выделить его из других сооружений и внести  в их  состав, создав новую композицию, новый архитектурный ансамбль.

Заключение

Наука геометрия  возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения. В конечном счете, в основе всей техники, так или иначе, лежит геометрия, потому что она появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.

И технику, и инженеру, и квалифицированному рабочему, и людям искусства геометрическое воображение необходимо, как геометру или архитектору. Математика, в частности геометрия, представляет собой могущественный инструмент познания природы, создания техники и преобразования мира.

Мое исследование показало, что проблема исследования многогранников была насущной всегда.  Правильные многогранники имеют красивые формы. Они являются удивительным символом симметрии, привлекавшим внимание выдающихся мыслителей. Этим объясняется непрекращающийся интерес человека к многогранникам.

История изучения и изображения многогранников являет собой яркий пример взаимопроникновения различных областей знания, неразрывности понятий «наука» и «искусство» как различных способов познания мира, двух основных составляющих единого целого — культуры, главного наследия человеческой цивилизации. 

Часто в архитектурном сооружении сочетаются различные геометрические фигуры, что позволяет создавать разнообразные архитектурные сооружения, непохожие друг на друга. Таким образом, можно говорить о пространственных геометрических фигурах, которые служат основой сооружения в целом или отдельных его частей.

Благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии. Формы многогранников придают зданиям особый вид. Многогранники в архитектуре необходимы. Ведь это не просто красивые и большие здания, это прочные, надёжные и уникальные сооружения, которые ещё много лет будут поражать своей точностью, величественностью и таинственностью. Правы арабы в том, что всё на свете страшится времени. Но больше всего они правы в том, что время страшится пирамид.

Математика предлагает архитектору ряд общих правил организации частей в целое, которые помогают расположить эти части в пространстве, так, что в них проявляется порядок.

Библиографический список

1. Кац Е.А. Искусство и наука — о многогранниках вообще и усеченном икосаэдре в частности, Издательство «Энергия», 2002, №10, с.42-47; №11, с.45-50; №12, с.56-60.

2. Литвиненко В.Н. Многогранники. Задачи и решения:- Москва: «Вита-Пресс», 1995.

3. Смирнова И.М. В мире многогранников: Книга для учащихся.- Москва: Просвещение, 1995.

4. Стахов А.П. «Код да Винчи», Платоновы и Архимедовы тела, квазикристаллы, фуллерены, решетки Пенроуза и художественный мир Матюшки Тейи Крашек // «Академия Тринитаризма», Москва, Эл № 77-6567, публ.12561, 07.11.2005.

5. Я познаю мир: Детская энциклопедия. Архитектура.1990

6. http://schools.techno.ru/sch758/2003/geomet/new!!/prav.html

7. http://slovari.yandex.ru/dict/bse/article/00048/75500.htm

8. http://architecturesss.blogspot.ru/2010/12/blog-post_14.html

9. http://ru. wikipedia. org

Приложение 1. Таблица . Связь вершин, ребер и граней

Название

Запись Шлефли

Число вершин

Число ребер

Число граней

Тетраэдр

{3,3}

4

6

4

Куб

{4,3}

8

12

6

Октаэдр

{3,4}

6

12

8

Икосаэдр

{3,5}

12

30

20

Додекаэдр

{5,3}

20

30

12

Приложение 2. Рисунки.

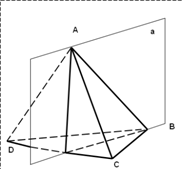
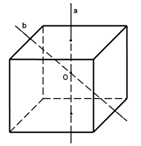
Рисунок 1. Симметрия тетраэдра

Рисунок 2. Оси симметрии куба

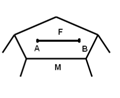
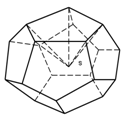
Рисунок 3. Отрезок целиком в многограннике М

Рисунок 4. Внутренняя точка S многогранника М

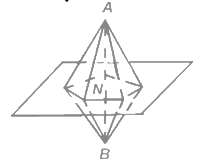
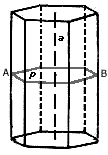
Рисунок 5.

Пирамиды с вершинами А и В

Рисунок 6.

Отражение многогранника

Приложение 2. Рисунок 7. Двойственность многогранников

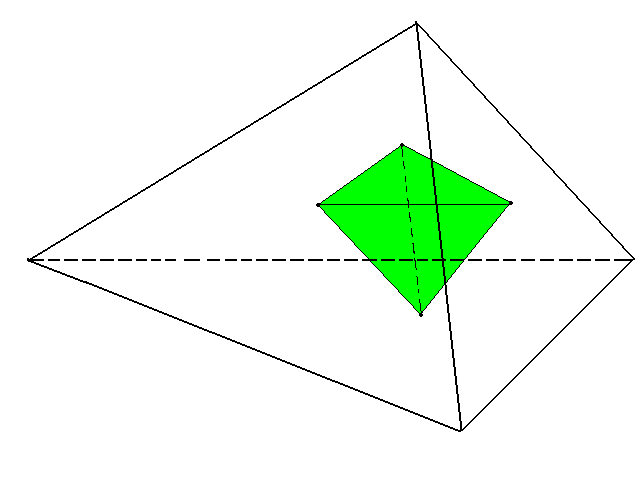
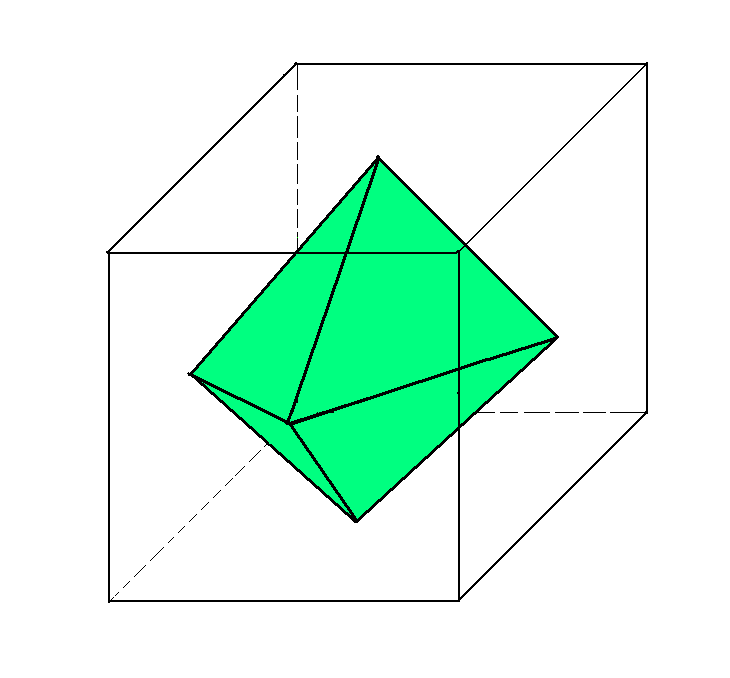
Тетраэдр

Куб

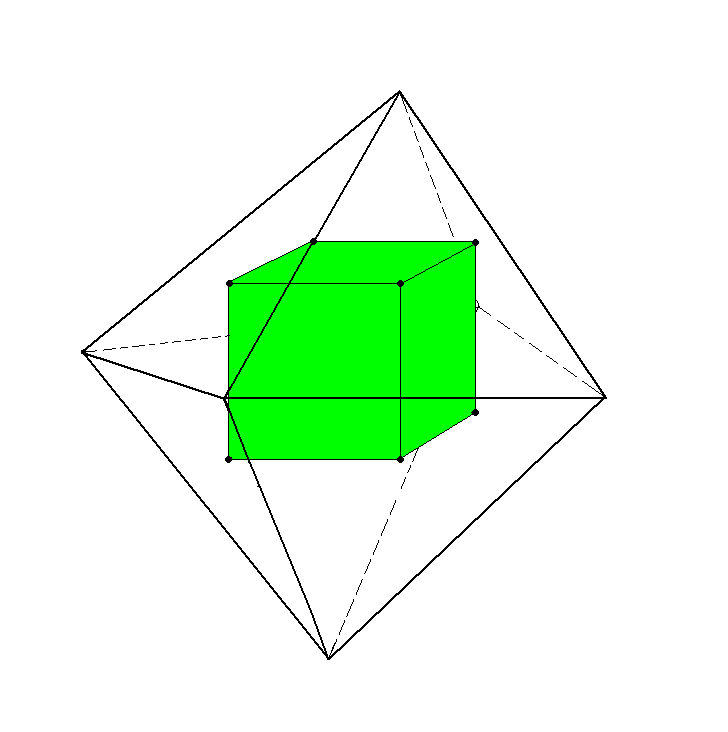
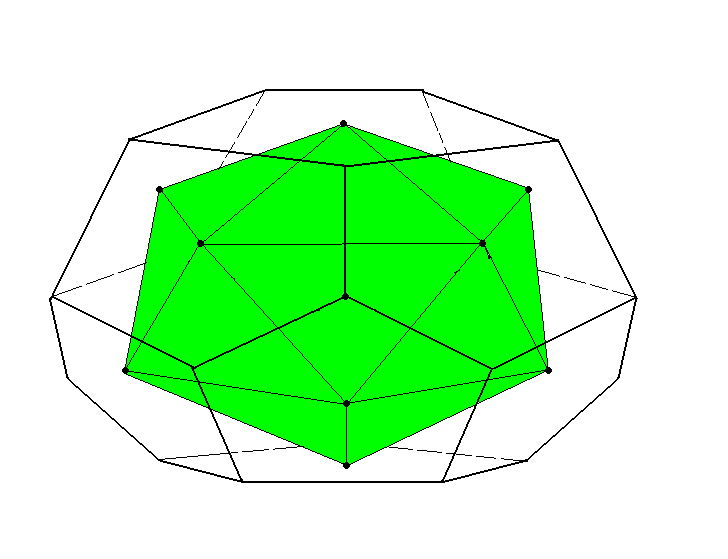
Октаэдр

Додекаэдр

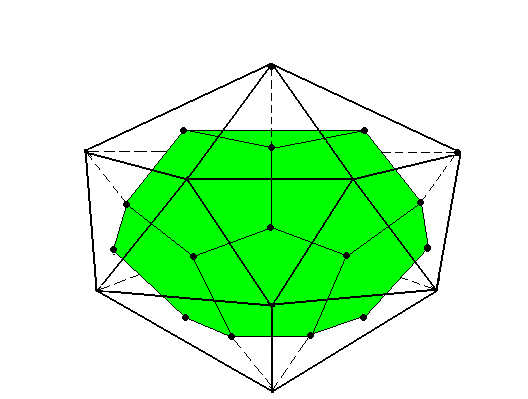
Икосаэдр

Приложение 2. Рисунок 8. Заполнение кубами пространства

Приложение 3. Фото.

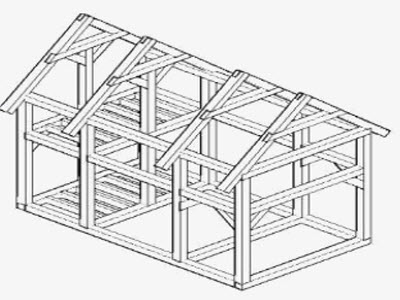
Фото 1. Великая пирамида в Гизе

Фото 2. Стоечно-балочный каркас

Фото 3. Готические сооружения

Фото 4. Сетчатая оболочка геодезического купола

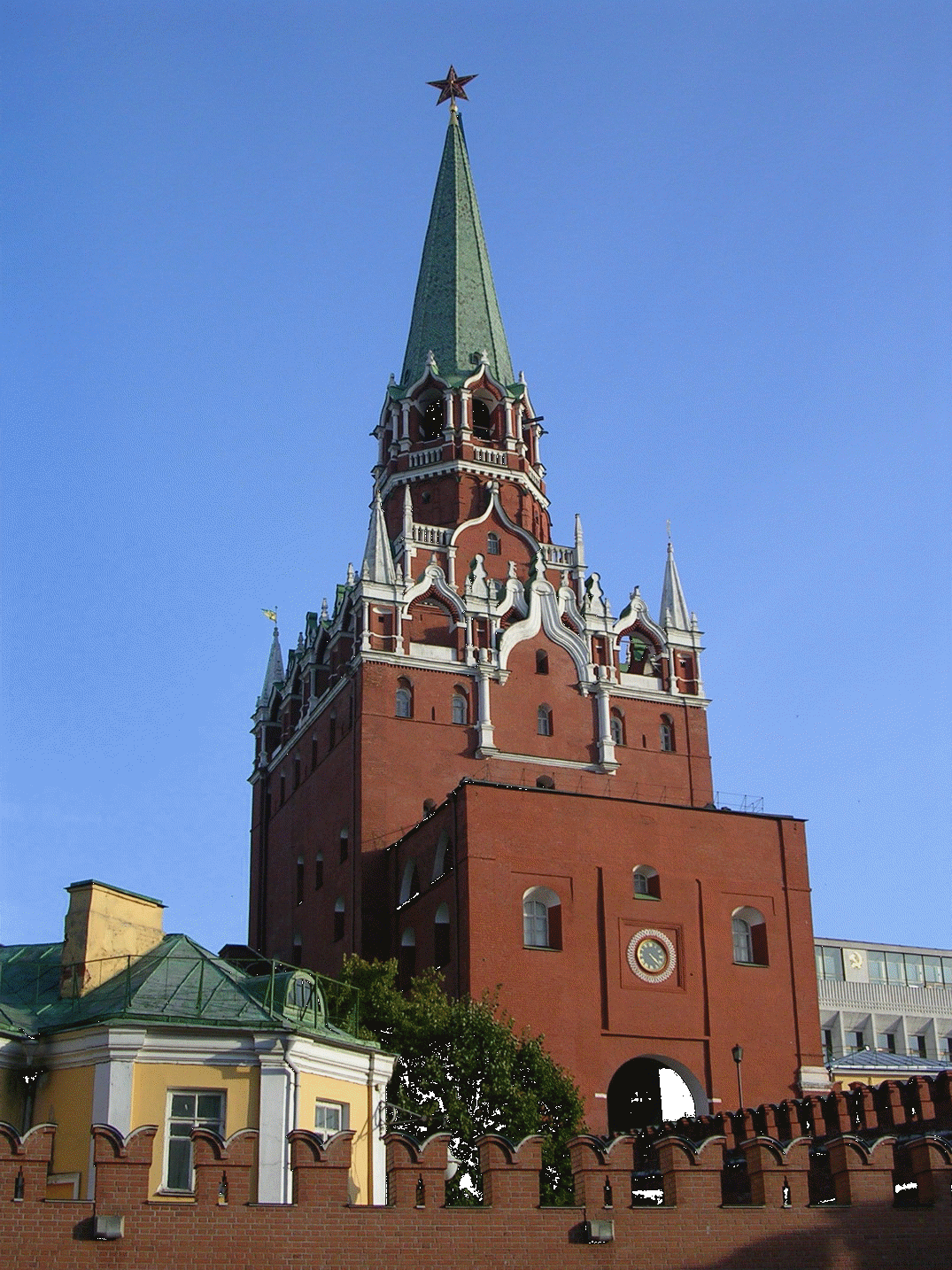
Фото 5. Куполообразный домик в штате Миссури

Фото 6. Спасская башня

Фото 7. Набатная башня

Фото 8. Здание Глазковской школы

Фото 9. Боголюбская церковь

Фото 10. Церковь Илии-пророка

Фото 11. Драмтеатр

Фото 12. Педагогический институт

Фото 13. Железнодорожный вокзал

Фото 14. Дом моей мечты

infourok.ru

Исследовательский реферат на тему "В мире многогранников"

МБОУ « Средняя общеобразовательная школа № 3»

В мире многогранников

Исследовательский реферат.

Выполнил: ученик 10 «Б» класса

Касумов РамизНаучные руководители:

Ханаша Любовь Николаевна,

Лянтор

Содержание

1. Введение...............................................................................................................................

2. История развития многогранников....................................................................................

3.Определение многогранника, его элементы..................................................................

4. Классификация многогранников.......................................................................................

5. Тела Платона.........................................................................................................................

6. Тела Архимеда.....................................................................................................................

7. Звездчатые многогранники................................................................................................

8. Многогранники в искусстве...............................................................................................

9. Многогранники в архитектуре...........................................................................................

10. Музей плодов в Яманаши.................................................................................................

12. Многогранники в природе ..............................................................................................

13. Заключение........................................................................................................................

16. Список используемой литературы……………………………………………………..

17. Приложение 1 …………………………………………………………………………...

18. Приложение 2 …………………………………………………………………………...

19. Приложение 3……………………………………………………………………………

20.Приложение 4…………………………………………………………………….………

Аннотация

Касумов Рамиз

г. Лянтор, МБОУ «СОШ №3», 10 б класс

«В мире многогранников»

руководители: Ханаша Любовь Николаевна, учитель математики

Гороховик Татьяна Георгиевна, учитель математики

Цель работы: изучить мир многогранников, выяснить проявление в природе и применение в искусстве и архитектуре.

Задачи:

1. изучить литературу по выбранной теме;

2. ознакомиться с различными видами многогранников, их свойствами;

3. выяснить, где они встречаются в природе и окружающем нас мире;

4. изготовить модели многогранников для кабинета математики.

Методы исследований: анализ научной литературы, сравнение, моделирование, исторический, фотофиксация.

Основные результаты исследований: изучил историю многогранников, рассмотрел различные виды многогранников, выяснил, где они встречаются в природе и окружающем нас мире, изготовил с одноклассниками модели многогранников для кабинета математики.

Введение

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Карбюзье в начале 20 века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека.

Стереометрия довольно сложный раздел геометрии для многих учеников школ, ведь пространственное воображение развито далеко не у всех. К тому же, сам предмет геометрии не вызывает особого энтузиазма у учащихся. «Предмет математики настолько серьезен, что полезно не упускать случая, делать его немного занимательным», говорил Блез Паскаль. Это и послужило причиной выбора темы моей работы: «Мир многогранников». Трудно найти человека, который не имел бы какого-либо представления о многогранниках. С многогранниками мы встречаемся везде - в природе, технике, искусстве, науке, архитектуре. Применение разнообразных геометрических форм придает строениям особый колорит, поднимает человечество на более высокую ступень развития.

Тема работы: «В мире многогранников».

Творческое название: «Глядя на мир нельзя не удивляться!»

Проблема: Существует ли гармония между красотой и многогранностью?

Задачи:

Изучить литературу о многогранниках.

Показать влияние правильных многогранников на возникновение философских теорий и гипотез.

Ознакомиться с различными видами многогранников, их свойствами.

Показать связь геометрии и природы.

Познакомиться с примерами применения многогранников в архитектуре и искусстве.

Систематизировать найденную информацию.

Изготовить модели многогранников для кабинета математики.

Создать презентацию к работе.

Объект исследования: Математика

Предмет исследования: Многогранники

Гипотеза: Без многообразия геометрических форм окружающий нас мир был бы скучен и однообразен.

История развития многогранников

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды. Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой.

Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.

Наше знакомство с многогранниками начинается уже в начальных классах (куб, прямоугольный параллелепипед) и продолжается до окончания школы. Многогранником называется тело, граница которого является объединением конечного числа многоугольников. [3]

Элементы многогранника

Грань многогранника – это некоторый многоугольник (многоугольником называется ограниченная замкнутая область, граница которой состоит из конечного числа отрезков).

Стороны граней называются ребрами многогранника, а вершины граней – вершинами многогранника. К элементам многогранника, кроме его вершин, ребер и граней, относятся также плоские углы его граней и двугранные углы при его ребрах. Двугранный угол при ребре многогранника определяется его гранями, подходящими к этому ребру. [1]

Классификация многогранников

Выпуклый многогранник - это многогранник, любые две точки которого соединимы в нем отрезком. Выпуклые многогранники обладают многими замечательными свойствами.

Теорема Эйлера: Для любого выпуклого многогранника В-Р+Г=2,

Где В – число его вершин, Р - число его ребер, Г - число его граней.

Теорема Коши: Два замкнутых выпуклых многогранника, одинаково составленные из соответственно равных граней равны.

Выпуклый многогранник считается правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер.

Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. [4]

«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»

Бертран Рассел

Тела Платона

Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. “Правильных многогранников так мало, - написал когда-то Л. Кэрролл, - но это весьма скромный по численности отряд сумел пробраться в самые глубины различных наук”.

Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. .

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии.. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный не выпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов. Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:

Вселенная — додекаэдр

Земля - куб

Огонь – тетраэдр

Вода - икосаэдр

Воздух – октаэдр

Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" – грань, гексаэдр (куб) имеет 6 граней, "гекса" – шесть, октаэдр - восьмигранник, "окто" – восемь, додекаэдр - двенадцатигранник, "додека" – двенадцать, икосаэдр имеет 20 граней, "икоси" - двадцать.

Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами. [4] Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии". Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх. Икосаэдр - воду, т.к. он самый "обтекаемый. Куб -землю, как самый "устойчивый. Октаэдр - воздух, как самый "воздушный". Пятый многогранник, додекаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным. Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы "стихий" настраивались Платоном в совершенных консонансах, как четыре струны лиры. Консонансом называется приятное созвучие. Надо сказать, что своеобразные музыкальные отношения в Платоновых телах являются чисто умозрительными и не имеют под собой никакой геометрической основы. Этими отношениями не связаны ни число вершин Платоновых тел, ни объемы правильных многогранников, ни число ребер или граней. В связи с этими телами уместно будет сказать, что первая система элементов, включавшая четыре элемента - землю, воду, воздух и огонь, - была канонизирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течение многих веков. Вполне возможно отождествить их, с известными нам, четырьмя состояниями вещества - твердым, жидким, газообразным и плазменным.

Важное место занимали правильные многогранники в системе гармоничного устройства мира И. Кеплера. Все та же вера в гармонию, красоту и математически закономерное устройство мироздания привела И. Кеплера к мысли о том, что поскольку существует пять правильных многогранников, то им соответствуют только шесть планет. По его мнению, сферы планет связаны между собой вписанными в них Платоновыми телами. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором будет находиться Солнце. Проделав огромную вычислительную работу, в 1596 г. И. Кеплер в книге "Тайна мироздания" опубликовал результаты своего открытия. В сферу орбиты Сатурна он вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера Меркурия. Тайна мироздания кажется открытой. Сегодня можно с уверенностью сказать, что расстояния между планетами не связаны ни с какими многогранниками. Впрочем, возможно, что без "Тайны мироздания", "Гармонии мира" И. Кеплера, правильных многогранников не было бы трех знаменитых законов И. Кеплера, которые играют важную роль в описании движения планет.

Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.

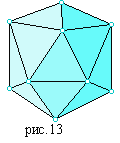
Все пять правильных многогранников перечислены в таблице, приведенной ниже. В трех последних столбцах указаны N0 – число вершин, N1 – число ребер и N2 – число граней каждого многогранника.

(число вершин)

N1

(число ребер)

N2

(число граней)

Тетраэдр

4

6

4

Куб

8

12

6

Октаэдр

6

12

8

Икосаэдр

12

30

20

Додекаэдр

20

30

12

Тела Архимеда

Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно-полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр,

ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр. [2]

усеченный тетраэдр усеченный октаэдр усеченный икосаэдр

усеченный гексаэдр усеч додекаэдр ромбоусеченный

кубооктаэдр

ромбоусеченный

икосододекаэдр ромбокубо-октаэдр ромбоикосо-додекаэдр

курносый додекаэдр кубо-октаэдр конусный куб

икосо-додекаэдр

Конструирование архимедова усеченного икосаэдра из платонова икосаэдра

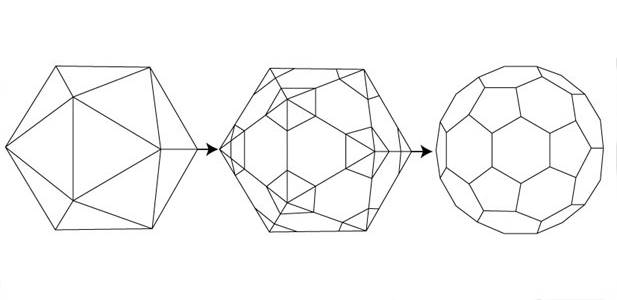
Звездчатые многогранники

Кроме правильных многогранников красивые формы имеют звёздчатые многогранники. Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. У звёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами. Их всего четыре. Первые два были открыты И. Кеплером (1571 - 1630), а два других почти 200 лет спустя построил Л. Пуансо (1777 - 1859). Именно поэтому правильные звёздчатые многогранники называются телами Кеплера - Пуансо.

Все они получаются «озвездыванием» Платонова т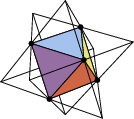ела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются.

Если же продлить все грани октаэдра до пересечения их друг с другом, то получится фигура, что возникает при взаимопроникновении двух тетраэдров - «стелла октангула», которая называется «продолженным октаэдром».

Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них - малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.

Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются. Людвиг Шлефли не изгонял геометрическое тело из семейства многогранников только за то, что его грани самопересекаются, тем не менее, оставался непреклонным, как только речь заходила про малый звездчатый додекаэдр. Довод его был прост и весом: это кеплеровское животное не подчиняется формуле Эйлера! Его колючки образованы д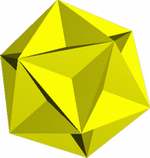венадцатью гранями, тридцатью ребрами и двенадцатью вершинами, и, следовательно, В+Г—Р вовсе не равняется двойке.

Шлефли был и прав, и не прав. Конечно же, геометрический ежик не настолько уж колюч, чтобы восстать против непогрешимой формулы. Надо только не считать, что он образован двенадцатью пересекающимися звездчатыми гранями, а взглянуть на него как на простое, честное геометрическое тело, составленное из 60 треугольников, имеющее 90 ребер и 32 вершины.

Тогда В+Г-Р=32+60-90 равно, как и положено, но зато тогда к этому многограннику неприменимо слово «правильный» - ведь грани его теперь не равносторонние, а всего лишь равнобедренные треугольники. Кеплер не додумался, что у полученной им фигуры есть двойник.

Многогранник, который называется «большой додекаэдр» - построил французский геометр Луи Пуансо спустя двести лет после кеплеровских звездчатых фигур.

Большой икосаэдр был впервые описан Луи Пуансо в 1809 году. И опять Кеплер, увидев большой звездчатый додекаэдр, честь открытия второй фигуры оставил Луи Пуансо. Эти фигуры также наполовину подчиняются формуле Эйлера. [2]

Многогранники в искусстве

«Поистине, живопись — наука и законная дочь природы,ибо она порождена природой»(Леонардо да Винчи)

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, архитекторы, художники. Леонардо да  Винчи (1452-1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он  проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли «О божественной пропорции».

Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471-1528гг.), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.

Голландский художник Мориц Корнилис Эшер, родившийся в 1989 году в Леувардене, создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника.

Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции - это окно, которое отражается левой верхней частью сферы.

Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он поместил внутрь центральной фигуры хамелеонов, чтобы затруднить восприятие всей фигуры. Таким образом, необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера. [2]

Многогранники в архитектуре

Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения.

Геометрия появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.

Страна

Архитектурные сооружения

Геометрические

фигуры

Применение в современной

архитектуре

Древний Египет

Мастаба

Ступенчатая пирамида

( фараона Джосера)

Классическая пирамида

Погребальные комплексы

Храм богу Амону-Ра

Обелиск

Усеченная пирамида

Четырехугольная пирамида

Параллелепипед

Цилиндры

Пирамиды в Лувре, Франция, 20 в.

Мавзолей Ленина,

Россия 20 в.

7. высотных зданий

8. в Москве 20 в.

Башни «Петронас»

в Малайзии

Древняя Греция

Храм

Ордера

Параллелепипед

Призма

Цилиндр

Усеченный конус

Колоннада театров,

дворцов, парковых

ансамблей

Древний Рим

Триумфальные арки

Триумфальные колонны

Купол

Амфитеатр (Колизей)

Термы

Арки

Мосты

Параллелепипед

Цилиндр

Сфера

Триумфальные арки и колонны в Москве,

Санкт – Петербурге

Цирк

Стадион

Арочные мосты

Сауны и бани

Средние века

Замки-крепости

Параллелепипед

Пирамида

Конус

Усеченный конус

Цилиндр

Дома-коттеджи

Являются элементами жилых домов

Музей Плодов в Яманаши

Этот музейно-развлекательный комплекс, созданный с помощью трехмерного моделирования, продолжает тему музеев без произведений искусств.Как объясняет создатель Музея Ицуко Хасегава, одна из немногих преуспевающих японских женщин-архитекторов, „геометрия трех оболочек” была проанализирована с помощью объемных компьютерных построений. Каждая форма была образована путем вращения простых геометрических форм до получения сложных объемов.[2]

Многогранники в природе

Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Например, кристаллы поваренной соли имеют форму куба.

При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.

Алмаз (октаэдр)

Шеелит (пирамида)

Хрусталь (призма)

Поваренная соль (куб)

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

П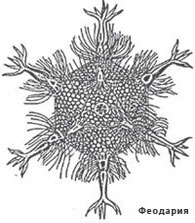равильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник. [2] Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.

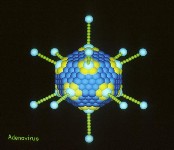
Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на  правильный двадцатигранник, или икосаэдр. Есть вирусы, размножающиеся в клетках животных (позвоночных и беспозвоночных), другие облюбовали растения, третьи (их называют бактериофагами или просто фагами) паразитируют в микробах, но икосаэдрическая форма встречается у вирусов всех этих трех групп.

Где еще можно увидеть эти удивительные тела? В очень красивой книге немецкого биолога начала нашего века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы". Cлайд№20

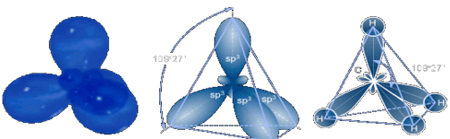
В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН4, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

Идеи Пифагора, Платона, И. Кеплера о связи правильных многогранников с гармоничным устройством мира уже в наше время нашли свое продолжение в интересной научной гипотезе, авторами которой (в начале 80-х годов) явились московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла,оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли , проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Их 62 вершины и середины ребер, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.

В трехмерном пространстве деления сферы ведут к созданию пяти правильных многогранников, так называемых пяти тел Платона. Формы Платона связаны с человеческим телом и природой сознания, раскрытие которой ведет не только к понимание интеллекта Вселенной, но и к эмпирическому восприятию Бога, даруя ощущение глубокой всеобщей взаимосвязи элементов бытия. Здесь особую роль играет число 5. Оно связано с зарождением жизни на земле и в то же время с бессмертием.

Первичные многоугольники и многогранники — фундаментальные образцы творения, представляющие творческие силы самоорганизации, которые формируют и определяют мир. Все в природе может быть описано в терминологии математических принципов, которые свойственны этим формам.

Какую форму могло бы иметь первое творение? Каковы изначально сотворенные объемные формы? Существует пять таких творений, которые являются наиболее существенными, потому что они — единственные тела, у которых все грани и все внутренние углы равны. Это тетраэдр, октаэдр, куб, додекаэдр и икосаэдр; производные от треугольника, квадрата и пятиугольника; воплощение чисел 3, 4 и 5. Все другие тела представляют собой только модификации эти пяти.

Заключение

Каков он, наш мир? Мы говорим: огромный, прекрасный, разнообразный…Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Если посмотреть вокруг, то можно заметить в обычных вещах такое, как что самая популярная форма современного здания, радиоприёмников, телевизоров, шкафов это-параллелепипед. Или в природе: цветах, бактериях, камнях и т.д. мы можем увидеть формы пространственных фигур. Эти формы фигур кажутся очень красивыми. Нас поражает красота, совершенство, гармония пространственных фигур.

Подбирая материал для своей работы, я познакомился с различными видами многогранников (правильные, неправильные, звездчатые) и их свойствами, узнал, где они встречаются в природе (кристаллы, соты, снежинки, феодария) и окружающем нас мире (головоломки, пирамиды, картины).

Решая поставленную проблему, я увидел, что многогранники окружают меня везде – это крупинки сахара и соли, камень в кольце мамы, форма зданий и деревьев и многое другое. Гармония между красотой и многогранностью существует.

Эта работа была для меня интересна. Думаю, что собранный материал будет полезен мне и моим одноклассникам.

Список использованной литературы

1. Атанасян Л.С.. Бутузов В.Ф. Геометрия 10-11; М. ; «Просвещение». 2000.

2. Интернет сайт www.уаndeх.ru

3 . Крайнева Л.Б. Построение правильных многогранников с использованием куба //Математика в школе.-1994.-2.-54-57

4. Смирнова И.М. Учебное пособие для10-11 классов гуманитарного профиля; «Просвещение» 1997.

5. Смирнова И.М. Уроки стереометрии в гуманитарных классах. Изучение многогранников//Математика в школе.-1934.- 4 .-41-47

Приложение 1

Архитектурные сооружения Древнего Египта, Древней Греции

«Ложная пирамида» Снефру

Пирамида Хефрена

Ступенчатая пирамида фараона Джосера

Приложение 2

Фото архитектурных сооружений города Лесосибирска

Приложение 3

Многогранники в деталях автомобиля

двигатель

капот

Приложение 4

Модели для изготовления многогранников

у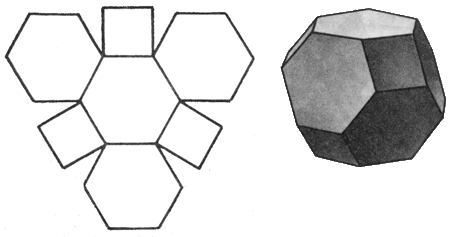сеченный октаэдр

Октаэдр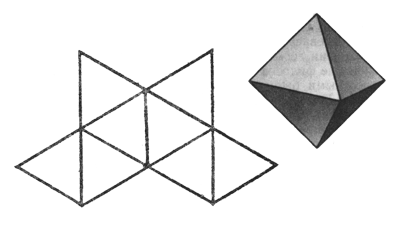

т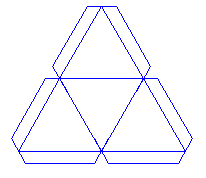етраэдр

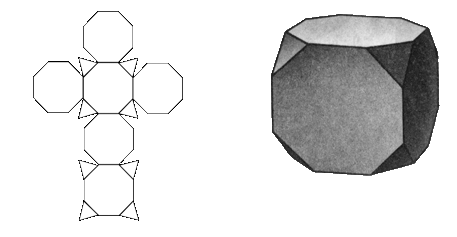
усеченный гексаэдр

infourok.ru

Многогранники в архитектуре | Блог «Твоей столицы»

Использовать многогранники в архитектуре люди стали очень давно, еще до новой эры. И по мере роста строительного мастерства в мире появлялись новые шедевры, основанные на сложных геометрических фигурах. Наша Национальная библиотека — одна из них. Но мы покажем вам еще 11 удивительных примеров.

Благодаря своей нетривиальной архитектуре Национальная библиотека попадала в самые различные рейтинги — от самых необычных зданий мира, до — не поверите! — самых уродливых. А все из-за формы книгохранилища — ромбокубооктаэдра.

Труднопроизносимое слово ромбокубооктаэдр обозначает многогранник, образованный 18 квадратами и 8 треугольниками. Кстати, библиотека — самый крупный из архитектурных ромбокубооктаэдров, возведенных в мире в настоящее время. Его высота составляет 73,6 м (23 этажа), а вес — 115 000 тонн.

Повторить в архитектуре сложные многогранники (особенно, архимедовы тела — к которым, в том числе, относится и ромбокубооктаэдр) действительно нелегко. И если случается, то в меньшем масштабе, чем Нацбиблиотека, и усеченной форме.

Например, музей архитектуры Тойо Ито на острове Омишима (Япония) — в основе дизайна музея лежат геометрические фигуры: октаэдр, тетраэдр и кубооктаэдр.

Или вот здание Международного экономического комитета в Киеве, где купол конференц-зала своими гранями напоминает нашу библиотеку.

Ботанический сад «Эдем» в Корнуолле (Великобритания) был построен в 2001 году на месте выработанного мелового карьера, а для конструкций сводов использовались формы шестигранных сот. А это еще один вид многогранников — усеченный икосаэндр. Состоит из 12-ти пятиугольников и 20-ти шестиугольников.

Дворец счастья в Ашхабаде (Туркменистан) выглядит величественно, но использует в конструкции более простые многогранники. 11-этажное здание представляет собой трехступенчатое сооружение, каждая сторона которого имеет вид восьмиконечной звезды. Куб, возвышающийся на больших колоннах, образует его верхнюю ступень и вбирает в себя шар диаметром 32 метра — символическую планету Земля с изображением карты Туркменистана.

Греческое слово «пентагон» стало нарицательным именем не только для здания министерства обороны США, которое в плане выглядит пятиугольником, но и для самого ведомства.

Современный стеклянный вход в Лувр, который появился во дворе ренессансного дворца 20 лет назад и до сих пор остается спорным новоделом, — это тоже многогранник, пирамида.

Усеченная пирамида пользуется популярностью у современных архитекторов. Например, в Индианополисе (США) в 1972 году закончили строительство офисного комплекса из трех зданий, который так и назвали — The Pyramids. Сейчас в нем расположен Институт искусства Индианополиса.

А башня из поставленных друг на друга параллелепипедов или пирамид представляет собой древнее архитектурное сооружение — зиккурат. Зиккураты известны со времен древней Месопотамии, конец IV тысячелетия до нашей эры. В архитектуре используются довольно часто. Для бывших граждан Советского Союза самый известный зиккурат — это мавзолей Ленина.

Но эта геометрическая форма вдохновляет архитекторов и на оригинальные здания. Как, например, здание британской разведки Ми-6 в Лондоне. Помните, как оно взорвалось в последней серии «бондианы»?

Контуры древнего зиккурата угадываются в очертаниях бизнес-центра «Авалон Плаза», построенного в Москве в 2008 году.

А замыкают наш рассказ два здания, где многогранники не стали основным объемом, а лишь использованы как плоскости поверхности. Что делает их поистине футуристическими, хотя у обоих назначение вполне мирное.

Вот так выглядит здание публичной библиотеки в Сиэтле (США).

А это парк развлечений Футуроскоп под Парижем (Франция).

Какой из них выглядит фантастичнее — решать вам!

Comments

comments

Powered by Facebook Comments

blog.t-s.by

Реферат на тему многогранники в архитектуре: Исследовательский реферат на тему В мире многогранников

С мастерской точностью художник нашел меру равновесия в композиции картины. Он противопоставил гибкую балансирующую фигурку юной гимнастки неподвижному, словно неотделимому от сиденья — куба, атлету на первом плане. Практическую геометрию изучали, отложив на время кисти и краски, величайшие художники и теоретики искусства Леонардо да Винчи и Альбрехт Дюрер.

Они использовали геометрическую технику в приложении к теории пропорций и перспективы в живописи. Федор Яковлевич Алексеев прославился городскими пейзажами, главным образом видами Петербурга и Москвы. Им были созданы также ряд видов провинциальных городов.

Вид Дворцовой набережной от Петропавловской крепости. Лука Пачоли Это был крупнейший европейский алгебраист Х V в. В Милане он подружился с выдающимся художником и ученым Леонардо да Винчи. По настоянию Леонардо в г. Сам Леонардо выполнил иллюстрации для этой книги, в том числе 59 изображений многогранников. Применения икосаэдров Титульный лист книги Ж.

Надгробный памятник в кафедральном соборе Солсбери. Титан Возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи — символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосимметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности.

Изображения Леонардо да Винчи додекаэдра методом жестких ребер а и методом сплошных граней б. Изящество многогранников в архитектуре……………. Определить место и роль многогранников в архитектуре, и насколько важна их роль в архитектурной жизни; Задача: Как архитекторы применяют многогранники в строительстве.

Строители очень ценят за его форму, которая предает зданию: Интересные новости Важные темы Обзоры сервисов Pandia. Основные порталы, построенные редакторами. Каталог авторов частные аккаунты. Все права защищены Мнение редакции может не совпадать с мнениями авторов. Минимальная ширина экрана монитора для комфортного просмотра сайта: Кроме того, любые два смежных треугольника образуют равные двугранные углы.

Точно такие правильные треугольники появляются во всех 12 вершинах прямоугольников, по пять в каждой. Таким образом, существует правильный многогранник, соответствующий символу 3, 5. Этот многогранник называется икосаэдром , что в переводе с греческого означает двадцатигранник. У икосаэдра 12 вершин. Чтобы построить правильный многогранник с символом 5, 3 , возьмем в качестве вершин этого многогранника центры всех двадцати треугольных граней икосаэдра.

Центры пяти треугольников, сходящихся в той или иной вершине икосаэдра, образуют вершины плоского правильного пятиугольника. Всего таких пятиугольников столько же, сколько вершин у икосаэдра - двенадцать. Эти правильные пятиугольники, сходящиеся по три в каждой вершине в центре треугольной грани икосаэдра , образуют двенадцатигранник - додекаэдр.

Все двугранные углы у этого додекаэдра равны. Поэтому этот многогранник является правильным. Два правильных многогранника - октаэдр и додекаэдр - строились при помощи других многогранников - куба и икосаэдра.

Причем каждая вершина, скажем, октаэдра соответствовала некоторой вершине куба. То же самое можно сказать и о паре многогранников икосаэдр - додекаэдр.

Два многогранника называются дуальными , если между множеством граней одного из них и множеством вершин другого существует взаимно однозначное соответствие, причем такое, что если две грани первого из них смежные ребру, то соответствующие этим граням вершины второго многогранника соединяются с ребром. Следует отметить, что у пары дуальных многогранников число вершин одного равно числу граней другого, а ребер у них поровну.

Дуальные многогранники состоят лишь из пяти- и шестиугольников, причем в каждой вершине сходятся по три грани. Такие многогранники называются фуллеренами.

Изучение фуллеренов очень важно для приложений в химии, медицине, архитектуре. Теорема Грюнбаума в переводе на язык фуллеренов означает, что во всяком фуллерене имеется в точности двенадцать пятиугольников, а шестиугольников может быть какое угодно число, не меньше двух.

Чрезвычайно важная задача - как перечислить всевозможные структуры фуллеренов с наперед заданным числом n шестиугольников и сколько их в зависимости от n - остается актуальной и по сей день. Полуправильные многогранники являются естественным расширением правильных многогранников. Это выпуклые многогранники, гранями которых являются правильные многоугольники, - возможно, с разным числом сторон, и в каждой вершине сходится одинаковое число граней.

Большинство из них были открыты еще Архимедом. Но открывались они и в ХХ веке. Так, если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр , имеющий восемь граней рис.

Из них четыре — правильные шестиугольники и четыре — правильные треугольники. В каждой вершине этого многогранника сходится три грани. Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр рис. Обратите внимание на то , что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и додекаэдра также можно получить усеченный куб рис. Для того, чтобы получить еще один правильный многогранник, проведем в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины.

В результате получим полуправильный многогранник, который называется кубооктаэдром рис. Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и название — кубооктаэдр. Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром рис.

У него двадцать граней — правильные треугольники и двенадцать граней — правильные пятиугольники, то есть все грани икосаэдра и додекаэдра. Еще два многогранника называются усеченный кубооктаэдр рис. Отсечение углов этих многогранников дает не квадраты, а прямоугольники. Мы рассмотрели 9 из 13 описанных Архимедом полуправильных многогранников.

Четыре оставшихся — многогранники более сложного типа. На рисунке 10 мы видим ромбокубооктаэдр. Его поверхность состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов. На рисунке 11 изображен ромбоикосододекаэдр, поверхность которого состоит из граней икосаэдра, додекаэдра и еще 30 квадратов. Сейчас известно несколько тысяч различных типов снежинок. П равильные многогранники встречаются так же и в живой природе.

Например, скелет одноклеточного организма феодарии Circjgjnia icosahtdra по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник. Это свойство помогает морскому организму преодолевать давление толщи воды.

Где еще можно увидеть эти удивительные тела? В очень красивой книге немецкого биолога начала нашего века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН 4 , очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра.

Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа. Идеи Пифагора, Платона, И. Кеплера о связи правильных многогранников с гармоничным устройством мира уже в наше время нашли свое продолжение в интересной научной гипотезе, авторами которой в начале х годов явились московские инженеры В. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете.

Лучи этого кристалла, а точнее, его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли , проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: Их 62 вершины и середины ребер, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.

В трехмерном пространстве деления сферы ведут к созданию пяти правильных многогранников, так называемых пяти тел Платона. Формы Платона связаны с человеческим телом и природой сознания, раскрытие которой ведет не только к понимание интеллекта Вселенной, но и к эмпирическому восприятию Бога, даруя ощущение глубокой всеобщей взаимосвязи элементов бытия.

Здесь особую роль играет число 5. Оно связано с зарождением жизни на земле и в то же время с бессмертием. Первичные многоугольники и многогранники — фундаментальные образцы творения, представляющие творческие силы самоорганизации, которые формируют и определяют мир.

Все в природе может быть описано в терминологии математических принципов, которые свойственны этим формам. Какую форму могло бы иметь первое творение? Каковы изначально сотворенные объемные формы?

Существует пять таких творений, которые являются наиболее существенными, потому что они — единственные тела, у которых все грани и все внутренние углы равны. Это тетраэдр, октаэдр, куб, додекаэдр и икосаэдр; производные от треугольника, квадрата и пятиугольника; воплощение чисел 3, 4 и 5.

Все другие тела представляют собой только модификации эти пяти. Каков он, наш мир? Если посмотреть вокруг, то можно заметить в обычных вещах такое, как что самая популярная форма современного здания, радиоприёмников, телевизоров, шкафов это-параллелепипед. И ли в природе: Эти формы фигур кажутся очень красивыми. Нас поражает красота, совершенство, гармония пространственных фигур. Подбирая материал для своей работы, я познакомился с различными видами многогранников правильные, неправильные, звездчатые и их свойствами, узнал, где они встречаются в природе кристаллы, соты, снежинки, феодария и окружающем нас мире головоломки, пирамиды, картины.

Решая поставленную проблему, я увидел, что многогранники окружают меня везде — это крупинки сахара и соли, камень в кольце мамы, форма зданий и деревьев и многое другое. Гармония между красотой и многогранностью существует. Эта работа была для меня интересна.

Думаю, что собранный материал будет полезен мне и моим одноклассникам. Уроки стереометрии в гуманитарных классах. Архитектурные сооружения Древнего Египта, Древней Греции. Ф ото архитектурных сооружений города Лесосибирска. Многогранники в деталях автомобиля. Модели для изготовления многогранников. Изящный пример звездчатого додекаэдра можно найти в работе "Порядок и хаос".

Гравюра "Звезды", на которой тела, полученные объединением тетраэдров, кубов и октаэдров. На картине изображён додекаэдр, образованный двенадцатью плоскими пятиконечными звёздами. Построить такое сооружение - трудная инженерная задача: Ошибка даже в два градуса могла бы привести в итоге к плачевным результатам. Вообще без геометрии не было бы ничего. Все здания, которые нас окружают — это геометрические фигуры.

Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.

referat-4all.ru

"Многогранники в архитектуре и живописи"

Слайд 1

Слайд 2

Эпиграф «Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.» Бертран Рассел

Слайд 3

Гипотеза Возможно ли применение правильных многогранников в архитектуре и живописи…

Слайд 4

Задачи Исследовать творчество художников -импрессионистов: Леонарда да Винчи, Сальвадора Дали; Узнать, о использовании форм многогранников в живописи и архитектуре; Изучить дополнительную литературу; Сделать проект

Слайд 5

Содержание * Эпоха геометрики * Живопись средних веков * Искусство Х VIII – Х I Х веков * Искусство ХХ века * Многогранники в искусстве. * Многогранники в архитектуре

Слайд 6

Многогранники в архитектуре Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения. Геометрия появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.

Слайд 7

Многогранники в архитектуре

Слайд 8

Евклид. Рельеф работы Андрея Пизано. 1334-1340гг.

Слайд 9

Троица. Фреска Мазаччо в соборе Санта-Мария Новелла. Флоренция. 1425-1426гг. Интерес к геометрии пространства в конечном итоге привел к открытию в живописи линейной перспективы с единой точкой схода.

Слайд 10

Примерно с Х III в. Художники начали экспериментировать с изображением пространства. Они «создавали» живописное пространство, изменяя размеры фигур, располагая по определенным правилам элементы архитектуры, детали ландшафта. Пьеро делла Франческа. Бичевание Христа. Х V в.

Слайд 11

Великая пирамида в Гизе. Эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности. Кроме того, это единственное из чудес, сохранившееся до наших дней. Во времена своего создания Великая пирамида была самым высоким сооружением в мире. И удерживала она этот рекорд, по всей видимости, почти 4000 л

Слайд 12

Царская гробница Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.

Слайд 13

.Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

Слайд 14

Ещё с давних времён зодчие использовали многогранники в строительстве различных архитектурных сооружений. Эти геометрические фигуры казались людям таинственными и завораживающими, им отдавалось высокое предпочтение, что видно из примера египетских пирамид, построенных ещё в древнейшие времена простыми рабами своим фараонам. Что так влекло простой народ к этим удивительным фигурам, не известно и по сей день, и учёным остаётся только предполагать.

Слайд 15

Вечные строения Во всем облике японского строения очевидна идея преобразования пространства, подчинения его новой логике - логике "завоевания" природного ландшафта, которому противопоставлена четкая геометрия проникающих архитектурных форм .

Слайд 16

Казанская церковь в Москве Многогранники в архитектуре Москвы

Слайд 17

Многогранники в архитектуре Москвы Собор непорочного зачатия Девы Марии на малой Грузинской Исторический музей

Слайд 18

В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров. Александрийский маяк

Слайд 19

Работы Фра Джовани да Верона, созданные для церкви Santa Maria in Organo в Вероне.

Слайд 20

Применение многогранников в живописи. • Некоторые художники использовали в изображениях своих картин многогранники. Этот приём положил начало целому направлению в искусстве - импрессионизму. Выделяют следующих художников: О. Моне, О. Ренуар, Э. Дега, К. Писсарро, С. Сислеи, Б. Моризо, С. Дали, Л. Да Винчи, Дюрер. В своих многофигурных композициях они стремились сохранить непревзойдённость, силу и свежесть первого впечатления, которое позволяло схватить в увиденном неповторимо характерное, не вдаваясь в отдельные детали. Кажущиеся случайность и неуравновешенность, асимметрия композиции, смелые срезы фигур, теряя глубину, пространство порой «выворачиваются» на плоскость или же уходят в бесконечность. Объёмные формы как бы растворяются в окутывающей их светло-воздушной оболочке.

Слайд 21

Предельно упрощенное изображение не предполагает в пейзаже таких «подробностей», как окна, двери. Дома здесь смотрятся россыпью кристаллов. Жорж Брак. Дома в Эстаке. 1906г.

Слайд 22

Пабло Пикассо. Девочка на шаре . С мастерской точностью художник нашел меру равновесия в композиции картины. Он противопоставил гибкую балансирующую фигурку юной гимнастки неподвижному, словно неотделимому от сиденья – куба, атлету на первом плане.

Слайд 23

Страница из «Руководства к измерению» А.Дюрера . Нюрнберг. 1525г. Практическую геометрию изучали, отложив на время кисти и краски, величайшие художники и теоретики искусства Леонардо да Винчи и Альбрехт Дюрер. Они использовали геометрическую технику в приложении к теории пропорций и перспективы в живописи.

Слайд 24

Федор Яковлевич Алексеев (1753-1824) прославился городскими пейзажами, главным образом видами Петербурга и Москвы. Им были созданы также ряд видов провинциальных городов. Вид Дворцовой набережной от Петропавловской крепости. 1794г.

Слайд 25

Архангел Гавриил. Фреска Х II в.

Слайд 26

Лука Пачоли . Картина неизвестного художника. Пачоли искал эти «божественные эффекты» в самых совершенных созданиях математики – пяти платоновых телах, строил их из стеклянных плиток, а затем раздавал «для коллекций разных вельмож».

Слайд 27

Лука Пачоли Это был крупнейший европейский алгебраист Х V в. В Милане он подружился с выдающимся художником и ученым Леонардо да Винчи. По настоянию Леонардо в 1497г. Пачоли написал книгу «О Божественной пропорции». Сам Леонардо выполнил иллюстрации для этой книги, в том числе 59 изображений многогранников. Первая страница «Суммы знаний» Л.Пачоли.

Слайд 28

Применения икосаэдров Титульный лист книги Ж. Кузена «Книга о перспективе». Надгробный памятник в кафедральном соборе Солсбери.

Слайд 29

Сальвадор Дали «Тайная вечеря».

Слайд 30

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.

Слайд 31

Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.

Слайд 32

Многогранники в искусстве «Поистине, живопись — наука и законная дочь природы, ибо она порождена природой» (Леонардо да Винчи)

Слайд 33

Титан Возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи (1452-1519) — символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосимметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности. Изображения Леонардо да Винчи додекаэдра методом жестких ребер (а) и методом сплошных граней(б )

Слайд 34

Вывод • Наша гипотеза подтвердилась. Изучив огромное количество литературы, познакомившись с различными понятиями, относящимися к данной теме, мы пришли к выводу, что действительно многогранники нашли широкое применение в архитектуре и живописи. Многогранные фигуры скрывают в себе некую тайну, встретившись с которой, человек считает необходимым разгадать её. Именно это завораживает и интригует взгляды людей.

Слайд 35

Информационные ресурсы • Геометрия 10-11. Учебник для общеобразовательных учреждений. Базовый и профильный уровни. Москва «Просвещение» 2007 Л. С. Атанасян, В. Ф. Бутузов • Русь деревянная. Москва «Детская литература» 1981. А. Ополовников, Г. Островский. • Мировая художественная культура от истоков до 17 века 10 класс. Учебник для общеобразовательных учреждений гуманитарного профиля. Дрофа Москва 2006. Г. И. Данилова. • Интернет.

nsportal.ru

Многогранники в архитектуре | Социальная сеть работников образования

Слайд 1

Слайд 2

Многогранником называется тело, граница которого является объединением конечного числа многоугольников Что же такое многогранник???

Слайд 3

Первые архитектурные сооружения строились из камней, кусков глины, дерева и влажного песка. Уже тогда человек выбирал самые выразительные по форме и величине камни, из которых возводил архитектурные шедевры. Всё это говорит о том, что дизайн архитектурного сооружения начинает свое развитие с древних времён. Пирамида Кукулькана Мексика Пирамида Луны Теотиуакан (Мексика)

Слайд 4

Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта. Слово «пирамида» — греческое, означает многогранник. Египетские пирамиды

Слайд 5

В древнем мире была популярная пирамидальная форма строения. Вся сложность такого сооружения заключалась в том что, края блоков должны быть очень точно вымерены и выровнены с самого начала строительства, иначе они не сойдутся в одной точке на вершине пирамиды . Египетские пирамиды

Слайд 6

Фаросский маяк состоял из трёх мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь. Александрийский маяк

Слайд 7

Музей архитектуры Тойо Ито на острове Омишима (Япония) Вообще без геометрии не было бы ничего. Все здания, которые нас окружают – это геометрические фигуры. Дворец счастья в Ашхабаде (Туркменистан)

Слайд 8

Смоленская крепость имела вид непрерывной замкнутой фигуры. В её состав входило 38 башен. Внизу стена сложена из правильных, хорошо отёсанных прямоугольных блоков белого камня длинной от 92 до 21 сантиметра и высотой от 34 до 20 сантиметров, а вверху из хорошо обожжённого кирпича, средние размеры которого 31х15х6 сантиметров. Первоначальная протяженность стен крепости была равна 6,5 километра . Многогранные башни Смоленской крепости

Слайд 9

Трудно найти подходящие слова, чтобы описать впечатления от готического собора. Они высоки и тянутся к небу бесконечными стрелами башен и башенок, вимпергов, фиалов, заостренных арок. Стены не ощущаются, их как бы и нет. Арки, галереи, башни, какие - то площадки с аркадами, громадные окна, все дальше и дальше бесконечно сложная, ажурная игра ажурных форм. «Искусство есть наука»,— считал еще в середине XII века Доминик Гундиссалинус . Готический собор в Милане(Италия)

Слайд 10

Готический собор. Кёльн (Германия) Готический собор. Кентербери (Англия)

Слайд 11

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. архитекторы, художники. Леонардо да Винчи (1452 - 1519) например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу Монаха Луки Пачоли ''О божественной пропорции.'' Леонардо да Винчи

Слайд 12

Современная архитектура 1)Отель( Дубай ) 3)Один из магазинов в Японии 1 2 3 2 2)Усеченная пирамида (США)

Слайд 13

1)Оперный театр(Сидней) 3)Публичная библиотека Сиэтл(США ) 1 3 2 2) Парк развлечений Футуроскоп в Париже (Франция )

Слайд 14

ФУЛЛЕР ( Fuller ) Ричард Бакминстер (1895-1983), американский архитектор и инженер. Разработал легкие и прочные «геодезические купола». Купола Б.Фуллера в современной архитектуре

Слайд 15

Идея «геодезических куполов» появилась в результате исследований в области картографии, а именно переноса сферической поверхности земли на плоскость с минимальными искажениями. Идея достаточно проста, сфера представляется в виде многогранника ( икосаэдра ), то есть двадцатигранника со сторонами в виде правильных треугольников. Павильон США на Экспо -67, ныне музей «Биосфера» в Монреале, Канада.

Слайд 16

«Геодезические купола» получили большое распространение, они продолжают использоваться и сейчас в крупных общественных сооружениях, например: «Проект Эдем» Всего построено около трехсот тысяч «геодезических куполов», они широко используются как ангары, склады, эксплуатируются как жилища в местах со сложными погодными условиями. Ботанический сад «Эдем» в Корнуолле (Великобритания)

Слайд 17

Математики считают, что пчёлы строили свои шестиугольные соты задолго до появления человека. Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Геометрические свойства икосаэдра позволяют экономить генетическую информацию.

Слайд 18

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ, т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.

Слайд 19

Одна из главных мусульманских мечетей республики Татарстан и Казани. Расположена на территории Казанского кремля. Архитектура этой мечети представляет собой сочетание различных многогранников. Мечеть Кул - Шариф

Слайд 20

Многогранники в архитектуре Москвы Собор непорочного зачатия Девы Марии на малой Грузинской Исторический музей

Слайд 21

Казанская церковь в Москве Многогранники в архитектуре Москвы

Слайд 22

Исходя из этого , я могу сделать вывод, что без геометрии не было бы столь прекрасных архитектурных сооружений! Мир многогранников велик, он составляет 1/3 всего составляющего на земле. Ведь все сооружения это геометрические фигуры , от самых простых до самых сложных. Так же могу сказать что роль многогранники в архитектуре велика, ведь многогранник – это величайшее открытие, которое использует человек . Вывод

nsportal.ru

Многогранники в архитектуре

Скачать эту презентацию

Скачать эту презентацию

Многогранники в архитектуре

Как уже известно, первые архитектурные сооружения строились из камней, кусков глины, дерева и влажного песка.Если мы рассмотрим первые архитектурные сооружения, которые строились человеком из камней, то можно отметить, что уже тогда человек выбирал самые выразительные по форме и величине камни. Всё это говорит о том, что дизайн архитектурного сооружения начинает своё развитие с древних времён. Пирамида Луны. Конец 1 тыс до н. э. — начало н. э. Высота 42 м. Теотиуакан.Тенаюка. Пирамида 12-15 вв. Культура ацтеков.Пирамида Кукулькана («Кастильо») в Чичен-Ица. Культура майя. 8-12 вв. Мексика.

Первое чудо света Пирамидальная форма в строительстве была популярна в древнем мире. Построить такое сооружение - трудная инженерная задача: края блоков должны быть очень точно выверены и выровнены с самого начала строительства, иначе они не сойдутся в одной точке на вершине пирамиды. Британский физик К. Мендельсон ставит вопрос: как без современных научных приборов древние египтяне могли определить направление на нужную точку в воздухе и строить прямо по направлению на нее? Ошибка даже в два градуса могла бы привести в итоге к плачевным результатам. Пирамида Хеопса, может быть, самое грандиозное сооружение на земле. Почти пять тысяч лет стоит эта огромная пирамида. Высота её достигала 147 м. Вплоть до конца XIX в. пирамида Хеопса являлась самым высоким сооружением на земле.

Египетские пирамиды хранят в себе огромное количество тайн и загадок. Однако загадки внешних характеристик пирамид - это еще цветочки. Поразительно также и то, что происходит внутри. До сих пор не известно точно, почему внутри пирамиды, ориентированной по сторонам света, проявляется эффект мумификации любой органики. Тела мелких животных, умерших в пирамиде, даже без бальзамирования мумифицируются и сохраняются очень длительное время. Важно заметить, что эффект мумификации наиболее сильно наблюдается в центре пирамиды, примерно на высоте 1/3 ее высоты. Примерно на этой высоте находились захоронения фараонов. Кроме того, в пирамиде тупые лезвия бритвы, положенные с сохранением ориентировки по сторонам света, в короткое время затачиваются.

Вообще без геометрии не было бы ничего. Все здания, которые нас окружают – это геометрические фигуры. Паросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров.

Многогранные башни Смоленской крепости В плане крепость имела вид неправильной замкнутой фигуры, которая как бы прижималась к Днепру. В состав крепости входило 38 прясел и столько же башен.Внизу стена сложена из правильных, хорошо отёсанных прямоугольных блоков белого камня длинной от 92 до 21 сантиметра и высотой от 34 до 20 сантиметров, а вверху из хорошо обожжённого кирпича, средние размеры которого 31х15х6 сантиметров.

ГОТИКА В XII в. архитектура понимается уже как наука, как знание, как геометрия, имеющая практическое приложение, как деятельность, требующая не только большого опыта, навыков и вкуса, но и основательных научных знаний. Усложнившаяся архитектурная практика готической эпохи, требовавшая от архитектора специальных математических знаний, вызвала это представление.

«Искусство есть наука»,— считал еще в середине XII века Доминик Гундиссалинус. Благодаря высокому уровню знаний готического архитектора были воздвигнуты величественные и обширные готические храмы, в которых единство и логика пропорционального строя пронизывали все многообразие архитектурных элементов. «Искусство без науки ничто»,— заключили в конце XIV века архитекторы, призванные на консультацию по строительству Миланского собора.

Современнаяархитектура

Новогодний хрустальный шар в Нью-Йорке обновили к 100-летнему юбилею Почти двухметровый в диаметре, состоящий из 672 хрустальных треугольников шар заиграл неповторяющимися цветовыми решениями, включая, конечно, звездно-полосатый американский флаг. Теперь шар светит вдвое ярче, потребляет энергии всего лишь как 20 фенов и, благодаря новым технологиям, имеет 16 миллионов цветовых комбинаций.

Купола Б.Фуллера в современной архитектуре ФУЛЛЕР (Fuller) Ричард Бакминстер (1895-1983), американский архитектор и инженер. Разработал легкие и прочные «геодезические купола».

Идея «геодезических куполов» достаточно проста, сфера представляется в виде многогранника (икосаэдра), то есть двадцатигранника со сторонами в виде правильных треугольников. Эта фигура и разворачивается на плоскость, давая неискаженные соотношения по всей поверхности.

Эта конструкция оказалась очень эффективной при том, что она позволяет перекрывать большие пространства практически без ограничений по площади, но еще ее экономическая целесообразность возрастает пропорционально размеру, также она обладает очень хорошими характеристиками прочности: может выдерживать порывы ураганного ветра до 210 миль/ч.

«Геодезические купола» получили большое распространение, они продолжают использоваться и сейчас в крупных общественных сооружениях, например: «Проект Эдем» (Николас Гримшоу, 2000-2001гг.)

Всего построено около трехсот тысяч «геодезических куполов», они широко используются как ангары, склады, эксплуатируются как жилища в местах со сложными погодными условиями (купол на Южном полюсе). Эта конструкция рассматривается как подходящая для организации постоянно обитаемых станций на Луне и Марсе.

Г. Цимлянск, ул. Будённого

Многогранники в животном мире «МОЙ ДОМ ПОСТРОЕН ПО ЗАКОНАМ САМОЙ СТРОГОЙ АРХИТЕКТУРЫ. САМ ЕВКЛИД МОГ БЫ ПОУЧИТЬСЯ, ПОЗНАВАЯ ГЕОМЕТРИЮ МОИХ СОТ», — говорит пчела в «Тысяче и одной ночи». Она права: пчелиная ячейка представляет собой нижнюю половину усечённого икосаэдра, одного из полуправильных архимедовых тел, и это решение с точки зрения экономии воска и строительных усилий настолько разумно, что во Французской академии в 18 в. решили: пчёлы используют достижения высшей математики, подчиняясь божественному указанию и руководству.

«Плоские черви», М. К. Эшер «Строительный кирпич имеет форму прямоугольного параллелепипеда, и это логично, потому что такие кирпичи соединять друг с другом проще всего. Но любой человек, любящий и понимающий красоту правильных тел, может пожалеть, что строители не используют другие формы.Например, тетраэдры, перемежающиеся с октаэдрами, могут складываться один с другим не хуже традиционных кирпичей. Вот дом, построенный из комбинаций этих двух форм. Он не имеет ни вертикальных, ни горизонтальных поверхностей, ни полов, ни стен, ни потолка — в обычном понимании этих слов. Вот почему он весь внутри заполнен какой-то жидкой средой, в которой плавают существа, напоминающие плоских червей — планарий».

Наш вывод Без геометрии не было бы ничего, ведь все здания, которые окружают нас –это геометрические фигуры. Сначала – более простые, такие как квадрат,прямоугольник, шар. Затем – более сложные : призмы, тетраэдры, пирамиды и т.д. Но мы не всегда обращаем внимание на окружающие нас здания. В далёкой древности, ещё не имея никакого представления о геометрии,люди строили себе жилища и дома различных форм. Формы многогранников придают зданиям особый вид. И мы считаем, что многогранники в архи- тектуре необходимы. Ведь это не просто красивые и большие здания, это прочные, надёжные и уникальные сооружения, которые ещё много лет будут поражать своей точностью, величественностью и таинственностью. Правы арабы в том, что всё на свете страшится времени. Но больше всего они правы в том, что время страшится пирамид. И мы с ними согласны!

Электронные ресурсы:http://pictoris.ruhttp://www.distedu.ru./mirror/_math/www.tmn.fio.ru/works/26x/304/d1_2.htmhttp://biosphere.ec.gc.ca/The_sphere/Richard_Buckminster_Fuller-WS30956246-1_En.htmhttp://100top.ru/encyclopedia/article/?articleid=12191

ppt4web.ru

Смотрите также

• 
  История развития телевидения реферат
• 
  История развития онкологии реферат
• 
  Жан поль марат реферат
• 
  Дружба народов казахстана реферат
• 
  Диспансеризация здоровых детей реферат
• 
  Витамины на грядке реферат
• 
  Бюджетирование в контроллинге реферат
• 
  Реферат искусство и реклама
• 
  Реферат что изучает математика
• 
  Анатомия лимфатическая система реферат
• 
  Реферат на тему гамбургеры