Методы решения линейных и квадратных уравнений были известны еще древним грекам. Решение уравнений третьей и четвертой степеней были получены усилиями итальянских математиков Ш. Ферро, Н. Тартальи, Дж. Картано, Л. Феррари в эпоху Возрождения. Затем наступила пора поиска формул для нахождения корней уравнений пятой и более высоких степеней. Настойчивые, но безрезультатные попытки продолжались около 300 лет и завершились благодаря работам норвежского математика Н. Абеля. Он доказал, что общее уравне6ие пятой и более высоких степеней неразрешимы в радикалах. Решение общего уравнения n-ой степени

a0xn +a1 xn-1 +…+an-1 x+an =0, a0¹0

при n³5 нельзя выразить через коэффициенты с помощью действий сложения, вычитания, умножения, деления, возведения в степень и извлечения корня.

Для неалгебраических уравнений типа

х–cos(x)=0

задача еще более усложняется. В этом случае найти для корней явные выражения, за редким случаем не удается.

В условиях, когда формулы «не работают», когда рассчитывать на них можно только в самых простейших случаях, особое значение приобретают универсальные вычислительные алгоритмы. Известен целый ряд алгоритмов, позволяющих решить рассматриваемую задачу.

Если записать уравнение в виде

f(x) =0,

то для применения этих алгоритмов нет необходимости накладывать какие-либо ограничения на функцию f(x), а предполагается только что она обладает некоторыми свойствами типа непрерывности, дифференцируемости и т.д.

Это итерационный численный метод нахождения корня (нуля) заданной функции.

Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом простой итерации.

1. Постановка задачи

Дано уравнение:

Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что корень существует). Предполагается, что F(X) непрерывна на отрезке [A;B].

Входным параметром алгоритма, кроме функции F(X), является также начальное приближение — некоторое X0, от которого алгоритм начинает идти.

Пример.

Найдем корень уравнения

Рисунок 1. Функция

Будем искать простой корень уравнения, находящийся на отрезке локализации [-0.4,0].

Приведем уравнение к виду x=f(x), где

Проверим условие сходимости:

Рисунок 2. График производной

Максимальное по модулю значение производной итерационной функции достигается в левом конце отрезка

Выполним 3 итерации по расчетной формуле

x= (x),

1 итерация .

2 итерация .

3 итерация .

2. Математические и алгоритмические основы решения задачи

2.1 Описание метода простых итераций

Рассмотрим уравнение

f(x)=0 (2.1)

с отделенным корнем X[a, b]. Для решения уравнения (2.1) методом простой итерации приведем его к равносильному виду:

x=φ(x). (2.2)

Это всегда можно сделать, причем многими способами. Например:

x=g(x) · f(x) + x ≡ φ(x),

где g(x) — произвольная непрерывная функция, не имеющая корней на отрезке [a,b].

Пусть x(0) — полученное каким-либо способом приближение к корню x (в простейшем случае x(0) =(a+b)/2). Метод простой итерации заключается в последовательном вычислении членов итерационной последовательности:

x(k+1) =φ(x(k) ), k=0, 1, 2,… (2.3)

начиная с приближения x(0) .

УТВЕРЖДЕНИЕ: 1 Если последовательность {x(k) } метода простой итерации сходится и функция φ непрерывна, то предел последовательности является корнем уравнения x=φ(x)

ДОКАЗАТЕЛЬСТВО: Пусть

. (2.4)

Перейдем к пределу в равенстве x(k+1) =φ(x(k) ) Получим с одной стороны по (2.4), что а с другой стороны в силу непрерывности функции φ и (2.4)

В результате получаем x* =φ(x* ). Следовательно, x* — корень уравнения (2.2), т.е. X=x* .

Чтобы пользоваться этим утверждением нужна сходимость последовательности {x(k) }. Достаточное условие сходимости дает:

ТЕОРЕМА 2.1: (о сходимости) Пусть уравнение x=φ(x) имеет единственный корень на отрезке [a,b] и выполнены условия:

1) φ(x) C1 [a,b];

2) φ(x)[a,b] " x [a,b];

3) существует константа q > 0: | φ '(x) | ≤ q < 1 x[a,b]. Tогда итерационная последовательность {x(k) }, заданная формулой x(k+1) = φ(x(k) ), k=0, 1,… сходится при любом начальном приближении x(0)[a,b].

ДОКАЗАТЕЛЬСТВО: Рассмотрим два соседних члена последовательности {x(k) }: x(k) = φ(x(k-1) ) и x(k+1) = φ(x(k) ) Tак как по условию 2) x(k) и x(k+1) лежат внутри отрезка [a,b], то используя теорему Лагранжа о средних значениях получаем:

x (k+1) — x (k) = φ(x (k) ) — φ(x (k-1) ) = φ '(c k )(x (k) — x(k-1) ),

где c k (x (k-1), x (k) ).

Отсюда получаем:

| x (k+1) — x (k) | = | φ '(c k ) | · | x (k) — x(k-1) | ≤ q | x (k) — x(k-1) | ≤

≤ q ( q | x (k-1) — x(k-2) | ) = q 2 | x (k-1) — x(k-2) | ≤… ≤ q k | x (1) — x(0) |. (2.5)

Рассмотрим ряд

S∞ = x (0) + ( x (1) — x (0) ) +… + ( x (k+1) — x (k) ) +…. (2.6)

Если мы докажем, что этот ряд сходится, то значит сходится и последовательность его частичных сумм

Sk = x (0) + ( x (1) — x (0) ) +… + ( x (k) — x (k-1) ).

Но нетрудно вычислить, что

Sk = x (k)). (2.7)

Следовательно, мы тем самым докажем и сходимость итерационной последовательности {x(k) }.

Для доказательства сходимости pяда (2.6) сравним его почленно (без первого слагаемого x(0) ) с рядом

q 0 | x (1) — x (0) | + q 1 |x (1) — x (0) | +… + |x (1) — x (0) | + ..., (2.8)

который сходится как бесконечно убывающая геометрическая прогрессия (так как по условию q < 1). В силу неравенства (2.5) абсолютные величины ряда (2.6) не превосходят соответствующих членов сходящегося ряда (2.8) (то есть ряд (2.8) мажорирует ряд (2.6). Следовательно ряд (2.6) также сходится. Tем самым сходится последовательность {x(0) }.

Получим формулу, дающую способ оценки погрешности

|X — x(k+1) |

метода простой итерации.

Имеем

X — x(k+1) = X — Sk+1 = S∞ — Sk+1 = (x(k+2) — (k+1) ) + (x(k+3) — x(k+2) ) +… .

Следовательно

|X — x(k+1) | ≤ |x(k+2) — (k+1) | + |x(k+3) — x(k+2) | +… ≤ qk+1 |x(1) — x(0) | + qk+2 |x(1) — x(0) | +… = qk+1 |x(1) — x(0) | / (1-q).

В результате получаем формулу

|X — x(k+1) | ≤ qk+1 |x(1) — x(0) | / (1-q). (2.9)

Взяв за x(0) значение x(k), за x(1) — значение x(k+1) (так как при выполнении условий теоремы такой выбор возможен) и учитывая, что при имеет место неравенство qk+1 ≤ q выводим:

|X — x(k+1) | ≤ qk+1 |x(k+1) — x(k) | / (1-q) ≤ q|x(k+1) — x(k) | / (1-q).

Итак, окончательно получаем:

|X — x(k+1) | ≤ q|x(k+1) — x(k) | / (1-q). (2.10)

Используем эту формулу для вывода критерия окончания итерационной последовательности. Пусть уравнение x=φ(x) решается методом простой итерации, причем ответ должен быть найден с точностью ε, то есть

|X — x(k+1) | ≤ ε.

С учетом (2.10) получаем, что точность ε будет достигнута, если выполнено неравенство

|x(k+1) -x(k) | ≤ (1-q)/q. (2.11)

Таким образом, для нахождения корней уравнения x=φ(x) методом простой итерации с точностью нужно продолжать итерации до тех пор, пока модуль разности между последними соседними приближениями остается больше числа ε(1-q)/q.

ЗАМЕЧАНИЕ 2.2: В качестве константы q обычно берут оценку сверху для величины

2.2 Геометрическая интерпретация

Рассмотрим график функции . Это означает, что решение уравнения и — это точка пересечения с прямой :

Рисунок 3.

И следующая итерация — это координата x пересечения горизонтальной прямой точки с прямой .

Рисунок 4.

Из рисунка наглядно видно требование сходимости . Чем ближе производная к 0, тем быстрее сходится алгоритм. В зависимости от знака производной вблизи решения приближения могут строится по разному. Если , то каждое следующее приближение строится с другой стороны от корня:

Рисунок 5.

3. Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунке 6, 7.

Используемые обозначения:

·FN, F – уравнение для поиска корня;

·X, START – начальное значение;

·E, PRECISION – точность вычисления;

·N, COUNT_ITER –количество итераций.

Рисунок 6 – Функциональная модель решения задачи для функции SIMPLE_ITER

Рисунок 7 – Функциональная модель решения задачи для поиска корня уравнения методом простой итерации

4. Программная реализация решения задачи

Файл SIMPLE_ITER.txt

; ФУНКЦИЯ, РЕАЛИЗУЮЩАЯ МЕТОД ПРОСТЫХ ИТЕРАЦИЙ

(DEFUN SIMPLE_ITER (N E X FN)

(COND

((AND (<= N 0) (> (ABS (- (FUNCALL FN X) X)) (* E (FUNCALL FN X)))) X)

(T (SIMPLE_ITER (- N 1) E (FUNCALL FN X) FN))

)

; ПОДГРУЖАЕМУРАВНЕНИЕ

(LOAD «D:\\FUNCTION.TXT»)

; РАССЧИТЫВАЕМ НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ К КОРНЮ

(SETQSTART (/ (- (CADRINTERVAL) (CARINTERVAL)) 2))

; ВЫЧИСЛЯЕМКОРЕНЬ

(SETQ ROOT (SIMPLE_ITER COUNT_ITER PRECISION START (FUNCTION F)))

; ОТКРЫВЕМФАЙЛДЛЯЗАПИСИ

(SETQ OUTPUT_STREAM (OPEN «D:\\ROOT.TXT» :DIRECTION :OUTPUT))

; ПЕЧАТАЕМВФАЙЛКОРЕНЬ

(PRINT 'ROOT OUTPUT_STREAM)

(PRINT ROOT OUTPUT_STREAM)

; ЗАКРЫВАЕМФАЙЛ

(TERPRI OUTPUT_STREAM)

(CLOSE OUTPUT_STREAM)

Файл FUNCTION.txt (пример 1)

; ФУНКЦИЯ

(DEFUN F (X)

(/ (+ (- (* X X) (* 5 (COS X))) 3.25) 3)

)

; КОЛИЧЕСТВО ИТЕРАЦИЙ

(SETQ COUNT_ITER 100)

; ПРОМЕЖУТОК, НА КОТОРОМ ИЩЕМ КОРЕНЬ

(SETQ INTERVAL '(-0.4 0))

; ТОЧНОСТЬ ВЫЧИСЛЕНИЯ

(SETQ PRECISION 0.0001)

Файл FUNCTION.txt (пример 2)

; ФУНКЦИЯ

(DEFUN F (X)

(- (* X X) (COS X))

)

; КОЛИЧЕСТВО ИТЕРАЦИЙ

(SETQ COUNT_ITER 60)

; ПРОМЕЖУТОК, НА КОТОРОМ ИЩЕМ КОРЕНЬ

(SETQ INTERVAL '(1 1.5))

; ТОЧНОСТЬ ВЫЧИСЛЕНИЯ

(SETQ PRECISION 0.0001)

5. Пример выполнения программы

Пример 1.

Рисунок 8 – Входные данные

Рисунок 9 – Выходные данные

Пример 2.

Рисунок 10 – Входные данные

Рисунок 11– Выходные данные

ЗАКЛЮЧЕНИЕ

Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.

Итогом работы можно считать созданную функциональную модель нахождения корней уравнения методом простой итерации. Данная модель применима к детерминированным задачам, т.е. погрешностью экспериментального вычисления которых можно пренебречь. Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы

1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н.Бронштейн, К.А.Семендяев. – М.: Наука, 2007. – 708 с.

2. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.: ЮНИТИ-ДАНА, 2006. C. 412.

3. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.

4. Поиск минимума функции [Электронный ресурс] – Режим доступа: solidbase.karelia.ru/edu/meth_calc/files/12.shtm

5. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.

6. Симанков, В.С. Основы функционального программирования [Текст] / В.С.Симанков, Т.Т.Зангиев, И.В.Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.

7. Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.

8. Хювенен Э. Мир Лиспа [Текст] / Э.Хювенен, Й.Сеппянен. – М.: Мир, 1990. – 460 с.

www.ronl.ru

1.2 Метод итераций. Решение нелинейных уравнений методом итераций

Метод итерации | Бесплатные курсовые, рефераты и дипломные работы

Из равенства

вычитаем сторонами уравнение (2.6.1)

Получаем

, (2.6.15)

где .

Метод итерации состоит в следующем. Задается начальное приближение . Затем последовательно вычисляются , , …, , … по формуле

, . (2.6.16)

Вычисления производятся до тех пор, пока не выполнится условие

, (2.6.17)

после чего приближенное решение принимается равным .

Достаточное условие сходимости метода.

…

Пусть – корень, – погрешность, тогда (по теореме Лагранжа):

Пусть

Тогда справедлива цепочка неравенств

откуда следует, что

т.к. и .

Следовательно, достаточным условием сходимости является

. (2.6.18)

Количество итераций , достаточное для получения приближенного решения уравнения с заданной точностью определяется из условия . Учитывая, что при и значения натурального логарифма от этих величин отрицательные (и ), получим следующую оценку

. (2.6.19)

Очевидно, что чем сильнее неравенство , т.е. чем меньше , тем меньше количество итераций , достаточное для получения приближенного решения уравнения с заданной точностью .

Обобщение. Если достаточное условие сходимости итераций (2.6.18) не выполняется, то вместо исходной задачи (2.6.1) можно рассмотреть эквивалентную ей задачу

, (2.6.20)

где – некоторая, специально подобранная, знакопостоянная на отрезке , функция.

Тогда в итерационном процессе (2.6.16) функция имеет вид

. (2.6.21)

Для сходимости так построенного итерационного процесса функция должна быть подобрана из достаточного условия сходимости (2.6.18).

Рассмотрим два примера метода итерации: метод простой итерации и метод Ньютона.

Метод простой итерации. В итерационном процессе можно, в частности, принять

, (2.6.22)

где – специально подобранное число (итерационный параметр).

Тогда алгоритм пересчета по методу простой итерации примет вид

, . (2.6.23)

Например, возможен следующий выбор параметра .

Пусть на отрезке существует только один корень, т.е.

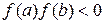и не меняет знак на .

Далее, пусть величина такая, что

для всех .

Тогда в качестве параметра можно взять значение

В этом случае имеем:

; , (2.6.24)

Откуда

. (2.6.25)

Для обеспечения на практике хорошей сходимости величина не должна сильно превышать по модулю значения . В этом случае неравенство будет существенно бόльшим.

Метод Ньютона. Этот метод представляется частным случаем общего метода итераций, если принять

. (2.6.26)

Следовательно,

(2.6.27)

и алгоритм пересчета по методу Ньютона имеет вид

, . (2.6.28)

Метод Ньютона имеет наглядую геометрическую интерпретацию. Формула касательной к кривой в точке имеет вид

(2.6.29)

Вместо корня уравнения (2.6.1)

определим корень уравнения

, (2.6.30)

или в развернутом виде

Из последнего выражения следует, что искомый корень, обозначим его , имеет вид

т.е. или

Следовательно, на -ом шаге итерации по методу Ньютона приближением корня функции является корень касательной к этой функции в точке , . Поэтому метод Ньютона известен также как метод касательных. Рис. 2.6.3 иллюстрирует геометрическую интерпретацию итераций по методу Ньютона при заданном начальном приближении корня .

Рис. 2.6.3. Геометрическая интерпретация метода Ньютона.

Рассмотрим выполнение достаточного условия сходимости итерационного процесса по методу Ньютона. В данном случае

откуда можно заключить, что достаточное условие сходимости имеет вид

или . (2.6.31)

Замечание. Заметим, что при достаточной близости начального приближения к корню уравнения метод Ньютона всегда сходится.

refac.ru

2. Метод простой итерации. Поиск нулей функции. Итерационные методы

Поиск нулей функции. Итерационные методы

Реферат по курсу “Численные методы”

Тема: “ Поиск нулей функции. Итерационные методы”

Содержание

Введение

1. Поиск нулей функции

2. Метод простой итерации

3. Итерационный процесс Ньютона

Литература

Ведение

Поиск нулей функции является важнейшей процедурой при исследовании и построении различных функций зависимостей, исследовании непрерывных процессов. Фактически поиск нулей функций сводится в постепенному приближению к области, в которой функция приобретает нулевое значение и исследованию ее.

Если уравнение представлено в форме , то нахождение корня такого уравнения формулируется как задача поиска такого значения (или таких значений) , при котором .

1. Поиск нулей функций

Характерным признаком наличия корня у функции в некотором интервале служит различие знаков у значений функции слева и справа от точки . Первой проблемой, непременно возникающей при поиске нулей функции, является обнаружение и минимизация размеров области нахождения нужного корня.

Многие уравнения благодаря пониманию физики описываемых ими явлений, как правило, дают представления об областях расположения нулей и обычно не требуют проведения аналитических исследований. В общем же случае, когда требуется найти все корни, область определения функции должна быть любыми известными эвристическими или аналитическими приемами расчленена на подобласти, включающие по одному корню. Это означает, что для каждой подобласти указаны границы возможного изменения каждой независимой переменной заданной системы нелинейных алгебраических уравнений. Для сжатия подобласти в точку, соответствующую корню, теперь могут быть предложены численные процедуры, из которых рассмотрим наиболее простые и популярные.

2. Метод простой итерации

где , матрица масштабирующих коэффициентов, в общем случае недиагональная.

Итерационный процесс начинается с подстановки в правую часть произвольного значения и вычисления очередного вектора для последующей подстановки:

Сходимость к решению такого процесса зависит от вида функции правой части и, следовательно, от величин масштабирующих коэффициентов . Сходимость будет, если скалярная функция , однозначно характеризующая изменение вектора за один цикл, больше значения этой функции при подстановке в нее соответствующих :

Если и , условие именуют условием Липшица.

Если – диагональная матрица, то величины можно выбрать из условия отрицательности скорости изменения . Для этого достаточно взять производную от рекуррентной формулы и установить соответствующее соотношение с нулем:

Таким образом, знание максимальных значений производных системы функций в области [a, b] нахождения корня , позволяет выбрать масштабирующие коэффициенты, обеспечивающие сходимость процесса.

3. Итерационный процесс Ньютона

Вторым по важности и популярности итерационным процессом для случая аналитического задания системы уравнений и локализации области нахождения корня является итерационный процесс Ньютона.

Пусть отклонение начального вектора искомого решения отличается от точного на величину , тогда, выполнив разложение в ряд Тейлора неявных функций в окрестности и ограничившись слагаемыми с частными производными первого порядка, получим систему уравнений для вычисления добавок к начальному вектору, приближающих последний к значению корня:

Обозначим частные производные (). Система уравнений для вычисления вектора будет:

где – матрица, обратная матрице Якоби из частных производных:

Итерационную процедуру Ньютона для вычисления корней нелинейной системы уравнений можно в результате представить так:

Здесь верхний индекс в обозначениях частных производных указывает на подстановку в них значения x , полученного на k-той итерации.

Остановка итерационного процесса осуществляется тогда, когда по всем компонентам вектора x достигнута заданная относительная погрешность , т.е. должна быть истинной конъюнкция:

В одномерном случае итерации для уравнения g(x)=0 выглядят так:

Нетрудно заметить одну и ту же природу коэффициентов, стоящих перед значением функций у трех вариантов итерационных процедур и обеспечивающих сходимость процесса : все они учитывают значение производных в области нахождения нулей функции.

Литература

1. Бахвалов Н.С. Численные методы в задачах и упражнениях / Н. С. Бахвалов А.В. Лапин, Е.В. Чижонков. М.: Высш. шк., 2000. 192 с.

2. Блинов И.Н., “Об одном итерационном процессе Ньютона”, Изв. АН СССР. Сер. матем., 33:1 (1969), 3–14

3. Вайнберг М.М., Треногин В.А. Теория ветвления решений нелинейных уравнений. М.: Наука, 1969. 528 с.

4. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш. шк., 2001. - 383с.

5. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1976. 544 с.

6. Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.: Наука, 1965. 250 с.

7. Шуп Т.Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. - 255с.

www.neuch.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..

Реферат: Поиск нулей функции. Итерационные методы. Метод итерации реферат

Реферат - Нахождение корней уравнения методом простой итерации (ЛИСП-реализация)

1.2 Метод итераций. Решение нелинейных уравнений методом итераций

Похожие главы из других работ:

2.3 Метод деления отрезка пополам (метод дихотомии, метод бисекции)

2.4 Метод простых итераций

2.1 Метод простых итераций

3.3.3 Метод наискорейшего спуска (метод Коши)

2.1 Метод итераций

2.1.1 Пример решения системы уравнений с помощью метода итераций

Глава 1 АПРИОРНЫЙ ВЫБОР ЧИСЛА ИТЕРАЦИЙ В МЕТОДЕ ПРОСТЫЙ ИТЕРАЦИЙ С ПОПЕРЕМЕННО ЧЕРЕДУЮЩИМСЯ ШАГОМ ДЛЯ УРАВНЕНИЙ I РОДА

Глава 2 СЛУЧАЙ НЕЕДИНСТВЕННОГО РЕШЕНИЯ В МЕТОДЕ ПРОСТЫХ ИТЕРАЦИЙ С ПОПЕРЕМЕННО ЧЕРЕДУЮЩИМСЯ ШАГОМ

Глава 3 АПОСТЕРИОРНЫЙ ВЫБОР ЧИСЛА ИТЕРАЦИЙ В МЕТОДЕ ПРОСТЫХ ИТЕРАЦИЙ С ПОПЕРЕМЕННО ЧЕРЕДУЮЩИМСЯ ШАГОМ ДЛЯ РЕШЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ

Глава 4 МЕТОД ПРОСТЫХ ИТЕРАЦИЙ С ПОПЕРЕМЕННО ЧЕРЕДУЮЩИМСЯ ШАГОМ ДЛЯ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ТЕОРИИ ПОТЕНЦИАЛА

Глава I. Исследование метода итераций

1.4 Решение нелинейного уравнения методом итераций

3.4.3 Метод CFOP (метод Джессики Фридрих)

Метод простых итераций

6. Метод Ньютона (Метод касательных, линеаризации)

Метод итерации | Бесплатные курсовые, рефераты и дипломные работы

2. Метод простой итерации. Поиск нулей функции. Итерационные методы

Похожие главы из других работ:

2.3 Метод деления отрезка пополам (метод дихотомии, метод бисекции)

2.5 Метод Ньютона (метод касательных)

2.6 Метод секущих (метод хорд)

1.1 Метод простой итерации

2. Простой отжиг проволок на встречных курсах в муфельном термоаппарате

1.1 Критерии согласия Колмогорова и омега-квадрат в случае простой гипотезы

1.2 Критерии согласия ?2 Пирсона для простой гипотезы

3.1.2 Метод поиска по координатной сетке с постоянным шагом и метод случайного поиска. Сравнение результатов вычислений

3.3.3 Метод наискорейшего спуска (метод Коши)

1.1 Метод простой итерации

2. Метод простой итерации

2. Метод простой итерации

3.4.3 Метод CFOP (метод Джессики Фридрих)

1. Решение систем линейных алгебраических уравнений методом простой итерации

6. Метод Ньютона (Метод касательных, линеаризации)

Поиск нулей функции. Итерационные методы

Смотрите также