|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Симплекс-метод c искусственным базисом. Метод искусственного базиса реферат
§3. «Метод искусственного базиса».. Математические методы в экономике
Похожие главы из других работ:
Использование среды MatLAB для решения линейной программы
2. СИМПЛЕКС-МЕТОД
...
Классические методы оптимизации
3.2 Метод Лагранжа
Пример 1...
Линейное программирование: методы решения задач
2.1 Графический метод
Графический метод решения задачи линейного программирования - основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач...
Линейное программирование: методы решения задач
2.2 Симплекс-метод
Двумерные задачи линейного программирования решаются графически. Для случая, когда неизвестны три переменные, можно рассмотреть трехмерное пространство...
Линейное программирование: методы решения задач
2.4 Метод потенциалов
Метод потенциалов - является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения...
Математические методы в экономике
§3. «Метод искусственного базиса».
Если ограничения исходной задачи содержат единичную матрицу порядка М, то при неотрицательности правых частей уравнений определен первоначальный план, из которого с помощью симплекс - таблиц находится оптимальный план...
Математическое моделирование экономических процессов на железнодорожном транспорте
3.2 Решение задачи симплекс - методом с использованием искусственного базиса
1. Необходимо составить оптимальную диету, запустив три вида продуктов В1, В2, В3 с заданными ценами С1, С2, С3...
Метод Зойтендейка
2. МЕТОД ЗОЙТЕНДЕЙКА
...
Нахождение минимальных затрат при распределении товаров среди магазинов методами решения транспортной задачи
1.2.3 Метод потенциалов
Наиболее простым методом ТЗ является метод потенциалов. Потенциалами называются условные числа Ui ,Vj , приписанные определённым образом каждому поставщику и потребителю...
Нейронные сети
1. Базовые понятия искусственного нейрона
...
Нейронные сети
1.1 Структура искусственного нейрона
Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона...
Оптимальный режим управления двухсекторной моделью экономики
3.1 Метод Эйлера
Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера...
Оптимизация транспортной работы, связанной с грузоперевозками, методами линейного программирования
1.1 Метод Хичкока
Алгоритм определения оптимальности: во всех загруженных клетках получаем нулевой потенциал, для этого по строчкам и столбцам таблицы, ко всем расстояниям, поставленным в верхних правых углах загруженных клеток, прибавляем такие числа...
Прогнозирование объема прибыли предприятия при наличии сезонной компоненты
1.2 Метод Четверикова
Эмпирический ряд выравниваетсяскользящей средней с периодом скольжения, т.е. берется (+1) членов исходного ряда, из которыхпервый и последний берутся с половинным весом:...
Решение задачи о коммивояжере
Метод решения
Для начала следует сказать, что в основе любого метода решения данной задачи лежит полный перебор всевозможных вариантов путей. [2]Мы проходимся по каждому маршруту: одни отбрасываем, другие сравниваем с минимальным путем...
em.bobrodobro.ru
Метод искусственного базиса — курсовая работа
Кемеровский филиал МЭСИ
Курсовой проект по
Математическим методам.
Кемерово 2012
Задание.
Для курсового проектирования _______________________________________
___________________________________________________________________
Студента____________ курса, группы__________________________________
Ф.И.О.____________________________________________________________
Тема курсового проекта______________________________________________
__________________________________________________________________
Для выполнения курсового проекта должны быть представлены
- Введениея______________________________________________________________________________________________________________________________________________________________________________
- Общая часть__________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
- Специальная часть_____________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
- Графическая часть_____________________________________________ __________________________________________________________________________________________________________________________
- Используемая литература _____________________________________________________________ __________________________________________________________________________________________________________________________________________________________________________________________________
Дата выдачи___________________ Срок окончания________________ Руководитель курсового проекта_______________________________
Содержание
- Введение_____________________________________________2
8. Список литературы____________________________________12
1. Введение.
Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторовича "Математические методы организации и планирования производства". Поскольку методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В.Канторовича осталась почти не замеченной.
Свое второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования. В 1975 году академик Л.В.Канторович и американец профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за "вклад в разработку теории и оптимального использования ресурсов в экономике".
В автобиографии, представленной в Нобелевский комитет, Леонид Витальевич Канторович рассказывает о событиях, случившихся в 1939 году. К нему, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда… Поэтому простой перебор вершин не годился. Леонид Витальевич писал: "оказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоков… Это настойчиво побудило меня к поиску эффективного метода их решения". И уже летом 1939 года была сдана в набор книга Л.В.Канторовича "Математические методы организации и планирования производства", в которой закладывались основания того, что ныне называется математической экономикой.
Американский математик А.Данциг в 1947 году разработал весьма эффективный конкретный метод численного решения задач линейного программирования (он получил название симплекс метода). Идеи линейного программирования в течении пяти шести лет получили грандиозное распространение в мире, и имена Купманса и Данцига стали повсюду широко известны.
2. Линейное программирование.
Линейное программирование – это раздел математики о методах решения задач связанных с нахождением экстремумов линейных функций, нескольких переменных при наличии линейных ограничений на ети переменные.
Задача линейного программирования – состоит из целевой функции системы ограничений и условий не отрицательности и формулируется следующим образом: Найти экстремум целевой функции и соответствующие ему переменные при условии, что эти переменные удовлетворяют системы ограничений и условия не отрицательности.
Виды задач линейного программирования.
Вид задачи определяется по системе ограничений.
- Задача называется стандартной, если система ограничений состоит только из неравенств.
- Задача называется канонической, если система ограничений состоит только из уравнений.
- Задача называется общей, если система ограничений состоит из уравнений и неравенств.
3. Методы решения задач.
Графический метод решения задач линейного программирования.
Графический метод – основан на геометрической интерпретации задачи и применяется для решения стандартных задач линейного программирования с двумя переменными.
Симплексный метод решения задач линейного программирования.
Этот метод является универсальным и решает любые задачи линейного программирования с любым числом переменных.
Геометрически он требует значения целевой функции в вершинах многогранника решений и выбирает оптимальное.
4. Искусственный базис.
Данный метод решения применяется при наличии в системе ограничений и условий-равенств, и условий-неравенств, и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных Ri со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами M, имеющими смысл "штрафов" за ввод искусственных переменных, а в задачи минимизации - с положительными M. Таким образом из исходной получается новая M-задача (поэтому метод искусственного базиса так же называют M-методом).
Если в оптимальном решении М-задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении M-задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.
Симплекс-таблица, которая составляется в процессе решения, используя метод искусственного базиса, называется расширенной. Она отличается от обычной тем, что содержит две строки для функции цели: одна – для составляющей F, а другая – для составляющей M. При составлении симплекс таблицы полагают что исходные переменные являются небазисными, а дополнительные(xn+m) и искусственные (Ri)- базисными.
Исходная таблица для "Метода искусственного базиса" имеет следующий вид:
|
Элементы дополнительной строки M расчитываются как сумма соответствующих коэффициентов условий-равенств (условий в которые после приведения к каноническому виду введены переменные Ri) взятая с противоположным знаком.
Правила преобразований симплексной таблицы
При составлении новой симплекс-таблицы в ней происходят следующие изменения:
- Вместо базисной переменной xk записываем xl; вместо небазисной переменной xl записываем xk.
- ведущий элемент заменяется на обратную величину ak,l'= 1/ak,l
- все элементы ведущего столбца (кроме ak,l) умножаются на -1/ak,l
- все элементы ведущей строки (кроме ak,l) умножаются на 1/ak,l
оставшиеся элементы симплекс-таблицы преобразуются по формуле ai,j'= ai,j- ai,l×ak,j/ ak,l
5. Алгоритм метода искусственного базиса.
Шаг 1. Приводим задачу ЛП к каноническому виду с неотрицательными правыми частями , i=1,..., m.
Шаг 2. Строим вспомогательную задачу ЛП
и приводим ее к специальному виду. Для этого целевую функцию выражаем через небазисные переменные.
Шаг 3. Решаем ВЗЛП симплекс-методом.
Шаг 4. Если , то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается.
Шаг 5. Если , то строим СЗЛП для исходной задачи на основе оптимальной симплекс-таблицы ВЗЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.
Шаг 6. Определить ведущий элемент
Шаг 7. Выполнить пересчёт матрицы
Шаг 8. Проверить результат пресчёта атрицы на оптимальность
Шаг 9. Если найденное решение оптимально,то вычисления прекратить и сформульровать ответ.
referat911.ru
2.5. Метод искусственного базиса
Симплекс-метод применяется для решения задач ЛП, представленных в специальной форме:
 (16)
(16)
Характерная особенность задачи (16) – известное базисное допустимое решение

Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо привести эту задачу к виду (16), т. е. выделить начальное допустимое базисное решение. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса и состоит в следующем [1,2,3].
Вычислительная схема метода искусственного базиса
Шаг 1. Приводим задачу ЛП к канонической форме с неотрицательными правыми частями  :
:
 (17)
(17)
Шаг 2. В каждую i-ю строку ограничений (17) вводим искусственную неотрицательную переменную  и строим вспомогательную задачу ЛП вида:
и строим вспомогательную задачу ЛП вида:
 (18)
(18)
В задаче (18)  – допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные
– допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные :
:

Шаг 3. Для вспомогательной задачи (18) строим симплексную таблицу
| b | | … | | |
| | | | … | |
| | | | … | |
| … | … | …………………. | ||
| | | | … | |
и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.
Шаг 4. Если  и все переменные
и все переменные являются небазисными, то m переменных из
являются небазисными, то m переменных из войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид
войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид
 (19)
(19)
Так как переменные  , то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи
, то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи через небазисные переменные
через небазисные переменные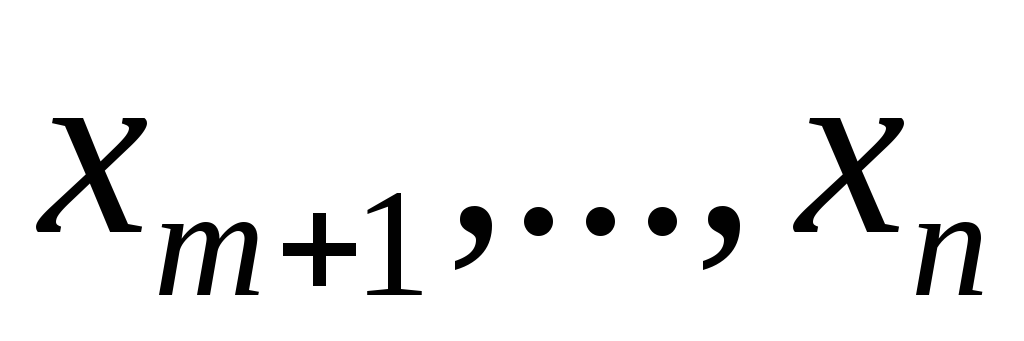 системы (19), получим исходную задачу (17) в виде (16).
системы (19), получим исходную задачу (17) в виде (16).
Шаг 5. Если  , но в базисе остались искусственные переменные
, но в базисе остались искусственные переменные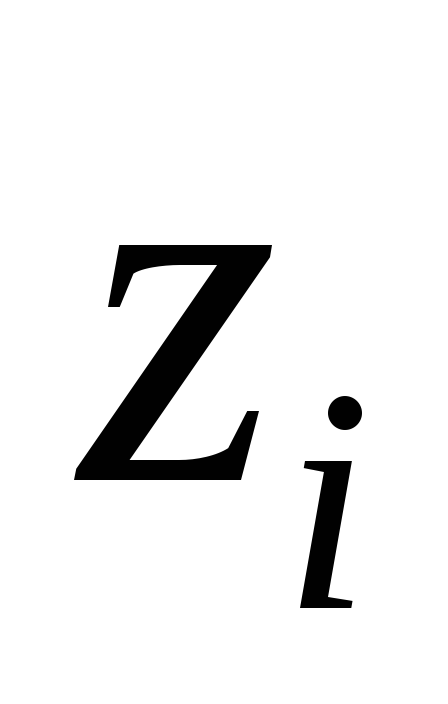 , для которых
, для которых (вырожденный случай), то проводим для каждой искусственной переменной
(вырожденный случай), то проводим для каждой искусственной переменной из базиса следующее преобразование симплексной таблицы.
из базиса следующее преобразование симплексной таблицы.
Выбираем ведущим столбцом столбец такой переменной  , для которой элемент индексной строки
, для которой элемент индексной строки , а элемент столбца
, а элемент столбца . В этом случае строка искусственной переменной
. В этом случае строка искусственной переменной будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная
будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.
выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.
Шаг 6. Если  , то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные
, то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.
быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.
Пример решения задачи методом искусственного базиса
Выделить допустимое базисное решение для задачи ЛП:

Приведем задачу к канонической форме на минимум с неотрицательными правыми частями:

Заметим, что переменные  и
и можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.
можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.
Во вторую строку ограничений вводим искусственную переменную z, потому что в этой строке нет переменной, которую можно взять базисной, не проводя при этом дополнительных преобразований всей системы ограничений.
Полученная вспомогательная задача имеет вид

Приведем задачу к виду (16):

Выпишем соответствующую симплексную таблицу:
| B | | | | |
| | 10 | 5 | 4 | -1 |
| | 3 | 3 | -2 | 0 |
| | 10 | 5 | 4 | -1 |
| | 5 | 2 | 1 | 0 |
Ведущий столбец рекомендуется выбирать не по максимальному положительному элементу строки целевой функции, а так, чтобы из базиса выводилась искусственная базисная переменная (соответствующая ведущая строка должна быть строкой искусственной переменной). Так, выбрав ведущим столбцом столбец переменной  , получим ведущую строку – строку с переменнойz (выбирая ведущим столбцом
, получим ведущую строку – строку с переменнойz (выбирая ведущим столбцом  , получили бы ведущую строку
, получили бы ведущую строку , и из базиса выводилась бы переменная
, и из базиса выводилась бы переменная ).
).
Итак, искусственная переменная z выйдет из базиса, а переменная  введется в базис.
введется в базис.
Симплексная таблица преобразуется к виду:
| B | | | | |
| | 0 | 0 | -1 | 0 |
| | 8 | 11/2 | 1/2 | -1/2 |
| | 5/2 | 5/4 | 1/4 | -1/4 |
| | 5/2 | 3/4 | -1/4 | 1/4 |
Так как значение  , то полученный базис
, то полученный базис является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию
является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию через небазисные переменные
через небазисные переменные , подставим значение базисной переменной
, подставим значение базисной переменной в целевую функцию. В результате получим:
в целевую функцию. В результате получим:

Тогда исходная задача будет иметь вид специальной формы задачи ЛП:

что и требовалось получить в результате решения вспомогательной задачи.
studfiles.net
Математическое программирование
МЕТОД ИСКУССТВЕННОГО БАЗИСА, ИЛИ М-МЕТОД
До сих пор мы всесторонне рассматривали задачу, решение которой осуществлялось на основе простейшего алгоритма симплексного метода, поскольку все ограничения имели вид меньше либо равно. В этом случае дополнительные переменные задачи образуют единичный базис. Но может получиться так, что система ограничений представлена в канонической форме, но она не приведена к единичному базису.
При решении таких задач был введен метод искусственного базиса. Он особенно удобен, когда число переменных значительно превосходит число уравнений.
Алгоритм решения задачи симплексным методом с искусственным базисом рассмотрим на примере.
Пример 1:  Найти максимум Z = 4Х1 + 2Х2 + ХзХ1 + Х2 + Х3 ? 82Х1 + Х2 + Х3 ? 83Х1 + 2Х2 + Х3 = 15Хj ? 0, j = 1,…,3.
Найти максимум Z = 4Х1 + 2Х2 + ХзХ1 + Х2 + Х3 ? 82Х1 + Х2 + Х3 ? 83Х1 + 2Х2 + Х3 = 15Хj ? 0, j = 1,…,3.
 Переходим к канонической форме:Х1 + Х2 + Х3 – Х4 = 82Х1 + Х2 + Х3 + Х5 = 83Х1 + 2Х2 + Х3 = 15Хj ? 0, j = 1,…,5Zmax = 4Х1 + 2Х2 + Х3 + 0*Х4 + 0*Х5.
Переходим к канонической форме:Х1 + Х2 + Х3 – Х4 = 82Х1 + Х2 + Х3 + Х5 = 83Х1 + 2Х2 + Х3 = 15Хj ? 0, j = 1,…,5Zmax = 4Х1 + 2Х2 + Х3 + 0*Х4 + 0*Х5.
Данная система ограничений не имеет единичного базиса, так как дополнительная переменная Х4 имеет коэффициент минус единица, а третье ограничение было представлено уравнением, и в нем отсутствует базисная переменная. Для того чтобы был единичный базис, вводим в соответствующие ограничения искусственные переменные У1 и У2 с положительными коэффициентами (+1).
Следует отметить, что искусственные переменные вводятся только для математической формализации задачи. Поэтому схема вычислений должна быть такой, чтобы искусственные переменные не могли попасть в окончательное решение в числе базисных переменных. С этой целью для искусственных переменных в целевой функции вводят коэффициент М, обозначающий очень большое число. На практике (особенно при решении задачи на ЭВМ) вместо М берут конкретное большое число, например 10 000. Причем при решении задачи на максимум этот коэффициент вводится в целевую функцию со знаком минус, а при решении на минимум — со знаком плюс. Теперь будем решать Т (М)-задачу, целевая функция которой содержит целевую функцию Z-задачи и искусственные переменные с коэффициентом ±М, то естьmТ = Z — М ? Уi при решении на максимум целевой функции иi =1mТ = Z + М ? Уi при решении на минимум целевой функции.i=1
В нашем случае: Х1 + Х2 + Х3 – Х4 + У1 = 82Х1 + Х2 + Х3 + Х5 = 83Х1 + 2Х2 + Х3 + У2 = 15Хj ? 0, j = 1,…,5Тmax = 4Х1 + 2Х2 + Х3 + 0*Х4 + 0*Х5 – М(У1 + У2).
Х1 + Х2 + Х3 – Х4 + У1 = 82Х1 + Х2 + Х3 + Х5 = 83Х1 + 2Х2 + Х3 + У2 = 15Хj ? 0, j = 1,…,5Тmax = 4Х1 + 2Х2 + Х3 + 0*Х4 + 0*Х5 – М(У1 + У2).
Эта задача решается в симплексных таблицах, но для удобства целевую функцию разбивают на 2 строки:
- в первую строку записываем оценки, которые не содержат коэффициент М;
- во вторую строку — оценки по каждой свободной переменной, содержащие коэффициент М.
Расчет элементов (оценок) этих двух строк производится по формуле (1). Только отличие:
- при расчете оценок Z-строки должны быть учтены коэффициенты Сj, входящие вфункцию Z;
- при расчете оценок М-строки этот коэффициент во внимание не берется, а М — выносится, как общий множитель.
Для того чтобы Т-задача и Z-задача были равны, нужно, чтобы значения Уi были равны нулю. Поэтому, пока Уi не равно нулю, разрешающий столбец выбирается по оценкам во второй строке, используя алгоритм симплексного метода.
Лишь после того, как все Уi станут равны нулю, дальнейший расчет будет вестись по первой индексной строке, то есть — обычная Z-задача.
Причем, когда искусственная переменная будет выводиться из базиса, ее выбросим из симплексной таблицы, а в следующей симплекс-таблице не будет бывшего разрешающего столбца.Между оптимальными решениями М-задачи и Z-задачи существует связь, устанавливаемая следующей теоремой:
1.Если в оптимальном решении М-задачи все искусственные переменные (Уi) равны нулю, то это решение будет являться оптимальным решением Z-задачи
2. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных отлична от нуля, то Z-задача не имеет решения по причине несовместности системы ограничений.
3. Если М-задача оказалась неразрешимой (Т>+? или-?), то исходная задача также неразрешима либо по причине несовместности системы ограничений, либо по причине неограниченности функции Z.
Составим первую симплексную таблицу. При решении М-методом разрешающий столбец можно выбирать в М-строке не по наибольшей, по абсолютной величине отрицательной оценке (при решении на максимум) и не по наибольшей положительной оценке (при решении на минимум), а по той из них, которая быстрее выводит У из базиса. В данном примере разрешающим столбцом будет столбец свободной переменной Х2 с оценкой (-3).
Таблица 3.1 Первая симплексная таблица
  Св.ПБ.П. Св.ПБ.П. | СjCi | 0 | 4 | 2 | 1 | 0 | ai0/aip |
| ai0 | X1 | X2 | X3 | X4 | |||
| У1 | -М | 8 | 1 | 1 | 1 | -1 | 8 |
| X5 | 0 | 8 | 2 | 1 | 1 | 0 | 8 |
| У2 | -М | 15 | 3 | (2) | 1 | 0 | 7,5 < |
| Z | 0 | -4 | -2 | -1 | 0 | ||
| М | -23 | -4 | -3 ^ | -2 | 1 |
Заполнение Z-строки осуществляется по формуле:a00 = 0*8-0=0a01 = 0*2-4=-4a02 = 0*1-2=-2a03 = 0*1-1=-1a04 = 0*0-0=0.
Заполнение М-строки:a?00 = -М*8+(-М)*15=-23Мa?01 = -М*1+(-М)*3=-4Мa?02 = -М*1+(-М)*2=-3Мa?03 = -М*1+(-М)*1=-2Мa?04 = -М*(-1)+(-М)*0=1М.М выносим как общий множитель.
В последнем столбце в разрешающей строке стоит 0, поэтому столбец свободной переменной Х4 переносим без изменений.
Таблица 3.2 Вторая симплексная таблица
  Св.ПБ.П. Св.ПБ.П. | СjCi | 0 | 4 | 1 | 0 | ai0/aip |
| ai0 | X1 | X3 | X4 | |||
| У1 | -М | 1/2 | -1/2 | (1/2) | -1 | 1(-2) < |
| X5 | 0 | 1/2 | 1/2 | 1/2 | 0 | 1(0) |
| Х2 | 2 | 15/2 | 3/2 | 1/2 | 0 | 15(0) |
| Z | 15 | -1 | 0 | 0 | ||
| М | -1/2 | 1/2 | -1/2 ^ | 1 |
Во второй таблице получаем вырожденное решение, так как получаются два одинаковых минимальных симплексных отношения. Поэтому находим отношения элементов столбца, следующего за разрешающим, к элементам разрешающего столбца с учетом знака.
Таблица 3.3 Третья симплексная таблица
  Св.ПБ.П. Св.ПБ.П. | СjCi | 0 | 4 | 0 | ai0/aip |
| ai0 | X1 | X4 | |||
| Х3 | 1 | 1 | -1 | -2 | — |
| X5 | 0 | 0 | (1) | 1 | 0 < |
| Х2 | 2 | 7 | 2 | 1 | 3,5 |
| Z | 15 | -1^ | 0 |
Теперь решаем обычным симплексным методом.Таблица 3.4
Четвертая симплексная таблица
  Св.ПБ.П. Св.ПБ.П. | СjCi | 0 | 0 | 0 |
| ai0 | X5 | X4 | ||
| Х3 | 1 | 1 | 1 | -1 |
| X1 | 4 | 0 | 1 | 1 |
| Х2 | 2 | 7 | -2 | -1 |
| Z | 15 | 1 | 1 |
В оценочной строке все элементы являются неотрицательными величинами, следовательно, получено оптимальное решение:Zmax = 15 Хопт (0,7,1,0,0).
Пример 2:Задача решалась на минимум (Z>min) целевой функции. На последней итерации получили следующую таблицу:
Таблица 3.5 Последняя симплексная таблица
  Св.ПБ.П. Св.ПБ.П. | СjCi | 0 | 4 | 1 | 0 |
| ai0 | X1 | X3 | X4 | ||
| У1 | М | -1/2 | -1/2 | -1/2 | -1 |
| X5 | 0 | 1/2 | 1/2 | 1/2 | 0 |
| Х2 | 2 | 15/2 | 3/2 | 1/2 | 0 |
| Z | 15 | -1 | 0 | 0 | |
| М | -1/2 | -1/2 | -1/2 | -1 |
В Т-задаче получено оптимальное решение, так как в М-строке нет больше положительных оценок, то есть выбор разрешающего столбца невозможен, а У1 находится в базисе. В этом случае исходная задача не имеет решения по причине несовместности системы ограничений.
kursach37.com
Симплекс-метод c искусственным базисом | Бесплатные курсовые, рефераты и дипломные работы
Читайте также:
|
Для построения исходного опорного плана при решении задачи симплекс-методом необходимо, чтобы матрица коэффициентов при переменных, имеющая «m» строк и «n» столбцов (m<n), содержала в себе единичную матрицу порядка «m». Такая матрица получалась после введения дополнительных переменных в исходные ограничения вида «≤». Однако, если исходные ограничения задаются сразу уравнениями, то нет никакой гарантии, что матрица коэффициентов содержит единичную матрицу порядка «m». То же относится и к системе неравенств … вида « ≥».
Дополнительные переменные входят в такую систему с коэффициентами «-1». В этих случаях для решения задачи применяется симплекс-метод с искусственным базисом.
В левую часть уравнений вводятся неотрицательные искусственные переменные ω1, ω2, …, ωm , коэффициенты при которых образуют единичную матрицу. Эти же переменные с большими по абсолютной величине отрицательными коэффициентами (-M) включаются в целевую функцию.
В результате расширенная задача принимает вид:


При условиях:

 ,
, 
Искусственные переменные необходимы для построения исходного плана задачи. В процессе решения они должны выводиться из базиса, т.к. в окончательном плане задачи должны соблюдаться исходные уравнения, а это возможно когда ωi=0.
Решение задачи линейного программирования методом искусственного базиса включает следующие этапы.
1. Составляют расширенную задачу.
2. Находят опорный план расширенной задачи.
3. С помощью обычных вычислений симплекс-методом исключают искусственные переменные из базиса. Анализ ведут по «m+2» строке. В результате находят опорный план исходной задачи, либо устанавливают ее неразрешимость.
4. Используя найденный опорный план исходной задачи симплекс-методом находят оптимальный план (анализ ведут по «m+1» строке) или устанавливают неразрешимость задачи.
Возможны случаи , когда при оптимизации опорного плана расширенной задачи в «m+2» строке еще остается отрицательное число, но в соответствующем ему столбце нет положительных коэффициентов, следовательно, в базисе остаются несколько искусственных переменных и они не могут быть выведены. Это означает, что исходная задача не имеет искомого решения. Полученный план не удовлетворяет всем поставленным условиям, и окончательный базис будет содержать искусственную переменную.
Пример:
Найти оптимальное решение задачи
F=-2x1+3x2−6x3−x4→min
при ограничениях


Приведем задачу к виду основной задачи линейного программирования, учитывая, что целевая функция должна стремиться к max
:
F=-2x1+3x2−6x3−x4→max


Среди векторов, составленных из коэффициентов при неизвестных, только два единичных (х4 и х5), поэтому в левую часть третьего уравнения добавим искусственную переменную ω и составим расширенную задачу:
F=-2x1+3x2−6x3−x4−М ω →max



Теперь задача содержит необходимое количество единичных векторов, образующих базис. Составим симплекс –таблицу

1-ая итерация
План можно улучшить . Анализ ведем по второй индексной строке . Вводимой переменной будет х3 ,а выводимой ω т.к.

Примечание.
Искусственную переменную всегда стараются вывести первой. Как только ω выведена из базиса , на последующих итерациях столбец ω не заполняется и индексная строка будет одна .
refac.ru
4. Метод искусственного базиса
1.4.3. Методы искусственного базиса
Многие практические задачи линейного программирования не содержат линейно независимой системы единичных векторов Рj, которую можно выбрать в качестве первого базиса задачи. В этом случае в задачу вводят дополнительно k единичных векторов Рn+1,...,Pn+к, образующих базис.
Пусть задана следующая основная задача линейного программирования:


Переменные хn+1,…,xn+k называются искусственными, а связанная с ними система векторов Pn+1,…,Рn+k - искусственным базисом вспомогательной задачи. Следует здесь заметить, что если среди векторов Рj есть векторы, которые могут быть элементами базиса, то в соответствующие равенства исходной системы ограничений нет смысла вводить искусственные переменные.
Теперь к вспомогательной задаче можно применить симплекс-метод и найти ее решение.
Теорема 1.6. Вспомогательная задача всегда разрешима. При этом mах  <= 0. Если mах
<= 0. Если mах = 0 и достигается на плане
= 0 и достигается на плане=(
1,...,
n,
n+1,...,
n+k), то вектор х=(
1,...,
n) является опорным планом исходной задачи (1.9), (l.10). Если mах
 < 0, то система условий (1.10) несовместна.
< 0, то система условий (1.10) несовместна.
Продолжая итерации симплекс-метода для модифицированной последней симплекс-таблицы вспомогательной задачи, найдем решение исходной задачи. Модификация симплекс-таблицы состоит в удалении искусственных переменных и замене коэффициентов целевой функции вспомогательной задачи на соответствующие коэффициенты целевой функции (1.9).
2-й метод. Рассмотрим следующую расширенную задачу, часто называемую М-задачей :

где М- некоторое достаточно большое положительное цисло, конкретное значение которого обычно не задается.
Переменные хn+1,..,xn+k также называют искусственными, а связанная с ними система векторов Pn+i ,…, Рn+к - искусственным базисом расширенной задачи.
Теорема 1.7. Если в оптимальном плане расширенной задачи (1.11), (1.12) все искусственные переменные равны нулю, то полученное оптимальное решение является решением исходной задачи (1.9), (1.10). Если в оптимальном плане расширенной задачи (1.11), (1.12) хотя бы одна искусственная переменная отлична от нуля, то исходная задача (1.9), (1.10) решения не имеет.
В этом методе, искусственного базиса исходные данные расширенной задачи заносятся в таблицу, которая содержит на одну строку больше, чем обычная симплекс-таблица. Это связано с тем, что разности : j (
j ( j =d+ еМ ) состоят из дух частей, одна из которых зависит от M, а другая - нет. В(k+2)-ю строку помещаются коэффициенты при М, а в (k+1)-ю - слагаемые, не содержащие М.
j =d+ еМ ) состоят из дух частей, одна из которых зависит от M, а другая - нет. В(k+2)-ю строку помещаются коэффициенты при М, а в (k+1)-ю - слагаемые, не содержащие М.
При переходе от одного опорного плана к другому в базис вводят переменную, соответствующую наименьшему отрицательному числу (k+2)-й строки. Искусственная переменная, исключенная из базиса в результате некоторой итерации, в дальнейшем не вводится ни в один из последующих базисов, и преобразование столбца симплексной таблицы, соответствующего этой переменной, не производится.
Пересчет симплекс-таблиц при переходе от одного опорного плана к другому производится по общим правилам симплекс-метода. Итерационный процесс по (k+2)-й строке ведут до тех пор, пока:
1) либо все искусственны е переменные не будут исключены из базиса;
2) либо не все искусственны е переменные исключены из базиса, но (k+2)-я строка не содержит больше отрицательных элементов в столбцах векторов Р1,..., Рn+к :
В первом случае базис отвечает некоторому опорному плану исходной задачи, и определение ее оптимального плана продолжают по (k+1)-й строке симплекс-таблицы.
Во втором случае, если элемент, стоящий в (k+2)-й строке столбца вектора Ро, отрицателен, то исходная задача не имеет решения; если же он равен нулю, то найденный опорный план исходной задачи является вырожденным и базис содержит по крайней мере один из векторов искусственного базиса.
studfiles.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|






























