Реферат: Математика в годы великой отечественной войны. Математика в военном деле реферат

Математика и военное дело

Математика и военное дело.

Начало использования математических знаний в военном деле относится к глубокой древности. Известно, что в Древнем Вавилоне арифметические сведения употреблялись при подсчете необходимых запасов для армии, геометрия же использовалась при строительстве укреплений и подсчете объема необходимых земельных работ.

В знаменитом диалоге Платона «Государство» говорится о том, что арифметика и геометрия необходимы каждому воину. Вот небольшие цитаты из текста этого диалога:

«Но ведь арифметика и счет целиком касаются числа?..

- Значит, они принадлежат к тем познаниям, которые мы искали. Воину их необходимо усвоить для войскового строя, а философу – для постижения сущности…» (Платон. Соч., т.3, ч. I с.335 М., «Мысль», 1971.)

«При устройстве лагерей, занятии местностей, стягивании и развертывании войск и разных других военных построениях, как во время сражения, так и в походах, конечно, скажется разница между знатоком геометрии и тем, кто ее не знает». (Там же, с. 336 – 337).

Мы хорошо знаем, что создание математического анализа – дифференциального и интегрального исчислений – в значительной мере было связано с задачами, выдвинутыми артиллерией, и что позднее, в свою очередь, развитие новой математики оказывало огромное влияние на прогресс самой артиллерии. Во все времена считалось, что артиллерийский офицер одновременно является хорошим знатоком математики. В этом плане прекрасное утверждение высказано в одном из древнерусских сочинений по артиллерии: «… начальное, во – первых, орудие, еще пушкарю подобает при себе имети – есть циркуль». (Цит. По кн.: А. Платов и Л. Кирпичев. Исторический очерк образования и развития артиллерийского училища. Спб., 1870).

Само собой разумеется, что авторы, говоря о циркуле, имели в виду не только и не столько этот простейший прибор для черчения, сколько математику с ее возможностями строгих логических выводов и расчетов.

Для создания армии, в начале XX века, необходимо было наряду с подготовкой командного состава, решить ряд научных и инженерно – технических проблем. Проблемы артиллерии по–прежнему оставались решающими. Но наряду с ними появились задачи, связанные с созданием собственной авиации, бронетанковых сил, организацией проводной и радиосвязи. Они требовали не только привлечения известных и уже хорошо разработанных математических методов, но и создания новых методов исследования.

В ту пору на первом месте стояли проблемы, связанные с полетом самолета. Теория полета позволила рассчитывать аэродинамические свойства конструкций до их постройки и испытания в воздухе. Эту работу возглавил выдающийся ученый Н.Е. Жуковский (1847-1921). Он и его ученики положили начало замечательному учреждению, получившему позднее наименование ЦАГИ (Центральный аэрогидродинамический институт).

В связи с исследованием механики полета при больших скоростях М.А. Лаврентьев разработал новую математическую теорию квазианалитических функций, позволяющую учитывать сжимаемость воздуха.

Совершенно естественно, что математическая теория полета самолета была лишь одной из проблем, которые требовали серьезного участия математиков. Другие проблемы были связаны с новыми аспектами теории стрельбы: стрельба из танка, стрельба из самолета и по самолету, рассеивание при бомбометании и так далее. Большое значение приобрели вопросы устойчивости движения (самолета, снаряда, корабля, торпеды и прочее). Военное дело потребовало широкого привлечения ряда новых методов математики, в частности теории устойчивости движения, начало которой было положено еще в XIX веке А.М. Ляпуновым (1857-1918). Ляпунов разрабатывал эту теорию в связи с задачами устойчивости Солнечной системы. Но в науке часто случается, что математические приемы, созданные для определенной задачи практики, находят позднее многочисленные новые применения, и в том числе в областях знания, очень далеких от первоначальной.

Чтобы поднять самолет в воздух, требуется создать легкую и одновременно прочную конструкцию корпуса и фюзеляжа. Вот почему большое значение для авиации, а также для морского дела получила проблема создания прочных и одновременно легких и тонких конструкций. Для ее решения необходимы не только физические эксперименты, но и математические расчеты, а также создание математических моделей интересующих нас реальных явлений.

С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые не доступны для понимания противником. История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Виету(1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, математической логики, алгебры.

Для решения проблем обороны страны еще перед Великой Отечественной войной начали широко использоваться (помимо экспериментальных исследований) математические методы. Если говорить о тех направлениях математической мысли, которые нашли особенно серьезное применение, то в первую очередь следует назвать теорию дифференциальных уравнений, теорию вероятностей, алгебру и математическую логику, теорию функций комплексного переменного, методы приближенных вычислений. Из прикладных математических дисциплин должны быть упомянуты теоретическая механика, аэро- и гидродинамика, теория упругости, математическая физика.

Но мы не должны упускать из вида и другой аспект использования математики – ее непременное присутствие при образовании офицера армии и флота. Без математики, без ее безукоризненного знания, и притом в весьма широком объеме, не может быть ни хорошего штурмана, ни артиллериста, ни связиста, ни строителя, ни приемщика военной продукции на заводах. Базой же любого математического образования является хорошо усвоенный курс математики средней школы.

Великая Отечественная война выдвинула перед всеми видами деятельности огромное число сложнейших проблем. Математика не осталась в стороне. Перед ней возникли многочисленные новые задачи, зачастую совершенно необычные. Нередко же появлялись вопросы, которые могли быть решены задолго до того, как они потребовались, но о них не думали, им не придавали значения. Например, перед войной все были увлечены созданием авиации, которая летела бы с огромными для того времени скоростями, на большой высоте и отличалась бы при этом большой маневренностью. Однако уже в первый период войны стало ясно, что при определенных условиях оказываются незаменимыми бомбардировщиками тихоходные самолеты, которые раньше использовались лишь как учебные. Но для них не было таблиц бомбометания, поскольку никто не помышлял о таком их использовании. Пришлось срочно эти таблицы составлять, а для этого было необходимо, для ускорения и упрощения вычислений, придумать хорошие формулы.

Известно, что еще К.Э. Циолковский (1857-1935) много занимался ракетной техникой. Им были предложены методы расчета движения ракет. Эти его результаты и результаты других исследователей были использованы при создании знаменитых «катюш». Таким образом, появлению на фронтах ракетного оружия предшествовала огромная работа не только конструкторской мысли, но и мысли математиков. А такого рода проблем возникало тысячи.

Необходимость выпуска огромной массы однородной продукции, с которой неизбежно связано военное производство, привела к постановке задачи исключительной важности: проверке качества больших количеств однородных изделий. При ее решении возникали трудности двоякого характера: во-первых, проверка качества каждого изделия требует некоторого времени и, во-вторых, проверка качества некоторых изделий приводить к их непоправимой порче. Нередко проверка качества одного – единственного изделия требует несравненно большего времени, чем его изготовление. Так, изготовить винтовочный патрон на соответствующем автомате можно за малую долю минуты, а проверка его качества отнимает много минут; проверка качества взрывателя приводит неминуемой его порчи. Как поступать в условиях, когда продукция нужна и ощущается острая нехватка рабочей силы? Выход был найден: использование статистических методов контроля за качеством продукции. Эти методы позволяют при проверке ничтожной доли изготовленных изделий давать достаточно точные заключения о качестве всей партии. При этом удается добиться выигрыша двоякого рода: значительного уменьшения времени на контроль качества изделий и огромного уменьшения порчи изделий при контроле.

Первые идеи статистического метода контроля за качеством принимаемых партий продукции принадлежали еще М.В. Остроградскому (1801-1862). Позднее они разрабатывались в Ташкенте В.И. Романовским (1879-1954). Во время Великой Отечественной войны этими вопросами занимались многие математики в нашей стране. Разработанные ими идеи легли в основу важной прикладной области теории вероятностей – теории статистических методов приемочного контроля.

Наряду с вопросами приемочного контроля ( то есть контроля качества уже изготовленной продукции) начали разрабатываться и проблемы управления качеством в процессе производства.

Несомненно, что послевоенный период начался в военном деле тремя событиями исключительной важности: появлением ядерного оружия, созданием электронных вычислительных машин и широким развитием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулось с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков.

Во время Великой Отечественной войны широкое употребление при стрельбе по танкам и другим бронированным целям получили так называемые кумулятивные снаряды (от латинского слова «кумуло» - накапливаю). Их пробивное действие оказалось несравненно большим, чем снарядов такого же калибра, и даже с большим количеством взрывчатых веществ, но обычных. Оказывается, что если в снаряде сделать выемку и эту выемку закрыть стальным конусом, то пробивное действие такого заряда резко увеличивается. Это явление было замечено еще во второй половине XIX века и тогда же нашло использование в горном деле. Первое военное применение этого эффекта относится к 1914 году, широкое же использование пришлось на войну 1941-1945 годов. Этим явлением заинтересовался выдающийся советский математик и механик М.А. Лаврентьев. После длительных экспериментов он разработал математическую теорию кумулятивного заряда. Выяснилось, что стальной конус при ударе о преграду с огромной скоростью превращается в тонкую направленную струю и, как иголка, пронзает броню. При соответствующих подборах угла конуса можно получить скорость струи до 90 км/с. Большие усилия Лаврентьев потратил на использование кумулятивного эффекта для разработки теории направленных взрывов при устройстве платин, прокладке каналов и прочее. Теория Лаврентьева позволила не просто использовать подмеченное опытным путем явление, а заранее рассчитывать его действие и при заданном усилии добиваться максимально возможного результата.

В период Великой Отечественной войны было широко использовано реактивное оружие. В качестве зажигательного средства ракеты появились еще в X веке. Первые боевые ракеты в России были изготовлены в 1815 году по проекту генерала А.Д. Засядко. Они с успехом применялись в период русско–турецкой войны 1828-1829 годов, а позднее в Крымской войне 1853-1856 годов. В настоящее время действие ракетного оружия распространяется на тысячи километров.

Трудно переоценить значение математики в деле обороны страны. Обратимся к фактам. 23 июня 1941 года состоялось внеочередное расширенное заседание Президиума Академии наук СССР. Советские ученые заявили, что отдадут «все свои знания, все свои силы, энергию и свою жизнь за дело нашего великого народа, за победу над врагом и полный разгром фашистских бандитов, осмелившихся нарушить священную границу нашей Родины».

Математический институт Академии наук СССР разрабатывает штурманские таблицы. Уже в 1943 году они находят широкое применение в боевой практике авиации дальнего действия. Какова их ценность? Расчеты всех дальних полетов, выполняемые по этим таблицам, значительно повысили точность самолетовождения.

Идет жестокая война. Фронт требует увеличения эффективности огня артиллерии, повышения меткости стрельбы. Эту проблему успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеивания артиллерийских снарядов. Математическая теория вероятностей использовалась во время Великой Отечественной войны и для определения наилучших методов нахождения самолетов, подводных лодок противника, и для указания путей, позволяющих избежать встречи с подводными лодками врага.

Математика помогала рассчитывать, сколько нужно сделать одновременных выстрелов по самолету противника для того, чтобы иметь наибольшую вероятность сбить его. Член-корреспондент АН СССР Н.Г. Четаев предложил наиболее выгодную крутизну нарезки стволов орудий, что позволило обеспечить кучность боя и устойчивость снарядов при полете.

Война требовала от авиации больших скоростей самолетов. Но увы! При освоении больших скоростей авиация столкнулась с внезапным разрушением самолетов из-за вибрации особого рода – флаттера. Опять новая проблема. И тут на помощь приходит математика. За решение данной задачи берется группа ученых во главе с М.В. Келдышем. Она разработала сложную математическую теорию флаттера. Сделано большое дело. Самолеты обеспечены надежной защитой от появления вибраций.

Благодаря немедленному использованию в производстве теоретических исследований видных наших ученых – академиков М.В. Келдыша, А.А. Дородницына и других – стали возможны большие темпы выпуска боевых самолетов.

Видная роль в деле обороны нашей страны принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы ВМС. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизни многих людей, сберечь большие материальные ценности.

Все преподаватели школ прекрасно знаю, что каждый год проводятся уроки Мужества, приуроченные ко Дню Победы. Каждый год мы вынуждены подбирать материал к ним. И этот материал очень редко имеет отношение к нашим предметам. Но приведенный выше материал отвечает всем необходимым требованиям. Он связан с событиями Великой Отечественной войны, рассказывает о подвиге нашего народа, о самоотверженном труде и в тоже время связан с изучаемым предметом. Весь материал подобран таким образом, что может быть использован в любом классе. Стоит еще привести материал к уроку посвященному блокаде Ленинграда и приуроченному к отмечавшемуся в 2003 году 300-летию города.

Повторение темы «Действия с обыкновенными дробями» проходит в конце апреля, как раз перед праздником Победы. Урок посвященный блокаде Ленинграда начинается вполне буднично, с упражнений на действия с дробями.

Выполните действия:

Найдите, на какую часть единицы

больше, чем ,

больше, чем .

После того как все задания выполнены, учитель демонстрирует буханку хлеба, разрезанную на 8 частей. Одна часть лежит отдельно. Одна такая «восьмушка» была дневным рационом ленинградцев в самые тяжелые дни блокады этого города. Блокада длилась 900 дней, но самым трудным периодом оказалась зима 1941-1942 годов, когда основные городские припасы были уничтожены немецкими самолетами, а увезти ослабевших детей и стариков, раненых и больных было невозможно, так как все пути из города были отрезаны врагом. Только зимой 1942 года стал лед на Ладожском озере, и по нему была проложена в город дорога, названная дорогой жизни.

Но Ленинград не сдавался. Героизм защитников города хорошо передан в стихах Юрия Воронова, пережившего все ужасы блокады.

Из писем на Большую землю.

Наш город в снег до пояса закопан.

Но если с крыш на город посмотреть,

То улицы похожи на окопы,

В которых побывать успела

Смерть…

Но в то, что умер город наш, -

Не верьте!

Нас не согнут отчаянье и страх.

Мы знаем от людей, сраженных смертью,

Что означает:

«Смертью

смерть

поправ».

Мы знаем:

Клятвы говорить не просто.

Но если в Ленинград ворвется враг,

Мы разорвем последнюю из простынь

Лишь на бинты, но не на белый флаг!

Февраль.

Какая длинная зима, как время медленно крадется!..

В ночи

Ни люди, ни дома не знают, кто из них проснется.

И поутру, когда ветра метелью застилают небо,

Опять короче, чем вчера, людская очередь за хлебом.

В нас голод убивает страх. Но он же убивает силы…

На Пискаревских пустырях все шире

Братские могилы…

Прочитав эти стихи, учитель просит ребят снова вспомнить о блокадной восьмушке хлеба. Задания:

Подсчитайте, сколько граммов весит восьмая часть буханки хлеба массой в 1 килограмм. [125грамм. ]

Подсчитайте какую часть буханки составляет одна треть от восьмушки? [одну двадцать четвертую. ]

Сколько граммов приходится на часть буханки? [примерно 41,66 грамма.]

Что больше: или ? Представьте, что этими дробями выражаются доли хлебного пайка. В каком пайке больше хлеба? На сколько граммов?[ В части буханки хлеба больше, чем в части примерно на 21 грамм.]

После этих подсчетов учитель читает ребятам рассказ «Кусочек хлеба» из книги Воскобойникова «Девятьсот дней мужества».

Погиб при обороне Ленинграда Петр Карпушкин. А в Ленинграде осталась его семья – жена и три дочери, младшей 3 года. Обессиленные от голода, в пустой промерзшей квартире они ждут прихода мамы. Ее слабые шаги за стеной возвращают утерянный, казалось, шанс на спасение. Анна Герасимовна торопливо делит принесенную ею осьмушку хлеба на 3 части и один кусочек подносит младшенькой – самой слабой из троих. Дочка надкусывает хлеб – на большее сил уже не хватает. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось… умерла дочка, но остались две других. Их надо спасать. Хлеба теперь стало больше: часть буханки вместо (60,5 грамм вместо 41,66 грамма. Это больше примерно на 20 грамм на каждого.). Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее детей неизмеримо важнее, чем маленький кусочек хлеба насущного.

Карпушкины выжили. А блокадный кусочек хлеба хранился в их семье более 30 лет. Потом уже внучка Анны Герасимовны Ира Федосик, поступив в ПТУ№13 Ленинграда, передала эту семейную реликвию училищному музею.

После такого рассказа и у учителя, и у учеников просто не остается душевных сил на обычную работу. Да в этом и нет нужды. Истекли 40 минут урока. Совсем мало было на уроке математики. Но почему же на следующий день так хорошо проходят обычные уроки математики? Почему те ребята, для которых дроби еще недавно были камнем преткновения, теперь явно с ними подружились?

Я нахожу ответ в том, что рассказ о блокадном хлебе оказался сильным эмоциональным ударом для многих ребят. Причем эмоционально окрасились самые обычные вычисления. Ими вряд ли когда-нибудь заинтересовались бы учителя литературы или истории, рассказывающие о той же Ленинградской блокаде. Учителя-гуманитарии сказали бы, что хлеба было мало, очень мало. А математик не станет причитать, а просто сосчитает, сколько же было хлеба. И этот сухой подсчет, который приходилось выполнять людям, бесконечно любящим друг друга, но вынужденным делить его между собой, ранит глубже, чем самые трогательные описания.

globuss24.ru

Статья на тему Математика и военное дело

Математика и военное дело.

Начало использования математических знаний в военном деле относится к глубокой древности. Известно, что в Древнем Вавилоне арифметические сведения употреблялись при подсчете необходимых запасов для армии, геометрия же использовалась при строительстве укреплений и подсчете объема необходимых земельных работ.

В знаменитом диалоге Платона «Государство» говорится о том, что арифметика и геометрия необходимы каждому воину. Вот небольшие цитаты из текста этого диалога:

«Но ведь арифметика и счет целиком касаются числа?..

- Значит, они принадлежат к тем познаниям, которые мы искали. Воину их необходимо усвоить для войскового строя, а философу – для постижения сущности…» (Платон. Соч., т.3, ч. I с.335 М., «Мысль», 1971.)

«При устройстве лагерей, занятии местностей, стягивании и развертывании войск и разных других военных построениях, как во время сражения, так и в походах, конечно, скажется разница между знатоком геометрии и тем, кто ее не знает». (Там же, с. 336 – 337).

Мы хорошо знаем, что создание математического анализа – дифференциального и интегрального исчислений – в значительной мере было связано с задачами, выдвинутыми артиллерией, и что позднее, в свою очередь, развитие новой математики оказывало огромное влияние на прогресс самой артиллерии. Во все времена считалось, что артиллерийский офицер одновременно является хорошим знатоком математики. В этом плане прекрасное утверждение высказано в одном из древнерусских сочинений по артиллерии: «… начальное, во – первых, орудие, еще пушкарю подобает при себе имети – есть циркуль». (Цит. По кн.: А. Платов и Л. Кирпичев. Исторический очерк образования и развития артиллерийского училища. Спб., 1870).

Само собой разумеется, что авторы, говоря о циркуле, имели в виду не только и не столько этот простейший прибор для черчения, сколько математику с ее возможностями строгих логических выводов и расчетов.

Для создания армии, в начале XX века, необходимо было наряду с подготовкой командного состава, решить ряд научных и инженерно – технических проблем. Проблемы артиллерии по–прежнему оставались решающими. Но наряду с ними появились задачи, связанные с созданием собственной авиации, бронетанковых сил, организацией проводной и радиосвязи. Они требовали не только привлечения известных и уже хорошо разработанных математических методов, но и создания новых методов исследования.

В ту пору на первом месте стояли проблемы, связанные с полетом самолета. Теория полета позволила рассчитывать аэродинамические свойства конструкций до их постройки и испытания в воздухе. Эту работу возглавил выдающийся ученый Н.Е. Жуковский (1847-1921). Он и его ученики положили начало замечательному учреждению, получившему позднее наименование ЦАГИ (Центральный аэрогидродинамический институт).

В связи с исследованием механики полета при больших скоростях М.А. Лаврентьев разработал новую математическую теорию квазианалитических функций, позволяющую учитывать сжимаемость воздуха.

Совершенно естественно, что математическая теория полета самолета была лишь одной из проблем, которые требовали серьезного участия математиков. Другие проблемы были связаны с новыми аспектами теории стрельбы: стрельба из танка, стрельба из самолета и по самолету, рассеивание при бомбометании и так далее. Большое значение приобрели вопросы устойчивости движения (самолета, снаряда, корабля, торпеды и прочее). Военное дело потребовало широкого привлечения ряда новых методов математики, в частности теории устойчивости движения, начало которой было положено еще в XIX веке А.М. Ляпуновым (1857-1918). Ляпунов разрабатывал эту теорию в связи с задачами устойчивости Солнечной системы. Но в науке часто случается, что математические приемы, созданные для определенной задачи практики, находят позднее многочисленные новые применения, и в том числе в областях знания, очень далеких от первоначальной.

Чтобы поднять самолет в воздух, требуется создать легкую и одновременно прочную конструкцию корпуса и фюзеляжа. Вот почему большое значение для авиации, а также для морского дела получила проблема создания прочных и одновременно легких и тонких конструкций. Для ее решения необходимы не только физические эксперименты, но и математические расчеты, а также создание математических моделей интересующих нас реальных явлений.

С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые не доступны для понимания противником. История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Виету(1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, математической логики, алгебры.

Для решения проблем обороны страны еще перед Великой Отечественной войной начали широко использоваться (помимо экспериментальных исследований) математические методы. Если говорить о тех направлениях математической мысли, которые нашли особенно серьезное применение, то в первую очередь следует назвать теорию дифференциальных уравнений, теорию вероятностей, алгебру и математическую логику, теорию функций комплексного переменного, методы приближенных вычислений. Из прикладных математических дисциплин должны быть упомянуты теоретическая механика, аэро- и гидродинамика, теория упругости, математическая физика.

Но мы не должны упускать из вида и другой аспект использования математики – ее непременное присутствие при образовании офицера армии и флота. Без математики, без ее безукоризненного знания, и притом в весьма широком объеме, не может быть ни хорошего штурмана, ни артиллериста, ни связиста, ни строителя, ни приемщика военной продукции на заводах. Базой же любого математического образования является хорошо усвоенный курс математики средней школы.

Великая Отечественная война выдвинула перед всеми видами деятельности огромное число сложнейших проблем. Математика не осталась в стороне. Перед ней возникли многочисленные новые задачи, зачастую совершенно необычные. Нередко же появлялись вопросы, которые могли быть решены задолго до того, как они потребовались, но о них не думали, им не придавали значения. Например, перед войной все были увлечены созданием авиации, которая летела бы с огромными для того времени скоростями, на большой высоте и отличалась бы при этом большой маневренностью. Однако уже в первый период войны стало ясно, что при определенных условиях оказываются незаменимыми бомбардировщиками тихоходные самолеты, которые раньше использовались лишь как учебные. Но для них не было таблиц бомбометания, поскольку никто не помышлял о таком их использовании. Пришлось срочно эти таблицы составлять, а для этого было необходимо, для ускорения и упрощения вычислений, придумать хорошие формулы.

Известно, что еще К.Э. Циолковский (1857-1935) много занимался ракетной техникой. Им были предложены методы расчета движения ракет. Эти его результаты и результаты других исследователей были использованы при создании знаменитых «катюш». Таким образом, появлению на фронтах ракетного оружия предшествовала огромная работа не только конструкторской мысли, но и мысли математиков. А такого рода проблем возникало тысячи.

Необходимость выпуска огромной массы однородной продукции, с которой неизбежно связано военное производство, привела к постановке задачи исключительной важности: проверке качества больших количеств однородных изделий. При ее решении возникали трудности двоякого характера: во-первых, проверка качества каждого изделия требует некоторого времени и, во-вторых, проверка качества некоторых изделий приводить к их непоправимой порче. Нередко проверка качества одного – единственного изделия требует несравненно большего времени, чем его изготовление. Так, изготовить винтовочный патрон на соответствующем автомате можно за малую долю минуты, а проверка его качества отнимает много минут; проверка качества взрывателя приводит неминуемой его порчи. Как поступать в условиях, когда продукция нужна и ощущается острая нехватка рабочей силы? Выход был найден: использование статистических методов контроля за качеством продукции. Эти методы позволяют при проверке ничтожной доли изготовленных изделий давать достаточно точные заключения о качестве всей партии. При этом удается добиться выигрыша двоякого рода: значительного уменьшения времени на контроль качества изделий и огромного уменьшения порчи изделий при контроле.

Первые идеи статистического метода контроля за качеством принимаемых партий продукции принадлежали еще М.В. Остроградскому (1801-1862). Позднее они разрабатывались в Ташкенте В.И. Романовским (1879-1954). Во время Великой Отечественной войны этими вопросами занимались многие математики в нашей стране. Разработанные ими идеи легли в основу важной прикладной области теории вероятностей – теории статистических методов приемочного контроля.

Наряду с вопросами приемочного контроля ( то есть контроля качества уже изготовленной продукции) начали разрабатываться и проблемы управления качеством в процессе производства.

Несомненно, что послевоенный период начался в военном деле тремя событиями исключительной важности: появлением ядерного оружия, созданием электронных вычислительных машин и широким развитием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулось с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков.

Во время Великой Отечественной войны широкое употребление при стрельбе по танкам и другим бронированным целям получили так называемые кумулятивные снаряды (от латинского слова «кумуло» - накапливаю). Их пробивное действие оказалось несравненно большим, чем снарядов такого же калибра, и даже с большим количеством взрывчатых веществ, но обычных. Оказывается, что если в снаряде сделать выемку и эту выемку закрыть стальным конусом, то пробивное действие такого заряда резко увеличивается. Это явление было замечено еще во второй половине XIX века и тогда же нашло использование в горном деле. Первое военное применение этого эффекта относится к 1914 году, широкое же использование пришлось на войну 1941-1945 годов. Этим явлением заинтересовался выдающийся советский математик и механик М.А. Лаврентьев. После длительных экспериментов он разработал математическую теорию кумулятивного заряда. Выяснилось, что стальной конус при ударе о преграду с огромной скоростью превращается в тонкую направленную струю и, как иголка, пронзает броню. При соответствующих подборах угла конуса можно получить скорость струи до 90 км/с. Большие усилия Лаврентьев потратил на использование кумулятивного эффекта для разработки теории направленных взрывов при устройстве платин, прокладке каналов и прочее. Теория Лаврентьева позволила не просто использовать подмеченное опытным путем явление, а заранее рассчитывать его действие и при заданном усилии добиваться максимально возможного результата.

В период Великой Отечественной войны было широко использовано реактивное оружие. В качестве зажигательного средства ракеты появились еще в X веке. Первые боевые ракеты в России были изготовлены в 1815 году по проекту генерала А.Д. Засядко. Они с успехом применялись в период русско–турецкой войны 1828-1829 годов, а позднее в Крымской войне 1853-1856 годов. В настоящее время действие ракетного оружия распространяется на тысячи километров.

Трудно переоценить значение математики в деле обороны страны. Обратимся к фактам. 23 июня 1941 года состоялось внеочередное расширенное заседание Президиума Академии наук СССР. Советские ученые заявили, что отдадут «все свои знания, все свои силы, энергию и свою жизнь за дело нашего великого народа, за победу над врагом и полный разгром фашистских бандитов, осмелившихся нарушить священную границу нашей Родины».

Математический институт Академии наук СССР разрабатывает штурманские таблицы. Уже в 1943 году они находят широкое применение в боевой практике авиации дальнего действия. Какова их ценность? Расчеты всех дальних полетов, выполняемые по этим таблицам, значительно повысили точность самолетовождения.

Идет жестокая война. Фронт требует увеличения эффективности огня артиллерии, повышения меткости стрельбы. Эту проблему успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеивания артиллерийских снарядов. Математическая теория вероятностей использовалась во время Великой Отечественной войны и для определения наилучших методов нахождения самолетов, подводных лодок противника, и для указания путей, позволяющих избежать встречи с подводными лодками врага.

Математика помогала рассчитывать, сколько нужно сделать одновременных выстрелов по самолету противника для того, чтобы иметь наибольшую вероятность сбить его. Член-корреспондент АН СССР Н.Г. Четаев предложил наиболее выгодную крутизну нарезки стволов орудий, что позволило обеспечить кучность боя и устойчивость снарядов при полете.

Война требовала от авиации больших скоростей самолетов. Но увы! При освоении больших скоростей авиация столкнулась с внезапным разрушением самолетов из-за вибрации особого рода – флаттера. Опять новая проблема. И тут на помощь приходит математика. За решение данной задачи берется группа ученых во главе с М.В. Келдышем. Она разработала сложную математическую теорию флаттера. Сделано большое дело. Самолеты обеспечены надежной защитой от появления вибраций.

Благодаря немедленному использованию в производстве теоретических исследований видных наших ученых – академиков М.В. Келдыша, А.А. Дородницына и других – стали возможны большие темпы выпуска боевых самолетов.

Видная роль в деле обороны нашей страны принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы ВМС. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизни многих людей, сберечь большие материальные ценности.

Все преподаватели школ прекрасно знаю, что каждый год проводятся уроки Мужества, приуроченные ко Дню Победы. Каждый год мы вынуждены подбирать материал к ним. И этот материал очень редко имеет отношение к нашим предметам. Но приведенный выше материал отвечает всем необходимым требованиям. Он связан с событиями Великой Отечественной войны, рассказывает о подвиге нашего народа, о самоотверженном труде и в тоже время связан с изучаемым предметом. Весь материал подобран таким образом, что может быть использован в любом классе. Стоит еще привести материал к уроку посвященному блокаде Ленинграда и приуроченному к отмечавшемуся в 2003 году 300-летию города.

Повторение темы «Действия с обыкновенными дробями» проходит в конце апреля, как раз перед праздником Победы. Урок посвященный блокаде Ленинграда начинается вполне буднично, с упражнений на действия с дробями.

Выполните действия: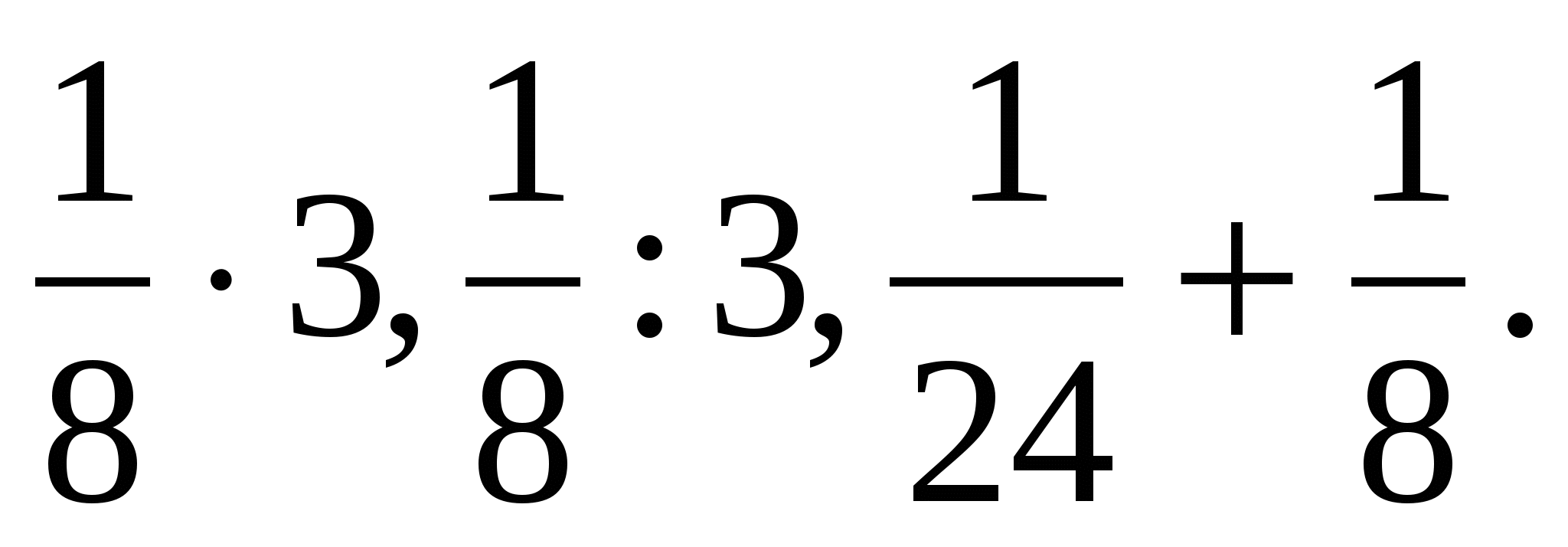

Найдите, на какую часть единицы

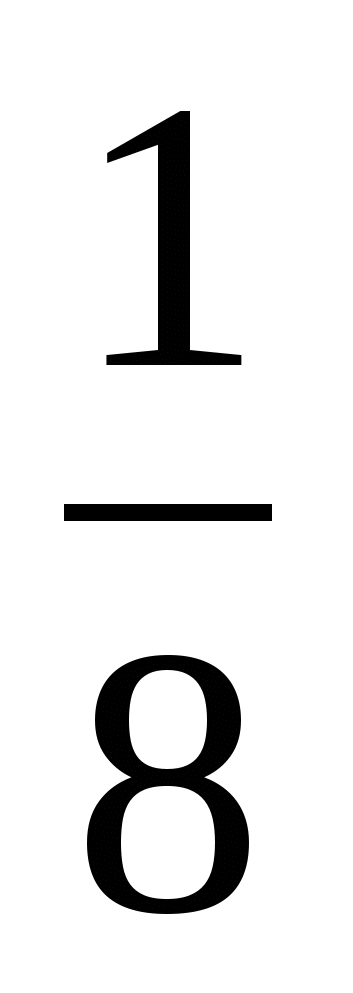больше, чем ,

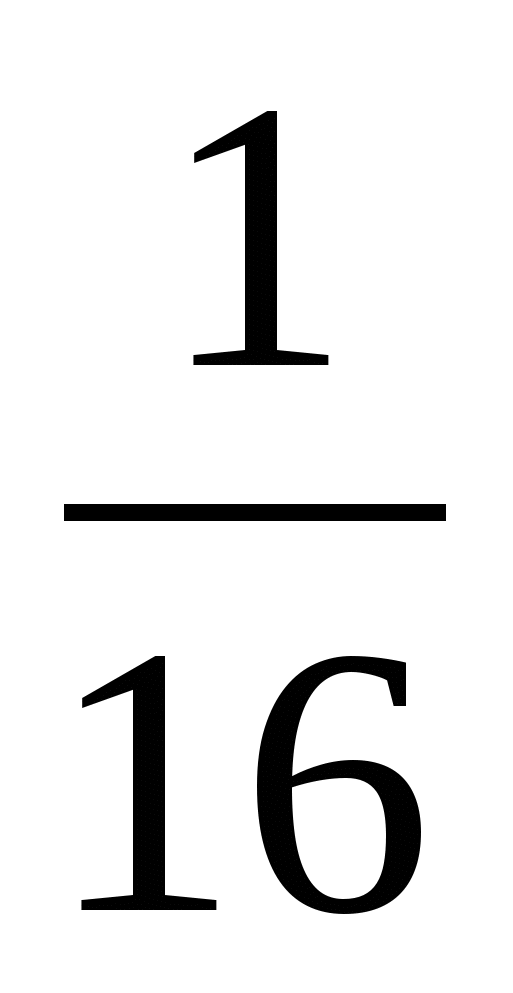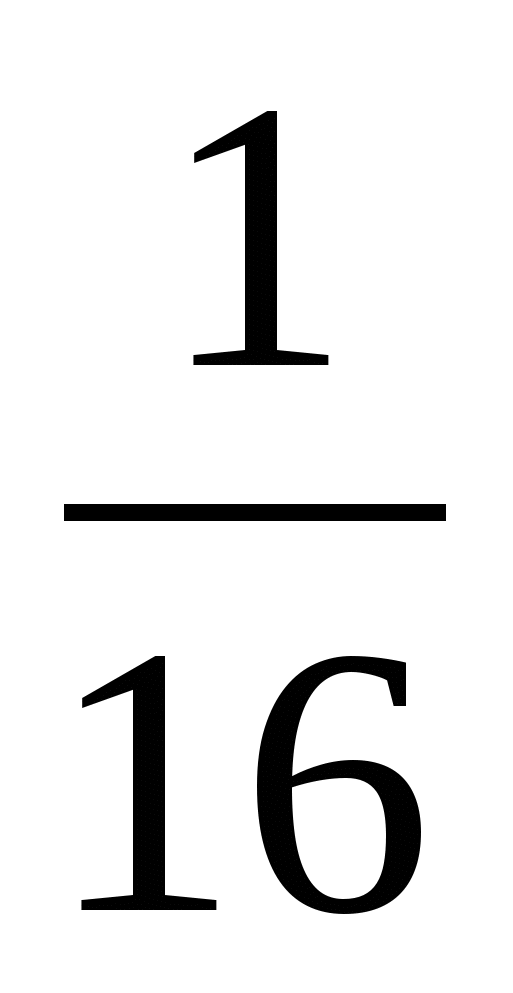больше, чем .

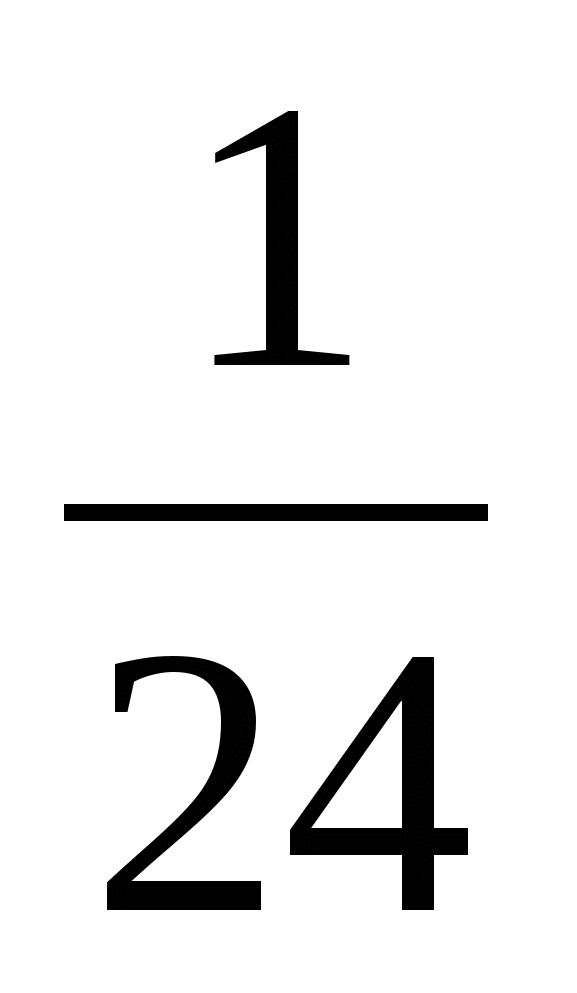После того как все задания выполнены, учитель демонстрирует буханку хлеба, разрезанную на 8 частей. Одна часть лежит отдельно. Одна такая «восьмушка» была дневным рационом ленинградцев в самые тяжелые дни блокады этого города. Блокада длилась 900 дней, но самым трудным периодом оказалась зима 1941-1942 годов, когда основные городские припасы были уничтожены немецкими самолетами, а увезти ослабевших детей и стариков, раненых и больных было невозможно, так как все пути из города были отрезаны врагом. Только зимой 1942 года стал лед на Ладожском озере, и по нему была проложена в город дорога, названная дорогой жизни.

Но Ленинград не сдавался. Героизм защитников города хорошо передан в стихах Юрия Воронова, пережившего все ужасы блокады.

Из писем на Большую землю.

Наш город в снег до пояса закопан.

Но если с крыш на город посмотреть,

То улицы похожи на окопы,

В которых побывать успела

Смерть…

Но в то, что умер город наш, -

Не верьте!

Нас не согнут отчаянье и страх.

Мы знаем от людей, сраженных смертью,

Что означает:

«Смертью

смерть

поправ».

Мы знаем:

Клятвы говорить не просто.

Но если в Ленинград ворвется враг,

Мы разорвем последнюю из простынь

Лишь на бинты, но не на белый флаг!

Февраль.

Какая длинная зима, как время медленно крадется!..

В ночи

Ни люди, ни дома не знают, кто из них проснется.

И поутру, когда ветра метелью застилают небо,

Опять короче, чем вчера, людская очередь за хлебом.

В нас голод убивает страх. Но он же убивает силы…

На Пискаревских пустырях все шире

Братские могилы…

Прочитав эти стихи, учитель просит ребят снова вспомнить о блокадной восьмушке хлеба. Задания:

Подсчитайте, сколько граммов весит восьмая часть буханки хлеба массой в 1 килограмм. [125грамм. ]

Подсчитайте какую часть буханки составляет одна треть от восьмушки? [одну двадцать четвертую. ]

Сколько граммов приходится на 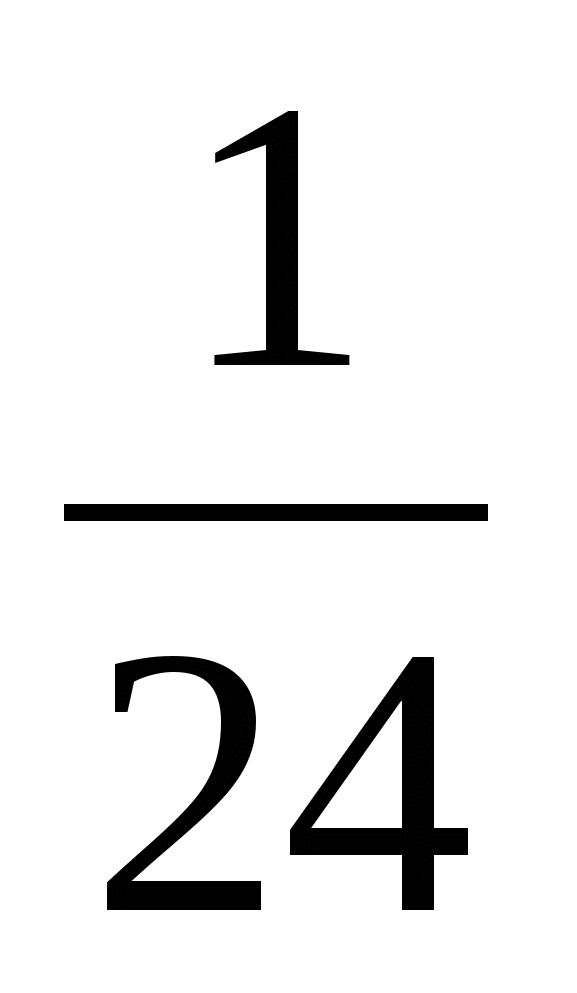часть буханки? [примерно 41,66 грамма.]

Что больше: 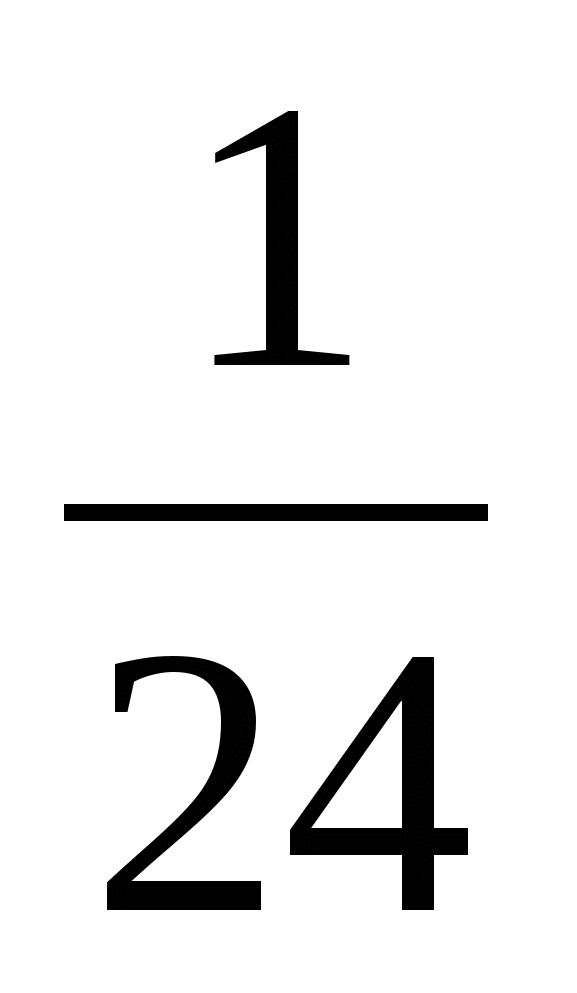или 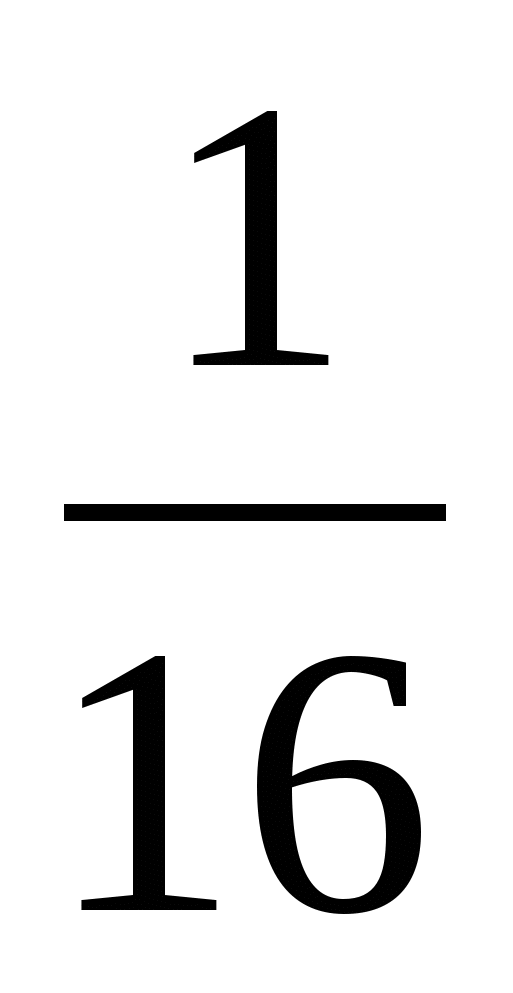? Представьте, что этими дробями выражаются доли хлебного пайка. В каком пайке больше хлеба? На сколько граммов?[ В 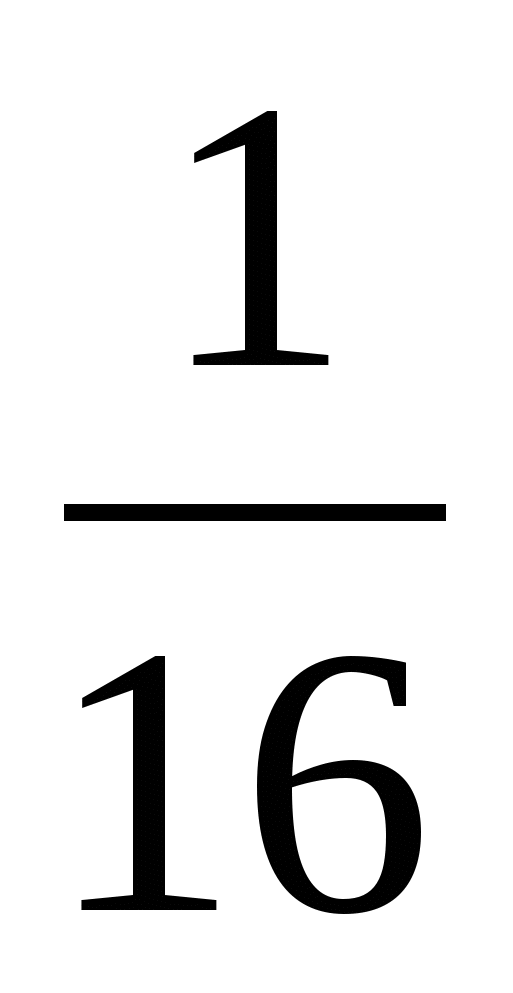части буханки хлеба больше, чем в 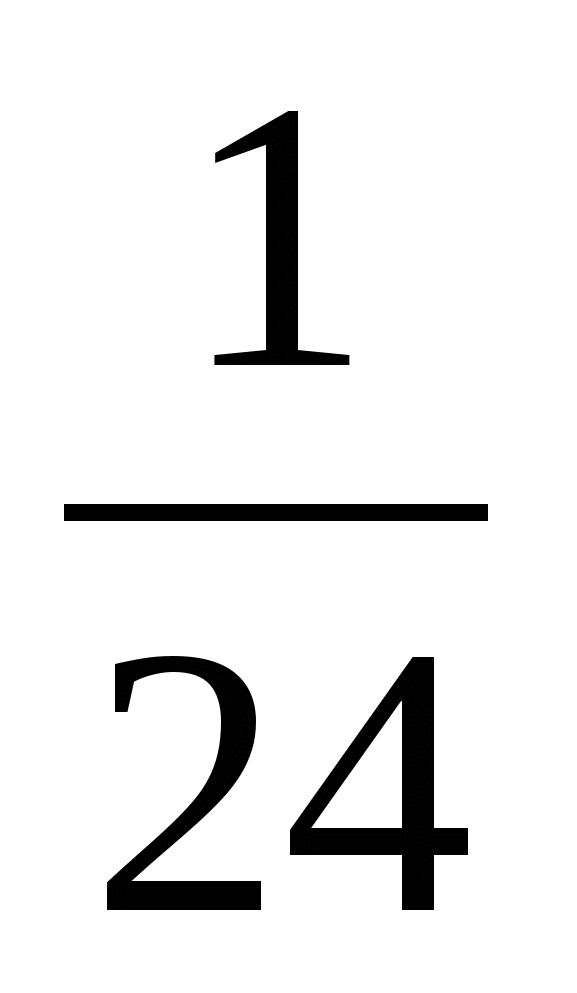части примерно на 21 грамм.]

После этих подсчетов учитель читает ребятам рассказ «Кусочек хлеба» из книги Воскобойникова «Девятьсот дней мужества».

Погиб при обороне Ленинграда Петр Карпушкин. А в Ленинграде осталась его семья – жена и три дочери, младшей 3 года. Обессиленные от голода, в пустой промерзшей квартире они ждут прихода мамы. Ее слабые шаги за стеной возвращают утерянный, казалось, шанс на спасение. Анна Герасимовна торопливо делит принесенную ею осьмушку хлеба на 3 части и один кусочек подносит младшенькой – самой слабой из троих. Дочка надкусывает хлеб – на большее сил уже не хватает. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось… умерла дочка, но остались две других. Их надо спасать. Хлеба теперь стало больше: 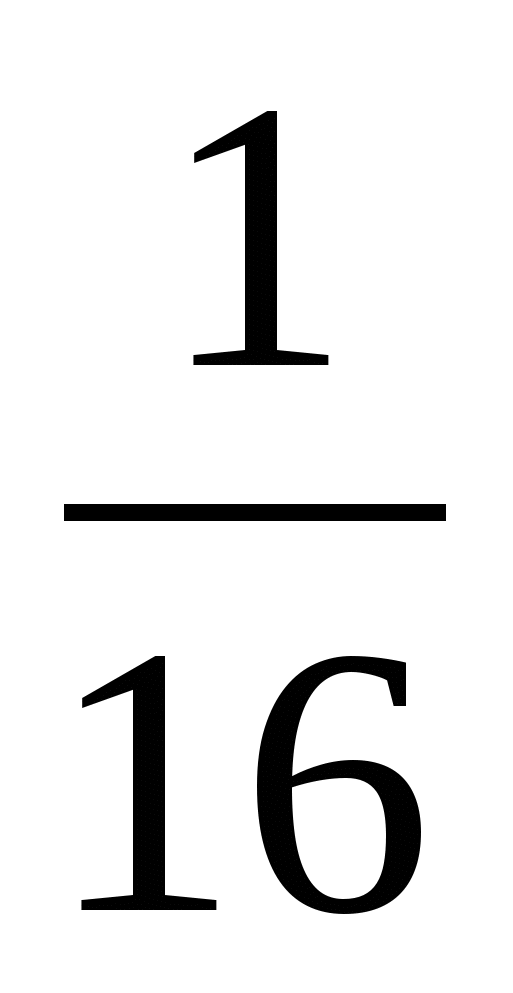часть буханки вместо 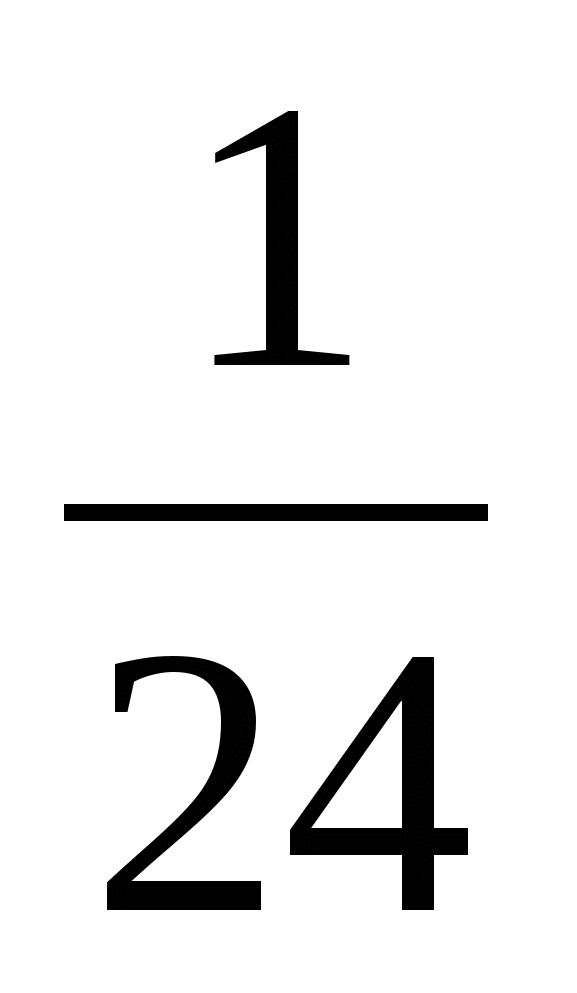(60,5 грамм вместо 41,66 грамма. Это больше примерно на 20 грамм на каждого.). Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее детей неизмеримо важнее, чем маленький кусочек хлеба насущного.

Карпушкины выжили. А блокадный кусочек хлеба хранился в их семье более 30 лет. Потом уже внучка Анны Герасимовны Ира Федосик, поступив в ПТУ№13 Ленинграда, передала эту семейную реликвию училищному музею.

После такого рассказа и у учителя, и у учеников просто не остается душевных сил на обычную работу. Да в этом и нет нужды. Истекли 40 минут урока. Совсем мало было на уроке математики. Но почему же на следующий день так хорошо проходят обычные уроки математики? Почему те ребята, для которых дроби еще недавно были камнем преткновения, теперь явно с ними подружились?

Я нахожу ответ в том, что рассказ о блокадном хлебе оказался сильным эмоциональным ударом для многих ребят. Причем эмоционально окрасились самые обычные вычисления. Ими вряд ли когда-нибудь заинтересовались бы учителя литературы или истории, рассказывающие о той же Ленинградской блокаде. Учителя-гуманитарии сказали бы, что хлеба было мало, очень мало. А математик не станет причитать, а просто сосчитает, сколько же было хлеба. И этот сухой подсчет, который приходилось выполнять людям, бесконечно любящим друг друга, но вынужденным делить его между собой, ранит глубже, чем самые трогательные описания.

infourok.ru

Математика в военном деле

Математика в военном деле

Выполнили: МОУ «СОШ №94»

Савочкин Дмитрий, Илларионова Екатерина

Руководители: Е. Н. Егорова, О. Е. Яковлева

Цель работы

1.Показать роль математики в военном деле

2. Показать связь математики с культурой родного края через вклад советских математиков во время войны

3. Повысить знания о роли математики в военном деле

Оглавление

1.Введение 2.Келдыш Мстислав Всеволодович 3.Крылов Алексей Николаевич 3.Андрей Николаевич Колмогоров

4.Турбулентность

5.Вывод

6.Список использованной литературы

Введение

Важнейшим фактором, приближавшим победу нашего народа в Великой Отечественной войне, следует считать решения важных прикладных задач, которые осуществили в предвоенные годы и в годы войны советские математики.

Ракетная установка «Катюша»

Математики и военные инженеры успешно решали важнейшие практические вопросы освоения природных богатств, проблемы, связанные с созданием новой совершенной военной техники, с увеличением выпуском танков, самолетов и другой продукции, в которой так нуждался фронт.

Келдыш Мстислав Всеволодович

Келдыш Мстислав Всеволодович (1911—1978) — российский учёный в области математики и механики, академик Академии Наук СССР.

В начале 40-х годов авиастроители столкнулись со странным и непонятным явлением.

Во время полёта самолёта при достижении им определённой скорости возникали сильные колебания отдельных его частей и через несколько секунд машина разваливалась на куски.

Этими проблемами занялся М.В.Келдыш.

М.В. Келдыш и его сотрудники исследовали причины флаттера и шимми и создали математическую теорию, которая позволила своевременно защитить от этих явлений конструкции скоростных самолетов. За это открытие учёный в 1942 году был удостоен Государственной премии, которая представлена на этом слайде.

Золотая медаль имени М.В. Келдыша Российской академии наук

8

Келдыш математически показал, что флаттер имеет резонансную природу, т. е. аналогичен эффекту резонанса, наблюдаемому при колебаниях упругой пружины с прикрепленной массой m и коэффициентом упругости k. 

Колебания пружинного маятника

9

Чтобы избежать резонанса при движении крыла в воздушном потоке, М. В. Келдыш предложил соответствующим образом перераспределить массы вдоль крыла и так расположить упругие элементы, чтобы избежать совпадения собственных частот колебаний крыла с частотами вынуждающих внешних сил. Первые же полеты самолетов, усовершенствованных по рекомендациям М. В. Келдыша, дали прекрасные результаты. Итак, математика снова выручила авиацию.

Крылов Алексей Николаевич

Крылов Алексей Николаевич (1863-1945), российский кораблестроитель, механик и математик, академик Академии Наук СССР, Герой Социалистического Труда. Участник проектирования и постройки первых русских линкоров.

Крылов А.Н. выпустил труды по теории корабля, магнитных и гироскопических компасов, артиллерии, механике, математике, истории науки. Создал ряд корабельных и артиллерийских приборов.

Академик Алексей Николаевич Крылов создал таблицу непотопляемости, по которой можно было рассчитать, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен и насколько это затопление  может улучшить  устойчивость корабля.

Алексей Николаевич Крылов по праву считается основоположником русской научной школы кораблестроения.

Обладая поистине энциклопедическими знаниями, он оставил заметный след в самых различных областях науки и , прежде всего в математике.

Андрей Николаевич Колмогоров

Андрей Николаевич Колмогоров (12  апреля 1903, Тамбов — 20 октября 1987, Москва) — русский советский математик, один из крупнейших математиков ХХ века. Профессор МГУ, доктор физико-математических наук, академик Академии наук СССР (1939 год). Президент Московского математического общества (ММО) в 1964—1966 и 1974—1985.

Проблему увеличения эффективности огня артиллерии решил академик Андрей Николаевич Колмогоров.

Теория вероятностей использовалась для местонахождения самолётов и подводных лодок противника, для указания путей, позволяющих избежать встречи с подводными лодками врага.

График эффективности стрельбы

Турбулентность

Ещё в конце тридцатых годов Колмогорова заинтересовали проблемы турбулентности. В работах 1941—1942 и 1962 годов он разработал теорию так называемой локально-изотропной турбулентности, которая позволила выяснить местную структуру развития турбулентного потока.

Турбулентность

Колмогоров ввёл важное понятие масштаба турбулентности, использование которого даёт, в частности, возможность оценивать влияние взвешенных частиц и полимерных растворов на развитие турбулентности. В 1946 году Колмогоров организует лабораторию атмосферной турбулентности в Геофизическом институте АН СССР

ВЫВОД:

Математика- это одна их точных наук , которая никогда не потеряет актуальность.

Проведя исследования мы поняли что математика играет в военной сфере очень большую роль. Именно от точности расчетов ученых в годы войны зависело большинство человеческих жизней . И именно благодаря их открытиям мы смогли одержать победу над достойным врагом , превосходившим нас как численно, так и технически.

Список использованной литературы:

http://festival.1september.ru/articles/633291/

http://5klass.net/matematika-7 klass / Matematika -v- voennom -dele/002-Rol-matematiki-v-voennom-dele.html

https://ru.wikipedia.org/wiki

Спасибо за внимание!!!

22

videouroki.net

Математика и военное дело

Математика и военное дело.

Начало использования математических знаний в военном деле относится к глубокой древности. Известно, что в Древнем Вавилоне арифметические сведения употреблялись при подсчете необходимых запасов для армии, геометрия же использовалась при строительстве укреплений и подсчете объема необходимых земельных работ.

В знаменитом диалоге Платона «Государство» говорится о том, что арифметика и геометрия необходимы каждому воину. Вот небольшие цитаты из текста этого диалога:

«Но ведь арифметика и счет целиком касаются числа?..

- Значит, они принадлежат к тем познаниям, которые мы искали. Воину их необходимо усвоить для войскового строя, а философу – для постижения сущности…» (Платон. Соч., т.3, ч. I с.335 М., «Мысль», 1971.)

«При устройстве лагерей, занятии местностей, стягивании и развертывании войск и разных других военных построениях, как во время сражения, так и в походах, конечно, скажется разница между знатоком геометрии и тем, кто ее не знает». (Там же, с. 336 – 337).

Мы хорошо знаем, что создание математического анализа – дифференциального и интегрального исчислений – в значительной мере было связано с задачами, выдвинутыми артиллерией, и что позднее, в свою очередь, развитие новой математики оказывало огромное влияние на прогресс самой артиллерии. Во все времена считалось, что артиллерийский офицер одновременно является хорошим знатоком математики. В этом плане прекрасное утверждение высказано в одном из древнерусских сочинений по артиллерии: «… начальное, во – первых, орудие, еще пушкарю подобает при себе имети – есть циркуль». (Цит. По кн.: А. Платов и Л. Кирпичев. Исторический очерк образования и развития артиллерийского училища. Спб., 1870).

Само собой разумеется, что авторы, говоря о циркуле, имели в виду не только и не столько этот простейший прибор для черчения, сколько математику с ее возможностями строгих логических выводов и расчетов.

Для создания армии, в начале XX века, необходимо было наряду с подготовкой командного состава, решить ряд научных и инженерно – технических проблем. Проблемы артиллерии по–прежнему оставались решающими. Но наряду с ними появились задачи, связанные с созданием собственной авиации, бронетанковых сил, организацией проводной и радиосвязи. Они требовали не только привлечения известных и уже хорошо разработанных математических методов, но и создания новых методов исследования.

В ту пору на первом месте стояли проблемы, связанные с полетом самолета. Теория полета позволила рассчитывать аэродинамические свойства конструкций до их постройки и испытания в воздухе. Эту работу возглавил выдающийся ученый Н.Е. Жуковский (1847-1921). Он и его ученики положили начало замечательному учреждению, получившему позднее наименование ЦАГИ (Центральный аэрогидродинамический институт).

В связи с исследованием механики полета при больших скоростях М.А. Лаврентьев разработал новую математическую теорию квазианалитических функций, позволяющую учитывать сжимаемость воздуха.

Совершенно естественно, что математическая теория полета самолета была лишь одной из проблем, которые требовали серьезного участия математиков. Другие проблемы были связаны с новыми аспектами теории стрельбы: стрельба из танка, стрельба из самолета и по самолету, рассеивание при бомбометании и так далее. Большое значение приобрели вопросы устойчивости движения (самолета, снаряда, корабля, торпеды и прочее). Военное дело потребовало широкого привлечения ряда новых методов математики, в частности теории устойчивости движения, начало которой было положено еще в XIX веке А.М. Ляпуновым (1857-1918). Ляпунов разрабатывал эту теорию в связи с задачами устойчивости Солнечной системы. Но в науке часто случается, что математические приемы, созданные для определенной задачи практики, находят позднее многочисленные новые применения, и в том числе в областях знания, очень далеких от первоначальной.

Чтобы поднять самолет в воздух, требуется создать легкую и одновременно прочную конструкцию корпуса и фюзеляжа. Вот почему большое значение для авиации, а также для морского дела получила проблема создания прочных и одновременно легких и тонких конструкций. Для ее решения необходимы не только физические эксперименты, но и математические расчеты, а также создание математических моделей интересующих нас реальных явлений.

С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые не доступны для понимания противником. История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Виету(1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, математической логики, алгебры.

Для решения проблем обороны страны еще перед Великой Отечественной войной начали широко использоваться (помимо экспериментальных исследований) математические методы. Если говорить о тех направлениях математической мысли, которые нашли особенно серьезное применение, то в первую очередь следует назвать теорию дифференциальных уравнений, теорию вероятностей, алгебру и математическую логику, теорию функций комплексного переменного, методы приближенных вычислений. Из прикладных математических дисциплин должны быть упомянуты теоретическая механика, аэро- и гидродинамика, теория упругости, математическая физика.

Но мы не должны упускать из вида и другой аспект использования математики – ее непременное присутствие при образовании офицера армии и флота. Без математики, без ее безукоризненного знания, и притом в весьма широком объеме, не может быть ни хорошего штурмана, ни артиллериста, ни связиста, ни строителя, ни приемщика военной продукции на заводах. Базой же любого математического образования является хорошо усвоенный курс математики средней школы.

Великая Отечественная война выдвинула перед всеми видами деятельности огромное число сложнейших проблем. Математика не осталась в стороне. Перед ней возникли многочисленные новые задачи, зачастую совершенно необычные. Нередко же появлялись вопросы, которые могли быть решены задолго до того, как они потребовались, но о них не думали, им не придавали значения. Например, перед войной все были увлечены созданием авиации, которая летела бы с огромными для того времени скоростями, на большой высоте и отличалась бы при этом большой маневренностью. Однако уже в первый период войны стало ясно, что при определенных условиях оказываются незаменимыми бомбардировщиками тихоходные самолеты, которые раньше использовались лишь как учебные. Но для них не было таблиц бомбометания, поскольку никто не помышлял о таком их использовании. Пришлось срочно эти таблицы составлять, а для этого было необходимо, для ускорения и упрощения вычислений, придумать хорошие формулы.

Известно, что еще К.Э. Циолковский (1857-1935) много занимался ракетной техникой. Им были предложены методы расчета движения ракет. Эти его результаты и результаты других исследователей были использованы при создании знаменитых «катюш». Таким образом, появлению на фронтах ракетного оружия предшествовала огромная работа не только конструкторской мысли, но и мысли математиков. А такого рода проблем возникало тысячи.

Необходимость выпуска огромной массы однородной продукции, с которой неизбежно связано военное производство, привела к постановке задачи исключительной важности: проверке качества больших количеств однородных изделий. При ее решении возникали трудности двоякого характера: во-первых, проверка качества каждого изделия требует некоторого времени и, во-вторых, проверка качества некоторых изделий приводить к их непоправимой порче. Нередко проверка качества одного – единственного изделия требует несравненно большего времени, чем его изготовление. Так, изготовить винтовочный патрон на соответствующем автомате можно за малую долю минуты, а проверка его качества отнимает много минут; проверка качества взрывателя приводит неминуемой его порчи. Как поступать в условиях, когда продукция нужна и ощущается острая нехватка рабочей силы? Выход был найден: использование статистических методов контроля за качеством продукции. Эти методы позволяют при проверке ничтожной доли изготовленных изделий давать достаточно точные заключения о качестве всей партии. При этом удается добиться выигрыша двоякого рода: значительного уменьшения времени на контроль качества изделий и огромного уменьшения порчи изделий при контроле.

Первые идеи статистического метода контроля за качеством принимаемых партий продукции принадлежали еще М.В. Остроградскому (1801-1862). Позднее они разрабатывались в Ташкенте В.И. Романовским (1879-1954). Во время Великой Отечественной войны этими вопросами занимались многие математики в нашей стране. Разработанные ими идеи легли в основу важной прикладной области теории вероятностей – теории статистических методов приемочного контроля.

Наряду с вопросами приемочного контроля ( то есть контроля качества уже изготовленной продукции) начали разрабатываться и проблемы управления качеством в процессе производства.

Несомненно, что послевоенный период начался в военном деле тремя событиями исключительной важности: появлением ядерного оружия, созданием электронных вычислительных машин и широким развитием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулось с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков.

Во время Великой Отечественной войны широкое употребление при стрельбе по танкам и другим бронированным целям получили так называемые кумулятивные снаряды (от латинского слова «кумуло» - накапливаю). Их пробивное действие оказалось несравненно большим, чем снарядов такого же калибра, и даже с большим количеством взрывчатых веществ, но обычных. Оказывается, что если в снаряде сделать выемку и эту выемку закрыть стальным конусом, то пробивное действие такого заряда резко увеличивается. Это явление было замечено еще во второй половине XIX века и тогда же нашло использование в горном деле. Первое военное применение этого эффекта относится к 1914 году, широкое же использование пришлось на войну 1941-1945 годов. Этим явлением заинтересовался выдающийся советский математик и механик М.А. Лаврентьев. После длительных экспериментов он разработал математическую теорию кумулятивного заряда. Выяснилось, что стальной конус при ударе о преграду с огромной скоростью превращается в тонкую направленную струю и, как иголка, пронзает броню. При соответствующих подборах угла конуса можно получить скорость струи до 90 км/с. Большие усилия Лаврентьев потратил на использование кумулятивного эффекта для разработки теории направленных взрывов при устройстве платин, прокладке каналов и прочее. Теория Лаврентьева позволила не просто использовать подмеченное опытным путем явление, а заранее рассчитывать его действие и при заданном усилии добиваться максимально возможного результата.

В период Великой Отечественной войны было широко использовано реактивное оружие. В качестве зажигательного средства ракеты появились еще в X веке. Первые боевые ракеты в России были изготовлены в 1815 году по проекту генерала А.Д. Засядко. Они с успехом применялись в период русско–турецкой войны 1828-1829 годов, а позднее в Крымской войне 1853-1856 годов. В настоящее время действие ракетного оружия распространяется на тысячи километров.

Трудно переоценить значение математики в деле обороны страны. Обратимся к фактам. 23 июня 1941 года состоялось внеочередное расширенное заседание Президиума Академии наук СССР. Советские ученые заявили, что отдадут «все свои знания, все свои силы, энергию и свою жизнь за дело нашего великого народа, за победу над врагом и полный разгром фашистских бандитов, осмелившихся нарушить священную границу нашей Родины».

Математический институт Академии наук СССР разрабатывает штурманские таблицы. Уже в 1943 году они находят широкое применение в боевой практике авиации дальнего действия. Какова их ценность? Расчеты всех дальних полетов, выполняемые по этим таблицам, значительно повысили точность самолетовождения.

Идет жестокая война. Фронт требует увеличения эффективности огня артиллерии, повышения меткости стрельбы. Эту проблему успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеивания артиллерийских снарядов. Математическая теория вероятностей использовалась во время Великой Отечественной войны и для определения наилучших методов нахождения самолетов, подводных лодок противника, и для указания путей, позволяющих избежать встречи с подводными лодками врага.

Математика помогала рассчитывать, сколько нужно сделать одновременных выстрелов по самолету противника для того, чтобы иметь наибольшую вероятность сбить его. Член-корреспондент АН СССР Н.Г. Четаев предложил наиболее выгодную крутизну нарезки стволов орудий, что позволило обеспечить кучность боя и устойчивость снарядов при полете.

Война требовала от авиации больших скоростей самолетов. Но увы! При освоении больших скоростей авиация столкнулась с внезапным разрушением самолетов из-за вибрации особого рода – флаттера. Опять новая проблема. И тут на помощь приходит математика. За решение данной задачи берется группа ученых во главе с М.В. Келдышем. Она разработала сложную математическую теорию флаттера. Сделано большое дело. Самолеты обеспечены надежной защитой от появления вибраций.

Благодаря немедленному использованию в производстве теоретических исследований видных наших ученых – академиков М.В. Келдыша, А.А. Дородницына и других – стали возможны большие темпы выпуска боевых самолетов.

Видная роль в деле обороны нашей страны принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы ВМС. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизни многих людей, сберечь большие материальные ценности.

Все преподаватели школ прекрасно знаю, что каждый год проводятся уроки Мужества, приуроченные ко Дню Победы. Каждый год мы вынуждены подбирать материал к ним. И этот материал очень редко имеет отношение к нашим предметам. Но приведенный выше материал отвечает всем необходимым требованиям. Он связан с событиями Великой Отечественной войны, рассказывает о подвиге нашего народа, о самоотверженном труде и в тоже время связан с изучаемым предметом. Весь материал подобран таким образом, что может быть использован в любом классе. Стоит еще привести материал к уроку посвященному блокаде Ленинграда и приуроченному к отмечавшемуся в 2003 году 300-летию города.

Повторение темы «Действия с обыкновенными дробями» проходит в конце апреля, как раз перед праздником Победы. Урок посвященный блокаде Ленинграда начинается вполне буднично, с упражнений на действия с дробями.

Выполните действия:

Найдите, на какую часть единицы

больше, чем ,

больше, чем .

После того как все задания выполнены, учитель демонстрирует буханку хлеба, разрезанную на 8 частей. Одна часть лежит отдельно. Одна такая «восьмушка» была дневным рационом ленинградцев в самые тяжелые дни блокады этого города. Блокада длилась 900 дней, но самым трудным периодом оказалась зима 1941-1942 годов, когда основные городские припасы были уничтожены немецкими самолетами, а увезти ослабевших детей и стариков, раненых и больных было невозможно, так как все пути из города были отрезаны врагом. Только зимой 1942 года стал лед на Ладожском озере, и по нему была проложена в город дорога, названная дорогой жизни.

Но Ленинград не сдавался. Героизм защитников города хорошо передан в стихах Юрия Воронова, пережившего все ужасы блокады.

Из писем на Большую землю.

Наш город в снег до пояса закопан.

Но если с крыш на город посмотреть,

То улицы похожи на окопы,

В которых побывать успела

Смерть…

Но в то, что умер город наш, -

Не верьте!

Нас не согнут отчаянье и страх.

Мы знаем от людей, сраженных смертью,

Что означает:

«Смертью

смерть

поправ».

Мы знаем:

Клятвы говорить не просто.

Но если в Ленинград ворвется враг,

Мы разорвем последнюю из простынь

Лишь на бинты, но не на белый флаг!

Февраль.

Какая длинная зима, как время медленно крадется!..

В ночи

Ни люди, ни дома не знают, кто из них проснется.

И поутру, когда ветра метелью застилают небо,

Опять короче, чем вчера, людская очередь за хлебом.

В нас голод убивает страх. Но он же убивает силы…

На Пискаревских пустырях все шире

Братские могилы…

Прочитав эти стихи, учитель просит ребят снова вспомнить о блокадной восьмушке хлеба. Задания:

Подсчитайте, сколько граммов весит восьмая часть буханки хлеба массой в 1 килограмм. [125грамм. ]

Подсчитайте какую часть буханки составляет одна треть от восьмушки? [одну двадцать четвертую. ]

Сколько граммов приходится на часть буханки? [примерно 41,66 грамма.]

Что больше: или ? Представьте, что этими дробями выражаются доли хлебного пайка. В каком пайке больше хлеба? На сколько граммов?[ В части буханки хлеба больше, чем в части примерно на 21 грамм.]

После этих подсчетов учитель читает ребятам рассказ «Кусочек хлеба» из книги Воскобойникова «Девятьсот дней мужества».

Погиб при обороне Ленинграда Петр Карпушкин. А в Ленинграде осталась его семья – жена и три дочери, младшей 3 года. Обессиленные от голода, в пустой промерзшей квартире они ждут прихода мамы. Ее слабые шаги за стеной возвращают утерянный, казалось, шанс на спасение. Анна Герасимовна торопливо делит принесенную ею осьмушку хлеба на 3 части и один кусочек подносит младшенькой – самой слабой из троих. Дочка надкусывает хлеб – на большее сил уже не хватает. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось… умерла дочка, но остались две других. Их надо спасать. Хлеба теперь стало больше: часть буханки вместо (60,5 грамм вместо 41,66 грамма. Это больше примерно на 20 грамм на каждого.). Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее детей неизмеримо важнее, чем маленький кусочек хлеба насущного.

Карпушкины выжили. А блокадный кусочек хлеба хранился в их семье более 30 лет. Потом уже внучка Анны Герасимовны Ира Федосик, поступив в ПТУ№13 Ленинграда, передала эту семейную реликвию училищному музею.

После такого рассказа и у учителя, и у учеников просто не остается душевных сил на обычную работу. Да в этом и нет нужды. Истекли 40 минут урока. Совсем мало было на уроке математики. Но почему же на следующий день так хорошо проходят обычные уроки математики? Почему те ребята, для которых дроби еще недавно были камнем преткновения, теперь явно с ними подружились?

Я нахожу ответ в том, что рассказ о блокадном хлебе оказался сильным эмоциональным ударом для многих ребят. Причем эмоционально окрасились самые обычные вычисления. Ими вряд ли когда-нибудь заинтересовались бы учителя литературы или истории, рассказывающие о той же Ленинградской блокаде. Учителя-гуманитарии сказали бы, что хлеба было мало, очень мало. А математик не станет причитать, а просто сосчитает, сколько же было хлеба. И этот сухой подсчет, который приходилось выполнять людям, бесконечно любящим друг друга, но вынужденным делить его между собой, ранит глубже, чем самые трогательные описания.

doc4web.ru

Статья на тему Математика и военное дело

Математика и военное дело.

Начало использования математических знаний в военном деле относится к глубокой древности. Известно, что в Древнем Вавилоне арифметические сведения употреблялись при подсчете необходимых запасов для армии, геометрия же использовалась при строительстве укреплений и подсчете объема необходимых земельных работ.

В знаменитом диалоге Платона «Государство» говорится о том, что арифметика и геометрия необходимы каждому воину. Вот небольшие цитаты из текста этого диалога:

«Но ведь арифметика и счет целиком касаются числа?..

- Значит, они принадлежат к тем познаниям, которые мы искали. Воину их необходимо усвоить для войскового строя, а философу - для постижения сущности…» (Платон. Соч., т.3, ч. I с.335 М., «Мысль», 1971.)

«При устройстве лагерей, занятии местностей, стягивании и развертывании войск и разных других военных построениях, как во время сражения, так и в походах, конечно, скажется разница между знатоком геометрии и тем, кто ее не знает». (Там же, с. 336 - 337).

Мы хорошо знаем, что создание математического анализа - дифференциального и интегрального исчислений - в значительной мере было связано с задачами, выдвинутыми артиллерией, и что позднее, в свою очередь, развитие новой математики оказывало огромное влияние на прогресс самой артиллерии. Во все времена считалось, что артиллерийский офицер одновременно является хорошим знатоком математики. В этом плане прекрасное утверждение высказано в одном из древнерусских сочинений по артиллерии: «… начальное, во - первых, орудие, еще пушкарю подобает при себе имети - есть циркуль». (Цит. По кн.: А. Платов и Л. Кирпичев. Исторический очерк образования и развития артиллерийского училища. Спб., 1870).

Само собой разумеется, что авторы, говоря о циркуле, имели в виду не только и не столько этот простейший прибор для черчения, сколько математику с ее возможностями строгих логических выводов и расчетов.

Для создания армии, в начале XX века, необходимо было наряду с подготовкой командного состава, решить ряд научных и инженерно - технических проблем. Проблемы артиллерии по-прежнему оставались решающими. Но наряду с ними появились задачи, связанные с созданием собственной авиации, бронетанковых сил, организацией проводной и радиосвязи. Они требовали не только привлечения известных и уже хорошо разработанных математических методов, но и создания новых методов исследования.

В ту пору на первом месте стояли проблемы, связанные с полетом самолета. Теория полета позволила рассчитывать аэродинамические свойства конструкций до их постройки и испытания в воздухе. Эту работу возглавил выдающийся ученый Н.Е. Жуковский (1847-1921). Он и его ученики положили начало замечательному учреждению, получившему позднее наименование ЦАГИ (Центральный аэрогидродинамический институт).

В связи с исследованием механики полета при больших скоростях М.А. Лаврентьев разработал новую математическую теорию квазианалитических функций, позволяющую учитывать сжимаемость воздуха.

Совершенно естественно, что математическая теория полета самолета была лишь одной из проблем, которые требовали серьезного участия математиков. Другие проблемы были связаны с новыми аспектами теории стрельбы: стрельба из танка, стрельба из самолета и по самолету, рассеивание при бомбометании и так далее. Большое значение приобрели вопросы устойчивости движения (самолета, снаряда, корабля, торпеды и прочее). Военное дело потребовало широкого привлечения ряда новых методов математики, в частности теории устойчивости движения, начало которой было положено еще в XIX веке А.М. Ляпуновым (1857-1918). Ляпунов разрабатывал эту теорию в связи с задачами устойчивости Солнечной системы. Но в науке часто случается, что математические приемы, созданные для определенной задачи практики, находят позднее многочисленные новые применения, и в том числе в областях знания, очень далеких от первоначальной.

Чтобы поднять самолет в воздух, требуется создать легкую и одновременно прочную конструкцию корпуса и фюзеляжа. Вот почему большое значение для авиации, а также для морского дела получила проблема создания прочных и одновременно легких и тонких конструкций. Для ее решения необходимы не только физические эксперименты, но и математические расчеты, а также создание математических моделей интересующих нас реальных явлений.

С глубокой древности в военном деле применялись различные способы передачи информации, в том числе и такие, которые не доступны для понимания противником. История использования различного рода кодов для шифровки сообщений насчитывает тысячелетия. Вспомним, что математику Ф. Виету(1540-1603) удавалось с большой легкостью разгадывать шифры, использовавшиеся испанским королем для передачи секретных сведений, направляемых посланнику при французском дворе и некоторым другим лицам.

Само собой разумеется, что эти вопросы в наши дни заняли несравненно большее значение. В последние десятилетия к проблемам шифрования и дешифрования широко привлекаются математики, особенно специалисты в области комбинаторики, математической логики, алгебры.

Для решения проблем обороны страны еще перед Великой Отечественной войной начали широко использоваться (помимо экспериментальных исследований) математические методы. Если говорить о тех направлениях математической мысли, которые нашли особенно серьезное применение, то в первую очередь следует назвать теорию дифференциальных уравнений, теорию вероятностей, алгебру и математическую логику, теорию функций комплексного переменного, методы приближенных вычислений. Из прикладных математических дисциплин должны быть упомянуты теоретическая механика, аэро- и гидродинамика, теория упругости, математическая физика.

Но мы не должны упускать из вида и другой аспект использования математики - ее непременное присутствие при образовании офицера армии и флота. Без математики, без ее безукоризненного знания, и притом в весьма широком объеме, не может быть ни хорошего штурмана, ни артиллериста, ни связиста, ни строителя, ни приемщика военной продукции на заводах. Базой же любого математического образования является хорошо усвоенный курс математики средней школы.

Великая Отечественная война выдвинула перед всеми видами деятельности огромное число сложнейших проблем. Математика не осталась в стороне. Перед ней возникли многочисленные новые задачи, зачастую совершенно необычные. Нередко же появлялись вопросы, которые могли быть решены задолго до того, как они потребовались, но о них не думали, им не придавали значения. Например, перед войной все были увлечены созданием авиации, которая летела бы с огромными для того времени скоростями, на большой высоте и отличалась бы при этом большой маневренностью. Однако уже в первый период войны стало ясно, что при определенных условиях оказываются незаменимыми бомбардировщиками тихоходные самолеты, которые раньше использовались лишь как учебные. Но для них не было таблиц бомбометания, поскольку никто не помышлял о таком их использовании. Пришлось срочно эти таблицы составлять, а для этого было необходимо, для ускорения и упрощения вычислений, придумать хорошие формулы.

Известно, что еще К.Э. Циолковский (1857-1935) много занимался ракетной техникой. Им были предложены методы расчета движения ракет. Эти его результаты и результаты других исследователей были использованы при создании знаменитых «катюш». Таким образом, появлению на фронтах ракетного оружия предшествовала огромная работа не только конструкторской мысли, но и мысли математиков. А такого рода проблем возникало тысячи.

Необходимость выпуска огромной массы однородной продукции, с которой неизбежно связано военное производство, привела к постановке задачи исключительной важности: проверке качества больших количеств однородных изделий. При ее решении возникали трудности двоякого характера: во-первых, проверка качества каждого изделия требует некоторого времени и, во-вторых, проверка качества некоторых изделий приводить к их непоправимой порче. Нередко проверка качества одного - единственного изделия требует несравненно большего времени, чем его изготовление. Так, изготовить винтовочный патрон на соответствующем автомате можно за малую долю минуты, а проверка его качества отнимает много минут; проверка качества взрывателя приводит неминуемой его порчи. Как поступать в условиях, когда продукция нужна и ощущается острая нехватка рабочей силы? Выход был найден: использование статистических методов контроля за качеством продукции. Эти методы позволяют при проверке ничтожной доли изготовленных изделий давать достаточно точные заключения о качестве всей партии. При этом удается добиться выигрыша двоякого рода: значительного уменьшения времени на контроль качества изделий и огромного уменьшения порчи изделий при контроле.

Первые идеи статистического метода контроля за качеством принимаемых партий продукции принадлежали еще М.В. Остроградскому (1801-1862). Позднее они разрабатывались в Ташкенте В.И. Романовским (1879-1954). Во время Великой Отечественной войны этими вопросами занимались многие математики в нашей стране. Разработанные ими идеи легли в основу важной прикладной области теории вероятностей - теории статистических методов приемочного контроля.

Наряду с вопросами приемочного контроля ( то есть контроля качества уже изготовленной продукции) начали разрабатываться и проблемы управления качеством в процессе производства.

Несомненно, что послевоенный период начался в военном деле тремя событиями исключительной важности: появлением ядерного оружия, созданием электронных вычислительных машин и широким развитием работ по ракетной технике. Каждое из указанных направлений конструкторской мысли столкнулось с необходимостью самого широкого привлечения к соответствующим разработкам представителей теоретических областей знания, в первую очередь физиков и математиков.

Во время Великой Отечественной войны широкое употребление при стрельбе по танкам и другим бронированным целям получили так называемые кумулятивные снаряды (от латинского слова «кумуло» - накапливаю). Их пробивное действие оказалось несравненно большим, чем снарядов такого же калибра, и даже с большим количеством взрывчатых веществ, но обычных. Оказывается, что если в снаряде сделать выемку и эту выемку закрыть стальным конусом, то пробивное действие такого заряда резко увеличивается. Это явление было замечено еще во второй половине XIX века и тогда же нашло использование в горном деле. Первое военное применение этого эффекта относится к 1914 году, широкое же использование пришлось на войну 1941-1945 годов. Этим явлением заинтересовался выдающийся советский математик и механик М.А. Лаврентьев. После длительных экспериментов он разработал математическую теорию кумулятивного заряда. Выяснилось, что стальной конус при ударе о преграду с огромной скоростью превращается в тонкую направленную струю и, как иголка, пронзает броню. При соответствующих подборах угла конуса можно получить скорость струи до 90 км/с. Большие усилия Лаврентьев потратил на использование кумулятивного эффекта для разработки теории направленных взрывов при устройстве платин, прокладке каналов и прочее. Теория Лаврентьева позволила не просто использовать подмеченное опытным путем явление, а заранее рассчитывать его действие и при заданном усилии добиваться максимально возможного результата.

В период Великой Отечественной войны было широко использовано реактивное оружие. В качестве зажигательного средства ракеты появились еще в X веке. Первые боевые ракеты в России были изготовлены в 1815 году по проекту генерала А.Д. Засядко. Они с успехом применялись в период русско-турецкой войны 1828-1829 годов, а позднее в Крымской войне 1853-1856 годов. В настоящее время действие ракетного оружия распространяется на тысячи километров.

Трудно переоценить значение математики в деле обороны страны. Обратимся к фактам. 23 июня 1941 года состоялось внеочередное расширенное заседание Президиума Академии наук СССР. Советские ученые заявили, что отдадут «все свои знания, все свои силы, энергию и свою жизнь за дело нашего великого народа, за победу над врагом и полный разгром фашистских бандитов, осмелившихся нарушить священную границу нашей Родины».

Математический институт Академии наук СССР разрабатывает штурманские таблицы. Уже в 1943 году они находят широкое применение в боевой практике авиации дальнего действия. Какова их ценность? Расчеты всех дальних полетов, выполняемые по этим таблицам, значительно повысили точность самолетовождения.

Идет жестокая война. Фронт требует увеличения эффективности огня артиллерии, повышения меткости стрельбы. Эту проблему успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеивания артиллерийских снарядов. Математическая теория вероятностей использовалась во время Великой Отечественной войны и для определения наилучших методов нахождения самолетов, подводных лодок противника, и для указания путей, позволяющих избежать встречи с подводными лодками врага.

Математика помогала рассчитывать, сколько нужно сделать одновременных выстрелов по самолету противника для того, чтобы иметь наибольшую вероятность сбить его. Член-корреспондент АН СССР Н.Г. Четаев предложил наиболее выгодную крутизну нарезки стволов орудий, что позволило обеспечить кучность боя и устойчивость снарядов при полете.

Война требовала от авиации больших скоростей самолетов. Но увы! При освоении больших скоростей авиация столкнулась с внезапным разрушением самолетов из-за вибрации особого рода - флаттера. Опять новая проблема. И тут на помощь приходит математика. За решение данной задачи берется группа ученых во главе с М.В. Келдышем. Она разработала сложную математическую теорию флаттера. Сделано большое дело. Самолеты обеспечены надежной защитой от появления вибраций.

Благодаря немедленному использованию в производстве теоретических исследований видных наших ученых - академиков М.В. Келдыша, А.А. Дородницына и других - стали возможны большие темпы выпуска боевых самолетов.

Видная роль в деле обороны нашей страны принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы ВМС. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизни многих людей, сберечь большие материальные ценности.

Все преподаватели школ прекрасно знаю, что каждый год проводятся уроки Мужества, приуроченные ко Дню Победы. Каждый год мы вынуждены подбирать материал к ним. И этот материал очень редко имеет отношение к нашим предметам. Но приведенный выше материал отвечает всем необходимым требованиям. Он связан с событиями Великой Отечественной войны, рассказывает о подвиге нашего народа, о самоотверженном труде и в тоже время связан с изучаемым предметом. Весь материал подобран таким образом, что может быть использован в любом классе. Стоит еще привести материал к уроку посвященному блокаде Ленинграда и приуроченному к отмечавшемуся в 2003 году 300-летию города.

Повторение темы «Действия с обыкновенными дробями» проходит в конце апреля, как раз перед праздником Победы. Урок посвященный блокаде Ленинграда начинается вполне буднично, с упражнений на действия с дробями.

Выполните действия:

Найдите, на какую часть единицы

больше, чем ,

больше, чем .

После того как все задания выполнены, учитель демонстрирует буханку хлеба, разрезанную на 8 частей. Одна часть лежит отдельно. Одна такая «восьмушка» была дневным рационом ленинградцев в самые тяжелые дни блокады этого города. Блокада длилась 900 дней, но самым трудным периодом оказалась зима 1941-1942 годов, когда основные городские припасы были уничтожены немецкими самолетами, а увезти ослабевших детей и стариков, раненых и больных было невозможно, так как все пути из города были отрезаны врагом. Только зимой 1942 года стал лед на Ладожском озере, и по нему была проложена в город дорога, названная дорогой жизни.

Но Ленинград не сдавался. Героизм защитников города хорошо передан в стихах Юрия Воронова, пережившего все ужасы блокады.

Из писем на Большую землю.

Наш город в снег до пояса закопан.

Но если с крыш на город посмотреть,

То улицы похожи на окопы,

В которых побывать успела

Смерть…

Но в то, что умер город наш, -

Не верьте!

Нас не согнут отчаянье и страх.

Мы знаем от людей, сраженных смертью,

Что означает:

«Смертью

смерть

поправ».

Мы знаем:

Клятвы говорить не просто.

Но если в Ленинград ворвется враг,

Мы разорвем последнюю из простынь

Лишь на бинты, но не на белый флаг!

Февраль.

Какая длинная зима, как время медленно крадется!..

В ночи

Ни люди, ни дома не знают, кто из них проснется.

И поутру, когда ветра метелью застилают небо,

Опять короче, чем вчера, людская очередь за хлебом.

В нас голод убивает страх. Но он же убивает силы…

На Пискаревских пустырях все шире

Братские могилы…

Прочитав эти стихи, учитель просит ребят снова вспомнить о блокадной восьмушке хлеба. Задания:

Подсчитайте, сколько граммов весит восьмая часть буханки хлеба массой в 1 килограмм. [125грамм. ]

Подсчитайте какую часть буханки составляет одна треть от восьмушки? [одну двадцать четвертую. ]

Сколько граммов приходится на часть буханки? [примерно 41,66 грамма.]

Что больше: или ? Представьте, что этими дробями выражаются доли хлебного пайка. В каком пайке больше хлеба? На сколько граммов?[ В части буханки хлеба больше, чем в части примерно на 21 грамм.]

После этих подсчетов учитель читает ребятам рассказ «Кусочек хлеба» из книги Воскобойникова «Девятьсот дней мужества».

Погиб при обороне Ленинграда Петр Карпушкин. А в Ленинграде осталась его семья - жена и три дочери, младшей 3 года. Обессиленные от голода, в пустой промерзшей квартире они ждут прихода мамы. Ее слабые шаги за стеной возвращают утерянный, казалось, шанс на спасение. Анна Герасимовна торопливо делит принесенную ею осьмушку хлеба на 3 части и один кусочек подносит младшенькой - самой слабой из троих. Дочка надкусывает хлеб - на большее сил уже не хватает. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось… умерла дочка, но остались две других. Их надо спасать. Хлеба теперь стало больше: часть буханки вместо (60,5 грамм вместо 41,66 грамма. Это больше примерно на 20 грамм на каждого.). Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее детей неизмеримо важнее, чем маленький кусочек хлеба насущного.

Карпушкины выжили. А блокадный кусочек хлеба хранился в их семье более 30 лет. Потом уже внучка Анны Герасимовны Ира Федосик, поступив в ПТУ№13 Ленинграда, передала эту семейную реликвию училищному музею.

После такого рассказа и у учителя, и у учеников просто не остается душевных сил на обычную работу. Да в этом и нет нужды. Истекли 40 минут урока. Совсем мало было на уроке математики. Но почему же на следующий день так хорошо проходят обычные уроки математики? Почему те ребята, для которых дроби еще недавно были камнем преткновения, теперь явно с ними подружились?

Я нахожу ответ в том, что рассказ о блокадном хлебе оказался сильным эмоциональным ударом для многих ребят. Причем эмоционально окрасились самые обычные вычисления. Ими вряд ли когда-нибудь заинтересовались бы учителя литературы или истории, рассказывающие о той же Ленинградской блокаде. Учителя-гуманитарии сказали бы, что хлеба было мало, очень мало. А математик не станет причитать, а просто сосчитает, сколько же было хлеба. И этот сухой подсчет, который приходилось выполнять людям, бесконечно любящим друг друга, но вынужденным делить его между собой, ранит глубже, чем самые трогательные описания.

botana.cc

Реферат - Математика в годы великой отечественной войны

Введение

Прошли почти 60 лет со дня победы советского народа в Великой Отечественной

войне. Неисчислимые жертвы понесла страна во имя неза­висимости, свободы и

общественных идеалов; миллионы погибших и раненых, страдания от голода,

тысячи разрушенных городов и деревень, сотни тысяч угнанных на фашистскую

каторгу.

Несмотря ни на что советский народ выстоял и победил.

С первых дней войны математики принимали участие в защите страны: призывались

в армию, записывались в народное ополчение, шли на фронт добровольцами. В

самые тяжелые для страны дни они показали себя верными сыновьями Родины,

способными на самопожертвование и готовыми отдать жизнь во имя свободы

Отчизны. И действительно, многие из тех, кто ушел па фронт, не возвратились

и не приступили к своей любимой работе. Среди погибших было много талантливых

математиков, подававших большие надежды, способных внести большой вклад в

прогресс наших знаний.

Как только стало известно о нападении фашистской Германии на наше Отечество,

всюду на заводах и в учреждениях прошли митинги» и возникло общенародное

движение по записи в народное ополчение. В ополчение за­писались

практически все студенты и аспиранты и подавляющее большин­ство ассистентов,

доцентов и профессоров, в том числе и те, кто по возрасту и состоянию

здоровья был освобожден от воинской службы. Позднее некоторые ополченцы были

вычеркнуты из списков, так как они имели профессорские звания или степени

доктора. В эту категорию попал и я, поскольку к тому времени мной была

защищена докторская диссертация. В результате мне пришлось не с оружием в

руках защищать страну, а участвовать в создании этого оружия, а также в

разработке методов рационального его использования.

1. На защиту Родины

Большое число математиков, как мы уже отмечали, были мобилизованы или ушли

на фронт добровольцами. Они храбро воевали и честно исполняли свой

гражданский долг. Несомненно, что при этом страна потеряла огромное число

талантливой молодежи, которая могла бы стать гордостью отечественной науки.

Об этом мы можем судить, во-первых, по тому, что среди возвратившихся после

участия в сражениях Великой Отечественной войны значитель­ное число стало

крупными учеными — профессорами, членами — корреспондентами и академиками

Всесоюзной и республиканских, академии наук. Достаточно назвать такие имена

как академики Ю. В. Линник, Ю.А. Митропольский, Г.Г. Черный, Н.П. Еругин,

О.С. Парасюк, чтобы убедиться в этом. А во-вторых, каждый из университетов

потерял многих молодых ученых, уже сумевших проявить себя и обещавших в

будущем очень многое, но не вернувшихся с войны. Так, Московский университет

потерял талантливых молодых математиков Г.М. Бавли, М.В. Бебутова, Н.В.

Веденисова, В.Н. Засухина и многих, многих других. Они могли бы стать

гордостью нашей науки, но воина прервала и зачеркнула раз­витие так славно

начатого ими научного пути.

Помимо преподавателей, аспирантов и студентов, получивших мобилизационные

извещения уже в первые дни войны и попавших в регулярные воинские части,

механико-математический факультет Московского университета дал 213 человек в

8-ю Краснопресненскую дивизию народного ополчения. Все они были зачислены в

975-и артиллерийский полк этой дивизии и после короткого обу­чения уже в

августе заняли оборонительный рубеж на ржевско-вяземском направлении. Вместе

со всеми наши товарищи создавали оборонительный рубеж: рыл и окопы,

противотанковые рвы, манные поля, устанавливали орудия. Но на фронте не все

происходит так, как предполагает обороняющийся.

2. В народном ополчении: бой под Ельней

В начале октября положение на ельнинском направлении резко обострилось,

поскольку немцы сосредоточили здесь большие свежие силы и начали

наступательную операцию, В связи с этим командование фронтом передало 8-ю

Краснопресненскую дивизию из 32-й в 24-ю армию и срочно перебросило ее с

подготовленных позиций в район деревни Уварово, расположенной несколько

южнее Ельни. К сожалению, подготовленных позиций там не оказалось и пришлось

задерживать врага буквально «с марша». Дивизия выполнила боевую задачу: она

задержала врага на несколько дней и тем самым оказала значительную помощь

обороне Москвы. По сохранившимся сведениям это сражение дорого обошлось

оккупантам: около 45 тысяч солдат и офицеров они потеряли под Ельней в

результате стойкой обороны советских солдат. Но и мы запла­тили за это

дорогую цену: около трети ополченцев 8-ой дивизии погибли в этих боях. Среди

них были аспиранты или уже защитившие диссертации А.И. Герчиков, М.Е.

Глезерман, В.II. Засухин, И.Р. Лепехин, X.М. Мильштейн, С.С. Кудашев, С.Я.

Карпов, А.Т. Павлов, М.И. Песин и ряд других. Трудно переоценить тяжесть этой

потери для страны и для советской науки, а нам, преподавателям факультета,

знавшим их лично, ценившим их способности и увлеченность наукой, эта потеря

особенно горька.

Академик и директор Института механики МГУ Г. Г. Черный рассказывал, что

975-й артиллерийский полк 5 октября отбивал ожесточенные атаки наседавшего

со всех сторон противника. Одно за другим выходили из строя орудия. Когда

был отдан приказ об отходе на новую позицию, из них осталось лишь шесть.

Отходить к лесу пришлось по открытому полю под огнем про­тивника; еще четыре

орудия были выведены из строя. Расчеты оставшихся двух орудий изготовились к

бою, а пехота залегла рядом, на опушке, в наспех вырытых окопчиках. В это

время разведка донесла, что вблизи от леса движется большая колонна

противника — машины с солдатами, самоходные орудия, минометы, боеприпасы.

Было принято немедленное решение — атаковать наличными средствами беспечного

противника. Наводчиком одного из орудий был Г.Г. Черный, другого — также

мехматовец И.Степанов. Тщательное прицеливание, зала и оба снаряда

разорвались в колонне. Дальше бешеный огонь но противнику, разбитые машины,

мотоциклы, уничтоженные солдаты. Однако растерянность врага прошла, и в

ответ полетели снаряды и мины. Дуэль длилась до тех пор, пока у наших

оставались снаряды.

3. Медсестры, летчицы и артиллеристы

Многие студентки после прохождения двухмесячных курсов медсестер были

направлены в госпитали, медсанбаты и непосредственно на пере­довую. Кроме

того, студентки университета откликнулись на призыв из­вестной летчицы Героя

Советского Союза Марины Расковой и стали штурманами и летчицами, в

частности, 46-го гвардейского полка ночных бомбардировщиков. Летали эти

летчицы на тихоходном и незащищенном от огня самолете «У-2», но наносили

противнику весьма значительный ущерб. Пяти летчицам вы­пускницам мехмата

было присвоено звание Героя Советского Союза. Вот их имена: Е. Руднева, Е.

Пасько, Р. Гашева, А. Зубкова, Е. Рябова. Еще три выпускника факультета были

Героями Советского Союза — Г. Барыков, Г.Волохов, Л. Ратушная.

Герой Советского Союза Екатерина Рябова перед боевым вылетом

Добровольцем пошел в Армию и профессор А.А. Ляпунов и, как многие мехматовцы,

стал артиллерийским офицером. Он не только храбро воевал, но и вносил много

ценного в правила стрельбы. Но здесь он использовал свой опыт математика,

которому свойственно искать самые лучшие решения. Его предложения позволили

увеличить эффективность стрельбы. За работы в области кибер­нетики, теории

множеств и программирования А. А. Ляпунов уже после войны был избран член-

корреспондентом АН СССР.

Математики нашей страны в период тягчайших испытаний проявили себя как

подлинные патриоты, проявляли величайшее мужество, были храбрыми и

расчетливыми воинами.

4. Математические задачи — для фронта

Мы должны преклоняться перед выдержкой, самоотверженностью и верностью

Отчизне» которую проявляли математики-воины. Однако нельзя забывать и о

другом вкладе математиков в победу советского народа над сильным и коварным

врагом. Этот вклад состоит в использовании тех специфических знаний и умений,

которыми обладают математики. Значение этого фактора особенно важно в наши

дни, когда война стала, в первую очередь, соревнованием ра­зума,

изобретательности и точного расчета. Дело в том, что для военных действии

привлекаются все достижения естествознания, а вместе с ними и математика во

всех ее проявлениях. Создание атомного и ракетного оружия потребовало не

только использования физических законов, но и обширных математических

расчетов, создания новых математических моделей и даже новых ветвей

математики. Без таких предварительных математических исследо­ваний не

создается ни одна техническая система и, чем она сложнее, тем разнообразнее

и шире ее математический аппарат. Для примера, крейсер представляет собой

такую сложную техническую систему. Прежде чем начать его постройку,

необходимо выявить геометрические обводы корпуса судна, чтобы при движении

не создавались дополнительные сопротивления и чтобы одновременно он был

послушен управляющим воздействиям руля. Предварительно не­обходимо

обеспечить живучесть корабля, надежность его управления, рассчитать влияние

на остойчивость расположения различного рода масс — машин, орудий, торпедных

аппаратов и пр. Но и этого мало — требуется обеспечить связь со всеми боевыми

единицами корабля, то есть создать эффективную систему управ­ления кораблем и

его оружием.

Мы перечислили лишь ничтожную долю тех задач, которые должен решить

математик, прежде чем корабль можно начать строить. Но серьезные задачи

необходимо решать и в период его эксплуатации — штурманские расчеты, расчеты

стрельб и т. д.

Академик М.А. Лавреньтев за изучением пробивного

действия взрывчатых веществ 1944г.

5. Совершенствование военной техники

В период Великой Отечественной войны техника была разнообразной и сложной.

Она также требовала широкого использования математических расчетов для ее

изготовления и эксплуатации. Увеличение спорости полета самолетов требовало

не только повышения мощности двигателей, но и выбора оптимального профиля

фюзеляжа и крыльев, а также решения многих других вопросов.

В России над этими вопросами еще с прошлого века работал ряд ученых и е

первую очередь Н. Е. Жуковский (1847 — 1921), названный В.И. Лениным отцом

русской авиации. Он закономерно считается основоположником новой

математической науки — аэродинамики, в которой ему удалось создать ряд

сильных методов исследования и решить многочисленные актуальные задачи,

основать большую научную школу, состоящую из ближайших учеников по

университету и старейшему высшему техническому заведению Москвы — Московскому

высшему техническому училищу.

Жуковский заложил основы Военно-воздушной академии, получившей впоследствии

его имя, а также Центральный аэрогидродинамический ин­ститут. Это научное

учреждение долгие годы работало под руководством одного из ближайших

учеников и сотрудников Н.Е. Жуковского — С.А. Чаплыгина (1869 —1942) и

объединили многих выдающихся исследователей — М. В. Келдыша (1911 — 1978).

В.В. Голубева (1884 —1954), М.А. Лаврентьева (1900—1980) и др. Теоретический

отдел разрабатывал многие важные проблемы, в том числе и для военной авиации.

Многие из этих разработок пригодились и были широко использованы для создания

новых систем истребителей, штурмовиков и бомбардировщиков, обладавших

повышенной маневренностью, скоростью, надежностью.

Большое значение получили теории двух явлений — штопора и шимми (или

флаттера), представлявших в ту пору основную опасность для авиаторов. Как

правило, самолет, попавший в состояние штопора или шимми (особые вибрации

самолета, приводившие к его разрушению) уже не могли из него выйти. Теорию

этих явлений создал М. В. Келдыш (впоследствии президент Академии наук СССР,

главный теоретик космонавтики). Однако он пошел дальше и на основании теории

сделал заключения о том, как устранять эти явления. В результате практика

полетов получила надежное средство для борьбы с шимми и штопором и за все

время войны практически не было в нашей авиации гибели само­летов и летчиков

по этим причинам. Переоценить результаты этих исследовании невозможно,

поскольку они помогли не только сохранить жизнь летчиков и самолеты, но и

позволили летать на больших скоростях.

6. Теория стрельбы

Традиционная область деятельности ученых нашей страны — исследование

артиллерийских систем.

Этим занимались М. В. Остроградский (1801 —1862) и П. Л. Чебышёв (1821—1894), и

последующие поколения ученых. Проблемы пристрелки, разработанные еще в XIX

веке в связи с появлением новых типов артиллерии потребовали в период Великой

Отечественной войны дополнительных исследований и состав­ления таблиц.

Стрельба с самолета по самолету и по наземным целям также привела к

математическим задачам, которые нужно было срочно решить. Ими занимались

упорно как специалисты в области артиллерии, так и математики. Проблемы

бомбометания привели к необходимости составления таблиц, позволяющих находить

оптимальное время для сброса бомб на цель, область, которую накроет бомбовой

удар. Такие таблицы были составлены еще до начала войны но

для самолетов, обладающих большими скоростями. Во время войны выявилась

полезная возможность использования тихоходных учебных самолетов для ночных

бомбежек. Были созданы специальные полки ночных бомбардировщиков, но для них

не было своевременно создано таблиц бомбометания. Возникла срочная задача

производства соответствующих расчетов. Таблицы были созданы и они оказали

несомненную помощь нашим летчикам и летчицам.

Интересная задача возникла у моряков в связи с желанием увеличить

вероятность попадания в цель при торпедном залпе. Возникла идея за счет

искусственного рассеивания увеличить эту вероятность. Этой задачей занялся

один из крупнейших нищих математиков академия А.Н. Кол­могоров. Ему удалось

найти полное решение задачи и довести его до практического использования.

Несомненно, что какую-то долю успехов наших моряков следует отнести и на

счет этой решенной Колмогоровым задачи. Позднее его выводы были перенесены и

на проблемы, связанные со стрельбой зенитной артиллерии по самолетам. Вообще

нужно сказать, что актуальная математическая задача, решенная в одной

практической ситуации, очень быстро находит и другие применения, порой очень

далекие от первоначального направления исследований.

7. Статистический контроль в военном производстве

Имеется еще один аспект работы советских математиков на помощь фронту, о

котором нельзя умалчивать — это работа по организации производственного

процесса, направленная на повышение производительности труда и на улучшение

качества продукции. Здесь мы столкнулись с огромным числом проблем, которые

по самому их существу нуждались в математических методах и в усилиях

математиков. Мы затронем здесь лишь одну проблему, получив­шую наименование

контроля качества массовой промышленной продукции и управления качеством в

процессе производства. Эта проблема со всей остротой возникла перед

промышленностью уже в первые дни войны, поскольку прошла массовая

мобилизация и квалифицированные рабочие стали солдатами. Им на смену пришли

женщины и подростки без квалификации и рабочего опыта.

Я вспоминаю такой случай: мне пришлось быть на одном из приборостроительных

заводов в Свердловске. Он изготовлял крайне необходимые приборы для авиации

и артиллерии. У станков я увидел практически только подростков 13 — 15 лет.

Увидел и также огромные кучи бракованных деталей. Сопро­вождавший меня мастер

пояснил, что эти детали выходят за пределы допуска и поэтому непригодны для

сборки. А вот если бы удилось собрать из этих «запоротых» деталей пригодные

приборы, мы бы смогли сразу ate удовлетворить потребности на месяц вперед.

Слова мастера не давали мне покоя. В результате общения с инженерами завода

родилась мысль разбить детали на 6 групп по размерам, которые уже было бы

возможно сопрягать между собой. В шестую группу входили детали совершенно

непригодные для сборки. Исследования показали, что так собранные приборы

оказались вполне пригодными для дела. Они обладали одним недостатком: если

какая-либо деталь выходила из строя, то ее можно было за­менять лишь деталью

той же группы, из деталей которой собран прибор. Но в ту пору и для тех

целей, для которых были предназначены приборы, можно было обойтись заменой

приборов, а не деталей. Нам удалось успешно использовать завалы» испорченных

подростками деталей.

Задача контроля качества изготовленной продукции состоит в следующем. Пусть

изготовлено N изделии, они должны удовлетворять некоторым требованиям.

Скажем, снаряды должны быть определенного диаметра, не выходящего за пределы

отрезка [D1, D2], иначе они будут непригодны для стрельбы. Они должны обладать определенной кучностью при стрельбе, иначе будут затруднения при стрельбе по цели. И если с первой задачей справиться легко —нужно замерить диаметры изготовленных снарядов и отобрать те из них, которые не удовлетворяют требованиям, то с другим требованием поло­жение значительно сложнее. Действительно, чтобы проверить кучность стрельбы, необходимо провести

стрельбы. А что же останется после испытаний? Испытания нужно произвести так,

чтобы подавляющая часть продукции осталась пригодной для дальнейшего

использования. Мы столкнулись с основным требованием; по испытанию малой части

изделий научиться судить о качестве всей партии. Методы, которые были для

этой цели предложены, получили название статистических. Их теория берет свое

начало с одной работы 1848 года академика М.В. Остроградского. Позднее этой

задачей занимались профессор В. И. Романовский (1879 — 1954) в Ташкенте и его

ученики. Во время войны их совершенствованием нанялся А.Н. Колмогоров и его

ученики.

Задача, о которой только что было рассказано, обладает одним дефектом в самой

ее постановке: партия продукции уже изготовлена и нужно сказать, можно ее

принять или же следует ее отвергнуть? Но, спрашивается, зачем же изготовлять

партию, чтобы ее затем браковать? Нельзя ли так организовать

производственный процесс, чтобы уже при изготовлении поставить заслон для

изготовления некачественной продукции? Такие методы были предложены и

получили название статистических методов тенящего контроля. Время oт времени

со станка берутся несколько (скажем, пять) только что наготовленных изделий и

замеряются параметры их качества. Если все эти параметры находятся в

допустимых пределах, то производственный процесс продолжается, если же хотя

бы одно изделие выходит за пределы допуска, то подается сигнал о

необходимой переналадке станка или о смене режущего инструмента. Какое

отклонение параметра от номинала допустимо, чтобы вся партия была изготовлена

качественно? Это требует специальных расчетов.

После окончания войны выяснилось, что аналогичные исследования проводили

математики США, Они подсчитали, что результаты их работы принесли за годы

войны стране миллиардную экономию. То же самое можно сказать и о работах

советских математиков и инженеров.

Заключение

До сих пор нет сводного труда, который бы показал, как много математики дали

фронту для победы, как их исследования помогали совер­шенствовать оружие,

которое использовали воины в боях. Этот пробел следует восполнить как можно

быстрее, поскольку многих из тех, кто это делал, уже нет в живых, поскольку

человеческая память несовершенна и многое забывается. А нам никак нельзя

забывать о том, что подвиг народа в Великой Отечественной войне не

ограничивается только славными делами фронтовиков, что основы победы ковались

и в тылу, где руками рабочих и их разумом, руками и разумом инженеров и ученых

создавалась и совершенствовалась военная техника. Нельзя нам забывать и того

, что по многим параметрам к концу войны наши танки, самолеты,

артиллерийские орудия стали совершеннее тех, которые противопоставлял нам

враг. Нельзя забывать, что в конце войны мы вынуждены, были вплотную заняться

созданием собственного атомного оружия, а для этого пришлось объединить

интеллектуальные усилия физиков, химиков, технологов, математиков,

металлургов и самостоятельно пройти тот путь, который уже был пройден США и их

западными союзниками. Мы его прошли сами, тогда как в США работали лучшие

ученые со всей Европы — Англии, Франции, Италии, Дании, Германии (эмигранты),

Польши, Венгрии и, конечно, самих Соединенных Штатов Америки,

Со времени Победы прошло почти 60 лет. Советские математики многое дали

восстановлению и развитию народного хозяйства, а также прогресс у

теоретической математики. К сожалению, и теперь положение в мире таково, что

страну, а имеете с ней и математики, вынуждены уделять внимание разработке

проблем обороны. Однако это не самоцель, а вынужденная необходимость. Каждый

же из нас мечтает о том времени, когда человечество забудет о войнах и о

подготовке к ним.

www.ronl.ru

Математики и математика в годы великой отечественной войны содержание: Стр. 1 Введение

23

МАТЕМАТИКИ И МАТЕМАТИКА

В ГОДЫ

ВЕЛИКОЙ ОТЕЧЕСТВЕННОЙ ВОЙНЫ

СОДЕРЖАНИЕ:

Стр.

1)Введение………………………………………………………………………..3

2)Глава 1.Участие учёных-математиков в боевых действиях……………4

3)Глава 2.Математические задачи для фронта и тыла……………………5

4)Глава 3. Вклад Челябинска в победу над фашистами…………………...9

5)Заключение……………………………………………………………………11

6)Приложение А. Фотографии…………………………………………….......12

7)Приложение Б. Задачи военной тематики…………………………….......16

8)Список литературы…………………………………………………………..22

ВВЕДЕНИЕ.

Прошло более 60 лет со дня победы советского народа в Великой Оте­чественной войне. Неисчислимые жертвы понесла страна во имя неза­висимости, свободы и общественных идеалов: миллионы погибших и ра­неных, страдания от голода, тысячи разрушенных городов и деревень, сотни тысяч угнанных на фашистскую каторгу.

Несмотря ни на что совет­ский народ выстоял и победил.

Великая Отечественная война не прошла мимо советских математиков: тысячи из них ушли на фронт по мобилизации или добровольцами, многие переключились на решение важных задач, необходимых для победы, остальные не переставали трудиться на своих постах, веря в разгром врага и создавая для будущего новые научные ценности.

Актуальность данного исследования состоит в том, что реальных участников тех событий почти не осталось в жизни, мои ровесники знают о войне лишь из книг и кинофильмов. Но память человеческая несовершенна, многие события забывают. Мы должны знать реальных людей, которые приближали победу и подарили нам будущее.

Цель данной работы: определить вклад математики и математиков в победу в Великой Отечественной войне.

В рамках этой цели ставились следующие задачи:

1) Выяснить, кто из учёных-математиков принимал участие в боевых действиях.

2) Определить, какие задачи приходилось решать математикам в годы Великой

Отечественной войны.

3) Выяснить вклад Челябинска в победу над фашистами.

Среди методов исследования я использовала такие, как:

изучение литературных источников,

сравнительный анализ полученной информации,

отбор информации для работы,

изучение и решение задач, которые могли решаться в годы войны,

создание задач военной тематики для использования на уроках и во внеклассной деятельности.

ГЛАВА 1. УЧАСТИЕ УЧЕНЫХ - МАТЕМАТИКОВ В БОЕВЫХ ДЕЙСТВИЯХ.

C первых же дней Великой Отечественной Войны огромное число математиков были мобилизова­ны или ушли на фронт доброволь­цами. Они храбро воевали и честно исполняли свой гражданский долг. При этом страна потеряла огромное число талантливой молодежи, которая могла бы стать гордостью отечественной науки. Об этом мы можем судить, во-первых, по тому, что среди возвратившихся после участия в сражениях Вели­кой Отечественной войны значитель­ное число стало крупными учены­ми - профессорами, членами - коррес­пондентами и академиками Всесоюз­ной и республиканских, академии на­ук.

Например, добровольцем ушел на фронт и участвовал в боях с фашистскими захватчиками в Крыму, на Украине, в Прибалтике и в Восточной Пруссии выдающийся математик и педагог А.А. Ляпунов (1911 – 1973). Он храбро воевал и внес много ценного в правила стрельбы. Здесь он ис­пользовал свой опыт математика, ко­торому свойственно искать самые лучшие решения. Его предложения увеличили эффективность стрельбы. За работы в области кибер­нетики, теории множеств и програм­мирования А.А.Ляпунов уже после войны (с 1964 г.) был избран член - корреспонден­том АН СССР.

В частях тяжелой артиллерии на Пулковских высотах отстаивал город Ленинград выдающийся специалист в области теории чисел, теории вероятностей и математической статистики, доктор физико – математических наук, а потом академик АН СССР Ю. В. Линник (1915 – 1972)

А во-вторых, каждый из университетов потерял многих мо­лодых ученых, уже сумевших про­явить себя и обещавших в будущем очень многое, но не вернувшихся с войны. Осенью 1941г. умер от ран и нечеловеческих условий вражеского плена Н.Б. Веденисов (1905 -1941). Свой путь в математике талантливый ученый начинал в области теории множеств и теории функций действительного переменного. Позже его научные интересы перешли в область теоретико – множественной топологии, где он получил ряд важных результатов. Война застала Веденисова преподавателем одной из военных академий. Не смотря на слабое здоровье и бронь, он принял твердое решение уйти в ополчение. В тяжелых боях под Ельней ученый был ранен и оказался в плену, где силы его быстро иссякли.

М. В. Бебутов (1913 – 1942) начал свою научную работу еще в студенческие годы. Его научные интересы были связаны с качественной теорией дифференциальных уравнений. Первая публикация относится к 1938г, а последняя опубликована посмертно в 1942г. И все же, несмотря на такой ограниченный промежуток научной деятельности, М. В. Бебутов получил в математике ряд важных результатов. Защищенная им в июне 1941г. диссертация была отмечена ученым советом как выдающаяся работа.

Не вернулись с войны и такие талантливые молодые мате­матики Московского университета, как Г.М. Бавли, В.Н. Засухин, А.И. Герчиков, М.Е. Глезерман, И.Р. Лепе­хин, X.М. Мильштейн, С.С. Кудашев, С.Я. Карпов, А.Т. Павлов, М.И. Песин и многие, многие другие.

Все они могли бы стать гордостью нашей науки, но война прервала и зачеркнула раз­витие так славно начатого ими науч­ного пути. Сколько замыслов осталось не осуществленными, какие россыпи математических сокровищ они унесли с собой. Справедливо говорят, что трудно даже представить, какой была бы сегодня математика, не понеси мы этих потерь.

ГЛАВА 2. МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ДЛЯ ФРОНТА И ТЫЛА.

Мы должны преклоняться перед вы­держкой, самоотверженностью и вер­ностью Отчизне, которую проявля­ли математики-воины. Однако нельзя забывать и о другом вкладе мате­матиков в победу советского народа над сильным и коварным врагом. Этот вклад состоит в использовании тех специфических знаний и умений, ко­торыми обладают математики. Зна­чение этого фактора особенно важ­но в наши дни, когда война стала, в первую очередь, соревнованием ра­зума, изобретательности и точного расчета. Дело в том, что для военных действии привлекаются все до­стижения естествознания, а вместе с ними и математика во всех ее прояв­лениях. Создание атомного и ракет­ного оружия потребовало не только использования физических законов, но и обширных математических расчетов, создания новых математи­ческих моделей и даже новых вет­вей математики. Без таких предва­рительных математических исследо­ваний не создается ни одна техни­ческая система и, чем она сложнее, тем разнообразнее и шире ее мате­матический аппарат.

Для примера, крейсер представляет собой очень сложную техническую систему. Преж­де чем его построить, надо выявить геометрические формы корпуса судна, чтобы при движе­нии не создавалось дополнительное сопротивления и чтобы одновременно судно слушалось руля. Также не­обходимо обеспечить живучесть ко­рабля, надежность его управления, рассчитать влияние расположения машин, орудий, торпедных аппаратов на устойчивость и пр. Но и этого мало — требуется обеспечить связь со всеми боевыми единицами корабля, то есть создать эффективную систему управ­ления кораблем и его оружием.

Здесь перечислена лишь ничтожная доля тех задач, которые должен ре­шить математик, прежде чем корабль можно начать строить. Но серьезные задачи необходимо решать и в период его эксплуатации — штурманские расчеты, расчеты стрельб и т. д.

Роль математики в военном деле велика. Обратимся к фактам прошлого.

2.1. Совершенствование военной техники.

В период Великой Отечественной войны техника была разнообразной и сложной. Она требовала широ­кого использования математических расчетов для ее изготовления и эксп­луатации.

Увеличение скорости поле­та самолетов требовало не только повышения мощности двигателей, но выбора оптимального профиля фюзе­ляжа и крыльев, а также решения многих других вопросов. Достижение блестящих результатов в совершенствовании боевых самолетов позволило А. С. Яковлеву и С.А.Лавочкину создать грозные истребители, С. В. Илюшину – неуязвимые штурмовики, А.Н. Туполеву, Н. Н. Поликарпову и В. М. Петлякову – мощные бомбардировщики.

Но, овладевая большими скоростями, авиаконструкторы столкнулись с неизвестным ранее явлениями в поведении самолета. В определенных режимах работы моторов в конструкциях самопроизвольно возникало возбуждение, причем с большой амплитудой, и это явление (флаттер) вело к разрушению самолета в воздухе. Опасности подстерегали скоростные машины и на земле. При взлете и посадке самолета колеса вдруг начинали вилять из стороны в сторону. Это явление, названное шимми, нередко вызывало катастрофы самолетов на аэродромах. Выдающийся советский математик М. В. Келдыш и возглавляемый им коллектив ученых исследовали причины флаттера и шимми. Созданная учеными математическая теория этих опасных явлений позволила советской авиационной науке своевременно защитить конструкции скоростных самолетов от появления таких вибраций. Ученые дали рекомендации, которые требовалось учитывать при конструировании самолетов. В результате наша авиация во время войны не знала случаев разрушения самолетов по причине неточного расчета конструкций, тем самым были спасены жизни многих летчиков и боевые машин.

Советские ученые опередили врага и в создании реактивной авиации.

Первый испытательный полет нашего реактивного истребителя был произведен в мае 1942 г., немецкий реактивный «Мессершмитт» поднялся в воздух через месяц после этого.

Видная роль в деле обороны нашей страны принадлежит выдающемуся математику – академику

А. Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно – Морскими силами. Он создал таблицу непотопляемости, по которой можно было рассчитать, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен и насколько это затопление может улучшить устойчивость корабля. Использование этих таблиц спасло жизнь многих людей, помогло сберечь огромные материальные ценности.

2.2. Теория стрельбы.

Традиционная область деятельно­сти ученых нашей страны — исследование артиллерийских систем.

• Проблемы пристрел­ки, разработанные еще в XIX веке, в связи с появлением новых типов

артиллерии потребовали в период Великой Отечественной войны до­полнительных исследований и состав­ления таблиц.

а) Стрельба с самолета по самолету и по наземным целям также привела к математическим

за­дачам, которые нужно было срочно решить. Ими занимались как специалисты в области

артиллерии, так и математики. Проблемы бом­бометания привели к необходимости составления

таблиц, позволяющих находить оптимальное время для сброса бомб на цель, а также область,

кото­рую накроет бомбовой удар. Такие таблицы были составлены еще до на­чала войны, но для

самолетов, об­ладающих большими скоростями. Во время войны были созданы специальные

полки ночных тихоходных бомбарди­ровщиков, но для них не было таблиц бомбометания.

На кафедре теории вероятностей МГУ были рассчитаны таблицы бомбометания с малых

высот при малых скоростях самолета. Они оказали несомненную помощь нашим

летчи­кам и летчицам.

б) В апреле 1942 г коллектив математиков под руководством основателя конструктивной

теории функции действительного переменного и первого аксиоматика теории вероятностей

академика С. Н. Бернштейна разработал и вычислил таблицы для определения местонахож-

дения судна по радиопеленгам. Таблицы ускоряли штурманские расчеты примерно в 10 раз.

В 1943 г были подготовлены штурманские таблицы, которые нашли широкое применение в

боевых действиях дальней авиации, значительно повысили точность самолетовождения. Штаб

авиации дальнего действия, дал высокую оценку работе математиков, отметив, что ни в

одной стране мира не были известны таблицы, равные этим по простоте и оригинальности.

Н. Г. Четаев определил наивыгоднейшую крутизну нарезки стволов орудия. Это обеспечивало максимальную кучность боя и непереворачиваемость снаряда при полете.

• Один из крупнейших наших математиков, академик А.Н. Кол­могоров, используя свои

работы по теории вероятности, разработал теорию наивыгоднейшего рассеивания артиллерийских снарядов. Он нашел полное решение этой задачи и довел его до практического использования. Полученные им результаты помогли повысить меткость стрельбы и тем самым увеличить эффектность действия артиллерии, которую заслуженно называли богом войны.

• Большое значение для решения практических задач, в том числе оборонных, имело развитие

номографии – одного из разделов математики, изучающей теорию и способы построения одного из видов чертежей – номограмм, которые экономят время для вычислений, упрощают их. Номограммы специального бюро при НИИ математики МГУ под руководством Н.А.Глаголева применялись при обороне городов, использовались для оптимального размещения зенитных батарей вокруг Москвы, в Военно-Морском Флоте.

2.3. Статистический контроль в военном производстве.

Имеется еще один аспект работы советских математиков на помощь фронту, о котором нельзя не вспомнить— это работа по организации производственного процесса, направ­ленная на повышение производитель­ности труда и на улучшение каче­ства продукции. Здесь было огромное число проблем, которые нуж­дались в математических методах и в усилиях математиков. Я рассмотрю только одну проблему – контроль качества продукции и управления качеством в процессе производства.

Эта проблема со всей остротой возникла перед промыш­ленностью уже в первые дни войны, поскольку прошла массовая мобили­зация и квалифицированные рабочие стали солдатами. Им на смену приш­ли женщины и подростки без квали­фикации и рабочего опыта.

Рассмотрим лишь один пример, имевший место на приборостроительном заводе в Свердловске. Здесь изготовлялись очень важные приборы для авиации и ар­тиллерии. У станков были только подростки 13 — 15 лет. Многие детали, которые они выпускали, выходили за пределы до­пуска и поэтому не использовались для сборки. Тогда все детали разбили на 6 групп по размерам, которые уже было бы возможно со­прягать между собой. Исследования показали, что так собранные прибо­ры оказались вполне пригодными для дела и удовлетворили потребности на месяц вперед.

Они обладали одним недостат­ком: если какая-либо деталь выходи­ла из строя, то ее можно было за­менять лишь деталью той же груп­пы, из деталей которой собран при­бор. Но в ту пору и для тех це­лей, для которых были предназначены приборы, можно было обойтись заменой приборов, а не деталей. Мастерам удалось успешно использовать зава­лы испорченных подростками де­талей.

Задача контроля качества изготов­ленной продукции состоит в следующем. Пусть изготовлено N изделий, они должны удовлетворять некото­рым требованиям. Скажем, снаряды должны быть определенного диамет­ра, не выходящего за пределы от­резка [D1, D2], иначе они будут не­пригодны для стрельбы. Они должны обладать определенной кучностью при стрельбе, иначе будут затруднения при стрельбе по цели. И если с первой задачей справиться легко — нуж­но замерить диаметры изготовленных снарядов и отобрать те из них, которые не удовлетворяют требова­ниям, то с другим требованием поло­жение значительно сложнее. Действи­тельно, чтобы проверить кучность стрельбы, необходимо провести стрельбы. А что же останется после испытаний? Испытания нужно произ­вести так, чтобы подавляющая часть продукции осталась пригодной для дальнейшего использования. Была поставлена задача – как по испытанию малой части изделий на­учиться судить о качестве всей пар­тии. Методы, которые были для этой цели предложены, получили название статистических. Их теория берет свое начало с одной работы 1848 года академика М.В. Остроградского. Позднее этой задачей занимались профессор В. И. Романовский (1879 — 1954) в Ташкенте и его ученики. Во время войны их совершенствованием занялся А.Н. Колмогоров и его уче­ники.

Задача, о которой только что было рассказано, обладает одним дефектом в самой ее постановке: партия про­дукции уже изготовлена и нужно выяснить, можно ее принять или же следует ее

отвергнуть? Но зачем изготовлять пар­тию, чтобы ее затем браковать? Возникла проблема, как организовать произ­водственный процесс, чтобы уже при изготовлении поставить заслон для изготовления некачественной про­дукции? Такие методы были предло­жены и получили название статисти­ческих методов текущего контроля. Время от времени со станка берутся несколько (скажем, пять) только что наготовленных изделий и замеряются параметры их качества. Если все эти параметры находятся в допустимых пределах, то производственный про­цесс продолжается, если же хотя бы одно изделие выходит за пределы до­пуска, то подается сигнал о необ­ходимой переналадке станка или о смене режущего инструмента. Какое отклонение параметра от номинала допустимо, чтобы вся партия была изготовлена качественно?

Это требует специальных расчетов.

После окончания войны выясни­лось, что результаты рабо­ты советских математиков и

инженеров принесли за годы войны стране миллиардную экономию.

ГЛАВА 3. ВКЛАД ЧЕЛЯБИНСКА В ПОБЕДУ НАД ФАШИСТАМИ.

В те тяжелые годы челябинцы делали немыслимое:

ставили цеха из остатков вывезенных сборных конструкций, рубя проволоку и вытесывая топором сложнейшие перекрытия;

возвращали в строй тысячи тяжелораненых, делая сложнейшие операции и отдавая свою кровь бойцам; снабжали армию хлебом и мукой, мясом и одеждой, получая по карточкам 800 граммов хлеба, 50 граммов крупы и 30 граммов мяса в день на работающего.

 45 тысяч южноуральцев ушли на фронт добровольцами;

600 тысяч участвовали в Великой Отечественной войне;

250 тысяч из них погибли.

Кроме этого Челябинск внес огромный вклад в оборону нашей страны.

Танкоград… Такого города не было на карте, но о нем сообщалось во всех сводках Совинформбюро, о нем знали солдаты на фронте.

Еще в 1940 г. Челябинский тракторный завод начал осваивать производство тяжелых танков

КВ (Клим Ворошилов),война потребовала их массового выпуска. Осенью 1941 г. в Челябинск с Украины прибыл Харьковский моторный завод, выпускающий танковые дизели, из Ленинграда – знаменитый Кировский завод. Новое объединенное предприятие представляло собой танковый комбинат и стало называться Уральским Кировским заводом, названным народом Танкоградом. В небывало сжатые сроки завод стал одним из главных арсеналов фронта.

Конструкторское бюро Танкограда возглавил Ж. Я. Котин (1908 – 1979) – талантливый конструктор и прекрасный организатор. Мозговой центр города – конструкторское бюро – работал не только над совершенствованием своего детища КВ – 1, но и над созданием новых, еще более грозных машин.

За годы войны Котиным Ж.Я и его коллективом были созданы 13 типов боевых машин.

Среди них такие, как:

Самоходная артиллерийская установка СУ – 152. Это мощное орудие, установленное на шасси тяжелого танка, выводило из строя «тигры» и «пантеры»;

Танки ИС -1 (Иосиф Сталин), ИС – 2, ИС – 3. Эти танки отличались от уже созданных, превосходили их по вооружению, боевой защите, скорости;

Артсамоход КВ – 7;

Танковый тягач ССС – 2Т и др;

6 типов танковых дизельмоторов.

За годы войны было выпущено 18 тысяч танков и самоходных установок, 48,5 тысяч танковых дизельмоторов, 17,7 миллионов заготовок боеприпасов. Впервые в мировой практике танкостроения сборка тяжелого танка была поставлена на конвейер.

Заводы Танкограда дали фронту:

 каждый третий снаряд;

каждый второй танк.

За создание отечественной научной школы танкостроения Ж. Я. Котину была присвоена ученая степень доктора технических наук. Конечно же, без отличного знания математики, без точных и правильных расчетов, это было бы невозможно.

Представители творческой интеллегенции других профессий также работали на оборону. Хотя многие ученые и преподаватели ушли на фронт, количество научных работников не уменьшилось, а возросло – за счет эвакуированных вузов.

Главным центром исследования стал Челябинский Дом ученых, в секциях которого шли напряженные научные поиски:

инженеры строители предложили использовать вместо кирпича шлакоблоки,

металлурги – заменители дорогостоящих цветных металлов,

механизаторы переводили трактора и автомобили с жидкого топлива на газ.

Все это невозможно без точных расчетов, знания математических методов исследования, законов математики.

ЗАКЛЮЧЕНИЕ.

Со времени Победы прошло более 60 лет. Вторая мировая война оказалась прежде всего войной танков, соревнования моторов, огня и брони, и от того, чья конструкторская мысль оказывалась точнее и глубже, зависел исход многих сражений. Советские математики многое сделали для восстановления и развития народ­ного хозяйства. За годы войны, в нечеловеческих условиях, наблюдался прогресс в теоретической математики. До сих пор нет сводного труда, который бы показал, как много ма­тематики дали фронту для победы, как их исследования помогали совер­шенствовать оружие, которое исполь­зовали воины в боях.

Этот пробел следует восполнить как можно быст­рее, поскольку многих из тех, кто это делал, уже нет в живых, поскольку человеческая память несовершенна и многое забывается. А нам никак нель­зя забывать о том, что подвиг на­рода в Великой Отечественной войне не ограничивается только славными делами фронтовиков, что основы побе­ды ковались и в тылу, где руками рабочих и их разумом, руками и разумом инженеров и ученых создава­лась и совершенствовалась военная техника. Нельзя нам забывать и то­го, что по многим параметрам к концу войны наши танки, самолеты, артиллерийские орудия стали со­вершеннее тех, которые противопо­ставлял нам враг. Нельзя забывать, что в конце войны мы вынуждены, были вплотную заняться созданием собственного атомного оружия, а для этого пришлось объединить интеллек­туальные усилия физиков, химиков, технологов, математиков, металлур­гов и самостоятельно пройти тот путь, который уже был пройден США и их западными союзниками.

К сожале­нию, и теперь положение в мире таково, что страны, а вместе с ней и математики, вынуждены уделять внимание разработке проблем обороны. Однако это не самоцель, а вы­нужденная необходимость. Каждый же из нас мечтает о том времени, когда человечество забудет о войнах и о подготовке к ним.

Таким образом, я считаю, что тема моей работы очень актуальна в наши дни, особенно для моих сверстников.

Во – первых, она приближает математику к истории моей страны, к жизни.

Показывает, что это не просто сухие цифры, это история, человеческие судьбы. Ведь от точности расчетов зависели человеческие жизни.

Во – вторых, эта работа помогает понять, что изучение математики необходимо, она соприкасается со всеми отраслями науки. И чем бы мы в дальнейшем не занимались, что бы мы не выбрали, знания математики нам будут необходимы.

ПРИЛОЖЕНИЕ А.

ФОТОГРАФИИ.

Академик М.А.Лавреньтев за изучением пробивного действия взрывчатых веществ 1944г.

Доктор физико – математических наук Выдающийся математик – педагог

Ю.В.ЛИННИК (1915 – 1972) А.А.ЛЯПУНОВ (1911 – 1973)

Ж.Я.КОТИН (1908 – 1979) конструктор танков.

КВ-7

ИС-2

Солдатские будни

ПРИЛОЖЕНИЕ Б.

ЗАДАЧИ ВОЕННОЙ ТЕМАТИКИ.

«Кусочек хлеба» (из книги Воскобойникова «Девятьсот дней мужества»)

Погиб при обороне Ленинграда Петр Карпушкин. А в Ленинграде осталась его семья – жена и три дочери, младшей 3 года. Обессиленные от голода, в пустой промерзшей квартире ждут прихода мамы. Ее слабые шаги за стеной возвращают утерянный, казалось, шанс на спасение. Анна Герасимовна торопливо делит принесенную ею осьмушку хлеба на 3 части и один кусочек подносит младшенькой – самой слабой из троих. Дочка надкусывает хлеб – на большее сил уже не хватает. Она умирает на глазах у мамы, на руках у сестренок. Это самая обычная смерть в голодном блокадном Ленинграде. Необычен поступок матери. Казалось… умерла дочка, но остались две других. Их надо спасать. Хлеба стало больше: 1/16 часть буханки вместо 1/24. Но мать поступает иначе. Она решает сохранить надкусанный ребенком кусочек хлеба как память. Она поняла, что сила духа ее, ее детей неизмеримо важнее, чем маленький кусочек хлеба насущного.

Карпушкины выжили. А блокадный кусочек хранился в их семье более 30 лет. Потом уже внучка Анны Герасимовны Ира Федосик, поступив в ПТУ № 13 Ленинграда, передала эту семейную реликвию училищному музею.

Задачи о блокадной восьмушке хлеба: (тема «Действия с обыкновенными дробями»)

• Подсчитать, сколько граммов весит 1/8 часть буханки хлеба массой в 1 кг. (125 г.)

• Какую часть буханки составляет 1/3 от восьмушки? (1/24 часть буханки)

• Сколько граммов приходится на 1/24 часть буханки? (Примерно 41,66 г.)

• На сколько граммов хлеба в1/16 части содержится больше, чем в 1/24 части хлебного пайка? ( Примерно на 21 г.)

Задачи на движение:

• Разведывательному кораблю (разведчику), двигавшемуся в составе эскадрильи, дано задание обследовать район моря на 70 миль в направлении движения эскадры. Скорость эскадрильи – 35 миль в час, скорость разведчика – 70 миль в час. Определить, через сколько времени разведчик возвратится к эскадре.

Решение: 1) 70 – 35= 35(км) – расстояние между кораблями через час.

2) 70 + 35 = 105(км/ч) – скорость сближения.

3) 35 : 105 = 1/3(ч) =20(мин) – необходимо на обратный путь кораблю.

4) 1ч +20мин = 1ч 20 мин – разведчик возвратится.

Ответ: корабль (разведчик) вернётся к эскадре через 1 час 20 минут после отбытия.

• Разведчик получил приказ произвести разведку впереди эскадрильи и вернуться через 3 часа. Через какое время после оставления эскадрильи разведывательный корабль должен повернуть назад, если его скорость 60 узлов, а скорость эскадрильи 40 узлов?

Ответ: корабль должен повернуть назад к эскадре через 2 часа 30 минут после отплытия.

Задачи, приводящие к квадратным уравнениям.

• Имеются два сплава меди с другим металлом, причём относительное содержание меди в одном из этих сплавов на 40% больше, чем во втором. Сплавляя кусок 1 сплава, содержащего 6 т. меди, с куском 2 сплава, содержащего 12 т. меди, получили слиток, содержащий 36% меди. Определить процентное содержание меди в каждом из первоначальных сплавов?

Ответ: 45% в первом сплаве, а во втором – 85%.

Линейные неравенства.

• Для выпуска военной продукции установлены станки-автоматы двух типов А и В, имеющие разную производительность. Работая совместно, три станка типа А и один станок типа В дают не более 10 т. продукции в час, а один станок типа А вместе с двумя станками типа В дают не менее 8 т. продукции в час. Найти, сколько тонн продукции в час даёт станок каждого типа (графическим способом).

Решение: Пусть производительность станка – автомата типа А х т/ч, а производительность станка – автомата типа В у т/ч. Из условия, что три станка типа А и один станок типа В дают не более 10 т. продукции в час, составим неравенство 3х + у ≤ 10. Из условия, что один станок типа А вместе с двумя станками типа В дают не менее 8 т. продукции в час, составим неравенство: х + 2у ≥ 8.

Изобразим графически эти неравенства:

По графику видим, что 0 ≤ x ≤ 2,4 4 ≤ y ≤ 10

Ответ: Станок типа А дает до 2,4т продукции в час, а станок типа В от 4 до 10 тонн.

Линейные уравнения.

• С самолёта, находящегося на высоте большей 320 м., для партизан был сброшен груз. За какое время груз долетит до земли? (ускорение свободного падения принять равным 10 м/с2 )

На каком расстоянии от деревни, занятой фашистами, должны находиться партизаны, чтобы забрать груз, если средняя скорость передвижения по лесу 5,4 км/ч и немцы увидели самолет за 10 минут до сброса груза?

Решение: Формула расстояния свободно падающего тела h = ½(gt2).

Выразим из нее t: t =

Имеем q = 10 м/с2, h >320м, значит t > , т.е. t > , t > 8.

Теперь выясним, на каком расстоянии от деревни могут быть партизаны. Расстояние вычисляется по формуле S = v ∙ t, 5,4 км/ч = 1,5 м/с. значит S > 1,5∙(8+600), S > 912.

Ответ: Груз будет лететь до земли больше 8 секунд, партизаны должны быть удалены от немцев более 912 м.

• Сигнальная ракета выпущена вертикально вверх с начальной скоростью V0=30 м /с. Определить через сколько секунд после запуска ракета достигает наибольшей высоты, если высоту можно найти по формуле: h=V0t – 1/2gt2 (ускорение свободного падения считать равным 10 м/с2). Вычислить эту высоту.

Решение: Траектория движения ракеты представляет собой параболу (график квадратичной функции у = 30х – 5х2), ветви которой опущены вниз. Наибольшее значение функция принимает в вершине. Значит, нам надо найти координаты вершины по параболы.

Это можно сделать по формулам: y = y(x)

= 3 у = 45

Ответ: Через 3 секунды ракета достигнет наибольшей высоты 45 м.

• При испытании двух двигателей было установлено, что расход бензина при работе первого двигателя составил 450 гр., а при работе второго 288 гр., причём второй двигатель работал на 3 часа меньше, расходовал бензина в час на 6 гр. меньше. Сколько граммов бензина расходует в час каждый двигатель?

Решение: Пусть первый двигатель расходует х гр./ч, а второй двигатель – (х – 6) гр./ч.

Расход бензина при работе первого двигателя составил 450 гр., а при работе второго 288 гр., значит, первый двигатель проработал 450/х ч, второй 288/(х – 6) ч.

Второй двигатель работал на 3 часа меньше, т.е. 450/х - 288/(х – 6) = 3.

Преобразовав это дробно – рациональное уравнение получим 3х2 - 180х +2700 = 0,

х2 - 60х + 900 = 0, (х – 30)2 = 0, х = 30.

Итак, первый двигатель расходует 30 гр./ч, второй двигатель расходует 24 гр./ч.

Ответ: 30 гр./ч и 24 гр./ч.

Задачи на сплавы.

Мне кажется, что во время войны на производстве приходилось решать задачи на сплавы.

• Имеется кусок сплава меди с оловом общей массой 12тонн, содержащей 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

Ответ: Надо добавить 1,5 тонны олова.

• Имеется два куска сплава меди и цинка с процентным содержанием меди 30% и 80% соответственно. В каком отношении надо взять эти сплавы, чтобы , переплавив взятые куски вместе, получить сплав, содержащий 60% меди?

Решение: Пусть х(т)- масса первого сплава, а у(т) – масса второго сплава, тогда (х + у) (т) – масса третьего сплава.

«Расщепим» с помощью весовых концентраций эти количества на компоненты:

х = 0,3х +0,7х у = 0,8у + 0,2у

Тогда (0,3х + 0,8у) (т) – меди в третьем сплаве.

(0,3х + 0,8у) ÷ (х + у) – концентрация меди в третьем сплаве. По условию задачи она равна 0,6.

Преобразовав уравнение, получим 3х + 8у = 6х + 6у, т.е. х ÷ у =2÷3

Ответ: Надо взять 2 части первого сплава и 3 части второго сплава.

Решение: Пусть х % - полезных веществ в руде. «Расщепим» массы руды и металла на компоненты 40 = (х/100)∙40 + ( 100-х )/100)∙40 20 = 0,94∙20 + 0,06∙20.

По условию все полезные вещества получены из 40 тонн руды, поэтому составляем уравнение (х/100)∙40 = 0,94∙20. Решая это уравнение, получаем х = 47.

Мы нашли, сколько процентов полезных веществ содержится в руде. Поэтому примесей там 53%.

Ответ: В руде 53% примесей.

• Имеется сталь двух сортов с содержанием никеля 5% и 40 %. Сколько стали каждого сорта следует взять, чтобы получить после переплавки 140 т стали с содержанием никеля 30%?

Решение: Пусть х(т) – масса первого сорта, у(т) – масса второго сорта, тогда (х + у) (т) – масса третьего сорта. По условию задачи х + у = 140.

«Расщепим» с помощью весовых концентраций массы двух первых сортов на компоненты:

х = 0,05х + 0,95х у = 0,4у+ 0,6у, тогда в третьем сплаве (0,05х + 0,4у) (т)- никеля в третьем сплаве.

По условию концентрация никеля в третьем сплаве равна 0,3, поэтому масса никеля в этом сплаве 140 ∙ 0,3 = 42(т). Составим уравнение 0,05х + 0,4у = 42

Решив систему уравнений х + у = 140. Получим х = 40 и у = 100

0,05х + 0,4у = 42

Ответ: Надо взять 40т стали первого сорта и 100т стали второго сорта.

СПИСОК ЛИТЕРАТУРЫ:

1)Гнеденко Б.В. Математика и оборона страны, - М.: 1978.

2)Гнеденко Б. В. Математика и контроль качества продукции М.: Знание, 1984.

3)Левшин Б.В. Советская наука в годы Великой Отечественной Войны - М.: Наука, 1983.

4)Оружие Победы.-2-е изд., перераб. И доп. - М: Машиностроение, 1986.

5)Челябинск. История моего города: учеб. Для учащихся общеобразоват. школ, гимназий, лицеев. - Челябинск: Издательство ЧГПУ, 1999.

refdb.ru

Смотрите также

• 
  Закономерности действия экологических факторов реферат
• 
  Духовность и здоровье семьи реферат
• 
  Видоизменение корней реферат 6 класс
• 
  Реферат история развития языка программирования
• 
  Реферат на тему виды приемов
• 
  Шотландия реферат на английском языке
• 
  Шотландия на английском языке реферат
• 
  Система питания инжекторного двигателя реферат
• 
  Реферат система питания инжекторного двигателя
• 
  Реферат предприятие как производственная система
• 
  Реферат неотложная помощь при утоплении