Исследовательская работа по географии "Математика в географии". Математика в географии реферат

Исследовательская работа по географии "Математика в географии"

Школьный конкурс проектных и исследовательских работ учащихся

"Мои первые шаги"

МБОУ "Смоленская СОШ №2"

Тема проектной работы:

"Математика в географии".

Выполнил:

Левашов Матвей,

ученик 7В класса

МБОУ "Смоленская СОШ №2"

Руководитель проекта:

Плотникова Анна Викторовна,

учитель географии

МБОУ "Смоленская СОШ №2".

2017 год

СОДЕРЖАНИЕ

Введение ............................................................................................................................3 1.Основная часть ...............................................................................................................4

1.1.Математика, как наука................................................................................................4 1.2.География, как наука...................................................................................................6 1.3. Взаимосвязь географии и математики......................................................................9

2. Практическая часть.......................................................................................................11 Заключение........................................................................................................................14 _

Список использованной литературы.........................................................................................................................15____________________________

ВВЕДЕНИЕ

Для начала я хотела сказать, почему я решился на эту работу. Я очень люблю математику. Конечно, не всегда все решается быстро, но в этом и прелесть этой науки. Нужно заставлять свой мозг трудиться. "Математика – гимнастика ума", это слова великого полководца Александра Васильевича Суворова. А Михаил Васильевич Ломоносов, человек уникального ума, говорил, что математику уже затем следует учить, что она ум в порядок приводит. Я думаю, к мнению таких людей стоит прислушаться. Математика и полезна тем, что она трудна.

Место математики в жизни и науке определяется тем, что она позволяет переводить обычные явления в природе, обществе, даже в нашем городе и стране, которые основываются на приблизительных описаниях, на язык точных формул, по которым можно получить не приблизительные, а точные цифры и выводы. Не случайно говорят, что степень научности той или иной дисциплины измеряется тем, насколько в ней применяется математика.

Своей работой я хотел показать, что математика это не трудная и скучная наука, а древний, надежный и важный помощник человека. На примере взаимодействия математики с такой древней наукой, как география, можно увидеть, что математика не существует отдельно от других наук. Роль математики в жизни человека огромна.

Цель исследования: доказать связь математики и географии.

Задачи исследования:

1. показать важность математики в географии и способы ее применения;

2. проведение сравнительного анализа и отбора статистического материала;

3. нахождение примеров использования математического метода в географии;

4. оценка эффективности применения математических методов с помощью анкетирования учащихся.

Гипотеза: математика и география очень тесно связаны между собой; без царицы всех наук – математики – географии было бы очень трудно существовать

Объект исследования: математика и география как самостоятельные науки.

Предмет исследования: математические методы в географии.

Методы исследования: информационный, социологический и аналитический.

1. Основная часть

   1. Математика, как наука.

«Математика - это язык, на котором написана книга природы».Г. Галилей

«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на­стойчивость и упорство в достижении цели.

А. И. Маркушевич, советский математик и педагог

Слово МАТЕМАТИКА произошло от греческого  mathema, что обозначает знание, учение, наука.

МАТЕМАТИКА – это наука о количественных  отношениях  и пространственных формах окружающего нас мира. 

Ученые поняли, что математика  это особая наука ещё в Древней Греции  в 6 - 5 вв. до нашей эры. Математика – древнейшая наука в истории человечества. Она демонстрирует возможности человеческого разума. Невозможно познать математику, не ознакомившись с историей её развития. Благодаря ученым, расшифровавшим древние рукописи, удаётся воссоздать пути становления математики и её возрастающую роль в развитии человечества.

Представления человека о числе относятся к очень далекой эпохе древнего каменного века. Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук  и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века,  изображает число 35 в виде выстроенных в ряд 35 палочек - пальцев.

Дальнейшее развитие математики происходило примерно  в  3000  до  н. э. благодаря вавилонянам и египтянам. В то время математика в основном была связана с ведением хозяйства. Математические знания использовались при обмене денег и расчетах за товары, для вычисления налогов и доли урожая, которую нужно было отдавать в пользу государства, храма или землевладельца. Многочисленные арифметические и геометрические задачи решались людьми при строительстве домов, храмов, каналов, хранилищ для зерна. Без применения математики невозможны были исследования движений Луны и планет. А это позволило людям предсказывать положения планет. Очень важной задачей математики был расчет календаря, поскольку календарь использовался для определения сроков сельскохозяйственных работ и религиозных праздников.

Греки в течение 1-2 столетий сумели овладеть математическим наследием своих предшественников, но они не остановились на достигнутом, и продолжали развивать математическую науку дальше. Греки были, прежде всего, геометрами. Геометрия буквально означает «землемерие». Многим из нас известны имена древнегреческих ученых Фалес Милетский, Пифагор, Евклид, Платон, Аристотель, Архимед. С тех времен математика стала не просто наукой для ведения простых хозяйственных подсчетов, а она стала инструментом для выявления сущности явлений и процессов.

Свой вклад в развитие математики внесли индийцы и арабы. Немаловажно было то, что арабские математики переписывали труды греческих математиков, комментировали и совершенствовали их. Многие их работы послужили основой для последующего развития математики в Европе.

В средние века основой развития математической науки служило интенсивное развитие ремесел, производства товаров и торговля. Для развития математики большую роль сыграли переводы на латинский язык сочинений арабских математиков. Европейцы смогли познакомиться с трудами Архимеда, Евклида и других греческих математиков. Открывались первые университеты.

В XVI-XVII вв. математика развивалась в Италии, Франции, Германии, Голландии. Появляются новые математические теории, математические вычисления становятся все более сложными. В математике начинают видеть метод изучения природы.

Какие бы крупные изменения не происходили за тысячи лет с человеческой цивилизацией, все время на помощь людям приходила математика. Ведь все события, происходящие с человечеством, не могли обойти стороной науку. Менялось общество, менялась и наука.

Сейчас человечество решает много разных вопросов. Это и политика, и экономика, и экология и многое другое. Все это, заставляет человеческий интеллект искать пути решения для того, чтобы управлять сложными системами природы. Здесь на помощь людям приходит прогнозирование.

Как выяснилось, решение прогнозных задач в большинстве случаев базируется на использовании математических моделей. В этом случае мы видим изменение целей математики: если ранее целью использования математических моделей было описание физических явлений, то теперь целью математического моделирования стала прогнозирование последствий принятия тех или иных решений. Математическое моделирование характеризуется тем, что процесс его проведения часто требует выполнения больших количеств вычисления. Проведение такого количества вычислений стало возможным только благодаря появлению и использованию компьютеров. Решения математических задач с помощью компьютеров потребовало средств «перевода» этих задач с математического языка на язык компьютеров. Так появилось программирование и вместе с ним и новый тип математики компьютерная математика.

Вот так возникла новая математика, отличная от греческой математики, и от европейской математики. Эту математику можно условно называть мировой математикой. Если греческая математика была обращена к человеку, европейская математика – к природе, то мировая математика – ко всей человеческой цивилизации в целом.

Математика дала возможность осуществить технологический прогресс человечества, она стала той самой необходимой частью этого прогресса. Возникновение и развитие мировой науки и компьютерной математики позволило и позволяет человечеству избежать ряда социальных, экономических и технических катастроф.

1. 2. География, как наука.

География – также как и математика является древнейшей наукой. Слово «география» произошло от греческого ge – «земля» и grapho – пишу. География (греч. - “землеописание”) - наука, изучающая поверхность Земли, облегающие и подстилающие её слои вещества, которые в совокупности образуют географическую оболочку. Истоки географии уходят вглубь веков гораздо дальше, чем, например, у физики, химии, биологии, геологии и многих других наук.

В течение многих веков география существовала как описательно-познавательная наука, географы открывали и описывали ранее неизвестные страны и земли. География столетиями накапливала факты и ее главная задача состояла в том, чтобы шаг за шагом создавать картину поверхности земного шара, т.е. нанести на карту и описать берега материков и островов, горы, реки, озера и т.д.

Не следует, конечно, думать, что географы в прошлом были только собирателями фактов, среди них были и выдающиеся мыслители. Уже в глубокой древности люди пытались объяснить разливы рек, приливы и отливы, происхождение ветров и течений и многие другие географические явления. Но общий уровень науки был таким, что ученые не могли экспериментально исследовать наблюдаемые явления, и им приходилось догадываться об их сущности и происхождении, полагаясь на свою интуицию или фантазию.

Только к концу прошлого века география смогла опереться на основные законы физики, химии и биологии, чтобы изучать и объяснять сложные явления и процессы, которые происходят в земной поверхности. Таким образом, география начала превращаться из описательной (“собирательной”) дисциплины в науку теоретическую.

Современная география – это целая “семья” наук, которые изучают природу, законы развития хозяйства, условия жизни населения. Одна из важнейших задач современной географии - изучение того, как существовать природе и человеку для правильного использования природных ресурсов и сохранения благоприятных условий для жизни человека на нашей планете.

Зачатки географических знаний появились еще у первобытных людей, ведь их жизнь зависела от того, как они умеют ориентироваться в пространстве и отыскивать естественные убежища, источники воды, места для охоты, камни для орудий и т.д. Первобытный человек отличался острой наблюдательностью и даже умением делать рисунки местности на шкурах, бересте, дереве - прообразы наших географических карт.

Уже на самых ранних стадиях своей хозяйственной деятельности первобытный человек вступил в сложные взаимодействия с окружающей природной средой. Исследования археологов в последние годы показали, что уже в конце каменного века человек уничтожил основную часть крупных млекопитающих в северном полушарии, и вызвал, тем самым, “первый экологический кризис” в истории нашей планеты. Он был вынужден перейти от собирательства и охоты к земледелию.

А первые географические письменные документы оставили нам земледельческие народы Древнего Востока: Египта, Двуречья, Северной Индии и Китая. Так, в Египте для определения сроков различных сельскохозяйственных работ стали проводиться регулярные астрономические наблюдения. Египтяне довольно точно определили продолжительность года и ввели солнечный календарь. Древним египтянам и вавилонянам были известны солнечные часы. Египетские и вавилонские жрецы, а также китайские астрономы установили закономерности повторения солнечных затмений и научились предсказывать их. Из Двуречья происходит деление года - на 12 месяцев, суток - на 24 часа, окружности - на 360 градусов; там же было введено понятие “лунная неделя”.

Древние знания о Земле опирались, прежде всего, на мифологические представления. Так, древним египтянам Земля представлялась в виде плоского вытянутого прямоугольника, окруженного со всех сторон горами. Некоторые народы считали, что Земля плоская и держится на трех китах, которые плавают и безбрежном всемирном океане. Следовательно, эти киты и были в их глазах основной основ, подножием всего мира.

 Древние индийцы представляли Землю в виде полусферы, которую держат четыре слона. Слоны стоят на огромной черепахе. Но когда люди стали путешествовать и плавать по морям, когда им стали известны простейшие астрономические данные, эти мифологические верования уходили в прошлое.

В Древней Греции около 500 г. до н.э. Аристотель впервые высказал идею о том, что Земля имеет форму шара. Он доказывал свою идею тем, что: у земной тени при лунных затмениях наблюдалась круглая форма и вид звездного неба при передвижении с севера на юг изменялся.

Около 165 г. до н.э. греческий ученый Кратес изготовил первую модель земного шара - глобус.

Аристарх Самосский в III в. до н.э. впервые приблизительно определил расстояние от Земли до Солнца. Он первым начал учить, что Земля движется вокруг Солнца и вокруг своей оси.

В Древней Греции зародились основные направления географической науки. Нужды мореплавания и торговли (греки основали в то время ряд колоний на берегах Средиземного и Черного морей) вызвали необходимость в описаниях суши и морских берегов.

В Греции возникло новое географическое направление, которое получило впоследствии название математической географии. Одним из первых представителей этого направления был Эратосфен из Кирены (276-194 гг. до н.э.). Древнегреческий учёный Эратосфен изобрел систему координат, покрыв свою карту сеткой из перекрещивающихся горизонтальных и вертикальных линий. Он первым ввел понятие параллели и меридиана. Немного линий было на карте Эратосфена, и нанесены они были на разном расстоянии друг от друга, все это мало походило на градусную сеть. И, тем не менее, новая страница познания Земли была открыта. Эратосфен показал на своих картах новые пути, например, путь в Индию, которым гораздо позже воспользовался Колумб.

В по­сле­ду­ю­щее время также было со­зда­но много гео­гра­фи­че­ских карт по мере от­кры­тия новых тер­ри­то­рий. Ко­неч­но, эти карты были да­ле­ки от иде­а­ла, но все равно имели огром­ное зна­че­ние и яв­ля­лись по­ка­за­те­лем про­грес­са гео­гра­фи­че­ских зна­ний.

В средние века (V-XV вв.) в Европе, учения античных ученых уничтожались христианской церковью как “языческие”. Однако в это время были открыты большие территории в разных уголках земного шара.

В 1271-1295 гг. итальянский купец и путешественник Марко Поло (1254-1324) совершил путешествие через Центральную Азию в Китай, где прожил около 17 лет. Находясь на службе у монгольского хана, он посетил разные части Китая. Он первым из европейцев описал Китай. Но его современники книгу сначала не приняли и к ее содержанию отнеслись с недоверием, зато позже она служила одним из основных источников для составления карты Азии.

К серии подобных путешествий следует отнести и путешествие русского купца Афанасия Никитина. С торговыми целями он отправился в 1466 г. из г.Твери по Волге до Дербента, пересек Каспийское море и через Персию достиг Индии. На обратном пути, через три года, он вернулся через Персию и Черное море. Записки, сделанные Афанасием Никитиным во время путешествия, известны под названием “Хожение за три моря”. Они содержат сведения о населении, хозяйстве, религии, обычаях и природе Индии.

Мор­ские пу­те­ше­ствия были очень опас­ны, но купцы, бо­га­тев­шие на за­мор­ской тор­гов­ле, и за­во­е­ва­те­ли, хо­тев­шие при­со­еди­нить новые тер­ри­то­рии, от­прав­ля­ли одну экс­пе­ди­цию за дру­гой.

В пе­ри­од Ве­ли­ких гео­гра­фи­че­ских от­кры­тий в Гер­ма­нии был со­здан пер­вый гло­бус. При­ме­ча­тель­ным яв­ля­ет­ся тот факт, что на нем не были изоб­ра­же­ны тер­ри­то­рии Се­вер­ной и Южной Аме­ри­ки, так как ле­ген­дар­ное пу­те­ше­ствие Хри­сто­фо­ра Ко­лум­ба еще было в бу­ду­щем.

Вер­сия Ари­сто­те­ля о том, что Земля имеет форму шара, окон­ча­тель­но под­твер­ди­лась толь­ко в 1522 году, когда кру­го­свет­ная экс­пе­ди­ция Ма­гел­ла­на пе­ре­сек­ла Тихий океан.

В XVII веке была от­кры­та Ав­стра­лия.

Ан­тарк­ти­да была от­кры­та 16 (28) ян­ва­ря 1820 года рус­ской экс­пе­ди­ци­ей под ру­ко­вод­ством Фад­дея Бел­линсгау­зе­на и Ми­ха­и­ла Ла­за­ре­ва, ко­то­рые на шлюп­ках «Во­сток» и «Мир­ный» по­до­шли к ма­те­ри­ку.

Имена пер­во­от­кры­ва­те­лей, ис­сле­до­ва­те­лей со­хра­ни­лись на гео­гра­фи­че­ских кар­тах, их име­на­ми на­зва­ны раз­лич­ные гео­гра­фи­че­ские объ­ек­ты (на­при­мер, ост­ров Кука, море Лап­те­вых, Ма­гел­ла­нов про­лив и т.д.).

Сей­час от­кры­ты все ма­те­ри­ки, ост­ро­ва, моря, оке­а­ны, и Земля видна как на ла­до­ни из кос­мо­са. В на­сто­я­щее время про­ис­хо­дит более по­дроб­ное изу­че­ние по­верх­но­сти пла­не­ты, дна оке­а­на, внут­рен­них ча­стей Земли, изучение кли­ма­ти­че­ских яв­ле­ний с по­мо­щью со­вре­мен­ных при­бо­ров и зна­ний. При изу­че­нии Земли ак­тив­но при­ме­ня­ют­ся не толь­ко гео­гра­фи­че­ские ме­то­ды и зна­ния, но и до­сти­же­ния мно­гих дру­гих наук.

1. 3. Взаимосвязь географии и математики.

Необходимость применения математики в географии возникла потому, что со времен возникновения человеческой цивилизации увеличивалось количество человеческих открытий, осваивались новые земли, строились города, и поток географической информации все увеличивался. Он охватывал множество стран, городов, народов, все части и явления природы, население, культуру и многое другое, и становился огромным и необозримым. Тогда на помощь географам пришла математика.

Первые опыты применения математики в географии, как отмечают исследователи, относятся к временам древнегреческих ученых Фалеса Милетского и Эратосфена. Так называемая, математическая география в те древние времена занималась вычислением параметров Земли как планеты, расчетом ее форм и размеров. На карте, созданной Эратосфеном, мы можем видеть вертикальные и горизонтальные линии - это меридианы и параллели.

Параллели и меридианы – это воображаемые линии на поверхности Земли, они проходят через любую точку поверхности Земли. Любая точка на Земле – это пересечение параллели и меридиана и она имеет свои координаты. Немного линий было на карте Эратосфена, и нанесены они были на разном расстоянии друг от друга, мало походя на современную градусную сеть. И, тем не менее, новая страница познания Земли была открыта.

Эратосфен показал на своих картах новые пути, например, путь в Индию, которым гораздо позже воспользовался Колумб. Сегодня мы не представляем нашу жизнь без географических координат. Координаты задает капитан в навигационной системе корабля, летчик в самолете, водитель в своем автомобиле пользуется навигатором.

Я упомянул о картах и координатах, но как человек научился наносить географические объекты на карту, ведь их размеры так отличаются друг от друга, а язык карты должен быть точным. И здесь на помощь людям приходит математика. Мы видим это из научного определения карты, которое гласит: «Карта – это уменьшенное, обобщенное изображение поверхности, построенное по математическому закону на плоскости и показывающее посредством условных знаков размещение и свойства объектов».

Для изображения географических объектов на карте применяется масштаб. Масштаб был придуман ещё до нашей эры Евклидом, а полное определение “масштаба” звучит так: «Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом». Масштаб (от немецкого - мера и Stab - палка) - это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности. Масштаб — это дробь, у которой в числителе единица, а знаменатель — число, указывающее, во сколько раз расстояние на карте меньше, чем сама местность.

Приведу простой пример: Итак, нам нужно изобразить на тетрадном листе реку длиной 30 км. «Но она же не поместиться!» - скажете вы. Поместиться, если мы применим масштаб. Выберем масштаб 1: 1 000 000, что означает, что в 1 см – 10 км, значит 1 см тетрадного листа соответствует 10 км реки. Теперь мы можем изобразить реку в тетради. На тетрадном листочке её длина будет составлять 3 см. Поместилась? Так при помощи МАСШТАБА поместились на наши карты - все реки, горы, моря и океаны нашей планеты. И помогла в этом людям МАТЕМАТИКА.

В средние века и во времена Великих географических открытий люди больше занимались землеописанием, связанным с открытием новых мест на планете Земля. И если в данный период и можно указать на ряд опытов применения математических методов в географии, то это скорее случайности, нежели закономерный процесс вхождения математики в географию.

Но уже, в начале XX в. появилась научная основа применения математики в географии. Появились ученые, которые серьезно работали в этой области. Чем они занимались? Они проводили статистические наблюдения, т.е. собирали сведения о каком-либо явлении, затем эти сведения обрабатывали при помощи математических формул. Таким образом, вырисовывалась картина закономерности многих явлений и процессов в географии.

Такую картину сейчас называют – «математическая модель». Это отображение географических явлений математическими формулами. Математические модели хорошо показывают, как с течением времени изменяются наблюдаемые географические явления. Модели позволяют «проигрывать» возможные ситуации развития какого-либо явления и получать самое лучшее решение, а также делать прогнозы. Такое математическое моделирование очень помогает при наблюдении за вулканами, землетрясениями, наводнениями и другими объектами. В настоящее время в географии используются достаточно сложные методы математического моделирования.

Сегодня наша жизнь очень быстро развивается, информации становится все больше и больше. Однажды на помощь человеку уже пришли компьютеры. Географы уже изучают землю, не путешествуя по морям и суше, а при помощи космических аппаратов. Человечество построило множество заводов и фабрик, нефтепроводов и газопроводов. А вся эта могучая техника воздействует на окружающую среду, нарушая нашу экологию. Чтобы разобраться во всех этих процессах, нужно наблюдать и понимать, как раз­вивается эта большая система ПРИРОДА-ЧЕЛОВЕК и как нам надо жить, чтобы все не испортить. И сейчас на помощь географии также приходит математика, только расчеты стали сложнее, а решение находятся быстрее, так как у человека в руках столько технических новинок.

2. Практическая часть

Приступая к работе, я задался вопросом: А знает ли кто – ни будь из моих одноклассников, что математика связана с географией»?

В связи с этим, я провел анкетирование среди учащихся 7-х классов и учителей МБОУ «Смоленская СОШ №2»

Анкета содержала следующие вопросы:

1. Связана ли математика с географией?

2. Приведите примеры такой связи

3. Можно ли изучать географию без применения математических законов?

Всего в анкетировании приняло участие 35 учеников 7-х классов и 5 учителей нашей школы.

Результаты анкетирования представлены в диаграмме, из которой видно,

что из 35 учащихся по первому вопросу:

6 человек не знают ответа (14%)

3 человека ответил нет (9%)

26 человек ответили «Да» (74%)

Все учителя 100% однозначно ответили "Да" - математика связана с географией.

На 2 вопрос Приведите примеры связи математики с географией учащиеся ответили так:

1. Площади океанов, материков

2. Абсолютная высота гор

3. Определение координат

4. Рассчитать расстояние между объектами на карте

5. Графики суточного хода температур, осадков

6. Определение масштаба

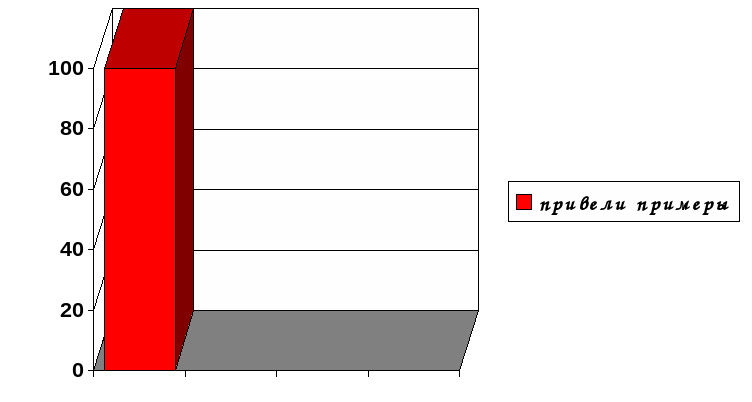
12 человек (34%) не дали ни одного правильного ответа.

23 человека (66%) привели примеры

Все учителя (100%) привели примеры связи математики с географией

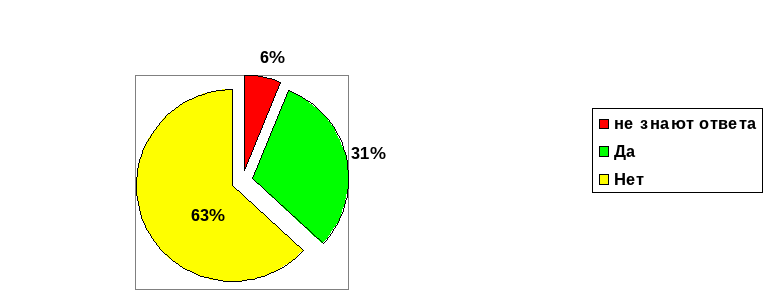
По третьему вопросу ребята ответили так:

2 человека не знают ответа (6%)

11 человек, считают что можно изучать географию без математики (31%)

22 ответили, что нельзя изучить географию без использования математических методов (63%)

Среди учителей полное согласие 100%, все уверены, что изучать географию без математики просто не возможно.

Такие результаты ответов среди учеников, ещё раз убедили меня в том, что моя работа необходима.

ЗАКЛЮЧЕНИЕ

В своей работе я постарался показать развитие математики и географии, как наук. Работая над этой темой, я постоянно находил доказательства тому, что с самых древних времён, с начала зарождения и математики и географии, эти науки были неразрывно связаны друг с другом. И сегодня, в наше высокотехнологичное время география и математика продолжают совместно работать на благо человечества.

Если бы математика тесно не сотрудничала с географией, география вообще как наука не смогла бы развиваться.

Доказательствами к этому являются такие факты:

1. Многие географические термины позаимствованы из математики

2. В географии используются простейшие основы математики

3. Все законы физики и химии сформировались в какой-то мере благодаря математике, а географии химические и физические законы помогают развиваться и занимать своё место в науках.

Пользуясь математическими знаниями, мы знаем, сколько нас на планете Земля. Больше 7 млн. человек.

В России – больше 146 000 000 человек.

В Алтайском крае – больше 2 млн. человек.

В нашей школе – больше 600 человек.

А в моем классе – 22 человека.

При помощи математики люди могут: считать и пересчитывать население земли, площади государств и городов; создавать карты; измерять высоту гор, глубину морей и океанов; определять координаты любых объектов, а значит летать на ракетах, самолетах, плавать на кораблях, ездить на автомобилях; наблюдать за погодой и делать прогнозы; изучать другие миры.

Эту работу можно продолжить: проследить как география связана с другими дисциплинами так, как все науки связаны друг с другом в большей или меньшей степени. Связи географии с другими науками довольно тесные. Особенно если речь идет о таких дисциплинах, как история, физика, химия, биология, экономика или экология.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. www.wikipedia.org

2. www.nperov.ru

3. www.activestudy.ru

4. www.youtube.com

5. www.rui-tur.r u - географический справочник.

6. www.40204s007.edusite.ru

7. www.geo-sfera.info

8. www.files.school-collection.ru

9. www.wikiversity.org

10. www.geograf-stud.ru

infourok.ru

34.Математические методы в географии.

НТР сопровождалась применением математических методов исследования во всех без исключения науках. Мат. Мышление стало важным для ученых всех специальностей, в т ч и для географов. ЭВМ постоянно совершенствуются и позволяют быстро обрабатывать разную информацию. Сильное влияние на развитие мат. Методов в географии первоночально оказало их более раннее использование в смежных науках. Стали формироваться собственные оригинальные пути исследования , когда в смежных с географией науках и в самой г. стали иполь-ся методы мат. статистики для анализа и обработки массового материала Существуют методы математической логики, которые используются при анализе основных определений науки. Мат.методы - это вспомогательное орудие, которое позволяет находить количественные закономерности, облегчает обработку научной информации. Приложение математики к географии не есть лишь подсобное средство исследования. Математика и география - сложные, целостные, обладающие внутренним единством системы. Взаимодействие математики и географии определяется изучением разных типов структур. В работах ряда географов выявляются структуры точечные, линейные и древовидные, или сетевые, стратиграфические, диффузные, зональные, региональные. Требуется еще большая работа по установлению географических структур для перехода к их исчислению на основе типологии мат. структур и раскрывающих их мат. теорий. Решение сложных задач, необходимое для географии, так же должно влиять на математику, как решение проблем , важных для техники, физики, биологии. Проблемы географии очень многогранны Мат теории оказываются слишком грубыми для географ. Систем и структур, для моделирования географических явлений и процессов.

studfiles.net

Применение математических методов в географических исследованиях

Применение математических методов в географических исследованиях

Содержание

Введение

. Теоретические аспекты изучения математизации географии

.1 Математизация географии, её причины и необходимость

.2 Современные направления применения математических методов

. Математическое моделирование в географии

. Использование математического моделирования в экономической географии

.1 Модель центральных мест В. Кристаллера

.2 Теория А. Лёша

.3 Модель изолированного государства И. Тюнена

.4 "Штандорт" промышленности Вебера

Заключение

Список использованных источников

Введение

Отношение к математическим методам в географии неоднозначно у различных исследователей. Оно колеблется от восхищенно-восторженного до непроглядно-пессимистического. Первые опыты применения математики в географии, как пишут П. Джеймс и Дж. Мартин, относятся ко временам Фалеса Милетского и Эратосфена, когда существовала и использовалась в качестве термина математическая география. Правда, в отличие от нашего времени в это понятие вкладывался несколько иной смысл. В область интересов математической географии входило решение геодезических и астрономо-геодезических задач, например вычисление параметров Земли как планеты, ее формы и другое. Средние века и даже времена Великих географических открытий не породили теорий, влекущих на путь математизации географии. И если в данный период и можно указать на ряд опытов применения количественных методов, то это скорее случайности, нежели закономерный процесс математизации географии. Но уже впервой половине XX в. сформировалась прочная основа, и появились ученые, постоянно работающие в области математизации в географии - это была статистическая обработка рядов наблюдений, а уже после второй мировой войны появились первые группы ученых, создавшие собственные школы.

Объект исследования - математические методы. Цель - изучение и применение математических методов в географических исследованиях.

Для достижения цели необходимо решить следующие задачи: охарактеризовать применение математических методов; выявить современные направления применения математических методов; обосновать применение математического моделирования в географических науках.

При написании данной работы применялись методы: описательный и метод обобщения. Основой написания курсовой работы послужили труды зарубежных ученых: А. Вебера, В. Кристаллера, А. Лёша, И. Тюнена.

1. Теоретические аспекты изучения математизации географии

.1 Математизация географии, её причины и необходимость

Математические методы не являются чем-то новым, свойственным только современному этапу развития географии. Математические методы в том или ином виде давно используются в географических исследованиях. Число, числовые характеристики - обязательный элемент географических описаний. Первые опыты, как было отмечено выше, относятся ко временам Фалеса Милетского и Эратосфена Киренского, когда существовала математическая география. В область математической географии входило решение геодезических и астрономо-геодезических задач. Конец 1950 -1960 гг. расцвет математизации. Без математических методов было не солидно издавать книги и защищать диссертации. Многие ученые видели в математизации географии одно из основных направлений развития её теории. В 1970-х годах стали появляться работы, в которых высказывались мнения о нецелесообразности и даже вредности математизации географии. Этому способствовало упрощенное описание сложных географических явлений без достаточного понимания их сути, применение математических алгоритмов без учета накладываемых ими ограничений, игнорирование традиционных для географии методов исследований и т.д.

Одним из первых в России математические методы в географические исследования стал внедрять Д.Л. Арманд. В настоящее время в географии используются достаточно сложные методы математического моделирования. Можно выделить два обстоятельства, которые первоначально обусловили стремление к математизации географии: во-первых, только математические методы позволяют придать количественных характер исследованиям, в географии накопилось большое количество фактического материала, требующего обобщения; во-вторых, только математический метод позволяет упорядочить исследования, а математический способ мышления делает исследование более объективным и достоверным.

Современная математизация - процесс, связанный с НТР, принесший во все науки ускорение сбора и обработки информации, улучшение методов ее хранения и способов объективизации полученных выводов.

В настоящее время математические методы активно привлекаются для географического прогноза. Эти методы делают прогнозы более объективными и достоверными. Существует ряд трудностей, не позволяющих широко использовать математические методы в географии:

1.Природные системы, явления, протекающие в них, представляют сложные динамические системы со множеством прямых и обратных связей, описать которые математическим языком достаточно трудно.

2.Слабая формализация понятий и терминов, используемых в исследовании. математизация география вебер тюнен

3.Отсутствие достаточной математической подготовки у специалистов географов.

.Необходимо пом

www.studsell.com

Реферат - Математическая основа карт

При изображении физической поверхности Земли на карте (плоскости) ее вначале проектируют отвесными линиями на уровенную поверхность (рисунок 74) а затем уже по определенным правилам это изображение развертывают на плоскость.

При изображении небольшого участка земной поверхности соответствующий участок уровенной поверхности принимают за горизонтальную плоскость и, спроектировав на нее этот участок, получают топографический план местности. Геометрическая сущность такого изображения заключается в следующем. Если из каждой точки какой-нибудь прямой АВ (рисунок 75), произвольно расположенной в.пространстве, опустить перпендикуляр на горизонтальную плоскость Р. (плоскость проекций), то точки пересечения перпендикуляров с плоскостью составят прямую ab которая и будет; плановым изображением прямой АВ. Изображение в плане точек и линий земной поверхности называется их горизонтальным, приложением или горизонтальной проекцией.

В том случае, когда проектируемая линия горизонтальна, ее изображение в плане равно длине самой линии. Если проектируемая прямая наклонна, то ее горизонтальное проложение всегда короче ее длины и уменьшается с увеличением угла наклона. Горизонтальное проложение вертикальной линии представляет точку.

Рисунок 74 – Проектирование физической поверхности Земли на уровенную поверхность

Рисунок 75 – Горизонтальное проложение (изображение в плане) точки, прямой, ломаной, и кривой линий.

При создании карты на нее наносят в заданном масштабе, то есть с определенным уменьшением, горизонтальные проложения всех-точек местности, линий, контуров, проектируя их на уровенную поверхность Земли, которую в пределах листа карты принимают за горизонтальную плоскость. На местности все линии, обычно наклонны, а, значит, их Горизонтальные проложения всегда короче самих линий.

Сущность картографических проекций. Сферическую поверхность развернуть на плоскости без разрывов и складок невозможно, то есть ее плановое изображение на плоскости нельзя представить без искажений, с полным геометрическим подобием всех ее очертаний. Полного подобия спроектированных на уровенную поверхность очертаний островов, материков и различных объектов можно, добиться лишь на шаре (глобусе). Изображение поверхности Земли на шаре (глобусе) обладает равномасштабностью, равноугольностью и равновеликостью.

Эти геометрические свойства одновременно и полностью сохранить на карте невозможно. Построенная на плоскости географическая сетка, изображающая меридианы и параллели, будет иметь определенные искажения, поэтому будут искажены изображения всех объектов земной поверхности. Характер и размеры искажений зависят от способа построения картографической сетки, на основе которой составляется карта.

Отображение поверхности эллипсоида или шара на плоскости называется картографической проекцией. Существуют различные виды картографических проекций. Каждому из них соответствуют определенная картографическая сетка и присущие ей искажения. В одном виде проекции искажаются размеры площадей, в другом – углы, в третьем – площади и углы. При этом во всех проекциях без исключения искажаются длины линий.

Картографические проекции классифицируют по характеру искажений, виду изображения меридианов и параллелей (географической сетке) и некоторым другим признакам.

Рисунок 76 – Карта мира в равноугольной проекции

По характеру искажений различают следующие: картографические проекции:

— равноугольные, сохраняющие равенство углов между направлениями на карте и в натуре. На рисунке 76 показана карта мира, на которой картографическая сетка сохраняет свойство равноугольности. На карте сохранено подобие углов, но искажены размеры площадей. Например, площади Гренландии и Африки на карте почти одинаковы, а в действительности площадь Африки примерно в 15 раз больше площади Гренландии;

— равновеликие, сохраняющие пропорциональность площадей на карте соответствующим площадям на земном эллипсоиде. На рисунке 77 показана карта мира, составленная в равновеликой проекции. На ней сохранена пропорциональность всех площадей, но искажено подобие фигур, то есть отсутствует равноугольность.

Взаимная перпендикулярность меридианов и параллелей на такой карте сохраняется только по среднему меридиану:

— равнопромежуточные, сохраняющие постоянство масштаба по какому-либо направлению;

— произвольные, не сохраняющие ни равенства углов, ни пропорциональности площадей, ни постоянства масштаба. Смысл применения произвольных проекций заключается в более равномерном распределении искажений на карте и удобстве решения некоторых практических задач.

По виду изображения сетки, меридианов и параллелей картографической проекции подразделяются на конические, цилиндрические, азимутальные и др. Причем в пределах каждой из этих групп могут быть разные по характеру искажений проекции (равноугольные, равновеликие).

Рисунок 77 – Карта мира в равновеликой проекции

Геометрическая сущность конических и цилиндрических проекций заключается в том, что сетка, меридианов и параллелей проектируется на боковую поверхность конуса или цилиндра с последующим развертыванием этих поверхностей в плоскость. Геометрическая сущность азимутальных проекций заключается в том, что сетка меридианов и параллелей проектируется на плоскость, касательную к шару в одном из полюсов или секущую по какой-либо параллели.

Картографическую проекцию, наиболее подходящую по характеру, величине и распределению искажений для той или иной карты, выбирают в зависимости от назначения, содержания карты, а также от размеров, конфигурации и географического положения картографируемой территории. Благодаря картографической сетке все искажения, как бы велики они ни были, сами по себе не влияют на точность определения по карте географического положения (координат) изображаемых на ней объектов. В то же время картографическая сетка, являясь графическим выражением проекции, позволяет при измерениях по карте учитывать характер, величину и распределение искажений. Поэтому любая географическая карта представляет собой математически определенное изображение земной поверхности.

www.ronl.ru

Смотрите также

• 
  Лао цзы философия реферат
• 
  История развития иммунологии реферат
• 
  Закономерности развития науки реферат
• 
  Горизонт реферат 3 класс
• 
  Экономика древнего рима реферат
• 
  Судебник 1497 года реферат
• 
  Смысл жизни счастье реферат
• 
  Реферат эпоха петра великого
• 
  Реферат способы улучшения памяти
• 
  Реферат особенности японского менеджмента
• 
  Проблема развития памяти реферат