dok.opredelim.com

Компьютерное моделирование в фармакологии - bioinformatics.ru

Обновлено 26.07.2010 Автор: Administrator

Введение

С самого начала научного подхода к познанию окружающего мира, математические модели использовались, чтобы придать нашим идеям простую и точную форму с целью предсказывать события в постоянно изменяющемся окружении. Физические науки достигли значительных успехов прежде всего с использованием количественных моделей в научном методе как средства для формулирования гипотез.

Методы, которые разрабатываются для применения математических моделей биологических систем в компьютерных имитационных исследованиях, позволяют выдвигать гипотезы относительно физиологии, фармакологии, и токсикологии живых систем. Также становится возможным экстраполировать результаты полученные в экспериментах на клетках и тканях in vitro на контекст всего организма. Оснащенные современной вычислительной техникой математические модели, имитирующие физиологические и фармакологические процессы используются для теоретических проверок гипотез относительно влияния локальных физиологических и фармакологических эффектов на организм в целом. Построенная модель служит в качестве объекта исследований для исследователей заинтересованных в изучении возможных эффектов фармакологических или токсичных субстанций. Таким образом, удается избежать избыточных экспериментов над лабораторнымив животными.

Математическое моделирование и анализ систем успешно используются в фармакологии и физиологии с целью лучше понять и выразить количественно идеи о взаимодействиях происходящих среди сложнейших биосистем. Такие модели часто служат как средство формального построения гипотез относительно предлагаемых механизмов физиологического функционирования. Использование гипотез в компьютерных имитационных исследованиях может дать понимание взаимодействий физиологических переменных, которое может не быть интуитивно очевидным.

Одной из главной целей всемирных организаций по охране животных является уменьшение количества подопытных животных используемых в медико-биологических исследованиях. Хотя вряд ли когда-нибудь компьютерные имитационные модели полностью заменят эксперимент на животном, они могут послужить в качестве средств для рационального планирования исследований проводимых на лабораторных животных. Рациональное исследование может быть выполнено с использованием алгоритма такого как, например, изображенного на рисунке.

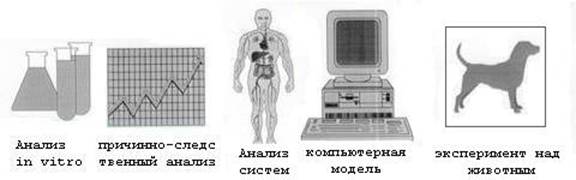
В предлагаемой схеме есть постоянное взаимодействие между информацией полученной из исследований in vitro, теоретическими соображениями, и обобщениями на уровне целого организма. Результаты экспериментов in vitro сначала переводятся в зависимости доза-ответ или в причинно-следственные отношения для органа или клеток. Эти отношения затем экстраполируются на уровень организма в целом с использованием математических моделей. Модели реализуются и изучаются с помощью компьютеров в имитационных исследованиях с целью предсказать динамические результаты in vivo исследований системы в целом. Запланированные эксперименты над животными могут сначала быть выполнены теоретически, чтобы протестировать целостность предлагаемых протоколов опытов и выявить потенциальные пробелы перед тем как лабораторные животные будут использованы. Этот метод также позволяет исследователю который не участвует в in vivo исследовании перевести результаты его или ее исследований на уровень организма.

Приведем несколько обоснований применения математического моделирования в фармакологии.

1. Математическое моделирование и компьютерная симуляция позволяют теоретически оценить и количественно измерить воздействие на весь организм в целом препарата, фармакологическое или токсическое воздействие которого измерено в экспериментах над клеткой, тканью или органом.

2. Модели позволяют теоретически определить возможные токсические эффекты препарата на органы и системы, на которые препарат напрямую не влияет, но которые могут быть косвенно затронуты из-за сложных и неочевидных взаимодействий присущих биологическим системам. Часто наиболее существенные токсические побочные эффекты препарата не обусловлены системой, непосредственно подвергающейся лечению. Только комплексный и всеобъемлющий подход с широкомасштабным моделированием может предсказать возможные побочные эффекты.

3. В некоторых случаях только компьютерный эксперимент, основанный на реальных данных, может быть запущен на сколь угодно длительное время, и позволяет предсказать побочные эффекты вещества которые проявятся только в будущем. Такие долгосрочные исследования токсических эффектов часто сложны для проведения над животными из-за своей продолжительности или из-за неоправданных страданий, причиняемых подопытным животным.

4. Компьютерное моделирование позволяет косвенно рассчитать влияние препарата на такие физиологические параметры, которые трудно или невозможно измерить напрямую.

В настоящее время математические модели и компьютерное моделирование еще не могут полностью вытеснить экспериментирование на подопытных животных в медико-биологических исследованиях. Обсуждается ряд теоретических и философских вопросов относительно их применения в биологических работах и по-прежнему существует много белых пятен в нашем понимании того, как функционирует организм, которые не разрешимы без реальных экспериментов над подопытными животными. Но по мере того как увеличивается наше знание о функционировании биологических систем, компьютерные модели усложняются, становятся более детализированными и все лучше отражающими реальные процессы.

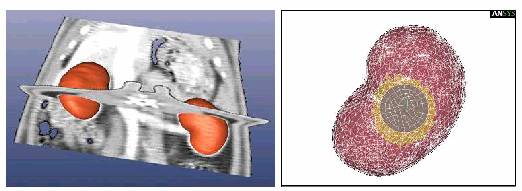
Создание 3D-модели почки крысы

Для создания функционирующих компьютерных моделей для физиологических и фармакологических приложений требуется

1. разработка соответствующего математического аппарата для описания моделируемых процессов

2. реализация этой модели на языке программирования или с применением электронных таблиц.

План моделирования должен включать в себя описания аппаратных средств и программного обеспечения использованного для разработки моделей, методику выполнения моделирования. Обычно следует более детализированно планировать применение "доморощенного" программного обеспечения чем для широко известных коммерчески-доступных программных продуктов. Рассмотрим подробнее некоторые специальные вопросы, имеющие отношение к моделированию.

1. Генерирование псевдослучайных чисел

Суть моделирования методом Монте-Карло состоит в возможности генерировать произвольные случайные числа. Важно отметить, что под словом “случайные” в компьютерном моделировании понимается нечто отличное от того, что мы вкладываем в это понятие в повседневной жизни. Случайные числа могут быть либо “истиными” случайными числами, которые основываются на аппаратных средствах (например, шум полупроводникового диода), или “псевдо-случайными“, которые генерируются компьютерной программой. Почти все статистические пакеты и языки программирования включают в себя генераторы псевдо-случайных чисел (RNGs – Random Number Generators), использующие тот или иной алгоритм для генерации чисел, которые ведут себя подобно “истиным” случайным числам выбранным из однородного распределения. Генератор случайных чисел, использующийся в фармакологическом моделировании должен быть соответствующим образом протестирован.

Повторение случайных последовательностей чисел или других паттернов может привести к моделированию, которое не представляет адекватно стохастическую природу индивидуумов в пределах исследуемой выборки (и событий в пределах испытаний). Генераторы псевдо-случайных чисел имеют недостаток в том, что они являются циклическими и при достаточном числе обращений дают повторяющиеся последовательности. Периодом генератора псевдо-случайных чисел называется количество вызовов, которые могут быть сделаны прежде, чем генератор повторит последовательность еще раз. Использующийся в фармакологическом моделировании генератор должен иметь период по крайней мере порядка квадрата количества вызовов. Таким образом, RNG, использующий модуль около 2**31 может не иметь достаточную "произвольность" для клинического моделирования.

2. Генерирование величин распределенных по определенному закону

Как только сгенерированы равномерно распределенные случайные величины, они должны быть трансформированы в соответствующее стохастическое распределение. Как минимум, общие имитационные пакеты программ должны включать нормальное, лог-нормальное, бета-, и пуассоновское распределения, способность создавать распределения из совокупности равномерно распределенных переменных. Также может потребоваться генерация соответствующих многомерных распределений.

3. Решение дифференциальных уравнений

Для описания детерминированных изменяющихся во времени явлений, большинство разработчиков компьютерных моделей в фармакологии используют дифференциальные уравнения (ДУ). Применение аппарата дифференциальных уравнений позволяет в максимальной степени “обобщить” программу, даже если нет необходимости использовать дифференциальные уравнения для всех моделирований. Использование ДУ делает код, который реализует данную подзадачу, более удобочитаемым, но и требует больших вычислительных затрат. Линейные системы могут иметь явные решения, которые могут затем быть модифицированы с использованием линейных операторов, с целью решить проблему аналитически. Например, используя однокомпартментные модели и принцип суперпозиции, можно сгенерировать профиль зависимости концентрации препарата в плазме крови при многократных инъекциях. Главное преимущество аналитического решения уравнений – скорость вычислений. Методы решения дифференциальных уравнений медленнее, чем методы для решений уравнений, заданных в явном виде. Если моделируемая динамическая система - нелинейная (и эта нелинейность имеет значение в имитировании, что обычно случается в “реальной” жизни), то аппарат дифференциальных уравненийо должен быть безусловно использован. Следствием этого является резкое увеличение вычислительных затрат.

Выбор метода для решения дифференциальных уравнений зависит от конкретной проблемы. Если интервал интегрирования достаточно большой (как это бывает в обычных случаях моделирования), тогда требуемая точность может быть получена с использованием метода Рунге-Кутты или метода Адамса с адаптацией 4-го порядка. Если отношение самой большой константы к самой маленькой достаточно велико (например, в фармакокинетическом моделировании с использованием компартментов), или если есть медленно и быстро изменяющиеся компоненты в пределах системы, то эта система требует очень специфических алгоритмов для ее решения, таких как, например, алгоритм Gear или Livermore Solver. Поскольку клиническое моделирование явно изучает эффект изменчивости, вероятно будут наблюдаться предельные величины параметра, поэтому часто следует использовать методы устойчивого (робастного) интегрирования. В любом случае, рекомендуется выполнять предварительную проверку того, что используюется адекватный задаче метод решения ОДУ. В некоторых случаях подходящая аппроксимация может существенно уменьшить вычислительные проблемы.

4. Требования к компьютеру

Быстрый центральный процессор CPU (чем быстрее, тем лучше) может быть необходим для того, чтобы выполнить имитационный проект в течение разумного периода времени, совместимого с графиками разработки лекарства. Имитационные исследования методом Монте-Карло обычно требуют большие размеры памяти и возможности хранения данных. Несколько пробных моделирований, каждое с использованием тысячи повторений, могут легко занять вплоть до сотен мегабайт дисковой памяти. Требуемый размер оперативной памяти (RAM) обычно должен быть достаточным для манипулирования массивами данных этого размера. Для настоящих моделирований фармакоцевтические компании применяют многопроцессорные сервера, работающие месяцами напролет.

Реализация

Стандартным способом реализации математической модели на компьютере является написание специальных программ на языках BASIC, C/C++, Delphi или даже на JavaScript. Однако это довольно трудоемкий способ, т.к. приходится писать большое количество программного кода, не относящееся непосредственно к конкретной модели. К достоинствам метода можно отнести то, что весь процесс моделирования контролируется непосредственно исследователем.

Альтернативный вариант – использование электронных таблиц, которые поддерживают итеративное решение уравнений. Здесь мировым стандартом является Microsoft Excel.

Для серьезного моделирования с применением сложных математических выкладок более целесообразно использование специальных математических пакетов. Наиболее популярны – Matlab, Mathematica, MathCAD, Maple. Их особенностью является богатейший арсенал математических методов, изощренная компьютерная графика и пользовательский интерфейс. Однако и здесь надо быть готовым к написанию программ на встроенных языках программирования.

Необходимо иметь в виду, что существует потенциальная трудность со всеми вышеописанными методами компьютерного моделирования: полученные результаты могут очень сильно зависеть от использованных в модели уравнений. В случае, когда уравнения известны из неких исходных принципов (например, альвеолярное газовое уравнение, закон сохранения вещества) это не должны быть препятствием, но если уравнение является эмпирическими, то использование альтернативных моделей может привести к совершенно другим результатам. Одним из примеров является уравнение для кривой диссоциации гемоглобина, для которого известно множество различных формулирово

Существуют также опасности допущения ошибок либо при построении математической модели, либо ошибки при программировании, особенно если реализацией модели занимается непрофессиональный программист. В таких случаях возможно появление эффектов, которые вовсе не имеют под собой фармакологического обоснования. Необходимо отделять такие эффекты от действительных предсказаний корректно построеной и реализованной модели.

В тех случаях когда существует более чем одно установленное уравнение для описания фармакологического отношения, исследователь может задаться целью изучить эффект влияния выбора уравнения на поведение модели. Если существуют несколько уравнений, которые все хорошо представляют основные данные, то выбор уравнения должен обычно не должен иметь сильно влиять на полученные результаты. Проводя виртуальные эксперименты в течение нескольких дней (или даже нескольких часов) экспериментатор может получить значимую информацию о взаимодействии нескольких физиологических переменных, при условии, что связи, описывающие эти переменные будут выражены в форме уравнения. С другой стороны, фактическое реальное экспериментирование требует времени, финансирования и усилий, которые могут быть не всегда возможными.

Если исследователь принимает эти базисные принципы, то полученные результаты должны также быть заслуживающими доверия (при условии, что проект модели и реализация была сделана правильно). В этом отношении существуют, по крайней мере, четыре пункта:

1. Насколько “разумные” уравнения использованы в модели?

2. Выражают ли уравнения какой-либо известный фармакологический принцип?

3. Как точно уравнения описывают данные, на которых они основаны?

4. Правильно ли модель была разработана и реализована?

Положительные ответы на каждый из вопросов должны быть получены еще до формулирования результатов моделирования.

Виртуальные больные

Компьютерные технологии достаточно широко распространены в немедицинских исследованиях. Различные ситуации в климатологии и геологии моделируются с помощью компьютеров, инженеры проектируют сложные конструкции, используя математическую симуляцию чаще, чем создание и тестирование реальных прототипов. Только в области науки, связанные с изучением человека, компьютерные технологии продвигались очень медленно. Однако ситуация меняется на глазах, и электронно-вычислительная техника находит все более широкое применение в биомедицинских исследованиях.

Билл и Аллен - пациенты, страдающие бронхиальной астмой. Несмотря на то, что они ни разу не были на приёме у врача, на зависть другим больным они имеют возможность использовать новейшие препараты и методики для лечения своей болезни. Правда, в ходе лечения их состояние может значительно ухудшиться, и они могут даже умереть, но эта проблема поправима и решается она всего лишь одним щелчком компьютерной "мышки", а все потому, что Билл и Аллен - пациенты виртуальные. Работа с такими электронными больными способна заменить собой крупные дорогостоящие исследования, позволяет испытывать препараты, которых даже ещё не существует в природе, не говоря уже о специальном разрешении на их применение у человека.

Так же, как и настоящие, виртуальные больные могут по-разному воспринимать назначенное лечение. Точное знание различий между электронными пациентами позволяет лучше учесть влияние большинства важных факторов на течение болезни и развитие осложнений.

Поскольку бронхиальная астма - очень сложное и не до конца изученное заболевание, в основе моделей виртуальных пациентов лежат различные взгляды на его патогенез, выбранные экспериментаторами. Так, при создании Билла использовали гипотезу о том, что сигнальная молекула интерлейкин-5 избыточно стимулирует клетки иммунной системы - эозинофилы, которые активируют процессы воспаления, приводящие в конечном итоге к приступу астмы. У Аллена же активация болезни происходит в том случае, когда макрофаги приводят к нарушению проходимости дыхательных путей.

Билл и Аллен были специально созданы для проверки возможности использования блокаторов интерлейкина-5 в лечении и профилактике приступов астмы. Оказалось, что при воздействии виртуальных аллергенов и без лечения приступ астмы у Билла продолжался более длительное время, чем это обычно бывает у реальных больных. Данный факт навёл экспериментаторов на мысль, что механизм астмы Билла, судя по всему, не является отражением действительности. Поскольку же симуляция введения блокатора интерлейкина-5 предотвращала развитие приступа у Билла, но не была эффективной у Аллена, чья модель ближе к реальности, фармацевтическая компания прекратила разработку таких препаратов для лечения астмы.

В то же время стоит обратить внимание на то, что любая модель не является совершенной. Чем глубже представления о проблеме, тем ближе симуляция реальности, но при полном отсутствии понимания смоделировать интересующую ситуацию практически невозможно.

Лабораторные животные в фармакологии

Лабораторные животные наиболее часто используются в следующих областях: медико-биологические эксперименты, испытания на безопасность и в образовательных целях. Исследователи используют животных в попытке понять различные уровни функционирования организма, его болезни и физиологическое состояние, создать новые вакцины и методы для лечения различных заболеваний. Такие исследования не направлены исключительно на заболевания человека, они также развивают ветеринарию.

Промышленность использует животных для тестирования безопасности и эффективности широкого ряда потребительских продуктов, включая фармакологические препараты, косметику, средства для ведения домашнего хозяйства, пестициды, различные химикалии и т.д.

В естественнонаучном образовании животные используются повсеместно – как часть обучающего процесса. Студент обязательно сталкивается со вскрытием лягушек и червей при изучении биологии, более тонкие методы используются при подготовке ветеринаров.

Во всех этих случаях, животные подвергаются насилию и боли в той или иной степени, что не является естественной частью их среды обитания. Поэтому мы должны быть заинтересованы в поиске новых альтернатив использованию животных в экспериментах, стараться уменьшить число животных, по возможности максимально облегчить их страдания.

Альтернативные методы делятся на 3 класса: замена, уменьшение, уточнение (в англоязычной литературе это называется правилом трех R: Replacement, Reduction, Refinement).

Замена использования животных включает в себя методы, в которых животные не используются совсем (абсолютная замена) или методы, в которых применяются ткани и клеточные культуры (относительная замена). При этом часто происходит отказ от методов in vivo в пользу методов in vitro.

К сожалению, абсолютная или относительная замена лабораторных животных не всегда возможна. Некоторые важные исследования (по крайней мере, в настоящее время) не могут быть произведены без использования животных. В таких случаях исследователи стараются уменьшить число животных, задействованных в эксперименте. Тщательное планирование эксперимента и применение современных методов статистического анализа данных часто позволяют существенно сократить число подопытных животных, сохраняя при этом значимость окончательного результата.

Компьютер в фармакологическорм образовании

Фармакология изучает взаимодействие живых организмов и химических агентов. Бесспорно, практические занятия являются одной из важнейших составляющих медико-биологического образования. Эксперименты in vivo и in vitro широко используются, чтобы помочь студентам в приобретении практических экспериментальных навыков, однако не менее важной задачей является закрепление и осмысление фактического материала, полученного на лекциях, семинарах, и из учебников. Хотя применение лабораторных животных для этой цели стало традицией, у этого подхода есть свои недостатки. Попробуем перечислить некоторые из них:

- постановка эксперимента достаточна сложна и подчас требует значительных затрат времени.

- из предыдущего пункта следует, что для данного промежутка времени может быть проверено только ограниченное число препаратов

- эксперимент может быть ресурсоемким, и экономические соображения могут оказаться превалирующими в организации исследования

- эксперимент на животных всегда сопряжен с морально-этическими ограничениями, тема которых также обсуждается в настоящем реферате.

Компьютерное моделирование, применяемое в медицинском образовании, может быть разбито на следующие категории:

- компьютерные текстовые симуляторы

- компьютерные графические симуляторы

- симуляторы с использованием манекенов

- симуляторы виртуальной реальности

Рассмотрим несколько подробнее каждый из классов.

Текстовые симуляторы создают словесное описание ситуации, в которой пользователь выбирает один из нескольких предопределенных ответов. Основываясь на полученном ответе, компьютер генерирует следующую ситуацию. Например, в ситуации, когда пациент жалуется на постоянные головные боли, студенту могут быть предложены в качестве выбора выписать НПВС или направить пациента на компьютерную томографию. Получив информацию о действиях студента, программа создает следующий бланк, где может быть представлено уже намного больше вариантов дальнейшего выбора. Будучи основываными только на текстовом режиме, такие симуляторы относительно просты для программирования и нетребовательны к компьютерным ресурсам. Однако в настоящее время это не является препятствием и сегодня текстовые симуляторы используются относительно редко.

Графические симуляторы воссоздают на дисплее графическое изображение ситуации, часто чтобы объяснить фармакокинетические и фармакодинамические процессы связанные с приемом препарата. Обычно используется только “мышь” в качестве интерфейсного устройства. Хотя такие симуляции способствуют пониманию и усвоению материала обычно они не развивают у студентов практических навыков. Главная цель их использования состоит в объяснении неких абстрактных концепций в доступной и недорогой форме. Такие симуляторы особенно подходят для моделирования физиологических и фармакологических процессов. Примеры таких программ приводятся в следующих разделах.

A - сердечная пункция с целью извлечения крови из сердца. B - техника выполнения разреза вдоль средней линии живота. C - деформация кожи из-за тургора, создающегося мягкими тканями. D – удаление сердца. E - разрез трахеи, который облегчает удаление легкого (кадр F).

Симуляторы с использованием манекенов могут быть выполнены с различной стапенью сложности и реалистичности, но обычно всегда дороги. Передовые модели включают физическую модель человеческого тела и непрерывно регистрируют сигналы, отражающие физиологические параметры, такие как электрокардиограмма, артериальное давление, капнограмма, пульсоксиметрия и т.д. Ранние системы такого рода требовали вмешательства обучаемого для изменения поведения в соответствии с предпринимаемыми действиями. Современные варианты используют сложные компьютерные модели физиологии и фармакологии человека для автоматической генерации ответов манекеном и сигнальными отведениями. В противоположность текстовому и графическому тренажерам, использование манекенов позволяет развить некоторые практические навыки, которые впоследствии будут применяться в клинике.

Технологии виртуальной реальности начали приобретать популярность последнее время, особенно для обучения хирургов. С их помощью возможен переход от двумерного руководства к миру трехмерных имитированных больных. Принципиальная сложность существует в трудности моделирования тактильных ощущений. Тем не менне эта проблема активно разрабатывается в многочисленных научно-исследовательских центрах с привлечением микро-технологий.

Для преподавания фармакологии было разработано большое количество компьютерных программ. Тем не менее, восприятие студентами виртуальной фармакологии как альтернативы экспериментальной – вопрос не столь очевидный. В австралийском Charles Sturt University проводился эксперимент по выявлению эффективности обучения фармакологии с применением компьютеров.

Традиционно для обучения в течение года использовались лекции и практические занятия в лабораториях. Эксперимент проводился в классе, оборудованном 16 компьютерами. Студенты работали парами на компьютере, и на постановку виртуальной лабораторной работы уходило 2-3 часа. После окончания курса было проведено исследование эффективности применения компьютерного моделирования в экспериментальной фармакологии. Всего принимали участие в исследовании 75 человек и из них 74 студента отметили, что их понимание фармакологии существенно улучшилось в результате применения компьютера. При этом 100% опрошенных предпочли виртуальные эксперименты традиционным, отмечая то, что компьютерные эксперименты позволяют легче понятьфармакологические концепции и, следовательно, запомнить.

Виртуальные эксперименты, использующиеся в практике преподавания фармакологии, позволяют получать более наглядные результаты, предоставляя гибкие возможности по изменению условий постановки эксперимента. Также, компьютер позволяет значительно снизить число умертвляемых в учебных целях подопытных животных.

Важно отметить, что в проведенных компьютерных симуляциях студенты были жестко ограничены временными рамками с целью улучшения качества обучения. Было обнаружено, что студенты, которым была предоставлена возможность работать без лимита времени, обычно хуже усваивали материал.

Другой важный вывод состоит в том, что цели и задачи эксперимента должны быть четко поставлены перед студентами непосредственно до самого процесса моделирования. Обучаемые должны уже быть подготовленными по теме лабораторной работы и нет необходимости повторять теоретический материал перед практической частью. В противном случае студентам может потребоваться значительное время для выполнения всех заданий лабораторной работы.

В заключение отметим, что компьютерные симуляции оказываются выполнимыми и эффективными как основная часть практических разделов фармакологии. Основной задачей применения компьютера является повышение понимания предмета студентами. Компьютерные модели могут также послужить в качестве альтернативы использования животных в традиционных экспериментах.

Виртуальная лаборатория

В контексте получения университетского образования для нас наиболее важным является вопрос – позволяет ли виртуальная лаборатория развить в будущем исследователе те же умения, знания, навыки и отношение к эксперименту, как и настоящая лаборатория? Здесь полезно обсудить, какие же познания приобретает студент в реальной лаборатории.

Заманчиво думать о лаборатории как о месте, где развиваются лабораторные навыки, однако после некоторого раздумья можно составить длинный список из пунктов, котрые студент получает в стенах настоящей лаборатории. Например, к ним относятся изолирование кровеносных сосудов, умение правильно обращаться с подопытными животными, выработка научного подхода к проблеме, оптимальная организация работы и распределение времени, социальное общение и совместная работа с другими исследователями. Студенту необходимо осознавать то, что ему требуется приложить значительные усилия для того, чтобы соответствовать высоким мировым стандартам, стараться быть самокритичным и непредубежденным.

Тем не менее, многие из вышеперечисленных навыков и умений могут быть успешно развиты и при применении виртуальной лаборатории. Новые знания приобретаются студентом непосредственно при постановке эксперимента (с использованием моделирования различных органов и тканей), опыт применения научного подхода таким же образом может быть получен при моделировании. Такие качества как решимость и осторожность могут быть развиты при виртуальном моделировании критических ситуаций. Есть ли такие навыки, которые могут быть получены только в реальной лаборатории? Умение обращаться с подопытными животными и, например, выделение сосудов, похоже, не может быть достигнуто в виртуальной лаборатории. Трудно смоделировать на компьютере акт убийства живого существа и таким образом поставить исследователя перед моральными вопросами так же, как это происходит в реальности. Некоторые студенты верят, что они способны убить животное и верят, что они компетентны в этом, зкспериментировав перед этим лишь на пластиковых моделях или на уже убитых животных. Однако часто случается, что даже самый подготовленный студент, столкнувшись с этим, неожиданно понимает, что существует отличие между реальностью и виртуальными моделями!

Виртуальное вскрытие в виртуальной лаборатории

Свойство, которое часто выявляется только в настоящей лаборатории – это “неуклюжесть”. Некоторые студенты - прогрессивные, творческие и компетентные в виртуальных лабораториях – становятся некоординированными и рассеяными при работе без компьютера. Только в реальной фармакологичекой лаборатории они обнаруживают, что не могут применять разнообразное мышление, наблюдательность, планирование и “работу руками”, которые требуются в реальном времени для успешной постановки эксперимента in vivo. Пригодность или неприспособленность для некоторых типов реальной лабораторной работы не обнаруживается в виртуальной реальности.

Sniffy – TheVirtualRat

В качестве одного из примеров моделирования лабораторного животного можно привести известную программу Sniffy - The Virtual Rat, которая позволяет симулировать поведение настоящей крысы, но без всех недостатков использования реального животного!

Моделирование лабораторной крысы в действии - Sniffy The Virtual Rat

Программа позволяет студентам воспроизводить классические эксперименты по изучению физиологии обучения (выработка условных рефлексов и т.д.). Возможна реализация собственного плана эксперимента, использование различных стимулирующих факторов и т.д. Можно отметить продуманный пользовательский интерфейс и великолепно выполненную компьютерную графику, которая очень похоже симулирует движения реальной крысы.

Rat CVS (Cardiovascular System)

Rat CVS разработана John Dempster, University of Strathclyde.

Программа Rat CVS (для реферата была использована версия 3.2.7) моделирует эксперимент по воздействию различных препаратов на сердечно-сосудистую систему крысы. Программа позволяет регистрировать изменения системного артериального давления, давления, создаваемого в левом желудочке, венозного давления, силу и частоту сердечного сокращения. Возможно также моделирование спинальной крысы.

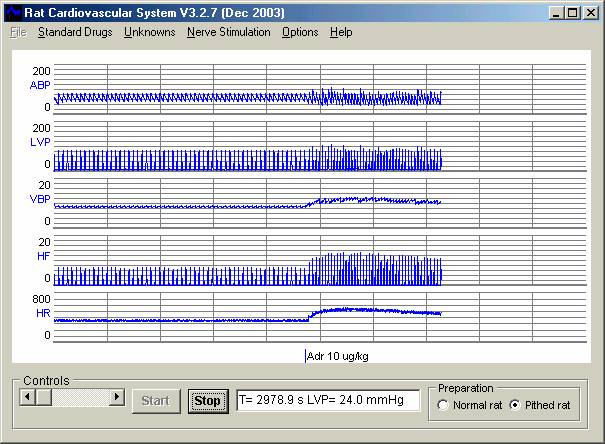
Rat CVS - введение адреналина в дозе 10 мкг/кг

 Экспериментатору возможно производить инъекции различных препаратов в требуемых дозах (дигоксин, атенолол, изопреналин, лозартан и т.д.), стимулировать нервную систему (блуждающий нерв и т.д.). Все это сопровождается визуализацией изменения параметров сердечно сосудистой системы в реальном времени.

Программа может быть использована как для обучения студентов, так и для контроля – можно “вводить” крысе неизвестные препараты с целью их определения студентом. Отдельно доступны для свободного доступа исходные файлы программы, если возникнет необходимость в изменении или дополнении модели. Модель реализована на языке программирования Object Pascal (Borland Delphi).

TheVirtualCat

 The Virtual Cat разработана John Dempster, University of Strathclyde.

Программа The Virual Cat (для реферата была использована версия 2.5.5) моделирует эксперимент по воздействию различных препаратов на сердечно-сосудистую и мышечную систему кошки. Программа позволяет регистрировать изменения системного артериального давления, частоту сердечных сокращений, силу и частоту сокращений m. tibialis.

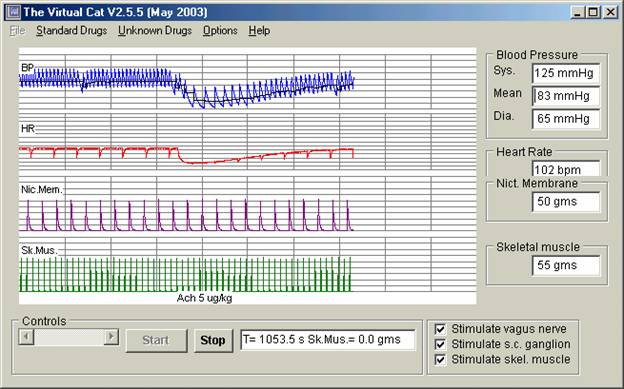
The Virtual Cat - введение ацетилхолина в дозе 5 мкг/кг

Экспериментатор может вводить широкий спектр препаратов (атропин, гистамин, морфин, тубокурарин) в необходимой дозе.

Так же, как и Rat CVS, программа Virtual Cat может быть использована и для обучения для контроля – возможен режим работы, при котором студенту необходимо определить “введенный” в кровоток или прямо в мышцу препарат.

Программа позволяет сохранять текущий эсперимент на диске в виде файла, распечатывать полученные временные зависимости, настраивать другие сервисные функции.

Литература

1. L. Wang, Сomputer-simulated pharmacology experiments for undergraduate pharmacy students: experience from an Australian university, Indian Journal Of Pharmacology, 2001

2. D.J Doyle, Simulation in Medical Education: Focus on Anesthesiology

1. Беллман Р. Математические методы в медицине. –М: Мир, 1987

2. Бейли Н. Математика в биологии и медицине. –М: Мир, 1970

3. R.Summers, S.Hudson et al, Computer Simulation Studies and Biomedical Research, Animal Welfare Information Center Newsletter, vol. 6

Начальная Windows Commander Far WinNavigator Frigate Norton Commander WinNC Dos Navigator Servant Salamander Turbo Browser Winamp, Skins, Plugins Необходимые Утилиты Текстовые редакторы Юмор		File managers and best utilites Главная » Реферат » Математика в фармакологии реферат Математика в фармацевтике. Математика в фармакологии реферат Математика в аптечном деле | Социальная сеть работников образования Слайд 1 Презентация подготовлена: ученицей 9 «Б» класса МОУ «СОШ №1 р.п. Новые Бурасы Новобурасского района Саратовской области» Тарабриной Анастасией. Руководитель: Боровикова Екатерина Ивановна . МАТЕМАТИКА НА СЛУЖБЕ МИРА И СОЗИДАНИЯ МАТЕМАТИКА В АПТЕЧНОМ ДЕЛЕ Слайд 2 ВВЕДЕНИЕ Когда мы говорим о лекарственных препаратах, то пытаемся понять истину человека и его жизни — и оценить эту истину с помощью инструментов и подходов точных наук и высокоточных технологий, применяемых в медицине: следовательно, эти инструменты и подходы являются определяющими жизнь самого человека. Главный принцип, сформулированный еще в клятве Гиппократа, остается неизменным: primum non nocere , главное — не навредить. Поэтому какими бы великолепными не были лекарственные препараты, нужно взвешивать все «за» и «против» их эффективности и безопасности . В данной работе я хочу наглядно показать как применяется математике в аптечном деле. Если изучить глубже тонкости работы аптеки, то понимаешь, насколько важна эта наука! Слайд 3 Исторически, начиная с самых древних времен, лекарства готовили в аптеках. Первыми упоминаниями об аптеке, как о месте хранения лекарств говорил Гиппократ . Наиболее прогрессивными в плане методики и систематизации научных аптечных знаний были монахи, которые работали в лабораториях и составляли специальные сборники лечебных рецептов: в них описана методика сбора, способы обработки и приемы терапевтического применения. Тогда лекари сами изучали свойства растений, минералов, продуктов животного происхождения и сами были авторами прописей, которые зачастую назывались по имени придумавшего эту пропись лекаря Естественно без математики и других наук , ничего у них не получилось бы ? Если бы они не понимали в каких дозах берется то или иное вещество яд, а в каких – лекарство, то нашему организму до сих пор бы приходилось обходиться своими силами в борьбе против вирусов, опухолей и др. болезней, а это порой очень трудно. Поэтому ещё в древности великие математики часто занимались алхимией, а алхимики прекрасно знали математику. ИСТОРИЯ АПТЕЧНОГО ДЕЛА Слайд 4 МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Математические приёмы, которые используются для анализа работы в аптеке: 1 . Какая берётся выручка и время по месяцам, при этом пик продаж приходятся на зиму . 2. Какое определяется количество заказанных препаратов их аналогов и синонимов. 3. Как определяется процент средней покупки , а именно: выручка за день, делённая на количество чеков по кассе. 4. Как ведется расчёт прибыли. 5. Как суммиру e тся стоимость нескольких товаров 6. И элементарно, как правильно выдать сдачу клиенту . Слайд 5 МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Математика прогнозирования: товары сезонного спроса в аптеке Среди большого разнообразия наименований товаров, реализуемых в аптеках, встречаются такие, которые обладают выраженными сезонными колебаниями продаж. Например, востребованность противопростудных и витаминных препаратов возрастает в осенне-зимне-весенний период, в то время как «средства от диареи» или косметика для загара в основном продаются летом. Задачи выявления сезонных колебаний спроса актуальны всегда, так как от этого инструмента управления ассортиментом и товарными запасами в немалой степени зависит эффективность любого торгового предприятия. Слайд 6 Составление отчётов о работе аптеки В ходе разработки аптеки выявилась необходимость в автоматизации ведения учетно-отчетной документации и решении задач, связанных со снабжением аптеки лекарственными средствами. В связи с этим, аптека составляет предполагаемый перечень задач, подлежащих автоматизации, которые необходимо решать начальнику аптеки. Заведующая аптекой обязана предоставлять отчёты о работе аптеки ежемесячно, и далеко не все денные и таблицы есть в компьютере. МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Слайд 7 С учетом динамики заболеваемости рекомендуется создавать противоэпидемические запасы лекарственных средств по расчетным графикам функции распределения времени. Спрос на лекарственные средства х -можно определить по формуле: Х = N·D , где N-количество заболевших, D-количество лекарственных средств на курс лечения. МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Слайд 8 МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Планирование закупок товара. Чтобы правильно составить заявку и избежать возврата товара из-за истечения его срока годности, или наоборот – нехватки товара, необходимо рассчитать сколько единиц данного лекарства в среднем уходит в неделю/в месяц, и заказать нужное количество. Анализ фальсифицированного товара. Ежемесячно нужно предоставлять отчёт по браку: рассчитывать сколько процентов от общего кол-ва товара выявлено брака. Это нужно для того, чтобы успешнее бороться с некачественным товаром. Слайд 9 Чтобы сдать выполнимый план выручки на месяц необходимо знать среднее количество покупателей в день/месяц. Неликвидный товар – ( товар , который лежит на прилавках, больше шести месяцев), нужно обязательно знать, сколько и какой это товар, чтобы больше его не заказывать. МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК Слайд 10 МАТЕМАТИКА В ОРГАНИЗАЦИИ РАБОТЫ АПТЕК В древности на латыни рецепты назывались Formula remediorum ( remedium - лекарственное средство ) или Formula medicinalis . ИЗГОТОВЛЕНИЕ РЕЦЕПТОВ В данном случае выписан рецепт на сложную комбинированную мазь. Rp .: - сокращение от латинского слова " recipe " - возьми. Далее идет список компонентов, которые необходимо взять для приготовления мази (компоненты пишутся на латинском языке в родительном падеже). Первый компонент пишется после двоеточия, все остальные компоненты - строго (!) под ним. Ментола и Новокаина - ( ana , сокращение аа с чертой над буквами) "поровну по" 0,1 г, то есть по 100 мг каждого. Раствора адреналина гидрохлорида 0,1% - капель ( guttas ) 10 (по традиции количество капель пишется римскими цифрами) Цинка оксида 1 г Ланолина 5 г - компонент основы мази как правило пишется в конце прописи Вазелина 15 г - второй компонент основы мази Misce ut fiat unguentum - Смешай, чтобы получилась мазь Da . Signa - Выдай. Обозначь. Мазь в нос. Слайд 11 Мы все прекрасно знаем, что здоровье нам необходимо! И очень часто мы можем поправить его прибегая к услугам аптек. Из всего ранее сказанного, стало ясно, что без математики многое было бы невозможно сделать в аптечной работе. А значит не все болезни лечились бы. П отому что, как бы создавались лекарства, если бы люди не могли правильно рассчитывать пропорции компонентов. ЗАКЛЮЧЕНИЕ Слайд 12 Используемые ресурсы http://www.remedium.ru/section/pharmwork/detail.php?ID=32046 http://www.google.ru/search?hl=ru&cp=6&gs_id=m&xhr=t&q=%D0%B0%D0%BF%D1%82%D0%B5%D0%BA%D0%B0&newwindow=1&bav=on.2,or.r_gc.r_pw.r_qf.&biw=1280&bih=658&um=1&ie=UTF-8&tbm=isch&source=og&sa=N&tab=wi&ei=CwN0UJP6FdL14QTUpYHgAg#um=1&hl=ru&newwindow=1&tbm=isch&sa=1&q=%D0%B0%D0%BF%D1%82%D0%B5%D0%BA%D0%B0+&oq=%D0%B0 %D0%BF%D1%82%D0%B5%D0%BA%D0%B0+&gs_l=img.3..0l10.989920.989920.2.990324.1.1.0.0.0.0.183.183.0j1.1.0...0.0...1c.1.8e04af4DNKA&pbx=1&bav=on.2,or.r_gc.r_pw.r_qf.&fp=bd51b760e89e29bd&biw=1280&bih=658 http://www.d22d.ru/load/29-1-0-714 nsportal.ru Математика в фармацевтике	Математика в фармацевтике. Цель: Выяснить нужна ли математика в моей будущей профессии. Выполнила: ученица 9 «Б» класса Василец Мария. Учитель: Гамаюнова Ирина Николаевна. Введение. Моя будущая профессия связана с медициной, а именно с аптечным делом, моя профессия – провизор. Казалось бы, не так уж и много места математике , но , если изучить глубже тонкости работы аптеки, то понимаешь, насколько важна эта наука, и без неё невозможно было бы осуществить производство и распространение лекарств. В данной работе я хочу наглядно показать где в фармацевтике нужна математика и доказать, что нельзя быть образованным и успешным человеком, абсолютно не зная этой важнейшей науки. Математика в биологии. На биологии нам рассказывают не только о строении и законах живой природы, но и учат решать генетические задачи, в которых очень важно, например, правильно вычислить процентное соотношение и определить степень влияния факторов на признаки живого организма. И также нередко применяются математические формулы в решении сложных задач. Пример задачи: Молодые родители удивлены, что у них, имеющих одинаковую (II) группу крови, появился непохожий на них ребенок с I группой крови. Какова была вероятность рождения такого ребенка в этой семье? Без математики не быть здоровью! Довольно смелое утверждение, скажете Вы. Однако, давайте подумаем, как бы учёные смогли создать лекарство, если бы не могли правильно рассчитать пропорции компонентов. Если бы они не понимали в каких дозах то или иное вещество яд, а в каких – лекарство, то нашему организму до сих пор бы приходилось обходиться своими силами в борьбе против вирусов, опухолей и др. болезней, а это порой очень трудно. Поэтому ещё в древности великие математики часто занимались алхимией, а алхимики прекрасно знали математику. изготовление лекарства по часто встречающейся прописи: Пример. Rp.: Dimedroli Ephedrini aa 0,03 Sacchari 0,25 Misce fiat pulvis Dentur tales doses N. 10 Signetur (латинский). Отвешивают 2,8 полуфабриката (состава: димедрол 0,03 + сахар 0,25) и смешивают его с 0,3 эфедрина по правилам смешивания сложных порошков. Приготовленную смесь развешивают на десять порций по 0,31. А теперь о главном: Математика в аптечном деле. В чём проявляется важность математики в аптеке? Начнём, опять-таки, с самого простого, дальше – сложнее. Итак: 1. Работа с клиентом: - суммирование стоимости нескольких товаров - выдача сдачи - вычитание % скидки, если таковая имеется. Да, вы можете сказать, что сейчас все вычислительные операции выполняет компьютер, и будете правы, но что, если он сломался, а работать-то надо. 2. Приём товара, наценка товара. 2. Приём товара, наценка товара. Иногда требуется проверять данные, занесённые в компьютер, ведь машины тоже ошибаются. 3. Составление отчётов о работе аптеки: кол-во заказанного товара, кол-во реализованного товара, средний чек и т.п. Заведующая аптекой обязана предоставлять отчёты о работе аптеки ежемесячно, и далеко не все денные и таблицы есть в компьютере. 4. Ежедневный расчёт выполнения месячного плана. 4. Ежедневный расчёт выполнения месячного плана. Каждой аптеке даётся индивидуальный план выручки на месяц и нужно ежедневно следить за его выполнением. 5.Анализ рентабельности. Для повышения рентабельности аптеке необходим постоянный анализ всей хозяйственной деятельности . Анализ проводится ежемесячно, но можно и чаще. Коэффициент рентабельности рассчитывается как отношение прибыли к активам. 6. Планирование закупок товара. 6. Планирование закупок товара. Чтобы правильно составить заявку и избежать возврата товара из-за истечения его срока годности, или наоборот – нехватки товара, необходимо рассчитать сколько единиц данного лекарства в среднем уходит в неделю/в месяц, и заказать нужное количество. 7. Анализирование фальсифицированного товара. Ежемесячно нужно предоставлять отчёт по браку: рассчитывать сколько процентов от общего кол-ва товара выявлено брака. Это нужно для того, чтобы успешнее бороться с некачественным товаром. 8.Анализ посещаемости аптеки. 8.Анализ посещаемости аптеки. Чтобы сдать выполнимый план выручки на месяц необходимо знать среднее количество покупателей в день/месяц. 9.Анализ неликвидного товара. Неликвидный товар – товар, который лежит на прилавках > 6 месяцев, и нужно обязательно знать, сколько и какой это товар, чтобы больше его не заказывать. Заключение. Спасибо за внимание!

Добавить комментарий

bioinformatics.ru

Смотрите также

• 
  Малые жанры фольклора реферат
• 
  Конституционное право франции реферат
• 
  История развития педиатрии реферат
• 
  Дополнительные устройства пк реферат
• 
  Военная доктрина рк реферат
• 
  Великая греческая колонизация реферат
• 
  Белки плазмы крови реферат
• 
  Библиотека конгресса сша реферат
• 
  Атомизм реферат по философии
• 
  Абсолютный идеализм гегеля реферат
• 
  3 поколение эвм реферат