Реферат: Комплексные числа. Комплексные числа реферат
Реферат - Комплексные числа - Математика
<a/>/> ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобысделать возможной операцию извлечения квадратного корня из любогодействительного числа. Это, однако, не является достаточным основанием длятого, чтобы вводить в математику новые числа. Оказалось, что если производитьвычисления по обычным правилам над выражениями, в которых встречаютсяквадратный корень из отрицательного числа, то можно прийти к результату, уже несодержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решениякубического уравнения. Оказалось, когда кубическое уравнение имеет тридействительных корня, в формуле Кардано встречается квадратный корень изотрицательного числа. Поэтому квадратные корни из отрицательных чисел сталиупотреблять в математике и назвали их мнимыми числами – тем самым они как быприобрели право на нелегальное существование. Полные гражданские права мнимымчислам дал Гаусс, который назвал их комплексными числами, дал геометрическуюинтерпретацию и доказал основную теорему алгебры, утверждающую, что каждыймногочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики,физики сводится к решению алгебраических уравнений. Поэтому исследованиеалгебраических уравнений является одним из важнейших вопросов в математике.Стремление сделать уравнения разрешимыми – одна из главных причин расширенияпонятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней.Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чиселразрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X+B=0 (A/>0). Однако алгебраические уравнениястепени выше первой могут не иметь рациональных корней. Например, такимиявляются уравнения X2=2, X3=5. Необходимостьрешения таких уравнений явилось одной из причин введения иррациональных чисел.Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чиселнедостаточно для того, чтобы решить любое алгебраическое уравнение. Например,квадратное уравнение с действительными коэффициентами и отрицательнымдискриминантом не имеет действительных корней. Простейшее из них – уравнение X2+1=0. Поэтомуприходится расширять множество действительных чисел, добавляя к нему новыечисла. Эти новые числа вместе с действительными числами образуют множество,которое называют множеством комплексных чисел.
Выясним предварительно, какой виддолжны иметь комплексные числа. Будем считать, что на множестве комплексныхчисел уравнение X2+1=0 имеет корень. Обозначим этот кореньбуквой i Таким образом, i– это комплексное число, такое, что i2= –1.
Как и для действительных чисел, нужноввести операции сложения и умножения комплексных чисел так, чтобы сумма ипроизведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B·iможно считать записью комплексногочисла в общем виде. Название «комплексное» происходит от слова «составное»: по виду выражения A+B·i.
Комплексными числами называют выражения вида A+B·i, где A и B –действительныечисла, а i –некоторый символ, такой что i2= –1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A+B·i, а число B – его мнимой частью. Число i называется мнимой единицей.
Например, действительная частькомплексного числа 2+3·i равна 2, а мнимая равна 3.
Для строгого определения комплексногочисла нужно ввести для этих чисел понятие равенства.
Два комплексных числа A+B·i и C+D·i называются равными тогда итолько тогда, когда A=C и B=D, т.е. когда равны их действительныеи мнимые части.
2.ГЕОМЕТРИЧЕСКАЯИНТЕРПРЕТАЦИЯ
КОМПЛЕКСНОГОЧИСЛА
/>
Рисунок 1
Действительные числа геометрическиизображаются точками числовой прямой. Комплексное число A+B·i можно рассматривать как парудействительных чисел(A;B).Поэтому естественно комплексное число изображать точками плоскости. Впрямоугольной системе координат комплексное число Z=A+B·i изображаетсяточкой плоскости с координатами (A;B),и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствиеявляется взаимно однозначным. Оно дает возможность интерпретировать комплексныечисла как точки плоскости на которой выбрана система координат. Такаякоординатная плоскость называется комплексной плоскостью. Осьабсцисс называется действительной осью, т.к. на ней расположеныточки соответствующие действительным числам. Ось ординат называется мнимойосью – на ней лежат точки, соответствующие мнимым комплексным числам.
/>
Рисунок 2
Не менее важной и удобной являетсяинтерпретация комплексного числа A+B·i как вектора, т.е. вектора с началом в точке
O(0;0) и с концом вточке М(A;B) (рисунок 2).
Соответствие установленное междумножеством комплексных чисел, с одной стороны, и множествами точек или векторовплоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A+B·i. СопряженнымсZ называется комплексное число A – B·i, которое обозначается />, т.е.
/>=/>=A – B·i.
Отметим, что />= A+B·i, поэтому для любого комплексного числа Z имеет место равенство />=Z.
Модулем комплексного числа Z=A+B·i называется число /> иобозначается />, т.е.
/>=/>=/> (1)
Из формулы (1) следует, что /> для любого комплексногочисла Z, причем />=0 тогда и толькотогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
/>
4.СЛОЖЕНИЕИ УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммойдвух комплексных чисел A+B·i и C+D·iназывается комплексное число (A+C)+(B+D)·i, т.е. (A+B·i)+(C+D·i)=(A+C)+(B+D)·i
Произведениемдвух комплексных чисел A+B·i и C+D·i называется комплексное число (A·C – B·D)+(A·D+B·C) ·i, т.е.
(A+B·i)·(C+D·i)=(A·C– B·D)+(A·D+B·C)·i
Из формул вытекает, что сложение иумножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложенияи умножения комплексных чисел обладают свойствами действительных чисел.Основные свойства:
Переместительное свойство:
Z1<sup/>+Z2=Z2+Z1, Z1·Z2=Z2·Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1·Z2)·Z3=Z1·(Z2·Z3)
Распределительное свойство:
Z1·(Z2+Z3)=Z1·Z2+Z1·Z3
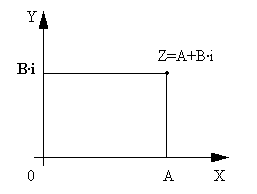
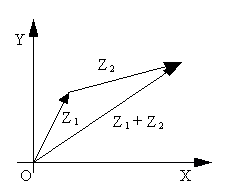
Геометрическое изображение суммыкомплексных чисел
/>
Рисунок 3
Согласно определению сложения двух комплексных чисел,действительная часть суммы равна сумме действительных частей слагаемых, мнимаячасть суммы равна сумме мнимых частей слагаемых. Точно также определяютсякоординаты суммы векторов:
Сумма двух векторов с координатами (A1;B1)и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор,соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы,соответствующие комплексным числам Z1 и Z2.
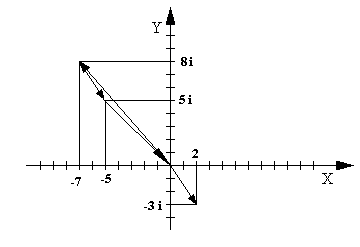
Пример1: Найти сумму и произведение комплексных чисел Z1=2 – 3×i и
1 Способ:
Z2= –7 + 8×i.
Z1 + Z2 = 2 – 7 + (–3 + 8)×i = –5 + 5×i
/>
Z1×Z2 = (2 – 3×i)×(–7 + 8×i) = –14 + 16×i + 21×i + 24 = 10 + 37×i
2 Способ:
5.ВЫЧИТАНИЕИ ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – этооперация, обратная сложению: длялюбых комплексных чиселZ1и Z2 существует, и притом только одно,число Z, такое, что:
Z+ Z2=Z1
Если к обеим частям равенстваприбавить (–Z2) противоположное числу Z2:
Z+Z2+(–Z2)=Z1+(–Z2), откуда
Z = Z1<sub/>– Z2
Число Z=Z1+Z2 называют разностью чиселZ1и Z2.
Деление вводится как операция,обратная умножению:
Z×Z2=Z1
Разделив обе части на Z2 получим:
Z=/>
Из этого уравнения видно, что Z2/>0
/>
Геометрическое изображениеразности комплексных чисел
Рисунок 4 Разности Z2 – Z1 комплексных чисел Z1 и Z2, соответствуетразность векторов, соответствующих числам Z1 и Z2. Модуль/> разности двух комплексныхчиселZ2 и Z1 по определению модуля есть длинавектора Z2 – Z1. Построим этот вектор, как суммувекторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двухкомплексных чисел есть расстояние между точками комплексной плоскости, которыесоответствуют этим числам.
Это важное геометрическоеистолкование модуля разности двух комплексных чисел позволяет с успехомиспользовать простые геометрические факты.
Пример 2: Даны комплексные числа Z1= 4 + 5·i и Z2= 3 + 4·i.Найти разность Z2 – Z1и частное />
Z2– Z1<sub/>= (3 + 4·i) – (4+ 5·i) = –1 – i
/>=/>=/>
6.ТРИГОНОМЕТРИЧЕСКАЯФОРМА
КОМПЛЕКСНОГОЧИСЛА
/>
Рисунок 5
Запись комплексного числа Z в виде A+B·i называется алгебраической формойкомплексногочисла. Помимо алгебраической формы используются и другие формы записикомплексных чисел.
Рассмотрим тригонометрическуюформу записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B·i выражаются через его модуль />= rи аргумент j следующим образом:
A=r·cosj; B= r·sinj.
Число Z можно записать так:
Z= r·cosj+i·/>·sinj = r·(cosj +i·sinj)
Z = r·(cosj +i·sinj) (2)
Эта запись называется тригонометрическойформой комплексного числа.
r =/>– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z/>0 называется величина угла междуположительным направлением действительной оси и вектором Z, причем величина угла считаетсяположительной, если отсчет ведется против часовой стрелки, и отрицательной,если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случаечисло задается только своим модулем.
Как уже говорилось выше />= r =/>, равенство (2)можно записать в виде
A+B·i=/>·cosj+i·/>·sinj, откуда приравнивая действительные имнимые части, получим:
cosj =/>, sinj =/> (3)
Если sinj поделить на cosj получим:
tgj=/> (4)
Эту формулу удобней использовать длянахождения аргумента j,чем формулы (3). Однако не все значения j, удовлетворяющие равенству (4),являются аргументами числа A+B·i. Поэтому при нахождении аргумента нужно учесть, вкакой четверти расположена точка A+B·i.
7.СВОЙСТВАМОДУЛЯ И АРГУМЕНТА
КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формыудобно находить произведение и частное комплексных чисел.
Пусть Z1= r1·(cosj1<sub/>+i·sinj1), Z2<sub/>= r2·(cosj2<sub/>+i·sinj2). Тогда:
Z1Z2= r1·r2[cosj1·cosj2 – sinj1·sinj2 + i·( sinj1·cosj2 + cosj1·sinj2)]=
=r1·r2[cos(j1+ j2) + i·sin(j1+ j2)].
Таким образом, произведениекомплексных чисел, записанных в тригонометрической форме, можно находить поформуле:
Z1Z2=r1·r2[cos(j1+ j2) + i·sin(j1+ j2)] (5)
Из формулы (5) следует, чтоприумножении комплексных чисел их модули перемножаются, а аргументы складываются.
Если Z1=Z2 то получим:
Z2=[r·(cosj+i·sinj)]2= r2·(cos2j+i·sin2j)
Z3=Z2·Z=r2·(cos2j+i·sin2j)·r·(cosj+i·sinj)=
=r3·(cos3j+i·sin3j)
Вообще для любого комплексного числа Z=r·( cosj+i·sinj)/>и любого натурального числа n справедлива формула:
Zn<sup/>=[ r·(cosj+i·sinj)]n= rn·(cosnj+i·sinnj), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел,записанных в тригонометрической форме, можно находить по формуле:
/>/>/>[ cos(j1– j2) + i·sin(j1– j2)]. (7)
/>= />=cos(–j2) + i·sin(–j2)
Используя формулу 5
/>(cosj1 +i·sinj1)×(cos(–j2) + i·sin(–j2)) =
cos(j1– j2) + i·sin(j1– j2).
Пример 3:
Z3 = –8
Число –8запишем в тригонометрической форме
8 = 8·(cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r3×(cos3j+ i×sin3j) = 8·(cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Тогда 3j =p + 2pk, kÎZ
j=/>, kÎZ
r3 = 8
r = 2
Следовательно:
Z = 2·( cos(/>) + i·sin(/>)), kÎZ
k = 0,1,2...
k = 0
Z1 = 2·( cos/> +i·sin/>) = 2·(/>i) = 1+/>×i
k = 1
Z2 = 2·( cos(/> + />) + i·sin(/> + />)) = 2·( cosp + i·sinp) = –2
k = 2
Z3 = 2·( cos(/> + />) + i·sin(/> + />)) = 2·( cos/> + i·sin/>) = 1–/>×i
Ответ: Z13 = />;Z2 = –2
Пример 4:
Z4 = 1
Число 1запишем в тригонометрической форме
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r4×(cos4j+ i×sin4j) =cos(2pk) + i·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j= />, kÎZ
r4= 1
r = 1
Z = cos />+ i×sin/>
k = 0,1,2,3...
k = 0
Z1 = cos0+ i×sin0= 1 + 0 = 1
k = 1
Z2 = cos />+ i×sin/> = 0 +i = i
k = 2
Z3 = cosp + i·sinp = –1+ 0 = –1
k = 3
Z4 = cos />+ i×sin/>
Ответ: Z13 = />1
Z24 = /> i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕКОРНЯ
Из формулы 6 видно, что возведениекомплексного числа r·( cosj +i·sinj) в целую положительную степень снатуральным показателем его модуль возводится в степень с тем же показателем,а аргумент умножается на показатель степени.
[r·(cosj +i·sinj)]n= rn·(cos nj +i·sin nj)
Число Zназывается корнем степениn из числа w ( обозначается />), если Zn =w.
Из данного определения вытекает, чтокаждое решение уравнения Zn =w является корнем степени n из числа w. Другими словами, для того, чтобыизвлечь корень степени nиз числа w, достаточнорешить уравнение Zn =w. Если w=0, то при любом nуравнение Zn=wимеет только одно решение Z=0. Если w/>0, то и Z/>, а, следовательно, и Zиw можно представить втригонометрической форме
Z = r·(cosj +i·sinj), w = p·(cosy +i·siny)
Уравнение Zn = w примет вид:
rn·(cos nj +i·sin nj) = p·( cosy +i·siny)
Два комплексных числа равны тогда итолько тогда, когда равны их модули, а аргументы отличаются слагаемыми,кратными 2p. Следовательно, rn = p и nj = y + 2pk, гдеkÎZ или r = /> иj = />,где kÎZ.
Итак, все решения могут быть записаныследующим образом:
ZK=/>[cos(/>) + i·sin(/>)], kÎZ (8)
Формулу 8 называют второйформулой Муавра.
Таким образом, если w/>0, то существует ровно n корней степени n из числа w: все они содержатся в формуле 8. Всекорни степениnиз числа w имеют один и тот же модуль />, но разные аргументы,отличающиеся слагаемым, кратным числу />.Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w, соответствует точкам комплекснойплоскости, расположенным в вершинах правильного n– угольника, вписанного в окружностьрадиуса /> с центром в точке Z = 0.
Символ /> неимеет однозначного смысла. Поэтому, употребляя его, следует четко представлятьсебе, что под этим символом подразумевается. Например, используя запись />, следует подумать о том,чтобы было ясно, понимается под этим символом пара комплексных чисел i и–i, или одно, то какое именно.
Уравнениявысших степеней
Формула 8 определяет все корнидвучленного уравнения степени n.Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнениястепени n:
an×Zn +an–1×Zn–1<sup/>+...+a1×Z1<sup/>+a0<sub/>= (9)
Где an,..., a0<sub/>– заданные комплексные числа.
В курсе высшей математикидоказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайнеймере один корень. Эта теорема была доказана немецким математиком Карлом Гауссомв 1779 году.
Опираясь на теорему Гаусса, можнодоказать, что левая часть уравнения 9 всегда может быть представлена в видепроизведения:
/>,
Где Z1,<sub/>Z2,...,<sub/>ZK – некоторые различные комплексные числа,
а a1,a2,...,ak<sub/>– натуральные числа, причем:
a1+ a2 +… + ak = n
Отсюда следует, что числа Z1,<sub/>Z2,...,<sub/>ZK являются корнями уравнения 9. При этом говорят, что Z1<sub/>является корнем кратности a1, Z2<sub/>– корнем кратности a2 и так далее.
Если условиться считать кореньуравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнениестепени nимеет в множестве комплексных чиселровноn корней.
Теорема Гаусса и только чтосформулированная теорема дают решения о существовании корней, но ничего неговорят о том, как найти эти корни. Если корни первой и второй степени могутбыть легко найдены, то для уравнений третей и четвертой степеней формулыгромоздки, а для уравнений степени выше четвертой таких формул вообще несуществует. Отсутствие общего метода не мешает отыскивать все корни уравнения.Для решения уравнения с целыми коэффициентами часто оказывается полезнойследующая теорема: целые корнилюбого алгебраического уравнения с целыми коэффициентами являются делителямисвободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an×Zn + an–1×Zn–1<sup/>+...+ a1×Z1<sup/>+ a0<sub/>= 0
с целыми коэффициентами. Тогда
an×kn + an–1×kn–1<sup/>+...+ a1×k1<sup/>+ a0<sub/>= 0
a0<sub/>= – k(an×kn–1 + an–1×kn–2 +...+ a1)
Число в скобках, при сделанныхпредположениях, очевидно, целое, значит k – делитель числа a0.
9.КВАДРАТНОЕУРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
1. имеет один корень, если a = 0.
2. имеет два действительных корня Z1,2=/>, если a > 0.
3. неимеет действительных корней, если a < 0. Но имеетдва комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2×/>=i2×(/>)2. Тогда уравнение Z2 = a запишется в виде: Z2 –i2×(/>)2= 0
т.е. (Z – i×/>)(Z + i×/>) = 0
Следовательно, уравнение имеет двакорня: Z1,2= /> i×/>
Введенное понятие корня из отрицательногочисла позволяет записать корни любого квадратного уравнения с действительнымикоэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2=/> (10)
Итак, при любых действительных a(a/>0), b, c корни уравнения можно находить поформуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен, то уравнение a×Z2 + b×Z + c = 0 два действительных различных корня.Если D = 0, то уравнение a×Z2 + b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z2 + b×Z + c = 0 имеет два различных комплексныхкорня.
Комплексные корни квадратногоуравнения обладают такими же свойствами, как и известные нам свойствадействительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2 + b×Z + c = 0, a/>0. Тогда справедливы свойства:
1. Теорема Виета: Z1+ Z2 = –/>
Z1×Z2 = />
2. При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 –6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 = />
Z1,2 =/>
Ответ: Z1= Z2 = 3 +i
Пример 6:
3·Z2 +2·Z+ 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = /> = />
Z1,2 =/>
Z1 = –(/>)
Z2 = –/>
Ответ: Z1 = Z2 = –/>
Пример 7:
Z4 –8·Z2 – 9 = 0
Z2 = t
t2 –8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = />= />= 4/>
t1 =9 t2 = – 1
Z2 =9 Z2 = – 1
Z1,2 =/>3 Z = />
Z3,4 =/>i
Ответ: Z1,2 =/>3, Z3,4=/>i
Пример 8:
Z4 + 2·Z2– 15 = 0
Z2 = t
t2 + 2·t –15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = />= />= –1/>4
t1 = –5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = –1·5 Z3,4 =/>/>
Z2 = i2·5
Z1,2 =/>i/>
Ответ: Z1,2 =/>i/>, Z3,4=/>/>
Пример 9:
Z2 = 24– 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i–Y2
X2 + 2·X·Y·i– Y2= 24 – 10·i
{
(X2 – Y2)+ 2·X·Y·i=24 – 10·i X2 – Y2 = 24
2·X·Y = – 10
Y = – />
X2 – />= 24
/> умножимна X2/>0
X4 – 24·X2– 25 = 0
X2 = t
t2 – 24·t –25 = 0
t1·t2= – 25
t1 + t2= 24
t1 =25 t2 = – 1
X2 =25 X2 = – 1 — нетрешений
X1,2 = />5
X1 =5 X2 = – 5
Y1 = – /> Y2= />
Y1 = –1 Y2 = 1
Тогда:
Z1,2 =/>(5 – i)
Ответ: Z1,2 =/>(5 – i)
ЗАДАЧИ:
{
1)/> X2 + 3·X·Y + Y2 = 6
X + Y = 2
/>
( 2 – Y)2+ 3·( 2 – Y)·Y + Y2 = 6
4 – 4·Y + Y2+ 6·Y – 3·Y2 + Y2 = 6
–Y2 +2Y – 2 = 0 /–1
Y2 – 2Y+ 2 = 0
Д = b2 – 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4·i2
Y1,2 = /> = /> = 1/> i
Y1 = 1–i Y2 = 1 + i
{
X1 = 1 + i X2 = 1–iОтвет: {1 +i; 1–i}
{1–i; 1 + i}
{
2)/> Z3 + w5 = 0
Z2×/>4 = 111/>4 = 1
{
Z3 = –w5
Z2×/>12 = 1
—Возведем в квадрат
—Возведем в куб
/>
w10×/>12= 1
w10×/>10×/>2 = 1
(w×/>)10×/>2= 1
(/>)10×/>2 = 1
т.к. w = A + B×i
/> = A – B×i
w×/> = (A + B×i)·( A – B×i) = A2 – (B×i)2= A2 + B2 = />2= w×/>
т.е. />20·/>2= 1
Возьмем модуль от обоихчастей последнего уравнения:
/>20·/>2 = 1
/>22 = 1
т.е.
/> = 1
Тогда из уравнения получим
/>2 = 1
т.е.
/> = />1
w1 =1 w2 = –1
Подставим эти значения впервое уравнение данной системы и найдем численное значение Z
1) w1 =1
Z6 = 1
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Z = r×(cosj+ i×sinj)
r6×(cos6j+ i×sin6j) = cos(2pk) +i·sin(2pk), kÎZ
r6= 1 6j = 2pk
r =1 j = />, kÎZ
Z = cos/>+ i·sin/>, kÎZ
k = 0,1,2...
k = 0
Z1 = cos0+ i×sin0= 1 + 0 = 1
Z1 = 1
k = 1
Z2 = cos/> +i·sin/> = />i= />i
Z2 =/>i
k = 2
Z3 =cos/>+ i·sin/> = –/>i
Z3 = –/>i
k = 3
Z4 = cosp + i·sinp = –1+ 0 = –1
Z4 = –1
k = 4
Z5 = cos/> +i·sin/> = –/>i
Z5 = –/>i
k = 5
Z6 = cos/> +i·sin/> = />i
Z6 = />i
Ответ: Z1 = 1, Z2=/>i, Z3 = –/>i, Z4 = –1, Z5= –/>i, Z6= />i
2) w2 = –1
Z6 = –1
–1 = 1·(cos(p + 2pk) +i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r6×(cos6j+ i×sin6j) = cos(p + 2pk) + i·sin(p + 2pk), kÎZ
r6 =1 6j = p + 2pk
r = 1 j = />, kÎZ
Z = cos(/>) + i·sin(/>), kÎZ
k = 0,1,2...
k = 0
Z1 = cos/> +i·sin/> = />i
Z1=/>i
k = 1
Z2= cos(/>) + i·sin(/>) = 0 + i= i
Z2=i
k = 2
Z3= cos(/>) + i·sin(/>) = –/>i
Z3= –/>i
k = 3
Z4= cos(/>) + i·sin(/>) = –/>i
Z4= –/>i
k = 4
Z5= cos(/>) + i·sin(/>) = 0 – i= –i
Z5= – i
k = 5
Z6= cos(/>) +i·sin(/>)= />i
Z6=/>i
Ответ: Z1 =/>i , Z2 =i, Z3= –/>i, Z4 = –/>i, Z5= – i, Z6 =/>i
3)
Доказать, что сумма двухкомплексных чисел не превосходит сумму модулей этих чисел.
1 СПОСОБ:
Пусть Z1=X+Y×i и Z2=U+V×i
Доказать что:
/>
/>
Предположим противоположное:
/>>/> / т.к. корень существует только из неотрицательного числа, то можно возвести вквадрат обе части неравенства.
X2+2·X·U+U2+Y2+2·Y·V+V2 > X2+Y2+U2+V2+2·/>
2·(X·U+Y·V) > 2·/>
Если мы предположили верно,то X·U+Y·V > 0, а поэтому возведем вквадрат:
X2·U2+2·XU·Y·V+Y2·V2> X2·U2 + X2·V2+Y2·U2+Y2·V2
2·X·Y·V·U > X2·V2+Y2·U2
X2·V2+Y2·U2– 2·X·Y·V·U < 0
(X·V + Y·U)2 < 0
Это невозможно, т.к. A2/> 0, значит полученное нами неравенство неверно.
/>
что и требовалось доказать
2 СПОСОБ:
/>
Пусть Z1 и Z2 – двапроизвольных комплексных числа. Z1– соответствует точке A, Z2 –соответствует точке B.
В силу неравенстватреугольника
/> т.е.
/>
Что и требовалось доказать.
www.ronl.ru
Комплексные числа | Рефераты KM.RU
Комплексные числа
ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A· X+B=0 (A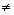 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X2+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X2+1=0 имеет корень. Обозначим этот корень буквой i Таким образом, i – это комплексное число, такое, что i 2= –1.
Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B· i можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A+B· i.
Комплексными числами называют выражения вида A+B· i, где A и B –действительные числа, а i – некоторый символ, такой что i2= –1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A+B· i, а число B – его мнимой частью. Число i называется мнимой единицей.
Например, действительная часть комплексного числа 2+3· i равна 2, а мнимая равна 3.
Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.
Два комплексных числа A+B· i и C+D· i называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА
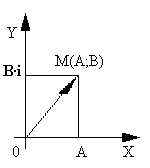
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B· i можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+B· i изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки, соответствующие мнимым комплексным числам.
Не менее важной и удобной является интерпретация комплексного числа A+B· i как вектора, т.е. вектора с началом в точке
O(0;0) и с концом в точке М(A;B) (рисунок 2).
Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A+B· i. Сопряженным с Z называется комплексное число A – B· i, которое обозначается 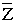 , т.е.
, т.е.
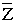 =
=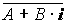 =A – B· i.
=A – B· i.
Отметим, что  = A+B· i, поэтому для любого комплексного числа Z имеет место равенство
= A+B· i, поэтому для любого комплексного числа Z имеет место равенство 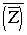 =Z.
=Z.
Модулем комплексного числа Z=A+B· i называется число 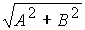 и обозначается
и обозначается  , т.е.
, т.е.
 =
=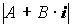 =
=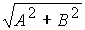 (1)
(1)
Из формулы (1) следует, что 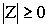 для любого комплексного числа Z, причем
для любого комплексного числа Z, причем 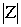 =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
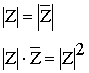
4.СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммой двух комплексных чисел A+B· i и C+D· i называется комплексное число (A+C) + (B+D)· i, т.е.(A+B· i) + (C+D· i)=(A+C) + (B+D)· i Произведением двух комплексных чисел A+B· i и C+D· i называется комплексное число (A· C – B· D)+(A· D+B· C) · i, т.е.
(A + B· i)· (C + D· i)=(A· C – B· D) + (A· D + B· C)· i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство:
Z1+Z2=Z2+Z1, Z1· Z2=Z2· Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1· Z2)· Z3=Z1· (Z2· Z3)
Распределительное свойство:
Z1· (Z2+Z3)=Z1· Z2+Z1· Z3
Геометрическое изображение суммы комплексных чисел
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:
Сумма двух векторов с координатами (A1;B1) и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы, соответствующие комплексным числам Z1 и Z2.
Пример 1: Найти сумму и произведение комплексных чисел Z1=2 – 3× i и
1 Способ:
Z2= –7 + 8× i.
Z1 + Z2 = 2 – 7 + (–3 + 8)× i = –5 + 5× i
Z1× Z2 = (2 – 3× i)× (–7 + 8× i) = –14 + 16× i + 21× i + 24 = 10 + 37× i
2 Способ:
5.ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1 и Z2 существует, и притом только одно, число Z, такое, что:
Z + Z2=Z1
Если к обеим частям равенства прибавить (–Z2) противоположное числу Z2:
Z+Z2+(–Z2)=Z1+(–Z2), откуда
Z = Z1– Z2
Число Z=Z1+Z2 называют разностью чисел Z1 и Z2.
Деление вводится как операция, обратная умножению:
Z× Z2=Z1
Разделив обе части на Z2 получим:
Z=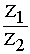
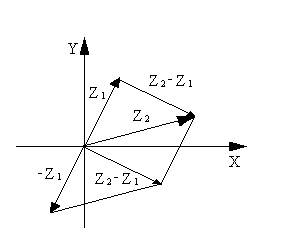
Из этого уравнения видно, что Z2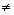 0
0
Геометрическое изображение разности комплексных чисел
Разности Z2– Z1 комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль  разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.
Пример 2: Даны комплексные числа Z1= 4 + 5· i и Z2= 3 + 4· i. Найти разность Z2 – Z1 и частное 
Z2 – Z1 = (3 + 4· i) – (4 + 5· i) = –1 – i
 =
= =
=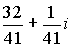
6.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА

Запись комплексного числа Z в виде A+B· i называется алгебраической формой комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.
Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B· i выражаются через его модуль 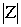 = r и аргумент j следующим образом:
= r и аргумент j следующим образом:
A= r· cosj ; B= r· sinj .
Число Z можно записать так:
Z= r· cosj + i· 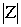 · sinj = r· (cosj + i· sinj )
· sinj = r· (cosj + i· sinj )
Z = r· (cosj + i· sinj ) (2)
Эта запись называется тригонометрической формой комплексного числа.
r =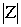 – модуль комплексного числа.
– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z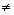 0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается только своим модулем.
Как уже говорилось выше 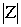 = r =
= r =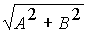 , равенство (2) можно записать в виде
, равенство (2) можно записать в виде
A+B· i=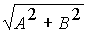 · cosj + i·
· cosj + i· 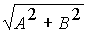 · sinj , откуда приравнивая действительные и мнимые части, получим:
· sinj , откуда приравнивая действительные и мнимые части, получим:
cosj =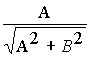 , sinj =
, sinj = (3)
(3)
Если sinj поделить на cosj получим:
tgj =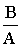 (4)
(4)
Эту формулу удобней использовать для нахождения аргумента j , чем формулы (3). Однако не все значения j , удовлетворяющие равенству (4), являются аргументами числа A+B· i . Поэтому при нахождении аргумента нужно учесть, в какой четверти расположена точка A+B· i.
7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.
Пусть Z1= r1· (cosj 1+ i· sinj 1), Z2= r2· (cosj 2+ i· sinj 2). Тогда:
Z1Z2= r1· r2[cosj 1· cosj 2 – sinj 1· sinj 2 + i· ( sinj 1· cosj 2 + cosj 1· sinj 2)]=
= r1· r2[cos(j 1 + j 2) + i· sin(j 1 + j 2)].
Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
Z1Z2= r1· r2[cos(j 1 + j 2) + i· sin(j 1 + j 2)] (5)
Из формулы (5) следует, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Если Z1=Z2 то получим:
Z2=[r· (cosj + i· sinj )]2= r2· (cos2j + i· sin2j )
Z3=Z2· Z= r2· (cos2j + i· sin2j )· r· (cosj + i· sinj )=
= r3· (cos3j + i· sin3j )
Вообще для любого комплексного числа Z= r· ( cosj + i· sinj )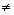 0 и любого натурального числа n справедлива формула:
0 и любого натурального числа n справедлива формула:
Zn=[ r· (cosj + i· sinj )]n= rn· ( cosnj + i· sinnj ), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
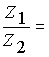

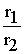 [ cos(j 1 – j 2) + i· sin(j 1 – j 2)]. (7)
[ cos(j 1 – j 2) + i· sin(j 1 – j 2)]. (7)
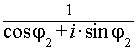 =
= 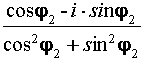 = cos(–j 2) + i· sin(–j 2)
= cos(–j 2) + i· sin(–j 2)
Используя формулу 5
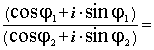 (cosj 1 + i· sinj 1)× ( cos(–j 2) + i· sin(–j 2)) =
(cosj 1 + i· sinj 1)× ( cos(–j 2) + i· sin(–j 2)) =
cos(j 1 – j 2) + i· sin(j 1 – j 2).
Пример 3:
Z3 = –8
Число –8 запишем в тригонометрической форме
8 = 8· ( cos(p + 2p k ) + i·sin(p + 2p k )), k Î Z
Пусть Z = r× (cosj + i× sinj ), тогда данное уравнение запишется в виде:
r3× (cos3j + i× sin3j ) = 8· ( cos(p + 2p k ) + i·sin(p + 2p k )), k Î Z
Тогда 3j =p + 2p k , k Î Z
j = 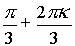 , k Î Z
, k Î Z
r3 = 8
r = 2
Следовательно:
Z = 2· ( cos(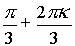 ) + i·sin(
) + i·sin(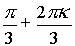 )), k Î Z
)), k Î Z
k = 0,1,2...
k = 0
Z1 = 2· ( cos + i·sin
+ i·sin ) = 2· (
) = 2· (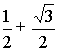 i) = 1+
i) = 1+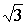 × i
× i
k = 1
Z2 = 2· ( cos( +
+  ) + i·sin(
) + i·sin( +
+  )) = 2· ( cosp + i·sinp ) = –2
)) = 2· ( cosp + i·sinp ) = –2
k = 2
Z3 = 2· ( cos( +
+ 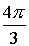 ) + i·sin(
) + i·sin( +
+ 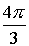 )) = 2· ( cos
)) = 2· ( cos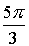 + i·sin
+ i·sin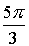 ) = 1–
) = 1–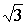 × i
× i
Ответ: Z13 =  ; Z2 = –2
; Z2 = –2
Пример 4:
Z4 = 1
Число 1 запишем в тригонометрической форме
1 = 1· ( cos(2p k ) + i·sin(2p k )), k Î Z
Пусть Z = r× (cosj + i× sinj ), тогда данное уравнение запишется в виде:
r4× (cos4j + i× sin4j ) = cos(2p k ) + i·sin(2p k )), k Î Z
4j = 2p k , k Î Z
j =  , k Î Z
, k Î Z
r4 = 1
r = 1
Z = cos  + i× sin
+ i× sin
k = 0,1,2,3...
k = 0
Z1 = cos0+ i× sin0 = 1 + 0 = 1
k = 1
Z2 = cos  + i× sin
+ i× sin = 0 + i = i
= 0 + i = i
k = 2
Z3 = cosp + i·sinp = –1 + 0 = –1
k = 3
Z4 = cos 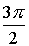 + i× sin
+ i× sin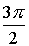
Ответ: Z13 = 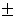 1
1
Z24 = 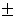 i
i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Из формулы 6 видно, что возведение комплексного числа r· ( cosj + i· sinj ) в целую положительную степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
[ r· (cosj + i· sinj )]n= rn· ( cos nj + i· sin nj )
Число Z называется корнем степени n из числа w ( обозначается  ), если Zn =w .
), если Zn =w .
Из данного определения вытекает, что каждое решение уравнения Zn = w является корнем степени n из числа w . Другими словами, для того, чтобы извлечь корень степени n из числа w , достаточно решить уравнение Zn = w . Если w =0, то при любом n уравнение Zn = w имеет только одно решение Z= 0. Если w 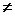 0, то и Z
0, то и Z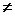 0, а, следовательно, и Z и w можно представить в тригонометрической форме
0, а, следовательно, и Z и w можно представить в тригонометрической форме
Z = r· (cosj + i· sinj ), w = p· (cosy + i· siny )
Уравнение Zn = w примет вид:
rn· ( cos nj + i· sin nj ) = p· ( cosy + i· siny )
Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемыми, кратными 2p . Следовательно, rn = p и nj = y + 2p k, где kÎ Z или r = 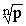 и j =
и j = 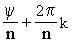 , где kÎ Z .
, где kÎ Z .
Итак, все решения могут быть записаны следующим образом:
ZK=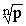 [cos(
[cos(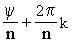 ) + i· sin(
) + i· sin(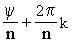 )], kÎ Z (8)
)], kÎ Z (8)
Формулу 8 называют второй формулой Муавра.
Таким образом, если w 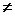 0, то существует ровно n корней степени n из числа w : все они содержатся в формуле 8. Все корни степени n из числа w имеют один и тот же модуль
0, то существует ровно n корней степени n из числа w : все они содержатся в формуле 8. Все корни степени n из числа w имеют один и тот же модуль 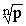 , но разные аргументы, отличающиеся слагаемым, кратным числу
, но разные аргументы, отличающиеся слагаемым, кратным числу  . Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w , соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса
. Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w , соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса 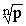 с центром в точке Z = 0.
с центром в точке Z = 0.
Символ  не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись
не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись  , следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно.
, следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно.
Уравнения высших степеней
Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнения степени n:
an× Zn + an–1× Zn–1+...+ a1× Z1+ a0= 0 (9)
Где an,..., a0– заданные комплексные числа.
В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.
Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9 всегда может быть представлена в виде произведения:
 ,
,
Где Z1,Z2,...,ZK– некоторые различные комплексные числа,
а a1,a2,...,ak – натуральные числа, причем:
a1 + a2 + ... + ak = n
Отсюда следует, что числа Z1,Z2,...,ZK являются корнями уравнения 9. При этом говорят, что Z1 является корнем кратности a1, Z2– корнем кратности a2 и так далее.
Если условиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел ровно n корней.
Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для уравнений третей и четвертой степеней формулы громоздки, а для уравнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни уравнения. Для решения уравнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an× Zn + an–1× Zn–1+...+ a1× Z1+ a0= 0
с целыми коэффициентами. Тогда
an× kn + an–1× kn–1+...+ a1× k1+ a0= 0
a0= – k(an× kn–1 + an–1× kn–2 +...+ a1)
Число в скобках, при сделанных предположениях, очевидно, целое, значит k – делитель числа a0.
9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
- имеет один корень, если a = 0.
- имеет два действительных корня Z1,2=
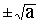 , если a > 0.
, если a > 0. - не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)× (– a) = i2× 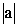 = i2× (
= i2× (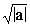 )2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2× (
)2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2× (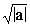 )2 = 0
)2 = 0
т.е. (Z – i× 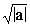 )(Z + i×
)(Z + i× 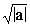 ) = 0
) = 0
Следовательно, уравнение имеет два корня: Z1,2 =  i×
i× 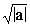
Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами
a× Z2 + b× Z + c = 0
По известной общей формуле
Z1,2=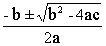 (10)
(10)
Итак, при любых действительных a(a 0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4× a× c
положителен , то уравнение a× Z2 + b× Z + c = 0 два действительных различных корня. Если D = 0, то уравнение a× Z2 + b× Z + c = 0 имеет один корень. Если D < 0, то уравнение a× Z2 + b× Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a× Z2 + b× Z + c = 0, a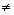 0. Тогда справедливы свойства:
0. Тогда справедливы свойства:
- Теорема Виета: Z1 + Z2 = –
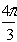
Z1× Z2 = 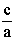
- При всех комплексных Z справедлива формула
a× Z2 + b× Z + c = a× (Z – Z1)× (Z – Z2)
Пример 5:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 = 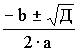
Z1,2 =
Ответ: Z1 = Z2 = 3 + i
Пример 6:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = 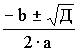 =
= 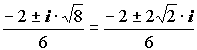
Z1,2 =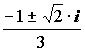
Z1 = – (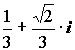 )
)
Z2 = –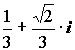
Ответ: Z1 = Z2 = –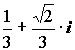
Пример 7:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = 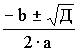 =
= 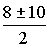 = 4
= 4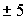
t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 =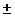 3 Z =
3 Z = 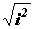
Z3,4 =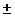 i
i
Ответ: Z1,2 =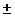 3, Z3,4 =
3, Z3,4 =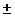 i
i
Пример 8:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = 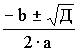 =
=  = –1
= –1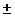 4
4
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 =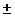
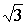
Z2 = i2·5
Z1,2 =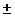 i
i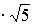
Ответ: Z1,2 =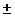 i
i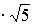 , Z3,4 =
, Z3,4 =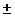
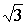
Пример 9:
Z2 = 24 10· i
Пусть Z = X + Y· i
(X + Y· i)2 = X2 + 2· X· Y· i Y2
X2 + 2· X· Y· i Y2 = 24 10· i
(X2 Y2) + 2· X· Y· i = 24 10· i
Y = 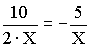
X2 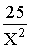 = 24
= 24
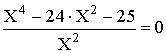 умножим на X2
умножим на X2 0
0
X4 – 24· X2 – 25 = 0
X2 = t
t2 – 24· t – 25 = 0
t1· t2 = – 25
t1 + t2 = 24
t1 = 25 t2 = – 1
X2 = 25 X2 = – 1 — нет решений
X1,2 = 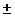 5
5
X1 = 5 X2 = – 5
Y1 = – 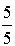 Y2 =
Y2 = 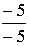
Y1 = – 1 Y2 = 1
Тогда:
Z1,2 =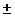 (5 – i)
(5 – i)
Ответ: Z1,2 =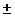 (5 – i)
(5 – i)
ЗАДАЧИ:
1)
( 2 – Y)2 + 3·( 2 – Y)·Y + Y2 = 6
4 – 4·Y + Y2 + 6·Y – 3·Y2 + Y2 = 6
–Y2 + 2Y – 2 = 0 /–1
Y2 – 2Y + 2 = 0
Д = b2 – 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4· i2
Y1,2 = 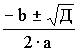 =
= 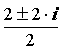 = 1
= 1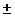 i
i
Y1 = 1– i Y2 = 1 + i
X1 = 1 + i X2 = 1– i
Ответ: {1 + i ; 1– i}
{1– i ; 1 + i}
2)
— Возведем в квадрат
— Возведем в куб
w 10× 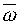 12 = 1
12 = 1
w 10× 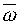 10×
10× 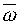 2 = 1
2 = 1
(w × 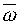 )10×
)10× 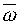 2 = 1
2 = 1
(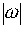 )10×
)10× 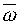 2 = 1
2 = 1
т.к. w = A + B× i
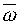 = A – B× i
= A – B× i
w × 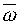 = (A + B× i)·( A – B× i) = A2 – (B× i)2 = A2 + B2 =
= (A + B× i)·( A – B× i) = A2 – (B× i)2 = A2 + B2 = 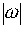 2 = w ×
2 = w × 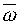
т.е. 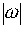 20·
20·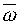 2 = 1
2 = 1
Возьмем модуль от обоих частей последнего уравнения:
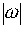 20·
20·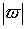 2 = 1
2 = 1
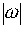 22 = 1
22 = 1
т.е.
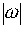 = 1
= 1
Тогда из уравнения получим
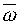 2 = 1
2 = 1
т.е.
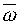 = +-1
= +-1
w 1 = 1 w 2 = –1
Подставим эти значения в первое уравнение данной системы и найдем численное значение Z
1) w 1 = 1
Z6 = 1
1 = 1· ( cos(2p k ) + i·sin(2p k )), k Î Z
Z = r× (cosj + i× sinj )
r6× (cos6j + i× sin6j ) = cos(2p k ) + i·sin(2p k ), k Î Z
r6 = 1 6j = 2p k
r = 1 j =  , k Î Z
, k Î Z
Z = cos + i·sin
+ i·sin , k Î Z
, k Î Z
k = 0,1,2...
k = 0
Z1 = cos0+ i× sin0 = 1 + 0 = 1
Z1 = 1
k = 1
Z2 = cos + i·sin
+ i·sin =
= 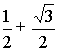 i =
i = 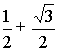 i
i
Z2 =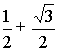 i
i
k = 2
Z3 = cos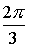 + i·sin
+ i·sin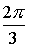 = –
= –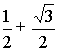 i
i
Z3 = –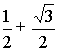 i
i
k = 3
Z4 = cosp + i·sinp = –1 + 0 = –1
Z4 = –1
k = 4
Z5 = cos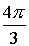 + i·sin
+ i·sin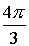 = –
= –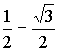 i
i
Z5 = –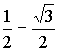 i
i
k = 5
Z6 = cos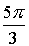 + i·sin
+ i·sin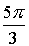 =
= 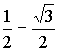 i
i
Z6 = 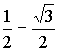 i
i
Ответ: Z1 = 1, Z2 =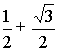 i, Z3 = –
i, Z3 = –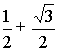 i, Z4 = –1, Z5 = –
i, Z4 = –1, Z5 = –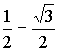 i, Z6 =
i, Z6 = 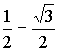 i
i
2) w 2 = –1
Z6 = –1
–1 = 1· ( cos(p + 2p k ) + i·sin(p + 2p k )), k Î Z
Пусть Z = r× (cosj + i× sinj ), тогда данное уравнение запишется в виде:
r6× (cos6j + i× sin6j ) = cos(p + 2p k ) + i·sin(p + 2p k ), k Î Z
r6 = 1 6j = p + 2p k
r = 1 j =  , k Î Z
, k Î Z
Z = cos( ) + i·sin(
) + i·sin( ), k Î Z
), k Î Z
k = 0,1,2...
k = 0
Z1 = cos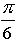 + i·sin
+ i·sin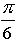 =
= 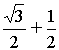 i
i
Z1 =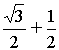 i
i
k = 1
Z2 = cos( ) + i·sin(
) + i·sin( ) = 0 + i = i
) = 0 + i = i
Z2 = i
k = 2
Z3 = cos(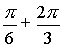 ) + i·sin(
) + i·sin(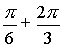 ) = –
) = –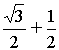 i
i
Z3 = –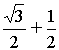 i
i
k = 3
Z4 = cos( ) + i·sin(
) + i·sin( ) = –
) = – i
i
Z4 = – i
i
k = 4
Z5 = cos( ) + i·sin(
) + i·sin( ) = 0 – i = – i
) = 0 – i = – i
Z5 = – i
k = 5
Z6 = cos(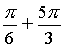 ) + i·sin(
) + i·sin(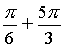 ) =
) =  i
i
Z6 = i
i
Ответ: Z1 =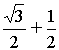 i , Z2 = i, Z3 = –
i , Z2 = i, Z3 = –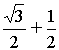 i , Z4 = –
i , Z4 = – i, Z5 = – i, Z6 =
i, Z5 = – i, Z6 = i
i
3)
Доказать, что сумма двух комплексных чисел не превосходит сумму модулей этих чисел.
1 СПОСОБ:
Пусть Z1=X+Y× i и Z2=U+V× i
Доказать что:
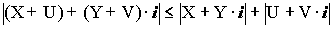
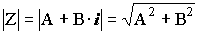
Предположим противоположное:
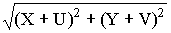 >
> 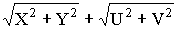 / т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
/ т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
X2+2· X· U+U2+Y2+2· Y· V+V2 > X2+Y2+U2+V2+2· 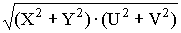
2· (X· U+Y· V) > 2· 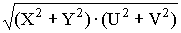
Если мы предположили верно, то X· U+Y· V > 0, а поэтому возведем в квадрат:
X2· U2+2· XU· Y· V+Y2· V2 > X2· U2 + X2· V2+Y2· U2+Y2· V2
2· X· Y· V· U > X2· V2+Y2· U2
X2· V2+Y2· U2 – 2· X· Y· V· U < 0
(X· V + Y· U)2 < 0
Это невозможно, т.к. A2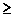 0, значит полученное нами неравенство неверно.
0, значит полученное нами неравенство неверно.
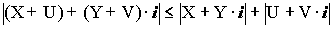
что и требовалось доказать
2 СПОСОБ:
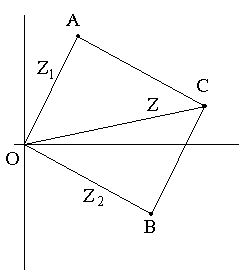
Пусть Z1 и Z2– два произвольных комплексных числа. Z1– соответствует точке A, Z2– соответствует точке B.
В силу неравенства треугольника
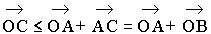 т.е.
т.е.
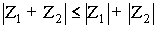
Что и требовалось доказать.
Дата добавления: 03.04.2001
www.km.ru
Доклад - Комплексные числа - Математика
<a/>/> ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобысделать возможной операцию извлечения квадратного корня из любогодействительного числа. Это, однако, не является достаточным основанием длятого, чтобы вводить в математику новые числа. Оказалось, что если производитьвычисления по обычным правилам над выражениями, в которых встречаютсяквадратный корень из отрицательного числа, то можно прийти к результату, уже несодержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решениякубического уравнения. Оказалось, когда кубическое уравнение имеет тридействительных корня, в формуле Кардано встречается квадратный корень изотрицательного числа. Поэтому квадратные корни из отрицательных чисел сталиупотреблять в математике и назвали их мнимыми числами – тем самым они как быприобрели право на нелегальное существование. Полные гражданские права мнимымчислам дал Гаусс, который назвал их комплексными числами, дал геометрическуюинтерпретацию и доказал основную теорему алгебры, утверждающую, что каждыймногочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики,физики сводится к решению алгебраических уравнений. Поэтому исследованиеалгебраических уравнений является одним из важнейших вопросов в математике.Стремление сделать уравнения разрешимыми – одна из главных причин расширенияпонятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней.Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чиселразрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X+B=0 (A/>0). Однако алгебраические уравнениястепени выше первой могут не иметь рациональных корней. Например, такимиявляются уравнения X2=2, X3=5. Необходимостьрешения таких уравнений явилось одной из причин введения иррациональных чисел.Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чиселнедостаточно для того, чтобы решить любое алгебраическое уравнение. Например,квадратное уравнение с действительными коэффициентами и отрицательнымдискриминантом не имеет действительных корней. Простейшее из них – уравнение X2+1=0. Поэтомуприходится расширять множество действительных чисел, добавляя к нему новыечисла. Эти новые числа вместе с действительными числами образуют множество,которое называют множеством комплексных чисел.
Выясним предварительно, какой виддолжны иметь комплексные числа. Будем считать, что на множестве комплексныхчисел уравнение X2+1=0 имеет корень. Обозначим этот кореньбуквой i Таким образом, i– это комплексное число, такое, что i2= –1.
Как и для действительных чисел, нужноввести операции сложения и умножения комплексных чисел так, чтобы сумма ипроизведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B·iможно считать записью комплексногочисла в общем виде. Название «комплексное» происходит от слова «составное»: по виду выражения A+B·i.
Комплексными числами называют выражения вида A+B·i, где A и B –действительныечисла, а i –некоторый символ, такой что i2= –1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A+B·i, а число B – его мнимой частью. Число i называется мнимой единицей.
Например, действительная частькомплексного числа 2+3·i равна 2, а мнимая равна 3.
Для строгого определения комплексногочисла нужно ввести для этих чисел понятие равенства.
Два комплексных числа A+B·i и C+D·i называются равными тогда итолько тогда, когда A=C и B=D, т.е. когда равны их действительныеи мнимые части.
2.ГЕОМЕТРИЧЕСКАЯИНТЕРПРЕТАЦИЯ
КОМПЛЕКСНОГОЧИСЛА
/>
Рисунок 1
Действительные числа геометрическиизображаются точками числовой прямой. Комплексное число A+B·i можно рассматривать как парудействительных чисел(A;B).Поэтому естественно комплексное число изображать точками плоскости. Впрямоугольной системе координат комплексное число Z=A+B·i изображаетсяточкой плоскости с координатами (A;B),и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствиеявляется взаимно однозначным. Оно дает возможность интерпретировать комплексныечисла как точки плоскости на которой выбрана система координат. Такаякоординатная плоскость называется комплексной плоскостью. Осьабсцисс называется действительной осью, т.к. на ней расположеныточки соответствующие действительным числам. Ось ординат называется мнимойосью – на ней лежат точки, соответствующие мнимым комплексным числам.
/>
Рисунок 2
Не менее важной и удобной являетсяинтерпретация комплексного числа A+B·i как вектора, т.е. вектора с началом в точке
O(0;0) и с концом вточке М(A;B) (рисунок 2).
Соответствие установленное междумножеством комплексных чисел, с одной стороны, и множествами точек или векторовплоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A+B·i. СопряженнымсZ называется комплексное число A – B·i, которое обозначается />, т.е.
/>=/>=A – B·i.
Отметим, что />= A+B·i, поэтому для любого комплексного числа Z имеет место равенство />=Z.
Модулем комплексного числа Z=A+B·i называется число /> иобозначается />, т.е.
/>=/>=/> (1)
Из формулы (1) следует, что /> для любого комплексногочисла Z, причем />=0 тогда и толькотогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
/>
4.СЛОЖЕНИЕИ УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммойдвух комплексных чисел A+B·i и C+D·iназывается комплексное число (A+C)+(B+D)·i, т.е. (A+B·i)+(C+D·i)=(A+C)+(B+D)·i
Произведениемдвух комплексных чисел A+B·i и C+D·i называется комплексное число (A·C – B·D)+(A·D+B·C) ·i, т.е.
(A+B·i)·(C+D·i)=(A·C– B·D)+(A·D+B·C)·i
Из формул вытекает, что сложение иумножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложенияи умножения комплексных чисел обладают свойствами действительных чисел.Основные свойства:
Переместительное свойство:
Z1<sup/>+Z2=Z2+Z1, Z1·Z2=Z2·Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1·Z2)·Z3=Z1·(Z2·Z3)
Распределительное свойство:
Z1·(Z2+Z3)=Z1·Z2+Z1·Z3
Геометрическое изображение суммыкомплексных чисел
/>
Рисунок 3
Согласно определению сложения двух комплексных чисел,действительная часть суммы равна сумме действительных частей слагаемых, мнимаячасть суммы равна сумме мнимых частей слагаемых. Точно также определяютсякоординаты суммы векторов:
Сумма двух векторов с координатами (A1;B1)и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор,соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы,соответствующие комплексным числам Z1 и Z2.
Пример1: Найти сумму и произведение комплексных чисел Z1=2 – 3×i и
1 Способ:
Z2= –7 + 8×i.
Z1 + Z2 = 2 – 7 + (–3 + 8)×i = –5 + 5×i
/>
Z1×Z2 = (2 – 3×i)×(–7 + 8×i) = –14 + 16×i + 21×i + 24 = 10 + 37×i
2 Способ:
5.ВЫЧИТАНИЕИ ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – этооперация, обратная сложению: длялюбых комплексных чиселZ1и Z2 существует, и притом только одно,число Z, такое, что:
Z+ Z2=Z1
Если к обеим частям равенстваприбавить (–Z2) противоположное числу Z2:
Z+Z2+(–Z2)=Z1+(–Z2), откуда
Z = Z1<sub/>– Z2
Число Z=Z1+Z2 называют разностью чиселZ1и Z2.
Деление вводится как операция,обратная умножению:
Z×Z2=Z1
Разделив обе части на Z2 получим:
Z=/>
Из этого уравнения видно, что Z2/>0
/>
Геометрическое изображениеразности комплексных чисел
Рисунок 4 Разности Z2 – Z1 комплексных чисел Z1 и Z2, соответствуетразность векторов, соответствующих числам Z1 и Z2. Модуль/> разности двух комплексныхчиселZ2 и Z1 по определению модуля есть длинавектора Z2 – Z1. Построим этот вектор, как суммувекторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двухкомплексных чисел есть расстояние между точками комплексной плоскости, которыесоответствуют этим числам.
Это важное геометрическоеистолкование модуля разности двух комплексных чисел позволяет с успехомиспользовать простые геометрические факты.
Пример 2: Даны комплексные числа Z1= 4 + 5·i и Z2= 3 + 4·i.Найти разность Z2 – Z1и частное />
Z2– Z1<sub/>= (3 + 4·i) – (4+ 5·i) = –1 – i
/>=/>=/>
6.ТРИГОНОМЕТРИЧЕСКАЯФОРМА
КОМПЛЕКСНОГОЧИСЛА
/>
Рисунок 5
Запись комплексного числа Z в виде A+B·i называется алгебраической формойкомплексногочисла. Помимо алгебраической формы используются и другие формы записикомплексных чисел.
Рассмотрим тригонометрическуюформу записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B·i выражаются через его модуль />= rи аргумент j следующим образом:
A=r·cosj; B= r·sinj.
Число Z можно записать так:
Z= r·cosj+i·/>·sinj = r·(cosj +i·sinj)
Z = r·(cosj +i·sinj) (2)
Эта запись называется тригонометрическойформой комплексного числа.
r =/>– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z/>0 называется величина угла междуположительным направлением действительной оси и вектором Z, причем величина угла считаетсяположительной, если отсчет ведется против часовой стрелки, и отрицательной,если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случаечисло задается только своим модулем.
Как уже говорилось выше />= r =/>, равенство (2)можно записать в виде
A+B·i=/>·cosj+i·/>·sinj, откуда приравнивая действительные имнимые части, получим:
cosj =/>, sinj =/> (3)
Если sinj поделить на cosj получим:
tgj=/> (4)
Эту формулу удобней использовать длянахождения аргумента j,чем формулы (3). Однако не все значения j, удовлетворяющие равенству (4),являются аргументами числа A+B·i. Поэтому при нахождении аргумента нужно учесть, вкакой четверти расположена точка A+B·i.
7.СВОЙСТВАМОДУЛЯ И АРГУМЕНТА
КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формыудобно находить произведение и частное комплексных чисел.
Пусть Z1= r1·(cosj1<sub/>+i·sinj1), Z2<sub/>= r2·(cosj2<sub/>+i·sinj2). Тогда:
Z1Z2= r1·r2[cosj1·cosj2 – sinj1·sinj2 + i·( sinj1·cosj2 + cosj1·sinj2)]=
=r1·r2[cos(j1+ j2) + i·sin(j1+ j2)].
Таким образом, произведениекомплексных чисел, записанных в тригонометрической форме, можно находить поформуле:
Z1Z2=r1·r2[cos(j1+ j2) + i·sin(j1+ j2)] (5)
Из формулы (5) следует, чтоприумножении комплексных чисел их модули перемножаются, а аргументы складываются.
Если Z1=Z2 то получим:
Z2=[r·(cosj+i·sinj)]2= r2·(cos2j+i·sin2j)
Z3=Z2·Z=r2·(cos2j+i·sin2j)·r·(cosj+i·sinj)=
=r3·(cos3j+i·sin3j)
Вообще для любого комплексного числа Z=r·( cosj+i·sinj)/>и любого натурального числа n справедлива формула:
Zn<sup/>=[ r·(cosj+i·sinj)]n= rn·(cosnj+i·sinnj), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел,записанных в тригонометрической форме, можно находить по формуле:
/>/>/>[ cos(j1– j2) + i·sin(j1– j2)]. (7)
/>= />=cos(–j2) + i·sin(–j2)
Используя формулу 5
/>(cosj1 +i·sinj1)×(cos(–j2) + i·sin(–j2)) =
cos(j1– j2) + i·sin(j1– j2).
Пример 3:
Z3 = –8
Число –8запишем в тригонометрической форме
8 = 8·(cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r3×(cos3j+ i×sin3j) = 8·(cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Тогда 3j =p + 2pk, kÎZ
j=/>, kÎZ
r3 = 8
r = 2
Следовательно:
Z = 2·( cos(/>) + i·sin(/>)), kÎZ
k = 0,1,2...
k = 0
Z1 = 2·( cos/> +i·sin/>) = 2·(/>i) = 1+/>×i
k = 1
Z2 = 2·( cos(/> + />) + i·sin(/> + />)) = 2·( cosp + i·sinp) = –2
k = 2
Z3 = 2·( cos(/> + />) + i·sin(/> + />)) = 2·( cos/> + i·sin/>) = 1–/>×i
Ответ: Z13 = />;Z2 = –2
Пример 4:
Z4 = 1
Число 1запишем в тригонометрической форме
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r4×(cos4j+ i×sin4j) =cos(2pk) + i·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j= />, kÎZ
r4= 1
r = 1
Z = cos />+ i×sin/>
k = 0,1,2,3...
k = 0
Z1 = cos0+ i×sin0= 1 + 0 = 1
k = 1
Z2 = cos />+ i×sin/> = 0 +i = i
k = 2
Z3 = cosp + i·sinp = –1+ 0 = –1
k = 3
Z4 = cos />+ i×sin/>
Ответ: Z13 = />1
Z24 = /> i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕКОРНЯ
Из формулы 6 видно, что возведениекомплексного числа r·( cosj +i·sinj) в целую положительную степень снатуральным показателем его модуль возводится в степень с тем же показателем,а аргумент умножается на показатель степени.
[r·(cosj +i·sinj)]n= rn·(cos nj +i·sin nj)
Число Zназывается корнем степениn из числа w ( обозначается />), если Zn =w.
Из данного определения вытекает, чтокаждое решение уравнения Zn =w является корнем степени n из числа w. Другими словами, для того, чтобыизвлечь корень степени nиз числа w, достаточнорешить уравнение Zn =w. Если w=0, то при любом nуравнение Zn=wимеет только одно решение Z=0. Если w/>0, то и Z/>, а, следовательно, и Zиw можно представить втригонометрической форме
Z = r·(cosj +i·sinj), w = p·(cosy +i·siny)
Уравнение Zn = w примет вид:
rn·(cos nj +i·sin nj) = p·( cosy +i·siny)
Два комплексных числа равны тогда итолько тогда, когда равны их модули, а аргументы отличаются слагаемыми,кратными 2p. Следовательно, rn = p и nj = y + 2pk, гдеkÎZ или r = /> иj = />,где kÎZ.
Итак, все решения могут быть записаныследующим образом:
ZK=/>[cos(/>) + i·sin(/>)], kÎZ (8)
Формулу 8 называют второйформулой Муавра.
Таким образом, если w/>0, то существует ровно n корней степени n из числа w: все они содержатся в формуле 8. Всекорни степениnиз числа w имеют один и тот же модуль />, но разные аргументы,отличающиеся слагаемым, кратным числу />.Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w, соответствует точкам комплекснойплоскости, расположенным в вершинах правильного n– угольника, вписанного в окружностьрадиуса /> с центром в точке Z = 0.
Символ /> неимеет однозначного смысла. Поэтому, употребляя его, следует четко представлятьсебе, что под этим символом подразумевается. Например, используя запись />, следует подумать о том,чтобы было ясно, понимается под этим символом пара комплексных чисел i и–i, или одно, то какое именно.
Уравнениявысших степеней
Формула 8 определяет все корнидвучленного уравнения степени n.Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнениястепени n:
an×Zn +an–1×Zn–1<sup/>+...+a1×Z1<sup/>+a0<sub/>= (9)
Где an,..., a0<sub/>– заданные комплексные числа.
В курсе высшей математикидоказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайнеймере один корень. Эта теорема была доказана немецким математиком Карлом Гауссомв 1779 году.
Опираясь на теорему Гаусса, можнодоказать, что левая часть уравнения 9 всегда может быть представлена в видепроизведения:
/>,
Где Z1,<sub/>Z2,...,<sub/>ZK – некоторые различные комплексные числа,
а a1,a2,...,ak<sub/>– натуральные числа, причем:
a1+ a2 +… + ak = n
Отсюда следует, что числа Z1,<sub/>Z2,...,<sub/>ZK являются корнями уравнения 9. При этом говорят, что Z1<sub/>является корнем кратности a1, Z2<sub/>– корнем кратности a2 и так далее.
Если условиться считать кореньуравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнениестепени nимеет в множестве комплексных чиселровноn корней.
Теорема Гаусса и только чтосформулированная теорема дают решения о существовании корней, но ничего неговорят о том, как найти эти корни. Если корни первой и второй степени могутбыть легко найдены, то для уравнений третей и четвертой степеней формулыгромоздки, а для уравнений степени выше четвертой таких формул вообще несуществует. Отсутствие общего метода не мешает отыскивать все корни уравнения.Для решения уравнения с целыми коэффициентами часто оказывается полезнойследующая теорема: целые корнилюбого алгебраического уравнения с целыми коэффициентами являются делителямисвободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an×Zn + an–1×Zn–1<sup/>+...+ a1×Z1<sup/>+ a0<sub/>= 0
с целыми коэффициентами. Тогда
an×kn + an–1×kn–1<sup/>+...+ a1×k1<sup/>+ a0<sub/>= 0
a0<sub/>= – k(an×kn–1 + an–1×kn–2 +...+ a1)
Число в скобках, при сделанныхпредположениях, очевидно, целое, значит k – делитель числа a0.
9.КВАДРАТНОЕУРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
1. имеет один корень, если a = 0.
2. имеет два действительных корня Z1,2=/>, если a > 0.
3. неимеет действительных корней, если a < 0. Но имеетдва комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2×/>=i2×(/>)2. Тогда уравнение Z2 = a запишется в виде: Z2 –i2×(/>)2= 0
т.е. (Z – i×/>)(Z + i×/>) = 0
Следовательно, уравнение имеет двакорня: Z1,2= /> i×/>
Введенное понятие корня из отрицательногочисла позволяет записать корни любого квадратного уравнения с действительнымикоэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2=/> (10)
Итак, при любых действительных a(a/>0), b, c корни уравнения можно находить поформуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен, то уравнение a×Z2 + b×Z + c = 0 два действительных различных корня.Если D = 0, то уравнение a×Z2 + b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z2 + b×Z + c = 0 имеет два различных комплексныхкорня.
Комплексные корни квадратногоуравнения обладают такими же свойствами, как и известные нам свойствадействительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2 + b×Z + c = 0, a/>0. Тогда справедливы свойства:
1. Теорема Виета: Z1+ Z2 = –/>
Z1×Z2 = />
2. При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 –6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 = />
Z1,2 =/>
Ответ: Z1= Z2 = 3 +i
Пример 6:
3·Z2 +2·Z+ 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = /> = />
Z1,2 =/>
Z1 = –(/>)
Z2 = –/>
Ответ: Z1 = Z2 = –/>
Пример 7:
Z4 –8·Z2 – 9 = 0
Z2 = t
t2 –8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = />= />= 4/>
t1 =9 t2 = – 1
Z2 =9 Z2 = – 1
Z1,2 =/>3 Z = />
Z3,4 =/>i
Ответ: Z1,2 =/>3, Z3,4=/>i
Пример 8:
Z4 + 2·Z2– 15 = 0
Z2 = t
t2 + 2·t –15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = />= />= –1/>4
t1 = –5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = –1·5 Z3,4 =/>/>
Z2 = i2·5
Z1,2 =/>i/>
Ответ: Z1,2 =/>i/>, Z3,4=/>/>
Пример 9:
Z2 = 24– 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i–Y2
X2 + 2·X·Y·i– Y2= 24 – 10·i
{
(X2 – Y2)+ 2·X·Y·i=24 – 10·i X2 – Y2 = 24
2·X·Y = – 10
Y = – />
X2 – />= 24
/> умножимна X2/>0
X4 – 24·X2– 25 = 0
X2 = t
t2 – 24·t –25 = 0
t1·t2= – 25
t1 + t2= 24
t1 =25 t2 = – 1
X2 =25 X2 = – 1 — нетрешений
X1,2 = />5
X1 =5 X2 = – 5
Y1 = – /> Y2= />
Y1 = –1 Y2 = 1
Тогда:
Z1,2 =/>(5 – i)
Ответ: Z1,2 =/>(5 – i)
ЗАДАЧИ:
{
1)/> X2 + 3·X·Y + Y2 = 6
X + Y = 2
/>
( 2 – Y)2+ 3·( 2 – Y)·Y + Y2 = 6
4 – 4·Y + Y2+ 6·Y – 3·Y2 + Y2 = 6
–Y2 +2Y – 2 = 0 /–1
Y2 – 2Y+ 2 = 0
Д = b2 – 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4·i2
Y1,2 = /> = /> = 1/> i
Y1 = 1–i Y2 = 1 + i
{
X1 = 1 + i X2 = 1–iОтвет: {1 +i; 1–i}
{1–i; 1 + i}
{
2)/> Z3 + w5 = 0
Z2×/>4 = 111/>4 = 1
{
Z3 = –w5
Z2×/>12 = 1
—Возведем в квадрат
—Возведем в куб
/>
w10×/>12= 1
w10×/>10×/>2 = 1
(w×/>)10×/>2= 1
(/>)10×/>2 = 1
т.к. w = A + B×i
/> = A – B×i
w×/> = (A + B×i)·( A – B×i) = A2 – (B×i)2= A2 + B2 = />2= w×/>
т.е. />20·/>2= 1
Возьмем модуль от обоихчастей последнего уравнения:
/>20·/>2 = 1
/>22 = 1
т.е.
/> = 1
Тогда из уравнения получим
/>2 = 1
т.е.
/> = />1
w1 =1 w2 = –1
Подставим эти значения впервое уравнение данной системы и найдем численное значение Z
1) w1 =1
Z6 = 1
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Z = r×(cosj+ i×sinj)
r6×(cos6j+ i×sin6j) = cos(2pk) +i·sin(2pk), kÎZ
r6= 1 6j = 2pk
r =1 j = />, kÎZ
Z = cos/>+ i·sin/>, kÎZ
k = 0,1,2...
k = 0
Z1 = cos0+ i×sin0= 1 + 0 = 1
Z1 = 1
k = 1
Z2 = cos/> +i·sin/> = />i= />i
Z2 =/>i
k = 2
Z3 =cos/>+ i·sin/> = –/>i
Z3 = –/>i
k = 3
Z4 = cosp + i·sinp = –1+ 0 = –1
Z4 = –1
k = 4
Z5 = cos/> +i·sin/> = –/>i
Z5 = –/>i
k = 5
Z6 = cos/> +i·sin/> = />i
Z6 = />i
Ответ: Z1 = 1, Z2=/>i, Z3 = –/>i, Z4 = –1, Z5= –/>i, Z6= />i
2) w2 = –1
Z6 = –1
–1 = 1·(cos(p + 2pk) +i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r6×(cos6j+ i×sin6j) = cos(p + 2pk) + i·sin(p + 2pk), kÎZ
r6 =1 6j = p + 2pk
r = 1 j = />, kÎZ
Z = cos(/>) + i·sin(/>), kÎZ
k = 0,1,2...
k = 0
Z1 = cos/> +i·sin/> = />i
Z1=/>i
k = 1
Z2= cos(/>) + i·sin(/>) = 0 + i= i
Z2=i
k = 2
Z3= cos(/>) + i·sin(/>) = –/>i
Z3= –/>i
k = 3
Z4= cos(/>) + i·sin(/>) = –/>i
Z4= –/>i
k = 4
Z5= cos(/>) + i·sin(/>) = 0 – i= –i
Z5= – i
k = 5
Z6= cos(/>) +i·sin(/>)= />i
Z6=/>i
Ответ: Z1 =/>i , Z2 =i, Z3= –/>i, Z4 = –/>i, Z5= – i, Z6 =/>i
3)
Доказать, что сумма двухкомплексных чисел не превосходит сумму модулей этих чисел.
1 СПОСОБ:
Пусть Z1=X+Y×i и Z2=U+V×i
Доказать что:
/>
/>
Предположим противоположное:
/>>/> / т.к. корень существует только из неотрицательного числа, то можно возвести вквадрат обе части неравенства.
X2+2·X·U+U2+Y2+2·Y·V+V2 > X2+Y2+U2+V2+2·/>
2·(X·U+Y·V) > 2·/>
Если мы предположили верно,то X·U+Y·V > 0, а поэтому возведем вквадрат:
X2·U2+2·XU·Y·V+Y2·V2> X2·U2 + X2·V2+Y2·U2+Y2·V2
2·X·Y·V·U > X2·V2+Y2·U2
X2·V2+Y2·U2– 2·X·Y·V·U < 0
(X·V + Y·U)2 < 0
Это невозможно, т.к. A2/> 0, значит полученное нами неравенство неверно.
/>
что и требовалось доказать
2 СПОСОБ:
/>
Пусть Z1 и Z2 – двапроизвольных комплексных числа. Z1– соответствует точке A, Z2 –соответствует точке B.
В силу неравенстватреугольника
/> т.е.
/>
Что и требовалось доказать.
www.ronl.ru
Реферат - Комплексные числа - Рефераты на репетирем.ру
Комплексные числа
ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X+B=0 (A  0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X2+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X2+1=0 имеет корень. Обозначим этот корень буквой i Таким образом, i – это комплексное число, такое, что i 2=–1.
Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B·i можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A+B·i.
Комплексными числами называют выражения вида A+B·i, где A и B –действительные числа, а i – некоторый символ, такой что i2=–1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A+B·i, а число B – его мнимой частью. Число i называется мнимой единицей.
Например, действительная часть комплексного числа 2+3·i равна 2, а мнимая равна 3.
Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.
Два комплексных числа A+B·iи C+D·i называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА

Рисунок 5 Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B·i можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+B·i изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки, соответствующие мнимым комплексным числам.

Рисунок 5 Не менее важной и удобной является интерпретация комплексного числа A+B·i как вектора, т.е. вектора с началом в точке
O(0;0) и с концом в точке М(A;B) (рисунок 2).
Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A+B·i. Сопряженным с Zназывается комплексное число A – B·i, которое обозначается  , т.е.
, т.е.
 =
=  =A – B·i.
=A – B·i.
Отметим, что  = A+B·i, поэтому для любого комплексного числа Z имеет место равенство
= A+B·i, поэтому для любого комплексного числа Z имеет место равенство  =Z.
=Z.
Модулем комплексного числа Z=A+B·i называется число  и обозначается
и обозначается  , т.е.
, т.е.
 =
=  =
=  (1)
(1)
Из формулы (1) следует, что  для любого комплексного числа Z, причем
для любого комплексного числа Z, причем  =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:

4.СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммой двух комплексных чисел A+B·iи C+D·i называется комплексное число (A+C) + (B+D)·i, т.е. (A+B·i) + (C+D·i)=(A+C) + (B+D)·i
Произведением двух комплексных чисел A+B·iи C+D·i называется комплексное число (A·C – B·D)+(A·D+B·C) ·i, т.е.
(A + B·i)·(C + D·i)=(A·C – B·D) + (A·D + B·C)·i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2= –1.Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство:
Z1+Z2=Z2+Z1, Z1·Z2=Z2·Z1
Сочетательное свойство:
(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1·Z2)·Z3=Z1·(Z2·Z3)
Распределительное свойство:
Z1·(Z2+Z3)=Z1·Z2+Z1·Z3
Геометрическое изображение суммы комплексных чисел

Рисунок 5 Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:
Сумма двух векторов с координатами (A1;B1) и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1и Z2 нужно сложить векторы, соответствующие комплексным числам Z1и Z2.
Пример 1: Найти сумму и произведение комплексных чисел Z1=2 – 3×i и
1Способ:
Z2= –7 + 8×i.
Z1 + Z2 = 2 – 7 + (–3 + 8)×i = –5 + 5×i
Z1×Z2 = (2 – 3×i)×(–7 + 8×i) = –14 + 16×i + 21×i + 24 = 10 + 37×i
2 Способ:

5.ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1и Z2существует, и притом только одно, число Z, такое, что:
Z + Z2=Z1
Если к обеим частям равенства прибавить (–Z2) противоположное числу Z2:
Z+Z2+(–Z2)=Z1+(–Z2), откуда
Z = Z1– Z2
Число Z=Z1+Z2 называют разностью чисел Z1и Z2.
Деление вводится как операция, обратная умножению:
Z×Z2=Z1
Разделив обе части на Z2получим:
Z= 
Из этого уравнения видно, что Z2  0
0

Геометрическое изображение разности комплексных чисел
Рисунок 5
Разности Z2– Z1комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль  разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам. Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.
Пример 2: Даны комплексные числа Z1= 4 + 5·i и Z2= 3 + 4·i. Найти разность Z2 – Z1и частное 
Z2 – Z1= (3 + 4·i) – (4 + 5·i) = –1 – i
 =
= =
=
6.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА

Рисунок 5
Запись комплексного числа Z в виде A+B·i называется алгебраической формой комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.
Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B·i выражаются через его модуль  = r и аргумент j следующим образом:
= r и аргумент j следующим образом:
A= r·cosj ; B= r·sinj.
Число Z можно записать так:
Z= r·cosj+ i·  ·sinj = r·(cosj + i·sinj)
·sinj = r·(cosj + i·sinj)
Z = r·(cosj + i·sinj) (2)
Эта запись называется тригонометрической формой комплексного числа.
r =  – модуль комплексного числа.
– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается только своим модулем.
Как уже говорилось выше = r =, равенство (2) можно записать в виде
A+B·i=·cosj + i··sinj,откуда приравнивая действительные и мнимые части, получим:
cosj =, sinj = (3)
Если sinj поделить на cosj получим:
tgj= (4)
Эту формулу удобней использовать для нахождения аргумента j, чем формулы (3). Однако не все значения j, удовлетворяющие равенству (4), являются аргументами числа A+B·i . Поэтому при нахождении аргумента нужно учесть, в какой четверти расположена точка A+B·i.
7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.
Пусть Z1= r1·(cosj1 + i·sinj1), Z2= r2·(cosj2 + i·sinj2). Тогда:
Z1Z2= r1·r2[cosj1·cosj2 – sinj1·sinj2 + i·( sinj1·cosj2 + cosj1·sinj2)]=
= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)].
Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
Z1Z2= r1·r2[cos(j1 + j2) + i·sin(j1 + j2)] (5)
Из формулы (5) следует, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Если Z1=Z2то получим:
Z2=[r·(cosj + i·sinj)]2= r2·(cos2j + i·sin2j)
Z3=Z2·Z= r2·(cos2j + i·sin2j)·r·(cosj + i·sinj)=
= r3·(cos3j + i·sin3j)
Вообще для любого комплексного числа Z= r·( cosj + i·sinj)0 и любого натурального числа n справедлива формула:
Zn =[ r·(cosj + i·sinj)]n= rn·( cosnj+ i·sinnj), (6)
которую называют формулой Муавра.
Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
[ cos(j1 – j2) + i·sin(j1 – j2)]. (7)
= = cos(–j2) + i·sin(–j2)
Используя формулу 5
(cosj1 + i·sinj1)×( cos(–j2) + i·sin(–j2)) =
cos(j1 – j2) + i·sin(j1 – j2).
Пример 3:
Z3 = –8
Число –8 запишем в тригонометрической форме
8 = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r3×(cos3j+ i×sin3j) = 8·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ
Тогда 3j =p + 2pk, kÎZ
j = , kÎZ
r3 = 8
r = 2
Следовательно:
Z = 2·( cos() + i·sin()), kÎZ
k = 0,1,2...
k = 0
Z1 = 2·( cos + i·sin) = 2·(i) = 1+×i
k = 1
Z2 = 2·( cos( + ) + i·sin( + )) = 2·( cosp + i·sinp) = –2
k=2
Z3 = 2·( cos( + ) + i·sin( + )) = 2·( cos + i·sin) = 1–×i
Ответ: Z13 = ; Z2 = –2
Пример 4:
Z4 = 1
Число 1 запишем в тригонометрической форме
1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ
Пусть Z = r×(cosj+ i×sinj), тогда данное уравнение запишется в виде:
r4×(cos4j+ i×sin4j) = cos(2pk) + i·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j = , kÎZ
r4 = 1
r = 1
Z = cos + i×sin
k = 0,1,2,3...
k = 0
Z1 = cos0+ i×sin0 = 1 + 0 = 1
k = 1
Z2 = cos + i×sin = 0 + i = i
k = 2
Z3 = cosp + i·sinp = –1 + 0 = –1
k = 3
Z4 = cos + i×sin
Ответ: Z13 = 1
Z24 = i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Из формулы 6 видно, что возведение комплексного числа r·( cosj + i·sinj) в целую положительную степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
[ r·(cosj + i·sinj)]n= rn·( cos nj + i·sin nj)
Число Z называется корнем степени n из числа w ( обозначается ), если Zn =w.
Из данного определения вытекает, что каждое решение уравнения Zn = w является корнем степени n из числа w. Другими словами, для того, чтобы извлечь корень степени n из числа w, достаточно решить уравнениеZn = w. Если w=0, то при любом n уравнение Zn = w имеет только одно решение Z= 0. Если w0, то и Z0, а, следовательно, и Z и w можно представить в тригонометрической форме
Z = r·(cosj + i·sinj), w = p·(cosy + i·siny)
Уравнение Zn = w примет вид:
rn·( cos nj + i·sin nj) = p·( cosy + i·siny)
Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемыми, кратными 2p. Следовательно, rn = p и nj=y+2pk, где kÎZ или r = и j = , где kÎZ.
Итак, все решения могут быть записаны следующим образом:
ZK=[cos() + i·sin()], kÎZ (8)
Формулу 8 называют второй формулой Муавра.
Таким образом, если w0, то существует ровно n корней степени n из числа w: все они содержатся в формуле 8. Все корни степени n из числа wимеют один и тот же модуль , но разные аргументы, отличающиеся слагаемым, кратным числу . Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w, соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса с центром в точке Z = 0.
Символ не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись , следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно.
Уравнения высших степеней
Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнения степени n:
an×Zn + an–1×Zn–1 +...+ a1×Z1 + a0 = 0 (9)
Где an,..., a0– заданные комплексные числа.
В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.
Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9 всегда может быть представлена в виде произведения:
,
Где Z1,Z2,...,ZK– некоторые различные комплексные числа,
а a1,a2,...,ak – натуральные числа, причем:
a1 + a2 + ... + ak = n
Отсюда следует, что числа Z1,Z2,...,ZK являются корнями уравнения 9. При этом говорят, что Z1 является корнем кратности a1, Z2– корнем кратности a2 и так далее.
Если условиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел ровно n корней.
Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для уравнений третей и четвертой степеней формулы громоздки, а для уравнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни уравнения. Для решения уравнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an×Zn + an–1×Zn–1+...+ a1×Z1+ a0= 0
с целыми коэффициентами.Тогда
an×kn + an–1×kn–1+...+ a1×k1+ a0= 0
a0= – k(an×kn–1 + an–1×kn–2 +...+ a1)
Число в скобках, при сделанных предположениях, очевидно, целое, значит k – делитель числа a0.
9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
имеет один корень, если a = 0.
имеет два действительных корня Z1,2=, если a > 0.
не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2×= i2×()2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2×()2 = 0
т.е. (Z – i×)(Z + i×) = 0
Следовательно, уравнение имеет два корня: Z1,2 = i×
Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами
a×Z2 + b×Z + c = 0
По известной общей формуле
Z1,2= (10)
Итак, при любых действительных a(a0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2– 4×a×c
положителен , то уравнение a×Z2 + b×Z + c = 0 два действительных различных корня. Если D = 0, то уравнение a×Z2 + b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z2 + b×Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2 + b×Z + c = 0, a0. Тогда справедливы свойства:
Теорема Виета: Z1 + Z2 = –
Z1×Z2 =
При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 5:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i2·4
Z1,2 =
Z1,2 =
Ответ: Z1 = Z2 = 3 + i
Пример 6:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2 = =
Z1,2 =
Z1 = – ()
Z2 = –
Ответ: Z1 = Z2 = –
Пример 7:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = = = 4
t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 =3 Z =
Z3,4 =i
Ответ: Z1,2 =3, Z3,4 =i
Пример 8:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = = = –14
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 =
Z2 = i2·5
Z1,2 =i
Ответ: Z1,2 =i, Z3,4 =
Пример 9:
Z2 = 24 10·i
Пусть Z = X + Y·i
(X + Y·i)2 = X2 + 2·X·Y·i Y2
X2 + 2·X·Y·i Y2 = 24 10·i
(X2 Y2) + 2·X·Y·i = 24 10·i
Y =
X2 = 24
умножим на X2 0
X4 – 24·X2 – 25 = 0
X2 = t
t2 – 24·t – 25 = 0
t1·t2 = – 25
t1 + t2 = 24
t1 = 25 t2 = – 1
X2 = 25 X2 = – 1 — нет решений
X1,2 = 5
X1 = 5 X2 = – 5
Y1 = – Y2 =
Y1 = – 1 Y2 = 1
Тогда:
Z1,2 =(5 – i)
Ответ: Z1,2 =(5 – i)
ЗАДАЧИ:
1)
( 2 – Y)2 + 3·( 2 – Y)·Y + Y2 = 6
4 – 4·Y + Y2 + 6·Y – 3·Y2 + Y2 = 6
–Y2 + 2Y – 2 = 0 /–1
Y2 – 2Y + 2 = 0
Д = b2 – 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4· i2
Y1,2 = = = 1 i
Y1 = 1– i Y2 = 1 + i
X1 = 1 + i X2 = 1– i
Ответ: {1 + i ; 1– i}
{1– i ; 1 + i}
2)
— Возведем в квадрат
— Возведем в куб
referat.store
Реферат - Комплексные числа - Математика
Средняя общеобразовательная школа №1 11 класс
<img src="/cache/referats/12808/image001.gif" v:shapes="_x0000_s1027"> <img src="/cache/referats/12808/image002.gif" " v:shapes="_x0000_s1028 _x0000_s1030">
<img src="/cache/referats/12808/image004.gif" align=«left» hspace=«12» v:shapes="_x0000_s1026"><span Arial",«sans-serif»; mso-bidi-font-family:«Times New Roman»">
“Помимо и даже против воли того или другого математика, мнимые числаснова и снова появляются на выкладках, и лишь постепенно, по мере того какобнаруживается польза от их употребления, они получают более и более широкоераспространение” Ф. Клейн.
Автор: Исаев Рома (полная версия реферата и много других полезных материалов на моём сайтеraycom.narod.ru/)Обязательно загляние!
Учитель:Моторина Дина Юрьевна
Дубна, 2002План:
1. Введение 2
2. Историявозникновения комплексных чисел 3
а) Развитие понятия очисле 3
б) На пути к комплекснымчислам 4
в) Утверждениекомплексных чисел в математике 5-6
3. Комплексные числа иих свойства 7
а) Понятие комплексногочисла 7
б) Геометрическоеизображение комплексных чисел 8-9
в) Тригонометрическаяформа комплексного числа 9
4. Действия с комплекснымичислами 10
а) сложение 11
б) вычитание 11
в) умножение 10-11
г) деление 11
5. Решение уравнений скомплексными переменными 12-13
6. Приложение 14
7. Заключение 15
8. Списоклитературы 15
Введение
Решение многих задач физики и техники приводит кквадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решениемногих таких задач имеет вполне определенный физический смысл. Значениевеличин, получающихся в результате решения указанных уравнений, назваликомплексными числами. Комплексные числа широко использовал отец русской авиацииН. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой онявляется. Комплексные числа и функции от комплексного переменного находятприменение во многих вопросах науки и техники.
Цельнастоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решениемуравнений с комплексным переменным.
Историявозникновения комплексных чисел1. Развитие понятия о числеДревнегреческие математикисчитали “настоящими” только натуральные числа. Постепенно складывалосьпредставление о бесконечности множества натуральных чисел.
В IIIвеке Архимед разработалсистему обозначения вплоть до такого громадного как <img src="/cache/referats/12808/image006.gif" v:shapes="_x0000_i1028">
Следующим важным этапом в развитии понятия очисле было введение отрицательных чисел — это было сделано китайскимиматематиками за два века до н. э. Отрицательные числа применяли в IIIвекедревнегреческий математик Диофант, знавший уже правила действия над ними, а в VIIвекеэти числа уже подробно изучили индийские ученые, которые сравнивали такие числас долгом. С помощью отрицательных чисел можно было единым образом описыватьизменения величин. Уже в VIIIвеке было установлено, чтоквадратный корень из положительного числа имеет два значения — положительное иотрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: неттакого числа <img src="/cache/referats/12808/image008.gif" v:shapes="_x0000_i1029">,чтобы <img src="/cache/referats/12808/image010.gif" v:shapes="_x0000_i1030">.
2. На пути к комплексным числамВ XVIвеке в связи с изучениемкубических уравнений оказалось необходимым извлекать квадратные корни из отрицательныхчисел. В формуле для решения кубических уравнений вида <img src="/cache/referats/12808/image012.gif" v:shapes="_x0000_i1031"> кубические иквадратные корни: <img src="/cache/referats/12808/image014.gif" v:shapes="_x0000_i1025"><img src="/cache/referats/12808/image016.gif" v:shapes="_x0000_i1032">.<img src="/cache/referats/12808/image018.gif" v:shapes="_x0000_i1033">
Эта формула безотказно действует в случае,когда уравнение имеет один действительный корень (<img src="/cache/referats/12808/image020.gif" v:shapes="_x0000_i1026"> x=1), а если оно имеет три действительных корня (<img src="/cache/referats/12808/image022.gif" v:shapes="_x0000_i1034"> x1=1x2,3 =<img src="/cache/referats/12808/image024.gif" v:shapes="_x0000_i1027">XVIIIи XIXвеков доказал, чтобуквенное уравнение пятой степени <img src="/cache/referats/12808/image026.gif" v:shapes="_x0000_i1035"> нельзя решить алгебраически;точнее: нельзя выразить его корень через буквенные величины a, b, c, d, eспомощью шести алгебраических действий (сложение, вычитание, умножение, деление,возведение в степень, извлечение корня).
В 1830 году Галуа (Франция) доказал, чтоникакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-йстепени имеет (если рассматривать и комплексные числа) nкорней (среди которых могутбыть и равные). В этом математики были убеждены еще в XVIIвеке (основываясь наразборе многочисленных частных случаев), но лишь на рубеже XVIIIи XIXвеков упомянутая теорема была доказана Гауссом.
Итальянский алгебраист Дж.Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что системауравнений <img src="/cache/referats/12808/image028.gif" v:shapes="_x0000_i1036">, не имеющая решений во множестве действительных чисел,имеет решения вида <img src="/cache/referats/12808/image030.gif" v:shapes="_x0000_i1037">,<img src="/cache/referats/12808/image032.gif" v:shapes="_x0000_i1038"><img src="/cache/referats/12808/image034.gif" v:shapes="_x0000_i1039">
3. Утверждение комплексных чисел в математикеКардано называл такиевеличины “чисто отрицательными” идаже “софистически отрицательными”,считал их бесполезными и старался их не употреблять. В самом деле, с помощьютаких чисел нельзя выразить ни результат измерения какой-нибудь величины, ниизменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянскогоалгебраиста Р. Бомбелли, в которой были установлены первые правилаарифметических операций над такими числами, вплоть до извлечения из них кубическихкорней. Название “мнимые числа” ввелв 1637 году французский математик и философ Р. Декарт, а в 1777 году один изкрупнейших математиков XVIIIвека — Л. Эйлер предложилиспользовать первую букву французского слова imaginaire(мнимый) для обозначениячисла <img src="/cache/referats/12808/image036.gif" v:shapes="_x0000_i1040"> (мнимой единицы). Этотсимвол вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексныечисла” так же был введен Гауссом в1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий,предметов, явлений и т. д. Образующих единое целое.
В течение XVIIвека продолжалосьобсуждение арифметической природы мнимых чисел, возможности дать им геометрическоеобоснование.
Постепенно развивалась техника операций надмнимыми числами. На рубеже XVIIи XVIIIвеков была построена общаятеория корней n-ых степеней сначала из отрицательных, а за тем излюбых комплексных чисел, основанная на следующей формуле английского математикаА. Муавра (1707): <img src="/cache/referats/12808/image038.gif" v:shapes="_x0000_i1041"><img src="/cache/referats/12808/image018.gif" v:shapes="_x0000_i1042">(подробнеесмотри приложение). С помощью этой формулы можно было так же вывестиформулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 годузамечательную формулу: <img src="/cache/referats/12808/image040.gif" v:shapes="_x0000_i1043"> которая связывалавоедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлераможно было возводить число eв любую комплекснуюстепень. Любопытно, например, что <img src="/cache/referats/12808/image042.gif" v:shapes="_x0000_i1044">.Можно находить sinи cosот комплексных чисел,вычислять логарифмы таких чисел, то есть строить теорию функций комплексногопеременного.
В конце XVIIIвека французский математик Ж. Лагранж смог сказать, что математический анализуже не затрудняют мнимые величины. С помощью мнимых чисел научились выражатьрешения линейных дифференциальных уравнений с постоянными коэффициентами. Такиеуравнения встречаются, например, втеории колебаний материальной точки в сопротивляющейся среде. Еще раньшешвейцарский математик Я. Бернулли применял комплексные числа для решенияинтегралов.
Хотя в течение XVIIIвека с помощью комплексныхчисел были решены многие вопросы, в том числе и прикладные задачи, связанные скартографией, гидродинамикой и т. д., однако еще не было строго логическогообоснования теории этих чисел. По этому французский ученый П. Лаплас считал,что результаты, полученные с помощью мнимых чисел, — только наведение,приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.
“Никто ведь не сомневается в точностирезультатов, получаемых при вычислениях с мнимыми количествами, хотя онипредставляют собой только алгебраические формы иероглифы нелепых количеств” Л.Карно.
После создания теории комплексных чиселвозник вопрос о существовании “гиперкомплексных” чисел — чисел с несколькими“мнимыми” единицами. Такую систему вида <img src="/cache/referats/12808/image044.gif" v:shapes="_x0000_i1045"><img src="/cache/referats/12808/image046.gif" v:shapes="_x0000_i1046"> (переместительности):например, <img src="/cache/referats/12808/image048.gif" v:shapes="_x0000_i1047"><img src="/cache/referats/12808/image050.gif" v:shapes="_x0000_i1048">
Большой вклад в развитие теории функцийкомплексного переменного внесли русские и советские ученые Н. И. Мусхелишвилизанимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев — каэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров — к проблемамквантовой теории поля.
Комплексные числа и их свойства1. О комплексных числах
В связи с развитием алгебры потребовалось ввестисверх прежде известных положительных и отрицательных чисел числа нового рода.Они называются комплексными. Комплексное число имеет вид a + bi; здесь aи b – действительныечисла, а i – числонового рода, называемое мнимой единицей. “Мнимые” числа составляют частный видкомплексных чисел (когда а = 0). С другой стороны, и действительные числаявляются частным видом комплексных чисел (когда b = 0).
Действительное число aназовем абсциссой комплексного числа a+ bi;действительное число b– ординатой комплексногочисла
a+ bi.Основное свойство числа iсостоит в том, чтопроизведение i*iравно –1, т.е.
i2= -1. (1)
Долгое время не удавалось найти такиефизические величины, над которыми можно выполнять действия, подчинённые тем жеправилам, что и действия над комплексными числами – в частности правилу (1). Отсюда названия: “мнимаяединица”, “мнимое число” и т.п. В настоящее время известен целый ряд такихфизических величин, и комплексные числа широко применяются не только в математике,но также и в физике и технике.
Правило каждого действия надкомплексными числами выводится из определения этого действия. Но определениядействий над комплексными числами не вымышлены произвольно, а установлены стаким расчетом, чтобы согласовались с правилами действий над вещественнымичислами. Ведь комплексные числа должны рассматриваться не в отрыве отдействительных, а совместно с ними.
Действительное число азаписывается также в виде a+ 0i(или a– 0i).
Примеры. Запись 3 + 0iобозначает то же, что запись 3. Запись –2 + 0iозначает –2.
Комплексное число вида 0 + biназывается “чисто мнимым”. Запись biобозначает то же, что 0 + bi. Два комплексных a+ bi, a’ + b’iсчитаются равными, если уних соответственно равны абсциссы иординаты, т. е. Если a= a’, b= b’. В противном случаекомплексные числа не равны. Это определение подсказывается следующим соображением. Если бы могло существовать,скажем, такое равенство:
2 + 5i= 8 +2i, то по правилам алгебры мы имели бы i= 2, тогда как iне должно батьдействительным числом.
2. Геометрическое изображение комплексных чисел
<img src="/cache/referats/12808/image052.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1033"> Действительные числа можно изобразить точкамипрямой линии, как показано на рис.2, где точка Kизображает число 5. Эточисло можно изобразить также отрезком ОK, учитывая не только его длину, но инаправление.
Каждая точка С “числовой прямой” изображаетнекоторое действительное число (рациональное, если отрезок ОС соизмерим с единицейдлины, и иррациональное, если несоизмерим). Таким образом, на “числовой прямой”не остаётся места для комплексных чисел.
Но комплексные числа можно изобразить на“числовой прямой”. Для этого мы выбираем на плоскости прямоугольную системукоординат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a+ biмы изображаемточкой М, у которой абсцисса х равна абсциссе а комплексного, аордината у равна ординате bкомплексного числа.
<img src="/cache/referats/12808/image054.jpg" align=«left» hspace=«12» v:shapes="_x0000_s1034">Примеры. На рис. 2 точка А сабсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. ТочкаВ (-4,-5) изображает комплексное число –4 — 5i.
Действительные числа (вкомплексной форме они имеют вид a+ 0i) изображают точками оси OХ, а чистомнимые – точками оси OУ.
Примеры. Точка К на рис. 2 изображает действительноечисло 5, точка L– чисто мнимое число 3i. Начало координатизображает число 0.
Сопряжённые комплексные числа изображаются паройточек, симметричных относительно оси абсцисс; так, точки А и А’ на рис. 2 изображаютсопряжённые числа 3 +5i и 3-5i.
Комплексные можно изображать также отрезками,начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости.Так, комплексное число a+ biможно изобразить не толькоточкой M (рис. 1), но также вектором ОM.
Замечание. Давая какому –либо отрезку наименование “вектор”, мы подчёркиваем, что существенное значениеимеет не только длина, но и направление отрезка.
Геометрическое истолкованиекомплексных чисел позволило определить многие понятия, связанные с функциейкомплексного переменного, расширило область их применения.
Стало ясно, что комплексныечисла полезны во многих вопросах, где имеют дело с величинами, которыеизображаются векторами <img src="/cache/referats/12808/image018.gif" v:shapes="_x0000_i1049">
3. Тригонометрическая формакомплексного числа.
Абсцисса а и ордината bкомплексного числа a+ biвыражаются через модуль r и аргумент q. Формулами
a =r cos q , r=a/cos q
b = r sin q, r=b/sin q
r–длина вектора (a+bi), q– угол, который он образуетс положительным направлением оси абсцисс (см. рис. 1).
Поэтому всякое комплексное число можно представитьв виде r(cosq+ isinq), где r> 0 т.е. z=a+bi или z=r*cosq+ r*sinq
Это выражение называется нормальнойтригонометрической формой или, короче, тригонометрической формой комплексногочисла.
Действия с комплексными числами
1. Сложение комплексных чисел Определение: Суммой комплексных чисел a+ biи a’ + b’iназываюткомплексное число (a+ a’) + (b+ b’)i.
Это определение подсказывается правиламидействий с обычными многочленами.
Пример 1. (-3 + 5i) +(4 – 8i) = 1 — 3i
Пример2. (2 + 0i) + (7 + 0i) = 9 + 0i.Так как запись 2 + 0iозначаетто же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой(2 + 7=9).
Пример3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Пример4. (-2 + 3i) + ( — 2 – 3i) = — 4
В примере 4 сумма двух комплексных чиселравна действительному числу. Два комплексных числа a+biи a-biназываются сопряженными.Сумма сопряженных комплексных чисел равна действительному числу.
Для комплексных чисел справедливыпереместительный и сочетательный законы сложения. Их справедливость следует изтого, что сложение комплексных чисел по существу сводится к сложению действительныхчастей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
2. Вычитание комплексныхчисел.
Определение.Разностью комплексных чиселa+ bi(уменьшаемое) и a’ + b’i(вычитаемое) называетсякомплексное число (a– a’) + (b– b’)i.
Пример1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
3. Умножение комплексныхчисел.
Определение. Произведением комплексных чисел a+ biи a’ + b’iназываетсякомплексное число
(aa’ – bb’) + (ab’ + ba’)i.
Замечание.На практике нет нуждыпользоваться формулой произведения. Можно перемножить данные числа, какдвучлены, а затем положить, что i2= -1.
Пример1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i2 = 3 – 6i + 2i + 4= 7 – 4i.
Пример2. (a + bi)(a – bi) = a2+ b2
Пример 2 показывает, что произведение сопряженныхкомплексных чисел есть действительное и притом положительное число.
Для умножения комплексныхчисел также справедливы переместительный и сочетательный законы, а такжераспределительный закон умножения по отношению к сложению.
4. Деление комплексныхчисел.
В соответствии с определением делениядействительных чисел устанавливается следующее определение.
Определение. Разделить комплексноечисло a+ biна комплексное число a’ + b’i– значит найти такое число x+ yi,которое, будучи помножено на делитель, даст делимое.
Конкретное правило деленияполучим, записав частное в виде дроби и умножив числитель и знаменатель этойдроби на число, сопряженное со знаменателем:(a+ bi):(c+ di)=<img src="/cache/referats/12808/image056.gif" v:shapes="_x0000_i1050">
Пример 1. Найти частное (7 – 4i):(3 + 2i).
Записав дробь (7 – 4i)/(3+ 2i), расширяем её на число 3 – 2i,сопряженное с 3 + 2i. Получим:
((7 – 4i)(3 — 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.
Пример 1 предыдущего пунктадаёт проверку.
Пример2.(-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)( -3 + 4i)) = (-14 –23i)/25= -0,56 – 0.92i.
Чтобы доказать, что праваячасть действительно является частным, достаточно помножить её на a’ + b’.Получим a+ bi.
<img src="/cache/referats/12808/image014.gif" v:shapes="_x0000_i1051">
Решениеуравнений с комплексными переменными
Рассмотримсначала простейшее квадратное уравнение z2 = a, где а — заданное число, z — неизвестное. На множестве действительных чисел это уравнение:
1) имеет один корень z= 0, если а = 0;
2) имеет два действительных корня z1,2 = <img src="/cache/referats/12808/image058.gif" v:shapes="_x0000_i1052">,если а>0;
3) не имеет действительных корней, если а<0.
Намножестве комплексных чисел это уравнение всегда имеет корень.
Задача 1. Найти комплексные корниуравнения z2 = a, если:
1) а = -1; 2)а = -25; 3) а = -3.
1) z2 = -1. Так как i2 = -1, то это уравнение можнозаписать в виде z2 = i2, или z2 — i2 = 0. Отсюда, раскладываялевую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i.Ответ. z1,2=<img src="/cache/referats/12808/image060.gif" v:shapes="_x0000_i1053">i.
2) z2 = -25. Учитывая, что i2 = -1, преобразуем этоуравнение:
z2= (-1)25,
z2= i2 52, z2 — 52 i2=0, (z-5i)(z+5i) = 0, откуда z1 =5i, z2 = -5i.Ответ:
z 1,2= <img src="/cache/referats/12808/image060.gif" v:shapes="_x0000_i1054">
3) z2= -3, z2 = i2(<img src="/cache/referats/12808/image062.gif" v:shapes="_x0000_i1055">2, z2 — (<img src="/cache/referats/12808/image062.gif" v:shapes="_x0000_i1056">2i2 = 0, (z -<img src="/cache/referats/12808/image062.gif" v:shapes="_x0000_i1057"> <img src="/cache/referats/12808/image062.gif" v:shapes="_x0000_i1058">
Ответ: z1,2 = <img src="/cache/referats/12808/image064.gif" v:shapes="_x0000_i1059">.
Вообщеуравнение z2 = a, где а < 0 имеет два комплексных корня: Z1,2=<img src="/cache/referats/12808/image058.gif" v:shapes="_x0000_i1060">i.
Используяравенство i2 = -1, квадратные корни из отрицательных чиселпринято записывать так: <img src="/cache/referats/12808/image067.gif" v:shapes="_x0000_i1061">i, <img src="/cache/referats/12808/image069.gif" v:shapes="_x0000_i1062">i, <img src="/cache/referats/12808/image071.gif" v:shapes="_x0000_i1063">i<img src="/cache/referats/12808/image073.gif" v:shapes="_x0000_i1064">
Итак, <img src="/cache/referats/12808/image075.gif" v:shapes="_x0000_i1065"> определен для любогодействительного числа а (положительного, отрицательного и нуля). Поэтому любоеквадратное уравнение az2 + bz+ c= 0, где а, b, с — действительные числа, а <img src="/cache/referats/12808/image077.gif" v:shapes="_x0000_i1066"> 0,имеет корни. Эти корни находятся по известной формуле:
Z1,2 = <img src="/cache/referats/12808/image079.gif" v:shapes="_x0000_i1067"> .
Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 = <img src="/cache/referats/12808/image081.gif" v:shapes="_x0000_i1068"><img src="/cache/referats/12808/image083.gif" v:shapes="_x0000_i1069"> = 2 <img src="/cache/referats/12808/image060.gif" v:shapes="_x0000_i1070">i.
Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3iи z2=2-3i. Найдем сумму ипроизведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.
Число 4 — это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположнымзнаком, а число 13- свободный член, то есть в этом случае справедлива теоремаВиета. Она справедлива для любого квадратного уравнения: если z1 и z2 — корни уравнения az2+bz+c= 0, z1+z2 = <img src="/cache/referats/12808/image085.gif" v:shapes="_x0000_i1071"> z1z2 = <img src="/cache/referats/12808/image087.gif" v:shapes="_x0000_i1072">
Задача 3. Составить приведенноеквадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i.
Второй корень z2уравнения является числом,сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим
P=-(z1+z2)=2, q=z1z2=5. Ответ z2-2z+5=0.
Приложение.
В качестве приложения яхочу рассмотреть формулу (иногда в литературе она имеет название теоремы)Муавра. Она имеет большое значение в тригонометрии, потому что позволяет выражать синусы и косинусы углов (n*x), где n– любое целое число, через простые функции sinx и cosx.
Формула: <img src="/cache/referats/12808/image038.gif" v:shapes="_x0000_i1073">
где i– мнимая часть комплексного числа, i2= -1
Пример:
cos3q+ i*sin3q =(cosq + i*sinq)3= cos3 q + 3i cos2 q * sinq + 3i2 *cosq * sin2 q + i3sin3 q = cos3 q — 3cosq *sin2 q+ i*(3cos2 q * sinq — sin3 q)
Приравнивая абсциссы и ординаты, получаем: cos3q= cos3 q — 3cosq *sin2 q
sin3q= 3cos2 q * sinq — sin3 q
Таким же образом можно значительно упростить sin4x, cos4x(sin5x, cos5xи т.д.) до выражений, содержащих sinxи cosx
Заключение *
Комплексныечисла, несмотря на их “лживость” и недействительность,имеют очень широкое применение. Они играют значительную роль не только вматематике, а также в таких науках, как физика, химия. В настоящее времякомплексные числа активно используются в электромеханике, компьютерной икосмической индустрии.
Именнопоэтому нам расширять свои знания о комплексных числах, их свойствах иособенностях. Основные элементы учения о комплексных числах рассмотрены мною вданном реферате.
* примечание:
комплексные числа не входят в базовую школьнуюпрограмму алгебры но, тем не менее, являются серьёзным разделом элементарнойматематики.
Список литературы.
А.П. Савин“Энциклопедический словарь юного математика”
М.Я. Выгодский “Справочник по элементарной математике”
И.С. Петраков“Математические кружки в 8-10 классах”
М.И. Сканави “Сборник задачпо математике (геометрия)”
www.ronl.ru
Реферат Комплексные числа
Средняя общеобразовательная школа №1 11 класс




“Помимо и даже против воли того или другого математика, мнимые числа снова и снова появляются на выкладках, и лишь постепенно, по мере того как обнаруживается польза от их употребления, они получают более и более широкое распространение” Ф. Клейн.
Автор: Исаев Рома (полная версия реферата и много других полезных материалов на моём сайте http://raycom.narod.ru/) Обязательно загляние!
Учитель: Моторина Дина Юрьевна
Дубна, 2002
План:
1. Введение 2
2. История возникновения комплексных чисел 3
а) Развитие понятия о числе 3
б) На пути к комплексным числам 4
в) Утверждение комплексных чисел в математике 5-6
3. Комплексные числа и их свойства 7
а) Понятие комплексного числа 7
б) Геометрическое изображение комплексных чисел 8-9
в) Тригонометрическая форма комплексного числа 9
4. Действия с комплексными числами 10
а) сложение 11
б) вычитание 11
в) умножение 10-11
г) деление 11
5. Решение уравнений с комплексными переменными 12-13
6. Приложение 14
7. Заключение 15
8. Список литературы 15
Введение
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.
Цель настоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решением уравнений с комплексным переменным.
История возникновения комплексных чисел
1. Развитие понятия о числе
Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.
В III веке Архимед разработал систему обозначения вплоть до такого громадного как  . Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в челом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
. Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в челом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа  , чтобы
, чтобы  .
.
2. На пути к комплексным числам
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида  кубические и квадратные корни:
кубические и квадратные корни: 
 .
.
Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень ( x=1), а если оно имеет три действительных корня (
x=1), а если оно имеет три действительных корня ( x1=1 x2,3 =
x1=1 x2,3 = ), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени
), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени  нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений  , не имеющая решений во множестве действительных чисел, имеет решения вида
, не имеющая решений во множестве действительных чисел, имеет решения вида  ,
,  , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что  .
.
3. Утверждение комплексных чисел в математике
Кардано называл такие величины “чисто отрицательными” и даже “софистически отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа  (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.
Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): 
 (подробнее смотри приложение). С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу :
(подробнее смотри приложение). С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу :  , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e в любую комплексную степень. Любопытно, например, что
, которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e в любую комплексную степень. Любопытно, например, что  . Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
. Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.
Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. По этому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.
“Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств” Л. Карно.
После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида  , где
, где  , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например,
, построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например,  , а
, а  . Гиперкомплексные числа не являются темой моего реферата, поэтому я лишь упоминаю об их существовании.
. Гиперкомплексные числа не являются темой моего реферата, поэтому я лишь упоминаю об их существовании.
Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.
Комплексные числа и их свойства 1. О комплексных числах
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они называются комплексными. Комплексное число имеет вид a + bi; здесь a и b – действительные числа , а i – число нового рода, называемое мнимой единицей. “Мнимые” числа составляют частный вид комплексных чисел (когда а = 0). С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).
Действительное число a назовем абсциссой комплексного числа a + bi; действительное число b – ординатой комплексного числа
a + bi. Основное свойство числа i состоит в том, что произведение i*i равно –1, т.е.
i2= -1. (1)
Долгое время не удавалось найти такие физические величины, над которыми можно выполнять действия, подчинённые тем же правилам, что и действия над комплексными числами – в частности правилу (1). Отсюда названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен целый ряд таких физических величин, и комплексные числа широко применяются не только в математике, но также и в физике и технике.
Правило каждого действия над комплексными числами выводится из определения этого действия. Но определения действий над комплексными числами не вымышлены произвольно, а установлены с таким расчетом, чтобы согласовались с правилами действий над вещественными числами. Ведь комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними.
Действительное число а записывается также в виде a + 0i (или a – 0i).
Примеры. Запись 3 + 0i обозначает то же, что запись 3. Запись –2 + 0i означает –2.
Комплексное число вида 0 + bi называется “чисто мнимым”. Запись bi обозначает то же, что 0 + bi. Два комплексных a + bi, a’ + b’i считаются равными, если у них соответственно равны абсциссы и ординаты, т. е. Если a = a’, b = b’. В противном случае комплексные числа не равны. Это определение подсказывается следующим соображением. Если бы могло существовать, скажем, такое равенство:
2 + 5i = 8 + 2i, то по правилам алгебры мы имели бы i = 2, тогда как i не должно бать действительным числом.
2. Геометрическое изображение комплексных чисел
 Действительные числа можно изобразить точками прямой линии, как показано на рис.2, где точка K изображает число 5. Это число можно изобразить также отрезком ОK, учитывая не только его длину, но и направление.
Действительные числа можно изобразить точками прямой линии, как показано на рис.2, где точка K изображает число 5. Это число можно изобразить также отрезком ОK, учитывая не только его длину, но и направление.
Каждая точка С “числовой прямой” изображает некоторое действительное число (рациональное, если отрезок ОС соизмерим с единицей длины, и иррациональное, если несоизмерим). Таким образом, на “числовой прямой” не остаётся места для комплексных чисел.
Но комплексные числа можно изобразить на “числовой прямой”. Для этого мы выбираем на плоскости прямоугольную систему координат с одним и тем же масштабом на обеих осях (рис. 1). Комплексное число a + bi мы изображаем точкой М, у которой абсцисса х равна абсциссе а комплексного, а ордината у равна ординате b комплексного числа.
П римеры. На рис. 2 точка А с абсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. Точка В (-4,-5) изображает комплексное число –4 - 5i.
римеры. На рис. 2 точка А с абсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. Точка В (-4,-5) изображает комплексное число –4 - 5i.
Действительные числа (в комплексной форме они имеют вид a + 0i) изображают точками оси OХ, а чисто мнимые – точками оси OУ.
Примеры. Точка К на рис. 2 изображает действительное число 5, точка L – чисто мнимое число 3i. Начало координат изображает число 0.
Сопряжённые комплексные числа изображаются парой точек, симметричных относительно оси абсцисс; так, точки А и А’ на рис. 2 изображают сопряжённые числа 3 +5i и 3 -5i.
Комплексные можно изображать также отрезками, начинающимися в точке О и оканчивающимися в соответствующей точке числовой плоскости. Так, комплексное число a + bi можно изобразить не только точкой M (рис. 1), но также вектором ОM .
Замечание. Давая какому – либо отрезку наименование “вектор”, мы подчёркиваем, что существенное значение имеет не только длина, но и направление отрезка.
Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.
Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами  на плоскости: при изучении течения жидкости, задач теории упругости.
на плоскости: при изучении течения жидкости, задач теории упругости.
3. Тригонометрическая форма комплексного числа.
Абсцисса а и ордината b комплексного числа a + bi выражаются через модуль r и аргумент q. Формулами
a = r cos q , r=a/cos q
b = r sin q , r=b/sin q
r – длина вектора (a+bi) , q – угол, который он образует с положительным направлением оси абсцисс (см. рис. 1).
Поэтому всякое комплексное число можно представить в виде r(cos q + i sin q), где r > 0 т.е. z=a+bi или z=r*cos q + r*sin q
Это выражение называется нормальной тригонометрической формой или, короче, тригонометрической формой комплексного числа.
Действия с комплексными числами
1. Сложение комплексных чисел
Определение: Суммой комплексных чисел a + bi и a’ + b’i называют комплексное число (a + a’) + (b + b’)i.
Это определение подсказывается правилами действий с обычными многочленами.
Пример 1. (-3 + 5i) + (4 – 8i) = 1 - 3i
Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i.Так как запись 2 + 0i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Пример 4. (-2 + 3i) + ( - 2 – 3i) = - 4
В примере 4 сумма двух комплексных чисел равна действительному числу. Два комплексных числа a+bi и a-bi называются сопряженными. Сумма сопряженных комплексных чисел равна действительному числу.
Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
2. Вычитание комплексных чисел.
Определение. Разностью комплексных чисел a + bi (уменьшаемое) и a’ + b’i (вычитаемое) называется комплексное число (a – a’) + (b – b’)i.
Пример 1. (-5 + 2i) – (3 – 5i) = -8 + 7i
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
3. Умножение комплексных чисел.
Определение. Произведением комплексных чисел a + bi и a’ + b’i называется комплексное число
(aa’ – bb’) + (ab’ + ba’)i.
Замечание. На практике нет нужды пользоваться формулой произведения. Можно перемножить данные числа, как двучлены, а затем положить, что i2 = -1.
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a2 + b 2
Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.
Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
4. Деление комплексных чисел.
В соответствии с определением деления действительных чисел устанавливается следующее определение.
Определение. Разделить комплексное число a + bi на комплексное число a’ + b’i – значит найти такое число x + yi, которое, будучи помножено на делитель, даст делимое.
Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем: (a + bi):(c + di)=
Пример 1. Найти частное (7 – 4i):(3 + 2i).
Записав дробь (7 – 4i)/(3 + 2i), расширяем её на число 3 – 2i, сопряженное с 3 + 2i. Получим:
((7 – 4i)(3 - 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.
Пример 1 предыдущего пункта даёт проверку.
Пример 2. (-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)( -3 + 4i)) = (-14 –23i)/25 = -0,56 – 0.92i.
Чтобы доказать, что правая часть действительно является частным, достаточно помножить её на a’ + b’. Получим a + bi.

Решение уравнений с комплексными переменными
Рассмотрим сначала простейшее квадратное уравнение z2 = a, где а - заданное число, z - неизвестное. На множестве действительных чисел это уравнение:
1) имеет один корень z = 0, если а = 0;
2) имеет два действительных корня z1,2 =  , если а>0;
, если а>0;
3) не имеет действительных корней, если а<0.
На множестве комплексных чисел это уравнение всегда имеет корень .
Задача 1. Найти комплексные корни уравнения z2 = a, если:
1) а = -1; 2) а = -25; 3) а = -3.
1) z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2 - i2 = 0. Отсюда, раскладывая левую часть на множители, получаем (z-i)(z+i) = 0, z1 = i, z2 = -i.Ответ. z1,2 =  i.
i.
2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение:
z2 = (-1)25,
z2 = i2 52, z2 - 52 i2= 0, (z-5i)(z+5i) = 0, откуда z1 = 5i, z2 = -5i.Ответ:
z 1,2 =  5i.
5i.
3) z2 = -3, z2 = i2( )2, z2 - (
)2, z2 - ( )2i2 = 0, (z -
)2i2 = 0, (z -  i)(z +
i)(z +  i) = 0
i) = 0
Ответ: z1,2 =  i.
i.
Вообще уравнение z2 = a, где а < 0 имеет два комплексных корня: Z1,2=  i.
i.
Используя равенство i2 = -1, квадратные корни из отрицательных чисел принято записывать так:  = i,
= i,  = 2i,
= 2i,  = i
= i  .
.
Итак,  определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с - действительные числа, а
определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с - действительные числа, а  0, имеет корни. Эти корни находятся по известной формуле:
0, имеет корни. Эти корни находятся по известной формуле:
Z1,2 =  .
.
Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2 =  =
=  = 2
= 2  3i.
3i.
Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.
Число 4 - это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13- свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 - корни уравнения az2+bz+c = 0, z1+z2 =  , z1z2 =
, z1z2 =  .
.
Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющие корень z1=-1-2i.
Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим
P=-(z1+z2)=2, q=z1z2=5. Ответ z2-2z+5=0.
Приложение.
В качестве приложения я хочу рассмотреть формулу (иногда в литературе она имеет название теоремы) Муавра. Она имеет большое значение в тригонометрии, потому что позволяет выражать синусы и косинусы углов (n*x), где n – любое целое число, через простые функции sin x и cos x.
Формула: 
где i – мнимая часть комплексного числа, i2 = -1
Пример:
cos3q + i*sin3q =(cosq + i*sinq)3 = cos3 q + 3i cos2 q * sinq + 3i2 * cosq * sin2 q + i3 sin3 q = cos3 q - 3cosq * sin2 q + i*(3cos2 q * sinq - sin3 q)
Приравнивая абсциссы и ординаты, получаем:
cos3q = cos3 q - 3cosq * sin2 q
sin3q = 3cos2 q * sinq - sin3 q
Таким же образом можно значительно упростить sin4x, cos4x (sin5x, cos5x и т.д.) до выражений, содержащих sinx и cosx
Заключение *
Комплексные числа, несмотря на их “лживость” и недействительность, имеют очень широкое применение. Они играют значительную роль не только в математике, а также в таких науках, как физика, химия. В настоящее время комплексные числа активно используются в электромеханике, компьютерной и космической индустрии.
Именно поэтому нам расширять свои знания о комплексных числах, их свойствах и особенностях. Основные элементы учения о комплексных числах рассмотрены мною в данном реферате.
* примечание:
комплексные числа не входят в базовую школьную программу алгебры но, тем не менее, являются серьёзным разделом элементарной математики.
Список литературы.
А.П. Савин “Энциклопедический словарь юного математика”
М.Я. Выгодский “Справочник по элементарной математике”
И.С. Петраков “Математические кружки в 8-10 классах”
М.И. Сканави “Сборник задач по математике (геометрия)”
nreferat.ru
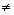 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел. 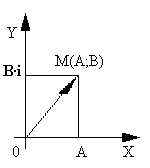

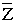 , т.е.
, т.е.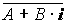 =A – B· i.
=A – B· i. = A+B· i, поэтому для любого комплексного числа Z имеет место равенство
= A+B· i, поэтому для любого комплексного числа Z имеет место равенство 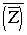 =Z.
=Z.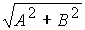 и обозначается
и обозначается  , т.е.
, т.е. 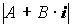 =
=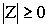 для любого комплексного числа Z, причем
для любого комплексного числа Z, причем 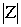 =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы: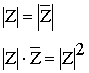


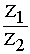

 разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
 =
=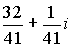

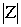 = r и аргумент j следующим образом:
= r и аргумент j следующим образом: 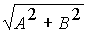 , равенство (2) можно записать в виде
, равенство (2) можно записать в виде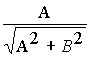 , sinj =
, sinj = (3)
(3)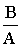 (4)
(4)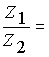

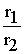 [ cos(j 1 – j 2) + i· sin(j 1 – j 2)]. (7)
[ cos(j 1 – j 2) + i· sin(j 1 – j 2)]. (7)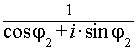 =
= 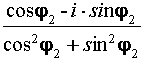 = cos(–j 2) + i· sin(–j 2)
= cos(–j 2) + i· sin(–j 2)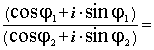 (cosj 1 + i· sinj 1)× ( cos(–j 2) + i· sin(–j 2)) =
(cosj 1 + i· sinj 1)× ( cos(–j 2) + i· sin(–j 2)) = 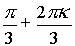 , k Î Z
, k Î Z  + i·sin
+ i·sin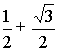 i) = 1+
i) = 1+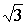 × i
× i ) + i·sin(
) + i·sin(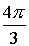 ) + i·sin(
) + i·sin(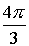 )) = 2· ( cos
)) = 2· ( cos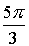 + i·sin
+ i·sin ; Z2 = –2
; Z2 = –2 , k Î Z
, k Î Z  + i× sin
+ i× sin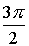 + i× sin
+ i× sin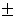 1
1 ), если Zn =w .
), если Zn =w .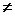 0, то и Z
0, то и Z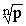 и j =
и j = 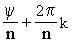 , где kÎ Z .
, где kÎ Z . . Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w , соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса
. Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w , соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса  , следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно.
, следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i и –i, или одно, то какое именно. ,
,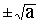 , если a > 0.
, если a > 0. 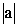 = i2× (
= i2× (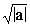 )2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2× (
)2. Тогда уравнение Z2 = a запишется в виде: Z2 – i2× ( i×
i× 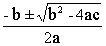 (10)
(10)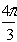
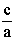
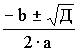

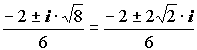
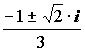
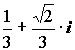 )
)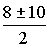 = 4
= 4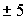
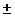 3 Z =
3 Z = 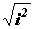
 = –1
= –1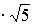
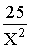 = 24
= 24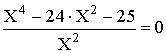 умножим на X2
умножим на X2 0
0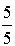 Y2 =
Y2 = 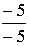
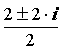 = 1
= 1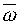 12 = 1
12 = 1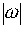 )10×
)10× 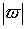 2 = 1
2 = 1 , k Î Z
, k Î Z 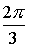 + i·sin
+ i·sin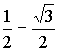 i
i , k Î Z
, k Î Z 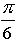 + i·sin
+ i·sin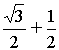 i
i  ) + i·sin(
) + i·sin(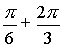 ) + i·sin(
) + i·sin( ) + i·sin(
) + i·sin( i
i  ) + i·sin(
) + i·sin(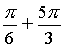 ) + i·sin(
) + i·sin(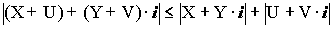
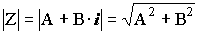
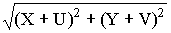 >
> 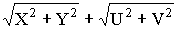 / т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
/ т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.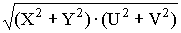
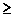 0, значит полученное нами неравенство неверно.
0, значит полученное нами неравенство неверно.
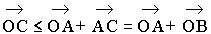 т.е.
т.е.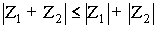
 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел. 

 , т.е.
, т.е. =
=  =A – B·i.
=A – B·i. = A+B·i, поэтому для любого комплексного числа Z имеет место равенство
= A+B·i, поэтому для любого комплексного числа Z имеет место равенство  =Z.
=Z. и обозначается
и обозначается  , т.е.
, т.е.  =
=  =
=  (1)
(1)  для любого комплексного числа Z, причем
для любого комплексного числа Z, причем  =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:



 0
0
 разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам. 
 =
= =
=

 = r и аргумент j следующим образом:
= r и аргумент j следующим образом:  ·sinj = r·(cosj + i·sinj)
·sinj = r·(cosj + i·sinj) – модуль комплексного числа.
– модуль комплексного числа.



 . Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в челом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
. Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в челом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.  , чтобы
, чтобы  .
. кубические и квадратные корни:
кубические и квадратные корни: 
 .
. x=1), а если оно имеет три действительных корня (
x=1), а если оно имеет три действительных корня ( x1=1 x2,3 =
x1=1 x2,3 = ), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени
), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени  нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня). , не имеющая решений во множестве действительных чисел, имеет решения вида
, не имеющая решений во множестве действительных чисел, имеет решения вида  ,
,  , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что
, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что  .
.  (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
 , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e в любую комплексную степень. Любопытно, например, что
, которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e в любую комплексную степень. Любопытно, например, что  . Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
. Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного. , где
, где  , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например,
, построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Правила действия над кватернионами напоминает правила обычной алгебры, однако их умножение не обладает свойством коммутативности (переместительности): например,  , а
, а  . Гиперкомплексные числа не являются темой моего реферата, поэтому я лишь упоминаю об их существовании.
. Гиперкомплексные числа не являются темой моего реферата, поэтому я лишь упоминаю об их существовании. Действительные числа можно изобразить точками прямой линии, как показано на рис.2, где точка K изображает число 5. Это число можно изобразить также отрезком ОK, учитывая не только его длину, но и направление.
Действительные числа можно изобразить точками прямой линии, как показано на рис.2, где точка K изображает число 5. Это число можно изобразить также отрезком ОK, учитывая не только его длину, но и направление. римеры. На рис. 2 точка А с абсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. Точка В (-4,-5) изображает комплексное число –4 - 5i.
римеры. На рис. 2 точка А с абсциссой х=3 и ординатой у=5 изображает комплексное число 3 + 5i. Точка В (-4,-5) изображает комплексное число –4 - 5i. 
 , если а>0;
, если а>0;  i.
i.  )2, z2 - (
)2, z2 - ( i.
i.  = i,
= i,  = 2i,
= 2i,  = i
= i  .
.  определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с - действительные числа, а
определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2 + bz + c = 0, где а, b, с - действительные числа, а  0, имеет корни. Эти корни находятся по известной формуле:
0, имеет корни. Эти корни находятся по известной формуле:  .
.  =
=  = 2
= 2  , z1z2 =
, z1z2 =  .
. 