Реферат Измерение постоянных токов. Измерение силы тока реферат

Электрический ток — реферат

Содержание

Стр.

Введение…………………………………………………………………..2

Основные характеристики……………………………………………….3

Законы постоянного тока………………………………………………...6

Измерение силы тока с помощью приборов…………………………....8

Источники постоянного тока…………………………………………….9

Заключение……………………………………………………………….11

Список использованных источников…………………………………..12

Введение

Электри́ческий ток — направленное движение заряженных частиц под воздействиемэлектрического поля[1]. Такими частицами могут являться: в проводниках — электроны, вэлектролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки(электронно-дырочная проводимость).

При изучении электрического тока, было обнаружено множество его свойств, которые позволили найти ему практическое применение в различных областях человеческой деятельности, и даже создать новые области, которые без существования электрического тока были бы невозможны. После того, как электрическому току нашли практическое применение, и по той причине, что электрический ток можно получать различными способами, в промышленной сфере возникло новое понятие - электроэнергетика.

В медицине электрический ток используют в реанимации, электростимуляции определённых областей головного мозга. Электрические разряды применяются для лечения таких заболеваний, как болезнь Паркинсона и эпилепсия, также дляэлектрофореза. Водитель ритма, стимулирующий сердечную мышцу импульсным током, используют при брадикардии и иных сердечных аритмиях.

1.Основные характеристики:

1. Сила тока - I, единица измерения - 1 А (Ампер).

Силой тока называется величина, равная заряду, протекающему через поперечное сечение проводника за единицу времени.

I = Dq/Dt . (1)

Формула (1) справедлива для постоянного тока, при котором сила тока и его направление не изменяются со временем. Если сила тока и его направление изменяются со временем, то такой ток называется переменным.

Для переменного тока:

I = lim Dq/Dt , (*) Dt - 0

т.е. I = q', где q' - производная от заряда по времени.

2. Плотность тока - j, единица измерения - 1 А/м2.

Плотностью тока называется величина, равная силе тока, протека-ющего через единичное поперечное сечение проводника:

j = I/S . (2)

3. Электродвижущая сила источника тока - э.д.с. ( e ), единица измерения - 1 В (Вольт). Э.д.с.- физическая величина, равная работе, совершаемой сторонними силами при перемещении по электрической цепи единичного положительного заряда:

e = Аст./q . (3)

4. Сопротивление проводника - R, единица измерения - 1 Ом.

Под действием электрического поля в вакууме свободные заряды двигались бы ускоренно. В веществе они движутся в среднем равномерно, т.к. часть энергии отдают частицам вещества при столкновениях.

Теория утверждает, что энергия упорядоченного движения зарядов рассеивается на искажениях кристаллической решетки. Исходя из природы электрического сопротивления, следует, что

R = r*l/S , (4)

где

l - длина проводника, S - площадь поперечного сечения, r - коэффициент пропорциональности, названный удельным сопротивлением материала.

Эта формула хорошо подтверждается на опыте.

Взаимодействие частиц проводника с движущимися в токе зарядами зависит от хаотического движения частиц, т.е. от температуры проводника. Известно, что

r = r0(1 + a t) , (5)

R = R0(1 + a t) . (6).

Коэффициент a называется температурным коэффициентом сопротив-ления:

a = (R - R0)/R0*t .

Для химически чистых металлов a > 0 и равно 1/273 К-1. Для сплавов температурные коэффициенты имеют меньшее значение. Зависимость r(t) для металлов линейная:

В 1911 году открыто явление сверхпроводимости, заключающееся в том, что при температуре, близкой к абсолютному нулю, сопротивление некоторых металлов падает скачком до нуля.

У некоторых веществ (например, у электролитов и полупроводников) удельное сопротивление с ростом температуры уменьшается, что объясняется ростом концентрации свободных зарядов.

Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью s

s = 1/r . (7)

5. Напряжение - U , единица измерения - 1 В.

Напряжение - физическая величина, равная работе, совершаемой сторонними и электрическими силами при перемещении единичного положительного заряда.

U = (Aст.+ Аэл.)/q . (8)

Так как Аст./q = e, а Аэл./q = f1-f2, то

U = e + (f1 - f2) . (9)

2. Законы постоянного тока

Закон Ома для участка цепи. Сопротивление проводников. Последовательное и параллельное соединение проводников. Электродвижущая сила. Закон Ома для полной цепи. Работа и мощность тока.

Всякое движение электрических зарядов называют электрическим током. В металлах могут свободно перемещаться электроны, в проводящих растворах - ионы, в газах могут существовать в подвижном состоянии и электроны, и ионы.

Условно за направление тока считают направление движения положительных частиц, поэтому в металлах это направление противоположно направлению движения электронов.

Плотность тока - величина заряда, проходящего в единицу времени через единицу поверхности, перпендикулярной к линиям тока. Эта величина обозначается j и рассчитывается следующим образом:

j=nev.

Здесь n - концентация заряженных частиц, e - заряд каждой из частиц, v - их скорость.

Сила тока i - величина заряда, проходящего в единицу времени через полное сечение проводника. Если за время dt через полное сечение проводника прошел заряд dq, то

i=(dq)/(dt).

По другому, сила тока находится интегрированием плотности тока по всей поверхности любого сечения проводника. Единица измерения силы тока - Ампер. Если состояние проводника (его температура и др.) стабильно, то между приложенным к его концам напряжением и возникающим при этом током существует однозначная связь. Она называется Закон Ома и записывается так:

I=U/R.

R - электрическое сопротивление проводника, зависящее от рода вещества и от его геометрических размеров. Единичным сопротивлением обладает проводник, в котором возникает ток 1 А при напряжении 1 В. Эта единица сопротивления называется Ом.

Закон Ома в дифференциальной форме:

j=sE,

где j - плотность тока, Е - напряженность поля, s - проводимость. В этой записи закон Ома содержит величины, характеризующие состояние поля в одной и той же точке.

Различают последовательное и параллельное соединения проводников. При последовательном соединении ток, протекающий по всем участкам цепи, одинаков, а напряжение на концах цепи складывается как алгебраическая сумма напряжений на всех участках.

R=S(Ri).

При параллельном соединении проводников постоянным остается напряжение, а ток складывается из суммы токов, протекающих по всем ветвям. В этом случае складываются величины, обратные сопротивлению:

1/R=S(1/Ri).

Для получения постоянного тока на заряды в электрической цепи должны действовать силы, отличные от сил электростатического поля; их называют сторонними силами.

Если рассматривать полную электрическую цепь, необходимо включить в нее действие этих сторонних сил и внутренне сопротивление источника тока r. В этом случае закон Ома для полной цепи примет вид:

I=E/(R+r).

Е - электродвижущая сила (ЭДС) источника. Она измеряется в тех же единицах, что и напряжение. Величину (R+r) называют иногда полным сопротивлением цепи.

Сформулируем правила Киркгофа: Первое правило: алгебраическая сумма сил токов в участках цепи, сходящихся в одной точке разветвления, равна нулю.

Второе правило: для любого замкнутого контура сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.

Мощность тока рассчитывается по формуле

P=UI=I2R=U2/R.

Закон Джоуля-Ленца. Работа электрического тока (тепловое действие тока) A=Q=UIt=I2Rt=U2t/R.

3. Измерение силы тока с помощью приборов

На практике для измерения силы тока используется специальный прибор, его называют амперметр (для приборов, которые предназначены для измерения в проводниках малых токов, используются более чувствительные приборы, такие как миллиамперметры, микроамперметры, гальванометры).

Такие приборы подключают последовательно к тому участку цепи, в котором необходимо измерить силу тока. Как уже отмечалось выше, за единицу силы тока принят 1 ампер (1 А). Что же представляет собой эта единица измерения?

За 1 ампер принимается сила такого тока, который проходя по двум прямым параллельным проводникам, которые имеют бесконечную длину и малый диаметр и расположены в вакууме в 1 метре друг от друга, вызывает силу взаимодействия на участке проводника в 1 метр, равную 0,0000002 H.

Мы уже привыкли, что единицы измерения тех или иных физических величин получили свои названия в честь великих ученых, и Ампер не исключение. Ему присвоено имя французского физика и математика Андре-Мари Ампера.

Этот ученый немало потрудился на благо науки, к примеру, именно он ввел такие понятия, как электродинамика, электростатика, соленоид, напряжение, ЭДС, гальванометр, электрический ток и т. п. Кроме того Ампер открыл такое явление, как механическое взаимодействие между проводниками с током, а также правило определения направления в нем электрического тока. Вот собственно и все.

4.Источники постоянного тока

Простейшим источником постоянного тока является химический источник (гальванический элемент или аккумулятор), поскольку полярность такого источника не может самопроизвольно измениться.

Для получения постоянного тока используют также электрические машины - генераторы постоянного тока.

В электронной аппаратуре, питающейся от сети переменного тока, для получения пульсирующего тока используют выпрямитель. Далее для уменьшения пульсаций может быть использован сглаживающий фильтр и, при необходимости, стабилизатор напряжения.

Усилитель постоянного тока (УПТ) — электронный усилитель, рабочий диапазон частот которого включает нулевую частоту (постоянный ток).

На верхнюю границу частотного диапазона усилителя никаких ограничений не накладывается, то есть она может находиться в области очень высоких частот. Таким образом, термин УПТ можно применять к любому усилителю, способному работать на постоянном токе.

В подавляющем большинстве случаев УПТ является усилителем не тока, как следует из названия, а напряжения. Путаница обусловлена тем, что термин ток употребляется для описания электрических процессов вообще.

Машины постоянного тока

Конструктивно машина постоянного тока состоит из неподвижного статора (индуктора) с полюсами и вращающегося ротора (якоря) с коллектором. Статор является источником магнитного поля и механическим остовом машины, якорь- часть машины, в обмотке которой индуцируется э. д. с.

На одном валу с якорем жестко закрепляется коллектор, электрически соединенный с его обмоткой. Коллектор - характерная деталь машины постоянного тока. Его медных пластин касаются неподвижные угольно-графитовые щетки, размещенные в щеткодержателях на траверсе и электрически соединенные с внешней цепью. Во избежание искрения щетки тщательно притираются к коллектору, а их умеренный нажим должен быть отрегулирован.

Принцип действия машин постоянного тока основан на законе электромагнитной индукции и законе Ампера. Магнитное поле машины создается постоянным током (током возбуждения) в обмотке полюсов или постоянными магнитами в машинах малой мощности. Его силовые линии замыкаются через стальные станину, сердечники полюсов и сердечник якоря, дважды преодолевая на своем пути воздушный зазор между ними. Магнитная цепь четырехполюсной машины постоянного тока разветвленная, симметричная. Плоскость, проходящую через ось машины под углом а, при котором она перпендикулярна к силовым линиям, называют геометрической нейтралью (при а. = 0 и 772).

Существует два режима работы эл. двигателей

а: режим генератора б: режим двигателя

В режиме генератора машина преобразует механическую энергию в электрическую: к обмотке возбуждения статора подводится постоянный ток возбуждения, а якорь вращается каким-либо первичным двигателем. При этом провода обмотки якоря пересекают магнитные силовые линии полюсов и в них индуцируются э. д. с. С помощью коллектора и щеток, которые являются механическим выпрямителем, эти переменные пульсирующие э. д. с. суммируются в постоянную по значению и направлению э. д. с. машины Е. Если к щеткам подключить приемник, то в нем установится постоянный ток I.

turboreferat.ru

Реферат Измерение постоянных токов

Vladimirs Bernatovičs

Kursa darbs

(Elektriskie mērījumi)

2002Saturs.1. Ievads 32. Teoretiskā daļa 4

3. Aprēķinu daļa 13 4. Secinājums 16 5. Literatūra 17 6. Pielikūms 18Ievads.Dota uzdevuva man jāizmēra līdzstrāvu ar šunta palidzību. Šunts plaši izmantas, lai paplašināt mērāmo strāvas intervālu. Vēl man jāizdara statistisko apstrādi un un aprēķināt kļudas.

Измерение постоянных токов

Общие замечания. Измерение постоянных токов в подавляющем большинстве случаев производится посредством магнитоэлектрических амперметров и вольтметров. Для этой цели применяют также электромагнитные, электродинамические, ферро-динамические и электростатические приборы, а также потенциометры постоянного тока и цифровые приборы.

Магнитоэлектрические амперметры. Измерительные механизмы магнитоэлектрических амперметров и вольтметров принципиально не различаются. В зависимости от назначения прибора (для измерения-тока или напряжения) меняется его измерительная цепь. В амперметрах измерительный механизм включается в цепь непосредственно или при помощи шунта. В вольтметрах последовательно с измерительным механизмом включается добавочный резистор, и прибор подключается к тем точкам схемы, между которыми необходимо измерить напряжение.

Амперметр без шунта применяется в том случае, если весь измеряемый ток можно пропустить через токоподводящие пружинки (или растяжки) и обмотку рамки измерительного механизма. Обычно значение этого тока не превышает 20—30 мА, т. е. такая схема возможна только для микро- и миллиамперметров.

Характер измерительной цепи в значительной степени определяется также допустимой температурной погрешностью и пределом измерения прибора.

Изменение температуры прибора сказывается на его работе следующим образом.

1. При повышении температуры удельный противодействующий момент пружинок (или растяжек) уменьшается примерно на 0,2— 0,4% на каждые 10 К повышения температуры. Магнитный поток постоянного магнита падает приблизительно на 0,2% на каждые 10 К повышения температуры.

Так как ослабление пружинок и уменьшение магнитного потока вызывают одинаковые изменения противодействующего и вращающего моментов по значению, но с разными знаками, то эти два явления практически взаимно компенсируют друг друга. .. и2. Изменяется- электрическое сопротивление обмотки рамки и пружинок. Это является основным источником температурной погрешности магнитоэлектрических приборов.

В большинстве случаев температурная погрешность вольтметров является незначительной. Это объясняется тем, что температурный коэффициент сопротивления (ТКС) цепи вольтметра определяется не только ТКС «медной» части обмотки измерительного механизма, но и добавочного резистора, выполняемого из материала с очень малым ТКС.

Наиболее неблагоприятным в отношении влияния температуры является амперметр с шунтом. При повышении температуры и неизменных значениях измеряемого тока и сопротивления шунта .Rш (шунт, как указывалось выше, выполняется из манганина) ток /, протекающий через измерительный механизм, уменьшается и появляется отрицательная погрешность.

Для компенсации температурной погрешности часто применяются специальные схемы. Наиболее широко используемые схемы для температурной компенсации представлены на рис. 3.23 и 3.24. Простейшим способом уменьшения температурной погрешности является включение последовательно с обмоткой рамки добавочного резистора Ra из манганина (рис. 3.23). Недостаток этой схемы заключается в том, что на рамку попадает только часть напряжения, снимаемого с шунта. Для прибора класса точности 0,2 напряжение, попадаемое на рамку, составляет всего 5%. Обычно этот способ применяется только для приборов класса точности не выше 1,0.

Рис. 3.23. Схемы для температурной

компенсации амперметров с

добавочным резистором Рис. 3.24. Последовательно-параллельная

схема для температурной компенсации

Последовательно-параллельная схема (рис. 3.24) широко используется в прибсрах высоких классов точности (0,5; 0,2; 0,1). В такой схеме последовательно с уедной рамкой включается резистор из манганина R3. Эта цепь шунтируется резистором R1 из материала с большим температурным коэффициентом (меди или никеля) и через последовательно включенный манганиновый резистор R2 подключается к шунту Rm. При повышении температуры возрастают сопротивления рамки и R1. Однако, поскольку последовательно с рамкой включен резистор R3, имеющий практически нулевой температурный коэффициент, то по сравнению с цепью рамки увеличение сопротивления в цепи R1 будет больше. Поэтому изменится распределение токов /2 и It таким образом, что в обмотку рамки будет ответвляться несколько большая часть общего тока, чем раньше. Так как сопротивление между точками a и с увеличивается, а ток !хне изменяется, напряжение Uac между этими точками несколько увеличится. Выбором сопротивлений можно добиться того, чтобы при изменении температуры ток в обмотке рамки менялся в пределах, определяемых допускаемым значением температурной погрешности.

При создании приборов для измерения очень малых напряжений (например, э. Д. с. термопар) желательно, чтобы всё напряжение подводилось непосредственно к цепи измерительного механизма. В этом случае температурная компенсация осуществляется не с помощью схем, а посредством термомагнитного шунта. Такой шунт выполняется из специальных магнитных материалов (сплавов меди с никелем или железа с никелем), у которых магнитная проницаемость существенно уменьшается при возрастании температуры. Конструктивно термомагнитный шунт представляет собой пластинки, которыми замыкаются полюсные наконечники постоянного магнита. При повышении температуры магнитное сопрот тивление шунта возрастает, что приводит к увеличению индукции в воздушном зазоре и к малой зависимости показаний от температуры.Магнитоэлектрические амперметры и вольтметры выпускают переносными и щитовыми. Переносные приборы в большинстве случаев делают высокоточными (классов 0,1—0,5), многопредельными (до нескольких десятков пределов) и часто комбинированными (например, вольтамперметрами). В качестве многопредельного комбинированного прибора можно указать, например, милливольт-.миллиамперметр типа М1109 класса точности 0,2. Прибор имеет 15 пределов измерений: 8 — по напряжению (от 15 мВ до 3 В) и 7 — по току (от 0,15 до 60 мА). Щитовые приборы выпускают обычно однопредельными, чаще всего классов точности 1,0 и 1,5.

Магнитоэлектрические гальванометры. Гальванометром называется электроизмерительный прибор с неградуированной шкалой, имеющий высокую чувствительность к току или напряжению.

Рис. 3.25. Схематическое

устройство гальванометра

на подвесе

Гальванометры широко используются в качестве нуль-индикаторов, а также для измерения малых токов, напряжений и количеств электричества, если известна постоянная гальванометра.

Кроме магнитоэлектрических существуют и некоторые другие виды гальванометров, например электростатические, называемые электрометрами. Однако их применение весьма ограничено.

Основное требование, предъявляемое к гальванометрам, — высокая чувствительность, которая достигается, главным образом, путем уменьшения противодействующего момента и использования светового указателя с большой длиной луча.

По конструктивному оформлению различают: а) гальванометры переносные (со встроенной шкалой), в которых используются как стрелочные, так и световые указатели; б) гальванометры зеркальные, с отдельной шкалой, требующие стационарной установки по уровню.

В переносных гальванометрах подвижная часть устанавливается на растяжках, а в зеркальных — на подвесе (рис. 3.25). В последнем случае токоподвод к обмотке рамки 1 осуществляется посредством подвеса 2 и безмоментной нити 4. Для измерения угла поворота рамки служит зеркальце 3, на которое фокусируется луч света от специального осветителя.

Постоянная зеркального гальванометра данной конструкции зависит от расстояния между зеркальцем и шкалой. Ее условились выражать для расстояния, равного 1 м, например: С1 = 1,2*10-6 А*м/мм. Для переносных гальванометров в паспорте указывают цену деления шкалы, например: 1 деление = 0,5*10-6 А.

Наиболее чувствительные современные зеркальные гальванометры имеют постоянную до 10-11 А*м/мм; у переносных гальванометров постоянная составляет примерно 10-8 — 10-9 А/дел.

Стандарт на гальванометры (ГОСТ 7324 — 68) допускает отклонение постоянной (или цены деления) от указанной в паспорте на ±10%.

Важной характеристикой гальванометра является постоянство, нулевого положения указателя, под которым понимают невозвращение указателя к нулевой отметке при плавном его движении от крайней отметки шкалы. По этому параметру гальванометры делят на разряды постоянства. Условное обозначение разряда постоянства нулевого положения указателя гальванометра, состоящее из цифрового обозначения разряда постоянства, заключенного в ромб, наносят на шкалу гальванометра при маркировке.

Многие гальванометры снабжают магнитным шунтом. Регулируя положение шунта посредством выведенной наружу ручки, можно менять значение магнитной индукции в рабочем зазоре. При этом изменяется постоянная, а также ряд других параметров гальванометра. По требованию стандарта, магнитный шунт должен изменять постоянную по току не менее чем в 3 раза. В паспорте гальванометра и в его маркировке указывают значения постоянной при двух крайних положениях шунта — полностью введенном и полностью выведенном.

Гальванометр должен иметь корректор, перемещающий при круговом вращении указатель в ту или другую сторону от нулевой отметки. Гальванометры с подвижной частью на подвесе должны быть снабжены арретиром (приспособлением для механической фиксации подвижной части), который включают, например, при переноске прибора.

Гальванометры ввиду высокой чувствительности необходимо защищать от помех. Так, от механических сотрясений гальванометры защищают, устанавливая их на капитальные стены или специальные фундаменты; от токов утечек — электростатическим экранированием и т. п.

Характер движения подвижной части гальванометра при изменении измеряемой величины зависит от его успокоения, которое определяется сопротивлением внешней цепи. Для удобства работы с гальванометром это сопротивление подбирают близким к так называемому внешнему критическому сопротивлению Rк, указанному в паспорте гальванометра. Если гальванометр замкнут на внешнее критическое сопротивление, то указатель плавно и за минимальное время подходит к положению равновесия, не переходит его и не совершает около него колебаний (см. § 3.10).

Баллистический гальванометр позволяет измерять малые количества электричества (импульс тока), протекающие в течение коротких промежутков времени — долей секунды. Таким образом, баллистический гальванометр предназначен для импульсных измерений. Теория баллистического гальванометра (см. § 3.10) показывает, что если принять допущение о том, что подвижная часть начинает свое движение после окончания импульса тока в обмотке подвижной рамки, то количество электричества Q, протекшее в цепи, пропорционально первому максимальному отклонению указателя alm, т. е.

Q = C6a1m, (3.36)

где Сб — баллистическая постоянная гальванометра, выражаемая в кулонах на деление.

Следует отметить, что Сб не остается неизменной для данного гальванометра, а зависит от сопротивления внешней цепи, что требует обычно ее определения в процессе измерений опытным путем.

Указанное выше допущение выполняется тем точнее, чем больше момент инерции подвижной части гальванометра и, следовательно, больше период свободных колебаний Т0. Для баллистических гальванометров Т0составляет десятки секунд (для обычных гальвано-,метров — единицы секунд). Это достигается увеличением момента {инерции подвижной части гальванометра с помощью дополнитель-|ной детали в виде диска.Магнитоэлектрические измерительные механизмы. В магнитоэлектрических измерительных механизмах вращающий момент создается в результате взаимодействия магнитного поля постоянного магнита и магнитного поля 'проводника с током, выполняемого обычно в виде катушки — рамки.

Обратимся к рассмотрению принципа действия магнитоэлектрических измерительных механизмов.

На рис. 3.1 показана подвижная рамка измерительного механизма, находящаяся в равномерном радиальном магнитном поле. При протекании по обмотке рамки тока возникают силы F, стремящиеся повернуть рамку так, чтобы ее плоскость стала перпендикулярной к направлению Ох— 02. При равенстве вращающего и противодействующего моментов подвижная часть останавливается.

Для получения зависимости между углом отклонения и током в рамке обратимся к уравнению (3.1), которое применительно к нашему случаю представляется так:

(3.5) где Ф — поток, сцепляющийся с обмоткой рамки; I — ток в обмотке рамки.

Величина Ф может быть подсчитана как произведение индукции В в воздушном зазоре, числа витков w обмотки рамки и суммы площадей двух боковых поверхностей, описанных активными сторонами подвижной катушки при ее повороте на угол а я от нейтрального положения (оси О1 — O2).В соответствии с рис. 3.1 активными сторонами обмотки рамки будут являться стороны, расположенные в плоскости, перпендикулярной рисунку. Стороны рамки, находящиеся в плоскости рисунка, при своем движении скользят

вдоль силовых линий, не пересекая их, и поэтому не будут участвовать в создании вращающего момента. Следовательно,

Ф = B2rlwa,

где r— радиус рамки относительно оси вращения; / — длина рамки; а — угол отклонения рамки от нейтрального положения. Обозначив площадь катушки через s, можем написать

Ф = Bswa.

Подставляя это выражение в формулу (3.5) и дифференцируя его, получим

(3.6)

Так как противодействующий момент создается упругими элементами, то можно воспользоваться формулой (3.2) и для режима установившегося отклонения написать

откуда

(3.7)

Как видно из выражения (3.7), при перемене направления тока в обмотке рамки меняется на обратное и направление отклонения подвижной части.

Для получения отклонения указателя в нужную сторону необходимо при включении прибора соблюдать указанную на приборе полярность.

Из выражения (3.7) и определения понятия чувствительности следует, что для магнитоэлектрических измерительных механизмов и, следовательно, для магнитоэлектрических приборов чувствительность

(3.8)

Из уравнения (3.8) видно, что чувствительность магнитоэлектрического прибора не зависит от угла отклонения и постоянна по всей шкале; отсюда следует, что магнитоэлектрические приборы имеют равномерную шкалу. Это позволяет выпускать их комбинированными и многопредельными.

Магнитоэлектрические приборы относятся к числу наиболее точных. Они изготовляются вплоть до класса точности 0,1. Высокая точность этих приборов объясняется рядом причин. Наличие равномерной шкалы уменьшает погрешности градуировки и отсчета. Благодаря сильному собственному магнитному полю влияние посторонних полей на показания приборов весьма незначительно. Внешние электрические поля на работу приборов практически не влияют. Температурные погрешности могут быть скомпенсированы с помощью специальных схем.

Большим достоинством магнитоэлектрических приборов является высокая чувствительность. В этом отношении магнитоэлектрические приборы не имеют себе равных. Известны магнитоэлектрические микроамперметры с током полного отклонения 0,1 мкА (например, типа М95, класса точности 1,0).

Благодаря этим достоинствам магнитоэлектрические приборы применяют с различными преобразователями переменного тока в постоянный для измерений в цепях переменного тока.

К недостаткам магнитоэлектрических приборов следует отнести несколько более сложную и дорогую конструкцию, чем, например, конструкция электромагнитных приборов, невысокую перегрузочную способность (при перегрузке обычно перегорают токоподводя-щие пружинки или растяжки для создания противодействующего момента) и, самое главное, отмеченную выше возможность применения в качестве амперметров и вольтметров лишь для измерений в цепях постоянного тока (при отсутствии преобразователей).

Магнитоэлектрические измерительные механизмы с механическим противодействующим моментом используются главным образом в амперметрах, вольтметрах и гальванометрах, а также в некоторых типах омметров.

Рассмотрим особенности устройства измерительных механизмов магнитоэлектрических логометров.

Как было указано выше, в логометрах противодействующий момент создается не механическим путем, а электрическим. Для этого в магнитоэлектрическом логометре (рис. 3.2) подвижная часть выполняется в виде двух жестко скрепленных между собой рамок 1 и 2, по обмоткам которых протекают токи I1 и I2. Пружинки для создания механического противодействующего момента не ставятся, а ток к обмоткам подводится с помощью безмоментных токопр оводов, выполняемых в виде тонких неупругих металлических ленточек.

Направления токов в обмотках выбираются так, чтобы моменты Мх и М2, создаваемые рамками, действовали навстречу друг другу. Один из моментов вращающий, а второй — противодействующий. Хотя бы один из моментов должен зависеть от угла поворота. Значит, один (или несколько) из параметров, определяющих значение момента, должен являться функцией угла а. Технически наиболее просто сделать зависящей от угла поворота индукцию Л. Для этого магнитное поле в зазоре должно быть неравномерным, что достигается неравномерностью зазора (с этой целью сердечник на рис. 3.2 сделан эллипсоидальным).

В общем виде выражения для моментов М1 и М2могут быть записаны так:

где и — функции, выражающие закон изменения индукции для рамок 1и 2 при перемещении их в зазоре. При установившемся равновесии моменты М1 и М2равны, т. е.

откуда

Выражение для угла поворота можно представить так:

(3.9)Из выражения (3.9) видно, что отклонение подвижной части логометра зависит от отношения токов в его обмотках.

Измерительные механизмы магнитоэлектрических логометров применяют прежде всего в омметрах.

Электромагнитные измерительные механизмы. Вращающий момент в электромагнитных измерительных механизмах возникает в результате взаимодействия магнитного поля катушки, по обмотке которой протекает измеряемый ток, с одним или несколькими ферромагнитными сердечниками, обычно составляющими подвижную часть механизма. В настоящее время наибольшее применение получили три конструкции измерительных механизмов: а) с плоской катушкой; б) с круглой катушкой; в) с замкнутым магнитопроводом.

На рис. 3.3 показан измерительный механизм с плоской катушкой. Катушка / наматывается медным проводом и имеет воздушный зазор, в который может входить эксцентрично укрепленный на оси сердечник 2. Материал сердечника должен обладать высокой магнитной проницаемостью, что способствует увеличению вращающего момента при заданном значении потребления мощности прибором, и минимальной коэрцитивной силой, что уменьшает погрешность от гистерезиса. Обычно материалом сердечника в щитовых приборах служит электротехническая (кремнистая) сталь, а в точных переносных приборах — пермаллой.

При наличии тока в катушке сердечник стремится расположиться в месте с наибольшей концентрацией поля, т. е. втягивается в зазор катушки. При этом закручиваются пружинки 3, в результате чего возникает противодействующий момент. Для успокоения движения подвижной части в электр-омагнитных измерительных механизмах применяют обычно воздушные или жидкостные успокоители. На рис. 3.3 представлен измерительный механизм с воздушным успокоителем, состоящим из камеры 4 и крыла 5.

Одним из существенных недостатков электромагнитных измерительных механизмов с плоской или с круглой катушкой является сильное влияние внешних магнитных полей. Это объясняется тем, что собственное магнитное поле невелико. Для защиты от внешних полей применяются в основном два способа — астазирование и экранирование.

В астатическом измерительном механизме на оси подвижной части укреплены два одинаковых сердечника, каждый из которых размещается в магнитном поле одной из катушек, включенных между собой последовательно. Направление обмоток выбрано так,

что магнитные поля Катушек, равные по значению и конфигурации, направлены навстречу друг другу. При этом подвижная часть будет находиться под действием суммы двух моментов, каждый из которых создается одним из сердечников и действующей на него катушкой. Если такой измерительный механизм попадает в равномерное внешнее поле, то один из моментов, для которого направления собственного и возмущающего полей будут совпадать, увеличится, а второй — соответственно уменьшится. Суммарный момент, а следовательно, и показания прибора при этом не изменяются. Недостатки астатического измерительного механизма заключаются в усложнении и удорожании конструкции, а также в том, что ас-тазирование исключает действие только равномерных полей.

При магнитном экранировании измерительный механизм помещается внутрь замкнутой оболочки из ферромагнитного материала с большой магнитной проницаемостью (чаще всего из пермаллоя). Действие экрана состоит в том, что магнитные линии внешнего поля, стремясь пройти по пути с наименьшим магнитным сопротивлением, сгущаются внутри стенок экрана, почти не проникая во внутреннюю область. Для улучшения магнитной защиты иногда применяются экраны из двух или нескольких оболочек.На рис. 3.4 показан электромагнитный измерительный механизм с замкнутым магнитопроводeом мещена на магнитопровод 2 с полюсными наконечниками 3. При наличии

тока в обмотке катушки подвижный сердечник 4 стремится повернуться по часовой стрелке вокруг оси 0, втягиваясь в рабочее пространство между полюсными накладками.

Достоинствами измерительного механизма с замкнутым магнитопроводом являются: повышенная чувствительность, уменьшение погрешности от влияния внешних магнитных полей, возможность относительно просто менять характер шкалы путем изменения положения левого полюсного наконечника относительно правого. Обычно в измерительных механизмах с замкнутым магнитопроводом применяют растяжки и жидкостное успокоение.

В заключение отметим, что по своему устройству электромагнитные измерительные механизмы являются самыми простыми .среди измерительных механизмов приборов разных групп.

На основании уравнения (3.1) определим вращающий момент электромагнитного измерительного механизма. Электромагнитная энергия катушки, по обмотке которой протекает ток,

где L — индуктивность катушки, зависящая от положения сердечника; / — ток в обмотке.

Выражение для вращающего момента будет

Если противодействующий момент создается с помощью упругих элементов, то для режима установившегося отклонения

откуда

(3.10)Из выражения (3.10) видно следующее:

1. Знак угла отклонения подвижной части не зависит от направления тока в обмотке. Это значит, что электромагнитные приборы могут применяться для измерений в цепях постоянного и переменного тока. В цепи переменного тока они измеряют действующее значение тока (или напряжение).

2. Шкала, электромагнитного прибора неравномерная, т. е. между измеряемой величиной (током) и.углом отклонения нет прямо пропорциональной зависимости. Характер шкалы зависит от множителя т. е. от закона изменения индуктивности с изменением

угла поворота сердечника и от квадрата тока в катушке. Меняя форму сердечника и его расположение в катушке, можно получить практически равномерную шкалу, начиная с 20 — 25% верхнего предела диапазона измерений.

Устройство измерительного механизма электромагнитного ло-гометра с катушками Л и £ представлено на рис. 3.5. Сердечники на оси укреплены так, что при повороте подвижной части в некоторых пределах индуктивность одной катушки увеличивается, а другой — уменьшается, вследствие чего вращающие моменты направлены в противоположные стороны. Взаимным влиянием одной катушки на другую пренебрегаем. Для статического равновесия можем написать

или Решая это уравнение относительно получим

(3.11)Электромагнитные измерительные механизмы используются в настоящее время в амперметрах, вольтметрах, в фазометрах и частотомерах. Кроме этих приборов, применяются резонансные электромагнитные приборы, в которых частота собственных колебаний подвижной части (сердечника) настраивается в резонанс с частотой тока в обмотке. К таким устройствам относятся вибрационные частотомеры.

Главными достоинствами электромагнитных приборов являются: простота конструкции и, как следствие, дешевизна и надежность в работе; способность выдерживать большие перегрузки, что объясняется отсутствием токоподводов к подвижной части; возможность применения для измерений в цепях постоянного и переменного тока (отдельных приборов до частоты примерно 10 000 Гц).

К недостаткам приборов относятся относительно малые точность и чувствительность.Aprēķinu daļa.

Izmantojama shēma.Pēc Oma līkuma: no tā

Tad Is aizmainām ar ,tad

Pēc tam pieņēmsim kā ,tad Mūsu gadījuma Apreķinu tabula.

N0	1	2	3	4	5	6	7	8	9	10
Ir(mA)	70	70	70.1	70.1	69.9	69.9	70	70	70.1	70.1
I(A)	0.2800	0.2800	0.2804	0.2804	0.2796	0.2796	0.2800	0.2800	0.2804	0.2804

N0	11	12	13	14	15	16	17	18	19	20
Ir(mA)	69.9	68.8	69.9	70	70.1	70.2	70.2	70.1	70	70
I(A)	0.2796	0.2752	0.2796	0.2800	0.2804	0.2808	0.2808	0.2804	0.2800	0.2800

Izmantojamas iekārtas:

Milliampermatrs – 75(mA), skāle (0-75), iekšēja pretestība r-28(Om), klase (1.0)

Šunts – iekšēja pretestība Rs-9.33(Om), klase (0.1)Pēc iegūtam datiem veicām statistisko apstrādi.

Xi	0.2792	0.2796	0.28	0.2804	0.2808
mi	1	4	7	6	2
pi	0.05	0.2	0.35	0.3	0.1

- eksperimentu skaits

Pēc tam atrodam , Ais - Strāvas īstā vertība

Tālāk atrodu ticamības intervālu ar izturību .

Tad mūsu rezultāts ir vienads: Aprēķinu kļudas.Ablolūta kļuda ir vienāda:

Relatīva kļūda ir vienāda:

Beigu rezultāti: Secinājums.Šajā darbā es veicu līdzstrāvas mērīšānu ar šunta palidzību. Pēc iegūtam datiem es atrodu absolūto un relatīvu kļudu , atrodu tīcamības intervālu. Pēc iegūtam datiem var sākt ,ka ar šunta palidzību var mērīt strāvas ar lielu precizitāti.Literatūra.1. A.В. Фремке и Е.М.Душина.-5-е изд., и доп.-Л.:Энергия. Лелингр. 1980.-392с.,ил.Pielīkums.

bukvasha.ru

Сила тока | Бесплатные курсовые, рефераты и дипломные работы

Сила тока — физическая величина , равная отношению количества заряда , прошедшего через некоторую поверхность за время , к величине этого промежутка времени[1]:

В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.

Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ. 1 А = 1 Кл/с.

По закону Ома сила тока для участка цепи прямо пропорциональна приложенному напряжению к участку цепи и обратно пропорциональна сопротивлению src=»http://ok-t.ru/studopediaru/baza5/2005988043.files/image061.png» /> проводника этого участка цепи:

Носителями заряда, движение которых, приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны, ионы или дырки. Сила тока зависит от заряда этих частиц, ихконцентрации , средней скорости упорядоченного движения частиц , а также площади и формы поверхности, через которую течёт ток.

Если и постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде

где — угол между скоростью частиц и вектором нормали к поверхности.

В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока , протекающего через малый элемент поверхности площадью :

Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности

В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид

где e — элементарный электрический заряд.

Вектор называют плотностью электрического тока. Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости , а направление совпадает с направлением упорядоченного движения заряженных частиц[2].

Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр,гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).

В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).

15. Закон Ома для участка цепи;

Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде :

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи Rи, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

где:

· — ЭДС источника напряжения,

· — сила тока в цепи,

· — сопротивление всех внешних элементов цепи,

· — внутреннее сопротивление источника напряжения.

Из закона Ома для полной цепи вытекают следствия:

· При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

· При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто[2] выражение

где есть напряжение или падение напряжения, (или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

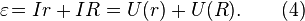
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.

refac.ru

Реферат: Измерение постоянных токов

Rīgas Tehniskā Universitāte

DMZC

Vladimirs Bernatovičs

Kursa darbs

(Elektriskie mērījumi)

Līdzstrāvas mērīšana ar šunta palīdzību

2002

Saturs.

1. Ievads 3

2. Teoretiskā daļa 4

3.Aprēķinu daļa 13

4.Secinājums 16

5. Literatūra 17

6. Pielikūms 18

Ievads.

Dota uzdevuva man jāizmēra līdzstrāvu ar šunta palidzību. Šunts plaši izmantas, lai paplašināt mērāmo strāvas intervālu. Vēl man jāizdara statistisko apstrādi un un aprēķināt kļudas.

Измерение постоянных токов

Изменение температуры прибора сказывается на его работе следующим образом.

2. Изменяется- электрическое сопротивление обмотки рамки и пружинок. Это является основным источником температурной погрешности магнитоэлектрических приборов.

Наиболее неблагоприятным в отношении влияния температуры является амперметр с шунтом. При повышении температуры и неизменных значениях измеряемого тока и сопротивления шунта .Rш(шунт, как указывалось выше, выполняется из манганина) ток /, протекающий через измерительный механизм, уменьшается и появляется отрицательная погрешность.

Для компенсации температурной погрешности часто применяются специальные схемы. Наиболее широко используемые схемы для температурной компенсации представлены на рис. 3.23 и 3.24. Простейшим способом уменьшения температурной погрешности является включение последовательно с обмоткой рамки добавочного резистораRaиз манганина (рис. 3.23). Недостаток этой схемы заключается в том, что на рамку попадает только часть напряжения, снимаемого с шунта. Для прибора класса точности 0,2 напряжение, попадаемое на рамку, составляет всего 5%. Обычно этот способ применяется только для приборов класса точности не выше 1,0.

Рис. 3.23. Схемы для температурной

компенсации амперметров с

добавочным резистором Рис. 3.24. Последовательно-параллельная

схема для температурной компенсации

Последовательно-параллельная схема (рис. 3.24) широко используется в прибсрах высоких классов точности (0,5; 0,2; 0,1). В такой схеме последовательно с уедной рамкой включается резистор из манганинаR3.Эта цепь шунтируется резистором R1из материала с большим температурным коэффициентом (меди или никеля) и через последовательно включенный манганиновый резисторR2подключается к шунтуRm.При повышении температуры возрастают сопротивления рамки и R1.Однако, поскольку последовательно с рамкой включен резисторR3,имеющий практически нулевой температурный коэффициент, то по сравнению с цепью рамки увеличение сопротивления в цепиR1будет больше. Поэтому изменится распределение токов /2иItтаким образом, что в обмотку рамки будет ответвляться несколько большая часть общего тока, чем раньше. Так как сопротивление между точками a и с увеличивается, а ток!хне изменяется, напряжениеUacмежду этими точками несколько увеличится. Выбором сопротивлений можно добиться того, чтобы при изменении температуры ток в обмотке рамки менялся в пределах, определяемых допускаемым значением температурной погрешности.

Магнитоэлектрические амперметры и вольтметры выпускают переносными и щитовыми. Переносные приборы в большинстве случаев делают высокоточными (классов 0,1—0,5), многопредельными (до нескольких десятков пределов) и часто комбинированными (например, вольтамперметрами). В качестве многопредельного комбинированного прибора можно указать, например, милливольт-.миллиамперметр типа М1109 класса точности 0,2. Прибор имеет 15 пределов измерений: 8 — по напряжению (от 15 мВ до 3 В) и 7 — по току (от 0,15 до 60 мА). Щитовые приборы выпускают обычно однопредельными, чаще всего классов точности 1,0 и 1,5.

Магнитоэлектрические гальванометры.Гальванометром называется электроизмерительный прибор с неградуированной шкалой, имеющий высокую чувствительность к току или напряжению.

Рис. 3.25. Схематическое

устройство гальванометра

на подвесе

В переносных гальванометрах подвижная часть устанавливается на растяжках, а в зеркальных — на подвесе (рис. 3.25). В последнем случае токоподвод к обмотке рамки 1 осуществляется посредством подвеса2и безмоментной нити4.Для измерения угла поворота рамки служит зеркальце3,на которое фокусируется луч света от специального осветителя.

Постоянная зеркального гальванометра данной конструкции зависит от расстояния между зеркальцем и шкалой. Ее условились выражать для расстояния, равного 1 м, например: С1= 1,2*10-6А*м/мм. Для переносных гальванометров в паспорте указывают цену деления шкалы, например: 1 деление = 0,5*10-6А.

Наиболее чувствительные современные зеркальные гальванометры имеют постоянную до 10-11А*м/мм; у переносных гальванометров постоянная составляет примерно 10-8— 10-9А/дел.

Характер движения подвижной части гальванометра при изменении измеряемой величины зависит от его успокоения, которое определяется сопротивлением внешней цепи. Для удобства работы с гальванометром это сопротивление подбирают близким к так называемому внешнему критическому сопротивлениюRк,указанному в паспорте гальванометра. Если гальванометр замкнут на внешнее критическое сопротивление, то указатель плавно и за минимальное время подходит к положению равновесия, не переходит его и не совершает около него колебаний (см. § 3.10).

Q=C6a1m,(3.36)

где Сб— баллистическая постоянная гальванометра, выражаемая в кулонах на деление.

Следует отметить, что Сбне остается неизменной для данного гальванометра, а зависит от сопротивления внешней цепи, что требует обычно ее определения в процессе измерений опытным путем.

Магнитоэлектрические измерительные механизмы.В магнитоэлектрических измерительных механизмах вращающий момент создается в результате взаимодействия магнитного поля постоянного магнита и магнитного поля 'проводника с током, выполняемого обычно в виде катушки — рамки.

Обратимся к рассмотрению принципа действия магнитоэлектрических измерительных механизмов.

На рис. 3.1 показана подвижная рамка измерительного механизма, находящаяся в равномерном радиальном магнитном поле. При протекании по обмотке рамки тока возникают силыF,стремящиеся повернуть рамку так, чтобы ее плоскость стала перпендикулярной к направлению Ох— 02. При равенстве вращающего и противодействующего моментов подвижная часть останавливается.

(3.5) где Ф — поток, сцепляющийся с обмоткой рамки; I — ток в обмотке рамки.

В соответствии с рис. 3.1 активными сторонами обмотки рамки будут являться стороны, расположенные в плоскости, перпендикулярной рисунку. Стороны рамки, находящиеся в плоскости рисунка, при своем движении скользят

Ф =B2rlwa,

где r—радиус рамки относительно оси вращения; / — длина рамки; а — угол отклонения рамки от нейтрального положения. Обозначив площадь катушки через s, можем написать

Ф =Bswa.

Подставляя это выражение в формулу (3.5) и дифференцируя его, получим

(3.6)

откуда

(3.7)

(3.8)

Рассмотрим особенности устройства измерительных механизмов магнитоэлектрических логометров.

Как было указано выше, в логометрах противодействующий момент создается не механическим путем, а электрическим. Для этого в магнитоэлектрическом логометре (рис. 3.2) подвижная часть выполняется в виде двух жестко скрепленных между собой рамок 1 и2,по обмоткам которых протекают токи I1и I2. Пружинки для создания механического противодействующего момента не ставятся, а ток к обмоткам подводится с помощью безмоментных токопр оводов, выполняемых в виде тонких неупругих металлических ленточек.

Направления токов в обмотках выбираются так, чтобы моменты Мхи М2, создаваемые рамками, действовали навстречу друг другу. Один из моментов вращающий, а второй — противодействующий. Хотя бы один из моментов должен зависеть от угла поворота. Значит, один (или несколько) из параметров, определяющих значение момента, должен являться функцией угла а. Технически наиболее просто сделать зависящей от угла поворота индукцию Л. Для этого магнитное поле в зазоре должно быть неравномерным, что достигается неравномерностью зазора (с этой целью сердечник на рис. 3.2 сделан эллипсоидальным).

В общем виде выражения для моментовМ1иМ2могут быть записаны так:

гдеи— функции, выражающие закон изменения индукции для рамок 1и2при перемещении их в зазоре. При установившемся равновесии моментыМ1иМ2равны, т. е.

откуда

Выражение для угла поворота можно представить так:

(3.9)

Из выражения (3.9) видно, что отклонение подвижной части логометра зависит от отношения токов в его обмотках.

Измерительные механизмы магнитоэлектрических логометров применяют прежде всего в омметрах.

Электромагнитные измерительные механизмы.Вращающий момент в электромагнитных измерительных механизмах возникает в результате взаимодействия магнитного поля катушки, по обмотке которой протекает измеряемый ток, с одним или несколькими ферромагнитными сердечниками, обычно составляющими подвижную часть механизма. В настоящее время наибольшее применение получили три конструкции измерительных механизмов: а) с плоской катушкой; б) с круглой катушкой; в) с замкнутым магнитопроводом.

На рис. 3.3 показан измерительный механизм с плоской катушкой. Катушка / наматывается медным проводом и имеет воздушный зазор, в который может входить эксцентрично укрепленный на оси сердечник2.Материал сердечника должен обладать высокой магнитной проницаемостью, что способствует увеличению вращающего момента при заданном значении потребления мощности прибором, и минимальной коэрцитивной силой, что уменьшает погрешность от гистерезиса. Обычно материалом сердечника в щитовых приборах служит электротехническая (кремнистая) сталь, а в точных переносных приборах — пермаллой.

При наличии тока в катушке сердечник стремится расположиться в месте с наибольшей концентрацией поля, т. е. втягивается в зазор катушки. При этом закручиваются пружинки3,в результате чего возникает противодействующий момент. Для успокоения движения подвижной части в электр-омагнитных измерительных механизмах применяют обычно воздушные или жидкостные успокоители. На рис. 3.3 представлен измерительный механизм с воздушным успокоителем, состоящим из камеры4и крыла 5.

На рис. 3.4 показан электромагнитный измерительный механизм с замкнутым магнитопроводeом мещена на магнитопровод2с полюсными наконечниками3.При наличии

тока в обмотке катушки подвижный сердечник4стремится повернуться по часовой стрелке вокруг оси0,втягиваясь в рабочее пространство между полюсными накладками.

где L — индуктивность катушки, зависящая от положения сердечника; / — ток в обмотке.

Выражение для вращающего момента будет

откуда

(3.10)

Из выражения (3.10) видно следующее:

2. Шкала, электромагнитного прибора неравномерная, т. е. между измеряемой величиной (током) и.углом отклонения нет прямо пропорциональной зависимости. Характер шкалы зависит от множителят. е. от закона изменения индуктивности с изменением

или

Решая это уравнение относительнополучим

(3.11)

Электромагнитные измерительные механизмы используются в настоящее время в амперметрах, вольтметрах, в фазометрах и частотомерах. Кроме этих приборов, применяются резонансные электромагнитные приборы, в которых частота собственных колебаний подвижной части (сердечника) настраивается в резонанс с частотой тока в обмотке. К таким устройствам относятся вибрационные частотомеры.

К недостаткам приборов относятся относительно малые точность и чувствительность.

Aprēķinu daļa.

Izmantojama shēma.

Pēc Oma līkuma:no tā

Tad Isaizmainām ar,tad

Pēc tam pieņēmsim kā,tad

Mūsu gadījuma

Apreķinu tabula.

N0	1	2	3	4	5	6	7	8	9	10
Ir(mA)	70	70	70.1	70.1	69.9	69.9	70	70	70.1	70.1
I(A)	0.2800	0.2800	0.2804	0.2804	0.2796	0.2796	0.2800	0.2800	0.2804	0.2804

N0	11	12	13	14	15	16	17	18	19	20
Ir(mA)	69.9	68.8	69.9	70	70.1	70.2	70.2	70.1	70	70
I(A)	0.2796	0.2752	0.2796	0.2800	0.2804	0.2808	0.2808	0.2804	0.2800	0.2800

Izmantojamas iekārtas:

Milliampermatrs – 75(mA), skāle (0-75), iekšēja pretestība r-28(Om), klase (1.0)

Šunts – iekšēja pretestība Rs-9.33(Om), klase (0.1)

Pēc iegūtam datiem veicām statistisko apstrādi.

Xi	0.2792	0.2796	0.28	0.2804	0.2808
mi	1	4	7	6	2
pi	0.05	0.2	0.35	0.3	0.1

- eksperimentu skaits

Pēc tam atrodam, Ais- Strāvas īstā vertība

Tālāk atrodu ticamības intervālu ar izturību.

Tad mūsu rezultāts ir vienads:

Aprēķinu kļudas.

Ablolūta kļuda ir vienāda:

Relatīva kļūda ir vienāda:

Beigu rezultāti:

Secinājums.

Šajā darbā es veicu līdzstrāvas mērīšānu ar šunta palidzību. Pēc iegūtam datiem es atrodu absolūto un relatīvu kļudu , atrodu tīcamības intervālu. Pēc iegūtam datiem var sākt ,ka ar šunta palidzību var mērīt strāvas ar lielu precizitāti.

Literatūra.

1. A.В. Фремке и Е.М.Душина.-5-е изд., и доп.-Л.:Энергия. Лелингр. 1980.-392с.,ил.

Pielīkums.

superbotanik.net

Реферат Измерение постоянных токов. Измерение силы тока реферат

Электрический ток — реферат

2. Законы постоянного тока

3. Измерение силы тока с помощью приборов

Машины постоянного тока

Реферат Измерение постоянных токов

Vladimirs Bernatovičs

Kursa darbs

Измерение постоянных токов

Сила тока | Бесплатные курсовые, рефераты и дипломные работы

Реферат: Измерение постоянных токов

Kursa darbs

Измерение постоянных токов

Смотрите также