|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Инерциальные системы отсчета. Первый закон Ньютона. Инерциальные системы отсчета первый закон ньютона реферат
Инерциальные системы отсчета. Первый закон Ньютона. Видеоурок. Физика 9 Класс
Тема: Законы взаимодействия и движения тел
Урок 13. Инерциальные системы отсчета. Первый закон Ньютона
Ерюткин Евгений Сергеевич
На предыдущем уроке мы говорили о важности выбора системы отсчета. Напомним, что от того, как мы выберем СО, будут зависеть траектория, пройденный путь, скорость. Есть еще ряд особенностей, связанных с выбором системы отсчета, именно о них поговорим.
В седьмом классе вы изучали понятия «инерция» и «инертность». Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние. Если оно двигалось, то оно должно стремиться к тому, чтобы сохранять скорость этого движения. А если оно покоилось, то будет стремиться сохранить свое состояние покоя.
Инертность – это свойство тела сохранять состояние движения. Свойство инертности характеризуется такой величиной, как масса. Чем тело тяжелее, тем его труднее сдвинуть с места или, наоборот, остановить.
Обратите внимание на то, что эти понятия имеют непосредственное отношение к понятию «инерциальная система отсчета» (ИСО), о которой будет идти речь ниже.
Рассмотрим движение тела (или состояние покоя) в случае, если на тело не действуют другие тела. Заключение о том, как будет вести себя тело в отсутствии действия других тел, впервые было предложено Рене Декартом: если тело движется и на него не действуют другие тела, то движение будет сохраняться, оно будет оставаться прямолинейным и равномерным. Если же на тело не действуют другие тела, а тело покоится, то будет сохраняться состояния покоя. Но известно, что состояние покоя связано с системой отсчета, в одной СО тело покоится, а в другой вполне успешно и ускоренно движется. Результаты опытов и рассуждений приводят к выводу о том, что не во всех системах отсчета тело будет двигаться прямолинейно и равномерно или находиться в состоянии покоя при отсутствии действия на него других тел. Следовательно, для решения главной задачи механики важно выбрать такую систему отчета, где все-таки выполняется закон инерции, где ясна причина, вызвавшая изменение движения тела. Если тело будет двигаться прямолинейно и равномерно в отсутствии действия других тел, такая система отсчета будет для нас предпочтительной, а называться она будет инерциальной системой отсчета (ИСО).
Можно провести следующие рассуждения относительно инерциальной системы отсчета. Представьте ситуацию, когда движется автомобиль, затем водитель выключает двигатель, и дальше автомобиль движется по инерции. Но это некорректное утверждение.
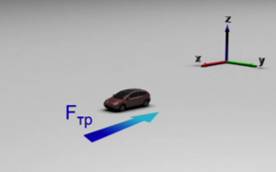
Рис.1. Скорость автомобиля меняется в результате действия силы трения
По той простой причине, что с течением времени автомобиль остановится в результате действия силы трения. Поэтому в данном случае не будет равномерного движения – одно из условий отсутствует.
Рассмотрим другой случай: с постоянной скоростью движется большой, крупный трактор при этом впереди тащит большой груз ковшом. Такое движение можно рассматривать как прямолинейное и равномерное.

Рис. 2. Экскаватор движется равномерно и прямолинейно. Действие всех тел скомпенсировано
Потому что в этом случае все силы, которые действуют на тело, скомпенсированы, уравновешивают друг друга. Значит, систему отсчета, связанную с этим телом, мы можем считать инерциальной.
Инерциальных систем отсчета может быть очень много. Реально же такая система отсчета все-таки идеализирована. Поскольку при ближайшем рассмотрении таких систем отсчета в полном смысле нет. ИСО – это некая идеализация, которая позволяет эффективно моделировать реальные физические процессы.
Для инерциальных систем отсчета справедлива формула сложения скоростей Галилея. Также заметим, что все системы отсчета, о которых мы говорили до этого, можно считать инерциальными в некотором приближении.
Впервые сформулировал закон, посвященный ИСО, Исаак Ньютон. Заслуга Ньютона заключается в том, что он первый научно показал, что скорость движущегося тела меняется не мгновенно, а в результате какого-то действия в течение времени. Вот этот факт и лег в основу создания закона, который называем первым законом Ньютона.
Первый закон Ньютона: существуют такие системы отсчета, в которых тело движется прямолинейно и равномерно или находится в состоянии покоя в том случае, если на тело не действуют силы или все силы, действующие на тело, скомпенсированы. Такие системы отсчета называются инерциальными.
По-другому иногда говорят следующее: инерциальной системой отсчета называется такая система, в которой выполняются законы Ньютона.
Большая часть систем, реальных систем отсчета – неинерциальные. Рассмотрим простой пример: сидя в поезде, вы положили на стол какое-либо тело (например, яблоко). Когда поезд трогается с места, мы будем наблюдать такую любопытную картину: яблоко будет двигаться, покатится в противоположную движению поезда сторону. В данном случае мы не сможем определить, какие же тела действуют, заставляют яблоко двигаться. В этом случае говорят, что система неинерциальная. Но можно выйти из положения, введя силу инерции.
Еще один пример: когда тело движется по закруглению дороги, то возникает сила, которая заставляет отклоняться тело от прямолинейного направления движения.

Рис. 3. Пример неинерциальной СО
В этом случае мы тоже должны рассмотреть неинерциальную систему отсчета, но, как и в предыдущем случае, тоже можем выйти из положения, вводя т.н. силы инерции.
Систем отсчета существует бесконечное множество, но среди них большинство – это те, которые мы инерциальными системами отсчета считать не можем. Инерциальная система отсчета – это идеализированная модель. Кстати, такой системой отсчета мы можем принять систему отсчета, связанную с Землей или какими-либо далекими объектами (например, со звездами).
Список дополнительной литратуры
- Галилей Г. Диалог о двух главнейших системах мира: Птолемеевой и Коперниковой. ОГИЗ-СССР, 1948
- Гиндикин С.Г. Рассказы о физиках и математиках. Библиотечка “Квант»”. Вып. 14. М.: Наука, 1982
- Лебедев В.И. Исторические опыты по физике. М.: КомКнига, 2007
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. М.: Просвещение
- Ньютон И. Математические начала натуральной философии. М.: Наука, 1989
- Слободянюк А.И. Физика 10. Часть 1. Механика. Электричество
- Физика. Механика. 10 класс. Под ред. Мякишева Г.Я. М.: Дрофа
- Филатов Е.Н. Физика 9. Часть 1. Кинематика. ВШМФ: Авангард
- Эйнштейн А., Инфельд Л. Эволюция физики. Развитие идей от первоначальных понятий до теории относительности и квантов. М.: Наука, 1965
interneturok.ru
Инерциальные системы отсчета: первый закон Ньютона
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое.
И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда». Галилей понял, что пребывание тела в состоянии покоя не является единственным следствием отсутствия внешних сил.
Тогда Галилей заявил: тело, на которое не действуют никакие силы, будет либо находиться в покое, либо двигаться равномерно прямолинейно. То есть, движение с одинаковой скоростью по прямой траектории, с точки зрения физики, равнозначно состоянию покоя.
Что есть состояние покоя?
В жизни этот факт наблюдать очень сложно, поскольку всегда имеет место сила трения, которая не дает предметам и вещам покидать свои места. Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой.
И в самом деле, на тело действую только две силы: сила тяжести и сила реакции опоры. Но расположены они на одной прямой и направлены друг против друга. Таким образом, по принципу суперпозиции, мы имеем, что общая сила, действующая на такое тело равна нулю.
Однако это идеальный случай. В жизни сила трения проявляет себя почти во всех случаях. Галилей сделал важное открытие, приравняв состояние покоя и движение с постоянной скоростью по прямой линии. Но этого было недостаточно. Оказалось, что условие это выполняется не во всех случаях.
Ясность в этот вопрос внес Исаак Ньютон, обобщивший исследования Галилея и, таким образом, сформулировавший Первый Закон Ньютона.
Первый закон Ньютона: формулируем сами
Существуют две формулировки первого закона Ньютона современная и формулировка самого Исаака Ньютона. В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон.
Современная формулировка звучит следующим образом: «Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго».
Инерциальные системы отсчета
Инерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела. Получается очень неудобоваримо, малопонятно и напоминает комичную ситуацию, когда на вопрос: “Где это «тут»?” отвечают: “Это здесь”, а на следующий логичный вопрос: “А где это «здесь»?” отвечают: “Это тут”. Масло масляное. Замкнутый круг.
Формулировка самого Ньютона такова: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
Однако на практике этот закон выполняется не всегда. Убедиться в этом можно элементарно. Когда человек стоит, не держась за поручни, в движущемся автобусе, и автобус резко тормозит, то человек начинает двигаться вперед относительно автобуса, хотя его не понуждает к этому ни одна видимая сила.
То есть, относительно автобуса первый закон Ньютона в изначальной формулировке не выполняется. Очевидно, что он нуждается в уточнении. Уточнением и является введение инерциальных систем отсчета. То есть, таких систем отсчета, в которых первый закон Ньютона выполняется. Это не совсем понятно, поэтому попробуем перевести все это на человеческий язык.
Инерциальные и неинерциальные системы отсчета
Свойство инерции любого тела таково, что до тех пор, пока тело остается изолированным от других тел, оно будет сохранять свое состояние покоя или равномерного прямолинейного движения. «Изолированным» - это значит никак не связанным, бесконечно удаленным от других тел.
На практике это означает, что если в нашем примере за систему отсчета принять не автобус, а какую-то звезду на окраине Галактики, то первый закон Ньютона будет абсолютно точно выполняться для беспечного пассажира, не держащегося за поручни. При торможении автобуса он будет продолжать свое равномерное движение, пока на него не подействуют другие тела.
Вот такие системы отсчета, которые никак не связаны с рассматриваемым телом, и которые никак не влияют на инертность тела, называются инерциальными. Для таких систем отсчета первый закон Ньютона в его исходной формулировке абсолютно справедлив.
То есть закон можно сформулировать так: в системах отсчета, абсолютно никак не связанных с телом, скорость тела при отсутствии стороннего воздействия остается неизменной. В таком виде первый закон Ньютона легко доступен для понимания.
Проблема заключается в том, что на практике очень сложно рассматривать движение конкретного тела относительно таких систем отсчета. Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
Поэтому за такую систему отсчета условно часто принимают Землю, хотя она и связана с находящимися на ней телами и влияет на характеристики их движения. Но для многих расчетов такое приближение оказывается достаточным. Поэтому примерами инерциальных систем отсчета можно считать Землю для расположенных на ней тел, Солнечную систему для ее планет и так далее.
Первый закон Ньютона не описывается какой-либо физической формулой, однако с помощью него выводятся другие понятия и определения. По сути, этот закон постулирует инертность тел. И таким образом выходит, что для инерциальных систем отсчета закон инерции и есть первый закон Ньютона.
Еще примеры инерциальных систем и первого закона Ньютона
Так, например, если тележка с шаром будет ехать сначала по ровной поверхности, с постоянной скоростью, а потом заедет на песчаную поверхность, то шар внутри тележки начнет ускоренное движение, хотя никакие силы на него не действуют (на самом деле, действуют, но их сумма равна нулю).
Происходит это от того, что система отсчета (в данном случае, тележка) в момент попадания на песчаную поверхность, становится неинерциальной, то есть перестает двигаться с постоянной скоростью.
Первый Закон Ньютона вносит важное разграничение между инерциальными и неинерциальными системами отсчета. Также важным следствием этого закона является тот факт, что ускорение, в некотором смысле, важнее скорости тела.
Поскольку движение с постоянной скоростью по прямой линии суть нахождение в состоянии покоя. Тогда как движение с ускорением явно свидетельствуют о том, что либо сумма сил, приложенных к телу, не равно нулю, либо сама система отсчета, в которой находится тело, является неинерциальной, то есть движется с ускорением.
Причем ускорение может быть как положительным (тело ускоряется), так и отрицательным (тело замедляется).
Нужна помощь в учебе?
 Предыдущая тема: Относительность движения: понятие и примеры Следующая тема:   Второй закон Ньютона: формула и определение + маленький опыт
Предыдущая тема: Относительность движения: понятие и примеры Следующая тема:   Второй закон Ньютона: формула и определение + маленький опытВсе неприличные комментарии будут удаляться.
www.nado5.ru
3.1.1. Первый закон Ньютона. Инерциальные системы отсчета
В качестве первого закона Ньютон взял принцип инерции Галилея (1632 год) и дополнил его понятием инерциальной системы отсчета. Согласно принципу инерции Галилея свободное тело сохраняет состояние, покоя или равномерного, прямолинейного движения пока воздействие других тел не выведет его из этого состояния.
Из этого принципа следует, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инерцией. Поэтому первый закон Ньютона называют законом инерции, а движение тела в отсутствие воздействий со стороны других тел - движением по инерции.
Первый закон Ньютона выполняется не во всех системах отсчета. Те системы, в которых он выполняется, называются инерциальными системами отсчета.
Экспериментально установлено, что практически инерциальной системой отсчета является гелиоцентрическая система отсчета, начало координат которой находится в центре Солнца, а оси проведены в направлении трех удаленных звезд, выбранных, например, так, чтобы они были взаимно перпендикулярны.
Для многих практических целей при движении макроскопических тел в качестве системы отсчета используется система, связанная с Землей. Такая система отсчета считается приближенно инерциальной из-за влияния суточного и годового вращения Земли.
Таким образом, можно дать следующую формулировку первого закона Ньютона: существуют такие системы отсчета, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие других тел не выведет его из этого состояния.
Покажем, что любая система отсчета, которая движется равномерно и прямолинейно относительно инерциальной системы, также является инерциальной. Пусть тело А покоится в инерциальной системе отсчета К (рис. 3.1). Система отсчета К' движется относительно системы К равномерно и прямолинейно со скоростью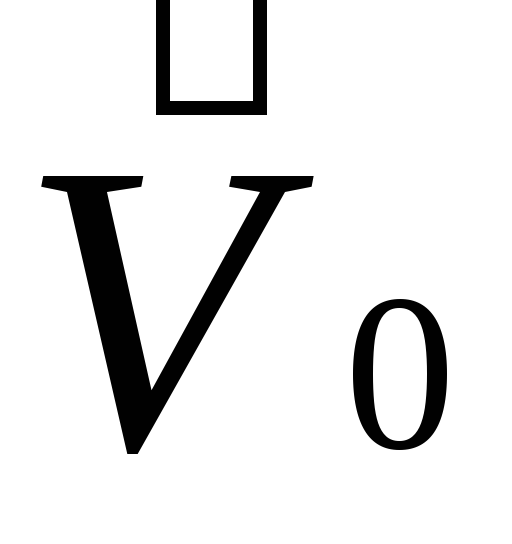 . Тело А относительно системы К' движется равномерно и прямолинейно со скоростью -
. Тело А относительно системы К' движется равномерно и прямолинейно со скоростью -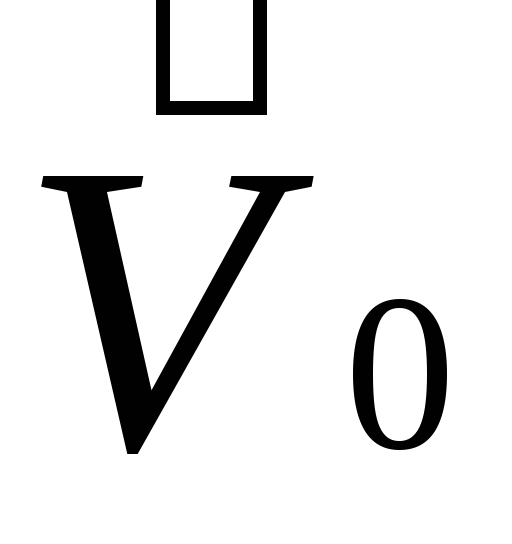 , что также удовлетворяет первому закону Ньютона. Следовательно, система отсчета К' является инерциальной. Таким образом, по известной одной инерциальной системе отсчета можно описанным выше способом построить их сколько угодно.
, что также удовлетворяет первому закону Ньютона. Следовательно, система отсчета К' является инерциальной. Таким образом, по известной одной инерциальной системе отсчета можно описанным выше способом построить их сколько угодно.
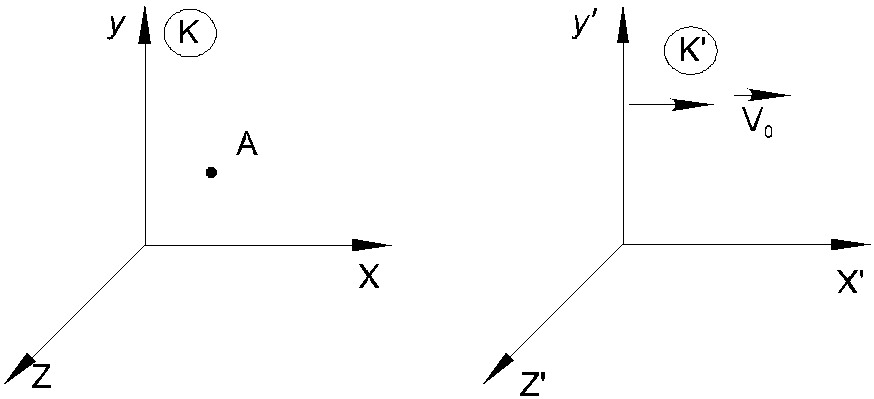
Рис 3.1
3.1.2. Второй закон Ньютона
Этот закон является основным законом динамики материальной точки и твердого тела, движущегося поступательно.
Закон устанавливает связь между силой, массой и ускорением.
Опыт показывает, что всякое изменение величины или направления скорости движения тела вызывается его взаимодействием с другими телами.
В механике сила определятся как количественная мера взаимодействия тел, которое приводит к изменению их скорости или деформации.
Сила характеризуется величиной, направлением и точкой приложения. Следовательно, сила является векторной величиной.
По современным представлениям, основанным на опыте, все наблюдаемые в природе взаимодействия могут быть сведены к четырем фундаментальным: гравитационному, слабому, электромагнитному и сильному.
Гравитационное взаимодействие присуще всем материальным объектам. Оно определяется наличием у материальных тел массы и подчиняется закону всемирного тяготения Ньютона. Радиус действия гравитационного взаимодействия неограничен. В области микромира роль гравитационного взаимодействия ничтожно мала.
Слабое взаимодействие - короткодействующее, существует в микромире и проявляется в том, что приводит к определенному виду нестабильности элементарных частиц.
Электромагнитное взаимодействие проявляется при взаимодействии токов и зарядов. Радиус действия электромагнитного взаимодействия неограничен. Оно является определяющим в образовании атомов, молекул и макроскопических тел.
Ядерное или сильное взаимодействие является самым интенсивным. Радиус сильного взаимодействия очень мал ~10-15 м. Благодаря этому взаимодействию протоны и нейтроны удерживаются в ядрах, несмотря на сильное отталкивание протонов.
К нефундаментальным силам относятся силы упругости, трения, сопротивления и другие. Все эти силы могут быть сведены к электромагнитным или гравитационным, однако, это приводит к существенному усложнению решения задач механики. По этой причине в механике силы упругости и трения рассматривают наряду с фундаментальными.
Опытным путем установлено еще одно важное свойство сил, проявляющееся при механическом взаимодействии. Силы в механике подчиняются принципу суперпозиции, который заключается в следующем: одновременное взаимодействие частицы М с несколькими другими n частицами с силами 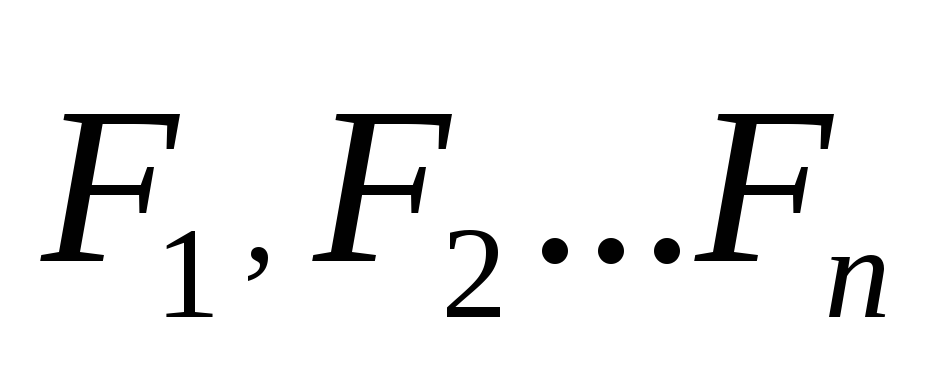 эквивалентно действию одной силы
эквивалентно действию одной силы , равной их векторной сумме.
, равной их векторной сумме.
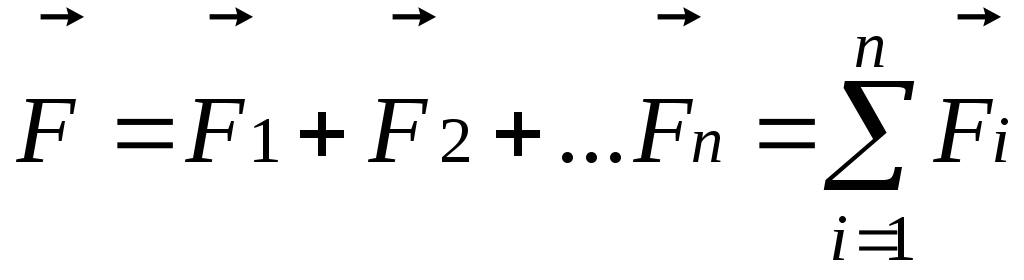 . (3.1)
. (3.1)
Силу  называют равнодействующей.
называют равнодействующей.
Как показывает опыт, все тела обладают свойством препятствовать изменению величины и направления скорости. Это свойство называется инертностью.
Массу можно определить двумя способами. Первый из них состоит в следующем. Выбирается эталонное тело, масса которого mэт принимается за единицу массы. Масса m исследуемого тела определяется из следующего соотношения, установленного опытным путем:
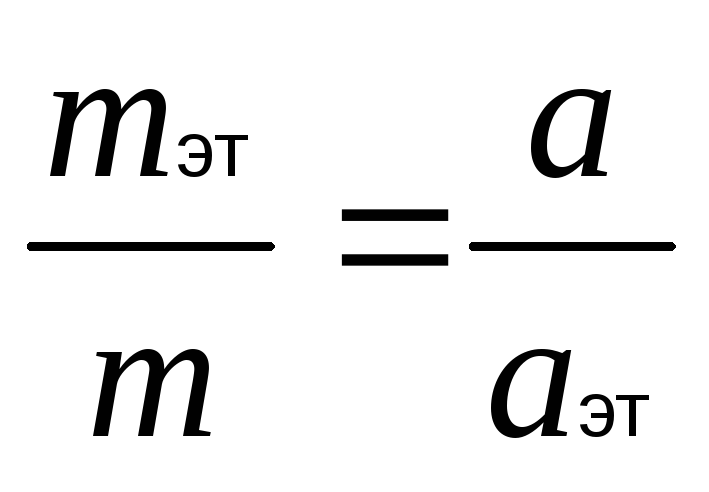 ,
,
где а и аэт - ускорения, вызываемые действием одной и той же силы на эталонное и исследуемое тела. При этом определяется так называемая инертная масса.
Второй способ основан на использовании закона всемирного тяготения. При этом определяется так называемая гравитационная масса.
А. Эйнштейн сформулировал принцип эквивалентности гравитационной и инертной массы: инертная и гравитационная массы одного и того же тела одинаковы.
Эквивалентность инертной и гравитационной масс позволяет выбрать для них одну единицу измерения. В качестве единицы массы в системе СИ принят килограмм (кг) - масса эталонного платиново-иридиевого тела, хранящегося во Франции в международном бюро мер и весов.
Динамическое воздействие движущегося тела на другие тела зависит от скорости и массы. Поэтому в качестве динамической характеристики интенсивности движения вводится векторная величина  , называемая импульсом (или количеством движения) тела и равная произведению его массы на скорость:
, называемая импульсом (или количеством движения) тела и равная произведению его массы на скорость:
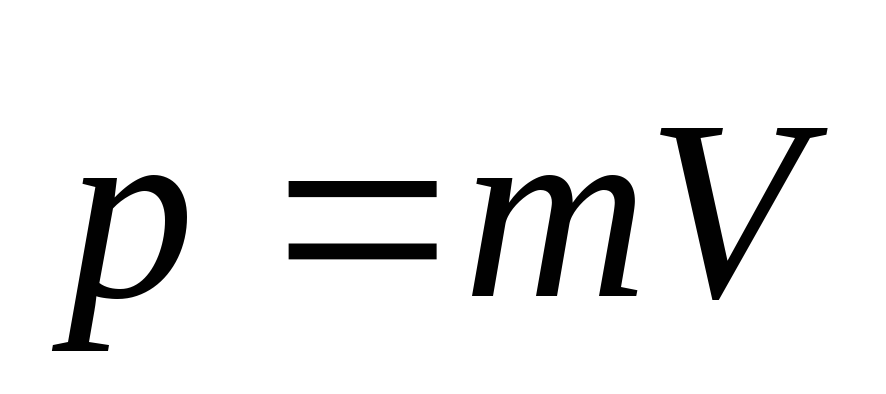 . (3.2)
. (3.2)
Единица импульса килограмм-метр, деленный на секунду (кг·м/с).
Согласно второму закону Ньютона, производная по времени от импульса тела равна равнодействующей всех приложенных к нему сил:
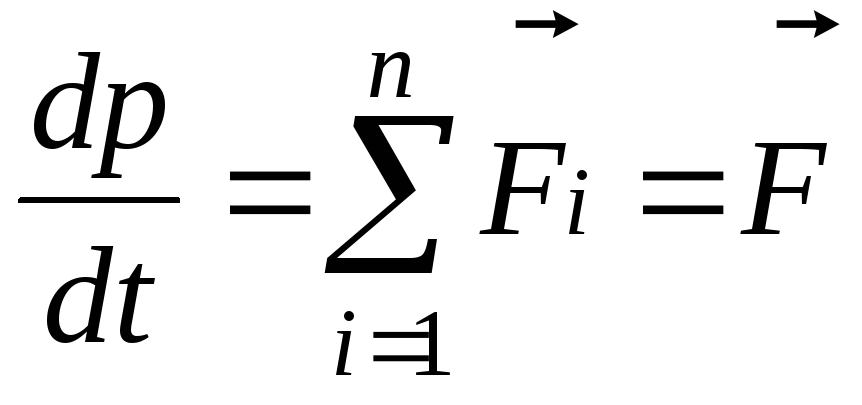 . (3.3)
. (3.3)
Из (3.3) следует, что изменение импульса происходит в направлении равнодействующей силы  . Отметим, что второй закон Ньютона в форме (3.3) допускает описание движения тела с переменной массой. Если масса тела постоянна, то из (3.2) и (3.3) получаем уравнение второго закона Ньютона в виде
. Отметим, что второй закон Ньютона в форме (3.3) допускает описание движения тела с переменной массой. Если масса тела постоянна, то из (3.2) и (3.3) получаем уравнение второго закона Ньютона в виде
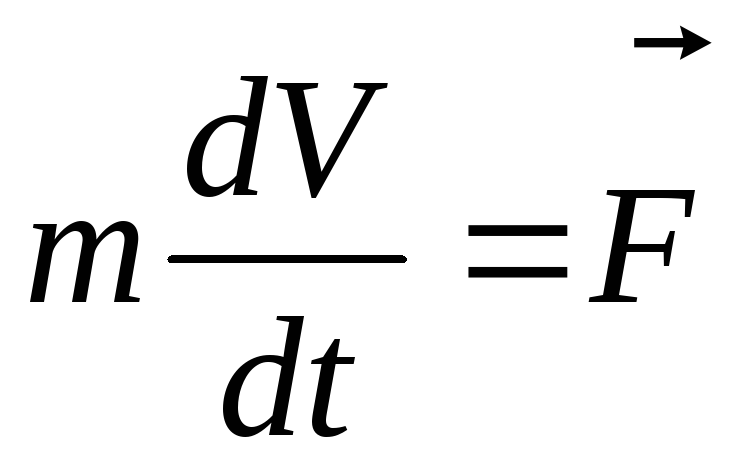 , (3.4)
, (3.4)
откуда с учетом формулы (2.21) получаем:
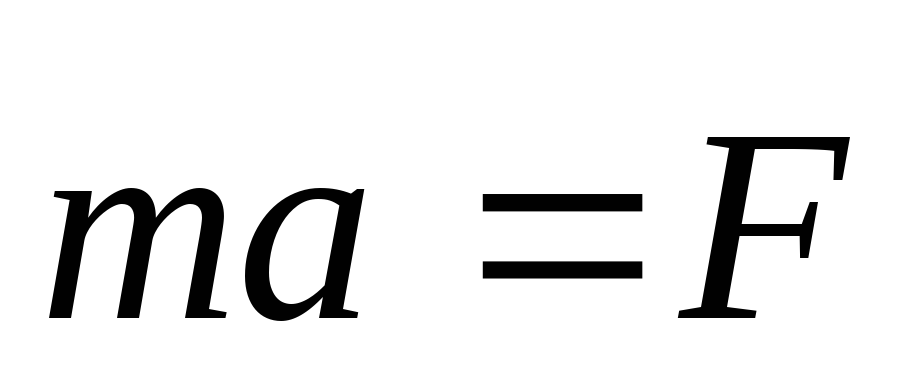 . (3.5)
. (3.5)
Единица силы в СИ является производной единицей, определение которой основано на формуле (3.5). Единица силы - 1 Ньютон (Н), это такая сила, которая телу с массой 1 кг сообщает ускорение 1м/с2.
Второй закон Ньютона часто называют основным законом динамики поступательного движения. С помощью этого закона в механике решаются две основные задачи:
1. Прямая основная задача - установление дифференциальных уравнений движения тела (точки) и их решение.
2. Обратная основная задача - нахождение зависимости сил взаимодействия тел от их координат, скоростей и времени, то есть установление законов взаимодействия.
studfiles.net
Реферат Первый закон Ньютона
скачатьРеферат на тему:
План:
- Введение
- 1 Формулировка
- 2 История
- 3 Смежные понятия ЛитератураПримечания
Введение
Ине́рция (от лат. inertia — бездеятельность, косность) — явление сохранения скорости тела в случае, если внешние воздействия на него отсутствуют или взаимно скомпенсированы.
1. Формулировка
Существование явления инерции в классической механике постулируется Первым законом Нью́тона, который также называется Зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:
Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Современная формулировка закона:
Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.
Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными. Проявлением неинерциальности в них является возникновение фиктивных сил, называемых «силами инерции».
2. История
Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте[1]:
| Никто не сможет сказать, почему [тело], приведенное в движение, где-нибудь остановится, ибо почему оно скорее остановится здесь, а не там? Следовательно, ему необходимо или покоиться, или двигаться до бесконечности. |
Однако сам Аристотель считал, что пустота в природе не может существовать, и в другом его труде, «Механике», утверждается[2]:
| Движущееся тело останавливается, если сила, его толкающая, прекращает свое действие. |
Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (сил трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.
Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку Аристотеля. В своем труде «Беседы о двух новых науках» он писал[2]:
| …скорость, однажды сообщенная движущемуся телу, будет строго сохраняться, поскольку устранены внешние причины ускорения или замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время, как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно |
Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то, при движении по горизонтальной плоскости, у тела нет причин ускоряться или замедляться, и оно должно пребывать в состоянии равномерного движения или покоя.
Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считал Аристотель и его последователи. Это открытие Галилея вошло в науку как Закон инерции. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.
3. Смежные понятия
Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведенной в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.
Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (примерами абстрактной модели служат абсолютно твердое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами и соответствие реально наблюдаемого движения тел в таких системах с результатами расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика и ограничивается лишь величиной искривления пространства-времени, которое было предсказано в рамках общей теории относительности (1915 год) и впервые зафиксировано в 1919 году при исследовании отклонения света в гравитационном поле Солнца.
Инертность — свойство тела, состоящее в том, что для изменения его скорости относительно инерциальной системы отсчёта необходимо определённое воздействие на него. Мерой инертности в физике выступает инертная масса.
Литература
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Том 1. Часть 1-я; Часть 2-я
- Том 2. Часть 1-я; Часть 2-я
- Кокарев С. С. Три лекции о законах Ньютона. Ярославль. Сб. трудов РНОЦ Логос, вып. 1, 45-72, 2006.
Примечания
- Физика (Аристотель)/Книга 4/Глава 8 - ru.wikisource.org/wiki/ru:Физика_(Аристотель)/Книга_4/Глава_8
- ↑ 12Эйнштейн А., Инфельд Л. Эволюция физики - eqworld.ipmnet.ru/ru/library/books/EinsteinInfeld1965ru.djvu. — М.: Наука, 1965. — С. 10-12.
wreferat.baza-referat.ru
Первый закон Ньютона





«Физика - 10 класс»
Какое явление называют инерцией?Что называют системой отсчёта?
Закон инерции относится к самому простому случаю движения — движению тела, которое не взаимодействует с другими телами, т. е. движению свободного тела.
Ответить на вопрос, как же движутся свободные тела, не обращаясь к опыту, нельзя. Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть?
Имеется лишь один выход. Надо поместить тело в условия, при которых влияние внешних взаимодействий можно делать всё меньшим и меньшим, и наблюдать, к чему это ведёт. Можно, например, наблюдать за движением гладкого камня на горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к Земле компенсируется действием поверхности, на которую он опирается; на скорость его движения влияет только трение.) При этом легко обнаружить, что, чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, не меняя заметно скорость. На основе подобных наблюдений можно сделать вывод: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсем не менял бы своей скорости. Именно к такому выводу пришёл впервые Галилей.
Первый закон Ньютона:
Существуют системы отсчёта, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, если на него не действуют другие тела.
Первыи закон, или закон инерции, как его часто называют, фактически был открыт Галилеем, но строгую формулировку дал и включил его в число основных законов механики Исаак Ньютон.
Этот закон, с одной стороны, содержит определение инерциальной системы отсчёта. С другой стороны, он содержит утверждение (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы отсчёта существуют в действительности.
Инерциальные и неинерциальные системы отсчёта.
До сих пор систему отсчёта мы связывали с Землёй, т. е. рассматривали движение относительно Земли. В системе отсчёта, связанной с Землёй, ускорение тела определяется только действием на него других тел. Система отсчёта, связанная с Землёй, является инерциальной.
Из формулировки первого закона следует, что если есть одна инерциальная система отсчёта, то любая другая движущаяся относительно неё прямолинейно и равномерно также является инерциальной.

Однако, помимо инерциальных систем отсчёта, есть и другие, в которых тело имеет ускорение даже в том случае, когда на него другие тела не действуют.
В качестве примера рассмотрим систему отсчёта, связанную с автобусом. При равномерном движении автобуса пассажир может не держаться за поручень, действие со стороны автобуса компенсируется взаимодействием с Землёй. При резком торможении автобуса стоящие в проходе пассажиры падают вперёд, получая ускорение относительно стенок автобуса (рис. 2.6). Однако это ускорение не вызвано какими-либо новыми воздействиями со стороны Земли или автобуса непосредственно на пассажиров. Относительно Земли пассажиры сохраняют свою постоянную скорость, но автобус начинает двигаться с ускорением, и пассажиры относительно него также движутся с ускорением. Ускорение появляется вследствие того, что движение их рассматривается относительно тела отсчёта (автобуса), движущегося с ускорением.

Рассмотрим маятник, находящийся на вращающемся диске (рис. 2.7). Нить маятника отклонена от вертикали, хотя сам он неподвижен относительно диска. Натяжение нити не может быть скомпенсировано силой притяжения к Земле. Следовательно, отклонение маятника нельзя объяснить только его взаимодействием с телами.
Рассмотрим ещё один маятник, находящийся в неподвижном вагоне. Нить маятника вертикальна (рис. 2.8, а). Шарик взаимодействует с нитью и Землёй, сила натяжения нити равна силе тяжести. С точки зрения пассажира в вагоне и человека, стоящего на перроне, шарик находится в равновесии вследствие того, что сумма сил, действующих на него, равна нулю.
Как только вагон начинает двигаться с ускорением, нить маятника отклоняется (шарик по инерции стремится сохранить состояние покоя). С точки зрения человека, стоящего на перроне, ускорение шарика должно быть равно ускорению вагона, так как нить не разрывается и шарик движется вместе с вагоном. Шарик по-прежнему взаимодействует с теми же телами, сумма сил этого взаимодействия должна быть отлична от нуля и определять ускорение шарика.
С точки зрения пассажира, находящегося в вагоне, шарик неподвижен, следовательно, сумма сил, действующих на шарик, должна быть равна нулю, однако на шарик действуют те же силы — натяжения нити и сила Рис. 2.8 тяжести. Значит, на шарик (рис. 2.8, б) должна действовать сила  ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).
ин, которая определяется тем, что система отсчёта, связанная с вагоном, неинерциальная. Эту силу называют силой инерции (см. рис. 2.8, б).
В неинерциальных системах отсчёта основное положение механики о том, что ускорение тела вызывается действием на него других тел, не выполняется.
Системы отсчёта, в которых не выполняется первый закон Ньютона, называются неинерциальными.
Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика - Физика, учебник для 10 класса - Класс!ная физика
Основное утверждение механики --- Сила --- Инертность тела. Масса. Единица массы --- Первый закон Ньютона --- Второй закон Ньютона --- Принцип суперпозиции сил --- Примеры решения задач по теме «Второй закон Ньютона» --- Третий закон Ньютона --- Геоцентрическая система отсчёта --- Принцип относительности Галилея. Инвариантные и относительные величины --- Силы в природе --- Сила тяжести и сила всемирного тяготения --- Сила тяжести на других планетах --- Примеры решения задач по теме «Закон всемирного тяготения» --- Первая космическая скорость --- Примеры решения задач по теме «Первая космическая скорость» --- Вес. Невесомость --- Деформация и силы упругости. Закон Гука --- Примеры решения задач по теме «Силы упругости. Закон Гука» --- Силы трения --- Примеры решения задач по теме «Силы трения» --- Примеры решения задач по теме «Силы трения» (продолжение) ---
Устали? - Отдыхаем!


Вверх
class-fizika.ru
Первый закон Ньютона. Инерциальные системы отсчета
Стр 1 из 3Следующая ⇒Вопрос №5
Первый закон Ньютона. Инерциальные системы отсчета
Основы классической динамики составляют 3 закона и 3 закона сохранения:
-импульса
-момента импульса
-полной механической энергии
Эти законы являются аксиомами (постулаты).
1-й закон Ньютона:
Любая материальная точка движется равномерно и прямолинейно или сохраняет состояние покоя до тех пор пока воздействие со стороны других тел (мат. точек) не изменит это состояние.
Этот закон также называют законом инерции.
1-й закон Ньютона выполняется не любой СО.
Системы отсчета ,в которых выполняется 1-й закон Ньютона называются инерциальными.
Способность тел двигаться или сохранять состояние покоя ,при отсутствии воздействия других те называется инерцией.
Все тела обладают инертностью.
В природе существуют инерциальные системы отсчета.
Вопрос №6 Масса, импульс, сила. Второй закон Ньютона для материальной точки. Единицы силы, массы и импульса.
Для количественного описания динамики движения вводятся понятия массы, импульса и силы.
Масса– количественная мера инертности тела. Это есть скалярная величина. Так же масса – величина аддетивная (суммируемая ) ,т.е. масса тела (системы) равна сумме масс отдельных ее частей m= m1+m2+…mn.
[m]= M; едm=кг
Импульс мат. точки – векторная величина, численно равная произведению массы мат. точки m на ее скорость v. Импульс суммируемая величина. Также импульс называют количеством движения.
p= mv
едp= (кг* м)/c
[p]=([m]*[l])/[t]=(M*L)/T=MLT-1
Сила– количественная мера воздействия одного тела на другое. Это векторная величина.
Если на одно тело действует несколько сил, то их действие можно заменить одной силой F , которая является суммой (векторной) всех сил, действующих на тело.
F=F1+F2+F3+…+Fn= ∑Fi
Сила F называется результирующей. В отдельных случаях можно указать точку приложения силы. Единица силы вводится из 2-го закона Ньютона для мат. точки.
Второй закон Ньютона для мат. точки.
1)Скорость изменения импульса мат. точки по времени равно результирующей силе, действующей на эту точку:
dP/dt=F
d(mv)/dt=F
Если m=const, то mdv/dt=ma=F
7.Третий закон Ньютона. Границы применимости законов Ньютона.
3-ий закон Ньютона: действие одного тела на другое всегда имеет характер взаимодействия. Две мат.точки действуют друг на друга с силами равными по величине, но противоположными по знаку.
механика Ньютона неприменима, если относительные скорости точек сравнимы со скоростью света [это область релятивистской или эйнштейновской механики]; неприменима механика классическая и к изучению явлений микромира [это область квантовой механики]. Но они основаны на классической механики. В остальных областях => классическая механика даёт достаточно точные результаты.
8. Масса, импульс и центр масс системы мат.точек и абсолютно твёрдого тела. Второй закон Ньютона для системы мат.точек и абсолютно твёрдого тела.
Сис-ма мат.точек – совокупность мат.точек взаимодействующих между собой.
Центр масс(центр инерции)- точка С радиус-вектор которой даётся 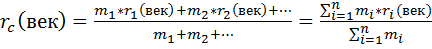
Скорость центра масс – производная скорости центра масс по времени.
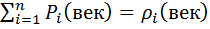 - импульс системы мат.точек.
- импульс системы мат.точек.
Импульс системы мат.точек – произведение m массы на скорость её центра масс.
Абсолютно твёрдое тело – тело, расстояние между двумя точками которого всегда остаётся неизменным. Поэтому а.т.т.можно рассматрвиать как совокупность мат.точек жёстко связанных между собой.
Рассмотри систему мат.точек и запишем для каждой точки входящей в систему второй закон Ньютона.
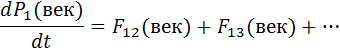
F1 – результатирующая всех внешних сил, действующих на первую точку.
2-ый закон Ньютона для абсолютно твёрдого тела: поступательное движение а.т.т.такое движение при котором любая прямая жёстко связанная с этим телом при движении тела перемещается параллельно самой себе.
При поступательном движении тела все точки тела имеют одинаковые скорости. Поэтому для любой точки тела скорость такая же как и у центра масс.
13.
При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды.
Существует внешнее и внутреннее трение (иначе называемое вязкостью). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.
Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.
Внешнее трение подразделяют на трение покоя (статическое трение) и кинематическое трение. Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения.
В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.
14.
Момент инерции тела относительно некоторой оси z – это сумма произведений масс м. т. Составляющих тело на квадрат их расстояния до оси z.
n
Iz=∑ mizi²
i=1
Момент инерции – это кол. Мера инертности тела при вращательном движении. зависит от массы и от распределения массы по телу.
Собственный момент инерции Ic – это момент инерции тела относ. оси проходящей через его центр масс.
Icк = 2/5 * mR²
Для вычисления мом. инерции тв. Тела исп. Теорема Штейнера
Iz۱=Ic+ma²
Мом. Инерции тв. тела относ. производной оси z۱ = собственному моменту инерции тела Ic + произведение массы тела m на квадрат расстояния a между осью z штрих и z проходящей через центр масс тела параллельно оси z۱
15. Кинематика вращательного движения. Угловая скорость и угловое ускорение. Связь между линейной и угловой скоростью.
Вращение движения тела – движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, назыв. осью вращения.
Траектория движения точки при этом лежит в плоскостях перпендикулярных оси вращения. Ось вращения проходит как внутри тела или быть в ей. Если ось вращения проходит внутри тела, то тела принадл. ось не вращения – неподвижны.
За равный промежуток времени все точки вращ.движ. поворачиваются а один и тот же угол. Для коллич. Оценки вращ.движ. вводится понятие угловой скорости. По определению угловая мгновенная скорость движения 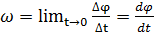 ( 1ая производная поворота ϕ по времени)Вектор угловой скорости направлен вдоль оси вращ. Так, если смотреть с конца, ω вращ. Тела происходит против часовой стрелки. Если угловая скорость постоянна, движение равномерное.Время, за которое тело совершает один полный поворот, поворачивается на угол 2π, назыв. период вращения.
( 1ая производная поворота ϕ по времени)Вектор угловой скорости направлен вдоль оси вращ. Так, если смотреть с конца, ω вращ. Тела происходит против часовой стрелки. Если угловая скорость постоянна, движение равномерное.Время, за которое тело совершает один полный поворот, поворачивается на угол 2π, назыв. период вращения. 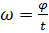
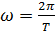
 =
=  единица измер.
единица измер. 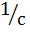 =
= 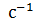 Величина V равная
Величина V равная  назыв. частотой.
назыв. частотой.
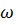 =
= 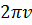 ед.измер
ед.измер 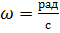
Для коллич. оценки быстроты изм.угловой скорости вводится понятие углового ускорения. По определению угловое мгновенное ускорении 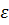 =
= 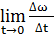 =
= 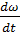
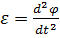 Вектор
Вектор 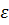 так же направле вдоль оси вращения и совпадает с направлением
так же направле вдоль оси вращения и совпадает с направлением 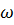 , если тело набирает обороты, противоп., если замедляет движение. Ед
, если тело набирает обороты, противоп., если замедляет движение. Ед 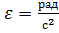 Если
Если 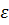 постоянно это будет равномерное вращ. Движение
постоянно это будет равномерное вращ. Движение 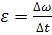
Связь между линейной и угловой скоростью: 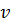 =
= 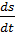
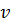 = [
= [ 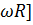
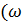 ^R) =90
^R) =90 
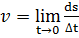 =
= 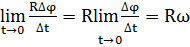
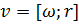
Вопрос № 18 Момент импульса
Момент импульса – динамическая величина.
Импульс – произведение массы материальной точки на её скорость.
P=mU
Момент импульса определяется аналогично моменту силы.
Момент импульса: L = [r1 P]
|L| = L = rˑRlim(r1 R)
Момент импульса относительно неподвижной оси Z – это проекция момента импульса относительно произвольной точки оси на эту ось .
Единица L = мˑНˑс =Нˑмˑс
Единица L = ((кгˑм)/с)ˑм = (кгˑм2)/с
Вопрос 19. Основной закон динамики вращательного движения для системы материальных точек и для тела, шарнирно закрепленного в одной точке .(уравнение моментов)
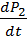 =
= 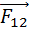 +
+ 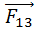 +
+ 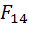 +
+ 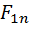 +
+ 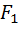
Для 2-ой точки
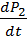 =
= 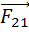 +
+ 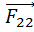 +
+ 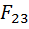 +…+
+…+ 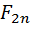 +
+ 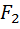 (1)
(1)
Для 3-ей точки
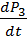 =
= 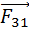 +
+ 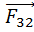 +
+ 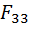 +…+
+…+ 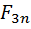 +
+ 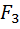
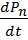 =
= 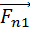 +
+  +
+  +…+
+…+ 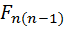 +
+ 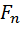
[ 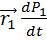 ]=[
]=[ 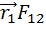 ]+
]+ 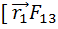 ]+…+[
]+…+[ 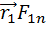 ]+[
]+[ 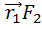 ]
]
[ 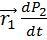 ]=[
]=[ 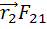 ]+
]+ 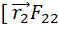 ]+[
]+[ 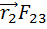 ]+…+[
]+…+[ 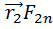 ]+
]+ 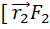 ] (2)
] (2)
……………………………………………………………………………
[ 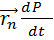 ]=[
]=[ 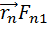 ]+
]+ 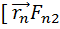 ]+[
]+[ 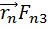 ]+…+[
]+…+[ 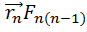 ]+
]+ 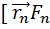 ]
]
[ 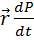 ]=
]= 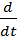 [
[ 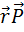 ]
]
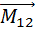 =[
=[ 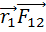 ]
]
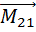 =[
=[ 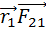 ]
]
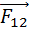 =-
=- 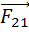
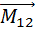 =-
=- 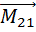
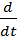 [
[ 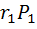 ]=
]=  +
+ 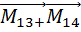 +…+
+…+ 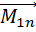 +
+ 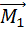
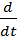 [
[ 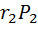 ]=
]= 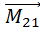 +
+ 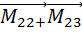 +
+ 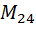 +…+
+…+ 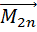 +
+ 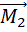 (3)
(3)
………………………………………………………………….
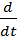 [
[ 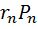 ]=
]= 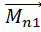 +
+ 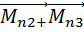 +…+
+…+ 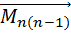 +
+ 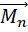
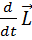 =
= 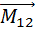 +
+ 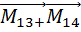 +…+
+…+ 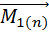 +
+ 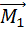
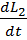 =
= 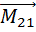 +
+ 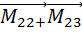 +…+
+…+ 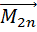 +
+ 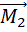 (4)
(4)
………………………………………………
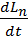 =
= 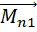 +
+ 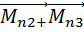 +…+
+…+ 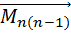 +
+ 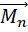
Сложим правую и левую часть этих ур-ний
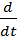 (
(  +
+  +
+  +…+
+…+  )= (
)= ( 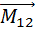 +
+ 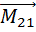 )+ (
)+ ( 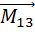 +
+ 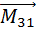 )+ (
)+ ( 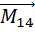 +
+ 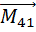 )+…+ (
)+…+ ( 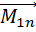 +
+ 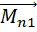 )+…+
)+…+ 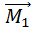 +
+ 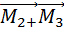 +
+ 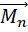
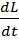 =
= 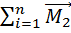 (5)
(5)
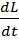 =
= 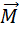 (6)
(6)
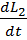 =
= 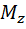 (7)
(7)
Скорость изменения момента импульса(1) для системы матер.точек,взятых относительно неподвижной точки О=результатирующему моменту М всех внешних сил,действующих на эту систему взятой той же точки О.
(6) справедливо также для твёрдого тела шарнирно-закрепленного в одной точке.
1. Вопрос 20. Момент импульса твердого тела относительно неподвижной оси. Основной закон динамики вращательного движения для тела, вращающегося относительно неподвижной оси.
Скорость изменения момента импульса твердого тела относительно неподвижной оси Z=результирующему моменту Мz всех внешних сил,действующих на тело относительно тойже осиZ.
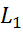 =
= 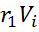 sin90=
sin90= 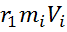 =
= 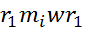 =
= 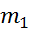 w
w 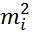 (8)
(8)
L= 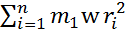 =w
=w 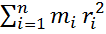 (9)- момент инерции твердого тела
(9)- момент инерции твердого тела
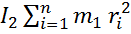 (10)
(10)
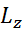 =
= 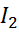 w (11)
w (11)
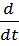 (
( 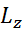 w)=
w)= 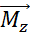 (12)
(12)
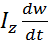 =
= 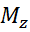 (13)
(13)
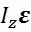 =
= 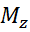 (14)
(14)
Произведение момента инерции твердого тела относительно неподвижной оси Z на его угловое ускорение w =результирующему моменту М,Z всех внешних сил,действующих на тело относительно тойже неподвижной оси Z.
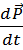 =
= 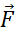
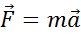
6,7,8,13-основной закон динамики(2-ой зокон Ньютона для вращающегося тела)
21.Момент инерции тела. Теорема Штейнера. Собственные моменты инерции диска, шара, стержня, кольца, цилиндра. Единица момента инерции.
Момент инерции тв. тела относительно некоторой оси z – это сумма произведения масс материальных точек, составляющих тело на квадрат расстояния до оси z .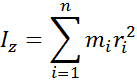
Момент инерции – количественная мера инертности тела при вращательном движении. Момент инерции зависит как от массы тела, так и от распредел. масс тела. Чем больше м. ин. тела, тел труднее остановить вращ. тело.
Собственный момент инерции – момент инерции тела относит. оси, проход. Через его центр масс С (Ic). Для м.т. понятие сотств. момента инерции отсуств.
Собственный моменты:
1. Шар: 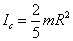 3. Стержень:
3. Стержень: 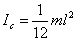 5. Цилиндр:
5. Цилиндр: 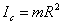
2. Диск: 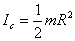 4. Кольцо:
4. Кольцо: 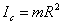
Теорема Штейнера. Момент инерции тв. Тела относительно произвольной оси z равен собств. Моменту инерции тела плюс произведение массы тела на квадрат расстояния между осью z’ и z, проходящей через центр масс.
23. Закон сохранения момента импульса
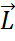 =[
=[ 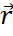
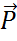 ]
]
Момент импульса на ось – проекция вектора на ось.
Lz= Izw
Момент импульса замкнутой системы – величина постоянная. (вектор 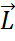 = const)
= const)
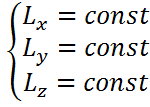
В незамкнутой системе могут сохраняться проекции импульса на отдельные направления.
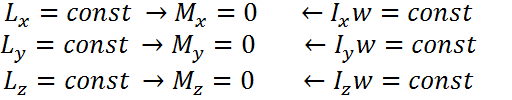
В незамкнутой системе момент импульса также сохраняется, если результирующий момент внешних сил, действующих на систему, равен 0.
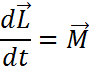
Закон сохранения момента импульса не выводится из основного закона динамики вращательного движения, а лишь согласуется с ним. Более того, закон сохранения момента импульса имеет более широкое значение, чем основной закон динамики(2-й закон Ньютона).
ЗСМИ является следствием изотропности пространства.
Вопрос №5
Первый закон Ньютона. Инерциальные системы отсчета
Основы классической динамики составляют 3 закона и 3 закона сохранения:
-импульса
-момента импульса
-полной механической энергии
Эти законы являются аксиомами (постулаты).
1-й закон Ньютона:
Любая материальная точка движется равномерно и прямолинейно или сохраняет состояние покоя до тех пор пока воздействие со стороны других тел (мат. точек) не изменит это состояние.
Этот закон также называют законом инерции.
1-й закон Ньютона выполняется не любой СО.
Системы отсчета ,в которых выполняется 1-й закон Ньютона называются инерциальными.
Способность тел двигаться или сохранять состояние покоя ,при отсутствии воздействия других те называется инерцией.
Все тела обладают инертностью.
В природе существуют инерциальные системы отсчета.
Читайте также:
lektsia.com
2. Динамика поступательного движения
С помощью кинематических уравнений можно вычислить положение движущегося тела в любой момент времени, если известны его начальное положение, скорость и ускорение. Но кинематика не даёт ответа на вопросы: по какой причине тело движется именно так? почему оно имеет именно такое ускорение?
Ответы на эти вопросы даёт динамика.
2.1. Первый закон ньютона. Инерциальные системы отсчёта
Первый закон Ньютона гласит: всякое тело покоится или движетсяравномерно и прямолинейно, если на него не действуют другие тела или их действие компенсируется.
Эта простая формулировка имеет глубокий смысл. Её можно рассматривать с разных точек зрения, обнаруживая различные аспекты этого закона.
Прежде всего следует отметить, что первый закон не может выполняться в любой системе отсчёта. Допустим, что имеется тело, на которое не действуют другие тела (или сумма действующих на тело сил равна нулю), и в некоторой системе отсчёта это тело покоится. В этой системе отсчёта первый закон выполняется. Пусть другая система движется относительно первой с постоянным ускорением а'. Как следует из преобразований Галилея (см. разд. 1.6), в такой системе отсчёта рассматриваемое тело будет иметь ускорение. Первый закон в этой системе не выполняется. Это означает, что первый закон Ньютона будет выполняться лишь в тех системах отсчёта, которые движутся равномерно и прямолинейно относительно той, в которой рассматриваемое тело покоится при отсутствии воздействий на него. Такие системы отсчёта называютинерциальными системами отсчёта.
Возникает вопрос: как определить, инерциальна ли какая-либо конкретная система отсчёта?
Ответ на этот вопрос содержится в формулировке первого закона Ньютона. С этой точки зрения закон и есть определение инерциальной системы отсчёта.
Инерциальной является такая система отсчёта, в которой сумма сил, действующих на неподвижное тело, равна нулю.
В неинерциальных системах отсчёта сумма сил, действующих на неподвижное тело, нулю не равна!
Рассмотрим пример. Пусть металлический шарик лежит на горизонтальном столике в вагоне движущегося поезда. Скорость шарика относительно столика по условию равна нулю.
Шарик, лежащий на столе, притягивается к Земле и взаимодействует с поверхностью стола. Если измерить результаты этих взаимодействий (сейчас совершенно не важно, как это можно сделать), то окажется, что воздействия компенсируют друг друга.
Следовательно, система отсчёта, связанная с вагоном, является инерциальной.
Теперь представьте себе, что поезд начал тормозить (или разгоняться, или поворачивать). Что будет с шариком? Шарик начнёт двигаться относительно столика, т.е. шарик изменит свою скорость относительно данной системы отсчёта.
Но ведь действие Земли на шарик по-прежнему компенсируется действием столика, а скорость движения шарика не остаётся постоянной.
Это означает, что теперь система отсчёта, связанная с вагоном, инерциальной не является.
Для большинства задач, встречающихся в науке и технике, инерциальной системой отсчёта является система, связанная с Землёй или движущаяся равномерно и прямолинейно относительно Земли.
Но в ряде случаев системы отсчёта, связанные с Землёй, считать инерциальными нельзя. Дело в том, что Земля вращается, следовательно любой предмет, неподвижный относительно Земли, движется ускоренно (равномерное движение по окружности является равноускоренным движением; при таком движении тело имеет центростремительное ускорение). Если пренебречь этим ускорением нельзя, инерциальной системой отсчёта считают систему отсчёта, связанную с Солнцем.
Однако смысл первого закона Ньютона не ограничен определением инерциальной системы отсчёта.
Согласно первому закону Ньютона, для того, чтобы тело двигалось равномерно и прямолинейно, никакие силы не нужны.
Можно возразить, что ни один предмет не начнёт двигаться, если его не толкать. Но обратите внимание: не начнёт, т.е. не изменит своюпредыдущуюскорость. Так что силы нужны не для того, чтобы тела двигались, а для того, чтобы они изменяли свою скорость.
studfiles.net
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


