Многообра́зие — топологическое пространство, которое локально выглядит как «обычное» евклидово пространство $\R^n$ . Евклидово пространство является самым простым примером многообразия. Более сложным примером может служить поверхность Земли. Возможно сделать карту какой-либо области земной поверхности, например карту полушария, но невозможно составить единую (без разрывов) карту всей её поверхности.

Исследования многообразий были начаты во второй половине XIX века, они естественно возникли при изучении дифференциальной геометрии и теории групп Ли. Тем не менее, первые точные определения были сделаны только в 30-х годах XX века.

Обычно рассматриваются так называемые гладкие многообразия, то есть те, на которых есть выделенный класс «гладких» функций — в таких многообразиях можно говорить о касательных векторах и касательных пространствах. Для того, чтобы измерять длины кривых и углы, нужна ещё дополнительная структура — риманова метрика.

В классической механике гладкие многообразия служат как фазовые пространства. В общей теории относительности четырёхмерные псевдоримановы многообразия используются как модель для пространства-времени.

1. Топологические многообразия

n-мерное топологическое многообразие без края — это хаусдорфово топологическое пространство со счётной базой, в котором каждая точка имеет открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , то есть n-мерного Евклидова пространства.

n-мерное топологическое многообразие — это хаусдорфово топологическое пространство со счётной базой, в котором каждая точка имеет окрестность, гомеоморфную открытому подмножеству замкнутого полупространства в $\R^n$ (считаем открытыми также объединения открытых подмножеств с пересечением их границы и граничной гиперплоскости).

Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество).
Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие без края.
Компактное связное многообразие без границы называется замкнутым
Некомпактное связное многообразие называется открытым.

1.1. Комментарии

Условие счётности базы эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности.
Иногда, вместо условия счётности базы используется более слабое условие паракомпактности, или, что эквивалентно, метризуемости пространства.
Введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

2. Гладкие многообразия

Гладкая структура, определённая ниже, обычно возникает в почти всех приложениях и при этом делает многообразие гораздо удобней в работе.

Начинаем с топологического многообразия M без границы. Назовём картой гомеоморфизм $\varphi$ из открытого множества $U\subset M$ на открытое подмножество $\R^n$ .

Набор карт, покрывающих всё M, называется атласом.

Если две карты $\varphi$ и ψ накрывают одну точку в M, то их композиция $\varphi\circ\psi^{-1}$ задаёт отображение «склейки» из открытого множества $\R^n$ в открытое множество $\R^n$ . Если все отображения склейки из класса Ck (то есть k раз непрерывно дифференцируемых функций), то атлас называется Ck атласом (можно также рассматривать $k=\infty$ или ω, что соответствует бесконечно дифференцируемым и аналитическим склейкам).

Пример: сфера может быть покрыта $C^\infty$ -атласом из двух карт на дополнениях северного и южного полюсов со стереографическими проекциями по отношению к этим полюсам.

Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.

Для таких многообразий можно ввести понятия касательного вектора, касательного и кокасательного пространств и расслоений.

Для заданной C1-гладкой структуры можно найти $C^\infty$ -гладкую структуру, задаваемую новым $C^\infty$ -атласом, который задаёт ту же C1-гладкую структуру. Более того, все такие полученные таким образом многообразия являются $C^\infty$ -диффеоморфными. Поэтому часто под гладкой структурой понимают C1-гладкую структуру.

Не каждое топологическое многообразие допускает гладкую структуру. Примеры таких «шершавых» многообразий появляются уже в размерности четыре. Также существуют примеры топологических многообразий, которые допускают несколько различных гладких структур. Первый такой пример нестандартной гладкой структуры, так называемая сфера Милнора, был построен Милнором на семимерной сфере.

3. Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Гомеоморфный класс замкнутой связной поверхности задаётся её Эйлеровой характеристикой и ориентируемостью. (Если ориентируемо, то это сфера с ручками (англ.), если нет, то связная сумма нескольких копий проективной плоскости)

Классификация замкнутых трёхмерных многообразий следует из гипотезы Тёрстона, которая была недавно доказана Перельманом.

Если размерность больше трёх, то классификация невозможна; более того, невозможно построить алгоритм, который определяет, является ли многообразие односвязным. Тем не менее существует классификация всех односвязанных многообразий во всех размерностях ≥ 5.

Можно также классифицировать гладкие многообразия.

В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, $\R^4$ допускают континуум различных гладких структур.
В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

4. Дополнительные структуры

Часто гладкие многообразия оснащают дополнительными структурами. Вот список наиболее часто встречаемых дополнительных структур:

Метрический тензор
Симплектическая форма
Комплексная структура

5. Вариации и обобщения

Орбиобразие
Псевдомногообразие

Литература

Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.

wreferat.baza-referat.ru

Реферат Многообразия

скачать

Реферат на тему:

План:

1 Топологические многообразия
- 1.1 Комментарии
2 Гладкие многообразия
3 Классификация многообразий
4 Дополнительные структуры
5 Вариации и обобщения

Введение

1. Топологические многообразия

Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество).
Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие без края.
Компактное связное многообразие без границы называется замкнутым
Некомпактное связное многообразие называется открытым.

1.1. Комментарии

Условие счётности базы эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности.
Иногда, вместо условия счётности базы используется более слабое условие паракомпактности, или, что эквивалентно, метризуемости пространства.
Введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

2. Гладкие многообразия

Набор карт, покрывающих всё M, называется атласом.

Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.

3. Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Можно также классифицировать гладкие многообразия.

В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, $\R^4$ допускают континуум различных гладких структур.
В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

4. Дополнительные структуры

Метрический тензор
Симплектическая форма
Комплексная структура

5. Вариации и обобщения

Орбиобразие
Псевдомногообразие

Литература

Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.

wreferat.baza-referat.ru

Реферат Многообразие (топология)

скачать

Реферат на тему:

План:

1 Топологические многообразия
- 1.1 Комментарии
2 Гладкие многообразия
3 Классификация многообразий
4 Дополнительные структуры
5 Вариации и обобщения

Введение

1. Топологические многообразия

Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество).
Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие без края.
Компактное связное многообразие без границы называется замкнутым
Некомпактное связное многообразие называется открытым.

1.1. Комментарии

Условие счётности базы эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности.
Иногда, вместо условия счётности базы используется более слабое условие паракомпактности, или, что эквивалентно, метризуемости пространства.
Введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

2. Гладкие многообразия

Набор карт, покрывающих всё M, называется атласом.

Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.

3. Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Можно также классифицировать гладкие многообразия.

В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, $\R^4$ допускают континуум различных гладких структур.
В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

4. Дополнительные структуры

Метрический тензор
Симплектическая форма
Комплексная структура

5. Вариации и обобщения

Орбиобразие
Псевдомногообразие

Литература

Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.

wreferat.baza-referat.ru

Реферат Многообразие

скачать

Реферат на тему:

План:

1 Топологические многообразия
- 1.1 Комментарии
2 Гладкие многообразия
3 Классификация многообразий
4 Дополнительные структуры
5 Вариации и обобщения

Введение

1. Топологические многообразия

Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество).
Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие без края.
Компактное связное многообразие без границы называется замкнутым
Некомпактное связное многообразие называется открытым.

1.1. Комментарии

Условие счётности базы эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности.
Иногда, вместо условия счётности базы используется более слабое условие паракомпактности, или, что эквивалентно, метризуемости пространства.
Введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

2. Гладкие многообразия

Набор карт, покрывающих всё M, называется атласом.

Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.

3. Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Можно также классифицировать гладкие многообразия.

В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, $\R^4$ допускают континуум различных гладких структур.
В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

4. Дополнительные структуры

Метрический тензор
Симплектическая форма
Комплексная структура

5. Вариации и обобщения

Орбиобразие
Псевдомногообразие

Литература

Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.

wreferat.baza-referat.ru

Реферат Замкнутое многообразие

скачать

Реферат на тему:

План:

1 Топологические многообразия
- 1.1 Комментарии
2 Гладкие многообразия
3 Классификация многообразий
4 Дополнительные структуры
5 Вариации и обобщения

Введение

1. Топологические многообразия

Точки, которые имеют открытую окрестность, гомеоморфную открытому подмножеству $\R^n$ , называются внутренними, а множество всех таких точек — внутренность многообразия (это всегда непустое множество).
Дополнение к внутренности называется краем, это — (n − 1)-мерное многообразие без края.
Компактное связное многообразие без границы называется замкнутым
Некомпактное связное многообразие называется открытым.

1.1. Комментарии

Условие счётности базы эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности.
Иногда, вместо условия счётности базы используется более слабое условие паракомпактности, или, что эквивалентно, метризуемости пространства.
Введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.

2. Гладкие многообразия

Набор карт, покрывающих всё M, называется атласом.

Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.

3. Классификация многообразий

Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности

Можно также классифицировать гладкие многообразия.

В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например, $\R^4$ допускают континуум различных гладких структур.
В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.

4. Дополнительные структуры

Метрический тензор
Симплектическая форма
Комплексная структура

5. Вариации и обобщения

Орбиобразие
Псевдомногообразие

Литература

Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.

wreferat.baza-referat.ru

01. Геометрия гладких многообразий | Решение задач по математике и дру

Пусть – гладкое -мерное многообразие и – произвольная точка в нем. Говорят, что на многообразии дана Кривая, если имеется непрерывное отображение интервала в Пусть – локальные координаты в окрестности точки . Тогда кривая в локальных координатах может быть записана в виде . Кривая называется Гладкой, если все функции , определяющие эту кривую, гладкие. Пусть кривая проходит через точку , мы можем считать, что .

Касательным вектором к кривой в точке 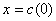называется вектор .

Пример 1. Отображение , заданное следующим образом

Называется винтовой линией в . Очевидно, что это гладкая кривая и касательный вектор к ней в точке есть .

Отметим, что выражение касательного вектора в данной точке зависит от координатной карты. Действительно, пусть – другие локальные координаты в окрестности точки . Тогда при переходе от карты к карте координаты вектора преобразуются по закону , который легко следует из правила дифференцирования сложной функции.

Различным кривым, проходящим через точку , соответствуют, вообще говоря, различные касательные векторы. Но возможна также ситуация, когда две различные кривые в общей точке имеют одинаковые касательные векторы, например винтовая линия из примера 1 и прямая в общей точке имеют одинаковые касательные векторы .

Все касательные векторы многообразия в точке образуют векторное пространство, которое называется Касательным пространством к в точке и обозначается . Размерность касательного пространства равна размерности гладкого многообразия .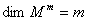

Мы можем рассмотреть следующую -ю координатную кривую в многообразии : и через 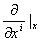обозначить ее касательный вектор в точке . Тогда векторы образуют базис касательного пространства в точке .

Любой вектор на многообразии можно рассматривать как Дифференциальный оператор, действующий на гладких функциях. Вектор переводит функцию в число . Производные вычисляются в той точке, где задан касательный вектор . Это определение не зависит от выбора карты. Действительно, . Здесь мы используем следующее сокращенное правило суммирования : если в некотором выражении индекс входит дважды, один раз как верхний, а другой раз как нижний, то по нему подразумевается суммирование.

Лемма. Если дифференциальный оператор Инвариантен относительно выбора карты, то его коэффициенты 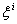Образуют вектор.

Доказательство. Из равенства следует, что . Отсюда следует, что , так как предыдущее равенство имеет место для любой функции .

Итак, векторы из находятся во взаимно однозначном соответствии с инвариантными операторами вида .

Говорят, что на многообразии задано Векторное поле , если в каждой его точке задан вектор. В локальных координатах векторное поле задается в виде , Векторное поле называется Гладким, если все функции являются гладкими.

Траекторией данного векторного поля называется такая кривая, что . Из общей теории обыкновенных дифференциальных уравнений следует, что найдется такое , что на интервале всегда существует траектория векторного поля . Каждая данная траектория может быть единственным образом продолжена на некоторый максимальный интервал . Если , то траектория называется Полной. Точка , в которой все координаты векторного поля обращаются в нуль , называется Особой точкой векторного поля.

Пример. Рассмотрим на единичной сфере векторное поле . Очевидно, что его траекториями будет семейство параллелей . Все траектории полные. У данного поля две особые точки: и . Из топологических соображений на двумерной сфере не существует гладкого векторного поля без особых точек.

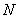Пусть – отображение класса двух гладких многообразий. Для точки определим линейное отображение следующим образом : пусть вектор , где – некоторая кривая в , проходящая через точку , тогда есть кривая в , проходящая через точку . Положим . Данное линейное отображение касательных пространств называется Дифференциалом гладкого отображения в точке и обозначается или .

В локальных координатах на многообразии дифференциал задается с помощью матрицы Якоби следующим образом:

Дифференциал отображения обладает следующим свойством.

Лемма. Имеет место равенство , где и .

Доказательство.

,ч. т.д.

Пример. Рассмотрим так называемые географические координаты на сфере . Пусть и задано отображение следующим образом: . Тогда дифференциал этого отображения в точке имеет вид . При этом дифференциал отображает касательный вектор в вектор , а вектор в вектор . Вектор касателен к параллелям на сфере, а вектор – к меридианам.

Теперь мы изучим геометрию ортогональной группы матриц. Напомним, что квадратная матрица размера с вещественными элементами называется Ортогональной, если . Множество всех ортогональных матриц образует группу, обозначаемую .

Группа вложена в пространство , поскольку любую матрицу можно записать в строку длины . Соотношение равносильно системе из уравнений. Пусть и рассмотрим отображение по формуле . Ясно, что в нулевую матрицу при данном отображении переводятся ортогональные матрицы, следовательно . Вычислим дифференциал отображения .

Для этого рассмотрим кривую , такую что и – данная матрица. Имеем Очевидно, что – симметрическая матрица. Любая симметрическая матрица представима в виде где для некоторой матрицы . Достаточно положить . Итак, образ отображения совпадает с пространством симметрических матриц, следовательно, ранг матрицы Якоби системы, описывающей группу – постоянен. По теореме о неявной функции множество представляет собой гладкое многообразие. Вычислим размерность этого многообразия. Имеем {пространства симметрических матриц}=. Поэтому . В частности, размерность группы являющейся связной компонентой единицы группы , равна 3.

Литература. 1. Трофимов В. В. гл.1 , параграфы 8,9.

2. Бишоп Р. Л., Криттенден Р. Дж. гл.1, 1.3,1.4.

matica.org.ua

Реферат Когомологии де Рама

скачать

Реферат на тему:

План:

1 Гладкие многообразия
- 1.1 Определения
  - 1.1.1 Через коцепной комплекс
  - 1.1.2 Как класс эквивалентности форм
- 1.2 Теорема де Рама
2 Алгебраические многообразия
- 2.1 Определение
3 Частные случаи когомологий де Рама
- 3.1 Относительные когомологии де Рама

Введение

Когомологии де Рама — теория когомологий, основанная на дифференциальных формах, и применяемая в теориях гладких и алгебраических многообразий.

Названы в честь швейцарского математика де Рама. k-мерная группа когомологий де Рама многообразия M обычно обозначается $H^k_{\mathrm{dR}}(M)$ .

1. Гладкие многообразия

1.1. Определения

1.1.1. Через коцепной комплекс

Комплексом де Рама называется коцепной комплекс внешних дифференциальных форм на гладком многообразии M с внешней производной $d\,^k$ в качестве дифференциала.

$0 \to\Omega^0(M)\stackrel{d\,^0}{\to}\Omega^1(M)\stackrel{d^1}{\to}\Omega^2(M)\stackrel{d^2}{\to}\Omega^3(M)\to\ldots$

Здесь Ω0(M) — пространство гладких функций на M, Ω1(M) — пространство 1-форм, то есть Ωk(M) — пространство k-форм. Заметим, что $d\,^{k+1} d\,^k=0$ . k-мерная группа когомологий Hk этого коцепного комплекса является его мерой точности в k-ом члене и определяется как

$H^k(\Omega^\bullet,\;d^\bullet)=\mathrm{Ker}\,d^k\,/\,\mathrm{Im}\,d^{k-1}.$

Заметим, что всякая точная форма является замкнутой.

1.1.2. Как класс эквивалентности форм

Более геометрически, идея когомологий де Рама состоит в том, чтобы классифицировать замкнутые формы на многообразии: две замкнутые формы α и β в Ωk(M) называются когомологичными, если они отличаются на точную форму, то есть их разность α − β = dγ является точной точной формой. Это определение порождает отношение эквивалентности на множестве замкнутых форм в Ωk(M).

Когомологическим классом [α] формы α называется множество всех замкнутых форм, отличающихся от α на точную форму — то есть множество форм вида α + dγ.

k-мерная группа когомологий де Рама $H^k_\mathrm{dR}(M)$ — это факторгруппа всех замкнутых форм в Ωk(M) по подгруппе точных форм.

Заметим, что для многообразия M, имеющего N связных компонент,

$H^0_\mathrm{dR}(M)\cong\mathbf{R}^N.$

Действительно, формы степени 0 — это скалярные функции. Замкнутость означает, что функции имеют нулевую производную, то есть постоянны на каждой компоненте связности многообразия.

1.2. Теорема де Рама

Теорема Стокса является выражением двойственности между когомологиями де Рама и гомологиями цепных комплексов. А именно, ключевое следствие из теоремы состоит в том, что «интегралы от замкнутой формы по гомологичным цепям равны»: если ω — замкнутая k-форма, а M и N — гомологичные k-цепи (то есть M − N является границей (k + 1)-мерной цепи W), то

$\int\limits_M\omega=\int\limits_N\omega,$

поскольку их разность есть интеграл

$\int\limits_{\partial W}\omega=\int\limits_W\,d\omega=\int\limits_W 0=0.$

Таким образом, спаривание дифференциальных форм и цепей посредством интегрирования определяет гомоморфизм из когомологий де Рама $H^k_\mathrm{dR}(M)$ в группу сингулярных когомологий $H^k(M;\;\mathbf R)$ . Теорема де Рама, доказанная Жоржем де Рамом в 1931 году, утверждает, что на гладких многообразиях это отображение является изоморфизмом:

$H^k_\mathrm{dR}(M)\cong H^k(M;\;\mathbf R).$

Внешнее произведение наделяет прямую сумму групп $H^k_\mathrm{dR}(M)$ структурой кольца. Аналогичную структуру в сингулярных когомологиях $H^k(M;\;\mathbf R)$ задаёт $\smile$ -умножение. Теорема де Рама утверждает также, что эти два кольца когомологий изоморфны как градуированные кольца.

2. Алгебраические многообразия

2.1. Определение

Совершенно аналогично гладкому случаю, с каждым алгебраическим многообразием X над полем k связывается комплекс регулярных дифференциальных форм.

Группами когомологий де Рама многообразия X называются группы когомологий $H^p_\mathrm{dR}(X/k)$ .

3. Частные случаи когомологий де Рама

Если X является гладким и полным многообразием, а характеристика поля $\mathrm{char}\,k=0$ , то когомологии де Рама являются когомологиями Вейля.
Если многообразие X есть гладкое аффинное многообразие, а поле $k=\C$ , то справедлив следующий аналог теоремы де Рама: $H^p_{\mathrm{dR}}(X/k)\cong H^p(X_{an},\;\mathbb{C}),$

где Xan — комплексное аналитическое многообразие, соответствующее алгебраическому многообразию X.

Например, если X — дополнение к алгебраической гиперповерхности в $P^n(\C)$ , то когомологии $H^p(X,\;\C)$ могут быть вычислены при помощи рациональных дифференциальных форм на $P^n(\C)$ с полюсами на этой гиперповерхности.

3.1. Относительные когомологии де Рама

Для любого морфизма $f\colon X\to S$ можно определить так называемый относительный комплекс де Рама

$\sum_{p\leqslant 0}\Gamma(\Omega^p_{X/S}),$

приводящий к относительным когомологиям де Рама $H^p_\mathrm{dR}(X/S)$ .

В случае, если многообразие X является спектром кольца $\mathrm{Spec}\,A$ , а $S=\mathrm{Spec}\,B$ и оба обладают аффинностью, то относительный комплекс де Рама совпадает с $\Lambda\Omega^1_{A/B}$ .

Когомологии $\mathcal{H}^p_\mathrm{dR}(X/S)$ комплекса пучков $\sum_{p\leqslant 0}f_*\Omega^p_{X/S}$ на S называется пучками относительных когомологий де Рама. Eсли f — собственный морфизм, то эти пучки когерентны на S.

Литература

Ботт, Р., Ту, Л. В. Дифференциальные формы в алгебраической топологии. — М.: Платон, 1997. — 336 с. — ISBN 5-80100-280-4.
Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: методы теории гомологий. — М.: Наука, 1984. — 343 с.
де Рам, Ж. Дифференцируемые многообразия = Varietes differentiables. — M.: КомКнига, 2006. — 250 с. — ISBN 5-484-00341-5.

wreferat.baza-referat.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..