Дифференциальные уравнения и их применение в медицинской практике. Дифференциальные уравнения и их применение в медицинской практике реферат

Дифференциальные уравнения и их применение в медицинской практике — реферат

                                      Ивановский Фармацевтический Колледж

                                                     Реферат

                            Тема: Дифференциальные уравнения и их применение в медицинской практике

Дисциплина: Математика

                                                                       Выполнил

                                                                       Данилова  Е.А., студент гр. 1А

                                                                       Проверил

                                                                Димакова И.В., преподаватель

                                                                       математики

                                                                       Оценка ___________

                                                                       Подпись_________                                                            

2014-2015 уч. год

                                                 Содержание

ВВЕДЕНИЕ………………………………………………………………………..3

Цели и задачи…………………………………………………………………….4

1. Применение математических методов в профессиональной деятельности среднего медицинского персонала…………………………………………….5

1.1 Моделирование с применением  дифференциальных уравнений………….6

1.2.Дифференциальные уравнения с разделяющимися переменными..……10

2. Линейность или нелинейность дифференциальных уравнений ……….....10

2.1. Пример применения дифференциальных уравнений в медицине……….11

2.2. Уравнения старших порядков. …………………………………….………12

Заключение……………….……………………………………………………..14

Список литературы……………………………………………………………………….15   

                                                        ВВЕДЕНИЕ

     Теория дифференциальных уравнений – раздел математики, который занимается изучением дифференциальных уравнений и связанных с ними задач. Её результаты применяются во многих естественных науках, особенно широко – в физике.

     Неформально  говоря, дифференциальное уравнение  – это уравнение, в котором  неизвестной величиной является  некоторая функция. При этом в  самом уравнении участвует не  только неизвестная функция, но  и различные производные от  неё. Дифференциальным уравнением  описывается связь между неизвестной  функцией и её производными. Такие  связи обнаруживаются в самых  разных областях знания: в механике, физике, химии, биологии, экономике  и других.

3

                                                Цели и задачи

1.Дать подробную информацию  о дифференциальных уравнениях

2.Рассмотреть примеры  дифференциальных уравнений

3.Узнать,где они используются

4.Разобрать виды дифференциальных  уравнений

4

Глава 1. Применение математических методов в профессиональной деятельности среднего медицинского персонала.

   При выполнении своих профессиональных обязанностей медицинским работникам часто приходится производить различные математические вычисления. От правильности проведённых расчётов зависит здоровье, а иногда и жизнь пациентов.

  В хозяйственных расчётах, во многих отраслях науки части  величин принято выражать в  процентах. Очень часто в лабораторной  практике приходится встречаться  со случаями приготовления растворов  с определённой массовой долей  растворённого вещества, смешением  двух растворов разной концентрации  или разбавлением крепкого раствора  водой.

 В медицинских приложениях  дифференциальные уравнения используются, например:

Для определения скорости кровотока, скорости движения клапанов и стенок сердца, определения вязкости крови и других параметров гемодинамики.

Для описания медико-биологических приложений ультразвука: эхоэнцефалограмма, УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография.

Для описания процессов физиологической акустики, которая изучает устройство и работу звуковоспринимающих и звуковоспроизводящих органов человека и животных.

Для определения функции изменения численности популяции микроорганизмов в зависимости от времени.[1]

5

1.1.Моделирование с применением дифференциальных уравнений

Скорость многих как нормальных, так и патологических процессов зависит от того, насколько далеко уже «продвинулось» развитие этих процессов за предшествующее время. Например, скорость роста объема опухоли зависит от того, какого объема опухоль уже достигла. Это объясняется тем, что скорость роста зависит от числа имеющихся опухолевых клеток, а этому числу пропорционален занимаемый ими объем. Если x(t)—зависимость результата некоторого процесса х от времени, то производная этой функции по времени х'(t) характеризует скорость этого процесса. Поскольку скорость процесса

часто находится в зависимости от его результата, в одном уравнении оказываются как x(t)так и x'(t). Подобные уравнения называются дифференциальными. В них могут входить вторые производные, характеризующие ускорения, с которыми происходят процессы, и производные еще более высоких порядков. Таким образом, дифференциальное уравнение для функции x(t)—это уравнение, в которое входят производные этой функции по аргументу t. Порядок дифференциального уравнения определяется наивысшим порядком производных, встречающихся в этом уравнении.

  Дифференциальные уравнения  являются одним из важнейших  разделов математики, который имеет  очень большое прикладное значение. Кроме общематематического и  теоретического интереса, дифференциальные  уравнения находят широкое практическое  применение. Например, при решении  задач, связанных с электродинамикой, распространением тепла, радиоактивным  распадом, оптимальным управлением  и т.д. 

  Традиционным примером  прикладной задачи, приводящей к  простейшему 

6

обыкновенному дифференциальному уравнению первого порядка, является задача о радиоактивном распаде вещества.   Дифференциальные уравнения описывают процессы распространения тепла и диффузии газов. Изучение электромагнитных полей базируется на знаменитых уравнениях Максвелла. Фундаментальную роль в квантовой механике играет дифференциальное уравнение, называемое уравнением Шредингера. Опираясь на решение системы дифференциальных уравнений, был сконструирован автопилот. Дифференциальные уравнения использовались при создании аппарата "искусственная почка", поскольку процесс гемодиализа (т.е. очищения крови при помощи искусственной почки) описывается системой дифференциальных уравнений. А ведь этот аппарат спасает жизни многих и многих. 

  Несколько десятков лет назад нелинейные уравнения мало кого интересовали. А сейчас они переживают взлет. Одиночные волны, которые описываются этими уравнениями, сейчас играют большую роль. Просто раньше такие уравнения не умели решать. 

  Теория дифференциальных  уравнений является самым большим  разделом современной математики. Чтобы охарактеризовать ее место  в современной математической  науке, прежде всего, необходимо  подчеркнуть основные особенности  теории дифференциальных уравнений, состоящей из двух обширных  областей математики: теории обыкновенных  дифференциальных уравнений и  теории уравнений с частными  производными. Для составления математической  модели в виде дифференциальных  уравнений нужно, как 

правило, знать только локальные связи, и не нужна информация обо всем физическом явлении в целом. Математическая модель дает возможность изучать явление в целом, предсказать его развитие, делать количественные оценки изменений, происходящих в нем с течением времени. Важно

7

отметить, что для проверки правильности математической модели очень важны теоремы существования решений соответствующих дифференциальных уравнений, так как математическая модель не всегда адекватна конкретному явлению и из существования решения реальной задачи (физической, химической, биологической и т.д.) не следует существование решения соответствующей математической задачи.

  Задачи различных  естественных наук снабжают теорию  дифференциальных уравнений проблемами, из которых вырастают богатые  содержанием теории. Однако бывает  и так, что математическое исследование, рожденное в рамках самой математики, через значительное время после  его проведения находит приложение  в конкретных «жизненных» проблемах  в результате их более глубокого  изучения. Таким примером может  служить задача Трикоми для  уравнений смешанного типа, которая  спустя более четверти века  после ее решения нашла важные  применения в задачах современной  газовой динамики при изучении  сверхзвуковых течений газа. Д. Гильберт  писал, что "математика сопровождала  по пятам физическое мышление  и, обратно, получила наиболее мощные  импульсы со стороны проблем, выдвигавшихся физикой". Таким  образом, дифференциальные уравнения  находятся как бы на перекрестке  математических дорог. 

  С одной стороны, новые  важные достижения в топологии, алгебре, функциональном анализе, теории  функций и других областях  математики сразу же приводят  к прогрессу в теории дифференциальных  уравнений и тем самым находят  путь к приложениям. С другой  стороны, проблемы физики и техники, биологии и медицины, химии и  т.д., сформулированные на языке  дифференциальных уравнений, вызывают  к жизни новые направления  в математике, приводят к необходимости  совершенствования математического  аппарата, дают начало новым математическим  теориям, имеющим 

8

внутренние законы развития, свои собственные проблемы. Ф. Клейн в книге «Лекции о развитии математики в XIX столетии» писал: "Математика в наши дни напоминает оружейное производство в мирное время. Образцы восхищают знатока. Назначение этих вещей отходит на задний план". Несмотря на эти слова, можно сказать, что нельзя стоять за "разоружение" математики. 

  Вспомним, например, что  древние греки изучали конические  сечения задолго до того, как  было открыто, что по ним движутся  планеты. Действительно, созданная  древними греками теория конических  сечений не находила своего  применения почти две тысячи  лет, пока Кеплер не воспользовался  ею для создания теории движения  небесных тел. Исходя из теории  Кеплера, Ньютон создал механику, являющуюся основой всей физики  и техники. Другим таким примером  может служить теория групп, зародившаяся  в конце XVIII века (Лагранж, 1771 год) в  недрах самой математики и  нашедшая лишь в конце XIX века  плодотворное применение сначала  в кристаллографии, а позднее  в теоретической физике и других  естественных науках. 

  Многие разделы теории  дифференциальных уравнений так  разрослись, что стали самостоятельными  науками. Можно сказать, что большая  часть путей, связывающих абстрактные  математические теории и естественнонаучные  приложения, проходит через дифференциальные  уравнения. Все это обеспечивает  теории дифференциальных уравнений  почетное место в современной  науке. Таким образом, в теории  дифференциальных уравнений ясно  прослеживается основная линия  развития математики: от конкретного  и частного через абстракцию  к конкретному и частному.

  Для реализации математических  моделей в настоящее время  широко используются компьютеры. С помощью ЭВМ проводят так  называемые 

9

«машинные эксперименты», при исследовании патологических процессов в кардиологии, развития эпидемий и т.д. При этом можно легко изменять масштаб по времени: ускорить или замедлить течение процесса, рассмотреть процесс в стационарном режиме, как это предложено в модели сокращения мышцы (модель Дещеревского) и по пространству. Например, ввести локальную пространственную неоднородность параметров, изменить конфигурацию зоны патологии. Изменяя коэффициенты или вводя новые члены в дифференциальные уравнения, можно учитывать те или иные свойства модулируемого объекта или теоретически создавать объекты с новыми свойствами, так,  например, получать лекарственные препараты более эффективного действия. С помощью ЭВМ можно решать сложные уравнения и прогнозировать поведение системы: течение заболевания, эффективность лечения, действия фармацевтического препарата и т.д.

yaneuch.ru

Дифференциальные уравнения и их применение в медицинской практике

Приложенные файлы

• file7Дифференциальные уравнения и их применение в медицинской практикеРазмер файла: 2 MB Загрузок: 144

educontest.net

10.7. Применение дифференциальных уравнений в биологии и медицине.

Задача 1. Закон размножения бактерий с течением времени.

Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Найти зависимость изменения количества бактерий от времени.

Обозначим количество бактерий, имеющихся в данный момент, через х. Тогда

где k — коэффициент пропорциональности.

В этом уравнении разделим переменные и проинтегрируем его:

Потенцируем последнее выражение:

Полагая, что при t=0 х=х0, получим С=x0. Следовательно,

(10.12)

Уравнение (9.7.1) выражает закон размножения бактерий с течением времени. Таким образом, при благоприятных условиях увеличение бактерий с течением времени происходит по экспоненциальному закону.

Этот закон представляет интерес не только с теоретической, но и с практической точки зрения. Он говорит о том, что, создавая для полезной популяции благоприятные условия, можно очень быстро получить популяцию с больший численностью. Весьма показательна в этом смысле история с пенициллином. Когда был открыт этот антибиотик, грибки, его выделяющие, стали выращивать в наилучших условиях. Их неограниченно подкармливали, следили, чтобы им не было тесно, и, конечно, оберегали от вредных видов. Будущий урожай можно было совершенно точно подсчитать по формуле. Размножаясь в соответствии с экспоненциальным законом, пенициллиновые грибки в короткий срок обеспечили весь мир ценным лекарством.

Экспоненциальному закону размножения подчиняется так называемый «экологический взрыв», когда тот или иной биологический вид, попав в благоприятные условия, за короткий срок достигает большой численности. Для примера можно указать на губительные нашествия полчищ насекомых (саранчи, шелкопряда и др.) или на неожиданные последствия акклиматизации кроликов в Австралии.

Задача 2. Закон роста клеток с течением времени.

Для палочковидных клеток, у которых отношение поверхности клетки к ее объему сохраняется постоянным, скорость роста клетки dl/dt пропорциональна длине клетки l в данный момент:

(10.13)

где  и β — постоянные, характеризующие процессы синтеза и распада.

В уравнении (9.7.2) разделим переменные и проинтегрируем его:

При t=0, l=l0 постоянная С=l0, и поэтому

т.е. рост палочковидных клеток происходит по экспоненциальному закону.

Задача 3. Закон разрушения клеток в звуковом поле.

Кавитация ультразвуковых волн проявляется в виде разрывов суспензионной среды и образования мельчайших пузырьков и пустот, плотность которых незначительна по сравнению с плотностью воды. Простейшие — бактерии, водоросли, дрожжи, лейкоциты и эритроциты — могут быть разрушены при кавитации, возникающей в интенсивном ультразвуковом ноле. В очень широком диапазоне частот относительные скорости разрушения биологических клеток различных видов остаются постоянными. Эти скорости могут характеризовать относительную хрупкость клеток различных видов. Чтобы выразить это количественно, нужно определить скорость разрушения клетки в постоянном звуковом поле. Изучение этого вопроса показывает, что, пока по крайней мере 1% популяции остается неразрушенным, можно написать, что

(10.14)

где N — концентрация клеток; t — время; R — постоянная.

Разделим в уравнении (9.7.3) переменные и проинтегрируем его:

Постоянную С найдем из условия, что при t=0 N=N0 и C=N0

Тогда

Разрушение клеток в постоянном звуковом поле происходит по экспоненциальному закону.

Задача 4. Составление и решение дифференциальных уравнений в теории эпидемий.

Рассмотрим составление и решение дифференциальных уравнений в теории эпидемий при условии, что изучаемое заболевание носит длительный характер. При этом процесс передачи инфекции значительно более быстрый, чем течение самой болезни, и зараженные особи не удаляются из колонии и передают при встречах инфекцию незаряженным особям.

Пусть в начальный момент t=0 a — число зараженных, b -число незаряженных особей, х(t)—число зараженных особей в момент времени t, a y(t) — число незараженных особей к моменту времени t.

В любой момент времени t для промежутка [0, Т], меньшего времени жизни одного поколения, имеет место равенство

(10.15)

При этих условиях нужно найти закон изменения числа незараженных особей с течением времени, т. е. найти y=f(t).

Так как инфекция передается при встречах зараженных особей с. незараженными, то число незараженных особей будет убывать с течением времени пропорционально количеству встреч между зараженными и незаряженными особями. Для, промежутка времени dt

Откуда

где β — коэффициент пропорциональности.

Подставив в это уравнение x из равенства (10.15), получим дифференциальное уравнение с разделяющимися переменными

После разделения дифференциалов и переменных в последнем уравнении получим

Преобразуем левую часть уравнения и проинтегрируем его:

или

Выполним в последнем уравнении потенцирование:

По начальным условиям: при t=0 y=b найдем постоян­ную интегрирования С:

Подставим значение С=b/a в последнее .равенство:

Разрешая это уравнение относительно у, окончательно получим

(10.16)

Формула (10.16) дает закон убывания числа незараженных особей с течением времени.

studfiles.net

Дифференциальные уравнения и их применение в медицинской практике

1. Дифференциальные уравнения и их применение в медицинской практике

en.ppt-online.org

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ИХ ПРИМЕНЕНИЕ В МЕДИЦИНСКОЙ ПРАКТИКЕ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ИХ ПРИМЕНЕНИЕ В МЕДИЦИНСКОЙ ПРАКТИКЕ

План: 1. Основные понятия и определения дифференциального уравнения 2. Методы решения дифференциальных уравнений. 3. Применение дифференциальных уравнений для решения задач.

1. Основные понятия и определения дифференциального уравнения Уравнения, в которых неизвестными являются не только сами функции, но и их производные называются дифференциальными уравнениями. y’+y+3 x=0

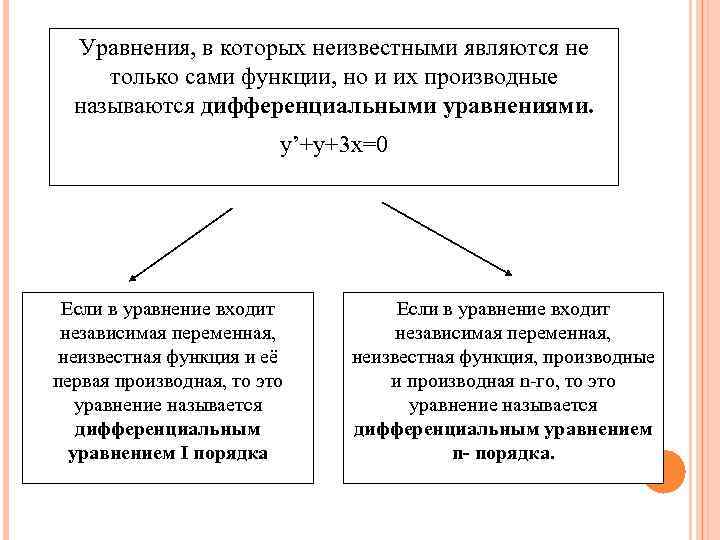Уравнения, в которых неизвестными являются не только сами функции, но и их производные называются дифференциальными уравнениями. y’+y+3 x=0 Если в уравнение входит независимая переменная, неизвестная функция и её первая производная, то это уравнение называется дифференциальным уравнением I порядка Если в уравнение входит независимая переменная, неизвестная функция, производные и производная n-го, то это уравнение называется дифференциальным уравнением n- порядка.

Пример: Решить уравнение у’=5 Решение: y=5 x+C – общее решение дифференциального уравнения Зададим начальные условия : х0=0, у0=1 и подставим в общее решение соответственно вместо х и у. Получаем у=5 х+1 -это частное решение дифференциального уравнения. 10 9 8 7 6 5 4 3 2 1 0 -1 -5 -4 -3. 5 -3 -2. 5 -2 -1. 5 -1 -0. 5 0 0. 5 1 1. 5 2 2. 5 3 3. 5 4 4. 5 5 -2 -3 -4 -5 -6 -7 -8 -9 -10 Геометрически общее решение y=5 x+C представляет собой семейство прямых

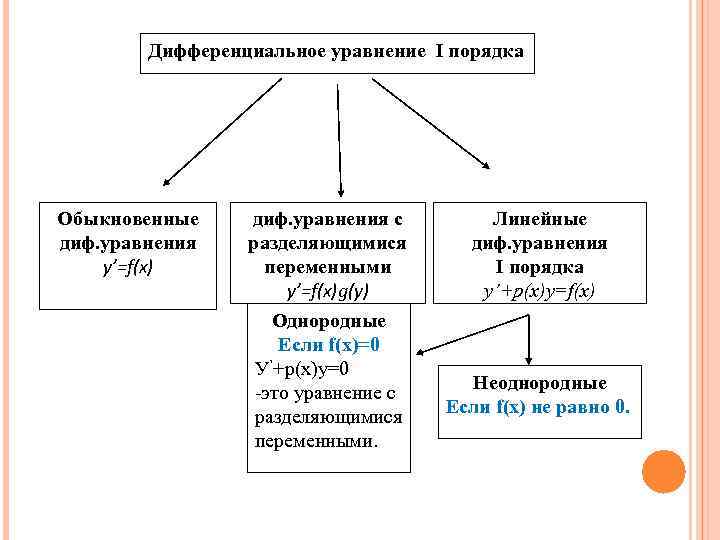Дифференциальное уравнение I порядка Обыкновенные диф. уравнения y’=f(x) диф. уравнения с разделяющимися переменными y’=f(x)g(y) Однородные Если f(x)=0 У’+p(x)y=0 -это уравнение с разделяющимися переменными. Линейные диф. уравнения I порядка y’+p(x)y=f(x) Неоднородные Если f(x) не равно 0.

2. Метоы решения дифференциального уравнения Обыкновенное дифференциальное уравнение y’=f(x)

Пример: Решить дифференциальное уравнение y’=5 х+2 Решение:

Дифференциальное уравнение с разделяющимися переменными y’=f(x)g(y) Решается это уравнение по шагам: 1. dy/dx=f(x)g(y) 2. dy/g(y)=f(x)dx 3. Интегрируем обе части выражения. 4. Находим первообразные. 5. Выражаем функцию у через х.

Пример: Решить дифференциальное уравнение: Решение: Выражаем функцию у через х:

Линейное дифференциальное уравнение I порядка y’+p(x)y=f(x) Если f(x)=0, то уравнение называется линейным однородным уравнением: y’+p(x)y=0

Пример: Найти общее решение дифференциального уравнения: y’+y 2 cosx=0 Решение: - формула общего решение уравнения Подставляем в формулу общего решения и получаем: - общее решение уравнения

Линейное дифференциальное уравнение I порядка y’+p(x)y=f(x) Если f(x)≠ 0, то уравнение называется линейным неоднородным уравнением. Общее решение неоднородного уравнения имеет вид:

Пример: Найти общее решение дифференциального уравнения: y’+yx=3 х Решение: Формула общего решения уравнения: Обозначим: p(x)=x, f(x)=3 x

3. Применение дифференциальных уравнений для решения задач.

Составление и применение дифференциальных уравнений Решение любой задачи с помощью математического анализа можно разбить на три этапа: 1. перевод условий задачи на язык математики; 2. решение задачи; 3. оценка результатов.

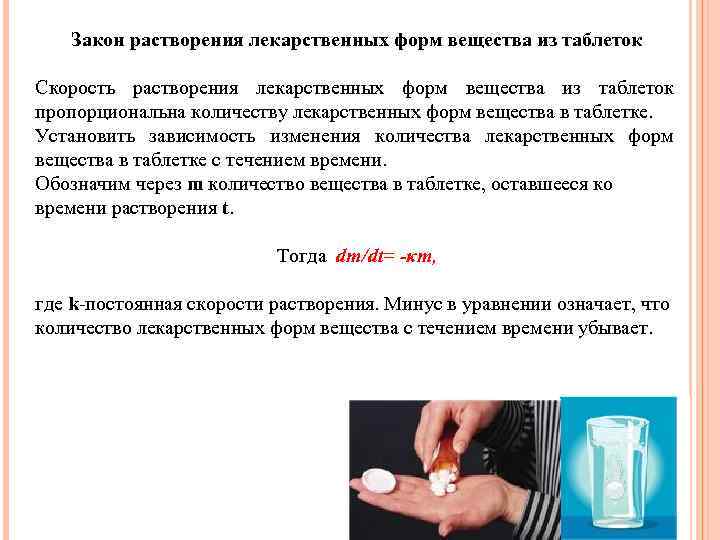Закон растворения лекарственных форм вещества из таблеток Скорость растворения лекарственных форм вещества из таблеток пропорциональна количеству лекарственных форм вещества в таблетке. Установить зависимость изменения количества лекарственных форм вещества в таблетке с течением времени. Обозначим через m количество вещества в таблетке, оставшееся ко времени растворения t. Тогда dm/dt= -κm, где k-постоянная скорости растворения. Минус в уравнении означает, что количество лекарственных форм вещества с течением времени убывает.

Закон размножения бактерий с течением времени Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Установить зависимость изменения количества бактерий от времени. Обозначим количество бактерий, имеющихся в данный момент, через х. Тогда dx/dt=kx, где k – коэффициент пропорциональности.

Закон роста клеток с течением времени Для палочковидных клеток, у которых отношение поверхности клетки к её объёму сохраняется постоянным, скорость роста клетки dl/dt пропорциональна длине клетки l в данный момент: dl/dt = (α - β) l где α, β – постоянные, характеризующие процессы синтеза и распада.

Закон разрушения клеток в звуковом поле Кавитация ультразвуковых волн проявляется в виде разрывов суспензионной среды и образования мельчайших пузырьков и пустот, плотность которых незначительна по сравнению с плотностью воды. Простейшие (бактерии, водоросли, дрожжи, лейкоциты, эритроциты) могут быть разрушены при кавитации, возникающей в интенсивном звуковом поле. Относительные скорости разрушения биологических клеток различных видов остаются постоянными в очень широком диапазоне частот. Эти скорости могут характеризовать относительную хрупкость клеток различных видов. Чтобы выразить это количественно, нужно определить скорость разрушения клетки в постоянном звуковом поле. Изучение этого вопроса показывает, что, пока по крайней мере 1% популяции остаётся неразрушенным, можно записать: d. N/dt = - RN где N – концентрация клеток; t –время; R - постоянная

Внутривенное введение глюкозы При внутривенном введении глюкозы с помощью капельницы скорость поступления глюкозы в кровь постоянна и равна С. В крови глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Дифференциальное уравнение, описывающее данный процесс: dx/dt=c-αx, где х-количество глюкозы в крови в текущий момент времени; с-скорость поступления глюкозы в кровь; α-положительная постоянная

Теория эпидемий В теории эпидемий при условии, что изучаемое заболевание носит длительный характер, процесс передачи инфекции значительно более быстрый, чем течение самой болезни, и зараженные особи не удаляются из колонии и передают при встречах инфекцию незараженным особям. Пусть в начальный момент t=0, а – число зараженных, b – число незараженных особей, x(t), y(t) – соответственно число зараженных и незараженных особей к моменту времени t. В любой момент времени t для промежутка, меньшего времени жизни одного поколения, имеет место равенство х+у=а+b Уравнение зомби-апокалипсиса (b. N)(S/N)Z = b. SZ, где N — общее число населения, S — число людей, восприимчивых к атакам зомби, Z — общее число самих зомби b — вероятность заражения вирусом. (1)

Теория эпидемий При этих условиях нужно установить закон изменения числа незаражённых особей с течением времени, т. е. найти y=f(x). Так как инфекция передаётся при встречах зараженных особей с незараженными, то число незараженных особей будет убывать с течением времени пропорционально количеству встреч между зараженными и незараженными особями. Для промежутка времени dt dy=-βxy, откуда dy/dt= - βxy, где β – коэффициент пропорциональности. Подставив в это уравнение значение х из равенства (1), получим дифференциальное уравнение с разделяющимися переменными: dy/dt= - βy (a+b-y)

Пример: Составьте дифференциальное уравнение и найдите частные решения: Концентрация лекарственного препарата в крови уменьшается вследствие выведения вещества из организма. Скорость уменьшения концентрации пропорциональна концентрации вещества в данный момент. Определить зависимость концентрации данного вещества в крови от времени, если в начальный момент времени она была равна 0, 2 мг/л, а через 23 часа уменьшилась вдвое Решение: Уравнение описывающее этот процесс: , где - скорость выведения вещества из организма, m - концентрация лекарственного препарата в крови в данный момент времени; k - коэффициент пропорциональности

Решение: Решая полученное уравнение, получаем: где m 0 -концентрация вещества в крови в начальный момент времени t=0, m – текущая концентрация вещества в крови в момент времени t.

Решение: Потенцируя, получим: По условию задачи m 0=0, 2 мг/л, m=m 0/2 мг/л, t=23 ч. Подставляем и находим: Зависимость концентрации данного вещества в крови от времени, описывается следующим законом:

Контрольные вопросы для закрепления: 1. Дайте понятие дифференциальному уравнению, его решению. 2. Назовите методы решения дифференциальных уравнений, охарактеризуйте каждый. 3. Приведете примеры обыкновенного дифференциального уравнения, уравнения с разделяющими переменными, линейного. 4. Приведите примеры дифференциального уравнения первого, второго, третьего порядка. 5. Каково практическое применение дифференциальных уравнений.

present5.com

Смотрите также

• 
  Реферат повседневная жизнь крестьян в россии в 19 веке
• 
  Реферат основные точки зрения ученых на поэму медный всадник
• 
  Реферат воздействие человека на биосферу в области использования транспорта
• 
  Особенности миграционных процессов во второй половине 20 века реферат
• 
  Ничто так не способствует людской добродетели как законодательство реферат
• 
  Реферат на тему русский язык национальный язык русского народа
• 
  Проблема жизни и смерти в духовном опыте человека реферат
• 
  Причины появления и основные черты развития постиндустриальной экономики реферат
• 
  Реферат первая волна русской эмиграции люди и их судьбы
• 
  Первая волна русской эмиграции люди и их судьбы реферат
• 
  Вирусы как неклеточная форма жизни и их значение реферат