V. Арифметическая и геометрическая прогрессия, проценты. Арифметическая прогрессия реферат

Доклад на научную конференцию по теме: «Арифметическая прогрессия».

VII районная научно — практическая

Конференция школьников

«Первые шаги в науку»

Секция:

«Математика».

Тема:

«Арифметическая

прогрессия».

Автор:

Миронец Маргарита

ученица 9 «В» класса

МОУ СОШ №20

имени Н.Е.Чернышева

станицы Казанской

Кавказского района

Краснодарского края

Руководитель:

Бондаренко Евгения

Леонидовна, учитель

математики первой

квалифицированной

категории

МОУ СОШ№20

имени Н.Г.Чернышева

станицы Казанской

Кавказского района

Краснодарского края.

Ст. Кавказская

2010г.

Содержание:

Аннотация……………………………………………………………………………………….. 3

Введение …………………………………………………………………………………………4

1.Определения и формулы……………………………………………………………………... 6

2. Примеры решения заданий на Тему: «Нахождение разности, суммы и п-го члена

арифметической прогрессии»………………………………………………………………….. 8

З. Решение задач на формулы арифметической прогрессии……………………………….. 10

Заключение…………………………………………………………………………………….. 11

Литература……………………………………………………………………………………... 12

Аннотация.

Тема актуальна, имеет широкое практическое применение. Арифметические прогрессии и их свойства изучались математиками с древних времен. Автор стремится, раскрыть в полной мере свои познания в этой области умело совершает экскурс в историю, решал задачу немецкого математика Карла Фридриха Гаусса. Хотя задачи на нахождение последовательностей начинают решать в 9 классе, автор выбрал эту тему, потому что математика имеет постоянно дело с бесконечностью. Опровержение известного изречения Нельзя объять необъятное, мы не только научимся задавать такие необъятные объекты, как бесконечные последовательности, но сумеем выделить некоторые их группы, такие как арифметическая прогрессия, но и опишем отдельные свойства. Знание свойств арифметической прогрессии позволяет решить немало различных задач. В работе автор уделил достаточное место теме арифметическая прогрессия: определению, свойствам делает вывод формулы суммы n первых членов арифметической прогрессии. Рассмотрены примеры решения заданий на тему:

«Нахождение разности, суммы и n-го члена арифметической прогрессию». Решены задачи на формулы арифметической прогрессии.

Автор исследует актуальную тему математики, решал сознательно задачи об арифметической прогрессии. Тема дана блоком. Идет отработка вычислительных навыков, даны задания трех уровней сложности, в том числе предлагаемые на ЕГЭ. Затем идет отработка применения знаний при решении задач практического содержания.

В работе подробно освещена теоретическая часть, доказаны теоремы, рассмотрен аналитический способ решения арифметической последовательности.

Особый интерес у автора вызвало решение нестандартных задач. Приведены примеры решения последовательности из сборника Подготовка к «малому ЕГЭ)» М.: Эксмо, 2008. Использована обширная литература. Данная работа заслуживает интерес, и лишь начало в исследовании важной и интересной темы. Эти исследования обеспечат молодому автору развитие математических способностей и знаний.

(Бондаренко Е.Л.)

Введение.

infourok.ru

Прогрессии

Содержание.

1) Введение __________________________________________________3

2) Глава 1. Прогрессии.

§1 Последовательность_________________________________________4

§2 Арифметическая прогрессия_________________________________6

§3 Геометрическая прогрессия__________________________________9

§4 Понятия гармонической прапорции и гармонической прогрессии__17

3) Глава 2. Задачи.____________________________________________19

4) Заключение _______________________________________________25

5) Литература ________________________________________________26

Введение.

Термин «прогрессия» имеет латинское происхождение (progression, что означает «движение вперед») и был введен римским автором Боэцием (VI в.). Этим термином в математике прежде именовали всякую последовательность чисел, построенную по такому закону, который позволяет неограниченно продолжать эту последовательность в одном направлении. В настоящее время термин «прогрессия» в первоначально широком смысле не употребляется. Два важных частных вида прогрессий – арифметическая и геометрическая – сохранили свои названия. Сами названия «арифметическая» и «геометрическая» были перенесены на прогрессии из теории непрерывных пропорций, изучением которых занимались древние греки. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.. Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым. Ариабхатта(v в.) применял формулы общего числа, суммы арифметической прогрессии....

Геометрическая прогрессия играет большую и важную роль не только в школьном курсе алгебры, но и в дальнейшем обучении в высших учебных заведениях. Важность этого на первый взгляд небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения, в частности он часто применяется в теории рядов, рассматриваемой на II-III курсах университета. Поэтому крайне важно дать полное описание этого курса, дабы читатель мог повторить уже известный ему из школьного курса материал, или даже почерпнуть много нового и интересного.

В своей работе я рассматриваю определения арифметической, геометрической и бесконечно убывающей геометрической прогрессий, а так же свойства членов прогрессий, сумму n-членов арифметической и геометрической прогрессий. Ввожу понятия гармонической пропорции и гармонической прогрессии. Так же в этой работе целая глава посвещана задачам по данной теме.

Цель курсовой работы упрощение решения практических задач и применение свойств арифметической и геометрической прогрессии при решении задач.

Глава 1.Прогрессии.

§1 Последовательность

ПОСЛЕДОВАТЕЛЬНОСТь-совокупность чисел (математических выражений и т.п.; говорят: элементов любой природы), занумерованных натуральными числами. Последовательность записывается в виде , ,..., ,... или коротко {}.

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n2можно записать:

y1 = 12 = 1;

y2 = 22 = 4;

y3 = 32 = 9;…yn = n2;…

Способы задания последовательностей.

Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.

1. Последовательность задана аналитически, если задана формула ее n-го члена:

yn = f(n).

Пример. yn= 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y1 = 3; yn = yn–1 + 4, если n = 2, 3, 4,….

Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: yn = 4n – 1.

Пример 2. y1 = 1; y2 = 1; yn= yn–2 + yn–1 , если n = 3, 4,….

Здесь: y1 = 1; y2 = 1; y3 = 1 + 1 = 2; y4 = 1 + 2 = 3; y5 = 2 + 3 = 5; y6 = 3 + 5 = 8;

Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .

На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n.

Свойства числовых последовательностей.

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y1 < y2 < y3 < … < yn < yn+1 < ….

Определение.Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y1 > y2 > y3 > … > yn > yn+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Пример 1. y1 = 1; yn = n2</SUP– последовательность.

Пример 2. y1 = 1; – убывающая последовательность. §2 Арифметическая прогрессия

Арифметической прогрессией называется такая последовательность, у которой каждый ее член, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d,которое называется разностью прогрессии.

Для всех элементов прогрессии, начиная со второго выполнимо равенство:

Если d > 0, то прогрессия является возрастающей. Если d < 0, то прогрессия является убывающей.

Арифметическая прогрессия считается конечной, если рассматриваются только ее первые несколько членов.

= + d = (+ d) + d = + 2d,

= + d = (+ 2d) + d = + 3d,

= + d(n-1) = + d(n-1) - формула n-го члена арифметической прогрессии.(n≥1)

Пример

3,6,9,12,15,18,21,24,27,30 — арифметическая прогрессия из десяти членов с шагом 3.

Свойства

2.Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.

3.Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии: $a_n={a_{n-1}+a_{n+1} \over 2} \quad \forall n \ge 2$ .

Обратное также верно, то есть это свойство является признаком арифметической прогрессии.
Доказательство:

$\Rightarrow : \forall n > 1 \quad a_n = a_1 + (n - 1)d = \frac{2\cdot (a_1 + (n - 1)d)}{2} = \frac{2a_1 + 2dn - 2d}{2} = \frac{a_1 + (n-2)d + a_1 + nd}{2} = \frac{a_{n-1}+ a_{n+1}}{2}$

Обратное аналогично

4.Сумма n первых членов арифметической прогрессии может быть выражена формулами

$S_n=\sum_{i=1}^n a_i ={a_1+a_n \over 2}n={2a_1 + d(n-1) \over 2}n$

Доказательство:

$\sum_{i=1}^na_i = \sum_{i=1}^n(a_1+d(i - 1)) = \sum_{n - i = 1}^n(a_1+d(n - i - 1)) = \sum_{i=1}^n(a_1 + dn - di) =$

$= \sum_{i=1}^n(2a_1 + d(n-1)) - \sum_{i=1}^n(a_1+d(i-1)) = n(2a_1 + d(n-1)) - \sum_{i=1}^n(a_1+d(i-1)) \quad \Rightarrow$

$\Rightarrow \sum_{i=1}^n(a_1+d(i-1)) = n\frac{2a_1+d(n-1)}{2} = n\frac{a_1+a_1+d(n-1)}{2} = n\frac{a_1+a_n}{2}$

$n = 1 :\quad S_1 = \sum_{i=1}^1(a_1+d\cdot 0) = a_1 = 1\cdot \frac{a_1+a_1}{2}$

$n \rightarrow n+1 :\quad S_{n+1} = \sum_{i=1}^{n+1}(a_1+d(i-1)) = \sum_{i=1}^n(a_1+d(i-1))+(a_1+dn)=$

$=S_n+(a_1+dn) = n\frac{a_1 + a_n}{2}+(a_1+dn) = \frac{na_1 + na_1+n^2d-nd+2a_1+2dn}{2}=$

$=(n+1)\frac{2a_1+dn}{2}=(n+1)\frac{a_1 + a_{n+1}}{2}$

5.Сумма n последовательных членов арифметической прогрессии начиная с члена k:

$S_n={a_k+a_{k+n-1} \over 2}n$

6.Пример суммы арифметической прогрессии является сумма ряда натуральных чисел до n включительно:

$S_n = \sum_{i=1}^n i = 1+2+3+4+5+...+n = {n(n+1) \over 2}$

Задача 1.При делении девятого члена арифметической прогрессии на второй член в частном получается 5, а при делении тринадцатого члена на шестой член в частном получается 2 и в остатке 5. Найти первый член и разность прогрессии.

Решение: …,- арифметическая прогрессия

: остаток 5)

Используя формулу n-го члена прогрессии получаем систему уравнений:

Откуда 4(2d-5)=3d,то 5d=20,то d=4

Ответ: d=4

Задача 2. Известно, что при любом n сумма Sn членов некоторой арифметической прогрессии выражается формулой Sn=4n²-3n. Найти три первых члена этой прогрессии.

Решение:

Пусть n=1 .

Пусть n=2 .

Так как ,то

Ответ: ,,

Задача 3. Найти сумму

Решение: перепишем сумму в виде:

Ответ:

Задача 4. Найти сумму =++ +…+

Решение: заметим,что =-

Тогда перепишем сумму в виде разности:

=(1 -)+( - )+( - )+…+( - )+( - )=1 - =

Ответ: =.

§3 Геометрическая прогрессия

Геометри́ческая прогре́ссия — последовательность чисел $b_1,\ b_2,\ b_3,\ \ldots$ (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число $q \quad$ (знаменатель прогрессии), где $b_1\not=0$ , $q\not=0$ и обычно предполагают, что $q\not=1$

$b_1,\ b_2=b_1q,\ b_3=b_2q,\ \ldots,\ b_n=b_{n-1}q$

www.coolreferat.com

V. Арифметическая и геометрическая прогрессия, проценты.

Арифметической прогрессией называется последовательность чисел N, у которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же постоянным для данной последовательности числом , т.е.

Формула 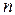-ого члена арифметической прогрессии:

где — первый член; — разность прогрессии, .- общий член.

При любом имеем:

Таким образом (при … ),

или ,

т.е. каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

Формула для общего члена арифметической прогрессии N связывает четыре величины: , , и . Если три из них заданы, то из этой формулы можно найти четвертую величину. Приведем соответствующие формулы нахождения , и :

; ; .

Сумма 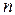первых членов арифметической прогрессии:

или .

При арифметическая прогрессия является монотонно возрастающей, а при монотонно убывающей.

Геометрической прогрессией называется последовательность чисел N, у которой каждый член, начиная со второго, получается из предыдущего умножением его на некоторое постоянное для этой последовательности число , т.е.

, N.

Число называется знаменателем геометрической прогресии, — первым членом; .- общим членом.

Любой член прогрессии можно выразить через соседние, как их среднее геометрическое: , где .

Сумма 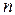первых членов геометрической прогрессии:

, если .

Для геометрической прогрессии со знаменателем имеют место следующие свойства монотонности:

— прогрессия является возрастающей, если выполнено одно из следующих условий:

— прогрессия является убывающей, если выполнено одно из следующих условий:

— если , то геометрическая прогрессия является знакопеременной: ее члены с нечетными номерами имеют тот же знак, что и ее первый член, а члены с четными номерами – противоположный ему знак. Знакопеременная геометрическая прогрессия не является монотонной.

Сумма бесконечно убывающей геометрической прогрессии :

Процентом называется сотая часть числа.

В экономике есть понятие простых и сложных процентов.

Простые проценты начисляются по формуле:

а сложные — по формуле:

где 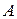— нарощенный капитал; — основной капитал; — процентная ставка; — время (число лет).

refac.ru

V. Арифметическая и геометрическая прогрессия, проценты.

Количество просмотров публикации V. Арифметическая и геометрическая прогрессия, проценты. - 65

Арифметической прогрессией принято называть последовательность чисел N, у которой каждый член, начиная со второго, равен предыдущему, сложенному с одним и тем же постоянным для данной последовательности числом , ᴛ.ᴇ.

Формула -ого члена арифметической прогрессии:

где - первый член; - разность прогрессии, .- общий член.

При любом имеем:

Таким образом (при ),

или ,

ᴛ.ᴇ. каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

Формула для общего члена арифметической прогрессии N связывает четыре величины: , , и . В случае если три из них заданы, то из этой формулы можно найти четвертую величину. Приведем соответствующие формулы нахождения , и :

; ; .

Сумма первых членов арифметической прогрессии:

или .

При арифметическая прогрессия является монотонно возрастающей, а при монотонно убывающей.

Геометрической прогрессией принято называть последовательность чисел N, у которой каждый член, начиная со второго, получается из предыдущего умножением его на неĸᴏᴛᴏᴩᴏᴇ постоянное для этой последовательности число , ᴛ.ᴇ.

, N.

Число принято называть знаменателем геометрической прогресии, - первым членом; .- общим членом.

Любой член прогрессии можно выразить через соседние, как их среднее геометрическое: , где .

Сумма первых членов геометрической прогрессии:

, в случае если .

Для геометрической прогрессии со знаменателем имеют место следующие свойства монотонности:

- прогрессия является возрастающей, в случае если выполнено одно из следующих условий:

- прогрессия является убывающей, в случае если выполнено одно из следующих условий:

- если , то геометрическая прогрессия является знакопеременной: ее члены с нечетными номерами имеют тот же знак, что и ее первый член, а члены с четными номерами – противоположный ему знак. Знакопеременная геометрическая прогрессия не является монотонной.

Сумма бесконечно убывающей геометрической прогрессии :

Процентом принято называть сотая часть числа.

В экономике есть понятие простых и сложных процентов.

Простые проценты начисляются по формуле:

а сложные - по формуле:

где - нарощенный капитал; - основной капитал; - процентная ставка; - время (число лет).

V. Арифметическая и геометрическая прогрессия, проценты. Арифметическая прогрессия реферат

Доклад на научную конференцию по теме: «Арифметическая прогрессия».

Прогрессии

V. Арифметическая и геометрическая прогрессия, проценты.

V. Арифметическая и геометрическая прогрессия, проценты.

Читайте также

Смотрите также