Геометрия, 10 класс: уроки, тесты, задания
Аксиомы стереометрии
-
Аксиомы стереометрии и их простейшие следствия
Параллельность прямых и плоскостей
-
Параллельность прямых, прямой и плоскости
-
 Угол между прямыми
Угол между прямыми
-
Параллельность плоскостей
-
Перпендикулярность прямых и плоскостей
-
Перпендикулярность прямой и плоскости
-
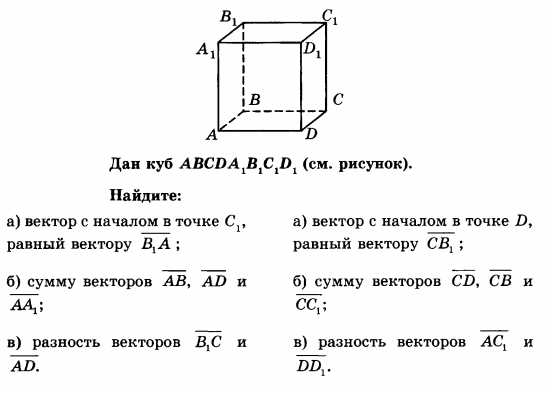 Угол между прямой и плоскостью
Угол между прямой и плоскостью
-
Двугранный угол. Перпендикулярность плоскостей
Многогранники
-
Понятие многогранника. Призма
-
Пирамида
-
Правильные многогранники
Векторы в пространстве
-
Понятие вектора в пространстве
-
Сложение и вычитание векторов.
 Умножение вектора на число
Умножение вектора на число
-
Компланарные векторы
ГДЗ по Геометрии 10 класс самостоятельные и контрольные работы Ершова
Авторы: Ершова А.П., Голобородько В.В..
Математика у многих школьников вызывает трудности, поэтому советуем использовать ГДЗ по геометрии 10 класс самостоятельные и контрольные работы Ершова. Особенно сложно становится в последние годы обучения, когда нужно готовиться к экзаменам. С этой целью и создали сборники. Здесь содержатся все знания, требуемые для учеников.
Решение заданий предоставляется в понятной форме. Каждое упражнение классифицируется по номеру и уроку для удобства поиска. Все составляется в соответствии с ФГОС. Учитывается рабочая программа для разных учебных заведений, распределяя материал по уровням сложности.
Каждое упражнение классифицируется по номеру и уроку для удобства поиска. Все составляется в соответствии с ФГОС. Учитывается рабочая программа для разных учебных заведений, распределяя материал по уровням сложности.
Особенности сборника по геометрии за 10 класс, самостоятельные и контрольные работы от Ершовой
Школьники зачастую жалуются на большую загруженность при посещении школы. Необходимо выполнять большое количество действий, изучать дисциплины. По ним задаются упражнения на каждый урок. Самостоятельно разобраться во всем без помощи посторонних достаточно сложно.
Решебник – это специальное пособие, которое содержит в себе правильные ответы на все вопросы. Теперь подготовка к занятиям становится более простой. Достаточно просто решить задачу, посмотреть ее номер, открыть и проверить себя. В результате будут выявлены ошибки, что поможет с их устранением в будущем. Такая форма контроля уже давно пользуется широкой популярностью. Это также удобный инструмент для преподавателей, позволяющий заниматься составлением рабочей программы, планов, методических указаний.
- изучение информации самостоятельно;
- просмотр верных ответов онлайн;
- готовиться к тестам, проверочным работам;
- широкий спектр задач разной степени сложности;
- воспитание дисциплины;
- улучшение оценок и общей успеваемости.
Справочник по геометрии для 10 класса, самостоятельные и контрольные работы (авторы: Ершова А.П., Голобородько В.В.) поможет ребенку подготовиться к предстоящим экзаменам. В нем содержатся примеры, понятное описание и объяснение всех алгоритмов. Теперь процесс обучения в школе станет немного проще и продуктивнее.
ГДЗ самостоятельные и контрольные работы по геометрии за 10 класс Ершова, Голобородько
Десятиклассники переживают непростой период, так как им остается всего два года до сдачи экзаменов.
А геометрия вообще доставляет школьникам больше всего сложностей, так как для успешного ее изучения нужно заучивать огромное количество формул, алгоритмов, постулатов и аксиом. Зато она благотворно влияет на интеллект человека: развивает вычислительные навыки, способности доказывать и делать выводы. Как сделать обучения более эффективным и быстрым? Этому поспособствует эвристический метод. Он состоит в том, что ребенок сам усваивает материал, с помощью средства-помощника, таким будет онлайн-решебник. Вашему вниманию предлагается отличный сборник, который долгое время со старанием разрабатывали и составляли опытные и профессиональные методисты, и выпустило издательство «Илекса» в 2014 году.
Вашему вниманию предлагается отличный сборник, который долгое время со старанием разрабатывали и составляли опытные и профессиональные методисты, и выпустило издательство «Илекса» в 2014 году.
По каким причинам пользователи выбирают учебно-методическицй комплекс по геометрии за 10 класс для самостоятельных и контрольных работ (авторы: Ершова А.П., Голобородько В.В.)
Этот справочник поможет не только учащимся. Отстающий сможет сам проходить разделы и усваивать темы, а отличник будет делать заранее перед уроками для того, чтобы в школе быть более уверенным. Родители смогут контролировать учебный процесс ребенка, а учителя- составлять классные задания. К тому же, все подано в интересной форме специально для детей. Другие преимущества:
- Можно научиться независимой работе, синтезу и анализу. Хотя, в этом возрасте, получение данного навыка достаточно тяжело дается детям. Поэтому если использовать решебник регулярно, обучающийся сможет научиться навыкам самоконтроля гораздо быстрее;
- самостоятельно рассматривать новый материал;
- закреплять пройденные на уроке темы;
- учтены европейские стандарты преподавания;
- исключительно правильные ответы;
- больше не потребуется ждать, когда мамы и папы вернутся с работы или учитель наконец-то освободится для того, чтобы объяснить вам принцип решения очередного примера.

Содержание решебника с ГДЗ по геометрии для 10 класса от Ершовой
Книга включает все главы, рекомендованные к изучению:
- планиметрия;
- стереометрия;
- многогранники.
Самостоятельная работа по физике Относительность движения 10 класс
Самостоятельная работа по физике Относительность движения 10 класс с ответами. Самостоятельная работа включает 5 вариантов, в каждом по 2 задания.
Вариант 1
1. Поезд длиной 240 м движется со скоростью 18 км/ч. За какое время он проедет мост, длина которого 720 м?
2. Какие векторы называют равными? В каком случае проекция вектора на координатную ось отрицательна?
Вариант 2
1. Поезд длиной 120 м движется со скоростью 72 км/ч. За какое время он проедет туннель длиной 3 км 480 м?
2. Какие действия можно производить с векторами? Как определить проекции вектора перемещения на координатные оси OX и OY?
Вариант 3
1. Поезд длиной 800 м движется со скоростью 20 м/с. В течение какого промежутка времени его будет видеть пассажир состава, движущегося во встречном направлении со скоростью 108 км/ч?
Поезд длиной 800 м движется со скоростью 20 м/с. В течение какого промежутка времени его будет видеть пассажир состава, движущегося во встречном направлении со скоростью 108 км/ч?
2. Какие векторы называют коллинеарными? В каком случае проекция вектора на координатную ось равна 0?
Вариант 4
1. Вагон длиной 30 м движется со скоростью 1 м/с. От конца вагона в том же направлении по платформе бежит человек со скоростью 3 м/с. Какое расстояние он пробежит, достигнув начала вагона?
2. Какие величины называют скалярными? Приведите примеры. Что называют проекцией вектора на координатную ось?
Вариант 5
1. Самолёт летит из пункта А в пункт В и обратно два раза. Первый раз в безветренную погоду, а второй раз при ветре, направление которого совпадает с направлением из пункта А в пункт В. В каком случае время полёта меньше?
2. Сформулируйте правило параллелограмма для сложения векторов.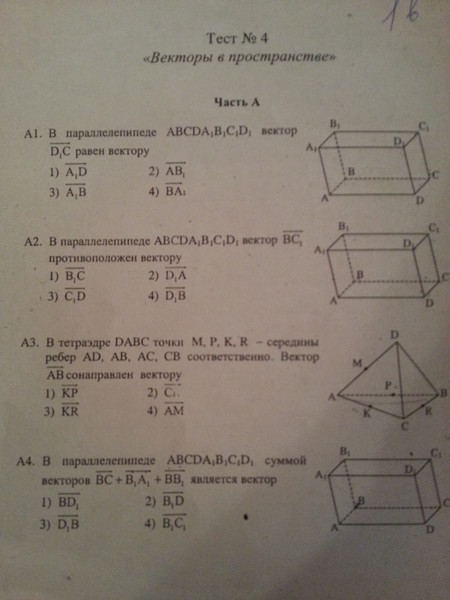 Поясните рисунком.
Поясните рисунком.
Ответы на самостоятельную работа по физике Относительность движения 10 класс
Вариант 1
1. 192 с
2. Два вектора называются равными, если они сонаправлены и имеют равные модули.
Вариант 2
1. 3 мин
2. Сложение векторов. Умножение скаляра на вектор.
Вариант 3
1. 16 с
2. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Вариант 4
1. 45 м
2. Примерами скалярных величин могут служить: масса, плотность, работа, сила тока, температура. Скаляры являются алгебраическими величинами и с ними можно производить любые алгебраические действия: сложение, вычитание.
Вариант 5
1. t2 > t2
2. Поместим начала векторов a и b в одну точку. Тогда вектор a + b, имея начало в той же точке, является диагональю параллелограмма, построенного на
векторах a и b.
Математика средней школы (10, 11 и 12 классы)
Математика средней школы для 10, 11 и 12 классов представлены вопросы и задачи для проверки глубокого понимания математических концепций и вычислительных процедур. Предоставляются подробные решения и ответы на вопросы.
12 класс
11 класс
10 класс
Онлайн-калькуляторы
- Онлайн-математические калькуляторы и решатели
- Онлайн-калькуляторы и решатели геометрии
- Калькулятор теста на делимость.
 Онлайн-калькулятор, проверяющий целые числа на видимость с помощью 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13.
Онлайн-калькулятор, проверяющий целые числа на видимость с помощью 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13. - Калькуляторы сложения, вычитания и умножения целых чисел. Три отдельных онлайн-калькулятора для сложения, вычитания и умножения целых чисел.
- Калькулятор частного и остатка. Онлайн-калькулятор, который вычисляет частное и остаток от деления двух целых чисел.
- Калькулятор наименьшего общего кратного (lcm). Вычислите наименьшее общее кратное двух натуральных чисел.
- Калькулятор наибольшего общего коэффициента (gcf).
 Вычислите наибольший общий делитель двух натуральных чисел.
Вычислите наибольший общий делитель двух натуральных чисел. - Калькулятор основных факторов. Разложите положительное целое число на простые множители.
- Калькулятор сложения дробей. Добавьте 2 или 3 дроби и уменьшите окончательный ответ.
- Калькулятор умножения дробей. Умножьте 2 дроби и уменьшите ответ.
- Калькулятор деления дробей. Разделите 2 дроби и уменьшите ответ.
- Калькулятор дробей.
 Перепишите дроби в уменьшенном виде.
Перепишите дроби в уменьшенном виде.
Больше начальной математики (4 и 5 классы) с бесплатными вопросами и задачи с ответами Домашняя страница
Автор — сообщите об этом по электронной почте ad
Vectors.pdf — Среднесрочный тест для 10-го класса Глава 1 Векторы СРЕДНЕСРОЧНЫЙ ТЕСТ ГЕОМЕТРИИ Глава 1 Векторы Задача 1 Противоположные векторы — это векторы с одинаковым
Предварительный просмотр неформатированного текста: Среднесрочный тест для 10 класса Глава 1: Векторы ГЕОМЕТРИЯ СРЕДНИЙ ТЕСТ Глава 1: Векторы Задача 1 Противоположные векторы — это векторы с A.та же отправная точка и противоположные направления. Б. та же отправная точка и направление. C. та же конечная точка и направление. D. одна и та же конечная точка и противоположные направления. Проблема 2 Равные векторы — это векторы, у которых A. одинаковая отправная точка и направление. Б. та же отправная точка и величина. C. одинаковая начальная и конечная точки. D. одинаковой величины и направления. Проблема 3 Два противоположных вектора должны иметь одинаковую начальную точку A. Задача 4 Б. направление. C. величина. Сколько векторов можно нарисовать из двух разных точек? А.1. B. 2. Задача 5 D. Конечная точка. C. 3. D. 4. Пусть ABCD — параллелограмм. Из 4 точек A, B, C и D можно нарисовать 3 ненулевых вектора, которые имеют ………….. с −− →
AB, кроме самого себя. А. в том же направлении. Б. такой же величины. C. та же отправная точка. D. противоположные направления. Задача 6 Пусть вектор −− →
AB — это представление для путешествия из A в B на карте. Если путешествие из C в D такое же, как путешествие из A в B, сколько мест на карте показано на карте
что D может быть?
А.0. Б. 1. Задача 7
А.
С.А.
C. Пусть ABC — треугольник с центром тяжести G и медианой AM. Какое утверждение — →
AB. — → −− → −− →
Б. GA + GB + GC = ~
0.
— → −− → −− →
D.
одинаковая отправная точка и направление. Б. та же отправная точка и величина. C. одинаковая начальная и конечная точки. D. одинаковой величины и направления. Проблема 3 Два противоположных вектора должны иметь одинаковую начальную точку A. Задача 4 Б. направление. C. величина. Сколько векторов можно нарисовать из двух разных точек? А.1. B. 2. Задача 5 D. Конечная точка. C. 3. D. 4. Пусть ABCD — параллелограмм. Из 4 точек A, B, C и D можно нарисовать 3 ненулевых вектора, которые имеют ………….. с −− →
AB, кроме самого себя. А. в том же направлении. Б. такой же величины. C. та же отправная точка. D. противоположные направления. Задача 6 Пусть вектор −− →
AB — это представление для путешествия из A в B на карте. Если путешествие из C в D такое же, как путешествие из A в B, сколько мест на карте показано на карте
что D может быть?
А.0. Б. 1. Задача 7
А.
С.А.
C. Пусть ABC — треугольник с центром тяжести G и медианой AM. Какое утверждение — →
AB. — → −− → −− →
Б. GA + GB + GC = ~
0.
— → −− → −− →
D. AG + BG + CG = ~
0. Пусть A, B, C, D — 4 различных точки, а векторы равны
А. −− → −− → —
→
AB + AD = AI.
−− → — → −− →
Г. AB + AC = AD. Б. — →
−− →
GA + 2GM = ~ 0.
−− →
−− →
AM + 2M G = ~ 0. Проблема 9 ~ u?
Б. Задача 10 Задача 11 −− →
CD. ложный? −− → −− → −− → −− →
~ u = AD — CD + CB — DB. Какой из нижеуказанных
С. −− →
ОБЪЯВЛЕНИЕ. Д. — →
AC. Пусть ABC — треугольник, а M, N, P — середины AB, AC и BC соответственно.−− → −− →
МП + НП =
−− →
ЯВЛЯЮСЬ . потом
А. Д. Бесконечно много. Дан параллелограмм ABCD с центром I. Какое из следующих утверждений верно? −− → −− → — →
AB + BC = AC.
— → −− → −− →
AC — AD = CD. Задача 8 C. 2. B. −− →
П. Б. С. — →
AP. Порыв ветра уносит воздушный шар в направлении D. ~ a −− →
MN. со скоростью 5 м / с. Другой порыв ветра также уносит шар, но в другом направлении со скоростью 4 м / с. Который из
следующие не могут A. 1 м / с. Проблема 12 — скорость, с которой летит воздушный шар?
Б.4 м / с. C. 5м / с. Д. 10м / с. На следующей карте показаны дом Алисы (A) и ее школа (B), а также некоторые другие места в городе (C, D, E, F, G).
AG + BG + CG = ~
0. Пусть A, B, C, D — 4 различных точки, а векторы равны
А. −− → −− → —
→
AB + AD = AI.
−− → — → −− →
Г. AB + AC = AD. Б. — →
−− →
GA + 2GM = ~ 0.
−− →
−− →
AM + 2M G = ~ 0. Проблема 9 ~ u?
Б. Задача 10 Задача 11 −− →
CD. ложный? −− → −− → −− → −− →
~ u = AD — CD + CB — DB. Какой из нижеуказанных
С. −− →
ОБЪЯВЛЕНИЕ. Д. — →
AC. Пусть ABC — треугольник, а M, N, P — середины AB, AC и BC соответственно.−− → −− →
МП + НП =
−− →
ЯВЛЯЮСЬ . потом
А. Д. Бесконечно много. Дан параллелограмм ABCD с центром I. Какое из следующих утверждений верно? −− → −− → — →
AB + BC = AC.
— → −− → −− →
AC — AD = CD. Задача 8 C. 2. B. −− →
П. Б. С. — →
AP. Порыв ветра уносит воздушный шар в направлении D. ~ a −− →
MN. со скоростью 5 м / с. Другой порыв ветра также уносит шар, но в другом направлении со скоростью 4 м / с. Который из
следующие не могут A. 1 м / с. Проблема 12 — скорость, с которой летит воздушный шар?
Б.4 м / с. C. 5м / с. Д. 10м / с. На следующей карте показаны дом Алисы (A) и ее школа (B), а также некоторые другие места в городе (C, D, E, F, G). Группа 3 1 Класс 10 Промежуточный тест Глава 1: Векторы Какой из следующих маршрутов ведет Алису из дома в школу? Задача 13 A. — → −− → −− → −− → −− → −− →
AF — BC + DG — BE — CF — EG B. — → −− → −− → −− → −− → −− →
AE — BC — DG + EG + CF + DF C. — → −− → −− → −− → −− → −− →
AC + CF — BC + BG — EG — BF D. −− → −− → −− → −− → −− → −− →
AD + CE + DF — CF + EG — BG В физике вектор может использоваться для представления силы, где направление и величина вектора представляют направление и мощность (в Ньютонах)
силу соответственно.На картинке воздушный змей приводится в движение натяжной веревкой.
~ 5 Н. В результате
из ~
s и w
~. Если
~ = 60o, cos (~ k, ~ s) =
√ (~ s, w)
7 19
Б.
.
19
√
23 166
Д.
.
166 и одновременно находясь под ветром
по направлению С. Задача 14
C. это сумма 3
.
7
3
14 А.А. ~ k ~ u и ~ v?
| ~ u |. | ~ v |. грех (~ u, ~ v).
Д. | ~
u |. | ~ v |. | грех (~ u, ~ v) |.
B. Дан треугольник ABC такой, что AB = 2, AC = 4, и середины AB и AC соответственно. Скалярное произведение
А. 5.
Группа 3 1 Класс 10 Промежуточный тест Глава 1: Векторы Какой из следующих маршрутов ведет Алису из дома в школу? Задача 13 A. — → −− → −− → −− → −− → −− →
AF — BC + DG — BE — CF — EG B. — → −− → −− → −− → −− → −− →
AE — BC — DG + EG + CF + DF C. — → −− → −− → −− → −− → −− →
AC + CF — BC + BG — EG — BF D. −− → −− → −− → −− → −− → −− →
AD + CE + DF — CF + EG — BG В физике вектор может использоваться для представления силы, где направление и величина вектора представляют направление и мощность (в Ньютонах)
силу соответственно.На картинке воздушный змей приводится в движение натяжной веревкой.
~ 5 Н. В результате
из ~
s и w
~. Если
~ = 60o, cos (~ k, ~ s) =
√ (~ s, w)
7 19
Б.
.
19
√
23 166
Д.
.
166 и одновременно находясь под ветром
по направлению С. Задача 14
C. это сумма 3
.
7
3
14 А.А. ~ k ~ u и ~ v?
| ~ u |. | ~ v |. грех (~ u, ~ v).
Д. | ~
u |. | ~ v |. | грех (~ u, ~ v) |.
B. Дан треугольник ABC такой, что AB = 2, AC = 4, и середины AB и AC соответственно. Скалярное произведение
А. 5. Б. -5. Задача 16 из 3 N, летит воздушный змей. Каково скалярное произведение 2 произвольных векторов | ~ u |.| ~ v |. cos (~ u, ~ v).
| ~ u |. | ~ v |. | cos (~ u, ~ v) |. Задача 15 ~ s −− →
BN и −− →
CM Aˆ = 60o. Пусть M и N — это C. 7. D. -7. Пусть скалярное произведение между двумя заданными векторами равно 0. Угол между двумя векторами равен
A. 0o B. Задача 17
А. 2 а. С. 2 а
2. C. (~ u, ~ v) = 150 D. −a
2 180o. −− →
AB и — →
AC равен 2
. Д. 2 2а. На рисунке показана упаковка закуски, разорванная в двух направлениях двумя разными силами. Если скалярное произведение сил меньше или равно o 90o.Дан правильный треугольник ABC такой, что AB = a. Скалярное произведение
Б. Задача 18 45o −9
,
2 упаковка откроется. Если первая сила равна 2 Н, и вторая сила должна быть …………., чтобы открыть упаковку. A. не менее C. не менее Задача 19 √
3 3
.
2 Б. не более 9
.
2 D. не более √
3 3
.
2
9
.
2 Если скалярное произведение сил в задаче 18 меньше -8, пакет будет вместо этого разорван на 2 части.
Б. -5. Задача 16 из 3 N, летит воздушный змей. Каково скалярное произведение 2 произвольных векторов | ~ u |.| ~ v |. cos (~ u, ~ v).
| ~ u |. | ~ v |. | cos (~ u, ~ v) |. Задача 15 ~ s −− →
BN и −− →
CM Aˆ = 60o. Пусть M и N — это C. 7. D. -7. Пусть скалярное произведение между двумя заданными векторами равно 0. Угол между двумя векторами равен
A. 0o B. Задача 17
А. 2 а. С. 2 а
2. C. (~ u, ~ v) = 150 D. −a
2 180o. −− →
AB и — →
AC равен 2
. Д. 2 2а. На рисунке показана упаковка закуски, разорванная в двух направлениях двумя разными силами. Если скалярное произведение сил меньше или равно o 90o.Дан правильный треугольник ABC такой, что AB = a. Скалярное произведение
Б. Задача 18 45o −9
,
2 упаковка откроется. Если первая сила равна 2 Н, и вторая сила должна быть …………., чтобы открыть упаковку. A. не менее C. не менее Задача 19 √
3 3
.
2 Б. не более 9
.
2 D. не более √
3 3
.
2
9
.
2 Если скалярное произведение сил в задаче 18 меньше -8, пакет будет вместо этого разорван на 2 части. Под каким углом должны быть приложены усилия, чтобы открыть упаковку с помощью силы 5 Н и 2 Н.
А.90o. Задача 20 √ A. a2 + b2. Группа 3 Б. 135o. Величина вектора √ B. a2 — b2. ~ u (a, b) C. 120o. Д. 150o С. a2 + b2. D. a 2 — b2. 2 класс 10 Промежуточный тест Задача 21
А.
C. 2 ненулевых вектора A. ac + bd = -1. Задача 23 A (xA, yA)
Б. (xA — xB, yA — yB).
D. (xA — yA, xB — yB). Даны 2 различные точки (xA + xB, yA + yB).
(xA + yA, xB + yB). Задача 22 Глава 1: Векторы ~ u (a, b) и ~ v (c, d) B. ac + bd = 0 (xB, yB). Координаты вектора −− →
AB перпендикулярны друг другу, если
С.ак-бд = -1. D. ac-bd = 0. Даны координаты 3 точек M (2,2), N (-4, -4) и P (5,5). Какое из утверждений верно? A. M находится между N и P.
B. N находится между M и P.
C. P находится между M и N.
D. M, N и P нелинейны. Задача 24 Даны 2 вектора наибольшего целого числа x, удовлетворяющих
А. -2. Задача 25 ϕ ~ a (−2x, 3) и ~ b (−3, x + 1). Пусть ϕ — угол между ~ a и ~ b. Угол тупой формы равен B. 1. C. -1. D. 0. Три большие площади города расположены в точках A (32,21 северной широты, 13,22 западной долготы), B (30,05 северной широты, 15,53 западной долготы) и C (34,5 северной широты, 14,62 западной долготы).
Под каким углом должны быть приложены усилия, чтобы открыть упаковку с помощью силы 5 Н и 2 Н.
А.90o. Задача 20 √ A. a2 + b2. Группа 3 Б. 135o. Величина вектора √ B. a2 — b2. ~ u (a, b) C. 120o. Д. 150o С. a2 + b2. D. a 2 — b2. 2 класс 10 Промежуточный тест Задача 21
А.
C. 2 ненулевых вектора A. ac + bd = -1. Задача 23 A (xA, yA)
Б. (xA — xB, yA — yB).
D. (xA — yA, xB — yB). Даны 2 различные точки (xA + xB, yA + yB).
(xA + yA, xB + yB). Задача 22 Глава 1: Векторы ~ u (a, b) и ~ v (c, d) B. ac + bd = 0 (xB, yB). Координаты вектора −− →
AB перпендикулярны друг другу, если
С.ак-бд = -1. D. ac-bd = 0. Даны координаты 3 точек M (2,2), N (-4, -4) и P (5,5). Какое из утверждений верно? A. M находится между N и P.
B. N находится между M и P.
C. P находится между M и N.
D. M, N и P нелинейны. Задача 24 Даны 2 вектора наибольшего целого числа x, удовлетворяющих
А. -2. Задача 25 ϕ ~ a (−2x, 3) и ~ b (−3, x + 1). Пусть ϕ — угол между ~ a и ~ b. Угол тупой формы равен B. 1. C. -1. D. 0. Три большие площади города расположены в точках A (32,21 северной широты, 13,22 западной долготы), B (30,05 северной широты, 15,53 западной долготы) и C (34,5 северной широты, 14,62 западной долготы). После матча болельщики решают встретиться у кетроид треугольника ABC, чтобы отпраздновать это событие.
победа. Координаты места празднования:
A. (48,38N, 21,69W) Группа 3 B. (32,25N, 14,46W) C. (39,56N, 17,4W). Д. (32,3,14,48). 3 …
После матча болельщики решают встретиться у кетроид треугольника ABC, чтобы отпраздновать это событие.
победа. Координаты места празднования:
A. (48,38N, 21,69W) Группа 3 B. (32,25N, 14,46W) C. (39,56N, 17,4W). Д. (32,3,14,48). 3 …
Просмотр
Полный документ
Изучение использования множественных представлений для обучения векторов в 10 классе по физическим наукам
Абстрактные
Целью данной статьи было изучить использование множественного представления
подход в качестве стратегии обучения для улучшения понимания учащимися векторов в
10 класс Физические науки.Исследование также хотело рассмотреть подход MR.
через призму учащихся. Выборка, состоящая из 45 учеников 10 класса из
Всего в исследовании приняли участие 160 учащихся 10-х классов физических наук. Обе
количественные и качественные данные были собраны и проанализированы. Учащиеся были первыми
прошли предварительный тест для установления их первоначального понимания векторов. Этот предварительный тест был
с последующим вмешательством в форме урока. Урок проводился по порядку
познакомить учащихся с обучением через множественные представления.Затем был проведен посттест
для определения воздействия вмешательства. Чтобы собрать и количественно оценить
восприятие учащимися использования множественных представлений в преподавании и обучении
векторов в 10 классе учащимся физических наук раздали анкеты
полный. Последним шагом было интервью с учащимися для триангуляции результатов
три инструмента. Исследование показало, что учащиеся испытывали трудности с
понимание векторов в их традиционных уроках разговорной речи и их
восприятие векторов было отрицательным.Исследование также показало, что множественные
Представления могут улучшить понимание и развить позитивное восприятие
учащихся к преподаванию и изучению векторов. Это улучшение происходит только
если несколько представлений используются правильно.
Учащиеся были первыми
прошли предварительный тест для установления их первоначального понимания векторов. Этот предварительный тест был
с последующим вмешательством в форме урока. Урок проводился по порядку
познакомить учащихся с обучением через множественные представления.Затем был проведен посттест
для определения воздействия вмешательства. Чтобы собрать и количественно оценить
восприятие учащимися использования множественных представлений в преподавании и обучении
векторов в 10 классе учащимся физических наук раздали анкеты
полный. Последним шагом было интервью с учащимися для триангуляции результатов
три инструмента. Исследование показало, что учащиеся испытывали трудности с
понимание векторов в их традиционных уроках разговорной речи и их
восприятие векторов было отрицательным.Исследование также показало, что множественные
Представления могут улучшить понимание и развить позитивное восприятие
учащихся к преподаванию и изучению векторов. Это улучшение происходит только
если несколько представлений используются правильно. Исследование также выяснило, что когда
Множественные представления используются неправильно, это ограничивает более глубокое понимание
ученики. По результатам исследования был сделан ряд рекомендаций.
Некоторые из них заключались в том, что при обучении следует использовать несколько представлений.
векторов, и советники по предметам и учителя должны быть должным образом подготовлены
использование нескольких представлений.Учебники по физическим наукам должны быть разработаны
для размещения нескольких представлений.
Исследование также выяснило, что когда
Множественные представления используются неправильно, это ограничивает более глубокое понимание
ученики. По результатам исследования был сделан ряд рекомендаций.
Некоторые из них заключались в том, что при обучении следует использовать несколько представлений.
векторов, и советники по предметам и учителя должны быть должным образом подготовлены
использование нескольких представлений.Учебники по физическим наукам должны быть разработаны
для размещения нескольких представлений.
Quiz Grade 10 октября | Евклидов вектор
Название экзамена ___________________________________
МНОЖЕСТВЕННЫЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос.
1)
Если вектор, направленный вверх, имеет положительную величину, вектор, направленный вниз, имеет отрицательную величину.1)
А)
Правда
Б)
Ложь
2)
Два вектора смещения имеют величину 5. 0 м и 7,0 м соответственно. Если эти два вектора сложить вместе, величина суммы2)
0 м и 7,0 м соответственно. Если эти два вектора сложить вместе, величина суммы2)
А)
равно 12 м.
Б)
равна 8,6 м.
В)
равна 2,0 м.
Г)
может быть от 2,0 м до 12 м.
3)
Два вектора величиной 20 мм и 50 мм складываются. Какое из следующих значений является возможным для величины результирующего? 3)
А)
20 мм
Б)
10 мм
C)
40 мм
Г)
80 мм
4)
Величина результирующего двух векторов не может быть меньше, чем величина любого из этих двух векторов.4)
А)
Правда
Б)
Ложь
КРАТКИЙ ОТВЕТ. Напишите слово или фразу, которые лучше всего завершают каждое утверждение или отвечают на вопрос.
5)
Учащийся складывает два вектора смещения, которые имеют величины 12,0 м и 5,0 м. Каков диапазон возможных ответов для величины результирующего вектора?
5)
МНОЖЕСТВЕННЫЙ ВЫБОР. Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос.
Выберите один вариант, который лучше всего завершает утверждение или отвечает на вопрос.
6)
Если
A
—
B
=
0, то векторы
A
и
B
имеют равные величины и направлены в одном направлении. 6)
А)
Правда
Б)
Ложь
7)
Если три вектора складываются в ноль, все они должны иметь равные величины.7)
А)
Правда
Б)
Ложь
8)
Сумма двух векторов фиксированных величин имеет наибольшую величину, когда угол между этими двумя векторами равен 8)
А)
60 °
Б)
90 °
C)
180 °
D)
270 °
E)
0 °
КРАТКИЙ ОТВЕТ.Напишите слово или фразу, которые лучше всего завершают каждое утверждение или отвечают на вопрос.
9)
Вектор скорости имеет компоненты 36 м / с на запад и 22 м / с на север. Какова величина и направление этого вектора?
Какова величина и направление этого вектора?
9)
1
Свойства векторов | Векторы и скаляры
Векторы — это математические объекты, и теперь мы изучим некоторые их математические свойства.
Если два вектора имеют одинаковую величину (размер) и в одном направлении, то мы называем их равными друг другу.Например, если у нас есть две силы, \ (\ vec {F_ {1}} = \ text {20} \ text {N} \) в восходящем направлении и \ (\ vec {F_ {2}} = \ text {20} \ text {N} \) в направлении вверх , тогда мы можем сказать, что \ (\ vec {F_ {1}} = \ vec {F_ {2}} \).
Так же, как скаляры, которые могут иметь положительные или отрицательные значения, векторы также могут быть положительными или отрицательными. Отрицательный вектор представляет собой вектор, который указывает направление, в противоположность в положительном направлении опорного . Например, если в конкретной ситуации, мы определяем направление вверх в качестве опорного положительного направления, то сила \ (\ VEC {F_ {1}} = \ текст {30} \ текст {N} \) вниз будет быть отрицательным вектором и также может быть записано как \ (\ vec {F_ {1}} = — \ text {30} \ text {N} \). В этом случае отрицательный знак (\ (- \)) указывает на то, что направление \ (\ VEC {Р- {1}} \) противоположно направлению опорного положительном направлении.
В этом случае отрицательный знак (\ (- \)) указывает на то, что направление \ (\ VEC {Р- {1}} \) противоположно направлению опорного положительном направлении.
Как и скаляры, векторы также можно складывать и вычитать. Мы исследуем, как это сделать дальше.
Сложение и вычитание векторов (ESAGO)
Сложение векторов
При добавлении векторов нам необходимо учесть и их величины, и направлений.
Например, представьте себе следующее.Вы с другом пытаетесь переместить тяжелую коробку. Вы стоите позади него и с силой толкаете вперед \ (\ vec {{F} _ {1}} \), а ваш друг становится впереди и тянет его к себе с силой \ (\ vec {{F} _ {2 }} \). Две силы действуют в направлении и (т.е. вперед), поэтому общая сила, действующая на коробку, составляет:
Очень легко понять концепцию сложения векторов через действие, использующее вектор смещения .
Смещение — это вектор, который описывает изменение положения объекта. Это вектор, который указывает от исходного положения до конечного положения.
Это вектор, который указывает от исходного положения до конечного положения.
Добавление векторов
Материалы
малярная лента
Метод
Приклейте полоску малярной ленты горизонтально через пол. Это будет вашей отправной точкой.
Задача 1 :
Сделать \ (\ text {2} \) шагов в прямом направлении. Используйте кусок малярной ленты, чтобы отметить конечную точку и обозначить ее A . Затем сделайте еще \ (\ text {3} \) шаг в прямом направлении.Используйте малярный скотч, чтобы отметить ваше конечное положение как B . Убедитесь, что вы стараетесь, чтобы ваши шаги были одинаковой длины!
Задача 2 :
Вернитесь на исходную линию. Теперь сделайте \ (\ text {3} \) шагов вперед. С помощью куска малярной ленты отметьте конечную точку и отметьте ее B . Затем сделайте еще \ (\ text {2} \) шаг вперед и используйте новый кусок малярной ленты, чтобы отметить ваше конечное положение как A .
Обсуждение
Что вы заметили?
В Задаче 1 первые \ (\ text {2} \) шаги вперед представляют вектор смещения, а вторые \ (\ text {3} \) шаги вперед также образуют вектор смещения.Если бы мы не остановились после первых \ (\ text {2} \) шагов, мы бы сделали \ (\ text {5} \) шагов в прямом направлении в целом. Следовательно, если мы добавим векторы смещения для шагов \ (\ text {2} \) и \ (\ text {3} \) шагов, мы должны получить в общей сложности \ (\ text {5} \) шагов в прямом направлении. направление.
Неважно, делаете ли вы \ (\ text {3} \) шаг вперед, а затем \ (\ text {2} \) шаг вперед, или два шага, за которыми следует еще один \ (\ text {3} \) шаг вперед .Ваша финальная позиция такая же! Порядок добавления значения не имеет!
Мы можем представить сложение векторов графически, основываясь на вышеизложенном действии. Нарисуйте вектор для первых двух шагов вперед, а затем вектор для следующих трех шагов вперед.
Нарисуйте вектор для первых двух шагов вперед, а затем вектор для следующих трех шагов вперед.
Мы добавляем второй вектор в конец первого вектора, так как это то место, где мы сейчас находимся после того, как первый вектор сработал. Вектор от хвоста первого вектора (начальная точка) до головы второго вектора (конечная точка) является тогда суммой векторов.
Как вы можете убедиться, порядок, в котором вы добавляете векторы, не имеет значения. В приведенном выше примере, если вы решили сначала сделать \ (\ text {3} \) шаг вперед, а затем еще один \ (\ text {2} \) шаг вперед, конечный результат все равно будет \ (\ text {5} \) шагает вперед.
Вычитание векторов
Вернемся к проблеме с тяжелым ящиком, который вы и ваш друг пытаетесь переместить. Если вы сначала не связались должным образом, вы оба можете подумать, что вам следует двигаться в своем собственном направлении! Представьте, что вы стоите за ящиком и с силой тянете его на себя \ (\ vec {{F} _ {1}} \), а ваш друг стоит перед ящиком и с силой тянет его к себе \ (\ vec {{F} _ {2}} \). В этом случае две силы действуют в против направлений. Если мы определим направление, в котором ваш друг тянет, как положительное , тогда сила, которую вы прикладываете, должна быть отрицательной , поскольку она имеет противоположное направление. Мы можем записать общую силу, приложенную к коробке, как сумму отдельных сил:
В этом случае две силы действуют в против направлений. Если мы определим направление, в котором ваш друг тянет, как положительное , тогда сила, которую вы прикладываете, должна быть отрицательной , поскольку она имеет противоположное направление. Мы можем записать общую силу, приложенную к коробке, как сумму отдельных сил:
Фактически вы вычли два вектора! Это то же самое, что и сложение двух векторов, имеющих противоположные направления.
Как и раньше, мы можем хорошо проиллюстрировать векторное вычитание, используя векторы смещения.Если вы сделаете \ (\ text {5} \) шагов вперед, а затем вычтите \ (\ text {3} \) шагов вперед, у вас останется только два шага вперед:
Что вы сделали физически, чтобы вычесть \ (\ text {3} \) шагов? Изначально вы сделали \ (\ text {5} \) шагов вперед, но затем вы сделали \ (\ text {3} \) шаги назад , чтобы вернуться назад, сделав только \ (\ text {2} \) шаги вперед. Это обратное смещение представлено стрелкой, указывающей влево (назад) длиной \ (\ text {3} \). Чистый результат сложения этих двух векторов — \ (\ text {2} \) шагов вперед:
Чистый результат сложения этих двух векторов — \ (\ text {2} \) шагов вперед:
Таким образом, вычитание одного вектора из другого аналогично добавлению вектора в противоположном направлении (т.е.е. вычитание \ (\ text {3} \) шагов вперед аналогично добавлению \ (\ text {3} \) шагов назад).
Вычитание одного вектора из другого аналогично добавлению вектора в противоположном направлении.
Результирующий вектор
Окончательная величина, которую вы получаете при сложении или вычитании векторов, называется результирующим вектором . Другими словами, отдельные векторы могут быть заменены результирующими — общий эффект тот же.
- Результирующий вектор
Результирующий вектор — это единственный вектор, действие которого такое же, как и у отдельных векторов, действующих вместе.
Мы можем проиллюстрировать концепцию результирующего вектора, рассмотрев две наши ситуации с использованием сил для перемещения тяжелого ящика. В первом случае (слева) вы и ваш друг прикладываете силы в одном направлении. Результирующая сила будет суммой двух ваших сил, приложенных в этом направлении. Во втором случае (справа) силы действуют в противоположных направлениях. Результирующий вектор снова будет суммой двух приложенных вами сил, однако после выбора положительного направления одна сила будет положительной, а другая отрицательной, и знак результирующей силы будет зависеть только от того, какое направление вы выбрали как положительное.Для наглядности посмотрите схемы ниже.
В первом случае (слева) вы и ваш друг прикладываете силы в одном направлении. Результирующая сила будет суммой двух ваших сил, приложенных в этом направлении. Во втором случае (справа) силы действуют в противоположных направлениях. Результирующий вектор снова будет суммой двух приложенных вами сил, однако после выбора положительного направления одна сила будет положительной, а другая отрицательной, и знак результирующей силы будет зависеть только от того, какое направление вы выбрали как положительное.Для наглядности посмотрите схемы ниже.
Силы действуют в том же направлении
(положительное направление вправо)
Силы применяются в противоположных направлениях
(положительное направление вправо)
Существует специальное имя для вектора, который имеет ту же величину, что и результирующий вектор, но направление противоположно направлению : равновесный . Если вы сложите результирующий вектор и равновесные векторы вместе, ответ всегда будет равен нулю, потому что равновесие отменяет результирующий.
- Равновесный
Равновесный вектор — это вектор, который имеет ту же величину , но направление противоположно результирующему вектору.
Если вы обратитесь к изображениям тяжелого ящика ранее, уравновешивающие силы для двух ситуаций будут выглядеть так:
КЛАССЫ: | Период 2 12 класс Исчисление и векторы: MCV4U1 07/77; Комната 2037 | Период 4 11 класс Университетская математика: MCR3U1 07/77; Комната 2026 | Период 5 12 класс Исчисление и векторы: MCV4U1 07/77; Комната 2026 |
ПРЕДСТОЯЩИЕ СОБЫТИЯ: | Обратите внимание на GC относится к Google Classroom Тест: среда, 17 февраля | Обратите внимание на GC относится к Google Classroom Тест: вторник, 16 февраля | Обратите внимание на GC относится к Google Classroom Тест: среда, 17 февраля |
Чт. | Вот примечания с дополнительными примерами ограничений. | Экспоненциальные уравнения, часть 2. HW: см. GC. | Вот примечания с дополнительными примерами ограничений. |
ср. 10 февраля | Пара предельных примеров здесь. HW: см. GC. | Экспоненциальные уравнения Часть 1. HW: см. GC. | Пара предельных примеров здесь. HW: см. GC. |
Вт. 9 февраля | Здесь еще один пример ограничения. HW: см. GC. | Обзор. HW: см. GC. | Здесь
еще один пример ограничения. HW: см. GC. |
пн. 8 февраля | Темп изменений. HW: P.29 # 4, 7, 8, 10-13, 15bc, 20, 22 | Брал HW. Упрощающие радикалы. | Темп изменений. HW: P.29 # 4, 7, 8, 10-13, 15bc, 20, 22 |
пт. 5 февраля | Наклон касательной линии. HW: см. GC | Обзор / HW: Законы экспонентов Рациональные экспоненты; HW: см. GC | Наклон касательной линии. HW: см. GC |
Чт. 4 февраля | Подробнее Обзор и рационализация знаменателей (и Нумераторы). HW: стр.9 (Упражнение
1. | Законы об обзоре и консолидации экспонентов. Вот обзор (с 10 класса). HW: см. GC | Подробнее Обзор и рационализация знаменателей (и Нумераторы). HW: стр.9 (Упражнение 1.1) # 1, 2ac, 3abdf, 4bc, 6abdf, 7; Рабочий лист / упражнение 2.8 # 5 (см. GC) |
ср. 3 февраля | Введение и ожидания от курса. HW: обзор плана курса и его организация, начало обзора. | Введение и ожидания от курса. HW: обзор плана курса и его организация, начало обзора. | Введение и ожидания от курса. HW: обзор плана курса и его организация, начало обзора. |
| 1 | Самооценка | Самооценка — MYP Grade 10–3 Pre Calculus | |
| Цель: оценка | |||
| 2 | Координатная геометрия-плоскость | Формула расстояния. | |
| Цель: По завершении урока ученик сможет рассчитать расстояние между любыми двумя точками на числовой плоскости и интерпретировать результаты. | |||
| 3 | Координата Геометрия-середина, наклон | Формула средней точки | |
| Задача: По завершении урока учащийся сможет понять формулу средней точки и использовать ее на практике. | |||
| 4 | Координатная геометрия-градиент | Градиент | |
| Цель: По завершении урока учащийся сможет вычислить градиент линии с учетом ее наклона или угла к положительному направлению оси x; или его взлет и бег. | |||
| 5 | Координатная геометрия-градиент | Формула градиента. | |
Задача: По завершении урока ученик сможет рассчитать уклон линии с учетом любых двух точек на линии, а также сможет проверить, лежат ли 3 или более точек на одной линии и какая неизвестная точка. сделаю параллельными линиями. сделаю параллельными линиями. | |||
| 6 | Координатная геометрия-прямая | Прямая. | |
| Цель: По завершении урока учащийся сможет нарисовать линию, параллельную любой оси, и прокомментировать ее градиент там, где этот градиент существует. | |||
| 7 | Координата Геометрия-наклон и т. Д. | Строки через начало координат. | |
| Задача: По завершении урока ученик сможет нарисовать линию, проходящую через начало координат формы y = mx, и прокомментировать ее градиент по сравнению с градиентами других линий через начало координат и использовать информацию для решать задачи. | |||
| 8 | Координатная геометрия-уравнение прямой | Общий вид линии и пересечения x и y. | |
| Задача: По завершении урока учащийся сможет преобразовать уравнение прямой из формы, записанной как y = mx + c, в общую форму и наоборот. | |||
| 9 | Координатная геометрия-пересечение | Форма пересечения линии с наклоном. | |
| Задача: По завершении урока учащийся сможет найти наклон и точку пересечения с учетом уравнения и с учетом наклона и точки пересечения и вывести уравнение. | |||
| 10 | Координатная геометрия — угол наклона | Точечный наклон формы прямой | |
| Цель: По завершении урока учащийся поймет, как вывести уравнение прямой линии с учетом градиента и точки на линии. | |||
| 11 | Геометрия координат — Формула двух точек | Двухточечная формула: уравнение прямой, соединяющей пару точек. | |
| Задача: По завершении урока учащийся сможет вычислить уравнение линии с учетом любых двух названных точек на линии. | |||
| 12 | Геометрия координат — форма пересечения | Форма пересечения прямой: найти уравнение при заданных x и y | |
Цель: По завершении урока учащийся получит эффективный и действенный метод расчета уравнения прямой. | |||
| 13 | Координатная геометрия — уравнения параллельных линий | Параллельные линии: определить уравнение прямой, параллельной другой | |
| Задача: По завершении урока ученик сможет решить, параллельны ли две или более прямых или нет, и решить задачи, связанные с параллельными линиями. | |||
| 14 | Геометрия с координатами — перпендикулярные линии | Перпендикулярные линии. | |
| Цель: По завершении урока ученик сможет вывести уравнение линии, учитывая, что она перпендикулярна другой указанной линии. | |||
| 15 | Одновременное использование | Одновременные уравнения | |
| Задача: По завершении урока ученик сможет решить 2 уравнения с 2 неизвестными переменными методом подстановки. | |||
| 16 | Одновременное использование | Метод исключения | |
Задача: По завершении урока ученик сможет решить 2 уравнения с 2 неизвестными переменными методом исключения. | |||
| 17 | Одновременное использование | Метод исключения часть 2 | |
| Задача: По окончании урока ученик сможет решить все типы одновременных уравнений с 2 неизвестными переменными методом исключения. | |||
| 18 | Одновременное использование | Приложения одновременных уравнений | |
| Цель: По завершении этого урока ученик сможет вывести системы уравнений из данной задачи, а затем решить эти уравнения. | |||
| 19 | Матрицы | Основные понятия — Матрицы | |
| Цель: По завершении урока учащийся ознакомится с матрицами | |||
| 20 | Матрицы | Сложение и вычитание матриц | |
| Цель: По завершении этого урока учащийся сможет определить, когда возможно сложение и вычитание матриц, и выполнить эти операции. | |||
| 21 | Матрицы | Умножение скалярных матриц | |
Задача: По завершении этого урока учащийся сможет выполнить скалярное умножение матрицы. | |||
| 22 | Матрицы | Умножение одной матрицы на другую | |
| Задача: По завершении урока учащийся сможет определить, возможно ли умножение матрицы на матрицу, предсказать порядок матрицы ответов, а затем выполнить умножение матрицы на матрицу. | |||
| 23 | Матрицы | Перевод в номерной плоскости | |
| Цель: По завершении урока ученик сможет поместить упорядоченные пары в матрицу, затем выполнить перевод путем сложения с использованием матрицы преобразования, а затем извлечь упорядоченные пары из матрицы ответов. | |||
| 24 | Матрицы | Перевод методом матричного умножения | |
| Задача: По завершении урока ученик сможет преобразовывать упорядоченные пары в элементы матрицы, умножать матрицы вместе, где это возможно, и интерпретировать матрицу ответов на числовой плоскости. | |||
| 25 | Преобразования | Специальные преобразования — отражения, вращения и увеличения. | |
| Цель: По завершении урока ученик сможет выполнять преобразования: вращать, отражать и изменять размер различных форм и / или точек, где это применимо. | |||
| 26 | Векторы | Векторы | |
| Цель: По завершении урока учащийся сможет представить вектор в матричной и схематической форме, а также сложить два вектора, используя матрицы и / или диаграмму. | |||
| 27 | Одновременные уравнения | Количество решений (2 этап) | |
| Задача: По завершении урока учащийся определит совместные, несовместимые или одинаковые системы уравнений. | |||
| 28 | Векторы | Сложение 2 векторов в 2 и 3D (этап 2) | |
| Задача: По завершении урока учащийся поймет и использует формы компонентов для векторного разрешения. | |||
| 29 | Линейные системы | Оптимальные решения (этап 2) — Векторы | |
Цель: По завершении урока ученик поймет процесс линейного программирования для поиска оптимальных решений. | |||
| 30 | Линейные системы | Линейные системы с матрицами (этап 2) | |
| Задача: По окончании урока ученик обработает матрицы, составленные из линейных систем уравнений. | |||
| 31 | Линейные системы | Рядно-эшелонная форма (2 этап) | |
| Задача: По завершении урока ученик обработает матрицы, сформированные из линейных систем уравнений, с использованием строчно-эшелонированной формы. | |||
| 32 | Алгебра-формулы | Изменение темы формулы. | |
| Задача: По завершении урока учащийся сможет перемещать местоимения по уравнению, используя все правила и операции, описанные ранее. | |||
| 33 | Алгебра-неравенства | Устранение неравенств. | |
Задача: По завершении урока учащийся поймет знаки «больше чем» и «меньше чем» и сможет выполнять простые неравенства. | |||
| 34 | Факторизация по алгебре | Упрощение простых алгебраических дробей. | |
| Цель: По завершении урока учащийся поймет, как можно упростить алгебраические дроби с помощью факторизации. | |||
| 35 | Алгебраические дроби | Упрощение алгебраических дробей с помощью законов индекса. | |
| Цель: По завершении урока учащийся сможет упростить большинство алгебраических дробей, используя различные методики. | |||
| 36 | Алгебраотрицательные индексы | Алгебраические дроби с отрицательными индексами. | |
| Цель: По завершении урока ученик сможет понять, как упростить алгебраическое дробное выражение с отрицательным индексом, а также как написать такое выражение без отрицательного индекса. | |||
| 37 | Факторизация | Факторизация алгебраических дробей, включая биномы. | |
| Цель: По завершении урока учащийся должен научиться упрощать более сложные алгебраические дроби, используя различные методы. | |||
| 38 | Алгебраические дроби-двучлены | Сокращение биномиальных множителей в алгебраических дробях. | |
| Цель: По завершении урока учащийся должен уметь разложить на множители биномы, чтобы упростить дроби. | |||
| 39 | Абсолютное значение или модуль | Упрощение абсолютных значений | |
| Цель: По завершении урока учащийся сможет упростить выражения, содержащие абсолютные значения или модуль действительных чисел. | |||
| 40 | Абсолютное значение или модуль | Решение для переменной | |
| Цель: По завершении урока учащийся сможет решать уравнения, содержащие одно абсолютное значение. | |||
| 41 | Абсолютное значение или модуль | Решение неравенств и построение графиков | |
Задача: По завершении урока учащийся сможет решить неравенства, содержащие одно абсолютное значение. | |||
| 42 | Неравенства геометрии координат | Неравенства на числовой плоскости. | |
| Задача: По завершении урока учащийся сможет вывести выражение для неравенства с учетом его графика.Студент также сможет решать некоторые задачи, используя неравенства. | |||
| 43 | Исчисление | Пределы | |
| Цель: По завершении урока ученик сможет решать задачи, используя правило предельной суммы. | |||
| 44 | Исчисление = 1-й прин | Дифференциация от первых принципов. | |
| Цель: По завершении урока ученик сможет применить формулу первых принципов (исчисление), чтобы найти градиент касательной в любой точке непрерывной кривой. | |||
| 45 | Исчисление = 1-й прин | Дифференцирование y = x в степени n. | |
Задача: По завершении урока «Исчисление» ученик сможет различать несколько выражений, в которых x возведен в степень n. | |||
| 46 | Дифференциальное исчисление, целое | Значение dy над dx — уравнения касательных и нормалей. | |
| Цель: По завершении урока математического анализа учащийся сможет применить навыки дифференцирования и алгебры, чтобы найти уравнение касательной и нормали к точке на кривой. | |||
| 47 | Дифференциальное исчисление, целое | Функция правила функции, правила произведения, правила частного. | |
| Цель: По завершении урока «Исчисление» учащийся поймет, как использовать правило цепочки, правило произведения и правило частного. | |||
| 48 | Дифференциальное исчисление, целое | Возрастающие, убывающие и стационарные функции. | |
Цель: По завершении урока учащийся поймет, как найти первую производную различных функций и использовать ее в различных ситуациях для определения возрастающих, убывающих и стационарных функций. | |||
| 49 | Исчисление | Первая производная — точки поворота и построение кривых | |
| Цель: По завершении урока «Исчисление» учащийся сможет использовать первую производную, чтобы находить и определять характер стационарных точек на кривой. | |||
| 50 | Графические полиномы | Построение графиков комплексных многочленов: квадраты без действительных корней | |
| Задача: По завершении урока учащийся сможет определить, имеет ли квадратичный корень действительный или комплексный, а затем построить график. | |||
| 51 | Графические полиномы | Общее уравнение круга: определите и изобразите уравнение | |
| Задача: По завершении урока ученик сможет решать эти типы задач. Работа с кругами также поможет студенту в теме геометрии круга, которая проверяет навыки студента в логике и рассуждении. | |||
| 52 | Графические кубические кривые | Графические кубические кривые | |
Цель: По завершении этого урока учащийся сможет построить график кубической формы с учетом ее уравнения или вывести уравнение кубической формы с учетом ее графика или другой соответствующей информации. | |||
| 53 | Уравнения абсолютных значений | Уравнения абсолютных значений | |
| Цель: По завершении этого урока учащийся сможет использовать графики с функцией абсолютного значения. Учащийся сможет построить график функции с учетом ее уравнения и уметь находить пересечение абсолютного значения функции | .|||
| 54 | Rect. Hyperbola | Прямоугольная гипербола. | |
| Задача: По завершении урока учащийся сможет проанализировать и построить график прямоугольной гиперболы и описать ее важные особенности. | |||
| 55 | Функции | Определение, домен и диапазон | |
| Цель: По завершении этого урока учащийся сможет выбирать функции из отношений, обращаясь к домену и диапазону. | |||
| 56 | Функции | Обозначения и оценки | |
Цель: По завершении урока учащийся научится понимать различные обозначения функций. | |||
| 57 | Функции | Подробнее о домене и диапазоне | |
| Цель: По завершении урока учащийся сможет описать область и диапазон, используя соответствующую систему обозначений. | |||
| 58 | Функции | Домен и диапазон графических представлений | |
| Цель: По завершении урока ученик сможет описать предметную область и диапазон, используя соответствующие обозначения набора из графических представлений. | |||
| 59 | Функции | Вычисление и построение графиков кусочных функций | |
| Цель: По завершении урока учащийся сможет оценивать и строить графики кусочных функций. | |||
| 60 | Функции | Комбинации функций | |
| Цель: По завершении урока учащийся сможет выполнять операции с функциями, работая со своими доменами. | |||
| 61 | Функции | Функциональный состав | |
Цель: По завершении урока учащийся поймет состав функций или функцию функции.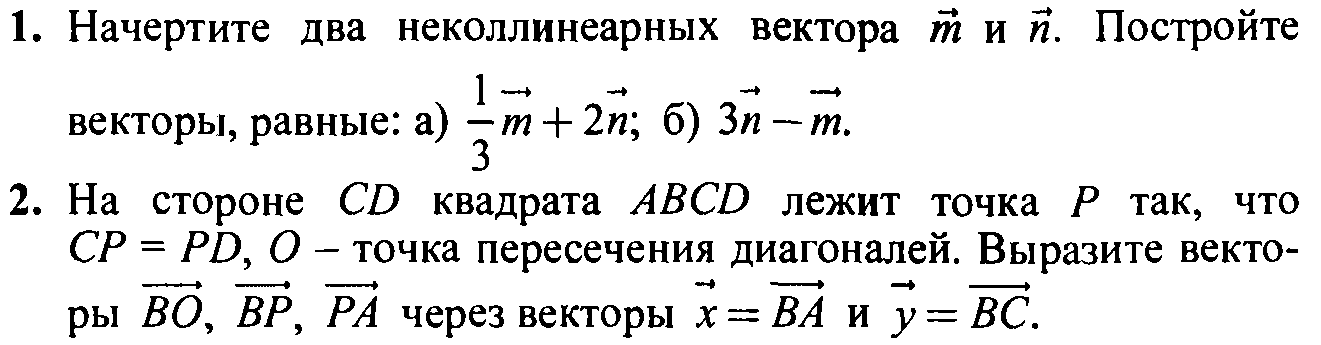 | |||
| 62 | Функции | Обратные функции | |
| Задача: По завершении урока ученик сможет находить обратные функции, правильно использовать обозначения и использовать тест горизонтальной линии. | |||
| 63 | Функции | Рациональные функции Часть 1 | |
| Цель: По завершении урока учащийся сможет работать с разделением функций и интерпретировать его на плоскости координатных чисел, показывая вертикальные и горизонтальные асимптоты. | |||
| 64 | Функции | Рациональные функции, часть 2 | |
| Цель: По завершении урока учащийся сможет использовать степень многочленов и деление многочленов для помощи в построении графиков рациональных функций на плоскости координатных чисел, показывая вертикальные, горизонтальные и наклонные асимптоты. | |||
| 65 | Функции | Сложение полиномов и т. Д. При объединении и упрощении функций (этап 2) Д. При объединении и упрощении функций (этап 2) | |
| Задача: По завершении урока учащийся получит несколько методов понимания и построения графиков с использованием алгебры. | |||
| 66 | Геометрия-парабола | Парабола: описать свойства параболы из ее уравнения | |
| Цель: По завершении урока учащийся сможет предсказать общую форму и важные характеристики параболы, а затем построить диаграмму параболы, чтобы проверить предсказания. | |||
| 67 | Функции и графики | Квадратичные многочлены вида y = ax. + bx + c. | |
| Цель: По завершении урока ученик сможет предсказать общую форму параболы и проверить предсказания, нарисовав параболу. Студент также познакомится с дискриминантом и осью. | |||
| 68 | Функции и графики | Построение полных квадратов: y = (a-x) в квадрате | |
Цель: По завершении урока учащийся сможет проанализировать кривую, а затем проверить свою работу, построив кривую. | |||
| 69 | Графические корни | Построение иррациональных корней | |
| Задача: По завершении урока ученик сможет решить любой многочлен, имеющий действительные корни, рациональные или иррациональные. | |||
| 70 | Координатная геометрия | Решить, построив график | |
| Задача: По завершении урока учащиеся будут использовать форму линии пересечения наклона, чтобы создавать графики и находить точки пересечения. | |||
| 71 | Разница 2 квадратов | Разница двух квадратов | |
| Задача: По завершении урока ученик понимает разницу между двумя квадратами и уметь распознавать факторы. | |||
| 72 | Общие факты и различия | Общий множитель и разность двух квадратов | |
Цель: По завершении урока учащийся будет знать общие факторы и распознавать разницу двух квадратов. | |||
| 73 | Квадратичные трехчлены | Квадратичные трехчлены [одночлены] — Случай 1. | |
| Цель: По завершении урока ученик поймет факторизацию квадратных трехчленных уравнений со всеми положительными членами. | |||
| 74 | Факторизация квадроциклов | Факторизация квадратичных трехчленов [одночлен] — Случай 2. | |
| Цель: По завершении урока ученик точно определит процесс, если средний член квадратичного трехчлена отрицательный. | |||
| 75 | Факторизация квадроциклов | Факторизация квадратичных трехчленов [одночлен] — Случай 3. | |
| Цель: По завершении урока учащийся получит более глубокие знания о факторизации квадратичных трехчленов и поймет, где второй член положительный, а третий — отрицательный. | |||
| 76 | Факторизация квадроциклов | Факторизация квадратичных трехчленов [одночлен] — Случай 4. | |
| Цель: По завершении урока ученик поймет, как разложить на множители все возможные типы одночленных квадратичных трехчленов и, в частности, где 2-й член и 3-й член отрицательны. | |||
| 77 | Факторизация квадроциклов | Факторизация немонических квадратичных трехчленов | |
| Цель: По завершении урока учащийся сможет разложить на множители любой квадратный трехчлен. | |||
| 78 | Факторизация квадроциклов | Факторизация немонических квадратичных трехчленов — метод Луны | |
| Цель: По завершении урока ученик выучит два метода факторизации квадратичных трехчленов, в том числе метод пересечения. | |||
| 79 | Квадратные уравнения | Введение в квадратные уравнения. | |
| Цель: По завершении урока ученик поймет простые квадратные уравнения. | |||
| 80 | Квадратные уравнения | Квадратные уравнения с факторизацией.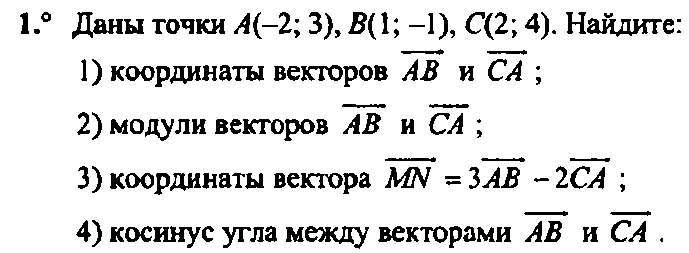 | |
| Задача: По завершении урока ученик сможет найти оба корня квадратного уравнения путем факторизации. | |||
| 81 | Квадратные уравнения | Решение квадратных уравнений. | |
| Цель: По завершении урока ученик приобретет больше уверенности в работе с квадратными уравнениями. | |||
| 82 | Квадратные уравнения | Завершение квадрата | |
| Задача: По завершении урока учащийся поймет, как заполняется квадрат. | |||
| 83 | Квадратные уравнения | Решение квадратных уравнений до квадрата | |
| Цель: По завершении урока учащийся поймет причину заполнения квадрата. | |||
| 84 | Квадратные уравнения | Квадратичная формула | |
| Задача: По завершении урока ученик выучит формулу корней квадратного уравнения. | |||
| 85 | Квадратные уравнения | Решение задач с квадратными уравнениями | |
Цель: По завершении урока учащийся сможет выразить задачу в виде квадратного уравнения, а затем решить его. | |||
| 86 | Квадратные уравнения | Графическое решение одновременных квадратных уравнений | |
| Цель: По завершении урока учащийся лучше поймет, почему квадратные уравнения имеют два решения, и сможет решать квадратные уравнения и задачи графически. | |||
| 87 | Алгебра-полиномы | Введение в многочлены | |
| Цель: По завершении урока ученик поймет всю терминологию, связанную с полиномами, и сможет судить, является ли какое-либо алгебраическое выражение полиномом или нет. | |||
| 88 | Алгебра-полиномы | Сумма, разность и произведение двух многочленов. | |
| Задача: По завершении урока ученик сможет складывать многочлены, вычитать и умножать и находить степени ответов. | |||
| 89 | Алгебра-полиномы | Полиномы и деление в столбик. | |
Цель: По завершении урока учащийся поймет процесс деления в столбик с полиномами. | |||
| 90 | Теорема об остатке | Теорема об остатке. | |
| Цель: По завершении урока ученик поймет, как работает теорема об остатке и как ее можно применить. | |||
| 91 | Теорема об остатке | Подробнее о теореме об остатке | |
| Цель: По завершении урока ученик поймет теорему об остатке и поймет, как ее можно применить для решения некоторых интересных вопросов о нахождении неизвестных коэффициентов многочленов. | |||
| 92 | Теорема о факторах | Факторная теорема | |
| Задача: По завершении урока учащийся сможет использовать теорему о факторах и определить, является ли член в форме x минус a множителем данного многочлена. | |||
| 93 | Теорема о факторах | Подробнее о теореме о факторах | |
Цель: По завершении урока ученик полностью поймет теорему о факторах и как ее можно применить для решения некоторых вопросов по нахождению неизвестных коэффициентов многочленов.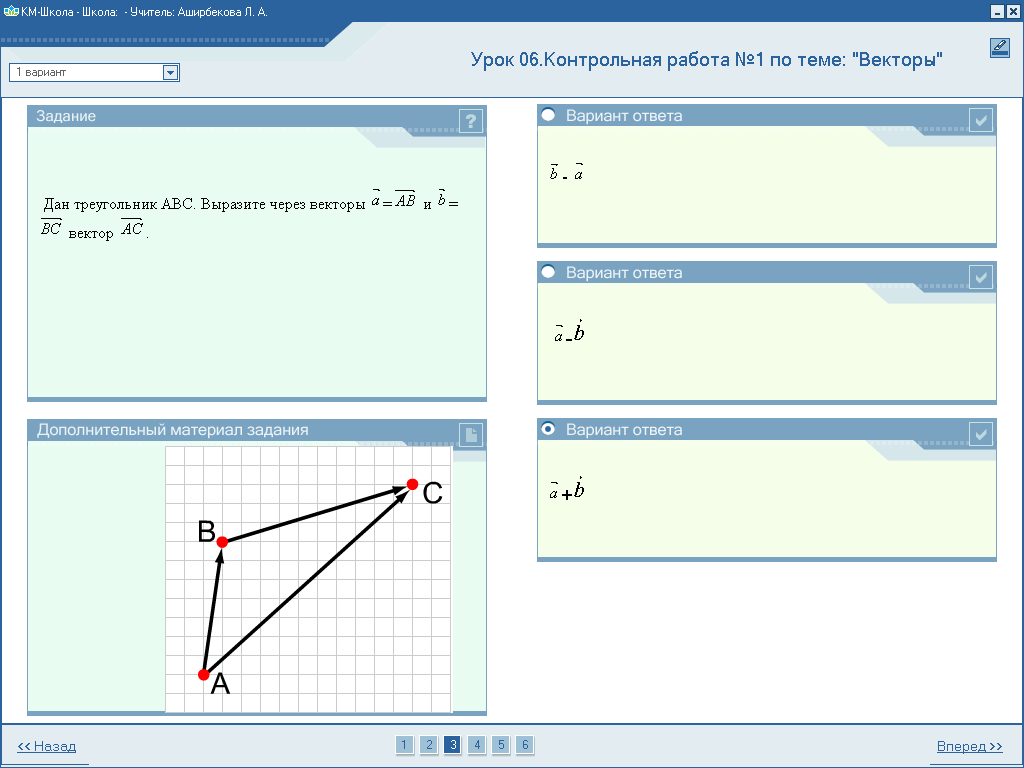 | |||
| 94 | Теорема о факторах | Полное разложение на множители с использованием теоремы о множителях | |
| Задача: По завершении урока ученик сможет разложить на множители многочлены более высокой степени, чем 2, и найти их нули. | |||
| 95 | Логарифмы-комплексные числа | Мнимые числа и стандартная форма | |
| Цель: По завершении урока ученик будет использовать форму a + bi комплексных чисел для сложения и вычитания. | |||
| 96 | Логарифмы-комплексные числа | Комплексные числа — умножение и деление | |
| Цель: По завершении урока ученик будет использовать форму a + bi комплексных чисел для умножения и деления. | |||
| 97 | Логарифмы-комплексные числа | Построение комплексных чисел и графическое представление | |
Задача: По завершении урока ученик будет использовать диаграмму аргандов, чтобы помогать в сложении и вычитании комплексных чисел.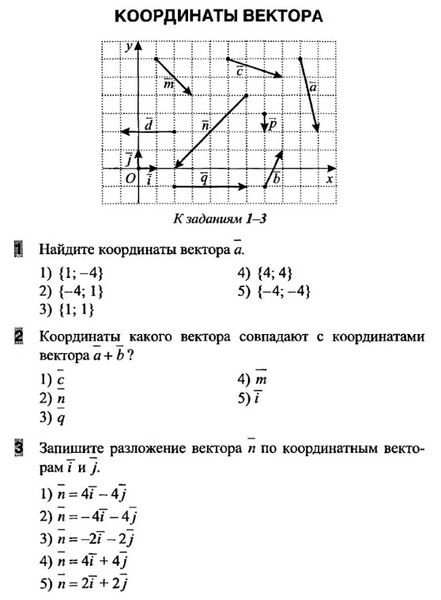 | |||
| 98 | Логарифмы-комплексные числа | Абсолютное значение | |
| Цель: По завершении урока ученик будет использовать абсолютное значение или модуль комплексных чисел | |||
| 99 | Логарифмы-комплексные числа | Тригонометрическая форма комплексного числа | |
| Задача: По завершении урока ученик напишет комплексные числа в тригонометрической или полярной форме.Это также может быть известно как модная форма. | |||
| 100 | Логарифмы-комплексные числа | Умножение и деление комплексных чисел в триггерной форме (этап 2) | |
| Задача: По завершении урока ученик будет использовать тригонометрическую форму комплексных чисел для умножения и деления. | |||
| 101 | Логарифмы-комплексные числа | Теорема ДеМуавра (этап 2) | |
Задача: По завершении урока ученик будет использовать теорему ДеМуавра, чтобы находить степени комплексных чисел в триггерной форме. | |||
| 102 | Логарифмы-комплексные числа | Корень n-й степени действительных и комплексных чисел (этап 2) | |
| Задача: По завершении урока ученик будет использовать теорему ДеМуавра, чтобы найти корни комплексных чисел в триггерной форме. | |||
| 103 | Логарифмы-комплексные числа | Основная теорема алгебры (этап 2) | |
| Цель: По завершении урока студент узнает и использует основную теорему алгебры, чтобы найти множители для многочленов с действительными коэффициентами над полем комплексных чисел. | |||
| 104 | Статистическая вероятность | Биномиальная теорема — треугольник Паскаля | |
| Цель: По завершении этого урока учащийся будет использовать треугольник Паскаля и биномиальную теорему, чтобы написать разложение биномиальных выражений в целых степенях. | |||
| 105 | Статистическая вероятность | Биномиальные вероятности с использованием биномиальной теоремы | |
| Задача: По завершении урока учащийся сможет решать определенные типы вероятностных вопросов, используя биномиальную теорему | |||
| 106 | Статистическая вероятность | Методы подсчета и упорядоченные выборки — перестановки | |
Задача: По завершении этого урока учащийся научится использовать некоторые новые методы счета, используемые для решения вероятностей. | |||
| 107 | Статистическая вероятность | Неупорядоченный выбор — комбинации | |
| Цель: По завершении урока учащийся сможет использовать формулу n c r как с калькулятором, так и без него, а также сможет использовать ее для решения вероятностных задач, в которых происходит неупорядоченный выбор. | |||
| 108 | Статистика — сгруппированные данные | Расчет среднего, режима и медианы на основе сгруппированных данных | |
| Цель: По завершении урока учащийся сможет определять центры классов, получать подсчеты частоты и определять средние и модовые значения. | |||
| 109 | Статистика с помощью калькулятора | Статистика и студенческий калькулятор | |
| Цель: По завершении урока ученик сможет использовать научный калькулятор в режиме статистики для вычисления ответов на статистические задачи. | |||
| 110 | Статистика — Дальность и разброс | Дальность как мера рассеивания | |
Задача: По завершении урока учащийся сможет определять диапазон и использовать его при принятии решений. | |||
| 111 | Статистика— Распространение | Меры распространения | |
| Цель: По завершении урока учащийся сможет найти стандартное отклонение, используя набор данных или таблицу частотного распределения и калькулятор. | |||
| 112 | Статистика — стандартное отклонение | Приложения стандартного отклонения | |
| Задача: По завершении урока ученик сможет использовать стандартное отклонение как меру отклонения от среднего значения. | |||
| 113 | Статистика — стандартное отклонение | Нормальное распределение | |
| Цель: По завершении урока учащийся сможет использовать стандартное отклонение нормального распределения, чтобы найти процентную долю баллов в пределах диапазона. | |||
| 114 | Статистика — Межквартильный размах | Меры разброса: межквартильный размах | |
| Задача: По завершении урока учащийся сможет найти верхний и нижний квартили и межквартильный размах | |||
| 115 | Статистика | Участки стебля и листьев вместе с участками коробок и усов | |
Цель: По завершении урока учащийся будет знаком со статистической лексикой, включая квартили, режимы, медианы, диапазон и представление этой информации на графике прямоугольников и усов. | |||
| 116 | Статистика | Диаграммы рассеяния | |
| Задача: По завершении урока учащийся сможет строить диаграммы рассеяния и делать из них выводы. | |||
| 117 | Тригонометрия-возвышение | Углы подъема и понижения. | |
| Цель: По завершении урока учащийся сможет определить углы впадения и углы подъема, а также взаимосвязь между ними. | |||
| 118 | Тригонометрия практическая | Тригонометрические соотношения в практических ситуациях. | |
| Задача: По завершении урока учащийся сможет использовать тригонометрические отношения для решения задач, связанных с пеленгом компаса, а также углами наклона и подъема. | |||
| 119 | Тригонометрические отношения | Использование калькулятора для определения угла с учетом тригонометрического отношения. | |
Цель: По завершении урока учащийся сможет использовать калькулятор для определения значения неизвестного угла при заданном тригонометрическом соотношении. | |||
| 120 | Тригонометрия- отношения | Используя тригонометрические соотношения, найдите угол в прямоугольном треугольнике. | |
| Задача: По завершении урока учащийся сможет найти значение неизвестного угла в прямоугольном треугольнике, учитывая длины двух сторон. | |||
| 121 | Тригонометрические-точные соотношения | Тригонометрические отношения 30., 45. и 60. — точные соотношения. | |
| Цель: По завершении урока ученик сможет найти точные отношения синуса, косинуса и тангенса для углов 30., 45 и 60 | |||
| 122 | Правило тригонометрии-косинуса | Правило косинуса для поиска неизвестной стороны. [Случай 1 SAS]. | |
| Цель: По завершении урока учащийся сможет использовать правило косинуса, чтобы найти длину неизвестной стороны треугольника, зная 2 стороны и входящий угол. | |||
| 123 | Правило тригонометрии-косинуса | Правило косинуса для нахождения неизвестного угла. [Случай 2 SSS]. [Случай 2 SSS]. | |
| Цель: По завершении урока ученик сможет найти размер неизвестного угла треугольника, используя правило косинуса, учитывая длины трех сторон. | |||
| 124 | Тригонометрия-правило синуса | Правило синуса для поиска неизвестной стороны. Дело 1. | |
| Цель: По завершении урока ученик сможет использовать правило синуса для определения длины определенной стороны, когда ученику даны размеры двух углов и одной из сторон. | |||
| 125 | Тригонометрия-правило синуса | Правило синуса для поиска неизвестного угла. Дело 2. | |
| Цель: По завершении урока учащийся сможет использовать правило синуса, чтобы найти неизвестный угол, если у него есть две стороны и угол без включения. | |||
| 126 | Тригонометрические области | Формула площади | |
Цель: По завершении урока учащийся сможет использовать формулу синуса для определения площади треугольника с учетом двух сторон и включенного угла. | |||
| 127 | Тригонометрические отношения | Обратные отношения. | |
| Задача: По завершении урока ученик сможет определить и использовать тригонометрические соотношения синуса, косинуса и тангенса, то есть косеканс, секанс и котангенс. | |||
| 128 | Дополнительные углы триггера | Дополнительные угловые результаты. | |
| Цель: По завершении урока учащийся поймет, как установить дополнительные угловые результаты для соотношений синуса и косинуса, а затем как использовать эти результаты для решения тригонометрических уравнений. | |||
| 129 | Идентификаторы триггеров | Тригонометрические идентификаторы | |
| Задача: По завершении урока учащийся сможет упростить тригонометрические выражения и решить тригонометрические уравнения, используя знание тригонометрических тождеств. | |||
| 130 | Триггер большие углы | Углы любой величины | |
Задача: По завершении урока ученик сможет найти тригонометрические значения углов любой величины, назначив углы четырем квадрантам круга. | |||
| 131 | Триггер большие углы | Тригонометрические отношения 0 °, 90 °, 180 °, 270 ° и 360 ° | |
| Цель: По завершении урока учащийся научится находить тригонометрические отношения 0, 90, 180, 270 и 360 градусов. | |||
| 132 | График синус | График тригонометрических отношений — I Синусоидальная кривая. | |
| Цель: По завершении урока ученик узнает и начертит синусоидальную кривую, исследуя изменения амплитуды и периода. | |||
| 133 | График косинус | Построение тригонометрических соотношений — II косинусная кривая. | |
| Цель: По завершении урока ученик научится распознавать и рисовать косинусоидальную кривую, исследуя изменения амплитуды и периода. | |||
| 134 | Графики кривой загара | График тригонометрических соотношений — III Касательная кривая. | |
Задача: По завершении урока ученик научится распознавать и рисовать кривую загара. | |||
| 135 | График обратных чисел | Построение тригонометрических соотношений — IV Обратные соотношения. | |
| Задача: По завершении урока ученик научится распознавать и рисовать кривые взаимных отношений: cosec, sec и cot. | |||
| 136 | Триггер большие углы | Использование одного соотношения для поиска другого. | |
| Задача: По завершении урока ученик найдет другие тригонометрические соотношения для одного триггерного соотношения и сможет работать с углами любой величины. | |||
| 137 | Триггерные уравнения | Решение тригонометрических уравнений — тип I. | |
| Задача: По завершении урока ученик будет решать простые триггерные уравнения с ограниченными областями. | |||
| 138 | Триггерные уравнения | Решение тригонометрических уравнений — Тип II. | |
Цель: По завершении урока ученик решит тригонометрические уравнения с кратными тета и ограниченными областями.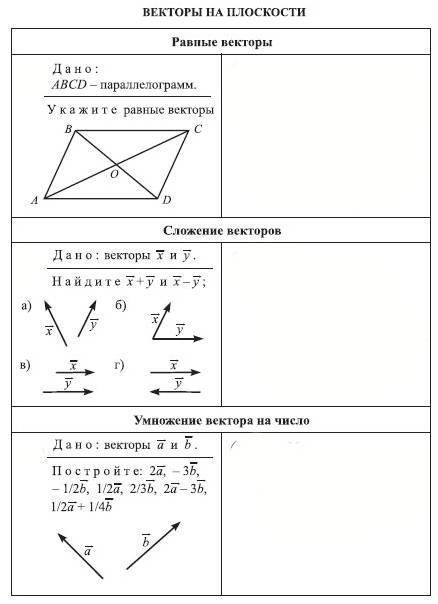 | |||
| 139 | Триггерные уравнения | Решение тригонометрических уравнений — Тип III. | |
| Задача: По завершении урока ученик решит тригонометрические уравнения с двумя тригонометрическими отношениями и ограниченными областями. | |||
| 140 | Полярные координаты | Построение полярных координат и преобразование полярных координат в прямоугольные | |
| Цель: По завершении урока ученик поймет полярную систему координат и свяжет ее с прямоугольной системой координат. | |||
| 141 | Полярные координаты | Преобразование прямоугольных координат в полярную форму | |
| Цель: По завершении урока ученик поймет полярную систему координат и представит ее в прямоугольных координатах. | |||
| 142 | Полярные координаты | Записать и обозначить точки в полярной форме с отрицательными векторами (этап 2) | |
Цель: По завершении урока ученик будет использовать отрицательные углы и отрицательные длины векторов.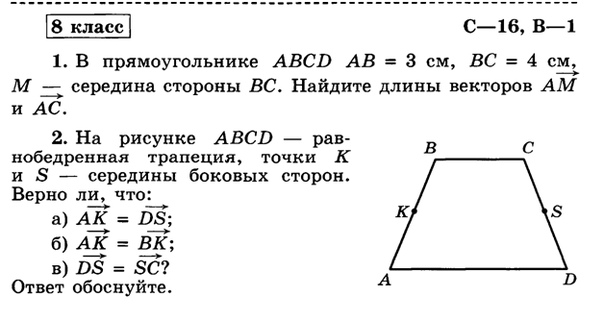 | |||
| 143 | Конические секции | Введение в конические сечения и их общее уравнение | |
| Задача: По завершении урока ученик определит коническое сечение по коэффициентам уравнения. | |||
| 144 | Конические секции | Парабола x. = 4 дня | |
| Задача: По завершении урока ученик определит фокус и направляющую для параболы, представленной в стандартной форме. | |||
| 145 | Конические секции | Круги | |
| Задача: По завершении урока учащийся определит радиус круга, указанный в стандартной форме. | |||
| 146 | Конические секции | Эллипсы | |
| Цель: По завершении урока ученик определит фокус, вершины и оси эллипса. | |||
| 147 | Конические секции | Гипербола | |
Задача: По завершении урока ученик определит фокус, вершины, оси и асимптоты гиперболы. | |||
| 148 | Последовательности и серии | Общие последовательности. | |
| Задача: По завершении урока учащийся сможет составить формулу на основе заданного числового шаблона, а затем найти конкретные члены этой последовательности, используя формулу. | |||
| 149 | Последовательности и серии | Нахождение Tn по Sn. | |
| Задача: По завершении урока ученик поймет, что сумма n членов ряда минус сумма n минус один член даст n-й член. | |||
| 150 | Арифметическая прогрессия | Арифметическая прогрессия | |
| Цель: По завершении урока учащийся сможет проверить, является ли данная последовательность арифметической прогрессией или нет, и сможет найти формулу для n-го термина, найти любой термин в A.П. и решить проблемы, связанные с этими понятиями. | |||
| 151 | Арифметическая прогрессия | Определение позиции термина в A. P. P. | |
| Задача: По завершении урока ученик сможет решить многие задачи, связанные с нахождением членов арифметической прогрессии. | |||
| 152 | Арифметическая прогрессия | Дайте два члена A.P., найдите последовательность. | |
| Задача: По завершении урока ученик сможет найти любой член арифметической прогрессии, если ему даны два члена | |||
| 153 | Арифметическая прогрессия | Средние арифметические | |
| Задача: По завершении урока учащийся сможет произвести арифметическую прогрессию между двумя заданными терминами.Это может включать поиск одного, двух или даже большего количества средних арифметических. | |||
| 154 | Арифметическая прогрессия | Сумма n членов А.П. | |
Цель: По завершении урока ученик поймет формулы для суммы арифметической прогрессии и научится их использовать при решении задач. | |||
| 155 | Геометрическая прогрессия | Геометрическая прогрессия. | |
| Задача: По завершении урока ученик сможет проверить, является ли данная последовательность геометрической прогрессией или нет, и сможет найти формулу для n-го термина, найти любой термин в G.П. и решить проблемы, связанные с этими понятиями. | |||
| 156 | Геометрическая прогрессия | Определение позиции термина в G.P. | |
| Цель: По завершении урока ученик поймет, как находить термины в геометрической прогрессии и как применять к ним различные типы задач. | |||
| 157 | Геометрическая прогрессия | Дайте два члена G.P., найдите последовательность. | |
| Цель: По завершении этого урока ученик сможет решить все задачи, связанные с нахождением общего отношения геометрической прогрессии. | |||
| 158 | Последовательности и ряды — геометрические средства | Средние геометрические. | |
| Задача: По завершении урока ученик сможет построить геометрическую прогрессию между двумя заданными семестрами. Это может включать поиск одного, двух или даже большего числа геометрических средних. | |||
| 159 | Последовательности и сумма серий gp | Сумма n членов G.P. | |
| Цель: По завершении урока ученик поймет формулы и научится использовать их для решения задач в суммировании геометрической прогрессии (G.П). | |||
| 160 | Последовательности и обозначение серий-сигма | Сигма-нотация | |
| Цель: По завершении проекта G.P. На уроке учащийся познакомится с сигма-нотацией и принципами ее действия. | |||
| 161 | Последовательности и серия-сумма-бесконечность | Ограничение суммы до бесконечности. | |
Цель: По завершении урока ученик выучит формулу предельной суммы G. Leave a Reply
| |||

 11 февраля
11 февраля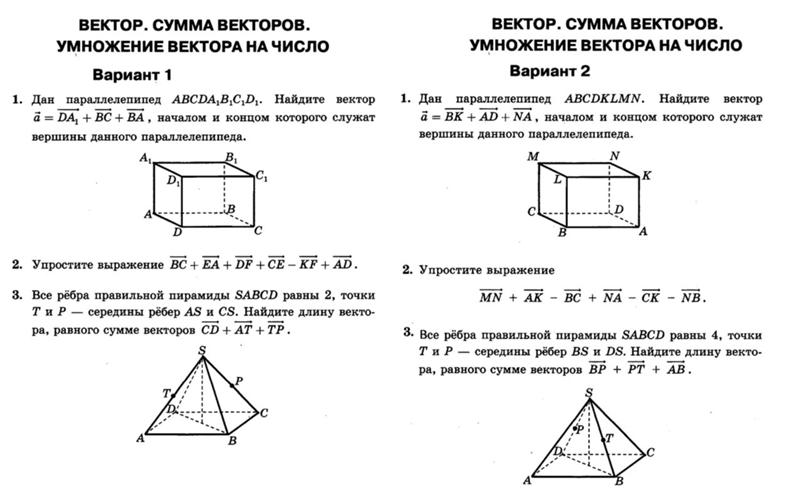
 1) # 1, 2ac, 3abdf, 4bc, 6abdf, 7; Рабочий лист / упражнение 2.8 # 5 (см. GC)
1) # 1, 2ac, 3abdf, 4bc, 6abdf, 7; Рабочий лист / упражнение 2.8 # 5 (см. GC)