Контрольная работа по теме «Скалярное произведение. Движения»
Просмотр
содержимого документа
Г-11 К/р № 2 «Скалярное произведение. Движения»
Вариант 1
- Даны векторы , = -5 + = — -2 + . Найдите : а) ∙ ; б) ( + ) ∙ 2 ; в) .
-
Даны точки А(5; -9; 6), В(-3; 4; -7), С(4; 0; -2). Запишите координаты точки, симметричной: а) точке В относительно начала координат; б) точке С относительно оси ОХ; в) точке А относительно плоскости ХОZ.

- Даны точки А(1; 3; 0), В(2; 3; -1), С(1; 2; -1), Е(4; 0; 1) . Найдите угол между прямыми АС и ВЕ .
Вариант 2
- Найдите угол между прямыми АВ и CD, если А(1; 1; 0), В(3; -1; 2), С(1; -1; 2) , D(0; 1; 0).
- Точка А симметрична точке В(6; 3; -2) относительно оси ОУ, точка С симметрична точке А относительно плоскости ХОZ. Найдите расстояние между точками А и С.
- Дан куб АВСDA1B1C1D1. Найдите угол между прямыми АСи DС1 используя метод координат.
Вариант 3
-
Найдите угол между прямыми АВ и CD, если А(3; -1; 3), В(3; -2; 2), С(2; 2; 3) , D(1; 2; 2).

- Точка В симметрична точке А(-5; -1; 3) относительно плоскости ХОУ, точка С симметрична точке В относительно оси ОZ. Найдите расстояние между точками В и С.
-
Дан куб АВСDA1B1C1D1. Найдите угол между прямыми АС1 и ВМ, где М-середина ребра DD
Контрольная работа «Решение треугольников. Скалярное произведение векторов» 9 класс
Контрольная работа по теме «Решение треугольников. Скалярное произведение
векторов»
Вариант 1.
1. Найдите скалярное произведение векторов
⃗а {2; -3 } , ⃗в { 4, -8 } ⃗а {3; -4 } , ⃗в { 5, -6 }
2. Будут ли векторы перпендикулярны?
⃗а {0,5; -2 } , ⃗в { -2, -0,5 } ⃗а {4; -0,5 } , ⃗в { -1, 8 }
3. В равнобедренном треугольнике боковая сторона равна
В равнобедренном треугольнике боковая сторона равна
8 см 9 см,
а угол при вершине треугольника
30
0
60
0
.
Найдите площадь треугольника.
4. Определите вид треугольника ( тупоугольный, остроугольный, прямоугольный), стороны
которого равны
13, 12 и 5 см 25, 20 и 15см.
5. Найдите значение выражения
√
3 соs 150
0
√2 sin 150
0
6. Найдите косинус угла между векторами
с ⃗ {1; 0 } и р⃗{ 0; 0,5 } х⃗{ 1, 7} и а⃗{ -0,5; 0,5}
7. Сторона треугольника равна 26 см ( 21см),а две другие образуют между собой угол
Сторона треугольника равна 26 см ( 21см),а две другие образуют между собой угол
60
0
(120
0 )
и относятся как 8 : 3 (5 : 3) .
Найдите периметр треугольника.
Контрольная работа по теме «Решение треугольников. Скалярное произведение
векторов»
Вариант 1. Вариант 2.
1. Найдите скалярное произведение векторов
⃗а {2; -3 } , ⃗в { 4, -8 } ⃗а {3; -4 } , ⃗в { 5, -6 }
2. Будут ли векторы перпендикулярны?
⃗а {0,5; -2 } , ⃗в { -2, -0,5 } ⃗а {4; -0,5 } , ⃗в { -1, 8 }
3. В равнобедренном треугольнике боковая сторона равна
8 см 9 см,
а угол при вершине треугольника
30
0
60
0
.
Найдите площадь треугольника.
4. Определите вид треугольника ( тупоугольный, остроугольный, прямоугольный), стороны
которого равны
13, 12 и 5 см 25, 20 и 15см.
5. Найдите значение выражения
√
3 соs 150
0
√2 sin 150
0
6. Найдите косинус угла между векторами
с ⃗ {1; 0 } и р⃗{ 0; 0,5 } х⃗{ 1, 7} и а⃗{ -0,5; 0,5}
7. Сторона треугольника равна 26 см ( 21см), а две другие образуют между собой угол
60
0
(120
0 )
и относятся как 8 : 3 (5 : 3) .
Найдите периметр треугольника.
Контрольная работа по геометрии в 11 классе «Метод координат в пространстве»
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми А D
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 1.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1.
 Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Найдите угол между прямыми А D1 и ВМ, где М – середина ребра D D1.
Контрольная работа
по теме: «Метод координат в пространстве»
Вариант 2.
Вычислите скалярное произведение векторов и , если =, , 60o,
Дан куб ABCDA1B1C1D1. Найдите угол между прямыми АС и D C1..
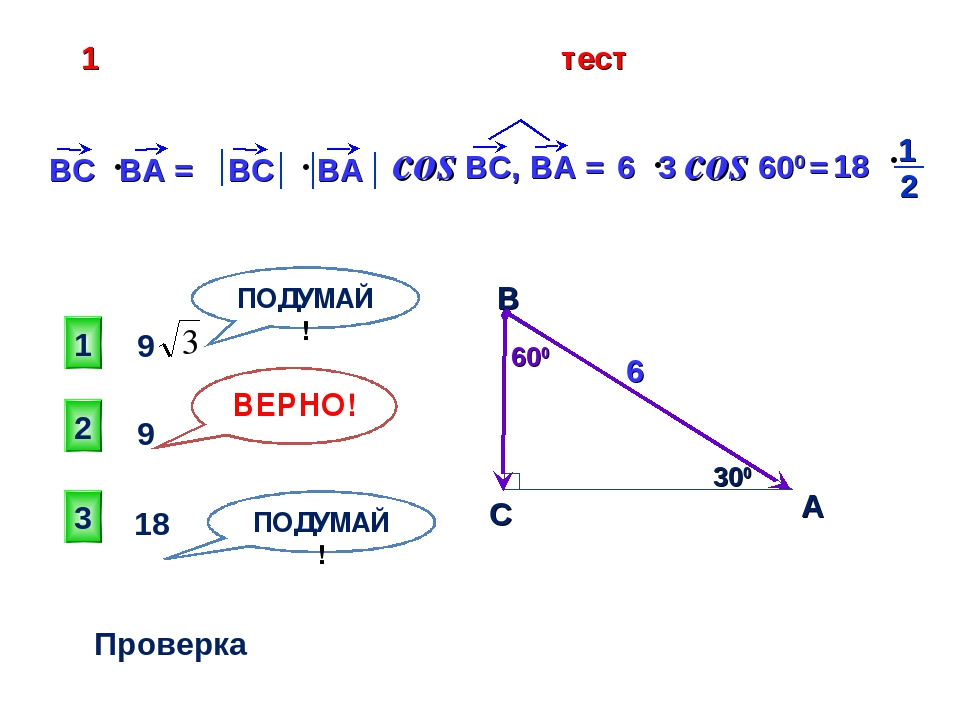
«Соотношения между сторонами и углами треугольника. Скалярное произведение векторов».
Содержимое публикации
Контрольная работа в 9 классе по теме: «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов». | |
3. 4.ЧетырехугольникABCD задан координатами своих вершин A(-1; 1), B(3; 3), C( 2; -2), D(-2; -1). Найдите косинус угла А | 3. ЧетырехугольникMNKP задан координатами своих вершин M( 5; -3), N(1; 2), K( 4; 4), P(6; 1). Найдите косинус угла М |
Вам также может понравиться:
Конкурсы 94 работы
Конкурсы 28 работ
и получите документ БЕСПЛАТНО! Подробнее
Если вам понравилась статья, лучший способ сказать cпасибо — это поделиться ссылкой со своими друзьями в социальных сетях 🙂
Также вас может заинтересовать
Контрольная работа №2 Соотношения между сторонами и углами треугольника.
 Скалярное произведение векторов
Скалярное произведение векторов
9 «а»
Контрольная работа №2
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.
Вариант 1
А1. В треугольнике АВС . Какая из сторон треугольника наибольшая, какая – наименьшая?
А2. В треугольнике АВС АВ = 12 см, АС = 6,5 см. Найдите его площадь.
А3. Найдите скалярное произведение векторов .
А4. Решите систему уравнений: а). б).
_______________________________________________________________
В1. Даны четыре точки А(1; 1), В(2; 3), С(0; 4), D(-1; 2). Докажите, что четырехугольник АВСD – прямоугольник.
В2. В треугольнике даны две стороны a = 10, b = 8
В3. Не выполняя построения, найдите координаты точек пересечения параболы и прямой .
________________________________________________________________
C1. В треугольнике АВС — тупой. АВ = 10, АС = 20. Площадь треугольника равна 96. Найдите медиану треугольника ВМ.
В треугольнике АВС — тупой. АВ = 10, АС = 20. Площадь треугольника равна 96. Найдите медиану треугольника ВМ.
Нормы оценок: «3» – 3А, «4» – 2А+1В, «5» – 2А+2В или 2А+1В+1С.
9 «а»
Контрольная работа №2
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.
А1. В треугольнике АВС АВ = 13 см, ВС = 9 см, АС = 15 см . Какой из углов треугольника наибольший, какой – наименьшаий?
А2. В треугольнике АВС АВ = 18 см, АС = 8,5 см. Найдите его площадь.
А3. Найдите скалярное произведение векторов .
А4. Решите систему уравнений:
а). б).
_______________________________________________________________
В1. Даны четыре точки А(0; 0), В(1; 1), С(0; 2), D(-1; 1). Докажите, что четырехугольник АВСD – квадрат.
В2. В треугольнике даны две стороны a = 6, b = 8 и противолежащий стороне а угол α = 300. Найдите остальные два угла и третью сторону.
В3. Не выполняя построения, найдите координаты точек пересечения параболы и прямой .
________________________________________________________________
C1. В треугольнике АВС — тупой. АВ = 10, АС = 20. Площадь треугольника равна 96. Найдите медиану треугольника ВМ.
Нормы оценок: «3» – 3А, «4» – 3А+1В, «5» – 2А+2В или 2А+1В+1С.
Контрольная работа по геометрии 11 класс Скалярное произведение
Контрольная работа № 2 по теме « Скалярное произведение векторов». Г – 11.
Вариант 1
№ 1. Даны векторы a и b, причем a =6i- 8k, b=1, ( a b ) = 600. Найти:
а) a ∙b ; б) значение m, при котором векторы a и c (4;1;m) перпендикулярны.
№ 2. Найдите угол между прямыми AB и СD, если A(3, — 1, 3), B(3, – 2, 2), C (2, 2, 3) и D (1, 2, 2).
№ 3. АВСDA1B1C1D1 – куб, DM = MD1. Найти угол между прямыми AD1 и BM.

Контрольная работа № 2 по теме « Скалярное произведение векторов». Г – 11.
Вариант 2
№ 1. Даны векторы a и b, причем a =4j- 3k, b=2, ( a b ) = 450. Найти:
а) a ∙b ; б) значение m, при котором векторы a и c {2;m;8} перпендикулярны.
№ 2. Найдите угол между прямыми AB и СD, если A(1, 1, 2), B(0, 1, 1), C(2, — 2, 2) и D (2, — 3, 1).
№ 3. АВСDA1B1C1D1 – куб. Найти угол между прямыми AB1 и A1D.
Контрольная работа № 2 по теме « Скалярное произведение векторов». Г – 11.
Вариант 3
№ 1. Найдите скалярное произведение a ∙ b, если a=3, b=14, a b= 60˚.
№ 2. Вычислите скалярное произведение векторов a ∙ b, если a4;-2;3 , b-1; -2; 5. Найдите
значение n, при котором векторы a и c {1, n, 5} перпендикулярны.
№ 3. Вычислите угол между прямыми АВ и CD, если А(3; 1; 0), С( 0; 2; 0 ), В(0; 0; 22 ), D(3; 1; 22 ).
Контрольная работа № 2 по теме « Скалярное произведение векторов». Г – 11.
Вариант 4
№ 1. Найдите скалярное произведение a ∙ b, если a=8, b=5, a b= 150˚.
№ 2. Вычислите скалярное произведение векторов a ∙ b, если a2;-1;3 , b-2; 2; 3. Найдите
значение m, при котором векторы a и c {-1, m, 5} перпендикулярны.
№ 3. Вычислите угол между прямыми АВ и CD, если А(6; -4; 8), С(12 ; -6 ; 4), В(8; -2; 4), D(14;-6; 2).
Приложенные файлы
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов
- Подробности
- Категория: Контрольные работы по геометрии. 9 класс
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ
9 КЛАСС
ТЕМА: СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ВАРИАНТ 1
1. Упростите выражение
Упростите выражение
Ответ: 1.
2. В треугольнике АВС угол А = α, угол В = β, АВ = с. Найдите площадь треугольника и радиус окружности, описанной около него.
Ответ:
3. В параллелограмме ABCD даны стороны АВ = 4 см, AD = 5√2 см и угол А = 45°. Найдите диагонали параллелограмма и его площадь.
Ответ: АС = √106 см, BD = √26 см и S = 20 см2.
4. Найдите координаты вектора
если
а угол между вектором
и положительным направлением оси абсцисс острый.
Ответ:
5. Вычислите скалярное произведение векторов
Ответ: −108.
ВАРИАНТ 2
1. Упростите выражение
Ответ: −1.
2. В треугольнике АВС угол А = α, угол В = β, ВС = а. Найдите площадь треугольника и радиус окружности, описанной около него.
Ответ:
3. В параллелограмме ABCD даны стороны АВ = 8 см, AD = 3√3 см и угол А = 60°. Найдите диагонали параллелограмма и его площадь.
В параллелограмме ABCD даны стороны АВ = 8 см, AD = 3√3 см и угол А = 60°. Найдите диагонали параллелограмма и его площадь.
Ответ: АС = √163 см, BD = √19 см и S = 36 см2.
4. Найдите координаты вектора
если
а угол между вектором
и положительным направлением оси ординат тупой.
Ответ:
5. Вычислите скалярное произведение векторов
Ответ: −33.
- < Назад
- Вперёд >
12.3: Точечное произведение — математика LibreTexts
Если мы прикладываем силу к объекту так, что объект перемещается, мы говорим, что работа выполняется за счет силы. Ранее мы рассматривали постоянную силу и предполагали, что сила приложена в направлении движения объекта. В этих условиях работа может быть выражена как произведение силы, действующей на объект, и расстояния, на которое объект перемещается. Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами.
Однако в этой главе мы увидели, что и сила, и движение объекта могут быть представлены векторами.
В этом разделе мы разрабатываем операцию, называемую скалярным произведением, которая позволяет нам вычислять работу в случае, когда вектор силы и вектор движения имеют разные направления. Точечный продукт по существу говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, встречаются ли два вектора под прямым углом.
Точечное произведение и его свойства
Мы уже научились складывать и вычитать векторы. В этой главе мы исследуем два типа умножения векторов. Первый тип умножения векторов называется скалярным произведением на основе обозначений, которые мы используем для него, и определяется следующим образом:
Определение: скалярное произведение
Точечное произведение векторов \ (\ vecs {u} = ⟨u_1, u_2, u_3⟩ \) и \ (\ vecs {v} = ⟨v_1, v_2, v_3⟩ \) дается как сумма изделий из комплектующих
\ [\ vecs {u} ⋅ \ vecs {v} = u_1v_1 + u_2v_2 + u_3v_3. \]
\]
Обратите внимание, что если \ (u \) и \ (v \) — двумерные векторы, мы вычисляем скалярное произведение аналогичным образом. Таким образом, если \ (\ vecs {u} = ⟨u_1, u_2⟩ \) и \ (\ vecs {v} = ⟨v_1, v_2⟩, \), то
\ [\ vecs {u} ⋅ \ vecs {v} = u_1v_1 + u_2v_2. \]
Когда два вектора объединяются при сложении или вычитании, результатом является вектор. Когда два вектора объединяются с использованием скалярного произведения, результатом является скаляр. По этой причине скалярное произведение часто называют скалярным произведением . Его также можно назвать внутренним продуктом .
Пример \ (\ PageIndex {1} \): вычисление скалярных произведений
- Найдите скалярное произведение \ (\ vecs {u} = ⟨3,5,2⟩ \) и \ (\ vecs {v} = ⟨− 1,3,0⟩ \).
- Найдите скалярное произведение \ (\ vecs {p} = 10 \ hat {\ textbf i} −4 \ hat {\ textbf j} +7 \ hat {\ textbf k} \) и \ (\ vecs {q} = −2 \ hat {\ textbf i} + \ hat {\ textbf j} +6 \ hat {\ textbf k}.
 \)
\)
Решение :
а. Подставьте компоненты вектора в формулу для скалярного произведения:
\ [\ begin {align *} \ vecs {u} ⋅ \ vecs {v} & = u_1v_1 + u_2v_2 + u_3v_3 \\ [4pt] & = 3 (−1) +5 (3) +2 (0) \ \ [4pt] & = — 3 + 15 + 0 \\ [4pt] & = 12.\ end {align *} \]
г. Вычисления такие же, если векторы записаны с использованием стандартных единичных векторов. У нас все еще есть три компонента для каждого вектора, которые нужно подставить в формулу для скалярного произведения:
\ [\ begin {align *} \ vecs {p} ⋅ \ vecs {q} & = u_1v_1 + u_2v_2 + u_3v_3 \\ [4pt] & = 10 (−2) + (- 4) (1) + (7 ) (6) \\ [4pt] & = — 20−4 + 42 \\ [4pt] & = 18. \ End {align *} \]
Упражнение \ (\ PageIndex {1} \)
Найдите \ (\ vecs {u} ⋅ \ vecs {v} \), где \ (\ vecs {u} = ⟨2,9, −1⟩ \) и \ (\ vecs {v} = ⟨− 3, 1, −4⟩.\)
- Подсказка
Умножьте соответствующие компоненты, а затем сложите их произведения.

- Ответ
\ (7 \)
Подобно сложению и вычитанию векторов, скалярное произведение имеет несколько алгебраических свойств. Мы докажем три из этих свойств, а остальные оставим в качестве упражнений.
Свойства точечного произведения
Пусть \ (\ vecs {u} \), \ (\ vecs {v} \) и \ (\ vecs {w} \) — векторы, а \ (c \) — скаляр.2 \]
Проба
Пусть \ (\ vecs {u} = ⟨u_1, u_2, u_3⟩ \) и \ (\ vecs {v} = ⟨v_1, v_2, v_3⟩. \) Тогда
\ [\ begin {align *} \ vecs {u} ⋅ \ vecs {v} & = ⟨u_1, u_2, u_3⟩⋅⟨v_1, v_2, v_3⟩ \\ [4pt] & = u_1v_1 + u_2v_2 + u_3v_3 \ \ [4pt] & = v_1u_1 + v_2u_2 + v_3u_3 \\ [4pt] & = ⟨v_1, v_2, v_3⟩⋅⟨u_1, u_2, u_3⟩ \\ [4pt] & = \ vecs {v} ⋅ \ vecs {u }. \ end {align *} \]
Ассоциативное свойство выглядит как ассоциативное свойство для умножения действительных чисел, но обратите внимание на разницу между скалярными и векторными объектами:
\ [\ begin {align *} c (\ vecs {u} ⋅ \ vecs {v}) & = c (u_1v_1 + u_2v_2 + u_3v_3) \\ [4pt] & = c (u_1v_1) + c (u_2v_2) + c (u_3v_3) \\ [4pt] & = (cu_1) v_1 + (cu_2) v_2 + (cu_3) v_3 \\ [4pt] & = ⟨cu_1, cu_2, cu_3⟩⋅⟨v_1, v_2, v_3⟩ \\ [4pt] & = c⟨u_1, u_2, u_3⟩⋅⟨v_1, v_2, v_3⟩ \\ [4pt] & = (c \ vecs {u}) ⋅ \ vecs {v}. 2 \)
2 \)
Решение
а.Обратите внимание, что это выражение запрашивает скалярное кратное \ (\ vecs {c} \) на \ (\ vecs {a} ⋅ \ vecs {b} \):
\ [\ begin {align *} (\ vecs {a} ⋅ \ vecs {b}) \ vecs {c} & = (⟨1,2, −3⟩⋅⟨0,2,4⟩) ⟨5, −1,3⟩ \\ [4pt] & = (1 (0) +2 (2) + (- 3) (4)) ⟨5, −1,3⟩ \\ [4pt] & = — 8⟨5 , −1,3⟩ \\ [4pt] & = ⟨− 40,8, −24⟩. \ End {align *} \]
г. Это выражение является скалярным произведением вектора \ (\ vecs {a} \) и скалярного кратного 2 \ (\ vecs {c} \):
\ [\ begin {align *} \ vecs {a} ⋅ (2 \ vecs {c}) & = 2 (\ vecs {a} ⋅ \ vecs {c}) \\ [4pt] & = 2 (⟨1 , 2, −3⟩⋅⟨5, −1,3⟩) \\ [4pt] & = 2 (1 (5) +2 (−1) + (- 3) (3)) \\ [4pt] & = 2 (−6) = — 12.2 = 53 \)
Использование точечного произведения для определения угла между двумя векторами
Когда два ненулевых вектора помещаются в стандартное положение, будь то в двух измерениях или в трех измерениях, они образуют угол между ними (рисунок \ (\ PageIndex {1} \)). Точечное произведение позволяет найти меру этого угла. Это свойство является результатом того факта, что мы можем выразить скалярное произведение через косинус угла, образованного двумя векторами.
Точечное произведение позволяет найти меру этого угла. Это свойство является результатом того факта, что мы можем выразить скалярное произведение через косинус угла, образованного двумя векторами.
Оценка скалярного произведения
Скалярное произведение двух векторов — это произведение величины каждого вектора и косинуса угла между ними:
\ [\ vecs {u} ⋅ \ vecs {v} = ‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ. \ label {evaldot} \]
Проба
Поместите векторы \ (\ vecs {u} \) и \ (\ vecs {v} \) в стандартное положение и рассмотрите вектор \ (\ vecs {v} — \ vecs {u} \) (Рисунок \ (\ PageIndex {2} \)). Эти три вектора образуют треугольник с длинами сторон \ (‖ \ vecs {u} ‖, ‖ \ vecs {v} ‖ \) и \ (‖ \ vecs {v} — \ vecs {u} ‖ \).2−2‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ \\ [4pt] −2 \ vecs {u} ⋅ \ vecs {v} & = — 2‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ \\ [4pt] \ vecs {u} ⋅ \ vecs {v} & = ‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ. \ end {align *} \]
\ end {align *} \]
□
Мы можем использовать форму скалярного произведения в уравнении \ ref {evaldot}, чтобы найти меру угла между двумя ненулевыми векторами, переставив уравнение \ ref {evaldot} для определения косинуса угла:
\ [\ cos θ = \ dfrac {\ vecs {u} ⋅ \ vecs {v}} {‖ \ vecs {u} ‖‖ \ vecs {v} ‖}. \ label {dot2} \]
Используя это уравнение, мы можем найти косинус угла между двумя ненулевыми векторами.Поскольку мы рассматриваем наименьший угол между векторами, мы предполагаем \ (0 ° ≤θ≤180 ° \) (или \ (0≤θ≤π \), если мы работаем в радианах). Обратный косинус уникален в этом диапазоне, поэтому мы можем определить меру угла \ (θ \).
Пример \ (\ PageIndex {3} \): определение угла между двумя векторами
Найдите угол между каждой парой векторов.
- \ (\ mathbf {\ hat i} + \ mathbf {\ hat j} + \ mathbf {\ hat k} \) и \ (2 \ mathbf {\ hat i} — \ mathbf {\ hat j} — 3 \ mathbf {\ hat k} \)
- \ (⟨2,5,6⟩ \) и \ (⟨− 2, −4,4⟩ \)
Решение
а.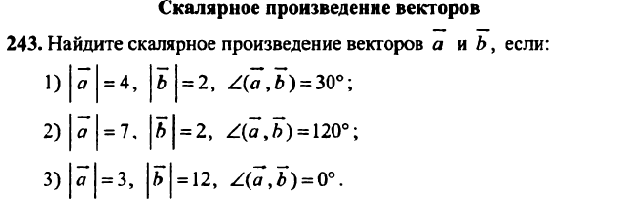 2}} \\ [4pt] & = \ dfrac {0} {\ sqrt {65} \ sqrt {36}} = 0. \ end {align *} \]
2}} \\ [4pt] & = \ dfrac {0} {\ sqrt {65} \ sqrt {36}} = 0. \ end {align *} \]
Теперь \ (\ cos θ = 0 \) и \ (0≤θ≤π \), поэтому \ (θ = π / 2 \).
Упражнение \ (\ PageIndex {3} \)
Найдите угол в радианах, образованный векторами \ (\ vecs {a} = ⟨1,2,0⟩ \) и \ (\ vecs {b} = ⟨2,4,1⟩ \). Округлить до ближайшей сотой.
- Подсказка
Используйте уравнение \ ref {dot2}.
- Ответ
\ (θ≈0.22 \) рад
Угол между двумя векторами может быть острым \ ((0 <\ cos θ <1), \) тупым \ ((- 1 <\ cos θ <0) \) или прямым \ ((\ cos θ = −1 ) \). Если \ (\ cos θ = 1 \), то оба вектора имеют одинаковое направление. Если \ (\ cos θ = 0 \), то векторы, помещенные в стандартное положение, образуют прямой угол (рисунок \ (\ PageIndex {3} \)). Мы можем формализовать этот результат в виде теоремы об ортогональных (перпендикулярных) векторах.
Ортогональные векторы
Ненулевые векторы \ (\ vecs {u} \) и \ (\ vecs {v} \) являются ортогональными векторами тогда и только тогда, когда \ (\ vecs {u} ⋅ \ vecs {v} = 0. \)
Проба
Пусть \ (\ vecs {u} \) и \ (\ vecs {v} \) ненулевые векторы, и пусть \ (θ \) обозначает угол между ними.Сначала предположим, что \ (\ vecs {u} ⋅ \ vecs {v} = 0. \), Тогда
\ [‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ = 0. \]
Однако \ (‖ \ vecs {u} ‖ ≠ 0 \) и \ (‖ \ vecs {v} ‖ ≠ 0, \), поэтому мы должны иметь \ (\ cos θ = 0 \). Следовательно, \ (θ = 90 ° \), и векторы ортогональны.
Теперь предположим, что \ (\ vecs {u} \) и \ (\ vecs {v} \) ортогональны. Тогда \ (θ = 90 ° \) и имеем
Тогда \ (θ = 90 ° \) и имеем
\ [\ begin {align *} \ vecs {u} ⋅ \ vecs {v} & = ‖ \ vecs {u} ‖‖ \ vecs {v} ‖ \ cos θ \\ [4pt] & = ‖ \ vecs { u} ‖‖ \ vecs {v} ‖ \ cos 90 ° \\ [4pt] & = ‖ \ vecs {u} ‖‖ \ vecs {v} ‖ (0) \\ [4pt] & = 0.\ end {align *} \]
□
Термины ортогональный, перпендикулярный, и нормальный каждый указывают, что математические объекты пересекаются под прямым углом. Использование каждого термина определяется главным образом его контекстом. Мы говорим, что векторы ортогональны, а прямые перпендикулярны. Термин нормальный используется чаще всего при измерении угла, образованного плоскостью или другой поверхностью.
Пример \ (\ PageIndex {4} \): определение ортогональных векторов
Определите, являются ли \ (\ vecs {p} = ⟨1,0,5⟩ \) и \ (\ vecs {q} = ⟨10,3, −2⟩ \) ортогональными векторами.
Решение
Используя определение, нам нужно только проверить скалярное произведение векторов:
\ [\ vecs {p} ⋅ \ vecs {q} = 1 (10) + (0) (3) + (5) (- 2) = 10 + 0−10 = 0. \ nonumber \]
\ nonumber \]
Поскольку \ (\ vecs {p} ⋅ \ vecs {q} = 0, \) векторы ортогональны (рисунок \ (\ PageIndex {4} \)).
Рисунок \ (\ PageIndex {4} \): Векторы \ (\ vecs {p} \) и \ (\ vecs {q} \) образуют прямой угол, когда их начальные точки выровнены.Упражнение \ (\ PageIndex {4} \)
Для какого значения \ (x \) \ (\ vecs {p} = ⟨2,8, −1⟩ \) ортогонально \ (\ vecs {q} = ⟨x, −1,2⟩ \)?
- Подсказка
Векторы \ (\ vecs {p} \) и \ (\ vecs {q} \) ортогональны тогда и только тогда, когда \ (\ vecs {p} ⋅ \ vecs {q} = 0 \).
- Ответ
\ (х = 5 \)
Пример \ (\ PageIndex {5} \): измерение угла, образованного двумя векторами
Пусть \ (\ vecs {v} = ⟨2,3,3⟩. \) Найдите меры углов, образованных следующими векторами.
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat i} \)
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat j} \)
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat k} \)
Решение
а. 2} \ sqrt {1}} = \ dfrac {3} {\ sqrt {22}} \\ [4pt] γ & = \ arccos \ dfrac {3} {\ sqrt {22}} ≈0.877 \, \ text { рад.} \ end {align *} \]
2} \ sqrt {1}} = \ dfrac {3} {\ sqrt {22}} \\ [4pt] γ & = \ arccos \ dfrac {3} {\ sqrt {22}} ≈0.877 \, \ text { рад.} \ end {align *} \]
Упражнение \ (\ PageIndex {5} \)
Пусть \ (\ vecs {v} = ⟨3, −5,1⟩. \) Найдите меру углов, образованных каждой парой векторов.
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat i} \)
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat j} \)
- \ (\ vecs {v} \) и \ (\ mathbf {\ hat k} \)
- Подсказка
\ (\ mathbf {\ hat i} = ⟨1,0,0⟩, \ mathbf {\ hat j} = ⟨0,1,0⟩, \) и \ (\ mathbf {\ hat k} = ⟨0 , 0,1⟩ \)
- Ответ
\ (г.α≈1,04 \) рад; б. \ (β≈2,58 \) рад; c. \ (γ≈1,40 \) рад
Угол, который вектор образует с каждой из координатных осей, называемый углом направления, очень важен в практических вычислениях, особенно в такой области, как инженерия. Например, в космонавтике угол запуска ракеты должен определяться очень точно. Очень маленькая ошибка в угле может привести к тому, что ракета отклонится от курса на сотни миль. Углы направления часто вычисляются с помощью скалярного произведения и косинусов углов, называемых направляющими косинусами.Поэтому мы определяем как эти углы, так и их косинусы.
Очень маленькая ошибка в угле может привести к тому, что ракета отклонится от курса на сотни миль. Углы направления часто вычисляются с помощью скалярного произведения и косинусов углов, называемых направляющими косинусами.Поэтому мы определяем как эти углы, так и их косинусы.
Определение: углы направления
Углы, образованные ненулевым вектором и осями координат, называются углами направления для вектора (рисунок \ (\ PageIndex {5} \)). Косинусы для этих углов называются направляющими косинусами .
Рисунок \ (\ PageIndex {5} \): Угол \ (α \) образован вектором \ (\ vecs {v} \) и единичным вектором \ (\ mathbf {\ hat i} \). Угол β образован вектором \ (\ vecs {v} \) и единичным вектором \ (\ mathbf {\ hat j} \).Угол γ образован вектором \ (\ vecs {v} \) и единичным вектором \ (\ mathbf {\ hat k} \). В примере, направляющие косинусы \ (\ vecs {v} = ⟨2,3,3⟩ \) равны \ (\ cos α = \ dfrac {2} {\ sqrt {22}}, \ cos β = \ dfrac {3} {\ sqrt {22}}, \) и \ (\ cos γ = \ dfrac {3} {\ sqrt {22}} \). Углы направления \ (\ vecs {v} \) равны \ (α = 1,130 \) рад, \ (β = 0,877 \) рад и \ (γ = 0,877 \) рад.
Углы направления \ (\ vecs {v} \) равны \ (α = 1,130 \) рад, \ (β = 0,877 \) рад и \ (γ = 0,877 \) рад.
До сих пор мы сосредоточились в основном на векторах, связанных с силой, движением и положением в трехмерном физическом пространстве. Однако векторы часто используются более абстрактно.Например, предположим, что продавец фруктов продает яблоки, бананы и апельсины. В определенный день он продает 30 яблок, 12 бананов и 18 апельсинов. Он может использовать вектор количества \ (\ vecs {q} = ⟨30,12,18⟩, \), чтобы представить количество фруктов, которые он продал в тот день. Точно так же он может захотеть использовать вектор цен \ (\ vecs {p} = ⟨0.50,0.25,1⟩, \), чтобы указать, что он продает свои яблоки по 50 центов за штуку, бананы за 25 центов и апельсины за 1 доллар за штуку. В этом примере, хотя мы по-прежнему можем изобразить эти векторы, мы не интерпретируем их как буквальные представления положения в физическом мире.Мы просто используем векторы, чтобы отслеживать отдельные фрагменты информации о яблоках, бананах и апельсинах.
Эта идея может показаться немного странной, но если мы просто будем рассматривать векторы как способ упорядочивания и хранения данных, мы обнаружим, что они могут быть довольно мощным инструментом. Возвращаясь к продавцу фруктов, давайте подумаем о скалярном произведении, \ (\ vecs {q} ⋅ \ vecs {p} \). Мы вычисляем это, умножая количество проданных яблок (30) на цену за яблоко (50 центов), количество проданных бананов на цену за банан и количество проданных апельсинов на цену за апельсин.Затем мы складываем все эти значения вместе. Итак, в этом примере скалярный продукт сообщает нам, сколько денег продавец фруктов имел от продаж в этот конкретный день.
Когда мы используем векторы в более общем смысле, нет причин ограничивать количество компонентов тремя. Что, если продавец фруктов решит начать продавать грейпфрут? В этом случае он хотел бы использовать четырехмерные векторы количества и цен для представления количества проданных яблок, бананов, апельсинов и грейпфрутов и их удельных цен. Как и следовало ожидать, для вычисления скалярного произведения четырехмерных векторов мы просто складываем произведения компонентов, как и раньше, но в сумме четыре члена вместо трех.
Как и следовало ожидать, для вычисления скалярного произведения четырехмерных векторов мы просто складываем произведения компонентов, как и раньше, но в сумме четыре члена вместо трех.
Пример \ (\ PageIndex {6} \): использование векторов в экономическом контексте
AAA Party Supply Store продает приглашения, праздничные сувениры, украшения и предметы общественного питания, такие как бумажные тарелки и салфетки. Когда AAA покупает свой инвентарь, он платит 25 центов за упаковку за приглашения и вечеринки. Украшения стоят 50 центов AAA каждое, а предметы общественного питания — 20 центов за упаковку.AAA продает приглашения по цене 2,50 доллара за пакет, а сувениры для вечеринок по цене 1,50 доллара за пакет. Украшения продаются по 4,50 доллара за штуку, а предметы общественного питания — по 1,25 доллара за упаковку.
В течение мая AAA Party Supply Store продает 1258 приглашений, 342 праздничных подарка, 2426 украшений и 1354 предмета общественного питания. Используйте векторы и точечные произведения, чтобы подсчитать, сколько денег AAA заработало на продажах в мае. Какую прибыль принес магазин?
Какую прибыль принес магазин?
Решение
Векторы затрат, цены и количества равны
.\ [\ begin {align *} \ vecs {c} & = ⟨0.25,0.25,0.50,0.20⟩ \\ [4pt] \ vecs {p} & = ⟨2.50,1.50,4.50,1.25⟩ \\ [4pt] \ vecs {q} & = ⟨1258,342,2426,1354⟩ . \ end {align *} \]
продаж AAA в мае можно рассчитать с помощью скалярного произведения \ (\ vecs {p} ⋅ \ vecs {q} \). У нас
\ [\ begin {align *} \ vecs {p} ⋅ \ vecs {q} & = ⟨2.50,1.50,4.50,1.251258,342,2426,1354⟩ \\ [4pt] & = 3145 + 513 + 10917 + 1692,5 \\ [4pt] & = 16267,5. \ end {align *} \]
Итак, AAA заработала 16 267,50 долларов в течение мая. Чтобы рассчитать прибыль, мы должны сначала подсчитать, сколько AAA заплатило за проданные предметы.Мы используем скалярное произведение \ (c⋅q \), чтобы получить
\ [\ begin {align *} \ vecs {c} ⋅ \ vecs {q} & = ⟨0.25,0.25,0.50,0.20⟩⋅⟨1258,342,2426,1354⟩ \\ [4pt] & = 314,5 + 85,5 + 1213 + 270,8 \\ [4pt] & = 1883,8. \ end {align *} \]
Итак, AAA заплатила 1883,30 доллара за проданные товары. Таким образом, их прибыль равна
Таким образом, их прибыль равна
\ [\ vecs {p} ⋅ \ vecs {q} — \ vecs {c} ⋅ \ vecs {q} = 16267,5−1883,8 = 14383,7. \ nonumber \]
Таким образом, магазин AAA Party Supply в мае заработал 14 383,70 долларов.
Упражнение \ (\ PageIndex {6} \)
1 июня магазин AAA Party Supply решил повысить цену, которую они взимают за праздничные сувениры, до 2 долларов за упаковку.Они также сменили поставщиков для своих приглашений и теперь могут покупать приглашения всего за 10 центов за упаковку. Все остальные затраты и цены остаются прежними. Если AAA продает 1408 приглашений, 147 сувениров для вечеринок, 2112 украшений и 1894 предмета общественного питания в июне, используйте векторы и точечные продукты для расчета их общих продаж и прибыли за июнь.
- Подсказка
Используйте четырехмерные векторы для определения стоимости, цены и количества проданных товаров.
- Ответ
Продажи = 15 685,50 долларов США; прибыль = 14 073,15 $
Прогнозы
Как мы видели, сложение объединяет два вектора для создания результирующего вектора. Но что, если нам дан вектор и нам нужно найти его составные части? Мы используем векторные проекции, чтобы выполнить противоположный процесс; они могут разбить вектор на составляющие. Величина проекции вектора — это скалярная проекция.Например, если ребенок тянет за ручку повозки под углом 55 °, мы можем использовать проекции, чтобы определить, какая часть силы, действующей на ручку, фактически перемещает повозку вперед (\ (\ PageIndex {6} \)) . Мы вернемся к этому примеру и узнаем, как его решить, после того, как увидим, как рассчитывать прогнозы.
Но что, если нам дан вектор и нам нужно найти его составные части? Мы используем векторные проекции, чтобы выполнить противоположный процесс; они могут разбить вектор на составляющие. Величина проекции вектора — это скалярная проекция.Например, если ребенок тянет за ручку повозки под углом 55 °, мы можем использовать проекции, чтобы определить, какая часть силы, действующей на ручку, фактически перемещает повозку вперед (\ (\ PageIndex {6} \)) . Мы вернемся к этому примеру и узнаем, как его решить, после того, как увидим, как рассчитывать прогнозы.
Определение: вектор и проекция
Проекция вектора из \ (\ vecs {v} \) на \ (\ vecs {u} \) — это вектор с меткой \ (\ text {proj} _ \ vecs {u} \ vecs {v} \) на рисунке \ (\ PageIndex {7} \).Он имеет ту же начальную точку, что и \ (\ vecs {u} \) и \ (\ vecs {v} \), и то же направление, что и \ (\ vecs {u} \), и представляет собой компонент \ (\ vecs {v} \), который действует в направлении \ (\ vecs {u} \). Если \ (θ \) представляет собой угол между \ (\ vecs {u} \) и \ (\ vecs {v} \), то по свойствам треугольников мы знаем длину \ (\ text {proj} _ \ vecs {u} \ vecs {v} \) равно \ (\ | \ text {proj} _ \ vecs {u} \ vecs {v} \ | = ‖ \ vecs {v} ‖ \ cos θ. \) Когда выражая \ (\ cos θ \) через скалярное произведение, получается
Если \ (θ \) представляет собой угол между \ (\ vecs {u} \) и \ (\ vecs {v} \), то по свойствам треугольников мы знаем длину \ (\ text {proj} _ \ vecs {u} \ vecs {v} \) равно \ (\ | \ text {proj} _ \ vecs {u} \ vecs {v} \ | = ‖ \ vecs {v} ‖ \ cos θ. \) Когда выражая \ (\ cos θ \) через скалярное произведение, получается
\ [\ | \ text {proj} _ \ vecs {u} \ vecs {v} \ | = ‖ \ vecs v‖ \ cos θ = ‖ \ vecs {v} ‖ \ left (\ dfrac {\ vecs {u } ⋅ \ vecs {v}} {‖ \ vecs {u} ‖‖ \ vecs {v} ‖} \ right) = \ dfrac {\ vecs {u} ⋅ \ vecs {v}} {‖ \ vecs {u} ‖.2} \ vecs {u}. \]
Длина этого вектора также известна как скалярная проекция вектора \ (\ vecs {v} \) на \ (\ vecs {u} \) и обозначается цифрой
.\ [\ | \ text {proj} _ \ vecs {u} \ vecs {v} \ | = \ text {comp} _ \ vecs {u} \ vecs {v} = \ dfrac {\ vecs {u} ⋅ \ vecs {v}} {‖ \ vecs {u} ‖.} \]
Рисунок \ (\ PageIndex {7} \): проекция \ (\ vecs {v} \) на \ (\ vecs {u} \) показывает компонент вектора \ (\ vecs {v} \) в направлении из \ (\ vecs {u} \).
Пример \ (\ PageIndex {7} \): поиск прогнозов
Найдите проекцию \ (\ vecs {v} \) на \ (\ vecs {u} \).2} (\ mathbf {\ hat i} +6 \ mathbf {\ hat j}) \\ [4pt] & = — \ dfrac {9} {37} (\ mathbf {\ hat i} +6 \ mathbf {\ hat j}) \\ [4pt] & = — \ dfrac {9} {37} \ mathbf {\ hat i} — \ dfrac {54} {37} \ mathbf {\ hat j}. \ end {align *} \]
Иногда полезно разложить векторы, то есть разбить вектор на сумму. Этот процесс называется разрешением вектора на компоненты в раз. Проекции позволяют нам идентифицировать два ортогональных вектора, имеющих желаемую сумму. Например, пусть \ (\ vecs {v} = ⟨6, −4⟩ \) и пусть \ (\ vecs {u} = ⟨3,1⟩.2} \ vecs {u} \\ [4pt] = \ dfrac {18−4} {9 + 1} \ vecs {u} \\ [4pt] = \ dfrac {7} {5} \ vecs {u} = \ dfrac {7} {5} ⟨3,1⟩ = ⟨\ dfrac {21} {5}, \ dfrac {7} {5}⟩. \ end {align *} \]
Теперь рассмотрим вектор \ (\ vecs {q} = \ vecs {v} — \ vecs {p}. \). У нас есть
\ [\ begin {align *} \ vecs {q} = \ vecs {v} — \ vecs {p} \\ [4pt] = ⟨6, −4⟩ − ⟨\ dfrac {21} {5}, \ dfrac {7} {5}⟩ \\ [4pt] = ⟨\ dfrac {9} {5}, — \ dfrac {27} {5}⟩. \ end {align *} \]
\ end {align *} \]
Ясно, что согласно тому, как мы определили \ (\ vecs {q} \), мы имеем \ (\ vecs {v} = \ vecs {q} + \ vecs {p}, \) и
\ [\ begin {align *} \ vecs {q} ⋅ \ vecs {p} = ⟨\ dfrac {9} {5}, — \ dfrac {27} {5} ⟩⋅⟨ \ dfrac {21} {5 }, \ dfrac {7} {5}⟩ \\ [4pt] = \ dfrac {9 (21)} {25} + — \ dfrac {27 (7)} {25} \\ [4pt] = \ dfrac { 189} {25} — \ dfrac {189} {25} = 0.\ end {align *} \]
Следовательно, \ (\ vecs {q} \) и \ (\ vecs {p} \) ортогональны.
Пример \ (\ PageIndex {8} \): преобразование векторов в компоненты
Выразите \ (\ vecs {v} = ⟨8, −3, −3⟩ \) как сумму ортогональных векторов, один из которых имеет то же направление, что и \ (\ vecs {u} = ⟨2,3 , 2⟩. \)
Решение
Пусть \ (\ vecs {p} \) представляет проекцию \ (\ vecs {v} \) на \ (\ vecs {u} \):
\ [\ begin {align *} \ vecs {p} & = \ text {proj} _ \ vecs {u} \ vecs {v} \\ [4pt] & = \ dfrac {\ vecs {u} ⋅ \ vecs {v}} {‖ \ vecs {u} ‖ ^ 2} \ vecs {u} \\ [4pt] & = \ dfrac {⟨2,3,2⟩⋅⟨8, −3, −3⟩} {∥ ⟨2,3,2⟩∥ ^ 2} ⟨2,3,2⟩ \\ [4pt] & = \ dfrac {16−9−6} {2 ^ 2 + 3 ^ 2 + 2 ^ 2} ⟨2, 3,2⟩ \\ [4pt] & = \ dfrac {1} {17} ⟨2,3,2⟩ \\ [4pt] & = ⟨\ dfrac {2} {17}, \ dfrac {3} {17 }, \ dfrac {2} {17}⟩. \ end {align *} \]
\ end {align *} \]
Затем,
\ [\ begin {align *} \ vecs {q} & = \ vecs {v} — \ vecs {p} = ⟨8, −3, −3⟩ − ⟨\ dfrac {2} {17}, \ dfrac {3} {17}, \ dfrac {2} {17}⟩ \\ [4pt] & = ⟨\ dfrac {134} {17}, — \ dfrac {54} {17}, — \ dfrac {53} { 17}⟩. \ end {align *} \]
Чтобы проверить нашу работу, мы можем использовать скалярное произведение, чтобы убедиться, что \ (\ vecs {p} \) и \ (\ vecs {q} \) — ортогональные векторы:
\ [\ begin {align *} \ vecs {p} ⋅ \ vecs {q} & = ⟨\ dfrac {2} {17}, \ dfrac {3} {17}, \ dfrac {2} {17}⟩ ⋅⟨ \ dfrac {134} {17}, — \ dfrac {54} {17}, — \ dfrac {53} {17}⟩ \\ [4pt] & = \ dfrac {268} {17} — \ dfrac { 162} {17} — \ dfrac {106} {17} = 0.\ end {align *} \]
Затем,
\ [\ vecs {v} = \ vecs {p} + \ vecs {q} = ⟨\ dfrac {2} {17}, \ dfrac {3} {17}, \ dfrac {2} {17}⟩ + ⟨\ Dfrac {134} {17}, — \ dfrac {54} {17}, — \ dfrac {53} {17}⟩. \ nonumber \]
Упражнение \ (\ PageIndex {7} \)
Выразите \ (\ vecs {v} = 5 \ mathbf {\ hat i} — \ mathbf {\ hat j} \) как сумму ортогональных векторов, один из которых имеет то же направление, что и \ (\ vecs { u} = 4 \ mathbf {\ hat i} +2 \ mathbf {\ hat j} \).
- Подсказка
Начните с поиска проекции \ (\ vecs {v} \) на \ (\ vecs {u} \).
- Ответ
\ (\ vecs {v} = \ vecs {p} + \ vecs {q}, \), где \ (\ vecs {p} = \ dfrac {18} {5} \ mathbf {\ hat i} + \ dfrac {9} {5} \ mathbf {\ hat j} \) и \ (\ vecs {q} = \ dfrac {7} {5} \ mathbf {\ hat i} — \ dfrac {14} {5} \ mathbf {\ hat j} \)
Пример \ (\ PageIndex {9} \): Скалярная проекция скорости
Контейнеровоз покидает порт, идя \ (15 ° \) к северу от востока. Его двигатель развивает скорость 20 узлов по этому пути (см. Следующий рисунок).Кроме того, океанское течение перемещает корабль на северо-восток со скоростью 2 узла. С учетом двигателя и течения, насколько быстро корабль движется в направлении \ (15 ° \) к северу от востока? Ответ округлите до двух десятичных знаков.
Решение
Пусть \ (\ vecs {v} \) будет вектором скорости, генерируемым двигателем, и пусть w будет вектором скорости течения. Мы уже знаем \ (‖ \ vecs {v} ‖ = 20 \) по желаемому маршруту. Нам просто нужно добавить скалярную проекцию \ (\ vecs {w} \) на \ (\ vecs {v} \).Получаем
Мы уже знаем \ (‖ \ vecs {v} ‖ = 20 \) по желаемому маршруту. Нам просто нужно добавить скалярную проекцию \ (\ vecs {w} \) на \ (\ vecs {v} \).Получаем
\ [\ begin {align *} \ text {comp} _ \ vecs {v} \ vecs {w} = \ dfrac {\ vecs {v} ⋅ \ vecs {w}} {‖ \ vecs {v} ‖} \\ [4pt] = \ dfrac {‖ \ vecs {v} ‖‖ \ vecs {w} ‖ \ cos (30 °)} {‖ \ vecs {v} ‖} = ‖ \ vecs {w} ‖ \ cos ( 30 °) = 2 \ dfrac {\ sqrt {3}} {2} = \ sqrt {3} ≈1.73 \, \ text {knots.} \ End {align *} \]
Корабль движется со скоростью 21,73 узла в направлении \ (15 ° \) к северу от востока.
Упражнение \ (\ PageIndex {8} \)
Повторите предыдущий пример, но предположите, что океанское течение движется на юго-восток, а не на северо-восток, как показано на следующем рисунке.
- Подсказка
Вычислите скалярную проекцию \ (\ vecs {w} \) на \ (\ vecs {v} \).
- Ответ
21 узел
Работа
Теперь, когда мы разбираемся в скалярных произведениях, мы можем увидеть, как применять их в реальных ситуациях.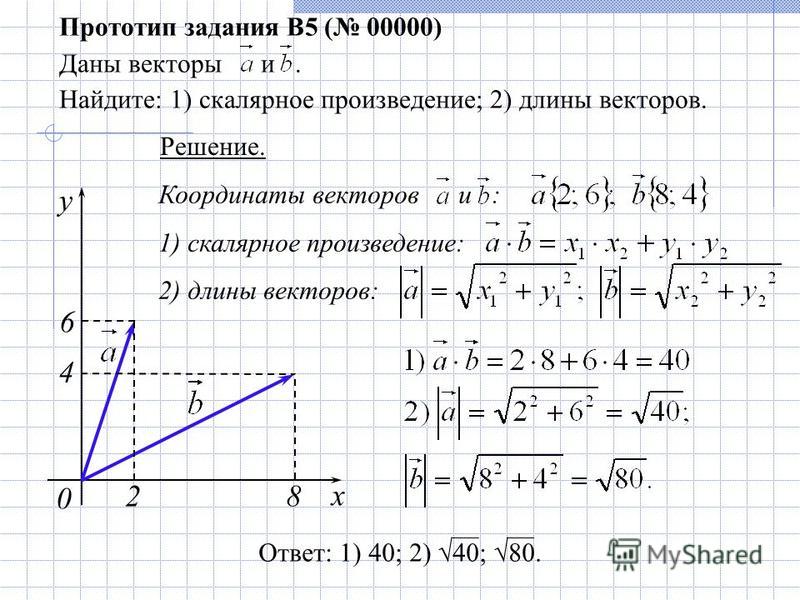 Наиболее распространенное применение скалярного произведения двух векторов — расчет работы.
Наиболее распространенное применение скалярного произведения двух векторов — расчет работы.
Из физики мы знаем, что работа совершается, когда объект перемещается силой.Когда сила постоянна и приложена в том же направлении, в котором движется объект, тогда мы определяем проделанную работу как произведение силы и расстояния, которое проходит объект: \ (W = Fd \). Мы видели несколько примеров этого типа в предыдущих главах. Теперь представьте, что направление силы отличается от направления движения, как в примере с ребенком, тянущим повозку. Чтобы найти проделанную работу, нам нужно умножить компонент силы, действующей в направлении движения, на величину смещения.Точечный продукт позволяет нам это делать. Если мы представим приложенную силу вектором \ (\ vecs {F} \), а смещение объекта вектором \ (\ vecs {s} \), то работа , выполненная силой , будет скалярным произведением из \ (\ vecs {F} \) и \ (\ vecs {s} \).
Определение: постоянная сила
Когда к объекту прикладывается постоянная сила, так что объект движется по прямой от точки \ (P \) к точке \ (Q \), работа \ (W \), совершаемая силой \ (\ vecs {F } \), действующий под углом θ от линии движения, определяется выражением
\ [W = \ vecs {F} ⋅ \ vecd {PQ} = ∥ \ vecs {F} ∥∥ \ vecd {PQ} ∥ \ cos θ. \]
\]
Вернемся к проблеме детской повозки, о которой говорилось ранее. Предположим, ребенок тянет тележку с силой в 8 фунтов на ручке под углом 55 ° . Если ребенок тянет повозку на 50 футов, найдите работу, выполняемую силой (Рисунок \ (\ PageIndex {8} \)).
Рисунок \ (\ PageIndex {8} \): Горизонтальная составляющая силы — это проекция \ (\ vecs {F} \) на положительную ось \ (x \) .У нас
\ [W = ∥ \ vecs {F} ∥∥ \ vecd {PQ} ∥ \ cos θ = 8 (50) (\ cos (55 °)) ≈229 \, \ text {ft⋅lb.} \ nonumber \]
В стандартных единицах США мы измеряем величину силы \ (∥ \ vecs {F} ∥ \) в фунтах. Величина вектора смещения \ (∥ \ vecd {PQ} ∥ \) говорит нам, как далеко переместился объект, и измеряется в футах. Таким образом, общепринятой единицей измерения работы является фут-фунт. Один фут-фунт — это объем работы, необходимый для перемещения объекта весом 1 фунт на расстояние 1 фут по вертикали. В метрической системе единицей измерения силы является ньютон (Н), а единицей измерения величины работы является ньютон-метр (Н · м) или джоуль (Дж).
Пример \ (\ PageIndex {10} \): расчет работы
Конвейерная лента создает силу \ (\ vecs {F} = 5 \ mathbf {\ hat i} −3 \ mathbf {\ hat j} + \ mathbf {\ hat k} \), которая перемещает чемодан из точки \ ( (1,1,1) \) в точку \ ((9,4,7) \) по прямой. Найдите работу, проделанную конвейерной лентой. Расстояние измеряется в метрах, а сила — в ньютонах.
Решение
Вектор смещения \ (\ vecd {PQ} \) имеет начальную точку \ ((1,1,1) \) и конечную точку \ ((9,4,7) \):
\ [\ vecd {PQ} = ⟨9−1,4−1,7−1⟩ = ⟨8,3,6⟩ = 8 \ mathbf {\ hat i} +3 \ mathbf {\ hat j} +6 \ mathbf {\ hat k}.\ nonumber \]
Работа — это скалярное произведение силы и смещения:
\ [\ begin {align *} W & = \ vecs {F} ⋅ \ vecd {PQ} \\ [4pt] & = (5 \ mathbf {\ hat i} −3 \ mathbf {\ hat j} + \ mathbf {\ hat k}) ⋅ (8 \ mathbf {\ hat i} +3 \ mathbf {\ hat j} +6 \ mathbf {\ hat k}) \\ [4pt] = 5 (8) + (- 3 ) (3) +1 (6) \\ [4pt] & = 37 \, \ text {N⋅m} \\ [4pt] & = 37 \, \ text {J} \ end {align *} \]
Упражнение \ (\ PageIndex {9} \)
Постоянная сила в 30 фунтов прикладывается под углом 60 °, чтобы тянуть ручную тележку на 10 футов по земле. Какую работу выполняет эта сила?
Какую работу выполняет эта сила?
- Подсказка
Используйте определение работы как скалярное произведение силы и расстояния.
- Ответ
150 фут-фунтов
ОПРЕДЕЛЕНИЕ СООТВЕТСТВИЯ: ИСПЫТАНИЕ ТОЧЕЧНОГО ПРОДУКТА
ОПРЕДЕЛЕНИЕ СООТВЕТСТВИЯ: ТЕСТ ТОЧЕЧНОГО ПРОДУКТАследующий: Что такое примыкание Up: Присоединенные операторы Предыдущая: Определение миграции
Между
зачатие идеи и воплощение ее в жизнь.Во время разработки что-то гораздо чаще выходит из строя.
Часто, когда что-то не получается,
необходимо много тестов, чтобы выявить причину сбоя.
Может быть, причину даже не найти.
Более коварно, что сбой может быть ниже порога обнаружения.
и низкая производительность страдала годами.
Я считаю, что тест скалярного произведения является чрезвычайно ценной контрольной точкой.
Концептуально идея транспонирования матрицы сводится к a ij ‘= a ji .Однако на практике мы часто сталкиваемся с матрицами слишком большого размера. поместиться в памяти любого компьютера. Иногда также не очевидно, как сформулировать рассматриваемый процесс. как матричное умножение. На практике мы обнаруживаем, что приложение и прилегающее к нему составляет две подпрограммы. Первая подпрограмма составляет умножение матриц. Сопряженная подпрограмма вычисляет, где — транспонированная матрица. В следующей главе мы будем решать огромные наборы одновременных уравнений. Тогда требуются обе подпрограммы.Мы с самого начала обречены, если практикующий предоставляет противоречивую пару подпрограмм. Тест скалярного произведения — это простой тест для проверки того, что два подпрограммы сопряжены друг с другом.
Ассоциативное свойство линейной алгебры говорит, что
нам не нужны круглые скобки в произведении вектор-матрица-вектор
нравится, потому что мы получаем то же самое
результат вне зависимости от того, где мы заключили круглые скобки. Они служат только для определения
последовательность вычислений.
Таким образом,
Они служат только для определения
последовательность вычислений.
Таким образом,
Я тестировал (9) на многих операторах
и был удивлен и обрадован, обнаружив
что часто выполняется с точностью, близкой к вычислительной
точность.Еще удивительнее то, что на некоторых компьютерах
уравнение (9)
иногда был удовлетворен вплоть до младший бит. Я не сомневаюсь, что могут возникнуть большие ошибки округления,
Но так далеко,
каждый раз, когда я сталкивался с относительным расхождением 10 -5 или более,
Позже мне удалось обнаружить концептуальную или программную ошибку. Естественно,
когда я провожу тесты скалярного произведения, я масштабирую подразумеваемую матрицу до
малый размер в порядке
чтобы ускорить процесс и убедиться, что
границы не перекрываются гораздо большим интерьером.
Естественно,
когда я провожу тесты скалярного произведения, я масштабирую подразумеваемую матрицу до
малый размер в порядке
чтобы ускорить процесс и убедиться, что
границы не перекрываются гораздо большим интерьером.
Не беспокойтесь, если у заданного вами оператора есть ошибки усечения. Такие ошибки в определении исходного оператора должно идентично совпадать с усечением ошибок в сопряженном.
Если ваш код проходит тест скалярного произведения , то вы действительно закодировали сопряженный оператор. В этом случае вы можете воспользоваться стандартными методами математики. для получения обратных операторов.
Мы можем говорить о непрерывной функции f ( t ) или дискретной f t .Для непрерывных функций мы используем интеграцию,
а для дискретных — суммирование.
В формальной математике тест скалярного произведения определяет сопряженный оператор,
за исключением того, что суммирование в скалярном произведении
может потребоваться изменить на интеграл. Вход или выход, или оба могут быть заданы
либо на континууме, либо в дискретной области.
Итак, тест скалярного произведения
может иметь интегрирование по одну сторону от знака равенства
а с другой — суммирование.
Теория линейных операторов богата концепциями,
но я не буду его здесь развивать.Я предполагаю, что вы изучали ее до того, как пришли читать эту книгу,
и что моя работа — показать вам, как его использовать.
Вход или выход, или оба могут быть заданы
либо на континууме, либо в дискретной области.
Итак, тест скалярного произведения
может иметь интегрирование по одну сторону от знака равенства
а с другой — суммирование.
Теория линейных операторов богата концепциями,
но я не буду его здесь развивать.Я предполагаю, что вы изучали ее до того, как пришли читать эту книгу,
и что моя работа — показать вам, как его использовать.
следующий: Что такое примыкание Up: Присоединенные операторы Предыдущая: Определение миграции Стэнфордский исследовательский проект
21.10.1998
Скалярное произведение — Точечное произведение
(Векторное произведение двух векторов)
Скалярное произведение , , также называемое скалярным произведением двух векторов , является одним из двух способов, с помощью которых мы узнаем, как умножить два вектора вместе, а другой способ — это перекрестное произведение, также называется векторным произведением.
Когда мы умножаем два вектора с помощью скалярного произведения , , , мы получаем скаляр (число, а не другой вектор !.
Обозначение
Для двух векторов \ (\ vec {u} \) и \ (\ vec {v} \) мы обращаемся к скалярному произведению , записывая:
\ [\ vec {u} \ bullet \ vec {v} \]
Другими словами, поставив точку между двумя векторами, что объясняет, почему мы также называем это скалярным произведением .Скалярное произведение: использование компонентов векторов
2D-векторы
Даны два вектора \ (\ vec {u} = \ begin {pmatrix} u_1 \\ u_2 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} v_1 \\ v_2 \ end {pmatrix} \) их скалярное произведение: \ [\ vec {u} \ bullet \ vec {v} = u_1v_1 + u_2v_2 \]
3D векторы
Даны два вектора \ (\ vec {u} = \ begin {pmatrix} u_1 \\ u_2 \\ u_3 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} v_1 \\ v_2 \\ v_3 \ end {pmatrix} \) их скалярное произведение: \ [\ vec {u} \ bullet \ vec {v} = u_1v_1 + u_2v_2 + u_3v_3 \]
Учебное пособие: как вычислить скалярное произведение
В этом руководстве мы узнаем, как вычислить скалярное произведение векторов \ (2 \), , используя их компоненты . Мы делаем это как для 2D, так и для 3D-векторов.
Мы делаем это как для 2D, так и для 3D-векторов.
Пример (2D-векторы)
Учитывая \ (\ vec {a} = \ begin {pmatrix} 2 \\ — 5 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 1 \\ -3 \ end {pmatrix} \), мы можем вычислить их скалярное произведение \ (\ vec {a} \ bullet \ vec {b} \) следующим образом: \ [\ begin {выровнено} \ vec {a} \ bullet \ vec {b} & = 2 \ times 1 + (-5) \ times (-3) \\ & = 2 + 15 \\ \ vec {a} \ bullet \ vec {b} & = 17 \ конец {выровнено} \]
Пример (3D-векторы)
Учитывая \ (\ vec {u} = \ begin {pmatrix} 2 \\ 1 \\ -3 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} 4 \\ 0 \\ 5 \ end {pmatrix} \), мы можем вычислить их перекрестное произведение \ (\ vec {u} \ bullet \ vec {v} \) следующим образом: \ [\ begin {выровнено} \ vec {u} \ bullet \ vec {v} & = 2 \ times 4 + 1 \ times 0 + (-3) \ times 5 \\ & = 8 + 0-15 \\ \ vec {u} \ bullet \ vec {v} & = -7 \ конец {выровнено} \]
Скалярное произведение: с использованием величин и угла
Для двух векторов \ (\ vec {u} \) и \ (\ vec {v} \) в 2D или в 3D их скалярное произведение (или скалярное произведение) можно вычислить по формуле:
\ [\ vec {u} \ bullet \ vec {v} = \ begin {vmatrix} \ vec {u} \ end {vmatrix}. {\ circ} \ end {pmatrix} \\
& = 20 \ умножить на 0,5 \\
\ vec {a} \ cdot {b} & = 10 \ end {align} \]
Скалярное произведение этих двух векторов равно \ (10 \).
{\ circ} \ end {pmatrix} \\
& = 20 \ умножить на 0,5 \\
\ vec {a} \ cdot {b} & = 10 \ end {align} \]
Скалярное произведение этих двух векторов равно \ (10 \).
Роль внутреннего угла \ (\ theta \)
Угол \ (\ theta \) между двумя векторами \ (\ vec {u} \) и \ (\ vec {v} \) играет важную роль в знаке скалярного произведения .
Это связано с тем, что \ (cos \ theta \) изменяется с положительный на ноль на отрицательный при изменении \ (\ theta \) с с острым на прямой угол , к тупой .
Глядя на формулу \ (\ vec {u} \ bullet \ vec {v} = \ begin {vmatrix} \ vec {u} \ end {vmatrix}. \ Begin {vmatrix} \ vec {v} \ end {vmatrix} cos \ theta \) ясно, что величины звездных величин \ (\ begin {vmatrix} \ vec {u} \ end {vmatrix} \) и \ (\ begin {vmatrix} \ vec {u} \ end {vmatrix} \) всегда положительны , поэтому \ (cos \ theta \) и, следовательно, \ (\ theta \) — это параметр, определяющий знак результата. {\ circ} \)
{\ circ} \)
Когда угол \ (\ theta \) между векторами \ (\ vec {u} \) и \ (\ vec {v} \) является прямым углом , скалярное произведение равно нулю : \ [\ vec {u} \ cdot \ vec {v} = 0 \]
ИСПЫТАНИЕ ДЛЯ ПЕРПЕНДИКУЛЯРНЫХ ВЕКТОРОВ
Для двух векторов \ (\ vec {u} \) и \ (\ vec {v} \) (в 2D или 3D) они перпендикулярны тогда и только тогда, когда: \ [\ vec {u} \ cdot \ vec {v} = 0 \]
Это дает очень полезный способ проверить, перпендикулярны ли два вектора.
Пример
Укажите, являются ли следующие пары векторов перпендикулярными:
- \ (\ vec {u} = \ begin {pmatrix} 3 \\ -2 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} -4 \\ -6 \ end {pmatrix} \)
- \ (\ vec {a} = \ begin {pmatrix} -5 \\ 2 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 1 \\ 3 \ end {pmatrix} \)
- \ (\ vec {a} = \ begin {pmatrix} 2 \\ 3 \\ 1 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 4 \\ -2 \\ -3 \ end {pmatrix} \)
- \ (\ vec {u} = \ begin {pmatrix} 2 \\ — 1 \\ 5 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} -3 \\ 4 \\ 2 \ end {pmatrix} \)
ПОСМОТРЕТЬ РЕШЕНИЯ +
- Мы нашли:
\ [\ begin {выровнено}
\ vec {u} \ cdot \ vec {v} & = \ begin {pmatrix} 3 \\ -2 \ end {pmatrix} \ cdot \ begin {pmatrix} -4 \\ -6 \ end {pmatrix} \\
& = 3 \ раз (-4) + (-2) \ раз (-6) \\
& = -12 + 12 \\
\ vec {u} \ cdot \ vec {v} & = 0
\ конец {выровнено} \]
Поскольку \ (\ vec {u} \ cdot \ vec {v} = 0 \), эти два перпендикулярны.
- Мы нашли: \ [\ begin {выровнено} \ vec {a} \ cdot \ vec {b} & = \ begin {pmatrix} -5 \\ 2 \ end {pmatrix} \ cdot \ begin {pmatrix} 1 \\ 3 \ end {pmatrix} \\ & = -5 \ раз 1 + 2 \ раз 3 \\ & = -5 + 6 \\ \ vec {a} \ cdot \ vec {b} & = 1 \ конец {выровнено} \] Поскольку \ (\ vec {a} \ cdot \ vec {b} \ neq 0 \) они не перпендикулярны.
- Мы нашли: \ [\ begin {выровнено} \ vec {a} \ cdot \ vec {b} & = \ begin {pmatrix} 1 \\ 3 \\ 1 \ end {pmatrix} \ cdot \ begin {pmatrix} 4 \\ -2 \\ -3 \ end { pmatrix} \\ & = 2 \ раз 4 + 3 \ раз (-2) + 1 \ раз (-3) \\ & = 8 + (-6) + (-3) \\ \ vec {a} \ cdot \ vec {b} & = -1 \ конец {выровнено} \] Поскольку \ (\ vec {a} \ cdot \ vec {b} \ neq 0 \) векторы \ (\ vec {a} \) и \ (\ vec {b} \) не перпендикулярны.
- Мы нашли:
\ [\ begin {выровнено}
\ vec {u} \ cdot \ vec {v} & = \ begin {pmatrix} 2 \\ -1 \\ 5 \ end {pmatrix} \ cdot \ begin {pmatrix} -3 \\ 4 \\ 2 \ end { pmatrix} \\
& = 2 \ раз (-3) + (-1) \ раз 4 + 5 \ раз 2 \\
& = -6 + (-4) + 10 \\
& = -6 — 4 + 10 \\
\ vec {u} \ cdot \ vec {v} & = 0
\ конец {выровнено} \]
Поскольку \ (\ vec {u} \ cdot \ vec {v} = 0 \) эти два вектора перпендикулярны.

Учебное пособие: вопрос стиля экзамена
Мы прорабатываем типичный вопрос в стиле экзамена , который несколько раз встречается на экзаменах (хотя и с разными номерами).
Учитывая векторы \ (\ vec {u} = \ begin {pmatrix} 0 \\ 5 \\ q \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} 0 \\ 10 \\ 14 \ end {pmatrix} \) найдите значение \ (q \), для которого \ (\ vec {u} \) и \ (\ vec {v} \) равны:
- Параллельный
- Перпендикуляр
Свойства скалярного произведения
Для любых векторов, таких как \ (\ vec {u} \), \ (\ vec {v} \) и \ (\ vec {w} \)
- Скалярное произведение равно коммутативному : \ (\ vec {u} \ bullet \ vec {v} = \ vec {v} \ bullet \ vec {u} \)
- Скалярное произведение подчиняется «обычным» законам распределенности \ (\ vec {u} \ bullet \ begin {pmatrix} \ vec {v} + \ vec {v} \ end {pmatrix} = \ vec {u } \ пуля \ vec {v} + \ vec {u} \ bullet \ vec {w} \)
- \ (\ vec {u} \ bullet \ vec {u} = \ begin {vmatrix} \ vec {u} \ end {vmatrix} ^ 2 \)
- Даны вектор \ (\ vec {u} \) и скаляр \ (k \ in \ mathbb {R} \): \ (\ begin {vmatrix} k.
 \ vec {u} \ end {vmatrix} = \ begin {vmatrix} k \ end {vmatrix}. \ begin {vmatrix} \ vec {u} \ end {vmatrix} \)
\ vec {u} \ end {vmatrix} = \ begin {vmatrix} k \ end {vmatrix}. \ begin {vmatrix} \ vec {u} \ end {vmatrix} \)
Пример 1
Учитывая два вектора \ (\ vec {a} = \ begin {pmatrix} 1 \\ 4 \\ -3 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 2 \\ 7 \\ 5 \ end {pmatrix} \), мы можем показать, что \ (\ vec {a} \ cdot \ vec {b} = \ vec {b} \ cdot \ vec {a} \):
\ [\ begin {выровнено} \ vec {a} \ cdot \ vec {b} & = 1 \ раз 2 + 4 \ раз 7 + (-3) \ раз 5 \\ & = 2 + 28 + (- 15) \\ & = 30-15 \\ \ vec {a} \ cdot \ vec {b} & = 15 \ конец {выровнено} \]
\ [\ begin {выровнено} \ vec {b} \ cdot \ vec {a} & = 2 \ раз 1 + 7 \ раз 4 + 5 \ раз (-3) \\ & = 2 + 28 + (- 15) \\ & = 30-15 \\ \ vec {b} \ cdot \ vec {a} & = 15 \ конец {выровнено} \]
мы ясно видим, что \ (\ vec {a} \ cdot \ vec {b} = \ vec {b} \ cdot \ vec {a} \).Пример 2
Учитывая два вектора \ (\ vec {u} = \ begin {pmatrix} 2 \\ 6 \\ 3 \ end {pmatrix} \), \ (\ vec {v} = \ begin {pmatrix} 5 \\ 1 \ \ -3 \ end {pmatrix} \) и \ (\ vec {w} = \ begin {pmatrix} 4 \\ -1 \\ 2 \ end {pmatrix} \) мы можем проверить, что \ (\ vec {u} \ cdot \ begin {pmatrix} \ vec {v} + \ vec {w} \ end {pmatrix} \) следующим образом:
\ [\ begin {выровнено} \ vec {u} \ cdot \ begin {pmatrix} \ vec {v} + \ vec {w} \ end {pmatrix} & = \ vec {u} \ cdot \ vec {v} + \ vec {u} \ cdot \ vec {w} \\ & = \ begin {pmatrix} 2 \\ 6 \\ 3 \ end {pmatrix} \ cdot \ begin {pmatrix} 5 \\ 1 \\ -3 \ end {pmatrix} + \ begin {pmatrix} 2 \\ 6 \ \ 3 \ end {pmatrix} \ cdot \ begin {pmatrix} 4 \\ -1 \\ 2 \ end {pmatrix} \\ & = \ underbrace {2 \ times 5 + 6 \ times 1 +3 \ times (-3)} _ {\ vec {u} \ cdot \ vec {v}} + \ underbrace {2 \ times 4 + 6 \ times (-1) + 3 \ times 2} _ {\ vec {u} \ cdot \ vec {w}} \\ & = 10 + 6 + (-9) + 8 + (-6) + 6 \\ & = 10 + 6-9 + 8-6 + 6 \\ & = 16-9 + 8-6 + 6 \\ & = 7 + 8-6 + 6 \\ & = 15-6 + 6 \\ & = 9 + 6 \\ \ vec {u} \ cdot \ begin {pmatrix} \ vec {v} + \ vec {w} \ end {pmatrix} & = 15 \ конец {выровнено} \]
\ [\ begin {выровнено} \ vec {u} \ cdot \ begin {pmatrix} \ vec {v} + \ vec {w} \ end {pmatrix} & = \ begin {pmatrix} 2 \\ 6 \\ 3 \ end {pmatrix} \ cdot \ begin {pmatrix} \ begin {pmatrix} 5 \\ 1 \\ -3 \ end {pmatrix} + \ begin {pmatrix} 4 \\ -1 \\ 2 \ end {pmatrix} \ end {pmatrix} \\ & = \ begin {pmatrix} 2 \\ 6 \\ 3 \ end {pmatrix} \ cdot \ begin {pmatrix} \ begin {pmatrix} 5 + 4 \\ 1 + (-1) \\ -3 + 2 \ end {pmatrix} \ end {pmatrix} \\ & = \ begin {pmatrix} 2 \\ 6 \\ 3 \ end {pmatrix} \ cdot \ begin {pmatrix} 9 \\ 0 \\ -1 \ end {pmatrix} \\ & = 2 \ раз 9 + 6 \ раз 0 + 3 \ раз (-1) \\ & = 18 + 0 + (-3) \\ & = 18 — 3 \\ \ vec {u} \ cdot \ begin {pmatrix} \ vec {v} + \ vec {w} \ end {pmatrix} & = 15 \ конец {выровнено} \]
Мы видим, что оба результата равны и что скалярное произведение подчиняется «обычным» законам дистибутивности.Упражнение 1
- Вычислите скалярное произведение каждой из следующих пар векторов:
- \ (\ vec {a} = \ begin {pmatrix} -2 \\ 1 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 3 \\ 7 \ end {pmatrix} \)
- \ (\ vec {u} = 3 \ vec {i} — 2 \ vec {j} + \ vec {k} \) и \ (\ vec {v} = — \ vec {i} + 4 \ vec {j } + 2 \ vec {k} \)
- \ (\ vec {c} = \ begin {pmatrix} 2 \\ 0 \\ — 5 \ end {pmatrix} \) и \ (\ vec {d} = \ begin {pmatrix} 1 \\ — 3 \\ 4 \ end {pmatrix} \)
- Учитывая векторы \ (\ vec {a} = \ begin {pmatrix} 2 \\ -3 \\ 4 \ end {pmatrix} \) и \ (\ vec {b} = \ begin {pmatrix} 1 \\ -2 \\ p \ end {pmatrix} \), найдите значение \ (p \), для которого \ (\ vec {a} \) и \ (\ vec {b} \) перпендикулярны.
- Учитывая векторы \ (\ vec {u} = \ begin {pmatrix} 0 \\ 5 \\ q \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} 0 \\ 10 \\ 14 \ end {pmatrix} \) найдите значение \ (q \), для которого \ (\ vec {u} \) и \ (\ vec {v} \) равны:
- параллельный
- перпендикуляр
- Покажите этот треугольник ABC, в котором вершины \ (A \), \ (B \) и \ (C \) имеют координаты \ (A (0, -3,9) \), \ (B (5, -10, 10) \) и \ (C (2, -4,6) \) находится под прямым углом к \ (C \).
- Учитывая \ (\ vec {u} = \ begin {pmatrix} 2k \\ — 1 \\ 1 \ end {pmatrix} \) и \ (\ vec {v} = \ begin {pmatrix} k \\ k \\ — 1 \ end {pmatrix} \) перпендикулярны и \ (k> 0 \), найдите значение \ (k \).
Выберите номер вопроса, для которого вы бы хотели видеть работу:
Qu.1 Qu. 2 Qu. 3 Qu. 4 Qu. 5
Умножение векторов
Векторы — что это такое? дает введение в предмет.
Есть два полезных определения умножения векторов в в одном произведение — скаляр, а в другом — произведение вектор. Нет операции деления векторов. В некоторых школьные программы вы встретите скалярные произведения, но не векторные продуктов, но мы обсуждаем оба типа умножения векторов в в этой статье, чтобы дать более полное представление об основах субъект
Скалярное умножение
Скалярное произведение векторы $ {\ bf u} = (u_1, u_2, u_3) $ и $ {\ bf v} = (v_1, v_2, v_3) $ является скаляром, определяемым как $$ {\ bf u.2 \ quad (2), $$ и если $ {\ bf i, j, k} $ — единичные векторы вдоль оси тогда $$ {\ bf i.i} = {\ bf j.j} = {\ bf k.k} = 1, \ quad {\ rm и} \ quad {\ bf i.j} = {\ bf j.k} = {\ bf k.i} = 0 \ quad (3). $$ Это оставлено читателю, чтобы проверить из определения, что $$ {\ bf u.v} = {\ bf v.u}, \ {\ rm и} \ ({\ bf u + v}). {\ bf w} = {\ bf u.w} + {\ bf v.w}. $$ Это показывает, что мы можем расширять или умножать $$ {\ bf u.v} = (u_1 {\ bf i} + u_2 {\ bf j} + u_3 {\ bf k}). (v_1 {\ bf i} + v_2 {\ bf j} + u_3 {\ bf k}) $$ дает девять членов. Используя уравнение (3), шесть из этих членов равны ноль, а остальные три дают выражение $ u_1v_1 + u_2v_2 + u_3v_3 $ в соответствии с определением в уравнении (1).{-1} \ left ({{\ bf u.v} \ over | {\ bf u} ||| {\ bf v} |} \ right) \ quad (7). $$ В трех измерениях мы можем использовать более интуитивное определение угла с точки зрения поворота, но в более высокие размеры необходимо иметь определение угла такие как формула (7). Если мы воспользуемся этой формулой для определения угла, тогда Правило косинуса следует прямо, поскольку они эквивалентны.
Обратите внимание, что произведение вектора-строки и вектора-столбца равно определяется в терминах скалярного произведения, и это согласуется с матричное умножение.$$ (u_1 \ u_2 \ u_3) \ left (\ begin {array} {cc} v_1 \\ v_2 \\ v_3 \ end {array} \ right) = u_1v_1 + u_2v_2 + u_3v_3. $$
Векторное умножение
Векторное произведение двух векторы $ {\ bf b} $ и $ {\ bf c} $, записываемые как $ {\ bf b} \ times {\ bf c} $ (и иногда называют крестом product), это вектор $$ {\ bf b} \ times {\ bf c} = \ left ( \ begin {array} {cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \ end {array} \ right) \ quad (8). $$ Существует альтернативное определение векторного произведения, а именно, что $ {\ bf b} \ times {\ bf c} $ является вектор величины $ | {\ bf b} || {\ bf c} | \ sin \ theta $ перпендикулярно $ {\ bf b} $ и $ {\ bf c} $ и подчиняясь «правилу правой руки», и докажем, что этот результат следует из данного определения и что эти два определения эквивалентны.Приведено доказательство позже для полноты, но сначала рассмотрим $ {\ bf b} \ times {\ bf c} $ выражается через компоненты в направлениях $ {\ bf i, j, k} $.
Из этого определения видно, что $ {\ bf b} \ times {\ bf c} = — {\ bf c} \ times {\ bf b} $, поэтому эта операция не коммутативна. Если $ {\ bf i, j, k} $ — единичные векторы вдоль осей, тогда из этого определения: $$ {\ bf i} \ times {\ bf i} = {\ bf j} \ times {\ bf j} = {\ bf k} \ times {\ bf k}, $$ и $$ \ eqalign {{\ bf i} \ times {\ bf j} & = {\ bf k}, \ quad {\ bf j} \ times {\ bf i} = — {\ bf k} \ cr {\ bf j} \ times {\ bf k} & = {\ bf i}, \ quad {\ bf k} \ times {\ bf j} = — {\ bf i} \ cr {\ bf k} \ times {\ bf i} & = {\ bf j}, \ quad {\ bf i} \ times {\ bf k} = — {\ bf j}.} $$ Из определения следует, что $$ k ({\ bf b} \ times {\ bf c}) = (k {\ bf b}) \ times {\ bf c} = {\ bf b} \ times (k {\ bf c}), \ quad \ quad ({\ bf a + b}) \ times {\ bf c} = ({\ bf a} \ times {\ bf c}) + ({\ bf b} \ times {\ bf c}). $$ Расширение выражения $$ {\ bf b} \ times {\ bf c} = (b_1 {\ bf i} + b_2 {\ bf j} + b_3 {\ bf k}) \ times (c_1 {\ bf i} + c_2 {\ bf j} + c_3 {\ bf k}) $$ дает $$ (b_2c_3-b_3c_2) {\ bf i} + (b_3c_1-b_1c_3) {\ bf j} + (b_1c_2-b_2c_1) {\ bf k} \ quad (9) $$ который — формула для векторного произведения, заданная в уравнении (8).
Теперь мы докажем, что два определения умножения векторов эквивалент. На схеме показаны направления векторов $ {\ bf b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $, которые образуют правую вручил набор ».
Вы можете закончить чтение здесь, и это действительно больше важно понимать, что есть два определения вектора продукт, который может быть доказан как эквивалентный, чем он механически проработать детали доказательства.
Теорема Вектор произведение двух векторов $ {\ bf b} $ и $ {\ bf c} $ является вектором $ {\ bf b} \ times {\ bf c} $ со следующими свойствами:
(i) $ {\ bf b} \ times {\ bf c} $ имеет величина $ | {\ bf b} || {\ bf c} | \ sin \ theta $, где $ \ theta $ — угол между направлениями $ {\ bf b} $ и $ {\ bf c} $;
(ii) $ {\ bf b} \ times {\ bf c} $ — это перпендикулярно $ {\ bf b} $ и $ {\ bf c} $ с направлением, таким, что векторы $ {\ bf b} $, $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $ образуют правый набор, как на схеме, так что $ {\ bf b} \ times {\ bf c} $ и $ {\ bf c} \ times {\ bf b} $ направлены в противоположные стороны.
Доказательство части (i) Рассмотрим площадь параллелограмма со сторонами, заданными векторы $ {\ bf b} $ и $ {\ bf c} $ и угол $ \ theta $ между ними стороны. Площадь этого параллелограмма равна $ | {\ bf b} || {\ bf c} | \ sin \ theta $. Вектор $ {\ bf b} $ можно разложить на вектор $ k {\ bf c} $ величины $ | {\ bf b} | \ cos \ theta $ в направлении $ {\ bf c} $ и $ {\ bf b} -k {\ bf c} $ величины $ | {\ bf b} | \ sin \ theta $ перпендикулярно $ {\ bf c} $, где $ k = | {\ bf b} | \ cos \ theta / | {\ bf c} | = ({\ bf b. 2 $.2} \ cr & = | {\ bf b} \ times {\ bf c} |. } $$
Доказательство части (ii) Кому показать, что $ {\ bf b} $ и $ {\ bf b} \ times {\ bf c} $ перпендикулярны покажем, что скалярное произведение равно нулю: $$ {\ bf b}. {\ bf b} \ times {\ bf c} = b_1 (b_2c_3-b_3c_2) + b_2 (b_3c_1-b_1c_3) + b_3 (b_1c_2-b_2c_1) = 0, $$ и аналогично скалярное произведение $ {\ bf c} $ и $ {\ bf b} \ times {\ bf c} $ равен нулю, поэтому эти векторы перпендикулярны.
Скалярное произведение (скалярное произведение) векторов
В скалярном произведении векторов компоненты вектора объединяются для получения скаляра.Скалярное произведение двух векторов — это произведение компоненты одного вектора (в направлении другого вектора) и второго вектора. Скалярное произведение в основном используется в физике. Скалярное произведение также известно как «скалярное произведение».
Математическое определение скалярного произведения двух векторов a и b обозначается a.b и определяется следующим образом.
a.b = | a | | б | Cos θ, где θ — угол между a и b .
Свойства скалярного произведения:
1) a.b — скаляр.
2) Из определения скалярного произведения имеем Cos θ = a.b / | a | | б |
3) a и b ортогональны, если a.b = 0.
4) a.b = b.a
5) ii = jj = kk = 1, где i , j и k являются взаимно ортогональными единичными векторами вдоль x , y и z — оси.
6) Точечный продукт является распределительным по сравнению с добавлением.
то есть a. (B + c) = a.b + b.c
7) Для любого скаляра m , (ma) .b = m (a.b)
8) Если a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k, то ab = a 1 b 1 + a 2 b 2 + a 3 b 3 .
(Это потому, что i.j = j.k = k.i = 0, потому что они взаимно ортогональны)
Пример:
Если a = 3i + 2j + 5k и b = 2i — 6j + 4k, то найдите a.б
Решение:
По объекту № 8,
а.б = 3 * 2 + 2 * -6 + 5 * 4 = 6-12 + 20 = 14.
Вам также нужна помощь с французским? Взгляните на наши услуги репетиторства французского языка.
SchoolTutoring Academy — ведущая компания по оказанию образовательных услуг для школьников и школьников. Мы предлагаем учебные программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Parlier, посетите: Tutoring in Parlier.
Понимание точечного произведения
Автор Роберт
Dunlop |
Введение
Скалярное произведение — это величина, выражающая угловое соотношение между двумя векторы. В этой статье мы узнаем, как рассчитывается это значение, его математическое значение и несколько способов использования этой функции в 3D-приложения.
Вычисление скалярного произведения
Скалярное произведение — это скалярное значение, являющееся результатом операции двух векторы с одинаковым количеством компонентов. Для каждого из двух векторов A и B с n компонентами, скалярное произведение рассчитывается как:
A B = A 1 B 1 + … + A n B n
Скалярное произведение, таким образом, представляет собой сумму произведений каждый компонент двух векторов.Например, если A и B были трехмерными векторами:
A B = A.x * B.x + A.y * B.y + A.z * B.z
Общая функция C ++ для реализации скалярного произведения на двух векторах с плавающей запятой любых размеров может выглядеть примерно так:
float dot_product (float * a, float * b, int size)
{
float dp = 0.0f;
для (int i = 0; i
return dp;
}
Этот образец кода предоставлен исключительно для демонстрации общего функция для уточнения способа вычисления скалярного произведения; DirectX предоставляет несколько реализаций этой функции для вас, как вы увидите в дальнейшем, хотя, если вам нужно было написать свой собственный функция (например, при использовании C ++ без библиотек D3DX) вы, скорее всего, просто напишите отдельные функции для обработки часто используемых векторных типов (2D, 3D, 4D) как встроенный код.
Так что это значит?
Ранее мы говорили, что скалярное произведение представляет собой угловую зависимость между двумя векторами, и оставим на этом. Теперь рассмотрим подробнее что представляет собой это значение.
Допустим, у нас есть два вектора, A и B, как показано слева. В значения | A | и | B | представляют длины векторов A и B, соответственно, и Θ — угол между двумя векторами. Точечный продукт векторов A и B будет иметь следующее отношение к этим значения:
A B = | A | * | B | * cos ( Θ )
То есть скалярное произведение двух векторов будет быть равным косинусу угла между векторами, умноженному на длину каждый из векторов.
Угловая область точечного произведения:
Учитывая характеристики функции косинуса, мы можем вывести три возможных условия:
- Если A и B перпендикулярны (под углом 90 градусов к друг друга), результат скалярного произведения будет равен нулю, потому что cos ( Θ ) будет ноль.
- Если угол между A и B меньше 90 градусов, точечное произведение будет положительным (больше нуля), так как cos ( Θ ) будет положительным, а длины векторов всегда будут положительными значениями.
- Если угол между A и B больше 90 градусов, точечное произведение будет отрицательным (меньше нуля), так как cos ( Θ ) будет отрицательным, а длины векторов всегда положительные.
Угол от скалярного произведения единичных векторов
Приведенные выше характеристики верны для любых векторов ненулевой длины. Кроме того, существует особый случай, когда оба вектора являются единичными векторами, т.е. есть, векторы длиной один (1.0). В этом случае длина векторов не влияет на уравнение, упрощая до:
A B = | A | * | B | * cos ( )
A B = 1 * 1 * cos ( Θ )
A B = cos ( )
В этом случае скалярное произведение равно косинус угла между векторами. Таким образом, угол между блоком векторы могут быть рассчитаны как:
Θ = acos (A B)
Угол от скалярного произведения неединичных векторов
Углы между неединичными векторами (векторами с длины не равны 1.0) можно вычислить либо предварительно нормализовав векторов, или путем деления скалярного произведения неединичных векторов на длину каждый вектор.
Точечное произведение вектора с самим собой
Взять скалярное произведение вектора на себя (т.е. A A) приводит к значению, равному квадрату длины вектора. Это знакомая часть уравнения расстояния, d = sqrt (x * x + y * y + z * z).
Проекция вектора на другой вектор
Если взять
скалярное произведение единичного вектора A и второго вектора B любой ненулевой длины,
результатом является длина вектора B, спроецированного в направлении вектора A (см.
рисунок слева).Это используется разными способами, например, при столкновении
отклик и преобразование векторов из одной системы координат в другую (это
лежит в основе матричных преобразований).
Реализации DirectX
DirectX Graphics предоставляет несколько реализаций функции скалярного произведения:
Кросс-произведение векторов— обзор
1.3 Основные концепции релятивистской квантовой механики
Третий вопрос, поставленный выше: «Как нужно модифицировать квантовую теорию, преподаваемую на курсах химии для студентов-бакалавров, чтобы учесть релятивистские эффекты?», Требует несколько более развернутый ответ.Рассмотрим нерелятивистский не зависящий от времени SE для электрона с потенциальной энергией V ,
(11) hˆnrelψnrel = V + Tˆψnrel = V + 12mepˆ⋅pˆψnrel = ψnrelEnrel
Как уже упоминалось, член кинетической энергии получается путем квантования нерелятивистская кинетическая энергия T = p 2 / (2 m e ), используя pˆ = −iℏ∇. Проблема с релятивистским случаем заключается в следующем: как квантовать выражение квадратного корня (6) для релятивистской энергии? Одна из возможностей — использовать расширение корня в c — 2 , как в уравнении.(7), а затем квантовать импульс. Однако это приводит к сильно сингулярным операторам, и спин, естественно, не возникает из этого подхода. Другая возможность заключается в квантовании W 2 уравнения. (5) и решим уравнение типа Hˆ2ψ = ψE2. Это действительно представляет собой релятивистское квантово-теоретическое уравнение (названное в честь Клейна и Гордона). Оказалось, что это неправильное уравнение для частиц со спином 1/2 (таких как электроны), и есть другие проблемы, связанные с уравнением, связанным с тем фактом, что в его зависящей от времени версии производные по времени имеют второй заказ [11].
Дирак утверждал, что релятивистский квантовый гамильтониан должен быть линейным по импульсу, так что временные и пространственные производные появляются в первом порядке в зависящем от времени волновом уравнении. 9 Соответственно, он предложил линеаризацию квадратного корня выражения (6) в виде
(12) W = me2c4 + c2p2 = mec2β + cα · p
Это приводит к гамильтониану Дирака при квантовании
(13 ) hˆD = V + mec2β + cα⋅pˆ
Тогда возникает вопрос: что такое β и вектор 10 α = ( α x , α y , α z )? Взяв квадрат с обеих сторон уравнения.(12) и предполагая, что p коммутирует с β и α , получаем ( u , v ∈ { x , y , z })
(14 ) m2c4 + c2p2 = me2c4β4 + c2∑u, vpupvαuαv + mec3∑upuβαu + αuβ
Отсюда следует, что 11
(15) β2 = 1, αuαv + αvαu = 2δuv, βα2 9 + αuβ000 таким образом, что правая часть уравнения. (14) равна левой части. Эти условия не могут быть выполнены, если β и α u являются числами.Вместо этого можно удовлетворить условиям с набором матриц 4 × 4 (или с матрицами более высокой четной размерности), потому что матричные произведения, в отличие от чисел, обычно не коммутируют. Стандартное представление матриц Дирака:
(16) β = 1000010000−10000−1, αx = 0001001001001000, αy = 000 − i00i00 − i00i000, αz = 0010000−110000−100
В уравнении. (15) «0» следует интерпретировать как матрицу, заполненную нулями, а «1» соответствует единичной матрице 4 × 4 (1 на диагонали, ноль в другом месте).См. Также упражнение 2.
Возможно, читатель заметил, что недиагональные блоки 2 × 2 матрицы α представляют собой спиновые матрицы Паули
(17) σx = 0110, σy = 0 − ii0, σz = 100−1
, которые можно сгруппировать в векторный оператор σ = ( σ x , σ y , σ z ). Оператор электронного спина Sˆ = 1 / 2σℏ. Существует удобное обозначение матриц Дирака в виде блоков 2 × 2, в которых используются матрицы Паули:
(18) β = 100-1, α = 0σσ0
Каждый элемент матриц в уравнении.(18) представляет собой блок 2 × 2, где «0» представляет блок нулей, а «1» представляет единичную матрицу (а не блок 2 × 2, заполненный единицей). В этих разделенных обозначениях одноэлектронный гамильтониан Дирака уравнения (13) читается как
(19) hˆD = V + mec2β + cα · pˆ = V + mec2cσ · pˆcσ⋅pˆV − mec2
Этот вид сильно отличается от нерелятивистской SE. Более того, поскольку гамильтониан Дирака имеет матричную структуру 4 × 4, волновая функция должна быть четырехкомпонентным объектом
(20) ψD = ψ1ψ2ψ3ψ4 = ψUψL, ψU = ψ1ψ2, ψL = ψ3ψ4
Каждая из ψ i — это функция трехмерного пространства.Квадратные скобки указывают разделение обозначений, соответствующих формуле. (19), где U обозначает два верхних, а L обозначает два нижних из четырех компонентов волновой функции. Обозначения, обозначающие «большой» и «малый» компоненты, чаще используются в соответствующей литературе, при этом малым компонентом является ψ L для электронных состояний. Волновая функция нормирована,
(21) 1 = ∫ψ † ψdV = ∫ (ψ1, ψ2, ψ3, ψ4) ⁎ψ1ψ2ψ3ψ4dV = ∫ψU † ψU + ψL † ψLdV
Не являются независимыми ψ i друг от друга, но взаимосвязаны пространственной и спиновой симметрией физической задачи и матричной структурой hˆD.Наличие оператора спина в hˆD указывает на то, что многокомпонентный характер оператора и волновой функции так или иначе связан со спиновыми степенями свободы электрона. Поэтому четырехкомпонентная волновая функция Дирака также называется четырехспинором. Верхняя и нижняя компоненты, ψ U , ψ L , являются двухспинорами.
Перед тем, как продолжить, мы установили нуль шкалы энергии на + mc 2 , как в уравнении.(8). Для согласованности нам нужно вычесть mc 2 из потенциальной энергии в уравнении. (19), что эквивалентно замене
(22) β = 100−1 → β ′ = 000−2
в уравнении. (19). В конечном итоге ДЭ для электрона составляет
(23) hˆDψD = Vcσ · pˆcσ · pˆV − 2mec2ψUψL = ψUψLE
Это уравнение может не иметь четко определенного нерелятивистского предела, c → ∞, потому что скорость света не фигурируют в знаменателях. Похоже, что весь оператор просто уходит в бесконечность при c → ∞.Однако нерелятивистский предел действительно содержится в формуле. (23). Давайте сначала напишем два уравнения для ψ U и ψ L явно:
(24a) VψU + cσ · pˆψL = ψUE
(24b) cσ · pˆψU + V − 2mec2ψL = ψLE
Из второго уравнения получаем
(25) ψL = XˆψU, ψU = Xˆ − 1ψL, где Xˆ = 12meckσ · pˆ
, где
(26) k = 1 − V − E2mec2−1 = 1 + ∑n = 1∞V − E2mec2n
Из-за множителя 1 / (2 c ) в уравнении. (25), ψ L традиционно называют «малым» компонентом.Это действительно обычно намного меньше, чем верхний компонент ψ U . Мы подставляем уравнение. (25) в уравнение. (24a) и получить релятивистское уравнение для верхних компонент
(27) hˆESCψU = V + 12meσ · pˆkcσ · pˆψU = ψUE
Исключаются нижние (малые) компоненты четырехкомпонентной волновой функции. Поэтому процедуру часто называют удалением мелких компонентов (ESC). Процедура показывает, что в принципе можно выполнять релятивистские квантовые вычисления только с одной из двухспинорных компонент, ψ U или ψ L , потому что другая компонента может быть создана с помощью оператора Xˆ или Xˆ − 1, как в уравнении.(25). Уравнение ESC не имеет большого практического значения, поскольку оператор зависит от энергии. Кроме того, нормализация волновой функции требует учета вкладов от обоих компонентов в уравнение. (21).
В последние годы был достигнут огромный прогресс в разработке процедур, позволяющих строить не зависящие от энергии формально точные двухкомпонентные релятивистские одноэлектронные гамильтонианы, которые можно использовать для релятивистских вычислений. Этот маршрут может быть более эффективным при четырехкомпонентных вычислениях, потому что нужно оптимизировать и хранить только две компоненты волновой функции вместо четырех, хотя четырехкомпонентные методы также становятся очень быстрыми. 12 Кроме того, существует множество эффективных с вычислительной точки зрения приближенных («квазирелятивистских») двухкомпонентных гамильтонианов, доступных в пакетах программ для квантовой химии, которые позволяют исследователям проводить достаточно точные релятивистские вычисления для атомов и молекул. Как это часто бывает, эффективность достигается за счет введения приближений.
Для конечного потенциала V (конечные ядра) k стремится к 1, когда скорость света стремится к бесконечности.Позже мы можем взять предел точечного ядра, что оставляет k → 1 в качестве нерелятивистского предела. Из уравнения. (27), тогда получаем
(28) hˆnrelψ = V + 12meσ⋅pˆσ⋅pˆψ = ψE
Читателю предлагается (Упражнение 3) использовать определение матриц Паули, чтобы подтвердить, что
(29) σ ⋅pˆσ⋅pˆ = 1001pˆ⋅pˆ
Следовательно, уравнение. (28) во многом эквивалентно нерелятивистской СЭ. Волновые функции могут быть выбраны в качестве собственных функций σ z или любой другой линейной комбинации матриц Паули, а двухспинорная природа имеет значение только для спиновых факторов.При σ z собственных функций,
ψr, «spin» = ψrtimes10or01
, где ψ ( r ) является решением уравнения. (11). Следовательно, ДЭ действительно включает нерелятивистский предел, хотя и не очевидным образом. Спин электрона естественным образом возникает из релятивистской теории электрона и входит в нерелятивистский предел по формуле (2). (28).
Вместо того, чтобы идти за нерелятивистским пределом, сохраняя некоторые члены в разложении k в уравнении.(26) дает приближенные двухкомпонентные релятивистские гамильтонианы. Например, в порядке c — 2 получается (см. Упражнения 4 и 5) 13
(30) hˆrel = hˆnrel + 14me2c2pˆV − Epˆ + i4me2c2σ⋅pˆV × pˆ
. Порядок c — 2 представляет собой скалярные релятивистские поправки. Последний член, зависящий от спина, отвечает за спин-орбитальное взаимодействие. Приближенный гамильтониан зависит от энергии и поэтому не имеет большого практического применения.Однако можно подумать об использовании его для теории возмущений, где сначала вычисляется нормированная нерелятивистская волновая функция, а затем используется уравнение. (30) с нерелятивистской энергией E для вычисления младшего порядка c — 2 поправки к энергии. В порядке возмущения выше, чем самый низкий, необходимо учитывать как расширения c — 2 из ψ L и ψ U , так и члены более высокого порядка в операторе.
С учетом перенормировки верхних компонент волновой функции (см. [12], глава 17) релятивистский двухкомпонентный гамильтониан порядка c — 2 превращается в оператор Паули
(31 ) hˆPauli = hˆnrel − pˆ48me3c2 + ℏ2∇2V8mec2 + i4me2c2σ⋅pˆV × pˆ
Энергия возмущения первого порядка, взятая с нерелятивистской волновой функцией, 〈ψnrel | hˆrel − hˆnrel | ψnrel | . (30) и (31) (операторы SO идентичны).Стоит выделить несколько особенностей оператора Pauli. Первый член, называемый членом массы-скорости, может рассматриваться как квантованная версия члена квадратного корня разложения в уравнении (1). (7). Этот термин обычно интерпретируется как поправка к кинетической энергии, связанной с релятивистским увеличением массы электрона (член массы-скорости). Второй оператор в правой части уравнения. (31) можно рассматривать как поправку к потенциальной энергии, которая возникает из-за того факта, что электростатическое взаимодействие между электроном и ядром не является мгновенным (термин Дарвина).Последний член — это оператор связи SO. Оператор Паули содержит сильно сингулярные члены, которые приводят к вариационному коллапсу и вызывают проблемы также при расчетах по теории возмущений, за исключением низшего порядка. Поэтому его использование не рекомендуется. Однако у него есть характерные компоненты двухкомпонентных релятивистских гамильтонианов, которые часто используются: есть скалярные релятивистские (бессиновые) члены и есть SO-связь. Для многоэлектронных систем есть дополнительные члены, похожие на члены одноэлектронного гамильтониана, но с потенциалом отталкивания электронов, заменяющим V , и новые спин-зависимые члены, которые возникают из релятивистских поправок к электрон-электронному взаимодействию.
Пример для вариационно устойчивого приближенного двухкомпонентного оператора получается следующим образом: Переписывая безразмерный объект k уравнения. (26) как
(32) k = 1 − V − E2mec2−1 = 2mec22mec2 − V1 + E2mec2 − V − 1
и аппроксимируем k как
(33) K = 2mec22mec2 − V≈k
взяв только нулевой порядок разложения правой части уравнения. (32) дает гамильтониан, который часто используется для релятивистских расчетов ЯМР. Это называется регулярным приближением нулевого порядка (ZORA) или гамильтонианом Чанга – Пелисье – Дюрана [13,14].Его версия без полей 14 читает
(34a) hˆZORA = V + 12meσ⋅pˆKσ⋅pˆ
(34b) = V + 12mepˆ⋅Kpˆ + i2meσ⋅pˆK × pˆ
Как и другие двухкомпонентные релятивистские операторы, гамильтониан ZORA можно разделить на скалярную и SO-часть (переход от формул 34a к 34b, см. упражнение 4). Нерелятивистский предел дается K → 1. Из-за потенциала V в выражении K зависит от положения. На рис. 3 показан график Kr для атома Hg. Видно, что K сильно отличается от K в областях, близких к ядру, где потенциал достигает значений, сравнимых с mc 2 .Для точечного ядра K → 0 при r → 0. Для конечного ядра K остается конечным, но небольшим, вблизи и внутри ядра. Видно, что электронный потенциал, экранирующий ядерный заряд, имеет значение для значений — , соответствующих внутреннему и внешнему ядру, валентной оболочке и далее. 15
Рис. 3. Кинематический фактор ZORA K для атома Hg как функция расстояния от ядра. Синий (сплошной): используется V ( r ) из численного расчета DFT с конечным ядром.Красный (пунктир): Использование V ( r ) = потенциал только ядра для точечного ядра с зарядом Z = 80 в выражении для K. Среднеквадратичный радиус ядра составляет 5,5 × 10 — 5 Å. [4].
ZORA, как известно, является хорошим приближением для валентных орбиталей в HAs, а также для связывания и орбиталей неподеленных пар в молекулах с HAs. Из уравнения. (32), нулевое усечение правой части оправдано, пока E мало. Это верно для валентных орбиталей, даже в HAs, но не верно для глубоких ядерных орбиталей в тяжелых элементах.Для расчетов молекулярных свойств, которые являются «химическими» в том смысле, что они определяются валентными орбиталями, ZORA является подходящим приближенным релятивистским методом. Существуют и другие вариационно устойчивые приближенные, а также формально точные двухкомпонентные подходы, которые используются для расчетов ЯМР (избранные ссылки см. В разделе 2.2). Эти операторы, как правило, не имеют компактных простых операторных представлений, в частности, для членов, зависящих от магнитного поля. Поэтому для целей этой главы структура ZORA, хотя и приблизительная, используется для иллюстрации различий между четырехкомпонентными, двухкомпонентными релятивистскими и нерелятивистскими операторами.
Прежде чем перейти к обсуждению параметров ЯМР, мы кратко обсудим еще несколько аспектов одноэлектронного SO-оператора. Для сферически-симметричного ядерного потенциала V ( r ) = — Ze 2 / (4 πε 0 r ) (т.е. для атомов 16 ) в операторе Паули СО
pˆV = −iℏ∇V = iℏZe24πε0rr3
(см. Упражнение 6). Напомним, что оператор углового момента имеет вид Lˆ = r × pˆ. Кроме того, σℏ = 2Sˆ.Таким образом, SO-оператор электрона для атома может быть записан как
(35) hˆSO = Ze28πε0me2c2Sˆ⋅Lˆr3 = Ze28πε0me2c2Lˆ⋅Sˆr3
В упражнениях 7 и 8 свойства этого оператора исследуются более подробно. В упражнении 9 читатель может рассчитать влияние взаимодействия SO на энергию атомизации молекулы TlH. Как уже упоминалось в разделе 1.2, оператор SO приводит к расщеплению вырожденных состояний в атомной оболочке с заданным угловым моментом ℓ . Собственные функции больше не являются проекциями спина в чистом виде, а смешивают спин α (↑) со спином β (↓).SO-взаимодействие в атомах также смешивает состояния с разными магнитными квантовыми числами m  . Как будет показано ниже, сочетание SO может иметь сильное влияние на химические сдвиги ЯМР в системах с тяжелыми элементами.
Наконец, необходимо отметить, что рассмотрение электронной корреляции в теории релятивистской электронной структуры является очень активной областью исследований (см. [15] и обзоры, перечисленные в разделе 6), как и расчет спектроскопические свойства, такие как параметры ЯМР с помощью методов релятивистской квантовой химии.В тематических исследованиях, представленных в этой главе, использовалась некоторая форма приближения к проблеме электронной корреляции. Для выбранных примеров этому способствовало использование ДПФ, а приближенный двухкомпонентный гамильтониан использовался для учета релятивистских эффектов в расчетах. Относительно конкретных вопросов ДПФ в релятивистских вычислениях, в частности, общего использования нерелятивистских функционалов в сочетании с релятивистскими плотностями, см. [16].
Подводя итог этому разделу:
- •
Релятивистское квантовое уравнение для электрона, разработанное Дираком, является четырехкомпонентным уравнением.Электронный спин естественно возникает из релятивистской теории.
- •
Уравнения можно преобразовать в двухкомпонентную форму. Для релятивистских квантово-химических расчетов доступны приближенные и (в принципе) точные двухкомпонентные гамильтонианы.
- •
Для c → ∞ решения ДУ и его двухкомпонентных версий становятся эквивалентными решениям ДУ (со спином).
- •
Для многоэлектронных систем необходимо также учитывать релятивистские эффекты для электрон-электронного взаимодействия.Это активный объект исследований, наряду с разработкой точных и эффективных четырех- и двухкомпонентных релятивистских методов для расчета спектроскопических свойств, таких как параметры ЯМР.
- •
Обычно существует различие между скалярными релятивистскими эффектами (от операторов без спина) и SO-связью.

