Контрольная работа по геометрии 8 класс «Прямоугольник. Ромб. Квадрат»
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
Вариант 1.
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 1400 . Определите углы ∆ AOD.
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Вариант 2.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 1000 .
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
Вариант 1.
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 140
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см. , найдите его площадь.
, найдите его площадь.
Вариант 2.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 100
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
Вариант 1.
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 140
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Вариант 2.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 100
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 600, найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Контрольная Работа Прямоугольник Ромб Квадрат 8 Класс – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
Контрольная Работа Прямоугольник Ромб Квадрат 8 Класс
Разработки
/
Математика
/
Уроки
/
8 класс
/ Контрольная работа по геометрии 8 класс «Прямоугольник. Ромб. Квадрат»
Ромб. Квадрат»
Продолжительность 72 часа
Документ: Удостоверение о повышении квалификации
Контрольная работа по геометрии 8 класс «Прямоугольник. Ромб. Квадрат» (12.75 KB)
Похожие файлы
Рабочая программа по математике (8-е классы)
Рабочая программа по математике 8-й класс
Система работы с высокомотивированными и одаренными учащимися по…
Развитие пространственных представлений школьников в обучении…
Учитель, преподаватель математики и информатики
Учитель, преподаватель физики и математики
Электронная тетрадь по математике 6 класс ФГОС
Лицензия на осуществление образовательной деятельности №5251 от 25.08.2017 г.
Скачивание сейчас начнётся…
Не забудьте поделиться материалом в социальных сетях с Вашими коллегами
Блог
Курсы
Комплекты
Олимпиады
Вебинары
Видеоучебник
Тесты
Разработки
Учительская
О проекте
Об организации
Обратная связь
Проверка документов
Друзьям
Вакансии
Пользовательское соглашение
Политика конфиденциальности
Рассылка
Регистрируясь Вы соглашаетесь с пользовательским
соглашением и
политикой конфиденциальности , а также даёте согласие на
получение информационных и рекламных писем от ООО “Мультиурок” на указанный Вами e-mail. Отказаться от рассылки Вы сможете в любой момент, кликнув на ссылку
Отказаться от рассылки Вы сможете в любой момент, кликнув на ссылку
«отказаться от рассылки», которая будет в каждом
письме.
Или войти с помощью аккаунта в соцсети
Или войти с помощью аккаунта в соцсети
Контрольная работа 8 класс к учебнику Атанасян. «Прямоугольник. Ромб. Квадрат» в 2 вариантах
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 140 0 . Определите углы ∆ AOD.
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 100 0 . Определите углы ∆ MON.
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 140 0 . Определите углы ∆ AOD.
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Периметр квадрата равен 46 см., найдите его площадь.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 100 0 . Определите углы ∆ MON.
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
Контрольная работа № . Тема «Прямоугольник. Ромб. Квадрат».
1. Периметр прямоугольника равен 16 см. Чему равны стороны прямоугольника, если известно, что одна его сторона в 3 раза больше другой?
2. В ромбе АВСD О – точка пересечения диагоналей, угол А равен 140 0 . Определите углы ∆ AOD.
3. В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=4см, ЕС=5 см. Найдите периметр прямоугольника.
Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 24 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
1. Одна из сторон прямоугольника в 4 раза больше другой. Его периметр равен 30 см. Чему равны стороны прямоугольника?
2. В ромбе MNPQ О – точка пересечения диагоналей, угол N равен 100 0 . Определите углы ∆ MON.
3.В прямоугольнике АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е, так что ВЕ=7см, ЕС=3 см. Найдите периметр прямоугольника.
4. Меньшая диагональ ромба равна 32 см, один из углов равен 60 0 , найдите сторону ромба
5. Периметр квадрата равен 46 см., найдите его площадь.
© 2008-2020, ООО «Мультиурок», ИНН 6732109381
Лицензия на право ведения
образовательной деятельности
№5251 от 25.08.2017 г.
Правообладатель товарного знака “Мультиурок”, свидетельство №660396
Введите вашу электронную почту, чтобы восстановить пароль!
Контрольная работа по геометрии 8 класс » Прямоугольник .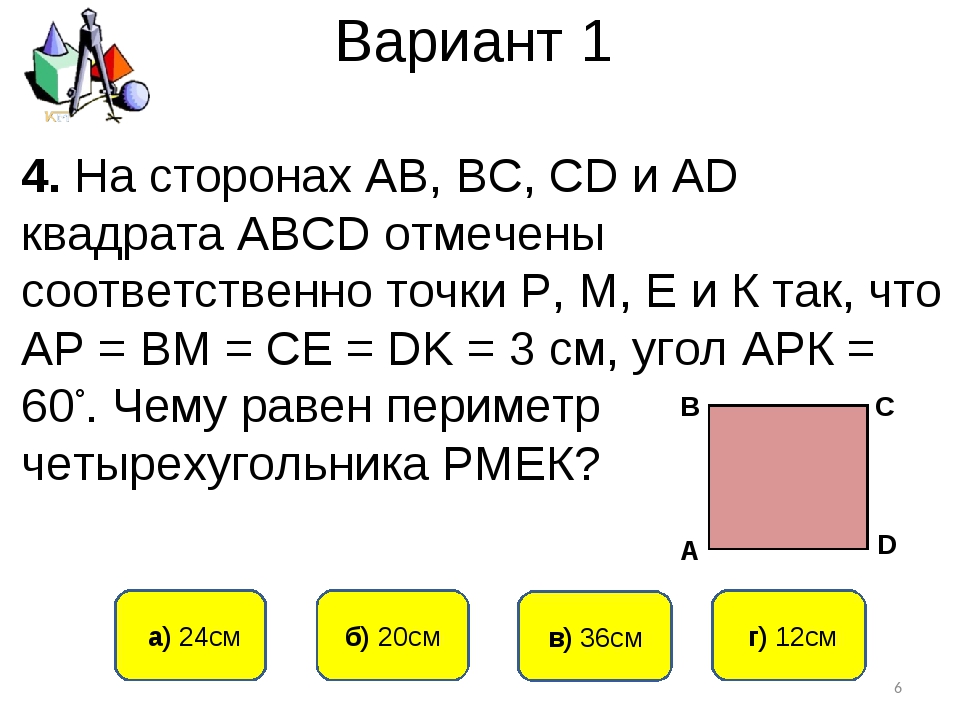 «
«
Тест по теме » Прямоугольник , ромб , квадрат » | Класс
Контрольная работа № 1 по геометрии ( 8 класс )
Контрольные работы по геометрии 8 класс | Методическая…
Геометрия 8 класс . Контрольная работа № 1 с ответами
Художественное Творчество Скифов Реферат
Реферат На Тему Языки Народов Мира
Қазақстан Тәуелсіз Мемлекет Эссе
Мини Сочинение Путешествие Капельки
Эссе На Тему Сонеты
Прямоугольник, ромб, квадрат
Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма. 0$, а $AB$ — общая сторона, то по I признаку равенства треугольников, $\triangle ABD=\triangle ABC$. Следовательно
0$, а $AB$ — общая сторона, то по I признаку равенства треугольников, $\triangle ABD=\triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $\angle DRC=\angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $\triangle DRC=\triangle ARB$. Значит, $\angle RDC=\angle RCD=\angle RAB={\rm \ }\angle RBA$.
Так как $\angle DRA=\angle CRB$, как вертикальные, то по I признаку равенства треугольников $\triangle DRA=\triangle CRB$. Значит, $\angle RDA=\angle RAD=\angle RCB={\rm \ }\angle RBC$.
Следовательно, $\angle A=\angle B=\angle C=\angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
Рисунок 3. Ромб
Рассмотрим свойство ромба.
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).
Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ — медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 2=50\] \[a=5\sqrt{2}\] \[P=4a=20\sqrt{2}\]
2=50\] \[a=5\sqrt{2}\] \[P=4a=20\sqrt{2}\]
Ответ: $20\sqrt{2}$.
Прямоугольник, ромб, квадрат тест по геометрии (8 класс)
Сложность: знаток.Последний раз тест пройден 1 час назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Чему равна сумма углов прямоугольника?
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросПодсказка 50/50ОтветитьВопрос 2 из 10
Выберите верное утверждение:
- Правильный ответ
- Неправильный ответ
- Вы и еще 70% ответили правильно
- 70% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 3 из 10
Диагонали пересекаются под прямым углом.
 Это верно:
Это верно:- Правильный ответ
- Неправильный ответ
- Вы и еще 70% ответили правильно
- 70% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 4 из 10
Выберите верное утверждение:
- Правильный ответ
- Неправильный ответ
- Вы и еще 54% ответили правильно
- 54% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 5 из 10
Могут ли углы квадрата быть равными 100⁰?
- Правильный ответ
- Неправильный ответ
- Вы и еще 86% ответили правильно
- 86% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 6 из 10
Ось симмтерии – это:
- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 7 из 10
Сколько осей симметрии имеет неразвернутый угол?
- Правильный ответ
- Неправильный ответ
- Вы и еще 58% ответили правильно
- 58% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 8 из 10
Точка О является центром симметрии отрезка АВ, если:
- Правильный ответ
- Неправильный ответ
- Вы и еще 57% ответили правильно
- 57% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 9 из 10
Какие из четырехугольников всегда имеют 4 равных угла?
- Правильный ответ
- Неправильный ответ
- Вы и еще 83% ответили правильно
- 83% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50ОтветитьВопрос 10 из 10
Является ли прямоугольником параллелограмм, у которго есть прямой угол?
- Правильный ответ
- Неправильный ответ
- Вы и еще 54% ответили правильно
- 54% ответили правильно на этот вопрос
В вопросе ошибка?
Подсказка 50/50Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Алла Гордеева
10/10
Vlad Turlov
9/10
Артемий Трифонов
8/10
Владислав Лавриненко
9/10
Denis Evdokimov
1/10
Руслан Хисамов
10/10
Белла Михайлова
10/10
Тест «Прямоугольник, ромб, квадрат» (8 класс), соответствующий министерским требованиям, поможет школьникам получить «отлично» за текущий урок или проверочную работу. Представленные вопросы охватывают всю теоретическую базу раздела. Более сложные задания являют собой задачи, требующие применения формул, теорем.
Прохождение теста подразумевает только выбор одного варианта из нескольких, поэтому справиться с ним можно очень быстро. Тематического вопросы разного уровня сложности позволяют самостоятельно, а главное объективно оценить свое владение материалом. Для удобства к подборке подаются правильные ответы, что позволяет сразу восполнять “пробелы”. При необходимости желательно дополнять ответы информацией из учебников. К заданиям легко получить онлайн доступ с любого гаджета. Представленные тесты могут использовать и старшие ученики (8-9 классы), если нужно повторить материал.
При необходимости желательно дополнять ответы информацией из учебников. К заданиям легко получить онлайн доступ с любого гаджета. Представленные тесты могут использовать и старшие ученики (8-9 классы), если нужно повторить материал.
Тест по геометрии «Прямоугольник. Ромб. Квадрат» – отличный инструмент для самостоятельного оценивания. Вопросы подобраны так, чтобы их можно было использовать не только для подготовки к тематическим контрольным, но и к итоговым промежуточным проверкам.
Рейтинг теста
Средняя оценка: 3.9. Всего получено оценок: 1334.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
8 класс Контрольная работа №1 Вариант 1
8 класс Контрольная работа №1 Вариант 1 Тема:
«Четырехугольники»
1.
Диагонали прямоугольника АВСD пересекается
в точке О, АВО =
36°. | 8 класс Контрольная работа №1 Вариант 2 Тема:
«Четырехугольники»
1. |
8класс Контрольная работа №2 Вариант 1 Тема: «Площадь» 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника. 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. 4. Смежные стороны параллелограмма равны 52 и 30 см, а острый угол равен 30°. Найдите площадь параллелограмма. 5. Вычислите площадь трапеции АВСD с  | 8класс Контрольная работа №2 Вариант 2 Тема: «Площадь» 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника. 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника. 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. 4. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если АD = 27см, ВС = 13 см, СD=10см, D=30˚. 5.
Высота ВК, проведенная к стороне АD
параллелограмма
АВСD,
делит эту сторону на отрезки АК=7см
КD=15см,
А=45˚. |
8класс Контрольная работа №3 Вариант 1 Тема: «Признаки подобия треугольников» 1. Дано: А=В, СО=4, DO=6, AO=5. (рис. 1) Найти: ОВ, АС: ВD, SAOC:SBOD. 2. В ΔАВС АВ =4, ВС=7, АС=6, а в ΔMNK MK=8, MN=12, KN=14. Найдите углы ΔMNK, если А= 80˚, В=60˚. 3. Дано: МК||АC, ВМ: АВ =1:4. Найдите периметр ΔВМК, если РАВС=25см. (рис.2) 4. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, АD=12см, ВС=4см. Найдите SВОС, если SАОD=45см2. | 8класс Контрольная работа №3 Вариант 2 Тема: «Признаки подобия треугольников» 1. Найти: МК, РЕ:NК, SМЕР:SMKN. 2. В ΔАВС АВ=12, ВС=18, В=70˚, а в ΔMNK NK=9, MN=6, N=70˚. Найдите АС и С , если МК=7, К=60˚ . 3. Дано: А=В, СО:ОD=2:3. Найдите периметр ΔАСО, если РВОD=21см. (рис.2) 4. В трапеции АВСD (АD и ВС основания)диагонали пересекаются в точке О, SАОD=32см2, SВОС=8см2. Найдите меньшее основание трапеции, если большее из них 10см |
8класс Контрольная работа №5 Вариант 1(1уров.) Тема: «Окружность» 1)Хорды MN и РК пересекаются в точке Е так, что МЕ=12 ,NЕ=3 , РЕ=9. Найти РК. 2) Дано: АОВ=130˚,АС=140˚. Найти: ВС , АСВ.(см. рис.) 3)
АВ и АС-отрезки касательных, проведенных
к окружности радиуса 3см, с центром в
точке О. | 8класс Контрольная работа №5 Вариант 2(1уров.) Тема: «Окружность» 1)Хорды АВ и СD пересекаются в точке F так, что AF=4 , BF=16 ,CF=32. Найти CD. 2) Дано:АСВ=60˚,ВС=130˚. (см рис)Найти: ВОА, АС. 3) MN и MК-отрезки касательных, проведенных к окружности радиуса 4см, с центром в точке О. Найдите длины отрезков МN и МК, если МО=5см. |
8класс Контрольная работа №5 Вариант 1(2уров.) Тема: «Окружность» 1) АВ и АС- отрезки касательных, проведенных к окружности радиуса 9см. Найдите длины отрезков АС и АО, если АВ=12см. 2) Дано: АС:ВС=11:12, АОВ=130˚. (см рис) Найти: ВСА, ВАС, АВС. 3) Хорды MN и РК пересекаются в точке Е так, что МЕ=12, NЕ=3, РЕ = КЕ. Найти РК. 4)
Окружность с центром О и радиусом 16см
описана около ∆АВС так, что
ОАВ=30˚,
ОСВ=45˚. | 8класс Контрольная работа №5 Вариант 2(2уров.) Тема: «Окружность» 1)MN и MК-отрезки касательных, проведенных к окружности радиуса 5см. Найдите длины отрезков МN и МК, если МО=13см. 2) Дано: АС:ВС=5:3, АСВ=60˚. (см рис) Найти: ВСА, ВАС, АВС. 3) Хорды АВ и СD пересекаются в точке F так, что AF=4, BF=16, CF=DF. Найти CD. 4) Окружность с центром О и радиусом 12см описана около ∆MNK так, что MОN=120˚, NОK=90˚. Найдите стороны MN и NK. |
8класс Контрольная работа №4 Вариант1(1уров.) Тема: «Применение подобия. Соотношения между сторонами и углами прямоугольного треугольника» 1.Средние
линии треугольника равны 5см, 7см и
12см. Найдите периметр этого треугольника. 2. Дано: АН=bc=16, НВ=aс=25. СН=h, АС=b, ВС=а, АВ=с. Найдите: СН, АС, ВС, АВ. 3. В прямоугольном треугольнике КМС (угол М-прямой) КМ=3, МС=4. Найти: sinС, cosС, tgС. | 8класс Контрольная работа №4 Вариант2(1ур.) Тема: «Применение подобия. Соотношения между сторонами и углами прямоугольного треугольника» 1.Средние линии треугольника равны 6см, 9см и 13см. Найдите периметр этого треугольника. 2. Дано: АН=bc=25, НВ=aс=36. СН=h, АС=b, ВС=а, АВ=с. Найдите: СН, АС, ВС, АВ. 3. В прямоугольном треугольнике КМС (угол С-прямой) КМ=5, МС=4. Найти: sinM, cosM, tgM. |
8класс Контрольная работа №4 Вариант1(2уров) Тема: «Применение подобия. Соотношения между сторонами и углами прямоугольного треугольника» 1. 2. В прямоугольном ∆АВС (С=90˚) АС=5см, ВС=5. Найдите: АВ, sin В. 3. В ∆АВС А=50˚, С=70˚, ВС=7см, ВН — высота . Найдите АН. 4. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем В- середина АК, АD=12см. Найдите: ВС+АD. 5. Медианы ∆АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС и пересекающая АВ и ВС в точках Е и F соответственно, АС=15см. Найдите ЕF. | 8класс Контрольная работа №4 Вариант2(2ур) Тема: «Применение подобия. Соотношения между сторонами и углами прямоугольного треугольника» 1. Средние линии треугольника ∆АВС относятся как 4:5:6, а Р∆АВС= 60см. Найдите стороны ∆АВС. 2.
В прямоугольном ∆АВС (В=90˚)
АВ=7см, ВС=7. 3. В ∆АВС А=50˚, С=70˚, ВН=4см, ВН — высота . Найдите АС. 4. В трапеции АВСD продолжения боковых сторон пересекаются в точке Е, причем В- середина АЕ, Вс=7см. Найдите: АD-ВС. 5. Медианы ∆АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС и пересекающая АВ и ВС в точках Е и F соответственно, ЕF=12см. Найдите АС. |
Самостоятельные работы
8 класс Самостоятельная работа Вариант 1(2ур) Тема: «Параллелограмм» 1. В четырехугольнике АВСD АВ||СD, BC||AD, АС = 20 см, ВD = 10 см, AВ = 13 см. Диагонали АВСD пересекаются в точке О. Найдите периметр ∆СОD. 2. Из вершины В параллелограмма АВСD с острым углом А проведен перпендикуляр ВК к прямой АD,
ВК = АВ/2. 3.Середина отрезка ВD является центром окружности с диаметром АС, причем точки А, В, С, D не лежат на одной прямой. Докажите, что АВСD — параллелограмм. | 8 класс Самостоятельная работа Вариант 2(2ур) Тема: «Параллелограмм» 1. В четырехугольнике АВСD АВ || СD, ВС||АD , О — точка пересечения диагоналей. Периметр ∆АОD равен 25 см, АС = 16 см, ВD = 14см. Найдите BС. 2. В параллелограмме АВСD с острым углом А из вершины В опущен перпендикуляр ВК к прямой АD, АK = ВК. Найдите С, D. 3. Дан параллелограмм АВСD. На продолжении диагонали АС за вершины А и С отмечены точки M и N соответственно так, что AM=CN. Докажите, что МBND- параллелограмм. |
8 класс Самостоятельная работа Вариант 1(1ур) Тема: «Параллелограмм» 1. В параллелограмме АВСD AВ = 13 см, ВС=24см Найдите периметр АВСD. 2. В параллелограмме АВСD А=56˚. Найдите C, D, В. 3. В параллелограмме АВСD АС = 20 см, ВD = 10 см, AВ = 13 см. Диагонали АВСD пересекаются в точке О. Найдите периметр ∆СОD. | 8 класс Самостоятельная работа Вариант 2(1ур) Тема: «Параллелограмм» 1. В параллелограмме АВСD AВ = 31 см, ВС=42см Найдите периметр АВСD. 2. В параллелограмме АВСD С=65˚. Найдите А, D, В. 3. В параллелограмме АВСD АС = 52 см, ВD = 74см, AВ = 16 см. Диагонали АВСD пересекаются в точке О. Найдите периметр ∆СОD. |
8 класс Самостоятельная работа Вариант 1(3) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике АВСD диагонали пересекаются в точке О. Точка Е-середина АВ, ВАС=50˚. Найдите ЕОD. 2) В ромбе АВСD диагонали пересекаются в точке О, А=31˚. Найдите углы ∆ВОС. 3) Дан отрезок, равный перпендикуляру, опущен-ному из вершины некоторого квадрата на диаго-наль. Постройте этот квадрат. | 8 класс Самостоятельная работа Вариант 2(3) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике МРКН диагонали пересека-ются в точке О. Отрезок ОА является высотой ∆МОР, АОР=15˚. Найдите ОНК. 2) В ромбе МРКН диагонали пересекаются в точке О. Один из углов ∆РКО равен 33˚. Найдите углы этого ∆РКО и РМН. 3) Дан отрезок, равный перпендикуляру, опущен-ному из точки пересечения диагоналей некоторого квадрата на его сторону. Постройте этот квадрат. |
8 класс Самостоятельная работа Вариант 1(2) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике АВСD диагонали пересекаются в точке О. Точка Е-середина АВ, ВАС=50˚. Найдите ЕОD. 2) В ромбе АВСD диагонали пересекаются в точке О, А=31˚. Найдите углы ∆ВОС. 3) Разделите отрезок на 10 равных частей. | 8 класс Самостоятельная работа Вариант 2(2) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике МРКН диагонали пересека-ются в точке О. Отрезок ОА является высотой ∆МОР, АОР=15˚. Найдите ОНК. 2) В ромбе МРКН диагонали пересекаются в точке О. Один из углов ∆РКО равен 33˚. Найдите углы этого ∆РКО и РМН. 3) Разделите отрезок на 9 равных частей. |
8 класс Самостоятельная работа Вариант 1(1) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике АВСD АВ=13см, ВС=24см. Найдите РАВСD 2) В ромбе АВСD А=31˚. Найдите остальные углы ромба. 3) Разделите отрезок на 10 равных частей. | 8 класс Самостоятельная работа Вариант 2(1) Тема: «Прямоугольник, ромб, квадрат» 1) В прямоугольнике АВСD АD=23см, DС=12см. Найдите РАВСD 2) В ромбе АВСD В=131˚. Найдите остальные углы ромба. 3) Разделите отрезок на 9 равных частей. |
8класс Самостоятельная работа Вариант1(2) Тема: «Вписанный угол» 1) Дано: А=50˚, АВ :АС=3:2. Найти: В, С, АОС.(см рис.) 2) Хорды АВ и СD пересекаются в точке Е. Найдите СD, если АЕ=4см, ВЕ=9см, а длина СЕ в 4 раза больше длины DЕ. | 8класс Самостоятельная работа Вариант2(2) Тема: «Вписанный угол» 1) Дано: В=60˚, АВ :ВС=7:5. Найти: А, С, ВОС.(см рис.) 2) Хорды MN и КP пересекаются в точке T. Найдите MN, если KT=6см, PT=8см, а длина MT в 3 раза меньше длины NТ. |
8класс Самостоятельная работа вариант 1 (1) Тема: «Касательная к окружности» 1) прямая КЕ касается окружности с центром в точке О, К-точка касания. Найдите ОЕ, если КЕ=8см, а радиус окружности равен 6см. 2) В ∆ АВС АВ=4, ВС=3, АС=5. Докажите, что АВ- отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом =3. | 8класс Самостоятельная работа вариант 2 (1) Тема: «Касательная к окружности» 1) прямая MN касается окружности с центром в точке О, M-точка касания. Найдите ОN, если MN=6см, а радиус окружности равен 8см. 2) В ∆ АВС АВ=6, ВС=8, АС=10. Докажите, что АВ- отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом =6. |
8класс Самостоятельная работа вариант 1 (2) Тема: «Касательная к окружности» 1) АВ и ВС – отрезки касательных, проведенных из точки В к окружности с центром в точке О и радиусом = 6. Найдите ВО, если АОС=60˚. (А и С- точки касания) 2) В ∆ АВС АВ=4, ВС=3, АС=5. Докажите, что АВ- отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом =3. 3) Даны угол и отрезок. Постройте окружность, касающуюся сторон данного угла, с центром, удаленным от вершины угла на расстояние, равное длине данного отрезка. | 8класс Самостоятельная работа вариант 2 (2) Тема: «Касательная к окружности» 1) MN и NK – отрезки касательных, проведенных из точки N к окружности с центром в точке О, MNK=90˚. Найдите радиус окружности, если ОN=2. (M и K- точки касания) 2) В ∆ АВС АВ=6, ВС=8, АС=10. Докажите, что АВ- отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом =6. 3) Даны угол и отрезок. Постройте окружность, касающуюся сторон данного угла, с центром, удаленным от вершины угла на расстояние, равное длине данного отрезка. |
8класс Самостоятельная работа вариант 1 (1ур) 1. Найдите сумму углов выпуклого двенадцати-угольника. 2. В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая -на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см. | 8класс Самостоятельная работа вариант 2 (1ур) 1. Найдите сумму углов выпуклого тринадцати-угольника. 2. В выпуклом шестиугольнике три стороны равны, четвертая в 2 раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая на ! см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см. |
8класс Самостоятельная работа вариант 1 (2ур) 1.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160°? 2. В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая -на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см. | 8класс Самостоятельная работа вариант 2 (2ур) 1.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2520°? 2. В выпуклом шестиугольнике три стороны равны, четвертая в 2 раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая на ! см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см. |
8класс Самостоятельная работа Вариант 1(1) | 8класс Самостоятельная работа Вариант 2(1) |
Дано: АН=bc=16, НВ=aс=25. Найдите: СН=h, АС=b, ВС=а, АВ=с. | Дано: АН=bc=25, НВ=aс=36. Найдите: СН=h, АС=b, ВС=а, АВ=с. |
8класс Самостоятельная работа Вариант 1(2) | 8класс Самостоятельная работа Вариант 2(2) |
Высота, проведенная из вершины прямого угла прямоугольного треугольника, равна 6см и делит гипотенузу на отрезки, один из которых больше другого на 5см. Найдите стороны треугольника. | В прямоугольном треугольнике (С=90˚) проведена высота СН так, что ВН на 4см больше СН, АН=9см. Найдите стороны треугольника. |
8 класс Самостоятельная работа Вариант 1 Тема: «Признаки подобия треугольников»
Доказать: ΔАВС ΔА1В1 2)Дано: DА=5, ВС=2, АО=25. Найти: ВО и отношение площадей ΔВОС и ΔАОD. | 8 класс Самостоятельная работа Вариант 2 Тема: «Признаки подобия треугольников»
С=60˚, С1=60˚, В1=70˚. Доказать: ΔАВС ΔА1В1С1
СО=30, DО=10, DВО=61˚. Найти: САО и отношение площадей ΔАОС и ΔВОD. |
8класс Самостоятельная работа Вариант 1 Тема: «Средняя линия треугольника» 1)Дано: К,М,N-середины АВ,ВС и АС. АВ=14см, ВС=12,4см, АС=8см,=72˚ Найдите: РКMN, . 2)В равнобедренном ΔАВС (ВС-основание) медианы пересекаются в точке О. Найдите ОВ, если АВ=АС=13см, ВС=10см. | 8класс Самостоятельная работа Вариант 2 Тема: «Средняя линия треугольника» 1)Дано: М,К,N-середины АВ,ВС и АС. АВ=14,8см, ВС=12см, АС=16см,=84˚. Найдите: РКMN, . 2)В равнобедренном ΔАВС (АС-основание) медианы пересекаются в точке О. Найдите ОС, если АВ=ВС=10см, АС=16см. |
8 класс Самостоятельная работа Вариант 1 Тема: « Синус, косинус, тангенс угла» 1. В прямоугольном треугольнике КМС (угол М-прямой) ∟С=41˚, КМ=5. Найти: МС, КС. 2. В прямоугольном треугольнике КМС (угол К-прямой) КМ=6, МС=10. Найти: sinM, cosM, tgM. 3. Стороны параллелограмма 4см и 5см, а угол между ними 45˚. Найдите площадь параллелограмма. | 8 класс Самостоятельная работа Вариант 2 Тема: « Синус, косинус, тангенс угла» 1. В прямоугольном треугольнике КМС (угол К-прямой) ∟М=61˚, КС=6. Найти: МС, МК. 2. В прямоугольном треугольнике КМС (угол С-прямой) КМ=10, МС=8. Найти: sinК, cosК, tgК. 3. Стороны параллелограмма 6см и 7см, а угол между ними 60˚. Найдите площадь параллелограмма. |
8 класс Самостоятельная работа
Тема: «Площадь треугольника»(1 уровень, 1вариант)
1. | Дано:АВ=8см, АС=6см,А=30˚. Найдите SАВС. | 2. | Дано: АО=4, ВО=9, СО=5, DО=8,SАОС=15. Найти SВОD. |
8 класс Самостоятельная работа
Тема: «Площадь треугольника»(1 уровень, 2вариант)
1. | Дано:АВ=12см, АС=9см,А=30˚. Найдите SАВС. | 2. | Дано: АО=10, ВО=8, СО=12, DО=6,SВОD=14. Найти SАОС. |
8 класс Самостоятельная работа
Тема: «Площадь треугольника»(2 уровень, 1вариант)
1. | Дано: АD=6см, DС=8см,А=45˚. ВС=10,ВD-высота. Найдите SАВС и высоту, прове-денную к ВС. | 2. | Дано: СО=DО, ВО=2ОА, SАОС=12. Найти SВОD. |
8 класс Самостоятельная работа
Тема: «Площадь треугольника»(2 уровень, 2вариант)
1. | Дано:АВ=10см, DС=9см,С=45˚ ВD=6,АD-высота. Найдите SАВС и высоту, прове-денную к АВ. | 2. | Дано: ОВ=ОС, ОD=3ОА, SАОС=16. Найти SВОD. |
8 класс 1 вариант ( 1 уровень) Самостоятельная работа
Тема: «Площадь»
1.Сторона параллелограмма равна 21см, а высота, проведенная к ней 15см. Найдите площадь
параллелограмма.
2.Сторона треугольника равна 5см, а высота, проведенная к ней, в 2 раза больше стороны.
Найдите площадь треугольника.
3.В трапеции основания равны 6 и 10см, а высота равна 8см. Найдите площадь трапеции.
4.Сторона квадрата равна 5см. Найдите площадь и периметр квадрата.
5.Площадь прямоугольника равна 36см2, одна сторона 3см. Найдите другую сторону и
периметр______________________________________________________________________
8 класс 2 вариант ( 1 уровень) Самостоятельная работа
Тема: «Площадь»
1.Сторона параллелограмма равна 12см, а высота, проведенная к ней 51см. Найдите площадь
параллелограмма.
2.Сторона треугольника равна 7см, а высота, проведенная к ней, в 3раза больше стороны.
Найдите площадь треугольника.
3.В трапеции основания равны 7 и 11см, а высота равна 6см. Найдите площадь трапеции.
4.Сторона квадрата равна 9см. Найдите площадь и периметр квадрата.
5.Площадь прямоугольника равна 48см2, одна сторона 6см. Найдите другую сторону и
периметр______________________________________________________________________
8 класс 1 вариант ( 2 уровень) Самостоятельная работа
Тема: «Площадь»
1.В равнобедренном ΔАВС высота ВH=12см, а основание АС в 3 раза больше ВH. Найдите
площадь ΔАВС.
2.В параллелограмме АВСD стороны равны 14 и 8см, высота, проведенная к большей стороне
равна 4см. Найдите площадь параллелограмма и вторую высоту.
3.Площадь трапеции равна 320см2, а высота равна 8см. Найдите основания трапеции, если
длина одного основания в 0,6 раза больше длины другого.
4.Диагонали ромба относятся как 3:5, а их сумма равна 8см. Найдите площадь ромба.
5.Прямоугольную площадку со сторонами 1,5м и 2,6м нужно выложить квадратной плиткой
со стороной 0,2м. Сколько плиток потребуется?______________________________________
8 класс 2 вариант ( 2 уровень) Самостоятельная работа
Тема: «Площадь»
1. В равнобедренном ΔАВС высота АH в 4 раза меньше основания ВС=16см. Найдите
площадь ΔАВС.
2. В параллелограмме АВСD высоты равны 10 и 5см, площадь параллелограмма равна 60см2.
Найдите стороны параллелограмма.
3. В равнобедренной трапеции АВСМ большее основание АМ=20см, ВH- высота, АH=6см,
ВАМ=45˚. Найдите площадь трапеции.
4.Диагонали ромба относятся как 2:3, а их сумма равна 25см. Найдите площадь ромба.
5.Квадратную площадку со стороной 2,6м нужно выложить прямоугольной плиткой
со сторонами 0,2 м и 0,3 м . Сколько плиток потребуется?__________________________
Прямоугольник, ромб, квадрат. Готовимся к ОГЭ по математике. Модуль 2. Урок 52
Прямоугольник — это параллелограмм, у которого все углы прямые (см. рис.1).
Рис.1
Признак прямоугольника: если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Рассмотрим рисунок 2. Если мы знаем, что — параллелограмм и , то мы можем утверждать, что — прямоугольник.
Рис.2
Площадь прямоугольника равна произведению его смежных сторон: (на рисунке 2).
Диагонали любого прямоугольника равны.
Другим видом параллелограмма является ромб — четырёхугольник, все стороны которого равны между собой (см. рис.3).
Рис.3
Ромб является параллелограммом, диагонали которого взаимно перпендикулярны ( на рисунке 4).
Рис.4
Признак ромба: если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом. Если — параллелограмм и , то — ромб (см. рис.4).
Площадь ромба равна половине произведения его диагоналей. для ромба ABCD на рисунке 4.
Квадрат — это такой прямоугольник, у которого все стороны равны (см. рис. 5).
Рис.5
Квадрат также является ромбом, а потому сочетает в себе свойства и прямоугольника, и ромба.
Диагональ квадрата , если — сторона квадрата.
Площадь квадрата равна квадрату его стороны, то есть (см. рис.5).
Задача 1. Найдите площадь и высоту ромба , изображённого на рисунке 6.
Рис.6
Решение.
, так как ромб — параллелограмм и диагонали точкой пересечения делятся пополам.
.
С другой стороны, , где — высота ромба.
Ответ: 96; 9,6.
Задача 2. Укажите номера верных утверждений.
1) В равностороннем треугольнике все углы равны 90°.
2) Любой прямоугольник является ромбом.
3) В равнобедренной трапеции углы при основании равны.
4) Диагонали параллелограмма точкой пересечения делятся пополам.
5) Сумма двух соседних углов ромба может быть больше 180°.
Решение.
Утверждение 1) неверно, так как в равностороннем треугольнике все углы равны 60°.
Утверждение 2) неверно, так как легко привести пример прямоугольника, который не является ромбом (см. рис.7).
Утверждение 3) верно, оно является свойством равнобедренной трапеции.
Рис.7
Утверждение 4) верно, оно является свойством параллелограмма.
Утверждение 5) неверно, так как сумма соседних углов любого параллелограмма равна 180°.
Ответ: 34.
Решение задач по теме «Прямоугольник. Квадрат. Ромб»
Цель урока: закрепить в процессе решения задач полученные знания и навыки.
Задачи урока:
- закрепить теоретический материал по теме “Прямоугольник. Ромб. Квадрат”;
- совершенствовать навыки решения задач;
- развитие элементов геометрического мышления и воспитание интереса к оперированию геометрическими понятиями;
- умение выполнять и оценивать выполненную работу;
- расширение кругозора, развитие чувства взаимопомощи, совершенствование навыков работы с компьютером.
Оборудование: доска, компьютеры, карточки с заданиями, тесты, справочный материал, таблицы.
Ход урока
1. Организационный момент.
– Сообщить тему урока, сформулировать цели урока.
- Какую тему мы изучаем?
- В процессе изучения темы вы должны знать:
Уметь:
Учащиеся должны:
Знать: определение прямоугольника и его свойства, определение и свойства
ромба, определение квадрата и все его свойства.
Уметь: доказывать особое свойство прямоугольника и ромба, применять
свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в
которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.
На сегодняшний день мы
знаем: определение прямоугольника и его свойства, определение и
свойства ромба, определение квадрата и все его свойства;
умеем: доказывать особое свойство прямоугольника и ромба.
Что не умеем? применять свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.
Поэтому целью нашего урока будет закрепить в процессе решения задач полученные знания и навыки.
2. Актуализация знаний учащихся.
Повторим знания, полученные на прошлом уроке. Предлагаю вам, работая в парах, дать определения параллелограмма, прямоугольника, ромба, квадрата и, вспомнив их свойства заполнить таблицу.
Теоретический опрос (работа в парах).
- Дать определения понятиям: параллелограмм, прямоугольник, ромб, квадрат.
- Вспомнить свойства и заполнить таблицу, отметив знаки + (да) и — (нет).
По первому вопросу оценить друг друга. Оценки выставляем в лист учета.
| Свойство | Параллелограмм | Прямоугольник | Ромб | Квадрат |
| Противолежащие стороны параллельны и равны. | ||||
| Все стороны равны. | ||||
| Противолежащие углы равны, сумма соседних углов равна 180. | ||||
| Все углы прямые. | ||||
| Диагонали пересекаются и точкой пересечения делятся пополам. | ||||
| Диагонали равны. | ||||
| Диагонали взаимно перпендикулярны и являются биссектрисами его углов. |
Произведите взаимопроверку и оцените друг друга.
Используя определения и свойства фигур, выполните математический диктант.
Математический диктант (графический).
Вариант 1.
- Является ли прямоугольником параллелограмм, у которого есть прямой угол?
- Верно ли, что каждый параллелограмм является прямоугольником?
- Диагонали параллелограмма равны 3 см и 5 см. Является и этот параллелограмм прямоугольником?
- Верно ли, что каждый ромб является параллелограммом?
- Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?
Вариант 2.
- Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
- Верно ли, что каждый прямоугольник является параллелограммом?
- Диагонали четырехугольника равны. Обязательно ли этот четырехугольник – прямоугольник?
- Верно ли, что каждый параллелограмм является ромбом?
- Две соседние стороны параллелограмма равны и образуют прямой угол. Называется ли такой параллелограмм — квадратом?
Проверьте правильность своих ответов и оцените свой диктант.
Итак, мы повторили определения и свойства параллелограмма, прямоугольника, квадрата, ромба. Но основной нашей целью является закрепить в процессе решения задач, полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.
Поэтому перейдем к решению задач с использованием теоретического материала.
3. Формирование умений и навыков. Решение задач.
Решение задач (устно и по готовым чертежам).(таблица 5).
1. Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.
Всегда ли при решении задач используем свойства?
(Определение).
Значит, для решения задач надо знать и свойства, и определения.
Выполнение задания – карточки с печатной основой (для коррекции знаний учащихся).
№ 11, 12, 14.
Решение задачи с комментированием.
1. В прямоугольнике АВСD диагонали АС и ВD пересекаются в точке О, причем, угол АОВ равен 40. Найдите угол DАО.
Обратите внимание на правильное оформление решения задачи. А теперь решим задачу с записью в тетради.
Решение задачи с комментированием в тетради. Учебник № 403.
4. Контроль за знаниями, умениями и навыками решения задач.
Мы повторили теоретический материал, разобрали решение задач с применением свойств фигур. А теперь предлагаю вам, решить самостоятельно задачи теста и задачи, предложенные компьютером.
1 вариант – у компьютера,
2 вариант – выполняет тест; затем поменялись местами.
Задания на карточках (тест, 2 варианта).
Вариант 1.
А1. Диагональ ромба образует с его стороной угол 26. Найдите наибольший угол ромба.
1) 128; 2) 154; 3) 104; 4) 52.
А2. Периметр параллелограмма равен 42 см, а одна из его сторон на 5 см больше другой. Найдите меньшую сторону параллелограмма.
1) 5 см; 2) 9 см; 3) 13 см; 4) 8 см.
А3. В прямоугольнике АВСD : ВD = 10 см, периметр треугольника ВОС равен 16 см. Найдите длину стороны ВС.
1) 5 см; 2) 6 см; 3) 7 см; 4) 8 см.
Вариант 2.
А1. Диагональ ромба образует с его стороной угол 32. Найдите наибольший угол ромба.
1) 148; 2) 64; 3) 126; 4) 116.
А2. Периметр параллелограмма равен 56 см, а одна из его сторон в 3 раза больше другой. Найдите большую сторону параллелограмма.
1) 14 см; 2) 12 см; 3) 21 см; 4) 16 см.
А3. В прямоугольнике АВСD : АВ = 5 см, АС = 12 см. Найдите периметр треугольника АОВ.
1) 15 см; 2) 25 см; 3) 17 см; 4) 7 см.
Оцените правильность ответов теста.
Проверка верных ответов.
Вариант 1: А1. – 1), А2 – 4), А3 – 2).
Вариант 2: А1 – 4), А2 – 3), А3 – 3).
Задания на компьютере.
В программе “ Планиметрия” открыть тему “ Четырехугольники”.
В разделе “ Контрольные вопросы” решить задачу. (3, 4, 7, 8, 11).
В журнале узнать свой средний бал и записать его в лист учета.
5. Итог урока.
Самооценка своей деятельности на уроке.
Урок подходит к концу, давайте подведем итоги. Посмотрим, удалось ли нам реализовать поставленную цель?
Какая была цель?
(Закрепить в процессе решения задач полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.)
Достигли ли мы ее?
Оцените, на сколько успешно каждый из вас справился с поставленной целью. Каждый, работая на уроке, оценивал свои знания теоретического материала.
У кого оценка “5”? “4”? “3”?, а есть оценка “2”?
Если ваши знания не на “5”, то дома вам еще раз необходимо проработать п. 45, 46, и ответить на вопросы 12–15.
Оценим свои умения по решению задач.
У кого оценка “5”? “4”? “3”?, а есть оценка “2”?
Для того, чтобы вы могли лучше решать задачи, дома необходимо решить следующие задачи № 405, 401 (а).
Запишите домашнее задание в дневник.
6. Домашнее задание.
Повторить п. 45, 46, вопросы 12–15, № 405, 401 (а).
Урок окончен. Спасибо за урок.
Литература
- Рабочая тетрадь по геометрии для 8 класса / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина — М.: Просвещение, 2003.
- Геометрия, 7–9: Учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2003.
- Современный учебно-методический комплекс “Планиметрия” 7–9. Просвещение – Медиа, 2003.
- Упражнения по планиметрии на готовых чертежах: Пособие для учителя / С. М. Саврасова, Г. А. Ястребинецкий. – М.: Просвещение, 1987.
Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция
В евклидовой геометрии четырехугольник — это четырехугольная двумерная фигура, сумма внутренних углов которой равна 360 °. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.
Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:
- Четырехугольник должен быть замкнутой формы с 4 сторонами
- Сумма всех внутренних углов четырехугольника составляет 360 °
В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь с их свойствами четырехугольников.
Это то, что вы прочитаете в статье:
Вот видео, объясняющее свойства четырехугольника:
На приведенной ниже схеме показан четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов составляет 360 °.
Таким образом, A + ∠B + ∠C + ∠D = 360 °
Различные виды четырехугольников
Существует 5 типов четырехугольников в зависимости от их формы. Эти 5 четырехугольников:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Трапеция
Давайте подробно обсудим каждый из этих пяти четырехугольников:
Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.
Прямоугольник
Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °). Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Свойства прямоугольников
Прямоугольник имеет три свойства:
- Все углы прямоугольника равны 90 °
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника — Площадь и периметр прямоугольника
Если длина прямоугольника L, а ширина B, то
- Площадь прямоугольника = длина × ширина или L × B
- Периметр прямоугольника = 2 × (L + B)
Эти практические вопросы помогут вам закрепить свойства прямоугольников
Планируете ли вы поступить в бизнес-школу США? Позвольте нам помочь вам пройти первый этап процесса i.е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Площадь
Квадрат — четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Объекты квадрата
Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:
- Все углы квадрата равны 90 °
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга пополам перпендикулярно
Формула квадрата — Площадь и периметр квадрата
Если сторона квадрата — «а», тогда
- Площадь квадрата = a × a = a²
- Периметр квадрата = 2 × (a + a) = 4a
Эти практические вопросы помогут вам закрепить свойства квадратов
Если вы наберете Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.
Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а его диагонали делят друг друга пополам.
Свойства параллелограмма
Четырехугольник, удовлетворяющий указанным ниже свойствам, будет классифицирован как параллелограмм.Параллелограмм имеет четыре свойства:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов составляет 180 °
Формулы параллелограмма — Площадь и периметр параллелограмма
Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:
- Периметр параллелограмма = 2 × (l + b)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма
Ромб
Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу.Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.
Свойства ромба
Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов составляет 180 °
Формулы ромба — Площадь и периметр ромб
Если сторона ромба — это, то периметр ромба = 4a
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба
Трапеция
Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Свойства трапеции
Трапеция — это четырехугольник, в котором одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции — Площадь и периметр трапеции
Если высота трапеции « h» (как показано на диаграмме выше), то:
- Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции
Свойства четырехугольника
В таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:
| Свойства четырехугольника | Прямоугольник | Квадрат | Параллелограмм | Ромб | Трапеция | |||||
| Все стороны равны | ✖ | 902 902 902 902 ✔ | 2 902 902 Стороны равны✔ | ✔ | ✔ | ✔ | ✖ | |||
| Противоположные стороны параллельны | ✔ | ✔ | ✔ | 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902✔ | ✔ | ✖ | ✖ | ✖ | ||
| Противоположные углы равны | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ двух смежных углов 902 ✔ | ✔ | ✔ | ✔ | ✖ |
| Разделить пополам | ✔ 9022 0 | ✔ | ✔ | ✔ | ✖ | |||||
| Перпендикулярно пополам | ✖ | ✔ | ✖ | ✔ | 0 ✖3✔ | 0 ✖3
Важные формулы четырехугольника
В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
| Формулы четырехугольника | Прямоугольник | Квадрат | Параллелограмм | Ромб | Ромб 902 902 9019 9035 b2 902 902 902 902 902 902 902 902 902 902 902 l × h | ½ × d1 × d2 | ½ × (Сумма параллельных сторон) × высота |
| Периметр | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Сумма всех сторон |
Дополнительная литература:
Четырехсторонние вопросы
Попрактикуемся в применении свойств четырехугольника на следующих типовых вопросах:
Вопрос 1
Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.Сколько метров забора нужно купить, чтобы ограждать весь сад?
- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
Шаг 1: Дано
- У Адама прямоугольный сад.
- Он имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: найти
- Длина, необходимая для ограждения всего сада.
Шаг 3: подход и разработка
Забор можно строить только вокруг внешней стороны сада.
- Итак, общая необходимая длина забора = Сумма длин всех сторон сада.
- Так как сад прямоугольный, сумма длин всех сторон — это не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Следовательно, необходимая длина забора — 50 метров.
Следовательно, вариант E — правильный ответ.
Вопрос: 2
Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если стена 25 метров в длину и 18 метров в ширину, то какова общая стоимость покраски стены?
- 300 долларов
- 350 долларов
- 450 долларов
- 600 долларов
- 675 долларов
Решение
Шаг 1: Дано
- Стив хочет покрасить одну стену своей комнаты.
- Стена 25 метров в длину и 18 метров в ширину.
- Стоимость покраски стены — 1,5 доллара за квадратный метр.
Шаг 2: найти
- Общая стоимость покраски стены.
Шаг 3: подход и разработка
- Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы сможем получить общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 $ = 675 $
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему времени вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь.
Вот еще несколько статей по математике:
- Повысьте точность ответов на вопросы по математике по многоугольникам
- Вопросы по геометрии — наиболее распространенные ошибки | GMAT Quant Prep
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Мы — самая обсуждаемая компания по подготовке к GMAT на gmatclub: мы получили более 2060 отзывов.
Почему бы вам не воспользоваться бесплатным испытанием и не судить сами?
Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.
Часто задаваемые вопросы
Какие бывают четырехугольники?Существует 5 типов четырехугольников: прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.
Где я могу найти несколько практических вопросов по четырехугольникам?В этой статье вы можете найти несколько практических вопросов о четырехугольниках.
Какова сумма внутренних углов четырехугольника?Сумма внутренних углов четырехугольника равна 360 °.
Свойства особых параллелограммов
Ромб — четырехугольник со всеми равными сторонами. Это также параллелограмм со всеми связанными с ним свойствами. Однако ромб имеет и дополнительные свойства.
Теорема 52: Диагонали ромба делят пополам противоположные углы.
Теорема 53: Диагонали ромба перпендикулярны друг другу.
В ромбе CAND (Рисунок 2), по теореме 52 , CN делят пополам ∠ DCA и ∠ ДНК. Кроме того, AD делит пополам ∠ CAN и ∠ CDN и по теореме 53 , CN ⊥ AD .
Рисунок 2 Диагонали ромба перпендикулярны друг другу и делят пополам противоположные углы.
Квадрат — четырехугольник со всеми прямыми углами и всеми равными сторонами.Квадрат также является параллелограммом, прямоугольником и ромбом и обладает всеми свойствами всех этих специальных четырехугольников. На рисунке 3 изображен квадрат.
Рисунок 3 У квадрата четыре прямых угла и четыре равные стороны.
На рисунке 4 показаны отношения этих четырехугольников друг к другу.
Рисунок 4 Отношения между различными типами четырехугольников.
Пример 1: Обозначьте следующие рисунки 5.
Рисунок 5 Определите эти многоугольники.
(a) пятиугольник, (b) прямоугольник, (c) шестиугольник, (d) параллелограмм, (e) треугольник, (f) квадрат, (g) ромб, (h) четырехугольник, (i) восьмиугольник, и (j) правильный пятиугольник
Пример 2 : На рисунке 6 найдите м ∠ A, м ∠ C, м ∠ D, CD, и AD .
Рисунок 6 Параллелограмм с одним заданным углом.
м ∠ A = м ∠ C = 80 °, поскольку последовательные углы параллелограмма являются дополнительными.
м ∠ D = 100 °, потому что противоположные углы параллелограмма равны.
CD = 8 и AD = 4, , потому что противоположные стороны параллелограмма равны.
Пример 3: На рисунке 7 найдите TR, QP, PS, TP, и PR .
Рисунок 7 Прямоугольник с указанной диагональю.
TR = 15, потому что диагонали прямоугольника равны.
QP = PS = TP = PR = 7,5, потому что диагонали прямоугольника делят друг друга пополам.
Пример 4: На рисунке 8 найдите м ∠ MOE, м ∠ NOE, и м ∠ MYO .
Рисунок 8 Ромб с указанным одним углом.
м ∠ MOE = m ∠ NOE = 70 °, потому что диагонали ромба делят пополам противоположные углы.
м ∠ MYO = 90 °, потому что диагонали ромба перпендикулярны.
Прямоугольник, ромб и квадрат
6,2 Что такое специальные параллелограммы? Стр. 9 Свойства ромбов, прямоугольников и квадратов 6.2 - Что такое специальные параллелограммы? ___ Свойства ромбов, прямоугольников и Квадраты На предыдущем уроке вы узнали, что параллелограммы имеют обе пары противоположных стороны параллельны. Вы также открыли много разные свойства параллелограммов.Сегодня вы собираетесь продолжить исследование с параллелограммами с четным более специальные свойства. 6.8 – ПАРАЛЛЕЛОГРАММЫ С ПРАВЫМИ УГЛАМИ а. Прямоугольники - это особые параллелограммы. Поскольку они параллелограммы, что вы уже знаете о прямоугольниках? противоположный параллельный Оба _____________ стороны ___________ Оба _____________ противоположный стороны конгруэнтный ________________ противоположные углы Оба _____________ конгруэнтный ________________ последовательные углы Оба _____________ дополнительный ________________ делить пополам Диагонали ________________ каждый Другой б.Марк хотел узнать об этом больше форма. Он заметил, что диагонали кажутся особенными отношениями помимо того, чтобы быть разделенным пополам. Он решил исследовать. Дважды нарисовал прямоугольник, добавление одной диагонали. Найдите длину AC и BD. Показать все работы. Что Вы уведомление? 2 8 + 2 15 2 Икс 2 Икс знак равно 289 = 17 = х 2 8 + 2 15 2 Икс 2 Икс знак равно 289 = 17 = х Диагонали совпадают c. Перечислите два специальных свойства Rectangles есть то, чего нет у общих параллелограммов. 4 прямых угла Диагонали конгруэнтный 6.9 – ПАРАЛЛЕЛОГРАММЫ С РАВНЫМ СТОРОНЫ а. Ромб - еще один вид особенного параллелограмм. Поскольку они параллелограммы, что ты уже знаете о ромбах? противоположный Оба _____________ параллельный стороны ________________ Оба _____________ противоположный стороны конгруэнтный ________________ противоположные углы Оба _____________ конгруэнтный ________________ последовательные углы Оба _____________ дополнительный ________________ x y 180 у Икс у Икс делить пополам Диагонали ________________ каждый Другой c.Одри хотела узнать о ней больше форма. Она заметила, что диагонали кажется, имеют особые отношения как хорошо. Она измерила стороны ромб и все они были длиной 5 единиц. Затем она измерила AC = 6 единиц и BD = 8 единицы измерения. Отметьте эти длины на картинке ниже. Есть ли способ определить, является ли ∆AEB прямоугольный треугольник? Объяснять. 2 5 5 5 3 4 3 5 4 5 2 3 2 4 = + 25 = 9 + 16 25 = 25 Диагонали являются перпендикуляр d. Одри заметила кое-что еще с угол в ромбе. Используя данный симметрия линий, обозначьте любые углы конгруэнтный.Что ты заметил? Диагонали делят углы пополам c. Перечислите две особые свойства Ромбы есть то, чего нет у общих параллелограммов. 4 конгруэнтных стороны Диагонали перпендикуляр Диагонали пополам углы 6.10 - ПАРАЛЛЕЛОГРАММЫ С РАВНЫМ СТОРОНЫ И ПРАВЫЕ УГЛЫ У мисс Мэтьюз есть любимый четырехугольник. Это ромб в сочетании с прямоугольником. а. Как зовут мисс Мэтьюз? форма? Нарисуйте картинку, чтобы поддержать отвечать. квадрат б. Эта форма имеет больше свойств, чем любой другой четырехугольник.Почему вы думаете это? Это параллелограмм, прямоугольник и ромб 6.11 - СПЕЦИАЛЬНЫЕ ПАРАЛЛЕЛОГРАММЫ Назовите тип параллелограмма. Объяснять как вы знаете, используя только маркировку. параллелограмм прямоугольник ромб ромб прямоугольник ромб квадрат ромб 6.12 - ОТСУТСТВИЕ ДЕТАЛЕЙ Найдите недостающую информацию на основе тип формы и ее особые свойства. а. Диагонали ромба PQRS пересекаются у Т. Найдите указанную меру. mQPR _____ 30 ° 90 ° mQTP _________ mPQT _________ 60 ° 12 RP = _________ SP = _________ 15 15 RS = _________ 15 60 ° 90 ° 30 ° 15 15 б.Диагонали прямоугольника WXYZ пересекаются в P. Учитывая, что XZ = 12, найти указанная мера. 40 ° WXZ _________ 40 ° 50 ° PYX _________ 80 ° 50 ° XPY _________ 80 ° 6 WP = _________ c. Диагонали квадрата DEFG пересекаются в H. Учитывая, что EH = 5, найти указанная мера. GHF 90 ° HGF 45 ° 45 ° HFG HF = 5 90 ° 45 ° 45 ° 6.13 - ПЛОЩАДЬ Найдите площадь ромба, найдя площадь каждого треугольника, а затем сложить. 22 275 275 25 275 275 A = 1100 фут2 1,5 7 42 = х2 + 32 16 = х2 + 9 7 1.5 7 1,5 7 7 3 1,5 7 7 = х2 7x A 6 7 см 2 8 4 8 4 84 8 A = 32 м2 4,5 3 3 4,5 3 3 3 4,5 3 3 3 4,5 3 3 6 A 18 3 футов 2 Параллелограмм Трапеция Прямоугольник Равнобедренный Трапеция Ромб летающий змей Квадрат Треугольник Прямоугольник • Все свойства параллелограмма • 4 прямых угла • Диагонали совпадают A bh Ромб • Все свойства параллелограмма • Диагонали перпендикулярны • Углы диагоналей делятся пополам Добавьте площадь каждого треугольника Квадрат • Все свойства, перечисленные выше A s 2 или A bh
[PDF] Geo — Практический тест CH6
1 Geo — H6 Практический тест Множественный выбор Выберите вариант, который лучше всего завершает утверждение или отвечает на вопрос.1 …
Geo — CH6 Практический тест Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. ________
____
____
1. Найдите размер каждого внешнего угла правильного десятиугольника. а. 45 ° с. 18 ° б. 22,5 ° д. 36 ° 2. На схеме показан элемент в форме параллелограмма, с помощью которого зеркало заднего вида крепится к автомобилю. В параллелограмме РГТУ UR = 25, RX = 16, m∠STU = 42,4o. Найдите ST, XT и m∠RST.
а. ST = 16, m∠RST = 42,4 °, XT = 25 б. ST = 25, m∠RST = 47,8 °, XT = 16 3. MNOP — параллелограмм. Найдите MP.
г. ST = 25, m∠RST = 137,6 °, XT = 16 дней. ST = 5, m∠RST = 137,6 °, XT = 4
а. МП = 25 гр. МП = 20 б. МП = 30 дн. MP = 6 4. Напишите доказательство в две колонки. Дано: ABDF и FBCD — параллелограммы. Доказательство: ∠BCD ≅ ∠ABF
Завершите доказательство.
Доказательство: Утверждения 1. ABDF и FBCD — параллелограммы. 2. ∠BCD ≅ ∠DFB 3. DF Ä AB 4. ∠DFB ≅ ∠ABF 5. ∠BCD ≅ ∠ABF
____
Причины 1.Дано 2. [1] 3. Противоположные стороны параллелограмма параллельны. 4. [2] 5. Замена
a. [1] В параллелограмме противоположные углы совпадают. [2] Теорема об альтернативных внутренних углах b. [1] Теорема о вертикальных углах [2] Теорема об альтернативных внешних углах c. [1] CPCTC [2] В параллелограмме противоположные углы совпадают. d. [1] В параллелограмме последовательные углы совпадают. [2] В параллелограмме все углы равны. 5. Покажите, что GHIJ — параллелограмм для x = 5 и y = 8.
Завершите объяснение.
HI = 5x — 10 ГДж = 7x — 20 HI = 5 (5) — 10 = [1] ГДж = 7 (5) −20 = [2]
Дано Заменить и упростить.
GH = 3y GH = 3 (8) = [3]
Дано Заменить и упростить.
JI = 5y — 16 JI = 5 (8) — 16 = [4]
Поскольку HI = GJ и GH = JI, GHIJ является параллелограммом, потому что [5]. а. [1] 15 [2] 15 [3] 24 [4] 24 [5] оба набора противоположных сторон конгруэнтны. б. [1] 15 [2] 24 [3] 15 [4] 24 [5] один набор противоположных сторон параллелен и конгруэнтен.c. [1] 15
____
[2] 15 [3] 24 [4] 24 [5] оба набора противоположных сторон параллельны. d. [1] 24 [2] 24 [3] 15 [4] 15 [5] оба набора противоположных углов совпадают. 6. Покажите, что четырехугольник DEFG является параллелограммом.
−7 наклон DE = 310− (−5) = 38
наклон FG = 48 −− 10 = 38 DE =
(3 — (−5)) 2 + (10-7) 2 =
FG =
(8-0) 2 + (4-1) 2 =
73
73
Завершите объяснение.
DE и FG имеют одинаковый наклон, поэтому [1].Поскольку DE = FG, [2]. Поскольку [3], DEFG — параллелограмм. а. [1] DE ⊥ FG [2] DE ≅ FG [3] Одна пара противоположных сторон равна и перпендикулярна. б. [1] DE Ä FG [2] DE ≅ FG [3] Одна пара противоположных сторон параллельна и конгруэнтна. c. [1] DE Ä FG
____
[2] DE ~ FG [3] Одна пара противоположных сторон параллельна и пропорциональна. d. [1] DE ⊥ FG [2] DE ≠ FG [3] Одна пара противоположных сторон не конгруэнтна, но перпендикулярна. 7. Художник создает прямоугольное лоскутное одеяло с различными типами лент, идущих от угла к центру лоскутного одеяла.Размеры прямоугольника: AB = 10 дюймов и AC = 14 дюймов. Найдите BX.
а. BX = 7 дюймов b. BX = 10 дюймов ____
c. BX = 5 дюймов d. BX = 14 дюймов
8. Покажите, что все четыре стороны квадрата ABCD равны и AB ⊥ BC.
а. AB = 3 5, BC = 3 5, CD = 3 5, DA = 3 5, наклон AB = 2, наклон BC = — 12. Поскольку произведение угловых коэффициентов равно −1, AB ⊥ BC. б. AB = 9, BC = 9, CD = 9, DA = 9, наклон AB = 2, наклон BC = — 1. Поскольку 2
2
2
2
2
произведение наклонов равно −1, AB ⊥ BC.c. AB = 3 5, BC = 3 5, CD = 3 5, DA = 3 5, наклон AB = 1, наклон 2
BC = −2. Поскольку произведение угловых коэффициентов равно −1, AB ⊥ BC. d. AB = 4, BC = 4, CD = 4, DA = 4, наклон AB = 2, наклон BC = 1. Поскольку произведение угловых коэффициентов равно 1, AB ⊥ BC. ____
9. Сторона деревянного сундука представляет собой четырехугольник с AB Ä CD и BC Ä DA. Если m∠A = 90 °, каково наиболее точное описание ABCD?
____
а. Обе пары противоположных сторон параллельны, поэтому ABCD — параллелограмм.Поскольку один угол равен 90 °, это прямой угол, а параллелограмм с одним прямым углом — это прямоугольник. б. Обе пары противоположных сторон параллельны, поэтому ABCD — параллелограмм. Поскольку один угол равен 90 °, это прямой угол, а параллелограмм с одним прямым углом — квадрат. c. Обе пары противоположных сторон параллельны, поэтому ABCD представляет собой ромб. Поскольку один угол составляет 90 °, это прямой угол, а ромб с одним прямым углом — это квадрат. d. Обе пары противоположных сторон параллельны, поэтому ABCD — параллелограмм.Один угол, измеряющий 90 °, не дает достаточно информации, чтобы изменить его описание. 10. Определите, верен ли вывод. Если нет, сообщите, какая дополнительная информация необходима, чтобы сделать его достоверным. Дано: AB ≅ CD, BC ≅ DA и AC ≅ BD. Заключение: ABCD — квадрат.
а. Противоположные стороны равны, поэтому ABCD — параллелограмм. Диагонали совпадают, поэтому ABCD представляет собой прямоугольник. Две последовательные стороны не совпадают, поэтому ABCD не является квадратом. б. Противоположные стороны совпадают, поэтому ABCD представляет собой ромб.Диагонали совпадают, поэтому ABCD представляет собой прямоугольник. Четырехугольник, представляющий собой ромб, и прямоугольник — это квадрат, поэтому ABCD — квадрат. c. Противоположные стороны равны, поэтому ABCD — параллелограмм. Диагонали совпадают, поэтому ABCD представляет собой ромб. Один угол не является прямым, поэтому ABCD не является квадратом. d. Противоположные стороны совпадают, поэтому ABCD представляет собой ромб. Диагонали совпадают, поэтому ABCD — квадрат.
____
11. Используйте диагонали, чтобы определить, является ли параллелограмм с вершинами A (−1, — 2), B (−2, 0), C (0, 1) и D (1, — 1) прямоугольник, ромб или квадрат.Назовите все подходящие имена. а. прямоугольник, ромб, квадрат c. прямоугольник b. прямоугольник, ромб d. квадрат
Числовой ответ 12. В параллелограмме LMNO NO = 10,2 и LO = 14,7. Каков периметр параллелограмма LMNO? 13. Найдите значение x в ромбе.
Соответствие Сопоставьте каждому термину словаря его определение. а. вогнутый b. выпуклый c. диагональ d. правильный многоугольник e. сторона многоугольника f. вершина многоугольника g. четырехугольник h. трапеция ____ ____ ____ ____ ____
14.15. 16. 17. 18.
сегмент, который соединяет любые две непоследовательные вершины многоугольника многоугольник, в котором ни одна диагональ не содержит точек на внешней стороне многоугольника, один из сегментов, образующих многоугольник, многоугольник, который является как равносторонним, так и равносторонний — общая конечная точка двух сторон многоугольника. Сопоставьте каждый словарный термин с его определением. а. воздушный змей b. трапеция c. прямоугольник
г. е. f. г. ____ ____ ____ ____ ____
19. 20. 21. 22. 23.
прямоугольник квадратный ромб параллелограмм
четырехугольник с четырьмя прямыми углами четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами четырехугольник с четырьмя равными сторонами четырехугольник с две пары параллельных сторон четырехугольник с ровно двумя парами совпадающих последовательных сторон
Geo — CH6 Раздел ответов практического теста НЕСКОЛЬКИЙ ВЫБОР 1.ОТВЕТ: D У десятиугольника 10 сторон и 10 вершин. сумма внешних углов = 360 °, мера одного внешнего угла =
360 = 36 ° 10
Теорема о сумме внешних углов многоугольника У правильного десятиугольника 10 одинаковых внешних углов, поэтому разделите сумму на 10.
Мера каждого внешний угол правильного десятиугольника 36 °. Обратная связь A B C D
Разделите на количество сторон многоугольника. Разделите 360 на количество сторон многоугольника. Разделите 360 на количество сторон.Верный!
PTS: 1 DIF: Среднее значение REF: Страница 384 OBJ: 6-1.4 Определение внешних углов в многоугольниках NAT: 12.3.3.f TOP: 6-1 Свойства и атрибуты многоугольников 2. ANS: C Чтобы найти ST: In параллелограмм, противоположные стороны равны. ST ≅ UR Определение конгруэнтных отрезков ST = UR Подставляем 25 вместо UR. ST = 25 Чтобы найти XT:
XT ≅ RX XT = RX XT = 16
В параллелограмме диагонали делят друг друга пополам. Определение конгруэнтных сегментов. Замените 16 на RX.
Чтобы найти m∠RST:
m∠RST + m∠STU = 180 ° В параллелограмме последовательные углы являются дополнительными.Заменить 42,4 ° на m∠STU. m∠RST + 42,4 ° = 180 ° Вычтите 42,4 ° с обеих сторон. m∠RST = 137,6 ° Обратная связь A B C
В параллелограмме последовательные углы являются дополнительными, противоположные стороны совпадают, а диагонали делят друг друга пополам. В параллелограмме последовательные углы являются дополнительными, а не дополнительными. Верный!
D
Противоположные стороны параллелограмма совпадают, а диагонали делят друг друга пополам.
PTS: 1 NAT: 12.3.3.f 3. ANS: B
MP ≅ NO
MP = NO
5x = 3x + 12 x = 6
MP = 5x = 5 (6) = 30
DIF: Среднее REF: Страница 392 TOP: 6-2 Свойства параллелограммов
OBJ: 6-2.1 Приложение
Противоположные стороны параллелограмма совпадают. Определение конгруэнтных отрезков Заменитель. Упростите и решите. Подставить и решить для измерения всего сегмента.
Обратная связь A B C D
Противоположные стороны параллелограмма совпадают. Верный! Установите выражения для противоположных сторон параллелограмма равными друг другу. Подставьте решение для x обратно в исходное выражение.
PTS: OBJ: NAT: 4. ANS: Proof:
1 DIF: Среднее значение REF: Страница 393 6-2.2 Использование свойств параллелограммов для поиска мер 12.3.3.f TOP: 6-2 Свойства параллелограммов A
Утверждения 1. ABDF и FBCD являются параллелограммами. 2. ∠BCD ≅ ∠DFB 3. DF Ä AB 4. ∠DFB ≅ ∠ABF 5. ∠BCD ≅ ∠ABF
Причины 1. Дано 2. В параллелограмме противоположные углы совпадают. 3. Противоположные стороны параллелограмма параллельны. 4. Теорема об альтернативных внутренних углах 5. Замена
Обратная связь A B C D
Правильно! Угол BCD и угол DFB не являются вертикальными углами.Конгруэнтность треугольников не доказана. В параллелограмме только противоположные углы должны совпадать.
PTS: OBJ: TOP: 5. ANS:
1 DIF: Среднее значение REF: Page 394 6-2.4 Использование свойств параллелограммов в доказательном NAT: 12.3.5.a 6-2 Свойства параллелограммов A Учитывая HI = 5x — 10 ГДж = 7x — 20 HI = 5 (5) — 10 = 15 ГДж = 7 (5) −20 = 15 Заменить и упростить.
GH = 3y GH = 3 (8) = 24
JI = 5y — 16 JI = 5 (8) — 16 = 24
Дано Заменить и упростить.
Поскольку HI = GJ и GH = JI, GHIJ — параллелограмм, поскольку оба набора противоположных сторон конгруэнтны. Обратная связь A B C D
Правильно! Вычислялась информация об обоих наборах противоположных сторон четырехугольника. Чтобы сделать вывод о параллельности сторон, необходимо рассчитать уклон. Будьте осторожны при определении того, какое число входит в какой пробел!
PTS: 1 DIF: Среднее значение REF: Страница 399 OBJ: 6-3.1 Проверка значений параллелограммов TOP: 6-3 Условия для параллелограммов 6.ОТВЕТ: B Найдите уклон и длину одной пары противоположных сторон. 10-7 3 — (−5)
=
наклон FG = 48 −− 10 =
3 8
наклон DE = DE =
NAT: 12.3.3.f
3 8
(3 — (−5)) 2 + (10-7) 2 =
73
FG = (8-0) 2 + (4-1) 2 = 73 DE и FG имеют одинаковый наклон, поэтому DE Ä FG. Поскольку DE = FG, DE ≅ FG. Поскольку одна пара противоположных сторон одновременно конгруэнтна и параллельна, DEFG представляет собой параллелограмм. Обратная связь A B C D
Когда наклоны одинаковые, линии параллельны.Верный! Если стороны равны по длине, то они равны. Перпендикулярные линии не имеют одинакового наклона.
PTS: OBJ: TOP: 7. ANS:
1 DIF: Среднее REF: Page 400 6-3.3 Доказательство параллелограммов в координатной плоскости NAT: 12.3.3.g 6-3 Условия для параллелограммов A Диагонали прямоугольника конгруэнтны. AC = BD = 14 1 Прямоугольник — это параллелограмм. Диагонали параллелограмма BX = 2 BD рассекают друг друга пополам. 1 BX = 2 (14) = 7 Подставить и упростить.
Обратная связь A B C D
Правильно! Диагонали прямоугольника равны.Диагонали прямоугольника равны. Диагонали прямоугольника делят друг друга пополам.
PTS: 1 NAT: 12.3.3.f 8. ANS: A
DIF: Basic REF: Страница 408 OBJ: 6-4.1 TOP: 6-4 Свойства специальных параллелограммов
AB =
(−1 — (−4)) 2 + (3 — (−3)) 2 = 3 5
BC =
(5 — (−1)) 2 + (0-3) 2 = 3 5
CD =
(2-5) 2 + (−6-0) 2 = 3 5
(−4-2) 2 + (−3 — (−6)) 2 = 3 5 3 — (−3) наклон AB = −1 — (−4) = 2
DA =
наклон BC =
0−3 5 — (−1)
= — 12
2 ⋅ ÊÁË — 12 ˜˜¯ = −1 Поскольку произведение наклонов равно −1, AB ⊥ BC.Обратная связь A B C D
Правильно! Используйте формулу расстояния, чтобы найти меры длин сторон квадрата. Наклон линии — это разница в координатах y, деленная на разницу в координатах x. Используйте формулу расстояния, чтобы найти меры длин сторон квадрата.
PTS: 1 DIF: Среднее REF: Страница 410 OBJ: 6-4.3 Проверка свойств квадратов NAT: 12.3.5.a TOP: 6-4 Свойства специальных параллелограммов 9. ANS: A Обе пары противоположных сторон параллельны, поэтому ABCD — параллелограмм.Поскольку один угол равен 90 °, это прямой угол, а параллелограмм с одним прямым углом — это прямоугольник. Обратная связь A B
C
Правильно! Квадрат — это параллелограмм с одним прямым углом и двумя последовательными равными сторонами. Найдите фигуру с одним прямым углом, но не обязательно с двумя последовательными конгруэнтными сторонами. У ромба есть параллельные противоположные стороны, но есть и другие ограничения. Найдите форму
D
без других ограничений. Параллелограмм с одним прямым углом ДЕЙСТВИТЕЛЬНО предоставляет достаточно информации, чтобы изменить его описание.
PTS: 1 DIF: Среднее REF: Страница 418 OBJ: 6-5.1 Application NAT: 12.3.3.f TOP: 6-5 Условия для специальных параллелограммов 10. ANS: A Противоположные стороны совпадают, поэтому ABCD — параллелограмм. Диагонали совпадают, поэтому ABCD представляет собой прямоугольник. Две последовательные стороны не совпадают, поэтому ABCD не является квадратом. Обратная связь A B C D
Правильно! Если противоположные стороны совпадают, четырехугольник не обязательно является ромбом. Найдите описание с меньшим количеством ограничений. Если диагонали параллелограмма совпадают, создается другая форма.Если противоположные стороны совпадают, четырехугольник не обязательно является ромбом. Найдите описание с меньшим количеством ограничений.
PTS: 1 DIF: Среднее значение REF: Страница 420 OBJ: 6-5.2 Применение условий для специальных параллелограммов TOP: 6-5 Условия для специальных параллелограммов 11. ANS: A Шаг 1 График ABCD.
NAT: 12.3.3.f
Шаг 2 Диагонали прямоугольника совпадают. Найдите AC и BD, чтобы определить, является ли ABCD прямоугольником.
AC =
(0 — (−1_) 2 + (1 — (−2)) 2 =
BD =
(1 — (−2)) 2 + (−1-0) 2 =
10 10
Поскольку AC = BD, ABCD — прямоугольник.Шаг 3 Диагонали ромба перпендикулярны. Найдите наклоны AC и BD, чтобы определить, является ли ABCD ромбом.
наклон AC =
1 — (−2) 0 — (−1)
= 3
наклон BD =
−1-0 1 — (−2)
= — 13
Так как (3) Á — 13
Ë
ˆ˜ = −1, AC ⊥ BD и ABCD — ромб. ¯
Поскольку ABCD одновременно является ромбом и прямоугольником, он также является квадратом. Обратная связь A B C D
Правильно! Четырехугольник, представляющий собой прямоугольник и ромб, — это тоже нечто иное.Найдите наклон диагоналей ABCD, чтобы определить, является ли форма ромбом. Определите, является ли четырехугольник прямоугольником, найдя размеры его диагоналей.
PTS: 1 DIF: Среднее значение REF: стр. 420 OBJ: 6-5.3 Определение особых параллелограммов в координатной плоскости NAT: 12.3.4.d TOP: 6-5 Условия для специальных параллелограммов ЧИСЛОВЫЙ ОТВЕТ 12. ANS: 49,8 PTS: 1 DIF: Среднее значение TOP: 6-2 Свойства параллелограммов 13. ANS: 0.5
NAT: 12.2.1.h
PTS: 1 DIF: Advanced NAT: 12.3.3.f TOP: 6-4 Свойства специальных параллелограммов MATCHING 14. ANS: TOP: 15. ANS: TOP: 16. ANS: TOP: 17. ANS: TOP: 18. ANS: TOP:
C PTS: 1 DIF : 6-1 Свойства и атрибуты многоугольников B PTS: 1 DIF: 6-1 Свойства и атрибуты многоугольников E PTS: 1 DIF: 6-1 Свойства и атрибуты многоугольников D PTS: 1 DIF: 6-1 Свойства и атрибуты Полигоны F PTS: 1 DIF: 6-1 Свойства и атрибуты полигонов
19. ANS: C
PTS:
1
DIF:
Basic
REF: Страница 382
Basic
REF: Page 383
Basic
REF: Страница 382
Basic
REF: Страница 382
Basic
REF: Страница 382
Basic
REF: Страница 408
20.21. 22. 23.
TOP: ANS: TOP: ANS: TOP: ANS: TOP: ANS: TOP:
6-4 Свойства специальных параллелограммов E PTS: 1 DIF: 6-4 Свойства специальных параллелограммов F PTS : 1 DIF: 6-4 Свойства специальных параллелограммов G PTS: 1 DIF: 6-2 Свойства параллелограммов A PTS: 1 DIF: 6-6 Свойства воздушных змеев и трапеций
Basic
REF: Page 410
Basic
REF: Страница 409
Basic
REF: Страница 391
Basic
REF: Страница 427
Является ли квадрат прямоугольником?
Сходство в свойствах квадрата и прямоугольника может помочь нам сделать вывод о запросе «Является ли квадрат прямоугольником».В геометрии мы узнали о различных типах форм, таких как квадрат, прямоугольник, цилиндр, ромб, кубоид, куб, конус, параллелограмм и т. Д. Многие из этих форм обладают определенными общими свойствами. Квадрат и прямоугольник являются примерами таких двумерных форм. Оба они подпадают под категорию четырехугольников.
Квадрат против прямоугольника
Квадрат: Квадрат — это двумерная плоская фигура с четырьмя равными сторонами, четырьмя внутренними прямыми углами и четырьмя углами.Другими словами, квадрат — это четырехугольник или четырехугольник. Все углы равны, поэтому четырехугольник считается равносторонним.
Прямоугольник: Прямоугольник — это двухмерная фигура с четырьмя сторонами, четырьмя внутренними прямыми углами и четырьмя углами. Противоположные стороны прямоугольника равны. Прямоугольник имеет четыре угла, каждый из которых составляет 90º. Подобно квадрату, прямоугольник также называют равносторонним четырехугольником.
Давайте посмотрим на изображение, данное здесь, чтобы лучше понять квадрат и прямоугольник.
Поскольку и квадрат, и прямоугольник имеют одинаковое количество сторон, т.е. 4, мы можем заключить, что и квадрат, и прямоугольник являются четырехугольниками. Мы можем наблюдать сходство свойств как квадрата, так и прямоугольника в следующем разделе.
Свойства квадрата и прямоугольника
И квадрат, и прямоугольник обладают некоторыми особыми свойствами, которые отличают их от обычного четырехугольника. Мы можем провести сравнение необходимых свойств обеих фигур из следующей таблицы и сделать вывод, обладает ли квадрат всеми свойствами, которые определяют прямоугольник.
Чем похожи квадрат и прямоугольник?
Из сравнения, проведенного выше для общих свойств, общих для квадрата и прямоугольника, мы видим, что квадрат имеет все свойства, которые определяют прямоугольник, что делает их определенным образом похожими. Это означает, что квадрат также можно назвать разновидностью прямоугольника.
Таким образом, мы можем окончательно заключить, что да, квадрат есть прямоугольник.
Что делает квадрат особым прямоугольником?
Да, квадрат — это особый тип прямоугольника, потому что он обладает всеми свойствами прямоугольника.Подобно прямоугольнику, квадрат имеет:
- внутренних углов размером 90 ∘ каждый.
- противоположных сторон, которые параллельны и равны.
- две диагонали, которые делят друг друга пополам и равны.
Квадрат называется особым видом прямоугольника, потому что он обладает некоторыми дополнительными свойствами, которые не применяются к прямоугольникам. Их:
- Все четыре стороны квадрата равны.
- Диагонали квадрата делятся пополам под прямым углом.
Важные примечания
Ниже приведены несколько важных замечаний по теме — квадрат прямоугольник.
- Все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
- Все квадраты — ромбы, но не все ромбы — квадраты.
Попробуйте нестандартно ответить на следующий вопрос:
- Каждая четырехгранная фигура является четырехугольником?
- Все ли прямоугольники квадраты?
- Все ли ромбы квадратные?
- Квадрат — это трапеция?
- Квадрат — это параллелограмм?
Часто задаваемые вопросы о том, является ли квадрат прямоугольником
Квадрат — это прямоугольник — да или нет?
Ответ — да.Квадрат — это прямоугольник, потому что он обладает всеми свойствами прямоугольника. Эти свойства:
- Внутренние углы размером 90 ∘ каждый.
- Противоположные стороны, которые параллельны и равны.
- Две диагонали, пересекающие друг друга и равные друг другу.
В чем разница между квадратом и прямоугольником?
Квадраты обладают некоторыми дополнительными свойствами, которые не применяются к прямоугольникам. У квадрата все четыре стороны равны, тогда как в прямоугольнике равны только противоположные стороны.
Квадрат — это прямоугольник и ромб?
Квадрат одновременно является прямоугольником и ромбом, потому что он обладает свойствами прямоугольников и ромбов. Если вы тоже ищете ответ на вопрос — ромб или прямоугольник, то ответ отрицательный.
Квадрат — это прямоугольник. Это утверждение верно или неверно?
Это утверждение верно. Квадрат — это прямоугольник, потому что он обладает всеми свойствами прямоугольника.
Почему квадрат — это особый тип прямоугольника?
Квадрат — это особый тип прямоугольника, поскольку он обладает всеми свойствами прямоугольника.Подобно прямоугольнику, квадрат имеет внутренние углы, каждый из которых составляет 90º. противоположные стороны, которые параллельны и равны.
Почему прямоугольник не квадрат?
У прямоугольника не обязательно все четыре стороны одинаковой меры. Это причина того, что прямоугольник не является квадратом.
Четырехугольники Недвижимости | Параллелограммы, Трапеция, Ромб
Нажмите здесь, чтобы посмотреть это проницательное видео.Лучшие университеты мира
В этом руководстве по основным понятиям геометрии мы рассмотрим типы и свойства четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапецию.
определение:
Четырехугольник — это простая замкнутая фигура с четырьмя сторонами.
Виды четырехугольников
Есть пять типов четырехугольников.
- Параллелограмм
- Прямоугольник
- Площадь
- Ромб
- Трапеция
Общим свойством всех четырехугольников является то, что сумма всех их углов равна 360 °.
Давайте посмотрим на свойства различных четырехугольников.
параллелограмм
Свойства параллелограмма
- Противоположные стороны параллельны и совпадают.
- Противоположные углы совпадают.
- Смежные углы являются дополнительными.
- Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два равных треугольника.
- Если один из углов параллелограмма — прямой, то все остальные углы прямые, и он становится прямоугольником.
Важные формулы параллелограммов
- Площадь = Д * В
- Периметр = 2 (L + B)
Прямоугольники
Свойства прямоугольника
- Противоположные стороны параллельны и совпадают.
- Все углы прямые.
- Диагонали совпадают и делят друг друга пополам (делят друг друга поровну).
- Противоположные углы, образованные в точке пересечения диагоналей, совпадают.
- Прямоугольник — это особый тип параллелограмма с прямыми углами.
Важные формулы для прямоугольников
- Если длина L, а ширина B, то
Длина диагонали прямоугольника = √ (L 2 + B 2 )
- Площадь = L * B
- Периметр = 2 (L + B)
квадратов
Объекты квадрата
- Все стороны и углы совпадают.
- Противоположные стороны параллельны друг другу.
- Диагонали совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Квадрат — это особый тип параллелограмма, все углы и стороны которого равны.
- Кроме того, параллелограмм становится квадратом, когда диагонали равны правым биссектрисам друг друга.
Важные формулы для квадратов
- Если «L» — длина стороны квадрата, тогда длина диагонали = L √2.
- Площадь = L 2 .
- Периметр = 4L
Ромб
Свойства ромба
- Все стороны совпадают.
- Противоположные углы совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Соседние углы являются дополнительными (например, A + ∠B = 180 °).
- Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу.
Важные формулы для ромба
Если a и b — длины диагоналей ромба,
- Площадь = (a * b) / 2
- Периметр = 4L
Трапеция
Свойства трапеции
- Основания трапеции параллельны друг другу (MN ⫽ OP).
- Нет сторон, углы и диагонали не совпадают.
Важные формулы трапеции
- Площадь = (1/2) ч (L + L 2 )
- Периметр = L + L 1 + L 2 + L 3
Обзор объектов недвижимости
Обобщая то, что мы узнали до сих пор, для удобства использования и запоминания:
| S. No. | Недвижимость | параллелограмм | Прямоугольник | Ромб | Квадрат |
| 1 | Все стороны совпадают | ✕ | ✕ | & проверить; | & проверить; |
| 2 | Противоположные стороны параллельны и совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 3 | Все углы совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 4 | Противоположные углы равны | & проверить; | & проверить; | & проверить; | & проверить; |
| 5 | Диагонали совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 6 | Диагонали перпендикулярны | ✕ | ✕ | & проверить; | & проверить; |
| 7 | Диагонали пересекают друг друга | & проверить; | & проверить; | & проверить; | & проверить; |
| 8 | Углы смежные дополнительные | & проверить; | & проверить; | & проверить; | & проверить; |
Продолжить изучение:
— Свойства линий и углов
— Свойства и формулы кругов
— Типы треугольников и свойства
Четырехугольники — Квадраты | Shmoop
Квадраты
Если вы думали, что прямоугольники особенные, вас ждет угощение.Их называют квадратами, и они идеальны во всех отношениях. Ну, не через каждые , потому что ни один четырехугольник не идеален. Но квадраты, безусловно, являются супермоделями четырехугольного мира. (Думайте только о здоровых углах, а не о болезненных.)
Квадрат — это прямоугольник с четырьмя равными сторонами. Или ромб с четырьмя равными углами. Или параллелограмм с четырьмя равными сторонами и четырьмя равными углами. Сделайте ваш выбор; они все одинаковые. Правильно: квадрат — это параллелограмм, прямоугольник и ромб в одном лице.Это все и пакет чипсов.
Равносторонний и равносторонний означают одно и то же, когда вы говорите о треугольниках, но четырехугольники немного разборчивее. Четырехугольник может быть равноугольным, но не равносторонним (прямоугольник) или равносторонним, но не равносторонним (ромб). Квадрат, однако, равен и . Все стороны квадрата имеют одинаковую длину (равносторонние), и все его углы имеют одинаковую меру (равносторонние). Это делает квадрат единственным равносторонним четырехугольником и .Конечно, мы можем просто назвать это «правильным четырехугольником».
Пример задачи
Внутренний угол квадрата имеет размер, в 18 раз превышающий длину его стороны. Каков периметр квадрата?
Мы знаем, что каждый внутренний угол в квадрате имеет меру 90 °. (Квадраты равносторонние и имеют 4 угла в сумме 360 °.) Чтобы найти периметр, нам нужно умножить длину стороны квадрата s на 4, потому что квадрат имеет четыре конгруэнтные стороны. Таким образом, P = 4 s .
Если размер одного угла в 18 раз больше размера стороны, мы знаем, что 18 с = 90. Мы можем найти значение с , найдя 90 ÷ 18. После вычисления с = 5, мы можем найти P = 4 с = 4 (5) = 20.
Пример задачи
Если четырехугольник — ромб, является ли он также квадратом?
Четырехугольник — это любая четырехугольная фигура. Ромб — это четырехугольник с четырьмя равными сторонами. Квадрат — это четырехугольник с четырьмя равными сторонами и четырьмя равными углами.Возникает вопрос: должен ли четырехугольник с четырьмя равными сторонами иметь четыре равных угла?
Прямой ответ — нет. Ромби — это параллелограммы, поэтому противоположные углы совпадают, а следующие друг за другом — дополнительные. Если один равен 90 °, то все они 90 °, но где написано, что они должны быть 90 °? Это не так. Во всяком случае, нигде мы не можем увидеть. Таким образом, хотя ромб может быть квадратом , это не обязательно.
Поскольку квадраты представляют собой просто прямоугольные ромбы (или ромбовидные прямоугольники), их диагонали имеют те же свойства, что и у ромбов и прямоугольников.А именно, диагонали квадрата равны серединным перпендикулярам друг к другу. Кроме того, они могут танцевать чечетку, играть на виолончели и заниматься паркуром. Разносторонне одаренные маленькие негодяи, не так ли?
Пример задачи
Четырехугольник JAIM — квадрат. Найдите длину x .
У нас есть два способа сделать это, и оба используют прямоугольные треугольники. Мы бы извинились за это, но пора к ним привыкнуть.
Во-первых, мы могли бы посмотреть на Δ JAI и найти длину его гипотенузы JI .Поскольку обе ветви ( JA и AI ) совпадают, мы знаем, что Δ JAI представляет собой треугольник 45-45-90 с катетами 4 см. Запомнили ли мы свойства этих треугольников или извлекли из теоремы Пифагора, мы должны получить длину в см для JI . Поскольку диагонали квадрата совпадают и делят друг друга пополам, мы знаем, что x составляет половину этой длины, или см ≈ 2,83 см.
Второй способ — понять, что квадрат также является ромбом, а это значит, что его диагонали перпендикулярны биссектрисам.Другими словами, не только сегмент ME имеет длину x , но и EI также имеет длину x . А поскольку ∠ MEI — прямой угол, у нас есть еще один треугольник 45-45-90: Δ MEI . Мы знаем гипотенузу ( MI = 4 см) и можем вычислить длину одной ножки, x . Будь то по теореме Пифагора или по особым свойствам треугольника, мы также должны получить cm ≈ 2,83 см.
Если в лесу упал квадрат, но его никто не услышит, в чем смысл жизни?
Мы не собираемся заниматься такими ужасающими экзистенциальными кризисами, как этот, но мы, , хотим знать, как отличить квадрат от квадрата — независимо от смысла жизни.Итак, если он выглядит как квадрат и катится как квадрат, это квадрат? (Вы когда-нибудь пробовали катить квадрат? Даже на спуске это непросто.) Мы можем сказать несколько разных способов.
- Если четырехугольник равносторонний и равносторонний, это квадрат.
- Если ромб равноугольный, это квадрат.
- Если прямоугольник равносторонний, это квадрат.
По сути, если вы можете доказать, что четырехугольник одновременно является ромбом и прямоугольником, вы доказали, что это квадрат.Конечно, мы можем использовать диагонали, чтобы доказать, что дело в ромбе и прямоугольнике, но мы оставим это вам.

 Найдите угол АОD 2.
Найдите углы прямоугольной трапеции,
если один из ее углов равен
20°.
3.
Стороны параллелограмма относятся
как 1 : 2, а его периметр равен
30 см. Найдите стороны параллелограмма.
4.
В равнобедренной трапеции сумма углов
при бо-льшем основании равна
96°. Найдите углы трапеции.
5.
Высота ВМ, проведенная
из вершины угла ромба АВСD образует
со стороной АВ угол
30°, АМ= 4
см. Найдите длину диагонали ВD ромба,
если точка М лежит
на стороне АD.
Найдите угол АОD 2.
Найдите углы прямоугольной трапеции,
если один из ее углов равен
20°.
3.
Стороны параллелограмма относятся
как 1 : 2, а его периметр равен
30 см. Найдите стороны параллелограмма.
4.
В равнобедренной трапеции сумма углов
при бо-льшем основании равна
96°. Найдите углы трапеции.
5.
Высота ВМ, проведенная
из вершины угла ромба АВСD образует
со стороной АВ угол
30°, АМ= 4
см. Найдите длину диагонали ВD ромба,
если точка М лежит
на стороне АD. Диагонали прямоугольника МNKР
пересекаются в точке О, МОN =
64°. Найдите угол ОМР. 2.
Найдите углы равнобедренной трапеции,
если один из ее углов равен 30°.
3.
Стороны параллелограмма относятся
как 3 : 1, а его периметр равен
40 см. Найдите стороны параллелограмма.
4.
В прямоугольной трапеции сумма углов
при мень-шем основании равна248°.
Найдите углы трапеции.
5.
Высота ВМ, проведенная
из вершины угла ромба АВСD образует
со стороной АВ угол
30°, длина диагонали АС равна
6 см. Найдите АМ9 если
точка М лежит на продолжении стороны АD.
Диагонали прямоугольника МNKР
пересекаются в точке О, МОN =
64°. Найдите угол ОМР. 2.
Найдите углы равнобедренной трапеции,
если один из ее углов равен 30°.
3.
Стороны параллелограмма относятся
как 3 : 1, а его периметр равен
40 см. Найдите стороны параллелограмма.
4.
В прямоугольной трапеции сумма углов
при мень-шем основании равна248°.
Найдите углы трапеции.
5.
Высота ВМ, проведенная
из вершины угла ромба АВСD образует
со стороной АВ угол
30°, длина диагонали АС равна
6 см. Найдите АМ9 если
точка М лежит на продолжении стороны АD.
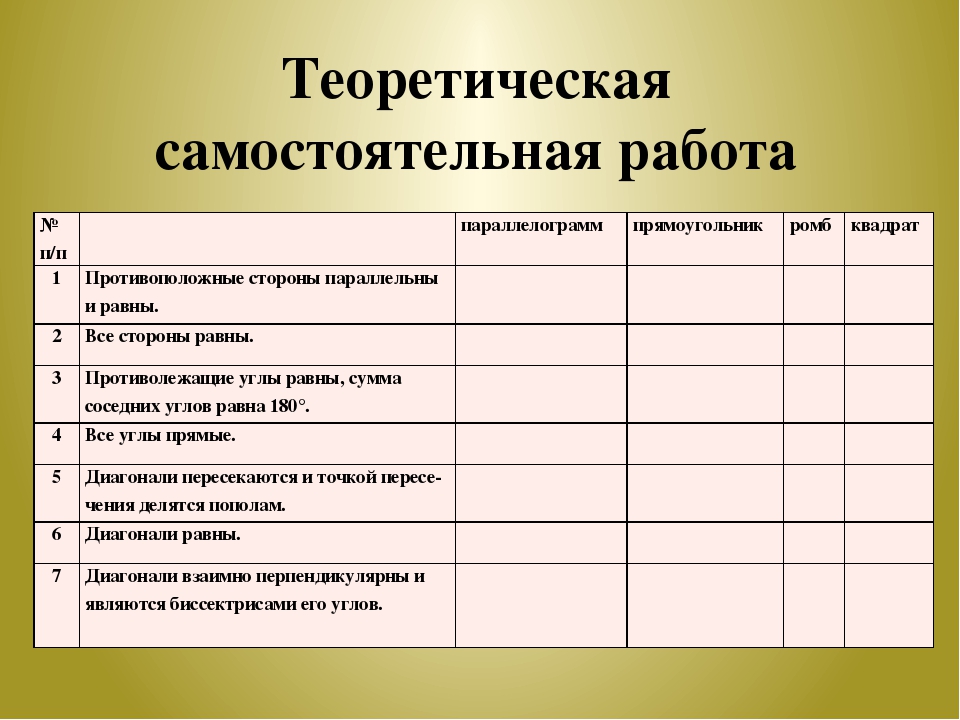
 Дано:
РЕ||NK,
МР=8, MN=12,
ME=6.
(рис. 1)
Дано:
РЕ||NK,
МР=8, MN=12,
ME=6.
(рис. 1) Найдите длины отрезков АС и
АО, если АВ=4см.
Найдите длины отрезков АС и
АО, если АВ=4см. Найдите стороны АВ и ВС.
Найдите стороны АВ и ВС.
 Средние линии треугольника ∆АВС
относятся как 2:3:4, а Р∆АВС=
45см. Найдите стороны ∆АВС.
Средние линии треугольника ∆АВС
относятся как 2:3:4, а Р∆АВС=
45см. Найдите стороны ∆АВС. Найдите: СА, sin
С.
Найдите: СА, sin
С. Найдите
C,
D.
Найдите
C,
D.