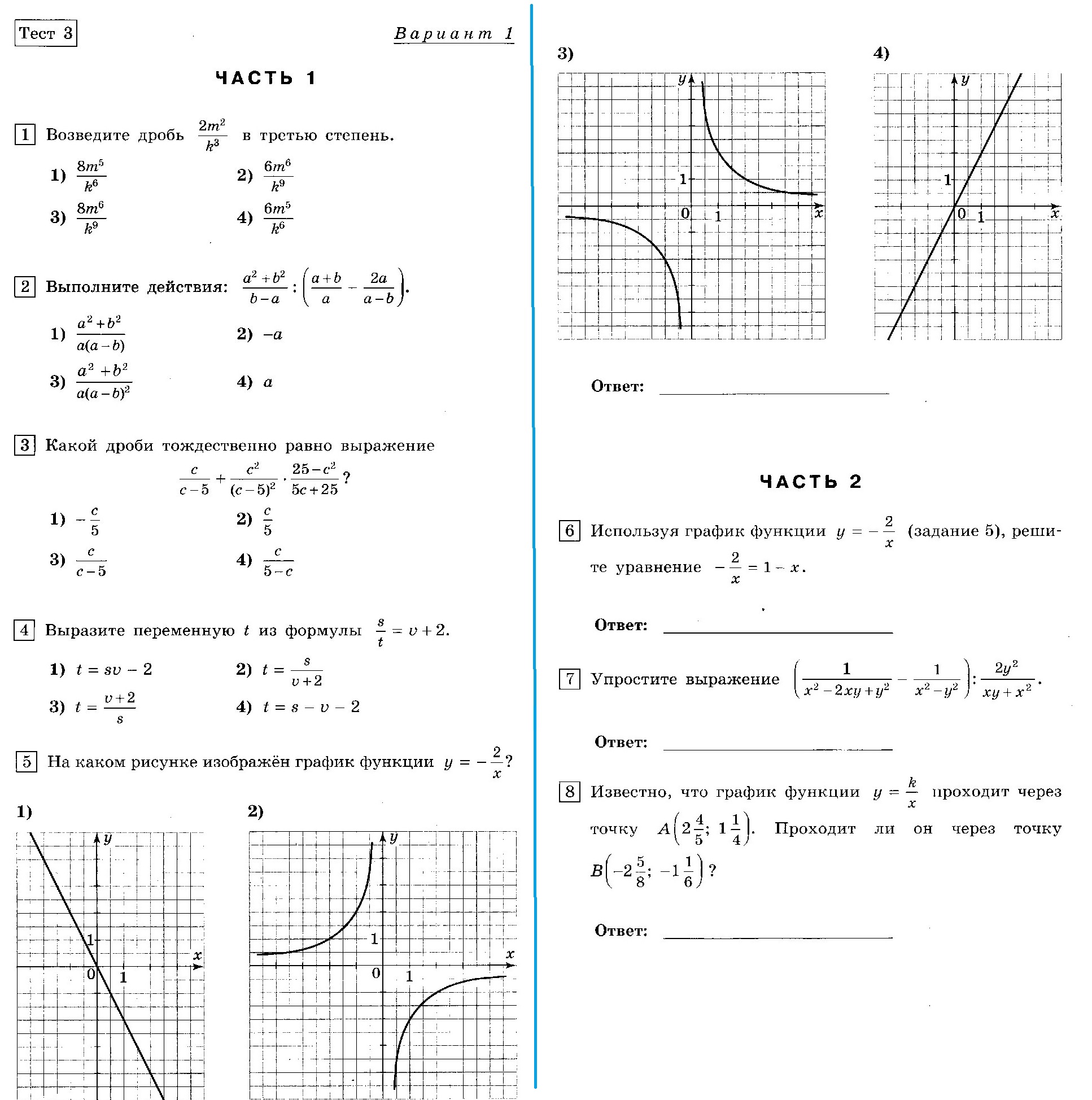
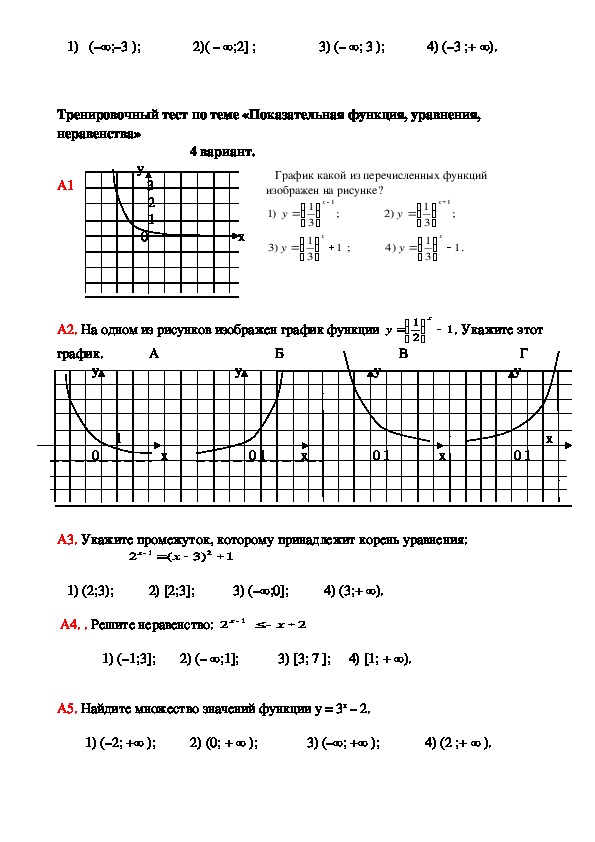
Показательная функция 10 класс контрольная работа: Контрольная работа по теме: Показательная функция 10 класс

Контрольная работа по теме: Показательная функция 10 класс

Контрольная работа по алгебре

«Показательная функция»

Вариант 1

Сравнить числа:

а) и ; б) ﴾и .

Решить уравнение:

а) ﴾ = 16; б) ; в) — 2• + 5 = 0

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾

Найти точку пересечения графиков у = и у = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция»

Вариант 2

Сравнить числа:

а) и ; б) и .

Решить уравнение:

а) ; б) ; в) — 5• + 3= 0.

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾.

Решить графически уравнение = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция» Вариант 1

Сравнить числа:

а) и ; б) ﴾и .

Решить уравнение:

а) ﴾ = 16; б) ; в) — 2• + 5 = 0

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾

Найти точку пересечения графиков у = и у = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция»Вариант 2

Сравнить числа:

а) и ; б) и .

Решить уравнение:

а) ; б) ; в) — 5• + 3= 0.

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾.

Решить графически уравнение = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция» Вариант 1

Сравнить числа:а) и ; б) ﴾ и .

Решить уравнение: а) ﴾ = 16; б) ; в) — 2• + 5 = 0

Решить неравенство .

Решить неравенство а) ; б) ; в) + ﴾

Найти точку пересечения графиков у = и у = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция»

Вариант 1

Сравнить числа:

а) и ; б) ﴾и .

Решить уравнение:

а) ﴾ = 16; б) ; в) — 2• + 5 = 0

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾

Найти точку пересечения графиков у = и у = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция»

Вариант 2

Сравнить числа:

а) и ; б) и .

Решить уравнение:

а) ; б) ; в) — 5• + 3= 0.

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾.

Решить графически уравнение = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция» Вариант 1

Сравнить числа:

а) и ; б) ﴾и .

Решить уравнение:

а) ﴾ = 16; б) ; в) — 2• + 5 = 0

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾

Найти точку пересечения графиков у = и у = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция»Вариант 2

Сравнить числа:

а) и ; б) и .

Решить уравнение:

а) ; б) ; в) — 5• + 3= 0.

Решить неравенство .

_________________________________________________________________

Решить неравенство

а) ; б) ; в) + ﴾.

Решить графически уравнение = х+ 4

Решить уравнение .

Контрольная работа по алгебре

«Показательная функция» Вариант 2

Сравнить числа: а) и ; б) и .

Решить уравнение: а) ; б) ; в) — 5• + 3= 0.

Решить неравенство .

Решить неравенство а) ; б) ; в) + ﴾.

Решить графически уравнение = х+ 4

Решить уравнение .

Контрольная работа по математике (Показательная функция) для 10-го класса от Колягина в 2016 году

Ответы

Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Статистика и загрузка

Скачать

Если загрузка не началась автоматически, повторите попытку или нажмите сюда!
Просмотров17660Загрузок
ДобавилГость23.09.2019Дата
ДеньПонедельник22:43Время

Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.

Все материалы сайта представлены исключительно в ознакомительных целях.

Источник/автор материала: БАЗА ОБРАЗОВАТЕЛЬНЫХ РЕСУРСОВ

Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.

Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.

Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]

Справочные материалы

Загрузка формул. ..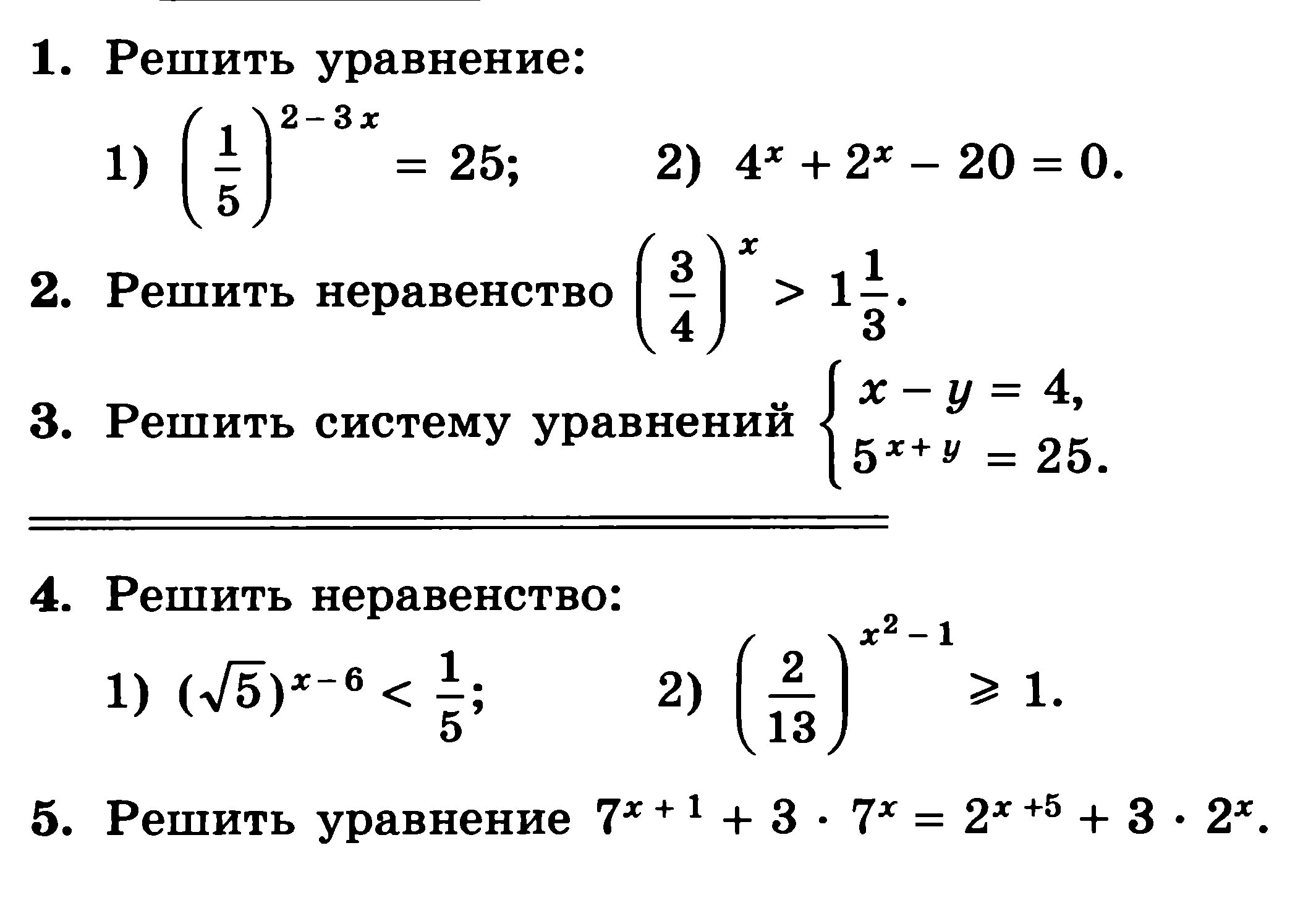

Загрузка тестирования…

Обсуждения

Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!

Контрольная работа по математике на тему «Показательная функция» (10 класс)

Контрольная работа по математике 10­11 класс. Тема: «Показательная функция. Решение показательных уравнений ». Вариант 1. 1. Дайте определение показательной функции. 2. Постройте график функции  3. Найдите область определения функции: 13  y  , если  a >1.  x xa y y а)  б)  y x 2  1  2  x    5 в) г) y  x 22  2 4. Упростите выражение: а)           б)  3 5 a  5 a  323b 3 55 3 52 : a в)  г)  4  bb  3 x a 4 x 8 : x b x 3 x : a 5. Вычислите:     43     4 а)  б)   1 4 5 2: 525  в)  г)  73 5 3 44 7 125 2 : 3 6. Решите уравнение: а)  5 x 125 б)     x  1  4  2 7. Решите уравнение: а)  16 x  45 4 x в)  8 4 x  1 37  x    1 8    г)  5 x 22  x  3 1 б)  x 4 4 x  3  x 2 4 2 x  9 Контрольная работа по математике 10­11 класс.

Тема: «Показательная функция. Решение показательных уравнений». Вариант 2. 1. Дайте определение показательной функции. 2. Постройте график функции  3. Найдите область определения функции: y  , если 0< a <1. xa а)  y 5 x б)  у 3  x 2 4. Упростите выражение: в)  y г)  y 2     1  3  1  x 3 2 x  1  6 4  3 43a а)  б)  5 32 5 x 3 : x 5. Вычислите:    а)  3 5      3 3 б)  7 132  49: 3      6. Решите уравнение: а)  б)   x 3  5 7 49 x  x  2 49 1 7 7. Решите сложное уравнение: 3 в)  b г)  b : x 52   b   2 b x 52 1 b    x в)  г)  65 3 4 39 6     1  243  4 27 в)  3 x 52  x г)  x 3 81  4 1 9 а)  x 25  56 x 5 б)  x 9  x 4  x 3 27  22 x Контрольная работа по математике. Тема: «Показательная функция. Решение показательных уравнений ». Вариант 3. 1. Дайте определение показательной функции.  2. Постройте график функции  3. Найдите область определения функции: 1  5  x 7 2    в)  а)   xa    5 y y у  1 x , если  a >1. б)  y 3 x 4.
 Упростите выражение: г)  y 5  x 3 3 17 4 3 2 17 x а)          б)  3 73 a : 72 a 2 в)  c 17 8  c  : c 2 17  2 5 x г)         1 b    x     7 x  b 5. Вычислите:    а)  4 3      8 8 б)  25 7 2 1   5 5  7 6. Решите уравнение: а)  б)  81 x 3 2 x 32 в)  г)     1 4    5 26 376   2 73 16 5 в)  г)  64 x x 2   5 3 2 72  x 10 7  x 1 49 7. Решите сложное уравнение: а)  676  x x 36 б)  x 25 2 x  9  x 5 5  x 81 Ответы. Вариант 1. 1) Показательная функция – это функция, заданная формулой  1a 2)  ). y  (где a >0, xa  ; в)  0;у  ; г)  2;у    у у    3) а)  ;0 4) а) 1; б)  5) а) 9; б)   ; б)  ;5 6b ; в)  2b ; г) 1. 1 ; в) 1; г) 16. 8 6) а) х=4; б)  7) а) х=1, х=0; б) х=­2. 1х 2 ; в) х=­8; г) х=3, х=­1. Вариант 2. 1) Показательная функция – это функция, заданная формулой  1a 2)  ). y  (где a >0,  xa ; в)  у  ;0   ; г)  6;у  .  0;у 4a ; б) 1; в) 3) а) 4) а)  5) а) 5; б)  ; б)   ;2 у  3b ; г)   xb3 .
  1 ; в) 1; г) 729. 7 1 ; б) х=­ 5 6) а) х= 7) а) х=1, х=0; б) х=­3. 1 ; в) х=4; г) х=2, х=3. 2 Вариант 3. 1) Показательная функция – это функция, заданная формулой  1a 2)  ). y  (где a >0, xa ; в)   ;0   у ; г)    ;3  у .  ;0  xb 2 .  у ; б)  1 ; в)  2 5;у 2х ; б)   3) а)  4) а)  8с ; г)  5) а) 9; б) 125; в) 8; г) 36. 6) а) х= 7) а) х=1, х=0; б) х=­1. 1 ; б) х=5; в) х=­1; г) х=­4, х=­3. 4

Контрольные работы для 10 класса

Приложение 2

Контрольные работы для 10 класса

Контрольные работы для разных профилей, соответст­вующие вариантам планирования из расчета 2, 5 ч, 3 ч, 4 ч и 5 ч в неделю, обозначены и устроены следующим образом .

Контрольные работы для базового уровня обозначены одной буквой К (с соответствующим номером работы). Контрольные работы, предназначенные для профильного уровня, обозначены двумя буквами

КП (с соответствующим номером работы).

В каждой контрольной работе раздел Асодержит задания для базо­вого уровня (планирование из расчета 2, 5 ч и 3 ч в неделю). Разделы Б и Всодержат задания для профильного уровня (при планировании из расчета 4 ч и 5 ч в неделю соответственно).

В зависимости от уровня подготовки класса, времени, отводимого на контрольную работу, и варианта планирова­ния учитель может объявить учащимся, какие задания работы он считает обя­зательными, а какие дополнительными (как правило, это последние задания в каждом разделе). За выполнение обязательной части работы ученику ставится одна отметка. Ставить отметку за выполнение дополнительных заданий нужно только в случае успеха и с согласия ученика.

При любом варианте планирования учитель может пред­ложить учащимся одного класса, имеющим различную подготовку по теме, посильный уровень контрольной работы. Тем самым разноуровневые контрольные работы позволяют учителю дифференцировать требования к учащимся.

Итоговую контрольную работу в 10 классе можно про­вести в форме теста, близкого по форме к ЕГЭ, или в форме традиционной контрольной работы.

Контрольная работа по теме «Функции, уравнения, неравенства»

(базовый уровень К 1, профильный уровень КП 1 )

Вариант А 1

Вариант А 2

Найдите область определения функции:

а) ;

б) .

а) ;

б) .

Постройте график функции:

а);

б) .

а);

б) .

Решите уравнение:

а) ;

б) .

а) ;

б) .

Решите неравенство:

а) ;

б) .

а) ;

б) .

а) Подберите корень уравнения . Докажите, что других корней это уравнение не имеет;

б) Постройте график неравенства

x +y 0

а) Подберите корень уравнения . Докажите, что других корней это уравнение не имеет;

б) Постройте график неравенства x –y 0

Вариант Б 1

Вариант Б 2

а) Найдите область определения функции:

;

;

б) Найдите область значений функции:

y = x2 – 6.

y = x2 + 9.

Постройте график функции:

а);

б) .

а);

б) .

Решите уравнение:

а) ;

б) .

а) ;

б) .

Решите неравенство:

а) ;

б) .

а) ;

б) .

а) Решите уравнение:

;

;

б) Постройте график неравенства:

x2 +y  0.

x2 –y

Вариант В 1

Вариант В 2

а) Найдите область определения функции:

;

;

б) Найдите область значений функции

.

.

а) Постройте график функции:

;

;

б) Постройте график уравнения:

.

.

Решите уравнение:

а) ;

б) .

а) ;

б) .

Решите неравенство:

а) ;

б) .

а) ;

б) .

а) Решите уравнение (и обоснуйте правильность решения):

;

б) Постройте график неравенства:

(x – 2)2 +y2 9.

x 2 + (y +5)2 16.

Контрольная работа 2 по теме «Функции, уравнения, неравенства»

(только профильный уровень КП 2 )

Вариант Б 1

Вариант Б 2

Выполните деление многочлена на многочлен , если

,

.

,

.

Найдите целые корни многочлена:

Многочлен при делении на двучлены и

дает остатки 4 и 4 соответственно.

дает остатки 2 и 6 соответственно.

Найдите остаток от деления многочлена на .

Докажите с помощью метода математической индукции, что при любом
натуральном справедливо равенство:

.

.

*

Найдите значения и такие, чтобы

число 2 было корнем не менее второй кратности для многочлена .

число 4 было корнем не менее второй кратности для многочлена .

Контрольная работа по теме «Тригонометрические функции»

(базовый уровень К 2, профильный уровень КП 3 )

Постройте график функции:

.

.

Постройте график функции:

.

.

Постройте график функции:

.

.

Контрольная работа по теме «Тригонометрические уравнения и неравенства»

(базовый уровень К 3, профильный уровень КП 4 )

Контрольная работа 2 по теме «Тригонометрические уравнения и неравенства»

(только профильный уровень КП 5)

Вариант Б 1

Вариант Б 2

Решите уравнение:

а) ;

б) ;

в) .

а)

б)

в) .

Решите неравенство:

а) ;

б) ;

в) .

а) ;

б) ;

в) .

Решите систему:

Решите уравнение:

.

.

*

Найдите все значения параметра , при которых уравнение имеет корни:

.

Вариант В 1

Вариант В 2

Решите уравнение:

а) ;

б) .

а) ;

в) .

Решите неравенство:

а) ;

б) ;

в) .

а) ;

б) ;

в) .

Решите систему:

Решите уравнение:

*

Найдите все значения параметра , при которых уравнение имеет корни:

Контрольная работа по теме «Степенная функция»

(базовый уровень К 4, профильный уровень КП 6 )

Контрольная работа по теме «Показательная и логарифмическая функции»

(базовый уровень К 5, профильный уровень КП 7 )

Контрольная работа 2 по теме «Показательная и логарифмическая функции»

(базовый уровень К 6, профильный уровень КП 8 )

Контрольная работа 3 по теме «Показательная и логарифмическая функции»

(только профильный уровень КП 9)

Вариант Б 1

Вариант Б 2

Решите показательно-степенное уравнение:

а) ;

б) .

а) ;

б) .

Решите показательно-степенное неравенство при x> 0:

.

.

Решите уравнение (и обоснуйте правильность решения):

.

.

*

Найдите все значения параметра , при которых уравнение имеет
единственное решение:

.

.

Вариант В 1

Вариант В 2

Решите показательно-степенное уравнение:

а) ;

б) .

а) ;

б) .

Решите показательно-степенное неравенство:

.

.

Решите уравнение:

.

.

*

Найдите все значения параметра , при которых уравнение имеет два
различных корня:

.

.

СПИСОК ЛИТЕРАТУРЫ

1. Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профильный уровни .– М.: Илекса, 2011, – 480 с.

2. Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профильный уровни.– М.: Илекса, 2011, – 432 с.

3. Ершова А.П., Нелин Е.П. Сборник самостоятельных и контрольных работ по алгебре и началам математического анализа для 10 класса.– М.: Илекса, 2011, – 96 с.

4. Нелин Е.П. Алгебра 7-11 классы. Определения, свойства, методы решения – в таблицах. Сер. Комплексная подготовка к ЕГЭ и ГИА. – М.: Илекса, 2011, – 128 с.

5. Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа в 10 классе: пособие для учителя .– М.: Илекса, 2011, – 96 с.

 Программа рассмотрена и одобрена научно-методическим советом по математике Минобрнауки России

 Серым цветом залиты номера тем, которые не являются обязательными при обучении на базовом уровне

4 $$ $$ B (4) = 100 * 1,12 * 1,12 * 1,12 * 1,12 $$ $$ B (4) = 157,35 … $$

На самом деле в числе много цифр после десятичной точки. В реальной проблеме обычно указывается, где следует округлить ответ, но в этом случае имеет смысл округление до ближайшего ВСЕГО числа. Зачем? Потому что здесь мы имеем дело с бактериями. Бактерий может быть только целое число, поэтому ответ лучше всего выразить как 157 после 4 часов роста.

DeepNotes | Демистификация глубокого обучения

Примечание. Полный исходный код можно найти здесь https: // github.com / parasdahal / deepnet

Функция Softmax

Функция Softmax принимает N-мерный вектор действительных чисел и преобразует его в вектор действительных чисел в диапазоне (0,1), который в сумме дает 1.

Как следует из названия, функция softmax является «мягкой» версией функции max. Вместо выбора одного максимального значения он разбивает все (1), при этом максимальный элемент получает наибольшую часть распределения, но другие более мелкие элементы также получают часть его.

Это свойство функции softmax, заключающееся в том, что она выводит распределение вероятностей, делает ее пригодной для вероятностной интерпретации в задачах классификации.

В Python код для функции softmax выглядит следующим образом:

  def softmax (X):
    exps = np.exp (X)
    возврат exps / np.sum (exps)

Следует отметить, что числовой диапазон чисел с плавающей запятой в numpy ограничен. Для float64 верхняя граница равна. Для экспоненты нетрудно превысить этот предел, и в этом случае python возвращает нан .

Чтобы сделать нашу функцию softmax численно стабильной, мы просто нормализуем значения в векторе, умножая числитель и знаменатель на константу.

Мы можем выбрать произвольное значение для члена, но обычно выбирается, поскольку он сдвигает все элементы в векторе от отрицательного к нулю, а отрицания с большими показателями насыщаются до нуля, а не до бесконечности, избегая переполнения и в результате .

Код нашего стабильного softmax следующий:

  def stable_softmax (X):
    exps = np.ехр (X - np.max (X))
    возврат exps / np. sum (exps)

Производная от Softmax

Из-за желаемого свойства функции softmax, выводящей распределение вероятностей, мы используем его в качестве последнего слоя в нейронных сетях. Для этого нам нужно вычислить производную или градиент и передать ее обратно на предыдущий уровень во время обратного распространения.

Из правила частного мы знаем, что у нас есть.

В нашем случае и. Всегда будет иметь, всегда будет.Но надо отметить, что в, будет только если, иначе его 0.

Если,

Для,

Таким образом, производная функции softmax задается как,

Или с помощью дельты Кронекера

Потеря перекрестной энтропии

Перекрестная энтропия указывает расстояние между тем, каким, по мнению модели, должно быть выходное распределение, и тем, чем на самом деле является исходное распределение. Это определяется как, Мера перекрестной энтропии — широко используемая альтернатива квадрату ошибки.Он используется, когда активация узла может пониматься как представляющая вероятность того, что каждая гипотеза может быть верной, то есть когда выход представляет собой распределение вероятностей. Таким образом, он используется как функция потерь в нейронных сетях, которые имеют активации softmax в выходном слое.

  def cross_entropy (X, y):
    "" "
    X - результат полностью подключенного уровня (num_examples x num_classes)
    y - метки (num_examples x 1)
    Обратите внимание, что y не является вектором с горячим кодированием.
    Его можно вычислить как y.argmax (axis = 1) из векторов меток с горячим кодированием, если это необходимо.
    "" "
    m = y.shape [0]
    p = softmax (X)
    # Мы используем индексацию многомерного массива для извлечения
    # softmax вероятность правильной метки для каждого образца.
    # См. Https://docs.scipy.org/doc/numpy/user/basics.indexing.html#indexing-multi-dimensional-arrays для понимания индексирования многомерных массивов.
    log_likelihood = -np.log (p [диапазон (м), y])
    потеря = np.sum (log_likelihood) / m
    обратные потери

Производная перекрестной потери энтропии с Softmax

Cross Entropy Loss с функцией Softmax широко используются в качестве выходного уровня. Теперь мы используем производную softmax, которую мы вывели ранее, чтобы получить производную функции потерь кросс-энтропии.

На основе производной от softmax, полученной нами ранее,

— это вектор с горячим кодированием для меток, поэтому и. Итак, у нас есть

— очень простое и элегантное выражение. Переводим в код

  def delta_cross_entropy (X, y):
    "" "
    X - результат полностью подключенного уровня (num_examples x num_classes)
    y - метки (num_examples x 1)
    Обратите внимание, что y не является вектором с горячим кодированием.При необходимости его можно вычислить как y.argmax (axis = 1) из векторов меток, закодированных в горячем режиме.
    "" "
    m = y.shape [0]
    град = softmax (X)
    град [диапазон (м), y] - = 1
    град = град / м
    вернуться град

Экспоненциальное распределение

Марко Табога, доктор философии

Экспоненциальное распределение — это непрерывное распределение вероятностей, используемое для смоделировать время, которое нам нужно подождать, прежде чем произойдет данное событие. Это постоянный аналог геометрический распределение, которое вместо этого является дискретным.

Иногда его еще называют отрицательным экспоненциальным распределением.

Содержание

  1. Введение

  2. Определение

  3. Параметр скорости и его интерпретация

  4. Ожидаемое значение

  5. Вариация

  6. Функция создания момента

  7. Функция создания момента

  8. Функция

  9. Подробнее

    1. Свойство без памяти

    2. Сумма экспоненциальных случайных величин является гамма-случайной величиной

  10. График плотности

  11. 52 Упражнения 9152

    12. Упражнение 2

  12. Упражнение 3

Введение

Сколько времени пройдет до землетрясения в данном регионе? Как как долго нам нужно ждать, пока покупатель зайдет в наш магазин? Как долго это будет принять до того, как колл-центр получит следующий телефонный звонок? Как долго будет кусок техники работать без поломок?

На подобные вопросы часто дает вероятностный ответ с использованием экспоненциального распределения.

Все эти вопросы касаются времени ожидания перед определенным событием. имеет место. Если это время ожидания неизвестно, часто уместно подумать о это как случайная величина, имеющая экспоненциальную распространение.

Грубо говоря, время нам нужно подождать, прежде чем произойдет событие, имеет экспоненциальное распределение, если вероятность того, что событие произойдет в течение определенного промежутка времени, равна пропорционально длине этого временного интервала.

Точнее, имеет экспоненциальное распределение, если условное вероятность примерно пропорционально длине временного интервала между временами а также , на любой момент времени .

Во многих практических ситуациях это свойство очень реалистично. Это причина, по которой экспоненциальное распределение так широко используется для моделирования ожидания раз.

Экспоненциальное распределение строго связано с распределением Пуассона. Если 1) событие может произойти более одного раза и 2) время, прошедшее между двумя последовательные вхождения распределены экспоненциально и не зависят от предыдущих вхождений, затем количество вхождений события в пределах данная единица времени имеет распределение Пуассона. Приглашаем читателя ознакомиться с лекция о распределении Пуассона для более подробной информации подробное объяснение и наглядное графическое представление этого факта.

Определение

Экспоненциальное распределение характеризуется следующим образом.

Определение Позволять быть непрерывным случайная переменная. Пусть это поддержка быть набором положительного реального числа: Пусть . Мы говорим что имеет экспоненциальное распределение с параметром если и только если это плотность вероятности функция это параметр называется параметром скорости .

Случайная величина, имеющая экспоненциальное распределение, также называется экспоненциальная случайная величина.

Следующее — доказательство того, что — допустимая функция плотности вероятности.

Проба

Неотрицательность очевидна. Нам нужно доказать что интеграл над равно . Это доказано как следует:

Чтобы лучше понять экспоненциальное распределение, вы можете взглянуть на его графики плотности.

Параметр скорости и его интерпретация

Мы упоминали, что вероятность того, что событие произойдет между двумя датами а также пропорционально (при условии, что это не произошло раньше ). Параметр скорости постоянная пропорциональность: где бесконечно малая более высокого порядка, чем (т.е. функция который доходит до нуля быстрее, чем делает).

Вышеуказанное условие пропорциональности также достаточно, чтобы полностью характеризуют экспоненциальное распределение.

Предложение Соразмерность условие удовлетворен только если имеет экспоненциальное распределение.

Проба

Условная вероятность можно написать asDenote от

Статистические функции (scipy.stats) — SciPy v1.5.4 Справочное руководство

alpha (* args, ** kwds)

Альфа-непрерывная случайная величина.

anglit (* args, ** kwds)

Непрерывная угловая случайная величина.

arcsine (* args, ** kwds)

Непрерывная арксинусная случайная величина.

argus (* args, ** kwds)

Распределение Argus

beta (* args, ** kwds)

Бета-непрерывная случайная величина.

Betaprime (* args, ** kwds)

Бета-простая непрерывная случайная величина.

bradford (* args, ** kwds)

Непрерывная случайная величина Брэдфорда.

заусенец (* args, ** kwds)

Непрерывная случайная величина заусенца (тип III).

burr12 (* args, ** kwds)

Непрерывная случайная величина заусенца (тип XII).

cauchy (* args, ** kwds)

Непрерывная случайная величина Коши.

chi (* args, ** kwds)

Непрерывная случайная величина с ци.

chi2 (* args, ** kwds)

Непрерывная случайная величина хи-квадрат.

косинус (* args, ** kwds)

Косинусная непрерывная случайная величина.

хрустальный шар (* args, ** kwds)

Распределение Crystalball

dgamma (* args, ** kwds)

Непрерывная случайная величина с двойной гаммой.

dweibull (* args, ** kwds)

Двойная непрерывная случайная величина Вейбулла.

erlang (* args, ** kwds)

Непрерывная случайная величина Эрланга.

expon (* args, ** kwds)

Экспоненциальная непрерывная случайная величина.

exponnorm (* args, ** kwds)

Нормальная непрерывная случайная величина, измененная экспоненциально.

exponweib (* args, ** kwds)

Возведенная в степень непрерывная случайная величина Вейбулла.

exponpow (* args, ** kwds)

Непрерывная случайная величина экспоненциальной степени.

f (* args, ** kwds)

Непрерывная случайная величина F.

fatiguelife (* args, ** kwds)

Непрерывная случайная величина усталостной долговечности (Бирнбаум-Сондерс).

fisk (* args, ** kwds)

Непрерывная случайная величина Фиска.

foldcauchy (* args, ** kwds)

Свернутая непрерывная случайная величина Коши.

foldnorm (* args, ** kwds)

Свернутая нормальная непрерывная случайная величина.

frechet_r (* args, ** kwds)

Сплошная непрерывная случайная величина справа Фреше (или минимум Вейбулла).

frechet_l (* args, ** kwds)

Левая непрерывная случайная величина Фреше (или максимум Вейбулла).

genlogistic (* args, ** kwds)

Обобщенная логистическая непрерывная случайная величина.

gennorm (* args, ** kwds)

Обобщенная нормальная непрерывная случайная величина.

genpareto (* args, ** kwds)

Обобщенная непрерывная по Парето случайная величина.

genexpon (* args, ** kwds)

Обобщенная экспоненциальная непрерывная случайная величина.

genextreme (* args, ** kwds)

Обобщенная непрерывная случайная величина с экстремальными значениями.

gausshyper (* args, ** kwds)

Гауссовская гипергеометрическая непрерывная случайная величина.

гамма (* args, ** kwds)

Гамма-непрерывная случайная величина.

gengamma (* args, ** kwds)

Обобщенная гамма-непрерывная случайная величина.

genhalflogistic (* args, ** kwds)

Обобщенная полулогистическая непрерывная случайная величина.

geninvgauss (* args, ** kwds)

Обобщенная обратная гауссовская непрерывная случайная величина.

гилбрат (* args, ** kwds)

Непрерывная случайная величина Гилбрата.

gompertz (* args, ** kwds)

Непрерывная случайная величина Гомперца (или усеченного Гамбеля).

gumbel_r (* args, ** kwds)

Непрерывная случайная величина Гамбеля со скосом вправо.

gumbel_l (* args, ** kwds)

Непрерывная случайная величина Гамбеля с наклоном влево.

полукоши (* args, ** kwds)

Непрерывная случайная величина наполовину Коши.

halflogistic (* args, ** kwds)

Полулогистическая непрерывная случайная величина.

halfnorm (* args, ** kwds)

Полунормальная непрерывная случайная величина.

halfgennorm (* args, ** kwds)

Верхняя половина обобщенной нормальной непрерывной случайной величины.

гипсеканс (* args, ** kwds)

Непрерывная случайная величина с гиперболическим секансом.

invgamma (* args, ** kwds)

Инвертированная гамма-непрерывная случайная величина.

invgauss (* args, ** kwds)

Обратная гауссовская непрерывная случайная величина.

invweibull (* args, ** kwds)

Инвертированная непрерывная случайная величина Вейбулла.

johnsonsb (* args, ** kwds)

Непрерывная случайная величина Джонсона С.Б.

johnsonsu (* args, ** kwds)

Непрерывная случайная величина Johnson SU.

каппа4 (* args, ** kwds)

Распределение по 4 параметрам Каппа.

каппа3 (* args, ** kwds)

Распределение параметров Каппа 3.

ksone (* args, ** kwds)

Распределение статистики одностороннего критерия Колмогорова-Смирнова.

kstwo (* args, ** kwds)

Двусторонний критерий распределения статистики Колмогорова-Смирнова.

kstwobign (* args, ** kwds)

Предельное распределение масштабированной статистики двустороннего критерия Колмогорова-Смирнова.

Laplace (* args, ** kwds)

Непрерывная случайная величина Лапласа.

сбор (* args, ** kwds)

Непрерывная случайная величина Леви.

levy_l (* args, ** kwds)

Скошенная влево непрерывная случайная величина Леви.

levy_stable (* args, ** kwds)

Устойчивая по Леви непрерывная случайная величина.

логистика (* args, ** kwds)

Логистическая (или возведенная в квадрат) непрерывная случайная величина.

логгамма (* args, ** kwds)

Логарифмическая гамма-непрерывная случайная величина.

loglaplace (* args, ** kwds)

Непрерывная случайная величина по лог-Лапласу.

lognorm (* args, ** kwds)

Логнормальная непрерывная случайная величина.

loguniform (* args, ** kwds)

Логарифмически однородная или обратная непрерывная случайная величина.

lomax (* args, ** kwds)

Непрерывная случайная величина Ломакса (Парето второго рода).

maxwell (* args, ** kwds)

Непрерывная случайная величина Максвелла.

mielke (* args, ** kwds)

Непрерывная случайная величина Mielke Beta-Kappa / Dagum.

мойал (* args, ** kwds)

Непрерывная случайная величина Мойала.

накагами (* args, ** kwds)

Непрерывная случайная величина Накагами.

ncx2 (* args, ** kwds)

Нецентральная непрерывная случайная величина хи-квадрат.

ncf (* args, ** kwds)

Непрерывная случайная величина с нецентральным F-распределением.

nct (* args, ** kwds)

Нецентральная непрерывная случайная величина Стьюдента.

norm (* args, ** kwds)

Нормальная непрерывная случайная величина.

norminvgauss (* args, ** kwds)

Нормальная обратная гауссовская непрерывная случайная величина.

pareto (* args, ** kwds)

Непрерывная по Парето случайная величина.

pearson3 (* args, ** kwds)

Непрерывная случайная величина типа III Пирсона.

Учебный центр

Это не предложение или ходатайство в какой-либо юрисдикции, где мы не уполномочены вести бизнес или где такое предложение или ходатайство противоречили бы местным законам и постановлениям этой юрисдикции, включая, помимо прочего, лиц, проживающих в Австралии, Канаде. , Гонконг, Япония, Саудовская Аравия, Сингапур, Великобритания и страны Европейского Союза.

Волатильность рынка, объем и доступность системы могут задерживать доступ к счету и исполнение сделок.

Прошлая эффективность ценной бумаги или стратегии не является гарантией будущих результатов или успеха инвестирования.

Торговля акциями, опционами, фьючерсами и валютой предполагает спекуляцию, и риск потери может быть значительным. Перед торговлей клиенты должны учитывать все соответствующие факторы риска, включая собственное финансовое положение. Маржинальная торговля иностранной валютой сопряжена с высоким уровнем риска, а также со своими уникальными факторами риска.

Опционы подходят не всем инвесторам, поскольку особые риски, присущие торговле опционами, могут подвергнуть инвесторов потенциально быстрым и значительным убыткам. Перед тем как торговать опционами, вам следует внимательно ознакомиться с характеристиками и рисками стандартизированных опционов.

Ордера на спреды, страддлы и другие многоплановые опционные заказы, размещенные в Интернете, будут нести комиссию в размере 0,65 доллара США за контракт по каждой части. Заказы, размещенные другими способами, будут иметь дополнительные транзакционные издержки.

Торговля фьючерсами и фьючерсными опционами носит спекулятивный характер и подходит не всем инвесторам.Пожалуйста, прочтите Уведомление о рисках для фьючерсов и опционов, прежде чем торговать фьючерсными продуктами.

Торговля на Форекс предполагает использование кредитного плеча, сопряжена с высоким уровнем риска и подходит не всем инвесторам. Пожалуйста, прочтите «Раскрытие информации о валютных рисках» перед тем, как торговать валютными продуктами.

Счета фьючерсов и форекс не защищены Корпорацией по защите инвесторов в ценные бумаги (SIPC).

Услуги по торговле фьючерсами, фьючерсными опционами и валютой, предоставляемые TD Ameritrade Futures & Forex LLC.Торговые привилегии подлежат рассмотрению и утверждению. Не все клиенты подойдут. Счета Forex недоступны для жителей Огайо или Аризоны.

Доступ к рыночной информации в режиме реального времени возможен при принятии соглашений об обмене. Профессиональный доступ отличается, и может взиматься плата за подписку. Подробнее см. Наши профессиональные тарифы и сборы.

Подтверждающая документация для любых заявлений, сравнений, статистических или других технических данных будет предоставлена ​​по запросу.TD Ameritrade не дает рекомендаций и не определяет пригодность какой-либо безопасности, стратегии или курса действий для вас посредством использования вами наших торговых инструментов. Вы несете исключительную ответственность за любое инвестиционное решение, которое вы принимаете в своей самостоятельной учетной записи.

No related posts.

Leave a Reply

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *