Контрольная работа по биологии 8 класс по теме: «Опорно-двигательная система»
Контрольная работа по теме «Опорно-двигательная система»
8 класс
Вариант 1.
Часть А
К каждому заданию части А дано несколько ответов, из которых только один верный.
Кость это – ……….. ткань
А – эпителиальная
Б – нервная ткань
В – соединительная
Г – поперечнополосатая мышечная
Органические вещества обеспечивают костям:
А – твёрдость и хрупкость
Б – твёрдость и гибкость
В – хрупкость и эластичность
Г – гибкость и эластичность
Неподвижно соединены:
А – кости верхней конечности
Б – позвонки грудного отдела позвоночника
В – кости черепа
Г – кости нижней конечности
Кости черепа, лопатки, тазовые кости относятся к ……….

А – плоским
Б — длинным трубчатым
В – коротким трубчатым
Г – губчатым
В состав стопы не входят:
А – плюсна
Б – запястье
В – предплюсна
Г – фаланги пальцев
Функцию кроветворения выполняет:
А – хрящ
Б – красный костный мозг
В – жёлтый костный мозг
Г – надкостница
К мозговому отделу черепа не относятся ………. кости:
А — височные
Б – затылочная
В – скуловые
Г – теменные
В связи с прямохождением у человека появилась:
А – пятипалая конечность
Б – мозговой отдел черепа стал больше лицевого
В – большой палец на руке противопоставлен остальным
Г – сводчатая стопа
Нарушение целостности кости – это
А – перелом
Б – ушиб
В – вывих
Г – растяжение
Для гладких мышц не характерно
А – медленное сокращение
Б – многоядерность
В – веретеновидная форма
Г – регуляция вегетативным отделом нервной системы
Что не является причиной нарушения осанки
А – не тренированность мышц
Б – нерациональное питание
В – переутомление
Г – несоответствующая росту мебель
Источником энергии, необходимой для движения, являются
А – вода
Б – витамины
В – минеральные вещества
Г – органические вещества
Часть В
В1. Установите соответствие между характеристикой мышечной ткани и её видом.
Установите соответствие между характеристикой мышечной ткани и её видом.
ХАРАКТЕРИСТИКА
ВИД ТКАНИ
Мышца, изменяющая размер зрачка
1 — гладкая мышечная
Скелетные мышцы
2 – поперечнополосатая
Клетки веретеновидные
Поперечно исчерчены
Сокращаются быстро
Сокращаются медленно
Выберите три верных ответа.
В2. К грудной клетке относятся:
А – ключицы
Б – 12 грудных позвонков
В – 12 пар ребер
Г – плечевая кость
Д – лопатки
Е – грудина
Часть С
С1. Дайте развёрнутый свободный ответ.
Как оказать первую помощь при переломе костей предплечья?
Контрольная работа по теме «Опорно-двигательная система»
8 класс
Вариант 2.
Часть А
 Выберите верный, по вашему мнению, ответ.
Выберите верный, по вашему мнению, ответ.Хрящ это – ……….. ткань
А – эпителиальная
Б – нервная ткань
В – соединительная
Г – поперечнополосатая мышечная
Неорганические вещества обеспечивают костям:
А – твёрдость и хрупкость
Б – твёрдость и гибкость
В – хрупкость и эластичность
Г – гибкость и эластичность
Полуподвижно соединены
А – кости верхней конечности
Б – позвонки грудного отдела позвоночника
В – кости черепа
Г – кости нижней конечности
Кости пясти и фаланги пальцев относятся к ………. костям
А – плоским
Б — длинным трубчатым
В – коротким трубчатым
Г – губчатым
В состав кисти не входят:
А – плюсна
Б – запястье
В – пясть
Г – фаланги пальцев
Рост костей в толщину происходит за счёт:
А – хряща
Б – красного костного мозга
В – жёлтого костного мозга
Г – надкостницы
К лицевому отделу черепа относятся ……….
А — височные
Б – затылочная
В – скуловые
Г – теменные
В связи с трудовой деятельностью у человека появилась:
А – чашеобразный таз
Б – S – образный позвоночник
В – большой палец на руке противопоставлен остальным
Г – сводчатая стопа
Изменение формы сустава и невозможность движения в нём – это
А – перелом
Б – ушиб
В – вывих
Г – растяжение
Для поперечнополосатых мышц характерно
А – медленное сокращение
Б – многоядерность
В – веретеновидная форма
Г – регуляция вегетативным отделом нервной системы
Что не является причиной плоскостопия
А – ношение обуви на высоких каблуках
Б – длительное пребывание на ногах
В – ожирение
Г – стресс
Гиподинамия – это:
А – активный образ жизни
Б – пониженная подвижность
В – нарушение осанки
Г – повышение работоспособности
Часть В
В1. Установите соответствие между характеристикой мышечной ткани и её видом.
Установите соответствие между характеристикой мышечной ткани и её видом.
ВИД ТКАНИ
Диафрагма
1 — гладкая мышечная
Мышца аорты
2 – поперечнополосатая
Многоядерные клетки
Одноядерные клетки
Регулируется соматическим отделом
Регулируется вегетативным отделом
В2. Выберите три верных ответа.
К скелету свободной верхней конечности относятся:
А – ключицы
Б – лучевая кость
В – плюсна
Г – плечевая кость
Д – лопатки
Е – запястье
Часть С
С1. Дайте развёрнутый свободный ответ.
Как оказать первую помощь при вывихе локтевого сустава?
Таблица 2. Правильные ответы.
Часть А
№ задания
1
2
3
4
5
6
7
8
9
10
11
12
Ответ Вариант 1
В
Г
В
А
Б
Б
В
Г
А
Б
В
Г
Ответ Вариант 2
В
А
Б
В
А
Г
В
В
В
Б
Г
Б
Часть В
№ задания
1
2
Ответ. Вариант 1.
Вариант 1.
121221
212121
Ответ. Вариант 2.
БГЕ
Часть С.
Вариант 1.
С 1. Как оказать первую помощь при переломе костей предплечья?
Содержание верного ответа и указания к оцениванию (допускаются иные формулировки ответа, не искажающие его смысл)
Баллы
Элементы ответа:
Обездвижить конечность – наложить шину.
Шина должна фиксировать два соседних сустава (лучезапястный и локтевой суставы). Шину накладывают поверх одежды и обуви, которые при необходимости разрезают; для предупреждения сдавливания тканей в местах костных выступов накладывают мягкий материал;
Немедленно доставить пострадавшего в медицинское учреждение
Ответ правильный и полный, включает все названные выше элементы, не содержит биологических ошибок
3
Ответ правильный, но не полный, включает 2 из названных выше элементов и не содержит биологических ошибок или ответ включает 3 из названных выше элементов, но содержит негрубые биологические ошибки
2
Ответ не полный, включает 1 из названных выше элементов и не содержит биологических ошибок или ответ включает 1-2 из названных выше элементов, но содержит негрубые биологические ошибки
1
Ответ неправильный
0
Максимальный балл
3
Вариант 2.
С1. Как оказать первую помощь при вывихе локтевого сустава?
Содержание верного ответа и указания к оцениванию (допускаются иные формулировки ответа, не искажающие его смысл)
Баллы
Элементы ответа:
1) На время транспортировки конечность иммобилизуется (фиксируется) в таком положении, в каком больной ее удерживает (наложить фиксирующую повязку по типу косынки или прибинтовать руку к туловищу).
2) К месту вывиха нужно приложить грелку с холодной водой или льдом, либо смоченное холодной водой полотенце.
3) Немедленно доставить пострадавшего в медицинское учреждение. Самим вправлять вывих нельзя!
Ответ правильный и полный, включает все названные выше элементы, не содержит биологических ошибок
3
Ответ правильный, но не полный, включает 2 из названных выше элементов и не содержит биологических ошибок или ответ включает 3 из названных выше элементов, но содержит негрубые биологические ошибки
2
Ответ не полный, включает 1 из названных выше элементов и не содержит биологических ошибок или ответ включает 1-2 из названных выше элементов, но содержит негрубые биологические ошибки
1
Ответ неправильный
0
Максимальный балл
3
Тестовая контрольная работа по теме: «Опорно-двигательный аппарат»
Тестовая контрольная работа по теме: «Опорно-двигательный аппарат»
Вариант 1.
1. К парным костям мозгового отдела черепа человека относится:
1) теменная; 2) лобная; 3) затылочная; 4) носовая.
2. Плечевая и бедренная кости относятся к группе:
1) смешанных костей; 2) губчатых костей; 3) плоских костей; 4) трубчатых костей.
3. Рост кости в длину осуществляется за счет:
1)хрящевой ткани; 2)надкостницы;
3) желтого костного мозга; 4) красного костного мозга.
4. Неподвижное соединение между собой имеют кости:
1) плечевая и локтевая; 2) мозгового отдела позвоночника;
3) грудного отдела позвоночника; 4) бедра и голени.
5. Мышечное утомление наступает быстрее:
1)при динамической работе; 2)смене поз; 3)умственной работе; 4)статической работе.
6. Скелет и мышцы не выполняют функцию:
1) защитную 2) двигательную 3) опорную 4) транспорта веществ
7. К поясу нижних конечностей человека относятся кости:
1)голени; 2)бедра; 3) таза; 4) позвоночника.
8. Изгибы позвоночника человека связаны с
1) прямохождением 2) трудовой деятельностью
3) общественным образом жизни 4) переносом тяжестей
9. Скелетные мышцы прикрепляются к костям с помощью:
1) миофибрилл; 2) сухожилий; 3) связок; 4) соединительнотканной оболочки.
10. Опорно-двигательный аппарат человека составляют:
1) кости скелета и сухожилия; 2) соединительная ткань;
3) кости, их соединения и мышцы; 4) только кости и их соединения.
11. Что из перечисленного характерно для скелета человека? (3 отв)
1) сводчатая стопа 2) прямой позвоночник без изгибов
3) позвоночник с S-образным изгибом 4) широкий чашевидный пояс нижних конечностей
5) сжатая с боков грудная клетка 6) массивные челюсти
12. Какие мышцы относятся к мышцам туловища? (3 отв)
1) межреберные мышцы; 2) икроножная мышца; 3) мышцы брюшного пресса
4) диафрагма; 5) височная мышца; 6) надчерепная мышца
В задании 13 Установите соответствие между костями и типом соединения
Кости скелета
Тип соединения
А) крестцовые позвонки
1) Неподвижное
Б) плечо и предплечье
2) Полуподвижное
В) грудные позвонки
З) Подвижное
Г) кости мозговой части черепа
Д) голень и стопа
Е) копчик
Задание 14. Вставьте пропущенные термины в текст
Вставьте пропущенные термины в текст
ЧЕРЕП ЧЕЛОВЕКА.
Череп состоит из ________(А) костей. Мозговой отдел представлен парными теменными и __________________(Б) костями и непарными ______________ (В) и затылочной. Кости черепа соединены ___________________(Г). Мозговой отдел преобладает над лицевым.
Перечень терминов: 1. скуловые 2. неподвижно (сращены) 3. 23 4. лонная 5. 220 6. лобная 7. Височные 8. неподвижно (швы).
Задание 15. Укажите номер неправильного предложения и исправьте ошибку.
Скелет плечевого пояса и верхних конечностей.
1. Благодаря тому, что верхние конечности прикреплены к надежной опоре, они обладают подвижностью во всех направлениях, способны выдерживать большие физические нагрузки. 2. Такую опору создают кости плечевого пояса – две лопатки и ключица. 3. Лопатки – большие кости треугольной формы, состоящие из компактного костного вещества. 4. Лопатки соединены с ребрами и позвоночным столбом только при помощи мышц. 5.Скелет верхних конечностей состоит из трех отделов: плеча, предплечья и кисти. 6.Плечо образовано двумя костями, а предплечье – одной.
4. Лопатки соединены с ребрами и позвоночным столбом только при помощи мышц. 5.Скелет верхних конечностей состоит из трех отделов: плеча, предплечья и кисти. 6.Плечо образовано двумя костями, а предплечье – одной.
Тестовая контрольная работа по теме: «Опорно-двигательный аппарат»
Вариант 2.
1. К поясу верхних конечностей человека относятся кости:
1) голени; 2) плеча; 3) предплечья; 4) ключицы.
2. За счет этой структуры происходит рост костей в толщину:
1) суставной хрящ; 2) надкостница; 3) желтый костный мозг; 4) красный костный мозг.
З. Основу скелетных мышц составляет ткань:
1) гладкая мышечная; 2) поперечнополосатая мышечная; 3) эпителиальная; 4) соединительная.
4. Парными костями черепа являются:
1) лобные и затылочные кости; 2) лобные и теменные;
3) только височные; 4) височные и теменные.
5. В состав грудной клетки входит
1) ключица 2) лопатка 3) грудина 4) кость плеча
6. Кости фаланг пальцев — это:
Кости фаланг пальцев — это:
1) трубчатые кости; 2) губчатые кости; 3) смешанные кости; 4) плоские кости.
7. Какую мышцу не относят к системе опоры и движения?
1) икроножная мышца 2) сердечная мышца
3) большая грудная мышца 4) двуглавая мышца плеча
8. Непарными костями мозгового отдела черепа человека являются:
1)лобная и теменная; 2)затылочная и теменная; 3)височная и теменная; 4)лобная и затылочная.
9. Явление, при котором происходит снижение работоспособности мышц в процессе длительной работы, называют:
1) замедлением; 2) утомлением; 3) усталостью; 4) торможением.
10. Какие функции выполняет красный костный мозг?
1)кроветворный орган; 2)часть нервной системы; 3)депо крови; 4)запасные органич. вещества
11. В чем состоит сходство скелета человека и скелетов млекопитающих животных?(3 отв)
1) позвоночник имеет пять отделов 2) стопа имеет свод
3) мозговой отдел черепа больше лицевого 4) имеются парные суставные конечности
5) в шейном отделе семь позвонков 6) форма позвоночника S–образная
12. Какие мышцы не относятся к мышцам туловища? (3 отв)
Какие мышцы не относятся к мышцам туловища? (3 отв)
1) межреберные мышцы; 2) икроножная мышца 3) мышцы брюшного пресса;
4) трапециевидная мышца; 5) височная мышца; 6) жевательные мышцы.
В задании 13 Установите соответствие между костями и типом соединения
А) кости таза1) Неподвижное
Б) фаланги пальца
2) Полуподвижное
В) кости мозгового отдела черепа
3) Подвижное
Г) позвонки шейного отдела позвоночника
Д) бедренная кость с костями таза
Е) кости рёбер с грудиной
Задание 14. Вставьте пропущенные термины в текст
МЫШЕЧНЫЕ ТКАНИ ЧЕЛОВЕКА
Волокна скелетных мышц под микроскопом ___________(А). Их длина составляет ___________(Б). Волокна сердечной мышечной ткани, в отличие от поперечнополосатой скелетной, имеют контактные участки. Совокупность клеток, образующих ткань мышц внутренних органов, называют ___________(В) мышечной тканью.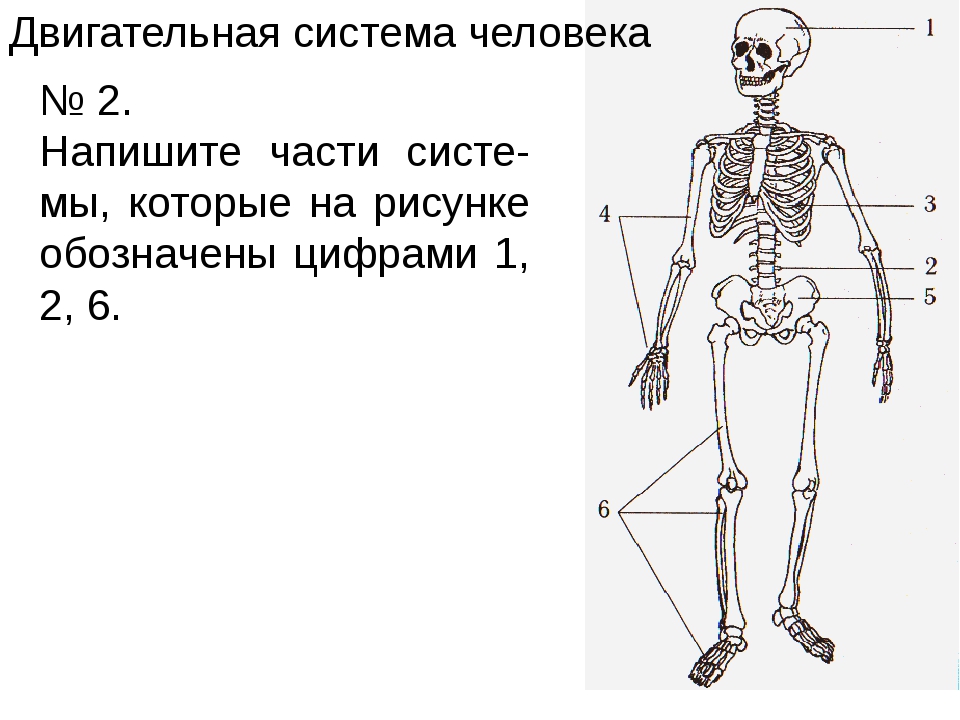 Для всех типов мышечных тканей характерные свойства — возбудимость и ___________(Г).
Для всех типов мышечных тканей характерные свойства — возбудимость и ___________(Г).
Перечень терминов: 1. поперечнополосатая 2. Гладкая 3. не поперечно исчерчены
4. поперечно исчерчены 5. 10-12 см 6. 0,1 мм 7. проводимость 8. сократимость
Задание 15. Укажите номер неправильного предложения и исправьте ошибку.
Скелет головы.
1. Скелет головы – череп – состоит из мозгового и лицевого отделов. 2. Лицевой отдел черепа преобладает над мозговым. 3. Кости черепа между собой соединены неподвижно путем сращения. 4. Височные, теменные и затылочные кости относятся к мозговому отделу черепа, а лобная, скуловые, челюстные – к лицевому отделу. 5. Верхнечелюстная кость неподвижная, нижнечелюстная кость – подвижная. 6. На этих костях находятся зубы, корни которых расположены в специальных костных ячейках.
Критерии оценивания работы обучающихся
Задания номер 1-10 оцениваются — 1 баллом
Задания 11-15 оцениваются — 2 баллами, выставляется 1 балл, если допущена одна ошибка, и 0 баллов, если допущено две и более ошибки
Максимальное количество баллов – 20
2 – в состав плечевого пояса входят две лопатки и две ключицы.
3 – лопатки плоские кости, состоящие из губчатого вещества.
6 – плечо образовано одной костью – плечевой, а предплечье – двумя: локтевой и лучевой
15
2. У человека мозговой отдел черепа преобладает над лицевым.
3. Кости черепа соединены между собой неподвижно с помощью швов.
4. Лобная кость относится к мозговому отделу черепа.
“2”- менее 50%
“3”- 50%-65%
“4”- 65%-85%
“5”- 85%-100%
2 | 3 | 4 | 5 | 6 | |
2 | 3 | 4 | 5 | 6 | |
При выполнении заданий 1-11 выберите один правильный ответ из четырех. | |||||||
1. Опорно-двигательный аппарат человека образован: | |||||||
а. только скелетом | в. | ||||||
б. только скелетными мышцами | г. скелетом и мышцами сердца и желудка | ||||||
2. Гибкость костей обеспечивается за счет: | |||||||
а. органических веществ | в. губчатого строения | ||||||
б. неорганических веществ | г. трубчатого строения | ||||||
3. К осевому скелету относятся: | |||||||
а. кости поясов конечностей и скелет свободных конечностей | |||||||
б. | |||||||
в. скелет туловища, кости поясов конечностей и скелет свободных конечностей | |||||||
г. череп и скелет туловища | |||||||
4. Шейный отдел позвоночника состоит из: | |||||||
а. 12 позвонков | б. 5 позвонков | в. 7 позвонков | г. 24 позвонков | ||||
5. Скелет свободной верхней конечности образуют: | |||||||
а. локтевая и лучевая кости, кости кисти | |||||||
б. | |||||||
в. лопатка и две ключицы | |||||||
г. лопатка, ключица, плечевая кость, кости предплечья и кости кисти | |||||||
6. Пояс нижних конечностей образуют: | |||||||
а. крестец | в. бедренная кость и крестец | ||||||
б. бедренная и берцовая кости | г. тазовые кости | ||||||
7. Цифрой 2 на рисунке обозначена кость: |
| ||||||
а. | |||||||
б. большая берцовая | |||||||
в. малая берцовая | |||||||
г. тазовая | |||||||
| |||||||
8. Ребра с грудиной соединены: | |||||||
а. посредством хряща | в. неподвижно, образуя шов | ||||||
б. посредством сустава | г. связками | ||||||
9. Какая мышца опускает плечо вниз и отводит руки за спину? | |||||||
а. | б. двуглавая плеча | в. дельтовидная | г. широчайшая спины | ||||
10. Для уменьшения отека и боли при вывихе сустава следует: | |||||||
а. согреть поврежденный сустав | |||||||
б. самостоятельно вправить вывих | |||||||
в. приложить лед к поврежденному суставу | |||||||
г. превозмогая боль разработать поврежденный сустав | |||||||
11. Пример динамической работы – это: | |||||||
а. | в. чтение книги за письменным столом | ||||||
б. ожидание автобуса на остановке | г. бег на длинную дистанцию | ||||||
При выполнении заданий 12-14 выберите три верных ответа из шести. | |||||||
12. Скелет человека в отличие от скелета млекопитающих животных имеет: | |||||||
а. прямой позвоночник без изгибов | г. позвоночник S-образной формы | ||||||
б. грудную клетку, сжатую в спинно-брюшном направлении | д. | ||||||
в. грудную клетку, сжатую с боков | е. массивный лицевой отдел черепа | ||||||
13. Неправильная осанка может привести к: | |||||||
а. смещению и сдавливанию внутренних органов | |||||||
б. нарушению кровоснабжения внутренних органов | |||||||
в. растяжению связок в тазобедренном суставе | |||||||
г. нарушению мышечного и связочного аппарата стопы | |||||||
д. деформации грудной клетки | |||||||
е. | |||||||
14. При динамической работе мышц человека, в отличие от статической, | |||||||
а. быстрее наступает утомление | г. работоспособность более продолжительна | ||||||
б. движения в суставах не происходит | д. уменьшается частота сердечных сокращений | ||||||
в. утомление наступает медленно | е. сокращение мышц чередуется с расслаблением | ||||||
При выполнении заданий 15-16 установите соответствие. | |||||||
15. | |||||||
КОСТИ ЧЕРЕПА | ОТДЕЛ ЧЕРЕПА | ||||||
а. лобная | 1. лицевой | ||||||
б. височная | 2. мозговой | ||||||
в. скуловая |
| ||||||
г. носовая | |||||||
д. нижнечелюстная | |||||||
16. Установите соответствие между примером соединения костей и типом, к которому оно относится. | |||||||
ПРИМЕР | ТИПЫ СОЕДИНЕНИЯ КОСТЕЙ | ||||||
а. бедренная и большая берцовая кости | 1. неподвижное | ||||||
б. лобная и теменная кости | 2. подвижное | ||||||
в. затылочная и височная кости |
| ||||||
г. нижняя челюсть и височная кость | |||||||
д. позвонки крестцового отдела | |||||||
При выполнении заданий 17-18 установите правильную последовательность. | |||||||
17. Установите последовательность расположения отделов позвоночника человека (сверху вниз): | |||||||
а. поясничный | в. грудной | г. крестцовый | |||||
б. шейный |
| д. копчиковый | |||||
18. Расположите в правильном порядке кости верхней конечности, начиная от плечевого пояса: | |||||||
а. кости пясти | в. плечевая кость | г. | |||||
б. лучевая кость |
| д. фаланги пальцев | |||||
При выполнении задания 19 вставьте в текст пропущенные термины. | |||||||
19. Вставьте в текст «Строение кости» пропущенные термины из предложенного перечня, используя для этого цифровые обозначения. | |||||||
СТРОЕНИЕ КОСТИ Кость покрыта соединительнотканной оболочкой – _____ (А). За счет деления ее клеток кость растет в _____ (Б), таким образом обеспечивается _____ (В) функция. Кроме этой функции, она выполняет еще _____ (Г) и трофическую, т.к. в ней много кровеносных и лимфатических сосудов, нервных волокон. | |||||||
1. толщина | 4. опорная | 6. костеобразующая | |||||
2. фасция | 5. надкостница | 7. длина | |||||
3. защитная |
| 8. образовательная | |||||
При выполнении задания 20 прочитайте текст и найдите в нем биологические ошибки. | |||||||
20. Внимательно прочитайте текст «Скелет головы» и найдите в нем предложения, в которых содержатся биологические ошибки. | |||||||
1. Скелет головы – череп – состоит из мозгового и лицевого отделов. 2. Лицевой отдел черепа человека преобладает над мозговым. 3. Кости черепа человека соединены неподвижно путем сращения. 4. Височные, теменные и затылочная кости относятся к мозговому отделу, а скуловые и челюстные – к лицевому. 5. Верхнечелюстная кость подвижная, а нижнечелюстная – неподвижная. 6. На этих костях находятся зубы, корни которых расположены в специальных костных ячейках. | |||||||
Контрольная работа по теме: «Опорно-двигательная система».
8 класс
Контрольная работа
по теме: «Опорно-двигательная система»
Вариант 2
Что защищает от повреждений спинной мозг?
А) черепная коробка
Б) позвоночник
В) грудная клетка
Г) лопатки
С помощью чего образуется полуподвижное соединение между позвонками шейного, грудного и поясничного отделов позвоночника?
А) с помощью межпозвоночных дисков
Б) с помощью сухожилий
В) с помощью суставной сумки
Г) с помощью сустава
Для предупреждения плоскостопия нужно носить обувь с каблуком не более:
А) 1-3 см.
Б) 3-5 см.
В) 5-8 см.
Г) без каблука.
До какого возраста кости растут в толщину?
А) до 18-20 лет
Б) до 20-25 лет
В) до 25-30 лет
Г) 30-35 лет
В каком положении следует транспортировать пострадавшего при подозрении на перелом позвоночника?
А) в горизонтальном
Б) в вертикальном
В) в сидячем
Г) на боку
В каком случае накладывают шину?
А) при ушибах
Б) при растяжениях
В) при кровотечениях
Г) при переломах, вывихах
Назовите основные свойства мышечной ткани
А) пластичность
Б) волокнистость
В) сократимость
Г) гибкость
Что руководит работой мышц?
А) опорно-двигательная система
Б) кровеносная система
В) нервная система
Г) система покровных органов
Что происходит, если поступление питательных веществ в организм превосходит энергозатраты?
А) образование жира
Б) образование жидкости
В) рост мышечной массы
Г) утолщение костей
Что развивают динамические упражнения?
А) силу
Б) выносливость
В) умение концентрироваться
Г) быстроту, точность движений
До какого возраста кости растут в длину?
А) до 16-18 лет
Б) до 18-20 лет
В) 20-23 лет
Г) 23-25 лет
Сочленение тазобедренного сустава:
А) цилиндрическое
Б) шаровое
В) эллиптическое
Кости черепа у новорожденного ребенка соединены:
А) подвижно
Б) неподвижно
В) полуподвижно
Структурной единицей кости является:
А) компактное вещество
Б) губчатое вещество
В) остеон
Г) миофибрилла
Скелет свободной верхней конечности состоит из:
А) плечевой кости, лучевой, малой берцовой и костей, образующих кисть.
Б) бедренной кости, локтевой, лучевой кости и костей, образующих кисть.
В) плечевой кости, лучевой кости, локтевой кости, а также костей запястья, пясть и фаланг пальцев.
Тело трубчатой кости внутри заполнено:
А) красным костным мозгом.
Б) желтым костным мозгом.
В) межклеточной жидкостью.
Г) лимфой.
Рост трубчатых костей в длину осуществляется за счет деления клеток, образующих:
А) головки костей
Б) тело кости
В) внутренний слой надкостницы
Г) хрящевую ткань, расположенную между головкой и телом кости.
Рост трубчатых костей в толщину осуществляется за счет деления клеток:
А) внутреннего слоя надкостницы.
Б) хрящевой ткани, расположенной между головкой и телом кости
В) тела кости
Работа гладких мышц регулируется:
А) соматической нервной системой
Б) вегетативной нервной системой
В) за счет импульсов, возникающих в самой мышце
Сердечная мышца характеризуется:
А) быстрыми ритмическими сокращениями и расслаблениями
Б) только быстрыми сокращениями
В) относительно медленными ритмическими сокращениями и расслаблениями
Поперечная исчерченность в сердечной мышечной ткани:
А) отсутствует
Б) имеется только в ткани, образующей стенки желудочков
В) имеется в тканях образующих как стенки желудочков, так и стенки предсердий
Количество ядер в клетке сердечной мышцы:
А) небольшое и они располагаются в центре клетки
Б) большое и они располагаются по периферии клетки
В) одно, располагающееся в центре клетки
Тип сократительной деятельности гладкой мышцы называется:
А) тетаническим
Б) тоническим
В) оба ответа неправильные
8 класс
Контрольная работа
по теме: «Опорно-двигательная система»
Вариант 1.
Как называется неподвижное соединение костей?
А) стык
Б) сустав
В) шов
Г) хрящ
Какая кость стопы самая крупная?
А) решетчатая
Б) лучевая
В) малоберцовая
Г) пяточная
В каком возрасте завершается рост и окостенение скелета?
А) в 16 лет
Б) в 18 лет
В) в 25 лет
Г) в 35 лет
Что развивает статические упражнения?
А) быстроту, точность движений
Б) силу, выносливость
В) ловкость
Г) скорость реакции
Что необходимо сделать при переломе костей черепа?
А) наложить гипсовую повязку
Б) наложить шину
В) наложить жгут
Г) немного приподнять голову и положить лед
Кто первым положил использовать эфирный наркоз для обезболивания во время операций?
А) Гиппократ
Б) Н.И. Пирогов
В) И.П. Павлов
Г) И. И. Мечников
И. Мечников
Из чего состоит средний слой стенки артерий, вен, желудка и кишечника?
А) из гладких мышц
Б) из скелетных мышц
В) из эпителиальной ткани
Г) из соединительной ткани
Какая мышца отвечает за сгибание руки в локтевом суставе?
А) двуглавая
Б) трехглавая
В) плечевая
Г) четырехглавая
Каким должно быть расстояние от глаз до рабочего места?
А) 10-15 м.
Б) 20-30 м.
В) 30-35 м.
Г) 40-45 м.
Что происходит, если поступление питательных веществ в организм превосходит энергозатраты?
А) образование жира
Б) образование жидкости
В) рост мышечной массы
Г) утолщение костей
К плоским костям скелета относят:
А) кости предплечья
Б) кости таза
В) фаланги пальцев
Кости голени относят к костям:
А) трубчатым
Б) плоским
В) смешанным
Г) губчатым
Основными неорганическими соединениями костей являются соли:
А) железа
Б) калия
В) кальция
Г) натрия
Лицевой отдел черепа образован костями:
А) скуловой, височной, теменной, лобной, затылочной
Б) парными: височными, теменными, непарными: затылочной, лобной, клиновидной и решетчатой
В) парными: височной, теменной, непарными: подъязычной, скуловой
Г) парными: верхнечелюстной, небной, скуловым и непарными: нижнечелюстной, решетчатой костью
Основным органическим веществом кости является.
А) оссеин.
Б) инсулин.
В) кератин.
Г) миозин.
Количество пар ребер, прикрепляющихся непосредственно к грудной клетке:
А) 8
Б) 10
В) 11
Г) 12
Клетки, образующие поперечно-полосатую мышечную ткань:
А) длинные, цилиндрической формы, с округлыми или заостренными концами
Б) вытянутые, веретеновидные, с заостренными концами
В) длинные, на концах разветвляются и соединяются с друг другом
Поперечно-полосатая мышечная ткань образует:
А) стенку сердца
Б) стенки пищеварительной и мочеполовой систем, дыхательных путей и кровеносных сосудов
В) скелетные мышцы
Утомление скелетной мышцы
А) наступает довольно быстро
Б) практически не возникает
В) нарастает очень медленно
Сокращение гладкой мышечной ткани:
А) подчиняется сознанию
Б) не подчиняется сознанию
В) оба ответа неправильны
Миофибриллы (волокна) поперечно-полосатой мышечной ткани:
А) длинной 1-4 мм и хорошо видны в световой микроскоп
Б) длинной 0,002-0,5 мм и хорошо видны в световой микроскоп
В) длинной 0,08 мм и не видны в световой микроскоп
Стойкое смещение суставных костей, при котором головка одной кости выходит из суставной ямки другой, называют:
А) вывих
Б) открытый перелом
В) закрытый перелом
Мышцы, обладающие противоположным действием, называются:
А) синергисты
Б) антагонисты
В) волангисты
Контрольная работа по биологии 9 класс по теме опорно-двигательная система
Контрольная работа по биологии 9 класс
Тема: « Опорно-двигательная система»
Ф. И. обучающегося дата
И. обучающегося дата
1. Какое значение имеет скелет? Выбери правильные ответы:
А) опора тела
Б) движение
В) переваривание пищи
Г) выделение
Д) защита органов
2. Подчеркни правильный ответ: «Из каких органов состоит опорно-
двигательная система?»
А) Нервы и мозг Б) Печень и почки В) Кости и мышцы.
3.Ответь на вопросы:
А ) Как называются кости, имеющие полость внутри?
Б) Какие вещества придают костям эластичность? (минеральные соли, вода, органические вещества)
4. На какие отделы можно разделить скелет человека?
I
I I
I II
I V
5.Определи тип соединения костей, запиши номера рисунков с их изображением.
Подвижное
Неподвижное
П олуподвижное
6.Подчеркни названия костей мозгового отдела черепа.
Теменные
Скуловые
Лобная
Затылочная
Носовая
Нижняя челюсть
Височные
7. Посмотри на рисунок. Исправь ошибки в названиях отделов позвоночника.
Посмотри на рисунок. Исправь ошибки в названиях отделов позвоночника.
8.Выбери из списка кости нижней и верхней конечностей. Запиши их в таблицу.
Плечевая кость, позвонок, ребра, бедренная кость, большая берцовая кость, кости кисти, лучевая кость, грудина, локтевая кость, малая берцовая кость, кости стопы , лопатка.
Кости верхних конечностей | Кости нижних конечностей |
9.Из какой мышечной ткани состоят скелетные мышцы? Подчеркни правильный ответ.
Гладкая Поперечнополосатая Сердечная
10. В каком отделе черепа находятся мимические мышцы? Подчеркни правильный ответ.
В лицевом В мозговом
11. Какие мышцы принимают участие в поворотах головы? Подчеркни правильные ответы.
Мышцы рук
Мышцы шеи
Мышцы спины
Мышцы лица
Мышцы живота
Мышцы груди
12. Какие факторы могут привести к утомлению мышц? Правильные ответы подчеркните.
Какие факторы могут привести к утомлению мышц? Правильные ответы подчеркните.
А) Монотонный физический труд
Б) Смена видов деятельности (умственный труд сменяется физическим)
В) Отдых
Г) Сон
Д) Спортивные тренировки длительное время.
13.Напиши какие ты знаешь травмы опорно-двигательной системы.
А)
Б)
В)
Г)
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/221406-kontrolnaja-rabota-po-biologii-9-klass-po-tem
Опорно-двигательный аппарат (Реферат) — TopRef.ru
Реферат по биологии на тему:
«Опорно-двигательный аппарат»
Ученика 9 «Г» класса
средней школы № 117
ЮЗАО г. Москва
Юдицкого Александра.
Москва 2004
План:
I. Введение.
II. Скелет.
1. Позвоночник.
Позвоночник.
2.Грудная клетка.
3.Конечности.
4.Нога и рука.
III. Два вида мышечной ткани.
1.Гладкие мышцы.
2.Мышцы скелета.
3.Нервные связи в мышцах.
4.Мышцы выделяют тепло.
5.Сила и скорость сокращения мышцы.
IV. Утомление и отдых.
1.Причины утомления.
V. Статика и динамика человеческого тела.
1.Условия равновесия.
VI. Спорт нужен каждому.
1.Тренировка мышц.
2.Труд и спорт.
3.Спортсменом может стать всякий.
VII. Великие люди о пользе физических упражнений.
VIII. Заключение.
XI. Список использованной литературы.
Опорно-двигательный аппарат
Опорно-двигательный
аппарат составляют кости скелета с
суставами, связки и мышцы с сухожилиями,
которые наряду с движениями обеспечивают
опорную функцию организма. Кости и
суставы участвуют в движении пассивно,
подчиняясь действию мышц, но играют
ведущую роль в осуществлении опорной
функции. Определённая форма и строение
костей придают им большую прочность,
запас которой на сжатие, расжатие,
сгибание значительно превышает нагрузки,
возможные при повседневной работе
опорно-двигательного аппарата. Например,
большеберцовая кость человека при
сжатии выдерживает нагрузку более
тонны, а по прочности растяжения почти
не уступает чугуну. Большим запасом
прочности обладают также связки и хрящи.
Кости и
суставы участвуют в движении пассивно,
подчиняясь действию мышц, но играют
ведущую роль в осуществлении опорной
функции. Определённая форма и строение
костей придают им большую прочность,
запас которой на сжатие, расжатие,
сгибание значительно превышает нагрузки,
возможные при повседневной работе
опорно-двигательного аппарата. Например,
большеберцовая кость человека при
сжатии выдерживает нагрузку более
тонны, а по прочности растяжения почти
не уступает чугуну. Большим запасом
прочности обладают также связки и хрящи.
Скелет
Скелет состоит из соединённых между собой костей. Он обеспечивает нашему телу опору и сохранение формы, а также защищает внутренние органы. У взрослого человека скелет состоит примерно из 200 костей. Каждая кость имеет определённую форму, величину и занимает определённое положение в скелете. Часть костей соединена между собой подвижными суставами. Они приводятся в движение прикреплёнными к ним мышцами.
Позвоночник. Оригинальной
конструкцией, составляющей основную
опору скелета, является позвоночник.
Если бы он состоял из сплошного костного
стержня, то наши движения были бы
скованными, лишёнными гибкости и
доставляли бы столь же неприятные
ощущения, как езда в телеге без рессор
по булыжной мостовой.
Оригинальной
конструкцией, составляющей основную
опору скелета, является позвоночник.
Если бы он состоял из сплошного костного
стержня, то наши движения были бы
скованными, лишёнными гибкости и
доставляли бы столь же неприятные
ощущения, как езда в телеге без рессор
по булыжной мостовой.
Упругость сотен связок, хрящевых прослоек и изгибов делает позвоночник прочной и гибкой опорой. Благодаря такому строению позвоночника человек может нагибаться, прыгать, кувыркаться, бегать. Очень сильные межпозвонковые связки допускают самые сложные движения и вместе с тем создают надёжную защиту спинному мозгу. Он не подвергается какому-либо механическому растяжению, давлению при самых невероятных изгибах позвоночника.
Изгибы позвоночного столба
соответствуют влиянию нагрузки на ось
скелета. Поэтому нижняя, более массивная
часть становится опорой при передвижении;
верхняя, при свободном движении, помогает
сохранять равновесие. Позвоночный столб
можно было бы называть позвоночной
пружиной.
Волнообразные изгибы позвоночника обеспечивают его упругость. Появляются они с развитием двигательных способностей ребёнка, когда он начинает держать голову, стоять, ходить.
Грудная клетка. Грудная клетка образована грудными позвонками, двенадцатью парами рёбер и плоской грудной костью, или грудиной. Рёбра представляют собой плоские изогнутые дугою кости. Их задние концы подвижно соединены с грудными позвонками, а передние концы десяти верхних рёбер при помощи гибких хрящей соединяются с грудной костью. Это обеспечивает подвижность грудной клетки при дыхании. Две нижние пары рёбер короче остальных и оканчиваются свободно. Грудная клетка защищает сердце и лёгкие, а также печень и желудок.
Интересно заметить, что окостенение
грудной клетки происходит позднее
других костей. К двадцати годам
заканчивается окостенение рёбер, и
только к тридцати годам происходит
полное слияние частей грудины, состоящей
из рукоятки, тела грудины и мечевидного
отростка.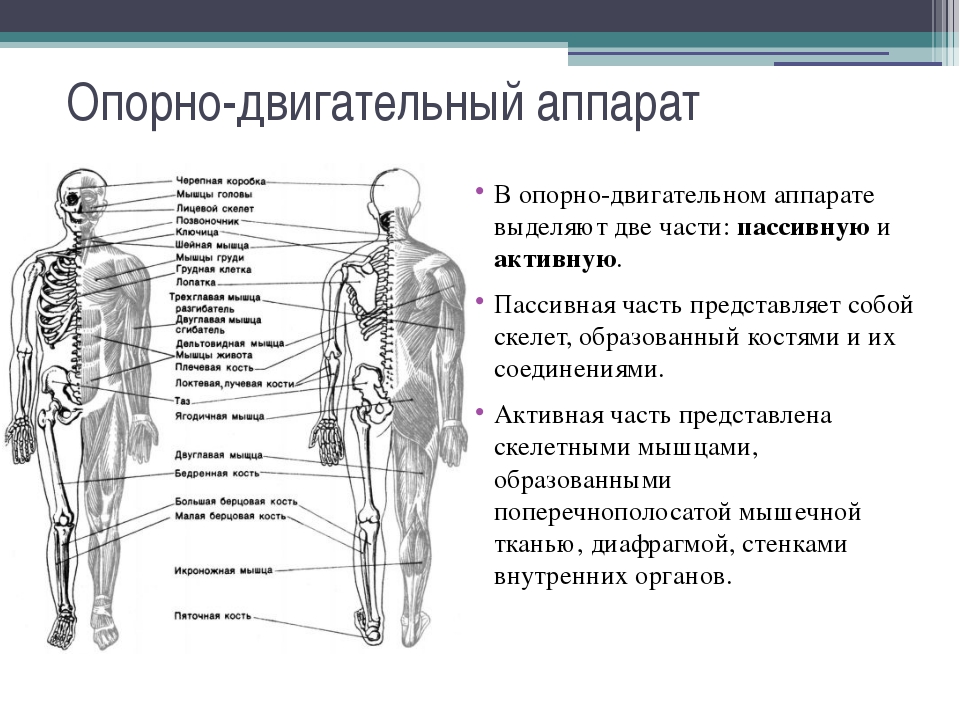
Форма грудной клетки с возрастом изменяется. У новорожденного она имеет, как правило, форму конуса с основанием, обращённым вниз. Потом окружность грудной клетки в первые три года увеличивается быстрее, чем длина туловища. Постепенно грудная клетка из конусообразной приобретает характерную для человека округлую форму. Поперечник её больше, чем длина.
Развитие грудной клетки зависит от образа жизни человека. Сравните спортсмена, пловца, атлета с человеком, не занимающимся спортом. Легко понять, что развитие грудной клетки, её подвижность зависят от развития мышц. Поэтому у подростков двенадцати-пятнадцати лет, занимающихся спортом, окружность грудной клетки на семь-восемь сантиметров больше, чем у их сверстников, не занимающихся спортом.
Неправильная посадка учащихся за партой, сдавливание грудной клетки могут привести к её деформации, что нарушает развитие сердца, крупных сосудов и лёгких.
Конечности. Благодаря тому,
что конечности прикреплены к надёжной
опоре, они обладают подвижностью во
всех направлениях, способны выдерживать
большие физические нагрузки.
Благодаря тому,
что конечности прикреплены к надёжной
опоре, они обладают подвижностью во
всех направлениях, способны выдерживать
большие физические нагрузки.
Лёгкие кости — ключицы и лопатки, лежащие на верхней части грудной клетки, охватывают её, точно пояс. Это опора рук. Выступы и гребни на ключице и лопатке являются местом прикрепления мышц. Чем больше сила этих мышц, тем больше развиты костные отростки и неровности. У атлета, грузчика продольный гребень лопатки более развит, чем у часовщика или счетовода. Ключица – перекидной мост между костями туловища и рук. Лопатка и ключица создают надёжную рессорную опору руки.
По положению лопаток и ключиц можно судить о положении рук. Анатомы помогли восстановить отломанные руки древнегреческой статуи Венеры Милосской, определив их положение по силуэтам лопаток и ключиц.
Кости таза толстые, широкие и
почти полностью сросшиеся. У человека
таз оправдывает своё название – он, как
чаша, поддерживает внутренние органы
снизу. Это одна из типичных черт
человеческого скелета. Массивность
таза пропорциональна массивности костей
ног, несущих основную нагрузку при
передвижении человека, поэтому скелет
таза человека выдерживает большую
нагрузку.
Это одна из типичных черт
человеческого скелета. Массивность
таза пропорциональна массивности костей
ног, несущих основную нагрузку при
передвижении человека, поэтому скелет
таза человека выдерживает большую
нагрузку.
Нога и рука. При вертикальной позе руки человека не несут постоянной нагрузки как опоры, приобретают лёгкость и разнообразие действия, свободу движения. Рука может совершать сотни тысяч различных двигательных операций. Ноги же несут всю тяжесть тела. Они массивны, имеют чрезвычайно прочные кости и связки.
Головка плеча не имеет ограничения в широких круговых движениях рук, Например при метании копья. Головка же бедра глубоко вдаётся в углубление таза, что ограничивает движения. Связки этого сустава самые прочные и удерживают на бёдрах тяжесть туловища.
Упражнением и тренировкой достигается большая свобода движений ног, несмотря на их массивность. Убедительным примером этого может быть балетное искусство, занятия гимнастикой, восточные единоборства.
Трубчатые кости рук и ног имеют огромный запас прочности. Интересно, что расположение ажурных перекладин Эйфелевой башни соответствует строению губчатого вещества головок трубчатых костей, словно Ж. Эйфель конструировал кости. Инженер пользовался теми же законами конструкции, которые обуславливают строение кости, придавая ей лёгкость и прочность. В этом причина сходства металлической конструкции и живой костной структуры.
Локтевой сустав обеспечивает сложные и многообразные движения руки в трудовой жизни человека. Только ему свойственна способность вращать предплечье вокруг своей оси, с характерным движением раскручивания или закручивания.
Коленный сустав направляет голень при ходьбе, беге, прыжках. Коленные связки у человека обуславливают прочность опоры при распрямлении конечности.
Кисть начинается группой косточек запястья. Эти кости не испытывают сильного давления, выполняют сходную функцию, поэтому они мелкие, однообразные, трудноразличимые. Интересно упомянуть, что великий анатом Андрей Везалий мог с завязанными глазами определить каждую запястную косточку и сказать, к левой или правой руке она относится.
Кости пясти умеренно подвижны, расположены они в виде веера и служат опорой пальцев. Фаланг пальцев — 14. Все пальцы имеют по три косточки, кроме большого — у него две косточки. У человека очень подвижен большой палец. Он может становиться под прямым углом по отношению ко всем остальным. Его пястная кость способна противопоставляться остальным костям руки.
Развитие большого пальца связано с трудовыми движениями кисти. Индейцы называют большой палец «матерью», яванцы -«старшим братом». В древности пленникам отрубали большой палец, чтобы унизить их человеческое достоинство и сделать негодными для участия в сражениях.
Кисть совершает самые тончайшие движения. При любом рабочем положении руки кисть сохраняет полную свободу движения.
Стопа в связи с ходьбой стала массивнее. Кости предплюсны очень большие и крепкие в сравнении с костями запястья. Наиболее крупные из них – таранная и пяточная кости. Они выдерживают значительную тяжесть тела. У новорожденных движения стопы и её большого пальца сходны с их движением у обезьян. Усиление опорной роли стопы при ходьбе привело к формированию её свода. При ходьбе, стоянии легко можно ощутить, как всё пространство между этими точками «висит в воздухе».
Свод, как известно в механике, выдерживает большое давление, чем площадка. Свод стопы обеспечивает упругость походки, устраняет давление на нервы и сосуды. Его образование в истории происхождения человека связано с прямохождением и является отличительной особенностью человека, приобретённой в процессе его исторического развития.
Артрит, боль в пояснице, кости, мышцы
Обзор
Что такое опорно-двигательный аппарат?
Ваша опорно-двигательная система включает кости, хрящи, связки, сухожилия и соединительные ткани. Ваш скелет обеспечивает основу для ваших мышц и других мягких тканей. Вместе они поддерживают вес вашего тела, поддерживают осанку и помогают двигаться.
Широкий спектр заболеваний и состояний может привести к нарушениям опорно-двигательного аппарата.Старение, травмы, врожденные аномалии (врожденные дефекты) и болезни могут вызывать боль и ограничивать движение.
Вы можете сохранить здоровье опорно-двигательного аппарата, уделяя особое внимание общему здоровью. Придерживайтесь сбалансированной диеты, поддерживайте здоровый вес, регулярно занимайтесь спортом и обращайтесь к врачу для проверки.
Функция
Как работает опорно-двигательный аппарат?
Нервная система (командный центр вашего тела) контролирует ваши произвольные движения мышц. Произвольные мышцы — это те мышцы, которыми вы управляете намеренно.Некоторые из них задействуют большие группы мышц для выполнения таких действий, как прыжки. Другие используют более мелкие движения, например, нажатие кнопки. Движение происходит, когда:
- Ваша нервная система (мозг и нервы) посылает сигнал для активации ваших скелетных (произвольных) мышц.
- Ваши мышечные волокна сокращаются (напрягаются) в ответ на сообщение.
- Когда мышца активируется или сжимается, она тянет за сухожилие. Сухожилия прикрепляют мышцы к костям.
- Сухожилие тянет кость, заставляя ее двигаться.
- Чтобы расслабить мышцы, ваша нервная система посылает другое сообщение. Это заставляет мышцы расслабляться или отключаться.
- Расслабленная мышца снимает напряжение, переводя кость в положение покоя.
Анатомия
Какие части опорно-двигательного аппарата?
Опорно-двигательный аппарат помогает вам стоять, сидеть, ходить, бегать и двигаться. В теле взрослого человека 206 костей и более 600 мышц, соединенных связками, сухожилиями и мягкими тканями.
Части опорно-двигательного аппарата:
- Кости: Кости всех форм и размеров поддерживают ваше тело, защищают органы и ткани, накапливают кальций и жир и производят клетки крови. Твердая внешняя оболочка кости окружает губчатый центр. Кости обеспечивают структуру и форму вашему телу. Они работают с мышцами, сухожилиями, связками и другими соединительными тканями, помогая вам двигаться.
- Хрящ: Тип соединительной ткани, хрящевая подкладка костей внутри суставов, вдоль позвоночника и в грудной клетке.Прочный эластичный хрящ защищает кости от трения друг о друга. У вас также есть хрящи в носу, ушах, тазу и легких.
- Суставы: Кости соединяются, образуя суставы. Некоторые суставы имеют большой диапазон движений, например, шаровидный плечевой сустав. Другие суставы, такие как колено, позволяют костям двигаться вперед и назад, но не вращаются.
- Мышцы: Каждая мышца состоит из тысяч эластичных волокон. Ваши мышцы позволяют вам двигаться, сидеть прямо и оставаться на месте.Некоторые мышцы помогают бегать, танцевать и поднимать тяжести. Вы используете других, чтобы написать свое имя, застегнуть пуговицу, поговорить и проглотить.
- Связки: Связки, изготовленные из прочных коллагеновых волокон, соединяют кости и помогают стабилизировать суставы.
- Сухожилия: Сухожилия соединяют мышцы с костями. Состоящие из фиброзной ткани и коллагена, сухожилия жесткие, но не очень эластичные.
Состояния и расстройства
Какие состояния и нарушения влияют на опорно-двигательный аппарат?
Сотни заболеваний могут вызвать проблемы с опорно-двигательным аппаратом.Они могут влиять на то, как вы двигаетесь, говорите и взаимодействуете с миром. Некоторые из наиболее распространенных причин скелетно-мышечной боли и проблем с движением:
- Старение: В процессе естественного старения кости теряют плотность. Менее плотные кости могут привести к остеопорозу и переломам костей (переломам костей). С возрастом мышцы теряют свою массу, а хрящи начинают изнашиваться, что приводит к боли, жесткости и уменьшению диапазона движений. После травмы вы можете не зажить так быстро, как в молодости.
- Артрит: Боль, воспаление и скованность суставов являются следствием артрита. У пожилых людей больше шансов заболеть остеоартритом из-за разрушения хрящей внутри суставов, но это заболевание может затронуть людей любого возраста. Другие типы артрита также вызывают боль и воспаление в суставах, включая ревматоидный артрит, анкилозирующий спондилит и подагру.
- Проблемы со спиной: Боль в спине и мышечные спазмы могут быть результатом растяжения мышц или травм, таких как грыжа межпозвоночного диска.Некоторые состояния, включая стеноз и сколиоз позвоночника, вызывают структурные проблемы в спине, что приводит к боли и ограничению подвижности.
- Рак: Несколько типов рака поражают опорно-двигательный аппарат, включая рак костей. Опухоли, которые растут в соединительной ткани (саркомы), могут вызывать боль и проблемы с движением.
- Врожденные аномалии: Врожденные аномалии, также известные как врожденные пороки, могут влиять на внешний вид, структуру и функции тела.Косолапость — одна из самых распространенных проблем с опорно-двигательным аппаратом, с которой рождаются дети. Это вызывает скованность и уменьшение диапазона движений.
- Болезнь: На работу костей, мышц и соединительных тканей влияет широкий спектр заболеваний. Некоторые из них, например остеонекроз, приводят к разрушению костей и их гибели. Другие заболевания, такие как фиброзная дисплазия и болезнь хрупкости костей (несовершенный остеогенез), вызывают легкое переломание костей. Состояния, которые влияют на скелетные мышцы (миопатии), включают более 30 типов мышечной дистрофии.
- Травмы: Сотни травм могут поражать кости, хрящи, мышцы и соединительные ткани. В результате чрезмерного использования могут возникать травмы, такие как синдром запястного канала, бурсит и тендинит. Растяжения, разрывы мышц, переломы костей и травмы сухожилий, связок и других мягких тканей могут быть результатом несчастных случаев и травм.
Насколько распространены эти состояния?
У всех время от времени возникают боли в мышцах и суставах. Одним из наиболее распространенных заболеваний опорно-двигательного аппарата является боль в спине, особенно боль в пояснице.Более 80% людей в Соединенных Штатах в какой-то момент жизни испытывают боли в спине. Артрит тоже очень распространен. Более 54 миллионов взрослых в США страдают артритом. Каждый год миллионы людей случаются с переломами, растяжениями и растяжениями. Большинство людей восстанавливаются после этих травм без длительных проблем со здоровьем.
Забота
Как сохранить здоровье опорно-двигательного аппарата?
Лучший способ заботиться о опорно-двигательном аппарате — поддерживать хорошее здоровье в целом.Чтобы ваши кости и мышцы были здоровыми, вам необходимо:
- Регулярно выполняйте упражнения, и обязательно включайте в себя сочетание упражнений с отягощением и сердечно-сосудистой деятельности. Укрепление мышц может поддержать суставы и защитить их от повреждений.
- Высыпайтесь достаточно , чтобы ваши кости и мышцы могли восстановиться и восстановиться.
- Поддерживайте здоровый вес. Лишние килограммы оказывают давление на кости и суставы, вызывая ряд проблем со здоровьем.Если у вас избыточный вес, поговорите со своим врачом о здоровом плане похудания.
- Выбирайте здоровую пищу , включая сбалансированную диету из фруктов и овощей, нежирного белка и молока для крепких костей.
- Бросьте курить и воздержитесь от табака. Курение снижает кровоток по всему телу. Ваши кости, мышцы и мягкие ткани нуждаются в адекватном кровотоке, чтобы оставаться здоровыми.
- Проходите регулярные осмотры и проверки здоровья в соответствии с возрастом. Если вам больше 65 лет, поговорите со своим врачом о сдаче теста на плотность костной ткани.
###
Часто задаваемые вопросы
Когда мне следует позвонить своему врачу?
Поговорите со своим врачом, если у вас есть боль, отек, скованность, ограниченный диапазон движений или проблемы с движением. Немедленно обратитесь к своему провайдеру, если какие-либо из этих изменений произойдут внезапно. Внезапные проблемы могут быть признаком серьезного состояния.
Записка из клиники Кливленда
У всех время от времени возникают боли в мышцах и мышцах.Хотя, возможно, вы не сможете предотвратить все растяжения, растяжения и переломы костей, вы сможете сохранить здоровье опорно-двигательного аппарата. Поддержание хорошего общего состояния здоровья снизит риск заболеваний и травм. А сохранение здоровья поможет вам быстрее выздороветь, если вы все-таки получите травму. Регулярно посещая врача, контролируя свой вес и заботясь о себе, вы защитите свои кости и мышцы, чтобы они могли и дальше защищать вас.
Структура, функции и контроль опорно-двигательного аппарата человека
Реферат
Человеческое тело представляет собой сложный организм, основные механические свойства которого обеспечиваются взаимосвязанной опорно-двигательной сетью, контролируемой нервной системой.Природа костно-мышечной взаимосвязи способствует стабильности, произвольным движениям и устойчивости к травмам. Однако фундаментальное понимание этой сети и ее контроля со стороны нейронных систем остается неуловимым. Здесь мы устраняем этот пробел в знаниях, используя медицинские базы данных и математическое моделирование, чтобы выявить организационную структуру, прогнозируемые функции и нейронный контроль опорно-двигательной системы. Мы построили очень упрощенную опорно-двигательную сеть всего тела, в которой отдельные мышцы соединяются с несколькими костями как через точки начала, так и через точки прикрепления.Мы продемонстрировали, что, используя эту упрощенную модель, роль мышцы в этой сети может предложить теоретическое предсказание восприимчивости окружающих компонентов к вторичным повреждениям. Наконец, мы проиллюстрировали, что наборы мышц группируются в сетевые сообщества, которые имитируют организацию модулей управления в первичной моторной коре. Этот новый формализм для описания взаимодействий между мышечной и скелетной системами служит основой для разработки и тестирования терапевтических реакций на травмы, вдохновляя будущие успехи в клиническом лечении.
Об авторе
Хотя сетевая наука часто используется для характеристики сетей на основе геномики, протеомики и коннектомики, ее полезность для понимания биомеханики, ортопедии и физиотерапии остается в значительной степени неизученной. Действительно, текущая клиническая практика и знания, касающиеся опорно-двигательного аппарата, в основном сосредоточены на отдельных областях тела, отдельных мышцах или отдельных травмах и поэтому остаются безразличными к мезомасштабным или глобальным особенностям архитектуры тела, которые могут иметь решающее значение для травм и восстановления.Мы устранили этот пробел, представив опорно-двигательный аппарат в виде графа или сети, в которой мы рассмотрели кости и мышечные связи между ними. Моделируя мышцы как пружины и кости как точечные массы, мы разработали пертурбативный подход, чтобы исследовать функцию этой сети. Используя эту модель, мы рассчитали сетевые эффекты возмущения отдельных мышц. Используя этот формализм, мы можем провести новые параллели между этой системой и первичной моторной корой, которая ее контролирует, и проиллюстрировать клинические связи между сетевой структурой и мышечным повреждением.
Введение
Взаимосвязанная природа человеческого тела долгое время была предметом научных исследований и суеверных верований. От древних юморов, связывающих сердце, печень, селезенку и мозг смелостью, спокойствием и надеждой [1], до современного понимания связи кишечника и мозга [2], люди склонны искать взаимосвязи между разрозненными частями тела, чтобы объяснять сложные явления. Тем не менее, напряжение остается между этой базовой концептуализацией человеческого тела и редукционизмом, неявным в современной науке [3].Понимание всей системы часто относят к футуристическому миру, в то время как отдельные эксперименты уточняют наше понимание мельчайших составных частей.
Опорно-двигательный аппарат человека не является исключением из этой дихотомии. В то время как медицинская практика сосредоточена на кистях, стопах или лодыжках, клиницисты знают, что травмы одной части опорно-двигательного аппарата обязательно влияют на работу других (даже отдаленно удаленных) частей [4]. Травма лодыжки может изменить характер походки, что приведет к хронической боли в спине; травма плеча может изменить осанку и вызвать дискомфорт в шее.Понимание фундаментальных отношений между фокальной структурой и потенциальными удаленными взаимодействиями требует целостного подхода.
Здесь мы подробно описываем такой подход. Наша концептуальная основа мотивирована недавними теоретическими достижениями в сетевой науке [5], которая представляет собой развивающуюся дисциплину, построенную на упорядоченном слиянии математики (в частности, теории графов [6]) и физики (в частности, статистической механики [7]), компьютеров. наука, статистика [8] и системная инженерия.Подход упрощает сложные системы, разграничивая их компоненты и отображая паттерн взаимодействия между этими компонентами [9]. Это представление кажется особенно подходящим для изучения опорно-двигательного аппарата человека, который состоит из костей и соединяющих их мышц. В этом исследовании мы использовали этот подход для оценки структуры, функции и контроля опорно-двигательного аппарата.
Использование сетевых наук для понимания опорно-двигательного аппарата в последние годы увеличилось [10].Однако этот каркас в основном использовался для исследования свойств локальных мышечных или костных сетей. Например, была исследована местная структура черепа, чтобы выяснить, как можно классифицировать кости [11]. Кроме того, были проведены исследования топологии костно-мышечной сети позвоночника для оценки напряжений и деформаций в костях [12]. Существует несколько исследований, посвященных всей опорно-двигательной системе, хотя они не используют математические инструменты, которые мы использовали здесь [13,14].Настоящее исследование отличается от предыдущих работ оценкой всей опорно-двигательной системы в сочетании с математическими инструментами науки о сетях.
В этом более широком контексте мы сосредоточили внимание на проблеме реабилитации после травм скелетных мышц или коры головного мозга. Прямое повреждение мышцы или связанного с ней сухожилия или связки влияет на другие мышцы через компенсаторные механизмы тела [15]. Точно так же потеря использования определенной мышцы или группы мышц из-за прямого повреждения коры головного мозга может привести к компенсаторному использованию альтернативных мышц [16,17].То, как структурированы взаимосвязи опорно-двигательного аппарата и как они функционируют, напрямую ограничивает то, как повреждение определенной мышцы повлияет на опорно-двигательный аппарат в целом. Понимание этих взаимосвязей может дать столь необходимое понимание того, какие мышцы больше всего подвержены риску вторичной травмы из-за компенсаторных изменений, возникающих в результате очаговой травмы, тем самым давая основу для более комплексных подходов к реабилитации. Кроме того, понимание того, как кора головного мозга отображается не только на отдельные мышцы, но и на группы топологически близких мышц, может помочь в будущих эмпирических исследованиях взаимосвязи между очаговыми повреждениями (включая инсульт) моторной коры и риском вторичного повреждения.
Материалы и методы
Построение сети
Используя таблицы Хосфорда Muscle [18], мы построили скелетно-мышечный гиперграф, представив 173 кости (некоторые из которых на самом деле являются связками и сухожилиями) как узлы и 270 мышц как гиперребра, соединяющие эти узлы ( происхождение и точки прикрепления мышцы перечислены в таблице S9). Этот гиперграф также можно интерпретировать как двудольную сеть, в которой мышцы являются одной группой, а кости — второй группой (). Матрица заболеваемости C 173 × 270 скелетно-мышечной сети, таким образом, определяется как C ij = 1, если v i ∈ e j , и 0 в противном случае, где V = {v 1 , · · ·, v 173 } — это набор узлов (костей), а E = {e 1 , · · ·, e 270 } — набор гиперребер (мышц).Это гиперграфическое представление тела устраняет большую часть сложности опорно-двигательного аппарата, кодируя только то, какие мышцы прикрепляются к каким костям. Весь анализ применялся только к одной половине (левой или правой) тела, потому что каждое полушарие головного мозга контролирует только противоположную сторону тела. Поэтому мы еще больше упростили нашу модель, допустив лево-правую симметрию; на любых фигурах, на которых изображены обе половины тела, вторая половина присутствует исключительно для визуальной интуиции.
Схема представлений данных и вычислительных методов.(a) Скелетно-мышечная сеть была сначала преобразована в двудольную матрицу, где 1/0 указывает на наличие / отсутствие связи между мышцами и костями. (b) Сообщества топологически связанных мышц идентифицируются путем (1) преобразования гиперграфа в граф мышца-мышцы, в котором каждая запись кодирует количество общих костей каждой пары мышц, и (2) впоследствии мышцы были разбиты на сообщества , в котором составляющие члены более плотно связаны с другими членами своего сообщества, чем с членами других сообществ.(c) Чтобы облегчить пертурбацию, опорно-двигательная сеть была физически встроена, так что кости (узлы) изначально располагались в их правильных анатомических положениях. (d) Чтобы понять влияние отдельных мышц на взаимосвязанную систему, все узлы, связанные выбранным гиперребром, были возмущены в четвертом пространственном измерении.
Костно-ориентированный график A и мышечный график B () — это просто одномодовые проекции C. Проекция на кости A = C T C, а проекция на мышцы B = CC T .Затем диагональные элементы были установлены равными нулю, в результате чего мы получили взвешенную матрицу смежности [5]. Мы получили оценочные анатомические местоположения центра масс каждой мышцы (и кости), изучив анатомические тексты [19] и оценив x-, y- и z-координаты для отображения на графическом представлении человеческого тела ().
Расчет оценки воздействия
Для измерения потенциальной функциональной роли каждой мышцы в сети мы использовали классический пертурбативный подход. Чтобы максимизировать простоту и потенциал для фундаментальной интуиции, мы смоделировали опорно-двигательную систему как систему точечных масс (костей) и пружин (мышц).Мы растянули мышечную пружину и наблюдали влияние этого возмущения на расположение всех остальных мышц. Физически, чтобы повредить мышцу, мы смещали все кости, связанные с этой мышцей, на одинаковую величину и в одном направлении, растягивая мышцу, и удерживали эти кости на новом месте. Этот процесс также математически эквивалентен простому изменению жесткости пружины, относящейся к конкретной мышечной пружине. Затем системе позволяли достичь равновесия. Мы зафиксировали кости по средней линии и по периферии в пространстве, чтобы предотвратить смещение системы.Чтобы количественно оценить влияние возмущения этой единственной мышечной пружины, мы определили движение узла и следующим образом:
mid2r → idt2 = ∑j ≠ i∈V [SijAijl → ij (xij-‖l → ij‖)] — βdr → idt,
где l ij — смещение между узлами i и j, x ij — невозмущенное расстояние между узлами i и j, m — масса узла (которую мы установили равной единице для всех узлов в сети) , β = 1 — коэффициент демпфирования, r i — положение узла i , A — взвешенная матрица смежности графа, ориентированного на кости, и S ij представляет собой сумму всех сил пружин мышцы, к которым подключены узлы i и j.Чтобы нормализовать восстанавливающую силу мышц на узлах, пусть сила пружины мышцы q 1 / (k — 1). Здесь мы установили, что все кости имеют равный вес, а все мышцы имеют одинаковую жесткость пружины, что является упрощением реальной физической анатомии. Для обсуждения того, как учесть дополнительные физические свойства, такие как масса кости и мышечная сила, а также дополнительные результаты с использованием этих свойств, см. S5 Text. Более того, образцы траекторий, которые дают интуитивное представление о динамике нашей модели, были включены в вспомогательную информацию (S8 рис.).
Чтобы измерить потенциальную функциональную роль каждой мышцы в сети, мы растянули гиперреберь мышцы и измерили влияние возмущения на остальную часть сети. Вместо того, чтобы возмущать сеть в каком-то произвольном трехмерном направлении, мы расширили объем нашей симуляции до четвертого измерения. При возмущении мышцы мы смещали все узлы (кости), содержащиеся в этом гиперребре мышцы, на постоянный вектор в четвертом измерении и удерживали их этим смещением ().Затем возмущение в ответ прокатилось по сети пружин. Мы последовательно растягивали каждую мышечную гиперреберь и определили оценку воздействия этого возмущения как общее расстояние, на которое все узлы опорно-двигательной сети перемещаются от их исходных положений. Величина смещения — это суммарное смещение по всем временным точкам, от начала возмущения до соответствующего отсечки для времени уравновешивания. Здесь мы нашли равновесие системы, позволив динамике выровняться в течение достаточного периода времени.Обратите внимание, что равновесие также может быть решено с использованием стационарного, нединамического подхода; мы решили использовать динамику в этом случае для более широкой поддержки будущих приложений.
Отклонение оценки удара
Для каждой мышцы мы рассчитали индекс, который количественно определяет, насколько оценка воздействия этой мышцы отклоняется от ожидаемой с учетом степени ее гиперребер; мы называем этот показатель «ударным отклонением». Мы начинаем с построения нулевой модели, которая определяет ожидаемое воздействие при наборе статистических допущений.В текущем исследовании мы использовали несколько различных нулевых моделей с разными наборами допущений, которые мы подробно рассмотрим в следующих разделах. Отклонение воздействия рассчитывалось следующим образом: мы вычисляли среднее значение, стандартное отклонение и 95% доверительные интервалы (ДИ) для каждой из категорий степени нулевого гиперграфа из ансамбля из 100 нулевых гиперграфов. Расстояние от данной мышцы до среднего значения ± 95% доверительного интервала (в зависимости от того, что ближе всего) было вычислено и разделено на стандартное отклонение этого распределения степеней нулевого гиперграфа.Таким образом, мы рассчитали отклонение от ожидаемого значения в стандартных отклонениях (аналогично z-баллу). содержит мышцы, которые лежат за пределами 95% ДИ коэффициентов отклонения относительно степени их гиперребер. Мышцы можно естественным образом сгруппировать в соответствии с гомункулом, грубым одномерным представлением того, как контрольные области мышц группируются в моторную кору. Для данной группы гомункулов мы рассчитали коэффициент отклонения как количество мышц с положительным отклонением, деленное на общее количество мышц в группе ().
Таблица 1
Мышцы с большей или меньшей нагрузкой, чем ожидалось в модели нулевого гиперграфа.Мышцы на левой стороне оказывают меньшее влияние, чем ожидалось, учитывая степень их гиперребер: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее влияние, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартных отклонений превышает среднее значение, в порядке от наибольшего к наименьшему.В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 20 | Брахиалис | ||||||||||
| 2 | 145 | Букцинатор | 22 | Anconeus | ||||||||||||
| 3 | 148 | 12 | Teres minor | |||||||||||||
| 5 | 11 | Infraspinatus | ||||||||||||||
| 6 | 13 | Te res major | ||||||||||||||
| 8 | 10 | Supraspinatus | ||||||||||||||
| 8 | 16 | большой грудной мышцы longus | ||||||||||||||
| 11 | 161 | Piriformis | ||||||||||||||
| 10 | 31 | Brachioradialis 9002 | 31 | Brachioradialis
| ||||||||||||
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 3 | Колено | ||||||
| 2 | 17 | Глазные мышцы | 4 | Бедро | ||||||||
| 3 | 18 | Мышцы лица | 19 | Мышцы губ | 7 | Локоть | ||||||
| 5 | 8 | Запястье | ||||||||||
| 6 | 10 | Мизинец | ||||||||||
| 8 | 21 | Язык | ||||||||||
Обнаружение сообщества
Чтобы понять как функцию, так и контроль над опорно-двигательной системой, мы были заинтересованы в определении групп плотно связанных между собой мышц с использованием подхода, основанного на данных.Мы выполнили тип обнаружения сообщества, максимизируя функцию качества модульности, введенную Ньюманом [20]:
Q = ∑ijBij − γPijδ (gi, gj),
где P ij — ожидаемый вес ребра в нулевой модели Ньюмана-Гирвана, узел i назначен сообществу g i , узел j назначен сообществу g j , а δ — дельта-функция Кронекера. Путем максимизации Q мы получили разделение узлов (мускулов) на сообщества, так что узлы в одном сообществе были более плотно взаимосвязаны, чем ожидалось в сетевой нулевой модели (справа).
Здесь мы также использовали параметр разрешения для настройки размера и количества обнаруженных сообществ таким образом, чтобы количество обнаруженных сообществ соответствовало количеству групп внутри гомункула, для прямого сравнения. В частности, мы использовали параметр разрешения γ = 4,3, чтобы разделить мышечно-ориентированную матрицу на 22 сообщества (см. Таблицу S8). Мы начали с переопределения исходной мышечно-ориентированной матрицы B, следуя Jutla et al. [21]; мы положим k = Σ i B i , j , а затем мы применили локально жадный алгоритм максимизации модульности типа Лувена к скорректированной матрице B ‘= B-γkTk∑ jkj [22].
Указанный выше метод обнаружения сообществ недетерминирован [23]. То есть одно и то же решение не будет достигнуто при каждом отдельном запуске алгоритма. Следовательно, необходимо убедиться, что используемые назначения сообщества хорошо представляют сеть, а не только локальный максимум ландшафта. Поэтому мы максимально увеличили функцию качества модульности в 100 раз, получив 100 различных заданий от сообщества. Из этого набора решений мы определили надежную репрезентативную консенсусную структуру сообщества [24].S1 Рис. Показывает, как обнаруженные сообщества изменяются в зависимости от параметра разрешения для мышечно-ориентированной сети.
Сетевые нулевые модели
Мы используем реконструированные графы в качестве нулевой модели, с которой сравниваем эмпирические данные. В частности, мы построили нулевой гиперграф, перемонтировав мышцы, которым присвоена одна и та же категория (определенная ниже) равномерно и случайным образом. Таким образом, мышцы мизинца будут перестроены только внутри мизинца, и аналогично для мышц других категорий.Важно отметить, что этот метод также сохраняет степень каждой мышцы, а также степень распределения всего гиперграфа.
Таблица 3
Категории гомункулов и связанные с ними идентификационные номера.
| Идентификатор категории | Название категории | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Пальцы | |||||||||||||||
| 2 | Лодыжка | 5 | Ствол | |||||||||||||
| 6 | Плечо | |||||||||||||||
| 7 | Колено | |||||||||||||||
| 8 | Запястье | |||||||||||||||
| 9 | Безымянный палец | |||||||||||||||
| 12 | Средний палец | |||||||||||||||
| 13 | Указательный палец | |||||||||||||||
| 14 | Большой палец | |||||||||||||||
| 15 | Бровь | 15 | Бровь | 17 | веко и глазное яблоко | |||||||||||
| 18 | F ace | |||||||||||||||
| 19 | Губы | |||||||||||||||
| 20 | Челюсть | |||||||||||||||
| 21 | Язык | |||||||||||||||
| Категории 22 | Глотание мышц | |||||||||||||||
| Мышцы | Недели восстановления | Источник | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Triceps brachii | 4 | Bateman (1962) | |||||||||||
| 9026 | Latissimus dorsi | 12 | Nagda (2011) | ||||||||||
| Двуглавая мышца плеча | 12 | Zafra (2009) | |||||||||||
| Голеностопный сустав | 2 | McC14 | Torg (1982) | ||||||||||
| Зубья | 0 | Beachy (2004) | |||||||||||
| Плечо | 2 | Bateman (1962) | |||||||||||
| 9026 | |||||||||||||
| Бедро | 12 | Niemuth (2005) | |||||||||||
| Глаз / веко | 1,4 | Leivo (2015) | |||||||||||
| Колено | 8 | Колено | 8 | 4Колено | 8 | 8 | Fleisig (2012) | ||||||
| Запястье / кисть | 1.4 | Логан (2004) |
Данные области соматотопической репрезентации
Мы вычислили корреляцию между отклонением оценки воздействия и площадью соматотопической репрезентации, посвященной определенной группе мышц. Ареалы представительства были собраны из двух отдельных источников [38,39]. Тома и соответствующие ссылки перечислены в. В обоих исследованиях испытуемых просили многократно артикулировать сустав, и регистрировались объемы областей первичной моторной коры, которые подверглись наибольшему изменению в BOLD-сигнале.Затем мы рассчитали коэффициент корреляции между объемами коры и средним воздействием всех мышц, связанных с этим суставом, как определено в таблицах Hosford Muscle. Мы обнаружили значительную линейную корреляцию между двумя показателями с помощью функции MATLAB, fitlm.m, с параметром «Robust», установленным на «on».
Таблица 5
Размеры и источники объема соматотопической репрезентации первичной моторной коры.
| Мышцы | Объем (мм 3 ) | Артикул | ||||
|---|---|---|---|---|---|---|
| Большой палец | 1,390 | Indovina (2000) | ||||
| Индекс | ||||||
| Средний | 650 | Indovina (2000) | ||||
| Рука | 5,566 | Alkadhi (2002) | ||||
| Пальцы | 2,972 | Alkadhi (2002) | ||||
| Elbow | 2,267 | Alkadhi (2002) |
Результаты
Структура опорно-двигательного аппарата человека
Для исследования структурных взаимосвязей костно-мышечной системы человека использовалась гипер-мышечная система. подход.Основываясь на последних достижениях сетевой науки [5], мы исследовали опорно-двигательную систему как сеть, в которой кости (сетевые узлы) соединены друг с другом мышцами (сетевые гиперребра). Гиперребро — это объект, соединяющий несколько узлов; мышцы соединяют несколько костей через точки начала и вставки. Степень гиперребра k равна количеству узлов, которые оно соединяет; таким образом, степень мышцы — это количество костей, с которыми она контактирует. Например, трапеция — это гиперребро высокой степени, которое связывает 25 костей лопатки и позвоночника; И наоборот, приводящий большой палец представляет собой гиперребро низкой степени, которое связывает 7 костей руки ().Набор гиперребер (мышц) с общими узлами (костями) называется гиперграфом: граф H = (V, E) с N узлами и M гиперребрами, где V = {v 1 , …, v N } — это набор узлов, а E = {e 1 , …, e M } — набор гиперребер.
Структура гиперграфа.(a) Слева: анатомический рисунок трапеции. Справа: преобразование трапеции в гиперребро (красный; степень k = 25), соединяющее 25 узлов (костей) на голове, плече и позвоночнике.(b) Приводящая мышца большого пальца, соединяющая 7 костей руки. (в) Пространственная проекция распределения степеней гиперребер на тело человека. Гиперребра высокой степени сконцентрированы в основном в ядре. (d) Скелетно-мышечная сеть отображается в виде двудольной матрицы (1 = соединена, в противном случае 0). (e) Распределение степени гиперребра для гиперграфа опорно-двигательного аппарата, которое значительно отличается от ожидаемого в случайном гиперграфе. Данные доступны для (e) в DOI : 10.5281 / zenodo.1069104.
Представление опорно-двигательного аппарата человека в виде гиперграфа позволяет количественно оценить его структуру (). Мы заметили, что распределение степени гиперребер носит тяжелый характер: большинство мышц связывают 2 кости, а несколько мышц связывают многие кости (). Наклон распределения степеней существенно отличается от такового случайных сетей (двухвыборочный критерий Колмогорова-Смирнова, KS = 0,37, p <0,0001, см. Материалы и методы) [5], что свидетельствует о наличии мышц неожиданно низкой и высокий градус ().
Функция опорно-двигательного аппарата человека
Чтобы исследовать функциональную роль мышц в опорно-двигательном аппарате, мы использовали упрощенную модель опорно-двигательного аппарата и выяснили, может ли эта модель генерировать полезные клинические корреляты. Мы реализовали физическую модель, в которой кости образуют основной каркас тела, а мышцы скрепляют эту структуру. Каждый узел (кость) представлен как масса, пространственное расположение и движение которой физически ограничены гиперребрами (мышцами), с которыми он связан.В частности, кости — это точки, расположенные в их центре масс, заимствованные из текстов по анатомии [19], а мышцы — это пружины (затухающие гармонические осцилляторы), соединяющие эти точки [40,41]; для гиперребра степени k мы создали k (k — 1) / 2 пружин, связывающих k узлов. То есть для мышцы, соединяющей k костей, мы разместили пружины так, чтобы каждая из k мышц имела прямое пружинное соединение с каждой из других k — 1 костей.
Затем мы взволновали каждую из 270 мышц тела и вычислили их оценку воздействия в сети (см. Материалы и методы и).Когда мышца физически смещается, она вызывает волнообразное смещение других мышц по всей сети. Оценка удара мышцы — это среднее смещение всех костей (и косвенно мышц) в результате его первоначального смещения. Мы наблюдали значительную положительную корреляцию между степенью мышц и оценкой воздействия (F (1,268) = 23,3, R 2 = 0,45, p <0,00001;), предполагая, что структура гиперребра определяет функциональную роль мышц в опорно-двигательной сети.Мышцы с большим количеством точек прикрепления и начала имеют большее влияние на опорно-двигательный аппарат, когда они нарушены, чем мышцы с небольшим количеством точек прикрепления и начала [42]. Мы можем получить более подробное представление о результатах этого анализа, подробно изучив взаимосвязь между оценкой воздействия и статистическими показателями топологии сети. На рис. S11 мы показываем, что функция сети, измеренная с помощью оценки воздействия, значительно коррелировала со средней длиной кратчайшего пути.Хотя сетевая статистика статична по своей природе, их функциональная интерпретация обеспечивается пертурбативным моделированием динамики системы.
Исследование опорно-двигательного аппарата.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 37,3, R 2 = 0,757, p <0.0001). Заштрихованные области указывают 95% доверительный интервал, а точки данных масштабируются в соответствии с количеством включенных мышц. График пронумерован следующим образом: трицепс (1), большой палец (2), широчайшая мышца спины (3), двуглавая мышца плеча (4), лодыжка (5), шея (6), челюсть (7), плечо (8). ), большая круглая (9), бедра (10), глазные мышцы (11), колено (12), локоть (13), запястье / кисть (14). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве руководства к интерпретации важно отметить, что оценка воздействия, хотя и значительно коррелирует со степенью мускулатуры, не может быть им полностью предсказана ().Вместо этого, структура локальной сети, окружающей мышцу, также играет важную роль в ее функциональном воздействии и способности восстанавливаться. Чтобы лучше количественно оценить влияние этой структуры локальной сети, мы спросили, существуют ли мышцы, которые имели значительно более высокие или значительно более низкие оценки воздействия, чем ожидалось в нулевой сети. Мы определили положительное (отрицательное) отклонение оценки воздействия, которое измеряет степень, в которой мышцы более (менее) воздействуют, чем ожидалось в сетевой нулевой модели (см. Материалы и методы).В результате этого расчета был получен показатель, который выражает влияние конкретной мышцы по сравнению с мышцами с идентичной степенью гиперребер в нулевой модели. Другими словами, этот показатель учитывает сложность конкретной мышцы ().
Является ли эта математическая модель клинически актуальной? Отвечает ли тело по-разному на травмы мышц с более высокой оценкой удара, чем на мышцы с более низкой оценкой удара? Чтобы ответить на этот вопрос, мы оценили потенциальную взаимосвязь между воздействием на мышцы и временем восстановления после травмы.В частности, мы собрали данные о спортивных травмах и времени между получением травмы и возвращением в спорт. Мы отметили, что время восстановления сильно коррелировало с отклонениями оценки удара отдельной мышцы или группы мышц (F (1,12) = 37,3, R 2 = 0,757, p <0,0001;), предполагая, что наши Математическая модель предлагает полезный клинический биомаркер реакции сети на повреждение. Мы отмечаем, что важно учитывать тот факт, что восстановление может быть медленнее у человека, которому требуются максимальные усилия в спортивном спорте, по сравнению с человеком, который стремится только функционировать в повседневной жизни.Поэтому, чтобы обобщить наши результаты для всего населения, мы также изучили данные о времени восстановления, полученные от не спортсменов, и представляем эти дополнительные результаты во вспомогательной информации (текст S6).
Наконец, чтобы получить интуитивное представление о том, как очаговая травма может вызывать отдаленные эффекты, потенциально замедляющие выздоровление, мы рассчитали влияние мышц голеностопного сустава и определили, какие другие мышцы были затронуты сильнее всего. То есть для каждой отдельной мышцы голеностопного сустава мы рассчитали воздействие на каждую из оставшихся 264 мышц, не относящихся к голеностопному суставу, а затем усреднили это значение по всем мышцам голеностопного сустава.Из 264 мышц, не связанных с голеностопным суставом, единственная мышца, на которую больше всего воздействует нарушение мышц голеностопного сустава, — это двуглавая мышца бедра, а второй по величине — латеральная широкая мышца колена. Кроме того, мышца бедра, на которую больше всего влияет нарушение, — это камбаловидная мышца.
Контроль опорно-двигательного аппарата человека
Какова взаимосвязь между функциональным воздействием мышцы на тело и нейронной архитектурой, которая влияет на контроль? Здесь мы исследуем отношения между опорно-двигательной системой и первичной моторной корой.Мы исследовали область карты коркового изображения головного мозга, посвященную мышцам с низким или высоким воздействием, опираясь на анатомию моторной полосы, представленной в моторном гомункуле [43] (), грубое одномерное представление тела в головном мозге [44 ]. Мы заметили, что области гомункула по-разному контролируют мышцы с положительной и отрицательной оценкой отклонения воздействия (). Более того, мы обнаружили, что области гомункула, контролирующие только положительно (отрицательно) отклоняющиеся мышцы, как правило, располагаются медиально (латерально) на моторной полосе, что предполагает наличие топологической организации ожидаемого воздействия мышцы на нервную ткань.Чтобы исследовать эту закономерность более глубоко, для каждой области гомункула мы рассчитали коэффициент отклонения как процент мышц, которые положительно отклонились от ожидаемой оценки воздействия (т. Е. Значение 1 для бровей, глаз, лица и значение 0 для колена , бедро, плечо; см.). Мы обнаружили, что коэффициент отклонения достоверно коррелировал с топологическим положением на моторной полосе (F (1,19) = 21,3, R 2 = 0,52, p <0,001;).
Зондирование опорно-двигательного аппарата.(а) Гомункул первичной моторной коры, сконструированный Пенфилдом.(b) Коэффициент отклонения достоверно коррелирует с гомункулярной топологией (F (1,19) = 21,3, R 2 = 0,52, p <0,001), уменьшаясь от медиального (область 0) к латеральному (область 22). (c) Отклонение оценки воздействия достоверно коррелирует с объемом активации моторной полосы (F (1,5) = 14,4, R 2 = 0,743, p = 0,012). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. График пронумерован следующим образом: большой палец (1), указательный палец (2), средний палец (3), рука (4), все пальцы (5), запястье (6), локоть (7).(d) Корреляция между пространственным упорядочением категорий гомункулов Пенфилда и линейной мышечной координатой из многомерного масштабного анализа (F (1,268) = 316, R 2 = 0,54, p <0,0001). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве более строгой проверки этой взаимосвязи между воздействием мышцы на сеть и нейронной архитектурой мы сопоставили данные о физических объемах функциональной активации на основе МРТ на моторной полосе, которые предназначены для отдельных движений (например,g., сгибание пальцев или моргание глаз). Объемы активации определяются как воксели, которые активируются (определяемые сигналом, зависящим от уровня кислорода в крови) во время движения [38,39]. Важно отметить, что мы обнаружили, что объем функциональной активации независимо предсказывает отклонение оценки удара мышц (, F (1,5) = 14,4, p = 0,012, R 2 = 0,743), что согласуется с интуицией, что мозг будет посвятите больше места в сером веществе контролю над мышцами, которые более эффективны, чем ожидалось в нулевой модели.Опять же, отклонение от удара — это показатель, который учитывает степень гиперреберности конкретной мышцы и относится к удару мышц с идентичной степенью гиперребер в нулевой модели. Таким образом, ударное отклонение измеряет топологию локальной сети, а не просто непосредственные соединения рассматриваемой мышцы.
В качестве финального теста этой взаимосвязи мы спросили, оптимально ли сопоставлена стратегия нервного контроля, воплощенная в моторной полоске, с группами мышц. Мы построили мышечно-ориентированный граф, соединив две мышцы, если они касаются одной и той же кости (, слева).Мы наблюдали наличие групп мышц, плотно связанных друг с другом, имеющих общие кости. Мы извлекли эти группы, используя метод кластеризации, разработанный для сетей [45,46], который обеспечивает разделение мышц на сообщества на основе данных (справа). Чтобы сравнить структуру сообщества, присутствующую в мышечной сети, с архитектурой системы нейронного контроля, мы рассмотрели каждую из 22 категорий моторного гомункула [18] как отдельное нейронное сообщество и сравнили эти присвоения сообществу, основанные на мозге, с заданиями сообщества. полученный из управляемого данными раздела мышечной сети.Используя коэффициент Рэнда [47], мы обнаружили, что распределение сообществ как для гомункула, так и для мышечной сети было статистически схожим (z Rand > 10), что указывает на соответствие между модульной организацией опорно-двигательного аппарата и структурой гомункула. Например, трицепс плеча и двуглавая мышца плеча принадлежат к одной гомункулярной категории, и мы обнаружили, что они также принадлежат к одному и тому же сообществу топологических мышечных сетей.
Затем, поскольку гомункулус имеет линейную топологическую организацию, мы спросили, был ли порядок сообществ внутри гомункула () подобен управляемому данными упорядочению групп мышц в теле, как определено с помощью MDS [48].Из сети, ориентированной на мышцы (), мы получили матрицу расстояний, которая кодирует наименьшее количество костей, которые необходимо пройти, чтобы перейти от одной мышцы к другой. MDS этой матрицы расстояний выявил одномерные линейные координаты для каждой мышцы, так что топологически близкие мышцы были близко друг к другу, а топологически далекие мышцы были далеко друг от друга. Мы заметили, что линейная координата каждой мышцы значительно коррелирует с ее категорией гомункула (, F (1,268) = 316, p <0.0001, R 2 = 0,54), что указывает на эффективное отображение между нейронным представлением мышечной системы и сетевой топологией мышечной системы в теле.
Наши результаты демонстрируют соответствие между топологией гомункула и упорядочением мышц на основе данных, полученным с учетом топологических расстояний между ними. Этот результат можно интерпретировать одним из двух способов: одна разумная гипотеза состоит в том, что, поскольку большинство соединений в опорно-двигательной сети являются короткодействующими, открытие в основном обусловлено связями ближнего действия.Вторая разумная гипотеза состоит в том, что, хотя соединения ближнего действия являются наиболее распространенными, соединения дальнего действия образуют важные внутримодульные связи, которые помогают определять организацию сети. Чтобы выбрать между этими двумя гипотезами, мы рассмотрели два варианта нашего эксперимента MDS: один включает только соединения, длина которых меньше средней длины соединения, а другой — только соединения, длина которых превышает среднюю длину соединения. Мы обнаружили, что упорядочение на основе данных, полученное только из коротких и только из длинных соединений, привело к значительным корреляциям с гомункулярной топологией (F (1,268) = 24.9, R 2 = 0,085, p <0,0001 и F (1,268) = 5, R 2 = 0,018, p = 0,026 соответственно). Примечательно, что включение как длинных, так и коротких соединений приводит к более сильной корреляции с гомункулярной топологией, чем рассмотрение любого из них независимо, что предполагает зависимость от соединений любой длины. В будущем было бы интересно проверить, в какой степени эта межсетевая карта изменяется у людей с двигательными нарушениями или изменениями после инсульта.
Обсуждение
Структура опорно-двигательного аппарата человека
Представляя сложную взаимосвязь опорно-двигательного аппарата в виде сети костей (представленных узлами) и мышц (представленных гиперребрами), мы получили ценную информацию об организации человеческого организма. тело. Изучение анатомических сетей с использованием аналогичных методов становится все более распространенным в области эволюционной биологии и биологии развития [10]. Однако этот подход обычно применялся только к отдельным частям тела, включая руку [49], голову [11] и позвоночник [12], тем самым предлагая понимание того, как развивалась эта часть организма [50, 51].Более того, даже после моделирования всей мускулатуры тела [13] и нервно-мышечно-скелетной системы [14] в более общем плане некоторые количественные утверждения могут остаться неуловимыми, в значительной степени из-за отсутствия математического языка, на котором можно было бы обсуждать сложность взаимосвязи. узоры. В этом исследовании мы предлагаем явное и экономное представление всей опорно-двигательной системы в виде графа узлов и ребер, и это представление позволило нам точно охарактеризовать сеть в целом.
При моделировании системы как сети важно начать последующее исследование с характеристики нескольких ключевых архитектурных свойств. Одним из наиболее фундаментальных показателей структуры сети является ее распределение по степеням [52], которое описывает неоднородность подключения узла к его соседям таким образом, который может дать представление о том, как формировалась система [7]. Мы заметили, что степень распределения опорно-двигательного аппарата значительно отличается от ожидаемого в нулевом графе (), показывая меньше узлов высокой степени и переизбыток узлов низкой степени.Несоответствие между графами реальной и нулевой модели согласуется с тем фактом, что опорно-двигательная система человека развивается в контексте физических и функциональных ограничений, которые вместе определяют ее явно неслучайную архитектуру [53]. Распределение степеней этой сети показывает пик примерно на второй степени, за которым следует относительно тяжелый хвост узлов высокой степени. Последняя особенность обычно наблюдается во многих типах реальных сетей [54], чьи концентраторы могут быть дорогостоящими в разработке, обслуживании и использовании [55,56], но играют критическую роль в надежности системы, обеспечивая быстрое реагирование [55], буферизация изменчивости окружающей среды [57] и облегчение выживания и воспроизводства [58].Первая особенность — пик распределения — согласуется с интуицией, что большинство мышц опорно-двигательного аппарата соединяются только с двумя костями, в первую очередь для функции простого сгибания или разгибания в суставе. Напротив, есть только несколько мышц, которые требуют высокой степени для поддержки очень сложных движений, таких как поддержание выравнивания и угла позвоночника за счет одновременного управления движением многих костей. Эти ожидаемые результаты обеспечивают важную проверку модели, а также предлагают полезную визуализацию опорно-двигательного аппарата.
Скелетно-мышечная сеть характеризуется особенно интересным свойством, которое отличает ее от нескольких других реальных сетей: тем фактом, что она встроена в трехмерное пространство [59]. Это свойство не наблюдается в семантических сетях [60] или World Wide Web [61], которые кодируют отношения между словами, концепциями или документами в некоторой абстрактной (и, скорее всего, неевклидовой) геометрии. Напротив, опорно-двигательная система представляет собой объем с узлами, имеющими определенные координаты, и краями, представляющими физически протяженные ткани.Чтобы лучше понять физическую природу опорно-двигательного аппарата, мы исследовали анатомическое расположение мышц с разной степенью (). Мы заметили, что мышечные центры расположены преимущественно в торсе, обеспечивая плотную структурную взаимосвязь, которая может стабилизировать ядро тела и предотвратить травмы [62]. В частности, мышцы высокой степени группируются вокруг средней линии тела, рядом с позвоночником, вокруг таза и плечевого пояса, что согласуется с представлением о том, что для маневренности и устойчивости этих областей требуется совокупность мышц с различной геометрией и свойствами тканей [63 ].Действительно, мышцы в этих местах должны поддерживать не только сгибание и разгибание, но также отведение, приведение и внутреннее и внешнее вращение.
Важно отметить, что в костно-мышечной системе у разных людей существуют значительные различия, и не все анатомические атласы согласуются с наиболее репрезентативным набором точек вставки и происхождения. Представленные здесь результаты отражают то, как опорно-двигательная система была представлена в тексте, из которого она была построена [19], и поэтому обеспечивают только одно возможное сетевое представление опорно-двигательной системы.Чтобы оценить надежность наших результатов при разумных вариациях конфигурации опорно-двигательного аппарата, мы создали вторую опорно-двигательную сеть из альтернативного атласа [64]. Используя этот второй атлас, мы наблюдали последовательные результаты и сообщаем об этом дополнительном анализе в S3 Text.
Также важно отметить, что мы сопоставили первый атлас [19] в скелетно-мышечный граф, состоящий как из костных, так и из некостных узлов. Этот выбор уравнивает структурные роли костей и определенных сухожилий и связок, что, по общему признанию, является упрощением биологии.Одним из оправданий такого упрощения является то, что некостные структуры часто служат важными точками прикрепления мышц (то есть подошвенной фасцией стопы). Таким образом, разумно разделить опорно-двигательную сеть на две категории мышц и структур, которые служат точками прикрепления мышц, как мы это сделали здесь. Тем не менее, эта вторая категория довольно неоднородна по составу, и в будущей работе можно было бы также рассмотреть возможность построения многослойного графа с отдельным слоем, учитывающим каждый тип структуры мышечного прикрепления.Чтобы подтвердить, что наши результаты и интерпретации существенно не меняются из-за наличия некостных мышечных точек прикрепления, мы удалили такие точки в альтернативном атласе и отметили, что наши основные результаты все еще остаются в силе (см. Текст S3).
Функция опорно-двигательного аппарата человека
Чтобы лучше понять функциональную роль отдельной мышцы во взаимосвязанной опорно-двигательной системе, мы реализовали основанную на физике модель свойств импульсного отклика сети, кодируя кости как точечные массы, а мышцы как пружины [65].Примечательно, что эта очень упрощенная модель опорно-двигательного аппарата способна идентифицировать важные функциональные особенности. Хотя мышцы высокой степени также имели тенденцию иметь большое влияние на реакцию сети (), было несколько заметных отклонений от этой тенденции ().
Мышца, оказывающая наименьшее воздействие по сравнению с ожидаемой, — это orbicularis oculi, мышца, используемая для управления движением века. Эта мышца небольшая и относительно изолированная в теле, берут начало и прикрепляются к костям черепа.Мышцы лица в целом образуют плотное и изолированное сообщество, с немногими связями, выходящими за пределы этого сообщества. Эти факторы, вероятно, способствуют слабому воздействию этой мышцы, и аналогичный аргумент может быть сделан в отношении оставшихся двух мышц с меньшим воздействием, чем ожидалось, которые также являются мышцами лица.
Мышцы с большей нагрузкой, чем ожидалось, более многочисленны, но почти полностью расположены в верхней конечности или поясе верхней конечности. Длинный разгибатель запястья, anconeus, brachioradialis и brachialis мышцы являются собственными мышцами руки, последние три действуют в локтевом суставе.Все эти мышцы могут иметь более сильное воздействие, чем ожидалось в нулевой модели, потому что они могут прямо или косвенно влиять на движение многих костей запястья и кисти. Наблюдаемое сильное воздействие этих мышц может быть результатом того факта, что они контролируют движение конечности, а на конце конечности находится множество костей, движение которых напрямую зависит от этих мышц. Остальные ударные мышцы, за исключением грушевидной мышцы, прикрепляют верхнюю конечность к осевому скелету.Этими мышцами являются коракобрахиальная, подостная, надостная, подлопаточная, малая круглая, большая круглая и большая грудная мышцы. Эти мышцы, как и предыдущие четыре, обладают тем свойством, что они контролируют движение всей конечности, что, вероятно, способствует их влиянию. В отличие от предыдущей группы, эти мышцы также соединяются с осевым скелетом, что также может усиливать их воздействие. Многие из этих мышц берут свое начало на костях плечевого пояса и могут влиять на все другие мышцы плечевого пояса и, возможно, на все кости, связанные с этими мышцами.Такая же динамика, вероятно, существует в нижней конечности, что отражается наличием грушевидной мышцы тазового пояса. Подробное обсуждение того, как структура локальной сети и конфигурация мышц могут взаимодействовать с отклонением от удара, представлено в S7 Text. В дополнение к нашей работе, представленной во вспомогательной информации, дальнейшее понимание свойств этих выбросов может быть получено путем проведения экспериментов по тщательному изучению костей, на которые сильнее всего воздействует каждая из этих мышц.
Хотя сетевое представление системы может дать базовую физическую интуицию благодаря своей скупости и простоте, оно также остается безразличным ко многим деталям архитектуры и функций системы. Извечный вопрос, могут ли эти базовые модели сложных систем обеспечить точные прогнозы реальных результатов. Мы рассмотрели этот вопрос, изучив взаимосвязь между оценкой удара мышцы и количеством времени, которое требуется человеку для восстановления после травмы.Мы количественно оценили время восстановления, суммируя (i) время восстановления после первичной инвалидности, вызванной первоначальным мышечным повреждением, и (ii) время восстановления после любых вторичных нарушений, вызванных изменением использования других мышц в сети из-за первоначального травма мышц [66]. Мы обнаружили, что отклонение от ожидаемой оценки воздействия в нулевой сети значительно коррелировало со временем восстановления (), подтверждая представление о том, что очаговая травма может иметь длительные воздействия на организм из-за изначально взаимосвязанной природы опорно-двигательной системы.
Действительно, известно, что мышечные изменения в одной части тела влияют на другие группы мышц. Например, укрепление мышц бедра может привести к улучшению функции колена после замены коленного сустава [67]. Изменение мышечной функции в голеностопном суставе после растяжения связок может вызвать изменение функции мышц бедра [68, 69], результат, воспроизведенный нашей моделью (которая показала, что двуглавая мышца бедра и латеральная широкая мышца бедра больше всего пострадали от травмы голеностопного сустава), а повреждение мышц конечностей может приводят к вторичному повреждению диафрагмы [70].Наша модель предлагает математически принципиальный способ предсказать, какие мышцы с большей вероятностью будут иметь такое вторичное влияние на более крупную опорно-двигательную систему, а какие мышцы подвержены риску вторичного повреждения, учитывая первичное повреждение в определенном участке мышцы. В будущем было бы интересно проверить, могут ли эти прогнозы повлиять на полезные корректировки клинических вмешательств, явно принимая во внимание риск вторичного повреждения определенных мышц. Ранее профилактика вторичных мышечных травм в основном сводилась к криотерапии [71,72] и еще не была мотивирована такой механистической моделью.Наконец, важный вопрос, который следует задать, заключается в том, насколько эта конфигурация опорно-двигательного аппарата является эволюционно выгодной и как эволюционное давление могло оптимизировать воздействие на мышцы. Интуитивно можно было ожидать, что эволюционное давление снижает мышечную нагрузку, возможно, за счет увеличения мышечной избыточности. Тщательное исследование эволюционных преимуществ топологии костно-мышечной сети было бы интересной темой для будущей работы.
Контроль опорно-двигательного аппарата человека
Учитывая сложность опорно-двигательного аппарата и его критическую роль в выживании человека, естественно задать вопрос о том, как эта сеть управляется человеческим мозгом.Действительно, изучение моторного контроля имеет долгую и яркую историю [73], которая дала важную информацию о том, как мозг может успешно и точно совершать произвольные движения, несмотря на такие проблемы, как избыточность, шум [74], задержки сенсорной обратной связи. [75], неопределенность окружающей среды [76], нервно-мышечная нелинейность [77] и нестационарность [78]. Здесь мы использовали отличный, но дополняющий друг друга подход и спросили, как топология опорно-двигательного аппарата может быть отображена на топологии моторной полосы в коре головного мозга.Мы начали с того, что отметили, что ударное отклонение мышцы положительно коррелирует с размером коркового объема, предназначенного для его контроля (). Одна из интерпретаций этой взаимосвязи состоит в том, что те мышцы, которые своими непосредственными связями оказывают большее влияние, чем ожидалось в нулевой модели, имеют тенденцию контролировать более сложные движения и, следовательно, требуют большего количества нейронов для управления этими движениями [79]. Вторая интерпретация основана на эволюционном аргументе о том, что мышцы с большей нагрузкой нуждаются в большей избыточности в их системах управления [80], и эта избыточность принимает форму большей корковой области.
Помимо локальных объемов коры [81], можно также захотеть понять, в какой степени крупномасштабная организация опорно-двигательной сети отражает организацию контролирующей ее моторной полосы. Основываясь на недавнем применении методов выявления сообществ к изучению анатомии черепа [11,82,83], мы сообщили о модульной организации мышечной сети: группы мышц, в которых мышцы одной группы с большей вероятностью соединяются с одной. кроме мышц в других группах.Что еще интереснее, мы наблюдали, что мышечные сообщества очень похожи на известную группу мышц моторной полоски (справа): мышцы, которые имеют тенденцию соединяться с теми же костями, что и друг друга, также имеют тенденцию контролироваться той же частью моторной полоски. Более того, естественное линейное упорядочение мышечных сообществ — такое, что сообщества располагаются близко друг к другу на линии, если они имеют общие сетевые соединения — имитирует порядок контроля в моторной полосе (). Эти результаты дополняют важную предыдущую работу, предполагающую, что одномерная организация моторной полосы связана как со структурной, так и со функциональной организацией скелетно-мышечной сети [84,85].Фактически, результаты более конкретно предлагают определение оптимального сетевого управления на уровне сети: согласованность линейной карты от сообществ опорно-двигательного аппарата до сообществ моторных полос.
Наконец, мы исследовали физическое расположение кортикального контроля ударных мышц. Мы заметили, что мышцы с большим воздействием, чем ожидалось, при нулевом графике, как правило, контролируются средними точками на моторной полосе, в то время как мышцы с меньшим воздействием, чем ожидалось, обычно контролируются боковыми точками на моторной полосе ().Эта пространственная специфика указывает на то, что организация моторной полосы ограничивается физическим расположением тела, а также аспектами функционирования мышц. Предыдущие исследования изучали общее временное соответствие между корковой активностью и мышечной активностью во время движения [86], но мало что известно о топологическом соответствии.
Методологические соображения
Построение гиперграфа на основе опорно-двигательного аппарата человека требует допущений и упрощений, которые влияют на гибкость текущей модели.Наиболее заметным является разделение системы на две категории: мышцы и кости. Эти категории не содержат дополнительной информации и, следовательно, не учитывают особенности внутренней архитектуры мышцы или кости. Это упрощение вводит несколько ограничений для пертурбативной модели, включая возможность моделирования функциональной архитектуры сложных мышц или мышц, обладающих способностью независимо сокращать подмножество волокон. Например, двуглавая двуглавая мышца плеча берет начало как на лопатке, так и на супрагленоидном бугорке, и можно сокращать волокна одной головки отдельно от волокон другой головки.Дальнейшая работа может расширить нашу структуру моделирования, чтобы представить эту сложную функциональную архитектуру. Более того, немышечные структуры мягких тканей, важные для опорно-двигательного аппарата, не могут быть четко учтены. Эти структуры, включая сухожилия и связки, могут быть либо (1) закодированы как кости, как в основной текстовой сети, либо (2) исключены из сети, как в приложении; ни один из вариантов не является полностью анатомически точным.
В случае костей модель не может учесть взаимодействия кость-кость (суставы).Большинство мышц действуют на суставы, и исключение суставов затемняет специфическую функцию мышц. То есть модель учитывает тот факт, что мышцы перемещают кости, но не то, как они движутся или в каком направлении. В пертурбативном моделировании отсутствие ограничений на суставы позволяет размещать кости под неестественными углами относительно соседних костей. Кроме того, кости моделируются как точечные массы, которые в пертурбативном моделировании могут позволить костям проходить траектории, связанные с прохождением через пространство, которое на самом деле занято другой костью.Дальнейшая работа может расширить нашу структуру моделирования, чтобы учесть эти дополнительные биофизические ограничения.
Аналитические данные, полученные с помощью этой модели, являются результатом входных данных. Поскольку индивидуальные вариации существуют в опорно-двигательном аппарате, они также существуют и в мышечных воздействиях. Мы попытались использовать два набора входных данных, чтобы оправдать наши основные выводы, но эти результаты не могут быть обобщены на все здоровые конфигурации опорно-двигательного аппарата. В частности, степень мышц, подверженная индивидуальным изменениям, может повлиять на воздействие этой мышцы.Каким образом нормативные индивидуальные вариации в степени мышечной массы связаны с вариациями прогнозируемого воздействия на мышцы, является важным вопросом, который, тем не менее, выходит за рамки настоящего исследования.
Наконец, опорно-двигательный аппарат человека представляет собой сложную и плотно взаимосвязанную сеть. Ни мышцы, ни кости не функционируют как независимые образования. Таким образом, трудно отделить функцию отдельной мышцы от воздействия окружающих мышц. Независимость мышц может быть частично устранена соответствующим выбором нулевой модели, и наши результаты остаются в силе при различных вариантах.Тем не менее, при интерпретации этих результатов следует учитывать представление о том, что мышцы — и факторы воздействия — не являются действительно независимыми.
Вспомогательная информация
S1 Text
Альтернативные нулевые модели.Этот текстовый файл подробно описывает построение альтернативных нулевых моделей.
(DOCX)
S2 Text
Разрешение обнаружения сообщества.Этот файл содержит описание выбора параметра разрешения обнаружения сообщества.
(DOCX)
S3 Text
Альтернативная опорно-двигательная сеть.Этот файл содержит описание альтернативной опорно-двигательной сети.
(DOCX)
S4 Текст
Динамика костей в результате мышечного пертурбации.(DOCX)
S5 Text
Учет веса костей и силы мышц.(DOCX)
S6 Text
Анализ восстановления мышц, не связанных со спортсменами.(DOCX)
S7 Text
Структура локальной сети и отклонение от воздействия.(DOCX)
S1 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в случайно перестроенных гиперграфах.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений выше среднего в порядке от наибольшего до наименьшего. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S2 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению со случайно перестроенными гиперграфами.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени.Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью. Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S3 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в гиперграфах, случайным образом перепрограммированы в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень.Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гипреберья: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение, в порядке от наибольшего к наименьшему. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S4 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению с гиперграфами, случайно перестроенными в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень. Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S5 Таблица
Мышцы с большей или меньшей нагрузкой, чем ожидалось в случайном гиперграфе.Эта нулевая модель требовала случайного назначения связей между костями и мышцами, сохраняя только общий уровень, а не индивидуальный уровень мышц. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение и упорядочено от наибольшего к наименьшему.
(XLSX)
S6 Таблица
Объемы мышц подсети голени.Здесь мы включаем название мышцы (столбец 1), объем мышцы (в см 3 ; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S7 Таблица
Масса костей подсети ноги.Здесь мы включаем название кости (столбец 1), массу кости (в граммах; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S8 Таблица
Присвоенные категории гомункулов и основанное на данных распределение мышц в сообществе.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S9 Таблица
Гиперграф мышц и костей из таблиц Hosford Muscle [18], используемых в основном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S10 Таблица
Гиперграф мышц и костей из атласа Гранта [64], использованный в дополнительном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S1 Рис.
Обнаружение сообщества с разными параметрами разрешения.На этом рисунке показано, как выбор параметра разрешения во время обнаружения сообществ изменит количество и размер обнаруженных сообществ.С увеличением параметра разрешения размер отдельных сообществ уменьшается, а количество сообществ увеличивается. (a-d) Обнаружение сообщества для сети, ориентированной на мышцы, с использованием значений γ, равных 1, 2, 8 и 16 соответственно. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S2 Рис.
Обнаружение сообщества с разными параметрами разрешения.Этот рисунок иллюстрирует стабильность при выбранном параметре настройки γ = 4.3. Здесь мы исследуем разбиения, созданные из близких параметров разрешения γ = 4,2 и γ = 4,4. Визуально кажется, что все три раздела имеют похожую структуру. Два соседних раздела также математически схожи: z-оценка коэффициента Рэнда [47] z Rand (γ = 4,2, γ = 4,3) = 105, z Rand (γ = 4,3, γ = 4,4) = 110 и z Rand (γ = 4,2, γ = 4,4) = 105. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S3 Рис.
Визуальное сравнение нулевых моделей.Этот рисунок иллюстрирует различия в нулевых двудольных графах. (A) Исходный непереставленный двудольный граф мышца-кость. (B) Случайный нулевой двудольный граф. (C) Случайно перестроенный двудольный граф. (D) Двудольный граф, случайно измененный внутри сообщества, используемый в основном тексте, который переставляет топологию локально, сохраняя при этом глобальную топологию.
(EPS)
S4 Рис.
Основные результаты как функция нулевой модели.Здесь мы показываем результаты с использованием модели случайного гиперграфа или модели гиперграфа с измененной связью (перестановкой), которая не поддерживает локальные связи. (A) Оценка удара, построенная как функция степени гиперребра для случайных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (B) Оценка удара, нанесенная на график как функция степени гиперребра для переставленных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (C) Коэффициент отклонения достоверно коррелирует с категорией гомункула (F (1,19) = 6.67, p = 0,018, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием случайной нулевой модели гиперграфа. (D) Коэффициент отклонения достоверно коррелирует с гомункулярной категорией (F (1,19) = 6,86, p = 0,017, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием пермутированного нулевая модель гиперграфа. (E) Отклонение оценки воздействия значимо коррелирует с площадью активации моторной полосы (F (1,5) = 13,4, p = 0,014, R 2 = 0.72) с использованием случайной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (F) Отклонение оценки воздействия значительно коррелирует с площадью активации моторной полосы (F (1,5) = 13,7, p = 0,022, R 2 = 0,73) с использованием пермутированной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (G) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 64.5, p = 6,3 × 10 −6 , R 2 = 0,85), используя случайную нулевую модель гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. (H) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 70,5, p <0,0001, R 2 = 0,86), больше, чем ожидалось при перестановке — основанная на нулевой модели гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S5 Рис.
Топология сети и гомункул.Линейные координаты мышц, определенные с использованием многомерного масштабирования без пороговой обработки с помощью взвешенной матрицы расстояний (рассчитанной с использованием distance_wei.m, включенного в Brain Connectivity Toolbox, https://sites.google.com/site/bctnet/). Без пороговой обработки также существует значимая корреляция между линейной координатой мышцы и площадью гомункула (F (1,268) = 303, p <0.0001, R 2 = 0,53). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S6 Рис.
Исследование функции опорно-двигательного аппарата для альтернативной сети.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 40,2, p <0,0001, R 2 = 0.77). Заштрихованные области указывают 95% доверительных интервалов, а точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S7 Рис.
Проверка опорно-двигательного аппарата для альтернативной сети.(a) Коэффициент отклонения значимо коррелирует с гомункулярной топологией (F (1,18) = 8,88, R 2 = 0,33, p = 0,0080), уменьшаясь от медиального (область 0) к латеральному (область 22) регионы. (b) Отклонение оценки воздействия достоверно коррелирует с площадью активации моторной полосы (F (1,5) = 23.4, R 2 = 0,82, p = 0,005). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S8 Рис.
Динамика возмущения двуглавой мышцы плеча.На этом рисунке показано движение ключицы, а также костей пальца и стопы в ответ на возмущение двуглавой мышцы плеча. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S9 Рис.
Сравнение моделей с утяжелением костей и силой мышц и без них.Воздействие мышц ног рассчитывалось с добавлением и без добавления анатомических значений массы кости и объема мышц. Было обнаружено, что эти воздействия существенно коррелировали друг с другом (F (1,25) = 6,83, R 2 = 0,0214, p = 0,015), что позволяет предположить, что по крайней мере в некоторых частях тела наше упрощенное сетевое представление обеспечивает разумное приближение для более биофизически точных сетевых представлений. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S10 Рис.
Исследование функции опорно-двигательного аппарата для не спортсменов.Набрано время восстановления после травм различных мышц не спортсменов. Мы наблюдали значительную корреляцию между временем восстановления мышц и отклонением от удара (F (1,14) = 5,02, R 2 = 0,264, p = 0,041). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S11 Рис.
Соответствие топологии сети и функции системы.Топология сети, в частности средняя длина кратчайшего пути, значительно отрицательно коррелирует с оценкой воздействия, оцененной на основе пертурбативного моделирования динамики системы (F (1,268) = 65,1, R 2 = -0,4422, p <0,0001). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S12 Рис.
Связь между мышечно-скелетными вариациями и мышечным воздействием через две скелетно-мышечные сети.Здесь мы сравниваем процентное изменение оценки и степени воздействия для каждой мышцы между опорно-двигательным аппаратом, указанным в основном тексте, и сообщенным в дополнительном тексте.Мы наблюдаем, что на оценку удара мышц больше влияют большие изменения степени, чем меньшие изменения степени (F (1,268) = 5,76, R = 0,1450, p = 0,017). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S13 Рис.
Альтернативный пертурбативный подход.Чтобы установить меру воздействия на гиперреберь мышцы, объекты были перемещены в четвертое пространственное измерение, чтобы избежать произвольного выбора в трех измерениях. Альтернативным подходом было бы возмущение каждой мышцы в каждом из трех ортогональных направлений, каждый раз вычисляя воздействие и вычисляя векторную сумму этих трех результатов.Чтобы ответить на вопрос о том, как эти два подхода сравниваются, мы провели этот эксперимент на двудольной матрице мышцы-кости, чтобы создать два вектора 270 × 1, один из которых кодировал оценки воздействия посредством смещения в четвертом измерении, а другой — векторную сумму три ортогональных смещения. Два вектора достоверно коррелировали друг с другом (F (1,268) = 1590, R 2 = 0,856, p <0,0001).
(PNG)
Структура, функции и контроль опорно-двигательного аппарата человека
Реферат
Человеческое тело представляет собой сложный организм, основные механические свойства которого обусловлены взаимосвязанной опорно-двигательной сетью, управляемой нервной системой.Природа костно-мышечной взаимосвязи способствует стабильности, произвольным движениям и устойчивости к травмам. Однако фундаментальное понимание этой сети и ее контроля со стороны нейронных систем остается неуловимым. Здесь мы устраняем этот пробел в знаниях, используя медицинские базы данных и математическое моделирование, чтобы выявить организационную структуру, прогнозируемые функции и нейронный контроль опорно-двигательной системы. Мы построили очень упрощенную опорно-двигательную сеть всего тела, в которой отдельные мышцы соединяются с несколькими костями как через точки начала, так и через точки прикрепления.Мы продемонстрировали, что, используя эту упрощенную модель, роль мышцы в этой сети может предложить теоретическое предсказание восприимчивости окружающих компонентов к вторичным повреждениям. Наконец, мы проиллюстрировали, что наборы мышц группируются в сетевые сообщества, которые имитируют организацию модулей управления в первичной моторной коре. Этот новый формализм для описания взаимодействий между мышечной и скелетной системами служит основой для разработки и тестирования терапевтических реакций на травмы, вдохновляя будущие успехи в клиническом лечении.
Об авторе
Хотя сетевая наука часто используется для характеристики сетей на основе геномики, протеомики и коннектомики, ее полезность для понимания биомеханики, ортопедии и физиотерапии остается в значительной степени неизученной. Действительно, текущая клиническая практика и знания, касающиеся опорно-двигательного аппарата, в основном сосредоточены на отдельных областях тела, отдельных мышцах или отдельных травмах и поэтому остаются безразличными к мезомасштабным или глобальным особенностям архитектуры тела, которые могут иметь решающее значение для травм и восстановления.Мы устранили этот пробел, представив опорно-двигательный аппарат в виде графа или сети, в которой мы рассмотрели кости и мышечные связи между ними. Моделируя мышцы как пружины и кости как точечные массы, мы разработали пертурбативный подход, чтобы исследовать функцию этой сети. Используя эту модель, мы рассчитали сетевые эффекты возмущения отдельных мышц. Используя этот формализм, мы можем провести новые параллели между этой системой и первичной моторной корой, которая ее контролирует, и проиллюстрировать клинические связи между сетевой структурой и мышечным повреждением.
Введение
Взаимосвязанная природа человеческого тела долгое время была предметом научных исследований и суеверных верований. От древних юморов, связывающих сердце, печень, селезенку и мозг смелостью, спокойствием и надеждой [1], до современного понимания связи кишечника и мозга [2], люди склонны искать взаимосвязи между разрозненными частями тела, чтобы объяснять сложные явления. Тем не менее, напряжение остается между этой базовой концептуализацией человеческого тела и редукционизмом, неявным в современной науке [3].Понимание всей системы часто относят к футуристическому миру, в то время как отдельные эксперименты уточняют наше понимание мельчайших составных частей.
Опорно-двигательный аппарат человека не является исключением из этой дихотомии. В то время как медицинская практика сосредоточена на кистях, стопах или лодыжках, клиницисты знают, что травмы одной части опорно-двигательного аппарата обязательно влияют на работу других (даже отдаленно удаленных) частей [4]. Травма лодыжки может изменить характер походки, что приведет к хронической боли в спине; травма плеча может изменить осанку и вызвать дискомфорт в шее.Понимание фундаментальных отношений между фокальной структурой и потенциальными удаленными взаимодействиями требует целостного подхода.
Здесь мы подробно описываем такой подход. Наша концептуальная основа мотивирована недавними теоретическими достижениями в сетевой науке [5], которая представляет собой развивающуюся дисциплину, построенную на упорядоченном слиянии математики (в частности, теории графов [6]) и физики (в частности, статистической механики [7]), компьютеров. наука, статистика [8] и системная инженерия.Подход упрощает сложные системы, разграничивая их компоненты и отображая паттерн взаимодействия между этими компонентами [9]. Это представление кажется особенно подходящим для изучения опорно-двигательного аппарата человека, который состоит из костей и соединяющих их мышц. В этом исследовании мы использовали этот подход для оценки структуры, функции и контроля опорно-двигательного аппарата.
Использование сетевых наук для понимания опорно-двигательного аппарата в последние годы увеличилось [10].Однако этот каркас в основном использовался для исследования свойств локальных мышечных или костных сетей. Например, была исследована местная структура черепа, чтобы выяснить, как можно классифицировать кости [11]. Кроме того, были проведены исследования топологии костно-мышечной сети позвоночника для оценки напряжений и деформаций в костях [12]. Существует несколько исследований, посвященных всей опорно-двигательной системе, хотя они не используют математические инструменты, которые мы использовали здесь [13,14].Настоящее исследование отличается от предыдущих работ оценкой всей опорно-двигательной системы в сочетании с математическими инструментами науки о сетях.
В этом более широком контексте мы сосредоточили внимание на проблеме реабилитации после травм скелетных мышц или коры головного мозга. Прямое повреждение мышцы или связанного с ней сухожилия или связки влияет на другие мышцы через компенсаторные механизмы тела [15]. Точно так же потеря использования определенной мышцы или группы мышц из-за прямого повреждения коры головного мозга может привести к компенсаторному использованию альтернативных мышц [16,17].То, как структурированы взаимосвязи опорно-двигательного аппарата и как они функционируют, напрямую ограничивает то, как повреждение определенной мышцы повлияет на опорно-двигательный аппарат в целом. Понимание этих взаимосвязей может дать столь необходимое понимание того, какие мышцы больше всего подвержены риску вторичной травмы из-за компенсаторных изменений, возникающих в результате очаговой травмы, тем самым давая основу для более комплексных подходов к реабилитации. Кроме того, понимание того, как кора головного мозга отображается не только на отдельные мышцы, но и на группы топологически близких мышц, может помочь в будущих эмпирических исследованиях взаимосвязи между очаговыми повреждениями (включая инсульт) моторной коры и риском вторичного повреждения.
Материалы и методы
Построение сети
Используя таблицы Хосфорда Muscle [18], мы построили скелетно-мышечный гиперграф, представив 173 кости (некоторые из которых на самом деле являются связками и сухожилиями) как узлы и 270 мышц как гиперребра, соединяющие эти узлы ( происхождение и точки прикрепления мышцы перечислены в таблице S9). Этот гиперграф также можно интерпретировать как двудольную сеть, в которой мышцы являются одной группой, а кости — второй группой (). Матрица заболеваемости C 173 × 270 скелетно-мышечной сети, таким образом, определяется как C ij = 1, если v i ∈ e j , и 0 в противном случае, где V = {v 1 , · · ·, v 173 } — это набор узлов (костей), а E = {e 1 , · · ·, e 270 } — набор гиперребер (мышц).Это гиперграфическое представление тела устраняет большую часть сложности опорно-двигательного аппарата, кодируя только то, какие мышцы прикрепляются к каким костям. Весь анализ применялся только к одной половине (левой или правой) тела, потому что каждое полушарие головного мозга контролирует только противоположную сторону тела. Поэтому мы еще больше упростили нашу модель, допустив лево-правую симметрию; на любых фигурах, на которых изображены обе половины тела, вторая половина присутствует исключительно для визуальной интуиции.
Схема представлений данных и вычислительных методов.(a) Скелетно-мышечная сеть была сначала преобразована в двудольную матрицу, где 1/0 указывает на наличие / отсутствие связи между мышцами и костями. (b) Сообщества топологически связанных мышц идентифицируются путем (1) преобразования гиперграфа в граф мышца-мышцы, в котором каждая запись кодирует количество общих костей каждой пары мышц, и (2) впоследствии мышцы были разбиты на сообщества , в котором составляющие члены более плотно связаны с другими членами своего сообщества, чем с членами других сообществ.(c) Чтобы облегчить пертурбацию, опорно-двигательная сеть была физически встроена, так что кости (узлы) изначально располагались в их правильных анатомических положениях. (d) Чтобы понять влияние отдельных мышц на взаимосвязанную систему, все узлы, связанные выбранным гиперребром, были возмущены в четвертом пространственном измерении.
Костно-ориентированный график A и мышечный график B () — это просто одномодовые проекции C. Проекция на кости A = C T C, а проекция на мышцы B = CC T .Затем диагональные элементы были установлены равными нулю, в результате чего мы получили взвешенную матрицу смежности [5]. Мы получили оценочные анатомические местоположения центра масс каждой мышцы (и кости), изучив анатомические тексты [19] и оценив x-, y- и z-координаты для отображения на графическом представлении человеческого тела ().
Расчет оценки воздействия
Для измерения потенциальной функциональной роли каждой мышцы в сети мы использовали классический пертурбативный подход. Чтобы максимизировать простоту и потенциал для фундаментальной интуиции, мы смоделировали опорно-двигательную систему как систему точечных масс (костей) и пружин (мышц).Мы растянули мышечную пружину и наблюдали влияние этого возмущения на расположение всех остальных мышц. Физически, чтобы повредить мышцу, мы смещали все кости, связанные с этой мышцей, на одинаковую величину и в одном направлении, растягивая мышцу, и удерживали эти кости на новом месте. Этот процесс также математически эквивалентен простому изменению жесткости пружины, относящейся к конкретной мышечной пружине. Затем системе позволяли достичь равновесия. Мы зафиксировали кости по средней линии и по периферии в пространстве, чтобы предотвратить смещение системы.Чтобы количественно оценить влияние возмущения этой единственной мышечной пружины, мы определили движение узла и следующим образом:
mid2r → idt2 = ∑j ≠ i∈V [SijAijl → ij (xij-‖l → ij‖)] — βdr → idt,
где l ij — смещение между узлами i и j, x ij — невозмущенное расстояние между узлами i и j, m — масса узла (которую мы установили равной единице для всех узлов в сети) , β = 1 — коэффициент демпфирования, r i — положение узла i , A — взвешенная матрица смежности графа, ориентированного на кости, и S ij представляет собой сумму всех сил пружин мышцы, к которым подключены узлы i и j.Чтобы нормализовать восстанавливающую силу мышц на узлах, пусть сила пружины мышцы q 1 / (k — 1). Здесь мы установили, что все кости имеют равный вес, а все мышцы имеют одинаковую жесткость пружины, что является упрощением реальной физической анатомии. Для обсуждения того, как учесть дополнительные физические свойства, такие как масса кости и мышечная сила, а также дополнительные результаты с использованием этих свойств, см. S5 Text. Более того, образцы траекторий, которые дают интуитивное представление о динамике нашей модели, были включены в вспомогательную информацию (S8 рис.).
Чтобы измерить потенциальную функциональную роль каждой мышцы в сети, мы растянули гиперреберь мышцы и измерили влияние возмущения на остальную часть сети. Вместо того, чтобы возмущать сеть в каком-то произвольном трехмерном направлении, мы расширили объем нашей симуляции до четвертого измерения. При возмущении мышцы мы смещали все узлы (кости), содержащиеся в этом гиперребре мышцы, на постоянный вектор в четвертом измерении и удерживали их этим смещением ().Затем возмущение в ответ прокатилось по сети пружин. Мы последовательно растягивали каждую мышечную гиперреберь и определили оценку воздействия этого возмущения как общее расстояние, на которое все узлы опорно-двигательной сети перемещаются от их исходных положений. Величина смещения — это суммарное смещение по всем временным точкам, от начала возмущения до соответствующего отсечки для времени уравновешивания. Здесь мы нашли равновесие системы, позволив динамике выровняться в течение достаточного периода времени.Обратите внимание, что равновесие также может быть решено с использованием стационарного, нединамического подхода; мы решили использовать динамику в этом случае для более широкой поддержки будущих приложений.
Отклонение оценки удара
Для каждой мышцы мы рассчитали индекс, который количественно определяет, насколько оценка воздействия этой мышцы отклоняется от ожидаемой с учетом степени ее гиперребер; мы называем этот показатель «ударным отклонением». Мы начинаем с построения нулевой модели, которая определяет ожидаемое воздействие при наборе статистических допущений.В текущем исследовании мы использовали несколько различных нулевых моделей с разными наборами допущений, которые мы подробно рассмотрим в следующих разделах. Отклонение воздействия рассчитывалось следующим образом: мы вычисляли среднее значение, стандартное отклонение и 95% доверительные интервалы (ДИ) для каждой из категорий степени нулевого гиперграфа из ансамбля из 100 нулевых гиперграфов. Расстояние от данной мышцы до среднего значения ± 95% доверительного интервала (в зависимости от того, что ближе всего) было вычислено и разделено на стандартное отклонение этого распределения степеней нулевого гиперграфа.Таким образом, мы рассчитали отклонение от ожидаемого значения в стандартных отклонениях (аналогично z-баллу). содержит мышцы, которые лежат за пределами 95% ДИ коэффициентов отклонения относительно степени их гиперребер. Мышцы можно естественным образом сгруппировать в соответствии с гомункулом, грубым одномерным представлением того, как контрольные области мышц группируются в моторную кору. Для данной группы гомункулов мы рассчитали коэффициент отклонения как количество мышц с положительным отклонением, деленное на общее количество мышц в группе ().
Таблица 1
Мышцы с большей или меньшей нагрузкой, чем ожидалось в модели нулевого гиперграфа.Мышцы на левой стороне оказывают меньшее влияние, чем ожидалось, учитывая степень их гиперребер: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее влияние, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартных отклонений превышает среднее значение, в порядке от наибольшего к наименьшему.В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 20 | Брахиалис | ||||||||||
| 2 | 145 | Букцинатор | 22 | Anconeus | ||||||||||||
| 3 | 148 | 12 | Teres minor | |||||||||||||
| 5 | 11 | Infraspinatus | ||||||||||||||
| 6 | 13 | Te res major | ||||||||||||||
| 8 | 10 | Supraspinatus | ||||||||||||||
| 8 | 16 | большой грудной мышцы longus | ||||||||||||||
| 11 | 161 | Piriformis | ||||||||||||||
| 10 | 31 | Brachioradialis 9002 | 31 | Brachioradialis
| ||||||||||||
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 3 | Колено | ||||||
| 2 | 17 | Глазные мышцы | 4 | Бедро | ||||||||
| 3 | 18 | Мышцы лица | 19 | Мышцы губ | 7 | Локоть | ||||||
| 5 | 8 | Запястье | ||||||||||
| 6 | 10 | Мизинец | ||||||||||
| 8 | 21 | Язык | ||||||||||
Обнаружение сообщества
Чтобы понять как функцию, так и контроль над опорно-двигательной системой, мы были заинтересованы в определении групп плотно связанных между собой мышц с использованием подхода, основанного на данных.Мы выполнили тип обнаружения сообщества, максимизируя функцию качества модульности, введенную Ньюманом [20]:
Q = ∑ijBij − γPijδ (gi, gj),
где P ij — ожидаемый вес ребра в нулевой модели Ньюмана-Гирвана, узел i назначен сообществу g i , узел j назначен сообществу g j , а δ — дельта-функция Кронекера. Путем максимизации Q мы получили разделение узлов (мускулов) на сообщества, так что узлы в одном сообществе были более плотно взаимосвязаны, чем ожидалось в сетевой нулевой модели (справа).
Здесь мы также использовали параметр разрешения для настройки размера и количества обнаруженных сообществ таким образом, чтобы количество обнаруженных сообществ соответствовало количеству групп внутри гомункула, для прямого сравнения. В частности, мы использовали параметр разрешения γ = 4,3, чтобы разделить мышечно-ориентированную матрицу на 22 сообщества (см. Таблицу S8). Мы начали с переопределения исходной мышечно-ориентированной матрицы B, следуя Jutla et al. [21]; мы положим k = Σ i B i , j , а затем мы применили локально жадный алгоритм максимизации модульности типа Лувена к скорректированной матрице B ‘= B-γkTk∑ jkj [22].
Указанный выше метод обнаружения сообществ недетерминирован [23]. То есть одно и то же решение не будет достигнуто при каждом отдельном запуске алгоритма. Следовательно, необходимо убедиться, что используемые назначения сообщества хорошо представляют сеть, а не только локальный максимум ландшафта. Поэтому мы максимально увеличили функцию качества модульности в 100 раз, получив 100 различных заданий от сообщества. Из этого набора решений мы определили надежную репрезентативную консенсусную структуру сообщества [24].S1 Рис. Показывает, как обнаруженные сообщества изменяются в зависимости от параметра разрешения для мышечно-ориентированной сети.
Сетевые нулевые модели
Мы используем реконструированные графы в качестве нулевой модели, с которой сравниваем эмпирические данные. В частности, мы построили нулевой гиперграф, перемонтировав мышцы, которым присвоена одна и та же категория (определенная ниже) равномерно и случайным образом. Таким образом, мышцы мизинца будут перестроены только внутри мизинца, и аналогично для мышц других категорий.Важно отметить, что этот метод также сохраняет степень каждой мышцы, а также степень распределения всего гиперграфа.
Таблица 3
Категории гомункулов и связанные с ними идентификационные номера.
| Идентификатор категории | Название категории | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Пальцы | |||||||||||||||
| 2 | Лодыжка | 5 | Ствол | |||||||||||||
| 6 | Плечо | |||||||||||||||
| 7 | Колено | |||||||||||||||
| 8 | Запястье | |||||||||||||||
| 9 | Безымянный палец | |||||||||||||||
| 12 | Средний палец | |||||||||||||||
| 13 | Указательный палец | |||||||||||||||
| 14 | Большой палец | |||||||||||||||
| 15 | Бровь | 15 | Бровь | 17 | веко и глазное яблоко | |||||||||||
| 18 | F ace | |||||||||||||||
| 19 | Губы | |||||||||||||||
| 20 | Челюсть | |||||||||||||||
| 21 | Язык | |||||||||||||||
| Категории 22 | Глотание мышц | |||||||||||||||
| Мышцы | Недели восстановления | Источник | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Triceps brachii | 4 | Bateman (1962) | |||||||||||
| 9026 | Latissimus dorsi | 12 | Nagda (2011) | ||||||||||
| Двуглавая мышца плеча | 12 | Zafra (2009) | |||||||||||
| Голеностопный сустав | 2 | McC14 | Torg (1982) | ||||||||||
| Зубья | 0 | Beachy (2004) | |||||||||||
| Плечо | 2 | Bateman (1962) | |||||||||||
| 9026 | |||||||||||||
| Бедро | 12 | Niemuth (2005) | |||||||||||
| Глаз / веко | 1,4 | Leivo (2015) | |||||||||||
| Колено | 8 | Колено | 8 | 4Колено | 8 | 8 | Fleisig (2012) | ||||||
| Запястье / кисть | 1.4 | Логан (2004) |
Данные области соматотопической репрезентации
Мы вычислили корреляцию между отклонением оценки воздействия и площадью соматотопической репрезентации, посвященной определенной группе мышц. Ареалы представительства были собраны из двух отдельных источников [38,39]. Тома и соответствующие ссылки перечислены в. В обоих исследованиях испытуемых просили многократно артикулировать сустав, и регистрировались объемы областей первичной моторной коры, которые подверглись наибольшему изменению в BOLD-сигнале.Затем мы рассчитали коэффициент корреляции между объемами коры и средним воздействием всех мышц, связанных с этим суставом, как определено в таблицах Hosford Muscle. Мы обнаружили значительную линейную корреляцию между двумя показателями с помощью функции MATLAB, fitlm.m, с параметром «Robust», установленным на «on».
Таблица 5
Размеры и источники объема соматотопической репрезентации первичной моторной коры.
| Мышцы | Объем (мм 3 ) | Артикул | ||||
|---|---|---|---|---|---|---|
| Большой палец | 1,390 | Indovina (2000) | ||||
| Индекс | ||||||
| Средний | 650 | Indovina (2000) | ||||
| Рука | 5,566 | Alkadhi (2002) | ||||
| Пальцы | 2,972 | Alkadhi (2002) | ||||
| Elbow | 2,267 | Alkadhi (2002) |
Результаты
Структура опорно-двигательного аппарата человека
Для исследования структурных взаимосвязей костно-мышечной системы человека использовалась гипер-мышечная система. подход.Основываясь на последних достижениях сетевой науки [5], мы исследовали опорно-двигательную систему как сеть, в которой кости (сетевые узлы) соединены друг с другом мышцами (сетевые гиперребра). Гиперребро — это объект, соединяющий несколько узлов; мышцы соединяют несколько костей через точки начала и вставки. Степень гиперребра k равна количеству узлов, которые оно соединяет; таким образом, степень мышцы — это количество костей, с которыми она контактирует. Например, трапеция — это гиперребро высокой степени, которое связывает 25 костей лопатки и позвоночника; И наоборот, приводящий большой палец представляет собой гиперребро низкой степени, которое связывает 7 костей руки ().Набор гиперребер (мышц) с общими узлами (костями) называется гиперграфом: граф H = (V, E) с N узлами и M гиперребрами, где V = {v 1 , …, v N } — это набор узлов, а E = {e 1 , …, e M } — набор гиперребер.
Структура гиперграфа.(a) Слева: анатомический рисунок трапеции. Справа: преобразование трапеции в гиперребро (красный; степень k = 25), соединяющее 25 узлов (костей) на голове, плече и позвоночнике.(b) Приводящая мышца большого пальца, соединяющая 7 костей руки. (в) Пространственная проекция распределения степеней гиперребер на тело человека. Гиперребра высокой степени сконцентрированы в основном в ядре. (d) Скелетно-мышечная сеть отображается в виде двудольной матрицы (1 = соединена, в противном случае 0). (e) Распределение степени гиперребра для гиперграфа опорно-двигательного аппарата, которое значительно отличается от ожидаемого в случайном гиперграфе. Данные доступны для (e) в DOI : 10.5281 / zenodo.1069104.
Представление опорно-двигательного аппарата человека в виде гиперграфа позволяет количественно оценить его структуру (). Мы заметили, что распределение степени гиперребер носит тяжелый характер: большинство мышц связывают 2 кости, а несколько мышц связывают многие кости (). Наклон распределения степеней существенно отличается от такового случайных сетей (двухвыборочный критерий Колмогорова-Смирнова, KS = 0,37, p <0,0001, см. Материалы и методы) [5], что свидетельствует о наличии мышц неожиданно низкой и высокий градус ().
Функция опорно-двигательного аппарата человека
Чтобы исследовать функциональную роль мышц в опорно-двигательном аппарате, мы использовали упрощенную модель опорно-двигательного аппарата и выяснили, может ли эта модель генерировать полезные клинические корреляты. Мы реализовали физическую модель, в которой кости образуют основной каркас тела, а мышцы скрепляют эту структуру. Каждый узел (кость) представлен как масса, пространственное расположение и движение которой физически ограничены гиперребрами (мышцами), с которыми он связан.В частности, кости — это точки, расположенные в их центре масс, заимствованные из текстов по анатомии [19], а мышцы — это пружины (затухающие гармонические осцилляторы), соединяющие эти точки [40,41]; для гиперребра степени k мы создали k (k — 1) / 2 пружин, связывающих k узлов. То есть для мышцы, соединяющей k костей, мы разместили пружины так, чтобы каждая из k мышц имела прямое пружинное соединение с каждой из других k — 1 костей.
Затем мы взволновали каждую из 270 мышц тела и вычислили их оценку воздействия в сети (см. Материалы и методы и).Когда мышца физически смещается, она вызывает волнообразное смещение других мышц по всей сети. Оценка удара мышцы — это среднее смещение всех костей (и косвенно мышц) в результате его первоначального смещения. Мы наблюдали значительную положительную корреляцию между степенью мышц и оценкой воздействия (F (1,268) = 23,3, R 2 = 0,45, p <0,00001;), предполагая, что структура гиперребра определяет функциональную роль мышц в опорно-двигательной сети.Мышцы с большим количеством точек прикрепления и начала имеют большее влияние на опорно-двигательный аппарат, когда они нарушены, чем мышцы с небольшим количеством точек прикрепления и начала [42]. Мы можем получить более подробное представление о результатах этого анализа, подробно изучив взаимосвязь между оценкой воздействия и статистическими показателями топологии сети. На рис. S11 мы показываем, что функция сети, измеренная с помощью оценки воздействия, значительно коррелировала со средней длиной кратчайшего пути.Хотя сетевая статистика статична по своей природе, их функциональная интерпретация обеспечивается пертурбативным моделированием динамики системы.
Исследование опорно-двигательного аппарата.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 37,3, R 2 = 0,757, p <0.0001). Заштрихованные области указывают 95% доверительный интервал, а точки данных масштабируются в соответствии с количеством включенных мышц. График пронумерован следующим образом: трицепс (1), большой палец (2), широчайшая мышца спины (3), двуглавая мышца плеча (4), лодыжка (5), шея (6), челюсть (7), плечо (8). ), большая круглая (9), бедра (10), глазные мышцы (11), колено (12), локоть (13), запястье / кисть (14). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве руководства к интерпретации важно отметить, что оценка воздействия, хотя и значительно коррелирует со степенью мускулатуры, не может быть им полностью предсказана ().Вместо этого, структура локальной сети, окружающей мышцу, также играет важную роль в ее функциональном воздействии и способности восстанавливаться. Чтобы лучше количественно оценить влияние этой структуры локальной сети, мы спросили, существуют ли мышцы, которые имели значительно более высокие или значительно более низкие оценки воздействия, чем ожидалось в нулевой сети. Мы определили положительное (отрицательное) отклонение оценки воздействия, которое измеряет степень, в которой мышцы более (менее) воздействуют, чем ожидалось в сетевой нулевой модели (см. Материалы и методы).В результате этого расчета был получен показатель, который выражает влияние конкретной мышцы по сравнению с мышцами с идентичной степенью гиперребер в нулевой модели. Другими словами, этот показатель учитывает сложность конкретной мышцы ().
Является ли эта математическая модель клинически актуальной? Отвечает ли тело по-разному на травмы мышц с более высокой оценкой удара, чем на мышцы с более низкой оценкой удара? Чтобы ответить на этот вопрос, мы оценили потенциальную взаимосвязь между воздействием на мышцы и временем восстановления после травмы.В частности, мы собрали данные о спортивных травмах и времени между получением травмы и возвращением в спорт. Мы отметили, что время восстановления сильно коррелировало с отклонениями оценки удара отдельной мышцы или группы мышц (F (1,12) = 37,3, R 2 = 0,757, p <0,0001;), предполагая, что наши Математическая модель предлагает полезный клинический биомаркер реакции сети на повреждение. Мы отмечаем, что важно учитывать тот факт, что восстановление может быть медленнее у человека, которому требуются максимальные усилия в спортивном спорте, по сравнению с человеком, который стремится только функционировать в повседневной жизни.Поэтому, чтобы обобщить наши результаты для всего населения, мы также изучили данные о времени восстановления, полученные от не спортсменов, и представляем эти дополнительные результаты во вспомогательной информации (текст S6).
Наконец, чтобы получить интуитивное представление о том, как очаговая травма может вызывать отдаленные эффекты, потенциально замедляющие выздоровление, мы рассчитали влияние мышц голеностопного сустава и определили, какие другие мышцы были затронуты сильнее всего. То есть для каждой отдельной мышцы голеностопного сустава мы рассчитали воздействие на каждую из оставшихся 264 мышц, не относящихся к голеностопному суставу, а затем усреднили это значение по всем мышцам голеностопного сустава.Из 264 мышц, не связанных с голеностопным суставом, единственная мышца, на которую больше всего воздействует нарушение мышц голеностопного сустава, — это двуглавая мышца бедра, а второй по величине — латеральная широкая мышца колена. Кроме того, мышца бедра, на которую больше всего влияет нарушение, — это камбаловидная мышца.
Контроль опорно-двигательного аппарата человека
Какова взаимосвязь между функциональным воздействием мышцы на тело и нейронной архитектурой, которая влияет на контроль? Здесь мы исследуем отношения между опорно-двигательной системой и первичной моторной корой.Мы исследовали область карты коркового изображения головного мозга, посвященную мышцам с низким или высоким воздействием, опираясь на анатомию моторной полосы, представленной в моторном гомункуле [43] (), грубое одномерное представление тела в головном мозге [44 ]. Мы заметили, что области гомункула по-разному контролируют мышцы с положительной и отрицательной оценкой отклонения воздействия (). Более того, мы обнаружили, что области гомункула, контролирующие только положительно (отрицательно) отклоняющиеся мышцы, как правило, располагаются медиально (латерально) на моторной полосе, что предполагает наличие топологической организации ожидаемого воздействия мышцы на нервную ткань.Чтобы исследовать эту закономерность более глубоко, для каждой области гомункула мы рассчитали коэффициент отклонения как процент мышц, которые положительно отклонились от ожидаемой оценки воздействия (т. Е. Значение 1 для бровей, глаз, лица и значение 0 для колена , бедро, плечо; см.). Мы обнаружили, что коэффициент отклонения достоверно коррелировал с топологическим положением на моторной полосе (F (1,19) = 21,3, R 2 = 0,52, p <0,001;).
Зондирование опорно-двигательного аппарата.(а) Гомункул первичной моторной коры, сконструированный Пенфилдом.(b) Коэффициент отклонения достоверно коррелирует с гомункулярной топологией (F (1,19) = 21,3, R 2 = 0,52, p <0,001), уменьшаясь от медиального (область 0) к латеральному (область 22). (c) Отклонение оценки воздействия достоверно коррелирует с объемом активации моторной полосы (F (1,5) = 14,4, R 2 = 0,743, p = 0,012). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. График пронумерован следующим образом: большой палец (1), указательный палец (2), средний палец (3), рука (4), все пальцы (5), запястье (6), локоть (7).(d) Корреляция между пространственным упорядочением категорий гомункулов Пенфилда и линейной мышечной координатой из многомерного масштабного анализа (F (1,268) = 316, R 2 = 0,54, p <0,0001). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве более строгой проверки этой взаимосвязи между воздействием мышцы на сеть и нейронной архитектурой мы сопоставили данные о физических объемах функциональной активации на основе МРТ на моторной полосе, которые предназначены для отдельных движений (например,g., сгибание пальцев или моргание глаз). Объемы активации определяются как воксели, которые активируются (определяемые сигналом, зависящим от уровня кислорода в крови) во время движения [38,39]. Важно отметить, что мы обнаружили, что объем функциональной активации независимо предсказывает отклонение оценки удара мышц (, F (1,5) = 14,4, p = 0,012, R 2 = 0,743), что согласуется с интуицией, что мозг будет посвятите больше места в сером веществе контролю над мышцами, которые более эффективны, чем ожидалось в нулевой модели.Опять же, отклонение от удара — это показатель, который учитывает степень гиперреберности конкретной мышцы и относится к удару мышц с идентичной степенью гиперребер в нулевой модели. Таким образом, ударное отклонение измеряет топологию локальной сети, а не просто непосредственные соединения рассматриваемой мышцы.
В качестве финального теста этой взаимосвязи мы спросили, оптимально ли сопоставлена стратегия нервного контроля, воплощенная в моторной полоске, с группами мышц. Мы построили мышечно-ориентированный граф, соединив две мышцы, если они касаются одной и той же кости (, слева).Мы наблюдали наличие групп мышц, плотно связанных друг с другом, имеющих общие кости. Мы извлекли эти группы, используя метод кластеризации, разработанный для сетей [45,46], который обеспечивает разделение мышц на сообщества на основе данных (справа). Чтобы сравнить структуру сообщества, присутствующую в мышечной сети, с архитектурой системы нейронного контроля, мы рассмотрели каждую из 22 категорий моторного гомункула [18] как отдельное нейронное сообщество и сравнили эти присвоения сообществу, основанные на мозге, с заданиями сообщества. полученный из управляемого данными раздела мышечной сети.Используя коэффициент Рэнда [47], мы обнаружили, что распределение сообществ как для гомункула, так и для мышечной сети было статистически схожим (z Rand > 10), что указывает на соответствие между модульной организацией опорно-двигательного аппарата и структурой гомункула. Например, трицепс плеча и двуглавая мышца плеча принадлежат к одной гомункулярной категории, и мы обнаружили, что они также принадлежат к одному и тому же сообществу топологических мышечных сетей.
Затем, поскольку гомункулус имеет линейную топологическую организацию, мы спросили, был ли порядок сообществ внутри гомункула () подобен управляемому данными упорядочению групп мышц в теле, как определено с помощью MDS [48].Из сети, ориентированной на мышцы (), мы получили матрицу расстояний, которая кодирует наименьшее количество костей, которые необходимо пройти, чтобы перейти от одной мышцы к другой. MDS этой матрицы расстояний выявил одномерные линейные координаты для каждой мышцы, так что топологически близкие мышцы были близко друг к другу, а топологически далекие мышцы были далеко друг от друга. Мы заметили, что линейная координата каждой мышцы значительно коррелирует с ее категорией гомункула (, F (1,268) = 316, p <0.0001, R 2 = 0,54), что указывает на эффективное отображение между нейронным представлением мышечной системы и сетевой топологией мышечной системы в теле.
Наши результаты демонстрируют соответствие между топологией гомункула и упорядочением мышц на основе данных, полученным с учетом топологических расстояний между ними. Этот результат можно интерпретировать одним из двух способов: одна разумная гипотеза состоит в том, что, поскольку большинство соединений в опорно-двигательной сети являются короткодействующими, открытие в основном обусловлено связями ближнего действия.Вторая разумная гипотеза состоит в том, что, хотя соединения ближнего действия являются наиболее распространенными, соединения дальнего действия образуют важные внутримодульные связи, которые помогают определять организацию сети. Чтобы выбрать между этими двумя гипотезами, мы рассмотрели два варианта нашего эксперимента MDS: один включает только соединения, длина которых меньше средней длины соединения, а другой — только соединения, длина которых превышает среднюю длину соединения. Мы обнаружили, что упорядочение на основе данных, полученное только из коротких и только из длинных соединений, привело к значительным корреляциям с гомункулярной топологией (F (1,268) = 24.9, R 2 = 0,085, p <0,0001 и F (1,268) = 5, R 2 = 0,018, p = 0,026 соответственно). Примечательно, что включение как длинных, так и коротких соединений приводит к более сильной корреляции с гомункулярной топологией, чем рассмотрение любого из них независимо, что предполагает зависимость от соединений любой длины. В будущем было бы интересно проверить, в какой степени эта межсетевая карта изменяется у людей с двигательными нарушениями или изменениями после инсульта.
Обсуждение
Структура опорно-двигательного аппарата человека
Представляя сложную взаимосвязь опорно-двигательного аппарата в виде сети костей (представленных узлами) и мышц (представленных гиперребрами), мы получили ценную информацию об организации человеческого организма. тело. Изучение анатомических сетей с использованием аналогичных методов становится все более распространенным в области эволюционной биологии и биологии развития [10]. Однако этот подход обычно применялся только к отдельным частям тела, включая руку [49], голову [11] и позвоночник [12], тем самым предлагая понимание того, как развивалась эта часть организма [50, 51].Более того, даже после моделирования всей мускулатуры тела [13] и нервно-мышечно-скелетной системы [14] в более общем плане некоторые количественные утверждения могут остаться неуловимыми, в значительной степени из-за отсутствия математического языка, на котором можно было бы обсуждать сложность взаимосвязи. узоры. В этом исследовании мы предлагаем явное и экономное представление всей опорно-двигательной системы в виде графа узлов и ребер, и это представление позволило нам точно охарактеризовать сеть в целом.
При моделировании системы как сети важно начать последующее исследование с характеристики нескольких ключевых архитектурных свойств. Одним из наиболее фундаментальных показателей структуры сети является ее распределение по степеням [52], которое описывает неоднородность подключения узла к его соседям таким образом, который может дать представление о том, как формировалась система [7]. Мы заметили, что степень распределения опорно-двигательного аппарата значительно отличается от ожидаемого в нулевом графе (), показывая меньше узлов высокой степени и переизбыток узлов низкой степени.Несоответствие между графами реальной и нулевой модели согласуется с тем фактом, что опорно-двигательная система человека развивается в контексте физических и функциональных ограничений, которые вместе определяют ее явно неслучайную архитектуру [53]. Распределение степеней этой сети показывает пик примерно на второй степени, за которым следует относительно тяжелый хвост узлов высокой степени. Последняя особенность обычно наблюдается во многих типах реальных сетей [54], чьи концентраторы могут быть дорогостоящими в разработке, обслуживании и использовании [55,56], но играют критическую роль в надежности системы, обеспечивая быстрое реагирование [55], буферизация изменчивости окружающей среды [57] и облегчение выживания и воспроизводства [58].Первая особенность — пик распределения — согласуется с интуицией, что большинство мышц опорно-двигательного аппарата соединяются только с двумя костями, в первую очередь для функции простого сгибания или разгибания в суставе. Напротив, есть только несколько мышц, которые требуют высокой степени для поддержки очень сложных движений, таких как поддержание выравнивания и угла позвоночника за счет одновременного управления движением многих костей. Эти ожидаемые результаты обеспечивают важную проверку модели, а также предлагают полезную визуализацию опорно-двигательного аппарата.
Скелетно-мышечная сеть характеризуется особенно интересным свойством, которое отличает ее от нескольких других реальных сетей: тем фактом, что она встроена в трехмерное пространство [59]. Это свойство не наблюдается в семантических сетях [60] или World Wide Web [61], которые кодируют отношения между словами, концепциями или документами в некоторой абстрактной (и, скорее всего, неевклидовой) геометрии. Напротив, опорно-двигательная система представляет собой объем с узлами, имеющими определенные координаты, и краями, представляющими физически протяженные ткани.Чтобы лучше понять физическую природу опорно-двигательного аппарата, мы исследовали анатомическое расположение мышц с разной степенью (). Мы заметили, что мышечные центры расположены преимущественно в торсе, обеспечивая плотную структурную взаимосвязь, которая может стабилизировать ядро тела и предотвратить травмы [62]. В частности, мышцы высокой степени группируются вокруг средней линии тела, рядом с позвоночником, вокруг таза и плечевого пояса, что согласуется с представлением о том, что для маневренности и устойчивости этих областей требуется совокупность мышц с различной геометрией и свойствами тканей [63 ].Действительно, мышцы в этих местах должны поддерживать не только сгибание и разгибание, но также отведение, приведение и внутреннее и внешнее вращение.
Важно отметить, что в костно-мышечной системе у разных людей существуют значительные различия, и не все анатомические атласы согласуются с наиболее репрезентативным набором точек вставки и происхождения. Представленные здесь результаты отражают то, как опорно-двигательная система была представлена в тексте, из которого она была построена [19], и поэтому обеспечивают только одно возможное сетевое представление опорно-двигательной системы.Чтобы оценить надежность наших результатов при разумных вариациях конфигурации опорно-двигательного аппарата, мы создали вторую опорно-двигательную сеть из альтернативного атласа [64]. Используя этот второй атлас, мы наблюдали последовательные результаты и сообщаем об этом дополнительном анализе в S3 Text.
Также важно отметить, что мы сопоставили первый атлас [19] в скелетно-мышечный граф, состоящий как из костных, так и из некостных узлов. Этот выбор уравнивает структурные роли костей и определенных сухожилий и связок, что, по общему признанию, является упрощением биологии.Одним из оправданий такого упрощения является то, что некостные структуры часто служат важными точками прикрепления мышц (то есть подошвенной фасцией стопы). Таким образом, разумно разделить опорно-двигательную сеть на две категории мышц и структур, которые служат точками прикрепления мышц, как мы это сделали здесь. Тем не менее, эта вторая категория довольно неоднородна по составу, и в будущей работе можно было бы также рассмотреть возможность построения многослойного графа с отдельным слоем, учитывающим каждый тип структуры мышечного прикрепления.Чтобы подтвердить, что наши результаты и интерпретации существенно не меняются из-за наличия некостных мышечных точек прикрепления, мы удалили такие точки в альтернативном атласе и отметили, что наши основные результаты все еще остаются в силе (см. Текст S3).
Функция опорно-двигательного аппарата человека
Чтобы лучше понять функциональную роль отдельной мышцы во взаимосвязанной опорно-двигательной системе, мы реализовали основанную на физике модель свойств импульсного отклика сети, кодируя кости как точечные массы, а мышцы как пружины [65].Примечательно, что эта очень упрощенная модель опорно-двигательного аппарата способна идентифицировать важные функциональные особенности. Хотя мышцы высокой степени также имели тенденцию иметь большое влияние на реакцию сети (), было несколько заметных отклонений от этой тенденции ().
Мышца, оказывающая наименьшее воздействие по сравнению с ожидаемой, — это orbicularis oculi, мышца, используемая для управления движением века. Эта мышца небольшая и относительно изолированная в теле, берут начало и прикрепляются к костям черепа.Мышцы лица в целом образуют плотное и изолированное сообщество, с немногими связями, выходящими за пределы этого сообщества. Эти факторы, вероятно, способствуют слабому воздействию этой мышцы, и аналогичный аргумент может быть сделан в отношении оставшихся двух мышц с меньшим воздействием, чем ожидалось, которые также являются мышцами лица.
Мышцы с большей нагрузкой, чем ожидалось, более многочисленны, но почти полностью расположены в верхней конечности или поясе верхней конечности. Длинный разгибатель запястья, anconeus, brachioradialis и brachialis мышцы являются собственными мышцами руки, последние три действуют в локтевом суставе.Все эти мышцы могут иметь более сильное воздействие, чем ожидалось в нулевой модели, потому что они могут прямо или косвенно влиять на движение многих костей запястья и кисти. Наблюдаемое сильное воздействие этих мышц может быть результатом того факта, что они контролируют движение конечности, а на конце конечности находится множество костей, движение которых напрямую зависит от этих мышц. Остальные ударные мышцы, за исключением грушевидной мышцы, прикрепляют верхнюю конечность к осевому скелету.Этими мышцами являются коракобрахиальная, подостная, надостная, подлопаточная, малая круглая, большая круглая и большая грудная мышцы. Эти мышцы, как и предыдущие четыре, обладают тем свойством, что они контролируют движение всей конечности, что, вероятно, способствует их влиянию. В отличие от предыдущей группы, эти мышцы также соединяются с осевым скелетом, что также может усиливать их воздействие. Многие из этих мышц берут свое начало на костях плечевого пояса и могут влиять на все другие мышцы плечевого пояса и, возможно, на все кости, связанные с этими мышцами.Такая же динамика, вероятно, существует в нижней конечности, что отражается наличием грушевидной мышцы тазового пояса. Подробное обсуждение того, как структура локальной сети и конфигурация мышц могут взаимодействовать с отклонением от удара, представлено в S7 Text. В дополнение к нашей работе, представленной во вспомогательной информации, дальнейшее понимание свойств этих выбросов может быть получено путем проведения экспериментов по тщательному изучению костей, на которые сильнее всего воздействует каждая из этих мышц.
Хотя сетевое представление системы может дать базовую физическую интуицию благодаря своей скупости и простоте, оно также остается безразличным ко многим деталям архитектуры и функций системы. Извечный вопрос, могут ли эти базовые модели сложных систем обеспечить точные прогнозы реальных результатов. Мы рассмотрели этот вопрос, изучив взаимосвязь между оценкой удара мышцы и количеством времени, которое требуется человеку для восстановления после травмы.Мы количественно оценили время восстановления, суммируя (i) время восстановления после первичной инвалидности, вызванной первоначальным мышечным повреждением, и (ii) время восстановления после любых вторичных нарушений, вызванных изменением использования других мышц в сети из-за первоначального травма мышц [66]. Мы обнаружили, что отклонение от ожидаемой оценки воздействия в нулевой сети значительно коррелировало со временем восстановления (), подтверждая представление о том, что очаговая травма может иметь длительные воздействия на организм из-за изначально взаимосвязанной природы опорно-двигательной системы.
Действительно, известно, что мышечные изменения в одной части тела влияют на другие группы мышц. Например, укрепление мышц бедра может привести к улучшению функции колена после замены коленного сустава [67]. Изменение мышечной функции в голеностопном суставе после растяжения связок может вызвать изменение функции мышц бедра [68, 69], результат, воспроизведенный нашей моделью (которая показала, что двуглавая мышца бедра и латеральная широкая мышца бедра больше всего пострадали от травмы голеностопного сустава), а повреждение мышц конечностей может приводят к вторичному повреждению диафрагмы [70].Наша модель предлагает математически принципиальный способ предсказать, какие мышцы с большей вероятностью будут иметь такое вторичное влияние на более крупную опорно-двигательную систему, а какие мышцы подвержены риску вторичного повреждения, учитывая первичное повреждение в определенном участке мышцы. В будущем было бы интересно проверить, могут ли эти прогнозы повлиять на полезные корректировки клинических вмешательств, явно принимая во внимание риск вторичного повреждения определенных мышц. Ранее профилактика вторичных мышечных травм в основном сводилась к криотерапии [71,72] и еще не была мотивирована такой механистической моделью.Наконец, важный вопрос, который следует задать, заключается в том, насколько эта конфигурация опорно-двигательного аппарата является эволюционно выгодной и как эволюционное давление могло оптимизировать воздействие на мышцы. Интуитивно можно было ожидать, что эволюционное давление снижает мышечную нагрузку, возможно, за счет увеличения мышечной избыточности. Тщательное исследование эволюционных преимуществ топологии костно-мышечной сети было бы интересной темой для будущей работы.
Контроль опорно-двигательного аппарата человека
Учитывая сложность опорно-двигательного аппарата и его критическую роль в выживании человека, естественно задать вопрос о том, как эта сеть управляется человеческим мозгом.Действительно, изучение моторного контроля имеет долгую и яркую историю [73], которая дала важную информацию о том, как мозг может успешно и точно совершать произвольные движения, несмотря на такие проблемы, как избыточность, шум [74], задержки сенсорной обратной связи. [75], неопределенность окружающей среды [76], нервно-мышечная нелинейность [77] и нестационарность [78]. Здесь мы использовали отличный, но дополняющий друг друга подход и спросили, как топология опорно-двигательного аппарата может быть отображена на топологии моторной полосы в коре головного мозга.Мы начали с того, что отметили, что ударное отклонение мышцы положительно коррелирует с размером коркового объема, предназначенного для его контроля (). Одна из интерпретаций этой взаимосвязи состоит в том, что те мышцы, которые своими непосредственными связями оказывают большее влияние, чем ожидалось в нулевой модели, имеют тенденцию контролировать более сложные движения и, следовательно, требуют большего количества нейронов для управления этими движениями [79]. Вторая интерпретация основана на эволюционном аргументе о том, что мышцы с большей нагрузкой нуждаются в большей избыточности в их системах управления [80], и эта избыточность принимает форму большей корковой области.
Помимо локальных объемов коры [81], можно также захотеть понять, в какой степени крупномасштабная организация опорно-двигательной сети отражает организацию контролирующей ее моторной полосы. Основываясь на недавнем применении методов выявления сообществ к изучению анатомии черепа [11,82,83], мы сообщили о модульной организации мышечной сети: группы мышц, в которых мышцы одной группы с большей вероятностью соединяются с одной. кроме мышц в других группах.Что еще интереснее, мы наблюдали, что мышечные сообщества очень похожи на известную группу мышц моторной полоски (справа): мышцы, которые имеют тенденцию соединяться с теми же костями, что и друг друга, также имеют тенденцию контролироваться той же частью моторной полоски. Более того, естественное линейное упорядочение мышечных сообществ — такое, что сообщества располагаются близко друг к другу на линии, если они имеют общие сетевые соединения — имитирует порядок контроля в моторной полосе (). Эти результаты дополняют важную предыдущую работу, предполагающую, что одномерная организация моторной полосы связана как со структурной, так и со функциональной организацией скелетно-мышечной сети [84,85].Фактически, результаты более конкретно предлагают определение оптимального сетевого управления на уровне сети: согласованность линейной карты от сообществ опорно-двигательного аппарата до сообществ моторных полос.
Наконец, мы исследовали физическое расположение кортикального контроля ударных мышц. Мы заметили, что мышцы с большим воздействием, чем ожидалось, при нулевом графике, как правило, контролируются средними точками на моторной полосе, в то время как мышцы с меньшим воздействием, чем ожидалось, обычно контролируются боковыми точками на моторной полосе ().Эта пространственная специфика указывает на то, что организация моторной полосы ограничивается физическим расположением тела, а также аспектами функционирования мышц. Предыдущие исследования изучали общее временное соответствие между корковой активностью и мышечной активностью во время движения [86], но мало что известно о топологическом соответствии.
Методологические соображения
Построение гиперграфа на основе опорно-двигательного аппарата человека требует допущений и упрощений, которые влияют на гибкость текущей модели.Наиболее заметным является разделение системы на две категории: мышцы и кости. Эти категории не содержат дополнительной информации и, следовательно, не учитывают особенности внутренней архитектуры мышцы или кости. Это упрощение вводит несколько ограничений для пертурбативной модели, включая возможность моделирования функциональной архитектуры сложных мышц или мышц, обладающих способностью независимо сокращать подмножество волокон. Например, двуглавая двуглавая мышца плеча берет начало как на лопатке, так и на супрагленоидном бугорке, и можно сокращать волокна одной головки отдельно от волокон другой головки.Дальнейшая работа может расширить нашу структуру моделирования, чтобы представить эту сложную функциональную архитектуру. Более того, немышечные структуры мягких тканей, важные для опорно-двигательного аппарата, не могут быть четко учтены. Эти структуры, включая сухожилия и связки, могут быть либо (1) закодированы как кости, как в основной текстовой сети, либо (2) исключены из сети, как в приложении; ни один из вариантов не является полностью анатомически точным.
В случае костей модель не может учесть взаимодействия кость-кость (суставы).Большинство мышц действуют на суставы, и исключение суставов затемняет специфическую функцию мышц. То есть модель учитывает тот факт, что мышцы перемещают кости, но не то, как они движутся или в каком направлении. В пертурбативном моделировании отсутствие ограничений на суставы позволяет размещать кости под неестественными углами относительно соседних костей. Кроме того, кости моделируются как точечные массы, которые в пертурбативном моделировании могут позволить костям проходить траектории, связанные с прохождением через пространство, которое на самом деле занято другой костью.Дальнейшая работа может расширить нашу структуру моделирования, чтобы учесть эти дополнительные биофизические ограничения.
Аналитические данные, полученные с помощью этой модели, являются результатом входных данных. Поскольку индивидуальные вариации существуют в опорно-двигательном аппарате, они также существуют и в мышечных воздействиях. Мы попытались использовать два набора входных данных, чтобы оправдать наши основные выводы, но эти результаты не могут быть обобщены на все здоровые конфигурации опорно-двигательного аппарата. В частности, степень мышц, подверженная индивидуальным изменениям, может повлиять на воздействие этой мышцы.Каким образом нормативные индивидуальные вариации в степени мышечной массы связаны с вариациями прогнозируемого воздействия на мышцы, является важным вопросом, который, тем не менее, выходит за рамки настоящего исследования.
Наконец, опорно-двигательный аппарат человека представляет собой сложную и плотно взаимосвязанную сеть. Ни мышцы, ни кости не функционируют как независимые образования. Таким образом, трудно отделить функцию отдельной мышцы от воздействия окружающих мышц. Независимость мышц может быть частично устранена соответствующим выбором нулевой модели, и наши результаты остаются в силе при различных вариантах.Тем не менее, при интерпретации этих результатов следует учитывать представление о том, что мышцы — и факторы воздействия — не являются действительно независимыми.
Вспомогательная информация
S1 Text
Альтернативные нулевые модели.Этот текстовый файл подробно описывает построение альтернативных нулевых моделей.
(DOCX)
S2 Text
Разрешение обнаружения сообщества.Этот файл содержит описание выбора параметра разрешения обнаружения сообщества.
(DOCX)
S3 Text
Альтернативная опорно-двигательная сеть.Этот файл содержит описание альтернативной опорно-двигательной сети.
(DOCX)
S4 Текст
Динамика костей в результате мышечного пертурбации.(DOCX)
S5 Text
Учет веса костей и силы мышц.(DOCX)
S6 Text
Анализ восстановления мышц, не связанных со спортсменами.(DOCX)
S7 Text
Структура локальной сети и отклонение от воздействия.(DOCX)
S1 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в случайно перестроенных гиперграфах.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений выше среднего в порядке от наибольшего до наименьшего. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S2 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению со случайно перестроенными гиперграфами.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени.Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью. Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S3 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в гиперграфах, случайным образом перепрограммированы в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень.Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гипреберья: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение, в порядке от наибольшего к наименьшему. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S4 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению с гиперграфами, случайно перестроенными в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень. Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S5 Таблица
Мышцы с большей или меньшей нагрузкой, чем ожидалось в случайном гиперграфе.Эта нулевая модель требовала случайного назначения связей между костями и мышцами, сохраняя только общий уровень, а не индивидуальный уровень мышц. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение и упорядочено от наибольшего к наименьшему.
(XLSX)
S6 Таблица
Объемы мышц подсети голени.Здесь мы включаем название мышцы (столбец 1), объем мышцы (в см 3 ; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S7 Таблица
Масса костей подсети ноги.Здесь мы включаем название кости (столбец 1), массу кости (в граммах; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S8 Таблица
Присвоенные категории гомункулов и основанное на данных распределение мышц в сообществе.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S9 Таблица
Гиперграф мышц и костей из таблиц Hosford Muscle [18], используемых в основном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S10 Таблица
Гиперграф мышц и костей из атласа Гранта [64], использованный в дополнительном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S1 Рис.
Обнаружение сообщества с разными параметрами разрешения.На этом рисунке показано, как выбор параметра разрешения во время обнаружения сообществ изменит количество и размер обнаруженных сообществ.С увеличением параметра разрешения размер отдельных сообществ уменьшается, а количество сообществ увеличивается. (a-d) Обнаружение сообщества для сети, ориентированной на мышцы, с использованием значений γ, равных 1, 2, 8 и 16 соответственно. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S2 Рис.
Обнаружение сообщества с разными параметрами разрешения.Этот рисунок иллюстрирует стабильность при выбранном параметре настройки γ = 4.3. Здесь мы исследуем разбиения, созданные из близких параметров разрешения γ = 4,2 и γ = 4,4. Визуально кажется, что все три раздела имеют похожую структуру. Два соседних раздела также математически схожи: z-оценка коэффициента Рэнда [47] z Rand (γ = 4,2, γ = 4,3) = 105, z Rand (γ = 4,3, γ = 4,4) = 110 и z Rand (γ = 4,2, γ = 4,4) = 105. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S3 Рис.
Визуальное сравнение нулевых моделей.Этот рисунок иллюстрирует различия в нулевых двудольных графах. (A) Исходный непереставленный двудольный граф мышца-кость. (B) Случайный нулевой двудольный граф. (C) Случайно перестроенный двудольный граф. (D) Двудольный граф, случайно измененный внутри сообщества, используемый в основном тексте, который переставляет топологию локально, сохраняя при этом глобальную топологию.
(EPS)
S4 Рис.
Основные результаты как функция нулевой модели.Здесь мы показываем результаты с использованием модели случайного гиперграфа или модели гиперграфа с измененной связью (перестановкой), которая не поддерживает локальные связи. (A) Оценка удара, построенная как функция степени гиперребра для случайных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (B) Оценка удара, нанесенная на график как функция степени гиперребра для переставленных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (C) Коэффициент отклонения достоверно коррелирует с категорией гомункула (F (1,19) = 6.67, p = 0,018, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием случайной нулевой модели гиперграфа. (D) Коэффициент отклонения достоверно коррелирует с гомункулярной категорией (F (1,19) = 6,86, p = 0,017, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием пермутированного нулевая модель гиперграфа. (E) Отклонение оценки воздействия значимо коррелирует с площадью активации моторной полосы (F (1,5) = 13,4, p = 0,014, R 2 = 0.72) с использованием случайной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (F) Отклонение оценки воздействия значительно коррелирует с площадью активации моторной полосы (F (1,5) = 13,7, p = 0,022, R 2 = 0,73) с использованием пермутированной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (G) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 64.5, p = 6,3 × 10 −6 , R 2 = 0,85), используя случайную нулевую модель гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. (H) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 70,5, p <0,0001, R 2 = 0,86), больше, чем ожидалось при перестановке — основанная на нулевой модели гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S5 Рис.
Топология сети и гомункул.Линейные координаты мышц, определенные с использованием многомерного масштабирования без пороговой обработки с помощью взвешенной матрицы расстояний (рассчитанной с использованием distance_wei.m, включенного в Brain Connectivity Toolbox, https://sites.google.com/site/bctnet/). Без пороговой обработки также существует значимая корреляция между линейной координатой мышцы и площадью гомункула (F (1,268) = 303, p <0.0001, R 2 = 0,53). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S6 Рис.
Исследование функции опорно-двигательного аппарата для альтернативной сети.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 40,2, p <0,0001, R 2 = 0.77). Заштрихованные области указывают 95% доверительных интервалов, а точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S7 Рис.
Проверка опорно-двигательного аппарата для альтернативной сети.(a) Коэффициент отклонения значимо коррелирует с гомункулярной топологией (F (1,18) = 8,88, R 2 = 0,33, p = 0,0080), уменьшаясь от медиального (область 0) к латеральному (область 22) регионы. (b) Отклонение оценки воздействия достоверно коррелирует с площадью активации моторной полосы (F (1,5) = 23.4, R 2 = 0,82, p = 0,005). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S8 Рис.
Динамика возмущения двуглавой мышцы плеча.На этом рисунке показано движение ключицы, а также костей пальца и стопы в ответ на возмущение двуглавой мышцы плеча. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S9 Рис.
Сравнение моделей с утяжелением костей и силой мышц и без них.Воздействие мышц ног рассчитывалось с добавлением и без добавления анатомических значений массы кости и объема мышц. Было обнаружено, что эти воздействия существенно коррелировали друг с другом (F (1,25) = 6,83, R 2 = 0,0214, p = 0,015), что позволяет предположить, что по крайней мере в некоторых частях тела наше упрощенное сетевое представление обеспечивает разумное приближение для более биофизически точных сетевых представлений. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S10 Рис.
Исследование функции опорно-двигательного аппарата для не спортсменов.Набрано время восстановления после травм различных мышц не спортсменов. Мы наблюдали значительную корреляцию между временем восстановления мышц и отклонением от удара (F (1,14) = 5,02, R 2 = 0,264, p = 0,041). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S11 Рис.
Соответствие топологии сети и функции системы.Топология сети, в частности средняя длина кратчайшего пути, значительно отрицательно коррелирует с оценкой воздействия, оцененной на основе пертурбативного моделирования динамики системы (F (1,268) = 65,1, R 2 = -0,4422, p <0,0001). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S12 Рис.
Связь между мышечно-скелетными вариациями и мышечным воздействием через две скелетно-мышечные сети.Здесь мы сравниваем процентное изменение оценки и степени воздействия для каждой мышцы между опорно-двигательным аппаратом, указанным в основном тексте, и сообщенным в дополнительном тексте.Мы наблюдаем, что на оценку удара мышц больше влияют большие изменения степени, чем меньшие изменения степени (F (1,268) = 5,76, R = 0,1450, p = 0,017). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S13 Рис.
Альтернативный пертурбативный подход.Чтобы установить меру воздействия на гиперреберь мышцы, объекты были перемещены в четвертое пространственное измерение, чтобы избежать произвольного выбора в трех измерениях. Альтернативным подходом было бы возмущение каждой мышцы в каждом из трех ортогональных направлений, каждый раз вычисляя воздействие и вычисляя векторную сумму этих трех результатов.Чтобы ответить на вопрос о том, как эти два подхода сравниваются, мы провели этот эксперимент на двудольной матрице мышцы-кости, чтобы создать два вектора 270 × 1, один из которых кодировал оценки воздействия посредством смещения в четвертом измерении, а другой — векторную сумму три ортогональных смещения. Два вектора достоверно коррелировали друг с другом (F (1,268) = 1590, R 2 = 0,856, p <0,0001).
(PNG)
Структура, функции и контроль опорно-двигательного аппарата человека
Реферат
Человеческое тело представляет собой сложный организм, основные механические свойства которого обусловлены взаимосвязанной опорно-двигательной сетью, управляемой нервной системой.Природа костно-мышечной взаимосвязи способствует стабильности, произвольным движениям и устойчивости к травмам. Однако фундаментальное понимание этой сети и ее контроля со стороны нейронных систем остается неуловимым. Здесь мы устраняем этот пробел в знаниях, используя медицинские базы данных и математическое моделирование, чтобы выявить организационную структуру, прогнозируемые функции и нейронный контроль опорно-двигательной системы. Мы построили очень упрощенную опорно-двигательную сеть всего тела, в которой отдельные мышцы соединяются с несколькими костями как через точки начала, так и через точки прикрепления.Мы продемонстрировали, что, используя эту упрощенную модель, роль мышцы в этой сети может предложить теоретическое предсказание восприимчивости окружающих компонентов к вторичным повреждениям. Наконец, мы проиллюстрировали, что наборы мышц группируются в сетевые сообщества, которые имитируют организацию модулей управления в первичной моторной коре. Этот новый формализм для описания взаимодействий между мышечной и скелетной системами служит основой для разработки и тестирования терапевтических реакций на травмы, вдохновляя будущие успехи в клиническом лечении.
Об авторе
Хотя сетевая наука часто используется для характеристики сетей на основе геномики, протеомики и коннектомики, ее полезность для понимания биомеханики, ортопедии и физиотерапии остается в значительной степени неизученной. Действительно, текущая клиническая практика и знания, касающиеся опорно-двигательного аппарата, в основном сосредоточены на отдельных областях тела, отдельных мышцах или отдельных травмах и поэтому остаются безразличными к мезомасштабным или глобальным особенностям архитектуры тела, которые могут иметь решающее значение для травм и восстановления.Мы устранили этот пробел, представив опорно-двигательный аппарат в виде графа или сети, в которой мы рассмотрели кости и мышечные связи между ними. Моделируя мышцы как пружины и кости как точечные массы, мы разработали пертурбативный подход, чтобы исследовать функцию этой сети. Используя эту модель, мы рассчитали сетевые эффекты возмущения отдельных мышц. Используя этот формализм, мы можем провести новые параллели между этой системой и первичной моторной корой, которая ее контролирует, и проиллюстрировать клинические связи между сетевой структурой и мышечным повреждением.
Введение
Взаимосвязанная природа человеческого тела долгое время была предметом научных исследований и суеверных верований. От древних юморов, связывающих сердце, печень, селезенку и мозг смелостью, спокойствием и надеждой [1], до современного понимания связи кишечника и мозга [2], люди склонны искать взаимосвязи между разрозненными частями тела, чтобы объяснять сложные явления. Тем не менее, напряжение остается между этой базовой концептуализацией человеческого тела и редукционизмом, неявным в современной науке [3].Понимание всей системы часто относят к футуристическому миру, в то время как отдельные эксперименты уточняют наше понимание мельчайших составных частей.
Опорно-двигательный аппарат человека не является исключением из этой дихотомии. В то время как медицинская практика сосредоточена на кистях, стопах или лодыжках, клиницисты знают, что травмы одной части опорно-двигательного аппарата обязательно влияют на работу других (даже отдаленно удаленных) частей [4]. Травма лодыжки может изменить характер походки, что приведет к хронической боли в спине; травма плеча может изменить осанку и вызвать дискомфорт в шее.Понимание фундаментальных отношений между фокальной структурой и потенциальными удаленными взаимодействиями требует целостного подхода.
Здесь мы подробно описываем такой подход. Наша концептуальная основа мотивирована недавними теоретическими достижениями в сетевой науке [5], которая представляет собой развивающуюся дисциплину, построенную на упорядоченном слиянии математики (в частности, теории графов [6]) и физики (в частности, статистической механики [7]), компьютеров. наука, статистика [8] и системная инженерия.Подход упрощает сложные системы, разграничивая их компоненты и отображая паттерн взаимодействия между этими компонентами [9]. Это представление кажется особенно подходящим для изучения опорно-двигательного аппарата человека, который состоит из костей и соединяющих их мышц. В этом исследовании мы использовали этот подход для оценки структуры, функции и контроля опорно-двигательного аппарата.
Использование сетевых наук для понимания опорно-двигательного аппарата в последние годы увеличилось [10].Однако этот каркас в основном использовался для исследования свойств локальных мышечных или костных сетей. Например, была исследована местная структура черепа, чтобы выяснить, как можно классифицировать кости [11]. Кроме того, были проведены исследования топологии костно-мышечной сети позвоночника для оценки напряжений и деформаций в костях [12]. Существует несколько исследований, посвященных всей опорно-двигательной системе, хотя они не используют математические инструменты, которые мы использовали здесь [13,14].Настоящее исследование отличается от предыдущих работ оценкой всей опорно-двигательной системы в сочетании с математическими инструментами науки о сетях.
В этом более широком контексте мы сосредоточили внимание на проблеме реабилитации после травм скелетных мышц или коры головного мозга. Прямое повреждение мышцы или связанного с ней сухожилия или связки влияет на другие мышцы через компенсаторные механизмы тела [15]. Точно так же потеря использования определенной мышцы или группы мышц из-за прямого повреждения коры головного мозга может привести к компенсаторному использованию альтернативных мышц [16,17].То, как структурированы взаимосвязи опорно-двигательного аппарата и как они функционируют, напрямую ограничивает то, как повреждение определенной мышцы повлияет на опорно-двигательный аппарат в целом. Понимание этих взаимосвязей может дать столь необходимое понимание того, какие мышцы больше всего подвержены риску вторичной травмы из-за компенсаторных изменений, возникающих в результате очаговой травмы, тем самым давая основу для более комплексных подходов к реабилитации. Кроме того, понимание того, как кора головного мозга отображается не только на отдельные мышцы, но и на группы топологически близких мышц, может помочь в будущих эмпирических исследованиях взаимосвязи между очаговыми повреждениями (включая инсульт) моторной коры и риском вторичного повреждения.
Материалы и методы
Построение сети
Используя таблицы Хосфорда Muscle [18], мы построили скелетно-мышечный гиперграф, представив 173 кости (некоторые из которых на самом деле являются связками и сухожилиями) как узлы и 270 мышц как гиперребра, соединяющие эти узлы ( происхождение и точки прикрепления мышцы перечислены в таблице S9). Этот гиперграф также можно интерпретировать как двудольную сеть, в которой мышцы являются одной группой, а кости — второй группой (). Матрица заболеваемости C 173 × 270 скелетно-мышечной сети, таким образом, определяется как C ij = 1, если v i ∈ e j , и 0 в противном случае, где V = {v 1 , · · ·, v 173 } — это набор узлов (костей), а E = {e 1 , · · ·, e 270 } — набор гиперребер (мышц).Это гиперграфическое представление тела устраняет большую часть сложности опорно-двигательного аппарата, кодируя только то, какие мышцы прикрепляются к каким костям. Весь анализ применялся только к одной половине (левой или правой) тела, потому что каждое полушарие головного мозга контролирует только противоположную сторону тела. Поэтому мы еще больше упростили нашу модель, допустив лево-правую симметрию; на любых фигурах, на которых изображены обе половины тела, вторая половина присутствует исключительно для визуальной интуиции.
Схема представлений данных и вычислительных методов.(a) Скелетно-мышечная сеть была сначала преобразована в двудольную матрицу, где 1/0 указывает на наличие / отсутствие связи между мышцами и костями. (b) Сообщества топологически связанных мышц идентифицируются путем (1) преобразования гиперграфа в граф мышца-мышцы, в котором каждая запись кодирует количество общих костей каждой пары мышц, и (2) впоследствии мышцы были разбиты на сообщества , в котором составляющие члены более плотно связаны с другими членами своего сообщества, чем с членами других сообществ.(c) Чтобы облегчить пертурбацию, опорно-двигательная сеть была физически встроена, так что кости (узлы) изначально располагались в их правильных анатомических положениях. (d) Чтобы понять влияние отдельных мышц на взаимосвязанную систему, все узлы, связанные выбранным гиперребром, были возмущены в четвертом пространственном измерении.
Костно-ориентированный график A и мышечный график B () — это просто одномодовые проекции C. Проекция на кости A = C T C, а проекция на мышцы B = CC T .Затем диагональные элементы были установлены равными нулю, в результате чего мы получили взвешенную матрицу смежности [5]. Мы получили оценочные анатомические местоположения центра масс каждой мышцы (и кости), изучив анатомические тексты [19] и оценив x-, y- и z-координаты для отображения на графическом представлении человеческого тела ().
Расчет оценки воздействия
Для измерения потенциальной функциональной роли каждой мышцы в сети мы использовали классический пертурбативный подход. Чтобы максимизировать простоту и потенциал для фундаментальной интуиции, мы смоделировали опорно-двигательную систему как систему точечных масс (костей) и пружин (мышц).Мы растянули мышечную пружину и наблюдали влияние этого возмущения на расположение всех остальных мышц. Физически, чтобы повредить мышцу, мы смещали все кости, связанные с этой мышцей, на одинаковую величину и в одном направлении, растягивая мышцу, и удерживали эти кости на новом месте. Этот процесс также математически эквивалентен простому изменению жесткости пружины, относящейся к конкретной мышечной пружине. Затем системе позволяли достичь равновесия. Мы зафиксировали кости по средней линии и по периферии в пространстве, чтобы предотвратить смещение системы.Чтобы количественно оценить влияние возмущения этой единственной мышечной пружины, мы определили движение узла и следующим образом:
mid2r → idt2 = ∑j ≠ i∈V [SijAijl → ij (xij-‖l → ij‖)] — βdr → idt,
где l ij — смещение между узлами i и j, x ij — невозмущенное расстояние между узлами i и j, m — масса узла (которую мы установили равной единице для всех узлов в сети) , β = 1 — коэффициент демпфирования, r i — положение узла i , A — взвешенная матрица смежности графа, ориентированного на кости, и S ij представляет собой сумму всех сил пружин мышцы, к которым подключены узлы i и j.Чтобы нормализовать восстанавливающую силу мышц на узлах, пусть сила пружины мышцы q 1 / (k — 1). Здесь мы установили, что все кости имеют равный вес, а все мышцы имеют одинаковую жесткость пружины, что является упрощением реальной физической анатомии. Для обсуждения того, как учесть дополнительные физические свойства, такие как масса кости и мышечная сила, а также дополнительные результаты с использованием этих свойств, см. S5 Text. Более того, образцы траекторий, которые дают интуитивное представление о динамике нашей модели, были включены в вспомогательную информацию (S8 рис.).
Чтобы измерить потенциальную функциональную роль каждой мышцы в сети, мы растянули гиперреберь мышцы и измерили влияние возмущения на остальную часть сети. Вместо того, чтобы возмущать сеть в каком-то произвольном трехмерном направлении, мы расширили объем нашей симуляции до четвертого измерения. При возмущении мышцы мы смещали все узлы (кости), содержащиеся в этом гиперребре мышцы, на постоянный вектор в четвертом измерении и удерживали их этим смещением ().Затем возмущение в ответ прокатилось по сети пружин. Мы последовательно растягивали каждую мышечную гиперреберь и определили оценку воздействия этого возмущения как общее расстояние, на которое все узлы опорно-двигательной сети перемещаются от их исходных положений. Величина смещения — это суммарное смещение по всем временным точкам, от начала возмущения до соответствующего отсечки для времени уравновешивания. Здесь мы нашли равновесие системы, позволив динамике выровняться в течение достаточного периода времени.Обратите внимание, что равновесие также может быть решено с использованием стационарного, нединамического подхода; мы решили использовать динамику в этом случае для более широкой поддержки будущих приложений.
Отклонение оценки удара
Для каждой мышцы мы рассчитали индекс, который количественно определяет, насколько оценка воздействия этой мышцы отклоняется от ожидаемой с учетом степени ее гиперребер; мы называем этот показатель «ударным отклонением». Мы начинаем с построения нулевой модели, которая определяет ожидаемое воздействие при наборе статистических допущений.В текущем исследовании мы использовали несколько различных нулевых моделей с разными наборами допущений, которые мы подробно рассмотрим в следующих разделах. Отклонение воздействия рассчитывалось следующим образом: мы вычисляли среднее значение, стандартное отклонение и 95% доверительные интервалы (ДИ) для каждой из категорий степени нулевого гиперграфа из ансамбля из 100 нулевых гиперграфов. Расстояние от данной мышцы до среднего значения ± 95% доверительного интервала (в зависимости от того, что ближе всего) было вычислено и разделено на стандартное отклонение этого распределения степеней нулевого гиперграфа.Таким образом, мы рассчитали отклонение от ожидаемого значения в стандартных отклонениях (аналогично z-баллу). содержит мышцы, которые лежат за пределами 95% ДИ коэффициентов отклонения относительно степени их гиперребер. Мышцы можно естественным образом сгруппировать в соответствии с гомункулом, грубым одномерным представлением того, как контрольные области мышц группируются в моторную кору. Для данной группы гомункулов мы рассчитали коэффициент отклонения как количество мышц с положительным отклонением, деленное на общее количество мышц в группе ().
Таблица 1
Мышцы с большей или меньшей нагрузкой, чем ожидалось в модели нулевого гиперграфа.Мышцы на левой стороне оказывают меньшее влияние, чем ожидалось, учитывая степень их гиперребер: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее влияние, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартных отклонений превышает среднее значение, в порядке от наибольшего к наименьшему.В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 20 | Брахиалис | ||||||||||
| 2 | 145 | Букцинатор | 22 | Anconeus | ||||||||||||
| 3 | 148 | 12 | Teres minor | |||||||||||||
| 5 | 11 | Infraspinatus | ||||||||||||||
| 6 | 13 | Te res major | ||||||||||||||
| 8 | 10 | Supraspinatus | ||||||||||||||
| 8 | 16 | большой грудной мышцы longus | ||||||||||||||
| 11 | 161 | Piriformis | ||||||||||||||
| 10 | 31 | Brachioradialis 9002 | 31 | Brachioradialis
| ||||||||||||
| Порядок ранжирования | Меньшее воздействие, чем ожидалось | Более эффективное воздействие, чем ожидалось | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число | Гигантское ребро | Название мышцы | Гибкое ребро | Название мышцы | 3 | Колено | ||||||
| 2 | 17 | Глазные мышцы | 4 | Бедро | ||||||||
| 3 | 18 | Мышцы лица | 19 | Мышцы губ | 7 | Локоть | ||||||
| 5 | 8 | Запястье | ||||||||||
| 6 | 10 | Мизинец | ||||||||||
| 8 | 21 | Язык | ||||||||||
Обнаружение сообщества
Чтобы понять как функцию, так и контроль над опорно-двигательной системой, мы были заинтересованы в определении групп плотно связанных между собой мышц с использованием подхода, основанного на данных.Мы выполнили тип обнаружения сообщества, максимизируя функцию качества модульности, введенную Ньюманом [20]:
Q = ∑ijBij − γPijδ (gi, gj),
где P ij — ожидаемый вес ребра в нулевой модели Ньюмана-Гирвана, узел i назначен сообществу g i , узел j назначен сообществу g j , а δ — дельта-функция Кронекера. Путем максимизации Q мы получили разделение узлов (мускулов) на сообщества, так что узлы в одном сообществе были более плотно взаимосвязаны, чем ожидалось в сетевой нулевой модели (справа).
Здесь мы также использовали параметр разрешения для настройки размера и количества обнаруженных сообществ таким образом, чтобы количество обнаруженных сообществ соответствовало количеству групп внутри гомункула, для прямого сравнения. В частности, мы использовали параметр разрешения γ = 4,3, чтобы разделить мышечно-ориентированную матрицу на 22 сообщества (см. Таблицу S8). Мы начали с переопределения исходной мышечно-ориентированной матрицы B, следуя Jutla et al. [21]; мы положим k = Σ i B i , j , а затем мы применили локально жадный алгоритм максимизации модульности типа Лувена к скорректированной матрице B ‘= B-γkTk∑ jkj [22].
Указанный выше метод обнаружения сообществ недетерминирован [23]. То есть одно и то же решение не будет достигнуто при каждом отдельном запуске алгоритма. Следовательно, необходимо убедиться, что используемые назначения сообщества хорошо представляют сеть, а не только локальный максимум ландшафта. Поэтому мы максимально увеличили функцию качества модульности в 100 раз, получив 100 различных заданий от сообщества. Из этого набора решений мы определили надежную репрезентативную консенсусную структуру сообщества [24].S1 Рис. Показывает, как обнаруженные сообщества изменяются в зависимости от параметра разрешения для мышечно-ориентированной сети.
Сетевые нулевые модели
Мы используем реконструированные графы в качестве нулевой модели, с которой сравниваем эмпирические данные. В частности, мы построили нулевой гиперграф, перемонтировав мышцы, которым присвоена одна и та же категория (определенная ниже) равномерно и случайным образом. Таким образом, мышцы мизинца будут перестроены только внутри мизинца, и аналогично для мышц других категорий.Важно отметить, что этот метод также сохраняет степень каждой мышцы, а также степень распределения всего гиперграфа.
Таблица 3
Категории гомункулов и связанные с ними идентификационные номера.
| Идентификатор категории | Название категории | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Пальцы | ||||||||||||
| 2 | Лодыжка | 5 | Ствол | ||||||||||
| 6 | Плечо | ||||||||||||
| 7 | Колено | ||||||||||||
| 8 | Запястье | ||||||||||||
| 9 | Безымянный палец | ||||||||||||
| 12 | Средний палец | ||||||||||||
| 13 | Указательный палец | ||||||||||||
| 14 | Большой палец | ||||||||||||
| 15 | Бровь | 15 | Бровь | 17 | веко и глазное яблоко | ||||||||
| 18 | F ace | ||||||||||||
| 19 | Губы | ||||||||||||
| 20 | Челюсть | ||||||||||||
| 21 | Язык | ||||||||||||
| Категории 22 | Глотание мышц |
| Мышцы | Недели восстановления | Источник | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Triceps brachii | 4 | Bateman (1962) | |||||||||||
| 9026 | Latissimus dorsi | 12 | Nagda (2011) | ||||||||||
| Двуглавая мышца плеча | 12 | Zafra (2009) | |||||||||||
| Голеностопный сустав | 2 | McC14 | Torg (1982) | ||||||||||
| Зубья | 0 | Beachy (2004) | |||||||||||
| Плечо | 2 | Bateman (1962) | |||||||||||
| 9026 | |||||||||||||
| Бедро | 12 | Niemuth (2005) | |||||||||||
| Глаз / веко | 1,4 | Leivo (2015) | |||||||||||
| Колено | 8 | Колено | 8 | 4Колено | 8 | 8 | Fleisig (2012) | ||||||
| Запястье / кисть | 1.4 | Логан (2004) |
Данные области соматотопической репрезентации
Мы вычислили корреляцию между отклонением оценки воздействия и площадью соматотопической репрезентации, посвященной определенной группе мышц. Ареалы представительства были собраны из двух отдельных источников [38,39]. Тома и соответствующие ссылки перечислены в. В обоих исследованиях испытуемых просили многократно артикулировать сустав, и регистрировались объемы областей первичной моторной коры, которые подверглись наибольшему изменению в BOLD-сигнале.Затем мы рассчитали коэффициент корреляции между объемами коры и средним воздействием всех мышц, связанных с этим суставом, как определено в таблицах Hosford Muscle. Мы обнаружили значительную линейную корреляцию между двумя показателями с помощью функции MATLAB, fitlm.m, с параметром «Robust», установленным на «on».
Таблица 5
Размеры и источники объема соматотопической репрезентации первичной моторной коры.
| Мышцы | Объем (мм 3 ) | Артикул | ||||
|---|---|---|---|---|---|---|
| Большой палец | 1,390 | Indovina (2000) | ||||
| Индекс | ||||||
| Средний | 650 | Indovina (2000) | ||||
| Рука | 5,566 | Alkadhi (2002) | ||||
| Пальцы | 2,972 | Alkadhi (2002) | ||||
| Elbow | 2,267 | Alkadhi (2002) |
Результаты
Структура опорно-двигательного аппарата человека
Для исследования структурных взаимосвязей костно-мышечной системы человека использовалась гипер-мышечная система. подход.Основываясь на последних достижениях сетевой науки [5], мы исследовали опорно-двигательную систему как сеть, в которой кости (сетевые узлы) соединены друг с другом мышцами (сетевые гиперребра). Гиперребро — это объект, соединяющий несколько узлов; мышцы соединяют несколько костей через точки начала и вставки. Степень гиперребра k равна количеству узлов, которые оно соединяет; таким образом, степень мышцы — это количество костей, с которыми она контактирует. Например, трапеция — это гиперребро высокой степени, которое связывает 25 костей лопатки и позвоночника; И наоборот, приводящий большой палец представляет собой гиперребро низкой степени, которое связывает 7 костей руки ().Набор гиперребер (мышц) с общими узлами (костями) называется гиперграфом: граф H = (V, E) с N узлами и M гиперребрами, где V = {v 1 , …, v N } — это набор узлов, а E = {e 1 , …, e M } — набор гиперребер.
Структура гиперграфа.(a) Слева: анатомический рисунок трапеции. Справа: преобразование трапеции в гиперребро (красный; степень k = 25), соединяющее 25 узлов (костей) на голове, плече и позвоночнике.(b) Приводящая мышца большого пальца, соединяющая 7 костей руки. (в) Пространственная проекция распределения степеней гиперребер на тело человека. Гиперребра высокой степени сконцентрированы в основном в ядре. (d) Скелетно-мышечная сеть отображается в виде двудольной матрицы (1 = соединена, в противном случае 0). (e) Распределение степени гиперребра для гиперграфа опорно-двигательного аппарата, которое значительно отличается от ожидаемого в случайном гиперграфе. Данные доступны для (e) в DOI : 10.5281 / zenodo.1069104.
Представление опорно-двигательного аппарата человека в виде гиперграфа позволяет количественно оценить его структуру (). Мы заметили, что распределение степени гиперребер носит тяжелый характер: большинство мышц связывают 2 кости, а несколько мышц связывают многие кости (). Наклон распределения степеней существенно отличается от такового случайных сетей (двухвыборочный критерий Колмогорова-Смирнова, KS = 0,37, p <0,0001, см. Материалы и методы) [5], что свидетельствует о наличии мышц неожиданно низкой и высокий градус ().
Функция опорно-двигательного аппарата человека
Чтобы исследовать функциональную роль мышц в опорно-двигательном аппарате, мы использовали упрощенную модель опорно-двигательного аппарата и выяснили, может ли эта модель генерировать полезные клинические корреляты. Мы реализовали физическую модель, в которой кости образуют основной каркас тела, а мышцы скрепляют эту структуру. Каждый узел (кость) представлен как масса, пространственное расположение и движение которой физически ограничены гиперребрами (мышцами), с которыми он связан.В частности, кости — это точки, расположенные в их центре масс, заимствованные из текстов по анатомии [19], а мышцы — это пружины (затухающие гармонические осцилляторы), соединяющие эти точки [40,41]; для гиперребра степени k мы создали k (k — 1) / 2 пружин, связывающих k узлов. То есть для мышцы, соединяющей k костей, мы разместили пружины так, чтобы каждая из k мышц имела прямое пружинное соединение с каждой из других k — 1 костей.
Затем мы взволновали каждую из 270 мышц тела и вычислили их оценку воздействия в сети (см. Материалы и методы и).Когда мышца физически смещается, она вызывает волнообразное смещение других мышц по всей сети. Оценка удара мышцы — это среднее смещение всех костей (и косвенно мышц) в результате его первоначального смещения. Мы наблюдали значительную положительную корреляцию между степенью мышц и оценкой воздействия (F (1,268) = 23,3, R 2 = 0,45, p <0,00001;), предполагая, что структура гиперребра определяет функциональную роль мышц в опорно-двигательной сети.Мышцы с большим количеством точек прикрепления и начала имеют большее влияние на опорно-двигательный аппарат, когда они нарушены, чем мышцы с небольшим количеством точек прикрепления и начала [42]. Мы можем получить более подробное представление о результатах этого анализа, подробно изучив взаимосвязь между оценкой воздействия и статистическими показателями топологии сети. На рис. S11 мы показываем, что функция сети, измеренная с помощью оценки воздействия, значительно коррелировала со средней длиной кратчайшего пути.Хотя сетевая статистика статична по своей природе, их функциональная интерпретация обеспечивается пертурбативным моделированием динамики системы.
Исследование опорно-двигательного аппарата.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 37,3, R 2 = 0,757, p <0.0001). Заштрихованные области указывают 95% доверительный интервал, а точки данных масштабируются в соответствии с количеством включенных мышц. График пронумерован следующим образом: трицепс (1), большой палец (2), широчайшая мышца спины (3), двуглавая мышца плеча (4), лодыжка (5), шея (6), челюсть (7), плечо (8). ), большая круглая (9), бедра (10), глазные мышцы (11), колено (12), локоть (13), запястье / кисть (14). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве руководства к интерпретации важно отметить, что оценка воздействия, хотя и значительно коррелирует со степенью мускулатуры, не может быть им полностью предсказана ().Вместо этого, структура локальной сети, окружающей мышцу, также играет важную роль в ее функциональном воздействии и способности восстанавливаться. Чтобы лучше количественно оценить влияние этой структуры локальной сети, мы спросили, существуют ли мышцы, которые имели значительно более высокие или значительно более низкие оценки воздействия, чем ожидалось в нулевой сети. Мы определили положительное (отрицательное) отклонение оценки воздействия, которое измеряет степень, в которой мышцы более (менее) воздействуют, чем ожидалось в сетевой нулевой модели (см. Материалы и методы).В результате этого расчета был получен показатель, который выражает влияние конкретной мышцы по сравнению с мышцами с идентичной степенью гиперребер в нулевой модели. Другими словами, этот показатель учитывает сложность конкретной мышцы ().
Является ли эта математическая модель клинически актуальной? Отвечает ли тело по-разному на травмы мышц с более высокой оценкой удара, чем на мышцы с более низкой оценкой удара? Чтобы ответить на этот вопрос, мы оценили потенциальную взаимосвязь между воздействием на мышцы и временем восстановления после травмы.В частности, мы собрали данные о спортивных травмах и времени между получением травмы и возвращением в спорт. Мы отметили, что время восстановления сильно коррелировало с отклонениями оценки удара отдельной мышцы или группы мышц (F (1,12) = 37,3, R 2 = 0,757, p <0,0001;), предполагая, что наши Математическая модель предлагает полезный клинический биомаркер реакции сети на повреждение. Мы отмечаем, что важно учитывать тот факт, что восстановление может быть медленнее у человека, которому требуются максимальные усилия в спортивном спорте, по сравнению с человеком, который стремится только функционировать в повседневной жизни.Поэтому, чтобы обобщить наши результаты для всего населения, мы также изучили данные о времени восстановления, полученные от не спортсменов, и представляем эти дополнительные результаты во вспомогательной информации (текст S6).
Наконец, чтобы получить интуитивное представление о том, как очаговая травма может вызывать отдаленные эффекты, потенциально замедляющие выздоровление, мы рассчитали влияние мышц голеностопного сустава и определили, какие другие мышцы были затронуты сильнее всего. То есть для каждой отдельной мышцы голеностопного сустава мы рассчитали воздействие на каждую из оставшихся 264 мышц, не относящихся к голеностопному суставу, а затем усреднили это значение по всем мышцам голеностопного сустава.Из 264 мышц, не связанных с голеностопным суставом, единственная мышца, на которую больше всего воздействует нарушение мышц голеностопного сустава, — это двуглавая мышца бедра, а второй по величине — латеральная широкая мышца колена. Кроме того, мышца бедра, на которую больше всего влияет нарушение, — это камбаловидная мышца.
Контроль опорно-двигательного аппарата человека
Какова взаимосвязь между функциональным воздействием мышцы на тело и нейронной архитектурой, которая влияет на контроль? Здесь мы исследуем отношения между опорно-двигательной системой и первичной моторной корой.Мы исследовали область карты коркового изображения головного мозга, посвященную мышцам с низким или высоким воздействием, опираясь на анатомию моторной полосы, представленной в моторном гомункуле [43] (), грубое одномерное представление тела в головном мозге [44 ]. Мы заметили, что области гомункула по-разному контролируют мышцы с положительной и отрицательной оценкой отклонения воздействия (). Более того, мы обнаружили, что области гомункула, контролирующие только положительно (отрицательно) отклоняющиеся мышцы, как правило, располагаются медиально (латерально) на моторной полосе, что предполагает наличие топологической организации ожидаемого воздействия мышцы на нервную ткань.Чтобы исследовать эту закономерность более глубоко, для каждой области гомункула мы рассчитали коэффициент отклонения как процент мышц, которые положительно отклонились от ожидаемой оценки воздействия (т. Е. Значение 1 для бровей, глаз, лица и значение 0 для колена , бедро, плечо; см.). Мы обнаружили, что коэффициент отклонения достоверно коррелировал с топологическим положением на моторной полосе (F (1,19) = 21,3, R 2 = 0,52, p <0,001;).
Зондирование опорно-двигательного аппарата.(а) Гомункул первичной моторной коры, сконструированный Пенфилдом.(b) Коэффициент отклонения достоверно коррелирует с гомункулярной топологией (F (1,19) = 21,3, R 2 = 0,52, p <0,001), уменьшаясь от медиального (область 0) к латеральному (область 22). (c) Отклонение оценки воздействия достоверно коррелирует с объемом активации моторной полосы (F (1,5) = 14,4, R 2 = 0,743, p = 0,012). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. График пронумерован следующим образом: большой палец (1), указательный палец (2), средний палец (3), рука (4), все пальцы (5), запястье (6), локоть (7).(d) Корреляция между пространственным упорядочением категорий гомункулов Пенфилда и линейной мышечной координатой из многомерного масштабного анализа (F (1,268) = 316, R 2 = 0,54, p <0,0001). Данные доступны в DOI : 10.5281 / zenodo.1069104.
В качестве более строгой проверки этой взаимосвязи между воздействием мышцы на сеть и нейронной архитектурой мы сопоставили данные о физических объемах функциональной активации на основе МРТ на моторной полосе, которые предназначены для отдельных движений (например,g., сгибание пальцев или моргание глаз). Объемы активации определяются как воксели, которые активируются (определяемые сигналом, зависящим от уровня кислорода в крови) во время движения [38,39]. Важно отметить, что мы обнаружили, что объем функциональной активации независимо предсказывает отклонение оценки удара мышц (, F (1,5) = 14,4, p = 0,012, R 2 = 0,743), что согласуется с интуицией, что мозг будет посвятите больше места в сером веществе контролю над мышцами, которые более эффективны, чем ожидалось в нулевой модели.Опять же, отклонение от удара — это показатель, который учитывает степень гиперреберности конкретной мышцы и относится к удару мышц с идентичной степенью гиперребер в нулевой модели. Таким образом, ударное отклонение измеряет топологию локальной сети, а не просто непосредственные соединения рассматриваемой мышцы.
В качестве финального теста этой взаимосвязи мы спросили, оптимально ли сопоставлена стратегия нервного контроля, воплощенная в моторной полоске, с группами мышц. Мы построили мышечно-ориентированный граф, соединив две мышцы, если они касаются одной и той же кости (, слева).Мы наблюдали наличие групп мышц, плотно связанных друг с другом, имеющих общие кости. Мы извлекли эти группы, используя метод кластеризации, разработанный для сетей [45,46], который обеспечивает разделение мышц на сообщества на основе данных (справа). Чтобы сравнить структуру сообщества, присутствующую в мышечной сети, с архитектурой системы нейронного контроля, мы рассмотрели каждую из 22 категорий моторного гомункула [18] как отдельное нейронное сообщество и сравнили эти присвоения сообществу, основанные на мозге, с заданиями сообщества. полученный из управляемого данными раздела мышечной сети.Используя коэффициент Рэнда [47], мы обнаружили, что распределение сообществ как для гомункула, так и для мышечной сети было статистически схожим (z Rand > 10), что указывает на соответствие между модульной организацией опорно-двигательного аппарата и структурой гомункула. Например, трицепс плеча и двуглавая мышца плеча принадлежат к одной гомункулярной категории, и мы обнаружили, что они также принадлежат к одному и тому же сообществу топологических мышечных сетей.
Затем, поскольку гомункулус имеет линейную топологическую организацию, мы спросили, был ли порядок сообществ внутри гомункула () подобен управляемому данными упорядочению групп мышц в теле, как определено с помощью MDS [48].Из сети, ориентированной на мышцы (), мы получили матрицу расстояний, которая кодирует наименьшее количество костей, которые необходимо пройти, чтобы перейти от одной мышцы к другой. MDS этой матрицы расстояний выявил одномерные линейные координаты для каждой мышцы, так что топологически близкие мышцы были близко друг к другу, а топологически далекие мышцы были далеко друг от друга. Мы заметили, что линейная координата каждой мышцы значительно коррелирует с ее категорией гомункула (, F (1,268) = 316, p <0.0001, R 2 = 0,54), что указывает на эффективное отображение между нейронным представлением мышечной системы и сетевой топологией мышечной системы в теле.
Наши результаты демонстрируют соответствие между топологией гомункула и упорядочением мышц на основе данных, полученным с учетом топологических расстояний между ними. Этот результат можно интерпретировать одним из двух способов: одна разумная гипотеза состоит в том, что, поскольку большинство соединений в опорно-двигательной сети являются короткодействующими, открытие в основном обусловлено связями ближнего действия.Вторая разумная гипотеза состоит в том, что, хотя соединения ближнего действия являются наиболее распространенными, соединения дальнего действия образуют важные внутримодульные связи, которые помогают определять организацию сети. Чтобы выбрать между этими двумя гипотезами, мы рассмотрели два варианта нашего эксперимента MDS: один включает только соединения, длина которых меньше средней длины соединения, а другой — только соединения, длина которых превышает среднюю длину соединения. Мы обнаружили, что упорядочение на основе данных, полученное только из коротких и только из длинных соединений, привело к значительным корреляциям с гомункулярной топологией (F (1,268) = 24.9, R 2 = 0,085, p <0,0001 и F (1,268) = 5, R 2 = 0,018, p = 0,026 соответственно). Примечательно, что включение как длинных, так и коротких соединений приводит к более сильной корреляции с гомункулярной топологией, чем рассмотрение любого из них независимо, что предполагает зависимость от соединений любой длины. В будущем было бы интересно проверить, в какой степени эта межсетевая карта изменяется у людей с двигательными нарушениями или изменениями после инсульта.
Обсуждение
Структура опорно-двигательного аппарата человека
Представляя сложную взаимосвязь опорно-двигательного аппарата в виде сети костей (представленных узлами) и мышц (представленных гиперребрами), мы получили ценную информацию об организации человеческого организма. тело. Изучение анатомических сетей с использованием аналогичных методов становится все более распространенным в области эволюционной биологии и биологии развития [10]. Однако этот подход обычно применялся только к отдельным частям тела, включая руку [49], голову [11] и позвоночник [12], тем самым предлагая понимание того, как развивалась эта часть организма [50, 51].Более того, даже после моделирования всей мускулатуры тела [13] и нервно-мышечно-скелетной системы [14] в более общем плане некоторые количественные утверждения могут остаться неуловимыми, в значительной степени из-за отсутствия математического языка, на котором можно было бы обсуждать сложность взаимосвязи. узоры. В этом исследовании мы предлагаем явное и экономное представление всей опорно-двигательной системы в виде графа узлов и ребер, и это представление позволило нам точно охарактеризовать сеть в целом.
При моделировании системы как сети важно начать последующее исследование с характеристики нескольких ключевых архитектурных свойств. Одним из наиболее фундаментальных показателей структуры сети является ее распределение по степеням [52], которое описывает неоднородность подключения узла к его соседям таким образом, который может дать представление о том, как формировалась система [7]. Мы заметили, что степень распределения опорно-двигательного аппарата значительно отличается от ожидаемого в нулевом графе (), показывая меньше узлов высокой степени и переизбыток узлов низкой степени.Несоответствие между графами реальной и нулевой модели согласуется с тем фактом, что опорно-двигательная система человека развивается в контексте физических и функциональных ограничений, которые вместе определяют ее явно неслучайную архитектуру [53]. Распределение степеней этой сети показывает пик примерно на второй степени, за которым следует относительно тяжелый хвост узлов высокой степени. Последняя особенность обычно наблюдается во многих типах реальных сетей [54], чьи концентраторы могут быть дорогостоящими в разработке, обслуживании и использовании [55,56], но играют критическую роль в надежности системы, обеспечивая быстрое реагирование [55], буферизация изменчивости окружающей среды [57] и облегчение выживания и воспроизводства [58].Первая особенность — пик распределения — согласуется с интуицией, что большинство мышц опорно-двигательного аппарата соединяются только с двумя костями, в первую очередь для функции простого сгибания или разгибания в суставе. Напротив, есть только несколько мышц, которые требуют высокой степени для поддержки очень сложных движений, таких как поддержание выравнивания и угла позвоночника за счет одновременного управления движением многих костей. Эти ожидаемые результаты обеспечивают важную проверку модели, а также предлагают полезную визуализацию опорно-двигательного аппарата.
Скелетно-мышечная сеть характеризуется особенно интересным свойством, которое отличает ее от нескольких других реальных сетей: тем фактом, что она встроена в трехмерное пространство [59]. Это свойство не наблюдается в семантических сетях [60] или World Wide Web [61], которые кодируют отношения между словами, концепциями или документами в некоторой абстрактной (и, скорее всего, неевклидовой) геометрии. Напротив, опорно-двигательная система представляет собой объем с узлами, имеющими определенные координаты, и краями, представляющими физически протяженные ткани.Чтобы лучше понять физическую природу опорно-двигательного аппарата, мы исследовали анатомическое расположение мышц с разной степенью (). Мы заметили, что мышечные центры расположены преимущественно в торсе, обеспечивая плотную структурную взаимосвязь, которая может стабилизировать ядро тела и предотвратить травмы [62]. В частности, мышцы высокой степени группируются вокруг средней линии тела, рядом с позвоночником, вокруг таза и плечевого пояса, что согласуется с представлением о том, что для маневренности и устойчивости этих областей требуется совокупность мышц с различной геометрией и свойствами тканей [63 ].Действительно, мышцы в этих местах должны поддерживать не только сгибание и разгибание, но также отведение, приведение и внутреннее и внешнее вращение.
Важно отметить, что в костно-мышечной системе у разных людей существуют значительные различия, и не все анатомические атласы согласуются с наиболее репрезентативным набором точек вставки и происхождения. Представленные здесь результаты отражают то, как опорно-двигательная система была представлена в тексте, из которого она была построена [19], и поэтому обеспечивают только одно возможное сетевое представление опорно-двигательной системы.Чтобы оценить надежность наших результатов при разумных вариациях конфигурации опорно-двигательного аппарата, мы создали вторую опорно-двигательную сеть из альтернативного атласа [64]. Используя этот второй атлас, мы наблюдали последовательные результаты и сообщаем об этом дополнительном анализе в S3 Text.
Также важно отметить, что мы сопоставили первый атлас [19] в скелетно-мышечный граф, состоящий как из костных, так и из некостных узлов. Этот выбор уравнивает структурные роли костей и определенных сухожилий и связок, что, по общему признанию, является упрощением биологии.Одним из оправданий такого упрощения является то, что некостные структуры часто служат важными точками прикрепления мышц (то есть подошвенной фасцией стопы). Таким образом, разумно разделить опорно-двигательную сеть на две категории мышц и структур, которые служат точками прикрепления мышц, как мы это сделали здесь. Тем не менее, эта вторая категория довольно неоднородна по составу, и в будущей работе можно было бы также рассмотреть возможность построения многослойного графа с отдельным слоем, учитывающим каждый тип структуры мышечного прикрепления.Чтобы подтвердить, что наши результаты и интерпретации существенно не меняются из-за наличия некостных мышечных точек прикрепления, мы удалили такие точки в альтернативном атласе и отметили, что наши основные результаты все еще остаются в силе (см. Текст S3).
Функция опорно-двигательного аппарата человека
Чтобы лучше понять функциональную роль отдельной мышцы во взаимосвязанной опорно-двигательной системе, мы реализовали основанную на физике модель свойств импульсного отклика сети, кодируя кости как точечные массы, а мышцы как пружины [65].Примечательно, что эта очень упрощенная модель опорно-двигательного аппарата способна идентифицировать важные функциональные особенности. Хотя мышцы высокой степени также имели тенденцию иметь большое влияние на реакцию сети (), было несколько заметных отклонений от этой тенденции ().
Мышца, оказывающая наименьшее воздействие по сравнению с ожидаемой, — это orbicularis oculi, мышца, используемая для управления движением века. Эта мышца небольшая и относительно изолированная в теле, берут начало и прикрепляются к костям черепа.Мышцы лица в целом образуют плотное и изолированное сообщество, с немногими связями, выходящими за пределы этого сообщества. Эти факторы, вероятно, способствуют слабому воздействию этой мышцы, и аналогичный аргумент может быть сделан в отношении оставшихся двух мышц с меньшим воздействием, чем ожидалось, которые также являются мышцами лица.
Мышцы с большей нагрузкой, чем ожидалось, более многочисленны, но почти полностью расположены в верхней конечности или поясе верхней конечности. Длинный разгибатель запястья, anconeus, brachioradialis и brachialis мышцы являются собственными мышцами руки, последние три действуют в локтевом суставе.Все эти мышцы могут иметь более сильное воздействие, чем ожидалось в нулевой модели, потому что они могут прямо или косвенно влиять на движение многих костей запястья и кисти. Наблюдаемое сильное воздействие этих мышц может быть результатом того факта, что они контролируют движение конечности, а на конце конечности находится множество костей, движение которых напрямую зависит от этих мышц. Остальные ударные мышцы, за исключением грушевидной мышцы, прикрепляют верхнюю конечность к осевому скелету.Этими мышцами являются коракобрахиальная, подостная, надостная, подлопаточная, малая круглая, большая круглая и большая грудная мышцы. Эти мышцы, как и предыдущие четыре, обладают тем свойством, что они контролируют движение всей конечности, что, вероятно, способствует их влиянию. В отличие от предыдущей группы, эти мышцы также соединяются с осевым скелетом, что также может усиливать их воздействие. Многие из этих мышц берут свое начало на костях плечевого пояса и могут влиять на все другие мышцы плечевого пояса и, возможно, на все кости, связанные с этими мышцами.Такая же динамика, вероятно, существует в нижней конечности, что отражается наличием грушевидной мышцы тазового пояса. Подробное обсуждение того, как структура локальной сети и конфигурация мышц могут взаимодействовать с отклонением от удара, представлено в S7 Text. В дополнение к нашей работе, представленной во вспомогательной информации, дальнейшее понимание свойств этих выбросов может быть получено путем проведения экспериментов по тщательному изучению костей, на которые сильнее всего воздействует каждая из этих мышц.
Хотя сетевое представление системы может дать базовую физическую интуицию благодаря своей скупости и простоте, оно также остается безразличным ко многим деталям архитектуры и функций системы. Извечный вопрос, могут ли эти базовые модели сложных систем обеспечить точные прогнозы реальных результатов. Мы рассмотрели этот вопрос, изучив взаимосвязь между оценкой удара мышцы и количеством времени, которое требуется человеку для восстановления после травмы.Мы количественно оценили время восстановления, суммируя (i) время восстановления после первичной инвалидности, вызванной первоначальным мышечным повреждением, и (ii) время восстановления после любых вторичных нарушений, вызванных изменением использования других мышц в сети из-за первоначального травма мышц [66]. Мы обнаружили, что отклонение от ожидаемой оценки воздействия в нулевой сети значительно коррелировало со временем восстановления (), подтверждая представление о том, что очаговая травма может иметь длительные воздействия на организм из-за изначально взаимосвязанной природы опорно-двигательной системы.
Действительно, известно, что мышечные изменения в одной части тела влияют на другие группы мышц. Например, укрепление мышц бедра может привести к улучшению функции колена после замены коленного сустава [67]. Изменение мышечной функции в голеностопном суставе после растяжения связок может вызвать изменение функции мышц бедра [68, 69], результат, воспроизведенный нашей моделью (которая показала, что двуглавая мышца бедра и латеральная широкая мышца бедра больше всего пострадали от травмы голеностопного сустава), а повреждение мышц конечностей может приводят к вторичному повреждению диафрагмы [70].Наша модель предлагает математически принципиальный способ предсказать, какие мышцы с большей вероятностью будут иметь такое вторичное влияние на более крупную опорно-двигательную систему, а какие мышцы подвержены риску вторичного повреждения, учитывая первичное повреждение в определенном участке мышцы. В будущем было бы интересно проверить, могут ли эти прогнозы повлиять на полезные корректировки клинических вмешательств, явно принимая во внимание риск вторичного повреждения определенных мышц. Ранее профилактика вторичных мышечных травм в основном сводилась к криотерапии [71,72] и еще не была мотивирована такой механистической моделью.Наконец, важный вопрос, который следует задать, заключается в том, насколько эта конфигурация опорно-двигательного аппарата является эволюционно выгодной и как эволюционное давление могло оптимизировать воздействие на мышцы. Интуитивно можно было ожидать, что эволюционное давление снижает мышечную нагрузку, возможно, за счет увеличения мышечной избыточности. Тщательное исследование эволюционных преимуществ топологии костно-мышечной сети было бы интересной темой для будущей работы.
Контроль опорно-двигательного аппарата человека
Учитывая сложность опорно-двигательного аппарата и его критическую роль в выживании человека, естественно задать вопрос о том, как эта сеть управляется человеческим мозгом.Действительно, изучение моторного контроля имеет долгую и яркую историю [73], которая дала важную информацию о том, как мозг может успешно и точно совершать произвольные движения, несмотря на такие проблемы, как избыточность, шум [74], задержки сенсорной обратной связи. [75], неопределенность окружающей среды [76], нервно-мышечная нелинейность [77] и нестационарность [78]. Здесь мы использовали отличный, но дополняющий друг друга подход и спросили, как топология опорно-двигательного аппарата может быть отображена на топологии моторной полосы в коре головного мозга.Мы начали с того, что отметили, что ударное отклонение мышцы положительно коррелирует с размером коркового объема, предназначенного для его контроля (). Одна из интерпретаций этой взаимосвязи состоит в том, что те мышцы, которые своими непосредственными связями оказывают большее влияние, чем ожидалось в нулевой модели, имеют тенденцию контролировать более сложные движения и, следовательно, требуют большего количества нейронов для управления этими движениями [79]. Вторая интерпретация основана на эволюционном аргументе о том, что мышцы с большей нагрузкой нуждаются в большей избыточности в их системах управления [80], и эта избыточность принимает форму большей корковой области.
Помимо локальных объемов коры [81], можно также захотеть понять, в какой степени крупномасштабная организация опорно-двигательной сети отражает организацию контролирующей ее моторной полосы. Основываясь на недавнем применении методов выявления сообществ к изучению анатомии черепа [11,82,83], мы сообщили о модульной организации мышечной сети: группы мышц, в которых мышцы одной группы с большей вероятностью соединяются с одной. кроме мышц в других группах.Что еще интереснее, мы наблюдали, что мышечные сообщества очень похожи на известную группу мышц моторной полоски (справа): мышцы, которые имеют тенденцию соединяться с теми же костями, что и друг друга, также имеют тенденцию контролироваться той же частью моторной полоски. Более того, естественное линейное упорядочение мышечных сообществ — такое, что сообщества располагаются близко друг к другу на линии, если они имеют общие сетевые соединения — имитирует порядок контроля в моторной полосе (). Эти результаты дополняют важную предыдущую работу, предполагающую, что одномерная организация моторной полосы связана как со структурной, так и со функциональной организацией скелетно-мышечной сети [84,85].Фактически, результаты более конкретно предлагают определение оптимального сетевого управления на уровне сети: согласованность линейной карты от сообществ опорно-двигательного аппарата до сообществ моторных полос.
Наконец, мы исследовали физическое расположение кортикального контроля ударных мышц. Мы заметили, что мышцы с большим воздействием, чем ожидалось, при нулевом графике, как правило, контролируются средними точками на моторной полосе, в то время как мышцы с меньшим воздействием, чем ожидалось, обычно контролируются боковыми точками на моторной полосе ().Эта пространственная специфика указывает на то, что организация моторной полосы ограничивается физическим расположением тела, а также аспектами функционирования мышц. Предыдущие исследования изучали общее временное соответствие между корковой активностью и мышечной активностью во время движения [86], но мало что известно о топологическом соответствии.
Методологические соображения
Построение гиперграфа на основе опорно-двигательного аппарата человека требует допущений и упрощений, которые влияют на гибкость текущей модели.Наиболее заметным является разделение системы на две категории: мышцы и кости. Эти категории не содержат дополнительной информации и, следовательно, не учитывают особенности внутренней архитектуры мышцы или кости. Это упрощение вводит несколько ограничений для пертурбативной модели, включая возможность моделирования функциональной архитектуры сложных мышц или мышц, обладающих способностью независимо сокращать подмножество волокон. Например, двуглавая двуглавая мышца плеча берет начало как на лопатке, так и на супрагленоидном бугорке, и можно сокращать волокна одной головки отдельно от волокон другой головки.Дальнейшая работа может расширить нашу структуру моделирования, чтобы представить эту сложную функциональную архитектуру. Более того, немышечные структуры мягких тканей, важные для опорно-двигательного аппарата, не могут быть четко учтены. Эти структуры, включая сухожилия и связки, могут быть либо (1) закодированы как кости, как в основной текстовой сети, либо (2) исключены из сети, как в приложении; ни один из вариантов не является полностью анатомически точным.
В случае костей модель не может учесть взаимодействия кость-кость (суставы).Большинство мышц действуют на суставы, и исключение суставов затемняет специфическую функцию мышц. То есть модель учитывает тот факт, что мышцы перемещают кости, но не то, как они движутся или в каком направлении. В пертурбативном моделировании отсутствие ограничений на суставы позволяет размещать кости под неестественными углами относительно соседних костей. Кроме того, кости моделируются как точечные массы, которые в пертурбативном моделировании могут позволить костям проходить траектории, связанные с прохождением через пространство, которое на самом деле занято другой костью.Дальнейшая работа может расширить нашу структуру моделирования, чтобы учесть эти дополнительные биофизические ограничения.
Аналитические данные, полученные с помощью этой модели, являются результатом входных данных. Поскольку индивидуальные вариации существуют в опорно-двигательном аппарате, они также существуют и в мышечных воздействиях. Мы попытались использовать два набора входных данных, чтобы оправдать наши основные выводы, но эти результаты не могут быть обобщены на все здоровые конфигурации опорно-двигательного аппарата. В частности, степень мышц, подверженная индивидуальным изменениям, может повлиять на воздействие этой мышцы.Каким образом нормативные индивидуальные вариации в степени мышечной массы связаны с вариациями прогнозируемого воздействия на мышцы, является важным вопросом, который, тем не менее, выходит за рамки настоящего исследования.
Наконец, опорно-двигательный аппарат человека представляет собой сложную и плотно взаимосвязанную сеть. Ни мышцы, ни кости не функционируют как независимые образования. Таким образом, трудно отделить функцию отдельной мышцы от воздействия окружающих мышц. Независимость мышц может быть частично устранена соответствующим выбором нулевой модели, и наши результаты остаются в силе при различных вариантах.Тем не менее, при интерпретации этих результатов следует учитывать представление о том, что мышцы — и факторы воздействия — не являются действительно независимыми.
Вспомогательная информация
S1 Text
Альтернативные нулевые модели.Этот текстовый файл подробно описывает построение альтернативных нулевых моделей.
(DOCX)
S2 Text
Разрешение обнаружения сообщества.Этот файл содержит описание выбора параметра разрешения обнаружения сообщества.
(DOCX)
S3 Text
Альтернативная опорно-двигательная сеть.Этот файл содержит описание альтернативной опорно-двигательной сети.
(DOCX)
S4 Текст
Динамика костей в результате мышечного пертурбации.(DOCX)
S5 Text
Учет веса костей и силы мышц.(DOCX)
S6 Text
Анализ восстановления мышц, не связанных со спортсменами.(DOCX)
S7 Text
Структура локальной сети и отклонение от воздействия.(DOCX)
S1 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в случайно перестроенных гиперграфах.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы с правой стороны оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений выше среднего в порядке от наибольшего до наименьшего. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S2 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению со случайно перестроенными гиперграфами.Эта нулевая модель потребовала случайной перестройки мускулов внутри гиперграфа с сохранением степени.Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью. Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S3 Таблица
Мышцы с большей или меньшей степенью воздействия, чем ожидалось в гиперграфах, случайным образом перепрограммированы в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень.Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гипреберья: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение, в порядке от наибольшего к наименьшему. В этой таблице показаны мышцы, которые имели наибольшую положительную и наибольшую отрицательную разницу в воздействии, по сравнению с контрольными группами подобранной степени.
(XLSX)
S4 Таблица
Категории гомункулов, мышцы-члены которых либо все оказывают большее влияние, чем ожидалось, либо все оказывают меньшее влияние, чем ожидалось, по сравнению с гиперграфами, случайно перестроенными в пределах их категории гомункулов.Эта нулевая модель потребовала случайной перестройки мускулов в пределах их категории гомункулов, сохраняя степень. Категории слева полностью состоят из мышц с меньшим воздействием, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.Категории справа полностью состоят из мышц, оказывающих большее воздействие, чем ожидалось, по сравнению с контрольными группами с подобранной степенью.
(XLSX)
S5 Таблица
Мышцы с большей или меньшей нагрузкой, чем ожидалось в случайном гиперграфе.Эта нулевая модель требовала случайного назначения связей между костями и мышцами, сохраняя только общий уровень, а не индивидуальный уровень мышц. Мышцы на левой стороне оказывают меньшее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие больше единицы.96 стандартных отклонений ниже среднего, что указывает на то, что они лежат за пределами 95% доверительного интервала распределения. Мышцы на правой стороне оказывают большее воздействие, чем ожидалось, учитывая степень их гиперреберности: их воздействие более чем на 1,96 стандартного отклонения превышает среднее значение и упорядочено от наибольшего к наименьшему.
(XLSX)
S6 Таблица
Объемы мышц подсети голени.Здесь мы включаем название мышцы (столбец 1), объем мышцы (в см 3 ; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S7 Таблица
Масса костей подсети ноги.Здесь мы включаем название кости (столбец 1), массу кости (в граммах; столбец 2) и ссылку, из которой была взята оценка.
(XLSX)
S8 Таблица
Присвоенные категории гомункулов и основанное на данных распределение мышц в сообществе.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S9 Таблица
Гиперграф мышц и костей из таблиц Hosford Muscle [18], используемых в основном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S10 Таблица
Гиперграф мышц и костей из атласа Гранта [64], использованный в дополнительном тексте.Также доступно по адресу DOI: 10.5281 / zenodo.1069104.
(XLSX)
S1 Рис.
Обнаружение сообщества с разными параметрами разрешения.На этом рисунке показано, как выбор параметра разрешения во время обнаружения сообществ изменит количество и размер обнаруженных сообществ.С увеличением параметра разрешения размер отдельных сообществ уменьшается, а количество сообществ увеличивается. (a-d) Обнаружение сообщества для сети, ориентированной на мышцы, с использованием значений γ, равных 1, 2, 8 и 16 соответственно. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S2 Рис.
Обнаружение сообщества с разными параметрами разрешения.Этот рисунок иллюстрирует стабильность при выбранном параметре настройки γ = 4.3. Здесь мы исследуем разбиения, созданные из близких параметров разрешения γ = 4,2 и γ = 4,4. Визуально кажется, что все три раздела имеют похожую структуру. Два соседних раздела также математически схожи: z-оценка коэффициента Рэнда [47] z Rand (γ = 4,2, γ = 4,3) = 105, z Rand (γ = 4,3, γ = 4,4) = 110 и z Rand (γ = 4,2, γ = 4,4) = 105. Окончательная структура сообщества для каждого γ представляет собой согласованное разделение 100 отдельных прогонов алгоритма обнаружения сообщества.
(EPS)
S3 Рис.
Визуальное сравнение нулевых моделей.Этот рисунок иллюстрирует различия в нулевых двудольных графах. (A) Исходный непереставленный двудольный граф мышца-кость. (B) Случайный нулевой двудольный граф. (C) Случайно перестроенный двудольный граф. (D) Двудольный граф, случайно измененный внутри сообщества, используемый в основном тексте, который переставляет топологию локально, сохраняя при этом глобальную топологию.
(EPS)
S4 Рис.
Основные результаты как функция нулевой модели.Здесь мы показываем результаты с использованием модели случайного гиперграфа или модели гиперграфа с измененной связью (перестановкой), которая не поддерживает локальные связи. (A) Оценка удара, построенная как функция степени гиперребра для случайных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (B) Оценка удара, нанесенная на график как функция степени гиперребра для переставленных гиперграфов и наблюдаемого гиперграфа опорно-двигательного аппарата. (C) Коэффициент отклонения достоверно коррелирует с категорией гомункула (F (1,19) = 6.67, p = 0,018, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием случайной нулевой модели гиперграфа. (D) Коэффициент отклонения достоверно коррелирует с гомункулярной категорией (F (1,19) = 6,86, p = 0,017, R 2 = 0,26), уменьшаясь от медиального (область 0) к латеральному (область 22) с использованием пермутированного нулевая модель гиперграфа. (E) Отклонение оценки воздействия значимо коррелирует с площадью активации моторной полосы (F (1,5) = 13,4, p = 0,014, R 2 = 0.72) с использованием случайной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (F) Отклонение оценки воздействия значительно коррелирует с площадью активации моторной полосы (F (1,5) = 13,7, p = 0,022, R 2 = 0,73) с использованием пермутированной нулевой модели гиперграфа. Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. (G) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 64.5, p = 6,3 × 10 −6 , R 2 = 0,85), используя случайную нулевую модель гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. (H) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,11) = 70,5, p <0,0001, R 2 = 0,86), больше, чем ожидалось при перестановке — основанная на нулевой модели гиперграфа. Точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S5 Рис.
Топология сети и гомункул.Линейные координаты мышц, определенные с использованием многомерного масштабирования без пороговой обработки с помощью взвешенной матрицы расстояний (рассчитанной с использованием distance_wei.m, включенного в Brain Connectivity Toolbox, https://sites.google.com/site/bctnet/). Без пороговой обработки также существует значимая корреляция между линейной координатой мышцы и площадью гомункула (F (1,268) = 303, p <0.0001, R 2 = 0,53). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(EPS)
S6 Рис.
Исследование функции опорно-двигательного аппарата для альтернативной сети.(a) Оценка удара, построенная как функция степени гиперребра для модели нулевого гиперграфа и наблюдаемого гиперграфа опорно-двигательного аппарата. (b) Отклонение оценки воздействия коррелирует со временем восстановления мышц после травмы мышц или групп мышц (F (1,12) = 40,2, p <0,0001, R 2 = 0.77). Заштрихованные области указывают 95% доверительных интервалов, а точки данных масштабируются в соответствии с количеством задействованных мышц. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S7 Рис.
Проверка опорно-двигательного аппарата для альтернативной сети.(a) Коэффициент отклонения значимо коррелирует с гомункулярной топологией (F (1,18) = 8,88, R 2 = 0,33, p = 0,0080), уменьшаясь от медиального (область 0) к латеральному (область 22) регионы. (b) Отклонение оценки воздействия достоверно коррелирует с площадью активации моторной полосы (F (1,5) = 23.4, R 2 = 0,82, p = 0,005). Точки данных имеют размер в соответствии с количеством мышц, необходимых для конкретного движения. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S8 Рис.
Динамика возмущения двуглавой мышцы плеча.На этом рисунке показано движение ключицы, а также костей пальца и стопы в ответ на возмущение двуглавой мышцы плеча. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S9 Рис.
Сравнение моделей с утяжелением костей и силой мышц и без них.Воздействие мышц ног рассчитывалось с добавлением и без добавления анатомических значений массы кости и объема мышц. Было обнаружено, что эти воздействия существенно коррелировали друг с другом (F (1,25) = 6,83, R 2 = 0,0214, p = 0,015), что позволяет предположить, что по крайней мере в некоторых частях тела наше упрощенное сетевое представление обеспечивает разумное приближение для более биофизически точных сетевых представлений. Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S10 Рис.
Исследование функции опорно-двигательного аппарата для не спортсменов.Набрано время восстановления после травм различных мышц не спортсменов. Мы наблюдали значительную корреляцию между временем восстановления мышц и отклонением от удара (F (1,14) = 5,02, R 2 = 0,264, p = 0,041). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S11 Рис.
Соответствие топологии сети и функции системы.Топология сети, в частности средняя длина кратчайшего пути, значительно отрицательно коррелирует с оценкой воздействия, оцененной на основе пертурбативного моделирования динамики системы (F (1,268) = 65,1, R 2 = -0,4422, p <0,0001). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S12 Рис.
Связь между мышечно-скелетными вариациями и мышечным воздействием через две скелетно-мышечные сети.Здесь мы сравниваем процентное изменение оценки и степени воздействия для каждой мышцы между опорно-двигательным аппаратом, указанным в основном тексте, и сообщенным в дополнительном тексте.Мы наблюдаем, что на оценку удара мышц больше влияют большие изменения степени, чем меньшие изменения степени (F (1,268) = 5,76, R = 0,1450, p = 0,017). Данные доступны в DOI: 10.5281 / zenodo.1069104.
(PNG)
S13 Рис.
Альтернативный пертурбативный подход.Чтобы установить меру воздействия на гиперреберь мышцы, объекты были перемещены в четвертое пространственное измерение, чтобы избежать произвольного выбора в трех измерениях. Альтернативным подходом было бы возмущение каждой мышцы в каждом из трех ортогональных направлений, каждый раз вычисляя воздействие и вычисляя векторную сумму этих трех результатов.Чтобы ответить на вопрос о том, как эти два подхода сравниваются, мы провели этот эксперимент на двудольной матрице мышцы-кости, чтобы создать два вектора 270 × 1, один из которых кодировал оценки воздействия посредством смещения в четвертом измерении, а другой — векторную сумму три ортогональных смещения. Два вектора достоверно коррелировали друг с другом (F (1,268) = 1590, R 2 = 0,856, p <0,0001).
(PNG)
Костно-мышечная система — мышечная система: TEAS || Зарегистрированныйorg
Глоссарий костно-мышечной системы — мышечные термины и терминология
Термин «опорно-двигательный аппарат» включает две основные и различные подсистемы, а именно мышечную систему и скелетную систему. В целях данного обзора каждая из этих систем будет рассмотрена и исследована отдельно.
- Ткань скелетных мышц: поперечно-полосатая мышца, обеспечивающая произвольные движения тела
- Гладкая мышечная ткань: Мышца без поперечно-полосатых полос и неподконтрольные произвольному контролю
- Ткань сердечной мышцы: поперечно-полосатая непроизвольная мышца, которая находится только в сердце.Эта ткань обеспечивает работу сердца.
- Похищение: движение от середины тела
- Приведение: движение к середине тела
- Сгибание: движение, уменьшающее или уменьшающее угол между двумя мышцами или суставами
- Разгибание: движение, увеличивающее угол между двумя мышцами или суставами
- Гиперфлексия: Сгибание сустава, выходящее за рамки обычного
- Гиперэкстензия: разгибание сустава, выходящее за рамки обычного
- Вращение: Круговое движение сустава или мышцы, которое позволяет части тела двигаться по кругу.
- Наружное вращение: движение мышц и суставов, которое включает в себя как круговые движения, так и движение от центра тела
- Внутреннее вращение: движение мышц и суставов, которое включает в себя как круговые движения, так и движение к центру тела
- Circumduction: Движение мышц и суставов, которое влечет за собой полное движение 3600
- Инверсия: поворот шарнира внутрь
- Eversion: поворот шарнира наружу
- Подошвенное сгибание: движение стопы (подошвенное) вниз
- Тыльное сгибание: движение стопы (подошвенное) вверх
Части мышечной системы
На виде спереди и сзади мышечной системы выше поверхностные мышцы (те, что на поверхности) показаны на правой стороне тела, а глубокие мышцы (те, что под поверхностными мышцами) показаны на левой половине тела.Для ног на виде спереди показаны поверхностные мышцы, а на виде сзади показаны как поверхностные, так и глубокие мышцы.
Мышечная система состоит из клеток, содержащих белок. Например, мясо и птица, которые мы потребляем в повседневной жизни, представляют собой мышцы животных и являются хорошим источником диетического белка. Все мышцы тела сокращаются и расслабляются в результате деятельности нервной системы.
Существуют разные клетки, которые составляют разные виды мышц человеческого тела.Мышечную систему можно описать как имеющую три различных типа мышц, каждый из которых анатомически различается:
Этими тремя типами мышц являются:
- Сердечная мышца
- Скелетная мышца
- Гладкая мышца
Сердечная мышца
Сердечная мышца находится только в сердце. Сердечная мышца — это поперечно-полосатая мышца, как и скелетные мышцы. Полосы определяются как линии или полосы в мышцах, как показано выше на изображении сердечной мышцы.Сердечная мышца непроизвольна. Работа сердца не подчиняется воле человека.
Типы клеток, обнаруженные в сердечной мышце, — это миокардиоциты, которые сокращают миокард, который является толстым мышечным слоем сердечной ткани; миокардиоциты также называют кардиомиоцитами.
Эти мышцы работают с импульсами и нервным воздействием.
Скелетные мышцы
Скелетные мышцы, вид сверху вниз.
Скелетная мышца, как и сердечная мышца, поперечно-полосатая; однако, в отличие от сердечной мышцы, скелетная мышца — это произвольная мышца, которая позволяет скелетным структурам двигаться.Эти мышцы также контролируются нервной системой, и большинство скелетных мышц прикреплены к костям тела с помощью сухожилий, что позволяет телу двигаться.
Гладкие мышцы
Слои стенки пищевода
Гладкая мускулатура, в отличие от сердечной и скелетной мускулов, не имеет поперечно-полосатой структуры, но, как и сердечная мышца, гладкая мускулатура не является произвольной. Гладкие мышцы — это непроизвольные мышцы, которые контролируют движения и действия внутренних органов и систем тела.Например, гладкие мышцы при активности нервной системы выполняют перистальтику желудочно-кишечного тракта, перемещая пищу и переваренную пищу по желудочно-кишечному тракту к анальному отверстию.
Роль мышечной системы
Роли мышц и мышечной системы многочисленны и разнообразны. Таким образом, эти роли включают:
- Произвольное движение тела скелетными мышцами
- Непроизвольные действия органов тела с гладкой мускулатурой
- Непроизвольные сокращения и расслабление сердца сердечными мышцами
Движение мышц
Мышцы двигаются несколькими разными движениями или движениями.Многие из этих движений или движений описаны со ссылкой на плоскости тела, как связанные с движением, когда это движение изменяет нормальное анатомическое положение, и, более того, просто описывают движение. Например, отведение — это движение от центра тела или медиальной плоскости, а круговое движение — это изменение нормального положения сустава, когда сустав находится в нормальном анатомическом положении.
Мышцы суставов обладают определенными движениями или движениями, на которые они способны.Диапазон движения — это термин, который описывает определенные движения или движения, на которые способна каждая мышца. Например, руки способны к отведению и приведению.
Движения и движения, на которые способны суставы и их мышцы:
- Похищение
- Приведение
- Сгибание
- Hyperflexion
- добавочный номер
- Гиперэкстензия
- Вращение
- Внутреннее вращение
- Наружное вращение
- Обращение
- инверсия
- Eversion
Как показано на рисунке выше, эти термины мышечного движения определены как:
- Похищение: движение от середины тела
- Приведение: движение к середине тела
- Сгибание: движение, уменьшающее или уменьшающее угол между двумя мышцами или суставами
- Разгибание: движение, увеличивающее угол между двумя мышцами или суставами
- Гиперфлексия: Сгибание сустава, выходящее за рамки обычного
- Гиперэкстензия: разгибание сустава, выходящее за рамки обычного
- Вращение: Круговое движение сустава или мышцы, которое позволяет части тела двигаться по кругу.
- Наружное вращение: движение мышц и суставов, которое включает в себя как круговые движения, так и движение от центра тела
- Внутреннее вращение: движение мышц и суставов, которое включает в себя как круговые движения, так и движение к центру тела
- Круговое движение: движение мышц и суставов, которое влечет за собой полное 360 0 движение
- Инверсия: поворот шарнира внутрь
- Eversion: поворот шарнира наружу
- Подошвенное сгибание: движение стопы (подошвенное) вниз
- Тыльное сгибание: движение стопы (подошвенное) вверх
Отведение — это противоположность приведению, когда эти термины используются для описания движения суставов и мышц к телу и от тела.Многие суставы способны на это движение. Отведение — это движение от тела, от центра тела и от срединно-сагиттальной плоскости, как обсуждалось выше и как показано на рисунке выше. Например, рука может отводить от центра тела.
Аддукция противоположна похищению; этот термин определяется как движение к телу, к центру тела и к срединно-сагиттальной плоскости, как обсуждалось выше и как показано на рисунке выше. Суставы и мышцы, способные к отведению, также способны к приведению.Например, рука может сводиться к центру тела.
Сгибание противоположно разгибанию и наоборот. Сгибание — это изгибающее движение сустава или мышцы, которое уменьшает или уменьшает угол между двумя мышцами или суставами, как показано на рисунке выше. Например, локоть может сгибаться, сгибаться и уменьшать угол между плечом и предплечьем. Родственный термин — гиперфлексия, что означает, что сгибание сустава превышает то, что он обычно должен делать. Гиперфлексия, например, может возникнуть в результате травматической автомобильной аварии, когда голова прижата к груди или согнута сверх того, что она обычно должна делать.
Разгибание, противоположное сгибанию, — это нормальное выпрямляющее движение сустава или мышцы, которое увеличивает угол между двумя мышцами или суставами, как показано на рисунке выше. Например, локоть может выпрямиться и увеличить угол между плечом и предплечьем. Суставы и мышцы, способные к сгибанию, также способны к разгибанию. . Родственный термин — гиперэкстензия, что означает, что сустав разгибается за пределы того, что он обычно должен делать. Гиперэкстензия, например, может возникнуть в результате травматической автомобильной аварии, когда голова откинута назад или вытягивается сверх того, что она обычно должна делать.
Вращение — это круговое движение сустава или мышцы, которое позволяет части тела двигаться по кругу. Голова имеет суставы и мышцы, которые позволяют ей вращаться по кругу вправо или влево, как показано на рисунке выше.
Вращение частей тела называется внутренним или внешним, имея в виду вращение к центру тела или от него. Два типа вращения — внутреннее вращение и внешнее вращение.
Поза лотоса в йоге, демонстрирующая внешнее вращение ноги в бедре.
Наружное вращение — это движение мышц и суставов, которое влечет за собой как круговое движение, так и движение от центра тела, как показано на рисунке выше. Внешнее вращение также называется боковым вращением.
Поворот руки ближе к телу — это внутреннее вращение.
Внутреннее вращение — это движение мышц и суставов, которое влечет за собой как круговое движение, так и движение к центру тела, как показано на рисунке выше.Внутренняя ротация также называется ротацией медалей.
Раскачивание во время теннисной подачи является примером циркумдукции.
Круговое движение — это движение мышц и суставов, которое влечет за собой полное движение на 360 0 . Шаровидные и шарнирные суставы, такие как суставы бедра и плеча, могут вращаться, как показано на рисунке выше. Например, округление бедер происходит, когда кто-то использует обруч hoola или когда они заводят и вращают руку, чтобы разогреться перед бейсбольным мячом или подать в игре в теннис, как показано на рисунке выше.
Заболевания, поражающие мышечную систему
- Деформации и растяжения
- Мышечная дистрофия
- Рассеянный склероз
- Атрофия мышц
СВЯЗАННЫЕ TEAS АНАТОМИЯ И ФИЗИОЛОГИЯ СОДЕРЖАНИЕ:
Alene Burke, RN, MSN
Alene Burke RN, MSN является национально признанным преподавателем сестринского дела. Она начала свою карьеру учителем начальной школы в Нью-Йорке, а затем поступила в общественный колледж Квинсборо, чтобы получить степень младшего специалиста по медсестринскому делу.Она работала дипломированной медсестрой в отделении интенсивной терапии местной общественной больницы, и в то время она решила стать преподавателем медсестер. Она получила степень бакалавра наук по медсестринскому делу в колледже Эксельсиор, который входит в состав Университета штата Нью-Йорк, и сразу после окончания школы она поступила в аспирантуру Университета Адельфи на Лонг-Айленде, штат Нью-Йорк. Она закончила Summa Cum Laude в Адельфи со степенью двойного магистра в области сестринского образования и сестринского администрирования и сразу же получила докторскую степень по сестринскому делу в том же университете.Она является автором сотен курсов для медицинских работников, включая медсестер, она работает медсестрой-консультантом в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также была членом Американской ассоциации медсестер. Целевая группа ассоциации по компетентности и обучению членов медсестер.
Последние сообщения Alene Burke, RN, MSN (посмотреть все)Скелетно-мышечная система и болезнь
Опорно-двигательный аппарат — это общий термин, который, как следует из названия, относится к мышцам и скелету тела.В частности, опорно-двигательная система включает кости, мышцы, суставы, хрящи, связки, сухожилия и сумки. Опорно-двигательный аппарат обеспечивает стабильность, а также позволяет телу двигаться.
Анатомия опорно-двигательного аппарата
Кости — В теле взрослого человека 206 костей. Структура кости состоит из твердой внешней части, состоящей из белков (в основном коллагена) и гидроксиапатита (в основном кальция и других минералов). Внутренняя часть кости, называемая губчатой костью, мягче, чем твердая внешняя кортикальная кость, но все же необходима для поддержания прочности кости.Хотя структура всех костей одинакова, кости выполняют различные функции в организме:
- Кости обеспечивают структурную поддержку тела (то есть каркас скелета для прикрепления органов и тканей) и защищают определенные органы (например, грудная клетка защищает сердце).
- Кости накапливают большую часть кальция в организме.
- Кости имеют внутреннюю полость, которая содержит костный мозг, в котором вырабатываются эритроциты, лейкоциты и другие компоненты крови.
Кости подвергаются процессу, известному как ремоделирование. Ремоделирование кости — это непрерывный процесс, при котором старая кость постепенно заменяется новой. Каждая кость полностью реформируется примерно за 10 лет. Ежегодно заменяется 20% кости тела.
Мышцы — Есть два типа мышц, которые являются частью опорно-двигательного аппарата — скелетные и гладкие. Третий тип мышц, сердечные, не является частью опорно-двигательного аппарата. Скелетные мышцы — это пучки сократительных волокон.Действие сокращающихся мышц — это то, что движет различными частями тела. Скелетные мышцы прикрепляются к костям и располагаются противостоящими группами вокруг суставов (например, мышцы, сгибающие локоть, располагаются напротив мышц, выпрямляющих локоть). Скелетные мышцы контролируются мозгом и действуют добровольно под сознательным руководством человека. Гладкие мышцы играют роль в определенных функциях организма, которые не находятся под контролем человека. Гладкие мышцы расположены вокруг некоторых артерий, сокращаясь для регулирования кровотока.Гладкие мышцы также окружают кишечник, сокращаясь, чтобы перемещать пищу и фекалии по тракту. Хотя гладкие мышцы также контролируются мозгом, это не является произвольным. Включение гладкой мускулатуры основано на телесных потребностях, а не на сознательном контроле.
Суставы — Суставы — это места соединения концов двух или более костей. Хотя есть суставы, которые не двигаются (например, между пластинами черепа), большинство суставов способны облегчить движение. Есть два типа суставов, которые облегчают движение: хрящевые и синовиальные.Синовиальные суставы знакомы большинству людей. Синовиальные суставы человека бывают нескольких видов: шарнирно-гнездовые, кондиллоидные, скользящие, шарнирные, шарнирные и седловидные. Концы костей в этом типе сустава покрыты хрящом. Суставы заключены в суставную капсулу, имеющую выстилку (синовиальную оболочку). Клетки синовиальной оболочки производят синовиальную жидкость, которая питает хрящи и помогает уменьшить трение во время движения.
Хрящ — Концы кости, образующие сустав, покрыты хрящом.Нормальный хрящ гладкий, прочный и защищает концы кости. Хрящ состоит из коллагена, воды и протеогликанов. Хрящ служит амортизатором и снижает трение при движении сустава.
Связки — Связки представляют собой жесткие фиброзные тяжи или полосы ткани, соединяющие кость с костью. Связки состоят из коллагеновых и эластичных волокон. Эластичные волокна придают связкам некоторую растяжимость. Связки окружают и поддерживают суставы, позволяя двигаться в определенных направлениях.
Сухожилия — Сухожилия представляют собой жесткие волокнистые ткани, соединяющие мышцы с костью. Сухожилия в основном состоят из коллагена. Сухожилия обычно находятся внутри оболочки (то есть оболочки сухожилия), которая позволяет сухожилиям двигаться без трения. Оболочка сухожилия состоит из двух слоев: синовиальной оболочки и фиброзной оболочки сухожилия.
Бурсы — Бурсы — это небольшие наполненные жидкостью мешочки, которые служат подушкой и скользящей поверхностью с низким коэффициентом трения между соседними движущимися частями тела, такими как кости, мышцы, сухожилия и кожа.Бурсы встречаются по всему телу. Бурсы различаются по размеру в зависимости от их расположения в теле. По всему телу насчитывается около 160 бурс.
Заболевания опорно-двигательного аппарата
Заболевания опорно-двигательного аппарата, среди прочего, включают артрит, бурсит и тендинит. Основные симптомы заболевания опорно-двигательного аппарата включают боль, скованность, отек, ограниченный диапазон движений, слабость, утомляемость и снижение физических функций. Ревматолог является специалистом по артриту и ревматическим заболеваниям.Врачи-ортопеды также лечат заболевания опорно-двигательного аппарата.
Скелетная, мышечная и нервная системы
Скелетная система
марафонцев преодолевают расстояние более 26 миль от старта до финиша. Бег так далеко бросает вызов телу как физически, так и морально. Те, кто финишируют, могут гордиться достижением такой сложной цели. Бег на марафон требует силы мышц и выносливости. Также требуется крепкая скелетная система для поддержки этих мышц.
Скелетная система — это каркас костей, который обеспечивает структуру вашего тела и защищает ваши внутренние органы.Скелет также служит резервуаром для хранения минералов, производит клетки крови и позволяет телу двигаться. Типичный человеческий скелет состоит из 206 костей.
Череп содержит кости, которые окружают и защищают мозг, а кости позвоночника поддерживают череп и позволяют двигаться в спине. Ребра защищают важные внутренние органы. Кости в руках позволяют выполнять множество задач, а кости ног поддерживают тело при ходьбе или беге.
Каждая кость состоит из живой растущей ткани.Если кость ломается, один тип костных клеток разрушает поврежденную ткань, в то время как другой тип костных клеток начинает восстанавливать кость. Кальций и витамин D — это питательные вещества, которые помогают укрепить кости. Вы можете думать о костях как о твердых твердых предметах. Хотя внешняя часть кости твердая, внутренняя часть заполнена мягкой тканью, называемой костным мозгом. Костный мозг производит новые клетки крови.
Два типа костного мозга, красный и желтый, проходят через центр многих длинных костей, например, в ногах и руках.Красный костный мозг производит красные кровяные тельца, которые переносят кислород по всему телу. Он также производит определенные типы белых кровяных телец, которые помогают бороться с болезнями. Желтый костный мозг состоит в основном из жировых клеток, которые являются источником запасенной энергии.
Кости бывают разных форм и размеров, в зависимости от их функций. Например, короткие тонкие косточки в пальцах позволяют пальцам двигаться и хватать предметы. Кости классифицируются как:
- длинные кости в ногах и руках
- короткие кости в пальцах рук и ног
- плоских костей, обнаруженных в черепе и тазу
- Кости неправильной формы, обнаруженные в позвоночнике и ушах
Соединения
Суставы — это места, где встречаются две или более костей.Крепкие нити соединительной ткани, называемые связками, соединяют кости в большинстве суставов. Кости в суставах покрыты гибким хрящом, который представляет собой жесткую эластичную соединительную ткань. Хрящ покрывает кости, чтобы они не терлись друг о друга.
Степень подвижности костей в суставах различается. Например, суставы черепа неподвижны, а суставы плеча допускают широкий диапазон движений. Соединения классифицируются по типу движения, которое они допускают, и по форме их частей.
- Шаровидные шарниры в плечах и бедрах позволяют двигаться практически во всех направлениях.
- Шарнирные соединения в локтях и коленях позволяют перемещаться в одном направлении.
- Скользящие суставы на запястьях и лодыжках позволяют ограниченное движение во многих направлениях.
- Шарнирные суставы, расположенные между позвонками в позвоночнике, в основном позволяют вращательное движение из стороны в сторону.
- Неподвижные суставы, обнаруженные в черепе, удерживают кости черепа вместе и не допускают никаких движений.
Мышечная система
Скелетная и мышечная системы взаимосвязаны. Мышечная система использует мышцы для перемещения костей скелетной системы. Мышцы — это ткани, которые сокращаются. Сокращение происходит, когда мышечные волокна укорачиваются и стягиваются. Многие мышцы прикрепляются к костям, что позволяет вам ходить, бегать, метаться, танцевать или заниматься любым другим видом деятельности. Другие мышцы позволяют сердцу биться или перемещать пищу по телу.
Произвольные мышцы
Скелетные мышцы, или мышцы, которые используются для управления движением костей, — это произвольные мышцы, которыми вы можете сознательно управлять.Эти мышцы соединены с костями сухожилиями, которые представляют собой полосы прочной волокнистой соединительной ткани. Поскольку мышца может только сокращаться, каждый сустав контролируется противоположными мышцами. Это позволяет совершать возвратно-поступательное движение. Как показано на изображении, вы сокращаете мышцу двуглавой мышцы, чтобы согнуть руку. Когда ваша двуглавая мышца сокращается, ваша трехглавая мышца расслабляется и растягивается. Вы сокращаете трехглавую мышцу, чтобы выпрямить руку. Когда ваша трицепс сокращается, ваша двуглавая мышца расслабляется и растягивается.
Непроизвольные мышцы
Мышцы легких, кишечника, мочевого пузыря, кровеносных сосудов и сердца — это непроизвольные мышцы. У вас ограниченный контроль над непроизвольными мышцами. Другими словами, эти мышцы функционируют без вашего сознательного контроля. Некоторые непроизвольные мышцы перемещают материалы внутрь, через или из тела, например гладкие мышцы кровеносных сосудов, легких или кишечника. Непроизвольная мышца сердца называется сердечной мышцей.Сердечная мышца заставляет сердце биться, которое перекачивает кровь по всему телу.
Нервная система
Когда вы хотите двигаться, что заставляет ваши мышцы сокращаться? Мышцы двигаются в ответ на электрические и химические сигналы, которые проходят через нервную систему. Нервная система включает головной и спинной мозг, а также сеть специализированных нервных клеток, называемых нейронами. Когда вы решаете переместить руку или ногу, ваш мозг посылает нервный импульс по спинному мозгу. Импульс достигает задействованных мышц, вызывая сокращение и движение мышц.
Нейроны
Нейрон состоит из трех основных частей: дендритов, которые получают сообщения от других нейронов, тела клетки, содержащего ядро, и аксона, который позволяет электрическому сигналу перемещаться к другим нейронам и мышцам. Аксоны окружены миелиновой оболочкой, которая изолирует аксон и улучшает скорость проведения импульсов. В промежутке между нейронами, называемом синапсом, электрическое сообщение меняется на химическое сообщение, которое улавливается следующей нервной клеткой.
Спинной мозг
Спинной мозг состоит из нервных волокон, которые посылают импульсы от головного мозга к остальным частям тела. Спинной мозг посылает множество сообщений из головного мозга, чтобы тело могло функционировать. Однако иногда спинной мозг функционирует как система защиты организма, немедленно реагируя на экстренное сообщение нервных клеток, не затрагивая мозг. Например, когда вы касаетесь горячей плиты, сенсорный нейрон посылает вашему спинному мозгу сообщение о том, что плита горячая.Спинной мозг немедленно посылает сообщение мотонейронам в руке и руке, которое заставляет вас убирать руку от плиты. Этот рефлекторный ответ используется для предотвращения травм, когда сообщение слишком долго дойдет до головного мозга, по спинному мозгу, а затем до пораженной области.
Мозг
Мозг — сложный орган, который содержит 90 процентов нейронов тела. Мозг контролирует все действия, кроме рефлекторных реакций. Различные части мозга контролируют разные функции тела.
В основании мозга есть три основные структуры. Мозжечок контролирует координацию, осанку и равновесие. Продолговатый мозг управляет непроизвольными функциями организма, такими как дыхание и пищеварение. Мост помогает контролировать частоту дыхания и передает сигналы между мозжечком и головным мозгом.
Головной мозг — это большая структура в верхней части головного мозга. Он контролирует координацию движений и интерпретацию сенсорной информации изнутри и снаружи тела.Головной мозг разделен на две половины, называемые полушариями.
Каждое полушарие содержит четыре доли, которые выполняют определенные функции:
- Лобная доля регулирует произвольные движения и участвует в принятии решений и решении проблем.
- Височная доля регулирует память, эмоции, слух и речь.
- Теменная доля обрабатывает сенсорные сигналы от тела.
- Затылочная доля отвечает за зрение и зрительную память.


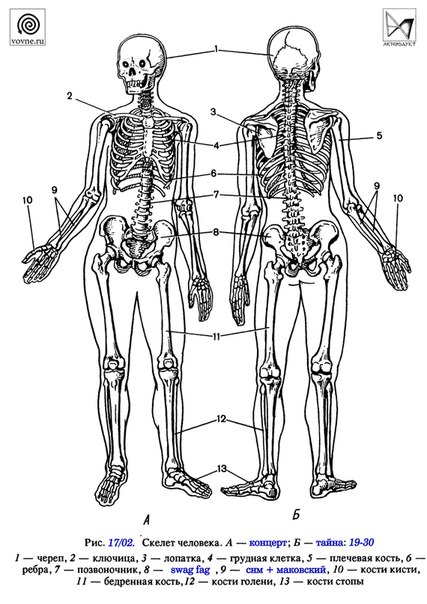 У здорового человека, в отличие от человека, страдающего плоскостопием,
У здорового человека, в отличие от человека, страдающего плоскостопием,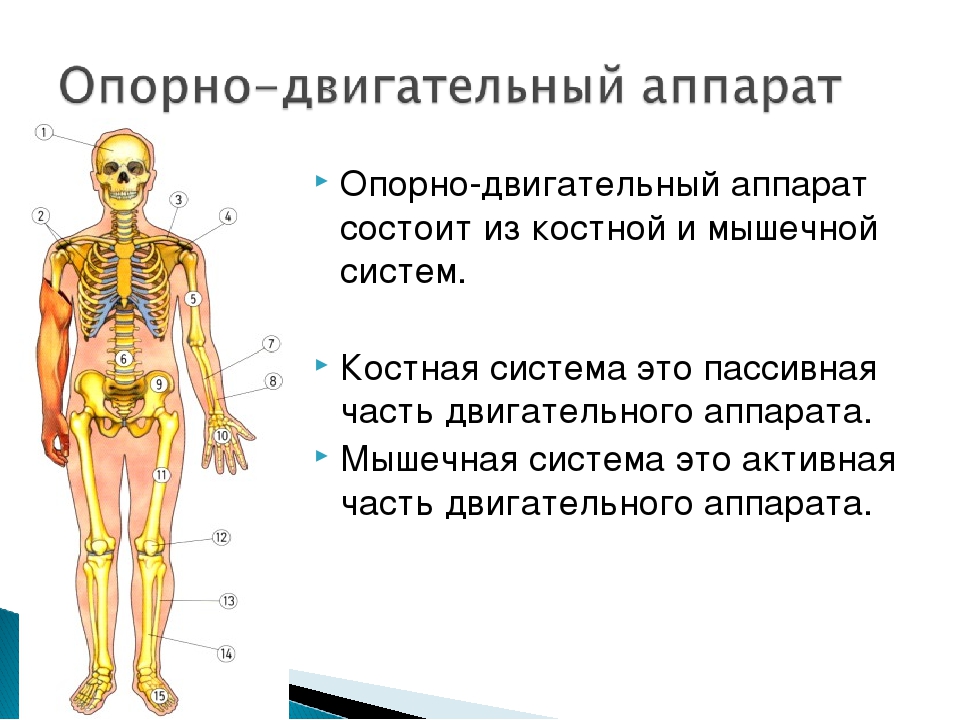 Укажите верные ответы на вопрос.
Укажите верные ответы на вопрос. В костной ткани межклеточное вещество
В костной ткани межклеточное вещество Широкий таз и 8-образный позвоночник сформировались у человека в процессе эволюции в связи с
Широкий таз и 8-образный позвоночник сформировались у человека в процессе эволюции в связи с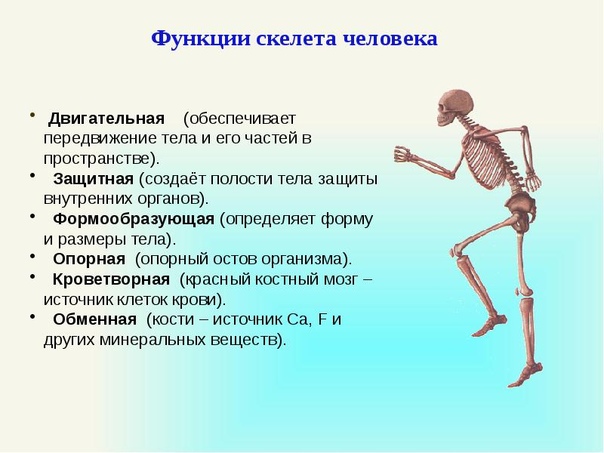
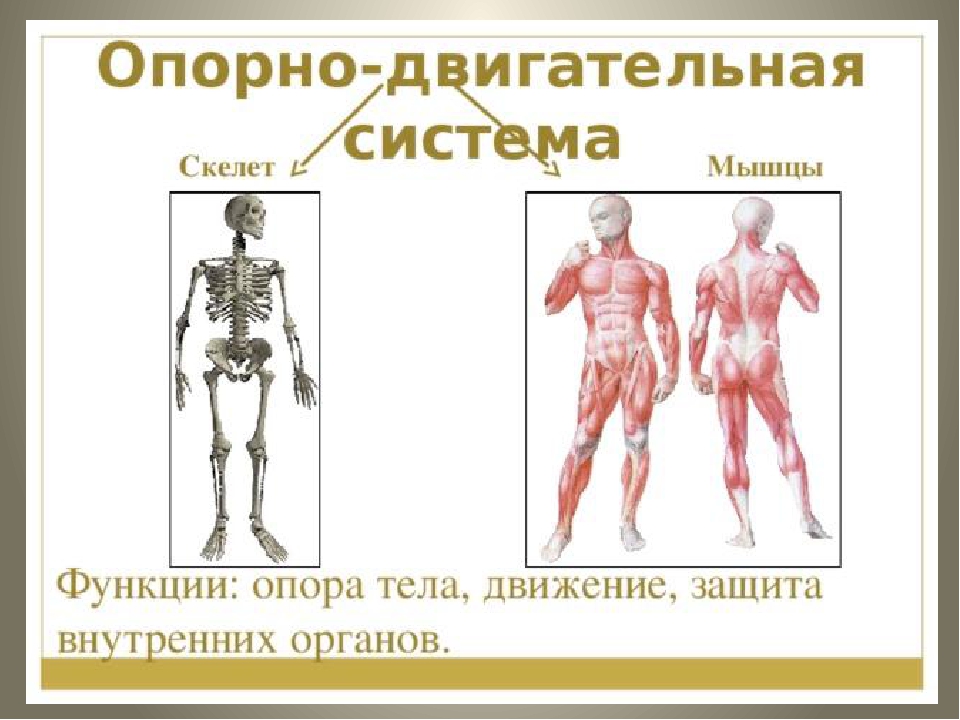 «Университет»Книжный дом», 1999г
«Университет»Книжный дом», 1999г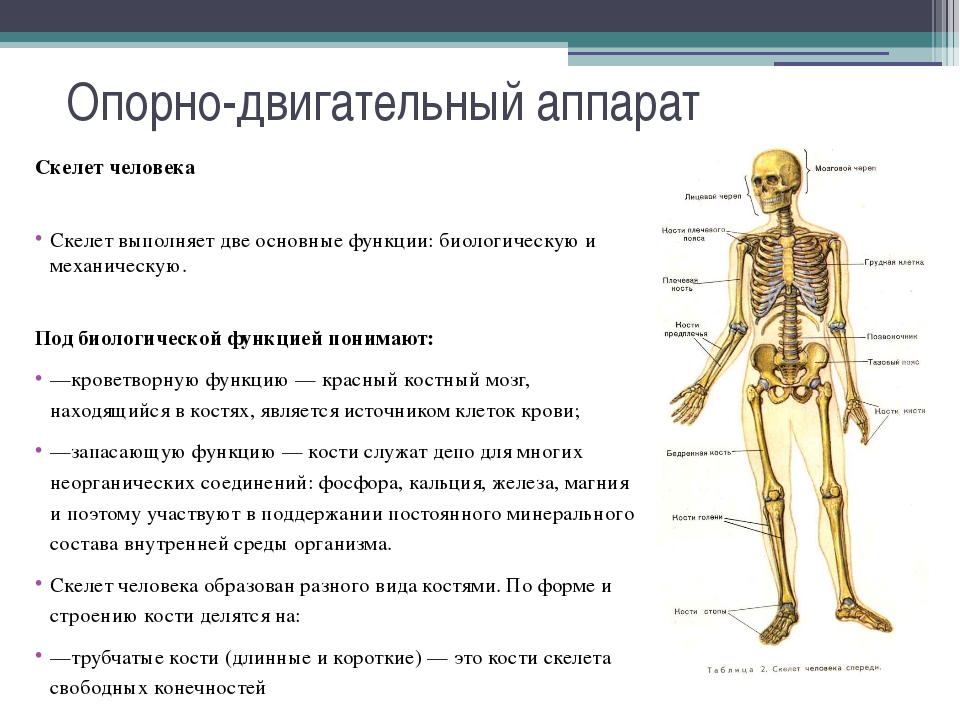 скелетом и скелетными мышцами
скелетом и скелетными мышцами череп и скелет свободных конечностей
череп и скелет свободных конечностей плечевая кость, кости предплечья и кости кисти
плечевая кость, кости предплечья и кости кисти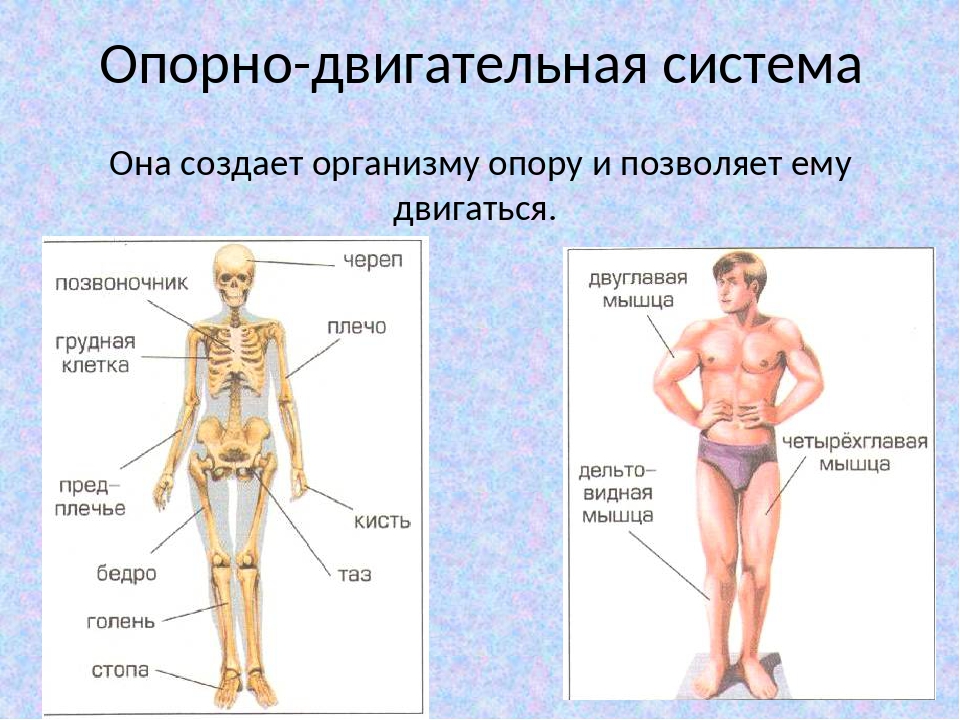 бедренная
бедренная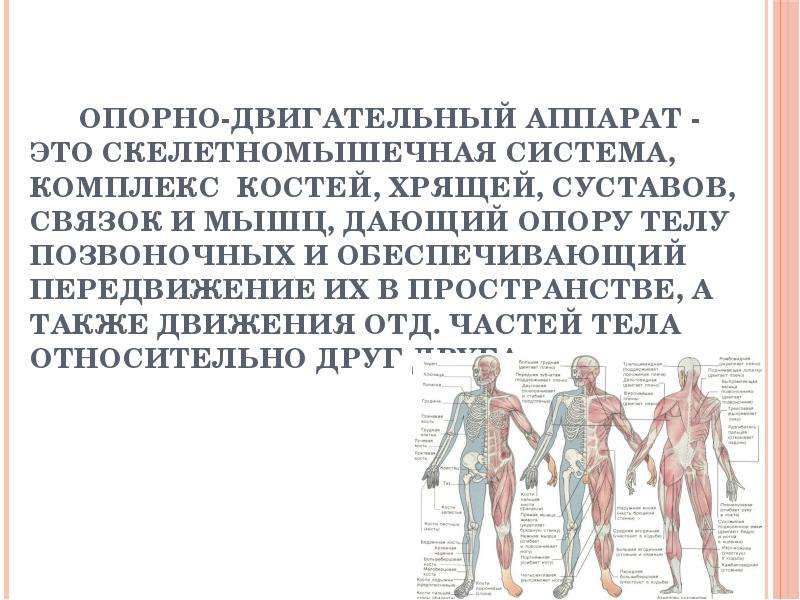 трехглавая плеча
трехглавая плеча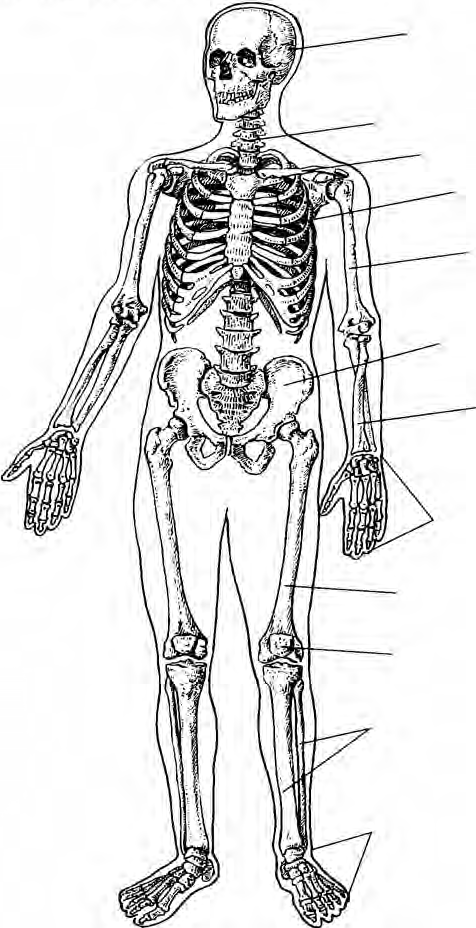 удержание поднятой штанги
удержание поднятой штанги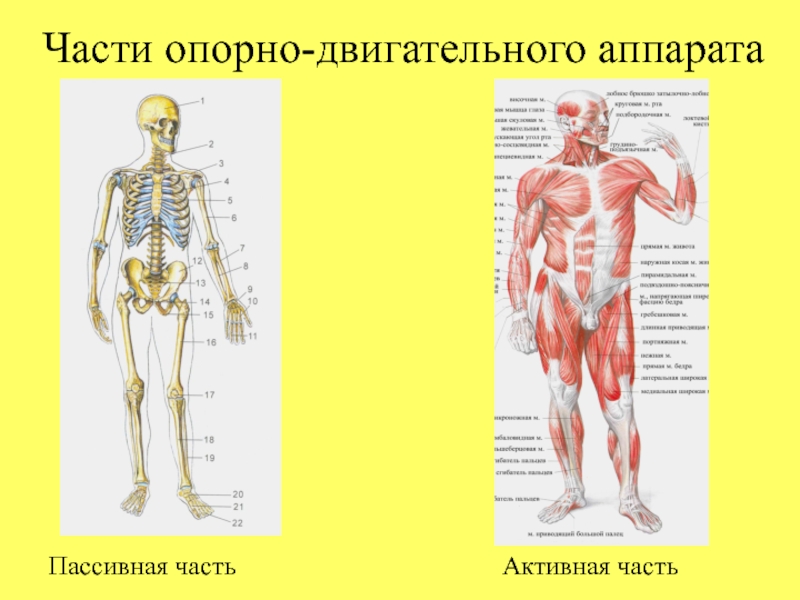 сводчатую стопу
сводчатую стопу увеличению количества минеральных веществ в костях
увеличению количества минеральных веществ в костях Установите соответствие между костью черепа человека и отделом черепа.
Установите соответствие между костью черепа человека и отделом черепа.
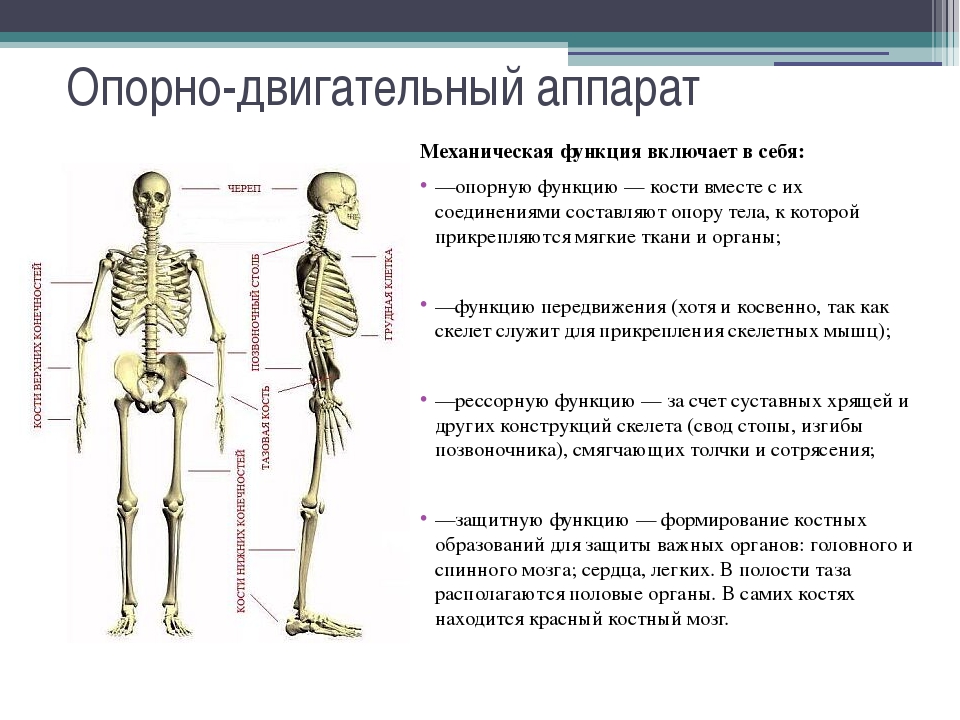
 кости запястья
кости запястья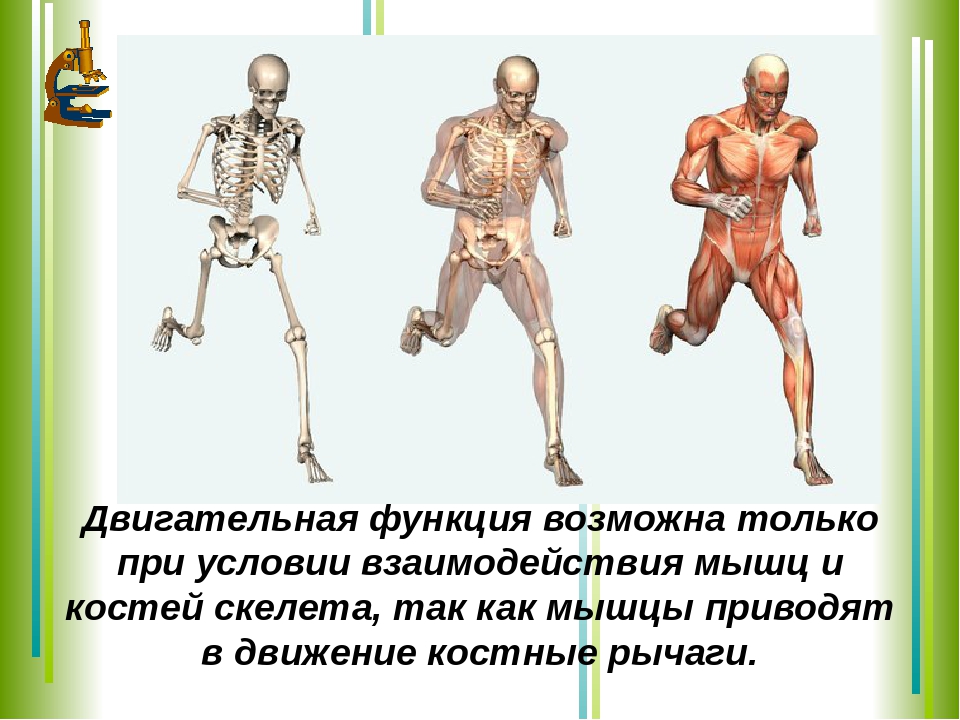
 Запишите сначала номера этих предложений, а затем сформулируйте их правильно.
Запишите сначала номера этих предложений, а затем сформулируйте их правильно.