Контрольная работа по теме: «Начальные геометрические сведения» | Методическая разработка по геометрии (7 класс):
Контрольная работа по теме: «Начальные геометрические сведения»
Вариант № 1
Часть 1
№ 1. Проведите прямую, обозначьте её буквой а и отметьте точки А и С, лежащие на этой прямой и точки К, Е, М, не лежащие на ней. Опишите взаимное расположение точек и прямой с помощью символов принадлежности.
№ 2. Начертите ∟МОК = 1400, ∟hk = 650, ∟М = 1800. Определите и подпишите вид угла. В тупом угле поставьте точки А, В, которые лежат на стороне угла, Е, Х – внутри угла, и точка Р – вне угла.
№ 3. Начертите отрезок АВ = 13 см. Отметьте точку С – середина отрезка АВ, а точка О – середина отрезка АС. Выпишите все получившиеся отрезки. Найдите длину отрезков: АС, СВ, АО, ОВ.
№ 4. Найдите угол, смежный с углом АВС, если угол АВС равен 1560 (сделать чертёж, выполнить решение)
№ 5. Начертите две пересекающие прямые, один из углов равен 1250.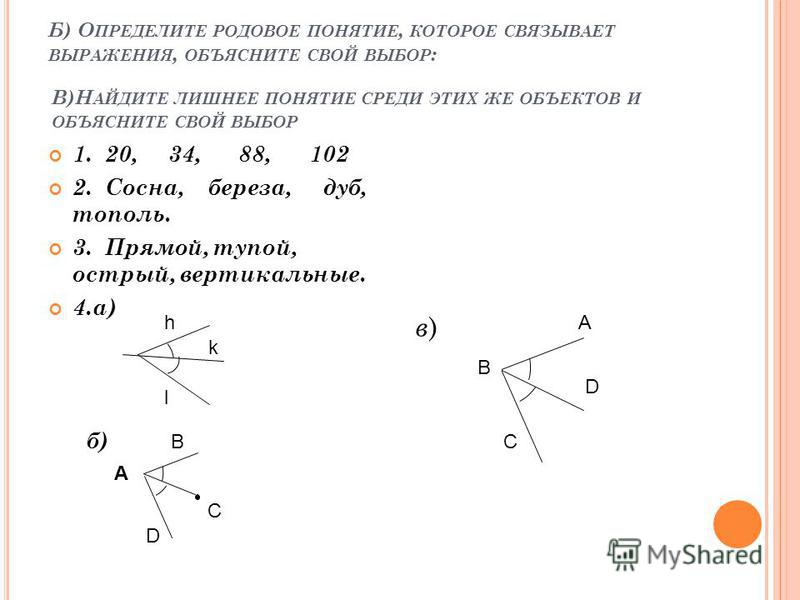 Найдите остальные три угла.
Найдите остальные три угла.
Часть 2
№ 6. На луче с началом в точке О отмечены точки А и В. Известно, что ОА = 11,7 см, а АВ = 3,9 см. Какую длину может иметь отрезок ОВ.
№ 7. Один из углов, образовавшихся при пересечении двух прямых, на 700 больше другого. Найдите эти углы
№ 8. Один из смежных углов в 8 раз больше другого. Найдите углы, которые образует биссектриса большего угла.
№ 9. Дано: угол ВОС равен 1480, ОМ ┴ ОС, ОК – биссектриса угла СОВ. Найти угол КОМ.
№ 10. Прямые АВ и СD пересекаются в точке О. ОК – биссектриса угла АОD, угол СОК равен 1180. Найдите угол ВОD.
Контрольная работа по теме: «Начальные геометрические сведения»
Вариант № 2
Часть 1
№ 1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой и точки О, F, К, не лежащие на ней. Опишите взаимное расположение точек и прямой с помощью символов принадлежности.
№ 2. Начертите ∟МОК = 1600, ∟hk = 550, ∟М = 1800. Определите и подпишите вид угла. В тупом угле поставьте точки С, В, которые лежат на стороне угла, Е, Н – внутри угла, и точка Х – вне угла.
В тупом угле поставьте точки С, В, которые лежат на стороне угла, Е, Н – внутри угла, и точка Х – вне угла.
№ 3. Начертите отрезок АВ = 15 см. Отметьте точку С – середина отрезка АВ, а точка О – середина отрезка АС. Выпишите все получившиеся отрезки. Найдите длину отрезков: АС, СВ, АО, ОВ.
№ 4. Найдите угол, смежный с углом АВС, если угол АВС равен 1360 (сделать чертёж, выполнить решение)
№ 5. Начертите две пересекающие прямые, один из углов равен 1150. Найдите остальные три угла.
Часть 2
№ 6. На луче с началом в точке О отмечены точки А и В. Известно, что ОА = 12,4 см, а АВ = 2,7 см. Какую длину может иметь отрезок ОВ.
№ 7. Один из углов, образовавшихся при пересечении двух прямых, на 220 меньше другого. Найдите эти углы
№ 8. Один из смежных углов в 8 раз меньше другого. Найдите углы, которые образует биссектриса меньшего угла.
№ 9. Дано: угол АОК равен 1540, ОС ┴ ОК, ОМ – биссектриса угла КОА. Найти угол МОС.
№ 10. Прямые АВ и СD пересекаются в точке О. ОК – биссектриса угла АОD, угол СОК равен 1160. Найдите угол ВОD.
ОК – биссектриса угла АОD, угол СОК равен 1160. Найдите угол ВОD.
Контрольная работа по геометрии на тему «Начальные геометрические сведения» (7 класс) с ответами и карточками для печати
Контрольная работа по геометрии (7 класс) №1
«Начальные геометрические сведения»
(Измерение отрезков и углов)
Задание 1. Найти угол в задаче, часть условия которой представлено на рисунке. 1 балл.
Задание 2. Сравнение / нахождение длины отрезка. 1 балл.
Задание 3. Применение знаний о смежных и вертикальных углах. Задача на доказательство. 2 балла.
Важно: задание считается решенным при соблюдении следующих условий:
получен верный ответ;
приведены все необходимые доказательства;
в процессе решения каждый шаг оправдан и следует из опорных знаний (определений, свойств, теорем и т.д.).
Оценивание:
«5» — 4 балла
«4» — 3 балла
«3» — 2 балла
«2» — 0-1 балл
Ключ:
1) BEK=23°, СЕР = 53°2) Нет.
1) РОВ = 40°, КОВ = 140°
2) Да.
Вариант 1
№1. На рисунке угол COD прямой. Найти угол АОС, если углы 1 и 2 равны.
№2. Точка N – середина отрезка PK, точка Е – середина отрезка NK. Найдите длину отрезка EK, если PK = 13,2 см.
№3. Отрезки AB и CD лежат на перпендикулярных прямых и пересекаются в точке Е. Внутри угла АЕС взята точка Р, а внутри угла DEB – точка К. AEP = 37°, DEK = 67°.
Найти углы BEK и СЕР.
Являются ли углы РЕА и ВЕК вертикальными? Ответ объясните.
Вариант 2
№1. На рисунке прямые AB и CD взаимно перпендикулярны, BON = 120°. Является ли луч ON биссектрисой угла АОС?
№2. Точка S является серединой отрезка PN, а точка N принадлежит отрезку SK. Найти длину отрезка PS, если PK = 74см, NK = 31 см.
№3. Развернутый угол АОВ делит плоскость на две части. Точка Р лежит в одной части, точка К в другой. АОР = 140°, АОК = 40°.
Найти углы РОВ и КОВ.
Вариант 1
№1. На рисунке угол COD прямой. Найти угол АОС, если углы 1 и 2 равны.
№2. Точка N – середина отрезка PK, точка Е – середина отрезка NK. Найдите длину отрезка EK, если PK = 13,2 см.
№3. Отрезки AB и CD лежат на перпендикулярных прямых и пересекаются в точке Е. Внутри угла АЕС взята точка Р, а внутри угла DEB – точка К. AEP = 37°, DEK = 67°.
Найти углы BEK и СЕР.
Являются ли углы РЕА и ВЕК вертикальными? Ответ объясните.
Вариант 2
№1.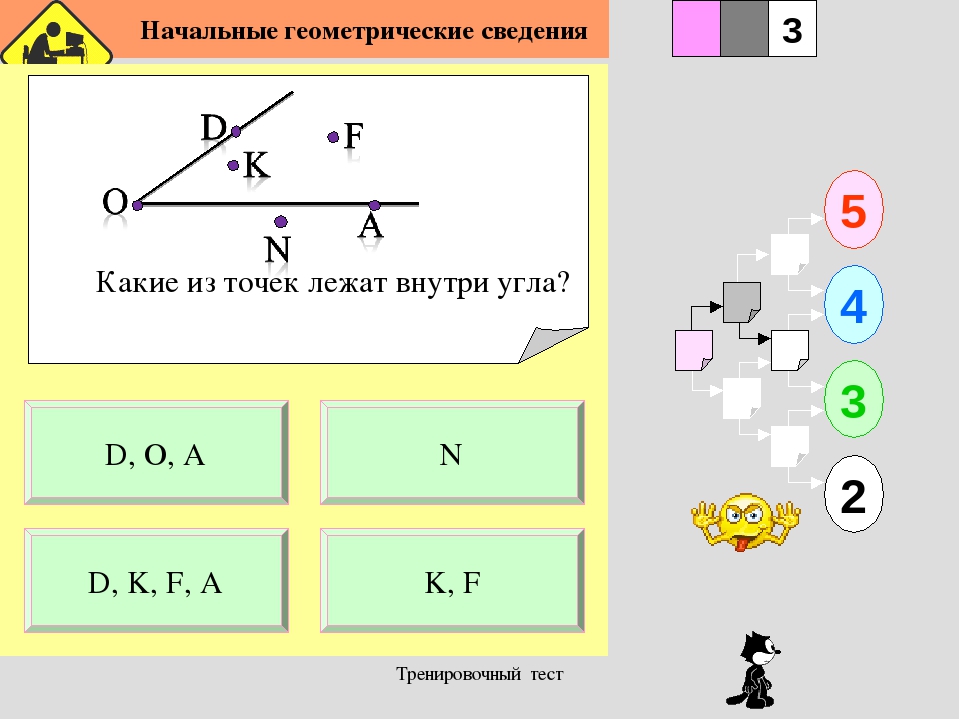 На рисунке прямые AB и CD взаимно перпендикулярны, BON = 120°. Является ли луч ON биссектрисой угла АОС?
На рисунке прямые AB и CD взаимно перпендикулярны, BON = 120°. Является ли луч ON биссектрисой угла АОС?
№2. Точка S является серединой отрезка PN, а точка N принадлежит отрезку SK. Найти длину отрезка PS, если PK = 74см, NK = 31 см.
№3. Развернутый угол АОВ делит плоскость на две части. Точка Р лежит в одной части, точка К в другой. АОР = 140°, АОК = 40°.
Найти углы РОВ и КОВ.
Являются ли углы АОК и РОВ вертикальными? Ответ объясните.
Геометрия 7 Атанасян К-1 В-2
Контрольная работа № 1 «Начальные геометрические сведения» по геометрии в 7 классе с ответами для УМК Атанасян. Вариант 2. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей. Геометрия 7 Атанасян К-1 В-2.
Геометрия 7 класс (Атанасян)
Контрольная работа № 1. Вариант 2.
К-1 «Начальные геометрические сведения» (транскрипт заданий)
Часть 1. Запишите номера верных ответов к заданию 1.
Запишите номера верных ответов к заданию 1.
№ 1. Используя рисунок, укажите верные утверждения:
1) ∠AKD и ∠BKD – смежные углы.
2) ∠BKD и ∠BKE – вертикальные углы.
3) ∠AKE – тупой угол.
4) ∠BKE – прямой угол.
Часть 2. Запишите ответ к заданию 2.
№ 2. Угол DC В равен 148°, СК – биссектриса этого угла. Найдите угол ∠BCK.
Часть 3. Запишите обоснованное решение задач 3–5.
№ 3. Найдите на рисунке ∠ADC, если ∠BDE = 138°.
№ 4. Найдите на рисунке длины отрезков BD и DC, если ВС = 24 см, а отрезок BD на 8 см больше отрезка DC.
№ 5*. Отрезки МР и ОК пересекаются в точке Е, один из углов при вершине Е равен 110°. Найдите угол КЕС, где ЕС – биссектриса угла РЕК.
Геометрия 7 Атанасян К-1 В-2
ОТВЕТЫ на контрольную работу:
№ 1. 1, 4.
№ 2. 74°.
№ 3. 138°.
№ 4. 8 см и 16 см.
8 см и 16 см.
№ 5. 55° или 35°.
Смотреть образец РЕШЕНИЯ заданий в тетради
Вы смотрели: Контрольная работа № 1 «Начальные геометрические сведения» по геометрии в 7 классе с ответами для УМК Атанасян. Дидактические материалы (упражнения) для учителей, учащихся и родителей.
К-1. Вариант 0 К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Вернуться на страницу: Контрольные работы по геометрии в 7 классе УМК Атанасян.
Перейти на страницу: Контрольные работы по геометрии в 7 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Геометрия 7 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.
Контрольная работа №1 по геометрии «Начальные геометрические сведения», ( 7 класс)
Геометрия – 7
Контрольная работа по теме «Начальные геометрические сведения»
Вариант 1.
№1. Запишите номера верных утверждений:
1)Углы ADF и ADN — смежные, 2)0, 3) Углы ADN и NDS – вертикальные, 4)< ADF = 1340, 5) -тупой. |
№2.Запишите ответ к номеру 2.
Угол DOM в два раза меньше угла AOD. Найти градусную меру угла AOM, если < AOD = 510. |
Записать обоснованное решение к номерам 3-5.
№3. Смежные углы KNM и KNP относятся как 5:4. Найти эти углы.
Дано: углы KNM и KNP-смежные, < KNM : < KNP= 5:4 Найти: < KNM , < KNP. |
№4. |
№5. Из точки А проведены три луча АС, АВ и АК. Найти угол КАВ, если
< САВ =710, а К= 120.
Геометрия – 7
Контрольная работа по теме «Начальные геометрические сведения»
Вариант 2.
№1. Запишите номера верных утверждений:
1)Углы ADF и FDS — смежные, 2)<AND =1290, 3)< FDS=510, 4) Углы ADF и NDS – вертикальные. 5)< FDS –острый. |
№2.Запишите ответ к номеру 2.
Угол AOD в четыре раза больше угла AOF. = 120. |
Записать обоснованное решение к номерам 3-5.
№3. Смежные углы KNM и KNP относятся как 7:2. Найти эти углы.
Дано: углы KNM и KNP-смежные, < KNM : < KNP= 7:2 Найти: < KNM , < KNP. | |
№4. Отрезок ВС на 0,8 см больше отрезка АС. Найти длину отрезка ВС, если известно, что длина отрезка DС=7,3 см, что на 2,1 см больше , чем длина отрезка АC. |
№5. Из точки N проведены три луча NС, NВ и NК. Найти угол КNВ, если
< СNВ =750, а <CNК= 140.
Геометрия 7 Атанасян К-1 Уровень 2 Контрольная работа № 1
Контрольная работа № 1 по геометрии в 7 классе «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы» с ответами УМК Атанасян Просвещение (средний уровень). Урок 10 поурочного планирования по геометрии. Геометрия 7 Атанасян К-1 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.
Смежные и вертикальные углы» с ответами УМК Атанасян Просвещение (средний уровень). Урок 10 поурочного планирования по геометрии. Геометрия 7 Атанасян К-1 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
Другие варианты контрольной работы № 1 в 7 классе:
К-1 Уровень 1 + Ответы
Контрольная работа № 1
Уровень 2 (средний). Геометрия 7 класс
Вариант 1 (транскрипт)
- На луче с началом в точке А отмечены точки В и С. Известно, что АВ = 10,3 см, ВС = 2,4 см. Какую длину может иметь отрезок АС?
- Разность двух углов, образовавшихся при пересечении двух прямых, равна 42°. Найдите все образовавшиеся углы.
- Один из смежных углов в пять раз больше другого. Найдите углы, которые образует биссектриса большего угла со сторонами меньшего.
- * Прямые АВ и CD пересекаются в точке О. ОК — биссектриса угла AOD, ∠COK = 118°. Найдите величину угла BOD.
Вариант 2 (транскрипт)
- На луче с началом в точке А отмечены точки В и С. Известно, что АС = 7,8 см, ВС = 2,5 см. Какую длину может иметь отрезок АВ?
- Один из углов, образовавшихся при пересечении двух прямых, на 22° меньше другого. Найдите все образовавшиеся углы.
- Один из смежных углов в четыре раза меньше другого. Найдите углы, которые образует биссектриса меньшего угла со сторонами большего.
- * Прямые MN и РК пересекаются в точке Е. ЕС — биссектриса угла MEP, ∠СЕК = 137°. Найдите величину угла КЕМ.
Решения и ответы на контрольную работу:
ОТВЕТЫ на Вариант 1
№ 1. Возможны два случая (рис. 1.139): а) АС = 12,7 см; б) АС= 7,9 см.
№ 2. ∠2 = ∠1 + 42°, ∠1 + ∠2 = 180°, отсюда ∠1 + ∠1 + 42° = 180°, ∠1 = ∠3 = 69°, ∠2 = ∠4 = 111° (рис. 1.140).
№ 3. Так как ∠KOB = 5∠AOK и ∠AOK + ∠KOB = 180°, то ∠AOK = 30°, ∠KOB = 150°. ∠KOC = ∠COB = 75°, тогда ∠AOC= 105° (рис. 1.141).
Ответ: ∠KOC = 75°, ∠AOC = 105°.
№ 4. ∠COK = 118°, ∠COK = ∠COA + ∠AOK. Так как ∠AOK = = X–∠AOD, a ∠AOD = 180° – ∠COA, тo ∠AOK= ½ • (180° – ∠COA), тогда ∠COK = ∠COA + ½ • (180° – ∠COA) = 118°. ∠COA = 56°, а значит, ∠BOD = 56° (рис. 1.142).
Ответ: 56°.
ОТВЕТЫ на Вариант 2
№ 1. Возможны два случая (рис. 1.143): а) АВ = 5,3 см; б) АВ = 10,3 см.
№ 2. ∠1 = ∠2 + 22°, ∠1 + ∠2 = 180°, отсюда ∠2 + ∠2 + 22° = 180°, ∠2 = ∠4 = 79°, ∠3 = ∠1 = 101° (рис. 1.144).
№ 3. Так как ∠COB = 4 ∠AOC и ∠COB+ ∠AOC = 180°, то ∠AOC = 36°, ∠COB = 144°. ∠COD = ∠DOA = 18°, тогда ∠BOD = 162° (рис. 1.145). ‘
№ 4. ∠CEK = 137°, ∠CEK = ∠CEM + ∠MEK. Так как ∠CEM = ½ ∠MEP, a ∠MEP =180° – ∠MEK, тo ∠CEM = ½ (180° – ∠MEK). Тогда ∠CEK = ½ (180° – ∠MEK) + ∠MEK = 137°. ∠MEK = 94°, т.e. ∠KEM = 94° (рис. 1.146).
Ответ: ∠KEM = 94°.
Информация для учителя:
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
Другие варианты контрольной работы № 1 в 7 классе:
К-1 Уровень 1 + Ответы К-1 Уровень 3 + Решения
Вы смотрели: Контрольная работа № 1 по геометрии в 7 классе
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Контрольная работа по геометрии на тему «Начальные геометрические сведения» 7 класс
Контрольная работа по теме «Начальные геометрические сведения» предназначена для учащихся 7 класса. Данная работа представлена в двух вариантах.
Просмотр содержимого документа
«Контрольная работа по геометрии на тему «Начальные геометрические сведения» 7 класс»
Геометрия 7 класс
Контрольная работа №1 на тему «Начальные геометрические сведения».
Работа учении____ _________________________________________________________
Дата проведения ___/ ___/ 20___ г
Вариант 1
Часть А. Запишите номера верных ответов к заданию 1.
1. Используя рисунок 1, укажите верные утверждения:
1) LAM и LAK — смежные углы.
2) LAM и NAM — вертикальные углы.
3) LAK — тупой угол.
4) MAN — прямой угол.
Рис 1.
Часть В. Запишите ответ к заданию 2.
2. Угол DCL равен 126°, СМ — биссектриса этого угла. Найдите угол MCL.
Часть С. Запишите обоснованное решение задач 3-5.
3. Найдите CPB, если BPK = 76°. (Рис. 2).
4. Найдите длины отрезков BP и DP, если BD = = 18 см, а отрезок DP на 4 см больше отрезка BP. (Рис. 2).
Рис. 2
5*. Из точки
Ответы.
Часть А | №№ правильных ответов | Часть В | Ответ |
Задание №1 | Задание №2 |
Часть С. Решения.
Геометрия 7 класс
Контрольная работа №1 на тему «Начальные геометрические сведения».
Работа учении____ _________________________________________________________
Дата проведения ___/ ___/ 20___ г
Вариант 2
Часть А. Запишите номера верных ответов к заданию 1.
1. Используя рисунок 1, укажите верные утверждения:
1) AKD и BKD — смежные углы.
2) BKD и BKE — вертикальные углы.
3) AKE — тупой угол.
4) BKE — прямой угол.
Рис. 1
Часть В. Запишите ответ к заданию 2.
2. Угол DCB равен 148°, СК — биссектриса этого угла. Найдите угол BCK.
Часть С. Запишите обоснованное решение задач 3-5.
3. Найдите ADC, если BDE равен 138°. (Рис. 2).
4. Найдите длины отрезков BD и DC, если ВС = 24 см, а отрезок BD на 8 см больше отрезка DC. (Рис. 2).
Рис. 2
5*. Отрезки MP и ОК пересекаются в точке Е, один из углов при вершине Е равен 110°. Найдите угол КЕС, где ЕС — биссектриса угла РЕК.
Ответы.
Часть А | №№ правильных ответов | Часть В | Ответ |
Задание №1 | Задание №2 |
Часть С. Решения.
Наш гид по экзаменам Trinity Grade 7
Есть четыре теста. В 7 классе пьесы могут быть в мажорной или минорной тональности:
7.1 — Размер, динамика, артикуляция
Вы услышите короткую пьесу, сыгранную дважды на фортепиано. Сначала определите размер, затем опишите динамику, затем прокомментируйте артикуляцию.
Размер
В 7-м классе вы должны уметь различать время 2/4, время 3/4, время 4/4 и тип времени 2, называемый временем 6/8 (или сложным временем дуплекса).За время 6/8 удары легко можно разделить на две группы по 3, что сделает их звучание «раскачивающимся».
К 7 классу вы уже будете практиковаться в распознавании всех этих размеров, но вот краткое содержание:
Послушайте этот пример за 2/4 раза:
Послушайте этот пример за 3/4 раза:
Прослушайте этот пример за 6/8 раз:
Послушайте этот пример за 4 раза:
Динамика и артикуляция
В 7 классе ожидается, что вы подробно опишете динамику и артикуляцию.Послушайте пример, затем прочтите описания, которые вы могли бы дать:
Dynamics — Пьеса начинается сильной стороной с акцентированных нот, которые затем имитируются в нижней части. На полпути происходит внезапное изменение фортепиано, но пьеса заканчивается форте.
Артикуляция — Артикуляция сначала стаккато, а затем частично невнятная. Более быстрые ноты обычно играются более плавно, чем более длинные.
7.2 — — Музыкальные особенности
После того, как вы дважды прослушаете произведение, вам будет предложено описать еще две особенности.
Рекомендуется заранее иметь в виду возможные функции, на которые вы могли бы обратить внимание, например:
Текстура — может быть или иметь элементы:
- Монофоническая фактура (одинарная линия без гармонии и аккомпанемента)
- Гомофоническая текстура (аккорд, в котором все звуки движутся вместе в одном ритме)
- Полифонический (несколько музыкальных линий или идей двигаются независимо друг от друга)
Структурные и композиционные приемы — вы можете указать длину фраз, последовательности, педальные ноты, хроматизм, точечные ритмы, повторение, имитацию, каденции, синкопы, орнаменты и то, начинается ли музыка с анакруса.
Персонаж — может быть танцевальным, маршевым или песенным, например.
Стиль — может быть барокко, классика, романтика, 20-21 века или джаз. После того, как вы описали другие характеристики, вероятно, легче предположить, в каком стиле находится изделие, потому что именно сочетание различных характеристик позволяет нам определить стиль.
Вот еще два примера, которые вы могли бы сказать о произведении, которое мы только что услышали:
Пьеса полифоническая — в ней есть однолинейные текстуры, каждая рука играет независимые строки, а левая рука имитирует правую в начале.Это танцевальный характер. Эти особенности позволяют предположить, что произведение принадлежит к эпохе музыки барокко.
Во время тренировки по аудиту вы услышите образцы музыки из разных эпох, чтобы лучше определять стиль.
Помощь со стилем и историей
Вот несколько индикаторов того, из какого стиля и периода происходит произведение. Конечно, не все они могут быть применимы к определенному произведению.
Барокко
- Использовался ограниченный диапазон клавиатуры
- Танцевальные ритмы
- Тщательно проработанная артикуляция
- Однолинейные текстуры с имитацией между частями
- Контрапункт — скрытые записи
- Нет педали или педаль очень маленькая
- Орнамент в стиле барокко
- Tempo остался прежним
- Никаких крайностей динамики
- Несложные гармонии
Возможные композиторы: Скарлатти, И. С. Бах, Гендель, Куперен, Пахельбель.
Классический
- Звучало как классический менуэт (если бы было в 3 раза)
- Он имел Alberti Bass (модель аккомпанемента с ломанными аккордами левой руки).
- Аккомпанемент основан на простых гармониях
- Очевидное использование гамм и арпеджио
- Динамика была оценена, чтобы сформировать фразы
- Мелодия изящная
- Использование элегантно невнятных нот
- С классическим орнаментом, как и витки
- Темп более-менее такой же — может немного подтормаживается в конце
- Обычная длина фразы, часто 4 такта
Возможные композиторы: Моцарт, Гайдн, ранний Бетховен, Клементи, Кухлау, Дуссек.
Романтический
- Очень выразительная игра
- … с большим количеством деталей, таких как упругое стаккато или широкие динамические изменения
- … с рубато (где темп гибкий — он становится немного быстрее, чем медленнее по фразе)
- Может сильно замедлиться в конце
- Кажется, выражает эмоции, такие как счастье / грусть / веселье / игривость
- Это может предложить сюжетную линию
- Богатые гармонии, иногда с плотными текстурированными аккордами (несколько нот одновременно)
- Расширенные фразы менее очевидной длины
- Лирическая мелодия, похожая на песню, с аккордовым или арпеджио-аккомпанементом
- Хроматизм в мелодиях или гармониях
- Использование педали сустейна
- Использовалась довольно широкая линейка клавиатуры
- Широкий динамический диапазон от очень громкого до очень тихого
Возможные композиторы: Шопен, Шуман, Григ, Брамс, Лист.
20 век и 21 век
- Гармония звучала достаточно современно, необычно, диссонансно или с нотками джаза
- Бодрые, иногда необычные ритмы
- Он имел джазовые ритмы — свинг или синкопированный
- Был хроматизм и цельные тональные шкалы (как Дебюсси или Равель).
- Смелые акценты
- Были большие динамические контрасты
- Внезапные изменения в динамике
- (Тем не менее, некоторые музыкальные произведения 20 века намеренно имеют очень мало изменений в динамике)
- Используется широкий компас — диапазон очень высоких и очень низких нот
Возможные композиторы: Прокофьев (ритмичный), Гершвин (джазовый), Барток (народное влияние, использование ладов, очень ритмичный) Дебюсси, Равель (импрессионист, мечтательный) Корник (джазовый), Нортон (джазовый), Скемптон (минималистский в идеях , повторяющиеся мотивы), Putz (плавный, сладко диссонирующий), McCabe & Hindemith (ударные, резкие изменения, сложные ритмы).
7.3 — Модуляция
Экзаменатор скажет вам, в какой тональности произведение, и сыграет ключевой аккорд. Затем вы снова услышите первые четыре такта и скажете, на какую тональность была модулирована музыка:
- субдоминантный ключ
- доминантный ключ
- относительный минорный ключ
- относительный мажорный ключ
Существуют различные способы идентификации новой тональности, например, некоторые люди пытаются удержать исходную ключевую ноту, напевая ее, а затем сравнивают ее с новой ключевой нотой.Для этого вам нужно уметь определять интервалы.
Более музыкальный способ решить, на какую тональность была модулирована музыка, — это слушать следующим образом:
Поддоминантный ключ
К субдоминанту, например От мажор до фа мажор — прислушайтесь к «нисходящему» эффекту добавленной квартиры. Впечатление немного похоже на идеальную или чумовую каденцию.
Доминантный ключ
К доминирующей тональности, напримерОт мажор до соль мажор — обратите внимание на «осветляющий» эффект добавленной резкости. Впечатление похоже на несовершенную каденцию, но сильнее.
Родственник несовершеннолетний
To the relative minor — послушайте изменение тональности от мажорной к минорной.
Родственник
Для относительного мажора — послушайте изменение тональности от минорной к мажорной.
7.4 — Изменения ритма и высоты звука
Экзаменатор даст вам распечатанную копию пьесы, которую вы слушали, и затем проиграет ее с тремя изменениями.Изменения могут касаться только высоты тона в мелодической линии, или могут относиться к ритму в любой части пьесы, или одновременно к мелодии и ритму.
Вы должны сказать, в каком такте происходило каждое изменение, и было ли это изменение ритма или высоты звука.
Вот пример трех изменений: сначала высота звука в такте 1, затем изменение ритма в такте 6, а затем изменение высоты звука в такте 7. Посмотрите видео в полноэкранном режиме:
Calculus II — Специальная серия
Онлайн-заметки ПавлаПримечания Быстрая навигация Скачать
- Перейти к
- Примечания
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Схождение / расхождение серий
- Интегральный тест
- Разделы
- Параметрические уравнения и полярные координаты
- Векторы
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер для комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущий раздел —
4.4 Геометрическое распределение (необязательно) | Техасский шлюз
Войдите во 2-й РАЙОН. Синтаксис инструкций следующий:
Чтобы вычислить вероятность значения P ( x = значение): используйте geometpdf ( p , число) . Здесь geometpdf представляет собой геометрическую функцию плотности вероятности. Он используется для определения вероятности того, что геометрическая случайная величина равна точному значению. p — вероятность успеха, а число — значение.
Чтобы вычислить кумулятивную вероятность P ( x ≤ значение): используйте geometcdf ( p , число) . Здесь geometcdf представляет собой геометрическую кумулятивную функцию распределения. Он используется для определения вероятности «не более» типа проблемы, вероятности того, что геометрическая случайная величина меньше или равна значению. p — вероятность успеха, а число — значение.
Чтобы найти P (x = 7) P (x = 7), введите 2nd DISTR, стрелку вниз до geometpdf (.Нажмите Ввод. Введите 0,02,7). Результат: P (x = 7) =. 0177P (x = 7) =. 0177.
Если нам нужно найти P (x≤7) P (x≤7), введите 2-й DISTR, стрелку вниз к geometcdf (. Нажмите ENTER. Введите .02,7). Результат: (x≤ = 7) =. 1319 (x≤ = 7) =. 1319.
График X ~ G (.02) —
Предыдущая гистограмма распределения вероятностей дает все вероятности X . Ось x каждой полосы — это значение X = количество компонентов компьютера, проверенных до обнаружения первого дефекта, а высота этой полосы — это вероятность появления этого значения.Например, значение x первого столбца равно 1, а высота первого столбца — 0,02. Это означает, что вероятность того, что первые протестированные компоненты компьютера неисправны, составляет 0,02.
Ожидаемое значение или среднее значение X равно E (X) = μ = 1p = 1.02 = 50E (X) = μ = 1p = 1.02 = 50.
Дисперсия X равна σ2 = (1p) (1p − 1) = (1.02) (1.02−1) = (50) (49) = 2,450σ2 = (1p) (1p − 1) = (1.02) (1.02 -1) = (50) (49) = 2,450.
Стандартное отклонение X составляет σ = σ2 = 2,450 = 49,5σ = σ2 = 2,450 = 49,5.
Вот как мы интерпретируем среднее значение и стандартное отклонение.Количество компонентов, которые вы ожидаете тестировать, пока не найдете первый дефектный, составляет 50 (это среднее значение). И вы ожидаете, что это будет отличаться в среднем примерно на 50 компонентов компьютера (что является стандартным отклонением).
Media aritmetica, media geometrya — Matera
1. Media aritmetică a două sau mai multe numere
Media aritmetică a două numere a și b este egală cu suma celor două numere, împărțită la doi.
m_a = \ frac {a + b} {2}
Media aritmetică a n numere este suma numerelor împărțită la numărul lor.
m_a = \ frac {x_1 + x_2 +… + x_n} {n}
Exerciii rezolvate cu media aritmetică
Exercițiul 1
Calculați media aritmetică a numerelor: 14, 21 și 37.
Rezolvare:
Exercițiul 2
Calculați media aritmetică a numerelor:
Rezolvare:
Exercițiul 3
La un concurs de informatică, elevii trebuie să susțină patru probe.Михай обинут ла простое пробуждение 6 точек, 8 точек и 9 точек. Câte puncte ar trebui să primească la ultima probă, pentru a avea o medie de 8 puncte?
Rezolvare:
2. Media aritmetică ponderată
Media aritmetică ponderată a n номер
având ponderile
se calculează folosind формула:
Exerciii rezolvate cu media ponderata
Exercițiul 1
Un Eve a cumpărat 3 caiete cu prețul de 5 лей / buc, 8 caiete cu prețul de 7 лей / buc și 9 caiete cu prețul de 8 лей / buc.Cât a plătit in medie pe un caiet?
Rezolvare:
Prin pondere înțelegem numărul de obiecte care au aceeași valoare / preț. Așadar, trebuie să calcăm media numerelor 5, 7 și 8 cu ponderile 3, 8 i 9.
Pe un caiet a plătit in medie 7,15 лей.
3. Медиа геометрическая a două numere reale
Media Geometrică sau media proporțională a două numere pozitive a și b este радикальный размер продукта:
Exerci reii rezolvate cu media geometry
Exercițiul 1
Calculați media geometryă a numerelor 4 și 9.2
Așadar, номер y va fi egal cu:
deoarece valoarea din modul e negativă:
Acum calcăm media aritmetică a celor două numere:
n Continuous Vom Calcula Media Geometrică a numerelor x și y .
4. Inegalitatea mediilor
Dacă a și b sunt două numere reale pozitive, atunci are loc următoarea inegalitate:
а \ leq m_g \ leq m_a \ leq b
Тест онлайн Медиа аритметика și медиа геометрическая
ncearcă să rezolvi acest test cu zece întrebări a câte un punct fiecare.Dacă răspunzi corect la toate întrebările, primești 10 puncte. Успехов!
геометрических последовательностей и серии
Геометрические последовательности
Геометрическая последовательность. Последовательность чисел, в которой каждое последующее число является произведением предыдущего числа и некоторой константы r ., Или геометрической прогрессии, используемой при ссылке на геометрическую последовательность., Представляет собой последовательность чисел, в которой каждое последующее число является произведением предыдущее число и некоторая постоянная r .
an = ran − 1 Геометрическая последовательность
И поскольку anan − 1 = r, постоянный множитель r называется общим отношением Константа r , которая получается делением любых двух последовательных членов геометрической последовательности; anan − 1 = r .. Например, следующая геометрическая последовательность,
9,27,81,243,729…
Здесь a1 = 9, а отношение между любыми двумя последовательными членами равно 3. Мы можем построить общий член an = 3an − 1, где,
a1 = 9a2 = 3a1 = 3 (9) = 27a3 = 3a2 = 3 (27) = 81a4 = 3a3 = 3 (81) = 243a5 = 3a4 = 3 (243) = 729 ⋮
В общем, с учетом первого члена a1 и общего отношения r геометрической последовательности мы можем записать следующее:
a2 = ra1a3 = ra2 = r (a1r) = a1r2a4 = ra3 = r (a1r2) = a1r3a5 = ra3 = r (a1r3) = a1r4 ⋮
Из этого мы видим, что любую геометрическую последовательность можно записать в терминах ее первого элемента, ее общего отношения и индекса следующим образом:
an = a1rn − 1 Геометрическая последовательность
Фактически, любой общий член, являющийся экспонентой в n , является геометрической последовательностью.
Пример 1
Найдите уравнение для общего члена данной геометрической последовательности и используйте его для вычисления 10 th члена: 3,6,12,24,48…
Решение:
Начнем с нахождения общего отношения,
г = 63 = 2
Обратите внимание, что соотношение между любыми двумя последовательными членами равно 2. Последовательность действительно представляет собой геометрическую прогрессию, где a1 = 3 и r = 2.
an = a1rn − 1 = 3 (2) n − 1
Следовательно, мы можем записать общий член an = 3 (2) n − 1, а член 10 th можно вычислить следующим образом:
a10 = 3 (2) 10−1 = 3 (2) 9 = 1,536
Ответ: an = 3 (2) n − 1; а10 = 1,536
Термины между данными элементами геометрической последовательности называются средними геометрическими. Термины между данными элементами геометрической последовательности..
Пример 2
Найдите все члены геометрической последовательности между a1 = −5 и a4 = −135. Другими словами, найдите все геометрические средние между 1 -м и 4 -м членами.
Решение:
Начнем с нахождения общего отношения r . В данном случае нам даны первый и четвертый слагаемые:
an = a1rn − 1 Используйте n = 4.

 Отрезок АВ на 0,9 см больше отрезка АС. Найти длину отрезка АВ, если известно, что длина отрезка АD=1,3 см, что на 2,9 см меньше, чем длина отрезка DC.
Отрезок АВ на 0,9 см больше отрезка АС. Найти длину отрезка АВ, если известно, что длина отрезка АD=1,3 см, что на 2,9 см меньше, чем длина отрезка DC. Найти градусную меру угла FOD, если
Найти градусную меру угла FOD, если