Методы оптимальных решений Контрольная работа
ТИПОВЫЕ ЗАДАЧИ ПО МИКРОЭКОНОМИКЕ U 1
ТИПОВЫЕ ЗАДАЧИ ПО МИКРОЭКОНОМИКЕ Задача Четыре индивида потребляют два блага в количествах и описываются функциями полезности U 0 0 ; U ln + ln; U ; U 4 4 Определить, какие индивиды имеют одинаковые предпочтения,
ПодробнееЭкономико-математические методы и модели
Частное образовательное учреждение высшего образования Приамурский институт агроэкономики и бизнеса Кафедра информационных технологий и математики ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ПО УЧЕБНОЙ ДИСЦИПЛИНЕ Экономико-математические
Экономико-математические методы и модели.

ИНСТИТУТ МИРОВОЙ ЭКОНОМИКИ И ИНФОРМАТИЗАЦИИ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Экономико-математические методы и модели. МОСКВА — 00 Практические задания
ПодробнееПроизводство экономических благ. Лекция 7
Южный федеральный университет Экономический факультет Лекция 7 Пять блоков вопросов 1. Производство. Производственные функции 2. Производство с одним переменным фактором 3. Производство с двумя переменными
Элементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль 6 Элементы линейного программирования
Подробнее3.3. БЮДЖЕТНАЯ ЛИНИЯ. ОПТИМУМ ПОТРЕБИТЕЛЯ
3. 3. Бюджетная линия. Оптимум потребителя 119 3.3. БЮДЖЕТНАЯ ЛИНИЯ. ОПТИМУМ ПОТРЕБИТЕЛЯ Карта безразличия представляет собой графическое отображение системы предпочтений потребителя. Естественно, потребитель
3. Бюджетная линия. Оптимум потребителя 119 3.3. БЮДЖЕТНАЯ ЛИНИЯ. ОПТИМУМ ПОТРЕБИТЕЛЯ Карта безразличия представляет собой графическое отображение системы предпочтений потребителя. Естественно, потребитель
ОТВЕТЫ Время выполнения заданий 90 минут
ОТВЕТЫ Время выполнения заданий 90 минут Часть А (задание 1-20) Выберите среди предложенных ответов единственный правильный и отметьте соответствующую ему цифру в бланке ответов на пересечении номера вопроса
ПодробнееЗадачи оптимизации. Кольцов С.Н
Задачи оптимизации. Кольцов С.Н 2014 www.linis.ru Задачи линейного программирования Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии
ЧАСТЬ Ii ПОТРЕБЛЕНИЕ И СПРОС
ЧАСТЬ Ii ПОТРЕБЛЕНИЕ И СПРОС 2. 1 Задачи Задача 1 Объем потребления некоторого товара домашним хозяйством (q) в зависимости от дохода (I) описывается равенством: 2 100I q =. 3 ( I + 10) Определить, при
1 Задачи Задача 1 Объем потребления некоторого товара домашним хозяйством (q) в зависимости от дохода (I) описывается равенством: 2 100I q =. 3 ( I + 10) Определить, при
Линейная алгебра
Линейная алгебра 22.12.2012 Линейные модели в экономике Линейное программирование Теория двойственности Линейная алгебра (лекция 15) 22.12.2012 2 / 28 Линейное программирование Каждой задаче линейного
задач Рабочая сила Латекс Гелий
5 задач, время 150 мин., 60 баллов. задач 1 3 4 5 Кол-во баллов 13 13 8 13 13 Задача 1. (13 баллов) На островах Иль де Бонѐр и Иль де Либертэ производят воздушные шарики, количество которых может выражаться
ПодробнееУсловия заданий и критерии оценивания
Олимпиада для студентов и выпускников вузов 3 г.
ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
Глава ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ.1. Эллипс, гипербола, парабола Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек F 1 и F есть постоянная
ПодробнееТема 4. Теория потребительского выбора
Тема 4. Теория потребительского выбора ПОТРЕБИТЕЛЬСКИЙ ВЫБОР решение потребителя о приобретении или какомлибо способе потребления некоторого блага (товара или услуги). Многие экономисты не разделяют понятий
Контрольная работа. F=6*x 1 +3*х 2, (3)
Контрольная работа Задача 5 На предприятии имеется сырье видов 1, 2, 3 Из него можно изготавливать изделия типов А и В Пусть запасы видов сырья на предприятии составляют b 1, b 2, b 3 ед соответственно,
ПодробнееДанный файл получен на сайте
ТЕСТ Ценообразование 1.
ЧАСТЬ v РЫНКИ ФАКТОРОВ ПРОИЗВОДСТВА
ЧАСТЬ v РЫНКИ ФАКТОРОВ ПРОИЗВОДСТВА 5.1 Задачи Задача 1 Функция полезности индивида U( I, F) = I + 200 R, где I суточный доход, R свободное время (часов в сутки). Найти объем предложения труда при следующих
ПодробнееТема 6. Теория потребительского выбора.
Тема 6. Теория потребительского выбора. Теория потребительского выбора описывает решения, формирующие индивидуальные кривые спроса и дает ответ на два вопроса: 1. Какое количество того или иного товара
Экономическая теория это наука:
1 Экономическая теория это наука: 2 Какая пара понятий отражает фундаментальную проблему экономической теории: 3 Ограниченность (редкость) ресурсов это проблема, которая: 4 Нормативная экономическая теория:
ПодробнееP, MR, MC MR 1 D 1 P 1 P 2 MR 2 D 2 P * Q * Q 1 Q 2
6.
( ) = , <. Тогда рыночный спрос,
Задания заочного тура Решите задания и заполните бланк ответов Будьте внимательны в заочном туре оцениваются только ответы Ответ на каждый из подпунктов задачи 1 оценивается в 2 балла ответ на каждый из
ПодробнееЭластичность спроса и предложения
Елена Александровна Давыдова кандидат экономических наук, доцент кафедры экономической теории факультета экономики НИУ ВШЭ Эластичность спроса и предложения Содержание Понятие эластичности Эластичность
S016-S020 S016. (1) (1)
Решения задач S016-S00 S016.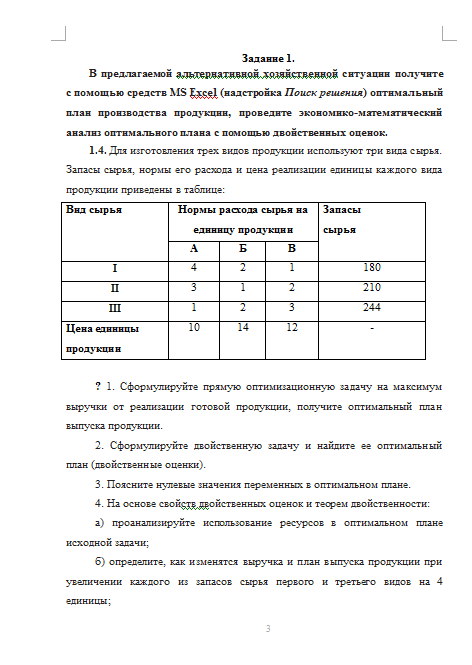 Долгое время фирма Х являлась единственным производителем уникального аппарата генератора закадрового смеха для комедийных сериалов. Фирма Х была легальным монополистом, так
Долгое время фирма Х являлась единственным производителем уникального аппарата генератора закадрового смеха для комедийных сериалов. Фирма Х была легальным монополистом, так
( ) Методы оптимальных решений Контрольная работа с подробным решением. Задача 1
Теория игр Решение контрольной работы
Теория игр Решение контрольной работы Задача Решить задачу графическим методом Решение Очевидно, матрица не имеет седловой точки, поэтому будем искать решение в смешанных стратегиях Решим задачу графическим
Подробнееопределяется матрицей A.

Задание.Мебельная фабрика планирует выпуск двух видов продукции А и Б. Спрос на продукцию не определен, однако можно предполагать, что он может принимать одно из трех состояний (I, II и III). В зависимости
ПодробнееЛекция 5. Игры с природой
Лекция 5. Игры с природой 09.10.2014 1 5.1. Понятие игры с природой 5.2. Принятие решений в условиях неопределенности 2 Как вы думаете, что такое неопределенность и риск в экономике? 3 Неопределенность
ПодробнееМатематический анализ Лекция 4.6
Московский Государственный Технический Университет им. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Лекция 4.6 к.ф.-м.н. Семакин А.Н. Математический анализ, Лекция
ПодробнееЛекция 2. Антагонистические игры.
Лекция 2. Антагонистические игры. 11.09.2014 1 2.1 Определение антагонистической игры 2.2 Понятие матричной игры 2.3 Выбор оптимальной стратегии в матричной игре 2.4 Ситуация равновесия в матричной игре
ПодробнееТеория принятия решений
Теория принятия решений Литература О.И. Ларичев «Теория и методы принятия решений» А.И. Орлов «Теория принятия решений» А.Т. Зуб «Принятие управленческих решений» А.Г. Мадера «Моделирование и принятие
ПодробнееБанк заданий для промежуточного контроля
Банк заданий для промежуточного контроля Тест. Тема «Линейное программирование» Состоит из — 3 теоретических вопроса по теме и 4 6 практических заданий, предусматривающих умения и навыки: составлять математические
ПодробнееЭкстремум функции двух переменных
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 11 Экстремум функции двух переменных Максимум или минимум функции называется её экстремумом Точка M 0, в которой функция имеет экстремум, называется точкой экстремума Если дифференцируемая
ПодробнееДинамическое программирование.

Лекция 7 Динамическое программирование. Задача распределения ресурсов. Динамическое программирование это математический метод нахождения оптимальных решений многошаговых (многоэтапных) задач. Динамическое
ПодробнееНелинейная задача оптимизации.
Нелинейная задача оптимизации. Кольцов С.Н 2014 www.linis.ru Задача безусловной оптимизации Задача оптимизации формулируется следующим образом: заданы множество Х (допустимое множество задачи) и функция
Подробнее3) Составление моделей экономических задач., стр , 3, 4,5,9,12. Домашнее задание. Теория:, стр Практика:, стр.20-25, 2,7,8,10.
5. Методические указания по подготовке к практическим занятиям при изучении дисциплины «Методы оптимальных решений» Направление подготовки 080100.62 «Экономика» Профиль «Экономика и управление инвестициями»
ПодробнееТЕОРИЯ ИГР В ЗАДАЧАХ
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ) М. Л. ОВЕРЧУК ТЕОРИЯ ИГР В ЗАДАЧАХ МЕТОДИЧЕСКИЕ УКАЗАНИЯ МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Л. ОВЕРЧУК ТЕОРИЯ ИГР В ЗАДАЧАХ МЕТОДИЧЕСКИЕ УКАЗАНИЯ МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Ситуационная задача 20 [K004140]
СЗ_Медицинская кибернетика_ч.2 17 СИТУАЦИОННЫЕ ЗАДАЧИ (часть 2) для первичной аккредитации выпускников, завершающих в 17 году подготовку по образовательной программе высшего медицинского образования в
ПодробнееЛокальная теорема Коши Пикара.
Локальная теорема Коши Пикара. Теорема (о существовании и единственности локального решения). Пусть дана задача Коши x = f(t, x) x(t 0 ) = x 0, (1) где правая часть f(t, x) определена и непрерывна в прямоугольнике
Подробнееmax f при условии, что g(x) = b i, (1)
Метод множителей Лагранжа Рассмотрим экстремальную задачу с ограничениями в виде равенств: найти a при условии что ) = ) на множестве допустимых значений описываемом системой уравнений где R : R R : R
ПодробнееМЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» Кафедра «Прикладная математика» И. А.
А.
Инвестиционная политика
УДК 336.051 ФОРМИРОВАНИЕ ОПТИМАЛЬНЫХ СТРАТЕГИЙ ИНВЕСТОРА НА РОССИЙСКОМ ФОНДОВОМ РЫНКЕ С ПОМОЩЬЮ МЕТОДОВ ТЕОРИИ ИГР Н. А. КЛИТИНА, ассистент кафедры фундаментальной и прикладной математики E-mal: kltnanna@yandex.
ПодробнееКонтрольная работа. F=6*x 1 +3*х 2, (3)
Контрольная работа Задача 5 На предприятии имеется сырье видов 1, 2, 3 Из него можно изготавливать изделия типов А и В Пусть запасы видов сырья на предприятии составляют b 1, b 2, b 3 ед соответственно,
ПодробнееПортфолио arcadynovosyolov: игры и решения
Портфолио arcadynovosyolov: игры и решения ОГЛАВЛЕНИЕ Типовые задачи… 2 Игры и решения… 2 Матричные игры… 2 Более сложные задачи… 7 Игры и решения… 7 Парето-оптимальное решение. .. 7 ТИПОВЫЕ ЗАДАЧИ
.. 7 ТИПОВЫЕ ЗАДАЧИ
равен k во всех точках множества Q.
17. Условный экстремум 17.1. Обратимся к рассмотрению нахождения условного (говорят также относительного) экстремума. Задача нахождения условного экстремума состоит в поиске локальных максимумов и минимумов
ПодробнееАВТОРЕФЕРАТ БАКАЛАВРСКОЙ РАБОТЫ
Министерство образования и науки Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПодробнееФондовый рынок 37 (565) 2013
37 (565) 3 УДК 33649 ФОРМИРОВАНИЕ ОПТИМАЛЬНОГО ПОРТФЕЛЯ ПРИ ЗАДАННОМ УРОВНЕ ДОХОДНОСТИ С ПОМОЩЬЮ ФУНКЦИИ ЛАГРАНЖА Н А КЛИТИНА, старший преподаватель кафедры фундаментальной и прикладной математики E-mal:
ПодробнееВведение.
 Каштанов В.А.
Каштанов В.А.Структурная надежность. Теория и практика Каштанов В.А. УПРАВЛЕНИЕ СТРУКТУРОЙ В МОДЕЛЯХ МАССОВОГО ОБСЛУЖИВАНИЯ И НАДЕЖНОСТИ С использованием управляемых полумарковских процессов исследуется оптимальная
ПодробнееДанный файл получен на сайте
Добавить вопрос МАТЕМАТИКА 1 Суммой (объединением) нескольких событий называется 2 Произведением (пересечением) двух событий А и В называется 3 Сколько существует различных пятизначных номеров, в которых
ПодробнееТеория принятия решений
Теория принятия решений Литература О.И. Ларичев «Теория и методы принятия решений» А.И. Орлов «Теория принятия решений» А.Т. Зуб «Принятие управленческих решений» А.Г. Мадера «Моделирование и принятие
ПодробнееВАРИАНТ 5 0,2 0,3 0,0 A 0,3 0,1 0, 2, 0,1 0, 0 0,3
ВАРИАНТ 5 Задание 1. Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс
Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс
ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
ИНФОРМАТИКА И ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА УДК 33:57.977. ББК 65в Б 7 З.У. Блягоз, А.Ю. Попова Принятие решений в условиях риска и неопределенности Аннотация: В статье рассматривается математическая модель игры,
ПодробнееДинамическое программирование.
Одесский национальний университет им. И.И.Мечникова Институт математики, экономики и механики Кафедра оптимального управления и экономической кибернетики Методические указания и задания для лабораторной
ПодробнееБиматричные игры. Решение игр 2 2
Биматричные игры Решение игр 2 2 Будем рассматривать 2 2 биматричную игру с матрицами выигрышей a a A = 2 b b, B = 2 a 2 a 22 b 2 b 22 Матрица A описывает выигрыши первого игрока, B, соответственно, второго
Подробнее1 ТЕМА 6: ТЕОРИЯ ИГР
1 ТЕМА 6: ТЕОРИЯ ИГР 2 Рекомендуемая литература: 1. Петросян Л. А. Теория игр. 2-е изд. СПб. : БХВ- Петербург, 2012. 424 с. 2. Колесник Г. В. Теория игр. 3-е изд. М. : Либроком, 2012. 152 с. 3. Лабскер
Петросян Л. А. Теория игр. 2-е изд. СПб. : БХВ- Петербург, 2012. 424 с. 2. Колесник Г. В. Теория игр. 3-е изд. М. : Либроком, 2012. 152 с. 3. Лабскер
Постановка и методы решения конечных игр
Постановка и методы решения конечных игр Методы теории игр рассматривают так называемые конфликтные ситуации, где сталкиваются интересы двух или более сторон, преследующих разные цели. Наибольшее распространение
ПодробнееКонтрольная работа по методам оптимальных решений Вариант 1.
1. Построить допустимую область для заданной системы линейных неравенств и найти координаты угловых вершин полученной области
2. Найти графическим способом наибольшее и наименьшее значение целевой функции zпри заданных условиях
z=x+y max (min)
при условии ( y—x 0, -2 x 0, y-0. 5x 0)
5x 0)
3. На трёх базах А1,А2 ,А3находится однородный груз в количествеа1,а2,а3. Этот груз необходимо развести пяти потребителямB1,B2,B3,B4,B5, потребности которых в данном грузе составляютb1,b2,b3,b4,b5соответственно. Стоимость перевозок пропорциональна расстоянию и количеству перевозимого груза. Матрица тарифовcij (тыс.руб./т.) и значенияа1,а2 ,а3;b1,b2,b3,b4,b5приведены ниже:
а1 = 200т; а2 = 250т; а3 = 250т; | b1 = 80т; b2 = 260т; b3 = 100т; b4 = 140т; b5 = 120т; |
Требуется спланировать
для транспортной задачи (ТЗ)
первоначальные планы перевозокxijдвумя способами (метод северо-западного
угла, метод минимальной стоимости) и
определить для полученных планов
значения целевой функции.
4. Методом потенциалов провести 2 шага улучшения первоначального плана ТЗ из задания 3, полученного по методу «северо-западного» угла. Записать полученное решение и вычислить для него значение целевой функции.
Контрольная работа по методам оптимальных решений Вариант 2.
1. Построить допустимую область для заданной системы линейных неравенств и найти координаты угловых вершин полученной области
2. Найти графическим способом наибольшее и наименьшее значение целевой функции zпри заданных условиях
z=-2x+y max (min)
при условии ( y—x 1, y+x 3, y 1, x 3)
3. На трёх базах А1,А2 ,А3находится однородный
груз в количествеа1,а2,а3. Этот груз необходимо
развести пяти потребителямB1,B2,B3,B4,B5, потребности которых в данном грузе
составляютb1,b2,b3,b4,b5соответственно.
Стоимость перевозок пропорциональна
расстоянию и количеству перевозимого
груза. Матрица тарифовcij (тыс.руб./т.) и значенияа1,а2 ,а3;b1,b2,b3,b4,b5приведены ниже:
Этот груз необходимо
развести пяти потребителямB1,B2,B3,B4,B5, потребности которых в данном грузе
составляютb1,b2,b3,b4,b5соответственно.
Стоимость перевозок пропорциональна
расстоянию и количеству перевозимого
груза. Матрица тарифовcij (тыс.руб./т.) и значенияа1,а2 ,а3;b1,b2,b3,b4,b5приведены ниже:
а1 = 150т; а2 = 200т; а3 = 150т; | b1 = 60т; b2 = 140т; b3 = 100т; b4 = 80т; b5 = 120т; |
Требуется спланировать
для транспортной задачи (ТЗ)
первоначальные планы перевозокxijдвумя способами (метод северо-западного
угла, метод минимальной стоимости) и
определить для полученных планов
значения целевой функции.
4. Методом потенциалов провести 2 шага улучшения первоначального плана ТЗ из задания 3, полученного по методу «северо-западного» угла. Записать полученное решение и вычислить для него значение целевой функции.
Контрольная работа по методам оптимальных решений Вариант 3.
1. Построить допустимую область для заданной системы линейных неравенств и найти координаты угловых вершин полученной области
2. Найти графическим способом наибольшее и наименьшее значение целевой функции zпри заданных условиях
z=x+2y max (min)
при условии ( y 3, y—x 0, 0 x 2)
3. На трёх базах А1,А2 ,А3находится однородный
груз в количествеа1,а2,а3. Этот груз необходимо
развести пяти потребителямB1,B2,B3,B4,B5, потребности которых в данном грузе
составляютb1,b2,b3,b4,b5соответственно.
Стоимость перевозок пропорциональна
расстоянию и количеству перевозимого
груза. Матрица тарифовcij (тыс.руб./т.) и значенияа1,а2 ,а3;b1,b2,b3,b4,b5приведены ниже:
а1 = 100т; а2 = 250т; а3 = 150т; | b1 = 70т; b2 = 140т; b3 = 100т; b4 = 70т; b5 = 120т; |
Требуется спланировать
для транспортной задачи (ТЗ)
первоначальные планы перевозокxijдвумя способами (метод северо-западного
угла, метод минимальной стоимости) и
определить для полученных планов
значения целевой функции.
4. Методом потенциалов провести 2 шага улучшения первоначального плана ТЗ из задания 3, полученного по методу «северо-западного» угла. Записать полученное решение и вычислить для него значение целевой функции.
Методы оптимальных решений РФЭИ Компьютерный практикум (3 задачи) + Контрольная работа (3 задачи) РФЭИ.
Фрагмент работы Введение Содержание Список литературы
Контрольная работа РФЭИ «Методы оптимальных решений» 3 задачиКонтрольный компьютерный практикум РФЭИ. Методы оптимальных решений
2 работы выполнены на ОТЛИЧНО!!!
Задания контрольного компьютерного практикумаЗадача 1
Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой машиной I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице 1.
Каждый продукт должен быть обработан каждой машиной I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице 1.
Таблица 1
I II III
А 0,5 0,4 0,2
В 0,25 0,3 0,4
Время работы машин I, II, III соответственно 40, 36 и 36 часов в неделю. Прибыль от изделий А и В составляет соответственно 5 и 3 доллара.
Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль.
Задача 2
Минимизировать функцию F (x) = 2×1 + 3×2 при следующих ограничениях:
5 x1 + 3×2 ≤ 15,
5 x1 + 4×2 ≥ 20,
x1 ≥ 0,
x2 ≥ 0,
x2 ≥ 5.
Задача 3
Максимизировать функцию F (x) = 7×1 – x2 при следующих ограничениях
3×1 + 5×2 ≤ 18,
4×1 + x2 ≤ 0,
Показать все 3×1 — 2×2 ≥ — 12,
— 7 x1 + x2 ≤ 2,
x1 ≥ 0,
x2 ≥ 0.
=========================
Задача 1
Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице 1.
Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице 1.
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного – 14 ден. ед. Определить количество мороженого каждого вида, которое
должна производить фирма, чтобы доход от реализации продукции был максимальным.
Задача 2
Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов и амортизация оборудования за один месяц и общий ресурс при каждом способе производства даны в таблице 2 (в ден. ед.).
При первом способе производства предприятие выпускает за один месяц 3 тыс.
Задача 3
Решить графическим способом задачу максимизации функции
F (x) = 2Х1 + 4Х2
при следующих ограничениях:
-2Х1 + 3Х2
Скрыть
…
…
Контрольная работа по методам оптимальных решений. Вариант 7
Краткое описание
Вариант № 7
Методы оптимальных решений:
6.3. Дана задача линейного программирования L (Х) = Х1 + Х2→ maх (min) при ограничениях:
7 х1 + 6х2 ≤ 42
— 2х1 + Х2 ≤ 4
3х1— 2х2 ≤ 0
— Х2 ≤ -2
Х1;Х2 ≥ 0
Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минимальному значениям.
6.6. Составить математическую модель и решить задачу симплексным методом.
В производстве пользующихся спросом двух изделий, А и В, принимают участие 3 цеха фирмы. На изготовление одного изделия А 1-й цех затрачивает a1 ч, 2-й цех — a2 ч, 3-й цех — а3 ч. На изготовление одного изделия В 1-й цех затрачивает d1 ч, 2-й цех — d2 ч, 3-й цех — d3 ч. На производство обоих изделий 1-й цех может затратить не более b1 ч, 2-й цех — не более b2 ч, 3-й цех — не более b3 ч.
От реализации одного изделия А фирма получает доход c1 р., изделия В — c2 р.
Определить максимальный доход от реализации всех изделий А и В.
6.7. Дана исходная задача при ограничениях:
7х1 + 8х2 ≤ 56
— 2х + 3х2 ≤ 6
— 2х1 + Х2 ≤ 0
Х1 ≤ 6
Х1;Х2 ≥ 0
Составить математическую модель симметричной двойственной задачи. По решению двойственной или исходной задачи найти решение другой с использованием основных теорем двойственности.
По решению двойственной или исходной задачи найти решение другой с использованием основных теорем двойственности.
6.11. Составить математическую модель транспортной задачи и решить ее.
Фирма имеет три магазина розничной торговли, расположенных в разных районах города (А, В, С). Поставки продукции в эти магазины осуществляются с двух складов D и Е, площади которых вмещают 30 и 25 т продукции соответственно. В связи с возросшим покупательским спросом фирма планирует расширить площади магазинов, поэтому их потребности в продукции с торговых складов составят 20, 35 и 15 т в день. Чтобы удовлетворить спрос на продукцию, предполагается строительство третьего склада, площади которого позволят хранить в нем 15 т продукции ежедневно. Руководство фирмы рассматривает два варианта его размещения. В таблице даны транспортные издержки, соответствующие перевозке продукции с двух существующих складов, и два варианта размещения нового склада.
Оценить две транспортные модели и принять решение, ка¬кой вариант размещения нового склада выгоднее. Предполагается, что остальные издержки сохраняют существующие значения.
Методы и модели в экономике:
8.2. Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, при¬надлежащих фирме.
Для модернизации предприятий совет директоров инвестирует средства в объеме 250 млн р. с дискретностью 50 млн р. Прирост выпуска продукции зависит от выделенной суммы, его значения представлены предприятиями и содержатся в таблице.
Найти распределение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.
8.3. В трех районах города предприниматель планирует строительство пользующихся спросом одинаковых по площади ми¬ни-магазинов «Продукты». Известны места, в которых их можно построить. Подсчитаны затраты на их строительство и эксплуатацию.
Известны места, в которых их можно построить. Подсчитаны затраты на их строительство и эксплуатацию.
Необходимо так разместить мини-магазины, чтобы затраты на их строительство и эксплуатацию были минимальные.
Таблица
|
Х |
1 |
2 |
3 |
4 |
|
g1(х)
g 2 (х)
g3(х) |
18
17
20 |
29
30
32 |
42
41
44 |
57
55
59 |
9. 3. Составить сетевой график выполнения работ и рассчитать временные параметры по данным, представленным в таблице.
3. Составить сетевой график выполнения работ и рассчитать временные параметры по данным, представленным в таблице.
Таблица
|
Содержание работы |
Обозначение |
Предыдущая работа |
Продолжительность, дни. |
|
Исходные данные на изделие |
|
15 |
|
|
Заказ комплектующих деталей |
10 |
||
|
Выпуск документации |
12 |
||
|
Изготовление деталей |
30 |
||
|
Поставка комплектующих деталей |
26 |
||
|
Сборка изделия |
, |
17 |
|
|
Выпуск документации на испытание |
19 |
||
|
Испытание и приемка изделия |
, |
18 |
10. 2. Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.
2. Торговая фирма разработала несколько вариантов плана продаж товаров на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.
1) Определить оптимальную стратегию фирмы в продаже товаров на ярмарке.
2) Если существует риск (вероятность реализации плана П1 — b% = 30, П2 — с% = 35, П3 — d% = 35), то какую стратегию фирме следует считать оптимальной?
Таблица
|
План продаж |
Величина дохода, ден. ед. |
||
|
|
Д1 |
Д2 |
Д3 |
|
П1 |
2 |
3 |
3 |
|
П2 |
4 |
2 |
1 |
|
П3 |
3 |
2 |
4 |
11. 2. Приходная касса городского района с временем работы А = 8 часов в день проводит прием от населения коммунальных услуг и различных платежей в среднем от В = 240 человек в день.
2. Приходная касса городского района с временем работы А = 8 часов в день проводит прием от населения коммунальных услуг и различных платежей в среднем от В = 240 человек в день.
В приходной кассе работают С = 3 оператора-кассира. Средняя продолжительность обслуживания одного клиента составляет D = 5 мин.
Определить характеристики работы приходной кассы как объекта СМО.
Контрольная работа по методам оптимальных решений. Вариант 3
Контрольная работа по методам оптимальных решений. Вариант 5
Контрольная работа по методам оптимальных решений. Вариант 6
Контрольная работа по методам оптимальных решений. Вариант 7
Контрольная работа по методам оптимальных решений. Вариант-8.
Контрольная работа по методам оптимальных решений. Вариант 10
Контрольная Методы оптимальных решений (вариант 6, НГУЭУ)
| Группа предметов | Технические |
| Предмет | Методы оптимальных решений |
| Тема/вариант работы | Контрольная Методы оптимальных решений (вариант 6, НГУЭУ) |
| Кол-во источников: | 0 |
| Кол-во страниц: | 11 |
| Тип работы: | Контрольная работа, 2017 |
| Цена работы | 350 руб |
Ситуационная (практическая) задача № 1
Для изготовления продукции двух видов А и В фирма расходует ресурсы, а от реализации этой продукции получает доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице.
Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении фирмы, и выручки от реализации продукции приведены в таблице.
Задача фирмы заключается в том, чтобы найти план выпуска, обеспечивающий получение максимальной выручки от реализации готовой продукции.
Требуется:
1. Построить математическую модель оптимизации выпуска продукции и записать ее в форме задачи линейного программирования.
2. Используя графический метод решения, найти оптимальный план выпуска продукции.
3. Составив двойственную задачу, к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения.
Ситуационная (практическая) задача № 2
Фирма может влиять дополнительным финансированием на скорость строительства своего торгового павильона. Очередность выполнения работ, их нормальная и ускоренная продолжительность выполнения, а также стоимость строительно-монтажных работ при нормальном и ускоренном режиме их выполнения приведены в таблицах.
Требуется:
1. С учетом технологической последовательности работ построить сетевой график выполнения этих работ.
2. Рассчитать временные характеристики сетевого графика при нормальном режиме выполнения работ. Найти критический путь и его продолжительность, указать все возможные критические пути, определить стоимость всего комплекса работ.
3. Указать стратегию минимального удорожания комплекса работ при сокращении сроков строительства на 2 дня. В какую итоговую сумму обойдется фирме ускоренная стройка павильона?
С данной контрольной работой также покупают
Билет №5 Методы оптимальных решений
Новую работу можно заказать здесь
Контрольная работа по «Методы оптимальных решений»
КОНТРОЛЬНАЯ РАБОТА
В а р и а н т 2
Задание 1. Пусть экономическая ситуация описывается как задача линейного программирования вида:
F = 3×1 + x2 ® max
2×1 + x2 ≤ 10 [pic 1]
1 ≤ x1 ≤ 4
x2 ≥ 1
x1 ≥ 0
Постройте графическую модель задачи и найдите ее решение графическим методом.
Р е ш е н и е :
Приведём задачу к стандартному виду ЗЛП :
F = 3×1 + x2 → max [pic 2]
2×1 + x2 ≤ 10
x1 ≥ 1
x1 ≤ 4
x2 ≥ 1.
Построим область допустимых решений (ОДP) Для этого построим прямые
( заменяем знаки неравенства на «=» )
2×1 + х2 = 10 (1)
х1 = 1 (2)
х1 = 4 (3)
х2 = 1 (4)
( прямую (1) cтроим по точкам (1; 8) и (5; 0) )
[pic 3]
Получили ОДР – трапецию ABCD. Направление максимизации целевой функкции (ЦФ) F = 3х1 + х2 задаёт вектор-градиент ( розовая стрелка ), его координаты – коэффициенты ЦФ, (3; 1) . Линии уровня ЦФ (краcный пунктир) – это прямые F = C, т.е. 3х1 + х2 = С, они перпендикулярны градиенту. Проводим произвольно линию уровня через начало координат ( при С = 0 короткий пунктир) или через конец вектора (3; 1) . При решении задачи на максимум нужно двигать эту прямую по градиенту до последнего касания этой прямой с ОДР в точке D.
При решении задачи на максимум нужно двигать эту прямую по градиенту до последнего касания этой прямой с ОДР в точке D.
[pic 4]
Так как точка D получена в результате пересечения прямых (1) и (3), то ее
координаты удовлетворяют уравнениям этих прямых:[pic 5]
2×1+ x2 = 10
x1 = 4
откуда получим: x1 = 4, x2 = 2 или Х* = (4; 2).
Тогда максимальное значение целевой функции:
max F = F(X*) = 3*4 + 1*2 = 14
Ответ : max F = F(4; 2 ) = 14
Задание 2
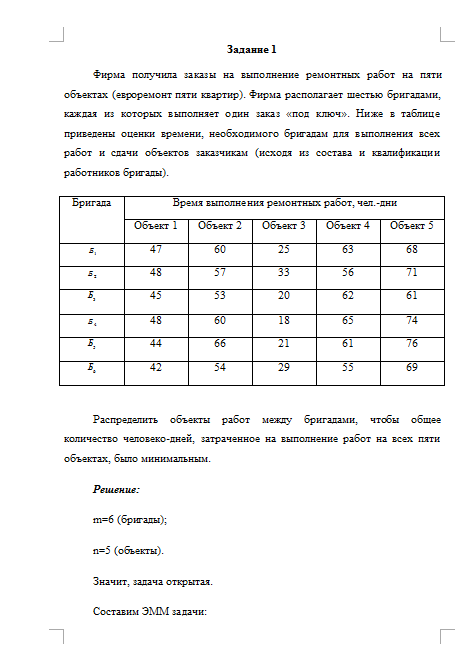
Для производства 4-х видов продукции используется 3 вида сырья. Нормы расхода сырья (кг), его запасы (кг), прибыль от реализации единицы продукции заданы таблицей.
Нормы расхода ресурсов на 1ед продукции | Запас ресурса | ||||
1 | 2 | 3 | 4 | ||
А | 4 | 5 | 10 | 2 | 30 |
В | 5 | 15 | 20 | 5 | 70 |
С | 40 | 10 | 15 | 20 | 150 |
Прибыль | 6 | 7,5 | 10 | 15 | МАХ |
1. Составить задачу линейного программирования, позволяющую определить оптимальный план выпуска продукции, обеспечивающий получение максимальной прибыли.
Составить задачу линейного программирования, позволяющую определить оптимальный план выпуска продукции, обеспечивающий получение максимальной прибыли.
2. Решить задачу, используя симплекс-метод. Записать решение и пояснить его экономический смысл. Важно: количество продукции каждого вида может принимать дробные значения.
3. Составить двойственную задачу. Найти решение двойственной задачи,
используя симплекс-таблицы, полученные при решении исходной задачи.
Пояснить экономический смысл решения.
Р е ш е н и е :
1. Обозначим : х1, x2 х3 х4 — план производства видов продукции И1 И2 И3 И4 соответственно. Тогда затраты ресурсов на план : А – (4х1+5х2+10х3+2х4),
В – (5х1+15х2+20х3+5х4), С – (40х1+10х2+15х3+20х4), прибыль равна:
6х1 + 7,5х2 + 10х3 + 15х4 (де.).
Получаем задачу ЛП :
F = 6х1 + 7,5х2 + 10х3 + 15х4 → max
4х1+5х2+10х3+2х4 ≤ 30[pic 6]
Excel Solver — Решения: выполнимые, «хорошие» и оптимальные
Решение (набор значений для переменных решения), для которого выполняются все ограничения в модели Solver, называется возможным решением . В некоторых проблемах уже известно возможное решение; в других случаях поиск приемлемого решения может быть самой сложной частью проблемы.
В некоторых проблемах уже известно возможное решение; в других случаях поиск приемлемого решения может быть самой сложной частью проблемы.
Оптимальное решение — это допустимое решение, в котором целевая функция достигает своего максимального (или минимального) значения — например, максимальной прибыли или наименьших затрат.Глобально оптимальное решение — это решение, в котором нет других возможных решений с лучшими значениями целевой функции. Локально оптимальное решение — это решение, в котором нет других возможных решений «поблизости» с лучшими значениями целевой функции — вы можете представить это как точку наверху «пика» или внизу «впадины». который может быть сформирован целевой функцией и / или ограничениями.
Solver предназначен для поиска возможных и оптимальных решений.В лучшем случае он найдет глобально оптимальное решение, но это не всегда возможно. В других случаях он найдет локально оптимальное решение, а в третьих, он остановится через определенный промежуток времени с лучшим решением, которое было найдено до сих пор. Но, как и многие пользователи, вы можете решить, что наиболее важно найти хорошее решение — то, которое лучше, чем решение или набор вариантов, которые вы используете сейчас.
Но, как и многие пользователи, вы можете решить, что наиболее важно найти хорошее решение — то, которое лучше, чем решение или набор вариантов, которые вы используете сейчас.
Тип решения, который может найти Решатель, зависит от характера математических соотношений между переменными, целевой функцией и ограничениями (и используемым алгоритмом решения).Как объясняется ниже, если ваша модель гладко выпуклая , вы можете рассчитывать найти глобально оптимальное решение; если он гладкий, но невыпуклый , вы обычно сможете найти локально оптимальное решение; если это негладкий , вам, возможно, придется довольствоваться «хорошим» решением, которое может быть или не быть оптимальным.
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Инструменты для валидации LP-моделирования
Что может пойти не так в процессе построения модели линейного программирования (LP)? Существуют потенциальные ловушки, влияющие на любое приложение LP; поэтому лицо, принимающее решение, и аналитик должны осознавать недостатки LP на этапе моделирования.
Для поиска на сайте попробуйте E dit | F ind на странице [Ctrl + f]. Введите слово или фразу в диалоговом окне, например « параметр» или « linear» Если первое появление слова / фразы не то, что вы ищете, попробуйте F ind Next .
МЕНЮ
- Введение
- Безграничность
- Множественные оптимальные решения (Бесчисленные оптимальные решения)
- Нет решения (невыполнимый LP)
- Вырождение
- Вырождение и двойные (теневые) цены
- У теневой цены может быть неправильный знак
- Избыточность среди ограничений
- Идентификация неограниченных возможных областей
- LP без вершины
- LP с неограниченными и множественными ограниченными оптимальными решениями
- Об основных и небазовых переменных решения
- LP без внутренних и граничных решений
- Оптимальное решение, созданное одним пакетом LP, не может быть получено другим
- Дает ли оптимальная симплексная таблица двойное решение?
- Решение целочисленного LP не может быть одной из целочисленных вершин
- Преобразование в стандартную форму может исказить возможную область
- Снятие ограничений равенства путем замены может изменить проблему
- Неправильная интерпретация теневой цены
- Всегда ли теневая цена неотрицательна?
- Альтернативные теневые цены
- Диапазон чувствительности стоимости с помощью графического метода
- Больше за меньшее и меньше за большее
- Электронные лабораторные работы по JavaScript
Сайтов-компаньонов:
Введение
Существуют потенциальные проблемы, которые влияют на любое приложение линейного программирования.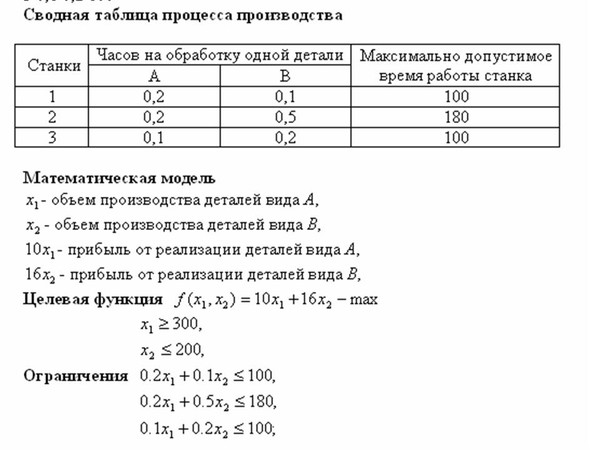 Оптимальное решение может быть невыполнимым или неограниченным, или может быть несколько решений. Также может произойти вырождение. На следующем рисунке представлена классификация LP для моделирования процесса валидации:
Оптимальное решение может быть невыполнимым или неограниченным, или может быть несколько решений. Также может произойти вырождение. На следующем рисунке представлена классификация LP для моделирования процесса валидации: Классификация решений линейных программ для моделирования процесса валидации
Эти и другие подводные камни не являются серьезным недостатком линейного программирования, поскольку это ситуации, о которых должен знать лицо, принимающее решения. Что может пойти не так в процессе построения ЛВ-модели?
Проблемы с пакетами LP: Большинство программных решателей LP испытывают трудности с распознаванием темной стороны LP и / или с какими-либо предложениями по их устранению.Примените следующие числовые задачи к WinQSB и обнаружите, а затем сообщите о том, что вы получили в качестве результата.
Неограниченность
Идентификация: В алгоритме симплексного решения, если вводится столбец j и все aij в этом столбце меньше или равны нулю, или соотношение столбцов (C / R) не может быть выполнено. См. Также случай вырождения.
См. Также случай вырождения.Например, рассмотрим следующую проблему:
Макс Y1
при условии:
Y1 + Y2 -2T = 0
Y1 -Y2 = 2
все переменные решения ³ 0.
После симплексных итераций мы попадаем в следующую таблицу:
| BVS | Y1 | Y2 | T | RHS | |
|---|---|---|---|---|---|
| Т | 0 | -1 | 1 | 1 | |
| Y1 | 1 | -1 | 0 | 2 | |
| Cj | 0 | 1 |
Хотя переменная Y2 должна входить в качестве базовой переменной, все элементы в этом столбце меньше нуля. Следовательно, проблема LP неограничена.
Следовательно, проблема LP неограничена.
Узнайте, что неограниченное Оптимальное решение означает наличие замкнутой неограниченной допустимой области, однако обратное этому утверждению может быть неверным. Несвязанное оптимальное решение означает, что ограничения не ограничивают оптимальное решение, а допустимая область эффективно простирается до бесконечности.
Разрешение: В реальной жизни такое бывает очень редко. Проверьте формулировку ограничений, одно или несколько ограничений отсутствуют.Также проверьте ограничения на наличие ошибок в спецификации в направлении ограничений неравенства и числовых ошибок.
Анализ чувствительности не применяется.
WinQSB и Lindo заявляют, что проблема неограниченна.
Возможная область неограниченности: Как упоминалось выше, знайте, что случай неограниченного решения требует неограниченной допустимой области. Обратное этому утверждению может быть неверным. Например, следующая задача LP имеет неограниченную допустимую область, однако решение ограничено:
Макс -4X1 -2X2
при условии:
X1 ³ 4
X2 £ 2
все переменные решения ³ 0.
Оптимальный вариант — X1 = 4 и X2 = 0.
Множественные оптимальные решения (Бесчисленные оптимальные решения)
Идентификация: В окончательной симплексной таблице, если строка Cj (последняя строка в таблице) равна нулю для одной или нескольких неосновных переменных, то у нас может быть более одного оптимального решения (следовательно, бесконечно много оптимальных решений ). Чтобы найти все остальные оптимальные угловые точки (если таковые имеются), поочередно вращайте каждый из неосновных столбцов с нулевым Cj.Необходимое условие для существования множественных решений LP. : Если общее количество нулей в приведенной стоимости вместе с количеством нулей в столбцах теневой цены превышает количество ограничений, то у вас может быть несколько решений.
Пример: следующая задача имеет много оптимальных решений:
Макс 6X1 + 4X2
при условии:
X1 + 2X2 16 фунтов стерлингов
3X1 + 2X2 £ 24
все переменные решения ³ 0.
Если вы запустите указанную выше проблему, скажем, на WinQSB или Lindo, вы найдете четыре нуля. Однако вы должны заметить, что это только необходимое условие, а не достаточное, как в приведенном выше числовом примере. К сожалению, QSB использует это необходимое условие. Поэтому иногда он дает неправильные сообщения.
Используя компьютерный пакет QSB, вы получите следующие два решения: (X1 = 8, X2 = 0) и (X1 = 4, X2 = 6). Обратите внимание, что наличие нескольких решений означает, что у нас есть бесчисленное множество оптимальных решений (а не только два).
Если имеется более одной вершин , которые являются оптимальными, мы всегда можем сгенерировать все другие оптимальные решения путем «линейной комбинации» координат всех оптимальных вершин. Например, для вышеупомянутой проблемы, основанной на двух решениях, полученных QSB, все следующие решения действительно являются оптимальными:
X1 = 8a + (1 — a) 4 = 4 + 4a, X2 = 0a + (1- a) 6 = 6 — a, для всех 0 £ a £ 1.
Разрешение: Проверьте коэффициенты целевой функции и ограничения.Могли быть ошибки округления.
Анализ чувствительности Не применяется. То есть анализ чувствительности, основанный на одном оптимальном решении, может быть неприменим для других.
Предупреждения об использовании пакетов программного обеспечения: К сожалению, Lindo не предоставляет никаких прямых предупреждений о существовании нескольких решений. WinQSB утверждает, что найдены альтернативные оптимальные решения. Однако такое заявление могло ввести в заблуждение.Например, следующая проблема имеет уникальное решение, WinQSB заявляет, что существует несколько решений!
Макс 30X1 — 4X2
S.T. 5X1 — X2 £ 30
X1 £ 5
X1 ³ 0
X2 не ограничен.
Единственное решение — X1 = 5, X2 = -5 с оптимальным значением 170.
Для следующей проблемы WinQSB предлагает 4 различных решения:
Свернуть X1 + X2 + 2X3
при условии:
X1 + X2 + X3 ³ 10
X1 + X2 + 2X3 ³ 13
X1, X2 неотрицательны.
Множество всех оптимальных решений этой задачи составляет полуплоскость. То есть все оптимальные решения лежат на плоскости X1 + X2 + 2X3 = 13, такой что X1 + X2 + X3 ³ 10, X1 ³ 0, X2 ³ 1 и X3 ³ 0.
Артикул:
Аппа Г., Об уникальности решений линейных программ, Журнал Общества операционных исследований , 53 (10), 1127-1132, 2002.
Стейнберг Д. и Д. Аукамп, О ранжировании коэффициентов стоимости в двойных вырожденных задачах линейного программирования, Decision Sciences , 14 (3), 440-441, 1983.
Нет решения (невыполнимая LP)
Невозможное решение означает, что ограничения слишком ограничивают и не оставили допустимой области.Например, не имеет решения следующая проблема:
Макс 5X1 + 3X2
при условии:
4X1 + 2X2 £ 8
X1 ³ 4
Х2 ³ 6.
Идентификация: Если вы не можете ввести какую-либо переменную, сохраняя выполнимость (т.е. значения RHS остаются неотрицательными).
Разрешение: Проверьте ограничения на наличие ошибок в спецификации в направлении ограничений неравенства и числовых ошибок. Если ошибки нет, значит, имеется конфликт интересов. Это должно быть решено путем поиска IIS (см. Примечание ниже) и последующего переформулирования модели.
Анализ чувствительности: Не применимо.
Примечание: Большинство коммерческих пакетов, таких как CPLEX и LINDO, имеют функцию, называемую IIS (Неприводимое недопустимое подмножество) i.е. минимальный набор ограничений, который нужно снять с задачи, чтобы сделать ее выполнимой. Этот набор ограничений недопустим, но подмножество IIS возможно. Следовательно, все ограничения в IIS способствуют невозможности реализации. Это означает, что необходимо удалить или изменить по крайней мере одно из ограничений в IIS, чтобы сделать модель возможной. Следовательно, поиск IIS просто помогает сосредоточить усилия по диагностике. В модели может быть несколько разных IIS, и одна ошибка может проявляться через разные IIS. Следовательно, вы должны отремонтировать модель следующим образом:
Следовательно, вы должны отремонтировать модель следующим образом:
Шаг 1: найдите IIS,
Шаг 2: устранение недопустимости в IIS и
Шаг 3: проверьте, возможна ли еще вся модель; в противном случае переходите к шагу 1.
В пакетах автоматической генерации расписания, например, полное устранение несоответствий в исходных входных данных является сложной задачей. Поэтому некоторые пакеты оснащены интерфейсным модулем, который действует как отладчик.Это устранит многие недостижимости на уровне поверхности во время первого запуска. Может потребоваться еще несколько прогонов, чтобы исключить более глубокую неосуществимость. В качестве альтернативного подхода проблема невозможности может быть обработана как проблема оптимизации с целью минимизации (возможно, взвешенного) количества нарушений ограничений. Когда ни одно решение не удовлетворяет всем ограничениям, находится близкое решение. Это близкое решение может выявить конфликтующие входные данные, которые необходимо исправить.
Извлеченный урок для принятия решений: Возможно, вы слышали, что «Если есть воля, значит, должен быть и способ».На самом деле совет должен быть в обратном порядке, т.е. «Если есть способ, то может быть воля». Это правильно, потому что допустимая область может быть пустой, и можно игнорировать одно или несколько ограничений, а затем оказаться в большой беде, например, о желании за пределами своих возможностей.
Вырождение
Рассмотрим ЛП с n переменными решения, вырожденная вершина — это вершина, через которую проходит более n гиперплоскостей. Например, 3 или более строк в 2-мерной пространственной задаче LP.В такой вершине такой метод, как симплекс, может переключаться с одного представления (с n гиперплоскостями) на другое и может даже возвращаться к первому и повторять этот «цикл». Теперь добавление небольших величин, скажем, к правым частям ограничений, немного сдвинет соответствующие гиперплоскости и «сместит» вершину. Вместо этого будет несколько соседних вершин, где обычно пересекаются n гиперплоскостей.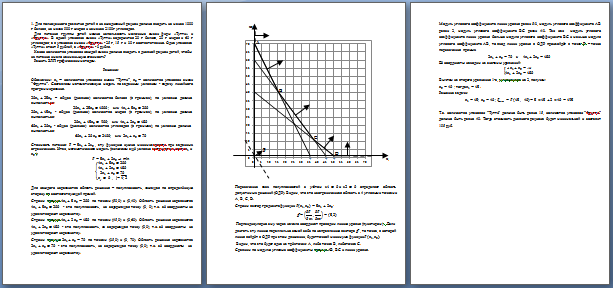 Теперь метод может переходить от одного к другому (каждый раз улучшая целевую функцию) и выходить из этой вырожденной области.Затем возмущение можно снова отключить в современной компьютерной реализации симплекс-методов и многих их вариаций.
Теперь метод может переходить от одного к другому (каждый раз улучшая целевую функцию) и выходить из этой вырожденной области.Затем возмущение можно снова отключить в современной компьютерной реализации симплекс-методов и многих их вариаций.Угловая точка в n-мерной задаче переменных решения называется вырожденной угловой точкой, если более n ограничений становятся связывающими (то есть активными) в этой угловой точке. То есть всякий раз, когда соприкасаются некоторые угловые точки. Например, в двумерной задаче угловая точка вырождается, если в этой угловой точке 3 или более ограничений становятся равенствами.
Например, рассмотрим следующую размерную задачу два :
Макс X1 + X2
при условии:
X1 £ 1
X2 £ 1
X1 + X2 £ 2
все переменные решения ³ 0.
Оптимальное решение — X1 = 1 и X2 = 1, при котором все три ограничения являются обязательными.
Когда оптимальное решение вырождается, у вас будет несколько теневых цен. Для вышеупомянутой проблемы два набора теневых цен — это (1, 1, 0) и (0, 0, 1), как вы можете убедиться, построив и решив двойную задачу.
Для вышеупомянутой проблемы два набора теневых цен — это (1, 1, 0) и (0, 0, 1), как вы можете убедиться, построив и решив двойную задачу.
Идентификация: Если есть хотя бы два равных и наименьших соотношения столбцов (b i / a ij ) при применении симплекс-метода, тогда решение вырождено, произвольно выберите исходящую переменную.
В редких случаях вырождение может вызвать зацикливание, как в следующей проблеме:
Макс 6X1 + 3X2
при условии:
X1 £ 1
X2 £ 1
Х1 — Х2 £ 1
-X1 + X2 £ 1
все переменные решения ³ 0.
И Lindo, и WinQSB занимают 3 итерации для решения этой простой вырожденной проблемы.
Разрешение: Добавьте к значению RHS небольшое число, скажем, 0,001. Это может решить проблему.
Анализ чувствительности: Анализ чувствительности может быть недействительным, и у вас могут быть альтернативные теневые цены.
И следующая задача, и двойственная к ней являются вырожденными:
Мин..jpg) X2
X2
при условии:
Х2 — 2Х3 + Х4 = 1
Х1 + 2Х2 — Х3 = 0
Х1 + Х2 + 3Х3 = 2
все переменные решения ³ 0.
Дополнительная литература:
Окамп Д. и Д. Стейнберг, Вычисление теневой цены в линейном программировании, Journal of Operational Research Society , 33, 557-565, 1982.
Эванс Дж. И Н. Бейкер, Вырождение и (неправильная) интерпретация анализа чувствительности в линейном программировании, Decision Sciences , 13, 348-354, 1982.
Гасс С. и С. Винджамури, Цикл в задачах линейного программирования, Computers & Operations Research , 31, 303-311, 2004.
Янсен Б., Анализ чувствительности в линейном программировании: просто будьте осторожны !, Европейский журнал операционных исследований , 101, 1997, 15-28.
Диапазон чувствительности стоимости с помощью графического метода
Широко распространено мнение, что можно вычислить диапазон чувствительности к стоимости, заключив в скобки (возмущенный) наклон целевой функции (изометрического значения) наклонами двух линий, являющихся результатом ограничений привязки. Этот графический метод расчета диапазонов чувствительности на основе наклона описан в популярных учебниках, таких как Anderson et al., (2007), Лоуренс и Пастернак (2002) и Тейлор (2006).
Этот графический метод расчета диапазонов чувствительности на основе наклона описан в популярных учебниках, таких как Anderson et al., (2007), Лоуренс и Пастернак (2002) и Тейлор (2006).К сожалению, это заблуждение. Следует предупредить, что их подход не является общим и работает тогда и только тогда, когда коэффициенты не меняют знак.
Предположим, что в LP с двумя переменными и ограничениями в виде неравенства у нас есть уникальный невырожденный оптимум на пересечении двух линий, как показано на следующем рисунке. Тогда диапазон объективных Коэффициенты, при которых это решение остается оптимальным, задаются наклонами двух прямых.
Следующее — контрпример. Это указывает на то, что нужно быть осторожным, чтобы указать, что коэффициенты не меняют знак.
Контрпример : Maximixe 5X 1 + 3X 2
Х 1 + Х 2 £ 2
х 1 — х 2 £ 0,
X 1 ³ 0, X 2 ³ 0.
Дополнительная литература:
Лоуренс Дж., Младший и Б. Пастернак, Прикладная наука управления: моделирование, анализ электронных таблиц и коммуникация для принятия решений , Джон Вили и сыновья, 2002.
Андерсон Д., Суини Д. и Уильямс Т., Введение в науку управления , West Publisher, 2007.
Тейлор III, Б., Введение в науку управления , Прентис Холл, 2006.
Вырождение и двойные (теневые) цены
Когда оптимальное решение является первично вырожденным, обычный анализ чувствительности не дает полной информации в вырожденном случае., то есть информация, которую можно получить от большинства пакетов LP, является подмножеством истинных интервалов чувствительности. Для решения этой проблемы существуют более продвинутые подходы к анализу чувствительности; однако они требуют гораздо больше вычислений, чем обычный анализ чувствительности.Например, рассматривая следующую ЛП с вырожденным оптимальным решением:
Макс 3X 1 + 9X 2
при условии:
х 1 + 4 х 2 £ 8
X 1 + 2X 2 £ 4
X 1 , X 2 ³ 0
При решении симплексным методом: введите X2 и разорвите ничью для выхода. переменная в пользу первой строки.Двойная (теневая) цена для RHS1 составляет 1,5, действительна в диапазоне [4, 8], а двойная цена для RHS2 — 1,5, действительна в диапазоне [4, 8]
переменная в пользу первой строки.Двойная (теневая) цена для RHS1 составляет 1,5, действительна в диапазоне [4, 8], а двойная цена для RHS2 — 1,5, действительна в диапазоне [4, 8]
Затем повторно решите проблему, изменив порядок R1 и R2, а также нарушение равенства уходящей переменной в пользу второй строки. Двойная цена для RHS1 равна 0, действительна в диапазоне [8, ¥), двойная цена для RHS2 — 4,5, действительна в диапазоне [0, 4]
Это показывает, что результирующие значения двойных цен могут зависеть от того, как разные решатели обрабатывают связи.Главный вопрос: если это модель распределения, какой из двух наборов двойственных решений применим? В этом простом примере кажется, что первый
набор двойных значений дает более полезную информацию, потому что он говорит, что RHS2 может быть увеличен до 4 единиц, при этом каждая единица увеличивает оптимальное значение на 1,5. Второй набор, с другой стороны, не показывает никакого преимущества в увеличении RHS1 или RHS2.
В обоих случаях первый диапазон представляет сокращение ресурса и следовательно, единичное уменьшение z на 1.5 и 4.5 соответственно. Второй диапазон представляет собой увеличение ресурса без влияния на оптимальное значение в RHS1 и увеличение единицы измерения RHS2 на 1,5. Эти результаты имеют смысл; однако процедура «перечисления» альтернативных вырожденных оптимумов не может быть и речи для практических задач.
Перечисление нескольких оптимумов в целом NP-сложно, но вам не нужно все оптимумы, чтобы получить полную картину теневой цены, по крайней мере, для изменений индивидуальных ограничений.Если вырождение приводит к «одностороннему» диапазону (текущая правая часть ограничения
Дополнительная литература:
Роос К., Т. Терлаки и Дж. Виал, Теория и алгоритмы линейной оптимизации: подход внутренней точки , John Wiley & Sons, 1997. Глава 19.
У теневых цен может быть неправильный знак
Некоторые программные пакеты LP не подчиняются строгой двойственности как для максимизации, так и для минимизации. Поэтому нужно это учитывать, соответственно корректировать знаки. Это можно сделать, изменив RHS на «маленькую» величину и найдя новое оптимальное значение, а затем используя определение теневой цены как скорости изменения оптимального значения по отношению к изменению RHS.
Поэтому нужно это учитывать, соответственно корректировать знаки. Это можно сделать, изменив RHS на «маленькую» величину и найдя новое оптимальное значение, а затем используя определение теневой цены как скорости изменения оптимального значения по отношению к изменению RHS.Например, рассматривая следующую LP с единственным оптимальным решением:
Свернуть 18X 1 + 10X 2
При условии:
12X 1 + 10X 2 ³ 120000
10X 1 + 15X 2 £ 150000
X 1 , X 2 ³ 0
Выполнив эту задачу с помощью LINDO, окончательный отчет дает теневые цены U 1 = -2.125 и U 2 = 0,75, а правильные — U 1 = 2,125 и U 1 = — 0,75. Эта досадная ошибка не ограничивается LINDO, например QM: Quantitative Methods для Windows дает те же результаты.
Дополнительная литература:
Аршам Х., Основы линейного программирования: управленческая перспектива от решения системы неравенств до реализации программного обеспечения, International Journal of Strategic Decision Sciences , 3 (3), 40-60, 2012.
Аршам Х., Алгоритм основного решения внутренних границ для линейных программ с областью чувствительности на основе оптимального решения, International Journal of Mathematics in Operational Research , 4 (4), 302-330, 2012.
Аршам Х., Инструмент валидации и проверки для оптимизирующих решателей, Journal of Information & Optimization Sciences , 29 (1), 57-80, 2008.
Избыточность среди ограничений
Избыточность означает, что некоторые ограничения не нужны, поскольку есть другие, более серьезные.Для простого случая LP с избыточным ограничением рассмотрим следующий числовой пример:Максимизировать 5X1 + 6X2
при условии: 3X1 + 6X2 £ 8, 6X1 + 4X2 £ 24, и оба X1, X2 ³ 0.
Идентификация: По крайней мере, строка в таблице имеет все элементы, включая значение RHS, равное нулю.
Разрешение: Удалите такие строки и продолжайте. Однако избыточность ограничений не абсолютная, а относительная.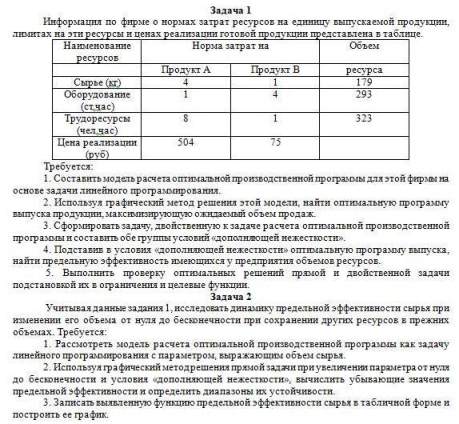 Кроме того, «минимальный» набор ограничений, то есть отсутствие избыточных ограничений для описания допустимой области, не обязательно означает, что количество ограничений является наименьшим.
Кроме того, «минимальный» набор ограничений, то есть отсутствие избыточных ограничений для описания допустимой области, не обязательно означает, что количество ограничений является наименьшим.
Анализ чувствительности: Анализ чувствительности RHS может быть недействительным, а для избыточных ограничений недоступны, кроме того, у вас могут быть альтернативные теневые цены. Например, почти во всех сетевых моделях одно из ограничений всегда является избыточным, поэтому результаты компьютерного программного обеспечения (такого как модуль QSB Nets) по анализу чувствительности для этих типов проблем могут быть неверными.
Идентификация неограниченно допустимой области
Прежде чем использовать какой-либо алгоритм решения, необходимо проявлять большую осторожность в процессе построения математической модели. Могут существовать потенциальные проблемы, влияющие на любой алгоритм решения оптимизации. Возможная область может быть неограниченной, хотя в реальной жизни неограниченная допустимая область встречается редко.
Учитывая следующую допустимую область стандартной формы F = {X: AX = b, X ³ 0}, где A — заданная матрица m на n, а b — m-вектор, нас интересует, является ли допустимая область неограниченной или нет.
Если множество F непусто, то F неограниченно тогда и только тогда, когда следующая задача LP имеет ненулевой вектор Y в качестве своего решения:
Увеличить S Y i
При условии: A Y = 0, 0 £ Y i £ 1, для всех i
Доказательство следует из леммы Фаркаша. Причем оптимальное решение Y * будет неограниченным направлением.
Обратите внимание, что решение простого LP с фиктивной целевой функцией, например:
Свернуть X 1
При условии: A X = b, X ³ 0
можно проверить условие непустоты F, если эта простая ЛП имеет ограниченное решение.
Теперь мы используем численный пример, чтобы проиллюстрировать описанную выше процедуру.
Рассмотрим следующую непустую допустимую область:
| 5X 1 | – | Х 2 | £ | 30 | |
| X 1 | £ | 5 | |||
| X 1 | ³ | 0 | , | Х 2 | не имеет ограничений в знаке |
Преобразование допустимой области в стандартную форму может быть достигнуто путем замены X2 — X3 на X2 и введения переменных резервирования X4 и X5 для двух ограничений £ соответственно. Стандартная форма региона:
Стандартная форма региона:
| 5X 1 | – | Х 2 | + | Х 3 | + | Х 4 | = | 30 |
| X 1 | + | Х 5 | = | 5 |
Все переменные неотрицательны.
Вышеупомянутая допустимая область неограничена тогда и только тогда, когда следующая LP имеет ненулевое Y * в качестве своего оптимального решения:
Развернуть Y 1 + Y 2 + Y 3 + Y 4 + Y 5
| 5Y 1 | – | Y 2 | + | Y 3 | + | Y 4 | = | 0 |
| Y 1 | + | Y 5 | = | 0 | ||||
| Y i | £ | 1 | , | для всех i, |
и все переменные неотрицательны.

Оптимальное решение — Y * = [0, 1, 1, 0, 0], которое не равно нулю. Следовательно, допустимая область действительно неограничена.
LP без Vertex
Следующий LP не имеет вершины:Увеличить X1 + X2
при условии: X1 + X2 £ 5, X1, X2 без ограничений.
Эта задача имеет замкнутую неограниченную допустимую область без вершины. Однако все множественные решения — это точки на прямой X1 + X2 = 5.
Стандартная форма : Теперь, преобразовав неравенство в равенство с переменной Slack S1 и ограничив переменные X1 — y и X2 -y, мы получили следующие основные решения:
| X1 | Х2 | y | S1 | Х1 + Х2 | |
| __________________________ | |||||
| 0 | 0 | 0 | -5 | невозможно | |
| 0 | 0 | -5/2 | 0 | невозможно | |
| 0 | 5 | 0 | 0 | 5 | |
| 5 | 0 | 0 | 0 | 5 | |
Это дает два основных возможных решения с равными целевыми значениями. Это указывает на то, что существует несколько решений, однако исходная допустимая область искажена!
Это указывает на то, что существует несколько решений, однако исходная допустимая область искажена!
Для этой проблемы WinQSB создает два различных оптимальных решения: (X1 = 5, X2 = 0) и (X1 = 0, X2 = 5), которые не являются вершинами. Примечательно, что для оптимальна не только любая выпуклая комбинация этих двух точек, но и точки за их пределами.
LP с неограниченными и множественными ограниченными оптимальными решениями
Рассмотрим следующую проблему LP:Увеличить X1 + X2
при условии: X1 + X2 = 5, и X1, и X2 не имеют ограничений по знаку.
Эта проблема имеет замкнутую неограниченную допустимую область. Оптимальные решения множественные, как ограниченные, так и неограниченные, которые представляют собой все точки на прямой X1 + X2 = 5.
Об основных и небазовых переменных решения
Верно ли, что при выполнении симплексных итераций «если переменная решения становится базовой переменной, то она остается базовой». Нет, не всегда. Неосновная переменная решения может стать базовой переменной в симплексной итерации, а на последней итерации она снова станет небазовой.Рассмотрим следующую проблему:
Нет, не всегда. Неосновная переменная решения может стать базовой переменной в симплексной итерации, а на последней итерации она снова станет небазовой.Рассмотрим следующую проблему:Максимизировать 5X1 + 6X2
при условии: 3X1 + 6X2 £ 8, 6X1 + 4X2 £ 24, и оба X1, X2 ³ 0.
Применяя симплексный метод для решения этой задачи, переменная решения X2 становится базовой переменной после первой симплексной итерации. Однако во второй итерации переменная решения X1 заменяет X2 в качестве новой базовой переменной. Вторая итерация для этой проблемы также обеспечивает оптимальное решение.Обратите внимание, что одно из ограничений является избыточным.
LP без каких-либо внутренних и граничных решений
Рассмотрим следующую проблему:Увеличить X1 + 2X2
при условии: X1 + X2 = 2, X1 — X2 = 0, X1³ 0 и X2 ³ 0.
Задача имеет допустимую область, которая представляет собой единственную точку (X1 = 1, X2 = 1) с оптимальным значением 3. Следовательно, эта задача не имеет ни внутренней точки, ни какой-либо граничной точки.У него есть только вершина.
Следовательно, эта задача не имеет ни внутренней точки, ни какой-либо граничной точки.У него есть только вершина.
Оптимальное решение, созданное одним пакетом LP, не может быть получено другим
Решение, полученное одним пакетом LP, может быть недоступно другим. Рассмотрим следующий числовой пример: Свернуть X1 + X2 + 2X3
при условии:
X1 + X2 + X3 ³ 10
X1 + X2 + 2X3 ³ 13
X1, X2 неограниченный знак
WinQSB: Используя пакет WinQSB, вы получите следующие несколько решений: A = (0, 7, 3) и B = (7, 0, 3).Это говорит о том, что все точки между этими сгенерированными оптимальными решениями также являются оптимальными. То есть все линейные комбинации этих двух решений также оптимальны:
X1 = 0a + (1 — a) 7 = 7 — 7a,
X2 = 7a + (1- a) 0 = 7a,
X3 = 3a + (1- a) 3 = 3,
для всех 0 £ a £ 1.
Однако обратите внимание, что оба ограничения являются обязательными, поэтому решения находятся на пересечении этих двух плоскостей, которое представляет собой линию. Более того, любые точки на всей прямой являются оптимальными, а не только точками между A и B.Другими словами, любые точки на линии пересечения (в параметрической форме):
Более того, любые точки на всей прямой являются оптимальными, а не только точками между A и B.Другими словами, любые точки на линии пересечения (в параметрической форме):
Х1 = т,
Х2 = 7 — т,
X3 = 3,
оптимальны для всех t, в том числе когда t является большим M.
Следовательно, эта задача LP не имеет вершины, имеет несколько ограниченных решений и неограниченные решения.
Линдо: Чтобы запустить эту задачу на Линдо, мы должны сначала удовлетворить условия неотрицательности, подставив для каждой неограниченной переменной Xi = xi — y.Результат:
мин. x1 + x2 + 2×3 — 5y
при условии:
x1 + x2 + x3 — 3y ³ 10
x1 + x2 + 2×3 — 5y ³ 13
Все переменные неотрицательны.
Запустив эту задачу на Lindo (или вашем WinQSB), мы получим x1 = 13, а все остальные переменные равны нулю. В терминах исходных переменных это дает: X1 = 13, X2 = 0 и X3 = 0. Как видите, решение, полученное Lindo, не может быть получено с помощью пакета WinQSB и наоборот. Очевидно, что результаты чувствительности для этой проблемы с использованием любого из пакетов недействительны. Множество всех оптимальных решений представляет собой полуплоскость, то есть:
Очевидно, что результаты чувствительности для этой проблемы с использованием любого из пакетов недействительны. Множество всех оптимальных решений представляет собой полуплоскость, то есть:
Макс 10U1 + 13U2
при условии:
U1 + U2 = 1
U1 + U2 = 1
U1 + 2U2 = 2
все переменные неотрицательны.
Запустив дуал на Lindo (или ваш WinQSB), мы получим U1 = 0, U2 = 1 с теневыми ценами (0, 13, 0), что является решением первичного, полученного ранее Lindo (или вашим WinQSB). Однако, удалив первое избыточное ограничение в двойной задаче, мы получим:
Макс 10U1 + 13U2
при условии:
U1 + U2 = 1
U1 + 2U2 = 2
все переменные неотрицательны.
Теперь, запустив эту задачу на Lindo (или на вашем WinQSB), мы получим U1 = 0, U2 = 1 с теневыми ценами (7, 3), которые являются решением (0, 7, 3) основной задачи, полученной ранее WinQSB. Другое решение невозможно.
Другое решение невозможно.
Используя WinQSB для двойной задачи, мы получаем U1 = 0, U2 = 1, с теневыми ценами (0, 7, 3), что является одним из решений для первичных, полученных ранее с помощью этого программного обеспечения.
Дает ли оптимальная симплексная таблица двойное решение?
Полезность последней симплексной таблицы для управленческих приложений заключается в том, что она содержит всю информацию, необходимую для выполнения анализа чувствительности, как вы увидите в последнем случае в этом курсе.Однако оптимальная симплексная таблица сама по себе не дает решения двойной задачи. Теневые цены — это решение двойной проблемы. Как вы уже знаете, теневая цена может быть положительной, нулевой или даже отрицательной, однако в окончательной симплексной таблице последняя строка всегда должна быть неположительной (в соответствии с требованиями алгоритмов решения). Следовательно, мы не можем просто считать теневые цены из окончательной таблицы, прежде чем сформулировать двойную задачу.
Числовой пример: рассмотрим следующую задачу,
Максимизировать 3X1 + 5X2
При условии:
X1 + 2X2 50 фунтов стерлингов
-X1 + X2 ³ 10,
Х1 ³ 0, Х2 ³ 0.
Вводя резервные и избыточные переменные, S1 и S2 соответственно, и следуя шагам алгоритма решения, не содержащего официальных лиц, мы получаем следующую окончательную симплексную таблицу:
| BVS | X1 | X2 | S1 | S2 | RHS | |
|---|---|---|---|---|---|---|
| X1 | 1 | 0 | 1/3 | 2/3 | 10 | |
| X2 | 0 | 1 | 1/3 | -1/3 | 20 | |
| Cj | 0 | 0 | 8/3 | 1/3 |
Теневых цен нет (8/3, 1/3). Вы видите это, построив двойную задачу:
Вы видите это, построив двойную задачу:
Свернуть 50Y1 + 10Y2
При условии:
Y1 — Y2 ³ 3,
2Y1 + Y2 ³ 5,
Y1 ³ 0,
и Y2 £ 0.
Имея двойную формулировку задачи, теперь вы можете правильно считывать теневые цены. Следовательно, теневые цены равны Y1 = 8/3 и Y2 = -1/3. Опять же, когда вы строите двойственную задачу, вы видите, что Y2 должен быть равен 0 £ в знаке.Вот почему вы берете -1/3 вместо 1/3 для Y2 из окончательной симплексной таблицы.
Решение для целочисленного LP не может быть одной из целочисленных вершин
Всякий раз, когда есть условие целостности для некоторой переменной решения, тогда оптимальное решение (если существует) может быть расположено в любом месте допустимой области. Это может быть одна из вершин, может быть на границе или даже внутри допустимой области.Рассмотрим следующую целочисленную линейную программу из Шеноя (1989):
Развернуть 100X1 + 160X2
При условии:
6X1 + 14X2 £ 42
7X1 + 7X2 £ 35
X1, X2 — целые неотрицательные числа.
Для этого небольшого примера можно найти все 14 возможных решений непосредственно из допустимой области, а затем, используя линии равных значений целевой функции, оптимальное решение находится в точке (X1 = 4, X2 = 1) с оптимальным значением 560 .
Это решение превосходит (X1 = 5, X2 = 0) с заданным в нем значением целевой функции 500. Обратите внимание, что оптимальное решение находится на граничной линии 7X1 + 7X2 = 35, но не на вершине, как в приведенной выше ссылке.
Дополнительная литература
Шеной Г.В., Линейное программирование: методы и приложения , John Wiley & Sons, 1989.
Преобразование в стандартную форму может исказить возможную область
Рассмотрим следующую задачу LP:Увеличить X1 + X2
при условии: X1 + X2 £ 5, X1, X2 без ограничений.
Эта задача имеет замкнутую неограниченную допустимую область без вершины.Однако все множественные решения — это точки на прямой X1 + X2 = 5.
Теперь посмотрим, что получится, если преобразовать эту задачу в стандартную форму, которая является требованием для запуска симплексного метода.
Стандартная форма : Теперь, преобразовав неравенство в равенство с переменной Slack S1 и ограничив переменные X1 — y и X2 -y, мы получили следующую стандартную форму:
Увеличить X1 + X2 -2y
при условии:
X1 + X2 -2y + S1 = 5, и все переменные ограничены по знаку.
Основные решения:
| X1 | Х2 | y | S1 | Х1 + Х2 | |
| _________________________ | |||||
| 0 | 0 | 0 | 5 | 0 | |
| 0 | 0 | -5/2 | 0 | невозможно | |
| 0 | 5 | 0 | 0 | 5 | |
| 5 | 0 | 0 | 0 | 5 | |
Это дает оптимальные вершины. Это указывает на то, что существует несколько решений. Однако исходная допустимая область теперь искажена !, то есть мы не можем произвести все решения, используя любую выпуклую комбинацию двух решений (0, 5) и (5, 0).
Это указывает на то, что существует несколько решений. Однако исходная допустимая область теперь искажена !, то есть мы не можем произвести все решения, используя любую выпуклую комбинацию двух решений (0, 5) и (5, 0).
Чтобы найти полное решение этой проблемы, нам нужно знать следующие два определения:
Луч: Луч — это полупрямая линия: {V + ah: a ³ 0}, где h — ненулевой вектор, содержащийся в S. Точка V называется корнем, и говорят, что луч является корневым. у В.
Extreme Ray: Крайний луч замкнутого множества S — это луч в S, который не может быть выражен как линейная комбинация других лучей в S.
Все оптимальные точки расположены на любом из двух крайних лучей, оба с корнем в V = (0, 5), в направлениях (1, -1) и (-1, 1):
(X 1 , X 2 ) = (0, 5) + a1 (1, -1) + a2 (-1, 1) =
(a1 — a2, 5 — a1 + a2),
для всех a1 ³ 0 и a2 ³ 0.
Вместо (0, 5) можно использовать любую точку на линии.
Однако для представления всех точек в допустимой области нам понадобится дополнительный член:
(X 1 , X 2 ) = (0, 5) + a1 (-1,1) + a2 (1, -1) + a3 (-1, -1),
для всех a1 ³ 0, a2 ³ 0 и a3 ³ 0.
Последний член необходим для всех точек ниже линии. Это происходит из-за того, что обе переменные неограничен в знаке [в направлениях [(0, -1) и (-1, 0)].
Общая идея параметрического представления состоит в том, что мы начинаем с вершины. Мы удаляемся от него в допустимом направлении каждого ребра к следующей возможной точке. Если такая точка существует (т.е. мы нашли другую вершину). В противном случае многогранник не ограничен в этом направлении, и это означает, что направление является крайним лучом. Обратите внимание, что многогранник без вершины всегда содержит прямую (или гиперплоскость). Для такого многогранника мы также должны добавить дополнительный луч, перпендикулярный этой прямой (или гиперплоскости), ЕСЛИ ограничение имеет форму неравенства (³ или £, как в приведенном выше примере.
Дополнительная литература
Чватал В., Линейное программирование , У. Х. Фриман и компания, Нью-Йорк (1983), Глава 18.
Снятие ограничений равенства путем замены может изменить проблему:
Всякий раз, когда в любой задаче LP есть какие-либо ограничения равенства, возникает соблазн уменьшить размер проблемы, удалив ограничения равенства с помощью подстановок. Проблема остается той же самой, если исключить неограниченную (ые) переменную (ы) с помощью любых ограничений равенства (если возможно).Однако, если нет неограниченных переменных, необходимо удалить ограничения равенства путем подстановки, потому что это может создать совершенно другую проблему LP. Вот встречный пример для удаления ограничения равенства:Макс X1
При условии:
Х2 + Х3 = -1
X1 — 2X2 + X3 £ 1
X1 + X2 £ 2
Все переменные неотрицательны.
У этой проблемы нет решения. Однако при замене, скажем, X3 = -1 — X2 везде проблема меняется на:
Макс X1
При условии:
X1 — 3X2 £ 2
X1 + X2 £ 2
Все переменные неотрицательны,
давая вам оптимальное решение (X1 = 2, X2 = 0) с оптимальным значением 2. Следовательно, эти две проблемы Не эквивалентны.
Следовательно, эти две проблемы Не эквивалентны.
Однако вы можете спросить: при каких условиях можно безопасно устранить ограничение равенства заменой? Ответ либо в неограниченной переменной, как упоминалось ранее, либо если все коэффициенты ограничения равенства имеют тот же знак, что и его RH, тогда будет безопасно исключить любую переменную путем подстановки, чтобы уменьшить количество переменных и ограничений. .
Дополнительная литература:
Аршам Х., Симплексный алгоритм без искусственного интеллекта для общих моделей LP, Математическое и компьютерное моделирование , 25 (1), 107-123, 1997.
Неправильная интерпретация цены теней
Теневая цена сообщает нам, насколько изменится целевая функция, если мы изменим правую часть соответствующего ограничения. Это часто называется «предельная стоимость», «двойная цена» или «двойная стоимость» для ограничения. Следовательно, теневая цена может не совпадать с «рыночной ценой».
Для каждого ограничения RHS теневая цена точно сообщает нам, насколько изменится целевая функция, если мы изменим правую часть соответствующего ограничения в пределах, указанных в диапазоне чувствительности на RHS.
Следовательно, для каждого значения RHS теневая цена представляет собой отношение изменения оптимального значения, вызванного любым допустимым увеличением или уменьшением RHS в пределах допустимого изменения.
К сожалению, существуют неправильные представления об определении теневой цены.Одно из таких неверных толкований заключается в следующем: «В задачах линейного программирования теневая цена ограничения — это разница между оптимизированным значением целевой функции и значением целевой функции, оцененным на необязательном базисе, когда правая часть (RHS) ограничение увеличивается на одну единицу «. Это относится к следующему веб-сайту: Design Decision Support Systems и Скрытые цены и штрафные санкции. Последний веб-сайт содержит следующие «Теневые цены: теневые цены для проблемы линейного программирования — это решения ее двойственности. I-я теневая цена — это изменение целевой функции в результате увеличения на единицу i-й координаты b. Теневая цена — это также сумма, которую инвестор должен был бы заплатить за одну единицу ресурса, чтобы выкупить производителя ».
I-я теневая цена — это изменение целевой функции в результате увеличения на единицу i-й координаты b. Теневая цена — это также сумма, которую инвестор должен был бы заплатить за одну единицу ресурса, чтобы выкупить производителя ». A Контрпример:
Рассмотрим следующий LP:
Макс X2
при условии:
X1 + X2 £ 2
2,5X1 + 4X2 £ 10
где обе переменные решения неотрицательны.
Эта проблема достигает своего оптимального решения в (0, 2) с оптимальным значением 2.
Предположим, мы хотим вычислить теневую цену первого ресурса, который является правой частью первого ограничения.
Изменение правой части первого ограничения путем увеличения на единицу приводит к:
Макс X2
при условии:
X1 + X2 £ 3
2,5X1 + 4X2 £ 10
где обе переменные решения неотрицательны.
Новая задача имеет оптимальное решение (0, 2,5) с оптимальным значением 2,5.
Таким образом, «как будто» теневая цена этого ресурса составляет 2,5 — 2 = 0,5. Фактически теневая цена этого ресурса равна 1, что можно найти, построив и решив двойную задачу.
Фактически теневая цена этого ресурса равна 1, что можно найти, построив и решив двойную задачу.
Причина этой ошибки становится очевидной, если мы заметим, что допустимое увеличение для поддержания действительности теневой цены первого ресурса равно 0.5. Увеличение на 1 превышает допустимое изменение первого значения RHS.
Теперь предположим, что мы изменили то же значение RHS, скажем, на + 0,1, что допустимо, тогда оптимальное значение для новой задачи — 2,1. Следовательно, теневая цена равна (2,1 -2) / 0,1 = 1. Мы должны быть немного осторожны при расчете теневых цен.
Если вы хотите вычислить теневую цену RHS, когда его диапазон чувствительности недоступен, вы можете получить оптимальные значения как минимум для двух возмущений.Если скорость изменения для обоих случаев дает вам одинаковые значения, то эта скорость действительно является теневой ценой. В качестве примера предположим, что мы возмущаем правую часть первого ограничения на +0,02 и -0,01. Решив проблему после этих изменений с помощью решателя LP, оптимальные значения составляют 2,02 и 1,09 соответственно. Поскольку оптимальное значение для номинальной задачи (без каких-либо возмущений) равно 2, скорость изменения для двух случаев составляет: (2,02 — 2) / 0,02 = 1 и (1,09 — 2) / (- 0,01) = 1 соответственно.Поскольку эти две ставки одинаковы, мы заключаем, что теневая цена на правую часть первого ограничения действительно равна 1.
Решив проблему после этих изменений с помощью решателя LP, оптимальные значения составляют 2,02 и 1,09 соответственно. Поскольку оптимальное значение для номинальной задачи (без каких-либо возмущений) равно 2, скорость изменения для двух случаев составляет: (2,02 — 2) / 0,02 = 1 и (1,09 — 2) / (- 0,01) = 1 соответственно.Поскольку эти две ставки одинаковы, мы заключаем, что теневая цена на правую часть первого ограничения действительно равна 1.
Всегда ли теневая цена неотрицательна?
Вы можете спросить: «Всегда ли теневая цена значения RHS неотрицательна?» Все зависит от формулировки первичного и его дуального. Важно помнить, что теневая цена данной RHS — это скорость изменения оптимального значения по отношению к изменению на этой RHS, при условии, что изменение находится в пределах чувствительности этой RHS.Рассмотрим следующий числовой пример:
Макс 3X1 + 5X2
При условии:
X1 + 2X2 £ 50
-X1 + X2 ³ 10
X1, X2 неотрицательны.
Мы заинтересованы в нахождении теневой цены RHS2 = 10. Двойная проблема:
Мин. 50U1 + 10U2
При условии:
U1 — U2 ³ 3
2U1 + U2 £ 5
U1 ³ 0, а U2 £ 0
Это можно проверить с помощью программного обеспечения WinQSB.Решение двойственного — U1 = 8/3, U2 = -1/3. Следовательно, теневая цена для RHS2 = 10 равна U2 = -1/3. То есть для каждого увеличения (уменьшения) значения RHS2 на единицу оптимальное значение для основной задачи уменьшается (увеличивается) на 1/3, учитывая, что изменение RHS2 находится в пределах его чувствительности.
Обратите внимание, что для другой версии той же основной задачи задачу можно записать эквивалентным образом, изменив направление второго ограничения неравенства:
Макс 3X1 + 5X2
При условии:
X1 + 2X2 £ 50
X1 — X2 £ -10
X1, X2 неотрицательны.
Двойная проблема для этой основной проблемы теперь такова:
Мин. 50Y1 — 10Y2
При условии:
Y1 + Y2 ³ 3
2Y1- Y2 £ 5
И Y1, и Y2 неотрицательны.
Опять же, двойную формулировку можно проверить с помощью программного обеспечения WinQSB. Решение этой двойной проблемы: Y1 = 8/3 и Y2 = 1/3. Следовательно, теневая цена для RHS2 = -10 составляет Y2 = 1/3. То есть для каждого увеличения (уменьшения) значения RHS2 оптимальное значение для увеличения (уменьшения) основной задачи на 1/3, учитывая, что изменение RHS2 находится в пределах его чувствительности.
Как вы уже заметили, обе двойные задачи совпадают при замене U1 = Y1 и U2 = -Y2. Это означает, что теневая цена, полученная для RHS2 = 10 и RHS2 = -10, имеет то же значение с противоположным знаком (как и ожидалось). Следовательно, знак теневой цены зависит от того, как вы формулируете дуальное, хотя значение и его интерпретация всегда одинаковы.
Также посетите
Ситуации «Больше за меньшее и меньше за большее».
Альтернативные теневые цены
Предположим, у нас есть ЛП, и у нее есть единственное оптимальное решение.Возможно ли иметь более одного набора двойных цен? Да, это возможно. Рассмотрим следующую проблему:
Рассмотрим следующую проблему:
Мин. 16X1 + 24X2
при условии:
X1 + 3X2 ³ 6
2X1 + 2X2 ³ 4
все переменные решения ³ 0.
Его дуал:
Макс 6U1 + 4U2
при условии:
U1 + 2U2 16 фунтов стерлингов
3U1 + 2U2 £ 24
все переменные решения ³ 0,
У этого двойника есть много альтернативных решений, таких как (U1 = 8, U2 = 0) и (U1 = 4, U2 = 6).Все выпуклые комбинации этих двух вершин также являются решениями.
Есть общие случаи, для которых теневые цены не уникальны. Как и в приведенном выше примере, всякий раз, когда между ограничениями присутствует избыточность или если оптимальное решение является «вырожденным», может быть более одного набора двойных цен. В общем, линейные независимые ограничения являются достаточным условием единственности теневых цен.
Рассмотрим следующую задачу LP с избыточным ограничением:
Макс 10X1 + 13X2
при условии:
Х1 + Х2 = 1
Х1 + Х2 = 1
Х1 + 2Х2 = 2
и все переменные неотрицательны.
Запуск дуала на Lindo (или на вашем WinQSB) приводит к X1 = 0, X2 = 1 с теневыми ценами (0, 13, 0).
Используя WinQSB для этой задачи, мы получаем X1 = 0, X2 = 1 с разными теневыми ценами (0, 7, 3).
В случае избыточности теневая цена, полученная одним пакетом LP, может не быть получена другим.
Дополнительная литература:
Аршам Х., Анализ устойчивости распределительных маршрутов транспортной задачи, Оптимизация , 43, 47-72, 1998.
Кларк Ф., Оптимизация и негладкий анализ , John Wiley & Sons, 1983.
Ситуации «больше за меньшее» и «меньше за большее»
Рассмотрим следующую производственную задачу LP: Увеличить X1 + 3X2 + 2X3
при условии: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = 9, все Xi неотрицательны.
Общее количество работ — 4 и 9. Оптимальное значение для этой задачи — 7 долларов.
Теперь, если вы измените вторую доступную рабочую силу с 9 на 12, оптимальной стоимостью будет 4 доллара. То есть вы отработали больше часов с меньшей прибылью.
То есть вы отработали больше часов с меньшей прибылью.
Эта ситуация возникает часто и известна как «Парадокс более-менее». Ресурс номер 2 имеет отрицательную теневую цену!
Чтобы определить наилучшее количество часов, вы должны работать над максимальным доходом, решая следующую параметрическую ЛП:
Увеличить X1 + 3X2 + 2X3
при условии: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 = L, L, и все Xi неотрицательны.
Используя LINDO (или ваш WinQSB), мы должны решить
Увеличить X1 + 3X2 + 2X3
при условии: X1 + 2X2 + X3 = 4, 3X1 + X2 + 2X3 — L = 0.
Оптимальный L — 8 часов, а оптимальное значение — 8 долларов!
Необходимым и достаточным условием существования ситуации «больше за меньшее / меньше за больше» является наличие ограничений (ограничений) равенства с отрицательными теневыми ценами для значений RHS.
Чтобы узнать больше об этом и других парадоксах, посетите:
Контрпримеры и объяснения мифов о LP.
Соответствующие ссылки на анализ чувствительности можно найти в Библиографии по оптимизации с анализом чувствительности.
Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Принципами добросовестного использования образовательных мультимедиа от 1996 года, разрешено только в некоммерческих и учебных целях.
Этот сайт может быть отражен в неизменном виде (включая эти уведомления) на любом сервере с общим доступом и иметь ссылки на другие веб-страницы. Все файлы доступны по адресу
http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.
Пожалуйста, пришлите мне по электронной почте свои комментарии, предложения и проблемы. Спасибо.
Этот сайт был запущен 25.02.1994, и его интеллектуальные материалы ежегодно тщательно обновлялись. Текущая версия — 8 th Edition.Все внешние ссылки проверяются раз в месяц.
Об уникальности решений линейных программ на JSTOR
Мы предлагаем конструктивный метод проверки того, имеет ли задача линейного программирования (LPP) единственное возможное или единственное оптимальное решение. Наш метод требует решения только одного дополнительного LPP, так что исходная проблема имеет альтернативные решения тогда и только тогда, когда оптимальное значение нового LPP положительно. Если исходное решение не является уникальным, отображается альтернативное решение.Обсуждаются возможные варианты применения.
Наш метод требует решения только одного дополнительного LPP, так что исходная проблема имеет альтернативные решения тогда и только тогда, когда оптимальное значение нового LPP положительно. Если исходное решение не является уникальным, отображается альтернативное решение.Обсуждаются возможные варианты применения.
Редакционная политика журнала Operational Research Society:
Журнал — это рецензируемый журнал, который издается 12 раз в год по поручению Общества операционных исследований. Целью журнала является публикация статей, в том числе статей, не являющихся членами Общества, которые имеют отношение к практикам, исследователям, преподавателям, студентам и потребителям операционных исследований и охватывают теорию, практику, историю или методологию исследование операций.Однако, поскольку оперативные исследования — это в первую очередь прикладная наука, основная цель журнала — привлечь и опубликовать отчеты о хороших практических примерах. Следовательно, статьи, иллюстрирующие применение OR к реальным проблемам, особенно приветствуются.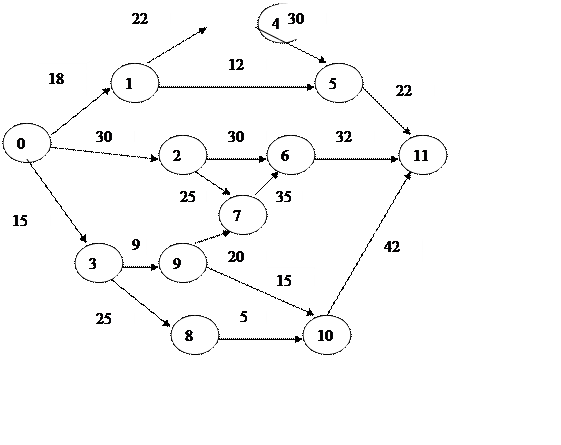
Palgrave Macmillan — глобальное академическое издательство, предлагающее обучение и стипендии в высшем образовании и профессиональном мире. Мы публикуем учебники, журналы, монографии, профессиональные и справочные работы в печати и в Интернете.Наша программа ориентирована на гуманитарные, социальные науки и бизнес. Как часть Macmillan Group, мы олицетворяем непрерывную 150-летнюю традицию независимой академической публикации, которая постоянно обновляется для будущего. Наша цель — быть избранным издателем для всех заинтересованных сторон — авторов, клиентов, деловых партнеров, академических сообществ, которые мы обслуживаем, и сотрудников, которые работают на нас. Мы стремимся сделать это, достигнув максимальной читательской аудитории произведениями высочайшего качества.
Линейное программирование | NEOS
Содержание
Назад к оптимизации с ограничениями или непрерывной оптимизации
Общая форма задачи линейного программирования (LP) заключается в минимизации линейной целевой функции непрерывных действительных переменных с учетом линейных ограничений. T x \) в допустимой области.п \, | \, Ax = b, x \ geq 0 \}. \]
T x \) в допустимой области.п \, | \, Ax = b, x \ geq 0 \}. \]
Любая спецификация значений для переменных решения — это решение ; возможное решение — это решение, для которого удовлетворены все ограничения. Оптимальное решение — это возможное решение, которое имеет наименьшее значение целевой функции для задачи минимизации. У LP может быть одно, более одного или ни одного оптимального решения. LP не имеет оптимальных решений, если у нее нет допустимых решений или если ограничения таковы, что целевая функция неограничена.Для получения дополнительной информации об обнаружении и диагностике невозможности см. Разделы линейного программирования.
В линейной программе переменная может принимать любое непрерывное (дробное) значение в пределах своих нижних и верхних границ. Для многих приложений дробные значения не имеют смысла. Целочисленное программирование Задачи (IP) — это задачи оптимизации, в которых целевая функция и все функции ограничений являются линейными, но некоторые или все переменные ограничены, чтобы принимать целочисленные значения. Целочисленное программирование Задачи часто имеют то преимущество, что они более реалистичны, чем задачи линейного программирования, но их недостатком является то, что их гораздо труднее решить. Хотя может быть неочевидным, что целочисленное программирование является гораздо более сложной проблемой, чем линейное программирование, это как в теории, так и на практике. Наиболее широко используемые универсальные методы решения IP-адресов используют решения серии LP для управления поиском целочисленных решений и доказательства оптимальности.Для получения дополнительной информации см. Целочисленное линейное программирование и связанные с ним страницы.
Целочисленное программирование Задачи часто имеют то преимущество, что они более реалистичны, чем задачи линейного программирования, но их недостатком является то, что их гораздо труднее решить. Хотя может быть неочевидным, что целочисленное программирование является гораздо более сложной проблемой, чем линейное программирование, это как в теории, так и на практике. Наиболее широко используемые универсальные методы решения IP-адресов используют решения серии LP для управления поиском целочисленных решений и доказательства оптимальности.Для получения дополнительной информации см. Целочисленное линейное программирование и связанные с ним страницы.
Важность линейного программирования проистекает как из его многочисленных приложений, так и из наличия эффективных методов общего назначения для поиска оптимальных решений. Эти методы являются универсальными, поскольку они принимают в качестве входных данных LP и определяют решение без ссылки на любую информацию, касающуюся происхождения LP или какой-либо специальной структуры LP. Они быстрые и надежные в широком диапазоне размеров задач и приложений.
Они быстрые и надежные в широком диапазоне размеров задач и приложений.
Хотя все линейные программы можно преобразовать в стандартную форму, обычно это не требуется для их решения. Большинство решателей LP могут обрабатывать другие формы, такие как
- общие границы : \ (l \ leq x \ leq u \), где \ (l \) и \ (u \) — векторы с известными нижними и верхними границами
- двусторонние ограничения : \ (b_1 \ leq Ax \ leq b_2 \) для произвольных \ (b_1 \) и \ (b_2 \)
- задач максимизации : вектор \ (c \) умножается на -1
Сегодня широко используются два семейства методов: симплексные методы и барьерные или методы внутренней точки .Оба метода генерируют улучшающуюся последовательность пробных решений до тех пор, пока не будет достигнуто решение, удовлетворяющее условиям для оптимального решения. Симплекс-методы были введены Джорджем Данцигом в 1940-х годах. Симплекс-методы обращаются к базовым решениям, вычисленным путем фиксации достаточного количества переменных на их границах, чтобы свести ограничения \ (Ax = b \) к квадратной системе, которую можно решить для уникальных значений остальных переменных. Базовые решения представляют собой крайние граничные точки допустимой области, определяемой \ (Ax = b \), \ (x> = 0 \), а симплекс-метод можно рассматривать как перемещение от одной такой точки к другой по краям границы. .Для получения дополнительной информации см. Симплексный метод.
Симплекс-методы обращаются к базовым решениям, вычисленным путем фиксации достаточного количества переменных на их границах, чтобы свести ограничения \ (Ax = b \) к квадратной системе, которую можно решить для уникальных значений остальных переменных. Базовые решения представляют собой крайние граничные точки допустимой области, определяемой \ (Ax = b \), \ (x> = 0 \), а симплекс-метод можно рассматривать как перемещение от одной такой точки к другой по краям границы. .Для получения дополнительной информации см. Симплексный метод.
Барьер или методы внутренней точки путем сравнения точек посещения во внутренней части возможной области. Эти методы основаны на методах нелинейного программирования, которые были разработаны и популяризированы в 1960-х годах Энтони Фиакко и Гартом МакКормиком. Их применение в линейном программировании восходит к инновационному анализу Нарендры Кармаркара в 1984 году. Для получения дополнительной информации см. Методы внутренних точек.
Благодаря достижениям в методах решения и вычислительной мощности за последние два десятилетия задачи линейного программирования с десятками или сотнями тысяч непрерывных переменных решаются регулярно.Коммерческие решатели LP, как правило, быстрее и надежнее, чем « бесплатные » решатели LP, но они, как правило, дороги, за исключением очень ограниченных оценочных и студенческих версий. Свободно доступные решатели, как правило, несколько менее надежны, но они все же полезны для решения многих задач. При использовании любого типа решателя способность решать любой конкретный класс проблем не может быть легко предсказана заранее, исходя только из размера проблемы; для установления трудности обычно требуется некоторое экспериментирование. Обзор программного обеспечения для линейного программирования, проведенный в OR / MS Today за 2013 год, предлагает обширный обзор коммерческих и бесплатных решателей.В сопутствующей статье Роберта Фурера освещаются некоторые вопросы, которые следует учитывать при выборе программного обеспечения.
Программное обеспечение для линейного программирования на сервере NEOS
Если у вас нет доступа к решателю LP в вашем учреждении и вы предпочитаете не загружать демо-версию или бесплатную решающую программу, вы можете получить доступ к бесплатно ряд коммерческих и свободно доступных решателей линейного программирования на NEOS Сервер.
- BDMLP: симплексный решатель, включенный в системы GAMS
- BPMPD: решатель алгоритма прямой и двойной внутренней точки для задач LP и выпуклых QP
- Clp: решатель с открытым исходным кодом с первичным и двойным симплексными алгоритмами
- Gurobi: коммерческое решение для LP (и многих других типов задач)
- MOSEK: коммерческое решение для LP (и других типов задач)
- OOQP: решатель алгоритма прямой и двойной внутренней точки для задач LP и выпуклых QP
- XpressMP: коммерческое решение для LP (и других типов задач)
Другие источники решателей LP
Дерево решений Ханса Миттельманна для программного обеспечения оптимизации содержит список дополнительных кодов общественного достояния и бесплатных кодов для исследований.
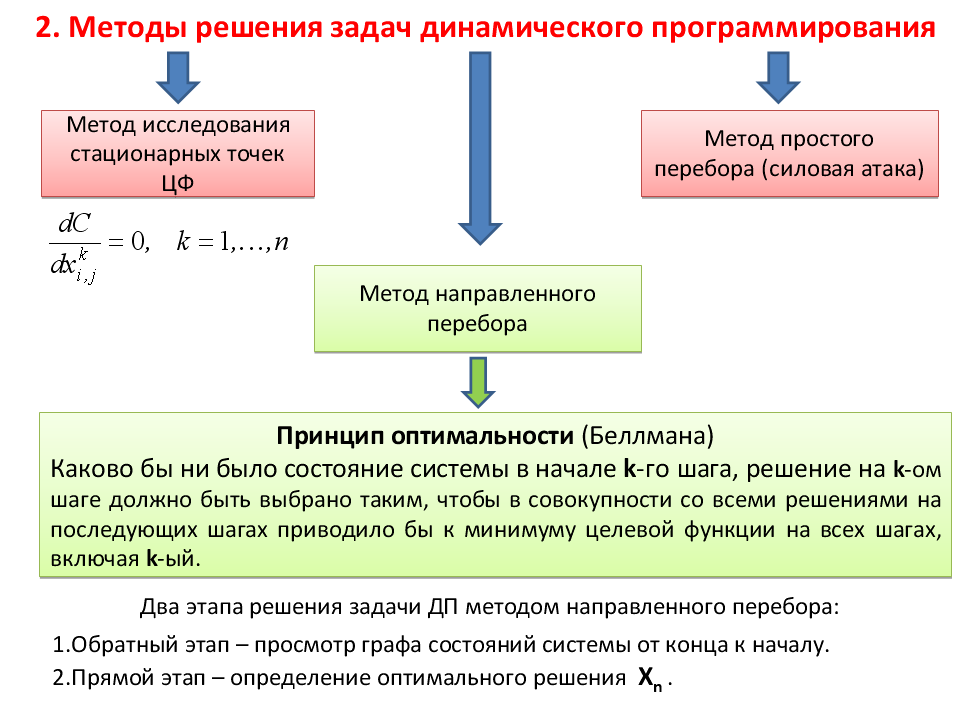 Список включает решатели LP / MILP, чистые решатели LP и точные решатели LP.
Список включает решатели LP / MILP, чистые решатели LP и точные решатели LP.В зависимости от программного обеспечения, доступного вам в вашем учреждении, у вас уже может быть доступ к решающим программам LP.
- Большинство программ для работы с электронными таблицами поставляются с ограниченным решателем линейного / целочисленного программирования в качестве функции или надстройки. Frontline Systems предлагает более мощные обновления решателя Excel. Lindo Systems, Inc. предлагает приложение What’sBest !, надстройку Excel для решения линейных, целочисленных и нелинейных моделей оптимизации. Программное обеспечение
- SAS / OR включает процедуры для решения задач линейного, целочисленного, сетевого потока и нелинейного программирования.
- Числовые библиотеки IMSL предлагают функции для задач линейного и нелинейного программирования.
- Если у вас есть MATLAB, вы можете запустить ряд полезных пакетов оптимизации, которые предоставляют некоторые функции линейного программирования:
- MAPLE предоставляет пакет оптимизации для решения различных типов задач оптимизации.

- Mathematica предлагает пакет исследования операций для решения задач линейной оптимизации, а также других типов задач оптимизации.
Инструменты и утилиты для линейного программирования
- Набор для тестирования NETLIB LP
- Набор для тестирования NETLIB LP в CUTE
- GAMS предлагает библиотеку моделей GAMS, которая включает модели многих различных типов, и библиотеку GAMS Testlib, которая включает модели, которые GAMS использует для тестирования и контроля качества.
- Джон Бисли из Университета Брюнеля поддерживает OR-библиотеку, в которой перечислено линейное программирование и более 3 десятков других категорий тестовых задач оптимизации.
Последнее обновление: 24 февраля 2014 г.
оптимизировать Транспортная проблема | В сторону науки о данных
Транспортная проблема (TP) с примером (NW Corner Rule, метод наименьшей стоимости, VAM, сбалансированная TP, несбалансированная TP)
Фотография Зейна Ли на Unsplash В этом быстро меняющемся мире потребность в товарах увеличивается день ото дня.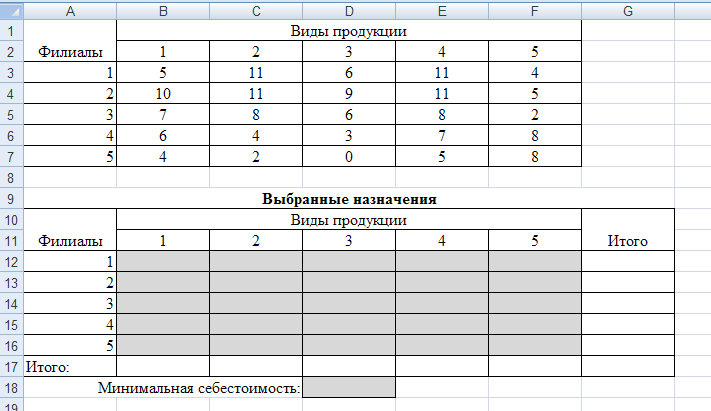 Соответственно, транспорт играет большую роль в обществе. Прибыль и состояние компаний, перевозящих товары из одного уголка страны в другой, определяются транспортом.Это особенно верно, когда транспортные расходы и время транспортировки превышают производственные затраты и время производства. Что, если перевозки во всех сферах будут выполняться профессионально и если соответствующие затраты будут оптимальными, производительность страны вырастет, даже если не будет затронут никакой другой фактор!
Соответственно, транспорт играет большую роль в обществе. Прибыль и состояние компаний, перевозящих товары из одного уголка страны в другой, определяются транспортом.Это особенно верно, когда транспортные расходы и время транспортировки превышают производственные затраты и время производства. Что, если перевозки во всех сферах будут выполняться профессионально и если соответствующие затраты будут оптимальными, производительность страны вырастет, даже если не будет затронут никакой другой фактор!
Исследование оптимальной транспортировки и распределения ресурсов; теория транспорта или теория транспорта. Французский математик Гаспар Монж формализовал эту задачу в 1781 году.Крупные успехи в этой области были сделаны во время Второй мировой войны советским математиком и экономистом Леонидом Канторовичем, известным как транспортная задача Монжа – Канторовича .
Важный тип транспортных проблем, которые решаются с помощью линейного программирования (LP), находится в области физического распределения товаров и услуг от нескольких центров предложения до центров спроса. Другими словами, транспортные проблемы связаны с перемещением товаров из разных источников в разные пункты назначения с общей целью минимизации транспортных расходов.Такая формулировка транспортной задачи с помощью линейного программирования также известна как транспортная задача Хичкока – Купманса.
Другими словами, транспортные проблемы связаны с перемещением товаров из разных источников в разные пункты назначения с общей целью минимизации транспортных расходов.Такая формулировка транспортной задачи с помощью линейного программирования также известна как транспортная задача Хичкока – Купманса.
Применение транспортной модели используется в авиационной отрасли, исследованиях и разработках, коммивояжере, перевалке и т. Д.
ПРЕДВАРИТЕЛЬНЫЕ УСЛОВИЯ
Для решения транспортной задачи необходимо предоставить следующую информацию:
- m = количество источников.
- n = количество пунктов назначения.
- Общее количество, доступное для каждого источника.
- Общее количество, необходимое в каждом пункте назначения.
- Стоимость перевозки одной единицы товара от каждого источника до каждого пункта назначения.
ПРЕДПОЛОЖЕНИЯ
Перед использованием любого метода транспортировки делаются следующие основные допущения:
- Общее количество, доступное во всех источниках, равно общему количеству, требуемому в пунктах назначения.
 Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные назначения.
Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные назначения. - Стоимость перевозки единицы из одного пункта отправления в пункт назначения известна и достоверна.
- Стоимость единицы не зависит от количества перевезенных товаров.
- Задача — минимизировать общие транспортные расходы.
- Хотя транспортные задачи могут быть сформулированы как LPP, для их решения разработаны другие более простые алгоритмы.
В основном есть 3 основных этапа
1. Формулировка транспортной модели в LPP
2.Найти базовое допустимое решение (BFS)
3. Тест на оптимальность
Давайте подробно рассмотрим
1. ФОРМУЛИРОВАНИЕ ТРАНСПОРТНОЙ МОДЕЛИ в LPP При решении задачи исследования эксплуатации ключевой частью было формулирование модели с помощью расшифровка проблемы. Для транспортной проблемы обычно проблема будет представлена в виде таблицы или матрицы, называемой транспортной таблицей или рентабельной матрицей.
Давайте проверим пример ниже.
Пример транспортной задачи с источником = {A, B, C} с общим предложением = 70 и пунктами назначения = {1,2,3} с общим спросом = 70 [изображение автора]Здесь
Source = { A, B, C}
Они представляют источники с производительностью 10,35,25 единиц товаров соответственно (выделены оранжевым цветом)
Следовательно, общее предложение = 10 + 35 + 25 = 70
Пункты назначения = {1,2 , 3}
Они представляют собой пункты назначения, для которых требуется 20,25,25 единиц товаров соответственно (выделены зеленым цветом).
Следовательно, общий спрос = 20 + 25 + 25 = 70
Элементы, представленные в матрице (выделены белым цветом), называются стоимостью. то есть стоимость единицы товара, связанная с перемещением единицы товара из одного пункта отправления в другой пункт назначения.
Например,
Затраты на перемещение 1 единицы товара из источника A в место назначения 1 = destination 2 / —
Затраты на перемещение 1 единицы товара из источника A в место назначения 1 = commod 2 / — (здесь мы смотрим на сечение источника A и пункта назначения 1 ) [изображение автора]Аналогично,
Затраты, понесенные при перемещении одной единицы товара из источника B в пункт назначения 2 = ₹ 4 / —
и так далее. [Здесь мы смотрим на сечение источника и назначения]
[Здесь мы смотрим на сечение источника и назначения]
ВИДЫ ПРОБЛЕМЫ ТРАНСПОРТИРОВКИ
Прежде чем продолжить, давайте рассмотрим различные типы транспортных проблем.
В основном существует 2 типа транспортных проблем:
1. Проблема сбалансированного транспорта
2. Проблема несбалансированного транспорта
Классификация транспортных проблем на сбалансированные и несбалансированные на основе имеющегося предложения и необходимого спроса. [изображение автора]Давайте заглянем в это.
1. Задача сбалансированного транспорта
общее доступное количество = общее требуемое количество
то есть, общее предложение = общий спрос
Давайте проверим пример ниже.
Пример сбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 75 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]Здесь
Общее предложение = 75
Общий спрос = 75
Следовательно, Общее предложение = Общий спрос
2. Проблема несбалансированного транспорта
Проблема несбалансированного транспорта
общее доступное количество ≠ общее требуемое количество
то есть общее предложение ≠ общий спрос
Общее количество, доступное во всех источниках, равно общему количеству, требуемому в пунктах назначения. Если они не совпадают, добавляются фиктивные источники или фиктивный пункт назначения, чтобы сделать это стандартной проблемой транспортировки.
Есть 2 ситуации, приводящие к этому несбалансированному состоянию
(i).Общее предложение> Общий спрос
(ii). Общее предложение <Общий спрос
(i). Общее предложение> Общий спрос
То есть, общее доступное количество> общее необходимое количество
Давайте проверим пример ниже.
Пример несбалансированной транспортной проблемы с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 60 [изображение автора]Здесь
Общее предложение = 65
Общий спрос = 60
Следовательно, Общее предложение> Общий спрос
В таких случаях мы добавляем фиктивный пункт назначения, дающий фиктивный спрос с каждой стоимостью, равной нулю (0), но фиктивный спрос для фиктивного пункта назначения в качестве общего предложения- общий спрос.
In в этом примере фиктивный спрос = 65–60 = 5
Таким образом, общее предложение = общий спрос
(ii). Общее предложение <Общий спрос
То есть общее доступное количество <общее требуемое количество
Давайте проверим пример ниже.
Пример несбалансированной транспортной проблемы с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]Здесь
Общее предложение = 65
Общий спрос = 75
Следовательно, Общее предложение <Общий спрос
В таких случаях мы добавляем фиктивный источник, дающий фиктивное предложение с каждой стоимостью, равной нулю (0), но фиктивное предложение для фиктивного пункта назначения как общий спрос- общий объем предложения.
In в этом примере фиктивное предложение = 75–65 = 10.
Таким образом, общее предложение = общий спрос
Решение, которое ищет каждая проблема при транспортировке, состоит в том, чтобы количество из каждого источника было направлено в какое место назначения, чтобы все потребности в одно и то же время сохранялись на уровне минимум.
Для этого мы должны преобразовать каждую проблему в стандартную, чтобы продвинуться дальше.
2. ОСНОВНОЕ ВОЗМОЖНОЕ РЕШЕНИЕ (BFS)Существуют различные методы, доступные для получения начального основного допустимого решения. Это:
(1). Северо-западное (С-З) угловое правило
(2). Метод наименьшей стоимости (или метод минимума матрицы)
(3). Метод приближения Фогеля [VAM] (или штрафной метод)
Метод приближения Фогеля [VAM] (или штрафной метод)
Давайте углубимся в каждый метод.
Для лучшего понимания рассмотрим пример задачи.
Вопрос дан ниже.
[изображение автора]Первым делом сделайте это стандартной транспортной задачей.
Для этого проверьте, является ли проблема при транспортировке сбалансированной или несбалансированной.
[изображение автора]Данная задача является сбалансированной транспортной задачей. Итак, приступим.
Теперь нам нужно найти простое возможное решение.Для одного и того же у нас есть 3 разных метода. Давайте по очереди проверим с помощью этой задачи.
(1). Правило северо-западного (С-З) угла
С-З направление [изображение автора]Выберите ячейку Северо-западного угла. т.е. стоимость пересечения 1-го ряда и 1-го столбца. [Здесь 5 (выделено синим цветом)]
Сравните спрос и предложение этой ячейки. [Здесь 65 и 70 (выделено красным)]
[изображение автора]Выделите ячейку с наименьшим значением [Здесь 65 (выделено желтым цветом)]
Вычтите исключенную ячейку с наименьшим значением. то есть выделенная ячейка. [Здесь 70–65 = 5]
то есть выделенная ячейка. [Здесь 70–65 = 5]
Удалите соответствующий столбец или строку, вычеркнув их. [Здесь столбец с пунктом назначения 1 (отмечен красной линией)]
Всегда общий спрос и предложение останутся неизменными. (Вы можете использовать этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы распределяем ячейки с новыми значениями таким образом, чтобы общий спрос и предложение остались прежними.
[т.е. здесь 42 + 43 + 65 = 150 (общий спрос) и 5 + 30 + 50 + 65 = 150 (общий объем предложения)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите ячейку Северо-Запад (С-З) и выполните те же действия, что и выше.
Давайте посмотрим на то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора] Здесь и спрос, и предложение будут одинаковыми, что будет далее распределено в оставшемся сингле клетка. [Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
[Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
Методы проверки правильности процесса:
Общий спрос и предложение останутся неизменными на протяжении всего шаги.
На последнем шаге отдельной ячейке будет присвоено значение либо со спросом, либо с предложением, поскольку обе будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, сделав другое значение равным нулю.(Какой из них выбрать, это выбор пользователя.)
Окончательная таблица со всеми выделенными ячейками будет такой.
Это дает начальное возможное решение по методу N-W Corner.
[изображение автора]Теперь давайте посчитаем стоимость, связанную с этим распределением.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (выделены желтым цветом) и стоимости соответствующей ячейки (показаны синим цветом).
т.е. Общая стоимость = (65×5) + (5×7) + (30×4) + (7×7) + (43×7)
= 325 + 35 + 120 + 49 + 301
= 830
Теперь давайте разберемся, что мы выяснили
₹ 830 — представляет собой общую стоимость, связанную с перемещением товаров.
Путь, по которому мы идем, обозначен красными стрелками, как мы обнаружили с помощью метода N-W Corner.
[изображение автора]Изобразим то же самое в таблице
таблица окончательного решения [изображение автора]Это может или не может представлять оптимальное решение для этой проблемы, т.е. могут существовать другие способы распределение, которое может дать лучшее решение с более низкой общей стоимостью.
Необходимо провести тест на оптимальность, чтобы проверить, является ли полученный ответ оптимальным.Если нет, то тест на оптимальность приводит нас к одному из возможных улучшений.
(2). Метод наименьшей стоимости (или метод минимума матрицы)
Давайте обсудим тот же пример.
Выберите наименьшее значение среди всех затрат (выделено белым цветом). т.е. минимальная стоимость. [Здесь 4 (выделено синим)]
Здесь две ячейки с наименьшей стоимостью. Какой из них выбрать, остается только за пользователем.
[изображение автора]Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, вы можете выбрать любой из них. (Какой из них выбрать — это выбор пользователя.)
Сравните спрос и предложение этой ячейки. [Здесь 30 и 65 (выделено красным цветом)] Назначьте ячейку с наименьшим значением [Здесь 30 (выделено желтым цветом)]
Вычтите исключенную ячейку с наименьшим значением. то есть выделенное значение ячейки. [Здесь 65–30 = 35]
Удалите соответствующий столбец или строку, удалив ее.[Здесь строка с источником B (отмечена красной линией)]
Всегда общий спрос и предложение останутся неизменными.
(Вы можете использовать этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы распределяем ячейки с новыми значениями таким образом, чтобы общий спрос и предложение остались прежними.
[то есть здесь 35 + 42 + 43 + 30 = 150 (общий спрос) и 70 + 50 + 30 = 150 (общий объем предложения)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите ячейку с наименьшей стоимостью и выполните те же действия, что и выше.
Давайте посмотрим на то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]Здесь и спрос, и предложение будут одинаковыми, что будет далее распределено в оставшемся сингле клетка. [Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
Методы проверки правильности процесса:
Общий спрос и предложение останутся неизменными через шаги.
На последнем шаге единичной ячейке будет присвоено значение либо со спросом, либо с предложением, так как обе будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, сделав другое значение равным нулю. (Какой из них выбрать, это выбор пользователя.)
Окончательная таблица со всеми выделенными ячейками будет такой.
Это дает изначально возможное решение методом наименьших затрат.
[изображение автора]Теперь давайте посчитаем стоимость, связанную с этим распределением.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (выделены желтым цветом) и стоимости соответствующей ячейки (показаны синим цветом).
т.е. Общая стоимость = (35×5) + (30×4) + (35×7) + (7×7) + (43×7)
= 175 + 120 + 245 + 49 + 301
= 890
Теперь давайте разберемся, что мы выяснили
₹ 890 — представляет собой общую стоимость, связанную с перемещением товаров.
Путь, по которому пройден, повторен красными стрелками, как мы нашли методом наименьших затрат.
[изображение автора]Изобразим то же самое в таблице.
таблица окончательных решений [изображение автора]Это может или не может представлять оптимальное решение для этой проблемы, т.е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью
Тест на оптимальность необходимо провести, чтобы проверить, является ли полученный ответ оптимальным.Если нет, то тест на оптимальность приводит нас к одному из возможных улучшений.
( 3). Метод аппроксимации Фогеля [VAM] (или штрафной метод)
Давайте обсудим тот же пример.
[изображение автора] Выбрать стоимостную ячейку для выделения в VAM не так просто, как если бы мы обсуждали метод N-W Corner и метод наименее затратной ячейки. (Успокойся, чувак, это не так уж сложно. «Но процесс немного длиннее, чем раньше».)
«Но процесс немного длиннее, чем раньше».)
В VAM мы должны сначала определить разницу между двумя наименьшими затратами в каждой строке и столбце.Они известны как штрафов / дополнительных расходов.
[изображение автора]Учитывается разница между двумя наименьшими значениями.
[Здесь Penalties = {2,0,1,1,3,1}]
Теперь найдите максимальное значение среди штрафов независимо от строки или столбца.
[Здесь max (штрафы) = 3 (выделено розовым цветом)]
[изображение автора]Если есть ничья, выберите любого. (Какой из них выбрать — это выбор пользователя.)
Теперь просмотрите соответствующую строку или столбец.
[Здесь столбец (выделен розовым цветом)]
Выберите наименьшее значение среди всех затрат (выделено розовым цветом). т.е. минимальная стоимость. [Здесь 4 (выделено синим цветом на рисунке ниже)]
[изображение автора]Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, вы можете выбрать любой из них.
(Какой из них выбрать — это выбор пользователя.)
Сравните спрос и предложение этой ячейки [Здесь 30 и 42 (выделены красным)]
[изображение автора ]Назначьте ячейку с наименьшим значением [Здесь 30 (выделено желтым)]
Вычтите исключенную ячейку с наименьшим значением.то есть выделенная ячейка. [Здесь 42–30 = 12]
Удалите соответствующий столбец или строку, удалив ее. [Здесь столбец с источником B (отмечен красной линией)]
Всегда общий спрос и предложение останутся неизменными. (Вы можете использовать этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы распределяем ячейки с новыми значениями таким образом, чтобы общий спрос и предложение остались прежними.
[то есть здесь 65 + 12 + 43 + 30 = 150 (общий спрос) и 70 + 50 + 30 = 150 (общий объем предложения)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите штраф и выполните те же действия, что и выше.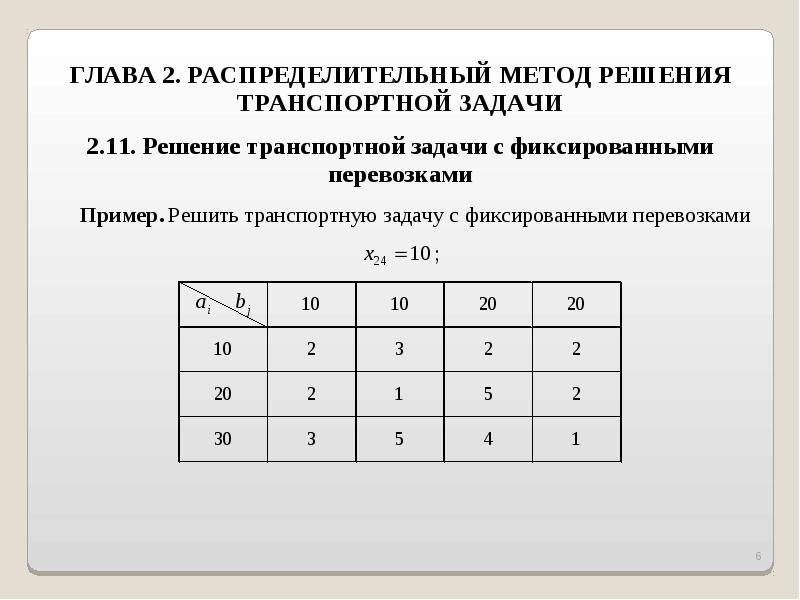
Давайте посмотрим на то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]Здесь и спрос, и предложение будут одинаковыми, что будет далее распределено в оставшемся сингле клетка. [Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
Методы проверки правильности процесса:
Общий спрос и предложение останутся неизменными через шаги.
На последнем шаге единичной ячейке будет присвоено значение либо со спросом, либо с предложением, так как обе будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, сделав другое значение равным нулю. (Какой из них выбрать, это выбор пользователя.)
Окончательная таблица со всеми выделенными ячейками будет такой.
Это дает начальное возможное решение от VAM.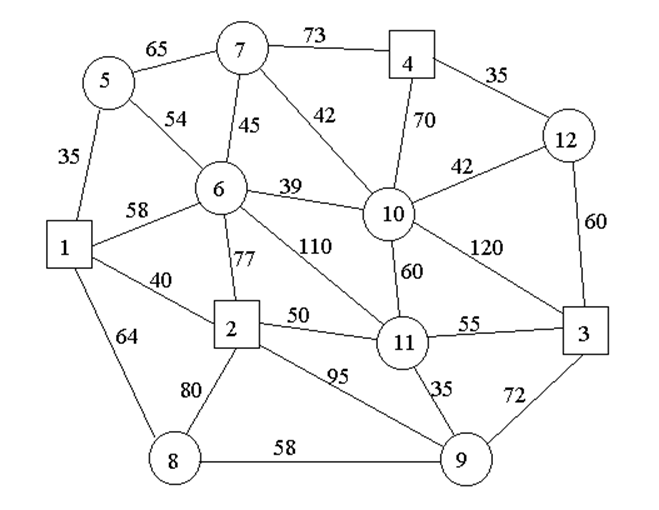
Теперь давайте посчитаем стоимость, связанную с этим распределением.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (выделены желтым цветом) и стоимости соответствующей ячейки (показаны синим цветом).
т.е. Общая стоимость = (65×5) + (5×7) + (30×4) + (7×7) + (43×7)
= 325 + 35 + 120 + 49 + 301
= 830
Теперь давайте разберемся, что мы выяснили
₹ 830 — представляет собой общую стоимость, связанную с перемещением товаров.
Путь, по которому мы идем, представлен красными стрелками, как мы обнаружили с помощью VAM.
[изображение автора]Изобразим то же самое в таблице.
таблица окончательных решений [изображение автора]Это может или не может представлять оптимальное решение для этой проблемы, т.е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью.

Необходимо провести тест на оптимальность, чтобы проверить, является ли полученный ответ оптимальным. Если нет, то тест на оптимальность приводит нас к одному из возможных улучшений.
3. Тест ОПТИМАЛЬНОСТИ
Хотя базовое выполнимое решение может учитывать все источники и ограничения местоположения, оно не обязательно должно давать решение с наименьшими затратами.Может быть несколько основных возможных решений, но оптимальным считается то, которое сводит к минимуму общие транспортные расходы. После того, как базовое возможное решение было определено любым из перечисленных выше методов, оно должно быть дополнительно протестировано, чтобы тесты на оптимальность проверили, является ли данное решение лучшим, а если нет, оно приведет нас к лучшему или оптимальному решению (I выбрал бы плохой вариант худшему.)
(Мы обсудим это подробно в другой статье, так как это само по себе кажется мне длинным.😂)
Оптимизация | математика | Britannica
Оптимизация , также известная как математическое программирование , набор математических принципов и методов, используемых для решения количественных задач во многих дисциплинах, включая физику, биологию, инженерию, экономику и бизнес. Этот предмет вырос из осознания того, что количественные задачи в явно разных дисциплинах имеют важные общие математические элементы. Благодаря этой общности многие проблемы могут быть сформулированы и решены с использованием единого набора идей и методов, составляющих область оптимизации.
Этот предмет вырос из осознания того, что количественные задачи в явно разных дисциплинах имеют важные общие математические элементы. Благодаря этой общности многие проблемы могут быть сформулированы и решены с использованием единого набора идей и методов, составляющих область оптимизации.
Исторический термин математическое программирование , в широком смысле синоним оптимизации, был придуман в 1940-х годах до того, как программирование стало приравниваться к компьютерному программированию. Математическое программирование включает изучение математической структуры задач оптимизации, изобретение методов решения этих задач, изучение математических свойств этих методов и реализацию этих методов на компьютерах. Более быстрые компьютеры значительно увеличили размер и сложность решаемых задач оптимизации.Развитие методов оптимизации сопровождалось успехами не только в компьютерных науках, но и в исследованиях операций, численном анализе, теории игр, математической экономике, теории управления и комбинаторике.
Проблемы оптимизации обычно состоят из трех основных элементов. Первый — это отдельная числовая величина или целевая функция, которая должна быть максимизирована или минимизирована. Целью может быть ожидаемая доходность портфеля акций, производственные затраты или прибыль компании, время прибытия автомобиля в указанный пункт назначения или доля голосов политического кандидата.Второй элемент — это набор переменных, то есть величин, значениями которых можно управлять для оптимизации цели. Примеры включают количество запасов, которые будут куплены или проданы, количество различных ресурсов, которые будут выделены для различных видов производственной деятельности, маршрут, которым должен следовать автомобиль через транспортную сеть, или политику, которую должен продвигать кандидат. Третий элемент задачи оптимизации — это набор ограничений, которые представляют собой ограничения на значения, которые могут принимать переменные.Например, для производственного процесса не может потребоваться больше ресурсов, чем доступно, и не может быть задействовано меньше нуля. В этих широких рамках задачи оптимизации могут иметь различные математические свойства. Задачи, в которых переменные являются непрерывными величинами (как в примере распределения ресурсов), требуют подхода, отличного от задач, в которых переменные являются дискретными или комбинаторными величинами (как при выборе маршрута транспортного средства из предопределенного набора возможностей).
Важный класс оптимизации известен как линейное программирование. Линейное указывает, что никакие переменные не возводятся в более высокие степени, например квадраты. Для этого класса задачи включают минимизацию (или максимизацию) линейной целевой функции, переменные которой являются действительными числами, которые ограничены, чтобы удовлетворять системе линейных равенств и неравенств. Другой важный класс оптимизации известен как нелинейное программирование. В нелинейном программировании переменные — действительные числа, а цель или некоторые ограничения — нелинейные функции (возможно, с использованием квадратов, квадратных корней, тригонометрических функций или произведений переменных).В этой статье обсуждается как линейное, так и нелинейное программирование. К другим важным классам задач оптимизации, не затронутым в этой статье, относятся стохастическое программирование, в котором целевая функция или ограничения зависят от случайных величин, так что оптимум находится в некотором «ожидаемом» или вероятностном смысле; оптимизация сети, которая включает оптимизацию некоторых свойств потока через сеть, например максимизацию количества материала, который может быть транспортирован между двумя заданными точками в сети; и комбинаторная оптимизация, при которой решение должно быть найдено среди конечного, но очень большого набора возможных значений, таких как множество возможных способов назначения 20 заводов-производителей 20 местам.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчасИстоки и влияние
Несмотря на то, что сегодня оно широко используется для решения повседневных задач принятия решений, до 1947 года линейное программирование было сравнительно неизвестным. До этой даты не проводилось никаких значительных работ, хотя французский математик Жозеф Фурье, казалось, знал о потенциале этого предмета еще в 1823 году. В 1939 году русский математик Леонид Витальевич Канторович опубликовал обширную монографию «Математические методы организации и планирования производства », которая теперь считается первым трактатом, признавшим эту достоверность. важные широкие классы задач планирования имели четко определенные математические структуры.К сожалению, предложения Канторовича почти два десятилетия оставались в основном неизвестными ни в Советском Союзе, ни в других странах. Между тем, линейное программирование значительно развилось в США и Западной Европе. В период после Второй мировой войны официальные лица в правительстве Соединенных Штатов пришли к выводу, что эффективная координация энергии и ресурсов целой нации в случае ядерной войны потребует использования научных методов планирования. С появлением компьютеров такой подход стал возможным.
Интенсивные работы начались в 1947 году в ВВС США. Модель линейного программирования была предложена, потому что она была относительно простой с математической точки зрения, и тем не менее она обеспечивала достаточно общую и практическую основу для представления взаимозависимых действий, которые разделяют ограниченные ресурсы. В модели линейного программирования разработчик модели рассматривает оптимизируемую систему как состоящую из различных видов деятельности, которые, как предполагается, требуют потока входов (например, рабочая сила и сырье) и выходов (например,g., готовая продукция и услуги) различных видов, пропорциональных уровню деятельности. Предполагается, что уровни активности могут быть представлены неотрицательными числами. Революционная особенность этого подхода заключается в выражении цели процесса принятия решений в терминах минимизации или максимизации линейной целевой функции — например, максимизация возможных самолето-вылетов в случае с военно-воздушными силами или максимизация прибыли в промышленности. До 1947 года все практическое планирование характеризовалось серией авторитетных правил процедуры и приоритетов.Общие цели никогда не были сформулированы, вероятно, из-за невозможности выполнения вычислений, необходимых для минимизации целевой функции при ограничениях. В 1947 году был представлен метод (описанный в разделе Симплексный метод), который оказался эффективным для решения практических задач. Интерес к линейному программированию быстро рос, и к 1951 году его использование распространилось на промышленность. Сегодня почти невозможно назвать отрасль, в которой математическое программирование в той или иной форме не используется, хотя приложения и масштабы его использования сильно различаются даже в пределах одной отрасли.
Интерес к линейному программированию распространился и на экономику. В 1937 году математик из Венгрии Джон фон Нейман проанализировал устойчиво развивающуюся экономику, основанную на альтернативных методах производства и фиксированных технологических коэффициентах. Что касается истории математики, то до 1936 г. изучение систем линейных неравенств практически не интересовало. В 1911 г. в качестве способа решения проблемы было предложено движение от вершины к вершине по ребрам многогранника (как это делается в симплекс-методе). решить задачу, связанную с оптимизацией, и в 1941 году движение по краям было предложено для задачи, связанной с транспортировкой.Заслуга за закладку большей части математических основ, вероятно, принадлежит фон Нейману. В 1928 году он опубликовал свою знаменитую статью по теории игр, а кульминацией его работы в 1944 году стала публикация в сотрудничестве с австрийским экономистом Оскаром Моргенштерном классической Теории игр и экономического поведения . В 1947 году фон Нейман предположил эквивалентность линейных программ и матричных игр, ввел важную концепцию двойственности и внес несколько предложений по численному решению линейного программирования и игровых задач.Серьезный интерес со стороны других математиков начался в 1948 году со строгого развития двойственности и связанных с ней вопросов.

