ГДЗ по Математике 3 класс Петерсон самостоятельные и контрольные работы
Авторы: Петерсон Л.Г., Поникарова Т.Ю..
Тип: Самостоятельные и контрольные работы, Перспектива
Школьники, которые пользуются ГДЗ по математике 3 класс самостоятельные и контрольные работы Петерсон не бояться тестирований. Почему? Потому что при помощи этого сборника они могут хорошо подготовиться к любым испытаниям. Математика — весьма непростой предмет, который многие дети воспринимают с трудом. Однако не учить его нельзя, ведь его знание понадобиться при сдаче ВПР, ГИА и ЕГЭ, при вступительных экзаменах в ВУЗ или институт, во время работы.
Хоть ребята еще толком не понимают этого, но математика окружает нас повсюду. Поэтому знания, которые закладываются в третьем классе имеют очень большое значение. Но недостаточно просто усвоить материал, учащимся необходимо еще доказать, что они поняли что к чему.
Онлайн-помощник по математике за 3 класс самостоятельные и контрольные работы Петерсона всегда поддержат в сложную минуту
Сборник состоит из двух частей, в каждой из которых по девяносто две страницы. Все приведенные работы соотносятся с тематическими параграфами или разделами. Каждый номер имеет понятное решение и детальный ответ, поэтому ученики могут:
- проследить алгоритм и уяснить его суть;
- понять в чем именно они допускают ошибки;
- дополнительно проработать материал, чтобы лучше его запомнить.
При помощи решебника каждый ребенок имеет возможность досконально изучить данную дисциплину, что облегчит выполнение домашних заданий и обеспечит получение хороших оценок.
Контрольные работы давно стали неотъемлемой частью обучения. Порой создается ощущение, что школьники только и делают, что проходят различные проверки, а не учатся. Порой так и происходит — учителя больше внимания уделяют этим тестированиям, чем разъяснению учебного материала. Не удивительно, что многие учащиеся имеют весьма средние показатели и оценки. А ведь для того, чтобы стать отличником много не надо — просто хорошо понимать то, что предстоит изучить.
Порой создается ощущение, что школьники только и делают, что проходят различные проверки, а не учатся. Порой так и происходит — учителя больше внимания уделяют этим тестированиям, чем разъяснению учебного материала. Не удивительно, что многие учащиеся имеют весьма средние показатели и оценки. А ведь для того, чтобы стать отличником много не надо — просто хорошо понимать то, что предстоит изучить.
Полноценное представление о каждой теме может дать
Годовая Контрольная Работа 3 Класс Перспектива – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Годовая Контрольная Работа 3 Класс Перспектива
Для всех учителей из 37 347 образовательных учреждений по всей стране
Получите деньги за публикацию своих
разработок в библиотеке «Инфоурок»
и получить бесплатное свидетельство о размещении материала на сайте infourok. ru
ru
репетиторы онлайн
от проекта «ИнфоУрок»
Онлайн-занятия с репетиторами
Подберём репетитора лично для Вас и запишем на бесплатное пробное занятие!
Инфоурок
›
Начальные классы
›
Другие методич. материалы
›
Годовая контрольная работа по математике 3 класс УМК «Перспектива»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Только сейчас Вы можете пройти дистанционное обучение прямо на сайте «Инфоурок» со скидкой 40% по курсу повышения квалификации «Организация работы с обучающимися с ограниченными возможностями здоровья (ОВЗ) в соответствии с ФГОС» (72 часа). По окончании курса Вы получите печатное удостоверение о повышении квалификации установленного образца (доставка удостоверения бесплатна).
Годовая контрольная работа по математике 3 класс УМК «Перспектива»
КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ ЗА 2016/2017 УЧЕБНЫЙ ГОД
Купили 300 г изюма, чернослива в 2 раза больше, чем изюма, а кураги на 500г меньше, чем чернослива. Сколько всего сухофруктов купили?
2. Определи порядок действий и вычисли значение выражений
(166 – 134) : (64 : 8) · (926 – 917)
3.Выполни вычисления, записывая выражения в столбик
5.Начерти прямоугольник со сторонами 2см и 5см. Найди его периметр.
6*** Расставь знаки действий так, чтобы получились верные записи
400 ….. 4 ….. 300 = 400 140….. 4 …… 40 = 600
600 ….200 …..2 = 200 270 ….30 ….. 2 = 210
Купили 200г шоколадных конфет, карамели в 2 раза больше, чем шоколадных конфет, а ирисок в 4 раза меньше, чем карамели. Сколько всего конфет купили?
2.Определи порядок действий и вычисли значение выражений
3.Выполни вычисления, записывая выражения в столбик
5. Начерти квадрат со стороной 4см. Найди его площадь.
6*** Расставь знаки действий так, чтобы получились верные записи
300 … 3 …. .300 = 600 240 …..4 …. 60 = 900
.300 = 600 240 …..4 …. 60 = 900
(500 …. 200) ….. 3 = 100 270 ….. 40 …. 3 = 150
Московский институт профессиональной переподготовки и повышения квалификации педагогов
Курс профессиональной переподготовки
Влияние сенсорной интеграции на ребенка с ОВЗ в дошкольный период
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категории
Алгебра
Английский язык
Астрономия
Биология
Внеурочная деятельность
Всеобщая история
География
Геометрия
Директору, завучу
Доп. образование
Дошкольное образование
Естествознание
ИЗО, МХК
Иностранные языки
Информатика
История России
Классному руководителю
Коррекционное обучение
Литература
Литературное чтение
Логопедия, Дефектология
Математика
Музыка
Начальные классы
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
Природоведение
Религиоведение
Родная литература
Родной язык
Русский язык
Социальному педагогу
Технология
Украинский язык
Физика
Физическая культура
Философия
Французский язык
Химия
Черчение
Школьному психологу
Экология
Другое
Выберите класс:
Все классы
Дошкольники
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
7 класс
8 класс
9 класс
10 класс
11 класс
также Вы можете выбрать тип материала:
Авторизуйтесь, чтобы задавать вопросы.
Знаете, что говорят коллеги из Вашего учебного заведения о КУРСАХ «Инфоурок»?
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Контрольные работы по математике 3 класс «Перспектива»
Контрольные работы по математике 3 класс УМК «Перспектива»
Итоговая контрольная работа по окружающему миру. 3 класс
3 класс
Контрольные работы по математике 3 класс (Перспектива)
Годовая контрольная работа по математике 3 класс УМК…
Сочинение Недоросль Невежда Без Души Зверь Про
Тюркский Язык Язык Науки Эссе
Отчет По Практике Медико Социальная Реабилитация
Реферат Карл Маркс Капитал
Титульный Лист Реферата Урфу Образец
ГДЗ по математике 3 класс самостоятельные и контрольные работы Петерсон Л.Г. Перспектива
Как часто у родителей бывают ситуации, когда они приходят домой после тяжелого рабочего дня и постоянных упреков начальника, а вместо отдыха предстоит проверять уроки у любимого сына, или дочки, помогать с подготовкой к проверочным. Конечно, дети – это цветы жизни, но такая картина все равно не приносит особой радости. Выход есть всегда и в данном случае, это — 
Но понять в такой онлайн решебник могут не только взрослые, но и школьники, которые в своих стремлениях к превосходным оценкам готовы прибегнуть ко всем мерам. Сборник станет отличным помощником в обучении, если с его помощью проверять уже готовые домашние задания, или разбираться с пропущенным, плохо усвоенным материалом. А за тем, чтобы ребенок использовал решебник по назначению, должны следить заботливые родители. Он особенно пригодится в периоды болезни, или сильной усталости, когда освоить пройденные темы самостоятельно порой невозможно, тем более для третьеклассника, который все еще искренне пытается найти время для всего, что его окружает, начиная от веселых прогулок и игр с друзьями, заканчивая уроками математики.
Данное пособие создавалась по всем правилам и включает в себя правильные ответы на Д/З и контрольные работы соответствующей книги. Благодаря профессиональному подходу и качественным решениям литература отлично подходит учителям для проверки тетрадок своих учеников.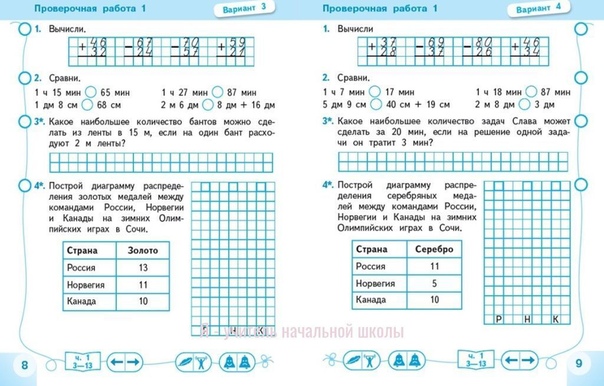
ГДЗ к учебнику по математике за 3 класс Петерсон Л.Г. (Перспектива) можно посмотреть здесь.
Контрольные работы по математике за 1 полугодие 3 класс
В третьем классе у учащихся по разным УМК теперь знания отличаются все больше и больше. К примеру, «Школа России» и «Школа 21 века» давали понятие уравнений с неизвестными и ребятишки научились их решать, а вот «Перспектива» не учила решать уравнения. Именно поэтому важно, чтобы контрольная соответствовала программе, а не была взята «с потолка». Мы предлагаем вам варианты контрольных работ для третьего класса за первое полугодие.
Именно поэтому важно, чтобы контрольная соответствовала программе, а не была взята «с потолка». Мы предлагаем вам варианты контрольных работ для третьего класса за первое полугодие.
Цель: проверить уровень математической подготовки, прочности усвоения и осознанности материала учащимися третьих классов по пройденным темам на конец 1 полугодия.
Контрольная работа по математике за 1 полугодие 3 класс по программе «Школа России»
1 вариант
1. В 4 наборах 32 листа цветной бумаги. В скольких наборах находятся 72 листа бумаги?
2. Вставьте в «окошки» знаки · или : и пропущенные числа так, чтобы примеры стали верными:
□ . . . 8 = 9 5 . . . □= 0 36 . . . □ = 6
3 . . . □ = 24 □ . . . 8 = 1 □ . . . 6 = 0
3. Найдите значение выражений:
45 : (33 – 24) · 6 63 + 27 : (30 : 10)
4. Площадь прямоугольника 42 см2, его ширина 6 см. Найдите длину и периметр этого прямоугольника.
Найдите длину и периметр этого прямоугольника.
5. Найдите значение выражения а + 27, если а = 8, а = 12, а = 16, а = 4.
6. В нашем доме живут Катя, Маша и Лена. Вчера я видел Катю и Машу. Одной из них 9 лет, другой – 8. Сегодня я видел Машу и Лену. Одной из них 10 лет, другой – 9. Кому сколько лет?
2 вариант
1. На 3 костюма идёт 9 м ткани. Сколько метров ткани пойдёт на 6 таких костюмов?
2. Вставьте в «окошки» знаки · или : и пропущенные числа так, чтобы примеры стали верными:
□ … 7 = 6 9 . . . □ = 0 5 . . . □ = 40
□ . . . 15= 1 56 . . . □= 7 □ . . .7 = 3
3. Найдите значение выражений:
60 – 18 : 2 · 3 96 – (35 – 5) : 6
4. Площадь прямоугольника 72 см2, его длина 8 см. Найдите ширину и периметр этого прямоугольника.
5. Найдите значение выражения 36 + в, если в = 9, в = 5, в = 29, в = 17.
6. Цветки картофеля бывают открыты от 6 ч утра до 14 ч дня, цветки льна – от 6 ч до 16 ч, а цветки календулы от 9 ч до 15 ч. В какие часы эти цветки раскрыты одновременно?
В какие часы эти цветки раскрыты одновременно?
Итоговая контрольная работа за 1 полугодие 3 класс. Программа «Школа 21 века»
1 вариант
1. Выпиши только верные неравенства:
(300 + 250 + 400) · 0 < 300 · 1
187 + 415 + 104 > 105 + 188 + 416
(80 — 66) : 2 = 7
2. Реши уравнения:
x + 135 = 582 72 : y = 8
3. Реши задачу:
В столовой израсходовали 18 кг риса, а гречневой крупы в 2 раза меньше, чем риса. Пшена израсходовали столько, сколько риса и гречневой крупы вместе. Сколько килограммов пшена израсходовали?
4. Выполни действия:
49 кг 32 г + 22 кг 59 г =
102 см 9 мм – 96 см 8 мм =
5. Вычисли по действиям:
180-81:9+6·4
324+189-205+18
2 вариант
1. Выпиши только верные равенства:
3 · 2 < 2 + 2 + 2
(56 — 48) · 4 = 24
83 + 2 · 4 = 91
2. Реши уравнения:
y — 104 = 289 5 * x = 35
3.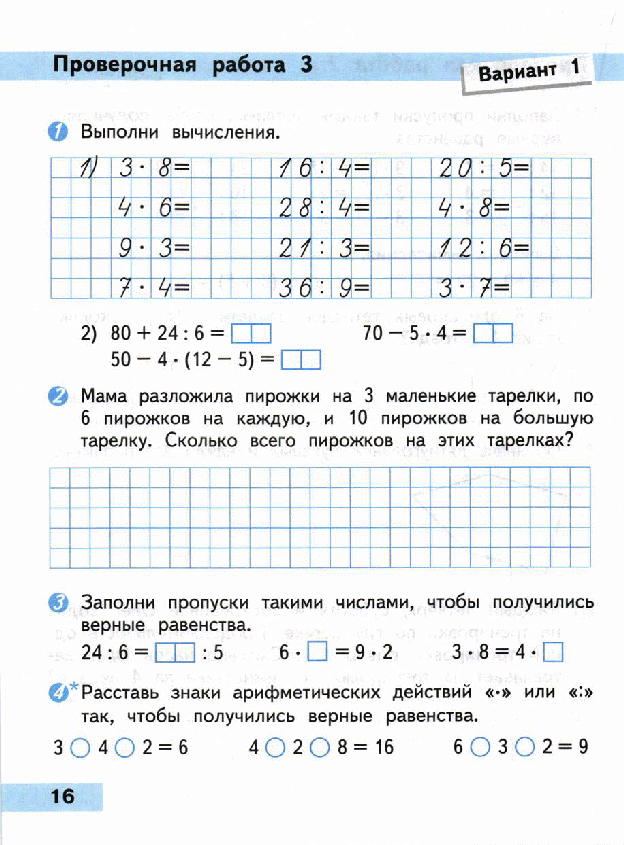 Реши задачу:
Реши задачу:
В субботу библиотеку посетили 24 читателя, а в воскресенье читателей было в 3 раза меньше, чем в субботу. В понедельник библиотеку посетило столько читателей, сколько в субботу и воскресенье вместе. Сколько читателей было в библиотеке в понедельник?
4. Выполни действия
158 см 5 мм + 42 см 4 мм =
101 кг 42 г – 64 кг 28 г =
5. Вычисли по действиям:
415-226+107-29
150-64:8+2·4
Контрольная за полугодие по УМК «Школа 21 века» (доп.вариант)
Вариант 1
1. Решите задачу:
Девочка прочитала в первый день 16 страниц, а во второй – 14. После этого ей осталось прочитать 18 страниц. Сколько всего страниц в этой книге?
2. Решите задачу:
Карандаш стоит 3 рубля. Сколько стоят 9 таких карандашей?
3. Решите примеры:
(17-8) · 2= 82-66=
(21-6) : 3= 49+26=
18 : 6 · 3= 28+11=
8 · 3 – 5= 94-50=
4. Найдите периметр и площадь прямоугольника со сторонами 4 см и 2 см.
5. Рассмотри таблицу.
Ниже приведено расписание уроков Насти на три дня.
Понедельник Вторник Среда
1 урок Русский язык Математика Русский язык
2 урок Физкультура Русский язык Математика
3 урок ИЗО Чтение Английский язык
4 урок Математика Музыка Чтение
5 урок История
Пользуясь таблицей, выбери верные утверждения.
1) Во вторник сразу после урока чтения идёт урок русского языка.
2) В понедельник урок математики не последний.
3) Каждый из этих трёх дней начинается с урока русского языка.
4) В понедельник уроков больше, чем во вторник.
В ответе запиши номера верных утверждений.
Вариант 2
1. Решите задачу:
В первый день школьники окопали 18 деревьев, во второй – 12 деревьев. После этого им осталось окопать 14 деревьев. Сколько деревьев было нужно окопать школьникам?
2. Решите задачу:
Решите задачу:
В пакете 7 кг картофеля. Сколько килограммов картофеля в 3 таких пакетах?
3. Решите примеры:
(24-6) : 2= 87-38=
(15-8) · 3= 26+18=
12 : 6 · 9= 73+17=
3 · 7 – 12= 93-40=
4. Найдите периметр прямоугольника со сторонами 3 см и 5 см
5. Рассмотри таблицу.
Ниже приведено расписание уроков Насти на три дня.
Понедельник Вторник Среда
1 урок Русский язык Математика Русский язык
2 урок Физкультура Русский язык Математика
3 урок ИЗО Чтение Английский язык
4 урок Математика Музыка Чтение
5 урок История
Пользуясь таблицей, выбери верные утверждения.
1) Во вторник сразу после урока математики идёт урок чтения
2) В среду урок английского языка не последний.
3) Каждый из этих трёх дней начинается с урока русского языка.
4) В понедельник уроков больше, чем во вторник.
В ответе запиши номера верных утверждений.
Контрольная работа по математике за 1 полугодие 3 класс «Перспективная начальная школа»
1 вариант
1. Укажите порядок действий и найдите значения выражений.
(145 – 45 : 5) · 7
158 · 6 – (468 + 354) : 3
297 – 209 + 73 · 8 – 329 : 7
2. Найдите значения выражений:
16457 – 7540 56 : 8
79596 + 49537 26 · 3
3. Найдите корни уравнений.
173 – х = 79 52 + х = 84 9 · х = 45
4. Реши задачу.
В подарке 2 шоколадки, а конфет – на 4 штуки больше. Сколько конфет в восьми таких подарках?
5. Начертите два отрезка: длина первого отрезка 12 см, длина второго – в 2 раза меньше.
2 вариант
1. Укажите порядок действий и найдите значения выражений.
(227 – 27 : 9) · 11
100 · 5 – (30 – 5) : 5
2. Найдите значения выражений:
56408+3592 6 · 7
723394–5639 32 : 4
3. Найдите корни уравнений.
Найдите корни уравнений.
284 – х = 84 83 + х = 100 5 · х = 30
4. Реши задачу.
В ящике 8 кг моркови. Сколько килограммов моркови в шести таких ящиках?
5. Начертите два отрезка: длина первого отрезка 12 см, длина второго – на 9 см меньше.
Контрольная работа (тест) по математике за 1 полугодие 3 класс, «Перспектива»
1 вариант
1. В каком числе 5 десятков 6 единиц.
1) 65 2) 56 3) 25 4) 61
2.Увеличь 60 на 37.
1) 97 2) 87 3) 78
3. Уменьшаемое 54, вычитаемое 40. Найди разность.
1) 94 2) 14 3) 4
4. Какое число нужно прибавить к трём десяткам, чтобы получилось 60?
1) 80 2) 30 3) 50 4) 58
5. Укажи значение произведения чисел 9 * 6
1) 52 2) 54 3) 63
6. Частное каких чисел равно 9 ?
1) 18 и 9 2) 3 и 3 3) 36 и 4
7. Чему равно произведение чисел 14 и 6 ?
1) 84 2) 20 3) 60
8. В каком выражении к числу 18 надо прибавить частное чисел 24 и 3?
1) 18 + 24 *3 2) 18 + 24 : 3 3) (18 + 24) : 3
9. Выяви закономерность и запиши следующие два числа
Выяви закономерность и запиши следующие два числа
3, 6, 9, 12, __________
10. Сравни выражения и поставь вместо звёздочки знак: >, <, =.
30+70 * 80+20
1) > 2) < 3) =
67-3 * 68-5
1) = 2) > 3) <
11. Сравни значения величин и поставь вместо звёздочки знак: >, <, ==.
8дм 8 см * 8 дм 5 см
1) > 2) < 3) =
12. Длина стороны квадрата равна 7 см. Чему равен периметр?
1) 12 см 2) 28 см 3) 14 см 4) 64 см
13. Реши задачу.
В 6 одинаковых наборах 48 карандашей. Сколько карандашей в 4 таких же наборах?
___________________________________________________________
___________________________________________________________
14. Запиши выражение и найди его значение.
Сумма чисел 16 и 24 разделить на 2.________________________
15. Какие два числа в указанном порядке надо записать в «окошки», чтобы равенство 9 х : =6
1) 2 и 6 2) 3 и 9 3) 4 и 6
16. Реши задачу выражением.
Реши задачу выражением.
Библиотекарь разложила на 8 полках по 6 новых книг и на 5 полках по 8 новых книг. Сколько всего новых книг разложила библиотекарь?
__________________________________________________________________
Ответ:____________________________________________________________
2 вариант
1. В каком числе 6 десятков 3 единиц.
1) 39 2) 93 3) 63 4) 91
2. Увеличь 64 на 6.
1) 69 2) 70 3) 58
3. Уменьшаемое 72, вычитаемое 50. Найди разность.
1) 22 2) 32 3) 42
4. Какое число нужно прибавить к двум десяткам, чтобы получилось 70?
1) 30 2) 50 3) 40 4) 4
5. Укажи значение частного 42 и 7
1) 7 2) 6 3) 8
6. В виде произведения каких чисел можно представить число 54 ?
1) 7 * 8 2) 6 * 8 3) 9 * 6
7. Чему равно произведение чисел 18 и 2 ?
1) 20 2) 36 3) 38
8. В каком выражении надо из числа 72 вычесть частное чисел 12 и 2?
1) 72 – 12 *2 2) 72 – 12 : 2 3) (72 – 12) : 2
9. Выяви закономерность и запиши следующие два числа
Выяви закономерность и запиши следующие два числа
4, 8, 12, 16, __________
10. Сравни выражения и поставь вместо звёздочки знак: >,<,=.
50+40 * 100-10
1) > 2) < 3) =
78-4 * 79-6
1) > 2) < 3) =
11. Сравни значения величин и поставь вместо звёздочки знак: >,<,=.
6 дм 4 см * 4 дм 6 см
1) > 2) < 3) =
12. Длина стороны квадрата равна 6 см. Чему равен периметр?
1) 24 см 2) 18 см 3) 36 см 4) 12 см
13. Реши задачу.
На 8 одинаковых кофтах 56 пуговиц. Сколько пуговиц на 5 таких кофтах?
___________________________________________________________________
___________________________________________________________________
14. Запиши выражение и найди его значение.
Разность чисел 27 и 18 умножить на 3.______________________________
15. Какие два числа в указанном порядке надо записать в «окошки», чтобы равенство 8 х : = 4
1) 5 и 8 2) 3 и 6 3) 3 и 4
16. Реши задачу выражением
Реши задачу выражением
Садовник посадил 5 рядов слив по 8 деревьев в каждом ряду и 7 рядов черешни по 6 деревьев в каждом ряду. Сколько всего деревьев посадил садовник?
______________________________________________________________
Ответ:________________________________________________________
Административная контрольная работа по математике за 1 полугодие 3 класса
Фамилия , имя __________________________________________
Контрольная работа по математике
3 класс, 1 полугодие
Вариант 1
1. Числа и величины.
Выбери четырехзначное число с цифрой 6 в разряде сотен. Обведи номер ответа.
1) 43 600
2) 7 562
3) 1 674
4) 260
2. Текстовые задачи.
Реши задачу.
На пошив 6 пальто ушло 24 метра ткани. Сколько ткани потребуется для пошива 8 таких пальто?
_____________________________________________________________________________
____________________________________________________________________________
3. Арифметические действия.
Арифметические действия.
Запиши примеры столбиком и вычисли.
824 * 6 138 * 40
4. Арифметические действия.
Вычисли :
240 – 640 : 8 * 2 =
5. Геометрические величины.
С помощью какого из перечисленных ниже числовых выражений можно найти периметр прямоугольника со сторонами 3 см и 4см? Отметь все верные ответы.
1) 3 + 4
2) 3 * 4
3) 3 * 4 *2
4) 3 * 2 + 4 * 2
5) (3 + 4) * 2
6. Работа с информацией.
Вася на протяжении двух недель в одно и то же время измерял температуру воздуха на улице и записывал результаты в таблицу.
Дни недели Первая неделя Вторая неделя
Понедельник +19 +20
Среда +25 +18
Пятница +17 +24
В какой день второй недели была самая низкая температура ?
Ответ: ____________________________
7. Три литра варенья надо разлить в пол-литровые банки. Хватит ли 5 таких банок ? Запиши ответ и объясни его.
Хватит ли 5 таких банок ? Запиши ответ и объясни его.
Ответ _________________________________
Объяснение _______________________________________________________
Фамилия , имя __________________________________________
Контрольная работа по математике
3 класс, 1 полугодие
Вариант 2
1. Числа и величины.
Выбери четырехзначное число с цифрой 2 в разряде десятков. Обведи номер ответа.
1) 3 200
2) 7 562
3) 624
4) 2 621
2. Текстовые задачи.
Реши задачу.
В 7 ящиках 56 кг яблок. Сколько кг яблок в 9 таких ящиках?
________________________________________________________________________
_______________________________________________________________________
3. Арифметические действия.
Запиши примеры столбиком и вычисли.
262 * 3 143 * 40
4. Арифметические действия.
Вычисли :
200 — 120: 3 * 2 =
5. Геометрические величины.
С помощью какого из перечисленных ниже числовых выражений можно найти площадь прямоугольника со сторонами 5 см и 4см? Отметь 2 верный ответ.
1) 5 + 4
2) 5 * 4
3) 5 * 2 + 4 * 2
4) (5 + 4) * 2
6. Работа с информацией.
В таблице представлены результаты учащихся 3 класса по легкой атлетике.
Имя ученика Прыжки в длину (см) Прыжки в высоту (см) Метание мяча (см)
Артем 295 85 28
Миша 305 105 33
Света 255 95 20
Карина 295 100 24
Участник, который показал лучшие результаты в трех видах соревнований, считается победителем и получает приз. Кто получил приз?
Ответ: ________________________________
7. Удобрение продается в упаковках. Одной упаковки достаточно для обработки посадок на площади 10 м2. Хватит ли 8 упаковок удобрения для обработки посадок площадью 75 м2 ? Запиши ответ и объясни его.
Удобрение продается в упаковках. Одной упаковки достаточно для обработки посадок на площади 10 м2. Хватит ли 8 упаковок удобрения для обработки посадок площадью 75 м2 ? Запиши ответ и объясни его.
Ответ :___________________
Объяснение :_______________________________________________________
ГДЗ по Математике за 3 класс Г.В. Дорофеев, Т.Н. Миракова Перспектива
авторы: Г.В. Дорофеев, Т.Н. Миракова.
Издательство: Просвещение 2015-2020 год.
В третьем классе учащимся предлагаются новые определения и правила для изучения более сложных задач. Если ученик сразу не успеет усвоить нужную информацию, в дальнейшем будет еще труднее постигать эту науку. Можно помочь ему в этом с приобретением надежного спутника в постижении нелегкой науки.
Из каких разделов состоит математика Г.В. Дорофеева и Т.Н. Мираковой за 3 класс
Материал представлен в двух частях. В каждой из них – упражнения, способы решений заданий, тесты, вопросы для самопроверки и многое другое. Здесь рассматриваются следующие темы:
В каждой из них – упражнения, способы решений заданий, тесты, вопросы для самопроверки и многое другое. Здесь рассматриваются следующие темы:
— натуральные числа до 100;
— умножение и деление от 2 до 9 в таблицах. Работа ведется с цифрами и числами до 100;
— трехзначные натуральные числа до 1000;
— отрабатываются методы развязывания задач на приведение к 1 и с использованием функции сравнения;
— приведены верные (правильные) ответы для самоконтроля.
Последовательное изучение материала поможет школьнику научиться приемам классификации и обобщения, синтеза и анализа, а также выполнять типовые упражнения для уверенного написания контрольных работв классе. В книге легко ориентироваться. Под отдельными номерами предлагаются те или иные темы, выделены пояснения и новые правила, тесты и проверочные работы.
Почему стоит приобрести издание?
Грамотно составленный учебник – это практичный инструмент как для самого учащегося, так и для взрослых: педагогов и родителей.
Школьнику решебник помогает:
— быстро находить правильные методы и верные ответы на заданные домой примеры и уравнения, без лишней траты времени, которое можно использовать на дополнительное развитие;
— полноценно готовится к уроку, и чувствовать себя более уверенно у доски и на самостоятельных;
— глубоко изучать тему с надежным закреплением знаний.
Для учителя – это отличное пособие в составлении рабочих программ по ФГОС. Родитель же с доступом к ГДЗ получает возможность со знанием дела проверять ребенка и помогать школьнику с разъяснениями. Ознакомиться с содержанием можно онлайн на специальных сайтах.
ГДЗ решебник Математика за 3 класс Миракова (Тесты) «Просвещение»
Математика 3 классТестыПерспективаМиракова«Просвещение»
Многим ученикам такой предмет, как математика, совсем не нравится, из-за чего они не хотят его учить и главное, понимать. Но контрольные и самостоятельные работы приходится писать всем, и никого не волнует, понял ученик тему или нет. Если углубиться в эту науку, то можно понять, что не настолько уж она и скучная и не понятная, как может показаться на первый взгляд. Если же школьник все же решил взяться за ум и учить математику, то ему поможет решебник к учебнику «Математика 3 класс тесты Миракова», от издательства «Просвещение» Перспектива.
Но контрольные и самостоятельные работы приходится писать всем, и никого не волнует, понял ученик тему или нет. Если углубиться в эту науку, то можно понять, что не настолько уж она и скучная и не понятная, как может показаться на первый взгляд. Если же школьник все же решил взяться за ум и учить математику, то ему поможет решебник к учебнику «Математика 3 класс тесты Миракова», от издательства «Просвещение» Перспектива.
Темы, на которые стоит обратить внимание
Особое внимание нужно обратить на такие темы как вычитание числа из суммы и умножение и деление различных чисел, ведь в будущем эти темы будут усложняться, поэтому если ребенок с самого начала не поймет что и как, не выучит таблицу умножения, то в будущем ему будет еще сложнее понять и решить задачку или пример. В 3 классе изучаются базовые знания, а это значит, что, не поняв тему сейчас, ученику сложно будет в дальнейшем.
Что в него включено:
Решебник состоит из готовых онлайн-ответов на все задания, которые не понятны для учащегося. Также некоторые задания имеют раскрытый ответ, то есть подробное описание действий.
Также некоторые задания имеют раскрытый ответ, то есть подробное описание действий.
Зачем он нужен
В первую очередь «ГДЗ по Математике 3 класс» нужен не для того, чтобы просто списать, а понять задание и номер, который не ясен для ученика. Есть еще несколько причин, для чего нужен этот решебник:
- Готовые ответы помогут хорошо усвоить ту или иную тему.
- В 3 классе школьники, не поняв тему, сразу бросают ее изучение, но узнав, что есть готовый ответ и объяснение к нему, они сразу берутся выполнять задание.
- Родители могут увидеть ответ и вспомнить то, что учили еще в школе, после чего объяснить ребенку что и как делается.
Также ученик может выполнить упражнение и через решебник его проверить. Самопроверка помогает в том случае, если родители заняты или не помнят ничего из школьного материала. А учителя не имеют времени на уроках каждому индивидуально объяснять то, что не понятно ребенку.
ГДЗ ответы к контрольным работам по математике 4 класс Дорофеев (Перспектива)
Страница 1 из 11
Из чего складывается оценка за четверть по математике? Из текущих оценок за работу на уроке, за домашнюю работу, за самостоятельные и контрольные работы. Вес последней оценки довольно велик, и она может значительно повлиять на общую успеваемость. А кому хочется из-за какой-то контрольной получить за четверть заниженную оценку? Никому! Вот потому и нужно готовиться к ним так же, как готовитесь к уроку, прорешать задания, которые может дать учитель. Как правило, задания похожи на те, которые вы уже решали на уроках, но могут быть и исключения.
И вот для исключения влияния на оценку таких «сюрпризов» мы вам позволяем заглянуть в книгу для учителя, в которой размещены все контрольные работы, которые вам, скорее всего, придется выполнять на уроках. Редко какая учительница будет придумывать их сама, легче и правильнее воспользоваться готовыми текстами из методического пособия, которое разработали непосредственно авторы учебников УМК «Перспектива» Дорофеев и Миракова.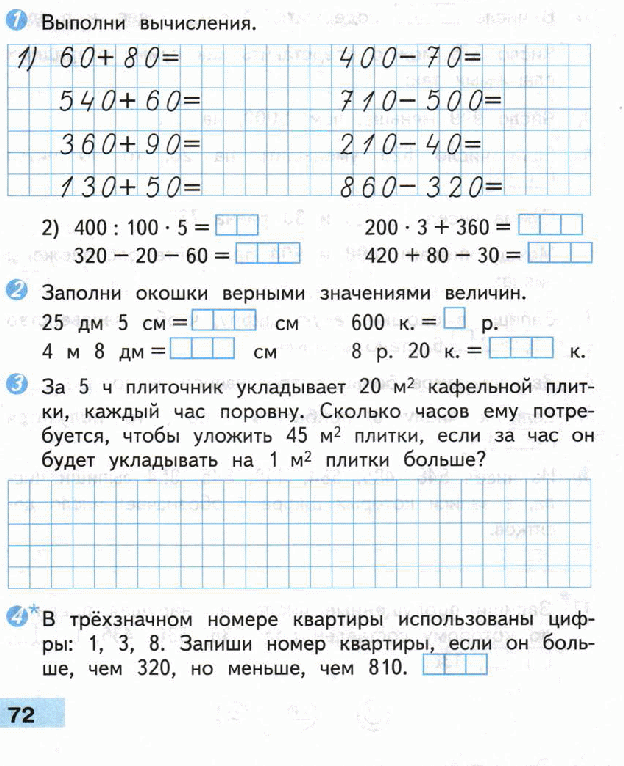 Может быть, особо щепетильный педагог заменит некоторые числа, но таких не много.
Может быть, особо щепетильный педагог заменит некоторые числа, но таких не много.
Поэтому, ознакомившись с будущей работой и порешав дома задания из нее, на уроке будет проще справиться с контрольной на хорошую и отличную отметку. Главное — понять принцип и логику решения. Контрольные работы из пособия «Математика. Методические рекомендации.» Авторы те же, что и у самого учебника математики (Дорофеев и Миракова), по которому учитель ведет уроки, поэтому контрольные синхронно согласуются с пройденной учебной программой. В каждой работе по 2 варианта, но учитель может расширить их количество за счет подобных заданий с другими значениями.
Для чего устраивают контрольные по математике в четвертом классе?
Контроль знаний учащихся еще никто не отменял. В самом начале и конце учебного года контролировать пытается администрация школы, в течение года — учитель. Процедура предполагает выдачу типовых заданий по пройденной теме. Где ученик допустит ошибки, там слабое место. Все ошибки прорабатываются детьми совместно с учителем после контрольной, при работе над ошибками. Так в идеале. На практике же получается, что контрольные пишутся просто для оценки. Дети, порой, видят этот листок перед собою первый и последний раз и знать не знают о том, какие именно ошибки в каких заданиях допустили. Согласитесь, что это распространенная практика, но это сводит на нет весь смысл контроля. Вот потому наш коллектив учителей и сделал ответы к контрольным работам по методичке для учителя за 4 класс. Написал ребенок в школе, получил оценку, пришел домой, мама распечатала нужную контрольную и поспрашивала, как решал. Так-то и так-то. Вот тут, малыш, ошибка, нужно решать вот так. С современной школой приходится изворачиваться…
Все ошибки прорабатываются детьми совместно с учителем после контрольной, при работе над ошибками. Так в идеале. На практике же получается, что контрольные пишутся просто для оценки. Дети, порой, видят этот листок перед собою первый и последний раз и знать не знают о том, какие именно ошибки в каких заданиях допустили. Согласитесь, что это распространенная практика, но это сводит на нет весь смысл контроля. Вот потому наш коллектив учителей и сделал ответы к контрольным работам по методичке для учителя за 4 класс. Написал ребенок в школе, получил оценку, пришел домой, мама распечатала нужную контрольную и поспрашивала, как решал. Так-то и так-то. Вот тут, малыш, ошибка, нужно решать вот так. С современной школой приходится изворачиваться…
Когда будут проводиться контрольные по математике в 4 классе?
Все номера уроков четко прописаны в методическом руководстве для учителя. Контрольная работа №1 предлагается примерно на 21-м уроке, после изучения темы Округление слагаемых. 2-я контрольная на 37-м уроке после темы Умножение двузначного числа на двузначное (письменные приемы вычисления). 3-я на 51-м уроке, после деления на двузначное число и уроков повторения. 64-й урок — контрольная №4, после задач на нахождение неизвестного по двум разностям, это предположительно конец второй четверти и первого полугодия. 5-я контрольная на 75-м уроке после сложения и вычитания величин, когда начали проходить вторую часть учебника. Контрольная №6 после таблицы единиц длины, урок 83. За задачами на движение в одном направлении следует проверочная работа №7, урок 97. На 112 уроке, после задач на движение по реке, идет 8-я контрольная. 9-я после особых случаев умножения и деления многозначных чисел и повторения за четвертую четверть, затем почти сразу пишем Итоговую контрольную работу за четвертый класс.
2-я контрольная на 37-м уроке после темы Умножение двузначного числа на двузначное (письменные приемы вычисления). 3-я на 51-м уроке, после деления на двузначное число и уроков повторения. 64-й урок — контрольная №4, после задач на нахождение неизвестного по двум разностям, это предположительно конец второй четверти и первого полугодия. 5-я контрольная на 75-м уроке после сложения и вычитания величин, когда начали проходить вторую часть учебника. Контрольная №6 после таблицы единиц длины, урок 83. За задачами на движение в одном направлении следует проверочная работа №7, урок 97. На 112 уроке, после задач на движение по реке, идет 8-я контрольная. 9-я после особых случаев умножения и деления многозначных чисел и повторения за четвертую четверть, затем почти сразу пишем Итоговую контрольную работу за четвертый класс.
Для кого ответы к контрольным по математике за 4 класс?
Естественно, что если ребенок увидит ответы до того, как прочитает вопросы, решать он уже ничего не захочет. Поэтому пользоваться ГДЗ ребенку в одиночку не стоит. Родитель может скопировать текст контрольной, распечатать на принтере и дать листок ученику для проработки. Готово? Можно свериться с правильными ответами. Решили, сравнили, смело можно идти на урок математики и получать пятерку. Не стоит пренебрегать подготовкой дома, потому что плохие оценки негативно влияют на морально-психическое состояние не только самого ребенка, но и учителя 😀 родителей. А уверенность в своих силах еще никому не помешала.
Поэтому пользоваться ГДЗ ребенку в одиночку не стоит. Родитель может скопировать текст контрольной, распечатать на принтере и дать листок ученику для проработки. Готово? Можно свериться с правильными ответами. Решили, сравнили, смело можно идти на урок математики и получать пятерку. Не стоит пренебрегать подготовкой дома, потому что плохие оценки негативно влияют на морально-психическое состояние не только самого ребенка, но и учителя 😀 родителей. А уверенность в своих силах еще никому не помешала.
В этом разделе сайта ГДЗответ.ру только контрольные по программе Перспектива к учебнику Дорофеева, Мираковой, Бука. Если хотите посмотреть другие программы, выбирайте в меню сайта класс и обложку с методическими рекомендациями нужной УМК и нужных авторов. К учебникам и тетрадям на печатной основе у нас так же есть ГДЗ, не поленитесь побродить по сайту и найдете много интересного, нужного и полезного.
Мы скрыли ответы к контрольным за первые 3 четверти, потому что они уже вами написаны. ГДЗ к заданиям четвертой четверти и за второе полугодие + годовые итоговые — все есть.
ГДЗ к заданиям четвертой четверти и за второе полугодие + годовые итоговые — все есть.
Ребенок борется с математикой? 12 знаков и 7 способов помочь
У многих родителей во всем мире, как и у вас, есть ребенка, который борется с математикой . Без надлежащих ресурсов или надежной системы поддержки эта реальность может быть устрашающей.
Но не волнуйтесь, ведь вы не одиноки! Дети, которые не любят математику, часто жалуются на то, что она слишком сложна или что они недостаточно умны. К сожалению, это убеждение может серьезно повлиять на успехи любого ребенка в математике.
Родители часто отмечают, что причины и симптомы могут варьироваться от ребенка к ребенку, поэтому мы кратко изложим и поможем вам понять:
- Что заставляет детей бороться с математикой
- Общие признаки среди детей, которые борются с математикой
- Как родители и учителя могут помочь ребенку, который борется с математикой
Давайте начнем помогать вашему ребенку добиться успеха, вместо того, чтобы бороться с математикой. 👇
👇
3 Основные причины, по которым ребенок испытывает трудности с математикой
Математика может быть сложной, потому что это совокупный предмет — он строится на себе год за годом.Вот почему так много родителей волнуются, когда кажется, что их дети теряют интерес к математике.
Родителям важно знать, что это не обязательно означает, что их ребенку не хватает ума или энергии. Вы не поверите, но дети, которые плохо понимают математику, часто прилагают большие усилия — умственно и физически.
Итак, что именно заставляет ребенка бороться с математикой? Исследования сузили ответ до трех вещей:
Отсутствие строительных блоков
Как упоминалось ранее, математика накапливается, поэтому изучение и понимание основ является обязательным.Если ребенок отстает в одной области из-за непонимания, переход к более сложным темам останется проблемой.
Например, если ребенок еще не понимает основ сложения, ему будет очень трудно понять концепцию умножения.
В 2015 году Университет Акрона опубликовал исследование под названием «Важность сильной математической основы». Исследователи проверили 39 девятых и десятиклассников на дроби, соотношения и пропорции.Участникам нужно было ответить на вопросы от третьего до седьмого класса.
Только семь участников смогли сдать экзамен. Увидев эти результаты, автор исследования Жасмин Ристон написала:
[Студентам] просто преподавали математические понятия, соответствующие их текущему уровню обучения, а не на основе текущих математических знаний, которые они приносили в класс. Из-за этого учащиеся не овладевали каждым стандартом уровня класса до того, как продолжили обучение на более высоком уровне.Этот недостаток мастерства создает огромные пробелы в понимании учащимися, не позволяя учащимся установить необходимые связи между содержанием и получить концептуальное понимание.
Беспокойство по поводу математики
В разгар трудностей легко чувствовать, что мы единственные, кто сталкивается с определенной проблемой. Для родителей ребенка, который испытывает трудности с математикой, это не исключение. И хотя это вызывает тревогу, мы надеемся, что родители во всем мире найдут утешение, зная, что их ребенок — не единственный, кто может испытывать беспокойство, когда дело касается математики.
Для родителей ребенка, который испытывает трудности с математикой, это не исключение. И хотя это вызывает тревогу, мы надеемся, что родители во всем мире найдут утешение, зная, что их ребенок — не единственный, кто может испытывать беспокойство, когда дело касается математики.
Чувство напряжения и беспокойства, которое мешает манипулировать числами и решать математические задачи в самых разных повседневных жизненных и академических ситуациях.
Фактически, наше руководство по преодолению математической тревожности подчеркивает, что около 93% из взрослых американцев испытывают математическую тревогу в той или иной степени, в то время как 17% американцев в целом страдают от высокого уровня математической тревожности.
Симптомы математической тревожности могут включать:
- Избегание
- Отсутствие реакции
- Низкое достижение
- Негативный разговор с самим собой
- Чувство постоянства
- Интенсивные эмоциональные реакции
- Психологические эффекты, такие как нервозность, липкие руки, учащенное сердцебиение скорость, расстройство желудка и головокружение
И по этой причине дети могут бороться с математикой с детства до взрослого возраста.
Трудности в обучении
Существуют многочисленные нарушения обучения математике, в том числе одна из наиболее распространенных: дискалькулия . Другие названия для него включают math или number dyslexia .
По словам доктора Даниэля Ансари, профессора когнитивной нейробиологии развития в Западном университете Канады, дети с дискалькулией:
- Часто борются с рабочей памятью
- Имеют проблемы с запоминанием математических фактов
- Может понимать логику математических фактов, но не знают, как и когда применить свои знания для решения проблем.
- Может не понимать количественные характеристики или понятия, такие как наибольшее и наименьшее, или разницу между словом пять и числом 5
Исследователи не совсем уверены, что вызывает дискалькулию но подозреваю, что это связано со структурой и функцией мозга.Поскольку могут быть задействованы различные факторы, такие как развитие человека, окружающая среда, генетическая структура или травма, то, как проявляются симптомы, вероятно, будет различаться, поскольку нет двух одинаковых детей.
12 Признаки того, что дети борются с математикой
1. Высказывает отрицательные отзывы о математике
Может быть сложно обнаружить ребенка, который борется с математикой. Один из наиболее заметных признаков заключается в том, что они говорят о предмете.
Когда ваш ребенок говорит что-то вроде «Я ненавижу математику» или «Я плохо разбираюсь в математике» и старается избегать занятий, связанных с математикой, это обычно признак того, что у него проблемы с предметом.
2. Тревога по математике
Будь то во время урока, теста или выполнения домашнего задания, ваш ребенок становится все более тревожным, когда приходит время заниматься математикой.
Несмотря на то, что они могут понимать концепции, математическая тревога приводит к тому, что они забывают то, что они узнали, или как их применять, когда придет время.
3. Низкие оценки по математике, но более высокие оценки по другим предметам
Слышите ли вы это от учителя или видите в его табеле успеваемости, ваш ребенок хорошо успевает по всем предметам, кроме математики.
Младшие оценки по математике могут побудить их сосредоточиться на предметах, в которых они уже преуспевают, и тратить мало времени на практику или изучение математики.
4. Проблемы при соединении математических семейств
По мере того, как учащиеся узнают больше математических фактов, они должны начать видеть взаимосвязь между определенными числами и уравнениями.
Ваш ребенок может испытывать трудности с математикой, если он не видит связи между, например, 2 + 3 = 5 и 5-3 = 2 .
5. Проблемы с управлением временем
Управление временем сложно для многих людей, в том числе для взрослых, поэтому этот знак может показаться несколько расплывчатым. Обратите внимание, нет ли у вашего ребенка проблем с оценкой временных интервалов, соблюдением установленного расписания или чтением часов — аналоговых или цифровых.
6. Проблемы с применением математических понятий к реальным задачам
Ваш ребенок может усвоить математические понятия, но ему трудно понять, как они применяются к вещам вне класса. Например:
Например:
- Узнать, сколько дней осталось до их дня рождения
- Расчет стоимости чего-либо и сколько сдачи они должны вернуть
- Определение количества определенного ингредиента, которое нужно использовать при приготовлении пищи
7 .Сложность с умственной математикой
Хотя это может быть полезно в первые годы, решение математических задач с использованием пальцев для счета может быть признаком того, что ваш ребенок испытывает трудности с математикой.
Это связано с тем, что по мере взросления дети будут сталкиваться с более крупными числами и более сложными уравнениями, которые требуют умственной математической практики — то, что может отпугнуть счет пальцев.
8. Не пытается найти альтернативные подходы к проблемам
В тот момент, когда возникает препятствие при решении математической задачи, ваш ребенок может разочароваться и уйти, прежде чем подумать или попытаться найти другое возможное решение.
9. Проблемы с базовыми математическими концепциями и вспоминанием фактов
Память может существенно повлиять на мышление с помощью чисел. Несмотря на то, что в прошлом его учили основам математических концепций и фактов, вашему ребенку сложно их запоминать и применять должным образом.
10. Проблемы с изучением сложных математических понятий и фактов
Из-за кумулятивного характера математики ключевым моментом является установление связей между предыдущими и новыми уроками.
Проблемы при построении более ранних математических понятий ограничивают способность ребенка закреплять новые математические навыки значимым и длительным образом.
11. Затруднения с обращением внимания
Каждый ребенок учится по-своему — некоторые могут сесть за стол и выполнить определенные задания, а другим будет полезна более активная практическая работа.
Если ваш ребенок нервничает, теряет свое место в задаче или кажется умственно уставшим, когда занимается математикой, возможно, он испытывает трудности с математикой (в той или иной форме).
12. Не достигают вехи
Как правило, дети достигают определенных вех в математике примерно в одном возрасте, но иногда у них возникают проблемы с развитием этих навыков с той же скоростью, и они отстают.
Учащиеся 1-го и 2-го классов, например, могут испытывать затруднения при переходе от счета по единицам к двойкам, пятеркам и десяткам, в то время как другие с легкостью берут это на себя.
Ознакомьтесь с инфографикой ниже, в которой показаны основные этапы математики и то, что вы можете ожидать в разном возрасте!
Щелкните, чтобы развернутьКак помочь ребенку, борющемуся с математикой (7 способов)
Как родитель, одна из ваших самых больших целей — помочь вашему ребенку добиться успеха. Однако важно помнить, что первым шагом к решению проблемы является ее определение.
Знание вышеперечисленных знаков поможет вам определить любые проблемы, с которыми ваш ребенок может столкнуться с математикой.
И чтобы сделать еще один шаг вперед, мы изложили семь советов, которые вы можете использовать дома, чтобы превратить математику в предмет, который ваш ребенок любит, а не страхи!
Сделайте математику забавой
Для некоторых детей достаточно изменить точку зрения, чтобы превратить математику из чего-то, чего боялись, во что-то любимое. Традиционный подход, основанный на ручке и бумаге, не всегда работает, и именно тогда вам нужно проявить творческий подход.
Традиционный подход, основанный на ручке и бумаге, не всегда работает, и именно тогда вам нужно проявить творческий подход.
Совет: Подумайте о том, чтобы заново познакомить вашего ребенка с математикой через призму игры. Это может принимать различные формы, такие как задачи со словами, учебники по математике, математические приложения и многое другое.
Или попробуйте Prodigy Math Game — увлекательное математическое приложение, ориентированное на учебную программу, которое любят более 100 миллионов студентов и учителей и которое, как было доказано, способствует повышению успеваемости по математике. Все внутриигровые образовательные материалы бесплатны, навсегда и доступны дома или в классе.
🌟 Кроме того, доступны планы Премиум-членства , которые позволят максимально эффективно практиковать математику и помогут вам с легкостью поддержать учебный путь вашего ребенка.Став участником, вы откроете дополнительные игровые награды для вашего ребенка. и предоставят вам доступ к новым родительским функциям, таким как обучение в классе, области практики и листы практики (без дополнительной оплаты).
и предоставят вам доступ к новым родительским функциям, таким как обучение в классе, области практики и листы практики (без дополнительной оплаты).
Находите ежедневные приложения
Математика окружает нас повсюду и присутствует в нашей повседневной жизни, но знают ли об этом ваши дети? Включение математики в их повседневную рутину может помочь им понять и оценить ее важность.
Итак, чего вы ждете? Начни учиться на практике!
Совет: Вовлекайте ребенка в такие дела, как покупки, готовка или садоводство! Каждое из этих реальных приложений включает числа, факты и концепции, которые могут помочь укрепить знания и понимание, а также получить удовольствие от математики.
Практикуйтесь с ребенком ежедневно
На первый взгляд этот совет может показаться таким же простым, как сидеть рядом с ребенком, пока он делает домашнее задание, и следить за тем, чтобы он его выполнил. Но участие в образовании вашего ребенка имеет много преимуществ.
Но участие в образовании вашего ребенка имеет много преимуществ.
По словам автора и психолога по развитию Ребекки Фрейзер-Тилл, участие родителей способствует академической успеваемости, улучшает социальные навыки и может повысить самооценку.
Совет: Выделяйте время для занятий математикой хотя бы 10 минут каждую ночь.Это поможет закрепить то, что они изучают в классе, и сосредоточить внимание на основополагающих концепциях, когда учителя знакомят их с более сложными концепциями в классе. Даже если у вашего ребенка нет домашних заданий по математике, попробуйте наши бесплатные, красочные и распечатанные рабочие листы:
Определите проблемные области
Если вы можете определить их самостоятельно, замечательно! Если нет, свяжитесь с учителем вашего ребенка, чтобы получить более близкое и точное представление о том, как вы можете помочь повысить его способности к успеху.
Совет: Вместе с учителем вашего ребенка разработайте план действий дома. Это также отличная возможность поделиться типами обучения, которые лучше всего подходят для вашего ребенка дома — то, о чем его учитель может не знать.
Это также отличная возможность поделиться типами обучения, которые лучше всего подходят для вашего ребенка дома — то, о чем его учитель может не знать.
Примите позитивное отношение
Хотя дети могут отрицательно относиться к математике, ваше отношение к предмету, возможно, сначала необходимо изменить. Исследование, проведенное в 2017 году в школе School Science and Mathematics , показало, что отношение родителей к математике может существенно предсказать отношение учащихся к математике.
В большинстве случаев негативное отношение возникает просто потому, что ученики говорят себе, что не могут заниматься математикой; в любом случае они никогда не воспользуются им; и так далее. Факторы, связанные с школой, усугубляются, когда они усиливаются дома, например, негативное отношение родителей к математике.
Совет: Даже если вы презираете математику, старайтесь изо всех сил поддерживать позитивное отношение к ней в отношении своего ребенка. Не просто восклицайте, что вы никогда не были хороши в математике, или отбросьте проблему и попросите их спросить своего учителя.Вместо этого поощряйте ребенка, когда он застревает, и пытайтесь вместе решить проблему, пока вы не придете к решению! Практикуя это, родители могут положительно влиять на отношение своего ребенка к математике. В результате это может повысить общую успеваемость и интерес детей к математике во взрослом возрасте.
Не просто восклицайте, что вы никогда не были хороши в математике, или отбросьте проблему и попросите их спросить своего учителя.Вместо этого поощряйте ребенка, когда он застревает, и пытайтесь вместе решить проблему, пока вы не придете к решению! Практикуя это, родители могут положительно влиять на отношение своего ребенка к математике. В результате это может повысить общую успеваемость и интерес детей к математике во взрослом возрасте.
Найти репетитора
Некоторые родители давно не ходят в школу и не знакомы с определенными методами обучения. Другим просто неудобно быть «учителем» дома.Вот почему некоторые родители решают пойти по пути онлайн-обучения.
Совет: Math Geek Mama предлагает несколько полезных способов найти репетитора по математике для вашего ребенка!
- Молва от друзей или семьи
- Проверьте доску объявлений библиотеки или общественного центра
- Спросите учителя вашего ребенка или школьного консультанта
- Найдите местного или онлайн-репетитора с помощью веб-сайтов
Prodigy также предлагает онлайн-обучение по математике один на один! Каждый ребенок учится по-своему. Репетиторы Prodigy по математике — это сертифицированные учителя, которые адаптируют свой стиль и уроки, чтобы научить вашего ребенка наилучшим образом.
Репетиторы Prodigy по математике — это сертифицированные учителя, которые адаптируют свой стиль и уроки, чтобы научить вашего ребенка наилучшим образом.
Изучите потенциальные проблемы с обучением
Если ваш ребенок действительно имеет нарушение обучаемости, чем раньше вы обратитесь за помощью, тем лучше!
Это может быть непросто решить проблему и поставить диагноз, но в долгосрочной перспективе своевременная и соответствующая поддержка может помочь обеспечить наилучший возможный образовательный путь для вашего ребенка.
Совет: Если с вами еще не связались, свяжитесь с учителем вашего ребенка или администратором школы, чтобы обсудить, как они могут помочь. Поскольку нарушения обучаемости обычно выявляются в школе, они могут использовать процесс, называемый реакцией на вмешательство, чтобы помочь точно определить, есть ли у ребенка нарушение обучаемости.
Заключительные мысли: Ваш ребенок борется с математикой?
Проблемы с математикой могут заставить детей чувствовать себя неразумными и влиять на их самооценку. Однако это обычная борьба.
Однако это обычная борьба.
Более того, есть практические способы помочь, как видите! Одна из величайших вещей, которые вы можете сделать сегодня — это дать им понять, что все борются, даже вы, и что у каждого есть свои сильные стороны!
Поделитесь личным примером того, как вы боролись с математикой и, если возможно, как вы ее преодолели. Затем попробуйте воспользоваться некоторыми из перечисленных выше полезных советов.
Математика может быть сложной задачей, но совместное путешествие поможет повысить уверенность вашего ребенка и побудит его продолжать попытки!
Вы хотите, чтобы ваш ребенок преуспел в математике.Мы можем помочь.
Да, Prodigy Math Game — это платформа, ориентированная на учебный план и вдохновленная фэнтези, которая нравится детям. Но он также содержит невероятно ценные инструменты и функции для таких родителей, как вы. Посмотрите одноминутное видео ниже
Готовы мотивировать вас и помочь поддержать их на этом пути?
Создайте бесплатную родительскую учетную запись сегодня!TRU Framework
В рамках проекта оценки по математике проводилось исследование того, как
материалы используются в классах, их влияние на учебную практику,
и как профессиональное развитие может быть использовано для достижения целей
материалы оценочного проекта по математике. Основное направление в этом было совместными усилиями с
изучение алгебры в
Калифорнийский университет в Беркли и штат Мичиган разработают программу Teaching for Robust
Понимание математики (TRU Math) набор инструментов для
Профессиональное развитие и исследования. Во время разработки TRU Math стало ясно, что концепции можно обобщить в структуру, применимую для разных предметов.
Основное направление в этом было совместными усилиями с
изучение алгебры в
Калифорнийский университет в Беркли и штат Мичиган разработают программу Teaching for Robust
Понимание математики (TRU Math) набор инструментов для
Профессиональное развитие и исследования. Во время разработки TRU Math стало ясно, что концепции можно обобщить в структуру, применимую для разных предметов.
Структура TRU
TRU — это структура для четкой и действенной характеристики мощной учебной среды.Это простой и доступный язык для обсуждения того, что происходит (и должно происходить) в классах, в процессе профессиональной подготовки и профессионального развития (PD). TRU соответствует тому, что мы считаем хорошей практикой; и он фокусирует внимание аудитории и администрации на том, что важно в обучении. В частности, это означает, что высококачественное обучение и PD будут соответствовать TRU — и что, если мы примем эту структуру и язык, параллели в обучении по дисциплинам будут очевидны.
Центральное место в TRU занимают 5 аспектов учебной деятельности. Классы, которые преуспевают в этих 5 измерениях, выпускают студентов, которые являются сильными мыслителями:
| Пять измерений мощных классных комнат | ||||
|---|---|---|---|---|
| Содержание | Когнитивная потребность | Равный доступ к контенту | Агентство, полномочия и личность | Формирующее оценивание |
| Степень, в которой структура учебной деятельности предоставляет учащимся возможности стать осведомленными, гибкими и находчивыми в дисциплинарной сфере мыслители.Обсуждения сфокусированы и последовательны, что дает возможность изучить дисциплинарные идеи, методы и точки зрения, установить связи и развить продуктивные дисциплинарные привычки. | Степень, в которой учащиеся имеют возможности осмыслить и осмыслить важные дисциплинарные идеи и их использование. Учащиеся лучше всего учатся, когда им бросают вызов таким образом, чтобы у них было пространство и поддержка для роста, при этом сложность задания варьируется от умеренной до сложной. Уровень сложности должен способствовать тому, что было названо «продуктивной борьбой».” | Степень, в которой структура классной деятельности приглашает и поддерживает активное участие всех учеников в классе, при этом класс решает основное дисциплинарное содержание. Классы, в которых небольшое количество учащихся получают большую часть «эфирного времени», не являются справедливыми, независимо от того, насколько богато их содержание: все учащиеся должны быть вовлечены осмысленным образом. | Степень, в которой учащимся предоставляется возможность «ходить и говорить, говорить» — участвовать в обсуждениях дисциплинарных идей, опираться на идеи других и заставлять других строить свои собственные — способами, которые способствуют развитию их свободы воли. (готовность участвовать), их владение контентом и развитие позитивной идентичности как мыслителей и учащихся. | Степень, в которой занятия в классе побуждают учащихся к мышлению и последующему взаимодействию, отвечают этим идеям, опираясь на продуктивные начинания и устраняя возникающие недопонимания. Эффективное обучение «встречает студентов там, где они есть» и дает им возможность углубить свое понимание. |
Пакет документов TRU
На этом веб-сайте доступны следующие материалы TRU:
Введение в TRU Framework
В этом введении представлен обзор основ структуры TRU и инструментов, поддерживающих ее использование.
Скачать Введение в TRU Framework (декабрь 2016 г.)
Инструменты профессиональной разработки TRU
Они могут использоваться учителем и коучем, профессиональным учебным сообществом или учителями, размышляющими о своей собственной практике, для улучшения обучения в соответствии с теми направлениями, которые, по мнению TRU Framework, важны. Два основных набора документов, руководства по беседе и наблюдению TRU, доступны в версиях для общей предметной области и для конкретных математических дисциплин.
Руководства по разговору по математике TRU предлагают пять наборов вопросов для размышления, каждый из которых посвящен ключевому аспекту, описанному в таблице 1. Цель этих вопросов — направлять дискуссии между учителями и другими поддерживающими людьми с целью улучшения понимания и емкость по каждому измерению.
Скачать TRU Domain-General Conversation Guide (бета, сентябрь 2016 г.)
Скачать TRU Mathematics Conversation Guide (бета, ноябрь 2016 г.)
Скачать TRU Mathematics Conversation Guide for Algebra (Alpha, March 2014)
«Обучение для устойчивого понимания» Руководства по наблюдению предназначены для поддержки коллегиальных наблюдений за обучением, будь то тренеры, учителя-наставники, администраторы или профессиональные учебные сообщества.Руководства по наблюдению обеспечивают серию «поисков» для каждого измерения и могут использоваться для облегчения планирования, наблюдения и совместного размышления над инструкциями.
Загрузить Общее руководство по наблюдению за доменом TRU (альфа, ноябрь 2016 г.)
Загрузить TRU Mathematics Observation Guide (Alpha, ноябрь 2016 г.)
TRU Math Рубрика
TRU Math Rubric , инструмент для исследователей для измерения успеваемости по математике в классе по шести критически важным параметрам (пять общих, одно специфическое для алгебры) учебной деятельности.
Скачать TRU Math Rubric (альфа, июль 2014 г.)
Вступительное занятие
Руководство для руководителей, слайды и материалы для семинара по ознакомлению с TRU, подходящие для широкой аудитории, включая учителей и руководство школы, доступны как часть проекта сети по улучшению математики: MathNIC.org
Дополнительные документы
Подробное описание идей, лежащих в основе структуры TRU, можно найти в следующих статьях:
Шенфельд, А.Х. (2013) Наблюдения в классе в теории и на практике ZDM , DOI 10.1007 / s11858-012-0483-1.
Шенфельд, А. Х. (2014, ноябрь).
Что делает классы эффективными и как мы можем поддержать учителей в их создании? Исследователь в области образования , 43 (8), 404-412. DOI: 10.3102 / 0013189X1455
Шенфельд, А.Х. (2015). Мысли о масштабе. ZDM , DOI 10.1007 / s11858-014-0662-3.
Schoenfeld, A.H. (2017).Роль видео в понимании и улучшении математического мышления и обучения. Публикация в журнале Journal of Mathematics Teacher Education.
по математике в DP — International Baccalaureate®
Программа требует, чтобы студенты изучали по крайней мере один курс математики.
В настоящее время доступны четыре курса по математике, и последняя оценка по этим курсам состоится в ноябре 2020 года:
- математические занятия стандартный уровень
- математика стандартный уровень
- математика высший уровень
- Дальнейшая математика, высший уровень (итоговая оценка май 2020 г.)
С августа 2019 года будут доступны следующие курсы, первая оценка которых состоится в мае 2021 года:
- Математика: анализ и подходы SL
- Математика: анализ и подходы HL
- Математика: приложения и интерпретация SL
- Математика: приложения и интерпретация HL
Студенты могут изучать только один курс математики.
Все курсы математики DP предназначены для удовлетворения разнообразных потребностей, интересов и способностей студентов, а также для удовлетворения требований различных университетов и карьерных устремлений.
Цели этих курсов — дать студентам возможность:
- развивать математические знания, концепции и принципы
- развивать логическое, критическое и творческое мышление
- используют и совершенствуют свои способности абстракции и обобщения.
Студентам также предлагается оценить международные аспекты математики и разнообразие ее культурных и исторических перспектив.
Все курсы математики DP требуют от студентов ценить использование технологий в математике и хорошо владеть калькуляторами с графическим дисплеем. [792 КБ]
Следующие курсы доступны онлайн:
Как записаться
Посетите эту страницу, чтобы узнать больше о процессе регистрации.
Читайте о группе 6: искусство
Узнайте больше о математике на семинаре DP для учителей.
Структура математического класса, которая способствует концептуальному обучению
В каждом выпуске нашей серии «Перспективы преподавателя» мы проводим интервью с учителями и администраторами по всей стране, которые уникальным образом привлекают, мотивируют и стимулируют своих учеников.Мы делимся их препятствиями, успехами и стратегиями, чтобы мы могли построить сообщество, лучше подготовленное к математической подготовке всех учеников.
Миган Эрвин была учителем начальной школы в течение 20 лет. В настоящее время она преподает в 3-м классе городских школ Колумбуса в Колумбусе, штат Огайо. Помимо обществознания и естественных наук, у нее есть 90 минут на преподавание математики каждый день.
90-минутное обучение математике с учащимися начальной школы с различным опытом позволяет решить некоторые задачи.Со временем Миган разработала структуру классов для ежедневного глубокого концептуального обучения математике.
90-минутная математическая модель Миган:
- Разминка (10-15 минут)
- Решение открытых задач (20-25 минут)
- Фокус-урок (10-15 минут)
- Вмешательство в малых группах (до 20 минут)
То, как вы начинаете свой урок математики, помогает определить ваши ожидания в отношении обучения. Миган использует спиральные контрольные вопросы и математические беседы, чтобы сразу же помочь ученикам решить проблемы.
Спиральный обзор состоит из периодического подъема вопросов по ранее изученным концепциям. Миган любит использовать вопросы из разных математических областей, потому что именно так студенты будут проходить тестирование по математике. В отличие, скажем, от понимания прочитанного, когда вопросы сгруппированы вокруг текста, в государственных тестах по математике от вопроса к вопросу часто пропускаются различные математические концепции.
«Спиральный обзор может помочь студентам постоянно практиковать концепции, полученные ранее в этом году, и сохранять эти стратегии свежими в памяти», — говорит Миган.Воспользовавшись предыдущими концепциями, он также помогает студентам наладить связи с тем, что они изучают в настоящее время, что способствует глубокому концептуальному пониманию.
Еще одно отличное упражнение для разминки, которое использует Миган, — это математические разговоры. Математические беседы — это короткие вопросы, которые довольно прямые, но также требуют некоторого обсуждения.
Раздел разминки сигнализирует о начале занятий по математике и сразу же заставляет учеников думать математически.
Открытое решение проблем (20-25 минут)У каждого ученика Эрвина есть свой математический журнал, который представляет собой сборник сочинений, в котором учащиеся вырезают и склеивают задачи дня.Иногда в проблеме будут персонажи Джиджи или друзей Джиджи. Иногда в нем участвуют ученики в классе или друзья в школе. Но проблемы всегда связаны с основным уроком дня.
«Я не говорю своим ученикам, как решать задачи, я просто говорю, что они пробуют разные вещи», — объясняет Миган. «Они могут сидеть одни или работать с партнером. Они могут использовать инструменты для решения проблем (манипуляторы) или рисовать наглядные пособия в своей записной книжке. Однако им всегда нужно записывать свой ответ и объяснение.”
Открытое решение проблем помогает студентам практиковать настойчивость — они должны все время работать над одним вопросом. Это также возможность для студентов попробовать разные стратегии и разные способы найти ответ.
Я не прошу студентов уметь применять каждый подход к решению разных типов задач. Но им действительно нужно найти стратегию, которая будет работать для них, способ, эффективный и точный.
— Миган Эрвин
Ближе к концу секции открытого решения проблем Миган просит студентов рассказать, как они решили проблему. Учащийся подойдет к камере для документов, чтобы поделиться страницей записной книжки с классом. Миган начинает год как ведущая, задавая уточняющие вопросы, но со временем другие студенты учатся задавать вопросы-фасилитаторы. Таким образом, учащиеся могут увидеть другие стратегии, которые используют их одноклассники, и, возможно, опробовать их на себе.
Фокус-урок (10-15 минут)Раздел целевого урока дает Миган возможность быть откровенным и дать прямые инструкции о том, что изучают ученики, и как это связано с другими концепциями. Это когда ее ученики развивают свои утверждения «Я могу». Например, в третьем классе одна из их целей — сказать: «Я могу использовать стратегию умножения».
Фокусным уроком может быть урок из учебника математики или разговор-головоломка из ST Math.
Разговоры-головоломки укрепляют уверенность, улучшают чувство числа и гибкость с числами. Разговоры-головоломки — отличный способ принести математические игры ST в ваш класс и использовать всю мощь визуальных моделей. Вы можете найти список уроков по логике ST Math на нашем справочном сайте.
«Я часто загадываю головоломки во время фокусных уроков, потому что ST Math предоставляет отличные интерактивные модели, которые я просто не могла воспроизвести самостоятельно», — делится Меган. «Я вытаскиваю пазл на экране в режиме учителя и прохожу его вместе с учениками.Сначала мы замечаем, что находится на экране. Затем, когда мы решаем, на что нажимать, мы видим, что анимация сразу же дает нам обратную связь. Я могу сделать паузу и задать студентам вопросы о том, что нам показывает Джиджи ».
Очень важно научить студентов говорить во время головоломок. Миган использует несколько разных стратегий, поэтому каждый день это не один и тот же формат. Она может попросить учащихся показать ответ, подняв доску или приложив пальцы к груди, когда они получат ответ. Или она может дать студентам время «подумать, спариться, поделиться» — обдумать свой ответ, спариться и обсудить с другим учеником, а затем поделиться с классом.
Использовать математику ST в классе? Найдите ресурсы для обсуждения головоломок на сайте помощи ST Math:
Вмешательство в малых группах (до 20 минут)Во время вмешательства в малых группах большинство учащихся работают в своем собственном темпе над ST Math, программой визуального обучения, в то время как Миган привлекает определенные группы учащихся для вмешательства.
Поскольку ST Math является наглядным, студенты с ограниченным знанием английского языка и плохо читающие имеют такой же доступ к программе, как и все остальные.Студенты работают самостоятельно на ноутбуке или планшете, но они делают больше, чем просто тренируются. Программа для самостоятельного обучения, основанная на мастерстве, обеспечивает индивидуальное обучение для каждого ученика, в то время как визуальные модели вовлекают учеников в активное построение стратегий и концептуальное понимание.
Миган пользуется этим, требуя от студентов использовать то, что они называют «бумагой для размышлений». Meagan скрепляет чистый лист бумаги и ресурсы (например, таблицу сотен) в специальной папке ST Math. Она поощряет студентов разгадывать головоломки на бумаге и использовать математические инструменты для поиска ответов.Найдите печатные ресурсы ST Math на нашем справочном сайте.
«Когда студенты проходили стандартизированные онлайн-тесты, мы видели, что студенты просто щелкали мышью, не задумываясь, потому что теперь все это находится на компьютере», — делится Миган. «Я ожидаю, что учащиеся будут использовать мыслящую бумагу каждый раз, когда мы используем ST Math, которая сохраняется при использовании компьютера для стандартизированных тестов. Теперь ученики видят в этих вопросах онлайн-теста еще одну головоломку, которую им нужно решить с помощью имеющихся у них инструментов.”
Вмешательство в малых группах позволяет Миган следить за тем, чтобы ни один студент не остался позади. Миган использует данные ST Math и различные тесты, а также наблюдения в классе, чтобы выявить пробелы в знаниях учащихся. Она собирает вместе 1–3 учащихся и разъясняет заблуждения, иногда с непосредственным инструктажем или разгадыванием головоломок из предыдущей цели или даже уровня обучения, если они пропустили основную концепцию в прошлом году.
Содействие концептуальному обучениюМиган со временем разработала структуру своего класса по математике, сознательно думая о том, чтобы сформировать концептуальное понимание математики у ее учеников.
Когда Миган попросили дать совет другим преподавателям, она сказала: «Если у вас есть доступ к ST Math, попробуйте загадать. Это изменило мою жизнь в классе. Это также отличный способ использовать ST Math для всего класса ».
Спасибо Миган Эрвин за ее преданность своим ученикам и за то, что она делилась своим опытом и знаниями с педагогами по всей стране!
Хотите узнать последние новости ST Math? Подпишитесь на нашу рассылку ST Math и узнавайте первыми о наших предложениях и объявлениях.
Основное различие с точки зрения учителя
В 2012 году я переехал из Миссисипи в Нью-Йорк, чтобы преподавать в чартерной начальной школе в Гарлеме. У моих 27 учеников пятого класса уровень чтения варьировался от третьего до восьмого класса. Они выросли, разговаривая на 14 разных языках в своих домах, которые были разбросаны от далеких пределов Бруклина до Южного Бронкса. Я говорил поэтам, мастерам Lego, танцорам и шахматистам. Один обнимал меня каждый час, каждый час.Остальных нужно было уговорить заговорить.
Каждый из этих учеников учился в разном темпе. Некоторым требовалось особое внимание, некоторым нужно было бросить вызов. Один студент умел вычислять умножение с 4-значным произведением в своей голове, в то время как другие все еще считали на пальцах.
Работа по дифференцированию обучения для удовлетворения потребностей разных учеников в моем классе принадлежала мне, их учителю. Я сделал это, разработав богатую учебную программу и организовав класс так, чтобы мои ученики были вовлечены — никогда не скучали.Мои студенты создавали архитектурные визуализации городских пейзажей как часть модуля по объему. Они исследовали литературные приемы, написав стихи «Откуда я» в стиле Джорджа Эллы Лайон. В рамках группы по анализу данных они использовали Google Maps, чтобы вычислить диапазон, среднее и медианное значение для их утренних поездок на работу. Они узнали, как предвзятость влияет на историю, прочитав биографию Клодетт Колвин, девочки-подростка, которая отказалась стоять в автобусе в Монтгомери за несколько месяцев до Розы Паркс.
Автор, преподающий в своем классе в Гарлеме.Все эти уроки основывались на Common Core, стандартах математики и английского языка, которые полностью вступят в силу в Миссисипи в следующем учебном году. Common Core дала мне гибкость в обучении в соответствии с индивидуальными потребностями моих студентов, не ставя под угрозу основные учебные цели, которые гарантировали, что они будут готовы к поступлению в колледж или карьере после окончания учебы.
Нью-Йорк был одним из первых, кто принял Общие основные стандарты штата (CCSS), и является одним из двух штатов, которые использовали тесты штата, соответствующие CCSS, с 2012-2013 учебного года.После двух лет преподавания в CCSS я уверен, что они внесут положительный вклад в штат Миссисипи, где неадекватные и неоднозначные стандарты уже давно позволяют школам придерживаться того, что Джордж Буш, как известно, назвал «мягким фанатизмом низких ожиданий».
Поэтому меня обеспокоило то, что губернатор Фил Брайант недавно присоединился к небольшому хору губернаторов-республиканцев, заявив о своем недовольстве стандартами Common Core. Вот что он сказал в заявлении в прошлом месяце (от AP):
Common Core — это неудавшаяся программа, и многие понимают, что эти стандарты не такие, как многие считали.Миссисипи несет ответственность и имеет право управлять своей собственной системой образования, а не делегировать этот контроль Вашингтону, округ Колумбия.
Помимо нелогичности называть программу «провальной» до того, как она была полностью реализована, утверждение Брайанта о том, что Common Core представляет собой образовательный аутсорсинг для федеральных органов власти, ставит под сомнение, насколько хорошо он на самом деле понимает эту проблему. Он не одинок. Почти вся политическая оппозиция CCSS, которую я видел и слышал, перекликается с дезинформированными преувеличениями Брайанта.Между тем опросы показывают, что около 75 процентов учителей поддерживают Common Core.
Назначение общего ядра
По правде говоря, эксперты в области образования призывают к более строгим образовательным стандартам с 1983 года, когда обширный отчет «Нация в опасности» впервые предупредил, что «нарастающая волна посредственности» в наших школах угрожает мировому превосходству Америки. Например, за 11-летний период с 1995 по 2006 год США опустились с первого на 14-е место по количеству выпускников колледжей и университетов.
Образование, основанное на стандартах, направлено на то, чтобы американские студенты соответствовали тем же ожиданиям, что и их зарубежные коллеги. Это был главный постулат реформ системы образования Билла Клинтона и Джорджа Буша, кульминацией которого стал Закон «Ни один ребенок не останется без внимания», подписанный в 2001 году. Закон впервые потребовал от всех штатов иметь набор стандартов, определяющих, что должны делать все учащиеся. знать и уметь делать по каждому предмету. В штате Миссисипи были разработаны рамки учебной программы по математике и языковым искусствам, дополненные серией стандартизированных тестов на конец года.
Вскоре после того, как реформы, основанные на стандартах, вступили в силу, 10 процентов беднейших американских студентов начали добиваться успехов в учебе, которые опережали общие средние показатели. Тем не менее США не смогли победить международных конкурентов, что заставило многих поверить в то, что штаты недостаточно высоко установили свои планки. Кроме того, лоскутное одеяло стандартов от штата к штату не имело большого значения для сравнений по границам штатов. По оценке консервативного Института Томаса Б. Фордхэма в 2010 году, стандарты штата Миссисипи получили C по математике и D по английскому языку, что вызвало беспощадную критику:
Стандарты Миссисипи загадочны, как будто они были созданы для того, чтобы запутать, а не прояснить ожидания студентов.Они организованы всего под двумя заголовками: чтение и письмо.
Экзамены, привязанные к государственным стандартам, также различались по сложности. Хотя большинство студентов из Миссисипи с легкостью сдали государственные экзамены, по общенациональным оценкам они получили почти самые низкие баллы.
В 2008 году, разочарованные годами застоя в образовании, Национальная ассоциация губернаторов, Совет директоров школ штата и Achieve, внепартийная некоммерческая группа по реформированию образования, начали процесс разработки стандартов математики и языковых искусств, которые в конечном итоге стали общепринятыми. Основные государственные стандарты.В то время как эти три группы возглавляли усилия, консультанты из двух крупнейших профсоюзов учителей страны, члены ACT и Совета колледжей, эксперты в области образования из 48 штатов (включая Миссисипи) и 10 000 комментариев общественности сыграли свою роль в окончательных стандартах, опубликованных в 2009.
В августе 2010 года Совет по образованию штата Миссисипи присоединился к 44 другим штатам и Вашингтону, округ Колумбия, когда он заменил предыдущие стандарты новыми стандартами Common Core, которые Институт Фордхэма описал как «значительно превосходящие то, что сегодня в штате Магнолия. .«С тех пор районы постепенно внедряют стандарты. Полное внедрение, вместе с новыми государственными тестами по математике и языку, согласованным с CCSS, должно произойти в течение 2014-15 учебного года.
Различия Common Core
Работа учеников в холле Eastside Elementary в округе Мэдисон демонстрирует метод «частичного произведения» для решения задачи умножения. Новые стандарты Common Core подчеркивают несколько способов решения проблем. (Фото: Джеки Мэдер, The Hechinger Report)CCSS намного более детализирован, чем исходящие рамки Миссисипи.Они четко разъясняют учителям, в чем заключаются их обязанности.
CCSS для языковых искусств отдает приоритет чтению и анализу различных текстов, письму с доказательствами и логическому мышлению. Они поощряют использование информационных текстов в младших классах и подчеркивают важность внимательного чтения определенных слов и фраз для понимания «авторского мастерства». В этом году мои ученики прочитали столько же документальной литературы, сколько и художественной, что позволило расширить словарный запас и получить базовые знания — ключевые компоненты понимания прочитанного.Внимательно изучая выбор авторов, мои ученики быстро стали лучшими писателями.
CCSS по математике значительно отличается от текущих государственных стандартов, потому что они требуют изменения подхода к обучению. Вместо того, чтобы сосредоточиться на способности вычислять и решать, стандарты Common Core делают упор на понимание лежащих в основе математических концепций. Дело не только в том, чтобы получить правильный ответ, но и в способности объяснить, как вы к нему пришли. Стандарты не предписывают конкретных стратегий или подходов, но они побуждают студентов решать задачи различными способами, а не просто с использованием стандартных алгоритмов, таких как деление в столбик или умножение с накоплением.
Как планировщик учебной программы по математике в своем классе, я изучал математические стандарты и особенно внимательно работал со студентами. Студенты, которые следовали строгим процедурам решения проблем, испытывали трудности, когда вопросы задавались иначе. Те, кто понимал лежащие в основе концепции, были гораздо более адаптивными. Это самое большое изменение, внесенное Common Core: оценки не просто проверяют способность учащихся находить правильные ответы; они нацелены на концептуальное понимание типов проблем, с которыми студенты столкнутся в реальном мире.
Позвольте мне показать вам, как это работает. Ниже приведен пример базовой задачи пятого класса, включающей деление дроби: 4 делить на = x. Если вы похожи на меня, вас учили «умножать на обратное» всякий раз, когда предъявляется делитель дроби. Этот процедурный подход (слева) выделен рядом с более концептуальным подходом, который требует Common Core (справа).
Умножение 4 на 3, обратное, слева даст вам правильный ответ (12, 0f конечно). Но вы заметите, что визуальная стратегия показывает, почему эта операция работает.В каждом целом есть 3 трети, поэтому в 4 целых будет в 4 раза больше третей; таким образом, 4 x 3 = 12. Это может показаться лишним шагов в этих основных вычислениях, но мои студенты, которые понимали концепции, лежащие в основе операций, добивались большего успеха, когда вопросы задавались в контексте реальных задач. Например:
Бенни пробегает 4 мили. Он останавливается за водой каждые 1/3 мили. Сколько всего раз Бенни будет останавливаться во время гонки (включая финиш)?
У студентов, которые полагались на процедуры, были проблемы с доступом к этому типу задач, потому что они не обязательно распознавали это как разделение.Беглость процедуры важна, и Common Core не отвергает ее, но исследования показывают, что учащиеся, у которых также есть сильные концептуальные основы, гораздо более успешны в математике, чем их сверстники, у которых ее нет. Чтобы понять, как Common Core трактует навык деления на дроби иначе, чем Math Framework Миссисипи, взгляните на два отрывка ниже.
Как и все остальное, переход на новые стандарты вызовет небольшое естественное трение. Обучить 21 000 учителей штата Миссисипи пониманию новых стандартов — непростая задача.В целом, штат уже провел более 100 обучающих семинаров, и многие округа постепенно вводят новые стандарты в существующую учебную программу — но впереди еще долгий путь, и внедрение будет ухабистым. Разочарование среди групп педагогов и родителей наверняка нарастет, поскольку CCSS полностью вступит в силу осенью, но, как я часто говорю своим ученикам, мы добьемся этого, если проявим терпение. Прелесть CCSS в том, что они позволяют продвигаться по учебной программе со скоростью, способствующей исследованию, исследованию и, в конечном итоге, устойчивому пониманию.Я знаю, что это можно сделать. В первый год обучения 96 процентов моих учеников сдали самый сложный государственный тест по математике в истории Нью-Йорка, а две трети получили наивысший возможный балл.
Губернатор Брайант и другие, кто скептически относятся к Common Core, должны понимать, что другое — не такое уж плохое слово, когда речь идет об образовании в Миссисипи, штате с самой низкой производительностью. Стандарты Common Core, бесспорно, более строгие, чем текущие государственные стандарты, и представляют собой сдвиг, который школы должны сделать, чтобы подготовить учащихся к возрастающей конкурентоспособности глобальной рабочей силы.Сами по себе стандарты не могут сделать этого, но в сочетании с сильными лидерами и преданными преподавателями они приведут нас к светлому будущему в сфере образования.
Эта история любезно предоставлена Rethink Mississippi. Воспроизведение запрещено.
Статьи по темеОтчет Хечингера предоставляет подробные, основанные на фактах, объективные отчеты об образовании, которые бесплатны для всех читателей. Но это не значит, что производить бесплатно. Наша работа информирует педагогов и общественность о насущных проблемах в школах и кампусах по всей стране.Мы рассказываем всю историю, даже если детали неудобны. Помогите нам продолжать делать это.
Присоединяйтесь к нам сегодня.
визуальных представлений в математике | CADRE
Визуальные представления (VR) используются в математике, чтобы помочь учащимся решать задачи или понимать абстрактные идеи. Графические данные, размещение чисел в строке или рисование словесной задачи — все это примеры использования VR. Несколько проектов из портфеля DRK – 12, финансируемых NSF, используют VR для улучшения математического понимания.В этом обзоре CADRE просит пять образовательных проектов по математике объяснить, как они используют виртуальную реальность в своих исследованиях и разработках.
КАРЬЕРА: Алгебраические знания для преподавания: межкультурная перспектива (классы: 1-4) 1. Как и почему роль VR критична в модели или вмешательстве, разрабатываемых и / или тестируемых вашим проектом?
VR играет важную роль в проекте «Алгебраические знания для преподавания: кросс-культурная перспектива».Цель проекта — собрать полезные алгебраических знаний для преподавания (AKT) на основе преподавания математики в классе опытных учителей начальных классов из США и Китая. Мы сосредоточились на трех аспектах AKT, включая использование репрезентаций учителями. В частности, нас интересует роль конкретных представлений, в том числе VR, и их связь с абстрактными представлениями. Таким образом, VR играют решающую роль в определении эффективного AKT в этом проекте и служат ключевым аспектом вмешательства проекта.
2. У вас есть примеры представлений? Как эти представления были реализованы в вашем проекте?
Один из важнейших типов VR, на который обращает внимание наш проект, — это линейные количественные модели, такие как «ленточная диаграмма». Этот тип представления широко используется в странах Восточной Азии из-за его эффективности в представлении количественных соотношений для улучшения способности учащихся решать проблемы. Таким образом, эта модель также подчеркивается государственным стандартом Common Core .В нашем проекте мы определили обучающие сегменты, которые включали использование ленточных диаграмм и других связанных линейных количественных моделей, таких как «предварительные ленты» (линейное расположение дискретных объектов) и числовые линии. Затем мы сравнили, как эти линейные количественные модели используются в классах США и Китая.
3. Какие аспекты использования VR тестировались или как они были связаны с исследуемыми исследовательскими вопросами?
Учитывая, что один из вопросов нашего исследования связан с использованием репрезентаций учителями, наш анализ линейных количественных моделей весьма актуален.Сосредоточившись на линейных количественных моделях, мы проанализировали типы, контексты и цели использования виртуальных машин учителями в классах США и Китая. Мы также изучили способы, которыми учащиеся участвуют в процессе моделирования. Выводы о межкультурных различиях в использовании линейных количественных моделей были доведены до сведения участников проекта на летних семинарах (раздел вмешательства в проекте). Затем учителя повторяли свои уроки, основываясь на советах, данных во время вмешательства.
4.Есть ли у вас какие-нибудь новые открытия?
Наше исследование выявило широкие возможности для дополнительного использования линейных количественных моделей в классах США. Однако основное различие в существующем использовании этих моделей между отобранными уроками для США и китайского заключается в учебной цели, для которой эти модели используются. В то время как на уроках китайского использовались линейные количественные модели (включая предварительные записи) с единственной целью моделирования лежащих в основе количественных соотношений сюжетных задач, в уроках в США линейные представления (как в контекстных, так и в неконтекстных проблемах) использовались в основном с целью прямого получения ответов (т.е. .g., подсчет предварительных лент для получения ответа, распределение точек на заданной ленте для получения ответа, прыжок по числовой строке для получения ответа). В тех случаях, когда линейные количественные модели используются для представления проблемных ситуаций в учебных классах США, эти модели часто используются только для нацеливания на отдельные количества, а не для взаимодействия между ними (т.е. количественные отношения). Кроме того, американские учителя, участвовавшие в этом исследовании, редко вовлекали студентов в обсуждение линейных моделей; тем не менее, китайские учителя потратили много времени, вовлекая студентов в со-построение, жестикулирование, сравнение и объяснение этих моделей.В совокупности эти результаты требуют переосмысления цели, для которой используются VR, и поиска новых способов взаимодействия учащихся с VR в классах США.
Ресурсы и продукты проекта:
- Сравнительная работа по использованию учителями линейных количественных моделей в настоящее время пересматривается для повторной публикации в исследовательском журнале.
- Исследование использования китайскими учителями ленточных диаграмм будет опубликовано в журнале Teaching Children Mathematics.
- В рамках проекта создано 25 аннотированных видеоклипов из США и Китая, иллюстрирующих межкультурные различия в использовании VR.
- В нашем видео на выставке NSF Video Showcase 2016 кратко упоминаются межкультурные различия в VR.
Разработка инструментов и процедур формирующего оценивания для аддитивного мышления (классы: K-3)
1. Как и почему роль VR критична в модели или вмешательстве, разрабатываемых и / или тестируемых вашим проектом?
VR играют центральную роль в процессе обучения числам, сложению и вычитанию в классах K – 3, которые мы разработали и проверили в полевых условиях в рамках нашего проекта DRK – 12 «Разработка инструментов формирующего оценивания и процедур для аддитивного мышления».Структурированные бусинки, десять рамок, числовые пути, числовые линии и открытые числовые линии используются в нашем проекте для поддержки студентов в развитии концептуального понимания чисел, сложения и вычитания. Что еще более важно, они обеспечивают обучающий мост, чтобы переместить учащихся от конкретных стратегий счета к более абстрактным стратегиям сложения и вычитания, основанным на прочном понимании чисел.
Исследование Института Фройденталя показало, что пустая или открытая числовая строка может помочь студентам разработать более сложные стратегии сложения и вычитания в процессе прогрессивной математизации.Однако, чтобы использовать числовую линию, дети должны понимать ее атрибуты (например, количество представлено как длина или расстояние; это непрерывная модель; между любыми двумя числами есть другие числа, которые не показаны). Основываясь на работе Адри Трефферса, мы строим понимание пустой или открытой числовой линии из понимания детьми счета с помощью структурированной нити бус (например, 100 бусинок с группами по 10 бусинок чередующихся цветов). Учителя учатся использовать бусинки, чтобы дети находили числа, разрабатывают более сложные стратегии счета (например,g., считая или прибавляя десятки), а затем перенесите это понимание в числовой путь и открытую числовую строку. Вот пример того, как перенести понимание разницы на бусинке на вычитание на открытой числовой прямой.
Мы предоставляем учителям подробное обучение использованию этих визуальных моделей и их роли в развитии понимания учащимися. Учителя учатся включать в свои инструкции конкретные и наглядные модели, распознавать модели и их назначение в учебных материалах и использовать формирующие задания для оценивания, которые просят детей взаимодействовать с визуальными моделями, чтобы постоянно оценивать и реагировать на развивающееся понимание учащимися.
2. У вас есть примеры представлений? Как эти представления были реализованы в вашем проекте?
Структура OGAP для аддитивного мышления включает в себя последовательность обучения для числа, сложения и вычитания. Эта структура является центральной для системы формирующего оценивания OGAP — учителя развивают понимание прогресса в обучении посредством профессионального развития, а затем используют структуру для выбора элементов формирующего оценивания, анализа работы студентов и инструктивного реагирования на доказательства, которые они видят в работе студентов.Вы можете видеть важность визуальных моделей на переходных уровнях.
OGAP Number Line Continuum — это инструмент, который учителя используют, чтобы понять, как они могут научить учащихся понимать и свободно владеть числовыми линиями, переходя от конкретного понимания счета по одному к объединению в группы и развитию системы десятичной системы. понимание и стратегии сложения и вычитания.
Мы разработали более 300 заданий формирующего оценивания (некоторые из которых включают визуальные модели), которые учителя используют для оценки понимания учащимися визуальных моделей.Он-лайн банк заданий и многие другие ресурсы доступны учителям после того, как они пройдут наше обучение.
3. Какие аспекты использования VR тестировались или как они были связаны с исследуемыми исследовательскими вопросами?
Наши прогрессии постоянно пересматриваются, чтобы отразить доказательства, которые мы видим в работе студентов на основе наших пилотных тестовых заданий. (Числовая прогрессия в настоящее время пересматривается на основе свидетельств того, что учащиеся используют визуальные модели, чтобы понять смысл задач на счет, сравнение и относительную величину.) Исследования того, как учителя используют эти инструменты и распорядки, чтобы понять смысл мышления учащихся и дать им инструкции, продолжаются. Результаты этого исследования используются как для улучшения инструментов и процедур, так и для того, чтобы больше узнать о возможностях и ограничениях инструментов и рутин для формирующего оценивания в школьных условиях.
4 . Есть ли у вас новые открытия, которыми вы можете поделиться?
Мы все еще находимся в процессе разработки и сбора и анализа данных для текущих исследований.Вот некоторые новые выводы в отношении VR:
- Визуальные модели играют ключевую роль в соединении понимания учащимися (1) числа как совокупности единиц с более сложным пониманием числа как состоящего из частей с числовыми значениями, и (2) подсчета к аддитивным рассуждениям и развитию более сложные стратегии сложения и вычитания.
- Основополагающее понимание детьми чисел, сложения и вычитания подтверждается стратегиями, которые они используют при взаимодействии с виртуальными машинами.
- Эти результаты отражены в нашей прогрессии и служат руководством для учителей, как инструктивно реагировать на доказательства мышления учащихся и поддерживать развитие аддитивного мышления.
- У учителей не так много возможностей узнать об исследованиях того, как маленькие дети изучают математику, или углубиться в содержание в классах K – 2. Повышение квалификации по этим темам и использованию наглядных моделей помогает информировать их инструктаж и использовать материалы учебной программы.
Ресурсы и продукты проекта:
- Набор инструментов и ресурсов доступен для обученных учителей на веб-сайте проекта: http://www.ogapmath.com/resources-for-ogap-schools
- Мы отправили рукопись на основе понимания base-10 в журнал NCTM Teaching Children Mathematics .
- Мы выступали на Ежегодной конференции по психологии математического образования в Северной Америке в 2017 г. и будем выступать на национальных конференциях NCSM и NCTM 23–25 апреля.
- Видео
INK-12: Преподавание и обучение с использованием интерактивных рукописных надписей в K-12 (классы: 3-5)
1. Как и почему роль VR критична в модели или вмешательстве, разрабатываемых и / или тестируемых вашим проектом?
Виртуальная реальность математических понятий — это ядро проектов ИНК – 12. Мы внедрили программную систему Classroom Learning Partner (CLP), в которой учащиеся начальной школы могли создавать виртуальную реальность мультипликативных ситуаций, используя комбинацию цифровых инструментов и рисования от руки.
2. У вас есть примеры представлений? Как эти представления были реализованы в вашем проекте?
Существовало три основных инструмента представления: штампы (несколько копий идентичных изображений), числовые линии и массивы, каждый из которых предоставлял математическую структуру, а также множество опций для студента-пользователя. Примеры всех наших представительств есть на нашем сайте INK-12.mit.edu. Их можно свободно использовать и делиться.
3. Какие аспекты использования VR тестировались или как они были связаны с исследуемыми исследовательскими вопросами?
В нашем проекте в значительной степени проводилось исследование, основанное на дизайне, пытаясь понять, какие виды представлений лучше всего поддерживают размышления учащихся о умножении и делении.Мы также изучали, как разрабатывать представления, которые давали студентам определенную свободу выражения и имели достаточную структуру, чтобы мы могли автоматически анализировать работу студентов, чтобы найти шаблоны использования.
4 . Есть ли у вас новые открытия, которыми вы можете поделиться?
Наши публикации содержат самые разные выводы. Самым всеобъемлющим (о котором мы все еще пишем) является то, что в пятинедельном испытании в классе четвертого класса с двумя контрольными классами учащиеся, которые использовали наше программное обеспечение, имели значительно более высокие результаты, чем учащиеся из контрольной группы.
Ресурсы и продукты проекта:
Математическое обучение посредством архитектурного проектирования и моделирования с использованием E-Rebuild (классы: 6-8) 1. Как и почему роль VR критична в модели или вмешательстве, разрабатываемых и / или тестируемых вашим проектом?
В проекте «Математическое обучение через архитектурное проектирование и моделирование с использованием E-Rebuild» мы исследовали игровую платформу обучения, которая обеспечивает множественное кодирование или мультимодальное представление решения математических задач для учащихся средней школы.Трехмерное динамическое визуально-пространственное представление является ключевым аспектом преобразования и координации мультимодальных внешних представлений в E-Rebuild. Этот проект направлен на вовлечение учащихся в осмысленное взаимодействие с системой мультимодальных (например, вербальных, обозначений и визуально-пространственных) внешних репрезентаций, которые, в свою очередь, стимулируют у студентов выполнение множественного кодирования и построение согласованной системы международные представления математических задач.
2.У вас есть примеры представлений? Как эти представления были реализованы в вашем проекте?
Учащиеся активно обрабатывают (например, интерпретируют двухмерные и трехмерные визуальные изображения архитектурных элементов и обратную связь) и управляют динамическими визуализациями (например, создают и конструируют визуализированные трехмерные игровые объекты) посредством обучения на основе игр. платформа при использовании математики и решения задач. Демо-игры доступны по адресу https://mileresearch.coe.fsu.edu/erebuildweb/
3.Какие аспекты использования VR тестировались или как они были связаны с исследуемыми исследовательскими вопросами?
Было записано игровое поведение пользователей (включая поведение при взаимодействии с виртуальной реальностью), и был проведен систематический анализ поведения для изучения их взаимодействия с виртуальными устройствами и связанными с ними процессами обучения.
4. Есть ли у вас новые выводы?
Мы все еще проводим анализ данных, две рукописи журнала отправлены и находятся на рассмотрении.
Ресурсы и продукты проекта:
Игровая площадка пропорций: динамичный мир для поддержки пропорционального мышления учителей (классы: 6-7)
1. Как и почему роль VR критична в модели или вмешательстве, разрабатываемых и / или тестируемых вашим проектом?
Это мероприятие посвящено тому, как учителя понимают и учатся на динамических виртуальных реальностях. Проект «Игровая площадка пропорций» возник в результате нашего наблюдения, что учителя рассуждали о пропорциональных ситуациях, когда они были представлены в динамической среде, иначе, чем когда они были представлены с использованием бумаги и карандаша.Мы решили, что это стоит того, чтобы лучше разобраться, поэтому создали набор интерактивных «игрушек» (в Интернете), призванных помочь учителям исследовать отдельные аспекты пропорционального мышления.
2. Как эти представления были реализованы в вашем проекте?
Представления будут использоваться в трехдневной программе профессионального развития, в которой мы сосредоточимся на некоторых крупных математических идеях, связанных с пропорциональным рассуждением. Мы попросим учителей поиграть с каждым из представлений, а затем решить с каждым хотя бы по одной задаче.В рамках этих усилий мы также будем просить участников создать одно или два дополнительных (статических) представления, которые описывают интересующие отношения из динамических настроек. Цель состоит в том, чтобы привлечь учителей таким образом, чтобы они могли развить свое понимание пропорций, установить связи между представлениями и между ними, а также способствовать общению, построению предположений и спорам о математических идеях.
3. Какие аспекты использования VR тестировались или как они были связаны с исследуемыми исследовательскими вопросами?
Наше внимание уделяется тому, как учителя взаимодействуют с динамическими VR.В частности, мы спрашиваем, как учителя рассуждают с помощью представлений и как они используют свое пропорциональное понимание, чтобы разобраться в ситуациях. Мы также заинтересованы в обнаружении доказательств того, что участники устанавливают связи между различными точными математическими идеями. Короче говоря, наша цель — лучше понять типы мышления, вызываемые динамическими виртуальными реальностями, и способы, с помощью которых работа с представлениями вызывает обширные дискуссии о математике, которую преподают эти учителя.
4. Есть ли у вас новые выводы?
Еще нет! Мы будем собирать данные летом и осенью.
Ресурсы и продукты проекта:
Глава 6 ответы на тесты по математике
Глава 6: Установка языка и обозначений — Mcqs по математике для 7 класса с ответами и пояснениями к контрольным экзаменам, другим тестам и т. Д. Эти решенные вопросы с несколькими вариантами ответов чрезвычайно полезны для подготовки к экзаменам, размещения в университетском городке все первокурсники, включая инженеров, студентов MBA и MCA, инженеров по компьютерам и ИТ и т. д.
См. Другие идеи о домашнем задании, ответах на тесты для детей, классе математики. Этот математический пакет включает в себя задачи со словами, координатные графики, задачи с расчетами / операциями и ключи ответов. Вы даете своему классу главу для романа, которую нужно прочитать в качестве домашнего задания, или, может быть, вы начинаете читать главу вместе в … Сказав это, он покинул Галилею и пошел в область Иудеи на другой берег Иордана. За ним следовали большие толпы, и он исцелял их там.Некоторые фарисеи приходили к нему, чтобы испытать его. Они спросили: «Законно ли мужчине разводиться со своей женой по любой и любой причине?» «Разве вы не читали, — ответил он, — что вначале Создатель …
Этот тест охватывает те же математические навыки, что и в разделе 3 SAT. Продолжайте подготовку к тесту прямо сейчас, задав эти бесплатные практические вопросы! Решите каждую проблему и выберите лучший из предложенных вариантов ответа. Поздравляю — вы выполнили.
Используйте тест в середине главы из книги в качестве практики и повторения.Проверьте свои решения. Покажите мне свою работу и задайте вопросы перед тем, как сдать тест на промежуточную оценку мастерства в классе.
Начните изучать ответы на главу 6. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения.
Этот тест состоит из 10 вопросов по решению проблем, которые необходимо выполнить за 12 минут.
