Математика 3 класс контрольные перспектива: Контрольные работы по математике 3 класс «Перспектива»

Контрольные работы по математике 3 класс УМК » Перспектива»

Вариант 1

1. Реши задачу:

Выкопали 60 кг моркови. В мешок высыпали 15 кг, а остальную морковь разложили в ящики по 9 кг в каждый. Сколько ящиков понадобилось ?

2. Вычисли:

5 ∙ 6 =                   48 : 6 =                     15 : 3 + 7 ∙ 4 =

7 ∙ 9 =                  64 : 8  =                    (21 + 28) : 7 =

3 ∙ 8 =                   40 : 5  =                   51 — 4 ∙ 9 + 21 =

8 ∙ 6 =                   30 : 3 =                    32 : 4 : 4 ∙ 6 =

3. Сравни, поставь знаки  >, <, =.

2 ч … 100 мин                          4 дм 9 см …  1м

68 мин … 1 ч 18мин                  1м … 99 см

1ч … 90мин                             70 см … 8 дм

4. Длина прямоугольника 5 см, а ширина 3 см. Начерти прямоугольник, найди его периметр.

5.* Периметр квадрата 24 см.

Начерти прямоугольник с таким же периметром.

Вариант 2

1. Реши задачу:

Купили 45 м ткани. Из 15 м сшили блузки, а из остальной ткани 5 платьев. Сколько метров ткани пойдёт на одно платье ?

2. Вычисли:

8 ∙ 2  =                 63 : 7  =               12 : 2 + 6 ∙ 6 =

7∙ 6  =                 18 : 3  =               (35 — 8) : 3 =

9 ∙ 3  =                21 : 3   =              43 — 4 ∙ 9 + 18 =

8 ∙ 8   =               42 : 7 =                 40 : 5 : 4 ∙ 8 =

3. Сравни, поставь знаки  > , < , =.

48 мин … 1ч                          100 см … 1 м

1ч 15 мин … 75мин                3 дм 9 см … 93 см

110 мин … 1ч 10мин               4дм 6см … 40 см

4. Длина прямоугольника 6 см, а ширина 2 см. Начерти прямоугольник, найди его периметр.

5.* Периметр квадрата 32 см. Начерти прямоугольник с таким же периметром.

Вариант 2

1. Реши задачу:

Купили 45 м ткани. Из 15 м сшили блузки, а из остальной ткани 5 платьев. Сколько метров ткани пойдёт на одно платье ?

2. Вычисли:

8 ∙ 2  =                 63 : 7  =               12 : 2 + 6 ∙ 6 =

7∙ 6  =                 18 : 3  =               (35 — 8) : 3 =

9 ∙ 3  =                21 : 3   =              43 — 4 ∙ 9 + 18 =

8 ∙ 8   =               42 : 7 =                 40 : 5 : 4 ∙ 8 =

3. Сравни, поставь знаки  > , < , =.

48 мин … 1ч                          100 см … 1 м

1ч 15 мин … 75мин                3 дм 9 см … 93 см

110 мин … 1ч 10мин               4дм 6см … 40 см

4. Длина прямоугольника 6 см, а ширина 2 см. Начерти прямоугольник, найди его периметр.

5.* Периметр квадрата 32 см. Начерти прямоугольник с таким же периметром.

Вариант 2

1. Реши задачу:

Купили 45 м ткани. Из 15 м сшили блузки, а из остальной ткани 5 платьев. Сколько метров ткани пойдёт на одно платье ?

2. Вычисли:

8 ∙ 2  =                 63 : 7  =               12 : 2 + 6 ∙ 6 =

7∙ 6  =                 18 : 3  =               (35 — 8) : 3 =

9 ∙ 3  =                21 : 3   =              43 — 4 ∙ 9 + 18 =

8 ∙ 8   =               42 : 7 =                 40 : 5 : 4 ∙ 8 =

3. Сравни, поставь знаки  > , < , =.

48 мин … 1ч                          100 см … 1 м

1ч 15 мин … 75мин                3 дм 9 см … 93 см

110 мин … 1ч 10мин               4дм 6см … 40 см

4. Длина прямоугольника 6 см, а ширина 2 см. Начерти прямоугольник, найди его периметр.

5.* Периметр квадрата 32 см. Начерти прямоугольник с таким же периметром.

ГДЗ по Математике 3 класс Петерсон 1, 2, 3 часть Учебник

В начальной общеобразовательной школе математике посвящено отнюдь не малое количество учебных часов. Это один из наиболее активно изучаемых предметов. В этом возрасте детям проще освоить арифметику и сформировать необходимый набор умений и навыков. Повышенное внимание к данному предмету не удивительно, ведь именно сейчас закладываются основы беглого обращения с числами, умения решать задачи практического толка.

В нелегком деле постижения азов поможет учебно-методический комплекс опытного педагога Людмилы Петерсон для третьего класса. Ее издание ориентировано на развитие мышления и творческих способностей, формирование прочных знаний, общих умений, а также развитие познавательного интереса и личностных качеств современного гражданина Российской Федерации.

Онлайн-решебник является частью УМК «Учусь учиться» для дошкольников и младших школьников. Материалы, которые приводит автор, соответствуют федеральному государственному образовательному стандарту (ФГОС), разработанному для начального общего образования. Методическую поддержку осуществляет Институт системно-деятельностной педагогики.

Почему ГДЗ Петерсон по математике нравится школьникам?

Это простой и понятный учебник, в котором все сложные темы расписаны понятным языком. Приведены многочисленные примеры практического использования полученных знаний. Автор ориентирует ребенка на ответственность и самостоятельную работу, на достижение конкретного результата. Сборники с верными ответами обладают следующими очевидными преимуществами:

• заданные на дом номера легко находить на нашем сайте;
• верные ответы приведены в соответствии со всеми требованиями на 2019-2020 годы;
• материалы на странице онлайн соответствуют школьной оценке «отлично»;
• круглосуточная доступность методической помощи.

Решенные задачи из пособия по математике Петерсона нельзя просто слепо переписывать. Над приведенными образцами выполнения и оформления необходимо рассуждать, систематизировать полученные умения и навыки.

Почему решебник (Петерсон) лучше, чем просто учебник для 3 класса?

Ребенку не всегда бывает всё понятно сразу. Например, во время урока можно отвлечься на короткий разговор с соседом по парте и пропустить важное пояснение учителя.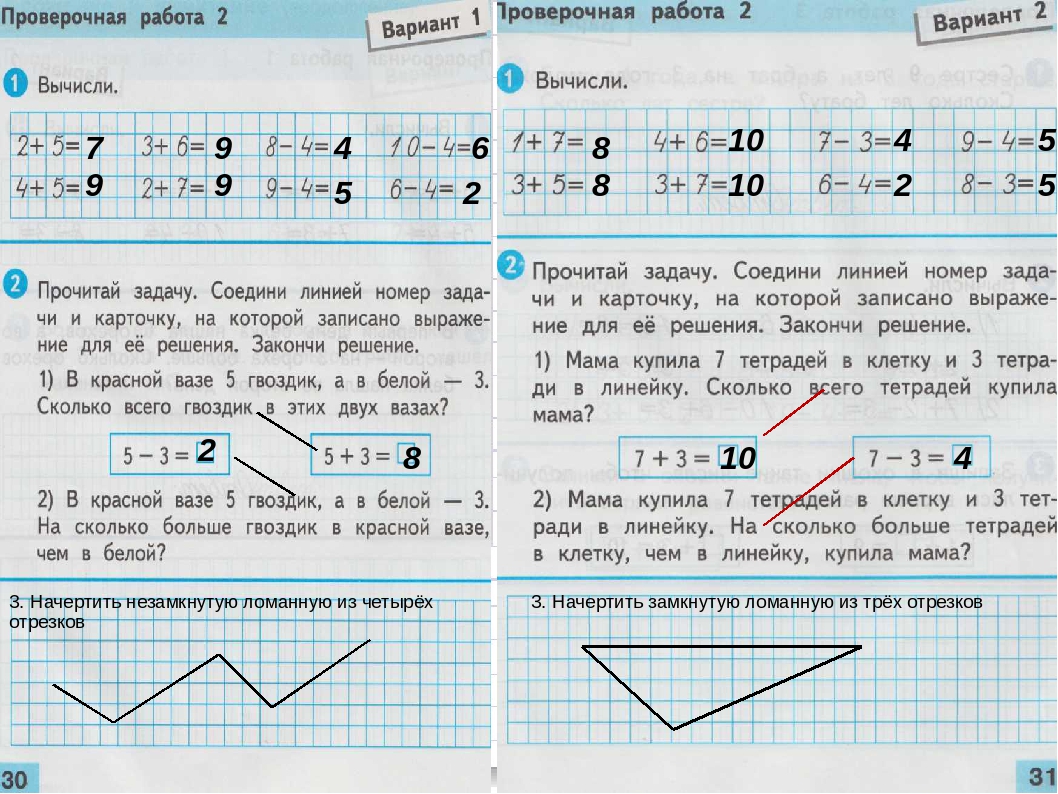 Из-за того, что в аудитории одновременно находится двадцать, а то и тридцать учеников, учитель не может уделить каждому достаточное количество внимания. Конечно, нужно вырабатывать навыки учебной работы в коллективе, сохранять дисциплину, уважительно относиться к педагогу.

Решебник способен исправить недостатки классно-урочной системы, ведь пропущенные пояснения можно найти в нем. К тому же, содержание отвечает соответствующему ФГОС, так что будет достойным дополнением к прочим материалам. С ГДЗ легко готовиться к контрольным, проверочным, диагностическим работам выполнять тесты по разным темам. Сейчас ученику крайне важно разобраться со следующими параграфами:

• выполнение операций в столбик;
• разряды числа и соответствующее разложение на них;
• элементы геометрии: отрезок, луч, прямая.

Пособие предназначено для всех третьеклассников. Оно повысит успеваемость и улучшит подготовку к тестам.

Контрольная работа по математике 3 класс 2 четверть перспектива :: wheeteharmilk

12. 11.2016 14:59

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

За 1, 2, 3 и 4 четверти. Начальные классы. Задачи по математике для 3 класса. Контрольные работы по математике за 3 класс, Перспектива.

Кг больше, чем с первого, а с третьего — в 2 раза меньше, чем со второго. Контрольная. Проводится в 1 четверти 3.

Вопросов, изученных в первом и во втором классах. Варианты контрольных работ. Контрольные работы по математике для 3 класса по учебнику Моро М. И.

Класса. Контрольная работа по математике за 2 четверть.1 вариант. С первого улья собрали 36 кг меда, со второго — на 12.

2. В шахматной секции 46 мальчиков, а девочек на 19 меньше. Контрольная по математике за 2 класс 3, 4 четверть.

Итоговые контрольные работы по математике 1, 2, 3 классы по УМК ПНШ. Итоговый тест по математике за первое полугодие для 2.

Класса. Итоговая контрольная работа по математике за 1 полугодие, 3 класс. Контрольная работа по литературному чтению.3 класс.3 четверть. Проводится после повторения.

 

Вместе с Контрольная работа по математике 3 класс 2 четверть перспектива часто ищут

 

контрольная работа по математике 3 класс 1 четверть.

контрольные работы по математике 3 класс моро.

контрольные работы по математике 4 класс.

контрольные работы по математике 3 класс школа россии.

контрольные работы по математике 3 класс школа 2100.

контрольные работы по математике 3 класс дорофеев.

контрольные работы по математике 3 класс петерсон.

контрольные работы по математике 3 класс перспектива дорофеев

 

Читайте также:

 

Гдз по немецкому языку 7 класс 85 учебника номер

 

Умк школа россии моро математика 4 класс урок 47 конспект скачать

 

Гдз по русскому 5 к упр 305 быстрова онлайн

 

rigifad итоговая контрольная работа по математике 3 класс перспектива дорофеев

итоговая контрольная работа по математике 3 класс перспектива дорофеев

Ссылка:

http://ufyvaka.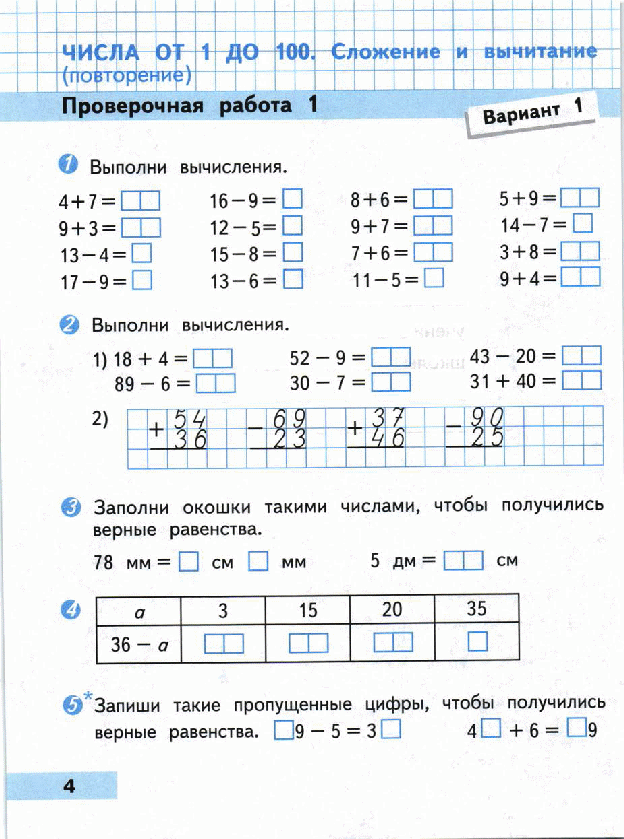 bemosa.ru/1/66/itogovaya-kontrolnaya-rabota-po-matematike-3-klass-perspektiva-dorofeev

.

итоговая контрольная работа по математике 3 класс перспектива дорофеев Контрольная работа по математике по итогам 3 четверти к учебникам Дорофеева Г. В. по программе Перспектива. Контрольная работа по математике, 3 класс,3. Данная комплексная итоговая контрольная работа составлена для 3 класса по учебнику Петерсон Л.Г. УМК Перспектива. Просмотр содержимого документа «Итоговая контрольная работа по математике 3 класс ». Варианты контрольных работ за 3 класс. Контрольная работа №1(Входная) (базовый уровень). . Итоговая контрольная работа за 3 класс (повышенный уровень). Дорофеев Г. В., Миракова Т. Н. Уроки математики. 3 кл. . Совместимость имени и даты 6+ 6+3+1+6+5+9+6+2+1 число фамилии , имени , отчества 8 . . Гороскоп на завтра рак работа (766) · Гороскоп весы … от других наличием широкой перспективы во всех начинаниях. … заданий по математике 11 класс Дорофеев Химия – это тяжелая . УМК Перспектива Дорофеев . по математике 3 класс . контрольная работа по . Итоговая контрольная работа по математике за 1 полугодие, 3 класс. Контрольные работы по математике, 2 класс, программа Перспектива. . Проверочная работа по математике, 2 класс, 3 четверть. Природные рекордсмены Южной Америки. . Контрольные работы по математике 4 класс умк перспектива дорофеев. по математике (1 класс) на тему: Контрольная работа по математике за 3 четверть 1 Входная контрольная работа по математике . (№1). Цель: установление фактического уровня теоретических знаний обучающихся по математике обязательного компонента учебного плана, их практических умений и навыков. Контрольные работы по математике для 3 класса за 3 четверть Математика 3 класс, контрольные работы с решениями Итоговая контрольная работа за 3 четверть Контрольная работа по математике 6 класс первое полугодие. Контрольная работа по литературе в 8 классе (за II полугодие). 26-04-2016, 12:41. Контрольная работа по теме Глагол, программа Перспектива. Дорофеев Г. В. Методическое пособие к учебнику МАТЕМАТИКА. 1 класс. ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ. Контрольная работа № 1 . 3. Сравни количество точек внутри и вне квадрата. Восстанови записи: .. Сколько всего яблонь и слив растет в саду? ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ЗА 1 КЛАСC . 24.5 КБ Входная контрольная работа по математике в 3 классе.doc 13.88 КБ Итоговая контрольная работа за 3 класс.docx Входная контрольная работа по математике в 3 классе. 1.Решите задачу. Контрольные работы по математике УМК Перспектива. Контрольные работы, представленные на странице, взяты из. ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА за 1 класс. 24.5 КБ Входная контрольная работа по математике в 3 классе.doc . 13.88 КБ Итоговая контрольная работа за 3 класс.docx . Входная контрольная работа по математике в 3 классе. 1.Решите задачу. . Итоговая контрольная работа по физической культуре. 3 класс. 1. Что из перечисленного не является спортивной обувью? . Данные тесты составлены на основе УМК Перспектива. . УМК Перспектива Дорофеев . . и проверочные работы по математике для 2 класса по УМК Перспектива . . было 3 монеты по 5 . . контрольная работа по математике 2четверть 2 класс г.в. дорофеев . . работы по ФГОС . Контрольные работы по математике 2 класс УМК Перспектива. Контрольные работы по математике 3 класс Планета знаний_18410 Итоговая контрольная работа за 3 класс (повышенный уровень). Дорофеев Г. В., Миракова Т. Н. Уроки математики. . Технологические карты к учебнику математики для 3 класса по программе Перспектива автор Дорофеева.. . . контрольная работа по математике 2четверть 2 класс г.в. дорофеев. . работа по математике . Контрольная работа по математике за 3 четверть 1 класс УМК Перспектива. . Конспект урока математики в 5 классе по теме Развертки УМК Г.В.Дорофеев. . ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ . Проверочная работа. Вариант 1. 1. Запиши выражения столбиком и выполни действия. 38 + 21 47 − 15. 74 + 16 63 − 28. 2. В шахматной секции 46 мальчиков, а девочек на 19 меньше. Сколько всего ребят в шахматной секции? контрольные работы по математике 4 класс дорофеев . работа по математике . Перспектива . Итоговая контрольная работа по . Тест по математике (2 класс) . Итоговая контрольная . Итоговая контрольная работа по математике для 1 класса. УМК « Перспектива» ФГОС 24 авг 2012 . Методическая разработка по математике (3 класс) на тему: . Контрольные работы по математике УМК «Школа России» (авторы . .. Итоговая контрольная работа включает в различные задания по основным . Контрольная работа по . Итоговая контрольная работа . по математике, 2 класс, 3 .

TRACKBACK http://rigifad.blog.fc2.com/tb.php/14-b5711b54

 

Официальный сайт университета имени А.И. Герцена

Факультет / Институт	Код	Наименовании специальности, направления подготовки	Наименование специальных* помещений и помещений для самостоятельной работы	Оснащенность специальных помещений и помещений для самостоятельной работы	Приспособленность помещений для использования инвалидами и лицами с ограниченными возможностями здоровья
Факультет безопасности жизнидеятельности	44.03.01	Педагогическое образование	19 аудиторий для проведения лекционных, семинарских и практических занятий, 3 компьютерных класса	Показать	данные уточняются
	44. 04.01	Педагогическое образование
Факультет биологии	05.03.06	Экология и природопользование	Полное оснащение учебного процесса,агробиостанция,зоологический музей, кабинет методики изучения  биологии и экологии, лаборатория	Показать	данные уточняются
	06.03.01	Биология
	44.03.01	Педагогическое образование
	05.04.06	Экология и природопользование
	06.04.01	Биология
	44.04.01	Педагогическое образование
Факультет географии	05.03.02	География	Учебные аудитории, компьютерные классы, ГЕОСТАНЦИЯ ЖЕЛЕЗО	Показать	данные уточняются
	05.03. 06	Экология и природопользование
	41.03.01	Зарубежное регионоведение
	44.03.01	Педагогическое образование
	05.04.02	География
	44.04.01	Педагогическое образование
	05.04.06	Экология и природопользование
Факультет изобразительного искусства	44.03.01	Педагогическое образование	Мастерские живописи и рисунка, скульптурная мастерская,эстампная мастерская, керамическая мастерская,мастерская компьютерной графики,текстильная мастерская,методический кабинет	Показать	данные уточняются
	44.04.01	Педагогическое образование
Факультет истории и социальных наук	39.03.01	Социология	Оборудованые учебные кабинеты,учебно -методическая информационная лаборатория	Показать	данные уточняются
	41. 03.04	Политология
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
	46.03.01	История
	46.04.01	История
	47.04.03	Религиоведение
	39.04.01	Социология
	41.04.04	Политология
Факультет математики	01.03.02	Прикладная математика и информатика	Оборудованые учебные кабинеты, объекты для проведения практических занятий	Показать	данные уточняются
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Факультет физики	03.03.02	Физика	5 лекционных аудиторий, оборудованных современными многофункциональными мультимедийными комплексами, 3 компьютерных класса и 20 учебных лабораторий	Показать	данные уточняются
	03. 04.02	Физика
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Филологический факультет	44.03.01	Педагогическое образование	Оборудованные учебные кабинеты, объекты для проведения практических занятий	Показать	данные уточняются
	44.04.01	Педагогическое образование
Факультет химии	04.03.01	Химия	Учебные кабинеты, объекты для проведения практических занятий	Показать	данные уточняются
	04.04.01	Химия
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Юридический факультет	37. 03.02	Конфликтология	Учебные кабинеты ,криминологическая лаборатория,криминалистическая лаборатория,лаборатория конфликтологии	Показать	данные уточняются
	40.03.01	Юриспруденция
	40.04.01	Юриспруденция
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Институт детства	44.03.01	Педагогическое образование	Учебные кабинеты, объекты для проведения практических занятий	Показать	данные уточняются
	44.04.01	Педагогическое образование
	44.03.02	Психолого-педагогическое образование
	44.04.02	Психолого-педагогическое образование
Институт дефектологического образования	44. 03.03	Специальное (дефектологическое) образование	Лаборатория  социально-реабилитационного сопровождения инклюзивного профессионального образования студентов с ограниченными возможностями здоровья и инвалидов	Показать	данные уточняются
	44.04.03	Специальное (дефектологическое) образование
Институт иностранных языков	45.03.02	Лингвистика	Специализированные учебные лаборатории (учебные комплексы) для обучения иностранному языку и переводу; презентационный зал с возможностью видеоконференцсвязи	Показать	данные уточняются
	45.04.02	Лингвистика
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Институт компьютерных наук и технологического образования	09. 03.01	Информатика и вычислительная техника	Лаборатория кафедры производственных  и компьютерных технологий, лаборатория мультимедиа, УМЛ «Музыкально-компьютерные технологии»	Показать	данные уточняются
	09.03.02	Информационные системы и технологии
	09.04.02	Информационные системы и технологии
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
Институт музыки, театра и хореографии	44.03.01	Педагогическое образование	Лекционные залы, классы для занятий, учебно-методическая лаборатория	Показать	данные уточняются
	44.04.01	Педагогическое образование
	52.03.01	Хореографическое искусство
	53. 03.02	Музыкально-инструментальное искусство
Институт народов Севера	44.03.01	Педагогическое образование	Специализированные учебные лаборатории (учебные комплексы) ,репетиционный зал фольклорного театра-студии «Северное сияние»	Показать	данные уточняются
	44.04.01	Педагогическое образование
Институт педагогики	44.03.01	Педагогическое образование	Учебные аудитории,компьютерное классы.. Учебно — методическая информационная лаборатория.	Показать	данные уточняются
	44.04.01	Педагогическое образование
	39.03.02	Социальная работа
	44.03.02	Психолого-педагогическое образование
	39.04.02	Социальная работа
Институт психологии	44. 03.02	Психолого-педагогическое образование	Имеются  учебные и лекционные аудитории,компьютерное оснощение. Учебно — методическая информационная лаборатория.	Показать	данные уточняются
	44.04.02	Психолого-педагогическое образование
	37.03.01	Психология
	37.04.01	Психология
	37.05.02	Психология служебной деятельности
	37.04.03	Клиническая психология
Институт физической культуры и спорта	44.03.01	Педагогическое образование	8 залов, 12 учебных аудиторий, из них: 5 лекционных, 7 учебно-методических.Имеются: компьютерный класс, научно-исследовательская лаборатория, методический кабинет, 14 административных помещений.	Показать	данные уточняются
	44. 04.01	Педагогическое образование
	49.03.01	Физическая культура
	49.03.02	Физическая культура для лиц с отклонениями в состоянии здоровья (адаптивная физическая культура)
Институт философии человека	42.03.01	Реклама и связи с общественностью	В наличии учебные аудитории: лекционные и учебно-методические,административные помещения.	Показать	данные уточняются
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование
	47.03.01	Филосифия
	47.04.01	Филосифия
Институт экономики и управления	38.03.01	Экономика	Специализированные учебные комплексы, компьютерные классы.	Показать	данные уточняются
	38. 04.01	Экономика
	38.03.02	Менеджмент
	38.04.03	Менеджмент
	38.03.03	Управление персоналом
	38.04.03	Управление персоналом
	38.03.04	Государственное и муниципальное управление
	38.04.04	Государственное и муниципальное управление
	43.03.02	Туризм
	44.03.01	Педагогическое образование
	44.04.01	Педагогическое образование

Средняя школа полностью ориентирована на девочек — ВМЕСТЕ — легче ВСЁ

Средняя школа полностью ориентирована на девочек

В педагогических книгах и статьях много пишут о том, что дети отличаются по темпераменту, способу усвоения материала, и другим характеристикам. Это все хорошо, только иногда забывается главное — что они отличаются по половому признаку. Мужчины и женщины физически устроены по-другому, и дело не только в тех самых органах.

«Я никогда не позволял, чтобы мои школьные занятия мешали моему образованию.» — Марк Твен

Мышление (а равно и остальные психические функции) мужчин и женщин (также мальчиков и девочек) работает совершенно по-разному. Отсюда бывает непонимание супругов («Я же ему сказала, а он не понимает!»), и отсюда бывают проблемы в учебе.

По вашим воспоминаниям — кто чаще в классе плохо учится, мальчик или девочка? Как правило, почти в каждом классе есть свой отпетый «двоечник», и это мальчишка. Современное школьное обучение (я имею в виду светские смешанные школы) целиком и полностью «женско-ориентированное». Начнем с того, что учитель-мужчина уже давно перешел в разряд раритетов. Разве что учитель физкультуры и труда у мальчиков, но там мыслительные процессы не особо задействованы. Учительница начальных классов, учительница математики, учительница физики.

..

Все основные дисциплины, где больше должна работать голова, не просто находятся в «женских руках», но и программу составляет кто? Вы когда-нибудь видели серпентарий методический кабинет? Там исключительно женский состав. (Я методист, я в курсе). Программа средней школы целиком и полностью ориентирована на «девочковое» мышление, поэтому так часто плохо учатся именно мальчики.

Программа построена на принципе «копипаст», то есть прочитай параграф и расскажи его, прочитай правило и сделай по нему упражнения, посмотри на образец и сделай по нему. Это типично женское мышление, которое тиражирует. Мужское мышление генерирует идеи и создает новые правила и новые образцы.

Именно поэтому девочкам так легко справляться с упражнениями на заданное правило, а мальчики не видят смысла в этом — они же усвоили идею, зачем ее теперь размусоливать?

Девочки обычно гораздо лучше отвечают у доски — вербальные центры у них лучше сформированы. Поэтому совершенно неправильно, когда мама говорит: «наш мальчик в два года не разговаривает, а у соседей девочка в год уже столько слов выдает!» — это нормально! Девочки в среднем начинают говорить раньше, и им легче сформулировать свои мысли, нежели мальчикам.

Мальчикам важно высказать суть, им незачем «растекаться мыслию по древу», в отличие от них девочки могут приукрашивать свои рассказы разными несущественными деталями, чем, конечно, радуют учителей и выглядят «более успешными» на фоне обрывочно отвечающих мальчиков.

Когда учительница русского языка проверяет сочинения, на что она первым делом обратит внимание? На объем! И если вместо заданного минимума «примерно полторы страницы» она увидит пять строчек, она даже читать не будет, а перечеркнет все жирной красной пастой и поставит «двойку».

Мальчикам год за годом на протяжении всего обучения внушают, что идея не важна, мысль не имеет ценности, важно только ее оформление и «копипаст» (Вспомним снижение оценок за помарки? Это исключительно женское извращение учительниц. Посмотрите на любого профессионала — как раскиданы стружки по столярной мастерской, как заляпано все в студии художника. Когда мальчики стремятся создать что-то новое, им совершенно некогда все «раскладывать по полочкам», это слишком низко для их высоких идей.

А в школе им вбивают, что помарка выше той мысли, которую они пытались выразить).

Конечно, и девочку нужно учить созидающему мышлению, но именно мальчики страдают больше от этой направленности обучения, когда нужно только усвоить информацию, а не добывать ее и не творить нечто новое.

Может показаться, что у меня есть противоречие — я столько писала о том, что на определенном этапе у детей наглядно-образное мышление, потом словесно-логическое? Это все верно. Но на одном и том же этапе у мальчиков и девочек оно работает немного по-разному в одних и тех же рамках. И те, и другие оперируют образами на стадии образного мышления, но при этом отличаются способы оперирования. Например,в игре девочки могут два часа устраивать домик для кукол, придумывать мебель и менять наряды, так и не начав сюжетных действий. Мальчики же сразу переходят именно к действиям — например, стали играть в машинки, тут же устраивают гонки и т.п.

У кого есть возможность посмотреть, как рисуют девочки и мальчики с комментариями, вы заметите примерно следующее:

Девочка будет подробно рассказывать про всякие красивости: «А это у принцессы такой дворец.

Тут будто у нее садик. Там такие цветочки (долгие перечисления с подбором цветовой гаммы). А тут живет ее собачка. собачку зовут…». На листе будет четкое разделение небо-земля с «ровными рядами» всех участников и предметов.

Мальчик будет больше выражаться звукоподражательными словами и междометиями, ему важно «закрутить сюжет», а не прорисовать каждый предмет: «а он такой — бац! — а они вжжжжжжжжж, а машина туда как поехала, этот бум-бум, а он такой побежал…». на листе будет неопределяемая мазня, по которой туда-сюда много раз «проехала машина».

И вот мальчик в первом классе приносит такой рисунок учительнице рисования (с «девочковым» мышлением), а она говорит: «Петров! Почему у тебя машина на воздухе висит? Почему у тебя человек вверх ногами? Ты где-нибудь видел человека на дороге вверх ногами? А почему ты залез за контур? Что, маленький, не научился раскрашивать?» (Класс хохочет). Таким образом мальчик не только получил попрание своей высокой идеи и динамичного сюжета, но и был выставлен «перед строем».

Подумайте, много у него останется желания созидать?

Как мы уже говорили, мышление мужчин требует новаторства, принципиально иных решений, мужчинам нужно «переворачивать мир», они, собственно, приходят к обучению для того, чтобы получить эти самые два кольца.

Как раз в начальной школе, когда у ребенка формируется словесно-логическое мышление, мужская логика-то и не нужна. Можно так пошутить, что у девочек в этом возрасте мышление «словесное» (именно они пересказывают желательные правильные ответы), а у мальчиков «логическое» — они ищут причинно-следственные связи между объектами, не всегда умея это сформулировать. Именно здесь даются готовые шаблоны и информация дается в готовом виде.

Это постоянное «делание по образцу» уничтожает стремление к самообразованию и любознательность в начальный период обучения (не нужно думать, что эти прекрасные качества формируются на пустом месте при окончании школы и начальная школа это лишь прописи, это как раз и формирование модели учебной деятельности, желательно на всю жизнь).

Плюс к тому, что обучение лишено стимула проявлять инициативу, заниматься поиском информации и искать собственное решение означенной проблемы, обучение построено именно на вербальном потоке, в обработке которого мальчики этого возраста не очень сильны (мы уже говорили, что они чаще девочек отвлекаются при слушании, хуже формулируют свои высказывания и т.п.).

В этом возрасте мальчикам нужно как можно больше «ставить экспериментов», они легче находят решение «путем проб и ошибок». Конечно, любая подобная деятельность исключена в начальной школе — чем экспериментировать? Счетными палочками? Мальчики дольше, чем девочки, находятся в периоде главенства кинестетического канала восприятия — им необходимо разобрать-собрать объект, чтобы узнать, как это устроено и почему оно так действует.

Но даже интеллектуальные трудности не так негативно сказываются, как психологические. Самая главная — соревновательность. Даже если это не подогревается учительницей, по законам развития группы в любом классе, пусть самом дружном, есть соревновательность и места «первого» и «последнего» в классе.

Соответственно, девочки в этом возрасте всегда и везде «быстрее-выше-сильнее», и в условиях современной акселерации даже и на физкультуре мальчикам не всегда удается одерживать победу (практически во всех знакомых мне первых классах самые высокие — девочки, а не мальчики).

Вообще то, что в классе ровесники мальчики и девочки — уже неправильно, потому что девочки гораздо опережают мальчиков в психическом развитии и других сферах. (Если почитать материалы о гендерных отличиях, вы найдете интересный факт — уже новорожденные девочки отличаются от мальчиков примерно на 2-3 недели по развитию — а ведь их еще никак «гендерно-ориентированно» не воспитывали! Девочки быстрее устанавливают контакт глаз, узнают лица близких и т.п.)

Конечно, к восьмому классу ситуация будет иная — в старших классах мальчики стремительно догоняют и обгоняют девочек в учебе. Но ведь и подсознание не будет ждать восемь лет!

В детсаду и начальной школе уже сформируются совершенно «немужские» пораженческие и зависимые позиции.

Такая ситуация, когда девочка публично доказывает свое превосходство, ломает мужское достоинство. А это происходит сплошь и рядом: мальчик не смог решить задачу у доски, вызвали дописывать девочку; девочки быстрее прорешают контрольную работу и сдадут тетрадки, а мальчики будут долго возиться; аккуратные работы девочек чаще оказываются на выставках, доске почета и т.п.; мальчики часто получают замечания за поведение и невнимательность, и им ставят в пример девочек; в конце концов, неуспевающие ученики-мальчики списывают уроки у отличниц-девочек.

Мы в самом начале темы говорили о том, что мужчине жизненно необходимо демонстрировать свои достижения и получать женское восхищение. И в том возрасте, когда у мальчиков формируются гендерные роли и поведенческие модели, они постоянно получают вербальные и невербальные негативные характеристики! Что особенно важно — в самом невыгодном сравнении с более успешными и социально принятыми девочками.

Мужчина должен демонстрировать достижения и получать женское восхищение, а получается все наоборот — мальчикам внушают, что они никчемные ничтожества на фоне главных и во всем превосходящих девочек.

Кроме того, что это провоцирует агрессию (уж действительно, хочется этих девчонок поколотить в углу на перемене), это еще и строит неправильные представления о себе и неадекватную самооценку.

У мальчика нет визуального подкрепления собственных достижений. Мальчик лишается представления, чем созидательным он может достичь успеха. Что это означает? Что мальчик чуть позже будет искать, чем же проявить свою маскулинность? Как вы понимаете, самый легкий и короткий путь всегда находится не очень хороший: если ты не куришь — ты не мужик, и т.п.

Марина Озерова

 

О параллельном обучении девочек и мальчиков

К настоящему времени в отечественной и мировой науке и образовательной практике накопилось достаточно аргументированных данных, указывающих на крайне негативное влияние смешанного обучения мальчиков и девочек на их духовное и физическое развитие и здоровье.

Заголовки авторитетных СМИ:

Исследование, проведенное в Великобритании, демонстрирует целесообразность раздельного обучения

Мальчики и девочки в школах должны обучаться отдельно. Таковы результаты правительственных исследований программы, которая проводилась в течение четырёх лет. Как показало исследование, отсутствие в классе девочек способствует тому, что мальчики показывают лучшие результаты на экзаменах. Связано это, по мнению учёных, с тем, что отсутствие представительниц противоположного пола позволяет мальчикам быть более раскрепощёнными…Исследование проведенное в 50 школах, где мальчики и девочки обучаются раздельно, показало, что при такой системе обучения мальчики показывают гораздо более впечатляющие результаты». (газета Independent).

• • • «Нью-Йорк Таймс» ( от 04. 03.2004) сообщает о предложенных новых правилах, которые открывают перед администрацией учебных заведений возможность создавать классы и школы с раздельным обучением».
    • «The Philadelphia Inquier»: психологи сообщают, что при раздельном обучении дети становятся более дисциплинированными, дружными и значительно повышается их успеваемость.
    • «Совместное с мальчиками обучение делает 94% девочек больными. К такому выводу пришли специалисты Института гигиены детей и подростков, которые 40 лет наблюдали за состоянием здоровья учеников нескольких московских школ» («Дуэль №» №3(300)
    • «В Китае опасаются поколения женоподобных мужчин и набирают учителей мужского пола» (RT, 9 февраля 2016)

Ещё в 80-е годы ХХ столетия Россия дала пример миру ни смешанного «бесполого», ни раздельного «изоляционного» образования. Была предложена модель параллельного образования мальчиков и девочек в параллельных классах (авторы В. Ф.Базарный и Дубровская Е.Н.)

Многолетними исследованиями, выполненными под руководством проф. В.Ф.Базарного установлено следующее:

Смешанное обучение – это основа деградации врожденных задатков мужской и женской личности, в т. ч. их функционального и духовного потенциала, инфантилизации и угасанию мужских качеств у юношей, снижению их трудового и оборонного потенциала, снижению детородного потенциала у молодых женщин, росту врожденной патологии у новорожденных, к взаимному отчуждению полов, деградации семейных устоев, росту социальных пороков.В настоящее время в странах СНГ около 1000 школ используют личностно-ориентированный подход обучения мальчиков и девочек в параллельных классах.

Используют на основе частных инициатив вне государственной политики и межведомственного (образование и здравоохранения) управления. Итоги обобщены и освещены в материалах 1-й Всероссийской научно – практической конференции «Опыт и перспективы поло-личностного (гендерного) образования в России» (г. Железногорск. 22-23 сентября 2009г.)

Понравилась статья? Подпишитесь на канал, чтобы быть в курсе самых интересных материалов

Подписаться

Молодые программисты создадут виртуальную выставку скульптур 18-19 веков в сквере Дзержинского

На смелый эксперимент решились в музее имени Врубеля.

Бронзовые скульптуры 19 века выставят под открытым небом! На смелый эксперимент решились в музее имени Врубеля. Экспонаты теперь сможет увидеть каждый, кто прогуливается по скверу Джержинского. За сохранность предметов искусства организаторы не переживают, выставка будет виртуальной. Для создания используют технологии дополненной реальности. Это совместный проект музея и ежегодной летней студенческой лаборатории, созданной омскими IT-компаниями. Журналист 12 канала познакомилась с начинающими компьютерными гениями.

«В реальности, в реальном сквере мы хотим расположить музейные экспонаты, чтобы на месте человек с телефоном, с айфоном ходил по скверу и на экране смартфона видел наши экспонаты. Их не нужно расставлять, мы их увеличим в размере. В самом приложении будет инструкция к какой точке нужно подойти, что нужно сделать», — рассказал студент ОмГУПС Ельаман Исаков.

Оцифровка лишь первый этап проекта. Теперь разработчикам приложения предстоит написать специальную программу. В ней ценители искусства смогут не только посмотреть на экспонат, но и узнать историю его создания или информацию об авторе. В первоначальной версии будет всего 6-7 работ. Большая часть из них сейчас представлены на выставке «Неизвестное столетие». Ещё несколько хранятся в заказниках музея и почти не выставлялись. Исправить это и сделать искусство доступнее — одна из главных целей проекта.

«Это возможность показать то, что у нас скрыто в фондах. Музей хранит более 32 тысяч экспонатов, это много, мы большие. И конечно, нам максимально много хотелось показать посетителям музея, горожанам. Такая возможность немножечко приоткрыть завесу в цифровом варианте. Я думаю, что этот эксперимент станет основой для большой долгой дружбы. Во всяком случае мы бы очень этого хотели», — поделилась заместитель директора по развитию основной деятельности музея изобразительных искусств имени Врубеля Ирина Гавриленко.

Разработкой приложения для музея начинающие программисты занимаются в рамках летней студенческой лаборатории, созданной омскими IT-компаниями. Ежегодно отбор сюда проходят почти три десятка талантливых ребят. Их делят на команды и предлагают различные проекты. В этом году таких 8. Это приложения и сайты для различных компаний. Партнёрство взаимовыгодное: фирмы по весьма демократичной цене получают качественный продукт, студенты — возможность заработать и заявить о себе.

«Очень круто, что после университета, а возможно, и обучаясь в университете, буду получать опыт, который потом пригодится в карьере. Лаборатория — это трамплин, акселератор талантов в первую очередь, чтобы заметили, позвали. Лаборатория, которую мы в 2013 году проводили, тому яркий пример, её выпускники сегодня очень успешны», — говорит технический директор IT-компании Алексей Коровянский.

Сдать проекты начинающие программисты должны до конца августа. Кстати, некоторые разработки организаторы студенческой лаборатории планируют презентовать на международном конкурсе. И, возможно, после этого омскими талантливыми студентами заинтересуются крупные корпорации.

Фото: pixabay.com.

---

Добавить в избранные источники Яндекс.Новостей

Подписаться на канал Яндекс.Дзен

Подписаться на канал Телеграм

Весна 2021 г. Ресурсы для администрирования тестов MCAS 3–8 классы и старшие классы ELA и математика (Next-Gen) и STE

Перейдите в центр ресурсов MCAS, чтобы получить следующее: ресурсов для подготовки студентов, включая учебное пособие для студентов, практические тесты, руководства по редактору формул и справочные листы по математике и STE учебных модулей для персонала и записи ранее предложенных учебных занятий Руководства по технологиям CBT и руководства пользователя, включая руководства для SR / PNP и испытаний инфраструктуры

Дополнительные политики / ресурсы

Правила участия на весну 2021 года

Обновленное руководство на весну 2021 года

Анкета для учащихся MCAS («Взгляды на климат и обучение [VOCAL], проект опроса учащихся)»

Образцы школьных материалов для координации проведения экзаменов MCAS

Полный список испытательных материалов (для использования при инвентаризации грузов для PBT и MCAS-Alt)

Слайд-шаблон для обучения администраторов тестирования

Ресурсы, связанные с технологиями для компьютерного тестирования

Рекомендации по настройке TestNav для учащихся в гибридном или удаленном обучении

PearsonAccess Следующие обновления на 2021 год

Обновления TestNav на 2021 год

Управляемые устройства Chromebook, необходимые для компьютерного тестирования

Ресурсы по цифровому обучению и технологиям

Планировщик компьютерных испытательных устройств 2021

Технические характеристики технологии

для компьютерного тестирования MCAS
Примечание. Регулярно проверяйте эту страницу на наличие обновлений.

Системные требования TestNav на 2020–2021 годы

Pearson, субподрядчик по тестированию, принял политику технологической поддержки для обновления операционной системы (ОС) устройства, которая согласовывает системные требования TestNav с поддерживаемыми производителем ОС и устройствами. Pearson будет основывать свою поддержку операционных систем и устройств на поддержке производителя с 15 июля. Технический персонал должен оценить поддержку производителя по состоянию на 15 июля , чтобы определить технологическое планирование на каждый предстоящий учебный год.Список устройств Chrome OS и даты истечения срока их действия можно найти в разделе «Управление политиками для устройств Chrome: политика автоматического обновления». Пожалуйста, обратитесь к Политике требований к системе TestNav компании Pearson и Системным требованиям TestNav для получения дополнительной информации.

Дополнительные правила / ресурсы для средних школ

Рекомендации по участию в программе MCAS для получения стипендии Адамса и Коплика

Дистанционное тестирование для 3–8 классов

Инструкции по изменению теста студента в PAN с дистанционного тестирования на личное тестирование

Настройка ProctorCache для удаленного тестирования (только для школ, использующих ProctorCache для личного тестирования)

Обновленное руководство по дистанционному тестированию

Руководство для дистанционного тестирования учащихся 3–8 классов для округов с удаленной академией

Инструкции администратора по дистанционному тестированию

Инструкции администратора тестирования для компьютерного удаленного тестирования

Образец письма и формы для дистанционного тестирования (рекомендуется для 6–8 классов) — на английском языке и переводы

Образец письма для родителей / опекунов удаленных учащихся 3–8 классов, которым требуется PBT — на английском языке и переводы

Последнее обновление: 1 июня 2021 г.

Оценка успеваемости для школ Аляски (PEAKS)

Стандарты искусств английского языка Аляски (ELA) демонстрируют ожидание того, что учащиеся будут развиваться в разных классах по чтению и анализу различных сложных текстов, четкому письму для различных целей, а также представлению и оценке идей и доказательств.Стандарты ELA разработаны, чтобы помочь студентам развить логическую последовательность в беглости речи, анализе и применении, продвигаясь к поступлению в колледж и карьере.

Стандарты математики Аляски предполагают, что навыки учащихся будут расти в зависимости от класса как по математике, так и по математическим практикам. Стандарты по математике разработаны, чтобы помочь учащимся развить логическую последовательность в математической беглости, концептуальном понимании и применении в реальном мире.

Научные стандарты K-12 для Аляски поддерживают обучение и понимание посредством осмысления и исследований, связанных с научными явлениями в науках о жизни, физических науках, науках о Земле и космосе, а также в инженерии и технологиях.В стандарты включены сквозные концепции, организационная структура для объединения знаний из различных научных дисциплин в последовательный и научно обоснованный взгляд на мир. Также включены научные и инженерные практики, Стандарты Аляски для школ с учетом культурных особенностей , а также аргументы, основанные на доказательствах, используемые в английском языке по искусству и математике.

Тесты по английскому языку и математике проводятся для учащихся 3–9 классов. Экзамен по естествознанию проводится учащимся 5, 8 и 10 классов.

Оценка науки PEAKS

В июне 2019 года на Аляске были приняты научные стандарты K-12 для Аляски , обеспечивающие новую основу для определения того, что студенты должны знать и уметь делать с точки зрения научных знаний и навыков. В результате началась работа по проектированию, разработке и внедрению новой оценки, которая заменит научную оценку Аляски оценкой, соответствующей научным стандартам K-12 для Аляски .

Оценка естественных наук PEAKS будет проводиться на территории всего штата для учащихся 5, 8 и 10 классов весной 2021 года.

Часто задаваемые вопросы о новой научной оценке PEAKS

Дизайн тестов и чертежи для экзаменов по английскому языку, математике и естествознанию, весна 2021 г.

Ресурсы по подготовке учащихся к экзаменам на бумаге или компьютере см. На вкладке «Подготовка учащихся».

Ресурсы для родителей и сообщества

Суммарные оценки Аляски

---

Подготовка студентов

---

Подготовка студентов

Следующие ресурсы были созданы, чтобы помочь подготовить учащихся и школы к экзаменам PEAKS и Alaska Science.Все ресурсы доступны для студентов, преподавателей, родителей и членов сообщества. DEED призывает всех использовать эти инструменты, чтобы ознакомиться с оценками.

Компьютерные тесты

Обучение онлайн-инструментам (OTT)

Учебное пособие для учащихся

Тесты на бумажной основе

Образцы заданий на бумаге

доступны для подготовки учащихся к экзаменам на бумаге. Тестовые буклеты и документы с ответами, а также сводные таблицы можно скачать из приведенной ниже таблицы.Сводные таблицы также предназначены для использования с компьютерным OTT.

Дизайн оценки

Департамент образования и раннего развития штата Аляска (DEED) лицензирует предметы из банка предметов для подготовки к колледжу и карьере (CCR) корпорации Data Recognition Corporation (DRC) для использования в экзаменах по английскому языку и математике. В августе 2017 года было проведено независимое стороннее исследование согласования, которое показало очень сильное соответствие между заданиями, используемыми при оценке, Аляскинским стандартам ELA и математике.Отчет об исследовании центровки предоставляется по запросу.

Ежегодно DRC составляет технический отчет, в котором содержится информация и анализ данных, подтверждающий достоверность и надежность итоговых оценок. Технический отчет предоставляется по запросу.

Дескрипторы уровня достижений (ALD)

Результаты

---

Родители

---

Педагоги

---

Дескрипторы уровня достижений (ALD)

Ресурсы для текстового анализа (TDA)

Раздел «Искусство английского языка» (ELA) программы PEAKS представляет учащимся вопрос «Текстозависимый анализ» (TDA).TDA был впервые включен в оценку ELA весной 2018 года, чтобы лучше согласовать оценку со стандартами ELA Аляски, принятыми в 2012 году. Стандарт написания W-9 связывает чтение для получения доказательств и анализ текста с возможностью записывать логические аргументы. TDA дает учащимся возможность продемонстрировать, что они могут интегрировать навыки грамотности и что чтение и письмо не являются отдельными навыками, а работают вместе.

Жилье и поддержка студентов

Поддержка студентов доступна для студентов, сдающих экзамены PEAKS и Alaska Science на компьютере и на бумаге.Универсальные инструменты — это поддержка или предпочтения, доступные всем учащимся. Адаптация — это практика и процедуры, которые обеспечивают равный доступ и используются регулярно и успешно во время инструктажа и оценок. Жилье должно быть доступно учащимся с ограниченными возможностями с планом IEP или 504, учащимся с преходящими нарушениями и учащимся EL, как указано в планах для учащихся. Дополнительную информацию можно найти на странице размещения.

Управление тестирования

Ресурсы по администрированию тестирования

обновляются ежегодно.

Руководства, руководства и политики

---

Формы оценки

---

DRC INSIGHT

---

Справочные листы

---

Ресурсы для DTC

Вход в Smartsheet — для доступа к DTC Corner Smartsheet.
Свяжитесь с Рэйчел, если вам нужен доступ.

Разъяснения об отказе от медицинских услуг (pdf)

Технологии

Alaska сотрудничает с Data Recognition Corporation (DRC) в проведении оценки успеваемости в школах Аляски, или PEAKS.DRC создала специальный номер телефона и адрес электронной почты для Аляски, чтобы помочь округам использовать портал DRC INSIGHT, тестовую систему INSIGHT и внедрять технологии.

Служба поддержки клиентов DRC

Телефон — 1-866-339-6390

Электронная почта — [email protected]

Технологические ресурсы для округов, такие как Руководство по использованию технологий (TUG) и Системные требования, доступны на портале DRC INSIGHT на вкладке «Документы» в разделе «Общая информация».

Бесплатная практика MAP для 3-го класса!

Что такое тест NWEA MAP для 3-го класса?

MAP Test для 3-го класса — это бессрочный компьютерный тест, разделенный на три предмета: математика, использование языка и чтение. Это отличный способ как для учителей, так и для родителей лучше понять успехи ученика в течение года, а также его учебные потребности. Это также способ для школ проверить, нужно ли ученикам быть помещенными в специальную программу.Узнайте больше о тестировании MAP.

NWEA MAP Test 3-го класса, согласованный с общим ядром

По мере того, как Common Core становится все более распространенным в школах США, многие стандартизированные и одаренные тесты адаптируются к его стандартам. Тест MAP для 3-го класса не исключение. По этой причине TestPrep-Online разработал практические тесты, которые следуют схеме Common Core MAP. С помощью нашего практического пакета MAP для 3-го класса вы можете убедиться, что ваш третий класс знакомится со всеми темами, соответствующими Общему ядру, и получает первоклассную практику для теста.

NWEA 3-й класс MAP Math Section

Раздел MAP Math для 3-го класса включает четыре общие области, которые обычно охватываются к тому времени, когда ученик достигает 3-го класса:

• Числа и операции: использование математики в уме для подсчета и вычислений
• Операции и алгебраическое мышление: применение основных функций дробей и десятичных дробей
• Алгебра: решение уравнений с недостающей информацией
• Геометрия: применение геометрических понятий, таких как симметричные и параллельные линии

Для большинства вопросов не требуется калькулятор, но для тех, кто требует, появится экранный калькулятор.Тестируемым также выдаются бумажки для решения задач. В среднем по математическому разделу 53 вопроса. Однако это число может быть изменено из-за адаптивного характера теста.

Раздел об использовании языка MAP NWEA

Раздел «Использование языка MAP» состоит из 53 вопросов с несколькими вариантами ответов. Взгляните на то, что описано в этом разделе:

Язык: демонстрирует понимание различных языковых соглашений, включая пунктуацию, регистр и орфографию
Грамматика и использование: демонстрирует понимание грамматических соглашений и точно их применяет
Письменные соглашения: демонстрирует, как планировать и организовывать написание

Нарисуйте путь вашего ребенка к успеху!
469 Вопросы и пояснения от $ 89

Подробнее

Раздел чтения карты NWEA MAP

Раздел MAP Reading для третьего класса адаптирован для того, чтобы задавать вопросы, на которые обычно способны ответить третьеклассники.Раздел для чтения разделен на три основных подраздела:

Распознавание слов и словарный запас: декодирование слов и распознавание структур слов и взаимосвязей
Литература: понимание ключевых структур и идей в литературных текстах, демонстрирующее способность анализировать ключевые ремесла и цели
Информационные тексты: , демонстрирующие понимание основных идеи и структура

Образцы вопросов теста MAP для 3-го класса

3)

Вопрос 8: понимание прочитанного

Прочтите историю. «Но я еще не хочу спать!» — причитал Ной. «Я хочу не ложиться спать и играть в свою новую игру!» Ной был младшим ребенком в семье. Ему уже разрешили ложиться спать позже, чем его брату и сестре, когда они были его возраста. «Если ты не пойдешь спать, зубная фея не сможет навестить тебя», — сказал отец Ноя. Услышав это, Ной побежал прямо в постель. Он заглянул под подушку, чтобы убедиться, что его зуб все еще там. Наконец, Ной заснул.Когда он проснулся, на улице было еще темно. Он увидел тень на стене и почувствовал, как кто-то тянется под его подушку. Ной очень плотно зажмурился, чтобы зубная фея все же отдала ему его подарок. Он фактически снова заснул еще до того, как почувствовал свое настоящее. Утром Ной проснулся очень взволнованным. Он пощупал подушку и нашел там новую красную игрушечную гоночную машинку! Он не видел зубную фею, но все еще чувствовал запах ее духов. Пахло духами его матери. Какое из следующих слов лучше всего можно использовать для заполнения поля? А) Он боялся зубной феи. Б) Он боялся, что зубная фея не придет. C) Время его сна уже прошло. D) Он очень устал.

Ответ и объяснение ▼ | ▲ Правильный ответ — Б. В этом отрывке упоминается, что после того, как отец Ноя сказал Ною, что, если он не ляжет спать, зубная фея не сможет навестить его, Ной сразу же побежал спать.Из этой информации можно сделать вывод, что Ной боялся, что зубная фея не навещает его, если он не ложится спать, и поэтому сразу побежал в постель. Следовательно, правильный ответ (B). Ответ (A) неверен, потому что в отрывке упоминается, что Ной ждал прихода зубной феи, поскольку он хотел получить подарок за свой зуб. Таким образом, он ее не боялся. Ответ (C) неверен, потому что в отрывке упоминается, что Ной уже пора спать, и он все еще не хотел ложиться спать. Ответ (D) неверен, потому что он представляет информацию, которая вообще не упоминается в отрывке.

Нарисуйте путь вашего ребенка к успеху!
469 Вопросы и объяснения
От $ 89

Подробнее

9 советов, которые помогут вашему ребенку успешно сдать MAP-тест 3-го класса

Перед тестом:

• Составьте учебный план. После того, как вы пройдете наш первоначальный образец теста, создайте иерархию предметов для изучения на основе сильных и слабых сторон вашего ребенка.
• Придерживайтесь распорядка. Помогите своему ребенку оставаться сосредоточенным. Сохраняйте фиксированный распорядок дня, выделяя для занятий одно и то же время каждый день. Это держит вашего ребенка морально подготовленным.
• Поддерживайте мотивацию вашего ребенка. Добавьте веселые занятия в учебный план, чтобы помочь вашему ребенку увлечься процессом обучения. Сидеть за столом полезно только короткое время, прежде чем оно станет утомительным. Мы рекомендуем игру с вопросами, в которой вы поощряете ребенка задавать определенное количество вопросов каждый день с обещанием вознаграждения в конце.
• Будьте позитивными. Отрицательное отношение может быть заразным, но и положительное тоже! Ваш ребенок будет в восторге от обсуждаемого предмета!

День проверки:

• Обзор — не учить. Надеемся, что на этом этапе вы уже получили много новой информации. Поэтому не рекомендуется начинать изучать что-то новое, так как это может помешать вашему ребенку использовать материал, который он / она уже выучил и который чувствует себя более комфортно, и получить оптимальные оценки, которых он / она заслуживает.
• Принесите закуски. Трудно сосредоточиться на пустой желудок; мы рекомендуем избегать этой проблемы, упаковывая различные полезные источники энергии, чтобы ваш ребенок мог их есть во время экзамена. Кто знает? Этот дополнительный толчок мог иметь значение между правильным и неправильным ответом.
• Приходите слоями. Ваш ребенок может отвлекаться, если в комнате слишком холодно или слишком тепло. Чтобы избежать этой проблемы, попросите ребенка одеться в легкую одежду и принести на тест свитер, который позволит ему чувствовать себя комфортно при любой температуре.
• Используйте идею «вознаграждения за участие». Ваш ребенок может испытывать давление перед обследованием. Постарайтесь избавиться от этого чувства, привнеся более прямой стимул — возможно, угощение после завершения теста, независимо от того, какие оценки получит ваш ребенок.
• Приходи пораньше. Выйдите из дома пораньше, чтобы дать время найти место и уладить неприятности, которые могут произойти по пути, например, невозможность определить местоположение или попасть в пробку.Кроме того, это даст вам возможность побеседовать с вашим ребенком, который так необходим.

Нарисуйте путь вашего ребенка к успеху!
469 Вопросы и объяснения
От $ 89

Подробнее

Практика тестирования MAP для 3-го класса

Получите больше примеров вопросов MAP для 3-го класса с помощью практического пакета MAP для 3-го класса TestPrep-Online! В нашем пакете 804 типовых вопроса, включая практические тесты для отдельных разделов, чтобы вы и ваш ребенок могли легко сосредоточиться на одном навыке за раз, если это необходимо.

Несмотря на то, что это стандартизованный тест, ребенок может — и должен — подготовиться к тесту MAP заранее, поскольку результаты тестирования MAP могут быть решающим фактором для помещения в обычные или одаренные классы. Чтобы помочь вам подготовиться, TestPrep-Online предлагает полный пакет практических занятий по тестированию MAP для 3-го класса.

MAP, CogAT и другие товарные знаки являются собственностью соответствующих владельцев товарных знаков. Ни один из владельцев товарных знаков не связан с TestPrep-Online или этим веб-сайтом.

Профессиональное развитие — Математические перспективы

Чтобы наши ученики были готовы встретить вызовы 21 века, классные учителя должны знать, как дети развивают понимание основных концепций математики и основных идей, которые являются вехами или препятствиями на пути к росту понимания. Кэти Ричардсон определила эти этапы обучения как критические фазы обучения ™. Учителям больше нет смысла обучать своих учеников методам решения математических задач без смысла и понимания.

Math Perspectives осознает важность профессиональной роли классных учителей, и мы знаем, что учителя нуждаются в постоянной поддержке и профессиональном развитии, чтобы справляться с растущими проблемами профессии, чтобы у детей был прочный фундамент и понимание математики, необходимой им для достижения успеха. математика высшего уровня и интеллектуальные преимущества, которых заслуживает каждый ученик.

Посмотреть наше текущее расписание

---

ИНСТИТУТЫ И КУРСЫ

Развитие математических понятий в Pre-K
Уровень класса: Pre-K
Продолжительность: 2 дня
Этот двухдневный курс посвящен учителям Pre-K тому, как создать позитивную среду, которая поддерживает изучение математики.Они получат знания о том, как исследуются математические идеи в среде Pre-K, посредством игры, активного участия и преднамеренных учебных заданий, а также научатся использовать методы опроса для развития математического мышления. Участники научатся предоставлять соответствующий опыт, который стимулирует математическое развитие и понимание и позволит им дифференцировать обучение в соответствии с рядом потребностей в их классе. Текст этого курса — Кэти Ричардсон «Развитие математических понятий в дошкольном возрасте».Подробнее…

---

Развитие числовых концепций
Уровень обучения: K-2
Продолжительность: 3 дня
Этот курс фокусирует внимание учителей K-2 на способах помочь детям развить понимание и компетентность в счетах, отношениях чисел, сложение, вычитание и разряд. Участники узнают, как вовлечь детей в значимые занятия, которые обеспечивают надлежащую практику и гарантируют, что у детей есть фундамент, в котором они нуждаются для будущего успеха.Участники узнают, как создать позитивную учебную среду в своих классах, а также узнают о практических методах предоставления занятий и материалов, отвечающих различным потребностям в их классах. Подробнее…

---

Институт оценки математических понятий (AMC)
Уровень обучения: K-3
Продолжительность: 5 дней
Институт оценки математических концепций (AMC) с точки зрения математики предназначен для преподавателей, тренеров по математике, математике координаторы, руководители учителей, профессиональные разработчики и другие педагоги, которые поддерживают профессиональное развитие детского сада через учителей математики третьего класса.AMC — это углубленное исследование того, как дети учат понятия чисел. Участники проводят неделю, погружаясь в изучение мышления и обучения детей, чтобы определить учебные потребности учащихся. Подробнее…

---

Курсы оценки математических понятий (AMC) для классов
Классы: K, 1 и 2
Продолжительность: 3 дня каждые
Несмотря на принятую школьную программу или используемые тесты, дети не все учатся в таком же темпе. В результате учителям необходимо определить, что их ученикам еще предстоит изучить, чтобы обеспечить им оптимальный и подходящий опыт.В ходе этих трехдневных курсов участники научатся использовать соответствующие оценки на уровне класса из серии «Оценка математических концепций» для определения учебных потребностей своих учеников. Они также научатся использовать информацию, полученную в результате оценивания, чтобы сосредоточить свое обучение и максимизировать обучение студентов, используя стратегии обучения из серии «Развитие числовых концепций» Кэти Ричардсон. Подробнее…

---

Преподавание для понимания
Уровень обучения: K-2 / 3-5
Продолжительность: 5 дней
Эти пятидневные курсы посвящены тому, как активно вовлекать учащихся в математику способами, которые выводят их за рамки процедуры для глубокого понимания основных математических понятий.Внимание уделяется созданию учебной среды, которая позволяет учителям определять учебные потребности отдельных детей и удовлетворять ряд потребностей в своих классах. Курс также посвящен тому, чтобы помочь учителям развить собственное понимание и знание ключевых математических понятий, которым они учат. Подробнее…

---

Числовые беседы: мышление числами K-2
Числовые беседы: мышление числами 3-5
Уровень оценки: K-2 и 3-5
Продолжительность: 3 дня
Во время этих трех- На дневных курсах учителя учатся помогать учащимся приобрести компетентность в вычислениях, используя визуальные модели и числовые отношения, чтобы развивать чувство числа и разрабатывать мощные численные стратегии, которые имеют смысл для учащихся.Учащиеся работают с числами, используя простые, но значимые и действенные стратегии. Учителя видят, что эти методы смоделированы, когда они наблюдают, как дети решают задачи во время разговоров с числами. Курс также посвящен тому, чтобы помочь учителям укрепить собственное понимание математики. Подробнее…

---

Понимание дробей
Уровень обучения: 3-5
Продолжительность: 3 дня
В этом курсе учителя научатся представлять ключевые концепции дробей таким образом, чтобы помочь учащимся глубже понять фундаментальные отношения, язык и символика дробей, десятичных знаков и процентов.Участники будут заниматься деятельностью, которая способствует разумным вычислениям со всеми четырьмя операциями. Подробнее…

---

Понимание чисел: развитие вычислительной техники
Уровень обучения: 3-5
Продолжительность: 3 дня
Этот трехдневный курс знакомит учителей 3-5 классов с методами и упражнениями, которые помогут их ученикам развиваться. понимание структуры чисел как основы для беглости вычислений. Темы включают в себя разряд, сложение и вычитание нескольких цифр, умножение и деление, а также первый взгляд на десятичные дроби.Подробнее…

Посмотреть наше текущее расписание

Оценка математических концепций: оценки

Краткие личные интервью

Оценки проводятся в виде коротких индивидуальных собеседований с учениками / учителями. Этот формат имеет решающее значение, поскольку «больше всего мы узнаем о том, как думают наши ученики и что они могут делать, когда мы сидим рядом с ними и наблюдаем за их математической работой». Из-за возраста и способностей юных учеников оценка по математике должна больше полагаться на наблюдение и беседу, а не на письмо.«То, что студенты пишут на бумаге, дает лишь представление о том, что они знают и думают» (Ричардсон, «Оценка математических концепций»). Каждая оценка может занять от пяти минут до пятнадцати минут.

Ответы студентов можно записать с помощью бумажных форм для собеседований со студентами или с помощью веб-программы. Учителя, использующие веб-версию, могут использовать любой настольный компьютер, iPad или ноутбук с доступом в Интернет.

AMC Уровни обучения

Уровни обучения по оценке математических понятий определяют конкретный уровень понимания и способности, которых студент достиг с данным математическим понятием.Щелкните здесь, чтобы прочитать о каждом из этих уровней для каждой из девяти оценок.

Ниже приведены отрывки из трех интервью со студентами AMC.

Рекомендации по использованию AMC

Поскольку числовые концепции развиваются относительно предсказуемым образом, существуют определенные концепции и важные этапы обучения, с которыми необходимо работать большинству детей в определенных классах.Учителя могут использовать оценки AMC для определения учебных потребностей своих учеников по мере развития их компетенции с конкретными концепциями. Этот документ представляет собой руководство для учителей, которые используют AMC, чтобы спланировать соответствующее обучение для всего класса, поскольку они сосредотачиваются на различных концепциях в течение года.
Скачать документ в формате PDF | 340 КБ

Книги AMC

В каждой книге содержится справочная информация учителя для постановки и использования заданий по оценке, инструкции по проведению наблюдений в классе, советы по организации информации и предложения по обучению.Учителя с черной линией включены и могут быть воспроизведены для оценивания в классе.
Подробнее »

Оценка на работе — мониторинг успеваемости ученика

Оценка математических концепций дает учителям задания «Оценка на работе» для каждой из оценок, чтобы дать учителям целенаправленный способ отслеживать текущую успеваемость ученика. Предоставляется все, что учителям необходимо для мониторинга успеваемости ученика. — инструкции, мастера черных линий и формы «Оценка на работе» есть в книгах AMC.

Посмотрите пример того, как Кэти Ричардсон демонстрирует задание AMC «Оценка на работе» с использованием карт комбинации номеров. Это задание из оценки AMC Combination Trains:

Отчетность и данные

Доступна мощная веб-система отчетности, которая суммирует результаты для учителей и администрации.
Подробнее »

Пожалуйста, звоните в отдел Math Perspectives с вопросами 1-360-715-2782

Тесты, которые мы уже создали для вас — Illuminate Education

Описание:

Эти 48 экзаменов Scott Foresman Reading Street предназначены для классов K-6 и включают контрольные показатели Unite и End of Year.

Оценок включено:

классы K-1: ISBN # 978-0-328-48542-0

2–3 классы: ISBN # 978-0-328-48543-7

4–6 классы: ISBN # 978-0-328-48899-5

Scott Foresman Reading Street PM Gr K Unit 1 BM

Scott Foresman Reading Street PM Gr K Unit 2 BM

Scott Foresman Reading Street PM Gr K Unit 3 BM

Scott Foresman Reading Street PM Gr K Unit 4 BM

Scott Foresman Reading Street PM Gr K Unit 5 BM

Scott Foresman Reading Street PM Gr K Unit 6 BM

Scott Foresman Reading Street PM Gr K EOY BM

Scott Foresman Reading Street PM Gr 1 Unit 1 BM

Scott Foresman Reading Street PM Gr 1 Unit 2 BM

Scott Foresman Reading Street PM Gr 1 Unit 3 BM

Scott Foresman Reading Street PM Gr 1 Unit 4 BM

Scott Foresman Reading Street PM Gr 1 Unit 5 BM

Scott Foresman Reading Street PM Gr 1 EOY BM

Scott Foresman Reading Street PM Gr 2 Unit 1 BM

Scott Foresman Reading Street PM Gr 2 Unit 2 BM

Scott Foresman Reading Street PM Gr 2 Unit 3 BM

Scott Foresman Reading Street PM Gr 2 Unit 4 BM

Scott Foresman Reading Street PM Gr 2 Unit 5 BM

Scott Foresman Reading Street PM Gr 2 Unit 6 BM

Scott Foresman Reading Street PM Gr 2 EOY BM

Scott Foresman Reading Street PM Gr 3 Unit 1 BM

Scott Foresman Reading Street PM Gr 3 Unit 2 BM

Scott Foresman Reading Street PM Gr 3 Unit 3 BM

Scott Foresman Reading Street PM Gr 3 Unit 4 BM

Scott Foresman Reading Street PM Gr 3 Unit 5 BM

Scott Foresman Reading Street PM Gr 3 Unit 6 BM

Scott Foresman Reading Street PM Gr 3 EOY BM

Scott Foresman Reading Street PM Gr 4 Unit 1 BM

Scott Foresman Reading Street PM Gr 4 Unit 2 BM

Scott Foresman Reading Street PM Gr 4 Unit 3 BM

Scott Foresman Reading Street PM Gr 4 Unit 4 BM

Scott Foresman Reading Street PM Gr 4 Unit 5 BM

Scott Foresman Reading Street PM Gr 4 Unit 6 BM

Scott Foresman Reading Street PM Gr 4 EOY BM

Scott Foresman Reading Street PM Gr 5 Unit 1 BM

Scott Foresman Reading Street PM Gr 5 Unit 2 BM

Scott Foresman Reading Street PM Gr 5 Unit 3 BM

Scott Foresman Reading Street PM Gr 5 Unit 4 BM

Scott Foresman Reading Street PM Gr 5 Unit 5 BM

Scott Foresman Reading Street PM Gr 5 Unit 6 BM

Scott Foresman Reading Street PM Gr 5 EOY BM

Scott Foresman Reading Street PM Gr 6 Unit 1 BM

Scott Foresman Reading Street PM Gr 6 Unit 2 BM

Scott Foresman Reading Street PM Gr 6 Unit 3 BM

Scott Foresman Reading Street PM Gr 6 Unit 4 BM

Scott Foresman Reading Street PM Gr 6 Unit 5 BM

Scott Foresman Reading Street PM Gr 6 Unit 6 BM

Scott Foresman Reading Street PM Gr 6 EOY BM

Преподавание математики посредством концептуальной мотивации и практического обучения

Это практический концептуальный документ, описывающий избранные средства для практического обучения и концептуальной мотивации на всех уровнях математического образования.В нем подробно описан подход, использованный авторами для разработки идей для практиков преподавания математики. В статье показано, что такой подход в математическом образовании, основанный на практическом обучении в сочетании с естественной мотивацией, проистекающей из здравого смысла, является эффективным. Кроме того, стимулирующие вопросы, компьютерный анализ (включая поиск в Интернете) и классические известные задачи являются важными инструментами мотивации в математике, которые особенно полезны в рамках практического обучения. Авторы утверждают, что вся учебная программа по математике K-20 под единым зонтом возможна, когда методы концептуальной мотивации и обучения действиям используются во всем этом широком спектре.Этот аргумент подтверждается различными примерами, которые могут быть полезны на практике школьным учителям и преподавателям вузов. Авторы нашли прагматическую причину для практического обучения в рамках математического образования практически на любом этапе академической жизни учащихся.

1. Введение

В настоящее время студентам требуется как познавательный, так и практический опыт на протяжении всего их математического образования, чтобы быть продуктивными гражданами 21 века. Происхождение этого утверждения можно проследить до работ Джона Дьюи, который подчеркивал важность образовательной деятельности, которая включает «развитие любого рода артистических способностей, особых научных способностей, эффективных гражданственности, а также профессиональных и деловых качеств». профессий »([1], с.307). Совсем недавно Биллетт [2], основываясь на своих исследованиях интеграции опыта обучения студентов высших учебных заведений в дисциплинах, связанных с сестринским уходом и подобными услугами в поддержку человеческих потребностей, предположил, что «возможно, можно полностью интегрировать практический опыт в совокупность опыта высшего образования, которая способствует развитию прочных и критических профессиональных знаний »(стр. 840). Главный аргумент данной статьи состоит в том, что в контексте математического образования практическое обучение (концепция, представленная в разделе 3) — это сам процесс передачи этого опыта в сочетании с концептуальной мотивацией (термин, введенный в разделе 2) при обучении математике. по всей учебной программе K-20.С этой целью в этом концептуальном документе, основанном на практических примерах, подробно описывается подход, использованный авторами для разработки идей для практикующих преподавателей математики, предлагается обзор избранных средств практического обучения в рамках формального континуума математического образования. В определенной степени эта статья продвигает идею обучения на практике [3] в контексте математического образования. Представлены аргументы, подтверждающие ценность практического обучения для всех участвующих лиц (на уровне колледжа, добавляя к дуэту из студента и преподавателя математики еще одного специалиста-нематематика из сообщества или университета) (разделы 2–4).Также рассматривается интеграция компьютерной педагогики подписи (CASP) и нецифровой технологии, а также эффективное опросы с обучением действием (разделы 5 и 6).

Студенты могут с радостью получать формальное математическое образование в течение двадцати и более лет, и они могут быть мотивированы повсюду с помощью обширных учебных программ по математике. Практическое обучение в математическом образовании в сочетании с механической теорией переносит математические темы в реальный мир. Естественно, что примеры начального уровня имеют основополагающее значение, и это подкрепляется практическим обучением на вторичном уровне (разделы 4.1.1 и 4.1.2). Открытые проблемы математики часто могут быть представлены учащимся начальных, средних и высших учебных заведений (Раздел 7). Традиционно классические результаты и открытые задачи мотивируют не только студентов, но и самих педагогов. Поскольку необходимы эффективные учителя математики, практическое обучение следует использовать на всех уровнях математического образования, зная, что будущие преподаватели входят в число нынешних учащихся. Конечно, возможность участвовать в открытиях очень мотивирует всех, включая студентов и учителей математики, по крайней мере.

2. Любопытство и мотивация

Хотя необходимость изучения математики в начальной, средней и высшей школе общеизвестна, вопрос о том, как преподавать математику, остается спорным. Как более подробно описано в [4] со ссылками на [5–10], разногласия вызваны неоднородностью программ подготовки учителей, разногласиями между формализмом и смыслом между преподавателями математики и различными взглядами на использование технологий. Мы считаем, что надлежащий способ преподавания математики на всех уровнях — это делать это через приложения, а не использовать традиционные лекции, подчеркивая формализм математического аппарата.Реальные приложения поддерживают мотивацию заинтересованных людей в изучении математики. Эту естественную мотивацию можно рассматривать как зависящий от возраста процесс, простирающийся от естественного детского любопытства в начальной школе до истинного интеллектуального любопытства на уровне высшего образования. Независимо от возраста учащихся, любопытство можно рассматривать как мотивацию «приобретать или преобразовывать информацию в обстоятельствах, которые не представляют немедленной адаптивной ценности для такой деятельности» ([11], с. 76). То есть любопытство и мотивация — тесно связанные психологические черты.

Большинство исследований по развитию любознательности касается начального образования. Однако эти исследования могут помочь нам понять, как любопытство превращается в мотивацию стать высококлассным профессионалом. Например, Видлер [12] проводил различие между эпистемическим и перцептивным любопытством, которые проявляются, соответственно, «запросом о знании» и проявляются, например, когда ребенок ломает голову над какой-то научной проблемой, с которой он столкнулся… [и] повышенное внимание дается объектам в ближайшем окружении ребенка, например, когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру на экране »(стр.18). Точно так же взрослые учащиеся на высшем уровне могут быть мотивированы призывом своего учителя математики задать вопросы, касающимся информации, которой они поделились, или их опытом общения с окружающим миром, когда они пытаются интерпретировать «ткань мира … [используя] какую-то причину максимум и минимум »(Эйлер, цит. по [13], с. 121).

Связанный с высшим уровнем, Видлер [14] определил мотивацию достижения как «образец… действий… связанных со стремлением достичь некоторого внутреннего стандарта качества» (стр.67). Есть также взрослые ученики, которые «заинтересованы в совершенстве ради него самого, а не ради вознаграждения, которое оно приносит» ([14], с. 69). Биггс [15] допускает, что внутренняя мотивация в изучении математики связана с «интеллектуальным удовольствием от решения проблем независимо от каких-либо вознаграждений, которые могут быть вовлечены… [предполагая, что] цели глубокого обучения и мотивации достижений в конечном итоге расходятся» (стр. 62). Классическим примером в поддержку этого предположения является решение (столетней давности) гипотезы Пуанкаре геометром Григорием Перельманом, который после почти десятилетия «глубокого обучения» отказался от нескольких международных наград за свою работу, включая медаль Филдса («Медаль Филдса»). Нобелевская премия ») и (1 миллион долларов) Clay Millennium Prize (https: // www.Claymath.org/).

Поскольку любопытство является источником мотивации к обучению, Мандельброт [16] в пленарной лекции по экспериментальной геометрии и фракталам на 7-м Международном конгрессе по математическому образованию посоветовал аудитории, в основном преподавателей математики дошкольного образования, как сосредоточиться на любопытстве, когда преподавание математики: «Мотивируйте студентов тем, что увлекательно, и надейтесь, что возникающий энтузиазм создаст достаточный импульс, чтобы продвинуть их через то, что не весело, но необходимо» (стр.86). Именно такую ​​мотивацию авторы называют концептуальной мотивацией. В частности, в этой статье термин «мотивация концепции» означает стратегию обучения, с помощью которой, используя любопытство учащихся в качестве стержня, введение новой концепции оправдывается использованием ее в качестве инструмента в приложениях для решения реальных проблем. Например, операция сложения может быть мотивирована необходимостью регистрации увеличения большого количества объектов другой такой величиной, концепция иррационального числа может быть мотивирована необходимостью измерения периметров многоугольных ограждений на плоскости решетки ( называется геодиской на начальном уровне), или концепция интеграла может быть мотивирована необходимостью найти области криволинейных плоских фигур.

Еще один математически значимый инструмент мотивации — конкретность. Согласно Дэвиду Гильберту, математика начинается с постановки задач в контексте конкретных действий, «подсказываемых миром внешних явлений» ([17], с. 440). Мы считаем, что «конкретность» является подходящим синонимом мотивации в отношении математического образования. Сам термин бетон указывает на то, что различные ингредиенты объединяются и синтезируются. Цель изучения математики — конкретизировать как теоретические, так и прикладные понятия.Полезно иметь четкое представление о чем-либо. Люди по своей природе хотят иметь «полное» знание определенных вещей. Зная детали и конкретизируя идеи, мы уменьшаем беспокойство, связанное с описанием и использованием этих идей. Конкретность мотивирует все стороны, вовлеченные в математическое образование. Даже на административном уровне существует понимание того, что «основная учебная программа FKL [Основы знаний и обучения] предоставит вам возможность изучить множество жизненно важных областей обучения, сделав вас более осведомленными и вовлеченными в понимание проблем, которые глобальные реалии требуют »([18], курсив, добавлено), где мы делаем упор на« реальности ».Это мотивация для всех, поскольку все мы хотели бы использовать математическую теорию или, по крайней мере, увидеть ее применение. Следовательно, мотивация у взрослых учеников пропорционально выше, чем у детей, которые могут не видеть «полезности» в математике. В Университете Южной Флориды преподавателей определенных курсов (например, последовательности исчисления) просят включить утверждение FKL в свои учебные планы.

До недавнего времени термины «промышленный» и «технический» имели довольно уничижительный оттенок в математическом образовании.Традиционное формальное чтение лекций по-прежнему преобладает в большинстве классных комнат. Однако при изучении математической теории часто используется некоторая «отрасль» или «техника», поэтому эти два понятия не дополняют друг друга. Трудно выделить часть огромного объема учебных программ по математике K-20, которая исключает использование теории или возможного практического применения. Кроме того, теория неявно включена в образование в области STEM из-за ее научного компонента.

В контексте подготовки учителей математики акцент на приложениях дает будущим учителям очень важную способность иллюстрировать математические идеи удобными для использования способами.Затем эту способность можно передать своим ученикам. Еще на уровне дошкольного образования можно понять, что математические знания возникают из необходимости разрешать реальные жизненные ситуации разной степени сложности. Принцип учебной программы, выдвинутый Национальным советом учителей математики [19], включает в себя представление о том, что всем учащимся на этом уровне следует предлагать опыт, «чтобы увидеть, что математика имеет мощное применение в моделировании и прогнозировании явлений реального мира» (стр. 15 -16). Этот акцент на приложениях выходит за рамки дошкольного уровня.Действительно, математика сильно развивалась и проникала во все сферы жизни, делая университетское математическое образование необходимым, но неоднозначным элементом современной культуры.

3. Обучение действием

Многие люди прагматичны, делая то, что работает. Когда что-то не работает, человек вынужден задавать вопросы, как заставить это работать. Начиная с 1940-х годов Реджинальд Реванс начал разрабатывать концепцию обучения действием, метод решения проблем, характеризующийся действием и размышлением о результатах, в качестве педагогической педагогики для развития бизнеса и решения проблем [20, 21].С тех пор обучение действием стало описывать различные формы, которые оно может принимать, и контексты, в которых его можно наблюдать. В контексте достижения высокого качества университетского обучения «целью практического обучения является обучение отдельного учителя» ([22], с. 7). В общем контексте повышения профессиональной результативности Дилворт [23] утверждает, что практическое обучение начинается с исследования реальной проблемы, поэтому независимо от того, является ли проблема «тактической или стратегической… [процесс] обучения является стратегическим» (стр.36). Практическое обучение в математическом образовании можно определить как обучение через индивидуальную работу учащихся над реальной проблемой с последующим размышлением над этой работой. В большинстве случаев эту работу поддерживает «более знающий друг».

В математическом образовании практическое обучение, зародившееся в раннем детстве, имеет естественный уровень зрелости. Прежде чем мы займемся повседневными обязанностями, связанными с взрослой жизнью, мы можем свободно рассмотреть практическое обучение в игровой форме.Наша страсть к играм и изучению выигрышных стратегий переносится в более позднюю жизнь как средство развлечения и как инструмент для обучения следующего поколения детей. Мотивация к практическому обучению в математическом образовании постепенно меняется от выигрыша в играх к успеху в реальных предприятиях. Залог успеха — умение решать проблемы. Исследования показывают, что любопытство можно охарактеризовать как волнение по поводу необычных наблюдений и неожиданных явлений [24].Кроме того, «то, что будет интересно детям, во многом зависит от природы окружающего их мира и их предыдущего опыта» ([12], с. 33). Учащиеся на всех уровнях образования стремятся к конкретности, естественно интересуются реальным миром и пользуются преимуществами практического обучения, особенно когда они неоднократно используют его в математическом образовании. В частности, в программе послесреднего математического образования для нематематических специальностей проблемы должны иметь применимость к реальности. Интересно, что мы, кажется, возвращаемся к «играм», когда имеем дело с чистой теорией, поскольку мы можем искать абстрактное решение ради самого решения.

Макс Вертхаймер, один из основателей гештальт-психологии, утверждал, что для многих детей «имеет большое значение, есть ли реальный смысл вообще ставить проблему» ([25], с. 273). Он привел пример 9-летней девочки, которая не училась в школе. В частности, она не могла решать простые задачи, требующие использования элементарной арифметики. Однако, когда ей давали проблему, которая возникла из конкретной ситуации, с которой она была знакома и решение которой «требовалось ситуацией, она не сталкивалась с необычными трудностями, часто проявляя превосходный смысл» ([25], с.273-274). Другими словами, лучшая стратегия развития у студентов интереса к предмету — это сосредоточить преподавание на темах, которые находятся в их сфере интереса. Как сказал Уильям Джеймс, классик американской психологии, который первым применил это к обучению учителей, «Любой объект, не интересный сам по себе, может стать интересным, если он станет ассоциироваться с объектом, к которому интерес уже существует» ( [26], стр. 62). Интерес также можно использовать для развития мотивации в образовании, поскольку он «относится к модели выбора среди альтернатив — моделей, которые демонстрируют некоторую стабильность во времени и которые, по-видимому, не являются результатом внешнего давления» ([27], с.132).

Отражение так же важно, как и действие. Способность размышлять о выполняемых действиях составляет так называемый внутренний контроль, когда люди считают себя ответственными за собственное поведение, что отличается от внешнего контроля, когда они видят, что другие или обстоятельства являются основной мотивацией индивидуального поведения [28 ]. Процесс практического обучения при решении реальной проблемы обычно начинается с трех основных вопросов. Мы спрашиваем: во-первых, что должно происходить? Во-вторых, что нам мешает это сделать? В-третьих, что мы можем сделать?

Практическое обучение (часто называемое в академических кругах практическим исследованием [29, 30]) традиционно использовалось для обучения управлению бизнесом и социальным наукам [31, 32], проведению научных исследований [33] и повышению квалификации учителей [22, 34–36].В математическом образовании [4, 37] практическое обучение как метод обучения было принято как педагогика, ориентированная на самостоятельное решение реальных проблем с последующей рефлексией. Обучение — это основная цель, даже если решение проблем реально и важно. Обучение облегчается за счет отказа от устоявшихся мировоззрений, тем самым создавая несколько незнакомую обстановку для проблемы. Теперь у нас есть методика практического обучения с использованием технологий для преподавания математики через реальные проблемы под руководством инструкторов STEM и специалистов сообщества, использующих компонент проекта [4].Цифровые технологии видны, по крайней мере, в рамках необходимой типологии рукописей. Конечно, он может пойти намного дальше и включать в себя важную утилиту (например, числовой интегратор, электронную таблицу или специализированное программное обеспечение). Наконец, действие действие обучение (берущее начало в бизнес-образовании [20, 21]) обеспечивает эффективный и четкий подход к математическому образованию. Этот подход был разработан на основе различных (и, как упоминалось в начале раздела 2, иногда спорных) активных методов обучения, которые повсеместно распространены среди преподавателей математики в различных контекстах обучения, ориентированных на конструктивизм и ориентированных на учащихся [38–41 ].

4. Практическое обучение на практике математического образования

Наша команда USF-SUNY [4] установила, что практическое обучение является положительной педагогической чертой на всех уровнях обучения (K-20). Кто-то может возразить, что, поскольку многие люди учатся на протяжении всей жизни, некоторые из нас могут использовать практическое обучение (возможно, в качестве преподавателей математики) за пределами K-20. Наша мотивация к практическому изучению математики может дать молодым ученикам возможность познакомиться с интересным, что известно о математике. Основные концепции могут быть довольно сложными, и студенты могут вернуться к идеям и развить их дальше по мере накопления опыта.Примеры практического обучения представлены в подразделах ниже по уровням обучения. Эти примеры даны с акцентом на конкретность, что, в свою очередь, мотивирует учащихся. Использование компонента проекта делает модель зонтика математики «один + два» доступной на высшем уровне (раздел 4.2.2).

4.1. Мотивация и обучение действиям на уровне начальной и средней школы

На уровне начальной школы математические концепции можно мотивировать с помощью надлежащим образом разработанных практических занятий, подкрепленных манипулятивными материалами.Такие действия должны объединять богатые математические идеи со знакомыми физическими инструментами. Как упоминалось выше, важным аспектом обучения действием является его ориентация на игру. Педагогическая характеристика игры в контексте обучения математике с помощью инструментов — это «нестандартное мышление», то есть то, что в присутствии учителя как «более знающего другого» открывает окно для будущего обучения учащихся. Тем не менее, отсутствие опоры можно наблюдать, как выразился Видлер [12], «когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру» (стр.18) интуитивно, через любопытство восприятия, осознавая, что устойчивость фигуры зависит от ее положения. То есть перцептивное любопытство в сочетании с творческим мышлением часто выходит за рамки деятельности, предназначенной для одного уровня, и сливается с изучением более продвинутых идей на более высоком когнитивном уровне. В следующих двух разделах показано, как использование двусторонних счетчиков и квадратных плиток, физических инструментов, обычно используемых в настоящее время в классе элементарной математики, может поддерживать, соответственно, введение чисел Фибоначчи, что позволяет с помощью вычислений открыть окно. к концепции золотого сечения и связать построение прямоугольников (из плиток) с обсуждением особых числовых соотношений между их периметрами и площадями.В обоих случаях переход от начального уровня к второстепенному может быть облегчен за счет использования цифровых технологий. То есть математические идеи, рожденные в контексте практического обучения с помощью физических инструментов, могут быть расширены на более высокий уровень с помощью вычислительных экспериментов, поддерживаемых цифровыми инструментами.

4.1.1. От двусторонних счетчиков к золотому сечению посредством обучения действием

Рассмотрим следующий сценарий обучения действиям:

Определите количество различных вариантов расположения одного, двух, трех, четырех и т. Д. На двусторонних (красных / желтых) счетчиках в котором не появляются две красные фишки подряд.

Экспериментально можно сделать вывод, что один счетчик можно расположить двумя способами, два счетчика — тремя способами, три счетчика — пятью и четыре счетчика — восемью (рис. 1). В частности, на рисунке 1 показано, что все комбинации с четырьмя счетчиками могут быть подсчитаны путем рекурсивного сложения 3 + 5 = 8, поскольку их можно разделить на две группы, так что в первой группе (с мощностью три) крайний правый счетчик равен красный, а во второй группе (мощность пять) крайняя правая фишка желтая.Реализуя эту идею под руководством учителя, молодой ученик может обнаружить, что следующая итерация (пять счетчиков — 13 способов, так как 13 = 5 + 8) согласуется с описанием на рисунке 1. Увеличение для единообразия последовательность 2, 3, 5, 8, 13 двумя единицами (при условии, что пустой набор счетчиков имеет только одно расположение) позволяет описать завершение вышеупомянутого сценария обучения действиям (то есть размышления о результатах воздействия на конкретный материалов согласно определенному правилу) через последовательность 1, 1, 2, 3, 4, 5, 8, 13,…, (в которой первые два числа равны единице, а каждое число, начиная с третьего, является суммой два предыдущих числа) — одна из самых известных числовых последовательностей во всей математике, названная в честь Фибоначчи (1270–1350), самого выдающегося итальянского математика своего времени.В рамках размышления над сценарием молодым студентам можно сказать, что, какими бы эзотерическими ни казались числа Фибоначчи, они, вероятно, столкнутся с ними снова.

Действительно, на уровне средней школы числа Фибоначчи можно исследовать в терминах отношений двух последовательных членов,. С этой целью можно использовать электронную таблицу, чтобы продемонстрировать, что отношения приближаются к числу 1,61803 по мере увеличения n , независимо от первых двух членов последовательности, и. Точное значение, число, известное как золотое сечение.Это пример того, как использование компьютера может предоставить ученикам и их учителям неформальный мост, соединяющий более низкий когнитивный уровень с более высоким. Без простоты вычисления соотношений двух последовательных чисел Фибоначчи, представленных в электронной таблице, было бы гораздо труднее связать простую обучающую деятельность по конкретному расположению двусторонних счетчиков с когнитивно более сложной идеей сходимости отношения к числу, известному с древности как золотое сечение.Золотое сечение, мотивированное компьютером, может быть обнаружено в контексте изучения специальной числовой последовательности, описывающей задачу обучения действиям, подходящую для маленьких детей. Другими словами, компьютер может естественным образом открыть окно для будущего практического обучения учащихся (см. Примечание об исследовании болезни Альцгеймера в Разделе 6 ниже).

В связи с использованием двусторонних счетчиков в контексте чисел Фибоначчи следует отметить, что многие кандидаты в учителя считают, что конкретные материалы можно использовать только на элементарном уровне, а за пределами этого уровня они бесполезны.Имея это в виду, авторы хотели бы утверждать, что, как и в случае с числами Фибоначчи, конкретные материалы могут использоваться для введения довольно сложных понятий, чтобы добавить фактор конкретности в изучение абстрактных идей. В частности, двусторонние счетчики могут служить воплощением двоичной арифметики во вводном курсе информатики. Более конкретно, если записать первые 16 натуральных чисел в двоичной форме, то при поддержке двусторонних счетчиков можно увидеть следующее.Имеются два однозначных числа, в которых в ряду не появляются никакие единицы (без красных жетонов подряд), три двузначных числа без единиц, стоящих подряд, пять трехзначных чисел без единиц, стоящих в ряду, и восемь четырехзначных чисел, в которых подряд не появляются единицы. Числа 2, 3, 5 и 8 — это последовательные числа Фибоначчи, которые, таким образом, могут быть использованы в качестве фрагментов предыдущих знаний учащихся при разработке новых идей посредством практического обучения. Более подробные исследования вторичного (и третичного) уровня с числами Фибоначчи см. В [43].

Очевидно, что мотивация связана с ожидаемым будущим успехом как следствие подросткового возраста. Теперь студенты стремятся к большей конкретизации понятий. Когда учащиеся средней школы имеют сильную мотивацию к практическому обучению, они могут создавать проекты уровня бакалавриата, как описано для студентов в Разделе 4.2 ниже. Постепенное ощущение «серьезности» сопровождает «зрелую» проектную работу. Прекрасные примеры практического обучения учащихся средних школ, выступающих на уровне колледжа, можно увидеть в проекте Publix Лорен Вудбридж «Pallet Physics» ([44], v.3, 2 (8)), проект квантовых вычислений Бо Муна «Проблема суммы подмножеств: уменьшение временной сложности NP-полноты с помощью квантового поиска» ([44], т. 4, 2 (2)), проект ракеты Логана Уайта « Моделирование полета ракеты в приближении низкого трения »([44], v. 6, 1 (5)), и проект Рошана Вармана по спиновым вычислениям« Spintronic Circuits: The Building Blocks of Spin-based Computing »([44] , т. 7, 1 (1)).

4.1.2. Креативность и обучение действиям

Люди творческие, когда они мотивированы, и можно проявить больше творчества после общей, формирующей конкретизации идей.Важно рано распознавать творческие способности студентов. Педагоги рассматривают творчество как «один из важнейших навыков 21 века… жизненно важный для индивидуального и организационного успеха» ([45], стр. 1). Способность учителей распознавать творческие способности своих учеников, которые могут быть скрыты за их незрелой успеваемостью в классе, имеет решающее значение для успешного преподавания и продуктивного обучения. Если скрытые творческие способности учеников не признаются и не поддерживаются учителем, они, скорее всего, останутся бездействующими, а то и исчезнут [46].Следующая история, взятая из класса второго класса, поддерживает идею о том, что учителя являются главными хранителями раскрытия творческого потенциала маленьких детей.

Кандидат в учителя начальной школы, работая индивидуально с учеником второго класса (под наблюдением классного руководителя), попросил его построить все возможные прямоугольники из десяти квадратных плиток (настоящая проблема для второго класса), ожидая, что ученик Постройте два прямоугольника, 1 на 10 и 2 на 5, каждый из которых представляет собой факт умножения числа 10, что будет изучено позже (в третьем классе).Кандидат в учителя был удивлен, увидев три прямоугольника, как показано на рисунке 2. Большое количество обучающих идей для практического обучения может быть связано с принятием прямоугольника с отверстием, которое демонстрирует скрытые творческие способности ребенка. Некоторые идеи могут быть связаны со вторичной математикой. Чтобы уточнить, подумайте о том, чтобы изучить взаимосвязь между площадью и периметром этого прямоугольника с отверстием, считая как внешний, так и внутренний периметры (размышление под руководством учителя о действиях ученика с использованием конкретных материалов).Видно, что площадь составляет 10 квадратных единиц, а периметр — 20 погонных единиц. То есть численно периметр в два раза больше площади. Сравнение площадей с периметрами прямоугольников известно еще со времен Пифагора [47]. В режиме обучения действием можно исследовать следующую ситуацию: существуют ли другие прямоугольники с прямоугольными отверстиями, у которых периметр в два раза больше площади? С этой целью на уровне средней школы можно ввести четыре переменные: a , b , c и d как длину и ширину большего и меньшего прямоугольников.Отсюда следует соотношение ab — cd = a + b + c + d . Используя Wolfram Alpha — вычислительную машину знаний, доступную бесплатно в Интернете, — можно попросить программу решить указанное выше уравнение над положительными целыми числами. Результат будет следующим:

Если задать a = b = 3, можно выбрать c = 1, откуда d = 1. Это дает нам квадрат с квадратным отверстием (рисунок 3).Этот пример показывает, как знание алгебры и возможности использования технологий могут помочь практикующим учителям в работе с маленькими детьми по развитию критического мышления и развитию творческих способностей. То есть, опять же, технологии служат неформальным мостом, мотивирующим связующим звеном между двумя разными классами учебной программы по математике. Принимая во внимание, что учитель может не обязательно видеть богатую среду обучения за нетрадиционным ответом ученика, сам факт того, что такой ответ был принят и похвален, будет мотивировать этого и других учеников продолжать мыслить нестандартно.

В заключение этого раздела отметим, что тройку, ученика начальной школы, классного учителя и кандидата в учителя, можно сравнить в контексте практического обучения с таковым студента бакалавриата, математического факультета и предмета. Area Advisor, как описано ниже в Разделе 4.2.2. Сходство этих двух сред (с разницей в несколько лет) заключается в двойном наблюдении за учеником, изучающим математику, дуэтом «других более знающих».

4.2. Бакалавриат по математике и практическому обучению

4.2.1. Понимание абстрактности с обучением на практике

Язык математики абстрактный с большей абстракцией на более высоких уровнях. Традиционно университетская математика для нематематических специальностей преподается, дистанцируясь от реальности, без связи с профессиональными интересами студентов. В этом контексте многие будущие профессионалы не видят важности математики в своих перспективных областях [48]. Кроме того, абстрактность в обучении часто приводит к проблемам в общении.Как отмечено в [49], в связи с преподаванием инженерной математики могут быть несоответствия между терминологией и идеями, используемыми математиком-преподавателем, и их интерпретацией студентами. Из-за того, что математическое образование на университетском уровне слишком теоретическое, оно становится неэффективным: нематематические специальности изучают предмет «потому что они должны». Альтернативный подход к математическому образованию основан на хорошо известном и прагматичном понятии «обучение на практике» (напр.g., [50–54]), что делает возможным конструктивное взаимодействие чистых и прикладных идей. Этот подход имеет большой потенциал для внедрения экспериментального обучения в математический анализ — базовую последовательность курсов в учебной программе по высшей математике.

4.2.2. Математика Umbrella Model

Вся университетская учебная программа по математике для нематематических специальностей может извлечь выгоду из практического обучения. Было обнаружено, что, особенно на университетском уровне, следует придерживаться «середины пути» в отношении относительных весов, придаваемых теории и применению.Математическая зонтичная группа (MUG) Университета Южной Флориды (USF), созданная Аркадием Гриншпаном в 1999 году [55], занимает эту «позицию». Он устраняет разрыв между математическим образованием и приложениями, одновременно вдохновляя студентов STEM на приобретение математических навыков, необходимых для успеха в их соответствующих дисциплинах. Эта инициатива привела к разработке модели «Зонтик математики» в образовании STEM, включающей сотни междисциплинарных (прикладных математических) студенческих проектов.За десять лет, прошедших с момента сообщения о том, что программа MUG была первой организацией, которая содействовала персонализированным математическим проектам, при поддержке консультантов по математике и предметным областям, для обучения нематематических дисциплин студентам STEM [56], MUG оставалась уникальной в этом отношении. Каждый проект выполняется под двойным контролем: консультант по математике (математический факультет) и консультант по предметной области (университетский или общественный специалист), который обычно предлагает проблему [4, 48, 55, 57–59].

Отличительной чертой MUG является уловка, заключающаяся в соединении одного студента бакалавриата с как минимум двумя профессионалами. Ситуация проиллюстрирована на Рисунке 4. В результате ученики получают доступ к более широкому кругу знаний, чем обычно предоставляется одному преподавателю математики.

Еще одной сильной стороной являются связи с сообществом, которые возможны, или междисциплинарные связи, которые, по крайней мере, имеют место за пределами математического факультета вуза.Практическое обучение привносит «реальность» в абстракции математики. Даже когда преподаватели математики пытаются решить задачи с помощью приложений, полезность не осознается из первых рук, пока студенты не начнут применять ее. Это мотивационный подход для всех участников трио. Позже студенты могут решить провести исследование в связи с их опытом работы в проекте. Кроме того, они, вероятно, сохранят задействованные концепции дольше, чем при подходе «чистой лекции».

4.2.3. Практическое обучение на курсах математического анализа верхнего уровня

Практическое обучение является сильным мотивирующим фактором для всех участников, участвующих в математической группе Umbrella. Этот фактор, кажется, является общей нитью во всем спектре практического обучения K-20. Заинтересованность участников в практическом обучении может быть пропорциональна индивидуальному опыту. Преподаватели математики потенциально могут получить наибольшую пользу, но от студентов ожидается, что они будут знать теорию достаточно, чтобы их можно было мотивировать. Что касается программ бакалавриата по математике, таких как математический анализ II и III, считается, что студентам достаточно пройти несколько небольших тестов и домашних заданий, а затем направить свою энергию на практическое обучение, а не требовать от них успешной сдачи выпускного экзамена.В частности, эта педагогика практического обучения помогает студентам, которые «незначительно преуспели», позволяя в их итоговые оценки включать компонент практического обучения, которому по праву придается значительный вес в общей оценке курса.

Чаще встречаются «успешные», которые могут быть очень продуктивными в своих проектах по практическому обучению. Есть вероятность, что работы студентов будут опубликованы или, возможно, даже отмечены [4, 57], как и многие студенты за последние два десятилетия.Это прекрасные мотиваторы для всех сторон, участвующих в практическом обучении. Поскольку действие проистекает из мотивации, важно осознавать роль «мотиваторов действия». Для студентов высших учебных заведений мощным мотиватором часто является изучение чего-то полезного и того, на чем можно построить или улучшить успешную карьеру.

Примечательно, что студенты естественным образом мотивированы успехом в изучении математики. Влияние практического обучения было проанализировано в Университете Южной Флориды на курсах инженерного исчисления, в которых участвовали тысячи студентов, прошедших эти курсы и последующие курсы с весны 2003 г. по весну 2015 г. [59].Некоторые результаты (сгруппированные по расе и этнической принадлежности) представлены на Рисунке 5 [59]. На этом рисунке показан эффект обучения действием, параллельных разделов обучения без действия и исторических (традиционных) разделов. В этой части исследования участвовали 1589 студентов, изучающих действие, и 1405 студентов, обучающихся на курсах, не использующих элемент обучения действием. Наконец, еще 2316 человек были отмечены как «исторические», что означает, что они прошли курс до весны 2003 г. (то есть до того, как было проведено различие в отношении использования или неиспользования практического обучения в своих курсах).Исследователи тщательно включили доверительные интервалы в свои результаты. Очевидно, что в этой относительно большой подгруппе из более крупного исследования все четыре категории расы / этнической принадлежности предпочитают быть участниками обучения действием. Для размышления есть много информации из [59]. Во всяком случае, этот и другие результаты демонстрируют академическое превосходство в действии над обучением без действия. Прагматический вывод — обучение действиям, поскольку оно работает.

4.2.4. Практическое обучение как универсальная образовательная концепция

Мотивация преподавателей математики возникает в результате знакомства с новым опытом практического обучения. В настоящее время зарегистрированы многие сотни проектов практического обучения, представляющих широкий круг тем. Кроме того, всегда происходит обучение тонким действиям, которое никогда не документируется. Из тех проектов, которые доступны в Журнале бакалавриата по математическому моделированию: один + два (UJMM) [44], очевидно, что практически во всех областях можно использовать практическое обучение.Есть проекты, посвященные очень специфическим отраслям инженерии, например, биомедицинским нанотехнологиям. Есть также много других проектов, не относящихся к «собственно инженерному делу», например, связанных с музыкой или даже образованием. Другие — это кросс-полевые типы, которые не поддаются четкой категоризации. Типы мостов часто представляют особый интерес. Это мотивирует преподавателей увидеть, что входит в смесь и какие области могут быть связаны посредством практического обучения. Это междисциплинарные особенности, желательные для всех учебных программ (в «вселенной учебных программ», то есть в образовании).Некоторые подробности доступны на главном веб-сайте Mathematics Umbrella Group (см. Центр промышленной и междисциплинарной математики). В журнале представлена ​​избранная подгруппа из более чем 2400 студенческих проектов, представленных с 2000 года. Признак разнообразия тематики проектов и участников студенческих работ очевиден из разнообразия тем, рассматриваемых в последних изданиях UJMM ([44], v. 8 , 1-2): «Применение простых гармоник для моделирования толчка» Кая Раймонда, «Силы, действующие на парусную лодку» Келли Стукбауэр, «Оптимизация топливного элемента» Эдуардо Гинеса, «Анализ осадков в Тампе» Эми Полен, «Аппроксимация площади поверхности колеблющихся липидных листочков с использованием взвешенной сеточной мозаики» Анаф Сиддики, «Рудиментарная модель реакции глюкозы на стресс» Нашей Риос-Гусман, «Органический сельскохозяйственный анализ: эффективность общепринятой практики» Брэдли Биега, «Использование Баланс скорости энтропии для определения теплопередачи и работы во внутренне обратимом, политрофическом, установившемся процессе потока »Саванна Гриффин,« Модельная функция улучшения мирового рекорда женщин на 1500 м с течением времени »Энни Аллмарк , «Максимальная мощность солнечного модуля из поликристаллического кремния» Джейнил Патель, «Оптимизация реакции сдвига водяного газа» Али Албулуши и «Волны цунами» Саманты Пеннино.

В дополнение ко многим опубликованным проектам бакалавриата существуют «сценарии практического обучения», которые можно рассматривать как совокупность различных практических занятий. Этот смешанный опыт имеет несколько идеалистических проблем. Проблемы можно считать типичными для того, что может рассматриваться в проекте, а не , а не реальными примерами. Эти сценарии мотивируют преподавателя математики включать практическое обучение в обычный теоретический курс.Этим опытом, вероятно, поделятся любые преподаватели математики, занимающие аналогичные должности в математическом образовании. Непосредственной мотивацией здесь является расширение нашего понимания взаимосвязи между теорией математики и решением актуальных проблем в реальном мире.

5. Мотивирующие вопросы как основное средство изучения математики

5.1. Вопросы как инструменты обучения действиям

Вопросы обычно становятся более сложными по мере взросления учащихся.Преподаватели на всех уровнях математического образования используют знания и опыт, чтобы ответить на вопросы. Желательны конкретные и уверенные ответы, при этом иногда (как правило, на более высоких уровнях) вопросы могут потребовать дополнительных размышлений перед их изложением. В контексте постановки проблем и их решения важно различать два типа вопросов, которые могут быть сформулированы так, чтобы стать проблемой: вопросы, требующие получения информации, и вопросы, требующие объяснения полученной информации [60].Подобно двум типам знаков — символам первого порядка и символизму второго порядка [61] — можно относиться к вопросам, ищущим информацию, как к вопросам первого порядка, а те, которые требуют объяснения, как к вопросам второго порядка [46]. В то время как на вопросы первого порядка можно ответить, используя разные методы, похоже, что не все методы могут быть использованы для объяснения того, что было получено при поиске информации, то есть для предоставления ответа на вопрос второго порядка. Часто просьба о объяснении является разумным размышлением о методе предоставления информации.

Что означает, что учителя должны обладать «глубоким пониманием» математики? Зачем им нужно такое понимание? У будущих учителей есть несколько причин, по которым они должны быть тщательно подготовлены к математике, чтобы иметь положительное влияние на успеваемость молодых изучающих математику. Во-первых, в современном классе математики ожидается, что ученики всех возрастов будут задавать вопросы, и их даже поощряют. В Соединенных Штатах национальные стандарты уже для классов pre-K-2 предполагают, что «необходимо воспитывать естественную склонность учащихся задавать вопросы… [даже] когда ответы не сразу очевидны» ([19], с.109). Это предложение подтверждается следующим комментарием кандидата в учителя начальной школы: «Не зная ответа на вопрос — это нормально, но нельзя оставлять этот вопрос без ответа». Кандидат описывает себя как «тот педагог, который всегда будет побуждать моих учеников задавать себе одни и те же вопросы, которые позволят им участвовать в глубоком размышлении».

5.2. Международный характер обучения посредством задавания вопросов

Министерство образования Онтарио в Канаде, расположенное на границе с США, в рамках своей программы математики для младших классов ожидает, что учителя будут иметь возможность «задавать ученикам открытые вопросы … поощряйте студентов задавать себе подобные вопросы… [и] моделируйте способы, которыми можно ответить на различные вопросы »([62], с.17). Для развития такого мастерства «учителя должны знать способы использования математических рисунков, диаграмм, манипулятивных материалов и других инструментов для освещения, обсуждения и объяснения математических идей и процедур» ([63], с. 33). В Чили учителя математики должны «использовать представления, опираться на предварительные знания, задавать хорошие вопросы и стимулировать любознательное отношение и рассуждение учащихся» ([64], с. 37). В Австралии учителя математики знают, как мотивировать «любопытство, бросить вызов мышлению учащихся, обсудить математический смысл и моделировать математическое мышление и рассуждения» ([65], с.4). Репертуар возможностей обучения, которые преподаватели предлагают своим ученикам, включает постоянный поиск альтернативных подходов к решению проблем, а также помощь ученикам в изучении конкретной стратегии решения проблем, с которой они боролись. В национальной учебной программе по математике в Англии используются такие термины, как «практика со все более сложными задачами с течением времени… [и] может решать задачи… с возрастающей степенью сложности» ([66], стр. 1). С этой целью учителя должны быть готовы иметь дело с ситуациями, когда естественный поиск вопросов приводит учеников к этой изощренности и усложнению математических идей.Необходимость такой подготовки учителей подтверждается кандидатом в учителя, который сформулировал это следующим образом: «Если ученик спрашивает, почему, а учитель не может объяснить, как что-то произошло, ученик теряет всякую веру и интерес к предмету и уважение к учителю ».

На уровне бакалавриата часто обсуждаются вопросы второго порядка. Преподаватели математики знают, что такие вопросы могут быть полезны для стимулирования дальнейших исследований. Возможно, правда, что математика, с которой приходится сталкиваться на уровне начальной и средней школы, должна быть безупречно понята преподавателями математики и что учащиеся могут быть «уверены» в том, что им преподают.Когда мы начинаем заниматься, скажем, теорией множеств или двумерной / трехмерной геометрией, могут быть загадочные результаты, которые действительно побуждают учащихся задуматься об изучении высшей математики. Любопытство математики — это то, что учащиеся, вероятно, сочтут привлекательным. Конечно, преподавателю математики полезно иметь глубокое понимание темы; однако в ответе могут быть детали, которые не поддаются немедленному описанию. В некоторых редких случаях ответ даже недоступен. Ожидается, что зрелость студентов позволит им признать, что на более высоких уровнях математики они не должны терять веру и уважение к преподавателю, если объяснение откладывается.На более ранних этапах математического образования учащиеся верят, что математика идеальна. Однако математика так же несовершенна, как и все остальное, изобретенное людьми. Студенты должны это знать.

6. Компьютерная сигнатурная педагогика и модель обучения и преподавания 3P

Любопытство и мотивация также могут быть поддержаны использованием цифровых инструментов в качестве инструментов практического обучения. Как было показано на примерах из дошкольного математического образования, компьютеры могут способствовать переходу с одного познавательного уровня на другой (более высокий).Это согласуется с современным использованием компьютеров в математических исследованиях, когда новые результаты возникают в результате вычислительных экспериментов. Например, радость перехода от визуального к символическому, когда двухсторонние счетчики были предложены как средство рекурсивного построения чисел Фибоначчи, которые затем можно было смоделировать в электронной таблице, где, возможно, благодаря интуиции, определился определенный образец в поведении соотношений могут быть обнаружены два последовательных члена. Это открытие мотивирует формальное объяснение того, почему отношения ведут себя определенным образом.Точно так же переход от числового описания прямоугольников с точки зрения периметра и площади приводит к их формальному представлению. В то время как прямоугольник с отверстием был обнаружен путем мышления «нестандартно», наличие цифрового инструмента облегчает переход от визуального к символическому с последующим использованием последнего представления в ситуации математического моделирования.

Мощь вычислительного моделирования может служить мотивацией для разработки, а затем исследования более сложных рекуррентных соотношений, чем у чисел Фибоначчи.Как обсуждалось в [58], использование моделирования электронных таблиц может быть применено в контексте исследования болезни Альцгеймера для изучения популяции трансгенных мышей с упором на финансовую осуществимость покупки двух родительских мышей (самца и самку) и выращивания популяции мышей определенного размер. Эффективный подход к этой проблеме включает теорию рекуррентных соотношений, которые первоначально были введены на вторичном уровне через числа Фибоначчи. Результаты, полученные с помощью моделирования в электронной таблице, затем могут быть использованы для проверки теоретических результатов.Подробнее об этом проекте см. [55].

Все это приводит к понятию компьютерной сигнатурной педагогики (CASP), когда побуждает размышлять и поддерживать анализ действий, предпринятых учеником в контексте практического обучения, обеспечивает CASP глубинную (а не поверхностную) структуру обучения [67] нанят учителем как «более знающий друг». Точно так же в более ранней публикации Биггс [15] проводил различие между поверхностной и глубокой структурой подходов студентов к обучению , описывая первый подход в терминах студента, «вкладывающего минимальное время и усилия в соответствии с видимостью соответствия требованиям… [ тогда как последний подход] основан на интересе к предмету задачи; стратегия максимального понимания »(стр.6). Адаптировав модель обучения в классе, предложенную Данкином и Биддлом [68], Биггс [15] представил теперь известную 3P модель обучения студентов, основанную на представлениях студентов об обучении в целом и их текущей учебной среде (прогноз), студенческий подход к обучению (процессу) и результат обучения студента (продукт). Исследование того, как первый P модели влияет на его второй P и, как следствие, третий P, было проведено Лиццио, Уилсоном и Саймонсом [69], которые выступили с семью теоретическими предложениями.Одно из этих предположений было основано на аргументе о том, что если студенты университетов воспринимают преподавание курсов их профессорами как надежное, то они с большей вероятностью выберут глубокий подход к обучению. Авторы пришли к выводу, что этот аргумент верен не только для учебных курсов по высшей математике, но и для курсов по методам математики для будущих школьных учителей. В современном преподавании математики правильное использование технологий является важной характеристикой учебной среды.В частности, в контексте студенческого подхода к обучению в глубокой структуре под эгидой CASP, можно расширить использование одного цифрового инструмента, такого как электронная таблица, другими современными технологиями, такими как Wolfram Alpha. С этой целью CASP, структурированный на основе глубоких подходов к преподаванию и обучению, может включать использование так называемых интегрированных электронных таблиц [70], которые поддерживают преподавание математики на всех образовательных уровнях с вычислительной надежностью обучения учащихся.

7.Проблемы и догадки, которые вдохновляют и мотивируют

Студент, изучающий математику (на любом уровне образования), скорее всего, столкнется с «бесполезностью» математического совершенства. В математике есть легко выражаемые вопросы (предположения), на которые нет ответов (доказательство). Это похоже на принцип неопределенности Гейзенберга, где есть «пределы точности», например, при нахождении как положения, так и импульса. Важное понятие состоит в том, что не всегда есть «стандартные» решения математических задач.Зная это, учащиеся могут продолжить изучение математики для решения некоторых задач. В этих случаях действует «нестандартное» обучение действиям. Первоначальные размышления носят в основном теоретический характер, но в конечном итоге будет вызвано приложение. Заметьте, что проблему даже не нужно решать, многое предстоит узнать в этой попытке. Это мотивационный процесс. Кроме того, размышления привносят конкретность в концепции проблемы и относятся к общей «природе» проблем и решению проблем.

Реальные приложения математики в значительной степени стимулируют различные виды исследований в предметной области, в которых участвуют как профессиональные математики, так и студенты разных специальностей. Это не означает, что прикладная математика является единственным значимым источником развития математической мысли. Действительно, в самой математике есть много проблем, которые раньше мотивировали и продолжают мотивировать тех, кто стремится получить полное представление о математике как о фундаментальной науке.Некоторые из этих задач (иногда называемых предположениями) можно рекомендовать для включения в учебную программу по математике для не математических специальностей, а также для кандидатов в учителя. Опыт авторов показывает, что теоремы и предположения, берущие начало как в чистой, так и в прикладной математике, могут запустить воображение и мыслительный процесс тех, чей ум открыт для оспаривания.

Например, формулировки и исторические подробности таких захватывающих проблем, как Великая теорема Ферма, доказанная Эндрю Уайлсом [71], и гипотеза Бибербаха, доказанная Де Бранжем [72] (см. Также [73]), могут быть включены в некоторые базовые курсы математики. для нематематических специальностей.Доказательства этих теорем требуют не только элементарных средств, но и чрезвычайно сложны. Однако, как заметил Стюарт [74], «тот факт, что доказательство важно для профессионального математика, не означает, что преподавание математики данной аудитории должно ограничиваться идеями, доказательства которых доступны этой аудитории» (стр. 187). . Давайте посмотрим на них.

Последняя теорема Ферма утверждает, что уравнение не имеет ненулевых целочисленных решений для x, y и z, когда .В частности, эта теорема может быть представлена ​​различным группам студентов-математиков как способ ответить на вопрос: Можно ли расширить интерпретацию троек Пифагора как разделение квадрата на сумму двух квадратов, чтобы включить аналогичные представления для более высоких степеней ? Как подробно описано в другом месте [75], использование электронной таблицы со второстепенными кандидатами в учителя позволяет визуализировать Великую теорему Ферма путем моделирования несуществующих решений вышеуказанного уравнения для почти таким же образом, как и для.Точно так же вполне возможно, что с помощью технологий или других средств естественный мост между утверждением Великой теоремы Ферма и некоторыми геометрическими свойствами модульных эллиптических кривых в доказательстве Уайлса станет доступным для будущих студентов-математиков.

Гипотеза Бибербаха утверждает, что для каждой аналитической функции, взаимно однозначной в единичном круге, неравенство выполняется. Этот легендарный результат с его потрясающими рекордами (см., Например, [76]) может пробудить интерес студентов к изучению таких важных математических понятий, как взаимно однозначные функции, степенные ряды, сходимость и коэффициенты Тейлора, которые, в частности, являются целесообразно обсудить с инженерами-майорами.Здесь также стоит упомянуть о глубоких геометрических корнях гипотезы Бибербаха. Например, его доказательство для основано на представлении плоской заданной области в виде контурного интеграла, и, таким образом, оно доступно для нематематических специальностей, зачисленных на курс исчисления верхнего уровня.

Существует также известная гипотеза Гольдбаха [77], которая утверждает, что каждое четное число больше двух может быть записано как сумма двух простых чисел (возможно, более чем одним способом). Было бы чудом, если бы эта гипотеза оказалась ложной.Пока встречных примеров не найдено. Хотя поиск противоположного примера кажется бесплодным, эмпирически было показано, что гипотеза Гольдбаха верна для всех четных чисел больше двух и меньше некоторого известного числа, состоящего из 17 цифр.

Другой известной, но простой для понимания проблемой является гипотеза Палиндрома [78]. Он имеет дело со свойством палиндромов (т. Е. Целых чисел, которые читаются так же, как вперед и назад) привлекать целые числа в соответствии со следующей процедурой: начать с любого целого числа, перевернуть его цифры и сложить два числа; повторите процесс с суммой и продолжайте видеть, что это приводит к палиндрому.Примечательно, что эта «игра с числами» недавно была упомянута как одна из двенадцати нерешенных проблем современной математики [79]. Именно эта проблема и, как отмечено в Принципах и стандартах школьной математики [19], ее образовательный потенциал для учащихся средних школ «ценить истинную красоту математики» (стр. 21) побудил кандидата в учителя средней школы работать с один из авторов по разработке вычислительных обучающих сред для учебных презентаций и экспериментов с большим классом развлекательных задач, как решенных, так и нерешенных [80].Как сказал Гаусс, «в арифметике самые элегантные теоремы часто возникают экспериментально в результате более или менее неожиданной удачи, в то время как их доказательства лежат настолько глубоко погруженными в темноту, что опровергают самые острые вопросы» (цитируется в [81]. ], стр. 112).

Похоже, что использование технологий для значимых экспериментов с числами под эгидой CASP может вдохновить и мотивировать студентов уже на уровне дошкольного образования к новым открытиям в элементарной теории чисел.Каким-либо образом расширяя наше понимание математики, мы потенциально расширяем нашу способность «процветать». Это неотъемлемая ценность и мотивация для обучения действиям. Предполагается, что вся математика может иметь приложения. Нам нужно только иметь мотивацию для разработки этих приложений.

8. Заключение

В этой статье, используя опыт авторов в преподавании математики и надзоре за приложениями этого предмета в практике государственных школ и промышленности, представлена ​​структура совместного использования практического обучения и концептуальной мотивации в контексте К-20 математического образования.Были представлены различные примеры практического обучения — индивидуальная работа над реальной проблемой с последующим размышлением под наблюдением «более знающего другого». Такой надзор может включать в себя «дуэт других» — классного учителя и кандидата в учителя в школе K-12, а также преподавателя математики и советника по предметной области в университете. В статье показано, что практическое изучение математики идет рука об руку с концептуальной мотивацией — методикой обучения, в которой введение математических концепций мотивируется (соответствующими классу) реальными приложениями, которые могут включать в себя действия учащихся над объектами, ведущие к формальному описанию этого. действие через символику математики.Этот подход основан на важных рекомендациях математиков [5, 16, 17] и педагогических психологов [1, 25, 26, 61].

Главный вывод статьи состоит в том, что за счет многократного использования концептуальной мотивации и практического обучения на всех уровнях математического образования общий успех учащихся имеет большой потенциал для улучшения. Это сообщение подкрепляется примерами творческого мышления молодых учащихся в классе, основанного на всестороннем сотрудничестве школьных учителей и преподавателей университета (в духе Группы Холмса [82]).Точно так же это сообщение было подкреплено примерами интереса студентов к изучению математического анализа посредством практического обучения в реальной жизни. Похоже, что растущий интерес студентов к математике связан с практическим обучением и концептуальной мотивацией, которые использовались для исправления широко распространенного формализма в преподавании математики, который, в частности, стал препятствием на пути к успеху STEM-образования [4, 7, 8] . Когда учащиеся имеют опыт практического изучения математики в школьные годы, они, вероятно, продолжат изучение предмета в том же духе, тем самым избежав многих препятствий на пути перехода от среднего образования к высшему.Как упоминалось в разделе 4.2.3, исследование по внедрению практического обучения инженерному исчислению с участием тысяч студентов Университета Южной Флориды [4, 59] показывает, что, хотя интерес студентов к практическому обучению может быть пропорционален индивидуальному опыту в этом случае их результаты обучения демонстрируют академическое превосходство практического обучения над другими педагогическими средствами проведения расчетов.

На начальном этапе формального математического образования школьники должны начать знакомство с практическим обучением и педагогикой концептуальной мотивации, усиленной, в зависимости от обстоятельств, задаванием вопросов и ответами на них, а также обучением использованию технологий.Как было показано в документе, не только учебные программы по математике K-12 во многих странах поддерживают обучение учащихся, задавая вопросы, но и их будущие учителя ценят такой вид математического обучения. Аналогичным образом, компьютерная сигнатурная педагогика [37] может использоваться для максимального понимания учащимися математики и поощрения их глубокого подхода к обучению [15]. У студентов университетов больше мотивации, чем у школьников, чтобы справляться с обязанностями взрослой жизни. Тем не менее, обе группы студентов все еще могут быть мотивированы своим естественным «бросающим вызов возрасту» любопытством.В этом отношении стимулирующие вопросы, склонность к использованию компьютеров и известные классические задачи являются важными инструментами мотивации при изучении математики. Объединение всей учебной программы по математике K-20 в единую систему возможно, когда методы концептуальной мотивации и обучения действиям используются во всем этом образовательном спектре. Наконец, очевидно, что есть прагматическая причина для того, чтобы знакомить учащихся с радугой обучения действием, и это потому, что среди сегодняшних учеников есть завтрашние учителя.Процесс должен и дальше развиваться.

No related posts.