Контрольная работа по теме:»Линейная функция» 7 класс
Контрольная работа по алгебре 7 класс по теме «Линейная функция»
Вариант 1
(5 баллов) Постройте график линейной функции у = -2х + 1. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
в) значения переменной х, при которых значения функции положительные
2. (3 балла) Найдите координаты точки пересечения прямых
у = 3 – х и у = 2х.
3. (3балла) а)Найдите координаты точки пересечения графика линейной
функции у = 2х – 6 с осями координат.
б) определите принадлежит ли графику данной функции точка М (10; 14)
4. (2 балла) В одной и той же системе координат постройте графики функций :
а) у = -2х; б) у = -5
5. (2 балла) Задайте линейную функцию у = кх
что ее график параллелен прямой у = 3х + 4.
Контрольная работа по алгебре 7 класс по теме «Линейная функция»
Вариант 2
(5 баллов)Постройте график линейной функции у = 2х — 3. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
в) значения переменной х, при которых значения функции отрицательные.
2. (3 балла) Найдите координаты точки пересечения прямых
у = – х и у = х — 8.
(3 балла) а) Найдите координаты точки пересечения графика линейной
функции у = — 2х + 6 с осями координат.
б) определите принадлежит ли графику данной функции точка М (15; -24)
4. (2 балла) В одной и той же системе координат постройте графики функций:
а) у = 2х; б) у = 4
5. (2 балла) Задайте линейную функцию у = кх формулой, если известно,
что ее график параллелен прямой у = -4х + 7.
6. (5баллов)Установите соответствие между графиками функций и формулами, которые их задают.
А)
Б)
В)
1) 2) 3) 4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
А
Б
В
6. (5 баллов) Установите соответствие между функциями и их графиками.
А) y = −2x − 4
Б) y = −2x + 4
В) y= 2x
1) 2) 3)
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
АБ
В
Контрольная работа по теме «Линейная функция» 7 класс алгебра
Контрольная работа по теме «Линейная функция»
Вариант 2
I часть (5 баллов)
Запишите верный ответ.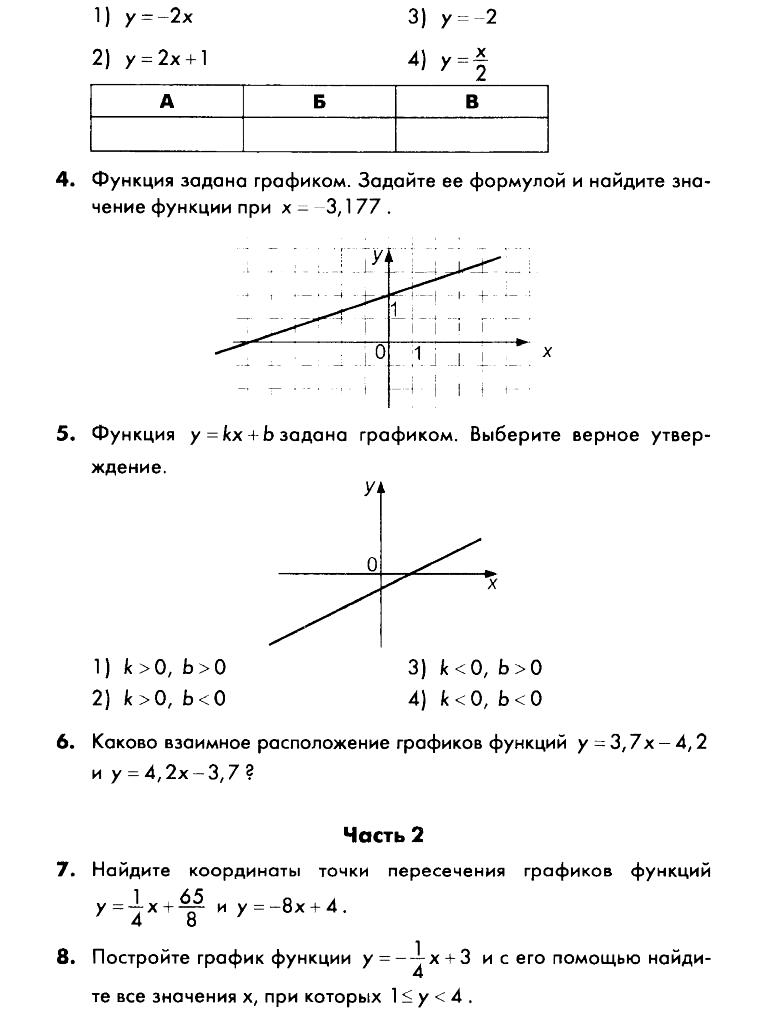
1 Какая из точек не принадлежит графику функции y = -5?
1) (0; -5)
2) (-5; -5)
3) (-5; 0)
4) (5; -5)
2. Найдите значение функции у = 3,7х — 8,3 при х = 2.
3. Найдите значение аргумента, при котором значение функции у = 187 — 218х равно -467.
4. Найдите координаты точки пересечения прямых у = 3 – х и у = 2х.
5. Найдите координаты точки пересечения графика линейной функции у = 2х – 6 с осями координат.
II часть (4 балла)
Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя
6.Постройте график линейной функции у = 2х — 3. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
7. Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен прямой у = 3х + 4.
III часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
8. При каком значении р решением уравнения 5х + ру – 3р = 0 является пара чисел (1; 1)
Контрольная работа по теме «Линейная функция»
Вариант 1
I часть (5 баллов)
Запишите верный ответ. Верный ответ каждого задания оценивается одним баллом.
1 Какая из точек не принадлежит графику функции y = -3?
1) (0; 3)
2) (-3; -3)
3) (-5; 0)
4) (-3; -5)
2. Найдите значение функции у = 4,7х — 6,3 при х = 2.
3. Найдите значение аргумента, при котором значение функции у = 187 — 21х равно -23.
4. Найдите координаты точки пересечения прямых у = – х и у = х — 8.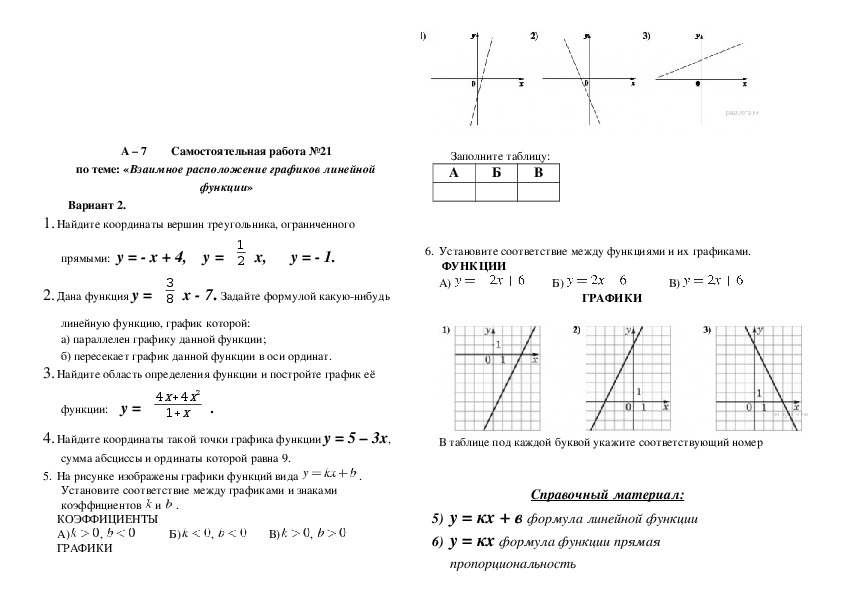
5. Найдите координаты точки пересечения графика линейной функции у = — 2х + 6 с осями координат.
II часть (4 балла)
Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
6. Постройте график линейной функции у = -2х + 1. С помощью графика найдите:
а) значение у, если х = 3;
б) значение х, если у = -1;
7. Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен прямой у = -4х + 7.
III часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
8. . При каком значении р решением уравнения -рх + 2у + р = 0 является пара чисел ( -1;2)
Алгебра 7 Макарычев К-3 Уровень 3
Контрольная работа № 3 по алгебре в 7 классе «Функции» с ответами по УМК Макарычев (сложный уровень). Глава II. ФУНКЦИИ И ИХ ГРАФИКИ. Урок 33 поурочного планирования — Алгебра 7 Макарычев К-3 Уровень 3 (варианты 5, 6).
Глава II. ФУНКЦИИ И ИХ ГРАФИКИ. Урок 33 поурочного планирования — Алгебра 7 Макарычев К-3 Уровень 3 (варианты 5, 6).
Перейти: Список контрольных по алгебре в 7 классе по УМК Макарычев (Оглавление)
Другие варианты контрольной работы № 3 «Функции»:
К-3 Уровень 1 + Ответы К-3 Уровень 2 + Ответы
Контрольная работа № 3 «Функции»
Уровень 3 (сложный). Варианты 5, 6
К-3. Вариант 5 (транскрипт)
- График линейной функции у = kх + b проходит через точки А (0; –3) и В (2; 0). Постройте график функции и определите функцию (найдите k и b).
- Укажите координаты точек пересечения графика функции у = 2х2 + 3х с осями координат.
- Найдите координаты точки графика функции у = 3х – 7, если эти координаты равны. Постройте график и укажите найденную точку.

- Постройте график зависимости |у – 2х + 1| = 2.
- Найдите точку пересечения графиков функций у = 7х – 31 и у = 2х – 6.
- Постройте график зависимости |х + 1| + |х – 1| = 2.
К-3. Вариант 6 (транскрипт)
- График линейной функции у = kх + b проходит через точки A (0; 2) и В (–3; 0). Постройте график функции и определите функцию (найдите k и b).
- Укажите координаты точек пересечения графика функции у = 3х2
- Найдите координаты точки графика функции у = –3х + 5, если эти координаты равны. Постройте график и укажите найденную точку.
- Постройте график зависимости |у + 2х – 2| = 1.
- Найдите точку пересечения графиков функций у = 9х – 43 и у = 3х – 7.
- Постройте график зависимости |у – 1| + |у + 1| = 2.
Решения и ответы на контрольную работу:
ОТВЕТЫ на Вариант 5
№ 1. у = 1,5х – 3.
у = 1,5х – 3.
№ 2. А (0; 0), В(–3/2; 0).
№ 3. А (3,5; 3,5).
№ 4. См. решение
№ 5. А (5; 4).
№ 6.
Смотреть РЕШЕНИЯ заданий Варианта 5
ОТВЕТЫ на Вариант 6
№ 1. у = 2/3 • х + 2 = 2х/3 + 2
№ 2. А (0; 0) и В(–2/3; 0).
№ 3. А(5/4; 5/4).
№ 4. См. решение
№ 5. А (6; 11).
№ 6. См. решение
Смотреть РЕШЕНИЯ заданий Варианта 6
Алгебра 7 Макарычев ОТВЕТЫ на К-3 В-2
Контрольная работа № 3 по алгебре с ответами (К-3 В-2)
Алгебра 7 Макарычев ОТВЕТЫ на К-3 В-2 — это задания, решения и ответы на контрольную работу № 3 «Функции и их графики. Линейная функция» (в 4-х вариантах) из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение, 2012», которое используется в комплекте с учебником по алгебре в 7 классе авторов: Ю. Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского.
Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под редакцией С.А. Теляковского.
Алгебра 7 класс (УМК Макарычев и др.)
Контрольная работа № 3. Вариант 2
Проверяемые темы учебника: § 5. Функции и их графики. § 6. Линейная функция.
Вариант 2. К—3 (§ 5, 6)
• 1. Функция задана формулой у = 4x – 30. Определите:
а) значение y, если x = –2,5; б) значение x, при котором у = –6; в) проходит ли график функции через точку В(7; –3).
• 2. а) Постройте график функции у = –3x + 3.
б) Укажите с помощью графика, при каком значении x значение у равно 6.
• 3. В одной и той же системе координат постройте графики функций: а) у = 0,5x; б) у = – 4.
4. Найдите координаты точки пересечения графиков функций у = –38x + 15 и у = –21x – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = – 5x + 8 и проходит через начало координат.
Контрольная работа № 3 по алгебре с ответами (К-3 В-2)
Решения и ответы на контрольную К-3 В-2
Вариант 2. ОТВЕТЫ:
ОТВЕТЫ:
№1. а) у = –40; б) х = 6; в) –2 ≠ –3; график функции не проходит через В(7;–3).
№2. х = –1
№3. а) у = 0,5х; б) у = –4.
№4. – 38х + 15 = –21х – 36; х = 3; у = –99. А(3, –99).
№5. b = 0. Ответ: у = –5x.
Смотреть РЕШЕНИЕ заданий Варианта 2
Алгебра 7 Макарычев ОТВЕТЫ на К-3 В-2. Задания, решения и ответы на контрольную работу из пособия для учащихся «Алгебра. Дидактические материалы. 7 класс / Звавич и др., 2012» (УМК Макарычев и др.).
Другие варианты: К-3. Вариант 1 К-3. Вариант 3 К-3. Вариант 4
Вернуться к Списку контрольных работ по алгебре 7 класс (ДМ — Звавич).
Алгебра 7 Макарычев КР-3 В2
Контрольная работа № 3 «Функции и их графики. Линейная функция» по алгебре в 7 классе с ответами и решениями Вариант 2. Представленные ниже работа ориентирована на учебник «Алгебра 7 класс» авторов Ю. Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Алгебра 7 Макарычев КР-3 В2.
Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Алгебра 7 Макарычев КР-3 В2.
Алгебра 7 класс (Макарычев)
Контрольная работа № 3. Вариант 2
КР-3 «Функции и их графики. Линейная функция» (транскрипт заданий)
- Функция задана формулой у = 4x – 30. Определите:
а) значение y, если x = –2,5; б) значение x, при котором у = –6; в) проходит ли график функции через точку В(7; –3). - а) Постройте график функции у = –3x + 3.
б) Укажите с помощью графика, при каком значении x значение у равно 6. - В одной и той же системе координат постройте графики функций: а) у = 0,5x; б) у = – 4.
- Найдите координаты точки пересечения графиков функций у = –38x + 15 и у = –21x – 36.
- Задайте формулой линейную функцию, график которой параллелен прямой у = – 5x + 8 и проходит через начало координат.
ОТВЕТЫ на контрольную работу
№1.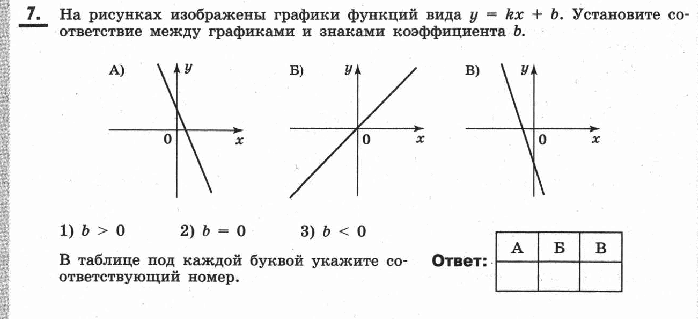 а) у = –40; б) х = 6; в) –2 ≠ –3; график функции не проходит через В(7;–3).
а) у = –40; б) х = 6; в) –2 ≠ –3; график функции не проходит через В(7;–3).
№2. х = –1
№3. а) у = 0,5х; б) у = –4.
№4. – 38х + 15 = –21х – 36; х = 3; у = –99. А(3, –99).
№5. b = 0. Ответ: у = –5x.
Смотреть подробные РЕШЕНИЯ заданий
Другие варианты: КР-3 Вариант 1 КР-3 Вариант 3 КР-3 Вариант 4
Вернуться на страницу: КОНТРОЛЬНЫЕ РАБОТЫ по алгебре в 7 классе (Макарычев).
Вы смотрели: Алгебра 7 Макарычев КР-3 В2. Контрольная работа по алгебре 7 класс «Уравнения с одной переменной» для УМК Макарычев и др. Цитаты из учебного пособия «Алгебра. Дидактические материалы. 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова — М.: Просвещение» использованы в учебных целях. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий.
Контрольная работа по математике (линейная функция и её график) для 7-го класса от Колягина в 2017 году
Ответы
Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 450 | 133 | Загрузок |
|---|---|---|---|
| Добавил | Гость | 09. 03.2019 03.2019 | Дата |
| День | Суббота | 01:56 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Колягин Ю.М.
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Математика для 8-х классов — Функции
Этот тест иллюстрирует диапазон сложности, ожидаемый следующими стандартами Common Core State (CCS):
Вопрос 1: Учитывая линейную функцию f 1 в таблице ниже и линейную функцию f 2 , представленную уравнением y = -3,2x +6, какая из функций имеет больший наклон?
f1
f2
Вопрос 2: Учитывая линейную функцию f 1 из вопроса 1 выше, что будет x для y = 0?
1/4
1/2
-1/2
-1/4
Вопрос 3: Учитывая линейную функцию f 1 , представленную уравнением y = -5, линейная функция f 2 , представленное уравнением y = -5 + x, и линейная функция f 3 , представленная уравнением y = 3x — 9, какая из функций имеет наименьшую скорость изменения?
f1
f2
f3
Вопрос 4: Какие из следующих уравнений представляют линейные функции?
y = 3xy + 2
y = 2 (3 — 2x)
y = x (x + 1)
y = x 2
Вопрос 5: Учитывая линейную функцию f (x) в в таблице ниже, каковы начальное значение и скорость изменения функции?
начальное значение: 0, скорость изменения: -3
начальное значение: 0, скорость изменения: 3
начальное значение: 6, скорость изменения: -3
начальное значение: 6, скорость изменения: -1
Вопрос 6: Определите, являются ли f (x), g (x), h (x) и i (x) функциями.
h (x) и i (x) — функции
f (x) и i (x) — функции
g (x) и h (x) — функции
f (x) и h (x) — функции
Вопрос 7: Учитывая четыре функции в таблице ниже, единственной линейной функцией между f 1 , f 2 , f 3 и f 4 является Select … f1f2f3f4.
| x | f 1 | f 2 | f 3 | f 4 |
| 0 | 0 | -1 | 4 | -2 |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 4 | 1 | -1 | 2 |
| 3 | 9 | 5 | 4 | 4 |
Вопрос 8: На рисунке ниже отображаемая функция является линейной и убывает при выборе… (- 3, -1) (- 1, 0) (0, 2) (2, 3) интервал.
Нажмите кнопку «Отправить», чтобы увидеть результаты.
Байесовская линейная регрессия в Python: использование машинного обучения для прогнозирования оценок учащихся Часть 2 | by Will Koehrsen
На практике вычисление точного апостериорного распределения для непрерывных значений затруднительно с вычислительной точки зрения, поэтому мы обращаемся к таким методам выборки, как Монте-Карло с цепью Маркова (MCMC), чтобы получить выборки из апостериорного распределения, чтобы аппроксимировать апостериорное.Монте-Карло относится к общей технике рисования случайных выборок, а цепь Маркова означает, что следующая отобранная выборка основана только на предыдущем значении выборки. Идея состоит в том, что по мере того, как мы отбираем больше выборок, аппроксимация апостериорного распределения в конечном итоге сходится к истинному апостериорному распределению параметров модели.
Конечным результатом байесовского линейного моделирования является не единичная оценка параметров модели, а распределение, которое мы можем использовать, чтобы делать выводы о новых наблюдениях.Это распределение позволяет нам продемонстрировать нашу неопределенность в модели и является одним из преимуществ методов байесовского моделирования. По мере увеличения количества точек данных неопределенность должна уменьшаться, показывая более высокий уровень уверенности в наших оценках.
Реализация байесовского линейного моделирования в Python
Лучшей библиотекой для вероятностного программирования и байесовского вывода в Python в настоящее время является PyMC3. Он включает множество утилит для построения байесовских моделей и использования методов MCMC для вывода параметров модели.Мы будем использовать модуль обобщенных линейных моделей (GLM) PyMC3, в частности, функцию GLM.from_formula , которая делает построение байесовских линейных моделей чрезвычайно простым.
Нам нужно сделать всего два шага, чтобы выполнить байесовскую линейную регрессию с помощью этого модуля:
- Построить формулу, связывающую функции с целью, и выбрать априорное распределение для правдоподобия данных
- Выборка из апостериорного распределения параметра с использованием MCMC
Формула
Вместо того, чтобы определять распределения вероятностей для каждого из параметров модели отдельно, мы передаем формулу R-стиля, связывающую функции (входные данные) с целевыми (выходными).Вот формула, связывающая оценку с характеристиками учащегося:
Оценка ~ неудачи + высшее_edu + mother_edu + учеба + отец_edu + пропуски
В этом синтаксисе ~ читается как «является функцией от». Мы говорим модели, что Grade — это линейная комбинация шести функций, расположенных справа от тильды.
Модель построена в контексте с использованием оператора with . В вызове GLM.from_formula мы передаем формулу, данные и семейство вероятностей данных (на самом деле это необязательно и по умолчанию используется нормальное распределение).Функция анализирует формулу, добавляет случайные величины для каждой функции (вместе со стандартным отклонением), добавляет вероятность данных и инициализирует параметры для разумной начальной оценки. По умолчанию априорные параметры модели моделируются как нормальное распределение.
После того, как модель GLM построена, мы производим выборку из апостериорного анализа с использованием алгоритма MCMC. Если мы не укажем, какой метод, PyMC3 автоматически выберет для нас лучший. В приведенном ниже коде я позволил PyMC3 выбрать сэмплер и указать количество выборок, 2000, количество цепочек, 2, и количество шагов настройки, 500.
В этом случае PyMC3 выбрал семплер без разворота и инициализировал семплер с помощью jitter + adap_diag. Честно говоря, я не совсем понимаю, что они означают, но полагаю, что кто-то намного умнее меня реализовал их правильно. Иногда просто знание того, как пользоваться инструментом, важнее, чем понимание каждой детали реализации!
Пробоотборник работает несколько минут, а наши результаты сохраняются в normal_trace . Он содержит все образцы для каждого из параметров модели (кроме образцов настройки, которые отбрасываются).Трассировка — это, по сути, наша модель, потому что она содержит всю информацию, необходимую для выполнения логического вывода. Чтобы получить представление о том, что делает байесовская линейная регрессия, мы можем исследовать трассировку с помощью встроенных функций в PyMC3.
График кривой показывает апостериорное распределение для параметров модели слева и прогрессию выборок, нанесенных на график для переменной справа. Два цвета представляют две выбранные цепочки разностей.
pm.traceplot (normal_trace)
Здесь мы видим, что параметры нашей модели — это не точечные оценки, а распределения.Среднее значение каждого распределения можно принять как наиболее вероятную оценку, но мы также используем весь диапазон значений, чтобы показать, что мы не уверены в истинных значениях.
Другой способ взглянуть на апостериорные распределения — это гистограммы:
pm.plot_posterior (normal_trace)
Здесь мы можем увидеть среднее значение, которое мы можем использовать в качестве наиболее вероятной оценки, а также все распределение. 95% HPD означает 95% наивысшей апостериорной плотности и соответствует достоверным интервалом для наших параметров.Достоверный интервал — это байесовский эквивалент доверительного интервала в статистике Frequentist (хотя и с разными интерпретациями).
Мы также можем увидеть сводку всех параметров модели:
pm.df_summary (normal_trace)
Мы можем интерпретировать эти веса во многом так же, как и веса линейной регрессии OLS. Например, в модели:
- Неудачи и пропуски предыдущих уроков имеют отрицательный вес
- Планы высшего образования и время учебы имеют положительный вес
- Образование матери и отца имеет положительный вес (хотя у матери гораздо более положительный вес)
Столбец стандартного отклонения и пределы hpd дают нам представление о том, насколько мы уверены в параметрах модели.Например, функция Father_edu имеет 95% hpd, которое изменяется от -0,22 до 0,27, что означает, что мы не совсем уверены, является ли эффект в модели отрицательным или положительным! Также существует большое стандартное отклонение (строка sd ) для правдоподобия данных, что указывает на большую неопределенность в целях. В целом мы видим значительную неопределенность в модели, потому что мы имеем дело с небольшим количеством выборок. Имея всего несколько сотен студентов, у нас недостаточно данных, чтобы точно определить параметры модели.
Чтобы увидеть влияние одной переменной на оценку, мы можем изменить значение этой переменной, оставив другие неизменными, и посмотреть, как изменяются оценочные оценки. Для этого мы используем функцию plot_posterior_predictive и предполагаем, что все переменные, кроме интересующей (переменной запроса), имеют медианное значение. Мы генерируем диапазон значений для переменной запроса, и функция оценивает оценку в этом диапазоне, выбирая параметры модели из апостериорного распределения.Вот код:
Результаты показывают примерную оценку в сравнении с диапазоном переменной запроса для 100 выборок из апостериорного анализа:
Байесовская линейная регрессия в Python: использование машинного обучения для прогнозирования оценок учащихся Часть 1 | by Will Koehrsen
Одно горячее кодирование является стандартным шагом в конвейерах машинного обучения, и его очень легко сделать с помощью библиотеки pandas:
# Выбрать только категориальные переменные
category_df = df.select_dtypes ('object') # Одно горячее кодирование переменные
dummy_df = pd.get_dummies (category_df) # Вернуть оценку в фрейм данных
dummy_df ['Grade'] = df ['Grade'] # Найти корреляции с оценкой
dummy_df.corr () ['Grade']. sort_values () upper_no -0.343742
school_MS -0.227632
Mjob_at_home -0.158496
reason_course -0.138195
internet_no -0.131408
address_R -0.128350
address_U 0.128350
internet_yes 0.131408
F_joteacher0000.1.173851
причина_репутация 0,185979
школа_GP 0,227632
высшее_да 0,343742
Мы снова видим интуитивно понятные отношения: высший_номер означает, что студент не хочет продолжать высшее образование, и отрицательно коррелирует с оценкой с высшим_ да студент действительно хочет получить высшее образование и показывает положительную корреляцию. Mjob_at_home означает, что мать остается дома, и имеет отрицательную корреляцию с оценкой, а Mjob_teacher указывает, что мать учит, и имеет положительную корреляцию.
В этой задаче мы будем использовать эти результаты, чтобы выполнить выбор функций, сохранив только 6 переменных, которые наиболее сильно коррелируют с итоговой оценкой. 6 — это своего рода произвольное число, которое, как я обнаружил, хорошо работает в модели, которая показывает, что машинное обучение — это просто эксперименты!
Последние шесть переменных, которые мы получаем после выбора функции (подробности см. В Блокноте), показаны на снимке нового фрейма данных. (Я переименовал столбцы, чтобы они были более интуитивно понятными):
Полные описания переменных находятся в репозитории машинного обучения UCI, но вот краткий обзор:
-
ошибки: предыдущие ошибки класса -
upper_edu: двоичный код, определяющий, будет ли студент получать высшее образование -
mother_edu: уровень образования матери -
учебное время: количество занятий в неделю -
Father_edu: уровень образования отца -
пропусков в школе: пропуски занятий в семестре
Пока мы выполняем выбор функций, мы также разделяем данные на набор для обучения и тестирования с помощью функции Scikit-learn.Это необходимо, потому что нам нужно иметь набор тестов удержания для оценки нашей модели и убедиться, что она не переоснащается для данных тестирования:
из sklearn.model_selection import train_test_split # df - это функции, а метки - цели
# Split поместив 25% в тестовый набор
X_train, X_test, y_train, y_test = train_test_split (df, labels,
test_size = 0.25,
random_state = 42)
Это оставляет нам 474 обучающих наблюдения и 159 точек данных тестирования.
Изучите выбранные элементы
Одна из моих любимых фигур — график пар, который отлично подходит для демонстрации как распределения переменных, так и отношений между парами переменных. Здесь я использую функцию seaborn PairGrid , чтобы показать график пар для выбранных функций:
Функция | Примечания, видео, контроль качества и тесты | 9 класс> Математика по выбору> Алгебра: упорядоченная пара и декартово произведение
Функция
Функция Источник: астрономия и физика.comФункция — это особая связь, в которой каждый вход имеет единственный выход. Пусть A и B — два множества. AB — это множество всех упорядоченных пар (a, b) таких, что a ∈ A и b ∈ B. Пусть f: AB — непустое подмножество AB. Тогда f является отношением от A к B. Этот f называется функцией от A к B, если f связывает каждый элемент B. Итак, функция — это особый тип отношения, которое связывает каждый элемент множества A с одним и только элемент Б.
Изображение и предварительное изображение
Пусть f = {(x, y): x ∈ A, y ∈ B} — функция из A в B.Первый элемент x упорядоченной пары (x, y) называется прообразом второго элемента y под функцией f, а y называется образом x под f. Мы пишем f (x) = y, что означает, что y является изображением x под f, и читается как f для x равно y или f для x равно y. Поскольку y является образом x при f, следовательно, f (x) является образом x при f.
Домен, ко-домен и диапазон функции
Домен, совместный домен и диапазон Источник: www.math-only-math.comПусть f — функция от множества A до множества B. Тогда A называется областью области f, а B называется областью области f. Набор всех изображений элементов под f называется диапазоном f. Диапазон значений f обозначается f (A).
Если A = {1,2,3}, B = {1,4,9}
f = {(1,1), (2,4), (3,9)}, тогда f — функция от A до B.
Здесь,
Домен f = A = {1,2,, 3}
Ко-домен f = B = {1,4,9}
Диапазон f = f (A) = {1,4,9}
Здесь диапазон f и ко-домен f — равные множества.т.е. f (A) = B.
Снова рассмотрим функцию g, которая определяется следующим образом:
Здесь
Домен g = A = {1,2,3}
Ко-домен g = {1,2,3,4}
В этом примере диапазон g, то есть g (A), является правильным подмножеством ко-домена g, то есть B.
Следовательно, диапазон функции может быть надлежащим подмножеством ее ко-домена или равным ко-домену.
Итак, для функции f из A в B мы пишем f (A) ≤B.
Типы функций
Типы функций Источник: www.kshitij-iitjee.com- Онто-функция
Пусть f — функция от A до B. Тогда f называется он-функцией, если каждый элемент B появляется как изображение хотя бы одного члена A
Здесь элемент B появляется как изображение элемента A. Итак, f является функцией.
В этом примере диапазон f и ко-домен f равны, поэтому функция f называется он-функцией, если ее диапазон и ко-домен равны, т. Е. F (A) = B. - В функцию
Пусть f — функция от A до B.Тогда f называется функцией into, если в B есть хотя бы один элемент, который не является изображением какого-либо элемента в функции.
Здесь диапазон f = {1,2,3} = A
Ко-домен f = {1,2,3,4} = B
Здесь диапазон f является правильным подмножеством его ко-домена.
Следовательно, функция f называется входящей функцией, если диапазон f является правильным подмножеством ее ко-области. - Функция один-к-одному
Пусть f — функция от A до B. Тогда f называется функцией один-к-одному, если никакие два разных элемента в A не имеют разумного представления в B. - Функция «многие к одному»
Пусть f будет функцией от A до B. Затем f вызывается функцией «многие к одному», если хотя бы два элемента A имеют одинаковое представление в B. - Равные функции
Две функции f и g, определенные в одной и той же области, называются равными, если f (a) = g (a) для каждого элемента a в области. - Независимая и зависимая переменная
Пусть f будет функцией от A до B, тогда переменная x, которая принимает значения в домене, называется независимой переменной, а переменная y, которая принимает значения в диапазоне, называется зависимой переменной .
Основные характеристики функции
Пусть f — функция от A до B, тогда
- для каждого x∈A существует элемент y∈B такой, что (x, y) ∈f, т.е. y является образом x при f, т.е. y = f (x).
- ни один элемент A не может иметь более одного изображения в B.
- могут быть элементы B, которые не связаны ни с одним элементом A.
- различных элементов A могут иметь одно и то же изображение в B.
Тестирование функции
Тестирование функции Источник: www.coolmath.comФункцию можно протестировать различными способами. Обычно мы проверяем это через определение, т.е.
а. Отношение называется функцией, если все элементы домена должны иметь изображение в ко-домену. В противном случае это не будет функция.
Функцию также можно проверить с помощью теста, известного как тест вертикальной линии. Для этого теста в любой точке графика рисуется вертикальная линия. Если вертикальная линия разрезает график только в одной точке, это функция, а если она разрезает более чем в одной точке, то это не функция.
Представление функции
- Форма реестра
В этой форме функция представлена набором всех упорядоченных пар, которые принадлежат данной функции.
Например, пусть A = {0,2,3,5,7} и
B = {0,2,4,5,7,9,10,15}, и f будет функцией «меньше чем» от A до B. тогда
f = {(0,2) (2,4) (3,5) (5,7) (7,9)} - Форма конструктора множеств
В этой форме функция представлена как {(): xA, yB, x … y}, пробел должен быть заменен правилом, которое связывает x и y.
Например, пусть A = {2,5,7,8}, B = {-3,0,1,2,3,4} и f = {(2, -3), (5,0) , (7,2), (8,3)}, тогда как f в форме построителя множеств может быть записано как
f = {(): x∈A, y∈B, x is more than y} - По формуле
В этой форме формула может использоваться для представления функции.
Например, уравнение y = 3x + 1 представляет функцию, где x принимает все значения из набора натуральных чисел N, а значения y получаются с помощью приведенного выше уравнения. - По таблице
В этой форме таблица может использоваться для представления функции.
Например, приведенная ниже таблица представляет функцию:х 1 2 3 4 5 6 7 y 1 4 9 16 25 36 49 - Стрелочная диаграмма
В этой форме функция представлена стрелками от первых компонентов ко вторым компонентам всех упорядоченных пар, которые принадлежат данной функции.
