Алгебра 8 Макарычев КР-3 Вариант 2
Контрольная работа по алгебре в 8 классе КР-3 В-2
Алгебра 8 Макарычев КР-3 Вариант 2. Задания, решения и ответы на контрольную работу «Арифметический квадратный корень. Свойства арифметического квадратного корня» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже контрольная работа в 2-х вариантах ориентирована на учебник «Алгебра 8» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки учебного пособия.
Алгебра 8 класс (Макарычев)
Контрольная работа № 3. Вариант 2
§ 5. Арифметический квадратный корень. § 6. Свойства арифметического квадратного корня.
К-3. Вариант 2 (транскрипт заданий)
- Вычислите: a) ½ √196 + 1,5 √0,36; б) 1,5 – 7 √[25/49]; в) (2 √1,5)2.
- Найдите значение выражения: a) √[0,36 • 25]; б) √8 • √18; в) √27 / √3; в) √[24 • 52].
- Решите уравнение: а) x2 = 0,64; б) x2 = 17.
- Упростите выражение: a) y3 √[4y2], где у ≥ 0; б) 7а √[16/a2], где а < 0.
- Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √38.
- При каких значениях переменной x имеет смысл выражение 2/(√x – 5) ?
ОТВЕТЫ на контрольную работу
КР-3. Ответы на Вариант 2.
№ 1. а) 7,9; б) –3,5; в) 6.
№ 3. а) –0,8; 0,8; б) –√17; √17.
№ 4. а) 2y4; б) –28.
№ 5. 6,1 и 6,2.
№ 6. x ∈ [0; 25) ∪ (25; +∞).
Смотреть РЕШЕНИЯ заданий Варианта 2
Алгебра 8 Макарычев КР-3 Вариант 2.
Контрольная работа по алгебре 8 класс (УМК Макарычев). Задания, решения и ответы на контрольную работу № 2 из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ Жохов, Макарычев, Миндюк — М.:Просвещение».
Другие варианты
Вернуться к Списку контрольных работ Алгебра 8 Макарычев (авт. В.И.Жохов и др.)
Алгебра 8 Контрольные работы Макарычев
Алгебра 8 Контрольные работы Макарычев — контрольные работы по алгебре в 8 классе с ответами и решениями по УМК Макарычев и др. (6 вариантов, 3 уровня сложности) В учебных целях использованы цитаты из пособия «Александр Рурукин: Алгебра. 8 класс. Поурочные разработки», которое используется в комплекте с учебником «Алгебра 8 класс / Макарычев Ю.Н., Миндюк Н.Г. и др (Просвещение)».
Алгебра 8 класс. Контрольные работы
по учебнику Макарычева
Глава I. РАЦИОНАЛЬНЫЕ ДРОБИ
РАЦИОНАЛЬНЫЕ ДРОБИК-1. Контрольная работа по алгебре с ответами
К-2. Контрольная работа по алгебре с ответами «Рациональные дроби»
Контрольная работа № 2
Глава II. КВАДРАТНЫЕ КОРНИ
К-3. Контрольная работа с ответами «Свойства квадратного арифметического корня»
Контрольная работа № 3К-4. Контрольная работа с ответами «Применение свойств квадратного корня»
Контрольная работа № 4
Глава III. КВАДРАТНЫЕ УРАВНЕНИЯ
К-5. Контрольная по алгебре с ответами «Квадратные уравнения»
Контрольная работа № 5К-6. Контрольная с ответами
Глава IV. НЕРАВЕНСТВА
НЕРАВЕНСТВАК-7. Контрольная работа с ответами «Числовые неравенства и их свойства»
Контрольная работа № 7К-8. Контрольная работа по алгебре с ответами «Неравенства»
Контрольная работа № 8
Глава V. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ.
ЭЛЕМЕНТЫ СТАТИСТИКИ
К-9. Контрольная работа с ответами «Степень с целым показателем»
Контрольная работа № 9К-10 «Итоговая контрольная работа» за курс 8 класса с ответами и решениями
Итоговая контрольная работа
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).
При проверке вариантов 1, 2 оценка «5» ставится за правильное решение пяти задач, оценка «4» — четырех задач и оценка «3» — трех задач. Одна задача является резервной (или запасной) и дает некоторую свободу выбора учащимся. При таких же критериях оценки за решение задач вариантов 3, 4 дается дополнительно 0,5 балла, вариантов 5, 6 — 1 балл (т. е. оценку «5» можно получить за правильное решение четырех задач).
Смотреть ВСЕ КОНТРОЛЬНЫЕ в 8 классе
Вы смотрели: Алгебра 8 Контрольные работы Макарычев — контрольные работы по алгебре в 8 классе с ответами по УМК Макарычев и др.
Вернуться к Списку уроков Тематического планирования в 8 классе.
Разноуровневые контрольные работы по алгебре для 8-х классов
Вариант 1.
Уровень 1.
- Решите неравенства:
- Решите систему неравенств:
- Решите двойное неравенство:
Уровень 2.
- Решите неравенства:
- Решите систему неравенств:
- Решите двойное неравенство:
Дополнительные задания.
- Известно, что . Оцените значение выражения
- Решите неравенства:
- Докажите неравенство:
Вариант 2.
Уровень 1.
- Решите неравенства:
- Решите систему неравенств:
- Решите двойное неравенство:
Уровень 2.
- Решите неравенства:
- Решите двойное неравенство:
Дополнительные задания.
- Известно, что . Оцените значение выражения
- Решите неравенства:
- Докажите неравенство:
Контрольная работа по теме “Квадратные корни”
Вариант 1.
Уровень 1.
- Упростите выражения:
- Сравните значения выражений: и .
- Освободитесь от иррациональности в знаменателе дроби:
- Сократите дроби:
- Решите уравнение, предварительно упростив его правую часть
Уровень 2.
- Упростите выражения:
- Сравните значения выражений: и .
- Освободитесь от иррациональности в знаменателе дроби:
- Сократите дроби:
- Докажите, что данное уравнение имеет целые корни, и найдите их
Вариант 2.
Уровень 1.
- Упростите выражения:
- Сравните значения выражений: и .
- Освободитесь от иррациональности в знаменателе дроби:
- Сократите дроби:
- Решите уравнение, предварительно упростив его правую часть
Уровень 2.
- Упростите выражения:
- Сравните значения выражений: и .
- Освободитесь от иррациональности в знаменателе дроби:
- Сократите дроби:
- Докажите, что данное уравнение имеет целые корни, и найдите их
Контрольная работа по теме “Квадратные уравнения”
Вариант 1.
Уровень 1
- Решите уравнения:
- Решите уравнение с помощью теоремы, обратной теореме Виета.
- Один из корней квадратного уравнения равен 2. Найдите второй корень и коэффициент а.
Уровень 2
- Решите уравнения:
Сборник контрольных работ по алгебре, (8 класс)
Контрольная работа № 1
По теме: «Арифметический квадратный корень».
Цель: проверить уровень усвоения ГОСО:
-умение применять определение квадратного корня;
—умение применять определение арифметического квадратного корня; -умение применять свойства арифметического квадратного корня; — умение решать уравнения с применением арифметического квадратного корня
1вариант. 2 вариант.
1.
Найдите значение выражения:
а); а) ;
б) 2 ; б) 1,5- 7;
в) в)
2. Вычислите, используя свойства корня:
а) ; а) ;
б) ; б) ;
в) ; в) г) ; г)
3. Решите уравнение :
а) ; б) а) ; б) .
4. При каких значениях х выражение имеет смысл:
а) б) а) ; б)
5.Укажите все целые числа, расположенные на координатной прямой между числами:
и 5 1 и
Критерии оценивания | |
«5» | 22-24 балла |
«4» | 18-21 балл |
«3» | 12-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Определение арифметического квадратного корня. | №1 | №4 | 40% | |
Свойства арифметического квадратного корня | №2 | 20% | ||
Решение уравнений | №3 | 20% | ||
Координатная прямая | №5 | 20% | ||
Итого | 60 % | 20 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | Найдите значение выражения | 1) Знание определения арифметического корня | 2балла | 4 балла |
2) Применение вычислительной техники | 2 балл | |||
2 | Вычислите, используя свойства корня | 1) Знание свойств арифметического корня. | 2 балла | 5 баллов |
2) Знание формулы 2=х, х≥0 | 2 балла | |||
3) Вычислительная техника | 1 балл | |||
3 | Решите уравнение | 1) Знание алгоритма решения уравнения | 1 балл | 5 баллов |
2) Знание определения квадратного корня | 2 балла | |||
3) Применение вычислительной техники | 1 балл | |||
4)Анализ и запись ответа | 1 балл | |||
4 | При каких значениях х выражение имеет смысл: | 1) Знание определения арифметического корня | 2 балла | 4 балла |
2) Умение возводить рациональные числа в четную степень | 2 балла | |||
5 | Решение задачи на рассуждение | 1) Знание понятия целых чисел | 2 балла | 6 баллов |
2) Умение располагать их координатнойпрямой | 2 балла | |||
3) Умение представить любое рациональное число в виде арифметического квадратного корня | 2 балла |
Контрольная работа № 2
По теме: «Квадратные корни».
Цель: проверить уровень усвоения ГОСО:
-знание определения и свойств арифметического квадратного корня;
-знание свойств и графика функции у=;
-умение освобождаться от иррациональности в знаменателе;
-выполнять преобразования, содержащие квадратные корни;
1вариант. 2 вариант.
1. Выполните действия:
а) ; а) ;б);б) ;
в) . в) .
2. Определите, какие из данных точек принадлежат графику функцииу= . . А(25; -5) В(1,21;1,1) А(36;-6), В(1,44;1,2)
3. Освободитесь от иррациональности в знаменателе:
а) ; а) ;
б) ; б)
4. Сократите дроби:
а) ; б) . а) ; б) .
5. Решите уравнение, предварительно упростив его правую часть:
Критерии оценивания | |
«5» | 20-22 балла |
«4» | 16-19 балл |
«3» | 10-15 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Выполнение действий, содержащие квадратные корни | №1 | 20% | ||
График функции | №2 | 20% | ||
Освободитесь от иррациональности в знаменателе | №3 | 20% | ||
Сокращение дробей | №4 | 20% | ||
Решение уравнений | №5 | 20% | ||
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | . | 1) Применение свойства корня из дроби. | 1 балл | 3балла |
2) Применение свойства корня из произведения. | 1 балл | |||
3) Применение формулы 2= │х│ | 1 балл | |||
2 | Графика функции. | 1) Принадлежность точки графику функции. | 2 балла | 3балла |
2) Вычислительная техника | 1 балл | |||
3 | Освобождение от иррациональности в знаменателе: | 1) Знание методов освобождения от иррациональности в знаменателе | 2 балла | 5 баллов |
2) Знание ФСУ | 2 балла | |||
3) Применение вычислительной техники | 1 балл | |||
4 | Сокращение дробей | 1)Умение раскладывать на множители | 3 балл | 5 баллов |
2) Умение сокращать дробь | 2 балл | |||
5 | Решение уравнения | 1) Свойства арифметического квадратного корня | 2 балла | 6 баллов |
2) Знание ФСУ | 2 балла | |||
3) Алгоритм решения уравнений | 1 балл | |||
4) Применение вычислительной техники | 1 балл |
Выполните действия
Контрольная работа №3
По теме: «Квадратные уравнения».
Цель: проверить уровень усвоения ГОСО:
-знание алгоритма решения неполных и полных квадратных уравнений;
-умение находить дискриминант и корни квадратного уравнения;
-умение применять прямую и обратную теоремы Виета.
1вариант. 2 вариант.
1.Найдите корни уравнений:
а) 8х-2х=0; а) 25х= 5х;
б) 9х=25; б) 100х- 16=0;
2.Решите уравнения:
3х2 -14х-5=0; 3х2 -11х-4=0;
3. Составьте квадратное уравнение,
корни которого равны
-5 и 8 9 и -4
4. При каком значении с уравнение
2х-2х+с=0 сх-6х+3=0
будет иметь один корень?
5. Один из корней уравнения
х-рх -18=0 равен -9. х+11х + q =0 равен -7
Найдите второй корень
и коэффициент р. и свободный член q
Критерии оценивания | |
«5» | 19-20 балла |
«4» | 15-18 баллов |
«3» | 9-14 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Квадратные уравнения | №1, №2 | 40% | ||
Теорема Виета | №3 | №5 | 40% | |
Зависимость количества корней квадратного уравнения от значения дискриминанта | №4 | 20% | ||
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | Найти корни уравнений | 1) Решение неполных квадратных уравнений | 2 балла | 3 балла |
2) Применение вычислительной техники | 1 балл | |||
2 | Решение уравнения. | 1) Решение полных квадратных уравнений | 2 балл | 3 балла |
2) Вычислительная техника | 1 балл | |||
3 | Составление квадратного уравнения по его корням | 1) Применение теоремы Виета | 2 балла | 4балла |
3) Применение вычислительной техники | 2 балла | |||
4 | Нахождение значения спри наличии одного корня в уравнении | 1) Нахождение дискриминанта | 1 балл | 5 баллов |
2) Знание условия: если Д=0,то корень: 1 | 2 балл | |||
3) Применение вычислительной техники | 2 балла | |||
5 | Нахождения одного из корней и коэффициента р | 1) Применение теоремы Виета | 2 балла | 5 баллов |
2)Нахождение второго корня уравнения | 2 балла | |||
3) Составление квадратного уравнения | 1 балл |
Контрольная работа №4
По теме: «Применение квадратных уравнений».
Цель: проверить уровень усвоения ГОСО:
-умение решать дробно-рациональные уравнения;
-умение решать биквадратные уравнения;
— умение решать уравненияметодом введения новой переменной;
-умение решать задачи с помощью дробно-рациональных уравнений.
1вариант. 2 вариант.
1.Решите уравнение:
=. =.
2. Решите биквадратное уравнение:
х4-8х2-9=0 у4-8у2+16=0
3.Решите задачу:
Катер прошел 80км по течению реки и вернулся обратно,
затратив на весь путь 9 часов.
Найдите собственную ско- Найдите скорость течения ре-
рость катера,если скорость ки, если скорость катера в стоячей
течения реки 2км/ч. воде равна 18км/ч.
4. Решите уравнение, используя введение новой переменной:
(5х+1)2+6(5х+1)-7=0 (6х-1)2-7(6х-1)-144=0
5.
Найдите корни уравнения:
+1=+1=.
Критерии оценивания | |
«5» | 22-24 балла |
«4» | 18-21 балл |
«3» | 12-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Рациональные уравнения | №1 | №5 | 40% | |
Биквадратные уравнения | №2 | 20% | ||
Уравнения, решаемые с помощью замены переменной | №4 | 20% | ||
Решение задач | №3 | 20% | ||
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | Решение рациональных уравнений | 1) Область допустимых значений | 1 балл | 4 балла |
2) Знание алгоритма | 1 балл | |||
3) Вычисления | 1 балл | |||
4) Анализ корней и запись ответа | 1 балл | |||
2 | Решение биквадратного уравнения | 1) Алгоритм решения биквадратного уравнения | 2 балла | 4 балла |
2) Анализ ответов и запись | 1балл | |||
3) Вычисления | 1 балл | |||
3 | Решение задачи | 1) Умение составить уравнение по тексту задачи | 2 балла | 6 баллов |
2) Алгоритм решения дробно-рациональных уравнений | 2 балла | |||
3) Анализ ответов и запись | 1 балл | |||
4) Вычисления | 1 балл | |||
4 | Уравнения, решаемые с помощью замены переменной | 1) Алгоритм решения уравнений с помощью замены переменной | 1 балл | 4 баллов |
2) Применение вычислительной техники | 2 балла | |||
3)Анализ и выбор ответа | 1 балл | |||
5 | Решение рациональных уравнений | 1) Область допустимых значений | 2 балла | 6 баллов |
2)Алгоритм решения дробно-рациональных уравнений | 2 балла | |||
3) Применение вычислительной техники | 1 балла | |||
4) Анализ корней и запись ответа | 1 балл |
Контрольная работа №5
По теме: «Квадритичная функция».
Цель: проверить уровень усвоения ГОСО:
-умение раскладыватьквадратный трехчлен на множители;
-уметь строить график квадратичной функции, читать график;
-уметь сокращать дроби;
-умение находить точки пересечения графиков.
1 вариант. 2 вариант.
Разложите на множители квадратный трехчлен :
а) а)
б) -2х2 + 5х – 3 б) -6х2 –х + 5
Постройте график функции
у . у= х2 — 4х -5
С помощью графика найдите:
найдите промежутки возрас- найдите промежутки убывания
тания функции. функции.
Сократите дробь:
. .
4.Не выполняя построения, определите пересекаются ли графики функций
у и у. у и у .
Если пересекаются, то найдите координаты точек пересечения.
5) Докажите, что любое значение квадратного трехчлена не менее 1.
.х2 — 4х + 6.
Критерии оценивания | |
«5» | 22-24 балла |
«4» | 18-21 балл |
«3» | 12-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Разложение на множители квадратного трехчлена | №1 | 20% | ||
Сокращение дробей | №3 | 20% | ||
Построение графика квадратичной функции | №2 | 20% | ||
Нахождение координат точки пересечения графиков | №4 | 20% | ||
Нахождение наименьшего значения | №5 | 20% | ||
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | Разложение на множители квадратного трехчлена | 1) Знание алгоритма разложения квадратного трехчлена на множители | 1 балла | 4 балла |
2) Умение решать квадратные уравнения | 2 балла | |||
3) Вычисления | 1 балл | |||
2 | Построение графика квадратичной функции | 1) Нахождение координат вершины параболы | 2 балл | 5 баллов |
2) Построение таблицы и графика | 2 балла | |||
3) Чтение графика | 1 балла | |||
3 | Сокращение дробей | 1) Применение формулы разложения квадратного трехчлена на множители | 2 балла | 5 баллов |
2) Сокращение дробей | 2 балла | |||
3) Вычисления | 1 балл | |||
4 | Нахождение координат точки пересечения графиков | 1) Составление и решение квадратного уравнения | 2 балла | 5 баллов |
2) Нахождение координат точек пересечения графиков | 2 балла | |||
3) Вычисления | 1 балл | |||
5 | Нахождение наименьшего значения | 1)Рассмотрение квадратного трехчлена как квадратичную функцию | 1 балл | 5 баллов |
2) Нахождение координат вершины параболы | 1 балл | |||
3) Обоснование ответа | 2 балла | |||
4) Вычисления | 1 балл |
Контрольная работа №6
По теме: «Квадратные неравенства.
»
Цель: проверить уровень усвоения ГОСО:
-умение решать квадратные неравенства методом интервалов,
графическим способом;
-нахождение области определения.
1вариант. 2 вариант.
1.Решите неравенства :
-9 0 -16
2. Решите неравенства методом интервалов:
а) (х+8)(х-4) а) (х+11)(х-9)
б) ; б) ;
3.Решить неравенство графическим способом:
х2+7х+10≥0 х2-3х-4≤0
4.При каком значении t уравнение
3 tх+3 имеет два корня? 2 tх+8 не имеет корней?
5.Найдите область определения функции
у . у
Критерии оценивания | |
«5» | 22-23 балла |
«4» | 18-21 балл |
«3» | 12-17 баллов |
Распределение заданий по содержанию и уровню сложности
Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция | % соотношение |
Квадратные неравенства | №1,№2 | №3 | 60% | |
Нахождения области определения | №5 | 20% | ||
Нахождение параметраt | №4 | 20% | ||
Итого | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемых элементов | Балл за выполнение задания | |
1 | Решение неравенства | 1) Знание методов решения неравенств и их применение | 2 балла | 4 балла |
2) Выбор и запись ответа | 1 балл | |||
3)Вычислительная техника | 1 балл | |||
2 | Решение неравенств методом интервалов | 1) Применение метода интервалов для произведения | 1 балл | 5 баллов |
2) Применение метода интервалов для дроби | 2 балла | |||
3) Выбор и запись ответа | 1 балл | |||
4) Вычислительная техника | 1 балл | |||
3 | Решение графическим способом | 1) Знание алгоритма графического метода | 2 балла | 4 балла |
2) Выбор и запись ответа | 1 балл | |||
3)Вычислительная техника | 1 балла | |||
4 | Прикаком зна-чении tуравне-ние имеет или не имеет корни | 1) Нахождение дискриминанта | 1 балл | 5 баллов |
2) Решение квадратного неравенства | 2 балла | |||
3) Вычислительная техника | 2 балла | |||
5 | Нахождение области определения | 1) Составление неравенства по определению квадратного корня | 2 балла | 5 баллов |
2) Решение квадратного неравенства | 2 балла | |||
3) Выбор и запись ответа | 1 балл |
Алгебра 8 класс К-2 (угл. ) с ответами . Контрольная работа
) с ответами . Контрольная работаКонтрольная 2 по алгебре 8 класс (угл.)
Алгебра 8 класс К-2 (угл.) с ответами. Контрольная работа по алгебре для 8 класса «Квадратные корни» с углубленным изучением математики (цитаты) из учебно-методического пособия «Самостоятельные и контрольные работы по алгебре для 8 класса с угл.изуч. математики / Е.Я. Карачинский». Цитаты из пособия указаны в учебных целях. При постоянном использовании контрольных рекомендуем купить указанное пособие.
Для увеличения изображения — нажмите на картинку ! Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»
Квадратные корни
Контрольная работа по алгебре 8 класс. К-2.
OCR-версия контрольной
К-2. 1 вариант
1. Вычислите:
2. Сравните числа: √11 — √10 и √6 — √5.
3. Постройте график функции:
4.
Упростите выражения:
5. Докажите неравенство:
К-2. 2 вариант.
1. Вычислите:
2. Сравните числа: √37 — √14 и √6 — √15.
3. Постройте график функции:
4. Упростите выражения:
5. Докажите неравенство:
К-2. 1 вариант
1. Вычислите:
2. Сравните числа: √11 — √10 и √6 — √5.
3. Постройте график функции:
4. Упростите выражения:
5. Докажите неравенство:
К-2. 2 вариант.
1. Вычислите:
2. Сравните числа: √37 — √14 и √6 — √15.
3. Постройте график функции:
4. Упростите выражения:
5. Докажите неравенство:
ОТВЕТЫ на контрольную работу
Вернуться к Списку контрольных работ по алгебре 8 класс (угл.изуч.)
Алгебра 8 класс К-2 (угл.) с ответами. Цитаты из учебно-методического пособия «Самостоятельные и контрольные работы по алгебре для 8 класса с угл.изуч. математики / Е.Я. Карачинский». Цитаты из пособия указаны в учебных целях.
При постоянном использовании контрольных рекомендуем купить указанное пособие.
контрольная работа квадратные корни и их свойства. действительные числа8 8 класс
4.1 417 контрольная работа квадратные корни и их свойства. действительные числа8 8 класс
КТП Математика алгебра 8 2018
Самостоятельные и контрольные работы : пособие для учителей учреждений общ. … Алгебра. 8 класс : пособие для учащихся учреждений общ. сред. образо … и их свойства. Действительные числа. 4. 5. 6. Квадратный корень из.
gymn.by Арифметический квадратный корень — урок. Алгебра, 8 класс.
Урок по теме Арифметический квадратный корень.
Теоретические
материалы и задания Алгебра, 8 класс. ЯКласс — онлайн-школа нового
поколения.
Квадратные корни. Действительные числа | Математика 8 класс …
Арифметический квадратный корень из произведения, дроби и степени. … Обосновывает свойства арифметического квадратного корня. … анализ соотношения между числовыми множествами и их элементами. … В первой главе своей работы я рассматриваю основное понятие многочлена, операци .
www.parta.com.ua Тесты по алгебре (8 класс), контрольная работа с ответами по …
Тест Рациональные дроби и их свойства 10 вопросов.
Уровень: знаток. … 3.
Квадратные корни … Тест Действительные числа (8 класс) 10 вопросов.
Самостоятельная работа «Действительные числа» 8 класс скачать
Скачать Самостоятельная работа «Действительные числа» 8 класс.
uchitelya.com Контрольная работ по теме «Квадратные корни и их свойства …
Контрольная работ по теме «Квадратные корни и их свойства. Действительные числа». Категория: Математика. 24.11.2018 21:14. Вариант 1. 1.
multiurok.ru Алгебра 8 Контрольные Макарычев (КИМ Глазков . ..
..Контрольные работы по алгебре 8 класс (УМК Макарычев и др.) … Алгебра 8 Контрольные Макарычев. Ответы на Контрольную работу 1 «Рациональные дроби и их свойства. Сумма … Арифметический квадратный корень … Алгебра 8 Макарычев. Ответы на Контрольную работу 3 «Действительные числа.
xn--b1agatflbfbtgq5jm.xn--p1ai Решайся! — YouTube
Здравствуйте, ребята, а так же их родители! Добро … Квадратные корни и их свойства. Действительные числа. 8 класс 2 вариант. — Duration: 22 minutes.
www.youtuКвадратный корень | Примечания, видео, контроль качества и тесты | 8 класс> Обязательная математика> Корни
Квадратный корень
Процесс, с помощью которого мы можем получить противоположное квадрату, называется нахождением квадратного корня.
Это противоположность квадрату. Это число, которое при умножении на себя указанное количество раз образует произведение, равное указанному числу.
Например:
- Квадратный корень из 9 равен 3 (потому что 3² = 3×3 = 9)
- Квадратный корень из 16 равен 4 (потому что 4 2 = 4×4 = 16)
- Квадратный корень из 36 равен 6 (поскольку 6² = 6×6 = 36)
- Квадратный корень из 81 равен 9 (потому что 9 2 = 9×9 = 81)
- Квадратный корень из 100 равен 10 (потому что 10² = 10×10 = 100)
\ (\ sqrt {} \) представляют собой квадратный корень.
\ (\ sqrt {25} \) означает квадратный корень из 25
\ (\ sqrt {64} \) означает квадратный корень из 64
Натуральное число — это точный квадратный корень. Некоторые из натуральных чисел: 1, 4, 9, 16 и т. Д.
Например: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 и т. Д. — полные квадраты.
Квадратный корень из числа можно получить двумя способами, которые упрощают процесс факторизации.
Два метода:
- Метод факторизации простых чисел
- Метод деления
Метод разложения на простые множители позволяет легко найти квадратный корень из натурального числа.
- Число должно быть множителем простого числа или должно быть выражено как множитель простого числа.
- Составьте пары из множителей, и каждая пара должна быть равна.
- Возьмите по одному множителю из каждой пары.
- Произведение на коэффициент — квадратный корень из заданного числа.
Это можно показать на числовых примерах:
1. Найдите квадратный корень из 36.
Решение:
\ (\ sqrt {36} \)
= \ (\ sqrt {6 \ times 6} \)
= 6
2.Найдите квадратный корень из 2025.
Решение:
\ (\ sqrt {2025} \)
= \ (\ sqrt {9 \ times 9 \ times 5 \ times 5} \)
= 9 × 5
= 45
Корень квадратный методом деления
Метод деления — это более быстрый способ найти квадратный корень из числа.
Это занимает меньше времени, чем метод факторизации. Например, число 512490 сгруппировано в три пары по 51, 24, 90. Если количество цифр в номере нечетное, то первая группа будет состоять из одной цифры, а остальные — из двух.Например, число 18021 сгруппировано в три группы по 1, 80, 21. Кубический корень.
В этом методе мы составляем пару цифр, для которой необходимо найти квадратный корень. При сопряжении цифры делаем это с правой стороны. Таким образом, если количество цифр четное, тогда вся группа будет иметь 2 цифры, а если количество цифр нечетное, то первая группа будет иметь одну, а другая будет иметь две цифры. Например, число 512490 сгруппировано в три пары по 51, 24, 90. Если количество цифр в номере нечетное, то первая группа будет состоять из одной цифры, а остальные — из двух.2} \)
= 4 × 2
= 8
Общие основные стандарты 8-го класса
Вот общие основные стандарты для 8-го класса со ссылками на ресурсы, которые их поддерживают.
Мы также поощряем много упражнений и книжную работу.
8 класс | Система счисления
Знайте, что есть числа, которые не являются рациональными, и округлите их рациональными числами.
8.NS.A.1 Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показывают, что десятичное расширение в конечном итоге повторяется, и преобразует десятичное расширение, которое в конечном итоге повторяется, в рациональное число.2). Например, усекая десятичное разложение квадратного корня из 2, покажите, что квадратный корень из 2 находится между 1 и 2, затем между 1,4 и 1,5, и объясните, как продолжить, чтобы получить более точные приближения.
Упражнение: Найдите приблизительное значение для Piкласса 8 | Выражения и уравнения
Работа с радикалами и целыми показателями.
8.EE.A.1 Знать и применять свойства целочисленных показателей для генерации эквивалентных числовых выражений.
3) = 1/27.9, и определяют, что население мира более чем в 20 раз больше.
8.EE.A.4 Выполнять операции с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используются как десятичные, так и экспоненциальные представления. Используйте научную нотацию и выбирайте единицы подходящего размера для измерений очень больших или очень малых количеств (например, используйте миллиметры в год для растекания по морскому дну). Интерпретируйте научные обозначения, созданные с помощью технологий.
Индексное обозначение — степень 10Поймите связи между пропорциональными отношениями, линиями и линейными уравнениями.
8.EE.B.5 График пропорциональных соотношений, интерпретируя удельный вес как наклон графика. Сравните два разных пропорциональных отношения, представленных разными способами. Например, сравните график расстояние-время с уравнением расстояние-время, чтобы определить, какой из двух движущихся объектов имеет большую скорость.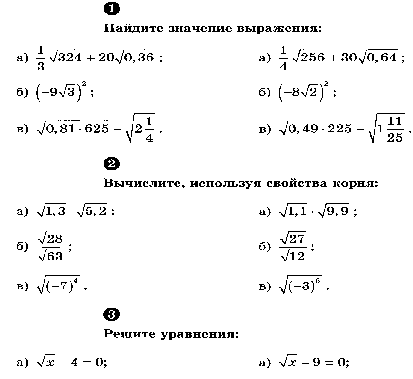
8.EE.B.6 Используйте аналогичные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b.
Анализируйте и решайте линейные уравнения и пары одновременных линейных уравнений.
8.EE.C.7 Решите линейные уравнения с одной переменной.
а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или без решений. Покажите, какая из этих возможностей имеет место, путем последовательного преобразования данного уравнения в более простые формы до тех пор, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
г. Решайте линейные уравнения с рациональными числовыми коэффициентами, включая уравнения, решения которых требуют расширения выражений с использованием свойства распределения и сбора похожих членов.
8.EE.C.8 Анализируйте и решайте пары одновременных линейных уравнений.
а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.
г. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения. Разбирайте простые случаи путем осмотра. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не могут одновременно быть 5 и 6.
c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными. Например, учитывая координаты двух пар точек, определите, пересекает ли линия, проходящая через первую пару точек, линию, проходящую через вторую пару.
8 класс | Функции
Определение, оценка и сравнение функций.
8.F.A.1 Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции — это набор упорядоченных пар, состоящих из входа и соответствующего выхода. (Обозначение функций не требуется для 8-го класса.)
Диапазон доменов и кодомен Инъективный сюръективный и биективный8.F.A.2 Сравнивают свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесных описаниях).Например, для линейной функции, представленной таблицей значений, и линейной функции, представленной алгебраическим выражением, определите, какая функция имеет большую скорость изменения.
Решения NCERT для класса 8 по математике Глава 6
Страница № 96:
Вопрос 1:
Какой будет агрегат цифра квадратов следующих чисел?
(i) 81 (ii) 272
(iii) 799 (iv) 3853
(v) 1234 (vi) 26387
(vii) 52698 (viii) 99880
(ix) 12796 (x) 55555
Ответ:
Мы знаем, что если
число имеет разрядную цифру a , затем квадрат
закончится единичной цифрой умножения a × а .
(я) 81
С в данном номере разрядная цифра единицы равна 1, а его квадрат будет заканчиваться единичной цифрой умножения (1 × 1 = 1) т.е. 1.
(ii) 272
С у данного числа разметочная цифра единицы — 2, квадрат будет заканчиваться единичной цифрой умножения (2 × 2 = 4) то есть 4.
(iii) 799
С у данного числа есть цифра разряда единицы как 9, его квадрат закончится единичной цифрой умножения (9 × 9 = 81) i.е., 1.
(iv) 3853
С у данного числа есть цифра разряда единицы как 3, его квадрат будет заканчиваться единичной цифрой умножения (3 × 3 = 9), то есть 9.
(в) 1234
С у данного числа есть цифра разряда единицы как 4, его квадрат будет заканчиваться единичной цифрой умножения (4 × 4 = 16), т.е. 6.
(vi) 26387
С у данного числа есть цифра разряда единицы как 7, его квадрат закончится единичной цифрой умножения (7 × 7 = 49) i.е., 9.
(vii) 52698
С
у данного числа есть цифра разряда единицы как 8, его квадрат
закончится единичной цифрой умножения (8 ×
8 = 64), то есть 4.
(viii) 99880
С для данного числа разрядная цифра единицы равна 0, а его квадрат в конце будет два нуля. Следовательно, единичная цифра квадрат данного числа равен 0.
(xi) 12796
С у данного числа есть цифра разряда единицы как 6, его квадрат будет заканчиваться единичной цифрой умножения (6 × 6 = 36) i.е., 6.
(х) 55555
С в данном числе разрядная цифра единицы — 5, квадрат будет заканчиваться единичной цифрой умножения (5 × 5 = 25), то есть 5.
Страница № 96:
Вопрос 2:
Следующие числа явно не идеальные квадраты. Обоснуйте.
(i) 1057 (ii) 23453
(iii) 7928 (iv) 222222
(v) 64000 (vi) 89722
(vii) 222000 (viii) 505050
Ответ:
Квадрат чисел
может заканчиваться любой из цифр 0, 1, 5, 6 или 9.Кроме того, идеальный
квадрат имеет четное число нулей в конце.
(i) 1057 имеет свой блок поместите цифру как 7. Следовательно, это не может быть идеальный квадрат.
(ii) 23453 имеет свое подразделение поместите цифру как 3. Следовательно, это не может быть идеальный квадрат.
(iii) 7928 имеет свое подразделение поместите цифру как 8. Следовательно, это не может быть идеальный квадрат.
(iv) 222222 имеет свой единица размещает цифру как 2. Следовательно, это не может быть идеальный квадрат.
(v) 64000 имеет в конце три нуля.Однако поскольку идеальный квадрат не может заканчиваться нечетным числом нулей, это не идеальный площадь.
(vi) 89722 имеет свой блок поместите цифру как 2. Следовательно, это не может быть идеальный квадрат.
(vii) 222000 содержит три нуля в конце. Однако поскольку идеальный квадрат не может заканчиваться нечетным числом нулей, это не идеальный квадрат.
(viii) 505050 имеет один ноль в конце. Однако поскольку идеальный
квадрат не может заканчиваться нечетным числом нулей, это не идеальный
площадь.
Страница № 96:
Вопрос 3:
Квадраты каких из следующих чисел будут нечетными?
(i) 431 (ii) 2826
(iii) 7779 (iv) 82004
Ответ:
Квадрат нечетного числа является нечетным, а квадрат четного числа — четным. Здесь 431 и 7779 — нечетные числа.
Таким образом, квадрат 431 и 7779 будет нечетным числом.
Видео решение для вычисления квадратов и квадратных корней (Страница: 96, Q.No .: 3)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 96, вопрос 3
Страница № 96:
Вопрос 4:
Соблюдайте следующую схему и найдите недостающие цифры.
11 2 = 121
101 2 = 10201
1001 2 = 1002001
100001 2 = 1… 2… 1
10000001 2 =…
Ответ:
В данном шаблоне можно заметить, что квадраты заданных чисел имеют такое же количество нулей до и после цифры 2, как и в исходном числе.
Следовательно,
100001 2 = 10000200001
10000001 2 = 100000020000001
Видео решение для вычисления квадрата и квадратного корня (Страница: 96, Q.No: 4)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 96, вопрос 4
Страница № 96:
Вопрос 5:
Обратите внимание на следующее шаблон и укажите недостающий номер.
11 2 = 121
101 2 = 10201
10101 2 = 102030201
1010101 2 =…
… 2 = 10203040504030201
Ответ:
Следуя данному выкройки, получаем
1010101 2 = 1020304030201
101010101 2 = 10203040504030201
Страница № 96:
Вопрос 6:
Используя данный
узор, найдите недостающие числа.
1 2 + 2 2 + 2 2 = 3 2
2 2 + 3 2 + 6 2 = 7 2
3 2 + 4 2 + 12 2 = 13 2
4 2 + 5 2 + _ 2 = 21 2
5 2 + _ 2 + 30 2 = 31 2
6 2 + 7 2 + _ 2 = __ 2
Ответ:
По заданному образцу, можно заметить, что,
(i) Третье число произведение первых двух чисел.
(ii) Четвертое число можно получить, прибавив 1 к третьему числу.
Таким образом, недостающие числа в шаблоне будут следующими.
4 2 + 5 2 + = 21 2
5 2 + + 30 2 = 31 2
6 2 + 7 2 + знак равно
Страница № 96:
Вопрос 7:
Без добавления найти сумма
(я) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Ответ:
Мы знаем, что сумма
первые n натуральные нечетные числа — это n 2 .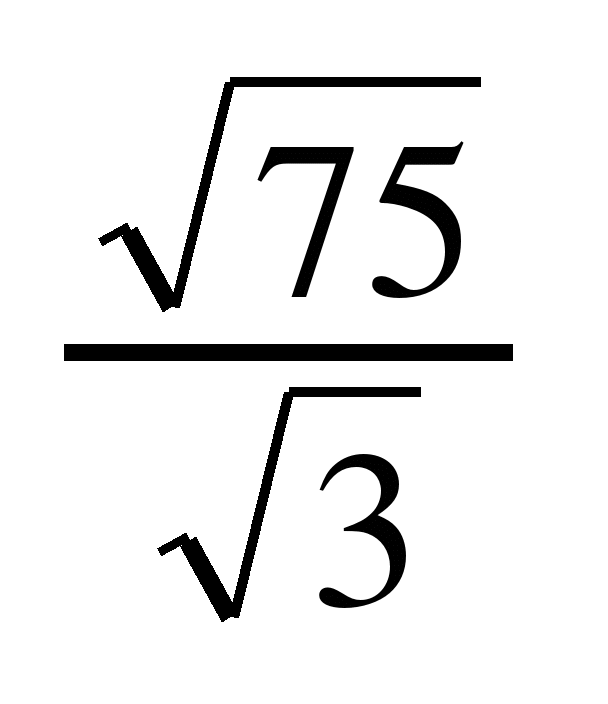
(i) Здесь мы должны найти сумму первых пяти нечетных натуральных чисел.
Следовательно, 1 + 3 + 5 + 7 + 9 = (5) 2 = 25
(ii) Здесь мы должны найти сумму первых десяти нечетных натуральных чисел.
Следовательно, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = (10) 2 = 100
(iii) Здесь мы должны найти сумму первых двенадцати нечетных натуральных чисел.
Следовательно, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 +17 + 19 + 21 + 23 = (12) 2 = 144
Страница № 96:
Вопрос 8:
(i) Экспресс 49 как сумма 7 нечетных чисел.
(ii) Экспресс 121 как сумма 11четных чисел.
Ответ:
Мы знаем, что сумма первые n натуральные нечетные числа — это n 2 .
(я) 49 = (7) 2
Следовательно,
49 — это сумма первых 7 нечетных натуральных чисел.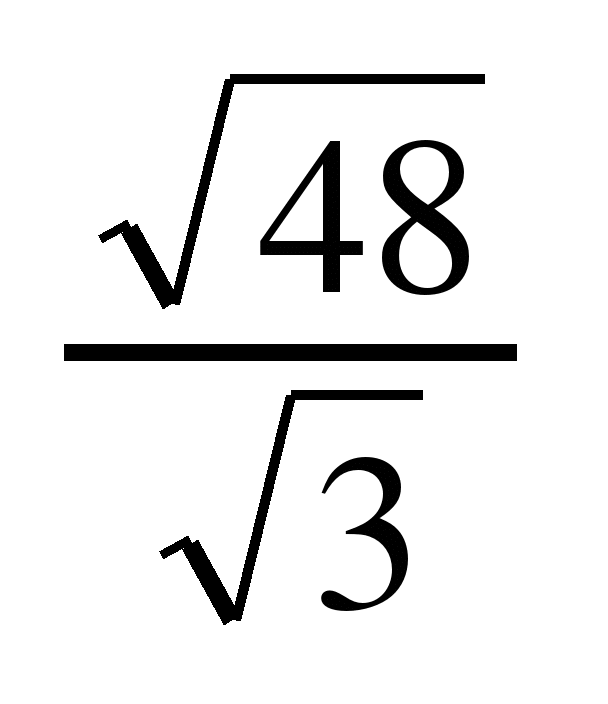
49 = 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii) 121 = (11) 2
Следовательно, 121 — это сумма первых 11 нечетных натуральных чисел.
121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
Страница № 96:
Вопрос 9:
Сколько чисел врут между квадратами следующих чисел?
(i) 12 и 13 (ii) 25 и 26 (iii) 99 и 100
Ответ:
Мы знаем, что будет быть 2 n число между квадратами чисел n и ( № + 1).
(i) Между 12 2 и 13 2 будет 2 × 12 = 24 числа
(ii) Между 25 2 и 26 2 будет 2 × 25 = 50 чисел
(iii) Между 99 2 и 100 2 будет 2 × 99 = 198 чисел
Страница № 98:
Вопрос 1:
Найдите квадрат из следующих чисел
(i) 32 (ii) 35
(iii) 86 (iv) 93
(v) 71 (vi) 46
Ответ:
(i) 32 2 = (30 + 2) 2
= 30 (30 + 2) + 2 (30 + 2)
= 30 2 + 30 × 2 + 2 × 30 + 2 2
= 900 + 60 + 60 + 4
= 1024
(ii) Число 35 имеет 5 вместо единицы.
Следовательно,
35 2 = (3) (3 + 1) сотни + 25
= (3 × 4) сотни + 25
= 1200 + 25 = 1225
(iii) 86 2 = (80 + 6) 2
= 80 (80 + 6) + 6 (80 + 6)
= 80 2 + 80 × 6 + 6 × 80 + 6 2
= 6400 + 480 + 480 + 36
= 7396
(iv) 93 2 = (90 + 3) 2
= 90 (90 + 3) + 3 (90 + 3)
= 90 2 + 90 × 3 + 3 × 90 + 3 2
= 8100 + 270 + 270 + 9
= 8649
(в) 71 2 = (70 + 1) 2
= 70 (70 + 1) + 1 (70 + 1)
= 70 2 + 70 × 1 + 1 × 70 + 1 2
= 4900 + 70 + 70 + 1
= 5041
(vi) 46 2 = (40 + 6) 2
= 40 (40 + 6) + 6 (40 + 6)
= 40 2 + 40 × 6 + 6 × 40 + 6 2
= 1600 + 240 + 240 + 36
= 2116
Видео решение для вычисления квадрата и квадратного корня (Страница: 98, Q. №: 1)
№: 1) Решение NCERT для математики класса 8 — квадраты и квадратные корни 98, вопрос 1
Страница № 98:
Вопрос 2:
Напишите триплет Пифагора, один член которого равен
(i) 6 (ii) 14
(iii) 16 (iv) 18
Ответ:
Для любого натурального числа м > 1, 2 м , м 2 — 1, м 2 + 1 образует пифагорову тройку.
(i) Если взять м 2 + 1 = 6, то м 2 = 5
Значение м не будет целым числом.
Если взять м 2 — 1 = 6, то м 2 = 7
Опять же, значение м не целое число.
Пусть 2 м = 6
м = 3
Следовательно, тройки Пифагора равны 2 × 3, 3 2 — 1, 3 2 + 1 или 6, 8 и 10.
(ii) Если взять м 2 + 1 = 14, то м 2 = 13
Значение м не будет целым числом.
Если взять м 2 — 1 = 14, то м 2 = 15
Опять же, значение м не целое число.
Пусть 2 м = 14
м = 7
Таким образом, м 2 — 1 = 49 — 1 = 48 и м 2 + 1 = 49 + 1 = 50
Следовательно, требуется триплет 14, 48 и 50.
(iii) Если взять м 2 + 1 = 16, то м 2 = 15
Значение м не будет целым числом.
Если взять м 2 — 1 = 16, то м 2 = 17
Опять же, значение м не целое число.
Пусть 2 м = 16
м = 8
Таким образом, м 2 — 1 = 64 — 1 = 63 и м 2 + 1 = 64 + 1 = 65
Следовательно, тройка Пифагора — это 16, 63 и 65.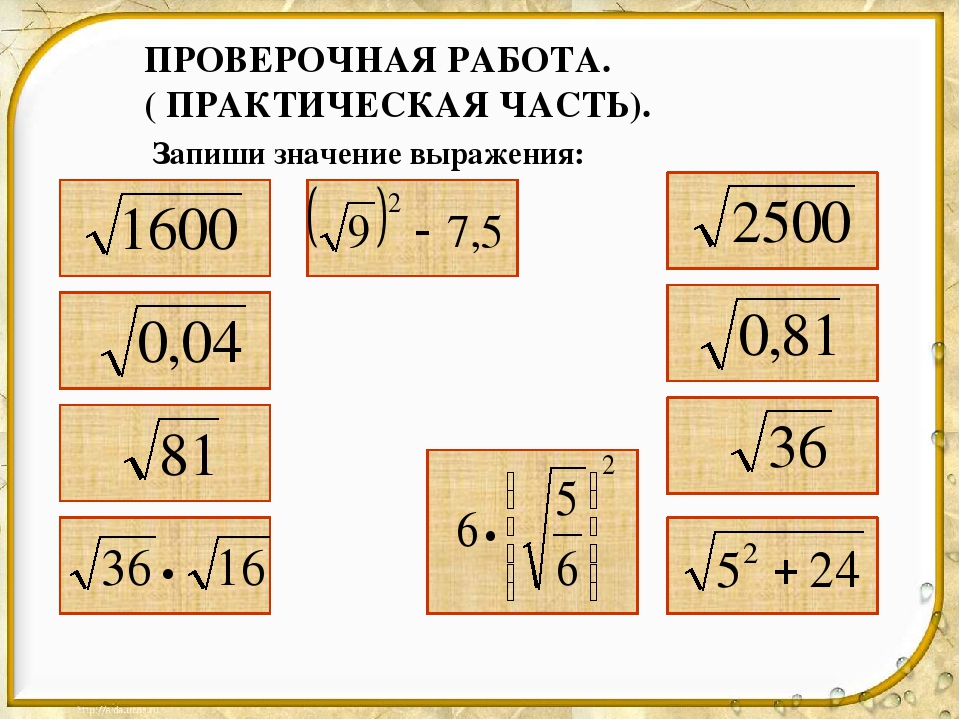
(iv) Если взять м 2 + 1 = 18,
м 2 = 17
Значение м не будет целым числом.
Если взять м 2 — 1 = 18, то м 2 = 19
Опять же, значение м не целое число.
Пусть 2 м = 18
м = 9
Таким образом, м 2 — 1 = 81 — 1 = 80 и м 2 + 1 = 81 + 1 = 82
Следовательно, тройка Пифагора — 18, 80 и 82.
Видео решение для вычисления квадрата и квадратного корня (Страница: 98, Q.No .: 2)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 98, вопрос 2
Страница № 102:
Вопрос 1:
Что может быть возможных «единичных» цифр квадратного корня каждого из следующих номеров?
(i) 9801 (ii) 99856
(iii) 998001 (iv) 657666025
Ответ:
(i) Если число заканчивается на 1, то единичная цифра квадратный корень из этого числа может быть 1 или 9.Следовательно, один цифра квадратного корня из 9801 равна 1 или 9.
(ii) Если число заканчивается на 6, то единичная цифра квадратный корень из этого числа может быть 4 или 6. Следовательно, цифра квадратного корня из 99856 равна 4 или 6.
(iii) Если номер заканчивается на 1, то единица цифры квадратный корень из этого числа может быть 1 или 9. Следовательно, цифра квадратного корня из 998001 равна 1 или 9.
(iv) Если число заканчивается на 5, то единичная цифра квадратный корень из этого числа будет 5.Следовательно, один цифра квадратного корня из 657666025 равна 5.
Страница № 102:
Вопрос 2:
Не делая никаких вычислений, найдите числа, которые точно не идеальные квадраты.
(i) 153 (ii) 257
(iii) 408 (iv) 441
Ответ:
Идеальные квадраты номер может заканчиваться любой из цифр 0, 1, 4, 5, 6 или 9 в единицах место.Кроме того, полный квадрат будет заканчиваться четным числом нулей, если любой.
(i) Поскольку число 153 имеет разрядную цифру 3, это не идеальный площадь.
(ii) Поскольку число 257 имеет разрядную цифру 7, это не идеальный площадь.
(iii) Поскольку число 408 имеет разрядную цифру 8, это не идеальный площадь.
(iv) Поскольку число 441 имеет разрядную цифру 1, это полный квадрат.
Страница № 102:
Вопрос 3:
Найдите квадратные корни из 100 и 169 методом повторного вычитания.
Ответ:
Мы знаем, что сумма первых n нечетных натуральных чисел равна n 2 .
Считай.
(i) 100 — 1 = 99 (ii) 99 — 3 = 96 (iii) 96 — 5 = 91
(iv) 91 — 7 = 84 (v) 84 — 9 = 75 (vi) 75 — 11 = 64
(vii) 64-13 = 51 (viii) 51-15 = 36 (ix) 36-17 = 19
(х) 19 — 19 = 0
Мы вычли последовательные нечетные числа, начиная с 1 до 100, и получили 0 на шаге 10 -го .
Следовательно,
Квадратный корень из 169 может быть получен методом повторного вычитания следующим образом.
(i) 169 — 1 = 168 (ii) 168 — 3 = 165 (iii) 165 — 5 = 160
(iv) 160 — 7 = 153 (v) 153 — 9 = 144 (vi) 144 — 11 = 133
(vii) 133 — 13 = 120 (viii) 120 — 15 = 105 (ix) 105 — 17 = 88
(x) 88 — 19 = 69 (xi) 69 — 21 = 48 (xii) 48 — 23 = 25
(xiii) 25–25 = 0
Мы вычли последовательные нечетные числа, начиная с 1 до 169, и получили 0 на шаге 13 -го .
Следовательно,
Видео решение для вычисления квадрата и квадратного корня (Страница: 102, Q.No .: 3)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 102, вопрос 3
Страница № 102:
Вопрос 4:
Найдите квадратные корни из следующих чисел простым числом Метод факторизации.
(i) 729 (ii) 400
(iii) 1764 (iv) 4096
(v) 7744 (vi) 9604
(vii) 5929 (viii) 9216
(ix) 529 (х) 8100
Ответ:
(i) 729 может быть факторизуется следующим образом.
3
729
3
243
3
81
3
27
3
9
3
3
1
729 = 3 × 3 × 3 × 3 × 3 × 3
∴ = 27
(ii) 400 может быть факторизуется следующим образом.
2
400
2
200
2
100
2
50
5
25
5
5
1
400 = 2 × 2 × 2 × 2 × 5 × 5
∴ = 20
(iii) 1764 может быть факторизуется следующим образом.
2
1764
2
882
3
441
3
147
7
49
7
7
1
1764 = 2 × 2 × 3 × 3 × 7 × 7
∴ = 42
(iv) 4096 может быть факторизуется следующим образом.
2
4096
2
2048
2
1024
2
512
2
256
2
128
2
64
2
32
2
16
2
8
2
4
2
2
1
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ знак равно 64
(в) 7744 может быть факторизуется следующим образом.
2
7744
2
3872
2
1936
2
968
2
484
2
242
11
121
11
11
1
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
∴ = 88
(vi) 9604 может быть факторизуется следующим образом.
2
9604
2
4802
7
2401
7
343
7
49
7
7
1
9604 = 2 × 2 × 7 × 7 × 7 × 7
∴ = 98
(vii) 5929 может быть факторизуется следующим образом.
7
5929
7
847
11
121
11
11
1
5929 = 7 × 7 × 11 × 11
∴ знак равно 77
(viii) 9216 может быть факторизуется следующим образом.
2
9216
2
4608
2
2304
2
1152
2
576
2
288
2
144
2
72
2
36
2
18
3
9
3
3
1
9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
∴ = 96
(ix) 529 может быть факторизуется следующим образом.
529 = 23 × 23
(x) 8100 может быть факторизуется следующим образом.
2
8100
2
4050
3
2025
3
675
3
225
3
75
5
25
5
5
1
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
∴ = 90
Страница № 102:
Вопрос 5:
Найдите наименьшее целое число для каждого из следующих чисел. на которое его следует умножить, чтобы получить идеальный квадрат число.Также найдите квадратный корень из полученного таким образом квадратного числа.
(i) 252 (ii) 180
(iii) 1008 (iv) 2028
(v) 1458 (vi) 768
Ответ:
(i) 252 можно разложить на множители следующим образом.
2
252
2
126
3
63
3
21
7
7
1
252 = 2 × 2 × 3 × 3 × 7
Здесь у простого множителя 7 нет пары.
Если у 7 выпадет пара, то число станет полным квадратом. Следовательно, 252 нужно умножить на 7, чтобы получить идеальное площадь.
252 × 7 = 2 × 2 × 3 × 3 × 7 × 7
Следовательно, 252 × 7 = 1764 — полный квадрат.
∴
(ii) 180 можно разложить на множители следующим образом.
2
180
2
90
3
45
3
15
5
5
1
180 = 2 × 2 × 3 × 3 × 5
Здесь у простого множителя 5 нет пары.Если 5 получит пару, тогда число превратится в правильный квадрат. Следовательно, 180 должен умножьте на 5, чтобы получить полный квадрат.
180 × 5 = 900 = 2 × 2 × 3 × 3 × 5 × 5
Следовательно, 180 × 5 = 900 — это полный квадрат.
∴ = 30
(iii) 1008 можно разложить на множители следующим образом.
2
1008
2
504
2
252
2
126
3
63
3
21
7
7
1
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
Здесь у простого множителя 7 нет пары.Если 7 получит пару, тогда число превратится в правильный квадрат. Следовательно, 1008 может быть умножить на 7, чтобы получить полный квадрат.
1008 × 7 = 7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
Следовательно, 1008 × 7 = 7056 — это полный квадрат.
∴ = 84
(iv) 2028 можно разложить на множители следующим образом.
2
2028
2
1014
3
507
13
169
13
13
1
2028 = 2 × 2 × 3 × 13 × 13
Здесь у простого множителя 3 нет пары.Если 3 получит пару, тогда число превратится в правильный квадрат. Следовательно, 2028 г. должен умножьте на 3, чтобы получить полный квадрат.
Следовательно, 2028 × 3 = 6084 — это полный квадрат.
2028 × 3 = 6084 = 2 × 2 × 3 × 3 × 13 × 13
∴ = 78
(в) 1458 может быть факторизуется следующим образом.
2
1458
3
729
3
243
3
81
3
27
3
9
3
3
1
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
Здесь у простого множителя 2 нет пары.Если 2 получит пару, тогда число превратится в правильный квадрат. Следовательно, 1458 г. умножьте на 2, чтобы получить полный квадрат.
Следовательно, 1458 × 2 = 2916 — это полный квадрат.
1458 × 2 = 2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
∴ = 54
(vi) 768 можно разложить на множители следующим образом.
2
768
2
384
2
192
2
96
2
48
2
24
2
12
2
6
3
3
1
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Здесь у простого множителя 3 нет пары.Если 3 получит пару, тогда число превратится в правильный квадрат. Следовательно, 768 должен умножьте на 3, чтобы получить полный квадрат.
Следовательно, 768 × 3 = 2304 — это полный квадрат.
768 × 3 = 2304 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
∴ = 48
Страница № 102:
Вопрос 6:
Для каждого из следующие числа, найдите наименьшее целое число, на которое он должен разделить так, чтобы получить точное квадратное число.Также найдите квадрат корень квадратного числа, полученного таким образом.
(i) 252 (ii) 2925
(iii) 396 (iv) 2645
(v) 2800 (vi) 1620
Ответ:
(i) 252 может быть факторизуется следующим образом.
2
252
2
126
3
63
3
21
7
7
1
Здесь, простой фактор 7 не имеет пары.
Если делим это число на 7, тогда число станет идеальным площадь. Следовательно, 252 нужно разделить на 7, чтобы получить идеальное площадь.
252 ÷ 7 = 36 — точный квадрат.
(ii) 2925 может быть факторизуется следующим образом.
3
2925
3
975
5
325
5
65
13
13
1
Здесь, у простого множителя 13 нет пары.
Если делим это число на 13, тогда число станет идеальным площадь. Следовательно, 2925 нужно разделить на 13, чтобы получить идеальное площадь.
2925 ÷ 13 = 225 — идеальный площадь.
(iii) 396 может быть факторизуется следующим образом.
2
396
2
198
3
99
3
33
11
11
1
Здесь, у простого множителя 11 нет пары.
Если делим это число на 11, тогда число станет идеальным площадь. Следовательно, 396 нужно разделить на 11, чтобы получить идеальное площадь.
396 ÷ 11 = 36 — идеальный площадь.
(iv) 2645 банка разложить на множители следующим образом.
Здесь, простой фактор 5 не имеет пары.
Если делим это число на 5, тогда число станет идеальным площадь.
Следовательно, 2645 нужно разделить на 5, чтобы получить полный квадрат.
2645 ÷ 5 = 529 — идеальный площадь.
(в) 2800 может быть факторизуется следующим образом.
2
2800
2
1400
2
700
2
350
5
175
5
35
7
7
1
Здесь, простой фактор 7 не имеет пары.
Если делим это число на 7, тогда число станет идеальным площадь.
Следовательно, 2800 нужно разделить на 7, чтобы получить полный квадрат.
2800 ÷ 7 = 400 — идеальный площадь.
∴
(vi) 1620 может быть факторизуется следующим образом.
2
1620
2
810
3
405
3
135
3
45
3
15
5
5
1
Здесь, простой фактор 5 не имеет пары.
Если делим это число на 5, тогда число станет идеальным площадь.
Следовательно, 1620 нужно разделить на 5, чтобы получить полный квадрат.
1620 ÷ 5 = 324 — идеальный площадь.
∴
Страница № 102:
Вопрос 7:
Учащиеся VIII класса школы пожертвовали в общей сложности 2401 рупий в Национальный фонд помощи премьер-министра.Каждый ученик пожертвовал столько рупий, сколько учеников в классе. Найдите количество учеников в классе.
Ответ:
Предполагается, что каждый ученик пожертвовал столько рупий, сколько ученик класса. Количество учеников в классе будет квадратным корнем из суммы, пожертвованной учениками класса.
Общая сумма пожертвования составляет 2401 рупий.
Количество учеников в классе =
∴
Следовательно, в классе 49 учеников.
Видео решение для вычисления квадрата и квадратного корня (Страница: 102, Q.No .: 7)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 102, вопрос 7
Страница № 103:
Вопрос 8:
2025 растений следует высаживать в саду таким образом, чтобы в каждом ряду было столько растений, сколько рядов.Найдите количество рядов и количество растений в каждом ряду.
Ответ:
Принято, что в саду каждый ряд содержит столько растений, сколько рядов.
Следовательно,
Количество рядов = Количество растений в каждом ряду
Общее количество растений = Количество рядов × Количество растений в каждом ряду
Количество рядов × Количество растений в каждом ряду = 2025
(количество строк) 2 = 2025
∴
Таким образом, количество рядов и количество растений в каждом ряду 45.
Видео решение для вычисления квадрата и квадратного корня (Страница: 103, Q.No .: 8)
Решение NCERT для математики класса 8 — квадраты и квадратные корни 103, вопрос 8
Страница № 103:
Вопрос 9:
Найти наименьшее квадратное число, которое делится на каждое из чисел 4, 9 и 10.
Ответ:
Число, которое будет НОК идеально делится на каждое из 4, 9 и 10.LCM из этих чисел выглядит следующим образом.
2 | 4, 9, 10 |
2 | 2, 9, 5 |
3 | 1, 9, 5 |
3 | 1, 3, 5 |
5 | 1, 1, 5 |
1, 1, 1 |
НОК 4, 9, 10 = 2 × 2 × 3 × 3 × 5 = 180
Здесь простой множитель 5 нет своей пары.Следовательно, 180 — не идеальный квадрат. Если мы умножьте 180 на 5, тогда число станет точным квадратом. Следовательно, 180 следует умножить на 5, чтобы получить идеальный площадь.
Следовательно, требуемый квадратное число 180 × 5 = 900
Страница № 103:
Вопрос 10:
Найдите самое маленькое квадратное число, которое делится на каждое из чисел 8, 15,
и 20.
Ответ:
Число, которое идеально делится на каждое из чисел 8, 15 и 20, их LCM.
2 | 8, 15, 20 |
2 | 4, 15, 10 |
2 | 2, 15, 5 |
3 | 1, 15, 5 |
5 | 1, 5, 5 |
1, 1, 1 |
НОК 8, 15 и 20 = 2 × 2 × 2 × 3 × 5 = 120
Здесь простые множители 2, 3 и 5 не имеют соответствующих пар.Следовательно, 120 не является идеальный квадрат.
Следовательно, 120 должны умножить на 2 × 3 × 5, т.е. 30, чтобы получить идеальное площадь.
Следовательно, требуемый квадратное число 120 × 2 × 3 × 5 = 3600
Страница № 107:
Вопрос 1:
Найдите квадратный корень из каждого из следующих чисел методом деления.
(i) 2304 (ii) 4489
(iii) 3481 (iv) 529
(v) 3249 (vi) 1369
(vii) 5776 (viii) 7921
(ix) 576 (x) 1024
(xi) 3136 (xii) 900
Ответ:
(i) Корень квадратный из 2304 можно вычислить следующим образом.
48
4
88
704
704
0
∴
(ii) Квадратный корень из 4489 можно вычислить следующим образом.
67
6
127
889
889
0
∴
(iii) Квадратный корень из 3481 можно вычислить следующим образом.
59
5
109
981
981
0
Следовательно,
(iv) Квадратный корень из 529 можно вычислить следующим образом.
23
2
43
129
129
0
∴
(v) Корень квадратный из 3249 можно рассчитать следующим образом.
57
5
107
749
749
0
∴
(vi) Квадратный корень из 1369 можно вычислить следующим образом.
37
3
67
469
469
0
∴
(vii) Квадратный корень из 5776 можно вычислить следующим образом.
76
7
146
876
876
0
∴
(viii) Квадратный корень из 7921 можно вычислить следующим образом.
89
8
169
1521
1521
0
∴
(ix) Корень квадратный из 576 можно вычислить следующим образом.
24
2
44
176
176
0
∴
(x) Корень квадратный из 1024 можно вычислить следующим образом.
32
3
62
124
124
0
∴
(xi) Квадратный корень из 3136 можно вычислить следующим образом.
56
5
106
636
636
0
∴
(xii) Квадратный корень из 900 можно вычислить следующим образом.
30
3
60
00
00
0
∴
Страница № 107:
Вопрос 2:
Найдите количество цифры квадратного корня каждого из следующих чисел (без любой расчет).
(i) 64 (ii) 144
(iii) 4489 (iv) 27225
(в) 3
Ответ:
(i) Размещая стержни, мы получить
С есть только одна полоса, квадратный корень из 64 будет иметь только одну цифру в этом.
(ii) размещая стержни, получаем
С есть два столбца, квадратный корень из 144 будет состоять из двух цифр.
(iii) размещая стержни, получаем
С есть две полосы, квадратный корень из 4489 будет состоять из двух цифр.
(iv) размещая стержни, получаем
С есть три столбца, квадратный корень из 27225 будет состоять из трех цифр в этом.
(v) Размещая баров, получаем
С есть три столбца, квадратный корень из 3 будет иметь 3 цифры в Это.
Страница № 108:
Вопрос 3:
Найдите квадратный корень из следующие десятичные числа.
(i) 2,56 (ii) 7,29
(iii) 51,84
Примечания для квадратов и квадратного корня класса 8 Скачать PDF
Важность квадратов и квадратного корня класса 8 Примечания и концепции к редакции
Внесение примечаний к исправлению для класса 8 поможет вам интерпретировать все, что вы Прочтите своими словами, чтобы лучше понять концепции класса 8. Были времена, когда ученики 8-х классов читали всю страницу безучастно, даже не понимая ни единого слова, но если вы сделаете заметок для 8-го стандарта , тогда ваш мозг попытается выжать смысл из каждого написанного вами предложения, что очень много. полезно для студентов.В заметках о редакции всегда фиксируется вся информация, которую вы узнали. Эти заметки во время экзамена будут действовать как готовые рекомендации для рассмотрения. Этот метод не только помогает сэкономить энергию и время учеников во время экзамена 8 класса, но также помогает им вспомнить все, что они изучали, за меньшее время. Заметки о пересмотре для класса 8 также помогли студентам запомнить то, что они изучали, потому что они могли прочитать каждое предложение строка за строкой и подготовить заметки.
Преимущества Примечания для квадратов и корней класса 8
a) Поможет вам своевременно пересмотреть все важные концепции перед школьными экзаменами 8 класса
b) Краткие примечания к каждой главе, приведенной в новейшие книги для класса 8 по квадратам и квадратным корням помогут вам изучить и повторить все основные концепции прямо у дверей экзаменационного зала.
c) Примечания, предоставленные Studiestoday.com, были подготовлены специально для студентов, сдающих экзамен Class 8 2020, чтобы они могли получить лучший результат на предстоящем экзамене Class 8
d) Вы почувствуете себя комфортно, потому что вы пересмотрели все важные темы Квадраты и квадратные корни , и вам не нужно будет носить с собой всю книгу на экзамене.
e) Загрузите все заметки в формате PDF для Квадраты и квадратные корни класса 8 и будьте уверены, что вы охватили все
Приведенные выше примечания будут поможет вам преуспеть на экзаменах.Вы всегда должны пересматривать концепции и заметки о квадратах и квадратных корнях для класса 8 перед экзаменами, они помогут вам обобщить все важные темы, и вы сможете получить более высокие оценки. Вы также можете щелкнуть ниже, чтобы загрузить решенные последние образцы работ, контрольные работы за прошлый год (за последние 10 лет) в формате pdf для печати, имитирующие онлайн-тесты, последние книги для класса 8, основанные на учебной программе и руководящих принципах, выпущенных CBSE NCERT KVS. Учебный материал подготовлен опытными преподавателями ведущих школ и институтов Индии и доступен для бесплатного скачивания в формате pdf.
Квадратный корень и кубический корень
Видео о квадратном корне и кубическом корне — ярлыки, советы и уловкиКвадратный корень и кубический корень
Важные моменты, о которых следует помнить: Квадратный корень: Если 2 = b, мы говорим, что квадратный корень из b равен
Он записывается как b = a
2) Кубический корень: Кубический корень из a обозначается как 3 a
3) ab = a × b
| 4) (a / b) = | a | = | a | × | b | = | ab | b | b |
5) Число, оканчивающееся на 8, никогда не может быть полным квадратом.
6) Запомните квадраты и кубы от 2 до 10. Это поможет легко решить задачи.
Найдите числа, которые имеют одинаковую цифру на месте единицы:
Советы и уловки
1) Поиск квадратного корня из 5-, 4- и 3-значных чисел
Как найти квадратный корень из 5-значного числа?
Как найти квадратный корень из 4-значного числа?
Как найти квадратный корень из трехзначного числа?
2) Нахождение квадрата больших чисел
Пример: 47 2 = 2209
Квадрат 47 можно легко определить, выполнив следующие шаги:
Шаг 1: Разделите число 47 на 4 и 7.
Шаг 2: Используйте формулу: (a + b) 2 = a 2 + 2ab + b 2
Здесь (4 + 7) 2 = 4 2 + 2 × 4 × 7 + 7 2
Без учета знака «плюс» напишите числа, как показано ниже:
[16] [56] [49]
Шаг 1. Запишите 9 из 49 и перенесите 4 в 56. . [—— 9]
Шаг 2: После прибавления 4 к 6 получаем 10. Поэтому запишите ноль и перенесите 1 (5 + 1 = 6) в 16.[—- 09]
Шаг 3: 6 + 6 = 12, запишите 2 и перенесите один. [— 209]
Шаг 4: Напишите ответ вместе с (1 + 1 = 2). [2209]
3) Нахождение кубического корня из 6-значного числа?
Примечание: Кубические корни из 6-, 5-, 4- или 3-значных чисел можно легко найти, используя тот же прием, который используется для нахождения квадратного корня из более крупных цифр.
Пример: 3 132651
Помните: последние 3 числа должны быть вырезаны, а ближайший куб первых оставшихся чисел должен быть найден.
Шаг 1: Разделите числа 132 и 651
Шаг 2: 125 — это куб 5, которое является ближайшим числом к 132. Следовательно, первое число, то есть число в разряде десятков, равно 5.
Шаг 3: 1 — это цифра вместо единицы. Следовательно, цифра на месте единицы равна 1.
Следовательно, кубический корень 132651 равен 51.
4) Как найти число, которое нужно добавить или вычесть, чтобы сделать число точным квадратом?
Для облегчения понимания рассмотрим пример.
Пример: 8888
Шаг 1: Разделим 8888 на 9. Мы получим остаток 7.
Шаг 2: Добавить делитель и коэффициент [9 + 9 = 18]
Шаг 3: Сейчас следующий делитель будет (18 и число x), который разделит следующее делимое. В этом случае 4 — это число x, и теперь делитель становится 184 × 4 = 736.
Шаг 4: Этот шаг должен выполняться в зависимости от количества цифр в делимом.
Случай 1: Если нам нужно найти число, которое нужно сложить, чтобы сделать число точным квадратом, тогда
Рассмотрим число, большее, чем частное.Ее частное 94, поэтому рассмотрим 95.
94 2 <8888 <95 2
8836 <8888 <9025
Число, которое нужно добавить = Большее число — данное число
Число, которое нужно добавить = 9025 — 8888 = 137
Случай 2: Если нам нужно найти число, которое нужно вычесть, чтобы сделать число точным квадратом, то
94 2 <8888 <95 2
8836 <8888 <9025
Число, которое нужно вычесть = Заданное число — Меньшее число
Число, которое нужно добавить = 8888 — 8836 = 52
Вариант вопросов
В основном задаются вопросы 4 типов. главу.Понимание и практика каждого из 4 типов поможет вам успешно справиться с проблемами из этой главы.
Тип 1. Найдите квадратный корень и кубический корень из заданных чисел
Q 1. Найдите квадратный корень из 5929
a. 49
г. 33
г. 77
г. 73
Посмотреть решение
Правильный вариант: (c)
Запомните прием, описанный в Кратких советах и приемах
Шаг 1: Разделите число 59 29
7 2 = 49 — ближайшее число к 59 .Следовательно, цифра в разряде десятков равна 7.
Шаг 2: Последняя цифра числа 29 — 9. Следовательно, 3 или 7 — это цифры вместо единицы.
Умножьте 3 на следующее по порядку большее число, например, 4
3 × 4 = 12
Но 12 Цифра на месте единицы равна 7.
Следовательно, квадратный корень из 5929 равен 77
Q 2. Найдите кубический корень из 1728
а. 12
г. 14
г. 16
г. 18
Посмотреть решение
Правильный вариант: (a)
Подсказка: Вопросы этого типа можно легко решить, решив данное число как произведение простых множителей и выбрав один общий множитель среди повторяющихся множителей.
Число 1728 легко делится на 2, 4, 8, 12 и т. Д. Выбор большего числа 12 уменьшит затраты на решение задачи.
1728 = 12 × 12 × 12 = 12 3
Q 3. Найдите значение 151
a. 12.459
г. 12.292
г. 13.591
г. Ни один из этих
Посмотреть решение
Правильный вариант: (b)
Подсказка:
Уловка для нахождения квадратного корня из чисел, не являющихся точными квадратами.
Шаг 1: Найдите квадрат туалета, равный 151. 144 — это ближайший квадрат, его квадратный корень равен 12.
Шаг 2: Теперь разделите полученное число на квадратный корень из ближайшего квадрата, т.е. 12
Шаг 3: Возьмите среднее значение 12,583 и извлеките квадратный корень из ближайшего числа.
| 12 + 12,583 | = 12,2915 = 12,292 |
| 2 |
Q 4. Найти — это значение
а. 9
б. 8
с. 6
г. 4
Просмотреть решение
Правильный вариант: (d)
Квадратный корень из 256 равен 16
Квадратный корень из 81 равен 9
Квадратный корень из 36 равен 6
10 + 6 = 16 = 4
Q 5. Найдите значение
a. 0,3
б. 0,7
г. 0,09
г. Ни один из этих
Просмотреть решение
Правильный вариант: (a)
Шаг 1: Сначала найдите 0.000729
Шаг 2:
Значение
Решения NCERT для математики класса 8 Глава 6 КВАДРАТНЫЕ И КВАДРАТНЫЕ КОРНИ
Решения NCERT для математики класса 8 Глава 6
| Класс: 43 | |
| Тема: | Математика — गणित |
| Глава 6: | Квадратные и квадратные корни |
Математика 8 класса Решения главы 6
Класс 8 Математика Глава 6 Квадратные и квадратные корни все упражнения ответы на вопросы на английском языке, а также на хинди Medium или View in Video Format обновлены для новой академической сессии 2020-21.Загрузите приложение «Математика для класса 8» или загрузите приложение कक्षा 8 गणित для автономного использования. После загрузки он работает без интернета.
8 Математика Глава 6 Решения на английском языке Средний
8 Математика Глава 6 Решения на хинди Средний
Математика класса 8 Упражнение 6.1 и 6.2 Решения в видео
Математика класса 8 Упражнение 6.1. Решения на видео Математика для класса 8 Упражнение 6.2. Решения на видеоМатематика для 8-го класса. Упражнение 6.Решения 3 и 6.4 в видео
Математика для класса 8 Упражнение 6.3 Решения в видео Математика для класса 8 Упражнение 6.4 Решения в видеоВажные термины о математике для класса 8 Глава 6
Какой будет единичная цифра квадратов из числа 81?
Число 81 содержит разрядную цифру единицы единицы. Итак, квадрат 1 равен 1.
Следовательно, цифра квадрата единицы единицы 81 равна 1.
Не прибавляя, найдите сумму 1 + 3 + 5 + 7 + 9.
Здесь пять нечетных чисел.2 = 25
बिना गणना किए बताएँ कि 153 वास्तव में पूर्ण वर्ग है या नहीं है।
हम जानते हैं कि संख्याओं के वर्गों में इकाई का अंक 0, 1, 4, 5, 6 और 9 होता है।
153 में इकाई का अंक 3 है, अतः यह संख्या पूर्ण वर्ग नहीं है।
बार-बार घटाने की विधि से 100 का वर्गमूल ज्ञात कीजिए।
बार-बार घटाने की विधि से 100 का वर्गमूल:
100–1 = 99
99–3 = 96
96–5 = 91
91–7 = 84
84–9 = 75
75–11 = 64
64-13 = 51
51-15 = 36
36-17 = 19
19-19 = 0
संख्या 1 से क्रमागत विषम को 100 में से घटाने पर 10 वाँ पद 0 प्राप्त होता है।
इसलिए, 100 का वर्गमूल = 10
В главе 6 «Квадратные и квадратные корни» мы найдем квадратные корни из разных чисел различными методами.