Контрольные работы алимов 11 класс: Контрольные работы по алгебре и началам анализа для 11 класса (Колягин Ю.М.)

Контрольные работы по алгебре и началам анализа для 11 класса (Колягин Ю.М.)

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 1

1. Найдите область определения и множество значений функции у = 2 cos x.

2. Выясните, является ли функция у = sin x – tg x четной или нечетной.

3. Изобразите схематически график функции у = sin x + 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = 3sin x ∙cos x + 1.

5. Постройте график функции у = 0,5 cos x – 2. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 2

1. Найдите область определения и множество значений функции у = 0,5 cos x.

2. Выясните, является ли функция у = cos x – x² четной или нечетной.

3. Изобразите схематически график функции у = cos x — 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = + 1.

5. Постройте график функции у = 2 sin x + 1. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 1

1. Найдите область определения и множество значений функции у = 2 cos x.

2. Выясните, является ли функция у = sin x – tg x четной или нечетной.

3. Изобразите схематически график функции у = sin x + 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = 3sin x ∙cos x + 1.

5. Постройте график функции у = 0,5 cos x – 2. При каких значениях х функция возрастает? Убывает?

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 2

1. Найдите область определения и множество значений функции у = 0,5 cos x.

2. Выясните, является ли функция у = cos x – x² четной или нечетной.

3. Изобразите схематически график функции у = cos x — 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = + 1.

5. Постройте график функции у = 2 sin x + 1. При каких значениях х функция возрастает? Убывает?

Контрольная работа № 2

по теме «Производная и ее геометрический смысл»

Вариант 1

1. Найдите производную функции: а) 3х² — б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = 8.

3. Запишите уравнение касательной к графику функции f(x) = sin x – 3x + 2 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x) = положительны.

5. Найдите точки графика функции f(x)= х³ – 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = .

Контрольная работа № 2

по теме «Производная и ее геометрический смысл»

Вариант 2

1. Найдите производную функции: а) 2х³ — б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = .

3. Запишите уравнение касательной к графику функции f(x) = 4x — sin x + 1 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x) = отрицательны.

5. Найдите точки графика функции f(x)= х³ + 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = cos .

Контрольная работа № 3

по теме «Применение производной к исследованию функций»

Вариант 1

1. Найдите стационарные точки функции f(x) = х³— 2х² +х +3.

2. Найдите экстремумы функции: а) f(x) =х³ – 2х² + х + 3; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х³— 2х² +х +3.

4. Постройте график функции f(x) = х³— 2х² +х +3 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³— 2х² +х +3 на отрезке .

6. Среди прямоугольников, сумма длин трех сторон которых равна 20, найдите прямоугольник наибольшей площади.

Контрольная работа № 3

по теме «Применение производной к исследованию функций»

Вариант 2

1. Найдите стационарные точки функции f(x) = х³— х² — х +2.

2. Найдите экстремумы функции: а) f(x) = х³— х² — х +2; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х

   3— х² — х +2.

4. Постройте график функции f(x) = х³— х² — х +2 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³— х² — х +2 на отрезке .

6. Найдите ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

Контрольная работа № 4

по теме «Интеграл»

Вариант 1

1. Докажите, что функция F(x) = 3х + sin x – e^2xявляется первообразной функции f (x) = 3 + cos x – 2e^2x на всей числовой оси.

2. Найдите первообразную F функции f (x) = 2, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 1 – 2х и графиком функции у = х² – 5х – 3.

Контрольная работа № 4

по теме «Интеграл»

Вариант 2

1. Докажите, что функция F(x) = х + cos x + e^3xявляется первообразной функции f (x) = 1 — sin x + 3e^3x на всей числовой оси.

2. Найдите первообразную F функции f (x) = — 3, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 3 – 2х и графиком функции у = х² + 3х – 3.

11 класс. Алгебра и начала анализа. Контрольные работы. Колягин Ю.М. | Учебно-методический материал по алгебре (11 класс):

Контрольная работа по алгебре и началам анализа №2

«Производная функции»       (базовый уровень)

1 вариант

1. Найти производную функции:  1) ,   2) ,

                        3) ,   4) .

2. Найти значение производной функции   в точке , если , .
3. Составить уравнение касательной к графику функции    в точке .
4. Найти значения   х, при которых значения производной функции  положительны.
5. Найти точки графика функции      в которых касательная к нему параллельна оси абсцисс.

Контрольная работа по алгебре и началам анализа №2

«Производная функции»       (базовый уровень)

2 вариант

1. Найти производную функции:  1) ,   2) ,

                     3) ,   4) .

2. Найти значение производной функции   в точке , если , .
3. Составить уравнение касательной к графику функции    в точке .
4. Найти значения   х, при которых значения производной функции  отрицательны.
5. Найти точки графика функции      в которых касательная к нему параллельна оси абсцисс.

…………………………………………………………………………………………………

Контрольная работа по алгебре и началам анализа №2

«Производная функции»       (профильный уровень)

1 вариант

1. Найти производную функции:  1) ,   2) ,

                     3) ,   4) .

2. Найти значение производной функции   в точке , если , .
3. Составить уравнение касательной к графику функции    в точке .
4. Найти значения   х, при которых значения производной функции  положительны.
5. Найти точки графика функции      в которых касательная к нему имеет заданный угловой коэффициент .
6. Найти все значения  а, при которых неравенство   не имеет действительных решений, если .

Контрольная работа по алгебре и началам анализа №2

«Производная функции»       (профильный уровень)

2 вариант

1. Найти производную функции:  1) ,   2) ,

                    3) ,   4) .

2. Найти значение производной функции   в точке , если , .
3. Составить уравнение касательной к графику функции    в точке .
4. Найти значения   х, при которых значения производной функции  отрицательны.
5. Найти точки графика функции      в которых касательная к нему имеет заданный угловой коэффициент .
6. Найти все значения  а, при которых неравенство   не имеет действительных решений, если .

…………………………………………………………………………………………………

Контрольная работа по алгебре и началам анализа  №3

«Исследование функции с помощью производной»

1 вариант

1. Найти экстремумы функции:  а) ,   б) .
2. Найти интервалы возрастания и убывания функции  .
3. Построить график функции  .
4. Найти наибольшее и наименьшее значения функции                    на отрезке .
5. В прямоугольный треугольник с катетами 5 см и 8 см вписан имеющий с ним общий угол прямоугольник наибольшей площади. Найти площадь прямоугольника.

Контрольная работа по алгебре и началам анализа  №3

«Исследование функции с помощью производной»

2 вариант

1. Найти экстремумы функции:  а) ,   б) .
2. Найти интервалы возрастания и убывания функции .
3. Построить график функции  .
4. Найти наибольшее и наименьшее значения функции                    на отрезке .
5. Найти наибольшую площадь ромба, сумма длин диагоналей которого равна 12 см. .

…………………………………………………………………………………………………..

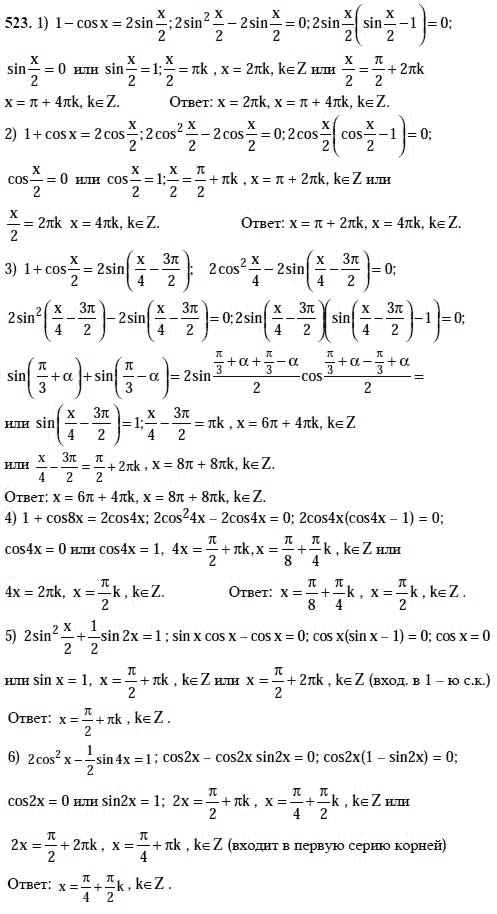Контрольная работа по алгебре и началам анализа №4

«Первообразная»

1 вариант

1. Доказать, что функция  является первообразной функции  на всей числовой оси.
2. Найти первообразную  функции , график которой проходит через точку .
3. Вычислить площадь фигуры, ограниченной линиями:

        а)  , ,  и осью ;

        б)  ,  и .

Контрольная работа по алгебре и началам анализа №4

«Первообразная»

2 вариант

1. Доказать, что функция  является первообразной функции  на всей числовой оси.
2. Найти первообразную  функции , график которой проходит через точку .
3. Вычислить площадь фигуры, ограниченной линиями:

        а)  , ,  и осью ;

        б)  ,  и .

…………………………………………………………………………………

Контрольная работа по алгебре и началам анализа №5

«Комбинаторика»

1 вариант

1. Найти   .
2. Сколькими способами из числа 15 учащихся класса можно выбрать культорга и казначея?
3. Сколько различных шестизначных чисел можно записать с помощью цифр 2, 3, 4, 5, 6, 7 таким способом, чтобы все цифры в числах были различны?
4. Записать разложение бинома .
5. Сколько существует различных кодов, состоящих из двузначного числа, цифры которого выбираются из цифр 1, 2, 3,  и  следующего за ним трехбуквенного слова, буквы которого выбираются из гласных букв русского алфавита? (Цифры и буквы в коде не повторяются.)

Контрольная работа по алгебре и началам анализа №5

«Комбинаторика»

2 вариант

1. Найти .
2. Сколькими способами 7 детей ясельной группы можно рассадить на 7 стульях.
3. Сколькими способами можно составить набор из 5 карандашей, выбирая их из 8 имеющихся карандашей восьми различных цветов?
4. Записать разложение бинома .
5. Шифр сейфа образуется из двух чисел. Первое,  двузначное число, образуется из цифр 1, 2, 3, 4. Второе трехзначное число, образуется из цифр 6, 7, 8 и 9 . Сколько различных шифров можно использовать в таком сейфе?

…………………………………………………………………………………………………

Контрольная работа по алгебре и началам анализа №6

«Вероятность событий»

1 вариант

1. Бросают 2 игральных кубика – большой и маленький. Какова вероятность того, что: 1) на обоих кубиках появятся четыре очка; 2) на большом кубике появится 2 очка, а на маленьком – четное число очков?
2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или белый, или красный шар?
3. Вероятность попадания по мишени стрелком равна . Какова вероятность: 1)непопадания по мишени при одном выстреле? 2) попадания по мишени в каждом из двух последовательных выстрелов? 3) попадания при первом и промахе – при втором выстреле?
4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?
5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трех случайным образом вынутых цветков окажется, по крайней мере, одна гвоздика?

Контрольная работа по алгебре и началам анализа №6

«Вероятность событий»

2 вариант

1. Бросают 2 игральных кубика – большой и маленький. Какова вероятность того, что: 1) на обоих кубиках появятся пять очков; 2) на маленьком кубике появится кратное 3 число очков, а на большом – 5 очков?
2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или черный, или красный шар?
3. Вероятность попадания по мишени стрелком равна . Какова вероятность: 1)непопадания по мишени при одном выстреле? 2) попадания по мишени в каждом из двух последовательных выстрелов? 3) попадания при первом и промахе – при втором выстреле?
4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты два черных шара?
5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трех случайным образом вынутых цветков окажется, по крайней мере, один нарцисс?

……………………………………………………………………………………………………

Контрольная работа по алгебре и началам анализа №7

«Комплексные числа»

1 вариант

1. Вычислить:  а) ,       б) .
2. Выполнить действия   и результат представить в тригонометрической форме.
3. Представить в тригонометрической форме число:  а) ;    б) .
4. Выполнить действия:   а) ,  

б) .

5. Найти множество точек комплексной плоскости, удовлетворяющих условию:  а) ,   б) .

6. Решить уравнение:  а) ,   б) .

Контрольная работа по алгебре и началам анализа №7

«Комплексные числа»

2 вариант

1. Вычислить:  а) ,       б) .
2. Выполнить действия   и  результат представить в тригонометрической форме.
3. Представить в тригонометрической форме число:  а) ;    б) .
4. Выполнить действия:   а) ,  

         б) .

5. Найти множество точек комплексной плоскости, удовлетворяющих условию:

         а) ,   б) .

6. Решить уравнение:  а) ,   б) .

………………………………………………………………………………………………….

Контрольная работа по алгебре и началам анализа №8 (базовый уровень)

«Уравнения и неравенства с двумя переменными»

 1 вариант

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению:  а),    б) .
2. Найти множество точек координатной плоскости, удовлетворяющих неравенству: а),    б) .
3. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств:

Контрольная работа по алгебре и началам анализа №8 (базовый уровень)

«Уравнения и неравенства с двумя переменными»

 2 вариант

Найти множество точек координатной плоскости, удовлетворяющих уравнению:  а),    б) .

Найти множество точек координатной плоскости, удовлетворяющих неравенству: а),    б).

Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств:

…………………………………………………………………………………………..

Контрольная работа по алгебре и началам анализа №8 (профильный уровень)

«Уравнения и неравенства с двумя переменными»

 1 вариант

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению .
2. Найти множество точек координатной плоскости, удовлетворяющих неравенству .
3. Найти площадь фигуры, заданной на координатной плоскости системой неравенств
4. (доп.) Найти все значения а, при которых система уравнений     имеет ровно два решения.

Контрольная работа по алгебре и началам анализа №8 (профильный уровень)

«Уравнения и неравенства с двумя переменными»

 2 вариант

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению .
2. Найти множество точек координатной плоскости, удовлетворяющих неравенству .
3. Найти площадь фигуры, заданной на координатной плоскости системой неравенств
4. (доп.) Найти все значения а, при которых система уравнений     имеет ровно два решения.

…………………………………………………………………………………………..

Контрольная работа «Применение производной к исследованию функций» Алгебра 11 класс. УМК Ш.А. Алимов.

Контрольная работа №3.

Вариант №1.

1.     Найти стационарные точки функции f(х) = 2х³ + 3х² – 1.

2.      Найти экстремумы функции

а) f(х) = х³ + 3х² – 2х + 2; б) f(х) = 2e^3х – 3е^2х .

3.     Найти интервалы возрастания и убывания функции f(х) = х⁴ – 18х² 

4.     Найти наибольшее и наименьшее значение функции f(х) = 2х³ + 3х² – 1 на отрезке [-1; 2].

5.     Исследовать функцию f(х) = х³

– 3х и построить ее график.

 

Вариант №2.

1.     Найти стационарные точки функции f(х) = х³ – х² + 1.

2.      Найти экстремумы функции

а) f(х) = х³ – 3х² + 2х + 4;  б) f(х) = 3e^2х – 2е^3х .

3.     Найти интервалы возрастания и убывания функции f(х) = х³ + 3х² – 24х + 1

4.     Найти наибольшее и наименьшее значение функции f(х) = х³– х² + 1 на отрезке                     [-2; 1].

5.      Исследовать функцию f(х) = х⁴ – 2х² и построить ее график.

 

Вариант №3.

1.     Найти стационарные точки функции f(х) = 2х³ – 3х² + 2.

2.      Найти экстремумы функции

а) f(х) = х³ – 3х² + 2х – 1;  б) f(х) = 4e^3х – 3е^4х.

3.     Найти интервалы возрастания и убывания функции f(х) = х⁴ – 2х² 

4.     Найти наибольшее и наименьшее значение функции f(х) = 2х³ – 3х² + 2 на отрезке [-1; 1].

5.     Исследовать функцию f(х) = х³ – 12х и построить ее график.

 

Вариант №4.

1.     Найти стационарные точки функции f(х) = 2х³ + 6х² – 1.

2.     Найти экстремумы функции

а) f(х) = х³ + х² – 2х + 1; б) f(х) = 3e^4х – 4е^3х.

3.     Найти интервалы возрастания и убывания функции f(х) = 2х³ – 6х² – 18х + 4

4.      Найти наибольшее и наименьшее значение функции f(х) = 2х³ + 6х² – 1на отрезке  [-3; 0].

5.     Исследовать функцию f(х) = х⁴ – 2х² + 2 и построить ее график.

 

Комбинаторика. Контрольная работа. Алгебра 11 класс. УМК Ш.А. Алимов и др.

Контрольная работа по теме «Комбинаторика»

Вариант 1

1. Сколькими способами из числа 25 учащихся класса можно выбрать старосту и физорга?

2. Сколько различных пятизначных чисел можно записать с помощью цифр 0,9,8,7,6,5?

3. Сколькими способами из 8 членов президиума можно выбрать председателя, его заместителя и секретаря?

4. Сколькими способами из 15 игроков можно выбрать стартовую шестерку?

5. Найти а); б); в).

6. Решить уравнение: а) = 25; б) (х – 1) = 42

Вариант 2

1. Сколькими способами из числа 24 учащихся класса можно выбрать двух дежурных?

2. Сколько различных пятизначных чисел можно записать с помощью цифр 9,8,7,6,5,4?

3. Сколькими способами из 12 учебных предметов можно составить расписание из шести различных уроков?

4. Сколькими способами можно составить букет из семи цветков, выбирая цветы из тринадцати имеющихся?

5. Найти а); б); в).

6. Решить уравнение: а) = 30; б) (х – 2) = 28

Вариант 3

1. Сколькими способами из числа 30 учащихся класса можно выбрать старосту и физорга?

2. Сколько различных четырехзначных чисел можно записать с помощью цифр 0, 1, 2, 3, 4?

3. Сколько существует способов для обозначения с помощью букв A, B, C, D, E, F, M, N вершин треугольника?

4. Сколькими способами из 25 учеников класса можно выбрать пятерых для участия в концерте?

5. Найти а); б); в).

6. Решить уравнение: а) = 42; б) (х – 3) = 50

Вариант 4

1. Сколькими способами из числа 28 учащихся класса можно выбрать двух дежурных?

2. Сколько различных четырехзначных чисел можно записать с помощью цифр 1, 2, 3, 4, 5?

3. Сколькими способами из 15 учебных предметов можно составить расписание из шести различных уроков?

4. Сколькими способами можно составить букет из пяти цветков, выбирая цветы из пятнадцати имеющихся?

5. Найти а); б); в).

6. Решить уравнение: а) = 56; б) (х + 3) = 32

 

Страница не найдена

Новости

23 июл

Мэр столицы Сергей Собянин рассказал о планах по созданию московского стандарта качества школ и поликлиник.

22 июл

Второй иностранный язык в российских школах не является обязательным, заявил министр просвещения России Сергей Кравцов.

21 июл

В Следственном комитете сообщили, что психолого-психиатрическая экспертиза, проводимая в отношении Ильназа Галявиева, ещё не завершена. В ведомстве не подтвердили информацию о признании невменяемым обвиняемого в массовом убийстве в казанской гимназии №175. При этом в ОНК Москвы сообщили, что Галявиев переведён из НИИ имени Сербского в психиатрическое отделение СИЗО «Бутырка», и не исключили, что следствие назначит повторную экспертизу.

21 июл

Самоубийства двух подростков в Липецкой области в июне 2021-го можно было предотвратить, если бы им вовремя оказали психологическую поддержку. Такие выводы специалисты сделали в ходе расследования громкой серии суицидов. За две недели на одной железнодорожной станции покончили с собой трое школьников: после 14-летней девочки из жизни ушёл сначала её парень, а затем подруга. Как отмечают эксперты, детские суициды опасны подражательным эффектом: после самоубийства одного подростка его примеру могут последовать несовершеннолетние одноклассники, друзья или члены семьи. Чтобы остановить эту «болезнь», необходима профилактика суицидов, однако в России до сих пор нет единой системы реагирования на такие трагедии.

19 июл

Вице-премьер России Дмитрий Чернышенко заявил, что правительство в текущем году намерено завершить программу подключения российских школ к высокоскоростному интернету.

19 июл

Первый заместитель председателя комитета Госдумы по образованию и науке Олег Смолин прокомментировал в беседе с RT сообщение о том, что в России до 2030 года планируется организовать проверку около 50% домашних заданий школьников с помощью искусственного интеллекта (ИИ).

19 июл

В России до 2030 года планируется организовать проверку порядка 50% домашних заданий школьников с помощью искусственного интеллекта (ИИ). Об этом информирует ТАСС со ссылкой на паспорт стратегии цифровой трансформации образования, подготовленный Минпросвещения России.

Семестровая контрольная работа по алгебре и началам математического анализа

 

Цель: проверка уровня знаний учебного материала за первый семестр 11 класса.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Контрольная работа содержит 2 варианта. Каждый состоит из трех частей, которые отличаются по сложности и форме тестовых заданий.

В І части контрольной работы предложено пять заданий с выбором одного правильного ответа, соответствующие начальному и среднему уровням учебных достижений учащихся. К каждому заданию дается четыре варианта ответа, из которых только один правильный. Задание считается выполненным верно, если ученик записал только букву, которой обозначен правильный вариант ответа. Правильный ответ за каждое из пяти заданий оценивается одним баллом. Ответы нужно записать в специальный бланк ответов. Если вы хотите изменить ответ, зачеркните его и рядом запишите новый.

II часть контрольной работы состоит из двух заданий, которые соответствуют достаточному уровню учебных достижений учащихся. Решение должно содержать краткую запись без обоснования. Правильное решение каждого из заданий этой части оценивается двумя баллами.

III часть контрольной работы состоит из одного задания, которое соответствует высокому уровню учебных достижений учащихся, его решение должно иметь развернутую запись с обоснованием. Правильное решение задачи оценивается тремя баллами.

Контрольная работа рассчитана на 45 минут. При выполнении работы необходимо указать номер задания, текст задач переписывать не обязательно.

Сумма баллов начисляется за правильно выполненные задания в соответствии с максимально возможным количеством предложенных баллов для каждой части (5; 4; 3 – всего 12 баллов). При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в отметку:

Баллы	1 – 4	5 – 7	8 – 10	11 – 12
Отметка	2	3	4	5

Вариант 1

І часть (5 баллов)

Задания 1 – 5 имеют по четыре варианта ответа, из которых только один правильный. Выберите правильный, по Вашему мнению, ответ. Верный ответ каждого задания оценивается одним баллом.

1. Решите уравнение

А) + n, nZ, Б) + n, nZ, В) + , nZ, Г) + 2n, nZ.

2. Найдите нули функции y

А) + n, nZ, Б) + n, nZ, В) + , nZ, Г) + 2n, nZ.

3. Найдите производную функции .

А) 4(3x – 7)3, Б) 12(3x – 7)3, В) 12(3x – 7)5, Г) (3x – 7)3.

4. Найдите производную функции .

А) , Б), В) другой ответ, Г) .

5. Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

А) 8, Б) 6, В) – 12, Г) 12.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

6. Решите уравнение

7. Найдите наименьшее и наибольшее значение функции на отрезке

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Исследуйте функцию y = 3x – x3 и постройте её график

Вариант 2

І часть (5 баллов)

Задания 1 – 5 имеют по четыре варианта ответа, из которых только один правильный. Выберите правильный, по Вашему мнению, ответ. Верный ответ каждого задания оценивается одним баллом.

1. Решите уравнение

А) + n, nZ, Б) + , nZ, В) (-1)n + , nZ, Г) + n, nZ.

2. Найдите нули функции

А) + n, nZ, Б) – + 2n, nZ, В) – + n, nZ, Г) – + n, nZ.

3. Найдите производную функции .

А) 12(4x + 5)2, Б) 12(4x + 5)3, В) 3(4x + 5)2, Г) (4x + 5)2.

4. Найдите производную функции .

А) , Б), В) , Г) другой ответ.

5. Найдите угловой коэффициент касательной к графику функции в точке с абсциссой

А) 5, Б) 10, В) 2, Г) 25.

II часть (4 балла)

Решение заданий 6-7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

6. Решите уравнение

7. Найдите наименьшее и наибольшее значение функции на отрезке

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

8. Исследуйте функцию y = 4×2 – x4 и постройте её график

Ответы:

І часть

	1	2	3	4	5
Вариант 1	В	А	Б	Г	В
Вариант 2	Б	Г	А	В	Б

ІІ часть

IІІ часть

Вариант 1	Вариант 2
y = 3x – x3	y = 4×2 – x4

 

Литература

1. Алгебра и начала математического анализа: 10-11 кл.: программа для общеобразоват. организаций: базовый уровень / сост. Коваленко Н.В., Федченко Л.Я., Маркина И.А.; ДИППО. – 2-е изд. – Донецк: Истоки, 2016. – 19 с.

2. Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – М.: Просвещение, 2016. – 384 с.

 

 

 

 

 

Ошибка 404

Внимательно ознакомьтесь с условиями пользования ресурсами сайта Домашняя школа InternetUrok.ru https://home-school.interneturok.ru/ (далее – Сайт). Пользуясь Сайтом ООО «ИНТЕРДА» (123317, г. Москва, Пресненская набережная, д. 8, стр. 1, этаж 8, помещение 17), Вы подтверждаете, что полностью принимаете следующие условия:

1. Под термином «содержание» в рамках настоящего Соглашения подразумеваются любые материалы, документы, изображения, схемы, аудиовидеоматериалы и любая другая информация, полученная на данном Сайте или размещенная на нем.

2. Данный Сайт представляет собой программное средство, позволяющее хранить, систематизировать и транслировать содержание научно-образовательного характера.

3. Сайт Домашняя школа InternetUrok.ru предоставляет возможность доступа к имеющимся на нем ресурсам исключительно в ознакомительных целях.

4. Информация, размещенная на Сайте, не является справочной и предоставляется исключительно в научно-образовательных целях.

5. Размещение видео и других материалов с сайта Домашняя школа InternetUrok.ru на сторонних ресурсах запрещено.

6. Администрация сайта Домашняя школа InternetUrok.ru оставляет за собой право в любой момент изменить содержание материалов (видео, тексты, задания и т.п.), размещенных на Сайте, без уведомления пользователей.

7. Администрация сайта Домашняя школа InternetUrok.ru не несет никакой ответственности за действия пользователей, связанные с использованием представленной на Сайте информации, и не возмещает убытков.

8. Информация на Сайте предоставляется также путем подключения третьих сторон к содержанию – предоставлением гиперссылок, указателей на другие сайты, поддерживаемые третьими лицами, предоставлением содержания сторонних сайтов обрамлением (фреймингом) и другими методами.

9. Подключение к содержанию сторонних сайтов предоставляется исключительно для удобства и информирования. Ответственность за содержание сторонних сайтов лежит на их создателях.

10. Если иное не указано в описании или титрах к видеоматериалу, все исключительные права на видеоматериал, размещенный на сайте Домашняя школа InternetUrok.ru (в том числе и конспект к нему), принадлежат ООО «ИНТЕРДА». Все исключительные права на записи онлайн-консультаций, домашние задания в виде вопросов, тестов, упражнений, задач, примеров принадлежат ЧОУ «Первая народная школа», если иное не указано в описании.

11. Если иное не указано прямо, услуги сайта предоставляются только для целей личного некоммерческого использования. Это означает, что без письменного разрешения Администрации сайта запрещается любое изменение, копирование, распространение, републикация, создание производных произведений, пересылка, продажа, лицензирование материалов сайта, за исключением трансляции материалов сайта исключительно в учебных учреждениях путём показа (трансляции) материалов или их частей напрямую с сайта Домашняя школа InternetUrok.ru.

12. Администрация Сайта приветствует гипертекстовые ссылки на сайт.

13. Запрещено использовать материалы и сервисы Сайта для любых целей, которые противоречат нормам морали и нравственности, целям создания данного Сайта, и/или нарушают (могут нарушить) запреты, предусмотренные настоящим Соглашением, и/или нарушают (могут нарушить) действующее законодательство РФ об авторских правах.

14. Запрещено использовать услуги Сайта любым способом, служащим для целей нанесения ущерба нормальному функционированию Сайта (включая флудинг, DOS-атаки, ограничение доступа к сайту третьих лиц, но не ограничиваясь ими).

15. Запрещено предпринимать попытки завладения чужими учетными записями (аккаунтами) на Сайте любыми способами (включая взлом пароля перебором, хакерство, фишинг, социальную инженерию, но не ограничиваясь ими).

16. Запрещена пропаганда наркотических средств, психотропных веществ. Не допускаются пропаганда или агитация, возбуждающие социальную, расовую, национальную или религиозную ненависть и вражду, пропаганда наркотических средств, психотропных веществ, а также иные виды пропаганды, запрещенные законами Российской Федерации. Запрещается пропаганда социального, расового, национального, религиозного или языкового превосходства.

17. Запрещено использование в сообщениях на Сайте и в данных при регистрации (логин, имя) ненормативной лексики, а также любых выражений, оскорбляющих личность собеседника или третьего лица (в том числе криптованный мат – латиницей, с использованием звёздочек, математических и иных символов). Администрация сайта имеет право блокировать любого Пользователя в случаях написания им нецензурной лексики или оскорблений во всех возможных каналах связи на сайте. Администрация сайта самостоятельно устанавливает срок блокировки конкретного Пользователя, нарушившего настоящий пункт Соглашения, в пределах периода от 1 до 7 дней, период блокировки компенсации не подлежит (продление доступа, возврат денежных средств).

18. Регистрируясь на Сайте, Пользователь дает свое согласие на участие в сборе диагностической информации, сведений об использовании Сайта, а также на обработку персональных данных, указанных на Сайте (ФИО, адрес электронной почты, пароль, возраст, место проживания, роль на Сайте), на любое действие (операцию) или совокупность действий (операций), совершаемых с персональными данными, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу (в т.ч. трансграничную и третьим лицам — партнерам), обезличивание, блокирование, удаление, уничтожение персональных данных с использованием средств автоматизации в целях информирования об услугах, предоставления и улучшения качества услуг, облегчения доставки обновлений ПО, поддержки Сайта и оказания других услуг, а также для проверки соблюдения условий настоящего Соглашения. Согласие вступает в силу с момента регистрации на Сайте и действует в течение сроков, установленных действующим законодательством РФ.

19. Администрация Сайта имеет право самостоятельно и без предварительного уведомления менять контент Сайта, в том числе транслируемые видеоуроки и условия настоящего Соглашения.

20. Администрация Сайта имеет право в одностороннем порядке менять политику использования своего контента Пользователем и партнерами, в том числе вводить платные Услуги.

ГДЗ по математическому анализу Алимова. Способ облегчить ученику

Издательство: Просвещение 2015 год.

Что делать, если вам трудно учиться?

Для одиннадцати классов каждый ученик сдает тесты. Кому-то сложнее подружиться, кто-то боится публичных выступлений. А школьникам, которых не отдают учиться, сложнее.

Как объясняют психологи, студенты с хорошими оценками — уверенные в себе люди, никогда не испытывают комплексов незавершенности.Чего нельзя сказать о тех, кому часто достается двое и трое. Из-за таких оценок учеников Близких в себе становятся неуверенными и замкнутыми. По этой причине их иногда травмируют одноклассники. Учителя не поддерживают, а надевают.

В этой ситуации вам нужно взять себя в руки и начать усердно работать: не пропустить ни одного урока выполнить любой заданный набор упражнение и написать тестов и тестовая работа на отлично ».

Способ помочь студенту

Однако иногда такая схема просто невозможна.Особенно если речь идет о алгебре . Это один из самых сложных объектов, так как он имеет огромное количество различных формул, правил и алгоритмов, которые необходимо запомнить.

Сделать это может далеко не каждый, поэтому многие пишут своим репетиторам своим детям, на самых разных кружках. Однако есть способ намного проще и проще. Вам понадобится дополнительное время, тетрадь и решебник к учебнику С.А.Алимова, Ю.М. Колягин, М.В. Ткачева ГЭФ за 10, 11 класс .

GDZ — Это пособие, где есть не только верных ответов на любой номер , но и решение задач . Их можно анализировать, выучить наизусть. Итак, школьник все умеет в одиночку А потом проверил по учебнику.

Такой подход даст:

Хорошо освоенная и закрепленная рабочая программа;

Положительные оценки за вход в плату и протестированные ноутбуки;

Отлично написано проверка.

Все желающие смогут найти это руководство, а также другие необходимые материалы в режиме онлайн . Все в открытом доступе — каждый может скачать себе на телефон и унести в школу. Это намного удобнее, чем тяжелый печатный формат.

ГДЗ к дидактическим материалам по алгебре для 10 класса Шабунин М.И. Ты можешь видеть.

ГДЗ к Дидактическим материалам по алгебре для 11 класса Шабунин М.И. Ты можешь видеть.

Алгебра 10-11 класс

Алимов, Колягин, Сидоров

Образование

Итак, в школьной жизни подростков начался самый тяжелый период.На горизонте маячит нелюбимый многими НГЭ, так что расслабляться ни в коем случае не стоит. Более того, в этот период знакомство с высшей математикой, которую не так просто понять, как обычную алгебру. Решебник к учебнику «Алгебра 10-11 класс» Алимов, Колягин, Сидоров Всегда приходит на помощь в сложных ситуациях, особенно когда подросток не получает всей информации на уроках.

Что в него входит.

В пособии подробно описаны все аспекты учебников, чтобы школьники могли найти и повторить любую тему в любое время, а также обновить этапы в памяти.Тщательность решения Б. ГДЗ по алгебре 10-11 класс способствует тому, что даже малейшие нюансы не ускользнут от внимания подростков, и эта тема больше не будет казаться такой классной.

Нужен Ли Решебник.

Многие тесты уже завершены, но впереди их еще много. Поэтому будет крайне обидно, если именно в этот период производительность резко упадет. А так как остальным школьникам предстоит пройти ОГЭ, то это совсем не так.Но, чтобы достойно пройти все препятствия, нужна не только внимательность к урокам, но и хорошее понимание материала. Для этого подойдет решебник к учебнику «Алгебра 10-11 класс» Алимов Ведь в этом пособии подростки смогут найти все необходимое для успешной учебы.

«Образование», 2012

Ученики ВУЗов никогда не знают, в какой момент у них могут возникнуть проблемы с учебой. На трудности способны сдать любой предмет, изучаемый в школе, начиная от русского языка и заканчивая ОБЖ.Одна из учебных дисциплин, регулярно заставляющая школьников потеть, — это алгебра. Алгебраика начинает терроризировать умы ребят с седьмого класса и продолжает это дело на десятом и одиннадцатом курсах. Подростки легко могут облегчить себе жизнь разными способами, в число которых неизменно входят решебники.

Сборник ГДЗ для 10-11 классов по алгебре (С.А. Алимов, Ю.М. Колягин, М.В. Ткачева) — Это прекрасное дополнение к основной книге.Благодаря предоставленной в нем справочной информации ученик готов решать любое упражнение. В заданиях предлагается анализ следующих тем:

• тригонометрические функции и уравнения;
• логарифм;
• градус.

Представленные ответы и комментарии являются необходимыми авторскими заметками, которые обязательно помогут ребенку.

Для чего нужен решебник

Издание дает возможность всем школьникам работать самостоятельно, а в случае недопонимания или пропуска какой-либо темы — пройти ее без ущерба для качества.Также справочные данные позволяют эффективно подготовиться к будущему самостоятельному и тестированию. Самые любознательные студенты могут идти по учебной программе вперед, что в дальнейшем положительно скажется на усвоении знаний и повышении среднего балла оценки.

Помимо десяти- и одиннадцатиклассников Пособие Алимова по алгебре для 10-11 классов Родители и учителя могут использовать: для первого оно будет инструментом контроля знаний ребенка, а для второго — базисом за разработку своих материалов и тестовых заданий для аудиторных занятий.

Как устроена коллекция

Ресурс полностью повторяет структуру учебника. Внутри у пользователя есть возможность просмотреть ответы на 1624 упражнения, а также задания из раздела «Проверь себя», разбитого на тринадцать глав. Ключи доступны круглосуточно, номер можно узнать через поле поиска или с помощью удобной навигации.

Алгебра входит в список предметов с 7 класса, и особенно вначале не любит школьников.Ведь вам нужно научить большому количеству математических и тригонометрических формул, правил и законов. Ребята считают, что это бесполезно в жизни, и на таких уроках невозможно найти что-либо толковое. Однако алгебра очень пригодится не только тем, кто хочет связать с ней жизнь. Развивает логическое мышление, искусство доказывать и делать выводы.

Точные науки многим даются непросто, потому что для того, чтобы добиться успеха на таких уроках, нужно знать множество формул и правил, а также уметь применять их на практике.Многие дети обладают гуманным складом ума и абсолютно не интересуются математикой и ее разделами или просто думают, что не могут ее понять, и теряют интерес и мотивацию.

Многие родители видят выход в репетиторе, но не каждая семья может позволить себе оплачивать дополнительные индивидуальные занятия. В такой ситуации целесообразно будет обратиться к решебнам. Актуально сегодня — это пособие, разработанное командой опытных и профессиональных методистов под руководством С.А.Алимова и выпущенное в 2015 году известным издательством «Просвещение».

Почему выбирают ГДЗ по алгебре для 10-11 классов (авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева)

Эта книга поможет не только отстающим по материалу, но и отличникам, которые углубят свои знания и улучшат навыки. Преимущества:

• простота использования (наличие линии для перемещения по частям учебника)
• поддержка мобильной версии для смартфона или телефона также может использоваться с компьютера или ноутбука.
• Все задания, приведенные в соответствующем учебно-методическом комплексе, соответствуют действительности.
• онлайн-режим позволяет открывать сайт в любое время и в любом месте.
• исключительно положительные отзывы пользователей

Содержание учебно-методического комплекса по алгебре ГПО для 10-11 классов от Алимовой С.А.

В эту книгу включены все главы и темы, присутствующие в школьной программе на данном этапе обучения:

• действительные номера;
• степенная функция;
• тригонометрических формул;
• производная и ее геометрическое значение;
• интегральный;
• комбинаторика

Таким образом, этот учебник принесет большую пользу учащимся, а их родители не будут беспокоиться об успеваемости.

3-е изд. — М .: Просвещение, 2016. — 464 с.

В данном учебнике развитие основных идей курса алгебры 7-9 классов авторов Ш.А. Алимова и другие. Элементарные функции изучаются в 10 классе классическими элементарными методами без привлечения производной; Числовая линия и линия трансформации развиваются параллельно с функционалом; Начало математического анализа положено в 11 классе. Система упражнений представлена ​​на трех уровнях сложности.Задания повышенной сложности в конце учебника содержат богатый материал для подготовки к университетам с повышенными требованиями к математике.

2016 , 3-е изд., 464с.)

Формат: PDF.

Размер: 9,1 МБ

Watch, скачать: ноябрь

Алгебра и начало математического анализа. ( 2012 г. , 18 изд., 464с.)

Формат: PDF.

Размер: 42.7 МБ

Watch, скачать: ноябрь .2019г, ссылки удалены по запросу Образования «Образование» (см. Примечание)

Алгебра и начало анализа. ( 2007 г. , 15 изд., 384с.)

Формат: PDF.

Размер: 10,3 МБ

Часы, скачать: ноябрь .2019г, ссылки удалены по запросу Образования «Образование» (см. Примечание)

СОДЕРЖАНИЕ
Глава 1.Фактические числа
§ 1. Целые и рациональные числа 3
§ 2. Фактические числа 7
§ 3. Бесконечно убывающая геометрическая прогрессия. . одиннадцать
§ 4. Арифметический корень натуральной степени 17
§ 5. Степень с рациональными и действительными показателями 24
Упражнения к главе I 35
Глава II. Степенная функция
§ 6. Степенная функция, ее свойства и диаграмма 39
§ 7. Взаимно обратные функции 47
§ 8. Аппаратные уравнения и неравенства 54
§ 9.Иррациональные уравнения 60
§ 10 *. Иррациональное неравенство 63.
Упражнения к главе II 69
Глава III. Показательная функция
§ одиннадцать. Индикативная функция, ее свойства и диаграмма 72
§ 12. Индикативные уравнения 77
§ 13. Индикативные неравенства 81
§ 14. Системы индикативных уравнений и неравенств … 84
Упражнения к главе III 87
Глава IV. . Логарифм
§ 15. Логарифмы 90
§ 16. Свойства логарифмов 94
§ 17.Десятичный и натуральный логарифмы 96
§ 18. Логарифмическая функция, ее свойства и график. . 100
§ 19. Логарифмические уравнения 105
§ 20. Логарифмические неравенства 109
Упражнения к главе IV 113
Глава V. Тригонометрические формулы
§ 21. Радианная мера угла 117
§ 22. Поверните точку вокруг начала координаты 121
§ 23. Определение синуса, косинуса и касательного угла …. 126
§ 24. Знаки синуса, косинуса и касания 132
§ 25.Зависимость между синусом, косинусом и тангенсом одного и того же угла 135
§ 26. Тригонометрические тождества 139
§ 27. Синус, косинус и тангенс его углов и — и 142
§ 28. Формулы сложения 144
§ 29. Синус, косинус и двойной угловой касательной 149
§ тридцать *. Синус, косинус и тангенс половинного угла 152
§ 31. Формулы утверждения 156
§ 32. Сумма и разность синусов. Сумма и разница в косинезе 161
Упражнения к главе V 164
Глава VI.Тригонометрические уравнения
§ 33. Уравнение COS X = A 168
§ 34. Уравнение SIN X = A 173
§ 35. Уравнение TG X = A 179
§ 36. Решение тригонометрических уравнений 184
§ 37 *. Примеры решения простейших тригонометрических неравенств 194
Упражнения к главе VI 197
Глава VII. Тригонометрические функции
§ 38. Область определения и множество тригонометрических функций 201
§ 39. Готовность, странность, частота тригонометрических функций 204
§ 40.Свойства функции y = COS X и ее расписание 208
§ 41. Свойства функции y = sin x и ее расписание 213
§ 42. Свойства функции y = TG X и ее расписание 217
§ 43 *. Обратные тригонометрические функции 223
Упражнения к главе VII 227
Глава VIII. Производная и ее геометрическое значение
§ 44. Производная 229
§ 45. Производная степенной функции 236
§ 46. Правила дифференцирования 240
§ 47. Производные некоторых элементарных функций.. . 245.
§ 48. Геометрическое значение производной 251
Упражнения к главе VIII 257
Глава IX. Применение производной функций
§ 49. Возрастание и убывание функции 261
§ 50. Функция экстремумов 265
§ 51. Применение производной к построению графиков функций 271
§ 52. Наибольшие и наименьшие значения \ функции …. 277
§ 53 *. Преобразование графики функции, точки перегиба…. 283
Упражнения к главе IX 287
Глава X Интеграл
§ 54. Пред-подобный 291
§ 55. Правила нахождения первичной 294
§ 56. Площадь криволинейной трапеции и интеграл …. 297
§ 57. Вычисление интегралов 301
§ 58. Вычисление площадей с помощью интегралов … 304
§ 59 *. Применение производной и интеграла для решения практических задач 309
Упражнения к главе x 315

Добавлено в новой редакции.

Глава XI Комбинаторика
§ 60. Правило производства 317
§ 61. Перестановки 320
§ 62. Размещение 323
§ 63. Комбайны и их свойства 326
§ 64. Бинин Ньютон 330
Упражнения к главе XI 333
Глава XII. Элементы теории вероятностей
§ 65. События 336
§ 66. Сочетания событий. Обратное событие. . 339.
§ 67. Вероятность события 343
§ 68. Сложение вероятностей 346
§ 69.Самостоятельные мероприятия. Умножение вероятностей. . . 350.
§ 70. Статистическая вероятность 354
Упражнения к главе XII 359
Глава XIII. Статистика
§ 71. Случайные переменные 364
§ 72. Центральные тенденции 370
§ 73. Меры рассеяния 375
Упражнения к главе XIII 383
приложение
§ 1. Набор 387
§ 2. Элементы математической логики 388
§ 3. Предел последовательности 390
§ 4. Дробная функция и ее расписание 393
§ 5.Уравнения и неравенства с двумя неизвестными. . . 395.
Упражнения для окончательного повторения курса алгебры и начала математического анализа. . . . 400.
Задания для внеклассной работы 426
Ответы и указания 432
Тема 460.

Предыдущая статья: «Я очень скучал по врагу в тот день … Следующая статья: «Пушкинская эпоха» русской культуры.

Гдз алимов 10 11 для общего образования. Нужен ли мне резольвер

3-е изд.- М .: Просвещение, 2016. — 464 с.

В данном учебнике развитие основных идей курса алгебры 7-9 классов авторами Ш.А. Алимов и другие. Элементарные функции изучаются в 10 классе классическими элементарными методами без привлечения производной; числовая линия и линия преобразований развиваются параллельно с функционалом; Начала математического анализа рассматриваются в 11 классе. Система упражнений представлена ​​на трех уровнях сложности.Задачи повышенной сложности в конце учебника содержат богатый материал для подготовки к вузам с повышенными требованиями по математике.

2016 , 3 изд., 464с.)

Формат: pdf

Размер: 9,1 МБ

Watch, скачать: ноябрь

Алгебра и начало математического анализа. ( 2012 г. , 18 изд., 464с.)

Формат: pdf

Размер: 42.7 МБ

Смотреть, скачать: ноябрь .2019, ссылки удалены по просьбе издательства «Образование» (см. Примечание)

Алгебра и начало анализа. ( 2007 г. , 15 изд., 384с.)

Формат: pdf

Размер: 10,3 МБ

Часы, скачать: ноябрь .2019, ссылки удалены по просьбе издательства «Образование» (см. Примечание)

СОДЕРЖАНИЕ
Глава 1.Действительные числа
§ 1. Целые и рациональные числа 3
§ 2. Действительные числа 7
§ 3. Бесконечно убывающая геометрическая прогрессия. … одиннадцать
§ 4. Арифметический корень натуральной степени 17
§ 5. Степень с рациональными и действительными показателями 24
Упражнения для главы I 35
Глава II. Степенные функции
§ 6. Степенная функция, ее свойства и график 39
§ 7. Взаимно обратные функции 47
§ 8. Эквивалентные уравнения и неравенства 54
§ 9.Иррациональные уравнения 60
§ десять *. Иррациональные неравенства 63
Упражнения к главе II 69
Глава III. Показательная функция
§ одиннадцать. Экспоненциальная функция, ее свойства и график 72
§ 12. Экспоненциальные уравнения 77
§ 13. Экспоненциальные неравенства 81
§ 14. Системы экспоненциальных уравнений и неравенств … 84
Упражнения к главе III 87
Глава IV. .Логарифмическая функция
§ 15. Логарифмы 90
§ 16.Свойства логарифмов 94
§ 17. Десятичные и натуральные логарифмы 96
§ 18. Логарифмическая функция, ее свойства и график. … сто
§ 19. Логарифмические уравнения 105
§ 20. Логарифмические неравенства 109
Упражнения к главе IV 113
Глава V. Тригонометрические формулы
§ 21. Радианная мера угла 117
§ 22. Вращение точки вокруг начала координат 121
§ 23. Определение синуса, косинуса и тангенса угла…. 126
§ 24. Знаки синуса, косинуса и тангенса 132
§ 25. Зависимость между синусом, косинусом и тангенсом одного и того же угла 135
§ 26. Тригонометрические тождества 139
§ 27. Синус, косинус и тангенс его углов и -a 142
§ 28. Формулы сложения 144
§ 29. Синус, косинус и тангенс двойного угла 149
§ тридцать *. Синус, косинус и полутангенс 152
§ 31. Формулы редукции 156
§ 32. Сумма и разность синусов. Сумма и разность косинусов 161
Упражнения к главе V 164
Глава VI.Тригонометрические уравнения
§ 33. Уравнение cos x = a 168
§ 34. Уравнение sin x = a 173
§ 35. Уравнение tan x = a 179
§ 36. Решение тригонометрических уравнений 184
§ 37 *. Примеры решения простейших тригонометрических неравенств 194
Упражнения к главе VI 197
Глава VII. Тригонометрические функции
§ 38. Область и множество значений тригонометрических функций 201
§ 39. Четность, нечетность, периодичность тригонометрических функций 204
§ 40.Свойства функции y = cos x и ее графика 208
§ 41. Свойства функции y = sin x и ее графика 213
§ 42. Свойства функции y = tg x и ее графика 217
Раздел 43 *. Обратные тригонометрические функции 223
Упражнения для главы VII 227
Глава VIII. Производная и ее геометрическое значение
§ 44. Производная 229
§ 45. Производная степенной функции 236
Раздел 46. Правила дифференцирования 240
§ 47.Производные некоторых элементарных функций. … … 245
§ 48. Геометрический смысл производной 251
Упражнения к главе VIII 257
Глава IX. Применение производной к изучению функций
§ 49. Увеличение и уменьшение функции 261
§ 50. Экстремумы функции 265
§ 51. Применение производной к построению графиков функций 271
§ 52. Наибольшее и наименьшее значение функции …. 277
§ 53 *.Выпуклость графика функции, точки перегиба … 283
Упражнения к главе IX 287
Глава X. Интеграл
§ 54. Первообразная 291
Раздел 55. Правила поиска первообразных 294
§ 56. Площадь криволинейная трапеция и интеграл …. 297
§ 57. Вычисление интегралов 301
§ 58. Вычисление площадей с помощью интегралов …. 304
§ 59 *. Применение производной и интеграла к решению практических задач 309
Упражнения к главе X 315

Добавлено в новой редакции.

Глава XI Комбинаторика
Раздел 60. Правило произведения 317
Раздел 61. Перестановки 320
§ 62. Размещение 323
Раздел 63. Комбинации и их свойства 326
§ 64. Бином Ньютона 330
Упражнения для главы XI 333
Глава XII. Элементы теории вероятностей
Раздел 65. События 336
§ 66. Сочетания событий. Обратное событие. … 339
Статья 67. Вероятность события 343
Статья 68. Сложение вероятностей 346
Статья 69.Независимые события. Умножение вероятностей. … … 350
Раздел 70. Статистическая вероятность 354
Упражнения для главы XII 359
Глава XIII. Статистика
§ 71. Случайные переменные 364
Раздел 72. Центральные тренды 370
Раздел 73. Меры дисперсии 375
Упражнения для приложения Глава XIII 383

§ 1. Наборы 387
§ 2. Элементы математической логики 388
§ 3. Предел последовательности 390
§ 4. Дробно-линейная функция и ее график 393
§ 5.Уравнения и неравенства с двумя неизвестными. … … 395
Упражнения для окончательного повторения курса алгебры и начала математического анализа. … … … 400
Задания для внеклассных занятий 426
Ответы и направления 432
Указатель 460

Обучение в современной школе требует от ученика много времени и сил. Особенно, если речь идет об изучении математических дисциплин, в том числе и алгебры.

Многие учителя не успевают эффективно контролировать уровень знаний учащихся.Домашнее задание оценивается схематично, и на первом месте стоит не формирование живого интереса к обучению и получению знаний, а отчет об успеваемости.

В этой ситуации ученики, от которых родители также требуют хорошей успеваемости, не находят ничего лучше, чем списывать выполненные домашние задания с решебников. Фактически, это только приводит к тому, что ребенок перестает понимать предмет. Чтобы ГДЗ приносили реальную пользу, необходимо методично их правильно использовать.

Как правильно использовать решение Алимова по алгебре 10-11 классов

Все ответы на домашние задания составляются тем же авторским коллективом, который создавал сам учебник. ГДЗ — это не просто возможность безрадостно списать безнадзорному школьнику, это, прежде всего, учебно-методическое пособие, которое должно улучшить дидактическую составляющую учебного процесса.

• Важно помнить, что домашнее задание — это не только примеры, но и теоретический материал, без усвоения которого невозможно успешно справиться.
• Готовые ответы следует использовать не для накрутки, а только для проверки правильности заданий.
• Решения для того или иного примера основаны на той или иной учебной теме, в руководстве есть ссылки на нее. Поэтому, если ученик испытывает затруднения, то в этом случае необходимо вернуться к предыдущему материалу и повторить его заново. Все это позволяет превратить решебник в эффективное средство контроля успеваемости, а также помочь студентам развить стимул к самостоятельному обучению.

Найди все ответы по алгебре для 10-11 класса Алимова онлайн

Мы стремимся сделать обучение более полным и эффективным. Для этого на нашем сайте размещены учебники, а также в ГДЗ по различным школьным дисциплинам.

Теперь вам не нужно покупать пачку бумажных руководств. Все доступно в электронном виде в любое время. Вы можете посетить наш сайт с ПК, смартфона или планшета. Это очень удобно, так как позволяет получать ответы на поставленные задачи, даже находясь в общественном транспорте или другом месте.

Алгебра 10-11 класс

Алимов, Колягин, Сидоров

Образование

Так начался самый тяжелый период в школьной жизни подростков. На горизонте маячит нелюбимый ОГЭ, так что расслабляться ни в коем случае не стоит. Более того, в этот период начинается знакомство с высшей математикой, которую не так легко понять, как обычную алгебру. Решебник для учебника «Алгебра 10-11 класс» Алимов, Колягин, Сидоров всегда придут на помощь в сложных ситуациях, особенно когда подросток не получает всю информацию на уроках.

Что включено.

В пособии подробно анализируется каждый аспект учебника, чтобы школьники могли найти и повторить любую тему в любое время, а также освежить в памяти уже пройденные этапы. Тщательность решений в ГДЗ в 10-11 классах алгебры способствует тому, что даже малейшие нюансы не ускользнут от внимания подростков, и эта тема больше не будет казаться такой устрашающей.

Нужен ли мне резольвер.

Многие тесты уже пройдены, но впереди их еще много. Поэтому будет крайне обидно, если именно в этот период резко упадет успеваемость. А поскольку остальным школьникам предстоит проходить ОГЭ, то это совсем не желательно. Но для того, чтобы достойно пройти все препятствия, потребуется не только внимательность к урокам, но и хорошее понимание материала. Для этого решебник как нельзя лучше подходит к учебнику «Алгебра 10-11 класс» Алимова , ведь именно в этом пособии подростки могут найти все необходимое для успешной учебы.

«Образование», 2012

Старшеклассники никогда не знают, в какой момент у них могут возникнуть проблемы с обучением. Любой предмет, изучаемый в школе, от русского до техники безопасности, может доставить трудности. Алгебра — одна из академических дисциплин, от которой у студентов регулярно появляется потливость. Алгебраика начинает терроризировать умы детей с седьмого класса и продолжает это дело на десятом и одиннадцатом годах обучения. Подростки могут облегчить себе жизнь разными способами, в том числе решебниками.

Сборник ГДЗ для 10-11 классов по алгебре (Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева) Прекрасное дополнение к основной книге. С помощью предоставленной в нем помощи ученик готов решать любое упражнение. Задания предполагают анализ следующих тем:

• тригонометрические функции и уравнения;
• логарифм;
• градус.

В представленных ответах и ​​комментариях есть необходимые авторские пометки, которые обязательно помогут ребенку.

Для чего нужен решебник?

Публикация дает всем студентам возможность проработать материал самостоятельно, а в случае недопонимания или упущения темы пройти его самостоятельно, не жертвуя качеством. Также справочные данные позволяют эффективно подготовиться к предстоящей самостоятельной и контрольной работе. Самые любознательные ученики могут продвинуться по учебной программе, что в будущем положительно скажется на усвоении знаний и повышении среднего балла.

После 10-11 классов Учебник Алимова по алгебре для 10-11 классов Родители и учителя вполне могут его использовать: для первых он станет инструментом контроля знаний ребенка, а для вторых станет основой для разработки собственных материалов и тестовых заданий для аудиторных занятий.

Как работает коллекция

Ресурс полностью повторяет структуру учебного пособия. Внутри пользователь имеет возможность просмотреть ответы на 1624 упражнения, а также на задания раздела «Проверьте себя», разбитого на тринадцать глав.Ключи доступны круглосуточно, номер можно найти через поле поиска или через удобную навигацию.

Алгебра входит в перечень предметов с 7 класса, и особенно в начале школьникам она не нравится. Ведь вам нужно выучить большое количество математических и тригонометрических формул, правил и законов. Ребята верят, что в жизни это не пригодится, и на таких уроках нельзя выучить ничего действенного. Однако алгебра очень полезна не только тем, кто хочет связать с ней свою жизнь.Развивает логическое мышление, искусство доказывать и делать выводы.

Точные науки многим даются непросто, потому что для того, чтобы добиться успеха на таких уроках, нужно знать множество формул и правил, а также уметь применять их на практике. Многие дети обладают гуманным складом ума и абсолютно не интересуются математикой и ее разделами или просто думают, что не могут ее понять, и теряют интерес и мотивацию.

Многие родители видят выход в репетиторе, но не каждая семья может позволить себе оплачивать дополнительные индивидуальные уроки.В такой ситуации было бы целесообразно обратиться в рещебники. Пособие разработано коллективом опытных и профессиональных методистов под руководством Ш.А. Алимова и опубликована в 2015 году известным издательством «Образование».

Почему стоит выбрать именно ГДЗ по алгебре для 10-11 классов (авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева)

Эта книга поможет не только тем, кто отстает в усвоении материала, но и отличникам, которые углубят свои знания и улучшат свои навыки.Преимущества:

• простота использования (наличие линейки для перемещения по частям учебника)
• поддержка мобильной версии для смартфона или телефона, также можно использовать с компьютера или ноутбука
• правильно решены все задачи, поставленные в соответствующий учебно-методический комплекс
• онлайн-режим дает возможность открывать сайт в любое время и в любом месте
• исключительно положительные отзывы пользователей

Содержание учебно-методического комплекса по гпо алгебре для 10-11 классов от Ш.Алимова А.

В эту книгу включены все главы и темы, присутствующие в школьной программе на данном этапе обучения:

• вещественные числа;
• степенных функций;
• тригонометрических формул;
Производная
• и ее геометрическое значение;
• интегральный;
• комбинаторика.

Таким образом, этот учебник принесет большую пользу учащимся, а их родители не будут беспокоиться об их успеваемости.

Сдам экзаменационные задания.Я решу. Этот раздел

Среднее общее образование

Линия Укк Г. К. Моравина. Алгебра и математический анализ (10-11) (угл.)

Линия Мерзляк. Алгебра и стартовый анализ (10-11) (у)

Математика

Разбираем задачи и решаем примеры с преподавателем

Уровень профиля экзаменационной бумаги Длится 3 часа 55 минут (235 минут).

Минимальный порог — 27 баллов.

Экзаменационная работа состоит из двух частей, различающихся по содержанию, сложности и количеству заданий.

Отличительной чертой каждой части работы является форма задач:

• часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целой или последней десятичной дроби;
• часть 2 содержит 4 задачи (задачи 9-12) с кратким ответом в виде целой или конечной десятичной дроби и 7 задач (задачи 13-19) с развернутым ответом (полная запись решения с обоснованием выполненных действий) .

Панова Светлана Анатольевна , учитель математики высшей категории школы, стаж работы 20 лет:

«Для получения аттестата школы выпускник должен сдать два обязательных экзамена в форме экзамена, один из Какая математика.В соответствии с концепцией развития математического образования в Российской Федерации Эге по математике делится на два уровня: базовый и профильный.Сегодня мы рассмотрим варианты профильного уровня.«

Задание № 1. — Проверяет У. У. У. У. У. У. У. У. У. У. Умение применять навыки, полученные в ходе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числа, Чтобы иметь возможность округлять десятичные дроби, уметь переводить одни единицы измерения в другие

Пример 1. В квартире, где живет Петр, установлен расход потребления холодной воды (счетчик).1 мая счетчик показал расход 172 кубометра. м воды, а на первое июня — 177 кубометров. Какую сумму должен заплатить Питер за холодную воду на май, если цена 1 куб. C холодной водой 34 рубля 17 копеек? Дайте ответ в рублях.

Решение:

1) Находим количество воды, потраченной за месяц:

177 — 172 = 5 (м.куб.)

2) Найдем сколько денег заплатят за израсходованную воду:

34.17,5 = 170,85 (руб)

Ответ: 170,85.

Задание №2. — Это одно из самых простых заданий экзамена. С ним успешно справляется большинство выпускников, что свидетельствует о владении понятием функции. Тип задания № 2 кодификатора требований — это задание на использование полученных знаний и навыков в практической деятельности и повседневной жизни. Задача № 2 состоит из описания с использованием функций различных фактических зависимостей между значениями и интерпретации их графиков.Задача № 2 проверяет возможность извлечения информации, представленной в таблицах в диаграммах, диаграммах. Выпускникам необходимо уметь определять значение функции по значению аргумента при различных методах настройки функции и описывать поведение и свойства функции в соответствии с ее графиками. Также необходимо уметь находить наибольшее или наименьшее значение в расписании и строить графики изученных функций. Допустимые ошибки случайны при чтении условий задания, чтении таблицы.

# Advertising_insert #

Пример 2. На рисунке показано изменение биржевой стоимости одной акции горнодобывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрел 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько бизнесменов потеряли в результате этих операций?

Решение:

2) 1000 · 3/4 = 750 (долей) — это 3/4 всех приобретаемых долей.

6) 247500 + 77500 = 325000 (руб) — предприниматель получил после продажи 1000 акций.

7) 340000 — 325000 = 15000 (руб) — Утерянный бизнесмен в результате всех операций.

В этом разделе мы готовимся к экзамену по математике как базовому, профильному уровню — у нас готовятся задания, тесты, описание экзамена и полезные рекомендации. Воспользовавшись нашим ресурсом, вы поймете минимум в решении задач и сможете успешно сдать экзамен по математике в 2019 году.Начинать!

Экзамен по математике является обязательным для любого ученика 11 класса, поэтому информация, представленная в этом разделе, актуальна для всех. Экзамен по математике делится на два типа — базовый и профильный. В этом разделе я анализирую каждый тип задач с подробным объяснением двух вариантов. Задачи еге строго тематические, поэтому по каждому номеру вы можете дать точные рекомендации и привести теорию, необходимую для решения такого типа задач. Ниже вы найдете ссылки на задачи, нажав на которые вы сможете изучить теорию и разобрать примеры.Примеры постоянно обновляются и обновляются.

Структура базового уровня ЕГЭ по математике

Экзамен по математике базового уровня состоит из за одно задание из них 20 задач с кратким ответом. Все задания направлены на проверку развития базовых навыков и практических навыков применения математических знаний в повседневных ситуациях.

Ответ на каждую из задач 1-20: целое число , конечная десятичная дробь , или последовательность чисел .

Задание с коротким ответом считается выполненным, если правильный ответ записан в бланке ответа №1 в форме, предусмотренной инструкцией по выполнению задания.

Наш портал дает вам такую ​​возможность!

В этом учебном году, как и в прошлом, многие предметы претерпели изменения и уточнения. Мы учли это при выборе материалов!

В этом разделе вы найдете задания, аналогичные официально утвержденным, которые предлагаются на экзаменах.К тому же у нас есть решения всех задач. Свою силу в онлайн-тестировании может попробовать любой пользователь портала: ответить на вопросы, узнать результат и получить направление для дальнейшей подготовки, обозначив свои слабые стороны.

Специально для поступающих организован календарь поступающих, содержащий наиболее полную и актуальную информацию обо всех важных событиях для сдачи экзамена и вступительных экзаменов. Здесь вы найдете подробное расписание. ЕГЭ-тестирование , принятые походы высших и специальных учебных заведений, сроки подачи документов и дата зачисления в различные учебные заведения.

Если после сдачи экзамена полученный балл оказался меньше ожидаемого, рекомендуем усилить подготовку. Вы всегда можете использовать ресурсы. Препараты к ЕГЭ разработаны на нашем портале специально для Вас!

Эге по математике является одним из основных тестов для выпускников школ перед получением аттестата и поступлением в высшее учебное заведение. Такой вариант контроля знаний используется для оценки знаний по дисциплинам, полученных в процессе.школьное обучение. Единый государственный экзамен Проходит в форме тестирования, подготовка заданий к итоговому тестированию осуществляется Рособрнадзором и другими уполномоченными органами в сфере образования. Проходной балл по математике зависит от индивидуальных требований вуза, в который поступает выпускник. Успешная сдача экзамена на высокий рейтинг — важный фактор успеха при поступлении.

Математика профильного уровня необходима при поступлении в вузы технической, экономической направленности.В основе экзаменационных заданий лежит базовый уровень Более сложные задания и к нему добавлены примеры. Предполагаются краткие и развернутые ответы:

• Первые задачи, не требующие глубоких знаний — это проверка знаний базового уровня;
• Следующие 5 являются более сложными, средний и высокий уровень владения предметом. Эти задачи проверяются с помощью компьютера, так как ответ на них краткий.

Развернутые ответы необходимы для последних семи задач.Для проверки соберите группу экспертов. Главное, чтобы, несмотря на сложность задач, которые входят в профильный уровень, они полностью соответствуют школьной программе. Почему они могут вызывать затруднения? Для успешного решения этих примеров и задач необходимы не только сухие знания, но и умение творчески подойти к решению, применить знания в нестандартной ситуации. Это формулировка вызывает затруднения.

Если студент выбирает этот уровень, это подразумевает его желание продолжить изучение точных наук в вузе.Выбор в пользу профильного экзамена говорит также о том, что уровень знаний студента достаточно высокий, то есть фундаментальная подготовка не нужна.
Процесс подготовки включает в себя повторение основных разделов, решение задач повышенной сложности, требующих нестандартного, творческого подхода.
Методика обучения

• Базовая подготовка осуществляется в школе, где ученик осваивает основы, иногда учитель проводит дополнительные факультативы для выпускников.Основная рекомендация — тщательно и основательно прорабатывать все темы, особенно в выпускном классе.
• Самостоятельная работа: Это требует особой самодисциплины, воли и самообладания. Вам нужно внимательно ознакомиться с. Проблема в направлении — только специалист может грамотно направить будущего соискателя на те темы, на которые нужно обратить внимание.
• Репетиторство: Профессиональный специалист поможет эффективно и быстро решить сложные задачи.
• Курсы и онлайн-обучение: современный и проверенный метод, экономящий время и деньги.Важное преимущество: вы можете проходить тестовые испытания онлайн, быстро получать ответы, тренироваться по разным заданиям.

«Решу по математике профильного уровня» — это возможность подготовиться к экзамену и успешно его сдать.

Экстремальных точек и их вывод. Экстремальная функция. Обновление знаний. «Мозговой штурм»

Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (учетную запись) Google и войдите в нее: https: // accounts.google.com

Подписи к слайдам:

EXTREME FUNCTIONS

Точки из области определения функции, в которых: f ′ (x) = 0 или не существует, называются критическими точками этой функции. Только они могут быть точками экстремума функции. (Рис. 1 и 2). f ′ (x 1) = 0 f ′ (x 2) = 0

Точки из области определения функции, в которых: f ′ (x) = 0 Extrema Не экстремум

Пусть x о — точка из области определения функции f (x) и f ′ (x о) = 0, если производная функции меняет знак с «+» на «-» в точке x о или наоборот, то эта точка это экстремум.X 1 X 2 X 1 max X 2 min

Экстремумы функции X 0 являются максимальной точкой (max) функции, если существует такая окрестность точки x 0, что для всех x ≠ x 0 из этой окрестности выполняется неравенство f (x) ˂ f (x 0). X 0 является точкой минимума (min) функции, если существует такая окрестность точки x 0, что для всех x ≠ x 0 из этой окрестности выполняется неравенство f (x) ˃ f (x 0).

Рисунок 1 Рисунок 2 Для приведенных графиков функции y = f (x) указывают: -критические точки; -стационарные точки; — экстремальные функции.

Алгоритм нахождения точек экстремума функции: 1. Найти производную функции; 2. Приравнять производную к нулю — найти стационарные точки; 3. Исследовать производную по «знаку» — сделать вывод.

Выполнить задачу 1. Найти точку максимума функции 2. Найти точку минимума функции в точке (0;) в точке (0;)

B 8 2 9 На рисунке показан график функции, определенной на интервале. . Найдите сумму точек экстремума функции.3. -2 1 4 5 8 10 -2 + 1 + 3 + 4 + 5 + 8 + 10 = …

На рисунке показан график производной функции f (x), определенной на интервале (-9; 8). Найти точку экстремума функции на интервале (-3; 3) -3 3 B8 — 2 + —

По теме: методические разработки, презентации и заметки

Презентация для уроков алгебры в 11 классе по теме «Возрастающие и убывающие функции. Экстремумы функции».

Презентация состоит из трех уроков.Часть материала я взял из презентаций других учителей, за что им очень благодарен. Для этого класса удобно скомпоновать уже сделанный материал по своему усмотрению …

0 \ nу> 0 \ n \ nФункция y = f (x) называется увеличивающейся на \ nterval, если при увеличении аргумента \\ n значение функции увеличивается на \\ n \\ n функция y = f (x) увеличивается, если большее \ n значение аргумента соответствует большему \ n значению функции \ ny = f (x) \ nу> 0 \ n \ n Теорема: Если производная на интервале \ n положительна, то функция y = f (x) в данном \ n интервале возрастает..jpg «,» smallImageUrl «:» http: \\ / \\ / pedsovet.su \\ / \\ / _ load-files \\ / load \\ / 38 \\ / 56 \\ / 9 \\ / f \\ /3-page-2_300.jpg «), (» number «: 3,» text «:» 2. Уменьшение функции \\ n \\ nФункция y = f (x) называется уменьшением на \\ девятый интервал , если значение функции уменьшается по мере увеличения аргумента \\ n. \\ n \\ nФункция уменьшается, если большее значение \\ n аргумента соответствует меньшему значению \\ very simple..jpg «,» smallImageUrl «:» http: \\ / \\ / pedsovet.su \\ / \\ / _ load-files \\ / load \\ / 38 \\ / 56 \\ / 9 \\ / f \\ / 3-page-4_300 .jpg «), (» number «: 5 , «текст»: «4. Минимальные точки \\ n \\ n Точка x = a называется точкой минимума и \\ n функции y = f (x), если производная в данной точке \\ n равна равным 0, и проходя через эту точку слева \\ n вправо, знак производной меняется с (-) на (+) \\ n \\ nf (x \\ n) \\ n \ \ nу> 0 \ nу> 0 \ n \ nу 0 \ n \ n– \ n \ nmi \ nn \ n \ n + \ n \ nx \\ n \\ nx0 \\ n \\ nРаспознавать \\ nминимальную точку по графику \\ nфункции очень просто.\\ nГрафик функции в \\ nокрестности \\ n минимальной точки выглядит \\ nподобно гладкому «дну» \\ n \\ nТочки минимума и максимума \\ n называются точками экстремума..jpg «,» smallImageUrl «:» http: \\ / \\ / pedsovet.su \\ / \\ / _ load-files \\ / load \\ / 38 \\ / 56 \\ / 9 \\ / f \\ / 3-страничный -5_300.jpg «), (» number «: 6,» text «:» Функция y = f (x) называется выпуклой на \\ девятом интервале, если все точки графика функции \\ n расположены ниже касательная. \\ n \\ n5 ..jpg «,» smallImageUrl «:» http: \\ / \\ / pedsovet.su \\ / \\ / _ load-files \\ Вогнутость функции \\ n \\ nФункция y = f (x) вызывается вогнутая на \\ интервале, если все точки графика функции \\ n расположены выше касательной. \\ N \\ ny «> 0 \\ n \\ ny»> 0 \\ n \ ny \ non \ nbody \\ n \ nth \\ nn \ nl \\ nе \\ nat \\ n \\ na \\ ncas \\ n \\ ns \\ nka \\ n \\ ny = f (x) \\ n \\ ny »> 0 \ ncasa \\ ntel \\ n \ \ ny \ n \\ nТЕОРЕМА: Функция y = f (x) является вогнутым \ n интервалом, если вторая производная в этом \ n интервале положительна..jpg «,» smallImageUrl «:» http: \\ / \\ / pedsovet.su \\ / \\ / _ load-files \\ / load \\ / 38 \\ / 56 \\ / 9 \\ / f \\ /3-page-7_300.jpg «), (» число «: 8,» текст «:» Точка P называется точкой перегиба \\ n функции y = f (x), если знак вторая производная \\ n изменяется при прохождении через эту \\ n точку слева направо. \\ n \\ n7. Точки перегиба \\ n \\ n \\ n \\ nP1 \\ nP2 \\ nу «0 \ \ nP1 \\ n \\ ny = f (x) \\ n \\ nу «0 \\ n \\ nТочку перегиба очень легко распознать по графику функции \\ n.\\ n График функции в \\ n среде \\ n точки перегиба выглядит как \\ n граница между \\ n «холмом» и «долиной» \\ n \\ nР \\ n \\ n » , «imageUrl»: «http: \\ / \\ / pedsovet.su \\ / \\ / _load-files \\ / load \\ / 38 \\ / 56 \\ / 9 \\ / f \\ / 3 -page-8..jpg «), (» number «: 9,» text «:» 8. Функциональные нули \\ n \\ / 38 \\ / 56 \\ / 9 \\ / f \\ / 3- page-9_300.jpg «), (» number «: 10,» text «:» Список \\ nСписок использованных источников: \\ nлитератур: \\ nУчебник: \\ nУчебник: Богомолов, \\ nБогомолов Н.\\ nNV .учреждения \\ nУчебные заведения \\ n \\ nПрезентация \\ nПрезентация может \\ n \\ nпредставлять \ nузнать \\ n \\ nуроки \\ nматематики \\ nматематики для \\ nдля \\ nсоставления \\ n функции, \\ nфункции для формулирования \\ nфункций \\ nсвойств \\ nсвойств \\ n \\ nприменение производной \\ nпроизводной согласно \\ nдвижению \\ nтеме «Производная. \\ n» Производная.

Пояснительная записка

Презентация по математике на тему: «Производная.Точки экстремума и перегиба. Увеличение и выпуклость функции »Предназначено для учащихся 1 курса средних профессиональных учебных заведений или учащихся 10-11 классов общеобразовательных школ.

Цель использования презентации в учебном процессе:

Наглядная демонстрация изложения на уроке с пояснениями учителя

Самостоятельное изучение материала по теме, (с возможностью конспектирования материала)

Многократное использование презентации в дистанционном обучении

Консолидация материала в процессе обучения, с самостоятельной формулировкой свойств графика функции.

Презентацию можно использовать на уроках в качестве наглядного пособия, для самостоятельного изучения темы, для заполнения пробелов в знаниях учащихся из-за пропусков занятий.

Презентация имеет удобный интерфейс, проста в использовании, содержит наглядность и информативность, использует гиперссылки и триггеры.

04.10.2013 Учитель математики ФАЛИНА Т.Б.

Презентационные скриншоты:

Слайд 1

ГБОУ СПО ПЕТРОЗАВОДСКИЙ ЛЕСОТЕХНИЧЕСКИЙ ТЕХНИКУМ «Производная.Точки экстремума и перегиба. Увеличение и выпуклость функции. Алгоритм работы: 1. Работа с презентацией позволяет сформировать основные понятия по теме, познакомиться со свойствами функции с позиции производной. 2. Презентация содержит определения, графики, свойства и теоремы, которые при необходимости можно обозначить, нажав на паузу. 3. Перейти к содержанию — управлять презентацией — одним щелчком мыши Презентационный конкурс «Интерактивная мозаика» на сайте сайта Интерактивное пособие выполнила учитель математики Петрозаводского лесотехнического техникума ФАЛИНА ТАТЬЯНА БОРИСОВНА Петрозаводск 2013

Слайд 2

Слайд 3

1.Увеличение функции y> 0 y> 0 Функция y = f (x) называется возрастающей на интервале, если при увеличении аргумента значение функции увеличивается Функция y = f (x) увеличивается если большее значение аргумента соответствует большему значению функции y = f (x) у> 0 Теорема: Если производная на отрезке положительна, то функция y = f (x) возрастает на заданный интервал.

Слайд 4

2.Уменьшение функции Функция y = f (x) называется убывающей в интервале, если значение функции уменьшается с увеличением аргумента. Функция уменьшается, если большее значение аргумента соответствует меньшему значению функции y

Слайд 5

3. Максимальные точки Точка x = a называется точкой максимума функции y = f (x), если производная в этой точке равна 0, а при переходе через эту точку слева направо знак производная меняется с (+) на (-) max f (x) y> 0 y> 0 + — xx y0 0 Очень легко распознать точку максимума на графике функции.График функции в окрестности точки максимума выглядит как плавный «холм» x xma

Слайд 6

4. Точки минимума Точка x = a называется точкой минимума функции y = f (x), если производная в этой точке равна 0, а при переходе через эту точку слева направо знак производная меняется с (-) на (+) f (x) y> 0 y> 0 y0 — mi n + x x0 На графике функции очень легко распознать точку минимума.График функции в окрестности точки минимума имеет вид гладкого «дна». Точки минимума и максимума называются точками экстремума. х хмин

Точка x1 называется точкой минимума
функция
f (x),
если
в
некоторая
окрестность точки x1,
неравенство
f (x) f (x1)
Значения функции в точках x0 и x1
соответственно назвал
максимум и минимум функции.
Максимум и минимум функции называется
экстремумом функции.

y

y f (x)
x1 x2
x3
x

На одном интервале функция может иметь

нескольких экстремумов, и может случиться так, что
минимум в одной точке больше, чем максимум в
в другой.
Максимум или минимум функции в некотором интервале
обычно не являются
функциями наибольшего и наименьшего значения.
Если в некоторой точке x0 дифференцируемая функция
f (x) имеет экстремум, то в некоторой
окрестности этой точки теорема
Ферма и производная функции в этой точке
равны нулю:
f (x0) 0

Однако функция может иметь экстремум в точке

, в которой она не дифференцируема.
Например, функция
y x
имеет минимум в точке
x 0
, но в этой точке она не дифференцируема.

Чтобы функция y = f (x) имела в точке x0 экстремум

, необходимо, чтобы
ее производная в этой точке была
нулем или не существовала.

Точки, в которых требуется условие экстремума

, называются
критическими или стационарными.
Таким образом, если в любой точке есть экстремум,
, то эта точка является критической.
Но переломный момент не обязательно является точкой экстремума
.

Поиск критических точек и экстремумов

функций:
1
y x
2

y (x) 2 x
y 2 x 0 при x 0
2
x 0
y 0
— критическая точка

y

x 0
y x
2
x

2

y x 1
3

Применим необходимое условие экстремума:

y (x 1) 3x
2
y 3x 0 при x 0
3
х 0
у 1
2
— критическая точка

y

y x
2
y 1
x

Если при переходе через точку x0 производная

дифференцируемой функции y = f (x) меняет знак
с плюса на минус, то x0 — точка
максимум, а если с минуса в плюс, то x0
есть точка минимума.

Пусть производная меняет знак с плюса на минус,

тех. на некотором интервале
а; х
0
f (x) 0
и на некотором интервале
x; b
0
f (x) 0
Тогда функция y = f (x) увеличится на
a; х
0

и уменьшится на

x; b
0
По определению возрастающей функции
f (x0) f (x) для всех
x a; x0
Для убывающей функции
f (x0) f (x) для всех
x0
x x0; b
— максимальная точка.
Доказательство аналогично минимуму.

1

Найти производную функции
y f (x)
2
Найдите критические точки функции на
, производная которой равна нулю или
не существует.

3

Изучите знак производной слева и
справа от каждых критических
точек.
4
Найдите экстремум функции.

Проверьте функцию на экстремум:

y x (x 1)
3

Применим схему

экстремум:
1
исследование
функция
на
Найдите производную функции:
y (x (x 1)) (x 1) 3x (x 1)
3
3
2
(x 1) (x 1 3x) (x 1) (4 x 1)
2
2

2

Найдите критические точки:
(x 1) (4 x 1) 0
2
х1 1
1
х2
4

3

Исследуем знак производной слева и
справа от каждых критических
точек:
y
y
1
4
1
Нет экстремума в точке x = 1.
x

4

Найти экстремум функции:
27
1
ж мин
256
4

Если первая производная

дифференцируемой функции y = f (x) в точке x0 равна нулю, а вторая производная
в этой точке
положительна, то x0 является точкой
минимум, а если вторая производная
отрицательна, тогда x0 — точка максимума.

Пусть

f (x0) 0
f (x0) 0
, следовательно,
f (x) f (x) 0
и в некоторой окрестности точки x0, т.е.е.

функция

f (x)
увеличится на
a; b
, содержащий точку x0.
Но
f (x0) 0
на интервале
a; x
f (x) 0
и на интервале
x; б
е (х) 0
0
0

Итак, функция

f (x)
при прохождении через точку x0 меняет знак с
минус на плюс, следовательно, эта точка
является точкой минимума.
Аналогично
доказал
максимум функции.
происходит
для

Схема исследования функции на экстремум в

в этом случае аналогична предыдущему, но
третий абзац следует заменить на:
3
Найдите вторую производную и
определите ее знак в каждой критической точке
.

Из второго достаточного условия следует, что

, если в критической точке вторая производная функции
не равна нулю, то эта точка является точкой экстремума
.
Обратное неверно: если в критической точке
вторая производная функции
равна нулю, то эта точка также
может быть точкой экстремума.
IN
В этом случае для изучения функции
достаточно первого условия экстремума
.

Задачи урока: Образовательные: — систематизировать знания и создать многоуровневые условия контроля (самоконтроль, взаимный контроль) усвоения знаний и навыков Развивающие: — способствовать формированию навыков применения полученных знаний в новой ситуации, развивать математическое мышление, речь; , мобильность, коммуникативные навыки

Памятка.Метод интервалов. Основные положения: 1. Знак продукта (частное) однозначно определяется знаками факторов (делимого и делителя). 2. Знак произведения не меняется (меняется на противоположный) при изменении знака четного (нечетного) числа множителей. 3. Знак линейной функции с ненулевым наклоном и знак квадратичной функции справа от большего (или единственного) корня совпадают со знаком их наивысшего коэффициента. 4. Если у строго возрастающей (убывающей) функции есть корень, то справа от корня он положительный (отрицательный) и меняет знак при переходе через корень.Примечания: 1. При отсутствии корней знак квадратичной функции совпадает со знаком ее старшего коэффициента по всей области определения этой функции. 2. Предложение 3 и замечание 1 справедливы для многочлена любой степени.

Работа с расписанием. Работа с расписанием. Рассмотрим рисунок, на котором изображен график функции y = x³-3x². Рассмотрим окрестность точки x = 0, т.е. некоторый интервал, содержащий эту точку.Из рисунка видно, что такая окрестность существует и функция принимает наибольшее значение в точке x = 0. Эта точка называется точкой максимума. Аналогично точка x = 2 называется точкой минимума, так как функция в этой точке принимает значение меньше, чем в любой точке окрестности x = 2. Рассмотрим рисунок, на котором изображен график функции y \ u003d x³-3x². Рассмотрим окрестность точки x = 0, т.е. некоторый интервал, содержащий эту точку.Из рисунка видно, что такая окрестность существует и функция принимает наибольшее значение в точке x = 0. Эта точка называется точкой максимума. Аналогично точка x = 2 называется точкой минимума, так как функция в этой точке принимает значение меньше, чем в любой точке окрестности x = 2.

Необходимо помнить: точка x 0 называется точкой максимума функции f (x), если существует такая окрестность точки x 0, что для всех x, отличных от x 0, из этой окрестности выполняется неравенство .Точка x 0 называется точкой максимума функции f (x), если существует такая окрестность точки x 0, что для всех x кроме x 0 из этой окрестности выполняется неравенство f (x) f (x 0) . (Рисунок 2) Точки максимума и минимума называются точками экстремума. Высокие и низкие точки называются крайними точками.

Немного истории математики: Пьер Ферма. (1601 — 1665) Работа советника в городском парламенте Тулузы не помешала Ферма изучать математику.Постепенно он приобрел известность как один из первых математиков Франции. Он соревновался с французским ученым Р. Декартом в создании аналитической геометрии, общих методов решения задач максимума и минимума. Его методы построения касательных к кривым, вычисления площадей криволинейных фигур, вычисления длин криволинейных фигур проложили путь к созданию дифференциального и интегрального исчисления. Работы Ферма положили начало новой математической науке — теории чисел.

Теорема Ферма.Если x 0 — точка экстремума дифференцируемой функции f (x), то f (x) = 0. Если x 0 — точка экстремума дифференцируемой функции f (x), то f (x) = 0. Теорема Ферма имеет ясный геометрический смысл: касательная к графику функции y = f (x) в точке (x 0; f (x 0)), где x 0 — точка экстремума функции y = f (x) параллельна оси абсцисс, поэтому его наклон f (x) равен нулю. Теорема Ферма имеет ясный геометрический смысл: касательная к графику функции y = f (x) в точке (x 0; f (x 0)), где x 0 — точка экстремума функции y = f (x) параллельна оси абсцисс, поэтому его наклон f (x) равен нулю.

Стационарные и критические точки Точки, в которых производная функции равна нулю, называются стационарными, т.е. если f (x) = 0, то этого недостаточно, чтобы утверждать, что x — точка экстремума. Точки, в которых функция имеет нулевую производную или недифференцируема, называются критическими точками этой функции. Рассмотрим функцию f (x) = x³. Ее производная f (x) = 3x², f (x) = 0. Однако x = 0 не является точкой экстремума, так как функция возрастает по всей числовой оси (рисунок 1).Сформулируйте достаточное условие того, что точка покоя является точкой экстремума.

0 слева от точки x 0 и f (x) «название =» (! LANG: Теорема: Пусть функция f (x) дифференцируема на интервале (a; b), x 0 є (a; б), а f (x) = 0. Тогда: 1) если при прохождении функции f (x) через точку покоя x 0 ее производная меняет знак с «плюс» на «минус», т.е. f (x )> 0 слева от точки x 0 и f (x) «> 10 !} Теорема: Пусть функция f (x) дифференцируема на интервале (a; b), x 0 є (a; b) и f (x) = 0.Тогда: 1) если при прохождении функции f (x) через точку покоя x 0 ее производная меняет знак с «плюс» на «минус», т.е. f (x)> 0 слева от точки x 0 и f (x) 0 слева от точки x 0 и f (x) 0 слева от x 0 и f (x) «> 0 слева от x 0 и f (x) 0 слева от x 0 и f (x) «> 0 слева от x 0 и f (x)» title = «(! LANG: Теорема: Пусть функция f (x) дифференцируема на интервале (a; b), x 0 є (a; b), а f (x) = 0. Тогда: 1) если при переходе через точку покоя x 0 функции f (x) ее производная меняет знак с «плюс» на «минус» «, я.е. f (x)> 0 слева от точки x 0 и f (x) «> title = «Теорема: Пусть функция f (x) дифференцируема на интервале (a; b), x 0 є (a; b) и f (x) = 0. Тогда: 1) если, когда функция f (x) проходит через точку покоя x 0, ее производная меняет знак с «плюс» на «минус», т.е. f (x)> 0 слева от точки x 0 и f (x) «> !}

План поиска экстремума функции. 1. Найдите производную функции. 2. Найдите стационарные точки функции, т.е.е. производная равна нулю. 3. Используя метод интервалов, выяснить, как меняются знаки производной. 4. Определите точки минимума или максимума по знакам перехода функции.

Рассмотрим задачу 1: Найти точки экстремума функции f (x) = 9x-3. Решение: 1) Найти производную функции: f ´ (x) = 9 2) Найти стационарные точки: Стационарных точек нет. 3) Эта функция линейна и возрастает по всей числовой оси, поэтому функция не имеет точек экстремума.Ответ: функция f (x) = 9x-3 не имеет точек экстремума.

Рассмотрим задачу 2: Найти точки экстремума функции f (x) = x ² -2x. Решение: 1) Найти производную функции: f ´ (x) = 2x-2 2) Найти стационарные точки: 2x-2 = 0X = 1. 3) Используя метод интервалов, найдем, как знак производной меняется (см. рисунок): 4) При переходе через точку x = 1 знак производной меняется со знака «-» на «+», поэтому x = 1 — точка минимума .Ответ: точка x = 1 — это точка минимума функции f (x) = x ² -2x.

Рассмотрим задачу 3: Найти точки экстремума функции f (x) = x -4x³. Решение: 1) Найти производную функции: f ´ (x) = 4x³-12x² 2) Найти стационарные точки: 4x³-12x² = 0 X1 = 0, x2 = 3. 3) Воспользоваться методом интервалов, находим, как меняется знак производной (см. рисунок): 4) При переходе через точку x = 0 знак производной не меняется, то эта точка не является точкой экстремума, а при переходе через в точке x 1 = 3 производная меняет знак с «-» на «+», поэтому x 2 = 3 — точка минимума.Ответ: точка x = 3 — это точка минимума функции f (x) = x -4x³.

Самостоятельно выполните следующие задачи: 1) На основании этого показателя определите точки максимума и минимума функции y = f (x). 2) Найдите стационарные точки: а) y = e ² -2e; б) у = 2х³-15х² + 36х; в) у = sinx-cosx; г) у = (2 + х²) / х. 3) Найдите экстремумы функции: а) f (x) = x³-x; б) f (x) = x -8x² + 3; в) f (x) = x + sinx; г) f (x) = x-cos2x.

Физическая культура. Студентам рекомендуется выполнять несколько физических упражнений для снятия усталости и стресса при длительной работе за компьютером. 1. Сидение на стуле: — руки за голову; — локти разведите шире, голову запрокиньте; — локти вперед, голова вперед; — руки расслаблены; — повторить упражнение 4 — 5 раз. 2. Сидя на стуле: — плавно отведите голову назад; — плавно наклоняйте голову вперед; — повторить упражнение 4 — 5 раз. 3. Упражнение для глаз: — быстро моргать; — закройте глаза и сядьте спокойно; — медленно сосчитайте до пяти; — повторить упражнение 4 — 5 раз.4. Упражнение для глаз: — плотно закройте глаза; — медленно сосчитайте до пяти; — откройте глаза и посмотрите вдаль; — повторить упражнение 4 — 5 раз. 5. Упражнение для глаз: — посмотрите на указательный палец вытянутой руки; — смотреть вдаль; — повторить упражнение 4 — 5 раз.

Тестирование: Чтобы запустить тест, вам необходимо открыть файл, расположенный в папке «Function extremes» на диске C: под именем «Test 1». В результате выполнения работы вы получаете оценку своих знаний.Также для систематизации знаний можно выполнить следующие тесты на повторение ранее изученного материала («Тест 2», «Тест 3», «Тест 4», «Тест 5»). Чтобы запустить тест, вам нужно открыть файл, расположенный в папке «Function extremes» на диске C: под именем «Test 1». В результате выполнения работы вы получаете оценку своих знаний. Также для систематизации знаний можно выполнить следующие тесты на повторение ранее изученного материала («Тест 2», «Тест 3», «Тест 4», «Тест 5»).

Урок и презентация «Экстремум функции». 11 класс. Учебник Алимова.

Просмотр содержимого документа

«8.12 экстремумов функции».

Тема: «Крайности функции»

Скажите, и я забуду.
Покажи мне, и я запомню.
Вовлеките меня, и я научусь.
Китайская мудрость.

Цели урока:

Образовательные:

На основе знаний учащихся о производной функции помочь сформулировать и понять определение понятий критических, стационарных точек и экстремальных точек; приводят к гипотезе: необходимое и достаточное условие существования экстремума функции.

Создать условие для первичного закрепления учащимися умения аналитически и графически определять наличие критических, стационарных точек и точек экстремума в функции.

Подготовить студентов к ЕГЭ.

Развивающая:

Способствовать развитию учебно-познавательной деятельности, логического мышления.

Образовательная:

Формировать умение наблюдать, замечать закономерности, обобщать, проводить рассуждения по аналогии.

Развивать мышление, внимание, речь студента.

Формировать общие трудовые навыки в условиях максимальной ответственности и ограниченного времени.

Воспитывать способность выслушивать другие мнения и отстаивать свою точку зрения.

Тип урока: урок ознакомления с новым материалом.

Во время занятий:

I … Организация времени (Информационно-отчетный метод)

Обновление знаний.«Мозговой штурм»

1. Вычислить производную функции: (задание выполняется самостоятельно, с дальнейшей самопроверкой, количество правильных заданий отмечается в листе самопроверки)

	f (x) = 3x 2 — 4x + 5
	f (x) = sin x — cos x
	f (x) = e x + ln x
	f (x) = e 2x — 6e x + 7
	ф (х) = — х 3 + 3х 2 + 9 х — 29

2.Решите неравенство: (у доски)

3. Определите интервалы монотонности функции: (у доски два ученика )

A) f (x) = 3x — 9 (1 точка)

B) f (x) = x 2 + 6x — 9 (2 балла)

II … Научно-исследовательская работа. (на миллиметровой бумаге)

Ответьте на вопросы:

IV … Формирование гипотезы (Частично исследовательская (эвристическая))

(студенты выдвигают гипотезу)

Если производная меняет знак с «-» на «+», и в самой точке равно 0, то эта точка будет точкой минимума функции.(за выдвижение гипотезы — 4 балла)

Ответьте на вопросы:

Назовите интервалы увеличения и уменьшения полученного графика.

Как ведет себя производная около этой точки при прохождении через эту точку? И именно здесь?

Работа с учебником.

P. 265 — 266. Найдите свою гипотезу в тексте.

Прочтите.

Минимальные и максимальные точки называются крайними точками.

Что мы будем делать на сегодняшнем уроке?

(научитесь находить точки экстремума функции)

Какова тема нашего урока?

Экстремумы функции. Записали тему урока.

Студенческое послание (методика стимулирования учебной активности школьников)

Выдвинутая вами гипотеза 4 века назад была подтверждена французским математиком Пьером Ферма.

(историческая справка)

Пьер Ферма (1601-1665) — французский математик, один из основоположников аналитической геометрии и теории чисел (теорема Ферма).Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

(студенты читают формулировку теоремы )

Работа с книгой стр. 267

Найдите, какие точки называются стационарными, критическими.

(Точки, в которых производная функции равна нулю, называются стационарными

Точки, в которых функция имеет производную, равную нулю или недифференцируема, называются критическими точками этой функции )

Работа с сигнальными картами .

Если утверждение верно — «да», если нет — «нет» (игра «ДА, НЕТ»

За правильный ответ 1 балл

Стр. 268 теорема … (ученики читают и объясните, как они это понимают)

Достаточный знак экстремума .

На доске: за правильное выполнение — 5 баллов.

Создайте алгоритм поиска точек экстремума функции .

1. Найдите область определения функции.

2. Найдите f «( x ).

x ) = 0 или f» ( x ) не существует.
(Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Поместите область определения и эти точки на координатную линию.

5. Определите знаки производной на каждом из интервалов

6. Примените знаки.

7. Запишите свой ответ.

(Практическая методика)

Работа с экзаменационными материалами

Функция y = f (x) определена на интервале (-4; 5).На рисунке показан график его производной. Найти точку минимума функции y = f (x)

Функция y = f (x) определена на интервале (- 6; 6). На рисунке показан график его производной. Найдите точки, в которых производная функции равна нулю (ответ : х = — 4; х = — 2; х = 1; х = 5).

Краткое содержание урока: выставление оценок (по листам самоконтроля)

Хотелось бы выучить получше…

Мне нравится …

Не нравится …

На уроке я почувствовал …

С домашним заданием …

Просмотр содержания презентации

«8,12 экстремума функции»

Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеките меня, и я буду учиться.

Китайская мудрость.

f (x) = 3x 2 — 4x + 5

f (x) = sin x — cos x

f (x) = ex + ln x

f (x) = e 2x — 6e x + 7

f (x) = — x 3 + 3x 2 + 9 x — 29

cos x + sin x

2e 2x — 6 e x

-3 х 2 + 6 х + 9

Постройте график функции: y = x 2 –6x + 8;

Ответьте на вопросы:

• Назовите интервалы увеличения и уменьшения полученного графика.
• Назовите точку минимума функции.

• Ответьте на вопросы:
• Назовите интервалы увеличения и уменьшения полученного графика.
• Назовите точку максимума функции.
• Как ведет себя производная около этой точки, проходя через эту точку? И именно здесь?

Ответьте на вопросы:

• Назовите интервалы увеличения и уменьшения полученного графика.
• Назовите точку максимума функции.
• Как ведет себя производная вблизи этой точки при прохождении через нее? И именно здесь?

Пьер Ферма (1601-1665) — французский математик, один из основоположников аналитической геометрии и теории чисел (теорема Ферма). Труды по теории вероятностей, исчислению бесконечно малых и оптике (принцип Ферма).

Пьер Ферма открыл методы нахождения экстремумов и касательных, которые, с современной точки зрения, сводятся к нахождению производной.

Необходимый признак экстремума .

Алгоритм поиска точек экстремума функции

1. Найдите область определения функции.

2. Найдите f «( x ).

3. Найдите критические точки, т.е. точки, где f «( x ) = 0 или f «( x ) не существует. (Производная равна 0 в нулях числителя, производная не существует в нулях знаменателя)

4. Поместите область определения и эти точки на координатную линию.

5. Определите знаки производной на каждом из интервалов

6. Примените знаки.

7. Запишите свой ответ.

д / з: п. 50, № 912 (2,4),

913 (2,4), 914 (2,4)

• Я могу…
• Я знаю…
• Я бы хотел узнать больше…
• Мне нравится…
• Не нравится…
• На уроке я чувствовал …
• С домашним заданием, Я …

Великий философ Конфуций однажды сказал: «Три пути ведут к знанию: путь размышления — самый благородный путь, путь подражания — самый легкий путь, а путь опыта — самый горький путь». Выполняя домашнее задание, каждый из вас пойдет своим путем к знаниям.

• Конфуций, Кун-цзы (родился около 551 г. — умер в 479 г. до н.э.), древнекитайский мыслитель, основатель конфуцианства.

Геометрический смысл производного представления алима. Презентация на тему «Геометрический смысл производной функции». Уравнение касательной к графику функции

Slide 2

Любая верная математическая идея рано или поздно находит применение в том или ином случае.Крылов А.Н.

Слайд 3

Цель урока

1) выяснить, что такое геометрический смысл производной, вывести уравнения касательной к графику функции 2) разработать ОУУН психической деятельности: анализ, обобщение и систематизация, логическое мышление, сознательное восприятие Учебный материал 3) формировать умение оценивать свой уровень знаний и желание его повышать, способствовать развитию потребности в самообразовании.Воспитание ответственности, коллективизма.

Slide 4

Словарь урока

производная, линейная функция, наклон, непрерывность, тангенсы углов (острые, тупые).

Slide 5

Сделайте по паре по 3 минуты каждый ученик работает самостоятельно, 2 минуты — в парах. Обсуждение результатов и запись в карточке ответов. (Карточка №1 остается у ученика для самоконтроля, карточка №2 должна быть возвращена учителю)

Слайд 6

Ответ.

Сделайте пару

Слайд 7

Определение

Функция, задаваемая формулой y = kx + b, называется линейной. Число k = tg называется наклоном прямой.

Слайд 8

y x -1 0 1 2 y = kx + b

Слайд 9

y x -1 0 1 2 y = kx + b

Слайд 10

y x 0 y = yₒ + к (х-xₒ)   x-xₒ y-yₒ xₒ x Mₒ (xₒ; yₒ) M (x; y) A (x; yₒ)

Slide 11

Уравнение прямой с наклоном k, проходящей через точку (x0; y0) y = y0 + k (x-x0) Уравнение прямой с наклоном k, проходящей через точку (x0; y0) ) y = y0 + k (x-x0) (1) Наклон прямой, проходящей через точки (x1; y1) и (x0; y0) (2)

Слайд 12

y x -1 0 1 2 Найдите наклон прямой y = kx + b

Слайд 13

Определение

Касательная к графику функции y = f (x) называется предельным положением секущей.рисунок

Слайд 14

касательная секущая

Слайд 15

Практическая работа Геометрический смысл производной

Назначение: По данным практической работы определить, в чем заключается геометрическое значение производной. Оборудование: линейки, транспортиры, микрокалькуляторы, миллиметровая бумага с нанесенным графиком.

Слайд 16

Задача

1. Постройте касательную к графику функции … в точке с абсциссой xₒ = 2 2.Измерьте угол, образованный касательной и положительным направлением оси oX. 3. Запишите  =…. 4. Рассчитать с помощью микрокалькулятора tg =…. 5. Вычислить f´ (xₒ), для этого найти f´ (x) 6. Записать: f´ (x) =…. ; f´ (xₒ) =…. 7. Выберите две точки на касательном графике и запишите их координаты. 8. Рассчитайте наклон прямой k по формуле 9. Результаты расчета занесите в таблицу

.

Slide 17

Геометрический смысл производной

Значение производной функции y = f (x) в точке x0 равно наклону касательной к графику функции y = f (x) в точке (x0; f (x0 ))

Слайд 18

Слайд 19

Слайд 20

Slide 21

Уравнение касательной к графику функции

1.Запишите уравнение прямой с наклоном k, проходящей через точку 2. Замените k на, а y = y0 + k (x-x0)

.

Чтобы просмотреть презентацию с изображениями, иллюстрациями и слайдами, загрузите соответствующий файл и откройте его в PowerPoint на своем компьютере.
Презентационные слайды Текстовое содержание: В.Н. Егорова, учитель математики КОУ «СОШ №1 (заочная форма)» Определение производной. Производная функции — одна из сложных тем в школьной программе.Не каждый выпускник ответит на вопрос, что такое производная ACBtg A-? Tg B -? ABC Работа устно Касательная — это отношение противоположной ноги к соседней

ACBtg A-? Tg B -? 47ABS Найдите меру в градусах

На рисунке показаны графики трех функций. Как вы думаете, какая из них растет быстрее? Устная работа Костя, Гриша и Матвей устроились одновременно. Посмотрим, как изменились их доходы за год: за полгода доход Кости увеличился более чем вдвое. И доход Гриши тоже увеличился, но незначительно.И доход Матвея упал до нуля. Условия запуска такие же, но скорость изменения функции другая. Что касается Матвея, то его доход в целом отрицательный.

Интуитивно мы можем легко оценить скорость изменения функции. Но как это сделать? На самом деле мы смотрим, насколько круто график функции идет вверх (или вниз). Другими словами, насколько быстро изменяется y при изменении x. Очевидно, что одна и та же функция в разных точках может изменяться быстрее или медленнее.
Производная — это скорость изменения функции.
Проблемы, ведущие к концепции производной 1. Задача о скорости изменения функции. Нарисован график некоторой функции. Возьмем точку с абсциссой. Проведем в этой точке касательную к графику функции. Для оценки наклона графика функции удобное значение — тангенс угла наклона касательной. За угол наклона берем угол между касательной и положительным направлением оси OX. Найти k = tan α∆АМN: N АNМ = 90˚, tgα = 𝐴𝑁𝑀𝑁 Геометрический смысл производной.

Производная функции в точке равна наклону касательной, проведенной к графику функции в этой точке. Геометрический смысл производной Производная функции равна тангенсу угла наклона касательной — это геометрический смысл производной
S Время пробега tАBU = S / t Проблемы, приводящие к концепции производная 2. Проблема скорости движения
ЗАДАЧА. Тело (материальная точка) движется по прямой, на которой задаются начало координат, единица измерения (метр) и направление.Закон движения задается формулой S = s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу координат (в метрах). Найдите скорость тела в момент времени t (в м / с). РЕШЕНИЕ. Предположим, что в момент t тело находилось в точке МОМ = S (t). Придадим аргументу t приращение ∆t и рассмотрим ситуацию в момент времени t + ∆t. Координата материальной точки будет другой, тело в этот момент будет в точке P: OP = s (t + ∆t) — s (t).Это означает, что за ∆t секунд тело переместилось из точки M в точку P. Имеем: MP = OP — OM = s (t + ∆t) — s (t). Полученная разность называется приращением функции: s (t + ∆t) — s (t) = ∆s. Итак, МП = ∆s (м). Тогда средняя скорость за интервал времени: 𝑣ср. = ∆𝑆∆𝑡 Средняя скорость S (t) S (t + ∆t) 0МР∆t
Производная функции y = f (x) в заданной точке x0 является пределом отношения приращения функции при это указывает на приращение аргумента, при условии, что приращение аргумента стремится к нулю.Обозначение производной: 𝑦′𝑥0 или ′𝑥0 𝑓′𝑥0 = lim∆ 𝑥 → 0∆𝑦∆𝑥 или 𝑓′𝑥0 = lim∆𝑥 → 0∆𝑓∆𝑥 Определение Аннотация
Мгновенная скорость — это средняя скорость в интервал, если ∆t → 0, т. е. гинст. = 𝒍𝒊𝒎∆𝒕 → 𝟎𝒗ср. = 𝒍𝒊𝒎∆𝒕 → 𝟎∆𝑺∆𝒕 Мгновенная скорость Аннотация Рассмотрим два значения аргумента x0 и ∆ x, где ∆х — приращение аргумента. Найдем приращение функции ∆f (x) = f (x0 + ∆х) — f (x0). Найдите отношение приращения функции к приращению аргумента ∆𝐟 (x) ∆х.Вычислить предел этого отношения при ∆х → 0 lim∆𝑥 → 0∆𝑓 (𝑥) ∆𝑥 = 𝑓 ′ (𝑥) Алгоритм нахождения производной (по определению) Пример вычисления производной Сводка решения

Пример 2 : Найти производную функции y = x Решение: f (x) = x.1. Возьмем два значения аргумента x и x + Δx. 2.∆𝑓 = 𝑓𝑥 + ∆𝑥 — 𝑓𝑥 = 𝑥 + ∆𝑥 — 𝑥 = ∆𝑥. 3.∆𝑓∆𝑥 = ∆𝑥∆𝑥 = 1,4.𝑓′𝑥 = lim∆𝑥 → 0∆𝑓∆𝑥 = lim∆𝑥 → 01 = 1. Отсюда (𝒙) ′ = 1 Пример вычисления производной Пример 3.Найти производную функции y = x2 Решение: f (x) = x2,1. Возьмем два значения аргумента x и x + Δx. 2.∆ = 𝑓𝑥 + ∆𝑥 — 𝑓𝑥 = (𝑥 + ∆𝑥) 2 — 𝑥2 = 𝑥2 + 2𝑥∆𝑥 + (∆𝑥) 2 — 𝑥2 = ∆𝑥 (2𝑥 + ∆𝑥). 3. ∆𝑓 (𝑥) ∆𝑥 = ∆𝑥 (2𝑥 + ∆𝑥) ∆𝑥 = 2𝑥 + ∆𝑥. 4. 𝑓′𝑥 = lim∆𝑥 → 0∆𝑓∆𝑥 = lim∆𝑥 → 0 (2𝑥 + ∆𝑥) = lim∆𝑥 → 02𝑥 + lim∆𝑥 → 0∆𝑥 = 2𝑥. Следовательно, (𝒙𝟐) ′ = 2x Пример вычисления производной Пример 4 Найти производную функции y = 𝒌𝒙 + 𝒎 Решение: f (x) = 𝑘𝑥 + 𝑚.1. Возьмите два значения аргумента x и x + Δx. 2.∆𝑓 = 𝑓𝑥 + ∆𝑥 — 𝑓𝑥 = 𝑘𝑥 + ∆𝑥 + 𝑚− 𝑘𝑥 — 𝑚 = 𝑘𝑥 + 𝑘∆𝑥 — 𝑘𝑥 = 𝑘∆𝑥.3.∆𝑓 (𝑥) ∆𝑥 = 𝑘∆𝑥∆𝑥 = 𝑘.4.𝑓′𝑥 = lim∆𝑥 → 0 ∆𝑓∆𝑥 = lim∆𝑥 → 0𝑘 = 𝑘. Следовательно, (𝒌𝒙 + 𝒎) ′ = k Пример вычисления производной Пример 5 Найти производную функции y = 𝟏𝒙 Решение: f (x) = 1𝑥.1. Возьмем два значения аргумента x и x + ∆x. 2. ∆𝑓 = 𝑓𝑥 + ∆𝑥 — 𝑓𝑥 = 1𝑥 + ∆𝑥 — 1𝑥 = 𝑥 — 𝑥 — ∆𝑥𝑥 (𝑥 + ∆𝑥) \ u003d — ∆𝑥𝑥 (𝑥 + ∆𝑥).3. ∆ 𝑓 (𝑥) ∆𝑥 = −∆𝑥𝑥 (𝑥 + ∆𝑥): ∆𝑥 = −∆𝑥𝑥 (𝑥 + ∆𝑥) ∆𝑥 = −1𝑥 (𝑥 + ∆𝑥). 4.𝑓′𝑥 = lim∆𝑥 → 0∆𝑓∆𝑥 = lim∆𝑥 → 0−1𝑥 (𝑥 + ∆𝑥) = — 1lim∆𝑥 → 01𝑥2 + 𝑥∆𝑥 = −lim∆𝑥 → 01lim∆𝑥 → 0𝑥2 + lim∆𝑥 → 0𝑥∆𝑥 = −1𝑥2. Следовательно, 𝟏𝒙 ′ = − Пример расчета производной Таблица производных ′ = 𝟎 𝒙 ‘= 1𝒙𝟐 ′ = 𝟐𝒙𝒌𝒙 + 𝒎 ′ = 𝒌𝟏𝒙 = − Закончите фразу: Наш сегодняшний урок был посвящен. .. На уроке я узнал, что … На уроке я узнал … Производная функции в точке равна… касательная, проведенная к графику функции в этой точке. Скорость изменения функции … Мне было трудно … УМНЫЕ МУЖЧИНЫ!
ppt_y

Прикрепленные файлы

аннотации других презентаций

«Тригонометрические формулы» — Cos x. Cos. F-ly преобразование суммы в произведение .. Sin (x + y). Формулы двойного аргумента. Формулы преобразования manuf. в количестве. Формулы сложения. Тригонометрия. Tg. Грех x. Соотношение между ф-ями. Ф-лы половинного аргумента. Тригонометрические уравнения.

«Расчет площади криволинейной трапеции» — Площади криволинейной трапеции. Формулы площади. Какая форма называется изогнутой трапецией. Повторение теории. Изогнутая область трапеции. Найдите первообразную функции. Какие из фигур являются криволинейными трапециями. Решение. Шаблоны функциональных графов. Подготовка к экзаменам. Фигура, не являющаяся изогнутой трапецией.

«Определить, является ли функция четной или нечетной» — Нечетные функции. Нет даже. Функция. График нечетной функции.Является четной функцией. Столбец. График четной функции. Даже функции. Функция нечетная. Осевая симметрия. Пример. Функция нечетная. Это не странно. Четные и нечетные функции.

«Логарифмы и их свойства» — Свойства степени. Таблицы логарифмов. Свойства логарифмов. История происхождения логарифмов. Повторите определение логарифма. Рассчитайте. Применение изученного материала. Проверить это. Определение логарифма. Открытие логарифмов. Найдите вторую половину формулы.

»« Логарифмические неравенства «11 класс» — Применение теоремы. журнал26 … журнал210 журнал0.36 … журнал0.310. Определение. > Т.К. 61, тогда logа f (x)> logа g (x)? Если 0logа g (x) ?.

«Множество первообразных» — Первоначальное. Выберите первообразную для функций. Определение уровня знаний. Решение нового типа задач. Фронтальный опрос. Проверка исполнения. Выходной контроль. Воспитательная самостоятельная работа. Концепция интеграции. Общий вид первообразных. Формулы.Оценочная система.

Муниципальное бюджетное образовательное учреждение

Глуховская общеобразовательная школа

Конспект открытого урока алгебры

на тему:

«Производная и ее геометрический смысл. Производная в ЕГЭ »

учитель математики и информатики

Дикалов Дмитрий Геннадьевич

2015

Краткое содержание урока по теме: Производная и ее геометрическое значение

Цели урока:

Образовательная:

• Просмотрите основные концепции раздела «Производная».
• Научить студентов, как быстро решать задачи по теме «Производная. «из вариантов ЕГЭ

Развивающие:

• Развитие познавательного интереса, логического мышления, развитие памяти, внимательности.
• вызывают интерес к структуре компьютерных сетей.

Образовательные:

• воспитывать сознательное отношение к работе, инициативу;
• Содействие дисциплине и организованности

Тип урока:

• урок по повторению и закреплению знаний

Структура урока:

• организация времени;
• обновление базовых знаний
• решение проблем
• домашнее задание

Оборудование: презентационная программа Microsoft Office PowerPoint, презентация, компьютер, мультимедийный проектор, интерактивная доска.

План урока:

1. Организационный момент (1 мин)
2. Обновление знаний (5 мин)
3. Решение проблем (34 мин)
4. Краткое содержание урока (4 мин)
5. Домашнее задание (1 мин)

Во время занятий:

I. Организационный момент

Учитель здоровается, знакомит с темой, целями и ходом урока.

II. Обновление знаний

1. 1. Каково геометрическое значение производной?
2. Как найти интервалы возрастания (убывания) функций?
3. Какой алгоритм нахождения точек экстремума?
4. Чем стационарные точки отличаются от точек экстремума?

III.Решаю задачи.

Решение задач нахождения производной в точке, нахождение интервалов увеличения и убывания, нахождение точек, в которых производная = 0, нахождение наибольшего и наименьшего значения функции.

Учащиеся решают эти задачи с помощью интерактивной доски, каждая задача изображена на отдельном слайде.

Студенты обсуждают нюансы решения задач по мере продвижения слайдов.

Студентам для самостоятельного решения предлагаются следующие задачи.

IV. Подведение итогов урока.

Для подведения итогов занятия вызывают к доске 1-2 ученика для решения задач из учебника № 956 (1,2): найти интервалы увеличения и уменьшения функции y = 2×3 + 3x 2 -2

Решение Стьюдента:

Чтобы найти интервалы увеличения и уменьшения функции, находим ее производную:

y` = 6x 2 + 6x

Чтобы найти стационарные точки, приравняйте производную к 0 и решите по этому уравнению получаем точки x = 0 и x = -1.Найдем среди этих точек точки экстремума. Для этого мы определяем знак производной на каждом из трех интервалов. На интервале х0 производная положительна, что означает, что на этих интервалах функция возрастает. На интервале

1

Студент записывает ответ.

V. Домашнее задание

№ 957, № 956 (на выполнение)

Оценка учащихся, активно проявивших себя на уроке.

Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (учетную запись) Google и войдите в нее: https: // accounts.google.com

Подписи к слайдам:

Геометрическое значение производной. Касательное уравнение. f (x)

Используя формулы и правила дифференцирования, найдите производные от следующих функций:

1. В чем геометрический смысл производной? 2. Можно ли провести касательную в любой точке графика? Какая функция называется дифференцируемой в точке? 3. Касательная наклонена под тупым углом к ​​положительному направлению оси Ox. Что можно сказать о знаке производной и характере монотонности функции? 4.Касательная наклонена под острым углом к ​​положительному направлению оси Ox. Что можно сказать о знаке производной и характере монотонности функции? 5 . Касательная наклонена под прямым углом к ​​положительному направлению оси Ox. А как насчет производной?

для дифференцируемых функций: 0 ° ≤ α ≤ 180 °, α ≠ 90 ° α — тупой тангенс угла α 0 f ´ (x 1)> 0 положение касательной не определено tan α несуб. f ´ (x 3) не n. α = 0 tan α = 0 f ´ (x 2) = 0

y = f / (x 0) (x — x 0) + f (x 0) (x 0; f (x 0) ) — координаты точки касания f ´ (x 0) = tan α = k — тангенс угла наклона касательной в заданной точке или наклоне (x; y) — координаты любой точки касательной Касательного уравнения

№1.Найти наклон касательной к кривой в точке с абсциссой x 0 = — 2. Задача B8 FBTZ USE

# 2. Задайте значение коэффициента k, при котором графики линейных функций y = 8x + 12 и y = kx — 3 параллельны. Ответ: 8. Задача B8 FBTZ USE

0 Y X 1 -1 1 -1 № 3. Функция y = f (x) определена на интервале (-7; 7). На рисунке ниже показан график его производной. Найдите количество касательных к графику функции y = f (x), параллельных оси абсцисс.Ответ: 3. Задание B8 FBTZ USE

№4. На рисунке изображена прямая, касательная к графику функции y = p (x) в точке (x 0; p (x 0)). Найдите значение производной при x 0. Ответ: -0,5. Задача B8 FBTZ USE

0 Y X 1 -1 1 -1 No. 5. Все касательные, параллельные прямой y = 2x + 5 или совпадающие с ней, нарисованы на графике функции f (x). Укажите количество точек касания. Ответ: 4. Задача B8 FBTZ USE

Запишите уравнения касательных к графику функции в точках его пересечения с осью абсцисс.Самостоятельная работа

Фамилия, имя Тестирование Творческое задание Урок +, -, :), 🙁 ,: |

1 группа №1. В чем геометрический смысл производной? № 2. Какими свойствами должна обладать функция y = f (x) имеют, заданные на отрезке (a; b), так что в точке с абсциссой x 0 Є (a; b) его график имеет касательную? № 3. Какой вид имеет уравнение касательной прямой Имеем? № 4. Составьте уравнение касательной к графику функции f (x) = 0,5 -4, если касательная образует угол 45 градусов с положительным направлением оси абсцисс.

2-я группа №1. В чем геометрический смысл производной? № 2. Какими свойствами должна обладать функция y = f (x), заданная на интервале (a; b), чтобы в точке с абсциссой x 0 Є (a; b) ее график имел касательную? № 3. Какой вид имеет уравнение касательной? № 4. Напишите уравнение касательной к графику функции f (x) =, параллельному прямой y = 9 x — 7.

3 группа №1. В чем геометрический смысл производной? № 2.Какими свойствами должна обладать функция y = f (x), заданная на интервале (a; b), чтобы в точке с абсциссой x 0 Є (a; b) ее график имел касательную? № 3. Каков вид уравнения касательной? № 4. Прямая, проходящая через начало координат, касается графика функции y = f (x) в точке A (-7; 14). Найти.

4-я группа №1. В чем геометрический смысл производной? № 2. Какими свойствами должна обладать функция y = f (x), заданная на интервале (a; b), чтобы в точке с абсциссой x 0 Є (a; b) ее график имел касательную? № 3.Какую форму имеет уравнение касательной? № 4. Прямая y = -4x-11 касается графика функции. Найдите абсциссу точки касания.

Предварительный просмотр:

Сценарий урока
по алгебре и принципам анализа в 10 классе.

Тема: «Геометрический смысл производной. Касательное уравнение »

Задачи: 1) продолжить формирование системы математических знаний и умений по теме« Уравнение касательной », необходимых для использования в практической деятельности, изучении смежных дисциплин, непрерывном обучении;

2) развитие навыков в использовании компьютерных и мультимедийных программ для организации собственной познавательной деятельности;

3) развивать логическое мышление, алгоритмическую культуру, критическое мышление;

4) воспитывать толерантность, общение.

Во время занятий.

1. Организация времени.
2. Размещение темы, постановка целей урока.
3. Проверка домашнего задания.

1. Базовые задания (сканированное задание)
2. Задание практического содержания повышенного уровня студенты решают трудности по своему выбору. Один из учеников представляет свое решение в виде мультимедийного проекта: «Строится параболический мост, соединяющий точки A и B, расстояние между которыми составляет 200 метров.Вход на мост и выход с моста должны быть прямыми участками пути, эти участки направлены к горизонту под углом 150. Указанные линии должны быть касательными к параболе. Приравнять профиль моста в заданной системе координат «

1. Обновление базовых знаний.

1. Дифференциальные функции:

• ()
• y = 4 ()
• y = 7x + 4 ()
• y = tg x + ()
• y = x 3 sin x ()
• y = ()

1. Ответьте на вопросы:

• Каков геометрический смысл производной?
• Можно ли провести касательную в любой точке графика? Какая функция называется дифференцируемой в точке?
• Касательная наклонена под тупым углом к ​​положительному направлению оси Ox.Что можно сказать о знаке производной и характере монотонности функции?
• Касательная наклонена под острым углом к ​​положительному направлению оси Ox. Что можно сказать о знаке производной и характере монотонности функции?
• Касательная наклонена под прямым углом к ​​положительному направлению оси OX. Что можно сказать о знаке производной и характере монотонности функции?
• Как должен выглядеть график функции, дифференцированной в точке?

1. Какова форма тангенциального уравнения? Объясните, что в этом уравнении (x0; f (x 0)), f ‘(x 0), (x; y)
2. Найдите наклон касательной к кривой y = 2×2 + x в точке с абсциссой x0 = -2 (-7).
3. Укажите значение коэффициента k, при котором графики линейных функций y = 8x + 12 и y = kx — 3 параллельны. (восемь)
4. Функция y = f (x) определена на интервале (-7; 7). На рисунке ниже показан график его производной. Найдите количество касательных к графику функции y = f (x), параллельных оси абсцисс. (3)
5. На рисунке изображена прямая, касательная к графику функции y = p (x) в точке (x0; p (x 0)).Найти значение производной в точке x0 . (-0,5)
6. Все касательные, параллельные прямой y = 2x + 5 или совпадающие с ней, проводились к графику функции f (x). Укажите количество точек касания. (4)

1. Самостоятельная работа с произвольной проверкой (один ученик выполняет задание за доской). Запишите уравнения касательных к графику функции f (x) = 4 — x 2 в точках его пересечения с осью абсцисс. (у = — + 4х + 8). Демонстрация иллюстрации.
2. Работа в творческих группах по 5-6 человек.

1. По очереди проходите компьютерное тестирование (Дополнительное тестирование к уроку 5, варианты 1 и 2 «Уроки алгебры Кирилла и Мефодия»). Результаты заносятся в диагностическую карту.
2. Заданий в тетрадях выполнить:

1-я группа

y = f (x) установить на интервале (a; b) так, чтобы в точке с абсциссаксом 0 Є (a; b

№ 4. Составьте уравнение касательной к графику функции f (x) = 0.5 x 2-4, если касательная составляет угол 45 с осью x 0 .

2-я группа

# 1. В чем геометрический смысл производной?

# 2. Какие свойства должна иметь функция y = f (x) на интервале (a; b), чтобы в точке с абсциссаксом 0 Є (a; b) ее график имел касательную?

№ 3. Как выглядит уравнение касательной?

№ 4. Запишите уравнение касательной к графику функции f (x) = x 3/3, параллельной прямой = 9 x — 7.

Группа 3

# 1. Каков геометрический смысл производной?

# 2. Какие свойства должна иметь функция y = f (x) на интервале (a; b), чтобы в точке с абсциссаксом 0 Є (a; b) ее график имел касательную?

№ 3. Как выглядит уравнение касательной?

№ 4. Прямая, проходящая через начало координат, касается графика функции
y = f (x) в точке A (-7; 14). Найдите … (Задание КИМ для подготовки к экзамену)

4 группа

# 1.В чем геометрический смысл производной?

# 2. Какие свойства должна иметь функция y = f (x) на интервале (a; b), чтобы в точке с абсциссаксом 0 Є (a; b) ее график имел касательную?

№ 3. Как выглядит уравнение касательной?

№ 4. Прямая y = -4x-11 касается графика функции f (x) = x3 + 7x 2 + 7x-6. Найдите абсциссу точки касания. (Задание КИМ для подготовки к экзамену)

Отчет о проделанной работе составляется на доске одним из участников группы.