Алгебра 9 Макарычев К-2 В-1
Контрольная работа по алгебре в 9 классе «Квадратичная функция и её график. Степенная функция. Корень n-й степени» с ответами и решениями. Алгебра 9 Макарычев К-2 В-1.
Алгебра 9 класс (Макарычев)
Контрольная работа № 2. Вариант 1
§ 3. Квадратичная функция и её график. § 4. Степенная функция. Корень n-й степени.
КР-2. Вариант 1 (транскрипт заданий)
1. Постройте график функции у = х2 – 6х + 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = –1;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, на котором функция возрастает.
2. Найдите наименьшее значение функции у = х2 – 8х + 7.
3. Найдите область значений функции у = х2 – 6х – 13, где х ∈ [–2; 7].
4. Не выполняя построения, определите, пересекаются ли парабола у = х2/4 и прямая у = 5х – 16.
Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения
Алгебра 9 Макарычев К-2 В-1 ОТВЕТЫ:
КР-2. Ответы на Вариант 1.
№2. –9.
№3. [–22; 3].
№4. Пересекаются в точках (4; 4) и (16; 64).
№5. 18,5.
Смотреть РЕШЕНИЯ заданий Варианта 1 в тетради
Алгебра 9 Макарычев К-2 В-1. Контрольная работа по алгебре 9 класс «Квадратичная функция и её график. Степенная функция. Корень n-й степени» с ответами и решениями.
Другие варианты: К-2 Вариант 2 К-2 Вариант 3 К-2 Вариант 4
В учебных целях использованы цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение». Представленная контрольная работа ориентирована на УМК Макарычева.
Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.
Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.Список контрольных работ по алгебре в 9 классе для УМК Макарычев (Оглавление)
Материал по алгебре (9 класс) на тему: Контрольные работы по математике 9 класс (Макарычев Ю.Н., Атанасян Л.С.)
Предварительный просмотр:
li{counter-increment:lst-ctn-kix_list_33-5}#doc8779917 ol.lst-kix_list_38-6{list-style-type:none}#doc8779917 ol.lst-kix_list_38-5{list-style-type:none}#doc8779917 .lst-kix_list_21-8>li{counter-increment:lst-ctn-kix_list_21-8}#doc8779917 ol.lst-kix_list_38-8{list-style-type:none}#doc8779917 ol.lst-kix_list_38-7{list-style-type:none}#doc8779917 ol.lst-kix_list_38-2{list-style-type:none}#doc8779917 ol.lst-kix_list_38-1{list-style-type:none}#doc8779917 ol.lst-kix_list_38-4{list-style-type:none}#doc8779917 ol.lst-kix_list_38-3{list-style-type:none}#doc8779917 ol.
lst-kix_list_38-0{list-style-type:none}#doc8779917 .lst-kix_list_5-0>li{counter-increment:lst-ctn-kix_list_5-0}#doc8779917 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc8779917 ol.lst-kix_list_37-2.start{counter-reset:lst-ctn-kix_list_37-2 0}#doc8779917 .lst-kix_list_45-2>li{counter-increment:lst-ctn-kix_list_45-2}#doc8779917 .lst-kix_list_42-1>li:before{content:»» counter(lst-ctn-kix_list_42-1,lower-latin) «. «}#doc8779917 .lst-kix_list_40-1>li{counter-increment:lst-ctn-kix_list_40-1}#doc8779917 ol.lst-kix_list_5-3.start{counter-reset:lst-ctn-kix_list_5-3 0}#doc8779917 .lst-kix_list_38-6>li{counter-increment:lst-ctn-kix_list_38-6}#doc8779917 .lst-kix_list_4-3>li{counter-increment:lst-ctn-kix_list_4-3}#doc8779917 .lst-kix_list_42-7>li:before{content:»» counter(lst-ctn-kix_list_42-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_17-1.start{counter-reset:lst-ctn-kix_list_17-1 0}#doc8779917 .lst-kix_list_42-5>li:before{content:»» counter(lst-ctn-kix_list_42-5,lower-roman) «.
«}#doc8779917 ol.lst-kix_list_8-8.start{counter-reset:lst-ctn-kix_list_8-8 0}#doc8779917 .lst-kix_list_42-3>li:before{content:»» counter(lst-ctn-kix_list_42-3,decimal) «. «}#doc8779917 .lst-kix_list_32-8>li{counter-increment:lst-ctn-kix_list_32-8}#doc8779917 ol.lst-kix_list_16-5{list-style-type:none}#doc8779917 ol.lst-kix_list_16-6{list-style-type:none}#doc8779917 .lst-kix_list_24-8>li:before{content:»» counter(lst-ctn-kix_list_24-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_16-7{list-style-type:none}#doc8779917 ol.lst-kix_list_16-8{list-style-type:none}#doc8779917 ol.lst-kix_list_16-1{list-style-type:none}#doc8779917 ol.lst-kix_list_16-2{list-style-type:none}#doc8779917 ol.lst-kix_list_16-3{list-style-type:none}#doc8779917 ol.lst-kix_list_16-4{list-style-type:none}#doc8779917 .lst-kix_list_24-2>li:before{content:»» counter(lst-ctn-kix_list_24-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_16-0{list-style-type:none}#doc8779917 .lst-kix_list_24-4>li:before{content:»» counter(lst-ctn-kix_list_24-4,lower-latin) «.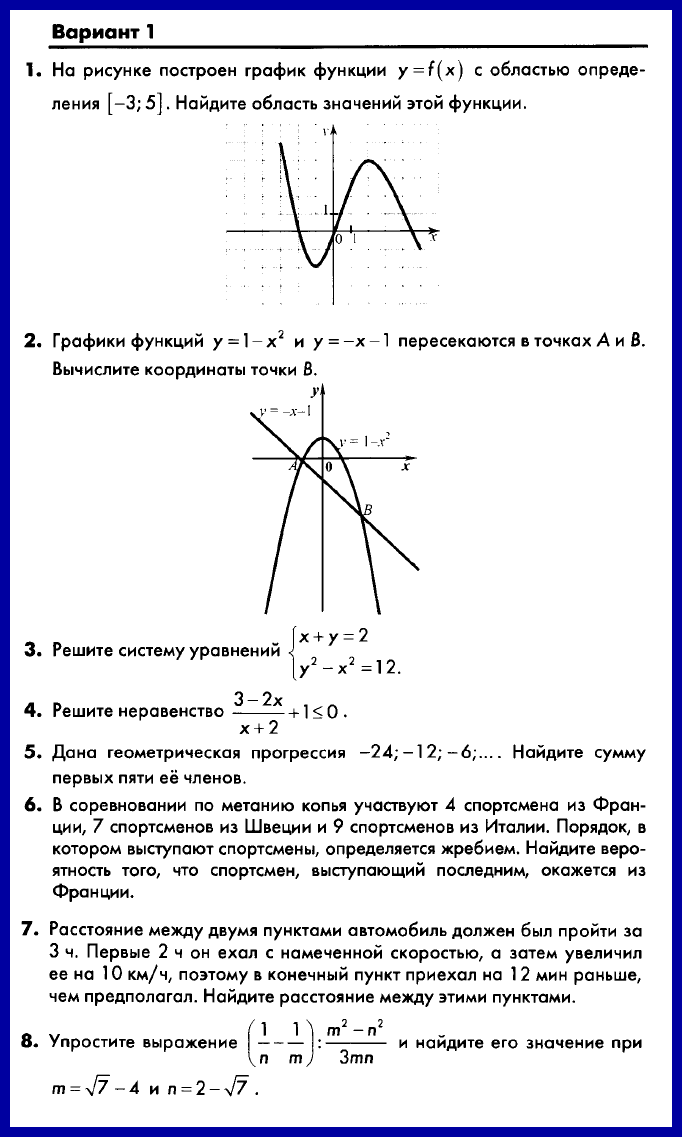
«}#doc8779917 ol.lst-kix_list_34-2.start{counter-reset:lst-ctn-kix_list_34-2 0}#doc8779917 .lst-kix_list_9-4>li{counter-increment:lst-ctn-kix_list_9-4}#doc8779917 .lst-kix_list_24-6>li:before{content:»» counter(lst-ctn-kix_list_24-6,decimal) «. «}#doc8779917 ol.lst-kix_list_14-1.start{counter-reset:lst-ctn-kix_list_14-1 0}#doc8779917 .lst-kix_list_23-6>li:before{content:»» counter(lst-ctn-kix_list_23-6,decimal) «. «}#doc8779917 .lst-kix_list_23-2>li:before{content:»» counter(lst-ctn-kix_list_23-2,lower-roman) «. «}#doc8779917 .lst-kix_list_23-0>li:before{content:»» counter(lst-ctn-kix_list_23-0,decimal) «) «}#doc8779917 .lst-kix_list_23-8>li:before{content:»» counter(lst-ctn-kix_list_23-8,lower-roman) «. «}#doc8779917 .lst-kix_list_3-6>li{counter-increment:lst-ctn-kix_list_3-6}#doc8779917 ol.lst-kix_list_44-0.start{counter-reset:lst-ctn-kix_list_44-0 0}#doc8779917 .lst-kix_list_24-0>li:before{content:»» counter(lst-ctn-kix_list_24-0,decimal) «) «}#doc8779917 .lst-kix_list_23-4>li:before{content:»» counter(lst-ctn-kix_list_23-4,lower-latin) «.
«}#doc8779917 .lst-kix_list_43-3>li:before{content:»» counter(lst-ctn-kix_list_43-3,decimal) «. «}#doc8779917 .lst-kix_list_22-2>li:before{content:»» counter(lst-ctn-kix_list_22-2,lower-roman) «. «}#doc8779917 .lst-kix_list_22-6>li:before{content:»» counter(lst-ctn-kix_list_22-6,decimal) «. «}#doc8779917 ol.lst-kix_list_31-2.start{counter-reset:lst-ctn-kix_list_31-2 0}#doc8779917 .lst-kix_list_43-7>li:before{content:»» counter(lst-ctn-kix_list_43-7,lower-latin) «. «}#doc8779917 .lst-kix_list_43-1>li:before{content:»» counter(lst-ctn-kix_list_43-1,lower-latin) «. «}#doc8779917 .lst-kix_list_22-0>li:before{content:»» counter(lst-ctn-kix_list_22-0,decimal) «) «}#doc8779917 .lst-kix_list_22-8>li:before{content:»» counter(lst-ctn-kix_list_22-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_9-7{list-style-type:none}#doc8779917 ol.lst-kix_list_22-5.start{counter-reset:lst-ctn-kix_list_22-5 0}#doc8779917 ol.lst-kix_list_9-8{list-style-type:none}#doc8779917 ol.lst-kix_list_9-3{list-style-type:none}#doc8779917 ol.
lst-kix_list_9-4{list-style-type:none}#doc8779917 .lst-kix_list_5-7>li{counter-increment:lst-ctn-kix_list_5-7}#doc8779917 ol.lst-kix_list_9-5{list-style-type:none}#doc8779917 ol.lst-kix_list_34-7.start{counter-reset:lst-ctn-kix_list_34-7 0}#doc8779917 ol.lst-kix_list_9-6{list-style-type:none}#doc8779917 ol.lst-kix_list_9-0{list-style-type:none}#doc8779917 .lst-kix_list_43-5>li:before{content:»» counter(lst-ctn-kix_list_43-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_9-1{list-style-type:none}#doc8779917 .lst-kix_list_22-4>li:before{content:»» counter(lst-ctn-kix_list_22-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_9-2{list-style-type:none}#doc8779917 ol.lst-kix_list_32-8.start{counter-reset:lst-ctn-kix_list_32-8 0}#doc8779917 ol.lst-kix_list_25-5.start{counter-reset:lst-ctn-kix_list_25-5 0}#doc8779917 .lst-kix_list_41-7>li:before{content:»» counter(lst-ctn-kix_list_41-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_24-4.start{counter-reset:lst-ctn-kix_list_24-4 0}#doc8779917 .lst-kix_list_6-4>li{counter-increment:lst-ctn-kix_list_6-4}#doc8779917 .
lst-kix_list_41-1>li:before{content:»» counter(lst-ctn-kix_list_41-1,lower-latin) «. «}#doc8779917 .lst-kix_list_40-7>li:before{content:»» counter(lst-ctn-kix_list_40-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_27-4.start{counter-reset:lst-ctn-kix_list_27-4 0}#doc8779917 ol.lst-kix_list_15-2.start{counter-reset:lst-ctn-kix_list_15-2 0}#doc8779917 .lst-kix_list_40-5>li:before{content:»» counter(lst-ctn-kix_list_40-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_42-1.start{counter-reset:lst-ctn-kix_list_42-1 0}#doc8779917 .lst-kix_list_41-5>li:before{content:»» counter(lst-ctn-kix_list_41-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_37-7.start{counter-reset:lst-ctn-kix_list_37-7 0}#doc8779917 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc8779917 .lst-kix_list_41-3>li:before{content:»» counter(lst-ctn-kix_list_41-3,decimal) «. «}#doc8779917 ol.lst-kix_list_29-8{list-style-type:none}#doc8779917 ol.lst-kix_list_29-7{list-style-type:none}#doc8779917 ol.lst-kix_list_29-4{list-style-type:none}#doc8779917 ol.
lst-kix_list_29-3{list-style-type:none}#doc8779917 ol.lst-kix_list_29-6{list-style-type:none}#doc8779917 ol.lst-kix_list_29-5{list-style-type:none}#doc8779917 ol.lst-kix_list_29-0{list-style-type:none}#doc8779917 ol.lst-kix_list_5-8.start{counter-reset:lst-ctn-kix_list_5-8 0}#doc8779917 ol.lst-kix_list_29-2{list-style-type:none}#doc8779917 ol.lst-kix_list_29-1{list-style-type:none}#doc8779917 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc8779917 .lst-kix_list_40-3>li:before{content:»» counter(lst-ctn-kix_list_40-3,decimal) «. «}#doc8779917 ol.lst-kix_list_12-2.start{counter-reset:lst-ctn-kix_list_12-2 0}#doc8779917 .lst-kix_list_40-1>li:before{content:»» counter(lst-ctn-kix_list_40-1,lower-latin) «. «}#doc8779917 .lst-kix_list_42-2>li{counter-increment:lst-ctn-kix_list_42-2}#doc8779917 ol.lst-kix_list_38-3.start{counter-reset:lst-ctn-kix_list_38-3 0}#doc8779917 .lst-kix_list_24-8>li{counter-increment:lst-ctn-kix_list_24-8}#doc8779917 ol.lst-kix_list_3-4.start{counter-reset:lst-ctn-kix_list_3-4 0}#doc8779917 ol.
lst-kix_list_19-0.start{counter-reset:lst-ctn-kix_list_19-0 0}#doc8779917 ol.lst-kix_list_34-6{list-style-type:none}#doc8779917 ol.lst-kix_list_34-5{list-style-type:none}#doc8779917 ol.lst-kix_list_34-8{list-style-type:none}#doc8779917 .lst-kix_list_7-1>li{counter-increment:lst-ctn-kix_list_7-1}#doc8779917 ol.lst-kix_list_34-7{list-style-type:none}#doc8779917 ol.lst-kix_list_34-2{list-style-type:none}#doc8779917 ol.lst-kix_list_34-1{list-style-type:none}#doc8779917 ol.lst-kix_list_34-4{list-style-type:none}#doc8779917 ol.lst-kix_list_34-3{list-style-type:none}#doc8779917 ol.lst-kix_list_34-0{list-style-type:none}#doc8779917 .lst-kix_list_21-8>li:before{content:»» counter(lst-ctn-kix_list_21-8,lower-roman) «. «}#doc8779917 .lst-kix_list_8-0>li{counter-increment:lst-ctn-kix_list_8-0}#doc8779917 ol.lst-kix_list_18-2.start{counter-reset:lst-ctn-kix_list_18-2 0}#doc8779917 .lst-kix_list_26-8>li:before{content:»» counter(lst-ctn-kix_list_26-8,lower-roman) «. «}#doc8779917 .lst-kix_list_21-0>li:before{content:»» counter(lst-ctn-kix_list_21-0,decimal) «) «}#doc8779917 .
lst-kix_list_13-1>li{counter-increment:lst-ctn-kix_list_13-1}#doc8779917 .lst-kix_list_26-4>li:before{content:»» counter(lst-ctn-kix_list_26-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_36-1.start{counter-reset:lst-ctn-kix_list_36-1 0}#doc8779917 .lst-kix_list_42-4>li{counter-increment:lst-ctn-kix_list_42-4}#doc8779917 .lst-kix_list_21-4>li:before{content:»» counter(lst-ctn-kix_list_21-4,lower-latin) «. «}#doc8779917 .lst-kix_list_26-0>li:before{content:»» counter(lst-ctn-kix_list_26-0,decimal) «) «}#doc8779917 .lst-kix_list_31-4>li{counter-increment:lst-ctn-kix_list_31-4}#doc8779917 ol.lst-kix_list_7-2.start{counter-reset:lst-ctn-kix_list_7-2 0}#doc8779917 .lst-kix_list_31-2>li{counter-increment:lst-ctn-kix_list_31-2}#doc8779917 ol.lst-kix_list_38-8.start{counter-reset:lst-ctn-kix_list_38-8 0}#doc8779917 ol.lst-kix_list_19-5.start{counter-reset:lst-ctn-kix_list_19-5 0}#doc8779917 ol.lst-kix_list_12-5{list-style-type:none}#doc8779917 ol.lst-kix_list_12-6{list-style-type:none}#doc8779917 ol.
lst-kix_list_12-7{list-style-type:none}#doc8779917 ol.lst-kix_list_12-8{list-style-type:none}#doc8779917 ol.lst-kix_list_12-1{list-style-type:none}#doc8779917 ol.lst-kix_list_12-2{list-style-type:none}#doc8779917 ol.lst-kix_list_12-3{list-style-type:none}#doc8779917 .lst-kix_list_35-8>li{counter-increment:lst-ctn-kix_list_35-8}#doc8779917 ol.lst-kix_list_12-4{list-style-type:none}#doc8779917 ol.lst-kix_list_39-6.start{counter-reset:lst-ctn-kix_list_39-6 0}#doc8779917 ol.lst-kix_list_45-6.start{counter-reset:lst-ctn-kix_list_45-6 0}#doc8779917 ol.lst-kix_list_26-3.start{counter-reset:lst-ctn-kix_list_26-3 0}#doc8779917 ol.lst-kix_list_12-0{list-style-type:none}#doc8779917 .lst-kix_list_25-0>li:before{content:»» counter(lst-ctn-kix_list_25-0,decimal) «) «}#doc8779917 .lst-kix_list_45-5>li:before{content:»» counter(lst-ctn-kix_list_45-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_10-8.start{counter-reset:lst-ctn-kix_list_10-8 0}#doc8779917 .lst-kix_list_39-0>li:before{content:»» counter(lst-ctn-kix_list_39-0,decimal) «.
«}#doc8779917 ol.lst-kix_list_40-7.start{counter-reset:lst-ctn-kix_list_40-7 0}#doc8779917 .lst-kix_list_37-0>li{counter-increment:lst-ctn-kix_list_37-0}#doc8779917 ol.lst-kix_list_21-4.start{counter-reset:lst-ctn-kix_list_21-4 0}#doc8779917 .lst-kix_list_44-1>li:before{content:»» counter(lst-ctn-kix_list_44-1,lower-latin) «. «}#doc8779917 .lst-kix_list_45-1>li:before{content:»» counter(lst-ctn-kix_list_45-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_20-6.start{counter-reset:lst-ctn-kix_list_20-6 0}#doc8779917 .lst-kix_list_13-8>li{counter-increment:lst-ctn-kix_list_13-8}#doc8779917 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc8779917 .lst-kix_list_44-5>li:before{content:»» counter(lst-ctn-kix_list_44-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_4-7.start{counter-reset:lst-ctn-kix_list_4-7 0}#doc8779917 ol.lst-kix_list_5-0{list-style-type:none}#doc8779917 ol.lst-kix_list_5-1{list-style-type:none}#doc8779917 .lst-kix_list_26-2>li{counter-increment:lst-ctn-kix_list_26-2}#doc8779917 ol.
lst-kix_list_5-2{list-style-type:none}#doc8779917 .lst-kix_list_40-8>li{counter-increment:lst-ctn-kix_list_40-8}#doc8779917 .lst-kix_list_20-2>li{counter-increment:lst-ctn-kix_list_20-2}#doc8779917 .lst-kix_list_27-4>li:before{content:»» counter(lst-ctn-kix_list_27-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-7.start{counter-reset:lst-ctn-kix_list_15-7 0}#doc8779917 .lst-kix_list_6-6>li{counter-increment:lst-ctn-kix_list_6-6}#doc8779917 .lst-kix_list_13-6>li{counter-increment:lst-ctn-kix_list_13-6}#doc8779917 ol.lst-kix_list_14-6.start{counter-reset:lst-ctn-kix_list_14-6 0}#doc8779917 .lst-kix_list_39-4>li:before{content:»» counter(lst-ctn-kix_list_39-4,lower-latin) «. «}#doc8779917 .lst-kix_list_39-8>li:before{content:»» counter(lst-ctn-kix_list_39-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_5-7{list-style-type:none}#doc8779917 ol.lst-kix_list_5-8{list-style-type:none}#doc8779917 ol.lst-kix_list_26-8.start{counter-reset:lst-ctn-kix_list_26-8 0}#doc8779917 .lst-kix_list_19-6>li{counter-increment:lst-ctn-kix_list_19-6}#doc8779917 ol.
lst-kix_list_5-3{list-style-type:none}#doc8779917 .lst-kix_list_8-7>li{counter-increment:lst-ctn-kix_list_8-7}#doc8779917 ol.lst-kix_list_5-4{list-style-type:none}#doc8779917 .lst-kix_list_27-0>li:before{content:»» counter(lst-ctn-kix_list_27-0,decimal) «) «}#doc8779917 ol.lst-kix_list_5-5{list-style-type:none}#doc8779917 ol.lst-kix_list_5-6{list-style-type:none}#doc8779917 .lst-kix_list_20-4>li{counter-increment:lst-ctn-kix_list_20-4}#doc8779917 ol.lst-kix_list_44-5.start{counter-reset:lst-ctn-kix_list_44-5 0}#doc8779917 ol.lst-kix_list_33-6.start{counter-reset:lst-ctn-kix_list_33-6 0}#doc8779917 ol.lst-kix_list_20-1.start{counter-reset:lst-ctn-kix_list_20-1 0}#doc8779917 .lst-kix_list_25-4>li:before{content:»» counter(lst-ctn-kix_list_25-4,lower-latin) «. «}#doc8779917 .lst-kix_list_19-4>li{counter-increment:lst-ctn-kix_list_19-4}#doc8779917 .lst-kix_list_35-1>li{counter-increment:lst-ctn-kix_list_35-1}#doc8779917 .lst-kix_list_46-5>li:before{content:»» counter(lst-ctn-kix_list_46-5,lower-roman) «.
«}#doc8779917 .lst-kix_list_24-1>li{counter-increment:lst-ctn-kix_list_24-1}#doc8779917 .lst-kix_list_25-8>li:before{content:»» counter(lst-ctn-kix_list_25-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_26-6.start{counter-reset:lst-ctn-kix_list_26-6 0}#doc8779917 .lst-kix_list_44-5>li{counter-increment:lst-ctn-kix_list_44-5}#doc8779917 .lst-kix_list_37-2>li{counter-increment:lst-ctn-kix_list_37-2}#doc8779917 .lst-kix_list_15-2>li{counter-increment:lst-ctn-kix_list_15-2}#doc8779917 .lst-kix_list_22-5>li{counter-increment:lst-ctn-kix_list_22-5}#doc8779917 .lst-kix_list_28-8>li:before{content:»» counter(lst-ctn-kix_list_28-8,lower-roman) «. «}#doc8779917 .lst-kix_list_24-6>li{counter-increment:lst-ctn-kix_list_24-6}#doc8779917 .lst-kix_list_17-3>li{counter-increment:lst-ctn-kix_list_17-3}#doc8779917 .lst-kix_list_28-4>li:before{content:»» counter(lst-ctn-kix_list_28-4,lower-latin) «. «}#doc8779917 .lst-kix_list_46-6>li{counter-increment:lst-ctn-kix_list_46-6}#doc8779917 .lst-kix_list_39-3>li{counter-increment:lst-ctn-kix_list_39-3}#doc8779917 ol.
lst-kix_list_25-0.start{counter-reset:lst-ctn-kix_list_25-0 0}#doc8779917 ol.lst-kix_list_25-8{list-style-type:none}#doc8779917 .lst-kix_list_28-3>li{counter-increment:lst-ctn-kix_list_28-3}#doc8779917 ol.lst-kix_list_25-7{list-style-type:none}#doc8779917 .lst-kix_list_35-6>li{counter-increment:lst-ctn-kix_list_35-6}#doc8779917 ol.lst-kix_list_25-4{list-style-type:none}#doc8779917 ol.lst-kix_list_25-3{list-style-type:none}#doc8779917 ol.lst-kix_list_13-0.start{counter-reset:lst-ctn-kix_list_13-0 0}#doc8779917 ol.lst-kix_list_25-6{list-style-type:none}#doc8779917 ol.lst-kix_list_25-5{list-style-type:none}#doc8779917 ol.lst-kix_list_32-3.start{counter-reset:lst-ctn-kix_list_32-3 0}#doc8779917 ol.lst-kix_list_25-0{list-style-type:none}#doc8779917 ol.lst-kix_list_25-2{list-style-type:none}#doc8779917 ol.lst-kix_list_25-1{list-style-type:none}#doc8779917 ol.lst-kix_list_8-3.start{counter-reset:lst-ctn-kix_list_8-3 0}#doc8779917 .lst-kix_list_11-5>li{counter-increment:lst-ctn-kix_list_11-5}#doc8779917 .
lst-kix_list_28-0>li:before{content:»» counter(lst-ctn-kix_list_28-0,decimal) «) «}#doc8779917 .lst-kix_list_27-8>li:before{content:»» counter(lst-ctn-kix_list_27-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_20-3.start{counter-reset:lst-ctn-kix_list_20-3 0}#doc8779917 .lst-kix_list_4-1>li{counter-increment:lst-ctn-kix_list_4-1}#doc8779917 .lst-kix_list_19-1>li:before{content:»» counter(lst-ctn-kix_list_19-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_46-2.start{counter-reset:lst-ctn-kix_list_46-2 0}#doc8779917 .lst-kix_list_27-8>li{counter-increment:lst-ctn-kix_list_27-8}#doc8779917 .lst-kix_list_19-3>li:before{content:»» counter(lst-ctn-kix_list_19-3,decimal) «. «}#doc8779917 ol.lst-kix_list_38-0.start{counter-reset:lst-ctn-kix_list_38-0 11}#doc8779917 .lst-kix_list_15-0>li{counter-increment:lst-ctn-kix_list_15-0}#doc8779917 ol.lst-kix_list_6-6.start{counter-reset:lst-ctn-kix_list_6-6 0}#doc8779917 .lst-kix_list_39-5>li{counter-increment:lst-ctn-kix_list_39-5}#doc8779917 .lst-kix_list_32-6>li{counter-increment:lst-ctn-kix_list_32-6}#doc8779917 ol.
lst-kix_list_29-6.start{counter-reset:lst-ctn-kix_list_29-6 0}#doc8779917 .lst-kix_list_11-0>li{counter-increment:lst-ctn-kix_list_11-0}#doc8779917 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc8779917 ol.lst-kix_list_9-6.start{counter-reset:lst-ctn-kix_list_9-6 0}#doc8779917 ol.lst-kix_list_16-3.start{counter-reset:lst-ctn-kix_list_16-3 0}#doc8779917 .lst-kix_list_22-7>li{counter-increment:lst-ctn-kix_list_22-7}#doc8779917 ol.lst-kix_list_4-5.start{counter-reset:lst-ctn-kix_list_4-5 0}#doc8779917 .lst-kix_list_37-0>li:before{content:»» counter(lst-ctn-kix_list_37-0,decimal) «. «}#doc8779917 .lst-kix_list_26-7>li{counter-increment:lst-ctn-kix_list_26-7}#doc8779917 .lst-kix_list_41-0>li{counter-increment:lst-ctn-kix_list_41-0}#doc8779917 .lst-kix_list_33-7>li{counter-increment:lst-ctn-kix_list_33-7}#doc8779917 .lst-kix_list_5-2>li{counter-increment:lst-ctn-kix_list_5-2}#doc8779917 .lst-kix_list_37-7>li{counter-increment:lst-ctn-kix_list_37-7}#doc8779917 .lst-kix_list_37-8>li:before{content:»» counter(lst-ctn-kix_list_37-8,lower-roman) «.
«}#doc8779917 .lst-kix_list_37-6>li:before{content:»» counter(lst-ctn-kix_list_37-6,decimal) «. «}#doc8779917 .lst-kix_list_28-5>li{counter-increment:lst-ctn-kix_list_28-5}#doc8779917 ol.lst-kix_list_35-0.start{counter-reset:lst-ctn-kix_list_35-0 4}#doc8779917 .lst-kix_list_22-0>li{counter-increment:lst-ctn-kix_list_22-0}#doc8779917 .lst-kix_list_46-1>li:before{content:»» counter(lst-ctn-kix_list_46-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_33-4.start{counter-reset:lst-ctn-kix_list_33-4 0}#doc8779917 .lst-kix_list_21-6>li{counter-increment:lst-ctn-kix_list_21-6}#doc8779917 .lst-kix_list_10-3>li{counter-increment:lst-ctn-kix_list_10-3}#doc8779917 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc8779917 ol.lst-kix_list_13-3.start{counter-reset:lst-ctn-kix_list_13-3 0}#doc8779917 .lst-kix_list_26-0>li{counter-increment:lst-ctn-kix_list_26-0}#doc8779917 ol.lst-kix_list_42-8{list-style-type:none}#doc8779917 ol.lst-kix_list_4-0.start{counter-reset:lst-ctn-kix_list_4-0 0}#doc8779917 ol.
lst-kix_list_42-6{list-style-type:none}#doc8779917 ol.lst-kix_list_42-7{list-style-type:none}#doc8779917 ol.lst-kix_list_42-4{list-style-type:none}#doc8779917 ol.lst-kix_list_42-5{list-style-type:none}#doc8779917 .lst-kix_list_27-4>li{counter-increment:lst-ctn-kix_list_27-4}#doc8779917 ol.lst-kix_list_42-2{list-style-type:none}#doc8779917 ol.lst-kix_list_42-3{list-style-type:none}#doc8779917 ol.lst-kix_list_42-0{list-style-type:none}#doc8779917 ol.lst-kix_list_42-1{list-style-type:none}#doc8779917 .lst-kix_list_38-2>li:before{content:»» counter(lst-ctn-kix_list_38-2,lower-roman) «. «}#doc8779917 .lst-kix_list_38-4>li:before{content:»» counter(lst-ctn-kix_list_38-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_43-2.start{counter-reset:lst-ctn-kix_list_43-2 0}#doc8779917 .lst-kix_list_16-1>li{counter-increment:lst-ctn-kix_list_16-1}#doc8779917 .lst-kix_list_27-1>li{counter-increment:lst-ctn-kix_list_27-1}#doc8779917 .lst-kix_list_38-4>li{counter-increment:lst-ctn-kix_list_38-4}#doc8779917 ol.
lst-kix_list_43-4.start{counter-reset:lst-ctn-kix_list_43-4 0}#doc8779917 .lst-kix_list_17-5>li{counter-increment:lst-ctn-kix_list_17-5}#doc8779917 ol.lst-kix_list_9-4.start{counter-reset:lst-ctn-kix_list_9-4 0}#doc8779917 ol.lst-kix_list_41-8.start{counter-reset:lst-ctn-kix_list_41-8 0}#doc8779917 .lst-kix_list_21-3>li{counter-increment:lst-ctn-kix_list_21-3}#doc8779917 ol.lst-kix_list_30-1.start{counter-reset:lst-ctn-kix_list_30-1 0}#doc8779917 .lst-kix_list_7-8>li{counter-increment:lst-ctn-kix_list_7-8}#doc8779917 .lst-kix_list_36-4>li:before{content:»» counter(lst-ctn-kix_list_36-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_13-5.start{counter-reset:lst-ctn-kix_list_13-5 0}#doc8779917 ol.lst-kix_list_20-8{list-style-type:none}#doc8779917 ol.lst-kix_list_13-8.start{counter-reset:lst-ctn-kix_list_13-8 0}#doc8779917 ol.lst-kix_list_20-5{list-style-type:none}#doc8779917 ol.lst-kix_list_20-4{list-style-type:none}#doc8779917 ol.lst-kix_list_20-7{list-style-type:none}#doc8779917 .lst-kix_list_11-7>li{counter-increment:lst-ctn-kix_list_11-7}#doc8779917 ol.
lst-kix_list_20-6{list-style-type:none}#doc8779917 ol.lst-kix_list_20-1{list-style-type:none}#doc8779917 ol.lst-kix_list_20-0{list-style-type:none}#doc8779917 ol.lst-kix_list_20-3{list-style-type:none}#doc8779917 ol.lst-kix_list_20-2{list-style-type:none}#doc8779917 .lst-kix_list_5-5>li{counter-increment:lst-ctn-kix_list_5-5}#doc8779917 .lst-kix_list_36-2>li:before{content:»» counter(lst-ctn-kix_list_36-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_43-7.start{counter-reset:lst-ctn-kix_list_43-7 0}#doc8779917 .lst-kix_list_44-7>li{counter-increment:lst-ctn-kix_list_44-7}#doc8779917 .lst-kix_list_16-8>li{counter-increment:lst-ctn-kix_list_16-8}#doc8779917 ol.lst-kix_list_33-7{list-style-type:none}#doc8779917 ol.lst-kix_list_33-6{list-style-type:none}#doc8779917 ol.lst-kix_list_33-8{list-style-type:none}#doc8779917 ol.lst-kix_list_33-3{list-style-type:none}#doc8779917 ol.lst-kix_list_33-2{list-style-type:none}#doc8779917 ol.lst-kix_list_33-5{list-style-type:none}#doc8779917 ol.lst-kix_list_33-4{list-style-type:none}#doc8779917 ol.
lst-kix_list_46-7.start{counter-reset:lst-ctn-kix_list_46-7 0}#doc8779917 .lst-kix_list_38-8>li{counter-increment:lst-ctn-kix_list_38-8}#doc8779917 ol.lst-kix_list_18-4.start{counter-reset:lst-ctn-kix_list_18-4 0}#doc8779917 ol.lst-kix_list_33-1{list-style-type:none}#doc8779917 ol.lst-kix_list_33-0{list-style-type:none}#doc8779917 ol.lst-kix_list_29-1.start{counter-reset:lst-ctn-kix_list_29-1 0}#doc8779917 .lst-kix_list_20-4>li:before{content:»» counter(lst-ctn-kix_list_20-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc8779917 ol.lst-kix_list_22-7.start{counter-reset:lst-ctn-kix_list_22-7 0}#doc8779917 .lst-kix_list_20-2>li:before{content:»» counter(lst-ctn-kix_list_20-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_6-1.start{counter-reset:lst-ctn-kix_list_6-1 0}#doc8779917 ol.lst-kix_list_16-8.start{counter-reset:lst-ctn-kix_list_16-8 0}#doc8779917 ol.lst-kix_list_33-1.start{counter-reset:lst-ctn-kix_list_33-1 0}#doc8779917 .lst-kix_list_4-8>li{counter-increment:lst-ctn-kix_list_4-8}#doc8779917 ol.
lst-kix_list_24-2.start{counter-reset:lst-ctn-kix_list_24-2 0}#doc8779917 ol.lst-kix_list_9-1.start{counter-reset:lst-ctn-kix_list_9-1 0}#doc8779917 .lst-kix_list_19-8>li{counter-increment:lst-ctn-kix_list_19-8}#doc8779917 .lst-kix_list_35-6>li:before{content:»» counter(lst-ctn-kix_list_35-6,decimal) «. «}#doc8779917 .lst-kix_list_36-5>li{counter-increment:lst-ctn-kix_list_36-5}#doc8779917 .lst-kix_list_3-2>li:before{content:»» counter(lst-ctn-kix_list_3-2,lower-roman) «. «}#doc8779917 .lst-kix_list_8-1>li:before{content:»» counter(lst-ctn-kix_list_8-1,lower-latin) «. «}#doc8779917 .lst-kix_list_18-0>li{counter-increment:lst-ctn-kix_list_18-0}#doc8779917 .lst-kix_list_30-7>li:before{content:»» counter(lst-ctn-kix_list_30-7,lower-latin) «. «}#doc8779917 .lst-kix_list_43-3>li{counter-increment:lst-ctn-kix_list_43-3}#doc8779917 .lst-kix_list_26-2>li:before{content:»» counter(lst-ctn-kix_list_26-2,lower-roman) «. «}#doc8779917 .lst-kix_list_21-6>li:before{content:»» counter(lst-ctn-kix_list_21-6,decimal) «.
«}#doc8779917 .lst-kix_list_41-3>li{counter-increment:lst-ctn-kix_list_41-3}#doc8779917 ol.lst-kix_list_35-3.start{counter-reset:lst-ctn-kix_list_35-3 0}#doc8779917 ol.lst-kix_list_16-0.start{counter-reset:lst-ctn-kix_list_16-0 0}#doc8779917 ol.lst-kix_list_4-2.start{counter-reset:lst-ctn-kix_list_4-2 0}#doc8779917 ol.lst-kix_list_27-2.start{counter-reset:lst-ctn-kix_list_27-2 0}#doc8779917 ol.lst-kix_list_18-7.start{counter-reset:lst-ctn-kix_list_18-7 0}#doc8779917 .lst-kix_list_25-5>li{counter-increment:lst-ctn-kix_list_25-5}#doc8779917 ol.lst-kix_list_11-6.start{counter-reset:lst-ctn-kix_list_11-6 0}#doc8779917 ol.lst-kix_list_6-4.start{counter-reset:lst-ctn-kix_list_6-4 0}#doc8779917 .lst-kix_list_17-1>li:before{content:»» counter(lst-ctn-kix_list_17-1,lower-latin) «. «}#doc8779917 .lst-kix_list_45-3>li:before{content:»» counter(lst-ctn-kix_list_45-3,decimal) «. «}#doc8779917 .lst-kix_list_32-3>li{counter-increment:lst-ctn-kix_list_32-3}#doc8779917 ol.lst-kix_list_27-1.start{counter-reset:lst-ctn-kix_list_27-1 0}#doc8779917 ol.
lst-kix_list_46-4.start{counter-reset:lst-ctn-kix_list_46-4 0}#doc8779917 .lst-kix_list_16-5>li:before{content:»» counter(lst-ctn-kix_list_16-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_22-2.start{counter-reset:lst-ctn-kix_list_22-2 0}#doc8779917 .lst-kix_list_30-7>li{counter-increment:lst-ctn-kix_list_30-7}#doc8779917 ol.lst-kix_list_41-5.start{counter-reset:lst-ctn-kix_list_41-5 0}#doc8779917 .lst-kix_list_44-7>li:before{content:»» counter(lst-ctn-kix_list_44-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_29-3.start{counter-reset:lst-ctn-kix_list_29-3 0}#doc8779917 .lst-kix_list_16-4>li{counter-increment:lst-ctn-kix_list_16-4}#doc8779917 ol.lst-kix_list_35-8.start{counter-reset:lst-ctn-kix_list_35-8 0}#doc8779917 .lst-kix_list_38-1>li{counter-increment:lst-ctn-kix_list_38-1}#doc8779917 ol.lst-kix_list_16-5.start{counter-reset:lst-ctn-kix_list_16-5 0}#doc8779917 .lst-kix_list_41-7>li{counter-increment:lst-ctn-kix_list_41-7}#doc8779917 ol.lst-kix_list_35-5.start{counter-reset:lst-ctn-kix_list_35-5 0}#doc8779917 .
lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc8779917 .lst-kix_list_14-5>li{counter-increment:lst-ctn-kix_list_14-5}#doc8779917 .lst-kix_list_7-5>li:before{content:»» counter(lst-ctn-kix_list_7-5,lower-roman) «. «}#doc8779917 .lst-kix_list_27-6>li:before{content:»» counter(lst-ctn-kix_list_27-6,decimal) «. «}#doc8779917 .lst-kix_list_23-2>li{counter-increment:lst-ctn-kix_list_23-2}#doc8779917 ol.lst-kix_list_30-4.start{counter-reset:lst-ctn-kix_list_30-4 0}#doc8779917 ol.lst-kix_list_11-1.start{counter-reset:lst-ctn-kix_list_11-1 0}#doc8779917 .lst-kix_list_30-0>li{counter-increment:lst-ctn-kix_list_30-0}#doc8779917 .lst-kix_list_18-5>li:before{content:»» counter(lst-ctn-kix_list_18-5,lower-roman) «. «}#doc8779917 .lst-kix_list_13-6>li:before{content:»» counter(lst-ctn-kix_list_13-6,decimal) «. «}#doc8779917 .lst-kix_list_10-6>li{counter-increment:lst-ctn-kix_list_10-6}#doc8779917 .lst-kix_list_1-7>li{counter-increment:lst-ctn-kix_list_1-7}#doc8779917 ol.
lst-kix_list_41-0.start{counter-reset:lst-ctn-kix_list_41-0 0}#doc8779917 .lst-kix_list_39-6>li:before{content:»» counter(lst-ctn-kix_list_39-6,decimal) «. «}#doc8779917 .lst-kix_list_7-5>li{counter-increment:lst-ctn-kix_list_7-5}#doc8779917 ol.lst-kix_list_24-7.start{counter-reset:lst-ctn-kix_list_24-7 0}#doc8779917 .lst-kix_list_29-0>li{counter-increment:lst-ctn-kix_list_29-0}#doc8779917 .lst-kix_list_31-3>li:before{content:»» counter(lst-ctn-kix_list_31-3,decimal) «. «}#doc8779917 .lst-kix_list_43-6>li{counter-increment:lst-ctn-kix_list_43-6}#doc8779917 .lst-kix_list_10-2>li:before{content:»» counter(lst-ctn-kix_list_10-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc8779917 .lst-kix_list_4-6>li:before{content:»» counter(lst-ctn-kix_list_4-6,decimal) «. «}#doc8779917 ol.lst-kix_list_29-8.start{counter-reset:lst-ctn-kix_list_29-8 0}#doc8779917 .lst-kix_list_25-6>li:before{content:»» counter(lst-ctn-kix_list_25-6,decimal) «. «}#doc8779917 .
lst-kix_list_46-7>li:before{content:»» counter(lst-ctn-kix_list_46-7,lower-latin) «. «}#doc8779917 .lst-kix_list_34-2>li{counter-increment:lst-ctn-kix_list_34-2}#doc8779917 .lst-kix_list_12-2>li{counter-increment:lst-ctn-kix_list_12-2}#doc8779917 .lst-kix_list_9-5>li:before{content:»» counter(lst-ctn-kix_list_9-5,lower-roman) «. «}#doc8779917 .lst-kix_list_29-6>li:before{content:»» counter(lst-ctn-kix_list_29-6,decimal) «. «}#doc8779917 ol.lst-kix_list_22-0.start{counter-reset:lst-ctn-kix_list_22-0 0}#doc8779917 .lst-kix_list_12-2>li:before{content:»» counter(lst-ctn-kix_list_12-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_41-3.start{counter-reset:lst-ctn-kix_list_41-3 0}#doc8779917 .lst-kix_list_11-6>li:before{content:»» counter(lst-ctn-kix_list_11-6,decimal) «. «}#doc8779917 .lst-kix_list_32-7>li:before{content:»» counter(lst-ctn-kix_list_32-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_30-6.start{counter-reset:lst-ctn-kix_list_30-6 0}#doc8779917 ol.lst-kix_list_11-3.start{counter-reset:lst-ctn-kix_list_11-3 0}#doc8779917 .
lst-kix_list_1-2>li:before{content:»» counter(lst-ctn-kix_list_1-2,lower-roman) «. «}#doc8779917 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc8779917 ol.lst-kix_list_41-2.start{counter-reset:lst-ctn-kix_list_41-2 0}#doc8779917 .lst-kix_list_18-7>li{counter-increment:lst-ctn-kix_list_18-7}#doc8779917 .lst-kix_list_29-7>li{counter-increment:lst-ctn-kix_list_29-7}#doc8779917 ol.lst-kix_list_11-4.start{counter-reset:lst-ctn-kix_list_11-4 0}#doc8779917 .lst-kix_list_28-2>li:before{content:»» counter(lst-ctn-kix_list_28-2,lower-roman) «. «}#doc8779917 .lst-kix_list_14-1>li:before{content:»» counter(lst-ctn-kix_list_14-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-6{list-style-type:none}#doc8779917 .lst-kix_list_25-8>li{counter-increment:lst-ctn-kix_list_25-8}#doc8779917 ol.lst-kix_list_15-7{list-style-type:none}#doc8779917 ol.lst-kix_list_15-8{list-style-type:none}#doc8779917 .lst-kix_list_14-4>li:before{content:»» counter(lst-ctn-kix_list_14-4,lower-latin) «. «}#doc8779917 ol.
lst-kix_list_15-2{list-style-type:none}#doc8779917 ol.lst-kix_list_15-3{list-style-type:none}#doc8779917 ol.lst-kix_list_15-4{list-style-type:none}#doc8779917 .lst-kix_list_14-5>li:before{content:»» counter(lst-ctn-kix_list_14-5,lower-roman) «. «}#doc8779917 .lst-kix_list_14-7>li:before{content:»» counter(lst-ctn-kix_list_14-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-5{list-style-type:none}#doc8779917 ol.lst-kix_list_45-4.start{counter-reset:lst-ctn-kix_list_45-4 0}#doc8779917 .lst-kix_list_37-5>li{counter-increment:lst-ctn-kix_list_37-5}#doc8779917 ol.lst-kix_list_15-0{list-style-type:none}#doc8779917 ol.lst-kix_list_15-1{list-style-type:none}#doc8779917 .lst-kix_list_34-6>li{counter-increment:lst-ctn-kix_list_34-6}#doc8779917 ol.lst-kix_list_32-1.start{counter-reset:lst-ctn-kix_list_32-1 3}#doc8779917 .lst-kix_list_20-7>li{counter-increment:lst-ctn-kix_list_20-7}#doc8779917 ol.lst-kix_list_35-6.start{counter-reset:lst-ctn-kix_list_35-6 0}#doc8779917 ol.lst-kix_list_28-3.start{counter-reset:lst-ctn-kix_list_28-3 0}#doc8779917 .
lst-kix_list_44-1>li{counter-increment:lst-ctn-kix_list_44-1}#doc8779917 .lst-kix_list_32-3>li:before{content:»» counter(lst-ctn-kix_list_32-3,decimal) «. «}#doc8779917 .lst-kix_list_14-8>li:before{content:»» counter(lst-ctn-kix_list_14-8,lower-roman) «. «}#doc8779917 .lst-kix_list_39-7>li{counter-increment:lst-ctn-kix_list_39-7}#doc8779917 .lst-kix_list_32-0>li:before{content:»» counter(lst-ctn-kix_list_32-0,decimal) «) «}#doc8779917 .lst-kix_list_3-2>li{counter-increment:lst-ctn-kix_list_3-2}#doc8779917 ol.lst-kix_list_15-5.start{counter-reset:lst-ctn-kix_list_15-5 0}#doc8779917 ol.lst-kix_list_22-3.start{counter-reset:lst-ctn-kix_list_22-3 0}#doc8779917 .lst-kix_list_5-4>li{counter-increment:lst-ctn-kix_list_5-4}#doc8779917 ol.lst-kix_list_24-6.start{counter-reset:lst-ctn-kix_list_24-6 0}#doc8779917 .lst-kix_list_5-1>li:before{content:»» counter(lst-ctn-kix_list_5-1,lower-latin) «. «}#doc8779917 .lst-kix_list_5-7>li:before{content:»» counter(lst-ctn-kix_list_5-7,lower-latin) «. «}#doc8779917 .
lst-kix_list_5-8>li:before{content:»» counter(lst-ctn-kix_list_5-8,lower-roman) «. «}#doc8779917 .lst-kix_list_5-4>li:before{content:»» counter(lst-ctn-kix_list_5-4,lower-latin) «. «}#doc8779917 .lst-kix_list_5-5>li:before{content:»» counter(lst-ctn-kix_list_5-5,lower-roman) «. «}#doc8779917 .lst-kix_list_6-1>li:before{content:»» counter(lst-ctn-kix_list_6-1,lower-latin) «. «}#doc8779917 .lst-kix_list_6-3>li:before{content:»» counter(lst-ctn-kix_list_6-3,decimal) «. «}#doc8779917 ol.lst-kix_list_32-6.start{counter-reset:lst-ctn-kix_list_32-6 0}#doc8779917 .lst-kix_list_6-8>li{counter-increment:lst-ctn-kix_list_6-8}#doc8779917 .lst-kix_list_6-0>li:before{content:»» counter(lst-ctn-kix_list_6-0,decimal) «) «}#doc8779917 .lst-kix_list_6-4>li:before{content:»» counter(lst-ctn-kix_list_6-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_14-8.start{counter-reset:lst-ctn-kix_list_14-8 0}#doc8779917 ol.lst-kix_list_15-0.start{counter-reset:lst-ctn-kix_list_15-0 0}#doc8779917 ol.lst-kix_list_44-7.
start{counter-reset:lst-ctn-kix_list_44-7 0}#doc8779917 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc8779917 .lst-kix_list_6-7>li:before{content:»» counter(lst-ctn-kix_list_6-7,lower-latin) «. «}#doc8779917 .lst-kix_list_6-6>li:before{content:»» counter(lst-ctn-kix_list_6-6,decimal) «. «}#doc8779917 ol.lst-kix_list_10-6.start{counter-reset:lst-ctn-kix_list_10-6 0}#doc8779917 ol.lst-kix_list_27-6.start{counter-reset:lst-ctn-kix_list_27-6 0}#doc8779917 .lst-kix_list_7-6>li:before{content:»» counter(lst-ctn-kix_list_7-6,decimal) «. «}#doc8779917 .lst-kix_list_18-5>li{counter-increment:lst-ctn-kix_list_18-5}#doc8779917 ol.lst-kix_list_19-7.start{counter-reset:lst-ctn-kix_list_19-7 0}#doc8779917 .lst-kix_list_15-5>li{counter-increment:lst-ctn-kix_list_15-5}#doc8779917 ol.lst-kix_list_6-2.start{counter-reset:lst-ctn-kix_list_6-2 0}#doc8779917 ol.lst-kix_list_24-1.start{counter-reset:lst-ctn-kix_list_24-1 0}#doc8779917 ol.lst-kix_list_36-3.start{counter-reset:lst-ctn-kix_list_36-3 0}#doc8779917 .
lst-kix_list_7-2>li:before{content:»» counter(lst-ctn-kix_list_7-2,lower-roman) «. «}#doc8779917 .lst-kix_list_7-6>li{counter-increment:lst-ctn-kix_list_7-6}#doc8779917 .lst-kix_list_27-2>li{counter-increment:lst-ctn-kix_list_27-2}#doc8779917 ol.lst-kix_list_22-8.start{counter-reset:lst-ctn-kix_list_22-8 0}#doc8779917 .lst-kix_list_31-0>li{counter-increment:lst-ctn-kix_list_31-0}#doc8779917 .lst-kix_list_34-8>li:before{content:»» counter(lst-ctn-kix_list_34-8,lower-roman) «. «}#doc8779917 .lst-kix_list_31-0>li:before{content:»» counter(lst-ctn-kix_list_31-0,decimal) «) «}#doc8779917 .lst-kix_list_12-6>li{counter-increment:lst-ctn-kix_list_12-6}#doc8779917 ol.lst-kix_list_23-0.start{counter-reset:lst-ctn-kix_list_23-0 0}#doc8779917 ol.lst-kix_list_28-8{list-style-type:none}#doc8779917 .lst-kix_list_13-4>li{counter-increment:lst-ctn-kix_list_13-4}#doc8779917 .lst-kix_list_9-8>li{counter-increment:lst-ctn-kix_list_9-8}#doc8779917 ol.lst-kix_list_28-5{list-style-type:none}#doc8779917 ol.lst-kix_list_28-4{list-style-type:none}#doc8779917 ol.
lst-kix_list_28-7{list-style-type:none}#doc8779917 ol.lst-kix_list_28-6{list-style-type:none}#doc8779917 ol.lst-kix_list_28-1{list-style-type:none}#doc8779917 ol.lst-kix_list_28-0{list-style-type:none}#doc8779917 .lst-kix_list_31-4>li:before{content:»» counter(lst-ctn-kix_list_31-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_28-3{list-style-type:none}#doc8779917 ol.lst-kix_list_28-2{list-style-type:none}#doc8779917 .lst-kix_list_15-7>li:before{content:»» counter(lst-ctn-kix_list_15-7,lower-latin) «. «}#doc8779917 .lst-kix_list_17-7>li{counter-increment:lst-ctn-kix_list_17-7}#doc8779917 .lst-kix_list_4-5>li:before{content:»» counter(lst-ctn-kix_list_4-5,lower-roman) «. «}#doc8779917 .lst-kix_list_15-1>li:before{content:»» counter(lst-ctn-kix_list_15-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc8779917 .lst-kix_list_15-3>li:before{content:»» counter(lst-ctn-kix_list_15-3,decimal) «. «}#doc8779917 .lst-kix_list_22-1>li{counter-increment:lst-ctn-kix_list_22-1}#doc8779917 .
lst-kix_list_42-7>li{counter-increment:lst-ctn-kix_list_42-7}#doc8779917 ol.lst-kix_list_4-4.start{counter-reset:lst-ctn-kix_list_4-4 0}#doc8779917 .lst-kix_list_33-2>li{counter-increment:lst-ctn-kix_list_33-2}#doc8779917 .lst-kix_list_40-5>li{counter-increment:lst-ctn-kix_list_40-5}#doc8779917 .lst-kix_list_30-2>li{counter-increment:lst-ctn-kix_list_30-2}#doc8779917 ol.lst-kix_list_9-2.start{counter-reset:lst-ctn-kix_list_9-2 0}#doc8779917 .lst-kix_list_11-2>li{counter-increment:lst-ctn-kix_list_11-2}#doc8779917 .lst-kix_list_33-8>li{counter-increment:lst-ctn-kix_list_33-8}#doc8779917 .lst-kix_list_12-3>li:before{content:»» counter(lst-ctn-kix_list_12-3,decimal) «. «}#doc8779917 ol.lst-kix_list_8-8{list-style-type:none}#doc8779917 ol.lst-kix_list_31-4.start{counter-reset:lst-ctn-kix_list_31-4 0}#doc8779917 .lst-kix_list_32-6>li:before{content:»» counter(lst-ctn-kix_list_32-6,decimal) «. «}#doc8779917 ol.lst-kix_list_8-4{list-style-type:none}#doc8779917 ol.lst-kix_list_8-5{list-style-type:none}#doc8779917 .
lst-kix_list_33-2>li:before{content:»» counter(lst-ctn-kix_list_33-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_8-6{list-style-type:none}#doc8779917 ol.lst-kix_list_8-7{list-style-type:none}#doc8779917 .lst-kix_list_16-3>li{counter-increment:lst-ctn-kix_list_16-3}#doc8779917 ol.lst-kix_list_8-0{list-style-type:none}#doc8779917 ol.lst-kix_list_8-1{list-style-type:none}#doc8779917 .lst-kix_list_13-3>li{counter-increment:lst-ctn-kix_list_13-3}#doc8779917 ol.lst-kix_list_8-2{list-style-type:none}#doc8779917 ol.lst-kix_list_8-3{list-style-type:none}#doc8779917 ol.lst-kix_list_40-5.start{counter-reset:lst-ctn-kix_list_40-5 0}#doc8779917 .lst-kix_list_10-4>li{counter-increment:lst-ctn-kix_list_10-4}#doc8779917 .lst-kix_list_14-1>li{counter-increment:lst-ctn-kix_list_14-1}#doc8779917 .lst-kix_list_34-4>li:before{content:»» counter(lst-ctn-kix_list_34-4,lower-latin) «. «}#doc8779917 .lst-kix_list_35-3>li{counter-increment:lst-ctn-kix_list_35-3}#doc8779917 .lst-kix_list_28-0>li{counter-increment:lst-ctn-kix_list_28-0}#doc8779917 .
lst-kix_list_13-5>li:before{content:»» counter(lst-ctn-kix_list_13-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_28-8.start{counter-reset:lst-ctn-kix_list_28-8 0}#doc8779917 .lst-kix_list_36-1>li{counter-increment:lst-ctn-kix_list_36-1}#doc8779917 .lst-kix_list_36-7>li{counter-increment:lst-ctn-kix_list_36-7}#doc8779917 .lst-kix_list_29-4>li{counter-increment:lst-ctn-kix_list_29-4}#doc8779917 .lst-kix_list_33-6>li:before{content:»» counter(lst-ctn-kix_list_33-6,decimal) «. «}#doc8779917 .lst-kix_list_32-4>li{counter-increment:lst-ctn-kix_list_32-4}#doc8779917 .lst-kix_list_33-8>li:before{content:»» counter(lst-ctn-kix_list_33-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_29-0.start{counter-reset:lst-ctn-kix_list_29-0 0}#doc8779917 .lst-kix_list_34-2>li:before{content:»» counter(lst-ctn-kix_list_34-2,lower-roman) «. «}#doc8779917 .lst-kix_list_34-5>li{counter-increment:lst-ctn-kix_list_34-5}#doc8779917 .lst-kix_list_30-5>li:before{content:»» counter(lst-ctn-kix_list_30-5,lower-roman) «.
«}#doc8779917 .lst-kix_list_35-0>li:before{content:»» counter(lst-ctn-kix_list_35-0,decimal) «. «}#doc8779917 .lst-kix_list_35-1>li:before{content:»» counter(lst-ctn-kix_list_35-1,lower-latin) «. «}#doc8779917 .lst-kix_list_35-4>li:before{content:»» counter(lst-ctn-kix_list_35-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_40-6.start{counter-reset:lst-ctn-kix_list_40-6 0}#doc8779917 ol.lst-kix_list_11-6{list-style-type:none}#doc8779917 ol.lst-kix_list_11-7{list-style-type:none}#doc8779917 .lst-kix_list_28-8>li{counter-increment:lst-ctn-kix_list_28-8}#doc8779917 ol.lst-kix_list_11-8{list-style-type:none}#doc8779917 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc8779917 .lst-kix_list_30-1>li:before{content:»» counter(lst-ctn-kix_list_30-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_11-2{list-style-type:none}#doc8779917 ol.lst-kix_list_11-3{list-style-type:none}#doc8779917 .lst-kix_list_3-0>li:before{content:»» counter(lst-ctn-kix_list_3-0,decimal) «) «}#doc8779917 ol.
lst-kix_list_11-4{list-style-type:none}#doc8779917 ol.lst-kix_list_11-5{list-style-type:none}#doc8779917 .lst-kix_list_30-2>li:before{content:»» counter(lst-ctn-kix_list_30-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_11-0{list-style-type:none}#doc8779917 ol.lst-kix_list_11-1{list-style-type:none}#doc8779917 .lst-kix_list_4-0>li{counter-increment:lst-ctn-kix_list_4-0}#doc8779917 .lst-kix_list_31-6>li{counter-increment:lst-ctn-kix_list_31-6}#doc8779917 ol.lst-kix_list_37-5.start{counter-reset:lst-ctn-kix_list_37-5 0}#doc8779917 .lst-kix_list_3-3>li:before{content:»» counter(lst-ctn-kix_list_3-3,decimal) «. «}#doc8779917 .lst-kix_list_38-3>li{counter-increment:lst-ctn-kix_list_38-3}#doc8779917 ol.lst-kix_list_10-7.start{counter-reset:lst-ctn-kix_list_10-7 0}#doc8779917 .lst-kix_list_17-1>li{counter-increment:lst-ctn-kix_list_17-1}#doc8779917 .lst-kix_list_11-1>li:before{content:»» counter(lst-ctn-kix_list_11-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_31-0.start{counter-reset:lst-ctn-kix_list_31-0 0}#doc8779917 .
lst-kix_list_11-0>li:before{content:»» counter(lst-ctn-kix_list_11-0,decimal) «) «}#doc8779917 ol.lst-kix_list_9-3.start{counter-reset:lst-ctn-kix_list_9-3 0}#doc8779917 .lst-kix_list_8-8>li:before{content:»» counter(lst-ctn-kix_list_8-8,lower-roman) «. «}#doc8779917 .lst-kix_list_35-4>li{counter-increment:lst-ctn-kix_list_35-4}#doc8779917 .lst-kix_list_43-5>li{counter-increment:lst-ctn-kix_list_43-5}#doc8779917 .lst-kix_list_4-8>li:before{content:»» counter(lst-ctn-kix_list_4-8,lower-roman) «. «}#doc8779917 .lst-kix_list_21-5>li{counter-increment:lst-ctn-kix_list_21-5}#doc8779917 .lst-kix_list_14-2>li{counter-increment:lst-ctn-kix_list_14-2}#doc8779917 .lst-kix_list_16-0>li:before{content:»» counter(lst-ctn-kix_list_16-0,decimal) «) «}#doc8779917 .lst-kix_list_40-6>li{counter-increment:lst-ctn-kix_list_40-6}#doc8779917 ol.lst-kix_list_4-8.start{counter-reset:lst-ctn-kix_list_4-8 0}#doc8779917 .lst-kix_list_8-4>li{counter-increment:lst-ctn-kix_list_8-4}#doc8779917 .lst-kix_list_16-3>li:before{content:»» counter(lst-ctn-kix_list_16-3,decimal) «.
«}#doc8779917 ol.lst-kix_list_46-8{list-style-type:none}#doc8779917 ol.lst-kix_list_37-4.start{counter-reset:lst-ctn-kix_list_37-4 0}#doc8779917 .lst-kix_list_41-1>li{counter-increment:lst-ctn-kix_list_41-1}#doc8779917 ol.lst-kix_list_46-6{list-style-type:none}#doc8779917 .lst-kix_list_44-0>li{counter-increment:lst-ctn-kix_list_44-0}#doc8779917 ol.lst-kix_list_46-7{list-style-type:none}#doc8779917 ol.lst-kix_list_46-4{list-style-type:none}#doc8779917 ol.lst-kix_list_46-5{list-style-type:none}#doc8779917 ol.lst-kix_list_46-2{list-style-type:none}#doc8779917 .lst-kix_list_17-8>li:before{content:»» counter(lst-ctn-kix_list_17-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_46-3{list-style-type:none}#doc8779917 ol.lst-kix_list_46-0{list-style-type:none}#doc8779917 ol.lst-kix_list_46-1{list-style-type:none}#doc8779917 .lst-kix_list_7-0>li:before{content:»» counter(lst-ctn-kix_list_7-0,decimal) «) «}#doc8779917 ol.lst-kix_list_27-7.start{counter-reset:lst-ctn-kix_list_27-7 0}#doc8779917 ol.lst-kix_list_19-6.
start{counter-reset:lst-ctn-kix_list_19-6 0}#doc8779917 ol.lst-kix_list_9-7.start{counter-reset:lst-ctn-kix_list_9-7 0}#doc8779917 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc8779917 .lst-kix_list_7-3>li:before{content:»» counter(lst-ctn-kix_list_7-3,decimal) «. «}#doc8779917 .lst-kix_list_9-7>li{counter-increment:lst-ctn-kix_list_9-7}#doc8779917 .lst-kix_list_13-8>li:before{content:»» counter(lst-ctn-kix_list_13-8,lower-roman) «. «}#doc8779917 .lst-kix_list_31-1>li:before{content:»» counter(lst-ctn-kix_list_31-1,lower-latin) «. «}#doc8779917 .lst-kix_list_18-7>li:before{content:»» counter(lst-ctn-kix_list_18-7,lower-latin) «. «}#doc8779917 .lst-kix_list_15-4>li:before{content:»» counter(lst-ctn-kix_list_15-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_19-1.start{counter-reset:lst-ctn-kix_list_19-1 0}#doc8779917 ol.lst-kix_list_24-8{list-style-type:none}#doc8779917 .lst-kix_list_10-4>li:before{content:»» counter(lst-ctn-kix_list_10-4,lower-latin) «.
«}#doc8779917 .lst-kix_list_10-8>li:before{content:»» counter(lst-ctn-kix_list_10-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_24-5{list-style-type:none}#doc8779917 ol.lst-kix_list_24-4{list-style-type:none}#doc8779917 ol.lst-kix_list_24-7{list-style-type:none}#doc8779917 .lst-kix_list_15-0>li:before{content:»» counter(lst-ctn-kix_list_15-0,decimal) «) «}#doc8779917 ol.lst-kix_list_24-6{list-style-type:none}#doc8779917 ol.lst-kix_list_24-1{list-style-type:none}#doc8779917 ol.lst-kix_list_14-3.start{counter-reset:lst-ctn-kix_list_14-3 0}#doc8779917 ol.lst-kix_list_24-0{list-style-type:none}#doc8779917 ol.lst-kix_list_24-3{list-style-type:none}#doc8779917 ol.lst-kix_list_24-2{list-style-type:none}#doc8779917 ol.lst-kix_list_44-2.start{counter-reset:lst-ctn-kix_list_44-2 0}#doc8779917 ol.lst-kix_list_32-5.start{counter-reset:lst-ctn-kix_list_32-5 0}#doc8779917 .lst-kix_list_12-8>li{counter-increment:lst-ctn-kix_list_12-8}#doc8779917 ol.lst-kix_list_4-0{list-style-type:none}#doc8779917 ol.
lst-kix_list_4-1{list-style-type:none}#doc8779917 ol.lst-kix_list_4-2{list-style-type:none}#doc8779917 ol.lst-kix_list_4-3{list-style-type:none}#doc8779917 ol.lst-kix_list_37-7{list-style-type:none}#doc8779917 ol.lst-kix_list_14-4.start{counter-reset:lst-ctn-kix_list_14-4 0}#doc8779917 ol.lst-kix_list_37-6{list-style-type:none}#doc8779917 .lst-kix_list_9-7>li:before{content:»» counter(lst-ctn-kix_list_9-7,lower-latin) «. «}#doc8779917 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc8779917 .lst-kix_list_29-4>li:before{content:»» counter(lst-ctn-kix_list_29-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_37-8{list-style-type:none}#doc8779917 ol.lst-kix_list_37-3{list-style-type:none}#doc8779917 ol.lst-kix_list_37-2{list-style-type:none}#doc8779917 ol.lst-kix_list_32-2.start{counter-reset:lst-ctn-kix_list_32-2 0}#doc8779917 ol.lst-kix_list_37-5{list-style-type:none}#doc8779917 ol.lst-kix_list_37-4{list-style-type:none}#doc8779917 .lst-kix_list_11-4>li:before{content:»» counter(lst-ctn-kix_list_11-4,lower-latin) «.
«}#doc8779917 ol.lst-kix_list_37-1{list-style-type:none}#doc8779917 ol.lst-kix_list_37-0{list-style-type:none}#doc8779917 ol.lst-kix_list_37-0.start{counter-reset:lst-ctn-kix_list_37-0 3}#doc8779917 .lst-kix_list_29-0>li:before{content:»» counter(lst-ctn-kix_list_29-0,decimal) «) «}#doc8779917 ol.lst-kix_list_4-8{list-style-type:none}#doc8779917 ol.lst-kix_list_19-2.start{counter-reset:lst-ctn-kix_list_19-2 0}#doc8779917 ol.lst-kix_list_4-4{list-style-type:none}#doc8779917 ol.lst-kix_list_4-5{list-style-type:none}#doc8779917 .lst-kix_list_12-0>li:before{content:»» counter(lst-ctn-kix_list_12-0,decimal) «) «}#doc8779917 ol.lst-kix_list_4-6{list-style-type:none}#doc8779917 ol.lst-kix_list_4-7{list-style-type:none}#doc8779917 .lst-kix_list_1-4>li:before{content:»» counter(lst-ctn-kix_list_1-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_44-3.start{counter-reset:lst-ctn-kix_list_44-3 0}#doc8779917 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc8779917 .lst-kix_list_34-5>li:before{content:»» counter(lst-ctn-kix_list_34-5,lower-roman) «.
«}#doc8779917 ol.lst-kix_list_45-8.start{counter-reset:lst-ctn-kix_list_45-8 0}#doc8779917 ol.lst-kix_list_19-3.start{counter-reset:lst-ctn-kix_list_19-3 0}#doc8779917 .lst-kix_list_33-5>li:before{content:»» counter(lst-ctn-kix_list_33-5,lower-roman) «. «}#doc8779917 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «) «}#doc8779917 ol.lst-kix_list_9-8.start{counter-reset:lst-ctn-kix_list_9-8 0}#doc8779917 .lst-kix_list_1-8>li:before{content:»» counter(lst-ctn-kix_list_1-8,lower-roman) «. «}#doc8779917 .lst-kix_list_34-1>li:before{content:»» counter(lst-ctn-kix_list_34-1,lower-latin) «. «}#doc8779917 .lst-kix_list_19-0>li:before{content:»» counter(lst-ctn-kix_list_19-0,decimal) «) «}#doc8779917 .lst-kix_list_8-1>li{counter-increment:lst-ctn-kix_list_8-1}#doc8779917 .lst-kix_list_7-0>li{counter-increment:lst-ctn-kix_list_7-0}#doc8779917 .lst-kix_list_19-0>li{counter-increment:lst-ctn-kix_list_19-0}#doc8779917 ol.lst-kix_list_44-6.start{counter-reset:lst-ctn-kix_list_44-6 0}#doc8779917 .
lst-kix_list_29-6>li{counter-increment:lst-ctn-kix_list_29-6}#doc8779917 ol.lst-kix_list_31-3.start{counter-reset:lst-ctn-kix_list_31-3 0}#doc8779917 ol.lst-kix_list_19-8.start{counter-reset:lst-ctn-kix_list_19-8 0}#doc8779917 ol.lst-kix_list_41-7{list-style-type:none}#doc8779917 ol.lst-kix_list_41-8{list-style-type:none}#doc8779917 ol.lst-kix_list_36-4.start{counter-reset:lst-ctn-kix_list_36-4 0}#doc8779917 ol.lst-kix_list_41-5{list-style-type:none}#doc8779917 ol.lst-kix_list_41-6{list-style-type:none}#doc8779917 ol.lst-kix_list_41-3{list-style-type:none}#doc8779917 ol.lst-kix_list_41-4{list-style-type:none}#doc8779917 ol.lst-kix_list_14-7.start{counter-reset:lst-ctn-kix_list_14-7 0}#doc8779917 ol.lst-kix_list_41-1{list-style-type:none}#doc8779917 ol.lst-kix_list_41-2{list-style-type:none}#doc8779917 ol.lst-kix_list_41-0{list-style-type:none}#doc8779917 .lst-kix_list_19-7>li:before{content:»» counter(lst-ctn-kix_list_19-7,lower-latin) «. «}#doc8779917 .lst-kix_list_9-2>li{counter-increment:lst-ctn-kix_list_9-2}#doc8779917 ol.lst-kix_list_23-8.start{counter-reset:lst-ctn-kix_list_23-8 0}#doc8779917 .lst-kix_list_24-5>li{counter-increment:lst-ctn-kix_list_24-5}#doc8779917 .lst-kix_list_46-3>li:before{content:»» counter(lst-ctn-kix_list_46-3,decimal) «. «}#doc8779917 .lst-kix_list_38-1>li:before{content:»» counter(lst-ctn-kix_list_38-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-6.start{counter-reset:lst-ctn-kix_list_15-6 0}#doc8779917 .lst-kix_list_37-2>li:before{content:»» counter(lst-ctn-kix_list_37-2,lower-roman) «. «}#doc8779917 .lst-kix_list_46-5>li{counter-increment:lst-ctn-kix_list_46-5}#doc8779917 .lst-kix_list_25-6>li{counter-increment:lst-ctn-kix_list_25-6}#doc8779917 .lst-kix_list_37-5>li:before{content:»» counter(lst-ctn-kix_list_37-5,lower-roman) «. «}#doc8779917 .lst-kix_list_46-0>li:before{content:»» counter(lst-ctn-kix_list_46-0,decimal) «. «}#doc8779917 ol.lst-kix_list_31-8.start{counter-reset:lst-ctn-kix_list_31-8 0}#doc8779917 .lst-kix_list_18-1>li:before{content:»» counter(lst-ctn-kix_list_18-1,lower-latin) «. «}#doc8779917 .lst-kix_list_38-8>li:before{content:»» counter(lst-ctn-kix_list_38-8,lower-roman) «. «}#doc8779917 .lst-kix_list_40-3>li{counter-increment:lst-ctn-kix_list_40-3}#doc8779917 .lst-kix_list_44-3>li{counter-increment:lst-ctn-kix_list_44-3}#doc8779917 .lst-kix_list_45-4>li{counter-increment:lst-ctn-kix_list_45-4}#doc8779917 .lst-kix_list_23-4>li{counter-increment:lst-ctn-kix_list_23-4}#doc8779917 ol.lst-kix_list_23-1.start{counter-reset:lst-ctn-kix_list_23-1 0}#doc8779917 ol.lst-kix_list_45-5.start{counter-reset:lst-ctn-kix_list_45-5 0}#doc8779917 ol.lst-kix_list_32-0.start{counter-reset:lst-ctn-kix_list_32-0 0}#doc8779917 .lst-kix_list_23-1>li{counter-increment:lst-ctn-kix_list_23-1}#doc8779917 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc8779917 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc8779917 .lst-kix_list_24-2>li{counter-increment:lst-ctn-kix_list_24-2}#doc8779917 ol.lst-kix_list_32-8{list-style-type:none}#doc8779917 ol.lst-kix_list_32-7{list-style-type:none}#doc8779917 .lst-kix_list_27-5>li:before{content:»» counter(lst-ctn-kix_list_27-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_32-4{list-style-type:none}#doc8779917 ol.lst-kix_list_32-3{list-style-type:none}#doc8779917 ol.lst-kix_list_32-6{list-style-type:none}#doc8779917 ol.lst-kix_list_32-5{list-style-type:none}#doc8779917 ol.lst-kix_list_10-3.start{counter-reset:lst-ctn-kix_list_10-3 0}#doc8779917 ol.lst-kix_list_32-0{list-style-type:none}#doc8779917 .lst-kix_list_22-3>li{counter-increment:lst-ctn-kix_list_22-3}#doc8779917 ol.lst-kix_list_32-2{list-style-type:none}#doc8779917 ol.lst-kix_list_32-1{list-style-type:none}#doc8779917 .lst-kix_list_39-7>li:before{content:»» counter(lst-ctn-kix_list_39-7,lower-latin) «. «}#doc8779917 .lst-kix_list_46-8>li{counter-increment:lst-ctn-kix_list_46-8}#doc8779917 .lst-kix_list_10-1>li:before{content:»» counter(lst-ctn-kix_list_10-1,lower-latin) «. «}#doc8779917 .lst-kix_list_18-4>li:before{content:»» counter(lst-ctn-kix_list_18-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-1.start{counter-reset:lst-ctn-kix_list_15-1 0}#doc8779917 ol.lst-kix_list_15-4.start{counter-reset:lst-ctn-kix_list_15-4 0}#doc8779917 ol.lst-kix_list_45-3.start{counter-reset:lst-ctn-kix_list_45-3 0}#doc8779917 .lst-kix_list_36-6>li:before{content:»» counter(lst-ctn-kix_list_36-6,decimal) «. «}#doc8779917 .lst-kix_list_36-0>li:before{content:»» counter(lst-ctn-kix_list_36-0,decimal) «. «}#doc8779917 ol.lst-kix_list_40-2.start{counter-reset:lst-ctn-kix_list_40-2 0}#doc8779917 ol.lst-kix_list_44-8.start{counter-reset:lst-ctn-kix_list_44-8 0}#doc8779917 .lst-kix_list_34-0>li{counter-increment:lst-ctn-kix_list_34-0}#doc8779917 ol.lst-kix_list_45-0.start{counter-reset:lst-ctn-kix_list_45-0 0}#doc8779917 .lst-kix_list_26-4>li{counter-increment:lst-ctn-kix_list_26-4}#doc8779917 ol.lst-kix_list_5-7.start{counter-reset:lst-ctn-kix_list_5-7 0}#doc8779917 ol.lst-kix_list_28-7.start{counter-reset:lst-ctn-kix_list_28-7 0}#doc8779917 .lst-kix_list_20-8>li:before{content:»» counter(lst-ctn-kix_list_20-8,lower-roman) «. «}#doc8779917 .lst-kix_list_39-1>li{counter-increment:lst-ctn-kix_list_39-1}#doc8779917 .lst-kix_list_46-6>li:before{content:»» counter(lst-ctn-kix_list_46-6,decimal) «. «}#doc8779917 .lst-kix_list_29-7>li:before{content:»» counter(lst-ctn-kix_list_29-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_10-7{list-style-type:none}#doc8779917 ol.lst-kix_list_10-8{list-style-type:none}#doc8779917 ol.lst-kix_list_10-3{list-style-type:none}#doc8779917 .lst-kix_list_9-4>li:before{content:»» counter(lst-ctn-kix_list_9-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_10-4{list-style-type:none}#doc8779917 .lst-kix_list_30-8>li{counter-increment:lst-ctn-kix_list_30-8}#doc8779917 ol.lst-kix_list_10-5{list-style-type:none}#doc8779917 ol.lst-kix_list_10-6{list-style-type:none}#doc8779917 ol.lst-kix_list_10-0{list-style-type:none}#doc8779917 ol.lst-kix_list_10-1{list-style-type:none}#doc8779917 ol.lst-kix_list_10-2{list-style-type:none}#doc8779917 ol.lst-kix_list_36-2.start{counter-reset:lst-ctn-kix_list_36-2 0}#doc8779917 .lst-kix_list_1-1>li:before{content:»» counter(lst-ctn-kix_list_1-1,lower-latin) «. «}#doc8779917 .lst-kix_list_11-7>li:before{content:»» counter(lst-ctn-kix_list_11-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_10-5.start{counter-reset:lst-ctn-kix_list_10-5 0}#doc8779917 .lst-kix_list_14-7>li{counter-increment:lst-ctn-kix_list_14-7}#doc8779917 ol.lst-kix_list_31-5.start{counter-reset:lst-ctn-kix_list_31-5 0}#doc8779917 ol.lst-kix_list_40-4.start{counter-reset:lst-ctn-kix_list_40-4 0}#doc8779917 .lst-kix_list_28-1>li:before{content:»» counter(lst-ctn-kix_list_28-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_19-6{list-style-type:none}#doc8779917 ol.lst-kix_list_19-7{list-style-type:none}#doc8779917 ol.lst-kix_list_19-8{list-style-type:none}#doc8779917 ol.lst-kix_list_19-2{list-style-type:none}#doc8779917 ol.lst-kix_list_19-3{list-style-type:none}#doc8779917 ol.lst-kix_list_19-4{list-style-type:none}#doc8779917 ol.lst-kix_list_19-5{list-style-type:none}#doc8779917 .lst-kix_list_30-8>li:before{content:»» counter(lst-ctn-kix_list_30-8,lower-roman) «. «}#doc8779917 .lst-kix_list_35-7>li:before{content:»» counter(lst-ctn-kix_list_35-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_19-0{list-style-type:none}#doc8779917 .lst-kix_list_30-5>li{counter-increment:lst-ctn-kix_list_30-5}#doc8779917 ol.lst-kix_list_19-1{list-style-type:none}#doc8779917 .lst-kix_list_26-6>li:before{content:»» counter(lst-ctn-kix_list_26-6,decimal) «. «}#doc8779917 .lst-kix_list_8-2>li:before{content:»» counter(lst-ctn-kix_list_8-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_36-7.start{counter-reset:lst-ctn-kix_list_36-7 0}#doc8779917 ol.lst-kix_list_31-6.start{counter-reset:lst-ctn-kix_list_31-6 0}#doc8779917 .lst-kix_list_46-2>li{counter-increment:lst-ctn-kix_list_46-2}#doc8779917 .lst-kix_list_12-0>li{counter-increment:lst-ctn-kix_list_12-0}#doc8779917 ol.lst-kix_list_45-1.start{counter-reset:lst-ctn-kix_list_45-1 0}#doc8779917 ol.lst-kix_list_40-0.start{counter-reset:lst-ctn-kix_list_40-0 0}#doc8779917 .lst-kix_list_8-5>li:before{content:»» counter(lst-ctn-kix_list_8-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_28-0.start{counter-reset:lst-ctn-kix_list_28-0 0}#doc8779917 .lst-kix_list_26-3>li:before{content:»» counter(lst-ctn-kix_list_26-3,decimal) «. «}#doc8779917 .lst-kix_list_3-6>li:before{content:»» counter(lst-ctn-kix_list_3-6,decimal) «. «}#doc8779917 .lst-kix_list_21-7>li:before{content:»» counter(lst-ctn-kix_list_21-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_5-0.start{counter-reset:lst-ctn-kix_list_5-0 0}#doc8779917 .lst-kix_list_39-4>li{counter-increment:lst-ctn-kix_list_39-4}#doc8779917 ol.lst-kix_list_31-7.start{counter-reset:lst-ctn-kix_list_31-7 0}#doc8779917 .lst-kix_list_16-6>li:before{content:»» counter(lst-ctn-kix_list_16-6,decimal) «. «}#doc8779917 ol.lst-kix_list_10-1.start{counter-reset:lst-ctn-kix_list_10-1 0}#doc8779917 .lst-kix_list_18-2>li{counter-increment:lst-ctn-kix_list_18-2}#doc8779917 .lst-kix_list_22-6>li{counter-increment:lst-ctn-kix_list_22-6}#doc8779917 ol.lst-kix_list_5-6.start{counter-reset:lst-ctn-kix_list_5-6 0}#doc8779917 .lst-kix_list_7-3>li{counter-increment:lst-ctn-kix_list_7-3}#doc8779917 .lst-kix_list_25-0>li{counter-increment:lst-ctn-kix_list_25-0}#doc8779917 .lst-kix_list_45-4>li:before{content:»» counter(lst-ctn-kix_list_45-4,lower-latin) «. «}#doc8779917 .lst-kix_list_45-7>li:before{content:»» counter(lst-ctn-kix_list_45-7,lower-latin) «. «}#doc8779917 .lst-kix_list_19-3>li{counter-increment:lst-ctn-kix_list_19-3}#doc8779917 ol.lst-kix_list_28-6.start{counter-reset:lst-ctn-kix_list_28-6 0}#doc8779917 ol.lst-kix_list_28-5.start{counter-reset:lst-ctn-kix_list_28-5 0}#doc8779917 .lst-kix_list_44-8>li:before{content:»» counter(lst-ctn-kix_list_44-8,lower-roman) «. «}#doc8779917 .lst-kix_list_23-7>li{counter-increment:lst-ctn-kix_list_23-7}#doc8779917 .lst-kix_list_44-6>li{counter-increment:lst-ctn-kix_list_44-6}#doc8779917 ol.lst-kix_list_10-2.start{counter-reset:lst-ctn-kix_list_10-2 0}#doc8779917 .lst-kix_list_40-0>li{counter-increment:lst-ctn-kix_list_40-0}#doc8779917 .lst-kix_list_17-2>li:before{content:»» counter(lst-ctn-kix_list_17-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_5-5.start{counter-reset:lst-ctn-kix_list_5-5 0}#doc8779917 ol.lst-kix_list_40-1.start{counter-reset:lst-ctn-kix_list_40-1 0}#doc8779917 .lst-kix_list_17-5>li:before{content:»» counter(lst-ctn-kix_list_17-5,lower-roman) «. «}#doc8779917 .lst-kix_list_45-7>li{counter-increment:lst-ctn-kix_list_45-7}#doc8779917 .lst-kix_list_6-2>li{counter-increment:lst-ctn-kix_list_6-2}#doc8779917 ol.lst-kix_list_36-6.start{counter-reset:lst-ctn-kix_list_36-6 0}#doc8779917 .lst-kix_list_27-2>li:before{content:»» counter(lst-ctn-kix_list_27-2,lower-roman) «. «}#doc8779917 .lst-kix_list_22-3>li:before{content:»» counter(lst-ctn-kix_list_22-3,decimal) «. «}#doc8779917 ol.lst-kix_list_28-4.start{counter-reset:lst-ctn-kix_list_28-4 0}#doc8779917 .lst-kix_list_43-8>li{counter-increment:lst-ctn-kix_list_43-8}#doc8779917 ol.lst-kix_list_23-3.start{counter-reset:lst-ctn-kix_list_23-3 0}#doc8779917 ol.lst-kix_list_5-4.start{counter-reset:lst-ctn-kix_list_5-4 0}#doc8779917 ol.lst-kix_list_5-1.start{counter-reset:lst-ctn-kix_list_5-1 0}#doc8779917 .lst-kix_list_25-3>li{counter-increment:lst-ctn-kix_list_25-3}#doc8779917 .lst-kix_list_16-6>li{counter-increment:lst-ctn-kix_list_16-6}#doc8779917 ol.lst-kix_list_28-1.start{counter-reset:lst-ctn-kix_list_28-1 0}#doc8779917 ol.lst-kix_list_10-0.start{counter-reset:lst-ctn-kix_list_10-0 0}#doc8779917 .lst-kix_list_31-7>li:before{content:»» counter(lst-ctn-kix_list_31-7,lower-latin) «. «}#doc8779917 .lst-kix_list_3-8>li{counter-increment:lst-ctn-kix_list_3-8}#doc8779917 .lst-kix_list_4-6>li{counter-increment:lst-ctn-kix_list_4-6}#doc8779917 ol.lst-kix_list_23-6.start{counter-reset:lst-ctn-kix_list_23-6 0}#doc8779917 .lst-kix_list_17-4>li{counter-increment:lst-ctn-kix_list_17-4}#doc8779917 .lst-kix_list_4-2>li:before{content:»» counter(lst-ctn-kix_list_4-2,lower-roman) «. «}#doc8779917 .lst-kix_list_36-3>li:before{content:»» counter(lst-ctn-kix_list_36-3,decimal) «. «}#doc8779917 .lst-kix_list_26-1>li{counter-increment:lst-ctn-kix_list_26-1}#doc8779917 .lst-kix_list_9-1>li:before{content:»» counter(lst-ctn-kix_list_9-1,lower-latin) «. «}#doc8779917 .lst-kix_list_15-8>li{counter-increment:lst-ctn-kix_list_15-8}#doc8779917 .lst-kix_list_40-8>li:before{content:»» counter(lst-ctn-kix_list_40-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_36-8.start{counter-reset:lst-ctn-kix_list_36-8 0}#doc8779917 .lst-kix_list_37-8>li{counter-increment:lst-ctn-kix_list_37-8}#doc8779917 .lst-kix_list_31-3>li{counter-increment:lst-ctn-kix_list_31-3}#doc8779917 .lst-kix_list_41-4>li:before{content:»» counter(lst-ctn-kix_list_41-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_23-5.start{counter-reset:lst-ctn-kix_list_23-5 0}#doc8779917 .lst-kix_list_10-1>li{counter-increment:lst-ctn-kix_list_10-1}#doc8779917 ol.lst-kix_list_28-2.start{counter-reset:lst-ctn-kix_list_28-2 0}#doc8779917 .lst-kix_list_12-6>li:before{content:»» counter(lst-ctn-kix_list_12-6,decimal) «. «}#doc8779917 ol.lst-kix_list_23-4.start{counter-reset:lst-ctn-kix_list_23-4 0}#doc8779917 .lst-kix_list_13-2>li:before{content:»» counter(lst-ctn-kix_list_13-2,lower-roman) «. «}#doc8779917 .lst-kix_list_32-1>li{counter-increment:lst-ctn-kix_list_32-1}#doc8779917 ol.lst-kix_list_5-2.start{counter-reset:lst-ctn-kix_list_5-2 0}#doc8779917 ol.lst-kix_list_7-0{list-style-type:none}#doc8779917 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc8779917 ol.lst-kix_list_33-5.start{counter-reset:lst-ctn-kix_list_33-5 0}#doc8779917 ol.lst-kix_list_9-0.start{counter-reset:lst-ctn-kix_list_9-0 0}#doc8779917 ol.lst-kix_list_30-0.start{counter-reset:lst-ctn-kix_list_30-0 0}#doc8779917 ol.lst-kix_list_13-4.start{counter-reset:lst-ctn-kix_list_13-4 0}#doc8779917 .lst-kix_list_30-6>li{counter-increment:lst-ctn-kix_list_30-6}#doc8779917 ol.lst-kix_list_40-3.start{counter-reset:lst-ctn-kix_list_40-3 0}#doc8779917 .lst-kix_list_42-8>li:before{content:»» counter(lst-ctn-kix_list_42-8,lower-roman) «. «}#doc8779917 .lst-kix_list_13-0>li{counter-increment:lst-ctn-kix_list_13-0}#doc8779917 ol.lst-kix_list_20-2.start{counter-reset:lst-ctn-kix_list_20-2 0}#doc8779917 ol.lst-kix_list_43-8.start{counter-reset:lst-ctn-kix_list_43-8 0}#doc8779917 ol.lst-kix_list_7-5{list-style-type:none}#doc8779917 ol.lst-kix_list_7-6{list-style-type:none}#doc8779917 ol.lst-kix_list_7-7{list-style-type:none}#doc8779917 ol.lst-kix_list_7-8{list-style-type:none}#doc8779917 ol.lst-kix_list_7-1{list-style-type:none}#doc8779917 ol.lst-kix_list_7-2{list-style-type:none}#doc8779917 ol.lst-kix_list_7-3{list-style-type:none}#doc8779917 ol.lst-kix_list_7-4{list-style-type:none}#doc8779917 ol.lst-kix_list_23-2.start{counter-reset:lst-ctn-kix_list_23-2 0}#doc8779917 .lst-kix_list_42-0>li:before{content:»» counter(lst-ctn-kix_list_42-0,decimal) «. «}#doc8779917 .lst-kix_list_42-2>li:before{content:»» counter(lst-ctn-kix_list_42-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_46-8.start{counter-reset:lst-ctn-kix_list_46-8 0}#doc8779917 .lst-kix_list_43-0>li{counter-increment:lst-ctn-kix_list_43-0}#doc8779917 .lst-kix_list_35-7>li{counter-increment:lst-ctn-kix_list_35-7}#doc8779917 .lst-kix_list_24-7>li{counter-increment:lst-ctn-kix_list_24-7}#doc8779917 .lst-kix_list_29-8>li{counter-increment:lst-ctn-kix_list_29-8}#doc8779917 .lst-kix_list_42-6>li:before{content:»» counter(lst-ctn-kix_list_42-6,decimal) «. «}#doc8779917 ol.lst-kix_list_30-5.start{counter-reset:lst-ctn-kix_list_30-5 0}#doc8779917 .lst-kix_list_42-4>li:before{content:»» counter(lst-ctn-kix_list_42-4,lower-latin) «. «}#doc8779917 .lst-kix_list_18-8>li{counter-increment:lst-ctn-kix_list_18-8}#doc8779917 ol.lst-kix_list_26-7.start{counter-reset:lst-ctn-kix_list_26-7 0}#doc8779917 ol.lst-kix_list_10-4.start{counter-reset:lst-ctn-kix_list_10-4 0}#doc8779917 .lst-kix_list_7-2>li{counter-increment:lst-ctn-kix_list_7-2}#doc8779917 .lst-kix_list_24-7>li:before{content:»» counter(lst-ctn-kix_list_24-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_36-5.start{counter-reset:lst-ctn-kix_list_36-5 0}#doc8779917 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc8779917 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc8779917 ol.lst-kix_list_9-5.start{counter-reset:lst-ctn-kix_list_9-5 0}#doc8779917 ol.lst-kix_list_40-8.start{counter-reset:lst-ctn-kix_list_40-8 0}#doc8779917 ol.lst-kix_list_20-7.start{counter-reset:lst-ctn-kix_list_20-7 0}#doc8779917 .lst-kix_list_24-3>li:before{content:»» counter(lst-ctn-kix_list_24-3,decimal) «. «}#doc8779917 .lst-kix_list_24-5>li:before{content:»» counter(lst-ctn-kix_list_24-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_43-3.start{counter-reset:lst-ctn-kix_list_43-3 0}#doc8779917 ol.lst-kix_list_16-4.start{counter-reset:lst-ctn-kix_list_16-4 0}#doc8779917 .lst-kix_list_6-5>li{counter-increment:lst-ctn-kix_list_6-5}#doc8779917 ol.lst-kix_list_27-6{list-style-type:none}#doc8779917 ol.lst-kix_list_27-5{list-style-type:none}#doc8779917 .lst-kix_list_23-3>li:before{content:»» counter(lst-ctn-kix_list_23-3,decimal) «. «}#doc8779917 .lst-kix_list_23-7>li:before{content:»» counter(lst-ctn-kix_list_23-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_27-8{list-style-type:none}#doc8779917 ol.lst-kix_list_27-7{list-style-type:none}#doc8779917 ol.lst-kix_list_27-2{list-style-type:none}#doc8779917 ol.lst-kix_list_23-7.start{counter-reset:lst-ctn-kix_list_23-7 0}#doc8779917 ol.lst-kix_list_27-1{list-style-type:none}#doc8779917 ol.lst-kix_list_27-4{list-style-type:none}#doc8779917 ol.lst-kix_list_27-3{list-style-type:none}#doc8779917 ol.lst-kix_list_46-3.start{counter-reset:lst-ctn-kix_list_46-3 0}#doc8779917 .lst-kix_list_23-1>li:before{content:»» counter(lst-ctn-kix_list_23-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_27-0{list-style-type:none}#doc8779917 .lst-kix_list_24-1>li:before{content:»» counter(lst-ctn-kix_list_24-1,lower-latin) «. «}#doc8779917 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc8779917 ol.lst-kix_list_26-2.start{counter-reset:lst-ctn-kix_list_26-2 0}#doc8779917 .lst-kix_list_23-5>li:before{content:»» counter(lst-ctn-kix_list_23-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_36-0.start{counter-reset:lst-ctn-kix_list_36-0 2}#doc8779917 .lst-kix_list_8-6>li{counter-increment:lst-ctn-kix_list_8-6}#doc8779917 ol.lst-kix_list_4-6.start{counter-reset:lst-ctn-kix_list_4-6 0}#doc8779917 ol.lst-kix_list_39-5.start{counter-reset:lst-ctn-kix_list_39-5 0}#doc8779917 ol.lst-kix_list_3-0.start{counter-reset:lst-ctn-kix_list_3-0 0}#doc8779917 ol.lst-kix_list_29-2.start{counter-reset:lst-ctn-kix_list_29-2 0}#doc8779917 .lst-kix_list_25-5>li:before{content:»» counter(lst-ctn-kix_list_25-5,lower-roman) «. «}#doc8779917 .lst-kix_list_25-7>li:before{content:»» counter(lst-ctn-kix_list_25-7,lower-latin) «. «}#doc8779917 .lst-kix_list_3-5>li{counter-increment:lst-ctn-kix_list_3-5}#doc8779917 ol.lst-kix_list_18-3.start{counter-reset:lst-ctn-kix_list_18-3 0}#doc8779917 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc8779917 ol.lst-kix_list_18-7{list-style-type:none}#doc8779917 ol.lst-kix_list_18-8{list-style-type:none}#doc8779917 ol.lst-kix_list_33-0.start{counter-reset:lst-ctn-kix_list_33-0 0}#doc8779917 ol.lst-kix_list_18-3{list-style-type:none}#doc8779917 ol.lst-kix_list_18-4{list-style-type:none}#doc8779917 ol.lst-kix_list_45-2.start{counter-reset:lst-ctn-kix_list_45-2 0}#doc8779917 ol.lst-kix_list_18-5{list-style-type:none}#doc8779917 ol.lst-kix_list_18-6{list-style-type:none}#doc8779917 ol.lst-kix_list_18-0{list-style-type:none}#doc8779917 ol.lst-kix_list_18-1{list-style-type:none}#doc8779917 ol.lst-kix_list_18-2{list-style-type:none}#doc8779917 .lst-kix_list_9-3>li{counter-increment:lst-ctn-kix_list_9-3}#doc8779917 ol.lst-kix_list_7-6.start{counter-reset:lst-ctn-kix_list_7-6 0}#doc8779917 ol.lst-kix_list_15-3.start{counter-reset:lst-ctn-kix_list_15-3 0}#doc8779917 ol.lst-kix_list_6-0.start{counter-reset:lst-ctn-kix_list_6-0 0}#doc8779917 .lst-kix_list_4-2>li{counter-increment:lst-ctn-kix_list_4-2}#doc8779917 ol.lst-kix_list_3-1{list-style-type:none}#doc8779917 ol.lst-kix_list_3-2{list-style-type:none}#doc8779917 ol.lst-kix_list_3-3{list-style-type:none}#doc8779917 .lst-kix_list_5-1>li{counter-increment:lst-ctn-kix_list_5-1}#doc8779917 ol.lst-kix_list_3-4{list-style-type:none}#doc8779917 ol.lst-kix_list_21-3.start{counter-reset:lst-ctn-kix_list_21-3 0}#doc8779917 ol.lst-kix_list_3-0{list-style-type:none}#doc8779917 .lst-kix_list_38-5>li{counter-increment:lst-ctn-kix_list_38-5}#doc8779917 ol.lst-kix_list_25-6.start{counter-reset:lst-ctn-kix_list_25-6 0}#doc8779917 ol.lst-kix_list_32-4.start{counter-reset:lst-ctn-kix_list_32-4 0}#doc8779917 .lst-kix_list_16-0>li{counter-increment:lst-ctn-kix_list_16-0}#doc8779917 .lst-kix_list_26-5>li:before{content:»» counter(lst-ctn-kix_list_26-5,lower-roman) «. «}#doc8779917 .lst-kix_list_10-0>li{counter-increment:lst-ctn-kix_list_10-0}#doc8779917 ol.lst-kix_list_3-5{list-style-type:none}#doc8779917 ol.lst-kix_list_3-6{list-style-type:none}#doc8779917 ol.lst-kix_list_3-7{list-style-type:none}#doc8779917 ol.lst-kix_list_3-8{list-style-type:none}#doc8779917 .lst-kix_list_26-1>li:before{content:»» counter(lst-ctn-kix_list_26-1,lower-latin) «. «}#doc8779917 .lst-kix_list_21-1>li:before{content:»» counter(lst-ctn-kix_list_21-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_15-8.start{counter-reset:lst-ctn-kix_list_15-8 0}#doc8779917 ol.lst-kix_list_45-7{list-style-type:none}#doc8779917 ol.lst-kix_list_45-8{list-style-type:none}#doc8779917 ol.lst-kix_list_45-5{list-style-type:none}#doc8779917 .lst-kix_list_34-3>li{counter-increment:lst-ctn-kix_list_34-3}#doc8779917 ol.lst-kix_list_45-6{list-style-type:none}#doc8779917 ol.lst-kix_list_45-3{list-style-type:none}#doc8779917 .lst-kix_list_45-3>li{counter-increment:lst-ctn-kix_list_45-3}#doc8779917 ol.lst-kix_list_45-4{list-style-type:none}#doc8779917 ol.lst-kix_list_45-1{list-style-type:none}#doc8779917 ol.lst-kix_list_45-2{list-style-type:none}#doc8779917 ol.lst-kix_list_45-0{list-style-type:none}#doc8779917 .lst-kix_list_10-2>li{counter-increment:lst-ctn-kix_list_10-2}#doc8779917 ol.lst-kix_list_45-7.start{counter-reset:lst-ctn-kix_list_45-7 0}#doc8779917 .lst-kix_list_21-5>li:before{content:»» counter(lst-ctn-kix_list_21-5,lower-roman) «. «}#doc8779917 .lst-kix_list_45-2>li:before{content:»» counter(lst-ctn-kix_list_45-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_27-8.start{counter-reset:lst-ctn-kix_list_27-8 0}#doc8779917 .lst-kix_list_21-0>li{counter-increment:lst-ctn-kix_list_21-0}#doc8779917 .lst-kix_list_25-1>li:before{content:»» counter(lst-ctn-kix_list_25-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_31-1.start{counter-reset:lst-ctn-kix_list_31-1 0}#doc8779917 .lst-kix_list_45-6>li:before{content:»» counter(lst-ctn-kix_list_45-6,decimal) «. «}#doc8779917 .lst-kix_list_44-6>li:before{content:»» counter(lst-ctn-kix_list_44-6,decimal) «. «}#doc8779917 ol.lst-kix_list_7-1.start{counter-reset:lst-ctn-kix_list_7-1 0}#doc8779917 ol.lst-kix_list_23-6{list-style-type:none}#doc8779917 .lst-kix_list_44-2>li:before{content:»» counter(lst-ctn-kix_list_44-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_23-5{list-style-type:none}#doc8779917 ol.lst-kix_list_23-8{list-style-type:none}#doc8779917 ol.lst-kix_list_23-7{list-style-type:none}#doc8779917 .lst-kix_list_39-1>li:before{content:»» counter(lst-ctn-kix_list_39-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_23-2{list-style-type:none}#doc8779917 .lst-kix_list_16-7>li{counter-increment:lst-ctn-kix_list_16-7}#doc8779917 ol.lst-kix_list_23-1{list-style-type:none}#doc8779917 ol.lst-kix_list_23-4{list-style-type:none}#doc8779917 ol.lst-kix_list_23-3{list-style-type:none}#doc8779917 .lst-kix_list_27-7>li{counter-increment:lst-ctn-kix_list_27-7}#doc8779917 .lst-kix_list_45-1>li{counter-increment:lst-ctn-kix_list_45-1}#doc8779917 ol.lst-kix_list_23-0{list-style-type:none}#doc8779917 .lst-kix_list_34-1>li{counter-increment:lst-ctn-kix_list_34-1}#doc8779917 .lst-kix_list_38-7>li{counter-increment:lst-ctn-kix_list_38-7}#doc8779917 .lst-kix_list_16-5>li{counter-increment:lst-ctn-kix_list_16-5}#doc8779917 .lst-kix_list_3-7>li{counter-increment:lst-ctn-kix_list_3-7}#doc8779917 .lst-kix_list_22-5>li:before{content:»» counter(lst-ctn-kix_list_22-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_36-8{list-style-type:none}#doc8779917 ol.lst-kix_list_36-7{list-style-type:none}#doc8779917 .lst-kix_list_43-2>li:before{content:»» counter(lst-ctn-kix_list_43-2,lower-roman) «. «}#doc8779917 .lst-kix_list_43-6>li:before{content:»» counter(lst-ctn-kix_list_43-6,decimal) «. «}#doc8779917 ol.lst-kix_list_36-4{list-style-type:none}#doc8779917 .lst-kix_list_21-2>li{counter-increment:lst-ctn-kix_list_21-2}#doc8779917 ol.lst-kix_list_36-3{list-style-type:none}#doc8779917 ol.lst-kix_list_36-6{list-style-type:none}#doc8779917 .lst-kix_list_45-8>li{counter-increment:lst-ctn-kix_list_45-8}#doc8779917 .lst-kix_list_22-1>li:before{content:»» counter(lst-ctn-kix_list_22-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_36-5{list-style-type:none}#doc8779917 ol.lst-kix_list_36-0{list-style-type:none}#doc8779917 ol.lst-kix_list_36-2{list-style-type:none}#doc8779917 ol.lst-kix_list_36-1{list-style-type:none}#doc8779917 .lst-kix_list_23-3>li{counter-increment:lst-ctn-kix_list_23-3}#doc8779917 .lst-kix_list_9-5>li{counter-increment:lst-ctn-kix_list_9-5}#doc8779917 .lst-kix_list_5-8>li{counter-increment:lst-ctn-kix_list_5-8}#doc8779917 .lst-kix_list_27-0>li{counter-increment:lst-ctn-kix_list_27-0}#doc8779917 .lst-kix_list_41-6>li{counter-increment:lst-ctn-kix_list_41-6}#doc8779917 ol.lst-kix_list_19-4.start{counter-reset:lst-ctn-kix_list_19-4 0}#doc8779917 .lst-kix_list_38-0>li{counter-increment:lst-ctn-kix_list_38-0}#doc8779917 .lst-kix_list_32-0>li{counter-increment:lst-ctn-kix_list_32-0}#doc8779917 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc8779917 ol.lst-kix_list_38-4.start{counter-reset:lst-ctn-kix_list_38-4 0}#doc8779917 ol.lst-kix_list_25-1.start{counter-reset:lst-ctn-kix_list_25-1 0}#doc8779917 ol.lst-kix_list_14-7{list-style-type:none}#doc8779917 ol.lst-kix_list_14-8{list-style-type:none}#doc8779917 ol.lst-kix_list_14-3{list-style-type:none}#doc8779917 ol.lst-kix_list_21-8.start{counter-reset:lst-ctn-kix_list_21-8 0}#doc8779917 ol.lst-kix_list_14-4{list-style-type:none}#doc8779917 ol.lst-kix_list_14-5{list-style-type:none}#doc8779917 ol.lst-kix_list_14-6{list-style-type:none}#doc8779917 .lst-kix_list_34-8>li{counter-increment:lst-ctn-kix_list_34-8}#doc8779917 ol.lst-kix_list_14-0{list-style-type:none}#doc8779917 ol.lst-kix_list_14-1{list-style-type:none}#doc8779917 .lst-kix_list_27-5>li{counter-increment:lst-ctn-kix_list_27-5}#doc8779917 .lst-kix_list_40-6>li:before{content:»» counter(lst-ctn-kix_list_40-6,decimal) «. «}#doc8779917 ol.lst-kix_list_44-4.start{counter-reset:lst-ctn-kix_list_44-4 0}#doc8779917 ol.lst-kix_list_14-2{list-style-type:none}#doc8779917 .lst-kix_list_41-6>li:before{content:»» counter(lst-ctn-kix_list_41-6,decimal) «. «}#doc8779917 .lst-kix_list_20-5>li:before{content:»» counter(lst-ctn-kix_list_20-5,lower-roman) «. «}#doc8779917 .lst-kix_list_41-2>li:before{content:»» counter(lst-ctn-kix_list_41-2,lower-roman) «. «}#doc8779917 .lst-kix_list_20-1>li:before{content:»» counter(lst-ctn-kix_list_20-1,lower-latin) «. «}#doc8779917 .lst-kix_list_12-3>li{counter-increment:lst-ctn-kix_list_12-3}#doc8779917 ol.lst-kix_list_8-4.start{counter-reset:lst-ctn-kix_list_8-4 0}#doc8779917 ol.lst-kix_list_3-5.start{counter-reset:lst-ctn-kix_list_3-5 0}#doc8779917 .lst-kix_list_21-7>li{counter-increment:lst-ctn-kix_list_21-7}#doc8779917 .lst-kix_list_14-4>li{counter-increment:lst-ctn-kix_list_14-4}#doc8779917 .lst-kix_list_10-7>li{counter-increment:lst-ctn-kix_list_10-7}#doc8779917 .lst-kix_list_25-4>li{counter-increment:lst-ctn-kix_list_25-4}#doc8779917 .lst-kix_list_18-1>li{counter-increment:lst-ctn-kix_list_18-1}#doc8779917 ol.lst-kix_list_14-5.start{counter-reset:lst-ctn-kix_list_14-5 0}#doc8779917 .lst-kix_list_32-7>li{counter-increment:lst-ctn-kix_list_32-7}#doc8779917 .lst-kix_list_40-2>li:before{content:»» counter(lst-ctn-kix_list_40-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_37-1.start{counter-reset:lst-ctn-kix_list_37-1 0}#doc8779917 .lst-kix_list_36-4>li{counter-increment:lst-ctn-kix_list_36-4}#doc8779917 .lst-kix_list_29-1>li{counter-increment:lst-ctn-kix_list_29-1}#doc8779917 .lst-kix_list_43-7>li{counter-increment:lst-ctn-kix_list_43-7}#doc8779917 ol.lst-kix_list_32-7.start{counter-reset:lst-ctn-kix_list_32-7 0}#doc8779917 .lst-kix_list_43-2>li{counter-increment:lst-ctn-kix_list_43-2}#doc8779917 ol.lst-kix_list_41-1.start{counter-reset:lst-ctn-kix_list_41-1 0}#doc8779917 .lst-kix_list_19-4>li:before{content:»» counter(lst-ctn-kix_list_19-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_37-8.start{counter-reset:lst-ctn-kix_list_37-8 0}#doc8779917 .lst-kix_list_31-5>li{counter-increment:lst-ctn-kix_list_31-5}#doc8779917 ol.lst-kix_list_24-5.start{counter-reset:lst-ctn-kix_list_24-5 0}#doc8779917 ol.lst-kix_list_27-5.start{counter-reset:lst-ctn-kix_list_27-5 0}#doc8779917 ol.lst-kix_list_22-4.start{counter-reset:lst-ctn-kix_list_22-4 0}#doc8779917 ol.lst-kix_list_11-2.start{counter-reset:lst-ctn-kix_list_11-2 0}#doc8779917 .lst-kix_list_42-1>li{counter-increment:lst-ctn-kix_list_42-1}#doc8779917 .lst-kix_list_19-6>li:before{content:»» counter(lst-ctn-kix_list_19-6,decimal) «. «}#doc8779917 .lst-kix_list_17-2>li{counter-increment:lst-ctn-kix_list_17-2}#doc8779917 ol.lst-kix_list_8-7.start{counter-reset:lst-ctn-kix_list_8-7 0}#doc8779917 ol.lst-kix_list_41-6.start{counter-reset:lst-ctn-kix_list_41-6 0}#doc8779917 .lst-kix_list_42-5>li{counter-increment:lst-ctn-kix_list_42-5}#doc8779917 .lst-kix_list_32-2>li{counter-increment:lst-ctn-kix_list_32-2}#doc8779917 .lst-kix_list_36-2>li{counter-increment:lst-ctn-kix_list_36-2}#doc8779917 ol.lst-kix_list_31-8{list-style-type:none}#doc8779917 .lst-kix_list_20-5>li{counter-increment:lst-ctn-kix_list_20-5}#doc8779917 ol.lst-kix_list_31-5{list-style-type:none}#doc8779917 ol.lst-kix_list_31-4{list-style-type:none}#doc8779917 ol.lst-kix_list_31-7{list-style-type:none}#doc8779917 ol.lst-kix_list_31-6{list-style-type:none}#doc8779917 ol.lst-kix_list_37-3.start{counter-reset:lst-ctn-kix_list_37-3 0}#doc8779917 ol.lst-kix_list_31-1{list-style-type:none}#doc8779917 ol.lst-kix_list_31-0{list-style-type:none}#doc8779917 ol.lst-kix_list_31-3{list-style-type:none}#doc8779917 .lst-kix_list_37-1>li:before{content:»» counter(lst-ctn-kix_list_37-1,lower-latin) «. «}#doc8779917 ol.lst-kix_list_31-2{list-style-type:none}#doc8779917 .lst-kix_list_46-2>li:before{content:»» counter(lst-ctn-kix_list_46-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_44-1.start{counter-reset:lst-ctn-kix_list_44-1 0}#doc8779917 ol.lst-kix_list_24-0.start{counter-reset:lst-ctn-kix_list_24-0 0}#doc8779917 .lst-kix_list_18-3>li{counter-increment:lst-ctn-kix_list_18-3}#doc8779917 .lst-kix_list_37-3>li:before{content:»» counter(lst-ctn-kix_list_37-3,decimal) «. «}#doc8779917 ol.lst-kix_list_35-7.start{counter-reset:lst-ctn-kix_list_35-7 0}#doc8779917 .lst-kix_list_37-3>li{counter-increment:lst-ctn-kix_list_37-3}#doc8779917 .lst-kix_list_18-0>li:before{content:»» counter(lst-ctn-kix_list_18-0,decimal) «) «}#doc8779917 .lst-kix_list_38-7>li:before{content:»» counter(lst-ctn-kix_list_38-7,lower-latin) «. «}#doc8779917 .lst-kix_list_3-0>li{counter-increment:lst-ctn-kix_list_3-0}#doc8779917 .lst-kix_list_18-2>li:before{content:»» counter(lst-ctn-kix_list_18-2,lower-roman) «. «}#doc8779917 ol.lst-kix_list_27-0.start{counter-reset:lst-ctn-kix_list_27-0 0}#doc8779917 ol.lst-kix_list_11-7.start{counter-reset:lst-ctn-kix_list_11-7 0}#doc8779917 ol.lst-kix_list_14-2.start{counter-reset:lst-ctn-kix_list_14-2 0}#doc8779917 .lst-kix_list_41-4>li{counter-increment:lst-ctn-kix_list_41-4}#doc8779917 .lst-kix_list_30-4>li{counter-increment:lst-ctn-kix_list_30-4}#doc8779917 .lst-kix_list_38-5>li:before{content:»» counter(lst-ctn-kix_list_38-5,lower-roman) «. «}#doc8779917 .lst-kix_list_25-2>li{counter-increment:lst-ctn-kix_list_25-2}#doc8779917 .lst-kix_list_27-1>li:before{content:»» counter(lst-ctn-kix_list_27-1,lower-latin) «. «}#doc8779917 .lst-kix_list_27-3>li:before{content:»» counter(lst-ctn-kix_list_27-3,decimal) «. «}#doc8779917 .lst-kix_list_18-8>li:before{content:»» counter(lst-ctn-kix_list_18-8,lower-roman) «. «}#doc8779917 ol.lst-kix_list_27-3.start{counter-reset:lst-ctn-kix_list_27-3 0}#doc8779917 .lst-kix_list_17-6>li{counter-increment:lst-ctn-kix_list_17-6}#doc8779917 ol.lst-kix_list_4-3.start{counter-reset:lst-ctn-kix_list_4-3 0}#doc8779917 .lst-kix_list_10-7>li:before{content:»» counter(lst-ctn-kix_list_10-7,lower-latin) «. «}#doc8779917 .lst-kix_list_20-1>li{counter-increment:lst-ctn-kix_list_20-1}#doc8779917 .lst-kix_list_10-5>li:before{content:»» counter(lst-ctn-kix_list_10-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_18-6.start{counter-reset:lst-ctn-kix_list_18-6 0}#doc8779917 .lst-kix_list_29-3>li{counter-increment:lst-ctn-kix_list_29-3}#doc8779917 .lst-kix_list_9-2>li:before{content:»» counter(lst-ctn-kix_list_9-2,lower-roman) «. «}#doc8779917 .lst-kix_list_46-4>li:before{content:»» counter(lst-ctn-kix_list_46-4,lower-latin) «. «}#doc8779917 ol.lst-kix_list_37-6.start{counter-reset:lst-ctn-kix_list_37-6 0}#doc8779917 ol.lst-kix_list_14-0.start{counter-reset:lst-ctn-kix_list_14-0 0}#doc8779917 .lst-kix_list_12-5>li{counter-increment:lst-ctn-kix_list_12-5}#doc8779917 .lst-kix_list_31-1>li{counter-increment:lst-ctn-kix_list_31-1}#doc8779917 .lst-kix_list_9-0>li:before{content:»» counter(lst-ctn-kix_list_9-0,decimal) «) «}#doc8779917 ol.lst-kix_list_24-3.start{counter-reset:lst-ctn-kix_list_24-3 0}#doc8779917 .lst-kix_list_23-5>li{counter-increment:lst-ctn-kix_list_23-5}#doc8779917 .lst-kix_list_11-3>li:before{content:»» counter(lst-ctn-kix_list_11-3,decimal) «. «}#doc8779917 .lst-kix_list_6-3>li{counter-increment:lst-ctn-kix_list_6-3}#doc8779917 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc8779917 .lst-kix_list_29-1>li:before{content:»» counter(lst-ctn-kix_list_29-1,lower-latin) «. «}#doc8779917 .lst-kix_list_29-3>li:before{content:»» counter(lst-ctn-kix_list_29-3,decimal) «. «}#doc8779917 .lst-kix_list_9-8>li:before{content:»» counter(lst-ctn-kix_list_9-8,lower-roman) «. «}#doc8779917 .lst-kix_list_28-6>li{counter-increment:lst-ctn-kix_list_28-6}#doc8779917 .lst-kix_list_28-7>li:before{content:»» counter(lst-ctn-kix_list_28-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_44-8{list-style-type:none}#doc8779917 .lst-kix_list_1-7>li:before{content:»» counter(lst-ctn-kix_list_1-7,lower-latin) «. «}#doc8779917 ol.lst-kix_list_44-6{list-style-type:none}#doc8779917 ol.lst-kix_list_44-7{list-style-type:none}#doc8779917 ol.lst-kix_list_44-4{list-style-type:none}#doc8779917 .lst-kix_list_1-5>li:before{content:»» counter(lst-ctn-kix_list_1-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_44-5{list-style-type:none}#doc8779917 .lst-kix_list_28-5>li:before{content:»» counter(lst-ctn-kix_list_28-5,lower-roman) «. «}#doc8779917 ol.lst-kix_list_44-2{list-style-type:none}#doc8779917 ol.lst-kix_list_44-3{list-style-type:none}#doc8779917 .lst-kix_list_5-6>li{counter-increment:lst-ctn-kix_list_5-6}#doc8779917 ol.lst-kix_list_44-0{list-style-type:none}#doc8779917 ol.lst-kix_list_22-6.start{counter-reset:lst-ctn-kix_list_22-6 0}#doc87799]]>
Контрольные работы по алгебре 9 класс (Макарычев Ю.Н.) | Материал по алгебре (9 класс) на тему:
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 1.
- Сократите дробь .
- Решите неравенство 5х – 7 ≥ 7х – 5.
- Решите уравнение х2 – 10х + 25 = 0.
- Сравните 56,78 ∙ 106 и 5,687 ∙ 107.
- Решите систему уравнений:
- Постройте график функции у = 7х – 5 и найдите, при каких значениях х значения у не меньше – 40.
- В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 2
- Сократите дробь .
- Решите неравенство 3х – 8 ≥ 8х – 3.
- Решите уравнение х2 – 14х + 49 = 0.
- Сравните 4,567 ∙ 109 и 45,76 ∙ 108.
- Решите систему уравнений:
- Постройте график функции у = 6х – 7 и найдите, при каких значениях х значения у не больше – 49.
- В арифметической прогрессии второй член равен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 21 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 1.
- Сократите дробь .
- Решите неравенство 5х – 7 ≥ 7х – 5.
- Решите уравнение х2 – 10х + 25 = 0.
- Сравните 56,78 ∙ 106 и 5,687 ∙ 107.
- Решите систему уравнений:
- Постройте график функции у = 7х – 5 и найдите, при каких значениях х значения у не меньше – 40.
- В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 2
- Сократите дробь .
- Решите неравенство 3х – 8 ≥ 8х – 3.
- Решите уравнение х2 – 14х + 49 = 0.
- Сравните 4,567 ∙ 109 и 45,76 ∙ 108.
- Решите систему уравнений:
- Постройте график функции у = 6х – 7 и найдите, при каких значениях х значения у не больше – 49.
- В арифметической прогрессии второй член равен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 21 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольные работы по алгебре 9 класс (Макарычев)
Контрольная работа №2 (пп.5 – 9) 9 класс( Макарычев)
Вариант 1.
Найдите значение выражения:
а) ; б) ; в) .
2. Сравните:
а) 1,37 и 1,47; в) ( — 2,7)6и 1,96;
б) ( — 0,5)7 и ( — 0,6)7; г) ( — 1,1)6и 1.
Изобразите схематически график функции:
а) у =- 3х2; б) у = 2х2 – 3.
Постройте график функции у = х2 – 5х + 6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значения функции.
5. Пересекаются ли прямая у = 2х -1 и парабола у = х2 + 3?
Контрольная работа №2 (пп.5 – 9) 9 класс( Макарычев)
Вариант 2.
Найдите значение выражения:
а) ; б) ; в) .
2. Сравните:
а) 1,28 и 1,58; в) (- 3,9)4и 3,54
б) (- 0,6)5 и ( — 0,4)5; г) ( — 1,2)7и — 1.
3. Изобразите схематически график функции:
а) у = 3х2; б) у = — 2(х + 1)2.
4. Постройте график функции у = х2 – х — 2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному — 1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значения функции.
5. Пересекаются ли прямая у = 5х -2 и парабола у = х2 + 4?
Контрольная работа №2 (пп.5 – 9) 9 класс( Макарычев)
Вариант 1.
Найдите значение выражения:
а) ; б) ; в) .
2. Сравните:
а) 1,37 и 1,47; в) ( — 2,7)6и 1,96;
б) ( — 0,5)7 и ( — 0,6)7; г) ( — 1,1)6и 1.
Изобразите схематически график функции:
а) у =- 3х2; б)
Постройте график функции у = х2 – 5х + 6. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значения функции.
5. Пересекаются ли прямая у = 2х -1 и парабола у = х2 + 3?
Контрольная работа №2 (пп.5 – 9) 9 класс( Макарычев)
Вариант 2.
Найдите значение выражения:
а) ; б) ; в) .
2. Сравните:
а) 1,28 и 1,58; в) (- 3,9)4и 3,54;
б) (- 0,6)5 и ( — 0,4)5; г) ( — 1,2)7и — 1.
3. Изобразите схематически график функции:
а) у = 3х2; б) у = — 2(х + 1)2.
4. Постройте график функции у = х2 – х — 2. С помощью графика найдите:
а) значение функции, соответствующее значению аргумента, равному — 1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значения функции.
5. Пересекаются ли прямая у = 5х -2 и парабола у = х2 + 4?
Алгебра 9 Макарычев Контрольные работы ДМ
Алгебра 9 Макарычев Контрольные работы с ответами (4 варианта). Цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева — М.: Просвещение» использованы в учебных целях. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия. Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены ответы на задания контрольной. При постоянном использовании данных контрольных работ рекомендуем КУПИТЬ книгу: Алгебра. Дидактические материалы 9 класс / Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева — М.: Просвещение (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки учебного пособия.
Алгебра 9 Макарычев Контрольные работы:
Контрольная работа № 1 + Ответы Контрольная работа № 2 + Ответы Контрольная работа № 3 + Ответы Контрольная работа № 4 + Ответы Контрольная работа № 5 + Ответы Контрольная работа № 6 + Ответы Контрольная работа № 7 + Ответы Контрольная работа № 8 + Ответы Итоговая контрольная работа + Ответы
Вы смотрели страницу Алгебра 9 Макарычев Контрольные работы. Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Алгебра. Дидактические материалы 9 класс / Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева — М.: Просвещение». Вернуться на страницу «Алгебра 9 класс».
Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.
Другие контрольные работы по алгебре в 9 классе:
УМК Мерзляк, Полонский, Якир — Дидактические материалы (только контрольные работы)
УМК Мордкович — Попов М.А. Дидактические материалы по алгебре 9 кл.
УМК Мордкович — Александрова Л.А. Контрольные работы по алгебре в 9 классе
УМК Никольский (МГУ — школе) — Потапов и др. Дидактические материалы по алгебре 9 кл.
Алгебра 9 Макарычев Контрольная № 2 с ответами
Контрольная работа № 2 по алгебре с ответами 9 класс по УМК Макарычев и др.2 и прямая у = 12 — х. Если точки пересечения существуют, то найдите их координаты.
ОТВЕТЫ на контрольную работу:
Вернуться к Списку контрольных работ по алгебре 9 класс (Макарычев)
Вы смотрели: Контрольная работа по алгебре 9 класс с ответами по УМК Макарычев и др. (Просвещение) Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Алгебра 9 Макарычев Контрольная № 2. Цитаты использованы в учебных целях.
Алгебраическое выражение | Примечания, видео, контроль качества и тесты | 9 класс> Обязательная математика> Алгебра
Алгебраическое выражение
Факторизация
Факторизация выражения формы a 2 -b 2
(i) Возьмите квадратный лист бумаги с единицей «а» на одной стороне, площадь которой равна квадратным единицам.
(ii) В одном из углов квадрата отрежьте небольшой квадрат со стороной «b».Площадь этого квадратика равна единицам.
(iii) Давайте разрежем 2 -b 2 по диагонали, как показано на рисунке.
(iv) Расположите две части, чтобы получился прямоугольник.
Длина прямоугольника = (a + b) ед.
Ширина прямоугольника = (a-b)
Итак, площадь прямоугольника = длина × ширина
= (а + б) (а-б)
= а 2 -b 2
∴ Площадь прямоугольника = (a 2 -b 2 ) кв.Установка
∴ a 2 -b 2 = (a + b) (a-b)
Что нужно помнить
Некоторая полезная формула
- (a + b) 2 = a 2 + 2ab + b 2 или (a + b) 2 + 4ab
- (a-b) 2 = a 2 -2ab + b 2 или, (a + b) 2 -4ab
- a 2 -b 2 = (a + b) (a-b)
- a 2 + b 2 = (a + b) 2 -2ab или, (a-b) 2 + 2ab
- Это включает в себя все отношения, которые установились между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которые нельзя увидеть или потрогать.
- общие интересы и общие цели не нужны обществу.
Видео для алгебраических выражений
Математические выходки — простое факторизация
Математика — Факторинг — Помощь по математике — Факторинг
Факторизация на простые числа | Факторы и мультипликаторы | Предалгебра | Хан Академия
Вопросы и ответы
Soln: 16x 4 -4x 2
= 4x 2 (4x 2 -1)
= 4x 2 {(2x 2 ) (1) 2 }
= 4x 2 (2x + 1) (2x-1) Отв.
Солнце: 3x 3 -48x
= 3x (x 2 -16)
= 3x (x 2 -4 2 )
= 3x (x + 4) (x-4) Ответ
Soln: a 4 -b 4
= (a 2 ) 2 — (a 2 ) 2 — (b 2 ) 2
= (a 2 + b 2 ) (a 2 -b 2 )
= (a 2 + b 2 ) (a + b) (ab) Ответ.
Солнце: (y + 1) 2 -4
= (y + 1) 2 — (2) 2
= (y + 1 + 2) (y + 1-2)
= (y + 3) (y-1) Ответ.
Солнце: 36- (x + 5) 2
= 6 2 — (x + 5) 2
= (6 + x + 5) (6-x-5)
= ( 11 + x) (1-x) Отв.
Soln: a 2 + 2ab + b 2 -c 2
= (a + b) 2 -c 2
= (a + b + c) (a + bc) Ответ
Soln: m 2 + n 2 -2mn-p 2
= m 2 -2mn + n 2 -p 2
= (m -n) 2 — п 2
= (m-n + p) (mnp) Отв.
Soln: ab 2 -b (ac) -c
= ab 2 -ab + bc-c
= ab (b-1) + c (b-1)
= (b-1) ) (ab + c) Ответ.
Soln: x 2 -2 (x + y) -y 2
= x 2 -y 2 -2 (x + y)
= (x + y) (xy) — 2 (x + y)
= (x + y) (xy-2) Отв.
Солн .: (32) 2 — (28) 2
= (32 + 28) (32-28)
= 60 × 4
= 240 Ответ.
Солн .: (51) 2 — (49) 2
= (51 + 49) (51-49)
= 100 × 2
= 200 Ответ.
Солн .: (101) 2 — (99) 2
= (101 + 99) (101-99)
= 200 × 2
= 400 Ответ.
Солнце: (7.9) 2 — (2.1) 2
= (7.9) 2 — (2.1) 2
= (7,9 +2,1) (7,9-2,1)
= 10,0 × 5,8
= 58 Ans
Солнце: 4x 2 + 9x + 5
= 4x 2 + 5x + 4x + 5
= 4x 2 + 5x + 4x + 5
= x (4x + 5) +1 (4x +5)
= (x + 1) (4x + 5) Ответ.
Soln: 4x 2 -12x + 5
= 4x 2 -10x -2x + 5
= 2x (2x-5) -1 (2x-5)
= (2x-1) (2x -5) Отв.
Soln: p 4 +4
= (p 2 ) 2 +2 2
= (p 2 ) 2 +2.p 2 .2 + 2 2 -4p 2
= (p 2 +2) 2 -4p 2 = (p 2 +2) 2 — (2p ) 2
= (p 2 + 2 + 2p) (p 2 + 2-2p)
= (p 2 + 2p + 2) (p 2 -2p + 2) Ответ
Soln: a 4 +4
= (a 2 ) 2 +2 2
= (a 2 ) 2 +2.a 2 .2 + 2 2 -4a5 2
= (a 2 +2) 2 -4a 2 = (a 2 +2) 2 — (2a ) 2
= (a 2 + 2 + 2a) (a 2 + 2-2a)
= (a 2 + 2a + 2) (a 2 -2a + 2) Ответ
Соотношение и пропорции| Примечания, видео, контроль качества и тесты | 9 класс> Обязательная математика> Алгебра
Соотношение и пропорции
Коэффициент
Отношение двух величин одного типа (пусть a и b) используется для выражения того, во сколько раз больше или меньше одно количество по сравнению с другим.Например, если a = 3 и b = 4, то мы можем написать \ (\ frac {a} {b} \) = \ (\ frac {3} {4} \). Кроме того, мы можем написать a = \ (\ frac {3} {4} \) b или a — это три четверти b. Соотношения 2: 5 и 8:20.
При соотношении a: b или \ (\ frac {a} {b} \) a называется антецедентом, а b называется консеквентом. Отношение b: a является обратным соотношением a: b и наоборот.
Соотношение соединений
Если a: b и c: d — любые два отношения. тогда a: b \ (\ times \) c: d = \ (\ frac {a} {b} \) \ (\ times \) \ (\ frac {c} {d} \) = \ (\ frac { ac} {bd} \) = ac: bd называется составным соотношением.2} \) = a 2 : b 2
И соотношение sup-duplicate \ (\ frac {a} {b} \) = √ \ (\ frac {a} {b} \)
Отношение в трех экземплярах и в трех экземплярах
Если a: b является соотношением, то соотношение в трех экземплярах \ (\ frac {a} {b} \) = (\ (\ frac {a} {b} \)) 3 и дробное соотношение \ (\ frac {a} {b} \) = 3 √ \ (\ frac {a} {b} \)
Пропорции
Аналогично, если два или более двух отношений равны, те количества, которые составляют отношения, пропорциональны.
Два соотношения a: b и c: d равны или \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), тогда a, b, c и d пропорциональны.
Теперь давайте изучим некоторые связанные примеры пропорции.
Пример: \ (\ frac {8} {20} \) = \ (\ frac {2} {5} \)
Или \ (\ frac {20} {8} \) = \ (\ frac {5 \ times 4} {2 \ times 4} \) = \ (\ frac {5} {2} \)
\ (\ следовательно \) \ (\ frac {20} {8} \) = \ (\ frac { 5} {2} \)
Продолжение пропорции
Если a, b и c — любые три числа, так что отношение a и b равно отношению b и c, то такое соотношение известно как a сложная пропорция.
\ (\ следовательно \) \ (\ frac {a} {b} \) = \ (\ frac {b} {c} \) называется непрерывной пропорцией. Тогда ac = b 2
a: b = b: c
Здесь a — 1 st пропорция
b средняя доля
c is 3 rd пропорция
Средняя доля (b) = √ac
Свойства пропорции
Если a, b, c и d пропорциональны, то мы можем проверить следующие шесть свойств пропорции.
- Invertendo
- Alternendo
- Componendo
- Дивидендо
- Componendo и Dividendo
- Приложение
a) Invertendo
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {b} {a} \) = \ (\ frac {d} {c} \) известно как инвертные свойства пропорции.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
Тогда 1 \ (\ div \) \ (\ frac {a} {b} \) = 1 \ (\ div \) \ (\ frac {c} {d} \) (1 делится на оба отношения)
1 \ (\ times \) \ (\ frac {b} {a} \) = 1 \ (\ times \) \ (\ frac {d} {c} \)
\ (\ следовательно \) \ (\ frac {b} {a} \) = \ (\ frac {d} {c} \)
Следовательно, если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {b} {a} \) = \ (\ frac {d } {c} \)
b) Alternendo
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a} {c} \) = \ ( \ frac {b} {d} \) известно как свойство alternendo пропорции.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
Умножая оба значения на \ (\ frac {b} {c} \), получаем \ (\ frac {a} {b} \) \ (\ times \) \ (\ frac {b} {c} \) = \ (\ frac {c} {d} \) \ (\ times \) \ (\ frac {b} {c} \)
или, \ (\ frac {a} {c} \) = \ (\ frac {b} {d} \)
\ (\ следовательно \) \ (\ frac {a} {c} \) = \ (\ frac {b} {d} \)
c) Componendo
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a + b} {b} \) = \ (\ frac {c + d} {d} \) известен как свойство пропорции componendo.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
Затем, прибавив по одной с обеих сторон, получим
\ (\ frac {a} {b} \) + 1 = \ (\ frac {c} {d} \) + 1
\ (\ frac {a + b} {b} \) = \ (\ frac {c + d} {d} \)
Следовательно, если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a + b} {b} \) = \ (\ frac {c + d} {d} \)
d) Дивидендо
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a — b} {b} \) = \ (\ frac {c — d} {d} \) известно как свойство пропорции делимого.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
вычитая 1 с обеих сторон, получаем
\ (\ frac {a} {b} \) — 1 = \ (\ frac {c} {d} \) — 1
или, \ (\ frac {a — b} {b} \) = \ (\ frac {c — d} {d} \)
\ (\ следовательно \) \ (\ frac {a — b} {b} \) = \ (\ frac {c — d} {d} \)
e) Componendo и дивиденды
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a + b} {a — b } \) = \ (\ frac {c + d} {c — d} \) известно как свойство пропорциональности и деления пропорции.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
По compendendo у нас есть,
\ (\ frac {a + b} {b} \) = \ (\ frac {c + d} {d} \) …………….. (1)
Опять же, по дивидендам имеем
\ (\ frac {a — b} {b} \) = \ (\ frac {c — d} {d} \) ……………….. . (2)
Теперь, разделив уравнение (1) на (2), получим
\ (\ frac {\ frac {a + b} b} {\ frac {ab} b} \) = \ (\ frac {\ frac {c + d} d} {\ frac {cd} d} \)
или, \ (\ frac {a + b} {b} \) \ (\ times \) \ (\ frac {b} {a — b} \) = \ (\ frac {c + d} {d} \) \ (\ times \) \ (\ frac {d} {c — d} \)
или, \ (\ frac {a + b} {a — b} \) = \ (\ frac {c + d} {c — d} \)
\ (\ следовательно \) \ (\ frac {a + b} {a — b} \) = \ (\ frac {c + d} {c — d} \)
f) Дополнение
Если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \) = \ (\ frac {a + c} {b + d} \) известно как свойство сложения пропорции.
Проба:
Здесь \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \)
По alternendo получаем,
\ (\ frac {a} {c} \) = \ (\ frac {b} {d} \)
По alternendo получаем,
\ (\ frac {a + c} {c} \) = \ (\ frac {b + d} {d} \)
Опять же, alternendo получаем,
\ (\ frac {a + c} {b + d} \) = \ (\ frac {c} {d} \)
\ (\ следовательно \) \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \) = \ (\ frac {a + c} {b + d} \)
Следовательно, если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \), то \ (\ frac {a} {b} \) = \ (\ frac {c } {d} \) = \ (\ frac {a + c} {b + d} \)
Аналогично, если \ (\ frac {a} {b} \) = \ (\ frac {c} {d} \) = \ (\ frac {e} {f} \), то \ (\ frac {a } {b} \) = \ (\ frac {c} {d} \) = \ (\ frac {e} {f} \) = \ (\ frac {a + c + e} {b + d + f }\) и так далее.
Решение прекращенной и продолжающейся пропорции (k-метод):
Прекращенная доля
Если a, b, c и d прерываются,
Пусть \ (\ frac ab \) = \ (\ frac cd \) = k
Затем,
\ (\ frac ab \) = k,
∴ a = bk ……………….. (i)
\ (\ frac cd \) = k,
∴ c = dk ………………… (ii)
В знаменателе с ‘k’ постоянное число, выразите два числителя.Решаем проблемы, связанные с пропорциями.
Продолжение пропорции
Если a, b, c и d находятся в непрерывной пропорции,
Пусть \ (\ frac ab \) = \ (\ frac bc \) = \ (\ frac cd \) = k
или, \ (\ frac cd \) = k
∴ c = dk ………………. (i)
или, \ (\ frac bc \) = k
∴ b = ck = d.k.k = dk 2 ………….. (II)
или, \ (\ frac ab \) = k,
∴ a = bk = dk 2 .k = dk 3 …………. (iii)
∴ a = dk 3 , b = dk 2 и c = dk
Итак, если a, b, c и d находятся в одинаковых пропорциях, мы выражаем a, b, c через d с константой k и решаем задачу.
Тест по математике для 9 классов
МАТЕМАТИЧЕСКИЙ ТЕСТ 9 КЛАССА
Задача 1:
Что больше ³√3 или ⁵√4
Решение
Задача 2:
Упростить √64 + √2500
Решение
Задача 3:
√3 + √2 и √3 — √2 называются ____________ сердами.
Решение
Проблема 4:
Два набора называются __________________ наборами, если они имеют одинаковое количество элементов.
Решение
Задача 5:
Найдите угол сектора с радиусом 21 см и длиной дуги 66 см.
Решение
Задача 6:
Отношение площади квадранта круга к площади полукруга равно.
Решение
Задача 7:
Найдите площадь заштрихованной части, если радиус круга OA равен 7 см и AB = DC = 7 см.
Решение
Задача 8:
Уравнения
3x-4y = 6, -6x + 8y = -12
имеет ______________ номер решения.
Решение
Задача 9:
Точка совпадения высот треугольника называется ___________.
Решение
Задача 10:
Сумма любых смежных углов параллелограмма равна ________
Решение
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
ответов
1. ³√3 2. 8√2 3. Конъюгат 4. Эквивалент 5. 180 ° | 6. 1: 2 7. 111,56 кв. См 8. бесконечный 9. Ортоцентр 10. 180 ° |
Если у вас есть отзывы о наших математических материалах, напишите нам:
v4formath @ gmail.com
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебра
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование общепринятых единиц словесные задачи
Преобразование метрических единиц текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
Word задачи по типам ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Тригонометрические проблемы со словами
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках 7
13
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
одностадийные задачи с уравнениями со словами
линейные неравенства со словами
Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Домен и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с использованием длинного di видение
L.Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
.