Контрольные работы 10 класс физика кинематика: Контрольная работа в новом формате. Кинематика. 10 класс.

Контрольные тесты по физике на тему «Кинематика» 10 класс

Тест по теме «Кинематика» Вариант 1.

1. Расстояние между начальной и конечной точками — это:

А) путь Б) перемещение В) смещение Г) траектория

2. В каком из следующих случаев движение тела нельзя рассматривать как движение материальной точки?

А) Движение Земли вокруг Солнца. Б) Движение спутника вокруг Земли.

В) Полет самолета из Владивостока в Москву. Г) Вращение детали, обрабатываемой на

станке

3. Какие из перечисленных величин являются скалярными? 
А) перемещение Б) путь В) скорость

4. Что измеряет спидометр автомобиля? 
А) ускорение; Б) модуль мгновенной скорости; 
В) среднюю скорость; Г) перемещение

5. Какая единица времени является основной в Международной системе единиц? 
А) 1час Б) 1 мин В) 1 с Г) 1 сутки.

6. Два автомобиля движутся по прямому шоссе в одном направлении. Если направить ось ОХ вдоль направления движения тел по шоссе, тогда какими будут проекции скоростей автомобилей на ось ОХ? 
А) обе положительные Б) обе отрицательные
В) первого — положительная, второго — отрицательная 
Г) первого — отрицательная, второго – положительная

7. Автомобиль объехал Москву по кольцевой дороге, длина которой 109 км. Чему равны пройденный путь l и перемещение S автомобиля? 
A) l = 109 км; S = 0 Б) l =218км S = 109 км В) l = 218 км; S = 0. Г) l=109км; S=218 км

8. Какой из графиков соответствует равномерному движению? ( Рис. 1).

А) 1 Б) 2 В) 3 Г) 4.

9. Определите путь, пройденный точкой за 5 с. (Рис. 2).

А) 2м Б) 2,5м В) 5м Г) 10м.

10.. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени.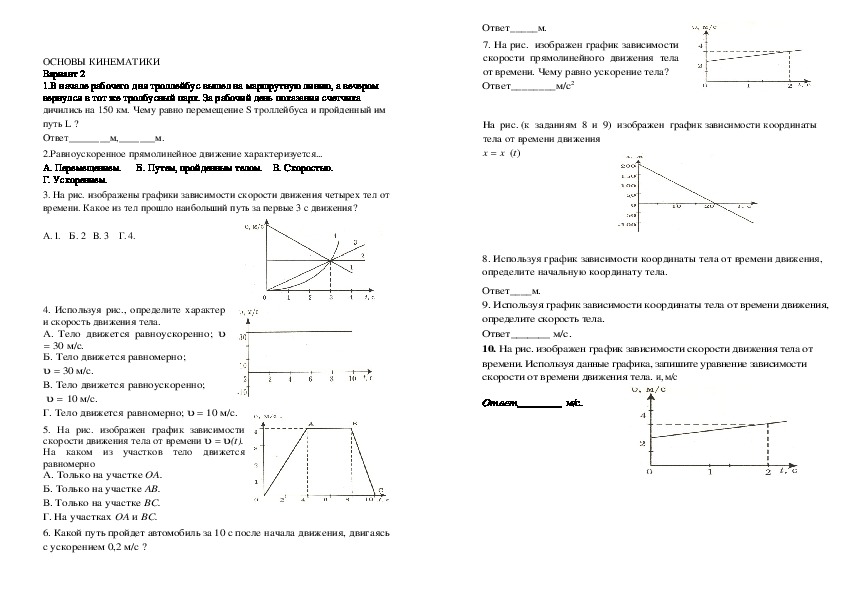 Определить путь, пройденный велосипедистом за интервал времени от t₁ = 1c до t₂ = 3с?

А) 9 м Б) 6 м В) 3 м. Г) 12 м

11. Если ускорение равно 2 м/с², то это:

А) равномерное движение Б) равнозамедленное движение

В) равноускоренное движение Г) прямолинейное

12. Ускорение характеризует изменение вектора скорости

А) по величине и направлению Б) по направлению В) по величине

13. Автомобиль, движущийся прямолинейно равноускоренно, увеличил свою скорость с 
3 м/с до 9 м/с за 6 секунд. С каким ускорением двигался автомобиль? 
А) 0 м/с² Б) 3 м/с² В) 2 м/с² Г) 1 м/с²

14. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с² через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?

А) 15м/с Б) 25м/с В) 10м/с Г) 20м/с.

Тест по теме «Кинематика» Вариант 2.

1. Велосипедист движется из точки А велотрека в точку В по кривой АВ. Назовите 
физическую величину, которую изображает вектор АВ. 
А) путь Б) перемещение В) скорость

2. Почему при расчетах можно считать Луну материальной точкой (относительно Земли)?

А) Луна — шар Б) Луна — спутник Земли В) Масса Луны меньше массы Земли

Г) Расстояние от Земли до Луны во много раз больше радиуса Луны.

3. . Физические величины бывают векторными и скалярными. Какая физическая величина из перечисленных является скалярной? 

А) ускорение Б) время В) скорость Г) перемещение

4. . Какие из перечисленных ниже величин являются векторными: 
1) путь 2) перемещение 3) скорость? 
А) 1 и 2 Б) 2 и 3 В) 2 Г) 3 и 1.

5. Основными единицами длины в СИ являются: 
А) метр Б) километр В) сантиметр Г) миллиметр

6. Два автомобиля движутся по прямому шоссе в противоположных направлении. Если направить ось ОХ вдоль направления движения первого автомобиля по шоссе, тогда какими будут проекции скоростей автомобилей на ось ОХ? 
А) обе положительные Б) обе отрицательные

В) первого — положительная, второго — отрицательная 
Г) первого — отрицательная, второго – положительная

7. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на 
землю. Чему равны путь l и перемещение S за все время его движения? 
A) l = 20 м, S = 0 м Б) l = 10 м, S = 0   B) l = 10 м, S = 20 м Г) l = 20 м, S = 10 м.

8. Какой из графиков соответствует равномерному движению? ( Рис. 1).

А) 3 Б) 4 В) 1 Г) 2

9. Определите путь, пройденный точкой за 3 с. (Рис. 2).

А) 2м Б) 6м В) 5м Г) 1,5м.

10.. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени. Определить путь, пройденный велосипедистом за интервал времени от t

1 = 2c до t₂ = 4с?

А) 9 м Б) 6 м В) 3 м. Г) 12 м

11. Если ускорение равно -3м/с², то это:

А) равномерное движение Б) равноускоренное движение

В) равнозамедленное движение Г) прямолинейное движение

12. Автомобиль трогается с места и движется с возрастающей скоростью прямолинейно. 
Какое направление имеет вектор ускорения? 
А) ускорение равно 0 Б) направлен против движения автомобиля
В) направлен в сторону движения автомобиля

13. Скорость автомобиля за 20с уменьшилась с 20м/с до 10м/с. С каким средним ускорением двигался автомобиль?

А) 0,5м/с² Б) 5м/с² В) -5м/с² Г) -0,5м/с²

14. Определить скорость тела при торможении с ускорением 0,2м/с² через 30с от начала движения, если начальная скорость его была равна 2м/с.

А) -4м Б) 4 м В) -6м Г) 8м.

Ответы

Вариант 1 Вариант 2

1 –б 1 -б

2 — г 2 – г

3 – а 3 – б

4 – б 4 – в

5 – в 5 – а

6 – а 6 – в

7 – в 7 – а

8 – б 8 – г

9 – г 9 – б

10 – б 10 – б

11 – в 11 – в

12 – а 12 – в

13 – г 13 – г

14 – б 14- а

1. Тело двигается вдоль оси x декартовой системы координат со скоростью 3 м/с и одновременно вдоль оси y со скоростью 4 м/с. Найти результирующую скорость.
   5 м/с;
   7 м/с;
   1 м/с.

1.13. Автомобиль трогается с места и движется с возрастающей скоростью прямолинейно. 
Какое направление имеет вектор ускорения? 
А) ускорение равно 0; Б) направлен против движения автомобиля; 
В) направлен в сторону движения автомобиля.

1.14. Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет 
вектор ускорения? 
А) ускорение равно 0; Б) направлен против движения автомобиля; 
В) направлен в сторону движения автомобиля.

1.16. Физические величины бывают векторными и скалярными. Какая физическая величина из перечисленных является скалярной? 
А) ускорение; Б) время; В) скорость; Г) перемещение.

1.18. Основными единицами длины в СИ являются: 
А) километр; Б) метр; В) сантиметр; Г) миллиметр.

1.19. Какие из перечисленных ниже величин являются векторными: 
1) путь, 2) перемещение, 3) скорость? 
А) 1 и 2; Б) 2; В) 2 и 3; Г) 3 и 1.

1.22. Двигаясь прямолинейно, одно тело за каждую секунду проходит путь 5 м, другое тело — за каждую секунду 10 м. Движения этих тел являются: 
А) равномерными; Б) неравномерными; 
В) первого неравномерным, второго равномерным; 
Г) первого равномерным, второго неравномерным

1 25. Модуль скорости тела за каждую секунду увеличивался в 2 раза. Какое утверждение будет правильным? 
А) ускорение уменьшалось в 2 раза; Б) ускорение не изменялось; 
В) ускорение увеличивалось в 2 раза

1.26. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на 
землю. Чему равны путь l и перемещение S за все время его движения? 
A) l = 10 м, S = 0 м; Б) l = 20 м, S = 0; 

B) l = 10 м, S = 20 м; Г) l = 20 м, S = 10 м.

1.35. При отходе от станции ускорение поезда составляет 1 м/с2. Какой путь проходит поезд за 10 с? 
А) 5 м; Б) 10 м; В) 50 м; Г) 100 м.

1.36. При равноускоренном движении в течение 5 с автомобиль увеличил скорость от 10 до 
15 м/с. Чему равен модуль ускорения автомобиля? 
А) 1 м/с2; Б) 2 м/с2; В) 3 м/с2; Г) 5 м/с2.

1.55. Какая из приведенных функций (v(t)) описывает зависимость модуля скорости от 
времени при равномерном прямолинейном движении тела вдоль оси ОХ со скоростью 5 м/с? 

A) v = 5t; Б) v = t; B) v = 5; Г) v = -5.

1.65. Находящемуся на горизонтальной поверхности стола бруску сообщили скорость 5 м/с. Под действием сил трения брусок движется с ускорением 1 м/с2. Чему равен путь, пройденный бруском за 6 секунд? 
А) 48 м; Б) 12 м; В) 40 м; Г) 30 м.

13. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени. Определить путь, пройденный велосипедистом за интервал времени от t₁ = 1c до t₂ = 4с?

А) 15 м. Б) 3 м. В) 12 м. Г) 9 м. Д) 20 м.

14. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени.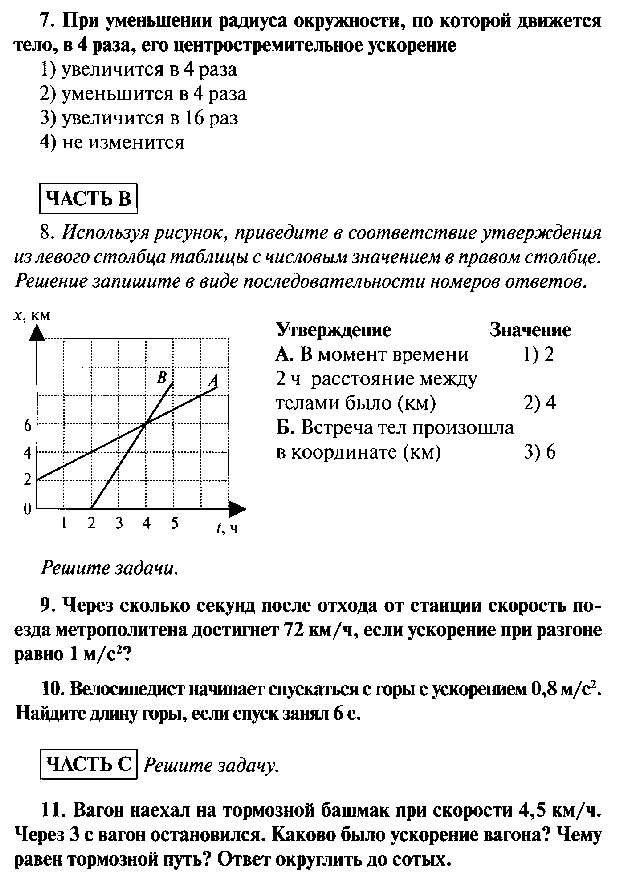 Определить скорость движения велосипедиста в момент времени t = 2c.

А) 2 м/с. Б) 6 м/с. В) 3 м/с. Г) 12 м/с. Д) 8 м/с.

18. Тело движется прямолинейно и уменьшает скорость. Куда направлено ускорение?

А) По ходу движения. Б) По нормали. В) Против движения. Г) По радиусу — вектору к данной точке траектории. Д) По касательной к траектории

20. Почему при расчетах можно считать Луну материальной точкой (относительно Земли)?

А) Луна — шар. Б) Луна — спутник Земли. В) Масса Луны меньше массы Земли.

Г) Расстояние от Земли до Луны во много раз больше радиуса Луны.

Д) Среди предложенных ответов нет правильного.

Скорость автомобиля за 20 с уменьшилась с 20 м/с до 10 м/с. С каким средним ускорением двигался автомобиль?   [−0,5 м/с²]

Контрольная работа «Кинематика» (профильный уровень) 10 класс

ВАРИАНТ 1

1. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем за 5 с.

2. Тело свободно падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения? Сопротивлением воздуха пренебречь.

3.

4. Тело, свободно падающее с некоторой высоты без начальной скорости, за время τ = 1 с после начала движения проходит путь в n = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

5. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

ВАРИАНТ 2

1. Тело движется вдоль оси Ох, причем проекция скорости _x меняется с течением времени по закону, приведенному на графике. Какой путь прошло тело за время от 4 до 16 с?

2. Поезд, двигаясь под уклон, прошел за 20 с путь 340 м и развил скорость 19 м/с. С каким ускорением двигался поезд и какова была скорость в начале уклона?

3. Мимо остановки по прямой улице с постоянной скоростью проезжает грузовик. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с ускорением 3 м/с², и догоняет грузовик на расстоянии 150 м от остановки. Какова скорость грузовика?

4. В последнюю секунду свободного падения тело прошло путь, в n = 2 раза больший, чем в предыдущую. Найдите полное время падения t, если начальная скорость тела равна нулю.

5. Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями α=30⁰. Маленькая шайба начинает движение вверх по наклонной плоскости из точки А с начальной скоростью υ₀ под углом β=60⁰ к прямой АВ. В ходе движения шайба съезжает на прямую АВ в точке В. Найдите υ₀, если АВ=1 м. Трением между шайбой и наклонной плоскостью пренебречь.

ВАРИАНТ 3

1. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем за 5 с.

2. Тело брошено вертикально вверх с высоты 20 м с начальной скоростью 3 м/с. На какой высоте окажется тело через 2 с после начала движения?

3. Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением, и догоняет грузовик на расстоянии 150 м от остановки. Каково ускорение мотоциклиста?

4. За последнюю секунду движения свободно падающее тело прошло своего пути. Найдите полное время падения, если начальная скорость равна нулю.

5. Мяч бросают горизонтально с высоты 1,25 м по направлению к вертикальной стене, находящейся на расстоянии 2,5 м от точки бросания. Какова должна быть начальная скорость мяча, чтобы после упругого удара о стену он приземлился под точкой бросания (см. рисунок)?

ВАРИАНТ 4

1. Первые 20 с лодка двигалась по течению реки, а затем – против течения. На всем пути модуль скорости лодки относительно воды оставался неизменным. График изменения координаты лодки относительно берега приведён на рисунке. Чему равна скорость течения реки?

2. Тело падает вертикально вниз с высоты 20м без начальной скорости. Определить путь, пройденный телом за последнюю секунду падения.

3. Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через некоторое время τ от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением 3 м/с². Он догоняет грузовик на расстоянии 150 м от остановки. Чему равно τ?

4. Тело, свободно падающее с некоторой высоты из состояния покоя, первый участок пути проходит за время τ=1 с, а такой же последний – за время τ. Найти полное время падения t, если начальная скорость равна нулю.

5. С отвесной скалы высотой H=10 м в горизонтальном направлении бросают камень с начальной скоростью υ₀. Одновременно с поверхности Земли под углом α=60⁰ к горизонту на встречу камень бросают мячик с той же начальной скоростью υ₀ (см. рисунок). В полете мячик столкнулся с камнем в воздухе. Определите на каком расстоянии L от скалы бросили мячик. Сопротивлением воздуха пренебречь.

Контрольная работа по теме Кинематика 10 класс

Контрольная работа по теме Кинематика для учащихся 10 класса с ответами. Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий.

1 вариант

A1. Какое тело, из перечисленных ниже, оставляет видимую траекторию?

1) Камень, падающий в горах
2) Мяч во время игры
3) Лыжник, прокладывающий новую трассу
4) Легкоатлет, совершающий прыжок в высоту

А2. Материальная точка, двигаясь прямолинейно, перемес­тилась из точки с координатами (-2; 3) в точку с коор­динатами (1; 7). Определите проекции вектора переме­щения на оси координат.

1) 3 м; 4 м
2) -3 м; 4 м
3) 3 м; -4 м
4) -3 м; -4 м

А3. Во время подъема в гору скорость велосипедиста, дви­гающегося прямолинейно и равноускоренно, изменилась за 8 с от 5 м/с до 3 м/с. При этом ускорение велосипеди­ста было равно

1) -0,25 м/с²
2) 0,25 м/с²
3) -0,9 м/с²
4) 0,9 м/с²

А4. При прямолинейном равноускоренном движении с на­чальной скоростью, равной нулю, путь, пройденный те­лом за три секунды от начала движения, больше пути, пройденного за первую секунду, в

1) 2 раза
2) 3 раза
3) 4 раза
4) 9 раз

А5.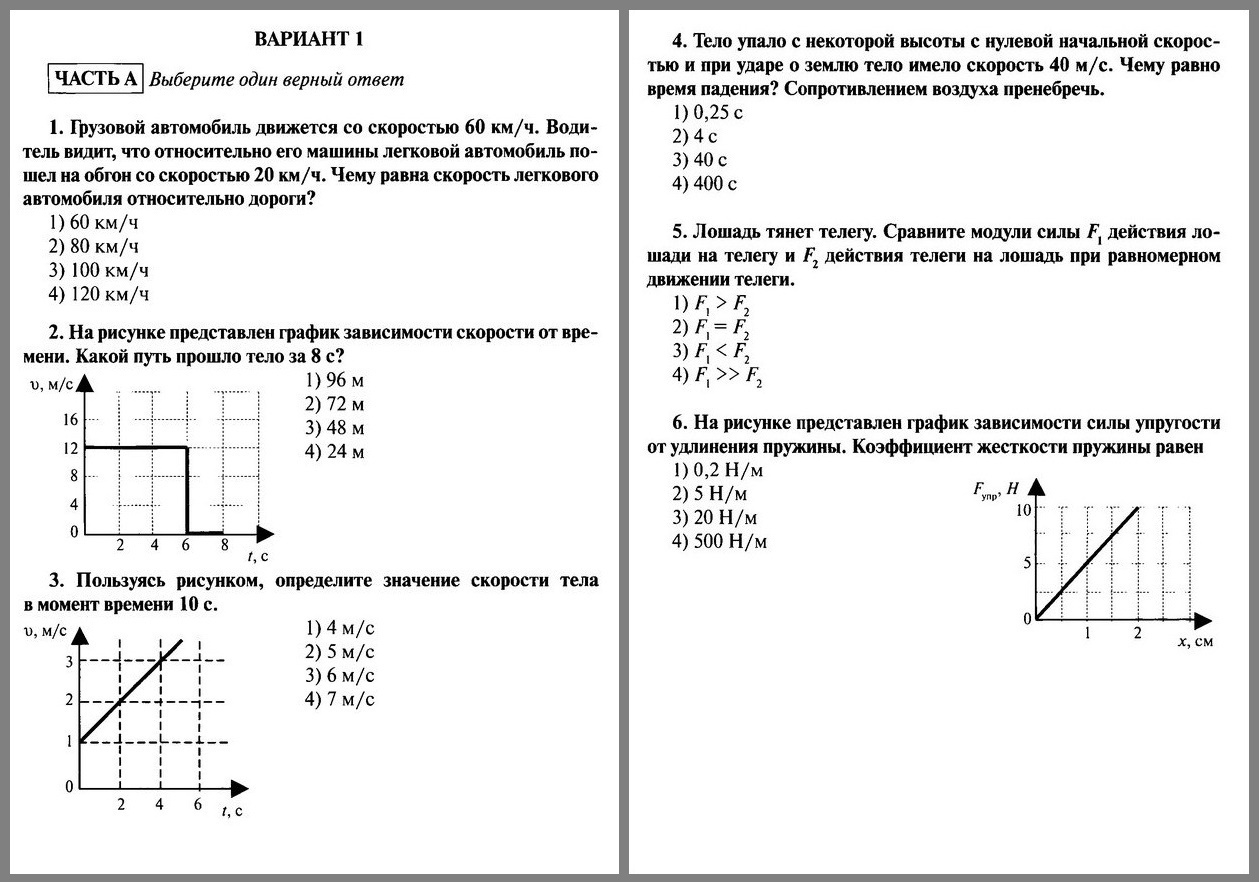 На графике изображена зависи­мость проекции скорости тела, движущегося вдоль оси ОХ, от времени.

Какое перемещение совершило тело к моменту времени t = 5 с?

1) 2 м
2) 6 м
3) 8 м
4) 10 м

B1. Вагон шириной 2,4 м, движущийся со скоростью 15 м/с, был пробит пулей, летевшей перпендикулярно к направлению движения вагона. Смещение отверстий в стенах вагона относительно друг друга 6 см. Найдите скорость пули.

В2. Два шкива разного радиуса со­единены ременной передачей и приведены во вращательное движение (см. рис.).

Как изменяются перечисленные в первом столбце физические величины при пере­ходе от точки А к точке В, если ремень не проскальзывает?

Физические величины

А) линейная скорость
Б) период вращения
В) угловая скорость

Их изменение

1) увеличится
2) уменьшится
3) не изменится

C1. В течение 20 с ракета поднимается с постоянным уско­рением 8 м/с², после чего двигатели ракеты выключаются. На какой максимальной высоте побывала ракета?

2 вариант

A1. Исследуется перемещение лошади и бабочки. Модель ма­териальной точки может использоваться для описания движения

1) только лошади
2) только бабочки
3) и лошади, и бабочки
4) ни лошади, ни бабочки

А2. В трубопроводе с площадью поперечного сечения 100 см² нефть движется со скоростью 1 м/с. Какой объем нефти проходит по трубопроводу в течение 10 мин?

1) 0,1 м³
2) 0,6 м³
3) 6 м³
4) 60 м³

А3. Автомобиль движется по шоссе с постоянной скоростью и начинает разгоняться. Проекция ускорения на ось, направленную по вектору начальной скорости автомо­биля

1) отрицательна
2) положительна
3) равна нулю
4) может быть любой по знаку

А4. Каретка спускается по наклонной плоскости, длиной 15 см в течение 0,26 с. Определите ускорение каретки, если движение начинается из состояния покоя.

1) 1,7 м/с²
2) 2,2 м/с²
3) 4,4 м/с²
4) 6,2 м/с²

А5. На рисунке представлен график зависимости пути s велосипедиста от времени t. В каком интервале времени велосипедист не двигался?

1) От 0 с до 1 с
2) От 1 с до 3 с
3) От 3 с до 5 с
4) От 5 с и далее

B1. На пути 60 м скорость тела уменьшилась в три раза за 20 с. Определите скорость тела в конце пути, считая ус­корение постоянным.

B2. На поверхность диска с центром в точке О нанесли две точки А и В (причем ОВ = ВА), и привели диск во вращение с постоянной линей­ной скоростью (см. рис.).

Как из­менятся перечисленные в первом столбце физические величины при переходе от точки А к точке В?

Физические величины

А) угловая скорость
Б) период обращения по окружности
В) центростремительное ускорение

Их изменения

1) увеличится
2) уменьшится
3) не изменится

C1. Аэростат поднимается с Земли с ускорением 2 м/с² вер­тикально вверх без начальной скорости. Через 20 с после начала движения из него выпал предмет. Определите, на какой наибольшей высоте относительно Земли побывал предмет.

3 вариант

A1. Решаются две задачи:

А) рассчитывается скорость погружения подводной лодки;
Б) рассчитывается время движения лодки от одной военной базы до другой.

В каком случае подводную лодку можно рассматривать как материальную точку?

1) Только в первом
2) Только во втором
3) В обоих случаях
4) Ни в первом, ни во втором

А2. Материальная точка, двигаясь прямолинейно, перемес­тилась из точки с координатами (-2; 3) в точку с коор­динатами (1; 7). Определите модуль вектора перемеще­ния на оси координат.

1) 1 м
2) 2 м
3) 5 м
4) 7 м

А3. Санки съехали с одной горки и въехали на другую. Во время подъема на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 43,2 км/ч до 7,2 км/ч. При этом модуль ускорения был равен

1) -2,5 м/с²
2) 2,5 м/с²
3) -3,5 м/с²
4) 3,5 м/с²

А4. К.Э. Циолковский в книге «Вне Земли», описывая по­лет ракеты, отмечал, что через 8 с после старта ракета находилась на расстоянии 3,2 км от поверхности Земли. С каким ускорением двигалась ракета?

1) 1000 м/с²
2) 500 м/с²
3) 100 м/с²
4) 50 м/с²

А5. По графику зависимости модуля скорости от времени определите путь, пройденный телом за 20 с.

1) 60 м
2) 80 м
3) 50 м
4) 40 м

В1. Охотник стреляет в птицу, летящую на расстоянии 36 м от него со скоростью 15 м/с в направлении перпендику­лярном линии прицеливания. Какой путь пролетит пти­ца от момента выстрела до попадания в нее дроби, если скорость дроби при вылете из ружья 400 м/с?

В2. Два шкива разного радиуса соеди­нены ременной передачей и при­ведены во вращательное движение (см. рис.).

Как изменяются пере­численные в первом столбце фи­зические величины при переходе от точки В к точке А, если ремень не проскальзывает?

Физические величины

А) линейная скорость
Б) период вращения
В) угловая скорость

Их изменение

1) увеличится
2) уменьшится
3) не изменится

С1. В течение 20 с ракета поднимается с постоянным уско­рением 8 м/с² после чего двигатели ракеты выключаются. Через какое время после этого ракета упадет на Землю?

4 вариант

А1. Какое тело из перечисленных ниже двигается прямоли­нейно?

1) Конец минутной стрелки
2) Автомобиль на крутом вираже
3) Мальчик на качелях
4) Взлетающая ракета

А2. Поезд длиной 350 м двигается равномерно со скоростью 15 м/с. Он проходит мост за 2 мин. Определите длину моста.

1) 335 м
2) 550 м
3) 1235 м
4) 1450 м

А3. Шарик скатывается по наклонному прямому желобу с постоянным ускорением, по модулю равным 2 м/с². 3а 3 с скорость шарика увеличивается на

1) 1,5 км/ч
2) 5,4 км/ч
3) 6,0 км/ч
4) 21,6 км/ч

А4. Гору длиной 50 м лыжник прошел за 10 с, двигаясь с ускорением 0,4 м/с². Чему равна скорость лыжника в начале и в конце горы?

1) 3 м/с и 6 м/с
2) 2 м/с и 8 м/с
3) 4 м/с и 7 м/с
4) 3 м/с и 7 м/с

А5. На рисунке приведен гра­фик зависимости проекции скорости тела от времени.

Проекция ускорения тела в интервале времени от 8 до 12 с представлена графиком

B1. Скорость материальной точки на пути 60 м увеличилась в 5 раз за 10 с. Определите ускорение тела, считая его постоянным.

В2. На поверхность диска с центром в точке О нанесли две точки А и В (причем ОВ = ВА), и привели диск во вращение с постоянной линей­ной скоростью (см. рис.).

Как из­менятся перечисленные в первом столбце физические величины при переходе от точки В к точке А?

Физические величины

А) угловая скорость
Б) период обращения по окружности
В) центростремительное ускорение

Их изменение

1) увеличится
2) уменьшится
3) не изменится

5 вариант

A1. Можно ли линейку принять за материальную точку?

1) Только при ее вращательном движении
2) Только при ее поступательном движении
3) Только при ее колебательном движении
4) Можно при любом ее движении

А2. Расход воды в канале за минуту составляет 16,2 м³ Ши­рина канала 1,5 м и глубина воды 0,6 м. Определите скорость воды.

1) 0,1 м/с
2) 0,2 м/с
3) 0,3 м/с
4) 18 м/с

А3. Легковой и грузовой автомобили одновременно начинают движение из состояния покоя. Ускорение легкового ав­томобиля в 4 раза больше, чем у грузового. Во сколько раз большую скорость разовьет легковой автомобиль за то же время?

1) В 2 раза
2) В 4 раза
3) В 8 раз
4) В 16 раз

А4. Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Определите примерно уско­рение пули внутри ствола, если считать ее движение рав­ноускоренным.

1) 312,5 км/с²
2) 114 км/с²
3) 1248 м/с²
4) 100 м/с²

А5. Тело, двигаясь вдоль оси ОХ прямолинейно и равноус­коренно, за некоторое время уменьшило свою скорость в 2 раза. Какой из графиков зависимости проекции уско­рения от времени соответствует такому движению?

B1. Аварийное торможение автомобиля заняло 4 с и происходило с постоянным ускорением 4 м/с². Найдите тормозной путь.

В2. Два шкива разного радиуса со­единены ременной передачей и приведены во вращательное дви­жение (см. рис.).

Как изменяются перечисленные в первом столбце физические величины при пере­ходе от точки А к точке В, если ремень не проскальзывает?

Физические величины

А) линейная скорость
Б) частота
В) угловая скорость

Их изменение

1) увеличится
2) уменьшится
3) не изменится

C1. Аэростат поднимается с Земли с ускорением 2 м/с² вер­тикально вверх без начальной скорости. Через 10 с после начала движения из него выпал предмет. Определите, через какое время после своего падения предмет окажется на высоте 75 м относительно Земли?

Ответы на контрольную работу по теме Кинематика 10 класс
1 вариант
А1-3
А2-1
А3-1
А4-4
А5-1
В1-600 м/с
В2-312
С1-2880 м
2 вариант
А1-3
А2-3
А3-2
А4-3
А5-3
В1-1,5 м/с
В2-332
С1-480 м
3 вариант
А1-2
А2-3
А3-2
А4-3
А5-1
В1-1,35 м
В2-321
С1-40 с
4 вариант
А1-4
А2-4
А3-4
А4-4
А5-3
В1-0,8 м/с²
В2-331
С1-8,37 с
5 вариант
А1-2
А2-3
А3-2
А4-1
А5-4
В1-32 м
В2-322
С1-5 с

Контрольная работа по физике Кинематика 9 класс

Контрольная работа по физике Кинематика Законы взаимодействия и движения тел 9 класс с ответами. Работа состоит из 4 вариантов в каждом варианте по 9 заданий.

1 вариант

1. Исследуется перемещение слона и мухи. Модель мате­риальной точки может использоваться для описания движения

1) только слона
2) только мухи
3) и слона, и мухи в разных исследованиях
4) ни слона, ни мухи, поскольку это живые существа

2. Вертолёт Ми-8 достигает скорости 250 км/ч. Какое время он затратит на перелёт между двумя населённы­ми пунктами, расположенными на расстоянии 100 км?

1) 0,25 с
2) 0,4 с
3) 2,5 с
4) 1440 с

3. На рисунках представлены графики зависимости коор­динаты от времени для четырёх тел, движущихся вдоль оси ОХ. Какое из тел движется с наибольшей по моду­лю скоростью?

4. Велосипедист съезжает с горки, двигаясь прямоли­нейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение ве­лосипедиста 0,5 м/с². Сколько времени длится спуск?

1) 0,05 с
2) 2 с
3) 5 с
4) 20 с

5. Лыжник съехал с горки за 6 с, двигаясь с постоянным ускорением 0,5 м/с². Определите длину горки, если из­вестно, что в начале спуска скорость лыжника была равна 18 км/ч.

1) 39 м
2) 108 м
3) 117 м
4) 300 м

6. Моторная лодка движется по течению реки со скоро­стью 5 м/с относительно берега, а в стоячей воде — со скоростью 3 м/с. Чему равна скорость течения реки?

1) 1 м/с
2) 1,5 м/с
3) 2 м/с
4) 3,5 м/с

7. Установите соответствие между физическими величи­нами и формулами, по которым эти величины опреде­ляются.

Физические величины

А) Ускорение
Б) Скорость при равномер­ном прямолинейном движении
В) Проекция перемещения при равноускоренном прямолинейном движе­нии

Формулы

8. На пути 60 м скорость тела уменьшилась в 3 раза за 20 с. Определите скорость тела в конце пути, считая ус­корение постоянным.

9. Из населённых пунктов А и В, расположенных вдоль шоссе на расстоянии 3 км друг от друга, в одном на­правлении одновременно начали движение велосипедист и пешеход. Велосипедист движется из пункта А со ско­ростью 15 км/ч, а пешеход со скоростью 5 км/ч. Опре­делите, на каком расстоянии от пункта А велосипедист догонит пешехода.

2 вариант

1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Пути, пройденные этими телами, отличаются на

1) 5 м
2) 20 м
3) 10м
4) 30 м

2. За 6 минут равномерного движения мотоциклист про­ехал 3,6 км. Скорость мотоциклиста равна

1) 0,6 м/с
2) 10 м/с
3) 15 м/с
4) 600 м/с

3. На рисунках представлены графики зависимости про­екции перемещения от времени для четырёх тел. Какое из тел движется с наибольшей по модулю скоростью?

4. Во время подъёма в гору скорость велосипедиста, дви­гающегося прямолинейно и равноускоренно, изменилась за 8 с от 18 км/ч до 10,8 км/ч. При этом ускорение ве­лосипедиста было равно

1) -0,25 м/с²
2) 0,25 м/с²
3) -0,9 м/с²
4) 0,9 м/с²

5. Аварийное торможение автомобиля происходило в тече­ние 4 с. Определите, каким был тормозной путь, если начальная скорость автомобиля 90 км/ч.

1) 22,5 м
2) 45 м
3) 50 м
4) 360 м

6. Пловец плывёт по течению реки. Определите скорость пловца относительно берега, если скорость пловца от­носительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

1) 0,5 м/с
2) 0,1 м/с
3) 0,5 м/с
4) 0,7 м/с

7. Установите соответствие между физическими величи­нами и их единицами измерения в СИ.

Физические величины

А) скорость
Б) ускорение
В) время

Единицы измерения СИ

1) мин
2) км/ч
3) м/с
4) с
5) м/с²

8. Поезд начинает равноускоренное движение из состоя­ния покоя и проходит за четвёртую секунду 7 м. Какой путь пройдёт тело за первые 10 с?

9. Катер, переправляясь через реку шириной 800 м, дви­гался перпендикулярно течению реки со скоростью 4 м/с в системе отсчёта, связанной с водой.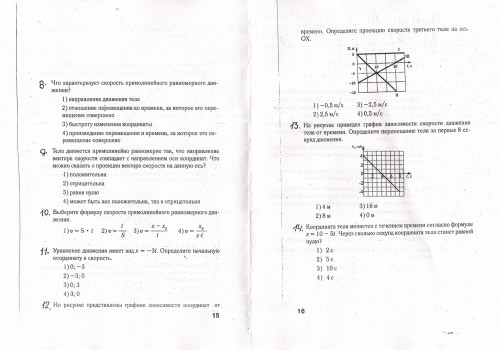 На сколько будет снесён катер течением, если скорость течения реки 1,5 м/с?

3 вариант

1. Решаются две задачи:

А: рассчитывается маневр стыковки двух космических кораблей;
Б: рассчитываются периоды обращения космических кораблей вокруг Земли.

В каком случае космические корабли можно рассмат­ривать как материальные точки?

1) Только А
2) Только Б
3) И А, и Б
4) Ни А, ни Б

2. Средняя скорость поезда метрополитена 40 м/ с. Время движения между двумя станциями 4 минуты. Опреде­лите, на каком расстоянии находятся эти станции.

1) 160 м
2) 1000 м
3) 1600 м
4) 9600 м

3. На рисунках представлены графики зависимости про­екции скорости от времени для четырёх тел, движу­щихся вдоль оси ОХ. Какое из тел движется с постоян­ной скоростью?

4. Ускорение велосипедиста на одном из спусков трассы равно 1,2 м/с² На этом спуске его скорость увеличилась на 18 м/с.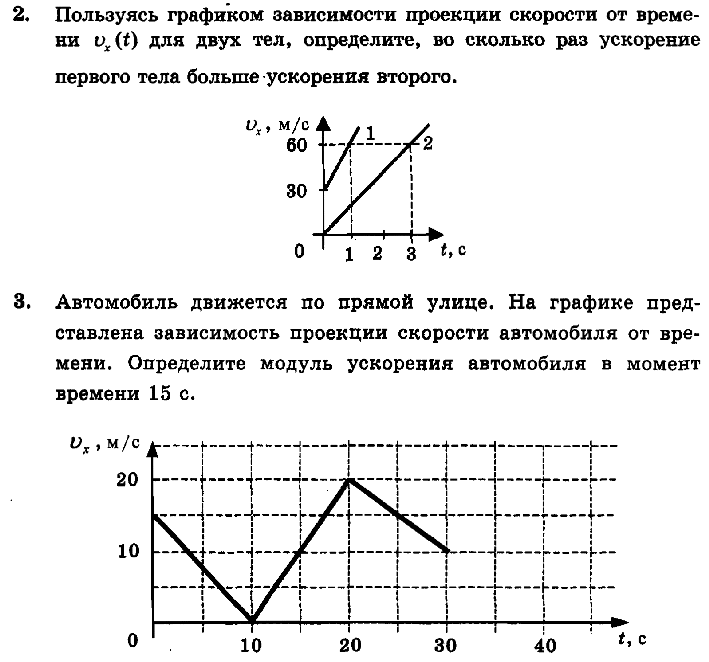 Велосипедист спускается с горки за

1) 0,07 с
2) 7,5 с
3) 15 с
4) 21,6 с

5. Какое расстояние пройдёт автомобиль до полной останов­ки, если шофёр резко тормозит при скорости 72 км/ч, а от начала торможения до остановки проходит 6 с?

1) 36 м
2) 60 м
3) 216 м
4) 432 м

6. Катер движется по течению реки со скоростью 11 м/с относительно берега, а в стоячей воде — со скоростью 8 м/с. Чему равна скорость течения реки?

1) 1 м/с
2) 1,5 м/с
3) 3 м/с
4) 13 м/с

7. Установите соответствие между физическими величи­нами и формулами, по которым эти величины определяются.

Физические величины

А) Проекция ускорения
Б) Проекция перемещения при равномерном прямолинейном движении
В) Проекция скорости при равноускоренном прямолинейном движении

Формулы

8. Скорость материальной точки на пути 60 м увеличи­лась в 5 раз за 10 с. Определить ускорение, считая его постоянным.

9. Товарный поезд едет со скоростью 36 км/ч. Спустя 30 минут с той же станции по тому же направлению выходит экспресс со скоростью 144 км/ч. На каком рас­стоянии от станции экспресс догонит товарный поезд?

4 вариант

1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Перемещения этих тел соответственно равны

1) 10 м, 20 м
2) 20 м, 40 м
3) Ом, Ом
4) Ом, 20 м

2. Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна

1) 12 км/ч
2) 24 км/ч
3) 36 км/ч
4) 60 км/ч

3. На рисунках представлены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?

4. Санки съехали с одной горки и въехали на другую. Во время подъёма на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с, при этом модуль ускорения был равен

1) -2,5 м/с²
2) 2,5 м/с²
3) -3,5 м/с²
4) 3,5 м/с²

5. При равноускоренном прямолинейном движении ско­рость катера увеличилась за 10 с от 5 м/с до 9 м/с. Ка­кой путь пройден катером за это время?

1) 50 м
2) 70 м
3) 80 м
4) 90 м

6. Пловец плывёт против течения реки. Определите скорость пловца относительно берега, если скорость пловца относи­тельно воды 0,4 м/с, а скорость течения реки 0,3 м/с.

1) 0,1 м/с
2) 0,2 м/с
3) 0,5 м/с
4) 0,7 м/с

7. Установите соответствие между физическими величи­нами и их единицами измерения в СИ.

Физические величины

А) перемещение
Б) скорость
В) время

Единицы измерения СИ

1) мин
2) км/ч
3) м/с
4) с
5) м

8. Тело, двигаясь равноускоренно, в течение пятой секун­ды от начала движения прошло путь 45 м. Какой путь оно пройдёт за 8 с от начала движения?

9. Пловец пересекает реку шириной 240 м. Скорость тече­ния реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направлена перпендикулярно к вектору тече­ния. На сколько метров пловец будет снесён течением к тому моменту, когда он достигнет противоположного берега?

Ответы на контрольную работу по физике Кинематика
1 вариант
1-3, 2-4, 3-4, 4-4, 5-1, 6-3, 7-425, 8-1,5 м/с, 9-4,5 км
2 вариант
1-2, 2-2, 3-3, 4-1, 5-3, 6-4, 7-354, 8-100 м, 9-300 м
3 вариант
1-2, 2-4, 3-1, 4-3, 5-2, 6-3, 7-431, 8-0,8 м/с², 9-24 км
4 вариант
1-3, 2-3, 3-4, 4-2, 5-2, 6-1, 7-534, 8-320 м, 9-192 м

Контрольная работа по физике в 10 классе (профильный уровень) «Основы кинематики»

Вариант 1.

1. Тело движется согласно уравнению х = At + Bt², где А = 4 м/с, В = — 0,05 м/с², t — время в секундах. Определить момент времени, в который скорость точки равна нулю.

2. Сосулька падает с крыши дома. Первую половину пути она пролетела за 1 с. Сколько времени ей осталось лететь?

3. Шкив трансмиссионного вала имеет диаметр 1 м. Сколько оборотов в минуту делает вал, если скорость ремня, охватывающего шкив, 6,28 м/с? Скольжением ремня пренебречь.

4. Из винтовки произведен выстрел в горизонтальном направлении с высоты 4 м над землей. Определить дальность и время полета, если скорость пули 100м/с.

5. Два тела были брошены с земли с одинаковыми по модулю начальными скоростями. Первое тело было брошено под углом 30⁰ к горизонту, второе — под углом 60⁰ к горизонту. Дальность полета первого тела S₁ = 24 м. Чему равна дальность полета второго тела

Вариант 4.

1. Материальная точка движется вдоль оси ОХ по закону: х = А+ Сt + Bt², где А = 7 м, В = 3 м/с², С = 0,5 м/с, t — время в секундах. Определить координату точки в тот момент, когда скорость точки будет равна нулю.

2. Тело, брошено вертикально вверх со скоростью 50 м/с. Какой путь пройдет тело за 4 с?

3. Линейная скорость точек на окружности колеса 10 м/с, а точек, находящихся на 20 см ближе к центру, — 5 м/с. Сколько оборотов за 6,28 с сделает колесо?

4. Пуля вылетает из орудия в горизонтальном положении со скоростью 1000м/с. Определить насколько сместится пуля в вертикальном направлении, если мишень находится на расстоянии 750м.

5. Мяч брошен с поверхности земли под углом 30⁰ к горизонту с начальной скоростью 20 м/с.

Сколько секунд длился полет мяча до его удара о землю и какова дальность полета?

Вариант 10.

1. Материальная точка движется по прямой со скоростью, проекция которой равна V_x = At + В м/с, где А = 4 м/с² В = — 2 м/с, t — время в секундах. Определить величину перемещения точки в интервале времени от t₁ = 1 с до t₂ = 3 с.

2. Мяч брошен вертикально вверх с начальной скоростью 30 м/с. Какой путь он пролетит за 4с.

3. При равномерном движении по окружности тело проходит 5 м за 2 с. Определить величину центростремительного ускорения тела, если период обращения равен 5 с.

4. Пуля вылетает из орудия в горизонтальном положении со скоростью 200м/с. Определить насколько сместится пуля в вертикальном направлении, если мишень находится на расстоянии 350м.

5. Два тела были брошены с земли с одинаковыми по модулю начальными скоростями. Первое тело было брошено под углом 30⁰ к горизонту, второе — под углом 45⁰ к горизонту. Дальность полета первого тела S₁ = 36 м. Чему равна дальность полета второго тела

Вариант 15.

1. Тело движется прямолинейно с ускорением 4 м/с². Начальная скорость равна 14 м/с. Какой путь проходит тело за третью секунду движения ?

2. Над колодцем глубиной 20 м бросают вертикально вверх камень со скоростью 15 м/с. Через сколько секунд он достигнет дна колодца.

3. Турбина имеет диаметр рабочего колеса 9 м и совершает 60 оборотов за 62,8 с. Определить линейную скорость концов лопаток турбины.

4. С какой скоростью надо бросить тело горизонтально с некоторой высоты, чтобы дальность полета равнялась высоте с которой брошено тело.

5.  Стрела, выпущенная с ровной горизонтальной поверхности земли под углом к горизонту, упала обратно на землю в 40 м от места выстрела. Чему равна скорость стрелы через 1с после выстрела, если в этот момент она была направлена горизонтально.

Вариант 2.

1. Самолет затрачивает на разбег 24 с. Рассчитать длину разбега самолета, если на половине длины разбега самолет имел скорость, равную 30 м/с. Движение самолета считать равноускоренным.

2. Тело брошено вертикально вверх со скоростью 30 м/с. За какое время оно пролетит 50 м?

3. Период вращения первого колеса вдвое меньше периода вращения второго колеса, а радиус первого колеса в 6 раз больше радиуса второго колеса. Во сколько раз центростремительное ускорение точек, лежащих на ободе первого колеса, больше центростремительного ускорения точек, лежащих на ободе второго колеса?

4. Мальчик бросил мячик горизонтально с высоты 20 м. С какой скоростью был брошен мяч и сколько он находился в полете если он упал на расстоянии 6м.

5. Тело брошено под углом 30 градусов к горизонту со скоростью 30 м/с. Определить минимальную скорость за все время движения.

Вариант 3.

1. Длина ствола винтовки 90 см. Скорость пули при вылете из дула равна 800 м/с. Какова будет скорость пули при вылете, если ствол укоротить на 30 см? Движение пули считать равноускоренным. Ответ округлить до целых.

2. Подъемный кран опускает бетонную плиту с постоянной скоростью 1 м/с. Когда плита находилась на расстоянии 4 м от поверхности земли, с нее упал небольшой камень. На сколько секунд камень раньше достигнет земли, чем плита?

3. Шар, прикрепленный к нити, описывает окружность радиусом 15 см с постоянным центростремительным ускорением 5 м/с². Определить линейную скорость шара.

4. Автомобиль движется со скоростью 60 м/с. Сколько оборотов за время 6,28 с сделают его колеса, если они катятся по шоссе без проскальзывания, а внешний диаметр покрышек колес равен 30 см?

5.  Стрела, выпущенная с ровной горизонтальной поверхности земли под углом к горизонту, упала обратно на землю в 20 м от места выстрела. Чему равна скорость стрелы через 2с после выстрела, если в этот момент она была направлена горизонтально.

Вариант 5.

1.Тело, двигаясь равнозамедленно, проходит за первую секунду путь, на 5 м больший, чем за вторую секунду. Определить абсолютную величину ускорения тела.

2. Тело брошено с высоты 38 м с начальной скоростью 9 м/с, направленной вертикально вниз. Какой путь пройдет тело за последнюю секунду движения?

3. Автомобиль движется со скоростью 30 м/с. Сколько оборотов за время 6,28 с сделают его колеса, если они катятся по шоссе без проскальзывания, а внешний диаметр покрышек колес равен 60 см?

4. Из винтовки произведен выстрел в горизонтальном направлении с высоты 5 м над землей. Определить дальность и время полета, если скорость пули 1000м/с.

5. Тело брошено под углом к горизонту , находилось в полете 4 секунды. Определите максимальную высоту.

Вариант 6.

1. Тело, двигаясь равноускоренно без начальной скорости, в последнюю секунду прошло путь в 5 раз больший, чем за первую секунду. Определить время движения.

2. Свободно падающее тело за последнюю секунду падения проходит путь 45 м. Определить высоту, с которой падало тело.

3. Ведущее колесо электровоза диаметром 1,2 м делает 5 оборотов за 1 секунду. С какой скоростью движется электровоз?

4. Пуля вылетает из орудия в горизонтальном положении со скоростью 200м/с. Определить насколько сместится пуля в вертикальном направлении, если мишень находится на расстоянии 350м.

5. Определить гол под которым нужно бросить тело, чтобы дальность полета была в раз больше чем максимальная высота.

Вариант 7.

1. Тело начинает двигаться из состояния покоя и движется 10 с равноускоренно с ускорением 4 м/с². Затем движение тела становится равнозамедленным с ускорением 2 м/с², и тело останавливается. Найти путь, пройденный телом.

2. Свободно падающий камень пролетел последние три четверти пути за 1 с. С какой высоты он падал?

3. Вычислить путь, который проехал велосипедист, двигавшийся с угловой скоростью 0,1 рад/с по окружности радиуса 100 м за 30 секунд.

4. Пуля вылетает из орудия в горизонтальном положении со скоростью 350м/с. Определить насколько сместится пуля в вертикальном направлении, если мишень находится на расстоянии 3500м.

5. Определить под каким углом к горизонту нужно бросить тело, чтобы максимальная высота полета была в раз больше чем дальность.

Вариант 8.

1. Самолет затрачивает на разбег 24 с. Рассчитать длину разбега самолета, если на половине длины разбега самолет имел скорость, равную 30 м/с. Движение самолета считать равноускоренным.

2. Два тела упали с разной высоты, но достигли земли одновременно, причем первое тело падало 1 с, а второе 2 с. На каком расстоянии от земли было второе тело в тот момент, когда первое тело начало падать?

3. Турбина имеет диаметр рабочего колеса 9 м и совершает 60 оборотов за 62,8 с. Определить линейную скорость концов лопаток турбины.

4. Камень, брошенный горизонтально со скоростью 20м/с, упал на землю под углом 300 к горизонту. Какова высота дома.

5. Мяч брошен под углом 60 градусов к горизонту с начальной скоростью 30 м/с. Определить модуль скорости через 2 с.

Вариант 9.

1. Длина ствола винтовки 90 см. Скорость пули при вылете из дула равна 800 м/с. Какова будет скорость пули при вылете, если ствол укоротить на 30 см? Движение пули считать равноускоренным. Ответ округлить до целых.

2. Мяч, брошенный вертикально вверх, упал на землю через 6 с. На какую высоту он поднялся?

3. Стержень вращается с угловой частотой 10 рад/с относительно оси, проходящей через точку, отстоящую от одного конца стержня на 1/3 его длины и на 2/3 от другого. Найти отношение линейных скоростей концов стержня (т. е. отношение большей скорости к меньшей).

4. Мальчик бросил мячик горизонтально с высоты 50 м. С какой скоростью был брошен мяч и сколько он находился в полете если он упал на расстоянии 16 м.

5. С какой минимальной скоростью следует бросить под углом 45° к горизонту камень, чтобы он достиг высоты 2,5 м?

Вариант 11.

1. Тело движется согласно уравнению х = At + Bt², где А = 4 м/с, В = — 0,05 м/с², t — время в секундах. Определить момент времени, в который скорость точки равна нулю.

2. Скорость тела, брошенного вертикально вверх, равна 30 м/с. Определить высоту, на которую тело поднимется через 2 с после броска, если сопротивлением воздуха пренебречь.

3. Шкив трансмиссионного вала имеет диаметр 1 м. Сколько оборотов в минуту делает вал, если скорость ремня, охватывающего шкив, 6,28 м/с? Скольжением ремня пренебречь.

4. Камень, брошенный горизонтально со скоростью 15м/с, упал на землю под углом 60⁰ к горизонту. Какова высота дома.

5. Мяч брошен под углом 30 градусов к горизонту с начальной скоростью 50 м/с. Определить модуль скорости через 2 с.

Вариант 12.

1. Материальная точка движется вдоль оси ОХ по закону: х = А+ Сt + Bt², где А = 4 м, В = 10 м/с², С = 0,5 м/с, t — время в секундах. Определить координату точки в тот момент, когда скорость точки будет равна нулю

.

2. Стрела, выпущенная из лука вертикально вверх, упала на землю через 6 с. Какова начальная скорость стрелы?

3. Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на 6 см ближе к оси колеса.

4.Камень, брошенный со скоростью 12 м/с в горизонтальном направлении, упал на землю через 2 с. Определить высоту и дальность его полета.

5. С какой минимальной скоростью следует бросить под углом 60° к горизонту камень, чтобы он достиг высоты 2 м?

Вариант 13.

1. Материальная точка движется по прямой со скоростью, проекция которой равна V_x = At + В м/с, где А = 6 м/с² В = — 3 м/с, t — время в секундах. Определить величину перемещения точки в интервале времени от t₁ = 1 с до t₂ = 5 с.

2. Тело брошено с высоты 45 м с начальной скоростью 8 м/с, направленной вертикально вниз. Какой путь пройдет тело за последнюю секунду движения?

3. Автомобиль движется со скоростью 30 м/с. Сколько оборотов за время 6,28 с сделают его колеса, если они катятся по шоссе без проскальзывания, а внешний диаметр покрышек колес равен 60 см?

4. С вертолета, находящегося на высоте 250 м, произведен выстрел в горизонтальном направлении со скоростью 90 км/ч. Определить расстояние на котором упадет снаряд.

5. С какой минимальной скоростью следует бросить под углом 15° к горизонту камень, чтобы дальность его полета равнялась 20м?

Вариант 14.

1. Тело движется прямолинейно с ускорением 4 м/с². Начальная скорость равна 10 м/с. Какой путь проходит тело за третью секунду движения ?

2. Сосулька падает с крыши дома. Первую половину пути она пролетела за 1 с. Сколько времени ей осталось лететь?

3. Стержень вращается с угловой частотой 10 рад/с относительно оси, проходящей через точку, отстоящую от одного конца стержня на 1/5 его длины и на 4/5 от другого. Найти отношение линейных скоростей концов стержня (т. е. отношение большей скорости к меньшей).

4. Камень, брошенный со скоростью 12 м/с в горизонтальном направлении, упал на землю через 2 с. Определить высоту и дальность его полета.

5. Определить под каким углом брошено тело к горизонту если минимальная скорость за все время полета равна 2 от ее максимального значения.

Физика 10 класс. Контрольная работа по теме «Кинематика»

10 класс Контрольная работа «Кинематика»

1 вариант

1.Какую систему координат выбрать для определения положения лифта?

А. одномерную (х) Б. двумерную (х;у)

В. трехмерную (х; у; z) Г. среди ответов нет правильного.

2.Вектор скорости при равномерном движении точки по окружности

А. постоянен по модулю и по направлению; Б. равен нулю;

В.постоянен по модулю, но непрерывно меняется по направлению;

Г. постоянен по направлению но непрерывно изменяется по модулю.

3. Какое из уравнений описывает равномерное движение:

А. х = 5- 3t², Б. х = 8+ 2t В. v_x =2+t² Г. v_x =4 t

4.Установите соответствие между параметрами движения и формулами, их описывающими,

для равноускоренного прямолинейного движения без начальной скорости.

А) Модуль перемещения Б) Скорость

1) x0 + aхt2/2 2) vхt 3) aхt 4) x0 + v0хt − 1/2aхt2 5) v0х + aхt

5. Зависимость от времени координаты точки, движущейся вдоль оси Х, имеет вид: Х= 10t — 2t².

а) Опишите характер движения.

б) Какова начальная скорость и ускорение?

в) Запишите уравнение зависимости проекции скорости от времени v_x(t).

г) Чему равно перемещение тела за 2с?

д) определите скорость через 2с и 4 с после начала движения

6. Движение материальной точки в плоскости ХОУ описывается уравнениями: х = 2t,

у = 4 — 2t. Чему равны начальные координаты движущейся точки? Запишите уравнение

траектории движения, т.е. зависимость координаты у от координаты х.

7. На рисунке представлен график зависимости скорости автомобиля от времени.

Опишите характер движения в интервалах времени 0-1с, 1-3 с, 3-5 с.

Запишите уравнение зависимости проекции скорости от времени в интервале 0-1 с,

определите путь, пройденный автомобилем в интервале времени от 0 до 1 с после

начала движения.

8.Шарик равномерно вращается по окружности радиусом 20 см с частотой 2 об/сек.

Найти период обращения шарика, его угловую и линейную скорости.

10 класс Контрольная работа «Кинематика»

2 вариант

1.Какую систему координат выбрать для определения положения самолета?

А. одномерную (х) Б. двумерную (х;у)

В. трехмерную (х; у; z) Г. среди ответов нет правильного.

2.Основная задача кинематики …

А. … установить причины движения тел; Б. … изучить условия равновесия тел;

В. … определить положение тел в пространстве в любой момент времени.

Г. … определить скорость движения.

3.Какие из уравнений описывают равноускоренное движение:

А. х = 6- 4t, Б. х = 2t + t² В. v_x =3+2t² Г. v_x = 2+ 4 t

4.Установите соответствие между параметрами движения и формулами, их описывающими,

для равнозамедленного движения с начальной скоростью v₀.

А) Координата Б) Скорость

1) x0 + vхt 2) v0х − aхt 3) vхt 4) x0 + v0хt − 1/2aхt2 5) v0х + aхt

5. Зависимость от времени координаты точки, движущейся вдоль оси Х, имеет вид: Х= 50 – 10t + 5t²

а) Опишите характер движения.

б) Какова начальная скорость и ускорение?

в) Запишите уравнение зависимости проекции скорости от времени v_x(t).

г) Чему равно перемещение тела за 3с?

д) определите скорость через 2с и 3 с после начала движения.

6. Движение материальной точки в плоскости ХОУ описывается уравнениями: х = 6 +3t,

у=4t. Чему равны начальные координаты движущейся точки? Запишите уравнение

траектории движения, т.е. зависимость координаты у от координаты х.

7. На рисунке представлен график зависимости скорости от времени для тела,

движущегося прямолинейно. Опишите характер движения в интервалах времени 0-1с,

1-4 с, 4-6 с,6-8с. Запишите уравнение зависимости проекции скорости от времени в

интервале 0-1 с, определите путь, пройденный автомобилем в интервале времени

от 0 до 1 с после начала движения.

8.Диск радиусом 30 см совершает один оборот за 0,5 с. Найти частоту обращения диска,

его угловую и линейную скорости точек, лежащих на краю диска?

Практический тест SAT Physics: Kinematics_cracksat.net

1. Объект, движущийся с постоянной скоростью, проходит один раз по круговой траектории. Что из нижеперечисленного относится к истинным утверждениям об этом движении?

I. Смещение равно нулю.

II. Средняя скорость равна нулю.

III. Ускорение нулевое.

A. I только
B. I и II только
C. I и III только
D. III только
E. II и III только

2. В момент времени t = t ₁ скорость объекта задается вектором v ₁ , показанным ниже.

Вскоре, при t = t ₂ , скорость объекта будет вектором v ₂ .

Если v ₁ и v ₂ имеют одинаковую величину, какой из следующих векторов лучше всего иллюстрирует среднее ускорение объекта между t = t ₁ и t = т ₂ ?

А.
B.
C.
D.
E.

3. Что из следующего должно всегда выполняться?

I. Если ускорение объекта постоянное, он должен двигаться по прямой линии.

II. Если ускорение объекта равно нулю, его скорость должна оставаться постоянной.

III. Если скорость объекта остается постоянной, то его ускорение должно быть нулевым.

A. Только I и II
B. Только I и III
C. Только II
D. Только III
E. Только II и III

4. Бейсбольный мяч брошен прямо вверх. Какое ускорение у мяча в самой высокой точке?

A. 0
B. г , вниз
C. г , вниз
D. г , вверх
E. г , вверх

5. Сколько времени займет автомобиль , начиная из состояния покоя и равномерно ускоряясь по прямой со скоростью 5 м / с ² , чтобы преодолеть расстояние 200 м?

A. 9,0 с
B. 10,5 с
C. 12,0 с
D. 15.5 с
E. 20,0 с

6. Камень падает со скалы и ударяется о землю со скоростью 30 м / с. Насколько высока была скала?

A. 15 м
B. 20 м
C. 30 м
D. 45 м
E. 60 м

7. По футбольному мячу, находящемуся на земле, наносится удар с начальной скоростью 10 м / с при угле пуска 30 °. Рассчитайте его общее время полета, предполагая, что сопротивление воздуха незначительно.

А. 0,5 с
Б. 1 с
В. 1.7 с
D. 2 с
E. 4 с

8. Камень бросается с моста горизонтально с начальной скоростью 30 м / с. Определите общую скорость камня, когда он войдет в воду через 4 секунды. (Не учитывать сопротивление воздуха).

A. 30 м / с
B. 40 м / с
C. 50 м / с
D. 60 м / с
E. 70 м / с

9. Какой из следующих утверждений верно относительно движения идеального снаряда, выпущенного под углом 45 ° к горизонтали?

А.Вектор ускорения направлен против вектора скорости на пути вверх и в том же направлении, что и вектор скорости на пути вниз.
B. Скорость на вершине траектории равна нулю.
C. Общая скорость объекта остается постоянной в течение всего полета.
D. Горизонтальная скорость уменьшается при подъеме и увеличивается при спуске.
E. Вертикальная скорость уменьшается по мере увеличения высоты. D ложно, потому что горизонтальная составляющая постоянна на протяжении всего движения.

Снаряд | Примечания, видео, контроль качества и тесты | 11 класс> Физика> Кинематика

Снаряд

Любой объект, брошенный в атмосферу так, что он попадает под действие только силы тяжести, называется снарядом. Его путь — траектория. Здесь сопротивлением воздуха пренебрегают, а ускорение силы тяжести направлено вниз. 2 \ sin 2 \ theta} {g} \\ \ end {align *}

Максимальный диапазон

Для данной начальной скорости u, горизонтальное расстояние зависит от угла проекции.o — \ theta \), но время полета при этих углах проекции будет другим.

Горизонтальный снаряд

Объект проецируется горизонтально с высоты h над землей с начальной скоростью u. Снаряд находится под действием силы тяжести. Таким образом, горизонтальная скорость постоянна, а вертикальная скорость продолжает увеличиваться. (начальная скорость = 0)

Снаряд, выпущенный горизонтально с высоты h от земли.

Path of Projectile

Пусть координата положения снаряда в P будет (x, y) после времени t его проекции.2 \\ \ text {или,} \: T & = \ sqrt {\ frac {2h} {g}} \\ \ end {align *}

Горизонтальный диапазон

Горизонтальный диапазон — это расстояние, покрытое за горизонтальное направление во время полета T.

\ begin {align *} R & = u \ times T \\ \ поэтому R & = u \ times \ sqrt {\ frac {2h} {g}} \\ \ end {align *}

Скорость снаряда в любой момент

Хотя снаряд изначально имеет горизонтальную скорость, он приобретает вертикальную скорость из-за силы тяжести.{-1} \ frac {gt} {u} \ end {align *}

терминов, касающихся движения | Примечания, видео, контроль качества и тесты | 11 класс> Физика> Кинематика

Условия, касающиеся движения

Движение и покой — понятия относительные. Они зависят от ситуации наблюдателя, наблюдателя и наблюдаемого объекта. Итак, покой и движение можно описать применительно к наблюдателю. Раздел механики, имеющий дело с телом в состоянии покоя, называется статическим. Раздел физики, который занимается движением, не зная его причины, известен как кинематика.

Расстояние

Длина фактического пути, по которому тело движется из исходного положения в конечное, называется расстоянием. Единица измерения S.I — метр (м). Это скалярная величина.

Смещение

Кратчайшее расстояние между начальным и конечным положением тела называется смещением. Его единица СИ — метр (м). Это векторная величина.

Разница между расстоянием и смещением

S.N	Расстояние	Смещение
1.	Расстояние — это длина фактического пути, пройденного объектом.	Смещение объекта — это кратчайшая длина от исходного положения до конечного положения объекта.
2.	Расстояние, пройденное объектом, всегда положительно.	Смещение может быть положительным, отрицательным или нулевым.
3.	Пройденное расстояние зависит от формы пути, по которому проходит объект.	Смещение не зависит от формы пути, по которому проходит объект.
4.	Расстояние — это скалярная величина.	Смещение — это векторная величина.

Скорость

Скорость изменения расстояния известна как скорость. Другими словами, расстояние, пройденное телом за единицу времени, называется скоростью. Его единица СИ — м / с. Это скалярная величина.

Математически

$$ \ text {Скорость} = \ frac {пройденное расстояние} {время} $$

Скорость

Скорость изменения смещения называется скоростью. Единица измерения — м / с. Это векторная величина.

Математически:

$$ \ text {Скорость} = \ frac {пройденное расстояние} {затраченное время} $$

Разница между скоростью и скоростью

S.N	Скорость	Скорость
1.	Это расстояние, пройденное телом за единицу времени.	Это скорость изменения смещения.
2.	Скорость всегда положительная.	Скорость может быть положительной, отрицательной или нулевой.
3.	Скорость тела равна или больше скорости тела.	Скорость тела равна или меньше скорости тела.
4.	Скорость — это скалярная величина.	Скорость — это векторная величина.

Равномерная и неравномерная скорость

Считается, что тело имеет равномерную скорость, если оно проходит равное расстояние за равные промежутки времени.В противном случае говорят, что тело имеет неравномерную скорость.

Равномерная и неоднородная скорость

Говорят, что тело имеет равномерную скорость, если оно совершает равное перемещение за равные промежутки времени. В противном случае говорят, что тело имеет неоднородную скорость.

Мгновенная скорость

Когда скорость тела непрерывно изменяется, мы должны определить скорость в конкретный момент времени. Такая скорость называется мгновенной скоростью. Математически это отношение смещения тела к методу очень малого времени.

\ begin {align *} \ text {т.е. Мгновенная скорость} (v) & = \ lim {\ Delta t \ to o} \ frac {\ Delta s} {\ Delta t} \\ & = \ frac {ds} {dt} \\ \ end {align *}

Средняя скорость и скорость

Средняя скорость определяется как отношение общего пройденного расстояния к общему затраченному времени. Средняя скорость определяется как отношение общего пройденного смещения к общему затраченному времени.

\ begin {align *} V_ {av} & = \ frac {\ text {total displacement}} {\ text {total time}} \\ & = \ frac {s_1 — s_2} {t_2 — t_2} = \ frac {\ Delta s} {\ Delta t} \ end {align *}

Ускорение

Ускорение определяется как скорость изменения скорости во времени.Пусть начальная скорость объекта равна u, а через интервал времени t она становится v. Тогда среднее ускорение равно

\ begin {align *} a & = \ frac {\ Delta v} {\ Delta t} = \ frac {v — u} {t} \\ at & = u — v \\ \ text {or} \: v & = u + at \ end {align *}

Deceleration

Retardation — это скорость уменьшения скорости. Поскольку конечная скорость меньше начальной, ускорение становится отрицательным, а замедление — отрицательным ускорением.

Равномерное ускорение

Считается, что объект движется с равномерным ускорением, если его скорость изменяется на равную величину за равный интервал времени f.Ускорение свободного падения является примером равномерного ускорения.

Переменное ускорение

Считается, что объект движется с переменным ускорением, если изменение скорости в равный интервал времени не одинаково.

Среднее ускорение

\

Среднее ускорение объекта для данного движения определяется как отношение общего изменения скорости ускорения объекта для данного движения, определяемого как отношение общего изменения в скорость объекта к общему временному интервалу.

Рассмотрим объект, движущийся по прямой от точки P до Q, как показано на рисунке. В точке P скорость равна v ₁ в момент времени t ₁ , а в точке Q скорость равна v ₂ в момент времени t ₂ .

$$ Тогда \; изменить \; in \; velocity = v_2 — v_1 = \ Delta v $$

$$ и \; change \; in \; time = t_2 — t_1 = \ Delta t $$

$$ \ поэтому среднее ускорение a_ {av} \; = \ frac {общее изменение скорости} {общий интервал времени} $$

$$ = \ frac {\ Delta v} {\ Delta t} $$

Мгновенное ускорение

Если скорость тела непрерывно изменяется во времени, мы определяем ускорение в определенный момент времени или в точке на его пути как мгновенное ускорение, которое задается предельным значением \ (\ frac {\ Delta v} {\ Delta t} \), когда \ (\ Delta t \) стремится к нулю.

\ end {align *} \ поэтому \ text {мгновенное ускорение,} a & = \ lim {\ Delta t \ to \ theta \ frac {\ Delta v} {\ Delta t} = \ frac {dv} {dt } \ begin {align *}

Ускорение — это векторная величина, единица измерения — мс ^-2 в единицах СИ и см ^-2 в системе CGS.

GRE Subject Test по физике (для участников)

Обзор

• Тест состоит примерно из 100 вопросов с пятью вариантами ответов, некоторые из которых сгруппированы в наборы и основаны на таких материалах, как диаграммы, графики, экспериментальные данные и описания физических ситуаций.
• Цель теста — определить степень понимания испытуемыми фундаментальных принципов и их способности применять эти принципы при решении задач.
• На большинство тестовых вопросов можно ответить, если вы освоили первые три года обучения физике.
• В тесте преимущественно используется международная система единиц (СИ). Таблица с информацией, представляющей различные физические константы и несколько коэффициентов преобразования между единицами СИ, представлена ​​в тестовой тетради.
• Приблизительный процент результатов теста по основным темам содержания был установлен экзаменационной комиссией с учетом результатов общенационального обзора программ бакалавриата по физике. Процентные показатели отражают определение комитетом относительного внимания, уделяемого каждой теме в типичной программе бакалавриата. Эти проценты приведены ниже вместе с основными подтемами, включенными в каждую категорию контента. В каждой категории подтемы перечислены примерно в порядке убывания важности для включения в тест.
• Почти все вопросы теста будут относиться к материалам этого списка; тем не менее, время от времени могут возникать вопросы по другим темам, не перечисленным здесь явно.
• Тест по физике, проводимый с сентября 2020 года, дает три дополнительных балла в дополнение к общему баллу: (1) классическая механика, (2) электромагнетизм и (3) квантовая механика и атомная физика. Вопросы, на которых основываются промежуточные оценки, распределяются по всему тесту; они не откладываются и помечаются отдельно, хотя несколько вопросов из одной области содержания могут появляться последовательно.

Характеристики содержимого

1. КЛАССИЧЕСКАЯ МЕХАНИКА — 20%
   (например, кинематика, законы Ньютона, работа и энергия, колебательное движение, вращательное движение вокруг фиксированной оси, динамика систем частиц, центральные силы и небесная механика, трехмерная динамика частиц, лагранжиан и Гамильтонов формализм, неинерциальные системы отсчета, элементарные вопросы гидродинамики)
2. ЭЛЕКТРОМАГНЕТИЗМ — 18%
   (например, электростатика, токи и цепи постоянного тока, магнитные поля в свободном пространстве, сила Лоренца, индукция, уравнения Максвелла и их приложения, электромагнитные волны, цепи переменного тока, магнитные и электрические поля в веществе)
3. ОПТИКА И ВОЛНОВЫЕ ЯВЛЕНИЯ — 9%
   (такие как свойства волн, суперпозиция, интерференция, дифракция, геометрическая оптика, поляризация, эффект Доплера)
4. ТЕРМОДИНАМИКА И СТАТИСТИЧЕСКАЯ МЕХАНИКА — 10%
   (например, законы термодинамики, термодинамические процессы, уравнения состояния, идеальные газы, кинетическая теория, ансамбли, статистические концепции и расчет термодинамических величин, тепловое расширение и теплопередача)
5. КВАНТОВАЯ МЕХАНИКА — 12%
   (такие как фундаментальные концепции, решения уравнения Шредингера (включая квадратные ямы, гармонические осцилляторы и водородные атомы), спин, угловой момент, симметрия волновой функции, элементарная теория возмущений)
6. АТОМНАЯ ФИЗИКА — 10%
   (такие как свойства электронов, модель Бора, квантование энергии, атомная структура, атомные спектры, правила отбора, излучение черного тела, рентгеновские лучи, атомы в электрическом и магнитном полях)
7. СПЕЦИАЛЬНАЯ ОТНОСИТЕЛЬНОСТЬ — 6%
   (например, вводные понятия, замедление времени, сокращение длины, одновременность, энергия и импульс, четыре вектора и преобразование Лоренца, сложение скоростей)
8. ЛАБОРАТОРНЫЕ МЕТОДЫ — 6%
   (такие как анализ данных и ошибок, электроника, приборы, обнаружение излучения, статистика подсчета, взаимодействие заряженных частиц с веществом, лазеры и оптические интерферометры, анализ размеров, фундаментальные приложения вероятности и статистики)
9. СПЕЦИАЛИЗИРОВАННЫЕ ТЕМЫ — 9%
   Ядерная физика и физика элементарных частиц (e.g., ядерные свойства, радиоактивный распад, деление и синтез, реакции, фундаментальные свойства элементарных частиц), конденсированное вещество (например, кристаллическая структура, дифракция рентгеновских лучей, тепловые свойства, электронная теория металлов, полупроводники, сверхпроводники), разное ( например, астрофизика, математические методы, компьютерные приложения)

Сдающие тест должны быть знакомы с некоторыми математическими методами и их приложениями в физике. Такие математические методы включают одно- и многомерное исчисление, системы координат (прямоугольные, цилиндрические и сферические), векторную алгебру и векторные дифференциальные операторы, ряды Фурье, уравнения в частных производных, краевые задачи, матрицы и определители, а также функции комплексных переменных.Эти методы могут появляться в тесте в контексте различных категорий контента, а также время от времени задавать вопросы, касающиеся только математики в указанной выше категории специализированных тем.

Скачать учебник

<Вернуться к: Содержание теста

Кинематика 11 класс Физика | Банкноты

Скорость и скорость:

Скорость:

Скорость изменения смещения во времени называется скоростью. Это векторная величина, и величина скорости равна величине смещения.Направление скорости совпадает с направлением смещения. Предположим, что если d — это полное перемещение тела за время t, , то его средняя скорость за время t будет :

$ {{\ rm {v}} _ {{\ rm {avg}}}} = \ frac {{\ rm {d}}} {{\ rm {t}}}

долларов США

Скорость:

Скорость, с которой объект преодолевает расстояние, называется его скоростью. Это скалярная величина. Например, быстро движущийся объект будет иметь высокую скорость и преодолевать большее расстояние за меньшее время, тогда как медленно движущийся объект будет иметь меньшую скорость и за это время он преодолеет меньшее расстояние

$ {\ rm {averagespeed}} = \ frac {{{\ rm {distance \: traveled}}}} {{{\ rm {timetaken}}}} $

Отдых и движение:

Движение:

Если объект меняет свое положение по отношению к окружающему за определенное время.Тогда говорят, что тело находится в состоянии движения.

$ {\ rm {motion}} = \ frac {{\ Delta {\ rm {d}}}} {{{\ rm {time}}}}

долларов США

Отдых:

Если объект не меняет своего положения по отношению к окружающей среде, то говорят, что тело находится в состоянии покоя.

Равномерное и неравномерное ускорение:

Равномерное ускорение:

Если скорость v тела изменяется на равную величину за равные интервалы времени t, то считается, что тело имеет равномерное ускорение для тела, движущегося с равномерным ускорением, его среднее ускорение равно мгновенному ускорению.

Неравномерное ускорение:

Если скорость v тела изменяется неравномерно в неравные интервалы f раз, то говорят, что тело имеет неравномерное ускорение.

Вывод уравнений:

(i) S = ut + $ \ frac {1} {2} $ при ²

(ii) v ² = u ² + 2as.

(i) Пусть «S» — расстояние, «u» — начальная скорость, «v» — конечная скорость, «a» — ускорение, «t» — время.Чтобы вывести уравнение движения, у нас есть скорость, которая выражается как

$ {\ rm {\ bar v}} $ = $ \ frac {{\ Delta {\ rm {x}}}} {{\ Delta {\ rm {t}}}}

долларов

Где Δx относится к изменению смещения во временном интервале Δt

Перестановка для вытеснения,

Δx = $ \ overline {{\ rm {v \:}}} $ Δt

x — x _i = $ {\ rm {\ bar v}} $ Δt

x = x _i + $ {\ rm {\ bar v}} $ Δt — уравнение 1

Средняя скорость дана как среднее значение начальной и конечной скоростей,

$ {\ rm {\ bar v}} $ = $ \ frac {1} {2} $ (u + v) — уравнение 2

Из первого уравнения движения имеем,

v = u + aΔt

Подставляя значение «v» в уравнение 2,

$ {\ rm {\ bar v}} $ = $ \ frac {1} {2} $ (u + v)

$ {\ rm {\ bar v}} $ = $ \ frac {1} {2} $ (u + u + a Δt)

$ {\ rm {\ bar v}} $ = $ \ frac {1} {2} $ (2u + a Δt)

$ {\ rm {\ bar v}} $ = u + $ \ frac {1} {2} $ a Δt — уравнение 3

Теперь подставляя уравнение 3 в уравнение 1, получаем

x = x _i + $ {\ rm {\ bar v}} $ Δt

x = x _i + (u + $ \ frac {1} {2} $ a Δt) Δt

x = x _i + u Δt + $ \ frac {1} {2} $ a Δt ²

x _i — это начальное смещение, им можно пренебречь, если мы не рассматриваем начальное смещение и можем представить смещение как «s».Далее Δt относится к промежутку времени и может быть записано просто как t. Таким образом, это уравнение движения можно записать как

s = u t + $ \ frac {1} {2} $ a t ²

(ii) Это уравнение движения может быть получено с помощью уравнений движения 1 ^st и 2 ^st . Имеем 1 ^st уравнение движения as,

v = u + a t

Переставляем по времени получаем,

t = $ \ frac {{{\ rm {v \:}} — {\ rm {\: u \:}}}} {{\ rm {a}}} $ — уравнение 1

И у нас есть 2 ^nd уравнение движения как,

s = u t + $ \ frac {1} {2} $ a t ² — уравнение 2

Подставляя значение t из уравнения 1 в уравнение 2, получаем

s = u $ \ frac {{{\ rm {v \:}} — {\ rm {\: u \:}}}} {{\ rm {a}}} $ + $ \ frac {1} { 2} $ a $ (\ frac {{{\ rm {v \:}} — {\ rm {\: u \:}}}} {{\ rm {a}}} $) ²

a s = u v — u ² + $ \ frac {1} {2} $ (v ² — 2 u v + u ² )

a s = $ \ frac {1} {2} $ (v ² — u ² )

В итоге получается,

2 a s = v ² — u ²

Относительная скорость:

Относительная скорость определяется как скорость одного объекта относительно другого объекта.

Если два тела A и B движутся со скоростью $ {{\ rm {V}} _ {\ rm {A}}} $ и $ {{\ rm {V}} _ {\ rm {B}}} {\ rm {\: \: in \: same \: \: direction \:}} $, тогда результирующая скорость или скорость A относительно B определяется как $ {{\ rm {V}} _ {{\ rm {AB}}}} {\ rm {\:}} = {{\ rm {V}} _ {\ rm {A}}} — {\ rm {\:}} {{\ rm {V}} _ {\ rm {B}}}

долларов США

Если два тела A и B движутся со скоростью $ {\ rm {V}} _ {\ rm {A}}} $ и $ {{\ rm {V}} _ {{\ rm {B \: \:}}}} {\ rm {in \: Against \: direction \: \:}} $, то результирующая скорость или скорость A w.rt B задается как $ {{\ rm {V}} _ {{\ rm {AB}}}} {\ rm {\:}} = {{\ rm {V}} _ {\ rm {A}} } — {\ rm {\:}} \ left ({- {{\ rm {V}} _ {\ rm {B}}}} \ right) $ = $ {{\ rm {V}} _ {\ rm {A}}} + {\ rm {\:}} {{\ rm {V}} _ {\ rm {B}}} $

Когда два тела образуют острый угол, чтобы получить относительную скорость объекта по отношению к закону параллельных векторов наблюдателя и закону треугольника векторов, можно использовать для вычисления относительной скорости. {}} $

Это уравнение параболы

Это показывает, что путь, по которому следует объект, является параболическим.2}

долларов США

0 = usin α + ½ (-g) T ² (поскольку вертикальное смещение равно 0)

T = $ \ frac {{2 {\ rm {usin \:}} \ alpha {\ rm {\: \:}}}} {{\ rm {g}}}

долларов

Горизонтальная дальность = горизонтальная скорость * время полета (Т)

R = ucos α * 2usin α / г

Путь снаряда, вылетающего горизонтально из вершины башни, параболический:

Когда объект выбрасывается в атмосферу, он попадает только под действие силы тяжести.{- 1}} \ frac {{{\ rm {gt}}}} {{\ rm {u}}} {\ rm {\: \:}}

долларов США

Метод расчета скорости тела A относительно другого тела B, когда они движутся под углом θ:

Пусть $ {{\ rm {v}} _ 1} {\ rm {\: and \:}} {{\ rm {v}} _ 2} {\ rm {\:}} $ a re скорость тела A и тело B и результирующая скорость $ {\ rm {v}} _ {{\ rm {AB}}}} $

Здесь $ {\ rm {\:}} \ mathop \ to \ limits _ {{{\ rm {V}} _ 1}} $ и $ {\ rm {\: \:}} \ mathop \ to \ limits_ { {{\ rm {V}} _ 2}} $ представлены сторонами параллелограмма OBCA, а $ {\ rm {\: \:}} \ mathop \ to \ limits _ {\ rm {V}} $ представлены OC такой, что $ {\ rm {\: \:}} \ mathop \ to \ limits _ {\ rm {v}} $ = $ \ mathop \ to \ limits _ {{{\ rm {V}} _ 1}} $ + $ {\ rm {\:}} \ mathop \ to \ limits _ {{{\ rm {V}} _ 2}} $.2}} $

Введение в физику и кинематика — Скачать PDF бесплатно

Эксперимент 6: трение

Эксперимент 6: Трение В предыдущих фунтах мы изучали значения силы тяжести Ньютона в идеальной настройке, то есть такой, при которой трение и сопротивление не учитывались.Однако из нашего повседневного опыта работы с движением мы знаем, что

Дополнительная информация

Руководство для учителя Acceleration Lab

Руководство учителя лаборатории Acceleraion Задачи :. Используйте графики зависимости расстояния от времени и скорости от времени, чтобы найти ускорение автомобиля. Обратите внимание на соотношение между углом наклона плоскости и ускорением

. Дополнительная информация

Транспортное уравнение

Уравнение переноса. Рассмотрим жидкость, текущую со скоростью V в пространстве, поперечное сечение которого обозначим буквой A.Предположим, что жидкость содержит конаминан, концентрация которого в любое время будет

. Дополнительная информация

Движение по прямой

Мойон вдоль линии срейга 6 сентября 993 года Дэйв Мандей, механик по дизельному топливу, во второй раз пересек канадский край Ниагарского водопада, свободно падая на 48 метров ниже (и скалывается). На его

Дополнительная информация

Исправление сигнала

9/3/25 Signal Recificaion.doc / Signal Recificaion. Применение переходных диодов — это прием сигналов. Вот и все приемники сигналов, полупроводниковые и полнофункциональные. Первые считают его идеальным

Дополнительная информация

Раздел 7-4 Перевод осей

62 7 ДОПОЛНИТЕЛЬНЫЕ ТЕМЫ В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ Раздел 7-4. Вычисление Aes. • Дополнительная информация

Законы движения Ньютона

Законы Моиона Ньюона MS4414 Теоретическая механика Закон Пихты велотр.В отсутствие внешних сил тело движется по прямой с консаном F = 0 = v = cons. Khan Academy Newon I. Орган второго закона.

Дополнительная информация

Векторы и векторное исчисление

Cprigh iuecm 6 Free dwnld & print от wwwiuecm D n воспроизводит ее мужские векторные изображения и ecr clculus Vecrs во внешних размерах Бесплатные ecrs: ECR является бесплатным, если я принимаю во внимание, что он находится под rnslin PQ бесплатный ecr

Дополнительная информация

Операции с многочленами

38 Глава P Предварительные требования стр.4 Операции с полиномами Что вам следует знать: Запишите полиномы в стандартной форме и определите коэффициенты передачи и степени полиномов Добавить и вычесть полиномы Умножить

Дополнительная информация

ЗАРЯДКА И РАЗРЯД КОНДЕНСАТОРА

СПИСОК ЛИТЕРАТУРЫ RC Circuis: Elecrical Insrumens: Mos Inroducory Physics exs (например, A. Halliday and Resnick, Physics; M. Sernheim и J. Kane, General Physics.) Это лабораторное руководство: Commonly Used Insrumens:

Дополнительная информация

Индуктивность и переходные схемы

Chaper H Inducance и Transien Circuis Blinn College — Physics 2426 — Терри Хонан Как следствие закона Фарадея изменение тока через одну катушку индуцирует ЭДС в другой катушке; он известен как muual

Дополнительная информация

Путешествие по Common Core Spelling Activities.Первый класс. Блоки 1, 2, 3, 4, 5,6 Полный год деятельности!

Firs Grde Unis 1, 2, 3, 4, 5,6 Целый год гражданских! Shor 1.m 2. 3.s 4.mn 5.dd Criss Cross Words c Wrie ech word five imes ech Урок 1 Что такое Pl? Его семья мемер распечатала слово за неделю с орфографией

Дополнительная информация

9. Цепи конденсатора и резистора.

ElecronicsLab9.nb 1 9. Схема включения конденсатора и резистора На данный момент мы рассмотрели резисторы в различных комбинациях с источником питания или батареей, которые обеспечивают постоянный источник напряжения или прямой ток

Дополнительная информация

Блок 6: Показатели и радикалы

Eponents nd Rdicls -: Rel Numer Sstem Unit: Eponents nd Rdicls Pure Mth 0 Примечания Nurl Numers (N): — счетные числа.{,,,,,} Целые числа (W): — подсчет чисел с 0. {0 ,,,,,,} Целые числа (I): —

Дополнительная информация

Векторы 2. 1. Обзор векторов

Векторы 2. Набор векторов Векторы являются направленными отрезками прямых — они могут быть представлены в виде компонентов или по направлению и величине. Мы можем использовать тригонометрию и теорему Пифгорса для переключения между формами

Дополнительная информация

УРАВНЕНИЯ ЛИНИЙ И ПЛОСКОСТЕЙ

УРАВНЕНИЯ ЛИНИЙ И ПЛОСКОСТЕЙ МАТЕМАТИЧЕСКАЯ 195, РАЗДЕЛ 59 (VIPUL NAIK) Соответствующий метерил в ООК: Раздел 12.5. Что студенты обязательно должны получить: Метрическое уравнение линии, заданной в двух точках и точках

. Дополнительная информация

Перестановки и комбинации

Пермуации и комбинации Combinaorics Copyrigh Sandards 006, Tes — ОТВЕТЫ Барри Мабийяр. 0 www.mah0s.com 1. Определите среднее значение в разложении (a b) Чтобы получить значение k для среднего значения, разделите

Дополнительная информация

РЕШЕНИЯ ДЛЯ КОНЦЕПЦИЙ ГЛАВА 5

1.m k S 10m Let, ccelertion, Начальная скорость u 0. S ut + 1 / t 10 ½ () 10 ½ () 10 5 м / с orce: m 5 10N (нс) 40000. u 40 км / ч 11,11 м / с. 3600 м 000 к; v 0; с 4 м осмот р е н и е РЕШЕНИЯ И КОНЦЕПЦИИ ТЭЦ 5 0 11,11

Дополнительная информация

Конденсаторы и индукторы

Емкости и индукторы Мы продолжаем наш анализ линейных цепей, вводя два новых пассивных и линейных элемента: конденсатор и индуктор. Все методы, разработанные до сих пор для анализа линейных

Дополнительная информация

Кручение тонких открытых сечений

EM 424: Кручение хин-секций 26 Кручение тонких, открытых секций Результаты, полученные нами для образования хин-прямоугольника, также могут быть использованы, с некоторыми уточнениями, для других открытых секций, таких как

Дополнительная информация

MATH 150 ДОМАШНЕЕ ЗАДАНИЕ 4 РЕШЕНИЯ

MATH 150 ДОМАШНЕЕ ЗАДАНИЕ 4 РЕШЕНИЯ Раздел 1.8 Покажите, что произведение двух чисел 65 1000 8 2001 + 3 177, 79 1212 9 2399 + 2 2001, nd 24 4493 5 8192 + 7 1777 неотрицательно. Ваше доказательство конструктивно

Дополнительная информация

Возврат инвестора Morningstar

Morningsar Invesor Reurn Morningsar Mehodology Paper 31 августа 2010 г. 2010 г. Morningsar, Inc. Все права защищены. Информация, содержащаяся в его документах, принадлежит компании Morningsar, Inc. Репродукция или выкуп

. Дополнительная информация

4.Условия международного паритета

4. Внутренние луковицы 4.1. За покупками, за покупками, за покупками (теория — одна из первых теорий обмена. Его теория основана на том, что он требует от страны

валюты. Дополнительная информация

9 НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ

9 НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ Любой случай, чья информация о том, что я знаю, является непрерывным, будет непрерывно распространяться.Непрерывные распределения относительно дискретных

Дополнительная информация

РУКОВОДСТВО ПО ОБЗОРУ РАЗМЕЩЕНИЯ МАТЕМАТИКИ

РУКОВОДСТВО ПО ОБЗОРУ РАЗМЕЩЕНИЯ МАТЕМАТИКИ Это руководство предназначено для вашего обзора перед прохождением теста. Вопросы, представленные здесь, я не участвую в тесте. Хотя si навыки lultor являются проверенным для вашего

Дополнительная информация .

No related posts.