Контрольные работы по алгебре и началам математического анализа 10-11 класс (базовый уровень). А.Г.Мордкович, В.И.Глизбург | Материал по алгебре (10 класс) на тему:
А.Г.Мордкович, В.И.Глизбург (Москва)
Контрольные работы по алгебре
и началам математического анализа
10-11 класс (базовый уровень)
В статье содержатся по два варианта контрольных работ по курсу «Алгебра и начала математического анализа 10-11 (базовый уровень)», ориентированных на учеб- ный комплект, готовящийся к публикации к началу 2008/09 уч. года издательством «Мнемозина» и включенный в Федеральный перечень учебников с грифом «Рекомен- довано»:
А.Г.Мордкович. Алгебра и начала математического анализа 10-11 (базовый уровень), часть 1. Учебник.
А.Г.Мордкович и др.Алгебра и начала математического анализа10-11 (базовый уровень), часть 2. Задачник.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания условно говоря базового, среднего (обязательного) уровня – до первой черты, задания уровня выше среднего – между первой и второй чертой, задания повышенной сложности – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий только до первой черты – оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) – оценка 4; ха успешное выполнение заданий всех трех уровней – оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение заданий только до первой черты – оценка 3; за успешное выполнение заданий базового уровня и одного дополнительного (после первой или после второй черты) – оценка 4; ха успешное выполнение заданий всех трех уровней – оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Тематическое планирование было опубликовано в журнале «Математика в школе» ……..
10 класс
Контрольная работа №1 «Действительные числа»
Вариант 1
- Задает ли указанное правило функцию:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 1, 3, – 1;
в) постройте график функции;
г) найдите промежутки монотонности функции.
- Исследуйте функцию на четность.
- На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ.
 Сделайте чертеж.
Сделайте чертеж. - Задайте аналитически и постройте график функции , у которой
______________________________________________________________
5. Найдите функцию, обратную функции . Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
- Известно, что функция убывает на R. Решите неравенство
.
Вариант 2
1. Задает ли указанное правило функцию:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0, 4;
в) постройте график функции;
г) найдите промежутки монотонности функции.
2. Исследуйте функцию на четность.
3. На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге АВ. Сделайте чертеж.
4. Задайте аналитически и постройте график функции , у которой
.
______________________________________________________________
5. Найдите функцию, обратную функции . Постройте
на одном чертеже графики указанных двух взаимно обратных функций.
_______________________________________
6.Известно, что функция возрастает на R. Решите неравенство
.
Контрольная работа № 2
По теме « Числовые функции»
Вариант 1
- Вычислите: а);
г) ; д) .
- Упростите выражение .
- Решите уравнение: а) ; б) .
____________________________________________________________
- Известно, что .
Найдите __________________________________
5. Расположите в порядке возрастания следующие числа:
.
Вариант 2
1. Вычислите: а);
г) ; д) .
2. Упростите выражение .
3. Решите уравнение: а) ; б) .
____________________________________________________________
4. Известно, что .
Найдите .
___________________________________
5. Расположите в порядке убывания следующие числа:
.
Контрольная работа № 3
По теме «Тригонометрические функции»
Вариант 1
- Не выполняя построения, установите, принадлежит ли графику функции точка: а) ; б) P .
- Исследуйте функцию на четность:
а) ; б) ; в) .
3. Исследуйте функцию на периодичность; укажите
основной период, если он существует.
4. Решите графически уравнение .
____________________________________________________________
5. Постройте график функции а) или б):
а) ; б) .
___________________________________
6. При каком значении параметра неравенство
имеет единственное решение? Найдите это решение.
Вариант 2
1. Не выполняя построения, установите, принадлежит ли графику функции точка: а) M ; б) P .
2. Исследуйте функцию на четность
а) ; б) , в) .
3. Исследуйте функцию на периодичность; укажите
основной период, если он существует.
- Решите графически уравнение .
____________________________________________________________
- Постройте график функции а) или б):
а) ; б) .
___________________________________
6. При каком значении параметра неравенство
имеет единственное решение? Найдите это решение.
Контрольная работа № 4
По теме «Тригонометрические уравнения»
Вариант 1
1. Вычислите: а) ; б) .
2. Решите уравнение: а) ; б) .
3. Найдите корни уравнения принадлежащие полуинтервалу .
____________________________________________________________
4. Решите уравнение .
___________________________________
5. Решите уравнение .
Вариант 2
1. Вычислите: а) ; б) .
2. Решите уравнение: а) ; б) .
3. Найдите корни уравнения принадлежащие
полуинтервалу .
____________________________________________________________
4. Решите уравнение .
___________________________________
- Решите уравнение .
Контрольная работа № 5
По теме «Преобразование тригонометрических выражений»
Вариант 1
1. Вычислите: а) б)
в)
2. Упростите выражение .
3. Решите уравнение .
4. Найдите корни уравнения принадлежащие
полуинтервалу.
____________________________________________________________
5. Решите уравнение .
___________________________________
6. Докажите, что для любого x справедливо неравенство .
Вариант 2
1. Вычислите: а) б)
в)
2. Упростите выражение .
3. Решите уравнение .
4. Найдите корни уравнения принадлежащие
промежутку .
____________________________________________________________
5. Решите уравнение .
___________________________________
- Докажите, что для любого x справедливо неравенство
.
Контрольная работа № 6
По теме «правила и формулы отыскания производных»
Вариант 1
- Вычислите первый, пятый и 100-й члены последовательности, если ее n-й член задается формулой .
2. Представьте бесконечную периодическую десятичную дробь 1,(18)
в виде обыкновенной дроби.
3. Найдите производную функции: а)
б) в) г) .
4. Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
____________________________________________________________
5. Докажите, что функция удовлетворяет соотношению
_________________________________
6. Найдите знаменатель бесконечно убывающей геометрической
прогрессии, у которой каждый член в 6 раз больше суммы всех ее последующих членов.
Вариант 2
- Вычислите первый, седьмой и 200-й члены последовательности, если ее n-й член задается формулой .
2. Представьте бесконечную периодическую десятичную дробь 2, (27)
в виде обыкновенной дроби.
3. Найдите производную функции: а)
б) в) г) .
4. Найдите угловой коэффициент касательной к графику функции
в точке с абсциссой .
____________________________________________________________
5. Докажите, что функция удовлетворяет соотношению
___________________________________
6. Сумма бесконечной геометрической прогрессии равна 4, а сумма
квадратов ее членов равна 48. Найдите первый член и знаменатель
прогрессии.
Контрольная работа № 7
По теме «Применение производной»
Вариант 1
1. Составьте уравнение касательной к графику функции
в точке
2. Составьте уравнения касательных к графику функции
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
Найдите точку пересечения этих касательных.
____________________________________________________________
3. Исследуйте функцию на монотонность и экстремумы и постройте ее график.
__________________________________
4. Найдите значение параметра , при котором касательная к графику
функции в точке с абсциссой параллельна
биссектрисе первой координатной четверти.
Вариант 2
1. Составьте уравнение касательной к графику функции
в точке
2. Составьте уравнения касательных к графику функции
в точках его пересечения с осью абсцисс.
____________________________________________________________
- Исследуйте функцию на монотонность и экстремумы
и постройте ее график.
___________________________________
4 Найдите значение параметра , при котором касательная к графику
функции в точке с абсциссой параллельна прямой
.
Контрольная работа № 8 (2 часа)
Итоговая контрольная работа
Вариант 1
- Найдите наименьшее и наибольшее значения функции
а) на отрезке ;
б) на отрезке .
2. Найдите диагональ прямоугольника наибольшей площади,
вписанного в прямоугольный треугольник с катетами 18см и 24 см
и имеющего с ним общий прямой угол.
____________________________________________________________
3. Исследуйте функцию на монотонность
и экстремумы.
________________________________
4. При каких значениях параметра уравнение имеет три
корня?
Вариант 2
- Найдите наименьшее и наибольшее значения функции:
а) на отрезке ;
б) на отрезке .
2. В прямоугольном треугольнике с катетами 36 и 48 на гипотенузе взята
точка. Из нее проведены прямые, параллельные катетам. Получился
прямоугольник, вписанный в данный треугольник. Где на гипотенузе
Где на гипотенузе
надо взять точку, чтобы площадь такого прямоугольника была
наибольшей?
____________________________________________________________
3. Исследуйте функцию на монотонность
и экстремумы.
___________________________________
- При каких значениях параметра уравнение имеет два
корня?
Контрольная работа № 1 | |
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
Контрольная работа № 2 | |
1 вариант 1). Вычислите: 2). 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
Контрольная работа № 3 | |
1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
Контрольная работа № 4 | |
1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
Контрольная работа № 5 | |
1 вариант 1). 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
Контрольная работа № 6 | |
1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
Контрольная работа № 7 ( итоговая ) | |
1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . | 2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
Контрольные работы для 10 класса по учебнику А.Г.Мордковича (профильный уровень)
Контрольная работа №1 по теме «Действительные числа» (1ч)
Вариант 1
Найдите остаток от деления на 11 числа 437.
Запишите периодическую дробь 0,(87) в виде обыкновенной дроби.
Сравните числа и .
Решите уравнение .
_____________________________________________
5. Решите неравенство .
______________________________________
6. Постройте график функции .
Вариант 2
Найдите остаток от деления на 19 числа 671.
Запишите периодическую дробь 0,(35) в виде обыкновенной дроби.
Сравните числа и .
Решите уравнение .
________________________________________
5. Решите неравенство .
________________________________________
6. Постройте график функции .
Вариант 3
Найдите остаток от деления на 13 числа 371.
Запишите периодическую дробь 0,21(8) в виде обыкновенной дроби.
Расположите следующие числа в порядке возрастания: .
Решите уравнение .
_____________________________________________
5. Найдите все двузначные нечетные делители числа 2184. ______________________________________________
6. Постройте график функции .
Вариант 4
Найдите остаток от деления на 17 числа 392.
Запишите периодическую дробь 2,35(7) в виде обыкновенной дроби.
Расположите следующие числа в порядке убывания: .
Решите уравнение .
______________________________________________
5. Найдите все двузначные четные делители числа 2772
_______________________________________________
6.Постройте график функции .
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 1
Задает ли указанное правило функцию , если:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ─ 2; 1; 5;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на четность.
периодическая функция с периодом Т = 3. Известно, что
а) Постройте график функции; б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции, определенной на открытом луче .
Известно, что функция возрастает на R. Решите неравенство.
______________________________________________________________
6. Найдите функцию, обратную функции . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________
7. Вычислите: .
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 2
Задает ли указанное правило функцию, если:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках ; 2; 6;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на четность.
периодическая функция с периодом Т = 2. Известно, что
а) Постройте ее график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции, определенной на луче .
Известно, что функция убывает на R. Решите неравенство.
_______________________________________________________________________
6. Найдите функцию, обратную функции . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
__________________________________________________
7. Вычислите: .
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 3
Задает ли указанное правило функцию, если:
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках 0; 1,5; 10;
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на четность.
периодическая функция с периодом Т = 4. Известно, что
а) Постройте график функции; б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции , определенной при всех , кроме точки x = 2.
Известно, что функция возрастает на
_______________________________________________________________
6. Найдите функцию, обратную функции . Постройте на одном чертеже графики указанных двух взаимно обратных функций.
______________________________________
7. Докажите, что для любого N справедливо равенство .
Контрольная работа № 2 по теме «Числовые функции». (2ч)
Вариант 4
Задает ли указанное правило функцию :
В случае положительного ответа:
а) найдите область определения функции;
б) вычислите значения функции в точках -0,75; 0; 3.
в) постройте график функции;
г) найдите промежутки монотонности функции.
Исследуйте функцию на четность.
периодическая функция с периодом Т = 2. Известно, что
а) Постройте график функции;
б) найдите нули функции;
в) найдите ее наибольшее и наименьшее значения.
Придумайте пример аналитически заданной функции определенной при всех , кроме точки .
Известно, что функция убывает на R. Решите неравенство .
______________________________________________________________
______________________________________________________________
7. Докажите, что для любого N справедливо равенство .
Контрольная работа № 3 по теме «Тригонометрические функции». (1ч)
Вариант 1
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге точки М1(-1; 0), М2 (0; -1), М3, М4 ?
Вычислите: .
Вычислите если .
Решите неравенство: а) б) .
Постройте график функции .
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
__________________________________________________
7. Сравните числа .
______________________________________
8. Решите неравенство .
Вариант 2
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге точки М1, М2 (0; 1), М3, М4 ?
Вычислите: .
Вычислите , если .
Решите неравенство: а)
Постройте график функции .
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
___________________________________________
7. Сравните числа .
__________________________________________
8. Решите неравенство .
Контрольная работа № 3 по теме «Тригонометрические функции». (1ч)
Вариант 3
Центр окружности единичного радиуса совпадает с началом координат плоскости хОу. Принадлежат ли дуге точки М1 (1; 0), М2, М3, М4 ?
Вычислите: .
Вычислите если .
Решите неравенство: а)
Постройте график функции .
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
_________________________________________________
7. Расположите в порядке возрастания следующие числа:
_____________________________________
8. При каком значении параметра уравнение имеет единственный корень? Чему он равен?
Вариант 4
Центр окружности единичного радиуса совпадает с началом координат плоскости XOY. Принадлежат ли дуге точки М1 (1; 0), М2, М3, М
Вычислите: .
Вычислите: , если .
Решите неравенство: а)
Постройте график функции .
Исследуйте функцию на четность и периодичность; укажите основной период, если он существует:
______________________________________________
7. Расположите в порядке возрастания следующие числа: .
_____________________________________
8. При каком значении параметра уравнение имеет единственный корень? Чему он равен?
Контрольная работа № 4 « Аксиомы стереометрии».
Вариант 1
Точки К, М, Р, Т не лежат в одной плоскости. Могут ли прямые КМ и РТ пересекаться?
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 13 м, ВВ1 = 7 м, причем отрезок АВ не пересекает плоскость α.
Точка Р не лежит в плоскости трапеции ABCD с основаниями AD и ВС. Докажите, что прямая, проходящая через середины отрезков РВ и PC, параллельна средней линии трапеции.
Вариант 2
Прямые EN и КМ не лежат на одной плоскости. Могут ли прямые ЕМ и NK пересекаться? (Ответ обоснуйте.)
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 3 м, ВВ1 = 17 м, причем отрезок АВ не пересекает плоскость α.
Точка Е не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков ЕА и ЕВ, параллельна стороне CD.
Контрольная работа № 5 по теме «Простейшие тригонометрические уравнения и неравенства». (2ч)
Вариант 1
Вычислите:
Постройте график функции .
Решите уравнение: а)
б) .
Найдите корни уравнения принадлежащие промежутку .
Постройте график функции .
__________________________________________________
6. Решите систему неравенств:
а) б)
___________________________________
7. Решите уравнение .
Вариант 2
1. Вычислите:
2. Постройте график функции .
3. Решите уравнение: а)
б) .
4. Найдите корни уравнения принадлежащие промежутку .
5. Постройте график функции .
__________________________________________________
6. Решите систему неравенств:
а) б)
___________________________________
7. Решите уравнение .
Контрольная работа № 5 по теме «Простейшие тригонометрические уравнения и неравенства». (2ч)
Вариант 3
1. Вычислите:
2. Постройте график функции .
3. Решите уравнение: а)
б) .
4. Найдите корни уравнения принадлежащие промежутку .
5. Постройте график функции .
_______________________________________________
6. Решите систему неравенств:
а) б)
___________________________________
7. Решите уравнение .
Вариант 4
1. Вычислите:
2. Постройте график функции .
3. Решите уравнения: а)
б) .
4. Найдите корни уравнения принадлежащие промежутку .
5. Постройте график функции .
__________________________________________________
6. Решите систему неравенств:
а) б)
___________________________________
7. Решите уравнение .
Контрольная работа №6 по теме «Параллельность в пространстве». (1ч)
Вариант 1
Плоскости α и β параллельны, причем плоскость α пересекает некоторую прямую а. Докажите, что и плоскость β пересекает прямую а.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, ВС, CD. Докажите, что плоскость КМР параллельна прямым АС и BD.
3. Даны две параллельные плоскости и не лежащая между ними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка B1B2, если
А1А2 = 6 см и РА1 : А1В1 = 3:2.
4. Постройте проекцию квадрата ABCD, зная проекции его вершин А, B и точки пересечения диагоналей О: точки A1, B1 и О1.
Вариант 2
1. Прямые а и b параллельны, причем прямая а пересекает некоторую плоскость α. Докажите, что и прямая b пересекает плоскость α.
2. Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, AC, AD. Докажите, что плоскости КМР и BCD параллельны.
3. Даны две параллельные плоскости и не лежащая между ними точка К. Две прямые, проходящие через точку К, пересекают ближнюю к точке К плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка В1В2, если А1А2 = 10 см и КА1 : А1В1 = 2:3.
4. Постройте проекцию правильного треугольника, зная проекции его вершины А и середин К, М сторон АВ и ВС: точки А1, К1 и М1.
Контрольная работа №7 по теме « Преобразование тригонометрических выражений». (2ч)
Вариант 1
Докажите тождество:
а) ,
б) .
Упростите выражение .
Вычислите .
Найдите .
Найдите корни уравнения принадлежащие промежутку .
Решите уравнение:
а) , б) .
_________________________________________
7. Вычислите .
___________________________________
8. Решите уравнение .
Вариант 2
1. Докажите тождество:
а) ,
б) .
2. Упростите выражение .
3. Вычислите .
4. Найдите .
5. Найдите корни уравнения
принадлежащие промежутку .
6. Решите уравнение:
а) ; б) .
_____________________________________
7. Вычислите .
___________________________________
8. Решите уравнение .
Контрольная работа №7 по теме « Преобразование тригонометрических выражений». (2ч)
Вариант 3
Докажите тождество:
а) ,
б) .
Упростите выражение .
Вычислите .
Найдите .
Найдите корни уравнения принадлежащие промежутку .
Решите уравнение: а) ;
б) .
____________________________________
7. Вычислите .
___________________________________
8. Решите уравнение .
Вариант 4
Докажите тождество:
а) ,
б) .
Упростите выражение .
Вычислите .
Найдите .
Найдите корни уравнения принадлежащие промежутку .
Решите уравнение:
а) ; б) .
__________________________________________________
7. Вычислите .
___________________________________
8. Решите уравнение .
Контрольная работа №8 по теме «Перпендикулярность прямой и плоскости». (1ч)
1 вариант
Концы отрезка АВ, не пересекающего плоскость, удалены от нее на расстояния 2,4м и 7,6м. Найдите расстояние от середины М отрезка АВ до этой плоскости.
Перекладина длиной 5м своими концами лежит на двух вертикальных столбах высотой 3м и 6м. Каково расстояние между основаниями столбов?
Из точки к плоскости проведены две наклонные, равные 17см и 15 см. Проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.
Из вершины равностороннего треугольника АВС проведен перпендикуляр АМ к плоскости треугольника. Чему равно расстояние от точки М до прямой ВС, если АМ =1м, ВС = 8м?
2 вариант
Точка А лежит в плоскости, точка В — на расстоянии 12,5м от нее. Найдите расстояние от плоскости до точки М, делящей отрезок АВ в отношении АМ : МВ = 2 : 3.
Какой длины нужно взять перекладину, чтобы ее можно было положить концами на два вертикальных столба высотой 4м и 8м, поставленные на расстоянии 3м один от другого?
Из точки к плоскости проведены две наклонные, одна из которых на 6см длиннее другой. Проекции наклонных равны 17см и 7см. Найдите наклонные.
Из вершины квадрата АВСК проведен перпендикуляр АМ к плоскости квадрата. Чему равно расстояние от точки М до прямой ВК, если АМ =2м, АВ = 8м?
Контрольная работа № 9 по теме «Комплексные числа». (1ч)
Вариант 1
Вычислите:
а), б).
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ;
б) множество точек z, удовлетворяющих условию
в) множество точек z, удовлетворяющих условию .
Запишите комплексное число в стандартной тригонометрической форме: а), б).
Решите уравнение .
Вычислите .
____________________________________
6. Решите уравнение .
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям:
Вариант 2
Вычислите:
а), б).
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ;
б) множество точек z, удовлетворяющих условию
в) множество точек z, удовлетворяющих условию .
Запишите комплексное число в стандартной тригонометрической форме: а), б).
Решите уравнение .
Вычислите .
__________________________________________________
6. Решите уравнение .
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям:
Контрольная работа № 9 по теме «Комплексные числа». (1ч)
Вариант 3
Вычислите: а), б).
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ;
б) множество точек z, удовлетворяющих условию
в) множество точек z, удовлетворяющих условию .
Запишите комплексное число в стандартной тригонометрической форме: а), б).
Решите уравнение .
Вычислите .
____________________________________
6. Решите уравнение .
___________________________________
7.Найдите множество точек, изображающих
комплексные числа, удовлетворяющие условиям:
Вариант 4
Вычислите: а), б).
Изобразите на комплексной плоскости:
а) середину отрезка, соединяющего точки ;
б) множество точек z, удовлетворяющих условию
в) множество точек z, удовлетворяющих условию .
Запишите комплексное число в стандартной тригонометрической форме: а), б).
Решите уравнение .
Вычислите .
____________________________________
6. Решите уравнение .
___________________________________
7. Найдите множество точек, изображающих комплексные числа, удовлетворяющие условиям:
Контрольная работа № 10 по теме «Перпендикулярность плоскостей». (1ч)
Вариант 1.
Отрезок АМ перпендикулярен плоскости квадрата АВСD со стороной 3 см. Найдите расстояние от точки М до диагонали ВD квадрата, если АМ=4см.
Перпендикулярные плоскости α и β пересекаются по прямой m. Точка А лежит в плоскости α, точка В – в плоскости β. АА1 перпендикулярен m, ВВ1 перпендикулярен m. Найти АВ, если АА1= 8см, ВВ1=12 см, А1В1=4см.
Плоскости равностороннего треугольника АВС и квадрата ВСDЕ перпендикулярны. Найти расстояние от точки А до стороны DЕ, если
АВ = 4 см.
Вариант 2.
Отрезок ВК перпендикулярен плоскости квадрата АВСD. Периметр квадрата равен 16 см. Найдите длину отрезка ВК, если расстояние от точки К до диагонали АС квадрата равно 5см.
Перпендикулярные плоскости α и β пересекаются по прямой n. Точка А лежит в плоскости α, точка В – в плоскости β. АМ перпендикулярен n, ВК перпендикулярен n. Найти МК, если АМ= 4см, ВК=6см, АВ=10см.
Плоскости равнобедренного треугольника АВС и квадрата АВDЕ перпендикулярны. Найдите расстояние от точки С до стороны DЕ, если АВ = 6см, < АВС=90°.
Контрольная работа №11 по теме «Декартовы координаты». (1ч)
Вариант 1
Даны точки А (0; 0; 2) и В(1; 1; -2), О — начало координат. На оси у найдите точку М (0; у; 0), равноудаленную от точек А и В.
В плоскости ху найдите точку С (х; у; 0), такую, чтобы векторы и были коллинеарными.
При каком значении х вектор (х; 2; 1) будет перпендикулярен вектору ?
Вариант 2
Даны точки А (0; -2; 0) и В (1; 2; -1), О — начало координат. На оси z найдите точку М (0; 0; z), равноудаленную от точек А и В.
Найдите точку С (х; у; z), такую, чтобы векторы и были равными.
При каком значении х вектор (х; 1; 2) будет перпендикулярен вектору ?
Контрольная работа № 12 по теме « Вычисление производных». (2ч)
Вариант 1
Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой .
Исследуйте последовательность на ограниченность и на монотонность.
Вычислите: а) ; б) .
Пользуясь определением, выведите формулу дифференцирования функции .
Пользуясь правилами и формулами дифференцирования, найдите производную функции:
.
Напишите уравнение касательной к графику функции в точке .
__________________________________________________________________
Докажите, что функция удовлетворяет соотношению .
_____________________________________________________________________
8. Найдите площадь треугольника, образованного осями координат и касательной к графику функции в точке .
Вариант 2
Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой .
Исследуйте последовательность на ограниченность и на монотонность.
Вычислите: а) ; б) .
Пользуясь определением, выведите формулу дифференцирования функции .
Пользуясь правилами и формулами дифференцирования, найдите производную функции:
6.Напишите уравнение касательной к графику функции в точке .
__________________________________________________________________
7. Докажите, что функция удовлетворяет соотношению .
______________________________________________________________________
8. Найдите площадь треугольника, образованного осями координат и касательной к графику функции в точке .
Контрольная работа № 12 по теме « Вычисление производных». (2ч)
Вариант 3
1. Вычислите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой .
2. Исследуйте последовательность на ограниченность и на монотонность.
3. Вычислите: ; б) .
4. Пользуясь определением, выведите формулу дифференцирования функции .
5. Пользуясь правилами и формулами дифференцирования, найдите производную функции:
.
6. Найдите угол, образованный касательной к графику функции в точке с абсциссой , с осью абсцисс.
____________________________________________________________________________
7. Докажите, что функция удовлетворяет соотношению .
__________________________________________________________________________
8. Найдите значение параметра , при котором касательная к графику функции в точке с абсциссой параллельна прямой . Напишите уравнение этой касательной.
Вариант 4
1. Напишите первый, тридцатый и сотый члены последовательности, если ее n-й член задается формулой .
2. Исследуйте последовательность на ограниченность и на монотонность.
3. Вычислите: а) ; б) .
4. Пользуясь определением, выведите формулу дифференцирования функции .
5. Пользуясь правилами и формулами дифференцирования, найдите производную функции:
.
Найдите угол, образованный касательной к графику функции в точке с абсциссой , с осью абсцисс.
____________________________________
Докажите, что функция удовлетворяет соотношению
___________________________________
8. Найдите значения параметра , при которых касательная к графику функции в точке с абсциссой параллельна касательной к этому графику в точке с абсциссой .
Контрольная работа № 13 по теме «Применения производной». (2ч)
Вариант 1
Исследуйте функцию у = на монотонность и экстремумы.
Постройте график функции у = 3x2 – х3.
Найдите наименьшее и наибольшее значения функции у = х3 — х2 + 1 на отрезке [-1; 1].
В полукруг радиуса 6 см вписан прямоугольник. Чему равна наибольшая площадь прямоугольника?
________________________________________
Докажите, что при х ϵ (0; справедливо неравенство cos х + х sin х > 1.
___________________________________________
При каких значениях параметра а функция у = 2 ах3 + 9х2 + 54 ах + 66 убывает на всей числовой прямой?
Вариант 2
Исследуйте функцию у = на монотонность и экстремумы.
Постройте график функции у = х3 — х2.
Найдите наименьшее и наибольшее значения функции у = х3 — х2 + 1 на отрезке [-1; 3].
В прямоугольный треугольник с гипотенузой 8 см и углом 60° вписан прямоугольник так, что одна из его сторон лежит на гипотенузе. Чему равна наибольшая площадь такого прямоугольника?
______________________________________
Докажите, что при х ϵ (0; справедливо неравенство sin х > х cos х.
__________________________________________
При каких значениях параметра а функция у = ах3 — 30х2 + 5(а+9)х — 7 возрастает на всей числовой прямой?
Контрольная работа № 13 по теме «Применения производной». (2ч)
Вариант 3
Исследуйте функцию у = 4(2 — х) на монотонность и экстремумы.
Постройте график функции у = + 4х2 — 15х.
Найдите наименьшее и наибольшее значения функции у = х — cos 2х на отрезке [-л; 0].
Периметр параллелограмма с острым углом 60° равен 8 см. Чему равна наибольшая площадь такого параллелограмма?
__________________________________________
Докажите, что при х > 0 справедливо неравенство cos х > 1 —
___________________________________
При каких значениях параметра а наименьшее на отрезке [0; 2] значение функции
у = 4х2 — 4ах + а2 — 2а + 2 равно 3?
Вариант 4
Исследуйте функцию у = 2на монотонность и экстремумы.
Постройте график функции у = +х2+3х
Найдите наименьшее и наибольшее значения функции у = sin х на отрезке [- ].
В треугольник с основанием а и высотой h вписан прямоугольник так, что одна его сторона принадлежит основанию треугольника. Чему равна наибольшая площадь такого прямоугольника?
____________________________________________
Докажите, что при х 3 справедливо неравенство 4х(х2 + 6) > 15(х2 + 3).
___________________________________________
При каких значениях параметра а наименьшее на отрезке [0; 2] значение функции у = х2 + (а + 4)х + 2а + 3 равно — 4?
Контрольная работа № 14 по теме « Комбинаторика и вероятность». (1ч)
Вариант 1
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?
Сколько четырехзначных чисел можно составить из цифр 1,2,3,4 при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3. Решите уравнение .
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
__________________________________________________
На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
В разложении бинома коэффициент третьего члена на 44 больше коэффициента второго члена. Найдите член, не зависящий от .
Вариант 2
1. В яхт-клубе состоит 9 человек. Из них надо выбрать председателя, заместителя, секретаря и казначея. Сколькими способами это можно сделать?
Сколько четырехзначных чисел можно составить из цифр 1,2,3,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
Решите уравнение .
Из колоды в 36 карт вытаскивают три карты. Какова вероятность того, что все они тузы?
________________________________________________
5. Сколько существует треугольников, у которых вершины являются вершинами данного выпуклого 8-угольника, но стороны не совпадают со сторонами этого n-угольника?
6.Сумма биномиальных коэффициентов разложения бинома равна 64. Найдите член, не зависящий от x.
Контрольная работа № 9 (1 час)
Вариант 3
Из 30 членов спортивного клуба надо не только составить команду из 4 человек для участия в четырехэтапной эстафете, но и определить порядок выхода спортсменов на этапы. Сколькими способами это можно сделать?
Сколько трехзначных чисел можно составить из цифр 1,2,3 при условии, что цифры могут повторяться?
Решите уравнение .
В урне находится 3 белых и 4 черных шара. Какова вероятность того, что вынутые из нее наудачу два шара окажутся белыми?
____________________________________________
На прямой взяты 6 точек, а на параллельной ей прямой – 7 точек. Сколько существует треугольников, вершинами которых являются данные точки?
В разложении бинома биномиальный коэффициент пятого члена относится к биномиальному коэффициенту третьего члена, как 1:2. Найдите член, не зависящий от х.
Вариант 4
В городской думе 30 человек. Из них надо выбрать председателя и трех его заместителей. Сколькими способами это можно сделать?
Сколько трехзначных чисел можно составить из цифр 1,2,3,4,0 при условии, что каждая цифра может содержаться в записи числа лишь 1 раз?
Решите уравнение .
В урне находится 2 белых, 3 красных и 16 черных шаров. Какова вероятность того, что из вынутых из нее наудачу двух шаров один окажется белым, а другой красным?
_____________________________________________
Сколько существует треугольников, у которых вершины являются вершинами данного выпуклого 10-угольника?
_______________________________________
В разложении бинома сумма биномиальных коэффициентов второго члена от начала и третьего члена от конца равна 78.
Найдите член, не зависящий от х.
Контрольная работа №15 по теме «Векторы». (1ч)
Вариант 1
Найдите координаты вектора , если А(5; -1; 3), В(2; -2; 4).
Даны векторы и . Найдите .
Изобразите систему координат Охуz и постройте точку А(1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
Вычислите скалярное произведение векторов и , если , ,
Вариант 2
Найдите координаты вектора , если С(6; 3; -2), D(2; 4; -5).
Даны векторы и . Найдите .
Изобразите систему координат Охуz и постройте точку B(-2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Вычислите скалярное произведение векторов и , если , ,
ГДЗ решебник Алгебра 10 класс
Алгебра считается одной из основных и наиболее важных отраслей математики, которая затрагивает следующие области, такие как структура, отношение и количество. Алгебра охватывает не только числовую сферу, но также символы, переменные и множества элементов. Будучи настолько сложным предметом, это вызывает проблемы у многих учеников. Наш сервис рад предложить «ГДЗ по алгебре 10 класс» всем, кто нуждается в профессиональной помощи.
Сущность и целевое назначение решебника по алгебре за 10 класс
Вам нужна помощь алгебры? Мы знаем, как ответить: «ГДЗ по алгебре 10 класс» – оптимальное решение для школьников, их родителей и учителей. ГДЗ по алгебре очень востребованы, потому что:
- домашнюю работу может быть трудно выполнить из-за особенностей науки;
- решить домашнюю работу по алгебре обычно занимает много времени и усилий.
Основные преимущества решебника
К основным преимущества современного решебника можно отнести следующие:
- Поможет вам решить сложные задачи, связанные с выполнением домашних заданий по алгебре.
- В решебнике по алгебре используются форматы, требуемые вашей школой, с тщательным вниманием к деталям.
Для того, чтобы правильно решить задания по алгебре, ученики должны иметь соответствующий склад ума. Это главная причина, почему вопросы алгебры иногда могут быть проблематичными. Каждый ученик хотя бы один раз в течение своей школьной или студенческой жизни испытывал проблемы с алгеброй либо из-за нехватки времени, либо в случае, если задания по алгебре не соответствуют программе и имеют тенденцию быть слишком сложными для выполнения. Решебник по алгебре избавит вас от сложностей и значительно сэкономит время. Полезно данное пособие будет и учителям – с целью нахождения оптимального решения математических задач.
С нашим сайтом легко получить знания и учиться на отлично! У нас вы найдете также решебники по другим предметам обще образовательной школы.
Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)
Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)
Просмотр содержимого документа
«Итоговая контрольная работа по алгебре и начала анализа за курс 10 класса (уч. Мордкович А.Г.)»
Пояснительная записка
к тексту годовой контрольной работы
по алгебре за курс 10 класса (уч. Мордкович А.Г.).
Базовый уровень
Годовая контрольная работа составлена в соответствии с программным материалом курса «Алгебра и начала анализа» и требованиями федеральных государственных образовательных стандартов. Задания данной работы отражают следующие основные темы курса алгебры: «Тригонометрические выражения», «Тригонометрические уравнения», «Производная», «Применение производной».
Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре текстов в формате ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. Использованы задания из открытого банка задач ЕГЭ по математике. На выполнение работы отводится 40 минут.
Элементы анализа:
Нахождение значения тригонометрического выражения.
Решение тригонометрического уравнения и нахождение наименьшего положительного корня.
Нахождение значения тригонометрического выражения. Применение формулы косинуса двойного угла.
Нахождение значения тригонометрической функции по известной кофункции
Нахождение значения производной рациональной функции в точке.
Нахождение значения производной тригонометрической функции в точке.
Применение производной. Нахождение точек экстремума.
а) Решение тригонометрического уравнения методом замены и сведением к квадратному
б) Нахождение корней уравнения, принадлежащих данному отрезку.
Применение производной.Нахождение наибольшего и наименьшего значения дробной функции на отрезке.
Несмотря на то, что всего в работе 9 заданий, элементов анализа всего 10. Поэтому критерии оценивания следующие:
«3» — верно выполнено 4-6 заданий
«4» — верно выполнено 7-8 заданий
«5» — верно выполнено 9-10 заданий
Итоговая контрольная работа
10 класс.
I вариант
Найдите значение выражения: 24.
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения:
Найдите и
Найдите значение производной функцииу = х2 – 6х + 1 в точке х0=-1.
Найдите значение производной функции в точке:
у = -3 + 2, х0 = .
Найдите точки экстремума и определите их характер:
у = х3 + 3х2 – 9х – 2.
а) Решите уравнение:
2
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Итоговая контрольная работа
10 класс.
II вариант
Найдите значение выражения: 46.
Решить уравнение: — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции в точке у = х2 – 5х + 2 в точке х0=-2.
Найдите значение производной функции в точке:
у = 3 -, х0 = .
Найдите точки экстремума и определите их характер: у = 2х3 — 10х2 + 6х.
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = 2х + на отрезке .
Итоговая контрольная работа
10 класс.
III вариант
Найдите значение выражения: 37
Решить уравнение — = 0 и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции у = х3 + 4х2 – 1 в точке х0=-1.
Найдите значение производной функции в точке: у = — 2, х0 = .
Найдите точки экстремума и определите их характер: у = х3 + х2 – 5х – 3.
а)Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Итоговая контрольная работа
10 класс.
IV вариант
Найдите значение выражения: 34.
Решить уравнение и укажите наименьший положительный корень уравнения в градусах.
Найдите значение выражения: .
Найдите и
Найдите значение производной функции у = х4 – 2х — 1 в точке х0=-2.
Найдите значение производной функции в точке: у = — 2, х0= .
Найдите точки экстремума и определите их характер: у = х3— х2 – х +3.
а) Решите уравнение:
б) Укажите корни, принадлежащие отрезку
Найдите наибольшее и наименьшее значения функции у = х + на отрезке .
Алгебра 10 Контрольные работы Рурукин
Контрольные работы по алгебре в 10 классе с ответами. Используются при работе по УМК А.Г. Мордкович и др., а также по УМК А.Н. Колмогоров и др. (при незначительном изменении порядка следования работ). Ответы адресованы родителям. Алгебра 10 Контрольные работы Рурукин + ответы.
Цитаты из пособия «Контрольно-измерительные материалы. Алгебра и начала анализа. 10 класс / А.Н. Рурукин — М.:ВАКО» использованы в учебных целях. При постоянном использовании контрольных работ по алгебре в 10 классе рекомендуем купить книгу: Рурукин: Контрольно-измерительные материалы. Алгебра и начала анализа. 10 класс. ФГОС, в которой кроме контрольных работ есть тесты и самостоятельные работы.
Алгебра и начала анализа. 10 класс
Контрольные работы (сост. А.Н. Рурукин)
Контрольная работа 1 К-1 «Числовые функции»
Контрольная работа 2 К-2 «Тригонометрические функции»
Контрольная работа 3 К-3 «Обратные тригонометрические функции»
Контрольная работа 4 К-4 «Простейшие уравнения, системы уравнений, неравенства»
Контрольная работа 5 К-5 «Преобразование тригонометрических выражений»
Контрольная работа 6 К-6 «Тригонометрия (итоговая работа)»
Контрольная работа 7 К-7 «Вычисление производных»
Контрольная работа 8 К-8 «Применения производной»
Контрольная работа 9 К-9 «Производная и ее применения»
Контрольная работа 10 ИТОГОВАЯ за 10 класс
Вы смотрели: Контрольные работы по алгебре в 10 классе с ответами. Используются при работе по УМК А.Г. Мордкович и др., а также по УМК А.Н. Колмогоров и др. (при незначительном изменении порядка следования работ). Цитаты из пособия «Контрольно-измерительные материалы. Алгебра и начала анализа. 10 класс / А.Н. Рурукин — М.:ВАКО» использованы в учебных целях Ответы адресованы родителям.
Алгебра 10 Контрольные работы Рурукин + ответы.
|
Каталог Поиск книг Электронные приложенияПодписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Социальные сети | Учебники написаны подробно, доступно, хорошим литературным языком, с большим числом тщательно разобранных примеров. Приоритетной содержательно-методической линией остаётся функционально-графическая, лучше отвечающая возрастным особенностям учащихся, чем традиционные установки на приоритет алгебраических формул. Все учебники полностью отвечают требованиям сегодняшнего дня:
|
Отделение школьных помещений — директора и учителя
Совместными усилиями группы ресурсов для сотрудников (ERG) Департамента образования Нью-Йорка (DOE) заключили партнерство с Отделом человеческого капитала (DHC) для проведения Третьей ежегодной недели развития карьеры (CDW) с понедельника, 17 мая 2021 г., по 21 мая 2021 г.CDW был создан для повышения осведомленности команд и офисов, дальнейшего продвижения нашей работы, уменьшения разрозненности и увеличения разнообразия, справедливости, инклюзивности и принадлежности, особенно в эти трудные времена.
Ресурсная группа по женщинам в менеджменте, которую в настоящее время возглавляют Джей Бастьен и Kimberley Coke, открыла первую в истории Неделю виртуального развития карьеры, проведя онлайн-мероприятие и семинар по сетям.
В ходе семинара «Женщины в менеджменте» поделились передовым опытом создания сетей в рамках Министерства энергетики; у них также была возможность пообщаться с другими участниками.
Ламсон Лам, старший исполнительный директор и старший спонсор групп ресурсов для сотрудников BLEND и AAPI, выступил с приветственным словом к мероприятию, особо выделив Специального гостя Рене Уильямс, основателя Недели развития карьеры.Ренэ подробно остановился на видении, миссии и целях Недели развития карьеры.
Рекомендуемый спикер Диана Феррер-Шварц, главный административный сотрудник отдела школьных помещений, поделилась практическими советами и ресурсами о том, как эффективно взаимодействовать в рамках DOE для карьерного роста.
Спикер Молли Криз, тренер по вопросам карьеры и сетевого взаимодействия, провела семинар «Как разработать лифт, который окажет положительное влияние».
Женщины в управлении впоследствии были представлены в информационном бюллетене Управления организационного развития и эффективности, где они поделились:
Группа ресурсов для сотрудников (ERG) «Женщины в менеджменте» (WIM) была создана, чтобы предложить женщинам путь для вступления и продвижения на руководящие и руководящие должности.В частности, WIM поддерживает женщин, которые хотят продвинуться в DOE, заинтересованы в развитии своих навыков и хотят создать инклюзивное сообщество. Ранее сегодня члены WIM организовали мероприятие, посвященное началу Недели карьерного роста, «Быстрое установление контактов, признание и создание возможностей». Ниже приведено видео, в котором соруководители группы, Кимберли Кока (Kimberley Coke) и Джейсмар Бастьен (Jaysmar Bastien) открывают сегодняшнюю сессию и задают позитивный тон для CDW 2021.
Видео о женщинах в менеджменте (WIM) Соруководители ERG, Кимберли Кокс и Джейсмар Бастьен, открывают сегодняшний семинар «Быстрое создание сетей, распознавание и создание возможностей» и задают позитивный тон для CDW 2021.”
Женщины в управлении работают под руководством Джона Ши, главного исполнительного директора Отдела школьных помещений, и старшего спонсора заместителя канцлера Адриенн Остин.
Текущее руководство:
Джей Бастьен, со-руководитель, председатель по связям с общественностью
Kimberley Coke, соруководитель, председатель производственного отдела
Элиза Бренман, секретарь и сопредседатель по мероприятиям
Джой Рифкин, сопредседатель мероприятий
Кимберли М. Де Вайн, сопредседатель мероприятий
Стефани Герц, «Младшие женщины в менеджменте», председатель
. Чтобы узнать больше о женщинах в менеджменте или стать участником, напишите нам на адрес wim @ schools.nyc.gov.
Это мероприятие было открыто для всех сотрудников Департамента образования г. Нью-Йорка.
% PDF-1.4 % 1653 0 объект > эндобдж xref 1653 168 0000000016 00000 н. 0000003716 00000 н. 0000008780 00000 н. 0000009014 00000 н. 0000010685 00000 п. 0000010740 00000 п. 0000011114 00000 п. 0000011168 00000 п. 0000014407 00000 п. 0000015183 00000 п. 0000015237 00000 п. 0000015292 00000 п. 0000015550 00000 п. 0000015944 00000 п. 0000015997 00000 п. 0000016040 00000 п. 0000016258 00000 п. 0000016663 00000 п. 0000016718 00000 п. 0000016773 00000 п. 0000017444 00000 п. 0000017498 00000 п. 0000017559 00000 п. 0000017614 00000 п. 0000017749 00000 п. 0000017803 00000 п. 0000017857 00000 п. 0000018115 00000 п. 0000018169 00000 п. 0000020144 00000 п. 0000020251 00000 п. 0000020305 00000 п. 0000020659 00000 п. 0000020712 00000 п. 0000023269 00000 п. 0000023674 00000 п. 0000023729 00000 п. 0000024097 00000 п. 0000024529 00000 п. 0000024582 00000 п. 0000024636 00000 п. 0000024912 00000 п. 0000024937 00000 п. 0000062939 00000 п. 0000062964 00000 н. 0000084301 00000 п. 0000084326 00000 п. 0000106832 00000 н. 0000106857 00000 н. 0000128268 00000 н. 0000128293 00000 н. 0000149522 00000 н. 0000149547 00000 н. 0000171447 00000 н. 0000171556 00000 н. 0000171664 00000 н. 0000174689 00000 н. 0000175030 00000 н. 0000175141 00000 н. 0000175548 00000 н. 0000176118 00000 н. 0000176442 00000 н. 0000176667 00000 н. 0000179860 00000 н. 0000180059 00000 н. 0000180432 00000 н. 0000180660 00000 н. 0000180992 00000 н. 0000181558 00000 н. 0000181583 00000 н. 0000203585 00000 н. 0000203610 00000 н. 0000232960 00000 н. 0000233017 00000 н. 0000233096 00000 н. 0000233223 00000 н. 0000233536 00000 н. 0000233593 00000 н. 0000233851 00000 п. 0000233931 00000 н. 0000234010 00000 н. 0000234201 00000 н. 0000234359 00000 п. 0000234480 00000 н. 0000234583 00000 п. 0000235075 00000 н. 0000235269 00000 н. 0000240321 00000 н. 0000243267 00000 н. 0000245946 00000 н. 0000246889 00000 н. 0000247483 00000 н. 0000247652 00000 н. 0000248277 00000 н. 0000248812 00000 н. 0000249520 00000 н. 0000357893 00000 н. 0000368677 00000 н. 0000368885 00000 н. 0000370674 00000 н. 0000375110 00000 н. 0000375957 00000 н. 0000377022 00000 н. 0000377385 00000 н. 0000378365 00000 н. 0000378592 00000 н. 0000379384 00000 н. 0000380901 00000 н. 0000381595 00000 н. 0000383058 00000 н. 0000385017 00000 н. 0000387218 00000 н. 0000388990 00000 н. 00003
00000 н. 0000392024 00000 н. 0000393489 00000 н. 0000394514 00000 н. 0000395602 00000 н. 0000396789 00000 н. 0000398076 00000 н. 0000398317 00000 н. 0000399483 00000 н. 0000401602 00000 н. 0000402254 00000 н. 0000403221 00000 н. 0000408519 00000 н. 0000422908 00000 н. 0000424066 00000 н. 0000426276 00000 н. 0000426685 00000 н. 0000428296 00000 н. 0000430949 00000 н. 0000431328 00000 н. 0000432279 00000 н. 0000432521 00000 н. 0000432779 00000 н. 0000433767 00000 н. 0000449453 00000 н. 0000450064 00000 н. 0000450272 00000 н. 0000451516 00000 н. 0000451713 00000 н. 0000452493 00000 н. 0000459477 00000 н. 0000459660 00000 н. 0000459899 00000 н. 0000460108 00000 п. 0000460397 00000 н. 0000463220 00000 н. 0000467185 00000 н. 0000477310 00000 н. 0000478203 00000 н. 0000479279 00000 н. 0000479521 00000 н. 0000482149 00000 н. 0000483099 00000 н. 0000483563 00000 н. 0000483752 00000 н. 0000484976 00000 н. 0000486058 00000 н. 0000400000 п. 00004
00000 п. 0000523707 00000 н. 0000571840 00000 н. 0000620249 00000 н. 0000621474 00000 н. 0000003817 00000 н. 0000008756 00000 н. трейлер ] >> startxref 0 %% EOF 1654 0 объект > эндобдж 1819 0 объект > поток H? Ӏ ߘ} 013 bmːksErgnB * Wls6 {F & $ t9ro * B?> ||Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
СОБСТВЕННЫХ функций онлайн. Область допустимых значений: теория и практика
Дробные уравнения.Нечетный
Внимание!
В этой теме есть доп.
Материалы в специальном разделе 555.
Для тех, кто сильно «не очень …»
И для тех, кто «очень …»)
Продолжаем изучать уравнения. Мы уже знаем, как работать с линейными уравнениями и квадратом. Остался последний вид — дробных уравнений . Или их еще называют гораздо более твердыми — дробно-рациональных уравнений . Это тоже самое.
Дробные уравнения.
Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дробь, а дробь, у которой неизвестно в знаменателе . Хотя бы в одном. Например:
Напомню, если в знаменателях всего числа Это линейные уравнения.
Как решить дробных уравнений ? Прежде всего — избавьтесь от дробей! После этого уравнение чаще всего превращается в линейное или квадратное.И тогда мы знаем, что делать … В некоторых случаях может превратиться в тождество типа 5 = 5 или в некорректное выражение типа 7 = 2. Но это случается редко. Ниже я об этом и говорю.
Но как избавиться от дробей !? Очень простой. Применяя все те же преобразования идентичности.
Нам нужно умножить все уравнения на одно и то же выражение. Чтоб все знаменатели притихли! Сразу все станет проще. Объясняю на примере. Нам нужно решить уравнение:
Как вы учились в младших классах? Несем все в одном направлении, приводим к общему знаменателю и т. Д.Забудьте, как страшный сон! Так нужно поступать, когда вы сворачиваете или вычитаете дробные выражения. Или работать с неравенством. А в уравнениях сразу обе части умножаем на выражение, что даст нам возможность сократить все знаменатели (то есть, по сути, на общий знаменатель). А что это за выражение?
В левой части для уменьшения знаменателя требуется умножение до x + 2. . А справа требуется умножение на 2.Итак, уравнение нужно умножить на 2 (x + 2) . Умножить:
Это обычное умножение дробей, но напишу подробно:
Обратите внимание, до сих пор не раскрываю планку (х + 2) ! Итак, напишу целиком:
В левой части уменьшено целиком (x + 2) , а в правой 2. Что и требовалось! После разрезания получаем линейный уравнение:
И это уравнение решит уже кто угодно! х = 2..
Решаю другой пример, посложнее:
Если вспомнить, что 3 = 3/1, а 2x = 2x / 1, то можно написать:
И снова избавляемся от того, что нам не очень нравится — от дробей.
Мы видим, что для уменьшения знаменателя с помощью XA необходимо умножить дробь на (x — 2) . И агрегаты нам не мешают. Что ж, размножайтесь. Все Левая часть I. все Правая часть:
Выше скобы (x — 2) не раскрываю.Работаю с брекетом целиком, как будто это одно число! Так надо делать всегда, иначе ничего не уменьшится.
С чувством глубокого удовлетворения сокращая (x — 2) И мы получаем уравнение без дробей, в Lineshek!
Но сейчас мы уже раскрываем скобки:
Отдаем эти вещи, переносим все влево и получаем:
Но прежде чем научиться решать другие задачи. Процентов.Кстати, еще грабли!
Если вам нравится этот сайт …Кстати, у меня для вас есть еще парочка интересных сайтов.)
К нему можно обратиться в примерах решения и узнать свой уровень. Тестирование с мгновенной проверкой. Узнай — с интересом!)
Вы можете ознакомиться с функциями и производными.
Для нас важно соблюдение конфиденциальности. По этой причине мы разработали политику конфиденциальности, в которой описано, как мы используем и храним вашу информацию.Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование личной информации
Под личной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица или общения с ним.
Вас могут попросить предоставить вашу личную информацию в любое время, когда вы связываетесь с нами.
Ниже приведены несколько примеров типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. Д.
Как мы используем вашу личную информацию:
- Собранная нами личная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и ближайших событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персонализированную информацию для внутренних целей, таких как аудит, анализ данных и различные исследования, чтобы улучшить качество наших услуг и предоставить вам рекомендации по нашим услугам.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном стимулирующем мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, в судебном порядке, в суде и / или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть вашу персональная информация. Мы также можем раскрыть информацию о вас, если мы определим, что такое раскрытие необходимо или целесообразно для целей безопасности, поддержания правопорядка или других социально значимых случаев.
- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем соответствующей третьей стороне — правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности — включая административные, технические и физические — для защиты вашей личной информации от потери, кражи и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение конфиденциальности на уровне компании
Чтобы убедиться, что ваша личная информация в безопасности, мы обеспечиваем соблюдение норм конфиденциальности и безопасности для наших сотрудников и строго следим за соблюдением мер конфиденциальности.
Решая различные задачи, нам часто приходится проводить одинаковые преобразования выражений. Но бывает, что одни трансформации в одних случаях допустимы, а в других — нет. Существенное содействие в части контроля допустимости проводимых преобразований оказывает ОТЗ. Давайте сосредоточимся на этом.
Суть подхода заключается в следующем: сравниваются переменные OTZ для исходного выражения с переменными OTZ для выражения, полученного в результате выполнения идентичных преобразований, и на основании результатов сравнения делаются соответствующие выводы сделаны.
В целом идентичные преобразования могут
- не влияют …
- приведет к расширению …
- приводит к сужению нечетного.
Разберем каждый случай на примере.
Рассмотрим выражение x 2 + x + 3 · x, переменная OTZ x для этого выражения — это множество R. Теперь мы выполнили с этим выражением следующее идентичное преобразование — мы представляем аналогичные термины, в результате оно примет вид х 2 + 4 · х. Очевидно, что OTZ-переменная x этого выражения также является множеством R.Таким образом, проведенная трансформация не изменила ОТЗ.
Идите дальше. Возьмем выражение x + 3 / x-3 / x. В этом случае OTZ определяется условием X ≠ 0, что соответствует набору (-∞, 0) ∪ (0, + ∞). Это выражение также содержит аналогичные термины, после ввода которых мы приходим к выражению X, для которого OZD равно R. Что мы видим: В результате преобразования произошло расширение OTZ (число нуля было добавлено к исходному выражению к исходному выражению).
Осталось рассмотреть пример сужения области допустимых значений после преобразований.Возьмите выражение. Эта переменная x определяется неравенством (X — 1) · (X — 3) ≥0, для своего решения она подходит, например, в результате имеем (-∞, 1] ∪∪; при ред. С.А. Веляковского. — 17-е изд. — М .: Просвещение, 2008. — 240 с .: Ил. — ISBN 978-5-09-019315-3.
Любое выражение с переменной имеет свою область допустимых значений, где она существует. ОСТ всегда нужно учитывать при решении. При его отсутствии можно получить неверный результат.
Эта статья покажет, как правильно найти OTZ, использовать на примерах. Также будет учтена важность индикации OTZ.
Допустимые и недопустимые значения переменных
Это определение связано с допустимыми значениями переменной.С введением определения посмотрим, к какому результату приведет.
Начиная с 7 класса начинаем работать с числами и числовыми выражениями. Исходные определения с переменными переходят к значению выражений с выбранными переменными.
Когда есть выражения с выбранными переменными, некоторые из них могут не выполняться. Например, выражение вида 1: a, если a = 0, то оно не имеет смысла, так как делить на ноль невозможно.То есть в выражении должны быть такие значения, которые подходят в любом случае и будут отвечать. Другими словами, имейте смысл с существующими переменными.
Определение 1.
Если есть выражение с переменными, оно имеет смысл только тогда, когда значение может быть вычислено при их подстановке.
Определение 2.
Если есть выражение с переменными, оно не имеет смысла, если значение не может быть вычислено при их подстановке.
То есть отсюда и полное определение
Определение 3.
Существующими допустимыми переменными называются такие значения, под которыми выражение имеет смысл. А если в этом нет смысла, то они считаются недопустимыми.
Чтобы уточнить вышесказанное: если переменных больше одной, тогда может быть пара подходящих значений.
Пример 1.
Например, рассмотрим выражение вида 1 x — y + z, где есть три переменные. В противном случае можно записать, как x = 0, y = 1, z = 2, другая запись имеет вид (0, 1, 2).Эти значения называются действительными, это означает, что вы можете найти значение выражения. Получаем, что 1 0 — 1 + 2 = 1 1 = 1. Отсюда видим, что (1, 1, 2) недопустимо. Подстановка дает деление на ноль, то есть 1 1 — 2 + 1 = 1 0.
Что такое ОЗ?
Область допустимых значений — важный элемент при вычислении алгебраических выражений. Поэтому при расчетах стоит обратить на это внимание.
Определение 4.
Область ONZE — Это набор значений, разрешенных для этого выражения.
Рассмотрим на примере выражения.
Пример 2.
Если у нас есть выражение вида 5 z — 3, то odb имеет вид (- ∞, 3) ∪ (3, + ∞). Это область допустимых значений, удовлетворяющих переменной z для заданного выражения.
Если существует выражение вида z x — y, то можно видеть, что X ≠ Y, Z принимает любое значение.Это называется нечетным выражением. Это нужно учитывать, чтобы при замене не получилось деление на ноль.
Область допустимых значений и область определения имеет то же значение. Только второй из них используется для выражений, а первый — для уравнений или неравенств. С помощью OTZ выражение или неравенство имеет смысл. Область определения поля совпадает с областью допустимых значений переменной x до выражения F (x).
Как найти odb? Примеры, решения
Найти OST означает нахождение всех допустимых значений, подходящих для данной функции или неравенства. Если эти условия не выполняются, возможно получение неверного результата. Чтобы найти OTZ, часто необходимо выполнить преобразование в данном выражении.
Есть выражения, вычисление которых невозможно:
- , если есть деление на ноль;
- удаление корня отрицательного числа;
- наличие отрицательного целого числа — только для положительных чисел;
- расчет логарифма отрицательного числа;
- область определения касательной π 2 + π · k, k ∈ Z и катангенса π · k, k ∈ Z;
- нахождение значений арксинуса и арксинуса числа со значением, не принадлежащим [- 1; один ] .
Все это говорит о том, насколько важен ADM.
Пример 3.
Найдите выражения OTZ x 3 + 2 · x · y — 4 .
Решение
В кубе можно построить любое число. В этом выражении нет дроби, поэтому значения x и y могут быть любыми. То есть ОТЗ — это любое число.
Ответ: X и Y — любые значения.
Пример 4.
Найдите выражения OTZ 1 3 — x + 1 0.
Решение
Видно, что дробь одна, где в знаменателе ноль. Это говорит о том, что при любом значении x мы получим деление на ноль. Значит, можно сделать вывод, что данное выражение считается неопределенным, то есть в нем нет …
Ответ: ∅.
Пример 5.
Найдите определенное odr выражение x + 2 · y + 3 — 5 · x.
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю.При отрицательном значении это не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0. То есть это искомая область допустимых значений.
Ответ: Множество x и y, где x + 2 · y + 3 ≥ 0.
Пример 6.
Определите выражения OTZ в форме 1 x + 1 — 1 + log x + 8 (x 2 + 3).
Решение
По условию у нас есть дробь, поэтому ее знаменатель не должен быть нулевым.Мы получаем, что x + 1 — 1 ≠ 0. Выражение кормления всегда имеет смысл, когда оно больше или равно нулю, то есть x + 1 ≥ 0. Поскольку оно имеет логарифм, его выражение должно быть строго положительным, т. Е. x 2 + 3> 0. Основание логарифма также должно иметь положительное значение и отличаться от 1, после чего добавить еще условия x + 8> 0 и x + 8 ≠ 1. Отсюда следует, что искомый OTZ примет значение форма:
x + 1-1 0, x + 1 ≥ 0, x 2 + 3> 0, x + 8> 0, x + 8 ≠ 1
Другими словами, они называют систему неравенств с одной переменной.Решение приведет к такому ОТЗ [- 1, 0) ∪ (0, + ∞).
Ответ: [- 1, 0) ∪ (0, + ∞)
Почему важно учитывать ОТЗ при проведении преобразований?
При одинаковых преобразованиях важно найти ОТЗ. Бывают случаи, когда существования OST не имеет места. Чтобы понять, имеет ли решение заданное выражение, необходимо сравнить переменные OTZ исходного выражения и полученного OTZ.
Идентичных преобразований:
- может не повлиять…
- может привести к расширению или дополнению …
- можно было сузить ОТЗ.
Рассмотрим на примере.
Пример 7.
Если у нас есть выражение вида x 2 + x + 3 · x, то оно определено для всей области определения. Даже при приведении таких компонентов и упрощении выражения odb не меняется.
Пример 8.
Если взять пример выражения X + 3 x — 3 x, то дело обстоит иначе. У нас есть дробное выражение.И мы знаем, что деление на ноль недопустимо. Тогда odb имеет вид (- ∞, 0) ∪ (0, + ∞). Видно, что ноль не является решением, поэтому добавьте его в круглую скобку.
Рассмотрим пример с наличием кормящего выражения.
Пример 9.
Если есть X — 1 · X — 3, то следует обратить внимание на OTZ, так как он должен быть записан в виде неравенства (x — 1) · (x — 3) ≥ 0. Можно решить интервальным методом, тогда получим, что ОТЗ примет вид (- ∞, 1] ∪ [3, + ∞).После преобразования X — 1 · X — 3 и использования свойств корней получаем, что OTZ можно дополнить и записать все в виде системы неравенств вида x — 1 ≥ 0, x — 3 ≥ 0. Когда она решена, мы получаем, что [3, + ∞). Это означает, что OTZ полностью записывается следующим образом: (- ∞, 1] ∪ [3, + ∞).
Необходимо избегать трансформаций, сужающих ОТЗ.
Пример 10.
Рассмотрим пример выражения X — 1 · X — 3, когда x = — 1.При подстановке получаем, что — 1 — 1 · — 1 — 3 = 8 = 2 2. Если это выражение преобразовать и привести к виду x — 1 · x — 3, то при вычислении получим, что 2 — 1 · 2–3 выражения не имеют смысла, так как выражение «кормление» не должно быть отрицательным.
Надо придерживаться идентичных преобразований, что ОТЗ не изменится.
Если есть примеры, расширяющие его, то его нужно добавить в OTZ.
Пример 11.
Рассмотрим дробь вида x x 3 + x.Если вы сократите x, то получим 1 x 2 + 1. Тогда odb расширится и станет (- ∞ 0) ∪ (0, + ∞). Причем при расчете уже работает вторая упрощенная дробь.
Если есть логарифмы, это немного другое.
Пример 12.
Если существует выражение вида Ln x + ln (x + 3), оно заменяется на Ln (x · (x + 3)) на основе свойства логарифма. Видно, что s (0, + ∞) нечетно до (- ∞, — 3) ∪ (0, + ∞). Следовательно, чтобы определить OTZ Ln (x · (x + 3)), необходимо вычислить OTZ, то есть (0, + ∞) множества.
При решении всегда необходимо обращать внимание на структуру и тип этого выражения по условию. При правильном участке определения результат будет положительным.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
В математике бесконечное множество функций. И у каждого в каждом — свой характер.) Для работы с самыми разными функциями нужно единичных, подходов. Иначе что это за математика ?!) И такой подход есть!
При работе с какой-либо функцией мы задаем стандартный набор вопросов.И первый, самый важный вопрос — это область определения функции . Иногда эту область называют множеством допустимых значений аргумента, областью функции функции и т. Д.
Какова функция определения функции? Как его найти? Эти вопросы часто бывают сложными и непонятными … Хотя на самом деле все предельно просто. Что вы можете увидеть лично, прочитав эту страницу. Перейти?)
Ну что тут сказать… только респект.) Да! Область определения естественного поля (о которой здесь идет речь) совпадают С … выражениями, входящими в функцию. Соответственно, их и ищут по одним и тем же правилам.
А теперь рассмотрим не совсем естественный участок определения.)
Дополнительные ограничения функции определения функции.
Здесь речь пойдет об ограничениях, которые накладывает задача. Те. В задаче есть некоторые дополнительные условия, которые придумал компилятор.Или плывут ограничения от способа настройки функции.
По поводу ограничений в задаче — все просто. Обычно, и искать не надо, в задаче все уже сказано. Напомню, что ограничения, написанные автором задания, не отменяют принципиальных ограничения математики. Просто не забудьте учесть сроки выполнения задачи.
Например, такая задача:
Найдите область определения поля:
на множестве положительных чисел.
Естественную область определения этой функции мы нашли выше. Эта площадь:
D (F) = ( -∞ ; -1) ∪ (-1; 2] ∪ ∪
При словесном способе настройки функции необходимо внимательно прочитать условие и найти ограничения для Xers. Иногда глаза ищут формулы, а слова просвистывают мимо сознания да …) Пример из предыдущего урока:
Функция задается условием: каждое значение натурального аргумента x ставится в соответствии с количеством чисел, из которых состоит значение x.
Здесь следует отметить, что речь идет только о О натуральных ценностях ИКСА. Затем I. D (F) Мгновенно записывает:
D (F): x ∈ Н.
Как видите, область определения поля — не такое уж сложное понятие. Поиск этой области сводится к проверке функции, регистрации системы неравенств и решению этой системы. Конечно, системы бывают и простыми, и сложными. Но…
Открою небольшой секрет. Иногда функция, для которой необходимо найти область определения, выглядит просто устрашающе. Хочу побледнеть и заплакать.) Но стоит написать систему неравенств … и вдруг система элементарная! Более того, чем ужасная функция, тем проще система …
Мораль: Глаза боятся, голова решает!)
Значение алгебраической дроби. Как решать алгебраические дроби? Теория и практика
В этом уроке рассматривается понятие алгебраической дроби.С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить определенный предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, всем достанется лучше торта. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В этом случае возникает понятие дробного выражения. С общими выражениями (не содержащими разделения на выражения с переменными) и их свойствами уже познакомился в 7 классе.Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные понятия
1. Определение и примеры алгебраических дробейРациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения. В первом выражении, например, роль числителя выступает, а знаменатель -.
Значение алгебраического дроби , как и любое алгебраическое выражение , зависит от числового значения переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
2. Расчет значения алгебраической дроби и две основные задачи на дробьРассмотрим первую типичную задачу: вычисление значения рационального дроби с разными значениями входящих в него переменных.
Пример 1. Вычислить значение дроби как а), б), Б)
Решение. Подставляем значения переменных в указанную дробь: а), б), в) — ее нет (так как делить невозможно).
Ответ: 3; один; не существует.
Как видите, есть две типовые задачи для любой дроби: 1) Расчет фруктов, 2) допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — Переменные, в которых выражение имеет смысл. Многие из всех допустимых значений переменных называются Нечетным или доменом .
3. Допустимые (ОТЗ) и недопустимые значения переменных в долях с одной переменнойЗначение буквенных переменных может быть неприемлемым, если знаменатель дроби при этих значениях равен нулю.Во всех остальных случаях значения переменных допустимы, так как дробь может быть вычислена.
Пример 2. Установить, при каких значениях переменная нет смысла ломать.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недопустимыми будут только те значения переменной, у которых знаменатель будет равен нулю. Знаменатель дроби, так пусть линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Решение примера следует правилу поиска недопустимых значений переменных — обозначение дроби равно нулю и расположены корни соответствующего уравнения.
Рассмотрим несколько похожих примеров.
Пример 3. Установить, при каких значениях переменной нет смысла ломать.
Решение. .
Ответ. .
Пример 4. Установить при каких значениях переменной не имеет смысла хилать.
Решение ..
Есть и другие постановки этой задачи — найти домен или область допустимых значений выражения (ОТЗ) . Это значит — найти все допустимые значения переменных. В нашем примере это все значения кроме. Область определения удобно отображать на числовой оси.
Для этого накидываем точку, как указано на картинке:
Таким образом, объем определения трещины Там будут все числа, кроме 3.
Ответ ..
Пример 5. Установить при каких значениях переменной не имеет смысла хилать.
Решение ..
Отображение полученного решения на числовой оси:
Ответ ..
4. Графическое изображение области допустимых (ОТЗ) и недопустимых значений переменных в дробяхПример 6. Установить при каких значениях переменных не имеет смысла хилать.
Решение .. Получили равенство двух переменных, приводим числовые примеры: или и т.д.
Показать это решение на расписании в декартовой системе координат:
Рис. 3. Функциональный график.
Координаты любой точки, лежащей на этом графике, не входят в область допустимых значений дроби.
Ответ. .
5. Шкаф типа «деление на ноль»В рассмотренных примерах мы столкнулись с ситуацией, когда деление возникало на ноль.Теперь рассмотрим случай, когда с типовым делением возникает более интересная ситуация.
Пример 7. Установить, при каких значениях переменных нет смысла ломать.
Решение ..
Оказывается, дробь не имеет смысла. Но можно утверждать, что это не так, потому что:.
Может показаться, что если конечное выражение равно 8 at, то можно вычислить и начальное, а значит, имеет смысл при. Однако, если подставить в исходное выражение, я понял — это не имеет смысла.
Ответ ..
Чтобы разобраться с этим примером более подробно с этим примером, следующая задача: при каких значениях указанная дробь равна нулю?
(дробь равна нулю, если ее числитель равен нулю). Но необходимо решить исходное уравнение с дробью, и это не имеет смысла при, потому что значение переменной равно нулю. Итак, это уравнение имеет только один корень.
6. Правило нахождения …Таким образом, можно сформулировать точное правило нахождения площади допустимых значений дроби: найти Нечетное дроби. Необходимо и достаточно приравнять его знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: расчет дробного значения при заданных значениях переменных и нахождение области допустимых значений троя .
Рассмотрим еще несколько задач, которые могут возникнуть при работе с дробями.
7. Разные задачи и выводыПример 8.Докажите, что в любых значениях переменной дроби.
Доказательства. Числитель — число положительное. . В итоге числитель и знаменатель — числа положительные, значит, и дробь — это положительное число.
Доказано.
Пример 9. Как известно, найти.
Решение. Делим долю замера. Уменьшать мы имеем право с учетом того, что является недопустимым значением переменной для этой дроби.
Ответ..
В этом уроке мы рассмотрели основные понятия, связанные с дробями. В следующем уроке мы рассмотрим — главное свойство трещины .
Библиография
1. Башмаков М. И. Алгебра 8 класс. — М .: Просвещение, 2004.
.2. Дорофеев Г.В., Суворова С.Б., Байнович Е.А. и другие. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс.Учебник для общеобразовательных учреждений. — М .: Просвещение, 2006.
.1. Фестиваль педагогических идей.
2. Старая школа.
3. Интернет-портал LIB2.Podelise. RU.
Домашнее задание
1. №4, 7, 9, 12, 13, 14. Дорофеев Г.В., Суворов С.Б., Байнович Е.А. и другие. Алгебра 8. — 5-е изд. — М .: Просвещение, 2010.
.2. Запишите рациональную дробь, площадь определения которой составляет: а) множество, б) множество, в) всю числовую ось.
3. Докажите, что при всех допустимых значениях переменной дробь неотрицательна.
4. Найдите область выражения. Примечание. Рассмотрим отдельно два случая: когда знаменатель младшей дроби равен нулю, и когда знаменатель исходной дроби равен нулю.
Когда ученик идет в старшую школу, математика делится на 2 предмета: алгебру и геометрию. Концепции становятся все более и более задачами. У некоторых возникают трудности с восприятием дробей.Они пропустили первый урок по этой теме, и вуаля. Фрукты? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраического дробления
Начнем с определения. Под алгебраической дробью понимается выражение P / Q, где p — числитель, а q — знаменатель. Под буквенной записью может быть скрыто число, числовое выражение, числовое выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала необходимо понять, что такое выражение является частью целого.
Как правило, целое равно 1. Число в знаменателе показывает, сколько частей было разделено на единицу. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробный знак соответствует знаку деления. Допускается записывать дробное выражение в виде математической операции «Решение». В этом случае числитель делится, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда ученики изучают эту тему в школе, им дают примеры для закрепления.Чтобы правильно их решать и находить различные пути из сложных ситуаций, необходимо применить основное свойство дробей.
Это звучит так: если умножить числитель и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является разделение обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.
Математические операции с дробями
Рассмотрим, как решить, главное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны придерживаться правил.
Итак, для операции сложения и вычитания необходимо найти дополнительный множитель, чтобы привести выражения к общему знаменателю.Если изначально дроби указаны с одинаковыми q выражениями, то вам нужно понизить этот пункт. Когда находят общий знаменатель, как решать алгебраические дроби? Вам нужно складывать или вычитать цифры. Но! Необходимо помнить, что если перед дробью стоит знак «-», то все знаки в числителе меняются на противоположные. Иногда не следует производить никаких замен и математических операций. Достаточно поменять знак перед дробью.
Часто используется такое понятие, как уменьшающая фракция .Это означает следующее: если числитель и знаменатель разделены на выражение, отличное от единицы (одинаковое для обеих частей), то получается новая дробь. Разделитель и разделитель меньше прежнего, но из-за основных правил дроби в исходном примере остаются равными.
Цель этой операции — получить новое неинтерпретируемое выражение. Вы можете решить эту задачу, если сократите числитель и знаменатель до наибольшего общего делителя. Алгоритм работы состоит из двух точек:
- Нахождение узла для обеих частей дроби.
- Деление числителя и знаменателя для найденного выражения и получение неустойчивой дроби, равной предыдущей.
Ниже представлена таблица, в которой расписаны формулы. Для удобства его можно распечатать и носить с собой в блокноте. Однако для того, чтобы решать контрольный или экзамен в будущем в будущем, не было затруднений решить, как решать алгебраические дроби, эти формулы нужно выучить наизусть.
Некоторые примеры с решениями
С теоретической точки зрения вопрос, как решать алгебраические дроби.Приведенные в статье примеры помогут лучше усвоить материал.
1. Преобразуйте дроби и приведите их к общему знаменателю.
2. Преобразуйте дроби и приведите их к общему знаменателю.
После изучения теоретической части и поиска практических вопросов больше не должно быть.
В § 42 было сказано, что если деление многочленов не может быть выполнено целенаправленно, частное записывается в форме дробного выражения, в котором делимое является числителем, а делитель — знаменателем.
Примеры дробных выражений:
Числитель и знаменатель дробного выражения и сами могут быть дробными выражениями, например:
Из дробных алгебраических выражений чаще всего приходится иметь дело с теми, в которых числитель и знаменатель являются многочленами (в частности, и одинарными). Каждое такое выражение называется алгебраической дробью.
Определение. Алгебраическое выражение, представляющее собой дробь, числитель и знаменатель которой являются полиномами, называется алгебраической дробью.
Как и в арифметике, числитель и знаменатель алгебраической дроби называются членами дроби.
В будущем, изучив действия над алгебраическими дробями, мы сможем преобразовать любое дробное выражение с помощью идентичных преобразований в алгебраическую дробь.
Примеры алгебраических дробей:
Обратите внимание, что целое выражение, то есть многочлен, можно записать в виде дроби, для этого достаточно записать в числителе это выражение, а в знаменателе — 1.Например:
2. Допустимые значения букв.
Буквы, входящие в числитель, могут принимать любые значения (если не введены дополнительные ограничения).
Для букв, входящих в знаменатель, действительны только те значения, которые не уплачены до нуля. Поэтому в будущем мы всегда будем предполагать, что знаменатель алгебраической дроби не равен нулю.
В этом уроке рассматривается понятие алгебраической дроби.С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить определенный предмет на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, всем достанется лучше торта. В данном случае мы сталкиваемся с понятием числовой дроби, однако возможна ситуация, когда объект делится на неизвестное количество частей, например, на x. В этом случае возникает понятие дробного выражения. С общими выражениями (не содержащими разделения на выражения с переменными) и их свойствами уже познакомился в 7 классе.Далее рассмотрим понятие рациональной дроби, а также допустимые значения переменных.
Рациональные выражения делятся на целых и дробных выражений.
Определение. Рациональная дробь — дробное выражение вида, где — многочлены. — знаменатель числителя.
Примеры рациональных выражений: — дробные выражения; — целые выражения.В первом выражении, например, роль числителя выступает, а знаменатель -.
Значение алгебраического дроби , как и любое алгебраическое выражение , зависит от числового значения переменных, которые в него включены. В частности, в первом примере значение дроби зависит от значений переменных и, а во втором только от значения переменной.
Рассмотрим первую типичную задачу: расчет значения рационального дроби с разными значениями входящих в него переменных.
Пример 1. Рассчитайте значение дроби в пунктах а), б), Б)
Решение. Подставляем значения переменных в указанную дробь: а), б), в) — ее нет (так как делить невозможно).
Ответ: а) 3; б) 1; Б) не существует.
Как видите, есть две типовые задачи для любой дроби: 1) Расчет фруктов, 2) допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных — Переменные, в которых выражение имеет смысл. Многие из всех допустимых значений переменных называются Нечетным или доменом .
Значение буквенных переменных может быть неприемлемым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значения переменных допустимы, так как дробь может быть вычислена.
Пример 2.
Решение. Чтобы это выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не был равен нулю. Таким образом, недопустимыми будут только те значения переменной, у которых знаменатель будет равен нулю. Знаменатель дроби, так пусть линейное уравнение:
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Решение примера следует правилу поиска недопустимых значений переменных — обозначение дроби равно нулю и расположены корни соответствующего уравнения.
Рассмотрим несколько похожих примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла .
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменная нет смысла ломать.
Решение. .
Есть и другие постановки этой задачи — найти домен или область допустимых значений выражения (ОТЗ) .Это значит — найти все допустимые значения переменных. В нашем примере это все значения кроме. Область определения удобно отображать на числовой оси.
Для этого накидываем точку, как указано на картинке:
Рис. Один
Таким образом, объем определения трещины Там будут все числа, кроме 3.
Ответ. .
Пример 5. Устанавливать при каких значениях переменной нет смысла ломать.
Решение. .
Отображение полученного решения на числовой оси:
Рис. 2.
Ответ. .
Пример 6.
Решение. . Получили равенство двух переменных, приводим числовые примеры: или и т. Д.
Показать это решение на расписании в декартовой системе координат:
Рис. 3. Функциональный график
Координаты любой точки, лежащей на этом графике, не входят в область допустимых значений дроби.
Ответ. .
В рассмотренных примерах мы столкнулись с ситуацией, когда деление возникало на ноль. Теперь рассмотрим случай, когда с типовым делением возникает более интересная ситуация.
Пример 7. Установить, при каких значениях переменных нет смысла ломать.
Решение. .
Оказывается, дробь не имеет смысла. Но можно утверждать, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 at, то можно вычислить и начальное, а значит, имеет смысл при. Однако, если подставить в исходное выражение, я понял — это не имеет смысла.
Ответ. .
Чтобы разобраться с этим примером более подробно с этим примером, следующая задача: при каких значениях указанная дробь равна нулю?
§ 1 Понятие алгебраической дроби
Алгебраической дроби называют выражение
, где расположены p и q; P — числитель алгебраической дроби, q — знаменатель алгебраической дроби.
Вот примеры алгебраических дробей:
Любой многочлен — это частный случай алгебраической дроби, потому что любой многочлен можно записать как
Например:
Значение алгебраической дроби зависит от значения переменных.
Например, вычисляем значение дроби
1)
2)
В первом случае получаем:
Обратите внимание, эту дробь можно разрезать:
Таким образом, расчет значения алгебраической дроби упрощается.Мы этим пользуемся.
Во втором случае получаем:
Как видно, значение алгебраической дроби изменилось с изменением переменных.
§ 2 Допустимые значения алгебраических дробей
Рассмотрим алгебраическую дробь
Значение x = -1 недопустимо для этой дроби, т.к. знаменатель дроби с таким значением x обращается к нулю. В этом случае значение переменной алгебраической дроби не имеет смысла.
Таким образом, значения переменных алгебраических дробей являются значениями переменных, в которых знаменатель не применяется к нулю.
Пусть решают некоторые примеры.
При каких значениях переменной не имеет смысла алгебраическая дробь:
Для поиска недопустимых значений переменных знаменатель равен нулю, а корни соответствующего уравнения равны.
При каких значениях переменной стоит нулевая алгебраическая дробь:
Дробь равна нулю, если числитель равен нулю.Приравниваем к нулю числитель нашей дроби и находим корни получившегося уравнения:
Таким образом, при x = 0 и x = 3 эта алгебраическая дробь не имеет смысла, а значит, мы должны исключить эти значения переменной из ответа.

 Монотонность функции;
Монотонность функции; Упростите:
Упростите: Найти наименьшее и наибольшее значения функций:
Найти наименьшее и наибольшее значения функций: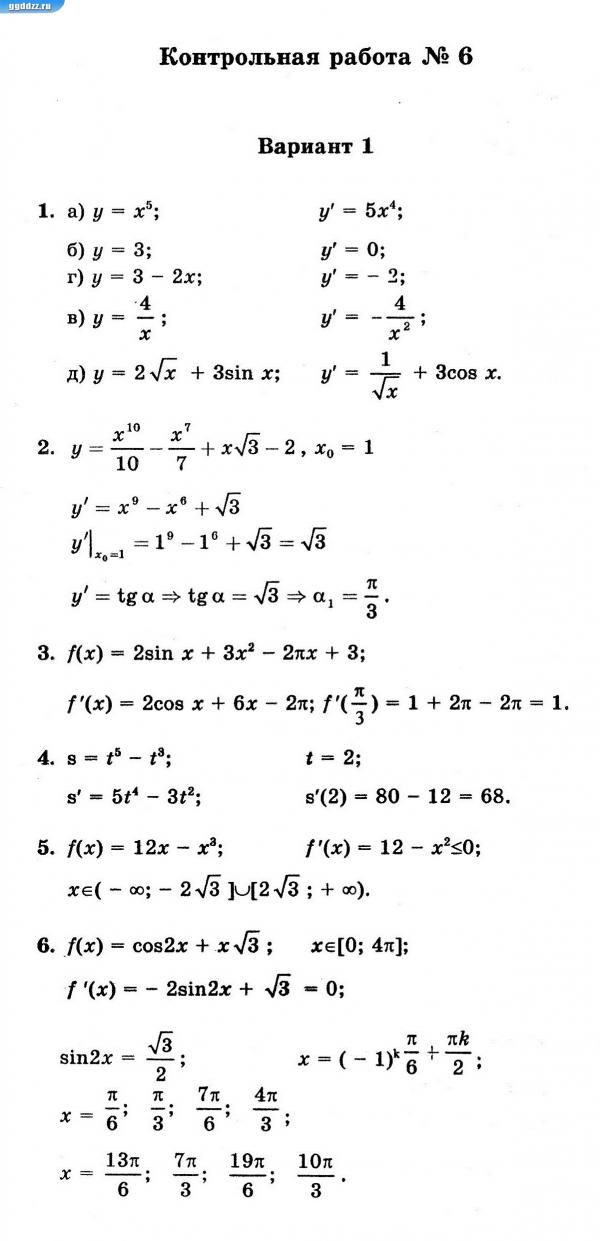 Вычислить:
Вычислить:
 Промежутки возрастания и убывания функции;
Промежутки возрастания и убывания функции;