Вариант 1 Часть 1. (Всего 6 баллов, каждое задание оценивается 1 баллом) Построить неколлинеарные векторы б) в) 2. Найти вектор, который равен сумме векторов Дан прямоугольник АВСД со сторонами 3 см и 5 см. а) Укажите пару коллинеарных противоположно направленных векторов, которые лежат на сторонах прямоугольника. б) Найдите длину вектора . в) Постройте суму векторов по правилу треугольника и по правилу параллелограмма. Часть 2. (Всего 4 балла, каждое задание оценивается 2 баллами) 3. АВСD – параллелограмм, диагонали которого пересекаются в точке О. через векторы 4. Точка М лежит на стороне ВС треугольника АВС и делит эту сторону в отношении 3:4. Выразить вектор . Часть 3. (Оценивается 3 баллами) 5. Основания равнобокой трапеции с боковой стороной 9 см относятся как 8:10. Найдите среднюю линии трапеции, если её периметр равен 54 см. | Вариант 2 Часть 1. (Всего 6 баллов, каждое задание оценивается 1 баллом) Построить неколлинеарные векторы б) в) 2. Найти вектор, который равен сумме векторов Дан прямоугольник MKNL со сторонами 6 см и 8 см. а) Укажите пару коллинеарных противоположно направленных векторов, которые лежат на сторонах прямоугольника. б) Найдите длину вектора . в) Постройте суму векторов по правилу треугольника и по правилу параллелограмма. Часть 2. (Всего 4 балла, каждое задание оценивается 2 баллами) 3. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Выразить векторы через векторы 4. Точка D лежит на стороне KN треугольника MKN и делит эту сторону в отношении 2:3. Выразить вектор . Часть 3. (Оценивается 3 баллами) 5. Основания равнобокой трапеции с боковой стороной 10 см относятся как 7:9. Найдите среднюю линии трапеции, если её периметр равен 100 см. | Вариант 1 Часть 1. (Всего 6 баллов, каждое задание оценивается 1 баллом) Построить неколлинеарные векторы б) в) 2. Дан прямоугольник АВСД со сторонами 3 см и 5 см. а) Укажите пару коллинеарных противоположно направленных векторов, которые лежат на сторонах прямоугольника. б) Найдите длину вектора . в) Постройте суму векторов по правилу треугольника и по правилу параллелограмма. Часть 2. (Всего 4 балла, каждое задание оценивается 2 баллами) 3. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Выразить векторы через векторы 4. Точка М лежит на стороне ВС треугольника АВС и делит эту сторону в отношении 3:4. Выразить вектор . Часть 3. (Оценивается 3 баллами) 5. Основания равнобокой трапеции с боковой стороной 9 см относятся как 8:10. Найдите среднюю линии трапеции, если её периметр равен 54 см. | Вариант 2 Часть 1. (Всего 6 баллов, каждое задание оценивается 1 баллом) Построить неколлинеарные векторы б) в) 2. Найти вектор, который равен сумме векторов Дан прямоугольник MKNL со сторонами 6 см и 8 см. а) Укажите пару коллинеарных противоположно направленных векторов, которые лежат на сторонах прямоугольника. б) Найдите длину вектора . в) Постройте суму векторов по правилу треугольника и по правилу параллелограмма. Часть 2. (Всего 4 балла, каждое задание оценивается 2 баллами) 3. АВСD – параллелограмм, диагонали которого пересекаются в точке О. Выразить векторы через векторы 4. Часть 3. (Оценивается 3 баллами) 5. Основания равнобокой трапеции с боковой стороной 10 см относятся как 7:9. Найдите среднюю линии трапеции, если её периметр равен 100 см. |
ОТВЕТЫ на КР-6 Геометрия 8 (Зив)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив)
Контрольная работа по геометрии «Векторы» (8 класс)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 6 «Векторы» (в 4-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Геометрия 8 класс (УМК Атанасян и др.)
Контрольная работа № 6 «Векторы».
К–6 Вариант 1
1.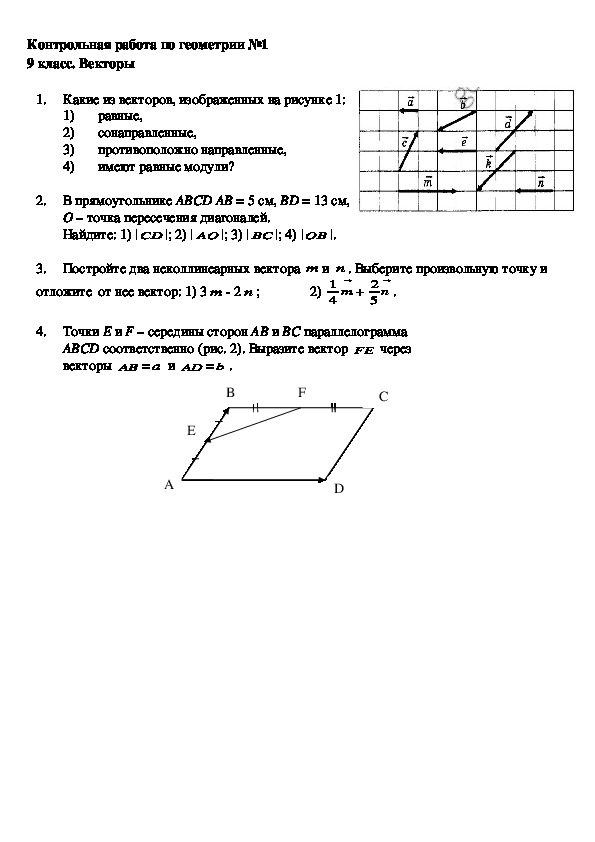 Начертите параллелограмм ABCD и постройте векторы .
Начертите параллелограмм ABCD и постройте векторы .
2. В треугольнике АВС В1 – середина АС, М – точка пересечения медиан.
г)* Используя векторы, покажите, что середина отрезка ВВ1 лежит на прямой АА1, если А1 ∈ ВС и ВА1 : А1С = 1 : 2.
К–6 Вариант 2
1. Начертите два неколлинеарных вектора а̅ и b̅, отложенных от разных точек. Постройте векторы
2. В трапеции ABCD основания AD и ВС относятся как 3 : 1. Диагонали трапеции пересекаются в точке О.
г)* Докажите, что DE < (2/3 DA + 1/2 DC), если точка Е – середина стороны АВ.
К–6 Вариант 3
1. Начертите треугольник АВС и постройте векторы
2. В параллелограмме ABCD точка М – середина стороны ВС, отрезки BD и AM пересекаются в точке О.
г)* Докажите, что OP < (2/3 AD + 1/6 АВ), если Р – середина отрезка CD.
К–6 Вариант 4
1. Начертите два неколлинеарных вектора а̅ и b̅, отложенных от разных точек. Постройте векторы
2. Основания ВС и АВ трапеции ABCD относятся как 1 : 2, Е – середина стороны CD, О – точка пересечения диагоналей.
г)* Используя векторы, докажите, что точка М, делящая отрезок АЕ в отношении 1 : 4, считая от точки Е, принадлежит прямой BD.
Геометрия 8 класс (УМК Атанасян и др.)
ОТВЕТЫ на КР-6 Геометрия 8 (Зив)
Контрольные работы по геометрии 8 класс (Атанасян) Векторы. Ответы и решения КР-6
ОТВЕТЫ на КР-6 Геометрия 8 (Зив) — это решения и ответы на контрольную работу № 6 «Векторы» (в 4-х вариантах) из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной.
Геометрия
Материалы для 7 класса
Самостоятельная работа «Нахождение углов», 7 класс — скачать
Задание по теме «Параллельные прямые», 7 класс — скачать
Материалы для 8 класса
Геометрия, 8 класс, к экзамену — скачать
Задание по теме «Площадь четырехугольника», 8 класс — скачать
Материалы для 9 класса
Самостоятельная работа «Понятие вектора», 9 класс — скачать
Самостоятельная работа «Правильные многоугольники», 9 класс — скачать
Дидактический материал по теме «Векторы», 9 класс — скачать
Задание по теме «Простейшие задачи в координатах», 9 класс — скачать
Контрольная работа «Метод координат», 9 класс — скачать
Перечень вопросов для проведения устного экзамена, 9 класс — скачать
Практическая работа по геометрии «Сложение и вычитание векторов», 9 класс — скачать
Тесты для 9 класса — скачать
Контрольная работа по теме «Правильные многоугольники», 9 класс — скачать
Материалы для 10 класса
Самостоятельная работа «Аксиомы стереометрии», 10 класс — скачать
Самостоятельная работа «Теорема о трех перпендикулярах» — скачать
Самостоятельная работа «Перпендикулярность прямой и плоскости» — скачать
Материалы для 11 класса
Раздаточный материал «Угол между двумя прямыми», 11 класс — скачать
Тест по теме «Призма», 11 класс — скачать
Цикл задач по теме «Цилиндр, конус», 11 класс — скачать
Задачи по теме «Объем пирамиды, призмы», 11 класс — скачать
Зачет по теме «Векторы в пространстве», 11 класс — скачать
Контрольная работа по теме «Тела вращения», 11 класс — скачать
Контрольные работы по геометрии для 11 класса — скачать
Дидактические материалы по геометрии (скачать с alleng. ru):
ru):
Геометрия. 7 класс. Сборник заданий для тематического и итогового контроля знаний. Ершова А.П. (2013, 112с.)
Геометрия. 8 класс. Дидактические материалы. Зив Б.Г., Мейлер В.М. (2010, 159с.)
Геометрия. 8 класс. Сборник заданий для тематического и итогового контроля знаний. Ершова А.П. (2013, 128с.)
Геометрия. 9 класс. Дидактические материалы. Зив Б.Г. (2009, 127с.)
Геометрия. Самостоятельные и контрольные работы: 7-9 классы. Иченская М.А. (2012, 144с.)
Геометрия. 10 класс. Дидактические материалы. Зив Б.Г. (2009, 159с.)
Геометрия. 11 класс. Дидактические материалы. Зив Б.Г. (2008, 128с.)
Самостоятельные и контрольные работы по геометрии для 10 класса. Ершова А.П., Голобородько В.В. (2013, 208с.)
Самостоятельные и контрольные работы по геометрии для 11 класса. Ершова А.П., Голобородько В.В. (2013, 208с.)
Добавить комментарий
Контрольные работы по геометрии 11 класс
Геометрия 11 класс
Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»
Вариант 1
Найдите координаты вектора , если А (5;-1; 3), В (2;-2; 4).

Даны векторы (3; 1;-2) и (1; 4;-3). Найдите .
Изобразите систему координат Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.
Вариант 2
Найдите координаты вектора , если С (6; 3;-2), D (2; 4;-5).
Даны вектора (5;-1; 2) и (3; 2;-4). Найдите .
Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.
Геометрия 11 класс
Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»
Вариант 1
Найдите координаты вектора , если А (5;-1; 3), В (2;-2; 4).
Даны векторы (3; 1;-2) и (1; 4;-3). Найдите .
Изобразите систему координат Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.

Вариант 2
Найдите координаты вектора , если С (6; 3;-2), D (2; 4;-5).
Даны вектора (5;-1; 2) и (3; 2;-4). Найдите .
Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.
Геометрия 11 класс
Контрольная работа № 2 по теме:
«Метод координат в пространстве»
Вариант 1
Вычислите скалярное произведение векторов , если
Дан куб АВСДА1В1С1Д1. Найдите угол между прямыми АД1 и ВМ, где М – середина ребра ДД1.
При движении прямая b отображается на прямую b1, а плоскость — на плоскость 1 и b׀׀1. Докажите, что b1׀׀1.

Вариант 2
Вычислите скалярное произведение векторов , если
Дан куб АВСДА1В1С1Д1. Найдите угол между прямыми АС и ДС1.
При движении прямая а отображается на прямую а1, а плоскость — на плоскость 1 и а. Докажите, что а11.
Геометрия 11 класс
Контрольная работа № 2 по теме:
«Метод координат в пространстве»
Вариант 1
Вычислите скалярное произведение векторов , если
Дан куб АВСДА1В1С1Д1. Найдите угол между прямыми АД1 и ВМ, где М – середина ребра ДД1.
При движении прямая b отображается на прямую b1, а плоскость — на плоскость 1 и b׀׀1.
 Докажите, что b1׀׀1.
Докажите, что b1׀׀1.
Вариант 2
Вычислите скалярное произведение векторов , если
Дан куб АВСДА1В1С1Д1. Найдите угол между прямыми АС и ДС1.
При движении прямая а отображается на прямую а1, а плоскость — на плоскость 1 и а. Докажите, что а11.
Контрольная работа №2 по теме: «Метод координат».
Вариант 1
С(-3,2,-4). Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.
Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.
При параллельном переносе точка А (-3;4;6) переходит в точку А1 (2;-4;5).
 Найдите сумму координат точки В1, в которую при этом параллельном переносе переходит точка В(-2;-4;1).
Найдите сумму координат точки В1, в которую при этом параллельном переносе переходит точка В(-2;-4;1).Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Вариант 2
А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.
Известны координаты вершин треугольника А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ – медиана треугольника. Найдите ВМ.
При параллельном переносе точка М (-3;2;-5) переходит в точку М1 (1;-3;-2). Найдите сумму координат точки К1, в которую при этом параллельном переносе переходит точка К(1;-2;-5).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Контрольная работа №2 по теме: «Метод координат».
Вариант 1
С(-3,2,-4).
 Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.
Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.
При параллельном переносе точка А (-3;4;6) переходит в точку А1 (2;-4;5). Найдите сумму координат точки В1, в которую при этом параллельном переносе переходит точка В(-2;-4;1).
Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Вариант 2
А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.
Известны координаты вершин треугольника А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ – медиана треугольника. Найдите ВМ.
При параллельном переносе точка М (-3;2;-5) переходит в точку М1 (1;-3;-2).
 Найдите сумму координат точки К1, в которую при этом параллельном переносе переходит точка К(1;-2;-5).
Найдите сумму координат точки К1, в которую при этом параллельном переносе переходит точка К(1;-2;-5).Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).
Геометрия 11 класс
Контрольная работа № 3 по теме:
«Цилиндр, конус и шар»
Вариант 1
Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см2. Найдите площадь поверхности цилиндра.
Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
б)площадь боковой поверхности конуса.Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Вариант 2
Осевое сечение цилиндра – квадрат, диагональ которого 4 см.
 Найдите площадь поверхности цилиндра.
Найдите площадь поверхности цилиндра.Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;
б) площадь боковой поверхности конуса.Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.
Геометрия 11 класс
Контрольная работа № 3 по теме:
«Цилиндр, конус и шар»
Вариант 1
Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см2. Найдите площадь поверхности цилиндра.
Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
б)площадь боковой поверхности конуса.
Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Вариант 2
Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;
б) площадь боковой поверхности конуса.Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.
Геометрия 11 класс
Контрольная работа № 4 по теме:
«Объемы тел»
Вариант 1
Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60.
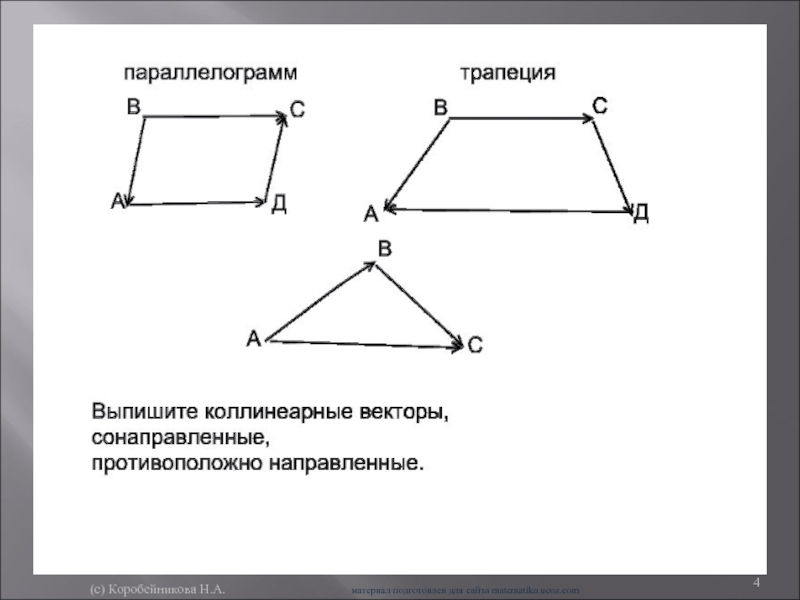 Найдите объем пирамиды.
Найдите объем пирамиды.В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.
Вариант 2
Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.
В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.
Геометрия 11 класс
Контрольная работа № 4 по теме:
«Объемы тел»
Вариант 1
Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60.
 Найдите объем пирамиды.
Найдите объем пирамиды.В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.
Вариант 2
Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.
В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.
Геометрия 11 класс
Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»
Вариант 1
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60.
 Найдите отношение объемов конуса и шара.
Найдите отношение объемов конуса и шара.Объем цилиндра равен 96 см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Вариант 2
В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
Геометрия 11 класс
Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»
Вариант 1
Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60. Найдите отношение объемов конуса и шара.
Объем цилиндра равен 96 см3, площадь его осевого сечения 48 см2.
 Найдите площадь сферы, описанной около цилиндра.
Найдите площадь сферы, описанной около цилиндра.
Вариант 2
В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
Геометрия 11 класс
Итоговая контрольная работа
Вариант 1
1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
;площадь описанной около пирамиды сферы;
угол между ВD и плоскостью DMC.
Вариант 2
1. В правильной треугольной пирамиде МАВС сторона основания равна
В правильной треугольной пирамиде МАВС сторона основания равна
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
, где Е – середина ВС;объем вписанного в пирамиду шара;
угол между стороной основания и плоскостью боковой грани.
Геометрия 11 класс
Итоговая контрольная работа
Вариант 1
1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
;площадь описанной около пирамиды сферы;
угол между ВD и плоскостью DMC.
Вариант 2
1. В правильной треугольной пирамиде МАВС сторона основания равна
В правильной треугольной пирамиде МАВС сторона основания равна
площадь боковой поверхности пирамиды;
объем пирамиды;
угол наклона боковой грани к плоскости основания;
скалярное произведение векторов
, где Е – середина ВС;объем вписанного в пирамиду шара;
угол между стороной основания и плоскостью боковой грани.
геометрических векторов — Precalculus
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Глава 11: Векторы и геометрия пространства
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8604
\ (\ newcommand {\ vecs} [1] {\ overset {\ scriptstyle \ rightharpoonup} {\ mathbf {# 1}}} \) \ (\ newcommand {\ vecd} [1] {\ overset {- \! — \! \ rightharpoonup} {\ vphantom {a} \ smash {# 1}}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \ ) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ kernel} {\ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {диапазон } \,} \) \ (\ newcommand {\ RealPart} {\ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand {\ norm} [1] {\ | # 1 \ |} \) \ (\ newcommand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \) \ (\ newcommand {\ Span} {\ mathrm {span} } \) \ (\ newcommand {\ kernel} {\ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {range} \,} \) \ (\ newcommand {\ RealPart} { \ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand {\ norm} [1] {\ | # 1 \ |} \) \ (\ newco mmand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \)
- Участники
- 11.
 1: Векторы на плоскости
1: Векторы на плоскости - Некоторые величины, такие как или сила, определяются как размером (также называемым величиной), так и направлением. Величина, имеющая величину и направление, называется вектором.
- 11.
- 11.2: Векторы в пространстве
- Векторы — полезные инструменты для решения двумерных задач. Однако жизнь существует в трех измерениях. Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства.
- 11.3: Точечное произведение
- Точечное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, встречаются ли два вектора под прямым углом.
- 11.
 4: Перекрестное произведение
4: Перекрестное произведение - В этом разделе мы разрабатываем операцию, называемую перекрестным произведением, которая позволяет нам найти вектор, ортогональный двум заданным векторам.Расчет крутящего момента — важное приложение для перекрестных произведений, и мы рассмотрим крутящий момент более подробно позже в этом разделе.
- 11.
- 11.5: Уравнения линий и плоскостей в пространстве
- Чтобы написать уравнение для линии, мы должны знать две точки на линии, или мы должны знать направление линии и хотя бы одну точку через которую проходит линия. В двух измерениях мы используем понятие уклона для описания ориентации или направления линии. В трех измерениях мы описываем направление линии, используя вектор, параллельный линии.В этом разделе мы исследуем, как использовать уравнения для описания линий и плоскостей в пространстве.
- 11.6: Квадрические поверхности
- Мы изучали векторы и векторные операции в трехмерном пространстве и разработали уравнения для описания линий, плоскостей и сфер.
 В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для исследования множества других поверхностей, которые можно изобразить в трехмерной системе координат.
В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для исследования множества других поверхностей, которые можно изобразить в трехмерной системе координат.
- 11.7: Цилиндрические и сферические координаты
- Декартова система координат обеспечивает простой способ описания местоположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Как следует из названия, цилиндрические координаты полезны при решении задач, связанных с цилиндрами. Точно так же сферические координаты полезны для решения задач, связанных со сферами.
- 11R: Упражнения на обзор главы 11
Участники
Гилберт Стрэнг (Массачусетский технологический институт) и Эдвин «Джед» Херман (Харви Мадд) со многими авторами.
 Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.
Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.
- Наверх
- Оглавление
- 11.1: Векторы на плоскости
- Была ли эта статья полезной?
- Да
- Нет
- Вид товара Глава
- .
- укрытие
- решения
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- расчетный график: да
Сложение вектора
С векторами и над векторами можно выполнять множество математических операций. Одна из таких операций — сложение векторов. Два вектора можно сложить вместе, чтобы определить результат (или результат). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомните в нашем обсуждении законов движения Ньютона, что чистая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект. То есть чистая сила была результатом (или результатом) сложения всех векторов силы.Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Одна из таких операций — сложение векторов. Два вектора можно сложить вместе, чтобы определить результат (или результат). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомните в нашем обсуждении законов движения Ньютона, что чистая сила , испытываемая объектом, была определена путем вычисления векторной суммы всех индивидуальных сил, действующих на этот объект. То есть чистая сила была результатом (или результатом) сложения всех векторов силы.Во время этого блока правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Эти правила суммирования векторов были применены к диаграммам свободного тела, чтобы определить результирующую силу (т. Е. Векторную сумму всех отдельных сил). Примеры приложений показаны на схеме ниже.
В этом модуле задача суммирования векторов будет расширена на более сложные случаи, в которых векторы направлены в направлениях, отличных от чисто вертикального и горизонтального направлений. Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. Векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Существует множество методов определения величины и направления результата сложения двух или более векторов. В этом уроке будут обсуждаться два метода, которые будут использоваться на протяжении всего модуля:
Теорема Пифагора
Теорема Пифагора — полезный метод для определения результата сложения двух (и только двух) векторов , образующих прямой угол друг к другу.Этот метод неприменим для добавления более двух векторов или для сложения векторов , а не под углом 90 градусов друг к другу. Теорема Пифагора — это математическое уравнение, которое связывает длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника.
Чтобы увидеть, как работает метод, рассмотрим следующую задачу:
Эрик покидает базовый лагерь и отправляется в поход на 11 км на север, а затем на 11 км на восток.Определите результирующее смещение Эрика.
В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу. Результат (или результат) ходьбы на 11 км на север и 11 км на восток — это вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток расположены под прямым углом друг к другу, теорема Пифагора может использоваться для определения результирующей (то есть гипотенузы прямоугольного треугольника).
Результат сложения 11 км, север плюс 11 км, восток — вектор с величиной 15,6 км. Позже будет обсуждаться метод определения направления вектора.
Давайте проверим ваше понимание с помощью следующих двух практических задач. В каждом случае используйте теорему Пифагора, чтобы определить величину векторной суммы . По завершении нажмите кнопку, чтобы просмотреть ответ.
Использование тригонометрии для определения направления вектора
Направление результирующего вектора часто можно определить с помощью тригонометрических функций. Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Синусоидальная функция связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, примыкающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Большинство студентов вспоминают значение полезной мнемоники SOH CAH TOA из своего курса тригонометрии. SOH CAH TOA — мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — синуса, косинуса и тангенса. Эти три функции связывают острый угол в прямоугольном треугольнике с отношением длин двух сторон прямоугольного треугольника. Синусоидальная функция связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы.Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Функция касательной связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, примыкающей к углу. Три уравнения ниже суммируют эти три функции в форме уравнения.
Эти три тригонометрические функции могут быть применены к задаче туриста, чтобы определить направление общего перемещения туриста.Процесс начинается с выбора одного из двух углов (кроме прямого) треугольника. После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После выбора угла любую из трех функций можно использовать для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
После определения меры угла можно определить направление вектора. В этом случае вектор составляет угол 45 градусов относительно востока.Таким образом, направление этого вектора записывается как 45 градусов. (Вспомните, как говорилось ранее в этом уроке, что направление вектора — это угол поворота против часовой стрелки, который вектор делает относительно востока.)
Расчетный угол не всегда соответствует направлению
Мера угла, определенная с помощью SOH CAH TOA, равна , а не всегда направлению вектора. Следующая векторная диаграмма сложения является примером такой ситуации.Обратите внимание, что угол внутри треугольника определен как 26,6 градуса с использованием SOH CAH TOA. Этот угол представляет собой угол поворота на юг, который вектор R делает по отношению к Западу. Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Тем не менее, направление вектора, выраженное условным обозначением CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Проверьте свое понимание использования SOH CAH TOA для определения направления вектора, попробовав следующие две практические задачи.В каждом случае используйте SOH CAH TOA для определения направления результирующего. По завершении нажмите кнопку, чтобы просмотреть ответ.
В приведенных выше задачах величина и направление суммы двух векторов определяется с помощью теоремы Пифагора и тригонометрических методов (SOH CAH TOA). Процедура ограничивается сложением двух векторов, образующих прямые углы друг к другу.Когда два вектора, которые должны быть добавлены, не находятся под прямым углом друг к другу, или когда необходимо сложить более двух векторов, мы будем использовать метод, известный как метод сложения векторов голова к хвосту. Этот метод описан ниже.
Этот метод описан ниже.
Величину и направление суммы двух или более векторов можно также определить с помощью точно нарисованной масштабированной векторной диаграммы.Используя масштабированную диаграмму, метод «голова к хвосту» используется для определения векторной суммы или результата. Обычная физическая лаборатория включает векторной прогулки . Либо используя смещения сантиметрового размера на карте, либо смещения метрового размера на большой открытой местности, ученик выполняет несколько последовательных смещений, начиная с назначенной начальной позиции. Предположим, вам дали карту вашего района и 18 направлений, по которым вам нужно следовать. Начиная с домашней базы , эти 18 векторов смещения могут быть сложены вместе последовательно, чтобы определить результат сложения набора из 18 направлений. Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда одно измерение заканчивалось, начиналось следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Возможно, первый вектор измеряется 5 см, восток. Когда это измерение закончится, начнется следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда одно измерение заканчивалось, начиналось следующее измерение. По сути, вы использовали бы метод сложения векторов «голова к хвосту».
Метод «голова к хвосту» включает рисование вектора для масштабирования на листе бумаги, начиная с заданной начальной позиции.Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были добавлены по направлению «голова к хвосту», результирующий результат протягивается от хвоста первого вектора к началу последнего вектора; т.е. от начала до конца. Как только результат нарисован, его длину можно измерить и преобразовать в реальных единиц, используя заданный масштаб. Направление полученного результата можно определить, используя транспортир и измерив его угол поворота против часовой стрелки с востока.
Направление полученного результата можно определить, используя транспортир и измерив его угол поворота против часовой стрелки с востока.
Пошаговый метод применения метода «голова к хвосту» для определения суммы двух или более векторов приведен ниже.
- Выберите масштаб и укажите его на листе бумаги. Наилучший выбор масштаба — такой, при котором диаграмма будет как можно больше, но при этом умещается на листе бумаги.
- Выберите начальную точку и нарисуйте первый вектор в масштабе в указанном направлении. Обозначьте величину и направление шкалы на диаграмме (например,г., МАСШТАБ: 1 см = 20 м).
- Начиная с того места, где заканчивается голова первого вектора, нарисуйте второй вектор в масштабе в указанном направлении. Обозначьте величину и направление этого вектора на диаграмме.
- Повторите шаги 2 и 3 для всех добавляемых векторов
- Нарисуйте результат от хвоста первого вектора к голове последнего вектора.
 Обозначьте этот вектор как Resultant или просто R .
Обозначьте этот вектор как Resultant или просто R . - Используя линейку, измерьте длину полученного результата и определите его величину путем преобразования в действительные единицы с помощью шкалы (4.4 см х 20 м / 1 см = 88 м).
- Измерьте направление результирующей, используя условное обозначение против часовой стрелки, о котором говорилось ранее в этом уроке.
Пример использования метода «голова к хвосту» проиллюстрирован ниже. Задача заключается в сложении трех векторов:
20 м, 45 град. + 25 м, 300 град. + 15 м, 210 град. МАСШТАБ: 1 см = 5 мМетод «голова к хвосту» используется, как описано выше, и определяется результат (выделен красным).Его величина и направление обозначены на схеме.
МАСШТАБ: 1 см = 5 м Интересно, что порядок, в котором добавляются три вектора, не влияет ни на величину, ни на направление результирующего. Результирующий по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
Результирующий по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
При сложении в этом другом порядке эти же три вектора по-прежнему дают результат с той же величиной и направлением, что и раньше (20. м, 312 градусов). Порядок, в котором векторы добавляются с использованием метода «голова к хвосту», не имеет значения.
МАСШТАБ: 1 см = 5 мДополнительные примеры сложения векторов методом «голова к хвосту» приведены на отдельной веб-странице.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», нашего интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» нашего веб-сайта и обеспечить интерактивный опыт с навыком добавления векторов.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», нашего интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» нашего веб-сайта и обеспечить интерактивный опыт с навыком добавления векторов.
Как построить результирующий вектор с помощью метода треугольника | Геометрия
Шаги для построения графика результирующего вектора с использованием метода треугольника
Шаг 1: Постройте оба вектора на одном графике. При вычитании векторов {eq} \ vec {u} — \ vec {v} {/ eq}, сначала перепишите задачу как {eq} \ vec {u} + (- \ vec {v}) {/ eq}, а затем нарисуйте векторы.
Шаг 2: Переместите второй вектор так, чтобы его начальная точка находилась в конечной точке первого вектора.
Шаг 3: Нарисуйте третий вектор, результирующий вектор, соединив начальную точку {eq} \ vec {u} {/ eq} до конечной точки {eq} \ vec {v} {/ eq} (или {eq} — \ vec {v} {/ eq}, если исходная задача включала вычитание).
Шаг 4: Запишите результирующий вектор в форме компонентов.
Словарь и уравнения для построения графика результирующего вектора с использованием метода треугольников
Вектор: Вектор — это математический объект, который имеет величину или размер и направление.Векторы обычно обозначаются стрелками.
Форма компонента: Форма компонента вектора {eq} \ vec {v} {/ eq} записывается как {eq} \ vec {v} = \ left
Метод треугольника для сложения векторов: Метод треугольника для сложения векторов — это метод, который мы можем использовать для сложения векторов, чтобы найти результирующий вектор графически. Этот метод сложения двух векторов, {eq} \ vec {u} + \ vec {v} {/ eq}, включает выстраивание начальной точки {eq} \ vec {v} {/ eq} с конечной точкой {eq} \ vec {u} {/ eq}, а затем завершение треугольника путем рисования вектора из начальной точки {eq} \ vec {u} {/ eq} до конечной точки {eq} \ vec {v} {/ экв}. Вектор, завершающий треугольник, является результирующим вектором {eq} \ vec {u} + \ vec {v} {/ экв}.
Этот метод сложения двух векторов, {eq} \ vec {u} + \ vec {v} {/ eq}, включает выстраивание начальной точки {eq} \ vec {v} {/ eq} с конечной точкой {eq} \ vec {u} {/ eq}, а затем завершение треугольника путем рисования вектора из начальной точки {eq} \ vec {u} {/ eq} до конечной точки {eq} \ vec {v} {/ экв}. Вектор, завершающий треугольник, является результирующим вектором {eq} \ vec {u} + \ vec {v} {/ экв}.
Мы будем использовать эти шаги, определения и уравнения для построения графика результирующего вектора с использованием метода треугольника в следующих двух примерах.
Пример задачи 1 — построение графика результирующего вектора с помощью метода треугольника — вычитание
График {eq} \ vec {u} — \ vec {v} {/ eq}, и запишите результирующий вектор в виде компонентов, если {eq} \ vec {u} = \ left <4, 1 \ right> {/ eq} и {eq} \ vec {v} = \ left <-3,2 \ right> {/ экв}.
Шаг 1: Постройте оба вектора на одном графике. При вычитании векторов {eq} \ vec {u} — \ vec {v} {/ eq}, сначала перепишите задачу как {eq} \ vec {u} + (- \ vec {v}) {/ eq}, а затем нарисуйте векторы.
Поскольку наша задача включает вычитание, нам сначала нужно переписать нашу задачу как сложение.
$$ \ begin {align} \ vec {u} — \ vec {v} {} & = \ vec {u} + (- \ vec {v}) \\ \\ & = \ left <4, 1 \ right> + (- \ left <-3,2 \ right>) \\ \\ & = \ left <4, 1 \ right> + \ left <3, -2 \ right> \ end {align} $$
Теперь мы можем построить график двух векторов, используя начало координат в качестве начальной точки и {eq} (4,1) {/ eq} и {eq} (3, -2) {/ eq} в качестве конечных точек для {eq} \ vec {u} \ text {и} — \ vec {v}, {/ eq} соответственно.
Шаг 2: Переместите второй вектор так, чтобы его начальная точка находилась в конечной точке первого вектора.
Рисунок {eq} — \ vec {v} {/ eq} так, чтобы его начальная точка находилась в конечной точке {eq} \ vec {u} {/ eq} показан на изображении.
Шаг 3: Нарисуйте третий вектор, результирующий вектор, соединив начальную точку {eq} \ vec {u} {/ eq} до конечной точки {eq} \ vec {v} {/ eq} (или {eq} — \ vec {v} {/ eq}, если исходная задача включала вычитание).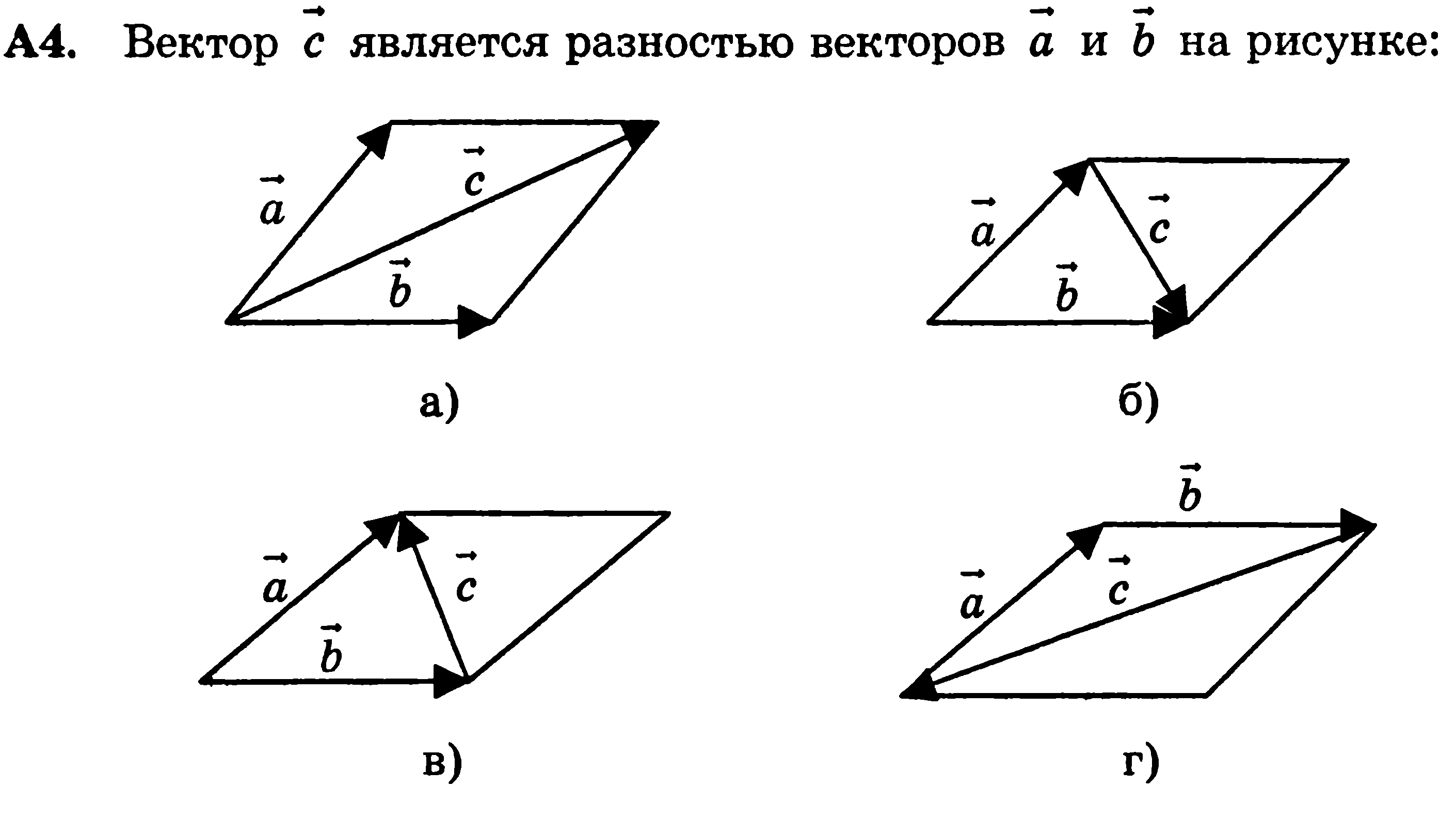
Подключение начальной точки {eq} \ vec {u} {/ eq} до конечной точки {eq} — \ vec {v} {/ eq}, мы создаем третий вектор, {eq} \ vec {u} + (- \ vec {v}) {/ eq}, как показано на рисунке.
Шаг 4: Запишите результирующий вектор в компонентной форме.
Горизонтальное смещение результирующего вектора равно 7, а вертикальное смещение равно -1. Следовательно, результирующий вектор:
$$ \ boxed {\ bf {\ vec {u} — \ vec {v} = \ left <7, -1 \ right>}} $$
Пример задачи 2 — Построение результирующего вектора с использованием метода треугольника — Дополнение
График {eq} \ vec {u} + \ vec {v} {/ eq}, и запишите результирующий вектор в виде компонентов, если {eq} \ vec {u} = \ left <-3, -2 \ right> {/ eq} и {eq} \ vec {v} = \ left <4,4 \ right> {/ экв}.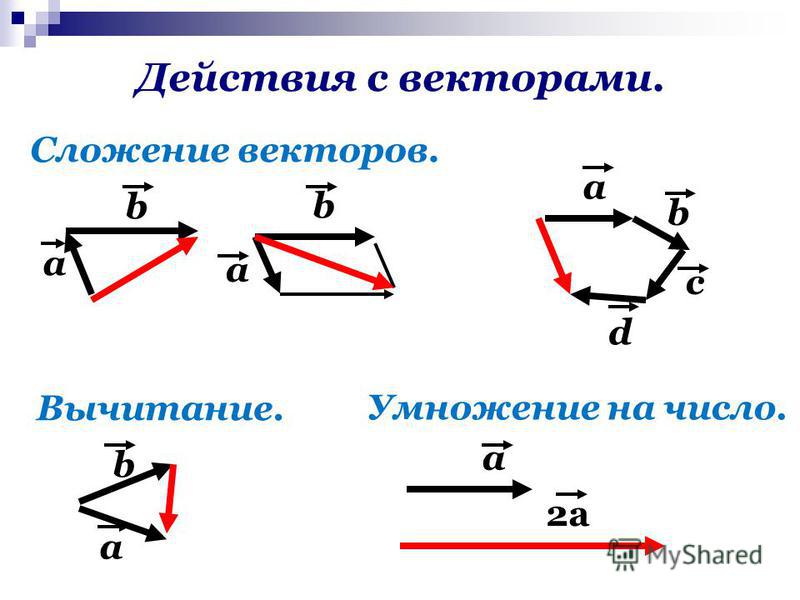
Шаг 1: Постройте оба вектора на одном графике. При вычитании векторов {eq} \ vec {u} — \ vec {v} {/ eq}, сначала перепишите задачу как {eq} \ vec {u} + (- \ vec {v}) {/ eq}, а затем нарисуйте векторы.
Поскольку эта задача включает в себя сложение векторов, мы просто строим графики векторов {eq} \ vec {u} \ text {и} \ vec {v} {/ экв}.
Шаг 2: Переместите второй вектор так, чтобы его начальная точка находилась в конечной точке первого вектора.
Шаг 3: Нарисуйте третий вектор, результирующий вектор, соединив начальную точку {eq} \ vec {u} {/ eq} до конечной точки {eq} \ vec {v} {/ eq} (или {eq} — \ vec {v} {/ eq}, если исходная задача включала вычитание).
Создание третьего вектора, {eq} \ vec {u} + \ vec {v} {/ eq}, имеем:
Шаг 4: Запишите результирующий вектор в компонентной форме.
$$ \ в коробке {\ bf {\ vec {u} + \ vec {v} = \ left <1,2 \ right>}} $$
Сложение и вычитание векторов: аналитические методы
Цели обучения
К концу этого раздела вы сможете:
- Изучите правила сложения и вычитания векторов с помощью аналитических методов.
- Применяйте аналитические методы для определения вертикальных и горизонтальных составляющих векторов.
- Примените аналитические методы, чтобы определить величину и направление результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации.Однако аналитические методы более краткие, точные и точные, чем графические методы, которые ограничены точностью, с которой можно сделать рисунок. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Разложение вектора на перпендикулярные компоненты
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения в перпендикулярных направлениях независимы. Нам очень часто требуется разделить вектор на перпендикулярные составляющие.Например, имея такой вектор, как A на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора, A x и A y , сложить для его создания.
Рис. 1. Вектор A с хвостом в начале системы координат x, y показан вместе с его компонентами x и y, A x и A y . Эти векторы образуют прямоугольный треугольник. Аналитические отношения между этими векторами резюмируются ниже.
A x и A y определены как компоненты A вдоль осей x и y -axes. Три вектора A , A x и A y образуют прямоугольный треугольник:
A x + A y = A
Обратите внимание, что эта взаимосвязь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление).Это соотношение не распространяется только на величины. Например, если A x = 3 м на восток, A y = 4 м на север и A = 5 м на северо-восток, то верно, что векторы A x + A y = A. Однако не верно, что сумма модулей векторов также равна. То есть
[латекс] 3 \ text {m} + 4 \ text {m} \ ne 5 \ text {m} \\ [/ latex]
Таким образом, A x + A y ≠ A Если вектор A известен, то его величина A (его длина) и угол θ ( его направление) известны.Чтобы найти A x и A y , его компоненты x — и y -компоненты, мы используем следующие отношения для прямоугольного треугольника.
[латекс] A_ {x} = A \ cos \ theta \\ [/ латекс]
и
[латекс] A_ {y} = A \ sin \ theta \\ [/ latex]
Рис. 2. Величины компонентов вектора Ax и A y могут быть связаны с результирующим вектором A и углом θ с тригонометрическими тождествами.Здесь мы видим, что [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex].
Предположим, например, что A — это вектор, представляющий полное перемещение человека, идущего по городу, рассматриваемое в «Кинематике в двух измерениях: введение» и «Сложение и вычитание векторов: графические методы».
Рис. 3. Мы можем использовать отношения [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex] для определения величина горизонтальных и вертикальных составляющих векторов в этом примере.{\ circ}) = 5.0 \ text {blocks} \\ [/ latex]
Вычисление результирующего вектора
Если известны перпендикулярные компоненты A x и A y вектора A , то A также можно найти аналитически. Чтобы найти звездную величину A и направление θ вектора из его перпендикулярных компонентов A x и A y , мы используем следующие отношения:
[латекс] A = \ sqrt {{A} _ {x ^ 2} + {A_ {y ^ 2}}} \\ [/ latex]
θ = tan — 1 ( A y / A x ).{2}} \ text {= 10} \ text {.} 3 \\ [/ latex] блока, опять же в соответствии с примером человека, идущего по городу. Наконец, направление θ = tan –1 (5/9) = 29,1º, как и раньше.
Определение векторов и компонентов вектора с помощью аналитических методовУравнения [латекс] A_ {x} = A \ cos \ theta \\ [/ latex] и [latex] A_ {y} = A \ sin \ theta \\ [/ latex] используются для нахождения перпендикулярных компонентов вектор, то есть переход от A и θ к A x и A y .{2}} \\ [/ latex] и θ = tan –1 ( A y / A x ) используются для нахождения вектора из его перпендикулярных компонентов — то есть перейти от A x и A y до A и θ . Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Добавление векторов с помощью аналитических методов
Чтобы увидеть, как складывать векторы с использованием перпендикулярных компонентов, рассмотрим рисунок 5, на котором векторы A и B складываются для получения результирующего R .
Рис. 5. Векторы A и B — это два этапа ходьбы, а R — результирующее или полное смещение. Вы можете использовать аналитические методы, чтобы определить величину и направление R .
Если A, и B представляют собой два этапа шага (два смещения), то R — это полное смещение. Человек, идущий на прогулку, получает чаевые R . Есть много способов прийти к одной и той же точке.{2}} \\ [/ latex] и θ = tan –1 ( A y / A x ). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси x и y, которые будут использоваться в проблеме. Затем найдите компоненты каждого вектора, которые нужно добавить вдоль выбранных перпендикулярных осей . Используйте уравнения A x = A cos θ и A y = A sin θ , чтобы найти компоненты.На рисунке 6 эти компоненты: A x , A y , B x и B y . Углы, которые векторы A, и B образуют с осью x , составляют θ A и θ B соответственно.
Рисунок 6. Чтобы сложить векторы A и B, сначала определите горизонтальные и вертикальные компоненты каждого вектора.Это пунктирные векторы A x , A y , B x и B y , показанные на изображении.
Шаг 2. Найдите компоненты результирующего по каждой оси, сложив компоненты отдельных векторов по этой оси . То есть, как показано на рисунке 7,
R x = A x + B x
и
R y = A y + B y .
Рис. 7. Величина векторов A, , x и B , x суммируется, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Точно так же величины векторов A x и B y складываются, чтобы получить величину R y результирующего вектора в вертикальном направлении. {2}} \\ [/ latex]
Шаг 4. Чтобы получить направление результата:
θ = tan −1 ( R y / R x ).
Следующий пример иллюстрирует эту технику добавления векторов с использованием перпендикулярных компонентов.
Пример 1. Добавление векторов аналитическими методами
Добавьте вектор A к вектору B , показанному на рисунке 8, используя перпендикулярные компоненты вдоль осей x — и y .Оси x и y расположены вдоль направлений восток-запад и север-юг соответственно. Вектор A представляет собой первый этап прогулки, во время которой человек проходит 53,0 м в направлении 20,0º к северу от востока. Вектор B представляет собой вторую ногу, смещение на 34,0 м в направлении 63,0º к северу от востока.
Рисунок 8.
Vector A имеет звездную величину 53,0 м и направление 20,0º к северу от оси x .Вектор B имеет звездную величину 34,0 м и направление 63,0º к северу от оси x . Вы можете использовать аналитические методы, чтобы определить величину и направление R .
СтратегияКомпоненты A и B вдоль осей x — и y представляют собой движение на восток и на север, чтобы добраться до той же конечной точки. Найденные, они объединяются для получения результата.
РастворСледуя описанному выше методу, мы сначала находим компоненты A и B по осям , x , и , y , . Обратите внимание, что A = 53,0 м, θ A = 20,0 º, B = 34,0 м и θ B = 63,0 º. Мы находим x -компоненты, используя [latex] A_ {x} = A \ cos \ theta \\ [/ latex], что дает
[латекс] \ begin {array} {c} A_ {x} = A \ cos \ theta_ {A} = (53.{\ circ}) \\ = (34,0 м) (0,891) = 30,3 \ text {m} \ end {array} [/ latex]
Компоненты результата x и y составляют
R x = A x + B x = 49,8 м + 15,4 м = 65,2 м
и
R y = A y + B y = 18.{2} \ text {m}} \\ [/ latex]
, так что
R = 81,2 м.
Наконец, находим направление результирующего:
θ = tan −1 ( R y / R x ) = + tan −1 (48,4 / 65,2).
Таким образом,
θ = tan -1 (0,742) = 36,6º.
Рис. 9. Используя аналитические методы, мы видим, что величина R равна 81.2 м, направление 36,6º к северу от востока.
ОбсуждениеЭтот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонентов очень похоже — это просто добавление отрицательного вектора. Вычитание векторов осуществляется добавлением отрицательного вектора. То есть A — B ≡ A + ( –B ). Таким образом, в метод вычитания векторов с использованием перпендикулярных компонентов идентичен методу сложения .Компоненты –B являются отрицательными элементами компонентов B . Компоненты x и y результирующего A — B = A , таким образом, составляют
[латекс] R_ {x} = A_ {x} + (-B_ {x}) \\ [/ latex]
и
[латекс] R_ {y} = A_ {y} + (-B_ {y}) \\ [/ latex]
, а остальная часть описанного выше метода идентична методу сложения. (См. Рисунок 10.)
Анализ векторов с использованием перпендикулярных компонентов очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга.Следующий модуль, Projectile Motion, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать изображение четким и упрощает физику.Рисунок 10. Вычитание двух векторов, показанных на рисунке 5. Компоненты –B являются отрицательными значениями компонентов B. Метод вычитания такой же, как и для сложения.
Исследования PhET: добавление векторов
Узнайте, как складывать векторы. Перетащите векторы на график, измените их длину и угол и просуммируйте их.Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Аналитический метод сложения и вычитания векторов включает использование теоремы Пифагора и тригонометрических тождеств для определения величины и направления результирующего вектора.
- Шаги для сложения векторов A и B с использованием аналитического метода следующие:
Шаг 1: Определите систему координат для векторов.Затем определите горизонтальные и вертикальные компоненты каждого вектора, используя уравнения
.[латекс] \ begin {массив} {lll} {A} _ {x} & = & A \ text {cos} \ theta \\ {B} _ {x} & = & B \ text {cos} \ theta \ end {array} \\ [/ latex]
и
[латекс] \ begin {array} {lll} {A} _ {y} & = & A \ text {sin} \ theta \\ {B} _ {y} & = & B \ text {sin} \ theta \ text {.} \ end {array} \\ [/ latex]
Шаг 2: Добавьте горизонтальные и вертикальные компоненты каждого вектора, чтобы определить компоненты R x и R y результирующего вектора, R :
[латекс] {R} _ {x} = {A} _ {x} + {B} _ {x} \\ [/ latex]
и
[латекс] {R} _ {y} = {A} _ {y} + {B} _ {y} \\ [/ latex]
Шаг 3: Используйте теорему Пифагора, чтобы определить величину R результирующего вектора R :
[латекс] R = \ sqrt {{{R} _ {x}} ^ {2} + {{R} _ {y}} ^ {2}} \\ [/ latex]
Шаг 4: Используйте тригонометрическую идентичность, чтобы определить направление [латекс] \ тета \ [/ латекс] R :
[латекс] \ theta = {\ text {tan}} ^ {- 1} \ left ({R} _ {y} / {R} _ {x} \ right) [/ latex].
Концептуальные вопросы
1. Предположим, вы складываете два вектора A и B . Какое относительное направление между ними дает результирующую с наибольшей величиной? Какая максимальная величина? Какое относительное направление между ними дает наименьшую величину равнодействующей? Какая минимальная величина?
2. Приведите пример ненулевого вектора с нулевой компонентой.
3. Объясните, почему вектор не может иметь компонент, превышающий его собственную величину.
4. Если векторы A и B перпендикулярны, каков компонент A вдоль направления B ? Каков компонент B в направлении A ?
Задачи и упражнения
1. Найдите следующее для пути C на рисунке 12: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
Рис. 12. Различные линии представляют собой пути, по которым идут разные люди в городе. Все блоки имеют ширину 120 м.
2. Найдите следующее для пути D на рисунке 12: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. В этой части задачи явно покажите, как вы следуете шагам аналитического метода сложения векторов.
3. Найдите северную и восточную составляющие смещения от Сан-Франциско до Сакраменто, показанные на рисунке 13.
Рисунок 13.
4. Решите следующую задачу, используя аналитические методы. Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от начальной точки и каково направление по компасу линии, соединяющей вашу отправную точку с конечным положением? (Если вы представляете два этапа прогулки как векторные смещения A, и B , как на рисунке 14, то в этой задаче вам предлагается найти их сумму R = A + B .)
Рис. 14. Два смещения A, и B складываются, чтобы получить общее смещение R, имеющее величину R и направление θ .
Обратите внимание, что вы также можете решить эту проблему графически. Обсудите, почему аналитический метод решения этой проблемы потенциально более точен, чем графический метод.
5. Повторите упражнение 4, используя аналитические методы, но поменяйте порядок двух этапов прогулки и покажите, что вы получите тот же конечный результат.(Эта задача показывает, что добавление их в обратном порядке дает тот же результат, то есть B + A = A + B .) Обсудите, как другой путь для достижения той же точки может помочь преодолеть препятствие, блокирующее вам другой путь.
6. Вы ведете [латекс] 7 \ text {.} \ Text {50 км} [/ latex] по прямой в направлении 15º к востоку от севера. (а) Найдите расстояния, на которые вам нужно проехать прямо на восток, а затем прямо на север, чтобы добраться до той же точки. (Это определение эквивалентно нахождению компонентов смещения в восточном и северном направлениях.) (b) Покажите, что вы все еще прибываете в одну и ту же точку, если восточный и северный этапы поменяны местами.
7. Снова выполните упражнение 4, используя аналитические методы, и измените второй этап прогулки на 25,0 м прямо на юг. (Это эквивалентно вычитанию B из A — то есть нахождению R ‘ = A — B ) (b) Повторите еще раз, но теперь вы сначала идете на 25,0 м на север, а затем на 18,0 м на восток. (Это эквивалентно вычитанию A из B, то есть нахождению 30.8 м, 35,8 к западу от севера. Это согласуется с вашим результатом?)
8. У нового землевладельца есть треугольный участок плоской земли, который она хочет оградить. Начиная с западного угла, она измеряет длину первой стороны 80,0 м, а следующей — 105 м. Эти стороны представлены как векторы смещения A от B на рисунке 15. Затем она правильно вычисляет длину и ориентацию третьей стороны C. Каков ее результат?
Рисунок 15.
9.Вы летите 32,0 км по прямой в неподвижном воздухе в направлении 35º к югу от запада. (а) Найдите расстояния, на которые вам придется лететь прямо на юг, а затем прямо на запад, чтобы прибыть в ту же точку. (Это определение эквивалентно нахождению компонентов смещения в южном и западном направлениях.) (B) Найдите расстояния, на которые вам придется пролететь сначала в направлении 45,0º к югу от запада, а затем в направлении 45,0º к западу от севера. . Это компоненты смещения по другому набору осей — одна повернута на 45 °.
10. Фермер хочет отгородить свой четырехсторонний участок плоской земли. Он измеряет первые три стороны, показанные как A, B и C на рисунке 16, а затем правильно вычисляет длину и ориентацию четвертой стороны D. Каков его результат?
Рисунок 16.
11. Пытаясь сбежать со своего острова, Гиллиган строит плот и отправляется в море. В течение дня ветер сильно меняется, и его дует по следующим прямым линиям: 2,50 км 45,0 ° к северу от запада; затем 4.70 км 60,0º к югу от востока; затем 1,30 км 25º к югу от запада; затем 5,10 км прямо на восток; затем 1,70 км 5,00º к востоку от севера; затем 7.20 к югу от запада; и, наконец, 2,80 км, 10,0 ºсеверо востока. Каково его окончательное положение относительно острова?
12. Предположим, пилот летит 40,0 км в направлении 60º к северу от востока, а затем летит 30,0 км в направлении 15º к северу от востока, как показано на рисунке 17. Найдите его общее расстояние R от начальной точки и направление θ. прямого пути до конечной позиции.Обсудите качественно, как этот полет будет изменен ветром с севера и как влияние ветра будет зависеть как от скорости ветра, так и от скорости самолета относительно воздушной массы.
Рисунок 17.
Глоссарий
- аналитический метод:
- Метод определения величины и направления результирующего вектора с использованием теоремы Пифагора и тригонометрических тождеств
Избранные решения проблем и упражнения
1.(а) 1,56 км (б) 120 м на восток
3. Северная составляющая 87,0 км, восточная составляющая 87,0 км
5. 30,8 м, 35,8 к западу от севера
7. (a) 30,8 м, 54,2 ° к югу от запада (b) 30,8 м, 54,2 ° к северу от востока
9. 18,4 км к югу, затем 26,2 км к западу (b) 31,5 км под углом 45,0 ° к югу от запада, затем 5,56 км под углом 45,0 ° к западу от севера
11. 7,34 км, 63,5º к югу от востока
| Имя | Описание | |
|---|---|---|
| конструктор (x: число = 0, y: число = 0, z: число = 0): Vector3d | ||
| addCrossProductToTargetsInPlace (ax: число, ay: число, az: число, bx: число, by: число, bz: число, cx: число, cy: число, cz: число): void | Накапливать вектор, который представляет собой векторы кросс-произведения от исходной точки (ax, ay, az) до целей (bx, by, bz) и (cx, cy, cz) | |
| angleFromPerpendicular (vectorB: Vector3d): Угол | Вернуть (строго типизированный) угол от этого вектора к плоскости, перпендикулярной planeNormal. | |
| angleTo (vectorB: Vector3d): Угол | Вернуть (строго типизированный) угол от этого вектора к vectorB. | |
| angleToXY (vectorB: Vector3d): Угол | Вернуть (строго типизированный) угол от этого вектора к вектору В, используя только части xy. | |
| клон (результат ?: Vector3d): Vector3d | Скопируйте xyz из этого экземпляра в новый (или, возможно, повторно используемый) Vector3d | |
| crossProduct (vectorB: Vector3d, результат ?: Vector3d): Vector3d | Вернуть произведение этого вектора на векторB. | |
| crossProductMagnitude (vectorB: XYAndZ): число | Вычислить величину перекрестного произведения (без выделения временного векторного объекта) | |
| crossProductMagnitudeSquared (vectorB: XYAndZ): номер | Вычислить квадрат величины перекрестного произведения (без выделения временного векторного объекта) | |
| crossProductStartEnd (pointA: Point3d, pointB: Point3d, результат ?: Vector3d): Vector3d | Перекрестное произведение с вектором из точки A в точку B | |
| crossProductStartEndXY (pointA: Point3d, pointB: Point3d): номер | Перекрестное произведение (только части xy) с вектором от точки A до точки B | |
| crossProductXY (vectorB: Vector3d): номер | Вернуть перекрестное произведение экземпляра и вектораB, используя только части x и y. | |
| crossProductXYZ (x: число, y: число, z: число, результат ?: Vector3d): Vector3d | возвращает векторное произведение , это с вектором (x, y, z) | |
| dotProduct (vectorB: XYAndZ): номер | Верните скалярное произведение этого вектора с помощью vectorB. | |
| dotProductStart3dEnd4d (pointA: Point3d, pointB: Point4d): номер | Возвращает скалярное произведение с вектором (pointB — pointA * pointB.ш) | |
| dotProductStartEnd (pointA: XYAndZ, pointB: XYAndZ): номер | Возвращает скалярное произведение этого вектора на вектор с от pointA к pointB | |
| dotProductStartEndXY (pointA: Point3d, pointB: Point3d): номер | Точечное произведение с вектором от точки A до точки B, используя только части xy | |
| dotProductStartEndXYZ (pointA: Point3d, x: число, y: число, z: число): число | Точечное произведение с вектором из точки A в точку B, с точкой B, заданной как x, y, z | |
| dotProductStartEndXYZW (pointA: Point3d, x: число, y: число, z: число, w: число): число | Точечное произведение с вектором из точки A в точку B, с точкой B, заданной как (взвешенные) x, y, z, w | |
| dotProductXY (vectorB: Vector3d): номер | Верните скалярное произведение экземпляра и вектораB, используя только части x и y. | |
| dotProductXYZ (x: число, y: число, z: число = 0): число | Точечное произведение с вектором (x, y, z) | |
| FractionOfProjectionToVector (target: Vector3d, defaultFraction: number = 0): number | Вернуть дробную проекцию spaceVector на этот | |
| интерполировать (дробь: число, vectorB: XYAndZ, результат ?: Vector3d): Vector3d | Вернуть вектор, вычисленный в дробной позиции между этим вектором и vectorB | |
| isParallelTo (other: Vector3d, AgainstIsParallel: boolean = false, returnValueIfAnInputIsZeroLength: boolean = false): boolean | Проверить, параллелен ли этот вектор другому. | |
| isPerpendicularTo (other: Vector3d, returnValueIfAnInputIsZeroLength: boolean = false): boolean | Проверить, перпендикулярен ли этот вектор другому. | |
| минус (вектор: XYAndZ, результат ?: Vector3d): Vector3d | Вернуть разность векторов this - vector | |
| отрицание (результат ?: Vector3d): Vector3d | Вернуть новый вектор с инвертированными компонентами из вызывающего экземпляра. | |
| normalize (результат ?: Vector3d): Vector3d | undefined | Верните единичный вектор, параллельный этому. | |
| normalizeInPlace (): логическое | Если этот вектор имеет ненулевую длину, разделите его на длину, чтобы получить единичный вектор. | |
| normalizeWithDefault (x: число, y: число, z: число, результат ?: Vector3d): Vector3d | Нормализовать этот вектор, используя заданный xyz по умолчанию, если длина равна нулю. | |
| normalizeWithLength (результат ?: Vector3d): {mag: number, v: Vector3d | undefined} | Вернуть объект пары, содержащий (a) свойство v , которое является единичным вектором в направлении | |
| planarAngleTo (вектор: Vector3d, planeNormal: Vector3d): Угол | Вернуть угол (как строго типизированный Angle) из этого вектора в vectorB. | |
| planarRadiansTo (вектор: Vector3d, planeNormal: Vector3d): число | Вернуть (радианы как простое число, не строго типизированный угол) радианы из этого вектора в vectorB. | |
| плюс (вектор: XYAndZ, результат ?: Vector3d): Vector3d | Вернуть векторную сумму this - vector | |
| plus2Scaled (vectorA: XYAndZ, scalarA: number, vectorB: XYAndZ, scalarB: number, result ?: Vector3d): Vector3d | Вернуть (строго типизированный Vector3d) this Vector3d + vectorA * scalarA + vectorB * scalarB | |
| plus3Scaled (vectorA: XYAndZ, scalarA: number, vectorB: XYAndZ, scalarB: number, vectorC: XYAndZ, scalarC: number, result ?: Vector3d): Vector3d | Вернуть (строго типизированный Vector3d) thisVector3d + vectorA * scalarA + vectorB * scalarB + vectorC * scalarC | |
| plusScaled (вектор: XYAndZ, scaleFactor: number, результат ?: Vector3d): Vector3d | Вектор возврата + вектор * скаляр | |
| rotate90Around (ось: Vector3d, результат ?: Vector3d): Vector3d | undefined | Поверните этот вектор на 90 градусов вокруг вектора оси. | |
| rotate90CCWXY (результат ?: Vector3d): Vector3d | Вернуть вектор такой же длины, но повернуть на 90 градусов против часовой стрелки | |
| rotate90Towards (цель: Vector3d, результат ?: Vector3d): Vector3d | undefined | Вернуть вектор (новый или предварительно выделенный), повернутый на 90 градусов в плоскости этого вектора и целевого вектора. | |
| rotateXY (угол: Угол, результат ?: Vector3d): Vector3d | Поверните части xy этого вектора вокруг оси z. | |
| safeDivideOrNull (знаменатель: число, результат ?: Vector3d): Vector3d | undefined | Разделить на знаменатель, но вернуть значение undefined, если знаменатель равен нулю. | |
| масштаб (масштаб: число, результат ?: Vector3d): Vector3d | Вектор возврата * скаляр | |
| scaleToLength (длина: число, результат ?: Vector3d): Vector3d | undefined | Возвращает вектор (необязательно новый или повторно используемый) в направлении , это , но с указанной длиной. | |
| setStartEnd (point0: XYAndZ, point1: XYAndZ): void | Установить (заменить) компоненты xzz так, чтобы они были вектором от point0 до point1 | |
| signedAngleTo (vector1: Vector3d, vectorW: Vector3d): Угол | Вернуть угол (строго типизированный угол) от этого вектора к вектору В, измеренный в плоскости, содержащей оба, с вектором W, указывающим, с какой стороны смотреть, чтобы контролировать знак угла. | |
| signedRadiansTo (vector1: Vector3d, vectorW: Vector3d): число | Возвращает угол (простое число радиан, не строго типизированный угол) от этого вектора к вектору В, измеренный в плоскости, содержащей оба, с вектором W, указывающим, с какой стороны смотреть, чтобы контролировать знак угла. | |
| sizeCrossProduct (vectorB: Vector3d, productLength: number, result ?: Vector3d): Vector3d | undefined | Вычислить перекрестное произведение с vectorB . | |
| меньшеUnorientAngleTo (vectorB: Vector3d): Угол | Вернуть наименьший (строго типизированный) угол из (двунаправленной) линии, содержащей , это , в (двунаправленную) строку, содержащую vectorB | |
| меньшеUnorientRadiansTo (vectorB: Vector3d): number | Вернуть наименьший угол (в радианах) из (двунаправленной) строки, содержащей , это , в (двунаправленную) строку, содержащую vectorB | |
| tripleProduct (vectorB: Vector3d, vectorC: Vector3d): число | Вернуть тройное произведение экземпляра, vectorB и vectorC | |
| tryNormalizeInPlace (smallestMagnitude: number = Geometry.smallMetricDistance): логическое | Попробуйте нормализовать (разделить на величину), сохранив результат на месте. | |
| unitCrossProduct (vectorB: Vector3d, результат ?: Vector3d): Vector3d | undefined | Вычислите перекрестное произведение этого вектора на vectorB . | |
| unitCrossProductWithDefault (vectorB: Vector3d, x: number, y: number, z: number, result ?: Vector3d): Vector3d | Вычислите перекрестное произведение этого вектора на vectorB . | |
| unitPerpendicularXY (результат ?: Vector3d): Vector3d | Возвращает вектор, который находится в плоскости xy, перпендикулярно xy части этого вектора, и имеет единичную длину. | |
| create (x: number = 0, y: number = 0, z: number = 0, result ?: Vector3d): Vector3d Static | возвращает Vector3d (новый или повторно использованный из необязательного результата) | |
| createAdd2Scaled (vectorA: XYAndZ, scaleA: number, vectorB: XYAndZ, scaleB: number, result ?: Vector3d): Vector3d Static | Вернуть (строго типизированный Vector3d) thisVector3d + vectorA * scalarA + vectorB * scalarB | |
| createAdd2ScaledXYZ (ax: number, ay: number, az: number, scaleA: number, bx: number, by: number, bz: number, scaleB: number, result ?: Vector3d): Vector3d Static | Вернуть (строго типизированный Vector3d) thisVector3d + vectorA * scalarA + vectorB * scalarB со всеми компонентами, представленными в виде чисел | |
| createAdd3Scaled (vectorA: XYAndZ, scaleA: number, vectorB: XYAndZ, scaleB: number, vectorC: XYAndZ, scaleC: number, result ?: Vector3d): Vector3d Static | Вернуть (строго типизированный Vector3d) thisVector3d + vectorA * scaleA + vectorB * scaleB + vectorC * scaleC | |
| createArrayFromPackedXYZ (данные: Float64Array): Vector3d [] Статический | Вернуть массив векторов, составленный из групп по 3 записи в Float64Array. | |
| createCrossProduct (ux: number, uy: number, uz: number, vx: number, vy: number, vz: number, result ?: Vector3d): Vector3d Static | Создайте вектор, который представляет собой произведение двух векторов, представленных как отдельные аргументы | |
| createCrossProductToPoints (origin: XYAndZ, pointA: XYAndZ, pointB: XYAndZ, result ?: Vector3d): Vector3d Static | Вернуть перекрестное произведение векторов из исходной точки в точку A и точку B. | |
| createFrom (data: XYAndZ | XAndY | Float64Array | number [], результат ?: Vector3d): Vector3d Static | Копирование содержимого из другого Point3d, Point2d, Vector2d или Vector3d | |
| createPolar (r: число, theta: угол, z ?: число): Vector3d Static | Возвращает вектор, определяемый расстоянием в полярных координатах и углом от оси x | |
| createRotateVectorAroundVector (вектор: Vector3d, ось: Vector3d, угол ?: Угол): Vector3d | undefined Статический | Вернуть вектор, который является входным вектором, повернутым вокруг вектора оси. | |
| createSpherical (r: число, theta: угол, phi: угол): Vector3d Static | Вернуть вектор, определенный в сферических координатах. | |
| createStartEnd (начало: XYAndZ, конец: XYAndZ, результат ?: Vector3d): Vector3d Static | Вернуть вектор, определенный начальной и конечной точками (конец — начало). | |
| createStartEndXYZXYZ (x0: число, y0: число, z0: число, x1: число, y1: число, z1: число, результат ?: Vector3d): Vector3d Static | Вернуть вектор (необязательно в предварительно выделенном результате, иначе вновь созданный) от [x0, y0, z0] до [x1, y1, z1] | |
| createZero (результат ?: Vector3d): Vector3d Static | Вернуть вектор с 000 частями xyz. | |
| dotProductAsXYAndZ (dataA: XYAndZ, dataB: XYAndZ): число Статический | Вернуть скалярное произведение компонентов xyz двух входов, которые являются XYAndZ, но не являются явно Vector3d | |
| из JSON (json ?: XYZProps): Vector3d Static | Преобразовать json в Vector3d. | |
| unitX (масштаб: число = 1): Vector3d Static | Вернуть единичный вектор X, необязательно умноженный на масштаб | |
| unitY (масштаб: число = 1): Vector3d Static | Вернуть единичный вектор Y | |
| unitZ (масштаб: число = 1): Vector3d Static | Вернуть единичный вектор Z |
Векторные операции
В физическом мире некоторые величины, такие как масса, длина, возраст и стоимость, могут быть представлены только величиной.Другие величины, такие как скорость и сила, также включают направление. Вы можете использовать векторы для представления тех величин, которые включают как величину, так и направление. Одним из распространенных способов использования векторов является определение фактической скорости и направления самолета с учетом его воздушной скорости и направления, а также скорости и направления попутного ветра. Другое распространенное использование векторов заключается в нахождении результирующей силы на объекте, на которую действуют несколько отдельных сил.
Любая величина, имеющая размер и направление, называется векторной величиной .Если A, и B — две точки, которые расположены на плоскости, то направленный отрезок линии от точки A до точки B обозначается. Точка A — это начальная точка , а точка B — конечная точка .
Геометрический вектор — это величина, которая может быть представлена направленным линейным сегментом. С этого момента вектор будет обозначаться жирным шрифтом, например v или u .Величина вектора вектора — это длина направленного линейного сегмента. Величину иногда называют нормой . Два вектора имеют одинаковое направление , если они параллельны и указывают в одном направлении. Два вектора имеют противоположных направления , если они параллельны и указывают в противоположных направлениях. Вектор, который не имеет величины и указывает в любом направлении, называется нулевым вектором . Два вектора называются эквивалентными векторами , если они имеют одинаковую величину и одинаковое направление.
На рисунке 1 показано сложение вектора с использованием правила хвостового конца . Чтобы сложить векторы v и u , переместите вектор u так, чтобы начальная точка u находилась в конечной точке v . Результирующий вектор от начальной точки v до конечной точки u является вектором v + u и называется результирующим . Векторы v и u называются компонентами вектора v + u .Если два добавляемых вектора не параллельны, то можно также использовать правило параллелограмма . В этом случае начальные точки векторов совпадают, а в результате получается диагональ параллелограмма, образованная двумя векторами в качестве смежных сторон параллелограмма.
Рисунок 1
Пример сложения векторов.
Чтобы умножить вектор u на действительное число q , умножьте длину u на | q | и измените направление u , если q <0.Это называется скалярным умножением на . Если вектор u умножается на -1, результирующий вектор обозначается как — u . Он имеет ту же величину, что и и , но в противоположном направлении. На рисунке 2 показано использование скаляров.
Рисунок 2
Примеры векторов.
Пример 1: Самолет летит строго на запад со скоростью 400 миль в час. Попутный ветер дует в юго-западном направлении со скоростью 50 миль в час.Нарисуйте диаграмму, отображающую путевую скорость и направление самолета (Рисунок 3).
Рисунок 3
Рисунок для примера 1 — векторное представление.
Вектор, представленный в предыдущем примере, известен как вектор скорости . Пеленг на вектора v — это угол, измеренный по часовой стрелке от правильного севера до v . В этом примере пеленг самолета составляет 270 °, а пеленг ветра — 225 °.Нарисовав фигуру в виде треугольника с использованием правила хвостового оперения, можно вычислить длину (путевую скорость самолета) и азимут полученного результата (Рисунок 4).
Рис. 4
Чертеж для примера 1 — угловое представление.
Во-первых, используйте закон косинусов, чтобы найти величину результирующей.
Затем используйте закон синусов, чтобы найти подшипник.
Таким образом, азимут β равен 270 ° — 4.64 °, или примерно 265,4 °.
Пример 2: Самолет летит со скоростью 300 миль в час. Ветер дует с юго-востока со скоростью 86 миль в час с пеленгом 320 °. На каком пеленге должна стоять плоскость, чтобы иметь истинный пеленг (относительно земли) 14 °? Какая будет путевая скорость самолета (рис. 5)?
Рисунок 5
Чертеж для примера 2.
Используйте закон синусов для расчета пеленга и путевой скорости.Поскольку эти альтернативные внутренние углы совпадают, угол 54 ° является суммой угла 14 ° и угла 40 °.
Следовательно, пеленг плоскости должен быть 14 ° + 13,4 ° = 27,4 °. Базовая скорость самолета составляет 342,3 мили в час.
Любой вектор может быть разбит на два вектора , горизонтальный компонент и вертикальный компонент. Эти составляющие векторы называются проекциями (Рисунок 6).
Рисунок 6
Пример проекций.

 Выразить векторы
Выразить векторы
 Найти вектор, который равен сумме векторов
Найти вектор, который равен сумме векторов
 Точка D лежит на стороне KN треугольника MKN и делит эту сторону в отношении 2:3. Выразить вектор .
Точка D лежит на стороне KN треугольника MKN и делит эту сторону в отношении 2:3. Выразить вектор .