Контрольная работа по тригонометрическим функциям: Контрольная работа по теме «Тригонометрические функции, их свойства и графики» (алгебра 10 класс)

Контрольная работа №1 по теме»Тригонометрические функции»

Вариант1 1.Найти область определения и множество значений функции у=5 cos х . 2. Выяснить является функция у=2sin x – tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 0,5. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 2. При каких значениях функция убывает; возрастает?

Вариант2 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -0,5. 4.Найти наибольшее и наименьшее значения функции у= 6cosx — 6sinх + 3 5. Построить график функции у= sin х + 2. При каких значениях функция убывает; возрастает?

Вариант3 1.Найти область определения и множество значений функции у= cos х + 4 2. Выяснить является функция у = 3sin x + tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = -1. 4.Найти наибольшее и наименьшее значения функции у= 8sin x cos х — 2 5. Построить график функции у= cos х — 1. При каких значениях функция убывает; возрастает?

Вариант6 1.Найти область определения и множество значений функции у=sin х — 3 2. Выяснить является функция у = cos x +3 x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 5cosx — 5sinх + 2 5. Построить график функции у= sin х — 1. При каких значениях функция убывает; возрастает?

Вариант5 1.Найти область определения и множество значений функции у= 5cos х . 2. Выяснить является функция у=sin x –5 tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 10sin x cos х + 2 . 5. Построить график функции у= cos х + 1. При каких значениях функция убывает; возрастает?

Вариант6 1.Найти область определения и множество значений функции у=sin х + 2 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = 1. 4.Найти наибольшее и наименьшее значения функции у= 8cosx — 8sinх + 3 5. Построить график функции у= sin х + 1. При каких значениях функция убывает; возрастает?

Вариант7 1.Найти область определения и множество значений функции у=cos х + 11 2. Выяснить является функция у=sin x –2tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 3. При каких значениях функция убывает; возрастает?

Вариант8 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 6cosx — 6sinх + 3 5. Построить график функции у= sin х +3. При каких значениях функция убывает; возрастает?

Контрольная Работа 1 По Теме Тригонометрические Функции – Telegraph

➡➡➡ ПОДРОБНЕЕ КЛИКАЙ ТУТ!

Контрольная Работа 1 По Теме Тригонометрические Функции
23 . 2019 — Контрольная работа по теме Тригонометрические функции .
4 . 2019 — Приложение . Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения:  . .
7 2019 — Контрольная работа по теме «Тригонометрические функции» . Вариант 1 . Постройте схематично функции у = 2cosx . Найдите область  . .
Контрольная работа по теме «Тригонометрические функции» — Тригонометрические функции — 1-е полугодие . Цель: проверить знания учащихся с  . .
30 . 2019 — Скачать — Контрольная работа №1 по теме » Тригонометрические функции» в 11 классе, алгебра и начала анализа . Контрольная  . .
12 . 2019 — «Контрольная работа по теме «Тригонометрические функции»» . Вариант 1 . 1 . Найти область определения функции . 1) у=sin 2) у=cos 3)  . .
26 . 2019 — Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 .
Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 . Сравните с нулём  . .
Контрольные работы с ответами к учебнику Мордковича А .Г . за 1, 2, 3, . . Контрольная работа №1 «Определение тригонометрических функций» .
Контрольная работа по теме «Тригонометрические функции» (итоговая за 1 полуг) . Вариант I . А1 . Упростите выражение . 1)cos(sin . 2 . . 1) 0 2) 1 3)  . .
23 . — Контрольная работа по теме: Тригонометрические функции . Вариант 1 . №1 . Вычислите : . №2 . Решите уравнение: . №3 . Найдите  . .
31 . — Контрольная работа по алгебре и началам анализа . по теме «Тригонометрические функции» . Вариант 1 . Найти область определения  . .
Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 . 2 . Сравните с нулём  . .
Контрольная работа №1 . Цели урока: проверить знания и умение учащихся по теме «Тригонометрические функции» . Ход урока: Организационный  . .
3 ав 2019 — Контрольная / проверочная работа для учителя-предметника для всех классов . . . Тригонометрические функции . 1 курс . Контрольная работа по математике . . Самостоятельная работа по теме «Преобразование  . .
Контрольная работа по алгебре и началам анализа Тема: . . Главная > Контрольная работа . . Тема: Тригонометрические функции . . 1 18 Контроль и коррекция знаний по теме «формулы суммы и разности тригонометрических  . .
Контрольная работа по теме «Тригонометрические функции» форма ЕГЭ . . . 1) Федеральный компонент государственного стандарта общего  . .
Контрольная работа . По теме «Тригонометрические функции и их свойства» . Выполнил ученик 9 класса . Вариант I . Результаты: 1-1 . 1-2 . 1-3 . 1-4 . 1-5 .
4 — Контрольная работа по теме «Тригонометрические функции» Материалы . . Изобразить график функции у = Sin x +1 на отрезке .
Контрольная работа № 3 по теме «Тригонометрические функции и тождества . Решение простейших тригонометрических уравнений» . 1 . Решите  . .
Контрольная работа по теме «Тригонометрические функции» (Алгебра 10класс) . . Помогите решить контрольную пж график надо начертить y=tg x -1  . .
Контрольная работа 11 класс . Тригонометрические функции . Варианты 1-4 .doc . Скачать 288 Кб . Автор: Мельникова И .Н .
уметь: решать простейшие тригонометрические уравнения по формулам; . . 14, Контрольная работа № 1по теме «Тригонометрические функции», 1 .
Глава 2 . Тригонометрические функции [А .Г . Мордкович (базовый уровень)] . . Контрольная работа № 1 . . Подготовка к контрольной работе №2 по теме «Тригонометрические функции» (Таженова У . С .) Контрольная работа № 2 .
Контрольная работа № 1 . Тригонометрические функции, их свойства . Содержание учебного материала . Радианная ме ра угла . Синус, косинус, тангенс  . .
Используемые в КОС оценочные средства представлены в таблице 1 . Таблица 1 . . Контрольная работа . Тема 2 .5 . Показательные уравнения и неравенства . . . тригонометрические функции . Самостоятельная работа . Тема 7 .2 .
Контрольная работа № 1 по теме «Числовые функции . Числовая окружность» (1 час) . • Контрольная работа № 2 по теме «Тригонометрические  . .
Тема . Время к/р . 1 урок . 20-25 мин . 1 урок . 1 урок . Тригонометрические . . следованию функции . Итоговая контрольная работа . 5 . 1 урок . 1 урок . 1 урок .
показательные, логарифмические и тригонометрические функции . . . сов . Контрольная работа №3 . МОДУЛЬ№1 . Тема 1 .6 .Тригонометрические  . .
Кр № 1 . Числовые функции . 10 . 10 . Кр № 2 . Тригонометрические функции . 24 . . 48 . Контрольная работа №2 .1 по теме . «Перпендикулярность прямой и  . .
Формулы суммы и разности одноименных тригонометрических функций . Представьте в виде произведения: 1) sin 40° + sin 60°; . 6) cos 2х + cos Зх; .
19 Контрольная работа 6 Тема контрольной работы: Формулы тригонометрических функций и их применение Дата 2 вариант 1 . Найдите значение  . .
Контрольная работа №1 (по повторению) . Тема 1 . Числовые функции (7/2/1) . . . Практическая работа №6 «Тригонометрические функции числового и  . .
15 . 2020 — Контрольная работа №1 по теме «Развитие понятия о числе» . . Выражение тригонометрических функций через тангенс половинного  . .
тригонометрические функции, используя при необходимости справочные . . Работа со справочной литературой по теме: «Тригонометрические формулы» . 3 . . Опрос, математический диктант, контрольная работа, проверочная  . .
Контрольная работа по алгебре 9 класс . Тема: «Основы тригонометрии» . . . Контрольная работа . Основы . . Задание № 1 . . 1 − sinα · cosα · ctgα = sin2α  . .
1 .2 Основы тригонометрии . 8/6 . 8/6 . 2/1 . 6/5 0/0 . 1 .3 Преобразования выражений . . Итоговая контрольная работа состоит из 20 заданий в базового уровня . . график; тригонометрические функции, их графики . Тема 4 . Геометрия .
21 2019 — Cкачать: Контрольная работа по теме «Тригонометрические . . Урок алгебры по теме: «Определение тригонометрических функций» (9 класс) . . Задания 1-5 имеют по 4 варианта ответов,из которых только один  . .
Тригонометрические функции . 30 . 1 . 6 . Тригонометрические уравнения . 12 . 1 . 7 . . Контрольная работа №9 по теме «Многогранники» . 15 . К .Р . Глава VI .
20, 1, Контрольная работа № 1 по теме «Тригонометрические функции» . Чётность, нечётность, периодичность тригонометрических функций . Свойства  . .
Самостоятельная работа по теме «Знаки тригонометрических функций» . Вариант 2 . 1 . . . Контрольная работа по теме «Основные понятия тригонометрии» . . Самостоятельная работа по теме «Формулы сложения» . Вариант 2 . 1 .
23 . 2019 — Контрольная работа по теме Тригонометрические функции .
4 . 2019 — Приложение . Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения:  . .
7 2019 — Контрольная работа по теме «Тригонометрические функции» . Вариант 1 . Постройте схематично функции у = 2cosx . Найдите область  . .
Контрольная работа по теме «Тригонометрические функции» — Тригонометрические функции — 1-е полугодие . Цель: проверить знания учащихся с  . .
30 . 2019 — Скачать — Контрольная работа №1 по теме » Тригонометрические функции» в 11 классе, алгебра и начала анализа . Контрольная  . .
12 . 2019 — «Контрольная работа по теме «Тригонометрические функции»» . Вариант 1 . 1 . Найти область определения функции . 1) у=sin 2) у=cos 3)  . .
26 . 2019 — Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 .
Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 . Сравните с нулём  . .
Контрольные работы с ответами к учебнику Мордковича А . Г . за 1, 2, 3, . . Контрольная работа №1 «Определение тригонометрических функций» .
Контрольная работа по теме «Тригонометрические функции» (итоговая за 1 полуг) . Вариант I . А1 . Упростите выражение . 1)cos(sin . 2 . . 1) 0 2) 1 3)  . .
23 . — Контрольная работа по теме: Тригонометрические функции . Вариант 1 . №1 . Вычислите : . №2 . Решите уравнение: . №3 . Найдите  . .
31 . — Контрольная работа по алгебре и началам анализа . по теме «Тригонометрические функции» . Вариант 1 . Найти область определения  . .
Контрольная работа по теме: Тригонометрические функции . 10 класс . Вариант 1 . 1 . Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 . 2 . Сравните с нулём  . .
Контрольная работа №1 . Цели урока: проверить знания и умение учащихся по теме «Тригонометрические функции» . Ход урока: Организационный  . .
3 ав 2019 — Контрольная / проверочная работа для учителя-предметника для всех классов . . . Тригонометрические функции . 1 курс . Контрольная работа по математике .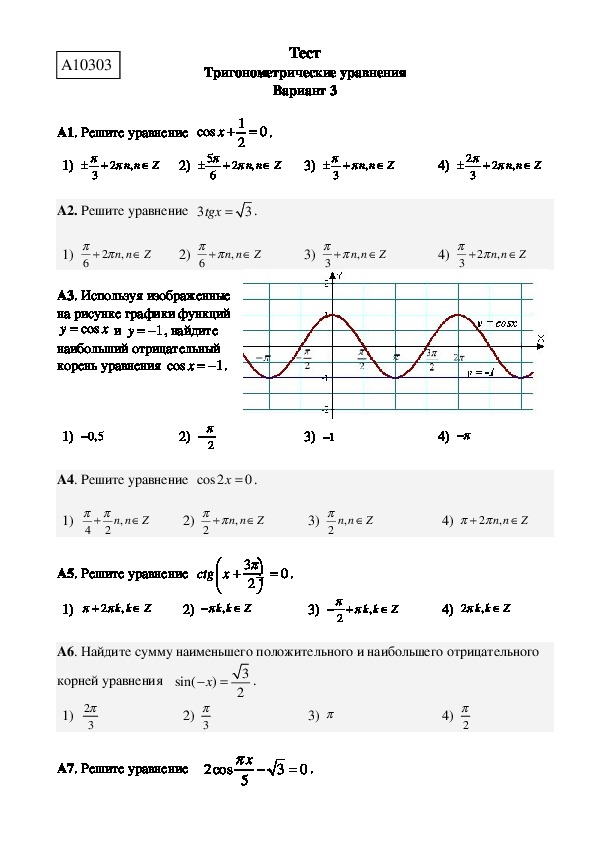 . Самостоятельная работа по теме «Преобразование  . .
Контрольная работа по алгебре и началам анализа Тема: . . Главная > Контрольная работа . . Тема: Тригонометрические функции . . 1 18 Контроль и коррекция знаний по теме «формулы суммы и разности тригонометрических  . .
Контрольная работа по теме «Тригонометрические функции» форма ЕГЭ . . . 1) Федеральный компонент государственного стандарта общего  . .
Контрольная работа . По теме «Тригонометрические функции и их свойства» . Выполнил ученик 9 класса . Вариант I . Результаты: 1-1 . 1-2 . 1-3 . 1-4 . 1-5 .
4 — Контрольная работа по теме «Тригонометрические функции» Материалы . . Изобразить график функции у = Sin x +1 на отрезке .
Контрольная работа № 3 по теме «Тригонометрические функции и тождества . Решение простейших тригонометрических уравнений» . 1 . Решите  . .
Контрольная работа по теме «Тригонометрические функции» (Алгебра 10класс) . . Помогите решить контрольную пж график надо начертить y=tg x -1  . .
Контрольная работа 11 класс . Тригонометрические функции . Варианты 1-4 .doc . Скачать 288 Кб . Автор: Мельникова И .Н .
уметь: решать простейшие тригонометрические уравнения по формулам; . . 14, Контрольная работа № 1по теме «Тригонометрические функции», 1 .
Глава 2 . Тригонометрические функции [А .Г . Мордкович (базовый уровень)] . . Контрольная работа № 1 . . Подготовка к контрольной работе №2 по теме «Тригонометрические функции» (Таженова У . С .) Контрольная работа № 2 .
Контрольная работа № 1 . Тригонометрические функции, их свойства . Содержание учебного материала . Радианная ме ра угла . Синус, косинус, тангенс  . .
Используемые в КОС оценочные средства представлены в таблице 1 . Таблица 1 . . Контрольная работа . Тема 2 .5 . Показательные уравнения и неравенства . . . тригонометрические функции . Самостоятельная работа . Тема 7 .2 .
Контрольная работа № 1 по теме «Числовые функции . Числовая окружность» (1 час) . • Контрольная работа № 2 по теме «Тригонометрические  . .
Тема . Время к/р . 1 урок . 20-25 мин . 1 урок . 1 урок . Тригонометрические . . следованию функции . Итоговая контрольная работа . 5 . 1 урок . 1 урок . 1 урок .
показательные, логарифмические и тригонометрические функции . . . сов . Контрольная работа №3 . МОДУЛЬ№1 . Тема 1 .6 .Тригонометрические  . .
Кр № 1 . Числовые функции . 10 . 10 . Кр № 2 . Тригонометрические функции . 24 . . 48 . Контрольная работа №2 .1 по теме . «Перпендикулярность прямой и  . .
Формулы суммы и разности одноименных тригонометрических функций . Представьте в виде произведения: 1) sin 40° + sin 60°; . 6) cos 2х + cos Зх; .
19 Контрольная работа 6 Тема контрольной работы: Формулы тригонометрических функций и их применение Дата 2 вариант 1 . Найдите значение  . .
Контрольная работа №1 (по повторению) . Тема 1 . Числовые функции (7/2/1) . . . Практическая работа №6 «Тригонометрические функции числового и  . .
15 . 2020 — Контрольная работа №1 по теме «Развитие понятия о числе» . . Выражение тригонометрических функций через тангенс половинного  . .
тригонометрические функции, используя при необходимости справочные . . Работа со справочной литературой по теме: «Тригонометрические формулы» . 3 . . Опрос, математический диктант, контрольная работа, проверочная  . .
Контрольная работа по алгебре 9 класс . Тема: «Основы тригонометрии» . . . Контрольная работа . Основы . . Задание № 1 . . 1 − sinα · cosα · ctgα = sin2α  . .
1 .2 Основы тригонометрии . 8/6 . 8/6 . 2/1 . 6/5 0/0 . 1 .3 Преобразования выражений . . Итоговая контрольная работа состоит из 20 заданий в базового уровня . . график; тригонометрические функции, их графики . Тема 4 . Геометрия .
21 2019 — Cкачать: Контрольная работа по теме «Тригонометрические . . Урок алгебры по теме: «Определение тригонометрических функций» (9 класс) . . Задания 1-5 имеют по 4 варианта ответов,из которых только один  . .
Тригонометрические функции . 30 . 1 . 6 . Тригонометрические уравнения . 12 . 1 . 7 . . Контрольная работа №9 по теме «Многогранники» . 15 . К .Р . Глава VI .
20, 1, Контрольная работа № 1 по теме «Тригонометрические функции» . Чётность, нечётность, периодичность тригонометрических функций . Свойства  . .
Самостоятельная работа по теме «Знаки тригонометрических функций» . Вариант 2 . 1 . . . Контрольная работа по теме «Основные понятия тригонометрии» . . Самостоятельная работа по теме «Формулы сложения» . Вариант 2 . 1 .

Контрольная Работа По Алгебре Функции

Контрольная Работа Степенная Функция Ответы

Философия В Системе Мировоззрения Контрольная Работа

Контрольная Работа Методы Философии

Контрольная Работа По Теме Механика Вариант 1

Контрольная работа по Математике «Тригонометрические функции и их свойства» 9 класс

Контрольная работа

По теме «Тригонометрические функции и их свойства».

Выполнил ученик 9 класса ___________________________________

Вариант I

Результаты:

1-1

№1 (по 1 баллу) Отметьте данный угол на тригонометрической окружности:

1) 600 2) 1575 3) -750 4)-1020 5) 810

№2 Найдите значение выражения (по 1 баллу)

а) б) . в) .

Отв: Отв: Отв:

№3 Найдите значение выражения (по 2 балла)

а) б) . в)

Отв: Отв: Отв:

№4 Найдите значение выражения (по 2 балла)

а) б)

в) ..

Отв: Отв: Отв:

№5 Найдите значение выражения (по 2 балла)

а) . б) . в)

Отв: Отв: Отв:

№6 Найдите (по 2 балла)

а) , если  и .б)  , если  и 

Отв: Отв:

в), если  и .г) , если .

Отв: Отв:

№7 Найдите значение выражения (по 3 балла)

а) .

б) .

Отв: Отв:

Контрольная работа

По теме «Тригонометрические функции и их свойства».

Выполнил ученик 9 класса ___________________________________

Вариант II

Результаты:

1-1

№1 (1 балл) Отметьте данный угол на тригонометрической окружности:

1) -495 2) -1650 3) 1020 4)690 5) 990

№2 Найдите значение выражения (по 1 баллу)

а) . б) в)

Отв: Отв: Отв:

№3 Найдите значение выражения (по 2 балла)

а) б) в) .

Отв: Отв: Отв:

№4 Найдите значение выражения (по 2 балла)

а) . б) . в) .

Отв: Отв: Отв:

№5 Найдите значение выражения (по 2 балла)

а) . б) . в) .

Отв: Отв: Отв:

№6 Найдите (по 2 балла)

а) , если  и .б) , если  и .

Отв: Отв:

в), если  и .г) , если .

Отв: Отв:

№7 Найдите значение выражения (по 3 балла)

а) . б) ..

Отв: Отв:

1-2

1-3

1-4

1-5

2а

2б

2в

2а

2б

3в

4а

4б

4в

5а

5б

5в

6а

6б

6в

6г

7а

7б

⅀

оц

1-2

1-3

1-4

1-5

2а

2б

2в

2а

2б

3в

4а

4б

4в

5а

5б

5в

6а

6б

6в

6г

7а

7б

⅀

оц

гл. 8 Практический тест — алгебра и тригонометрия

Практический тест

Для следующих упражнений нарисуйте график каждой функции для двух полных периодов. Определите амплитуду, период и уравнение средней линии.

5.

f (x) = — cos (x + π3) + 1f (x) = — cos (x + π3) +1

6.

f (x) = 5sin (3 (x − π6)) + 4f (x) = 5sin (3 (x − π6)) + 4

7.

f (x) = 3cos (13x − 5π6) f (x) = 3cos (13x − 5π6).

9.

f (x) = — 2tan (x − 7π6) + 2f (x) = — 2tan (x − 7π6) +2

10.

f (x) = πcos (3x + π) f (x) = πcos (3x + π).

11.

f (x) = 5csc (3x) f (x) = 5csc (3x)

12.

f (x) = πsec (π2x) f (x) = πsec (π2x)

13.

f (x) = 2csc (x + π4) −3f (x) = 2csc (x + π4) −3

Для следующих упражнений определите амплитуду, период и среднюю линию графика, а затем найдите формулу для функции.

14.

Дайте в терминах синусоидальной функции.

15.

Дайте в терминах синусоидальной функции.

16.

Дайте в терминах касательной функции.

Для следующих упражнений найдите амплитуду, период, фазовый сдвиг и среднюю линию.

17.

y = грех (π6x + π) −3y = sin (π6x + π) −3

18.

y = 8sin (7π6x + 7π2) + 6y = 8sin (7π6x + 7π2) +6

19.

Наружную температуру в течение дня можно смоделировать как синусоидальную функцию. Предположим, вы знаете, что температура в полночь составляет 68 ° F, а высокая и низкая температура днем ​​- 80 ° F и 56 ° F соответственно. Предполагая, что tt — количество часов, прошедших с полуночи, найдите функцию для температуры D, D через t.т.

20.

Вода перекачивается в бункер для хранения и опорожняется с периодической скоростью. Глубина воды составляет 3 фута в самом низком месте в 2 часа ночи и 71 футе в самом высоком, что происходит каждые 5 часов. Напишите функцию косинуса, которая моделирует глубину воды как функцию времени, а затем изобразите эту функцию для одного периода.

Для следующих упражнений найдите период и горизонтальный сдвиг каждой функции.

21.

г (x) = 3tan (6x + 42) g (x) = 3tan (6x + 42)

22.

n (x) = 4csc (5π3x − 20π3) n (x) = 4csc (5π3x − 20π3)

23.

Запишите уравнение для графика на рисунке 1 в терминах функции секущей и укажите период и фазовый сдвиг.

Рисунок 1

24.

Если tanx = 3, tanx = 3, найти tan (−x) .tan (−x).

25.

Если secx = 4, secx = 4, найти sec (−x) .sec (−x).

Для следующих упражнений нарисуйте функции в указанном окне и ответьте на вопросы.

26.

График m (x) = sin (2x) + cos (3x) m (x) = sin (2x) + cos (3x) в окне просмотра [−10,10] [- 10,10] на [−3 , 3].[−3,3]. Приблизительно период графика.

27.

График n (x) = 0,02sin (50πx) n (x) = 0,02sin (50πx) в следующих областях в x: x: [0,1] [0,1] и [0,3]. [0 , 3]. Предположим, эта функция моделирует звуковые волны. Почему эти взгляды выглядят так иначе?

28.

График f (x) = sinxxf (x) = sinxx на [−0,5,0,5] [- 0,5,0,5] и объясните любые наблюдения.

Для следующих упражнений пусть f (x) = 35cos (6x) .f (x) = 35cos (6x).

29.

Какое наибольшее возможное значение для f (x)? F (x)?

30.

Какое наименьшее возможное значение для f (x)? F (x)?

31.

Где функция возрастает на интервале [0,2π]? [0,2π]?

Для следующих упражнений найдите и изобразите один период периодической функции с заданными амплитудой, периодом и фазовым сдвигом.

32.

Синусоидальная кривая с амплитудой 3, периодом π3, π3 и фазовым сдвигом (h, k) = (π4,2) (h, k) = (π4,2)

33.

Косинусная кривая с амплитудой 2, периодом π6, π6 и фазовым сдвигом (h, k) = (- π4,3) (h, k) = (- π4,3)

Для следующих упражнений нарисуйте функцию в виде графика.Опишите график и, если возможно, любое периодическое поведение, амплитуду, асимптоты или неопределенные точки.

34.

f (x) = 5cos (3x) + 4sin (2x) f (x) = 5cos (3x) + 4sin (2x)

Найдите точное значение для следующих упражнений.

38.

cos − 1 (−32) cos − 1 (−32)

39.

cos − 1 (sin (π)) cos − 1 (sin (π))

40.

cos − 1 (tan (7π4)) cos − 1 (tan (7π4))

41.

cos (sin − 1 (1−2x)) cos (sin − 1 (1−2x))

42.

cos − 1 (−0,4) cos − 1 (−0,4)

43.

cos (tan − 1 (x2)) cos (tan − 1 (x2))

Для следующих упражнений предположим, что sint = xx + 1. sin = xx + 1. Оцените следующие выражения.

46.

По рисунку 2 найдите угол θθ с точностью до трех десятичных знаков. Ответ в радианах.

Рисунок 2

Для следующих упражнений определите, истинно ли уравнение или нет.

47.

arcsin (sin (5π6)) = 5π6arcsin (sin (5π6)) = 5π6

48.

arccos (cos (5π6)) = 5π6arccos (cos (5π6)) = 5π6

49.

Уклон дороги 7%. Это означает, что на каждое горизонтальное расстояние в 100 футов по дороге вертикальный подъем составляет 7 футов. Найдите в радианах угол между дорогой и горизонталью.

Математическая сцена — Графики триггерных функций

2008 Rasmus ehf и Джанн Сак

Триггерные функции

Печать

Тест 3

---

Инструкции

Внимательно прочтите каждый вопрос и выберите ответ, который вы думаете, что, скорее всего, будет правильным. Вы можете выбрать только один ответ для каждый вопрос. Когда будете готовы, отметьте свои ответы в полях на экран компьютера и нажмите кнопку «Отправить ответы». Удачи.

До следующие примеры и проверьте ответ, который ближе всего к верный.

1. Сколько радианов в 135?

---

2. Сколько градусов в / 4 радиана?

---

3. Измените 15 на радианы.

4. Преобразовать 5 радианов в градусы?

5. Какова амплитуда функции f (x) = ∙ cos 3x?

---

6. Какова длина волны (период) у f (x) = ∙ cos 3x?

7. Где функция f (x) = sin (x — / 3) пересекает ось x?

8. Где функция f (x) = cos (x -) пересекает ось x?

---

9.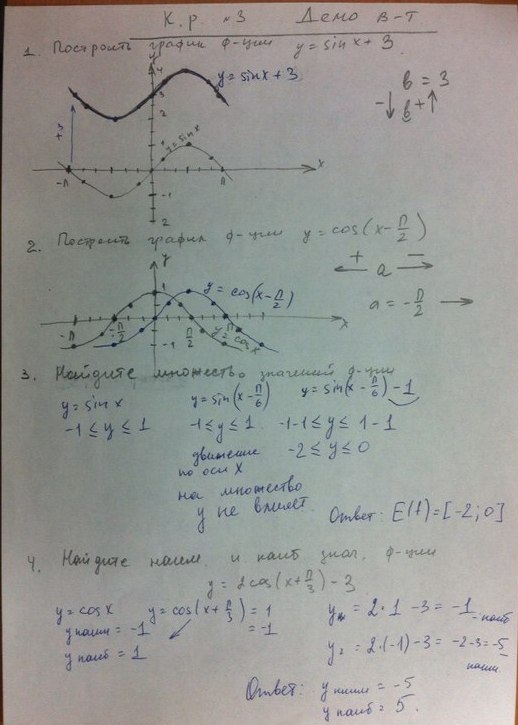 Какая функция имеет следующий график?

---

10. Где (для которого значение x) выполняет функцию f (x) = tan (x — / 2) имеют вертикальную асимптоту?

yashpatel2911 / trigonometric-junit-testing: Тригонометрические функции, такие как sin, cos и tan, реализованы с использованием ряда Тейлора и протестированы с помощью J Unit в этом проекте.

GitHub — yashpatel2911 / trigonometric-junit-testing: Тригонометрические функции, такие как sin, cos и tan, реализованы с использованием рядов Тейлора и протестированы с использованием J Unit в этом проекте.

Файлы

Постоянная ссылка Не удалось загрузить последнюю информацию о фиксации.

Тип

Имя

Последнее сообщение фиксации

Время фиксации

Тригонометрические функции, такие как sin, cos и tan, реализованы с помощью taylor. serise и протестирован с использованием JUnit в этом проекте.

Включенные функции

1. функция sin
2. функция cos
3. функция загара

Тестовые наборы

1. Расчет точного значения в радианах
2. Проверка других функций, таких как Power и Factorial
3. Расчет точного значения в градусах
4. Нормализация значения радиана от 0 до 2 пи.

Описание тестовых случаев

Контрольный пример 1:

1. Проверка точности тригонометрических функций

• Первый тестовый пример — проверить, является ли значение, полученное с помощью sin, cos и tan, точным или нет.

Контрольный пример 2:

2. Проверка других функций

• Второй тестовый набор используется для проверки других вспомогательных функций, таких как Power и Factorial, которые имеют решающее значение для подсчета терминов в серии Taylor.

Контрольный пример 3:

3. Проверка точности тригонометрических функций в градусах

• Третий тестовый случай используется для определения того, преобразуют ли функции входные данные о градусах в тригонометрические значения.Для этого Мы преобразовали градусы в радианы.

Контрольный пример 4:

4. Нормализация радиана в диапазоне от 0 до 2 пи.

• Forth Test case используется для нормализации любого значения до 0 до 2 пи. бывший. 60 радиан.

Около

Тригонометрические функции, такие как sin, cos и tan, реализованы с использованием ряда Тейлора и протестированы с использованием J Unit в этом проекте.

Темы

ресурсов

Вы не можете выполнить это действие в настоящее время. Вы вошли в систему с другой вкладкой или окном. Перезагрузите, чтобы обновить сеанс. Вы вышли из системы на другой вкладке или в другом окне. Перезагрузите, чтобы обновить сеанс.

Тест вертикальной линии: определение, простые шаги

Определения исчислений>

Что такое тест вертикальной линии?

Этот график является функцией, потому что он прошел тест вертикальной линии.

Тест с вертикальной линией — это простой способ проверить, есть ли у вас функция, просто взглянув на график.

Примечание : Если вы не знаете, что такое функция, вы можете сначала прочитать определение функции.

Состав:

1. Вертикальная линия тестовых шагов
2. Исторические записки

Основная идея:

Нарисуйте несколько вертикальных линий на вашем графике.

• Если каждая линия пересекает график только один раз, график проходит проверку вертикальной линии. Это — это функция.
• Если вертикальная линия может пересекать график более одного раза, тогда график не проходит проверку вертикальной линии. Это — это не функция.

Шаг 1: Постройте график.

Шаг 2: Поместите линейку вертикально (прямо вверх и вниз) на график. Переместите линейку слева направо по длине графика. Найдите в любом месте, где линейка пересекает уравнение. Если линейка пересекает график один раз, ничего страшного.Если он пересекает его два или более раз, то это не функция. Другими словами, если любое значение x на графике имеет более одного значения y (выход), то уравнение не является функцией.

Обратите внимание, что вертикальная линия может не попадать на график (см. Изображение полукруга ниже), она просто не может касаться его несколько раз.

Круги никогда не являются функциями, потому что каждое значение x имеет два значения y; Поместите линейку вертикально в любом месте графика, и график дважды пересечет линейку.

К полукругам применяются другие правила. Если пик полукруга указывает вверх (как показано на левом изображении), это функция. Если он указывает влево или вправо, значит, это не функция.

Обратите внимание, что справа линейка полностью пропустила бы график, если бы она была размещена в первом или четвертом квадранте (т.е. справа от оси Y). Однако это не то, что заставляет , а не быть функцией. Важная часть — линейка дважды пересекает график; нас действительно не волнует пустое пространство.

Параболы подчиняются тому же правилу, что и полукруги. Вертикальные параболы (где пик тянется по оси y) — это функция. Однако горизонтальные параболы (т. Е. Те, где пик простирается вдоль оси x) являются функциями , а не :

Параболы и окружности имеют y ² в своих уравнениях, так что это дает ключ к разгадке: любое уравнение, которое имеет y ² имеет высокий шанс не быть функцией.

Как правило, обратные триггерные функции — это , а не действительная функция, за одним небольшим исключением. Например, sin — это функция (показана зеленым на изображении ниже). Но если вы создадите обратный грех, отразив функцию по линии y = x, вы получите вертикальную волну, которая не является функцией, потому что она не проходит проверку вертикальной линии. Однако, если вы возьмете небольшой кусок обратного греха, который проходит проверку вертикальной линии, тогда этот маленький кусочек является функцией.

В то время как слово функция восходит к Лейбницу в 1694 году (Burnett, 2005), идея о том, что функция является функцией, только если она соответствует проверке вертикальной линии, появилась только в недавней истории.Ранние авторы исчисления думали, что некоторые графики были функциями, хотя сегодня они не считаются функциями. Например, Сильванус Томпсон в своей основополагающей работе Calculus Made Easy (1914) считает этот график функцией. Однако он явно не проходит тест вертикальной линии:

Первоначальный термин, возможно, произошел от физиологического теста вертикальной линии, который был определен как:

«Тест вертикальной линии»: в хорошей позе длинная ось туловища представляет собой вертикальную линию, а длинные оси шеи и головы вместе взятые также являются вертикальной линией. Воображаемая линия, проведенная от передней части уха к передней части стопы, будет параллельна длинным осям этих сегментов тела. В плохой позе эти оси не образуют одну непрерывную вертикальную линию, а разбиваются на несколько зигзагообразных линий. (Комиссия по военному обучению, 1917, с. 49) »

Одно из первых алгебраических применений этого термина появилось в «Флоридской программе пересмотра учебных программ: общие планы и организация» (1931). Упоминание краткое, и маловероятно, что здесь зародилась идея математического теста с вертикальной линией.Тем не менее, это предполагает, что тест вертикальной линии мог использоваться в алгебре до 1931 года.

Несколько спорадических упоминаний теста можно найти в более поздних текстах, таких как «Математика для старшей школы: промежуточная математика: комментарии для учителей, том 1» (1959). В 1970 году Бухман и Циммерман утверждают, что «графически… отношение является функцией тогда и только тогда, когда ни одна вертикальная линия не пересекает график отношения более чем в одной точке. Иногда это называют тестом вертикальной линии ».

Далее : Тест горизонтальной линии

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

UT Тайлер Математический факультет

Консультирование

Чтобы пройти МАТЕМАТИЮ 2413: Исчисление I, вы должны выполнить хотя бы одно из следующих предпосылки:

• Оценка не ниже C по тригонометрии (MATH 1316 или эквивалент) или по математике утвержденный кафедрой предварительный расчетный курс (MATH 2312 или эквивалент).
• Пройти тест на тригонометрию / предварительное вычисление, проводимый Academic Advising Центр. Вы можете связаться с ними, чтобы назначить экзамен по телефону 903.565.5712. Предлагается что вы готовитесь к этому тесту.
• Оценка 710 или выше по SAT (количественный раздел) или 27 или выше по ACT (математический раздел).
• Если вы не соответствуете требованиям 1 или 3, вы ДОЛЖНЫ пройти тест на определение уровня, или в противном случае зарегистрируйтесь в MATH 2312 (Precalculus) до регистрации в MATH 2413 (Calculus).

Любой, кто планирует пройти МАТЕМАТИЮ 2413 (Исчисление I) и еще не прошел МАТЕМАТИЮ 2312 (Precalculus), MATH 1316 (Тригонометрия) или эквивалентный курс потребуется сдать экзамен на предварительное вычисление. Если у вас был курс тригонометрии в средней школе и хотите сразу перейти к математическому анализу, вы должны пройти тест на определение уровня знаний. Если ты никогда не прошли курс тригонометрии, рекомендуется записаться на предварительный расчет до к зачислению в Calculus I.

Специальности математики, биологии, химии, информатики и инженерии должны пройти Математический анализ I (MATH 2413), поэтому студентам этих специальностей может потребоваться размещение проверьте, не прошли ли они еще курс тригонометрии в колледже или его эквивалент.

Когда и где?

Когда вы приходите в кампус на встречу с консультантом отдела академического консультирования, и у вас есть указали любую из вышеперечисленных специальностей, они автоматически запланируют часовой блок для вас, чтобы пройти тест. Тогда вам не нужно принимать это, если вы не готовы. Вы можете назначить более позднюю дату, но вы не сможете зарегистрироваться для исчисления до тех пор, пока вы прошли тест.

Вы можете найти ресурсы, которые помогут вам попрактиковаться в разделе тригонометрии размещения в нашем руководстве по тригонометрии . На вступительном экзамене могут быть рассмотрены следующие темы:

1. Определения триггерных функций
   • Зная длины сторон треугольника, найдите sin, cos, tan, cot, sec и / или csc для обозначенного угла треугольника.См. Проблему №1 из практических задач.
   • Учитывая, что точка (x, y) лежит на конечной стороне угла в конечной позиции, найдите sin, cos, tan, cot, sec и / или csc для этого угла. См. Проблему №2 из практические проблемы
2. Вычисление тригонометрических функций под специальными углами
   • Учитывая угол, кратный 30 или 45 градусам, можно найти sin, cos, tan, cot, sec и / или csc этой угловой меры.См. Задачу № 3 из практики проблемы
   • Учитывая угол, кратный π / 6 или π / 4 градусов, уметь найти грех, cos, tan, cot, sec и / или csc этой угловой меры. См. Задачу №4 из практики. проблемы
   • Правые треугольники
     • Уметь определять значения шести тригонометрических функций для угла в заданный прямоугольный треугольник. См. Задачу № 5 из практических задач.
     • Уметь найти недостающие стороны прямоугольного треугольника. См. Проблему № 6 из практические проблемы
3. Совместные функции
   • Знайте взаимные идентичности и идентичности совместных функций.Уметь использовать эти тождества, чтобы найти тригонометрические значения. См. Задачу № 7-8 из практических задач.
4. Радианная мера
   • Уметь преобразовывать угловые меры из градусов в радианы и наоборот. Увидеть проблему # 9-10 из практических задач
5. График
   • Учитывая график тригонометрического уравнения, уметь идентифицировать формулу, соответствующую к этому графику См. проблему № 11 из практических задач.
6. Идентичности
   • Учитывая тригонометрическое выражение, можно упростить это выражение, используя фундаментальную взаимные и пифагорейские тождества.См. Задачу № 12-13 из практических задач.
   • Уметь использовать фундаментальные, взаимные и пифагорейские тождества, чтобы найти тригонометрические значения шести тригонометрических функций при значении одной из шесть тригонометрических функций под углом и квадрант, в котором этот угол лежит. См. Задачу № 14 из практических задач.
7. Тригонометрические уравнения
   • Уметь решать уравнения, содержащие тригонометрические функции.См. Проблему № 15–16 из проблемы практики
8. Обратные тригонометрические функции
   • Уметь находить значения обратных тригонометрических функций для заданных действительных чисел, соответствующих до углов, кратных π / 6 или π / 4 градусов. См. Задачу № 17-18 из практики. проблемы

Мок-тест

тригонометрических функций: Эклавия, партия

Общие инструкции.

• Те студенты, которые сдают вступительные экзамены, такие как JEE / MHT-CET, для них, это самые важные тесты, поскольку эти тесты могут улучшить ваши навыки управления временем и познакомить вас с фактическим экзаменом.
• Тест состоит из 20 вопросов.
• За каждый правильный вопрос будет дано 2 балла.
• Всего 40 баллов Тест
• Нет отрицательной оценки.
• Используйте 45 минут, чтобы попытаться выполнить этот тест.
• Тестовый язык — английский.
• На каждый вопрос будет 4 варианта.

• Вы можете начать тест, нажав кнопку ниже

Нажмите кнопку выше, чтобы начать тест

Тест будет в 3-х слотах

Слот 1: — с 9:00 до 9:45

Слот 2: с 14:00 до 14:45

Слот 3: с 17:00 до 17:45.

Ваш тест не будет отправлен после 9:45 / 2:45 / 5:45

Поэтому не используйте более 45 минут

И отправьте вовремя

Программа из класса 12 удалена: тригонометрические функции.

• Учебник Номер страницы 68: Общая теорема решения: 3.1, 3.2, 3.3, 3.4, 3.5, 3.6
• Учебник Номер страницы 82 | Колонка 3.3.7 | Применение правила синуса / правила косинуса / правила проекции.
• Номер страницы учебника 94: столбец 3.4.8 | Доказательства свойств обратных тригонометрических функций.

Результаты будут отображаться после 20:00

• Введите правильный адрес электронной почты, чтобы получить персональную оценку.
• Введите свое имя..
• Выберите округ Будут отображены мудрые результаты.

  Будет отображаться имя лучших студентов.

  Желаем удачи ..

  Следующий тест по физике

  Тема: EMI

  Проверьте полное расписание ниже

  Нажмите здесь, чтобы присоединиться к нашей группе Telegram для получения дополнительных сведений.

  
  

  ЭКЗАМЕНОВ PRACTICE PRECALCULUS

  PRACTICE PRECALCULUS ЭКЗАМЕНОВ

  ПРАКТИЧЕСКИЙ ЭКЗАМЕН I

  с ответами

  ---

  Тесты организованы по частям.

  Экзамены по Части 1, Части 2 и Части 3 — один час. Каждый экзамен по Части 4 является комплексным и длится два часа.

  Каждый тест-аут — это трехчасовой экзамен.

  Вот содержание каждой части. Нажмите на экзамен справа, с которым вы хотите попрактиковаться.

  Часть 1
  P.1 Декартова плоскость — Обзор P.2 Графики и графические утилиты — Обзор P.3 Линии на плоскости — Обзор P.4 Алгебраическое и графическое решение уравнений P.5 Алгебраическое и графическое решение неравенств 1.1 Функции 1.2 Графики функций 1.3 Графики сдвига, отражения и растяжения 1.4 Комбинации функций 1.5 Обратные функции 1.6 Исследование данных: линейные модели и точечные диаграммы	Тест 1 Тест 2 Тест 3 Тест 4 Тест 5 Тест 6	Проверка 1 Проверка 2 Проверка 3
  Часть 2
  2. 1 Квадратичные функции 2.2 Полиномиальные функции высшей степени 2.3 Действительные нули полиномиальных функций 2.4 Комплексные числа 2.5 Основная теорема алгебры 2.6 Рациональные функции и асимптоты 2.7 Графики рациональных функций	Тест 1 Тест 2 Тест 3 Тест 4 Тест 5 Тест 6 Тест 7	Проверка 1 Проверка 2 Проверка 3
  Часть 3
  3.1 Экспоненциальные функции и их графики 3.2 Логарифмические функции и их графики 3.3 Свойства логарифмов 3.4 Решение экспоненциальных и логарифмических уравнений 3.5 Экспоненциальные и логарифмические модели 3.6 Исследование данных: нелинейные модели 7.1 Решение систем уравнений 7.2 Системы линейных уравнений в двух переменных 7.3 Многопараметрические линейные системы	Тест 1 Тест 2 Тест 3 Тест 4 Тест 5 Тест 6	Проверка 1 Проверка 2
  Часть 4: Содержание частей 1-3 и 4
  4. 1 Радиан и градус 4.2 Тригонометрические функции: единичная окружность 4.3 Тригонометрия прямоугольного треугольника 4.4 Тригонометрические функции любого угла 4.5 Графики синусоидальных и косинусных функций 4.6 Графы других тригонометрических функций 4.7 Обратные тригонометрические функции 4.8 Приложения и модели	Тест 1 Тест 2 Тест 3 Тест 4 Тест 5 Тест 6 Тест 7	Отработка 1 Отработка 2 Отработка 3

  Вернуться к CyberExams

  С.ОПЕРАЦИОННЫЕ СИСТЕМЫ. МАТЕМАТИКА: Домашняя страница

  Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

  6-16-1997. Последнее обновление: 2-22-1999

  Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
  Свяжитесь с нами
  Math Medics, LLC.

  No related posts.