Контрольная работа по теме тригонометрия: Контрольная работа «Тригонометрия»

Контрольная работа «Тригонометрия»

Контрольная работа «Тригонометрия»

Вариант № 1.

1. Выразите в радианах: а) 10°; б) 210°.

2. Выразите в градусах: а) ; б) .

3. Вычислить значение каждой из тригонометрических функций, если: .

4. Упростите выражение: ;

5. Докажите тождество: ;

6. Вычислите значение sin2x, если cosx = и

– ; 2) ; 3) ; 4) – .

7. Найдите значение выражения при

8. Упростите выражение

9. Найдите значение выражения: при x=

а); б) ; в) ; г) 0.

10. Вычислите:

а) ; б) ; в) ; г)1.

11. Решите уравнение

а) π\2n; б) ; в) πn; г) 0.

12. Решите уравнение

а) π\2+πn; б) πn; в) π\2n; г) πn+2πn.

13. Решите уравнение

а) x=(-1)n+1π\3+πn; б) x=(-1)nπ\6+πn; в) x=(-1)nπ\3+πn; г) x=(-1)n+1π\2+πn.

14. Решите уравнение

а) x=π\3+πn; б) x=π\2+2πn; в) x=π\6+2πn; г) x=2π\3+πn.

15. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют … числа t.

16. Угол в один радиан – это … угол, опирающийся на дугу, длина которой равна радиусу окружности.

17. Какая из тригонометрических функции является четной функцией?

18. Решите уравнение .

Вариант № 2.

1. Выразите в радианах: а) 15°; б) 225°.

2. Выразите в градусах: а) ; б) .

3. Вычислить значение каждой из тригонометрических функций, если: .

4. Упростите выражение: ;

5. Докажите тождество: ;

6. Вычислите значение cos2 , если sin = – и

– ; 2) ; 3) – 0,5 ; 4) 0,5.

7. Найдите значение выражения при cos =

8. Упростите выражение

9. Найдите значение выражения: при x=

а) 1; б) 0,5; в) ; г) 1,5.

10. Вычислите:

а)0; б) ; в)1; г) .

11. Решите уравнение

а) π\2n; б) π\2+2πn; πn. в) 2π\3+2πn; 2πn.; г) π+2πn; πn.

12. Решите уравнение

а) π\2n; б) 2πn, в) π\3+πn; г) πn.

13. Решите уравнение

а) ±π\2n; б) ±π\2+2πn; в) ±π\4+2πn; г) ±π+2πn; πn.

14. Решите уравнение

а) π\2 +2πn; б) 2πn. в) π\3+πn; г) π+2πn.

15. Если точка М числовой окружности соответствует числу t, то ординату точки М называют … числа t. 16. Если функция ограничена и снизу и сверху, то её называют … . 17. Какие тригонометрические функции являются нечетными функциями?

18. Решите уравнение . Записать полное решение.

Эталон ответов

контрольной работы «Тригонометрия»

Вариант № 1 Вариант № 2

1. π\18, 7π\6 1. π\12, 5π\4

2. 12,140 2. 15,120

3. -5\13, -12\3, -5\12 3. -2√6\5, 2√6, √6\12

4. 1\cos2α 4. — tg2α

5. верное 5. верное

6. 4 6. -1\2

7. -1,4 7. 1,5

8.1 8. 1

9.г, 9. а,

10.г, 10.а,

11.в, 11.в,

12.б, 12.б,

13.а, 13.в,

14.б, 14.г,

15.косинусом, 15.синусом,

16.центральный, 16.ограниченной,

17.косинус, 17.синус, тангенс, котангенс.

18. х = 2πп 18. х = π\2 + 2πп

х = -arcctg7+πп х = arcctg1\3+πп

Критерии оценивания

Отметка «2» выставляется, если выполнено менее 10 (от 1 до 9) заданий работы.

Отметка «3» выставляется, если верно выполнено 10 — 13 заданий работы.

Отметка «4» выставляется, если верно выполнено 14 — 16 заданий работы.

Отметка «5» выставляется, если верно выполнено 17-18 заданий работы.

Контрольная работа по теме «Тригонометрия. Решение уравнений»

Контрольная работа №2

Вариант 1

1. Вычислите:

2. Вычислите с помощью формулы приведения:

3. Решите графически уравнение:

4. Решите уравнение:

5. Решите уравнение:

6. Докажите, что верно равенство:

7. Решить уравнение:

8. ^*Решить уравнение:

Критерии оценок:

оценка «5» — при выполнении всех заданий

оценка «4» — при выполнении шести заданий

оценка «3» — при выполнении любых четырех примеров.

Контрольная работа №2

Вариант 2

1. Вычислите:

2. Вычислите с помощью формулы приведения:

3. Решите графически уравнение:

4. Решите уравнение:

5. Решите уравнение:

6. Докажите, что верно равенство:

7. Решить уравнение:

8. ^*Решить уравнение:

Критерии оценок:

оценка «5» — при выполнении всех заданий

оценка «4» — при выполнении шести заданий .

оценка «3» — при выполнении любых четырех примеров

Контрольная работа №2

Вариант 3

1. Вычислите:

2. Вычислите с помощью формулы приведения:

3. Решите графически уравнение:

4. Решите уравнение:

5. Решите уравнение:

6. Докажите, что верно равенство:

7. Решить уравнение:

8. ^*Решить уравнение:

Критерии оценок:

оценка «5» — при выполнении всех заданий

оценка «4» — при выполнении шести заданий

оценка «3» — при выполнении любых четырех примеров.

Контрольная работа №2

Вариант 4

1. Вычислите:

2. Вычислите с помощью формулы приведения:

3. Решите графически уравнение:

4. Решите уравнение:

5. Решите уравнение:

6. Докажите, что верно равенство:

7. Решить уравнение:

8. ^*Решить уравнение:

Критерии оценок:

оценка «5» — при выполнении всех заданий

оценка «4» — при выполнении шести заданий

оценка «3» — при выполнении любых четырех примеров

Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. 

 

Простейшие тригонометрические уравнения.

 

 

Методы решения тригонометрических уравнений.

Решение тригонометрического уравнения состоит из двух этапов:  преобразование уравнения для получения его простейшего вида ( см. выше ) и  решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения  тригонометрических уравнений.

 

1. Алгебраический метод.  Этот метод нам хорошо известен из алгебры

   ( метод замены переменной и подстановки ).

  

2. Разложение на множители.

  Этот метод рассмотрим на примерах.

 

    П р и м е р  1.  Решить уравнение:  sin x + cos x = 1 .

 

    Р е ш е н и е .   Перенесём все члены уравнения влево:

 

                                                               sin x + cos x – 1 = 0 ,

 

                               преобразуем и разложим на множители выражение в

                               левой части уравнения:

                             

    П р и м е р   2.   Решить уравнение:  cos ²x + sin x · cos x = 1.

 

    Р е ш е н и е .     cos

2 x + sin x · cos x – sin ² x – cos ² x = 0 ,

 

                                            sin x · cos x – sin ²x = 0 ,

 

                                            sin x · ( cos x – sin x ) = 0 ,

                              

    П р и м е р   3.   Решить уравнение:  cos 2x – cos 8x + cos 6x = 1.  

     Р е ш е н и е .    cos 2x + cos 6x = 1 + cos 8x ,

 

                               2 cos 4

x cos 2x = 2 cos ² 4x ,

 

                               cos 4x · ( cos 2x –  cos 4x ) = 0 ,

    

                               cos 4x · 2 sin 3x · sin x = 0 ,

                              1).  cos 4x = 0 ,               2).  sin 3x = 0 ,          3). sin x = 0 ,

                           

3.

Приведение к однородному уравнению.

Уравнение называется однородным относительно  sin  и  cos, если все его члены одной и той же степени относительно sin

  и cos  одного и того же угла. Чтобы решить однородное уравнение, надо:

 

   а)  перенести все его члены в левую часть;

   б)  вынести все общие множители за скобки;

   в)  приравнять все множители и скобки нулю;

   г)  скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на 

        cos ( или sin ) в старшей степени; 

   д)  решить полученное алгебраическое уравнение относительно tan .  

 

    П р и м е р .   Решить уравнение:  3sin ²x + 4 sin x · cos x + 5 cos ² x = 2.

 

    Р е ш е н и е .  3sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ² x ,

 

                             sin ²x + 4 sin x · cos x + 3 cos ²x = 0 ,

 

                             tan ² x + 4 tan x + 3 = 0 ,  отсюда  y ² + 4y +3 = 0 ,

 

                             корни этого уравнения:  y₁ = -1,  y

₂ = -3,  отсюда

                             1)   tan x = –1,                  2)   tan x = –3,

                              

 

4. Переход к половинному углу.

Рассмотрим этот метод на примере:

 

    П р и м е р .   Решить уравнение:  3 sin x – 5 cos x = 7. 

    Р е ш е н и е .  6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

                                                                         = 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

                             2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

                             tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

                                     .   .   .   .   .   .   .   .   .   .

5. Введение вспомогательного угла. Рассмотрим уравнение вида:

 

                                           a sin x + b cos x = c ,

 

    где  a, b, c – коэффициенты;  x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1.

Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:

 

 

6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.

    

    П р и м е р .  Решить уравнение:  2 sin 2x · sin 6x = cos 4x.

 

    Р е ш е н и е .  Преобразуем левую часть в сумму:

 

                                        cos 4

x – cos 8x = cos 4x ,

 

                                                 cos 8x = 0 ,

 

                                                 8x = p / 2 + pk ,

 

                                                 x = p / 16 + pk / 8 .

 

7. Универсальная подстановка. Рассмотрим этот метод на примере.

                                                                                                                                             

      П р и м е р .    Решить уравнение:  3 sin x – 4 cos x = 3 .

  

           

                             Таким образом, решение даёт только первый случай.

Контрольная работа №5. Тригонометрия

Контрольная работа №5. Тригонометрия.

I вариант

1. Вычислите:

а) ;

б) .

2. Упростите выражение:

а) ;

б)

3. Вычислите:

а)

б) если

4. Найдите такие углы α, для каждого из которых выполняется равенство:

а) б)

в) г)

5. Вычислите:

а) если

б) если

6. Вычислите

7. В прошлом году в городской думе заседали 50 депутатов от двух партий и 5 независимых депутатов. После выборов в этом году общее число депутатов не изменилось, но число депутатов первой партии увеличилось на 10%, число депутатов второй партии уменьшилось на 10%, число независимых депутатов уменьшилось на 1. Сколько депутатов от каждой из этих партий избрано в городскую думу в этом году?

Контрольная работа №5. Тригонометрия.

II вариант

1. Вычислите:

а)

б)

2. Упростите выражение:

а)

б)

3. Вычислите:

а)

б) если

4. Найдите все такие углы α, для каждого из которых выполняется равенство:

а) б)

в) г)

5. Вычислите:

а) если

б) если

6. Вычислите

7. В пансионате в прошлом году отдыхало 700 мужчин и женщин и 100 детей. В этом году число мужчин уменьшилось на 10%, а число женщин увеличилось на 10%, число детей увеличилось на 10. В результате общее число отдыхающих не изменилось. Сколько мужчин и сколько женщин отдыхало в пансионате в этом году?

Контрольная работа №5. Тригонометрия.

III вариант

1. Вычислите:

а)

б)

2. Упростите выражение:

а)

б)

3. Вычислите:

а)

б) если

4. Найдите все такие углы α, для каждого из которых выполняется равенство:

а) б)

в) г)

5. Вычислите:

а) если

б) если

6. Вычислите

7. Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 60% большей. На сколько процентов время движения оказалось меньше запланированного?

Контрольная работа №5. Тригонометрия.

IV вариант

1. Вычислите:

а)

б)

2. Упростите выражение:

а)

б)

3. Вычислите:

а)

б) если

4. Найдите все такие углы α, для каждого из которых выполняется равенство:

а) б)

в) г)

5. Вычислите:

а) если

б) если

6. Вычислите

7. Некоторое расстояние планировали проехать с постоянной скоростью, а проехали расстояние на 40% большее и со скоростью на 75% большей. На сколько процентов время движения оказалось меньше запланированного?

▶▷▶ тригонометрические функции контрольная работа ответы

▶▷▶ тригонометрические функции контрольная работа ответы

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	26-11-2018

тригонометрические функции контрольная работа ответы — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа по теме «Тригонометрические функции» infourokru/kontrolnaya-rabota-po-teme Cached Приложение Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Контрольные работы по алгебре 10 класс, контрольные по mathematics-testscom/algebra-10-klass/ Cached Дополнительные материалы по алгебре Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Контрольная работа по теме «Тригонометрические функции compendiumsu/mathematics/algebra10/17html Cached 1-е полугодие Глава 2 Тригонометрические функции Уроки 27-28 Контрольная работа по теме Тригонометрические Функции Контрольная Работа Ответы — Image Results More Тригонометрические Функции Контрольная Работа Ответы images Контрольная работа «Основные тригонометрические формулы» 10 uchitelyacom/algebra/90176-kontrolnaya-rabota-osnovnye Cached Скачать Контрольная работа «Основные тригонометрические формулы» 10 класс Ширина блока px контрольная работа по алгебре за 10 класс тема тригонометрия кампусятарф/blog/132589html Cached контрольная работа по алгебре за 10 класс тема тригонометрия ответы Блог им opyfos Тест по геометрии на тему «Параллельные прямые»; 7 класс Самостоятельные и контрольные работы по алгебре и началам allengorg/d/math/math2495htm Cached Самостоятельные и контрольные работы по алгебре и началам математического анализа для 10 класса Подготовка к контрольной работе «Тригонометрические функции wwwuchmetru/library/material/154153 Cached Следующий урок- контрольная работа по дидактическим материалам к указанному УМК , варианты 1-2 обычной сложности, варианты 3-4 средней сложности, варианты 5-6 можно предложить учащимся Контрольные работы по алгебре и началам анализа 10 класс Алимов infourokru/kontrolnie-raboti-po-algebre-i Cached Контрольная работа № 1 по теме «Действительные числа» Характеристика контрольной работы Номер задания Контрольная работа «Тригонометрические функции сложения школа-пифагорарф/publ/kontrolnye_raboty Cached Информатика для школьников Уроки математики Сайт для учителя математики Контрольная работа по Математике «Тригонометрические функции globuss24ru/doc/kontrolynaya-rabota-po Cached №1 (по 1 баллу) Отметьте данный угол на тригонометрической окружности: 1) 600 2) 1575 3) -750 4)-1020 5) 810 Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 14,800 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

3

«Свойства и графики тригонометрических функций «

• smarter
• smarter
• не забывайте оставлять свои комментарии

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Контрольная работа по теме » Тригонометрические » infourokru › …rabota…trigonometricheskie-funkcii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте 10 Решите систему: Контрольная работа по теме: Тригонометрические уравнения и неравенства 11 Найдите производную функции Контрольная работа по теме: Производная Применение производной Читать ещё 10 Решите систему: Контрольная работа по теме: Тригонометрические уравнения и неравенства 10 класс 2 вариант 1 Вычислите: arcsin ( ) + 0,5arctg (- ) 1) ; 2) ; 3) ; 4) — 2 Вычислите: arcos ( ) + arcctg ( ) 1) ; 2) ; 3) ; 4) 11 Найдите производную функции Контрольная работа по теме: Производная Применение производной 10 класс 2 Вариант 1 Найдите производную функции 1) 2) 3) 4) 2 Найдите значение производной функции в точке Скрыть 2 Контрольная работа » Тригонометрические функции » 10 uchitelyacom › …rabota-trigonometricheskie-funkcii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа по теме: Тригонометрические функции 10 класс Выберите правильную серию ответов Читать ещё Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Выберите правильную серию ответов : 1) + – – 2) – – + 3) + + – 4) + – + 3 Вычислите Скрыть 3 Контрольная работа по тригонометрии videourokinet › Разработки › kontrolnaya-rabota-po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа №2 « Тригонометрические функции » Вариант №1 В контрольной работе 7 заданий Критерий оценивания: «3» — верно выполнены 2 или 3 задания , «4» — верно выполнены 4 или 5 заданий , «5» — верно выполнены 6 или 7 заданий Задание 1 Вычислить: если Задание 2 Упростит Читать ещё Контрольная работа №2 « Тригонометрические функции » Вариант №1 В контрольной работе 7 заданий Критерий оценивания: «3» — верно выполнены 2 или 3 задания , «4» — верно выполнены 4 или 5 заданий , «5» — верно выполнены 6 или 7 заданий Задание 1 Вычислить: если Задание 2 Упростит выражение: Задание 3 Доказать тождество: Задание 4 Найти заданную точку на числовой окружности Скрыть 4 Контрольные работы по алгебре 10 класс, контрольные mathematics-testscom › Онлайн Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ за 1, 2, 3, 4 четверти Контрольные на темы: «Определение тригонометрических функций «, «Свойства и графики тригонометрических функций » Читать ещё Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ за 1, 2, 3, 4 четверти Контрольные на темы: «Определение тригонометрических функций «, «Свойства и графики тригонометрических функций «, » Тригонометрические уравнения», » Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций » и др Дополнительные материалы по алгебре Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Все материалы проверены антив Скрыть 5 Контрольная работа № 2 Тригонометрические тождества e-osnovaru › PDF/osnova_3_26_4346pdf Показать ещё с сайта Пожаловаться Информация о сайте Тригонометрические функции числового аргумента Обратные тригонометрические функции : определение Ответы к контрольным работам Контрольная работа № 1 Читать ещё Тригонометрические функции числового аргумента Основные соотношения между тригонометрически -ми функциями одного аргумента Периодичность функций Свойства и графики тригонометрических функций 8 Вариант 1 1 ° Вычислите: 2 Обратные тригонометрические функции : определение, свойства, графики Простейшие тригонометри — ческие уравнения Ответы к контрольным работам Контрольная работа № 1 8 Вариант 1 1 2 2 − 5 3 Чётная Скрыть pdf Посмотреть Сохранить на ЯндексДиск 6 Тригонометрические функции контрольная работа ответы — смотрите картинки ЯндексКартинки › тригонометрические функции контрольная работа Пожаловаться Информация о сайте Ещё картинки 7 Контрольная работа по теме « Тригонометрические » урокрф › …kontrolnaya_rabota…trigonometricheskie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная / проверочная работа для учителя-предметника для всех классов Административная контрольная работа по математике для 1 курса ППКРС Рубежный контроль по Основам геодезии Итоговая контрольная работа по дисциплине «Эффективное поведение на рынке труда» Читать ещё Контрольная / проверочная работа для учителя-предметника для всех классов Учебно-дидактические материалы для всех классов Административная контрольная работа по математике для 1 курса ППКРС Рубежный контроль по Основам геодезии Итоговая контрольная работа по дисциплине «Эффективное поведение на рынке труда» Контрольные работы МДК0202 учет и контроль технологических процессов Деловая игра по предпринимательству Скрыть 8 Учебно-методический материал по алгебре (11 класс) на nsportalru › …kontrolnaya…teme-trigonometricheskie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Контрольная работа по алгебре и началам анализа в 11 классе по теме » Тригонометрические функции » 2 варианта Читать ещё Контрольная работа по алгебре и началам анализа в 11 классе по теме » Тригонометрические функции » 2 варианта Контрольная работа по алгебре и началам анализа в 11 классе по теме » Тригонометрические функции » 2 варианта Скачать Скрыть 9 КОНТРОЛЬНАЯ РАБОТА school195orgru › …59…trigonometricheskie_funktsii… Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 1 по теме ,, Тригонометрические функции ” 11 класс (10 – 11) I вариант 4 Найдите наименьшее целoе значениe функции у = 2 sin x cosx 13 5 Постройте график функции у = 0,5sin x − 2 Найдите Читать ещё Контрольная работа № 1 по теме ,, Тригонометрические функции ” 11 класс (10 – 11) I вариант II вариант 1 Найдите область определения и множество значений функций : а) у=−9 4 Найдите наименьшее целoе значениe функции у = 2 sin x cosx 13 5 Постройте график функции у = 0,5sin x − 2 Найдите промежутки возрастания и наименьший положительный период Скрыть pdf Посмотреть Сохранить на ЯндексДиск 10 Контрольная работа №1 по теме» Тригонометрические » kopilkaurokovru › matematika/testi…rabota…funktsii Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Просмотр содержимого документа « Контрольная работа №1 по теме» Тригонометрические функции «» Вариант1 1Найти область определения и множество значений функции у=5 cos х 2 Выяснить является функция у=2sin x – tg x четной или нечетной? 3Изобразить график функции у= sin x на Читать ещё Просмотр содержимого документа « Контрольная работа №1 по теме» Тригонометрические функции «» Вариант1 1Найти область определения и множество значений функции у=5 cos х 2 Выяснить является функция у=2sin x – tg x четной или нечетной? 3Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 0,5 4Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5 Построить график функции у= cos х + 2 При каких значениях функция убывает; возрастает? Вариант2 Скрыть Контрольная работа по теме: » Тригонометрические » multiurokru › Обо мне › …-naia-rabota-po-tiemie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Данная контрольная работа предназначена для проверки знаний, полученных по теме : » Тригонометрические функции » для учащихся Просмотр содержимого документа « Контрольная работа по теме: » Тригонометрические функции «» Контрольная работа по теме: Тригонометрические Читать ещё Данная контрольная работа предназначена для проверки знаний, полученных по теме : » Тригонометрические функции » для учащихся класса Просмотр содержимого документа « Контрольная работа по теме: » Тригонометрические функции «» Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Скрыть Тестовые задания по теме » Тригонометрические » uchportalru › load/27-1-0-42374 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте задания по теме » Тригонометрические функции » по предмету Математика 10 Умение находить значения обратных тригонометрических функций Автор: Янес Светлана Юрьевна Место работы : МБОУ «ЗСОШ№1 Завьяловского района» Читать ещё Методическая разработка Тестовые задания по теме » Тригонометрические функции » по предмету Математика Категория: Печатные тесты по математике 10 Умение находить значения обратных тригонометрических функций Целевая аудитория: для 10 класса Автор: Янес Светлана Юрьевна Место работы : МБОУ «ЗСОШ№1 Завьяловского района» Добавил: yanessu Скачать с портала (2213 Kb) Смотрите также: Компьютерная программа для учителей математики «Транспарант Обратные тригонометрические функции » Тест «Обратные тригонометрические функции » в 4 — х вариантах Конспект и презентация к уроку » Тригонометрические формулы» Презентация к уроку математики » Тригонометрия Скрыть Тест 2 Тригонометрические функции pandiaru › text/78/188/20988php Показать ещё с сайта Пожаловаться Информация о сайте Тест 2 Тригонометрические функции Вариант 1 А Выберите правильный ответ В3Сколько целых чисел из промежутка принадлежит области определения функции ? С Для каждого задания приведите решение и укажите ответ С1 Найдите все значения х, при которых функция у = 1 – 2cos2 x принимает Читать ещё Тест 2 Тригонометрические функции Вариант 1 А Выберите правильный ответ A1 Найдите область определения функции у = 2sin x + tg x 1) х – любое число; 2) х R, кроме х=0; 3) х R, кроме ; 4) х R, кроме х=1 А2 Какими свойствами обладает функция у = 2 – sin 3x ? 1) нечетная, периодическая; 2) ни четная ни нечетная, непериодическая В3Сколько целых чисел из промежутка принадлежит области определения функции ? С Для каждого задания приведите решение и укажите ответ С1 Найдите все значения х, при которых функция у = 1 – 2cos2 x принимает положительные значения С2 Найдите множество значений функции у = 2sin x , если х принадлежит промежутку Скрыть Контрольная работа » Тригонометрические функции » easyenru › load…rabota…trigonometricheskie_funkcii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа составлена к 1 главе » Тригонометрические функции » учебника ЮМКолягина, МВТкачева, НЕФёдорова, МИШабунина Алгебра-11 Материал контрольной работы составлен на основе учебника Тест : Тригонометрические функции | Ответы Вариант 1 4egeru › …gia…test-trigonometricheskie-funkciihtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тест : Тригонометрические функции Пробные работы ОГЭ по математике В каком варианте ответа правильно указаны все цифры, на месте которых в предложении должны стоять запятые? Читать ещё Тест : Тригонометрические функции Пробные работы ОГЭ по математике 2 варианта для 9-11 классов test-trfdoc [1545 Kb] (cкачиваний: 241) Ответы Вариант 1: 1 2 2 1 3 4 4 2 5 4 6 2 7 4 8 1 9 2 10 4 Просмотров: 2566 | 27 августа 2017 Тест : Тригонометрические уравнения и неравенства Тематические тесты по экономике Тест по русскому языку 14 вариантов ОГЭ онлайн Русский язык ← Задание 17 В каком варианте ответа правильно указаны все цифры, на месте которых в предложении должны стоять запятые? Женщина за прилавком (1) как будто (2) только ждала подходящего повода выразить Скрыть Контрольная работа №5 Тригонометрия doc4webru › …kontrolnaya-rabota-trigonometriyahtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте К уроку алгебры Контрольная работа №5 Тригонометрия — скачать бесплатно На сколько процентов время движения оказалось меньше запланированного? Контрольная работа №5 Тригонометрия Вместе с « тригонометрические функции контрольная работа ответы » ищут: тригонометрические формулы тригонометрические уравнения обратные тригонометрические функции тригонометрические тождества формулы приведения тригонометрия тригонометрический круг синус обратные тригонометрические функции их свойства и графики тригонометрическая таблица 1 2 3 4 5 дальше Браузер Все новые вкладки с анимированным фоном 0+ Установить

Контрольная работа по тригонометрии

Контрольная работа №2

«Тригонометрические функции».

Вариант №1

В контрольной работе 7 заданий. Критерий оценивания: «3» — верно выполнены 2 или 3 задания, «4» — верно выполнены 4 или 5 заданий, «5» — верно выполнены 6 или 7 заданий.

Задание 1 Вычислить:

Задание 2 Упростит выражение:

Задание 3 Доказать тождество:

Задание 4 Найти заданную точку на числовой окружности:

Задание 5

Известно, что. Вычислите: .

Задание 6 Решите уравнение:

Задание 7 Решите неравенство:

Контрольная работа №2

«Тригонометрические функции».

Вариант №2

В контрольной работе 7 заданий. Критерий оценивания: «3» — верно выполнены 2 или 3 задания, «4» — верно выполнены 4 или 5 заданий, «5» — верно выполнены 6 или 7 заданий.

Задание 1 Вычислить:

Задание 2 Упростит выражение:

Задание 3 Доказать тождество:

Задание 4 Найти заданную точку на числовой окружности:

Задание 5

Известно, что. Вычислите: .

Задание 6 Решите уравнение:

Задание 7 Решите неравенство:

Контрольная работа №2

«Тригонометрические функции».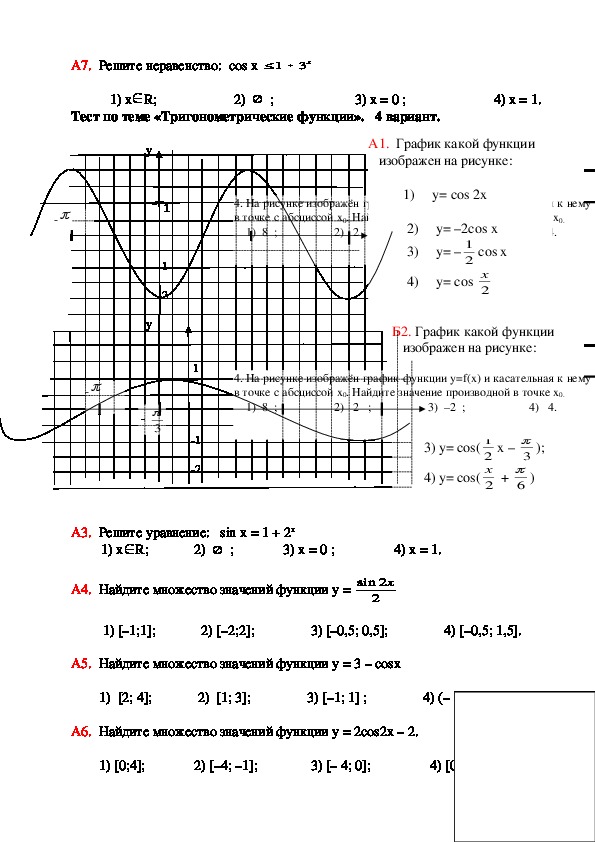

Вариант №1

В контрольной работе 7 заданий. Критерий оценивания: «3» — верно выполнены 2 или 3 задания, «4» — верно выполнены 4 или 5 заданий, «5» — верно выполнены 6 или 7 заданий.

Задание 1 Вычислить:

Задание 2 Упростит выражение:

Задание 3 Доказать тождество:

Задание 4 Найти заданную точку на числовой окружности:

Задание 5

Известно, что. Вычислите: .

Задание 6 Решите уравнение:

Задание 7 Решите неравенство:

Контрольная работа №2

«Тригонометрические функции».

Вариант №2

В контрольной работе 7 заданий. Критерий оценивания: «3» — верно выполнены 2 или 3 задания, «4» — верно выполнены 4 или 5 заданий, «5» — верно выполнены 6 или 7 заданий.

Задание 1 Вычислить:

Задание 2 Упростит выражение:

Задание 3 Доказать тождество:

Задание 4 Найти заданную точку на числовой окружности:

Задание 5

Известно, что. Вычислите: .

Задание 6 Решите уравнение:

Задание 7 Решите неравенство:

Контрольная работа По теме Теорема Пифагора.

Тригонометрические функции
Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 1

1. 
   Диагонали ромба равны 6см и 8см. Найдите сторону ромба.
   
2. 
   Найдите сторону АВ прямоугольного треугольника АВС , если ВС=√3 см, АС=1см,
   

С=90.

3. В прямоугольном треугольнике cos=0,6. Найдите sin, tg, ctg.

4. Основания равнобокой трапеции равны 11 см и

21 см, боковая сторона – 13 см. Найдите высоту трапеции.

Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 1

1. 
   Диагонали ромба равны 6см и 8см. Найдите сторону ромба.
   
2. 
   Найдите сторону АВ прямоугольного треугольника АВС , если ВС=√3 см, АС=1см,
   

С=90.

3. В прямоугольном треугольнике cos=0,6. Найдите sin, tg, ctg.

4. Основания равнобокой трапеции равны 11 см и

21 см, боковая сторона – 13 см. Найдите высоту трапеции.

Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 1

1. 
   Диагонали ромба равны 6см и 8см. Найдите сторону ромба.
   
2. 
   Найдите сторону АВ прямоугольного треугольника АВС , если ВС=√3 см, АС=1см,
   

С=90.

3. В прямоугольном треугольнике cos=0,6. Найдите sin, tg, ctg.

4. Основания равнобокой трапеции равны 11 см и

21 см, боковая сторона – 13 см. Найдите высоту трапеции.

Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 2

1. Найдите диагонали прямоугольника со сторонами 9см и 12см.

2. Найдите гипотенузу АВ прямоугольного треугольника АВС на рисунке, если АС=1см, ВС=√2 см, С=90.

3. В прямоугольном треугольнике sin =. Найдите tg, ctg, cos.

4. Основания равнобокой трапеции равны 30 см и

72 см, а боковая сторона 35см. Найдите высоту трапеции.

Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 2

1. Найдите диагонали прямоугольника со сторонами 9см и 12см.

2. Найдите гипотенузу АВ прямоугольного треугольника АВС на рисунке, если АС=1см, ВС=√2 см, С=90.

3. В прямоугольном треугольнике sin =. Найдите tg, ctg, cos.

4. Основания равнобокой трапеции равны 30 см и

72 см, а боковая сторона 35см. Найдите высоту трапеции.

Контрольная работа

По теме Теорема Пифагора. Тригонометрические функции.

Вариант 2

1. Найдите диагонали прямоугольника со сторонами 9см и 12см.

2. Найдите гипотенузу АВ прямоугольного треугольника АВС на рисунке, если АС=1см, ВС=√2 см, С=90.

3. В прямоугольном треугольнике sin =. Найдите tg, ctg, cos.

4. Основания равнобокой трапеции равны 30 см и

72 см, а боковая сторона 35см. Найдите высоту трапеции.

Контрольна робота з тригонометрії — pro100vkusn0.

ru

Скачать контрольна робота з тригонометрії txt

Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций: у = sin x ; y = cos 3x ; y = 3 sin (x) ; y = cos +. Решите.  Просмотр содержимого документа «Алгебра. 10 класс. Контрольная работа № 3 по теме: «Тригонометрический функции»».

Контрольная работа № 3. по теме: «Тригонометрический функции». Вариант 1. Данный тест предназначен для проверки уровня усвоения темы «Тригонометрические уравнения», проверяет основные знания и умения по теме, поможет подготовиться к контрольной работе.

Некоторые уравнения соответствуют уровню 13 задания ЕГЭ математика профильный уровень. Данный тест расчитан на учащихся старших классов и студентов 1 курсов СПО. Контрольная работа №2.Тригонометрические функции числового аргумента. Формулы приведения. Самостоятельная работа по теме «Тригонометрические уравнения и неравенства» состоит из 16 вариантов. Дает возможность проверить освоение основных навыков при решении тригонометрических уравнений.

Просмотр содержимого документа. Самостоятельная работа на 16 вариантов. по теме «Тригонометрические уравнения и неравенства». Самостоятельная работа по теме. Тригонометрические уравнения и неравенства. 1 вариант. Тригонометрия. Определение и свойства тригонометрических функций.

Градусная и радианная меры угла. Поддержать Проект.

Контрольные / проверочные работы для учителя-предметника для всех классов по ФГОС. Учебно-дидактические материалы для всех классов.  Контрольная работа «Тригонометрия». Нажмите, чтобы скачать публикацию в формате MS WORD (*.DOC).

Размер файла: Кбайт. Конкурсная работа. Всероссийский конкурс педагогического мастерства для школьных учителей «Контрольная работа в формате теста по математике».

Контрольная работа «Тригонометрия». Вариант № 1. 1. Выразите в радианах: а) 10°; б) °. Контрольная 10 класс. Тригонометрия. Перейти к файлу. Заказать учебную работу. 1 вариант 1. Найдите наименьшее целое значение функции. Найдите значение, если.   Контрольная работа по теме «Тригонометрия». 10 класс тригонометрия. 8 класс-тригонометрия. Опорные конспекты тригонометрия 10 класс. Урок обобшчение.тригонометрия 10 класс.

Электронный учебник. Тригонометрия. Тригонометрические тождества. Контрольная работа 2. Поддержать Проект: pro100vkusn0.ru Мои Контрольная работа по тригонометрии 2.  Контрольная работа 1 плейлиста Тригонометрия содержит тригонометрические уравнения и в видео показано решение Контрольная работа по тригонометрии №2.

Valery Volkov. lượt xem 6 N năm trước. Тригонометрические тождества. Контрольная работа 2. Задание 3. Докажите тождество. Поддержать Проект: ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА 10 класс тригонометрия. физика ОГЭ математика ЕГЭ — Романов Владимир. lượt xem 38 N năm trước.

PDF, fb2, fb2, fb2

Похожее:

Гдз літературне читання 4 клас віра науменко зошит

Збірник тестів з української мови для 5 класу

Алгебра 9 клас мерзляк сборник гдз

Контрольна робота з хімії 9 клас по темі вуглеводні

Презентація на тему штучні квіти

Практические тесты по тригонометрии

Пройдите бесплатный диагностический тест Varsity Learning Tools по тригонометрии, чтобы определить, какой академический концепции, которые вы понимаете, а какие требуют вашего постоянного внимания. Каждая проблема тригонометрии привязана к основной, основной концепции, которая проходит тестирование. Результаты диагностического теста тригонометрии показывают, как вы выполняли каждую область теста. Затем вы можете использовать результаты для создания индивидуального учебного плана, основанного на вашей конкретной области потребностей.

Классы тригонометрии в средней школе подробно знакомят учащихся с различными тригонометрическими тождествами, свойствами и функциями. Студенты обычно изучают тригонометрию после завершения предыдущего курса по алгебре и геометрии, но перед тем, как пройти предварительное исчисление и исчисление. Информация, которую студенты изучают в тригонометрии, помогает им преуспеть в более поздних курсах математики более высокого уровня, а также в таких научных курсах, как физика, где тригонометрические функции используются для моделирования определенных физических явлений.

Как и классы предалгебры, алгебры I и алгебры II, классы тригонометрии сосредоточены на функциях и графах. Тригонометрия, в частности, изучает тригонометрические функции и в процессе учит студентов, как построить график синуса, косинуса, секанса, косеканса, тангенса, котангенса, арксинуса, арккосуса и арктангенса, а также как выполнять фазовые сдвиги и вычислять их периоды и амплитуды. . Также обсуждаются тригонометрические операции, и студенты также узнают о тригонометрических уравнениях, в том числе о том, как понимать, устанавливать и учитывать тригонометрические уравнения, как решать отдельные тригонометрические уравнения, а также системы тригонометрических уравнений, как находить тригонометрические корни и как использовать квадратную формулу для тригонометрических уравнений.

Тригонометрические тождества также обсуждаются в классах тригонометрии; студенты узнают о тождествах суммы и произведения, а также тождества обратных операций, квадратов тригонометрических функций, половинных и удвоенных углов. Студенты также учатся работать с идентичностями с суммами углов, дополнительными и дополнительными идентичностями, пифагорейскими идентичностями, а также основными и определяющими идентичностями.

Другая важная часть тригонометрии — это научиться анализировать особые виды особых треугольников.Студенты учатся определять углы и длины сторон в прямоугольных треугольниках 30-60-90 и 45-45-90, используя закон синусов и закон косинусов, а также узнают, как определять похожие треугольники и определять пропорции, используя пропорциональность.

Тригонометрия также знакомит студентов с единичными кругами и радианами, уделяя особое внимание тому, как преобразовать градусы в радианы и наоборот. Обсуждаются дополнительные, дополнительные и котерминальные углы. Этот акцент на углах в единичном круге также применяется к координатной плоскости, когда исследуются углы в разных квадрантах.

Как теперь может быть очевидно, многие студенты очень опасаются проходить курс тригонометрии и не отставать от него. Такие ресурсы, как бесплатные практические тесты по тригонометрии для преподавателей университетской школы, могут помочь им направить любую нервозность, которую они испытывают по поводу курса, в процесс активного обзора, который принесет им пользу. Каждый практический тест по тригонометрии включает в себя дюжину вопросов по тригонометрии с несколькими вариантами ответов, и каждый вопрос сопровождается полным пошаговым объяснением, чтобы помочь учащимся, пропустившим его, изучить тестируемые концепции.Вопросы организованы в практических тестах, которые основаны на различных темах, преподаваемых в тригонометрии; вопросы также сгруппированы по концепциям. Итак, если студент хочет сосредоточиться только на ответах на вопросы об использовании закона синусов, вопросы, организованные по концепциям, делают это возможным. Используя бесплатные практические тесты по тригонометрии от Varsity Tutors, студенты могут попрактиковаться в материале, который им кажется трудным, и уменьшить опасения, которые они могут испытывать по поводу тригонометрии.

Наши совершенно бесплатные практические тесты по тригонометрии — идеальный способ улучшить свои навыки.Брать один из наших многочисленных практических тестов по тригонометрии для ответов на часто задаваемые вопросы. Ты получат невероятно подробные результаты оценки в конце вашего практического теста по тригонометрии, чтобы поможет вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по тригонометрии прямо сейчас и начнем!

Практические тесты по концепции

тригонометрия-угол-приложения

Вопросы : 8

Сложность теста :

тригонометрия-угловая скорость

Вопросы : 8

Сложность теста :

Среднее время нахождения : 2 минуты 36 секунд

длина дуги тригонометрии

Вопросы : 8

Сложность теста :

Среднее время нахождения : 7 минут

тригонометрия-площадь-сектора

Вопросы : 8

Сложность теста :

тригонометрические углы

Вопросы : 4

Сложность теста :

Среднее время нахождения : 16 минут

тригонометрические углы в разных квадрантах

Вопросы : 2

Сложность теста :

Среднее время нахождения : 41 секунда

тригонометрические дополнительные и дополнительные углы

Вопросы : 1

Сложность теста :

Среднее время нахождения : 23 секунды

тригонометрия-терминальные-углы

Вопросы : 1

Сложность теста :

Среднее время нахождения : 33 секунды

тригонометрия-найти-все-углы-в-диапазоне-заданном-конкретном-выходе

Вопросы : 7

Сложность теста :

тригонометрия-комплексные-числа-полярная форма

Вопросы : 11

Сложность теста :

Среднее время нахождения : 5 минут

комплексные числа тригонометрии

Вопросы : 11

Сложность теста :

Среднее время нахождения : 4 минуты

тригонометрия-де-муавр-s-теорема-и-нахождение-корней-комплексных-чисел

Вопросы : 7

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-полярная-форма-комплексных чисел

Вопросы : 8

Сложность теста :

тригонометрия-практические-приложения

Вопросы : 8

Сложность теста :

тригонометрический пеленг

Вопросы : 7

Сложность теста :

тригонометрия, наклонные самолеты и аэронавигация

Вопросы : 7

Сложность теста :

тригонометрические векторы

Вопросы : 8

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-сумма-разность-и-произведения-тождества

Вопросы : 8

Сложность теста :

тригонометрия-полное-доказательство-с использованием-сумм-разностей-или-произведений-синусов и косинусов

Вопросы : 10

Сложность теста :

тригонометрическое произведение синусов и косинусов

Вопросы : 8

Сложность теста :

Среднее затраченное время : 21 секунда

тригонометрия-сумма-и-разность-синусов и косинусов

Вопросы : 8

Сложность теста :

Среднее время нахождения : 4 минуты

тригонометрия-треугольники

Вопросы : 5

Сложность теста :

Среднее время нахождения : 9 минут

тригонометрия-площадь-треугольник

Вопросы : 8

Сложность теста :

Среднее время нахождения : 7 минут

тригонометрия-поиск-площадь-треугольника с помощью тригонометрии

Вопросы : 8

Сложность теста :

тригонометрия-закон косинусов и закон синусов

Вопросы : 4

Сложность теста :

Среднее время нахождения : 9 минут

тригонометрия-неоднозначные-треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрия-закон косинусов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 12 минут

тригонометрия-закон синусов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-правые треугольники

Вопросы : 7

Сложность теста :

Среднее время нахождения : 1 д 17 часов

тригонометрия-30-60-90-треугольники

Вопросы : 3

Сложность теста :

Среднее время нахождения : 4 минуты

тригонометрия-45-45-90-треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 17 минут

тригонометрия-решение-задач-слов-с-тригонометрией

Вопросы : 4

Сложность теста :

тригонометрия-тригонометрические-приложения

Вопросы : 7

Сложность теста :

Среднее время нахождения : 7 минут

тригонометрия-использование-специальные-треугольники-сделать-выводы

Вопросы : 10

Сложность теста :

тригонометрические-подобные-треугольники

Вопросы : 1

Сложность теста :

Среднее время нахождения : 24 секунды

тригонометрические идентифицирующие-похожие-треугольники

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 минута 14 секунд

тригонометрия-пропорции-в-подобных-треугольниках

Вопросы : 1

Сложность теста :

Среднее время нахождения : 13 секунд

тригонометрия-решающие треугольники

Вопросы : 4

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрические углы нахождения

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 45 секунд

тригонометрические поисковые стороны

Вопросы : 1

Сложность теста :

Среднее время нахождения : 22 секунды

тригонометрия-тригонометрические-уравнения

Вопросы : 5

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-решение-тригонометрические-уравнения

Вопросы : 3

Сложность теста :

Среднее время нахождения : 52 минуты

тригонометрические поисковые тригонометрические корни

Вопросы : 2

Сложность теста :

Среднее время нахождения : 41 секунда

тригонометрия-квадратичная-формула-с тригонометрией

Вопросы : 2

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрические системы тригонометрических уравнений

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 минута 58 секунд

тригонометрия-понимание-тригонометрические-уравнения

Вопросы : 2

Сложность теста :

Среднее затраченное время : 2 минуты 0 секунд

тригонометрия-факторизация-тригонометрические-уравнения

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 37 секунд

тригонометрия-установка-тригонометрические-уравнения

Вопросы : 6

Сложность теста :

Среднее время нахождения : 2 минуты 45 секунд

тригонометрия-тригонометрические-функции-и-графики

Вопросы : 5

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрия-тригонометрические функции

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 56 секунд

тригонометрия определить, какие значения тригонометрических функций не определены

Вопросы : 1

Сложность теста :

тригонометрия-графики-обратных-тригонометрических-функций

Вопросы : 8

Сложность теста :

тригонометрические упрощающие тригонометрические функции

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 47 секунд

тригонометрия-решите-тригонометрическую-функцию-возведением в квадрат обе стороны

Вопросы : 8

Сложность теста :

тригонометрия-тригонометрические функции

Вопросы : 1

Сложность теста :

Среднее время нахождения : 3 минуты

тригонометрия-понимание-знаки-6-тригонометрических функций в каждом квадранте

Вопросы : 1

Сложность теста :

тригонометрия-тригонометрические-графики

Вопросы : 2

Сложность теста :

Среднее время нахождения : 32 секунды

тригонометрия-определение-вертикальные сдвиги

Вопросы : 7

Сложность теста :

Среднее время нахождения : 2 минуты 48 секунд

тригонометрия, построение графиков, секанс и косеканс

Вопросы : 2

Сложность теста :

Среднее время нахождения : 59 секунд

тригонометрия-график-синус-косинус

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 13 секунд

тригонометрия-график-касательная-и-котангенс

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 мин 59 сек

тригонометрия-период и амплитуда

Вопросы : 2

Сложность теста :

Среднее затраченное время : 33 секунды

тригонометрия-фазовые сдвиги

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 мин 28 сек

тригонометрия-тригонометрические-тождества

Вопросы : 4

Сложность теста :

Среднее время нахождения : 2 минуты 27 секунд

тригонометрия-применить-основные-и-определения-тождества

Вопросы : 6

Сложность теста :

Среднее время нахождения : 12 минут

тригонометрические дополнительные и дополнительные тождества

Вопросы : 2

Сложность теста :

Среднее время нахождения : 53 секунды

тригонометрия-полная-основная-тригонометрическая-доказательства

Вопросы : 1

Сложность теста :

тригонометрические тождества удвоенных углов

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 11 секунд

тригонометрические тождества половинных углов

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 54 секунды

тригонометрические тождества обратных операций

Вопросы : 6

Сложность теста :

Среднее время нахождения : 5 минут

тригонометрические тождества квадратов тригонометрических функций

Вопросы : 3

Сложность теста :

Среднее время нахождения : 14 минут

тригонометрические тождества с суммами углов

Вопросы : 4

Сложность теста :

Среднее время нахождения : 6 минут

тригонометрия-пифагорейские тождества

Вопросы : 3

Сложность теста :

Среднее затраченное время : 1 минута 44 секунды

тригонометрические тождества суммы и произведения

Вопросы : 2

Сложность теста :

Среднее время нахождения : 2 минуты 5 секунд

тригонометрия-тригонометрические-операции

Вопросы : 1

Сложность теста :

Среднее затраченное время : 1 минута 4 секунды

тригонометрия-arcsin-arccos-arctan

Вопросы : 1

Сложность теста :

Среднее время нахождения : 2 минуты 8 секунд

тригонометрия-sec-csc-ctan

Вопросы : 3

Сложность теста :

Среднее время нахождения : 2 минуты 4 секунды

тригонометрия-грех-кос-загар

Вопросы : 2

Сложность теста :

Среднее затраченное время : 1 минута 10 секунд

тригонометрия-единица-круг-и-радианы

Вопросы : 2

Сложность теста :

Среднее время нахождения : 45 секунд

тригонометрические углы в единичной окружности

Вопросы : 2

Сложность теста :

Среднее время нахождения : 45 секунд

тригонометрия-радианы-и-преобразования

Вопросы : 2

Сложность теста :

Среднее время нахождения : 40 секунд

тригонометрия-единица-круг

Вопросы : 2

Сложность теста :

Среднее время нахождения : 28 секунд

Все ресурсы по тригонометрии

Основы тригонометрии, Sin, Cos, Tan Test

Выберите лучший ответ. Тригонометрические отношения округлены до ближайшей тысячной.

1. $ Sin A = \ frac {12} {16} $ для какого из следующих треугольников?

2. $ Tan A = \ frac {13} {12} $ для какого из следующих треугольников?

3. $ Cos B = \ frac {13} {33} $ для какого из следующих треугольников?

4. Какая тригонометрическая функция может быть больше или равна 1.000?
Синус
Косинус
Касательная
ничего из вышеперечисленного

5. Самолет поднимается под углом 40 °. Когда он достигает высоты в сто футов, какое расстояние по земле он преодолел? Для решения используйте тригонометрическую диаграмму. Округлите ответ до ближайшей десятой.
64.3 футов
76.6 футов
80.1 футов
119,2 футов

6. 20-футовая балка прислонена к стене. Луч достигает стены на высоте 13,9 фута над землей. Какова мера угла, образованного балкой и землей?
44 °
35 °
55 °
46 °

7. Какой набор углов имеет такое же тригонометрическое соотношение?
Sin 45 и загар 45
Sin 30 и cos 60
Cos 30 и загар 45
Тан 60 и грех 45

8. Какова сумма тригонометрических соотношений Sin 54 и Cos 36?
0,809
1,618
1.000
1,536

9. Какова сумма тригонометрических соотношений Sin 33 и Sin 57?
0,545
1.000
1,090
1,383

10. Какова сумма тригонометрических соотношений Cos 16 и Cos 74?
0,276
0,961
1,237
1,922

11. В △ ABC вершина C — прямой угол. Какое тригонометрическое соотношение имеет то же тригонометрическое значение, что и Sin A?
Sin B
Косинус A
Косинус B
Tan A

12. In ABC, Tan ∠A = 3/4. Гипотенуза треугольника ABC равна
3
4
5
9

13. In ABC, Sin ∠B = 14/17.Гипотенуза треугольника ABC равна
14
17
√485
0,824

14. In ABC, Cos ∠C = 22/36. Гипотенуза
22
36
0,611
2√445

Обведите каждый ответ «Верный» или «Неверный».

15. Если Sin∠A = 358, то m∠A = 21 °.
Верно
Ложь

16. Сумма синуса угла и косинуса его дополнения всегда больше 1.000.
Верно
Ложь

17. Тригонометрические отношения sin 45, cos 45 и tan 45 равны.
Верно
Ложь

Практические вопросы по тригонометрии

Если мы наблюдаем прямоугольный треугольник, где a и b — его катеты, а c — его гипотенуза, мы можем использовать тригонометрические функции, чтобы установить связь между углами и сторонами прямоугольного треугольника.

Если прямой угол прямоугольного треугольника ABC находится в точке C, то синус ( sin ) и косинус ( cos ) углов α (в точке A) и β (в точке B) можно найти так:

sinα = кондиционер sinβ = b / c

cosα = b / c cosβ = a / c

Обратите внимание, что sinα и cosβ равны, и то же самое касается sinβ и cosα. Итак, чтобы найти синус угла, мы делим сторону, противоположную этому углу, и гипотенузу. Чтобы найти косинус угла, мы разделим сторону, образующую этот угол (прилегающую сторону), на гипотенузу.

Есть еще 2 важные тригонометрические функции, тангенс и котангенс:

tgα = sinα / cosα = a / b

ctgα = cosα / sinα = b / a

Для функций синуса и косинуса существует таблица со значениями некоторых углов, которую следует запомнить, так как она очень полезна для решения различных тригонометрических задач.Вот эта таблица:

√

	0	30⁰	45⁰	60⁰	90⁰
sinα	0	1/2	√2 / 2	√3 / 2	1
cosα	1	√3 / 2	√2 / 2	1/2	0

Рассмотрим один пример:

Если a равно 9 см и c 18 см, найдите α.

Мы можем использовать синус для этой задачи:

sinα = a / c = 9/18 = 1/2

Из таблицы видно, что если sinα равно 1/2, то угол α равен 30⁰.

В дополнение к градусам мы можем записать углы с помощью π, где π представляет 180⁰. Например, угол π / 2 означает прямой угол 90⁰.

Правила и задачи по тригонометрии | Формулы треугольника Sin, Cos, Tan

Правила тригонометрии Страница

На этой странице есть правила тригонометрии, формулы треугольников sin, cos и tan, а также задачи для экзамена.

Тригонометрия включена в экзамен Next Generation по продвинутой алгебре и функциям.

Задачи тригонометрии

Инструкции: Ответьте на вопросы об угле a в правом треугольнике ниже. Длина гипотенузы составляет Y единиц. Две другие стороны имеют длину x и z.

Вы можете обратиться к формулам тригонометрии, особенно к приведенным ниже формулам треугольников sin, cos и tan, прежде чем отвечать на вопросы.

1) загар а =?

2) cos a =?

3) sin ² a =?

4) cos ² a =?

5) sin ² a + cos ² a =?

Ответы на тригонометрические задачи

1) напротив / рядом = Z / X

2) смежный / гипотенуза = X / Y

3) (противоположный / гипотенуза) ² = (Z / Y) ²

4) (рядом / гипотенуза) ² = (X / Y) ²

5) sin ² a + cos ² a всегда равно 1.

Другие задачи тригонометрии

Калькулятор тригонометрии

Правила и формулы тригонометрии:

Запомните следующие правила и формулы тригонометрии для экзамена.

Sin, Cos & Tan — Формулы треугольников

Для экзамена вам нужно будет понять формулы треугольников sin, cos и tan.

Помните, что гипотенуза — это сторона треугольника, противоположная прямому углу.

Соседняя сторона находится рядом с измеряемым углом.

Противоположная сторона находится напротив измеряемого угла.

Итак, наши формулы треугольника sin, cos и tan выглядят следующим образом:

Sin, Cos & Tan — законы треугольника

Вам также будут заданы вопросы о тригонометрических отношениях на экзамене.

Убедитесь, что вы знаете основные правила и формулы тригонометрии.

Это правила тригонометрии, относящиеся к формулам sin, cos и tan для прямоугольных треугольников:

cos ² A + sin ² A = 1

cos ² A = 1 — sin ² A

sin ² A = 1 — cos ² A

тангенс = sin ÷ cos

Правила тригонометрии для радианов

Это правила тригонометрии для радианов.

Радиан можно рассматривать как частичную длину окружности.

θ = s ÷ r [где θ = радианы вытянутого угла; s = длина дуги; и r = радиус]

π × 2 × радиан = 360 °

π × радианы = 180 °

π ÷ 2 × радиан = 90 °

π ÷ 4 × радиан = 45 °

π ÷ 6 × радиан = 30 °

Упражнения «Больше греха, тона и загара» (формула треугольника)

Дополнительная математическая практика

Бесплатный онлайн-тест Advanced Math Test

Получите 400 дополнительных математических задач Accuplacer — PDF

Продвинутые правила математики и тригонометрии, включая формулы треугольников sin, cos и tan, более подробно рассматриваются в нашем бесплатном онлайн-тесте.

% PDF-1.4 % 104 0 объект > эндобдж xref 104 99 0000000016 00000 н. 0000002331 00000 п. 0000002425 00000 н. 0000003279 00000 н. 0000004057 00000 н. 0000004087 00000 н. 0000004117 00000 н. 0000004139 00000 н. 0000005036 00000 н. 0000005058 00000 н. 0000005782 00000 н. 0000005804 00000 н. 0000006478 00000 н. 0000006500 00000 н. 0000007204 00000 н. 0000007226 00000 н. 0000007978 00000 н. 0000008780 00000 н. 0000009030 00000 н. 0000009349 00000 п. 0000009643 00000 п. 0000010443 00000 п. 0000011301 00000 п. 0000011634 00000 п. 0000012480 00000 п. 0000012555 00000 п. 0000012623 00000 п. 0000012645 00000 п. 0000013413 00000 п. 0000013473 00000 п. 0000013829 00000 п. 0000014616 00000 п. 0000014639 00000 п. 0000015725 00000 п. 0000015747 00000 п. 0000016194 00000 п. 0000018437 00000 п. 0000018997 00000 п. 0000022163 00000 п. 0000024154 00000 п. 0000026748 00000 н. 0000027277 00000 н. 0000027729 00000 н. 0000028517 00000 п. 0000028942 00000 п. 0000029625 00000 п. 0000029742 00000 п. 0000030167 00000 п. 0000030850 00000 п. 0000030976 00000 п. 0000031401 00000 п. 0000032084 00000 п. 0000032210 00000 п. 0000032635 00000 п. 0000033318 00000 п. 0000033445 00000 п. 0000033870 00000 п. 0000034553 00000 п. 0000034681 00000 п. 0000035106 00000 п. 0000035789 00000 п. 0000035917 00000 п. 0000036342 00000 п. 0000037025 00000 п. 0000037151 00000 п. 0000037576 00000 п. 0000038259 00000 п. 0000038387 00000 п. 0000038812 00000 п. 0000039495 00000 п. 0000039623 00000 п. 0000039830 00000 н. 0000040255 00000 п. 0000040938 00000 п. 0000041064 00000 п. 0000041489 00000 п. 0000042172 00000 п. 0000042298 00000 п. 0000042723 00000 п. 0000043406 00000 п. 0000043533 00000 п. 0000043958 00000 п. 0000044641 00000 п. 0000044769 00000 п. 0000045194 00000 п. 0000045877 00000 п. 0000046003 00000 п. 0000046428 00000 н. 0000047111 00000 п. 0000047239 00000 п. 0000047664 00000 н. 0000048347 00000 п. 0000048475 00000 п. 0000048572 00000 н. 0000048659 00000 н. 0000048751 00000 п. 0000471769 00000 н. 0000002573 00000 н. 0000003257 00000 н. трейлер ] >> startxref 0 %% EOF 105 0 объект > эндобдж 106 0 объект > / Кодировка> >> / DA (/ Helv 0 Tf 0 г) >> эндобдж 201 0 объект > ручей HSMhAfw1ԤEh =] * ͭnM? H @ EB1zE = y + I) vQ? F:

SAT Тригонометрия: SOHCAHTOA и радианы

Тригонометрия и радианы — это новые дополнения к разделу SAT Math! Вы любите измерения углов SOHCAHTOA и $ {π} $? Вы ненавидите тригонометрию и радианы и не знаете, что означает SOHCAHTOA или $ {π} / {2} $? Независимо от того, как вы относитесь к тригонометрии SAT, не стоит подчеркивать. В этом руководстве я расскажу вам все, что вам нужно знать о тригонометрии и радианах для теста SAT Math, и расскажу о некоторых практических задачах.

Тригонометрические формулы: синус, косинус, тангенс

Хотя тригонометрия составляет менее 5% всех математических вопросов , вы все равно хотите правильно ответить на эти вопросы, и вы не сможете правильно ответить ни на какие вопросы по тригонометрии, не зная следующие формулы:

Найдите синус угла по размерам сторон треугольника.

$$ \ sin (x) = {\ (Измерение \: из \: \: противоположной \: стороны \: до \: \: угла)} / {\ (Измерение \: из \: \: гипотенузы )} $$

На рисунке выше синус обозначенного угла будет $ {a} / {h} $

.

Найдите косинус угла по размерам сторон треугольника.

$$ \ cos (x) = {\ (Измерение \: of \: \: прилегающая \: сторона \: к \: \: угол)} / {\ (Измерение \: of \: \: гипотенуза )} $$

На рисунке выше косинус обозначенного угла будет $ {b} / {h} $.

Найдите тангенс угла по размерам сторон треугольника.

$$ \ tan (x) = {\ (Измерение \: из \: \: противоположной \: стороны \: до \: \: угла)} / {\ (Измерение \: из \: \: смежного \: side \: to \: the \: angle)} $$

На рисунке выше тангенс обозначенного угла будет $ {a} / {b} $.

Полезный трюк с памятью — это аббревиатура: SOHCAHTOA.

S In равно O pposite более H ypotenuse

C osine равно A djacent выше H ypotenuse

Угол T равен O pposite над A djacent

Вы также должны знать соотношение дополнительных углов для синуса и косинуса, которое составляет $ \ sin (x °) = \ cos (90 ° −x °) $.

Как применить навыки тригонометрии к SAT Math

Есть два основных типа вопросов по тригонометрии , которые вы увидите в тесте. Я научу вас обращаться к каждому.

Вопрос типа 1 попросит вас найти синус, косинус или тангенс, используя размеры сторон треугольника. Чтобы ответить на эти вопросы, вам нужно будет использовать диаграмму (то есть нарисовать ее, если она вам не дана). Давайте рассмотрим этот пример:

Треугольник ABC — это прямоугольный треугольник, угол B которого равен 90 °; гипотенуза равна 5, а сторона AB равна 4.Что такое косинус А?

Сначала создайте этот треугольник, используя данную информацию:

Затем укажите необходимую информацию. В этом случае вопрос, заданный для косинуса A. Мы знаем, основываясь на предыдущих формулах, что $ \ cos (A) = {\ (Measure \: of \: the \: смежная \: сторона \: to \: the \: angle)} / {\ (Измерение \: of \: \: гипотенуза)} $. Определите, что вам нужно: угол, сторона, прилегающая к углу, и гипотенуза:

.

У нас есть вся необходимая информация, поэтому нам просто нужно подставить ее в формулу:

$ \ cos (A) = {\ (Измерение \: of \: \: прилегающая \: сторона \: к \: \: угол)} / {\ (Измерение \: of \: \: гипотенуза) } = {4} / {5} $. 2)} = √ {(25) — (16)} = √ {9} = 3 $$

Знайте, что мы знаем, что сторона BC равна 3, нам просто нужно подставить это в формулу:

$$ \ sin (A) = {\ (Измерение \: of \: \: противоположной \: стороны \: до \: \: угла)} / {\ (Измерение \: of \: \: гипотенузы )} = {3} / {5} $$

Вопрос типа 2 попросит вас найти синус, косинус или тангенс угла, используя другой заданный синус, косинус или тангенс угла.Как и в случае с вопросом первого типа, чтобы ответить на эти вопросы, вам нужно будет использовать диаграмму (то есть нарисовать ее, если она вам не дана). Посмотрите этот пример:

В прямоугольном треугольнике ABC, где B — прямой угол, $ \ cos (A) = {4} / {5} $. Что такое грех (С)?

Вы хотите решить эти проблемы, нарисовав диаграмму, но сначала вам нужно выяснить, что и куда должно идти. Используйте формулу косинуса, чтобы выяснить, как нарисовать диаграмму.

$$ \ cos (A) = {\ (Измерение \: of \: \: прилегающая \: сторона \: к \: \: угол)} / {\ (Измерение \: of \: \: гипотенуза )} = {4} / {5} $$

Размер прилегающей стороны (AB) = 4

Измерение гипотенузы (AC) = 5

Вы можете заметить, что это тот же треугольник из предыдущего примера. В этом случае мы хотим найти косинус C. На основе предыдущих формул мы знаем, что $ \ sin (C) = {Измерение \: of \: \: противоположная \: сторона \: до \: \: угол } / {Мера \: of \: the \: hypotenuse} $. Определите, что вам нужно: угол, сторона, прилегающая к углу, и гипотенуза.

$$ \ sin (C) = {\ (Измерение \: of \: \: противоположной \: стороны \: до \: \: угла)} / {\ (Измерение \: of \: \: гипотенузы )} = {4} / {5} $$

$ {4} / {5} $ — это ответ.

Немного более сложная версия этого вопроса может попросить вас ввести касательную C вместо синуса C.2)} = √ {(25) — (16)} = √ {9} = 3 $$

Знайте, что мы знаем, что сторона BC равна 3, нам просто нужно подставить это в формулу:

$$ \ tan (C) = {\ (Измерение \: из \: \: противоположной \: стороны \: до \: \: угла)} / {\ (Измерение \: из \: \: смежного \: side \: to \: the \: angle)} = {4} / {3} $$

Теперь, когда мы знаем, как применять необходимые формулы для решения триггерных вопросов, давайте попробуем применить их к некоторым реальным практическим задачам SAT.

Практические задачи по тригонометрии SAT

Пример № 1

Объяснение ответа: Треугольник ABC — это прямоугольный треугольник с прямым углом в B.Следовательно, AC — гипотенуза прямоугольного треугольника ABC, а AB и BC — катеты прямоугольного треугольника ABC. Согласно теореме Пифагора,

$$ AB = √ (202) — (162) = √ (400) — (256) = √144 = 12 $$

Поскольку треугольник DEF подобен треугольнику ABC, с вершиной F, соответствующей вершине C, мера угла F равна мере угла C. Следовательно, $ \ sin‌F = \ sin‌C $. От длин сторон треугольника ABC, $ \ sin C = {\ (Измерение \: of \: \: противоположной \: стороны \: до \: угла \:)} / {\ (Измерение \: of \: \: гипотенуза)} = {\ AB} / {\ AC} = {12} / {20} = {3} / {5} $.Следовательно, $ \ sin‌F = {3} / {5} $.

Окончательный ответ: $ {3} / {5} $ или 0,6.

Пример # 2

Ответ Explanation: Есть два способа решить эту проблему. Более быстрый способ — если вы знаете дополнительное угловое соотношение для синуса и косинуса, которое составляет $ \ sin (x °) = \ cos (90 ° −x °) $. Следовательно, $ \ cos (90 ° −x °) = {4} / {5} $ или 0,8.

Однако вы также можете решить эту проблему, построив диаграмму, используя предоставленную информацию. Это прямоугольный треугольник (который должен быть для использования синуса / косинуса), а синус угла x равен $ {4} / {5} $, если $ \ sine = {\ (напротив \: side)} / {\ hypotenuse} $, тогда длина противоположной стороны равна 4, а длина гипотенузы — 5:

Поскольку два угла треугольника имеют размер x ° и 90 °, третий угол должен иметь размер $ 180 ° −90 ° −x ° = 90 ° −x ° $.Как видно из рисунка, $ \ cos (90 ° −x °) $, которое равно $ {смежная \: side} / {\: hypotenuse} $, также равно $ {4} / {5} $ или 0,8.

Пример № 3

Ответ Explanation: Как и в другой задаче тригонометрии, есть два способа решить эту проблему.

Более быстрый способ — понять, что x и y являются дополнительными углами (в сумме получается 90 °). Затем, используя соотношение дополнительных углов для синуса и косинуса, равное $ \ sin (x °) = \ cos (90 ° −x °) $, вы понимаете, что $ \ cos (y °) = 0.6 $.

Однако вы также можете решить эту проблему, построив диаграмму, используя предоставленную информацию. Это прямоугольный треугольник (который должен быть синусом / косинусом), а синус угла x равен 0,6. Следовательно, отношение стороны, противоположной углу x °, к гипотенузе равно 0,6.

Сторона, противоположная углу x °, является стороной, смежной с углом y °. $ \ cos (y °) = {\ (\: сторона \: смежная \: к \: \: y ° \: угол)} / {\ (\: гипотенуза)} = {6} / {10 } $, равно 0,6.

Ответ — 0.6.

Готовы выйти за рамки простого чтения о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Наша программа SAT, разработанная и написанная экспертами PrepScholar SAT , адаптируется к вашему уровню навыков по более чем 40 вспомогательным навыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.

Нажмите кнопку ниже, чтобы попробовать!

Радианы

Радианы будут составлять лишь небольшую часть (около 5%) вопросов по математике SAT , но вы все равно хотите ответить на эти вопросы правильно! Радианы — одна из самых сложных концепций.Что вам нужно знать о радианах?

Определение радианной меры

Простое определение: Радиан — это мера угла (точно так же, как градус — это мера угла).

Подробная / концептуальная версия: Радиан — это мера угла, основанная на длине дуги, которую угол пересекает на единичной окружности. Я знаю, это звучит как тарабарщина. Позвольте мне сломать это. Единичный круг — это круг радиусом в 1 единицу.Смотрите изображение:

Густавб / Викимедиа

Окружность (или длина вокруг) этой единичной окружности равна $ {2π} $, поскольку $ {C = 2πr} $ и r = 1.

Если бы угол был 360 °, то в радианах было бы $ {2π} $, поскольку длина дуги, которую угол 360 ° пересекает на единичной окружности, была бы всей окружностью окружности (что мы уже установили было $ {2π} $). Вот несколько хороших основных радианов, которые стоит запомнить:

Градусов	Радианы (точное)
30 °	$ {π} / {6} долл. США
45 °	{π} долл. США / {4} долл. США
60 °	{π} долл. США / {3} долл. США
90 °	{π} долл. США / {2} долл. США

Преобразование углов в градусы и радианы

Чтобы перейти от градусов к радианам, нужно умножить на $ {π} $, разделить на 180 °.Вот как преобразовать 90 ° в радианы:

$$ {90 ° π} / {180 °} $$

$$ = {π} / {2} $$

Чтобы перейти от радианов к градусам, нужно умножить на 180 °, разделить на $ {π} $. Вот как преобразовать $ {π} / {4} $ в градусы:

$$ {({π} / {4}) (180 °)} / {π} $$

$$ = {({180 ° π} / {4}) / {π} $$

$$ = 45 ° $$

Как вычислить тригонометрические функции с помощью контрольных угловых мер

Контрольные угловые меры (согласно определению College Board) равны 0, $ {π} / {6} $, $ {π} / {4} $, $ {π} / {3} $, $ {π} / {2} $ радиан, равный углу, равному 0 °, 30 °, 45 °, 60 ° и 90 ° соответственно.

У вас должна быть возможность использовать их с тригонометрическими функциями, описанными в предыдущем разделе тригонометрии (синус, косинус и тангенс). Вам не будут предлагаться значения тригонометрических функций, для которых требуется калькулятор.

Помните, что дополнительное угловое соотношение для синуса и косинуса, равное $ \ sin (x °) = \ cos (90 ° −x °) $, будет $ \ sin (x) = \ cos ({π} / {2 } −x) $ при преобразовании в радианы.

Проблемы практики SAT Radians

Пример # 1

Объяснение ответа: Правильный ответ — 6.2)} = √ {3 + 1} = √ {4} = 2 $. Таким образом, $ \ sin (∠AOB) = {1} / {2} $.

Следовательно, ∠AOB равно 30 °, что равно $ 30 ({π} / {180}) = {π} / {6} $ радиан. Следовательно, значение a равно 6.

Пример # 2

Ответ Пояснение: Полный оборот вокруг точки составляет 360 ° или $ {2π} $ радиан. Поскольку центральный угол AOB имеет меру $ {5π} / {4} $ радиан, он представляет $ / {2π} = {5} / {8} $ полного вращения вокруг точки O. Следовательно, сектор, образованный центральным углом AOB имеет площадь, равную $ {5} / {8} $ площади всего круга.Ответ — $ {5} / {8} $ или в десятичной форме 0,625.

Пример № 3

Что из следующего эквивалентно $ \ cos ({3π} / {10}) $?

A) $ \ — cos ({π} / {5}) $
B) $ \ sin ({7π} / {10}) $
C) $ \ — sin ({π} / {5}) $
D) $ \ sin ({π} / {5}) $

Объяснение ответа: Чтобы правильно ответить на этот вопрос, вам необходимо понимать тригонометрию и радианы. Синус и косинус связаны уравнением $ \ sin (x) = \ cos ({π} / {2} -x) $.

Чтобы узнать, что эквивалентно $ \ cos ({3π} / {10}) $, вам нужно изменить $ {3π} / {10} $ в форму $ {π} / {2} — х $.Для этого вам нужно задать уравнение:

$$ {3π} / {10} = {π} / {2} -x $$

Затем решите относительно x.

$$ {3π} / {10} — {π} / {2} = — x $$

$$ {3π} / {10} — {5π} / {10} = — x $$

$$ — {2π} / {10} = — x $$

$$ {2π} / {10} = x $$

$$ {π} / {5} = x $$

Следовательно, $ \ cos ({3π} / {10}) = \ cos ({π} / {2} — {π} / {5}) = \ sin ({π} / {5}) $. D — правильный ответ.

Проверьте себя с помощью вопросов по SAT тригонометрии!

Практика № 1

В треугольнике DCE угол C равен 90 °, $ \ DC = 5 $ и $ \ CE = 12 $.Какое значение имеет $ \ sin (D) $?

Практика №2

В прямоугольном треугольнике $ \ cos ({π} / {2} -x) = {6} / {8} $. Что такое $ \ sin (x) $?

Практика № 3

В окружности O центральный угол AOB имеет меру $ {3π} / {4} $ радиан. Какую долю площади круга составляет площадь сектора, образованного центральным углом AOB?

Ответы: # 1: $ {12} / {13} $, # 2: $ {6} / {8} $, 3) $ {3} / {8}

долларов

Что дальше?

Теперь, когда вы знаете, как обращаться с тригонометрией и радианами, убедитесь, что вы готовы ко всем другим математическим темам, которые вы увидите на SAT.Все наши математические руководства познакомят вас со стратегиями и практическими задачами по всем темам, затронутым в математическом разделе, от целых чисел до соотношений, кругов и многоугольников (и многого другого!).

Беспокоитесь о тестовом дне? Убедитесь, что вы точно знаете, что делать, и принесите с собой облегчение и успокоение нервов, прежде чем придет время сдавать экзамен SAT.

Не хватает времени на сдачу экзамена по математике? Не ищите ничего, кроме нашего руководства, которое поможет вам опередить время и максимизировать свой результат SAT по математике.

Рыбалка, чтобы получить наивысший балл? Ознакомьтесь с нашим руководством по получению идеального 800-го балла, написанным отличным бомбардиром.

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.

Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно. Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

Сдать онлайн-экзамен по тригонометрии | Викторина

Этот онлайн-курс объединяет раздел математики, посвященный сторонам сферических треугольников / плоскостей, углам и взаимосвязям между ними.

Изучая этот онлайн-курс, вы сможете улучшить свои навыки и добиться больших успехов в своей карьере. Это также означает, что онлайн-курс тригонометрии — это непростой курс. Многие студенты не проходят этот курс в течение года, поэтому этому курсу придается большое значение. Если вы записались на этот курс, вам необходимо быть пунктуальным и всегда показывать высшую успеваемость. Если вы отстаете от курса или опасаетесь, что не пройдете этот курс, вам лучше связаться с TAKEMYONLINEEXAMS.COM. Мы профессионалы своего дела и знаем, как помочь студентам, которые отчаянно нуждаются в нашей помощи. В знак доверия к нам приходят студенты со своими вопросами, такими как , пройти мой онлайн-тест по тригонометрии для меня или сдать онлайн-экзамен по тригонометрии для меня.

Пройдите за меня онлайн-тест по тригонометрии

---

Обеспокоены завтрашней викториной по тригонометрии? Что ж, вам просто нужно расслабиться, потому что TAKEMYONLINEEXAMS.COM присутствует, чтобы предоставить вам свою надежную помощь. Вам просто нужно связаться с нами с запросом «пройдите мой онлайн-тест для меня», и мы назначим вам нашего лучшего профессора. Будьте уверены, что такие запросы, как «пройдите мой онлайн-тест для меня», лучше всего обрабатывает на TAKEMYONLINEEXAMS.COM.

Тестируемые онлайн

---

Мы — ваши профессиональные тестируемые онлайн. Студенты, подобные вам, обращаются к нам со своими вопросами, такими как , например, пройти мой онлайн-тест по тригонометрии для меня или сдать онлайн-экзамен по тригонометрии для меня. Мы сдадим ваш тест и поставим вам оценку A или B. Мы помогаем сдать тесты и убедиться, что мы сдали их задолго до крайнего срока. Если у вас есть тест по вашему предмету, свяжитесь с TAKEMYONLINEEXAMS.COM, и мы сделаем это за вас. Будьте уверены, что вам не придется беспокоиться о своих онлайн-тестах или выпускном экзамене.

Заплатите кому-нибудь за мой онлайн-экзамен

---

У вас бессонные ночи перед выпускным экзаменом по тригонометрии? Вы беспокоитесь о том, что можете потерпеть неудачу на этом курсе и потратить впустую свое время и деньги? Если ответ на эти вопросы положительный, то лучше всего связаться с TAKEMYONLINEEXAMS.COM с вашим запросом «сдайте мой онлайн-экзамен для меня». У нас есть многолетний опыт в этой онлайн-поддержке, и мы сдадим ваш экзамен за вас и поставим вам оценку A или B. Вам просто нужно связаться с TAKEMYONLINEEXAMS.COM с запросом «пройдите мою онлайн-викторину».

Почему выбирают нас?

---

• Мы гарантируем Вам 100% качественную работу в любое время и всегда!
• Команда высококвалифицированных специалистов, которые являются выпускниками и аспирантами
• Ваши учетные данные на 100% безопасны
• Нет абсолютно НИКАКИХ шансов попасться
• Наш веб-сайт использует протокол HTTPS, поэтому все ваши логины и платежные реквизиты остаются в безопасности
• Мы в режиме онлайн обеспечиваем первоклассную работу
• У нас есть к.D. Обладатели степени в нашей команде
• Что бы ни случилось, мы никогда не идем на компромисс в отношении качества
• Мы можем гарантировать вам оценку A или B на ваших тестах и ​​выпускном экзамене

Свяжитесь с нами по электронной почте, в чате или свяжитесь с нами бесплатная цитата.

No related posts.