Контрольная работа по теме кинематика физика: Контрольная работа по физике 10 класс Кинематика

Контрольная работа №1 по теме «Оновы кинематики»(9 КЛАСС, ФИЗИКА)

Контрольная работа «Основы кинематики» Вариант №1 1.Велосипедист, двигаясь равномерно, проезжает 20 м за 2 с. Определите, какой путь он  проедет при движении с той же скоростью за 10 с. 2. По графику   определите скорость движения велосипедиста в момент времени t = 2 с.        .3. На рисунке 2 представлены графики зависимости проекций ско­ рости от времени для трёх тел, движущихся прямолинейно. Какое тело двигалось с  наибольшим ускорением? Вычислить ускорения. Какое тело двигалось прямолинейно  равномерно? ­ 4. С каким ускорением должен затормозить автомобиль, движущийся со скоростью 36  км/ч, чтобы через 10 с остановиться? . 5. За какое время велосипедист проедет 30 м, начиная движение с ускорением 0,75 м/с2? 6. Какую скорость приобретает троллейбус за 5 с, если он трогается с места с ускорением  1,2 м/с2? 7. Поезд через 10 с после начала движения приобретает скорость 0,6 м/с. Через какое  время от начала движения скорость поезда станет равна 9 м/с? Какой путь пройдет поезд  за это время? 8.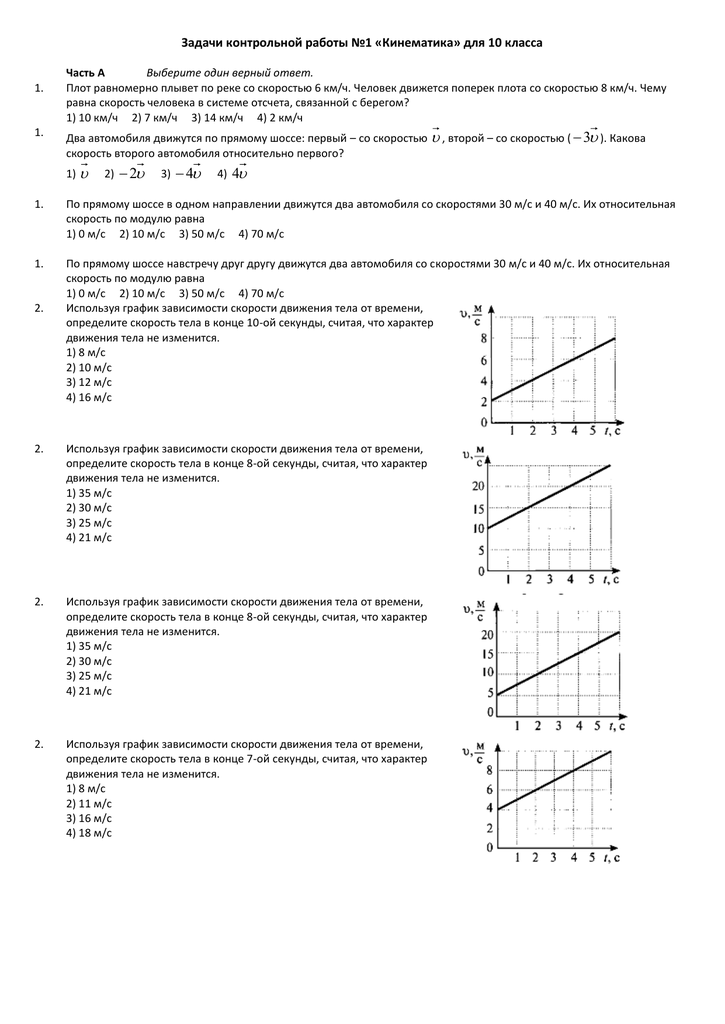

 Автомобиль, двигаясь равномерно, проходит путь 20 м за 4 с, после чего он начинает  тормозить и останавливается через 10 с. Определите ускорение и тормозной путь  автомобиля.      Контрольная работа «Основы кинематики» Вариант №2 1. Автомобиль, двигаясь равномерно, проехал 50 м за 2 с. Какой путь он проедет за 20 с,  двигаясь с той же скоростью? 2. По графику (см. рис. 1) определите скорость движения тела в момент времени t = 4 с.   3.  На рисунке 2 представлены графики зависимости проекций ско­ рости от времени для трёх тел, движущихся прямолинейно. Ка­ кое тело двигалось с наибольшим ускорением? Вычислить ускорения.. Какое тело  двигалось прямолинейно равномерно? 4. Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после  начала торможения. С каким ускорением двигался поезд? 5. Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния  покоя с ускорением 1,3 м/с2. 6. Какой должна быть длина взлетной полосы, если известно, что самолет для взлета  должен приобрести скорость 240 км/ч, а время разгона самолета равно примерно 30 с? 7.

 Спортсмен съехал на лыжах с горы длиной 40 м за 5 с. Определите ускорение движения и скорость спортсмена у подножия горы. 8. Тормоз легкового автомобиля считается исправен, если при скорости движения 8 м/с  его тормозной путь равен 7,2 м. Каково время торможения и ускорение автомобиля?

Контрольная Кинематика 9 📝 класс Физика

1. Сколько стоит помощь?

Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.

2. Каковы сроки?

Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.

3. Выполняете ли вы срочные заказы?

Да, у нас большой опыт выполнения срочных заказов.

4. Если потребуется доработка или дополнительная консультация, это бесплатно?

Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.

5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?

Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.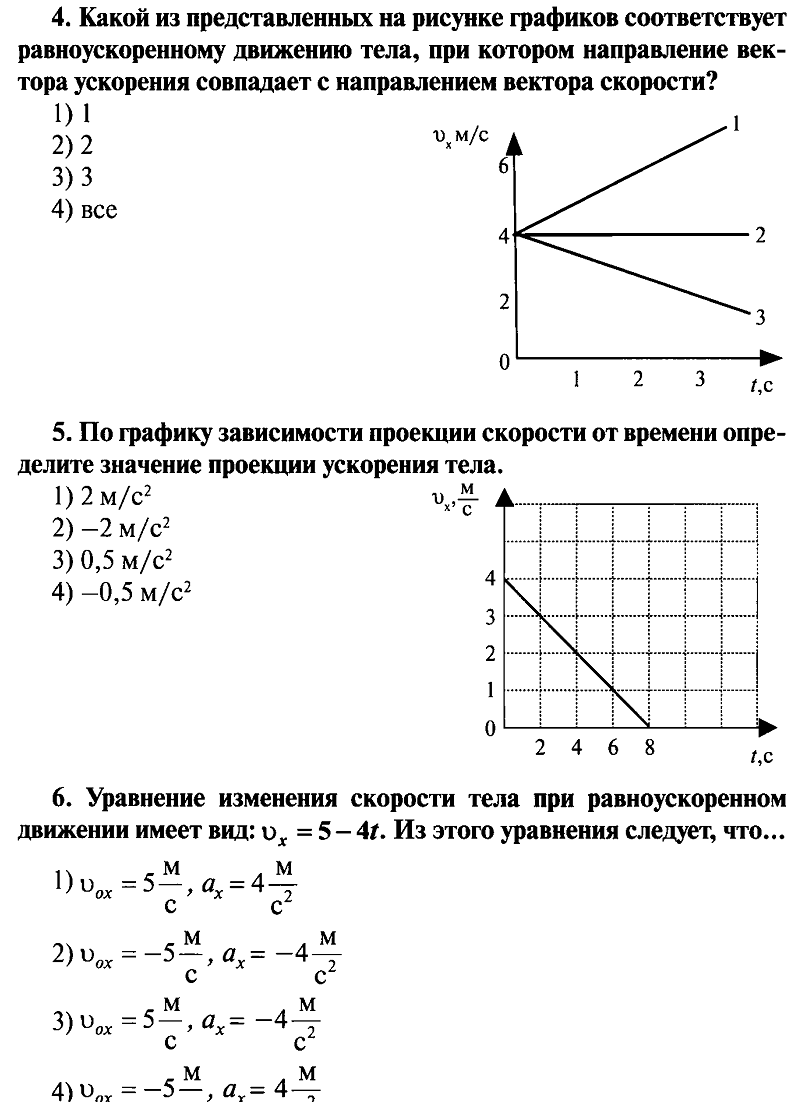

6. Каким способом можно произвести оплату?

Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.

7. Предоставляете ли вы гарантии на услуги?

На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.

8. Какой у вас режим работы?

Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.

Контрольные работы. 9 класс Контрольная работа по теме «Кинематика материальной точки». Вариант 1

А1. Линию, вдоль которой движется тело, называют

А. Пройденным путем Б. Перемещением В. Траекторией.

А2. Буксирный катер, двигаясь равномерно, за 3ч. прошёл путь 54км. Скорость катера равна …

А. 18м/с Б. 5м/с В. 15м/с

А3. Используя график зависимости скорости движения тела от времени, определите путь, пройденный телом за 3с.

А. 12м Б. 15м В. 18м.

А4. По графику координаты определите положение первого тела в момент t=5с.

А. 5м Б. 0 м В. 15м

А5. Решают две задачи:

А) рассчитывают выталкивающую силу, действующую на спортсмена,

плывущего дистанцию 400м,

Б) рассчитывают скорость спортсмена, бегущего дистанцию 400м.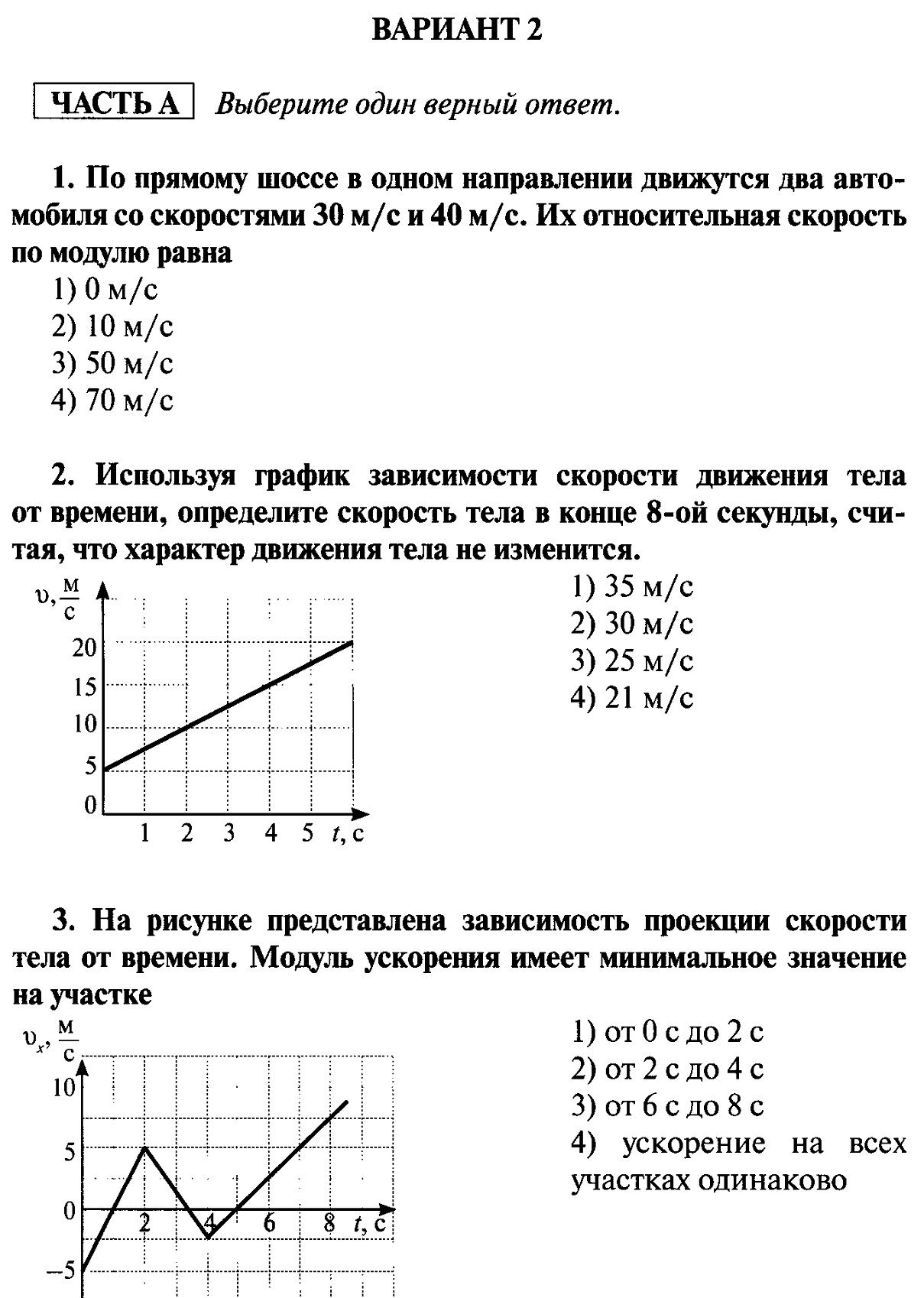

При решении какой задачи спортсмена можно принять за материальную точку?

А. И А, и Б. Б. А. В. Б.

А6. Какой из графиков соответствует равноускоренному движению тела, при котором вектор ускорения направлен противоположно вектору скорости?

А. 1 Б. 2 В. 3

А7. Мяч, упав с высоты 2м и отскочив от Земли, был пойман на высоте 1м. В обоих направлениях мяч двигался вдоль вертикальной прямой. Определите путь мяча за всё время движения.

А. 3м Б. 1м В. 0м

Часть 2.

В1. Три человека соревновались в беге. Первый бежал 20мин. со скоростью 12км/ч, второй пробежал 5км за полчаса, третий пробежал 6км со скоростью 11км/ч. Кто бежал быстрее всех?

В2. С каким ускорением движется гоночный автомобиль, если его скорость за 5с увеличивается от 144 до 216км/ч?

Часть 3.

С1. Рассчитайте длину взлетной полосы, если скорость самолета при взлете 300км/ч, а время разгона равно 40с.

Вариант 2

А1. Расстояние, пройденное телом в течение некоторого промежутка времени, называют…

А. Траекторией движения

Б. Пройденным путем В. Перемещением.

А2. Велосипедист, двигаясь равномерно, за 1,5ч проехал 27км. Скорость велосипедиста равна…

А. 18м/с Б. 5м/с В. 15м/с

А3. Используя график зависимости скорости движения тела от времени, определите путь, пройденный телом за 4с.

А. 12м Б. 24м В. 18м.

А4. По графику координаты определите положение второго тела в момент времени t=5с.

А. 15м Б. 5м В. 0 м.

А5. Решают две задачи:

А) рассчитывают время движения поезда между двумя станциями,

Б) рассчитывают время движения поезда вдоль железнодорожной

платформы.

При решении какой задачи поезд можно принять за материальную точку?

А. И А, и Б Б. А В. Б

А6. Какой из графиков соответствует равноускоренному движению тела, при котором вектор ускорения совпадает по направлению с вектором скорости?

А. 1 Б. 2 В. 3

А7. Мяч, упав с высоты 2м и отскочив от Земли, был пойман на высоте 1м. В обоих направлениях мяч двигался вдоль вертикальной прямой. Определите перемещение мяча за всё время движения.

А. 3м Б. 1м В. 0м

Контрольная работа №1 по теме «Кинематика» Вариант 1

Контрольная работа №1 по теме «Кинематика» Вариант 1 1.Какую скорость приобретает троллейбус за 10 с, если он трогается с места с ускорением 1,2 м/с2? 2. Поезд движется оп закруглению радиусом 500 м со скоростью 36 км/ч. Чему равно его центростремительное ускорение ? 3. Лыжник начинает спускаться с горы и за 20 с проходит путь 50 м .Определите ускорение лыжника и его скорость в конце спуска. 4. При аварийном торможении автомобиль остановился через 2 с. Найдите тормозной путь автомобиля, если он начал торможение при скорости 54 км/ч. 5. Тело, двигаясь из состояния покоя с ускорением 6м/с2 , достигло скорости 36 м/с, а затем остановилось через 5 с. Определите путь пройденный телом за все время движения ?

Контрольная работа №1 по теме «Кинематика» Вариант 2 1. Поезд, идущий со скоростью 18 км/ч, останавливается при торможении в течение 10 с. Найти его ускорение ? 2. Найти центростремительное ускорение автобуса, движущегося по выпуклому мосту с радиусом кривизны 30 м со скоростью 54 км /ч. 3. Первые 40 м пути 25 м автомобиль прошел за 10 с С каким ускорением он двигался и какую скорость при этом развил? 4. Какова длина пробега при посадке самолета, если его посадочная скорость равна 144 км/ч, а время торможения равно 20 с ? 5. Мотоциклист начал движение из состояния покоя и в течение 5 с двигался с ускорением 2 м/с2, затем 5 мин он двигался равномерно и,начав торможение, остановилось через 10 с. Определите весь пройденный им путь?

Контрольная работа №1 по теме «Кинематика» Вариант 1 1.Какую скорость приобретает троллейбус за 10 с, если он трогается с места с ускорением 1,2 м/с2? 2. Поезд движется оп закруглению радиусом 500 м со скоростью 36 км/ч. Чему равно его центростремительное ускорение ? 3. Лыжник начинает спускаться с горы и за 20 с проходит путь 50 м .Определите ускорение лыжника и его скорость в конце спуска. 4. При аварийном торможении автомобиль остановился через 2 с. Найдите тормозной путь автомобиля, если он начал торможение при скорости 54 км/ч. 5. Тело, двигаясь из состояния покоя с ускорением 6м/с2 , достигло скорости 36 м/с, а затем остановилось через 5 с. Определите путь пройденный телом за все время движения ?

Контрольная работа №1 по теме «Кинематика» Вариант 2 1. Поезд, идущий со скоростью 18 км/ч, останавливается при торможении в течение 10 с. Найти его ускорение ? 2. Найти центростремительное ускорение автобуса, движущегося по выпуклому мосту с радиусом кривизны 30 м со скоростью 54 км /ч. 3. Первые 40 м пути 25 м автомобиль прошел за 10 с С каким ускорением он двигался и какую скорость при этом развил? 4. Какова длина пробега при посадке самолета, если его посадочная скорость равна 144 км/ч, а время торможения равно 20 с ? 5. Мотоциклист начал движение из состояния покоя и в течение 5 с двигался с ускорением 2 м/с2, затем 5 мин он двигался равномерно и,начав торможение, остановилось через 10 с. Определите весь пройденный им путь?

Контрольная работа №1 по теме «Кинематика» Вариант 1 1.Какую скорость приобретает троллейбус за 10 с, если он трогается с места с ускорением 1,2 м/с2? 2. Поезд движется оп закруглению радиусом 500 м со скоростью 36 км/ч. Чему равно его центростремительное ускорение ? 3. Лыжник начинает спускаться с горы и за 20 с проходит путь 50 м .Определите ускорение лыжника и его скорость в конце спуска. 4. При аварийном торможении автомобиль остановился через 2 с. Найдите тормозной путь автомобиля, если он начал торможение при скорости 54 км/ч. 5. Тело, двигаясь из состояния покоя с ускорением 6м/с2 , достигло скорости 36 м/с, а затем остановилось через 5 с. Определите путь пройденный телом за все время движения ?

Контрольная работа №1 по теме «Кинематика» Вариант 2 1. Поезд, идущий со скоростью 18 км/ч, останавливается при торможении в течение 10 с. Найти его ускорение ? 2. Найти центростремительное ускорение автобуса, движущегося по выпуклому мосту с радиусом кривизны 30 м со скоростью 54 км /ч. 3. Первые 40 м пути 25 м автомобиль прошел за 10 с С каким ускорением он двигался и какую скорость при этом развил? 4. Какова длина пробега при посадке самолета, если его посадочная скорость равна 144 км/ч, а время торможения равно 20 с ? 5. Мотоциклист начал движение из состояния покоя и в течение 5 с двигался с ускорением 2 м/с2, затем 5 мин он двигался равномерно и,начав торможение, остановилось через 10 с. Определите весь пройденный им путь?

Контрольная работа по физике для 10 класса по теме «Кинематика материальной точки»

Контрольная работа по физике для 10 класса по теме «Кинематика материальной точки»

1.  Чему равно центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 10 м/с?

2.  Скорость поезда за 10 с уменьшилась с 20 до 10 м/с. Чему равно ускорение тела?

3.  Уравнение движения материальной точки имеет вид: х=50+5t. Определите:
а) начальную координату       
б) постройте график движения тела              
в) найдите перемещение тела за 10 с
г) найдите координату тела через 20 с.

4.  Свободно падающее тело  в момент удара о землю имело скорость 20 м/с. С какой высоты падало тело? Сколько времени длилось падение?

5.   Автомобиль первую половину пути проехал со скоростью 72 км/ч, а вторую половину пути со скоростью 54 км/ч. Найдите среднюю скорость автомобиля.

Контрольная работа по физике для 10 класса по теме: «Основы динамики»

1.  Объясните причину равномерного движения автомобиля по горизонтальному участку дороги.

2.  Масса человека на Земле 80 кг. Чему будут равны его масса и вес на поверхности Марса, если ускорение свободного падения на Марсе 3,7 м/с² ?

3.      Найдите силу притяжения двух тел массами по 10 кг, находящимися на расстоянии 100 м.

4.    Пружина длиной 25 см растягивается с силой 40 Н. Найдите конечную длину растянутой пружины, если ее жесткость 100 Н/м.

5.    Чему равна масса Луны, если ускорение свободного падения на Луне 1,6 м/с² , а ее радиус 1,74* 10⁶ м.

Контрольная работа по теме «Законы сохранения»     

1.  Найдите импульс грузового автомобиля массой 10 т, движущегося со скоростью 36 км/ч

2.   На какой высоте потенциальная энергия тела массой 60 кг равна 300 Дж?

3.  Упряжка собак, протащив сани по горизонтальному пути 
длиной 5 км, совершает работу 400 кДж. Считая коэффициент трения равным 0,02, найдите массу саней.

4.  Мяч брошен вертикально вверх с начальной скоростью 36 км/ч. На какую максимальную высоту он поднимется?

5.  С лодки массой 150 кг, движущейся со скоростью 2 м/с, прыгает мальчик массой 50 кг, двигаясь в горизонтальном направлении. Какой станет скорость лодки после прыжка мальчика, если он прыгнет с кормы со скоростью 4 м/с?

Контрольная работа по физике для 10 класса по теме: «Молекулярная физика и термодинамика»

1. 
   Во сколько раз изменится средняя квадратичная скорость движения молекул азота, если температура газа уменьшилась в 4 раза? Ответ обоснуйте.
   

2. 
   Найдите давление, которое оказывает 45 г неона при температуре 0⁰С, если его объем составляет 1 л.
   

3. 
   Совершается ли работа при изохорическом нагревании газа? Изобарическом охлаждении газа? Ответ обоснуйте.
   

4. 
   При изобарном расширении газа на 0,5 м³ ему было передано 0,3 МДж количество теплоты. Вычислите изменение внутренней энергии газа, если его давление равно 2*10⁵ Па.
   

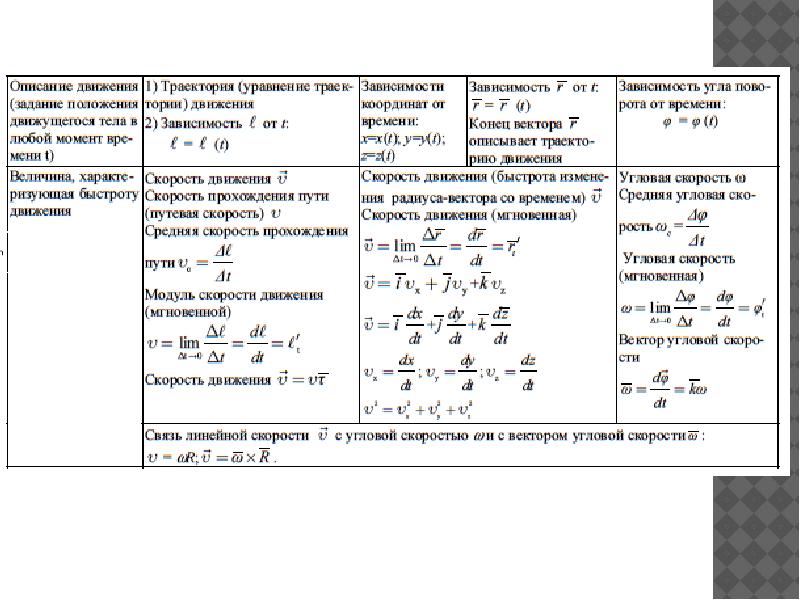
Кинематика. Теория и формулы для ЕГЭ + шпаргалка

КИНЕМАТИКА.
Теория и формулы (кратко и сжато)

Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.

---

Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.

Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.

---

---

Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.

Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).

---

---

Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.

Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.

 

---

---

Типы движений

1. Равномерное движение

1.1. Равномерное прямолинейное движение

Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.

Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.

Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.

Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.

Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.

1.2 Равномерное движение по окружности (равномерное вращение)

Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

---

 

2. Движение с постоянным ускорением

Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.

Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.

Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.

Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt  показывает, что скорость линейно зависит от времени.

Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.

---

 

3. Гармоническое движение

---

 

---

 

Виды движений

Прямолинейное движение

Криволинейное движение

Частные случаи равноускоренного движения под действием силы тяжести

Частные случаи решения задач

---

Дополнительные материалы по кинематике

Кинематика. Таблица кратко.

---

 

---

 

Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

Kinematics — документация SymPy 1.6.2

Этот документ дает некоторые математические основы к описанию кинематики системы, а также к тому, как представлять кинематику в sympy.physics.vector .

Введение в кинематику

Первая тема — кинематика жесткого движения. Твердое тело — это идеализированное представление физического объекта, имеющего инерцию массы и вращения. Очевидно, что твердые тела не гибкие. Мы можем сломать движение твердого тела в поступательное движение и вращательное движение (при работе с частицами мы есть только поступательное движение).Вращательное движение может быть далее разбито на простые вращения и общие вращения.

Смещение твердого тела определяется как движение, при котором ориентация тело не меняется при движении; или во время движения любой отрезок линии будет параллельно самому себе в начале движения.

Простые вращения — это вращения, при которых ориентация тела может изменяться, но всегда есть одна линия, которая остается параллельной самой себе в начале движение.{\ mathbf {B}} \) или угловая скорость \ (\ mathbf {B} \) в \ (\ mathbf {N} \), который является вектором. Обратите внимание, что здесь использовался термин твердое тело, но системы отсчета могут также иметь угловые скорости. Дальнейшее обсуждение различия между твердым телом и опорный кадр появится позже при описании представления кода.

Угловая скорость определяется как положительная в направлении, вызывающем углы ориентации для увеличения (для простых вращений или серии простых вращения).

Вектор угловой скорости представляет собой производную от ориентации по времени. В качестве векторной величины, производной по времени, например, описанных в разделе Vector & В документации ReferenceFrame эта величина (угловая скорость) должна быть определяется в системе отсчета. Это то, что \ (\ mathbf {N} \) находится в приведенное выше определение угловой скорости; кадр, в котором угловая скорость определено в. {\ mathbf {B}} = w_x \ mathbf {\ hat {b} _x} + w_y \ mathbf {\ hat {b} _y} + w_z \ mathbf {\ hat {b} _z} \]

Есть несколько дополнительных важных моментов, касающихся угловой скорости.{\ mathbf {D}} & = \ dot {q_1} \ mathbf {\ hat {a} _x} — \ dot {q_2} \ mathbf {\ hat {b} _z} + \ dot {q_3} \ mathbf {\ hat {c} _y} \\\ end {split} \]

Обратите внимание на знаки, используемые в определениях угловой скорости, которые относятся к как в этом случае определяется угол смещения.

Эта теорема значительно затрудняет определение угловых скоростей многотельных систем. проще, так как угловая скорость тела в цепочке нужно только определить к предыдущему телу, чтобы быть полностью определенным (а первое тело нуждается в быть определенным в желаемой системе отсчета).{\ mathbf {B}} \ times \ mathbf {v} \]

Вектор \ (\ mathbf {v} \) может быть любой векторной величиной: вектором положения, вектор скорости, вектор угловой скорости и т. д. Вместо того, чтобы брать время производная вектора в \ (\ mathbf {N} \), берем ее в \ (\ mathbf {B} \), где \ (\ mathbf {B} \) может быть любой системой отсчета или тело, обычно такое, в котором легко взять производную от \ (\ mathbf {v} \) в (\ (\ mathbf {v} \) обычно состоит только из базиса векторный набор, принадлежащий \ (\ mathbf {B} \)). {\ mathbf {B}} & = \ dot {w_x} \ mathbf {\ hat {b} _x} + \ dot {w_y} \ mathbf {\ hat {b} _y} + \ dot {w_z} \ mathbf {\ hat {b} _z} \\\ end {split} \ end {align} \ end {align} \]

Опять же, это только для случая, когда угловая скорость тела равна определены в фиксированных компонентах кузова.

Скорость точки и ускорение

Рассмотрим точку \ (P \): мы можем определить некоторые характеристики точки. Во-первых, мы можем определить вектор положения из некоторой другой точки в \ (P \). Во-вторых, мы можем определить вектор скорости \ (P \) в системе отсчета наш выбор.{OP} & = q_x

гл. 3 Введение в двумерную кинематику — College Physics

Ch. 3 Введение в двумерную кинематику — Физика колледжа | OpenStaxSkip к контенту

1. Предисловие
2. 1 Введение: Природа науки и физики
   1. Введение в науку и область физики, физических величин и единиц
   2. 1.1 Физика: введение
   3. 1.2 Физические величины и единицы
   4. 1. 3 Точность, прецизионность и значащие цифры
   5. 1.4 Приближение
   6. Глоссарий
   7. Краткое содержание раздела
   8. Концептуальные вопросы
   9. Задачи и упражнения
3. 1. Введение в одномерную кинематику
   2. 2.1 Смещение
   3. 2.2 Векторы, скаляры и системы координат
   4. 2.3 Время, скорость и скорость
   5. 2.4 Ускорение
   6. 2.5 Уравнения движения для постоянного ускорения в одном измерении
   7. 2.6 Основы решения проблем для одномерной кинематики
   8. 2.7 падающих объектов
   9. 2.8 Графический анализ одномерного движения
   10. Глоссарий
   11. Сводка раздела
   12. Концептуальные вопросы
   13. Задачи и упражнения
4. 3 Двумерная кинематика
   1. Введение в двумерную кинематику
   2. 3.1 Кинематика в двух измерениях: введение
   3. 3.2 Сложение и вычитание векторов: графические методы
   4. 3.3 Сложение и вычитание векторов: аналитические методы
   5. 3.4 Движение снаряда
   6. 3.5 Добавление скоростей
   7. Глоссарий
   8. Сводка раздела
   9. Концептуальные вопросы
   10. Задачи и упражнения
5. 4 Динамика: сила и законы движения Ньютона
   1. Введение в динамику: законы движения Ньютона
   2. 4.1 Развитие концепции силы
   3. 4.2 Первый закон движения Ньютона: инерция
   4. 4.3 Второй закон движения Ньютона: концепция системы
   5. 4.4 Третий закон движения Ньютона: симметрия сил
   6. 4.5 Нормальные, растягивающие и другие примеры сил
   7. 4.6 Стратегии решения проблем
   8. 4.7 Дальнейшие применения законов движения Ньютона
   9. 4.8 Расширенная тема: Четыре основных силы — Введение
   10. Глоссарий
   11. Краткое содержание раздела
   12. Концептуальные вопросы
   13. Задачи и упражнения
6. 5 Дальнейшее применение законов Ньютона: трение, сопротивление и эластичность
   1. Введение: дальнейшее применение законов Ньютона
   2. 5.1 Трение
   3. 5.2 Силы сопротивления
   4. 5.3 Упругость: напряжение и деформация
   5. Глоссарий
   6. Краткое содержание раздела
   7. Концептуальные вопросы
   8. Задачи и упражнения
7. 6 Равномерное круговое движение и гравитация
   1. Введение в равномерное круговое движение и гравитацию
   2. 6,1 Угол вращения и угловая скорость
   3. 6,2 Центростремительное ускорение
   4. 6,3 Центростремительная сила
   5. 6,4 Фиктивные силы и неинерциальные системы координат: сила Кориолиса
   6. 6.5 Универсальный закон тяготения Ньютона
   7. 6.6 Спутники и законы Кеплера: аргумент в пользу простоты
   8. Глоссарий
   9. Краткое содержание раздела
   10. Концептуальные вопросы
   11. Проблемы и упражнения
8. 7 Работа, энергия и энергетические ресурсы
   1. Введение в Работа, энергия и энергетические ресурсы
   2. 7.1 Работа: научное определение
   3. 7.2 Кинетическая энергия и теорема работы-энергии
   4. 7.3 Гравитационная потенциальная энергия
   5. 7.4 Консервативные силы и потенциальная энергия
   6. 7.5 Неконсервативные силы
   7. 7.6 Сохранение энергии
   8. 7.7 Энергия
   9. 7.8 Работа, энергия и мощность у людей
   10. 7.9 Использование энергии в мире
   11. Глоссарий
   12. Резюме раздела
   13. Концептуальные вопросы
   14. Задачи и упражнения
9. 8 Линейный импульс и столкновения
   1. Введение в линейный импульс и столкновения
   2. 8.1 Линейный импульс и сила
   3. 8.2 Импульс
   4. 8.3 Сохранение импульса
   5. 8.4 Упругие столкновения в одном измерении
   6. 8.5 Неупругие столкновения в одном измерении
   7. 8.6 Столкновения точечных масс в двух измерениях
   8. 8.7 Введение в ракетное движение
   9. Глоссарий
   10. Краткое содержание раздела
   11. Концептуальные вопросы
   12. Задачи и упражнения
10. 1. Введение в статику и крутящий момент
    2. 9.1 Первое условие равновесия
    3. 9.2 Второе условие равновесия
    4. 9.3 Стабильность
    5. 9.4 Приложения статики, включая стратегии решения проблем
    6. 9.5 Простые механизмы
    7. 9.6 Силы и моменты в мышцах и суставах
    8. Глоссарий
    9. Резюме раздела
    10. Концептуальные вопросы
    11. Задачи и упражнения
11. 10 Вращательное движение и угловой момент
    1. Введение в вращательное движение и угловой момент
    2. 10.1 Угловое ускорение
    3. 10.2 Кинематика вращательного движения
    4. 10.3 Динамика вращательного движения: вращательная инерция
    5. 10.4 Кинетическая энергия вращения: новый взгляд на работу и энергию
    6. 10,5 Угловой момент и его сохранение
    7. 10,6 Столкновения протяженных тел в двух измерениях
    8. 10.7 Гироскопические эффекты: векторные аспекты углового момента
    9. Глоссарий
    10. Сводка раздела
    11. Концептуальные вопросы
    12. Задачи и упражнения
12. 1. Введение в статику жидкости
    2. 11.1 Что такое жидкость?
    3. 11.2 Плотность
    4. 11.3 Давление
    5. 11.4 Изменение давления по глубине в жидкости
    6. 11.5 Принцип Паскаля
    7. 11.6 Манометрическое давление, абсолютное давление и измерение давления
    8. 11.7 Принцип Архимеда
    9. 11.8 Когезия и адгезия в жидкостях : Поверхностное натяжение и капиллярное действие
    10. 11.9 Давления в теле
    11. Глоссарий
    12. Сводка раздела
    13. Концептуальные вопросы
    14. Проблемы и упражнения
13. 12 Динамика жидкости и ее биологические и медицинские приложения
    1. Введение в динамику жидкости и ее Биологические и медицинские приложения
    2. 12.1 Расход и его связь со скоростью
    3. 12.2 Уравнение Бернулли
    4. 12.3 Наиболее общие приложения уравнения Бернулли
    5. 12.4 Вязкость и ламинарный поток; Закон Пуазейля
    6. 12.5 Начало турбулентности
    7. 12.6 Движение объекта в вязкой жидкости
    8. 12.7 Явления молекулярного переноса: диффузия, осмос и связанные процессы
    9. Глоссарий
    10. Краткое содержание раздела
    11. Концептуальные вопросы
    12. Проблемы и упражнения
14. 13 Температура, кинетическая теория и законы газа
    1. Введение в температуру, кинетическую теорию и законы газа
    2. 13.1 Температура
    3. 13.2 Термическое расширение твердых тел и жидкостей
    4. 13.3 Закон идеального газа
    5. 13.4 Кинетическая теория: атомное и молекулярное объяснение давления и температуры
    6. 13,5 Фазовые изменения
    7. 13,6 Влажность, испарение и кипение
    8. Глоссарий
    9. Краткое содержание раздела
    10. Концептуальные вопросы
    11. Задачи и упражнения
15. 14 Методы теплопередачи и теплопередачи
    1. Введение в методы теплопередачи и теплопередачи
    2. 14.1 Тепло
    3. 14.2 Изменение температуры и теплоемкость
    4. 14.3 Фазовое изменение и скрытая теплота
    5. 14.4 Методы теплопередачи
    6. 14,5 Проводимость
    7. 14,6 Конвекция
    8. 14,7 Излучение

Исследование моделирования в анимации персонажей на основе физики Engine

Компьютерная 3D-анимация персонажей — это, по сути, продукт, который сочетается с компьютерной графикой и робототехникой, физикой, математикой и искусством. Он основан на компьютерном оборудовании и графических алгоритмах, а в смежных науках быстро развиваются новые технологии.В настоящее время основная технология анимации персонажей основана на искусственном производстве ключевых технологий и захвата кадров на основе технологии устройств захвата движения. 3D-анимация персонажей широко используется не только в производстве фильмов, анимации и других коммерческих областях, но также в виртуальной реальности, компьютерном обучении, моделировании полета, инженерном моделировании, военном моделировании и других областях. В этой статье мы пытаемся изучить анимацию персонажей, основанную на физике, чтобы решить такие проблемы, как плохое взаимодействие в реальном времени, которое проявляется в персонаже, низкая степень использования и сложное производство.В статье глубоко изучаются кинематика, технология динамики и технология производства на основе данных движения. В то же время он проанализировал ODE, PhysX, Bullet и другие разнообразные основные физические движки и изучил дерево ограничивающих рамок иерархии OBB, иерархическое дерево AABB и другие алгоритмы обнаружения столкновений. Наконец, реализована анимация персонажей на основе ODE, которая представляет собой симуляцию движения и процесса столкновения трехколесного велосипеда.

1. Предпосылки и значение исследования

Основные технологии производства анимации — это технология ключевых кадров, основанная на искусственном производстве, и технология захвата движения, основанная на оборудовании захвата.Технология ключевых кадров, основанная на искусственном производстве, — это оригинальная технология комбинирования анимации. Это зависит от создания ключевых кадров и интерполяции между ключевыми кадрами для управления непрерывным воспроизведением анимации. Технология позволяет дизайнерам создавать анимацию по собственному желанию с максимальной степенью свободы, но продукты этой технологии не очень хороши с точки зрения естественного исполнения; кроме того, процесс производства довольно сложен [1]. С тех пор как появилось оборудование для захвата движения, его можно использовать для захвата данных движения в качестве источника информации для создания анимации, так что эффективность создания анимации персонажей и ощущение реальности анимации персонажей могут быть значительно улучшены.Однако, поскольку технологии нужны подлинные персонажи для участия в процессе захвата информации о движении, область ее применения становится весьма ограниченной. При использовании этой технологии подлинным действующим лицам не разрешается совершать опасные действия. Кроме того, высокая стоимость такого оборудования также ограничивает широкое использование технологии.

На фоне растущего промышленного спроса, повышенных требований к опыту пользователей и быстрого развития компьютерных технологий, вышеупомянутые два вида обычных традиционных методов производства анимации становятся все менее и менее возможными для удовлетворения требований дизайна и использования. .Основная причина заключается в том, что два вида технологий используют автономный способ в процессе объединения и хранения анимации, а затем для использования в постпродакшене; таким образом, анимация будет загружена соответствующим огромным пространством для хранения данных, учитывая ее высокое качество и длительность. Более того, самая большая проблема этого метода — низкая скорость с точки зрения производительности в реальном времени и самоадаптации, так что анимацию, на которую уходит много времени и денег, можно просто использовать для конкретных обстоятельств один раз.Все эти проблемы не вписываются в текущую тенденцию быстрого увеличения компьютерной обработки и пользовательского опыта [2].

В этой статье для решения проблем низкой производительности в реальном времени, низкого коэффициента использования и сложной процедуры, существующих в процессе создания анимации персонажей, исследуется метод моделирования анимации персонажей, основанный на физическом движке, и пример реализации метода.

2. Основание смежных исследований

В настоящее время анимация персонажей всегда находится в центре внимания и является трудностью в исследованиях компьютерной графики.В исследовании используются различные методы создания анимации, которые можно разделить на следующие категории [3]: (i) Метод создания анимации на основе кинематики (ii) Метод создания анимации на основе динамики (iii) Метод создания анимации на основе данные о движении

Далее следует краткое введение в перечисленные выше три вида анимации персонажей.

2.1. Принцип создания анимации персонажей на основе кинематики

Кинематика — очень важный раздел в физике и механике.В ходе исследования объект абстрагируется как модель твердого тела и модель частицы [4]. Эти модели используются для изучения движения объектов. Ключевым моментом модели твердого тела является исследование угловой скорости твердого тела, его вращательного движения, линейной скорости и т. Д. Основное внимание при исследовании модели частицы уделяется уравнению скорости, ускорения, замедления и движения частицы в указанной системе отсчета. Кроме того, не обязательно учитывать факторы влияния динамики, такие как качество и сила.

Метод кинематики делится на прямую кинематику и обратную кинематику.

2.1.1. Метод прямой кинематики [5]

В простой кинематической системе часто бывает два конца. Они бывают со свободным концом и фиксированным концом. Прямая кинематика описывает движение свободного конца с фиксированным концом системы в качестве отправной точки. Метод прямой кинематики: первый шаг — установить иерархическую структуру объекта, а затем установить поворот и положение каждого объекта в иерархии.

2.1.2. Метод обратной кинематики

Другой метод моделирования, основанный на кинематике, — это метод обратной кинематики [5]. Обратная кинематика прямо противоположна прямой кинематике. Обратная кинематика — это движение, при котором неподвижный конец движется за свободный конец.

Используйте следующую формулу, чтобы выразить основные принципы обратной кинематики [6]:

Формула (1) — это основная формула обратной кинематики, в которой смещение конца шарнирной цепи — это поворот угол конца шарнирной цепочки, — матрица Якоби.По формуле, приведенной выше, смещение сустава равно произведению, углу поворота концов цепочки сустава и матрице Якоби. Но формула (2) часто используется в обратной кинематике [6]:

В формуле, и аналогично находятся в формуле (1). псевдообратная матрица матрицы Якоби в линейной алгебре. является единичной матрицей. — постоянная оптимизации. — потребление энергии суставами для минимизации движения. Обратная кинематика рассчитывается от конца всей шарнирной цепи.По сравнению с прямой кинематикой, обратная кинематика больше подходит для создания более сложных движений и легче позволяет переворачивать объект в анимации. Однако обратная кинематика не универсальна. Некоторые задачи, которые подходят для прямой кинематики, не подходят для обратной кинематики.

2.2. Принцип создания анимации на основе динамики

Динамика также является очень важным разделом физики, изучающим взаимосвязь между силой и движением.Основная теория кинетических исследований — это закон движения Ньютона. Объект исследования динамики — макроскопический объект, скорость которого намного меньше скорости света. Анимация, созданная этим методом, имеет сильную физическую реальность, поскольку основана на законах физики.

При моделировании анимации персонажей кинематический метод заключается в вычислении положения и угла поворота каждого сустава персонажей, а ключевые кадры состоят из данных двух типов.

При моделировании анимации персонажа динамический метод сначала придает объекту физические свойства и применяет различные силы, а затем использует закон движения Ньютона для вычисления состояния персонажа.Суть этого метода — вычислить ускорение объекта силой. В динамике тип силы можно разделить на два типа: точечная сила и сила поля [7].

Помимо силы, столкновение также является важным фактором, влияющим на движение персонажа. В реальном мире, когда два объекта сталкиваются, они сталкиваются, но не проникают друг в друга. Когда происходит столкновение, сила взаимодействия изменит исходное состояние двух объектов, такое как положение, траектория и направление.Следовательно, при моделировании анимации персонажа, если столкновение происходит между объектами, исходное состояние движения персонажа будет изменено из-за силы взаимодействия.

2.3. Принцип создания анимации персонажей на основе данных движения

2.3.1. Захват движения

Вышеупомянутые методы анимации реализованы с использованием механики, биомеханики и повседневного жизненного опыта. В технологии захвата движения данные исходят из реальной производительности актера через оборудование захвата движения для получения данных о действиях.Поскольку обрабатываемые данные производятся людьми, технология захвата движения может сделать анимацию более реальной и естественной. Искусственных данных от захвата и обработки не было. Но оборудование для захвата движения очень дорогое и сложное в эксплуатации. Во время сбора данных конечности, тело и голова модели движения обычно устанавливают точки датчиков, и эти совокупные данные являются очень важной частью всей технологии захвата движения [8].

Динамические и кинематические методы, представленные в этой статье, используются для анимации физических законов движения.Однако сложность движения человека с физическими законами, особенно с точки зрения механизма координации движений человека, делает работу моделирования очень сложной, что приводит к нереалистичной анимации и отсутствию подробной подробной информации о реальном движении человеческого тела. В последние годы технология захвата движения вошла в поле зрения; он преодолевает недостатки двух вышеуказанных методов анимации и стал одной из самых многообещающих технологий в человеческой анимации.

2.3.2. Motion Blend

Технология смешивания движений — это технология, основанная на специальной базе данных и алгоритме движения. Чтобы использовать этот метод для работы с анимацией, нам обычно необходимо использовать алгоритм интерполяции и параметры интерполяции.

Основным преимуществом технологии Motion Blend является ее низкая вычислительная сложность. И он основан на данных захвата движения, чтобы сохранить исходное динамическое движение. Его главный недостаток состоит в том, что, например, напряжение, беспокойство и другие действия слишком зависят от существующих рабочих данных, и объем данных увеличивается.Если персонаж ходит походкой, которая не слишком утомлена или утомлена, необходимо иметь данные о нормальной ходьбе, а также данные об очень усталой ходьбе. В процессе интерполяции производители обычно имеют дело с переходом и преобразованием между набором параметров постоянным и линейным представлениями по умолчанию [9].

2.3.3. Деформация движения

Деформация движения — это технология для изменения и использования существующей информации о движении. Popoivc и Witkin используют интерактивные методы для смещения и масштабирования выбранных ключевых кадров для изменения существующих данных.По сравнению с траекторией во временной области, Уильямс и Брудерлин используются для настройки, изменения и повторного использования существующих данных анимации в частотной области. По сравнению с технологией движущейся анимации и технологией технологической анимации преимущество технологии микширования движений состоит в том, что она может использовать существующие реальные данные захвата для создания анимации. Более того, эта технология обеспечивает совместимость создателя анимации и анимации по ключевым кадрам с инструментом, с которым будет очень удобно работать.

По сравнению с технологией кинематической анимации и технологией технологической анимации преимущество технологии смешивания движений, которая относится к технологии технологической анимации, состоит в том, что она может использовать существующие реальные данные захвата для создания анимации [10]. Более того, эта технология совместима с технологией анимации по ключевым кадрам.

3. Исследования, связанные с физическим движком

Как правило, существует два типа физических движков: физический движок с открытым исходным кодом и коммерческий физический движок.

Обычно используемые профессиональные физические движки включают ODE, PhysX, Bullet, Havork, Newton и Vortex. Эти физические движки широко используются в таких областях, как инструменты графического моделирования, разработки игр, систем виртуальной реальности и так далее.

Обнаружение столкновений — это техническое ядро ​​физического движка, поэтому большая часть исследований физического движка — это исследования алгоритма обнаружения столкновений. В реальной жизни некоторые реакции происходят естественным образом при столкновении объектов и после них [11].Однако в виртуальном мире проблема столкновения требует решения некоторых алгоритмов. Обнаружение столкновений — важная часть таких областей, как робот, виртуальная реальность и т. Д. Его основная цель — определить, проникнут ли два или более объекта в контакт или войдут в контакт. Исследование обнаружения столкновений с помощью определенного алгоритма позволяет двум или более объектам не занимать одну и ту же пространственную область одновременно, не повреждая объекты.

В настоящее время во всем мире существуют две основные категории исследований по обнаружению столкновений: метод пространственной декомпозиции и метод ограничивающего прямоугольника.Метод ограничивающего прямоугольника моделирует объект сложной формы в приближенном простом трехмерном пространстве. Метод иерархической ограничивающей рамки метода ограничивающей рамки подходит для обнаружения столкновений в сложной среде.

ODE (Open Dynamics Engine) — это библиотека динамики твердого тела с открытым исходным кодом, которая часто используется при моделировании суставных соединений. ODE можно применять для имитации движущихся объектов в среде VR, существ на ногах и транспортных средств на земле.Он надежный, гибкий и быстрый. Гибкость отражается в портативности; Можно использовать Unix / Linux, Windows и MacOS. И он имеет встроенную систему обнаружения столкновений.

4. Исследование и разработка моделирования анимации персонажей на основе ODE

4.1. Моделирование динамики смоделированного транспортного средства на основе ODE

В ODE существует особый тип соединения, показанный на рисунке 1.

Шарнирный шарнир-2 состоит из двух несоосных шарниров. Полезная модель состоит из двух вращающихся валов и опоры.Среди них Axis 2 может вращаться только вокруг оси; однако ось 1 не только может вращаться вокруг оси, но также может ограничивать диапазон ее вращения.

Модель автомобиля состоит из кузова и колес. Согласно типу шарнира шарнира-2, тело 1 может представлять тело, а тело 2 может представлять колесо; аналогично, ось 1 может представлять рулевое колесо колеса, а ось 2 может представлять вал качения колеса. В динамическом проектировании системы ODE создается жесткий объект ODE с качеством и положением, и одновременно создается геометрия ODE, соответствующая твердому телу.Наконец, корпус и колеса соединяются шарниром Hinge-2. Построена простая модель автомобиля.

4.2. Моделирование столкновения символов на основе ODE

Процесс моделирования столкновения символов на основе ODE выглядит следующим образом.

4.2.1. Пространственная инициализация в моделировании столкновений

На этом этапе необходимо установить тип пространства столкновений и соответствующие свойства контактной поверхности, такие как гибкость, упругость и трение.

4.2.2. Инициализация данных при моделировании столкновений

На этом этапе необходимо проделать некоторую работу по инициализации и очистке данных перед моделированием столкновений [12].

Очистка данных о столкновениях . Очистите все виды информации о столкновениях, включая очистку данных о столкновениях, очистку группы контактов и удаление текущего пространства столкновений. Затем сбросьте все свойства контактной поверхности в соответствии с потребностями пользователя.

В соответствии с потребностями пользователя создайте пространство дерева с четырьмя ветвями, пространство хеширования и простое пространство.Эти три новых типа пространства коллизий используют разные алгоритмы обнаружения коллизий и разные структуры данных. Различная геометрия хранится с использованием разных структур данных.

Обнаружение данных коллизии . Данные столкновения — это настраиваемая переменная, в которой хранятся все данные, необходимые для геометрии столкновения. Символьный объект является источником данных. Перед симуляцией столкновения вам необходимо настроить данные столкновения для каждого объекта столкновения и добавить эти данные в список столкновений.Наконец, информация о столкновении передается в функцию столкновения, когда выполняется моделирование столкновения.

4.2.3. Старт моделирования столкновения

Процесс моделирования принимает временной шаг как единицу. В симуляторе ODE при моделировании для завершения временного шага для эффекта столкновения единиц необходимо использовать текущее состояние до воздействия и роль данных, а затем эффект столкновения, оказанный на роль тела [13, 14]. Эта ссылка должна вызывать существующую функцию столкновения пространства в ODE.Наконец, в соответствии с данными контактных узлов, созданных двумя контактными твердыми телами при столкновении, ODE завершает столкновение [15]. Функция космического столкновения — очень важная функция в этой ссылке. Прототипом его функции является Void dSpaceCollide (dSpaceID space, void, dNearCallback).

Эта функция определяет, какие геометрии могут возникнуть в пространстве, а затем вызывает функцию обратного вызова для обработки пары геометрий и, наконец, завершает столкновение.

Тип функции обратного вызова — dNearCallback, определенный следующим образом: Typedef void dNearCallback (void, dGeomID 1, dGeomID 2)

Среди них данные — это параметры, определяемые пользователем, непосредственно из прохода dSpaceCollide.Пара геометрий, обнаруживающая возможное столкновение, представлена ​​параметрами 1 и 2 [16]. Эта функция обратного вызова затем использует dCollide для создания точки контакта между геометриями. Затем эти точки контакта будут добавлены в процесс моделирования как контактное соединение.

Следующая операция будет выполняться внутри обратного вызова [17]: (i) Используйте функцию dCollide для создания выбранных точек контакта между геометриями, возвращая при этом количество точек контакта. (Ii) На основе всех данных о столкновениях в предыдущая ссылка, для каждой точки контакта выполняется поиск двух подходящих точек данных столкновения.(iii) ODE завершает эффект столкновения в соответствии с информацией о контактном соединении, содержащейся в этих двух столкновениях, и снова показывает изображение.

4.2.4. Конец моделирования столкновений

В конце моделирования ODE имитация столкновений также действует как движущая сила, чтобы остановить характер силы. Эта ссылка выполнит некоторую связанную с этим работу по очистке данных, которая поможет в следующем моделировании.

5. Реализация и тестирование симуляции анимации персонажей

5.1. Создание примера в анимации персонажа

Откройте программное обеспечение физического движка, отредактируйте и запустите программу на языке C, чтобы получить сценарий, показанный на рисунке 2.

На рисунке 2 вы можете увидеть основные элементы сцены , включая небо, землю, машину и препятствия.

Пример моделирования состоит из простых элементов: мощность транспортного средства поступает от двигателя; мощность и рулевое управление установлены на переднее колесо; соединение колеса и кузова автомобиля через шарнир; транспортное средство может иметь силы взаимодействия при касании любого объекта сценария; в автомобиле есть устройство обнаружения столкновения.

5.2. Тестирование

Путем настройки мощности транспортного средства можно реализовать силу взаимодействия между транспортным средством и объектами в сценарии, а также скорость скольжения по грунту, моделирование движения транспортного средства и процесс столкновения.

Тестирование производительности показано на рисунках 3, 4 и 5.

В ходе тестирования измените транспортное средство или различные параметры окружающей среды и посмотрите, изменится ли характер в Картинка соответствует кинетическому принципу.

5.2.1. Тестирование на трение

Когда автомобиль соприкасается с землей, измените кулоновский коэффициент трения mu с исходного dInfinity (скользящего контакта не будет) на 0 (отсутствие контакта трения). Этот коэффициент необходимо установить. И результат тестирования — колесо работает на холостом ходу. В это время переднее колесо в качестве выходной мощности может работать только на холостом ходу, поскольку нет трения, поэтому транспортное средство не может двигаться [18].

5.2.2. Тест на проникновение

Когда автомобиль находится в контакте с землей, soft_cfm является параметром нормальной гибкости контакта, который используется для регулировки гибкости объекта.Увеличение значения soft_cfm с исходного 0,3 до 1 указывает, что будет очень очевидный феномен проникновения объекта; результат тестирования показан на рисунке 6; возникает очень очевидный феномен проникновения между колесом и землей [18].

5.2.3. Проверка коэффициента скольжения

Установите FDS (коэффициент скольжения, зависящий от силы) на ноль. После того, как модель перевернется, продолжайте подавать питание на транспортное средство, и транспортное средство не имеет бокового скольжения, но остается неподвижным.(FDS указывает на явление бокового скольжения из-за боковой внешней силы при движении объекта, а расстояние скольжения пропорционально скорости движения объекта и внешней силе, поэтому FDS также называют коэффициентом скольжения боковой силы [18, 19 ].)

Если коэффициент трения скольжения FDS установлен на 0,1, продолжайте подавать питание на транспортное средство после его опрокидывания, и оно все еще может двигаться вбок. Результат тестирования показан на рисунке 7.

Когда мир создан, направление ускорения силы тяжести по оси-оси, установленное на 0, может быть получено, как на рисунке 8.

Судя по результатам испытаний, из-за ускорения свободного падения 0 имитация подвески в транспортном средстве.

Посредством моделирования автомобиля и окружающей среды с различными наборами параметров вы можете выполнять различные симуляции анимации на основе физического движка.

6. Резюме

Что касается исследований по моделированию анимации персонажей, в стране и за рубежом было сделано много достижений. На основе изучения имеющихся достижений научных исследований в данной статье выполнены следующие работы: углубленное исследование основных технологий производства компьютерной анимации персонажей; углубленный анализ и исследование основных физических движков; углубленное исследование соответствующих алгоритмов обнаружения столкновений; проектирование и построение архитектуры симуляции, чтобы сделать симуляцию анимации персонажей возможной с помощью движка ODE; построение платформы экспериментов по моделированию и успешных примеров реализации моделирования анимации персонажей на основе ODE; и проведение теста и анализа с разными параметрами.

В центре внимания следующих исследований: от модернизации модели движения транспортного средства до более сложной модели движения человеческого тела, имитирующей более сложные и точные движения человеческого тела; создание разных контроллеров для разных моделей персонажей и состояний движения и реализация более эффективного и реалистичного моделирования с помощью более интеллектуальных контроллеров; включение естественного выключения персонажа с помощью технологии смешивания анимации.

Конфликт интересов

Авторы заявляют, что у них нет конфликта интересов.

PPT — ФИЗИЧЕСКИЙ БЛОК 1: КИНЕМАТИКА (описание движения) Презентация в PowerPoint

ФИЗИЧЕСКИЙ БЛОК 1: КИНЕМАТИКА (описание движения)

ДВИЖЕНИЕ ПО ЛИНИИ ?

ДВИЖЕНИЕ ПО ЛИНИИ • Кто движется?

ДВИЖЕНИЕ ПО ЛИНИИ • Движение: изменение положения объекта по сравнению с системой отсчета («неподвижная» опорная точка) • Измерение движения (вдоль линии) • положение, x: положение относительно origin Начало координат (x = 0), единица измерения: м • смещение, s = Dx: изменение положения Dx = xf — xidisplacement = final position — исходное положение

ДВИЖЕНИЕ ПО ЛИНИИ • примеры смещения

ДВИЖЕНИЕ ПО ЛИНИИ • время, t: время с начала движения, единицы: с (в тексте используется Dt) • скорость, v: скорость перемещения по времени, единица: м / с • средняя скорость, vav = (xf-xi ) / t • имеет тот же знак +/-, что и смещение — показывает направление движения вдоль линии • мгновенная скорость, v: фактическая скорость в определенный момент времени, наклон по оси x в зависимости отt график. • при постоянной скорости, v = vav • для изменения скорости, vvav

ДВИЖЕНИЕ ПО ЛИНИИ • Скорость: величина скорости S = ​​d / t • Скорость — это скорость и направление (+/- вдоль линия), скорость не имеет направления. V = ∆x / t • скорость -24 м / с не то же самое, что +24 м / с (в противоположных направлениях), но оба имеют одинаковую скорость (24 м / с). • автомобильный спидометр показывает только скорость; для скорости вам понадобится спидометр и компас.

РЕШЕНИЕ ПРОБЛЕМ • Стратегия решения проблем • Дано: Какую информацию дает мне проблема? • Вопрос: В чем проблема? • Уравнение: какие уравнения или принципы я могу использовать, чтобы найти то, что требуется? • Решить: выяснить ответ.• Проверить: правильно ли работают агрегаты? Ответ кажется разумным?

ГРАФИЧЕСКОЕ ДВИЖЕНИЕ • интерпретация графика зависимости x от t (положение относительно времени) + константа v = 0 константа –v изменение + изменение v + v (движение вперед) (замедление) (не движется) (движение назад) (ускорение)

x t ГРАФИЧЕСКОЕ ДВИЖЕНИЕ • интерпретация графика x от t (положение от времени) • для линейных графиков x от t: наклон = подъем / ход = Dx / Dt , поэтому подъем = Dx наклон = vav run = Dt

x t ДВИЖЕНИЕ НА ГРАФИКЕ • интерпретация x vs.График t (положение в зависимости от времени) • для кривых графиков x в зависимости от t: наклон касательной линии = постоянное значение

ГРАФИЧЕСКОЕ ДВИЖЕНИЕ • интерпретация постоянной графика av в зависимости от t (скорость и время) + постоянная v v = 0 постоянный –v изменение + v изменение + v (замедление) (движение назад) (ускорение) (не движется) (движение вперед)

ГРАФИЧЕСКОЕ ДВИЖЕНИЕ • сравнение x с t и av с t график

постоянная скорость постоянное ускорение УСКОРЕНИЕ

УСКОРЕНИЕ • Ускорение, a: скорость изменения скорости • единица измерения: (м / с) / с или м / с2 • увеличение скорости (+ a) , уменьшение скорости (–a), изменение направления (какие три ускорителя в автомобиле?) • среднее ускорение, aav = (vu) / t = Dv / t • мгновенное ускорение, a: фактическое ускорение в определенной точке в время

время (с) 0 1 2 3 4 5 6 скорость (м / с) 0 2 4 6 8 10 12 положение (м ) 0 1 4 9 16 25 36 УСКОРЕНИЕ • Пример постоянного ускорения (a = aav): a = 2 м / с2 v  t, x  t2

термины: t: прошедшее время xf: конечное положение xo: начальное позиция s: изменение положения (xf-xi) термины: a: ускорение vavg: средняя скорость vf: конечная скорость u, vo: начальная скорость Dv: изменение скорости (vu) УСКОРЕНИЕ

определенные уравнения: a = Dv / t vav = Dx / t vav = (v + u) / 2 производных уравнения: s = ½ (v + u) tv = u + at xf = xi + ut + ½at2 v2 = u2 + 2as УСКОРЕНИЕ

ГРАФИЧЕСКОЕ ДВИЖЕНИЕ • интерпретация av vs.График t (скорость в зависимости от времени) Для линейных графиков v в зависимости от t наклон = постоянная a = 0 константа –a постоянная + a (замедление) (ускорение) (постоянная скорость)

GRAPHING MOTION • сравнение графиков v против t и a против t

PHYSICS UNIT 1: KINEMATICS (Describing Motion)

FREE FALL • Свободное падение: все падающие объекты постоянно ускоряются под действием силы тяжести • из-за ускорения гравитации, g, одинаково для всех объектов • используйте y вместо x, значение up положительно • g = –9.2

ФИЗИКА БЛОК 1: КИНЕМАТИКА (описание движения)

Старт от Старой лагуны Идите на 50 шагов на восток, на 25 шагов на север, на 15 шагов на запад, на 30 шагов на север, на 20 шагов на юго-восток X отмечает Место! ДВИЖЕНИЕ В ПЛОСКОСТИ

ДВИЖЕНИЕ В ПЛОСКОСТИ • Тригонометрия • синус: sin q = opp / hyp • косинус: cos q = adj / hyp • тангенс: tan q = opp / adj

MOTION IN A PLANE • Векторы • скаляры: показывают только количество (положение, время, скорость, масса) • векторы: показывают, сколько и в каком направлении • смещение, r или x: расстояние и направление • скорость, v: скорость и направление • ускорение, a: изменение скорости и направления

q v НОВОСТИ ДВИЖЕНИЕ В ПЛОСКОСТИ • Векторы • стрелки: вектор скорости v = v (скорость), q (направление) • длина пропорциональна величине • направление в координатах карты • между полюсами укажите градусы северной широты, западной долготы и т. Д.

ДВИЖЕНИЕ В ПЛОСКОСТИ шайба v относительно земли = шайба v относительно стола + таблица v относительно земли

ДВИЖЕНИЕ В ПЛОСКОСТИ • Комбинирование векторов • Нарисуйте диаграмму и обозначьте начало координат / оси ! • Коллинеарные векторы: v1 v2 v1 v2 • результирующий: vnet = v1 + v2 (направление: + или -) • Пример: самолет летит со скоростью 40 м / с E при встречном ветре W 10 м / с. Какая чистая скорость? • Пример: самолет летит со скоростью 40 м / с в.д. с попутным ветром 10 м / с.Какая чистая скорость?

ДВИЖЕНИЕ НА ПЛОСКОСТИ • Перпендикулярные векторы: величина результирующего: направление результирующего:

ФИЗИКА БЛОК 1: КИНЕМАТИКА (описание движения)

ОБЪЕКТ • ПРОВЕРКА • 1 ТЕСТ • 1 ОБЪЕКТ движение, положение, время • скорость (средняя, ​​мгновенная) • графики x против t, графики v против t, графики a против t • векторы, скаляры, смещение, скорость • добавление коллинеарных и перпендикулярных векторов • ускорение • свободное падение, сопротивление воздуха

ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР ТЕСТА БЛОКА 1 • Что на тесте: • 21 множественный выбор, 12 задач Dx = ½ (vf + vi) t vf = vi + at xf = xi + vit + ½at2 vf2 = vi2 + 2aDx

Контрольные вопросы

Размеры и оценки Знакомит учащихся с идеей составления оценок, повсеместное владение физикой.Также хорошо сочетается с обсуждение размеров, обработка больших чисел и, возможно, размерный анализ.	Размеры и смета	Размеры и оценка: решения
Смещение и скорость Позволяет учащимся изучить понятие средней скорости. (Не требует знания ускорения.)	Рабочий объем и скорость	Рабочий объем и скорость: решения
Скорость и ускорение Концептуально проверяет понимание учащимися графического представления скорость и ускорение.	Скорость и разгон	Скорость и ускорение: решения
Путешествие на Луну Студенты используют основные кинематические уравнения, чтобы вычислить время полета к Луне и Альфе Центавра.	Путешествие на луну	Путешествие на Луну: решения
Пожарные самолеты Использование кинематических уравнений, студенты исследуют независимость направления движения. (Можно связать с демонстрацией класса для большей ясности.)	Пожаротушение самолеты	Пожаротушение самолеты: решения
Гонка на двух автомобилях Далее практика с кинематикой.Использует онлайн-апплет Java созданный профессором физики BU Эндрю Даффи.	А гонка на двух автомобилях	А гонка на двух автомобилях: решения
Пловец, находящийся в стрессовом состоянии Исследование кинематики, сложения векторов и независимость направлений движения.	The напряженный пловец	The пловец в стрессовом состоянии: решения
Силы и Ньютона Законы
Тягач трактора Включает Второй закон Ньютона и векторное сложение.Немного сложная проблема для студентов в их ранних встречах с Законы Ньютона.	Трактор потянув	Трактор вытягивание: решения
Вертикальный прыжок Немного более комплексная проблема, опирающаяся как на студентов знание законов Ньютона и кинематики.	The вертикальный прыжок	The вертикальный прыжок: решения
Акселерометр Использование Второй закон Ньютона, студенты изучают, как измерить ускорение. Требуется хорошее понимание Ньютона. законы, а также синус и косинус.	An акселерометр	An акселерометр: решения
Энергия и работа
Levers Обучает студентов как работают рычаги.Студенты проходят через математический вывод с использованием немного геометрии и концепция работы.	Рычаги	Рычаги: решения
Скорость эвакуации Использование сохранение энергии, студенты находят убегающую скорость Земли и оцените радиус черной дыры.	Побег скорость	Побег скорость: решения
Импульс Консервация
Остались на берегу озера Учащиеся используют сохранение импульса и простые кинематика, чтобы выяснить, как выйти из озера, когда все они имейте с собой их книгу по физике!	Мель на озере	Мель на озере: решения
Взрыв в воздухе Еще одна проблема сохранения импульса, на этот раз имея дело с гранатой, разбивающейся на более мелкие части в в воздухе.Также вкратце исследует сохранение импульса. в двух измерениях.	Взрыв в воздухе	В воздухе взрыв: решения
Универсальный закон Плотность
Взвешивание Солнца Используя универсальный закон всемирного тяготения, студенты определить массу нашего Солнца.Эта же техника также используется для определения массы других звезд в нашей галактика.	Взвешивание Солнца	Взвешивание Солнце: решения
Гравитация на Земле Студенты показывают, что универсальный закон всемирного тяготения сводится к хорошо известным мг на Земле поверхность.Они также вычисляют г на Земле, на вершина Mt. Эверест и на Луне.	Гравитация на Земле	Сила тяжести на Земле: решения
Нагрев
Mystery Substance Пример того, как простая калориметрия определяется неизвестные материалы.	Таинственная субстанция	Mystery Substance: решения
Вода и климат Эта проблема объединяет концепции, изученные в физика в географических условиях прибрежный климат и внутренние суши климат. Студенты также оценивают наихудший глобальный сценарий потепления.	Вода и климат	Вода и климат: решения
Электричество и схемы
Электрические и гравитационные силы Студенты сравнивают электростатическое притяжение между протоном и электроном к их гравитационному притяжение и подумайте, почему гравитация доминирует во Вселенной на длинных весах.	Электричество против гравитации	Электричество против гравитации: решения
Три заряда на линии Более сложная задача закона Кулона с участием трех обвинения. Студенты исследуют, как разместить третью зарядите рядом с двумя другими так, чтобы третий заряд в равновесие.	Три заряда на линии	Три заряда на линии: решения
Резисторы Сложная проблема схемы, которая проверяет понимание студентами последовательного и параллельного резистора схемы. Также исследуются предельные случаи подключения бесконечно много резисторов, подключенных параллельно или последовательно.	Резисторы	Резисторы: решения
Мощность и электричество Зная P = IV и закон Ома, студенты получают два другие проявления силы и применяйте их, чтобы найти силу рассеивается как в последовательной, так и в параллельной цепи.	Сила и электричество	Сила и электричество: решения
Волны, звук и свет
Звук в воздухе и воде Студенты изучают выражение для модуля объемного сжатия и узнайте, как скорость звука зависит от этого модуля и плотность среды.Затем они находят скорость звук в воде, и используйте его для решения простой проблемы сонара.	Звук в воздухе и воде	Звук в воздухе и воде: решения
Удивительные летучие мыши Эта проблема связана с тем, как летучие мыши используют звук для перемещаться.Он исследует как можно использовать сонар для определения дальности до объекта и имеет более сложная часть об эффекте Доплера.	Удивительный Летучие мыши	Удивительный Летучие мыши: решения
Световые помехи Введение в спектроскопию.Ученики исследуйте, как свет преломляется на решетке, используйте известные длина волны света для характеристики решетки и использование эта решетка для определения длины волны неизвестного света источник.	Вмешательство света	Вмешательство света: решения

Заметки по физической кинематике NEET и движению снаряда PDF Скачать

Важность физической кинематики NEET и движению снаряда Заметки и концепции по редакции

Внесение изменений в NEET поможет вам интерпретировать все, что вы читаете, своими словами вы лучше понимаете концепции NEET Physics.Были времена, когда студенты NEET читали всю страницу тупо, даже не понимая ни единого слова, но если вы сделаете заметок для экзамена NEET , тогда ваш мозг попытается выжать смысл из каждого написанного вами предложения, что очень полезно для Студенты-медики . В заметках о редакции всегда фиксируется вся информация, которую вы узнали. Эти заметки во время экзамена будут действовать как готовые рекомендации для рассмотрения. Этот метод не только помогает сэкономить энергию и время студентов во время вступительного экзамена NEET, но также помогает им вспомнить все, что они изучали, за меньшее время.Примечания к редакции NEET также помогли студентам запомнить то, что они изучали, потому что они могли прочитать каждое предложение строка за строкой и подготовить примечания.

Преимущества Примечания для кинематики NEET и движения снаряда

a) Поможет вам своевременно пересмотреть все важные концепции перед вступительными экзаменами NEET

b) Краткие заметки по каждой главе, приведенной в последней версии NEET книги по физике помогут выучить и повторить все основные концепции прямо у дверей экзаменационного зала.

c) Примечания, предоставленные Studiestoday.com, были подготовлены специально для студентов, сдающих экзамен NEET 2020, чтобы они могли получить лучший рейтинг на предстоящем вступительном экзамене NEET

d) Вы почувствуете себя комфортно, что вы пересмотрели все важные темы из Kinematics and Projectile Motion , и вам не придется носить с собой всю книгу на экзамене

e) Загрузите все примечания в формате PDF для NEET Kinematics and Projectile Motion и будьте уверены, что вы охватили все

Приведенные выше примечания NEET помогут Вы сможете сдать экзамены NEET.Вы всегда должны пересматривать концепции и примечания NEET Physics Kinematics и Projectile Motion перед экзаменами, они помогут вам обобщить все важные темы, и вы сможете получить более высокие оценки. Вы также можете щелкнуть ниже, чтобы загрузить NEET Physics Kinematics и Projectile Motion, чтобы загрузить решенные последние образцы документов, вопросы за прошлый год (за последние 10 лет), рабочие листы для печати в формате pdf, имитирующие онлайн-тесты, последние книги NEET для NEET Physics Kinematics и Projectile Motion на основе учебной программы и руководящие принципы, выпущенные NEET.

No related posts.