Методическая разработка по физике: Контрольная работа по кинематике
Контрольная работа носит тематический характер. Каждый вариант содержит задачи разных уровней сложности. Учащийся может ознакомиться со всеми заданиями и самостоятельно выбрать уровень сложности, приемлемый для него в данный момент.
Каждый вариант включает 6 заданий.
1,2,3 задачи — первый уровень сложности. Эти задания рассчитаны на усвоение основных понятий, на простое отображение материала или несложные расчеты при узнавании и воспроизведении.
4.5 задачи- второй уровень сложности. Эти задания на 2-4 логических шага. Решение этих заданий требует более глубоких знаний по курсу физики и позволяет их применять в стандартных ситуациях.
6 задача- третий уровень сложности –задания, решения которых требует творческого использования приобретенных знаний и позволяет применять их в нестандартных ситуациях.
Правильность выполнения каждого задания оценивается в баллах:
1,2,3 задачи: по 1-2 балла
4-5 задачи: по 3 балла
6 задача: по 4 балла
Для оценивания результатов контрольной работы следует использовать следующие критерии:
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
1 вариант | 2 вариант |
Автомобиль движется со скоростью 72км/ч.Определить ускорение автомобиля, если через 20минут он остановится. (1балл) | Троллейбус трогается с места с ускорением 1,2 м/с2 . Какую скорость приобретает троллейбус за 1 минуту? (1 балл) |
Точка вращается по окружности радиусом 0,2м с периодом 2с. Определить линейную скорость.(2 балла) | Чему равен период колеса ветродвигателя, если за 2 минуты колесо сделало 50 оборотов?(2 балла) |
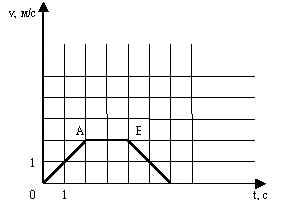
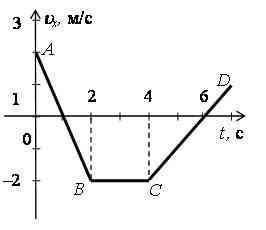
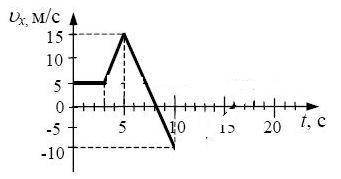
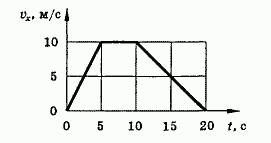
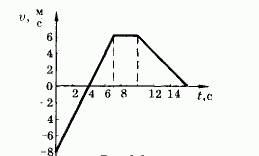
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла) | По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
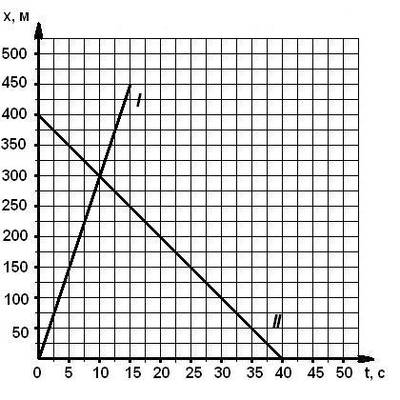
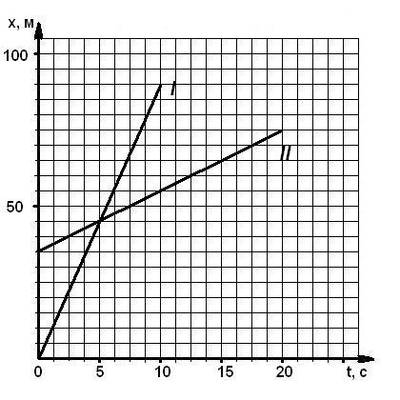
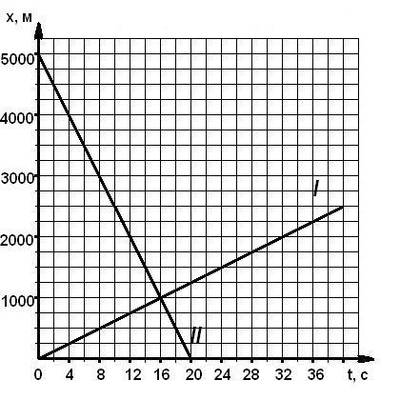
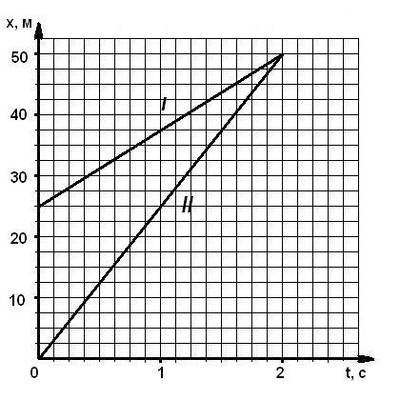
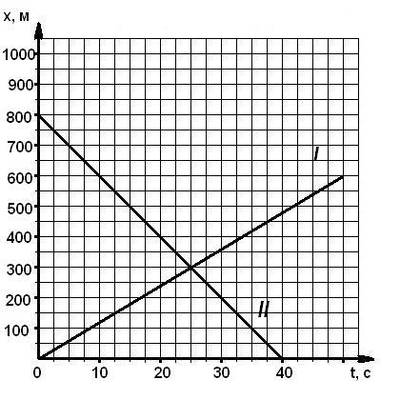
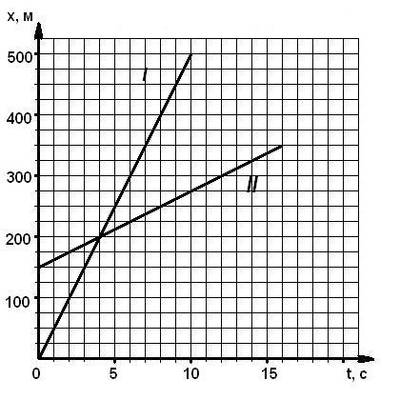
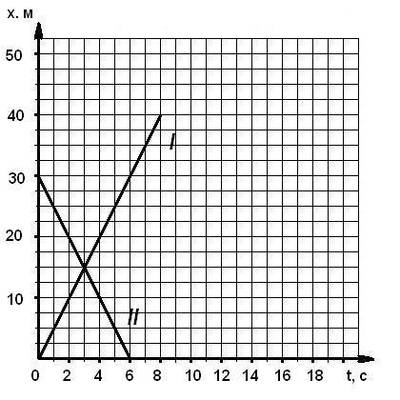
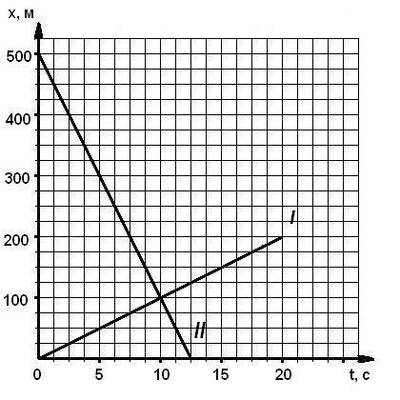
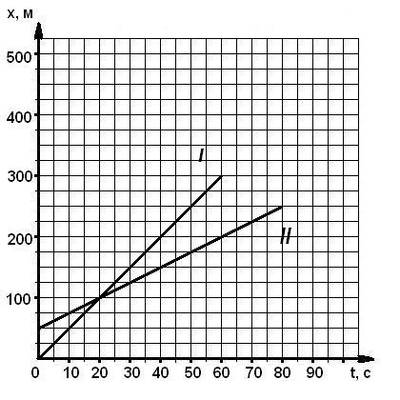
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла) | Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
|
Самолет при посадке коснулся посадочной полосы аэродрома при скорости 252 км/ч.Через 30 секунд он остановился. Определить путь , пройденный самолетом при посадке. | Тело брошено вертикально вниз со скоростью 5м/с с высоты 20м. Определить время падения тела на землю и скорость тела в момент падения. |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t)
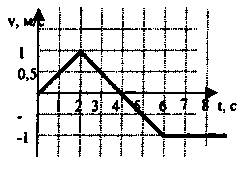
| По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) |
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
3 вариант | 4 вариант |
Автомобиль при разгоне за 10 секунд приобретает скорость 54 км/ч. Определить ускорение автомобиля. (1балл) | Вагонетка движется из состояния покоя с ускорением 0,25 м/с2. Какую скорость будет иметь вагонетка через 2 минуты от начала движения? (1 балл) |
Определить период вращающегося диска, если он за 10секунд делает 40 оборотов. (2 балла) | Какова скорость трамвайного вагона,движущегося по закруглению радиусом 50 метров с центростремительным ускорением 0,5м/с2.(2 балла) |
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2балла) | По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
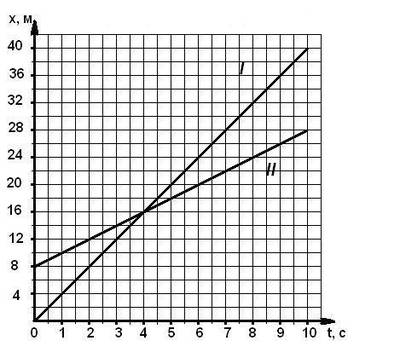
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
| Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла) |
Тело свободно падает с высоты 24 метра(без начальной скорости). Определить время падения тела и скорость тела в момент падения на землю.(3 балла) | Автомобиль , двигаясь со скоростью 43,2 км/ч, останавливается при торможении в течение 3 секунд. Какое расстояние он пройдет до остановки?(3 балла) |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
| По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
|
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
5 вариант | 6 вариант |
Поезд тронулся с места и через 10секунд разогнался до 54 км/ч. Определить ускорение поезда. (1балл) | Автомобиль ,трогаясь с места, движется с ускорением 0,25 м/с2. Какую скорость будет иметь автомобиль через 4 минуты от начала движения? (1 балл) |
Определить период вращающегося колеса, если он за 2минуты делает 60 оборотов. (2 балла) | Какова скорость автомобиля ,движущегося по закруглению радиусом 60 метров с центростремительным ускорением 1м/с2.(2 балла) |
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2балла)
| По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
| Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
|
Автомобиль , двигаясь в течение некоторого отрезка времени с ускорением 0,6 м/с2, совершил перемещение 400м. Какова конечная скорость автомобиля ,если его начальная скорость 20,5 м/с?(3 балла) | Камень свободно падает с высоты 56 метров(без начальной скорости). Определить время падения камня и скорость в момент падения на землю(3 балла) |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
| По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
|
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
7 вариант | 8 вариант |
Поезд ,трогаясь с места, движется с ускорением 1м/с2. Какую скорость будет иметь поездчерез 5 минут от начала движения? (1 балл) | Автомобиль тронулся с места и через 30 секунд разогнался до 60 км/ч. Определить ускорение автомобиля. (1балл) |
Точка обращается по окружности радиуса 1,5 метра с центростремительным ускорением 25 м/с2 Определить скорость точки. (2 балла) | Каково центростремительное ускорение тела при его равномерном движении по окружности радиусом 10 см, если при этом тело совершает 30 оборотов в минуту.(2 балла) |
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2балла)
| По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла) | Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла) |
Автомобиль , двигаясь в течение некоторого отрезка времени со скоростью 90 м/с, снижает свою скорость до 72 км/ч на пути длиной 56,25 4м. Каково ускорение автомобиля при торможении и время торможения?(3 балла) | Тело, двигавшееся со скоростью 108км/ч,тормозит с ускорением 2м/с2 на пути длиной 200метров. Определить конечную скорость тела и время торможения.(3 балла) |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
| По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) (4 балла)
|
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
9 вариант | 10 вариант |
Автомобиль движется со скоростью 108 км/ч.Определить ускорение автомобиля, если через 3 минуты он остановится. (1балл) | Троллейбус трогается с места с ускорением 2 м/с2 . Какую скорость приобретает троллейбус за 7 минут? (1 балл) |
Точка вращается по окружности радиусом 2м с периодом 10 с. Определить линейную скорость.(2 балла) | Чему равен период колеса ветродвигателя, если за 3 минуты колесо сделало 10 оборотов?(2 балла) |
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла) | По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
| Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
|
Вертолет при посадке коснулся посадочной полосы аэродрома при скорости 126 км/ч.Через 15 секунд он остановился. Определить путь , пройденный вертолетом при посадке.(3 балла) | Тело брошено вертикально вниз со скоростью 15м/с с высоты 30м. Определить время падения тела на землю и скорость тела в момент падения.(3 балла) |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t) | По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t)
|
Контрольная работа по теме: «Кинематика»
оценки | 5 | 4 | 3 | 2 |
баллы | 11-15 | 8-10 | 5-7 | 0-4 |
11 вариант | 12 вариант |
Автобус трогается с места с ускорением 0,4м/с2 . Какую скорость приобретает автобус за 3 минуты? (1 балл) | Поезд движется со скоростью 60 км/ч.Определить ускорение поезда, если через 0,5 минут он остановится. (1балл) |
Точка вращается по окружности радиусом 5м с частотой 2 Гц. Определить линейную скорость.(2 балла) | Чему равна частота колеса ветродвигателя, если за 3 минуты колесо сделало 10 оборотов?(2 балла) |
По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла) | По графику зав-ти скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке (2 балла)
|
Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
| Найти место и время встречи двух тел 2 способами (графич. и аналит.)(3 балла)
|
Вертолет при посадке коснулся посадочной полосы аэродрома при скорости 126 км/ч.Через 15 секунд он остановился. Определить путь , пройденный вертолетом при посадке.(3 балла) | Тело брошено вертикально вниз со скоростью 15м/с с высоты 30м. Определить время падения тела на землю и скорость тела в момент падения.(3 балла) |
По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t)
| По графику зав-ти скорости движения тела от времени построить графики зависимости ах(t), Sx(t)
|
Физика 9 Перышкин КР-1 В4 . Контрольная с ответами
Контрольная работа № 1 по физике с ответами в 9 классе «Кинематика» (вариант 3) для УМК Перышкин. Ответы адресованы родителям. Цитаты из пособия использованы в учебных целях. Физика 9 Перышкин КР-1 В4 + ОТВЕТЫ.
Физика 9 класс (УМК Перышкин).
Контрольная работа № 1. Вариант 4
КР-1 «Кинематика» (транскрипт):
№ 1. Два тела, брошенные с поверхности земли вертикально вверх, достигли высот 10 м и 20 м и упали на землю. Перемещения этих тел соответственно равны:
1) 10 м, 20 м 2) 20 м, 40 м 3) 0 м, 0 м 4) 0 м, 20 м
№ 2. Велосипедист, двигаясь равномерно по шоссе, проехал 1800 м за 3 минуты. Скорость велосипедиста равна
1) 12 км/ч 2) 24 км/ч 3) 36 км/ч 4) 60 км/ч
№ 3. На рисунках представлены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению?
№ 4. Санки съехали с одной горки и въехали на другую. Во время подъёма на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 12 м/с до 2 м/с, при этом модуль ускорения был равен
1) –2,5 м/с2 2) 2,5 м/с2 3) –3,5 м/с2 4) 3,5 м/с2
№ 5. При равноускоренном прямолинейном движении скорость катера увеличилась за 10 с от 5 м/с до 9 м/с. Какой путь пройден катером за это время?
1) 50 м 2) 70 м 3) 80 м 4) 90 м
№ 6. Пловец плывёт против течения реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с.
1) 0,1 м/с 2) 0,2 м/с 3) 0,5 м/с 4) 0,7 м/с
№ 7. Установите соответствие между физическими величинами и их единицами измерения в СИ.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
№ 8. Тело, двигаясь равноускоренно, в течение пятой секунды от начала движения прошло путь 45 м. Какой путь оно пройдёт за 8 с от начала движения?
№ 9. Пловец пересекает реку шириной 240 м. Скорость течения реки 1,2 м/с. Скорость пловца относительно воды 1,5 м/с и направлена перпендикулярно к вектору течения. На сколько метров пловец будет снесён течением к тому моменту, когда он достигнет противоположного берега?
Физика 9 Перышкин КР-1 В4 ОТВЕТЫ:
№ 1). 3.
№ 2). 3.
№ 3). 4.
№ 4). 2.
№ 5). 2.
№ 6). 1.
№ 7). 534.
№ 8). 320 м.
№ 9). 192 м.
Другие варианты: КР-1. Вариант 1 КР-1. Вариант 2 КР-1. Вариант 3
Вернуться с Списку контрольных работ по физике в 9 классе (УМК Перышкин)
Вы смотрели: Контрольная работа № 1 по физике с ответами в 9 классе «Кинематика». Цитаты из пособия для учащихся «Контрольные и самостоятельные работы по физике 9 класс к учебнику А.В. Перышкина Физика 9 класс ФГОС» (авт. О.И. Громцева, изд-во «Экзамен») использованы в учебных целях. Физика 9 Перышкин КР-1 В4 + ОТВЕТЫ.
Физика 10 класс. Контрольная работа по теме «Кинематика»
10 класс Контрольная работа «Кинематика»
1 вариант
1.Какую систему координат выбрать для определения положения лифта?
А. одномерную (х) Б. двумерную (х;у)
В. трехмерную (х; у; z) Г. среди ответов нет правильного.
2.Вектор скорости при равномерном движении точки по окружности
А. постоянен по модулю и по направлению; Б. равен нулю;
В.постоянен по модулю, но непрерывно меняется по направлению;
Г. постоянен по направлению но непрерывно изменяется по модулю.
3. Какое из уравнений описывает равномерное движение:
А. х = 5- 3t2, Б. х = 8+ 2t В. vx =2+t2 Г. vx =4 t
4.Установите соответствие между параметрами движения и формулами, их описывающими,
для равноускоренного прямолинейного движения без начальной скорости.
А) Модуль перемещения | 1) x0 + aхt2/2 |
5. Зависимость от времени координаты точки, движущейся вдоль оси Х, имеет вид: Х= 10t — 2t2.
а) Опишите характер движения.
б) Какова начальная скорость и ускорение?
в) Запишите уравнение зависимости проекции скорости от времени
г) Чему равно перемещение тела за 2с?
д) определите скорость через 2с и 4 с после начала движения
6. Движение материальной точки в плоскости ХОУ описывается уравнениями: х = 2t,
у = 4 — 2t. Чему равны начальные координаты движущейся точки? Запишите уравнение
траектории движения, т.е. зависимость координаты у от координаты х.
7. На рисунке представлен график зависимости скорости автомобиля от времени.
Опишите характер движения в интервалах времени 0-1с, 1-3 с, 3-5 с.
Запишите уравнение зависимости проекции скорости от времени в интервале 0-1 с,
определите путь, пройденный автомобилем в интервале времени от 0 до 1 с после
начала движения.

8.Шарик равномерно вращается по окружности радиусом 20 см с частотой 2 об/сек.
Найти период обращения шарика, его угловую и линейную скорости.
10 класс Контрольная работа «Кинематика»
2 вариант
1.Какую систему координат выбрать для определения положения самолета?
А. одномерную (х) Б. двумерную (х;у)
В. трехмерную (х; у; z) Г. среди ответов нет правильного.
2.Основная задача кинематики …
А. … установить причины движения тел; Б. … изучить условия равновесия тел;
В. … определить положение тел в пространстве в любой момент времени.
Г. … определить скорость движения.
3.Какие из уравнений описывают равноускоренное движение:
А. х = 6- 4t, Б. х = 2t + t2 В. vx =3+2t2 Г. vx = 2+ 4 t
4.Установите соответствие между параметрами движения и формулами, их описывающими,
для равнозамедленного движения с начальной скоростью v0.
А) Координата | 1) x0 + vхt 3) vхt 4) x0 + v0хt − 1/2aхt2 5) v0х + aхt |
5. Зависимость от времени координаты точки, движущейся вдоль оси Х, имеет вид: Х= 50 – 10t + 5t2
а) Опишите характер движения.
б) Какова начальная скорость и ускорение?
в) Запишите уравнение зависимости проекции скорости от времени vx(t).
г) Чему равно перемещение тела за 3с?
д) определите скорость через 2с и 3 с после начала движения.
6. Движение материальной точки в плоскости ХОУ описывается уравнениями: х = 6 +3t,
у=4t. Чему равны начальные координаты движущейся точки? Запишите уравнение
траектории движения, т.е. зависимость координаты у от координаты х.
7. На рисунке представлен график зависимости скорости от времени для тела,
движущегося прямолинейно. Опишите характер движения в интервалах времени 0-1с,
1-4 с, 4-6 с,6-8с. Запишите уравнение зависимости проекции скорости от времени в
интервале 0-1 с, определите путь, пройденный автомобилем в интервале времени
от 0 до 1 с после начала движения.

8.Диск радиусом 30 см совершает один оборот за 0,5 с. Найти частоту обращения диска,
его угловую и линейную скорости точек, лежащих на краю диска?
Контрольная работа «Кинематика» 10 класс
Контрольная работа «Кинематика», 10 класс
1вариант
1. Лыжник спускается с горы с начальной скоростью 6 м/с и ускорением 0,5 м/с2. Какова длина горы, если спуск с неё продолжался 12 с.
2. Автобус движется со скоростью 54 км/ч. На каком расстоянии от остановки водитель должен начать торможение, если для удобства пассажиров ускорение не должно превышать 1,2 м/с
3.Тело за 4 секунды изменило свою координату с 2 до 18 метров. Какова скорость тела
4. Два автомобиля перемещаются навстречу друг другу по параллельным дорогам со скоростями 36 км/ч и 12 м/с. Чему равна скорость одного автомобиля относительно другого
5. По данному уравнению υ = 5 + 6t определите, чему равно ускорение тела
6. Автомобиль движется со скоростью 20 м/с по закруглению дороги радиусом 50 метров. Чему равно центростремительное ускорение автомобиля

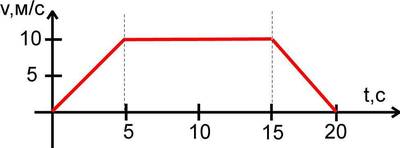
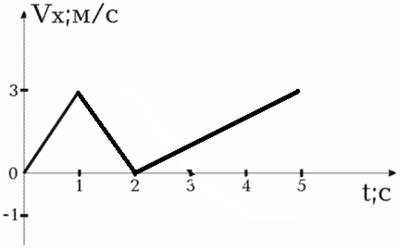
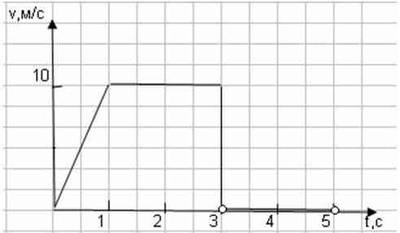
7. По графику скорости материальной точки определите:
а) начальную скорость тела и скорость через 10 с
после начала движения,
б) ускорение тела,
в) запишите уравнение скорости тела
8. Координата движущегося тела с течением времени меняется по следующему закону: x=-1+3t-t2. Определите начальную координату тела, проекцию начальной скорости и проекцию ускорения. Укажите характер движения тела.
9. Троллейбус двигался со скоростью 18 км/ч и, затормозив, остановился через 4 с. Определите ускорение и тормозной путь троллейбуса.
Контрольная работа «Кинематика», 10 класс
1. При какой скорости самолет может приземлиться на посадочной полосе аэродрома длиной 800 м при торможении с ускорением 5 м/с2?
2. Через сколько секунд после отправления от станции скорость поезда метрополитена достигнет 72 км/ч, если ускорение при разгоне равно 1 м/с2?
3. Тело, имея координату 3 метра, перемещается в течении 4 секунд со скоростью 1,2 м/с. Какова конечная координата тела
4. Два автомобиля двигаются равномерно по параллельным дорогам, в одном направлении, со скоростями 72 км/ч и 15 м/с. Чему равна скорость одного автомобиля относительно другого?
5. По данному уравнению x = 8 – 2t определите, чему равна скорость тела.
6
7. По графику скорости материальной точки определите:
а) начальную скорость тела и скорость через 20 с
после начала движения,
б) ускорение тела,
в) запишите уравнение скорости тела.
8. Координата движущегося тела с течением времени меняется по следующему закону: х=10-t-2t2. Определите начальную координату тела, проекцию начальной скорости и проекцию ускорения. Укажите характер движения тела.
9. За время торможения, равное 5 с, скорость автомобиля уменьшалась с 72 км/ч до 36 км/ч. Определите ускорение автомобиля при торможении и длину тормозного пути.
Контрольная работа по теме Кинематика. Динамика
Контрольная работа по теме «Кинематика. Динамика»
Вариант 1.
Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид: . Чему равна скорость тела в момент времени t = 2c при таком движении?
1) 2) 3) 4)
Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на . Ускорение велосипедиста 0,5 м\с² Сколько времени длился спуск?
Мяч, брошенный вертикально вверх, падает на землю. Найдите график зависимости от времени проекции скорости на вертикальную ось, направленную вверх.
1) 2) 3) 4)
Точка движется по окружности радиусом R с частотой обращения . Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
1) увеличить в 4 раза 2) уменьшить в 4 раза 3) уменьшить в 2 раза 4) увеличить в 2 раза
. На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху).
Каков модуль равнодействующей этих сил, если .
1) Н 2) Н 3) Н 4) Н
Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?
1) 50 Н 2) 5 Н 3) 0,5 Н 4) 0,05 Н
После удара хоккеиста начальная скорость шайбы 12,5 м/с. Шайба скользит по горизонтальной поверхности льда, и через 2,5с будет иметь скорость v. Коэффициент трения скольжения 0,1.
Под действием силы 3Н пружина удлинилась на 4 см. Чему равен модуль силы, под действием которого удлинение этой пружины составит 6 см?
Контрольная работа по теме «Кинематика. Динамика»
Вариант 2.
Зависимость координаты x тела от времени t имеет вид: .
Чему равна проекция скорости тела на ось Ox в момент времени при t = 3c таком движении?
1) 2) 3) 4)
Мальчик съезжает на санках равноускоренно со снежной горки. Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с², начальная скорость равна нулю. Найти длину горки.
Мяч брошен с вершины скалы без начальной скорости. Найдите график зависимости модуля перемещения от времени. Сопротивлением воздуха пренебречь.
1) 2) 3) 4)
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится величина её центростремительного ускорения, если скорость увеличить в 2 раза, а радиус окружности уменьшить в 2 раза?
1) увеличится в 8 раз 2) увеличится в 4 раза 3) увеличится в 2 раза 4) не изменится
На тело в инерциальной системе отсчета действуют две силы. Какой из векторов, изображенных на правом рисунке, правильно указывает направление ускорения тела в этой системе отсчета?
1) 1 2) 2 3) 3 4) 4
Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине . На канат со стороны груза действует сила, которая
1) равна 2) меньше 3) больше
4) равна силе тяжести, действующей на груз
Мотоциклист проходит поворот со скоростью 15 км\ч. Найдите радиус поворота, если коэффициент трения скольжения 0,5.
К пружине динамометра подвешен груз 0,1 кг. При этом пружина удлинилась на 2,5 см. Каким будет удлинение пружины при добавлении ещё двух таких же грузов?
Контрольная работа по теме «Кинематика. Динамика»
Вариант 3.
Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид: . Чему равна скорость тела в момент времени t = 1c при таком движении?
1) 2) 3) 4) свой ответ
Автомобиль трогается с места и движется с постоянным ускорением 5 м/с². Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?
3. Камень падает с высокого обрыва, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени
1) увеличивается 2) уменьшается 3) не изменяется
4) сначала увеличивается, а затем начинает уменьшаться
4. Материальная точка движется по окружности радиусом R со скоростью v. Как нужно изменить скорость её движения, чтобы при увеличении радиуса окружности в 2 раза центростремительное ускорение точки осталось прежним?
1) увеличить в 2 раза 2) уменьшить в 2 раза 3) увеличить в раза 4) уменьшить в раза
5. Брусок лежит на шероховатой наклонной опоре (см. рисунок). На него действуют три силы: сила тяжести , сила реакции опоры , и сила трения . Чему равен модуль равнодействующей сил и ?
1) 2) 3) 4)
6. Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой
1) меньше 100 Н, направленной вниз 2) больше 100 Н, направленной вниз
3) 100 Н, направленной вниз 4) 100 Н, направленной вверх
После удара хоккеиста начальная скорость шайбы 8,5 м/с. Шайба скользит по горизонтальной поверхности льда, и через 2,5с будет иметь скорость 12 м\с. Чему равен коэффициент трения скольжения ?
Под действием груза пружина удлинилась на 1 см. Этот же груз подвесили к пружине с вдвое большей жёсткостью. Какое получим удлинение пружины?
Контрольная работа по теме «Кинематика. Динамика»
Вариант 4.
Зависимость координаты x тела от времени t имеет вид: .
Чему равна проекция скорости тела на ось Ox в момент времени при t = 2c таком движении?
1) 2) 3) 4) свой ответ
При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Ускорение автомобиля равно…
3. Камень подброшен вверх и летит, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени
1) увеличивается 2) уменьшается 3) не изменяется
4) сначала увеличивается, а затем начинает уменьшаться
4. Точка движется по окружности радиусом R со скоростью v. Если скорость уменьшить в 2 раза, а радиус окружности увеличить в 2 раза, то центростремительное ускорение точки
1) не изменится 2) увеличится в 2 раза 3) уменьшится в 8 раз 4) уменьшится в 2 раза
5. На левом рисунке представлены векторы скорости и ускорения тела в инерциальной системе отсчёта. Какой из четырёх векторов на правом рисунке указывает направление вектора равнодействующей всех сил, действующих на это тело в этой системе отсчёта?
1) 1 2) 2 3) 3 4) 4
6. Мимо Земли летит астероид в направлении, показанном на рисунке пунктирной стрелкой. Вектор показывает силу притяжения астероида Землёй. Известно, что масса Земли в 10раз больше массы астероида. Вдоль какой стрелки (1 или 2) направлена и чему равна по модулю сила, действующая на Землю со стороны астероида?
1) вдоль стрелки 1, равна 2) вдоль стрелки 1, равна 10
3) вдоль стрелки 2, равна 10 4) вдоль стрелки 2, равна
7. По результатам исследования построен график зависимости силы трения от удлинения пружины. Каким будет удлинение, если к пружине подвесить груз массой 2 кг?
8. Мотоциклист проходит поворот со скоростью 20 км\ч. Коэффициент трения скольжении 0,6. Определите радиус поворота?
Проверочная работа по кинематике
Проверочная работа носит тематический характер. Каждый вариант содержит задачи разных уровней сложности. Учащийся может ознакомиться со всеми заданиями и самостоятельно выбрать уровень сложности, приемлемый для него в данный момент.
Каждый вариант включает 5 заданий.
1 задача — первый уровень сложности задания. Это задания рассчитаны на усвоение основных понятий.
5 задача — третий уровень сложности задания, решения которого требует творческого использования приобретенных знаний и позволяет применять их в нестандартных ситуациях.
Правильность выполнения каждого задания оценивается в баллах: 1 задача: по 1 балла;
2,3,4 задачи: по 2 балла;
5 задача: по 3 балла.
Для оценивания результатов контрольной работы следует использовать
следующие критерии:
оценки | баллы |
5 | 9 — 10 |
4 | 7 — 8 |
3 | 5 — 6 |
2 | 0 — 4 |
Проверочная работа по кинематике
Вариант – 1
1.Заполните таблицу.
Определение физической величины | Единица измерения | Формула для расчета данной величины |
Скорость | ||
Период |
2.Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 40 секунд. По неподвижному эскалатору пассажир мог бы подняться за 1 минуту 80 секунд. За какое время поднимается пассажир по движущемуся эскалатору?
3.Автомобиль первую половину времени двигался со скоростью 35 км/ч, а вторую половину времени со скоростью 18 м/с. Определите среднюю скорость автомобиля.
4 .Шкив делает 124 оборота за 1 минуту 18 секунд, барабан сепаратора 6200 оборотов за 3 минуты 10 секунд. Вычислите период и частоту вращения?
.Шкив делает 124 оборота за 1 минуту 18 секунд, барабан сепаратора 6200 оборотов за 3 минуты 10 секунд. Вычислите период и частоту вращения?
5.По графику зависимости скорости от времени, постройте график зависимости ускорения от времени и координаты от времени.
Проверочная работа по кинематике
Вариант – 2
1.Заполните таблицу.
Определение физической величины | Единица измерения | Формула для расчета данной величины |
Путь | ||
Частота |
2.Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 54 секунд. По неподвижному эскалатору пассажир мог бы подняться за 2 минуты 20 секунд. За какое время поднимается пассажир по движущемуся эскалатору?
3 .Катер первую половину пути двигался со скоростью 14 м/с, а вторую половину пути со скоростью 122 км/ч. Определите среднюю скорость катера.
4.Определите модуль скорости и центростремительного ускорения точек земной поверхности на экваторе. Радиус Земли принять равным 6356 км.
5.По графику зависимости ускорения от времени, постройте график зависимости скорости от времени и координаты от времени.
Проверочная работа по кинематике
Вариант – 3
1.Заполните таблицу.
Определение физической величины | Единица измерения | Формула для расчета данной величины |
Ускорение | ||
Угловая скорость |
2.Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 30 секунд. По неподвижному эскалатору пассажир мог бы подняться за 1 минуту 8 секунд. За какое время поднимается пассажир по движущемуся эскалатору?
3.Велосипедист две трети времени двигался со скоростью 14 км/ч, а одну третью времени 7 м/с. Определите среднюю скорость велосипедиста за весь промежуток времени.
4 .Каков радиус кривизны закругления дороги, если по ней самосвал движется с центростремительным ускорением 6 м/с2 при скорости 120 км/ч?
.Каков радиус кривизны закругления дороги, если по ней самосвал движется с центростремительным ускорением 6 м/с2 при скорости 120 км/ч?
5.По графику зависимости скорости от времени, постройте график зависимости ускорения от времени и координаты от времени.
Проверочная работа по кинематике
Вариант – 4
1.Заполните таблицу.
Определение физической величины | Единица измерения | Формула для расчета данной величины |
Перемещение | ||
Угловое ускорение |
2.Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 72 секунд. По неподвижному эскалатору пассажир мог бы подняться за 3 минуты 12 секунд. За какое время поднимается пассажир по движущемуся эскалатору?
3.Первую четверть пути локомотив шел со скоростью 33 м/с, остальной путь со скоростью 70 км/ч. Определите среднюю скорость локомотива на всем пути.
 4.Какую скорость имеют точки обода колеса автомобиля радиусом 80 см, если они движутся с ускорением 0,005 км/с2?
4.Какую скорость имеют точки обода колеса автомобиля радиусом 80 см, если они движутся с ускорением 0,005 км/с2?
5.По графику зависимости ускорения от времени, постройте график зависимости скорости от времени и координаты от времени.
Задачи физики: кинематика
Задача 1.
Поезд проходит 60 миль с 14:00. и 16:00 Как быстро все шло в 15:00?
Решение
Задача 2.
Возможно ли, что автомобиль мог разогнаться до 55 миль в час в пределах 268 метров, если автомобиль может разогнаться от 0 до 60 миль в час только за 15 секунд?
Решение
Задача 3.
Автомобиль движется в гору с постоянной скоростью 37 км / ч и возвращается вниз с холма с постоянной скоростью 66 км / ч. Рассчитайте среднюю скорость за всю поездку.
Решение
Задача 4.
Лучник стреляет стрелой со скоростью 30 м / с под углом 20 градусов по отношению к горизонту. Помощник, стоящий на ровной поверхности в 30 м от точки запуска, бросает яблоко прямо вверх с минимальной начальной скоростью, необходимой для встречи с траекторией стрелки.Какова начальная скорость яблока и в какое время после пуска стрелки нужно бросить яблоко так, чтобы стрела попала в яблоко?
Решение
Задача 5.
Ящик стоит на горизонтальной деревянной доске. Коэффициент статического трения между коробкой и доской 0,5. Вы берете один конец доски и поднимаете его, удерживая другой конец доски на земле.Какой угол между доской и горизонтальным направлением, когда ящик начинает скользить по доске?
Решение
Задача 6.
Блок 8 кг покоится на горизонтальном полу. Если вы толкнете блок весом 8 кг горизонтально с усилием 20 Н, он просто начнет двигаться.
(а) Что такое коэффициент трения покоя?
(b) Блок 10,0 кг укладывается наверх блока 8 кг. Какова величина F силы, действующей горизонтально на 8-килограммовый блок, как и раньше, которая требуется для того, чтобы два блока начали двигаться?
Решение
Задача 7.
Автомобиль ускоряется в. Найдите его ускорение в.
Решение
Задача 8.
Едем 1 км со скоростью 16 км / ч. Затем мы проезжаем еще 1 км со скоростью 32 км / ч. Какая у нас средняя скорость?
Решение
Задача 9.
Авиалайнер достигает взлетной скорости 163 миль в час за 36,2 с. Какова величина его среднего ускорения.
Решение
Задача 10.
Автомобиль изначально движется на север со скоростью 23 м / с.
(a) Найдите скорость автомобиля через 4 с, если он ускоряется на север.
(b) Найдите скорость автомобиля через 4 с, если его ускорение направлено на юг.
Решение
Найдите свою проблему в базе данных решенных физических задач (БЕСПЛАТНО) |
Бесплатно решаемых физических задач: кинематика
1.Кинематика:
В кинематике мы описываем только движение. Мы либо знаем скорость или ускорение, либо зависимость скорости от времени или ускорение от времени, но нам нужно найти что-то еще об этом движении.
Например, мы знаем, что скорость составляет 30 миль в час в течение 5 часов и 50 миль в час в течение 1 часа, и нам нужно знать пройденное расстояние. Мы не знаем, почему скорость постоянна; мы не знаем, почему ускорение имеет данное значение.Нам неизвестно происхождение движения. Эти вопросы рассматриваются в Dynamics. В кинематике нам просто нужно найти параметры связи движения между скоростью, ускорением и расстоянием.
Обычно в задачах кинематики рассматриваются только два типа движений:
- Движение с постоянной скоростью и
- Движение с постоянным ускорением.
Движение с переменным ускорением довольно сложно.Только в некоторых частных случаях мы можем легко решить такие проблемы, но обычно нам нужно решить дифференциальные уравнения второго порядка, чтобы получить ответ в этих проблемах.
Все уравнения движения в задачах кинематики выражаются в терминах векторов или координат векторов. Это самая сложная часть в задачах кинематики: как выразить начальные или конечные значения через переменные в кинематических уравнениях. Еще одна сложная часть кинематических задач связана с описанием относительного движения.
терминов, касающихся движения | Примечания, видео, контроль качества и тесты | 11 класс> Физика> Кинематика
Термины, касающиеся движения
 Движение и покой — понятия относительные.Они зависят от ситуации наблюдателя, наблюдателя и наблюдаемого объекта. Итак, покой и движение можно описать применительно к наблюдателю. Раздел механики, имеющий дело с телом в состоянии покоя, называется статическим. Раздел физики, который занимается движением, не зная его причины, известен как кинематика.
Движение и покой — понятия относительные.Они зависят от ситуации наблюдателя, наблюдателя и наблюдаемого объекта. Итак, покой и движение можно описать применительно к наблюдателю. Раздел механики, имеющий дело с телом в состоянии покоя, называется статическим. Раздел физики, который занимается движением, не зная его причины, известен как кинематика.
Расстояние
Длина фактического пути, по которому тело движется из исходного положения в конечное, называется расстоянием. Единица измерения S.I — метр (м).Это скалярная величина.
Смещение
Кратчайшее расстояние между начальным и конечным положением тела называется смещением. Его единица СИ — метр (м). Это векторная величина.
Разница между расстоянием и смещением
S.N | Расстояние | Смещение   |
1. | Расстояние — это длина фактического пути, пройденного объектом. | Смещение объекта — это кратчайшая длина от исходного положения до конечного положения объекта. |
2. | Расстояние, пройденное объектом, всегда положительно. | Смещение может быть положительным, отрицательным или нулевым. |
3. | Пройденное расстояние зависит от формы пути, по которому проходит объект. | Смещение не зависит от формы пути, по которому проходит объект. |
4. | Расстояние — это скалярная величина. | Смещение — это векторная величина. |
Скорость
Скорость изменения расстояния известна как скорость. Другими словами, расстояние, пройденное телом за единицу времени, называется скоростью. Его единица СИ — м / с. Это скалярная величина.
Математически:
$$ \ text {Скорость} = \ frac {пройденное расстояние} {затраченное время} $$
Скорость
Скорость изменения смещения называется скоростью. Единица измерения — м / с. Это векторная величина.
Математически,
$$ \ text {Скорость} = \ frac {пройденное расстояние} {затраченное время} $$
Разница между скоростью и скоростью
SN | Скорость | Скорость |
1. | Это расстояние, которое проходит тело за единицу времени. | Это скорость изменения смещения. |
2. | Скорость всегда положительная. | Скорость может быть положительной, отрицательной или нулевой. |
3. | Скорость тела равна или больше скорости тела. | Скорость тела равна или меньше скорости тела. |
4. | Скорость — это скалярная величина. | Скорость — это векторная величина. |
Равномерная и неравномерная скорость
Говорят, что тело имеет равномерную скорость, если оно проходит равное расстояние за равные промежутки времени. В противном случае говорят, что тело имеет неравномерную скорость.
Равномерная и неоднородная скорость
Говорят, что тело имеет равномерную скорость, если оно проходит равное смещение за равные промежутки времени.В противном случае говорят, что тело имеет неоднородную скорость.
Мгновенная скорость
Когда скорость тела непрерывно изменяется, мы должны определить скорость в конкретный момент времени. Такая скорость называется мгновенной скоростью. Математически это отношение смещения тела к методу очень малого времени.
\ begin {align *} \ text {т.е. Мгновенная скорость} (v) & = \ lim {\ Delta t \ to o} \ frac {\ Delta s} {\ Delta t} \\ & = \ frac {ds} {dt} \\ \ end {align *}
Средняя скорость и скорость
Средняя скорость определяется как отношение общего пройденного расстояния к общему затраченному времени.Средняя скорость определяется как отношение полного пройденного смещения к общему затраченному времени.
\ begin {align *} V_ {av} & = \ frac {\ text {total displacement}} {\ text {total time}} \\ & = \ frac {s_1 — s_2} {t_2 — t_2} = \ frac {\ Delta s} {\ Delta t} \ end {align *}
Ускорение
Ускорение определяется как скорость изменения скорости во времени. Пусть начальная скорость объекта равна u, а через интервал времени t она становится v. Тогда среднее ускорение составит
\ begin {align *} a & = \ frac {\ Delta v} {\ Delta t} = \ frac {v — u} {t} \\ at & = u — v \\ \ text {or} \: v & = u + at \ end {align *}
Deceleration
Retardation — это скорость уменьшения скорости.Поскольку конечная скорость меньше начальной скорости, ускорение становится отрицательным, а замедление — отрицательным ускорением.
Равномерное ускорение
Считается, что объект движется с равномерным ускорением, если его скорость изменяется на равную величину за равный интервал времени f. Ускорение свободного падения является примером равномерного ускорения.
Переменное ускорение
Говорят, что объект движется с переменным ускорением, если изменение скорости за равный интервал времени не одинаково.
Среднее ускорение
 \
\
Среднее ускорение объекта для данного движения определяется как отношение общего изменения скорости к ускорению объекта для данного движения, которое определяется как отношение общего изменения по скорости объекта к общему временному интервалу.
Рассмотрим объект, движущийся по прямой от P до Q, как показано на рисунке. В точке P скорость равна v 1 в момент времени t 1 , а в точке Q скорость равна v 2 в момент времени t 2 .
$$ Тогда \; изменить \; in \; velocity = v_2 — v_1 = \ Delta v $$
$$ и \; change \; in \; time = t_2 — t_1 = \ Delta t $$
$$ \ поэтому среднее ускорение a_ {av} \; = \ frac {общее изменение скорости} {общий интервал времени} $$
$$ = \ frac {\ Delta v} {\ Delta t} $$
Мгновенное ускорение
Если скорость тела непрерывно изменяется во времени, мы определяем ускорение в определенный момент времени или в точке на его пути как мгновенное ускорение, которое задается предельным значением \ (\ frac {\ Delta v} {\ Delta t} \), когда \ (\ Delta t \) стремится к нулю.
\ end {align *} \ поэтому \ text {мгновенное ускорение,} a & = \ lim {\ Delta t \ to \ theta \ frac {\ Delta v} {\ Delta t} = \ frac {dv} {dt } \ begin {align *}
Ускорение — это векторная величина, единица измерения — мс -2 в единицах СИ и -2 см в системе CGS.
Физика — Кинематика — Мартин Бейкер
Кинематика: Изучение и описание движения без учета его причин, например, мы можем вычислить конечную точку манипулятора робота из углов все его суставы.В качестве альтернативы, учитывая конечную точку манипулятора робота, мы могли бы рассчитать углы и параметры всех его стыков, необходимых для его установки (обратная кинематика — И.К.). Кинематику можно изучать без учета массы или физические величины, зависящие от массы.
О динамике поговорим позже. Один из способов подумать о разнице между кинематика и динамика заключается в том, что динамика является причиной движения и кинематики это эффект.
Кинематика включает положение, скорость и ускорение (а также их вращательное эквиваленты).
- Позиция — это точка в пространстве, которую занимает объект, это должно быть определенный в некоторой координате система.
- Скорость — это скорость изменения положения во времени.
- Ускорение — это скорость изменения скорости во времени.
Хотя я оставляю динамику на потом, здесь стоит упомянуть, что если на объект нет действующих сил, то он будет иметь постоянную скорость.Также, если на объект действует постоянная чистая сила, например гравитация например, тогда он будет иметь постоянное ускорение. Итак, эти частные случаи постоянной скорости и постоянного ускорения заслуживают рассмотрения в более деталь.
Движение в одном измерении
Если объект движется по прямой, и если мы измеряем его положение по эта линия, то ее положение, скорость и ускорение могут быть представлены скалярными величинами.Это значительно упрощает анализ, так что давайте начнем с этого.
Постоянная скорость (без чистой силы)
Скорость — скорость изменения позиции:
v = dp / dt
| где: | |||
символ | описание | тип | шт. |
| v | скорость | вектор | м / с |
| п. | позиция, расстояние от заданной точки | вектор | м |
| т | раз | скаляр | с |
| г… / dt | скорость изменения | ||
Таким образом, интеграция обеих сторон дает:
p = ∫v dt
, поэтому, если v постоянно:
p = p 0 + v t
| где: | |||
символ | описание | тип | шт. |
| v | скорость | вектор | м / с |
| п. | позиция, расстояние от заданной точки | вектор | м |
| т | раз | скаляр | с |
| п. 0 | позиция в момент времени t = 0 | вектор | м |
Постоянное ускорение (постоянная сила)
Скорость — скорость изменения позиции:
а = дв / дт
Таким образом, интеграция обеих сторон дает:
v = ∫a dt
, поэтому, если a постоянно:
v = v 0 + a * t
| где: | |||
символ | описание | тип | шт. |
| v | скорость | вектор | м / с |
| ускорение (дв / дт) | вектор | м | |
| т | раз | скаляр | с |
| v 0 или u | скорость в момент времени t = 0 (иногда пишется u) | вектор | м / с |
Итак, интегрирование ускорения дает скорость, чтобы получить позицию, которую мы нужно снова интегрировать:
p = ∫v dt
p = ∫ (v 0 + a * t) dt
p = p 0 + v 0 t + ½ a t 2
Переменное ускорение — приблизительные методы
Если у нас есть уравнение для ускорения как функции времени, мы можем применить интегрирование, чтобы найти скорость и положение, если нет, то мы можем использовать приближенные методы, такие как метод конечных разностей, метод Эйлера или Рунге-Кутта Метод.Если мы оживляем компьютерное моделирование, то это может быть очень хорошим методом, потому что нам нужно в любом случае сгенерировать позицию для каждого кадра, поэтому сгенерировать намного проще следующий кадр из кадра перед ним.
v n + 1 = v n + a * dt
| где: | |||
символ | описание | тип | шт. |
| v n + 1 | скорость на кадре n + 1 | вектор | м / с |
| v n | скорость на кадре n | вектор | м / с |
| ускорение | вектор | м / с 2 | |
| дт | время между кадром n и кадром n + 1 | скаляр | с |
и снова суммируя:
p n + 1 = p n + v n * dt
| где: | |||
символ | описание | тип | шт. |
| п п + 1 | позиция в кадре n + 1 | вектор | м / с |
| p n | Позицияв кадре n | вектор | м / с |
| v n | скорость на кадре n | вектор | м / с |
| дт | время между кадром n и кадром n + 1 | скаляр | с |
Эти приближения можно сделать более точными, используя метод Эйлера или Рунге-Кутта. Метод
Положение в трех измерениях (расположение и ориентация)
Когда мы работаем в трех измерениях, скалярные величины в одномерном случае p,
v и необходимость замены на 3D-векторы,  ,
,  и
и  .Также, чтобы определить положение объекта в трех измерениях, нам необходимо
знать как его местоположение, так и его ориентацию. Это дает максимум 6 градусов.
свободы (6DOF) 3 для линейного перемещения, 3 для вращения.
.Также, чтобы определить положение объекта в трех измерениях, нам необходимо
знать как его местоположение, так и его ориентацию. Это дает максимум 6 градусов.
свободы (6DOF) 3 для линейного перемещения, 3 для вращения.
Итак, следующий вектор состояния полностью определяет позицию, используя 6 скалярных количества.
Примечание: здесь смешанные единицы, верхние 3 — радианы, нижние 3 — метры.
Если объект ограничен, например, он может быть связан с другими объектами шарниром или другим типом соединения, то он может иметь менее 6 градусов свобода.
Может быть полезно представить местоположение и ориентацию как единый вектор, особенно когда мы переходим к уравнениям ускорения и динамики, это не так полезно для позиции, потому что мы не можем использовать векторное сложение для представления вращения. Я включил его сюда, чтобы начать знакомство с пространственным вектором Featherstone. обозначение (см. http://www.syseng.anu.edu.au/~roy/technical.html) Спасибо Майклу Шанцу, рассказавшему мне об этом (см. Файл hybridgdc.pdf на http: // michaelshantz.com).
Когда мы определяем положение твердого объекта, нам нужно сделать это относительно некоторая точка на объекте, также это точка, вокруг которой объект вращается. Итак, нам нужно определить локальную систему координат на теле. Если взять планетарный Например, в случае с Землей мы могли бы выбрать измерение относительно середины ядра Земли, или места на поверхности, или любого другого Другое место. Теперь, когда Земля движется, и перевод, и ориентация являются функциями времени.
Если мы выберем измерение локальной системы координат относительно точки на поверхности, то перевод будет сложной функцией времени, но если мы измеряем местную систему координат относительно центра Земли тогда перевод будет менее сложной функцией времени. Итак, в этом случае лучше, но не обязательно иметь локальную систему координат относительно к центру земли. Ориентация как функция времени не зависит локальной опорной точки, в случае земли, один оборот в сутки.
Преобразовывает
Матрицымогут использоваться для выполнения различных операций с объектами, таких как перевод, вращение, масштабирование и отвес. Когда мы представляем твердые объекты, мы хотим чтобы ограничить наши преобразования только перемещениями и поворотами, поэтому матрица 4×4 содержит избыточную информацию, и мы должны быть осторожны, чтобы не делать других операции на нем.
Сложные соединенные объекты, например рука робота, могут быть представлены в иерархии. групп преобразований, подробнее см. здесь.
Теоретически мы могли бы указать наше перемещение / вращение с помощью одного 6-мерного вектор, однако, как объяснялось в разделе «Вращение», это не так полезно, как могло бы кажется, что множественные преобразования не могут быть представлены простыми арифметическими операциями на векторах.
Примечание: здесь смешанные единицы, верхние 3 — радианы, нижние 3 — метры.
Множественные преобразования могут быть представлены только сложением их векторов, если преобразования бесконечно малы.Это означает, что 6-мерные векторы полезны для комбинирования скоростей и ускорений.
Равномерная угловая скорость
Хотя векторное сложение не может использоваться для углов, оно начинает приближать правильное значение по мере уменьшения угла, для вектора бесконечно малых вращений Можно использовать алгебру, поэтому векторную алгебру можно использовать для объединения вращений. Вектор вращения [w] содержит 3 значения: вращение вокруг x, вращение вокруг y и вращение вокруг z.
6d Вектор скорости
Может быть полезно иметь один вектор состояния, который может представлять угловой и линейные скорости. Так что операции с этой скоростью можно представить одним уравнением, которое включает как линейные, так и вращательные эффекты.
Примечание: здесь смешанные единицы измерения, верхние 3 — радианы / сек, нижние 3 — метры / сек.
Например, если объект двигался в рамках системы отсчета и системы отсчета сам двигался, мы могли вычислить вектор, представляющий абсолютную скорости путем сложения векторов, представляющих скорость системы отсчета и относительная скорость.Однако здесь нужно быть очень осторожными, это работает. Хорошо для линейного компонента (при условии, что мы используем ньютоновскую теорию относительности и не относительность Эйнштейна), но в отношении вращательной части мы должны быть осторожны если вращения не в одной и той же точке, в этом случае движение может может быть какое-то сложное спиральное или планетарное движение, но сложение все еще может работать для мгновенных значений.
Равномерное угловое ускорение
Вектор углового ускорения — это скорость изменения угловой скорости.Вектор ускорения 6D
Единый вектор состояния, представляющий как угловое, так и линейное ускорение. Это может быть очень полезно в динамике (см. здесь), например, это единственное уравнение связывает крутящие моменты, силы и ускорение объекта.

Моделирование программой
Я определил предлагаемый узел кинематики для представления поведения кинематики, поскольку VRML и Java3D еще нет такого узла.
Посмотреть, как это сделать в программе goto kinematics репетитор
Эти уравнения равномерного ускорения можно решить аналитически и получить:
- v = v 0 + a * t
- p = p 0 + v 0 t + ½ a t 2
- v 2 = v0 2 + 2 * a * p
где v0 = начальная скорость и s = дельта x (т.е. пройденное расстояние)
Однако при моделировании в реальном времени численное интегрирование выполняется быстрее, это делается программой в kinematicsBean, алгоритм для этого объясняется здесь.
Полное руководство по физике NEET: Советы по решению численных задач


Найдите или спросите Eduncle
1- Попробовать Бесплатные загрузки (текущие)
- Курсы
- UGC NET
- Коммерция
- Компьютерные науки и приложения
- Экономика Английский
- Образование Общий документ 1
- Управление человеческими ресурсами
- Закон
- Библиотека и информатика
- Менеджмент
- Политология
- История
- IIT JAM
- Биологические науки (BL)
- Математическая статистика (MS)
- Математика (MA)
- Физика (PH)
- Геология (GG)
- Химия (CY)
- Экономика
- UGC NET
- CSIR NET
- Химический al Sciences
- Науки о Земле
- Науки о жизни
- Математические науки
Онлайн-имитационные тесты NEET Physics Kinematics and Projectile Motion
Вышеупомянутые ссылки для NEET Mock Tests для 9000 Physics Kinematics and Projectile Motion поможет вам провести тесты на основе MCQ и проверить ваше понимание всех важных концепций, которые были подготовлены на основе последней учебной программы NEET 2020.Студенты должны использовать бесплатные пробные онлайн-тесты для NEET Physics, чтобы проверить их понимание своих концепций NEET Physics. На сайте StudiesToday.com представлена самая большая коллекция онлайн-тестов на основе MCQ по физике для экзаменов NEET 2020, которые помогут вам правильно подготовиться и получить наивысший рейтинг на экзаменах. Студенты могут пройти пробные тесты по NEET Physics столько раз, сколько захотят, а также загрузить сертификат о прохождении теста после прохождения онлайн-теста. Эти имитирующие онлайн-тесты для NEET Physics были разработаны преподавателями StudiesToday.com после тщательного изучения последней книги и на основе набора вопросов на предстоящих экзаменах для студентов NEET.
Преимущества он-лайн имитационных тестов для физической кинематики NEET и движения снаряда
a) имитационных онлайн-тестов для физической кинематики NEET и движения снаряда были разработаны опытными преподавателями после серьезных исследований по всем темам.
b) Онлайн-тесты NEET Physics с ответами были созданы таким образом, чтобы предоставить полные и всесторонние знания по каждой теме на легком и простом для понимания языке.
c) Вы также обнаружите, что некоторые вопросы, которые задаются в наших онлайн-тестах, могут появиться и на предстоящих экзаменах NEET Physics .
г) Тысячи студентов NEET прошли эти онлайн-тесты и получили отличные результаты и высокие оценки на экзаменах по физике NEET.
Пробные онлайн-тесты для физической кинематики NEET и движения снаряда доступны бесплатно всем учащимся, желающим участвовать в предстоящих вступительных экзаменах. Studiestoday.com предлагает самую эксклюзивную и самую большую последнюю базу данных бесплатных онлайн-пробных тестов для всех студентов. Повторение вопросов снова и снова в тестах даст дополнительное преимущество студентам NEET Physics . Большинство вопросов взяты из предыдущих экзаменов NEET , поэтому их практика в условиях экзамена определенно поможет вам получить более высокий рейтинг.
Для получения более бесплатных учебных материалов щелкните по ссылкам ниже, чтобы получить Physics Kinematics and Projectile Motion , чтобы загрузить образцы решенных документов, вопросы прошлого года с решениями, рабочие листы в формате pdf, NEET Книги и решения для кинематики и движения снаряда на основе физики по учебной программе и руководящим принципам, выпущенным NEET .Учебный материал и решенные образцы документов для NEET Physics for Kinematics and Projectile Motion были подготовлены опытными преподавателями ведущих институтов Индии и доступны для бесплатного скачивания.
.