Контрольная работа по физике механические колебания: КОНТРОЛЬНАЯ РАБОТА «МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ». ВАРИАНТ 4 — ФИЗИКА 9 КЛАСС — КОНТРОЛЬНЫЕ РАБОТЫ В НОВОМ ФОРМАТЕ — МАТЕРИАЛЫ ДЛЯ УЧИТЕЛЯ

Содержание

Контрольная работа по физике 11 класс механические колебания и волны

1. Кто предложил ядерную модель строения атома?

А. Н. Бор;            Б. М. Планк;   В. А. Столетов;   Г. Э. Резерфорд.

2. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Как при этом изменилась энергия атома?

А. энергия системы электрон – ядро возросла;

Б. энергия системы электрон – ядро уменьшилась;

В. энергия системы электрон – ядро не изменилась.

3. Ядерные силы притяжения действуют:

1. между протоном и протоном;

2. между нейтроном и протоном;

3. между нейтроном и нейтроном.

А. только в 1;                Б. только во 2;

В. только в 3;                Г. действуют во всех трех случаях.

4. В каком приборе след движения быстрой заряженной частицы в газе делается видимым в результате конденсации перенасыщенного пара на ионах?

А. в счетчике Гейгера-Мюллера;            Б. в сцинтилляционном счетчике;

В.

в камере Вильсона;                    Г. в пузырьковой камере.

5. Ядро состоит из 90 протонов и 144 нейтронов. После испускания двух β частиц, а затем одной α частицы, это ядро будет иметь:

А. 85 протонов, 140 нейтронов;               Б. 87 протонов, 140 нейтронов;

В. 90 протонов, 140 нейтронов;               Г. 87 нейтронов, 140 протонов.

6. Какое недостающее ядро надо вставить вместо Х в ядерную реакцию?

А. ;        Б. ;        В. ;        Г. .

7. Чему равна частота фотона, поглощаемого атомом при переходе из основного состояния с энергией Е0 в возбужденное состояние с энергией Е1?

А. ;        Б. ;                В. ;                Г.

8. Какой заряд Z и массовое число А будет иметь атомное ядро изотопа урана  после α – распада и двух β – распадов?

А. Z = 92, A = 234;                Б. Z = 92, A = 238;

B. Z = 94, A = 234;                Г. Z = 88, A = 236.

9. Каков состав ядра германия ? (Z – протонов, N – нейтронов)

А.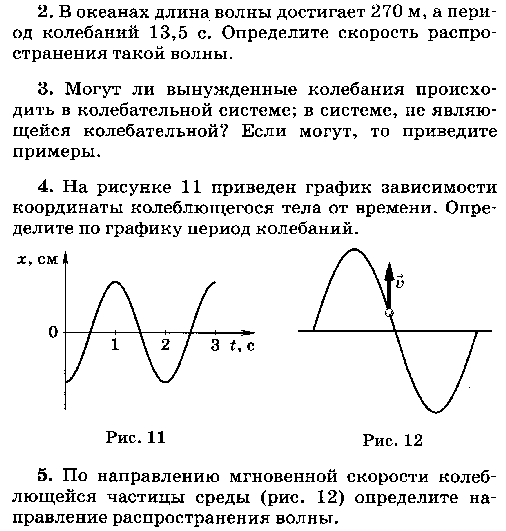 Z = 32, N = 73;        Б. Z = 32, N = 41;

B. Z = 73, N = 32;        Г. Z = 41, N = 32.

10. Найдите в мегаэлектронвольтах энергию связи ядра изотопа лития .

А. 20 МэВ;                Б. 3,92 МэВ;           В. 39 МэВ;            Г. 2,5 МэВ.

11. Имеется 106 атомов радиоактивного изотопа с периодом полураспада 10 мин. Сколько примерно атомов из них не испытает превращение за 20 мин.?

А. 106;                Б. 5 ∙ 105;        В. 7,5 ∙ 105;                Г. 2,5 ∙ 105.

12.Какая доля радиоактивных атомов распадается через интервал времени, равный двум периодам полураспада?

А.25%.

Б. 50%.

в. 75%.

Г. Все атомы распадутся.

13. К началу радиоактивного распада имели 1г радия. Через сколько минут его останется 0,125г, если его период полураспада равен 3 минуты?

Урок 1. механические колебания — Физика — 11 класс

Физика, 11 класс

Урок 1. Механические колебания

Перечень вопросов, рассматриваемых на уроке:

Механические колебания;

Виды механических колебаний;

Характеристики колебательных движений;

Явление резонанса.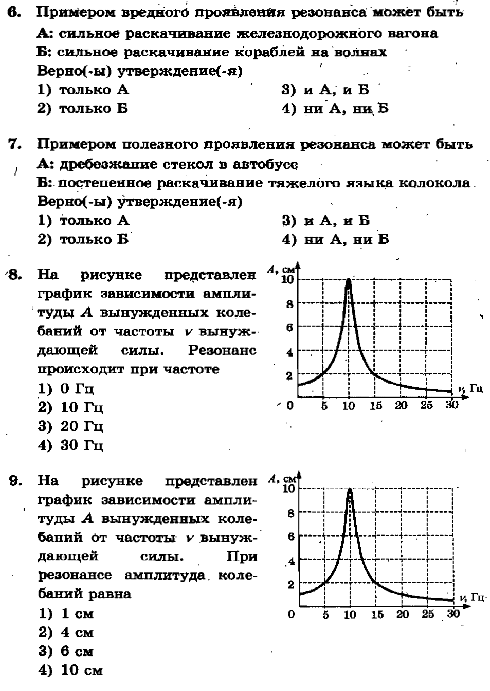

Глоссарий по теме

Механические колебания – это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени.

Колебания, происходящие под действием внутренних сил в колебательной системе, называют свободными.

Вынужденные колебания – это колебания, происходящие под действием внешней периодически меняющейся силы.

Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия.

Период – это время одного полного колебания.

Частота колебаний – это число колебаний за единицу времени.

Фаза колебаний – это физическая величина определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени.

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему с частотой свободных колебаний.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б. Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 53 – 73.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009. – С. 59 – 61.

  • Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
  • Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Мир удивителен и многообразен. Мы каждый день наблюдаем разные движения тел. Все мы видели, как раскачивается ветка на ветру, лодка на волнах, качели, деревья при ветре. Чем эти движения отличаются от движения тележки движущейся прямолинейно? Мы видим, что в отличие от движения тележки движущейся прямолинейно, движения всех этих тел повторяются через определенный промежуток времени.

Механические колебания – это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени.

Колебания играют огромную роль в нашей жизни. Примерами колебаний в нашем организме являются биение сердца, движение голосовых связок. Колебания происходят и в жизни нашей планеты (приливы, отливы, землетрясения) и в астрономических явлениях (пульсации звезд). Одним из грозных явлений природы является землетрясение – колебание земной поверхности. Строители рассчитывают возводимые ими сооружения на устойчивость при землетрясении.

Без знания законов колебаний нельзя было бы создать, телевидение, радио и многие современные устройства и машины. Неучтенные колебания могут привести к разрушению сложных технических сооружений и вызвать серьезные заболевания человека. Все это делает необходимым их всестороннее изучение.

Основным признаком колебательного движения является его периодичность. Колеблющееся тело за одно колебание дважды проходит положение равновесия. Колебания характеризуются такими величинами как период, частота, амплитуда и фаза колебаний.

Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия.

При малых амплитудах путь пройденный телом за одно полное колебание равен примерно четырем амплитудам.

Промежуток времени, в течение которого тело совершает одно полное колебание, называют периодом колебаний.

Период – это время одного полного колебания.

Чтобы найти период колебаний нужно разделить время колебаний на число колебаний.

[T] = 1с

Частота колебаний – это число колебаний за единицу времени.

[v] = 1 Гц (герц)

Единица частоты названа в честь немецкого ученого Г. Герца.

Фаза колебаний – это физическая величина определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени.

[ω] = 1 рад/ с

Во всех колебательных системах действуют силы, стремящиеся вернуть тело в состояние устойчивого равновесия. Существуют несколько типов маятников: нитяные и, пружинные и т.д. Под словом «маятник» понимают твердое тело способное совершать колебания под действием приложенных сил около неподвижной точки или вокруг оси.

Мы с вами будем рассматривать пружинный и математический маятники.

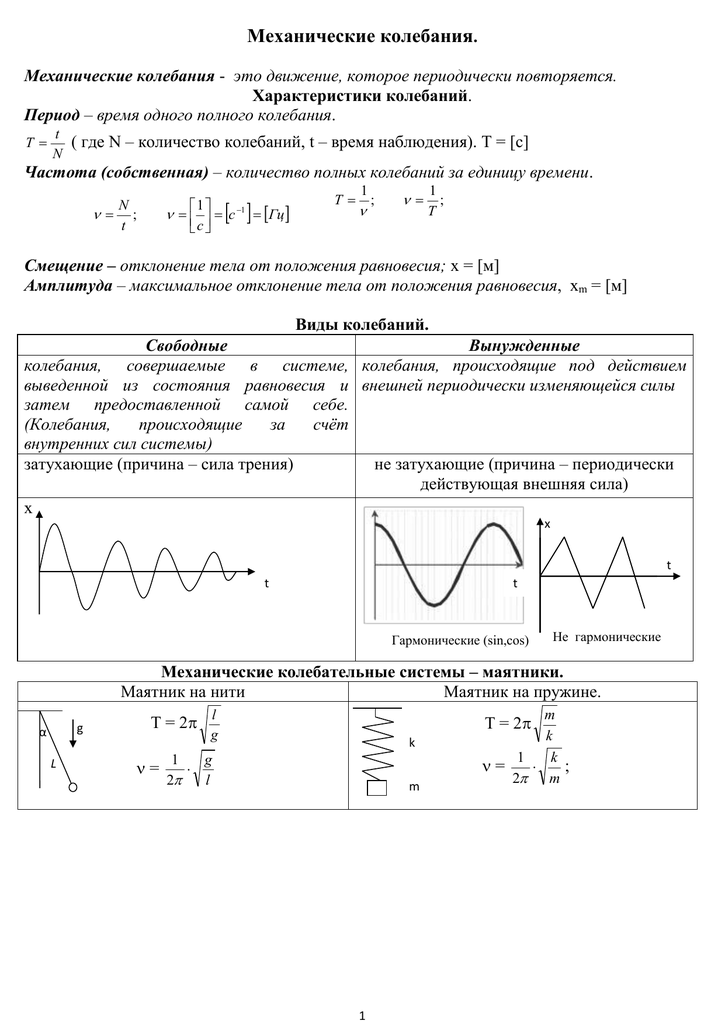
Пружинный маятник. Колебательная система в этом случае представляет собой тело, прикрепленное к пружине. Колебания в таком маятнике возникают под действием силы упругости пружины и силы тяжести.

Период колебаний пружинного маятника:

T- период колебаний пружинного маятника

m – масса подвешенного груза

𝑘 – жесткость пружины

Математический маятник.

Математический маятник – это материальная точка, подвешенная на длинной нерастяжимой нити.

Математический маятник — это идеализированная модель. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного тела и масса нити ничтожна по сравнению с массой тела. Колебания такого маятника происходят под действием силы натяжения нити и силы тяжести. Формула для расчета периода колебаний математического маятника была выведена Гюйгенсом.

T – период колебаний математического маятника

𝑙 – длина нити маятника

𝑔 – ускорение свободного падения

Гюйгенс доказал, что период малых колебаний маятника не зависят от времени. Используя это свойство, названное изохронностью маятника Гюйгенс в тысяча шестьсот пятьдесят седьмом году, сконструировал первые маятниковые часы. Это свойство маятника было открыто 19-летним Галилеем более чем за 20 лет до открытия Гюйгенса. Наблюдая за тем, как раскачиваются в соборе светильники, подвешенные на нитях одинаковой длины, он заметил, что их период колебаний не зависит от времени. Наручных часов тогда не было, и юный Галилей пришёл к решению, которое для многих поколений будет служить образцом блеска и остроумия человеческой мысли: он сравнил колебания маятника с частотой биения собственного сердца.

Гармоническими являются колебания, происходящие под действием силы пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению. Уравнение гармонических колебаний:

x – координата колеблющейся величины

– амплитуда колебаний

ω — циклическая частота

При наличии сил трения в системе колебания затухают. Амплитуда колебаний в этом случае со временем уменьшается.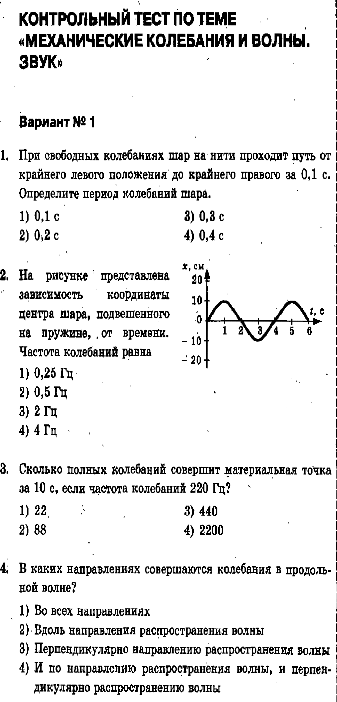 Иногда возникает необходимость в гашении колебаний, к примеру колебания кузова, на рессорах при езде на автомобиле. Для гашения колебаний применяют специальные амортизаторы. С кузовом связывают поршень, который при колебаниях движется в цилиндре, заполненном жидкостью. Большое сопротивление жидкости приводит к гашению колебаний.

Колебания, происходящие под действием внешней периодической силы, называются вынужденными.

Если частота изменения внешней силы не равна частоте свободных колебаний системы, то внешняя сила будет действовать не в такт со свободными колебаниями самой системы. В этом случае амплитуда колебаний будет определяться максимальным значением действующей на систему внешней силы.

Если частота изменения внешней силы совпадет с частотой свободных колебаний, то будет наблюдаться резкое возрастание амплитуды колебаний, так как внешняя сила в этом случае будет действовать в такт со свободными колебаниями этой системы.

ω — частота изменения внешней силы.

ω0 – частота свободных колебаний системы.

Впервые явление резонанса было описано Галилеем. Явление резонанса играет большую роль в природе, технике и науке. Большинство сооружений и машин обладая определенной упругостью, способно совершать свободные колебания. Поэтому внешние периодические воздействия могут вызвать их резонанс, что может стать причиной катастроф. Известно много случаев, когда источником опасных колебаний были люди, идущие в ногу. Так, в 1831 году в городе Манчестер при прохождении по мосту колонны солдат строевым шагом мост разрушился. Аналогичный случай был в г. Петербурге в 1905 году. При прохождении моста через реку Фонтанка эскадроном гвардейской кавалерии мост обрушился. Для предотвращения резонансных явлений используют разные способы гашения вынужденных колебаний. Один способ состоит в изменении частоты свободных колебаний в системе. Другой способ состоит в увеличении силы трения в системе: чем больше сила трения, тем меньше амплитуда резонансных колебаний

Разбор тренировочных заданий

1. Найдите массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за 16 с.

Дано:

𝑘=250 Н/м

N= 20

t= 16 с

_______

m=?

Решение:

Напишем формулу периода пружинного маятника

T=2π√(m/k)

Из этой формулы выразим массу

Период колебаний груза найдём через время колебаний и число колебаний по формуле:

Подставляем числовые значения величин

T=0,8 с.

Следовательно масса равна:

m=4 кг

Ответ: m=4 кг

2. На нити подвешен шарик массой 0,1 кг. Шарик отклонили на высоту 2,5 см (по отношению к положению равновесия) и отпустили. Определите максимальную скорость шарика.

Дано:

m= 0,1 кг

h=2,5 см = 0.025 м

_________

vm=?

Решение:

Скорость колеблющегося шарика максимальна в момент прохождения положения равновесия.

Для решения задачи применим закон сохранения энергии:

Подставляем числовые значения величин:

Ответ:

«Механические колебания» 📕- Механические колебания

Цель урока: проконтролировать умение учащихся самостоятельно применять полученные знания при решении задач.

1. Организационный момент (тетради с домашними заданиями сдаются для проверки учителю)

Выполнение контрольной работы.

Вариант -1.

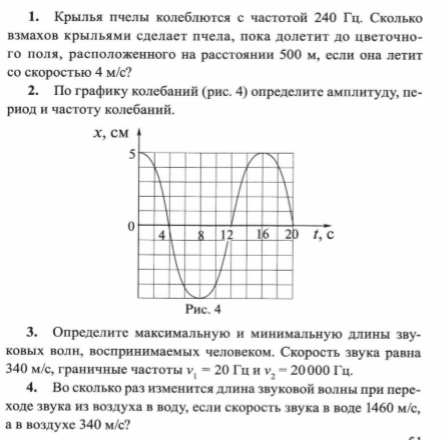
№1. На рисунке представлен график зависимости координаты гармонического колебания от времени. Определить, используя график:

а. амплитуду колебаний, которая равна…

б. период колебаний…

в.

частоту колебаний …

№2. Груз, подвешенный на нити, совершает незатухающие малые колебания.

Выпишите все правильные утверждения.

а. период колебаний не зависит от массы шарика;

б. чем короче нить подвеса, тем меньше период колебания;

в. период колебаний не зависит от амплитуды.

№3. Вдоль оси Ох материальная точка совершает гармонические колебания, амплитуда которых 20см. Рассчитать путь, пройденный материальной точкой за 5 полных колебаний.

№4. Два математических маятника колеблются с одинаковыми угловыми амплитудами. Длина одного

маятника 10 см, а другого – 20 см. Вычислить периоды колебаний этих маятников, а также отношение их энергий, если массы шариков одинаковы.

№5. Записать какое колебание является вынужденным: 1) груз на нити, однажды выведенный из положения равновесия, 2) качели с ребенком ритмично раскачиваемые, взрослым человеком.

Вариант – 2.

№1 На рисунке представлен график зависимости координаты гармонического колебания от времени. Используя график определить:

а амплитуду колебаний, которая равна…

б. период колебаний…

в. частоту колебаний…

№2. Что называется математическим маятником?

Выбрать и записать правильный ответ.

а. Физическое тело, совершающее колебания.

б. Подвешенная на невесомой нерастяжимой нити материальная точка.

в. Грузик, который подвесили к пружине.

№3. Определить амплитуду гармонических колебаний, для тела, которое совершает колебания вдоль оси Ох. Расстояние между точками, в которых скорость равна нулю, составляет 4 см.

№4. На невесомой нерастяжимой нити длиной 1 м подвесили небольшой шарик, который вывели из положения равновесия, так, чтобы нить составила с вертикалью небольшой угол и отпустили. Определить через какое время угол уменьшится вдвое.

№5. Записать, какие колебания являются свободными: 1) голосовые связки при пении; 2) груз, подвешенный на пружине, один раз, выведенный из положения равновесия.

Ответы к задачам (необходимые для быстрой проверки контрольной работы учителем)

Вариант -1.

№1 Xm=20 cм =0,2 м; T= 8 c; γ=0,125 Гц.

№2 Правильные утверждения — а ; б.

№3 Дано: Xm=0,2 м; n=5 колебаний; S — ? Решение. Sʹ=2 Xm; S= 5 Sʹ; Sʹ=0,4 м; S= 0,4·5=2м.

№4 Дано: m1=m2; L1= 0,1 м; L2= 0,2 м. T1-?; T2 -?; W1/W2 -?

Решение. T =2π QUOTE T1=6,28 c; T2=0,9 c; QUOTE = QUOTE = h₁/h₂; W₁/W₂= 1/2.

№5 Правильный ответ – 2

Вариант -2

№1. Хm= 0,1 м; T = 0,2 c; γ = 5 Гц

№2. Правильное утверждение: б.

№3. Дано: V=0; S= 0,04 м; Xm-?; S = 2 Xm; Xm= 0,02 м.

№4. Дано: L = 1 м; t — ?

Решение. V= — ω Xm QUOTE ; V= 0; ω t + π/2 =π; t = π/2ω = π T/2·2·π; t = T/4;

T =2π QUOTE ; t = T/4 = QUOTE QUOTE ; t = 1,57·0,3 =0,47c.

№5.Правильный ответ: 2

Подведем итоги урока

Домашнее задание: на стр. 73 – 74, «Краткие итоги главы»

Тест «Механические и электромагнитные колебания» по физике для 11 класса

Автор: Самойлова Людмила Ивановна

Место работы: МОКУ «Покровская средняя общеобразовательная школа Октябрьского района»

Должность: учитель физики

Дополнительные сведения: тест разработан по содержанию общеобразовательной программы для 11 класса средней школы

Тест №2 «Механические и электромагнитные колебания»

Вариант №1

  1. Дети раскачиваются на качелях. Какой это вид колебаний?

А. свободные Б. вынужденные В. Автоколебания

  1. Тело массой m на нити длиной l совершает колебания с периодом Т. Каким будет период колебаний тела массой m/2 на нити длиной l/2?

А. ½ Т Б. 2Т В. 4Т Г. ¼ Т Д. Т

  1. При подвешивании груза массой 1кг пружина в состоянии равновесия удлинилась на 5см. Какая максимальная энергия груза при колебаниях его на пружине с амплитудой 10см?

А. 1Дж Б. 10Дж В. 5Дж Г. 2Дж Д. 200Дж Е. 100Дж

  1. Совокупность точек, до которых дошло возмущение к моменту времени t, называют…

А. фронтом волны Б. длиной волны В. Волновой поверхностью Г. Лучом

  1. Скорость звука в воде 1470м/с. Какова длина звуковой волны при периоде колебаний 0,01с?

А. 147км Б. 1,47см В. 14,7м Г. 0,147м

  1. Как называют число колебаний за 2πс?

А. частота Б. период В. Фаза Г. Циклическая частота

  1. За какое примерно время свет может пройти расстояние от Земли до Солнца, равное 150 000 000км?

А. 0с Б. 1,3*103с В. 0,5с Г. 1,3с Д. 1200с Е. 8,3мин

  1. В положении равновесия механическая колебательная система обладает…

А. потенциальной энергией Б. кинетической энергией В. Магнитной энергией

Г. Не обладает энергией

  1. Какова резонансная частота в цепи из катушки индуктивностью в 9Гн и конденсатора электроемкостью 4Ф?

А. 72πГц Б. 12πГц В. 36Гц Г. 6Гц Д. 1/12πГц Е. 1/6Гц

  1. Движутся четыре электрона: 1 – равномерно и прямолинейно; 2 – равномерно по окружности; 3 – прямолинейно равноускоренно; 4 – совершает гармонические колебания вдоль прямой. В каком случае излучаются электромагнитные волны?

А. только 1 Б. только 2 В. Только 3 Г. Только 4 Д. 1 и 2 Е. 3 и 4

Ж. 2, 3 и 4 З. во всех случаях

  1. Мальчик услышал эхо через 10с после выстрела пушки. Скорость звука в воздухе 340м/с. На каком расстоянии от мальчика находится препятствие?

А. 1700м Б. 850м В. 136м Г. 68м

  1. Световая волна характеризуется длиной волны, частотой и скоростью. Какие из этих параметров изменяются при переходе из одной среды в другую?

А. длина волны Б. частота В. Скорость Г. Длина волны и частота

Д. длина волны и скорость Е. частота и скорость Ж. все З. никакие

  1. Величина, стоящая перед знаком синуса или косинуса называется…

А. период Б. частота В. Фаза Г.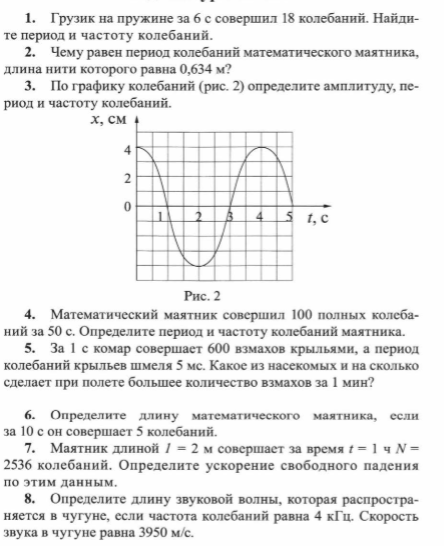 Циклическая частота Д. амплитуда

  1. Определить период свободных электромагнитных колебаний, если колебательный контур содержит катушку индуктивностью 1мкГн и конденсатор емкостью 36пФ.

А. 40нс Б. 3*10-18с В. 3,768*10-8с Г. 37,68*10-18с

  1. Определить, на какую резонансную частоту настраивается колебательный контур, содержащий конденсатор емкостью 1мкФ и катушку индуктивностью 4Гн.

А. 2000рад/с Б. 500 рад/с В. 5*10-4 рад/с Г. 500Гц

  1. Простейшая колебательная система, содержащая конденсатор и катушку индуктивности, называется…

А. автоколебательной системой Б. колебательной системой

В. Колебательным контуром

Тест №2 «Механические и электромагнитные колебания»

Вариант №2

  1. Какой вид колебания наблюдается при качании маятника в часах?

А.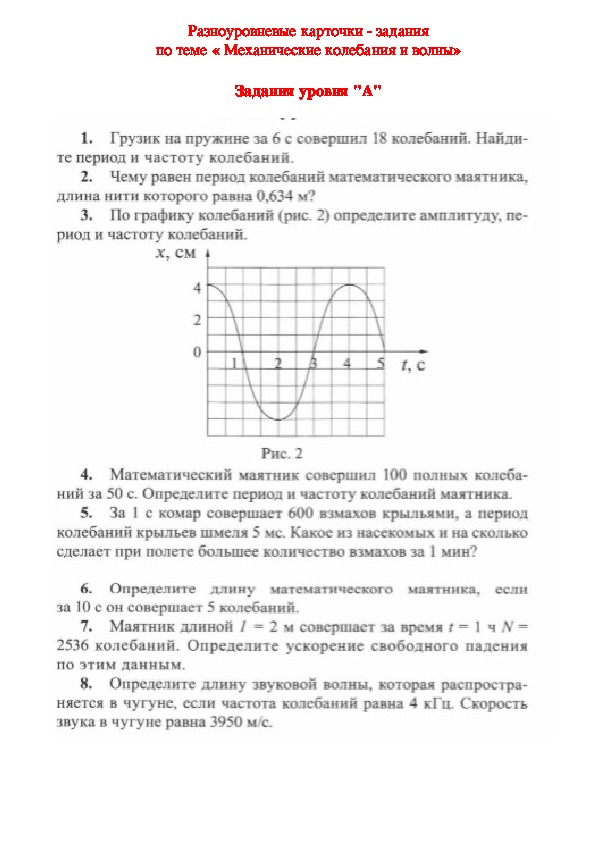 свободные Б. вынужденные В. Автоколебания Г. Упругие колебания

  1. Скорость звука в воздухе 330м/с. Какова частота звуковых колебаний, если длина волны равна 33см?

А. 1000Гц Б. 100Гц В. 10Гц Г. 10 000Гц Д. 0,1Гц

  1. В окружающем нас пространстве существует…

А. только электрическое поле Б. только магнитное поле В. Только электромагнитное поле

Г. Никакого поля

  1. Конденсатор электроемкостью С и катушка индуктивностью L включены параллельно в цепь переменного тока с частотой ω, амплитуда колебаний напряжения Um. Чему равны амплитуды колебаний силы тока через конденсатор и через катушку?

А. UmωC, UmωL Б. Um/ωC, Um/ωL В. UmωC, Um/ωL Г. Um/ωC, UmωL

  1. Через активное сопротивление R и идеальную катушку индуктивностью L протекает переменный ток частотой ω с амплитудой силы тока Im. Каковы средние значения мощности за один период на активном сопротивлении и на катушке?

А. Im2R, Im2ωL Б. Im2R/2, Im2ωL/2 В. Im2R/2Т, Im2ωL/2Т Г. Im2R, 0 Д. 0, Im2ωL

  1. Определить частоту излучаемых волн системой, содержащей катушку индуктивностью 9Гн и конденсатор электроемкостью 4Ф.

А. 72πГц Б. 12πГц В. 36Гц Г. 6Гц Д. 1/12πГц Е. 1/6Гц

  1. Движутся четыре электрона: 1 – равномерно и прямолинейно; 2 – равномерно по окружности; 3 – прямолинейно равноускоренно; 4 – совершает гармонические колебания вдоль прямой. В каком случае не излучаются электромагнитные волны?

А. только 1 Б. только 2 В. Только 3 Г. Только 4 Д. 1 и 2 Е. 3 и 4

Ж. 2, 3 и 4 З. во всех случаях

  1. По какой из характеристик световой волны определяется ее цвет?

А. по длине волны Б. по частоте В. По фазе Г. По амплитуде

  1. Световая волна характеризуется длиной волны, частотой и скоростью. Какие из этих параметров не изменяются при переходе света из одной среды в другую?

А. длина волны Б. частота В. Скорость Г. Длина волны и частота

Д. длина волны и скорость Е. частота и скорость Ж. все З. никакие

  1. Незатухающие колебания, происходящие за счет источника энергии, находящегося внутри системы, называются…

А. свободные Б. вынужденные В. Автоколебания Г. Упругие колебания

  1. Определите, на какую частоту нужно настроить колебательный контур, содержащий катушку индуктивностью 4мкГн и конденсатор емкостью 9пФ, чтобы он улавливал электромагнитные волны длиной 300м.

А. 9,6*10-10Гц Б. 1МГц В. 900кГц Г. 653Гц

  1. Определить период собственных колебаний контура, если он настроен на частоту 500кГц.

А. 1мкс Б. 1кс В. 2мкс Г. 2кс

  1. Мальчик услышал гром через 2,5с после вспышки молнии. Скорость звука в воздухе 340м/с. На каком расстоянии от мальчика вспыхнула молния?

А. 1700м Б. 850м В. 136м Г. 68м

  1. Определить период свободных электромагнитных колебаний, если колебательный контур содержит конденсатор емкостью 1мкФ и катушку индуктивностью 4Гн.

А. 4*10-8с Б. 3*10-18с В. 3,768*10-8с Г. 37,68*10-18с

  1. Определить резонансную частоту колебательного контура, содержащего конденсатор емкостью 1мкФ и катушку индуктивностью 4Гн.

А. 2000рад/с Б. 500рад/с В. 5*10-4рад/с Г. 500Гц

  1. Число колебаний в единицу времени называется…

А. частота Б. период В. Фаза Г. Циклическая частота

Тест №2 «Механические и электромагнитные колебания»

Вариант №3

  1. Люстра раскачивается после одного толчка. Какой это тип колебаний?

А. свободные Б. вынужденные В. Автоколебания Г. Упругие колебания

  1. Тело массой m на нити длиной l совершает колебания с периодом Т. Каким будет период колебаний тела массой 2m на нити длиной 2l?

А. ½ Т Б. 2Т В. 4Т Г. ¼ Т Д. Т

  1. При подвешивании груза массой 1кг пружина в состоянии равновесия удлинилась на 10см. Какая максимальная энергия груза при колебаниях его на пружине с амплитудой 20см?

А. 1Дж Б. 10Дж В. 5Дж Г. 2Дж Д. 200Дж Е. 100Дж

  1. Совокупность точек равной фазы называют…

А. фронтом волны Б. длиной волны В. Волновой поверхностью Г. Лучом

  1. Скорость звука в воздухе равна 330м/с. Какова длина световой волны при частоте колебаний 100Гц?

А. 33км Б. 33см В. 3,3м Г. 0,3м

  1. Как называют время одного полного колебания?

А. частота Б. период В. Фаза Г. Циклическая частота

  1. За какое время свет проходит расстояние от Земли до Луны, равное 400 000км?

А. 0с Б. 1300с В. 0,5с Г. 1,3с Д. 1200с Е. 8,3мин

  1. Конденсатор емкостью С и катушка индуктивностью L включены последовательно в цепь переменного тока частотой ω, амплитуда колебаний силы тока Im. Чему равны амплитуды колебаний напряжения на конденсаторе и на катушке?

А. ImωС, ImωL Б. Im/ ωС, Im/ωL В. ImωС, Im/ωL Г. Im/ωС, ImωL

  1. В крайних точках механическая колебательная система обладает…

А. потенциальной энергией Б. кинетической энергией В. Магнитной энергией

Г. Не обладает энергией.

  1. Какова резонансная частота ν0 в цепи из катушки индуктивностью в 4Гн и конденсатора с электроемкостью 9Ф?

А. 72πГц Б. 12πГц В. 36Гц Г. 6Гц Д. 1/12πГц Е. 1/6Гц

  1. Движутся четыре электрона: 1 – равномерно и прямолинейно; 2 – равномерно по окружности; 3 – прямолинейно равноускоренно; 4 – совершает гармонические колебания вдоль прямой. В каком случае излучаются электромагнитные волны?

А. только 1 Б. только 2 В. Только 3 Г. Только 4 Д. 1 и 2 Е. 3 и 4

Ж. 2, 3 и 4 З. во всех случаях

  1. Мальчик услышал гром через 5с после вспышки молнии. Скорость звука в воздухе 340м/с. На каком расстоянии от мальчика вспыхнула молния?

А. 1700м Б. 850м В. 136м Г. 68м

  1. Световая волна характеризуется длиной волны, частотой и скоростью. Какие из этих параметров изменяются при переходе из одной среды в другую?

А. длина волны Б. частота В. Скорость Г. Длина волны и частота

Д. длина волны и скорость Е. частота и скорость Ж. все З. никакие

  1. Величина, стоящая под знаком синуса или косинуса называется…

А. частота Б. период В. Фаза Г. Циклическая частота

  1. Определить период свободных электромагнитных колебаний, если колебательный контур содержит катушку индуктивностью 4мкГн и конденсатор емкостью 9пФ.

А. 4*10-8с Б. 3*10-18с В. 3,768*10-8с Г. 37,68*10-18с

  1. Определить резонансную частоту колебательного контура, содержащего конденсатор емкостью 1мкФ и катушку индуктивностью 4Гн.

А. 2000рад/с Б. 500рад/с В. 5*10-4рад/с Г. 500Гц

Тест №2 «Механические и электромагнитные колебания»

Вариант №4

  1. Какой тип колебаний наблюдается при отклонении груза, подвешенного на нити, от положения равновесия?

А. свободные Б. вынужденные В. Автоколебания Г. Упругие колебания

  1. Скорость звука в воздухе 660м/с. Какова частота звуковых колебаний, если длина волны равна 66см?

А. 1000Гц Б. 100Гц В. 10Гц Г. 10 000Гц Д. 0,1Гц

  1. В окружающем неподвижный заряд пространстве существует…

А. только электрическое поле Б. только магнитное поле В. Только электромагнитное поле

Г. Никакого поля

  1. Конденсатор электроемкостью С и катушка индуктивностью L включены параллельно в цепь переменного тока частотой ω, амплитуда колебаний напряжения Um. Чему равны амплитуды колебаний силы тока через конденсатор и через катушку?

А. UmωC, UmωL Б. Um /ωC, Um /ωL В. UmωC, Um /ωL Г. Um /ωC, UmωL

  1. Определить частоту излучаемых системой волн, если она содержит катушку индуктивностью 9Гн и конденсатор электроемкостью 4Ф.

А. 72πГц Б. 12πГц В. 36Гц Г. 6Гц Д. 1/12πГц Е. 1/6Гц

  1. Движутся четыре электрона: 1 – равномерно и прямолинейно; 2 – равномерно по окружности; 3 – прямолинейно равноускоренно; 4 – совершает гармонические колебания вдоль прямой. В каком случае не излучаются электромагнитные волны?

А. только 1 Б. только 2 В. Только 3 Г. Только 4 Д. 1 и 2 Е. 3 и 4

Ж. 2, 3 и 4 З. во всех случаях

  1. Световая волна характеризуется длиной волны, частотой и скоростью. Какие из этих параметров не изменяются при переходе из одной среды в другую?

А. длина волны Б. частота В. Скорость Г. Длина волны и частота

Д. длина волны и скорость Е. частота и скорость Ж. все З. никакие

  1. Незатухающие колебания, происходящие за счет источника энергии, находящегося внутри системы, называются…

А. свободные Б. вынужденные В. Автоколебания Г. Упругие колебания

  1. Определите, на какую частоту нужно настроить колебательный контур, содержащий катушку индуктивностью 4мкГн и конденсатор емкостью 9пФ, чтобы он улавливал электромагнитные волны длиной 300м.

А. 9,6*10-10Гц Б. 1МГц В. 900кГц Г. 653Гц

  1. По какой из характеристик волны определяется ее цвет?

А. по длине волны Б. по частоте В. По фазе Г. По амплитуде

  1. Определить период собственных колебаний контура, если он настроен на частоту 500кГц.

А. 1мкс Б. 1кс В. 2мкс Г. 2кс

  1. Через активное сопротивление R и идеальную катушку индуктивностью L протекает переменный ток частотой ω с амплитудой силы тока Im. Каковы средние значения мощности за один период на активном сопротивлении и на катушке?

А. Im2R, Im2ωL Б. Im2R/2, Im2ωL/2 В. Im2R/2Т, Im2ωL/2Т Г. Im2R, 0 Д. 0, Im2ωL

  1. Мальчик услышал гром через 2,5с после вспышки молнии. Скорость звука в воздухе 340м/с. На каком расстоянии от мальчика вспыхнула молния?

А. 1700м Б. 850м В. 136м Г. 68м

  1. Определить период свободных электромагнитных колебаний, если колебательный контур содержит катушку индуктивностью 4мкГн и конденсатор емкостью 9пФ.

А. 4*10-8с Б. 3*10-18с В. 3,768*10-8с Г. 37,68*10-18с

  1. Определить резонансную частоту колебательного контура, содержащего конденсатор емкостью 4мкФ и катушку индуктивностью 1Гн.

А. 2000рад/с Б. 500рад/с В. 5*10-4рад/с Г. 500Гц

  1. Число колебаний в единицу времени называют..

А. частота Б. период В. Фаза Г. Циклическая частота

Список литературы:

  1. Физика: Учеб. для 11 кл. общеобразоват. учреждений / Г.Я. Мякишев, Б.Б. Буховцев. — 15-е изд. -М.: Просвещение, 2009.-381с.

  2. Физика. Задачник. 10-11 кл.: Пособие для общеобразоват. учреждений / Рымкевич А. П. — 12-е изд., стереотип. — М.: Дрофа, 2008. — 192 с.

  3. Самостоятельные и контрольные работы. Физика. Кирик, Л. А П.-М.:Илекса,2005.

Контрольная работа по теме: «Механические колебания и волны»

скачать Контрольная работа по теме: «Механические колебания и волны»

вариант 1

Часть 1
При выполнении заданий этой части в бланке ответов под номером выполняемого вами задания (А1 – А15) поставьте знак «  » в клеточку, номер которой соответствует номеру выбранного вами ответа.


А 6

А 1
Периодичное движение является:


  1. повторяющимся

  2. равномерным

  3. равноускоренным

  4. прямолинейным


А 2


А 7
Какие из перечисленных движений не являются колебательными:


  1. движение качелей

  2. движение струны гитары

  3. движение маятника часов

  4. движение мяча, падающего на землю.


А 3

Период колебаний –



  1. число колебаний в единицу времени

  2. время, за которое совершаются колебания

  3. время, за которое совершается одно полное колебание


А 8
модуль максимального смещения от положения равновесия.


А 4

Свободные колебания могут совершатся…



  1. в колебательной системе

  2. в не колебательной системе


А 9
и в колебательной системе и в не колебательной системе

  1. в любой системе тел, в которой действует внешняя периодичная

сила.


А 5


А 10
Будет ли шарик совершать колебания, находясь на дне сферической чаши (а),

на её вершине (б)



  1. в случае (а) будет, а в случае (б) не будет

  2. будет и в случае (а) и в случае (б)

  3. не будет в обоих случаях

  4. в случае (а) не будет, а в случае (б) будет.

а

б

Какие характеристики вынужденных колебаний остаются неизменными в процессе колебаний?



  1. Только период

  2. Только частота

  3. Только амплитуда

  4. Период, частота и амплитуда.

Тело на нити отклонили от положения равновесия и отпустили. Опишите превращение энергии за половину периода.



  1. Кинетическая энергия превращается в потенциальную

  2. Потенциальная превращается в кинетическую

  3. Потенциальная – в кинетическую, а кинетическая – в потенциальную

  4. Кинетическая – в потенциальную, а потенциальная – кинетическую.

Длину нитяного маятника увеличили. Его период…



  1. увеличился

  2. уменьшился

  3. не изменился

  4. определить невозможно

Длину нитяного маятника уменьшили. Его период…



  1. увеличился

  2. уменьшился

  3. не изменился

  4. определить невозможно

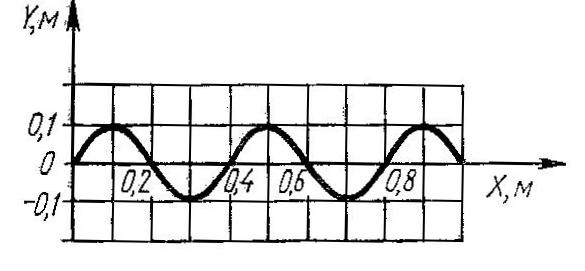
Что называют длиной волны?



  1. Расстояние, проходимое волной за половину периода.

  2. Расстояние, проходимое волной за один период.

  3. Расстояние, проходимое волной за определённое время.

  4. Расстояние, проходимое волной за четверть периода.


А 13

А 11
Выберите свойства, относящиеся к продольным волнам:

  1. эти волны могут распространяться только в газах

  2. эти волны могут распространяться только в газах и жидкостях


А 14
эти волны могут распространяться в газах, жидкостях и твёрдых телах

  1. эти волны возникают при деформации сдвига


А 12
Какие из перечисленных волн не относятся к поперечным?


  1. Волны на поверхности воды.

  2. Звуковые волны.


А 15
Волны на поверхности воды и радио волны.

  1. Свет.

Чем определяется высота тона звука?



  1. Частотой колебаний

  2. Амплитудой колебаний

  3. Скоростью распространения

  4. Длинной звуковой волны

Ультразвуковые волны– это …



  1. поперечные волны с частотой больше 20 000 Гц

  2. поперечные волны с частотой меньше 20 000 Гц

  3. продольные волны с частотой меньше 20 000 Гц

  4. волны с частотой больше 20 000 Гц

От каких характеристик звука зависит его громкость?



  1. От частоты звука

  2. От амплитуды

  3. От среды, в которой распространяется звук

  4. От всех вышеуказанных

Часть 2


При выполнении заданий В1 – В5 ответ (число) надо записать справа от номера соответствующего задания, начиная с первой клеточки, выразив его в указанных единицах. Единицы физических величин писать не нужно.


В 1
Определите период свободных колебаний, если за 2 с маятник совершил 20 полных колебаний.

В 2
Частота колебаний равна 20 кГц. Определите период колебаний.

В 3

Найдите длину волны, распространяющейся с скоростью v = 12 м/с, если частицы в волне колеблются с частотой 0,6 Гц.



В 4
Рыболов заметил, что за промежуток времени t = 10 с поплавок совершил на волнах N= 20 колебаний, а расстояние между соседними гребнями волн λ =1,2 м. Определите скорость распространения волн.

В 5
Камень с берега бросили в воду на расстояние 24 метра. Определите время необходимое волне, чтобы достичь берега, если расстояние между ближайшими гребнями возникшей волны 3 метра, частота колебаний 0,5 Гц

Контрольная работа по теме: «Механические колебания и волны»

вариант 2

Часть 1
При выполнении заданий этой части в бланке ответов под номером выполняемого вами задания (А1 – А15) поставьте знак «  » в клеточку, номер которой соответствует номеру выбранного вами ответа.


А 6

А 1
Колебательное движение является:


  1. равномерным

  2. равноускоренным

  3. прямолинейным

  4. периодичным.


А 2

Какие из перечисленных движений являются колебательными:


А 7
движение автомобиля


  1. движение луны вокруг земли

  2. движение качелей

  3. движение мяча, падающего на землю.


А 3


А 8
Число колебаний в единицу времени называется:


  1. периодом колебаний

  2. частотой колебаний

  3. амплитудой колебаний

  4. фазой колебаний.


А 4

Амплитуда колебаний –



  1. число колебаний в единицу времени

  2. время, за которое совершаются колебания

  3. время, за которое совершается одно полное колебание


А 9
модуль максимального смещения от положения равновесия.


А 5

Вынужденные колебания могут совершаться…



  1. в колебательной системе

  2. в не колебательной системе


А 10
и в колебательной системе и в не колебательной системе

  1. в любой системе тел, в которой действует внешняя периодичная сила

Почему маятник, пройдя положение равновесия, продолжает своё движени

Тематическое оценивание по теме «Механические колебания и волны» — Механические колебания и волны МЕХАНИКА — ВСЕ УРОКИ ФИЗИКИ 10 класс — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике

2-й семестр

 

МЕХАНИКА

 

4. Механические колебания и волны

Урок 8/67

Тема. Тематическое оценивание по теме «Механические колебания и волны»

 

Цель урока: контроль и оценка знаний, умений и навыков учащихся по теме «Механические колебания и волны»

Тип урока: контроля и оценивания знаний

 

РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКА

Учащимся можно предложить контрольную работу, состоящую из шести вариантов.

Ниже предлагается один из вариантов контрольной работы.

 

ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ №4

Задание 1 (0,5 балла)

Которая из шаров, изображенных на рисунках, может после кратковременного воздействия на нее рукой совершать колебания.

 

 

A. Шарик, изображена на рисунке 1.

Б. Шарик, изображена на рисунке 2.

В. Шарик, изображена на рисунке 3.

Г. Любая из шаров, изображенных на рисунках.

Задача 2 (1 балл)

Подвешенный на пружине груз совершает небольшие колебания в вертикальном направлении.

А. Чем больше жесткость пружины, тем больше период колебаний.

Б. Период колебаний груза зависит от амплитуды.

В. Чем меньше масса колеблющегося груза, тем больше период колебаний.

Г. Скорость груза изменяется с течением времени периодически.

Задание 3 (1,5 балла)

В каких средах могут возникать и распространяться поперечные волны? продольные волны? Приведите примеры.

Задание 4 (2 балла)

По поверхности воды в озере волна распространяется со скоростью 6 м/с. Каковы период и частота колебаний лодки на поверхности озера, если длина волны — 3 м?

Задание 5 (3 балла)

Задача 5 имеет целью установить соответствие (логические пары). К каждой строке, обозначенного буквой, подберите утверждение, обозначенное цифрой.

 

A. Период колебаний математического маятника

 

1.

Б. Период колебаний пружинного маятника

 

2.

В. Скорость волны

 

3.

Г. Период волны

 

4.

 

5.

 

 

Задание 6 (4 балла)

За один период времени один математический маятник совершает 50 колебаний, а другой — 30. Вычислите длины маятников, если один из них на 32 см короче другого.

Вибрация | физика | Britannica

Узнайте, как технология увеличения при движении позволяет исследователям отслеживать крошечные вибрации в инфраструктуре.

Узнайте, как прорывы в области увеличения при движении позволяют инженерам лучше отслеживать почти незаметные вибрации, вызываемые такими силами, как ветер и дождь, в инфраструктуре зданий.

© Массачусетский технологический институт (партнер по изданию Britannica) См. Все видео для этой статьи

Вибрация , периодическое возвратно-поступательное движение частиц упругого тела или среды, обычно возникающее, когда практически любая физическая система смещается из состояния равновесия и позволяет реагировать на силы, которые стремятся восстановить равновесие.

Подробнее по этой теме

Механика твердого тела: Свободные колебания

Предположим, что балка имеет длину L, имеет однородные свойства и опирается на шарниры на концах при X = 0 и X = …

Вибрации делятся на две категории: свободные и принудительные. Свободные колебания возникают, когда систему на мгновение нарушают, а затем позволяют двигаться без ограничений.Классический пример — груз, подвешенный на пружине. В состоянии равновесия система имеет минимальную энергию, а вес находится в состоянии покоя. Если груз опустить и отпустить, система ответит вертикальной вибрацией.

Колебания пружины имеют особенно простой вид, известный как простое гармоническое движение (SHM). Это происходит всякий раз, когда возмущению системы противодействует восстанавливающая сила, которая точно пропорциональна степени возмущения. В этом случае восстанавливающая сила — это растяжение или сжатие пружины, которое (согласно закону Гука) пропорционально смещению пружины.В простом гармоническом движении периодические колебания имеют математическую форму, называемую синусоидальными.

Большинство систем, в которых возникают небольшие нарушения, противодействуют им, применяя ту или иную форму восстанавливающей силы. Часто хорошим приближением является предположение, что сила пропорциональна возмущению, так что в предельном случае малых возмущений СТМ является характерной чертой колеблющихся систем. Одной из характеристик SHM является то, что период колебаний не зависит от их амплитуды.Поэтому такие системы используются для регулирования часов.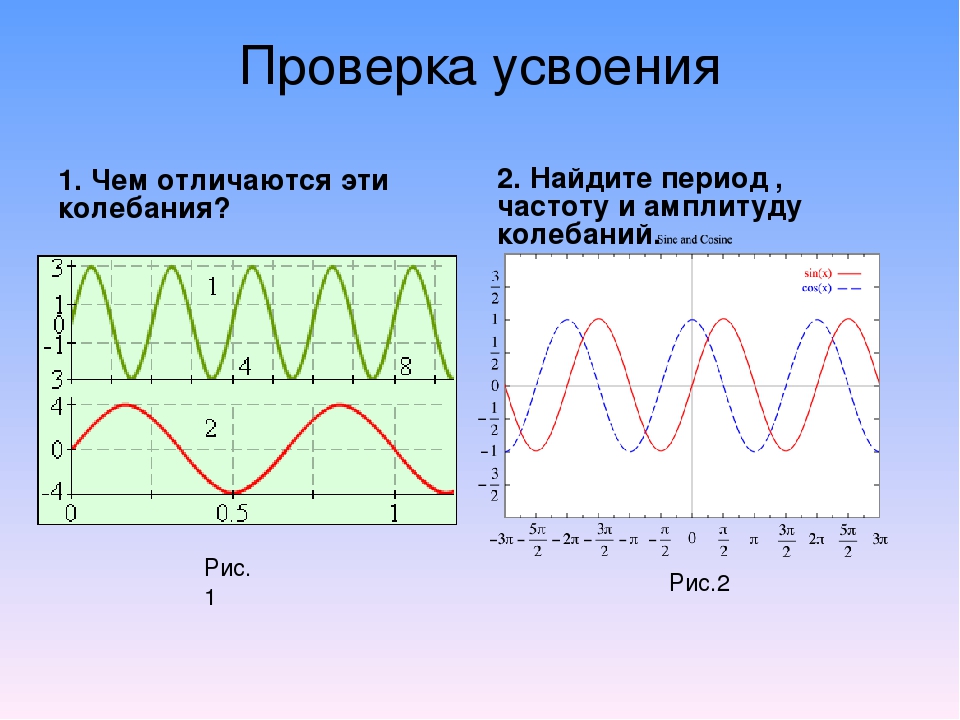 Колебание маятника, например, приближает SHM, если амплитуда мала.

Сэкономьте 50% на подписке Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сегодня Изучение обнаружения вибрации в зданиях

Обзор современных технологий, используемых для измерения вибрации в строительных материалах.

Encyclopædia Britannica, Inc. Посмотрите все видео по этой статье

Универсальной особенностью свободных колебаний является гашение.Все системы подвержены действию сил трения, которые постепенно истощают энергию колебаний, вызывая уменьшение амплитуды, обычно экспоненциально. Поэтому движение никогда не бывает точно синусоидальным. Таким образом, покачивающийся маятник, оставленный неуправляемым, в конечном итоге вернется в состояние покоя в положении равновесия (минимальной энергии).

Вынужденные вибрации возникают, если система постоянно приводится в действие внешним агентом. Простой пример — детские качели, которые толкают при каждом махе вниз. Особый интерес представляют системы, подвергающиеся SHM и управляемые синусоидальным воздействием.Это приводит к важному явлению резонанса. Резонанс возникает, когда частота возбуждения приближается к собственной частоте свободных колебаний. Результатом является быстрое поглощение энергии колебательной системой с соответствующим увеличением амплитуды колебаний. В конечном итоге рост амплитуды ограничен наличием затухания, но на практике отклик может быть очень большим. Говорят, что солдаты, идущие по мосту, могут создавать резонансные колебания, достаточные для разрушения конструкции.Подобный фольклор существует об оперных певцах, разбивающих бокалы.

Электрические колебания играют важную роль в электронике. Схема, содержащая как индуктивность, так и емкость, может поддерживать электрический эквивалент SHM, включающий синусоидальный ток. Резонанс возникает, если цепь приводится в действие переменным током, частота которого совпадает с частотой свободных колебаний цепи. Это принцип настройки. Например, радиоприемник содержит схему, собственная частота которой может варьироваться.Когда частота совпадает с частотой радиопередатчика, возникает резонанс, и в цепи возникает большой переменный ток этой частоты. Таким образом, резонирующие контуры могут использоваться для фильтрации одной частоты из смеси.

В музыкальных инструментах движение струн, мембран и воздушных колонн состоит из суперпозиции SHM; в инженерных сооружениях вибрации — обычное, хотя и нежелательное явление. Во многих случаях сложные периодические движения можно понимать как суперпозицию SHM на многих разных частотах.

Рао, Руководство для инструкторов по механической вибрации

  • Тематический каталог

DIFFYQS Механические колебания

Подраздел 2.4.1 Некоторые примеры

Наш первый пример — груз на пружине. Предположим, у нас есть масса \ (m> 0 \) (в килограммах), связанная пружиной с жесткостью пружины \ (k> 0 \) (в ньютонах на метр) к неподвижной стене. На массу может действовать некоторая внешняя сила \ (F (t) \) (в ньютонах). Наконец, есть некоторое трение, измеряемое как \ (c \ geq 0 \) (в ньютон-секундах на метр), когда масса скользит по полу (или, возможно, подключен демпфер).

Пусть \ (x \) будет смещением массы (\ (x = 0 \) — это положение покоя), при этом \ (x \) растет вправо (от стены).Сила, прилагаемая пружиной, пропорциональна сжатию пружины по закону Гука. Следовательно, это \ (kx \) в отрицательном направлении. Точно так же сила трения пропорциональна скорости массы. По второму закону Ньютона мы знаем, что сила равна массе, умноженной на ускорение, и, следовательно, \ (mx » = F (t) -cx’-kx \) или

\ begin {уравнение *} mx » + cx ‘+ kx = F (t). \ end {уравнение *}

Это линейное ОДУ с постоянным коэффициентом второго порядка. Мы говорим, движение

  1. принудительно , если \ (F \ not \ Equiv 0 \) (если \ (F \) не равно нулю тождественно),

  2. без принуждения или бесплатно , если \ (F \ Equiv 0 \) (если \ (F \) тождественно равен нулю),

  3. с демпфированием , если \ (c> 0 \ text {,} \) и

  4. без демпфирования , если \ (c = 0 \ text {.} \)

Эта система появляется во многих приложениях, даже если сначала она не кажется такой. Многие сценарии из реального мира можно упростить до массы на пружине. Например, тарзанка — это, по сути, система массы и пружины (вы — масса). Было бы хорошо, если бы кто-нибудь посчитал, прежде чем вы прыгнете с моста, верно? Приведем еще два примера.

Вот пример для инженеров-электриков. Рассмотрим изображенную схему RLC.Имеется резистор с сопротивлением \ (R \) Ом, индуктор с индуктивностью \ (L \) Генри и конденсатор емкостью \ (C \) фарад. Также имеется электрический источник (например, аккумулятор), подающий напряжение \ (E (t) \) вольт в момент времени \ (t \) (измеряется в секундах). Пусть \ (Q (t) \) — заряд конденсатора в кулонах, а \ (I (t) \) — ток в цепи. Связь между ними следующая: \ (Q ‘= I \ text {.} \) По элементарным принципам мы находим \ (L I’ + RI + \ nicefrac {Q} {C} = E \ text {.} \) Продифференцируем, чтобы получить

\ begin {уравнение *} L I » (t) + R I ‘(t) + \ frac {1} {C} I (t) = E’ (t). \ end {уравнение *}

Это неоднородное линейное уравнение с постоянными коэффициентами второго порядка. Поскольку \ (L, R \ text {,} \) и \ (C \) все положительны, эта система ведет себя так же, как система массы и пружины. Положение массы заменяется текущим. Масса заменяется индуктивностью, демпфирование заменяется сопротивлением, а жесткость пружины заменяется единицей, превышающей емкость.Изменение напряжения становится форсирующей функцией — для постоянного напряжения это движение без принуждения.

Наш следующий пример ведет себя как система массы и пружины только приблизительно. Предположим, что масса \ (m \) висит на маятнике длины \ (L \ text {.} \). Мы ищем уравнение для угла \ (\ theta (t) \) (в радианах). Пусть \ (g \) — сила тяжести. Элементарная физика требует, чтобы уравнение было

\ begin {уравнение *} \ theta » + \ frac {g} {L} \ sin \ theta = 0. \ end {уравнение *}

Давайте выведем это уравнение, используя второй закон Ньютона: сила равна массе, умноженной на ускорение.Ускорение равно \ (L \ theta » \), а масса — \ (m \ text {.} \), Поэтому \ (mL \ theta » \) должно быть равно тангенциальной составляющей силы, создаваемой силой тяжести. , что равно \ (mg \ sin \ theta \) в обратном направлении. Итак, \ (mL \ theta » = -mg \ sin \ theta \ text {.} \) \ (M \) любопытным образом сокращается из уравнения.

Теперь сделаем наше приближение. Для маленьких \ (\ theta \) мы имеем примерно \ (\ sin \ theta \ приблизительно \ theta \ text {.} \). Это можно увидеть, взглянув на график. На рисунке 2.1 мы видим, что приблизительно для \ (- 0.5 <\ theta <0.5 \) (в радианах) графики \ (\ sin \ theta \) и \ (\ theta \) почти одинаковы.

Рисунок 2.1. Графики \ (\ sin \ theta \) и \ (\ theta \) (в радианах).

Следовательно, когда колебания малы, \ (\ theta \) мало, и мы можем моделировать поведение с помощью более простого линейного уравнения

\ begin {уравнение *} \ theta » + \ frac {g} {L} \ theta = 0. \ end {уравнение *}

Ошибки из этого приближения нарастают. Таким образом, через долгое время состояние реальной системы может существенно отличаться от нашего решения.Также мы увидим, что в системе масса-пружина амплитуда не зависит от периода. Это не так для маятника. Тем не менее, для достаточно коротких периодов времени и небольших колебаний (то есть только малых углов \ (\ theta \)) приближение достаточно хорошее.

В реальных задачах часто бывает необходимо делать такие упрощения. Мы должны понимать как математику, так и физику ситуации, чтобы увидеть, действительно ли упрощение в контексте вопросов, на которые мы пытаемся ответить.2} \) и \ (\ tan \ gamma = \ nicefrac {B} {A} \ text {.} \) Следовательно, пусть \ (C \) и \ (\ gamma \) будут нашими произвольными константами, и запишем \ (x (t) = C \ cos (\ omega_0 t — \ gamma) \ text {.} \)

Упражнение 2.4.1.

Обоснуйте тождество \ (A \ cos (\ omega_0 t) + B \ sin (\ omega_0 t) = C \ cos (\ omega_0 t — \ gamma) \) и проверьте уравнения для \ (C \) и \ (\ gamma \ text {.} \). Подсказка: начните с \ (\ cos (\ alpha- \ beta) = \ соз (\ альфа) \ соз (\ beta) + \ sin (\ alpha) \ sin (\ beta) \) и умножьте на \ (C \ text {.} \) Тогда какими должны быть \ (\ alpha \) и \ (\ beta \)?

Хотя обычно проще использовать первую форму с \ (A \) и \ (B \) для решения начальных условий, вторая форма намного более естественна. Константы \ (C \) и \ (\ gamma \) имеют красивую физическую интерпретацию. Запишите решение как

\ begin {уравнение *} х (t) = C \ cos (\ omega_0 t — \ gamma). \ end {уравнение *}

Это колебание чистой частоты (синусоида). Амплитуда равна \ (C \ text {,} \) \ (\ omega_0 \) — это (угловая) частота , а \ (\ gamma \) — это так называемый фазовый сдвиг .Фазовый сдвиг просто сдвигает график влево или вправо. Мы называем \ (\ omega_0 \) естественную (угловую) частоту . Вся эта установка называется простым гармоническим движением .

Сделаем паузу, чтобы объяснить слово угловой перед словом частота . Единицы измерения \ (\ omega_0 \) — это радианы в единицу времени, а не циклы в единицу времени, как это обычно бывает при измерении частоты. Поскольку один цикл равен \ (2 \ pi \) радиан, обычная частота задается как \ (\ frac {\ omega_0} {2 \ pi} \ text {.} \) Это просто вопрос того, где мы поместим константу \ (2 \ pi \ text {,} \), и это дело вкуса.

Период движения равен единице по частоте (в циклах в единицу времени) и, следовательно, \ (\ frac {2 \ pi} {\ omega_0} \ text {.} \) Это количество времени, которое требуется для завершения одного полного цикла.

Пример 2.4.1.

Предположим, что \ (m = \ unit [2] {kg} \) и \ (k = \ unitfrac [8] {N} {m} \ text {.} \) Вся установка массы и пружины находится на грузовик, который ехал в 1 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text {.} \) Грузовик падает и, следовательно, останавливается. Груз удерживался на 0,5 метра вперед от положения покоя. Во время аварии масса расшатывается. То есть теперь масса движется вперед на 1 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text {,} \), в то время как другой конец пружины удерживается на месте. Таким образом, масса начинает колебаться. Какова частота возникающих колебаний? Какая амплитуда? Единицы измерения — единицы mks (метры-килограммы-секунды).

Установка означает, что во время аварии масса находилась на расстоянии полуметра в положительном направлении и относительно стены, к которой крепится пружина, масса двигалась вперед (в положительном направлении) на 1 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text {.} \) Это дает нам начальные условия.

Итак, уравнение с начальными условиями —

\ begin {уравнение *} 2 x » + 8 x = 0, \ qquad x (0) = 0,5, \ qquad x ‘(0) = 1. \ end {уравнение *}

Мы непосредственно вычисляем \ (\ omega_0 = \ sqrt {\ nicefrac {k} {m}} = \ sqrt {4} = 2 \ text {.} \) Следовательно, угловая частота равна 2. Обычная частота в Герцах (циклах в секунду) составляет \ (\ nicefrac {2} {2 \ pi} = \ nicefrac {1} {\ pi} \ приблизительно 0,318 \ text {.} \)

Общее решение —

\ begin {уравнение *} х (t) знак равно A \ cos (2t) + B \ sin (2t).2} = \ sqrt {0,25 + 0,25} = \ sqrt {0,5} \ приблизительно 0,707 \ text {.} \) Решение:

\ begin {уравнение *} х (t) = 0,5 \ cos (2t) + 0,5 \ sin (2t). \ end {уравнение *}

График \ (x (t) \) показан на рисунке 2.2.

Рисунок 2.2. Простое незатухающее колебание.

В общем, для свободного незатухающего движения решение вида

\ begin {уравнение *} х (т) = А \ соз (\ омега_0 т) + В \ грех (\ омега_0 т), \ end {уравнение *}

соответствует начальным условиям \ (x (0) = A \) и \ (x ‘(0) = \ omega_0 B \ text {.} \) Следовательно, \ (A \) и \ (B \) легко определить из начальных условий. Затем амплитуду и фазовый сдвиг можно вычислить из \ (A \) и \ (B \ text {.} \). В этом примере мы уже нашли амплитуду \ (C \ text {.} \). Давайте вычислим фазовый сдвиг. Мы знаем, что \ (\ tan \ gamma = \ nicefrac {B} {A} = 1 \ text {.} \) Мы берем арктангенс 1 и получаем \ (\ nicefrac {\ pi} {4} \) или приблизительно 0,785. Нам все еще нужно проверить, находится ли этот \ (\ gamma \) в правильном квадранте (и добавить \ (\ pi \) к \ (\ gamma \), если это не так).Поскольку и \ (A \), и \ (B \) положительны, то \ (\ gamma \) должен быть в первом квадранте, \ (\ nicefrac {\ pi} {4} \) радианы в первом квадранте, так что \ (\ gamma = \ nicefrac {\ pi} {4} \ text {.} \)

Примечание. Многие калькуляторы и компьютерные программы имеют не только функцию atan для арктангенса, но также то, что иногда называют atan2 . Эта функция принимает два аргумента, \ (B \) и \ (A \ text {,} \), и возвращает \ (\ gamma \) в правильном для вас квадранте.

Подраздел 2.{-pt}. \ end {уравнение *}

Поведение системы с критическим демпфированием очень похоже на систему с избыточным демпфированием. В конце концов, критически демпфированная система в некотором смысле является пределом сверхдемпфированных систем. Поскольку эти уравнения на самом деле являются лишь приближением к реальному миру, в действительности мы никогда не испытываем критического затухания, это место, куда мы можем попасть только в теории. Мы всегда немного недемпфированы или немного передемпфированы. На критическом затухании лучше не останавливаться.

Подраздел 2.{-pt} \ text {.} \) Решением является колеблющаяся линия между двумя огибающими кривыми. Огибающие кривые показывают максимальную амплитуду колебаний в любой момент времени. Например, если вы прыгаете с тарзанки, вам действительно интересно вычислить огибающую кривую, чтобы не удариться головой о бетон.

Фазовый сдвиг \ (\ gamma \) сдвигает колебание влево или вправо, но в пределах огибающих кривых (огибающие не меняются при изменении \ (\ gamma \)).

Обратите внимание, что угловая псевдочастота 1 становится меньше, когда затухание \ (c \) (и, следовательно, \ (p \)) становится больше.2 \) приближается к \ (4 км \ text {,} \), мы хотим, чтобы \ (\ omega_1 \) приблизился к нулю.

Мы не называем \ (\ omega_1 \) частотой, поскольку решение на самом деле не является периодической функцией.

С другой стороны, когда \ (c \) становится меньше, \ (\ omega_1 \) приближается к \ (\ omega_0 \) (\ (\ omega_1 \) всегда меньше, чем \ (\ omega_0 \)), и решение все больше и больше напоминает установившееся периодическое движение незатухающего корпуса. Огибающие кривые становятся более пологими и пологими, когда \ (c \) (и, следовательно, \ (p \)) стремится к 0.

Подраздел 2.4.4 Упражнения

Упражнение 2.4.2.

Рассмотрим систему массы и пружины с массой \ (m = 2 \ text {,} \) постоянной пружины \ (k = 3 \ text {,} \) и постоянной демпфирования \ (c = 1 \ text {.} \ )

  1. Настройте и найдите общее решение системы.

  2. Система недостаточно демпфирована, чрезмерно демпфирована или критически демпфирована?

  3. Если система не имеет критического демпфирования, найдите \ (c \), который делает систему критически демпфированной.

Упражнение 2.4.3.

Выполните упражнение 2.4.2 для \ (m = 3 \ text {,} \) \ (k = 12 \ text {,} \) и \ (c = 12 \ text {.} \)

Упражнение 2.4.4.

Используя единицы измерения mks (метры-килограммы-секунды), предположим, что у вас есть пружина с жесткостью пружины 4 \ (\ nicefrac {\ text {N}} {\ text {m}} \ text {.} \) Вы хотите используйте его для взвешивания предметов. Предполагайте отсутствие трения. Вы кладете массу на пружину и приводите ее в движение.

  1. Вы посчитаете и обнаружите, что частота составляет 0,8 Гц (циклов в секунду). Какая масса?

  2. Найдите формулу для массы \ (m \) с учетом частоты \ (\ omega \) в Гц.

Упражнение 2.4.5.

Предположим, мы добавляем возможное трение к упражнению 2.4.4. Кроме того, предположим, что вы не знаете жесткость пружины, но у вас есть два контрольных веса 1 кг и 2 кг для калибровки вашей установки. Вы приводите в движение каждую пружину и измеряете частоту. Для веса 1 кг вы измерили 1,1 Гц, для веса 2 кг вы измерили 0,8 Гц.

  1. Найдите \ (k \) (жесткость пружины) и \ (c \) (постоянную демпфирования).

  2. Найдите формулу для массы через частоту в Гц. Обратите внимание, что для данной частоты может быть более одной возможной массы.

  3. Какова масса неизвестного объекта с частотой 0,2 Гц? Предположим, вы знаете, что масса неизвестного объекта превышает килограмм.

Упражнение 2.4.6.

Предположим, вы хотите измерить трение, которое испытывает масса весом 0,1 кг, когда она скользит по полу (вы хотите найти \ (c \)). У вас есть пружина с жесткостью пружины \ (k = \ unitfrac [5] {N} {m} \ text {.} \) Вы берете пружину, прикрепляете ее к массе и прикрепляете к стене. Затем вы натягиваете пружину и отпускаете массу. Вы обнаружите, что масса колеблется с частотой 1 Гц. Что такое трение?

Упражнение 2.4.101.

Масса в \ (2 \) килограмма находится на пружине с жесткостью пружины \ (k \) ньютонов на метр без демпфирования. Предположим, что система находится в состоянии покоя, и в момент времени \ (t = 0 \) масса выбрасывается и начинает двигаться со скоростью 2 метра в секунду. Насколько большим должен быть \ (k \), чтобы груз не уходил дальше 3 метров от положения покоя?

Ответ

\ (k = \ nicefrac {8} {9} \) (и больше)

Упражнение 2.4.102.

Предположим, у нас есть RLC-цепь с резистором 100 миллиом (0,1 Ом), индуктивностью 50 миллигенри (0,05 генри) и конденсатором 5 фарад с постоянным напряжением.

  1. Установите уравнение ODE для текущего \ (I \ text {.} \)

  2. Найдите общее решение.

  3. Решите относительно \ (I (0) = 10 \) и \ (I ‘(0) = 0 \ text {.} \)

Ответ

a) \ (0,05 I » + 0,1 I ‘+ (\ nicefrac {1} {5}) I = 0 \) b) \ (I = C e ^ {- t} \ cos (\ sqrt {3 } \, t — \ gamma) \) c) \ (I = 10 e ^ {- t} \ cos (\ sqrt {3} \, t) + \ frac {10} {\ sqrt {3}} e ^ {-t} \ sin (\ sqrt {3} \, t) \)

Упражнение 2.4.103.

Вагон массой 5000 кг ударяется о бампер (пружину) в точке 1 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text {,} \), и пружина сжимается на 0,1 м. Предположим, что нет демпфирования.

  1. Найти \ (k \ text {.} \)

  2. Насколько сильно сжимается пружина, если вагон массой 10000 кг ударяет о пружину с той же скоростью?

  3. Если пружина сломается при сжатии более чем на 0,3 м, какова максимальная масса вагона, который может ударить ее при 1 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text { ?} \)

  4. Какая максимальная масса вагона может ударить по рессоре, не сломавшись при 2 \ (\ nicefrac {\ text {m}} {\ text {s}} \ text {?} \)

Ответ

a) \ (k = 500000 \) b) \ (\ frac {1} {5 \ sqrt {2}} \ приблизительно 0.141 \) в) 45000 кг г) 11250 кг

Упражнение 2.4.104.

Масса \ (m \) кг находится на пружине с \ (k = \ unitfrac [3] {N} {m} \) и \ (c = \ unitfrac [2] {Ns} {m} \ text {.} \) Найдите массу \ (m_0 \), для которой существует критическое затухание. Если \ (m Ответ

\ (m_0 = \ frac {1} {3} \ text {.} \) Если \ (m

Демонстраций по физике — Движение

Демонстрация по физике — Движение Движение, более правильное название «механика», — это старейший раздел физики. поставленный на прочную количественную основу Исааком Ньютоном (1642-1727) которые к 24 годам также развили исчисление, которое впоследствии стало незаменимый инструмент науки.Изучение движения часто рассматривается как относительно приземленный, но Альберт Эйнштейн (1879-1955) в возрасте 26 лет, в то время как работающий в Швейцарском патентном ведомстве, глубоко задумывался о движении света и произвел революцию в нашем понимании отношения пространства и время. Изучение движения дает возможность развить такие концепции. как сохранения энергии, актуальные для всех разделов физики. В движении эти концепции часто проявляются в наименее абстрактной форме. и наиболее легко визуализируемая форма.

1,1

Маятник шара для боулинга

Шар для боулинга подвешен к потолку на тонкой проволоке из нержавеющей стали. иллюстрирует простой гармонический осциллятор и сохранение энергии.
МАТЕРИАЛЫ
  • шар для боулинга: 16 фунтов, диаметр 8,5 дюйма
  • тонкая проволока из нержавеющей стали
  • подставка для ног
  • секундомер (опционально)
  • софтбол (по желанию)
ПРОЦЕДУРА
Волонтер, приглашенный из зала, стоит на затылке. у стены с шаром для боулинга, плотно прижатым к носу.Боулинг мяч отпускается (не толкается!), и инструктор просит волонтера положить руки по бокам и не двигаться, пока мяч возвращается в в пределах нескольких сантиметров от носа. Лучше всего, если маятник будет как как можно дольше, если волонтер далеко от точки отстранения а если зрители смотрят со стороны. Точка на стене должна быть помечены, чтобы указать правильное положение головы, а волонтер должен быть выбранной примерно правильной высоты, чтобы голова находилась в правильное положение или подставка для ног.Очки на волонтера добавить к драме. Посуда или другое хрупкое оборудование, которое может быть всего на миллиметры ниже траектории полета мяча усиливает интерес.

С помощью секундомера или простого подсчета секунд время, которое требуется можно определить качание мяча назад и вперед. Демонстрация затем можно повторить с мячами разного размера и массы (софтбол работает хорошо), чтобы показать, что период, но не обязательно фрикционный потери, зависят только от длины маятника.Аудитория может быть попросили проголосовать, будет ли более легкий мяч длиться дольше или короче время вернуться к исходной точке. Выбирая разные отправные точки для мяча, или внимательно наблюдая за периодом, когда мяч медленно приближается для отдыха можно продемонстрировать, что период не зависит от амплитуды, при условии, что амплитуда мала. Демонстрация может использоваться, чтобы подчеркнуть детерминированный характер классической физики и точность, с которой некоторые (но не все) физические системные системы можно предсказать.

ОБСУЖДЕНИЕ
Эта демонстрация иллюстрирует преобразование потенциальной энергии, когда мяч поднимается над своим положением покоя в кинетическую энергию, когда мяч приобретает скорость, и обратно, с потерями энергии из-за трения с воздух. Путем измерения или оценки количества промахов по мячу нос добровольца, можно определить дробную потерю энергии за цикл. Период маятника равен 2pi (л / г) ½ , где L — длина маятника, а g — ускорение свободного падения. (9.8 м / с 2 ). Период не зависит от массы маятника. или от амплитуды движения, по крайней мере до тех пор, пока амплитуда достаточно маленький. Если маятник поворачивается на угол 45 ° от по вертикали период примерно на 4% больше расчетного. На 90 °, период примерно на 18% больше.
ОПАСНОСТИ
Проволока должна иметь предел прочности на разрыв, по крайней мере, в несколько раз превышающий вес. шара и должен быть надежно закреплен.Убедитесь, что мяч не может ударить что-нибудь во время его взмаха и встать в положение, чтобы оно могло быть остановленным, если доброволец дает толчок, а не просто отпускает.

1,2

Вернуться назад банка

Банка, перекатываясь по столу, останавливается, а затем откатывается обратно в где это началось, иллюстрируя концепцию накопленной внутренней энергии.
МАТЕРИАЛЫ
  • банка цилиндрическая со съемной непрозрачной крышкой
  • резинка
  • груз с отверстием в центре
ПРОЦЕДУРА
Банка состоит из резиновой ленты, натянутой между ее центром. концы и груз, прикрепленный к ленте, чтобы заставить ленту мотаться вверх, когда банка катится [1,2].Банка останавливается, а затем откатывается обратно в где это началось. Видно, что стол не ровный, но он можно катить в любом направлении с одинаковым результатом. Помогает вращать баллончик на оборот или два перед тем, как отпустить его, чтобы компенсировать трение убытки как катится. Это также позволяет банке скручивать небольшой наклон. Один конец банки должен легко сниматься, чтобы открыть ее содержимое и чтобы объяснить его работу.
ОБСУЖДЕНИЕ
Эта демонстрация иллюстрирует преобразование кинетической энергии в потенциальную. и назад.Потенциальная энергия хранится внутри скрученной резины. группа. На микроскопическом уровне энергия хранится в электрическом потенциале заряженных частиц, составляющих молекулы каучука. Аналогии может производиться на заводе часов, на заправку автомобильного бензобака, к запасенной энергии в атомах и молекулах и энергии самой массы (E = mc 2 ).

С точки зрения специальной теории относительности масса банка и ее внутренний механизм немного увеличиваются, поскольку резинка заводится, и именно эта увеличенная масса превращается в кинетическую энергия, когда банка начинает катиться с остановки.Можно было оценить изменение массы от (дельта) mc 2 = mv 2 /2, чтобы показать, почему это обычно не обнаруживается для медленно движущихся объектов по сравнению с скорость света. Например, если банка имеет начальную скорость 1 м / с, частичное увеличение его массы в состоянии покоя составляет меньше чем 1 часть из 10 17 !

ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКИ
1.T. L. Liem, Приглашения на научные исследования , Ginn Press: Lexington, Массачусетс (1981).

2. J. P. VanCleave, Teaching the Fun of Physics , Prentice Hall Пресса: Нью-Йорк (1985).

1,3

Велосипедный гироскоп

Велосипедное колесо прикреплено к проволоке с помощью шарнирной лески и подвешено. из опоры получается впечатляющий гироскоп.
МАТЕРИАЛЫ
  • гироскоп колеса велосипеда *
  • проволока из нержавеющей стали
  • вертлюг для лески
  • вращающийся стул или платформа * или вращающийся стул (опция)
  • чемодан с внутренним гироскопом (опция)
* Можно приобрести в компании Carolina Biological Supply Company, Central Scientific Company, Fisher Scientific, Frey Scientific Company и Sargent-Welch Научная компания
ПРОЦЕДУРА
Гироскоп велосипедного колеса раскручивается до высокой скорости вручную или с помощью веревки. и подвешивается к потолку на проволоке с вертлюжком лески прикреплен к одному концу его оси [1-3].Вертлюг лески позволяет прецессировать. По мере прецессии гироскопа его ось может подниматься вверх. и вниз в движении, известном как нутация. Если гироскоп велосипедного колеса недоступно, те же эффекты можно увидеть в меньшем масштабе с игрушкой гироскоп или даже игрушечный волчок [4].

Можно попросить сильного волонтера из зала провести спиннинг. колесо велосипеда за один конец оси горизонтально на расстоянии вытянутой руки, а затем поднять его вертикально над головой, сначала с не вращающимся колесом а затем с быстрым вращением.Сделать это без немного практики. Вращающийся гироскоп, установленный внутри чемодана, обеспечивает особенно зрелищная и незабываемая демонстрация человеку кто пытается резко повернуться, неся чемодан.

Велосипедное колесо также можно держать в руках, сидя на вращающейся стул или вращающийся стул или стоя на вращающейся платформе, чтобы проиллюстрировать Третий закон Ньютона (действие и противодействие) и сохранение угловой импульс.Табурет можно заставить вращаться в одном или другом направлении, поворот оси велосипедного колеса в разные стороны. Человек на табурете может передать колесо кому-нибудь другому, который переворачивает его и передает обратно к человеку на стуле, который снова переворачивает его, и так далее, пока стул довольно быстро вращается.

Гироскоп имеет много интересных свойств. Можно показать, что это ось будет оставаться в горизонтальном положении до тех пор, пока ей будет позволена прецессия.Когда прецессия прекращается, она падает. Сила, необходимая, чтобы заставить его двигаться внутрь определенное направление должно применяться под прямым углом к ​​этому направлению. Когда колесо раскачивается как маятник, оно стремится оставаться в плоскости. Этот принцип инерциального наведения ракет, гирокомпаса и др. навигационные инструменты [5]. Можно отметить, что гироскопическое действие колес — одна из причин, по которой велосипед остается в вертикальном положении [6,7]. В таком случае прецессии нет, поскольку колесо подвешено к центру сила тяжести.Можно катать колесо велосипеда по полу, чтобы проиллюстрировать что он остается в вертикальном положении намного дольше, чем если бы он был выпущен из состояния покоя.

Увеличенная версия гироскопа на автомобильной шине, заполненной водой и другие недорогие детали, которые легко достать на свалках [8].

ОБСУЖДЕНИЕ
Гироскоп представляет собой интересный и необычный пример сохранения углового момента. Угловой момент — это вектор, направленный вдоль ось, вокруг которой вращается гироскоп (в смысле, заданном правой правило).При отсутствии внешних крутящих моментов направление, а также величина этого вектора останется постоянной. Трение создает крутящий момент что уменьшает величину вектора и в конечном итоге приводит к тому, что гироскоп перестать вращаться. Гравитация создает крутящий момент, перпендикулярный обеим осям. гироскопа и вертикали, и, таким образом, вызывает горизонтальную прецессию. На менее абстрактном уровне прецессию можно объяснить с точки зрения нисходящее притяжение силы тяжести, которое пытается заставить колесо вращаться быстрее при снизу, чем вверху.Поскольку колесо жесткое, это может произойти только если колесо движется горизонтально в том направлении, в котором низ колесо крутится. Земля — ​​это большой гироскоп, прецессирующий однажды каждые 26000 лет из-за гравитационного момента, прилагаемого Солнцем к небольшая выпуклость на экваторе.

Обратите внимание, что частота прецессии обратно пропорциональна частота вращения гироскопа. Этот факт можно проиллюстрировать внимательно наблюдая за прецессией при замедлении гироскопа.Более того, частота прецессии не зависит от угла, который ось составляет с горизонтальным. Крутящий момент наибольший, когда ось расположена горизонтально, но равно как и расстояние, на которое он должен пройти, чтобы прецессировать один раз, и эффекты просто отменяются.

Кинетическая энергия, связанная с прецессией, должна откуда-то поступать. Это происходит от гравитационной потенциальной энергии самого гироскопа. Когда гироскоп выходит из исходного фиксированного горизонтального положения, он начинает падать обычным образом.Это падающее движение быстро преобразует в прецессию, с центром масс чуть ниже, чем было изначально. Фактически, при падении он немного выходит за пределы своего положения равновесия. и колеблется вверх и вниз относительно этого равновесия, что приводит к нутации. Нутация обычно довольно быстро затухает, но может быть возбуждена от быстрый рывок вверх или вниз на свободном конце оси гироскопа. Если есть трение, замедляющее прецессию, центр масс постепенно падает, пока в конце концов колесо не свисает прямо вниз.

ОПАСНОСТИ
Вращающееся колесо велосипеда громоздко, и его трудно контролировать из-за уникальные свойства гироскопа. Вращение можно остановить, коснувшись колесо против чего-то (рубашка не рекомендуется!). Головокружение может быть вызывается очень быстро вращающимся стулом. Если это не делает предмет больной, человек может упасть после того, как встал со стула. А Перед выходом рекомендуется сделать паузу на несколько мгновений для восстановления равновесия.
ССЫЛКИ
1. Х. В. Доссо, Р. Х. Видал, Am. Journ. Phys. 30 , 528 (1962).

2. J. R. Prescott, Am. Journ. Phys. 31, , 393 (1963).

3. К. Т. Леондес, Scientific American 222 , 80 (март 1970 г.).

4. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

5. Х. Ф. Майнерс, Демонстрационные эксперименты по физике , Том I, Рональд Пресс Компани: Нью-Йорк (1970).

6. Д. Э. Х. Джонс, Physics Today 23 , 34 (апрель 1970 г.).

7. S. S. Wilson, Scientific American 228 , 81 (март 1973).

8. H. A. Daw, Am. Journ. Phys. 56, , 657 (1988).

1,4

Гвинея и перо

В вакуумированной стеклянной трубке объекты падают с одинаковой скоростью. независимо от их размера, формы и массы.
МАТЕРИАЛЫ
  • цилиндрическая стеклянная трубка со съемным концом и откачивающей насадкой *
  • пенни или другой небольшой плотный предмет
  • перо или ватный клубок
  • вакуумный насос
  • манометр (опция)
  • толстая книга и лист бумаги (по желанию)
* Можно приобрести в компании Carolina Biological Supply Company, Central Scientific Company, Frey Scientific Company и Sargent-Welch Scientific Компания
ПРОЦЕДУРА
Стеклянная трубка длиной не менее метра оснащена клапаном и насадкой. через которую трубка может быть откачана с помощью механического вакуумного насоса.Такая трубка называется морской и перьевой, потому что это были предметы, которые традиционно использовались во время демонстрации в Англии. столетия назад. Гвинея — английская золотая монета, выпущенная с 1663 по 1813 г. и оценена в 21 шиллинг. В наши дни современная монета и перо или ватный шарик.

Демонстрация начинается с вопроса аудитории, которая падает быстрее, перо или монета. (Вопрос напоминает старый анекдот про который весит больше, фунт перьев или фунт свинца.) Какой бы ответ дается либо правильно, либо неправильно, в зависимости от того, выполняется на воздухе или в вакууме. Можно отметить, что в науке часто встречаются противоположные теории, и в таких случаях требуются эксперименты чтобы определить, какие теории верны. Собственно, эксперимент обычно не может доказать, что теория верна, только то, что она неверна.

Два объекта помещаются в трубку при атмосферном давлении и быстро переворачивает трубку, давая ожидаемый результат.Затем трубка откачивается, и демонстрация повторилась. Оба будут падать с одинаковой скоростью, когда трубка откачана. Конечно, часть демонстрации, не требующая вакуум может быть сделан без использования трубки с демонстратором стоя на лекционном столе для немного дополнительной драмы.

Если вакуумный насос недоступен, альтернативная форма демонстрации можно сделать, используя тяжелую книгу и лист бумаги (меньшего размера, чем книга) [1]. Сначала они падают рядом.Книга упадет намного быстрее. Затем бумагу кладут плашмя на книгу и отпускают. все вместе. Они будут падать с той же скоростью, потому что книга устраняет сопротивление воздуха, которое иначе испытала бы бумага.

ОБСУЖДЕНИЕ
Легенда гласит, что этот эксперимент проводил Галилео Галилей (1564-1642). сбросив два ядра, одно в десять раз тяжелее другого, из Пизанская башня [2]. Легенда почти наверняка ложна, хотя он, как известно, проводил подобные эксперименты в молодости, всегда получая обратный результат, который он объяснил тем, что рост было недостаточно [3].Его аргументы больше основывались на мысленных экспериментах. например, упадут ли два идентичных объекта, соединенных вместе, с той же скоростью, что и по отдельности, а не в реальных экспериментах. Тем не менее, он провел много экспериментов, расстроивших аристотелевскую физику. и проложил путь Ньютону в его разработке законов движения [4,5]. 2 августа 1971 года астронавт Дэвид Скотт повторил эксперимент с молот геолога и соколиное перо стоя на безвоздушном поверхность Луны пока весь мир смотрел по телевизору.

Тот факт, что легкий объект падает в вакууме так же быстро, как тяжелый. озадачивает многих людей, которые правильно считают, что гравитация должна тянуть сильнее на тяжелом предмете. Однако из второго закона Ньютона (F = ma) труднее тяга требуется для ускорения более тяжелого объекта, и эффекты просто отменяются. Эта демонстрация является иллюстрацией эквивалентности гравитационного и инертной массы и является основой принципа эквивалентности, на котором основана общая теория относительности [6].В 1890 г. венгерский физик Барон Лоранд фон Этвеш (1848-1919) уточнил эксперимент Галилея и показал, что инерционная и гравитационная масса равны в одной части в 10 8 и более поздних экспериментах [7], мотивированных поиском для новой формы силы [8] достигли пяти частей в 10 10 .

Для большинства объектов сопротивление воздуха заметно влияет на скорость с которыми они падают. Для больших объектов, движущихся с высокой скоростью в воздухе, сила сопротивления определяется выражением F d = C (rho) Av 2 /2, где v — скорость, A — площадь поперечного сечения объекта, измеренная в плоскость, перпендикулярная его движению, rho — плотность воздуха и C — коэффициент лобового сопротивления.Коэффициент лобового сопротивления составляет около 0,5 для сферических объекты, но может достигать 1 для объектов неправильной формы. Приравнивая сопротивление к весу (F d = мг), конечная скорость вычисляется должно быть v t = [2 мг / C (rho) A] ½ . Плавучая сила Воздух оказывает на объект небольшую дополнительную силу, направленную вверх.

ОПАСНОСТИ
Значительная опасность этой демонстрации — поломка стеклянной трубки, особенно если он ударяется о твердый предмет, когда он быстро переворачивается во время эвакуированы.Следует использовать прочное стекло и проявлять большую осторожность. во время обращения.
ССЫЛКИ
1. T. L. Liem, Invitations to Science Inquiry , Ginn Press: Lexington, Массачусетс (1981).

2. Л. Купер, Аристотель, Галилей и Пизанская башня , Корнелл University Press: Итака, Нью-Йорк (1935).

3. Х. Баттерфилд, Истоки современной науки , Macmillan: Нью-Йорк (1960).

4.А. Р. Холл, От Галилея до Ньютона, 1630-1720 гг. , Харпер и Ряд: Нью-Йорк (1963 г.).

5. С. Дрейк, Scientific American 228 , 84 (май 1973 г.).

6. D. Sciame, Scientific American 196 , 99 (февраль 1957 г.).

7. Т. М. Нибауэр, М. П. МакХью и Дж. Э. Фаллер, Phys. Rev. Letters 59, , 609 (1987).

8. Э. Фишбах, Д. Сударский, А. Шафер, К. Талмадж и С. Х. Аронсон, Phys. Ред.Письма 56 , 3 (1986).

1,5

Обезьяна и кокос

Снаряд, направленный в чучело обезьяны, попадает в обезьяну, несмотря на то, что что обезьяна начинает падать в момент выстрела снаряда.
МАТЕРИАЛЫ
  • пистолет подпружиненный или пневматический
  • фаршированная обезьяна
  • электромагнит
  • микровыключатель или оптический датчик
ПРОЦЕДУРА
Эта популярная демонстрация обычно носит название «Обезьяна и Хантер «, но здесь изменено, чтобы апеллировать к чувствительности этически против убийства обезьян.Зрителей просят подумать о том, чтобы бросить кокосовый орех на обезьяну, которая падает с дерева в тот момент, когда кокос брошен и пытается поймать кокос. Если кокос бросили прямо у обезьяны на дереве можно было ожидать, что она будет выше обезьяны, так как обезьяна падает. С другой стороны, кокос не следует прямая линия. Зрителей просят проголосовать за то, нацелился ли кокос прямо на обезьяну будет идти выше или ниже обезьяны, когда она падает.Те кто воздерживается от голосования, конечно правы, потому что расстояние упало обезьяной и кокосом абсолютно одинаковы (без учета сопротивления воздуха) пока кокос находится в полете. Лучше всего это проиллюстрировать рисунком прямая линия к положению обезьяны на дереве. Кокос падает ниже этой линии на такое же расстояние, на которое обезьяна падает в данном время. Проблема немного причудливая, потому что обезьяна вряд ли мгновенно реагировать на выброс кокоса, и действует сопротивление воздуха по-разному на обезьяне и кокосе.

Аппарат для этой демонстрации * обычно состоит из какая-либо форма подпружиненного или пневматического пистолета, который может быть электрически активирован и электромагнит для поддержки чучела обезьяны [1-4]. В качестве альтернативы пистолет может быть запущен механически и отключен от магнита с помощью микровыключателя или оптический датчик. Полезное украшение — возможность изменить вертикальный угол между ружьем и обезьяной и возможность изменения скорость снаряда.Ни то, ни другое не должно влиять на результат демонстрации. Эффект наиболее драматичен при значительном расстояние между ружьем и обезьяной, но допустимое расстояние определяется точностью, с которой сконструирован аппарат. Лучше всего каждый раз бить обезьяну, даже если нужно сократить расстояние.

* Поставляется в Fisher Scientific

ОБСУЖДЕНИЕ
Эта демонстрация иллюстрирует тот факт, что вертикальный и горизонтальный компоненты независимы в движении снаряда.Вертикальное ускорение движения объекта не зависит ни от его горизонтальной, ни от вертикальной скорости. Другой распространенный пример этой идеи — проблема того, где выпустить объект из движущегося самолета для поражения цели на земле а затем найти, где находится самолет по отношению к цели, когда он попал.

Обратите внимание, что коллизия произойдет, только если v o sin (theta) o > (gd / 2) ½ , где v o — начальная скорость кокосовый орех, (theta) o — его начальный угол по отношению к по горизонтали, d — начальная высота обезьяны над землей и g — ускорение свободного падения (9.8 м / с 2 ). Если v o sin (theta) o меньше этого значения, обезьяна не может поймать кокос, потому что кокос ударится о землю прежде, чем достигнет его. Также обратите внимание, что горизонтальная составляющая количества движения должна сохраняться, когда кокос ударяется обезьяна, заставляя обезьяну и кокосовый орех продолжать движение в направлении кокоса, но с меньшей скоростью.

Те, кто имеет опыт обращения с оружием, знают, что оружие «прицельно» в «на заданном расстоянии (например, 100 метров), чтобы учесть нисходящую смещение пули при движении.Таким образом, когда фиксированная цель ближе, чем расстояние, на которое наведено ружье, необходимо прицелиться ниже цели, чтобы поразить ее [5]. В таком случае при падении цель, всегда нужно было целиться ниже нее.

ОПАСНОСТИ
Опасность этой демонстрации в том, что снаряд поразит кого-нибудь в аудитории либо сразу, либо после отражения чего-либо путь его траектории. Следует соблюдать осторожность при наведении ружья и предметы, которые могут отклонить снаряд, следует убрать с пути.
ССЫЛКИ
1. Б.Ф. Гриффинг, Дж. Р. Прист, Am. Journ. Phys. 38, , 1160 (1970).

2. А. А. Бартлетт, Х. Кларк, Р. Столлер, К. Зафиратос, Г. Фладстол и L. Laingor, Am. Journ. Phys. 43, , 561 (1975).

3. Б. Штальберг и Э. Персонен, Am. Journ. Phys. 50, , 470 (1982).

4. Х. Ф. Майнерс, Демонстрационные эксперименты по физике , том I, Рональд Пресс Компани: Нью-Йорк (1970).

5. Эглер Р.А., Phys. Учить. 27, , 356 (1989).

1,6

Баллистика Автомобиль

Машина, катящаяся по столу, выпускает снаряд прямо вверх, а затем улавливает это, показывая, что горизонтальная скорость объекта не зависит вертикальной силы.
МАТЕРИАЛЫ
  • автомобиль с подпружиненным механизмом *
  • стальной шар *
  • картон или другой туннель (по желанию)
* Можно приобрести в компании Carolina Biological Supply Company, Central Scientific Company и Sargent-Welch Scientific Company
ПРОЦЕДУРА
Маленькая машинка, которую можно катать по столу, оснащена подпружиненным механизм, толкающий стальной шар вертикально вверх.Как катится машина через стол веревка, которая надежно прикреплена к чему-то на стол, натягивается и вытаскивает штифт, освобождая пружину без значительно изменяя скорость автомобиля. При падении мяч поймали на машине.

Сначала слушателям объясняется принцип действия устройства, а затем штифт вытаскивается, когда автомобиль стоит. Наконец-то машина катится через стол, чтобы завершить демонстрацию. В качестве украшения машину можно заставить пройти через короткий туннель, пока мяч проходит через верх туннеля.В более крупномасштабной демонстрации достаточно большой автомобиль для проезда лектора можно использовать [1].

ОБСУЖДЕНИЕ
Эта демонстрация иллюстрирует независимость вертикального и горизонтального движение снарядов. Поскольку мяч запускается из машины, движущейся с постоянная горизонтальная скорость, мяч имеет такую ​​же горизонтальную скорость как автомобиль и, таким образом, остается прямо над ним (игнорируя трение колеса и возможное различное сопротивление воздуха шара и автомобиля).В качестве альтернативы можно использовать эту демонстрацию, чтобы проиллюстрировать преобразование систем координат. В инерционной системе, движущейся вместе с автомобилем, мяч движется прямо вверх и вниз. В системе, закрепленной в помещении, мяч следует по параболической траектории.
ОПАСНОСТИ
Следует позаботиться о том, чтобы машина не скатывалась с края стола, не столько потому, что это может кого-то травмировать, сколько потому, что машина может получить повреждения, если упадет на пол.Также держите пространство над автомобилем свободным чтобы мяч не касался чего-либо.
ССЫЛКА
1. Х. Ф. Майнерс, Демонстрационные эксперименты по физике , Том I, Рональд Пресс Компани: Нью-Йорк (1970).

1,7

Ведро с водой

Ведро с водой можно вращать по вертикальному кругу без воды. разлив, чтобы проиллюстрировать первый закон движения Ньютона.
МАТЕРИАЛЫ
  • ведро воды с надежной ручкой
  • ведро конфетти (по желанию)
  • поднос с несколькими рюмками, наполненными водой (по желанию)
ПРОЦЕДУРА
Идея центростремительных и центробежных сил и ускорений может быть наглядно показано ведро, частично заполненное водой.Ведро можно крутить по вертикальному кругу, не проливая воду. Один может тайно обменять ведра на ведро с конфетти, которое затем его бросили в аудиторию. Другие более опасные демонстрации тоже можно сделать. Ведро можно заменить на поддон, вмещающий несколько фужеры с водой. Веревка, прикрепленная к лотку через отверстия на каждый из четырех углов используется для поворота подноса по кругу [1]. Однажды аспирант-физик принес своего маленького сына в корзину но передумал, когда его родительские инстинкты (и, возможно, ужас его жены) лишил его веры в законы физики!
ОБСУЖДЕНИЕ
Согласно первому закону движения Ньютона, движущиеся объекты имеют тенденцию оставаться в движении, если на него не действует внешняя сила.В этом случае Ньютон Закон требует, чтобы вода продолжала двигаться по касательной к окружности. Таким образом, требуется сила, чтобы он всегда поворачивался к центру круг. Интерпретация этой демонстрации потенциально сбивает с толку если учесть, что в верхней части дуги вода ускоряется вниз из-за движения, но сила тяжести также направлена ​​вниз. Можно объяснить, что F = ma, таким образом, выполняется без выхода воды. ведро.Эта демонстрация дает возможность обсудить неинерциальные (ускоренные) системы отсчета и инерционные (фиктивные) силы (такие как центробежная сила).
ОПАСНОСТИ
Опасности этой демонстрации довольно очевидны. Убедитесь, что область полностью свободен от препятствий и что ручка надежно закреплена в ведро. Кроме того, не качайте ведро слишком медленно!
ССЫЛКА
1. T. L. Liem, Invitations to Science Inquiry , Ginn Press: Lexington, Массачусетс (1981).

1,8

Инерционные шары

Свойство инертной массы иллюстрируется натягиванием за привязанную веревку. на дно тяжелого мяча, подвешенного на идентичной веревке пока одна из струн не порвется.
МАТЕРИАЛЫ
  • тяжелый железный шар с крючками на противоположных сторонах (второй шар опционально) *
  • несколько длин веревки
  • жесткая опора
  • резиновая прокладка
* Можно получить в компании Central Scientific, Fisher Scientific и Sargent-Welch Scientific Company
ПРОЦЕДУРА
Подвешены два одинаковых тяжелых стальных шара с крючками на противоположных сторонах. от подставки струнами [1].Важно, чтобы опора была достаточно жесткий. Снизу каждого шара свисает веревка. Слушателям говорят что все строки идентичны и попросили проголосовать за то, какая строка будет сломаться первым, если нижняя струна натянута на один из шаров. Если аудитория голосов за то, что верхняя струна порвется первой, один протягивает руку и дает дергать струну рывком, чтобы она порвалась ниже мяча. Пока зрители ломают голову над тем, почему их интуиция ошибалась, предлагают повторить поэкспериментируйте со вторым мячом, отметив важность повторения научные эксперименты, но на этот раз струна натянута очень осторожно чтобы веревка порвалась над мячом.Зрителей просят объяснить почему результат был другим. Если бы голосование было противоположным, можно было бы поменяйте порядок демонстраций. Важность контроля можно обсудить все соответствующие переменные в эксперименте. Один мяч можно использовать, если вы потратите время, чтобы перевязать веревку между каждым демонстрация.
ОБСУЖДЕНИЕ
Объяснение связано с инерцией мяча. Быстрым рывком мяч должен ускоряться, и для этого требуется значительная сила если масса шара большая (F = ma).С другой стороны, с медленным тянуть, ускорение незначительно, а верхняя струна поддерживает вес мяча плюс натяжение нижней струны, в результате чего верхнюю струну порвать. Из второго закона Ньютона, T u — T l = m (g-a), где T u — натяжение верхней струны, T l — натяжение нижней струны, m — масса мяча, g — ускорение свободного падения (9,8 м / с 2 ), a — нисходящий ускорение мяча.Таким образом, верхняя струна рвется, когда нисходящая ускорение мяча менее 9,8 м / с 2 ; в противном случае рвется нижняя струна.
ОПАСНОСТИ
Опасность состоит в том, что при обрыве верхней струны мяч падает на человека. рука или нога. Демонстрацию следует проводить с резиновой прокладкой под ней. чтобы поймать мяч, и руку нужно быстро убрать, когда веревка перерывы.
ССЫЛКА
1. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

1,9

Вращающийся шарик и отрезная струна

Требование, чтобы объект двигался по прямой линии при отсутствии внешняя сила иллюстрируется выпуском вращающегося шара в определенном точка на своей орбите.
МАТЕРИАЛЫ
  • шар из пенополистирола, яркий цвет
  • двигатель с поворотным рычагом
  • домкрат
  • лезвие бритвы или острый нож
  • светлая струна или нить
ПРОЦЕДУРА
Шарик из пенополистирола, желательно яркого цвета, прикрепляется к легкой веревке. или нити и закрутите по кругу на конце руки, которая мотором.На домкрат устанавливается острый нож или лезвие бритвы, чтобы что его можно медленно поднять до точки, где он перерезает струну. При перерезании струны мяч улетает по касательной к окружности. Направление, в котором движется мяч, контролируется размещением нож.
ОБСУЖДЕНИЕ
Эта демонстрация иллюстрирует первый закон Ньютона. Когда веревка перерезана, больше нет радиально направленной внутрь силы, заставляющей мяч двигаться внутрь круг, и мяч продолжает двигаться по прямой траектории, кроме за эффект гравитации.

Угроза перерезания струны обычно заставляет зрителей съежиться на своих местах, так как мяч выглядит тяжелым и опасным, и поскольку интуитивно кажется, что направление, в котором пойдет мяч, не может быть точно предсказал. Однако мяч всегда улетает под прямым углом. до линии между ножом и центром круга. Таким образом, можно достаточно точно выстроить его траекторию. В любом случае мяч легкий достаточно, чтобы не причинить травм.

ОПАСНОСТИ
Основная опасность — для человека, проводящего демонстрацию. Винт домкрата должен располагаться рядом с вращающимся рычагом, поэтому следует соблюдать осторожность не ударяться вращающимся рычагом.

1,10

Игрушечные ракеты

Третий закон Ньютона и сохранение импульса иллюстрируются использование игрушечных ракет.
МАТЕРИАЛЫ
  • игрушечные ракеты *
  • дождеватель газона и сжатый воздух (опция)
  • огнетушитель двуокиси углерода (опция)
* Можно приобрести в компании Carolina Biological Supply Company, Central Scientific Company, Fisher Scientific, Frey Scientific Company, Nasco и Estes Industries (П.О. Box 227, Penrose, CO 81240)
ПРОЦЕДУРА
Игрушечные ракеты доступны во многих магазинах игрушек, а также у поставщиков научных товаров. аппарат. Ракеты, подходящие для демонстрации в помещении, используют сжатый воздух. и воду [1] или картридж со сжатым диоксидом углерода в качестве пропеллента. Твердотопливные ракеты наиболее безопасно демонстрировать на открытом воздухе. Скромнее демонстрации можно проводить с воздушными шарами, которые быстро выбрасывают воздух. С помощью водяной ракеты можно изучить эффект от использования различных пропорции воздуха и воды.

Ракета может быть прикреплена к проводу, протянутому через комнату или до потолок, чтобы контролировать направление полета ракеты. Ракета может также быть помещенным на конец вращающегося рычага для управления его траекторией [1]. Альтернативная демонстрация работы дождевателя газона на сжатом воздухе того же принципа, а также демонстрация сохранения угловой момент. Толпа думает, что спринклер подключен к воде а не воздух быстро обращает на себя внимание при включении!

Огнетушитель из углекислого газа обеспечивает тягу, достаточную для впечатляющих ракетные демонстрации.Сидя на вращающемся стуле или стоя на вращая платформу, можно заставить вращаться очень быстро. Углекислый газ огнетушитель, установленный на тележке [2] или велосипеде, сдвинет один на несколько сто футов. Роликовые коньки — еще одна возможность.

ОБСУЖДЕНИЕ
Обсуждение эффективно начинается с противопоставления ракеты и все другие транспортные средства, которые движутся за счет приложения силы к среде через через которые или через которые они движутся.Автомобиль движется вперед благодаря силы реакции между колесами и землей. Самолет движется вперед за счет силы реакции воздуха, который толкается назад лопасти пропеллера или турбины. Многие люди неправильно понимают и думают, что ракета работает, отталкиваясь от чего-то. Бросая баскетбольный мяч Стоя на платформе, которая может свободно вращаться, помогает развеять это представление.

Ракета движется вперед за счет силы реакции выбрасываемого выхлопа. самой ракеты.Другими словами, общий импульс ракеты и выхлоп постоянный. Общая ситуация описывается (нерелятивистской) уравнение ракеты v f = v i + v e ln (M i / M f ), где v i и v f — начальная и конечная скорости ракеты соответственно, v e — скорость истечения относительно ракеты и M i и M f являются начальными и конечные массы ракеты соответственно с учетом потери массы из-за выброшенного топлива.С другой стороны, можно объяснить движение ракета с точки зрения центра масс ракеты и движения выхлопа с постоянной скоростью. Тяга ракеты определяется величиной величины v e dM / dt и имеет те же единицы, что и сила. В тяга должна превышать вес (Mg), чтобы ракета оторвалась от земли. Кинетическая энергия ракеты исходит из запасенной потенциальной энергии. в виде сжатого газа (давление умноженное на объем) или химических связей, в зависимости от типа пороха.

ОПАСНОСТИ
Игрушечные ракеты могут быть очень опасными, если на них нацелены. Надо знать характеристики ракеты, которая будет использоваться, и отработка стрельбы в направлении, которое никому не причинит вреда и не повредит находящееся поблизости оборудование.
ССЫЛКИ
1. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

2. Ф. Холт, Г. Аманн, Phys. Учить. 27, , 560 (1989).

1,11

Роликовая цепь

Вращающаяся цепь сохраняет свою круглую форму при движении по лекции. стол и предметы на его пути.
МАТЕРИАЛЫ
  • небольшая гибкая цепочка (длиной около 60 см), завернутая в петлю
  • деревянный диск для цепи
  • электродвигатель
  • деревянная палка
ПРОЦЕДУРА
Цепь наматывалась на деревянный цилиндр и закручивалась до большого вращательного Скорость электродвигателя может быть сбита с цилиндра палкой [1,2].Цепочка сохранит круглую форму и будет катиться по лекции. стол и объекты на своем пути, пока в конечном итоге не остановится в куча на полу на некотором расстоянии. Цепь можно заставить лазить пандус и перелететь через комнату. Цилиндр диаметром 20 см с частотой вращения 2500 rpm делает эффективную демонстрацию.
ОБСУЖДЕНИЕ
Цепочка сохраняет свою форму за счет инерции каждого из ее звеньев. которые стремятся двигаться по прямой касательной к окружности.Эта тенденция часто приписывают центробежной силе, направленной наружу, но это не сила совсем. Фактически сила — это центростремительная сила, действующая к центру. круга, чтобы цепь не разлетелась. Альтернативно, можно описать поведение цепочки в терминах сохранения углового момента, который требует, чтобы он продолжал вращаться до тех пор, пока момент трения приводит его в состояние покоя.
ОПАСНОСТИ
Достаточно легкая цепь, вращающаяся с умеренной скоростью, относительно безвредна. и даже может быть забавным, если пытается сбить человека, но даже в этом случае Лучше всего направить его на стену и подальше от хрупкого оборудования.Это будет двигайтесь по достаточно прямой линии, если не отклонитесь.
ССЫЛКИ
1. Х. А. Робинсон, изд., Демонстрации лекций по физике , американский Институт физики: Нью-Йорк (1963).

2. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

1,12

Подвижная шпуля

Большая деревянная катушка (или йо-йо) с обмотанной снизу веревкой можно заставить двигаться либо в том направлении, в котором натянута струна или в обратном направлении в зависимости от угла струны с относительно горизонтали.
МАТЕРИАЛЫ
  • деревянная шпуля или йо-йо
  • строка
  • штангенциркуль и транспортир (опционально)
ПРОЦЕДУРА
Демонстрация [1] эффективно вводится, предлагая аудитории предсказать, катушка будет двигаться вперед или назад при натяжении струны. какой бы ни так как большинство голосов аудитории, катушка может быть в противоположном направлении, потянув за шнур под соответствующим углом.Маленький угол (тета) между тетивой и горизонталью сделает катушку двигайтесь в направлении тяги, и большая (тета) заставит катушку отойдите от тяги. Изменение угла настолько мало, что публика не замечать меняет направление. Поведение шпули довольно загадочно.
ОБСУЖДЕНИЕ
Объяснение включает рассмотрение сил и моментов на катушка (см. схему). Проще всего рассмотреть случай, когда строка тянут с силой и под таким углом, чтобы катушка находилась как раз на граница скольжения без перекатывания.Есть четыре силы: вес (мг), направленная вверх нормальная сила стола (Н), натяжение струны (Т) и сила трения (мкН). Если катушка еще не двигается, чистая горизонтальная сила равна нулю, или T cos (theta) = мкН. Только двое из силы создают крутящий момент вокруг центра золотника (Т и мкН), и эти моменты должны быть равны и противоположны, если катушка должна проскальзывать. чем повернуть. Уравнивание крутящих моментов дает r 1 T = r 2 мкН. Разделив это уравнение на предыдущее, получим cos (theta) = r 1 / r 2 .Таким образом, критический угол, определяющий направление вращения катушки. зависит только от соотношения двух радиусов и не зависит от массы катушки, натяжения струны и коэффициента трения. С помощью штангенциркуля и транспортира можно проверить предсказанный критический угол. Это особенно интересный пример равновесия жесткого тело.
ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКА
1.Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

1,13

Стопка карт

Статическое равновесие твердого тела иллюстрируется стопкой карточек. которые имеют внушительный свес.
МАТЕРИАЛЫ
  • стопка карточек, блоков или счетчиков
ПРОЦЕДУРА
Для небольшой аудитории можно использовать колоду обычных игральных карт.За большая группа, несколько десятков одинаковых квадратов картона или блоков дерево обеспечивает лучшую видимость. Более количественная демонстрация может быть это делается с помощью стопки метровых палочек, которые также можно подвесить в форма мобильного [1,2]. Самая верхняя карта колоды сдвигается по горизонтали. пока он не собирается опрокинуться (половина должна поддерживаться карточка внизу). Затем две верхние карты сдвигаются в одном направлении. и так далее, пока самые верхние карты не будут выходить на удивительно большое расстояние за основанием колоды.Для большей драмы позвольте стеку висеть над край стола [3]. Затем публике остается недоумевать, почему колода не опрокидывается. Пара колоды карт размещены рядом и стрижены в противоположных направлениях можно использовать для создания впечатляющего отдельно стоящего арка.
ОБСУЖДЕНИЕ
Правило состоит в том, что стопка карт находится в стабильном равновесии, пока центр тяжести всех карт выше определенной точки лежит над часть карты прямо под этой точкой.Центр тяжести верхняя карта находится в середине, поэтому она может нависать на половину своего ширина. В таком положении центр тяжести двух верхних карт оказывается таким что вторая карта может выступать на четверть своей ширины. Третий карта может выступать на одну шестую своей ширины, четвертая — на одну восьмую и так далее (см. схему). Таким образом, общий выступ верхней карты в колоде из N карточек определяется суммированием 1/2 + 1/4 + 1/6 + 1/8 + ··· + 1 / 2N, который представляет собой гармонический ряд с суммой, равной 0.5 (0,5772 + lnN) для больших N. Таким образом, можно получить сколь угодно большой вылет, используя достаточно большое количество карточек. С 52 картами максимально стабильный свес в 2,27 раза больше ширины карты. При наличии поверхностного натяжения который может быть довольно большим, если у карточек гладкая поверхность, можно добиться даже больший вылет, чем предполагалось вышеупомянутым расчетом.
ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКИ
1.Р. Эрлих, Phys. Учить. 23 , 489 (1985).

2. I. MacInnes, Phys. Учить. 27, , 42 (1989).

3. J. P. VanCleave, Teaching the Fun of Physics , Prentice Hall Пресса: Нью-Йорк (1985).

1,14

Маятник Wilberforce

Пружинный маятник, сконструированный таким образом, чтобы крутильные и продольные частоты почти идентичны, медленно передает свою энергию туда и обратно между двумя режимами колебаний.
МАТЕРИАЛЫ
  • пружинный маятник со специально сконструированной массой *
* Можно получить в Центральной научной компании
ПРОЦЕДУРА
Явление резонанса можно продемонстрировать с помощью простого, но умного устройство, названное маятником Уилберфорса [1-6], названное в честь Лайонела Роберта Уилберфорса (1861-1944), демонстратор в Кавендишской лаборатории в Кембридже, Англия. на рубеже веков.Он состоит из подвешенной сверху массы к весне. Такой маятник имеет три режима колебаний: 1) обычный режим качания, 2) колебание вдоль оси пружины и 3) крутильный (крутильный) режим. Если резонансные частоты двух вторых моды почти идентичны, и одна мода первоначально возбуждена, другая режим будет медленно накапливать энергию, и энергия будет медленно передаваться обратно и вперед между режимами.
ОБСУЖДЕНИЕ
Угловая частота режима качания определяется как (г / л) ½ , где g = 9.8 м / с 2 , а L — длина маятника. В частота колебаний пружины определяется как (к / м) ½ где k — жесткость пружины, а m — масса, поддерживаемая пружиной. Наконец, крутильная частота определяется выражением (K / I) ½ , где K — постоянная кручения, I — момент инерции подвешенного масса. Обычно момент инерции контролируется несколькими болтами. ввинчивается в массу симметрично.Гайки с резьбой затем болты можно перемещать вперед и назад, чтобы изменить момент инерции без изменения массы. Таким образом, две частоты можно сделать почти равно.

Если не было связи между модами, энергия в каждой моде останется постоянным, игнорируя трение, и моды могут быть возбуждены в любой комбинации без последующего взаимодействия. На самом деле растяжение пружины создает небольшой крутящий момент, который возбуждает крутильный режим.Торсионный режим, в свою очередь, попеременно растягивает и сжимает пружину, захватывающий весенний режим. Необходимость иметь частоты почти равно то, что связь между модами мала, и, следовательно, энергия должны быть перенесены в течение нескольких циклов. Эффект весьма впечатляющий если частоты тщательно отрегулированы. Это пример гармонического Генератор приводится в действие на своей резонансной частоте небольшой движущей силой.

Есть много других примеров связанных осцилляторов [7-16].Обычно они состоят только из двух согласованных частот. Пара соседних маятников (спаренная маятник) соединены вместе вверху резинкой или слабая пружина — еще одна распространенная демонстрация.

ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКИ
1. Л. Р. Уилберфорс, Philos. Mag. 38 , 386 (1894).

2. Л. Р. Уилберфорс в Гармонические колебания и фигуры вибрации , под редакцией Герберта К.Ньютон, Ньютон и другие производители научных приборов: Лондон (1909).

3. V. Kopf, Am. J. Phys. 58, , 833 (1990).

4. Дж. Уильямс, Р. Кейл, Phys. Учить. 21, , 257 (1983).

5. R. J. Whitaker, Phys. Учить. 26, , 37 (1988).

6. Р. Э. Берг, Т. С. Маршалл, Am. J. Phys. 59, , 32 (1991).

7. Х. А. Робинсон, изд., Демонстрации лекций по физике , американский Институт физики: Нью-Йорк (1963).

8. M. G. Olsson, Am. Journ. Phys. 44, , 1211 (1976).

9. T. E. Clayton, Am. Journ. Phys. 45, , 723 (1977).

10. J. G. Lipham, V. Pollak, Am. Journ. Phys. 46, , 110 (1978).

11. L. Falk, Am. Journ. Phys. 46, , 1120 (1978).

12. L. Falk, Am. Journ. Phys. 47, , 325 (1979).

13. M. G. Rusbridge, Am. Journ. Phys. 48, , 146 (1980).

14. H. M. Lai, Am. Journ. Phys. 52, , 219 (1984).

15. P. A. Bender, Am. Journ. Phys. 53, , 1114 (1985).

16. Х. Ф. Мейнерс, Демонстрационные эксперименты по физике , Том I, Компания Рональда Пресс: Нью-Йорк (1970).

1,15

Время реакции

Расстояние, на которое объект падает в гравитационном поле Земли, может использоваться как чувствительная мера коротких временных интервалов.
МАТЕРИАЛЫ
  • метр
  • хрустящая долларовая банкнота
ПРОЦЕДУРА
Обычная демонстрация состоит в том, чтобы держать измерительную линейку вертикально от верх, в то время как доброволец стоит, готовый поймать его большим пальцем и указательный палец [1]. Если пальцы находятся напротив отметки 50 см, например, при падении измерителя положение пальцев при падении измерителя палка поймана дает меру расстояния, на которое палка упала до того, как волонтер мог отреагировать.Затем время рассчитывается из d = gt 2 /2, или t = (2d / g) ½ , где g = 9,8 м / с 2 и d равно сброшенное расстояние (в метрах). Для дополнительного интереса демонстрация можно сделать с помощью хрустящей долларовой банкноты большим и указательным пальцами волонтера напротив портрета Джорджа Вашингтона. Купюру можно сложить вдоль чтобы он падал прямо вниз, не отклоняясь от воздуха. Только небольшой фракция добровольцев может оплатить счет.Без особого риска, можно предложить счет волонтеру, если его поймают.

Учащимся можно предложить попробовать этот эксперимент дома, возможно, используя критерий и сравнить их время реакции с их друзьями и родственники. Их можно попросить сравнить время реакции людей. разного возраста и сообщить результаты.

ОБСУЖДЕНИЕ
Помимо иллюстрации движения объекта при постоянном ускорении, можно использовать такую ​​демонстрацию для обсуждения сбора и анализа научных данных.Проведя эксперимент с несколькими добровольцами и табулируя результаты, можно объяснить концепции среднего, среднего и стандартное отклонение. Результаты могут быть представлены в виде гистограммы. В самым быстрым волонтерам, находящимся в хвосте распределения, можно приказать идти гоночные машины. На самом деле время реакции — лишь один из факторов успеха автогонщик.

Время, необходимое для падения предмета, обеспечивает практический способ измерить, скажем, глубину колодца.Бросьте камень в колодец и измерьте время, необходимое для достижения дна. Дана глубина в футах by 16t 2 , где t — время в секундах. Высота обрыва можно определить аналогичным образом, бросив камень горизонтально с края обрыва.

ОПАСНОСТИ
Эта демонстрация не несет никакой опасности, кроме как для эго самые медленные волонтеры. Не роняйте и не бросайте камни, если есть опасность люди или собственность ниже.
ССЫЛКА
1. Х. Ф. Майнерс, Демонстрационные эксперименты по физике , Том I, Рональд Пресс Компани: Нью-Йорк (1970).

1,16

Стакан и скатерть

Стеклянный стакан, частично наполненный водой, стоит у края стола. на ткань, которую быстро вытаскивают из-под стакана без проливание воды или поломка стакана.
МАТЕРИАЛЫ
  • большой стеклянный стакан с гладким дном
  • гладкое полотно без шва
ПРОЦЕДУРА
Стакан наполняется водой примерно на две трети и кладется на ткань. некоторое расстояние от края стола.Убедитесь, что ткань, стол и мензурки чистые и полностью сухие. Стол и дно стакана должно быть гладким, а ткань не должна иметь шва по краю. Медленно потяните ткань до тех пор, пока стакан не окажется примерно в 2 см от края стола а затем быстро выдерните ткань из-под стакана. Стакан должен оставаться на столе, вода не должна проливаться. Когда обретешь уверенность, демонстрация может проводиться с другими объектами, такими как весь стол настройка, но проще всего, если у объектов гладкая нижняя поверхность.А бумажное полотенце можно использовать вместо ткани.
ОБСУЖДЕНИЕ
Согласно первому закону Ньютона, покоящийся объект стремится оставаться в покое. пока не подвергнется действию внешней силы. В этом случае внешняя сила сила трения между стаканом и движущейся тканью. Трение сила имеет максимальное значение, пропорциональное массе стакана и его содержание, F = µmg, где µ — коэффициент трения (обычно несколько десятых), а g — ускорение свободного падения (9.8 м / с 2 ). Согласно второму закону Ньютона, эта сила вызывает максимальное ускорение. из a = F / m = µg. Таким образом, если ткань потянуть осторожно (ускорение менее мкг) стакан ускоряется вместе с ним, но если ткань внезапно дергается (ускорение больше мкг) ткань удаляется прежде, чем стакан сможет разогнаться до значительной скорости. Какой маленький скорость, которую он действительно набирает, быстро сводится к нулю за счет трения между стакан и стол после того, как ткань была удалена.Вдобавок эффект, который способствует успеху демонстрации, заключается в том, что коэффициент трения скольжения меньше коэффициента статического трение. Обратите внимание, что масса объекта отменяется, в отличие от популярных заблуждение [1], так что трюк с тяжелым объект, чем со светлым. Этот факт можно проиллюстрировать повторением демонстрация с пустым стаканом.
ОПАСНОСТИ
Эту демонстрацию следует практиковать, чтобы развить уверенность в том, что стакан не сломается.Важно не бояться тянуть ткань. Даже в этом случае лучше всего организовать демонстрацию таким образом, чтобы стакан действительно сломается, опасность травмирования отсутствует. В частности, не тяните ткань к аудитории.
ССЫЛКА
1. T. L. Liem, Invitations to Science Inquiry , Ginn Press: Lexington, Массачусетс (1981).

1,17

Наклонная плоскость

Предметы, скользящие или катящиеся по наклонной плоскости, используются для иллюстрации трение и момент инерции.
МАТЕРИАЛЫ
  • доска прямая, гладкая, длиной не менее метра
  • блоки из различных материалов
  • разные цилиндры, сферы и обручи
  • транспортир (опция)
ПРОЦЕДУРА
На плоскости размещаются блоки из различных материалов (по одному или одновременно), и самолет наклоняется под углом, при котором блоки только начинают горка.Один показывает, что угол разный для разных материалов. например, гладкое дерево и резина. Покажите, что для данного материала критическая угол не зависит от массы объекта и площади контакта. Покажите, что угол, под которым блок начинает скользить, немного больше чем угол, необходимый для его скольжения во время движения. Угол можно измерить транспортиром.

При наклоне плоскости под фиксированным углом катятся цилиндры, сферы и обручи вниз по самолету [1].Прежде чем это будет сделано, попросите аудиторию предсказать который сначала достигнет дна. Повторите с объектами разного размера и той же массы и с объектами одинакового размера и разной массы. Покажите, что если самолет наклонен слишком круто, объекты будут скользить скорее. чем катиться.

Сравнить скорость качения объекта без скольжения и одного скольжения без трения (моделируется большой массой с маленькими колесами). Оба случая примерно экономят механическую энергию, но скользящий объект всегда достигает дна перед катящимся объектом, потому что весь начальный потенциал энергия преобразуется в поступательную энергию без потерь во вращении.

ОБСУЖДЕНИЕ
Трение создает силу в направлении, противоположном направлению, в котором что-то движется или пытается двигаться. Сила трения пропорциональна к нормальной силе, которая в данном случае является составляющей гравитационного сила на объект в направлении, перпендикулярном плоскости. Если самолет наклонен под углом (тета) к горизонтали, так что объект скользит или вот-вот скользит, сила трения направлена вверх по плоскости и имеет величину f = µW cos (theta), где W — вес, а µ — коэффициент трения.Количество µ обычно находится в диапазоне от 0,01 до 1,0 и зависит от материалов. и состояние (шероховатость) поверхностей, но не в зоне контакта. Коэффициент трения несколько зависит от скорости движения объекта. и, в частности, больше, когда объект находится в состоянии покоя (статическое трение) чем когда он находится в движении (кинетическое трение).

Блок начнет скользить, когда компонент гравитационного сила в направлении вдоль плоскости (W sin (theta)) просто равна трению сила, и, таким образом, tan (theta) = sin (theta) / cos (theta) = 1 / µ, независимый веса W.Измерение критического угла (тета), при котором блок начинает скользить, таким образом, измеряется коэффициент трения. Трение преобразует потенциальную энергию блока в верхней части уклона. в тепло, когда блок скользит вниз, так что он может достичь дна без потенциальной энергии и с очень небольшой кинетической энергией.

Когда угол наклона плоскости достаточно мал, что объект может катиться по самолету без проскальзывания, нет относительной скорости между точка на объекте, которая соприкасается с плоскостью и плоскостью, и, таким образом, трение не действует на объект, и все механические энергия сохраняется.Однако, когда объект скатывается по плоскости, его первоначальная потенциальная энергия преобразуется как в поступательную энергию центра масс. а также в энергию вращения. Отношение вращательного к поступательному энергия I / mr 2 где I — момент инерции, m — масса и r — радиус объекта. Момент инерции MR 2 для обруча, mr 2 /2 для цилиндра и 2mr 2 /5 для сфера. Таким образом, обруч приобретает наибольшую энергию вращения и наименьшую поступательная энергия (и скорость) и, таким образом, требуется больше всего времени, чтобы спуститься самолет.Сфера — самая быстрая, а цилиндр — промежуточный. Поскольку начальная потенциальная энергия и конечная кинетическая энергия равны пропорциональные массе и не зависящие от радиуса, объекты одного и того же форма, но разная масса и радиус, движутся по плоскости с одинаковой скоростью. Если самолет наклонен слишком круто, объект будет скользить, трение будет делать работу, и скорость, с которой катятся предметы, предсказать труднее.

ОПАСНОСТИ
В этой демонстрации нет никаких опасностей, за исключением того, что когда объекты достигают нижней части склона, они захватываются таким образом, чтобы предотвратить их нанесение ущерба.
ССЫЛКА
1. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

1,18

Связанный Pendula

Два жестких маятника с одинаковой резонансной частотой соединены около сверху с резинкой, заставляя энергию переключаться туда и обратно между два.
МАТЕРИАЛЫ
  • две одинаковые жесткие маятники, поддерживаемые перекладиной сверху
  • резинки или слабые пружины
ПРОЦЕДУРА
После снятия резинки видно, что две маятники идентичны. с одним и тем же периодом, и каждый из них колеблется независимо от другого.Между ними прикреплена резинка или пружина, и обе маятники доведен до покоя. Затем запускают один маятник, раскачивающийся в плоскости, перпендикулярной к резинке. Через некоторое время первый маятник перестанет раскачиваться, а другой будет раскачиваться с большой амплитудой. Тогда первая будет медленно начните снова раскачиваться, пока второй успокоится и так далее пока энергия не будет погашена трением. Демонстрация может повторяется с соединенными резинками или пружинами разной жесткости на разном расстоянии от оси [1].
ОБСУЖДЕНИЕ
Резинка обеспечивает слабую связь между двумя маятниками, что позволяет энергия медленно передается от одного к другому. Чем сильнее сцепление (более жесткая резинка, чем дальше от оси), тем быстрее энергия переводы. Явление такое же, как и в маятнике Уилберфорса.

Идея может быть расширена на любое количество маятников и служит введение в движение волн. В электрических цепях энергия часто передается из одного резонансного контура в другой, настроенный на тот же частота за счет очень слабой электрической связи.Для радио и телевидения передачи, передатчик и приемник должны быть настроены на одну и ту же частоту и имеют узкую полосу пропускания.

ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКА
1. Дж. С. Миллер, Physics Fun and Demonstrations , Central Scientific Компания: Чикаго (1974).

1,19

Случайное блуждание

Несколько раз подбрасывая монету, чтобы определить направление поворота, можно выполнить случайное блуждание.
МАТЕРИАЛЫ
ПРОЦЕДУРА
Спросите аудиторию, был ли кто-нибудь когда-либо на случайной прогулке (иногда называемой «прогулка пьяницы»). Тогда предложите взять их на одного. Бросить монетку. Это это поднимается головы, поворачивает направо и делает большой шаг. Если выпадет решка, поверните налево и сделайте большой шаг. Повторите процесс много раз. Альтернативно, проиллюстрируйте метод одним или двумя шагами и побудите людей пойти выйти в большое поле и попробовать сами.Другой метод, который требует дольше, но хорошо работает, когда улицы в районе выстроены в линию в правильном прямоугольном шаблоне — ставить блок между каждым переворотом монета.

Так как эта демонстрация требует времени и наскучит после нескольких шагов, он идеально подходит для компьютерного моделирования. Легко программировать с помощью генератор случайных чисел, доступный на большинстве компьютерных языков. Например, короткая программа, которая будет работать под интерпретируемым BASIC на большинстве IBM-совместимых следующее:

10 ЭКРАН 1
20 CLS
30 Х = 160
40 Y = 100
50 А = INT (4 * RND)
60 ЕСЛИ A = 0 ТО X = X + 1
70 ЕСЛИ A = 1 ТО X = X-1
80 ЕСЛИ A = 2, ТО Y = Y + 1
90 ЕСЛИ A = 3 ТО Y = Y-1
100 PSET (X, Y)
110 GOTO 50

Зрителям можно сказать, что это то, что можно увидеть из самолет, летящий высоко над кем-то, совершающим случайное блуждание.В Полученный узор представляет собой фрактал с размерностью 1,5. Это на полпути между линия и поверхность. Молекулы в воздухе, которым мы дышим, движутся в случайном блуждании, за исключением трехмерного, а не двумерного Космос. Они меняют направление, когда сталкиваются с соседями, хотя изменение направления не всегда под прямым углом, и расстояние, на котором они переходить между столкновениями не всегда одинаково.

ОБСУЖДЕНИЕ
Хотя законы классической физики детерминированы, там, где есть много частиц, взаимодействующих друг с другом, например, в газе при атмосферном плотности, количество уравнений очень велико, и это практически невозможно. чтобы решить их все.В таких случаях более уместны статистические методы, и частицы в таком наборе будут перемещаться эффективно случайным образом. Если частицы ведут себя как твердые сферы, как они обычно ведут себя, если они электрически нейтральные, они движутся по прямой, пока не произойдет столкновение, после чего частицы разлетаются в произвольных направлениях. Механическая энергия обычно сохраняется при столкновении, хотя энергия может передаваться от одна частица к другой. Если частицы электрически заряжены, силы действуют на большие расстояния, а отклонение от прямой линии постепенное и непрерывно, но конечный результат тот же.То же верно, если частицы — это массивные астрономические объекты, управляемые дальнодействующими гравитационные силы.

Случайное блуждание характеризуется расстоянием d, называемым средним свободным путь (среднее расстояние, которое проходит частица до столкновения), и время (тау), называемое временем столкновения (среднее время между последовательными столкновения). Отношение двух и есть скорость частицы, v = d / (тау). Среднее расстояние, на которое частица проходит от исходного положения после время t определяется как r = d [t / (tau)] ½ (длина свободного пробега умноженное на квадратный корень из числа столкновений).Причина квадратного корня становится ясной, если рассмотреть частицу который перемещается на расстояние d, затем сталкивается на 90 ° и перемещается другое расстояние d. Согласно теореме Пифагора частица, таким образом, имеет переместился на расстояние d (2) ½ за время t = 2 (тау). Таким образом, если один подбрасывает монету 100 раз и каждый делает шаг в случайном направлении время, среднее расстояние, которое человек проходит, составляет 10 шагов. Не ожидайте, что это сработает после одного испытания, но в среднем по большому количеству испытаний следует приблизиться к ожидаемому результату.

ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.

1,20

Хаотический маятник

Различные маятники могут показывать хаотическое движение при воздействии нелинейная восстанавливающая сила.
МАТЕРИАЛЫ
  • два дисковых магнита
  • стальной шарик на конце струны
  • теннисный мяч (по желанию)
  • диапроектор (опция)
ПРОЦЕДУРА
Стальной шар или другой ферромагнитный предмет подвешен на веревке так, чтобы что он находится примерно в двух сантиметрах от пары дискообразных магнитов примерно в пяти сантиметрах друг от друга [1].Стальной шар можно поместить внутрь теннисный мяч, чтобы движения казались более загадочными. Весь аппарат может быть установлен на диапроектор для улучшения видимости. При отпускании маятник движется хаотично. Движение в конечном итоге останавливается с мячом над одним из магнитов, но траектория зависит чутко в исходной точке.

Эту демонстрацию лучше всего проводить после обсуждения и сопоставления периодическое движение обычного маятника.Укажите, что разница возникает потому, что возвращающая сила, создаваемая магнитом, очень нелинейна. в отличие от гравитационной силы, тангенциальная составляющая которой приблизительно равна пропорциональна углу, который маятник образует с вертикалью. Каждый магнит связал с ним область притяжения, которая определяет, какой начальный условия приблизятся к этому магниту. Граница бассейна — фрактал.

ОБСУЖДЕНИЕ
Хаотическое движение возникает всякий раз, когда детерминированная система демонстрирует поведение это выглядит случайным и чувствительно зависит от начальных условий.Только недавно стало широко известно, что даже очень простые уравнения могут быть такие решения. Однако уравнения должны включать нелинейность. В этом случае нелинейность возникает из-за притяжения магнитного поля. диполь магнита к наведенному магнитному диполю в стальном шаре. Такая сила очень сильна, но очень близка. С помощью одного магнита движение всегда будет распадаться до уникального конечного состояния, называемого «стабильным фиксированная точка ». Второй магнит допускает два конечных состояния, бассейны которых притяжение встречаются на фрактальной границе.Граница показывает структуру независимо от того, насколько сильно увеличены. Таким образом, две отправные точки вблизи границы могут иметь совершенно разные конечные условия. Эта чувствительность к начальному условия были названы «эффектом бабочки», потому что атмосфера предположительно хаотическая, детерминированная система, и, следовательно, хлопанье бабочки его крылья, скажем, в Бразилии могут вызывать торнадо в Техасе. Фактически, один из самых ранних примеров хаос был обнаружен в компьютерной модели атмосферного конвекция [2].
ОПАСНОСТИ
Эта демонстрация не представляет значительных опасностей.
ССЫЛКИ
1. Р. Эрлих, Поворачивая мир наизнанку, , Принстонский университет Пресса: Принстон, Нью-Джерси (1990).

2. Э. Н. Лоренц, J. Atmos. Sci. 20 , 130 (1963).

[Следующая глава] [Предыдущая Глава] [Главная страница сервера]

Дж. К. Спротт

Механическая вибрация | Статья о механической вибрации по The Free Dictionary

Механическая вибрация

Продолжающееся, повторяющееся и часто периодическое движение твердого или жидкого тела в определенных пространственных пределах.Вибрация часто возникает в различных природных явлениях, таких как приливное движение океанов, во вращающихся и неподвижных механизмах, в конструкциях, столь же разнообразных по своей природе, как здания и корабли, в транспортных средствах, а также в комбинациях этих различных элементов в более крупных системах. Источники вибрации и типы вибрационного движения и их распространение являются сложными предметами и во многом зависят от конкретных характеристик исследуемых систем. Кроме того, существует сильная связь между понятиями механической вибрации и распространением вибрации и акустических сигналов как через землю, так и через воздух, что создает возможные источники дискомфорта, раздражения и даже физического ущерба людям и строениям, прилегающим к источнику. вибрации.

Система масса-пружина-демпфер

Хотя явления вибрации сложны, некоторые основные принципы можно распознать в очень простой линейной модели системы масса-пружина-демпфер (см. Иллюстрацию). Такая система содержит массу M , пружину с жесткостью пружины k , которая служит для восстановления массы в нейтральное положение, и демпфирующий элемент, который противодействует движению колебательного отклика с силой, пропорциональной скорости движения. системы, где коэффициент пропорциональности равен постоянной демпфирования c .Эта демпфирующая сила является диссипативной по своей природе, и без ее присутствия реакция этой системы масса-пружина была бы полностью периодической.

Сложные системы

Вышеупомянутая модель линейной системы пружина-масса-демпфер содержит в себе ряд упрощений, которые никак не отражают условия реального мира. Эти упрощения включают периодичность как ввода, так и, в некоторой степени, отклика; дискретный характер входных данных, то есть предположение, что они временны по своей природе без привязки к пространственному распределению; и предположение, что для описания массы, жесткости и демпфирования требуются только одна резонансная частота и один набор параметров.Реальный мир намного сложнее. Многие источники вибрации непериодичны. К ним относятся импульсные силы и ударная нагрузка, когда к системе внезапно прикладывается сила на очень короткое время; случайные возбуждения, при которых сигнал колеблется во времени таким образом, что его амплитуда в любой данный момент может быть выражена только в терминах вероятностного ожидания; и апериодические движения, в которых флуктуация во времени может быть некоторой предписанной непериодической функцией или некоторой другой функцией, которая не всегда считается периодической.

Источники вибрации

Существует множество источников механической и структурной вибрации, с которыми инженер должен бороться как при анализе, так и при проектировании инженерных систем. Наиболее распространенная форма проблемы механической вибрации — это движение, вызванное механизмами различных типов, часто, но не всегда, вращающимися. К другим источникам вибрации относятся: распространение по земле в результате строительства; вибрация от тяжелых транспортных средств на обычном покрытии, а также вибрационные сигналы от железнодорожных систем, распространенные во многих городских районах; и вибрации, вызванные природными явлениями, такими как землетрясения и силы ветра.Волновое движение является источником вибрации в механических и конструкционных системах, связанных с морскими сооружениями.

Влияние вибрации

Наиболее серьезным эффектом вибрации, особенно в случае машинного оборудования, является то, что достаточно высокие переменные напряжения могут вызвать усталостное разрушение деталей машин и конструкций.

No related posts.

Leave a Reply

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *