Контрольная работа определение тригонометрических функций: Алгебра – 10 класс. Контрольные работы с ответами к учебнику Мордковича А.Г. за 1, 2, 3, 4 четверти

Содержание

Алгебра 10 клас контрольна робота 3

Скачать алгебра 10 клас контрольна робота 3 rtf

Контрольные работы по алгебре для 10 класса с ответами для любого учебника по курсу «Алгебра и начала анализа классы (базовый уровень)». Цитаты из пособия «Дидактические материалы по алгебре для классов / Зив, Гольдич» использованы в учебных целях. Алгебра 10 Контрольные работы Зив. Ответы адресованы родителям. Алгебра 10 класс (любой УМК) Контрольные работы (базовый уровень).

Контрольная работа № 1. Контрольная № 1 «Действительные числа» + Ответы. Контрольная работа № 2. Контрольная № 2 «Степенная функция» + Ответы. Контрольная работа № 3. Контрольная № 3 «Показательная функция» +. Контрольная работа по построению и преобразованию графиков тригонометрических функций.

Определения нулей функции и промежутков монотонности. Проверка на четность нечетность. Нахождения области определ. Контрольная работа по построению и преобразованию графиков тригонометрических функций.

Определения нулей функции и промежутков монотонности. Проверка на четность нечетность. Контрольная по алгебре 10 класса, контрольные работы по Мордковичу с ответами за 1, 2, 3, 4 четверти. Алгебра – 10 класс.

Контрольные работы с ответами к учебнику Мордковича А.Г. за 1, 2, 3, 4 четверти. Контрольные на темы: «Определение тригонометрических функций», «Свойства и графики тригонометрических функций», «Тригонометрические уравнения», «Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций» и др. Дополнительные материалы по алгебре Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.

Готовые Домашние Задания по Алгебре классы. Контрольные работы. Мордкович ГДЗ Решебник Контрольные работы Алгебра 10 класс Глизбург. Алгебра 10 классКонтрольные работыГлизбург«Мнемозина». Зачастую обучение в школе проходит не так гладко, как хотелось бы большинству родителей. Да это и не удивительно, учитывая сложность учебной программы. Поэтому учащимся может весьма пригодится решебник к учебнику «Алгебра 10 класс Контрольные работы, авторы: Глизбург» от издательства Мнемозина, которое входит в серии УМК «».

В сборнике подробно приводятся решения всех заданий, которые так же сопровождаются условиями. ГДЗ «Алгебра 10 класс Контрольные работы, авторы: Глизбург» помож.

Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразовательных организаций (базовый и углубленный уровни) / В. И. Глизбург ; под ред. А. Г. Мордковича. — 3-е изд., стер.

— М., — 64 с. Сборник контрольных работ составлен в полном соответствии с УМК А. Г. Мордковича и П. В. Семенова по алгебре и началам математического анализа для х классов с углубленным изучением математики. Каждый вариант контрольной работы выстроен по одной схеме: задания базового (обязательного) уровня — до первой черты, задания уровня выше среднего — между первой и второй чертой, задания повышенной сложности — после второй черты.

А Контрольная работа №1. Действительные числа. Вариант 1. 1. Вычислите: ; 2. Упростите выражение. 3. Решите уравнение. 4. Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной. дроби. 5. Сократите дробь. 6. Сравните числа: и 1; 7*. Упростите выражение. 1. Контрольная работа №1.

Действительные числа. Вариант 2. 1. Вычислите. Контрольная работа № 3 по алгебре в 10 классе с ответами. Используется при работе по УМК Никольский. Цитаты из пособия «Алгебра и начала математического анализа.

Дидактические материалы. 10 класс: базовый и углубленный уровни / Потапов, Шевкин» использованы в учебных целях. Ответы адресованы родителям. Алгебра 10 Никольский Контрольная 3 + ответы. Алгебра и начала анализа. 10 класс Контрольная работа № 3 (Никольский). Алгебра 10 Никольский Контрольная 3. К Вариант 3 (транскрипт). Найдите значение выражения (а1/2: а2/3)30 при а = (1/2)–2/5. Вычислите (21/3 • 9–1/3) / (6–2/3 • 43/2). Постро.

PDF, djvu, fb2, txt

Похожее:

О.

г стадник географія

Людовик 14 презентація

Основні положення еволюційного вчення чарльза дарвіна презентація

Практична робота користування засобами пожежогасіння

Нерівність доходів курсова

Контрольна робота 4 тригонометричні функції 10 клас

Скачать контрольна робота 4 тригонометричні функції 10 клас rtf

Пособие содержит самостоятельные и контрольные работы по всем важнейшим темам курса математики классов. Работы состоят из 6 вариантов трех уровней сложности. Дидактические материалы предназначены для организации дифференцированной самостоятельной работы учащихся. Контрольная работа 1 плейлиста Тригонометрия содержит тригонометрические уравнения и в видео показано решение Определение тригонометрических функций и их свойства.

Алгебра классы. Видеоурок #1. Видеоуроки математики. В данном видео содержится разбор контрольной работы по теме: Тригонометрические формулы в 10 классе. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. 1-класс 2-класс 3-класс 4-класс 5-класс 6-класс 7-класс 8-класс 9-класс класс класс. Решебники для го класса. Учебники для го класса. Решебники за 10 класс > Алгебра > А.Г. Мерзляк, В.Б.

Полонський, Ю.М. Рабінович, М.С. Якір. А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір. Загрузка Контрольні роботи. + Варіант 1. Контрольна робота 1№ Контрольна робота 2№ Контрольна робота 3№ Контрольна робота 4№ Контрольна робота 5№ Контрольна робота 6№ Контрольна робота 7№ Просмотр содержимого документа «Контрольная работа №1 по теме»Тригонометрические функции»». Вариант1. 1.Найти область определения и множество.

значений функции у=5 cos х. 2. Выяснить является функция у=2sin x – tg x. четной или нечетной? 3.Изобразить график функции у= sin x на. интервале (- 2п; 2п) и решить уравнение. sin x = 0,5. Ответы к контрольным и домашним самостоятельным работам приводятся в конце книги. 5. Тематика и содержание работ охватывают требования всех основных отечественных учебников алгебры и начал анализа 10—11 класса.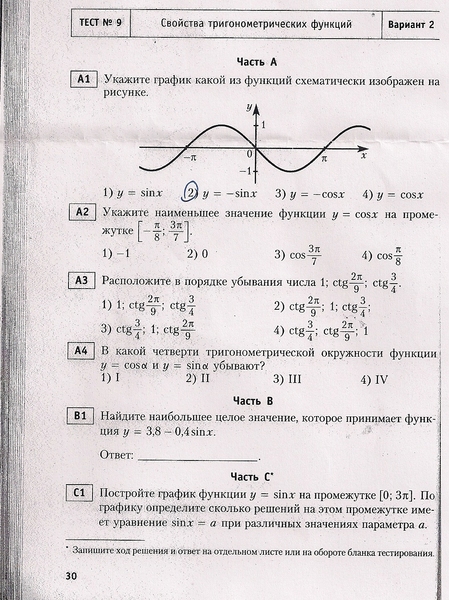

Для удобства пользования книгой приводится таблица тематического распределения работ по учебникам А. Н. Колмогорова и др., Н. Я. Виленкина и др. Наш адрес в Интернете: kinderugolok.ru ТРИГОНОМЕТРИЯ с Определение и свойства тригонометрических функций.

Головна» Професійна діяльність» Контрольні роботи» 10 клас, алгебра. У категорії матеріалів: 8 Показано матеріалів: Сортувати за: Даті · Назві · Рейтингу · Коментарям · Завантаженням · Переглядам.

КР 4 Означення та властивості тригонометричних функцій (2). КР 4 Означення та властивості тригонометричних функцій (2). КР 4.

Означення та властивості тригонометричних функцій. Контрольна робота №4 з алгебри та початків аналізу для 10 класу. Означення та властивості тригонометричних функцій. 10 клас, алгебра | Переглядів: | Завантажень: | Додав: petrovich | Дата: | Коментарі (0). КР 3. Степенева функція. Контрольна робота №3 з алгебри та початків аналізу. Контрольная работа 1 плейлиста Тригонометрия содержит тригонометрические уравнения и в видео показано решение Определение тригонометрических функций и их свойства.

Алгебра классы. Видеоурок #1. Видеоуроки математики. В данном видео содержится разбор контрольной работы по теме: Тригонометрические формулы в 10 классе. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Алгебра 10 класс. Контрольные работы. Глизбург. Мнемозина. В десятом классе школьникам предстоит ознакомиться с тригонометрией и производными. Темы сами по себе весьма сложные, так что отвлекаться во время уроков просто не рекомендуется.

Проверочные испытания и вовсе превращаются в настоящую полосу препятствий. Поэтому учащимся не стоит игнорировать призывы преподавателей дополнительно потренироваться дома. В качестве вспомогательного средства прекрасно подойдет решебник к учебнику «Алгебра. Контрольные работы 10 класс (базовый уровень)» Глизбург, в котором приведены все предстоящие работы.

PDF, doc, PDF, rtf

Похожее:

Планування інформатика 10 клас академічний рівень

Видатні люди буковини презентація

Економічна та соціальна географія україни 9 клас книга

Дпа 2014 9 клас фізика засєкіна

Природознавство 6 клас робочий зошит князева

5.

Определение тригонометрических функций

Функция косинус — это функция, которая ставит в соответствие каждому числу t абсциссу точки М(t) координатной окружности.

Функция синус — это функция, которая ставит в соответствие каждому числу

t ординату точки М(t) координатной окружности.

Если М(t) = М(х; у), то х = cos t, у = sin t

Таким образом,

М(t) = М(cos t; sin t)

Запись М(t) показывает положение точки М на координатной окружности, а запись М(cos t; sin t) – положение той же точки на координатной плоскости.

Функция тангенс — это частное от деления функции синус на функцию косинус.

Функция котангенс — это частное от деления функции косинус на функцию синус.

Поскольку деление на нуль невозможно, функции tg t и ctg t определены не для всех значений аргумента. Тангенс определен лишь для значений аргумента, при которых cos t  0, котангенс определен при sin t  0:

Тригонометрические функции — это общее название функций синус, косинус, тангенс и котангенс.

I. Основное тригонометрическое тождество и следствия из него:

II. Формулы (теоремы) сложения аргументов:

III. Формулы приведения:

1) функция меняется на кофункцию при переходе через вертикальную ось и не меняется при переходе через горизонтальную;

2) перед приведенной функцией ставится знак приводимой функции, считая  углом первой четверти.

IV. Формулы двойного аргумента:

V. Формулы понижения степени:

Значения тригонометрических функций некоторых углов

таблица 1

	0			
sin 	0		1	0	–1
cos 	1		0	–1	0
tg 	0	1	—	0	—
ctg 	—	1	0	—	0

Связь между тригонометрическими функциями одного аргумента

таблица 2

Искомая функция	Выражение искомой функции через
Искомая функция	sin 	cos 	tg 	сtg 
sin  =	sin 
cos  =		cos 
tg  =			tg 
сtg  =				сtg 

6.

Графики тригонометрических функций

Тригонометрический набор координат:

у = sin x синусоида

у = cos x косинусоида

у = tg x у = ctg x

тангенсоида котангенсоида

Контрольная работа № 4. «Тригонометрические уравнения». Вариант 2. Контрольная работа по теме «Тригонометрические формулы сложения аргументов».

Пояснительная записка
Рабочая программа по алгебре и началам анализа составлена в соответствии со стандартом общего образования (приказ Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного общего образования» от 05.

03.2004 года №1089), с авторской программой для общеобразовательных учреждений И. И. Зубаревой, А.Г. Мордкович «Программа. Алгебра и начала математического анализа.10-11 классы» — Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2011.
Всего часов 102
Количество часов в неделю 3
Количество учебных недель 34
Количество плановых контрольных работ 9
Из компонента образовательного учреждения на предмет «математика» выделен 1 час для развития содержания учебного материала на базовом уровне.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.

Цели
Изучение математики в старшей школе направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса
Задачи учебного предмета
Содержание образования, представленное в основной школе, развивается в следующих направлениях:
совершенствование техники вычислений
развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем
систематическое изучение свойств геометрических тел в пространстве, развитие пространственных представлений учащихся, освоение способов вычисления практически важных геометрических величин и дальнейшее развитие логического мышления учащихся
систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин
Общеучебные умения, навыки и способы деятельности
В ходе изучения математики в старшей школе учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:
проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решения широкого класса задач из различных разделов курса;
планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера;
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.

Основное содержание авторских программ полностью нашло отражение в данной рабочей программе, которая дает распределение учебных часов по разделам.
Основное содержание
Числовые функции (9 ч)
Основная цель Содержание
– формирование представления понятия об обратной функции.
– формирование умения задавать функцию различными способами; построение функций; задания обратной функции.
–развитие творческих способностей при работе с обратной функцией. Определение функции, способы ее задания, свойства функций. Обратная функция.
Тригонометрические функции (26 ч)
– формирование представления о числовой окружности, о числовой окружности на координатной плоскости;
– формирование умения находить значение синуса, косинуса, тангенса и котангенса на числовой окружности;
– овладение умением применять тригонометрические функции числового аргумента, при преобразовании тригонометрических выражений;
– овладение навыками и умениями построения графиков функций y = sin x, y = cos x, y = tg x,
y = ctg x;
– развитие творческих способностей в построении графиков функций y = m  f(x), y = f(k x), зная
y = f(x) Числовая окружность.

Длина дуги единичной окружности. Числовая окружность на координатной плоскости. Синус и коси-нус. Тангенс и котангенс. Тригонометрические функции числово-го аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Функция у = sin х, ее свойства и график. Функция у = cos x, ее свойства и график. Периодичность функ-ций у = sin x, у = cos х. Построение графика функций у = mf(x) и у = f(kx) по известному графику функции у = f(x). Функции у = tg х и у = ctg х, их свойства и графики.
Тригонометрические уравнения (10 ч)
– формирование представлений о решении тригонометрических уравнений на числовой окружности, об арккосинусе, арксинусе, арктангенсе и арккотангенсе;
– овладение умением решения тригонометрических уравнений методом введения новой переменной, разложения на множители;
– формирование умений решения однородных тригонометрических уравнений;
– расширение и обобщение сведений о видах тригонометрических уравнений Первые представления о решении тригонометрических урав-нений.

Арккосинус. Решение уравнения cos t ‘= а. Арксинус. Решение уравнения sin t = а. Арктангенс и арккотангенс. Реше-ние уравнений tg х = а, ctg x = а. Простейшие тригонометрические уравнения. Два метода решения тригономет-рических уравнений: введение новой пере-менной и разложение на множители. Однородные тригонометри-ческие уравнения.
Преобразования тригонометрических выражений (15 ч)
– формирование представлений о формулах синуса, косинуса, тангенса суммы и разности аргумента, формулы двойного аргумента, формулы половинного угла, формулы понижения степени;
– овладение умением применение этих формул, а также формулы преобразования суммы тригонометрических функций в произведение и формулы преобразования произведения тригонометрических функций в сумму;
– расширение и обобщение сведений о преобразовании тригонометрических выражений с применением различных формул Синус и косинус суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразова-ние сумм тригонометрических функций в произведение.

Преоб-разование произведений тригонометрических функций в суммы.
Производная (31 ч)
– формирование умений применения правил вычисления производных и вывода формул производных элементарных функций;
– формирование представления о понятии предела числовой последовательности и функции;
– овладение умением исследования функции с помощью производной, составлять уравнения касательной к графику функции Определение числовой последовательности и способы ее зада-ния. Свойства числовых последовательностей. Определение предела последовательности. Свойства сходящих-ся последовательностей. Вычисление пределов последовательно-стей. Сумма бесконечной геометрической прогрессии.
Итоговое повторение (11 ч)

Планирование учебного материала
Алгебра (102 ч)
Содержание материала Количество часов
Глава 1. Числовые функции
1. Определение числовой функции. Способы ее задания
2. Свойства функций
3. Обратная функция 9
3
3
3
Глава 2. Тригонометрические функции
4. Числовая окружность
5. Числовая окружность на координатной плоскости
Контрольная работа № 1
6. Синус и косинус. Тангенс и котангенс
7. Тригонометрические функции числового аргумента
8. Тригонометрические функции углового аргумента
9. Формулы приведения
Контрольная работа № 2
10. Функция у = sin х, ее свойства и график
11. Функция у = cos х, ее свойства и график
12. Периодичность функций у = sin х, у = cos x
13. Преобразования графиков тригонометрических функций 14. Функции у = tg х, у = ctg х, их свойства и графики
Контрольная работа № 3 26
2
3
1
3
2
2
2
1
2
2
1
2
2
1
Глава 3. Тригонометрические уравнения
15. Арккосинус и решение уравнения cos t = а 16. Арксинус и решение уравнения sin t = а
17. Арктангенс и арккотангенс. Решение уравнений tg х = а, ctg х = а
18. Тригонометрические уравнения
Контрольная работа № 4 10
2
2
1
4
1
Г л а в а 4. Преобразование тригонометрических выражений
19. Синус и косинус суммы и разности аргументов
20. Тангенс суммы и разности аргументов 21. Формулы двойного аргумента
22. Преобразование сумм тригонометрических функций в произведения
Контрольная работа № 5
23. Преобразование произведений тригонометрических функций в суммы 15
4
2
3
3
1
2
Г л а в а 5. Производная
24. Числовые последовательности и их свойства. Предел последовательности
25. Сумма бесконечной геометрической прогрессии
26. Предел функции
27. Определение производной
28. Вычисление производных
Контрольная работа № 6
29. Уравнение касательной к графику функции
30. Применение производной для исследований функций
31. Построение графиков функций
Контрольная работа № 7
32. Применение производной для отыскания наибольшего
и наименьшего значений непрерывной функции на промежутке
Задачи на отыскание наибольших и наименьших значений величин
Контрольная работа № 8
31
2
2
3
3
3
1
2
3
3
1
3
3
2
Обобщающее повторение 11

Аттестация обучающихся проводится в соответствии с Положением о системе оценок. Осуществляется текущий, тематический, итоговый контроль. Текущий контроль уровня усвоения материала осуществляется по результатам выполнения учащимися самостоятельных работ, решения задач, выполнения тестов. Промежуточная аттестация проводится в соответствии с Уставом образовательного учреждения в форме контрольной работы.
КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1. «Числовая окружность»
Контрольная работа № 2. «Тригонометрические функции»
Контрольная работа № 3. «Свойства и графики тригонометрических функций»
Контрольная работа № 4. «Тригонометрические уравнения»
Контрольная работа № 5. «Преобразование тригонометрических выражений»
Контрольная работа № 6. «Вычисление производной»
Контрольная работа № 7. «Применение производной для исследований функций»
Контрольная работа № 8. «Применение производной для отыскания наибольшего и наименьшего значения функции»
Контрольная работа № 9. «Итоговая»
Учебно-методический комплект и дополнительная литература
Мордкович. А.Г. Алгебра и начала математического анализа. 10-11 классы: учебник для учащихся общеобразовательных учреждений (базовый уровень) / [А. Г. Мордкович и др.]; под ред.А.Г. Мордковича — М: «Мнемозина», 2011
Мордкович. А.Г. и др. Алгебра и начала математического анализа. 10-11 класс: задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович и др.]; под ред.А.Г. Мордковича — М.: Мнемозина, 2011
Мордкович А.Г. Тульчинская Е.Е. Алгебра и начала анализа. 10-11 класс.: Контрольные работы для общеобразоват. учреждений.-М.: Мнемозина, 2000
Мордкович. А.Г. Алгебра и начала анализа. 10 –11 кл. Методическое пособие для учителя. – М.: Мнемозина, 2000
Математика: ежемесячный научно-методический журнал издательства «Первое сентября»
Интернет-ресурсы: электронные образовательные ресурсы из единой коллекции цифровых образовательных ресурсов (http://school-collection.edu.ru/), каталога Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/): информационные, электронные упражнения, мультимедиа ресурсы, электронные тесты (для подготовки к ЕГЭ)
Контрольные работы по алгебре и началам анализа в 10 классе.
Контрольная работа по теме «Определение тригонометрических функций»

Вариант 2

Контрольная работа по теме «Свойства и графики тригонометрических функций»
Вариант 1.

Вариант 2.

Контрольная работа по теме «Тригонометрические уравнения».
Вариант 1.

Вариант 2.

Контрольная работа по теме «Тригонометрические формулы сложения аргументов».
Вариант 1.

Вариант 2.

Контрольная работа по теме «Формулы тригонометрии».
Вариант 1.

Вариант 2.

Контрольная работа по теме «Правила и формулы отыскания производных»
Вариант 1.

Вариант 2.

Контрольная работа по теме «Применение производной к исследованию функций».
Вариант 1.

Вариант 2.

Домашня контрольна робота 10 клас

Скачать домашня контрольна робота 10 клас rtf

Алгебра Алгебра и начала анализа. Контрольные работы Мордкович А.Г. 10 класс. Задание не найдено. Контрольная работа №1. Вариант 1. 1. Контрольная работа № Вариант 1. 1. РДР по математике для 10 класса — сентябрь, октябрь года; Условия заданий, решение, ответы, критерии; Страница 1. Диагностическая работа по математике по разделу теория вероятностей и статистика 8 класс Сентябрь ВПР по математике 7 класс сентябрь ВПР по математике 8 класс сентябрь Тренировочная работа в формате ВПР по математике 7 класс Статград.

Диагностическая работа по математике 8 класс Контрольная работа по математике 8 класс за первое полугодие. Контрольная работа по математике 7 класс за первое полугодие. ВПР по математике 8 класс демовариант. 7 класс Входная мониторинговая контрольная работа Контрольная по алгебре 10 класса, контрольные работы по Мордковичу с ответами за 1, 2, 3, 4 четверти. Домашние задания. Мордкович А.Г. 10 КЛАСС. Контрольные работы. Мордкович А.Г. Атанасян Л.С. Алгебра – 10 класс.

Контрольные работы с ответами к учебнику Мордковича А.Г. за 1, 2, 3, 4 четверти. Контрольные на темы: «Определение тригонометрических функций», «Свойства и графики тригонометрических функций», «Тригонометрические уравнения», «Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций» и др. Если сомневаетесь, стоит ли школьникам пользоваться ГДЗ по алгебре 10–11 класс Мордкович, то подумайте – многим ли в жизни пригодились школьные знания по основам матанализа, комбинаторики или тригонометрии?

Только тем, кто поступил в профильные ВУЗы и нашел работу по специальности. Решебник позволит остальным не тратить зря время на зубрежку. Смотря в нем ответы и подробный ход решения задач, старшеклассники смогут качественно подготовиться к действительно нужным предметам, пообщаться с друзьями, заняться спортом. Самостоятельные и контрольные работы. Алгебра и начала анализа, 10 класс. Математика 10 класс. • 10 класс • проверка знаний, конспект. Комплект из 12 самостоятельных и 8 контрольных работ для проверки усвоения знаний по курсу алгебры и начал анализа для УМК А.Г.Мордковича, 10 класс (базовый уровень).

Все работы в 4-х вариантах. Самостоятельные работы составлены Александровой, контрольные работы — Л.А.Глизбургом под редакцией автора УМК А.Г.Мордковича. ©. Коломина Наталья Николаевна.

Контрольные работы. Экзамены. Виртуальная шпаргалка. Test on line. Additional reserve. Алгебра 10 кл. Муравины Г.К. и О.В. Главная» Единая система оценки качества образования. ВПР. ДКР» Диагностические контрольные работы (ДКР) в 10 классе в учебном году (федеральный уровень). Диагностические контрольные работы (ДКР) в 10 классе в учебном году (федеральный уровень).

Письмо Федерального центра тестирования от № О проведении ДКР в 10 crystal-zvon.ru (скачать) (посмотреть). Письмо Министерства образования и МП СО от № О проведении диагностических crystal-zvon.ru (скачать) (посмотреть). crystal-zvon.ru (скачать) (посмотреть). Домашняя контрольная работа по теме «Тригонометрические уравнения» 10а класс.

I вариант II вариант. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему.

djvu, txt, djvu, djvu

Похожее:

Математика 2 клас задача 153

Беларуская мова 4 класс 2 частка решебник

Гдз з укр літ 5 клас авраменко

Збірник завдань з української мови для 2 класу

Рос мова 4 клас нова програма

Божинова ф. я. фізика. 9 клас комплексний зошит для контролю

Определение и графики тригонометрических функций

Углы (аргументы функций): \ (\ alpha \), \ (x \)
Тригонометрические функции: \ (\ sin \ alpha \), \ (\ cos \ alpha \), \ (\ tan \ alpha \), \ (\ cot \ alpha \), \ (\ sec \ alpha \), \ (\ csc \ alpha \)
Набор действительных чисел: \ (\ mathbb {R} \)
Координаты точек на окружности: \ (х \), \ (у \)

Радиус круга: \ (r \)
Целые числа: \ (k \)

Тригонометрические функции — это элементарные функции, аргументом которых является угол. Тригонометрические функции описывают соотношение сторон и углов прямоугольного треугольника. Приложения тригонометрических функций чрезвычайно разнообразны. Например, любые периодические процессы можно представить в виде суммы тригонометрических функций (рядов Фурье). Эти функции часто встречаются при решении дифференциальных и функциональных уравнений.
Тригонометрические функции включают следующие функции \ (6 \): синус, косинус, тангенс, котангенс, секанс и косеканс.Для каждой из этих функций существует обратная тригонометрическая функция.
Тригонометрические функции могут быть определены с помощью единичной окружности. На рисунке ниже показан круг радиуса \ (r = 1 \). На окружности есть точка \ (M \ left ({x, y} \ right) \). Угол между радиус-вектором \ (OM \) и положительным направлением оси \ (x \) — равен \ (\ alpha \).
Синус угла \ (\ alpha \) — это отношение \ (y \) — координаты точки \ (M \ left ({x, y} \ right) \) к радиусу \ (r: \)
\ (\ грех \ альфа = у / г \).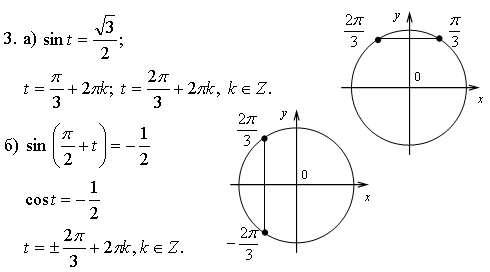
Поскольку \ (r = 1 \), синус равен \ (y \) — координате точки \ (M \ left ({x, y} \ right) \).
Косинус угла \ (\ alpha \) — это отношение \ (x \) — координаты точки \ (M \ left ({x, y} \ right) \) к радиусу \ (r: \)
\ (\ соз \ альфа = х / г \)
Тангенс угла \ (\ alpha \) — это отношение \ (y \) — координаты точки \ (M \ left ({x, y} \ right) \) к \ (x \) -координата:
\ (\ tan \ alpha = y / x, \; \) \ (x \ ne 0 \)
Котангенс угла \ (\ alpha \) — это отношение \ (x \) — координаты точки \ (M \ left ({x, y} \ right) \) к \ (y \) -координата:
\ (\ cot \ alpha = x / y, \; \) \ (y \ ne 0 \)
Секущая угла \ (\ alpha \) — это отношение радиуса \ (r \) к \ (x \) — координате точки \ (M \ left ({x, y} \ right) \ ):
\ (\ сек \ альфа = r / x = 1 / x, \; \) \ (x \ ne 0 \)
Косеканс угла \ (\ alpha \) — это отношение радиуса \ (r \) к \ (y \) — координате точки \ (M \ left ({x, y} \ right) \ ):
\ (\ csc \ alpha = r / y = 1 / y, \; \) \ (y \ ne 0 \)
Соотношение сторон и углов в прямоугольном треугольнике
В единичном круге проекции \ (x \), \ (y \) точки \ (M \ left ({x, y} \ right) \) и радиус \ (r \) образуют прямоугольный треугольник, в котором \ (x, y \) — катеты, а \ (r \) — гипотенуза. Поэтому приведенные выше определения сформулированы следующим образом:
Синус угла \ (\ alpha \) — это отношение противоположного катета к гипотенузе.
Косинус угла \ (\ alpha \) — это отношение соседнего катета к гипотенузе.
Тангенс угла \ (\ alpha \) — это отношение противоположного отрезка к соседнему отрезку.
Котангенс угла \ (\ alpha \) — это отношение соседнего отрезка к противоположному отрезку.
Секанс угла \ (\ alpha \) — это отношение гипотенузы к соседнему катету.
Косеканс угла \ (\ alpha \) — это отношение гипотенузы к противоположному катету.
График функции синуса
\ (y = \ sin x \), область определения: \ (x \ in \ mathbb {R} \), диапазон: \ (- 1 \ le \ sin x \ le 1 \)
График функции косинуса
\ (y = \ cos x \), область определения: \ (x \ in \ mathbb {R} \), диапазон: \ (- 1 \ le \ cos x \ le 1 \)
График касательной функции
\ (y = \ tan x \), область определения: \ (x \ in \ mathbb {R}, \) \ (x \ ne \ left ({2k + 1} \ right) \ pi / 2 \), диапазон: \ (- \ infty \ lt \ tan x \ lt \ infty \)
График функции котангенса
\ (y = \ cot x \), область определения: \ (x \ in \ mathbb {R}, \) \ (x \ ne k \ pi \), диапазон: \ (- \ infty \ lt \ cot x \ lt \ infty \)
График функции секанса
\ (y = \ sec x \), область определения: \ (x \ in \ mathbb {R}, \) \ (x \ ne \ left ({2k + 1} \ right) \ pi / 2 \), диапазон: \ (\ sec x \ in \) \ (\ left ({- \ infty, -1} \ right] \ cup \ left [{1, \ infty} \ right) \)
График функции косеканса
\ (y = \ csc x \), область определения: \ (x \ in \ mathbb {R}, \) \ (x \ ne k \ pi \), диапазон: \ (\ csc x \ in \) \ (\ left ({- \ infty, -1} \ right] \ cup \ left [{1, \ infty} \ right) \)

5.

3 Другие тригонометрические функции — Precalculus

Цели обучения

В этом разделе вы:

Найдите точные значения секанса, косеканса, тангенса и котангенса тригонометрических функций для π3, π3, π4, π4 и π6. π6.
Используйте опорные углы для оценки тригонометрических функций секанс, косеканс, тангенс и котангенс.
Используйте свойства четных и нечетных тригонометрических функций.
Распознавать и использовать основные идентичности.
Оценивайте тригонометрические функции с помощью калькулятора.

Пандус для инвалидных колясок, отвечающий требованиям Закона об американцах с ограниченными возможностями, должен образовывать угол с землей, касательная которого равна 112112 или меньше, независимо от его длины. Касательная представляет собой коэффициент, поэтому это означает, что на каждый 1 дюйм подъема уклон должен иметь 12 дюймов пробега. Тригонометрические функции позволяют нам указывать формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла.Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.

Нахождение точных значений секанса, косеканса, тангенса и котангенса тригонометрических функций

Чтобы определить остальные функции, мы еще раз нарисуем единичный круг с точкой (x, y) (x, y), соответствующей углу t, t, как показано на рисунке 1.Как и в случае с синусом и косинусом, мы можем использовать координаты (x, y) (x, y), чтобы найти другие функции.

Рисунок 1

Первая функция, которую мы определим, — это касательная. Тангенс угла — это отношение значения y к значению x соответствующей точки на единичной окружности. На рисунке 1 тангенс угла tt равен yx, x ≠ 0.yx, x ≠ 0. Поскольку значение y равно синусу t, t, а значение x равно косинусу t, t, тангенс угла tt также можно определить как sintcost, cost ≠ 0. синткост, стоимость ≠ 0. Функция касательной обозначается как tan.tan. Остальные три функции могут быть выражены как обратные функциям, которые мы уже определили.

Секущая функция обратна функции косинуса. На рисунке 1 секущая угла tt равна 1cost = 1x, x ≠ 0,1cost = 1x, x ≠ 0. Секущая функция сокращается до sec.sec.
Функция котангенса обратна функции тангенса. На рисунке 1 котангенс угла tt равен costint = xy, y 0.costint = xy, y ≠ 0. Функция котангенса сокращенно обозначается cot.cot.
Функция косеканса обратна функции синуса. На рисунке 1 косеканс угла tt равен 1sint = 1y, y ≠ 0,1sint = 1y, y ≠ 0. Функция косеканса сокращенно обозначается как csc.csc.

Функции касания, секанса, косеканса и котангенса

Если tt — действительное число и (x, y) (x, y) — точка, в которой конечная сторона угла tt радиан пересекает единичный круг, то

tant = yx, x ≠ 0sect = 1x, x ≠ 0csct = 1y, y ≠ 0cott = xy, y ≠ 0tant = yx, x ≠ 0sect = 1x, x ≠ 0csct = 1y, y ≠ 0cott = xy, y ≠ 0

Пример 1

Нахождение тригонометрических функций из точки единичной окружности

Точка (−32,12) (- 32,12) находится на единичной окружности, как показано на рисунке 2.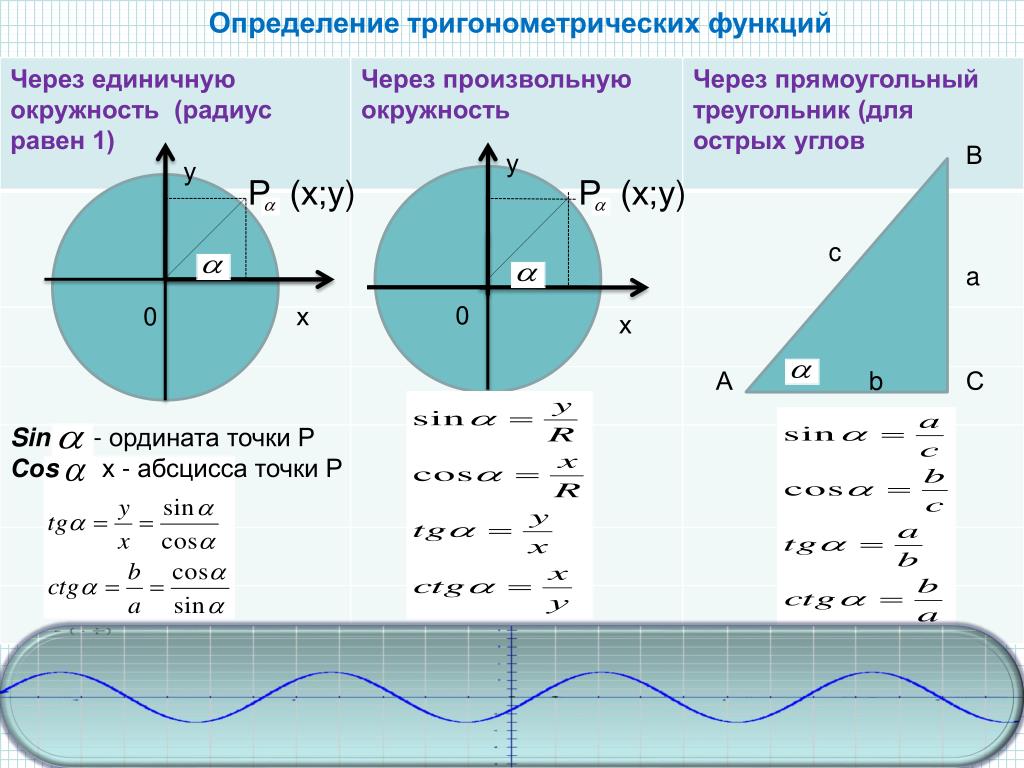 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott.

Рисунок 2

Решение

Поскольку нам известны координаты (x, y) (x, y) точки на единичной окружности, обозначенной углом t, t, мы можем использовать эти координаты для нахождения шести функций:

sint = y = 12cost = x = −32tant = yx = 12−32 = 12 (−23) = — 13 = −33sect = 1x = 1−32 = −23 = −233csct = 1y = 112 = 2cott = xy = — 3212 = −32 (21) = — 3sint = y = 12cost = x = −32tant = yx = 12−32 = 12 (−23) = — 13 = −33sect = 1x = 1−32 = −23 = −233csct = 1у = 112 = 2котт = ху = −3212 = −32 (21) = — 3

Попробуйте # 1

Точка (22, −22) (22, −22) находится на единичной окружности, как показано на рисунке 3.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott.

Рисунок 3

Пример 2

Нахождение тригонометрических функций угла

Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π6. t = π6.

Решение

Ранее мы использовали свойства равносторонних треугольников, чтобы продемонстрировать, что sinπ6 = 12sinπ6 = 12 и cosπ6 = 32.cosπ6 = 32.Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функций синуса и косинуса, чтобы найти остальные значения функции.

tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33 секунды π6 = 1cosπ6 = 132 = 23 = 233secπ6 = 1cosπ6 = 132 = 23 = 233 cscπ6 = 1sinπ6 = 112 = 2cscπ6 = 1sinπ6 = 112 = 2 cotπ6 = cosπ6sinπ6 = 3212 = 3cotπ6 = cosπ6sinπ6 = 3212 = 3

Попробуй # 2

Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π3.t = π3.

Поскольку нам известны значения синуса и косинуса для общих углов первого квадранта, мы можем найти другие значения функций для этих углов, установив xx равным косинусу и yy равным синусу, а затем используя определения тангенса, секанс, косеканс и котангенс. Результаты представлены в таблице 1.

Угол	00	π6, или 30 ° π6, или 30 °	π4, или 45 ° π4, или 45 °	π3, или 60 ° π3, или 60 °	π2, или 90 ° π2, или 90 °
Косинус	1	3232	2222	1212	0
Синус	0	1212	2222	3232	1
Касательная	0	3333	1	33	Неопределенный
Секант	1	233233	22	2	Неопределенный
Косеканс	Неопределенный	2	22	233233	1
Котангенс	Неопределенный	33	1	3333	0

Таблица 1

Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса

Мы можем оценивать тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже делали с функциями синуса и косинуса. Процедура такая же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке 4 показано, какие функции в каком квадранте положительны.

Чтобы помочь нам запомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера.Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который равен « A », 11 из шести тригонометрических функций положительны. В квадранте II « S mart» положительны только s ine и его обратная функция, косеканс. В квадранте III, «установка T », только угол t и его обратная функция, котангенс, положительны.Наконец, в квадранте IV « C девушка» положительны только осин c и его реципрокная функция, секанс.

Рисунок 4

Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций.

Измерьте угол, образованный конечной стороной данного угла и горизонтальной осью. Это опорный угол.
Оцените функцию под опорным углом.
Обратите внимание на квадрант, в котором находится конечная сторона исходного угла. Основываясь на квадранте, определите, будет ли выходной сигнал положительным или отрицательным.

Пример 3

Использование опорных углов для поиска тригонометрических функций

Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −5π6. − 5π6.

Решение

Угол между конечной стороной этого угла и осью x равен π6, π6, так что это опорный угол.Поскольку −5π6−5π6 находится в третьем квадранте, где и xx, и yy отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будут положительными.

cos (−5π6) = — 32, sin (−5π6) = — 12, tan (−5π6) = 33sec (−5π6) = — 233, csc (−5π6) = — 2, cot (−5π6) = 3cos ( −5π6) = — 32, sin (−5π6) = — 12, tan (−5π6) = 33sec (−5π6) = — 233, csc (−5π6) = — 2, детская кроватка (−5π6) = 3

Попробуй # 3

Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −7π4. − 7π4.

Использование четных и нечетных тригонометрических функций

Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций как с положительными, так и с отрицательными угловыми входами, мы должны изучить, как каждая функция обрабатывает отрицательный вход. Как оказалось, в этом отношении между функциями есть важное различие.

Рассмотрим функцию f (x) = x2, f (x) = x2, показанную на рисунке 5. График функции симметричен относительно оси y . На всем протяжении кривой любые две точки с противоположными значениями x имеют одинаковое значение функции. Это соответствует результату расчета: (4) 2 = (- 4) 2, (4) 2 = (- 4) 2, (−5) 2 = (5) 2, (- 5) 2 = (5) 2 , и так далее. Таким образом, f (x) = x2f (x) = x2 — четная функция, такая функция, что два противоположных входа имеют одинаковый выход.Это означает, что f (−x) = f (x) .f (−x) = f (x).

Рисунок 5 Функция f (x) = x2f (x) = x2 является четной функцией.

Теперь рассмотрим функцию f (x) = x3, f (x) = x3, показанную на рисунке 6. График несимметричен относительно оси y . На всем протяжении графика любые две точки с противоположными значениями x также имеют противоположные значения y . Итак, f (x) = x3f (x) = x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f (−x) = — f (x).f (−x) = — f (x).

Рисунок 6 Функция f (x) = x3f (x) = x3 — нечетная функция.

Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углом, как на рис. 7. Синус положительного угла равен y.y. Синус отрицательного угла — y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице 2.

Рисунок 7

sint = ysin (−t) = — ysint ≠ sin (−t) sint = ysin (−t) = — ysint ≠ sin (−t)	стоимость = xcos (−t) = xcost = cos (−t) стоимость = xcos (−t) = xcost = cos (−t)	tan (t) = yxtan (−t) = — yxtant ≠ tan (−t) tan (t) = yxtan (−t) = — yxtant ≠ tan (−t)
sect = 1xsec (−t) = 1xsect = sec (−t) sect = 1xsec (−t) = 1xsect = sec (−t)	csct = 1ycsc (−t) = 1 − ycsct ≠ csc (−t) csct = 1ycsc (−t) = 1 − ycsct ≠ csc (−t)	cott = xycot (−t) = x − ycott ≠ cot (−t) cott = xycot (−t) = x − ycott ≠ cot (−t)

Таблица 2

Четные и нечетные тригонометрические функции

Четная функция — это функция, в которой f (−x) = f (x). f (−x) = f (x).

Нечетная функция — это функция, в которой f (−x) = — f (x) .f (−x) = — f (x).

Косинус и секанс четные:

cos (−t) = costsec (−t) = sectcos (−t) = costsec (−t) = sect

Синус, тангенс, косеканс и котангенс нечетны:

sin (−t) = — sinttan (−t) = −tantcsc (−t) = — csctcot (−t) = — cottsin (−t) = — sinttan (−t) = — tantcsc (−t) = — csctcot (−t) = — cott

Пример 4

Использование четных и нечетных свойств тригонометрических функций

Если секанс угла tt равен 2, каков секанс угла −t? −t?

Решение

Секанс — четная функция.Секущая угла — это то же самое, что секанс его противоположности. Так, если секанс угла t равен 2, секанс −t − t также равен 2.

Попробуйте # 4

Если котангенс угла tt равен 3,3, каков котангенс угла −t? −t?

Распознавание и использование основных идентичностей

Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности.Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность может быть получена из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.

Фундаментальные личности

Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции могут быть связаны с функциями синуса и косинуса с помощью следующих основных соотношений:

tant = sintcosttant = sintcost cott = 1tant = costintcott = 1tant = costint

Пример 5

Использование идентичностей для вычисления тригонометрических функций

Учитывая sin (45 °) = 22, cos (45 °) = 22, sin (45 °) = 22, cos (45 °) = 22, вычислите tan (45 °). загар (45 °).
Дано sin (5π6) = 12, cos (5π6) = — 32, вычисляем sec (5π6) .sin (5π6) = 12, cos (5π6) = — 32, оцениваемsec (5π6).

Решение

Поскольку нам известны значения синуса и косинуса для этих углов, мы можем использовать тождества для оценки других функций.

tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1
сек (5π6) = 1cos (5π6) = 1−32 = −23 = −233sec (5π6) = 1cos (5π6) = 1−32 = −23 = −233

Попробуй # 5

Оценить csc (7π6).csc (7π6).

Пример 6

Использование тождеств для упрощения тригонометрических выражений

Упростите secttant.secttant.

Решение

Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.

secttant = 1costsintcostЧтобы разделить функции, мы умножаем их на обратную величину. = 1costcostsintРазделим косинусы. = 1sintУпростите и используйте тождество. = csctsecttant = 1costsintcost Чтобы разделить функции, мы умножаем на обратную величину.= 1costcostsintРазделите косинусы. = 1sint Упростите и используйте тождество. = Csct

Показав, что secttantsecttant можно упростить до csct, csct, мы фактически установили новую идентичность.

secttant = csctsecttant = csct

Попробуй # 6

Упростить (тант) (стоимость). (Тант) (стоимость).

Альтернативные формы пифагорейской идентичности

Мы можем использовать эти фундаментальные тождества, чтобы вывести альтернативные формы пифагорейской идентичности, cos2t + sin2t = 1.cos2t + sin2t = 1. Одна форма получается делением обеих частей на cos2t: cos2t:

cos2tcos2t + sin2tcos2t = 1cos2t1 + tan2t = sec2tcos2tcos2t + sin2tcos2t = 1cos2t1 + tan2t = sec2t

Другая форма получается делением обеих частей на sin2t: sin2t:

cos2tsin2t + sin2tsin2t = 1sin2tcot2t + 1 = csc2tcos2tsin2t + sin2tsin2t = 1sin2tcot2t + 1 = csc2t

Альтернативные формы пифагорейской идентичности

1 + tan2t = sec2t1 + tan2t = sec2t cot2t + 1 = csc2tcot2t + 1 = csc2t

Пример 7

Использование тождеств для связи тригонометрических функций

Если cos (t) = 1213 cos (t) = 1213 и tt находится в квадранте IV, как показано на рисунке 8, найдите значения других пяти тригонометрических функций.

Рисунок 8

Решение

Мы можем найти синус, используя тождество Пифагора, cos2t + sin2t = 1, cos2t + sin2t = 1, и остальные функции, связав их с синусом и косинусом.

(1213) 2 + sin2t = 1 sin2t = 1− (1213) 2 sin2t = 1−144169 sin2t = 25169 sint = ± 25169 sint = ± 25169 sint = ± 513 (1213) 2 + sin2t = 1 sin2t = 1− (1213 ) 2 sin2t = 1−144169 sin2t = 25169 sint = ± 25169 sint = ± 25169 sint = ± 513

Знак синуса зависит от значений y в квадранте, где расположен угол.Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицательный, -513.-513.

Остальные функции можно вычислить, используя тождества, связывающие их с синусом и косинусом.

tant = sintcost = −5131213 = −512sect = 1cost = 11213 = 1312csct = 1sint = 1−513 = −135cott = 1tant = 1−512 = −125tant = sintcost = −5131213 = −512sect = 1cost = 11213 = 1312csct = 1sint = 1−513 = −135cott = 1tant = 1−512 = −125

Попробуй # 7

Если sec (t) = — 178sec (t) = — 178 и 0

Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция. Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или 2π, 2π, приведет к одинаковым выводам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.

Другие функции также могут быть периодическими.Например, продолжительность месяцев повторяется каждые четыре года. Если xx представляет собой продолжительность, измеряемую в годах, а f (x) f (x) представляет количество дней в феврале, тогда f (x + 4) = f (x). F (x + 4) = f ( Икс). Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 года назад. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом. Период — это самый короткий интервал, в течение которого функция завершает один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней.

Период функции

Период PP повторяющейся функции ff — это число, представляющее интервал, такой что f (x + P) = f (x) f (x + P) = f (x) для любого значения x.x.

Период функций косинуса, синуса, секанса и косеканса равен 2π.2π.

Период функций касательной и котангенса равен π.π.

Пример 8

Нахождение значений тригонометрических функций

Найдите значения шести тригонометрических функций угла tt по рисунку 9 .

Рисунок 9

Решение

sint = y = −32cost = x = −12tant = sintcost = −32−12 = 3sect = 1cost = 1−12 = −2csct = 1sint = 1−32 = −233cott = 1tant = 13 = 33sint = y = −32cost = x = −12tant = sintcost = −32−12 = 3sect = 1cost = 1−12 = −2csct = 1sint = 1−32 = −233cott = 1tant = 13 = 33

Попробуй # 8

Найдите значения шести тригонометрических функций угла tt. на основе рисунка 10 .

Рисунок 10

Пример 9

Нахождение значения тригонометрических функций

Если sin (t) = — 32sin (t) = — 32 и cos (t) = 12, cos (t) = 12, найти sec (t), csc (t), tan (t), cot (t) .sec (t), csc (t), tan (t), cot (t).

Решение

sect = 1cost = 112 = 2csct = 1sint = 1−32−233tant = sintcost = −3212 = −3cott = 1tant = 1−3 = −33sect = 1cost = 112 = 2csct = 1sint = 1−32−233tant = sintcost = — 3212 = −3cott = 1tant = 1−3 = −33

Попробуй # 9

Если sin (t) = 22sin (t) = 22 и cos (t) = 22, cos (t) = 22, найти sec (t), csc (t), tan (t) и cot (t) .sec (t), csc (t), tan (t) ) И кроватка (t).

Оценка тригонометрических функций с помощью калькулятора

Мы научились оценивать шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве опорных углов для углов в других квадрантах. Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение. Если калькулятор имеет режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем производить расчет.

Вычисление тангенциальной функции с помощью научного калькулятора, в отличие от графического калькулятора или системы компьютерной алгебры, похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для обратных функций может не быть каких-либо специальных клавиш с надписью CSC, SEC или COT.В этом случае функция должна быть вычислена как обратная величина синуса, косинуса или тангенса.

Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования π180π180, чтобы преобразовать градусы в радианы. Чтобы найти секущую 30 °, 30 °, мы могли бы нажать

(для научного калькулятора): 130 × π180COS (для научного калькулятора): 130 × π180COS

или

(для графического калькулятора): 1cos (30π180) (для графического калькулятора): 1cos (30π180)

Учитывая угловую меру в радианах, используйте научный калькулятор, чтобы найти косеканс.

Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
Введите: 1/1 /
Введите значение угла в круглых скобках.
Нажать клавишу SIN.
Нажмите кнопку =.

Учитывая угловую меру в радианах, используйте графическую утилиту / калькулятор, чтобы найти косеканс.

Если в графической утилите есть режим градусов и режим радиан, установите его в режим радиан.
Введите: 1/1 /
Нажать клавишу SIN.
Введите значение угла в круглых скобках.
Нажмите клавишу ENTER.

Пример 10

Оценка косеканса с использованием технологии

Вычислите косеканс 5π7.5π7.

Решение

Для научного калькулятора введите следующую информацию:

1 / (5 × π / 7) SIN = 1 / (5 × π / 7) SIN = csc (5π7) ≈1.

279csc (5π7) ≈1,279

Попробуйте # 10

Вычислите котангенс −π8. − π8.

5.3 Секционные упражнения

Устные

Могут ли значения синуса и косинуса радианной меры когда-либо быть равными в интервале [0,2π), [0,2π)? Если да, то где?

Каким должен быть косинус ππ градусов? Объясните свои рассуждения.

Для любого угла в квадранте II, если бы вы знали синус угла, как бы вы могли определить косинус угла?

Опишите секущую функцию.

Тангенс и котангенс имеют период π.π. Что это говорит нам о выходе этих функций?

Алгебраические

Для следующих упражнений найдите точное значение каждого выражения.

В следующих упражнениях используйте опорные углы для оценки выражения.

38.

Если sint = 34, sint = 34 и tt находится в квадранте II, найдите cost, sect, csct, tant, cott.cost, sect, csct, tant, cott.

39.

Если cost = −13, cost = −13 и tt находится в квадранте III, найдите sint, sect, csct, tant, cott.sint, sect, csct, tant, cott.

40.

Если tant = 125, tant = 125 и 0≤t <π2,0≤t <π2, найдите sint, cost, sect, csct, sint, cost, sect, csct и cott.cott.

41.

Если sint = 32sint = 32 и cost = 12, cost = 12, найдите sect, csct, tant, sect, csct, tant и cott.Котт.

42.

Если sin40 ° ≈0,643 sin40 ° ≈0,643 и cos40 ° ≈0,766 cos40 ° ≈0,766 найти sec40 °, csc40 °, tan40 °, sec40 °, csc40 °, tan40 °, и cotand40 ° .cotand40 °.

43.

Если sint = 22, sint = 22, что такое sin (−t)? Sin (−t)?

44.

Если стоимость = 12, стоимость = 12, что такое cos (−t)? Cos (−t)?

45.

Если sect = 3.1, sect = 3.1, что такое sec (−t)? Sec (−t)?

46.

Если csct = 0,34, csct = 0,34, что такое csc (−t)? Csc (−t)?

47.

Если tant = −1,4, tant = −1,4, что такое tan (−t)? Tan (−t)?

48.

Если cott = 9,23, cott = 9,23, что такое детская кроватка (−t)? Cot (−t)?

Графический

В следующих упражнениях используйте угол в единичной окружности, чтобы найти значение каждой из шести тригонометрических функций.

50.

Технологии

Для выполнения следующих упражнений используйте графический калькулятор.

Расширения

В следующих упражнениях для оценки выражения используйте личности.

62.

Если tan (t) ≈2,7, tan (t) ≈2,7 и sin (t) ≈0,94, sin (t) ≈0,94, найти cos (t) .cos (t).

63.

Если tan (t) ≈1,3, tan (t) ≈1,3 и cos (t) ≈0,61, cos (t) ≈0,61, найти sin (t) . sin (t).

64.

Если csc (t) ≈3,2, csc (t) ≈3,2 и cos (t) ≈0,95, cos (t) ≈0,95, найти tan (t) .tan (t).

65.

Если cot (t) ≈0,58, cot (t) ≈0,58 и cos (t) ≈0,5, cos (t) ≈0,5, найти csc (t) .csc (t).

66.

Определите, является ли функция f (x) = 2sinxcosxf (x) = 2sinxcosx четной, нечетной или ни одной из них.

67.

Определите, является ли функция f (x) = 3sin2xcosx + secxf (x) = 3sin2xcosx + secx четной, нечетной или ни одной из них.

68.

Определите, является ли функция f (x) = sinx − 2cos2xf (x) = sinx − 2cos2x четной, нечетной или ни одной из них.

69.

Определите, является ли функция f (x) = csc2x + secxf (x) = csc2x + secx четной, нечетной или ни одной из них.

В следующих упражнениях используйте идентификаторы, чтобы упростить выражение.

Реальные приложения

72.

Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 15cos (1600d), h = 15cos (1600d), где hh представляет количество солнечных часов, а dd — день в году. Используйте уравнение, чтобы определить, сколько часов солнечного света 10 февраля, 42 ^-й день в году. Укажите период функции.

73.

Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 16cos (1500d), h = 16cos (1500d), где hh представляет часы солнечного света, а dd это день года.Используйте это уравнение, чтобы определить, сколько часов солнечного света 24 сентября, 267 ^-й день в году. Укажите период функции.

74.

Уравнение P = 20sin (2πt) + 100P = 20sin (2πt) +100 моделирует артериальное давление, P, P, где tt представляет время в секундах. (а) Определите артериальное давление через 15 секунд. б) Какое максимальное и минимальное артериальное давление?

75.

Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 6, y = 2cosx + 6, где xx представляет угол поворота коленвала.Найдите высоту поршня, когда угол поворота коленвала составляет 55 ° 0,55 °.

76.

Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 5, y = 2cosx + 5, где xx представляет угол поворота коленвала. Найдите высоту поршня, когда угол поворота коленвала составляет 55 ° 0,55 °.

Math.com Обзор триггеров

Триггерные функции: обзор

Согласно простейшему определению, тригонометрический (буквально «треугольник, измеряющий») функция, является одной из многих функций, которые связаны с одним непрямым углом прямоугольного треугольника к отношению длин любых двух сторон треугольника (или наоборот).

Следовательно, любая тригонометрическая функция (f) всегда удовлетворяет либо следующих уравнений:

f (q) = a / b OR f (a / b) = q,

где q — мера определенного угла в треугольник, а a и b — длины двух определенных сторон.

Это означает, что

Если первое равенство выполняется, мы можем выбрать любой прямоугольный треугольник, затем измерьте один из непрямых углов, а когда мы оцениваем тригонометрическую функцию под этим углом , результатом будет отношение длин двух треугольников, равное . стороны .
Однако, если последнее равенство выполняется, мы можем выбрать любой прямоугольный треугольник, затем вычислите отношение длин двух определенных сторон, а когда мы оцениваем тригонометрическую функцию при любом соотношении , результатом будет измерение одного из не прямых углов треугольника. (Эти функции называются обратными триггерами , поскольку они выполняют обратная или наоборот предыдущая триггерная функция.)

Это соотношение между углом и соотношением сторон в прямоугольном треугольнике — одна из важнейших идей тригонометрии. Кроме того, тригонометрический функции работают для любого прямоугольного треугольника . Следовательно — для прямоугольного треугольника — если мы измеряем один из непрямоугольных треугольников, мы можем математически вывести соотношение длин любых двух из стороны треугольника с помощью триггерных функций.

И если мы измеряем любое соотношение сторон, мы можем математически вывести меру одного из неправильных треугольников. углы с помощью обратных триггерных функций.Что еще более важно, если мы знаем размер одного из углов треугольника, а затем воспользуемся тригонометрической функцией чтобы определить соотношение длин двух сторон треугольника, и , мы знаем длину одной из этих сторон в отношение, тогда мы можем алгебраически определить длину другого этих двух сторон. (т.е. если мы определим, что a / b = 2, и мы знаем a = 6, то получаем, что b = 3.)

Так как в прямоугольном треугольнике три стороны и два непрямых угла, тригонометрическим функциям потребуется способ указать, какие стороны связаны с каким углом. (Не очень полезно знать, что соотношение длины двух сторон равняется 2, если мы не знаем, какая из мы говорим о трех сторонах. Точно так же, если мы определим это углов составляет 40 °, хотелось бы знать, какой угол это утверждение верно.

По определенному соглашению мы маркируем стороны как напротив , примыкает к , и гипотенуза относительно к нашему углу представляющий интерес q. полный объяснение

Как упоминалось ранее, первый тип тригонометрической функции, который связывает угол с отношением сторон, всегда удовлетворяет следующему уравнение:

f (q) = а / б.

Поскольку для любого угла q существует три способа выбор числителя (а) и три способа выбора знаменателя (б) мы можем создать следующие девять тригонометрических функций:

f (q) = opp / opp	f (q) = opp / adj	f (q) = opp / hyp
f (q) = прил / опп	f (q) = прил. / Прил.	f (q) = прил / гип
f (q) = hyp / opp	f (q) = hyp / adj	f (q) = hyp / hyp

Три диагональные функции, показанные красным, всегда равны одной. Они есть вырождены и, следовательно, бесполезны для нас. Поэтому мы удаляем эти вырожденные функции и присваивают метки оставшимся шести, обычно пишется в следующем порядке:

синус (q) = opp / hyp	косеканс (q) = hyp / opp
косинус (q) = adj / hyp	секанс (q) = hyp / adj
тангенс (q) = opp / adj	котангенс (q) = adj / opp

Кроме того, функции обычно сокращаются: синус (sin), косинус (cos), касательная (tan), косеканс (csc), секущая (sec) и котангенс (cot).

Не удивляйтесь. Безусловно, две наиболее важные триггерные функции запомнить — это синус и косинус. Все остальные триггерные функции первый вид может быть получен из этих двух функций. Например, функции справа — это просто мультипликативная обратная соответствующая функция слева (что делает их менее полезными). Кроме того, sin (x) / COs (x) = (opp / hyp) / (adj / hyp) = opp / adj = загар (х).Следовательно, касательная функция — это то же самое, что и частное функций синуса и косинуса (касательная функция по-прежнему удобно).

синус (q) = opp / hyp	CSC (q) = 1 / sin (q)
COs (q) = adj / hyp	сек (q) = 1 / COs (q)
tan (q) = sin (q) / COs (q)	кроватка (q) = 1 / tan (q)

Рассмотрим эти функции подробнее.Вы заметите, что там — функции синуса, секанса и касательной, и есть соответствующие «co» -функции. Они получили свои странные имена из разных схожих идей. в геометрии. Вы можете предположить, что совместные функции должны быть переименованы в мультипликативные инверсии соответствующего синуса, секущая и касательная функции. Однако в этом безумии есть своя методика. Кофункция данной триггерной функции (f) по определению функция, полученная после , дополняет ее параметр.Поскольку дополнение любого угла q равно 90 ° — q, тот факт, что следующие соотношения можно показать:

синус (90 ° — q) = косинус (q)

секанс (90 ° — q) = косеканс (q)

тангенс (90 ° — q) = котангенс (q)

таким образом оправдывая соглашение об именах.

Триггерные функции оцениваются по-разному в зависимости от единиц на q, например градусов, радиан или градусов.Например, sin (90 °) = 1, а sin (90) = 0,89399 …. объяснение

Так же, как мы можем определить тригонометрические функции вида

f (q) = a / b

которые принимают в качестве параметра не прямой угол и возвращают соотношение длины двух сторон треугольника, мы можем сделать обратное: определить триггерные функции формы

ж (а / б) = q

которые принимают отношение длин двух сторон в качестве параметра и возвращают измерение одного из непрямых углов.

**Обратные функции**
арксинус (opp / hyp) = q	арккосеканс (hyp / opp) = q
арккозин (прил / гип) = q	арксеканс (hyp / adj) = q
арктангенс (опп / прил) = q	арккотангенс (adj / opp) = q

Как и раньше, функции обычно сокращаются: арксинус (arcsin), арккосинус (arccos), арктангенс (arctan), арккосеканс (arccsc), арксеканс (arcsec) и аркотангенс (arccot).Согласно общепринятым обозначениям для обратных функций (f ^-1) вы также часто будете видеть эти записывается как sin ^-1, cos-1 ^{, tan ^-1 csc-1 ^{, сек ^-1 и детская кроватка ^-1. Остерегайтесь : есть еще один общепринятая нотация, которая записывает квадрат триггерных функций, например (sin (x)) ² как sin ² (x). Это может сбивать с толку, поскольку тогда вы могли бы тогда думать, что грех ^-1 (x) = (sin (x)) ^-1, то есть не соответствует истине .Отрицательный надстрочный индекс здесь — специальное обозначение, обозначающее обратные функции (не мультипликативные обратные).}}

Тригонометрия

Тригонометрия (от греч. Тригонон «треугольник» + метрон «мера»)

Хотите изучить тригонометрию? Вот краткое изложение.
Чтобы узнать больше, перейдите по ссылкам или перейдите в Индекс тригонометрии

Тригонометрия … всего около треугольников.

Тригонометрия помогает нам находить углы и расстояния и часто используется в науке, технике, видеоиграх и многом другом!

Прямоугольный треугольник

Наибольший интерес представляет прямоугольный треугольник. Прямой угол обозначен прямоугольником в углу:

Другой угол часто обозначается как θ, и тогда три стороны называются:

Соседний : рядом (рядом) угол θ
Напротив : напротив угла θ
, а самая длинная сторона — Гипотенуза

Почему прямоугольный треугольник?

Почему этот треугольник так важен?

Представьте, что мы можем измерять вдоль и поперек, но хотим знать прямое расстояние и угол:

Тригонометрия может найти недостающий угол и расстояние.

Или, может быть, у нас есть расстояние и угол, и нам нужно «нарисовать точку» вдоль и вверх:

Подобные вопросы часто встречаются в инженерии, компьютерной анимации и т. Д.

И тригонометрия дает ответы!

Синус, косинус и тангенс

Основные функции в тригонометрии: Синус, косинус и тангенс

Это просто одна сторона прямоугольного треугольника, разделенная на другую.

Для любого угла « θ «:

(Синус, косинус и тангенс часто сокращаются до sin, cos и tan.)

Пример: Что такое синус 35 °?

Используя этот треугольник (длины до одного десятичного знака):

sin (35 °) = Противоположно Гипотенуза = 2,8 4,9 = 0,57 …

Треугольник может быть больше, меньше или повернутым, но этот угол всегда будет иметь это соотношение .

У калькуляторов

в помощь нам есть sin, cos и tan, так что давайте посмотрим, как ими пользоваться:

Пример: насколько высокое дерево?

Мы не можем добраться до вершины дерева, поэтому мы уходим и измеряем угол (с помощью транспортира) и расстояние (с помощью лазера):

Мы знаем Гипотенузу
И мы хотим знать напротив

Синус — это отношение Противоположность / Гипотенуза :

грех (45 °) = Напротив Гипотенуза

Возьмите калькулятор, введите «45», затем нажмите клавишу «sin»:

sin (45 °) = 0. 7071 …

Что означает 0,7071 … ? Это отношение длин сторон, поэтому Противоположность примерно на 0,7071 раз длиннее Гипотенузы.

Теперь мы можем поставить 0,7071 … вместо sin (45 °):

0,7071 … = Напротив Гипотенуза

И мы также знаем, что гипотенуза равна 20 :

0,7071 … = Напротив 20

Чтобы решить, сначала умножьте обе части на 20:

20 × 0.7071 … = Напротив

Наконец:

Напротив = 14,14 м (до 2 знаков после запятой)

Когда вы наберетесь опыта, вы сможете сделать это быстро следующим образом:

Пример: насколько высокое дерево?

Начать с: sin (45 °) = Напротив Гипотенуза

Мы знаем: 0,7071 … = Напротив 20

Поменять местами: Напротив 20 = 0. 7071 …

Умножить обе стороны на 20 : Противоположное = 0,7071 … × 20

Вычислить: напротив = 14,14 (с точностью до 2 десятичных знаков)

Дерево 14,14 м высотой

Попробуйте Sin Cos and Tan

Поиграйте с этим некоторое время (перемещайте мышь) и ознакомьтесь со значениями синуса, косинуса и тангенса для разных углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °.

Также попробуйте 120 °, 135 °, 180 °, 240 °, 270 ° и т. Д. И обратите внимание, что позиции могут быть положительными или отрицательными по правилам декартовых координат, поэтому синус, косинус и тангенс также изменяются между положительным и отрицательным .

Итак, тригонометрия — это тоже окружности !

Единичный круг

То, с чем вы только что играли, — это Unit Circle.

Это круг с радиусом 1 с центром в 0.

Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.

Здесь мы видим синусоидальную функцию единичной окружности:

Примечание: вы можете увидеть красивые графики, состоящие из синуса, косинуса и тангенса.

Градусов и радианов

Углы могут быть в градусах или радианах. Вот несколько примеров:

Уголок	градусов	Радианы
Прямой угол	90 °	π / 2
__ Прямой угол	180 °	π
Полное вращение	360 °	2π

Повторяющийся узор

Поскольку угол равен , вращающемуся вокруг и вокруг окружности , функции синуса, косинуса и тангенса повторяются один раз при каждом полном повороте (см. Амплитуда, Период, Фазовый сдвиг и Частота).

Когда мы хотим вычислить функцию для угла, большего, чем полный оборот на 360 ° (2π радиан), мы вычитаем столько полных оборотов, сколько необходимо, чтобы вернуть его ниже 360 ° (2π радиан):

Пример: что такое косинус 370 °?

370 ° больше 360 °, поэтому вычтем 360 °

370 ° — 360 ° = 10 °

cos (370 °) = cos (10 °) = 0,985 (до 3 знаков после запятой)

А когда угол меньше нуля, просто добавьте полные обороты.

Пример: какой синус у −3 радиан?

−3 меньше 0, поэтому добавим 2π радиан

−3 + 2π = −3 + 6,283 … = 3,283 … радиан

sin (−3) = sin (3,283 …) = −0,141 (до 3 знаков после запятой)

Решение треугольников

Тригонометрия также полезна для обычных треугольников, а не только для прямоугольных.

Это помогает нам разгадывать треугольники. «Решение» означает поиск недостающих сторон и углов.

Мы также можем найти недостающие длины сторон.Общее правило:

Когда мы знаем какие-либо 3 стороны или углы, мы можем найти остальные 3
(кроме случая с тремя углами)

См. «Решение треугольников» для более подробной информации.

Другие функции (котангенс, секанс, косеканс)

Подобно синусу, косинусу и касательности, есть еще три тригонометрические функции , которые выполняются делением одной стороны на другую:

Косеканс, функция:	csc ( θ ) = Гипотенуза / Напротив
Секущая функция:	сек ( θ ) = Гипотенуза / Соседний
Функция котангенса:	детская кроватка ( θ ) = рядом / напротив

Тригонометрические и треугольные идентичности

И по мере того, как вы станете лучше разбираться в тригонометрии, вы сможете выучить эти:

Станьте экспертом в области треугольников (и кругов)!

ACT Тригонометрия: полное руководство

Тригонометрия — это раздел математики, который занимается прямоугольными треугольниками и отношениями между их сторонами и углами. (Слово «триггер» связано со словом «треугольник», чтобы помочь вам запомнить.)

Обычно в тесте ACT есть около 4-6 вопросов, связанных с тригонометрией (официальные инструкции по ACT говорят, что задачи тригонометрии составляют 7% теста). На первый взгляд они могут показаться сложными, но большинство из них сводятся к нескольким простым концепциям.

Эта статья будет вашим исчерпывающим руководством по тригонометрии, которое вам нужно знать для ACT. Мы расскажем вам о значении тригонометрии, формулах и объяснениях, которые вам нужно знать, а также о том, как решать некоторые из наиболее сложных тригонометрических задач ACT.

Что такое тригонометрия и как ее использовать?

Тригонометрия изучает отношения между сторонами и углами прямоугольных треугольников. Соотношения между размерами сторон прямоугольного треугольника и размерами его углов постоянны, независимо от того, насколько большой или маленький треугольник.

Некоторые из множества различных возможных типов прямоугольных треугольников.

Если вы знаете размер одной стороны и один угол, отличный от 90 ° для прямоугольного треугольника, вы сможете определить остальные стороны и углы треугольника.2 = 340 $

$ c = √340 $ или $ c = 2√85 $

Но что, если у нас есть только одна длина стороны и один из углов (не девяносто градусов)?

Несмотря на то, что у нас есть длина только одной стороны, мы все же можем найти другие, используя тригонометрию, потому что у нас есть мера одного из острых углов.

Итак, здесь мы можем сказать $ sin 34 ° = 12 / \ hypotenuse \ $

Итак, $ \ hypotenuse \ = 12 / {sin 34 °} $

Не волнуйтесь, если это еще не имеет для вас смысла! Мы разберем каждый шаг по мере продвижения в руководстве.

(Примечание: чтобы найти фактическую величину угла в градусах с использованием двух длин сторон, вам нужно будет выполнить вычисление обратной функции (также называемой функцией «дуги»). Но НЕ БОЙТЕСЬ — ACT никогда не заставит вас Сделайте это! Что касается вашей подготовки к математике ACT, поймите, что тест будет предлагать вам только вычислить достаточно далеко, чтобы сказать, например, «$ Cosine‌x = 4/5 $». Вам никогда не придется находить действительную величину угла из х по АКТ.

Мы находим эти меры, понимая отношение определенных сторон треугольника к их соответствующим углам. Это так называемые тригонометрические функции, и вам следует запомнить три функции для АСТ: синус, косинус и тангенс. Самый простой способ понять это — использовать мнемоническое устройство SOH, CAH, TOA , которое мы немного обсудим.> / P>

Тригонометрия широко используется в навигации, а также для расчета высот и расстояний. (На случай, если вам интересно, нужен ли вам триггер в реальной жизни.)

Наиболее распространенные триггерные вопросы ACT

Вопросы по тригонометрии ACT можно разделить на несколько категорий. Мы предоставили несколько реальных математических примеров ACT, чтобы продемонстрировать каждую концепцию.

# 1: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла из заданной прямоугольной треугольной диаграммы.

# 2: Нахождение синуса, косинуса или тангенса прямоугольного треугольника из задачи со словами.

Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены?

А.10 $ ‌tan‌23 ° $

Б. 10 $ sin‌23 ° $

C. 10 $ cos‌23 ° $

D. $ cos‌ {10/23} $

E. $ sin {10/23}

# 3: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла от заданного sin, cos или tan и диапазона, в который попадает угол.

Если $ tan‌Θ = 3/4 \ и 180 ° <Θ <270 ° $, что такое $ sinΘ $?

A. $ 4/3 $

Б. $ -4 / 3 $

C. $ -3 / 4 $

Д.$ 3/5 $

-3 Э. $ / 5

# 4: Определение периода или амплитуды графика.

Какова амплитуда графика?

А. 1

Б. 2

К. π

Д. 2π

E. 0

# 5: Закон синусов или закон косинусов.

Для такого вопроса, , вам дадут формулы закона синусов или закона косинусов , так что вам не придется беспокоиться об их запоминании.Однако наличие формулы не очень поможет, если вам она покажется или звучит как тарабарщина. По мере того, как вы будете изучать это руководство, выполнять практические вопросы ACT по математике, которые мы предоставили, и знакомиться с языком тригонометрии, используемым в этих вопросах, их станет намного легче решать.

Мы рассмотрим, как решить каждую из этих проблем, , но это даст вам представление о том, как будут выглядеть триггерные проблемы ACT в тесте.

SOH, CAH, TOA

Помните эту знаменитую мнемонику? Это спасет вашу жизнь.Давайте пройдемся по каждому.

SOH (синус)

Синус — это функция, в которой значение синуса (также называемое «грехом») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, к гипотенузе треугольника.

SOH : S in $ Θ $ = O противоположная сторона треугольника / H yпотенуза треугольника

Итак, в этом треугольнике $ sin‌Θ = b / c $, потому что сторона, противоположная углу $ Θ $, равна b , а гипотенуза равна c .

CAH (косинус)

Косинус — это функция, в которой значение косинуса (также называемого «$ cos $») угла тета ($ Θ $) можно найти, используя отношение стороны треугольника, примыкающей к углу $ Θ $ (т. Е. а не гипотенуза) над гипотенузой треугольника.

CAH : C os $ Θ $ = A смежная сторона треугольника / H yпотенуза треугольника

Примечание: смежный означает, что сторона треугольника касается угла / помогает создать угол $ Θ $.

В этом же треугольнике $ cos‌Θ = a / c $, потому что сторона, примыкающая к углу $ Θ $, равна a , а гипотенуза равна c .

TOA (касательная)

Касательная — это функция, в которой значение тангенса угла тета (также называемое тангенсом) можно найти, используя отношение стороны треугольника, противоположной углу тета, по соседней стороне треугольника к тета (что не является гипотенуза).

TOA : T и $ Θ $ = O заданная сторона треугольника / A смежная сторона треугольника.

В этом же треугольнике $ tan‌Θ = b / a $, потому что сторона, противоположная углу $ Θ $, равна b , а смежная сторона — a .

Теперь, когда вы знакомы со своими мнемоническими устройствами, вы можете составлять вопросы в несколько этапов. Например, немного более сложный вопрос может выглядеть примерно так:

Вам даны длины двух сторон треугольника, но для решения задачи вам нужна длина третьей стороны. 2 = 21 $

$ x = √21 $

Теперь, когда у вас есть измерение третьей стороны, вы можете найти $ tan‌B $.

$ Tan‌B = \ напротив / \ Соседний $

$ TanB = √21 / 2 $

Итак, ответ: F , √21 / 2 $

Какие стороны противоположны или смежны?

Гипотенуза треугольника всегда остается неизменной, но противоположные или смежные стороны меняются в зависимости от угла фокусировки.

Например, если вы пытаетесь найти $ sin $ угла $ γ $, вы должны использовать соотношение $ b / c $; если вы пытаетесь найти грех угла $ ξ $, вы должны использовать соотношение $ a / c $.2 = 44 $

$ x = √44 $

Теперь $ sin $ = $ \ Against / \ hypotenuse $, поэтому $ sin‌M = √44 / 12 $.

Итак, ответ — K.

Нет необходимости находить градусную меру (арксинус или обратный синус) угла M на вашем калькуляторе — это все, что вам нужно.

Вам также может быть предоставлено значение угла и длины стороны знаменателя вашего отношения. В этом случае управляйте уравнением, как алгебраическим уравнением, и умножайте противоположную сторону на знаменатель.

$ sin Θ = \ напротив / \ гипотенуза $

$ гипотенуза $ * sinΘ = $ напротив

Поскольку вас спрашивают о длине лодки до причала, а эта сторона составляет против под углом 52 °, вы знаете, что вам понадобится либо sin, либо tan (cos использует смежную и гипотенузу, а не противоположную).

Вам также дается смежных длины, 30 миль, поэтому вы будете использовать tan. (Вы можете сказать, что эта сторона смежная, потому что сторона, противоположная углу 90 °, является гипотенузой, поэтому 30 миль должны быть еще одним катетом треугольника).

$ tan‌Θ = \ напротив / \ рядом $

So $ tan‌52 ° = x / 30 $

30‌ $ тан52 ° = x

долл. США

Итак, ответ — F , длина лодки до причала 30 тангенциальных 52 °.

И снова проблема со словом из ранее.

А.10 ‌ $ загар‌23 ° $

Б. 10‌ $ sin‌23 ° $

C. 10 $ cos‌23 ° $

D. $ cos‌10 / 23 $

E. $ sin‌10 / 23 $

Сначала нарисуйте свою картинку, чтобы легче было представить, о чем вас просят.

Итак, у нас есть расстояние между лестницей и землей в 23 ° $. Также мы работаем с длинами соседней стороны треугольника и гипотенузы. Это означает, что нам понадобится косинус, так как $ cos‌Θ = \ Again / \ hypoteneuse $

Итак, $ cos‌23 ° = \ смежный / 10 $ (Почему 10? Длина лестницы 10 футов)

Это становится 10 $ ‌cos‌23 ° = \ смежный $

Итак, ответ: C , 10 $ ‌cos‌23 ° $

Придется ли мне определять угол?

Короткий ответ: нет, вас не попросят определить точную меру угла с помощью тригонометрии.2)}

долларов США

Когда Sin, Cos и Tan являются положительными или отрицательными?

В зависимости от того, где расположен треугольник в двумерном пространстве, значения sin, cos и tan будут отрицательными или положительными.

В двухмерном пространстве есть четыре квадранта, разделенных по осям x и y.

В квадранте I и x, и y положительны.
В квадранте II x отрицательный, а y положительный
В квадранте III оба значения x и y отрицательны
А в квадранте IV x положительный, а y отрицательный

Как и в случае со значениями x и y, sin, cos и tan могут быть положительными или отрицательными в зависимости от квадранта, в котором находится треугольник / угол.

В квадранте I все положительные
В квадранте II sin положителен, а cos и tan отрицательны
В квадранте II tan положительный, а sin и cos отрицательные
В квадранте IV cos положительна, а sin и tan отрицательны

Хороший способ запомнить это по мнемонической аббревиатуре ASTC — A ll S tudents T ake C hemistry — чтобы увидеть, какая из функций является положительной в зависимости от квадранта.

Итак, A ll положительны в квадранте I, S in положительны в квадранте II, T an положительны в квадранте III, а C os положительны в квадранте IV

Если $ tan‌Θ = 3/4 $ и $ 180 ° <Θ <270 ° $, что такое $ sinΘ $?

A. $ 4/3 $

Б. $ −4 / 3 $

C. $ -3 / 4 $

D. $ 3/5 $

-3 Э. $ / 5

Чтобы решить эту проблему, сначала определите длины сторон треугольника, используя теорему Пифагора (или используя свои знания о 3-4-5 треугольниках).2 = 25 9000 долларов США 6

$ c = 5

Итак, наша гипотенуза равна 5.

Мы знаем, что $ sin Θ = \ Against / \ hypotenuse $. Итак, $ sin‌Θ = 3/5 $.

Но подождите! Мы еще не закончили. Поскольку они сказали нам, что $ Θ $ лежит между $ 180 ° $ и $ 270 ° $, мы знаем, что значение sin для $ Θ $ отрицательно. Согласно ASTC, только загар угла $ Θ $ будет положительным в диапазоне от 180 ° $ до 270 ° $.

Итак, , наш окончательный ответ — E , $ — 3/5 $

Вторичные триггерные функции

В редких случаях на ACT вас попросят указать одну из вторичных триггерных функций.Это косеканс, секанс и котангенс. Максимум один вопрос за тест.

Вы могли заметить, что они похожи на основные триггерные функции, которые вы изучили выше. Фактически, эти вторичные функции являются обратными (обратными) sin, cos и касательной.

Чтобы помочь вам запомнить, что есть что, обратите внимание на третью букву каждого слова:

Co s ecant = обратная величина s ine
Se c ant = аналог c osine
Co t Угол = обратный t Угол

Косеканс

Косеканс — величина, обратная синусу.$ Косеканс Θ = \ гипотенуза / \ напротив $

Секант

Секанс — величина, обратная косинусу. $ Секанс Θ = \ гипотенуза / \ смежный $

Котангенс

Котангенс — величина, обратная касательной. $ Котангенс Θ = \ смежный / \ напротив $

Полезные формулы с Sin, Cos и Tan

Две формулы будут время от времени появляться на ACT. Если вы чувствуете, что не можете больше запоминать тригонометрию, не беспокойтесь об их запоминании — они могут ответить максимум на один вопрос за тест .2 {x}) $, что также равно 1.

Итак, мы имеем 1 + 1 = 2

Окончательный ответ: H , 2.

$$ (sin‌Θ) / (cos‌Θ) = tan‌Θ $$

Это уравнение имеет логический смысл, если представить его в виде диаграммы. Допустим, у вас есть треугольник, который выглядит так

$ Sin Θ $ будет 5 $ / 13 $. $ Cos Θ $ будет $ 12/13 $. $ Tan Θ $ составит 5 долларов США / 12%.

Вы также можете сказать $ tan‌Θ = {sin‌Θ} / {cos‌Θ} = {5/14} / {12/13} = (5/13) (13/12) = 65/156 $ (вы также можете просто отменить обе 13s, чтобы было проще) = 5 $ / 12 $

Графические триггерные функции

ACT не будет запрашивать у вас график триггерной функции, но вам нужно распознать, как каждая функция выглядит в виде графика.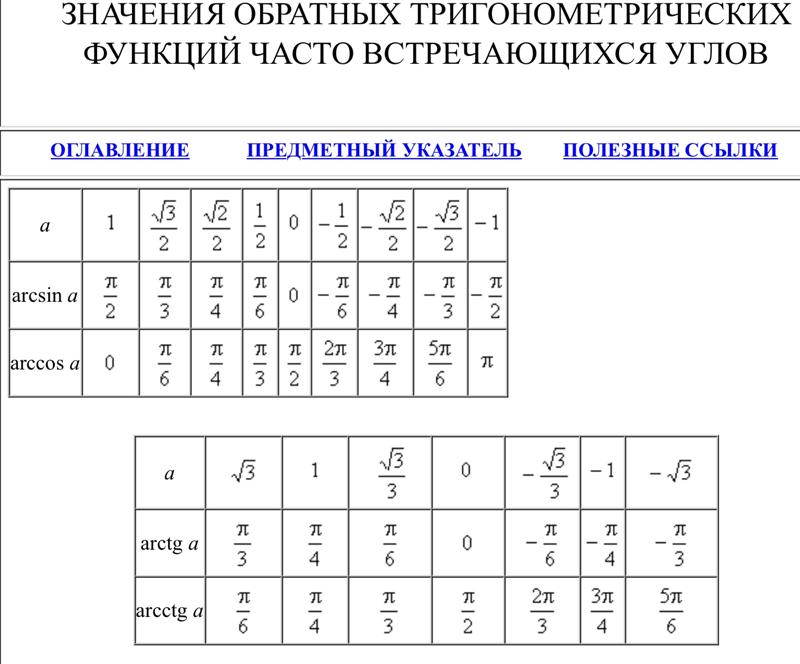

Синус

Синусоидальный график пересекает начало координат в виде волны. Он всегда повышается после $ x = 0 $, после того, как пересекает начало координат.

Это «нечетная» функция, потому что она не симметрична относительно оси y.

Косинус

График косинуса похож на «волнистый», но не пересекает начало координат. Он спускается после $ x = 0 $.

Это может помочь вам вспомнить, что косинус убывает после x = 0, если подумать, что « co — low »

Косинус является «четной» функцией, поскольку он симметричен относительно оси y.Это означает, что для всех значений $ x $ $ f (x) = f (-x) $.

Например, на приведенном выше графике $ y = 0,7 $ как при $ x = 1 $ , так и при $ x = -1 $

Иногда все, что вам зададут, — это определить, является ли график четным или нечетным, а также является ли график sin или cos. Вам будет легко понять это, если вы помните основные элементы триггерных графиков.

Хотя вы можете понять этот вопрос из представленной информации, это займет гораздо меньше времени, если вы узнаете, что график является косинусным и, следовательно, четным.А на ACT время ограничено и ценно.

Касательная

Касательный график выглядит совсем иначе, чем графики sin и cos — вам просто нужно уметь распознавать касательный график, когда вы его видите.

Периоды и амплитуды

ACT иногда просит вас найти период или амплитуду синусоидального или косинусного графика.

Период

Период графика — это расстояние по оси x, с которого график начинает повторяться.Найдите расстояние по оси x, на котором точка возвращается в исходное положение после завершения полного цикла .

Период синусоидального графика здесь равен 2π. Он должен идти как вверх, так и вниз, прежде чем окончательно вернуться к $ y = 0 $.

Период косинусного графика здесь также равен 2π. Он должен сначала спуститься, а затем снова подняться, чтобы вернуться в исходное положение при $ y = 1 $.

Амплитуда

Амплитуда графика — это его высота от оси x, расстояние между его наивысшим значением $ y $ и $ x = 0 $.

Итак, чтобы использовать тот же график, что и выше:

И синус, и косинус имеют амплитуду 1 (и, опять же, период 2π).

Радианы

Радианы — это еще один (более точный) способ измерения расстояния по окружности, а не градусы. Вместо градусов радианы выражаются через π (и доли π).

Если у вас есть полный круг, то это 360 градусов. Это также 2π радиан.

Почему 2π радиан? Что ж, придумайте формулу длины окружности. С = 2πr. Если ваш радиус равен 1, тогда ваша окружность равна 2π, что совпадает с вашей мерой в радианах.

Окружность с радиусом 1 и центром в начале координат называется «единичной окружностью». Радианы удобно рассматривать, помещая их на единичный круг.

Итак, если у вас есть полукруг, это 180 ° или π радиан.

И так далее. 90 ° — это $ π / 2 $ радиан, 270 ° — $ (3π) / 2 $ радиан.

Для преобразования градусов в радианы проще всего использовать преобразование между 180 ° и π .

Преобразовать 45 ° в радианы => $ (45) {π / 180} = π / 4 $ ‌радиан

Преобразовать $ (3π) / 4 $ радиан в градусы => $ {(3π) / 4} (180 / π) $ = 135 °

Шаги к решению триггерного вопроса

Итак, давайте рассмотрим, как разбить триггерный вопрос

# 1: Определите, требует ли проблема тригонометрии. Вы можете сказать, что проблема потребует триггера, когда:

Проблема упоминает sin, cos или tan в вопросе или в вариантах ответа

Задача дает вам диаграмму или описывает прямоугольный треугольник, а затем просит вас найти значение, которое нельзя найти, используя только теорему Пифагора.

Как мы видели в этой задаче ранее — вы можете использовать теорему Пифагора в как задачу тригонометрии, но вы не можете решить тригонометрическую задачу с помощью только , используя теорему Пифагора.

Проблема показывает вам «волнистый» график по осям x и y

Задача запрашивает период или амплитуду графика

# 2: Помните SOH, CAH, TOA.2 {‌Θ} и др.

# 4 :. Вспомните, как выглядят графики синуса, косинуса и тангенса.

И знайте, что:

Период = горизонтальное расстояние

Амплитуда = вертикальное расстояние

# 5: Празднуйте, потому что вы ответили на триггерные вопросы ACT!

На вынос

Хотя проблемы тригонометрии могут показаться устрашающими, почти каждый вопрос о тригонометрии ACT может быть решен, если вы знаете основные строительные блоки тригонометрии.

Чтобы извлечь максимальную пользу из подготовки к математике ACT, запомните эти три триггерные концепции: SOH, CAH, TOA, как управлять своими уравнениями и как распознавать графики функций. Если вы запомните их, вы обнаружите, что решаете практически все триггерные вопросы, которые ACT может вам бросить.

Что дальше?

Хотите больше математических стратегий и руководств ACT? Прочтите нашу статью по всем математическим темам, протестированным на ACT, чтобы убедиться, что вы их хорошо усвоили. Вы знаете твердотельную геометрию ACT? Обязательно освежите свои знания, если вы ищете каждую последнюю точку.

Хотите получить идеальный результат по математике в ACT? Ознакомьтесь с нашей статьей о том, как набрать 36 баллов в разделе ACT Math от 36 ACT-Scorer.

Чувствуете себя разбитым? Не знаете с чего начать? Не ищите дальше наших статей о том, что считается хорошей, плохой или отличной оценкой ACT. Не знаете, в какие дни предлагается ACT? Ознакомьтесь с полным списком дат тестирования ACT, чтобы найти подходящие для вашего расписания.

И если вы обнаружите, что у вас не хватает времени на математический раздел, посмотрите нашу статью о том, как перестать не хватать времени на математику ACT.

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.

Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

Тригонометрические функции и единичная окружность

Радианы

Радианы — это еще один способ измерения углов. Мера угла может быть преобразована из градусов в радианы.

Цели обучения

Объясните определение радиан с точки зрения длины дуги единичного круга и используйте его для преобразования между градусами и радианами.

Основные выводы

Ключевые моменты

Один радиан — это мера центрального угла окружности, при которой длина дуги равна радиусу
окружности.\ circ} {\ pi}} [/ латекс].
Радианная мера угла — это отношение длины дуги к радиусу круга [латекс] \ displaystyle {\ left (\ theta = \ frac {s} {r} \ right)} [/ latex] . Другими словами, если [latex] s [/ latex] — длина дуги круга, а [latex] r [/ latex] — радиус круга, то центральный угол, содержащий эту дугу, измеряется в радианах.

Ключевые термины

дуга : Непрерывная часть окружности круга.
окружность : длина линии, ограничивающей круг.
радиан : Стандартная единица измерения углов в математике. Мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.

Введение в радианы

Напомним, что деление круга на 360 частей дает измерение в градусах. Это произвольное измерение, и мы можем выбрать другие способы разделить круг.Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы останавливаетесь до того, как круг замкнется. Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.

Окружность круга

[латекс] C = 2 \ pi r [/ латекс]

Если мы разделим обе части этого уравнения на [латекс] r [/ латекс], мы получим отношение длины окружности, которое всегда равно [латексу] 2 \ pi [/ латексу] к радиусу, независимо от длины радиус.Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных длин струны и чуть больше четверти седьмой, как показано на диаграмме. ниже.

Длина окружности по сравнению с радиусом : Длина окружности немногим более чем в 6 раз превышает длину радиуса.

Это подводит нас к нашей новой угловой мере. Радиан — это стандартная единица измерения углов в математике. Один радиан — это мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.

Один радиан: Угол [латекс] t [/ латекс] выметает величину в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса круга.

Поскольку общая длина окружности круга равна [латексу] 2 \ пи [/ латекс], умноженному на радиус, полный круговой поворот составляет [латекс] 2 \ пи [/ латекс] радиан.\ circ [/ латекс].

Обратите внимание, что когда угол описывается без конкретной единицы измерения, он относится к радианам. {\ circ}} [/ latex].

Измерение угла в радианах

Длина дуги [латекс] s [/ латекс] — это длина кривой вдоль дуги. Точно так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.

Это отношение, называемое радианной мерой, одинаково независимо от радиуса окружности — оно зависит только от угла. Это свойство позволяет нам определить меру любого угла как отношение длины дуги [latex] s [/ latex] к радиусу [latex] r [/ latex].

[латекс] \ displaystyle {\ begin {align} s & = r \ theta \\ \ theta & = \ frac {s} {r} \ end {align}} [/ latex]

Измерительные радианы: (a) в угле 1 радиан; длина дуги равна радиусу [латекса] r [/ латекса]. (b) Угол в 2 радиана имеет длину дуги [латекс] s = 2r [/ латекс]. (c) Полный оборот составляет [латекс] 2 \ pi [/ латекс], или около 6,28 радиана.

Пример

Какова мера данного угла в радианах, если длина его дуги [латекс] 4 \ pi [/ latex], а длина [латекс] [/ латекс] 12?

Подставьте значения [latex] s = 4 \ pi [/ latex] и [latex] r = 12 [/ latex] в формулу угла:

[латекс] \ displaystyle {\ begin {align} \ theta & = \ frac {s} {r} \\ & = \ frac {4 \ pi} {12} \\ & = \ frac {\ pi} {3 } \\ & = \ frac {1} {3} \ pi \ end {align}} [/ latex]

Угол имеет размер [latex] \ displaystyle {\ frac {1} {3} \ pi} [/ latex] радиан.

Определение тригонометрических функций на единичной окружности

Определение точек на единичной окружности позволяет применять тригонометрические функции к любому углу.

Цели обучения

Используйте прямоугольные треугольники, нарисованные в единичной окружности, чтобы определить тригонометрические функции для любого угла

Основные выводы

Ключевые моменты

Координаты [latex] x [/ latex] — и [latex] y [/ latex] в точке на единичной окружности, заданной углом [latex] t [/ latex], определяются функциями [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex].{\ circ} [/ латекс].
Единичный круг демонстрирует периодичность тригонометрических функций, показывая, что они приводят к повторяющемуся набору значений через равные промежутки времени.

Ключевые термины

периодичность : качество функции с повторяющимся набором значений через равные промежутки времени.
единичная окружность : окружность с центром в начале координат и радиусом 1.
квадранты : Четыре четверти координатной плоскости, образованные осями [латекс] x [/ latex] — и [latex] y [/ latex].

Тригонометрические функции и единичная окружность

Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичной окружности. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1. Угол [латекс] t [/ латекс] (в радианах) образует дугу длиной [латекс] s [/ латекс].

Оси x- и y- делят координатную плоскость (и единичную окружность, поскольку она центрирована в начале координат) на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором развернется положительный угол. Четыре квадранта обозначены I, II, III и IV.

Для любого угла [latex] t [/ latex] мы можем обозначить пересечение его стороны и единичного круга его координатами, [latex] (x, y) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:

[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ y & = \ sin t \ end {align}} [/ latex]

Эти координаты показаны на диаграмме единичного круга.

Единичный круг: Координаты точки на единичной окружности, центральный угол которой составляет [латекс] t [/ латекс] радиан.

Обратите внимание, что значения [latex] x [/ latex] и [latex] y [/ latex] задаются длинами двух сторон треугольника, окрашенных в красный цвет. Это прямоугольный треугольник, и вы можете видеть, как длины этих двух сторон (и значения [latex] x [/ latex] и [latex] y [/ latex]) задаются тригонометрическими функциями [latex] t [/латекс].

Для примера того, как это применяется, рассмотрим диаграмму, показывающую точку с координатами [latex] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] по единичной окружности.

Точка на единичном круге: точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] на единичном круге .

Мы знаем, что для любой точки единичного круга координата [latex] x [/ latex] равна [latex] \ cos t [/ latex], а координата [latex] y [/ latex] — [latex] ] \ sin t [/ латекс]. Применяя это, мы можем определить, что [latex] \ displaystyle {\ cos t = — \ frac {\ sqrt2} {2}} [/ latex] и [latex] \ displaystyle {\ sin t = — \ frac {\ sqrt2} {2}} [/ латекс] для угла [латекс] t [/ латекс] на схеме.

Напомним, что [латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]. Применяя эту формулу, мы можем найти тангенс любого угла, обозначенного единичной окружностью. Для угла [латекс] т [/ латекс], указанного на диаграмме единичного круга, показывающей точку [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2 } \ right)} [/ latex], касательная:

[латекс] \ displaystyle {\ begin {align} \ tan t & = \ frac {\ sin t} {\ cos t} \\ & = \ frac {- \ frac {\ sqrt2} {2}} {- \ гидроразрыв {\ sqrt2} {2}} \\ & = 1 \ end {align}} [/ latex]

Ранее мы обсуждали тригонометрические функции применительно к прямоугольным треугольникам. {\ circ} [/ латекс].

Дальнейшее рассмотрение единичной окружности

Координаты определенных точек на единичной окружности и мера каждого угла в радианах и градусах показаны на диаграмме координат единичной окружности. Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.

Координаты единичной окружности : Единичная окружность, показывающая координаты и угловые размеры определенных точек.

Мы можем найти координаты любой точки единичной окружности.Учитывая любой угол [латекс] t [/ латекс], мы можем найти координату [latex] x [/ latex] или [latex] y [/ latex] в этой точке, используя [latex] x = \ text {cos} t [/ latex] и [latex] y = \ text {sin} t [/ latex].

Единичный круг демонстрирует периодичность тригонометрических функций. Периодичность относится к способу, которым тригонометрические функции приводят к повторяющемуся набору значений через равные промежутки времени. Взгляните на [latex] x [/ latex] -значения координат в единичном круге выше для значений [latex] t [/ latex] от [latex] 0 [/ latex] до [latex] 2 {\ pi} [/ latex]:

[латекс] {1, \ frac {\ sqrt {3}} {2}, \ frac {\ sqrt {2}} {2}, \ frac {1} {2}, 0, — \ frac {1} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {\ sqrt {3}} {2}, -1, — \ frac {\ sqrt {3}} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {1} {2}, 0, \ frac {1} {2}, \ frac {\ sqrt {2}} {2}, \ frac { \ sqrt {3}} {2}, 1} [/ латекс]

Мы можем определить закономерность в этих числах, которые колеблются между [латекс] -1 [/ латекс] и [латекс] 1 [/ латекс]. Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.

Пример

Решите [латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)}} [/ latex].

Похоже, это будет сложно решить. Однако обратите внимание, что диаграмма единичного круга показывает координаты в [latex] \ displaystyle {t = \ frac {7 \ pi} {6}} [/ latex].Поскольку координата [latex] y [/ latex] соответствует [latex] \ sin t [/ latex], мы можем определить, что

[латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)} = — \ frac {1} {2}} [/ latex]

Специальные уголки

Единичный круг и набор правил можно использовать для вызова значений тригонометрических функций специальных углов.

Цели обучения

Объясните, как свойства синуса, косинуса и тангенса и их знаки в каждом квадранте дают свои значения для каждого из специальных углов

Основные выводы

Ключевые моменты

Тригонометрические функции для углов единичной окружности можно запомнить и вызвать с помощью набора правил.
Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Умный класс триггера» используется для определения того, какие функции в каком квадранте положительны.
Базовые углы в квадранте I используются для определения значения любого угла в квадрантах II, III или IV. Базовый угол образует с осью [latex] x [/ latex] тот же угол, что и рассматриваемый угол.
В единичную окружность включаются только функции синуса и косинуса для особых углов.Однако, поскольку тангенс получается из синуса и косинуса, его можно вычислить для любого из специальных углов.

Ключевые термины

специальный угол : угол, кратный 30 или 45 градусам; тригонометрические функции легко записываются под этими углами.

Тригонометрические функции специальных углов

Напомним, что определенные углы и их координаты, которые соответствуют [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex] для данного угла [latex] t [/ latex], можно идентифицировать на единичном круге. {\ circ} \ right)} & = 1 \\ \ end {align}} [/ latex]

Выражения для косинусных функций этих специальных углов также просты.

Обратите внимание, что, хотя только синус и косинус определяются непосредственно единичной окружностью, тангенс можно определить как частное, включающее эти два:

[латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ латекс]

Касательные функции также имеют простые выражения для каждого из специальных углов.

Мы можем наблюдать эту тенденцию на примере.{\ circ} \ right)}} \\ & = \ frac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \\ & = \ frac {\ sqrt {3 }} {2} \ cdot \ frac {2} {1} \\ & = \ sqrt {3} \ end {align}} [/ latex]

Запоминание тригонометрических функций

Понимание единичной окружности и способность быстро решать тригонометрические функции для определенных углов очень полезно в области математики. Применение правил и ярлыков, связанных с единичным кругом, позволяет быстро решать тригонометрические функции. Ниже приведены некоторые правила, которые помогут вам быстро решить такие проблемы.

Признаки тригонометрических функций

Знак тригонометрической функции зависит от квадранта, в который попадает угол. Чтобы помочь запомнить, какие из тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который является «А», все тригонометрических функций положительны.В квадранте II, «Умный», только синус является положительным. В квадранте III «Триггер» только , касательная положительна. Наконец, в квадранте IV «Класс» только косинус положителен.

Знаковые правила для тригонометрических функций: Каждая тригонометрическая функция перечислена в тех квадрантах, в которых она положительна.

Определение значений с использованием опорных углов

Внимательно посмотрите на единичный круг и обратите внимание, что [latex] \ sin t [/ latex] и [latex] \ cos t [/ latex] принимают определенные значения, поскольку они колеблются между [latex] -1 [/ latex] и [латекс] 1 [/ латекс].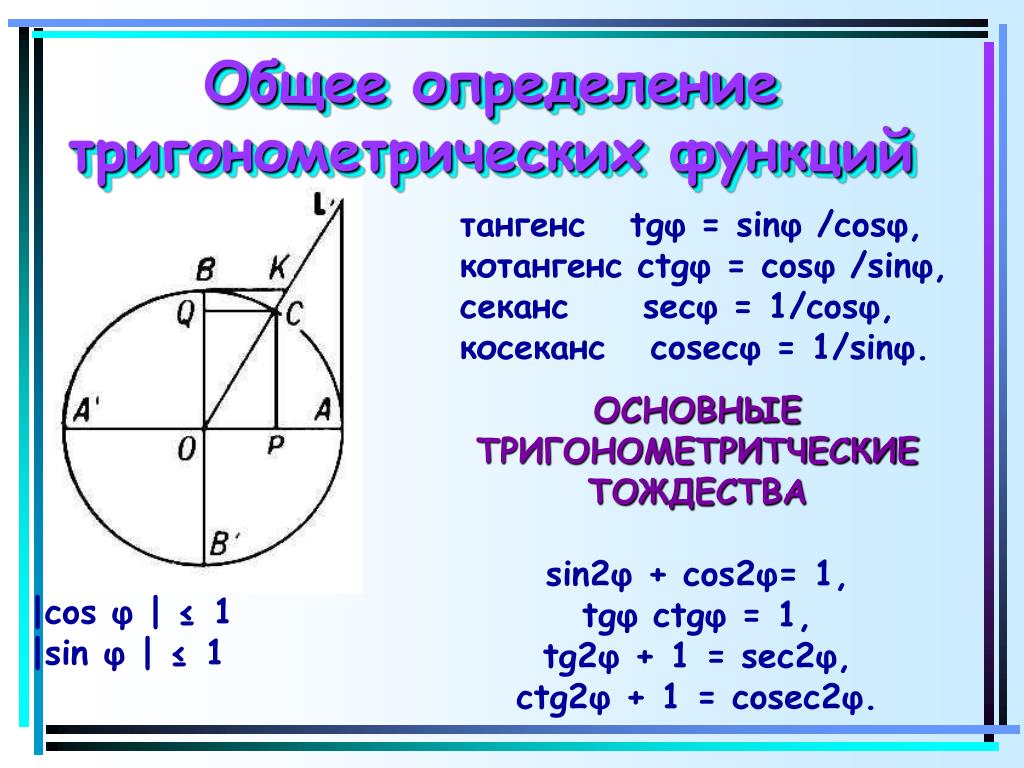 {\ circ} [/ латекс].

Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса является координатой [latex] y [/ latex] на единичной окружности, другой угол с таким же синусом будет иметь такое же значение [latex] y [/ latex], но будет иметь противоположное значение [latex] x [/ latex] -значение. Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.

Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол.Угол с таким же косинусом будет иметь одинаковое значение [latex] x [/ latex], но будет иметь противоположное значение [latex] y [/ latex]. Следовательно, его значение синуса будет противоположным значению синуса исходного угла.

Как показано на диаграммах ниже, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.

[латекс] \ Displaystyle {\ begin {align} \ sin t = \ sin \ alpha \ quad & \ text {and} \ quad \ cos t = — \ cos \ alpha \\ \ sin t = — \ sin \ beta \ quad & \ text {and} \ quad \ cos t = \ cos \ beta \ end {align}} [/ latex]

Контрольные углы: На левом рисунке [латекс] t [/ latex] является контрольным углом для [латекс] \ альфа [/ латекс].{\ circ} [/ latex] или [latex] 0 [/ latex] и [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex] радиан. Для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.

Базовые углы в каждом квадранте: Для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.

Таким образом, чтобы вызвать любой синус или косинус особого угла, вам необходимо определить его угол с осью [latex] x [/ latex], чтобы сравнить его с опорным углом.{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]

Синус и косинус как функции

Функции синуса и косинуса можно изобразить, используя значения из единичного круга, и на обоих графиках можно наблюдать определенные характеристики.

Цели обучения

Опишите характеристики графиков синуса и косинуса

Основные выводы

Ключевые моменты

Как синусоидальную функцию [latex] (y = \ sin x) [/ latex], так и косинусную функцию [latex] (y = \ cos x) [/ latex]) можно изобразить, нанеся точки, полученные из единичной окружности, с каждая координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] представляет собой соответствующее значение функции под этим углом.
Синус и косинус — периодические функции с периодом [латекс] 2 \ пи [/ латекс].
И синус, и косинус имеют домен [latex] (- \ infty, \ infty) [/ latex] и диапазон [latex] [- 1, 1] [/ latex].
График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция, в то время как график [latex] y = \ cos x [/ latex] симметричен относительно [latex ] y [/ latex] -axis, потому что это четная функция.

Ключевые термины

период : интервал, содержащий значения, повторяющиеся в функции.
четная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = f (x) [/ latex], с симметрией относительно оси [латекс] y [/ латекс].
нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , с симметрией относительно начала координат.
периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], который повторяется через равные промежутки времени.

Графические функции синуса и косинуса

Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами [latex] x [/ latex] и [latex] y [/ latex] точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции [latex] y = \ sin x [/ latex]. Мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения для синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ sin х [/ латекс]:

[латекс] \ displaystyle {(0, 0) \ quad (\ frac {\ pi} {6}, \ frac {1} {2}) \ quad (\ frac {\ pi} {4}, \ frac { \ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {2}, 1 ) \\ (\ frac {2 \ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {3 \ pi} {4}, \ frac {\ sqrt {2} } {2}) \ quad (\ frac {5 \ pi} {6}, \ frac {1} {2}) \ quad (\ pi, 0)} [/ latex]

Построение точек из таблицы и продолжение по оси [latex] x [/ latex] дает форму синусоидальной функции.

График синусоидальной функции: График точек с координатами [latex] x [/ latex], являющимися углами в радианах, и координатами [latex] y [/ latex], являющимися функцией [latex] \ sin x [/ latex] .

Обратите внимание на положительные значения синуса между [latex] 0 [/ latex] и [latex] \ pi [/ latex], которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичной окружности, и синусоидальной значения отрицательны между [латекс] \ пи [/ латекс] и [латекс] 2 \ пи [/ латекс], которые соответствуют значениям синусоидальной функции в квадрантах III и IV на единичной окружности.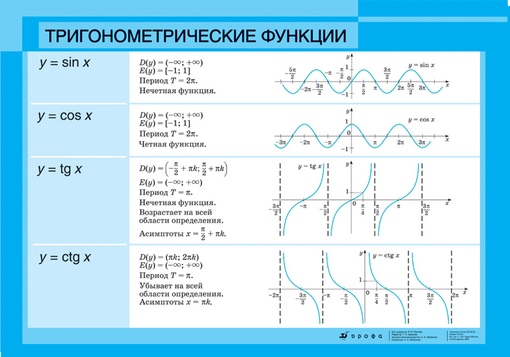

Построение значений синусоидальной функции: Точки на кривой [латекс] y = \ sin x [/ latex] соответствуют значениям синусоидальной функции на единичной окружности.

Теперь давайте аналогичным образом рассмотрим функцию косинуса, [latex] f (x) = \ sin x [/ latex]. Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:

[латекс] \ displaystyle {(0, 1) \ quad (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {4} , \ frac {\ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {1} {2}) \ quad (\ frac {\ pi} {2}, 0 ) \\ (\ frac {2 \ pi} {3}, — \ frac {1} {2}) \ quad (\ frac {3 \ pi} {4}, — \ frac {\ sqrt {2}} { 2}) \ quad (\ frac {5 \ pi} {6}, — \ frac {\ sqrt {3}} {2}) \ quad (\ pi, -1)} [/ latex]

Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса.

График функции косинуса: Точки на кривой [latex] y = \ cos x [/ latex] соответствуют значениям функции косинуса на единичной окружности.

Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичном круге, становится ясно, что диапазон обеих функций должен быть интервалом [latex] \ left [-1, 1 \ right] [/ latex].

Определение периодических функций

На графиках для синусоидальной и косинусной функций форма графика повторяется после [latex] 2 \ pi [/ latex], что означает, что функции являются периодическими с периодом [latex] 2 \ pi [/ latex].Периодическая функция — это функция с повторяющимся набором значений через равные промежутки времени. В частности, это функция, для которой определенный горизонтальный сдвиг, [латекс] P [/ латекс], приводит к функции, равной исходной функции:

[латекс] f (x + P) = f (x) [/ латекс]

для всех значений [latex] x [/ latex] в домене [latex] f [/ latex]. Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с [latex] P> 0 [/ latex] периодом функции. На диаграмме ниже показаны несколько периодов функций синуса и косинуса.

Периоды функций синуса и косинуса: Функции синуса и косинуса являются периодическими, что означает, что определенный горизонтальный сдвиг, [latex] P [/ latex], приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ латекс].

Четные и нечетные функции

Еще раз взглянув на функции синуса и косинуса в домене с центром на оси [latex] y [/ latex], можно выявить симметрии. Как мы видим на графике синусоидальной функции, она симметрична относительно начала координат, что указывает на нечетную функцию.На всем протяжении графика любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex]. Это характерно для нечетной функции: два входа, которые являются противоположными, имеют выходы, которые также являются противоположными.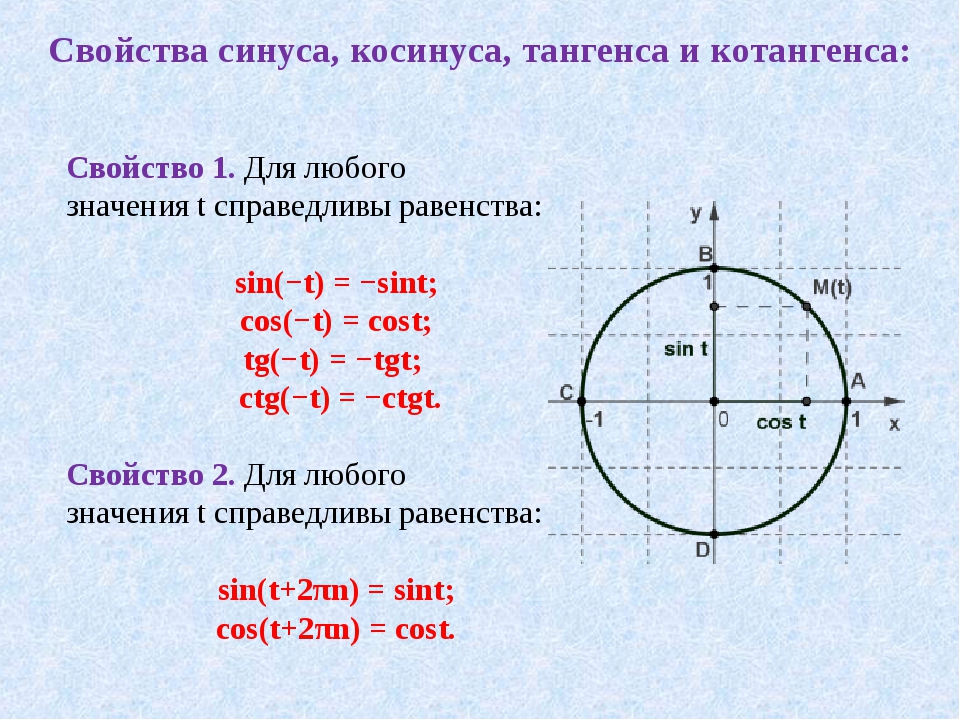 Другими словами, если [латекс] \ sin (-x) = — \ sin x [/ latex].

Нечетная симметрия синусоидальной функции: Синусоидальная функция нечетная, что означает, что она симметрична относительно начала координат.

График функции косинуса показывает, что он симметричен относительно оси y .Это означает, что это четная функция. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Другими словами, [латекс] \ cos (-x) = \ cos x [/ latex]. Мы можем видеть из графика, что это правда, сравнивая [latex] y [/ latex] -значения графика с любыми противоположными значениями [latex] x [/ latex].

Четная симметрия функции косинуса: Функция косинуса четная, что означает, что она симметрична относительно оси [latex] y [/ latex].

Касательная как функция

Характеристики касательной функции можно увидеть на ее графике.

Цели обучения

Опишите характеристики графика касательной функции

Основные выводы

Ключевые моменты

Функция касательной не определена при любом значении [latex] x [/ latex], где [latex] \ cos x = 0 [/ latex], и ее график имеет вертикальные асимптоты при этих значениях [latex] x [/ latex] .
Касательная — периодическая функция с периодом [латекс] \ пи [/ латекс].
График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией.

Ключевые термины

периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex] с набором значений, которые повторяются через равные промежутки времени.
период : интервал, содержащий минимальный набор значений, которые повторяются в периодической функции.
нечетная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , и есть симметрия относительно начала координат.
вертикальная асимптота : прямая линия, параллельная оси [латекс] y [/ латекс], к которой кривая приближается произвольно близко по мере того, как кривая уходит в бесконечность.

Построение касательной функции

Касательную функцию можно изобразить, построив точки [latex] \ left (x, f (x) \ right) [/ latex]. Форму функции можно создать, найдя значения касательной под определенными углами. Однако невозможно найти касательные функции для этих особых углов с единичной окружностью.Мы применяем формулу [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], чтобы определить касательную для каждого значения.

Мы можем проанализировать графическое поведение тангенциальной функции, посмотрев на значения некоторых специальных углов. Рассмотрим точки ниже, для которых координаты [latex] x [/ latex] представляют собой углы в радианах, а координаты [latex] y [/ latex] — [latex] \ tan x [/ latex]:

[латекс] \ displaystyle {(- \ frac {\ pi} {2}, \ text {undefined}) \ quad (- \ frac {\ pi} {3}, — \ sqrt {3}) \ quad (- \ frac {\ pi} {4}, -1) \ quad (- \ frac {\ pi} {6}, — \ frac {\ sqrt {3}} {3}) \ quad (0, 0) \\ (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {3}) \ quad (\ frac {\ pi} {4}, 1) \ quad (\ frac {\ pi} {3 }, \ sqrt {3}) \ quad (\ frac {\ pi} {2}, \ text {undefined})} [/ latex]

Обратите внимание, что [latex] \ tan x [/ latex] не определено в [latex] \ displaystyle {x = — \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ латекс]. Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются, когда [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы можем видеть, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.

Напомним, что существует несколько значений [latex] x [/ latex], которые могут дать [latex] \ cos x = 0 [/ latex]. В любой такой точке [latex] \ tan x [/ latex] не определено, потому что [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex]. При значениях, при которых функция касательной не определена, на ее графике наблюдаются разрывы. При этих значениях график касательной имеет вертикальные асимптоты.

График функции касательной: функция касательной имеет вертикальные асимптоты в [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ пи} {2}} [/ латекс].

Характеристики графика касательной функции

Как и функции синуса и косинуса, тангенс является периодической функцией. Это означает, что его значения повторяются через определенные промежутки времени. Период касательной функции равен [latex] \ pi [/ latex], потому что график повторяется на [latex] x [/ latex] -осных интервалах [latex] k \ pi [/ latex], где [latex] k [/ latex] — это константа. На графике функции касательной на интервале [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex] к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex], мы можем увидеть поведение графика за один полный цикл функции. Если мы посмотрим на
любой больший интервал, мы увидим, что характеристики графика повторяются.

График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией. Другими словами, [latex] \ text {tan} (- x) = — \ text {tan} x [/ latex] для любого значения [latex] x [/ latex]. Любые две точки с противоположными значениями [latex] x [/ latex] дают противоположные значения [latex] y [/ latex]. Мы можем видеть, что это правда, рассматривая значения [latex] y [/ latex] графика при любых противоположных значениях [latex] x [/ latex].Рассмотрим [латекс] \ displaystyle {x = \ frac {\ pi} {3}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ pi} {3}} [/ latex]. Выше мы уже определили, что [латекс] \ displaystyle {\ tan (\ frac {\ pi} {3}) = \ sqrt {3}} [/ latex] и [latex] \ displaystyle {\ tan (- \ frac { \ pi} {3}) = — \ sqrt {3}} [/ latex].

Секанс и тригонометрические функции

Тригонометрические функции имеют обратные величины, которые можно вычислить с помощью единичной окружности.

Цели обучения

Расчет значений тригонометрических функций, являющихся обратными синусу, косинусу и тангенсу

Основные выводы

Ключевые моменты

Секущая функция обратна функции косинуса [latex] \ displaystyle {\ left (\ sec x = \ frac {1} {\ cos x} \ right)} [/ latex].Его можно найти для угла [латекс] t [/ latex], используя координату [latex] x [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ sec t = \ frac { 1} {x}} [/ латекс].
Функция косеканса является обратной функцией синусоидальной функции [latex] \ displaystyle {\ left (\ csc x = \ frac {1} {\ sin x} \ right)} [/ latex]. Его можно найти для угла [латекс] t [/ latex], используя координату [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ csc t = \ frac { 1} {y}} [/ латекс].
Функция котангенса является обратной функцией касательной [латекс] \ displaystyle {\ left (\ cot x = \ frac {1} {\ tan x} = \ frac {\ cos t} {\ sin t} \ right) }[/латекс]. 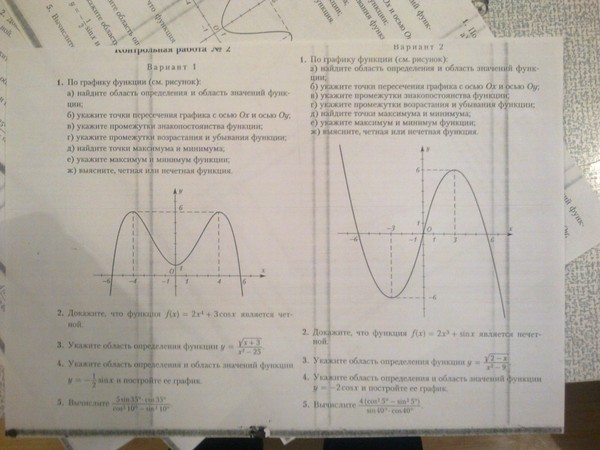Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].

Ключевые термины

секанс : величина, обратная функции косинуса
косеканс : величина, обратная синусоиде
котангенс : обратная величина касательной функции

Введение в взаимные функции

Мы обсудили три тригонометрические функции: синус, косинус и тангенс.Каждая из этих функций имеет обратную функцию, которая определяется обратной величиной отношения исходной тригонометрической функции. Обратите внимание, что обратные функции отличаются от обратных функций. Обратные функции — это способ работать в обратном направлении или определять угол с учетом тригонометрического отношения; они предполагают работу с теми же соотношениями, что и исходная функция.

Три взаимные функции описаны ниже.

Секант

Секущая функция является обратной функцией косинусной функции и обозначается сокращенно как [латекс] \ сек [/ латекс].
Его можно описать как отношение длины гипотенузы к длине соседней стороны в треугольнике.

[латекс] \ displaystyle {\ begin {align} \ sec x & = \ frac {1} {\ cos x} \\ \ sec x & = \ frac {\ text {hypotenuse}} {\ text {смежный}} \ end {align}} [/ latex]

Секанс легко вычислить со значениями в единичной окружности. Напомним, что для любой точки окружности значение [latex] x [/ latex] дает [latex] \ cos t [/ latex] для соответствующего угла [latex] t [/ latex].Следовательно, секущая функция для этого угла равна

.
[латекс] \ displaystyle {\ sec t = \ frac {1} {x}} [/ латекс]
Косеканс
Функция косеканса является обратной функцией синусоиды и обозначается сокращенно как [latex] \ csc [/ latex]. Его можно описать как отношение длины гипотенузы к длине противоположной стороны треугольника.
[латекс] \ displaystyle {\ begin {align} \ csc x & = \ frac {1} {\ sin x} \\ \ csc x & = \ frac {\ text {hypotenuse}} {\ text {напротив}} \ end {align}} [/ latex]
Как и секанс, косеканс может быть вычислен со значениями в единичной окружности.Напомним, что для любой точки круга значение [latex] y [/ latex] дает [latex] \ sin t [/ latex]. Следовательно, функция косеканса для того же угла равна
[латекс] \ displaystyle {\ csc t = \ frac {1} {y}} [/ латекс]
Котангенс
Функция котангенса обратна функции тангенса и обозначается сокращенно как [latex] \ cot [/ latex]. Его можно описать как отношение длины прилегающей стороны к длине гипотенузы в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ cot x & = \ frac {1} {\ tan x} \\ \ cot x & = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align}} [/ latex]
Также обратите внимание, что поскольку [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], его обратное значение равно
[латекс] \ displaystyle {\ cot x = \ frac {\ cos x} {\ sin x}} [/ латекс]
Котангенс также может быть вычислен со значениями в единичной окружности. Применяя координаты [latex] x [/ latex] и [latex] y [/ latex], связанные с углом [latex] t [/ latex], получаем
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ \ cot t & = \ frac {x} {y} \ end {align}} [/ латекс]
Вычисление обратных функций
Теперь мы распознаем шесть тригонометрических функций, которые можно вычислить, используя значения в единичном круге. Напомним, что мы использовали значения функций синуса и косинуса для вычисления функции тангенса.Мы будем следовать аналогичному процессу для обратных функций, ссылаясь на значения в единичном круге для наших расчетов.
Например, давайте найдем значение [latex] \ sec {\ left (\ frac {\ pi} {3} \ right)} [/ latex].
Применяя [latex] \ displaystyle {\ sec x = \ frac {1} {\ cos x}} [/ latex], мы можем переписать это как:
[латекс] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)} = \ frac {1} {\ cos {\ left ({\ frac {\ pi} {3}} \ right)}}} [/ латекс]
Из единичной окружности мы знаем, что [latex] \ displaystyle {\ cos {\ left ({\ frac {\ pi} {3}} \ right)} = \ frac {1} {2}} [/ latex] . Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ sec {\ left (\ frac {\ pi} {3} \ right)} & = \ frac {1} {\ frac {1} {2}} \\ & = 2 \ end {align}} [/ латекс]
Остальные взаимные функции могут быть решены аналогичным образом.
Пример
Используйте единичный круг для вычисления [латекс] \ sec t [/ latex], [latex] \ cot t [/ latex] и [latex] \ csc t [/ latex] в точке [latex] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex].
Точка на единичном круге: Точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex] , показанный в единичном круге.
Поскольку нам известны координаты [latex] (x, y) [/ latex] точки на единичной окружности, обозначенной углом [latex] t [/ latex], мы можем использовать эти координаты для нахождения трех функций.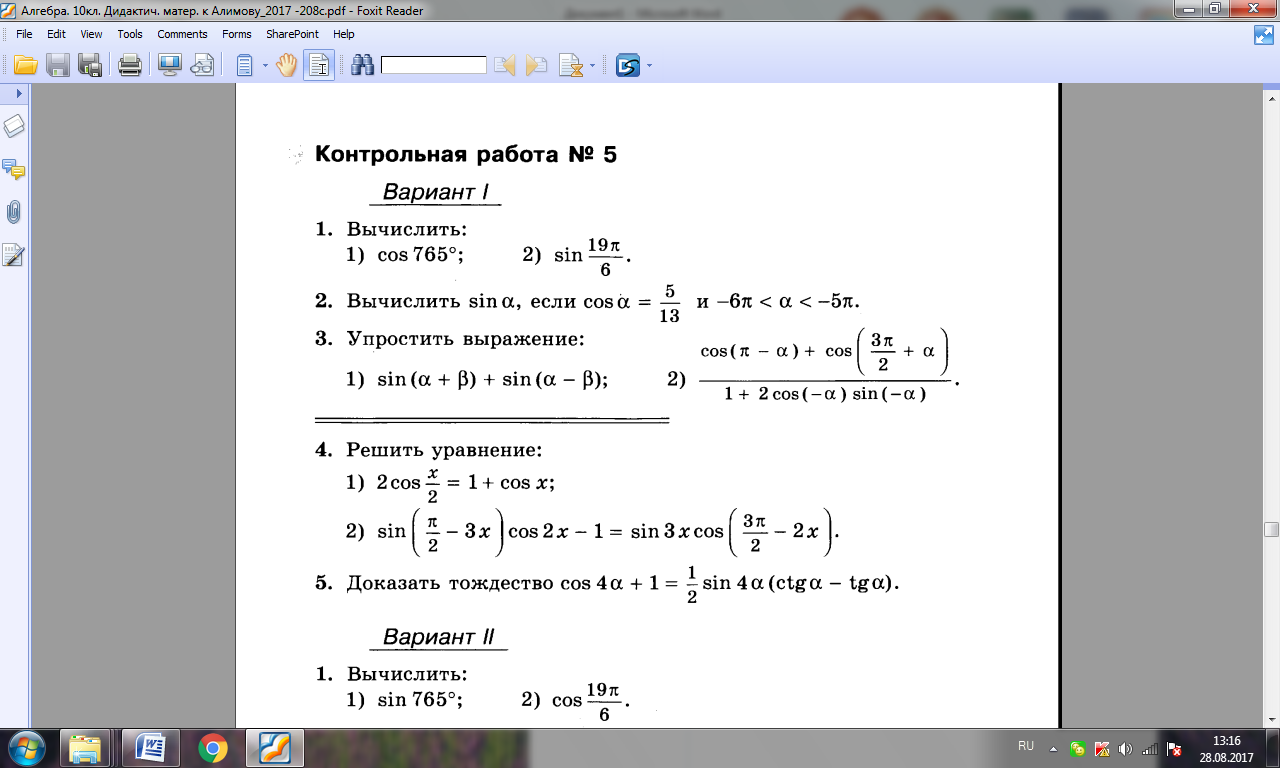
Напомним, что координата [latex] x [/ latex] дает значение для функции косинуса, а координата [latex] y [/ latex] дает значение для функции синуса.Другими словами:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
и
[латекс] \ displaystyle {\ begin {align} y & = \ sin t \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Используя эту информацию, можно вычислить значения обратных функций под углом [латекс] t [/ латекс]:
[латекс] \ displaystyle {\ begin {align} \ sec t & = \ frac {1} {\ cos t} \\ & = \ frac {1} {x} \\ & = \ left (\ frac {1 } {- \ frac {\ sqrt {3}} {2}} \ right) \\ & = — \ frac {2} {\ sqrt {3}} \\ & = \ left (- \ frac {2} { \ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} \ right) \\ & = — \ frac {2 \ sqrt {3}} {3} \ end {align} } [/ латекс]
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ & = \ frac {x} {y} \\ & = \ left (\ frac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \ right) \\ & = \ left (- \ frac {\ sqrt {3}} {2} \ cdot \ frac {2} {1} \ right) \\ & = — \ sqrt {3} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} \ csc t & = \ frac {1} {\ sin t} \\ & = \ frac {1} {y} \\ & = \ left (\ frac {1 } {\ frac {1} {2}} \ right) \\ & = 2 \ end {align}} [/ latex]
Обратные тригонометрические функции
У каждой тригонометрической функции есть обратная функция, которую можно изобразить. {- 1} x = y [/ latex].{-1} [/ латекс]
взаимно однозначная функция : функция, которая никогда не сопоставляет отдельные элементы своего домена с одним и тем же элементом своего диапазона.
Введение в обратные тригонометрические функции
Обратные тригонометрические функции используются для нахождения углов треугольника, если нам заданы длины сторон. Обратные тригонометрические функции могут использоваться, чтобы определить, какой угол даст определенное значение синуса, косинуса или тангенса.
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{-1} (б) = а [/ латекс]. Однако функции синуса, косинуса и тангенса — это , а не взаимно однозначные функции. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в своем диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно.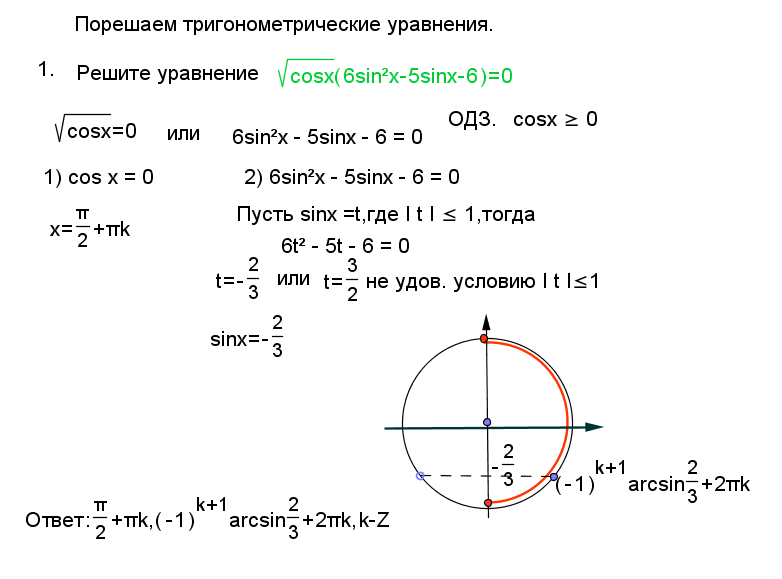 Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область определения каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем домен для каждой функции, который включает число [latex] 0 [/ latex].
Функции синуса и косинуса в ограниченных областях: (a) Синус-функция, показанная в ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ справа] [/ латекс]; (b) Функция косинуса, показанная в ограниченной области [latex] \ left [0, \ pi \ right] [/ latex].
График синусоидальной функции ограничен областью [latex] [- \ frac {\ pi} {2}, \ frac {\ pi} {2}] [/ latex] и графиком косинусной функции ограничено [латексом] [0, \ pi] [/ латексом]. График касательной функции ограничен [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Касательная функция в ограниченной области
Функция касательной, показанная в ограниченной области [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].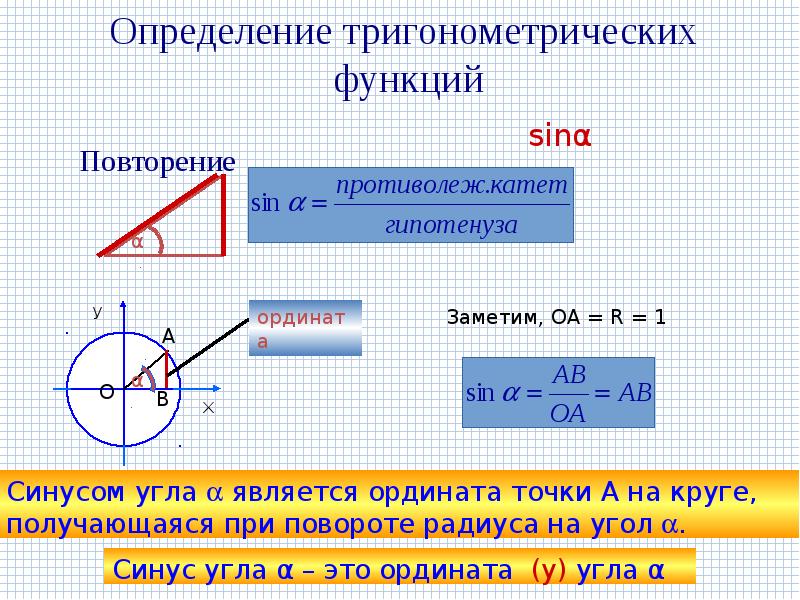
Эти варианты ограниченных доменов в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает обратимую функцию «один к одному». Традиционный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он распространяется от одной вертикальной асимптоты к другой, вместо того, чтобы разделяться на части асимптотой.{-1} x \ quad \ text {имеет домен} \ quad \ left (- \ infty, \ infty \ right) \ quad \ text {и диапазон} \ quad \ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right)} [/ latex]
Графики обратных тригонометрических функций
Функция синуса и функция обратного синуса (или арксинуса): функция арксинуса является отражением функции синуса относительно линии [latex] y = x [/ latex].
Чтобы найти область определения и диапазон обратных тригонометрических функций, мы меняем область определения и диапазон исходных функций.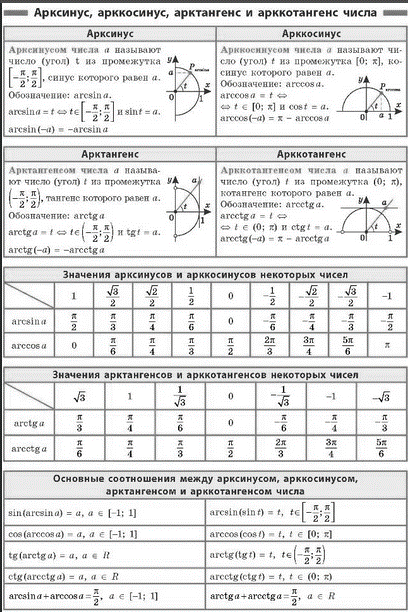
Функция косинуса и функция обратного косинуса (или арккосинуса): Функция арккосинуса является отражением функции косинуса относительно линии [латекс] y = x [/ latex].
Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Функция тангенса и функция арктангенса (или арктангенса): Функция арктангенса является отражением функции касательной относительно линии [латекс] y = x [/ latex].{-1} х = у [/ латекс].
Обзор Algebra Trig
Показать мобильное уведомление Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Оценка триггерной функции
Одна из проблем с большинством классов триггеров состоит в том, что они имеют тенденцию концентрироваться на триггерах прямоугольного треугольника и делать все в терминах степеней.Затем вы перейдете к курсу исчисления, где почти все делается в радианах, а единичная окружность — очень полезный инструмент.
Итак, сначала давайте посмотрим на следующую таблицу, чтобы соотнести градусы и радианы.
Степень 0 30 45 60 90 180 270 360
радианы 0 \ (\ displaystyle \ frac {\ pi} {6} \) \ (\ displaystyle \ frac {\ pi} {4} \) \ (\ displaystyle \ frac {\ pi} {3} \) \ (\ displaystyle \ frac {\ pi} {2} \) \ (\ Displaystyle \ пи \) \ (\ displaystyle \ frac {{3 \ pi}} {2} \) \ (\ Displaystyle 2 \ пи \)
Знай эту таблицу! Конечно, есть много других углов в радианах, которые мы увидим на этом занятии, но большинство из них будут связаны с этими несколькими углами. Итак, если вы сможете справиться с этими углами, вы сможете справиться с большинством других.
Предупреждаем, все в большинстве классов исчисления будут делаться в радианах!
Теперь давайте посмотрим на единичный круг. Ниже показан единичный круг с заполненным только первым квадрантом. Принцип действия единичного круга заключается в рисовании линии от центра круга наружу, соответствующей заданному углу. Затем посмотрите на координаты точки пересечения линии и круга.Первая координата — это косинус этого угла, а вторая координата — синус этого угла. Обычно используется пара из основных углов . Это \ (0, \ frac {\ pi} {6}, \ frac {\ pi} {4}, \ frac {\ pi} {3}, \ frac {\ pi} {2}, \ pi, \ frac {{3 \ pi}} {2} \) и \ (2 \ pi \) и показаны ниже вместе с координатами пересечений. Итак, из единичного круга ниже мы видим, что \ (\ cos \ left ({\ frac {\ pi} {6}} \ right) = \ frac {{\ sqrt 3}} {2} \) и \ ( \ sin \ left ({\ frac {\ pi} {6}} \ right) = \ frac {1} {2} \).
Вспомните, как работают знаки углов. Если вы вращаете против часовой стрелки, угол будет положительным, а если вы вращаетесь по часовой стрелке, угол будет отрицательным.
Напомним также, что один полный оборот равен \ (2 \ pi \), поэтому положительная ось \ (x \) может соответствовать либо углу 0, либо \ (2 \ pi \) (или \ (4 \ pi \), или \ (6 \ pi \), или \ (- 2 \ pi \), или \ (- 4 \ pi \), и т.д. . в зависимости от направления вращения). Точно так же угол \ (\ frac {\ pi} {6} \) (чтобы выбрать угол полностью наугад) также может быть любым из следующих углов:
\ (\ Displaystyle \ frac {\ pi} {6} + 2 \ pi = \ frac {{13 \ pi}} {6} \) (начать с \ (\ displaystyle \ frac {\ pi} {6} \ ) затем один раз поверните против часовой стрелки)
\ (\ displaystyle \ frac {\ pi} {6} + 4 \ pi = \ frac {{25 \ pi}} {6} \) (начать с \ (\ displaystyle \ frac {\ pi} {6} \ ) затем дважды поверните вокруг часовой стрелки)
\ (\ displaystyle \ frac {\ pi} {6} — 2 \ pi = — \ frac {{11 \ pi}} {6} \) (начинается с \ (\ displaystyle \ frac {\ pi} {6}) \) затем поверните один раз по часовой стрелке)
\ (\ displaystyle \ frac {\ pi} {6} — 4 \ pi = — \ frac {{23 \ pi}} {6} \) (начинается с \ (\ displaystyle \ frac {\ pi} {6}) \) затем дважды поверните по часовой стрелке)
и т. Д.
Фактически, \ (\ frac {\ pi} {6} \) может быть любым из следующих углов \ (\ frac {\ pi} {6} + 2 \ pi \, n \ ,, \; \; n = 0, \, \ pm 1, \, \ pm 2, \, \ pm 3, \, \ ldots \) В этом случае \ (n \) — это количество полных оборотов, которые вы делаете вокруг единичной окружности, начиная с \ (\ frac {\ pi} {6} \). Положительные значения \ (n \) соответствуют вращению против часовой стрелки, а отрицательные значения \ (n \) соответствуют вращению по часовой стрелке.
Итак, почему я ввел только первый квадрант? Ответ прост.Если вы знаете первый квадрант, вы можете получить все остальные квадранты из первого. Вы увидите это в следующих примерах.
Найдите точное значение каждого из следующего. Другими словами, не пользуйтесь калькулятором. Показать все решенияСкрыть все решения
\ (\ sin \ left ({\ frac {{2 \ pi}} {3}} \ right) \) и \ (\ sin \ left ({- \ frac {{2 \ pi}} {3}) } \правильно)\)
Показать решение
В первой оценке здесь используется угол \ (\ frac {{2 \ pi}} {3} \). Обратите внимание, что \ (\ frac {{2 \ pi}} {3} = \ pi — \ frac {\ pi} {3} \). Итак, \ (\ frac {{2 \ pi}} {3} \) находится путем поворота \ (\ frac {\ pi} {3} \) вверх от отрицательной оси \ (x \). Это означает, что линия для \ (\ frac {{2 \ pi}} {3} \) будет зеркальным отображением линии для \ (\ frac {\ pi} {3} \) только во втором квадранте. Координаты для \ (\ frac {{2 \ pi}} {3} \) будут координатами для \ (\ frac {\ pi} {3} \), за исключением того, что координата \ (x \) будет отрицательной.
Аналогично, для \ (- \ frac {{2 \ pi}} {3} \) мы можем заметить, что \ (- \ frac {{2 \ pi}} {3} = — \ pi + \ frac {\ pi } {3} \), поэтому этот угол можно найти, повернув вниз \ (\ frac {\ pi} {3} \) от отрицательной оси \ (x \).Это означает, что линия для \ (- \ frac {{2 \ pi}} {3} \) будет зеркальным отображением линии для \ (\ frac {\ pi} {3} \) только в третьем квадранте и координаты будут такими же, как координаты для \ (\ frac {\ pi} {3} \), за исключением того, что оба будут отрицательными.
Оба этих угла вместе с их координатами показаны на следующем единичном круге.
Из этого единичного круга видно, что \ (\ sin \ left ({\ frac {{2 \ pi}} {3}} \ right) = \ frac {{\ sqrt 3}} {2} \) и \ (\ sin \ left ({- \ frac {{2 \ pi}} {3}} \ right) = — \ frac {{\ sqrt 3}} {2} \).
Это приводит к интересному факту о синусоидальной функции. Функция синуса называется функцией с нечетным числом , поэтому для ЛЮБОГО угла мы имеем
\ [\ sin \ left ({- \ theta} \ right) = — \ sin \ left (\ theta \ right) \]
\ (\ cos \ left ({\ frac {{7 \ pi}} {6}} \ right) \) и \ (\ cos \ left ({- \ frac {{7 \ pi}} {6}}) \правильно)\)
Показать решение
В этом примере обратите внимание, что \ (\ frac {{7 \ pi}} {6} = \ pi + \ frac {\ pi} {6} \), это означает, что мы повернем вниз \ (\ frac {\ pi } {6} \) от отрицательной оси \ (x \), чтобы попасть в этот угол.Также \ (- \ frac {{7 \ pi}} {6} = — \ pi — \ frac {\ pi} {6} \), это означает, что мы должны повернуть вверх \ (\ frac {\ pi} {6} \) от отрицательной оси \ (x \) — до этого угла. Оба они показаны на следующем единичном круге вместе с соответствующими координатами точек пересечения.
Из этого единичного круга видно, что \ (\ cos \ left ({\ frac {{7 \ pi}} {6}} \ right) = — \ frac {{\ sqrt 3}} {2} \) и \ (\ cos \ left ({- \ frac {{7 \ pi}} {6}} \ right) = — \ frac {{\ sqrt 3}} {2} \).В этом случае функция косинуса называется функцией и даже , поэтому для ЛЮБОГО угла мы имеем
\ [\ cos \ left ({- \ theta} \ right) = \ cos \ left (\ theta \ right) \]
\ (\ tan \ left ({- \ frac {\ pi} {4}} \ right) \) и \ (\ tan \ left ({\ frac {{7 \ pi}} {4}} \ right) \)
Показать решение
Здесь мы должны отметить, что \ (\ frac {{7 \ pi}} {4} = 2 \ pi — \ frac {\ pi} {4} \), поэтому \ (\ frac {{7 \ pi}} {4 } \) и \ (- \ frac {\ pi} {4} \) фактически под одним углом! Единичный круг для этого угла составляет
.
Теперь, если мы вспомним, что \ (\ tan \ left (x \ right) = \ frac {{\ sin \ left (x \ right)}} {{\ cos \ left (x \ right)}}}), мы можно использовать единичную окружность, чтобы найти значения функции касательной.Итак,
\ [\ tan \ left (\ frac {7 \ pi} {4} \ right) = \ tan \ left (- \ frac {\ pi} {4} \ right) = \ frac {\ sin \ left (- { \ pi} / {4} \; \ right)} {\ cos \ left (- {\ pi} / {4} \; \ right)} = \ frac {- {\ sqrt {2}} / {2} \;} {{\ sqrt {2}} / {2} \;} = — 1 \]
Кстати, обратите внимание, что \ (\ tan \ left ({\ frac {\ pi} {4}} \ right) = 1 \), и мы видим, что касательная функция также называется нечетной функцией и поэтому для ЛЮБОГО угла у нас будет
\ [\ tan \ left ({- \ theta} \ right) = — \ tan \ left (\ theta \ right) \]
\ (\ sin \ left ({\ frac {{9 \ pi}} {4}} \ right) \)
Показать решение
Для этой задачи заметим, что \ (\ frac {{9 \ pi}} {4} = 2 \ pi + \ frac {\ pi} {4} \).Напомним, что один полный оборот равен \ (2 \ pi \). Таким образом, это означает, что \ (\ frac {{9 \ pi}} {4} \) и \ (\ frac {\ pi} {4} \) находятся в одной точке на единичной окружности. Следовательно,
\ [\ sin \ left ({\ frac {{9 \ pi}} {4}} \ right) = \ sin \ left ({2 \ pi + \ frac {\ pi} {4}} \ right) = \ sin \ left ({\ frac {\ pi} {4}} \ right) = \ frac {{\ sqrt 2}} {2} \]
Это приводит нас к очень интересному факту о функции синуса. Синусоидальная функция является примером периодической функции . Периодические функции — это функции, которые повторяются снова и снова.«Расстояние», на которое вам нужно переместиться вправо или влево, прежде чем функция начнет повторяться, называется периодом функции.
В случае синуса период равен \ (2 \ pi \). Это означает, что функция синуса будет повторяться каждые \ (2 \ pi \). Это приводит к красивой формуле для синусоидальной функции.
\ [\ sin \ left ({x + 2 \ pi n} \ right) = \ sin \ left (x \ right) \ hspace {0,25 дюйма} \, \, \, \, \, \, \, \, п = 0, \, \ pm 1, \, \, \ pm 2, \, \ ldots \]
Обратите внимание, что поскольку
\ [csc \ left (x \ right) = \ frac {1} {{\ sin \ left (x \ right)}} \]
то же самое можно сказать и о косеканте.
\ [\ csc \ left ({x + 2 \ pi n} \ right) = \ csc \ left (x \ right) \ hspace {0,25 дюйма} \, \, \, \, \, \, \, \, п = 0, \, \ pm 1, \, \, \ pm 2, \, \ ldots \]
Что ж, на самом деле нам следует быть осторожными. Мы можем сказать это при условии \ (x \ ne n \ pi \), поскольку синус будет равен нулю в этих точках, и поэтому косеканс там не будет!
\ (\ sec \ left ({\ frac {{25 \ pi}} {6}} \ right) \)
Показать решение
Здесь мы должны заметить, что \ (\ frac {{25 \ pi}} {6} = 4 \ pi + \ frac {\ pi} {6} \).Другими словами, мы начали с \ (\ frac {\ pi} {6} \) и дважды повернулись вокруг, чтобы вернуться в ту же точку на единичной окружности. Это означает, что
\ [\ sec \ left ({\ frac {{25 \ pi}} {6}} \ right) = \ sec \ left ({4 \ pi + \ frac {\ pi} {6}} \ right) = \ сек \ left ({\ frac {\ pi} {6}} \ right) \]
А теперь давайте не будем увлекаться секансом. {\ sqrt {3}} / {} _ {2}} = \ frac {2} {\ sqrt {3} } \]
Следует также отметить, что косинус и секанс — периодические функции с периодом \ (2 \ pi \).Итак,
\ [\ begin {align *} \ begin {align} \ cos \ left ({x + 2 \ pi n} \ right) & = \ cos \ left (x \ right) \\ \ sec \ left ({x + 2 \ pi n} \ right) & = \ sec \ left (x \ right) \ end {выровнено} & \ hspace {0,5in} n = 0, \ pm 1, \ pm 2, \, \ ldots \ end { выровнять *} \]
\ (\ tan \ left ({\ frac {{4 \ pi}} {3}} \ right) \)
Показать решение
Для решения этой задачи полезно знать, что тангенс (и, следовательно, котангенс) также является периодической функцией, но, в отличие от синуса и косинуса, она имеет период \ (\ pi \).
\ [\ begin {align *} \ begin {align} \ tan \ left ({x + \ pi n} \ right) & = \ tan \ left (x \ right) \\ \ cot \ left ({x + \ pi n} \ right) & = \ cot \ left (x \ right) \ end {выровненный} & \ hspace {0,5in} n = 0, \ pm 1, \ pm 2, \, \ ldots \ end {align * } \]
Итак, чтобы решить эту задачу, отметим, что \ (\ frac {{4 \ pi}} {3} = \ pi + \ frac {\ pi} {3} \).
No related posts.

Степень	0	30	45	60	90	180	270	360
радианы	0	\ (\ displaystyle \ frac {\ pi} {6} \)	\ (\ displaystyle \ frac {\ pi} {4} \)	\ (\ displaystyle \ frac {\ pi} {3} \)	\ (\ displaystyle \ frac {\ pi} {2} \)	\ (\ Displaystyle \ пи \)	\ (\ displaystyle \ frac {{3 \ pi}} {2} \)	\ (\ Displaystyle 2 \ пи \)