Контрольная работа номер 8 по алгебре: Алгебра 8 Контрольные Макарычев — Жохов

Содержание

Контрольные работы по алгебре 8 класс А.Г. Мордкович

Контрольная работа №1

Сложение и вычитание алгебраических дробей

Вариант 1

Контрольная работа №1

Сложение и вычитание алгебраических дробей

Вариант 2

Контрольная работа №2

Преобразование рациональных выражений

Вариант 1

Контрольная работа №2

Преобразование рациональных выражений

Вариант 2

Контрольная работа №3

Квадратичная функция. Функция .

Вариант 1

Контрольная работа №3

Квадратичная функция. Функция .

Вариант 2

Контрольная работа №4

Квадратичная функция. Функция .

Вариант 1

Контрольная работа №4

Квадратичная функция. Функция .

Вариант 2

Контрольная работа №5

Функция . Свойства квадратного корня

Вариант 1

Контрольная работа №5

Функция . Свойства квадратного корня

Вариант 2

Контрольная работа №6

Квадратные уравнения

Вариант 1

  1. Решите уравнение:

  2. Сократите дробь: .

  3. Один из корней уравнения равен 5. Найдите другой корень и коэффициент k.

  4. Поезд должен был пройти 480 км в определенное время. На половине пути он был задержан на 30 мин из-за технической неисправности. Чтобы прибыть вовремя, ему пришлось увеличить скорость на 2 км/ч. Сколько времени поезд находился в пути?

Контрольная работа №6

Квадратные уравнения

Вариант 2

  1. Решите уравнение:

  2. Сократите дробь: .

  3. Один из корней уравнения равен 12. Найдите другой корень и свободный член q.

  4. Из города А в город В выехал велосипедист и мотоциклист. Скорость велосипедиста на 10 км/ч меньше скорости мотоциклиста, поэтому он потратил на весь путь на 6 ч больше. С какой скоростью ехал мотоциклист, если расстояние между городами 120 км?

Контрольная работа №7

Действительные числа

Вариант 1

  1. Найдите значение выражения: .

  2. Упростите выражение:

.

  1. Вычислите: .

  2. Решите уравнение: .

  3. Упростите выражение: .

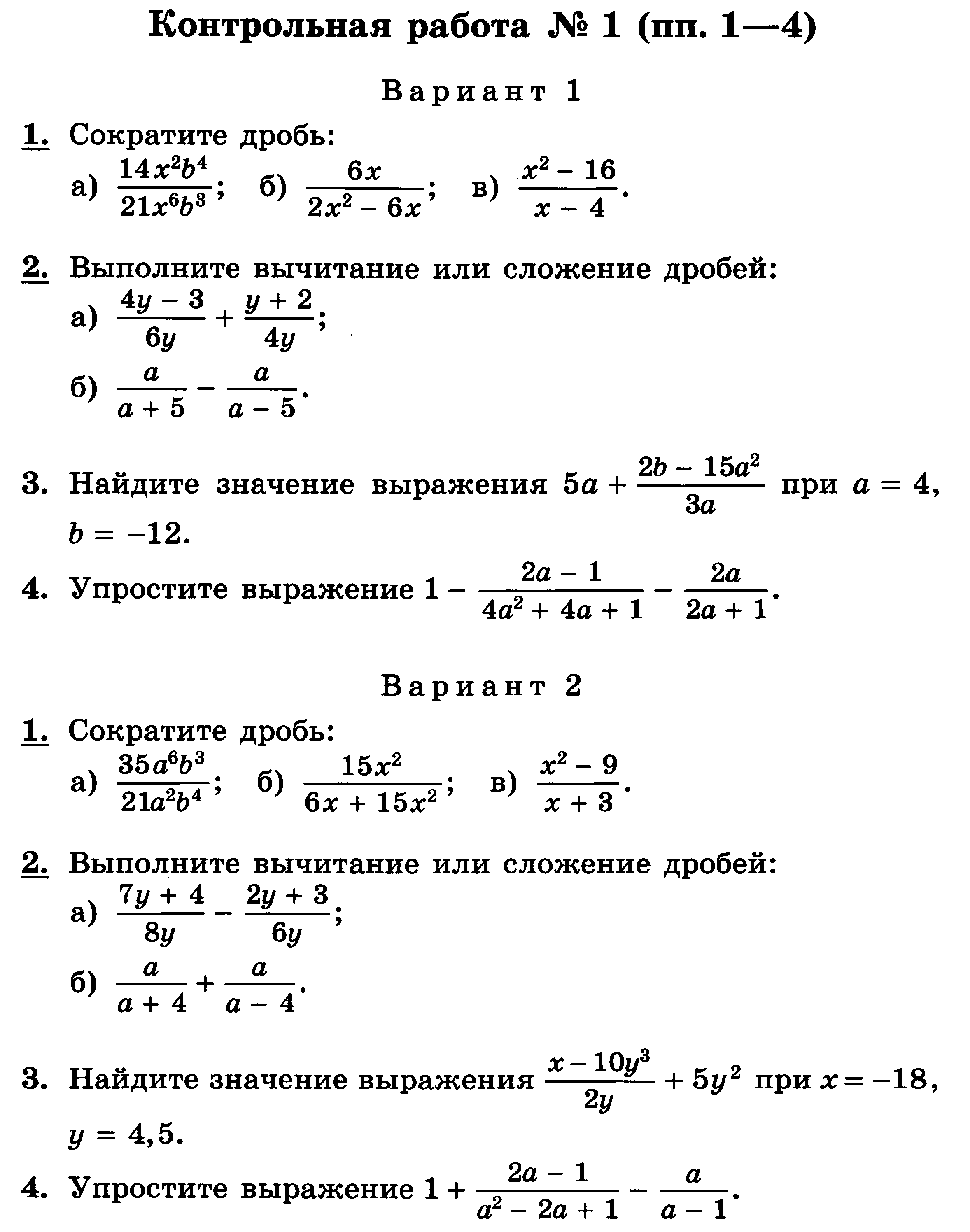
  4. Упростите выражение: .

Контрольная работа №7

Действительные числа

Вариант 2

  1. Найдите значение выражения: .

  2. Упростите выражение:

.

  1. Вычислите: .

  2. Решите уравнение: .

  3. Упростите выражение: .

  4. Упростите выражение: .

Контрольная работа №8

Неравенства

Вариант 1

Контрольная работа №8

Неравенства

Вариант 2

Контрольная работа №9

Итоговая контрольная работа

Вариант 1

Контрольная работа №9

Итоговая контрольная работа

Вариант 2

Гдз и решебник Алгебра 8 класс Мерзляк, Полонский, Рабинович — Дидактические материалы

Алгебра 8 класс

Тип пособия: Дидактические материалы

Авторы: Мерзляк, Полонский, Рабинович

Издательство: «Вентана-Граф»

Алгебра – это раздел математики, который изучает общие свойства числовых систем и методы решения задач с помощью уравнений. Здесь, в отличие от арифметики используется буквенное обозначение величин, которые позволяет записать действия над числами в краткой форме.

Что усвоят ученики на уроках

В рамках школьной программы ученики восьмого класса вначале приступят к изучению рациональных дробей и квадратного корня, а также рассмотрят их свойства и действия над ними. Далее они познакомятся с числовыми неравенствами и свойствами степеней с целыми показателями. Восьмиклассники научатся:

  1. Решать задачи и линейные уравнения.
  2. Работать с алгебраическим текстом, правильно использовать символику и определения.
  3. Описывать свойства функции, и строить графики.
  4. Пользоваться изученными формулами.
  5. Применять на практике полученные знания.

Уроки алгебры развивают логическое и абстрактное мышление, тренируют память, а также учат анализировать и делать выводы.

Для чего нужен решебник

Изучение дисциплины – это сложный и трудоемкий процесс, с которым к сожалению многие ребята не справляются. Неудовлетворительные оценки, пробелы в понимании учебного материала негативным образом влияют на уровень успеваемости. Для того, чтобы исправить ситуацию в лучшую сторону специалисты советуют использовать в процессе обучения «ГДЗ по Алгебре 8 класс Дидактические материалы Мерзляк, Полонский, Рабинович (Вентана-граф)»

. Сборник содержит правильные и досконально расписанные онлайн-ответы, которые помогут понять все тонкости и нюансы предмета. Пользуясь решебником ученик сможет:

  • правильно выполнить работу заданную на дом;
  • вовремя подготовиться к проверке знаний на уроке;
  • понять алгоритм решения задач и уравнений.

Работать с ГДЗ легко и просто. Расположение номеров упражнений полностью соответствует учебному изданию и найти нужную информацию не составит никакого труда. Это во многом экономит время и силы. Постоянно применяя решебник школьник добьётся высоких результатов и всегда будет во всеоружии перед предстоящим уроком.

Краткое описание учебника

Одним из полезных дополнительных пособий считаются дидактические материалы по алгебре за 8 класс авторы Мерзляк, Полонский. Здесь имеется большое количество разноплановых заданий, которые помогут не только закрепить теоретическую часть предмета, но и провести контроль навыков и умений по каждой теме в отдельности.

Скачать

Похожие ГДЗ Алгебра 8 класс

Алгебра 8 класс Самостоятельные и контрольные работы Мерзляк

Твитнуть

Поделиться

Плюсануть

Поделиться

Отправить

Класснуть

Запинить

 

Аннотация

Это пособие вместе с учебником для углублённого изучения математики «Алгебра. 8 класс» авторов А.Г. Мерзляка, В.М. Полякова входят в один учебно-методический комплект.

Первая часть пособия — «Самостоятельные работы» — разделена на четыре однотипных варианта по 41 работе в каждом (самостоятельные работы, имеющие одинаковые номера, являются однотипными). Каждая самостоятельная работа соответствует определённому параграфу учебника, что отражено в названии этой работы. К параграфам учебника, изучение которых предполагает рассмотрение задач многих типов, предлагаются две самостоятельные работы. Наличие аналогичных задач в самостоятельных работах с одинаковыми номерами также позволяет использовать этот материал для отработки навыков решения основных типов задач. Вторая часть пособия содержит задания для контрольных работ.

Пример из учебника

1. Докажите, что количество трёхзначных чисел равно количеству пятизначных чисел, в записи которых вторая и четвёртая цифры ( считая слева направо) соответственно равны 2 и 7.
2. В 8 классе 26 учеников. Все ученики этого класса увлекаются математикой или химией. Математикой увлекаются 18 человек, а химией – 14 человек. Сколько учеников увлекаются и математикой, и химией?
Самостоятельная работа № 4
Равно мощные множества. Счётные множества

Содержание

От авторов 3
Самостоятельные работы 4
Вариант 1 4
Вариант 2 25
Вариант 3 46
Вариант 4 67
Контрольные работы 88
Вариант 1 88
Вариант 2 98
Справочный материал 108

 

Учебник можно просто читать в онлайн режиме, переходя сразу на тот параграф или раздел, который Вам сейчас нужен.

Контрольно- измерительные материалы по алгебре 8 класс

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ

ШКОЛА С. БЕРЕЗОВО ПУГАЧЕВСКОГО РАЙОНА

САРАТОВСКОЙ ОБЛАСТИ»

 

 

 

«Рассмотрено»

Руководитель МО

_____ /__________ /

                ФИО

Протокол №____от

«__» ______ 20__г.

 

 

«Согласовано»

Заместитель директора по УВР МОУ СОШ  с.Березово

_____ /_________/

                ФИО

«__» ______ 20__г.

 

«Утверждено»

Директор МОУ СОШ с.Березово

_____ /________/

                ФИО

Приказ №___ от

«___» ______ 20__г.

 

 

 

Контрольно-измерительный материал

по алгебре в 8 классе

на 2018-2019 учебный год

 

 

 

                                                             

Рассмотрено на заседании

педагогического совета

протокол № __

«      »_______20     г.

 

 

 

 

Контрольно-измерительные материалы

 по алгебре 8 класс

(к учебнику В.Г.Дорофеева)

Контрольно-измерительные материалы ориентированы на учебник «Алгебра» для учащихся 7  класса под редакцией Г.В.Дорофеева и С.Б.Суворовой. Система контроля охватывает все изучаемые в курсе алгебры вопросы.

Структурирование контрольных работ имеет дифференцируемый подход к обучению и контролю знаний и умений учащихся. Каждая работа предусматривает проверку достижения школьниками уровня базовых требований и дает возможность учащимся проявить свои знания на более высоких уровнях.

Задания разного уровня обозначены в работе специальными значками:

       — задания базового уровня, их число варьируется в зависимости от темы и объема проверяемого материала, они аналогичны заданиям, представленным в учебнике;

       — задания более высокого уровня, в каждой работе их три;

       — дополнительное задание, предназначенное для учащихся, быстро справившихся с контрольной работой, выполняется по желанию на отдельную отметку.

В каждой контрольной работе приводятся критерии оценивания, в которых указаны нижние границы выставления отметок «3», «4», «5». Критерии оценивания открыты для учащихся, важно, чтобы они понимали, как и за что выставляется оценка. Контрольные работы и критерии оценки разработаны таким образом, чтобы у учащихся было право на ошибку: для получения «3» не обязательно правильно выполнить все задания базового уровня, точно так же и для получения пятерки не обязательно решить все задачи контрольной работы.

Содержание итоговых проверок охватывает изученные к этому времени темы курса. Итоговые контрольные работы направлены на проверку владения основным материалом и в определенной степени выяснение прочности знаний, приобретенных за продолжительный промежуток времени, и ориентированы на итоговые результаты. Как и тематические, они рассчитаны на один урок, предложенные тесты не содержат дополнительного задания, которое учитель может включать по своему усмотрению в зависимости от уровня подготовки класса или отдельных учащихся.

 

Наименование составленных работ

 

Кол-во

Контрольные работы

 

10

 

 

 

 

I ЧЕТВЕРТЬ

Стартовый контроль

ВАРИАНТ 1

 

ЧАСТЬ А

 

(Подчеркните правильный ответ). За каждый правильный ответ 1 балл

 

  1. Найдите значение выражения при а= -1,5; b=1

А.   Б.     В. – 3                              Г. 3

 

  1. Упростите выражение 3ху-3х-(х+3ху).

А. ху-3х;  Б. 3ху+х   В. -4х-6ху;                             Г. – 4х

 

  1. Представьте выражение (5a-2)2 в виде многочлена.

А. 25а2-10а+4  Б. 25а2+20а+4  В. 25а2-4                                          Г. 25а2-20а+4

 

  1. Выполните умножение: (5b-3а)(5b+3а)

А. 25b2+9а2  Б. 25b2-9a2   B. 25b2-30ab+9a2                            Г. 5b2-3a2

 

  1. Вынесите за скобки общий множитель 15a3-3a2b

А. 3а2(15а-b)  Б. 3a2(5-b)   B. 3a2(5a-1)                             Г. 3a2(5a-b)

 

ЧАСТЬ В

 

(Запишите только ответ, без решения). За каждый правильный ответ 2 балла

 

  1. Решить уравнение 2х-7=10-3(х+2)

Ответ: ___________________________________

 

  1. Упростить выражение  х5(х2)4

Ответ: ___________________________________

 

  1. Упростить выражение (а-4)2-а(2а-8)

Ответ: ____________________________________

 

  1. Разложить на множители 2ху+6у-хс-3с

Ответ: ____________________________________

 

  1. Сократить дробь:

 

 

Ответ: ________________________________

 

  1. Изобразите на координатной плоскости множество точек, удовлетворяющих условию: 1<у≤3

 

 

ЧАСТЬ С (Выполните полное решение)

 

  1. Решить уравнение –   (3 балла)

 

  1. В 15 одинаковых пакетов и 5 одинаковых коробок расфасовали 2400 г конфет. В каждую коробку уместилось на 20 г конфет больше, чем в каждый пакет. Сколько граммов конфет было в каждом пакете и каждой коробке? (4 балла)
  2. Решите уравнение -(3х-1)2+2(5+х)(х-5)+7х2=3  (6 баллов)

 

 

 

ВАРИАНТ 2

 

ЧАСТЬ А

 

(Подчеркните правильный ответ). За каждый правильный ответ 1 балл

 

  1. Найдите значение выражения при а= 1,5; с= -3,5

А

Контрольные работа алгебра 8 класс

КОНТРОЛЬНАЯ РАБОТА №1 «Сумма и разность дробей»

Вариант 1

10.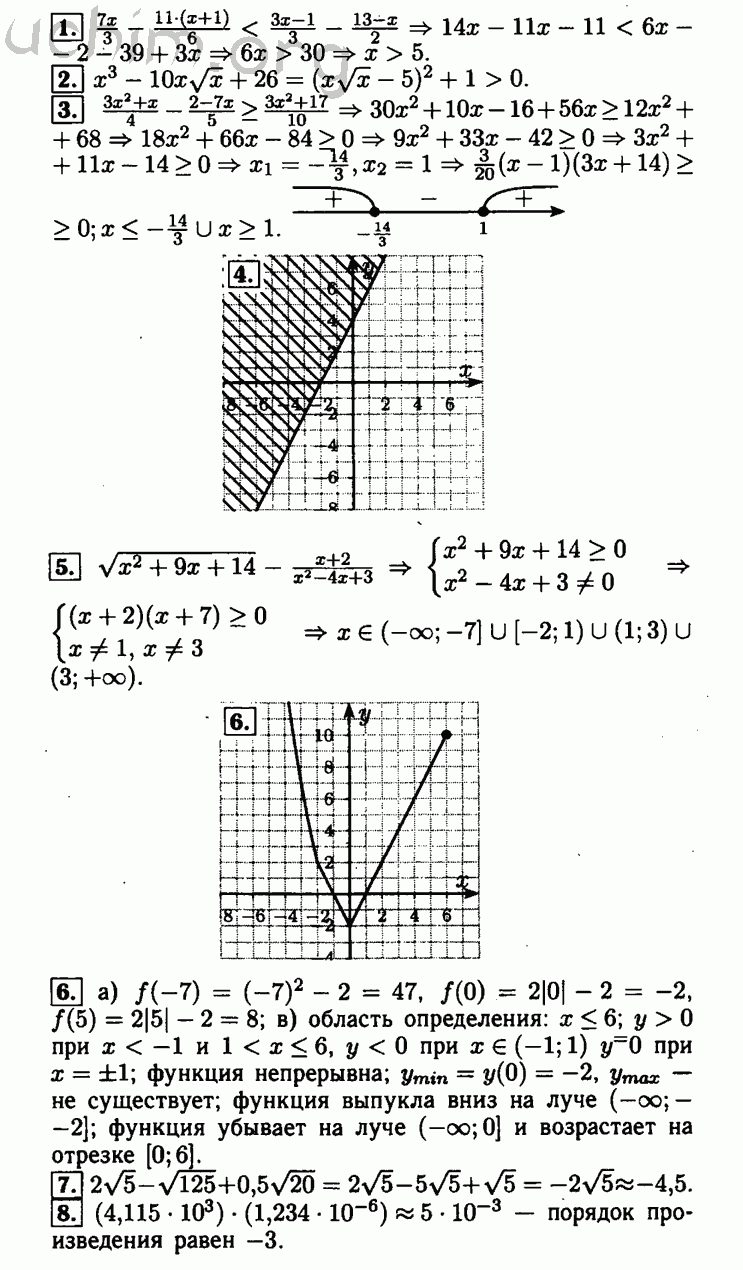 Сократите дробь: а) ; б) ; в) .

20.Выполните вычитание или сложение дробей: а) ; б) .

3.Найдите значение выражения при а = 4, b = –12.

4. Упростите выражение .

Вариант 2

10.Сократите дробь: а) ; б) ; в) .

20.Выполните вычитание или сложение дробей: а) ; б) .

3.Найдите значение выражения при х = –18, у = 4,5.

4.Упростите выражение .

КОНТРОЛЬНАЯ РАБОТА №2 «Рациональные дроби»

Вариант 1

10.Представьте в виде дроби выражение: а) ; б) ; в) .

2.Постройте график функции .

а) Укажите область определения и область значений функции.

б) При каких значениях х функция принимает положительные значения?

в) Принадлежат ли графику данной функции точки А(–4; 2), В(8; 1), С(64; –0,125)?

  1. Постройте график функции .

Вариант 2

10.Представьте в виде дроби выражение: а) ; б) ; в) .

2. Постройте график функции .

а) Укажите область определения и область значений функции.

б) При каких значениях х функция принимает отрицательные значения?

в) Принадлежат ли графику данной функции точки А(4; –2), В(–8; –1), С(–64; –0,125)?

3. Постройте график функции .

КОНТРОЛЬНАЯ РАБОТА №3 «Арифметический квадратный корень»

Вариант 1

10.Вычислите: а) ; б) ; в)

20.Найдите значение выражения: а) ; б) ; в) ; г) ; д) .

30.Постройте график функции у = . Какие из точек А (25; –5), В (1,21; 1,1), С (–4; 2)

принадлежат графику этой функции?

4. Решите уравнение: а) х2 = 25; б) у2 = 19.

5.Упростите выражение , если b < 0.

Вариант 2

10.Вычислите: а) ; б) ; в)

20.Найдите значение выражения: а) ; б) ; в) ; г) ; д)

30.Постройте график функции у = . Какие из точек А (–36; 6), В (1,44; 1,2), С (4; –2) принадлежат графику этой функции?

4. Решите уравнение: а) х2 = 64; б) а2 = 61.

5. Упростите выражение , если k < 0.

КОНТРОЛЬНАЯ РАБОТА №4 «Применение свойств квадратного корня»

Вариант 1

10.Упростите выражение: а) ; б) .

20.Сократите дробь: а) ; б) .

30.Освободитесь от знака корня в знаменателе: а) ; б) .

4. Докажите, что значение выражения является рациональным числом.

5. Упростите выражение: а) ; б) ; в) .

6. Внесите множитель под знак корня: а) ; б) , а  0; в) .

Вариант 2

10.Упростите выражение: а) ; б) .

20.Сократите дробь: а) ; б) .

30.Освободитесь от знака корня в знаменателе: а) ; б) .

4. Докажите, что значение выражения является рациональным числом.

5. Упростите выражение: а) ; б) ; в) .

6. Внесите множитель под знак корня: а) ; б) , а < 0; в) .

КОНТРОЛЬНАЯ РАБОТА №5 «Квадратные уравнения»

Вариант 1

10.Решите уравнение: а) 5х2 + 8х – 4 = 0; б) 25х2 – 4 = 0;в) 6х2 = 18х; г) (х + 3)2 – 2(х + 3) – 8 = 0.

2. Найдите два последовательных натуральных числа, произведение которых равно 132.

3.Один корень квадратного уравнения х2 – 4х + с = 0 равен . Найдите другой корень и значение с.

Вариант 2

10.Решите уравнение: а) 5х2 + 14х – 3 = 0; б) 36х2 – 25 = 0;в) 4х2 = 16х; г) (х – 3)2 – 2(х – 3) – 15 =

2. Одно из двух натуральных чисел на 3 больше другого. Найдите эти числа, если их произведение равно 180.

3.Корни уравнения х2 – х + q = 0 удовлетворяют условию 3х1 + 2х2 = 0. Найдите значение q.

КОНТРОЛЬНАЯ РАБОТА №6 «Дробные рациональные уравнения»

Вариант 1

10.Решите уравнение: а) ; б) .

2. Теплоход прошел 60 км по течению реки и 36 км против течения, затратив на весь путь 3 ч 30 мин. Какова собственная скорость теплохода, если скорость течения реки равна 3 км/ч?

3. Решите графически уравнение .

Вариант 2

10.Решите уравнение: а) ; б) .

2. Туристы проплыли на моторной лодке против течения реки 12 км и вернулись обратно. На все путешествие
они затратили 2 ч 30 мин. Какова собственная скорость лодки, если скорость течения реки 2 км/ч?

3.Решите графически уравнение .

КОНТРОЛЬНАЯ РАБОТА №7 «Числовые неравенства»

Вариант 1

10. Известно, что a > b. Сравните: а) а + 8 и b + 8; б) 0,6а и 0,6b; в) 4 – а и 5 – b.

20.Докажите неравенство: а) 4а2 + 1  4а; б) (а + 2)(а + 4) < (а + 3)2.

3. Зная, что 7,2 < а < 8,4 и 2 < b < 2,5, оцените: а) ab; б) –2а + b; в) .

4.Докажите неравенство при а > 0.

Вариант 2

10.Известно, что a < b. Сравните: а) а – 5 и b – 5; б) –0,6а и –0,6b; в) а – 2 и b – 1.

20.Докажите неравенство: а) 9b2 + 1  6b; б) (b – 1)(b – 3) < (b – 2)2.

3. Зная, что 1,5 < а < 1,8 и 1,2 < с < 1,5, оцените: а) aс; б) 4а – с; в) .

4.Докажите неравенство d 3 + 1  d 2 +

Ключевой ответ Глава 8 — Алгебра и тригонометрия

Перейти к содержаниюАлгебра и тригонометрияАлгебра и тригонометрияГлава 8 Содержание Мои основные моменты Распечатать Содержание
  1. Предисловие
  2. 1 Предварительные требования
    1. Введение в предварительные условия
    2. Условные обозначения
    3. Основные сведения
    4. Алгебра
    6. Основные сведения
    7. 1. 3 Радикалы и рациональные экспоненты
    8. 1.4 Полиномы
    9. 1.5 Факторинговые многочлены
    10. 1.6 Rational Expressions
    11. Обзор главы
      1. Ключевые термины
      2. Ключевые уравнения
      3. Ключевые концепции
    12. Упражнения
      1. Обзорные упражнения
      2. Практический тест
  3. 2 Equalities and Equalities
  4. 2 Equalities
    1. 2.1 Прямоугольные системы координат и графики
    2. 2.2 Линейные уравнения в одной переменной
    3. 2.3 Модели и приложения
    4. 2.4 Комплексные числа
    5. 2.5 Квадратичные уравнения
    6. 2.6 Другие типы уравнений
    7. 2.7 Линейные неравенства и неравенства абсолютных значений
    8. Обзор главы
      1. Ключевые термины
      2. Ключевые уравнения
      3. Ключевые понятия
      3
        Упражнения
        1. Практический тест
    9. 3 Функции
      1. Введение в функции
      2. 3.1 Функции и обозначение функций
      3. 3. 2 Домен и диапазон
      4. 3.3 Темпы изменений и поведение графиков
      5. 3.4 Состав функций
      6. 3.5 Преобразование функций
      7. 3.6 Абсолютные функции
      8. 3.7 Обратные функции
      9. Обзор глав
        1. Ключевые термины
        2. Ключевые уравнения
        3. Ключевые концепции
      10. Упражнения
        1. Упражнения на обзор
        2. Практический тест
    10. 4 Линейные функции
      1. Введение в линейные функции
      2. 4.1 Линейные функции
      3. 4.2 Моделирование с помощью линейных функций
      4. 4.3 Подгонка линейных моделей к данным
      5. Обзор главы
        1. Ключевые термины
        2. Ключевые концепции
      6. Упражнения
        1. Обзор упражнений
        4. Тестирование
          5. 9004 Полиномиальные и рациональные функции
          1. Введение в полиномиальные и рациональные функции
          2. 5.1 Квадратичные функции
          3. 5.2 Степенные и полиномиальные функции
          4. 5. 3 Графики полиномиальных функций
          5. 5.4 Деление многочленов
          6. 5.5 Нули полиномиальных функций
          7. 5.6 Рациональные функции
          8. 5.7 Инверсии и радикальные функции
          9. 5.8 Моделирование с использованием вариаций
          10. Глава
          11. Обзор
          12. Основные уравнения
          13. Ключевые слова
          15. Концепции
        5. Упражнения
          1. Обзор упражнений
          2. Практический тест
      7. 6 Экспоненциальные и логарифмические функции
        1. Введение в экспоненциальные и логарифмические функции
        2. 6.1 Экспоненциальные функции
        3. 6.2 Графики экспоненциальных функций
        4. 6.3 Логарифмические функции
        5. 6.4 Графики логарифмических функций
        6. 6.5 Логарифмические свойства
        7. 6.6 Экспоненциальные и логарифмические уравнения
        8. 6.7 Экспоненциальные и логарифмические уравнения
        9. 6.74 Экспоненциальные модели
        10. 6.74 Экспоненциальные данные модели
        11. Обзор главы
          1. Ключевые термины
          2. Ключевые уравнения
          3. Ключевые понятия
        12. Упражнения
          1. Обзор упражнений
          2. Практический тест
      8. 7 Круговая окружность: синус и косинус 3 Введение
          Функции единиц : Функции синуса и косинуса
        1. 7. 1 Углы
        2. 7.2 Тригонометрия по прямоугольному треугольнику
        3. 7.3 Единичная окружность
        4. 7.4 Другие тригонометрические функции
        5. Обзор главы
          1. Ключевые термины
          2. Ключевые уравнения
          3. Ключевые концепции
        6. Упражнения
          7. Практика
        7. Обзор
    11. 8 Периодические функции
      1. Введение в периодические функции
      2. 8.1 Графики функций синуса и косинуса
      3. 8.2 Графики других тригонометрических функций
      4. 8.3 Обратные тригонометрические функции
      5. Обзор главы
        1. Ключевые термины
        2. Ключевые уравнения
        3. Ключевые концепции
      6. Упражнения
        1. Обзор упражнений
        2. 0003
        4. Практический тест
          5. Тождества и уравнения
          1. Введение в тригонометрические тождества и уравнения
          2. 9.1 Решение тригонометрических уравнений с тождествами
          3. 9.2 Тождества суммы и разности
          4. 9. 3 Формулы двойного угла, полуугла и редукции
          5. 9.4 Формулы суммирования и произведения и суммы
          6. 9.5 Решение тригонометрических уравнений
          7. Обзор главы
            1. Ключевые термины
            2. Ключевые уравнения
            3. Ключевые концепции
          8. Упражнения
            1. Обзор упражнений
            2. Практический тест
        5. 10 Дальнейшие применения тригонометрии
          1. Введение в дальнейшие применения тригонометрии
          2. 10.1 Непрямые треугольники: закон синусов
          3. 10.2 Непрямые треугольники: закон косинусов
          4. 10.3 Полярные координаты
          5. 10.4 Полярные координаты: графики
          6. 10.5 Полярная форма комплексных чисел
          7. 10.6 Параметрические уравнения
          8. 10.7 Параметрические уравнения 10.7 Параметрические уравнения 10.7 : Графики
          9. 10.8 Векторы
          10. Обзор глав
            1. Ключевые термины
            2. Ключевые уравнения
            3. Ключевые концепции
          11. Упражнения
            1. Упражнения на обзор
            2. Практические тесты
        7. к системам уравнений и неравенств
        8. 11. 1 Системы линейных уравнений: две переменные
        9. 11.2 Системы линейных уравнений: три переменные
        10. 11.3 Системы нелинейных уравнений и неравенств: две переменные
        11. 11.4 Частные дроби
        12. 11,5 Матрицы и матричные операции
        13. 11.6 Системы исключения с помощью системы исключения по Гауссу
        14. 11.7 Решение систем с инверсиями
        15. 11.8 Решение систем с помощью правила Крамера
        16. Обзор главы
          1. Ключевые термины
          2. Ключевые уравнения
          3. Ключевые концепции
        17. Упражнения
          1. Обзор упражнений
            2. 00030003 12 Аналитическая геометрия
            1. Введение в аналитическую геометрию
            2. 12.1 Эллипс
            3. 12.2 Гипербола
            4. 12.3 Парабола
            5. 12.4 Вращение осей
            6. 12.5 Конические сечения в полярных координатах
              7. Обзор главы
              1. Ключевые термины
              2. Ключевые уравнения
              5. Ключевые понятия
              7. Обзорные упражнения
              8. Практический тест

          Числа со знаком. Целые числа — Полный курс алгебры

          2

          Положительные и отрицательные

          Алгебраический знак и модуль

          Вычитание большего числа из меньшего

          Номер строки

          Отрицательное значение любого числа

          Алгебраическое определение минуса числа

          В АРИФМЕТИКЕ мы не можем вычесть большее число из меньшего.

          2–3.

          Но в алгебре мы можем. И для этого мы изобретаем «отрицательные» числа.

          2-3 = -1.

          Теперь, чтобы получить положительные числа, мы начинаем с 0 и последовательно добавляем 1:

          0, +1, +2, +3, +4, +5 и т. Д.

          Чтобы получить отрицательные числа, мы начинаем с 0 и последовательно вычитаем 1:

          0, −1, −2, −3, −4, −5 и так далее.

          Мы называем все эти числа — положительные, отрицательные и 0 — целыми.Мы называем эти целые числа целыми числами, чтобы отличать их от дробей и десятичных знаков. Положительные целые числа больше 0. Отрицательные целые числа меньше. Мы называем их обоими номерами со знаком.

          1. Какие две части числа со знаком?

          Его алгебраический знак, + или -, и его абсолютное значение, которое является просто арифметическим значением, то есть числом без знака.

          Алгебраический знак +3 («плюс 3» или «положительный 3») равен +, а его абсолютное значение равно 3.

          Алгебраический знак −3 («минус 3» или «минус 3»): -. Абсолютное значение −3 также равно 3.

          Знак минус — это не только алгебраический знак. Это также знак операции вычитания. Скоро мы увидим, как эти двое связаны.

          Что касается алгебраического знака +, обычно мы его не пишем. Например, алгебраический знак 2 понимается как +.

          Что касается 0, полезно сказать, что он имеет оба знака: −0 = +0 = 0.
          (см. Урок 5, проблема 9 и Урок 11, Задача 11.)

          Когда мы помещаем число в вертикальные линии, | −3 |, это означает его абсолютное значение.

          | −3 | = 3.
          | 3 | = 3.

          Проблема 1. Оцените каждое из следующих действий.

          Чтобы увидеть ответ, наведите указатель мыши на цветную область.
          Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
          Сначала решите проблему сами!

          а) | 6 | = 6 б) | −6 | = 6 в) | 0 | = 0
          г) | 3 — 1 | = 2 д) | 1 — 3 | = 2

          2.Как вычесть большее число из меньшего?

          5–8

          1. Какой будет знак ответа?

          Было бы неправильно сказать, что мы не можем взять 8 из 5. Мы, конечно, можем взять 5 из 8 — и это то, что мы делаем — но мы сообщаем ответ со знаком минус!

          5-8 = −3.

          Даже в алгебре мы можем заниматься только обычной арифметикой. Но тогда мы должны выбрать правильный знак.

          Можно сказать, что это первое правило чисел со знаком:

          Чтобы вычесть большее число из меньшего,
          вычтите меньшее из большего, но ответ
          будет отрицательным.

          1 — 5 = −4.

          На самом деле мы делаем 5 — 1.

          Это было для того, чтобы вычесть большее число из меньшего, что были придуманы отрицательные числа.

          Проблема 2. В чем разница между 8 — 5 и 5 — 8?

          Алгебраические знаки.У них одинаковое абсолютное значение.

          8 — 5 = 3. 5 — 8 = −3.

          Задача 3. Вычесть.

          а) 3-5 = −2 б) 1 — 8 = −7
          c) 8 — 14 = −6 г) 20 — 65 = −45

          Проблема 4.У вас есть 20 долларов в банке, и вы выписываете чек на 25 долларов. Каков ваш баланс?

          20,00 — 25,00 = −5,00

          Номер строки

          То, что вы видите выше, называется числовой линией. Мы воображаем, что он простирается в обоих направлениях настолько далеко, насколько нам угодно. Отрицательные числа падают слева от 0. Положительные числа падают справа.

          Когда мы рисуем числовую линию, мы обычно помещаем целые числа.Однако мы представляем себе каждое число на числовой прямой. Таким образом, дробь ½ окажется между 0 и 1; дробь −½ находится между 0 и −1; и так далее.

          Фактически, именно в числовой строке мы начинаем видеть практическое использование чисел со знаком. В общем, они показывают некоторое количество «направления». Этой величиной может быть температура: больше или меньше определенной температуры, обозначенной как 0. Или это может быть положение или «адрес» некоторого объекта: слева или справа от некоторого фиксированного положения, выбранного как 0.Или это может быть время: до или после определенного момента, который снова выбирается равным 0. Или, как мы все знаем, отрицательные числа могут указывать на остаток на текущем счете

          Задача 5. Запуск ракеты запланирован ровно на 9:16 утра, что обозначается т (для времени) = 0, а т будет измеряться в минутах.

          а) Который час при т = −10? 9:06 утра.

          б) Который час при t = −1? 9:15.

          в) Который час при т = +5? 9:21 утра.

          г) Какова стоимость т в 9:00? т = −16.

          д) Какова стоимость т в 9:30? т = 14.

          Отрицательное значение любого числа

          Каждое число будет иметь отрицательное значение. Отрицательное число 3, например, будет найдено на том же расстоянии от 0, но с другой стороны.

          Это −3.

          Итак, какое число отрицательное у −3?

          Отрицательное значение −3 будет таким же расстоянием от 0 на другой стороне . Это 3.

          — (- 3) = 3.

          «Отрицательное значение −3 равно 3.»

          Это будет верно для любого числа a :

          «Отрицательное значение −a равно a .«

          То, что находится в коробке, называется формальным правилом. Это означает, что всякий раз, когда мы видим что-то похожее на это —

          — (- a )

          — что-то, что имеет форму от , мы можем переписать его в таком виде:

          Например,

          — (- 12) = 12.

          Изучить алгебру — значит изучить ее формальные правила. Что такое расчеты, как не записывать вещи в другой форме? В арифметике мы перепишем 1 + 1 как 2.В алгебре мы перепишем — (- a ) как a .

          См. Урок 5.

          Проблема 6. Оцените следующее.

          а) — (- 10) = 10 б) — (2-6) = 4

          в) — (1 + 4-7) = 2 г) — (- х ) = х

          Алгебраическое определение минуса числа

          Наконец, мы определяем отрицательное число в алгебре следующим образом.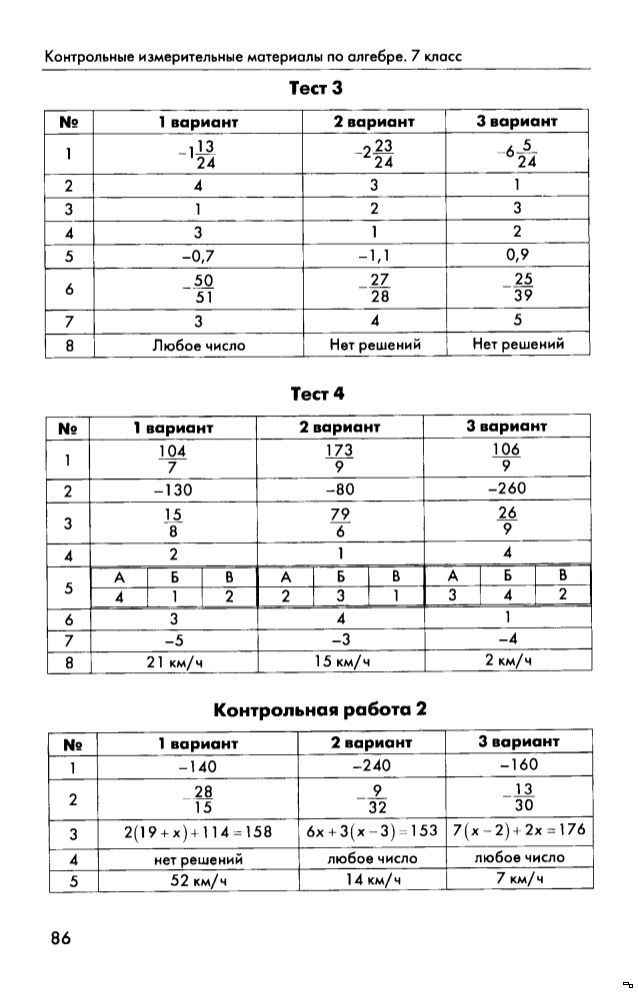 Например, −5 — это число, которое при добавлении к самому 5 дает 0.

          5 + (−5) = 0.

          То есть каждому числу a соответствует одно и только одно число — a , называемое отрицательным. И когда мы добавляем его к , мы получаем 0.

          a + (- a ) = — a + a = 0

          Задача 7. Какое число нужно прибавить к 8, чтобы получить 0?

          Проблема 8.Какое число нужно прибавить к −6, чтобы получить 0?

          6

          Задача 9. Какое число отрицательное — q ? Зачем?

          Отрицательное значение — q равно q , потому что — q + q = 0.

          То есть

          — (- q ) = q .

          Проблема 10. Если

          с + т = 0,

          тогда какая связь между t и s ?

          Проблема 11.Если бы вам нужно было доказать, что

          b — a отрицательное значение a — b ,

          как бы вы это сделали?

          Покажем, что a — b + b — a = 0.

          Чтобы доказать свойство чего-либо, будь то математика, логика или закон, мы должны просто показать, что оно удовлетворяет определению этого свойства.

          Следующий урок: сложение и вычитание чисел со знаком

          Содержание | Дом

          Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
          Даже 1 доллар поможет.

          Авторские права © 2020 Лоуренс Спектор

          Вопросы или комментарии?

          Эл. Почта: [email protected]


          Базы чисел: введение и двоичные числа

          Purplemath

          Преобразование между различными системами счисления на самом деле довольно просто, но идея, лежащая в основе этого, поначалу может показаться немного запутанной.И хотя тема различных основ может показаться вам несколько бессмысленной, рост компьютеров и компьютерной графики увеличил потребность в знаниях о том, как работать с различными (недесятичными) базовыми системами, особенно с двоичными системами (с единицами и нулями) и шестнадцатеричная система (числа от нуля до девяти, за которыми следуют буквы от A до F).

          MathHelp.com

          В нашей обычной десятичной системе есть цифры для чисел от нуля до девяти. У нас нет однозначного числа для «десяти». (Римляне использовали иероглиф «X».) Да, мы пишем «10», но это означает «1 десять и 0 единиц». Это две цифры; у нас нет ни одной единственной цифры, обозначающей «десять».

          Вместо этого, когда нам нужно считать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на один больше, чем девять десятков и девяти единиц («99»), мы обнуляем столбцы десятков и единиц и добавляем единицу к десятикратным или сотням. , столбец. Следующий столбец — это столбец десять раз десять, или тысячи. И так далее, причем каждый столбец большего размера в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, сообщая нам, сколько копий этой степени десяти нам нужно.

          Единственная причина, по которой математика с основанием десять кажется «естественной», а другие — нет, заключается в том, что вы использовали десятичный алгоритм с детства. И (почти) каждая цивилизация использовала математику по основанию десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мире мультфильмов, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы система с основанием восемь, или «восьмеричный».

          двоичный

          Давайте посмотрим на числа с основанием два или двоичные числа. Как бы вы записали, например, 12 10 («двенадцать по основанию десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять. В десятичной системе координат у вас есть столбцы или «места» для 10 0 = 1, 10 1 = 10, 10 2 = 100, 10 3 = 1000 и так далее. Точно так же в основании два у вас есть столбцы или «места» для 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16 и т. вперед.

          Первый столбец в математике с основанием два — это столбец единиц. Но в колонке единиц может быть только «0» или «1». Когда вы дойдете до «два», вы обнаружите, что не существует единственной цифры, которая обозначает «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец двоек и «0» в столбец единиц, указывая «1 два и 0 единиц». Двойка по основанию десять (2 10 ) записывается в двоичной системе как 10 2 .

          «Тройка» в основании два на самом деле означает «1, 2 и 1, 1», поэтому записывается как 11 2 .«Четыре» на самом деле означает дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и помещаем «1» в столбец четверок; 4 10 записывается в двоичной форме как 100 2 . Вот список первых чисел:

          Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.

          • Преобразует 101100101 2 в соответствующее десятичное число.

          Я перечислю цифры по порядку, так как они появляются в номере, который они мне дали. Затем в другом ряду я отсчитываю эти цифры от ПРАВА, начиная с нуля:

          Первая строка выше (помеченная как «цифры») содержит цифры из двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень двойки (основание), соответствующую каждой цифре. Я буду использовать этот список, чтобы преобразовать каждую цифру в степень двойки, которую она представляет:

          1 × 2 8 + 0 × 2 7 + 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0

          = 1 × 256 + 0 × 128 + 1 × 64 + 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1

          = 256 + 64 + 32 + 4 + 1

          = 357

          Затем 101100101 2 преобразуется в 357 10 .

          Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.

          • Преобразует 357 10 в соответствующее двоичное число.

          Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:

          Приведенный выше рисунок анимирован на «живой» веб-странице.

          Как видите, после многократного деления на 2 я получил следующие остатки:

          Эти остатки говорят мне, что такое двоичное число. Я читаю числа с внешней стороны деления, начиная сверху с конечного значения и его остатка, и заканчиваю свой путь вокруг и вниз по правой части последовательного деления. Тогда:

          СЕГОДНЯ В АЛГЕБРЕ…  Разминка: половина листа научной нотации  СТАТИСТИКА Гл.8 Промежуточный тест  Задача обучения 1: 8.4 Вы будете читать и записывать числа в научном формате.

          Презентация на тему: «СЕГОДНЯ В АЛГЕБРЕ…  Разминка: половина листа с научными обозначениями  СТАТИСТИКИ Глава 8 Промежуточный тест  Учебная цель 1: 8.4 Вы будете читать и писать числа в научном формате» — стенограмма презентации:

          1 СЕГОДНЯ В АЛГЕБРЕ…  Разминка: половина листа научной нотации  СТАТИСТИКИ, гл.8 Промежуточный тест  Учебная цель 1: 8.4 Вы будете читать и записывать числа в экспоненциальном представлении  В классе 8.4 ЗАДАТЬ СЕГОДНЯ Target Учебная цель 2: 8.5 Введение в функции экспоненциального роста # HW # 3, сдать сегодня

          2 Разминка: у вас есть 10 минут, чтобы заполнить половину листа. 10 минут.

          3 КАК ВЫ «СОЗДАЛИ» ?? Результаты для ВСЕХ моих классов алгебры: ЧИСЛО УЧАЩИХСЯ СРЕДНЕГО КЛАССА.8 ТЕСТ 1-Й ПЕРИОД 6-Й ПЕРИОД ИТОГО A / A-13922 B + / B / B-4610 C + / C / C-134 D + / D224 F8210 Среднее значение 22,5524,7023,63

          4 .

          No related posts.

Leave a Reply

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *