1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. | 1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую ме |
Сборник контрольных работ по геометрии, (10 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
10 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
Контрольная работа №1 10 класс.
Тема: «Аксиомы и их следствия».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач аксиомы стереометрии и их следствия;
— умение оформлять рисунки по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1.Могут ли две различных плоскости иметь три общие точки, не лежащие на одной прямой? 2.Прямая а лежит в плоскости α. Плоскость β пересекает плоскость α по прямой b. Известно, что прямая a пересекает плоскость β в точке b. Где лежит точка 3.Прямые a, b и c, не лежащие в одной плоскости, проходят через одну и ту же точку. Сколько различных плоскостей можно провести через эти прямые, взятые по две. 4.Точки A, B и прямая CD не лежат в одной плоскости. Каково взаимное расположение прямых CD и AB ? 5.Две соседние вершины и точка пересечения диагоналей квадрата лежат в плоскости α. Докажите, что и две других вершины квадрата лежат в этой же плоскости. |
II вариант. |
1. Плоскости α и β пересекаются по прямой 2.Прямая AB и точки С и D не лежат в одной плоскости. Докажите, что прямые AB и CD пересекаются. 3.Плоскости α и β пересекаются по прямой AB. Плоскости β и γ по прямой BC, а плоскости α и γ по прямой АС. Докажите, что A, B, C лежат на одной прямой. 4.Даны точки А и В. Доказать, что существуют такие точки C и D, что четыре точки A, B, C, D не лежат в одной плоскости. 5.Сторона АВ и диагональ BD прямоугольника ABCD лежат в плоскости α. Докажите, что и вершина С этого прямоугольника лежит в этой же плоскости. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
№1,2 | №3,4 | 80% | ||
Прямоугольник. Признаки и свойства | №5 | 20 % | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 3 балла |
Логичность обоснования. | 1 балл | |||
Запись решения. | 1 балл | |||
2 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 3 балла |
Логичность обоснования. | 1 балл | |||
Запись решения. | ||||
3 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 5 баллов |
Логичность обоснования. | 2 балла | |||
Запись решения. | 2 балла | |||
4 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 5 баллов |
Логичность обоснования. | 2 балла | |||
Запись решения. | 2 балла | |||
5 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 5 баллов | |
Логичность обоснования. | 2 балла | |||
Запись решения. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 балла – «4»
20-21 балл – «5»
Контрольная работа №2 10 класс.
Тема: «Параллельность прямых, прямой и плоскости, плоскостей».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач определения и признаки параллельных прямых, параллельных прямой и плоскости, плоскостей;
— умение оформлять рисунки по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1. Известно, что точки A, B, C, D лежат в одной плоскости. Определите, могут ли прямые AB и CD: а) быть параллельными; ;б) пересекаться в) быть скрещивающимися. проведена плоскость α. Известно, что BCA = CAD. Докажите, что BC параллельно α. 3.Квадрат ABCD и трапеция BEFC не лежат в одной плоскости. Точки M и N середины отрезков BE и FC соответственно. а) докажите, что MN параллельно AD б) найдите MN, если AD=10 см, EF=6 см. 4. На стороне AD параллелограмма ABCD выбрана точка А1 так, что DA1=4 см. Плоскость, параллельная диагонали АС, проходит через точку А1 и пересекает сторону CD в точке С1. а) Докажите подобие треугольников C1DA1 и ABC б) Найдите АС, если ВС=10 см, А1С1=6см. 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите А2В2 и АА2, если А1В1=18, АА1=24, АА2=⅔А1А2. |
II вариант. |
1. Известно, что точки A, B, C, D не лежат в одной плоскости. Определите, могут ли прямые AB и CD: а) быть параллельными; б) пересекаться; в) быть скрещивающимися. 2.Через сторону AD четырехугольника ABCD проведена плоскость α. Известно, что ABC + DAB = 180º .Докажите, что BC параллельно α. 3. Треугольник BEC и прямоугольник ABCD не лежат в одной плоскости. Точки M и N середины отрезков BE и EC соответственно. а) докажите, что AD параллельно MN б) найдите AD, если MN=5 см. 4. На стороне ВС параллелограмма ABCD выбрана точка С1 так, что С1В=3 см.Плоскость параллельная диагонали АС, проходит через С1 и пересекает сторону АВ в точке А1. а) Докажите подобие треугольников ADС и C1ВA1 б) Найдите АD, если А1С1=4 см, АС=12см. 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Расположение прямых в пространстве | №1 | № 3 | 40% | |
Расположение прямой и плоскости | №2 | № 4 | 40% | |
Параллельные плоскости | № 5 | 20% | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Расположение прямых в пространстве. | Знание определения. | 1 балл | 3 балла |
Логическое обоснование ответа. | 2 балла | |||
2 | Расположение прямой и плоскости. | Знание признака параллельности прямой и плоскости. | 1 балл | 3 балла |
Оформление решения задачи. | 2 балла | |||
3 | Расположение прямых в пространстве. | Знание признака параллельности прямых. | 1 балл | 5 баллов |
Свойство средней линии. | 2 балла | |||
Оформление решения задачи. | 2 балла | |||
4 | Расположение прямой и плоскости. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Свойства прямой параллельной плоскости. | 1 балл | |||
Подобие треугольников. | 1 балл | |||
Оформление решения задачи. | 2 балла | |||
5 | Свойства параллельных плоскостей. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
Подобие треугольников. | 2 балла | |||
Оформление решения задачи. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №3 10 класс.
Тема: «Параллельность плоскостей».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач определение, признаки и свойства параллельных плоскостей;
— знания и умения применять при решении задач свойства параллельного проектирования;
— умение выполнять чертежи по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1. Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1С и С1С не лежащие в плоскости параллелограмма. Докажите параллельность плоскостей А1АВ и С1СD. 2. Основания трапеции параллельны некоторой плоскости. Верно ли, что боковые стороны трапеции так же параллельны этой плоскости? Ответ объясните. 3. Постройте проекцию квадрата ABCD, зная проекции его вершин А, В и точки пересечения диагоналей О, точки А1, В1 и О1. 4. Параллельные прямые а и b пересекают одну из двух параллельных плоскостей в точках А1 и В1, а другую в точках А2 и В2 соответственно. а) Докажите, что А1В1 параллельно А2В2 б) Найдите А2А1В1, если А1А2В2=140ᴼ 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите А2В2 и АА2, если А1В1=18, АА1=24, АА2=⅔А1А2. |
II вариант. |
1. Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1С и С1С не лежащие в плоскости параллелограмма. Докажите параллельность плоскостей А1АD и C1CB. 2. Боковые стороны трапеции параллельны некоторой плоскости. Верно ли, что основания трапеции так же параллельны этой плоскости? Ответ объясните. 3. Постройте проекцию правильного треугольника АВС, зная проекции его вершины А и середины К, М сторон АВ и ВС, точки А1, К1 и М1. 4. Параллельные прямые а и b пересекают одну из двух параллельных плоскостей в точках А1 и В1, а другую в точках А2 и В2 соответственно. а) Докажите, что А1В1 равно А2В2 б) Найдите В1В2А2, если В1А1А2=50ᴼ 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5. |
Распределение заданий по содержанию и уровню сложности
Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
Параллельные плоскости | №1,2 | №4 | №5 | 80% |
Параллельное проектирование | №3 | 20% | ||
Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
№ задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
1 | Признак параллельности плоскостей | Выполнение чертежа по условию задачи | 1 балл | 3 балла |
Применение признака параллельности плоскостей | 1 балл | |||
Оформление решения задачи | 1 балл | |||
2 | Признак параллельности плоскостей | Применение признака параллельности плоскостей | 1 балл | 3 балла |
Оформление решения задачи | 2 балла | |||
3 | Параллельное проектирование | Знание и применение свойств параллельного проектирования | 3 балла | 5 баллов |
Выполнение построения | 1 балл | |||
Оформление решения задачи | 1 балл | |||
4 | Свойства параллельных плоскостей | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
Применение свойств параллельных плоскостей | 1 балл | |||
Свойство углов | 1 балл | |||
Оформление решения задачи | 2 балла | |||
5 | Квадрат. Признаки и свойства | Выполнение чертежа по условию задачи | 2 балла | 5 баллов |
Подобие треугольников | 2 балла | |||
Оформление решения задачи | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №4 10 класс.
Тема: «Перпендикулярность прямых, прямой и плоскости».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач определение, признаки и свойства перпендикулярных прямых, прямой и плоскости;
-знания и умения применять при решении задач теорему о трех перпендикулярах;
— умение выполнять чертежи по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1. Дано: АВ ┴ α, CD ┴ α, AB=CD.Определить вид четырехугольника ABCD. 2. Дан куб ABCDA1B1C1D1. Докажите что: AD ┴ (DCC1). 3. Из точки S к плоскости α проведе |
Проверочные работы по геометрии для 10 класса
Проверочные работы по геометрии для 10 класса охватывают несколько тем по учебнику Атанасян, Геометрия для 10-11 классов. Работа включает в себя также ключ к вопросам. В каждой проверочной работе по 8 вопросов. Всего 9 проверочных работ по каждому разделу.
Просмотр содержимого документа
«Проверочные работы по геометрии для 10 класса »
Самостоятельные работы по геометрии |
10 класс |
Подготовила: преподаватель математики ГАПОУ МО «Мурманский колледж экономики и информационных технологий» Конурова Алёна Николаевна, г. Мурманск |
Проверочная работа №1.
Аксиомы стереометрии и следствия из них
Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?
Могут ли две плоскости иметь общую точку, но не иметь общей прямой?
Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.
Даны точки А, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α?
В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?
*Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?
*Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?
*Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.
Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.
да | нет | АМ | три | одну или бесконечно много | нет | да | три или не одной |
Проверочная работа №2.
Параллельные прямые в пространстве.
Параллельность прямой и плоскости
Верно ли, что две параллельные прямые лежат в одной плоскости?
Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?
Определите взаимное расположение прямой а и плоскости α, если:
a || b и прямая b пересекает плоскость α.
Дана плоскость β и прямые а, b, с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если:
а || с , прямые b и с пересекаются, а прямая с лежит в плоскости β.
Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?
Определите взаимное расположение прямой а и плоскости α, если в плоскости α не существует прямой, пересекающей а.
Верно ли, что две прямые, параллельные одной плоскости, параллельны?
Могут ли прямые AB и CD быть параллельными, если прямые AD и BC пересекаются?
да | нет | пересекаются | а | да | параллельны | нет | да |
Проверочная работа №3.
Взаимное расположение прямых в пространстве
Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
Может ли угол в пространстве быть тупым?
Определите взаимное расположение прямых a и b , если прямая а лежит в плоскости α, а прямая b пересекает плоскость α в точке, не лежащей на прямой а.
Прямая l пересекает плоскость треугольника АВС в точке В. Назовите прямую, скрещивающуюся с l и содержащую сторону данного треугольника.
Определите, верно ли на плоскости, в пространстве или и на плоскости, и в пространстве данное утверждение:
«Если две различные прямые не пересекаются, то они параллельны.
Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?
Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?
Определите, какой из случаев взаимного расположения прямых a и b невозможен, если прямая а пересекается с с, а b||с.
нет | нет | скрещивающиеся | АС | на плоскости | да | да | параллельность |
Проверочная работа №4.
Параллельность плоскостей.
Тетраэдр и параллелепипед
Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?
Могут ли рёбра тетраэдра лежать на параллельных прямых?
Параллельные плоскости α и β пересекают плоскость γ по прямым a и b соответственно. Определите взаимное расположение прямых a и b .
Определите вид сечения параллелепипеда плоскостью, проходящей через середины четырёх боковых рёбер.
Дана плоскость α и точка А вне данной плоскости. Определите, какую фигуру в пространстве образуют все прямые, параллельные данной плоскости и проходящие через данную точку. Как расположена эта фигура по отношению к плоскости α?
Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?
Может ли в тетраэдре DABC грань DBC содержать прямую, параллельную ребру DA?
Плоскость γ пересекает параллельные плоскости α и β по прямым a и b соответственно. Прямая с скрещивается с прямой b . Укажите, какой из случаев взаимного расположения прямых а и с невозможен.
Определите, какую фигуру в пространстве образуют середины всех отрезков с концами на двух данных скрещивающихся прямых. Как расположена эта фигура по отношению к данным прямым?
да | нет | параллельны | параллелограмм | плоскости – параллельно – α | нет | нет | параллельны | плоскость параллельна данным прямым |
,
Проверочная работа №5.
Перпендикулярность прямой и плоскости
Верно ли, что две прямые, перпендикулярные к одной плоскости, параллельны?
Может ли прямая, перпендикулярная к плоскости, быть параллельной прямой, лежащей в этой плоскости?
Даны прямые a и b и плоскость α. Определите угол между данными прямыми, если a α, b || α.
ОА – прямая, перпендикулярная к плоскости равностороннего треугольника АВС. Назовите отрезок, равный отрезку ОС.
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?
Даны прямые a, b, c и плоскость α. Укажите среди данных прямых прямую, перпендикулярную к двум другим, если a α, b || α, с лежит в плоскости α.
Прямая a лежит в плоскости α, α. Вставьте вместо пропусков обозначения a, b или α так, чтобы данное утверждение было верным:
«Если прямая перпендикулярна к …, то она перпендикулярна к … и параллельна …»
да | нет | 90° | ОВ | нет | а | α – a — b |
Проверочная работа №6.
Перпендикуляр и наклонные.
Угол между прямой и плоскостью
Верно ли, что длина перпендикуляра меньше длины наклонной, проведённой из этой же точки?
Может ли угол между прямой и плоскостью быть тупым?
SA – перпендикуляр к плоскости треугольника АВС. Определите вид треугольника АВС, если SB ВС.
SA – перпендикуляр к плоскости прямоугольника АВСD. Назовите отрезок, изображающий расстояние от точки S до прямой СD.
Через сторону ВС треугольника АВС проведена плоскость α. АО – перпендикуляр к плоскости α. Назовите угол между АС и плоскостью α.
*Верно ли, что расстояние между параллельными плоскостями равно расстоянию от любой прямой одной плоскости до другой плоскости?
*Могут ли две прямые, образующие с данной плоскостью неравные углы, быть параллельными?
* SA – перпендикуляр к плоскости треугольника АВС. Назовите наибольшую сторону треугольника, если SС ВС.
да | нет | прямоуг. | SD | угол АСО | да | нет | АВ |
Проверочная работа №7.
Двугранный угол.
Перпендикулярность плоскостей.
Прямоугольный параллелепипед
Верно ли, что любая прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к другой плоскости?
Может ли диагональ прямоугольного параллелепипеда быть меньше одного из рёбер?
Плоскости α и β перпендикулярны. Прямая а не лежит в плоскости α. Определите взаимное расположение прямой а и плоскости α, если а β.
Равносторонние треугольники АВС и АDС не лежат в одной плоскости. М – середина АС. Назовите линейный угол двугранного угла между плоскостями треугольников.
*Верно ли, что если одна из двух плоскостей проходит через прямую, перпендикулярную к линии пересечения плоскостей, то эти плоскости перпендикулярны?
*Может ли сечение прямоугольного параллелепипеда плоскостью, перпендикулярной к основаниям, не являться прямоугольником?
*DА – перпендикуляр к плоскости прямоугольного треугольника АВС. Назовите линейный угол двугранного угла между плоскостями АВС и DВС, если АВ – гипотенуза треугольника АВС.
нет | нет | а ||α | ВМD | нет | нет | DСА |
Проверочная работа №8.
Призма. Пирамида
Верно ли, что основания любой призмы лежат в параллельных плоскостях?
Может ли высота пирамиды быть больше её бокового ребра?
Определите количество сторон многоугольника, лежащего в основании, если она имеет семь граней.
Определите вид четырёхугольника (прямоугольник, ромб, трапеция), который является сечением правильной треугольной призмы, если это сечение проходит через ребро нижнего основания и пересекает две стороны верхнего основания.
Могут ли три боковых грани пирамиды быть перпендикулярными к плоскости основания?
Верно ли, что параллелепипед является четырёхугольной призмой?
Может ли площадь боковой поверхности пирамиды быть равной площади её основания?
да | нет | 5 | трапеция | нет | да | нет |
Проверочная работа №9.
Векторы. Действия с векторами в пространстве
Верно ли что векторы, имеющие равные длины, равны?
Могут ли коллинеарные векторы лежать на скрещивающихся прямых?
В тетраэдре DАВС назовите вектор, равный сумме .
Диагонали куба АВСD пересекаются в точке О. Найдите число из равенства .
Даны точки А, В, С и D, причём никакие три из них не лежат на одной прямой. Определите взаимное расположение прямых АВ и СD, если векторы сонаправлены.
SО – высота правильной четырёхугольной пирамиды SАВСD. Найдите число 𝝀 из равенства .
Даны точки А, В, С и D, причём никакие три из них не лежат на одной прямой. Определите взаимное расположение прямых АВ и СD, если векторы не коллинеарны, а векторы коллинеарны.
нет | нет | 0,5 | параллельны | -0,5 | пересекаются |
При подготовки данного материала использовался учебник по геометрии Атанасян, 10-11кл., Геометрия.
ГДЗ к учебнику Атанасяна / контрольные работы / КА-1 А1 геометрия 10 класс самостоятельные и контрольные работы Ершова, Голобородько
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язы
Геометрия 10-й класс — Контрольная работа
Геометрия 10-й класс.
УЧЕБНИК:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г.
“Геометрия 10 — 11”
(М.: Просвещение, 1992 и последующие издания)
Примерное поурочное планирование
(2 часа в неделю, всего 68 часов)
Тема | Кол-во часов | Примечание (изменения, которые планирует учитель) | ||
Введение (2ч.) | ||||
Параллельность прямых и плоскостей (19ч.) | ||||
Параллельность прямых, прямой и плоскости. Контролирующая самостоятельная работа. | 3 | |||
Зачет №1. | 1 | |||
Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Контролирующая самостоятельная работа. | 3 | |||
Решение задач. | 1 | |||
Контрольная работа №1. | 1 | |||
Параллельность плоскостей. Контролирующая самостоятельная работа. | 3 | |||
Зачет №2. | 1 | |||
Тетраэдр и параллелепипед. | 5 | |||
Контрольная работа №2. | 1 | |||
Перпендикулярность прямых и плоскостей (16ч.) | ||||
Перпендикулярность прямой и плоскости. | 4 | |||
Перпендикуляр и наклонные. Угол между прямой и плоскостью. Контролирующая самостоятельная работа. | 4 | |||
Зачет №3. | 1 | |||
Двугранный угол. Перпендикулярность плоскостей. Контролирующая самостоятельная работа. | 4 | |||
Решение задач. | 2 | |||
Контрольная работа №3. | 1 | |||
Многогранники (16ч.) | ||||
Понятие многогранника. Призма. Контролирующая самостоятельная работа. | 4 | |||
Пирамида. Контролирующая самостоятельная работа. | 5 | |||
Правильные многогранники. | 2 | |||
Зачет №4. | 1 | |||
Решение задач. | 3 | |||
Контрольная работа №4. | 1 | |||
Векторы в пространстве (11ч.) | ||||
Понятие вектора в пространстве. | 2 | |||
Сложение и вычитание векторов. Умножение вектора на число. Контролирующая самостоятельная работа. | 2 | |||
Компланарные векторы. Контролирующая самостоятельная работа. | 3 | |||
Зачет №5. | 1 | |||
Решение задач. | 2 | |||
Контрольная работа №5. | 1 | |||
Итоговое повторение (4ч.) | ||||
КОНТРОЛЬНЫЕ, САМОСТЯТЕЛЬНЫЕ РАБОТЫ И ЗАЧЕТЫ
ГЕОМЕТРИЯ
10-й КЛАСС
Глава I. Параллельность прямых и плоскостей
Контролирующая самостоятельная работа к § 1
I вариант Задания № 23, 28 из учебника.
II вариант Задания № 24, 27 из учебника.
Зачет № 1
Образцы карточек к зачету
Карточка 1
1. Сформулируйте аксиомы А1 — А3, разъясните их смысл.
2. Сформулируйте и докажите признак параллельности прямой и плоскости.
3. Вершины B и С треугольника AВС лежат в плоскости , а вершина А не лежит в этой плоскости. Прямая а параллельна прямой АС и пересекает сторону АВ в точке М так, что AM:MB =3 : 4. а) Докажите, что прямая а пересекает плоскость . б) Найдите сторону AC, если длина отрезка прямой а от точки М до плоскости равна 7 см.
Карточка 2
1. Опишите все случаи взаимного расположения прямой и плоскости.
2. Сформулируйте и докажите теорему о плоскости, проходящей через две пересекающиеся прямые.
3. На сторонах АВ и АС треугольника AВС взяты соответственно точки Р и T; РТ = 4 см, АР : РВ =1 : 3. Плоскость проходит через точки Р и T и параллельна отрезку ВС. а) Докажите, что отрезки РТ и ВС параллельны, б) Найдите отрезок ВС.
Контролирующая самостоятельная работа к § 2
I вариант
Задание № 45 из учебника.
II вариант
Задание № 46 из учебника.
Контрольная работа № 1
I вариант
1. Середины сторон CD и BD треугольника BCD лежат в плоскости , а сторона ВС не лежит в этой плоскости: Докажите, что прямая ВС и плоскость параллельны.
2. Точки А, В, С и D не лежат в одной плоскости. Докажите, что любые три из них не лежат на одной прямой.
3. Прямая КМ параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости AВС. Выясните взаимное расположение прямых КМ и AВ и найдите угол между ними, если AВС = 110°.
II вариант
1. Середины сторон CD и АВ параллелограмма ABCD лежат в плоскости , а сторона ВС не лежит в этой плоскости. Докажите, что прямая AD и плоскость параллельны.
2. Точки А, В, С и D не лежат в одной плоскости. Докажите, что любые три из них являются вершинами треугольника.
3. Прямая КМ параллельна стороне ВС треугольника AВС и не лежит в плоскости АВС.Выясните взаимное расположение прямых КМ и АВ и найдите угол между ними, если АВС = 105°.
Контролирующая самостоятельная работа к § 3
I вариант
1. Отрезки АВ, AC, AD не лежат в одной плоскости. Точки К, М, N — соответственно их середины, а) Докажите, что плоскости BCD и KMN параллельны, б) Найдите площадь треугольника BCD, если площадь треугольника KMN равна 36 м2.
2. Задача 63 (а) из учебника.
II вариант
1. Три прямые, проходящие через точку М и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А, В и С, а вторую — в точках A1, B1, C1.а) Докажите, что треугольники АВС и A1B1C1подобны, б) Найдите АВ : А1В1, если МС =CC1.
2. Задание № 63 (б) из учебника.
Зачет № 2
Образцы карточек к зачету
Карточка 1
1. Сформулируйте определение скрещивающихся прямых.
2. Сформулируйте и докажите признак параллельности двух плоскостей.
3. Через вершины треугольника АВС проведены параллельные прямые, пересекающие плоскость , параллельную плоскости АВС, соответственно в точках А1, B1 и С1 Найдите стороны треугольника A1B1C1, если АВ = 5 см, АС = 4 см, ВАС = 60°.
Карточка 2
1. Перечислите все случаи взаимного расположения двух прямых.
2. Сформулируйте и докажите теорему об отрезках параллельных прямых, заключенных между двумя параллельными плоскостями.
3. Даны треугольник АОВ и параллелограмм ABCD, не лежащие в одной плоскости. Найдите угол между прямыми АО и CD, если ОАВ = 130°.
Контрольная работа № 2
I вариант
1. В тетраэдре ABCD точки М, К и Р— середины ребер АВ, BD и ВС. Докажите, что плоскость МКР параллельна плоскости ACD, и найдите площадь треугольника МКР, если площадь треугольника ACD равна 48 см2.
2. Дан параллелепипед ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра АВ параллельно плоскости ACC1.
3. Верно ли утверждение, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости? Ответ обоснуйте.
II вариант
1. В тетраэдре ABCD точки М, К и Р— середины ребер AD, BD и DC. Докажите, что плоскость МКР параллельна плоскости ABС, и найдите площадь треугольника AВС, если площадь треугольника МКР равна 48 см2.
2. Дан параллелепипед ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра AВ параллельно плоскости DBB1.
3. Прямые а и b расположены соответственно в параллельных плоскостях и . Верно ли, что эти прямые не имеют общих точек? Ответ обоснуйте.
Глава II. Перпендикулярность прямых и плоскостей
Контролирующая самостоятельная работа к§ 2
I вариант
Задания № 141, 149, 158 из учебника.
II вариант
Задания № 198, 154, 157 из учебника.
Зачет № 3
Образцы карточек к зачету
Карточка 1
1. Сформулируйте определение угла между прямой и плоскостью.
2. Сформулируйте и докажите теорему отрехперпендикулярах.
3. Из точки A, удаленной на расстояние 5 см от плоскости, проведены к этой плоскости наклонные AВ и AС под углом 30° к плоскости. Найдите угол между наклонными, если ВС = 10 см.
Карточка 2
1. Объясните, что такое перпендикуляр и наклонная, проведенные из точки к плоскости, основание перпендикуляра, основание и проекция наклонной.
2. Сформулируйте и докажите признак перпендикулярности прямой и плоскости.
3. Через вершину А правильного треугольника AВС проведена прямая AM, перпендикулярная к его плоскости. Найдите расстояние от точки М до стороны ВС, если АВ = 4 см, AM = 2 см.
Контролирующая самостоятельная работа к § 3
I вариант
Задания № 171, 189 (а), 193 (б), 196 (а) из учебника.
II вариант
Задания № 172, 189 (б), 193 (а), 196 (б) из учебника.
Контрольная работа № 3
I вариант
1. Через вершину К треугольника МКР проведена прямая KN, перпендикулярная к плоскости треугольника. Известно, что KN = 15см, МК = КР = 10 см, МР = 12 см. Найдите расстояние от точки N до прямой МР.
2.Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол B1ADB, если AС = 6м,AВ1 = 4 м, ABCD — квадрат.
II вариант
1. Через вершину прямого угла С в равнобедренном треугольнике CDE проведена прямая СA, перпендикулярная к плоскости треугольника. Известно, что СA = 35 дм, CD = 12 дм. Найдите расстояние от точки A до прямой DE.
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол ADCA1,
если AС=13 см, DC =5 см, AA1 = 12 см.
Глава III. Многогранники
Контролирующая самостоятельная работа к § 1
I вариант
1. Основание прямой призмы — ромб со стороной 12 см и углом 60°. Меньшая диагональ параллелепипеда равна 13 см. Найдите площадь: а) боковой поверхности призмы; б) полной поверхности призмы; в) диагонального сечения, содержащего меньшую диагональ призмы.
II вариант
Основание прямой призмы — ромб с меньшей диагональю 5 см и углом 120°. Меньшая диагональ параллелепипеда образует угол 45° с плоскостью основания. Найдите площадь: а) боковой поверхности призмы; б) полной поверхностипризмы; в) диагонального сечения, содержащего меньшую диагональ призмы.
Контролирующая самостоятельная работа к § 2
I вариант
Задания № 250, 257 из учебника.
II вариант
Задания № 251, 258 из учебника.
Зачет № 4
Образцы карточек к зачету
Карточка 1
1. Какая призма называется: а) прямой, б) наклонной, в) правильной?
2. Сформулируйте и докажите теорему о площади боковой поверхности правильной пирамиды.
3. Докажите, что прямая, проходящая через середины двух противоположных ребер правильного тетраэдра, перпендикулярна к ним. Найдите длину отрезка, соединяющего середины противоположных ребер правильного тетраэдра, если ребро тетраэдра равно 1 м.
Карточка 2
1. Какие точки называются симметричными относительно плоскости? Приведите пример многогранника, имеющего плоскость симметрии.
2. Сформулируйте и докажите теорему о площади боковой поверхности прямой призмы.
3. В правильной треугольной пирамиде высота равна стороне основания. Найдите угол между боковым ребром и плоскостью основания.
Контрольная работа № 4
I вариант
1. Основанием прямой призмы ABCDA1B1C1D1является параллелограмм ABCD со сторонами 6 дм и 12 дм и углом, равным 60°. Диагональ B1D призмы образует с плоскостью основания угол в 30°. Найдите площадь боковой поверхности призмы.
2. Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45°. Найдите площадь полной поверхности пирамиды.
II вариант
1. Основанием прямой призмы ABCD A1B1C1D1является параллелограмм ABCD со сторонами 4 см и 4 см и углом, равным 30°. Диагональ AC1 призмы образует с плоскостью основания угол в 60°. Найдите площадь боковой поверхности призмы.
2. Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45°. Найдите площадь полной поверхности пирамиды.
Глава IV. Векторы в пространстве
Контролирующая самостоятельная работа к § 2
I вариант
Задания № 335 (в), 336 (б), 337 (в), 339 (б), 351 (а), 382 (а, в).
II вариант
Задания № 335 (г), 336 (в), 337 (б), 339 (а), 351 (б), 382 (б, г).
Контролирующая самостоятельная работа к § 3
I вариант
Задания № 358 (б), 382 (а, г), 388 (б), 393 (а).
II вариант
Задания № 358 (в), 382 (б, в), 388 (а), 393 (б).
Зачет № 5
Образцы карточек к зачету
Карточка 1
1. Объясните правила треугольника и параллелограмма сложения двух векторов. Докажите, что сумма двух векторов не зависит от выбора точки, от которой откладывается первый вектор.
2. Дан параллелепипед ABCDA1B1C1D1, . Найдите вектор с началом и концом в вершинах параллелепипеда, равный сумме векторов и .
3. Даны параллелограмм ABCD и произвольная точка O пространства. Докажите, что
.
Карточка 2
1. Что значит разложить вектор по трем некомпланарным векторам? Сформулируйте и докажите теорему о разложении вектора по трем некомпланарным векторам.
2. Упростите выражение: .
3. Даны четыре произвольные точки пространства А, В, С иD. Докажите, что .
Контрольная работа № 5
I вариант
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах
параллелепипеда, равный: а) , б) .
2. Дан тетраэдр DABC. Точка М — середина ребра ВС, точка N—середина отрезка DM.
Выразите вектор через векторы и .
3. В параллелепипеде ABCDA1B1C1D1 медианы треугольника ABD пересекаются в точке Р.
Разложите вектор по векторам .
II вариант
1. Дан параллелепипедABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: а) , б) .
2. Дан тетраэдр DABC. Медианы треугольника BDC пересекаются в точке Р, точка К—
середина отрезка АР. Выразите вектор через векторы .
3. В параллелепипеде ABCDA1B1C1D1 точка O лежит на отрезке B1D1, причем В1О :OD1 = 2 : 1. Разложите вектор по векторам .
Устные упражнения по геометрии 10-й класс.
Сентябрь
1. Катеты в прямоугольном треугольнике равны 6 и 8 см.
Вычислсте гипотенузу. 10 см
2. Измерения прямоугольного параллелепипеда равны 2, 3 и 5 см.
Вычислите его объем. 30 см3
3. Ребро куба равно 2 см. Вычислите сумму длин всех ребер куба. 24 см
4. Как называется геометрическое место точек на плоскости, одинаково
удаленных от концов отрезка? Перпендикуляр к отрезку через его середину
5. Стороны прямоугольника равны 12 и 10 см. Вычислите площадь
прямоугольника. 120 см2
6. Основание треугольника равно 6 см, высота — 4 см. Вычислите площадь
треугольника. 12 см2
7. Сколько центров гомотетии имеют два равных параллельных отрезка? Один
8. В прямоугольном треугольнике острые углы относятся как 1 : 2. Как
относится меньший катет к гипотенузе? 1:2
9. Периметр прямоугольника равен 60 см, длина его вдвое больше ширины.
Вычислите площадь прямоугольника. 50 см2
10. Периметр большего треугольника равен 36 см. Вычислите периметр
подобного меньшего треугольника, если коэффициент подобия равен 3. 12 см
11. Катеты прямоугольного треугольника равны 3 и 4 см. Вычислите
радиус описанной окружности. 2,5 см
12. Угол при основании в равнобедренном треугольнике равен 72°.
Вычислите угол при вершине. 36°
13. Сколько градусов составляет угол между диагоналями ромба? 90°
14. Периметр равнобедренного, треугольника равен 100 см, боковая
сторона его в два раза больше основания. Чему равны стороны
треугольника? 20, 40 и 40 см
15. Площадь грани куба равна 16 см. Вычислите его объем. 64 см3
16. Чему равно отношение длины окружности к диаметру?
17. Из точки выходят три луча. Сколько можно провести плоскостей,
чтобы по крайней мере два из них принадлежали плоскости? 1 или 3
18. Координаты точки А(2; 1). Укажите координаты точки В, симметричной
относительно начала координат. В(- 2; -1)
19. Сколько осей симметрии имеет окружность? Бесчисленное множество
20. Катеты треугольника равны 9 и 12 см. Вычислите синус меньшего угла. 0,6
21. Для каких углов в прямоугольном треугольнике sin A ? А 30о
22. Чему равна сумма углов выпуклого шестиугольника? 540°
23. В прямоугольной трапеции большая боковая сторона равна 10 см,
а основания — 2 и 8 см. Вычислите вторую боковую сторону. 8 см
24. Диагонали ромба равны 6 и 8 см. Вычислите сторону ромба. 5 см
25. Ребро куба равно 2 см. Вычислите поверхность куба. 24 см2
26. Основание параллелограмма равно 12 см, а высота — 4 см.
Вычислите площадь параллелограмма. 48 см2
27. Сколько прямых в пространстве можно провести через три точки,
если каждая из них проходит через две точки? 3
28. Сколько плоскостей можно провести через две точки? Бесчисленное множество
29. Могут ли прямая и плоскость иметь лишь две общие точки? Нет
30. Две равнобедренные трапеции имеют соответственно равные углы.
Будут ли эти трапеции подобными? Не всегда
Октябрь
1. Ребро куба равно 2 см. Вычислите его объем. 8 см3
2. Площадь прямоугольника равна 120 см2, а ширина 8 см. Вычислите
длину прямоугольника. 15 см
3. Гипотенуза в прямоугольном треугольнике равна 10 см, катет 6 см.
Вычислите другой катет. 8 см
4. Как изменится площадь круга, если радиус его увеличить в два раза? Увеличится
в 4 раза
5. Могут ли две плоскости иметь одну общую точку? Нет
6. Стороны треугольника относятся как 5 : 4 ; 3, а периметр подобного
ему треугольника равен 60 см. Вычислите стороны подобного
треугольника. 25, 20 и 15 см
7. Высота треугольника в два раза меньше основания, а площадь его
равна 36 см2. Вычислите высоту треугольника. 6 см
8. Стороны параллелограмма равны 8 и 10 см, а угол между ними 150°.
Вычислите площадь параллелограмма. 40 см2
9. Координаты точек на плоскости А(- 2; 4) и B(4; 2). Вычислите
координаты середины отрезка AB. (1; 3)
10. Какой угол образует прямая у = x — 1 с осью абсцисс? 45°
11. На каком расстоянии находятся точки А(- 3; 1) и B(5; I)? 8 единиц
12. Укажите кратчайшее расстояние прямой у — 4 = 0 до начала координат. 4 единицы
13. Разность двух углов параллелограмма равна 40o. Вычислите его углы. 70 и 110o
14. Координаты точки М(5; 2). Укажите координаты точки K, симметричной
относительно оси ординат. К(- 5; 2)
15. Четыре точки не лежат в одной плоскости. Сколько различных плоскостей
можно провести через них, если три из них принадлежат плоскости? 4
16. Ребро куба равно 3 см. Вычислите его поверхность. 54 см2
17. Площадь круга равна 100 см2. Вычислите его диаметр. 20 см
18. Известно, что = 4 см, = 2 см, а угол между ними 60°. Вычислите
скалярное произведение векторов. 4
19. Можно ли через точку пересечения двух прямых в пространстве
провести еще одну прямую, которая не лежала бы с ними в этой
плоскости? Да
20. Длина прямоугольника равна 20 см, а ширина составляет 40% длины.
Вычислите площадь прямоугольника. 160 см2
21. Углы треугольника относятся, как 3:4:5. Вычислите углы треугольника. 45o, 60oи 75°
22. Периметр равнобедренного треугольника равен 65 см, а основание на
5 см больше боковой стороны. Вычислите стороны треугольника. 20, 20 и 25 см
23. Диагонали ромба равны 6 и 10 см. Вычислите площадь ромба. 30 см2
24. Верно ли утверждение, что прямые, которые пересекают
пересекающиеся прямые а и b не в общей точке, лежат в одной
плоскости с ними? Да
25. Две силы 6 и 8 Н приложены к одной точке и действуют под прямым
углом. Вычислите равнодействующую силу. 10Н
26. Прямые а и b лежат в параллельных плоскостях. Могут ли эти прямые
быть скрещивающимися? Да
27. Напишите уравнение окружности с центром в начале координат и
радиусом 4 см. x2 + у2 = 16
28. В равностороннем треугольнике проведены две медианы. Вычислите
наименьший угол между ними. 600
29. Найдите координаты точки пересечения прямых x + y = 2 и x – y = 2. (2; 0)
30. Площадь данного многоугольника равна 45 см2. Большая сторона его
равна 15 см, а сходственная сторона подобного многоугольника равна
5 см. Вычислите площадь подобного многоугольника. 5 см2
Ноябрь
1.Измерения прямоугольного параллелепипеда равны 3, 4 и 5 см.
Вычислите его объем. 60 см3
2. Радиус окружности равен 2 см. Вычислите длину окружности. 4 см
3. Катеты в прямоугольном треугольнике равны 5 и 12 см. Вычислите
гипотенузу. 13 см
4. Основание равнобедренного треугольника равно 6 см, а боковые
стороны — по 5 см. Вычислите площадь треугольника. 12см2
5. Площадь прямоугольника равна 150 см2, а длина 25 см. Вычислите
ширину прямоугольника. 6 см
6. Могут ли пересекаться плоскости, параллельные одной и той же прямой? Да
7. Точка D вне плоскости, проходящей через точки A, В, С. Может ли быть
трапецией четырехугольник ABCD? Нет
8. Стороны угла A пересечены двумя параллельными прямыми ВС и B1C1,
причем АВ = 8 см, ВВ1 = 4 см и АС = 12 см. Вычислите длину отрезка СС1 6см
9. Для каких углов А в прямоугольном треугольнике cos A ? 60° А
10. Два угла с соответственно параллельными сторонами относятся,
как 4:5. Вычислите эти углы. 80° и 100°
11. Угол ромба равен 30°, а высота 10 см. Вычислите площадь ромба. 200 см2
12. В прямоугольной трапеции большая боковая сторона равна 10 см, а
основания 4 и 10 см. Вычислите меньшую боковую сторону. 8 см
13. Проходит ли прямая у = x — 2 через точку А(4; 2)? Да
14. На каком расстоянии на плоскости находятся точки А(2; — 2) и B(2; 6)? 8 единиц
15. Известно, что на плоскости прямая, которая пересекает одну из
параллельных прямых, пересекает и другую. Будет ли это справедливо
для пространства? Нет
16. Поверхность куба равна 24 см2. Вычислите его объем. 8 см3
17. Четыре точки не лежат в одной плоскости. Могут ли какие-нибудь три
точки лежать на одной прямой? Нет
18. Всегда ли можно провести плоскость через прямую и две точки вне этой
прямой? Не всегда
19. Сколько центров гомотетии имеют два неравных параллельных отрезка? 1
20. Катеты треугольника равны 8 и 6 дм. Вычислите радиус описанного круга. 5 дм
21. Прямая l параллельна плоскости а. Существует ли на плоскости а прямая,
не параллельная l? Да
22. Координаты точки А(2; 4). Укажите координаты точки В, симметричной
относительно оси абсцисс. В(2; — 4)
23. Три плоскости пересекаются попарно. Сколько получится линий
пересечения? 3
24. Вершина угла находится внутри окружности, а дуги между сторонами
и продолжением сторон равны 50° и 100°. Вычислите угол. 75°
25. В равнобедренной трапеции углы относятся, как 5:7. Вычислите эти углы. 75o и 100o
26. Уравнение окружности х2 + у2 = 16. На каком расстоянии находятся точки
окружности от начала координат? 4
27. На каком расстоянии от начала координат находится точка М(6; — 8)? 10
28. Диагонали ромба равны 60 и 80 см. Вычислите сторону ромба. 50 см
29. Сколько сторон у выпуклого многоугольника, если сумма углов равна 540°? 5
30. Периметр равнобедренного треугольника равен 16 см, а сторона его
равна 6 см. Вычислите другие его стороны. по 5 см или 6 и 4 см
Декабрь
1. Площадь прямоугольника равна 180 см2 , а его длина 15 см. Вычислите
ширину прямоугольника. 12см
2. Ребро куба равно 3 дм. Вычислите его объем. 27 дм3
3. Гипотенуза в прямоугольном треугольнике равна 5 дм, а катет 4 дм.
Вычислите другой катет. 3 дм
4. Две окружности лежат в одной плоскости. Какие центры гомотетии
имеют эти окружности, если они не концентрические и у них неравные
диаметры? Внутренний и внешний
5. Напишите формулу Герона для вычисления площади треугольника.
S =
6. Вычислите вписанный угол, если он опирается на треть окружности. 60°
7. Один из внутренних углов треугольника равен 60°, а один из его внешних
углов равен 100°. Найдите два других угла треугольника. 80o и 40°
8. В равностороннем треугольнике медианы равны 12 см. На какие отрезки
точка их пересечения делит медиану? 4 и 8 см
9. Вычислите расстояние между центрами окружностей, имеющих
внутреннее касание, если их радиусы равны 7 и 4 см. 3 см
10. В треугольнике AВС сторона АВ равна 12 см, а сторона АС равна 15 см.
В каком отношении биссектриса угла А делит сторону ВС? 4 : 5
11. Укажите координаты точки пересечения прямой у = 0,5х + 2 с осью
ординат. (0; 2)
12. Две плоскости и пересекаются. Прямая l пересекает плоскость .
Всегда ли прямая l пересечет плоскость ? Нет
13. Перпендикулярны ли векторы ||(3; 2) и ||(2; — 3)? Да
14. Найдите геометрическое место точек пространства, равноудаленных от
двух точек А и В. [Плоскость, перпендикулярная АВ, проходящая через середину отрезка АВ]
15. Площадь круга равна 36 см 2. Вычислите радиус круга. 6 см
16. Прямая l не перпендикулярна плоскости . Можно ли на плоскости
найти прямую, которая будет перпендикулярна прямой l? Можно
17. Площадь трапеции равна 30 см2, ее средняя линия равна 6 см.
Вычислите высоту трапеции. 5 см
18. Известно, что || = 6 см, || = 5 см, а угол между ними 45°. Вычислите
скалярное произведение векторов. 15
19. Сторона равностороннего треугольника равна 4 дм. Вычислите его
площадь. 4 см2
20. Является ли диагональ параллелограмма осью cимметрии? Нет
21. Векторы (12; ,4) и (6; у) параллельны. Определите у. 2
22. Две прямые а и b параллельны плоскости . Параллельны ли прямые
а и b? Нет
23. Сколько прямых, перпендикулярных данной прямой, можно провести
из точки, лежащей на этой прямой? Бесчисленное множество
24. Сколько плоскостей можно провести через три точки, которые лежат
на одной прямой? Бесчисленное множество
25. Силы 9 Н и 12 Н действуют из одной точки и направлены под прямым
углом. Вычислите равнодействующую силу. 15 Н
26. Может ли параллельная проекция параллелограмма на плоскость
быть квадратом? Да
27. Вычислите углы равнобедренного треугольника, если угол при вершине
в два раза больше угла при основании. 45 o, 45 o и 90°
28. Хорда пересекает диаметр окружности под пряным углом и делит его на
отрезки 3 и 12 см. Вычислите длину хорды. 12 см
29. Радиусы двух окружностей равны 8 и 3 см, а длина общей внешней
касательной равна 12 см. Вычислите расстояние между центрами
окружностей. 13 см
30. Биссектриса одного из углов прямоугольника делит сторону пополам,
а его периметр равен 60 см. Вычислите стороны прямоугольника. 10 и 20 см
Январь
1. В равностороннем треугольнике сторона равна 8 см. Вычислите площадь
треугольника. 16 см2
2. Найдите геометрическое место точек пространства, равноудаленных от
всех точек окружности. [Перпендикуляр к плоскости окружности, проходящей через
центр окружности]
3. Основания трапеции равны 6 и 14 см, а высота 10 см. Вычислите площадь
трапеции. 100 см3
4. Могут ли две плоскости, которые проходят через непараллельные
прямые, быть параллельными? Да
5. Концы отрезка длиной 15 см принадлежат двум параллельным плоскостям,
расстояние между которыми равно 12 см. Вычислите проекцию отрезка
на плоскость. 9 см
6. Радиус окружности 3 дм. Вычислите длину окружности. 6 дм
7. Основание равнобедренного треугольника равно 8 см, а боковые стороны –
по 5 см. Вычислите площадь треугольника. 12 см2
8. Точки А, В, С и D не лежат в одной плоскости. Могут ли прямые АВ и CD
пересекаться? Нет
9. Катеты прямоугольного треугольника равны 30 и 40 см. Вычислите радиус
описанной окружности. 25 см
10. Сторона AD параллелограмма ABCD принадлежит плоскости , а сторона
ВС отстоит от нее на 12 см. Вычислите расстояние от точки пересечения
диагоналей параллелограмма до плоскости . 6 см
11. В равностороннем треугольнике сторона равна 6 см. Вычислите площадь
треугольника. 9 см2
12. Во сколько раз окружность длиннее радиуса? В 2 раз
13. Координаты точек на плоскости А(6; 1) и В(2; 3). Найдите координаты
середины отрезка АВ. С(4; 2)
14. Какой угол образует прямая у = х с осью ординат? 60°
15. Является ли точка пересечения диагоналей параллелограмма центром
симметрии? Да
16. Вычислите координаты точки пересечения прямых х + у = 5 и х — у = 1. (3; 2)
17. Вычислите вписанный угол, если он опирается на диаметр. 90°
18. Поверхность куба равна 54 дм2. Вычислите его объем. 27 дм3
19. Назовите геометрическое место точек, равноудаленных от двух
параллельных плоскостей? Параллельная плоскость
20. Концы отрезка длиной 10 см лежат в параллельных плоскостях.
Параллельная проекция отрезка равна 6 см. Вычислите расстояние
между плоскостями. 8 см
22. Диагонали ромба равны 160 и 120 см. Вычислите сторону ромба. 100 см
23. На тело в точке О действуют две силы 12 Н и 5 Н, а угол между их
направлениями прямой. Вычислите равнодействующую силу. 13 Н
24. Площадь параллелограмма равна 60 см2, а основание 15 см. Вычислите
высоту параллелограмма на основание. 4 см
25. Координаты точки К( — 3; 2). Укажите координаты точки М симметричной
точке К относительно начала координат. М(3; — 2)
26. Прямые а и b принадлежат пересекающимся плоскостям. Могут ли прямые
а и b быть параллельны? Да
27. Как изменится площадь прямоугольника, если измерения уменьшить в два
раза? Уменьшится в 4 раза
28. В параллелограмме углы относятся, как 2 : 3. Вычислите эти углы. 72°, 108°
29. Радиусы двух кругов равны 3 и 4 см. Их общие внутренние касательные
взаимно перпендикулярны. Вычислите длину этих касательных. По 7 см
30. Две хорды пересекаются. Первая делится точкой пересечения на отрезки
6 см и 2 см. Один из отрезков второй хорды равен 4 см. Вычислите вторую
хорду. 7 см
Февраль
1. Даны четыре различные точки A, В, С и D Три из них лежат на одной
прямой. Могут ли все точки лежать в одной плоскости? Да
2. Ребро куба равно 4 см. Выислите объем куба. 64 см3
3. Гипотенуза в прямоугольном треугольнике равна 13 см, а катет 5 см.
Вычислите другой катет. 12 см
4. Концы отрезка не пересекают плоскость и удалены от нее на расстояние
10 и 20 см. На каком расстоянии находится середина этого отрезка? 15 см
5. На каком расстоянии находится точка пересечения диагоналей куба от
его ребра длина которого 10 см? 5 см
6. Биссектриса угла параллелограмма делит его сторону пополам. Меньшая
сторона равна 6 см. Вычислите периметр параллелограмма. 36 см
7. Два угла с соответственно параллельными сторонами относятся, как 7 : 2.
Вычислите эти углы. 140° и 40°
8. Проходит ли прямая у = 2х — 3 через точку А(2; 3)? Нет
9. Сколько осей симметрии у ромба? 2
10. Диагонали четырехугольника, пересекаясь, делятся пополам. Можно ли
считать его параллелограммом? Да
11. Координаты точек А(2; 1) и В(8; 2). Определите координаты вектора АВ. (6;1)
12. Из концов дуги в 200° проведены касательные до взаимного пересечения.
Под каким углом пересекаются эти касательные? 20°
13. Хорда длиной 10 см стягивает дугу в 60°. Вычислите длину окружности. 20 см
14. Является ли точка пересечения диагоналей в равнобедренной трапеции
центром симметрии? Нет
15. В пространстве расположена трапеция. Чем является его параллельная
проекция на плоскость? Трапеция или отрезок
16. Площадь круга равна 16 см2. Вычислите радиус круга. 4 см
17. Какая линия представляет множество точек ху = 0 на плоскости? Оси координат
18. Хорда пересекает диаметр окружности под прямым углом и делит его
на отрезки 4 и 9 см. Вычислите длину хорды. 12 см
19. Параллельны ли прямые 2х — у = 1 и 4x — 2у = 1? Да
20. Вершина угла находится внутри окружности, а дуги между сторонами и
продолжением сторон равны 40° и 80°. Вычислите угол. 60°
21. Стороны ромба равны по 12 см, а угол между ними 60°. Вычислите
площадь ромба. 72 см2
22. Известно, что || = 5 см, || = 10 см, а угол между а и b равен 30°.
Вычислите скалярное произведение векторов. 25
23. В равностороннем треугольнике проведены две высоты. Вычислите
наименьший угол между высотами. 60°
24. Стороны параллелограмма относятся, как 2 : 3. Сколько процентов
составляет большая сторона от периметра? 30%
25. Проекция отрезки на плоскость равна 12 см, а длина отрезка 24 см.
Вычислите угол между отрезком и плоскостью. 60°
26. В треугольнике ABC стороны АВ и АС соответственно равны 20 и 30 см.
В каком отношении биссектриса угла А делит сторону ВС? 2 : 3
27. Определите множество точек на плоскости, заданное равенством ху = 4. Гипербола
28. Из точки А к окружности проведена касательная и секущая, равная 12 см.
Внешний отрезок секущей равен 3 см. Вычислите длину касательной. 6 cм
29. Вычислите объем прямоугольного параллелепипеда, если его измерения
равны 5, 4 и 3 см. 60 см 3
30. Две прямые 2х – у = 4 и 2х + у = 8 пересекаются. Вычислите координаты
точки пересечения этих прямых. (3; 2)
Март
1. Основания трапеции равны 4 и 12 см, а высота 10 см. Вычислите площадь
трапеции. 80 см2
2. Радиус окружности равен 4 см. Вычислите длину окружности. 8 см
3. Измерения прямоугольного параллелепипеда равны 5, 6 и 7 дм. Вычислите
его объем.. 210 дм3
4. Прямая АВ и точки С, D не принадлежат одной плоскости. Пересекаются
ли прямые АB и CD? Не всегда
5. Основание равнобедренного треугольника равно 10 см, а боковые стороны –
по 13 см. Вычислите площадь треугольника. 60 см2
6. Катеты в прямоугольном треугольнике равны 8 и 15 см. Вычислите
гипотенузу. 17 см
7. Может ли быть правильный треугольник сечением куба? Да
8. Для каких углов А в прямоугольном треугольнике ctg А 1? 45° А
9. Стороны угла пересекают окружность, а дуги между его сторонами
равны 30° и 90°. Вычислите угол. 30°
10. Назовите геометрическое место точек на плоскости х2 + у2 4. Круг с R = 2
11. Гипотенуза треугольника равна 10 см, а один катет 6 см. На какие
отрезки биссектриса угла делит второй катет? 5 и 3 см
12. В треугольнике АВС соs А = . Чему равен угол А? 60°
13. Координаты точек на плоскости А(- 1; 1) и B(5; 3). Вычислите координаты
середины отрезка AB. (2; 2)
14. Дано уравнение прямой у = — 3х + 6. Определите координаты точек
пересечения прямой с осью абсцисс. (2; 0)
15. Сколько осей симметрии у круга? Бесконечное множество
16. Площадь треугольника равна 362 дм. Вычислите площадь подобного ему
треугольника, стороны которого вдвое меньше, чем у заданного. 9 дм2
17. Определите вид треугольника в зависимости от углов, если его стороны
равны 4, 6 и 8 см. Тупоугольный
18. На каком расстоянии находятся точки A(7; 5) и B(3; 2)? 5 единиц
19. Две силы 8 Н и 15 Н приложены к одной точке и действуют под прямым
углом. Вычислите равнодействующую силу. 17 Н
20. Вычислите объем прямоугольного параллелепипеда, если его измерения
равны 6, 3 и 2 см. 36 см2
21. Поверхность куба равна 96 см2. Вычислите его объем. 64 см3
22. Стороны параллелограмма равны 10 и 12 см, а угол между ними 30°.
Вычислите площадь параллелограмма. 60 см2
23. Известно, что || = 4 см, || = 5 см, а угол между ними 60°. Вычислите
скалярное произведение векторов. 10
24. Стороны треугольника равны 5, 6 и 7 см. Определите вид треугольника в
зависимости от углов. Остроугольный
25. Радиус круга, описанного около прямоугольного треугольника равен 5 см,
а катет равен 6 см. Вычислите площадь треугольника. 24 см2
26. Назовите на плоскости геометрическое место точек, заданное неравенством
х2 — 5х + 6 0. Полоса на плоскости между прямыми х = 2, х = 3
27. Отрезок длиной 30 см образует с плоскостью угол 60°. Вычислите
проекцию отрезка на плоскость. 15 см
28. Вычислите угол, вписанный в дугу, которая составляет 5/12 окружности. 75°
29. Назовите геометрическое место точек на плоскости | у | = 3. Прямые y = 3 и y = -3
30. Две хорды пересекаются. Первая хорда делится на отрезки 3 и 12 см.
Один отрезок второй хорды равен 4 см. Вычислите вторую хорду. 13 см
Апрель
1. Стороны треугольника равны 2, 3 и 4 дм. Определите вид треугольника в
зависимости от углов. Тупоугольный
2. Вычислите углы треугольника, если они относятся как 1 : 2 : 3. 30°, 60°, 90°
3. Катет прямоугольного треугольника равен 20 дм, а гипотенуза 25 дм.
Вычислите другой катет. 15 дм
4. Площадь грани куба равна 9 дм2. Вычислите его объем. 27 дм3
5. Радиус окружности 6 см. Вычислите площадь круга. 36 см2
6. Угол при вершине равнобедренного треугольника равен 40°. Вычислите
угол при основании. 70°
7. Отрезок в 20 см образует с плоскостью угол 60°. Вычислите проекцию
отрезка на плоскость. 10 см
8. У двух связанных между собой шестерен имеется 60 зубцов и 20 зубцов.
На сколько градусов повернется большая шестерня, если меньшая сделает
один оборот? 120°
9. Площадь равностороннего треугольника равна 25 дм2. Вычислите
его сторону. 10 дм
10. Напишите уравнение окружности радиуса 6 см с центром в начале
координат. х2 + у2 = 36
11. Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, а
катет АС равен 12 см. На какие отрезки биссектриса угла А делит другой
катет? 6 и 10 см
12. На каком расстоянии от начала координат находится точка А(12; 5)? 13 см
13. Координаты точек А(- 2; — 1) и B(7; 1). Укажите координаты вектора . (9; 2)
14. Дуга содержит 160°. Под каким углом из точек этой дуги видна ее хорда? 100°
15. Может ли быть в сечении куба правильный шестиугольник? Да
16. Площадь трапеции равна 24 см2, а высота 4 см. Вычислите среднюю
линию трапеции. 6 см
17. Верно ли утверждение, что «прямая перпендикулярна плоскости, если
она перпендикулярна двум сторонам трапеции, лежащей в этой
плоскости»? Не всегда
18. Из точки окружности проведены равные хорда и радиус. Найдите
угол между ними. 60°
19. Отрезок пересекает плоскость, а концы его удалены от плоскости на 2 и
8 см. На каком расстоянии находится середина отрезка от плоскости? 3 см
20. В равностороннем треугольнике проведены две биссектрисы. Вычислите
наименьший угол между биссектрисами. 60°
21. Сторона ромба равна 8 см, а угол между eе сторонами равен 150°.
Вычислите площадь ромба. 32 см2
22. Один угол параллелограмма составляет 25% другого угла. Вычислите
углы параллелограмма. 36о и 144°
23. Хорда пересекает диаметр окружности под прямым углом и делит его
на отрезки 2 и 4,5 см. Вычислите длину хорды. 6 см
24. Сторона треугольника АВС АВ равна 6 см, сторона АС равна 10 см. В
каком отношении биссектриса угла А делит третью сторону ВС? 3 : 5
25. Назовите множество точек на плоскости, заданное уравнением х2 — 4 = 0.
Прямые х = 2 и х = -2
26. Какой угол образует прямая 2х — 2у = 5 с ось абсцисс? 45°
27. В треугольнике АВС cos А = — 0,5. Вычисли угол А. 120°
28. Параллельны ли прямые 3x — у = 3 и 6х — 2у = 3? Да
29. Площадь основания прямоугольного параллелепипеда равна 12 см2, а
его объем 36 см3. Вычислите высоту параллелепипеда. 3 см
30. Сколько осей симметрии у квадрата? 4
Май
1. Площадь грани куба равна 4 см2. Вычислите его объем. 8 см3
2. Длина окружности равна 10 см. Вычислите радиус окружности. 5 см
3. Основание равнобедренного треугольника равно 24 см, а боковые
стороны — по 13 см. Вычислите площадь треугольника. 60 см2
4. Дуга содержит 100°. Под каким углом из точек этой дуги видна ее хорда? 130°
5. Измерения прямоугольного параллелепипеда равны 3, 5 и 8 дм. Вычислите
его объем. 120 дм3
6. Катеты прямоугольного треугольника равны 30 и 40 дм. Вычислите
гипотенузу. 50 дм
7. Даны координаты точек А(2; 1; 3) и В(5; 4; 3). Найдите координаты вектора
. (3;3;0)
8. Вычислите расстояние точки А(4; 4; — 2) до начала координат. 6
9. Перпендикулярны ли векторы (3; 1; 1) и (1; 2; — 5)? Да
10. В прямоугольном треугольнике sin A = 0,6. Вычислите tg A. 3/4
11. Вычислите вписанный угол, опирающийся на дугу, которая составляет
четверть окружности. 45°
12. Хорда пересекает под прямым углом диаметр окружности и делит его на
отрезки 2 и 8 см. Вычислите длину хорды. 8 см
13. Концы отрезка АВ, равного 20 см, принадлежат параллельным плоскостям.
Отрезок и его проекция образуют угол 45°. Вычислите расстояние между
плоскостями. 10см
14. Радиус круга, описанного около прямоугольного треугольника, равен 10 см,
его катет равен 16 см. Чему равен синус меньшего угла треугольника? 0,6
15. Основания трапеции равны 8 и 12 см, а ее высота 5 см. Вычислите
площадь трапеции. 50 см2
16. Точка М лежит на перпендикуляре к плоскости и удалена от нее на
расстояние 12 см, а точка А принадлежит этой же плоскости и удалена
от основания перпендикуляра на 5 см. Вычислите расстояние AM. 13 см
17. Принадлежит ли точка А(0; 5; 0) плоскости 2х + у — z — 5 = 0? Да
18. Коллинеарны ли векторы (4; 4; 2) и (2; 2; 1)? Да
19. Параллельны ли плоскости 2х + 4у + 6z — 12 = 0 и х + 2у + 3z — 3 = 0? Да
20. Напишите уравнение плоскости, проходящей через точку М(4; 1; 2) и
перпендикулярной вектору (1; 3; 2). x + 3у + 2z — 11 = 0
21. Стороны параллелограмма равны 15 и 6 см, а угол между ними равен
1500. Вычислите площадь параллелограмма. 45 см2
22. Может ли катет равнобедренного прямоугольного треугольника образовать
угол 60° с плоскостью, проходящей через гипотенузу? Нет
23. Один конец отрезка длиной 20 дм принадлежит плоскости. Отрезок
образует с плоскостью угол в 30°. На какой высоте от плоскости находится
другой конец отрезка? 10 дм
24. Даны координаты векторов (2; 3; 4) и (1; 4; 2). Вычислите координаты
вектора . (3; 7; 6)
25. Площадь треугольника равна 60 см2. Его плоскость составляет угол 60° с
плоскостью . Вычислите площадь проекции треугольника на плоскость . 30см2
26. В пространстве квадрат. Что является параллельной проекцией квадрата
на плоскость? Параллелограмм или отрезок
27. Напишите уравнение сферы с центром в начале координат и
радиусом 4 см. х2 + у2 + z2 = 16
28. Координаты точки М(1; 2; 2). Вычислите расстояние точки М до начала
координат. 3
29. Перпендикулярны ли плоскости 2х — 5у + z + 4 = 0 и 3x + 2y + 4z — 1 = 0? Да
30. Как изменится объем прямоугольного параллелепипеда, если измерения
увеличить в два раза? Увеличится в 8 раз
Тесты по геометрии для 10-го класса онлайн
- Вход
- Тесты
- Опросы
- Кроссворды
- Диалоги
- Уроки
- Диалоги Уроки
- Онлайн тесты
Аналитическая геометрия Grade 10
Аналитическая геометрия, основные понятия и расчеты.
- 1. КЛАСС АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ: 10Laja Plaatjies201248629
2. ИСТОРИЯ Представленное в 1630-х годах важное математическое развитие, заложило основы современной математики, а также способствовало развитию вычислений РЕН ДЕКАРТ (1596-1650) и ПЬЕР ДЕ ФЕРМА (1601-1665), французские математики, независимо разработали основы аналитической геометрии 3.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Раздел математики, в котором алгебраические уравнения используются для описания размера и положения геометрических фигур в системе координат. 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Связь между алгеброй и геометрией стала возможной благодаря развитию системы координат, которая позволила описывать геометрические идеи, такие как точка и линия, в алгебраических терминах, таких как действительные числа и уравнения. Также известна как декартова геометрия или координатная геометрия. 5. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Использование системы координат для связи геометрических точек с действительными числами является центральной идеей аналитической геометрии.Определив каждую точку с помощью уникального набора действительных чисел, геометрические фигуры, такие как линии, круги и коники, можно описать с помощью алгебраических уравнений. 6. ДЕКАРТОВАЯ ПЛОСКОСТЬ Декартова плоскость, основа аналитической геометрии, позволяет графически представлять алгебраические уравнения в процессе, называемом построением графиков. Фактически, это графическое представление алгебраического уравнения любой формы — графики многочленов, рациональные функции, конические сечения, гиперболы, экспоненциальные и логарифмические функции, тригонометрические функции и даже векторы.7. КАРТСИАНСКАЯ ПЛОСКОСТЬ Ось x (горизонтальная ось), по которой отложены значения x. Ось y (вертикальная ось), по которой отложены значения y. origin, обозначенный символом 0, отмечает значение 0 координат обеих осей, заданных в форме (x, y) и используется для представления различных точек на плоскости. 8. НАКЛОН ЛИНИИ Наименьший угол, больший или равный 0, который линия составляет с положительным направлением оси x (0 <180) Наклон горизонтальной линии равен 0. Тангенс угла наклона m = tan 9 .НАКЛОН ЛИНИИ yy L LOMxOMx 10. УГОЛ МЕЖДУ ДВУМЯ ЛИНИЯМИ 11. УГОЛ МЕЖДУ ДВУМЯ ЛИНИЯМИ Если это угол, измеренный против часовой стрелки, между двумя линиями, то где m2 - наклон конечной стороны, а m1 - наклон начальной стороны 12. Точка - это упорядоченная пара чисел, записанная как (x; y). Расстояние - это мера длины между двумя точками. Формула для нахождения расстояния между любыми двумя точками: 13. Формула для нахождения середины. точка между двумя точками: 14.НАКЛОН ЛИНИИ Наклон или уклон линии описывает крутизну, уклон или уклон. Более высокое значение наклона указывает на более крутой наклон. Уклон обычно описывается отношением подъема, деленного на пробег между двумя точками на линии. Наклон обозначается. 15. Градиент между двумя точками Градиент между двумя точками определяется отношением вертикального изменения к горизонтальному изменению. Формула для определения градиента линии: 16. НАКЛОН ЛИНИИ Если линия поднимается слева направо, Если линия идет справа налево, если линия параллельна оси x, если линия параллельна оси y,> <= = 17.Две невертикальные линии параллельны тогда и только тогда, когда их наклоны равны. Две наклонные линии перпендикулярны тогда и только тогда, когда наклон одной является отрицательной обратной величиной наклона другой. (Если две линии перпендикулярны, произведение их градиентов равно 1.) Для горизонтальных линий градиент равен 0. Для вертикальных линий градиент не определен. 18. Если две линии с градиентами m1 и m2 перпендикулярны, то m1 m2 = -1. И наоборот: если m1 m2 = -1, то две линии с градиентами m1 и m2 перпендикулярны.19. ФАКТЫ ПРЯМОЙ ЛИНИИ y = mx + c y2 - y1 Градиент = x2 - ось x1Y Пересечение 20. Найдите уравнение прямой, которая проходит через точку (-1, 3) и перпендикулярна прямой с уравнением 4x y 1 0 21. РЕШЕНИЕ Найти градиент данной линии: 4 xy 1 0 y 4 x 1 m 4 Найти градиент перпендикуляра: Найти уравнение: m1 (используя формулу mm 1) 1 2 4y b = m (xa) y 3 = (x (-1)) 4y 12 = x + 1 4 yx 13 0 22. Эта презентация представляет собой смесь из 6 различных источников. Это: Фелипе, Н, М.(2014). Основные понятия аналитической геометрии [Презентация в PowerPoint]. Доступно по адресу: http://www.slideshare.net/NancyFelipe1/analyticgeometry-basic-concepts. Доступ: 6 марта 2014 г. Демирдаг, Д. (2013). Лекция №4 по аналитической геометрии [PowerPoint Presentation]. Доступно по адресу: http://www.slideshare.net/denmarmarasigan/lecture-4-analytic-geometry. Доступ: 6 марта 2014 г. Share, S. (2014). Аналитическая геометрия [презентация в PowerPoint]. Доступно по адресу: http://www.slideshare.net/SuziShare/analytical-geometry.Доступ: 6 марта 2014 г. Дерирдаг Д. (2012). Аналитическая геометрия [презентация в PowerPoint]. Доступно по адресу: http://www.slideshare.net/mstfdemirdag/analytic-geometry. Дата доступа: 6 марта 2014 г. Ноласко, К. М. Аналитическая геометрия [презентация в PowerPoint]. Доступно по адресу: http://www.slideshare.net/CecilleMaeNolasco/analytical-geometry. Дата обращения: 6 марта 2014 г. Siyavula_Education. (2012). Аналитическая геометрия Everything Maths, 10 класс [PowerPoint Presentation}. Доступно по адресу: http://www.slideshare.net/Siyavula_Education/analyticalgeometry?qid=9526d5d1-098f-45da-90b6d503de7f2db5&v=default&b=&from_search=4).Дата обращения: 6 марта 2014 г.
Геометрия | математика | Britannica
Самые ранние известные однозначные примеры письменных записей — датируемые Египтом и Месопотамией около 3100 г. до н.э. — демонстрируют, что древние народы уже начали разрабатывать математические правила и методы, полезные для съемки земельных участков, строительства зданий и измерения контейнеров для хранения. Начиная примерно с VI века до нашей эры, греки собрали и расширили эти практические знания и на их основе обобщили абстрактный предмет, ныне известный как геометрия, из сочетания греческих слов geo («Земля») и metron («мера»). ) для измерения Земли.
В дополнение к описанию некоторых достижений древних греков, в частности, логического развития геометрии Евклидом в Elements , в этой статье рассматриваются некоторые приложения геометрии к астрономии, картографии и живописи от классической Греции до средневекового ислама и Европы эпохи Возрождения. . Он завершается кратким обсуждением расширений неевклидовой и многомерной геометрии в современную эпоху.
Древняя геометрия: практическая и эмпирическая
Происхождение геометрии лежит в повседневной жизни.Традиционный отчет, сохранившийся в книге Геродота « History » (V век до н. Э.), Приписывает египтянам создание геодезических изысканий с целью восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекает из необходимости оценивать дань, хранить нефть и зерно и строить плотины и пирамиды. Даже три сложные геометрические задачи древних времен — удвоение куба, разрезание угла и квадрат круга, которые будут обсуждаться позже, — вероятно, возникли из практических вопросов, из религиозных ритуалов, хронометража и строительства, соответственно, в догреческие общества Средиземноморья.И главный предмет поздней греческой геометрии, теория конических сечений, обязана своим общим значением, а, возможно, и своим происхождением, своим приложением к оптике и астрономии.
В то время как многие древние люди, известные и неизвестные, внесли свой вклад в эту тему, ни один из них не сравнится с влиянием Евклида и его Элементов геометрии, книги, которой сейчас 2300 лет и которая является объектом столь же болезненного и кропотливого изучения, как Библия. Однако об Евклиде известно гораздо меньше, чем о Моисее.Фактически, единственное, что известно с достаточной степенью уверенности, — это то, что Евклид преподавал в Александрийской библиотеке во время правления Птолемея I (323–285 / 283 гг. До н. Э.). Евклид писал не только по геометрии, но также по астрономии и оптике, а также, возможно, по механике и музыке. Только Elements , который был широко скопирован и переведен, уцелел.
Евклид « Elements» был настолько полным и ясно написанным, что буквально перечеркнул работу его предшественников.То, что известно о греческой геометрии до него, происходит главным образом из отрывков, цитируемых Платоном и Аристотелем, а также более поздними математиками и комментаторами. Среди других ценных вещей, которые они сохранили, — некоторые результаты и общий подход Пифагора ( ок. 580– ок. 500 до н. Э.) И его последователей. Пифагорейцы убедили себя, что все вещи являются числами или обязаны своим отношением к числам. Доктрина придавала математике первостепенное значение в исследовании и понимании мира.Платон развивал аналогичную точку зрения, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключах к интерпретации Вселенной. Таким образом, древняя геометрия приобрела ассоциацию с возвышенным, чтобы дополнить ее земное происхождение и репутацию образца точного рассуждения.
Нахождение прямого угла
Древним строителям и геодезистам нужно было уметь строить прямые углы в поле по запросу. Метод, применявшийся египтянами, принес им в Греции прозвище «съемники каната», по-видимому, потому, что они использовали веревку для составления инструкций по строительству.Один из способов, которым они могли использовать веревку для построения прямоугольных треугольников, заключался в том, чтобы пометить веревку с петлей с узлами, чтобы веревка, удерживая ее за узлы и сильно натянув, образовывала прямоугольный треугольник. Самый простой способ выполнить трюк — взять веревку длиной 12 единиц, завязать узел на 3 единицы с одного конца и еще 5 единиц с другого конца, а затем связать концы вместе, чтобы образовать петлю, как показано на анимация. Однако египетские писцы не оставили нам инструкций об этих процедурах, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой напротив прямого угла равен сумме квадратов на двух других. стороны.Точно так же ведические писания древней Индии содержат разделы, называемые сульвасутра s, или «правила веревки», для точного расположения жертвенных алтарей. Необходимые прямые углы были сделаны веревками, отмеченными для получения триад (3, 4, 5) и (5, 12, 13).
В вавилонских глиняных табличках ( ок. 1700–1500 гг. До н. Э.) Современные историки обнаружили проблемы, решения которых указывают на то, что теорема Пифагора и некоторые особые триады были известны более чем за тысячу лет до Евклида.Однако у прямоугольного треугольника, составленного наугад, очень маловероятно, что все его стороны будут измеряться одной и той же единицей измерения, то есть, каждая сторона будет целым числом, кратным некоторой общей единице измерения. Этот факт, который был шокирован пифагорейцами, породил концепцию и теорию несоизмеримости.
Обнаружение недоступного
Согласно древней традиции, Фалес Милетский, живший до Пифагора в 6 веке до нашей эры, изобрел способ измерения недоступных высот, таких как египетские пирамиды.Хотя ни одно из его сочинений не сохранилось, Фалес, возможно, хорошо знал о вавилонском наблюдении, что для одинаковых треугольников (треугольников, имеющих одинаковую форму, но не обязательно одинаковый размер) длина каждой соответствующей стороны увеличивается (или уменьшается) на одно и то же число. Определение высоты башни с помощью подобных треугольников показано на рисунке. Древние китайцы достигли измерения недоступных высот и расстояний другим путем, используя «дополнительные» прямоугольники, как показано на следующем рисунке, который, как можно показать, дает результаты, эквивалентные результатам греческого метода с использованием треугольников.
Сравнение китайской и греческой геометрических теорем На рисунке показана эквивалентность китайской теоремы о дополнительных прямоугольниках и греческой теоремы о подобных треугольниках.
Encyclopædia Britannica, Inc.Оценка богатства
Вавилонская клинопись, написанная около 3500 лет назад, посвящена проблемам плотин, колодцев, водяных часов и раскопок. В нем также есть упражнение на круглых ограждениях с предполагаемым значением π = 3. Подрядчик по плавательному бассейну царя Соломона, который сделал пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение.Однако евреям следовало взять π у египтян до того, как пересечь Красное море, так как папирус Ринда ( ок. 2000 до н.э .; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.
Знание площади круга имело практическую ценность для чиновников, которые вели учет дани фараона, а также для строителей алтарей и бассейнов. Ахмес, писец, который скопировал и комментировал папирус Райнда ( c. 1650 до н.э.), много говорит о цилиндрических зернохранилищах и пирамидах, целых и усеченных.Он мог вычислить их объемы, и, как следует из его египетского seked , горизонтального расстояния, связанного с вертикальным подъемом в один локоть, в качестве определяющей величины для наклона пирамиды, он кое-что знал о подобных треугольниках.
Тестовая геометрия: Squab
Адаптироваться к местности
Адаптирует скелет персонажа к ландшафту.
Адаптивный чернослив
Удаляет элементы, пытаясь сохранить общий вид.
Добавить
Создает точки или полигоны, или добавляет точки / полигоны к входным данным.
Агент
Создает примитивы агента.
Агент Анимация Распаковка
Извлекает анимацию или клипы движения из примитива агента.
Распаковка персонажа агента
Извлекает остальную геометрию, скелет и анимацию из примитива агента.
Агент клип
Добавляет новые клипы в примитивы агентов.
Свойства клипа агента
Определяет, как должны воспроизводиться анимационные клипы агентов.
График переходов клипов агента
Создает геометрию, описывающую возможные переходы между анимационными клипами.
Уровень столкновения агентов
Создает новый слой агента, подходящий для обнаружения столкновений.
Агент настраивает соединения
Создает точечные атрибуты, определяющие пределы вращения суставов агента.
Сеть ограничений агента
Создает сеть ограничений, чтобы скрепить конечности агента.
Кэш определений агентов
Записывает файлы определения агента на диск.
Агент Править
Редактирует свойства примитивов агентов.
Уровень агента
Добавляет новый слой к примитивам агента.
Агент смотреть на
Регулирует голову агента, чтобы он смотрел на определенный объект или положение.
Поза агента из Рига
Обновляет позу примитива агента из геометрического скелета.
Подготовка агента
Добавляет агентам различные атрибуты общих точек для использования другими узлами скопления людей.
Прокси-агент
Предоставляет простую прокси-геометрию для агента.
Агентские отношения
Создает родительско-дочерние отношения между агентами.
Агент Адаптация к местности
Приспосабливает ноги агентов к местности и предотвращает скольжение ступней.
Группа преобразования агента
Добавляет новые группы преобразований в примитивы агента.
Агент Распаковка
Извлекает геометрию из примитивов агента.
Агент Веллум Распаковать
Извлекает геометрию из примитивов агентов для моделирования Веллума.
Агент с буровой установки
Создает примитив агента из геометрического каркаса.
Перегонный куб
Загружает геометрию из файла архива сцены Alembic (.abc) в геометрическую сеть.
Alembic Group
Создает геометрическую группу для примитивов Alembic.
Алембический примитив
Изменяет внутренние свойства примитивов Alembic.
Драйвер вывода Alembic ROP
Выровнять
Выравнивает группу примитивов друг с другом или с дополнительным входом.
Собрать
Очищает серию операций разрыва и создает получившиеся части.
Присоединить контрольную геометрию
Создает управляющую геометрию для установок KineFX на основе SOP.
Атрибут Adjust Float
Изменяет значения атрибутов с плавающей запятой для входящей геометрии.
Атрибут Adjust Integer
Изменяет целочисленные значения атрибутов входящей геометрии.
Атрибут Adjust Vector
Изменяет значения атрибута векторного типа входящей геометрии.
Размытие атрибутов
Размывает (или «расслабляет») точки в сетке или облаке точек.
Атрибут Cast
Изменяет размер / точность, которые Houdini использует для хранения атрибута.
Составной атрибут
Объединяет вершину, точку, примитив и / или подробные атрибуты между двумя или более выборками.
Копия атрибута
Копирует атрибуты между группами вершин, точки или примитивы.
Атрибут Создать
Добавляет или редактирует определенные пользователем атрибуты.
Атрибут Удалить
Удаляет точечные и примитивные атрибуты.
Выражение атрибута
Позволяет простым выражениям VEX изменять атрибуты.
Атрибут Fade
Изменяет точечный атрибут с течением времени.
Атрибут из пьес
Присваивает точкам атрибут, определяющий, какая модель из набора моделей должна быть скопирована / инстансирована в эту точку, случайным образом или на основе различных правил.
Атрибут Интерполировать
Интерполирует атрибуты внутри примитивов или на основе явных весов.
Зеркало атрибутов
Копирует и переворачивает атрибуты с одной стороны плоскости на еще один.
Атрибутный шум
Добавляет или генерирует шум в геометрических атрибутах.
Атрибут Paint
Интерактивное рисование атрибутов точек, например значений цвета или маски деформации, непосредственно на геометрии.
Attribute Promote
Повышает или понижает атрибуты с одного геометрического уровня на другой.
Атрибут случайный
Генерирует случайные значения атрибутов различных распределений.
Переназначение атрибутов
Подгоняет значения атрибута к новому диапазону.
Переименовать атрибут
Переименовывает или удаляет точечные и примитивные атрибуты.
Переориентировать атрибут
Изменяет атрибуты точки на основе различий между двумя моделями.
Строка атрибута Править
Edits stri
| Поезда с атрибутами — Узнайте о формах и цветовых узорах, собрав ряды блоков. | |
| Cob Web Plot — Измените переменные и наблюдайте закономерности из этого графического моделирования. | |
| конгруэнтных треугольников — строите похожие треугольники, комбинируя стороны и углы. | |
| Фракталы — Итерационные — Создание шести различных фракталов. | |
| Фракталы — Кох и Серпинский — Измените цвета и приостановите это фрактальное моделирование в любой момент. | |
| Фракталы — Множества Мандельброта и Жюлиа — Исследуйте отношения между этими двумя фрактальными множествами. | |
| Fractals — Polygonal — Измените параметры, чтобы создать новый фрактал. | |
| Geoboard — Используйте геодоски для иллюстрации концепций площади, периметра и рациональных чисел. | |
| Geoboard — Circular — Используйте круговые геодоски для обозначения углов и градусов. | |
| Geoboard — Coordinate — Прямоугольная геодоска с координатами x и y. | |
| Географическая доска — Изометрическая — Используйте геодиску для иллюстрации трехмерных фигур. | |
| Золотой прямоугольник — иллюстрирует итерации золотого сечения. | |
| Great Circle — Используйте трехмерный глобус, чтобы визуализировать и измерить кратчайший путь между городами. | |
| Насколько высоко? — Попробуйте свои силы в классическом тесте сохранения объема Пиаже. | |
| Ladybug Leaf — Запрограммируйте божью коровку, чтобы она пряталась за листом. | |
| лабиринты божьей коровки — запрограммируйте божью коровку на перемещение по лабиринту. | |
| Узорчатые блоки — Используйте шесть общих геометрических фигур для построения узоров и решения проблем. | |
| Пентамино — Используйте 12 комбинаций пентамино для решения задач. | |
| Платоновы тела — Определите характеристики Платоновых тел. | |
| Платоновы тела — Двойники — Определяют двойники платоновых тел. | |
| Platonic Solids — Slicing — Откройте для себя формы и отношения между частями платоновых тел. | |
| Полимино — построение и сравнение характеристик биомино, триомино, квадромино и т. Д. | |
| Теорема Пифагора — Решите две головоломки, иллюстрирующие доказательство теоремы Пифагора. | |
| Space Blocks — Создавайте и открывайте шаблоны, используя трехмерные блоки. | |
| Танграммы — Используйте все семь китайских пазлов, чтобы создавать формы и решать задачи. | |
| Тесселяции — Использование регулярных и полурегулярных мозаик для мозаики плоскости. | |
| Tight Weave — Визуализируйте создание ковра Серпинского, повторяющегося геометрического рисунка, напоминающего тканый коврик. | |
| Transformations — Composition — Изучите эффект применения композиции преобразования перемещения, поворота и отражения к объектам. | |
| Преобразования — Расширение — Динамически взаимодействуйте с преобразованием расширения и просматривайте его результат. | |
| Transformations — Reflection — Динамически взаимодействуйте и просматривайте результат преобразования отражения. | |
| Преобразования — Вращение — Динамически взаимодействуйте с преобразованием поворота и просматривайте его результат. | |
| Transformations — Translation — Динамически взаимодействуйте с преобразованием перевода и просматривайте его результат. | |
| Triominoes — Управляйте кусочками головоломки и находите множество решений. | |
| Turtle Geometry — Исследуйте числа, формы и логику, запрограммировав черепаху на движение. | |
| Cob Web Plot — Измените переменные и наблюдайте закономерности из этого графического моделирования. | |
| Фракталы — Итерационные — Создание шести различных фракталов. | |
| Фракталы — Кох и Серпинский — Измените цвета и приостановите это фрактальное моделирование в любой момент. | |
| Фракталы — Множества Мандельброта и Жюлиа — Исследуйте отношения между этими двумя фрактальными множествами. | |
| Fractals — Polygonal — Измените параметры, чтобы создать новый фрактал. | |
| Geoboard — Используйте геодоски для иллюстрации концепций площади, периметра и рациональных чисел. | |
| Geoboard — Circular — Используйте круговые геодоски для обозначения углов и градусов. | |
| Geoboard — Coordinate — Прямоугольная геодоска с координатами x и y. | |
| Географическая доска — Изометрическая — Используйте геодиску для иллюстрации трехмерных фигур. | |
| Золотой прямоугольник — иллюстрирует итерации золотого сечения. | |
| Great Circle — Используйте трехмерный глобус, чтобы визуализировать и измерить кратчайший путь между городами. | |
| Узорчатые блоки — Используйте шесть общих геометрических фигур для построения узоров и решения проблем. | |
| Плитка с вертушкой — Постройте и исследуйте очень необычную мозаику плоскости прямоугольными треугольниками. | |
| Платоновы тела — Определите характеристики Платоновых тел. | |
| Платоновы тела — Двойники — Определяют двойники платоновых тел. | |
| Platonic Solids — Slicing — Откройте для себя формы и отношения между частями платоновых тел. | |
| Полимино — построение и сравнение характеристик биомино, триомино, квадромино и т. Д. | |
| Теорема Пифагора — Решите две головоломки, иллюстрирующие доказательство теоремы Пифагора. | |
| Решатель прямоугольного треугольника — Попрактикуйтесь в использовании теоремы Пифагора и определений тригонометрических функций для поиска неизвестных сторон и углов прямоугольного треугольника. | |
| Space Blocks — Создавайте и открывайте шаблоны, используя трехмерные блоки. | |
| Танграммы — Используйте все семь китайских пазлов, чтобы создавать формы и решать задачи. | |
| Тесселяции — Использование регулярных и полурегулярных мозаик для мозаики плоскости. | |
| Tight Weave — Визуализируйте создание ковра Серпинского, повторяющегося геометрического рисунка, напоминающего тканый коврик. | |
| Transformations — Composition — Изучите эффект применения композиции преобразования перемещения, поворота и отражения к объектам. | |
| Преобразования — Расширение — Динамически взаимодействуйте с преобразованием расширения и просматривайте его результат. | |
| Transformations — Reflection — Динамически взаимодействуйте и просматривайте результат преобразования отражения. | |
| Преобразования — Вращение — Динамически взаимодействуйте с преобразованием поворота и просматривайте его результат. | |
| Transformations — Translation — Динамически взаимодействуйте с преобразованием перевода и просматривайте его результат. | |
| Triangle Solver — Попрактикуйтесь в использовании закона синусов и закона косинусов для определения неизвестных сторон и углов треугольника. | |
| Turtle Geometry — Исследуйте числа, формы и логику, запрограммировав черепаху на движение. |
КЛАСС 10 Геометрия
- Ресурс исследования
- Исследовать
- Искусство и гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- История
- Математика
- Наука
- Социальная наука
Лучшие подкатегории
- Продвинутая математика
- Алгебра
- Базовая математика
- Исчисление
- Геометрия
- Линейная алгебра
- Предалгебра
- Предварительный расчет
- Статистика и вероятность
- Тригонометрия
- другое →
Лучшие подкатегории
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Науки о здоровье
- Физика
- другое →
Лучшие подкатегории
- Антропология
- Закон
- Политология
- Психология
- Социология
- другое →


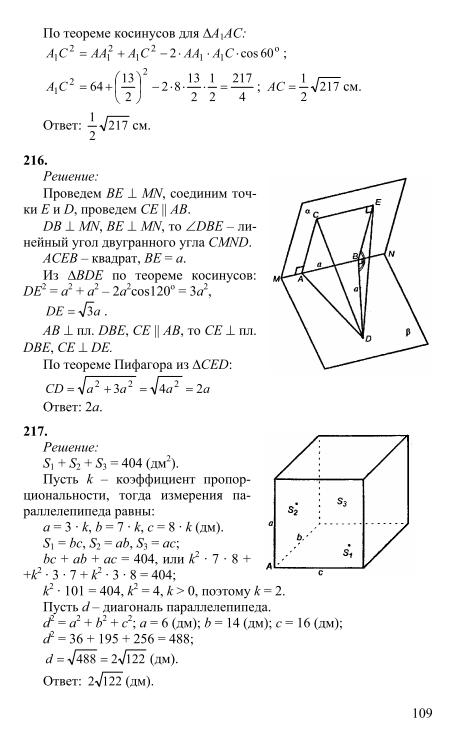 Могут ли эти прямые быть:
Могут ли эти прямые быть: