Контрольная работа «Двоичная система счисления»
Просмотр содержимого документа
«Контрольная работа «Двоичная система счисления»»
Контрольная работа
«Двоичная система счисления»
1 вариант
1. Перевести в двоичную систему счисления десятичные числа
37610 77710 101010
2. Перевести в десятичную систему счисления двоичные числа
1010112 11111112 11010010012
3. Сложить двоичные числа
111+111 101011+100110
4. Перемножить двоичные числа
111*111 1010*1010
2 вариант
1. Перевести в двоичную систему счисления десятичные числа
37510 77610 110010
2.
Перевести в десятичную систему счисления двоичные числа
1101012 11100112 10110101102
3. Сложить двоичные числа
101+111 110110+100111
4. Перемножить двоичные числа
101*111 1010*1000
3 вариант
1. Перевести в двоичную систему счисления десятичные числа
37410 77510 111010
2. Перевести в десятичную систему счисления двоичные числа
1110002 10101112 11111111112
3. Сложить двоичные числа
110+111 110111+100100
4. Перемножить двоичные числа
110*111 1010*1001
4 вариант
1. Перевести в двоичную систему счисления десятичные числа
37310 77410 111110
2. Перевести в десятичную систему счисления двоичные числа
1111112 11110012 11100011102
3. Сложить двоичные числа
101+101 111111+101011
4.
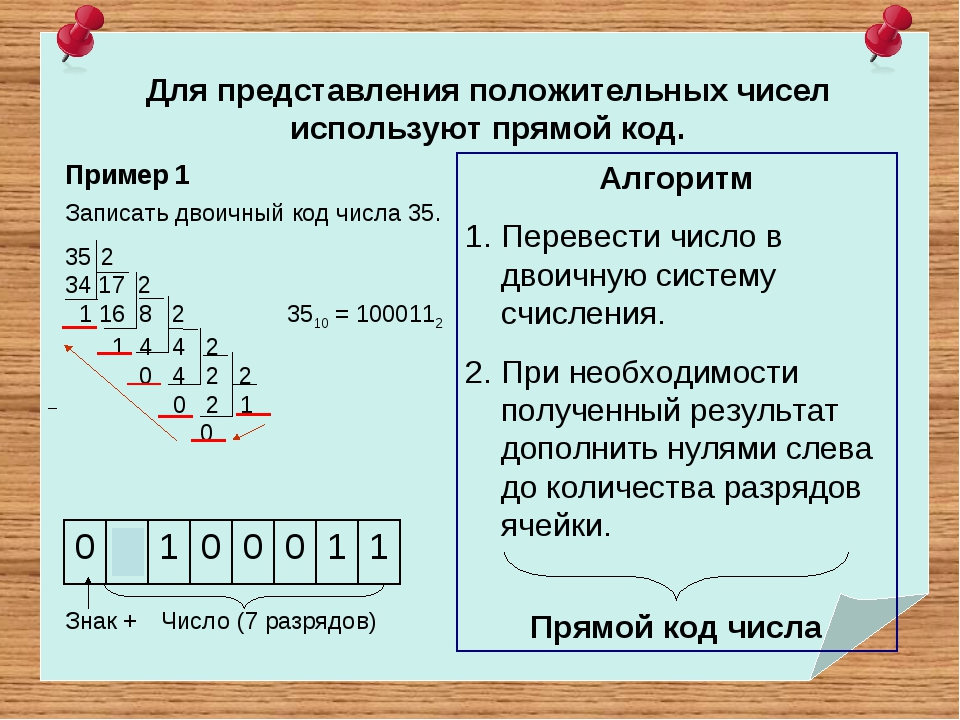Перемножить двоичные числа
101*101 1010*1100
Задание | Решение (варианты ответа) | Время | Тип | Возможные ошибки | Критерии оценки |
1) Какие цифры используются в двоичной системе? 1) 0 2) 1 3) 3 4) 2 | Ответ: 1, 2 | 1 мин | Знание, понимание | Нет знаний | 1 балл |
2) При сложении двух единиц в двоичной системе получится: 1) 2 2) 0 3) 1 4) 10 | Ответ: 4 | 2 мин | Знание, понимание | Нет знаний | 1 балл |
3) Сумма чисел 1112 + 1002 счисления равняется: 1) 1111002 2) 10112 3) 101110 4) 1010101 | Ответ: 2 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
4) Какое десятичное число в двоичной системе счисления записывается как 1000? 1) 10 2) 8 3) 11 4) 110 | Ответ: 2 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
5) Сколько единиц содержит число 10010 при переводе в двоичную: 1) 1 2) 2 3) 10 4) 3 | Ответ: 4 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
6) Переведите число в двоичную систему 11110 | Ответ: 11011112 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
7) Переведите число 100002 в десятичную систему счисления | Ответ: 16 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3 балла |
8) Переведите число 10510 в двоичную систему счисления | Ответ: 1101001 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
9) Сложите числа 10110+102 и запишите ответ в десятичной системе счисления | Ответ: 103 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
10) Умножьте числа 510*1012 = Ответ запишите в десятичной системе | Ответ: 25 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
Задание | Решение (варианты ответа) | Время | Тип | Возможные ошибки | Критерии оценки |
1) При сложении двух единиц в двоичной системе получится: 1) 10 2) 2 3) 1 4) 0 | Ответ: 10 | 2 мин | Знание, понимание | Нет знаний | 1 балл |
2) Сумма чисел 1002 + 1112 счисления равняется: 1) 1111002 2) 10112 3) 101110 4) 1010101 | Ответ: 2 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
3) Какие цифры используются в двоичной системе? 1) 10 2) 11 3) 1 4) 0 | Ответ: 3,4 | 1 мин | Знание, понимание | Нет знаний | 1 балл |
4) Какое десятичное число в двоичной системе счисления записывается как 1001? 1) 10 2) 8 3) 11 4) 9 | Ответ: 4 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
5) Сколько нулей содержит число 10010 при переводе в двоичную: 1) 1 2) 4 3) 10 4) 3 | Ответ: 2 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 2-3 балла |
6) Переведите число в двоичную систему 11010 | Ответ: 11011102 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3 балла |
7) Переведите число 10310 в двоичную систему счисления | Ответ: 11001112 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
8) Переведите число 100012 в десятичную систему счисления | Ответ: 17 | 5-7 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3 балла |
9) Сложите числа 112 +10110 и запишите ответ в десятичной системе счисления | Ответ: 104 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
10) Умножьте числа 610*1002 = Ответ запишите в десятичной системе | Ответ: 24 | 4 мин | Знание, применение, анализ | Нет знаний, ошибки в вычислениях | 3-4 балла |
Контрольная работа «Система Счисления» 8 класс
8 класс
I вариант
1.
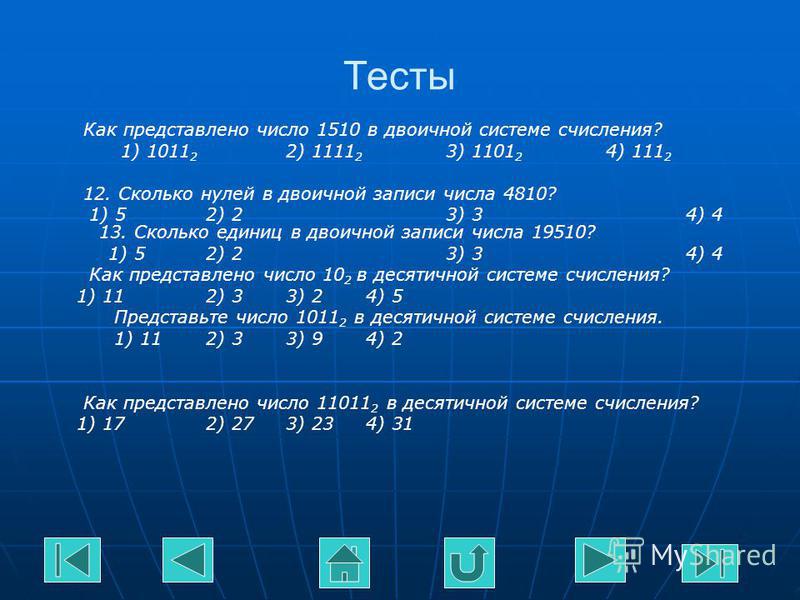Переведи числа из восьмиричной в десятичную систему счисления
А) 103
Б)147
2. Переведите числа в восьмеричную системы счисления:
А) 2910;
Б) 9910.
А) 11110;
Б) 9510;
4. Переведите числа в десятичную системы счисления:
А) 1D16
5. Переведите из двоичной системы счисления в десятичную
А)11010112
II
1.
Переведи числа из восьмиричной в десятичную систему счисления
А) 1208
Б) 1138;
2. Переведите числа в восьмеричную системы счисления:
А) 2410;
Б) 8910.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 8510;
Б) 99
4 Переведите в шестнадцатиричную систему счисления.
А) 15610
5. Переведите из двоичной системы счисления в десятичную
А) 1000012
III вариант
1.
. Переведи числа из восьмиричной в десятичную систему счисления
А) 2018
Б) 1178;
2. Переведите числа в восьмеричную системы счисления:
А) 5510;
Б) 11110.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 6410;
Б) 10010;
4. Переведите в шестнадцатиричную систему счисления
А) 33310 ;
А)111002
IV вариант
1.
Переведи числа из восьмиричной в десятичную систему счисления
А) 338
Б) 1238
2. Переведите числа в восьмеричную системы счисления:
А) 87
Б) 17710.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 4710;
Б) 11010;
4. Переведите в шестнадцатиричную систему счисления
А)25310;
5. Переведите из двоичной системы счисления в десятичную
А) 10111110012;
V вариант
1.
Переведи числа из восьмиричной в десятичную систему счисления
А)1748;
Г) 338
2. Переведите числа в восьмеричную системы счисления:;
А) 7910;
б) 18510.
А) 6710;
Б) 7310;
4. Переведите в шестнадцатиричную систему счисления
А) 25210.
5. Переведите из двоичной системы счисления в десятичную
А) 101011110102;
Проверочная работа по теме «Двоичная системы счисления»
Двоичная система счисления
Вид работы: проверочная работа
Автор: Шевченко Е.
Предмет: информатика
аудитория: 8 класс
Описание: данная работа может быть использована в качестве текущего, тематического контроля и направлена на закрепление и коррекцию знаний, умений, полученных в процессе изучения данной темы. Учащимся предлагается шесть вариантов проверочной работы. Каждый вариант состоит из одного теоретического вопроса на проверку знаний о системах счисления, их видах и пяти практических заданий для проверки навыков перевода чисел из десятичной системы счисления в двоичную и наоборот. Каждое задание оценивается в один балл.
Задачи: сформировать навыки по переводу чисел из десятичной системы счисления и наоборот; выявить качество и уровень овладения знаниями и умениями по теме «Двоичная система счисления»; развитие навыков индивидуальное практической деятельности; развитие познавательного интереса и внимания учащихся, умение оценивать правильность выполнения задания
Ожидаемые результаты:
умение давать определения основным понятиям систем счисления;
формирование устойчивых навыков перевода из десятичной системы счисления в двоичную и наоборот;
умение действовать по заданному алгоритму, оценивать правильность выполнения задания;
формирование ответственного отношения к обучению;
Вариант 1
1 Как называется количество символов в алфавите позиционной системы счисления?
2 Запишите числа в двоичной системе счисления: 27 38
3 Запишите числа в десятичной системе счисления: 11102 101102
4 Сколько единиц в двоичной записи числа 12
Вариант 2
1 Значение цифры не зависит от ее положения в числе в _____________ системе счисления
2 Запишите числа в двоичной системе счисления: 24 41
3 Запишите числа в десятичной системе счисления: 10112 101112
4 Сколько значащих нулей в двоичной записи числа 13
Вариант 3
1 Система счисления в которой для записи любых чисел используется два символа -это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 22 37
3 Запишите числа в десятичной системе счисления: 11012 100112
4 Сколько единиц в двоичной записи числа 14
Вариант 4
1 Десятичная система счисления — это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 26 42
3 Запишите числа в десятичной системе счисления: 11002 110012
4 Сколько значащих нулей в двоичной записи числа 11
Вариант 5
1 Система счисления в которой для записи любых чисел используется всего один символ -это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 25 43
3 Запишите числа в десятичной системе счисления: 10012 110112
4 Сколько единиц в двоичной записи числа 13
Вариант 6
1 Значение цифры зависит от ее положения в числе в _____________ системе счисления
2 Запишите числа в двоичной системе счисления: 21 33
3 Запишите числа в десятичной системе счисления: 11112 100102
4 Сколько значащих нулей в двоичной записи числа 14
2) Перевести число 0,824 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой)
| |||
3) Перевести число 671,7 из восьмеричной системы счисления в двоичную систему счисления
| 4) Перевести двоичное число 1111101 в десятичную систему счисления
| ||
5) Перевести двоичное число 110111,111 в шестнадцатеричную систему счисления
| 6) Сложить два восьмеричных числа 165+37=?
| ||
7) Сложить два двоичных числа 1111 + 1101 = ?
| 8) Найти разность двоичных чисел 101010 — 1011 = ?
| ||
9) Произвести умножение двоичных чисел 1011 * 111 = ?
| 10) Произвести деление двоичных чисел 1101110 : 1011 = ?
| 2) Перевести число 0,8125 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой)
| |
3) Перевести число 751,5из восьмеричной системы счисления в двоичную систему счисления
| 4) Перевести двоичное число 10000111 в десятичную систему счисления
| ||
5) Перевести двоичное число 101101,111 в шестнадцатеричную систему счисления
| 6) Сложить два восьмеричных числа 165+47=?
| ||
7) Сложить два двоичных числа 1001 + 1101 = ?
| 8) Найти разность двоичных чисел 100010 — 1011 = ?
| ||
9) Произвести умножение двоичных чисел 1101 * 111 = ?
| 10) Произвести деление двоичных чисел 1111001 : 1011 = ?
| 2) Перевести число 0,4375 из десятичной системы счисления в двоичную систему счисления (до 4-х знаков после запятой)
| |
3) Перевести число 401,5 из восьмеричной системы счисления в двоичную систему счисления
| 4) Перевести двоичное число 1101101 в десятичную систему счисления
| ||
5) Перевести двоичное число 1100101,11 в шестнадцатеричную систему счисления
| 6) Сложить два восьмеричных числа 175+45=?
| ||
7) Сложить два двоичных числа 1111 + 1101 = ?
| 8) Найти разность двоичных чисел 100010 — 1101 = ?
| ||
9) Произвести умножение двоичных чисел 1110 * 111 = ?
| 10) Произвести деление двоичных чисел 1001101 : 1011 = ?
| Вариант1 | Вариант2 | Вариант3 |
10000111 | 10100101 | 10100001 | |
0,1101 | 0,1101 | 0,0111 | |
110111001,111 | 111101001,101 | 100000001,101 | |
125 | 135 | 109 | |
27,Е | 2D,Е | 65,С | |
224 | 234 | 242 | |
11100 | 10110 | 11100 | |
11111 | 10111 | 10101 | |
1001101 | 1011011 | 1100010 | |
1010 | 1011 | 111 |
Контрольная работа по информатике.
«Системы счисления. Двоичная арифметика».
1 вариант
- Данные числа из различных систем счислений перевести в двоичную систему:
a) 3248 (11010100)
b) AF116(101011110001)
c) 8710 (1010111)
2. Данные числа из различных систем счисления перевести в шестнадцатеричную систему:
a) 110110112 (DB16)
b) 2238 (9316)
c) 19910 (C716)
3. Даны пары чисел. Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления
a) 23410 и 910 (11101010 и 1001) сум: 11110011 раз. 11100001 прз. 100000111010 частн. 1101
4. Даны дробные числа. Перевести числа в двоичную систему счисления.
a) 76,08710 (1001100,0001011)
b) 34, 9910 (100010,111111)
2 вариант
1 Данные числа из различных систем счислений перевести в двоичную систему:
d) 3258 (11010101)
e) FA116(111110100001)
f) 8910 (1011001)
2 Данные числа из различных систем счисления перевести в шестнадцатеричную систему:
d) 110111112 (DF16)
e) 2328 (9A16)
f) 20110 (C916)
3 Даны пары чисел.
Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления
57610 и 1210 (1001000000 и 1100) (1001001100) (1000110100) (1101100000000) (110000)
4 Даны дробные числа. Перевести числа в двоичную систему счисления.
a) 76,8710 (1001100,110111)
b) 34, 09910 (100010,000110)
Контрольная работа по информатике. «Системы счисления. Двоичная арифметика». на Сёзнайке.ру
1 вариант
- Данные числа из различных систем счислений перевести в двоичную систему:
a) 3248 (11010100)
b) AF116(101011110001)
c) 8710 (1010111)
2. Данные числа из различных систем счисления перевести в шестнадцатеричную систему:
a) 110110112 (DB16)
b) 2238 (9316)
c) 19910 (C716)
3.
Даны пары чисел. Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления
a) 23410 и 910 (11101010 и 1001) сум: 11110011 раз. 11100001 прз. 100000111010 частн. 1101
4. Даны дробные числа. Перевести числа в двоичную систему счисления.
a) 76,08710 (1001100,0001011)
b) 34, 9910 (100010,111111)
2 вариант
1 Данные числа из различных систем счислений перевести в двоичную систему:
d) 3258 (11010101)
e) FA116(111110100001)
f) 8910 (1011001)
2 Данные числа из различных систем счисления перевести в шестнадцатеричную систему:
d) 110111112 (DF16)
e) 2328 (9A16)
f) 20110 (C916)
3 Даны пары чисел.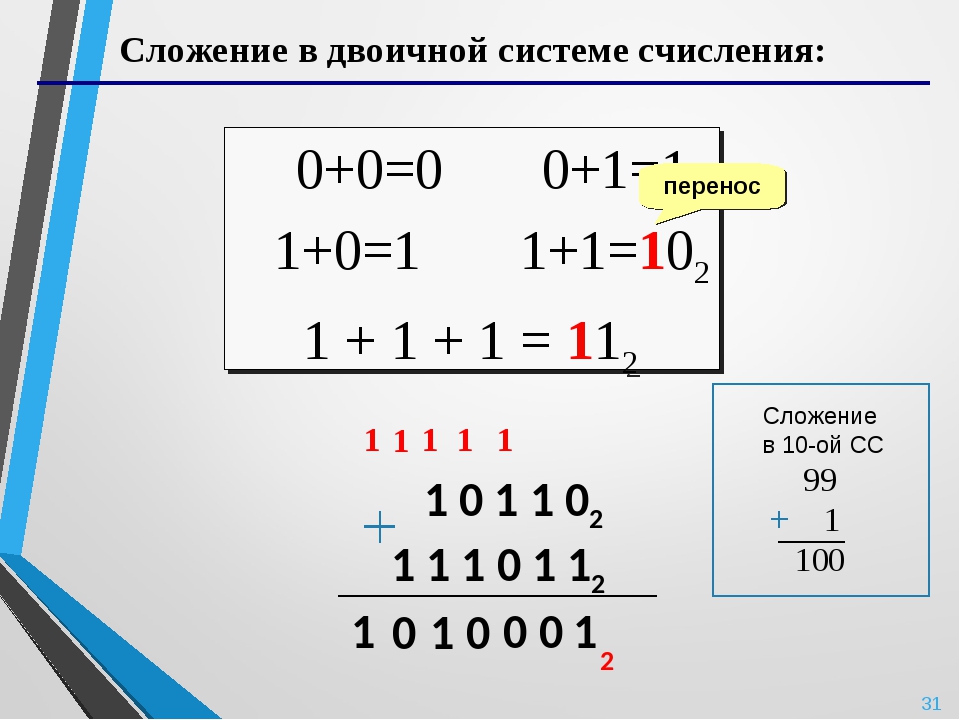
Перевести числа в двоичную систему счисления и проделать над ними операции сложения, вычитания, умножения и деления
57610 и 1210 (1001000000 и 1100) (1001001100) (1000110100) (1101100000000) (110000)
4 Даны дробные числа. Перевести числа в двоичную систему счисления.
a) 76,8710 (1001100,110111)
b) 34, 09910 (100010,000110)
Двоичная система счисления
Двоичное число состоит только из 0 с и 1 с.
110100 |
| Пример двоичного числа |
В двоичном формате нет 2, 3, 4, 5, 6, 7, 8 или 9!
Двоичные числа имеют множество применений в математике и не только.
Фактически в цифровом мире используются двоичные цифры.
Как мы считаем, используя двоичный код?
Это похоже на десятичный счет, за исключением того, что мы достигаем 10 гораздо раньше.
| Двоичный | ||
| 0 | Начинаем с 0 | |
| 1 | Затем 1 | |
| ??? | Но тогда нет символа для 2 … что нам делать? |
| ну как считать в десятичной системе счисления? | |||
| 0 | Начать с 0 | ||
| … | Посчитайте 1,2,3,4,5,6,7,8, а затем … | ||
| 9 | Это последняя цифра в десятичном формате | ||
| 10 | Итак, мы снова начинаем с 0, но добавляем 1 слева | ||
То же самое делается в двоичном формате …
| двоичный | |||
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 10 | Теперь начните снова с 0, но добавьте 1 слева | |
| ••• | 11 | 1 еще | |
| •••• | ??? | А СЕЙЧАС что. ..? |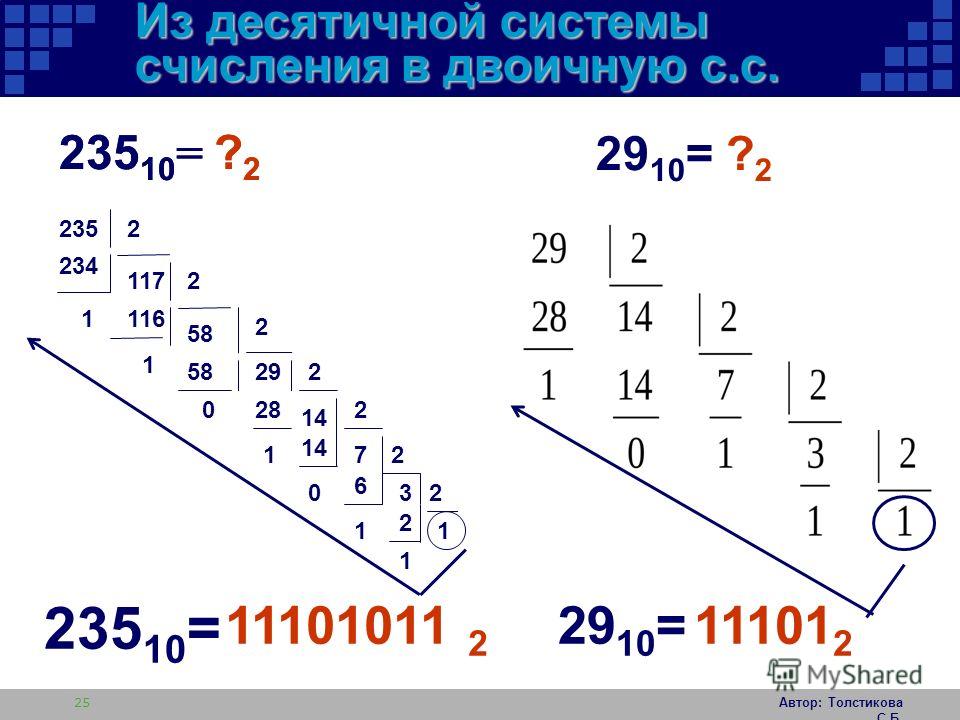
| Что происходит в десятичном формате? | |||
| 99 | Когда у нас заканчиваются цифры, мы … | ||
| 100 | … начните снова с 0, но добавьте 1 слева | ||
И это то, что мы делаем в двоичном формате …
| двоичный | |||
| 0 | Начать с 0 | ||
| • | 1 | Затем 1 | |
| •• | 10 | Начните снова с 0, но добавьте 1 слева | |
| ••• | 11 | ||
| •••• | 100 | снова начните с 0 и прибавьте единицу к числу слева. .. … но это число уже равно 1, поэтому оно также возвращается к 0 … … и 1 добавляется к следующей позиции слева | |
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1000 | Снова начать с 0 (для всех 3 цифр), добавить 1 слева | |
| •••••••••• | 1001 | И так далее! |
Посмотрите, как это делается, на этой небольшой демонстрации (нажмите кнопку воспроизведения):
Десятичное и двоичное
Вот несколько эквивалентных значений:
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Симметрия
Двоичные числа также имеют красивый и элегантный узор:
Вот несколько больших значений:
| Десятичный: | 20 | 25 | 30 | 40 | 50 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| Двоичный: | 10100 | 11001 | 11110 | 101000 | 110010 | 1100100 | 11001000 | 111110100 |
«Бинарный — это так же просто, как 1, 10, 11.
«
Теперь посмотрим, как использовать двоичный код для подсчета на пальцах больше 1000:
Позиция
В десятичной системе есть единицы, десятки, сотни и т. Д.
В Binary есть единицы, двойки, четверки и т. Д., Например:
Это 1 × 8 + 1 × 4 + 0 × 2 + 1 + 1 × (1/2) + 0 × (1/4) + 1 × (1/8)
= 13,625 в десятичной системе счисления
Цифры можно размещать слева или справа от точки, чтобы отображать значения больше единицы и меньше одного.
| 10,1 | |
| Число слева от точки целое число (например, 10) | |
| По мере продвижения влево каждое числовое место получает 2 раз больше . | |
| Первая цифра справа означает половину (1/2). | |
| По мере продвижения вправо каждое число становится в 2 раза меньше (вдвое меньше).  | |
Пример: 10.1
- «10» означает 2 в десятичной системе счисления,
- «.1» означает половину,
- Итак, «10,1» в двоичном формате равняется 2,5 в десятичном.
Вы можете преобразовывать двоичные числа в десятичные в шестнадцатеричные.
слов
Слово в двоичном формате происходит от слова «Bi-», означающего два. Мы видим «би-» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).
| Когда вы произносите как двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» , или иногда «один ноль один» ). Таким образом, люди не запутаются с десятичным числом. |
Одна двоичная цифра (например, «0» или «1») называется «битом».
Например, 11010 имеет длину пять бит.
Слово бит состоит из слов « b inary dig it »
Как показать, что число является двоичным
Чтобы показать, что число является двоичным числом , поставьте за ним маленькую двойку, например: 101 2
Таким образом, люди не подумают, что это десятичное число «101» (сто один).
Примеры
Пример: что такое 1111
2 в десятичном формате?- «1» слева находится в позиции «2 × 2 × 2», то есть 1 × 2 × 2 × 2 (= 8)
- Следующая «1» находится в позиции «2 × 2», то есть 1 × 2 × 2 (= 4)
- Следующая «1» находится в позиции «2», то есть 1 × 2 (= 2)
- Последняя «1» находится в разряде единиц, то есть 1
- Ответ: 1111 = 8 + 4 + 2 + 1 = 15 в десятичной системе счисления
Пример: что такое 1001
2 в десятичном формате?- «1» слева находится в позиции «2 × 2 × 2», то есть 1 × 2 × 2 × 2 (= 8)
- «0» находится в позиции «2 × 2», то есть 0 × 2 × 2 (= 0)
- Следующий «0» находится в позиции «2», то есть 0 × 2 (= 0)
- Последняя «1» находится в разряде единиц, то есть 1
- Ответ: 1001 = 8 + 0 + 0 + 1 = 9 в десятичной системе счисления
Пример: Что такое 1.1
2 в десятичной системе счисления?- «1» на левой стороне находится в позиции единиц, так что это означает 1.
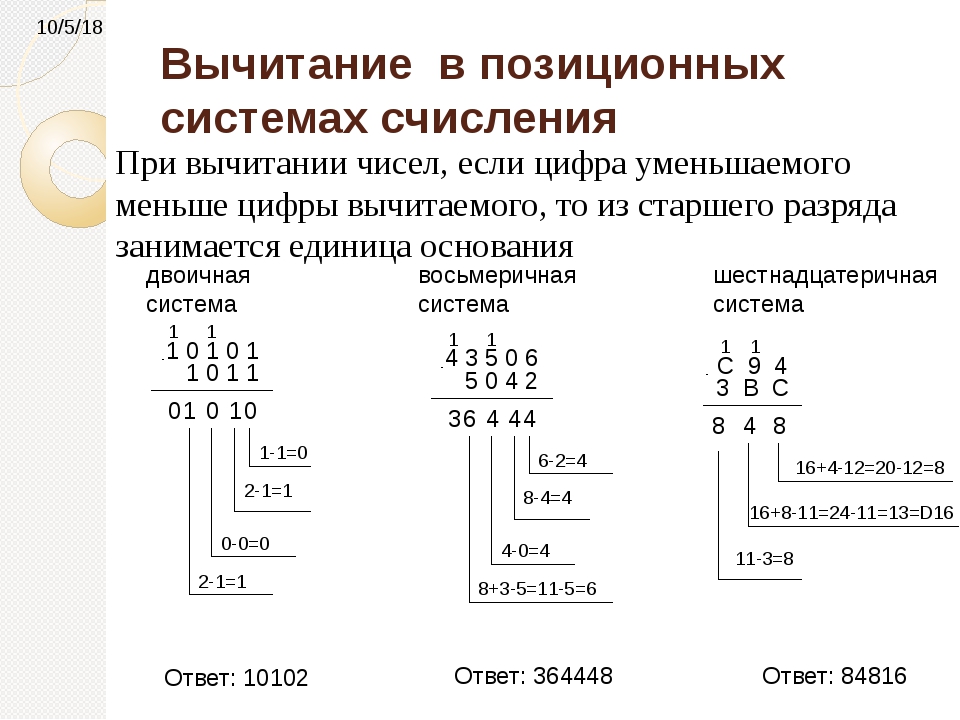
- 1 на правой стороне находится в положении «половинки», то есть 1 × (1/2)
- Итак, 1,1 — это «1 и 1 половина» = 1,5 в десятичном формате
Пример: Что такое 10,11
2 в десятичном формате?- «1» находится в позиции «2», то есть 1 × 2 (= 2)
- «0» находится в разряде единиц, то есть 0
- «1» справа от точки находится в положении «половинки», то есть 1 × (1/2)
- Последняя «1» справа находится в позиции «четверти», то есть 1 × (1/4)
- Итак, 10.11 равно 2 + 0 + 1/2 + 1/4 = 2,75 в десятичной системе счисления
«В мире есть 10 типов людей:
тех, кто понимает двоичные числа, и тех, кто не понимает».
Как работает двоичная система?
Как часто вы пользуетесь компьютером? Если вы подумаете обо всех гаджетах, которыми пользуетесь каждый день, вы, вероятно, поймете, что используете больше компьютеров, чем думаете. Помимо портативных или настольных компьютеров, которые вы используете в школе или дома, вы также можете использовать калькуляторы, смартфоны, планшеты, музыкальные плееры, электронные устройства для чтения, цифровые видеомагнитофоны, видеоигры и всевозможные другие устройства.
В современном мире, наполненном технологиями, трудно избежать использования компьютеров. На самом деле, мы держим пари, что многие из наших Wonder Friends однажды будут работать на работе, требующей от вас постоянного использования компьютеров. Некоторые из вас могут даже создавать компьютеры или писать код для создания программного обеспечения, видеоигр и приложений для смартфонов!
Когда вы изучаете основы компьютерного программирования, вы рано понимаете, что в основном все, что входит (ввод) или выходит (вывод) компьютера, состоит из последовательности нулей и единиц.В этом суть цифровых данных, и они основаны на двоичной системе.
Когда вы изучаете математику в школе, вы используете десятичную систему счисления. Это означает, что ваша система счисления состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Когда вы добавляете один к девяти, вы перемещаете 1 на одну позицию влево в десятки. поместите и поставьте 0 вместо единиц: 10.
С другой стороны, двоичная система счисления — это система счисления с основанием 2.
Это означает, что здесь используются только два числа: 0 и 1. Когда вы прибавляете единицу к единице, вы перемещаете 1 на одну позицию влево на место двоек и ставите 0 на место единиц: 10.Итак, в системе с основанием 10 10 равно десяти. В системе с основанием 2 10 равно двум.
В системе base-10, с которой вы знакомы, значения разряда начинаются с единиц и переходят к десяткам, сотням и тысячам при движении влево. Это потому, что система основана на степени 10.
Точно так же в системе с основанием 2 значения разряда начинаются с единиц и переходят к двойкам, четверкам и восьмеркам при перемещении влево. Это потому, что система base-2 основана на степени двойки. Каждая двоичная цифра называется битом.
Не волнуйтесь, если двоичная система сейчас сбивает с толку. Это довольно легко понять, если вы немного поработаете с этим. Поначалу это просто сбивает с толку, потому что все числа состоят только из нулей и единиц. Знакомая система с основанием 10 так же проста, как 1-2-3, а двоичная система с основанием 2 так же проста, как 1-10-11.
Вы можете ЗАДАВАТЬСЯ, почему компьютеры используют двоичную систему. Компьютеры и другие электронные системы работают быстрее и эффективнее, используя двоичную систему, потому что система, использующая только два числа, легко дублируется системой включения / выключения.
Электричество либо включено, либо выключено, поэтому устройства могут использовать выключатель в электрических цепях для простой обработки двоичной информации. Например, off может быть равен 0, а on — 1.
.Каждая буква, цифра и символ на клавиатуре представлены восьмибитным двоичным числом. Например, для вашего компьютера буква A на самом деле 01000001!
Чтобы помочь вам лучше понять двоичную систему и ее отношение к десятичной системе, с которой вы знакомы, вот как десятичные числа 1-10 выглядят в двоичной системе:
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
Binary Tutorial — Понятие и управление двоичными числами
Системы счисления!
Теория чисел и принцип работы двоичных чисел.
Введение
Числа окружают нас повсюду, и по большей части мы принимаем их как должное. Если бы я предложил вам 1337 долларов, вы были бы счастливы, потому что знаете, что это довольно разумная сумма. Система счисления — это средство представления количества вещей. Десятичная дробь — это лишь одна из нескольких систем счисления, а другие, в частичной двоичной системе, важны для понимания в различных областях, особенно в вычислительной технике.
В нашем введении для начинающих в двоичные, шестнадцатеричные и восьмеричные числа вы изучите двоичные преобразования и арифметику с интерактивными демонстрациями и подробными объяснениями.
Наброски
Это двоичное руководство разделено на 3 раздела. В общем, я рекомендую вам проработать их по порядку, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, тогда кто я такой, чтобы вас тормозить, просто идите прямо вперед.
- Системы счисления — Прочтите ниже, чтобы узнать о теории чисел.
- Преобразования — Как преобразовать двоичное в десятичное, шестнадцатеричное и восьмеричное числа.
- Арифметика — Узнайте, как выполнять различные арифметические операции с двоичными числами.
- Отрицательные числа — Узнайте, как работать с отрицательными числами в двоичном формате.
- Плавающая точка и дроби — Узнайте, как преобразовывать десятичные числа в двоичные дроби и числа с плавающей запятой и обратно.
Паттерны и ярлыки
Когда вы работаете с системами счисления, вы можете сделать много сокращений по адресу:
- упростят работу с ними.
- поможет проверить вашу работу / выявить глупые ошибки, которые вы могли совершить.
Я буду указывать на некоторые из них, когда мы прорабатываем материал, но вы всегда должны искать их сами (не только при работе с числами, но и в других областях).
В общем, вы хотите следить за шаблонами, а затем думать о том, как вы можете использовать эти шаблоны для своей выгоды.
Со временем вы научитесь их замечать.
Десятичная система
Десятичная система счисления — это та, с которой мы наиболее знакомы, мы используем ее каждый день.Десятичная дробь — это то, что мы называем позиционной системой счисления. То есть положение цифр придает значение представляемому ими значению. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также являются позиционными, поэтому, как только мы поймем основную теорию десятичной системы, мы сможем легко применить ее для понимания других систем.
Давайте посмотрим на пример:
Если у меня есть число 31415, на самом деле это означает:
30 000 + 1 000 + 400 + 10 + 5
Или точнее:
| 3 * 10 4 | 30 000 |
| 1 * 10 3 | 1 000 |
| 4 * 10 2 | 400 |
| 1 * 10 1 | 10 |
| 5 * 10 0 | 5 |
Десятичное число — по основанию 10 .Это означает, что у нас есть 10 символов для представления значений (0–9). По мере того, как мы перемещаемся по каждой позиции, мы умножаем это число на 10 в степень этой позиции (начиная с 0 в крайнем правом углу).
Помните: все, что больше нуля, всегда равно 1.
Десятичная система удобна как система счисления, так как каждый раз, когда мы увеличиваем степень, все, что нам нужно сделать, это добавить еще 0. Для каждой цифры в числе добавьте количество нулей, требуемых для позиции, и вы получите ее позиционное значение.Затем каждая цифра естественным образом совпадает с общим числом.
двоичный
Binary следует тому же шаблону, что и Decimal, за исключением того, что вместо основания 10 это base 2 . Вместо 10 символов для представления значений у нас есть два (0 и 1).
Итак, Decimal — это система счисления с основанием 10, у нас есть 10 символов и умножается на степень 10. Отсюда следует, что Binary — это система счисления с основанием 2, у нас есть два символа и умножается на степень 2.
Давайте посмотрим на пример:
Если у меня есть двоичное число 101010, оно переводится в десятичное как:
32 + 0 + 8 + 0 + 2 + 0 = 42
или:
| 1 * 2 5 | 32 |
| 0 * 2 4 | 0 |
| 1 * 2 3 | 8 |
| 0 * 2 2 | 0 |
| 1 * 2 1 | 2 |
| 0 * 2 0 | 0 |
Как видно из этого примера, двоичный код не так удобен для чтения и работы, как десятичный.Вы можете спросить, зачем тогда вообще возиться с двоичным кодом? Ответ заключается в том, что это более простой формат для работы с компьютерами. Его также можно использовать в других областях как ярлык для представления настроек.
Поскольку все степени двойки, кроме 0, приводят к четному числу, единственный способ получить нечетное число — это иметь самую правую цифру, равную 1. Это можно использовать в качестве быстрой проверки при выполнении преобразований, которые вы еще не сделали. глупая ошибка.
Шестнадцатеричный и восьмеричный
Две другие системы счисления, которые обычно используются в вычислениях, — это шестнадцатеричная и восьмеричная.Это обе системы счисления.
- Шестнадцатеричная система счисления по основанию 16
- Восьмеричное число — основание 8
Оба они тесно связаны с двоичным кодом. Вы заметите, что:
Это не относится к десятичным (нет степени 2, равной 10). Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичным, которых нет у десятичных. Мы исследуем их в следующем разделе, преобразования.
Для шестнадцатеричного числа мы увеличиваем до 15 (помните, что мы начинаем с 0).Как только мы дойдем до 9, мы добавим буквы алфавита A — F, чтобы представить 10-15 (см. Справочную таблицу ниже).
Возьмем десятичное число 27.
В шестнадцатеричном формате это будет 1B, что в десятичном формате означает:
.1 * 16 1 + 11 * 16 0 = 16 + 11
В восьмеричном формате это будет 33, что в десятичном представлении означает:
.3 * 8 1 + 3 * 8 0 = 24 + 3
Префиксы
Как видно из приведенных выше примеров, числа потенциально могут выглядеть одинаково, независимо от того, являются ли они двоичными, десятичными, восьмеричными или шестнадцатеричными.Если бы я дал вам число 2F7, вы бы сразу узнали, что оно шестнадцатеричное, но если бы я дал вам число 101, оно будет:
- 101 в двоичном формате и 5 в десятичном формате
- 101 в десятичной системе
- 101 в шестнадцатеричной системе счисления и 257 в десятичной системе счисления
- 101 в восьмеричной системе и 65 в десятичной системе счисления
??
Как видите, количество, которое представляет 101, сильно различается в зависимости от используемой базы. Чтобы избежать этой двусмысленности, мы добавляем префиксы к номерам, чтобы идентифицировать их основу.
- Десятичное число не имеет префикса.
- Шестнадцатеричный имеет префикс Ox, например: Ox1B
- Octal имеет префикс O, например: O421
- Binary имеет префикс Ob, например: Ob1101
Некоторые люди вместо этого используют суффикс, но они не так популярны:
- Decimal не имеет суффикса.
- Шестнадцатеричный имеет суффикс H, например: 1BH
- Octal имеет суффикс O, например: 421O
- Binary имеет суффикс B, например: 1101B
Примечание: для префиксов и суффиксов выше это заглавная буква o, а не ноль.
На протяжении большей части этого урока я не буду использовать префиксы, а буду определять базу напрямую, чтобы сделать ее более понятной.
Справочная таблица
Вот справочная таблица для различных систем счисления.
| Десятичное число | двоичный | восьмеричное | Шестнадцатеричный |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | С |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Вы заметите, что в двоичном файле есть шаблон.Крайний правый столбец чередуется между 0 и единицей. Следующий столбец делает то же самое, но по два за раз. Третий столбец делает то же самое, но по четыре за раз. Крайний левый столбец делает то же самое, но по 8 за раз. Этот шаблон позволяет легко проверить, что он написан правильно.
Если вы сдаете экзамен по двоичной системе, вам часто не разрешают зачитывать материал, но ничто не мешает вам самостоятельно составить эту таблицу после начала экзамена. Это может быть хороший справочник, особенно для конверсий, которые мы рассмотрим в следующем разделе.
Совет
Этот материал может быть немного трудным для понимания. Если вы обнаружите, что чтение материала немного напрягает, вот что я предлагаю:
- Проработайте примеры на бумаге. Изучение двоичного кода похоже на езду на велосипеде. Лучший способ — просто сделать это.
- Оставьте это на день или два, затем вернитесь и попробуйте еще раз.
Системы счисления
Системы счисления
Структуры данных и системы счисления
© Авторские права Брайан Браун, 1984–1999.Все права
сдержанный.
В этом учебном курсе используются расширения HTML 3.0
Введение
Система счисления определяет набор значений, используемых для представления количество. Мы говорим о количестве людей, посещающих занятия, количество модулей, взятых на одного студента, а также используйте числа для представляют собой оценки, полученные учащимися на тестах.
Количественная оценка значений и предметов по отношению друг к другу является помогает нам разобраться в окружающей среде.Мы делаем это в ранний возраст; выясняя, есть ли у нас еще игрушки, с которыми можно поиграть, еще подарки, еще леденцы и так далее.
Изучение систем счисления не ограничивается компьютерами. Мы применяем числа каждый день, и, зная, как работают числа, мы дать нам представление о том, как компьютер манипулирует и хранит числа.
Человечество на протяжении веков использовало знаки и символы для представляют собой числа. Ранние формы были прямыми линиями или группами линий, как в фильме Робинзон Крузо , где группа из шести вертикальных линий с диагональной линией поперек представлена одна неделя.
Сложно представить большие или очень маленькие числа с помощью такой графический подход. Еще в 3400 г. до н.э. в Египте и в 3000 г. до н.э. в Месопотамии они разработали символ, представляющий единицу 10. Это было большим достижением, поскольку уменьшило количество обязательные символы. Например, 12 можно представить как 10 и два юнита (три символа вместо 12, что требовалось ранее).
Римляне изобрели систему счисления, которая могла представлять все числа от 1 до 1000000 с использованием всего семи символов
- I = 1
- В = 5
- Х = 10
- L = 50
- С = 100
- D = 500
- M = 1000
Маленькая полоса над символом указывает на то, что номер умножить на 1000.
Наиболее распространенной сегодня системой счисления является арабский система. Впервые он был разработан индусами и использовался как еще в 3 веке до нашей эры. Введение символа 0, используется для обозначения позиционного значения цифр, было очень важный. Таким образом, мы познакомились с концепцией групп единиц, десятков единиц, сотен единиц, тысяч единиц и скоро.
В системах счисления часто полезно думать о повторяющихся устанавливает , где набор значений повторяется снова и снова.
В десятичной системе счисления имеет набор значений. диапазон от 0 до 9. Этот базовый набор повторяется снова и снова. над, создавая большие числа.
Обратите внимание, как повторяется набор значений от 0 до 9, и для каждого повторить, столбец слева увеличивается (с 0 до 1, затем 2).
Каждое увеличение значения происходит до значения наибольшего число в наборе (9), на этом этапе следующее значение является наименьшим в наборе (0), и новое значение создается в левый столбец (то есть следующее значение после 9 — 10).
09, 10 - 19, 20 - 29, 30 - 39 и т. Д.
Мы всегда записываем цифру с наибольшим значением на слева от номера
База
Значения
Базовое значение системы счисления — это количество различных
значения, которые имеет набор до повторения. Например, десятичный
имеет базу из десяти значений от 0 до 9.
- Двоичный = 2 (0, 1)
- Восьмеричное число = 8 (0-7)
- Десятичное число = 10 (0-9)
- Двенадцатеричный = 12 (используется для некоторых целей римлянами)
- Шестнадцатеричный = 16 (0-9, A-F)
- Vigesimal = 20 (используется майя)
- Шестидесятеричный = 60 (используется вавилонянами)
Взвешивание
Фактор
Весовой коэффициент — это значение множителя, применяемое к каждому
положение столбца номера.Например, десятичное число имеет
весовой коэффициент TEN в каждом столбце слева
указывает на увеличение значения умножения на 10 по сравнению с предыдущим
столбец справа, т.е. каждый столбец перемещается влево увеличивается
с коэффициентом умножения 10.
200 = ----- 0 * 10 0 = 0 * 1 = 0 ------ 0 * 10 1 = 0 * 10 = 0 ------- 2 * 10 2 = 2 * 100 = 200 ----- 200 (суммируя) -----
Рассмотрим еще один пример десятичного числа 312.
312 = ----- 2 * 10 0 = 2 * 1 = 2 ------ 1 * 10 1 = 1 * 10 = 10 ------- 3 * 10 2 = 3 * 100 = 300 ----- 312 (суммируя) -----
десятичный
Система счисления [Base-10]
В этой системе счисления используется ДЕСЯТЬ.
разные символы для представления значений.Установленные значения, используемые в
десятичный:
0 1 2 3 4 5 6 7 8 9
, где 0 имеет наименьшее значение, а девять — наибольшее. стоимость. Цифра или столбец слева имеет наибольшее значение, в то время как цифра справа имеет наименьшее значение.
Если при вычислении высшая цифра (9)
превышен, происходит перенос, который переносится в следующий столбец
(Слева).
Пример добавления и превышения диапазона базовой установки 8 + 4 8 9 +1 10 +2 Примечание 1: 11 +3 12 +4 Примечание 1: при превышении 9 мы возвращаемся к началу набора (0), и перенесите значение 1 в следующий столбец слева. Еще один пример добавления и превышения диапазона базового набора 198 + 4 198 199 +1 200 +2 Примечание 2: 201 +3 202 +4 Примечание 2: при превышении 9 мы возвращаемся к началу набора (0), и перенесите значение 1 в следующий столбец слева. Таким образом в средний столбец (9) добавлен 1, следующее значение в наборе - 0, и мы переносим 1 (потому что набор был превышен) в следующий левый столбец.Добавление значение переноса от 1 до 1 в крайнем левом столбце дает.
Позиционные значения [единицы, десятки, сотни, тысячи и т. Д.
Колонны]
Наверное, в школе нас учили позиционным ценностям,
столбцы представляют степени 10. Это выражается нам как
столбцы единиц (0-9), десятков (группы по 10), сотен (группы
100) и так далее.
237 = (2 группы по 100) + (3 группы по 10) + (7 групп по 1) = (100 + 100) + (10 + 10 + 10) + (1 + 1 + 1 + 1 + 1 + 1 + 1) = (200) + (30) + (7) = 237
Каждый столбец, перемещаемый влево, в 10 раз превышает предыдущее значение.
двоичный
Система счисления [База-2]
В двоичной системе счисления используются ДВА
значения для представления чисел. Значения:
, где 0 имеет наименьшее значение, а 1 — наибольшее. стоимость. Столбцы используются так же, как и в десятичная система, в которой крайний левый столбец используется для представления наибольшего значения.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0 1 10 Примечание: перейти к наименьшему значению в наборе, перенести влево 11 100 Примечание: перейти к наименьшему значению в наборе, перенести влево 101 110 Примечание: перейти к наименьшему значению в наборе, перенести влево 111
. В компьютере двоичная переменная, способная хранить двоичные данные. значение (0 или 1) называется BIT.
В десятичной системе столбцы представляют умножение.
значения 10.Это произошло потому, что было 10 значений (0–9) в
набор. В этой двоичной системе всего два значения (0 — 1)
в наборе, поэтому столбцы представляют собой значения умножения 2.
1011 = ---- 1 * 2 0 = 1 ----- 1 * 2 1 = 2 ------ 0 * 2 2 = 0 ------- 1 * 2 3 = 8 ---- 11 (в десятичной системе)
Диапазоны чисел в двоичном формате с использованием указанного количества бит
Сколько разных значений может быть представлено определенным числом
бит?
количество различных значений = 2 n где n - количество бит например.2 8 = 256 разных значений
Правила сложения двоичных файлов
| Эксплуатация | Результат |
| 0 + 0 | 0 |
| 0 + 1 | 1 |
| 1 + 0 | 1 |
| 1 + 1 | 0 и Carry 1 |
1011 + 101 = 1011 101 1.Начните с самого правого столбца и примените правила. 2. 1 + 1 равно 0 и переносит 1 в следующий столбец слева. 1011 101 ------ 0 и нести 1 что действительно похоже 1011 111 ------ 0 3. Теперь займитесь вторым столбцом. 4. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 ------ 00 и нести 1 что действительно похоже 1011 111 1 ------ 00 5.Теперь сделайте третий столбец 6. 1 + 1 равно 0, перенесите 1 в следующий столбец слева. 1011 111 1 ------ 000 и нести 1 что действительно похоже 1011 111 1 ------ 000 7. Теперь займитесь последней колонкой слева. 8. 1 + 1 равно 0 и переносится 1 слева. 1011 101 ------ 10000
Правила двоичного вычитания
| Эксплуатация | Результат |
| 0-0 | 0 |
| 0–1 | 1 и займ 1 |
| 1-0 | 1 |
| 1–1 | 0 |
Правила двоичного умножения
| Эксплуатация | Результат |
| 0 * 0 | 0 |
| 0 * 1 | 0 |
| 1 * 0 | 0 |
| 1 * 1 | 1 |
Примеры задач для двоичного сложения
и вычитание
Преобразование
Десятичное в двоичное
Существует несколько способов преобразования между десятичным и двоичным числами.Начнем с преобразования десятичного значения 254 в
двоичный.
Метод 1: Разделите число на 2, а затем разделите полученное. осталось на 2 и так далее, пока ничего не останется (0). Записывать остаток (равный 0 или 1) на каждом этапе деления. Как только делений больше нет, перечислите оставшиеся значения в обратный порядок. Это двоичный эквивалент.
254/2, что дает 127 с остатком 0 127/2, что дает 63 с остатком 1 63/2 получается 31 с остатком 1 31/2 получается 15 с остатком 1 15/2 получается 7 с остатком 1 7/2 дает 3 с остатком 1 3/2 дает 1 с остатком 1 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент 11111110 Другой пример, 132 десятичное 132/2, что дает 66 с остатком 0 66/2, что дает 33 с остатком 0 33/2, что дает 16 с остатком 1 16/2 - 8 с остатком 0 8/2 - 4 с остатком 0 4/2 дает 2 с остатком 0 2/2 дает 1 с остатком 0 1/2 дает 0 с остатком 1 таким образом, двоичный эквивалент 10000100
Метод 2: Каждый столбец представляет степень двойки, поэтому используйте
это как основа для расчета числа.Иногда бывает
называется подходом 8: 4: 2: 1.
Запишите двоичное число. Где 1 появляется в
столбец, добавьте значение столбца как степень двойки к итоговому значению.
| Взвешивание | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 0 | 1 | 1 | 11 |
| Взвешивание | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 0 | 1 | 1 | 1 | 7 |
| Взвешивание | 32 | 16 | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 1 | 1 | 0 | 1 | 1 | 59 |
| Взвешивание | 32 | 16 | 8 | 4 | 2 | 1 | Ответ |
| Двоичное значение | 1 | 0 | 1 | 0 | 1 | 0 | 42 |
Примеры задач для преобразования десятичных чисел в двоичные
Преобразование
Двоичные числа — это
- громоздко записывать
- длинный
- не имеет большого значения для обычного пользователя
- понимаются компьютерами
O кталл
Система счисления [База-8]
В восьмеричной системе счисления используется ВОСЕМЬ
значения для представления чисел.Значения:
0 1 2 3 4 5 6 7
, где 0 имеет наименьшее значение, а семь — наибольшее. стоимость. Столбцы используются так же, как и в десятичной системе, в этом крайнем левом столбце используется для представления наибольшего значения.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0-7, 10-17, 20-27, 30-37......
Задача: Преобразовать восьмеричное число 176 в десятичное.
Каждый столбец представляет степень 8, 176 = ---- 6 * 8 0 = 6 ----- 7 * 8 1 = 56 ------ 1 * 8 2 = 64 ---- 126
Octal широко использовался в ранних мэйнфреймах. системы.
шестнадцатеричный
Система счисления [Base-16]
В шестнадцатеричной системе счисления используется ШЕСТНАДЦАТЬ.
значения для представления чисел.Значения:
0 1 2 3 4 5 6 7 8 9 A B C D E F
, где 0 имеет наименьшее значение, а F — наибольшее значение. Столбцы используются так же, как и в десятичной системе счисления. система, в которой крайний левый столбец используется для представления наибольшая ценность.
Как мы видели в десятичной системе,
значения в наборе (0 и 1) повторяются как по вертикали, так и по
горизонтальные направления.
0 - F, 10 - 1 этаж, 20 - 2 этаж, 30 - 3 этаж......
Шестнадцатеричный формат часто используется для представления значений [чисел и адреса памяти] в компьютерных системах.
| Десятичное | двоичный | Шестнадцатеричный |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Преобразование шестнадцатеричного числа в десятичное
Задача: Преобразование 176 из шестнадцатеричного числа в десятичное.
Каждый столбец представляет степень 16, 176 = ---- 6 * 16 0 = 6 ----- 7 * 16 1 = 112 ------ 1 * 16 2 = 256 ---- 374
Преобразование двоичного числа в шестнадцатеричное
Проблема: Преобразование 10110 в шестнадцатеричное.
Каждая шестнадцатеричная цифра представляет 4 двоичных бита. Разделить двоичное число на группы по 4 бита, начиная справа.1 0110 = 1 = 6 = 16 в шестнадцатеричной системе счисления
Преобразование десятичного числа в шестнадцатеричное
Проблема: Преобразование десятичного числа 232 в шестнадцатеричное.
Используйте тот же метод, который использовался ранее, чтобы разделить десятичную дробь на двоичный, но разделить на 16. 232/16 = 14 с остатком 8 14/16 = 0 с остатком E (14 в десятичной системе = E) = E8 16
Во избежание путаницы мы часто добавляем суффикс для обозначения основания числа
162 ч ч означает шестнадцатеричный 162 16 16 означает основание 16 162 d d означает десятичное число 162 10 10 означает основание 10 162 o o означает восьмеричное 162 8 8 означает основание 8 101 b b означает двоичный 101 2 2 означает основание 2
Примеры задач для шестнадцатеричной системы
Преобразование
Представляя положительные и
отрицательные числа в двоичном формате
Когда для хранения значений используется несколько битов, наиболее
значащий бит [бит, имеющий наибольшее значение в
крайний левый столбец] используется для хранения знака [положительный или
отрицательный] числа.Остальные биты содержат фактические
стоимость.
Если число отрицательное, знак равен 1 , а для положительные числа, знак 0 .
Вопрос: Что такое диапазон чисел, доступных при использовании 8 бит.
Для 8 бит один бит предназначен для знака, 7 для числа, поэтому диапазон значений равен 2 7 = 127 комбинаций
Из-за проблем с сложением и вычитанием отрицательный числа обычно хранятся в формате, отличном от положительного числа.
Дополнительная информация о представлении чисел
Единицы Дополнение
Дополнение до 1 — это метод хранения отрицательных значений. Это просто
инвертирует все 0 в 1 и все 1 в 0.
| Оригинальный номер | Двоичное значение | Дополняющее значение до 1 |
| 7 | 00000111 | 11111000 |
| 32 | 00100000 | 11011111 |
| 114 | 01110010 | 10001101 |
Дополнение до двоек
Дополнение до 2 — это еще один метод хранения отрицательных значений.Это
получается добавлением 1 к значению дополнения 1.
| Оригинальный номер | Двоичное значение | Дополняющее значение до 1 | Дополняющее значение 2 |
| 7 | 00000111 | 11111000 | 11111001 |
| 32 | 00100000 | 11011111 | 11100000 |
| 114 | 01110010 | 10001101 | 10001110 |
Другой способ создания дополнительного числа до 2 — начать наименьший значащий бит и скопируйте все 0 до достигается первая 1.Скопируйте первую 1, затем инвертируйте все оставшиеся биты.
В следующей таблице показаны как единицы, так и двойки.
дополнить, используя диапазон 4 бита.
| Двоичный | Дополнение до 1 | Дополнение по 2 | Без знака |
| 0111 | 7 | 7 | 7 |
| 0110 | 6 | 6 | 6 |
| 0101 | 5 | 5 | 5 |
| 0100 | 4 | 4 | 4 |
| 0011 | 3 | 3 | 3 |
| 0010 | 2 | 2 | 2 |
| 0001 | 1 | 1 | 1 |
| 0000 | 0 | 0 | 0 |
| 1111 | -0 | -1 | 15 |
| 1110 | -1 | -2 | 14 |
| 1101 | -2 | -3 | 13 |
| 1100 | -3 | -4 | 12 |
| 1011 | -4 | -5 | 11 |
| 1010 | -5 | -6 | 10 |
| 1001 | -6 | -7 | 9 |
| 1000 | -7 | -8 | 8 |
Примечание: Посмотрите, как в случае дополнения до 1 есть два представления для 0
Серый код
Это циклический взвешенный код с переменным весом .Это означает, что он устроен так
что каждый переход от одного значения к следующему включает
только изменение одного бита .
Код Грея иногда называют отраженным двоичным кодом , потому что первые восемь значений сравниваются с последними 8 значения, но в обратном порядке.
| Десятичное | Двоичный | Серый |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Код Грея часто используется в механических приложениях, таких как энкодеры вала.
Арифметика по модулю 2
Это двоичное сложение, но перенос игнорируется.
Преобразование серого в двоичное
- запишите номер серым кодом
- старший бит двоичного числа является самым старшим значащий бит кода Грея
- добавить (используя по модулю 2) следующий значащий бит двоичное число до следующего значащего бита серого закодированное число для получения следующего двоичного бита
- повторяйте шаг 3 до тех пор, пока все биты серого закодированного числа не будут добавлено по модулю 2
- результирующее число является двоичным эквивалентом серого число
Пример преобразования 1101101 кода Грея в двоичный код Серый двоичный 1.1101101 2. 1 101101 1 копия в старшем разряде 3. 1 1 1101 1 0 1 по модулю 2 1 = 0 4. 11 0 1101 1 0 0 0 по модулю 2 0 = 0 3/4 110 1 101 10 0 1 0 по модулю 2 1 = 1 3/4 1101 1 01100 1 0 1 по модулю 2 1 = 0 3/4 11011 0 1 1001 0 0 0 по модулю 2 0 = 0 3/4 110110 1 10010 0 1 0 по модулю 2 1 = 1 Ответ: 1001001
Преобразование двоичного изображения в серый
- запишите число в двоичном коде
- старший бит серого числа является самым старшим значащий бит двоичного кода
- добавить (используя по модулю 2) следующий значащий бит двоичное число до следующего значащего бита двоичного число для получения следующего бита с серым кодом
- повторяйте шаг 3 до тех пор, пока все биты двоичного числа не закодированы. добавлены по модулю 2
- , результирующее число является серым эквивалентом двоичное число
Пример, преобразование двоичного кода 1001001 в код Грея Бинарный серый 1.1001001 2. 1 001001 1 копировать вниз старший бит 3. 10 01001 11 1 по модулю 2 0 = 1 4. 1 00 1001110 0 по модулю 2 0 = 0 3/4 10 01 001 1101 0 по модулю 2 1 = 1 3/4 100 10 01 11011 1 по модулю 2 0 = 1 3/4 1001 00 1 110110 0 по модулю 2 0 = 0 3/4 10010 01 1101101 0 по модулю 2 1 = 1 Ответ 1101101
Превышение 3 Серый код
Во многих приложениях желательно иметь код, который является двоично-десятичным кодом, а также единицей расстояния.Единица код расстояния получил свое название от того факта, что существует
изменение только одного бита между двумя последовательными числами. Превышение 3
код Грея является таким кодом, значения для нуля и девяти различаются
только 1 бит, как и все значения для последовательных чисел.
Выходы линейных устройств или угловых энкодеров могут кодироваться более 3 кодов Грея для получения многозначных чисел BCD.
| Десятичное | Излишек 3 Серый |
| 0 | 0010 |
| 1 | 0110 |
| 2 | 0111 |
| 3 | 0101 |
| 4 | 0100 |
| 5 | 1100 |
| 6 | 1101 |
| 7 | 1111 |
| 8 | 1110 |
| 9 | 1010 |
Главная | Другие курсы | Обратная связь | Примечания | Тесты
© Copyright B Brown / Peter Henry.1984–1999 годы.
Все права защищены.
Создание собственной электронной таблицы для преобразования двоичного числа в десятичное
Предлагаемые шаги
Предварительные знанияДля выполнения этого задания ожидается, что учащиеся будут разбираться в двоичных числах и понимать, как считать в двоичном формате. Обратитесь к введению к бинарному уроку.
Быстрая проверкаПроверьте, что учащиеся знают о двоичном счете, если возможно, используйте двоичные карты или напишите на доске десятичное число, например «21», чтобы смоделировать, как представить это число в двоичном формате, то есть 10101.Используйте следующую таблицу с заголовками, чтобы показать прогрессию двоичной системы счисления, похожую на единицы, 10, 100, 1000 для десятичной системы. Бинарный — это шаблон удвоения 1, 2, 4, 8, 16 и т. Д.
Используйте таблицу, чтобы убедиться, что все учащиеся могут считать в двоичном формате и представлять десятичные числа в двоичном.
Примечание. Не забывайте начинать слева при использовании таблицы для создания десятичного числа. Например, чтобы сделать число 21, мне нужно 16, ДА. Надо ли мне и 8, НЕТ. Мне нужен 4, ДА.Мне нужен 2, НЕТ. Мне нужен 1, ДА. Таким образом, двоичное число — 10101. Повторите этот процесс для других чисел. Попробуйте составить числа 1-21. Спросите, какое наибольшее число, чем может быть получено в этой таблице.
Числа больше 21. Если мы добавим еще один столбец, как мы можем сделать число 43?
| 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
Как сделать число 251? Обсудите схему удвоения, чтобы получить 64 и 128, и добавьте эти два новых столбца.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
С помощью электронной таблицы дифференцируйте задачи в зависимости от уровня знаний и навыков учащегося.Создайте основу для обучения, предоставив файл листовой бумаги, настройка которого частично завершена. Предоставляемые файлы — это MS Excel.
Некоторые студенты, которые хорошо владеют электронными таблицами, могут разработать свой собственный конвертер, и им может не понадобиться файл для поддержки своего обучения.
Предоставьте этот файл студентам, которые имеют базовые представления о том, как использовать электронную таблицу. В качестве отправной точки попросите учащихся протестировать лист, чтобы увидеть, как он работает. Могут ли они понять, как рассчитывается десятичное число ASCII? Спросите студентов, могут ли они заставить свой конвертер работать до десятичного числа 255.Предложите учащимся протестировать и проверить правильность автоматического суммирования и вывод в ячейке правильного десятичного числа ASCII.
Этот файл предназначен для студентов, которые хотят добавить условный оператор if для автоматического представления o или 1 как «включено» или «выключено». В этом примере условный оператор читает, если ячейка (см. Выше) = 1, затем отображается значение «Вкл.», Иначе, если ячейка = 0, отображается значение «выкл.».
Завершенная версия может выглядеть примерно так, см. Файл здесь.
Этот пример предназначен для студентов, которые заинтересованы в создании интерфейса.
Обратитесь к этой версии заполненной электронной таблицы с советами, объясняющими, как она настроена.
Эта версия включает бинарные карты с точками, которые можно использовать как дополнительную задачу.
У меня к вам вопрос.
Преобразования системы счисления
При написании программ для микроконтроллеров мы обычно используем 3 разных системы счисления: десятичную, двоичную и шестнадцатеричную (или шестнадцатеричную). Мы используем десятичные числа, потому что они естественны; так мы считаем.К сожалению, компьютеры так не считают. Поскольку компьютеры и микроконтроллеры могут использовать только единицы и нули, для их подсчета используются последовательности этих чисел. Это двоичная система счисления. Двоичные числа обычно начинаются с символа «0b», который не является частью числа. Иногда они также подразделяются на группы по 4 цифры, чтобы облегчить их чтение, а также облегчить их привязку к шестнадцатеричной системе счисления. Пример двоичного числа: 0b0100.1011. Точки в номере ничего не обозначают, они просто облегчают чтение числа.
Двоичная система проста для понимания, но для использования двоичной системы для представления больших чисел требуется много цифр. Шестнадцатеричная система может представлять гораздо большие числа с использованием меньшего количества символов и очень напоминает двоичные числа. Шестнадцатеричные числа обычно начинаются с префикса «0x», который не является частью числа. Одна шестнадцатеричная цифра может представлять четыре двоичных цифры!
Двоичные числа могут состоять только из единиц и нулей; обычно двоичное число состоит из 8 цифр (или кратно 8), если оно используется в каком-либо компьютере (или микроконтроллере).0). Есть два важных числа, которые мы должны знать, чтобы «деконструировать» число — основание системы счисления и расположение цифры в числе. Основание десятичного числа — 10. Когда мы преобразуем число 268, 2 — это вторая цифра, 6 — первая цифра, а 8 — нулевая цифра. Каждую цифру необходимо масштабировать в соответствии с ее местом в числе. Масштаб цифры — это основание системы счисления, возведенное в степень расположения цифры в числе. Таким образом, каждое число масштабируется, а затем все масштабированные цифры складываются, чтобы найти общее значение числа.0), что равно 181.
0b1011.0101. Какой совершенно неэффективный способ набора числа! Но мы можем представить одно и то же двоичное число, используя только 2 шестнадцатеричные цифры. Однако сначала мы начнем с преобразования шестнадцатеричного (шестнадцатеричного) числа в десятичное, как мы это сделали для двоичного числа. А как насчет 0xB5? Чего ждать?! Префикс 0x используется в коде, чтобы указать, что число записывается в шестнадцатеричном формате. Но что там делает «Би»? Шестнадцатеричный формат имеет основание 16, что означает, что каждая цифра может представлять до 16 различных значений.0) или 181.
Знание того, как преобразовать двоичное и шестнадцатеричное в десятичное, важно, но наиболее полезным преобразованием чисел, вероятно, является преобразование между шестнадцатеричным и двоичным. Эти две системы нумерации действительно очень хорошо работают вместе. Системы счисления связаны таким образом, что одна шестнадцатеричная цифра представляет ровно 4 двоичных цифры, и поэтому две шестнадцатеричные цифры могут представлять 8 бит (или двоичных цифр). Вот таблица, которая показывает, как каждая шестнадцатеричная цифра связана с двоичной системой:
| Двоичное значение | Шестнадцатеричное значение |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Например, чтобы преобразовать шестнадцатеричное число 0x1C в двоичное, мы должны найти соответствующее двоичное значение для 1 и C и объединить их.Итак, 0x1C в двоичном формате — это 0b0001.1100. Если бы мы хотели вычислить шестнадцатеричное значение двоичного числа, мы просто пошли другим путем. Чтобы найти шестнадцатеричное представление двоичного числа 0b0010.1011, мы сначала находим шестнадцатеричное значение для 0010, затем шестнадцатеричное значение для 1011 и объединяем их; шестнадцатеричное значение будет 0x2B.
Существует множество бесплатных инструментов для преобразования между этими системами нумерации, просто «преобразование шестнадцатеричных чисел в Google». Если вы используете Windows в качестве операционной системы, у вас есть отличный инструмент, встроенный в калькулятор.Просто переключите калькулятор в научный режим, и вы можете конвертировать между системами счисления, набрав число, а затем изменив формат калькулятора!
Двоичные числа
Обзор
На этом уроке студенты будут практиковаться в представлении чисел в двоичном формате (основание 2), переходя от представлений круг-квадрат, которые они сделали на прошлом уроке. Студенты создадут и будут использовать «Flippy Do», инструмент для манипуляций, который помогает студентам конвертировать между двоичными (основание 2) и десятичными (основание 10) числами.Они будут практиковаться в преобразовании чисел и изучат концепцию разряда в контексте двоичных чисел.
Назначение
Этот урок разработан для того, чтобы дать учащимся как можно больше времени, используя Flippy Do, чтобы освоиться с взаимосвязью между двоичными и десятичными числами и концепцией разряда.
Повестка дня
Модификации урока
Разминка (5 минут)
Активность (35 минут)
Подведение итогов (5 минут)
Посмотреть на Code Studio
Цели
Студенты смогут:
- Представление десятичных чисел с использованием комбинаций двоичных (основание 2) цифр 0 и 1
- Представление двоичных чисел с использованием комбинаций десятичных (основание 10) цифр 0-9
- Объясните, как позиция каждой двоичной цифры определяет ее разрядное и числовое значение
Препарат
Ссылки
Внимание! Сделайте копии всех документов, которыми вы планируете поделиться со студентами.
Учителям
Студентам
Модификации урока
Внимание, учителя! Если вы преподаете виртуально или в классе с социальной дистанцией, пожалуйста, прочтите полный план урока ниже, а затем щелкните здесь, чтобы получить доступ к изменениям.
Разминка (5 минут)
Цель обсуждения
Цель: На предыдущих уроках учащиеся представляли информацию двумя способами. Это быстро обдумываемый вопрос, позволяющий задействовать предыдущие знания и опыт учащихся. После того, как учащиеся отметили несколько пунктов ниже, они могут двигаться дальше.
- Ответ на вопрос «да / нет» или «правда / ложь»
- Включение / выключение переключателя
- Комбинации ответов да / нет с использованием нескольких символов в строке
- Мы можем добавлять больше одинаковых символов, поэтому единственным ограничением является то, сколько места у нас есть для записи или хранения этих символов
Подсказка: Вчера вы создали свою собственную систему счисления, используя круги и квадраты.
- О чем можно общаться, используя только два символа? Есть ли предел?
Обсудить: Ученики должны спокойно написать ответ, затем поделиться с партнером, а затем обсудить его со всем классом.
Активность (35 минут)
Дисплей: Используйте слайды деятельности для этого урока, чтобы познакомить студентов с двоичной системой счисления. Используйте заметки докладчика в качестве руководства для объяснения того, как фигуры, которые мы использовали в предыдущем уроке, соотносятся с двоичными числами.В этих слайдах используется много анимации.
Ищите этот символ на слайдах, чтобы показать, когда при их представлении воспроизводится анимация:. Обязательно просмотрите слайды перед уроком.
| Слайды | Заметки докладчика |
|---|---|
| Say: Сегодня мы собираемся изучить, как работают двоичные числа. | |
| Say: Имея только одно разрядное значение, у нас есть только два возможных шаблона: круг или квадрат. Анимация по клику Скажем: Я начал с круга, но мы могли бы легко начать с квадрата. | |
| Анимация перехода по клику Say: С двумя значениями разряда мы можем создать два набора предыдущих шаблонов. Затем вставьте круги перед первым набором и квадраты перед вторым набором. Это дает четыре возможных шаблона. | |
| Анимация перехода по щелчку мыши Say: Для трех шаблонов значений разряда мы можем сделать две копии двух шаблонов значений разряда.Затем, как мы делали раньше, заполните первый набор кругами впереди, а второй набор квадратами впереди. Это 8 аранжировок. Примечание: Компьютерные специалисты любят начинать счет с 0! | |
| Say: Что, если бы у нас было 10 фигур? | |
| Анимация по клику Say: Мы могли бы использовать больше геометрических фигур или мы могли бы использовать буквы, но формы, которые мы привыкли, представляют собой числа от 0 до 9. | |
| Say: С двумя местами у нас есть сотня 2-х фигурных узоров. Это числа от 00 до 99. Анимация по клику | |
| Say: Что происходит, когда мы считаем до последней фигуры? Сделайте это: Быстрая викторина! Что идет после этого числа? | |
| Скажи: 100! Когда мы подбегаем к последней фигуре, 9, мы возвращаемся к 0 и добавляем единицу в следующем месте слева.Это точечная стоимость, которую мы использовали всю свою жизнь. | |
| Say: Где этот заголовок? Анимация по клику | |
| Say: Двоичная система счисления состоит из двух форм. Анимация по клику | |
| Анимация по клику Скажем: Вместо фигур мы используем нули и единицы. В этом примере каждому шаблону соответствует десятичное число от 0 до 7. | |
| Say: Сегодня вы будете создавать свой собственный Flippy Do. Это инструмент, который позволит вам быстро и легко переводить между десятичной системой счисления, к которой мы привыкли как люди, и двоичной системой счисления, которую используют компьютеры. Раздайте: Раздайте шаблоны Flippy Do — по одному на каждого учащегося. Сделайте следующее: Проведите студентов по выполнению их Flippy Do, используя слайд в качестве руководства. | |
| Say: Каждое разрядное значение представляет один «бит», что является сокращением от «двоичной цифры». Двоичная цифра может быть нулем или единицей. В твоем легкомыслии восемь «бит». Анимация перехода по щелчку мыши Скажем: Вместе восьмизначные значения или «биты» составляют один «байт». Поскольку компьютеры представляют информацию в цифровом виде, компоненты информации самого низкого уровня являются битами. | |
| Do This: Используйте Flippy Do, чтобы попробовать эти шесть задач. Примечание: Может потребоваться продемонстрировать, как можно вычислить значения, подняв «1» для каждого значения, необходимого для получения суммы значений, равной десятичному числу. Например, чтобы преобразовать десятичное число 10, я бы перевернул единицу в позиции 8, потому что восемь может поместиться в 10 (следующий бит слева — 16, что слишком велико). Потом у меня осталось 2. Я переворачиваю единицу в позиции двойки. Это дает мне двоичное число «1010», что означает 10 в десятичной системе счисления. Если учащимся трудно понять правила системы, напомните им о концепции числовой ценности и используйте базу 10. | |
| Say: Давайте продолжим практику с нашими двумя основами счисления, десятичной и двоичной. После того, как вы закончите каждую из четырех частей Руководства по занятиям, я хочу, чтобы вы проверили свою работу со своим партнером. Не стесняйтесь использовать Flippy Do во время работы. Распространить: Практическое руководство Примечание: Поощряйте студентов использовать Flippy Do в качестве ресурса.
Примечание: По мере распространения воспользуйтесь возможностью стать ведущим обучающимся. Помогите учащимся найти указанные ниже элементы, используя предлагаемые вопросы:
|
Подведение итогов (5 минут)
Учебный совет
Числовые базы помогают нам выражать данные и рассуждать о количествах.С десятью цифрами на руках и ногах, основание десятичного числа (основание 10) было естественным для человеческого развития. Десять символов, которые мы используем для этой числовой базы, — это цифры от 0 до 9. Однако для компьютера имеет смысл представлять данные в двоичном формате (основание 2), поскольку это можно легко интерпретировать с помощью электрических переключателей, установленных в два состояния: ВКЛ или ВЫКЛ. Два символа, которые мы используем для этой числовой базы, — это цифры 0 и 1.
Обе числовые базы используют концепцию разряда.В десятичном формате числа состоят из десятичных степеней, возрастающих справа налево. Двоичный код аналогичен, однако мы используем степени двойки (1, 2, 4, 8, 16 и т. Д.). В двоичном формате это значения 1, 10, 100, 1000, 10000 и т. Д. Они составляют инкрементальные разряды в двоичной системе счисления.
На следующем уроке учащиеся увидят, как компьютеры используют двоичные числа для представления электрических сигналов в проводе. Для провода всегда устанавливается один из двух вариантов: включен или выключен.Выкл. Может быть обозначено 0, а вкл. — 1.
Примечания
Важно знать разницу между двоичной и десятичной системами счисления. В качестве обзора используется десятичная система счисления по основанию 10. Для обозначения чисел (0–9) используются десять различных символов. Система двоичных чисел — основание-2. Для обозначения чисел (0-1) используются два разных символа. Используя нашу Flippy Do, мы можем конвертировать между двоичной и десятичной системами счисления.
Хотя людям проще использовать десятичную систему счисления в повседневной жизни, позже в этом разделе мы увидим, как электрические сигналы внутри компьютеров могут быть наилучшим образом представлены с помощью двоичной системы счисления.
Цель обсуждения
Цель: Используйте это упражнение, чтобы оценить, что учащиеся узнали и что необходимо уточнить. Некоторые заблуждения можно визуально прояснить с помощью виджета двоичного одометра в следующем уроке.
Подсказка: Теперь, когда у нас была возможность попрактиковаться, давайте выясним, что мы узнали и о чем у нас остались вопросы. Запишите:
- 3 вещи, которые вы узнали сегодня
- 2 вещи, которые вы нашли интересными
- У вас остался 1 вопрос.
Журнал: Добавьте в свой журнал определения слов для бита и байта.
Оценка
: проверка понимания
Проверка понимания вопросов и решений можно найти в каждом уроке Code Studio. Эти вопросы можно использовать для выходного билета.
Вопрос: Сколько бит потребуется для подсчета всех учеников в классе сегодня?
Вопрос: Каждый раз, когда мы добавляем еще один бит, что происходит с количеством чисел, которое мы можем составить?
Вопрос: В чем сходство и различие между двоичной и десятичной системами счисления?
.